DYNAMIC PREDICTION OF RESIDUAL LIFE WITH LONGITUDINAL COVARIATES USING LONG SHORT-TERM MEMORY NETWORKS

Abstract

Sepsis, a complex medical condition that involves severe infections with life-threatening organ dysfunction, is a leading cause of death worldwide. Treatment of sepsis is highly challenging. When making treatment decisions, clinicians and patients desire accurate predictions of mean residual life (MRL) that leverage all available patient information, including longitudinal biomarker data. Biomarkers are biological, clinical, and other variables reflecting disease progression that are often measured repeatedly on patients in the clinical setting. Dynamic prediction methods leverage accruing biomarker measurements to improve performance, providing updated predictions as new measurements become available. We introduce two methods for dynamic prediction of MRL using longitudinal biomarkers. in both methods, we begin by using long short-term memory networks (LSTMs) to construct encoded representations of the biomarker trajectories, referred to as “context vectors.” In our first method, the LSTM-GLM, we dynamically predict MRL via a transformed MRL model that includes the context vectors as covariates. In our second method, the LSTM-NN, we dynamically predict MRL from the context vectors using a feed-forward neural network. We demonstrate the improved performance of both proposed methods relative to competing methods in simulation studies. We apply the proposed methods to dynamically predict the restricted mean residual life (RMRL) of septic patients in the intensive care unit using electronic medical record data. We demonstrate that the LSTM-GLM and the LSTM-NN are useful tools for producing individualized, real-time predictions of RMRL that can help inform the treatment decisions of septic patients.

1. Introduction.

When making treatment decisions, clinicians and patients often desire accurate predictions of remaining life expectancy that leverage all available patient information, including longitudinal biomarker data. The National Institutes of Health (NIH) defines a biomarker as “a characteristic that is objectively measured and evaluated as an indicator of normal biological processes, pathogenic processes, or pharmacologic responses to a therapeutic intervention (Strimbu and Tavel (2010)).” Longitudinal biomarker measurements, such as blood pressure, ventilator dependence, and white blood cell count, are commonly available in electronic medical records (EMRs). The recent proliferation of EMRs has led to a growing interest in using longitudinal biomarker data with “dynamic” prediction methods which provide updated predictions as new biomarker measurements become available. Clinicians and patients are especially interested in using longitudinal biomarker data to dynamically predict mean residual life (MRL), the remaining life expectancy of a patient at time $t$, given the patient has survived up to time $t$.

MRL prediction is of particular interest for patients diagnosed with sepsis, a complex medical condition that involves severe infections with life-threatening organ dysfunction (Singer et al. (2016)). Sepsis is a leading cause of death worldwide (Singer et al. (2016)). Although international guidelines for sepsis treatment have been established, treating septic patients remains highly challenging (Evans et al. (2021)). The heterogeneity of septic patient populations results in differing responses to medical intervention László et al. (2015)). Dynamic predictions of mean residual life provide clinicians with individualized, real-time information that can help inform the treatment decisions of septic patients.

We dynamically predict the restricted mean residual life (RMRL) of septic patients in the intensive care unit (ICU) from EMR data. We conduct our study using a data set constructed from the Multiparameter Intelligent Monitoring Intensive Care (MIMIC-III) database. MIMIC-III is a freely-available database comprised of deidentified health records for over 40,000 patients who stayed in the critical care units at Beth Israel Deaconess Medical Center between 2001 and 2012 (Johnson et al. (2016)). MIMIC-III contains data on patients’ demographics, vital signs, laboratory measurements, medications, imaging reports, chart notes, procedure codes, diagnostic codes, hospital stay, and survival. For a complete description of the MIMIC-III database, refer to Johnson et al. (2016).

In 2016, the definitions and clinical criteria for sepsis and septic shock were updated in the Third International Consensus Definitions for Sepsis and Septic Shock (Sepsis-3) (Singer et al. (2016)). Sepsis-3 defines sepsis as a “life-threatening organ dysfunction caused by a dysregulated host response to infection” and provides clinical criteria for diagnosing septic patients (Singer et al. (2016)). Komorowski (2019) developed code to identify patients in MIMIC-III fulfilling the Sepsis-3 criteria. Komorowski’s code pulls relevant physiological parameters for each patient from up to 24 hours preceding their sepsis diagnosis until 48 hours after. The code aggregates the data into four-hour time windows, recording an appropriate summary statistic when several measurements were taken in the same time window. We use the code to construct our studied data set which contains 48 covariates measured on 20,954 patients. We observe time of death for less than 15% of the septic patients.

Due to the computational burden of repeated model fitting for performance evaluation, we study a reduced set of covariates that were identified to be important predictors of mortality for septic patients in relevant studies and exploratory data analysis (Carrara, Baselli and Ferrario (2015), Hou et al. (2020)). The selected covariates include a single baseline covariate and 15 longitudinal biomarkers. The baseline covariate of interest is an indicator of whether the patient was previously admitted to the ICU during the given hospital stay. The longitudinal biomarkers of interest include two treatment variables: the median dosage of vasopressors provided to the patient in the given four-hour time-window and the cumulative amount of intravenous (IV) fluid administered to the patient since hospital admission. We also study a longitudinal indicator of mechanical ventilator dependence as well as 12 vital signs and laboratory values: albumin, calcium, magnesium, hemoglobin, arterial lactate, arterial pH, fraction of inspired oxygen (FiO2), peripheral oxygen saturation (SpO2), Sequential Organ Failure Assessment (SOFA) score, respiratory rate, heart rate, and systolic blood pressure.

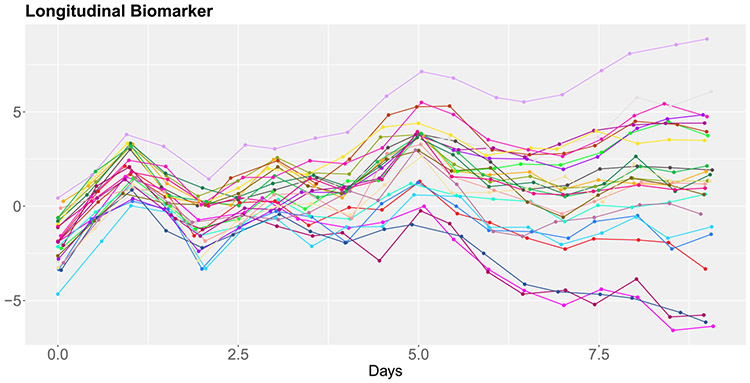
Biomarker trajectories of 25 randomly selected patients are illustrated in Figure 1. The longitudinal biomarker trajectories are sophisticated functions of time that exhibit notable variation among patients. Additionally, the number of biomarker measurements differs among patients. These complexities make it difficult to formulate a parametric model that fully captures the biomarker processes and their relationship with MRL.

Fig. 1.

The biomarker trajectories of magnesium (left) and systolic blood pressure (right) for 25 randomly selected septic patients in MIMIC-III.

The body of literature addressing how to model MRL with covariates measured only at baseline is vast. Popular baseline MRL models include proportional MRL models (Maguluri and Zhang (1994)), additive MRL models (Chen (2007)), and transformed MRL models (Sun and Zhang (2009)). Although Sun, Song and Zhang (2012) extended the family of transformed MRL models to accommodate time-dependent coefficients, none of the aforementioned models accommodate time-dependent covariates. Thus, they cannot be used to conduct dynamic prediction of MRL with longitudinal biomarker data.

A number of dynamic prediction models for survival risk have been developed via the landmarking approach (Zheng and Heagerty (2005), Van Houwelingen (2007), van Houwelingen and Putter (2012), Rizopoulos, Molenberghs and Lesaffre (2017), Zhu, Li and Huang (2019)). In a landmark analysis, a prediction model is fit at a series of time points, referred to as “landmark times,” using only data collected prior to the landmark time on patients at risk at the landmark time. Lin et al. (2018) used the landmarking approach to incorporate longitudinal covariates into the transformed MRL model presented by Sun, Song and Zhang (2012), effectively creating a dynamic prediction model for MRL.

To synthesize the longitudinal biomarker trajectories, Lin et al. (2018) proposed modeling the biomarkers using functional principal components analysis (FPCA). FPCA extracts dominant features from longitudinal trajectories as functional principal component (FPC) scores. Under the FPCA framework, Lin et al. (2018) introduced “window-specific FPC scores” that summarize a given longitudinal biomarker trajectory from baseline to the time of prediction. The authors proposed including the window-specific FPC scores as time-dependent covariates in their dynamic prediction model for MRL.

To calculate window-specific FPC scores at a given prediction time, Lin et al. (2018) presented a method that uses measurements collected from baseline to maximum follow-up time. Consequently, when the window-specific FPC scores are included as predictors in a dynamic MRL model, information collected after the time of prediction is used to predict MRL. This is undesirable in the dynamic prediction setting, where we wish to predict MRL using only the information available at the time of prediction.

Building on the work of Lin et al. (2018), we introduce two new methods to dynamically predict MRL from longitudinal biomarkers. The methods offer two potential advantages. First, the proposed methods uphold the dynamic nature of prediction. Second, the proposed methods may more effectively synthesize the complex longitudinal biomarker trajectories observed in MIMIC-III.

The proposed methods use long short-term memory networks (LSTMs) to construct “window-specific context vectors” which summarize the biomarker trajectories from baseline to the time of prediction. LSTMs are especially suitable for constructing summaries of biomarker trajectories because they are capable of modeling complex, heterogeneous functions. Thus, LSTMs are an attractive alternative to FPCA for synthesizing the MIMIC-III biomarkers. To uphold the dynamic nature of prediction, the LSTMs construct the window-specific context vectors using only the information available at the time of prediction.

The first proposed method, the long short-term memory generalized linear model (LSTM-GLM), dynamically predicts MRL using a dynamic transformed MRL model that includes the baseline covariates and window-specific context vectors as predictors. The second proposed method, the long short-term memory neural network (LSTM-NN), dynamically predicts MRL from the baseline covariates and window-specific context vectors using a feed-forward neural network. We apply the LSTM-GLM and the LSTM-NN to dynamically predict the RMRL of septic patients in MIMIC-III. We demonstrate that the LSTM-GLM and the LSTM-NN produce accurate, individualized, dynamic predictions. Thus, the LSTM-GLM and the LSTM-NN can be used to inform the challenging treatment decisions of patients diagnosed with sepsis.

In Section 2, we introduce the dynamic transformed MRL model, and we present the LSTM-GLM and the LSTM-NN. In Section 3, we describe the procedure used to evaluate prediction performance. In Section 4, we present simulation studies, and in Section 5, we apply the proposed methods to predict the RMRL of septic patients in MIMIC-III. We conclude with a discussion of implications and open problems in Section 6.

2. Methods.

2.1. Notation.

Let there be $i=1,\dots ,m$ patients, and let $t_{ij}\ge 0$ denote the time at which biomarker measurement $j$ was collected on patient $i$, $j=1,\dots n_i$. We study $m=20,954$ septic patients with $n_i\in [1,20]$ measurements. Let $T_i>0$ and $C_i>0$ denote the potential times to death and censoring, respectively, for patient $i$. We observe only $Y_i=\text{min}(T_i,C_i)$ and ${\Delta }_i=I(T_i\le C_i)$, the indicator of whether the death of patient $i$ was observed (${\Delta }_i=1$) or censored (${\Delta }_i=0$). Let ${\mathbf{X}}_i$ denote the $q$-dimensional vector of baseline covariates measured on patient $i$. We study $q=1$ indicator of whether patient $i$ was previously admitted to the ICU during the given hospital stay. Let ${\mathbf{Z}}_i(t)=\{Z_{i1}(t),\dots ,Z_{ip}(t)\}$ denote the $p$-dimensional vector of longitudinal biomarkers measured on patient $i$ at time $t\ge 0$. We study $p=15$ longitudinal biomarkers, including two treatment variables, an indicator of mechanical ventilator dependence, and 12 vital signs and laboratory values. Denote the covariate history of patient $i$ at time $\tau \ge 0$ as ${\mathscr{H}}_i(\tau )=\{{\mathbf{X}}_i,{\mathbf{Z}}_i(t_{i1}),\dots ,{\mathbf{Z}}_i(t_{i{\tau }_i})\}$, where ${\tau }_i={\text{argmax}}_j(t_{ij}<\tau )$. At time $\tau \ge 0$, the observed data for patient $i$ are {$Y_i,{\Delta }_i,{\mathscr{H}}_i(\tau )$}. The mean residual life (MRL) of patient $i$ at time $\tau \ge 0$, given the patient’s covariate history, is $E\{T_i-\tau \mid T_i>\tau ,{\mathscr{H}}_i(\tau )\}$.

To avoid infinite remaining life expectancy and extreme propensity weights (see Section 2.2), we set a restricted lifetime of $L=40$ days. Our potential survival time of interest is then $T_i^{\ast }=\text{min}(T_i,L)$, and the restricted mean residual life (RMRL) for patient $i$ at time $\tau \ge 0$, given the patient’s covariate history, is $E\{T_i^{\ast }-\tau \mid T_i>\tau ,{\mathscr{H}}_i(\tau )\}$. We use the dynamic prediction methods presented in Section 2 to predict the RMRL of septic patients by redefining $Y_i=\text{min}(T_i^{\ast },C_i)=\text{min}(T_i,C_i,L)$ and ${\Delta }_i=I(T_i^{\ast }\le C_i)=I(T_i,\le C_i)+I\{L\le \text{min}(T_i,C_i)\}\{1-I(T_i\le C_i)\}$.

2.2. Dynamic transformed MRL model.

Building on the work of Lin et al. (2018), we present a dynamic transformed MRL model that regresses residual life only on information collected prior to the time of prediction on patients at risk at the time of prediction. Let $f(\cdot )$ be a vector-valued function, and specify a prediction time $\tau \ge 0$. For patients with $Y_i>\tau$, define the $v$-dimensional vector ${\zeta }_i(\tau )=f\{{\mathbf{Z}}_i(t_{i1}),\dots ,{\mathbf{Z}}_i(t_{i{\tau }_i})\}$. Additionally, let $g(\cdot )$ be a prespecified, nonnegative link function that is twice continuously differentiable and strictly increasing. We specify the dynamic transformed MRL model as

$$E\{T_i-\tau \mid T_i>\tau ,{\mathscr{H}}_i(\tau )\}=g\{\eta (\tau )+\gamma {(\tau )}^T{\mathbf{X}}_i+\alpha {(\tau )}^T{\zeta }_i(\tau )\},$$ (1)

where $\eta (\cdot )$ is a scalar, time-dependent parameter, $\gamma (\cdot )$ is a $q$-dimensional, time-dependent parameter vector, and $\alpha (\cdot )$ is a $v$-dimensional, time-dependent parameter vector.

Define $w_i=\{{\Delta }_{i}I(Y_i>\tau )\}∕\widehat{G}(Y_i)$, where $\widehat{G}(\cdot )$ is an estimate of the survival function of censoring time. We estimate the parameters in equation (1) via a landmarking approach. Contrary to Lin et al. (2018), we do not adopt a supermodel approach for parameter estimation (Van Houwelingen (2007), van Houwelingen and Putter (2012)). Instead, we prespecify a set of positive prediction times $𝒯$. For each $\tau \in 𝒯$, we use penalized maximum likelihood methods (Friedman, Hastie and Tibshirani (2010)) to compute the values of $\eta (\cdot )$, $\gamma (\cdot )$, and $\alpha (\cdot )$ that minimize the objective function

$$\frac{1}{2{\sum }_i{w}_i}\sum _{i=1}^m{w}_i{\left[(Y_i-\tau )-g\left\{\eta (\tau )+{\gamma (\tau )}^T{\mathbf{X}}_i+{\alpha (\tau )}^T{\zeta }_i(\tau )\right\}\right]}^{{}^{{}^2}}+\lambda {\Vert \{\gamma (\tau ),\alpha (\tau )\}\Vert }_1,$$

where $\lambda$ is a scalar tuning parameter and ${\Vert \cdot \Vert }_1$ represents the $L_1$-norm. The inverse probability of censoring weights $w_i$ account for censoring in the data. We assume censoring time is independent of the baseline covariates and longitudinal biomarkers, and we estimate $\widehat{G}(\cdot )$ using the Kaplan–Meier estimator. Alternatively, if censoring time is assumed to depend on only the baseline covariates, a Cox regression model can be used to estimate $\widehat{G}(\cdot )$.

We impose an $L_1$-penalty on $v+q$ regression parameters in the objective function to prevent overfitting. To ensure fair penalization, we apply proportion-of-maximum scaling (POMS) to the longitudinal biomarkers such that

$${Z_{ik}(t)}^{\text{POMS}}=\frac{Z_{it}(t)-{\text{min}}_{i,u}\{Z_{ik}(u)\}}{{\max }_{i,u}\{Z_{ik}(u)\}-{\text{min}}_{i,u}\{Z_{ik}(u)\}}.$$

Conducting dynamic prediction of MRL with ${\zeta }_i(\tau )={\mathbf{Z}}_i(\tau )$ is difficult in practice. Often, not all patients have longitudinal measurements ${\mathbf{Z}}_i(\tau )$ available at all desired prediction times $\tau \in 𝒯$. In the MIMIC-III data set, longitudinal measurements are recorded at four-hour time intervals. Over 80% of patients are missing at least one measurement, and over 25% of patients are missing at least 10 measurements for all studied longitudinal biomarkers. Parametric models of ${\mathbf{Z}}_i(\cdot )$ that could be used to impute missing measurements are likely to be misspecified due to the complex, heterogeneous nature of biomarker processes. Moreover, regressing MRL only on the biomarker measurements taken at the time of prediction discards the information contained in the history of measurements.

Intuitively, it is desirable to select a function $f(\cdot )$ that summarizes the biomarker trajectories from baseline to prediction time $\tau$. However, a simple summary function, such as average or slope, is unlikely to capture the complex trajectories of the longitudinal biomarkers. To address these complications, Lin et al. (2018) proposed summarizing the biomarker trajectories from baseline to prediction time using window-specific FPC scores. Alternatively, we propose summarizing the trajectories using window-specific context vectors constructed by LSTM autoencoders.

2.3. Context vector construction.

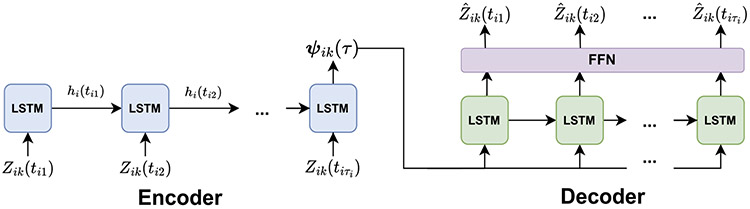
The window-specific context vector ${\psi }_{ik}(\tau )$ is an encoded representation of the trajectory of biomarker $k$ from baseline to prediction time $\tau$ for patient $i$. At each prediction time $\tau$, a distinct LSTM autoencoder is used to construct each of the $k=1,\dots ,p$ sets of window-specific context vectors. An LSTM autoencoder is an unsupervised neural network that learns how to best encode temporal input into a context vector, so it can then reconstruct the original input from that context vector. To uphold the dynamic nature of prediction, the LSTM autoencoder used to construct ${\psi }_{ik}(\tau )$ only accepts as input the biomarker measurements collected prior to time $\tau$ on patients at risk at time $\tau$, where patient $i$ is defined to be at risk at time $\tau$ if $Y_i>\tau$.

An LSTM autoencoder, which consists of an encoder and a decoder, is illustrated in Figure 2. Proportion-of-maximum scale the biomarker data, and let ${\mathbf{Z}}_{ik}^{\tau }=\{Z_{ik}(t_{i1}),\dots ,Z_{ik}(t_{i{\tau }_i})\}$ be the $n_{ik}^{\tau }$-dimensional vector of scaled measurements of biomarker $k$ collected on patient $i$ prior to time $\tau$. For each patient $i$ with $Y_i>\tau$, input ${\mathbf{Z}}_{ik}^{\tau }$ into the encoder. The encoder compresses ${\mathbf{Z}}_{ik}^{\tau }\in {\mathbb{R}}^{n_{ik}^{\tau }}$ into the window-specific context vector ${\psi }_{ik}(\tau )\in {\mathbb{R}}^s$. The decoder then constructs an estimate of the input scaled biomarker measurements, ${\widehat{\mathbf{Z}}}_{ik}^{\tau }$, from ${\psi }_{ik}(\tau )$. The autoencoder is trained to minimize the reconstruction error

$$\sum _{i:Y_i>\tau }\sum _{j=1}^{{\tau }_i}{\left\{Z_{ik}(t_{ij})-{\widehat{Z}}_{ik}(t_{ij})\right\}}^{{}^{{}^{{}^2}}}.$$

Fig. 2.

An LSTM autoencoder at time $\tau$, comprised of an encoder and a decoder. Both the encoder and decoder consist of a series of LSTM temporal units, labelled “LSTM.” The decoder also contains a feed-forward neural network layer, labelled “FFN.” The encoder compresses the input biomarker measurements $Z_{ik}(\cdot )$ into the window-specific context vector ${\psi }_{ik}(\tau )$, and the decoder attempts to reconstruct the original biomarker measurements from ${\psi }_{ik}(\tau )$. Information is passed between the LSTM temporal units via the hidden vectors $h_i(\cdot )$.

After training the autoencoder, the decoder can be removed from the network, so the encoder outputs the context vector ${\psi }_{ik}(\tau )$ directly to the user.

In an LSTM autoencoder, both the encoder and decoder are a type of recurrent neural network called a “long short-term memory network.” Recurrent neural networks (RNNs) are a class of artificial neural networks designed to process sequential data. RNNs contain a feedback loop that enables information from previous time steps to be passed to future time steps. The information is passed in an $s$-dimensional vector ${\mathbf{h}}_i(\cdot )$, referred to as a “hidden vector.” The parameters in an RNN are estimated via the back propagation through time (BPTT) algorithm (Werbos (1990)). In the BPTT algorithm, derivatives are multiplied across time steps. Consequently, in RNNs with a large number of time steps, if the derivatives are large, the gradients will increase exponentially and “explode.” If the derivatives are small, the gradients will decrease exponentially and “vanish.” This is referred to as the “vanishing and exploding gradient problem (Aggarwal (2018)).” The vanishing and exploding gradient problem makes it difficult for simple RNNs to capture long-term dependencies. LSTMs were designed especially to mitigate the vanishing and exploding gradient problem.

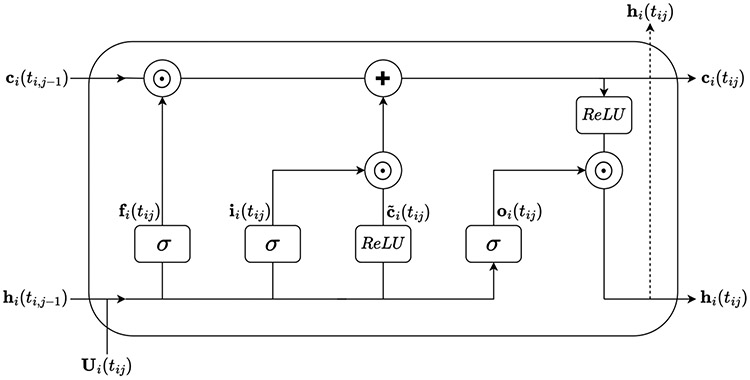
An LSTM can be conceptualized as a network of temporal units, with a single temporal unit corresponding to each time step in the data. Figure 3 depicts the LSTM temporal unit corresponding to time $t_{ij}$. LSTM networks mitigate the vanishing and exploding gradient problem using an $s$-dimensional vector ${\mathbf{c}}_i(\cdot )$, referred to as the “cell state.” Conceptually, the cell state can be thought of as a pseudo long-term memory that retains information from previous time steps (Aggarwal (2018)). The cell state is controlled by three $s$-dimensional gate control signals, the input gate ${\mathbf{i}}_i(\cdot )$, the forget gate ${\mathbf{f}}_i(\cdot )$, and the output gate ${\mathbf{o}}_i(\cdot )$. These gate control signals determine which information in the cell state is updated, discarded, and output to the next time step, respectively. Let ${\mathbf{U}}_i(t_{ij})$ represent the $r$-dimensional input vector for patient $i$ at time $t_{ij}$, and let ${\mathbf{h}}_i(t_{i,j-1})$ represent the $s$-dimensional hidden vector output for patient $i$ at time $t_{i,j-1}$. Then the three gate control signals for patient $i$ are characterized by the equations

$${\Omega }_i(t_{ij})=\sigma \left\{{\mathbf{W}}_{\Omega }{\mathbf{U}}_i(t_{ij})+{\mathbf{Q}}_{\Omega }{\mathbf{h}}_i(t_{i,j-1})+{\mathbf{v}}_{\Omega }\right\},\sigma (x)={(1+e^{-x})}^{-1},$$

where $\Omega =\mathbf{i}$, $\mathbf{f}$, $\mathbf{o}$, ${\mathbf{W}}_{\Omega }$ is an $s\times r$ parameter matrix, ${\mathbf{Q}}_{\Omega }$ is an $s\times s$ parameter matrix, and ${\mathbf{v}}_{\Omega }$ is an $s\times 1$ bias vector. Note, ${\mathbf{W}}_{\Omega }$, ${\mathbf{Q}}_{\Omega }$, and ${\mathbf{v}}_{\Omega }$ are gate-specific and temporally-shared.

Fig. 3.

An LSTM temporal unit at time $t_{ij}$.

At time $t_{ij}$, an $s$-dimensional candidate cell state for patient $i$, ${\tilde{\mathbf{c}}}_i(t_{ij})$, is computed as

$${\tilde{\mathbf{c}}}_i(t_{ij})=\text{ReLU}\{{\mathbf{W}}_c{\mathbf{U}}_i(t_{ij})+{\mathbf{Q}}_c{\mathbf{h}}_i(t_{i,j-1})+{\mathbf{v}}_c\},\text{ReLU}(x)=\max (0,x),$$

where ${\mathbf{W}}_c$ is an $s\times r$ parameter matrix, ${\mathbf{Q}}_c$ is an $s\times s$ parameter matrix, and ${\mathbf{v}}_c$ is an $s\times 1$ bias vector. Again, ${\mathbf{W}}_c$, ${\mathbf{Q}}_c$, and ${\mathbf{v}}_c$ are temporally-shared parameters.

At time $t_{ij}$, the cell state for patient $i$, ${\mathbf{c}}_i(t_{ij})$, is then computed as

$${\mathbf{c}}_i(t_{ij})={\mathbf{f}}_i(t_{ij})\odot {\mathit{c}}_i(t_{i,j-1})+{\mathbf{i}}_i(t_{ij})\odot {\tilde{\mathbf{c}}}_i(t_{ij}),$$

where $\odot$ represents the Hadamard product.

Ultimately, each temporal unit outputs a hidden vector for patient $i$, ${\mathbf{h}}_i(t_{ij})$, computed as

$${\mathbf{h}}_i(t_{ij})={\mathbf{o}}_i(t_{ij})\odot \text{ReLU}\{{\mathbf{c}}_i(t_{ij})\}.$$

The hidden vector is then passed to the next temporal unit. Additionally, it may be output to the next layer in the LSTM autoencoder.

At each prediction time $\tau$, for each of the $k=1,\dots ,p$ biomarkers, we train a separate LSTM autoencoder to construct the window-specific context vectors ${\psi }_{ik}(\tau )$ for all patients $i$ such that $Y_i>\tau$. Let the superscript $e$ signify elements of the encoder, and let the superscript $d$ signify elements of the decoder. Each encoder accepts as input the scaled measurements of biomarker $k$ collected at times $t_{ij}<\tau$ on patients with $Y_i>\tau$. For a given patient $i$, each biomarker measurement is input into a separate LSTM temporal unit, so ${\mathbf{U}}_i^e(t_{ij})=Z_{ik}(t_{ij})$ and $r=1$ for $j=1,\dots ,{\tau }_i$. The hidden vector for patient $i$ output by the last temporal unit is taken to be the context vector for patient $i$, so ${\psi }_{ik}(\tau )={\mathbf{h}}_i^e(t_{i{\tau }_i})$.

Similar to the encoder, the decoder contains an LSTM temporal unit corresponding to each biomarker measurement. In the decoder, each LSTM temporal unit accepts the context vector for patient $i$ as input, so ${\mathbf{U}}_i^d(t_{ij})={\psi }_{ik}(\tau )$ and $r=s$ for $j=1,\dots ,{\tau }_i$. Each temporal unit outputs the hidden vector ${\mathbf{h}}_i^d(t_{ij})$ which is fed into a feed-forward neural network (FFN) layer. At each measurement time $j=1,\dots ,{\tau }_i$, the FFN layer constructs an estimate of the scaled biomarker measurement for patient $i$, ${\widehat{Z}}_{ik}(t_{ij})$, from the hidden vector ${\mathbf{h}}_i^d(t_{ij})$ via linear regression. Specifically,

$${\widehat{Z}}_{ik}(t_{ij})={\mathbf{W}}_n{\mathbf{h}}_i^d(t_{ij})+v_n,$$

where ${\mathbf{W}}_n$ is an $s$-dimensional, temporally-shared parameter vector, and $v_n$ is a temporally-shared scalar bias.

As previously mentioned, the LSTM autoencoder is trained to minimize the reconstruction error ${\sum }_{i:Y_i>\tau }{\sum }_{j=1}^{{\tau }_i}{\{Z_{ik}(t_{ij})-{\widehat{Z}}_{ik}(t_{ij})\}}^2$. After training the autoencoder for biomarker $k$ at prediction time $\tau$, the window-specific context vector ${\psi }_{ik}(\tau )$ can be extracted for each patient $i$ such that $Y_i>\tau$. Because each window-specific context vector is constructed using only measurements taken at times $t_{ij}<\tau$ on patients with $Y_i>\tau$, ${\psi }_{ik}(\tau )$ can be used to conduct dynamic prediction. Moreover, since the number and timing of biomarker measurements can differ between patients, imputation of missing or irregularly measured biomarkers is unnecessary.

Each LSTM autoencoder has several hyperparameters that influence how well the output window-specific context vectors summarize the input biomarker trajectories. Important hyperparameters include the dimension of the window-specific context vector, $s$, and the number of times the BPTT algorithm processes the entire data set, referred to as the number of “training epochs.” Too many training epochs can lead to overfitting the data, and too few can lead to underfitting. These hyperparameters can be selected via traditional tuning methods such as hold-out validation or cross-validation. In Section 1 of the Supplementary Material (Rhodes, Davidian and Lu (2023)), we present an automated approach for selecting these hyperparameters for the LSTM-GLM.

2.4. LSTM-GLM.

First, we dynamically predict MRL using a dynamic transformed MRL model that includes the baseline covariates and window-specific context vectors as predictors. Let ${\psi }_i(\tau )=\{{\psi }_{i1}(\tau ),\dots ,{\psi }_{ip}(\tau )\}$ be an $sp$-dimensional vector containing the $p$ biomarker-specific, window-specific context vectors for patient $i$ at prediction time $\tau$. Additionally, let $g(\cdot )$ be a prespecified, nonnegative link function that is twice continuously differentiable and strictly increasing. The LSTM-GLM is specified as

$$E\{T_i-\tau \mid T_i>\tau ,{\mathscr{H}}_i(\tau )\}=g\{\eta (\tau )+{\gamma (\tau )}^T{\mathbf{X}}_i+\alpha {(\tau )}^T{\psi }_i(\tau )\}.$$ (2)

The LSTM-GLM is a special case of the dynamic transformed MRL model, specified in equation (1), where ${\zeta }_i(\tau )={\psi }_i(\tau )$. Accordingly, we estimate the parameters in equation (2) via penalized maximum likelihood by adopting the landmarking approach detailed in Section 2.2. Because a separate context vector is constructed for each biomarker, the parameter estimates of the LSTM-GLM can be used to gain insight into the relationship between the longitudinal biomarkers and mean residual life.

2.5. LSTM-NN.

Next, we introduce an alternative method for dynamic prediction of MRL from window-specific context vectors. The LSTM-NN dynamically predicts MRL using a feed-forward neural network that accepts the baseline covariates and window-specific context vectors as input. Compared to generalized linear models, feed-forward neural networks are more capable of modeling complex functional relationships. In fact, a neural network with a single nonlinear hidden layer and a single linear output layer can compute almost any function (Aggarwal (2018)). This makes neural networks ideal for modeling the complex relationship between MRL and the biomarker processes.

The LSTM-NN is a feed-forward neural network comprised of one or more hidden layers and an output layer. The first hidden layer takes the baseline covariates and context vectors as input, and the output layer produces estimates of MRL. Additional hidden layers can be added to the LSTM-NN to tailor the network’s flexibility to the complexity of the studied data set. For our simulation studies and MIMIC-III data application, we consider an LSTM-NN with two hidden layers, as illustrated in Figure 4.

Fig. 4.

The LSTM-NN at prediction time $\tau$.

For a given prediction time $\tau$, the first hidden layer, FFN1, accepts the baseline covariates ${\mathbf{X}}_i$ and the window-specific context vectors ${\psi }_i(\tau )$ as input. FFN1 then computes and outputs the $u$-dimensional hidden vector ${\mathbf{O}}_{i1}(\tau )$, which is calculated as

$${\mathbf{O}}_{i1}(\tau )=\tanh [{\mathbf{W}}_1\{{\mathbf{X}}_i,{\psi }_i(\tau )\}+{\mathbf{v}}_1],\tanh (x)=\frac{e^x-e^{-x}}{e^x+e^{-x}},$$

where ${\mathbf{W}}_1$ is a $u\times (q+sp)$ parameter matrix and ${\mathbf{v}}_1$ is a $u$-dimensional bias vector.

The second hidden layer, FFN2, then accepts ${\mathbf{O}}_{i1}(\tau )$ as input. FFN2 computes and outputs the $u$-dimensional hidden vector ${\mathbf{O}}_{i2}(\tau )$, which is calculated as

$${\mathbf{O}}_{i2}(\tau )=\tanh [{\mathbf{W}}_2{\mathbf{O}}_{i1}(\tau )+{\mathbf{v}}_2],$$

where ${\mathbf{W}}_2$ is a $u\times u$ parameter matrix and ${\mathbf{v}}_2$ is a $u$-dimensional bias vector.

The output layer, FFN3, then accepts ${\mathbf{O}}_{i2}(\tau )$ as input. FFN3 computes and outputs the estimate of MRL for patient $i$ at time $\tau$ as

$${\widehat{R}}_i(\tau )={\mathbf{W}}_3{\mathbf{O}}_{i2}(\tau )+v_3,$$

where ${\mathbf{W}}_3$ is a $u$-dimensional parameter vector and $v_3$ is a scalar bias.

As with the LSTM-GLM, we estimate the parameters of the LSTM-NN via a landmarking approach. First, we specify a set of positive prediction times $𝒯$. Then for each $\tau \in 𝒯$, we train the LSTM-NN to minimize the objective function

$${\left[\sum _{i=1}^m\frac{{\Delta }_{i}I(Y_i>\tau )}{\widehat{G}(Y_i)}\right]}^{{}^{{}^{{}^{{}^{{}^{{}^{-1}}}}}}}\sum _{i=1}^m\frac{{\Delta }_{i}I(Y_i>\tau )}{\widehat{G}(Y_i)}{\left[(Y_i-\tau )-{\widehat{R}}_i(\tau )\right]}^{{}^{{}^2}}+\lambda {\Vert {\mathbf{W}}_1\Vert }_2^2+{\lambda \Vert {\mathbf{W}}_2\Vert }_2^2.$$

Again, we use inverse probability of censoring weights to account for censoring, where $\widehat{G}(\cdot )$ is the Kaplan–Meier estimate of the survival function of censoring time. Additionally, we apply an $L_2$-penalty to the parameter matrices ${\mathbf{W}}_1$ and ${\mathbf{W}}_2$ to prevent overfitting. Here ${\Vert \cdot \Vert }_2$ represents the $L_2$-norm, and $\lambda$ is a tuning parameter for the $L_2$-penalties.

The LSTM-NN provides more flexibility in modeling the relationship between MRL and the longitudinal biomarkers than the LSTM-GLM. However, the complexity of the feed-forward neural network makes it difficult to interpret the relationship between the biomarkers and MRL. Moreover, the LSTM-NN has a number of hyperparameters that must be tuned, including the dimension of the parameter matrices $u$, the tuning parameter for the $L_2$-penalty $\lambda$, and the number of epochs used to train the LSTM-NN. These hyperparameters can be tuned using traditional processes, such as hold-out validation or cross-validation. However, these processes are computationally-intensive, and imperfect tuning can result in poor prediction performance.

3. Performance evaluation.

3.1. Comparative methods.

For the LSTM-GLM and the LSTM-NN to have utility in the clinical setting, the models must produce accurate dynamic predictions of MRL relative to competing dynamic prediction methods. Consequently, we evaluate the prediction performance of the LSTM-GLM and the LSTM-NN relative to six variations of the dynamic transformed MRL model specified in equation (1). For each of the six dynamic transformed MRL models, we define a distinct function of the history of longitudinal biomarker measurements, ${\zeta }_i(\tau )=f\{{\mathbf{Z}}_i(t_{i1}),\dots ,{\mathbf{Z}}_i(t_{i{\tau }_i})\}$. To maintain the dynamic nature of prediction, we construct ${\zeta }_i(\tau )$ using only biomarker measurements taken at times $t_{ij}<\tau$ on patients with $Y_i>\tau$. First, we define ${\zeta }_i^{(B)}(\tau )$ to be a vector of the baseline biomarker measurements. Second, we define ${\zeta }_i^{(L)}(\tau )$ to be a vector of the biomarker measurements collected most recently before prediction time $\tau$ (i.e., the “last-value carried forward”). Third, we define ${\zeta }_i^{(A)}(\tau )$ to be a vector of the average value of each biomarker prior to time $\tau$. Next, we define two vectors containing the intercept and slope of each biomarker regressed against time. The first vector, ${\zeta }_i^{(S)}(\tau )$, is formed by conducting an independent linear regression on each patient for each biomarker. The second vector, ${\zeta }_i^{(M)}(\tau )$, is formed by fitting a single linear mixed effects model with a random intercept and slope to all patients for each biomarker. Lastly, we define ${\zeta }_i^{(F)}(\tau )$ to be a vector of FPC scores computed independently on each biomarker. For each biomarker, ${\zeta }_i^{(F)}(\tau )$ contains the minimum number of FPC scores required to explain 99% of the total variance of that biomarker. We provide technical specifications for each comparative method in Section 2 of the Supplementary Material (Rhodes, Davidian and Lu (2023)).

3.2. Performance metrics.

To evaluate prediction performance, we focus on measures of calibration and discrimination. In the MIMIC-III data set, the survival time of interest $T_i^{\ast }$ was observed for only 14.99% of patients. Consequently, it is important for the measures of calibration and discrimination to account for censoring. Let ${\widehat{\text{RMRL}}}_i(\tau )$ represent a given model’s estimate of RMRL for patient $i$ at time $\tau$. We assess the calibration of each model via the inverse probability of censoring weighted mean square error

$$\frac{1}{{\sum }_i\frac{{\Delta }_{i}I(Y_i>\tau )}{\widehat{G}(Y_i)}}\sum _i\frac{{\Delta }_{i}I(Y_i>\tau )}{\widehat{G}(Y_i)}{\left[(Y_i-\tau )-{\widehat{\text{RMRL}}}_i(\tau )\right]}^{{}^{{}^2}}.$$

We refer to this quantity as the “testing loss.”

In addition to calibration, we assess each model’s discrimination, that is, its ability to accurately predict who among a given pair of patients will live longer. We compute the following discrimination metric based on Harrell’s C-Index (Harrell, Lee and Mark (1996)):

$$\frac{{\sum }_{i\ne j}I\{c_i(\tau )>c_j(\tau )\}I\{{\widehat{c}}_i(\tau )>{\widehat{c}}_j(\tau )\}{\Delta }_j}{{\sum }_{i\ne j}I\{c_i(\tau )>c_j(\tau )\}{\Delta }_j},$$

where $c_i(\tau )=Y_i-\tau$ and ${\widehat{c}}_i(\tau )={\widehat{\text{RMRL}}}_i(\tau )$. We refer to this quantity as the “testing C-index.”

3.3. Software.

We conduct the simulation studies and MIMIC-III data application in Python and R. We build and train the LSTM autoencoders and LSTM-NNs in Python using the Keras library (Chollet et al. (2015)). We fit the LSTM-GLMs and the six dynamic transformed MRL models in R using the glmnet package (Friedman, Hastie and Tibshirani (2010)). We compute the Kaplan–Meier estimate of the survival function of censoring time, $\widehat{G}(\cdot )$, in R using the survival package (Therneau and Grambsch (2000)). We leverage the fdapace R package (Gajardo et al. (2021)) to construct the FPCA vectors ${\zeta }_i^{(F)}$, and we use the lme4 R package (Bates et al. (2015)) to construct the linear regression vectors ${\zeta }_i^{(S)}$ and the mixed effects vectors ${\zeta }_i^{(M)}$.

4. Simulations.

We conduct simulation studies to assess the prediction performance of the LSTM-GLM and the LSTM-NN relative to the performance of the six dynamic transformed MRL models described in Section 3.1. We generate a single data set of covariates for $m=5000$ patients. For each patient we generate a single baseline covariate $X_i\stackrel{\text{iid}}{\sim }\mathbb{U}(0,1)$, where $\mathbb{U}$ denotes the uniform distribution. Let $({\tau }_1,{\tau }_2,\dots ,{\tau }_{19})=(0,0.5,\dots ,9)$, and let $𝒩(\mu ,\Sigma )$ denote a normal distribution with mean $\mu$ and variance-covariance $\Sigma$. For each patient we generate a single longitudinal biomarker at $j=1,2,\dots ,19$ patient-specific measurement times $t_{ij}=\text{min}(0,{\tau }_j+{\epsilon }_{ij})$, where ${\epsilon }_{ij}\stackrel{\text{iid}}{\sim }𝒩(0,{0.05}^2)$. We generate the longitudinal biomarker measurements as $Z_i(t_{ij})=B_i(t_{ij})+{ϵ}_{ij}$, where ${ϵ}_{ij}\stackrel{\text{iid}}{\sim }𝒩(0,{0.5}^2)$ represents the measurement error, and $B_i(\cdot )$ is a piecewise linear mixed effects model with eight interior knots. Specifically,

$$B_i(t)=a+b_{i0}+(c_1+b_{i1})t+\sum _{j=2}^{10}I\{t>(j-1)\}(c_j+b_{ij})\{t-(j-1)\},$$

where $a=-2$ and $(c_1,c_2,\dots ,c_{10})=(4,-7,5,-2.5,3.5,-5,1.5,2,-2,1)$. Let rep($(x,y)$) denote a vector containing $x$ repeated $y$ times. Then $(b_{i0},b_{i1},\dots ,b_{i10})\sim 𝒩(0,\mathbf{D})$, where $\mathbf{D}$ is the diagonal matrix $\mathbf{D}=\text{diag}\{1,\text{rep}(0.05,5),\text{rep}(0.01,5)\}$. Figure 5 illustrates the longitudinal biomarker trajectories of 25 randomly selected patients in the generated data set of covariates.

Fig. 5.

The biomarker trajectories of 25 randomly selected patients in the simulated covariate data set.

We conduct two simulation studies. In each study, we conduct 500 simulations using the aforementioned data set of covariates. For each of the 500 simulations, we generate a new data set of survival times $T_i$ and censoring times $C_i$ for all patients $i=1,2,\dots ,5000$. In both studies, we generate the censoring times as $C_i\stackrel{\text{iid}}{\sim }\mathbb{U}(0,100)$. Conversely, we generate the survival times $T_i$ using a different model for each study. In the first study, we generate $T_i$ according to the accelerated failure time (AFT) model ${\nu }_i={\int }_0^{T_i}\text{exp}\{{\beta }_1{B}_i(s)+{\beta }_2{X}_i\}ds$, where ${\beta }_1={\beta }_2=1$, ${\nu }_i=\text{exp}({\theta }_i)$, and ${\theta }_i\stackrel{\text{iid}}{\sim }𝒩(3,1)$. In the second study, we generate $T_i$ according to a Cox proportional hazards model with an exponential baseline hazard function. Specifically, $h_i(t\mid B_i(t),X_i)=\lambda \text{exp}\{{\beta }_1{B}_i(t)+{\beta }_2{X}_i\}$, where ${\beta }_1={\beta }_2=1$ and $\lambda =0.05$. In both studies, we impose a restricted lifetime of $L=50$. We describe the technical details of the survival time generation process in the Supplementary Material, Section 3 (Rhodes, Davidian and Lu (2023)).

We conduct prediction at time $\tau =5$, so $n_i\in \{10,11\}$. Across the 500 simulated AFT data sets, between 1824 and 1958 (mean = 1886) patients are at risk at $\tau =5$. Across the 500 simulated Cox data sets, between 1368 and 1502 (mean = 1438) patients are at risk at $\tau =5$. For both the AFT and Cox simulations, between 14% and 20% (mean = 17%) of the patients at-risk at $\tau =5$ are censored.

We log-transform the observed restricted residual lifetimes $Y_i-\tau$, and we define the link function for the LSTM-GLM and the six dynamic transformed MRL models to be the identity $g(x)=x$. Since we consider only a single longitudinal biomarker, we are not concerned with overfitting the data. Consequently, we set the tuning parameter to $\lambda =0$ in all dynamic prediction models.

We specify the dimension of the window-specific context vectors to be $s=5$, and we train the LSTM autoencoders for 500 epochs. We specify the dimension of the LSTM-NN parameter matrices to be $u=3$, and we train the LSTM-NNs for 5000 epochs. We train all neural networks using the Adam optimization algorithm (Kingma and Ba (2017)). For the LSTM autoencoders, we use cross-validation to adaptively select the learning rate from the options {$1{\mathrm{e}}^{-3},1{\mathrm{e}}^{-4}$} (O’Malley et al. (2019)). For the LSTM-NNs, we select a fixed learning rate of 1e⁻³.

For each simulation we randomly divide the data into a training data set and a testing data set, stratifying on the censoring status ${\Delta }_i$. We specify the training and testing data sets to each include 50% of the patients at risk at time $\tau =5$. We estimate the survival function of censoring time $\widehat{G}(\cdot )$ independently on the training and testing data sets. We then fit each model on the training data set and compute the performance metrics specified in Section 3.2 on the testing data set. We provide the Python and R code used to conduct the simulation studies in the Supplementary Material (Rhodes, Davidian and Lu (2023)).

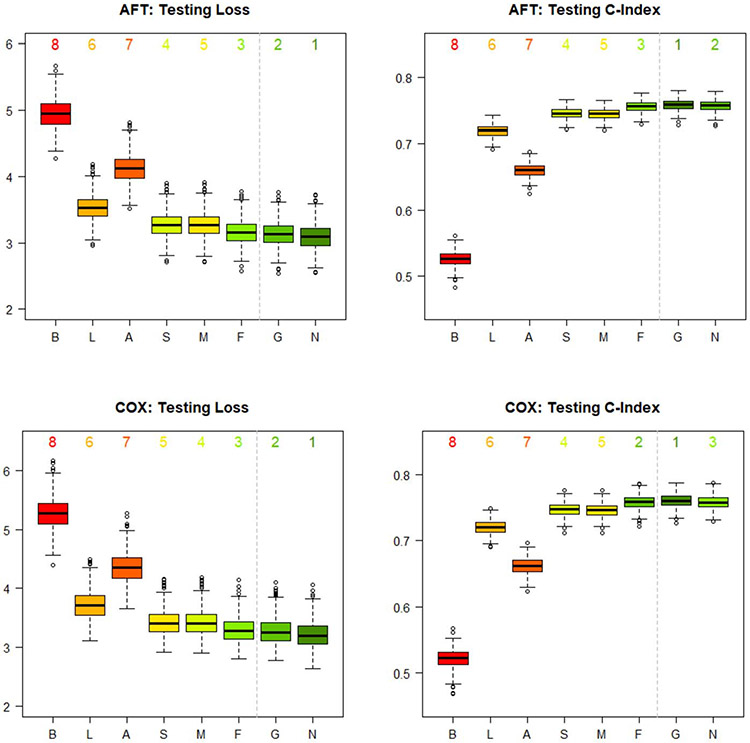
We plot the distributions of the 500 testing losses and 500 testing C-indexes for each of the eight studied dynamic prediction models in Figure 6. For both the AFT and Cox simulations, the LSTM-NN results in the lowest median testing loss, followed by the LSTM-GLM. The LSTM-GLM consistently results in the highest median testing C-index. The LSTM-NN results in the second-highest median testing C-index for the AFT simulations and in the third-highest for the Cox simulations, where it is surpassed by the FPCA model. Overall, the simulation studies indicate that the LSTM-GLM and the LSTM-NN exhibit better calibration and discrimination than the baseline, last-value carried forward, average, linear regression, and mixed effects models, and that they exhibit at least comparable performance to the FPCA model. Thus, the simulation studies support that the LSTM-GLM and the LSTM-NN are useful tools for dynamically predicting MRL from longitudinal biomarker data.

Fig. 6.

Distributions of the 500 testing losses and 500 testing C-indexes for each of the eight dynamic prediction models in the simulation studies. The models resulting in the lowest median testing loss and the highest median testing C-index are labelled 1. The models resulting in the highest median testing loss and the lowest median testing C-index are labelled 8. The six dynamic transformed MRL models are labelled according to their formulation of ${\zeta }_i(\tau )$. “B” represents the baseline vector. “L” represents the last-value carried forward vector. “A” represents the average vector. “S” represents the linear regression vector. “M” represents the mixed effects vector. “F” represents the FPCA vector. Furthermore, “G” represents the LSTM-GLM, and “N” represents the LSTM-NN.

In Section 4 of the Supplementary Material, we repeat the simulation studies, reducing both the measurement error and the variation in measurement times (Rhodes, Davidian and Lu (2023)). Compared to the simulations studies described above, the supplemental simulation studies demonstrate a more significant improvement in calibration and discrimination for the LSTM-GLM and the LSTM-NN relative to competing methods. Thus, the supplemental simulation studies indicate that the LSTM-GLM and the LSTM-NN are especially useful for producing accurate dynamic predictions of MRL in settings where the longitudinal biomarkers are measured using precise instruments.

5. Application to MIMIC-III.

5.1. Data analysis.

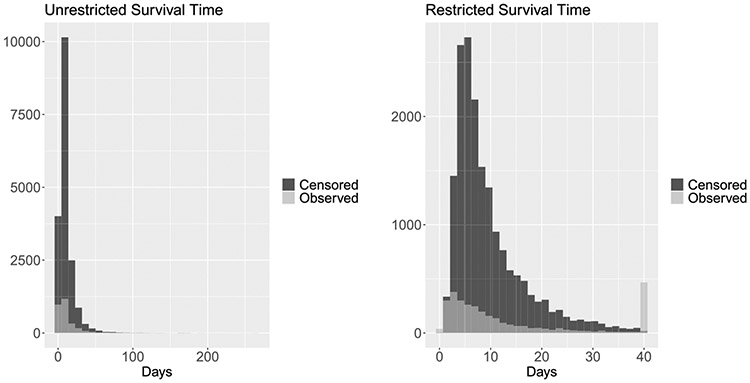
We dynamically predict the RMRL of septic patients in the ICU from EMR data using the LSTM-GLM and the LSTM-NN. To evaluate the utility of the proposed methods in this clinical setting, we compare the prediction performance of the LSTM-GLM and the LSTM-NN to the performance of the six dynamic transformed MRL models described in Section 3.1. We conduct the study on the MIMIC-III data set described in Section 1. The distributions of the unrestricted and restricted survival times of the septic patients are depicted in Figure 7. Because the distribution of restricted survival times is notably right skewed and RMRL is nonnegative by definition, we log-transform the observed restricted residual lifetimes $Y_i-\tau$. We then define the link function for the LSTM-GLM and the six dynamic transformed MRL models to be the identity $g(x)=x$. Because we conduct our study using $p=15$ longitudinal biomarkers, we face the risk of overfitting the data. Consequently, we select the $L_1$-penalty tuning parameter $\lambda$ via five-fold cross-validation for the LSTM-GLM and the six dynamic transformed MRL models.

Fig. 7.

LEFT: The distribution of unrestricted survival time, stratified by censoring status. RIGHT: The distribution of survival time restricted to L = 40 days, stratified by censoring status.

We provide a detailed description of the hyperparameter selection process for the LSTM-GLM and the LSTM-NN in the Supplementary Material, Section 5 (Rhodes, Davidian and Lu (2023)). Let $s$ denote the dimension of the window-specific context vectors, and let ${\text{ep}}_a$ denote the number of epochs used to train the LSTM autoencoders. At each prediction time $\tau \in 𝒯$, we construct four sets of window-specific context vectors using the hyperparameter settings $(s,{\text{ep}}_a)\in \{(3,150),(5,150),(5,300),(7,300)\}$, and we fit four LSTM-GLMs that each regress on one of the four sets of context vectors. For each $\tau \in 𝒯$, we define the LSTM-GLM that results in the lowest median testing loss to be the “best” LSTM-GLM at time $\tau$. The hyperparameter settings of the best LSTM-GLM at each $\tau \in 𝒯$ can be seen in Table 1.

Table 1.

The hyperparameter settings of the best LSTM-GLM and the best LSTM-NN at each prediction time $\tau \in 𝒯$, where the “best” model is defined to be the one resulting in the lowest median testing loss

Prediction Time	LSTM-GLM		LSTM-NN
Days	$s$	${\text{ep}}_a$	$s$	${\text{ep}}_a$	$\lambda$	$u$	${\text{ep}}_n$
1	3	150	7	300	0.01	1	2000
1.5	7	300	7	300	0.005	2	3000
2	3	150	7	300	0.005	2	2000
2.5	5	300	7	300	0.01	2	2000
3	7	300	7	300	0.01	2	3000

Additionally, we fit an “automated” LSTM-GLM which selects the hyperparameter settings of the window-specific context vectors via cross-validation. We describe the technical details of the automated hyperparameter selection process in the Supplementary Material, Section 1 (Rhodes, Davidian and Lu (2023)).

Let $\lambda$ denote the LSTM-NN $L_2$-penalty tuning parameter, let $u$ denote the dimension of the LSTM-NN parameter matrices, and let ${\text{ep}}_n$ denote the number of LSTM-NN training epochs. We train eight LSTM-NNs on the window-specific context vectors constructed with hyperparameter settings (7, 300) using all eight possible combinations of $\lambda \in \{0.005,0.01\}$, $u\in \{1,2\}$, and ${\text{ep}}_n\in \{2000,3000\}$. For each $\tau \in 𝒯$, we define the LSTM-NN that results in the lowest median testing loss to be the “best” LSTM-NN at time $\tau$. The hyperparameter settings of the best LSTM-NN at each $\tau \in 𝒯$ can be seen in Table 1.

We train all LSTM autoencoders and LSTM-NNs using the Adam optimization algorithm (Kingma and Ba (2017)). For each LSTM autoencoder, we use Bayesian optimization to adaptively select the learning rate from the options {$1{\mathrm{e}}^{-2},1{\mathrm{e}}^{-3},1{\mathrm{e}}^{-4}$} (O’Malley et al. (2019)). For the LSTM-NN, we select a fixed learning rate of 1e⁻⁴.

We conduct prediction at five prediction times, $\tau =\{1,1.5,2,2.5,3\}$, where $\tau \in 𝒯$ represents the number of days passed since the time of the given patient’s first record in the data set. At prediction time $\tau \in 𝒯$, we randomly divide the data into a training data set and a testing data set, stratifying on the censoring status ${\Delta }_i$. The training data set is specified to include 70% of the patients at risk at time $\tau$, and the testing data set is defined to include the other 30% of patients at risk. We estimate the survival function of censoring time $\widehat{G}(\cdot )$ independently on the training and testing data sets. We then fit each model on the training data set and compute the performance metrics, specified in Section 3.2, on the testing data set. We repeat this process 100 times, using 100 unique divisions of the data.

5.2. Results.

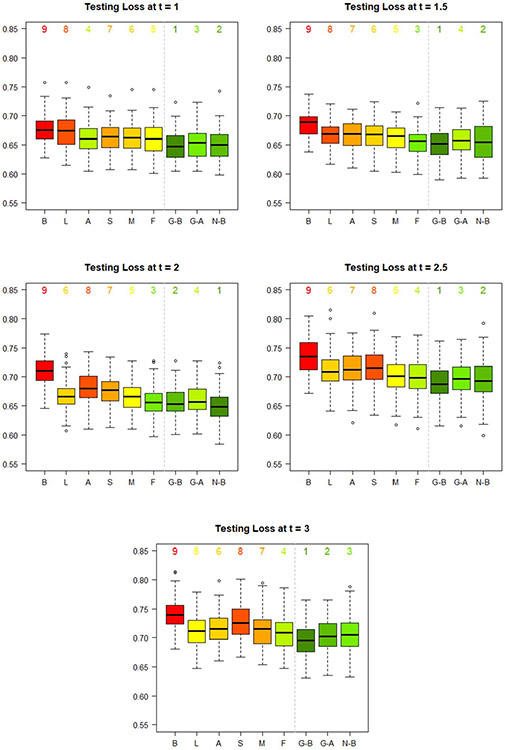
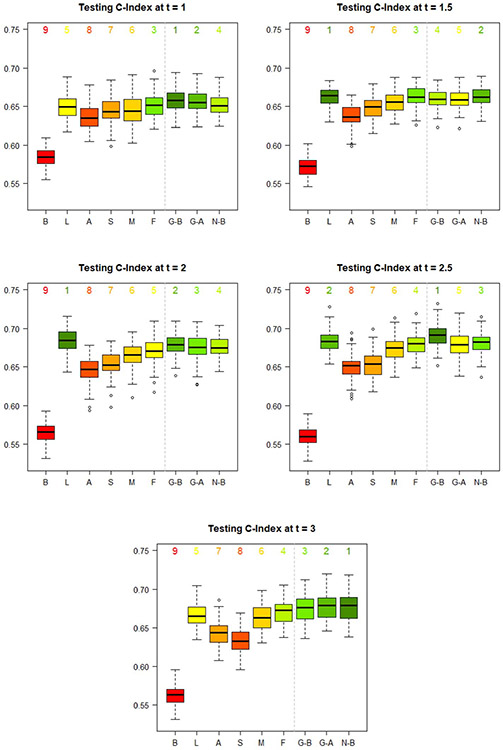
For each prediction time $\tau \in 𝒯$, we plot the distribution of 100 testing losses for the best LSTM-GLM, the automated LSTM-GLM, the best LSTM-NN, and the six dynamic transformed MRL models in Figure 8, and we plot the distribution of 100 testing C-indexes in Figure 9.

Fig. 8.

Distribution of the 100 testing losses for each of the nine studied dynamic prediction models at each prediction time $\tau \in 𝒯=\{1,1.5,2,2.5,3\}$. The model resulting in the lowest median testing loss is labelled 1. The model resulting in the highest median testing loss is labelled 9. The six dynamic transformed MRL models are labelled according to their formulation of ${\zeta }_i(\tau )$. “B” represents the baseline vector. “L” represents the last-value carried forward vector. “A” represents the average vector. “S” represents the linear regression vector. “M” represents the mixed effects vector. “F” represents the FPCA vector. The best LSTM-GLM is labelled “G-B.” The automated LSTM-GLM is labelled “G-A. ” The best LSTM-NN is labelled “N-B.”

Fig. 9.

Distribution of the 100 testing C-indexes for each of the nine studied dynamic prediction models at each prediction time $\tau \in 𝒯=\{1,1.5,2,2.5,3\}$. The model resulting in the highest median testing C-index is labelled 1. The model resulting in the lowest median testing C-index is labelled 9. The six dynamic transformed MRL models are labelled according to their formulation of ${\zeta }_i(\tau )$. “B” represents the baseline vector. “L” represents the last–value carried forward vector. “A” represents the average vector. “S” represents the linear regression vector. “M” represents the mixed effects vector. “F” represents the FPCA vector. The best LSTM-GLM is labelled “G-B.” The automated LSTM-GLM is labelled “G-A.” The best LSTM-NN is labelled “N-B.”

First, we compare the calibration of the nine dynamic prediction models via the testing loss. Generally, the best LSTM-GLM, the automated LSTM-GLM, the best LSTM-NN, and the FPCA model result in the lowest median testing losses. The baseline model consistently results in the highest median testing loss.

At prediction times $\tau =1,1.5,2.5,3$, the best LSTM-GLM results in the lowest median testing loss. At $\tau =2$, the best LSTM-NN results in the lowest median testing loss. In this application, the added flexibility of the LSTM-NN does not offset the cost of imperfect hyperparameter tuning.

In practice, we do not know which hyperparameter settings result in the “best” LSTM-GLM and the “best” LSTM-NN. Consequently, we use cross-validation to automatically select hyperparameters for the LSTM-GLM, as detailed in Section 1 of the Supplementary Material (Rhodes, Davidian and Lu (2023)). Generally, the automated hyperparameter selection process performs well. Disregarding the best LSTM-GLM and the best LSTM-NN, the automated LSTM-GLM results in the lowest median testing loss at prediction times $\tau =1,2.5,3$, and in the second-lowest median testing loss at $\tau =1.5,2$, where it is beat only by the FPCA model.

Second, we compare the discrimination of the nine dynamic prediction models via the testing C-index. As with calibration, the best LSTM-GLM, the automated LSTM-GLM, the best LSTM-NN, and the FPCA model generally result in good discrimination, and the baseline model consistently results in the poorest discrimination. Interestingly, the last-value carried forward model results in the highest median testing C-index at prediction times $\tau =1.5$, 2.

The best LSTM-NN results in a higher testing C-index than the best LSTM-GLM only at prediction times $\tau =1.5$, 3. Again, this indicates that the added flexibility of the LSTM-NN is offset by imperfect hyperparameter tuning.

The automated hyperparameter selection process for the LSTM-GLM performs well with respect to discrimination. Disregarding the best LSTM-GLM and the best LSTM-NN, the automated LSTM-GLM results in the highest median testing C-index at prediction times $\tau =1,3$, the second-highest at $\tau =2$, and the third-highest at $\tau =1.5,2.5$. In this case, the discrimination of the automated LSTM-GLM is beat only by the last-value carried forward model and the FPCA model.

In clinical application, calibration performance is often valued over discrimination performance. Typically, it is more important to accurately predict one septic patient’s remaining life expectancy than to accurately predict which of two septic patients has a longer remaining life expectancy. Taking this into consideration, these results suggest that the LSTM-GLM and the LSTM-NN exhibit the best performance when dynamically predicting the RMRL of septic patients in the ICU from EMR data, as compared to the baseline, last-value carried forward, average, linear regression, and mixed effects models. Moreover, the LSTM-GLM and the LSTM-NN exhibit at least comparable performance to the FPCA model, and if their hyperparameters are properly tuned, the LSTM-GLM and the LSTM-NN exhibit better performance than the FPCA model. This study demonstrates that the LSTM-GLM and the LSTM-NN are useful models for producing individualized, real-time predictions of the RMRL of septic patients in the ICU from EMR data.

6. Discussion.

Sepsis is a leading cause of death worldwide and remains highly challenging to treat (Singer et al. (2016)). We introduce two methods, the LSTM-GLM and the LSTM-NN, to dynamically predict the RMRL of septic patients in the ICU from EMR data. Through simulation studies and application to the MIMIC-III data set, we demonstrate that the LSTM-GLM and the LSTM-NN exhibit superior prediction performance relative to six competing methods. Thus, the LSTM-GLM and the LSTM-NN offer an automatic method to synthesize complex longitudinal biomarker trajectories and produce accurate predictions of MRL, all while upholding the dynamic nature of prediction. By producing individualized, real-time predictions of the RMRL of septic patients, the LSTM-GLM and the LSTM-NN can help clinicians make informed treatment decisions, potentially improving septic patient care.

The LSTM-GLM and the LSTM-NN can process data containing a large number of patients and biomarkers, like that typically found in EMRs. However, the methods can be computationally expensive relative to the baseline, last-value carried forward, average, linear regression, mixed effects, and FPCA dynamic transformed MRL models.

Because we propose training a distinct LSTM autoencoder to construct the context vector for each longitudinal biomarker, the relative computational cost of the LSTM-GLM and the LSTM-NN is most notable in settings with a large number of longitudinal biomarkers. To improve the computational efficiency of the proposed methods, a context vector summarizing multiple biomarkers could be constructed by training a single LSTM autoencoder on multiple biomarkers. However, this approach further obfuscates the relationship between MRL and the biomarkers. Additional research needs to be conducted to evaluate the feasibility and utility of this approach.

Alternative to the presented methods, a joint model could be constructed to connect the longitudinal biomarkers with the hazard function of death (Tsiatis and Davidian (2004)), and MRL predictions could be derived from the hazard function. However, this procedure can make it difficult to interpret the relationship between the biomarkers and MRL. Additionally, constructing joint models with a large number of longitudinal biomarkers can be computationally challenging (Hickey et al. (2016)).

In this work, we assume censoring time is independent of the baseline covariates and longitudinal biomarkers, and we estimate the survival function of censoring time $\widehat{G}(\cdot )$ via the Kaplan–Meier method. If censoring time is dependent on both baseline and longitudinal covariates, a time-dependent Cox regression model can be used to estimate $\widehat{G}(\cdot )$. However, further research should be conducted to determine how best to incorporate the history of longitudinal biomarker measurements into the Cox regression model. Potentially, the window-specific context vectors could be used as predictors in the Cox model.

We present an automated hyperparameter selection process for the LSTM-GLM in the Supplementary Material, Section 1 (Rhodes, Davidian and Lu (2023)). Further research is required to formulate satisfactory methods for tuning the hyperparameters of the LSTM-NN.

In this paper, we focus on obtaining accurate predictions of MRL. Consequently, we impose an $L_1$-penalty on the parameters of the LSTM-GLM to prevent overfitting. To conduct variable selection with the LSTM-GLM, a group LASSO penalty could instead be imposed to ensure that the entire context vector for a given longitudinal biomarker is either included in or removed from the model (Yuan and Lin (2006)). Further research is needed to determine the efficacy of using the LSTM-GLM to conduct variable selection.

NIHMS1945187-video-Code.zip ^{(18.7KB, zip)}