TRIBAL: Tree Inference of B cell Clonal Lineages

Abstract

B cells are a critical component of the adaptive immune system, responsible for producing antibodies that help protect the body from infections and foreign substances. Single cell RNA-sequencing (scRNA-seq) has allowed for both profiling of B cell receptor (BCR) sequences and gene expression. However, understanding the adaptive and evolutionary mechanisms of B cells in response to specific stimuli remains a significant challenge in the field of immunology. We introduce a new method, TRIBAL, which aims to infer the evolutionary history of clonally related B cells from scRNA-seq data. The key insight of TRIBAL is that inclusion of isotype data into the B cell lineage inference problem is valuable for reducing phylogenetic uncertainty that arises when only considering the receptor sequences. Consequently, the TRIBAL inferred B cell lineage trees jointly capture the somatic mutations introduced to the B cell receptor during affinity maturation and isotype transitions during class switch recombination. In addition, TRIBAL infers isotype transition probabilities that are valuable for gaining insight into the dynamics of class switching.

Via in silico experiments, we demonstrate that TRIBAL infers isotype transition probabilities with the ability to distinguish between direct versus sequential switching in a B cell population. This results in more accurate B cell lineage trees and corresponding ancestral sequence and class switch reconstruction compared to competing methods. Using real-world scRNA-seq datasets, we show that TRIBAL recapitulates expected biological trends in a model affinity maturation system. Furthermore, the B cell lineage trees inferred by TRIBAL were equally plausible for the BCR sequences as those inferred by competing methods but yielded lower entropic partitions for the isotypes of the sequenced B cell. Thus, our method holds the potential to further advance our understanding of vaccine responses, disease progression, and the identification of therapeutic antibodies.

1. Introduction

B cells play a pivotal role in the adaptive immune response, producing antibodies that neutralize foreign substances and infections [1, 2]. These antibodies, consisting of a heavy chain and a light chain, are initially formed as sequence-specific B cell receptors (BCRs) (Fig. 1a). The generation of specific BCR genes stems from a process known as V(D)J recombination, where DNA segments are rearranged to ensure a wide spectrum of antibodies to counter various pathogens [3]. To enhance their effectiveness, B cells undergo affinity maturation (Fig. 1b) [4], a a micro-evolutionary process involving repeated cycles of somatic hypermutation (SHM) and cellular divisions. SHM introduces mutations in the BCR genes, selecting for B cells expressing high-affinity BCRs, while eliminating those with low affinity. Concurrently, B cells have the ability for class switch recombination (CSR) (Fig.1b) [5], which diversifies their response by altering the antibody’s functional class or isotype.

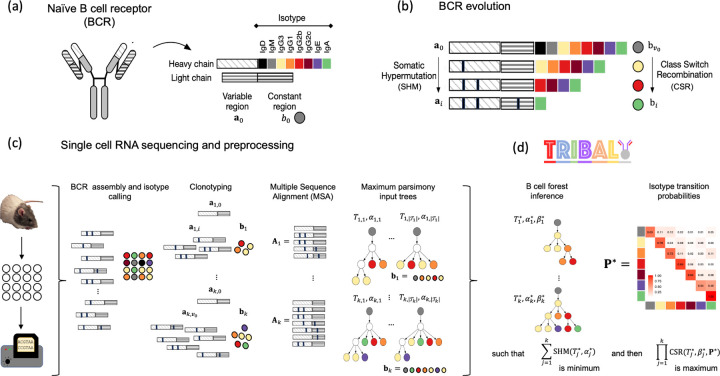
Figure 1: TRIBAL infers B cell lineage trees and isotype transition probabilities for scRNA-seq data.

(a) A BCR consists of paired heavy and light immunoglobulin chains, each consisting of a variable and constant region. The isotype is the heavy chain constant locus that is transcribed. (b) The BCR of B cells undergo somatic hypermutation/affinity maturation, where point mutations are introduced into the variable region of the heavy and light chains, and class switch recombination, where the heavy chain constant locus undergoes recombination and beings transcribing a different isotype. (c) After scRNA-seq, the variable regions for the light and heavy immunoglobulin alleles are assembled, the isotypes are called and the B cells are clustered into k clonotypes. A multiple sequence alignment ${\mathbf{\text{A}}}_j$ is found for each clonotype $j$ and used to infer a set of input trees with maximum parsimony. The leafs of each input tree are labeled by isotypes $\mathbf{\text{b}}$. (d) TRIBAL jointly infers a B cell lineage tree $T_j^{\ast }$ for each clonotype $j$ and population-specific isotype transition probabilities ${\mathbf{\text{P}}}^{\ast }$ with maximum parsimony for MSA ${\mathbf{\text{A}}}_j$ and maximum likelihood for isotypes ${\mathbf{\text{b}}}_j$.

Understanding the evolutionary history of B cells during these adaptive processes is integral to better understanding B cell response to infection and vaccination. However, the selection pressures applied to B cells during the affinity maturation process necessitate more specialized analytical approaches than those utilized for species phylogeny inference [6–9]. Specifically, Hoehn et al. developed HLP17 [10] and HLP19 [11], which are specialized codon substitution models for use with maximum likelihood inference via IgPhyML. Another important difference between B cell and species evolution is the lower mutation rate and the relatively short length of the BCR sequence (≈ 600 bp). These properties imply that maximum parsimony inference methods are viable [12–14] but typically result in a large solution space of many plausible phylogenies for the same data. In addition, these solutions exhibit additional tree uncertainty in the form of polytomies, i.e., multifurcating nodes with more than two children. This is counter to the underlying cell lineage tree, which is bifurcating as cell division results in exactly two daughter cells.

One approach to resolve phylogenetic uncertainty is the inclusion of additional data. This approach has proven effective in other areas, such as the use of physical location for studying cancer migration and metastasis [15], or geographical location for the inference of gene flow [16]. More related to B cell lineage inference, sequence abundance has been utilized by both GCTree [12] and ClonalTree [17] to discriminate between candidate solutions. However, both methods were originally developed for bulk RNA sequencing data and consequently were restricted to analysis of only the heavy chain sequences. With single cell RNA-sequencing (scRNA-seq), it is now possible to efficiently assemble BCR sequences that includes both heavy and light chain from a population of B cells [18] (Fig. 1c). As a result, the evolution of BCRs during affinity maturation can now be tracked with scRNA-seq with higher fidelity [19].

In addition, scRNA-seq yields another valuable data source in the form of the expressed isotype of the constant region of the heavy chain (Fig. 1c) [19]. Isotype data extracted from scRNA-seq has been helpful in related immunological domains, such as inferring dynamic cellular trajectories [20]. However, isotype expression is an especially useful marker of B cell evolution. When a B cell undergoes class switching from its current isotype to a new isotype, any heavy chain constant region locus between the current isotype and the new isotype in the genome is cut out or removed via a recombination process (Fig. 1b). Consequently, CSR is an irreversible process and the isotype state of a B cell offers a distinct milestone in its evolutionary history. Therefore, the inclusion of isotype information into the problem of B cell lineage inference has the potential to help minimize phylogenetic uncertainty by both reducing the size of the solution space and yielding more refined B cell lineage trees with fewer polytomies.

In this work, we present TRIBAL, which stands for Tree Inference of B cell Clonal Lineages (Fig. 1d). TRIBAL utilizes both the BCR sequence and isotype information from sequenced cells to infer a B cell lineage tree that jointly models the evolutionary processes of SHM and CSR. Additionally, TRIBAL infers the underlying isotype transition probabilities providing valuable insight into the dynamics of CSR (Fig. 1d). We demonstrate the accuracy of TRIBAL on simulated data and show that it is effective on experimental single cell data generated from the 5’ 10x Genomics platform. TRIBAL is available open source and has the potential to improve understanding of vaccine responses, track disease progression, and identify therapeutic antibodies.

2. Problem Statement

Suppose that we have sequenced and subsequently aligned the variable regions of the heavy and light chain of the B cell receptor (BCR) of $n$ B cells that descend from the same naive B cell post V(D)J recombination, resulting in a multiple sequence alignment (MSA) $\mathbf{\text{A}}$ composed of $m$ columns — the typical alignment length is $m\approx 650$ (Fig. 1c). That is, for each B cell $i$, we are given the concatenated sequence ${\mathbf{\text{a}}}_i\in {\mathrm{\Sigma }}^m$ where $\mathrm{\Sigma }=\left\{A,G,C,T,-\right\}$. In addition, we are given the isotype $b_i\in \left[r\right]=\left\{1,\dots ,r\right\}$, determined using tools such as Cell Ranger [21]. For humans, there are $r=8$ isotypes ordered as IgM/D, IgG3, IgG1, IgA1, IgG2, IgG4, IgE and IgA2, whereas for mice there are $r=7$ isotypes ordered as IgM/D, IgG3, IgG1, IgG2b, IgG2c (2a), IgE, IgGA. Finally, we are given sequence ${\mathbf{\text{a}}}_0$ and isotype $b_0=1$ of the ancestral naive B cell of the $n$ B cells — note that ${\mathbf{\text{a}}}_0$ and $b_0$ is post V(D)J recombination but prior to somatic hypermutation (SHM) and class switch recombination (CSR) and thus $b_0=1$. (Fig. 1a).

To study the evolutionary history of these $n$ cells, we aim to construct a B cell lineage tree $T$ that jointly describes the evolution of the DNA sequences $\mathbf{\text{A}}={\left[{\mathbf{\text{a}}}_0,{\mathbf{\text{a}}}_1,\dots ,{\mathbf{\text{a}}}_n\right]}^{\top }$ and their isotypes $\mathbf{\text{b}}={\left[b_0,b_1,\dots ,b_n\right]}^{\top }$. As such, each node $v$ of $T$ will be labeled by a sequence $\alpha \left(v\right)\in {\mathrm{\Sigma }}^m$ and isotype $\beta \left(v\right)\in \left[r\right]$. In particular, the root $v_0$ will be labeled by $\alpha \left(v_0\right)=b_0=1$ and $\beta \left(v_0\right)=b_0=1$ while the $n$ leaves $L\left(T\right)=\left\{v_1,\dots ,v_n\right\}$ of $T$ will be labeled by sequence $\alpha \left(v_i\right)={\mathbf{\text{a}}}_i$ and isotype $\beta \left(b_i\right)=b_i$ for each $i\in \left[n\right]$. A key property of isotype evolution is that it is irreversible. As such, the isotype $\beta \left(u\right)$ of an ancestral cell $u$ must be less than or equal to the isotype $\beta \left(v\right)$ of its descendants $v$. More formally, we have the following definition of a B cell lineage tree.

Definition 1. A rooted tree $T$ whose nodes are labeled by sequences $\alpha :V\left(T\right)\to {\mathrm{\Sigma }}^m$ and isotypes $\beta :V\left(T\right)\to \left[r\right]$ is a B cell lineage tree for MSA $\mathbf{\text{A}}={\left[{\mathbf{\text{a}}}_0,{\mathbf{\text{a}}}_1,\dots ,{\mathbf{\text{a}}}_n\right]}^{\top }$ and isotypes $\mathbf{\text{b}}={\left[b_0,b_1,\dots ,b_n\right]}^{\top }$ provided (i) $T$ has $n$ leaves $L\left(T\right)=\left\{v_1,\dots ,v_n\right\}$ such that each leaf $v_i\in L\left(T\right)$ is labeled by sequence $\alpha \left(v_i\right)={\mathbf{\text{a}}}_i$ and isotype $\beta \left(v_i\right)=b_i$, (ii) the root node $v_0$ of $T$ is labeled by sequence $\alpha \left(v_0\right)={\mathbf{\text{a}}}_0$ and isotype $\beta \left(v_0\right)=b_0$, and (iii) for all nodes $u$, $v\in V\left(T\right)$ such that $u$ is ancestral to $v$ it holds that $\beta \left(u\right)\le \beta \left(v\right)$.

In the following, we will refer to B cell lineage trees as lineage trees. Lineage trees typically have shallow depth due to the limited number of mutations introduced during SHM, making parsimony a reasonable optimization criterion [12–14]. Given a lineage tree $T$, the SHM parsimony score is computed as

$$\text{SHM}\left(T,\alpha \right)=\sum _{\left(u,v\right)\in E\left(T\right)}D\left(\alpha \left(u\right),\alpha \left(v\right)\right),$$ (1)

where $D\left(\alpha \left(u\right),\alpha \left(v\right)\right)$ is the Hamming distance [22] between sequences $\alpha \left(u\right)$ and $\alpha \left(v\right)$. However, one common challenge of using parsimony to model SHM is that it often results in a large number of candidate lineage trees with equal optimal parsimony score. In addition, many inferred lineage trees contain polytomies, or internal nodes with out-degree greater than 2. To overcome these two challenges, we propose to infer lineage trees that optimize both sequence evolution (SHM) and isotype evolution (CSR).

Similarly to SHM, one could model the evolution of CSR using unweighted parsimony. That is, one would prefer lineage trees $T$ with isotypes $\beta :V\left(T\right)\to \left[r\right]$ that minimize the number of isotype changes, i.e., ${\sum }_{\left(u,v\right)\in E\left(T\right)}D\left(\beta \left(u\right),\beta \left(v\right)\right)$. However, there are two issues with this approach. First, it does not appropriately penalize lineage trees that violate the irreversible property of isotype evolution [13]. Second, it does not account for the fact that given an isotype starting state the probability of transitioning to each of the possible isotype states is not necessarily equal. In fact, knowing these probability distributions is useful for researchers looking to gain basic insight into the patterns and casual factors of class switch recombination [23]. Therefore, we seek to develop an appropriate evolutionary model for CSR that captures the irreversible property of class switching and models preferential isotype class transitions.

We propose a state or tree dependence model [24, 25] evolutionary model for CSR, which models the joint probability distribution of a random variable vector under Markov-like assumptions on a given tree (Appendix A). Here, the random variables of interest in this state tree model are the isotypes $\beta \left(v\right)$ of each node $v$ in lineage tree $T$. This model is parameterized by a probability distribution over the isotype of the root and isotype transition probabilities. As the root $v_0$ of a lineage tree $T$ is a naive B cell post V(D)J recombination, the isotype $\beta \left(v_0\right)$ is always 1 (IgM) and the probability distribution of $\beta \left(v_0\right)$ is defined as $\text{Pr}\left(\beta \left(v_0\right)=1\right)=1$ and 0 otherwise. Intuitively, isotype transition probabilities captures the conditional probability of a descendant isotype given the isotype of its parent subject to irreversible isotype evolution. Next, we give a formal definition of isotype transition probabilities.

Definition 2. An $r\times r$ matrix $\mathbf{\text{P}}=\left[p_{s,t}\right]$ is an isotype transition probability matrix provided for all isotypes $s,t\in \left[r\right]$ it holds that (i)$p_{s,t}\ge 0$, (ii) $p_{s,t}=0$ if $s>t$, and (iii) ${\sum }_{t=1}^r{p}_{s,t}=1$ for all isotypes $s\in \left[r\right]$.

We define the joint likelihood $\text{CSR}\left(T,\beta ,\mathbf{\text{P}}\right)$ of the observed isotypes $\mathbf{\text{b}}$ for isotype transition probabilities $\mathbf{\text{P}}$ and any lineage tree $T$ whose leaves have isotypes $\mathbf{\text{b}}$ as

$$\text{CSR}(T,\beta ,\mathbf{P})=\mathrm{Pr}(\mathbf{b}|T,\alpha ,\beta ,\mathbf{P})=\mathrm{Pr}(\mathbf{b}|T,\beta ,\mathbf{P})=\prod _{\left(u,v\right)\in E\left(T\right)}{p}_{\beta (u),\beta (v)}.$$ (2)

We consider the problem of simultaneously inferring a lineage tree $T$ with nodes labeled by sequences $\alpha \left(v\right)$ and isotypes $\beta \left(v\right)$ given MSA $\mathbf{\text{A}}$ and isotypes $\mathbf{\text{b}}$ that optimizes both $\text{SHM}\left(T,\alpha \right)$ and $\text{CSR}\left(T,\beta ,\mathbf{\text{P}}\right)$. However, a significant barrier to solving this problem is that isotype transition probabilities $\mathbf{\text{P}}$ are unknown and need to be inferred. While there have been experimental studies that estimate these quantities under specific biological conditions [23], there currently exists no computational methods to infer these probabilities directly from a sequencing experiment. Here, we will leverage that typical single-cell sequencing experiments yield data from a set of diverse B cell lineages, where each lineage is commonly referred to as a clonotype. A common pre-processing step is to first cluster the $n$ sequenced cells into k clonotypes, where each clonotype $j$ contains $n_j$ cells (Fig. 1c). We follow convention and group B cells based on shared V(D)J alleles in heavy and light chains into a clonotype. Moreover, we reason that under many experimental conditions, the transition probabilities between isotypes will be similar to those within clonotypes. Thus, inferring these isotype transition probabilities for k clonotypes will yield higher accuracy than inferring isotype transition probabilities for a single lineage in isolation. This leads to the following problem statement.

Problem 1 (B cell Lineage Forest Inference (BLFI)). Given MSAs ${\mathbf{\text{A}}}_1,\dots ,{\mathbf{\text{A}}}_k$ and isotypes ${\mathbf{\text{b}}}_1,\dots ,{\mathbf{\text{b}}}_k$ for k clonotypes, find isotype transition probabilities ${\mathbf{\text{P}}}^{\ast }$ for $r$ isotypes and lineage trees $T_1^{\ast },\dots ,T_k^{\ast }$ for $\left({\mathbf{\text{A}}}_1,{\mathbf{\text{b}}}_1\right),\dots ,\left({\mathbf{\text{A}}}_k,{\mathbf{\text{b}}}_k\right)$ whose nodes are labeled by sequences ${\alpha }_1^{\ast },\dots ,{\alpha }_k^{\ast }$ and isotypes ${\beta }_1^{\ast },\dots ,{\beta }_k^{\ast }$, respectively, such that ${\sum }_{j=1}^k\text{SHM}\left(T_j^{\ast },{\alpha }_j^{\ast }\right)$ is minimum and then ${\prod }_{j=1}^k\text{CSR}\left(T_j^{\ast },{\beta }_j^{\ast },{\mathbf{\text{P}}}^{\ast }\right)$ is maximum.

In other words, we prioritize the SHM objective and then among all solutions with minimum SHM score we prefer those that additionally maximize the CSR objective. It is easy to see that the BLFI problem is NP-hard via a simple reduction from the Large Parsimony problem — see Appendix B.1 for more details.

3. Methods

We introduce Tree Inference of B cell Clonal Lineages, or TRIBAL, a method to solve the BLFI problem. This method is based on two key ideas that allow us to effectively solve the BLFI problem.

First, the lexicographical ordering of our two objectives — optimizing for SHM followed by CSR — enables one to use the following two-stage approach (Fig. 1c). In the first stage, we use existing maximum parsimony methods to generate a set $𝓣$ of input trees — also called a maximum parsimony forest — for each clonotype such that each tree $T\in 𝓣$ minimizes the objective $\text{SHM}\left(T,\alpha \right)$. To do so, we provide these methods only the sequence information $\mathbf{\text{A}}$ to enumerate a solution space $𝓣$ of trees whose nodes are labeled by sequences ${\alpha }_1,\dots ,{\alpha }_{\left|𝓣\right|}$. In the second stage, we incorporate isotype information $\mathbf{\text{b}}$ to further operate on the set $𝓣$ and additionally optimize $\text{CSR}\left(T,\beta ,\mathbf{\text{P}}\right)$ in such a manner that maintains optimality of the SHM objective. We note that a lexicographically optimal lineage tree $T^{\ast }$ does not necessarily need to be an element of $𝓣$, but instead it suffices that the evolutionary relationships in tree $T^{\ast }$ are a refinement of the evolutionary relationships described by some tree $T$ among the set $𝓣$ of input trees. More specifically, a refinement $T^{\prime }$ of tree $T$ is obtained by a series of expand operations such that an expand operation of node $v$ consists of splitting node $v$ into $v$ and $v^{\prime }$, joining them with an edge $\left(v,v^{\prime }\right)$ and then redistributing the children of $v$ to be descendants of either $v$ or $v^{\prime }$. We have the following key proposition and corollary.

Proposition 1. For any tree $T$ labeled by sequences $\alpha$ and refinement $T^{\prime }$ of $T$, there exists a sequence labeling ${\alpha }^{\prime }$ for $T^{\prime }$ such that $\text{SHM}\left(T,\alpha \right)=\text{SHM}\left(T^{\prime },{\alpha }^{\prime }\right)$.

Proof. The sequencing labeling ${\alpha }^{\prime }$ is found by setting ${\alpha }^{\prime }\left(v\right)=\alpha \left(v\right)$ and ${\alpha }^{\prime }\left(v^{\prime }\right)=\alpha \left(v\right)$ during each expand operation. By construction, the new edge $\left(v,v^{\prime }\right)$ has $D\left({\alpha }^{\prime }\left(v\right),{\alpha }^{\prime }\left(v^{\prime }\right)\right)=0$ and every original edge maintains its original Hamming distance in $T^{\prime }$. Therefore, $\text{SHM}\left(T,\alpha \right)=\text{SHM}\left(T^{\prime },{\alpha }^{\prime }\right)$. ☐

Corollary 1. Any lineage tree $T^{\prime }$ that lexicographically optimizes $\text{SHM}\left(T^{\prime },{\alpha }^{\prime }\right)$ and then $\text{CSR}\left(T^{\prime },{\beta }^{\prime },\mathbf{\text{P}}\right)$ must be a refinement of some tree $T$ optimizing only $\text{SHM}\left(T,\alpha \right)$.

Therefore, our sought lineage tree $T^{\ast }$ that lexicographically optimizes both objectives must be a refinement of some tree $T$ in the set $𝓣$.

The second key idea is that the inference of optimal lineage trees $T_1^{\ast },\dots ,T_k^{\ast }$ is conditionally independent when given isotype transition probabilities $\mathbf{\text{P}}$. This motivates the use of a coordinate ascent algorithm where we randomly initialize isotype transition probabilies ${\mathbf{\text{P}}}^{\left(1\right)}$ (Sec. 3.1 and Fig. 2a). Then, at each iteration $\ell$, we use isotype transition probabilities ${\mathbf{\text{P}}}^{\left(\ell \right)}$ and the input set ${𝓣}_j$ of trees to independently infer an optimal lineage tree $T_j^{\left(\ell \right)}$ for each clonotype $j$ (Sec. 3.2 and Fig. 2b). This is then followed by estimating updated isotype transition probabilities ${\mathbf{\text{P}}}^{\left(\ell +1\right)}$ given trees $T_1^{\left(\ell \right)},\dots ,T_k^{\left(\ell \right)}$ (Sec. 3.3 and Fig. 2c). We terminate upon convergence of our CSR objective or when exceeding a specified number of maximum iterations.

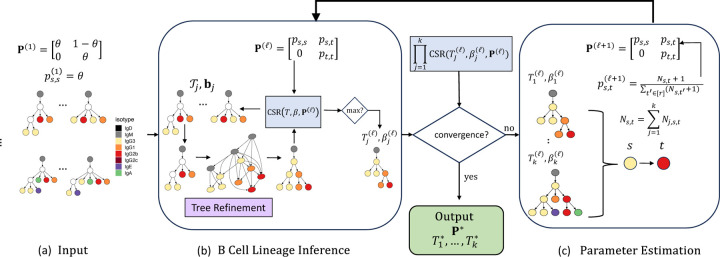
Figure 2: TRIBAL infers B cell lineage forest $T_1^{\ast },\dots ,T_k^{\ast }$ and isotype transitions ${\mathbf{\text{P}}}^{\ast }$ for k clonotypes utilizing coordinate ascent.

(a) The inputs to TRIBAL are isotype transition probabilities ${\mathbf{\text{P}}}^{\left(1\right)}$, which are initialized given a parameter $\theta \in \left[0.5,1\right]$, and a tuples $\left({𝓣}_1,{\mathbf{\text{b}}}_1\right)\dots ,\left({𝓣}_k,{\mathbf{\text{b}}}_k\right)$, where set ${𝓣}_j$ are maximum parsimony trees for MSA ${\mathbf{\text{A}}}_j$ and ${\mathbf{\text{b}}}_j$ are the observed isotypes of the $n_j$ cells of clonotype $j$. (b) Conditioning on isotype transition probabilities ${\mathbf{\text{P}}}^{\left(\ell \right)}$, a B cell lineage tree $T_j^{\left(\ell \right)}$ with nodes labeled by isotypes ${\beta }_j^{\left(\ell \right)}$ is inferred for each clonotype $j$ by solving the MPTR problem for each tree in the input set ${𝓣}_j$. (c) Convergence between ${\prod }_{j=1}^k\text{CSR}\left(T_j,{\beta }_j,\mathbf{\text{P}}\right)$ for iterations $\ell$ and $\ell -1$ is checked. If the difference has not converged, isotype transition probabilities ${\mathbf{\text{P}}}^{\left(\ell +1\right)}$ are updated using maximum likelihood estimation. If the difference has converged, the current inferred B cell lineage forest and isotype transition probabilities $\mathbf{\text{P}}$ are output. Multiple restarts may be performed for different values of $\theta$.

TRIBAL is implemented in Python 3, is open source (BSD-3-Clause license), and is available at https://github.com/elkebir-group/tribal.

3.1. Input

The input to TRIBAL is a set of k clonotypes with corresponding maximum parsimony forest ${𝓣}_j$ for each clonotype $j$. In addition, we are given isotypes ${\mathbf{\text{b}}}_j$ labeling the leaves of trees ${𝓣}_j$ for each clonotype $j$ (Fig.1c, Fig. 2a). Obtaining this input requires a number of preprocessing steps of a scRNA-seq dataset (Fig. 1), including (i) BCR assembly and isotype calling of each sequenced cell, (ii) clonotyping or clustering the cells based on a shared germline alleles for both the heavy and light chains, (iii) obtaining an MSA for sequences within a clonotype and (iv) finding a parsimony forest for each MSA of a clonotype. There preprocessing steps are not part of TRIBAL.

For our coordinate ascent approach, we also require an initialization for the isotype transition probabilities (Fig. 2a). We set the initial transition probabilities to reflect the observation that under baseline conditions, the probability of a B cell undergoing class switching is lower than the probability of it maintaining its original antibody class. [4, 23]. Thus, we initialize ${\mathbf{\text{P}}}^{\left(1\right)}$ such that $p_{s,s}>p_{s,t}$ for all isotypes $s$ and $t$. Let $\theta \in \left[0.5,1\right]$ be the probability that a B cell does not class switch, i.e., $p_{s,s}=\theta$ for each isotype $s<r$ and $p_{s,s}=1$ if $s=r$. We enforce irreversibility such that $p_{s,t}=0$, if $s>t$. We then initialize the remaining parameters uniformly, i.e., $p_{s,t}=\left(1-p_{s,s}\right)/\left(r-s\right)$ where $r$ is the total of number isotypes. We conduct multiple restarts, varying $\theta \in \left[0.5,1\right]$ in each restart.

3.2. B cell lineage tree inference via refinement

As described above, the inference of optimal lineage trees $T_1^{\left(\ell \right)},\dots ,T_k^{\left(\ell \right)}$ is conditionally independent given isotype transition probabilities ${\mathbf{\text{P}}}^{\left(\ell \right)}$. We therefore focus our discussion on how TRIBAL infers a B cell lineage tree $T_j^{\left(\ell \right)}$ for a single clonotype $j$ during iteration $\ell$ given isotype transition probabilities ${\mathbf{\text{P}}}^{\left(\ell \right)}$. By Corollary 1, we solve this problem by finding an optimal refinement $T^{\prime }$ and corresponding isotype labeling ${\beta }^{\prime }$ for each tree $T$ in the input set ${𝓣}_j^{\left(\ell \right)}$ and select the one that maximizes our CSR objective (Fig. 2b). Maximizing the log-likelihood of $\text{CSR}\left(T,\beta ,\mathbf{\text{P}}\right)$ is equivalent to maximizing a weighted parsimony criterion. This leads to the following problem statement.

Problem 2 (Most Parsimonious Tree Refinement (MPTR)). Given a tree $T$ on $n$ leaves, isotypes $\mathbf{\text{b}}=\left[b_0,\dots ,b_n\right]$ and isotype transition probabilities $\mathbf{\text{P}}$, find a tree $T^{\prime }$ with root $v_0^{\prime }$ and isotype labels ${\beta }^{\prime }:V\left(T^{\prime }\right)\to \left[r\right]$ such that (i) $T^{\prime }$ is a refinement of $T$, (ii) ${\beta }^{\prime }\left(v_0^{\prime }\right)=b_0=1$, (iii) ${\beta }^{\prime }\left(v_i^{\prime }\right)=b_i$ for each leaf $v_i^{\prime }\in \left\{v_1^{\prime },\dots ,v_n^{\prime }\right\}$ and (iv) $\log \hspace{0.33em}\text{CSR}\left(T^{\prime },{\beta }^{\prime },\mathbf{\text{P}}\right)$ is maximum.

We prove in Appendix B.1 that the MPTR problem is NP-hard. Therefore, we convert this problem to a graph problem (Fig. S2). For each node $u$ in tree $T$, multiple copies $\left(u,s\right)$ are added to the expansion graph $G_{T,\mathbf{\text{b}}}$, one for each possible isotype $s\in \left[r\right]$ subject to additional constraints depending on the observed isotypes of the leaves descendant from $u$. The edges $\left(\left(u,s\right),\left(v,t\right)\right)$ in this graph have weight $\log p_{s,t}$. We then solve the MPTR problem by finding a valid, maximum weight subtree $\left(T^{\prime },{\beta }^{\prime }\right)$ in the expansion graph $G_{T,\mathbf{\text{b}}}$ such that $T^{\prime }$ with isotype labels ${\beta }^{\prime }$ is a most parsimonious refinement of $T$. This is achieved via a mixed-integer linear programming (MILP) formulation, similar to that used to solve the Steiner minimal tree problem [26]. See Appendix C.1 for more details on the construction of the expansion graph from tree $T$ and leaf isotypes $\mathbf{\text{b}}$, proof of correctness for this algorithm and the MILP formulation.

To obtain outputs $\left(T_1^{\left(\ell \right)},{\beta }_1^{\left(\ell \right)}\right),\dots ,\left(T_k^{\left(\ell \right)},{\beta }_k^{\left(\ell \right)}\right)$, we set $\left(T_j^{\left(\ell \right)},{\beta }_j^{\left(\ell \right)}\right)$ to the tree $T^{\prime }$ and corresponding isotype labeling ${\beta }^{\prime }$ that maximize $\text{CSR}\left(T^{\prime },{\beta }^{\prime },{\mathbf{\text{P}}}^{\left(\ell \right)}\right)$ among all input trees ${𝓣}_j^{\left(\ell \right)}$ for each clonotype $j\in \left[k\right]$.

3.3. Parameter estimation

In the next step, given tuples $\left(T_1^{\left(\ell \right)},{\beta }_1^{\left(\ell \right)}\right),\dots ,\left(T_k^{\left(\ell \right)},{\beta }_k^{\left(\ell \right)}\right)$ of lineage trees and isotype labels for iteration $\ell$, we seek updated isotype transition probabilities ${\mathbf{\text{P}}}^{\left(\ell +1\right)}$ for iteration $\ell +1$ such that ${\prod }_{j=1}^k\text{CSR}\left(T_j^{\left(\ell \right)},{\beta }_j^{\left(\ell \right)},{\mathbf{\text{P}}}^{\left(\ell +1\right)}\right)$ is maximum (Fig. 2c). This is achieved via maximum likelihood estimation. For fixed lineage trees $T_1,\dots ,T_k$ and isotypes ${\beta }_1,\dots ,{\beta }_k$, our CSR objective can be rewritten as

$$\prod _{j=1}^k\text{CSR}\left(T_j,{\beta }_j,\mathbf{\text{P}}\right)=\prod _{j=1}^k\prod _{\left(u,v\right)\in E\left(T_j\right)}{p}_{{\beta }_i\left(u\right),{\beta }_i\left(v\right)}=\prod _{\left(s,t\right)\in \left[r\right]\times \left[r\right]}{p}_{s,t}^{N_{s,t}}$$ (3)

where $N_{s,t}={\sum }_{j=1}^k{\sum }_{\left(u,v\right)\in E\left(T_j\right)}\text{1}\left({\beta }_j\left(u\right)=s,{\beta }_j\left(v\right)=t\right)$ is the number of transition from $s$ to $t$ across all selected trees and clonotypes. Thus, we seek isotype transition probabilities $\mathbf{\text{P}}$ that maximize (3) subject to the constraints that ${\sum }_{t\in \left[r\right]}{p}_{s,t}=1$ for every isotype $s$. This constrained optimization problem is easily solved with the aid of Lagrange multipliers (see Appendix C.2 for details). Additionally, we add pseudocounts of 1 to avoid overfitting the data in the event of unobserved transitions, yielding the following updated probabilities $p_{s,t}^{\left(\ell +1\right)}$ for iteration $\ell +1$.

$$p_{s,t}^{(\ell +1)}=\frac{N_{s,t}+1}{{\sum }_{t^{\prime }\in \left[r\right]}\left(N_{s,t^{\prime }}+1\right)}.$$ (4)

After estimating ${\mathbf{\text{P}}}^{\left(\ell +1\right)}$, we then infer $\left(T_1^{(\ell +1)},{\beta }_1^{(\ell +1)}\right),\dots ,\left(T_k^{(\ell +1)},{\beta }_k^{(\ell +1)}\right)$, as discussed in Section 3.2.

4. Results

We evaluated TRIBAL on both in silico experiments (Sec. 4.1) and two sets of experimental scRNA-seq data. The first assessed performance on a model immunological system for affinity maturation (Sec. 4.2) and the second on a study of the relationship between age-associated B cells and autoimmune disorders (Sec. 4.3).

4.1. In silico experiments

We designed in silico experiments to evaluate TRIBAL with known ground-truth isotype transition probabilities $\mathbf{\text{P}}$ and lineage trees $T$ labeled by sequences $\alpha$ and isotypes $\beta$. Specifically, we used an existing BCR phylogenetic simulator [13] that models SHM but not CSR. We generated isotype transition probabilities $\mathbf{\text{P}}$ with $r=7$ isotypes (as in mice) under two different models of CSR. Briefly, both CSR models assume the probability of not transitioning is higher than the probability of transitioning, but in the sequential model there is clear preference for transitions to the next contiguous isotype, while in the direct model the probabilities of contiguous and non-contiguous class are similar. Given $\mathbf{\text{P}}$, we evolved isotype characters down each ground truth lineage tree $T$. We generated 5 replications of each CSR model for $k=75$ clonotypes and $n\in \left\{35,65\right\}$ cells per clonotype, resulting in 20 in silico experiments, yielding a total of 1500 ground truth lineage trees. In addition to comparing TRIBAL to existing methods including dnapars [7], dnaml [7] and IgPhyML [10], we also compared to a version of TRIBAL without tree refinement, denoted as tribal-No refinement (tribal-nr). To obtain the input set ${𝓣}_j$ of trees with maximum parsimony for each clonotype $j$, we utilized dnapars [7]. We refer to Appendix D for additional details on the simulations. In the following we focus our discussion on in silico experiments with $n=35$ cells per clonotype (see Fig. S5 for $n=65$).

To evaluate accuracy of isotype transition probability inference, we used Kullback–Leibler (KL) divergence [27] to compare the inferred transition probability distribution ${\widehat{\mathbf{p}}}_s$ of each isotype $s$ to the simulated ground truth distribution ${\mathbf{\text{p}}}_s$. KL divergence is defined as $D_{\text{KL}}\left({\widehat{\mathbf{p}}}_s||{\mathbf{\text{p}}}_s\right)={\sum }_{q\in \left[r\right]}{\widehat{p}}_{s,t}\log \left({\widehat{p}}_{s,t}/p_{s,t}\right)$; the lower the KL divergence, the more similar the two distributions. Since no existing methods infer isotype transition probabilities, we restricted this analysis to TRIBAL and TRIBAL-NR. Overall, we observed good concordance between simulated and TRIBAL inferred isotype transition probabilities (Fig. 3a). Specifically, TRIBAL had lower median KL divergence than TRIBAL-NR for all isotype starting states, except IgA, which is trivially 0, under both direct and sequential CSR models (direct: median of 0.15 vs. 0.73; sequential: median of 0.099 vs. 0.55). We observed improved performance of TRIBAL (but not for TRIBAL-NR) for $n=65$ cells per clonotype (Fig. S5a and Fig. S6). To assess the sensitivity of TRIBAL to infer isotype transition probabilities with fewer than $k=75$ clonotypes, we downsampled the 75 clonotypes to 25 and 50 clonotypes per experiment. We observed similar trends for experiments with $k\in \left\{25,50\right\}$ clonotypes, with TRIBAL continuing to outperform TRIBAL-NR while still achieving small KL divergences even as $k$ decreases (Fig. S7). These findings demonstrate that tree refinement is key to accurately estimate isotype transition probabilities.

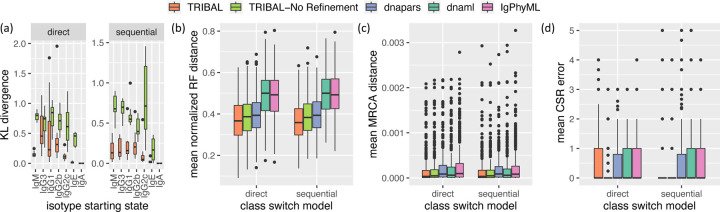
Figure 3: TRIBAL accurately infers isotype transition probabilities on simulated data while outperforming existing methods on lineage tree inference.

Simulation results shown are for 5 replications with $k=75$ clonotypes per replication and $n=35$ cells per clonotype. (a) KL divergence between inferred isotype transition probabilities and the reference ground truth distribution. (b) mean Robinson-Foulds distance between ground truth and inferred lineages tree per clonotype. (c) mean MRCA distance (26) between ground truth and inferred lineage trees per clonotype. (d) mean CSR error between ground truth and inferred B cells.

Next, we assessed the accuracy of lineage tree inference using the Robinson-Foulds (RF) distance [28] normalized by the total number of bipartitions in the ground truth $T$ and inferred lineage tree $\widehat{T}$ (25). Since TRIBAL, TRIBAL-NR and dnapars return multiple optimal solutions, we report the mean of the lineage tree inference metrics over all optimal solutions. We found TRIBAL had the lowest mean normalized RF distance for both direct and sequential CSR models (Fig. 3b). Overall, dnaml (median: 0.5) and IgPhyML (median: 0.49) had the worst performance on normalized RF. Interestingly, even though the starting trees of dnapars are used by TRIBAL, both TRIBAL (median: 0.36) and TRIBAL-NR (median: 0.38) outperformed dnapars (median: 0.39), showing the importance of using isotype information to resolve phylogenetic uncertainty.

While normalized RF distance only assesses the accuracy of the tree topology, it is important to also assess the accuracy of the ancestral sequence reconstruction. To that end, we used a metric called Most Recent Common Ancestor (MRCA) distance (26) introduced by Davidsen and Matsen [13]. For any two simulated B cells (leaves), the MRCA distance is the Hamming distance between the MRCA sequences of these two B cells in both the ground truth and inferred lineage trees. This distance is then averaged over all pairs of simulated B cells — see Appendix D.4 and Fig. S4a for additional details. Again, we report the mean of over all optimal solutions for TRIBAL, TRIBAL-NR and dnapars. We found TRIBAL outperformed all other methods (Fig. 3c), achieving the lowest overall median MRCA distance (3.46 × 10⁻⁵), followed by TRIBAL-NR (4.63 × 10⁻⁵). IgPhyML had the worst performance with a median of 8.78 × 10⁻⁵. Performance trends were consistent between methods across both CSR models.

Lastly, we assessed the accuracy of isotype inference by a new metric called CSR error, which is computed for each B cell $i$ and clonotype $j$ and is the absolute difference between the number of ground-truth class switches and inferred number of class switches that occurred along its evolutionary path from the root — see Appendix D and Fig S4b for additional details. Since dnaml, dnapars and IgPhyML do not infer isotypes for internal nodes, we pair these methods with the Sankoff algorithm [29] using $w_{s,t}$ equals 1 if $s=t,0$ if $s<t$ and $\infty$ otherwise. We account for the presence of multiple solutions by taking the mean across solutions. All methods had a median CSR error of 0 for both the direct and sequential models (Fig. 3d). Therefore, we utilized the third quartile for a more robust comparison. We found that under the direct model TRIBAL-NR (third quartile: 0) was the best performing method, while dnapars was second best (third quartile 0.8) and all other methods, including TRIBAL had a third quartile of 1. We observed a slight tendency of TRIBAL to overestimate the number of transitions due to the tree refinement step, while other methods tended to underestimate the number of transitions. However, under a sequential model, where refinement is helpful in accurately capturing sequential state transitions, we found that TRIBAL was tied with TRIBAL-NR for the best performance (third quartile: 0). All other methods had similar performance between both CSR models for this metric.

We observed similar trends on these metrics for in silico experiments containing $n=65$ cells per clonotype for $k=75$ clonotypes (Fig. S5). In summary, these results suggests that the incorporation of isotype data and the use of tree refinement are beneficial for both lineage tree inference and ancestral sequence and class switch reconstruction.

4.2. Keyhole limpet haemocyanin (NP-KLH) antigen immune response studies

We applied TRIBAL as well as IgPhyML to 10 × 5^′ scRNA-seq data of B cells extracted from mice immunized with nucleoprotein keyhole limpet haemocyanin (NP-KLH), a commonly used antigen in the study of antibody affinity maturation [30]. Our goal was to determine whether these methods recapitulate known patterns of B cell lineage evolution for this well-studied antigen using data from two studies and to compare the lineage trees inferred by each method. The first dataset (NP-KLH-1) was generated from C57BL/6 mice that were immunized with NP-KLH and total germinal center B cells were extracted 14 days after immunization [20]. The other two datasets came from a single study in which C57BL/6 mice were immunized with NP-KLH (NP-KLH-2a and NP-KLH-2b) and NP-specific germinal center B cells were extracted 13 days after immunization [31]. We utilized the standard 10× Cell Ranger [21] single-cell bioinformatics pipeline to generate sequence ${\mathbf{\text{a}}}_i$ and isotype $b_i$ for each cell $i$. We used Dandelion [32] to remove doublets, reassign alleles, and cluster the cells into clonotypes. We identified clonotype MSAs ${\mathbf{\text{A}}}_1,\dots ,{\mathbf{\text{A}}}_k$ based on shared V(D)J alleles for the heavy chain using the dowser package [14]. Finally, we excluded clonotypes with fewer than 5 cells. This yielded a total of $n=2670$ sequenced B cells clustered into $k=295$ clonotypes. We exclude methods that rely on sequence abundance as a key signal, such as GCTree [12] and ClonalTree [17] as we observed very few duplicated sequences within each clonotype. Fig. 4a shows the distribution of isotypes by dataset and Table S1 includes a more detailed summary of each dataset.

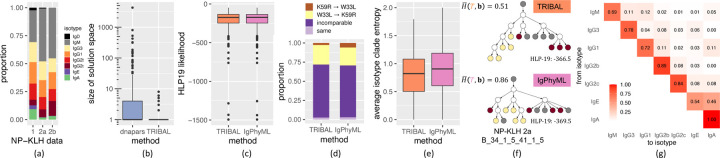
Figure 4: Comparison between TRIBAL and IgPhyML on the NP-KLH data.

(a) The distribution of isotypes $\mathbf{\text{b}}$ in each dataset. (b) A comparison of the solution space of dnapars versus TRIBAL. (c) The distribution of the HLP19 codon-substitution likelihood [11] for lineage trees inferred by TRIBAL and IgPhyML. (d) Observed distribution of evolutionary relationships between the W33L and K59 in clonotypes where both mutations are present. (e) The distribution of the average clade entropy with respect to an isotype labeling $\mathbf{\text{b}}$ of the leafset. (f) A comparison of lineage trees inferred for clonotype NP-KLH-2a B_34_1_5_41_1_5 with the average isotype clade entropy $\overline{H}\left(T,\mathbf{\text{b}}\right)$ reported for each inferred tree. (g) TRIBAL inferred isotype transition probabilities $\mathbf{\text{P}}$ for NP-KLH-1.

We used dnapars [7] to infer TRIBAL’s input set ${𝓣}_j$ for each clonotype $j$. We found that TRIBAL’s use of isotype information significantly reduced the number of optimal solutions identified by dnapars (mean: 31.5 vs. 1.3, max: 4310 vs. 8) — see Fig 4b. While IgPhyML, a maximum likelihood method using the HLP19 codon-substitution model [10, 11], infers only a single tree per clonotype, it is important to note that there might be multiple trees with maximum likelihood in the solution space. Indeed, we found high concordance of HLP19 likelihoods between the TRIBAL and IgPhyML inferred lineage trees, with a small overall mean absolute deviation of 0.97 (Fig. 4c, Fig. S8). We even observed that TRIBAL had a greater likelihood than IgPhyML in 59.3% of the clonotypes. Thus, TRIBAL resulted in a significant reduction in the size of the solution space compared to the maximum parsimony method dnapars with similar (and sometimes better) HLP19 likelikelihood as IgPhyML, illustrating how isotype information can be used to effectively reduce phylogenetic uncertainty.

Next, we assessed whether the lineage trees inferred by TRIBAL recapitulated expected biological trends for the NP-KLH model system. Previous research has indicated that the IGHV1–72*01 (VH186.2) variable gene in the heavy chain is preferentially used in the anti-NP response in C57BL/6 mice [33] via two distinct mutation paths: one in which a W33L mutation greatly increases affinity to NP, and another in which high affinity is achieved through K59R and the accumulation of several other mutations, such as S66N [34, 35]. Consequently, we expect that for clonotypes containing both W33L and K59R, these mutations would tend towards occurring in distinct lineages of the tree. We analyzed the inferred pairwise relationships between W33L & K59R in the 26 lineage trees that contained both mutations. Specifically, we categorized the relationship as K59R → W33L if K59R was ancestral to W33L, W33L → K59R if W33L was ancestral to K59R, incomparable if W33L and K59R occurred on distinct lineages of the tree and same if they were introduced on the same edge of the lineage tree. Indeed, we confirmed the tendency for mutual exclusivity of W33L and K59R by finding that the proportion of pairwise introductions categorized as incomparable was 0.69 and 0.67 for TRIBAL and IgPhyML, respectively (Fig. 4d). Additionally, it has been suggested that W33L mutations appear relatively early during the anti-NP response, whereas the K59R and S66N mutations typically appear later in the evolutionary history [36]. Defining level as the length of the shortest path from the MRCA of all B cells, we observed that W33L occurred at a median level of 1 for both TRIBAL and IgPhyML while both the K59R and S66N mutation occurred at a median level 2 for both methods (Fig. S9). This indicated that W33L was typically introduced earlier in the evolutionary history of a clonotype than K59R and S66N. Thus, both TRIBAL and IgPhyML trees recapitulate expected mutation patterns for this model system.

We next assessed the extent of agreement with isotype information. While TRIBAL infers isotype labels of ancestral nodes, IgPhyML does not have this capability. Therefore, we developed a new metric called average isotype clade entropy, which is computed with respect to the isotype labeling of the leaf set. For this metric, we compute the entropy of clade $u$ in tree $T$ with respect to all isotype leaf labels that are descendants of node $u$, taking the average entropy over all non-trivial clades, which excludes the root and the leaves (Appendix E.1). As IgPhyML returns bifurcating trees, we collapse edges with zero branch length for a more fair comparison of this metric. We observed lower average isotype clade entropy for TRIBAL (median: 0.82) versus IgPhyML (median 0.91) 4f. Fig. 4e depicts the lineage tree inferred by TRIBAL and IgPhyML for the NP-KLH-2a dataset (clonotype B_34_1_5_41_1_5). The TRIBAL inferred tree for this clonotype had lower isotype clade entropy than IgPhyML (TRIBAL: 0.51 vs IgPhyML: 0.86) while also resulting in a greater HLP19 likelihood (TRIBAL: −366.5 vs IgPhyML: −369.5). Thus, we find that the trees identified by TRIBAL are in better agreement with the leaf isotypes than IgPhyML.

In addition to the inferred B cell lineage trees, TRIBAL also inferred isotype transition probabilities $\mathbf{\text{P}}$ for each dataset (Fig. 4g, Fig S10). All three inferred isotype transition probability matrices more closely matched a CSR model of direct switching as opposed to a strictly sequential model. To compare the consistency of these estimates across datasets, we computed the Jensen-Shannon divergence (JSD) between the distribution of isotype transition probabilities for each isotype starting state IgM through IgG2c for each dataset pair. We observed low JSD (median: 0.029) across a total of 15 pairwise comparisons, suggesting consistent estimates between isotype transition probabilities.

In summary, these analyses show that the inclusion of isotype information and tree refinement has the potential to yield high quality lineage tree inference, even under a simpler model of SHM, i.e., parsimony. Moreover, the TRIBAL inferred lineage trees additionally optimize an evolutionary model of CSR, yielding lower isotype entropy partitions of the leaf set than IgPhyML. Finally, the additional inference of isotype transitions probabilities $\mathbf{\text{P}}$ has the potential to distinguish between direct versus sequential switching events.

4.3. Age-associated B cell (ABC) datasets

We evaluated TRIBAL on three scRNA-seq datasets with V region sequencing that investigated the relationship between age-associated B cells (ABCs) and autoimmune disorders [37]. For each dataset, B cells were extracted from the spleen of a MRL/lpr female mouse and sequenced using 10× 5′ scRNA-seq. The data was processed by the 10× Cell Ranger [21] single-cell bioinformatics pipeline to generate sequence ${\mathbf{\text{a}}}_i$ and isotype $b_i$ for each cell $i$. Nickerson et al. [37] identified clonotype MSAs ${\mathbf{\text{A}}}_1,\dots ,{\mathbf{\text{A}}}_k$ based on shared V(D)J alleles for the heavy chain using the dowser package [14] and inferred B cell lineage trees using IgPhyML for each clonotype. After filtering out clonotypes with fewer than 5 sequences, we retained 599 B cells and 54 clonotypes across the three datasets (Table S2). Fig. 5a shows the proportion of isotypes and annotations by mouse for the retained B cells. Of these 54 clonotypes, 35 had more than one distinct isotype across the sequenced B cells, with a median of 3 distinct isotypes per clonotype.

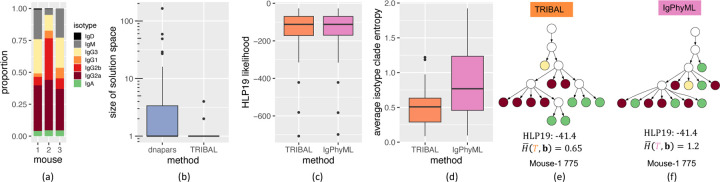
Figure 5: Comparison between TRIBAL and IgPhyML on ABC data.

(a) Distribution of B cell isotypes. (b) A comparison of the solution space of dnapars versus TRIBAL. (c) The distribution of the HLP19 codon-substitution likelihood [11] for lineage trees inferred by TRIBAL and IgPhyML. (d) Comparison of average isotype clade entropy for TRIBAL versus IgPhyML. (e,f) Comparison of inferred B cell lineage trees by TRIBAL (e) and IgPhyML (f) for clonotype Mouse-1 775 — see (a) for color legend.

We ran TRIBAL separately on each of the three mouse datasets, obtaining a maximum parsimony forest ${𝓣}_j$ for each clonotype $j$ via dnapars. Similar to our NP-KLH analysis, we found that TRIBAL effectively utilized the additional isotype data to reduce the number of optimal solutions identified by dnapars (mean: 8.1 vs. 1.3, max: 165 vs. 4) — see Fig. 5b. The HLP19 likelihood of the TRIBAL inferred lineage trees had high concordance with the IgPhyML inferred trees (mean absolute deviation: 0.97), with TRIBAL yielding a higher likelihood for 53% of the clonotypes (Fig. 5c, Fig. S11). The average isotype clade entropy for the 35 clonotypes with more than one distinct isotype was significantly lower for TRIBAL than for IgPhyML (median: 0.49 vs. 0.77) — see Fig. 5d. An example comparison is shown in Fig. 5e,f for clonotype Mouse-1 775. The tree refinement step of TRIBAL yielded a tree with a significantly lower average isotype clade entropy when compared to IgPhyML (0.65 vs. 1.2) while both trees had identical HLP19 likelihoods (−41.4). Finally, we observed that the isotype transition probabilities reveal evidence for both direct and sequential switching of isotypes (Fig. S12).

In summary, both TRIBAL and IgPhyML yield lineage trees with very similar HLP19 likelihoods, giving support for the validity of the TRIBAL inferred lineage trees in terms of sequence evolution. However, TRIBAL jointly optimizes evolutionary models for both SHM and CSR, yielding trees with lower average isotype clade entropy.

5. Conclusion

The development and application of methods for inferring B cell lineage trees and isotype transition probabilities from scRNA-seq data is crucial for advancing our understanding of the immune system. In this work, we introduced TRIBAL, a method to infer B cell lineage trees and isotype transition probabilities from scRNA-seq data. TRIBAL makes use of existing maximum parsimony methods to optimize an evolutionary model for SHM, then incorporates isotype data to find the most parsimonious refinement, i.e., maximizing the CSR likelihood, among the input set of trees. We proved that the subproblem of finding a refinement maximizing the CSR likelihood is NP-hard. We demonstrated the effectiveness of TRIBAL via in silico experiments and on experimental data. On in silico experiments, we showed the importance of tree refinement for both accurately estimating isotype transition probabilities and lineage tree inference. Furthermore, we demonstrated on experimental data that TRIBAL returns lineage trees that have similar HLP19 likelihoods, despite utilizing a less complex model for sequence evolution but yield a reduction in the entropy of the isotype leaf labelings.

There are several directions for future research. First, integration of germline “sterile” transcripts may offer a way to initialize the TRIBAL inferred isotype transition probabilities [38]. Second, many existing B cell lineage inference methods, such as IgPhyML, yield multifurcating trees when zero length branches are collapsed. There exists an opportunity to combine likelihood or distance based inference methods with the tree refinement step of TRIBAL. Third, the MPTR problem has a more general formulation with the potential for wider applications beyond the problem of B cell lineage inference. For example, sample location is useful in refining tumor phylogeny with polytomies [15]. On a related note, we hypothesize that there are special cases of the MPTR problem and its more general formulation that are in P. Such special cases may include a weight matrix with unit costs and an upper triangular weight matrix that adheres to the triangle inequality. Fourth, the assumption that a single isotype transition probability matrix is shared by all clonotypes could be relaxed to allow the inference of multiple matrices per experiment and an assignment of clonotypes to an inferred matrix. Fifth, TRIBAL could be extended to allow for the correction of inaccurately clonotyped B cells. Finally, more robust evolutionary models for SHM are needed to capture the presence of complex mutations, such as indels, introduced during affinity maturation [39, 40].

Availability:

TRIBAL is available at https://github.com/elkebir-group/tribal