Abstract
Prediction of enzyme kinetic parameters is essential for designing and optimizing enzymes for various biotechnological and industrial applications, but the limited performance of current prediction tools on diverse tasks hinders their practical applications. Here, we introduce UniKP, a unified framework based on pretrained language models for the prediction of enzyme kinetic parameters, including enzyme turnover number (kcat), Michaelis constant (Km), and catalytic efficiency (kcat / Km), from protein sequences and substrate structures. A two-layer framework derived from UniKP (EF-UniKP) has also been proposed to allow robust kcat prediction in considering environmental factors, including pH and temperature. In addition, four representative re-weighting methods are systematically explored to successfully reduce the prediction error in high-value prediction tasks. We have demonstrated the application of UniKP and EF-UniKP in several enzyme discovery and directed evolution tasks, leading to the identification of new enzymes and enzyme mutants with higher activity. UniKP is a valuable tool for deciphering the mechanisms of enzyme kinetics and enables novel insights into enzyme engineering and their industrial applications.
Subject terms: Computational models, Enzymes, Synthetic biology, Metabolomics, Protein design
Prediction of enzyme kinetic parameters is essential for designing and optimising enzymes for various biotechnological and industrial applications. Here, authors presented a prediction framework (UniKP), which improves the accuracy of predictions for three enzyme kinetic parameters.
Introduction
The study of enzyme catalysis efficiency to a specific substrate is a fundamental biological problem that has a profound impact on enzyme evolution, metabolic engineering, and synthetic biology1–3. The in vitro measured values of kcat and Km, the maximal turnover rate and Michaelis constant, are the indicators of the efficiency of an enzyme in catalyzing a specific reaction and can be used to compare the relative catalytic activity of different enzymes4. Currently, the measurement of the enzyme kinetic parameters relies primarily on experimental measurements, which are time-consuming, costly, and labor-intensive, resulting in a small database of experimentally measured kinetic parameters values5. For instance, the sequence database UniProt contains over 230 million enzyme sequences, while enzyme databases BRENDA and SABIO-RK contain tens of thousands of experimentally measured kcat values6–8. The integration of Uniprot identifiers in these enzyme databases has facilitated the connection between measured parameters and protein sequences. However, these connections are still far smaller in scale compared to the number of enzyme sequences, limiting the advancement of downstream applications such as directed evolution and metabolic engineering.
Researchers have attempted to utilize computational methods to accelerate the process of enzyme kinetic parameters prediction, but current approaches have exclusively concentrated on addressing one of these issues, overlooking the similarity of both tasks in reflecting the relationship of protein sequences towards substrate structures. A statistical approach has been proposed to infer Km values across species based on the known parameters of related enzymes9. An organism-independent model has been built which successfully predicts Km values for natural enzyme–substrate combinations using machine learning and deep learning10. Machine learning has also been demonstrated to be able to predict catalytic turnover numbers in Escherichia coli based on enzyme biochemistry, protein structure, and network context11. In addition, a deep learning-based method for kcat prediction from substrate structures and protein sequences has been developed, enabling high-throughput prediction12. Despite various prediction tools for kcat and Km, they often fail to accurately capture the relationship between these two parameters. Consequently, the calculated kcat / Km values from these models often deviate significantly from the experimental measurements. This discrepancy highlights the importance of a demonstration of a unified method for calculating or predicting kcat / Km, which is a crucial parameter reflecting catalytic efficiency. As a result, this has hindered the practical application of these methods in biotechnological and industrial contexts. Additionally, current models have failed to account for environmental factors such as pH and temperature, which can significantly impact enzyme kinetics13. Furthermore, the present models struggle to address high-value prediction problems due to imbalanced datasets, despite their importance in various biological research applications14,15. All these limitations have confined the current use of these tools to data analysis and model development, with no substantial impact on practical challenges such as enzyme discovery and directed evolution, which are of significant relevance to associated fields.
To overcome these limitations, a unified enzyme kinetic parameters prediction model with high accuracy needs to be developed. Recent breakthroughs in deep learning, particularly in the area of unsupervised learning from natural language processing, have led to novel data representation approaches that have been applied to biological problems with great success16–20. The advancement of pretrained language models for proteins and small molecules, represented using SMILES notation18–20, has illuminated the path towards a more effective model for predicting enzyme kinetic parameters. The absence of datasets documenting the impact of environmental factors on kinetic parameters constitutes a major impediment to the prediction of parameter values under these conditions. Constructing a dataset that encompasses this information, and employing a two-layer ensemble model that integrates information from multiple models12,21, is crucial to enhance the accuracy of these predictions. The distribution of experimentally measured kinetic parameters is imbalanced12, characterized by a scarcity of high-value kinetic parameter samples, much like imbalanced and long-tailed datasets commonly encountered in the field of visual recognition, where a few categories are heavily populated, while most categories only contain a limited number of samples22. In visual recognition problems, researchers have utilized various techniques to improve the accuracy of the model in predicting high values23,24. One effective and straightforward approach is the re-weighting method, which enhances the significance of underrepresented categories by increasing their weight in the model25.
Here, we present a pretrained language model-based enzyme kinetic parameters prediction framework (UniKP), which improves the accuracy of predictions for three enzyme kinetic parameters, kcat, Km, and kcat / Km, from a given enzyme sequence and substrate structure. We conducted a comprehensive comparison of 16 diverse machine learning models and 2 deep learning models, and demonstrated its remarkable improvement over previous prediction methods. Additionally, we have proposed a two-layer framework to consider environmental factors and validated its effectiveness on two representative datasets, including pH and temperature. We also applied typical re-weighting methods to the kcat dataset and successfully reduced the error of high value prediction. Lastly, we employed UniKP to assist the mining and directed evolution of tyrosine ammonia lyase (TAL), leading to the discovery of one TAL homolog from a database exhibiting significant enhanced kcat, and the identification of two TAL mutants with the highest kcat / Km values reported to date. We also validated that EF-UniKP consistently identifies highly active TAL enzymes with remarkable precision, when accounting for environmental factors.
Results
Overview of UniKP
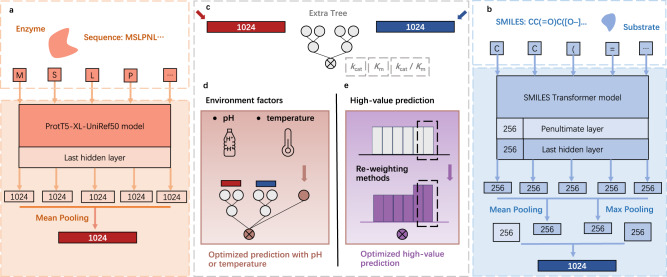
The UniKP framework is comprised of two key components: a representation module and a machine learning module (Fig. 1). The representation module is used to encode information about enzymes and substrates using pretrained language models. Specifically, the amino acids in the enzyme sequence are transformed into a 1024-dimensional vector using the ProtT5-XL-UniRef50 model (Fig. 1a). Mean pooling is applied to obtain per-protein representation, which has been found to be the most effective method for per-protein tasks18. On the other hand, the substrate structure is converted to a simplified molecular-input line-entry system (SMILES) format and processed by the pretrained SMILES transformer, resulting in a 256-dimensional vector for each symbol. The mean and max pooling of the last layer and the first outputs of the last and penultimate layers are then concatenated to generate a per-molecular representation vector of 1024 dimensions20 (Fig. 1b). The concatenated representation vector of both the protein and substrate are then fed into the following machine learning module. Here, the projections of t-distributed Stochastic Neighbour Embedding (t-SNE) with different perplexity and iterations demonstrated that a solely concatenated representation vector cannot discriminate well between high and low kcat values26, further emphasizing the need for the machine learning model (Supplementary Fig. 1).
Fig. 1. The overview of UniKP.
a Enzyme sequence representation module: Information about enzymes was encoded using a pretrained language model, ProtT5-XL-UniRef50. Each amino acid was converted into a 1024-dimensional vector on the last hidden layer, and the resulting vectors were summed and averaged by mean pooling, generating a 1024-dimensional vector to represent the enzyme. b Substrate structure representation module: Information about substrates was encoded using a pretrained language model, SMILES Transformer model. The substrate structure was converted into a simplified molecular-input line-entry system (SMILES) representation and input into a pretrained SMILES transformer to generate a 1024-dimensional vector. This vector was generated by concatenating the mean and max pooling of the last layer, along with the first outputs of the last and penultimate layers. c Machine learning module: An explainable Extra Trees model took the concatenated representation vector of both the enzyme and substrate as input and generated a predicted kcat, Km or kcat / Km value. d EF-UniKP: A framework that considers environmental factors to generate an optimized prediction. It is validated on two representative datasets: pH and temperature datasets. e Various re-weighting methods were used to adjust the sample weight distribution to generate an optimized prediction for high-value prediction task.
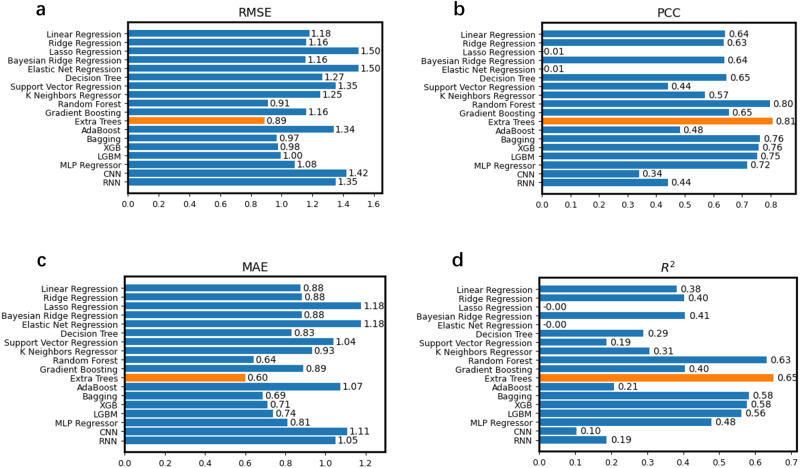
For the machine learning module, in order to explore the performance of different models, we conducted a comprehensive comparison of 16 diverse machine learning models, including basic linear regression to complex ensemble models, as well as 2 representative deep learning models, the Convolutional Neural Network (CNN) and the Recurrent Neural Network (RNN) (Fig. 2). Overall, the results showed that simpler models like linear regression displayed relatively poor prediction performance (Linear Regression R2 = 0.38). In contrast, ensemble models demonstrated better performance. Notably, random forests and extra trees significantly outperformed other models, with extra trees exhibiting the highest performance (Extra Trees R2 = 0.65). However, both categories of deep learning models, due to their demanding requirements for intricate network design and fine-tuning, did not perform as effectively in comparison (CNN R2 = 0.10, RNN R2 = 0.19). The results confirmed the significant advantage of ensemble models, with the extra trees model standing out as the best model. It’s worth noting that the datasets are relatively small (~10 k) and the features are high-dimensional (2048d), making ensemble models more suitable. Simpler linear models exhibit lower fitting capability, while more complex neural networks require a large amount of labelled data, potentially making them unsuitable for this problem. Therefore, the concatenated representation vectors of both the protein and substrate are subsequently input into the interpretable extra trees model for the prediction of three distinct enzyme kinetic parameters (Fig. 1c).
Fig. 2. Performance comparison of different models.
Comparison of Root Mean Square Error (RMSE) (a), Pearson Correlation Coefficient (PCC) (b), Mean Absolute Error (MAE) (c), and R2 (Coefficient of Determination) (d) values between experimentally measured kcat values and predicted kcat values of 16 diverse machine learning models and 2 deep learning models. The kcat values of all samples were predicted independently using 5-fold cross-validation. Each bar in the graph represents the models’ performance with respect to this metric. The “Extra Trees” model is highlighted in yellow, while other models are depicted in blue. The corresponding numerical values for each bar are provided on the right side. Source data are provided as a Source Data file.
Furthermore, to address two specific subproblems, we have fine-tuned the model for a better enzyme kinetic parameter prediction. One focuses on improving prediction performance by considering environmental factors (Fig. 1d). The other emphasizes optimization within the high-value range with higher error (Fig. 1e).
High accuracy of UniKP in enzyme kcat prediction
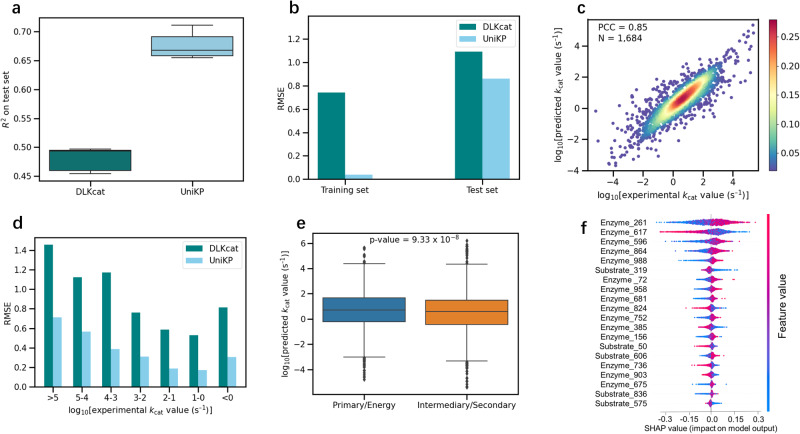
We first validated our proposed framework, UniKP, on a kcat prediction task, using the DLKcat dataset, which comprises 16,838 samples. The results were compared with those of DLKcat using the same evaluation metrics in the original publication12. Without any additional optimization of parameters, the average coefficient of determination (R2) value on the test set from five rounds of random splitting was 0.68, a 20% improvement over DLKcat (Fig. 3a). Additionally, the highest value of DLKcat in these five rounds was 16% lower than the lowest value of UniKP, further demonstrating the robustness of UniKP. The root mean square error (RMSE) between predicted and experimentally measured kcat values was also lower in UniKP compared to DLKcat, both in the training and test sets (Fig. 3b). We found a strong correlation between the predicted and experimentally measured kcat values in the test set (Fig. 3c; Pearson correlation coefficient (PCC) = 0.85) and the entire dataset (Supplementary Fig. 2a; PCC = 0.99), which were higher than those of DLKcat by 14% and 11%, respectively. Additionally, UniKP showed better prediction performance on a more stringent test set where either the enzyme or substrate was not present in the training set (Supplementary Fig. 2b; PCC = 0.83 vs. 0.70). UniKP also demonstrated superior performance in various kcat numerical intervals (Fig. 3d). In conclusion, UniKP outperforms DLKcat in enzyme kcat prediction across multiple evaluation metrics.
Fig. 3. High accuracy of UniKP in enzyme kcat prediction.
a Comparison of average coefficient of determination (R²) values for DLKcat and UniKP after five rounds of random test set splitting (n = 1684). b Comparison of the root mean square error (RMSE) between experimentally measured kcat values and predicted kcat values of DLKcat and UniKP for training (n = 15,154) and test sets (n = 1684). Dark bars represent RMSE of DLKcat and light bars for UniKP. c Scatter plot illustrating the Pearson coefficient correlation (PCC) between experimentally measured kcat values and predicted kcat values of UniKP for the test set (N = 1684), showing a strong linear correlation. The color gradient represents the density of data points, ranging from blue (0.02) to red (0.28). d Comparison of RMSE between experimentally measured kcat values and predicted kcat values of DLKcat and UniKP in various experimental kcat numerical intervals. Dark bars represent RMSE of DLKcat and light bars for UniKP. e Enzymes with significantly different kcat values between primary central and energy metabolism, and intermediary and secondary metabolism. An independent two-sided t-test to determine whether the means of two independent samples differ significantly. Primary central and energy metabolism (n = 3098) and intermediary and secondary metabolism (n = 4201) were examined in this analysis. f Shapley additive explanations (SHAP) analysis for the top 20-feature Extra Trees model. The impact of each feature on kcat values is illustrated through a swarm plot of their corresponding SHAP values. The color of the dot represents the relative value of the feature in the dataset (high-to-low depicted as red-to-blue). The horizontal location of the dots shows whether the effect of that feature value contributed positively or negatively in that prediction instance (x-axis). In each box plot (a, e), the central band represents the median value, the box represents the upper and lower quartiles and the whiskers extend up to 1.5 times the interquartile range beyond the box range. Source data are provided as a Source Data file.
Furthermore, to demonstrate UniKP’s ability to distinguish enzymes from different metabolic contexts, we separated the enzymes and their corresponding substrates into two categories, primary central and energy metabolism, and intermediary and secondary metabolism. Theoretically, the former should exhibit higher values27,28. Our results found that the primary central and energy metabolism category was significantly higher than the latter, consistent with expectations (Fig. 3e; p = 9.33 × 10−8). To gain insights into the model’s learning process, we used SHapley Additive exPlanations (SHAP) to analyze feature importance29. Higher values indicate more significant features. We calculated the SHAP value of each enzyme and substrate feature in the test set based on the trained UniKP. Our findings showed that 15 out of the top 20 features belonged to the enzyme category, while the rest belonged to the substrate (Fig. 3f). This confirms that the embedded enzyme features are more critical than those of the substrate. Furthermore, among the top 20 features, 12 were positively correlated with predicted kcat values, and 8 were negatively correlated. These results indicate that UniKP has a distinct preference for enzyme features, underscoring the decisive role of enzyme information.
In order to evaluate the potential data leakage, we used a reported method to compare the performance of UniKP with the geometric mean of experimental data which represent the potential data leakage30. The result demonstrated a clear advantage (higher correlation and lower RMSE) of UniKP over the geometric means, indicating the absence of data leakage in the training process (Supplementary Fig. 3).
UniKP markedly discriminates between kcat values of enzymes and their mutants
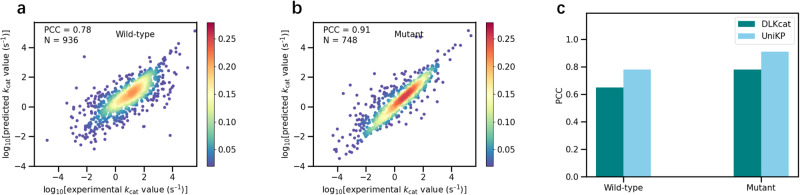
The ability to screen mutated enzymes is crucial in the process of enzyme evolution and its downstream applications. To further validate the discriminative power of UniKP, the dataset was segregated into wild-type and mutated enzymes based on DLKcat annotation12. The prediction results of UniKP were remarkable for both wild-type (Fig. 4a for the test set, PCC = 0.78; Supplementary Fig. 4a for the whole dataset, PCC = 0.98) and mutant enzymes (Fig. 4b for the test set, PCC = 0.91; Supplementary Fig. 4b for the whole dataset, PCC = 0.99). On the test set for both wild-type and mutant enzymes, the PCC of UniKP was found to be 13% higher than that of DLKcat (Fig. 4c). Moreover, we obtained R2 values of 0.60 for wild-type enzymes and 0.81 for mutant enzymes, along with RMSE values of 0.90 for wild-type enzymes and 0.67 for mutant enzymes. In order to further validate the ability of the proposed UniKP framework, we conducted additional experiments. We randomly selected 5 groups of enzymes for each category of Enzyme Commission (EC) number, with each group consisting of two enzymes and their corresponding kcat values for one specific substrate6. Our framework was found to outperform DLKcat in differentiating the kcat values of different enzymes for a given substrate (Supplementary Fig. 4c; 80% vs 53%).
Fig. 4. UniKP markedly discriminates kcat values of enzymes and their mutants.
Scatter plot illustrating the Pearson coefficient correlation (PCC) between experimentally measured kcat values and predicted kcat values of UniKP for wild type enzymes (a) (N = 936) and mutated enzymes (b) (N = 748). The color gradient represents the density of data points, ranging from blue (0.02) to red (0.28). c PCC values of wild-type and mutated enzymes on the test set of DLKcat and UniKP. Dark bars represent PCC values of DLKcat and light bars for UniKP. Source data are provided as a Source Data file.
A two-layer framework considering environmental factors
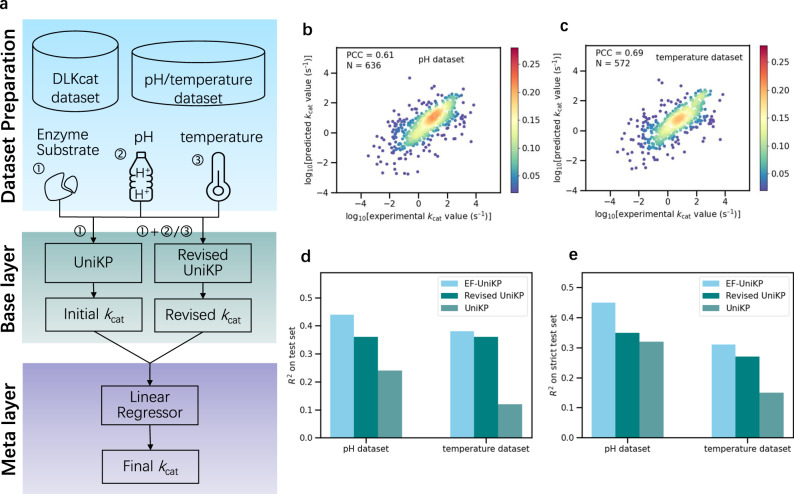
In order to simulate a more realistic biological experiment and predict more accurate kcat values considering environmental factors, we proposed a two-layer framework called EF-UniKP (Fig. 5a). This strategy is based on a two-layer framework that considers the influence of environmental factors such as pH and temperature. The base layer of the framework consists of two individual models, namely UniKP and Revised UniKP. The UniKP was trained using a dataset without environmental information to predict a rough kcat value, while the Revised UniKP was trained using a smaller dataset that considered an arbitrary environmental factor, such as pH or temperature. The input of the Revised UniKP is a concatenated representation vector of the protein and substrate, in combination with the pH or temperature value. The meta layer of the framework is a linear regression model that takes the predicted kcat values from both the UniKP and Revised UniKP as inputs. By considering information from both datasets with and without environmental information, the final predicted kcat value is more accurate.
Fig. 5. A two-layer framework considering environmental factors.
a A two-layer framework called EF-UniKP that consists of a base layer and a meta layer. The base layer contains two models, namely UniKP and Revised UniKP. The UniKP takes the concatenated representation vector of the enzyme and substrate as input, while the Revised UniKP uses a concatenated representation vector of the enzyme and substrate, combined with the pH or temperature value. Both models are trained using the Extra Trees algorithm. The meta layer of this framework includes a linear regressor that uses the predicted kcat values from both the UniKP and Revised UniKP to predict the final kcat value. Scatter plot illustrating the Pearson coefficient correlation (PCC) between experimentally measured kcat values and predicted kcat values of Revised UniKP for pH set (b) (N = 636) and temperature set (c) (N = 572). The color gradient represents the density of data points, ranging from blue (0.02) to red (0.28). d Coefficient of determination (R2) values between experimentally measured kcat values and predicted kcat values on pH and temperature test sets of EF-UniKP, Revised UniKP and UniKP. Light bars represent R2 of EF-UniKP, dark bars for Revised UniKP and darkish bars for UniKP. e R2 values between experimentally measured kcat values and predicted kcat values on more strict pH and temperature test sets of EF-UniKP, Revised UniKP and UniKP. These are the samples in the test set where at least either the substrate or enzyme was not included in the training set, resulting in 62 and 61 samples for pH and temperature, respectively. Light bars represent R2 of EF-UniKP, dark bars for Revised UniKP and darkish bars for UniKP. Source data are provided as a Source Data file.
To prospectively evaluate our proposed strategy, we assessed the influence of pH and temperature on enzyme-substrate reactions by creating two datasets. These contained enzyme sequences, substrate structures, and corresponding pH or temperature values and were sourced from UniProt and PubChem6,31. The pH and temperature datasets comprised 636 and 572 samples, respectively, and exhibited a wide range of values from 3 to 10.5 and 4 to 85 degrees (Supplementary Fig. 5a, b). To validate the effectiveness of the Revised UniKP, we conducted five-fold cross-validation on both datasets. Our results showed a strong correlation between predicted and experimentally measured kcat values (Fig. 5b, c), with a PCC of 0.61 and 0.69 for pH and temperature, respectively. Moreover, the R2 value was 0.36 and 0.47 for pH and temperature, respectively, indicating that the Revised UniKP performs well.
Furthermore, we divided the two datasets into training and test sets, allocating 80% and 20% respectively. Our results on independent test sets revealed that EF-UniKP outperforms both UniKP and Revised UniKP (Fig. 5d; R2 = 0.44, R2 = 0.38). On the pH dataset, the R2 values for EF-UniKP were 20% and 8% higher than for UniKP and Revised UniKP, respectively. On the temperature dataset, the R2 values were 26% and 2% higher, respectively. This was further supported by smaller errors and high correlation (Supplementary Fig. 6a, b). To prevent overfitting on the training set, we performed a stricter analysis and selected only those samples in the test set where at least either substrate or enzyme was not included in the training set, resulting in 62 and 61 samples for pH and temperature, respectively. Our results showed that EF-UniKP outperformed both UniKP and Revised UniKP, with R2 values 13% and 10% higher on the pH dataset and 16% and 4% higher on the temperature dataset (Fig. 5e; R2 = 0.45, R2 = 0.31). The advantages in RMSE and PCC also confirmed the effectiveness of EF-UniKP (Supplementary Fig. 6c, d). Overall, our newly established pH and temperature dataset confirmed that our two-layer framework can effectively consider environmental factors and improve model performance.
Enhancing high kcat prediction through re-weighting methods
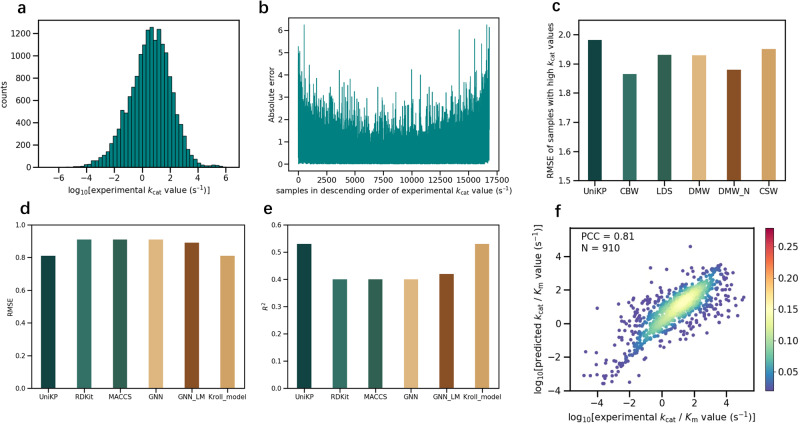
We further analyzed the kcat value distribution of the dataset used and found that it was highly imbalanced, with only a few samples at both ends and most samples in the middle, resembling a normal distribution (Fig. 6a). This presented a challenge for a machine learning model to extract the critical information23. However, predicting high kcat values has been essential in enzymology and synthetic biology14,15. To illustrate this, we implemented five-fold cross-validation on the entire dataset to independently scan the predicted kcat for all samples, from which we observed that the error was higher at both ends of the dataset compared to the middle (Fig. 6b). To address this issue, we utilized representative re-weighting methods, including Directly Modified sample Weight (DMW), Cost-Sensitive re-Weighting methods (CSW), Class-Balanced re-Weighting methods (CBW), and Label Distribution Smoothing (LDS), on the kcat dataset24,32,33. For each method, we applied several commonly used hyperparameters to the entire dataset and performed five-fold cross-validation using UniKP to predict kcat values for all samples, whereas 149 samples with kcat greater than 4 were selected to represent high kcat samples for DMW optimization and downstream comparison (Supplementary Figs. 7–11). We found that all of these methods outperformed the initial UniKP, with CBW being the most effective. The RMSE of high kcat samples was 6.5% lower with CBW than with the initial model (Fig. 6c). We further subdivided the high kcat value samples into two numerical intervals, higher than 5 and between 4 and 5, and found that the smaller errors in both intervals confirmed the effectiveness of our approach (Supplementary Fig. 12). Overall, our use of representative re-weighting methods enabled us to adjust the sample weight distribution and effectively improve high kcat value prediction.
Fig. 6. Enhancing high kcat prediction through re-weighting methods and unified framework for Km and kcat / Km predictions.
a The distribution of kcat values in the kcat dataset. All samples are divided into 50 bins. b The absolute error between experimentally measured kcat values and predicted kcat values of each sample. The kcat values of all samples were predicted independently using five-fold cross-validation. c Root mean square error (RMSE) between experimentally measured kcat values and predicted kcat values of 149 samples with kcat values higher than 4 (logarithm value) using various re-weighting methods and the initial UniKP. d, e RMSE, coefficient of determination (R2) between experimentally measured Km values and predicted Km values on Km test set. f Scatter plot illustrating the Pearson coefficient correlation (PCC) between experimentally measured kcat / Km values and predicted kcat / Km values of UniKP for kcat / Km dataset (N = 910). The color gradient represents the density of data points, ranging from blue (0.02) to red (0.28). Source data are provided as a Source Data file.
Unified framework for Km and kcat / Km predictions
Next, we investigated the performance of UniKP on Km and kcat / Km prediction. Although kcat is traditionally considered as independent of Km, in light of the principle that the primary sequence of a specific protein determined its three-dimensional structure, and therefore its function, we believed that hidden information in the primary sequence could also be used to predict its Km and kcat / Km values. For the prediction of Michaelis constant Km values, a reported representative dataset was selected10, consisting of 11,722 natural enzyme-substrate combinations and their corresponding Km values. The dataset was randomly divided into a training set (80%) and a test set (20%) which was used to train a predictor capable of predicting Km with enzyme sequence. The results showed that the Km predictor trained by UniKP outperformed most baseline models and achieved the prediction performance of the state-of-the-art model, with R2 = 0.530 and a RMSE value smaller than or equal to the previous models on the test set (Fig. 6d, e). There was also a high correlation between the predicted Km values and experimentally measured Km values (PCC = 0.73).
For kcat / Km prediction, an additional dataset was collected from BRENDA, UniProt and PubChem6,7,31, containing 910 enzyme sequences, substrate structures, and their corresponding kcat / Km values. Five-fold cross-validation was performed and a high correlation was found between the predicted values and real values (Fig. 6f; PCC = 0.81). The R2 was 0.65 and the RMSE was 1.07. As there was no predictor available to directly predict kcat / Km value from enzyme sequence and substrate structures, the state-of-the-art kcat predictor and Km predictor were used to predict the corresponding kcat and Km parameters which were used to calculate the kcat / Km values10,12. The PCC of these calculated kcat / Km values with the corresponding experimentally measured ones was −0.02, demonstrating the significant advantages of UniKP. The advantage of UniKP can be attributed to the high prediction consistency of its unified framework. In conclusion, the generalizability of UniKP on similar tasks with small molecule-protein interactions was verified.
UniKP assisted enzyme mining and evolution
Discovering alternative enzymes with enhanced activity for specific biochemical reactions and improving known enzyme efficiency through directed evolution are vital in synthetic biology and biochemistry research. However, enzyme mining and evolution processes can be time-consuming and labour-intensive. Tyrosine ammonia lyase (TAL), a key rate-limiting enzyme in flavonoid biosynthesis, has been extensively studied to identify superior TAL variants. For example, one study selected 107 representative TALs from 4729 unique sequences found in over ten distinct microbial species through bioinformatic analysis34. However, enzymatic assays revealed that only four TALs displayed higher activities, with the highest kcat of 4.32 s−1, considerably lower than the kcat of 114 s−1 reported for a TAL from Rhodotorula glutinis, identified from bacterial and fungal TAL enzymes based on empirical knowledge35–37. Directed evolution of RgTAL resulted in only a slight improvement in its kcat, from 114 to 142 s−1, from laborious screening of 4800 mutants36.
To employ UniKP for enzyme mining, we first used RgTAL as a template to perform BLASTp search and identified the top 1000 TAL sequences with high similarity. UniKP then predicted the kcat values for each sequence. The top 5 sequences with the highest predicted kcat values were selected for experimental validation. The results demonstrated that 5 RgTAL analogues can be successfully expressed in E. coli, of which 4 samples exhibited catalytic activity (Table 1, entry 1). Interestingly, 2 of the 4 samples surpassed RgTAL, with AsTAL from Armillaria solidipes displayed the highest kcat of 448.8 s−1, four times greater than RgTAL.
Table 1.
UniKP and EF-UniKP assisted enzyme mining and evolution
| Entry | Category | TALs | kcat (s−1) | Km (mM) | kcat / Km (s−1⋅mM−1) |
|---|---|---|---|---|---|
| 1 | UniKP: Enzyme mining | RgTAL | 117.8 | 0.36 | 327.2 |
| HiTAL | NA | NA | NA | ||
| PcTAL | 66.57 | 0.17 | 391.6 | ||
| SsTAL | 58.87 | 0.17 | 346.3 | ||
| AsTAL | 448.8 | 0.54 | 831.1 | ||
| IsTAL | 119.7 | 0.57 | 210.0 | ||
| 2 | UniKP: Enzyme evolution | RgTAL | 117.8 | 0.36 | 327.2 |
| MT-613P | NA | NA | NA | ||
| MT-603P | 52.57 | 1.15 | 45.71 | ||
| MT-366H | 40.31 | 0.48 | 83.98 | ||
| MT-366W | 31.02 | 0.85 | 36.49 | ||
| MT-587V | 162.9 | 0.33 | 493.6 | ||
| MT-10Y | 884.4 | 0.82 | 1079 | ||
| MT-337C | 96.81 | 6.48 | 14.94 | ||
| MT-668S | 53.60 | 3.85 | 13.92 | ||
| MT-489T | 816.8 | 0.71 | 1150 | ||
| MT-337D | 34.77 | 0.85 | 40.91 | ||
| 3 | EF-UniKP | TALclu | 16.54 | 0.05 | 330.80 |
| TrTAL | 34.54 | 0.04 | 863.50 | ||
| HiTAL | 76.00 | 0.21 | 361.90 | ||
| LeTAL | 33.85 | 0.07 | 483.57 | ||
| PpTAL | 28.09 | 0.04 | 702.25 | ||
| AaTAL | 25.24 | 0.03 | 841.33 |
Entry 1) The kinetic characteristics of wild-type Tyrosine ammonia lyase (RgTAL) from Rhodotorula glutinis and newly discovered TALs mined from non-redundant protein database by performing BLASTp. The top 5 sequences with the highest predicted kcat values by UniKP were selected for experimental validation, including HiTAL from Heterobasidion irregulare TC 32-1 (XP_009553370.1), PcTAL from Puccinia coronata f. sp. avenae (PLW06342.1), SsTAL from Sporidiobolus salmonicolor (CEQ38810.1), AsTAL from Armillaria solidipes (BK74450.1), IsTAL from Ilyonectria sp. MPI-CAGE-AT-0026 (KAH6995648.1). NA denotes the enzyme that was not soluble and showed no catalytic activity. Entry 2) The kinetic characteristics of RgTAL and mutants generated by UniKP. All variants of single-point mutations were generated for RgTAL, where each variant involved mutating an amino acid at a specific position to one of the other 19 canonical amino acids, which resulted in a total number of variants equal to the product of 19 and the length of the sequence (19*693 = 13,167). Through an in-silico screening of all 13,167 single-point mutations of RgTAL using UniKP, the top 5 mutants ranked by their predicted kcat or kcat / Km values were chosen from each screening (kcat or kcat / Km) for experimental validation. NA denotes the enzyme that was not soluble and showed no catalytic activity. And MT denotes the mutated form of RgTAL. Entry 3) The kinetic characteristics of wild-type Tyrosine ammonia lyase from Chryseobacterium luteum sp. nov (TALclu) and newly discovered TALs mined from non-redundant protein database by performing BLASTp. The top 5 sequences with the highest predicted kcat values by UniKP were selected for experimental validation, including TrTAL from Tephrocybe rancida (KAG6920185.1), HiTAL from Heterobasidion irregulare TC 32-1 (XP_009553370.1), LeTAL from Lentinula edodes (KAF8828722.1), PpTAL from Pleurotus pulmonarius (KAF4563271.1), AaTAL from Aspergillus arachidicola (KAE8337485.1). All the experiments were conducted under a pH of 9.5.
To showcase UniKP’s ability to assist directed evolution, we generated all variants with single-point RgTAL mutation, where each variant involved mutating an amino acid at a specific position to one of the other 19 canonical amino acids. This resulted in a total number of variants equal to the product of 19 and the length of the sequence (19*693 = 13,167). We performed an in-silico screening of all 13,167 single-point RgTAL mutations using UniKP by predicting their corresponding kcat and kcat / Km values. A total of 10 sequences, with the top 5 hits with highest predicted kcat and 5 with highest kcat / Km, were chosen for experimental validation (Table 1, entry 2). Among the mutants with highest predicted kcat, one exhibited a slightly higher kcat / Km of 493.6 mM−1s−1, indicating increased efficiency compared to the wild-type enzyme. In contrast, among the mutants with highest predicted kcat / Km, two mutants, RgTAL-10Y and RgTAL-489T, displayed significantly higher kcat / Km of 1079 mM−1s−1 and 1150 mM−1s−1, respectively. RgTAL-489T was 3.5-fold more efficient than the wild-type enzyme, representing the most efficient TAL reported to date. Moreover, through BLASTp analysis, the result showed that the most similar sequence in the whole dataset for kcat / Km predictor shares only a 35.42% identity. This demonstrates that UniKP indeed captures deep-level information, enabling effective screening of enzyme-substrate combinations that have not been presented in training set. These results confirm that UniKP is a rapid and effective method for mining new enzymes or improving existing enzymes for specific substrates.
Furthermore, in order to illustrate the effectiveness of EF-UniKP, we also conducted wet-lab experimental validations, using pH as an example. Specifically, we selected the TALclu38, which exhibited an optimal catalytic pH of 9.5. We employed a similar enzyme mining approach as before against TALclu and selected the top 5 sequences with the highest predicted kcat values by EF-UniKP for experimental validation. Remarkably, we found that the kcat and kcat / Km values of all 5 sequences exceeded those of TALclu. The kcat value of HiTAL from Heterobasidion irregulare TC 32-1 was the highest at 76.00 s−1, which is 4.6 times greater than that of TALclu. Additionally, the kcat / Km value of TrTAL from Tephrocybe rancida was the highest at 863.50 mM−1s−1, representing a 2.6-fold increase compared to TALclu (Table 1, entry 3). This result further demonstrates that EF-UniKP, when considering environmental factors, consistently identifies highly active TAL enzymes with remarkable precision.
Discussion
The traditional method of measuring enzyme kinetic parameters of diverse enzymes and their substrates through labor-insentive and time-consuming experiments hampers the development of enzymology and synthetic biology applications. To address this challenge, we present a pretrained language model-based enzyme kinetic parameters prediction framework, UniKP, which improves the accuracy of predictions for three essential enzyme kinetic parameters, kcat, Km, and kcat / Km, using only the enzyme sequence and substrate structure. Here, we conducted a comprehensive comparison of 16 diverse machine learning models and 2 deep learning models on the machine learning module of UniKP, with the extra trees emerging as the best model. We speculated that tree-based ensemble models are better suited for this issue, with relatively small datasets (~10k) and high-dimensional features (2048d). They utilized decision trees to efficiently break down high-dimensional data into smaller subsets, enabling more efficient feature selection and data segmentation. The combination of multiple decision trees reduced model variance, thereby balancing the instability of individual trees and decreasing the model’s sensitivity to training data, contributing to improving the model’s generalization abilities. The simpler models may be limited by insufficient fitting capabilities, while deep learning models rely on a large number of labelled samples, complicated network designs, and tedious parameter tuning.
UniKP demonstrated remarkable performance compared to the previous state-of-the-art model, DLKcat, in the kcat prediction task with an average coefficient of determination of 0.68, which was 20% higher. We speculated that pretrained models have greatly contributed to the performance of UniKP by creating an easily learnable representation of enzyme sequences and substrate structures using unsupervised information from the entire database18. Our analysis of model learning showed that protein information has a dominant effect, possibly due to the complexity of enzyme structure compared to substrate structure. Additionally, UniKP can effectively capture the small differences in kcat values between enzymes and their mutants, including experimentally measured cases, which is crucial for enzyme design and modification. And The disparity between the high identity region (>70 identity) and low identity region (<50 identity) of the R2 of UniKP predicted values and R2 of the gmean method underscores the adeptness of UniKP in extracting deeper interconnected information, thereby demonstrating a higher predictive accuracy in these tasks.
Moreover, the current models do not consider environmental factors, which is a critical limitation in simulating real experimental conditions. To address this issue, we propose a two-layer framework, EF-UniKP, which takes into account environmental factors. Based on two newly constructed datasets with pH and temperature information, respectively, EF-UniKP shows improved performance compared to the initial UniKP. To our knowledge, this is an accurate, high-throughput, organism-independent, and environment-dependent kcat prediction. Additionally, this approach has the potential to be extended to include other factors, such as cosubstrate and NaCl concentration39,40. However, existing models do not account for the interplay between these factors due to the lack of combined data. As experimental techniques advance, including biofoundry lab automation and continuous evolution methods41,42, we anticipate a surge in enzyme kinetic data. This influx will not only enrich the field but also enhance the accuracy of prediction models. Additionally, due to the high imbalance in the kcat dataset, which results in a high error on high kcat value predictions, we systematically explored four representative re-weighting methods to mitigate this issue. The results showed that the hyperparameter settings for each method were critical in improving high kcat value prediction. Compared to the initial UniKP, all of the methods resulted in lower errors, with CBW being the optimal method. CBW argues that as the number of samples increases, the additional benefit of a newly added data point will diminish, indicating information overlap among the data33. Therefore, it further optimizes the weight by taking into account this issue. In the kcat dataset, enzymes with high homology, substrates with similar structures, and enzyme mutants contain overlapping information, which could explain why CBW is effective in this particular case. Overall, these findings demonstrate that re-weighting methods can assist biologists in improving specific value predictions they focus on.
Furthermore, we confirmed the strong generalizability of the current framework on Michaelis constant (Km) prediction and kcat / Km prediction. UniKP achieved state-of-the-art performance in predicting Km values and, even more impressively, outperformed the combined results of current state-of-the-art models in predicting kcat / Km values. Furthermore, we validated the UniKP framework based on experimentally measured kcat / Km values and kcat / Km values calculated using kcat and Km prediction models on kcat / Km dataset. It is to be noted that the correlation observed between the values derived from UniKP kcat / UniKP Km and the experimental kcat / Km is relatively low (PCC = −0.01). This discrepancy is likely attributable to the disparate datasets employed in constructing the respective models, necessitating the development of a distinct model for predicting kcat / Km values. In the future, with the availability of a unified dataset encompassing both kcat and Km values, it is anticipated that the calculated outputs from the kcat and Km models would closely align with those generated by a dedicated model for kcat / Km.
The application of UniKP to Tyrosine ammonia lyase (TAL) enzyme mining and directed evolution demonstrated its potential to revolutionize synthetic biology and biochemistry research. This study showed that UniKP effectively identified high-activity TALs and rapidly improved catalytic efficiency of an existing TAL, with RgTAL-489T exhibiting a kcat / Km value 3.5 times higher than the wild-type enzyme. Additionally, the derived framework EF-UniKP, when considering environmental factors, consistently identifies highly active TAL enzymes with remarkable precision, with TrTAL from Tephrocybe rancida exhibiting a kcat / Km value 2.6 times higher than the wild-type enzyme. The result showed that the kcat and kcat / Km values of all 5 sequences exceeded those of the wild-type enzyme. By expediting enzyme discovery and optimization processes, UniKP holds promise as a powerful tool for advancing biocatalysis, drug discovery, metabolic engineering, and other fields that rely on enzyme-catalyzed processes.
However, there are still some limitations to the current version of UniKP. For instance, while UniKP is capable of differentiating kcat values of experimentally measured enzymes and their variants, the predicted kcat values are not sufficiently accurate. This may be due to an insufficient dataset compared to the number of known protein sequences and substrate structures. Although re-weighting methods can somewhat relieve the prediction bias caused by the imbalanced kcat dataset (~6.5% improvement), more significant improvement may be achieved through the synthetic minority oversampling technique and other sample synthesis methods43,44. A central objective in synthetic biology is the development of a digital cell, poised to revolutionize our methods of studying biology. A critical prerequisite for this endeavour is the meticulous determination of enzymatic parameters for all enzymes within the pathway. Tools assisted by artificial intelligence illuminate this challenge, offering a high-throughput approach to predicting enzymatic kinetics. However, despite the reduced errors in UniKP predictors compared to earlier models, inaccuracies remain a significant hurdle in crafting a precise metabolic model. The inclusion of a growing number of experimentally determined kcat and Km values, sourced from cutting-edge high-throughput experimental techniques like those employed in modern biofoundries, can enhance model accuracy. Furthermore, we intend to incorporate state-of-the-art algorithms, such as transfer learning, reinforcement learning, and other small sample learning algorithms to effectively process imbalanced datasets45,46. Moreover, we aim to explore more applications, including enzyme evolution and global analysis of organisms.
Methods
Dataset source and preprocessing
To evaluate the UniKP framework, we selected several representative datasets and constructed several datasets to verify its accuracy.
DLKcat dataset. The DLKcat dataset was prepared as in the original publication12. Specifically, we began by utilizing the DLKcat dataset, which is the most comprehensive and representative dataset based on enzyme sequences and substrate structures from BRENDA and SABIO-RK databases. Initially, the dataset contained 17,010 unique samples, but we excluded samples with substrate simplified molecular-input line-entry system (SMILES) containing “.” or kcat values less than or equal to 0, as per the DLKcat instruction. This resulted in 16,838 samples, which encompassed 7822 unique protein sequences from 851 organisms and 2672 unique substrates. All kcat values were converted to a logarithmic scale. The dataset was divided into training and test sets, with a ratio of 90% and 10%, respectively, which was repeated five times to obtain 5 randomized datasets for downstream model training and test, keeping the same as in the previous publication.
pH and temperature datasets. To predict the influence of environmental factors to kcat, we constructed two datasets that contain enzyme sequences, substrate structures, and their corresponding pH or temperature values. We obtained the enzyme sequences, substrate names, and pH or temperature values from the Uniprot database6. To obtain the corresponding substrate structure, we downloaded it from the PubChem database based on the substrate name and generated a SMILES representation via a python script31. The pH dataset comprised 636 samples, consisting of 261 unique enzyme sequences and 331 unique substrates, which resulted in 520 unique enzyme-substrate pairs. The pH values ranged from 3 to 10.5. The temperature dataset contained 572 samples, consisting of 243 unique enzyme sequences and 302 unique substrates, which resulted in 461 unique enzyme-substrate pairs. The temperature values ranged from 4 to 85 degrees. To evaluate the performance of UniKP on these datasets, we divided each dataset into an 80% training set and a 20% test set.
Michaelis constant (Km) dataset. To assess the generalizability of UniKP on related tasks, we utilized a representative dataset obtained from a previous publication with SOTA results10, which contains data retrieved from BRENDA. This dataset consists of 11,722 samples, comprising of enzyme sequences, substrate molecular fingerprints, and corresponding Km values. We converted the substrate structures into SMILES representations and log10-transformed all Km values. To evaluate the performance of UniKP on this dataset, we randomly divided the entire dataset into 80% training data and 20% test data, keeping the same as in the previous publication.
kcat / Km dataset. We constructed an additional dataset using information sourced from the BRENDA, UniProt, and PubChem databases6,7,31. This dataset comprises 910 samples consisting of enzyme sequences, substrate structures, and their corresponding kcat / Km values. We first obtained the UniProt ID of the enzyme and the name of the substrate along with their kcat / Km values from the BRENDA database. Then, the corresponding enzyme sequences and substrate structures were obtained from the UniProt and PubChem databasesusing the UniProt ID and the name of the substrate, repsectively. We divided the entire dataset into five parts randomly to evaluate the performance of UniKP.
Construction of UniKP
We implemented the UniKP framework using torch v. 1.10.1+cu113 and sklearn v. 0.24.2. UniKP consists of a representation module and a machine learning module. The representation module is responsible for generating effective representations of the enzyme sequences and substrate structures. We used the ProtT5-XL-UniRef50 protein language model, which has been shown to be effective in predicting peptide and protein function, to generate an embedded vector for the enzyme sequence18. Every amino acid was converted into a 1024-dimensional vector on the last hidden layer, and the resulting vectors were summed and averaged. The final enzyme representation was a 1024-dimensional vector. For the substrate structure, we generated a SMILES and used a pretrained SMILES transformer to create a 1024-dimensional vector by concatenating the mean and max pooling of the last layer and the first outputs of the last and penultimate layers20. The representation module converted the enzyme sequence or substrate structure into a numerical representation using an unsupervised learning process, making it easier for machine learning models to learn. The second module was an Extra Trees model, a machine learning method that can effectively capture the relationship between the concatenated representation vectors of the enzyme sequence and substrate structure and the kcat value. All experiments were conducted in a Linux environment running Ubuntu 20.04.5 on a server with 64 cores and 4 NVIDIA GeForce RTX 3080 GPUs. We used a single core and GPU for training.
Model setting
The 16 machine learning models includes Linear Regression, Ridge Regression, Lasso Regression, Bayesian Ridge Regression, Elastic Net Regression, Decision Tree, Support Vector Regression, K Neighbors Regressor, Random Forest, Gradient Boosting, Extra Trees, AdaBoost, Bagging, XGBoost (XGB), LightGBM (LGBM), MultiLayer Perceptron (MLP) Regressor. Here, the MLP Regressor was regarded as a traditional machine learning due to its shallow network design. We implemented all machine models using sklearn v. 1.1.1, utilizing default parameters, without additional optimization. The Convolutional Neural Network (CNN) architecture employed in this study comprises a 1D convolutional layer (conv1) with 16 output channels and a kernel size of 3 for feature extraction, followed by a max-pooling layer (pool) with a kernel size of 2 for downsampling. Then the model further includes two fully connected layers (fc1 and fc2), with fc1 having 16 * 1023 input features and 64 output features, and fc2 having 64 input features and 1 output feature. The architecture of Recurrent Neural Network (RNN) utilized in this study involves an RNN layer (rnn) with 2048 input features, 128 hidden units, and 1 layer. Following the RNN layer, there are two fully connected layers (fc1 and fc2). The first layer (fc1) has 128 input features and 64 output features, while the second layer (fc2) has 64 input features and 1 output feature. During the training process, deep learning models were optimized using an Adam optimizer with a learning rate of 0.0001, employing Mean Square Error as the loss function. The batch size was configured to be 8192. All deep learning models were implemented using Python 3.6.9 with pytorch 1.10.1+cu113.
Construction of EF-UniKP
We developed a framework, called EF-UniKP, which takes into account environmental factors such as pH and temperature. This two-layer framework comprises a base layer with two individual models: UniKP and Revised UniKP. The UniKP takes as input a concatenated representation vector of the protein and substrate, while the Revised UniKP uses a concatenated representation vector of the protein and substrate, combined with the pH or temperature value. Both models were trained using the Extra Trees algorithm. The meta layer of the framework consists of a linear regression model that utilizes the predicted kcat values from both the UniKP and Revised UniKP as inputs. The pH and temperature datasets were divided into training and test sets, with the former being 80% of the dataset. The training set was further split into two subsets: the first training set was 80% of the training set (or 64% of the entire dataset) and the second training set was 20% of the training set (or 16% of the entire dataset). The training process involved two steps. In the first step, UniKP was trained using the DLKcat dataset without environmental factors, while Revised UniKP was trained using the first training set of pH or temperature dataset. In the second step, a linear regression model was trained using the second training set of pH or temperature dataset, and the outputs from both models in the first layer. The evaluation was performed using the test data of the pH or temperature dataset. As the model’s performance may be influenced by different training and test set division, which were generated randomly, we have taken the precaution to average the results three times to mitigate this risk.
Evaluation metrics
To evaluate the performance of our framework, we utilized various metrics to compare the predicted kcat value and experimentally measured kcat. Our selected metrics included the coefficient of determination (R2) in Eq. 1, the pearson correlation coefficient (PCC) in Eq. (2), the root mean square error (RMSE) in Eq. (3), and the mean absolute error (MAE) in Eq. (4). These equations utilize variables such as for the experimentally measured kcat value, for the predicted kcat value, for the average of the experimentally measured kcat values, for the average of the predicted kcat values, and n for the number of samples (which depends on the size of the selected dataset). In this manuscript, we have presented various metrics in different sections for the comparison with existing models.
| 1 |
| 2 |
| 3 |
| 4 |
Feature importance analysis by SHAP
We utilized SHapley Additive exPlanations (SHAP), a unified framework for analyzing model interpretability, to compute the importance value of each feature29. The assigned SHAP value represents the significance of the feature, with higher values indicating greater importance. Moreover, SHAP can also indicate the positive or negative effects of features. This framework has been widely used to interpret the importance of various biological problems, including Type IV Secreted Effectors prediction and anticancer peptide prediction47,48. We applied SHAP on the kcat test set, which comprises 1684 samples, based on the trained UniKP. The SHAP summary produced by TreeExplainer displayed the magnitude, distribution, and direction of every feature effect. Each dot on the graph represents a dataset sample, and the x-axis position denotes the SHAP value, while the change in color represents different feature values. The implementation of SHAP was achieved through a freely available Python package.
t-SNE visualization
To better understand the distribution of embedded enzyme and substrate representations and explore the necessity of using machine learning, we utilized t-distributed stochastic neighbor embedding (t-SNE) to visualize the embedded enzyme and substrate vectors26. This widely used method has been employed to analyze feature distributions in biological tasks, such as antimicrobial peptide recognition and protein subcellular location49–51. We calculated embedded vectors for all 16,838 samples, which were concatenated and inputed into the t-SNE algorithm, which transformed them into two-dimensional vectors. We used the default parameters for the algorithm and normalized the resulting numerical values of the two-dimensional vector for each sample to display, as shown in Eq. 5, where denotes the value of the ith projected vector and denotes all values of the projected vector.
| 5 |
Sample weight redistribution methods
We explored four different methods to adjust the weight of the samples for accurate high kcat prediction. These representative weight redistribution methods included Directly Modified Sample Weight (DMW), Cost-Sensitive re-Weighting methods (CSW), Class-Balanced re-Weighting methods (CBW), and Label Distribution Smoothing (LDS)24,32,33. To enable fair comparison of the methods, we employed 5-fold cross-validation on the entire dataset to ensure that all samples could be predicted independently. We then divided the predicted kcat values into different intervals and calculated RMSE and MAE separately for kcat values higher than 4 (logarithm value) and kcat values higher than 5 (logarithm value).
DMW method
The DMW method is a weight redistribution approach where the weight of samples with kcat values higher than 4 (logarithm value) is directly enhanced. We explored several parameters, including weight multipliers (2, 5, 10, 20, 50, 100) and whether to normalize the weights. Through this process, we analyzed twelve optimized model combinations, which revealed that a weight coefficient of 10 without normalization was optimal. Increasing or decreasing the coefficient resulted in higher RMSE and MAE in predicting high kcat values.
CSW method
The CSW method assigns different weights to different classes to guide the model to pay more attention to minority categories. Three CSW variants, including CSW, root CSW, and square CSW, were applied to all samples. All the samples were divided into 131 bins, each covering an equal numeric interval. For CSW, the weight of each sample was set to the reciprocal of the sample size in each bin. The root CSW and square CSW methods reset the weight of each sample by its square root and its square, respectively. We found that the root CSW was the most effective method.
CBW method
The CBW method posits that the value of adding new data points will decrease as the size of the dataset increases. To reflect this, the effective number of samples can be calculated using Eq. (6), where n is the number of samples and β is a hyperparameter that ranges between 0 and 1. The weighting of each sample is then set to 1 divided by the effective number of samples. We evaluated the CBW method using different beta values (0.7, 0.75, 0.8, 0.85, 0.9, 0.99, 0.999, 0.9999) and found that the optimal value was 0.9, which resulted in the lowest prediction RMSE and MAE compared to other settings.
| 6 |
LDS methods
LDS is a simple, effective, and interpretable algorithm for tackling the problem of unbalanced datasets that exploits the similarity of the nearby label space. It had been verified to be very effective in sections where only a few samples exist, and the predicted error would be reduced dramatically. LDS convolves a symmetric kernel with the empirical density distribution to generate a kernel-smoothed effective density distribution in Eq. 7, where denotes the number of appearances of label y in the training data, denotes the effective density of label , and denotes the symmetric kernel. Similarly, we selected a Gaussian kernel and set various kernel sizes (3, 5, 7) and sigma values (1, 2). The optimal kernel size and sigma were 5 and 1, respectively.
| 7 |
Experimental validation of UniKP
We attempted to utilize UniKP to boost the enzyme mining process. Specifically, we selected a crucial enzyme in the naringenin synthetic pathway, tyrosine ammonia lyase (TAL).
BLASTp
Basic Local Alignment Search Tool protein (BLASTp) is a widely used bioinformatics tool for sequence similarity search52. It is a protein-protein BLAST algorithm that compares the query protein sequence against a non-redundant protein database and retrieves similar sequences based on their E-value, which estimates the probability of observing the alignment by chance. In this study, we utilized the BLASTp algorithm with RgTAL from Rhodotorula glutinis (AGZ04575) as the template to identify sequences with high similarity to TAL, and subsequently selected the top 1000 sequences based on E value for kcat prediction using the UniKP. The parameters used were default, employing a BLOSUM62 scoring matrix, a word size of 5, and an expectation threshold of 0.05 for the setting.
Experimental materials
The plasmids and strains used in the experiment are detailed in Supplementary Tables 1–2. For strain maintenance, Luria-Bertani (LB) medium, which contains 10 g/L tryptone, 10 g/L NaCl, and 5 g/L yeast extract, was utilized. In order to produce naringenin in diverse strains, MOPS (3-(N-morpholino)propanesulfonic acid) medium was used. All of the chemicals used in the experiment were reagent grade and purchased from Sigma-Aldrich (St. Louis, MO, USA). NEBuilder® HiFi DNA Assembly Kit (E2621S) was purchased from NEB (Beverly, MA, USA) for the purpose of plasmid constructions.
Determination of enzymatic kinetic parameters
The predicted TALs were codon-optimized for expression in BL21(DE3)36. These TALs were respectively synthesized and cloned into the pET32a plasmid by Genewiz (Suzhou, China). The enzyme kinetic parameters of the different TAL enzymes were also evaluated as the following processes. Specifically, the candidate enzymes were tested in a 200 μL reaction volume with purified protein (1 μg), different concentrations of L-tyrosine, and Tris-HCl buffer (90 μL 50 mM pH 8.5). The mixture was incubated at 40 °C for 30 min and monitored for the appearance of coumaric acid at 315 nm36. One unit of enzyme activity was defined as 1 μM p-coumaric acid production in one minute. The kinetic curves of experimental results were included in Supplementary Fig. 13–16. The chemicals in this study were analytical reagent grade and purchased from Sigma-Aldrich (Steinheim, Germany).
HPLC methods for naringenin detection
HPLC methods for detecting naringenin involved the use of an Agilent 1260 HPLC system (Waldbronn, Germany) equipped with a diode array detector (DAD) 1260 model VL + (G7115A) and a C18 column (3 × 100 mm 2.7 μm). The detection was performed at 290 nm and 30 °C. A gradient elution condition was employed with the following steps: 10% to 40% acetonitrile/water (vol/vol) for 5 min, 40% acetonitrile (vol/vol) for 7 min, 40% to 95% acetonitrile (vol/vol) for 3 min, and 95% to 10% acetonitrile (vol/vol) for 3 min. The elution rate was 0.3 mL/min. Additionally, 0.3% acetic acid (vol/vol) was added to the mobile phases to facilitate the separation of naringenin.
Statistics and reproducibility
The source of the dataset and the division criteria presented in this paper are detailed in each results section. Statistical analyses were performed using the packages in Python 3 (https://www.python.org/). No statistical method was used to predetermine sample size. We excluded samples with substrate simplified molecular-input line-entry system (SMILES) containing “.” or kcat values less than or equal to 0, as per the DLKcat instruction12. All datasets were randomly split into training and test sets to ensure a fair comparison. And based on the goal of enzyme evolution, samples with the highest enzyme kinetic parameters predicted by UniKP were selected for experimental validation. We were not blinded to allocation during experiments and outcome assessment.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.
Supplementary information
Source data
Acknowledgements
We would like to acknowledge the support from National Key R&D Program of China (2018YFA0903200 to X.L.), National Natural Science Foundation of China (32071421 to X.L.), Guangdong Basic and Applied Basic Research Foundation (2021B1515020049 to X.L.), Shenzhen Science and Technology Program (ZDSYS20210623091810032 and JCYJ20220531100207017 to X.L. and H.D.), and Shenzhen Institute of Synthetic Biology Scientific Research Program (ZTXM20203001 to X.L. and H.Y.). We also want to thank Miss Z. Wei for the support in handling administrative affairs.
Author contributions
H.Y. and X.L. conceived and designed the study, analyzed and interpreted the data, drafted and revised the manuscript. H.D. contributed to the conception and design of the study, wet-lab experiments and data analysis, and critical revisions of the manuscript. J.H. contributed to the wet-lab experiments and data analysis. J.D.K. revised the manuscript. All authors read and approved the final manuscript.
Peer review
Peer review information
Nature Communications thanks Iván Domenzain, Bian Wu and Ruibo Wu for their contribution to the peer review of this work. A peer review file is available.
Data availability
All relevant data supporting the key findings of this study are available within the article and its Supplementary Information files. All the data analysed in this study is publicly available from either public databases, including BRENDA (https://www.brenda-enzymes.org/search_result.php?a=305), UniProt (https://www.uniprot.org/), PubChem (https://www.uniprot.org/) databases or supplementary datasets of referenced articles (https://github.com/SysBioChalmers/DLKcat, https://github.com/AlexanderKroll/KM_prediction). The data described in this manuscript are available for download at https://github.com/Luo-SynBioLab/UniKP. The data is also available on Zenodo: 10.5281/zenodo.1011549853. Source data are provided with this paper.
Code availability
In order to facilitate additional utilization, we have made available all of the codes and thorough instructions in our GitHub repository located at https://github.com/Luo-SynBioLab/UniKP. Furthermore, a user-friendly example for predicting enzyme kinetic parameters has also been included in the repository. The code is also available on Zenodo: 10.5281/zenodo.1011549853.
Competing interests
X.L. has a financial interest in Demetrix and Synceres. J.D.K. has a financial interest in Amyris, Lygos, Demetrix, Napigen, Maple Bio, Apertor Labs, Zero Acre Farms, Berkeley Yeast, and Ansa Biotechnology. The remaining authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
These authors contributed equally: Han Yu, Huaxiang Deng.
Supplementary information
The online version contains supplementary material available at 10.1038/s41467-023-44113-1.
References
- 1.Kuchner O, Arnold FH. Directed evolution of enzyme catalysts. Trends Biotechnol. 1997;15:523–530. doi: 10.1016/S0167-7799(97)01138-4. [DOI] [PubMed] [Google Scholar]
- 2.Adadi R, Volkmer B, Milo R, Heinemann M, Shlomi T. Prediction of Microbial Growth Rate versus Biomass Yield by a Metabolic Network with Kinetic Parameters. PLoS Comput. Biol. 2012;8:e1002575. doi: 10.1371/journal.pcbi.1002575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Currin A, Swainston N, Day PJ, Kell DB. Synthetic biology for the directed evolution of protein biocatalysts: navigating sequence space intelligently. Chem. Soc. Rev. 2015;44:1172–1239. doi: 10.1039/C4CS00351A. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Briggs GE, Haldane JBS. A note on the kinetics of enzyme action. Biochem. J. 1925;19:338. doi: 10.1042/bj0190338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Nilsson A, Nielsen J, Palsson BO. Metabolic Models of Protein Allocation Call for the Kinetome. Cell Systems. 2017;5:538–541. doi: 10.1016/j.cels.2017.11.013. [DOI] [PubMed] [Google Scholar]
- 6.The UniProt Consortium et al. UniProt: the Universal Protein Knowledgebase in 2023. Nucleic Acids Res.51, D523–D531 (2023). [DOI] [PMC free article] [PubMed]
- 7.Scheer M, et al. BRENDA, the enzyme information system in 2011. Nucleic Acids Res. 2010;39:D670–D676. doi: 10.1093/nar/gkq1089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Wittig U, et al. SABIO-RK—database for biochemical reaction kinetics. Nucleic Acids Res. 2012;40:D790–D796. doi: 10.1093/nar/gkr1046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Borger S, Liebermeister W, Klipp E. Prediction of enzyme kinetic parameters based on statistical learning. Genome Inform. 2006;17:80–87. [PubMed] [Google Scholar]
- 10.Kroll A, Engqvist MKM, Heckmann D, Lercher MJ. Deep learning allows genome-scale prediction of Michaelis constants from structural features. PLoS Biol. 2021;19:e3001402. doi: 10.1371/journal.pbio.3001402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Heckmann D, et al. Machine learning applied to enzyme turnover numbers reveals protein structural correlates and improves metabolic models. Nat. Commun. 2018;9:5252. doi: 10.1038/s41467-018-07652-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Li F, et al. Deep learning-based kcat prediction enables improved enzyme-constrained model reconstruction. Nat. Catal. 2022;5:662–672. doi: 10.1038/s41929-022-00798-z. [DOI] [Google Scholar]
- 13.Bar-Even A, et al. The Moderately Efficient Enzyme: Evolutionary and Physicochemical Trends Shaping Enzyme Parameters. Biochemistry. 2011;50:4402–4410. doi: 10.1021/bi2002289. [DOI] [PubMed] [Google Scholar]
- 14.Iqbal WA, Lisitsa A, Kapralov MV. Predicting plant Rubisco kinetics from RbcL sequence data using machine learning. J. Exp. Botany. 2023;74:638–650. doi: 10.1093/jxb/erac368. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Tcherkez GGB, Farquhar GD, Andrews TJ. Despite slow catalysis and confused substrate specificity, all ribulose bisphosphate carboxylases may be nearly perfectly optimized. Proc. Natl. Acad. Sci. USA. 2006;103:7246–7251. doi: 10.1073/pnas.0600605103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Vaswani, A. et al. Attention is all you need. In Advances in neural information processing systems. p. 5998–6008 (2017).
- 17.Devlin, J. et al. Bert: Pre-training of deep bidirectional transformers for language understanding. arXiv preprint arXiv:1810.04805 (2018).
- 18.Elnaggar, A. et al. ProtTrans: Towards Cracking the Language of Lifes Code Through Self-Supervised Deep Learning and High Performance Computing. IEEE Trans. Pattern Anal. Mach. Intell. 1–1 (2021) 10.1109/TPAMI.2021.3095381.
- 19.Rives A, et al. Biological structure and function emerge from scaling unsupervised learning to 250 million protein sequences. Proc. Natl. Acad. Sci. USA. 2021;118:e2016239118. doi: 10.1073/pnas.2016239118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Honda, S. et al. Smiles transformer: Pre-trained molecular fingerprint for low data drug discovery. arXiv preprint arXiv:1911.04738 (2019).
- 21.Sagi, O., and Lior R. Ensemble learning: A survey. Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery 8.4, e1249 (2018).
- 22.Deng, J. et al. Imagenet: A large-scale hierarchical image database. 2009 IEEE conference on computer vision and pattern recognition 248-255. Ieee (2009).
- 23.Zhang, Y., Wei, X.-S., Zhou, B. & Wu, J. Bag of Tricks for Long-Tailed Visual Recognition with Deep Convolutional Neural Networks. AAAI 35, 3447–3455 (2021).
- 24.Yang, Y., et al. Delving into deep imbalanced regression. International Conference on Machine Learning 11842−11851. PMLR (2021).
- 25.Anand A, Pugalenthi G, Fogel GB, Suganthan PN. An approach for classification of highly imbalanced data using weighting and undersampling. Amino Acids. 2010;39:1385–1391. doi: 10.1007/s00726-010-0595-2. [DOI] [PubMed] [Google Scholar]
- 26.Van der Maaten L, Hinton G. Visualizing data using t-SNE. J. Mach. Learning Res. 2008;9:11. [Google Scholar]
- 27.Notebaart RA, Kintses B, Feist AM, Papp B. Underground metabolism: network-level perspective and biotechnological potential. Curr. Opin. Biotechnol. 2018;49:108–114. doi: 10.1016/j.copbio.2017.07.015. [DOI] [PubMed] [Google Scholar]
- 28.Kuznetsova E, et al. Genome-wide analysis of substrate specificities of the Escherichia coli haloacid dehalogenase-like phosphatase family. J. Biol. Chem. 2006;281:36149–36161. doi: 10.1074/jbc.M605449200. [DOI] [PubMed] [Google Scholar]
- 29.Lundberg, S. M. & Lee, S.-I. A unified approach to interpreting model predictions. Proc. 31st Int. Conf. Neural Inf. Process. Syst.31, 4768–4777 (2017).
- 30.Kroll, A. and Lercher, M. J. Machine learning models for the prediction of enzyme properties should be tested on proteins not used for model training. bioRxiv10.1101/2023.02.06.526991 (2023).
- 31.Kim S, et al. PubChem Substance and Compound databases. Nucleic Acids Res. 2016;44:D1202–D1213. doi: 10.1093/nar/gkv951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Japkowicz N. & and Stephen, S. The class imbalance problem: A systematic study. Intell. Data Anal. 2002;6:429–449. doi: 10.3233/IDA-2002-6504. [DOI] [Google Scholar]
- 33.Cui, Y., Jia, M., Lin, T.-Y., Song, Y. & Belongie, S. Class-Balanced Loss Based on Effective Number of Samples. in 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) 9260–9269 (IEEE, 2019). 10.1109/CVPR.2019.00949.
- 34.Jendresen CB, et al. Highly Active and Specific Tyrosine Ammonia-Lyases from Diverse Origins Enable Enhanced Production of Aromatic Compounds in Bacteria and Saccharomyces cerevisiae. Appl. Environ. Microbiol. 2015;81:4458–4476. doi: 10.1128/AEM.00405-15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Vannelli T, Xue Z, Breinig S, Qi WW, Sariaslani FS. Functional expression in Escherichia coli of the tyrosine-inducible tyrosine ammonia-lyase enzyme from yeast Trichosporon cutaneum for production of p-hydroxycinnamic acid. Enzyme Microb. Tech. 2007;41:413–422. doi: 10.1016/j.enzmictec.2007.03.013. [DOI] [Google Scholar]
- 36.Zhou S, et al. Characterization of mutants of a tyrosine ammonia-lyase from Rhodotorula glutinis. Appl. Microbiol. Biotechnol. 2016;100:10443–10452. doi: 10.1007/s00253-016-7672-8. [DOI] [PubMed] [Google Scholar]
- 37.Vannelli T, Wei Qi,W, Sweigard J, Gatenby AA, Sariaslani FS. Production of p-hydroxycinnamic acid from glucose in Saccharomyces cerevisiae and Escherichia coli by expression of heterologous genes from plants and fungi. Metab. Eng. 2007;9:142–151. doi: 10.1016/j.ymben.2006.11.001. [DOI] [PubMed] [Google Scholar]
- 38.Brack Y, Sun C, Yi D, Bornscheuer UT. Discovery of Novel Tyrosine Ammonia Lyases for the Enzymatic Synthesis of p‐Coumaric Acid. ChemBioChem. 2022;23:e202200062. doi: 10.1002/cbic.202200062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Caccuri AM, et al. Structural flexibility modulates the activity of human glutathione transferase P1−1: influence of a poor co-substrate on dynamics and kinetics of human glutathione transferase. J. Biol. Chem. 1996;271:16193–16198. doi: 10.1074/jbc.271.27.16193. [DOI] [PubMed] [Google Scholar]
- 40.Trapp S, et al. Plant uptake of NaCl in relation to enzyme kinetics and toxic effects. Environ. Exp. Botany. 2008;64:1–7. doi: 10.1016/j.envexpbot.2008.05.001. [DOI] [Google Scholar]
- 41.Hillson N, et al. Building a global alliance of biofoundries. Nature Commun. 2019;10:2040. doi: 10.1038/s41467-019-10079-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Wei T, et al. Exploiting spatial dimensions to enable parallelized continuous directed evolution. Mol. Syst. Biol. 2022;18:e10934. doi: 10.15252/msb.202210934. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Chawla NV, Bowyer KW, Hall LO, Kegelmeyer WP. SMOTE: Synthetic Minority Over-sampling Technique. Jair. 2002;16:321–357. doi: 10.1613/jair.953. [DOI] [Google Scholar]
- 44.Kotsiantis SB, Zaharakis I, Pintelas P. Supervised machine learning: A review of classification techniques. Emerg. Artif. Intell. Appl. Comput. Eng. 2007;160:3–24. [Google Scholar]
- 45.Kouw, W. M., & Loog, M. An introduction to domain adaptation and transfer learning. arXiv preprint arXiv:1812.11806 (2018).
- 46.Li, Y. Deep reinforcement learning: An overview. arXiv preprint arXiv:1701.07274 (2017).
- 47.Chen T, et al. T4SE-XGB: Interpretable Sequence-Based Prediction of Type IV Secreted Effectors Using eXtreme Gradient Boosting Algorithm. Front. Microbiol. 2020;11:580382. doi: 10.3389/fmicb.2020.580382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Lv Z, Cui F, Zou Q, Zhang L, Xu L. Anticancer peptides prediction with deep representation learning features. Brief Bioinform. 2021;22:bbab008. doi: 10.1093/bib/bbab008. [DOI] [PubMed] [Google Scholar]
- 49.Veltri D, Kamath U, Shehu A. Deep learning improves antimicrobial peptide recognition. Bioinformatics. 2018;34:2740–2747. doi: 10.1093/bioinformatics/bty179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Pan X, et al. Identification of Protein Subcellular Localization With Network and Functional Embeddings. Front. Genet. 2021;11:626500. doi: 10.3389/fgene.2020.626500. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Yu H, Luo X. IPPF-FE: an integrated peptide and protein function prediction framework based on fused features and ensemble models. Brief. Bioinform. 2023;24:bbac476. doi: 10.1093/bib/bbac476. [DOI] [PubMed] [Google Scholar]
- 52.Altschul SF, Gish W, Miller W, Myers EW, Lipman DJ. Basic local alignment search tool. J. Mol. Biol. 1990;215:403–410. doi: 10.1016/S0022-2836(05)80360-2. [DOI] [PubMed] [Google Scholar]
- 53.Yu, H. et al. UniKP: A unified framework for the prediction of enzyme kinetic parameters. Zenodo 10.5281/zenodo.10115498 (2023). [DOI] [PMC free article] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All relevant data supporting the key findings of this study are available within the article and its Supplementary Information files. All the data analysed in this study is publicly available from either public databases, including BRENDA (https://www.brenda-enzymes.org/search_result.php?a=305), UniProt (https://www.uniprot.org/), PubChem (https://www.uniprot.org/) databases or supplementary datasets of referenced articles (https://github.com/SysBioChalmers/DLKcat, https://github.com/AlexanderKroll/KM_prediction). The data described in this manuscript are available for download at https://github.com/Luo-SynBioLab/UniKP. The data is also available on Zenodo: 10.5281/zenodo.1011549853. Source data are provided with this paper.
In order to facilitate additional utilization, we have made available all of the codes and thorough instructions in our GitHub repository located at https://github.com/Luo-SynBioLab/UniKP. Furthermore, a user-friendly example for predicting enzyme kinetic parameters has also been included in the repository. The code is also available on Zenodo: 10.5281/zenodo.1011549853.