Abstract
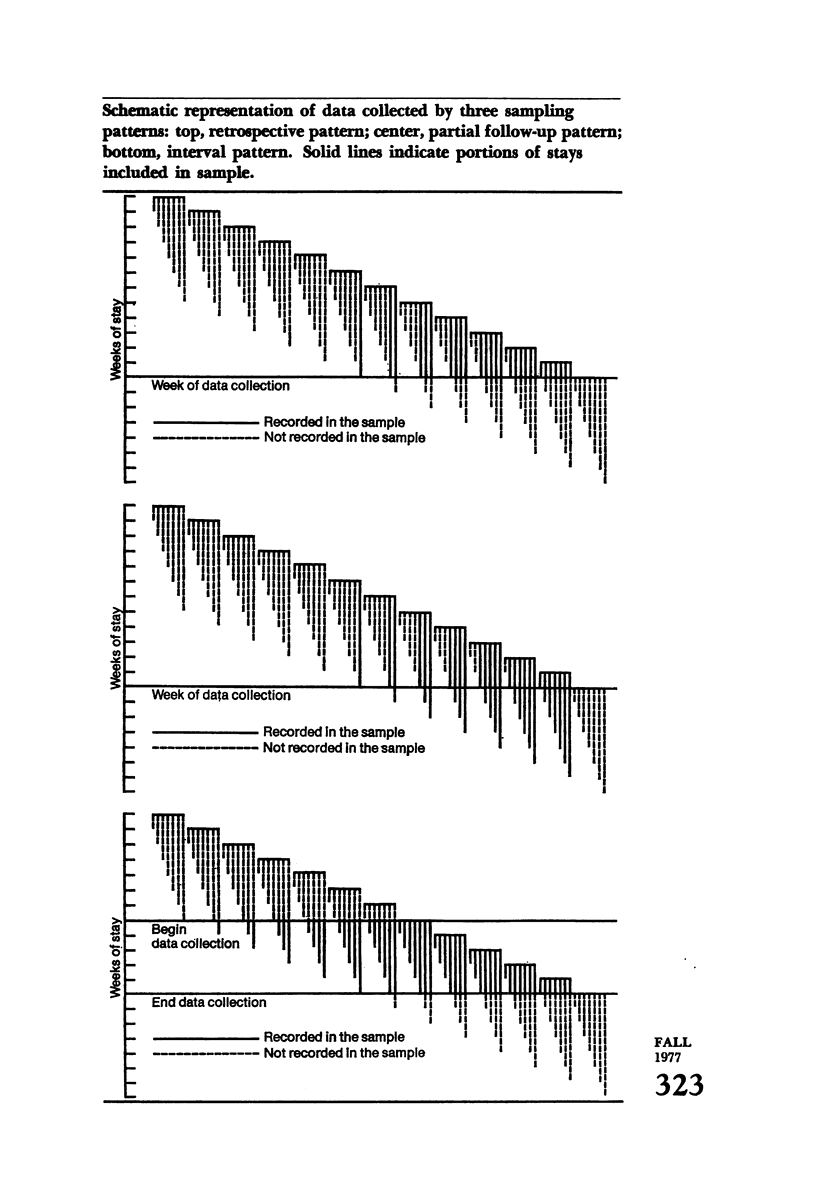
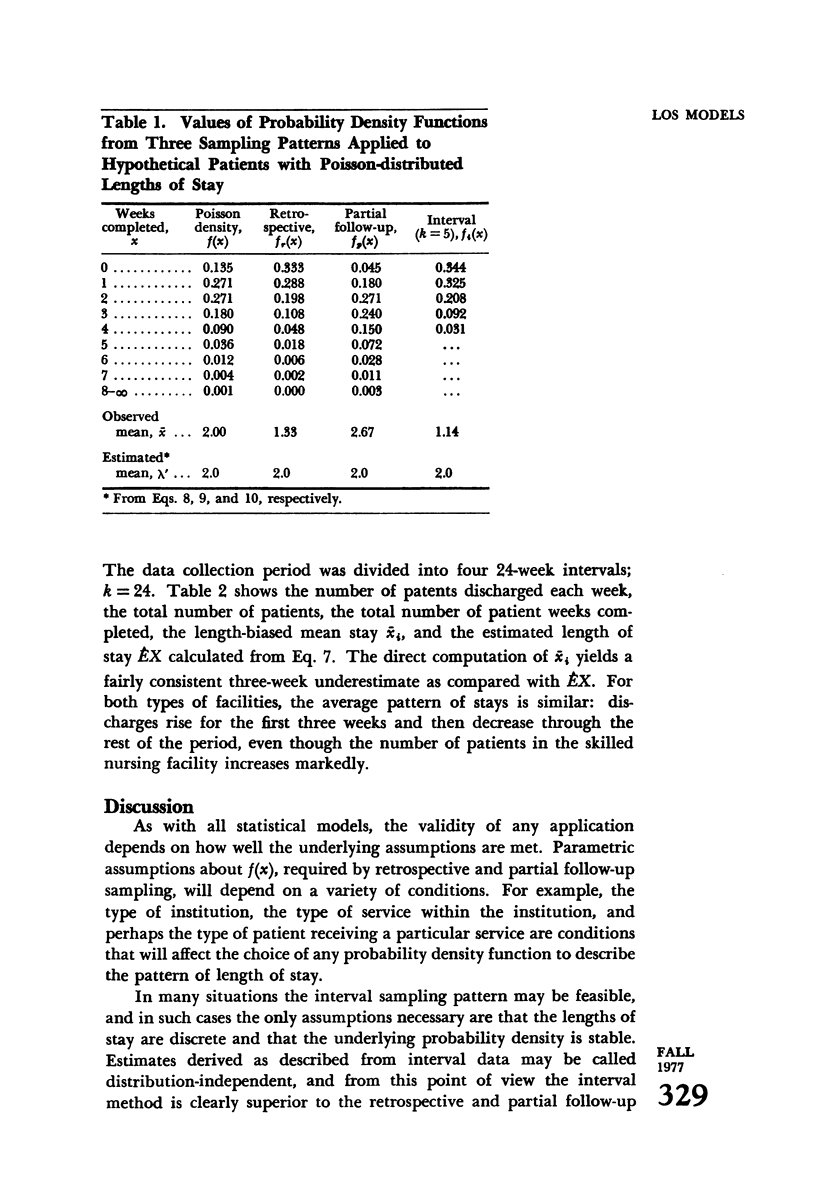
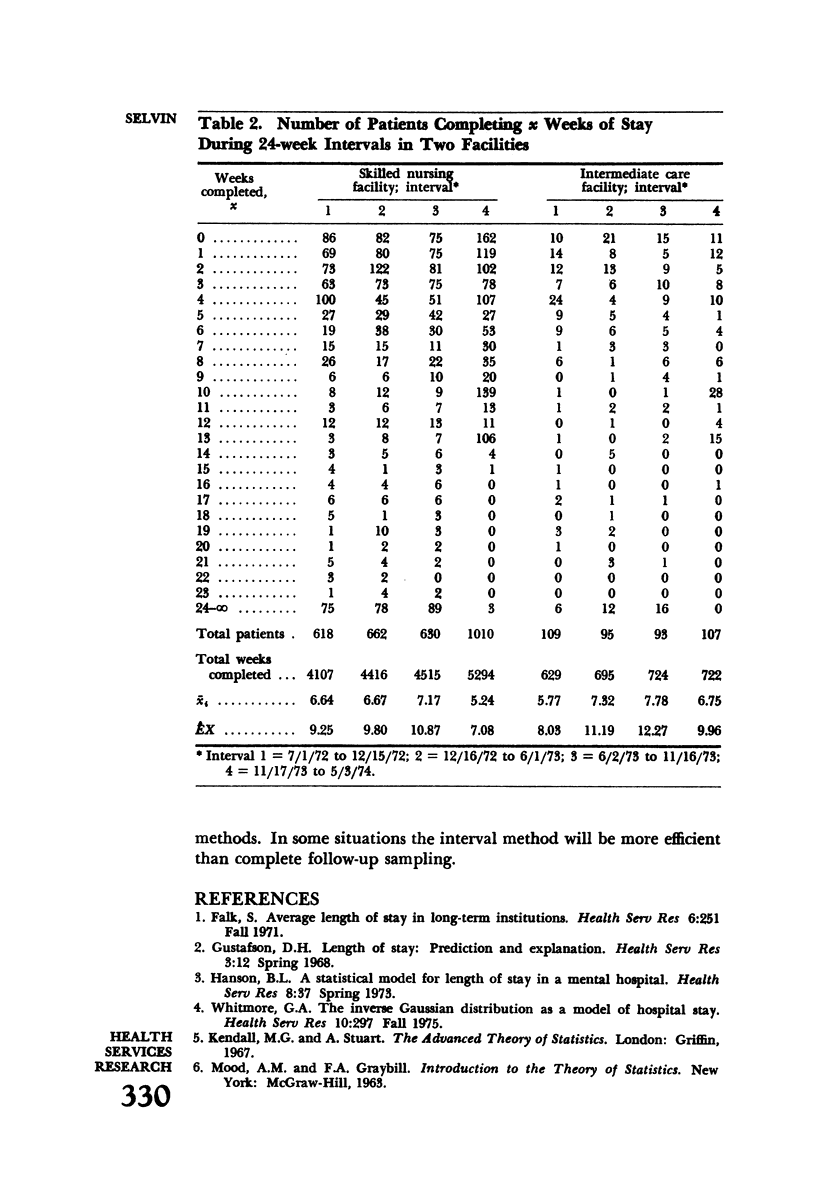
The probability density functions implied by three methods of collecting data on the length of stay in an institution are derived. The expected values associated with these density functions are used to calculate unbiased estimates of the expected length of stay. Two of the methods require an assumption about the form of the underlying distribution of length of stay; the third method does not. The three methods are illustrated with hypothetical data exhibiting the Poisson distribution, and the third (distribution-independent) method is used to estimate the length of stay in a skilled nursing facility and in an intermediate care facility for patients enrolled in California's MediCal program.
Full text
PDF





Selected References
These references are in PubMed. This may not be the complete list of references from this article.
- Falk S. Average length of stay in long-term institutions. Health Serv Res. 1971 Fall;6(3):251–255. [PMC free article] [PubMed] [Google Scholar]
- Gustafson D. H. Length of stay: prediction and explanation. Health Serv Res. 1968 Spring;3(1):12–34. [PMC free article] [PubMed] [Google Scholar]
- Hanson B. L. A statistical model for length of stay in a mental hospital. Health Serv Res. 1973;8(1):37–45. [PMC free article] [PubMed] [Google Scholar]
- Whitmore G. A. The inverse Gaussian distribution as a model of hospital stay. Health Serv Res. 1975 Fall;10(3):297–302. [PMC free article] [PubMed] [Google Scholar]


