The role of dynamics in heterogeneous catalysis: Surface diffusivity and N₂ decomposition on Fe(111)

Significance

Industrial catalysis is key to the green revolution. However, the chemistry underlying such processes is still poorly understood due to the high temperatures at which they take place. Using state-of-the-art methods, we simulate the dissociative chemisorption of nitrogen on a clean Fe(111) surface, which is relevant to the Haber–Bosch process. We find that the dynamical behavior of the surface strongly influences how the reaction occurs as a function of temperature. The atomistic insight gained suggests the importance of using dynamic approaches to accurately describe catalytic processes.

Abstract

Dynamics has long been recognized to play an important role in heterogeneous catalytic processes. However, until recently, it has been impossible to study their dynamical behavior at industry-relevant temperatures. Using a combination of machine learning potentials and advanced simulation techniques, we investigate the cleavage of the N₂ triple bond on the Fe(111) surface. We find that at low temperatures our results agree with the well-established picture. However, if we increase the temperature to reach operando conditions, the surface undergoes a global dynamical change and the step structure of the Fe(111) surface is destabilized. The catalytic sites, traditionally associated with this surface, appear and disappear continuously. Our simulations illuminate the danger of extrapolating low-temperature results to operando conditions and indicate that the catalytic activity can only be inferred from calculations that take dynamics fully into account. More than that, they show that it is the transition to this highly fluctuating interfacial environment that drives the catalytic process.

One of the remarkable features of industrial catalysts is their stability under extreme conditions of temperature and pressure, while being at the same time subjected to a constant flow of reactants and products. In fact, a heterogeneous catalyst can be described as a functional material that continuously creates active sites with its reactants under reaction conditions (1). To explain this behavior, already 40 y ago, Spencer proposed a picture of heterogeneous catalysis (2) in which a dynamical steady state is established. This can happen in two ways: Either surface atoms become highly mobile or, more dramatically, a surface instability sets in. However, the study of catalytic processes in such a scenario is very challenging and until recently has proven impossible. In fact, experimental investigations have been limited to studying temperatures and pressures much lower than industrial ones. In the same way, theoretical studies have assumed idealized conditions, possibly treating the dynamic effect as a perturbation. In the lack of other information, the microscopic behavior of the catalyst in operando conditions had to be inferred from the low-temperature low-pressure results or from indirect interpretation of high-temperature kinetic data.

Only recently are new technologies providing access to in situ and in operando characterization of catalytic materials (3–5), revealing the impact that such conditions have on their structure and corresponding activity (6, 7). In parallel, theoretical calculations have suggested that dynamics needs to be taken into account (8–13). However, they are often limited either by the short timescales investigated or by the fact that they treat dynamically only a subset of the system’s degrees of freedom. To overcome such limitations, we have recently developed new strategies combining machine learning potentials and enhanced sampling methods to model reactive events in realistic conditions (14–17).

We shall make use of this progress to simulate a classical catalytic process, namely the breakage of the $N_2$ triple bond on the (111) iron surface. This is a crucial step of the famed Haber–Bosch catalysis, and as such, it has been intensively studied (18–35). We briefly summarize the available experimental and theoretical findings that are mostly based on low-temperature investigations. From a microscopic point of view, Ertl et al. (20, 22) have investigated the nature of the molecularly adsorbed $N_2$, measuring the change of the bond vibration frequency. They concluded that the absorbed molecules are oriented either perpendicular or parallel to the surface. This was supported by the theoretical work of Itoh et al. (36), which showed that the N-N bond is weakened as a consequence of the charge transfer from the 3d orbitals of Fe to the anti-bonding orbitals ${\pi }^{\ast }$ of $N_2$, whose amount depends on the adsorption geometry. This interpretation was later confirmed by Freund et al. (25).

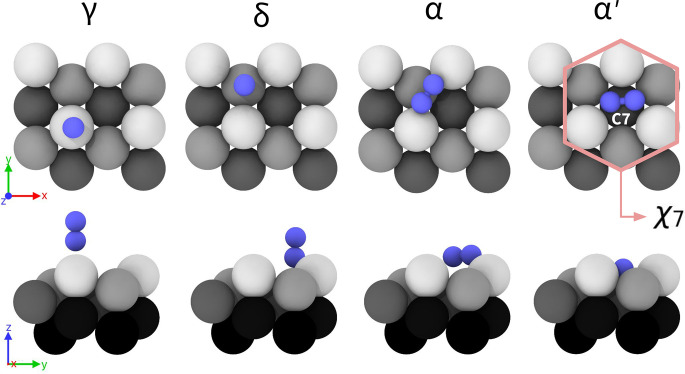
Later, Norskov et al. (28) performed static Density Functional Theory (DFT) calculations, confirming the scenario suggested by Ertl, but enriching it with new atomistic details. They distinguished between two different vertically adsorbed $N_2$ sites ($\gamma$ and $\delta$) depending on whether the molecule sits on top of a first or second layer atom (Fig. 1). Similarly, they predicted the existence of two different horizontal absorption sites. In one, $N_2$ is in a bridge position between first layer atoms ($\alpha$), while in the other, it sits in a hollow position on top of an atom of the third layer (${\alpha }^{\prime }$). The latter state is particularly relevant since it is believed to be the precursor to dissociation. According to ref. 28, such a state can be accessed either directly from the gas phase or via the sequence $\gamma \to \delta \to \alpha \to {\alpha }^{\prime }$. Along this pathway, the triple bond is progressively weakened: In the $\alpha$ state, a first $\pi$ bond is transferred to two surface atoms, followed by another one in the ${\alpha }^{\prime }$ state (33). Indeed, in the ${\alpha }^{\prime }$ site the molecule is in contact with seven-fold coordinated iron atoms ($C_7$) that can more easily donate electrons to the $N_2$ molecule.

Fig. 1.

$N_2$ adsorption sites on Fe(111) from T = 0 K calculations, Top and side view. Iron atoms are colored as a function of the perpendicular z position. From Left to Right: ($\gamma$) and ($\delta$) refer to the $N_2$ on top of first and second layer atoms, respectively. ($\alpha$) refer to a bridge site between first-layer atoms. (${\alpha }^{\prime }$) refer to a hollow site on top of the third layer.

The higher activity of the (111) surface has been attributed to the step structure that stabilizes the $\alpha$ structure and the high density and easy accessibility of $C_7$ atoms in the open Fe(111) surface (37, 38). Later on, we shall refer to the set of Fe atoms that surrounds the $N_2$ molecule in ${\alpha }^{\prime }$ as the ${\chi }_7$ environment (Fig. 1). There are good reasons to regard this set of atoms as a catalytic site. Indeed, when the $N_2$ molecule moves toward the ${\alpha }^{\prime }$ position, the amount of charge transferred from the iron surface to the nitrogen molecule increases. Furthermore, once inside the site, it can rotate between different equivalent orientations until the electronic orbitals are properly aligned for the reaction to take place. Thanks to these classical experiments and calculations, it can be said that the low-temperature behavior of $N_2$ on the Fe(111) surface is quite well understood.

Unfortunately, there are no experiments or calculations that can confirm the chemisorption mechanism of nitrogen in the industrial temperature and pressure range, i.e., T = 650 to 850 K and P = 10 to 300 bar. An attempt has been made to extract such information from the kinetics of ammonia synthesis, under the assumption that the rate-determining step is $N_2(\alpha )\to 2N$ (39–41). However, the kinetic parameters thus extracted appear irreconcilable with those fitted by Ertl at low temperatures, suggesting a different microscopic behavior influenced by the “chemical dynamics” (1, 2) emerging at high temperatures and possibly also by lateral interactions with other adsorbed nitrogen (18).

Here, we use modern simulation methods to investigate the temperature dependence of the surface dynamics and the $N_2$ dissociative chemisorption. A number of methodological innovations have made it possible to simulate such a challenging process. The first hurdle to be cleared is that in a catalytic process, chemical bonds are broken and formed; thus, the use of an ab initio approach is essential. However, due to their high computational cost, ab initio simulations can only be carried out in small systems and for short simulation times, while realistic modeling requires studying larger systems for longer times. A satisfactory compromise between accuracy and efficiency can be achieved if one follows the pioneering work of Behler and Parrinello (42) and optimize a machine learning (ML) potential to reproduce a suitably chosen set of quantum mechanical calculations. However, although the use of ML-based potentials reduces the cost of ab initio-quality simulations by orders of magnitude, these calculations are still too expensive, and it is not possible to explore the time scales over which these reactive processes occur. This makes the collection of reference configurations and thus the construction of interatomic potentials challenging. Combining this strategy with state-of-the-art enhanced sampling methodologies allows the time scale problem to be circumvented (14–17, 43–49). Enhanced sampling techniques are used here not only to bridge the time scales but also to harvest the appropriate set of configurations on which to train the potential. It is the fruitful combination of these two sets of techniques that allows performing DFT-quality reactive simulations of rare events which would otherwise be outside the scope of both classical and ab initio simulations. Here, we use the recently developed On-the-fly Probability Enhanced Sampling (OPES) method (50) which is an evolution of the widely used metadynamics technique (51, 52). Once the simulations were completed, due to the observed high-temperature complex behavior new analysis methods were required to understand and describe the catalytic behavior. In particular, we monitor the charge transferred from the metal to the molecule. To this effect, we trained a second machine learning model that is able to predict the charges without the need for expensive quantum mechanical calculations.

Armed with these tools, we study the dynamics of the Fe(111) surface and its influence on the $N_2$ adsorption and decomposition function of temperature. In particular, we find two contrasting behaviors. At low temperatures, the surface is relatively rigid, and the reaction proceeds as described in the literature. However, at higher temperatures, the atoms on the surface become highly mobile and the stepped structure of the surface becomes unstable. The ${\chi }_7$ cavities are continuously formed and broken, with the consequence that the precursor state ${\alpha }^{\prime }$ is destabilized, altering the reaction profile. Still, the transition state remains the one predominantly discussed in the literature. This dynamical scenario is in agreement with Spencer’s dynamical picture and shows that there are no static active sites. Rather, the $N_2$ dissociation takes place when the mobile reagent encounters the crucial surface fluctuations.

Results

A Reliable Potential to Study $N_2$ on Fe(111).

The first step of this work is the construction of a potential able to describe the properties of iron surfaces and their interaction with $N_2$ molecules during the adsorption and dissociation processes. To this effect, we trained a neural network-based potential on a set of single-point calculations so as to reproduce at best DFT energies and forces. For this procedure to be successful, a careful choice of the training dataset is needed, especially to model correctly the reactive pathways. Following our previous experience in modeling rare events with ML potentials (14–16), we started from a combination of enhanced and standard ab initio molecular dynamics (MD) simulations. Then, we used an active learning procedure accelerated by metadynamics (Materials and Methods). In this way, we are able to collect much more diverse and uncorrelated samples than more conventional approaches based on standard MD simulations and at the same time have control over the uncertainty of our potential. In fact, whenever a configuration is encountered in this procedure that is not well described by the potential, an ab initio calculation is performed and these data are added to the training set. The result of this procedure is a collection of all the relevant configurations for studying the surface dynamics and dissociative chemisorption of nitrogen on the Fe(111) surface. Using the Deep Potential Molecular Dynamics (53, 54) scheme our potential obtains a mean absolute error (MAE) on energies of 0.60 meV/atom and on forces of 31 meV/A, while the root mean squared error (RMSE) is 0.81 meV/atom and 40 meV/A for energies and forces, respectively. In SI Appendix, we report the detailed composition of the dataset (SI Appendix, Table S1) and extensive validation of the ML potential (SI Appendix, Figs. S1–S3), with emphasis on benchmarking the behavior of the surface against the underlying DFT electronic structure calculations (SI Appendix, Fig. S4).

Temperature Dependence of Fe Surface Morphology.

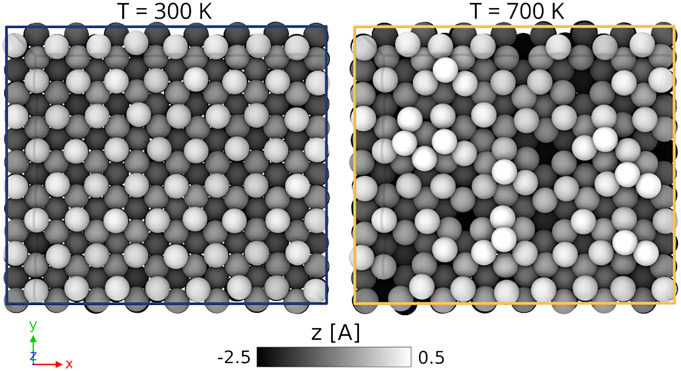
We first investigate the behavior of the pristine Fe(111) surface as a function of temperature. This study offers a number of surprises, as evident from Fig. 2, where we compare two surface snapshots taken at T = 300 K and T = 700 K after 20 ns of MD simulations. The former is hardly distinguishable from the equilibrium structure, while the latter exhibits a considerable amount of disorder. At high temperature, the surface is no longer flat, the formation of hills and holes is clearly visible, and the ordered step structure of the (111) surface is at first sight lost. Although revealing, these snapshots are unable to fully reflect the complex dynamics that takes place in the operando range of temperatures, and the reader is invited to see the movies illustrating the dynamics (Movies S1 and S2).

Fig. 2.

Fe(111) morphology: room temperature vs. in operando condition. Top view of final structures obtained from 20-ns molecular dynamics simulations of the Fe(111) at T = 300 K (Left) and T = 700 K (Right). Atoms are colored as a function of the Z position. Bright regions indicate adatoms, while dark regions the formation of vacancies on the surface. The atomistic snapshots are made with OVITO (55).

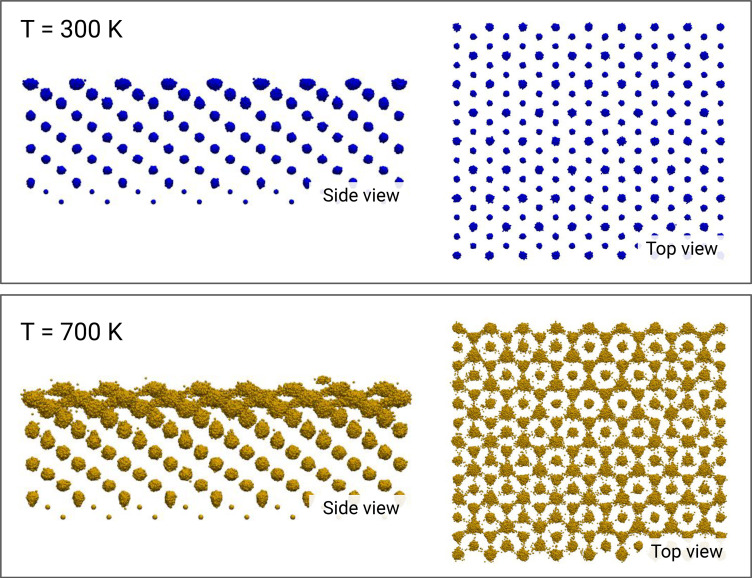
We turn this initial impression into a quantitative study and follow how the surface changes as a function of temperature. In Fig. 3A, we plot the temperature dependence of the density of surface-exposed atoms along the (111) direction. In the low-temperature regime, we observe only the expected thermal broadening. However, at temperatures above 500 K, a number of atoms move to the adlayer, leaving vacancies behind. This signals a very different behavior between a low-temperature regime $T<500$ K and a high-temperature one $T>600$ K, which is also reflected in the increase of surface roughness (Fig. 3B). The change in these two properties is accompanied by an increase of the surface atom diffusion coefficient (Fig. 3C). At $T=500$ K, the surface begins to disorder, but since the diffusion is still slow, its disorder is basically static. Above $T=600$ K, the surface dynamics is fully developed and the self-diffusion coefficient reaches large values. This is in agreement with the behavior of metallic surfaces well below the melting point (56–60). Indeed, the temperature at which surface diffusion sets in is known as the Hüttig temperature, which, for iron, is estimated to be around 600 K (2). In addition, our simulations allow us to further characterize the diffusion mechanism. Despite the high mobility, the system maintains its crystalline order, as can be clearly seen from the scatter diagram of atomic positions in Fig. 4 (see also SI Appendix, Fig. S6 for the other temperatures). Indeed, the BCC structure is locally preserved (SI Appendix, Fig. S5), and atoms undergo a jump-like diffusion between different crystallographic sites (SI Appendix, Fig. S7).

Fig. 3.

Fe(111) morphology and dynamics analysis as a function of temperature. (A) Atomic layer distribution of atoms belonging to the surface as a function of z. The emergence of new peaks at high temperatures denotes a roughening of the surface with the formation of adatoms (rightmost peak at 0.9 Å) and vacancies (leftmost peak at $-$2.2Å). The distribution is shown only for surface atoms dynamically identified at each time step by the Alpha-Shape method. (B) Mean and SD of the surface roughness measured as the SD of the surface atoms’ height. (C) Logarithm of the diffusion coefficient of surface atoms as a function of inverse temperature (main panel) and diffusion vs. temperature (Inset).

Fig. 4.

Scatter plot of atomic positions of Fe atoms. Results for the $T$ = 300 K (Top) and 700 K (Bottom) trajectories, both from a side and top view. The atom positions are recorded every 2.5 ps. Even at low temperature, the Debye–Waller factor of the surface-exposed atoms appears to be larger than that of the bulk atoms. The early occurrence of this dynamical behavior is facilitated by the lower density of the (111) surface and the reduced coordination (4) of the atoms in the topmost layer. At T = 700 K, a significant mobility is reached (side view), with the formation of an adlayer, while the long-range order is preserved (top view). Made with VMD (61).

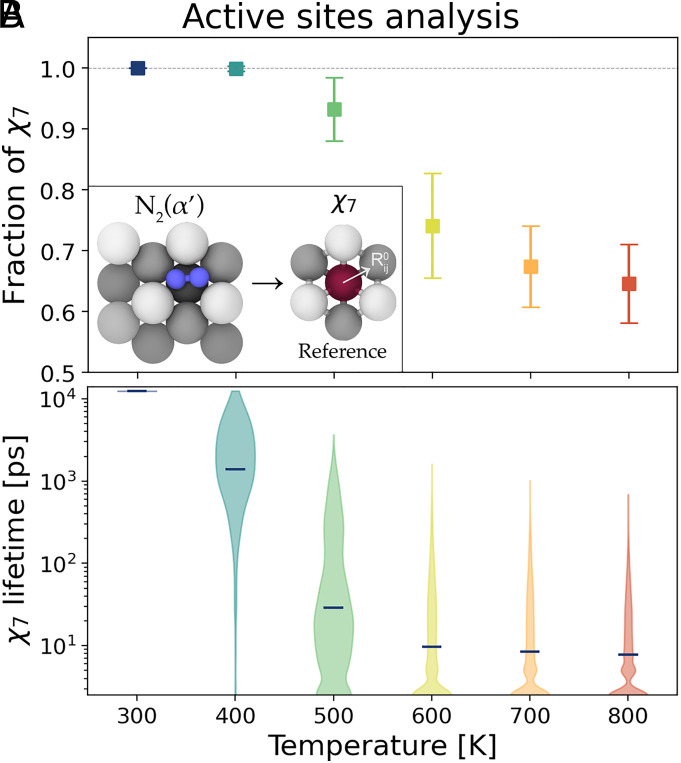
So far, our description has been based on analysis tools that are standard in surface physics. However, our main interest is understanding how dynamics influences surface reactivity. Thus, we study the temperature effect on the geometry of the ${\chi }_7$ sites, which we recall are associated with the precursor ${\alpha }^{\prime }$ state. To this effect, we use the similarity measure $\mathcal{S}(\chi ,{\chi }_7)$ between the atomic environments $\{\chi \}$ of surface atoms and the ${\chi }_7$ environment as defined in the Materials and Methods. By counting the number of surface atoms with high similarity, we can identify the potentially active sites. From Fig. 5A it can be seen that at the operando temperatures, the number of active sites decreases by about one-third as compared to low temperatures. However, looking at the number of sites only gives a partial view of the phenomenon. To fully capture the behavior of the ${\chi }_7$ sites, we need to measure also their lifetime (Fig. 5B). In fact, the active sites are continuously created and destroyed with a lifetime distribution that is far from being Gaussian. As a consequence, the average values of the lifetime are not at all representative of the typical dynamics of ${\chi }_7$ at high temperatures. In fact, the average lifetime is of the order of the tens of picoseconds, but the distributions have tails that reach the nanoseconds regime; thus, the reaction is still allowed.

Fig. 5.

Number and lifetime of ${\chi }_7$ active sites. (A) Average and SD of the number of ${\chi }_7$ sites exposed on the surface with respect to ideal surface. Inset: Construction of reference environment ${\chi }_7$ from the ${\alpha }^{\prime }$ adsorption site. (B) Violin plot with the distribution of lifetimes of ${\chi }_7$ sites. Line markers identify the average lifetime, while the width describes the distribution of the points.

Nitrogen Adsorption and Dissociation Mechanism.

We now study the interaction of an incoming nitrogen molecule with the surface, its adsorption, and subsequent splitting. Regarding the thermodynamic conditions, we study the temperature dependence in the zero-coverage limit which has been studied by Ertl’s group. The gas partial pressure is taken into account by constraining the accessible volume to the $N_2$ molecule to a value compatible with a pressure of P = 10 bar. To study this process, we perform a set of OPES simulations enhancing the fluctuations of two distinct collective variables. One is the nitrogen–nitrogen interatomic distance $d(N,N)$, which is a necessarily part of the reaction coordinate. The other is the coordination number between Fe and N atoms, which is meant to account for the geometric arrangement of the molecule relative to the surface.

While at low temperatures, the adsorption geometries are easily identified (Fig. 1), at high temperatures, the continuous movement of surface atoms makes it difficult to find a variable able to identify the $N_2$ pose. Previous experience (62) together with the findings of Itoh et al. (36) have shown that the electronic structure is a very sensitive indicator of the atomic environment. For this reason, we monitor the charge $q$ transferred from the metallic surface to the molecule. Partial charges are measured using the Bader electronic density decomposition (63, 64) and defined as the deviation of the Bader charges from their formal value. To be able to compute them in large systems, we trained a neural network on a set of DFT calculations (Materials and Methods) to predict partial charges given only the atomic positions. This allows us to monitor the MD simulations through the lens of underlying chemical changes.

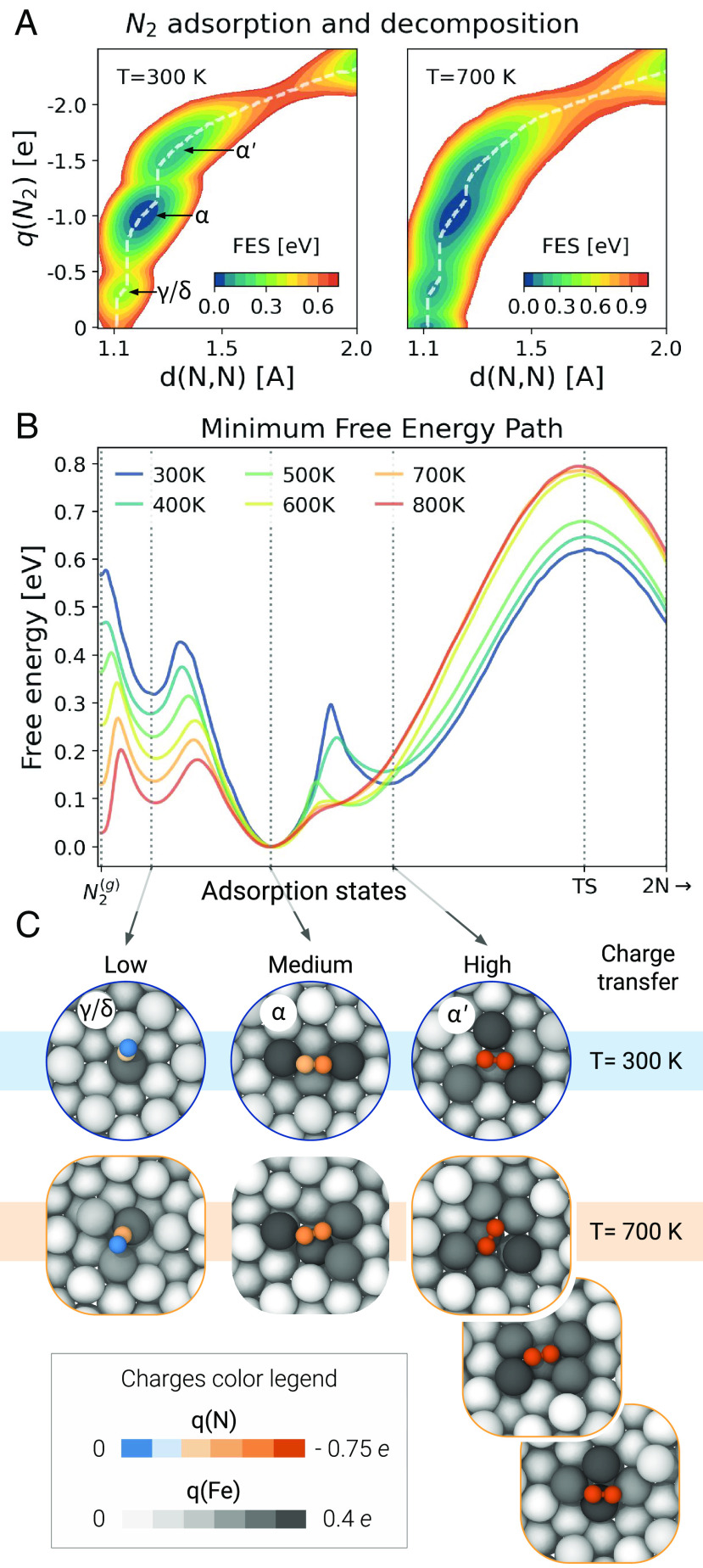
Performing the OPES simulations along these two collective variables results in effective sampling of all adsorbed states and the dissociation process (SI Appendix, Fig. S12). The resulting free energy surfaces (FES) are plotted in Fig. 6A for two contrasting temperatures as a function of the N-N distance $d$ and the sum of the N charges $q=q(N_2)$. Let us begin by analyzing the low-temperature one, where we clearly find metastable states that are characterized by distinct $N_2$ charges. In the gas phase, we have $q=0$, but as soon as the molecule interacts with the surface the charge changes. Indeed, it goes from a low value ($q\approx 0.3$) when the molecule is adsorbed perpendicular to the surface, be it $\delta$-like or in a $\gamma$-like vertical arrangement, to a medium value ($q\approx 1$), which corresponds to a $\alpha$-like horizontal position, and finally to a very high value ($q\approx 1.6$) where one can recognize the $\alpha$’ precursor state. This is evident when looking at the geometries in Fig. 6C, where atoms are colored on the basis of their charge. In particular, we observe how the charge transfer is asymmetrical between the two N atoms in the vertical states and symmetrical in the horizontal ones. The vertical adsorption states identified by calculations at T = 0 K ($\gamma$ and $\delta$) are characterized by the same charge transfer. To resolve them, it is necessary to project the free energy along the distance of $N_2$ from the surface (SI Appendix, Fig. S9). There we see how, over the entire temperature range, the free energy barrier between the two is so small that they can be considered as part of the same metastable state. Furthermore, this shows that the only possible path to reach the precursor ${\alpha }^{\prime }$ state is to pass first a vertical position and then a horizontal one.

Fig. 6.

Adsorption and decomposition mechanism. (A) Free energy as a function of N-N distance and the $N_2$ partial charge. Local minima represent the metastable states, and white dashed lines denote the minimum free energy pathways in this plane. (B) Free energy calculated along the minimum free energy pathways in the $d-q$ space, from the gas phase ($N_2^{(g)}$) to the adsorption states to the dissociated state ($2N$). See SI Appendix, Fig. S15 for the free energies scaled by the thermal energy $k_{B}T$. The uncertainty on the free energy profiles is below 0.02 eV for all temperatures; see SI Appendix, Fig. S13 for a block average analysis. Free energies are shown only up to an N-N distance of 2 $\mathrm{\AA }$, from which a harmonic restraint is applied. (C) Snapshots of representative geometries of the adsorption states based on the amount of charge transferred for T = 300 K and T = 700 K. Atoms are colored according to charges predicted by the neural network model, with two different color scales for the N and Fe atoms.

The free energy profiles reported in Fig. 6A also show that the increase in charge transfer is accompanied by a weakening of the N-N bond, as discussed by Ertl et al. (18, 36). If we focus on the dissociation barrier, we see that beyond the high charge basins, a narrow tube leads the transition state which is located at values $q\approx 2$ and $d\approx 1.7$ which are highly consistent with the chemistry of the process (31).

If we analyze the free energy surface at high temperature, we find that the shape is about the same, with similar metastable states as a function of charge and distance, albeit less defined. However, there is no longer a correspondence between free energy minima and classical adsorption states. As can be seen from the snapshots of T = 700 K geometries shown in Fig. 6C, the metastable states now correspond to an ensemble of mostly disordered and defected structures. Consequently, if we set out to enumerate all the minima of potential energy, we would find countless geometrically distinct states. Using the charge $q$ as a collective variable allows us to group all geometrically different configurations according to their ability to weaken the N-N bond, which is the driving force of the process.

We have computed similar two-dimensional free energy plots in the range of temperature from 300 to 800 K (SI Appendix, Fig. S10). To make a detailed comparison between all these free energies, it is better to make a one-dimensional projection along the minimum free energy paths. Remarkably these pathways can all be superimposed in the (d, q) plane (SI Appendix, Fig. S14) in spite of the different underlying dynamical behavior. In Fig. 6B, all these free energy curves are aligned to the $\alpha$ state minimum, and we see once again a strong difference in behavior between low and high temperature (SI Appendix, Fig. S15). The low-temperature behavior is essentially that predicted by Mortensen et al. modulo the merging of the vertical $\gamma$ and $\delta$ states. Notably, the free energy barrier between the $\alpha$ state and the dissociated one is close to that obtained from static DFT calculations (28, 33, 35, 65). However, if we increase the temperature above 500 K, things change significantly. The free energy barrier to dissociate from the $\alpha$ adsorption state increases by about 0.2 eV between low and high temperatures. Even more importantly, it is the very way in which the dissociative chemisorption occurs that is altered. In fact, the $\alpha$’ state, which is the low-temperature precursor, is no longer metastable. As a result, the $N_2(\alpha )$ to $2N$ reaction changes from a two-step process, in which the triple bond is progressively weakened (33), to one in which the molecule must find a critical configuration that can transfer all the necessary charge. The destabilization of the precursor state is due to the temperature-induced disruption of the ${\chi }_7$ cavities discussed earlier. In fact, if we artificially fix the iron atoms, the ${\alpha }^{\prime }$ state remains metastable at high temperature (SI Appendix, Fig. S11).

Transition State Characterization.

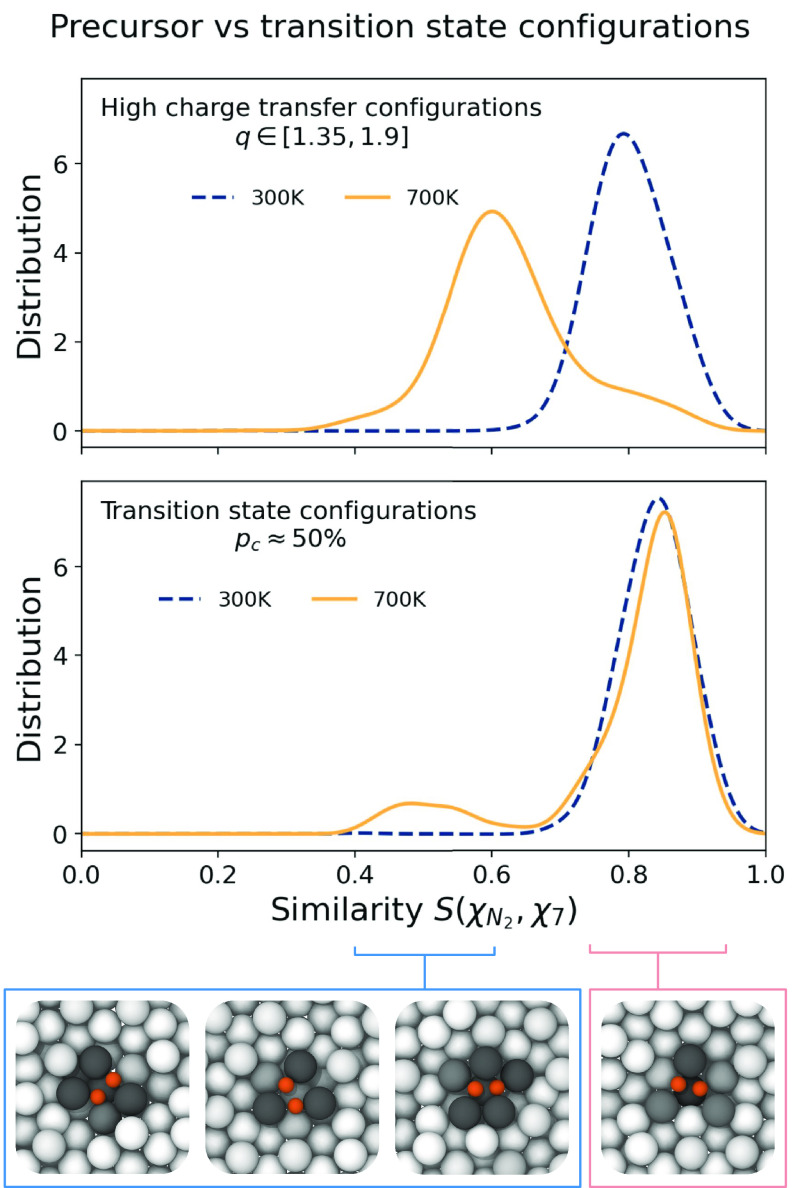
To deepen our analysis of the fate of the ${\alpha }^{\prime }$ site, we compute the distribution of the similarity $S({\chi }_{N_2},{\chi }_7)$ between the environment of the Fe atom that sits below the $N_2$ (Materials and Methods) and the active site reference ${\chi }_7$. We restrict this analysis to the high-charge (precursor) region by selecting only configurations with $q>1.35e$. At room temperature the distribution peaks at values close to 1, which means that $N_2$ is effectively adsorbed inside the ${\chi }_7$ environment (i.e., ${\alpha }^{\prime }$ state); see Fig. 7, Top panel. In contrast, at T = 700 K, the distribution peaks at smaller values, not compatible with the traditional site, and only a small shoulder is associated with the ${\chi }_7$ site. Thus, at T = 700 K, the probability of being adsorbed in the ${\chi }_7$ cavity is highly suppressed relative to room temperature. In particular, this reduction is greater than the decrease in the number of active sites alone reported in Fig. 5. This reinforces our argument that at high temperature we cannot rely on the correspondence with local minima of potential energy at T = 0 K, as surface dynamics leads to a distortion of adsorption configurations.

Fig. 7.

High charge vs. transition state configurations. Distribution of the similarity between the neighborhood of the Fe atom on which $N_2$ is located and the ${\chi }_7$ state for highly charged configurations (Top) and for those in the transition state ensemble (Bottom). They are computed with a Gaussian kernel density estimation, and reweighted to reflect the equilibrium distribution (Materials and Methods). All curves are normalized such that their integral sums to 1. The snapshots below the figure are samples of the two peaks of the distribution of transition states at T = 700 K, representing configurations with high similarity (${\chi }_7$ type, Right) and low similarity (defected structures, Left). More structures are shown in SI Appendix, Fig. S17. Atoms are colored according to the charge transfer with the same color scheme as in Fig. 6.

We then study the nature of the states that pertain to the transition region for $N_2$ dissociation. For each temperature, we performed a committor analysis on a subset of configurations extracted around the maxima of the minimum free energy pathways (Materials and Methods). This allows to identify an ensemble of transition state configurations, defined as atomic realizations for which the probability to go into the reactant or in the product states is equal. If we plot the histogram of these configurations as a function of the charge transferred, the resulting distribution is centered around the $q=2$ value at all temperatures (SI Appendix, Fig. S16). This is a reassuringly meaningful value since the transfer of two electrons is needed to break the $N_2$ triple bond (31). In the Fig. 7, Bottom, we report the distribution of transition states’ similarity with the ${\chi }_7$ arrangement for T = 300 and T = 700 K. At low temperature, the reactive configurations are only of the ${\chi }_7$ type, while at the higher temperature, a number of new atomic arrangements capable of transferring two electrons are activated by the dynamical roughening of the surface (Movie S3). However, even in this second regime, the distribution remains peaked at a value compatible with the ${\chi }_7$ state, unlike in the previous analysis of high-charge transfer configurations. This tells us that although the dynamics of surface atoms significantly suppresses the ${\alpha }^{\prime }$ state, the formation of the ${\chi }_7$ active site remains crucial for nitrogen decomposition, in confirmation of previous studies. We can thus describe it as the eye of the needle through which the $N_2$ must pass to break the bond.

Temperature Dependence of Chemical Reactivity.

In order to understand the consequences that the increase of the free energy barriers has on the chemical reactivity, we estimate the rate coefficients of the $N_2(\alpha )\to 2N$ reaction step using the Eyring–Polanyi equation:

$$\begin{array}{c}\hfill k=\kappa \frac{k_{B}T}{h}exp-\frac{\mathrm{\Delta }{G}^{†}}{\mathit{RT}},\end{array}$$ [1]

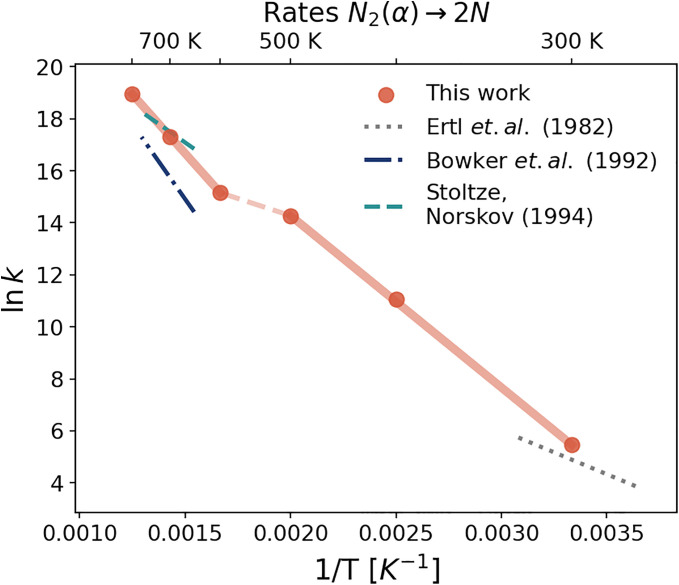
where the $\mathrm{\Delta }{G}^{†}$ values at each temperature are taken from the free energies computed from the MD simulations (Fig. 6), and the transmission coefficient $\kappa$ is taken equal to 1. The corresponding rate coefficients are reported in Fig. 8. Once again, one can clearly notice two distinct regimes where the rates can be linearly interpolated. These results can be contrasted with an extrapolation using only T = 300 K data, which overestimates the reaction rates at high temperatures (SI Appendix, Fig. S18).

Fig. 8.

Kinetic rates for the $N_2(\alpha )\to 2N$ step. Logarithm of the reaction rates as a function of inverse temperature. Red dots indicate the values estimated from the free energy profiles using the Eyring–Polanyi equation. To highlight the existence of two different behaviors, the solid red lines represent linear interpolations of the data in the low (300 to 500 K) and high temperature (600 to 800 K) regimes, while the dashed red line connects the two regimes. Literature data are calculated from the Arrhenius equation $k=Aexp-E_a/RT$, using the pre-exponential factors $A$ and the activation energies $E_a$ from refs. 18, 40, and 66. High-temperature data are plotted between 650 and 770 K, while low-temperature data between 275 and 325 K.

We can also compare our results with available kinetic models built to reproduce the experimental data, which refer to two very different regimes. In the case of Ertl et al. (18), they were obtained from experiments done in ultrahigh vacuum and low temperatures, between 120 and 150 K for $N_2$ molecular adsorption and between 214 and 423 K for dissociative chemisorption. In the case of Bowker et al. (41) and Stoltze and Norskov (40), the kinetic models were optimized to reproduce the rates of ammonia synthesis under industrial conditions (650 to 770 K and 1 to 300 bar), thus also taking into account lateral interactions with adsorbed species. Each model can therefore be applied only in the narrow range of temperatures considered. Even considering the uncertainty in the modeling of the experimental data and the different pressure conditions under which calculations and experiments were performed, we find it rather satisfactory that we can reconcile the two limiting behaviors in a single model.

Conclusions.

Dynamics has a disruptive effect on the morphology of the Fe (111) surface, with great consequences on the adsorption and dissociation of nitrogen molecules. This results in a drastic change in the behavior of the catalyst when going from low to high temperature, a change that takes place in a highly nonlinear way. This shows the danger of extrapolating high-temperature behavior from low-temperature experiments or theories.

More generally, our work puts into question a static approach to catalysis, especially industrial catalysis. It is not a static atomic arrangement that induces catalysis, but catalytic sites are continuously formed and disrupted. While this may seem detrimental at first, this diffusive behavior will be instrumental in establishing a catalytic steady state that is essential for long-term stability (2).

Even though it was not our intention to unveil the full complexity of the Haber–Bosch process, which involves multiple reaction steps where lateral interactions, adsorption intermediates as well as promoters play a crucial role, the dynamical scenario unveiled here allows drawing important conclusions. The transient existence of the dissociation site for nitrogen might prevent the resulting reactive species from forming a stable nitride (67) thus poisoning the catalyst. Likewise, any co-adsorbate that hinders the dynamic rearrangement of the iron surface would act as a strong poison. The extreme sensitivity of the catalysts (68) against oxygen, water, or sulphur species reducing the performance, already at concentrations way below the onset of phase formation as oxide or sulphide, would find a functional explanation. The detailed analysis of the charge re-distribution between iron and nitrogen presented here defines a successful ammonia synthesis catalyst to be bi-functional. As potent as the high availability of negative charge is for the reductive dissociation of di-nitrogen, as much a different active site will be needed to allow bond formation between the resulting nitrido-ion with the hydride form of activated hydrogen being omnipresent on the catalyst surface. This request may explain part (69) of the crucial role of “promoters” that was found (70) experimentally. These promoters may function by forming nitride-metallate (71) intermediates allowing hydrogenation by partly anionic hydrogen species. The present work forms an excellent basis for elucidating optimal configurations of iron and its co-catalysts operating under realistic pressures and temperatures with gases of realistic chemical composition and opens a way toward circumventing the scaling relation barrier (72) limiting the performance of metal catalysts for ammonia synthesis.

Materials and Methods

DFT Simulations.

The database needed to train the ML potential consists of a set of ab initio molecular dynamics (AIMD) trajectories, as well as single-point calculations of configurations generated by the ML potential during the active learning procedure (see below). In both cases, simulations are performed using the PWscf code of Quantum ESPRESSO (73–75) supplemented by the PLUMED plugin (76) which is an open-source, community-developed library (77) for enhanced sampling calculations.

In the lack of a golden standard for metallic systems like iron, we use PBE (78) as exchange-correlation functional. It has been shown that it reproduces well both the bulk (79) and surface properties (80) of iron. Of particular relevance here are surface energies, which are in good agreement with experimental data (80). It also provides a good description of both the interaction of $N_2$ with the surface (28) and the adsorption of nitrogen (29). Furthermore, the interaction with other small molecules is also well described, as reported by Carter et al. (81–83). We note in passing that machine learning potentials can also be used to investigate in a computationally efficient way the performance of different functionals by learning corrections to the PBE model in a delta-learning scheme (84).

Ultrasoft RRKJ pseudopotentials (85) replace explicit core-valence electron interactions, while electron density and wavefunctions are expanded in plane waves with energy cutoffs of 640 and 80 Ry, respectively. Occupation is treated by the cold smearing technique of Marzari et al. (86) with a Gaussian spreading of 0.04 Ry. Spin polarization is included to correctly describe the magnetic properties of iron. We checked whether there was an influence of temperature and pressure on the lattice constant, and this was negligible. Convergence against cutoff energy, Monkhost–Pack sampling, and occupation was tested, and the setup described was chosen as a compromise between feasibility and accuracy. Simulations were carried out with a time step of 1.0 fs in a constant volume and temperature (NVT) ensemble using the stochastic velocity rescaling thermostat (87). In order to span a larger portion of the configurational space, we simulated the systems at different temperatures ranging between 600 and 800 K. Slab models with 5, 8, and 12 atomic layers ( 45, 72, and 108 atoms respectively) are built, and a vacuum layer of at least 10 Å is set in the z-direction, thus avoiding the need to correct for dipole interactions. The first two lowest Fe layers are kept fixed during optimization and molecular dynamics calculations. The Brillouin zone was sampled using a $2\times 2\times 1$ Monkhost–Pack k-point grid (88). The same setup is adopted to analyze the cleavage of the $N_2$ bond on the Fe(111) surface. Enhanced sampling simulations are employed to speed up ab initio simulations and include configurations of adsorption/desorption events and especially of the cleavage of the $N_2$ bond (more details below).

Machine Learning Potential.

Given a set of DFT reference calculations, we optimize a neural network-based potential as to reproduce at best energies and forces given only the atomic positions and the chemical species. We used the Deep Potential Molecular Dynamics Smooth Edition scheme (53, 54) as implemented in DeePMD-kit software (89). The energy is decomposed as a sum of atomic contributions that depend on local environments within a cut-off range. Two different networks are used, one for embedding the atomic positions into symmetry invariant descriptors and the other for the regression task. The embedding network has three hidden layers and [30, 60, 120] nodes per layer, with an embedding matrix size of 20. The fitting network has three hidden layers and [240,240,240] nodes per layer. The cutoff radius was set to 6.0 Å with a switching function that decays from 5.7 Å to ensure continuity. The learning rate decays from $0.001$ to $3.5·{10}^{-8}$ with a decay constant of 4 epochs. The loss function used is a weighted root mean square error (RMSE) on energy and forces, with prefactors varying during training from 0.02 to 1 for energy and from 1,000 to 1 for forces. The potentials used during the active learning phase are trained for 200 epochs, while the final one is trained for 800 epochs. The database is divided into training, validation, and test (80-15-5%). Four different models are trained on different permutations of the training and validation databases, while the test portion is used only to assess the accuracy of the model at the end of the fitting procedure.

Active Learning Protocol.

After training an initial ML model on standard and enhanced AIMD simulations, an active learning strategy is used (90). This means using the ML model to collect new configurations through MD simulations, rather than from AIMD. Specifically, we can use the SD of predictions provided by a committee of NN models as a proxy for uncertainty. This allows us to select for DFT calculations only a subset of structures that are not already well described by the potential and add them to the training set. Nevertheless, performing active learning using only standard MD simulations is of limited effectiveness in this context, as it does not allow the reactive events to be thoroughly sampled. For this reason, we have coupled this procedure with enhanced sampling methods which allow to collect all the relevant geometric structures, providing an ab initio-grade description of the whole reaction pathway (16).

We used the metadynamics method to accelerate the sampling of the adsorption/desorption process as well as the cleavage of the $N_2$ bond using the collective variables and the parameters described below. Starting with the training set generated at T = 700 K, we performed simulations at the other temperatures as well to be sure that both the surface and the $N_2$ chemisorption are well described throughout the temperature range. To minimize the number of costly single-point DFT calculations, only configurations for which the SD of a force component (calculated from 4 models) is greater than 200 meV/A are considered. In total, five different active learning iterations were performed. At each round, we selected about 2k configurations for which we computed single-point DFT calculations, resulting in a total of about 10k structures collected via active learning.

Molecular Dynamics Simulations.

Classical molecular dynamics simulations were performed with Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS) software (91), patched with DeepMD-kit 2.1 (89) and PLUMED (76). NVT simulations were performed with an integration time step of 0.5 fs. The temperature was controlled using stochastic velocity scaling thermostat (87) with a coupling constant of 100 fs.

During the active learning phase, simulations of small systems were performed with a $3\times 3\times N_l$ slab and $N_l$ is the number of layers equal to 5, 8 or 12, such that their energy and forces can be computed with DFT calculations. When the potential is optimized, simulations lasting 20 ns were performed with an $8\times 8\times 12$ slab corresponding to 768 Fe atoms together with an $N_2$ molecule for the adsorption/dissociation simulations. In all simulations, the bottom two layers were fixed to impose a boundary condition that mimics a semi-infinite slab. Periodic boundary conditions were applied in the x- and y-directions, while along z a reflecting wall was applied above the surface. The distance of the wall from the top layer of the surface depends on the temperature and is such that a partial pressure of $N_2$ equal to 10 bar, according to the equation of state for ideal gases, is maintained. Input and results of the MD simulations, have been deposited in Zenodo.

Surface Analysis.

To analyze the morphology and dynamics of the iron surface, we first apply the Alpha-Shape method (92), as implemented in OVITO (55), to reconstruct the surface from the atomic positions. This method constructs a three-dimensional surface mesh using a virtual sphere to identify the surface separating the accessible volume (void) from the inaccessible volume (slab). The radius of the sphere used is equal to 2 Å. This makes it possible to identify the atoms that belong to the surface at each time step and limit the subsequent analysis to these, even if they change over time as is the case here due to high mobility.

Surface roughness is calculated as the SD of the heights of the atoms on the surface:

$$\begin{array}{c}\hfill S_q(t)=\sqrt{\frac{1}{n}{\displaystyle \sum _{i=1}^{N_s(t)}}{(z_i-\overline{z})}^2},\end{array}$$ [2]

where the sum runs over the $N_s(t)$ surface atoms identified by the Alpha-Shape method at time t.

The diffusion coefficient of surface atoms is computed from the time-lagged displacement as follows:

$$\begin{array}{c}\hfill D=\frac{{⟨{(\mathbf{x}(t+\tau )-\mathbf{x}(t))}^2⟩}_{\mathit{surf}}}{2\tau },\end{array}$$ [3]

where the average is calculated only on surface atoms. In SI Appendix, we show the dependence of the diffusion coefficient on the lag-time and its asymptotic convergence. Similar values can be extracted from the asymptotic behavior of the mean square displacement; however, we believe this method is better suited to the nature of diffusion, which occurs as jumps between lattice sites.

Environment Similarity.

To compare the environment around an atom with a reference, we use the environment similarity measure introduced by Piaggi and Parrinello (93). This measure can be viewed as a non-rotationally invariant version of the popular SOAP (Smooth Overlap of Atomic Positions) kernel (94). First, we define a smooth local density around the central atom by fitting a Gaussian to the position of each neighbor $i$:

$$\begin{array}{c}\hfill {\rho }_{\chi }(\mathbf{r})=\sum _{i\in \chi }exp\left(-\frac{|{\mathbf{r}}_i{-\mathbf{r}|}^2}{2{\sigma }^2}\right).\end{array}$$ [4]

Here, $\sigma$ is a broadening parameter and ${\mathbf{r}}_i$ the position of atom $i$ with respect to the central atom. We then define the environment similarity between $\chi$ and a reference ${\chi }_{\mathit{ref}}$ as:

$$\begin{array}{c}\hfill S(\chi ,{\chi }_{\mathit{ref}})=\int d\mathbf{r}{\rho }_{\chi }(\mathbf{r}){\rho }_{{\chi }_{\mathit{ref}}}(\mathbf{r}),\end{array}$$ [5]

which becomes:

$$\begin{array}{c}\hfill S(\chi ,{\chi }_{\mathit{ref}})=\frac{1}{n}\sum _{i\in \chi }\sum _{j\in {\chi }_{\mathit{ref}}}exp\left(-\frac{|{\mathbf{r}}_i-{\mathbf{r}}_j^0{|}^2}{4{\sigma }^2}\right),\end{array}$$ [6]

once we perform integration and we normalize the kernel such that $S({\chi }_{\mathit{ref}},{\chi }_{\mathit{ref}})=1$. Here, $n$ represents the number of atoms in the environment ${\chi }_{\mathit{ref}}$.

The environment chosen here as reference for the analysis of active sites is the ${\chi }_7$ environment defined in Fig. 5. This is the environment of a surface atom of the third layer corresponding to the cavity in which the $N_2$ is adsorbed in the ${\alpha }^{\prime }$ state, surrounded by 7-coordinated Fe atoms. As for the computational parameters, we included all Fe neighbors up to 3.5 Å for constructing the local density. To remove thermal fluctuations, we first performed a moving average of the atomic positions with a window of 2.5 ps. Furthermore, we used different values of the broadening parameter $\sigma$ depending on the simulation temperature. Specifically, we used $\sigma =0.15$ for $T\le 500$ K, $\sigma =0.17$ for $T=600$, $\sigma =0.185$ for $T=700$ and $\sigma =0.2$ for $T=800$ K. These numbers were chosen so that the position of the peak of ${\chi }_7$ atoms is approximately the same for the ideal case (i.e., for a surface with only thermal fluctuations and no observed diffusion, see the dashed lines in SI Appendix, Fig. S8).

Once we have calculated the environment similarity for each atom on the surface, we define the sites ${\chi }_7$ as those environments that have $S(\chi ,{\chi }_7)\ge 0.8$. The choice of the threshold value is based on the minima of the ideal distribution of environment similarity at each temperature (SI Appendix, Fig. S8) where the ideal environments are defined above.

Neural Network Charge Model.

In order to predict the atomic charges from the atomic positions generated by the ML-based molecular dynamics, we fitted a second neural network on a dataset of charges computed with DFT. This allows us to predict the charges given only the atomic positions and the chemical species. To extract the charges from the electron charge density, we used the Bader decomposition scheme (63, 64) to compute the number of valence electrons. Then, charges were defined as the deviation of Bader charges from their formal value. Here, the reference values were taken to be equal to $8e$ and $5e$ for Fe and N atoms, respectively. The charges were computed for a subset of configurations taken from those used to train the potential, for a total of about 10k configurations, which were split into training and validation sets (80 to 20%).

To fit the charges, we used the deep tensor neural network SchNet architecture (95), which was proposed for fitting ML potentials, as implemented in the SchNetPack library (96). To represent the local atomic environment, we used a SchNet module with five interaction layers, a 3.5 Å cosine cutoff with pairwise distances expanded on 30 Gaussians and 64 atom-wise features and convolution filters. As for the output, we used an atom-wise module with two hidden layers and (64,64) nodes per layer. The loss function used was the mean square error between the predicted charges $\{q_i\}$ and the reference ones $\{q_i^{\mathit{DFT}}\}$:

$$\begin{array}{c}\hfill \mathcal{L}=\frac{1}{N_{\mathit{at}}}{\displaystyle \sum _i}{(q_i-q_i^{\mathit{DFT}})}^2.\end{array}$$ [7]

We trained the NN using the optimizer Adam (97) and a learning rate of 0.001 with the early stopping criterion. The model obtained with these parameters has a root mean square error on the validation set equal to ${10}^{-4}e$.

Enhanced Sampling Simulations.

Even with the availability of a machine learning potential, many important processes such as chemical reactions continue to occur on time scales much longer than those accessible to standard molecular dynamics simulations. To enable these rare events to be simulated, numerous advanced sampling methods have been developed, and in particular, one family of these is based on the so-called collective variables $\mathbf{s}(R)$ (CVs). The CVs are functions of the atomic coordinates $R$ and are chosen to be the most difficult to sample modes of the system. Once they are identified, an external bias potential $V(s(R))$ is added to the system. The role of the bias is to enhance the $s$ fluctuations and speed up their sampling. Thus, with an appropriate choice of $s$, large energy barriers can be overcome so that rare events are accelerated and take place in an affordable computational time. In this work, we have used two such techniques: Metadynamics (51, 52) and the more recent OPES (50). The bias potential was added to the MD engine via the PLUMED plugin (76), be it Quantum Espresso (73–75) or LAMMPS (91).

Metadynamics.

Is a well-established method (51) in which a history-dependent bias potential $V(\mathbf{s},t)$ is constructed as a sum of repulsive Gaussians centered at the visited points in the collective space. The effect is to discourage the system from visiting already explored configurations. In particular, we consider its Well-Tempered variant (52), where the height of the hills is decreased over time as a function of the already deposited bias with a rate that is determined by the parameter $\gamma$. During the training data collection with ab initio simulations, we used well-tempered metadynamics to accelerate both adsorption and cleavage of the $N_2$ molecule on the Fe(111) surface. This allowed us to collect configurations along the reactive paths and teach the NN how to represent the potential along the chemical reaction. In these calculations, we used as CV the distance in the z direction between the $N_2$ center of mass and the bottom of the slab to accelerate $N_2$ adsorption, and the N-N distance to speed up $N_2$ dissociation. In both cases, a new Gaussian was deposited every 50 steps, with an initial height equal to 6 kJ/mol and a SD equal to 0.04 Å, with a $\gamma =30$.

OPES.

In the second stage in which we studied the adsorption and decomposition of $N_2$ with the ML potential, we used the On-the-fly Probability Enhanced Sampling (OPES) method (50). OPES is an evolution of metadynamics that converges faster and requires fewer hyperparameters to be chosen. It also allows us to limit the amount of bias that is deposited to avoid exploring high free energy regions (98). In this approach, rather than building on the fly the bias $V(s(R))$, the equilibrium probability distribution $P(\mathbf{s})$ is reconstructed using a Gaussian Kernel density estimator (KDE). Given a preassigned target distribution $p^{\mathit{tg}}(\mathbf{s})$, the bias is then defined as:

$$\begin{array}{c}\hfill V\left(\mathit{s}\right)=-\frac{1}{\beta }log\frac{p^{\mathit{tg}}(\mathit{s})}{P(\mathit{s})}.\end{array}$$ [8]

At convergence, $V\left(\mathit{s}\right)$ drives the $s$ distribution to the target $p^{\mathit{tg}}(\mathbf{s})$. The target distribution is chosen to be the well-tempered one: $p^{\mathit{tg}}(\mathbf{s})\propto P{(\mathbf{s})}^{\frac{1}{\gamma }}$, in which the equilibrium distribution is broadened and the free energy barriers are lowered by a bias factor $\gamma$. OPES simulations for studying the adsorption and decomposition of $N_2$ used the N-N distance and iron–nitrogen coordination number as collective variables. We used the iron–nitrogen coordination number as a proxy for the charge transfer. As can be seen in SI Appendix, Fig. S12, these two quantities are highly correlated in the $N_2$ state, while the coordination number fails to describe the charge transfer in the transition region and beyond. In this second regime, the second collective variable used (N-N distance) is able to describe the reaction progress, so it is essential to use both. The coordination number is calculated in a continuous and differentiable manner as follows:

$$\begin{array}{c}\hfill C_{N,Fe}={\displaystyle \sum _{i\in \{N\}}}{\displaystyle \sum _{j\in \{Fe\}}}\frac{1-{\left(\frac{r_{\mathit{ij}}}{r_0}\right)}^n}{1-{\left(\frac{r_{\mathit{ij}}}{r_0}\right)}^m}.\end{array}$$ [9]

The parameters used are $r_0=2.5$ Å, $n=6$, and $m=12$. The update of the OPES bias was performed every 1,000 steps, with the initial width of the kernels equal to 0.025 for $d(N,N)$ and 0.25 for $C_{N,Fe}$. The barrier parameter was set to 80 kJ/mol. Finally, it should be noted that a harmonic restraint was applied at $d\ge 2$ Å with an elastic constant equal to 2,000 kJ/mol/Ų. This was to facilitate the reversible sampling of the adsorption states and the dissociation barrier, without the need to wait for the recombination to occur. Note that the equilibrium value of the N-N distance in the 2N state is greater than 2 Å, and therefore, it is not sampled.

Free Energy Calculations.

At convergence, the free energy surface (FES) along the collective variables used for biasing can be recovered from the OPES simulation as:

$$\begin{array}{c}\hfill F(\mathit{s})=-k_{B}TlogP(\mathit{s}).\end{array}$$ [10]

A more general way, which also allows the FES to be calculated along CVs other than those used for bias, is through a reweighting procedure (50). When the bias is in a quasi-static regime, we can recover the expectation value of any quantity such as:

$$\begin{array}{c}\hfill ⟨O\left(\mathit{R}\right)⟩=\frac{⟨O\left(\mathit{R}\right)e^{\beta V\left(\mathit{s}\left(\mathit{R}\right)\right)}{⟩}_V}{{⟨e^{\beta V\left(\mathit{s}\left(\mathit{R}\right)\right)}⟩}_V}.\end{array}$$ [11]

In particular, if we are interested in the free energy profile along a given collective variable $s$, we have $P(s)=⟨\delta (s-s(\mathbf{R})⟩$. To approximate $P(s)$ from the simulation data, we use a weighted Gaussian density estimator, with the weights corresponding to $w_t=e^{-\beta V(s_t)}$. For the calculation of the minimum free energy pathways from the two-dimensional FES, we used the MEPSA (Minimum Energy Path Surface Analysis) package (99).

Committor Analysis.

To identify the transition state (TS) configurations, we selected a range around the dissociation barrier in the minimum free energy path and randomly chose within this range $n$ configurations from the simulation trajectories at each temperature. For each of the selected configurations, $m$ short MD simulations are started by initializing the velocities with a different random seed. The committor probability $p_c$, i.e., the probability of first committing to the dissociated 2$N$ state rather than falling back into the $N_2$ state, is then monitored. Configurations that have a committor probability $p_c\approx 0.5$ are part of the transition state ensemble. In practice, at each temperature studied, we extracted $n=500$ configurations, and for each of them, we tested the committor behavior running $m=50$ unbiased simulations with different initial velocities. We classified as belonging to the transition state ensemble those configurations for which $0.25\le p_c\le 0.75$. In such a way, we harness 100 to 150 transition state configurations for each temperature.

Supplementary Material

Appendix 01 (PDF)

Movie S1.

Surface dynamics at T=300 K vs T=700 K.

Movie S2.

Surface atoms diffusion at T=700 K.

Movie S3.

N₂ decomposition at T=300 K and T=700 K.

Data, Materials, and Software Availability

Input files and results of MD simulations as well as the code used for the analysis have been deposited in Zenodo (https://doi.org/10.5281/zenodo.10000226) (100).