Tutorial on model selection and validation of model input into precision dosing software for model‐informed precision dosing

Abstract

There has been rising interest in using model‐informed precision dosing to provide personalized medicine to patients at the bedside. This methodology utilizes population pharmacokinetic models, measured drug concentrations from individual patients, pharmacodynamic biomarkers, and Bayesian estimation to estimate pharmacokinetic parameters and predict concentration‐time profiles in individual patients. Using these individualized parameter estimates and simulated drug exposure, dosing recommendations can be generated to maximize target attainment to improve beneficial effect and minimize toxicity. However, the accuracy of the output from this evaluation is highly dependent on the population pharmacokinetic model selected. This tutorial provides a comprehensive approach to evaluating, selecting, and validating a model for input and implementation into a model‐informed precision dosing program. A step‐by‐step outline to validate successful implementation into a precision dosing tool is described using the clinical software platforms Edsim++ and MwPharm++ as examples.

INTRODUCTION TO MODEL‐INFORMED PRECISION DOSING

In 2015, President Barack Obama launched the Precision Medicine Initiative that outlined efforts to move beyond the “one‐size‐fits‐all” approach of modern medicine and into the realm of individualized, tailored dosing. ¹ , ² Precision medicine is the concept of designing therapeutic recommendations for an individual patient based on their demographics, clinical variables, and desired therapeutic outcomes. ¹ , ² , ³ , ⁴

Model‐informed precision dosing (MIPD) has been defined as a “state‐of‐the‐art” science that falls under the umbrella of precision medicine. ⁵ , ⁶ The goal of MIPD is to improve drug treatment outcomes in patients by achieving the optimal balance between beneficial effect and toxicity for the individual patient. ³ , ⁴ , ⁵ , ⁶ , ⁷ This goal is achieved by leveraging available clinical data with dedicated pharmacometric software capable of applying mathematical models to recommend a personalized dose. ³ , ⁴ , ⁵ , ⁶ , ⁷ These mathematical models are often developed with population pharmacokinetic (PopPK) modeling using various methodologies that include but are not limited to nonlinear mixed effects modeling (NONMEM, NLME), ⁸ nonparametric adaptive grid (Pmetrics) ⁹ approaches, regression models, decision trees, and other algorithms. ⁵ These models can be integrated into precision‐dosing software that can use the Bayesian estimation to facilitate MIPD. Bayesian estimation is a statistical method that leverages prior knowledge (a priori information; i.e., a PopPK model) and observed information (a posteriori information; i.e., individual patient data) to determine the individual's pharmacokinetic (PK) parameters and relative uncertainty that best describes the patient's data. Once obtained, one can forecast a drug's concentration at a specific time (i.e., estimating a patient's concentration‐time profile) or optimize a dosing regimen to improve the target attainment for the given drug. ¹⁰ , ¹¹ , ¹² , ¹³

PopPK modeling is a well‐established, quantitative method to describe the PKs (and pharmacodynamics [PD], if applicable) of a drug at the population level. ³ , ¹⁴ , ¹⁵ The goal of PopPK modeling is to describe the PK properties of the given drug and identify intrinsic and extrinsic sources of variability that affect a drug's PK. ³ , ¹⁴ This type of modeling provides us with a basic understanding of how the “average” or “typical” patient will behave, in addition to interpatient variability in drug disposition and parameter distributions. PopPK modeling entails several components, including: (1) a dataset; (2) a structural model, often a compartmental model, describing the typical concentration‐time profile within the population; (3) a covariate model quantifying the impact of patient‐specific covariates on a drug's PK; and (4) error models delineating the between‐subjects (interindividual) variability (BSV), between‐occasion variability (BOV), and residual unexplained variability (RUV). ⁶ , ¹⁶ , ¹⁷ , ¹⁸

Tutorials detailing the workflow for PopPK modeling have been previously discussed and are not within the scope of this tutorial. ¹⁰ , ¹⁵ , ¹⁷ , ¹⁸ , ¹⁹ , ²⁰ Rather, this tutorial will (1) highlight the importance of model selection for MIPD, (2) demonstrate how to select a model for MIPD, and (3) provide a step‐by‐step process to translate and validate input of a selected model into a precision dosing software prior to clinical implementation. This tutorial is intended to help clinicians and pharmacometricians understand how to critically analyze models for the implementation into clinical care or MIPD program. We will use the clinical PK/PD modeling software, Edsim++, ²¹ and its precision dosing plugin, MwPharm++ ²² (Mediware, Czech Republic), as an example application for this tutorial. However, the framework in this paper outlines the steps to evaluate published models for use in any MIPD program, including but not limited to DoseMeRx, ²³ InsightRX Nova, ²⁴ and PrecisePK. ⁷ , ²⁵ A roadmap for incorporating an MIPD program into clinical care will be provided in a separate tutorial.

WHY MODEL SELECTION IS IMPORTANT

For MIPD to be used for decision making in the clinical world, dosing recommendations must ensure that therapeutic targets are accurately achieved in a timely fashion, while also minimizing possible harm from toxicities. Concentrations that are too high or too low can have a critical impact on patient safety, outcomes, and therapeutic decision making. The key to appropriate MIPD is using the right model for the right patient at the right time. Lessons learned from vancomycin PopPK modeling in the recent past highlight this concept.

Vancomycin is a commonly used antibiotic that plays a critical role in treating severe infections with Gram positive bacteria, especially methicillin‐resistant organisms. It also has well known and clinically significant risk of causing kidney injury. ²⁶ The most recent consensus is that effectiveness of vancomycin is dependent on the area under the concentration‐curve (AUC) to minimum inhibitory concentration ratio (AUC/MIC). ²⁷ Practice recommendations have recently shifted from using trough‐only dosing guidance to model driven Bayesian estimation of AUC. ²⁷ , ²⁸ Whereas consensus recommendations suggest an “[…] approach to monitor AUC involv[ing] the use of Bayesian software programs, embedded with a PK model based on richly sampled vancomycin data […]” ²⁷ guidance on which model to use is less readily available.

There are dozens of published PopPK models for vancomycin, that greatly differ from one another in terms of patient population and clinical scenario in which the PK data were collected. Broeker et al. ²⁹ recently showed that for intermittent vancomycin dosing, there was significant variability in the outputs of 31 different PopPK models for both a priori model prediction and a posteriori Bayesian forecasting utilizing observed vancomycin concentrations from patients. The authors emphasize that each of these models were derived from data collected from different patient populations, used different structural models, and had varying degrees of optimal study designs.

As PopPK models are increasingly being developed for many drugs, and practice is shifting toward the use of MIPD, this tutorial seeks to help clinicians, clinical pharmacologists, pharmacists, and all members of a clinical team to choose the right model(s) to give the most accurate predictions for their specific target patient population. This tutorial will provide a systematic method to evaluate a model that may be considered for use in a precision dosing software for clinical use.

HOW TO SELECT A MODEL

What is the ideal model for MIPD?

An ideal model to use for precision dosing software is one that was developed in a similar population to the population in which one intends to perform precision dosing. Dosing regimens and indications would also be similar. Ideally, the sampling strategy used to obtain data would yield both a large quantity and high quality of samples using assays that can be replicated at one's own institution. The published model would have a well‐developed population modeling analysis plan described by the pharmacometricians so that one can evaluate the structural model, error model, and covariates. In the following subsections, we provide more details on what should be considered in the selection of a model.

Selecting the model based on the target population

One primary aspect to consider when evaluating a model for an MIPD program is the target patient population that provided the data for the model. Ideally, one should select a population model that recapitulates the intended population in which precision dosing will be implemented. That is, the modeled populations have received care in a similar clinical care environment, have similar demographics, are of equal diversity, and are receiving the same dosing regimens via the same route of administration used for the same indication. However, given the heterogeneity in real‐world patient populations, it is unlikely a published model will match perfectly with the intended population. Therefore, one needs to consider the generalizability and translatability of the model toward the population of interest. If the selected model contrasts (i.e., published model describes adults, but intended population is in pediatrics) from the population of interest, one should use caution when implementing the model or should confirm that the model is suitable for their use by assessing its use on example data.

When considering whether the modeled population can serve to describe the intended population, one should consider the following ³⁰ :

Distribution of ages in the population

• Age‐specific physiology can lead to substantial differences in PKs and PDs. The rapid physical growth, organ maturation, and ontogenesis (study of an organism's development) experienced early in life is physiologically unique to younger patients. ³¹ , ³² , ³³ Conversely, the physiology in mid‐ to late‐stages of life can be impacted by comorbidities (polypharmacy), epigenetic effects, and slowed organ function ³⁴ , ³⁵ , ³⁶ . These differences are often accounted for through allometry (weight) and age (e.g., postmenstrual age, organ maturation/deterioration, and ontogeny profiles) to account for differences in body size and organ function (maturation effect). ³⁷

• Even if the selected model does not exactly recapitulate the population of interest, one can confirm the model's appropriateness by evaluating its performance using example data from the intended population then alter the model's equations to describe the data as needed.

Ethnicity and race of the population

• Although it is recognized that self‐reported race is a social construct, it is important to consider the potential effect of ancestry and probability of genetic polymorphisms, which can lead to variations in PKs. ³⁸ , ³⁹ , ⁴⁰

• Depending on a drug's elimination pathway, the effects of race and ethnicity may be marginal, and a model that does not describe the effects of self‐reported race or ethnicity could be fit‐for‐purpose. Conversely, race and ethnicity could predispose genetic polymorphisms that alter a drug's elimination. If the selected model fails to include these effects for these select races and ethnicities, then it is not fit‐for‐purpose in the intended population. One could test the selected model's performance on example data from the desired population to confirm it is fit‐for‐purpose.

Dose amount, number of courses, route of administration, infusion duration, and time of administration, if applicable

• Differences in treatment strategies can result in altered PKs and PDs that limits the translatability to the intended population.

  • ○
    For intravenously administrated drugs: (1) Is the infusion an intermittent infusion or a continuous infusion? (2) Are there start/stop times recorded for the infusion? Are there differences in the infusion duration? (3) Is there a loading dose being administered prior to the maintenance dose? (4) What type of fluid (solvent) is being administered with the drug?
  • ○
    It is important to consider the time of day that the treatment is administered. Depending on the drug's metabolic pathway, the PKs and PDs might be impacted by the diurnal variation of various metabolic enzymes and transporters. ⁴¹ , ⁴²

• For enterally administered drugs: (1) How does the model describe any delay observed in absorption, if any? (2) Is food effect considered? ⁴³ Is the food status (fed or fasted) consistent among subjects included in the study? (3). Did the study use the formulation of interest? Many drugs have various formulations, including extended‐release versus standard‐release, and pill versus capsule versus liquid. (4) Did they use the same route of administration? Enteric tubes (e.g., nasogastric tube and gastrostomy tube) may affect variability in absorption.

• If the selected model does not align with these various factors, then one should reconsider the applicability of the selected model as it may not be fit‐for‐purpose.

Indication being treated

• Disease state can affect PKs and PDs (i.e., critical illness vs. healthy volunteers).

• Different indications (e.g., osteomyelitis or meningitis) can result in different dosing strategies and target exposures.

• If the selected model does not align with these various factors, then one should reconsider the applicability of the selected model as it may not be fit‐for‐purpose.

Comorbidities

• Certain comorbidities, like obesity, diabetes, and heart disease, have been shown to influence classes of medications, by either affecting the clearance (CL) or volume of distribution (V).

• Polypharmacy increases the likelihood of drug–drug interactions (DDIs).

  • ○
    Inducers

    • ■
      Medications that induce, or increase, the activity of a given metabolic enzyme or transporter, which results in an increase in the metabolism or elimination of the drug.
  • ○
    Inhibitors

    • ■
      Medications that inhibit the activity of a metabolic enzyme or transporter, resulting in the delayed metabolism or elimination of the given drug.

• Organ dysfunction, particularly liver or kidney disease, may have significant effects on drug metabolism and CL, especially when extracorporeal support devices are required for CL.

• It is unlikely that the population for the selected model will share an identical list of comorbidities with the intended population. Therefore, it is important to be aware of these differences and how they may affect a patient's PKs, PDs, and interpretation of results when modeling patient data for an MIPD program.

It is likely that no model will represent the patient population of interest on all the aforementioned factors, so it is important to judge which factors are the most likely to affect PK and PD variability and most important to take into account.

Sampling strategy

After determining that the population of a model is an appropriate representation for the intended population, one must also consider the study's sampling strategy.

Was the study retrospective or prospective in nature?

• PopPK models that are constructed via retrospective studies use clinical data that were likely not collected with the intention to describe the drug's behavior. With this potential limitation in mind, one should consider the sample size of the retrospective population and the sampling strategy used. The original sampling strategy may not have collected enough samples across the concentration‐time interval for the given drug and therefore does not provide the optimal quality nor quantity to adequately describe the desired PK parameters (see Sample size and D‐optimal design below). Additionally, clinical data captured in this nature may have inaccurate times documented for the administered dose or collected samples due to busy clinical activities, resulting in biased concentration‐time profiles. Collection of samples in retrospective studies may also be subject to errors of samples being drawn off the same line that the drug is infused or inadequate wasted blood, leading to higher concentrations.

• Retrospective studies may not demonstrate the same exclusion criteria that a prospective study would implement. This design increases the likelihood of comorbidities and polypharmacy confounding the PK results. However, these variables can be explored during covariate modeling.

• Conversely, prospective studies are often optimally designed to collect appropriate PK samples. Furthermore, attention is often given when recording the times for dose administration and sample collection. It is important to note that some prospective PK studies are performed in healthy subjects, especially in early drug development. Depending on the nature of the intended disease state, PKs in healthy subjects may be different from that in the intended population.

• If prospective studies were performed using scavenged opportunistic sampling ⁴⁴ , ⁴⁵ to limit blood draws in vulnerable populations (e.g., neonates, young children, and critically ill children), it is important to consider if the sample size and timing of sample collection were adequate to capture the entire concentration‐time profile and the variability.

• Sample size: Did the authors perform a power analysis to determine the appropriate number of patients, doses, and samples needed to construct a reliable model? Did they incorporate an optimal sampling strategy over an appropriate time course to reliably address the specific PK parameters of interest? ¹⁴ One should review the sample size justification in the original PopPK papers and determine if the quantity of samples per patient is adequate based on rich or sparse sampling when using the US Food and Drug Administration (FDA) guidance as a resource. If unable to determine the sample size, they should contact the authors for more details. Additional guidance has been provided specifically for pediatric studies by the FDA. ⁴⁶ , ⁴⁷

What is the PK parameter(s) or metric(s) of interest being investigated? Does the sampling strategy provide optimal design to accurately estimate the PK parameter(s) or metric(s) of interest?

• Are the authors interested in the maximum concentration (C _max) and/or describing the absorption phase? If so, does the sampling strategy provide sufficient quality and quantity of samples to describe this process for a non‐parenteral administered drug? Is concurrent intravenous data available to estimate absolute bioavailability and evaluate for potential flip‐flop kinetics? ¹⁴ , ¹⁹ These are helpful data, but not always available.

• Are the authors interested in the AUC for exposure‐response relationships, describing CL, or finding time to elimination threshold? If so, was an optimal sampling strategy used to optimally establish the exposure metric while limiting the number of samples? ⁴⁸

• Determinant optimal (D‐optimal) design: Optimization of sample strategy can be used to determine the ideal number and timing of sample collection that accurately determines the PK profile of the drug. ⁴⁹ The D‐optimal design is the most used criterion for optimization. ⁵⁰ More information regarding the maximization of the determinant of the population Fisher information matrix and minimization of the variance–covariance matrix of estimation, ⁴⁹ , ⁵¹ as well as software for D‐optimal design, ⁵⁰ can be found elsewhere. In short, the D‐optimal design can identify the timepoints that will provide the most information about the drug's PKs and help to minimize the number of samples needed for the study.

Data handling

It is important to evaluate how the authors handled the data before creating the model. Did the authors use all relevant and available data? If the authors state an omission of data, is the rationale for the omission appropriate? Do patients with omitted data differ from remaining patients? Omitted data are often a result of being classified as an outlier. ¹⁴ PopPK outliers often take two forms: (1) a true empirical outlier and (2) a statistical outlier. A true empirical outlier typically results from an error in the data collection process. This can occur when the time of the administered dose or collected sample are incorrectly reported in the electronic health record, as a result of assay error producing drug concentrations that are not clinically feasible, or inappropriately drawn samples (i.e., drawn from same line without adequate waste). Empirical outliers are often omitted from the PopPK analysis to refrain from impacting the PK parameter estimates. Statistical outliers are often visually identified during the review of goodness‐of‐fit (GOF) plots and residuals. Great consideration needs to be given when determining if a statistical outlier should be omitted from the PopPK analysis ¹⁵ ; typical omission results from a normalized weighted residual greater than five. ¹⁴ Statistical outliers can result from empirical error or simply represent variability in the population, which needs to be explored. However, removing statistical outliers for the sole purpose of improving the model's performance is poor practice and would call into question the technical adequacy of the model.

Measured drug

Three details that need to be considered are (1) whether the PopPK model under review measured the amount of drug in the serum, plasma, or whole blood (some papers may use the terms plasma and serum interchangeably, which can lead to another source of variability ⁵² ), (2) whether total concentrations unbound drug concentrations were measured, and (3) whether the same type of assay is accessible at one's institution. Subtle differences in the type of sample analyzed, type of assay, and assay variability can result in differences in the measured drug. Therefore, when one attempts to incorporate the given model in an institution's MIPD program, there will be an increase in uncertainty when interpreting the results.

Structural model

The structural model, or compartmental model, is the first element of the model output that one needs to evaluate when reviewing a proposed model for an MIPD program. The structural model defines the typical concentration‐time profile of the given drug and outlines the differential equations to provide estimates for each of the desired PK parameters. ¹⁹ , ²⁰ This fundamental step in the modeling process serves as the foundation for all succeeding steps – a misspecification or incorrect assumption at this stage can bias the findings from the model. When reviewing a structural model, one needs to consider the following:

What type of structural model was used?

• Were various structural models considered? Was justification provided for why the authors decided on the specific model they ultimately published?

• Does the selected model adequately describe the population data?

  • ○
    This step is evaluated visually by interpreting GOF plots. See Evaluation of model performance for additional information.

• Are there previously available data to support the use of this structural model?

• If the structural model is novel, do the authors provide statistical (and possibly physiological) rationale that supports this approach?

Covariate modeling

The covariate modeling process attempts to define the relationship between the PK parameters and patient‐specific variables. ¹⁹ These covariates attempt to improve the description of the population by explaining additional BSV in the PK parameters. The covariates investigated during this step in the modeling process are often outlined during the experimental design and can comprise both intrinsic and extrinsic sources of variability. ¹⁹ Intrinsic sources of variability are those innate to the patient and can include age, sex, race, ethnicity, body size, and genetics. ⁵³ Variation in body size is often described using body weight and indexes parameters to a 70 kg patient. The principle of allometric scaling is often applied to body weight to capture the body size variations in the developing population of pediatric patients so appropriate comparisons to adult patients can be made. Variations in body size have been described by body surface area, which has often been selected for oncology drugs or drugs with a high dependence on renal function for elimination from the body. The use of either body weight or body surface area to describe variation in body size and serve as a size scalar for PK parameters needs to be empirically justified during the covariate modeling process. Extrinsic sources of variability are exogenously applied to the patient and can include the dose amount, dosing frequency, route of administration, concurrent medications, medication history (e.g., medication failure), and the institution providing the treatment. ⁵³ The covariate modeling process is a dynamic step in the modeling building process. The identification, quantification, and quantitation of meaningful covariates can provide key insights into optimizing treatment outcomes and often personifies the “personalized” in personalized medicine. However, this step can also provide substantial model error if covariates are incorrectly incorporated into the model. When reviewing the covariate modeling for a prospective MIPD model, one should consider the following:

How did they analyze covariates?

• How did they select the covariates for analysis? Was there a predefined analysis plan?

  • ○
    The lack of a predefined analysis plan can introduce selection bias for the covariate analysis.
• Did they use a stepwise covariate approach ¹⁹ , ²⁰ or a full covariate modeling approach? ¹⁹ , ²⁰ If they used the least absolute shrinkage and selection operator (LASSO) approach, then do they demonstrate reproducibility? ⁵⁴ Is there sufficient power to quantify the effects of the selected covariates?

  • ○
    Although there is generally no preference in the method used to analyze covariates, the method should be explained and justified in accordance with good modeling practice. ⁵⁵

• Was co‐linearity of covariates on PK parameters explored? ¹⁹

• Were covariates tested on all PK parameters? Do they provide rationale if the covariates were tested on a specific PK parameter?

  • ○
    Rationale can include objective values (Evaluation of model performance) or a support (predefined) analysis plan.

Which covariates does the model include?

• Did they highlight the number of patients with the covariate? Is the covariate considered rare or common?

  • ○
    It limits the generalizability and translatability of the given model if their equations for each PK parameter include a rare covariate that was measured in only a small percentage of patients included in the model.
• Which type of covariate: continuous versus categorical? ¹⁹

  • ○
    If continuous, is there good spread of the data?

    • ■
      Does sampling provide a wide range of the covariate? Or are variable values narrow, with limited range?
    • ■
      Are there differences in the assay used to measure the continuous variable? Different assays, institutions, or patient ages can create differences that alter the categorization of variables. For example, the below limit of quantification may be different between institutions and lead to different cutoff points for categorization of variables.
  • ○
    If categorical, are there sufficient patients/samples in each group?

    • ■
      Did they convert a continuous variable into a categorical variable? If so, is the categorization appropriate or clinically meaningful?
• Covariate significance

  • ○
    Individual covariates are often added in a forward stepwise approach if the covariate reached the statistical significance criteria defined by the change in objective function value (∆OFV) ¹⁹ of:

    • ■
      1 degree of freedom:

      • p < 0.05: ΔOFV of at least −3.841
      • p < 0.01: ΔOFV of at least −6.635
    • ■
      2 degrees of freedom:

      • p < 0.05: ΔOFV of at least −5.99
      • p < 0.01: ΔOFV of at least −9.21
  • ○
    Although the inclusion of a significant covariate improves the model's description of the data, it is important to determine whether the covariate carries a significant clinical impact. Discussing the results with a clinical team can help determine if a statistically significant finding is clinically meaningful. ¹⁹ , ⁵⁶
• Did they provide information on how they handled covariate data that was missing or below the limit of quantitation?

  • ○
    Details on how to handle missingness can be found elsewhere. ¹⁵ , ¹⁹ , ²⁰

    • ■
      Options include omitting observations with any missing data, imputing based on mean/median/mode, regression imputation, or encoding missing data as their own variable in the model.
  • ○
    If there are missing data, do their methods of handling missing data make sense in accordance with the type of missing data (e.g., missing at random, missing completely at random, and missing not at random). ⁵⁷
• Are the covariates incorporated in the model readily collected at the study institution or does the institution have the infrastructure to collect them?

  • ○
    If the covariates are not readily available at one's institution, do the covariates improve the model significantly to justify the clinical cost to outsource the measurement of these covariates or to develop an in‐house method to measure the covariate?
• Does the model over‐parameterize?

  • ○
    Model over‐parameterization occurs when a model incorporates too many model parameters to describe the population. The addition of several model parameters may improve the performance, but it also increases the risk of over‐fitting the data with a model that is too complex for its fit‐for‐purpose. This limits the model's generalizability and increases the prospective variance surrounding parameter estimates. In brief, standard error less than 30% for fixed effects and less than 50% for random effects is considered acceptable. ¹⁹
  • ○
    The use of Akaike's information criterion (AIC) and Bayesian information criterion (BIC) can help inform whether the inclusion of the covariate over‐parameterizes the model by penalizing the model for each added parameter. ¹⁹ , ⁵⁸

Are the covariates incorporated into the model in a reasonable manner?

• If included as a time‐varying covariate, multiple samples over the entire time‐course need to be collected in order make appropriate estimations.

• Does the model use a mechanistic approach to incorporate the covariate into the model, rather than relying on specific “reference” values for certain covariates (e.g., renal function)?

• If the model includes a covariate that uses a population reference value, how does that reference value compare to the population of interest?

  • ○
    Example: Serum creatinine in high dose methotrexate (MTX): In one specific NONMEM model, the population reference value that adjusted clearance based on the time‐varying for serum creatinine corresponded to a typical value for a 4‐year‐old patient. ⁵⁹ However, adult patients usually have higher serum creatinine ⁶⁰ —therefore, the model, without the use of Bayesian estimation, would have a tendency to provide negative residuals, that is, slower CL and higher predicted concentrations than what is actually being observed due to the bias created by a low reference value.

Error modeling

Another key aspect in the model building process is the incorporation of an error model. There are two forms of “explained” variability: (1) BSV and (2) BOV. The BSV represents the degree of variability observed between patients and is added to the model's equations to describe the variability across patients. ¹⁹ The BOV represents the degree of variability within a patient, but across multiple occasions or drug courses/administrations and is included in the model's equations to describe the variability in a patient's drug absorption, metabolism, and elimination across multiple administrations of a drug. ¹⁹ , ⁶¹ The quantification of BOV is not as commonly investigated due to the quantity of sampling during each occasion and the longitudinal nature of these studies, but should be included, if available, to improve the Bayesian estimates of PK parameters. How to incorporate BOV for MIPD has been previously addressed. ⁶¹

Last, the RUV represents the PK variability within patients that cannot be explained by either the structural or covariate models. ¹⁹ RUV can be incorporated into the model‐building process via several different equations. Mould and Upton describe these models in detail, ¹⁹ but, in brief, RUV can be applied as an additive error, proportional error, exponential error or a combination of these error models. Although each of these applications have their advantages and disadvantages, often, the description of the population's RUV is empirically determined. ¹⁹ The importance of the error model cannot be understated. Therefore, one should consider the following when reviewing a prospective model's error model:

What type of error models were used? ¹⁹

• How did the author's incorporate BSV?

• Did the model include BOV? If so, was the sampling strategy optimized to adequately characterize this variability?

• How did the author's incorporate RUV into the model?

  • ○
    Did they use an additive, proportional, a combined approach, or an exponential model?

    • ■
      Additive and proportional error typically viewed as a constant form of error into the model and often represents assay error. ¹⁰ , ¹⁹
    • ■
      Exponential error models are like proportional error models but evaluate error on log‐transformed data. Exponential error models are also prone to the same over‐weighting of higher concentrations like proportional error models. A way to address this over‐weighting is to perform the log‐transformed both sides approach. ¹⁰ , ¹⁹
  • ○
    Were different residual error models explored?
  • ○
    Did the authors provide rationale for the used error models?
  • ○
    How large are these error values?

    • ■
      Large error values suggest that the model description of the data need improvement or the data have a lot of noise.
    • ■
      If used in clinical practice, it is critical to recognize that high variability will provide dosing recommendations or forecasted concentrations with a large confidence interval – therefore, lacking the possible precision needed for successful clinical use.
    • ■
      If residual unexplained variability is large (i.e., >30%), the impact of observed concentrations is relatively low. When using the model for Bayesian estimation, a certain degree of intrinsic error should be assumed in observed concentrations, which is reflective of the validation of the assay. The assay variability is typically less than 15% at most concentrations and less than 20% at the lowest measurable concentrations. ⁶²

Shrinkage ¹⁹

• Individual parameters that tend to shrink toward the population averages are typically seen in patients with sparse sampling.

• When the shrinkage is high (>20%–30%), individual data become less informative (individual predicted concentrations [IPREDs] and individual weighted residuals [IWRES]) and individual analyses need to be carefully considered. ¹⁹ Instead, “simulation‐based, diagnostic plots are not affected by shrinkage in a similar manner and can be more informative for diagnostic purposes when shrinkage is high.” ¹⁹

Evaluation of model performance

The Structural model, Covariate modeling, and Error model sections all outlined important aspects to consider when evaluating a model for an MIPD program. This final section will cover how to critically assess the prospective model's descriptive performance of the given population by evaluating the standard assessments (e.g., GOF plots), simulation‐based diagnostics, bootstrap analysis, and external validation. These aspects of model performance will provide confirmation that the developed model is reliable.

GOF plots

• GOF plots (Figure 1) illustrate how the model describes the data and is a visual method of assessing model bias and model misspecification ¹⁹ , ⁶³

• There are four typical GOF plots that evaluate a model's performance:

  • ○
    IPRED (model predicted concentrations based on individual covariates and accounts for unexplained variability) versus observed concentrations.
  • ○
    Population predicted concentrations (PREDs; model predicted concentrations based on individual covariates but still contains unexplained variability) versus observed concentrations.
  • ○
    Conditional weighted residuals (CWRES; a measure of difference between individual data and model predicted data) versus PREDs.
  • ○
    CWRES versus time (time after last dose).
• Model Bias ¹⁹ , ⁶³ , ⁶⁴

  • ○
    Does the IPRED and PRED display good linearity with the dependent variable (DV)?

    • ■
      Are the predicted versus observed concentrations in good agreement with the line of identity?
    • ■
      Ideally, the relationship between predicted and observed should display linearity across all concentrations.
    • ■
      If significant deviation from the line of identity is observed, then the model displays bias toward those concentrations.
  • ○
    Does the CWRES display a zero‐slope across PRED and time?

    • ■
      The plot of the CWRES versus population predicted and CWRES versus time should result in a line of best fit with a slope close to zero. A significant, non‐zero slope suggests that the model displays bias for certain concentrations/time.
• Model misspecification ⁶³ , ⁶⁴

  • ○
    Similar to model bias, except this refers to a systematic error in the model building process that results in nonlinearity of the GOF plots. Plots that display a sigmoidal or parabolic‐like relationship with the line of best fit suggest a misspecification within the structural, covariate, or error models used.

FIGURE 1.

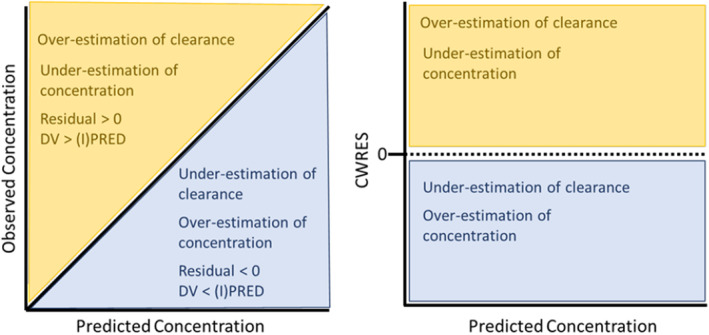
Visuals of GOF plots and what biases may be elucidated on these plots. The left plot illustrates interpretations from the visual evaluation of a (population or individual) predicted concentration versus observed concentration GOF plot. Data that fall above the line of identity (yellow region) will generate a residual greater than zero, implying that the observed concentration is greater than the predicted concentration. This means that the model provided an overestimation of clearance or an underestimation of the predicted concentration. Data that fall below the line of identify (blue region) will generate a residual less than zero, implying that the observed concentration is less than the predicted concentration. This means that the model provided an underestimation of clearance or an overestimation of concentration. These colors and their implications are consistent when reviewing the right plot, which displays a graph that evaluates the concentration versus CWRES. CWRES, conditioned weighted residuals; DV, dependent variable; GOF, goodness of fit.

Simulation‐based diagnostics ⁶³

• Do the authors provide a simulation‐based diagnostic plot of their model?

• Simulation‐based diagnostics are used to confirm the parameter estimates and include posterior predictive checks (PPCs), visual predictive checks (VPCs), numerical (numeric) predictive checks (NPCs) and normalized predictive distribution error (NPDE). ¹⁹ , ⁶³

• The process entails simulating new data sets using the selected database design. Prediction intervals (usually 95%) are constructed from simulated concentration time profiles and compared with observed data. ⁶³ Visual comparisons between the simulated data and observed are made. There should be good consistency between the simulated data and the observed data.

• VPCs can ensure that simulated data are consistent with observed data. ¹⁹

• These simulation‐based diagnostics are unaffected by high individual shrinkage.

Bootstrap analysis ⁶³

• Do the authors provide the results from a bootstrap analysis?

  • ○
    Bootstrap methods are resampling techniques that provide an alternative for estimating parameter precision. They are useful to verify the robustness of standard approximations for parameter uncertainty in PopPK models ¹⁹ , ⁶⁵ Bootstrapping avoids parametric assumptions made when computing the lower 2.5% and the upper 97.5% value of each parameter estimate.

• Results from the bootstrap analysis should be in good agreement with the derived model parameters.

External qualification (commonly called external validation) ⁶³

• Authors may also report the use of external qualification, assessing their model's performance using a dataset that was not included in the model‐building process. There are prespecified criteria that should be used to determine the validity of an external qualification/validation.

• This can either be done by using a split‐data file analysis (large population datasets can be divided into a development dataset and a test dataset – typically considered as internal validation) or a true external analysis using a dataset from a collaboration. ⁶³ It is recognized that external qualification can be difficult if the specific population of interest is not very large and would take a long period to enroll new patients for validation.

  • ○
    If the authors used a split‐data approach, does each dataset provide sufficient sample size for model building?
  • ○
    Do the authors provide an external qualification? If so, how did they select the external dataset? Do they provide sufficient materials to review the model's performance?
  • ○
    The use of a collaborator's dataset is often an attempt at assessing the model's performance on a population that differs from the original cohort.

    • ■
      Consider the age, ethnicity, race, and all aspects that are relevant when looking at a particular model of the external population.
    • ■
      If the model under review does not offer a population with good generalizability, but uses a more generalizable/relatable external cohort for validation, this opportunity could lend itself to be a suitable model for your clinical needs.

One must consider the individual aspects above when critiquing the model's performance of the external dataset.

Considering a model to meet the unmet medical need

At this point, one has fully evaluated and critiqued the performance of a published PopPK model with the intent of integrating it with a precision dosing software for further model validation and eventual incorporation into an MIPD program. Many of the above questions should be answered in the journal publication and should be considered simultaneously with priority given to certain considerations over others depending on the purpose of using the model. If the publication does not provide answers to help evaluate the model fully, consider communicating with the authors to obtain answers for key questions to ensure the model fits one's needs. Unfortunately, it is not uncommon that the drug of interest has few available PopPK models or the quality of the available models are poor. Therefore, one may be left wondering, “How do I know if an imperfect model is good enough?” or “Should I build my own PopPK model to address this medical need?”

An imperfect PopPK model would have to be considered on a case‐by‐case basis regarding its use in an MIPD program based on the drug, patient population, and availability of data from actual patients. A model developed using sound modeling practice could be performing poorly due to a suboptimal sampling strategy or a small population in the original study. Models that fall under this category could still be considered for model evaluation in a precision dosing software, but with caution. ³⁰ Imperfect models that do not follow good modeling practice should not be considered, as fallacies in their underlying assumptions can lead to unreliable results. ³⁰

Choosing to build one's own PopPK model is also an option. If one has access to high quality and a large quantity of PK data within one's institution for a given drug and the available PopPK models are scarce or lack desired performance, then it might be worth developing a new PopPK model, especially because the model will be developed using PK samples from the intended population of the MIPD program. One can also leverage previously published PopPK models as frameworks for initial structural and error models. ¹⁹ Once an in‐house PopPK model has been developed, it is still advised to evaluate the model by (1) comparing its performance to an external dataset of a published model and (2) using a precision dosing software. The former point will encourage collaboration with the modeling group of a previously published model and allow access to an external dataset that was not used in the model. One can compare the two models as discussed above in the Evaluation of model performance, but can also expand upon those analyses with the inclusion of metrics for model bias (mean/median prediction error) and model precision (mean/median absolute prediction error and root mean squares error). ⁶⁴

MODEL EVALUATION IN A PRECISION DOSING SOFTWARE

Implementation and validation of pharmacometric models into precision‐dosing software

Once a model has been evaluated and selected (e.g., a previously published PopPK model or a PopPK model developed in‐house), the model can now be entered into an MIPD software. However, several considerations must first be made to validate that the parameters are correctly entered into the software prior to clinical implementation. We outline the following steps to ensure the accurate entry of the parameters for the PopPK model into the precision dosing software and that the outputs (individualized PK parameters and concentration‐time profiles) are reliable: (1) extract model parameters from the literature, (2) define parameters, (3) define residual error, (4) define covariates and covariate parameter equations, (5). define the reference patient, (6) implement covariate models, (7) design and execute test scenarios, (8) confirm the plausibility of model output, and (9) visually validate concentration‐time profiles. For this tutorial, we use Edsim++ ²¹ and MwPharm++ ²² (Mediware, Czech Republic). Edsim++ uses an object‐oriented graphical user interface to allow for users to create PopPK and PK/PD models within the program. The defined model can then be imported into MwPharm++, an MIPD tool that has a user‐friendly interface that is accessible to pharmacometricians and clinicians, for implementation into clinical care. Although this paper precludes a complete tutorial on Edsim++ and MwPharm++, these steps are applicable to any precision dosing software. The Supplementary File outlines each of these steps using an intravenous one‐compartment linear vancomycin model with combined proportional and additive unknown residual error by Roberts et al. ⁶⁶ This model has been previously evaluated against other models and performed satisfactorily. ⁶⁷ Further, this Supplementary File can serve as a template for validating other PopPK models in an Excel spreadsheet for implementation into a precision‐dosing software.

Extract model parameters from the literature

First, we extract the final model parameters of a PopPK model of vancomycin from the literature. We find it easiest to screenshot the final parameter estimates from the paper of interest and embed them into an Excel spreadsheet, in addition to the reference for the paper. Generally, the parameters are often found in a table, along with bootstrap estimates, as in the vancomycin model. ⁶⁶

Define parameters

The standard PK parameters from the paper should be tabulated into the Excel spreadsheet and can be referred to as the Standard Parameter table. For this example, the model defines two fixed effects, CL and V, which have THETA (or median) values of 4.58 L/h and 1.53 L/kg, respectively. The BOV, represented as the SD; BSV, represented as the coefficient of variation (CV%); and units should also be calculated or copied from the paper (Table 1). As a reminder, SD = CV%/100 * mean because SD may not be reported.

TABLE 1.

Final model standard parameter estimates.

Parameter	Mean	SD	CV (%)	Unit
CL	4.58	1.782	38.9	L/h
V	1.53	0.572	37.4	L/kg

Note: Adapted with permission from “Vancomycin dosing in critically ill patients: robust methods for improved continuous‐infusion regimens,” by Roberts et al. ⁶⁶

Abbreviations: CL, clearance; CV (%), coefficient of variation; V, volume of distribution.

Define residual error

The residual error from the model was best explained using a combined proportional and additive random error component. The additive error and proportional errors were 2.4 mg/L and 0.199, respectively, and should be tabulated (Table 2).

TABLE 2.

Error model parameters.

Parameter	Value	Unit
Additive	2.4	mg/L
Proportional	0.199	–

Note: Adapted with permission from Roberts et al., ⁶⁶ volume of distribution. Error model parameters are assumed to not be log‐transformed.

Define covariates

Covariates can explain a significant amount of individual patient PK variability and are often independently estimated or included in a model as a normalized value on the PK parameters of a model. In this example, accounting for creatinine clearance normalized to body surface area (CLcrN) on CL and body weight (BW) on V improved the estimations of the model. Similar to defining the standard PK parameters, the covariates should be tabulated in the Excel spreadsheet and can be referred to as the Covariate table (Table 3). We recommend including a column for the individual patient values, which can be adjusted based on actual patient values, in addition to the reference patient values used from the paper and covariate units. For this specific case, the CLcrN reference value is 100 mL/min/1.73 m², which was determined by noting that the value is divided by 100 in the CL equation. Because a reference BW is not used in any of the covariate equations (i.e., BW is not normalized by a certain value), we chose 70 kg, which is a standard reference weight for adults (see more details see the section “Define the Reference Patient”).

TABLE 3.

Final model covariate values.

Covariate	Individual patient value	Reference patient value a	Unit
CLcrN	100	100	mL/min/1.73 m2
BW	70	70	kg

Note: Adapted with permission from Roberts et al. ⁶⁶

Abbreviations: BW, body weight; CLcrN, creatinine clearance normalized to body surface area.

^a See section on reference patient for more details on reference patient values.

Define parameter equations with covariates

All equations that were used to define the final population model should be included as formulas in the Excel spreadsheet for reference. These two equations, as represented in Roberts et al., ⁶⁶ are as follows:

$$\mathrm{CL}=4.58\times \frac{\text{CLcrN}}{100}$$

$$V=1.53\times \mathrm{BW}$$

Define the reference patient

Defining the reference patient of a model can often present challenges and requires reviewing the parameter equations and population demographics. For covariates that are normalized to a reference value, one can deduce the reference covariate value. In the case of Roberts et al., ⁶⁶ CLcrN is normalized to 100 mL/min/1.73 m², thus the reference patient has a CLcrN of 100 mL/min/1.73 m² and has a vancomycin CL of 4.58 L/h. For those covariates that are not normalized to a reference value, the next best step is to use the median value of the population. If the median value is not provided in the demographics’ table of the study, it is important to contact the authors of the model for this information. Another option, specific to weight, is to use a standard value of 70 kg for adults. In our example, the BW in the V equation is not normalized by a standard BW, so we selected 70 kg as the reference but we could have selected the median weight of the population found in the manuscript (74.8 kg). Thus, the reference patient for our model has a weight of 70 kg with a vancomycin V of 107.1 L.

Implement formulas for covariate effects to determine the parameter formulation

After defining all PK and covariate parameters from the model of interest, the equations we previously defined from the paper can be implemented to calculate the relative effects of each covariate on the CL and V. Referencing the population median (THETA) estimates for the PK parameters (Table 1) and covariate equations, we can calculate the effect of individual patient covariate values on the population CL and V. In the Excel spreadsheet, two cells corresponding to the calculated covariate effect (i.e., the new PK parameter value as a result of a specific covariate value's effect) can be created under the Standard Parameter table. If the value of the covariate is changed relative to the reference value in the Covariates table, this change in effect in the Standard Parameter table will be calculated. For example, if a patient has a CLcrN of 120 mL/min/1.73 m² and BW of 62.5 kg, the calculated covariate effect for CL and V would be 5.496 L/h and 95.625 L, respectively (Table 4).

TABLE 4.

Calculated covariate and parameter modulation effects.

Parameter	Mean	SD	CV (%)	Covariate Applied to Parameter	Patient covariate value	Calculated covariate effect	Parameter modulation effect
CL (L/h)	4.58	1.782	38.9	CLcrN (mL/min/1.73 m2)	120	5.496	1.2
V (L/kg)	1.53	0.572	37.4	BW (kg)	62.5	95.625	62.5

Note: Adapted with permission from Roberts et al. ⁶⁶

Of note, this table combines the “Standard Parameter” Table and “Covariates” Table in the Supplementary File Excel Spreadsheet.

Abbreviations: BW, body weight; CL, clearance; CLcrN, creatinine clearance normalized to body surface area; CV (%), coefficient of variation; V, volume of distribution.

After implementing the formulas to calculate the covariate effects, an additional column to calculate the overall effect on the population CL and V is available, denoted as the “Parameter Modulation Effect” (i.e., the fold‐increase or ‐decrease in the PK parameter as a result of a specific covariate value's effect) in the Standard Parameter table. These values are determined by dividing the calculated covariate effects by the mean population CL and V accordingly. Again, using a patient with a CLcrN of 120 mL/min/1.73 m² and BW of 62.5 kg, the overall parameter modulation effect for the CL is 1.2 and the V is 62.5 (Table 4).

Design and execute test scenarios

At this point, we can create and enter the model parameters from Roberts et al. ⁶⁶ into Edsim++. Figure 2a shows the developed, object‐oriented model in Edsim++, along with the defined CL (Figure 2b) and V (Figure 2c) parameters with associated covariates, CLcrN and BW, respectively. In order to validate that the parameters were correctly inputted into our precision dosing software (i.e., model qualification), we can create test scenarios in the Excel spreadsheet that can be compared to the values in Edsim++. These test scenarios are provided in the Excel spreadsheet and Table 5. Test 1 shows the calculated effects that correspond to the reference values, which are the normalized covariate values for CLcrN (e.g., 100 mL/min/1.73 m²) and BW (e.g., 70 kg) on the CL and V, respectively. This can serve as a comparator to subsequent test scenarios where the individual patient covariate value is adjusted to be different from the reference values, as shown in tests 2A, 2B, 3A, and 3B. For example, in test 2A, the CLcrN for the individual patient covariate value was kept at 100 mL/min/1.73 m², whereas the BW was changed to 35 kg, resulting in a calculated covariate effect for the V to be 53.55 L and a parameter modulation effect of 35. Although this scenario is a simple instance of this, where there was a 50% reduction in the V, these effects can become more complex if the final model parameter equations contain multiple covariates. Therefore, we recommend creating scenarios for each covariate that was included in the final model of the paper. The values from the Excel spreadsheet can be compared to our developed model in Edsim++ to validate that there are no data entry errors and the Edsim++ model is performing correctly.

FIGURE 2.

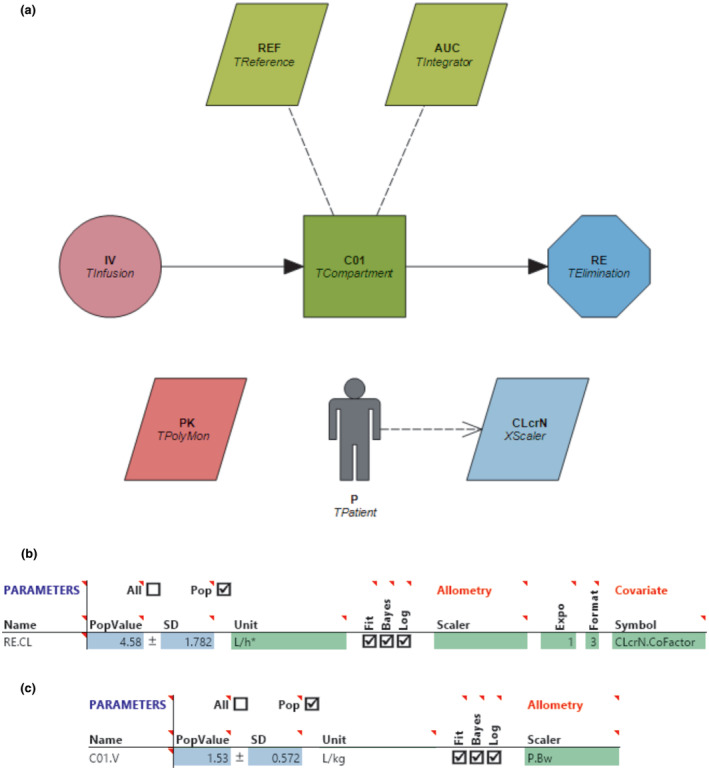
(a) Object‐oriented diagram of Roberts et al., 2011 ⁶⁶ intravenous one‐compartment linear vancomycin model defined in Edsim++. Each object corresponds to various PK, covariate, or miscellaneous components to define the PK parameters for a model of interest. The purple circle (“IV”) represents the intravenous vancomycin infusion, the green square (“C01”) represents the central compartment and V of the model, and the blue octagon (“RE”) represents the renal CL. The gray person (“P”) contains information about the individual and population (reference) patient and is linked to a light blue trapezoid (“CLcrN”) defining the CLcrN covariate. The two, light green rhombuses (“REF” and “AUC”), and pink rhombus (“PK”) correspond to additional parameters for the model (e.g., target concentration monitoring). (b) Screenshot of model parameters corresponding to object “RE,” with “CLcrN” applied as a covariate on the CL. (c) Screenshot of model parameters corresponding to object “C01,” with the covariate BW applied as a scaling function on the V. AUC, area under the concentration‐curve; BW, body weight; CL, clearance; CLcrN, creatinine clearance normalized to body surface area; PK, pharmacokinetic; RECL, renal clearance in L/h; REF, reference model parameters; V, volume of distribution.

TABLE 5.

Test scenarios evaluating covariate effects on final model parameters.

Parameter	Covariate applied to parameter	Individual patient covariate value	Excel calculated covariate effect	Parameter modulation effect
Test 1 (Reference values)
CL	CLcrN	100	4.58	1
V	BW	70	107.1	70
Test 2A
CL	CLcrN	100	4.58	1
V	BW	35 a	53.55	35
Test 2B
CL	CLcrN	100	4.58	1
V	BW	140 a	214.2	140
Test 3A
CL	CLcrN	50 a	2.29	0.5
V	BW	70	107.1	70
Test 3B
CL	CLcrN	150 a	6.87	1.5
V	BW	70	107.1	70

Abbreviations: BW, body weight; CL, clearance; CLcrN, creatinine clearance normalized to body surface area; V, volume of distribution.

^a Indicates individual patient value differs from the reference patient value.

Confirming the plausibility of model output

When assessing and testing a model for possible clinical use, one must consider the outputs the model generates for a patient of interest against what might be reasonably expected for the model “reference” patient. In many models, the reference patient is a healthy patient of a specific weight and other covariates, whereas the test patient (reflecting the particular target population of interest for model use in the clinical world) may have non‐mean values of these covariates due to various clinical reasons (e.g., organ dysfunction, sepsis, or comorbid conditions, for example). Comparing the PK outputs between the patient of interest and reference patient allows a model user to have a frame of reference for when a model makes real‐world sense, versus when there may be an error somewhere in how the model was entered or derived. For example, a patient with acute kidney injury and creatinine above baseline should have lower drug CL and thus higher drug concentrations across a dosing interval when compared to a reference patient with normal kidney function.

There are two specific considerations to highlight when using a model for pediatric purposes: the use of allometric scaling to relate patient size and CL, and the use of maturation effect functions describe the impact of development in organ functions on CL in infants and young children. Ideally, one can select a pediatric‐specific model that already incorporates allometric scaling and/or maturation effect. However, if such a pediatric‐specific model is unavailable, extrapolation from an adult model by incorporating allometric scaling and maturation function often works enough to fit‐for‐purpose. ⁶⁸ A recent 2016 study looked at published models for midazolam, a classically hepatically cleared medication, and gentamicin, a classically renally cleared medication, to see if any of their derived age or maturation parameters performed better than standard allometric scaling of CL (allometric weight exponent of 0.75) with sigmoidal maturation function (estimating time in weeks of postmenstrual age to reach half of the mature value), and found that the standard performed just as well as models that customized size and maturation as parameters. ⁶⁸ As models are entered into MIPD software, it can be to the user's advantage to practically add an allometric scale and/or maturation effect function if not already incorporated into the published model.

Visual validation of concentration‐time profiles

The Excel spreadsheet provided allows for validation of only the covariate model. To further ensure that the all the model components implemented within the MIPD software are appropriately estimating the drug's concentration, we can map the coordinates corresponding to the concentration‐time profile from the published PopPK model (a process known as “digitization”) and visually compare these coordinates to what is output by the precision‐dosing software. Several publicly available programs exist to digitize graph data, such as “WebPlotDigitizer” ⁶⁹ or “ScanIt.” ⁷⁰ Using figure 2 from Roberts et al., ⁶⁶ we digitize the concentration‐time curves for the 5 mg/kg loading dose over 1 h and 40 mg/kg loading dose over 3 h, followed by a 35 mg/kg/day continuous infusion. The digitized points should capture the entire PK profile to ensure adequate comparison. Then, using the parameters and corresponding loading dose from the paper, we simulated the concentration‐time curve in Edsim++ based on the reference patient (i.e., a patient with a body weight of 70 kg and CLcrN of 100 mL/min/1.73 m). The digitized points from the paper and the simulated concentration‐time curve from Edsim++ can then be overlaid to determine whether the implemented model reflects the published PopPK model (Figure 3). If the concentration‐time curve adequately matches the digitized points, we can assume the model was correctly implemented into Edsim++ and is now validated for clinical implementation using MwPharm++.

FIGURE 3.

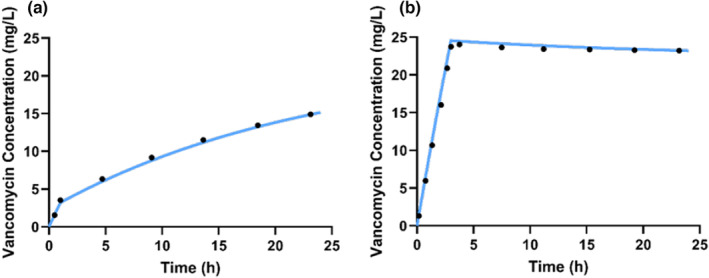
Overlay of simulated concentration‐time curves from Edsim++ and digitized points from the concentration‐time curves for the 5 mg/kg loading dose over 1 h and 40 mg/kg loading dose over 3 h, followed by a 35 mg/kg/day continuous infusion from Roberts et al. ⁶⁶ to validate accurate input of model into Edsim++.

After completing the process of selecting and validating models through the steps we have outlined, it is important to note that a model's performance should continually be evaluated after implementation. As Ron Keizer and colleagues have commented, “We recommend evaluation of the predictive ability of the intended model for its intended use before applying it in the clinic, and to continuously monitor it once deployed.” ³⁰ Newly generated data can be incorporated into existing models for better predictions and new models published in the literature should be evaluated for possible incorporation into precision dosing tools.

MIPD APPLICATIONS

Through this tutorial, we hope to have demonstrated how to select and validate the input of a PopPK model to be implemented for MIPD for a multitude of drugs in various clinical scenarios. In our institution, we have used MIPD for clinical applications of multiple drugs, including sirolimus, ⁷¹ methotrexate, ⁷² hydroxyurea, ⁷³ morphine in neonates, ⁷⁴ and infliximab. ⁷⁵

Challenges of MIPD

Although there are numerous MIPD applications that can be realized, there are several barriers to implementation. In order to apply MIPD to patients in real time, samples must be available for concentration measurements. Depending on the drug of interest, assays can be quite expensive, time‐consuming, or difficult to access. Some institutions might have the ability to run assays in‐house, but this also takes time to validate and requires significant financial support. Most drug monitoring assays require a blood draw which can be limiting due to lack of consent or daily blood draw limits based on patient size, particularly in critically ill patients who require many blood draws for clinical care. Selective sampling strategies, such as scavenged opportunistic sampling or sparse sampling, ⁴⁴ , ⁴⁵ can greatly minimize the amount of blood draws needed for informative therapeutic drug monitoring that can be applied to MIPD. The lack of standardization and training in the field of MIPD is a challenge preventing widespread applications. Finally, when considering the use of MIPD in pediatric patients, it is important to recognize that the majority of the data used to generate the models comes from adults which generates for some inherent discrepancies based on differences in physiology.

Solutions to move MIPD forward

Collaborative programs that integrate groups with advanced training in clinical pharmacology with clinicians can bring together individuals to best tailor models for effective implementation of MIPD. One such example of bringing “bench to bedside” is the PK Consult service in place at our institution. This service is accessible to clinicians for real‐time analysis of individual patient PK data and provides recommendations for dose alterations to achieve desired target exposure to ensure adequate beneficial effect while minimizing toxicity. The consult service allows for dose optimization of high‐risk drugs, including immunosuppressive agents in post solid organ transplantation or auto‐immune disease patients, biologic agents, chemotherapeutic drugs, and other drugs in patients that may have underlying organ dysfunction. This consult service will be described in a future tutorial.

In conclusion, we have outlined a path to the development of robust and dynamic model informed precision dosing using Edsim++ and MwPharm++ and as an example in efforts to provide personalized care to patients to improve outcomes.

FUNDING INFORMATION

Z.L.T., K. Paice, K. Pavia and K.S. have been supported by the National Institute of Child Health and Development T32 Cincinnati Pediatric Clinical Pharmacology Training Program (T32HD069054) during the writing of this manuscript. E.A.P. is supported by the National Institute of Mental Health of the National Institutes of Health under award number F31MH132265. S.T.G is supported by the National Institute of General Medical Sciences of the National Institutes of Health under award number R35GM146701.

CONFLICT OF INTEREST STATEMENT

N.P. is the President of Medimatics, the company that develops Edsim++ and MwPharm++. All other authors declared no competing interests for this work.

Supporting information

Data S1

Taylor ZL, Poweleit EA, Paice K, et al. Tutorial on model selection and validation of model input into precision dosing software for model‐informed precision dosing. CPT Pharmacometrics Syst Pharmacol. 2023;12:1827‐1845. doi: 10.1002/psp4.13056