The emergence of economic rationality of GPT

Significance

It is increasingly important to examine the capacity of large language models like Generative Pre-trained Transformer model (GPT) beyond language processing. We instruct GPT to make risk, time, social, and food decisions and measure how rational these decisions are. We show that GPT’s decisions are mostly rational and even score higher than human decisions. The performance is affected by the way questions are framed, but not by settings of demographic information and randomness. Moreover, the estimated preference parameters of GPT, compared to those of human subjects, are slightly different and exhibit a substantially higher degree of homogeneity. Overall, these findings suggest that GPT could have the potential in assisting human decision-making, but more research is needed to fully assess their performance and underpinnings.

Abstract

As large language models (LLMs) like GPT become increasingly prevalent, it is essential that we assess their capabilities beyond language processing. This paper examines the economic rationality of GPT by instructing it to make budgetary decisions in four domains: risk, time, social, and food preferences. We measure economic rationality by assessing the consistency of GPT’s decisions with utility maximization in classic revealed preference theory. We find that GPT’s decisions are largely rational in each domain and demonstrate higher rationality score than those of human subjects in a parallel experiment and in the literature. Moreover, the estimated preference parameters of GPT are slightly different from human subjects and exhibit a lower degree of heterogeneity. We also find that the rationality scores are robust to the degree of randomness and demographic settings such as age and gender but are sensitive to contexts based on the language frames of the choice situations. These results suggest the potential of LLMs to make good decisions and the need to further understand their capabilities, limitations, and underlying mechanisms.

ChatGPT is a sophisticated chatbot application developed by OpenAI, which employs the state-of-the-art Generative Pre-trained Transformer model (hereafter referred to as “GPT”). As one of the most representative examples of large language models (LLMs), GPT uses transformer architecture and deep learning techniques to learn from vast web-based text corpora that contain 175 billion parameters (1, 2). Thanks to its massive volume of training data, GPT can generate human-like text with remarkable accuracy and fluency, to the extent that human evaluators find it difficult to distinguish GPT output from text written by humans (2). In addition to their natural language-generation capabilities, LLMs have demonstrated impressive abilities in a wide range of domains. For instance, they can generate computer code (3), engage in human-like conversations on various topics (4), solve university-level math problems (5), exhibit theory of mind ability (6), and possess psychological characteristics similar to humans (7, 8). LLMs have also shown their aptitude in performing high-level reasoning tasks (9). The impressive capabilities of LLMs reveal their remarkable potential, which can be likened to the emergence of a new species: “Homo silicus” (10). Because these achievements signify a major milestone in the development of LLMs, it is important that we understand how GPT performs in various high-level reasoning tasks.

Here, we present a study on the economic rationality of GPT. Rationality has been central to the methodological debate throughout various disciplines and is the fundamental assumption in economics and related social sciences. Here, we use a classic notion of economic rationality in revealed preference analysis that captures the extent to which a decision maker maximizes some well-behaved utility functions for the given budget constraints (11–17). Prior studies have computed rationality score based on choice data in risky, intertemporal, and social decision-making in laboratory environments (18–25) as well as expenditure data from survey and grocery stores in the field (26–29). Economic rationality has also been measured in children (23, 30), monkeys (31), rats, and pigeons (32). Moreover, it has been proposed as a measure of decision-making quality and linked to a wide range of economic outcomes, such as occupation, income, and wealth differences across individuals, and development gaps across countries (22, 33–39). Nevertheless, the rationality of GPT remains unexplored.

We instruct GPT to act as a decision maker to make budgetary decisions in choice environments with varying characteristics. The basic framework contains 25 decision tasks to allocate 100 points between two commodities with different prices, which is commonly used in experimental economics. The rationality of GPT is measured by the consistency of these 25 decisions with the generalized axiom of revealed preference (GARP), a necessary and sufficient condition under which a set of decisions are in accordance with utility maximization (11, 12, 14, 15). Therefore, a rationality score is derived from each group of 25 tasks within a given environment. Building on this framework, we construct four environments by specifying the nature of the two commodities—two risky assets; two rewards with one for now and 1 for 1 mo later; two payments with one for the decision maker and one for another randomly paired subject; and two types of food with meat and tomatoes. Each environment is repeated 100 times, which generates 10,000 tasks for GPT. This design allows us to systematically measure GPT’s rationality in different choice domains. Moreover, we incorporate a series of variations in the randomness of GPT, the framing of decision tasks (40), the structure of the choice format (41), and the demographic settings of GPT (42). In order to compare the economic rationality between GPT and humans, we conduct a parallel experiment with 347 human subjects from a representative US sample.

We find that GPT demonstrates a high level of rationality in all four decision-making tasks concerning risk, time, social, and food, and it outperforms human subjects in the rationality score documented in both our human subject experiment and those reported in the literature. Furthermore, we find that GPT’s rationality scores are consistent across different demographic characteristics and invariant to the specification of the randomness of GPT. However, the level of rationality drops significantly when we employ a different price framing and when we use a discrete choice setting. These findings suggest that GPT obtains high rationality score but has some potential limitations in its decision-making abilities. Moreover, we estimate the preference parameters of GPT and human subjects. We find that the estimated preference parameters of GPT have some minor distinctions from human subjects and show a substantially higher degree of homogeneity.

Taken together, we use tools from revealed preference analysis and experimental economics to study increasingly capable artificial agents. There is growing interest in understanding these agents’ behavior (43) and ongoing debate about their performance compared with humans (44). Even though these artificial agents exhibit surprisingly excellent performance on many cognitive tests, some have expressed concern that such models are still far from achieving human-level understanding of language and semantics and exhibit considerable levels of behavioral bias (45, 46). We contribute to the understanding of the capacities and caveats of LLMs, by demonstrating that LLMs can act as if they are rational decision makers. We observe that rationality decreases when alternative price framing or discrete choice are used. This is line with some studies which show that GPT response can be highly sensitive to contexts (7, 10, 45, 47, 48, 49). Our study also highlights the need for more investigation and refinement of its decision-making mechanisms to ensure reliable and effective decision-making in various domains.

Methods

We examine GPT’s decision-making in different environments using the public OpenAI application programming interface (API). Multiple GPT variants are accessible through this API. For our exercise, we focus on the GPT-3.5-Turbo, which powers ChatGPT and is the most popular, stable, and cost-effective model in the GPT family. We use APIs with Python instead of ChatGPT, since APIs enable us to adjust the parameters of the model and conduct massive experiments in an efficient manner.

Below, we describe how we ask GPT to “make decisions” by introducing the construction of prompts through which GPT returns a text in response to an input text. We then outline multiple variations of our design to examine the robustness of our results.

Design of the Baseline Condition.

Instruct GPT to “make decisions".

Each input prompt in GPT-3.5-turbo includes the specifications of a role (system, assistant, or user) and corresponding contents. We instruct GPT to make decisions in three steps. First, we specify the system’s role as “a human decision maker” and notify the system that “you should use your best judgment to come up with solutions that you like most”. Second, we explain the role of assistant with respect to the decision format: selecting a bundle of commodities from a standard budget line with varying prices, which will be explained in detail later, without requesting responses for any decision. This assists in storing information about the tasks. Afterward, we assign a series of decision-making tasks to the role of user in order to ask GPT to make decisions.

Moreover, to confirm that GPT has understood the instructions, we ask three testing questions, in which we either directly ask it to recall the decision format or ask about the consequence of certain decision scenarios. For each question, we simulate 25 times and GPT constantly provides correct answers. This confirms that GPT understands the decision environment. Detailed prompts to instruct GPT and obtain GPT responses are provided in SI Appendix.

Decision task.

GPT decision tasks follow a typical budgetary experiment, in which a decision maker (DM) is endowed with 100 points to select a bundle of commodities, commodity $A$ and commodity $B$. The prices of the two commodities are based on different exchange rates between points and payoffs. Thus, a decision $i$ obtains a tuple $\left(p^i,x^i\right)$ whereby a DM selects a bundle $\left(x_A^i,x_B^i\right)$ under the prices $\left(p_A^i,p_B^i\right)$. Since measuring rationality requires a collection of such decisions, we include 25 tasks with randomly generated prices (22). After that, we measure the economic rationality of these 25 decisions ${\left(p^i,x^i\right)}_{i=1}^{25}$, based on the extent to which there exist some well-behaved utility functions to rationalize them.

To measure rationality across different preference domains, we vary the commodities in the decision tasks. In the first domain, the two commodities are specified as two contingent securities, in which the decisions capture the DM’s risk preference (21). In the second domain, the two commodities are rewards for today and 1 mo later, which are designed to examine the DM’s time preference (19). In the third domain, the two commodities are payoffs for the DM and another randomly matched subject, and thus the allocation captures the DM’s social preference (18, 25). Finally, in the fourth domain, the two commodities are the amount of meat and tomatoes, which captures the DM’s food preference (23).

We incorporate four preference domains of decisions, each consisting of 25 tasks. To examine GPT’s consistency in behavior, we simulate this process 100 times, resulting in 10,000 tasks for GPT. We refer to these 10,000 tasks, the 100 GPT observations in each preferences domain, as the baseline condition. A detailed description of tasks and parameters for prices are provided in SI Appendix. We set the temperature parameter to 0 (see the explanation below) and keep the default values for all other parameters.

Design of Conditions with Variations.

To enrich our understanding of GPT’s economic rationality, based on the baseline condition, we introduce variations in the temperature and the decision tasks. We also include demographic information in the text of the prompt as explained below.

Variations of temperature.

Temperature plays a critical role in regulating the level of stochasticity and creativity in the responses generated by GPT (50). It ranges from 0 to 1, with a higher number indicating higher randomness. We set the temperature to be 0 in the baseline condition, in which the model gives deterministic answers (7, 9, 10). Some studies on GPT incorporate the variation in temperature to investigate the impact of randomness in creating text (3, 51). Following their practice, we conduct two additional sets of conditions, with the parameter set to be 0.5 and 1.

Variations of decision task.

We design two variations of decision tasks to change the framing of prices and to switch from continuous to discrete choice, respectively. A detailed description is provided in SI Appendix.

In the baseline condition, we use “1 point = X units of commodity” to present price information, which is used in many existing experiments with human subjects (18, 19, 33, 35). In the price framing condition, we change it to “Y points = 1 unit of commodity”, which is an alternative framing used in the experimental literature (52). Since the budget sets remain constant, this allows us to examine whether framing affects the rationality of GPT.

In the baseline condition, the DM makes choices under the continuous budget sets. In the discrete choice condition, we change these to discrete choices: The DM is presented with 11 discrete options chosen from the budget line and is asked to choose one of them rather than directly choose from the budget line (37, 53). Specifically, the third prompt changes to the following: “In this round, there are 11 options, which are $(A_0,B_0)$, $(A_1,B_1)$, ..., and $(A_{10},B_{10})$. Please only tell me your best option in every round”. This allows us to examine whether rationality of GPT is robust to the change from continuous to discrete choice sets.

Response to demographic information.

We also investigate whether the rationality exhibited by GPT varies with the embedded demographic information. To achieve this, we include demographic information which varies in gender, age, education level, and minority group status. We change the input content of the system’s role in GPT to be “I want to you to act as a [demographic] decision maker, ...”. Variations are gender: “female decision maker” versus “male decision maker”; age: “young child decision maker” versus “elderly decision maker”; education: “decision maker with an elementary school education” versus “decision maker with a college education”; and minority: “Asian decision maker” versus “African American decision maker”. By doing so, we can examine whether GPT is responsive to demographic information and whether it performs differently under different individual characteristics. The responsiveness, if any, is relevant to the discussion about algorithm bias (42).

Design of the Human Experiment.

To obtain a better understanding of the behavior of GPT, we also conduct a human subject experiment with identical decision tasks, in which 347 human subjects from a representative US sample are randomly assigned to the baseline, price framing, and discrete choice conditions.^* We keep the experimental instructions between human subjects and GPT as similar as possible. SI Appendix provides the design and instructions of this pre-registered human experiment (AEARCTR-0011750). This experiment was approved by The Institutional Review Board of Finance and Economics Experimental Laboratory in The Wang Yanan Institute of Studies in Economics, Xiamen University (FEEL230701), and all subjects provided informed consent before they started the experiment. SI Appendix, Table S1 shows the demographic characteristics of our human subjects.

Revealed Preference Analysis.

Generalized axiom of revealed preference.

Consider a DM who selects a bundle $x^i\in {\mathbb{R}}_{+}^K$ from a budget line $\{x:p^i·x\le p^i·x^i$, $p^i\in {\mathbb{R}}_{++}^k\}$. A dataset $\mathcal{O}={\left(p^i,x^i\right)}_{i=1}^N$ represents a collection of $N$ decisions made by the DM. We say that a utility function $U:{\mathbb{R}}_{+}^k\to \mathbb{R}$ rationalizes the dataset $\mathcal{O}$ if for every bundle $x^i$, we have:

$$\begin{array}{c}\hfill U(x^i)\ge U(x)\text{for all} x\in \mathbb{R}{+}^K\text{s.t.}{p}^i·x\le p^i·x^i.\end{array}$$

Let $\mathcal{X}={\{x^i\}}_{i=1}^N$ be the set of bundles selected by the DM. We say that $x^i$ is directly revealed to be preferred to $x^j$, denoted by $x^i{\succsim }^{\ast }{x}^j$, if the DM chooses $x^i$ when $x^j\in \mathcal{X}$ is affordable (i.e., $p^i·x^j\le p^i·x^i$). We denote ${\succ }^{\ast }$ as the relation of directly strictly revealed preference. We denote ${\succsim }^{\ast \ast }$ as the transitive closure of ${\succsim }^{\ast }$, which refers to the revealed preferred relation.

A utility function is well behaved if it is continuous, concave, and strictly increasing. Afriat’s theorem (11, 14) states that a dataset $\mathcal{O}$ can be rationalized by a well-behaved utility function if and only if the dataset obeys the generalized axiom of revealed preference (GARP):

$$\begin{array}{c}\hfill \text{for all}{x}^i\text{and}{x}^j,x^i{\succsim }^{\ast \ast }{x}^j\text{implies} x^j{\nsucc }^{\ast }{x}^i.\end{array}$$

Apart from GARP, two closely related notions are the weak axiom of revealed preference (WARP): for all $x^i$ and $x^j$ in a dataset $\mathcal{O}$, $x^i{\succsim }^{\ast }{x}^j\text{implies} x^j{\underset{~}{\nsucc }}^{\ast }{x}^i.$, and the strong axiom of revealed preference (SARP): for all $x^i$ and $x^j$ in a dataset $\mathcal{O}$, $x^i{\succsim }^{\ast \ast }{x}^j\text{implies} x^j{\underset{~}{\nsucc }}^{{}^{\ast \ast }}{x}^i$, which works by exploiting transitivity. In our setting with two goods, checking WARP is equivalent to checking SARP (54). In our discrete setting, (23) shows that a locally non-satiated, strictly monotonic, continuous, and concave utility may violate GARP and demonstrates the need to use the assumption of strong monotonicity (see also ref. 55 for discussions).

Rationality score.

Afriat’s theorem provides a powerful tool for analyzing choice behavior. A popular approach for measuring the departure from rationality is the critical cost efficiency index (CCEI) proposed by Afriat (12). A subject has a CCEI $e\in \left[0,1\right]$ if $e$ is the largest number with a well-behaved $U$ that rationalizes the data set for every $x^i\in \mathcal{X}:$

$$\begin{array}{c}\hfill U(x^i)\ge U(x)\text{for all} x\in {\mathbb{R}}_{+}^K\text{s.t.}{p}^i·x\le e·p^i·x^i.\end{array}$$

A CCEI of 1 indicates passing GARP perfectly. A CCEI less than 1—say, 0.95—indicates that there is a utility function for which the chosen bundle $x^i$ is preferred to any bundle that is cheaper than $x^i$ for more than 5%. Put differently, the CCEI can be viewed as the amount by which a budget constraint must be relaxed in order to remove all violations of GARP, because the DM can achieve her utility targets by spending less money (12, 15). We compute CCEI to obtain a score of rationality for each domain with 25 decisions.

In the revealed preference literature, there are several other indices to score rationality (departure from GARP). These indices include the Houtman–Maks index (HMI) (56), money pump index (MPI) (28), and minimum cost index (MCI) (29). We also compute these indices and report the results as robustness checks.

Structural Estimation for Preferences.

In addition to rationality score, we further examine the underlying preferences using structural estimation.

Risk and time preferences estimation.

In the domain of risk preference, suppose that the DM chooses the contingent security $(x_A,x_B)$, we denote $x_1=max\{x_A,x_B\}$ as the high outcome and $x_2=min\{x_A,x_B\}$ as the low outcome. In the domain of time preference, suppose that the DM chooses the payment schedule $(x_A,x_B)$, we denote $x_1=x_A$ as the payment for today and $x_2=x_B$ as the payment for 1 mo later. For these two domains, we assume that the underlying utility function is given by:

$$\begin{array}{c}\hfill U(x_1,x_2)=\alpha u(x_1)+(1-\alpha )u(x_2),\end{array}$$

where the utility function $u(z)=\left\{\begin{array}{c}\frac{1}{\rho }{z}^{\rho },\rho \le 1(\rho \ne 0)\hfill \\ ln(z),\rho =0\hfill \end{array}\right.$ and $\alpha \in [0,1]$. For risk preference, $\alpha$ captures the decision weight placed on the better outcome (24, 57). When $\alpha =0.5$, we have a standard expected utility function and when $\alpha >0.5$ ($\alpha <0.5$), the better outcome is over(under)-weighted relative to the objective probability of 0.5. The parameter $\rho$ captures risk attitude with the parameter $\theta =1-\rho$ being the Arrow–Pratt measure of relative risk aversion.^† For time preference, $\alpha$ captures the weight placed on the payment today (19). When $\alpha >0.5$ ($\alpha <0.5$), it corresponds to positive (negative) time preference. The parameter $\rho$ is the curvature of the period function. When $\rho =1$, the DM allocates all expenditure to the time period with lower price, and as $\rho$ decreases, the DM is more desired to smooth payments across periods.

Social and food preferences estimation.

Regarding social preference, suppose that the DM chooses the allocation $(x_A,x_B)$, we denote $x_1=x_A$ as the payment for self and $x_2=x_B$ as the payment for the other. In the domain of food preference, assuming that the DM chooses the bundle $(x_A,x_B)$, we denote $x_1=x_A$ as the consumption of meat and $x_2=x_B$ as the consumption of tomatoes. Moreover, we assume that the underlying utility function is a member of the CES family and is given by:

$$\begin{array}{c}\hfill U(x_1,x_2)={[\alpha x_1^{\rho }+(1-\alpha )x_2^{\rho }]}^{\frac{1}{\rho }},\end{array}$$

where $\rho \le 1$ and $\alpha \in [0,1]$. For social preference, the parameter $\alpha$ captures the weight placed on the self’s payment relative to the other’s payment. $\alpha =1$ implies pure selfishness, $\alpha =0.5$ indicates fair-mindedness, and $\alpha =0$ refers to pure altruistic (18, 25). $\rho$ represents the curvature of the indifference curves, which measures equality efficiency orientation. $\rho =1$ indicates that the two payments are perfectly substitute with $U(x_1,x_2)=\alpha x_1+(1-\alpha )x_2$, which means that the DM is efficiency orientated. When $\rho \to 0$, the utility function approaches the Cobb–Douglas utility function, and shares of expenditures to self and to the other are constant. When $\rho \to -\infty$, it approaches to the Leontief utility function $min\{\alpha x_1,(1-\alpha )x_2\}$, which implies that the two payments are perfectly complemented and the DM is equality orientated (18, 25). In a similar vein, the parameter $\alpha$ in the food preference domain captures the weight placed on meat relative to tomatoes and the parameter $\rho$ represents the curvature of the indifference curves as that for social preference. We provide further details on estimation methods in SI Appendix.

Results

In this section, we first present the results from the baseline condition, and then report whether and how the results change with the variations in the decision tasks.

Results from the Baseline Condition.

Rationality score.

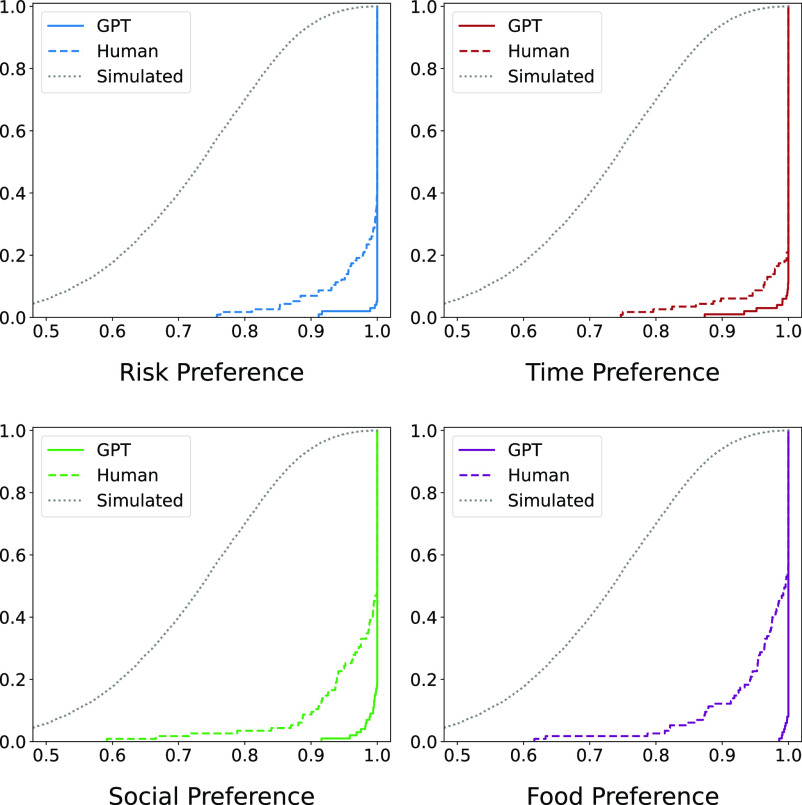
Fig. 1 presents the cumulative distributions of CCEI—the rationality score—for each of the four preference domains. We find that 95, 89, 81, and 92 out of 100 GPT observations for risk, time, social, and food preferences exhibit no violations of GARP; that is, CCEI equals 1. The average CCEI is 0.998, 0.997, 0.997, and 0.999 for risk, time, social, and food preferences, respectively. Meanwhile, in our human experiment, the average CCEI among human subjects is 0.980, 0.985, 0.967, and 0.963 for risk, time, social, and food preferences, respectively. Fig. 1 displays a consistent trend that GPT outperforms human subjects in terms of rationality. In each of the four preference domains, GPT obtains higher CCEI than human subjects ($P<0.01$, two-sided two-sample $t$-tests). In addition, we summarize studies in the revealed preference literature. SI Appendix, Fig. S1 plots CCEI values documented in prior studies, which range from 0.81 to 0.99 with an average of 0.918. Consistently, we find that CCEI of GPT also surpasses those of human subjects in all domains ($P<0.01$, two-sided one-sample t-tests).

Fig. 1.

Cumulative distributions of the CCEI values. This figure consists of four subplots for four preference domains. Each subplot depicts a cumulative distribution function (CDF) plot, which shows the proportion of CCEI values less than or equal to a specific threshold. The light dotted lines represent simulated subjects, the dark dashed lines represent human subjects, and the solid lines represent GPT observations.

To confirm that our chosen parameters have sufficient power to measure rationality, we adopt the test proposed by Bronars (58) as a benchmark, in which we generate simulated subjects by uniformly drawing random allocations along each of the budget lines and examine their rationality. We find that 99.9% of simulated subjects violate GARP. Fig. 1 shows the cumulative distributions of CCEI of simulated subjects, which are lower than both GPT observations and human subjects. We also conduct the power analysis using the predictive success (59), the Selten score (29), as well as bootstrapping from the sample of subjects (18). We show that the chosen parameters have the power to detect rationality violations, in support of the empirical validity of our study (see SI Appendix for more information).

In addition to CCEI, we calculate other indices to measure rationality including the Houtman–Maks index (HMI) (56), money pump index (MPI) (28), and minimum cost index (MCI) (29), and construct cumulative distribution plots for each index of GPT observations, human subjects, and simulated subjects in SI Appendix, Figs. S2–S5. Consistent with the observations based on CCEI, results from these indices show that GPT observations exhibit a high level of rationality across the four preference domains and surpass those of human subjects across all domains ($P<0.1$, two-sided two-sample t-tests).

Downward-sloping demand.

While GPT exhibits a high level of rationality, it is possible that its decisions are simply clustered at the corners or in certain areas. To address such concern, we examine whether GPT behavior respects the property of downward-sloping demand, a fundamental principle in the analysis of consumer behavior whereby the demand for a commodity decreases with its price (21, 25, 60).

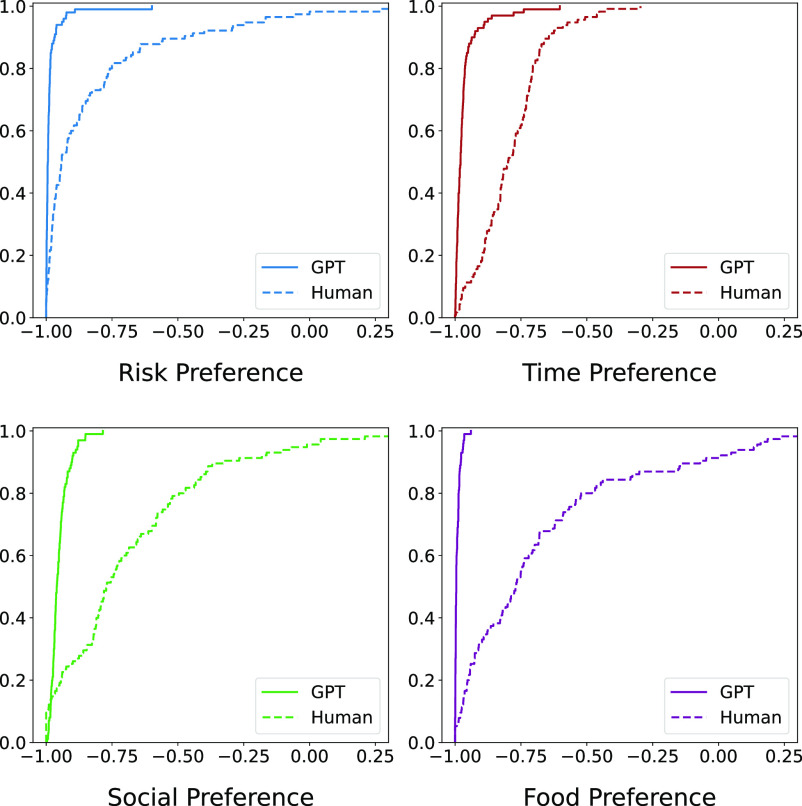
We measure the degree of compliance with downward-sloping demand for GPT observations and human subjects. This principle requires that when the relative price of a commodity increases, the consumer should not increase its consumption. More specifically, we measure whether each DM’s decisions respect this principle by calculating the Spearman’s correlation coefficient of $ln(x_A/x_B)$ and $ln(p_A/p_B)$ (60). A negative correlation indicates an appropriate response to price fluctuations, and zero or positive correlation indicates no response or irregular response to price changes. Note that $ln(x_A/x_B)$ is not defined in the corners. We adjust corner choices by a small constant, 0.1% of the budget, in each choice (60). We plot the cumulative distribution of the Spearman’s correlation coefficients of $ln(x_A/x_B)$ and $ln(p_A/p_B)$ as a proxy for the degree of downward-sloping demand for each of the four preference domains in Fig. 2.

Fig. 2.

Cumulative distributions of the spearman’s correlation coefficient of $ln(x_A/x_B)$ and $ln(p_A/p_B)$. This figure contains four subplots for four preference domains. The dashed (solid) lines represent human subjects (GPT observations).

For GPT observations, the coefficients for risk, time, social, and food preferences have a mean of $-$0.984, $-$0.966, $-$0.951, and $-$0.992, while these are $-$0.826, $-$0.788, $-$0.681, and $-$0.673 for human subjects, respectively. Overall, GPT is more responsive to price changes than human subjects in each preference domain ($P<0.01$, two-sided two-sample t-tests). Fig. 2 further illustrates that GPT observations always have negative Spearman’s correlation coefficients, while human has a lower proportion having negative Spearman’s correlation coefficients (96.1% on average). This strengthens our findings based on the rationality score and suggests that GPT is more capable of making reasonable responses to the changes in prices than human subjects.

In addition, for each GPT observation, SI Appendix, Figs. S6–S9 provide comprehensive visual representations by showing scatter diagrams and fitted lines of the shares of quantities $x_A/(x_A+x_B)$ and the log-price ratio $ln(p_A/p_B)$.

Preference estimation.

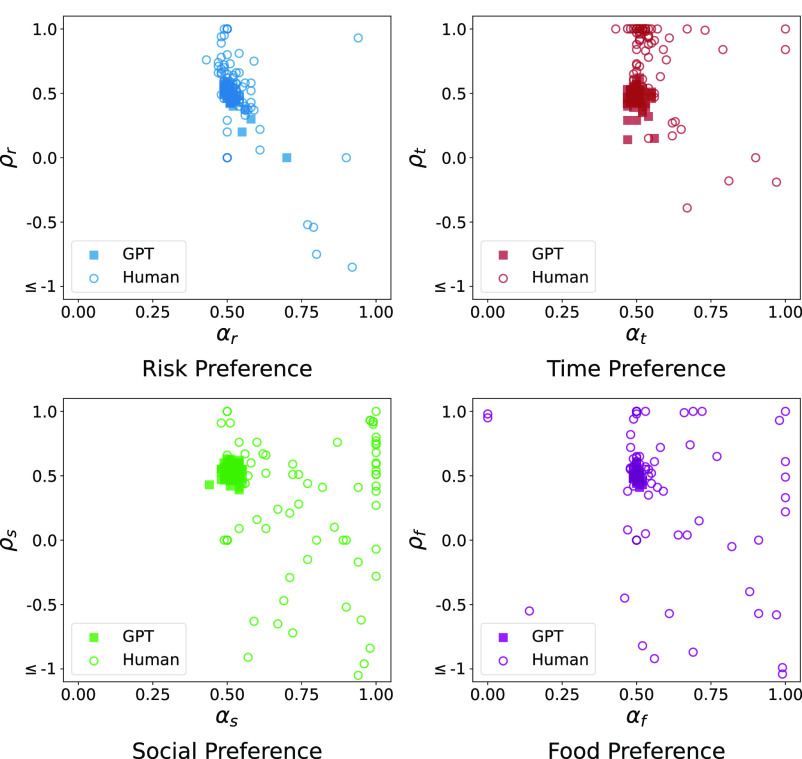
Since choices of GPT and human subjects are mostly consistent with well-behaved utility functions, we proceed to estimate the underlying risk, time, social, and food preferences.^‡ In total, we have eight estimated parameters: decision weight of the better outcome (${\alpha }_r$) and utility curvature (${\rho }_r$) for risk preference, weight of today (${\alpha }_t$) and utility curvature (${\rho }_t$) for time preference, weight for self’s payment (${\alpha }_s$) and utility curvature (${\rho }_s$) for social preference, weight for meat (${\alpha }_f$), and utility curvature (${\rho }_f$) for food preference. We first estimate the preference parameters at the aggregate level by pooling all responses of GPT observations and human subjects, respectively (SI Appendix, Table S2). Results show that, compared to human subjects, GPT is closer to an expect-utility maximizer (${\alpha }_r$: 0.618 vs. 0.508 for Human vs. GPT) and has a more linear utility curve (${\rho }_r$: 0.335 vs. 0.488) in risk preference; is more patient (${\alpha }_t$: 0.513 vs. 0.504) and has a less linear utility curve (${\rho }_t$: 0.981 vs. 0.466) in time preference; is more other-regarding (${\alpha }_s$: 0.735 vs. 0.512) and more efficiency-orientated (${\rho }_s$: 0.330 vs. 0.520) in social preference; and is less fond of meat (${\alpha }_f$: 0.583 vs. 0.501) and more efficiency-orientated (${\rho }_f$: 0.386 vs. 0.491) in food preference. Similar patterns can be observed in the individual-level estimations, in which we estimate preference parameters for each GPT decision maker and human subject, as shown in Fig. 3 and SI Appendix, Table S3. Moreover, the scatter plots of human subjects are more dispersed, which suggests a significantly higher level of preference heterogeneity among human subjects than GPT observations.

Fig. 3.

Scatter plots of estimated parameters. This figure contains four subplots for four preference domains. Each hollow circle (solid square) points represent a human subject (a GPT observation).

Results from the Conditions with Variations.

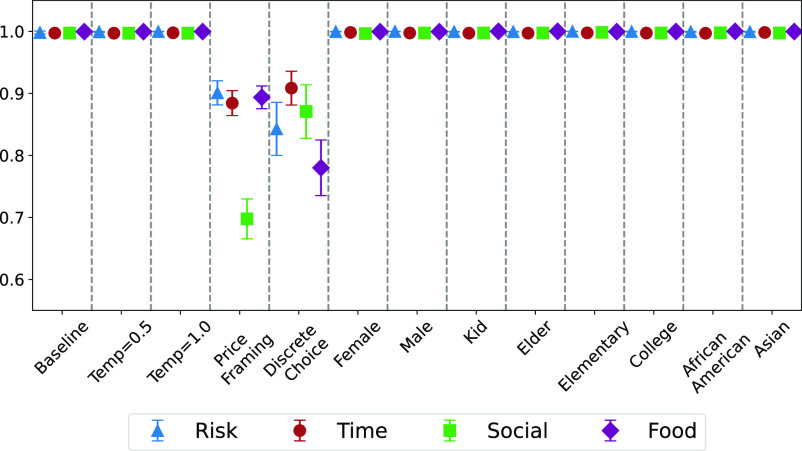
We examine variations in the temperature, decision tasks, and demographic information. Fig. 4 presents the mean CCEI values and 95% CIs across variations, and SI Appendix, Fig. S24 shows the mean Spearman’s correlation coefficients of $ln(x_A/x_B)$ and $ln(p_A/p_B)$ and their 95% CIs. We report these results in detail below.

Fig. 4.

Mean CCEI values of GPT observations across different variations. This figure displays the average CCEI values and 95% CIs for GPT observations under different conditions: baseline, temperature of 0.5, temperature of 1, price framing, and discrete choices, and various demographic settings.

Insensitive to variations in temperature.

When the temperature increases from 0 to 0.5 and 1, there is a higher number of invalid responses, namely, GPT does not provide an answer to the specified question (invalid response rate is 4.7% for temperature of 0.5 and 9.8% for temperature of 1). Therefore, we analyze the data conditional on those providing valid answers. We find that as the randomness increases, the level of rationality is similar to that in the baseline condition (Fig. 4). For each temperature and each preference domain, we plot the cumulative distributions of the CCEI values of GPT observations and simulated subjects for Bronars’ test in SI Appendix, Fig. S10 and the cumulative distributions of the Spearman’s correlation coefficients in SI Appendix, Fig. S11. These findings suggest that randomness increases the stochasticity and creativity in language presentations of GPT, but not the rationality score.

There are no significant differences for the estimated Spearman’s correlation coefficients of $ln(x_A/x_B)$ and $ln(p_A/p_B)$ between the baseline and the higher temperature (SI Appendix, Fig. S24) at the 10% level (two-sided two-sample t-tests). Similarly, the mean of estimated preference parameters is statistically indifferent to changes in temperature. However, the SDs of some parameters increase with temperature (${\rho }_r$, ${\rho }_t$, ${\rho }_s$, ${\rho }_f$: $P<0.01$, two-sample Levene tests), which suggests that high temperature may generate greater heterogeneity in the behavior of GPT.

Sensitive to variation in the decision tasks.

First, we compare the baseline and the price framing conditions. Changing the price framing significantly reduces GPT’s rationality level in all four tasks (Fig. 4). Remarkably, the average CCEI for risk preference declines to 0.901, with 34% exhibiting a CCEI below 0.9. These values are 0.884 (48%), 0.698 (88%), and 0.894 (49%) for time, social, and food preferences, respectively.^§ In each preference domain, CCEI values are significantly higher in the baseline condition than in the price framing condition ($P<0.01$, two-sided two-sample t-tests). Moreover, the downward-sloping demand property is impaired under the alternative price framing, with the key Spearman’s correlation coefficients being $-$0.053, $-$0.116, 0.267, and $-$0.499 for risk, time, social, and food preferences, respectively (SI Appendix, Fig. S24). SI Appendix, Figs. S13–S16 show the disordered responses of GPT observations to price changes in the price framing condition, which appear to be flatter compared to those in the baseline condition.

In SI Appendix, Figs. S17 and S18, we display the CDFs of CCEI (Spearman’s correlation coefficients) in the four conditions: baseline and price framing conditions in both the GPT experiment and the human experiment. We find that the alternative price framing also reduces the rationality level and the downward-sloping demand property in the human subjects experiment ($P<0.05$, two-sided two-sample t-tests in risk and time preferences). However, the figures suggest that these reductions are larger in the GPT experiment than in the human experiment, which is further verified in OLS regression analyses (SI Appendix, Table S4).

Second, we compare the baseline and the discrete choice conditions. When we present GPT with a set of 11 options, we also observe a decrease in rationality levels for discrete choices of GPT observations for all four tasks in Fig. 4 (risk: 0.998 vs. 0.843, $P<0.01$; time: 0.997 vs. 0.908, $P<0.01$; social: 0.997 vs. 0.871, $P<0.01$; food: 0.999 vs. 0.780, $P<0.01$, two-sided two-sample t-tests). Additionally, 51%, 32%, 33%, and 55% of GPT observations demonstrate a CCEI below 0.9 in risk, time, social, and food preferences, respectively. SI Appendix, Figs. S19–S22 show the demand curves of GPT observations, which exhibit significantly more corner solutions. Consistently, the Spearman’s correlation coefficients are $-$0.589, $-$0.497, $-$0.519, and $-$0.533 for risk, time, social, and food preferences (SI Appendix, Fig. S24; $P<0.01$ when compared to the baseline condition, two-sided two-sample t-tests). These suggest that GPT is less responsive to price changes under discrete choices than continuous choices.

SI Appendix, Figs. S23 and S24 shows the CDFs of the CCEI (Spearman’s correlation coefficients) in baseline and discrete choice conditions in the GPT experiment and human experiment. Human subjects’ rationality level and the downward-sloping demand property reduce in the discrete setting, compared to the baseline condition ($P<0.05$, two-sided two-sample t-tests in risk and time preferences). As shown in the figures, these reductions are larger in the GPT experiment than in the human experiment. We also verify this observation through OLS regression analyses (SI Appendix, Table S4). These results suggest that GPT’s decision-making is more significantly affected by both the framing of prices and discrete choices than human subjects.

Insensitive to demographic information.

Comparing the baseline condition and variations in demographics in the GPT experiment, we find that CCEI values, Spearman’s correlation coefficients of $ln(x_A/x_B)$ and $ln(p_A/p_B)$, and estimated preference parameters are all insensitive to variations of demographic factors embedded in the prompts to request responses from GPT (Fig. 4, SI Appendix, Fig. S24 and Tables S2 and S3).

These are in contrast to results of our human experiment (SI Appendix, Tables S5 and S6) and prior studies where rationality score and preference have been shown to differ across demographic groups (22, 28, 61). The fact that GPT’s decision-making process remains consistent across demographic variables suggests that GPT does not exhibit algorithmic bias in terms of decision-making quality, which provides a measure of reassurance regarding its fairness and consistency across diverse user groups.

Discussion

We conduct a study to assess the rationality of GPT, a popular large language model, using revealed preference analysis. Our findings demonstrate that GPT is able to display a high level of rationality in decision-making related to risk, time, social, and food preferences. We also observe that increasing the randomness of GPT does not significantly impact its performance. Furthermore, our analysis reveals that the level of rationality of GPT remains constant across different demographic characteristics, which indicates that it does not exhibit an algorithm bias. However, we observe a significant drop in rationality when we use a less standard presentation of prices or change the choice set from continuous to discrete. This suggests that GPT may have limitations in terms of sensitivity to contexts and frames.

Our study contributes to the ongoing discussions of the performance of GPT in various domains; these include reasoning, logic, math, language processing, and identifying factual errors (45). In addition to cognitive techniques and practical skills, some researchers have explored whether GPT can exhibit human-like decision-making abilities or perceive others’ thoughts (6, 10). Our study adds to these parallel studies by subjecting GPT to traditional decision-making tasks and employing a set of measures to systematically describe its behavior. Our work aligns with recent calls to study machine behavior to “reap their benefits and minimize their harms” (43). By providing insights into GPT’s decision-making capacity, we can better understand how to optimize its performance and address potential limitations.

Our study is situated within the growing literature on AI-based decision support tools. Many researchers have explored the usefulness of leveraging AI in various decision-making domains, such as bail decisions (62); clinical diagnosis (63); work arrangements (64); stock price forecasts (65); job recruitment (66); product or content consumption (67, 68); and mathematics development (69). Unlike these algorithms, which require data input and training, GPT is a language-based model that provides a direct question-and-answer service for normal users. Given its high level of rationality in decision-making across various domains, our study proves the potential of GPT as a general AI-based decision-support tool. The user-friendly interface and versatility of GPT render it a promising option for individuals and organizations seeking easy-to-use AI-based advice.

Our paper makes contributions to the literature on rationality and experimental methods. First, we demonstrate the effectiveness of experimental economics methods in studying choice behavior of artificial intelligence (43), which adds earlier studies of children (23, 30), monkeys (31), rats, and pigeons (32). Second, our work highlights the potential of large language models like GPT to streamline experimental research and yield new data and insights (10). Finally, studying the choice behavior of artificial intelligence can provide an important benchmark for understanding natural intelligence. For example, our understanding of how LLMs make decisions could help reveal general principles that govern both language intelligence and decision intelligence (70). By synthesizing insights from these various domains, our paper offers a unique perspective on the nature of rationality and broadens the methods that can be used to study it.

As an initial assessment of the economic rationality of GPT, our study has several limitations. First, our study examines the choice behavior of GPT but does not explore the mechanisms that underlie our observations. For example, we find that GPT responses are highly sensitive to contexts and frames. This may be due to the reflection of biases presented in the existing data (71, 72), the insufficient training of texts of the alternative contexts and frames (3, 5), or the tendency for LLMs to exploit spurious correlations or statistical irregularities in the data set under dissimilar tasks (73). In particular, ref. 74 suggests that a significant source of LLMs bias originates from a corpus-based heuristic using the relative frequencies of words. The “50-50 split” or “equal split” are high-frequency texts in allocation settings, and GPT can adapt this corpus-based heuristic and exhibit the tendency to choose the midpoint under an “unfamiliar” task with the alternative price framework. Similarly, “all or nothing” can be high-frequency texts under the presentation of options context, so GPT exhibits the tendency to choose the first or last option under an “unfamiliar” discrete choice condition. Recent studies have documented similar patterns in different environments (7, 10, 48, 49, 75).

In addition, our study reveals that demographic factors do not significantly impact GPT’s rationality or estimated preference parameters. This contrasts with the majority of the empirical literature, including our human subject experiment, where demographic factors often play a significant role. The lack of responsiveness to demographics aligns with the concept of hyperaccuracy distortion (76), which refers to the distortion resulting from the extensive efforts to align LLMs with human ethics such as the censorship of demographic information to reduce and prevent problematic outputs. In conclusion, with some speculative conjectures, we leave it to future studies to explore the mechanisms that underlie GPT’s choice behavior and open the black-box of this technology.

Second, we focus on economic rationality as defined by revealed preference analysis, whereas rationality is often defined more broadly in the literature to include various decision rules and heuristics (40, 77, 78). Third, we use a simple experimental environment with only two commodities to present budgetary decisions. However, studying rationality in more realistic settings, such as shopping behavior in a supermarket and portfolio choices in the financial markets would be more challenging yet important. Our study shows that economic rationality can emerge in GPT when decision contexts are simple and framed in specific ways. Future research is needed to investigate the broader applications of artificial intelligent agents as they continue to evolve.

Materials and Methods

Preference Utility Estimation.

Once the DM’s CCEI is sufficiently to justify treating the data as generated utility functions of well-behaved behavior, another interest is to estimate the preference parameters of the DM. Our estimations will be made for each DM separately on the assumption of the underlying utility function commonly employed found in the prior literature to capture risk, time, social, and food preferences.

Risk preference.

For the DM’s choice of contingent securities $x:\left(x_A,x_B\right)$, referring to ref. 24, we assume $x_1$ is the better outcome, $x_1=max\{x_A,x_B\}$, and $x_2$ is the worse outcome, $x_2=min\{x_A,x_B\}$. We estimate the risk preference of the DM by a functional form of disappointment aversion (DA) introduced by ref. 57:

$$U(x_1,x_2)=\alpha u(x_1)+(1-\alpha )u(x_2),$$

where $u(z)$ is the CRRA utility function:

$$u(z)=\left\{\begin{array}{cc}\frac{1}{\rho }{z}^{\rho }\hfill & \rho \le 1(\rho \ne 0)\hfill \\ ln(z)\hfill & \rho =0.\hfill \end{array}\right.$$

The parameter $\alpha \in [0,1]$ is the weight placed on the better outcome. For $\alpha >0.5$ ($\alpha <0.5$), the better (worse) outcome is over weighted relative to the objective probability (of 0.5). If $\alpha =0.5$, we have a standard expected utility decision maker. The parameter $\theta =1-\rho \ge 0$ is the Arrow–Pratt measure of relative risk aversion.

Time preference.

Following the method of ref. 19, we use a time separable period utility function to estimate the DM’s time preference from intertemporal decisions of the payoff between today and 1 mo later $x:(x_A,x_B)$, with the assumption that background income is zero:

$$U(x_A,x_B)=\alpha u(x_A)+(1-\alpha )u(x_B),$$

where $u(z)$ is the period utility function:

$$u(z)=\left\{\begin{array}{cc}\frac{1}{\rho }{z}^{\rho }\hfill & \rho \le 1(\rho \ne 0)\hfill \\ ln(z)\hfill & \rho =0.\hfill \end{array}\right.$$

The parameter $\alpha \in [0,1]$ is the weight placed on the today. For $\alpha >0.5$ ($\alpha <0.5$), today is over weighted relative to 1 mo later. The parameter $\rho \le 1$ is the curvature of the period utility function.

Social preference.

For capturing DM’s social preferences in choice $x:\left(x_A,x_B\right)$, the payoff of self and the other, following the method of refs. 18 and 25, we assume that $U(x_A,x_B)$ is a member of the CES family. It is given by

$$U(x_A,x_B)={\left[\alpha {\left(x_A\right)}^{\rho }+(1-\alpha ){\left(x_B\right)}^{\rho }\right]}^{1/\rho }.$$

The CES specification is very flexible, spanning a range of well-behaved utility. The parameter $\alpha \in \left[0,1\right]$ represents the relative weight on the payoff for the self of the DM. $\alpha =0.5$ indicates fair-mindedness, whereas $\alpha =1$ indicates pure selfishness and $\alpha =0$ indicates pure selflessness. The parameter $\rho \le 1$ represents the curvature of the indifference curves (equality-efficiency tradeoffs, an important implication in social preference). $\rho \to 0$ indicates a Cobb–Douglas function. When $\rho \to 1$, the utility approaches perfect substitutes: $\alpha x_A+$$(1-\alpha )x_B$; when $\rho \to -\infty$, the utility approaches Leontief: $min\{\alpha x_A,(1-\alpha )x_B\}$. $\rho$ represents “equality–efficiency” trade offs. $\rho >0$ ($\rho <0$) indicates toward efficiency (increasing total payoffs) because the expenditure decreases when the relative price increases.

Food preference.

For DM’s choice $x:(x_A,x_B)$ in food preference, the quantities of meat, and the quantities of tomatoes, we assume that $U(x_A,x_B)$ is a member of the CES family. It is given by:

$$U(x_A,x_B)={\left[\alpha {\left(x_A\right)}^{\rho }+(1-\alpha ){\left(x_B\right)}^{\rho }\right]}^{1/\rho }.$$

The parameter $\alpha \in \left[0,1\right]$ represents the relative weight on the utility of meat. The parameter $\rho \le 1$ represents the curvature of the indifference curves. $\rho \to 0$ indicates a Cobb–Douglas function, which implies that expenditures on meat and tomatoes are equal to fractions $\alpha$ and $1-\alpha$, respectively. $\rho >0$ ($\rho <0$) indicates a decrease in the relative price of meat and tomatoes ($p_A/p_B$) lowers (raises) the fraction of tomatoes in total expenditure.

Econometric specification.

For the four utility functions above, the first-order conditions at the optimal choice $(x_A,x_B)$, given $(p_A,p_B)$^¶, can be written as follows:

$$ln(x_A/x_B)=\frac{1}{\rho -1}\left[ln(p_A/p_B)+ln\frac{1-\alpha }{\alpha }\right].$$

Because $ln(x_1/x_2)$ is not well defined in corner solutions, referring to the method of refs. 25, 38, and 39, the demand function is given by:

$$x_A=\left[\frac{g}{{(p_A/p_B)}^r+g}\right]\frac{E}{p_A},$$

where $E$ is the expenditure, $r=\rho /(1-\rho )$, and $g={\left[\alpha /(1-\alpha )\right]}^{1/(1-\rho )}$. This generates the following econometric specification: $\frac{p_A{x}_A}{E}=\frac{g}{{(p_A/p_B)}^r+g}$. Note again that expenditure shares are bounded between zero and one. We can generate estimates of $g$ and $r$ using nonlinear tobit maximum likelihood and use this to infer the values of the underlying $\alpha$ and $\rho$ for four preference domains.

Supplementary Material

Appendix 01 (PDF)

Data, Materials, and Software Availability

Code and data for the current study are publicly available through https://www.dropbox.com/scl/fo/572ptz57vjis5cqkczj9l/h?rlkey=hhpsgdb6ghdzsrvj35mafdnwc&dl=0 (79).