Abstract
We have developed the CADLIVE (Computer-Aided Design of LIVing systEms) Simulator that provided a rule-based automatic way to convert biochemical network maps into dynamic models, which enables simulating their dynamics without going through all of the reactions down to the details of exact kinetic parameters. The simulator supports the biochemical reaction maps that are generated by the previously developed GUI editor. Notice that the part of the GUI editor had been previously published, but, as yet, not the simulator. To directly link biochemical network maps to dynamic simulation, we have created the strategy of three layers and two stages with the efficient conversion rules in an XML representation. This strategy divides a molecular network into three layers, i.e., gene, protein, and metabolic layers, and partitions the conversion process into two stages. Once a biochemical map is provided, CADLIVE automatically builds a mathematical model, thereby facilitating one to simulate and analyze it. In order to demonstrate the feasibility of CADLIVE, we analyzed the Escherichia coli nitrogen-assimilation system (64 equations with 64 variables) that consists of multiple and complicated negative and positive feedback loops. CADLIVE predicted that the glnK gene is responsible for hysteresis or reversibility of nitrogen-related (Ntr) gene expression with respect to the ammonia concentration, supporting the experimental observation of the runaway expression of the Ntr genes.
A challenge created by systems biology is to understand how all of the cellular molecules work in concert as a living system (Kitano 2002). An attempt to clarify the dynamics within cells not only predicts the consequences for mutations, alterations in available metabolites, or environmental changes, but also reveals some design principles underlying their molecular architectures, e.g., a general mechanism of how cells acquire complex systems showing robust properties to survive strict environmental variations (Barkai and Leibler 1997; Yi et al. 2000; Tyson et al. 2003). Major objectives of systems biology are to build molecular-interaction networks and to predict or understand the dynamics at the molecular-interaction level, where mathematical simulation plays an important role. These efforts contribute to advances in genetic engineering for rationally designing useful organisms (Becskei and Serrano 1999; Gardner et al. 2000; McAdams and Arkin 2000; Atkinson et al. 2003).
Advances in biological, analytical, and computational technologies contribute to developing a mathematical model to explore the dynamics of complex biological systems. Various levels of biochemical details, from very abstract models such as Boolean networks (Kauffman 1993; Bhattacharjya and Liang 1996) to very concrete models that include the full biochemical interactions with their exact kinetic parameters (Bhalla and Lyengar 1999; Kholodenko et al. 1999; Chen et al. 2000; Hasty et al. 2001; Schoeberl et al. 2002; Hatakeyama et al. 2003), have been proposed to understand molecular architectures and their dynamic features. The abstract model can deal with a large-scale network, analyzing the dynamics to the point where one can predict the attractor of a molecular network and know enough about the network architecture to connect these networks to attractors of choice, but there is a doubt whether this model truly represents biological reality. The concrete model closely fits the biological reality and may carry more weight with experimental biologists, but its complexity requires decades of research to obtain the exact kinetic parameters of detailed molecular mechanisms in vivo, resulting in restricting the application of the model.
Generally, there are two approaches to build molecular systems, reverse engineering and forward engineering. The very abstract model generally uses reverse engineering, whereas the concrete model adopts forward engineering. Reverse engineering typically requires the use of simplistic parametric models of a large-scale network, e.g., Bayesian networks and Boolean networks, the parameters of which are adjusted to fit real-world data (D'Haeseleer et al. 2000; Csete and Doyle 2002; Dougherty et al. 2002; Hartemink et al. 2002; Gardner et al. 2003). In forward engineering, a dynamic model is built based on detailed molecular interactions with exact kinetic parameters to achieve biological reality. This requires extensive knowledge of the system being studied.
Ideally, we would like to gain access to the activities of all-important molecular species including complexes and modified molecules. There is a strong need for methods that can handle concrete and complicated molecular systems at an intermediate level without going all the way down to exact biochemical reactions (D'Haeseleer et al. 2000). A solution for such a requirement is to combine forward engineering and reverse engineering. Forward engineering builds mathematical models with kinetic-related parameters from biochemical maps, and reverse engineering explores the kinetic parameters to fit to experimental data. From this viewpoint, the model would focus on capturing the intrinsic architecture of molecular networks rather than their detailed kinetics, where gene regulatory and metabolic network maps should play a central role in simulating their dynamics. The research of “biochemical maps to dynamics” is a promising field. However, there has been a big gap between the two, because the gene regulatory and metabolic networks within a cell appear too complicated and heterogeneous to automatically convert into plain mathematical models. Thus, most of the previous simulators begin with the description of mathematical equations with the assistance of GUI, and they have not supported the automatic conversion of biochemical network maps into dynamic models (Mendes 1993; Goryanin et al. 1999; Tomita et al. 1999; Hucka et al. 2002; Sauro et al. 2003).
In order to directly link biochemical networks to dynamic models, we have developed the CADLIVE (Computer-Aided Design of LIVing systEms) Simulator that provided a rule-based automatic way to convert biochemical network maps into dynamic models with mechanism-related parameters, supporting the biochemical maps generated by the previously developed GUI editor (Kurata et al. 2003). The aim of CADLIVE is to simulate qualitative features of dynamic models, not to reproduce the details of exact behaviors. To efficiently convert the maps into dynamic models, the technology of three layers and two stages has been originally developed with the elaborately designed rules in an XML representation, which divides a biochemical network into three layers, i.e., gene, protein, and metabolic layers, and partitions the conversion process into two stages. The simulation consists of forward and reverse engineering; forward engineering converts gene regulatory and metabolic networks into dynamic models, and reverse engineering explores the kinetic parameters of the model to fit to experimental data. Once a biochemical map is provided, CADLIVE automatically builds a dynamic model, thereby facilitating simulation and analysis. In order to demonstrate the feasibility of the CADLIVE Simulator, we analyzed the Escherichia coli nitrogen-assimilation system that consists of multiple and complicated negative and positive feedback loops, where the activity and synthesis of glutamine synthetase is regulated to adapt to the great changes in the ammonia concentration. CADLIVE predicted that the glnK gene is responsible for hysteresis or reversibility of nitrogen-related (Ntr) gene expression with respect to ammonia concentration, supporting the experimental observation of the runaway expression of the Ntr genes (Blauwkamp and Ninfa 2002b).
Methods
Regulator-reaction equations
In order to construct gene regulatory and metabolic networks, the CADLIVE Simulator uses a regulator-reaction equation, Regulator (Modifier) -0 Reactants → Products, which clearly shows the relationship between regulators and their regulated reactions (Kurata et al. 2003). Systems Biology Markup Language (SBML) level 2 supports this formula (Hucka et al. 2002). The symbols indicate a catalyst (-0), an activator (->>), and an inhibitor (-II). Reversible and irreversible reactions are described by the arrows (↔) or (→), respectively.
Forward engineering based on three layers and two stages
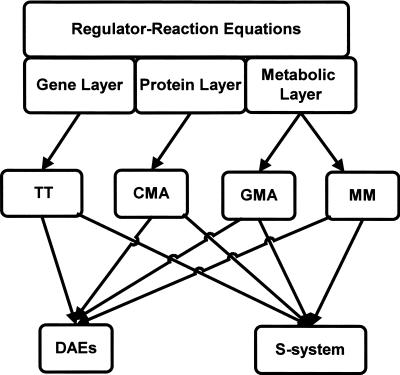
As shown in Figure 1 and Table 1, we classified biochemical reactions into three layers, i.e., gene, protein, and metabolic layers, and divided the conversion process into two stages. In the conversion of metabolic networks into General Mass Action (GMA) or simplified Michaelis-Menten equations (MM), the concentrations of enzyme–metabolite complexes are cancelled, because they are far less than those of metabolites in vivo. In the protein layer, since most proteins function in a complex or modified form, it is not practical to neglect the concentrations of complexes or modified proteins. Thus, Conventional Mass Action (CMA) is used to describe detailed protein signal-transduction pathways. In the gene layer, since various molecules such as proteins, amino acids, nucleic acids, and RNAs act in concert for transcription and translation, it is difficult to mathematically describe such reactions based on their complicated molecular mechanism. The use of ordinary transcription and translation equations (TT) is a rational choice for taking in gene expression within a cell. The combination of CMA and TT is able to describe gene regulatory networks. Problems for CMA are that its differential equations are stiff, due to the huge differences in values of kinetic parameters and molecular concentrations, and that many kinetic parameters are required.
Figure 1.
Strategy for three layers and two stages. A flow of the mathematical conversion according to three layers and two stages. The reactions are classified into three layers, i.e., gene, protein, and metabolic layers, and the conversion process is divided into two stages. At the first stage, both gene and protein networks are converted into the ordinary transcription and translation equations (TT), Conventional Mass Action (CMA), respectively, whereas the metabolic network uses General Mass Action (GMA) or simplified Michaelis-Menten equations (MM). At the second stage, such ordinary differential equations are further converted into differential and algebraic equations (DAEs) or S-system (Supplemental Method 1).
Table 1.
Simple examples of conversion from regulator-reaction equations to mathematical equations

(Km) Michaelis constant, (Vmax) maximum rate constant, (k) rate constant, (g1, g2) power coefficients, (ka) association rate constant, (ks) dissociation rate constant, (kx) conversion rate constant, (km) transcription rate constant, (kp) translation rate constant. The square brackets [] indicate the molar concentration and the suffix 0 indicates the total concentration. Actually, since biochemical networks include various complicated reactions, such as transcription regulations with multiple activators and suppressors, formation/degradation of multicomponent molecules, and complex modifications, the detailed rules must be created (Supplemental Method 1).
At the second stage, in order to overcome such problems, we applied the Two-Phase Partition (TPP) method to the conversion of CMA with TT to differential and algebraic equations (DAEs), thereby reducing not only the stiffness, but also decreasing the number of kinetic parameters (Kurata and Taira 2000). The TPP method divides the kinetics of molecular interactions into two phases, the molecular-binding phase and the reaction phase, assuming association/dissociation rates between proteins to be quite fast compared with the rates of synthesis/degradation of mRNAs or proteins. This is a commonly used assumption in biological systems. Consequently, TPP substitutes algebraic equations for stiff differential equations. In addition to DAEs, CADLIVE is able to convert the ordinary differential equations of TT, CMA, GMA, and MM into S-system at the steady state, which is useful for analyzing the sensitivity and stability in symbolic form.
The strategy of three layers and two stages is performed according to the elaborately defined rules that are implemented in XML as the “sanac” (synthesis and analysis of networks architecture in computer) representation. This format is designed by using the framework of Systems Biology Markup Language (SBML) (Hucka et al. 2002). The use of these rules enables the conversion of various complicated reactions, such as transcription regulations with multiple activators and suppressors, formation/degradation of multicomponent molecules, and complex modifications.
Reverse engineering for exploring kinetic parameters
In order to build dynamic models, it is required to fit the kinetic parameters to experimental data. The problem is that the values of most kinetic parameters remain to be measured because of experimental difficulties. Instead of measuring kinetic parameters one by one, we estimate the values for unmeasured parameters so that the dynamic simulation agrees with experimental data. In order to adjust the kinetic parameters to the experimental data, we used a search by genetic algorithms (GAs), where a fitness function is defined to characterize how correctly the estimated values of the parameters explain experimental data. First, a random search, which gives the kinetic parameters random values within specific regions, is used as the initial screening to find the kinetic parameter sets that provide a relatively high fitness. The obtained parameters are used as the initial individuals for the search by GAs. The GA is known as one of the algorithms that can seek out the global minimum, based on the heuristic assumptions that best solutions will be found in the regions of the parameter space that contains a high proportion of the solutions showing a high fitness. The use of the genetic operators of selection, crossover, and mutation explores the parameter spaces efficiently.
CADLIVE simulator
Overview
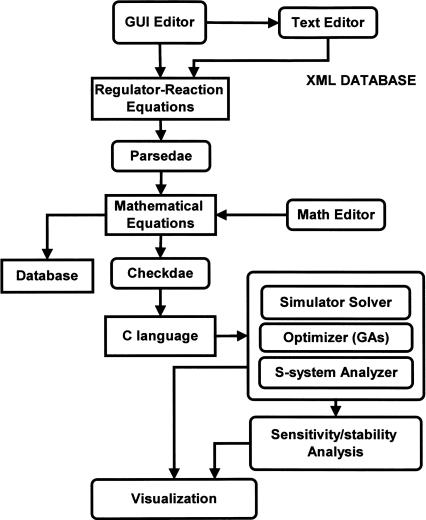
Figure 2 shows the process flow of the CADLIVE Simulator. The details are described in Supplemental Method 1. The simulator consists of the editors that describe regulator-reaction models, the parser (parsedae) that converts the regulator-reaction equations into a mathematical model, the converter (checkdae) that changes the mathematical model into the subroutine of the C programming language, the simulator engine (solver), the optimizer for estimating the values of biochemical parameters so as to reproduce experimental behaviors, the analyzer that carries out sensitivity/stability analysis and S-system analysis, the visualizer that draws simulated results, and the database for storing mathematical models.
Figure 2.
A process flow of the conversion of a biochemical network map to mathematical equations in the CADLIVE Simulator. The parsedae module parses the regulator-reaction equations that are described by the GUI Editor, converting into mathematical equations (checkdae file). The checkdae module converts the mathematical equations into the user functions available for the C language and the parameter file that is used for input of the initial concentrations of the species, the kinetic parameters, and the control parameters for the simulator. These functions and parameters are compiled to link to the simulation engine. In the checkdae file, one is allowed to edit mathematical models directly, because the checkdae file is written in the text format that consists of the variable declaration part and the equation part. The simulator supports dynamic simulation, steady state analysis, S-system analysis, and optimization of kinetic parameters.
Editor and notation of biochemical networks
We developed the editors to construct the regulator-reaction model for a concrete biochemical network according to the established rules that are implemented in “sanac” format. By registering the species and reactions with their attributes, we construct regulator-reaction equations. The CADLIVE Simulator has two kinds of editors. One is a GUI editor, and the other a text editor. The editor consists of two tables, i.e., the regulatorreaction equation table and the species table (see CADLIVE Web page) (Kurata et al. 2003).
Parsedae module
Based on three layers and two stages, the parsedae module parses and converts the “sanac” file for regulator-reaction equations with the various elements and attributes into mathematical models (a checkdae file) according to the selected mathematical formulas. In this module, the gene and protein layers are converted into CMA, including TT equations. The choice of the TPP method converts the regulator-reaction equations into DAEs through CMA, where the two conversion processes are carried out sequentially. The metabolic layers are converted into GMA or MM equations. The rules provided by the elements and attributes in XML enable computers to parse and convert regulator-reaction equations into a mathematical model accurately and efficiently. The parsedae module generates the checkdae file that describes mathematical models, TT, CMA, GMA, MM, and DAEs. Through the interface of php, one is allowed to edit mathematical models directly according to the instruction of CADLIVE, because the checkdae file is written in the text format that consists of the variable declaration part and the equation part. In other words, users can write their own mathematical models in the checkdae file. This greatly facilitates the flexibility for editing a mathematical model.
Checkdae module
The checkdae module converts a mathematical model, which is written in the checkdae file, into the user functions that will be complied by the C language to link to simulation libraries and the parameter setting file, where one sets the initial concentrations of the molecules, the kinetic parameters, and the parameters for controlling simulation. In the parameter-setting file, users are allowed to merge another file to update the current data. The checkdae module also converts ordinary differential equations including CMA, GMA, and MM into S-system at the steady state. Once the steady-state solutions of the differential equations are obtained, they can be converted into S-system at the steady state, where the coefficients of the S-system are provided automatically in symbolic form. Simultaneously, the checkdae module generates the various functions of sensitivities and stability, whereby users analyze the sensitivities and stability at the steady state.
The checkdae module also implements the function for surveying kinetic parameters to investigate the behavior of a model over a specific range of the values of some parameters. This allows users to effectively study the dependency of the model's behavior on the kinetic parameters, and is therefore a very effective means of forecasting the effects of parameter perturbations. The capability to predict the effect of the change in parameters or the activity that is becoming attainable in silico is an essential requisite for the rational design of engineered organisms.
Solver
Two distinct types of simulation can be carried out as follows: (1) time course simulation, where the values of variables are determined as a time series; (2) steady-state analysis, where the values of variables are determined for a state in which metabolite concentration does not change. For differential equations, the CADLIVE Simulator implements the Runge-Kutta method, the step-adaptive Runge-Kutta method, and the NDF that can be applied to highly stiff differential equations. The NDF has been programmed based on ode15s of MATLAB. The Runge-Kutta or the step-adaptive Runge-Kutta method is used for nonstiff differential equations. The Newton-Raphson algorithm is used to solve algebraic equations. The combination of the Newton-Raphson algorithm with the Runge-Kutta or with the step-adaptive Runge-Kutta method, or the NDF solves DAEs. The solver not only simulates dynamic behaviors of biochemical networks, but also solves the steady-state solutions by applying a quasi-steady state approximation to all the differential equations, resulting in generating algebraic equations. The Newton-Raphson method solves such algebraic equations to obtain the steady-state concentrations. In order to enhance the calculation rate, the CADLIVE Simulator uses the Message-Passing Interface (MPI) for parallel calculation.
Optimizer
CADLIVE implements a search by genetic algorithms (GAs), where a fitness function is defined to characterize how correctly the estimated values of the kinetic parameters explain experimental data. In the CADLIVE Simulator, the GA module has many sophisticated algorithms, e.g., crossover algorithms including UNDX, UNDXm, SPX, and BLX, and algorithms for generation alternation including MGG and island model, which show high capability to fit the simulated results to experimental data. Users operate the optimizer on command lines on LINUX, using the user functions and parameter setting files that are generated by the checkdae module.
Sensitivity and stability analysis
Sensitivity and stability analyses show how a biochemical system responds to perturbations or uncertainties. Among many methods for system analysis, the sensitivity and stability analyses are useful for characterizing the robustness of the mathematical at a steady-state level, and allows one to determine which parameters have the most effect on the model, or which factors cause the system to oscillate. The CADLIVE Simulator makes it possible to discover the steady state of the system, and to analyze how the changes in pool sizes from defined initial conditions affect the steady-state values.
Interactive simulation software
The simulator aims at simulating a dynamic model and analyzing sensitivity and stability at the steady state. Since there have been various system analyses, such as bifurcation and stochastic analyses (Hucka et al. 2002), CADLIVE does not implement such analyzers. Instead, the checkdae module produces the user function and parameter-setting files for the generated mathematical model, which is written in C. Therefore, users are able to use these mathematical equation files for further analysis on their own programs or analyzers. Users are also allowed to download the time course data and steady-state solutions to their PCs. In addition, since each CADLIVE module can be executed on command lines on Linux, users utilize the respective module for their purpose, separately.
Client and server model
The CADLIVE Simulator is a client-server model, supporting Internet Explorer. Users access a server through php, and operate on Web pages. The system functions on LINUX (Red Hat Version 7.1), and uses Xerces2 Java Parser for parsing the regulator-reaction equations in XML, postgreSQL for managing database, the C programming language for calculating differential and algebraic equations and matrixes, and Message-Passing Interface (MPI) for parallel computing.
Nitrogen-assimilation system
A schematic diagram of the E. coli nitrogen-assimilation system is shown in Figure 3. E. coli absolutely needs ammonia for synthesizing glutamine and glutamate, which are the sources for almost all nitrogen-containing compounds, including amino acids and nucleotides. Glutamine and glutamate are synthesized through glutamine synthetase (GS), glutamate synthase (GOGAT), and glutamate dehydrogenase (GDH) by adding ammonia to 2-ketoglutarate that is an intermediate of the TCA cycle. Among them, GS plays a major role in the ammonia assimilation. Multiple feedback loops control the activity and synthesis of glnA (GS) and the transcription of nitrogen-regulated (Ntr) genes, glnG (NRI), glnL (NRII), glnK (GlnK), and nac, whose products facilitate the adaptation to ammonia deficiency, monitoring the concentrations of nitrogenous and carboneous components. The feedback loops are conventionally divided into two major loops for controlling the activity and synthesis of GS. The former module consists of UTase/UR, PII, GlnK, PI, and GS; the latter consists of UTase/UR, PII, GlnK, NRI, NRII, and GS. A central regulator of PII is the key to coordinate the two loops, which transduces the information regarding glutamine and 2-ketoglutarate to both regulations for the GS activity and GS synthesis (Ninfa and Atkinson 2000). The functions of most Ntr genes have been assigned, but a physiological function of GlnK remains to be elucidated. GlnK is a PII homolog in function, but its transcription regulation is governed by NRI-P, whereas PII is synthesized constitutively (Blauwkamp and Ninfa 2002b).
Figure 3.
A schematic diagram of the E. coli nitrogen-assimilation system. (:), (-) Binding complexes and modification, respectively. The arrows indicate the reactions: binding and conversion ( ), catalyzing the reactions (
), catalyzing the reactions ( ), inhibiting the reactions (
), inhibiting the reactions ( ), activating the reactions (
), activating the reactions ( ), and transcription (
), and transcription ( ).
).
In this study, we focus on the function of GlnK, whose physiological role has been attractive (Atkinson et al. 2002; Blauwkamp and Ninfa 2002b). In the cells lacking GlnK, a very high expression of the Ntr promoters occur in nitrogen-starved cells, but the Ntr expression displays “runaway expression” when the ammonia is fed. This overexpression of the Ntr genes causes growth defects, because the products of overexpressed nac genes inhibit serine synthesis (Blauwkamp and Ninfa 2002a). On the other hand, the nac expression closely coordinates with nitrogen-starved cells of a wild type. The nitrogen-starved wild type does not display such a runaway expression very much when ammonia is added, i.e., the cells quickly return to a growth phase. The role of GlnK, a homolog of PII, is suggested to involve quick or reversible response. In order to assign the function of GlnK and to elucidate the mechanism of the runaway expression, CADLIVE analyzed Ntr gene expression with regard to the changes in the ammonia concentration in the absence or presence of GlnK.
Construction of the nitrogen-assimilation system
On the GUI editors of CADLIVE, registering the species and reactions with their associated elements and attributes constructed the regulator-reaction equations of the nitrogen-assimilation system. Based on the strategy of three layers and two stages, the simulator parsed the regulator-reaction equations, converting them into mathematical equations with kinetic parameters according to the TPP Method (Supplemental Method 2). The nitrogen-assimilation system consists of three layers, e.g., gene, protein, and metabolic layers. The gene and protein layers were converted into DAEs through CMA with TT. The metabolic layer was converted into MM. In order to connect the protein–gene layer to the metabolic layer, the enzymes, GS, GOGAT, and GDH, in the differential equations of the metabolic layer were defined as time-dependent variables, which are common to those of the gene–protein layer.
Optimization of the nitrogen-assimilation system
Search parameter
In order to determine the kinetic parameters for the dynamic model of the nitrogen-assimilation system, we carried out GAs. We classified two types of kinetic parameters, i.e., the values assumed/provided from literatures, and the values estimated in the model. In order to further decrease the number of the parameters to estimate, we considered the dependence relations among such parameters. The parameters to estimate can be divided into two classes, some parameters that are the key to govern the dynamics and the other parameters irrelevant to it. We focus on the key parameters, while we give the values assumed from literatures to the remaining ones. We exemplify a simple enzyme reaction to illustrate how to select key parameters. An enzyme reaction can be divided into an association between an enzyme and a substrate, and a conversion of the enzyme–substrate complex into a product. The reaction rate is determined by an association constant and by a conversion rate constant. However, we can make different reaction rates by varying the association constant, while the conversion rate constant is fixed. In this optimization, we mainly explore the association constants between components (K[1-28]) as the critical parameters; the rate constants of conversions such as protein syntheses and phosphorylations are assigned representative values assumed form literatures (Bremer and Dennis 1996). Since the function of GlnK is the same as that of PII, the corresponding kinetic parameters except transcriptions are assumed as the same value as follows: K[3] = K[4], K[5] = K[6], K[7] = K[8], K[9] = K[10], K[11] = K[12], K[13] = K[14], and K[15] = K[16]. The transcription-rate constant for GlnK is set so that the concentration of GlnK is smaller than PII, because the nitrogen-assimilation system shows the Ntr response without GlnK, but not without PII.
Fitness function
Assuming that the nitrogen-assimilation system is able to maintain the ratio of glutamine to 2-ketoglutarate against the remarkable change in the ammonia concentration, the fitness function is defined by:
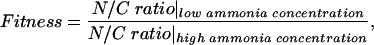 |
where the N/C ratio is the ratio of the glutamine concentration to the 2-ketoglutarate concentration at the steady state. After obtaining the parameters' sets that show a high fitness, we adjust the dynamic model to experimental data by using the second fitness function:
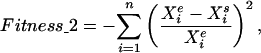 |
where Xi is the concentration of a component i and n is the number of data (e, experimental data; s, simulated data).
Module decomposition
Since the full nitrogen-assimilation system had many critical parameters to explore, we decomposed the system into functional modules. First, we separated the metabolic module that consisted of GS, GDH, and GOGAT out of the full system, exploring the metabolic module so that the glutamine and 2-ketoglutarate concentrations achieved the steady-state level at the high ammonia concentration, then fixing the values of these kinetic parameters. Second, we conveniently decomposed the full model into the GS activity-controlling module and the GS synthesis-controlling module. The former module consists of UTase/UR, PII, GlnK, PI, and GS; the latter consists of UTase/UR, PII, GlnK, NRI, NRII, and GS. How to divide the kinetic parameters into the two modules is shown in Supplemental Method 2. Twenty-eight parameters of K[1-28] were selected to estimate. Each module was optimized regarding the first fitness function by GAs (Yoshida and Kurata 2004). For the GS activity-controlling module and the GS synthesis-controlling module, the kinetic parameters of K[1-14] and of K[1-6,15-28] were explored, respectively. After obtaining a high-fitness value (0.5–1), we merged the parameters of both modules, where the overlapped parameters of K[1-6] were averaged. The GAs used the merged parameters as the initial individuals to optimize the full model. After 100 generations were calculated, we obtained a high fitness value (0.5–1). Using this full model, we optimized the second fitness function (Fitness_2), i.e., the difference between the target data and simulated data, by searching the critical parameters within relatively narrow ranges. In the series of GAs, we used a simple GA with UNDX as a crossover method.
Results
Construction of dynamic model
In order to demonstrate how the CADLIVE Simulator links a biochemical network map to dynamic simulation without going all pathways down to the details of exact kinetics, we exemplified the E. coli nitrogen-assimilation system, whose biochemical map has been presented, but there have been few kinetic data in vivo (Ninfa et al. 2000). By using CADLIVE we constructed the regulator-reaction equations of the nitrogen-assimilation system, parsing them to generate DAEs through CMA according to the TPP Method (Supplemental Method 2). The DAEs with 113 kinetic parameters were converted from the CMA with 141 kinetic parameters at the second stage. The rules provided by the elements and attributes in the “sanac” notation were satisfactory for directly linking gene regulatory and metabolic networks to dynamic models.
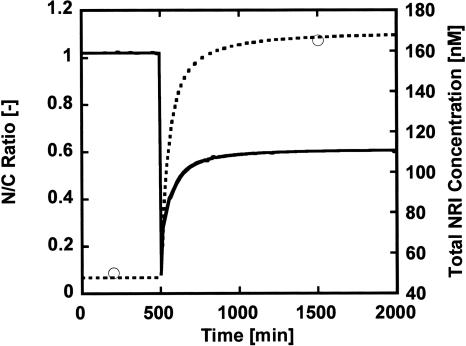
Although the biochemical network map has been described at the molecular-interaction level, most of the kinetic parameters remain to be measured in vivo. In order to estimate the kinetic parameters, we carried out genetic algorithms (GAs). Figure 4 shows the time course of the optimized model, where the ammonia concentration decreased to one fifth at 500 min. The ratio of the glutamine concentration to the 2-ketoglutarate concentration (N/C ratio) and the NRI concentration were simulated so that they agreed with experimental data at the steady state (Senior 1975; Reitzer and Magasanik 1983; Ikeda et al. 1996). The concentration of NRI (one of the Ntr proteins) was restored within several hours after ammonia depletion, which explains qualitative features of the transient response (Atkinson et al. 2002). Assigning the values assumed from literatures to the kinetic parameters regarding protein synthesis and conversions would reproduce such dynamic features (Bremer and Dennis 1996).
Figure 4.
Simulation for the time course of the ratio of glutamine to 2-ketoglutarate (—) and the total NRI concentration (-------) in wild-type cells. The concentration of ammonia decreases to one-fifth at 500 min. The circles are the targets for the total NRI concentration assumed from literatures.
Transient response and robustness
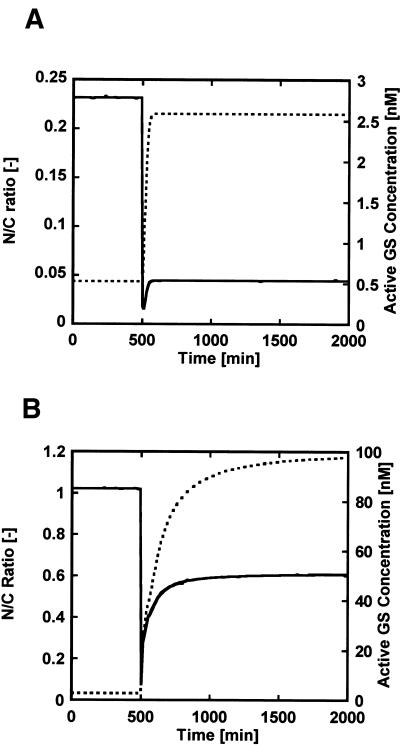
The nitrogen-assimilation system can be conveniently divided into two feedback regulator modules for controlling the GS activity and controlling the GS synthesis. Note that these two modules are the same as those that we divide the full system into to optimize the dynamic model. The GS activity feedback regulator is implemented through the protein interactions without any protein synthesis, it is intuitively expected to achieve a fast response, and the N/C ratio is supposed to be limited, because the total GS concentration is fixed. In contrast, the GS synthesis feedback regulator can increase the N/C ratio by synthesizing GS through positive-feedback loops, and we expect a slow response because it requires gene expressions. These features are reasonable in terms of the molecular architectures. In order to validate the dynamic model, we investigated whether these regulators showed such rational regulations in terms of a transient response and robustness. As shown in Figure 5, we simulated how these regulators provided a fast response and a robust property to the N/C ratio against the changes in the ammonia concentration. For the transient response, the GS activity feedback module regulated the GS activity at minute-scale (Fig. 5A), whereas the GS synthesis control required several hours to restore the active GS concentration (Fig. 5B), which was consistent with the experimental observation (Atkinson et al. 2002). For the N/C ratio, the feedback loop for GS activity enhanced the robustness of the N/C ratio to the change in the ammonia concentration more than the nonfeedback system (the metabolic module that consists of GS, GDH, and GOGAT) (data not shown). The addition of the GS synthesis feedback module to the GS activity module was able to further recover the N/C ratio due to the synthesis of the total GS. Both controls contribute to fast responses or enhanced robustness, but they show tradeoffs. The GS activity control indicates a fast response, but the N/C ratio is limited. In contrast, the GS synthesis control increases the N/C ratio by synthesizing GS, but it does not achieve fast response. These features are consistent with the experimental observation or the rational expectation in terms of the molecular architecture of the system (Atkinson et al. 2002). Thus, our model captures the intrinsic features of transient response and the robustness to the changes in the ammonia concentration.
Figure 5.
Model validation in terms of transient response and robustness. (A) Transient responses for the ratio of glutamine to 2-ketoglutarate (N/C ratio) (—) and the active GS concentration (.....) in the cells lacking the GS synthesis control module (the regulation with the GS activity control module alone). The active GS indicates nonadenylylated GS that catalyzes the conversion from glutamate and ammonia to glutamine. The ammonia concentration was decreased to one-fifth at 500 min. The GS activity module was obtained by setting the kinetic parameters K[15,16], which are the association constant between PII or GlnK and NRII, as zero in the full model. (B) Transient responses of the ratio of glutamine to 2-ketoglutarate (N/C ratio) (—) and the active GS concentration (.....) in the full model that consists of the GS activity control and GS synthesis control modules. The ammonia concentration was decreased to one-fifth at 500 min.
Model validation by knockout mutants
In order to demonstrate the validity of the dynamic model, we compared the simulated results of various knockout mutants with the experimental data (Ninfa et al. 2000), as shown in Table 2, where the GS concentrations were simulated under an ammonia-rich or ammonia-limiting medium. We focused on qualitative behaviors of GS, since few kinetic data have been measured in vivo, and the simulation does not aim at reproducing the exact dynamic behaviors. Except for ΔglnD mutant (Table 2A), the simulated GS concentrations for a wild type and the mutants, ΔglnG (ΔNRI), ΔglnL (ΔNRII), ΔglnB (ΔPII), and ΔglnK (ΔGlnK), agreed with the experimental data. The simulated and experimental features of the wild type and mutants can be deduced intuitively by tracing reaction pathways.
Table 2.
Model validations using knockout mutants
|
A
|
|
|
|---|---|---|
|
Changes in GS when cells are transferred to an ammonia-limiting medium
|
||
| Cell type | Experiment | Simulation |
| Wild type | ++ | ++ |
| ΔglnG (ΔNRI) | ± | ± |
| ΔglnL (ΔNRII) | ± | ± |
| ΔglnD (ΔUTase/UR) | ++ | + |
| ΔglnB (ΔPII) | ± | ± |
| ΔglnK (ΔGlnK) | ++ | ++ |
|
B
|
|
|
|---|---|---|
|
The GS concentration of mutants is compared with that of a wild type in the ammonia-rich medium
|
||
| Mutant | Experiment | Simulation |
| ΔglnL (ΔNRII) | + | + |
| ΔglnD (ΔUTase/UR) | – | – |
| ΔglnB (ΔPII) | ++ | ++ |
| ΔglnK (ΔGlnK) | ± | ± |
The GS concentrations of a wild-type and knockout mutants were simulated in an ammonia-limiting or ammonia-rich medium to compare with those of experimental data.
(A) The GS concentrations were compared between an ammonia-rich medium and an ammonia-limiting medium, where a wild type greatly increased the GS concentration due to the Ntr response. When the cells were transferred from an ammonia-rich medium to an ammonia-limiting medium, the GS concentration increased more than five-fold (++), increased five- to two-fold (+), and hardly changed (less than two-fold) (±). (B) The GS concentrations of the mutants were compared with those of a wild type in an ammonia-rich medium. Compared with the wild type, the GS concentration of mutants increased five-fold (++), increased five- to two-fold (+), hardly changed (±), and decreased (–).
First, we verify the consistent data between experiments and simulations. In Table 2A, for ΔglnG, ΔglnL, and ΔglnB, the decrease in the ammonia concentration hardly affects the GS synthesis, i.e., the Ntr response does not occur, whereas the ΔglnK mutant shows the Ntr response. The ΔglnG mutant has no transcription factor (NRI), and the ΔglnL mutant is not able to phosphorylate NRI due to lack of NRII, thus, these mutants deregulate the GS synthesis. Due to lack of PII, the ΔglnB mutant is not able to sufficiently transmit the change in the ammonia concentration to the NRII–NRI phosphorylation cascade, which deregulates the GS synthesis. In the ΔglnB mutant, GlnK, which has the same function as PII, does not supplement the role of PII, because the effect of GlnK is smaller than that of PII. For the same reason, ΔglnK shows the Ntr response. In Table 2B, for ΔglnL, phosphoarylated NRI is not dephosphorylated due to lack of NRII:PII, resulting in the increased GS synthesis. For ΔglnD, nonuridylylated PII suppresses the phosphorylation of NRII and NRI, resulting in the decease in the GS synthesis. For ΔglnB, NRII and NRI are phosphorylated, which increases the GS synthesis. For ΔglnK, the GS concentration is almost consistent with that of the wild type, because GlnK is not expressed at a high-ammonia concentration. Second, we investigate the inconsistent data for ΔglnD mutant. In our model, the depletion of the sensor protein (glnD) for 2-ketoglutarate and glutamine leads to deregulation of GS, but the real cells are able to sense the change of 2-ketoglutarate through PII, resulting in enhancing GS synthesis. The inconsistency is caused by the fact that our model does not consider the sensory reaction of PII.
The comparisons between experimental data and simulated results demonstrate that the dynamic model is able to predict not only the qualitative behaviors of the wild type, but also those of several mutants. For the inconsistent data, we understand the reason why the inconsistency is derived from lack of the sensory pathway. Consequently, using the experimental data of those knockout mutants demonstrates the validity of the dynamic model.
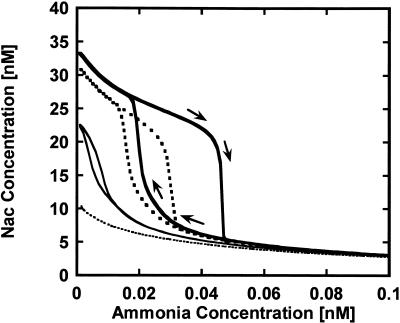
Prediction of hysteresis
Using the validated model, we simulated and analyzed the dynamics of the mutant lacking GlnK and a wild type in order to predict the mechanism for “runaway expression” of the Ntr genes. In Figure 6, the steady-state concentration of the nac proteins was plotted as a function of ammonia concentration. Nac is one of the Ntr proteins, and is controlled by NRI-P. Between two threshold concentrations of ammonia, the control system has two stable steady states. With the decrease in ammonia concentration, nac expression showed an abrupt increase at the low-threshold concentration. Conversely, with the increase in ammonia concentration, nac expression decreased rapidly at the high-threshold concentration. The minimum concentration of ammonia necessary to drive nac expression into a high level is distinctly lower than the maximum concentration necessary to hold nac proteins at a high level. Both threshold concentrations are different, indicating the bistability between both of the threshold values. This is a typical hysteresis curve, which explains the runaway expression of the Ntr genes.
Figure 6.
Hysteresis curves of nac protein with respect to ammonia concentration in the wild-type and the GlnK mutants. The mutant lacking GlnK ( ), the wild type: transcription rate for GlnK = 0.09 min-1 (
), the wild type: transcription rate for GlnK = 0.09 min-1 ( ), the mutant overexpressing GlnK: transcription rate for GlnK = 0.45 min-1 (—), and the mutant that greatly overexpresses GlnK: transcription rate for GlnK = 0.9 min-1 (-------).
), the mutant overexpressing GlnK: transcription rate for GlnK = 0.45 min-1 (—), and the mutant that greatly overexpresses GlnK: transcription rate for GlnK = 0.9 min-1 (-------).
Such a hysteresis curve is closely related to GlnK, because the region showing bistability becomes narrow with the increase in the transcription rate for GlnK. In the wild type that expresses GlnK, the hysteresis curve attenuates greatly. GlnK is a homolog of PII, but its transcription is controlled by NRI-P, whereas PII expresses constitutively (Ninfa and Atkinson 2000). A meaningful difference between GlnK and PII is transcription regulation. The increased synthesis of GlnK by NRI-P suppresses the phosphorylation of NRI by GlnK dephosphorylating NRII-P, indicating that it weakens the effect of the positive-feedback loop for NRI-P-activated transcription of the Ntr genes. When the effect of GlnK becomes strong, the hysteresis is changed into a reversible reaction, where the ammonia concentration uniquely determines Ntr expression. The negative feedback loop of GlnK is shown to be indispensable for a reversible response to the change in ammonia concentration. Thus, the experimental observation of “runaway expression” can be explained by the hysteresis of the mutant lacking GlnK (Blauwkamp and Ninfa 2002b). In addition, the hysteresis curves involved the cooperative binding of NRI-P to the promoter glnAp2. With the decrease in the number of cooperatively bound NRI-P, the hysteresis curves attenuate. Multiple NRI-Ps are known to bind the promoter cooperatively, indicating an ultrasensitive transcription, i.e., switch-like dynamics.
Irreversible transition into and out of ammonia starvation is driven by hysteresis in the mutant lacking GlnK. Hysteresis refers to toggle-like switching behavior in a dynamic system. Hysteresis transitions are discontinuous. Once a system has been switched on by moving the control parameter (ammonia) across the activation threshold, it cannot be switched off by bringing the control parameter back across the activation threshold in the opposite direction (Ferrell Jr. 2002; Tyson et al. 2003). Non-hysteresis switches behave differently, switching on and off at the same values. In general, positive and negative feedback loops can generate a bistable system that shows hysteresis. The ingredients required for bistability include some sort of feedback, e.g., positive feedback, double-negative feedback, autocatalysis, or the equivalent, but feedback alone does not guarantee that a system will be bistable. A bistable system must also possess some types of nonlinearity within the feedback circuits. Some of the enzymes in the feedback circuits must respond to their upstream regulators cooperatively, or in an ultrasensitive manner. As expected, the nitrogen-assimilation system satisfies such a requirement, because NRI-P cooperatively binds to the promoter of glnAp2 to synthesize GS, NRI, and NRII in a positive feedback manner. In the two loops, the positive and negative feedback must be properly balanced for the circuit to exhibit bistability. The positive-feedback loops create alternative states of low and high NRI-P activity, while the negative-feedback loops drive the control system back and forth between these states. GlnK is a critical balancer between the positive and negative-feedback loops and is responsible for hysteresis or reversibility. Bistability and hysteresis are new ways of looking at the Ntr response in E. coli.
Discussion
Feasibility of CADLIVE
Not only molecular biology, but also systems biology have produced detailed molecular interactions to construct concrete maps of gene regulatory and metabolic networks, which lead to an understanding of the dynamic molecular architectures within cells. Mathematical simulation plays a major role, but a problem has been how to connect biochemical maps to dynamic simulations. Since mathematical modeling appears complicated and technical, and requires many exact kinetic parameters, there has been a big gap between the biochemical maps and the dynamic simulations.
The CADLIVE Simulator has been demonstrated to handle gene regulatory and metabolic networks at an intermediate level without going all the way down to exact biochemical reactions. The aim of CADLIVE is to simulate the qualitative features of dynamic models, not to reproduce the details of exact behaviors. CADLIVE constructs a general model that includes protein complexes and modified molecules based on their individual mechanisms. This creates a promising modeling methodology at the intermediate level between very abstract models and very concrete models with exact kinetic parameters. The strategy of CADLIVE-based modeling consists of forward and reverse engineering. In the forward engineering, CADLIVE builds the mathematical model with kinetics-related parameters from a biochemical map, and then reverse engineering estimates the kinetic parameters that express the qualitative features of the biological system, thereby simulating the dynamic model. Further, since a CADLIVE-built model is a collective body of plain differential and algebraic equations, it is able to use powerful control engineering methods such as sensitivity, stability, bifurcation, and hysteresis analyses to explore design principles of molecular architectures. In this article, the use of the CADLIVE Simulator built a mathematical model for the nitrogenassimilation system, and estimated the kinetic parameters by genetic algorithms. The generated model was able to satisfy the behaviors of a wild-type and knockout mutants or the biological rationalities in terms of transient responses and robustness. Using this validated model, we analyzed the mechanism for the “runaway expression” of the nitrogen-related (Ntr) genes, which had been observed with respect to the reversible change in the ammonia concentration. In terms of control engineering, we predicted the mechanism for hysteresis of the Ntr gene expression. The negative-feedback control by GlnK is clarified to be responsible for quickly adapting to the changes in the ammonia concentration by reducing the hysteresis.
Breakthroughs in forward engineering
One of the most important breakthroughs for CADLIVE is the proposition of efficient and practical rules to integrate all possible molecular interactions into mathematical models, thereby simulating the dynamic features underlying their molecular architectures. Complicated mathematical models are successfully classified according to the strategy of three layers and two stages, which enables a simulator to automatically parse and convert biochemical network maps into mathematical models. Another great advantage for mathematical simulations is the use of TPP that converts biochemical networks into DAEs, which decrease the number of kinetic parameters and reduces the stiffness of differential equations.
In the nitrogen-assimilation system, TPP converted the CMA with 141 kinetic parameters into DAEs with 113 parameters. Twenty percentages of the parameters were reduced, which seems a small reduction. However, it greatly contributes to the enhanced efficiency of optimization, because the number of the critical parameters, which are used as the parameters to explore, has been reduced by one-half, i.e., 56 association and dissociation rate constants in CMA were reduced to 28 association constants in DAEs. For stiffness, the simulation of CMA failed when the ammonia concentration was changed at 1000 min (data not shown), indicating that CMA is not applicable to a great change in the ammonia concentration. This problem has not been solved by any solvers (Runge-Kutta, step-adaptive Runge-Kutta, or NDF). In contrast, the simulation of DAEs was completed successfully (the step-adaptive Runge-Kutta is the best solver), because stiff CMA with the association and dissociation rate constants that have huge differences in the values was replaced by algebraic equations in the DAEs. The TPP method contributes to the reduced number of parameters and solving the stiffness of differential equations for biochemical systems.
Reverse engineering
For the problem of how to obtain the values of unmeasured parameters, we present the optimizer that implements Genetic Algorithms (GAs). Since it is hard to develop a fully automatic optimizer, we implement the basic tools for optimization. It is important for an efficient optimization to define a fitness function and to reduce the number of kinetic parameters to estimate. In addition to those, decomposing a network plays an important role for optimization. In the nitrogen-assimilation system, the N/C ratio was an effective fitness function, because an optimization of this criterion generated the dynamic model that well agreed with experimental data of a wild-type and various knockout mutants. In order to reduce the number of the kinetic parameters to estimate, we divided the parameters into some critical parameters that govern dynamics and the others irrelevant to it, considering the kinetics. In this simulation, we mainly explored the association constants as critical parameters, and the rate constants of conversions such as protein syntheses and phosphorylations were assigned representative values assumed/provided form literatures (Bremer and Dennis 1996). This idea is very useful not only for reducing the number of the parameters to explore, but also for expressing the transient response with a biological reality. In addition to these, decomposing networks is a critical solution for optimizing the large-scale model with 113 kinetic parameters. We divide the nitrogen-assimilation system into three modules in terms of feedback control architectures, the metabolic circuits, the GS activity feedback loop, and the GS synthesis feedback loop, so that each module uses the common fitness functions (N/C ratio) (Yoshida and Kurata 2004). This leads to a successful decomposition for optimization.
Versatility and exchangeability
In order to demonstrate the versatility of the CADLIVE Simulator, we simulated the various kinds of biological models, e.g., the heat-shock response, the circadian clock, and metabolic circuits, as shown in the simulator Web site. These mathematical models that consist of DAEs captures the essences of their dynamic features, showing that the formalism of DAEs is useful for simulating gene regulatory networks. In CADLIVE, DAEs are automatically generated by applying a rapid equilibrium approximation to binding reactions. It is a common assumption, since binding reactions occur at a faster time scale than production and degradation of proteins in vivo. A typical example is the Michaelis-Menten equation, which is derived by applying a rapid equilibrium approximation or a quasi steady-state approximation to enzyme and substrate complex formations.
If DAEs are not preferred, i.e., neither rapid equilibrium approximations nor quasi steady-state approximations are appropriate, one can select other formalisms such as CMA. As an alternative, using the editor can change the type of reactions from a binding reaction to a reversible reaction. In such a case, CADLIVE converts a reversible reaction into CMA. The CADLIVE Simulator is able to directly link many kinds of biochemical reactions to mathematical equations. Thus, we expect that our conversion methods are elaborately designed to produce general dynamic models. Nevertheless, CADLIVE allows users to directly edit a mathematical model, which guarantees that they make their own mathematical model freely. This optional edition is useful for users who want to make very concrete models or to modify the CADLIVE-derived model at a lower level. Note that the nitrogen-assimilation model in this study (also the models in our Web pages) never uses such an optional edition.
In order to construct a large-scale model, it is necessary to combine or merge various biochemical networks. The important thing is to unify a data format among researchers. Systems Biology Markup Language (SBML) is a candidate of such universal data representations for biochemical networks. Thus, we designed the “sanac” representation as an extension of SBML at level 2, which enables combining SBML-related files to ours. It is a great advantage for the construction of a large-scale biochemical network and the subsequent simulation.
Systems biology aims at understanding the whole cell as dynamic molecular systems. The CADLIVE Simulator has provided a promising tool from a map to dynamic simulation. Once biochemical reaction maps are built, CADLIVE produces dynamic models. The use of CADLIVE analyzes the dynamic features of biochemical systems, thereby elucidating how the molecular processes act in concert within a cell. In the future, CADLIVE will be a core system to integrate various biochemical reactions into large-scale dynamic systems, and may construct virtual cells that produce all possible features of real biological systems at the molecular interaction levels.
Acknowledgments
We are very grateful for collaborations and discussions with Dr. Hiroaki Kitano. The CADLIVE Simulator has been developed together with Surigiken Co. Ltd. This study is mainly supported by the Rice Genome Project of National Institute of Agrobiological Sciences, and partially by The Project for Development of a Technological Infrastructure for Industrial Bioprocesses on R&D of New Industrial Science and Technology Frontiers by the Ministry of Economy, Trade & Industry (METI), and entrusted by the New Energy and Industrial Technology Development Organization (NEDO).
Article and publication are at http://www.genome.org/cgi/doi/10.1101/gr.3463705.
Footnotes
[Supplemental material is available online at www.genome.org. CADLIVE is freely available at http://kurata21.bio. kyutech.ac.jp/cadlive/menu.htm or http://www.cadlive.jp/.]
References
- Atkinson, M.R., Blauwkamp, T.A., Bondarenko, V., Studitsky, V., and Ninfa, A.J. 2002. Activation of the glnA, glnK, and nac promoters as Escherichia coli undergoes the transition from nitrogen excess growth to nitrogen starvation. J. Bacteriol. 184: 5358-5363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Atkinson, M.R., Savageau, M.A., Myers, J.T., and Ninfa, A.J. 2003. Development of genetic circuitry exhibiting toggle switch or oscillatory behavior in Escherichia coli. Cell 113: 597-607. [DOI] [PubMed] [Google Scholar]
- Barkai, N. and Leibler, S. 1997. Robustness in simple biochemical networks. Nature 387: 913-917. [DOI] [PubMed] [Google Scholar]
- Becskei, A. and Serrano, L. 1999. Engineering stability in gene networks by autoregulation. Nature 405: 590-593. [DOI] [PubMed] [Google Scholar]
- Bhalla, U. and Lyengar, R. 1999. Emergent properties of networks of biological signaling pathway. Science 283: 381-387. [DOI] [PubMed] [Google Scholar]
- Bhattacharjya, A. and Liang, S. 1996. Power laws in some random Boolean networks. Phys. Rev. Lett. 77: 1644. [DOI] [PubMed] [Google Scholar]
- Blauwkamp, T.A. and Ninfa, A.J. 2002a. Nac-mediated repression of the serA promoter of Escherichia coli. Mol. Microbiol. 45: 351-363. [DOI] [PubMed] [Google Scholar]
- ———. 2002b. Physiological role of the GlnK signal transduction protein of Escherichia coli: Survival of nitrogen starvation. Mol. Microbiol. 46: 203-214. [DOI] [PubMed] [Google Scholar]
- Bremer, H. and Dennis, P.P. 1996. Modulation of chemical composition and other parameters of the cell by growth rate. In Escherichia coli and Salmonella cellular and molecular biology (ed. F.C. Neidehardt), pp. 1553-1569. ASM Press, Washington, D.C.
- Chen, K.C., Csikasz-Nagy, A., Gyorffy, B., Val, B. Novak, J., and Tyson, J.J. 2000. Kinetic analysis of a molecular model of the budding yeast cell cycle. Mol. Biol. Cell 11: 369-391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Csete, M.E. and Doyle, J.C. 2002. Reverse engineering of biological complexity. Science 295: 1664-1669. [DOI] [PubMed] [Google Scholar]
- D'Haeseleer, P., Liang, S., and Somogyi, R. 2000. Genetic network inference: From co-expression clustering to reverse engineering. Bioinformatics 16: 707-726. [DOI] [PubMed] [Google Scholar]
- Dougherty, E.R., Barrera, J., Brun, M., Kim, S., Cesar, R.M., Chen, Y., Bittner, M., and Trent, J.M. 2002. Inference from clustering with application to gene-expression microarrays. J. Comput. Biol. 9: 105-126. [DOI] [PubMed] [Google Scholar]
- Ferrell Jr., J.E. 2002. Self-perpetuating states in signal transduction: Positive feedback, double-negative feedback and bistability. Curr. Opin. Cell. Biol. 14: 140-148. [DOI] [PubMed] [Google Scholar]
- Gardner, T.S., Cantor, C.R., and Collins, J.J. 2000. Construction of a genetic toggle switch in Escherichia coli. Nature 403: 339-342. [DOI] [PubMed] [Google Scholar]
- Gardner, T.S., di Bernardo, D., Lorenz, D., and Collins, J.J. 2003. Inferring genetic networks and identifying compound mode of action via expression profiling. Science 301: 102-105. [DOI] [PubMed] [Google Scholar]
- Goryanin, I., Hodgman, T.C., and Selkov, E. 1999. Mathematical simulation and analysis of cellular metabolism and regulation. Bioinformatics 15: 749-758. [DOI] [PubMed] [Google Scholar]
- Hartemink, A.J., Gifford, D.K., Jaakkola, T.S., and Young, R.A. 2002. Combining location and expression data for principled discovery of genetic regulatory network models. Pac. Symp. Biocomput. 437-449. [PubMed]
- Hasty, J., McMillen, D., Isaacs, F., and Collins, J.J. 2001. Computational studies of gene regulatory networks: In numero molecular biology. Nat. Rev. Genet. 2: 268-279. [DOI] [PubMed] [Google Scholar]
- Hatakeyama, M., Kimura, S., Naka, T., Kawasaki, T., Yumoto, N., Ichikawa, M., Kim, J.H., Saito, K., Saeki, M., Shirouzu, M., et al. 2003. A computational model on the modulation of mitogen-activated protein kinase (MAPK) and Akt pathways in heregulin-induced ErbB signalling. Biochem. J. 373: 451-463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hucka, M., Finney, A., Sauro, H.M., Bolouri, H., Doyle, J., and Kitano, H. 2002. The ERATO Systems Biology Workbench: Enabling interaction and exchange between software tools for computational biology. Pac. Symp. Biocomput. 450-461. [DOI] [PubMed]
- Ikeda, T.P., Shauger, A.E., and Kustu, S.G. 1996. Salmonella typhimurium apparently perceives external nitrogen limitation as internal glutamine limitation. J. Mol. Biol. 259: 589-607. [DOI] [PubMed] [Google Scholar]
- Kauffman, S.A. 1993. The origin of order, self-organization and selection in evolution. Oxford University Press,
- Kholodenko, B.N., Demin, O.V., Moehren, G., and Hoek, J.B. 1999. Quantification of short term signaling by the epidermal growth factor receptor. J. Biol. Chem. 274: 30169-30181. [DOI] [PubMed] [Google Scholar]
- Kitano, H. 2002. Systems biology: A brief overview. Science 295: 1662-1664. [DOI] [PubMed] [Google Scholar]
- Kurata, H. and Taira, K. 2000. Two-phase partition method for simulating a biological system at an extremely high speed. Genome Inform. Ser. Workshop Genome Inform. 11: 185-195. [PubMed] [Google Scholar]
- Kurata, H., Matoba, N., and Shimizu, N. 2003. CADLIVE for constructing a large-scale biochemical network based on a simulation-directed notation and its application to yeast cell cycle. Nucleic Acids Res. 31: 4071-4084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McAdams, H.H. and Arkin, A. 2000. Towards a circuit engineering discipline. Curr. Biol. 10: R318-R320. [DOI] [PubMed] [Google Scholar]
- Mendes, P. 1993. GEPASI: A software package for modeling the dynamics, steady state and control of biochemical and other systems. Comput. Appl. Biosci. 9: 563-571. [DOI] [PubMed] [Google Scholar]
- Ninfa, A.J. and Atkinson, M.R. 2000. PII signal transduction proteins. Trends Microbiol. 8: 172-179. [DOI] [PubMed] [Google Scholar]
- Ninfa, A.J., Jiang, P., Atkinson, M.R., and Peliska, J.A. 2000. Integration of antagonistic signals in the regulation of nitrogen assimilation in Escherichia coli. Curr. Top. Cell Reg. 36: 31-75. [DOI] [PubMed] [Google Scholar]
- Reitzer, L.J. and Magasanik, B. 1983. Isolation of the nitrogen assimilation regulator NtrI, the product of the glnG gene Escherichia coli. Proc. Natl. Acad. Sci. 80: 5554-5558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sauro, H.M., Hucka, M., Finney, A., Wellock, C., Bolouri, H., Doyle, J., and Kitano, H. 2003. Next generation simulation tools: The Systems Biology Workbench and BioSPICE integration. OMICS 7: 355-372. [DOI] [PubMed] [Google Scholar]
- Schoeberl, B., Eichler-Jonsson, C., Gilles, E.D., and Muller, G. 2002. Computational modeling of the dynamics of the MAP kinase cascade activated by surface and internalized EGF receptors. Nat. Biotechnol. 20: 370-375. [DOI] [PubMed] [Google Scholar]
- Senior, P.J. 1975. Regulation of nitrogen metabolism in Escherichia coli and Klebsiella aerogenes: Studies with the continuous-culature technique. J. Bacteriol. 123: 407-418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tomita, M., Hashimoto, K., Takahashi, K., Shimizu, T., Matsuzaki, Y., Miyoshi, F., Saito, K., Tanida, S., Yugi, K., Venter, J.C., et al. 1999. Software environment for whole cell simulation. Bioinformatics 15: 72-84. [DOI] [PubMed] [Google Scholar]
- Tyson, J.J., Chen, K.C., and Novak, B. 2003. Sniffers, buzzers, toggles and blinkers: Dynamics of regulatory and signaling pathways in the cell. Curr. Opin. Cell. Biol. 15: 221-231. [DOI] [PubMed] [Google Scholar]
- Yi, T.-M., Huang, Y., Simon, M.I., and Doyle, J. 2000. Robust perfect adaptation in bacterial chemotaxis through integral feedback control. Proc. Natl. Acad. Sci. 97: 4649-4653. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yoshida, K. and Kurata, H. 2004. Decomposition and integration of functional modules optimizes a dynamic model of large-scale biochemical networks. ISPJ Symp. Series 2004: 97-102. [Google Scholar]