Avian obligate brood parasitic lineages evolved variable complex polycrystalline structures to build tougher eggshells

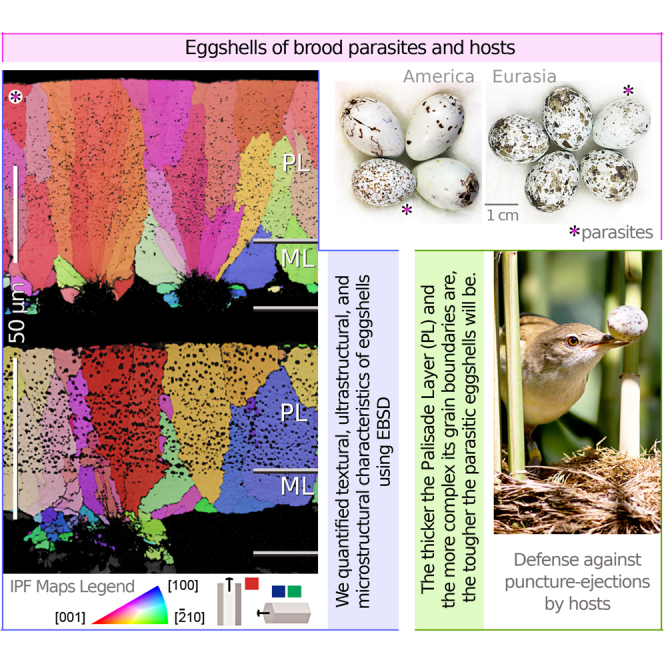
Summary

Avian brood parasites and their hosts display varied egg-puncture behaviors, exerting asymmetric co-evolutionary selection pressures on eggshells’ breaking strength. We investigated eggshell structural and textural characteristics that may improve its mechanical performance. Parasitic eggshell calcified layers showed complex ultra- and microstructural patterns. However, stronger parasitic eggshells are not due to lower textural severity (characterized by lower preferred crystallographic orientation, larger local grain misorientation and smaller Kearns factor), but rather to grain boundary (GB) microstructure characteristics within the eggshell outermost layer (palisade layer, PL). Accordingly, the thicker the PL and the more complex the GB pathways are, the tougher the parasitic eggshells will be. These characteristics, which we can identify as a “GB Engineering” driven co-evolutionary process, further improve eggshell breaking strength in those parasitic species that suffer relatively high frequencies of egg-puncturing by congeneric or hosts. Overall, plain textural patterns are not suitable predictors for comparing mechanical performance of bioceramic materials.

Graphical abstract

Highlights

• •Parasitic eggshell calcified layers show variable complex structural patterns
• •Stronger parasitic eggshells did not show lower textural severity than host eggshells
• •Grain boundary (GB) structure provides a better understanding for shell brittleness
• •The more complex the GB paths are, the tougher breaking the parasitic shells will be

Zoology; Ornithology; Evolutionary biology

Introduction

The avian eggshell is a complex bioceramic structure that combines inorganic crystalline compounds (e.g., ∼95% CaCO₃, ∼1% MgCO₃) and includes a sparse organic matrix (∼3.5%).^1,2 Eggshell fulfills several important physiological functions for embryonic development. However, the eggshell mechanical performance to maintain its integrity against external aggressions and damage is also of vital importance. Bird eggs have evolved an unusual combination of mechanical properties^3,4 to reduce the likelihood of eggshell breaking due to external physical forces. These contrary selection pressures on eggshell damage are achieved via mechanical properties such as having a high elastic modulus versus low fracture toughness³ (compared to other natural mineralized tissues⁴), and a high anisotropy in both breaking strength⁵ and fracture toughness.⁶ This renders eggshell cracking during the hatching process relatively easier than eggshell breakage due to external aggressions. Despite a reasonable amount of information on the cellular and biochemical mechanisms underlying eggshell mineralization process,² relatively few studies⁷ have explored how external selection pressures have driven the evolution of eggshell mechanical properties.

Avian obligate brood parasitism is an alternative reproductive strategy to parental care that provides a suitable model system to study the evolution of species-specific eggshell mechanical properties.⁸ Obligate brood parasitic birds lay their eggs in other (parental) species’ nests without participating in the incubation and nestling-care processes.⁹ In response to the parasitism costs, many host species have evolved anti-parasitic defenses, such as recognition and puncture-rejection of foreign eggs.^9,10,11 In turn, parasites have evolved counter-defenses,^9,11 such as mimetic eggs and also hyper-allometrically thick-shelled eggs, which are considered as adaptive advantages for this reproductive strategy.¹²

Since at least 1874, parasitic eggs have been considered to have greater eggshell breaking strength than host eggs.^{13,14,15,16,17,18} However, these inferences typically relied on eggshell thickness as a proxy of strength, which underestimates and trivializes the complex eggshell ultra- and microstructure and its specific functional performances. More recent evidence suggests that the eggshell microstructural and crystallographic textural organizations may further influence its mechanical properties.^1,19 Yet, the few studies that compared eggshell crystallographic structures in avian clades have shown occasionally disparate conclusions^8,20,21,22 (see Results and Discussion). These findings suggest that a comprehensive study is warranted, particularly in avian brood parasitism systems where parasites and/or hosts rely on egg puncturing to reduce competition for their respective hatchlings.

Differences in the egg-puncturing behavior patterns could exert differential selection on eggshell mechanical properties even between congeneric parasites and hosts.^8,23,24,25 For example, South American screaming cowbird and shiny cowbird (Icteridae: Molothrus rufoaxillaris and M. bonariensis) frequently puncture eggs already laid in host nests, including the eggs of hosts and other parasites. By contrast, North American brown-headed cowbird (M. ater) also punctures host eggs in nest, but these events are infrequent. Instead, the female brown-headed cowbird typically removes (by grasp-ejection) one host egg when it lays its own egg. Likewise, relatively few brown-headed cowbird host species are puncture-ejectors.^26,27 Thus, unlike the other two congeneric cowbirds, brown-headed cowbird and their hosts should be under a relatively lower selection pressure for enhanced eggshell breaking strength. Parasitic cuckoos (Cuculidae: Cuculus, from Africa and Eurasia) do not puncture eggs already laid in the nests of their hosts. However, cuckoos usually remove (by grasp-ejecting) and consume 1–2 host eggs before laying their own egg.²⁸ Instead, most cuckoo hosts have beaks that are too small to grasp-ejecting the parasitic eggs, therefore they often peck and puncture eggs before ejecting them from the nest (puncture-ejections).²⁹

To fully understand how parasite and host eggs have adapted greater functional and mechanical performance than expected for their sizes, we must consider the structural characteristics of the eggshell material. New techniques can shed light on how eggshell ultrastructural, microstructural and crystallographic textural shifts provide additional adaptive advantages during egg laying and incubation stages.

In terms of ultrastructure, the eggshell outermost calcified layer (palisade layer or effective thickness, PL) serves as a major factor contributing to breaking strength.^30,31 However, the innermost calcified layer (mammillary layer, ML) does not appear to directly affect the eggshell mechanical properties.^30,31 Instead, certain aspects of ML morphology seem to critically influence the early PL formation, affecting eggshell microstructure and texture.^30,32 ML morphology is characterized mainly by the density and distribution of organic nucleation sites (or cores) on the organic membranes (OMs). Spherulitic calcite grains (or crystals) grow out radially from these sites, giving rise to mammillary cones (MCs) during the early ML formation.^30,33 Calcite grain morphology, including the size and shape distributions, grain boundary (GB) characteristics (e.g., low- and high-energy GB densities, GB atomic array, GB triple junctions, see next section) and how they are arranged and oriented define the eggshell microstructure and crystallographic texture patterns.^{34,35,36,37,38} If such textures are non-random, local grain misorientations arise, and several related parameters (as Kearns factors and GB misorientations, see later in discussion)^{34,35,36,37,38} allow to introduce new ways for evaluating eggshell strength.

In materials science, Grain Boundary Engineering (GBE) has been conceptually investigated as a tool for improving diverse “non-natural” material properties. GBE is used to describe material processing methods to modify GB misorientation characteristics and control material properties.^39,40,41 Given the concept of “engineering” involved in the name, no one has ever explored the possibility of having that process modifying natural materials. Blind as it is, evolution can provide unexpected ways to solve optimization problems by selecting structural characteristics to improve mechanical properties.

Here we investigate the eggshell characteristics that may enhance the bioceramic material breaking strength. To do so, we quantify eggshell ultrastructural, microstructural and textural features using electron backscatter diffraction (EBSD) in a scanning electron microscope (SEM). Furthermore, we introduce new concepts for a further description of eggshell calcite crystals, such as Kernel Average Misorientation (KAM) and Crystallographic Preferred Orientation (CPO) (Figures 1, 2, 3, and S1–S3), which supplement conventional GB maps.

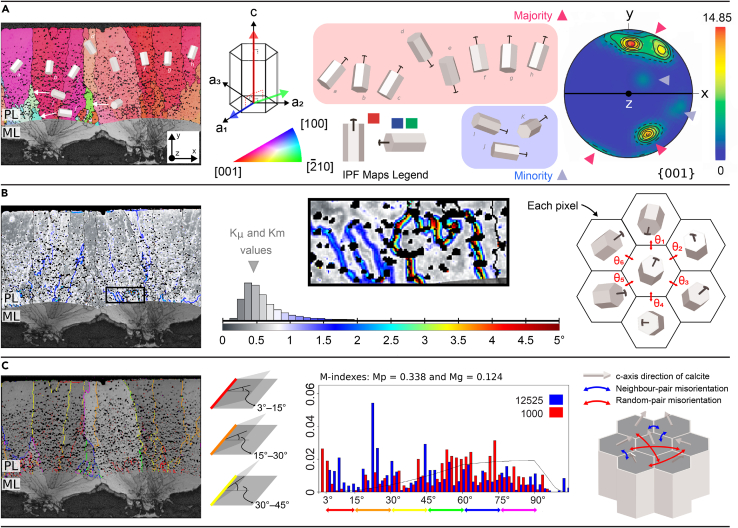
Figure 1.

Examples of EBSD maps and their interpretation

(A) Inverse Pole Figure (IPF) map showing calcite grains, from the Palisade Layer (PL), colored with the IPF map component. Grains with their c-axis that tend to be perpendicular to the eggshell surface (parallel to y-direction) are colored in reddish tones (majority); whereas the grains that tend to be parallel to the eggshell surface (x-, z-directions) are colored in greenish and bluish tones (minority). The majority reddish grains contribute to the hotspots of {001} pole figures at the polar regions. The minority bluish and greenish grains contribute to the weak signals at the equatorial parts of the pole figure. The value above the color bar (14.85) represents the multiple of uniform distribution density (MUD) value (high MUD value indicates strong crystallographic alignment and MUD value of 1 represents random distribution). Transverse direction Kearns texture factors (f_T) values were extracted from {001} pole figures. The pfJ-index values were extracted from {001}, {2$\overline{1}$0} and {100} pole figures.

(B) Kernel Average Misorientation (KAM) map identifying regions with KAM values between 0° (grayish tones) and 5° (dark reddish tones). These values represent the misorientation calculated by mean orientation between a point and its designated number of neighboring pixels, mapped according to the colored scale (KAM value = mean{θ_i, 1 ≤ i ≤ 6}). The set of all these KAM values for a studied sample is shown in a frequency distribution histogram (central schematic). From the histogram, we obtain the average and median KAM values (Kμ and Km) per eggshell sample.

(C) On a grain boundary (GB) map, misorientation angles between grains are represented by colors: 3° < θ ≤ 15° in red, 15° < θ ≤ 30° in orange, 30° < θ ≤ 45° in yellow, 45° < θ ≤ 60° in green, 60° < θ ≤ 75° in blue, and 75° < θ ≤ 90° in purple. The frequency distribution of (neighbour-pair and random-pair) misorientation is represented as a histogram. The continuous curve on the histogram shows the theoretical random distribution. The numbers next to blue and red boxes show the number of neighbour-pair (correlated) and random-pair (uncorrelated) misorientations. M-indexes (Mp and Mg) are defined on the base of the distribution of uncorrelated misorientation angles and theoretical random distribution. Legend, PL: Palisade Layer, ML: Mammillary Layer. For additional information, see STAR Methods.

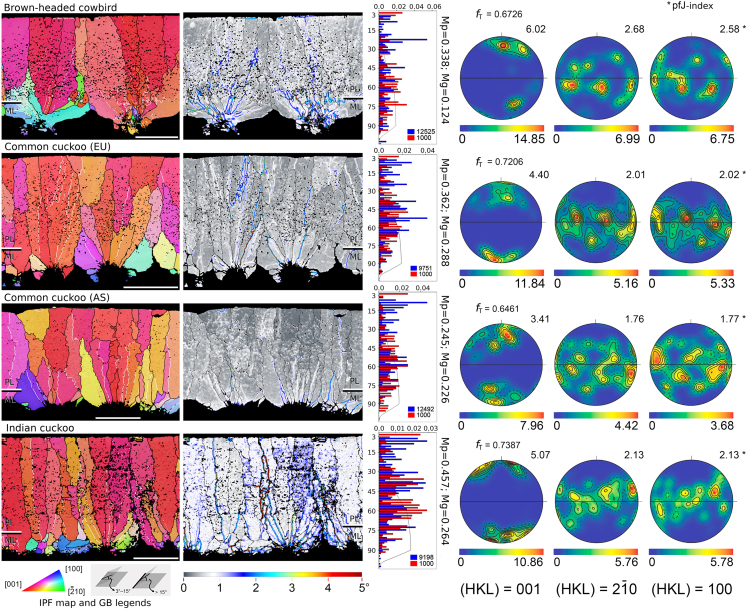
Figure 2.

EBSD maps for brood parasite eggshells

Profiles were obtained by (left to right): IPF maps, KAM maps, misorientation histograms, and {hkl} pole figures. Transverse direction Kearns texture factors (f_T) were extracted from {001} pole figure. White scale bar in the IPF maps indicate a reference length of 40μm. The numbers at the upper right corners of each pole figure are pfJ values extracted from each pole figure. Mp and Mg next to histograms mean M-index by point and by grain, respectively. For additional information, see Figure 1 and STAR Methods. Additional eggshell structural images are in Figures S6, S7, and S9.

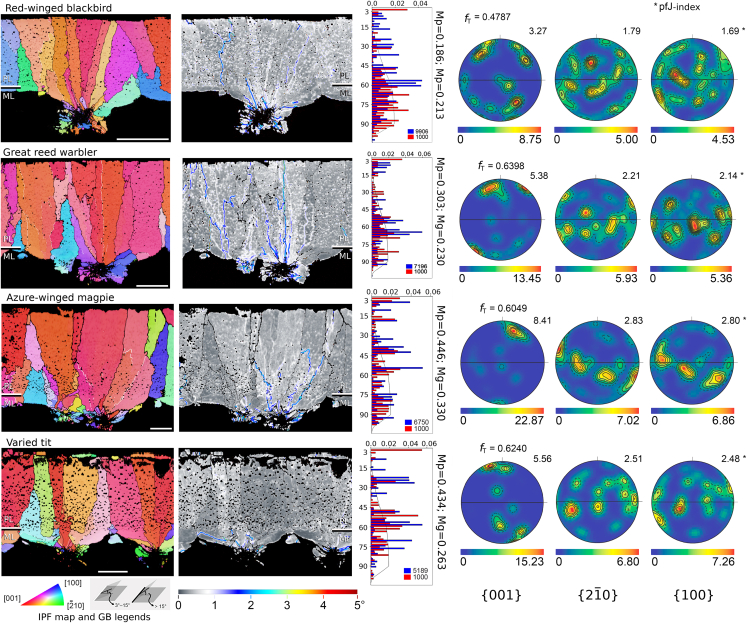
Figure 3.

EBSD maps for host eggshells

Profiles were obtained by (left to right): IPF maps, KAM maps, misorientation histograms, and {hkl} pole figures. White scale bar in the IPF maps indicate a reference length of 40μm (top) and 20μm (rest of the cases). Details are in Figure 2. Red winged blackbird is a frequent host of brown-headed cowbird (North America), great reed warbler is a frequent host of common cuckoo (Europe), azure winged magpie is a host shared by common cuckoo and Indian cuckoo (Asia), and varied tit is a frequent host of Indian cuckoo (Asia). For complete host eggshell samples, see Figures S1–S3. Additional eggshell structural images are in Figures S6, S7, and S9.

Using this comprehensive approach for eggshell crystallography, we perform a comparative study of eggshell characteristics across in avian clades, specifically emphasizing several obligate brood parasite–host systems where asymmetrical co-evolutionary selection pressures should have selected for different mechanical properties in host and parasite lineages. We include eggshell samples of egg-removal brood parasites (the common cuckoo C. canorus, the Indian cuckoo C. micropterus, and the brown-headed cowbird) and twelve of their host species (Figure S4). We also include additional data on egg-puncturing parasitic cowbirds.^8,25

Results and discussion

Thicker-shelled eggs of lineage-independent parasites

As has been shown in previous works,¹² both parasitic groups (cowbirds and cuckoos) exhibited relatively thicker-shelled eggs. This structural variable, represented here by the eggshell thickness relative to egg size (Rel. Shell_vol; variable definitions are in Table 1) showed significant differences from hosts’ groups (Figure 4A; pairwise Bayesian contrast values are in Table 2), according to our comparative analysis (via GLMMs; see STAR Methods).

Table 1.

Nomenclature and description of parameters and response variables

Parameters and Variables	Acronym	Definition	Description
Eggshell ultrastructure parameters	Shell	Mineralized eggshell	Total eggshell thickness (μm)
	PL	Palisade Layer	Outermost layer thickness of the eggshell or effective thickness (μm)
	ML	Mammillary Layer	Innermost layer thickness of the eggshell (μm)
	MCs	Mammillary Cones	Number of mammillary cones
Grain size and shape indexes	$\overline{A}$	Mean grain area	Mean value from all individual grain Ai measurements per shell sample (μm2)
	CED	Circle Equivalent Diameter	Diameter of a circle with area value $\overline{A}$ (μm) (Equation 1)
	Ei	grain Ellipticity	1-x/y; where (x,y) are short and long axes of the fitted ellipse for each grain Ai constituting a shell sample (dimensionless variable) (Equation 2)
Grain boundary (GB) parameters	LAB density	Low-Angle Boundary density	Low-energy intra-crystalline boundaries (3° < ω < 15°) per unit of scanned area (μm−1)
	HAB density	High-Angle Boundary density	High-energy inter-crystalline boundaries (15° < ω < 110°) per unit of scanned area (μm−1)
	TAB density	Total-Angle Boundary density	Low- and high-energy intra- and inter-crystalline boundaries (3° < ω < 110°) per unit of scanned area (μm−1)
Ultrastructure variables	Rel. Shellvol	Relative shell thickness	Residual values of the egg volume (independent variable) on shell thickness (response variable) regression line
	Rel. PLvol	Relative PL thickness	Residual values of the egg volume (independent variable) on PL thickness (response variable) regression line
	Rel. MLvol	Relative ML thickness	Residual values of the egg volume (independent variable) on ML thickness (response variable) regression line
	Rel. PLshell	Relative PL thickness	Residual values of the shell thickness (independent variable) on PL thickness (response variable) regression line
	Rel. MLshell	Relative ML thickness	Residual values of the shell thickness (as independent variable) on ML thickness (response variable) regression line
	PL ratio	Proportional thickness of the PL	100(PL thickness/shell thickness), dimensionless variable
	MC density	Mammillary Cone density	Number of MC per mm of cross-sectional eggshell profile (#MC/mm) (Figure S6)
	Rel. MC	Relative MC	Multiplication of the MC density by the eggshell perimeter (dimensionless variable)
Microstructure variables	Rel. CED	Relative CED	Division of the CED by the PL thickness (dimensionless variable independent of the scanned area and egg size)
	$\overline{E}$	Mean grain Ellipticity	Mean value from all individual grain ellipticity (Ei) measurements per shell sample (dimensionless variable)
	Rel. $\overline{E}$PL	Relative Ellipticity	Residual values of the PL thickness (as independent variable) on $\overline{E}$ (response variable) regression line
	Rel. LAB	Relative LAB	Multiplication of LAB density by the PL thickness (dimensionless variable independent of the scanned area and egg size)
	Rel. HAB	Relative HAB	Multiplication of HAB density by the PL thickness (dimensionless variable independent of the scanned area and egg size)
	Rel. TAB	Relative TAB	Multiplication of TAB density by the PL thickness (dimensionless variable independent of the scanned area and egg size)
Textural severity variables	Kμ	Average of all KAM values per shell sample	Each KAM value is calculated as average misorientation between a point and its designated number of neighboring points (Figure 1)
	Km	Median of all KAM values per shell sample	Each KAM value is calculated as average misorientation between a point and its designated number of neighboring points (Figure 1)
	pfJ	J-index (pfJ-index)	pfJ-index quantifies the sharpness of a pole figure (Equation 3)
	Mp	M-index	Mp quantifies the crystallographic preferred orientation (CPO) strength, and it was calculated for all points analyzed by EBSD to evaluate the dependence of fabric strength on the intracrystalline microstructure (Equation 4)
	Mg	M-index	Mg quantifies the CPO strength, and it was calculated for one point per grain by mean orientation of each grain to exclude the influence of intracrystalline microstructures on the strength of the eggshell (Equation 4)
	fT	Transverse direction Kearns texture factor	fT is defined as a weighted average of the basal pole figure intensity with respect to the sample normal direction (Equation 5)

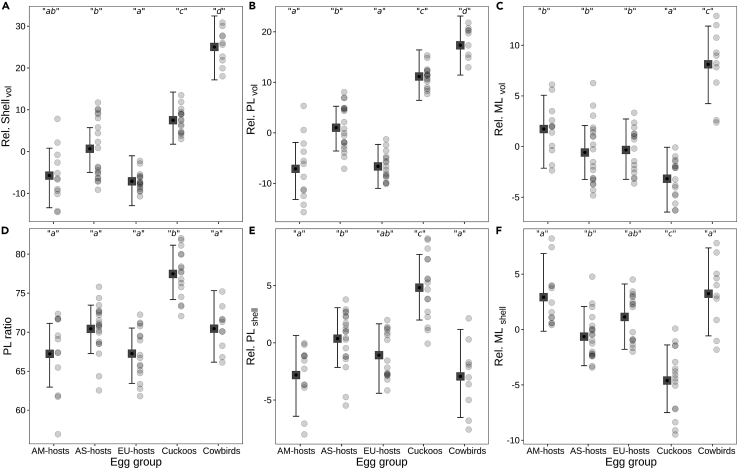
Figure 4.

Plots showing difference between egg groups in terms of eggshell ultrastructure variables

(A) Eggshell thickness relative to egg volume, (B) PL thickness relative to egg volume, (C) ML thickness relative to egg volume, (D) PL proportional thickness, (E) PL thickness relative to eggshell thickness, and (F) ML thickness relative to eggshell thickness against egg groups. Data are represented as means of posterior densities (squares) and associated 95% credible intervals (bars). Lowercase letters indicate significant differences between the means of groups (p ≤ 0.05). Legend, AM-hosts: American hosts, AS-hosts: Asian hosts, EU-hosts: European hosts. Response variable definitions are in Table 1 and STAR Methods. For additional comparative numerical data, see Tables 2 and S3–S8.

Table 2.

Summary of generalized linear mixed-effects models (GLMMs) significance and Bayesian contrasts (BCs)

Response variable	Overall p-MCMC	Pairwisea
		cowbirds – cuckoos	cuckoos – EU-hosts	cuckoos – AS-hosts	cuckoos – AM-hosts	cowbirds – EU-hosts	cowbirds – AS-hosts	cowbirds – AM-hosts
Rel. Shellvol	<0.001	17.5 [13.4, 21.7]	14.6 [11.0, 18.3]	6.9 [3.3, 10.2]	3.3 [9.3, 17.2]	32.1 [28.0, 36.4]	24.4 [20.3, 28.3]	30.8 [26.3, 35.2]
Rel. PLvol	<0.001	6.2 [2.9, 9.5]	17.8 [15.0, 20.7]	10.1 [7.5, 12.8]	18.3 [15.2, 21.3]	24.0 [20.8, 27.2]	16.3 [13.2, 19.5]	24.4 [20.9, 27.8]
Rel. MLvol	<0.001	11.3 [9.2, 13.5]	−2.8 [−4.7, −1.0]	−2.6 [−4.4, −0.8]	−4.9 [−7.0, −2.9]	8.5 [6.3, 10.6]	8.7 [6.6, 10.8]	6.4 [4.1, 8.7]
PL ratio	<0.001	−7.0 [−9.8, −4.3]	10.2 [7.7, 12.6]	7.0 [4.8, 9.5]	10.2 [7.6, 12.8]	3.2 [−0.1, 6.0]	0.0 [−2.7, 2.7]	3.2 [−0.1, 6.3]
Rel. PLshell	<0.001	−7.8 [−9.9, −5.7]	5.9 [4.1, 7.7]	4.5 [2.7, 6.2]	7.6 [5.7, 9.6]	−1.9 [−4.0, 0.2]	−3.3 [−5.3, −1.4]	−0.1 [−2.3, 2.1]
Rel. MLshell	<0.001	7.9 [5.8, 9.9]	−5.7 [−7.5, −3.9]	−4.0 [−5.7, −2.3]	−7.5 [−9.5, −5.6]	2.1 [−0.1, 4.1]	3.9 [1.9, 5.8]	0.3 [−1.9, 2.5]
MC density	<0.001	−12.7 [−14.7, −10.7]	7.4 [5.8, 9.0]	7.9 [6.2, 9.6]	10.1 [8.4, 11.5]	−5.3 [−7.3, −3.3]	−4.8 [−6.9, −2.7]	−2.6 [−4.5, −0.7]
Rel. MC	<0.001	−724 [−825, −625]	534 [451, 614]	636 [549, 726]	506 [432, 586]	−189 [−294, −92]	−88 [−191, 20]	−218 [−314, −120]
Rel. LAB	<0.001	0.39 [−0.41, 1.18]	0.99 [0.27, 1.66]	1.48 [0.83, 2.13]	−0.04 [−0.81, 0.70]	1.38 [0.61, 2.20]	1.86 [1.10, 2.62]	0.35 [−0.46, 1.21]
Rel. HAB	<0.001	−2.00 [−3.19, −0.80]	4.55 [3.51, 5.60]	4.27 [3.27, 5.25]	2.00 [0.84, 3.09]	2.55 [1.36, 3.74]	2.28 [1.13, 3.41]	0.003 [−1.25, 1.26]
Rel. TAB	<0.001	−2.15 [−3.89, −0.37]	5.51 [4.04, 7.08]	5.74 [4.21, 7.17]	1.96 [0.35, 3.67]	3.37 [1.61, 5.13]	3.60 [1.84, 5.27]	−0.18 [−2.09, 1.70]
Rel. CED	<0.001	0.024 [−0.019, 0.064]	−0.070 [−0.105, −0.031]	−0.059 [−0.095, −0.025]	−0.102 [−0.143, −0.064]	−0.047 [−0.088, −0.006]	−0.036 [−-0.076, 0.006]	−0.078 [−0.122, −0.034]
$\overline{E}$	0.016	0.034 [−0.017, 0.082]	0.046 [−0.001, 0.087]	0.029 [−0.014, 0.069]	0.035 [−0.013, 0.081]	0.080 [0.031, 0.132]	0.063 [−0.001 0.112]	0.069 [−0.001 0.123]
Kμ	0.077	overall mean value: 0.720, range: 0.400–1.150
Km	0.086	overall mean value: 0.443, range: 0.270–0.820
pfJ	0.055	overall mean value: 5.384, range: 3.270–8.840
Mp	0.196	overall mean value: 0.364, range: 0.184–0.624
Mg	0.300	overall mean value: 0.269, range: 0.075–0.687
fT	0.066	overall mean value: 0.606, range: 0.393–0.789

GLMMs were performed to determine whether consistent differences exist between egg groups (American hosts, Asian hosts, European hosts, parasitic cuckoos and parasitic cowbirds) on each eggshell structural feature (response variable). BCs were performed by multiple (pairwise) comparison post-hoc tests (BCs) for mean differences. The numerical values indicate the estimated mean difference and associated 95% credible interval (BC [95%CrI]). The BCs were considered statistically significant when the 95%CrI did not overlap zero. Finally, to determine which aspects of eggshell structural variations best explain the differences between egg groups, we also conducted Multivariate analysis of variance (MANOVA) and linear discriminant analysis (LDA). The subset of selected response variables (avoiding collinearities) were: Rel. PL_vol, Rel. ML_vol, Rel. PL_shell, Rel. CED, $\overline{E}$, Rel. LAB, Rel. HAB, and f_T (see Figure S5; Tables S1 and S2). For additional details, see STAR Methods.

^aBC outputs for host group pairs are not shown here, but see Figures 4 and 5.

Eggshell thickness is clearly an important factor positively affecting breaking strength⁴² and stiffness of parasitic birds.^8,25 Evolved hyper-allometrically thick-shelled eggs appears to be a parsimonious mechanism (see later in discussion) when calcium natural sources are not a limiting factor, and “exceptional” selective pressures (like usual egg-puncturing behaviors) are not acting significantly on egg phenotypes. However, more thorough studies of eggshell ultrastructure indicate that each mineralized layer (ML and PL, see Introduction) contributes differently to eggshell performance under mechanical loading.^20,22,43

Characterization of eggshell ultrastructure: palisade layer and mineralized layer relative thicknesses

We found that the brown-headed cowbird eggshells had ultrastructural characteristics that were distinct over cuckoo and hosts’ species, such as PL thickness and ML thickness relative to egg size (Rel. PL_vol, and Rel. ML_vol, Table 1), in addition to Rel. Shell_vol (Figures 4A–4C; Table 2). Furthermore, Rel. PL_vol (which was correlative with Rel. Shell_vol, r = 0.930, p < 0.001) and Rel. ML_vol were two of the most important contributors in the significant differentiation between parasites versus hosts and cowbirds versus cuckoos, according to our multivariate analysis (via LDA; see STAR Methods, Tables S1 and S2; Figure S5). The mean values of these three relative variables were significantly higher in the cowbird than in the cuckoo and hosts’ groups (Figures 4A–4C; Tables 2 and S3–S8).

This finding suggests that brown-headed cowbird eggs achieves greater eggshell thickness by proportionally increasing contributions to both the PL and ML, which should be sufficient to contribute to an extra breaking strength and/or stiffness differential. We also found that the proportional increases in both mineralized layers implies that the mean values of PL and ML absolute thicknesses show no statistical differences between this parasite and their large hosts (Table S3) (see later in discussion).

A structural variable unrelated to egg size is the proportional thickness of PL (PL ratio; Table 1). Eggshells from cuckoo species had significantly higher PL ratio values compared to eggshells from brown-headed cowbird and hosts’ groups (Figure 4D; Tables 2 and S4). In addition, eggshells from cuckoos and egg-puncturing parasites (screaming and shiny cowbirds) showed no significant differences in their PL ratio values (Table S4). Interestingly, the latter two parasitic groups achieved high PL proportional thickness through different mechanisms.

Egg-puncturing cowbirds achieved this higher ratio by only increasing PL thickness.²⁵ By contrast, our focal cuckoos showed a specific structural pattern that is more complex to interpret. That is, we detected that the PL ratio does not provide the necessary and sufficient information to describe this distinctive pattern. Thus, we define two complementary variables, the PL thickness and ML thickness, both relative to eggshell thickness (Rel. PL_shell and Rel. ML_shell; Table 1).

Our comparative analyses (via GLMMs; see STAR Methods) showed that cuckoo eggs had the lowest ML thickness values relative to egg size and to shell thickness (Rel. ML_vol, and Rel. ML_shell; Figures 4C and 4F; Table 2). Also, cuckoo eggs had the highest PL thickness values relative to shell thickness (Rel. PL_shell; Figure 4E and Table 2). However, these parasitic eggs had values of eggshell thickness and PL thickness, relative to egg size (Rel. Shell_vol and Rel. PL_vol), that were intermediate between brown-headed cowbird and hosts’ groups (Figures 4A and 4B; Table 2).

Specifically, these results suggest that cuckoos achieved a higher PL ratio through a combined effect of both layers, which can be explained as follows: (a) there is a considerable decrease in ML thickness, and that space is occupied by PL (which explains the lowest Rel. ML_vol and Rel. ML_shell values), (b) in addition to this layer substitution, there is also a slight extra increase in PL thickness (which explains the slightly high Rel. Shell_vol and moderately high Rel. PL_vol values), and (c) the combined effect of both layers can explain the highest Rel. PL_shell values and, consequently, the resulting PL ratio (Figure 4; Tables 2 and S4–S8).

This complex ultrastructural pattern allows cuckoo eggshells to undergo an increase in PL absolute thickness without an excessive increase in total shell thickness and, consequently, egg size. Such a mechanism could be the result of co-evolutionary pressures in opposite directions. Cuckoo eggs are under known selective pressures for already reduced allometric egg size to increase the likelihood that their smaller hosts will accept their eggs.⁴⁴ Simultaneously, in the opposite direction, cuckoo eggs are under pressures to provide increased interior egg space for embryonic development, such that parasite chicks will be sufficiently large and with necessary musculoskeletal strength for evicting the eggs and nestmates after hatching^45,46 (see later in discussion).

Unlike eggs of egg-puncturing cowbirds and their large hosts,^8,25 eggs of brown-headed cowbirds and their large hosts showed no relevant differences in the absolute thicknesses of total eggshell, PL and ML, in ultrastructural relative variables (such as PL ratio, Rel. PL_shell, and Rel. ML_shell), and even in the microstructural and textural characterizations (see next sections) (Table S3). Therefore, eggshells of brown-headed cowbirds and their large hosts are expected to show no relevant differences in mechanical performance. In fact, they showed no statistical differences in eggshell breaking strength or stiffness.^8,25

Parasitic cowbird lineage displays varied egg-damage behaviors (see Introduction). Parasite-imposed intraspecific competitive damage is especially frequent in nests parasitized by the screaming and shiny cowbirds. Thus, a stronger and stiffer eggshell may provide an adaptive advantage over the eggs of their hosts (regardless of relative egg dimensions), preventing successful puncture of the parasitic eggs by successive cowbird conspecifics. By contrast, brown-headed cowbird eggshell breaking strength (or puncture resistance)⁸ would not be directionally selected as their larger hosts typically reject the parasitic eggs through grasp-ejection and conspecific parasitic puncture events are infrequent.⁸

Simply increasing brown-headed cowbird eggshell thickness seems to be sufficient to contribute an additional strength and/or stiffness⁸ differential (since both are functions of eggshell thickness^42,47,48) necessary to provide an adaptive advantage over the eggs of their small hosts. We consider this mechanism as a species-specific adaptation comparatively parsimonious, since other possible mechanisms that strengthen the eggshells would involve complex processes at the ultra- and microstructural levels (shifts in ML morphology and in PL crystallography, see next sections). This additional mechanical performance would act as a counter-defense against the few small host species that do puncture-eject parasitic eggs,¹⁵ and would also protect against eggshell damage due to egg-collisions during parasitic egg laying from above nest rims of many small hosts.⁴⁹

Although such counter-defenses are not suitable to evaluate against their large hosts during the laying stage, the parasitic shell thickness shifts would act as an adaptive advantage during the incubation stage. For example, an increase in the parasitic egg $C$-number⁴⁷ could ensure safe large host contact incubation. $C$-number is a measure of how stiff an eggshell is with respect to egg mass after removing the egg shape effect ($C\equiv p_e·K$, where $K$ is eggshell stiffness, and $p_e$ is an egg shape and size dependent parameter; see Juang et al.⁴⁷). We calculated the $p_e$ values in 41 hosts larger than their parasite, the brown-headed cowbird (using raw data from Hung et al.⁷ and Juang et al.⁴⁷). We estimated that the hosts’ mean $p_e$ value was 293mN⁻¹ (range: 191–391) against 401mN⁻¹. That is, if an extra eggshell thickness implies an increase in stiffness such that there are no significant differences between this cowbird and their large hosts,^8,25 then the cowbird egg should have a $C$-number value 37% (range: 3–110) higher than the $C$-number values of their large hosts. Therefore, adaptive shifts in eggshell thickness (and consequently stiffness) would minimize the chances of crush damage to parasitic eggs during their incubation in the nests of their large hosts.

Common reed warbler (Acrocephalus scirpaceus) and great reed warbler (A. arundinaceus) are small hosts that frequently puncture-eject common cuckoo eggs. Despite finding statistical differences in their breaking strength (F: 0.69 ± 0.03N, 0.89 ± 0.01N, and 2.27 ± 0.01N, respectively),²⁴ these species do not appear to show differences in their $C$-number (∼19001, 20584, and 19391, respectively).^7,47 These findings suggest that there are eggshell structural characteristics that are specifically affecting the parasitic eggshell breaking strength, although great reed warblers and common cuckoos show no differences in their egg size, eggshell thickness and stiffness^7,24,47 (see later in discussion).

Characterization of eggshell ultrastructure: mineralized layer morphology

We previously showed that cuckoo eggshells had the lowest ML relative thickness (Rel. ML_vol, and Rel. ML_shell), and Rel. ML_vol mainly contributed in the differentiation between cuckoos and cowbirds (via LDA, see Figure S5; Tables S1 and S2). Furthermore, although the mean size of cuckoo eggs was ∼2.1 times larger than that their small hosts that lay smaller eggs (see STAR Methods), they showed no statistical difference in ML absolute thickness (GLS: F_2,49 = 9.108, p < 0.001, post-hoc test: p = 0.557). This supports that cuckoos had unusually low ML thickness regardless of relative egg and shell dimensions (Table S4).

Through backscattered electron (BSE) eggshell images (Figure S6), we determined a suite of ML morphological differences between cuckoos, cowbirds and hosts, which may have several relevant implications for cuckoo eggs. Despite complementary methodologies being necessary for a detailed morphological characterization of this innermost calcified layer (e.g., optical profilometry⁵⁰), we observed that internal eggshell surface pattern of cuckoo eggs is distributed in a more uniform and compact way (Figures S6 and S7). That is, MLs in brown-headed cowbird and hosts’ species showed visible differences in their local thickness given by the gaps between the tips of MCs (anchor point to OMs) and the inter-cone grooves (Figures S6 and S7). By contrast, greater uniformity in calcium distribution on the cuckoo eggshell internal surfaces may be attributed to a higher number of compact and smaller MCs, which reduces the gaps between MCs (Figures S6 and S7). We found that MLs from cuckoo eggshells contained a significantly higher number of cones (represented by MC density and Rel. MC variables; see Table 1, and STAR Methods) compared to the eggshells of cowbird and hosts’ groups (Tables 2 and S6–S8; Figure S8).

Each MC can be seen as a functional unit that provides a limited amount of calcium to an embryo,⁵¹ and the mechanisms of the calcium transport from the eggshell, respiratory gas exchange, and H₂O reabsorption are mediated by chorioallantoic membrane adjacent to the MC tips.^51,52,53,54 Then, a higher MC density may generate a greater and uniform contact with the chorioallantoic membrane. This would allow the apparent accelerated rates of calcium mobilization and respiratory gas exchange (since number of gas exchange pores and MCs are positively correlated^55,56,57).

For example, the "Extra calcium for chick vigor" hypothesis⁵⁸ suggests that some cuckoo nestlings require significant energy and strength to evict host eggs or nestlings. They may rely on extra calcium to build their musculoskeletal systems within their eggs to accomplish this task soon after hatching.⁵⁸ Unfortunately, this hypothesis has failed to receive support because the eggs of the non-evicting Clamator cuckoos are thicker-shelled than nest-mate-evicting cuckoos (Cuculus, Cacomantis, and Chrysococcyx spp.).^16,59 Just as the mechanical performance cannot be determined solely by comparing eggshell thickness, it does not seem appropriate either to dismiss this hypothesis by such an inference. Indeed, physiological calcium requirements for developing embryos are provided from the ML before hatching,⁶⁰ and the number of MCs determines the quantity of calcium available for bone formation for the developing embryo.⁶¹

Biomineralization heterochronic studies at the molecular and morphological levels will be necessary to explore the existence of evolutionary differences that could alter the embryonic development pattern. Such a pattern could affect the musculoskeletal formation rates^62,63 and/or physical strength levels⁶⁴ between hatchling parasitic species that vary in their parental care monopolization behaviors (evicting versus non-evicting strategies). Our prediction that nest-mate-evicting cuckoos should have more access to embryonic calcium sources than non-evictors (e.g., Clamator, and Molothrus spp.) is thus borne out by the current data.

In the meantime, at mechanical performance level, Simons³³ observed that hen (Gallus sp.) eggs having superior eggshell quality (low shell mechanical deformation) had a higher MC density than poor eggs, indicating that eggshell quality is improved by having more compact and smaller MCs. He further observed that guinea fowl (Numida sp.), whose eggs have quite a high breaking strength, also have MLs with reduced inter-MCs space. However, van Toledo et al.³¹ noted that the characteristics of calcite columnar grains (which form PL) appeared to be regulated by the speed at which MCs fuse; and early fusion of the MCs results in shorter inter-cones spaces (reduced gaps) that may strengthen the eggshells.²⁰ The early fusion phenomenon may account for a significant portion of the resulting eggshell strength.^20,43 Based on these findings, we characterized PL at microstructural and textural levels.

Characterization of eggshell microstructure and texture: palisade layer morphology

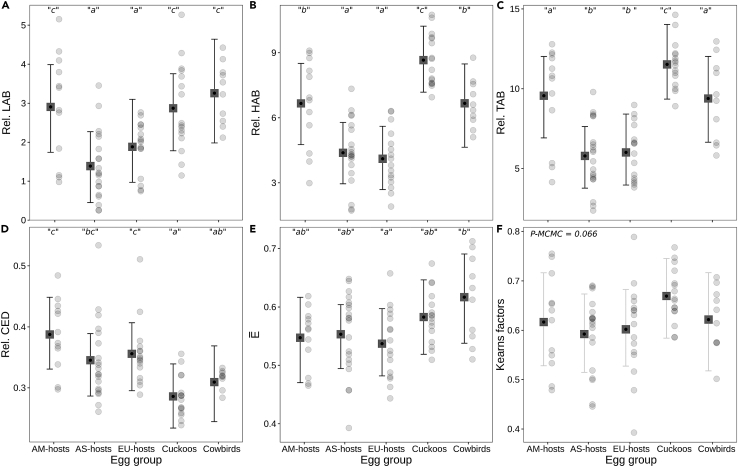
A relatively higher density of closely spaced MCs (Figures S6–S8) would explain the lower ML thickness in cuckoo eggshells, in accordance with the early fusion phenomenon.^20,21,43 These ML morphological differences would have a varied effect on PL microstructure as calcite columnar grains form at the point where individual MCs fuse. In fact, we found that PLs from cuckoo eggshells had (a) visually thinner polycrystalline units (or shell units⁶⁵) compared to brown-headed cowbird and hosts’ groups (Figure S7), (b) significantly smaller grains compared to brown-headed cowbirds (i.e., mean grain area $\overline{A}$, Table S4), and (c) significantly smaller grains compared to hosts’ groups (i.e., relative grain size represented by Rel. CED, see Tables 1 and 2; Figure 5D). More relevantly though, PLs from cuckoo eggshells had significantly longer GB lines relatively to brown-headed cowbird and hosts’ groups (i.e., Rel. HAB and Rel. TAB; see, Tables 1 and 2; Figures 5B and 5C).

Figure 5.

Plots showing difference between egg groups in terms of eggshell microstructure and textural variables

(A) Relative density of low-angle boundaries, (B) relative density of high-angle boundaries, (C) relative density of total- (low and high) angle boundaries, (D) relative calcite grain size, via circle equivalent diameter, (E) relative calcite grain shape, via ellipticity, and (F) transverse direction Kearns texture factor against egg groups. Data are represented as means of posterior densities (squares) and associated 95% credible intervals (bars). Lowercase letters indicate significant differences between the means of groups (p ≤ 0.05). Legend, AM-hosts: American hosts, AS-hosts: Asian hosts, EU-hosts: European hosts. Response variable definitions are in Table 1 and STAR Methods. For additional comparative numerical data, see Tables 2 and S3–S8.

The relative lengths of high-angle GB lines (Rel. HAB, which were correlative to Rel. TAB, r = 0.950, p < 0.001) together with Rel. PL_vol and Rel. ML_vol, were the variables that contributed to the differentiation between cuckoos versus hosts and, mainly, between cuckoos versus brown-headed cowbirds (via LDA, see Tables S1 and S2; Figure S5).

However, shifts in ML morphology did not imply significant differences in grain shape between eggs’ groups (i.e., grain ellipticity $\overline{E}$, Tables 1 and 2; Figure 5E). That is, calcite grains in eggshells of the brown-headed cowbird and hosts’ species were not wider (in relation to length) than those of the cuckoo species, as expected by the early fuse model.⁴³ Furthermore, unlike Dunn et al.,⁴³ our results did not provide support either for significant relationships between the grain size, total shell thickness or ML thickness versus crystallographic texture severity (see later in discussion).

Soler et al.²¹ showed that eggshells of the parasitic great spotted cuckoo (Clamator glandarius) were composed of smaller calcite grain units (analyzed focusing on both ML and PL), having lower intensity grain orientation distribution function (ODF; i.e., less severe texture) than two of their host species. The authors suggested these characteristics may contribute to make cuckoo eggs structurally stronger than non-parasitic eggs. In contrast, eggshells of egg-puncturing cowbirds (but not the egg-removal cowbird) were composed of smaller grains (analyzed focusing only on PL) than hosts’ species. However, López et al.⁸ found no evidence of differences in texture factors between all studied cowbirds’ and hosts’ species, despite finding strong differences in their major mechanical properties. These results are consistent with those shown by Rodríguez-Navarro et al.,²⁰ who found no statistical differences in grain orientation (nor in shell thickness) between two hen egg groups that strongly differed in their eggshell mechanical strength, even though the authors concluded that shells formed by randomly oriented grains should be stronger. Furthermore, Chiang et al.,²² when comparing eggshells of several avian species, found that the grain orientations have no effect on elastic modulus, and these results are consistent with those found by López et al.⁸

Our EBSD maps showed that the majority of calcite grains exhibited c-axes perpendicular to the eggshell surface (or parallel to the y-direction; see Figure 1). This was reflected in the pole figures for calcite c-axis {001}, with maximum intensities strongly oriented toward the poles (y-axis, radial direction) and weakest intensities around the equator zone (x-, z-axes), with no obvious orientation patterns (Figures 1, 2, 3, and S1–S3). As expected in avian eggshells, texture was characterized by a single fiber component with the radial direction mostly along the radial direction (Figures 1, 2, 3, and S1–S3). Misorientation angles between neighboring grains had deviations from random distributions, showing no tendency to follow the theoretical curve (Figures 1, 2, 3, and S1–S3). These deviations are due to the presence of discreet peaks appearing at low angles (3° < φ < 15°; see Figure 1), related to the presence of subgrains derived from a common parent microstructure (inheritance), the MC. Indeed, KAM maps showed the variations of local misorientations inside each grain (intragrain). The KAM maps were mostly in grayish tones (θ < 1°, occurring by the intragrain non-homogeneous occlusion of organic material) which means that local change in crystal orientation (0° < θ < 5°) was relatively small (Figures 1, 2, 3, and S1–S3).

Our comprehensive texture severity comparative analysis (via GLMMs, see STAR Methods) did not find evidence of variation between egg groups, in terms of local grain misorientation (KAM, represented by Kμ and Km indexes, Table 1), preferred orientation strength (CPO, represented by pfJ, Mp and Mg indexes, Table 1), and texture factor (i.e., transverse direction Kearns factor f_T, Table 1; Figure 5F) (see Table 2). Our results show consistent evidence that crystallographic texture patterns do not determine eggshell mechanical properties. In contrast to the conclusions of Rodríguez-Navarro et al.,²⁰ Soler et al.,²¹ and Dunn et al.,⁴³ our findings suggest that extra eggshell strengthening should not be related solely to lower textural severity parameters.

Together with describing further results and discussing the main disparate conclusions, we need to carefully discuss the basics of fracture and failure in fragile materials, as currently understood by materials science.

Textural severity and grain boundaries influence on bioceramic material mechanical performance

It is well-known that crystalline structure controls the cracking behaviors, and the structural “defects” have significant effects in controlling the mechanical properties.^{36,37,38,66,67} That is, a nano-micro crack will progress by choosing between different structures included in the atomic array, from less ordered regions (e.g., weak GB bonds) to perfect well-ordered crystalline regions (e.g., ionic-covalent bonds). In turn, the crack can be deterred by interposing “defects” (e.g., triple junctions, pores, precipitates and organic materials, amorphous crystal phases, perfect crystal plane barriers, among others).^38,67 However, GBs are the most likely candidates for dissipating energy during fracture, although still there are a few other possible ways to marginally augment the breaking strength. Then, the question is if those other ways are profusely present in polycrystalline eggshells, in a sort of naturally happening GBE process, and how to detect them. Unfortunately, from the viewpoint of materials characterization, and particularly from EBSD technique capabilities, many microstructure quantities overlap fuzzily spreading among the different kinds of defects and scales (texture severity, studied here by pfJ-index, K-indexes, M-indexes, texture factor f_T). For instance, (a) small grains may show a severe texture or not, although not as severe as a few well oriented crystals can appear. So, the fact that we observe weak textures because of the small grain size can or cannot be related to GBs or, alternatively, to texture itself, (b) KAM values would reflect the presence of small grain sizes because of the many pixels located on the neighborhoods of GBs, although they are not designed to measure texture, neither grain size, but internal misorientations, (c) The same can be said about M- or pfJ-indexes. From single crystals (an extreme) to finely divided polycrystals (opposite extreme), texture severity would decrease and all parameters to describe misorientation would increase, although their behavior is far from being linear or monotonous. So, orientation and misorientation distributions can be very misleading when not adequately used to predict fracture behavior, particularly when average values and not local ones are calculated.

Furthermore, the crystalline structure of calcite is rhombohedral (space group 167, R-32/c) with six faces, each nucleated on the {104} crystal plane,⁶⁸ where they also tend to twin and grow chemically easily, provided the appropriate organic matrix is available. Other twin planes are {001}, {012} and {018}, which, when they are tangent to the eggshell surface, will tend to favor cracks that will be also almost tangent to the eggshell surface and will not penetrate radially. Because of the crystallography itself, they are at low angles with the {001} planes, so, if the <001> directions are perpendicular to the eggshell, all the known cleavage planes will tend to be tangent to the eggshell surface.⁶⁹ If we assume that the most important feature to provide the eggshell with high breaking strength is to orient the cleavage planes tangent to the eggshell surface, that is <001> directions along radial egg direction, so we need a parameter, preferably a single number, to measure that preferential orientation conferring the eggs with such strength. For example, texture factor f_T is a measure of the relative number of <001> directions in coincidence with the radial direction of the eggshell surfaces. However, there are not differences in the crystallographic texture among egg groups (see Table 2) and/or species that differ strongly in their eggshell breaking strength, fracture toughness, elastic modulus, among other mechanical properties.^8,20,22

Crystallographic texture directly influences mechanical plastic deformation in polycrystalline metals,^37,70,71 but in fragile polycrystalline ceramics (such as calcite and biogenic minerals not subject to geological processes), plasticity is absent.⁷² Besides the obvious fact that crystallographic texture cannot directly influence fracture toughness and breaking strength in brittle polycrystalline ceramic materials, understanding fracture at the atomic level suggests that more local variables, directly linked to the failure phenomena, should be used.

Fortunately, EBSD provides the means to calculate those variables. Furthermore, the extreme decrease of grain sizes (e.g., like those that make up the ML) could mislead one to think that GBs would be so much abundant that strength should be higher. However, beyond certain grain size threshold, the presence of many GB paths would allow to go easily through eggshell thickness, in the direction it has even solicited, by almost straight, slightly waiving, cracks with much less energy expenditure.

Ultra-, micro- and nanostructures have been concepts sometimes defined differently in materials, biology and earth sciences. We talk about ultrastructure when observing, by optical or SEM imaging, scales that are invisible at naked eye. Meanwhile, since we are mainly working with a technique such as EBSD, allowing to quantitatively differentiate between micro- and nano-sized features, it will be pretty clear which are our definitions of microstructure and nanostructure (see Introduction). It will also be clear the meaning of large, small, larger or smaller, since they will always be related to a particular size determined by a concrete measurement and not to an undefined eye appreciation that could be misleading. The information about the presence of nanocrystals¹ is available, although not as an image. Whenever the resolution of our technique allows to clearly identify them (i.e., ∼30nm), will contribute to the determination of GBs (e.g., LAB, HAB and TAB) and their use for the calculation of related variables.

The optimum combination of relatively large columnar crystal (e.g., like those that make up the PL, compared to the ML) with path diversions (e.g., high frequency of triple junctions, as a “defect”, or eventual nanocrystals quite aligned with them but misoriented between each other, in cuckoo eggshells; see Figure S9) makes the choice of GBs in the PL, suitable for the physical understanding of fragile polycrystalline materials, such as eggshells. Moreover, GB fracture is always associated with low toughness and low ductility (i.e., high brittleness).⁷³ Indeed, the avian eggshell is characterized by relatively high Young’s modulus and low fracture toughness, what might render them stiff and strong but still brittle enough to fracture when required for hatching.³ Therefore, because of the weakness of the GB bonds, weaker than the bonds on cleavage plans, we again argue that GBs are better candidates for eggshell fracture toughness (K_c) improvement and, consequently, for breaking strength (F) evaluation. F is the maximum force needed to fracture the egg, and describes the response of the eggshell as a composite complex structure.²⁰ K_c describes the ability of a material to resist the propagation of small cracks^,3,48 and it is related to F and T (${F\propto K}_c{·T}^{3/2}$, T is eggshell thickness; see Bain⁴⁸).

Grain boundaries on control of brood parasitic eggshell breaking strength

Accordingly to the previous section, GB path lengths are microstructural features related to the cracking probability, suitable for evaluating fracture process in eggshell materials. Propagating fissures along these weaker paths is a process for releasing energy along every path on the eggshell. The longer these paths are (i.e., due to greater complexity and density of GB networks, Figure S9), the tougher (by K_c) and, consequently, stronger (by F), the eggshell will be. That is, it will take extra energy to go completely through GB tortuous labyrinths, causing a growing crack or fissure to deflect from side to side, or even in an opposite direction, greatly increasing both the energy consumed in the way and K_c value. Figure S9 shows a visual eye guide for judging the tortuosity of those labyrinths with dots marking the triple junctions, providing a hint for the expected results obtained by rigorous mathematical calculations of their lengths.

Eggs of the brown-headed cowbird and cuckoo species showed no statistical differences in PL absolute thicknesses, while these species showed differences with the two egg-puncturing cowbirds (Table S4). In parallel, cuckoo and brown-headed cowbird eggs showed differences in the TAB density, while cuckoo and egg-puncturing cowbird eggs showed no differences (Table S4). These patterns can be interpreted as follows.

Given a stress (mechanical load) on the egg equatorial section (see STAR Methods), the cracks produced in the shell are expected to propagate in the radial egg direction, and for a similar PL thickness, it is expected that a larger GB density greatly increases the energy consumed in crack or fissure propagation. Therefore, we expect an increase of the stress concentration factor K_c for increasing F (i.e., ${F\propto K}_c{·T}^{3/2}$)⁴⁸ in cuckoo eggshells compared to brown-headed cowbirds, since K_c depends on microstructure, and consequent increase of GBs, for increasing energy dissipation during fracture. Analogously, for the same TAB density, it is expected that a greater PL thickness should increase the GB lengths producing a longer pathway and greatly increasing the energy consumed in crack or fissure propagation. In this case, we also expect an increase of K_c for increasing F in egg-puncturing cowbird eggshells compared to the cuckoos. In fact, the egg-puncturing cowbirds, cuckoos and brown-headed cowbirds showed statistical differences in their Rel. TAB values (∼13.1, 11.5, and 9.4, respectively; Figure 5C; Tables 2 and S4). Therefore, we expect the intrinsic macro-mechanical K_c in cuckoo eggshells to be intermediate between the egg-puncturing and egg-removal cowbirds. Indeed, unlike the egg-puncturing cowbird eggs (F: overall 4.6 ± 0.1N),⁸ the brown-headed cowbird and common cuckoo eggs do not seem to show differences in their eggshell breaking strengths (F: 2.4 ± 0.4N vs. 2.3 ± 0.1N, respectively),^23,24 despite brown-headed cowbird eggs have thicker shells than common cuckoo eggs (Table S4) and show the highest relative shell thickness values (Figure 4A). Furthermore, the common cuckoo and their egg-puncturing host, the great reed warbler, show no differences in egg size, shell thickness,²⁴ $C$-number, and stiffness,^7,47 despite the fact that common cuckoo eggshells are statistically stronger than host eggshells²⁴ (see above).

These results clearly do not support indirect inferences on thicker implying stronger eggshells. Actually, these results indicate a K_c increment in cuckoo eggshells, what should increase F. In fact, the ability of common cuckoo eggshells to resist the propagation of small cracks (using Equation 3 in López et al; ⁸) was 1.25 and 1.82 times higher than eggshells of brown-headed cowbirds and their main hosts (warblers; see also Table S7), respectively. In turn, K_c values in both egg-puncturing cowbird eggshells were overall 1.43 times higher than brown-headed cowbird eggshells.⁸ These two independent results strongly support, as previously expected, that K_c and F are larger in cuckoos than in egg-removal cowbirds, but smaller than in egg-puncturing cowbirds.

Conclusions

We detected eggshell ultra- and microstructural differences leading to better functional and mechanical performance in those parasitic species with eggs having relatively high breaking-puncture frequencies. Our results revealed that stronger eggshells should not only be due to lower texture severity. This study demonstrates GBs within the outermost calcified layer (PL) of eggshells are microstructural and textural features suitable for physical foundation understanding of fragile polycrystalline eggshells. That is, the thicker the PL, and the longer and more complex the GB paths are, the stronger and tougher-breaking the eggshell will be. These characteristics, which we can identify as a GBE driven process, making it selectively chosen, depending on the many other texture related variables, has been positively identified as an utterly natural mechanism to further improve eggshell breaking strength in egg-puncturing cowbirds (that impose strong inter- and intraspecific competitive egg damage), followed by the cuckoos (with relatively high probabilities of egg breaking-puncture by their small hosts). Finally, eggs of parasitic cuckoos with "nestmate evicting" strategies (which implies greater physical exertion in their nestlings), showed morphological shifts in the innermost calcified layer (ML) of eggshells, although further investigations on biomineralization at the molecular and physiological levels are needed to determine how these shifts influence the calcium availability during embryonic development.

Limitations of the study

This study investigated the eggshells of a wide range of species but could not use many egg specimens per species due to limited availability. A few more replicative studies will be very useful to test the reproducibility of this research. The replicative study may investigate either the same parasite-host pairs or another lineage of parasites–host pairs (such as greater honeyguide). EBSD was the main analytical method used in this study, but settings of EBSD analysis that we used might have affected the quality of data. Future researchers are recommended to analyze an eggshell of a taxon used in this study and compare the data with ours (those uploaded in Data repository; see key resources table) to guarantee the reproducibility of our and their future works.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited data
EBSD raw data	This study	https://data.mendeley.com/datasets/xs364mt7wj/draft?a=85caa301-394b-46e6-a3d1-c58c45f48cb2, doi:10.17632/xs364mt7wj.1
Processed numerical data and R script	This study	https://data.mendeley.com/datasets/xs364mt7wj/draft?a=85caa301-394b-46e6-a3d1-c58c45f48cb2
Software and algorithms
ATEX (v. 3.30)	Beausir and Fundenberger 2017	http://www.atex-software.eu/
AZtec (v. 4.3)	Oxford Instruments	https://nano.oxinst.com/products/aztec
ImageJ (v. 1.51)	National Institute of Health	https://imagej.nih.gov/ij/download.html
MTEX (v. 5.8.1)	Hielscher and Schaeben 2008	https://mtex-toolbox.github.io/index
R Project	R Core Team 2020	https://www.r-project.org/
Unicef careware software package	Michibayashi and Mainprice 2004	http://www.gm.univ-montp2.fr/PERSO/mainprice/W_data/CareWare_Unicef_Programs/

Resource availability

Lead contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact, Seung Choi (seung0521@gmail.com).

Materials availability

All research materials (eggshells and prepared EBSD specimens) are deposited in the School of Earth and Environmental Sciences, Seoul National University (Seoul, South Korea). The used materials are listed in the key resources table.

Data and code availability

• •EBSD raw data, numerical data extracted from EBSD raw data and R scripts for statistical analysis have been deposited at Mendeley Data and are publicly available as of the date of publication. DOIs are listed in the key resources table.
• •This paper does not report original code.
• •Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.

Method details

Egg collection and study species

Egg samples were sourced from field collections and museum specimens in North America, Europe, and East Asia. We analyzed eggshells from the following parasite-host systems: (1) North America: brown-headed cowbird (Icteridae: Molothrus ater; adult female body mass: 38.1 ± 0.6g, egg vol: 2.9 ± 0.1ml, shell samples N = 10) and its host species, northern cardinal (Cardinalidae: Cardinalis cardinalis; 41.8 ± 0.4g, 4.7 ± 0.1ml, N = 4), red-winged blackbird (Icteridae: Agelaius phoeniceus; 39.5 ± 0.6g, 3.8 ± 0.1ml, N = 4) and house finch (Fringillidae: Haemorhous mexicanus; 21.4 ± 0.1g, 2.2 ± 0.1ml, N = 4); (2) Europe: common cuckoo (Cuculidae: Cuculus canorus; 106 ± 2g, 3.0 ± 0.1ml, N = 4) and its host species, great reed warbler (Acrocephalidae: Acrocephalus arundinaceus; 30.0g, range 23–45.5, 3.1 ± 0.1ml, N = 4), common reed warbler (Acrocephalus scirpaceus; 12.3g, range 9–19.7, 1.78 ± 0.1ml, N = 4), dunnock (Prunellidae: Prunella modularis; 19.7 ± 0.1g, 2.0 ± 0.1ml, N = 4) and white wagtail (Motacillidae: Motacilla alba; 21 ± 0.2g, 2.3 ± 0.1ml, N = 4), (3) East Asia: the common cuckoo (C. canorus; 3.4 ± 0.1ml, two eggshell morphotypes: blue eggshell, N = 4,and spotted beige eggshell, N = 4) and the Indian cuckoo (C. micropterus; 119g, range 112–129, 3.9 ± 0.2ml, N = 4) and their hosts, azure-winged magpie (Corvidae: Cyanopica cyanus; 92g, range 76–112, 5.4 ± 0.3ml, N = 4), Japanese tit (Paridae: Parus minor; 17.6 ± 0.1g, 1.4 ± 0.1ml, N = 4), varied tit (Paridae: Sittiparus varius; 17g, range 15.9–18.2, 1.69 ± 0.1ml, N = 4), vinous-throated parrotbill (Paradoxornithidae: Sinosuthora webbiana; 10.9 ± 0.2g, 1.31 ± 0.1ml, N = 4), and Daurian redstart (Muscicapidae: Phoenicurus auroreus; 16.2g, range 11–20, 1.70 ± 0.1ml, N = 4). Body mass values⁷⁴ correspond to the mass of adult females. The phylogenetic relationships are shown in Figure S4. All eggshells were cleaned with 70% ethanol and stored in a cool dark place until material preparation.

Preparation of EBSD specimens

We obtained EBSD data following the established methodology for fossil and modern eggshell preparation.⁷⁵ Specifically, we fragmented eggshells (N = 74) along the egg equatorial axis. We chose this access because it represents the most uniform and weakest part of the eggshell, and therefore it provides the best estimate of the lower limits of eggshell strength.⁷⁶ Additionally, both adults (parasites and hosts, personal observations) and embryos⁷⁷ peck at an egg’s equatorial section.

The eggshell fragments were embedded in epoxy resin with a drop of hardener. The embedded eggshells were cut and lapped on a glass plate with 400-, 600-, 1000-, and 3000-grit aluminum compounds. The lapped surfaces were polished with 0.5μm diamond paste and finally with colloidal silica (0.06μm) for 20min for each sample. The resulting surfaces were coated with an optimal carbon coating.⁷⁸ EBSD analysis was performed using a Symmetry detector (Oxford Instruments; https://nano.oxinst.com/symmetry), which is an attached accessory of FE-SEM (JEOL JSM-7100F), housed in the School of Earth and Environmental Sciences, Seoul National University. The Kikuchi lines⁷⁹ were automatically indexed using AZtecSynergy (v.4.3) software (Oxford Instruments) with a step size of 0.11–0.20μm depending on the thickness of eggshells. The orientation of each scanned pixel was determined by indexing Kikuchi patterns,⁷⁹ and the whole crystalline map was reconstructed by the proper processing of data. Crystallographic orientation data obtained by systematically scanning⁷⁹ the polished eggshell surface enable the spatial distribution of GB networks to be mapped and correspondingly, the spatial arrangement of crystalline orientations (texture) to be displayed.

Data curation methods

EBSD data were mainly presented in inverse pole figure (IPF) maps with GB information and kernel average misorientation (KAM) maps. The maps and transverse Kearns factor (f_T) were extracted using ATEX-software (v.3.30).⁸⁰ The {001}, {2$\overline{1}$0} and {100} pole figures and the frecuency distribution of misorientations (graphed as histograms, Figure 1) were extracted from HKL Channel 5 (v.5.12.74.0) software package (Oxford Instruments). We also used the Unicef careware software package of David Mainprice (www.gm.univ-montp2.fr/PERSO/mainprice/W_data/CareWare_Unicef_Programs) to extract pfJ-index and multiple of uniform distribution density (MUD) value and used MTEX-software (v.5.8.1, MATLAB toolbox)⁸¹ to acquire M-index values. From the EBSD data, we quantified the following eggshell parameters (Table 1).

Measurements of eggshell layers and mammillary cones

Eggshell ultrastructure was analyzed based on the EBSD maps. For the measurements, we used the ruler functionality on ImageJ (downloadable from http://rsb.info.nih.gov/ij/). The total thickness of each eggshell specimen was measured as the cross-sectional distance from its outermost surface to the point where the basal MCs get inserted into the organic membranes (OMs).

Thicknesses of both eggshell layers (ML and PL) were also assessed. ML thickness being the distance from the basal cones to the point at which the palisade columns first fuse. The layers were differentiated by visual comparison of rounded vesicle density and topographic roughness^82,83 (Figure S6). We also calculated the PL thickness relative to the eggshell total thickness as a percentage (PL ratio, [%]). For each eggshell cross-sectional profile micrograph (backscattered electron BSE images, Figure S6), we estimated the linear density of MCs (#MCs/mm), and defined the dimensionless variable Rel. MC as the multiplication of the MCs per mm by the eggshell perimeter (calculated as πB; where B is the egg breadth). We note that one of the limitations of this linear method is that we do not take into account the MCs’ size (e.g., volume) or its area in contact with the shell organic membranes.

Measurements of calcite grain size

From IPF maps, we treated pixels as grain candidates when more than ten continuous pixels have consistent crystallographic orientation, with a tolerance of ∼1–2° of misorientation.⁸⁴ If these candidates were bounded by a boundary angle ω > 15° (High-angle grain boundary), we considered the candidate a valid grain.⁸⁵ Whereas, when candidates were bounded by a boundary ω < 15° (Low-angle grain boundary) the candidate was considered an intra-GB (or sub-grain).⁸⁵ We measured grain size ($A,{[\mu m}^2]$) for all valid grains. For each eggshell sample, the mean value from all individual grain measurements was recorded as mean grain area $\left(\overline{A},{[\mu m}^2]\right)$. $\overline{A}$ was converted to a circle equivalent diameter (CED, $\left[\mu m\right]$) variable (Equation 1).

$$\text{CED}=d_c\left(\overline{A}\right)=2\sqrt{\frac{\overline{A}}{\pi }}$$ (Equation 1)

EBSD grain size data have often been reported in the literature by converting area measurements into a 'circle equivalent diameter' to obtain a more intuitive units of distance.⁸⁶ The c-axis of most calcite grains in PLs are columnar in shape and tend to be perpendicular to the eggshell surface (see Figure 1). Therefore, grains that tend to be larger may be positively correlated with greater PL thickness. Using circle equivalent diameter allows us to correct the effect given by the PL thickness (i.e. Rel. CED; Table 1) as a dimensionless variable and independent of the scanned area and eggshell thickness.

Measurements of Grain shape (Ellipse fitting)

Calcite grain shape was quantitatively expressed using aspect ratio.⁸⁷ Knowing the gravity center of each valid grain A_i, it was fitted by an ellipse. From the fitted ellipse, the short and long axes (x, y) as well as the angle of the long axis with the radial direction of the sample is obtained. The ellipticity (E_i) of each grain is calculated as follow:

$$E_i=1-\frac{x}{y}$$ (Equation 2)

For each eggshell sample, the mean value from all individual grain ellipticity measurements was summarized as mean grain ellipticity $\overline{E}$. When $y\approx x$, $\overline{E}$ tends to 0 (circular shape), and when $y\gg x$, $\overline{E}$ tends to 1 (elongated shape). Note that the grains on the map borders are not considered because they do not represent true grain shapes.

Measurements of grain boundary line network

The GB networks were separated by setting values of the angular misorientation ω. Low-angle boundaries (LAB, 3° < ω < 15°) are low-energy boundaries and high-angle boundaries (HAB, 15° < ω < 110°) are high-energy boundaries.³⁵ Total-angle boundaries (TAB, 3° < ω < 110°) are both low- and high-energy boundaries. We tailored the LAB, HAB and TAB densities, dividing the lengths of these boundaries by the scanned area (LAB, HAB and TAB density [μm⁻¹], respectively).

Measurements of grain local misorientation

Kernel average misorientation (KAM) is calculated as the average misorientation between a point and its designated number of neighbouring points (Figure 1). KAM shows the consistency of crystallographic direction of local areas. For example, when a point is surrounded by neighbouring points with drastically different crystallographic configuration, the point yields high KAM value, but, if it were surrounded by neighbouring points with very similar crystallographic configuration, the point would yield low KAM value. ATEX automatically provides descriptive statistics of KAM maps, via frequency distributions graphed as histograms. From the histograms, we obtained the average and median KAM values (Kμ and Km, respectivety) per eggshell sample (for graphical summary, see Figure 1). KAM maps allow to visualise minute local misorientation variations (θ < 1°). This is a useful complementary technique to GB maps, since the GB maps can be inefficient (by the presence of "noises") for low angle values (θ < 3°). The positions of smaller GBs (mostly 3° < θ < 5°) are overlapping with the positions with higher KAM values (mostly 1° < θ), but KAM maps additionally show that there are diverse variations of local misorientations inside each grain (intragrain) and they can be quantitatively measured.

Measurements of crystallographic preferred orientation

The pole figure J-index (pfJ-index) quantify the sharpness of a pole figure.^23,88 The pfJ-index (Equation 3) values were extracted from the orientations of grains in the {001}, {2$\overline{1}$0} and {100} pole figures using the Unicef Careware software package as follow:

$$pfJ=\int {\left[P_{hkl}\left(\alpha ,\beta \right)\right]}^{2}d\omega$$ (Equation 3)

where α and β are the spherical co-ordinates of the considered direction in the pole figure, $P_{hkl}\left(\alpha ,\beta \right)$ is the density in that direction for a given crystallographic pole defined by {hkl}, and dω = 1/2π sin α dαdβ is the fractional volume of integration. By definition, the pfJ-index theoretically ranges from 1 (corresponding to a completely random distribution) to infinity (a single crystal). The misorientation index (M-index)⁸⁹ quantify the crystallographic preferred orientation (CPO) strength based on the difference between the distribution of uncorrelated misorientation angles for the observed grains and the theoretical random distribution of uncorrelated misorientation angles (Figure 1). The M-index (Equation 4) values were calculated using MTEX (v.5.8.1, MATLAB toolbox)⁸¹ as follow:

$$M=\frac{1}{2}\int \left|R^T\left(\phi \right)-R^0\left(\phi \right)\right|d\phi$$ (Equation 4)

where $R^T\left(\phi \right)$ is the theoretical distribution of uncorrelated misorientation angles for a random fabric, $R^0\left(\phi \right)$ is the observed distribution of uncorrelated misorientation angles for a sample fabric from EBSD data, and φ is the misorientation angle of uncorrelated grain pair. The M-index ranges from 0 (corresponding to a completely random distribution) to 1 (a single crystal fabric). The M-index Mp was calculated for all points analyzed by EBSD to evaluate the dependence of fabric strength on the intracrystalline microstructure. In contrast, the M-index Mg was calculated for one point per grain by mean orientation of each grain to exclude the influence of intracrystalline microstructures on the strength of the eggshell.

Measurements of Kearns texture factor

Kearns texture factor (f, Equation 5) is the integral polar value taking in account the fiber-like intensity of <001> crystal direction (or radial direction) with respect to the radial egg direction.⁹⁰ It is defined as a weighted average of the basal pole figure intensity with respect to the sample normal direction:

$$f=\frac{{\int }_0^{\pi }I\left(\vartheta \right){\mathit{cos}}^2\vartheta \mathit{sin}\vartheta d\vartheta }{{\int }_0^{\pi }I\left(\vartheta \right)\mathit{sin}\vartheta d\vartheta }$$ (Equation 5)

where $I\left(\vartheta \right)$ is the average pole figure intensity at an angle $\vartheta$ from the sample normal. The function $I\left(\vartheta \right)$ used by Kearns is equivalent to the integral ${\int }_0^{2\pi }I\left(\phi ,\vartheta \right)d\phi$ over the pole figure intensity $I\left(\phi ,\vartheta \right)$, which is a function of both spherical angles.⁹¹

Kearns texture factors are typically measured in three orthogonal sample directions. For example, rolling f_R, transverse f_T, and normal f_N directions for a rolled sheet.⁹² For the eggshell analysis, only the angle of the basal pole to the sample normal was needed. The f_T values were extracted from {001} pole figures using ATEX-software. Kearns factor values vary between 1 (all the crystals are aligned pointing with their c-axis perpendicular to the shell surface) and 0 (all the crystals are aligned pointing with their c-axis parallel to the eggshell surface), and constitute an additional dimensionless variable for representing texture effects in a compact way.

Note that the microstructure and texture measurements were estimated by focusing on PL (Figure 1). PL shows the greatest variability among species, suggesting that this layer is suitable candidate for comparative analysis. By contrast, ML is composed of numerous small radial growth crystals (random orientations) with relatively few microstructural and mechanical differences between species.^8,22

Quantification and statistical analysis

Statistical analyses were conducted using R software (v.3.6.3).⁹³ A set of 1000 topologies was obtained from the Bayesian posterior distribution⁹⁴ provided in www.birdtree.org. A unique phylogenetic consensus tree was generated (Figure S4) via consensus.edges function from 'phytools' package (v.0.7.47),⁹⁵ and used as a framework for performing the Bayesian analyses, while plots were generated using the 'ggplot2' package (v. 3.3.5).⁹⁶

Confounding variable control

Different statistical techniques are suggested to test the main effects of a categorical variable on a continuous dependent variable (response) controlling for the effects of another selected continuous independent variable (covariate), which co-varies with the response variable. Such as ANOVA on covariate-adjusted residuals and ANCOVA.^97,98 Although ANCOVA is well-established and recommended,⁹⁷ it has important specific considerations, in addition to the common assumptions for any linear model, which are crucial for its use.^98,99,100 For example, the independence between the covariate and the treatment factors is an often-ignored assumption, resulting in incorrect inferences.^98,99 Specifically, our selected covariates, egg volume and shell thickness, and egg groups (categorical variable) exhibited dependence (GLS: F_1,4 = 6.502, p < 0.001, and F_1,4 = 87.105, p < 0.001, respectively), hence ANCOVA is not appropriate.^98,99,100 Instead, the residual analysis (phylogenetic size-correction,¹⁰¹ see below) is conservative which might be viewed as an advantage in order not to reach spurious and confused conclusions.⁹⁹

Phylogenetic size-correction

We fitted overall evolutionary regression lines⁸⁷ (via phylogenetic GLMMs,¹⁰² see below) to the entire data set and obtained the residual values (covariate-adjusted residuals). We define each set of residual values as: (a) Rel. Shell_vol (residuals from eggshell thickness vs. egg volume regression), (b) Rel. PL_vol (PL thickness vs. egg volume), (c) Rel. ML_vol (ML thickness vs. egg volume), (d) Rel. PL_shell (PL thickness vs. shell thickness), and (e) Rel. ML_shell (ML thickness vs. shell thickness). Each regression was performed using the phylogeny (given by the phylogenetic variance-covariance matrix) and species (as species-specific effect) as the random effect variables. We estimated R² as an indicator of goodness of fit within a Bayesian framework.¹⁰³ Regressions were significant and positively correlated (see following). We then tested the main effects of egg groups on the obtained residuals (hereafter, relative variables; see below).

Summary of regression outputs: (a) slope = 12.996, p-MCMC < 0.001, R² = 0.641; (b) slope = 10.288, p-MCMC < 0.001, R² = 0.565; (c) slope = 2.566, p-MCMC = 0.003, R² = 0.292; (d) slope = 0.802, p-MCMC < 0.001, R² = 0.923; and (e) slope = 0.198, p-MCMC < 0.001, R² = 0.487.

Comparative analyses

We performed phylogenetic generalized linear mixed-effects models (GLMMs) with Gaussian error, using the Markov chain Monte Carlo (MCMC) approach by Bayesian statistics, via the MCMCglmm function from the 'MCMCglmm' package (v.2.29)¹⁰³ to determine whether consistent differences exist between egg groups (American hosts, Asian hosts, European hosts, parasitic cuckoos and parasitic cowbirds) on each eggshell structural feature (response variable). The response variable for each model was: (a) Rel. Shell_vol, (b) Rel. PL_vol, (c) Rel. ML_vol, (d) Rel. PL_shell, (e) Rel. ML_shell, (f) PL ratio, (g) MC density, (h) Rel. MC, (i) Rel. LAB, (j) Rel. HAB, (k) Rel. TAB, (l) Rel. CED, (m) $\overline{E}$, (n) Kμ, (o) Km, (p) pfJ, (q) Mp, (r) Mg, and (s) f_T (Tables 1 and 2).

Each GLMM was performed using the phylogeny (given by the phylogenetic variance-covariance matrix) and/or species (as species-specific effect) as the random effect variables, according Deviance Information Criterion (DIC) criteria. DIC is an approximate model selection method which tries to explicitly balance model complexity with fit to the data.¹⁰⁴ We compared a model with no random factors, a phylogenetic model without intraspecific correlation structure, a model with only intraspecific structure, and a model with both phylogenetic and intraspecific structure.

All selected GLMMs were run for 5 million iterations with a burn-in of 500 and a thinning interval of 100. This generated 50,000 samples from each chain from which parameters were estimated. Before fitting the models, we explored the normality and homogeneity of variance. The violations to these assumptions were addressed by the log-transformation of the variables. For the model diagnosis, we analyzed the Markov chain to check reliability of the posterior approximation through Trace-plot and Autocorrelation-plot.¹⁰² We also applied the Heidelberg stationary test with the 'coda' package in R (v.0.19.3),¹⁰⁵ as a diagnostic test of convergence that uses the Cramér–von Mises statistic to test the null hypothesis that the sampled values come from a stationary distribution.¹⁰⁵

Fitted models were considered statistically significant when p-MCMC ≤ 0.05¹⁰² (Table 2). We then performed multiple (pairwise) comparison post-hoc tests for mean differences (Bayesian contrasts). Posterior distribution mean and associated 95% credible interval [95%CrI] (Figures 4 and 5), and Bayesian contrasts BCs (estimated mean differences and associated [95%CrI], via HPDinterval method, Table 2) values were obtained using the tidyMCMC function from the 'broom' and 'broom.mixed' packages in R (v.0.2.6).¹⁰⁶ BCs were considered statistically significant when [95%CrI] did not overlap zero⁹⁸ (Table 2).

Complementary comparative analyses

We also performed complementary comparisons as support of our main results and discussions. The egg groups to be compared were: the parasitic cuckoos [four levels: common cuckoo (blue eggshell, Asia), common cuckoo (beige eggshell, in Asia), common cuckoo (Europe), and Indian cuckoo (Asia)], and each parasite and their hosts [brown-headed cowbird and their hosts, northern cardinal, red-winged blackbird and house finch (North America); common cuckoo and its hosts, azure-winged magpie, vinous-throated parrotbill and Daurian redstart (Asia); common cuckoo and their hosts, great reed warbler, reed warbler, dunnock and white wagtail (Europe); Indian cuckoo and their hosts, azure-winged magpie, Japanese tit and varied tit (Asia)], and parasitic species [three levels: cuckoos (Eurasia), brown-headed cowbird (North America), and shiny and screaming cowbirds (South America)].

Because the complementary comparisons varied between low and unbalanced sample sizes, we explore differences among groups using alternative approaches such as frequentist statistics and non-parametric methods.

We analyzed the data using generalized least squares (GLS) fitted by a restricted maximum likelihood (REML) via gls function from the 'nlme' package in R (v.3.1.149).¹⁰⁷ The heteroscedastic variance was controlled by modeling the variance structure using the appropriate function (among varIdent, varPower, and varExp) according to the Akaike’s Information Criterion (AIC).^108,109 The anova function was used on the GLS models to determine its significance, and multiple comparisons (Tukey’s post-hoc tests) were performed via the glht function in the 'multcomp' package (v.1.4.17) with adjusted p-values.¹¹⁰

We also performed Randomization tests through non-parametric bootstrap (BS). Based on 1000 bootstrap replicates, we estimate bootstrap statistics (t) and 95% confidence intervals (using different methods) via the boot and boot.ci functions from 'boot' package (v.1.3.25),^111,112 and we used the typical tests, Welch's t-test, via oneway.test function from 'MASS' package (v.7.3.53)¹¹³ and Kruskal-Wallis test, via the kruskal.test function from 'stats' package (v.3.6.3).⁹³ All these alternative statistics methods were consistent, and we only showed the summary from GLS and Tukey’s post hoc tests (Tables S3–S8).

Multivariate analysis of variance and linear discriminant analysis

The multiple eggshell structural features studied in current work, can be integrated into a multivariate analysis comprehensive model (i.e., linear discriminant analysis LDA^114,115), making it possible to synthesize the eggshell ultrastructural, microstructural and microtextural information, thereby retaining/explaining most amount of existing variability among egg groups on fewer dimensions, and also assisting interpreting which specific eggshell structural variables best explain differences between parasites and hosts. We first tested for multivariate differences among egg groups (American hosts, Asian hosts, European hosts, cuckoos, and brown-headed cowbirds) by a multivariate analysis of variance (MANOVA) with Pillai’s statistic, via manova function (from ‘stats’ package) and using a subset of dependent variables. All candidate variables were previously standardized, and the multi-collinearity problem was avoided by the investigation of pairwise correlations, using rcorr function from 'Hmisc' package (v.4.4).¹¹⁶ The model assumptions were investigated using the Shapiro-Wilk test for multivariate normality and Box’s M-test for homogeneity covariance matrices, and was addressed by the log-transformation of the variables. Post hoc t-tests with Holm sequential Bonferroni correction for multiple levels were carried out using the 'lsmeans' package (v. 2.30.0),¹¹⁷ to reveal significant difference between egg groups. The α level was set at p ≤ 0.05. Then, we tested for a LDA (via lda function from 'MASS' package) to find the best combination of a subset of dependent variables (Table 2) that characterize, discriminate and maximize the differences among egg groups, through creation of new variables (discriminate functions LDs) that are linear combinations of the original variables. Standardized coefficients (canonical coefficients or weights) of each LD inform the relative contribution of each original variable in the linear combination (Table S1), and these were used to explain LDs’ biplots. Structure coefficients (Pearson’s r correlation between original dependent variables and canonical coefficients, Table S2) reports which of the original variables contributes more to the discriminant power.

Published: November 22, 2023