Exploring Optimal Objective Function Weightings to Predict Lifting Postures Under Unfatigued and Fatigued States

Abstract

Objective

To explore whether the optimal objective function weightings change when using a digital human model (DHM) to predict origin and destination lifting postures under unfatigued and fatigued states.

Background

The ability to predict human postures can depend on state-based influences (e.g., fatigue). Altering objective function weightings within a predictive DHM could improve the ability to predict tasks specific lifting postures under unique fatigue states.

Method

A multi-objective optimization-based DHM was used to predict origin and destination lifting postures for ten anthropometrically scaled avatars by using different objective functions weighting combinations. Predicted and measured postures were compared to determine the root mean squared error. A response surface methodology was used to identify the optimal objective function weightings, which was found by generating the posture that minimized error between measured and predicted lifting postures. The resultant weightings were compared to determine if the optimal objective function weightings changed for different lifting postures or fatigue states.

Results

Discomfort and total joint torque weightings were affected by posture (origin/destination) and fatigue state (unfatigued/fatigued); however, post-hoc differences between fatigue states and lifting postures were not sufficiently large to be detected. Weighting the discomfort objective function alone tended to predict postures that generalized well to both postures and fatigue states.

Conclusion

Lift postures were optimal predicted using the minimization of discomfort objective function regardless of fatigue state.

Application

Weighting the discomfort objective can predict unfatigued postures, but more research is needed to understand the optimal objective function weightings to predict postures during a fatigued state.

INTRODUCTION

Design of workspaces, equipment and clothing, including physical prototyping, is expensive, and particularly so within the military sector. Using the military sector as an example, millions of dollars are spent each year on projects related to the design and evaluation of physical prototypes in the United States alone (Department of Defense, 2017). Additionally, costs rise considerably as the number of physical prototype variations evaluated is increased, especially when only one option will ultimately be selected for production (Ahmed et al., 2019; Duffy, 2012; Hofbauer et al., 2011; Jun et al., 2019). Computer aided engineering (CAE), or the use of computer software to simulate performance in order to improve design, also referred to as virtual prototyping, can substantially reduce costs. By increasing the use of CAE, equipment, workspaces and clothing design, iterations can be developed and evaluated virtually, reducing the need for more extensive, costly physical prototyping (Bordegoni & Rizzi, 2011). However, the ability to evaluate human interactions with new workspace designs or equipment is often poorly considered within CAE, and is often only considered during more costly physical prototype design stages (Chaffin, 2009). Digital human modelling (DHM) software can be used to identify and evaluate human-systems integration concerns within CAE. This allows designers to identify and correct possible human factors and ergonomics concern before physical prototypes are built, saving time and money. Such issues would otherwise go unnoticed until the later physical prototype stage of development. Though DHM software is readily available to evaluate human-systems integration within CAE, use and uptake remain limited, partially due to limited guidance on how to predict postures for individuals under unique physiological states such as fatigue (Davidson et al., 2021).

One method that DHMs use to predict and simulate human postures is by leveraging optimization-based models. Optimization-based DHMs assume that humans inherently choose postures that minimize or maximize physiologically relevant performance criteria, an assumption well supported by current theories motor control (Abdel-Malek & Arora, 2013; Cashaback & Cluff, 2015; Scott, 2004; Todorov & Jordan, 2002; Yang, 2009). The mathematical formulations of the physiologically relevant performance criteria being optimized are considered objective functions. In emerging DHM’s, multiple objective functions are available for users to include within their predictions. Yet, little evidence is available to guide end-users in deciding which objective functions best predict realistic postures, particularly when considering individual state factors such as fatigue.

Selecting physiologically relevant objective functions that represent plausible goals of the sensorimotor system is a challenge. Multiple physiologically relevant performance criteria may compete and/or cooperate and their relative priority may alter with changes in task demands or an individual’s state (Berret et al., 2019; Cashaback & Cluff, 2015; Jin et al., 2019; Sparrow & Newell, 1998; Yang, 2009). Human gait is an example where associated objective functions are relatively well-defined during steady state walking, where commonly used performance criteria include minimizing muscle activations and maximizing gait stability and smoothness (Miller et al., 2012; Nguyen, Johnson, Sup, & Umberger, 2019). However, objective functions that best predict postures specific to the completion of occupational tasks, such as lifting, overhead reaching, pushing, and pulling remain poorly defined. A relatively unstudied consideration is how individual states, such as fatigue, may alter the relative weightings of objective functions (Davidson et al., 2021; Ma et al., 2009). Identifying optimal objective function weightings and understanding prospective differences in underlying objective functions and weightings will improve the ability to utilize DHMs to support virtual prototyping for a wider range of design characteristics.

Santos Pro (SantosHuman Inc., Coralville, Iowa) is a current and widely used DHM solution that allows user to predict postures by using a multi-objective optimization approach. Users can select and weight up to 7 different objective functions, depending on what objectives might be most relevant to a situation. These objective functions include the minimization of 1) discomfort, 2) maximum joint torque, 3) total joint torque, 4) change in potential energy, 5) effort, 6) joint displacement and 7) the maximization of vision. These objectives were selected as the mathematical representations of objectives that past research has identified as most likely to inform human movement solutions (see Abdel-Malek & Arora, 2013 for a more complete review). However, objectives including the minimization of discomfort, maximum joint torque, and total joint torque may have the most support when considering both the DHM-based optimization literature and the broader motor control literature. Discomfort is a well-established objective function within the literature (Marler, Rahmatalla, et al., 2005; Rochambeau et al., 2008). While discomfort is usually measured as a subjective phenomenon, the perception of discomfort seems to be linked to three underlying phenomena, the tendency to prefer more neutral postures, the tendency to require joint angles near end range and the tendency to move distal segments more readily than proximal segments (Marler, Rahmatalla, et al., 2005). Additionally, an extensive body of literature supports objective functions that have similar aims to the minimization of maximum joint torques (squared joint torque normalized to max torque producing capacity) and total joint torques (squared joint torques) (Crowninshield & Brand, 1981; Dul et al., 1984). Joint torque related objectives are particularly interesting when considering fatigue, or the reduction in torque generating capacity over time during a task. Where discomfort might serve as a good objective function to predict postures under unfatigued states, we speculate that under fatigued states it is possible that joint torque related objective functions may better predict postures. Understanding which objective functions are best suited to predict postures under specific states (like unfatigued or fatigued) remain an open question.

The purpose of this study was to identify the objective function weightings that best predict origin and destination postures in unfatigued and fatigued states during a floor-to-shoulder height box lifting. Additionally, we investigated if optimal objective function weightings were different when predicted origin relative to destination lifting postures, or when predicting postures in unfatigued or fatigued states. We hypothesized that the fatigued state postures would be better predicted with higher weightings towards the torque-based objective functions compared to the unfatigued states in both the origin and destination lifting postures.

METHODOLOGY

We used a combination of in silico and in vivo data to address our research question which we briefly summarize here before describing detailed methodology below. First, we used a commercially available software (Santos Pro) to predict postures at the origin and destination of a floor-to-shoulder lifting task (in silico data). We varied the settings in the software to systematically change the weighting factors for three objective functions, where each iteration generated a unique lifting posture for the prescribed lift origin and destination characteristics. Not knowing which iteration, or weighting factor combination generated the best prediction, we then compared each predicted posture (defined as a vector of joint angles) to postures measured experimentally (in vivo data) (also defined as a vector of joint angles). These postures were compared for participants lifting from an origin to a destination with the same characteristics used to constrain the predicted origin and destination postures. By plotting the resultant differences between predicted and measured postures (where measured postures were participant specific), we identified the weighting combinations corresponding to the predicted postures that were most similar (least deviation in joint angles) to each participant’s measured data, which we term optimal weightings. We then used the optimal weightings as our dependent measure to understand how the optimal weightings differed when predicting: i) origin versus destination postures, and ii) posture in unfatigued or fatigued states.

Generating in silico Data

Santos Pro software was used to predict postures at the origin and destination of a floor to shoulder height lift. Santos Pro is a physics-based human simulation software that uses a multi-objective optimization algorithm to predict joint angles (design variable) subject to internal (e.g., joint range of motion limits) and external (e.g., feet must remain on floor, hands must be on box handles) constraints. Users are able to select from and/or alter the weighting of several unique objective functions, termed performance measures in the software, based on the needs of the analysis. However, limited evidence is available to help users determine the objective function settings that best predicts realistic human postures. To address this concern during lifting, we used Santos Pro to predict origin and destination floor-to-shoulder height lifting postures for ten unique avatars. Each avatar was anthropometrically scaled (height and weight) to create a digital twin for each participant that had completed a 60-minute repetitive floor-to-shoulder height lifting protocol (Oomen et al., 2022). Origin and destination postures were predicted for each avatar 1,331 times, where the objective function settings were varied on each iteration to change the weighting allocated to each of three objective functions.

We focussed on manipulating the weightings of three objective functions available in the Santos Pro software including the minimization of: Discomfort, Maximum Joint Torque and Total Joint Torque. The word discomfort is often referred to in the literature but is typically poorly defined given its subjective nature (Abdel-Malek & Arora, 2013). However, for the purpose of being consistent with the setting labels in the Santos Pro software, we maintain the use of the discomfort term throughout. More specifically, the discomfort objective function included three factors (Equation (1)): the tendency to maintain a comfortable neutral position (standing with arms at the side); the tendency to move body segments sequentially (limbs, then spine and then sterno-clavicular); and the tendency to avoid joint end ranges of motion.

Equation 1

Shows the discomfort objective function. Firstly, optimizing for the tendency to settle towards a neutral position where q represents a posture, ∆q _i ^norm is the normalized (to range of motion) change in joint angle for a degree of freedom from the neutral position where the avatars are modelled with a total of 215 degrees of freedom. Secondly, variable γ _i is a weight used to prioritize the movement of specific joints over others (Marler, Yang, et al., 2005). G is a coefficient equal to 10 ⁶ . Lastly, QU and QL are penalty terms associates with values approaching the joint upper and lower range of motion limits, respectively.

$$f_1\left(\mathit{q}\right)=\frac{1}{G} {\displaystyle \sum }_{i=1}^{DoF}\left[{\gamma }_i\left(\mathrm{\Delta }{q}_i^{norm}\right)+G\times Q{U}_i+G\times Q{L}_i\right]$$ (1)

The minimization of total joint torque aimed to minimize effort defined as the square of all joint torques (Equation (2)) and the minimization of maximum joint torque minimized the squared torque normalized to the torque limit of the respective degree of freedom adapted from Marler, Knake, and Johnson (2011) (Equation (3)).

Equation 2

Shows the objective function for minimizing total joint torque (dynamic effort) adapted from Xiang et al., (2012) where variable τ _i represents the torque for a given degree of freedom, variable (q) is the resultant posture.

$$f_2\left(\mathit{q}\right)=\mathit{ }\sum _{i=1}^{DoF}{\mathit{\tau }}_i^2$$ (2)

Equation 3

Shows the minimization of maximum joint torque objective function equation where τ _i represents the torque for a given degree of freedom, (q) is the posture and τ _max represents the maximum torque limit of a degree of freedom.

$$f_3\left(\mathit{q}\right)={\displaystyle \sum }_{i=1}^{DoF}{\left(\frac{{\mathit{\tau }}_{\mathit{i}}}{{\mathit{\tau }}_{max}}\right)}^2$$ (3)

Within the software, priority can be given to different objective functions by selecting a weighting percentage between 0% and 100%. Different objective function weightings can alter the relative prioritization of the specified objective and therefore alter the predicted posture (defined by joint angles). The combinations of the various objective functions within the Santos Pro software are not required to add to 100%, but rather work more like manipulating hot and cold taps to output water of a preferred temperature. Where each tap can be manipulated between 0 and 100%, each objective can contribute 0–100% of its possible effect on the predicted posture. For this analysis, objective function combinations were iteratively simulated at 10% weighting increments from 0 to 100% for each of the three objective functions. Each combination (n = 1331) yielded a unique predicted posture.

The participant specific avatars were subject to internal and external constraints. Internal constraint included the joint range of motion and joint torque limit data defaults within Santos Pro which are based on previous research (Cahalan et al., 1989; Gill et al., 2002; Kaminski et al., 1999; Kumar, 1996). Predictions were also constrained to remain in balance using the zero-moment point stability constraint in the software. This constraint requires that a predicted posture be subject to the avatar maintaining the centre of pressure at the feet within their base of support. Previous research highlights the importance of considering this internal constraint when predicting postures for lifting tasks (Xiang et al., 2008).

To contextualize the predictions to the experimental data (Oomen et al., 2022), we used three external constraints. First, we used end effector and marker target pairings within the software to enforce the hand position (defined using end effectors on the second and fifth metacarpals of each hand) of each digital twin to be in a position within the virtual environment software that was equivalent to the actual hand position of the participant within the lab coordinate system. Second, we enforced a similar external constraint on the feet (defined using end effectors on the first and fifth metatarsals of each foot) to ensure that the feet of the digital twin avatar were in the same relative location as their companion live participant. Third, point loads were added to the third metacarpal-phalangeal joint of each digital twin, equivalent to the loads handled by their live human counterpart. Loads were applied bilaterally assuming an equal distribution of mass between the hands. Postures (joint angles for all degrees of freedom between the fixed hands and feet) were then predicted for all 1,331 objective function weighting configurations.

Description of in vivo Data

Previously measured motion capture data were obtained from ten participants (six female and four male) recruited from a university population who were completing a 60-minute repetitive lifting protocol for the purpose of evaluating movement variability and fatigue (Oomen et al., 2022). Complete details of the study protocol are reported by Oomen et al., (2022). Here, we only summarize salient details specific to our modelling efforts. Participant demographics data are described in Table 1. The experimental study protocol complied with the American Psychological Association and was approved by the University of Waterloo Office of Research Ethics Committee (ORE# 41674). Informed consent was obtained from each participant.

TABLE 1:

Demographics Information for the Participants Who Completed the Fatigued Lifting Protocol and Who Were Included in the Simulations

Demographic	Male (N = 4)	Female (N = 6)
Age (years)	26.8 ± 3.9	22.2 ± 4.0
Height (cm)	176.3 ± 11.5	162.2 ± 4.0
Weight (kg)	64.5 ± 11.0	61.9 ± 10.2

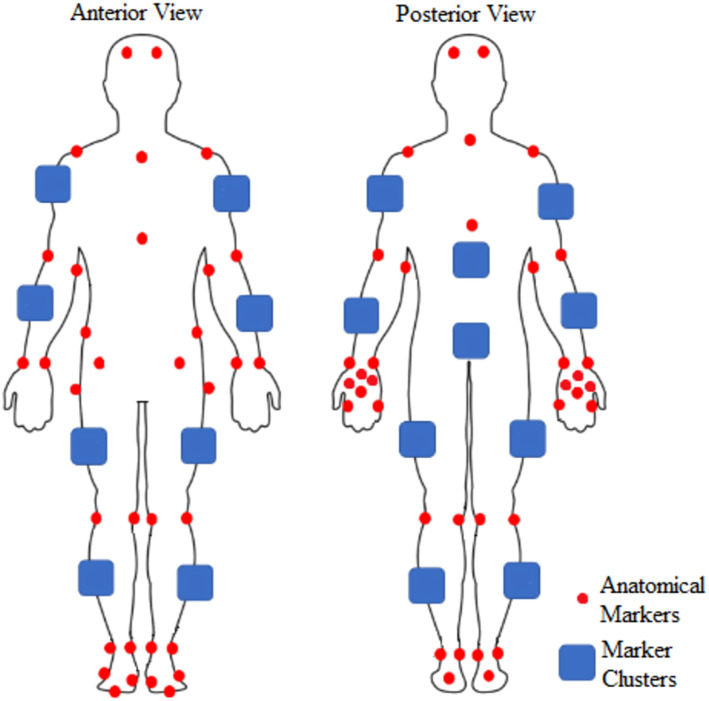
In brief, participants were instrumented with a whole-body, passive reflective, motion capture marker set (Figure 1) to define the kinematic skeleton (anatomical markers) and to track lifting kinematics (marker clusters). A static calibration trial (Vicon, Centennial, Co, USA) was collected with the full marker set. Following calibration, the marker clusters remained on the participants for the duration of the lifting task and the anatomical landmarks were removed with the exception of the head, hand, radial styloid, ulnar styloid, trunk markers (C7, T7, Xyphoid and suprasternal notch) and foot markers. Consistent with best practice for limiting skin motion artefact when measuring human movement (Leardini et al, 2005), marker clusters were used to track segment motions and to reconstruct the anatomical landmarks based on the relationships quantified from static calibration trial. Box motion was also tracked using passive reflective markers placed on the four corners of the box. The passive reflective marker trajectories were captured using a 12-camera Vicon motion capture system (Vicon, Centennial, Co, USA) sampled at 100 Hz.

Figure 1.

Locations of the passive reflective motion capture anatomical markers and marker clusters (Davidson et al., 2022).

Participants completed two-handed, floor-to-shoulder height lifting at a self-selected pace and technique for a duration of 60 minutes or until volitional fatigue (Figure 2). Each participant’s required lifting load corresponded to 30% of their maximum lifting capacity as determined using the EPIC Lifting Capacity test (Matheson et al., 1995). Every 15 lifts, participants were asked to provide their rating of perceived exertion (RPE) based on the Borg 6–20 scale (Borg, 1982). For this study, lift data were extracted from the first completed lift (unfatigued) and the last completed lift prior to volitional fatigue, or at the end of the 60-minute duration (fatigued).

Figure 2.

A participant performing the floor-to-shoulder height box lift while in the lift origin posture.

Marker trajectories for the first (unfatigued) and last (fatigued) lifts were labelled and gap filled within Vicon Nexus software (Vicon, Centennial, CO, USA). After the marker trajectories were visually assessed for quality, the marker trajectory data were imported into Visual3D (v.6.01.03, C-Motion, Germantown, MD, USA). Visual3D was used to create subject specific kinematic models that enabled us to reconstruct the required anatomical landmark data including, medial and lateral malleoli, medial and lateral femoral condyles, left and right anterior superior iliac spines, left and right acromion, medial and lateral epicondyles (upper arms). Marker trajectories were filtered with a zero-lag, second order, low pass Butterworth filter with an effective cut-off frequency of 6 Hz (Winter, 2009).

Our focus was on the posture at the origin and destination of lift, so we extracted the marker trajectory data from those two frames. The origin and destination of the lift were defined using the bottom left box marker position and velocity data, respectively. Lift origin was defined when the box marker was displaced by 5 cm in the global Z-position (using the standard engineering convention) from its resting position on the bottom shelf height. The lift destination was defined as the time point after origin when the velocity (norm of the x, y and z trajectory velocities) of the box marker reached zero.

As noted above, Santos Pro can be used to predict a posture in the absence of motion data by using multi-objective optimization, where the posture is defined as a vector of angles for each degree of freedom, or joints within the model. In addition to predicting postures, Santos can also be used as an inverse kinematic model when motion capture data is available. We used our motion capture data as an input into the Santos Pro inverse kinematic model to calculate the joint angles that corresponded to the measured motion capture data. In this way, the joint angle definitions for the predicted postures and for the postures calculated using measured data were consistent and could not be a source of error.

To use Santos Pro as a kinematic model, we needed map subject specific measured landmark data to each digital avatar. Virtual markers (referred to as anatomical hardpoints within Santos Pro) were added to each digital twin avatar over the same anatomical locations where anatomical markers were placed on the live participants. Measured anatomical marker trajectories were paired with their respective anatomical hardpoints to posture the avatar. Two anatomical markers were mapped per segment with the exception of one anatomical marker for the left and right clavicle and shoulder blade segment. All chosen anatomical landmarks can be seen in Figure 3. Joint angles (Table 2) that corresponded to the motion capture driven posture were extracted as the in vivo dataset. Joint angle data derived from the motion capture driven postures were compared against predicted joint angles from in silico simulation.

Figure 3.

Shows the anatomical hardpoints placed on the avatar in the same positions as the anatomical markers of the experimental participants. The following anatomical markers were mapped to their associated anatomical hardpoints for each body segment: first and fifth metatarsal (feet), medial and lateral malleoli (shanks), medial and lateral femoral condyles (thighs), left and right anterior superior iliac spines (pelvis), C7 and centre of manubrium (trunk), left and right acromion (clavicles and shoulder blades), medial and lateral epicondyles (upper arms), ulnar and radial styloid processes (lower arms), second and fifth metacarpals (hands), left and right forehead (head).

TABLE 2:

Joints and Associated Degrees of Freedom for Each Joint Included Within the Analysis

Joint	Number of Degrees of Freedom	Degrees of Freedom
Ankle	2	Plantarflexion/Dorsiflexion
		Inversion/Eversion
Knee	1	Flexion/Extension
Hip	3	Abduction/Adduction
		Flexion/Extension
		Internal/External Rotation
Trunk	3	Lateral Bending
		Flexion/Extension
		Rotation
Shoulder	3	Abduction/Adduction
		Flexion/Extension
		Internal/External Rotation
Elbow	1	Flexion/Extension

Response Surface Methodology

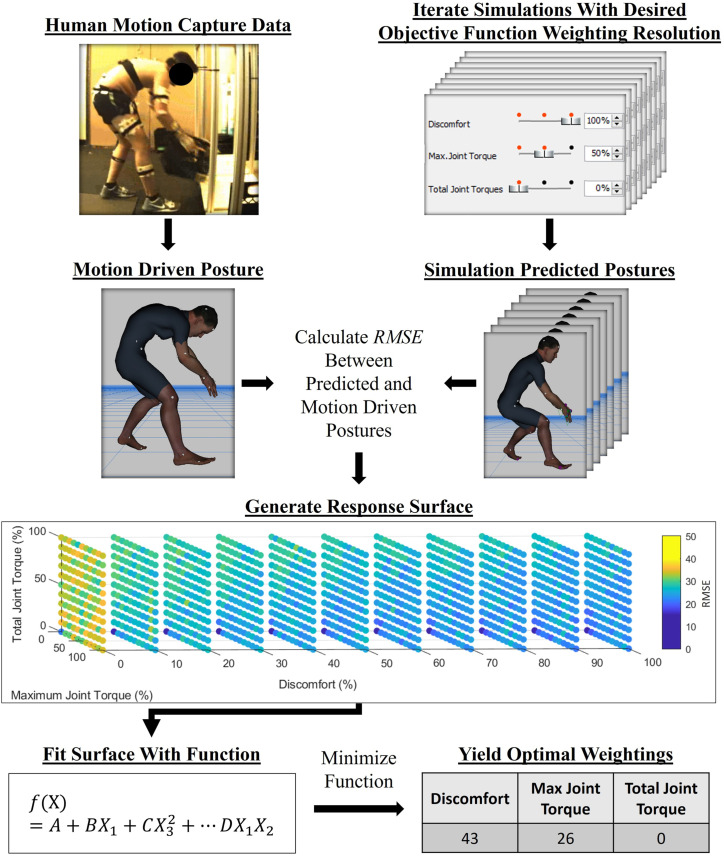
We had joint angle data defining origin and destination lifting postures in unfatigued and fatigued states for ten participants. Using digital twin avatars, we predicted 1331 unique postures for each origin and destination posture, by systematically varying the weighting of three objective functions available in the Santos Pro software. We used a response surface methodology (RSM), consistent with our previously description of the method (Davidson et al., 2021). The RSM was used to identify which origin and destination predicted postures and corresponding weighting factor combination, produced joint angles that were the closest to the joint angles observed by participants in the in vivo study during an unfatigued and fatigued state. The aim of the RSM approach was to define a surface that mapped the error between predicted postures and motion capture driven postures across different combinations and permutations of the discomfort, maximum joint torque, and total joint torque objective functions. The resultant error response surface (specific to each participant at each position in each fatigue state) was fit with a regression function, where the resultant functions were minimized to identify the optimal objective function weighting combination that minimized the error between predicted and motion capture driven postures (Figure 4).

Figure 4.

RSM approach for determining the optimal objective function weightings to allow simulation predicted postures to match empirical motion capture data (Davidson et al., 2022). Adapted from Davidson et al., (2021), motion capture data was mapped onto an avatar via anatomical hardpoints. The global position of the avatar’s hands and feet were then used as constraints for the predicted postures. Objective functions weightings were iteratively simulated at a set resolution and each predicted posture was compared to the origin motion capture driven posture to determine an error. All errors for a given posture and prediction set produced a surface which was fit with a regression function and then optimized to find the best objective function weighting.

Based on our previous analysis of different methods for estimating the difference in joint angles from measured and predicted postures (Davidson et al., 2021), we calculated a singular, representative root mean squared error term, for each comparison. To generate a singular term, for unique degrees of freedom at each joint (Table 2) we subtracted the joint angles defining the predicted posture from joint angles defining the motion capture driven posture. We then divided each difference by the total range of motion for each specific degree of freedom to normalize the joint angle differences relative to the joint range of motion and squared the quotient (Equations (4)–(6)). Degree of freedom specific error terms were averaged across all the different degrees of freedom within a joint to produce an average squared joint error term. In total, six joints were included to produce a total joint error similar to methods described by Xiang et al., (2010). To create the root mean squared error (RMSE), the average of the normalized squared error differences for each joint were calculated, the square root was taken, and the resultant values were expressed as a percentage.

Equation 4

Shows the calculation for normalized difference between the predicted and motion capture driven joint angles ( $\mathit{q})$ . This calculation was completed for all degrees of freedom (DoF) with each of their respective ranges of motion (RoM). All normalized differences were squared.

$$Normalized\hspace{0.17em}Joint\hspace{0.17em}DoF\hspace{0.17em}Squared\hspace{0.17em}Error={\left(\frac{Predicted\hspace{0.17em}DoF\hspace{0.17em}\mathit{q} -Simulated\hspace{0.17em}DoF\hspace{0.17em}\mathit{q}}{DoF\hspace{0.17em}RoM}\right)}^2$$ (4)

Equation 5

Shows the calculation of the average normalized joint error $\left(\mathrm{\in }\right)$ across all degrees of freedom within a joint.

$$\text{Average Joint Squared Error}(\in )=\frac{{{\displaystyle \sum }}^{\text{}}Normalized\hspace{0.17em}Joint\hspace{0.17em}DoF\hspace{0.17em}Difference}{nDoF}$$ (5)

Equation 6

Shows the root mean squared error (RMSE) for the combination of six joints of interest. Where the mean of the six average joint squared errors were calculated and the square root of that value was found and expressed as a percentage.

$$\text{RMSE }=\sqrt{\frac{\left({\in }_{Ankle}+ {\in }_{Knee}+ {\in }_{Hip}+ {\in }_{Trunk}+ {\in }_{Shoulder}+ {\in }_{Elbow}\right) }{6}} \ast 100$$ (6)

Consistent with Davidson et al., (2021), normalized RMSE response surfaces were fit with multivariate regression functions. R² values were output for linear, quadratic, cubic and quartic powers to determine the best fit. A predicted R² was calculated using a leave one out (LOO) cross validation approach as a metric of model over-fitting. Two criteria were used to determine which regression model’s equation would be used to determine the best objective function weighting coefficients. Firstly, the highest R² was chosen assuming it was an improvement over the lower power by an R² of at least 0.05. Secondly, the highest R² was only chosen if the difference between the R² and the predicted R² was 0.05 or less. Once the best regression model was chosen, the associated regression equation was optimized, using fmincon in MATLAB, to find the objective function coefficients with the least error (Mathworks, R2020, Natrick, MA). The objective function configuration with the least error as determined by the optimized regression equations were retained as the dependent variables for statistical analysis.

Statistical Methods

To determine if systematic changes in the optimal objective function weightings were observed between fatigue states for both the origin and destination postures, Friedman’s analysis of variance tests were applied to each objective function weighting using IBM SPSS Statistics (Version 27.0, IBM Corporations, Armonk, NY). The dependent variables were the participant specific optimal objective function weighting coefficients (discomfort, maximum joint torque and total joint torque) and the two independent variables were the position (origin and destination) and state (unfatigued and fatigued). An alpha value of less than 0.05 determined if significant differences were detected between an objective function’s weighting coefficients across location or fatigue state conditions. Post-hoc Wilcoxon pairwise comparisons were conducted with a Holm–Bonferroni correction to determine significance between conditions within an objective function.

RESULTS

Five participants met volitional fatigue throughout the fatigue lifting protocol and 5 completed a total of 60-minutes of lifting; however, all participants reported an RPE value greater than 14 by the end of the lifting protocol, where RPE values greater than 14 have been associated with muscle fatigue (Jakobsen et al., 2014; Sundelin & Hagberg, 1992). Lift protocol completion time, total number of lifts and peak final RPE values can be seen in Table 3.

TABLE 3:

Participant’s Protocol Completion Time, Number of Lifts Completed and Final RPE Score

Participant	Completion Time (min)	Total Lifts	Final RPE
1	38	333	19
2	35	285	20
3	60	510	16
4	59	615	19
5	60	540	17
6	60	495	17
7	27	255	20
8	60	510	18
9	60	495	18
10	57	345	20

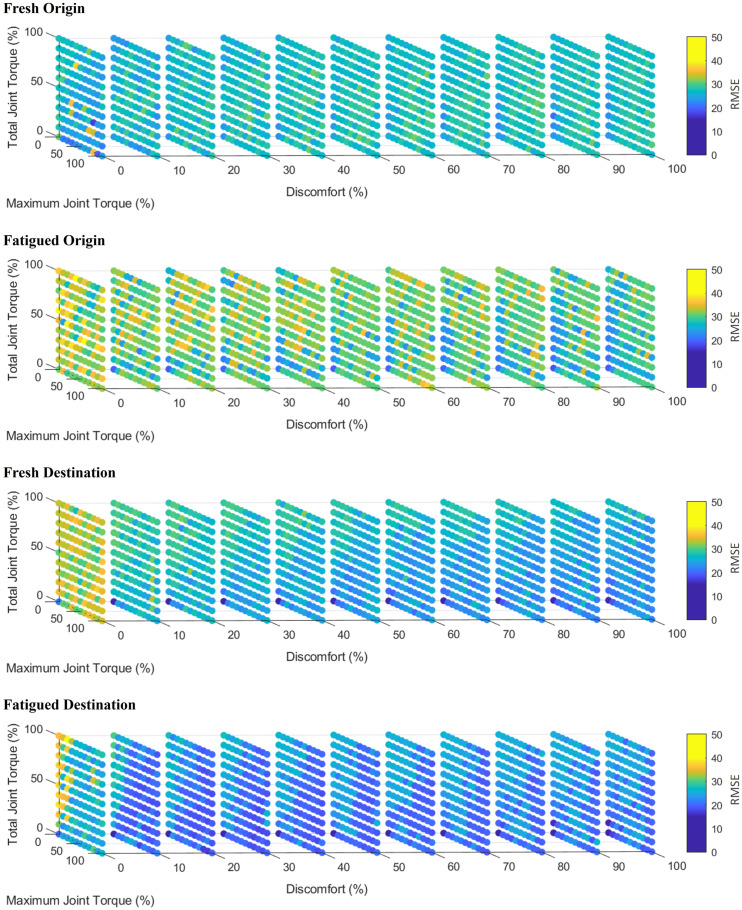
RMSE was plotted as a function of objective function weightings for each participant, specific to each location (origin and destination) and fatigue state (unfatigued and fatigued). Figure 5 demonstrates an exemplar RMSE plot for Participant 3. Based on the exemplar plots optimal objective function weighting configurations (dark blue data points) tended to prioritize the minimization of discomfort objective function with minimal contributions of the minimization of maximum and total joint torque objective functions.

Figure 5.

Normalized RMSE response for participant 3. Each axis represents a respective objective function weighting within the multi-objective optimization model. The colour bar corresponds to the normalized RMSE calculated at each objective function weighting where dark blue represents the lowest error and dark red represents the highest error.

Response surfaces were fit with multivariate regression models. The type of model was specific to each RMSE surface where four RMSE surfaces were best fit using a linear model, eight using a quadratic model, 17 using a cubic model, and 11 using quartic a model (Table 4). The mean R-squared model fit across all models was 0.46 ± 0.20. Mean predicted R-squared, using the LOO-CV approach across all models was 0.44 ± 0.20. Mean residual RMSE across all models was as 3.35% ± 1.29% normalized RMSE. Model fits varied between participant, lifting posture and fatigue state.

TABLE 4:

Multivariate Model Statistics for Each Participant Under Each Condition

Participant Number	Un-Fatigued Origin				Fatigued Origin
	Power	R 2	PR2	RMSE	Power	R 2	PR2	RMSE
1	4	0.46	0.43	2.93	4	0.55	0.52	2.85
2	4	0.55	0.52	3.26	3	0.37	0.35	5.02
3	3	0.60	0.58	2.24	4	0.67	0.64	2.84
4	2	0.73	0.73	4.48	3	0.44	0.42	3.66
5	2	0.42	0.41	2.09	2	0.14	0.12	3.52
6	1	0.04	0.03	2.70	1	0.02	0.02	8.19
7	3	0.16	0.13	2.94	2	0.18	0.16	3.68
8	4	0.74	0.72	3.10	1	0.23	0.22	5.32
9	4	0.79	0.77	2.27	3	0.46	0.44	3.06
10	3	0.62	0.61	3.27	4	0.49	0.44	3.37
1	3	0.47	0.45	3.08	2	0.37	0.36	3.98
2	2	0.41	0.40	3.54	3	0.61	0.60	3.66
3	3	0.72	0.71	1.78	3	0.62	0.60	2.12
4	1	0.26	0.26	4.84	2	0.26	0.25	5.27
5	3	0.44	0.42	2.94	3	0.35	0.33	5.18
6	4	0.69	0.67	1.80	3	0.47	0.45	2.66
7	2	0.25	0.23	4.56	4	0.62	0.59	1.75
8	3	0.30	0.27	4.12	3	0.68	0.66	1.74
9	3	0.36	0.34	3.03	3	0.35	0.33	2.95
10	4	0.62	0.59	2.38	4	0.73	0.70	1.83

Note: PR² is the predicted R² value calculated with a leave one out cross validation. RMSE (degrees normalized to total range of motion) is the root mean squared error of the residuals between the actual input values and the model predicted values.

Resultant optimal objective function weighting coefficients were not normally distributed, so the median and interquartile range of the regression predicted lowest normalized RMSE for each posture and fatigue state was calculated. Friedman’s tests were conducted to compare weightings for each objective function between location (origin and destination) and fatigue states (unfatigued and fatigued) detected significant differences for discomfort (Friedman’s Q (3) = 8.152, p = .043) and total joint torque (Friedman’s Q (3) = 8.143, p = .043). Maximum joint torque showed no differences between postures and fatigue states (Friedman’s Q (3) = 2.426, p = .489). However, post-hoc Wilcoxon pairwise comparisons revealed no statistically significant differences in objective function weightings between postures or fatigue states. The pairwise comparison closest to significance was found within the discomfort objective function between fatigued origin and unfatigued destination (Z = 1.4, p = .092). Optimal objective function weighting coefficients for each participant within each lift posture and fatigue state are shown in Table 5.

TABLE 5:

Shows the Model Predicted Objective Function Weighting Coefficients to Minimize Normalized RMSE. Optimal Objective Function Weighting Medians and Interquartile Ranges (IQR) are Also Shown

Participant Number	Discomfort				Maximum Joint Torque				Total Joint Torque
	Un-Fatigued Origin	Fatigued Origin	Un-Fatigued Destination	Fatigued Destination	Un-Fatigued Origin	Fatigued Origin	Un-Fatigued Destination	Fatigued Destination	Un-Fatigued Origin	Fatigued Origin	Un-Fatigued Destination	Fatigued Destination
1	82	32	46	57	0	0	18	40	0	0	0	0
2	31	36	100	50	0	55	0	13	0	0	0	0
3	53	30	100	100	0	0	0	0	0	0	0	0
4	42	48	100	62	22	25	100	49	0	0	0	0
5	71	100	100	43	100	0	0	26	0	0	0	0
6	100	0	45	100	0	100	0	0	0	0	0	0
7	53	64	74	50	0	71	42	15	100	51	0	0
8	26	100	100	100	0	100	0	0	11	0	0	0
9	22	48	100	100	0	0	0	0	0	0	0	0
10	57	27	100	38	23	9	0	0	26	0	0	0
Median	53	42	100	60	0	17	0	7	0	0	0	0
IQR	33	19	30	50	17	67	13	23	8	0	0	0

DISCUSSION

Weighting minimization of discomfort, not maximum or total joint torque, best predicted lift origin and destination postures in an unfatigued state. Counter to our hypothesis, weighting minimization of discomfort, in the absence of maximum or total joint torque, also best predicted lift origin and destination postures in a fatigued state suggesting that no statistically significant systematic shift in objective function weightings was present with fatigue. These results, however, may be more nuanced. The median optimal weighting for discomfort did seemingly, although not statistically significantly, decrease (group level change) to best predict fatigued lifting postures relative to when predicting unfatigued lifting postures. However, the optimal weighting for maximum joint torque only increased for a selection of the participant sample (individual level change). This may suggest considerable inter-participant variability in sensorimotor control responses to fatigue, or inter-participant variability in the accumulation of fatigue, and in turn, the need to adapt sensorimotor control strategies. It remains important to consider inter-participant variability in sensorimotor control strategies for lifting and inter-participant variability in fatigue accumulation when attempting to use DHMs to predict fatigued lifting actions in a manner that is representative of a population.

The inherent multi-objective nature of the discomfort weighting, the overlapping goals of the discomfort and joint torque objectives, and inter-participant variability may all explain why we observed that the singular use of discomfort best predicted lift origin and destination postures. Previous research investigating multi-objective optimization to predict lifting postures when using a DHM have observed that approaches which integrate more than one objective function reduce prediction errors when compared to single-objective (i.e., minimizing jerk, joint torque or stability) optimization (Song et al., 2016; Xiang et al., 2010). However, it may not be surprising that discomfort played a dominate role in our study because discomfort was inherently formulated as a multi-objective function combining the tendency to maintain a comfortable neutral position (standing with arms at the side); the tendency to move body segments sequentially (limbs, then spine and then sterno-clavicular joint); and the tendency to avoid joint end ranges of motion. As a result, our data support that lifting postures are likely best predicted by using multi-objective optimization, or alternatively when optimizing singular functions which are inherently multi-objective, like the mathematical formulation of discomfort in our study.

We may not have observed a more compelling shift from discomfort to maximum joint torque with the onset of fatigue due to the overlapping goals of these two objectives. As observed by Fischer et al., (2015) lifters indeed tend to lean forward at the destination when fatigued, in part to reduce the moment arm at the shoulder, consistent with maintaining the shoulder closer to the neutral posture (i.e. avoiding end range). One aim of the minimization of discomfort objective function tested in our study is to avoid joint end ranges of motion which may predict postures that reduce the moment arms thereby decreasing the resultant torque. If minimizing the tendency to use joint end ranges of motion indirectly minimizes the torques, this may explain why previous research has found minimization of total and maximum joint torques to be good predictors of lifting postures (Ayoub, 1998; Song et al., 2016; Xiang et al., 2012, 2010). Having aspects of torque-based objectives within discomfort may also explain why it tended to predict the lowest normalized RMSE between motion seeded and optimization predicted postures.

Inter-participant variability may also explain why there was an observed a trend towards the singular use of discomfort to best predict lifting postures. Previous work (Marler et al., 2009; Marler, Yang, et al., 2005) has suggested that prediction accuracy can be improved when combining another objective functions with the discomfort objective function; however that work only used one participant and therefore did not capture between participant variability. At the individual participant level, it was clear that some participants (e.g., participant 1) followed the findings reported by Marler et al., (2009) and Marler, Yang, et al. (2005), where others did not (e.g., participant 3). Therefore, multiple objectives may be best for predicting an individual’s behaviour; however, when taking the mean across a group of participant responses, discomfort appears to consistently predict well while the other objectives vary more in their performance.

As further explanation of the role of inter-participant variability, it is possible that individuals within the sample varied in how they accumulated fatigue, or how they adapted their sensorimotor control strategies with the onset of fatigue. A varied response to fatigue during lifting has been seen in the literature where Bonato et al. (2003) and Fischer et al. (2015), found that individuals moved from stoop style (larger trunk segment angle) lifting postures to more squat style (smaller trunk segment angle) lifting postures. In contrast, Fogleman and Smith (1995), Sparto et al., (1997), and Van Dieën et al., (1998), found increased lumbar flexion and less knee joint angle changes with prolonged lifting bouts as fatigue progressed. Variation across studies is likely explained by variation in the underlying samples in terms of control strategies and the accumulation of fatigue. With these contrasting results present in the literature it is likely that participants within this study experienced similar differences in their fatigue progression leading to the high variability in optimal objective function weightings to predict their lifting postures.

Median objective function weightings for the minimization of discomfort trend towards higher values for the destination lift postures than origin lift. Although there were no significant differences found between the two posture conditions, the trend showing potential for unique objective function weightings for an origin and destination posture within a single movement or task is an important consideration. However, when choosing objective function weighting configurations to best predict full movement profiles or the postures of a number of different movements’ movement, end-users may find it cumbersome to be frequently changing their objective function weighting configurations. Further analysis is needed to investigate the extent to which optimal objective function weightings change within movements or tasks.

Ultimately, our goal is to aid end-users in making decisions about which objective functions to select and how they should be weighted when predicting lifting postures. Variability in our data highlights that the median values may or may not be appropriate depending on the intended design goals. When predicting group behaviour for lifting tasks, prioritizing the minimization of discomfort will be helpful to predict realistic postures. This is because median values for discomfort ranged between 42% and 100%, and only one participant’s optimal objective function weighting combination included a 0% weighting for discomfort. The use of maximum and total joint torque objective functions was not as clear and appears to depend on the individual and fatigue state. Trying to predict fatigue responses and individual specific postures may not be feasible given the current data due to the high variability in the postural adaptations that each individual may have to fatigue.

Limitations

A sample of ten total participants may have limited our resolution to observe differences in the optimal weighting coefficients between an unfatigued to a fatigued state when considering pairwise comparisons. This is the first study aimed at identifying optimal objective functions weightings to predict lifting postures. Unfortunately, we did not know a priori, that the optimal objective function weightings would vary as much as we observed based on this sample. We hope our data can inform more targeted sample size calculations in future work. Additionally, participants may have varied in the amount of fatigue that accumulated during the 60-minute protocol, which may help explain the between participant variability. Although RPE values greater than 14 have previously been associated with muscle fatigue (Jakobsen et al., 2014; Sundelin & Hagberg, 1992); RPE is a perception based measure, and other factors such as boredom or changes in a participant’s attention could have influenced the perceived exertion. Given the observed between participant variability, it may be necessary that future work aiming to identify optimal objective function weightings considers a large sample size to get sufficient statistical power. Additionally, the participants were all recruited within the university and therefore were all university aged. While a wider range of ages may further increase between participant variability, age as a trait factor, may play an important role objective function weightings (Song et al., 2016). Only one lifting range (floor-to-shoulder height) was used for the purposes of this analysis and other lifting ranges may have yielded divergent results thereby potentially limiting the generalizability of these results.

The anthropometry of the digital human model avatar was scaled to the height of the participants based on the ISO-3411 anthropometric survey. Unlike the Visual3D model development, the subject link lengths were only scaled based on participant height rather than segment lengths as determined by anatomical landmark markers. This difference in segment length estimation may have led to postural differences between the experimentally collected data and the avatar seeded motion data. It is not known the specific segment length errors that were present between the participants and their unique avatars; however, segment length measures or estimates may be useful in the future to scale the avatar segments of interest for improved validity in seeding avatar motion with motion capture. The hand loads were also assumed to be evenly distributed between left and right hands of the avatars. Since a specific lifting technique was not prescribed, this may not be the case for our participants. If participants chose to use lift the box in a way that did not evenly distribute the load between their hands, this may have explained some potential differences between the experimental postures and the predicted postures. In the future, hand load estimations for non-constrained lifting tasks that allow for asymmetric movement may help improve the accuracy of the predicted postures, due to the improved load modelling accuracy.

CONCLUSION

Origin and destination lifting postures were best predicted when weighting the minimization of discomfort objective function, without weighting towards joint torque-based objective functions. As researchers continue to uncover and mathematically model constructs that humans tend to optimize for when performing occupational tasks, in the near term, this evidence supports that a discomfort based objective function (inclusive of tendency to maintain a neutral position, to move body segments sequentially, and to avoid joint end ranges of motion) may optimally predict lifting postures. Additionally, these data suggest that lifters may begin to prioritize different objectives as they fatigue, where some participant’s fatigued postures were better predicted by reducing the weighting towards discomfort and increasing the weighting towards minimizing maximum joint torque. However, between participant variability may play an important role in how a lifter may experience fatigue, and subsequently alter their postures with fatigue. This may limit the ability to robustly predict fatigued lifting motions at a group level in the near term. Continued research is important to ensure that DHMs can adequately consider the physiological states (fatigue) and environmental effects on human-system interactions that designers are interested in (Davidson et al., 2021) to improve the utility of DHMs to support virtual prototype assessments for both military and industry sectors alike.

Biography

Justin B. Davidson is affiliated with the department of Kinesiology and Health Sciences at the University of Waterloo in Ontario, Canada. He is a thesis-based PhD student in the Occupational Biomechanics and Ergonomics Lab (OBEL) and holds a MSc degree from the University of Waterloo (Obtained in 2021).

Joshua Cashaback is an Assistant Professor in the Department of Biomedical Engineering at the University of Delaware, where he directs the Neuromechanics and Learning Research Group. He received his BHK at the University of Windsor, a PhD in Biomechanics at McMaster University, and postdoctoral training in computational neuroscience at Western University and the University of Calgary.

Steven Fischer, RKin, CCPE is an Associate Professor in the Department of Kinesiology and Health Sciences at the University of Waterloo and directs research in the Occupational Biomechanics and Ergonomics Lab (https://uwaterloo.ca/obel/). He received his BSc in Kinesiology, MSc in Sport and Exercise Science from the University of New Brunswick and PhD in Occupational Biomechanics from the University of Waterloo.

ORCID iDs

Justin B. Davidson https://orcid.org/0000-0002-7895-8222

Steven L. Fischer https://orcid.org/0000-0002-3347-5403