Identifying low-dimensional trajectories of mechanically-ventilated patient systems: Empirical phenotypes of joint patient+care processes to enhance temporal analysis in ARDS research

Abstract

Mechanically ventilated patients generate waveform data that corresponds to patient interaction with unnatural forcing. This breath information includes both patient and apparatus sources, imbuing data with broad heterogeneity resulting from ventilator settings, patient efforts, patient-ventilator dyssynchronies, injuries, and other clinical therapies. Lung-protective ventilator settings outlined in respiratory care protocols lack personalization, and the connections between clinical outcomes and injuries resulting from mechanical ventilation remain poorly understood. Intra- and inter-patient heterogeneity and the volume of data comprising lung-ventilator system (LVS) observations limit broader and longer-time analysis of such systems. This work presents a computational pipeline for resolving LVS systems by tracking the evolution of data-conditioned model parameters and ventilator information. For individuals, the method presents LVS trajectory in a manageable way through low-dimensional representation of phenotypic breath waveforms. More general phenotypes across patients are also developed by aggregating patient-personalized estimates with additional normalization. The effectiveness of this process is demonstrated through application to multi-day observational series of 35 patients, which reveals the complexity of changes in the LVS over time. Considerable variations in breath behavior independent of the ventilator are revealed, suggesting the need to incorporate care factors such as patient sedation and posture in future analysis. The pipeline also identifies structural similarity in pressure-volume (pV) loop characterizations at the cohort level. The design invites active learning to incorporate clinical practitioner expertise into various methodological stages and algorithm choices.

1. Introduction

Modern critical care often involves mechanical ventilation (MV) to manage patients with disorders such as acute respiratory distress syndrome (ARDS), which is characterized by inflammation and pulmonary edema. MV is also used to sustain highly sedate or comatose patients including those with traumatic brain injury (TBI) and impaired autonomic breath control. Modern respiratory care protocols and technologies [1] emphasize lung-protective strategies [2], as MV may cause ventilator-induced lung injury (VILI,[3]). MV lung-protection relies on such factors as increased positive end-expiratory pressure (PEEP), decreased tidal volume, or reduced driving pressure [4, 5, 6] based on understanding of lung physiology. Technological advances in MV have not eliminated ventilator dyssynchrony (VD), a mismatch in patient-ventilator delivery and respiratory effort timing. VD may play a role in the development and propagation of VILI, a known contributor to mortality in ARDS patients [7]. Reduction in ARDS-related mortality has plateaued in recent decades [8] compared with significant curtailment in the two decades prior [9]. The desire to further mortality reduction motivates the continued study of MV effects as VILI and VD contribute to residual ARDS mortality.

Clinical observables, including airway pressure (p), volume (V ), and flow, are generated by the human lung-ventilator system (LVS), which encompasses the dynamic interaction between patient lungs and an engineered apparatus. This biomechanical LVS combines the components relevant for studying the effects of mechanical ventilation (MV) on longer timescales, particularly regarding physiological derangement under technological management. Non-ventilator aspects of patient care can also affect lung-ventilator dynamics and associated observables. Despite the temporal richness of waveform data, analyzing them within the LVS context proves challenging due to factors such as data volume (high sample rates yield millions of data points per patient per day), data heterogeneity influenced by patient-specific factors and care-originating ventilator setting changes, and the multi-scale nature of the problem that require consideration of intra-breath scale events over extended periods to detect signatures of injuries like VILI.

Notable previous works [10, 11] used supervised machine learning directly on ventilator data to identify the frequency and occurrence of different ventilator dyssynchronies. In addition to internal ventilator metrics, the analyses also used breath properties such as peak inspiratory pressure, inspiratory-to-expiratory time ratio (I:E), etc. to coarsely characterize waveform features via features familiar to practitioners [12, 13] Although such descriptors facilitate operational management of respiratory care, they may be insufficient to distinguish breath characteristics related to pathological lung mechanics or the timing of dyssynchronous patient efforts. Identification alone does not address the evolution of breath types and effects of VD.

Recent approaches to LVS data analysis have focused on hybrid methods of empirical parameter fitting [14, 15, 16] with attention to patient-ventilator dyssynchrony resolution at the waveform level. Purely rule-based mechanistic models targeting specific breath features require many parameters to overcome confounding influences [16] or define models of specific VD types [14]. These research strategies have converged on data-informed modeling methods as a robust tool to express waveform data through automated parametric representations. The present study uses a flexible model-based approach together with unsupervised ML to empirically discriminate Mv breaths and begins to account for heterogeneous LVS factors. It is targeted to reveal the structure and complexity of LVS evolution, and the focus on temporal factors contrasts related works in ARDS research that seek to identify cohort-scale VD [10] or infer respiratory mechanics through physiologic modeling [17, 14].

Development of relevant waveform representation models and analysis methods provide pathways for informatics research to pursue minimizing VILI. Continuing toward that goal, this work presents a framework for analyzing the evolution of MV breath types over extended time periods. It extends the analysis of LVS behavior from the breath level to the scale of hours-to-days while considering the context of ventilator settings. The method combines a model-based waveform digitization [16] with an unsupervised segmentation pipeline [18], although other sufficiently flexible parametrization frameworks and variations on the theme may be employed. This study’s hypothesis is that respiratory behavior or other patient properties may be identified from joint LVS data by separating the influence of changes in MV. Investigation proceeds by examining changes in observable data that occur independently of ventilator management within the context of the joint patient-ventilator system. Analysis of ARDS patient data through this perspective demonstrates compact descriptions of LVS evolution, broadly categorizes MV breaths, and identifies LVS heterogeneity sources that must be incorporated for further development.

2. Method

The root approach involves analyzing LVS data, including waveforms and ventilator settings, through a computational pipeline that begins with model-based inference. The method projects individual LVS waveform data onto personalized parametric representations and identifies patient-specific breath phenotypes without consideration of sequential ordering. The evolution of LVSs may be examined through phenotypes when co-labeled according to time.

2.1. Data

Mechanically-ventilated patient data were collected under the University of Colorado Multiple Institutional Review Board (COMIRB, protocol #18–1433). These data include airway pressure, volume, and flow and ventilator settings for 36 patients, all of whom had ARDS diagnoses and substantial risk of VILI as featured in [19]. Children, pregnant women, and age-censored elders, and the imprisoned were excluded. Esophageal pressures were recorded but used in this work; collection imposed additional exclusion criterion (viz. esophageal fistula, variceal bleeding or banding, facial fracture, and recent gastric/esophageal surgery). Source patients include 14 women and 22 men with median[IQR] age 59[25] years; 72% are white, 35% of which identify as Hispanic or Latino. Table 1 summarizes clinical and demographic characteristics of patients. Data total 1.74 million breaths over 71.14 recording-days (median 1.97[1.56] days per patient) recorded at 32 millisecond sampling (31.25 Hz) from Hamilton G5 ventilators (https://www.hamilton-medical.com). Adaptive pressure and pressure-controlled ventilation modes (APVcmv and P-CVM, respectively) account for 85–98% of breaths in most patients and over 94% in total. Ventilator management throughout employs the ARDSnet protocols [7].

Table 1:

Tabular summmary of the patient cohort and associated data. ‘Monitored’ and ‘Recorded’ durations denote the number of hours spanned by data and length continuous data contents, respectively. P:F ratio is the PaO₂/FiO₂ ratio at admission, AA = African-American, AI = American-Indian, AK = Alaska, NMB = Neuromuscular Blockade

Detail	Count	%	Median	IQR
Monitored (hrs)			47.0	37.2
Recorded (hrs)			43.1	40
Age (years)	36		58.5	24.5
Gender
Female	14	38.9	54.5	25.0
Male	22	61.1	58.5	26.0
Race/Ethicity
White	26	72.2
Unknown/NA	5	13.9
Black/AA	3	8.3
AI or AK Native	1	2.8
More than one race	1	2.8
ARDS risk
Pneumonia	12	33.3
COVID	11	30.6
Sepsis	6	16.7
Other	3	8.3
Pancreatitis	2	5.6
Aspiration	2	5.6
P:F ratio			135.9	81.0
Mortality	9	25.0
NMB use	9	25.0

Dyssynchrony labels.

An existing supervised ML technique [10, 19] identifies breath-wise VD to enrich LVS evolution context and provide comparison for newly calculated labels. Type-specific VD models each label breaths according to features characterizing dyssynchronous breaths (see ibid. SI). VD labels include normal (NL), reverse triggered (RT) with early (RTe) and middle (RTm) subtypes, early flow limited (eFL) with intermediate (eFLi) and severe (eFLs) subtypes, double trigger (DT) with reverse- (DTr) and patient- (DTp) subtypes, and early vent termination (EVT); breath mechanics of these VDs are described in [11]. Breath label vectors flag likely VD occurrence and can be summarized statistically over time intervals.

2.2. Windowed Model-based Inference on Individuals

The analysis begins with a continuous-time dynamical model that transforms observed waveform data into discrete parameters via inferential methods [16]. The differential equation governing the model state $y$ is:

$$\frac{dy}{dt}+g\cdot \left(y\left(t\right)-y_0\right)=\varphi (t,\omega )$$ (1)

where $t$ is time, $g$ is a smoothing parameter, $y_0$ is a reference state (such as PEEP when $y$ represents pressure), and $\varphi$ is a time-dependent function of parameters $\omega$. Optimizing the state $y$ to fit observed LVS waveform data over short windows yields parameters $\omega$ that encode waveform data. The relationship between parameters $\omega$ and simulated state $y$ is defined by the function $\varphi$. This work chooses a locally periodic piecewise constant function using parameters $\omega :=\left(a_1,\cdots ,a_M,\theta \right)$ where $\theta$ is the breath cycle length determined from the data, independent of the model and $M$ is independent hyperparameter representing the number of parameters in $a$. Time within the breath, defined by $\widehat{t}:=t-t_0\left(\mathrm{m}\mathrm{o}\mathrm{d}\theta \right)$, is divided into $M$ local time epochs whose lengths $\left\{\mathrm{\Delta }t\right\}$ depend on the model resolution $M$, breath length $\theta$, and partition function $\mathrm{{\rm Y}}$. Each epoch is associated with an amplitude $a_i$, so that $M$ determines model resolution. The piecewise-constant function $\varphi$ can be written as

$$\varphi \left(t;a,\theta \right)=\sum _{i=1}^M{a}_i\frac{1-e^{-g\text{Δ}{t}_i}}{g}\left[\left[\text{Υ}\left(i-1\right)\text{Δ}{t}_i\le \widehat{t}<\text{Υ}\left(i\right)\text{Δ}{t}_i\right]\right].$$ (2)

The fixed function $\mathrm{{\rm Y}}$ apportions epoch lengths using the I:E ratio to resolve the shorter, more valuable inspiratory phase at higher resolution. Optimal parameters $a$ are inferred from the data $y^{obs}$ using a windowed ensemble Kalman-like smoother over short, disjoint 10-second windows of data (see [16]), although other methods suffice. The framework uses the model to infer parameters from waveform data segments and map parameters to representative waveform characterizations.

2.3. Pipeline

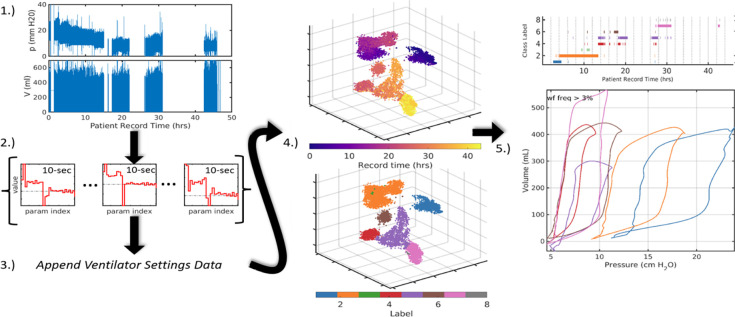
The computational pipeline extracts low-dimensional representations of LVS data that effectively encode relevant features of both breath waveform data and the ventilator settings associated with them. The method (Figure 1) follows [18] using model-inferred parameter distributions to uncover latent system similarities from data. The four stages of application to LVS data focus on changing system representation.

Figure 1:

Broad pipeline organization. Raw data (1.) are digitally parametrized (2.) over short windows. Summaries of these vectors are computed and appended with the contextual data of ventilator settings (3.) which include information such as ventilator operation mode, PEEP, flow and pressure triggers, and minimum mandatory breath rate. Augmented LVS descriptors are projected into three dimensions using tSNE (4.) where they can be analyzed based on time ordering (top) and structural similarity via segmentation (bottom). Finally, in (5.), temporal evolution of the system is compactly encoded in the time-ordered LVS descriptor labels and their associated waveform characterizations. The process transforms raw data (1.) into a more easily comprehensible form such as (5.).

1.). Waveform parametrization:.

Individual clinical records of continuous pressure (p) and volume (V) waveforms are inferred using a model (§2.2) with moderate resolution ($M=24$). Non-overlapping ten second windows are each encoded into M parameters by fitting the data over 1.6 second (50 points) moving sub-windows with 0.8 second overlaps (25 points, for 32 millisecond sampling). The resulting estimates are distributional samples of the 10-second windows totaling 4% fewer points than the source data.

2.). Parameter Distribution Summarization:.

The parameter distributions for each interval of data aim to retain enough information to allow differentiation based on measures of relative similarity. The 2M parameters are independently transformed into vectorized descriptors that collectively summarize the waveform behavior within each data window. Descriptor components include mean, quartiles, variance, and mode as well as non-gaussian measures (skewness, kurtosis, and Kolmogorov-Smirnov distance) to capture bimodal or asymmetric parameters distributions characterizing non-stationary LVS behavior. For $M=24$, these descriptors summarize content during each 10-second interval using 38.24% less volume than the original data. The strategy reduces the temporal sampling rate (from 31.25Hz to 0.1Hz) by depicting each window of 2D states as a larger vector that summarizes parameter distributions. Reduction in the overall data volume (see SIAppendix B) is governed by summary window length (under weaker stationarity assumptions) and model resolution ($M$).

3.). Augmentation:.

Appending ventilator setting data to the parametric descriptor vectors of each window contextualizes them in the health-care process. Ventilator settings detail the mode of operation (volume control, pressure control, spontaneous, etc.), supplied targets (tidal volume) as well as various machine settings (trigger thresholds, ramp time, PEEP). Some ventilator settings are already represented in parametric waveform descriptors, and therefore, need not be explicitly included. For example, ARDSnet protocols bind FiO₂ and PEEP ranges while realized I:E is a waveform property. Other available factors such as ventilator delivery power are not considered here but may be included as needed in specific applications. Ventilator mode is a nominal variable represented as set of binary variables using one-hot encoding. Interval summaries reflect the most frequent ventilator data found for breaths in each window. Ventilator settings change infrequently, and summary errors are therefore rare among estimated intervals.

4.). Cluster Labeling:.

Segmentation labels groups of LVS descriptors based on content similarity and can be applied at individual patient or aggregated cohort levels. Several methodological approaches can accomplish this goal (e.g., see [20]). However, direct segmentation is computationally expensive when descriptors are large (~ 400-dimensional for M = 24). Dimensional reduction is further motivated by the desire to visually inspect the quality and structure of label assignment. The t-distributed Stochastic Neighborhood Embedding (tSNE,[21]) reduces high-dimensional vectors into a low-dimensional space (here, 3D) by optimizing the KL-divergence between an assumed-normal distribution of the data and a t-distribution of the points in R³. The organization of embedded points approximates the local and global similarity structure [22], the targets of label assignment under a given metric.

LVS descriptors comprise mixed variable types so the the Gower distance is a natural choice of metrics. It averages over range-normalized absolute differences of continuous variables and binary dissimilarity of ventilator modes (categorical variables). Uniform Manifold Approximation and Projection (UMAP,[23, 24]) and tSNE produce similar dimensional reductions [25] in this application (SIAppendix A.3) All individualized results use the Matlab-native tSNE algorithm with parameters near default values (exaggeration=4, perplexity=50).

Unsupervised learning algorithms then assigns segmentation labels to the LVS descriptors. In both tSNE and UMAP LVS applications, Density-Based Spatial Clustering of Applications with Noise (DBSCAN, [26, 27]) identifies groups of similar LVS descriptors from point densities in the reduced coordinate space. A brief grid-search over DBSCAN parameters (min. core point neighbors 4–12; neighborhood radius 1.5–5 by 0.5) samples different label assignment possibilities, adopting the one that minimizes total distance between cluster centroids. Experimentally, such flexible assignment sought to capture the unknown degree of variation that tends to increases with the LVS record length. Use of k-means and k-medioids [28] was considered for efficiency but, unlike DBSCAN, could not capture non-convex groupings that typically emerged from LVS descriptors in reduced dimensions. Support vector clustering [29, 30] required too much computation time to be practical for day-scale analysis.

5.). Defining phenotypes.

Descriptor labels are directly associated with LVS data elements including the parameter estimation windows and the waveforms contained within them. Direct interpretation of labeled points is prevented by the dimensional reduction step, which embeds joint LVS descriptors into abstract, similarity-determined coordinates. However, points tacitly associated with the pipeline elements used to construct them, including the window times that link observations, parameters samples, summaries, and tSNE coordinates The LVS data can then be analyzed based on common or central properties characterizing features of each labeled group. Specifically, waveform data in a particular cluster are characterized and visualized by applying the model (Eq.(2.2)) to e.g., median parameters associated with a label. These k characterizations, along with their associated ventilator settings, define phenotypes of the LVS observables.

2.4. Phenotypes and Characterizations of LVS data

The phenotyping pipeline identifies elements of LVS states with similar structure, organizing short intervals of data into discrete categories for analysis over longer timescales. Cluster labels identify LVS state phenotypes of the observable data, and co-evolution of the patient-ventilator system is captured in the temporal progression through these categories. A stated objective is to identify changes originating from the patient-side of the system with no corresponding ventilator changes. These indicate the presence of confounding factors not recorded in the data such as changes in patient expectation and breathing pattern (e.g., patient effort, respiratory drive), lung mechanical function (e.g., VILI progression or recovery from ARDS), or another aspect of physiology.

Phenotype evolution is presented in the context of ventilator settings and in relation to VD identified via [10]. Additionally, pressure-volume (pV) characterizations defined by the model image of descriptors nearest to the phenotype center (viz. median) provide a familiar synopsis of associated waveform data for each window represented in the data. Such visualizations intend to summarize key features and notable changes defining the LVS trajectory.

Subsequent analysis and discussions employ principal component analysis (PCA), an empirical signal factorization based on variance minimization [31, 32]. This tool is used to show the LVS variance occurring under ventilator stationarity for qualitative analysis, as the empirically-determined basis may not represent physical or relevant LVS features. Here, their intended use is to reveal the temporal structure of LVS variation as these may relate to patient-side changes.

3. Results

The clinical LVS data of patients with ARDS (Table 1) is an important and practical target to test, demonstrate, and document the computational phenotyping pipeline in cases which may be prone to ventilator dyssynchronies and VILI. The pipeline ties labeled breath types to specific points in time during the patient record, which permits analyzing data and syntheses throughout the process. Results in this section consider LVS data together with time-ordered waveform characterizations to examine LVS evolution during the recorded hours of individual patients. Sequences of dyssynchrony labels generated as in [10] provide additional context for exploring breath behavior.

Briefly, most LVS patient data are identified with 20[14] (median[IRQ]) clusters using the fixed hyper-parameters across the cohort. About half of these groups are infrequent and represent less than 1% of the data. A median of 8[6.5] core clusters each representing more than 3% of the data account for the remainder of the data of each patient. Modifying ML hyper-parameters to eliminate the low-occurrence groups may consequently reduce label resolution. However, the number of labels needed to capture the main LVS behaviors of each patient depend on heterogeneous factors including patient health status, the number of changes in vent settings, and the total duration of the data. As recording durations span 0.7–92 hrs (medain[IQR] 46.8[35] hrs), the over-segmenting some LVS records to prevent loss of resolution in longer ones was a preferred alternative to fully optimized individual segmentation.

3.1. Simple, Individual Examples

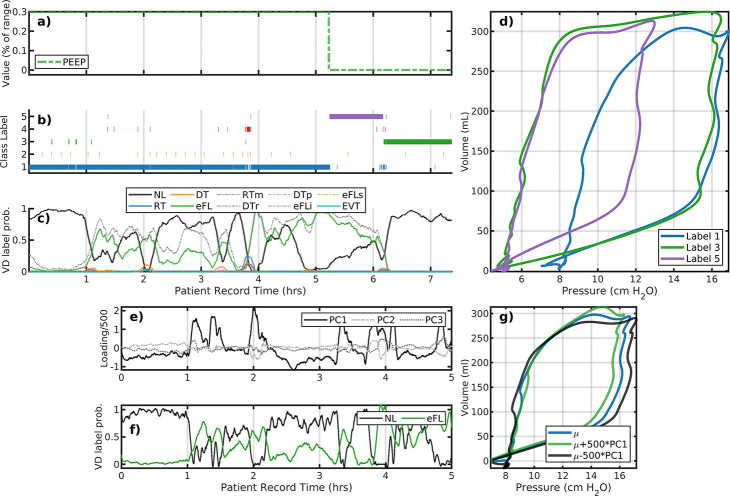
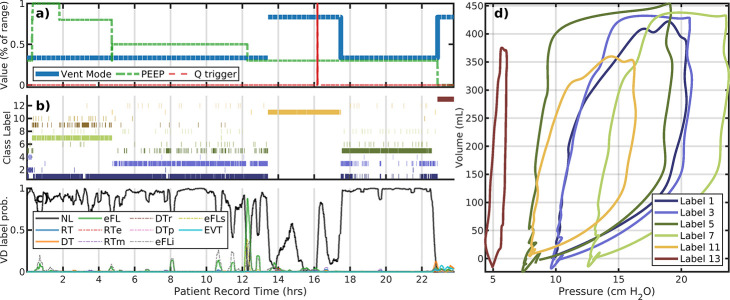
Figure 2 panels a–d illustrate the analysis of Patient #103 whose data consists of 7 record hours with one simple ventilator setting change. Only ventilator PEEP (a) is changed while there are three primary behaviors identified (b,d). The reduction of PEEP occurs about 2 hours following a rise in early flow limited breaths (eFL, panel c). This PEEP change (from 8 to 5 cmH₂O) shifts peak pressure from 16 to 12 cmH₂O for about an hour, at which time higher esophageal pressures returns. These breaths are identified as normal (NL) [10]. Increased specificity may be pursued by local segmentation or other dimensional reduction methods.

Figure 2:

Analysis of patient #103 LVS data (a–d) and the initial a 5-hour interval (e–g). Panels a–c correspond to changes in ventilator settings, segmentation labels, and identified VD type, respectively. The horizontal axis for these panels is the patient record time in hours. The panel (d) shows the model image of segmented data median parameters, which characterize the pV loops of breaths with that label (shown with the same color). Evolution of the LVS can be parsed pictorially from these figures. Large positive variations in the first principal component loading (e, black) for the initial 5-hour period align with VD labels indicating eFL type breaths (f) for this period. Specifically, this suggests discrimination of breaths shapes (g) can be differentiated using qualitatively criterion on local loadings or other segmentation.

A closer look at label 1 of patient #103:.

The first principal component loadings (panel e, black) for LVS descriptors over the first 5-hour period track the sequence of normal and eFL VD labels (f, shown as 5 minute statistics for clarity). Within the same breath phenotype (label 1), the sign of the component loading statistically the eFL VD labels (AUROC=0.8718); high positive values are associated with eFL breaths (f,g; green) where pressure maxima proceed volume maxima. These LVS variations result from changes in the patient component, as there is no change of ventilator settings. Note that direct correlation between continuous loading values on 10 second windows and statistical breath-wise binary VD label is not well-defined while binary-to-binary comparison is.

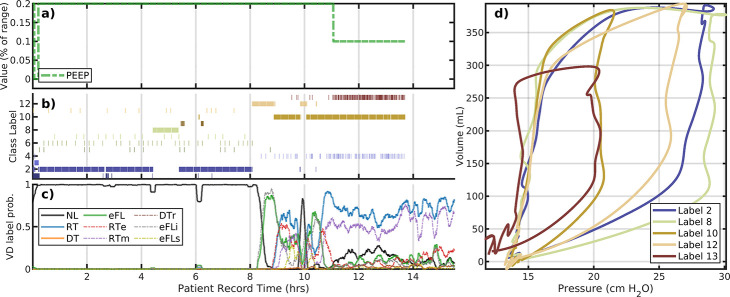
The patient #113 (Figure 3) dataset is nearly twice as long with again only one PEEP change occurring after 10.5 hours of the 15.6 hour record. Breaths are stably identified as normal-type until about 8 hours, occupying two cluster-identified similar breath shapes. This is followed briefly by eFL breaths and a transition to a new characterization (label 8, light green) for about 30 minutes. In the following period (9–14 hours), breaths are characterized by lower pressure maxima (label 10, gold); these are associated/identified with reverse-trigger breaths (primarily RTm) and waveforms featuring pronounced inspiratory pressure drop. The reduction in PEEP slightly increases the incidence of normal breaths during 11–14 hours although this results in the more frequent appearance of shallow breaths (label 13, red).

Figure 3:

The patient #113 evolution also includes only PEEP changed. The layout is the same as panels a–d of the previous figure. Under constant ventilator settings, breaths undergo transition several times including intervals of VD prior to PEEP change around 10.5 hours. A 1-hour long shift from label 2 to 8 occurs around 8 hours during which breaths decrease peak pressure and includes an increase in eFL and RT VD occurrence. After the PEEP change, breaths remain highly dyssynchronous and primarily centered around the characterization with label 10.

3.2. More complex LVS evolution examples

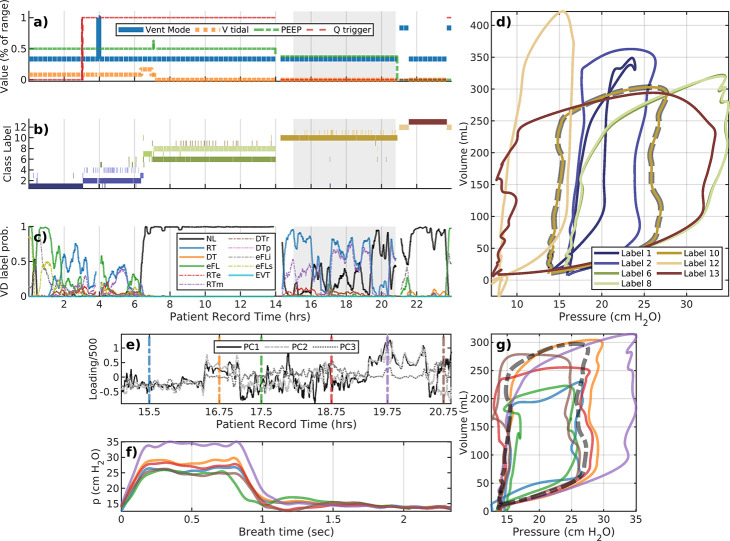
Cases presented in the previous subsection are atypical in that patient records in the data set are typically longer (>24 hours), include many ventilator settings changes, and segment into a larger collection of phenotypic breaths. Figure 4 illustrates the analysis of patient #114 whose LVS undergoes multiple changes over a 24-hour data period. The portion during 7–14.5 hours is dominated by normal breaths that spans two labels with similar characterizations as pV loops but differ in mean respiratory rate. The difference is minor (the mean difference is less than 20 milliseconds), although this affects model parameter and could combined via posterior analysis, with small DBSCAN hyper-parameter changes, or coarser period binning. Changes in flow trigger settings occur around 3 hours and reduce the occurrence of eFL near the star of the record, associated with caving in pV loops (label 1, dark blue). Dyssynchronies return when the flow trigger is returned to its initial value, near 15 hours. PEEP and tidal volume targets are also adjusted several times. Brief ventilator changes in ventilator mode around 20 and 23 hours allow spontaneous breathing which have a profoundly different pV characterizations (label 12,tan). The interim period (20.5–22.5 hours) consists of primarily normal breaths (label 13, brown) under the default pressure-control mode.

Figure 4:

A representative example: patient #114. The upper plot layout is the same as the previous figure. The lower plot examines the variability, and a shortcoming of low resolution segmentation to capture changes that may be highly diverse at a local level. The mean– the dashed black line – coincides with the golden pV loop (cluster #10) in the upper plot. The many distinct breath subtypes identified are more similar than to other main types in the upper plot; as a result, they are grouped together at this choice of hyperparameters.

A closer look at Label 10 of patient #114.

Breath phenotype analysis of patient #114 indicates no ventilator setting changes during the record interval 15–21 hours. Although one phenotypic breath dominates this period, ML-labeled dyssynchronies intimates much more variability. Principal components during this interval (Fig. 4b) suggest that the evolution is irregular. While pressure characterizations suggest the differences are largely attributed to pressure and inspiration duration, full characterizations indicate that breaths in this period are very heterogeneous in pV relationships. The continuous evolution through these subtypes – and their comparative differences to the other types – leads to their identification as a consistent group. SI Figure A.7 provides another case using principal components to further differentiate breath types with implications.

Figure 5 features data of the patient #149 LVS has little identified dyssynchrony. While most breaths as identified as normal, the system evolution diagram indicates irregularities in breath properties. In particular, label 1 (dark blue) regularly present under multiple PEEP settings in the pressure-controlled volume targeting mode, and are intermixed with other labels (e.g., 3,5, and 7) whose waveform characterizations are dissimilar. System heterogeneity within the patient makes parsing the evolution more complicated, as spontaneous breathing is possible during 12–16 hours and 23–24 hours under different PEEP values. Nevertheless, the space of breaths is considerably reduced in labels.

Figure 5:

The LVS evolution of patient 149 label#1 is discontinuous in time and occurs under different PEEP values. There is a lot of waveform variation present within the largely VD-less evolution, and significant changes in non-ventilator aspects of the LVS.

3.3. Cohort scale phenotypes of breath shapes

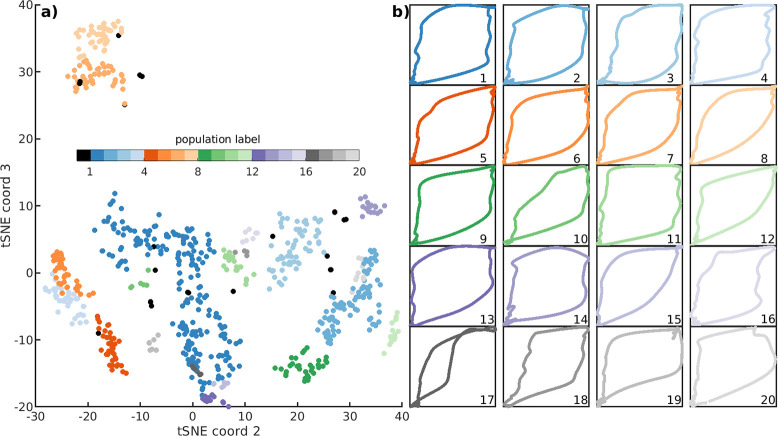
A cohort level breath characterization is achieved by further segmenting the population of individuals characterizations in non-dimensinoal form. The phenotyping pipeline yields a total of 721 patient-specific LVS characterizations across the cohort. Attempts to directly cluster these full characterizations was unsuccessful. Secondary tSNE-DBSCAN grouping could not identify cross-patient commonalities of these characterizations due to LVS-specific heterogeneities such as tidal volume (a target set by patient sex, height), PEEP (e.g., whether even or odd values are used), and respiratory rate (patient and sedation dependent). However, these factors may be accounted for by segmentation of pV loop shape rather than full LVS behavior. Pressure and volume characterizations are sampled in pV-space and then translated and scaled into the range [0,1]. The pV normalization accounts for differences in PEEP, tidal volume, and respiratory rate while preserving the differences in the pressure-volume relationship to extract the phenotypic shapes of breaths occurring throughout the estimated entire dataset. Using this method, a cohort-scale tSNE-DBSCAN analysis identifies 20 breath shape phenotypes along with a collection of 27 outliers. Figure 6 illustrates this normalized reorganization along with the median pV representatives and pressure traces for each identified group.

Figure 6:

Cohort scale breath types via segmentation of batched individual data. In panel a, each dots corresponds to one of N = 721 normalized pV loop characterizations extracted at an individual level. Labels (colors) identify 20 fundamental breath shapes comprising the dataset of 1.74M breaths. Un-grouped individual characterizations correspond to 27 outliers (black). The 20 pV trace shapes nearest to groupwise medians are shown at right (b) (see SI Fig. A.8 for outliers). Note that the xy-axes are the normalized pressure and volume in non-dimensional form.

Meta-characterization depends on several hyper-parameters associated with tSNE and DBSCAN which influence label granularity as well as thresholds defining outlier groups (SI Fig. A.8). Selected parameters aimed to maximize the number of phenotypes while minimizing the number of outliers with number of labels easily presented in an array; the results are qualitatively similar for nearby parameters. Table 2 summarizes the occurrence and contents of this grouping.

Table 2:

Tabulated occurrence of labels within the cohort. Columns indicate the cohort label (with 0 indicating the group of unrelated outliers), occurrence percentage, the number of patients represented in the label, and the number of individual LVS phenotypes comprising each label. Eleven non-outlier groups with occurrences greater than >2.5% constitute 87% of the data with outliers (Label 0) occupying an additional ~3.5%. Two breath types (italics) contain only phenotypes of patient #141, whose average inspiration compliance is consistently ~ 7.5 ml/cm H₂O) and distinct from the 1.5–3 ml/cm H₂O range typical across other patients.

Label	Percent	N pat	N pheno	Label	Percent	N pat	N pheno
0	3.48	14	27	-	-	-	-
1	29.68	28	200	11	2.51	6	20
2	11.10	12	85	12	2.19	1	16
3	9.74	13	58	13	1.69	2	14
4	6.52	4	38	14	1.69	5	18
5	5.51	4	39	15	1.43	1	6
6	5.31	7	39	16	1.29	2	7
7	5.30	10	48	17	0.88	4	5
8	4.74	3	43	18	0.19	4	4
9	3.66	4	32	19	0.10	3	7
10	2.93	4	6	20	0.07	4	9

3.4. Synthesis

Variations in pressure and volume observations of MV patients result from ventilator setting changes and patient dynamics. To understand the evolution of this system, one must jointly consider both patient and care processes. Analyzing patient state through breath data, especially for VILI detection and to track ARDS progression, requires considering ventilator settings. LVS evolution is primarily influenced by ventilator setting changes (e.g., PEEP, mode, tidal volume), with secondary changes indicative of patient progression or non-ventilator care. Analyzing periods of ventilator stationarity showed local breath evolution unrelated to MV changes, and empirically-identified breath variations agreed with ML-derived statistical labels of VD (patient 103 in Fig 2; patient 111 in Fig SI A.7). Local analysis or sub-phenotyping may resolve cases with more complicated evolution (e.g., patient 114 in Fig. 4b, although additional factors such as sedation and patient restfulness may be required to characterize and differentiate them.

Cohort-level segmentation of LVS behavior phenotypes was confounded by heterogeneities in patients as well as ventilator settings that depend on patient-specific properties. Specifically, tidal volume and breath rate differences among and within patients could not be accounted for, leading to partitioning of both patients and LVS behavior. However, secondary clustering of normalized 721 individual pV characterizations yielded 20 pV shapes and a collection of 27 outliers. As ventilator settings and breath rate factor into individual LVS segmentation, resulting pV characterization phenotypes inherit some aspect of those data indirectly.

Results and following conclusions naturally depend on algorithm hyperparameters that should be chosen in relation to targeted applications. The proposed methodology supports clinical expert guidance in selecting guidance of application, identifying specific features to be resolved in models, and phenotype interpretation; each stage of Fig. 1 supports expert-in-the loop refinement. Use of the phenotyping pipeline and subsequent analysis leads to methodological conclusions regarding application to real, clinical LVS data:

1. In application to a cohort of ARDS patient clinical data, system evolution is much easier to visualize, track, assess, and understand when the LVS is represented in a discrete, low-dimensional form as an evolution of phenotypes and waveform characterizations.

2. LVS-individual phenotypes depend on hyper-parameters of the dimensional reduction and labeling stages. Parameters affect the granularity of resolved phenotypes, and should be chosen flexibly to account for the desired quality of LVS temporal resolution as well as the length and complexity of the target dataset.

3. Sub-segmentation of phenotypes is possible, and may be used to align phenotype definitions with additional information streams such as VD identification. Cohort scale analysis is also possible from batched individual phenotyping to provide a coarser but unified basis for analyzing common trends and evolution of LVSs.

4. Discussion

Research into ARDS and VILI involves studying patient-ventilator interactions and may benefit from representation of the lung-ventilator system (LVS) over time. Typically, the available data include airway pressure, volume (or flow), and ventilator settings. This study introduces a framework to transform these LVS data into meaningful, low-dimensional characterizations of LVS state that facilitate analysis of LVS behavior and its evolution during patient care. The process involves aggregating segmented analyses of individual patient over short (10-second) intervals. Consequently, the observable LVS data is condensed into a small set of patient-level phenotypes, making it discrete and more manageable compared to continuous high-resolution waveforms and breath-wise ventilator settings.

Experiments conducted on clinical data of 35 patients with strong ARDS risks, including 8 2020 patients with COVID-19, found the automated phenotyping process sufficient to discern between changes in the ventilator and the patient components of the LVS system. Individual LVS phenotypes were primarily determined by ventilator setting changes, given that changes in mode, PEEP, and tidal volume profoundly affect waveform shapes. However, temporal changes in phenotype uncoordinated with ventilator changes were also present in nearly all patients with more than 12 hours of data, revealing changes in the patient side of the LVS system. Unlike the rapid and instantaneous transitions related to MV changes, patient-side changes were often a more continuous but non-monotonic progression together with transient behavior. These behaviors could be detected through principal component analysis of data over intervals of static MV, but additional EHR data required to adequately explain them are presently unavailable.

In cases with limited complexity, LVS phenotypes corresponded well with ML-labeled VD, as appear related to ventilator setting and behavior in response to changes. For more complex cases, breath phenotypes did not consistently differentiate normal and dyssynchronous breaths (Figs. 3,4). Signatures of VD can be subtle but remain discernible through empirical analysis (such as PCA) or sub-segmentation of individual phenotypes, and in the original data associated with each phenotype. Nevertheless, an important consideration for future work is the optimization of phenotype resolution, which is defined by of easily tunable hyper-parameters (viz. those of tSNE, UMAP, and DBSCAN) as well as deeper factors discussed below.

While granular refinement is accessible through targeted sub-segmentation of LVS phenotypes, batch analysis makes convenient a cohort analysis to assess the frequency of different breath shapes. For specific choice of hyper-parameters, the ~1.5M breaths reduce to a small set of 20 pV loop shapes and a set of 27 outliers. Signs of dyssynchrony are apparent in these core shapes such as ineffective triggering (10,18), and mild and severe flow limitation or patient effort (14,16, and 17 respectively). (Also, types 19 and 20 qualitatively suggest RT with late insufflation pressure drops indicative of patient effort.) This qualitative VD classification remains formally unvalidated in this work, as cohort scale breath shapes mask important considerations such as PEEP, tidal volume, and respiratory rate. Additionally, esophageal pressures were not encoded into phenotypes but are required to identify certain VD types [11]. Although individual phenotypes were often too coarse to differentiate normal and dyssynchronous breaths, this coarser segmentation could be refined by scaling to larger cohorts and longer patient data series.

4.1. Method Choices, Variations, and phenotype consolidation

The pipeline presented makes several choices regarding application-specific details. Algorithm choices such as model resolution, estimation/summary window length, the intra-breath partition (viz. $\mathrm{{\rm Y}}$ of Eqn.(2)), and omission of certain data are needed to balance efficiency with the quality of results. These choices were influenced by practical consideration such as stationarity over 3–4 breaths and model consistency [16]. Many modifications and changes to latter stages of the labeling process are possible including: hierarchical analysis of specific times at individual or cohort scales, characterizing breath types occurring under particular ventilator settings or modes, or incorporating other factors such as patient sedation level.

It remains essential for certain applications to examine breath shape independently of ventilator settings. For example, investigating signatures of ventilator dyssynchrony [11] may require normalizing breath features to account for ventilator settings that affect pressure and volume waveform maxima. To account for PEEP and tidal volume in this process, normalization during data segmentation requires a similarity measure to be invariant under translation and scaling, respectively. Use of parametrized waveform descriptors does not eliminate this problem. Circumventing these obstacles is possible by comparing waveform characterizations and merging labels based on characterization similarity, gauged by the difference between normalized characterized pV loops. This approach, explored in §3.3, applies to experiments that differ significantly in scale, and is motivated by the desire to link uncontrolled human LVS data with in vivo animal experiments (e.g. [33]).

4.2. Limitations and Improvements

Combining data assimilation-based parametrization with unsupervised learning ([18]) overcomes primary shortcomings of existing approaches. In particular, the mechanism-free encoding of waveform data into parameters with a priori definition circumvents patient- and care-dependent heterogeneity which strongly limit physiological model use in this domain ([16]). This greatly alters the representation LVS system: the rapid temporal sampling in two dimensions (p,V) is transformed into a low-frequency sampling of model parameter distributions (SIAppendix B) under stationarity assumptions. Accounting for irregularity in sample dimensions (viz. the number of points representing each breath) caused by variable respiratory rate in these breath-wise analyses is unnecessary in the continuous-time windowed approach.

An important limitation of this work and its clinical application regards the dependence on hyperparameters and a distance function used in dimensional reduction and group labeling. Fixed tSNE parameters and a very narrow DBSCAN parameter range not adequately account for individual record length, internal waveform heterogeneity, or the number of unique ventilator settings. Examples showed that chosen parameters of the segmentation processes were insufficient to produce phenotypes that corresponded with VD types using a known method, while also generating many smaller, low occurrence phenotypes. Selecting algorithm parameters to align identified phenotypes with VD labels is likely achievable as an application-specific optimization. This topic is important for clinical use but lies beyond the present scope focused on low-dimensional representation of LVS evolution. Additionally, the uniform weighting of components in the similarity metric used for dimensional reduction may not be optimal. Strategic weighting would require objective criteria compatible with mixed variables to apportion LVS descriptors correctly. However, a well-specified metric may improve low-dimensional tSNE or UMAP representation so that estimating VD severity is feasible within the LVS phenotyping results.

Algorithmically-defined LVS phenotypes did not include several important factors that limit the strength of conclusions about them. The pipeline process ignored esophageal pressure data because their rarity limits generalizability, their highly-localized features require high resolution to capture parametrically, and record inconsistencies (gaps, calibration) prevent continuous time characterization. Exclusion of this variable, essential to defining certain types of VD [11], limits phenotype ability to distinguish certain types of VD from airway observations. In addition, the model parameter definitions relies on ventilator-identified breath rate, and the pipeline therefore lacks the flexibility needed to identify double-triggered VD events that occur over multiple ventilator cycles.

Most importantly, the analysis did not consider extra-LVS influences on observable data, such as patient sedation, neuromuscular blockade use, posture, and airway moisture and secretions. These patient-state variations undoubtedly impact observed data and must be included to properly vet phenotypes identified under ventilator stationarity (cf. Figs. 2e–g and 4e–g).

Appropriate Normalization.

Cohort-scale segmentation of Sec3.3 normalized pressure and volume to a standard interval for inter-comparison. This waveform rescaling depends on local tidal volume, peep, and driving pressure which could be included as feature components to improve discrimination. Scaling volumes by predicted body weight accounts for patient invariants (sex and height) while pressure scaling remains co-dependent patient+care processes (viz. plateau pressure and assigned PEEP, assigned tidal volume per kg in adaptive pressure modes). Waveform data and their parametric summaries dominate the dimension of feature vectors. Unreported experiments using naive normalization yielded cohort breath labels that segmented patients rather than refining breath types groupings. The topic warrants investigation to identify appropriate cohort scale normalizations in addition to metrics and weights needed to balance the roles of normalized waveforms and associated scaling factors in label identification.

4.3. Concluding Remarks

This work demonstrates an effective operationalization of lung-ventilator systems for analyzing patient-ventilator interactions and breath types over extended timescales to facilitate the study of VILI and its connection VD. Computationally defined phenotypes consolidate LVS states into classes, reducing patient-ventilator dynamics to evolution of discrete phenotypic states. The development permits investigation of time-dependent changes in MV patients within the context of applied care from observable data. The approach encourages hypothesis formulation regarding the role of VD and MV duration on VILI by preserving time-ordered links between LVS data and low-dimensional representations that are easier to analyze and study. The pipeline organization is structured around active learning to incorporate domain expert knowledge info waveform feature targets, ventilator setting inclusion, and group similarity definitions.

The hybrid method incorporates model-based data assimilation and unsupervised machine learning to simplify LVS data into empirically-grouped rule-based descriptors. A suitable next step for understanding LVS evolution is the use of symbolic dynamics [34, 35, 36] to examine and identify common temporal patterns arising within patient cohorts. An initial step toward this goal is systematizing individual LVS evolutions within cohort-scale phenotypes (cf. §3.3) and tuning hyper-parameters for the resolution needed target this specific research goal.