A Semiparametric Cox-Aalen Transformation Model with Censored Data

Summary:

We propose a broad class of so-called Cox-Aalen transformation models that incorporate both multiplicative and additive covariate effects on the baseline hazard function within a transformation. The proposed models provide a highly flexible and versatile class of semiparametric models that include the transformation models and the Cox-Aalen model as special cases. Specifically, it extends the transformation models by allowing potentially time-dependent covariates to work additively on the baseline hazard and extends the Cox-Aalen model through a predetermined transformation function. We propose an estimating equation approach and devise an Expectation-Solving (ES) algorithm that involves fast and robust calculations. The resulting estimator is shown to be consistent and asymptotically normal via modern empirical process techniques. The ES algorithm yields a computationally simple method for estimating the variance of both parametric and nonparametric estimators. Finally, we demonstrate the performance of our procedures through extensive simulation studies and applications in two randomized, placebo-controlled HIV prevention efficacy trials. The data example shows the utility of the proposed Cox-Aalen transformation models in enhancing statistical power for discovering covariate effects.

1. Introduction

Censored failure time data are frequently encountered in epidemiological and biomedical studies. In the literature, the multiplicative and additive hazards models provide two principal frameworks for analyzing such data. The most popular multiplicative hazards model is the proportional hazards model (Cox, 1972), where the covariates are assumed to act multiplicatively on an unknown baseline hazard function. In contrast, the additive hazards models furnish an additive effect between the covariates and the baseline hazard function, enabling a direct reflection of the risk increase or decrease (Aalen, 1980; Huffer and McKeague, 1991; Lin and Ying, 1994). Without prior domain knowledge, it is hard to determine which approach is preferable among multiplicative and additive hazards models. In fact, both models may often be used to complement each other and provide more complete insights. Therefore, various multiplicative-additive hazard models have been proposed to capture both multiplicative and additive effects (Lin and Ying, 1995; Martinussen and Scheike, 2002). In particular, Scheike and Zhang (2002) suggested a Cox-Aalen model by replacing the baseline hazard function in the Cox model with Aalen’s additive model. The Cox-Aalen model has been studied for various types of censored data, e.g., right-censored (Scheike and Zhang, 2002), interval-censored (Boruvka and Cook, 2015), left-truncated and right-censored (Shen and Weng, 2018), left-truncated and mixed interval-censored (Shen and Weng, 2019), and recurrent-event (Qu and Sun, 2019).

Transformation models have also received wide attention in survival analysis. Dabrowska and Doksum (1988) introduced the class of linear transformation models, which includes the proportional hazards and proportional odds models (Pettitt, 1982; Bennett, 1983). Estimators for this class of models were proposed by Dabrowska and Doksum (1988), Cheng et al. (1995), Fine et al. (1998), Chen et al. (2002), among others. Zeng and Lin (2006) extended the linear transformation models to allow time-dependent covariates. Hereafter, we refer to this class of transformation models as Zeng and Lin’s model to avoid confusion. There is rich literature investigating Zeng and Lin’s model. Zeng and Lin (2006) proposed a nonparametric maximum likelihood estimator (NPMLE) in the presence of right-censored data. Zeng and Lin (2007) derived a system of self-consistent equations for the jump sizes of the baseline cumulative hazard function at exact failure times through an expectation-maximization (EM) algorithm. Chen (2009) showed that the self-consistent estimator derived in Zeng and Lin (2007) is asymptotically equivalent to a weighted Breslow-type estimator, which can be solved by a computationally-efficient iterative reweighting algorithm. Liu and Zeng (2013) investigated variable selection procedures by minimizing a weighted negative partial log-likelihood function plus an adaptive lasso penalty. More recently, Zeng et al. (2016) and Zhou et al. (2021) studied the nonparametric maximum likelihood estimation of Zeng and Lin’s model with interval-censored and partly interval-censored data, respectively.

However, one limitation of Zeng and Lin’s model is that all covariate effects are assumed to be multiplicative within the transformation function. This assumption is too restrictive in some applications. For example, in an analysis of risk factors on mortality among patients with myocardial infarction, Scheike and Zhang (2003) showed that some covariates (e.g., ventricular fibrillation and congestive heart failure) have additive effects while others (e.g., age and sex) have multiplicative effects. In addition, they pointed out that naively treating all covariates as multiplicative led to incorrect results when predicting survival probabilities. Another example is HIV prevention efficacy trials, for which HIV incidence varies across geographic regions and by sex/gender; thus, the different regions/sex/gender subgroups have different baseline hazard functions (Corey et al., 2021). Moreover, a Kaplan-Meier plot shows that survival curves for different regions cross, potentially suggesting an additive region effect. To the best of our knowledge, no existing work considers a class of semiparametric transformation models in which the baseline hazard function is allowed to depend on some potentially time-varying covariates additively. Therefore, it is desirable to provide a larger class of semiparametric transformation models that can accommodate both multiplicative and additive covariate effects under one unified framework.

The EM algorithm is a powerful tool for performing maximum likelihood estimation in the presence of latent variables or missing data (Dempster et al., 1977). In particular, various EM-type algorithms have been proposed to find NPMLE for semiparametric transformation models (Zeng and Lin, 2007; Liu and Zeng, 2013; Zeng et al., 2016; Zhou et al., 2021). In analogy to EM, Elashoff and Ryan (2004) proposed an expectation-solving (ES) algorithm that handles missing data for general estimating equations, greatly facilitating its application to a broader framework. When the complete-data estimating equations correspond to the score functions from the likelihood, the ES algorithm essentially reduces to the EM. The ES algorithm dramatically improves computational efficiency for solving estimating equations involving frailty or latent variables. For example, Johnson and Strawderman (2012) developed a smoothing expectation and substitution algorithm for the semiparametric accelerated failure time frailty model. Henderson and Rathouz (2018) considered an approximate EM procedure for a longitudinal latent class model for count data.

In this article, we propose a broad class of so-called Cox-Aalen transformation models that incorporate both multiplicative and additive covariate effects upon the baseline hazard function within a transformation. The proposed class of models is very flexible and contains Zeng and Lin’s model and the Cox-Aalen model as special cases. However, the multiplicative-additive structure within the transformation and the need to estimate several nonparametric functions simultaneously impose additional challenges for model estimation. To alleviate such difficulties, we devise an ES-type algorithm, which iterates between an E-step wherein functions of complete data are replaced by their expectations and an S-step where these expected values are substituted into the complete-data estimating equations, which are then solved. More specifically, within the S-step, the high-dimensional parameters are calculated explicitly, while the low-dimensional parameters are updated via the Newton-Raphson method. Consequently, the proposed ES algorithm is fast and stable even under a high percentage censoring rate, as evidenced by our simulation studies and real data applications. Another attraction of our approach is that we provide simple variance estimators for both parametric and nonparametric estimates. Furthermore, the theoretical properties of the proposed estimators are rigorously studied via modern empirical process techniques.

The rest of the article is organized as follows. In Section 2, we present the proposed Cox-Aalen transformation models. In Section 3, we formally describe the estimation procedure and establish the asymptotic properties of the proposed estimators. In Section 4, simulation studies are conducted to evaluate the finite-sample performance of the proposed method. In Section 5, we apply our method to two randomized HIV prevention efficacy trials. Section 6 concludes with a discussion.

2. Semiparametric Cox-Aalen Transformation Models

Let $X\left(\cdot \right)={\left(X_1\left(\cdot \right),\dots ,X_q\left(\cdot \right)\right)}^{\top }$ and $Z\left(\cdot \right)={\left(Z_1\left(\cdot \right),\dots ,Z_d\left(\cdot \right)\right)}^{\top }$ denote $q\times 1$ and $d\times 1$ vectors of potentially time-varying covariates, and $T$ denote the failure time of interest. We propose a broad class of so-called Cox-Aalen transformation models such that the cumulative hazard function for $T$ conditional on $X\left(\cdot \right)$ and $Z\left(\cdot \right)$ takes the form

$$\text{Λ}\left(t\left|X\left(\cdot \right),Z\left(\cdot \right)\right.\right)=G\left[{{\displaystyle \int }}_0^t\exp \left\{{\beta }^{\top }Z\left(s\right)\right\}d{\text{Λ}}_X\left(s\right)\right],$$ (1)

where $\beta$ is a $d\times 1$ vector of unknown regression coefficients, ${\text{Λ}}_X\left(s\right)={\int }_0^s\left\{X^{{ }^{\top }}\left(v\right)\alpha \left(v\right)\right\}dv$ is an unknown increasing function with $\alpha \left(v\right)={\left({\alpha }_1\left(v\right),\dots ,{\alpha }_q\left(v\right)\right)}^{\top }$, and $G\left(\cdot \right)$ is a pre-specified transformation function that is strictly increasing and thrice continuously differentiable with $G\left(0\right)=0$, $G^{\prime }\left(0\right)>0$ and $G\left(\infty \right)=\infty$. In addition, let $A\left(t\right)={\int }_0^t\alpha \left(s\right)ds={\left(A_1\left(t\right),\dots ,A_q\left(t\right)\right)}^{\top }$, where $A_j\left(t\right)={\int }_0^t{\alpha }_j\left(v\right)dv$ for $j=1,\dots ,q$. With $X_1\left(\cdot \right)$ fixed at 1, ${\alpha }_1\left(t\right)$ can be interpreted as a reference level of the risk. Generally, it is not meaningful to have $X\left(\cdot \right)$ equal or proportional to $Z\left(\cdot \right)$. For the choices of $G$, it is useful to consider the class of frailty-induced transformations

$$G\left(x\right)=-\log {{\displaystyle \int }}_0^{\infty }\exp \left(-x\xi \right)f\left(\xi \right)d\xi ,$$ (2)

where $f\left(\xi \right)$ is a density function of a nonnegative random variable $\xi$ with support $\left[0,\infty \right)$. The choice of the gamma density with unit mean and variance $r$ for $f\left(\xi \right)$ yields the logarithmic transformations $G\left(x\right)=r^{-1}\log \left(1+rx\right)\left(r⩾0\right)$ with $r=0$ specifying $G\left(x\right)=x$. The choice of the positive stable distribution with parameter $0<\rho <1$ yields the class of Box-Cox transformations $G\left(x\right)=\left\{{\left(1+x\right)}^{\rho }-1\right\}/\rho$. Note that $G\left(x\right)=\log \left(1+x\right)$ is often considered to be a member of the above class with $\rho =0$. By treating the latent variable $\xi$ as missing, the frailty-induced transformations are particularly useful in deriving EM type algorithms (Zeng and Lin, 2007; Liu and Zeng, 2013; Zeng et al., 2016; Zhou et al., 2021). Some remarks regarding the Cox-Aalen transformation models are as follows:

Remark 1: When ${\alpha }_j\left(t\right)=0\left(j=2,\dots ,q\right)$ for any $t$, the right-hand side of (1) reduces to

$$G\left[{{\displaystyle \int }}_0^t\exp \left\{{\beta }^{\top }Z\left(s\right)\right\}d{A}_1\left(s\right)\right].$$ (3)

Hence, Zeng and Lin’s model is a special case of the proposed model. Moreover, when $Z$ is time-invariant, (3) further reduces to a class of linear transformation models with the form $\log A_1\left(T\right)=-{\beta }^{\top }Z+\log G^{-1}\left(-\log {ϵ}_0\right)$, where ${ϵ}_0$ has a uniform distribution (Chen et al., 2002). The choices $G\left(x\right)=x$ and $G\left(x\right)=\log \left(1+x\right)$ yield the proportional hazards model and proportional odds model, respectively.

Remark 2: When $G\left(x\right)=x$, according to (1), the cumulative hazard function on the left-hand side can be written as

$${{\displaystyle \int }}_0^t\left\{X^{{ }^{\top }}\left(s\right)\alpha \left(s\right)\right\}\exp \left\{{\beta }^{\top }Z\left(s\right)\right\}ds.$$ (4)

Thus, the conditional hazard function of $T$ is $X^{\top }\left(t\right)\alpha \left(t\right)\exp \left\{{\beta }^{\top }Z\left(t\right)\right\}$. Therefore, the Cox-Aalen model is a special case of the proposed models. In particular, when $X_2,\dots ,X_q$ represent levels in a set of factors, model (4) further reduces to the stratified Cox model (Kalbfleisch and Prentice, 2002, Section 4.4).

Remark 3: for $G\left(x\right)=\log \left(1+x\right)$, the odds of surviving beyond time $t$ based on (1) are

$$\gamma \left(t\left|X,Z\right.\right)=\frac{\mathrm{Pr}\left(T>t\left|X,Z\right.\right)}{\mathrm{Pr}\left(T⩽t\left|X,Z\right.\right)}={\left\{{{\displaystyle \int }}_0^t\exp \left\{{\beta }^{\top }Z\left(s\right)\right\}d{\text{Λ}}_X\left(s\right)\right\}}^{-1}.$$

In the special case where $Z$ are time-independent covariates,

$$\gamma \left(t\left|X,Z\right.\right)=\gamma \left(t\left|X,Z_0\right.\right)\exp \left\{-{\beta }^{\top }\left(Z-Z_0\right)\right\},$$

which is a stratified proportional odds model when $X$ is a random variable indicating strata.

As illustrated above, our proposed class of semiparametric models is very flexible and contains many popular models in survival analysis. To motivate our approach, we first set up the observed data likelihood and derive the NPMLE for a special case. Then, for more general situations, we propose estimating the parameters $\beta$ and $A\left(\cdot \right)$ using estimating equations along with an easily-implemented ES algorithm. Finally, the asymptotic properties of the resulting estimators are derived via modern empirical process theory (van der Vaart and Wellner, 1996).

3. Methods

3.1. Notations

For the $i$th individual, let $T_i$ and $C_i$ be the failure time and censoring time, respectively. Let ${\tilde{T}}_i=\min \left(T_i,C_i\right)$ be the observed time and define ${\text{Δ}}_i=I\left(T_i⩽C_i\right)$. Thus, ${\text{Δ}}_i=1$ indicates that the exact failure time for the $i$th individual was observed while ${\text{Δ}}_i=0$ implies censoring. For a random sample of $n$ participants, the observed data consist of ${\text{𝒪}}_i=\left\{{\text{Δ}}_i,{\tilde{T}}_i,X_i\left(t\right),Z_i\left(t\right),t\in \left[0,\tau \right]\right\}$ for $i=1,\dots n$, where $\tau$ denotes the duration of the study. Moreover, we define $Y_i\left(t\right)=I\left({\tilde{T}}_i⩾t\right)$ and $N_i\left(t\right)={\text{Δ}}_{i}I\left({\tilde{T}}_i⩽t\right)$.

3.2. Nonparametric Maximum Likelihood Estimation

Assume that $T_i$ and $C_i$ are conditionally independent given $X_i\left(\cdot \right)$ and $Z_i\left(\cdot \right)$. Under the proposed Cox-Aalen transformation model (1), the likelihood for the observed data is

$$\begin{array}{l}{L}_n\left(\beta ,{\text{Λ}}_X\right)=\underset{i=1}{\overset{n}{\Pi }}\{{\left({{\text{Λ}}^{\prime }}_{X_i}\left({\tilde{T}}_i\right)\text{exp}\left\{{\beta }^{\top }{Z}_i\left({\tilde{T}}_i\right)\right\}{G}^{\prime }\left[{\int }_0^{{\tilde{T}}_i}\text{exp}\left\{{\beta }^{\top }{Z}_i\left(s\right)\right\}d{\text{Λ}}_{X_i}\left(s\right)\right]\right)}^{{\text{Δ}}_i}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\times \text{exp}\left(-G\left[{\int }_0^{{\tilde{T}}_i}\text{exp}\left\{{\beta }^{\top }{Z}_i\left(s\right)\right\}d{\text{Λ}}_{X_i}\left(s\right)\right]\right)\},\end{array}$$ (5)

where ${{\text{Λ}}^{\prime }}_X\left(\cdot \right)$ and $G^{\prime }\left(\cdot \right)$ are the derivatives of ${\text{Λ}}_X\left(\cdot \right)$ and $G\left(\cdot \right)$, respectively. The likelihood (5) involves $\beta$ and $q$ infinite dimensional parameters $A_j\left(j=1,\dots ,q\right)$, and it may not be concave in these parameters. Thus, the nonparametric maximum likelihood techniques are usually employed to restrict the parameter space.

To establish a simple and efficient estimation procedure, we adopt the idea in Zeng and Lin (2007) by treating $\xi$ as a latent variable in the class of frailty-induced transformations (2). Note that model (1) is equivalent to the survival time $T$ with cumulative hazard function

$$\text{Λ}\left(t\left|X\left(\cdot \right),Z\left(\cdot \right),\xi \right.\right)=\xi {\int }_0^t\text{exp}\left\{{\beta }^{\top }Z\left(s\right)\right\}d{\text{Λ}}_X\left(s\right),$$ (6)

because

$$\begin{array}{l}\text{Pr}\left(T>t\left|X\left(\cdot \right),Z\left(\cdot \right)\right.\right)=E\left[Pr\left\{T>t\left|X\left(\cdot \right),Z\left(\cdot \right),\xi \right.\right\}\left|X\left(\cdot \right),Z\left(\cdot \right)\right.\right]\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=E\left(\text{exp}\left[-\xi {\int }_0^t\text{exp}\left\{{\beta }^{\top }Z\left(s\right)\right\}d{\text{Λ}}_X\left(s\right)\right]\left|X\left(\cdot \right),Z\left(\cdot \right)\right.\right)\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}={\int }_0^{\infty }\text{exp}\left[-\xi {\int }_0^t\text{exp}\left\{{\beta }^{\top }Z\left(s\right)\right\}d{\text{Λ}}_X\left(s\right)\right]f\left(\xi \right)d\xi \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=\text{exp}\left(-G\left[{\int }_0^t\text{exp}\left\{{\beta }^{\top }Z\left(s\right)\right\}d{\text{Λ}}_X\left(s\right)\right]\right).\end{array}$$

Based on (2), it can be shown that the likelihood (5) is equivalent to

$$\underset{i=1}{\overset{n}{\Pi }}{\int }_{{\xi }_i}\left({\left[{\xi }_i{{\text{Λ}}^{\prime }}_{X_i}\left({\tilde{T}}_i\right)\text{exp}\left\{{\beta }^{\top }{Z}_i\left({\tilde{T}}_i\right)\right\}\right]}^{{\text{Δ}}_i}\text{exp}\left[-{\xi }_i{\int }_0^{{\tilde{T}}_i}\text{exp}\left\{{\beta }^{\top }{Z}_i\left(s\right)\right\}d{\text{Λ}}_{X_i}\left(s\right)\right]f\left({\xi }_i\right)\right)d{\xi }_i.$$

Now we consider nonparametric maximum likelihood estimation of $\beta$ and $A\left(\cdot \right)$. Let $0=t_0<t_1<\cdots <t_m<\infty$ denote the uniquely observed event times among the $n$ observations. Assume that the estimator for $A_j\left(j=1,\dots ,q\right)$ is a step function with jump size $a_{jk}$ at $t_k$. By the observation that $d{\text{Λ}}_X\left(t\right)=X^{\top }\left(t\right)dA\left(t\right)$, the estimator for ${\text{Λ}}_X$ is a step function with jump size $X^{\top }\left(t_k\right)a_k$ at $t_k$ where $a_k={\left(a_{1k},\dots ,a_{qk}\right)}^{\top }$ for $k=1,\dots ,m$. Let ${\mathcal{O}}_i^C=\left\{{\text{Δ}}_i,{\tilde{T}}_i,X_i\left(t\right),Z_i\left(t\right),{\xi }_i,t\in \left[0,\tau \right]\right\}$ be the complete data for the $i$th participant. The complete-data log-likelihood function can be written as

$$\begin{array}{l}\sum _{i=1}^n\{\sum _{k=1}^m\left({\text{Δ}}_{i}I\left({\tilde{T}}_i=t_k\right)\left[log\left\{{\xi }_i\left(X_{ik}^{\top }{a}_k\right)\right\}+{\beta }^{\top }{Z}_{ik}\right]\right)\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}-{\xi }_i\sum _{t_k⩽{\tilde{T}}_i}\text{exp}\left({\beta }^{\top }{Z}_{ik}\right)\left(X_{ik}^{\top }{a}_k\right)+log\hspace{0.17em}f\left({\xi }_i\right)\},\end{array}$$ (7)

where $Z_{ik}=Z_i\left(t_k\right)$ and $X_{ik}=X_i\left(t_k\right)$.

To obtain the NPMLE of $\beta$ and $A\left(\cdot \right)$, we propose an EM-type algorithm by treating $\xi$ as missing data. In the E-step, we evaluate the posterior mean of ${\xi }_i$ given the observed data, denoted by $\widehat{E}\left({\xi }_i\right)$. The detailed calculations are given in the next subsection. In the M-step, we maximize the expectation of (7) conditional on the observed data. More specifically, we set the derivatives of the conditional expectation of (7) with respect to $a_k\left(k=1,\dots ,m\right)$ and $\beta$ to zeros, respectively. Then one can solve for the estimates through the following equations:

$${\displaystyle \sum }_{i=1}^n\left\{{\text{Δ}}_{i}I\left({\tilde{T}}_i=t_k\right)\frac{X_{ik}}{X_{ik}^{\top }{a}_k}-I\left({\tilde{T}}_i⩾t_k\right)\widehat{E}\left({\xi }_i\right)\exp \left({\beta }^{\top }{Z}_{ik}\right)X_{ik}\right\}=0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{for}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}k=1,\dots ,m,$$ (8)

$${\displaystyle \sum }_{i=1}^n{\displaystyle \sum }_{k=1}^m\left\{{\text{Δ}}_{i}I\left({\tilde{T}}_i=t_k\right)-I\left({\tilde{T}}_i⩾t_k\right)\widehat{E}\left({\xi }_i\right)\left(X_{ik}^{\top }{a}_k\right)\exp \left({\beta }^{\top }{Z}_{ik}\right)\right\}{Z}_{ik}=0.$$ (9)

The dimension of the unknown parameters $\left(a_1,\dots ,a_m,\beta \right)$ depends on $m$, which could be a large number when $n$ is large or the censoring rate is low. Therefore, (8) and (9) are a system of high-dimensional nonlinear equations that is notoriously difficult to solve due to the curse of dimensionality. For a special case, i.e., $X$ is a vector of design variables for categories, there exist explicit formulae for calculating the high-dimensional parameters $a_k\left(k=1,\dots ,m\right)$. See Web Appendix A for details. However, such explicit formulae do not exist for more general scenarios; hence we consider an alternative estimating equation approach to overcome the aforementioned computational difficulties.

3.3. Estimating Equations

Following Elashoff and Ryan (2004), we develop an expectation-solving (ES) algorithm for model (1) in this section. We begin by constructing a system of complete-data estimating equations based on model (6), which is equivalent to the proposed model (1) under the frailty-induced transformations (2). The connection between the proposed ES algorithm and the EM algorithm is discussed at the end of this section. Note that the intensity for $N_i\left(t\right)$ is $Y_i\left(t\right){\xi }_i\exp \left\{{\beta }^{\top }{Z}_i\left(t\right)\right\}{X}_i^{\top }\left(t\right)\alpha \left(t\right)$ if ${\xi }_i$ is known. Let

$$M_i\left(t\right)=N_i\left(t\right)-{{\displaystyle \int }}_0^t{Y}_i\left(s\right){\xi }_i\exp \left\{{\beta }_0^{\top }{Z}_i\left(s\right)\right\}{X}_i^{\top }\left(s\right)d{A}_0\left(s\right),$$

where (${\beta }_0$, $A_0$) are the true values of ($\beta$, $A$). It is clear that $E\left\{X_i\left(t\right)d{M}_i\left(t\right)\right\}=0$ for any $0⩽t⩽\tau$ and ${\rm E}\left\{{\int }_0^{\tau }{Z}_i\left(t\right)d{M}_i\left(t\right)\right\}=0$. By treating ${\xi }_i$ as missing, we consider the following complete-data estimating equations

$${\displaystyle \sum }_{i=1}^n{X}_i\left(t\right)\left[d{N}_i\left(t\right)-Y_i\left(t\right){\xi }_i\exp \left\{{\beta }^{\top }{Z}_i\left(t\right)\right\}{X}_i^{\top }\left(t\right)dA\left(t\right)\right]=0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\left(0⩽t⩽\tau \right),$$ (10)

$${\displaystyle \sum }_{i=1}^n{{\displaystyle \int }}_0^{\tau }{Z}_i\left(t\right)\left[d{N}_i\left(t\right)-Y_i\left(t\right){\xi }_i\exp \left\{{\beta }^{\top }{Z}_i\left(t\right)\right\}{X}_i^{\top }\left(t\right)dA\left(t\right)\right]=0.$$ (11)

By the previous arguments that the nonparametric estimator for ${\text{Λ}}_X$ is a step function with jump size $X^{\top }\left(t_k\right)a_k$ at $t_k\left(k=1,\dots ,m\right)$, it follows that (10) and (11) can be written as

$$\left\{\begin{array}{l}{\sum }_{i=1}^n\left\{{\text{Δ}}_{i}I\left({\tilde{T}}_i=t_1\right)-I\left({\tilde{T}}_i⩾t_1\right){\xi }_i\left(X_{i1}^{\top }{a}_1\right)\exp \left({\beta }^{\top }{Z}_{i1}\right)\right\}{X}_{i1}=0\hfill \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\dots \hfill \\ {\sum }_{i=1}^n\left\{{\text{Δ}}_{i}I\left({\tilde{T}}_i=t_m\right)-I\left({\tilde{T}}_i⩾t_m\right){\xi }_i\left(X_{im}^{\top }{a}_m\right)\exp \left({\beta }^{\top }{Z}_{im}\right)\right\}{X}_{im}=0\hfill \\ {\sum }_{i=1}^n{\sum }_{k=1}^m\left\{{\text{Δ}}_{i}I\left({\tilde{T}}_i=t_k\right)-I\left({\tilde{T}}_i⩾t_k\right){\xi }_i\left(X_{ik}^{\top }{a}_k\right)\exp \left({\beta }^{\top }{Z}_{ik}\right)\right\}{Z}_{ik}=0.\hfill \end{array}\right.$$ (12)

Write $\theta ={\left(a_1^{\top },\dots ,a_m^{\top },{\beta }^{\top }\right)}^{\top }$. We propose to estimate $\theta$ through an ES-type algorithm by treating ${\xi }_i$ as missing. The ES algorithm iterates between an E-step wherein the functions of the complete data are replaced by their expectations, and an S-step where these expected values are substituted into the complete-data estimating equations (12), which are then solved. After specifying initial values of the unknown parameters $\theta$, say ${\theta }^{\left(0\right)}$, the proposed ES algorithm iterates between the following two steps until convergence:

E-step. Evaluate the posterior means $\widehat{E}\left({\xi }_i\right)$. When ${\text{Δ}}_i=1$, the posterior density of ${\xi }_i$ given the observed data $\left({\text{Δ}}_i=1,T_i,X_i,Z_i\right)$ is proportional to ${\xi }_i\exp \left(-{\xi }_i{S}_{i1}\right)f\left({\xi }_i\right)$, where $S_{i1}={\text{Δ}}_i{\sum }_{t_k⩽T_i}\left(X_{ik}^{\top }{a}_k\right)\exp \left({\beta }^{\top }{Z}_{ik}\right)$. Hence we obtain

$$\widehat{E}\left({\xi }_i\right)=G^{\prime }\left(S_{i1}\right)-\frac{G^{″}\left(S_{i1}\right)}{G^{\prime }\left(S_{i1}\right)},$$

by taking the derivative twice of the equation $\exp \left\{-G\left(x\right)\right\}={\int }_0^{\infty }\exp \left(-x\xi \right)f\left(\xi \right)d\xi$, where $G^{\prime }\left(\cdot \right)$ and $G^{″}\left(\cdot \right)$ are the first and second derivatives of $G\left(\cdot \right)$, respectively. When ${\text{Δ}}_i=0$, the posterior density of ${\xi }_i$ given the observed data (${\text{Δ}}_i=0$, $C_i$, $X_i$, $Z_i$) is proportional to $\exp \left(-{\xi }_i{S}_{i2}\right)f\left({\xi }_i\right)$, where $S_{i2}=\left(1-{\text{Δ}}_i\right){\sum }_{t_k⩽C_i}\left(X_{ik}^{\top }{a}_k\right)\exp \left({\beta }^{\top }{Z}_{ik}\right)$. One can obtain $\widehat{E}\left({\xi }_i\right)=G^{\prime }\left(S_{i2}\right)$. Therefore, the E-step can be summarized as

$$\widehat{E}\left({\xi }_i\right)={\text{Δ}}_i\left\{G^{\prime }\left(S_{i1}\right)-\frac{G^{″}\left(S_{i1}\right)}{G^{\prime }\left(S_{i1}\right)}\right\}+\left(1-{\text{Δ}}_i\right)G^{\prime }\left(S_{i2}\right).$$

S-step. After replacing $\xi$ by $\widehat{E}\left({\xi }_i\right)$, we solve (12) for $\theta$. To this end, we propose the following nonlinear Gauss-Seidel method (Ortega and Rheinboldt, 1970; Ortega, 1972).

Step 1. Fix $\beta$, update $a_k\left(k=1,\dots ,m\right)$ by solving

$$\left\{\begin{array}{l}{{\displaystyle \sum }}_{i=1}^n\left\{{\text{Δ}}_{i}I\left({\tilde{T}}_i=t_1\right)-I\left({\tilde{T}}_i⩾t_1\right)\widehat{E}\left({\xi }_i\right)\left(X_{i1}^{\top }{a}_1\right)\exp \left({\beta }^{\top }{Z}_{i1}\right)\right\}{X}_{i1}=0\hfill \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\dots \hfill \\ {{\displaystyle \sum }}_{i=1}^n\left\{{\text{Δ}}_{i}I\left({\tilde{T}}_i=t_m\right)-I\left({\tilde{T}}_i⩾t_m\right)\widehat{E}\left({\xi }_i\right)\left(X_{im}^{\top }{a}_m\right)\exp \left({\beta }^{\top }{Z}_{im}\right)\right\}{X}_{im}=0.\hfill \end{array}\right.$$ (13)

Note that for fixed $\beta$, (13) is a system of linear equations with respect to $a_k\left(k=1,\dots ,m\right)$ and updating $a_k$ is independent of updating $a_j$ for $k\ne j\left(k,j=1,\dots ,m\right)$. In particular, we have explicit formulae for updating $a_k\left(k=1,\dots ,m\right)$, i.e.,

$$a_k={\left\{\sum _{i=1}^{n}I\left({\tilde{T}}_i⩾t_k\right)\widehat{E}\left({\xi }_i\right)\exp \left({\beta }^{\top }{Z}_{ik}\right)X_{ik}{X}_{ik}^{\top }\right\}}^{-1}\left\{\sum _{i=1}^n{\text{Δ}}_{i}I\left({\tilde{T}}_i=t_k\right)X_{ik}\right\},$$ (14)

for $k=1,\dots ,m$.

Step 2. Fix $a_1,\dots ,a_m$, we update $\beta$ by solving the following equation using the Newton-Raphson method:

$${\displaystyle \sum }_{i=1}^n{\displaystyle \sum }_{k=1}^m\left\{{\text{Δ}}_{i}I\left({\tilde{T}}_i=t_k\right)-I\left({\tilde{T}}_i⩾t_k\right)\widehat{E}\left({\xi }_i\right)\left(X_{ik}^{\top }{a}_k\right)\exp \left({\beta }^{\top }{Z}_{ik}\right)\right\}{Z}_{ik}=0.$$

Note that within the S-step, we iterate between Step 1 and Step 2 until convergence. The S-step is declared convergent when the sum of the absolute differences of the estimates at two successive iterations is less than a small positive number, say 10⁻³.

We iterate between the E- and S-steps until convergence and denote the final estimates by $\widehat{\theta }={\left({\widehat{a}}_1^{\top },\dots ,{\widehat{a}}_m^{\top },{\widehat{\beta }}^{\top }\right)}^{\top }$. A natural estimator of $A\left(t\right)$ is $\widehat{A}\left(t\right)={\sum }_{t_k⩽t}{\widehat{a}}_k$ for $0⩽t⩽\tau$. Moreover, recall that $A\left(t\right)={\int }_0^t\alpha \left(s\right)ds$, hence we can estimate $\alpha \left(t\right)$, $0⩽t⩽\tau$ via a kernel estimator

$$\widehat{\alpha }\left(t\right)={\displaystyle \sum }_{k=1}^m{h}^{-1}K\left(\frac{t-t_k}{h}\right){\widehat{a}}_k,$$

where $K\left(x\right)$ is the kernel function and h is the bandwidth. Throughout this article, we choose the Epanechnikov kernel function, i.e., $K\left(x\right)=\frac{3}{4}\max \left\{1-x^2,0\right\}$.

The proposed ES algorithm has several desirable features. First, a closed-form formula for computing $\widehat{E}\left({\xi }_i\right)$ is obtained in the E-step. Second, it avoids solving a large system of nonlinear equations in the S-step because the high-dimensional parameters $a_k\left(k=1,\dots ,m\right)$ are calculated explicitly while the low-dimensional parameter $\beta$ is updated via the Newton-Raphson method. Accordingly, the proposed ES algorithm performs stably and satisfactorily without calculating the inverse of any high-dimensional matrices. Third, when $X$ is a vector of design variables for categories, the corresponding ES algorithm coincides with the EM algorithm proposed in Section 3.2 by observing that for fixed $\beta$, (8) and (13) share the same solution in terms of $a_k\left(k=1,\dots ,m\right)$. This implies that the proposed ES estimator is also efficient under this special case. See Web Appendix B for detailed justifications. Similarly, it can be shown that the ES algorithm coincides with the EM algorithm When $X=1$, i.e., $q=1$. Finally, we remark that (13) can be considered as a weighted version of (8), where each participant $i$ is assigned weight $X_{ik}^{\top }{a}_k$.

3.4. Variance Estimator

In this section, we provide easy-to-compute variance estimators for both the parametric estimates $\widehat{\beta }$ and the nonparametric estimates $\widehat{A}\left(t\right)$, $\widehat{a}\left(t\right)$. Note that $\widehat{E}\left({\xi }_i\right)$ is a function of the observed data ${\mathcal{O}}_i$ and the unknown parameter $\theta :\widehat{E}\left({\xi }_i\right)=g\left({\mathcal{O}}_i,\theta \right)$. With $\mathcal{O}$ the collection of ${\mathcal{O}}_i\left(i=1,\dots n\right)$, the proposed ES estimator is intrinsically equivalent to solving the following observed-data estimating equation: $U\left(\mathcal{O},\theta \right)=0$, where $U\left(\mathcal{O},\theta \right)=\left(U_{a_1},\dots ,U_{a_m},U_{\beta }\right)$,

$$\left\{\begin{array}{l}{U}_{a_1}={\sum }_{i=1}^n\left\{{\text{Δ}}_{i}I\left({\tilde{T}}_i=t_1\right)-I\left({\tilde{T}}_i⩾t_1\right)g\left({\mathcal{O}}_i,\theta \right)\left(X_{i1}^{\top }{a}_1\right)\exp \left({\beta }^{\top }{Z}_{i1}\right)\right\}{X}_{i1}\hfill \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\dots \hfill \\ U_{a_m}={\sum }_{i=1}^n\left\{{\text{Δ}}_{i}I\left({\tilde{T}}_i=t_m\right)-I\left({\tilde{T}}_i⩾t_m\right)g\left({\mathcal{O}}_i,\theta \right)\left(X_{im}^{\top }{a}_m\right)\exp \left({\beta }^{\top }{Z}_{im}\right)\right\}{X}_{im}\hfill \\ U_{\beta }={\sum }_{i=1}^n{\sum }_{k=1}^m\left\{{\text{Δ}}_{i}I\left({\tilde{T}}_i=t_k\right)-I\left({\tilde{T}}_i⩾t_k\right)g\left({\mathcal{O}}_i,\theta \right)\left(X_{ik}^{\top }{a}_k\right)\exp \left({\beta }^{\top }{Z}_{ik}\right)\right\}{Z}_{ik}.\hfill \end{array}\right.$$ (15)

Note that $U_{a_1},\dots ,U_{a_m},U_{\beta }$ also depend on the observed data $\mathcal{O}$ and the unknown parameter $\theta$. Here, we compress the notation when there is no confusion. From (15), one can easily note that $U\left(\mathcal{O},\theta \right)$ can be expressed as the sum of independent terms:

$$U\left(\mathcal{O},\theta \right)={\displaystyle \sum }_{i=1}^n{U}_i\left({\mathcal{O}}_i,\theta \right).$$

Let $D\left(\mathcal{O},\theta \right)$ be the derivative of $U\left(\mathcal{O},\theta \right)$ with respect to $\theta$. The covariance matrix of $\widehat{\theta }$ is consistently estimated by

$$D{\left(\mathcal{O},\theta \right)}^{-1}\left\{{\displaystyle \sum }_{i=1}^n{U}_i\left({\mathcal{O}}_i,\theta \right)U_i^{\top }\left({\mathcal{O}}_i,\theta \right)\right\}{\left\{D{\left(\mathcal{O},\theta \right)}^{-1}\right\}}^{\top }\left|{ }_{\theta =\widehat{\theta }}\right..$$ (16)

Therefore, the variance covariance matrix of $\widehat{\beta }$ can be consistently estimated by the $d\times d$ lower right-hand corner of (16). The variance covariance matrix of ${\widehat{a}}_k\left(k=1,\dots ,m\right)$ can be consistently estimated by the $\left(qm\right)\times \left(qm\right)$ upper left-hand corner of (16).

In addition, recall that $\widehat{A}\left(t\right)={\sum }_{t_k⩽t}{\widehat{a}}_k$ and $\widehat{\alpha }\left(t\right)={\sum }_{k=1}^m{h}^{-1}K\left(\frac{t-t_k}{h}\right){\widehat{a}}_k$ for $0⩽t⩽\tau$, such that the variance for $\widehat{A}\left(t\right)$ and $\widehat{\alpha }\left(t\right)$ are

$$\text{Var}\left\{\widehat{A}\left(t\right)\right\}={\displaystyle \sum }_{t_k⩽t}{\displaystyle \sum }_{t_j⩽t}\text{Cov}\left({\widehat{a}}_k,{\widehat{a}}_j\right),$$

$$\text{Var}\left\{\widehat{\alpha }\left(t\right)\right\}={\displaystyle \sum }_{k=1}^m{\displaystyle \sum }_{j=1}^m{h}^{-2}K\left(\frac{t-t_k}{h}\right)K\left(\frac{t-t_j}{h}\right)\text{Cov}\left({\widehat{a}}_k,{\widehat{a}}_j\right).$$

Variance estimators are obtained by replacing $\text{Cov}\left({\widehat{a}}_k,{\widehat{a}}_j\right)$ by $\widehat{Cov}\left({\widehat{a}}_k,{\widehat{a}}_j\right)$ in the above expressions.

3.5. Asymptotic Properties

In this subsection, we present the asymptotic properties of the proposed ES estimator. let $\varphi \left(t\right)=G^{\prime }\left(t\right)$, $\psi \left(t\right)=G^{″}\left(t\right)/G^{\prime }\left(t\right)$ and $\rho \left(t;\beta ,A\right)={{\displaystyle \int }}_0^{t}Y\left(s\right)\exp \left\{{\beta }^{\top }Z\left(s\right)\right\}{X}^{\top }\left(s\right)dA\left(s\right)$. Hence, the posterior mean of $\xi$ can be written as $g\left(\tau ;\beta ,A\right)=\varphi \left(\rho \left(\tau ;\beta ,A\right)\right)-\text{Δ}\psi \left(\rho \left(\tau ;\beta ,A\right)\right)$.

Let $P$ denote the true probability measure and ${\mathbb{P}}_n$ denote the empirical measure. In addition, let $\theta =\left(\beta ,A\right)$ be the parameters of interest and ${\theta }_0=\left({\beta }_0,A_0\right)$ be the true values of the parameters. Then the proposed ES estimator $\widehat{\theta }=\left(\widehat{\beta },\widehat{A}\right)$ is a Z-estimator solving the following observed-data estimating equation

$${\mathbb{P}}_n\text{Φ}\left(\beta ,A\right)\left(t\right)\equiv {\mathbb{P}}_n\left(\begin{array}{c}{\text{Φ}}_1\left(\beta ,A\right)\\ {\text{Φ}}_2\left(\beta ,A\right)\left(t\right)\end{array}\right)=0,$$

for $0⩽t⩽\tau$, where

$${\text{Φ}}_1\left(\beta ,A\right)={{\displaystyle \int }}_0^{\tau }\left[Z\left(t\right)dN\left(t\right)-Y\left(t\right)\exp \left\{{\beta }^{\top }Z\left(t\right)\right\}g\left(\tau ;\beta ,A\right)Z\left(t\right)X^{\top }\left(t\right)dA\left(t\right)\right],$$

$${\text{Φ}}_2\left(\beta ,A\right)\left(t\right)=X\left(t\right)dN\left(t\right)-Y\left(t\right)\exp \left\{{\beta }^{\top }Z\left(t\right)\right\}g\left(\tau ;\beta ,A\right)X\left(t\right)X^{\top }\left(t\right)dA\left(t\right).$$

Let $h$ be a function in $B{V}_1\left[0,\tau \right]$, where $B{V}_1\left[0,\tau \right]$ denotes the set of functions with total variation bounded by 1 on $\left[0,\tau \right]$. Define

$${\text{Φ}}_2\left(\beta ,A\right)\left[h\right]={{\displaystyle \int }}_0^{\tau }h\left(t\right)\left[X\left(t\right)dN\left(t\right)-Y\left(t\right)\exp \left\{{\beta }^{\top }Z\left(t\right)\right\}g\left(\tau ;\beta ,A\right)X\left(t\right)X^{\top }\left(t\right)dA\left(t\right)\right].$$

Similar to Gao et al. (2017) and van der Vaart and Wellner (1996, Section 3.3.1), the proposed ES estimator ($\widehat{\beta }$, $\widehat{A}$) is equivalent to the root of the estimating equation

$${\mathbb{P}}_n\text{Φ}\left(\beta ,A\right)\left[h\right]\equiv {\mathbb{P}}_n\left(\begin{array}{c}{\text{Φ}}_1\left(\beta ,A\right)\\ {\text{Φ}}_2\left(\beta ,A\right)\left[h\right]\end{array}\right)=0,$$

for all $h\in B{V}_1\left[0,\tau \right]$.

Write $\text{Ψ}\left(\theta \right)=P\text{Φ}\left(\beta ,A\right)\left[h\right]$ and ${\text{Ψ}}_n\left(\theta \right)={\mathbb{P}}_n\text{Φ}\left(\beta ,A\right)\left[h\right]$. Note that $\text{Ψ}\left(\theta \right)$ and ${\text{Ψ}}_n\left(\theta \right)$ are actually $h$-dependent. Rigorously speaking, we should write $\text{Ψ}\left(\theta \right)\left[h\right]=P\text{Φ}\left(\beta ,A\right)\left[h\right]$ and ${\text{Ψ}}_n\left(\theta \right)\left[h\right]={\mathbb{P}}_n\text{Φ}\left(\beta ,A\right)\left[h\right]$, but in the rest of the article, we suppress the letter $h$ when there is no confusion. The proposed ES estimator is a Z-estimator that satisfies ${\text{Ψ}}_n\left(\widehat{\theta }\right)=0$. To establish the asymptotic properties, we assume the following regularity conditions:

Condition 1. With probability one, $X\left(\cdot \right)$ and $Z\left(\cdot \right)$ have bounded total variation in $\left[0,\tau \right]$.

Condition 2. Let $\mathcal{B}$ be a compact set of ${\mathcal{R}}^d$ and $BV\left[0,\tau \right]$ be the class of functions with bound variation over $\left[0,\tau \right]$. The true parameter (${\beta }_0$, $A_0$) belongs to $\mathcal{B}\times B{V}^q\left[0,\tau \right]$ with ${\beta }_0$ an interior point of $\mathcal{B}$ and $A_0\left(t\right)={\left(A_{01}\left(t\right),\dots ,A_{0q}\left(t\right)\right)}^{\top }$ is continuous over $\left[0,\tau \right]$ with $A_0\left(0\right)=0$. Here $B{V}^q\left[0,\tau \right]$ denotes the product space $BV\left[0,\tau \right]\times \cdots \times BV\left[0,\tau \right]$.

Condition 3. With probability one, there exists a positive constant $\epsilon$ such that $P\left(Y\left(\tau \right)=1\left|X\left(\cdot \right),Z\left(\cdot \right)\right.\right)>\epsilon$ and $P{N}^2\left(\tau \right)<\infty$. If there exists a vector $\gamma$ and a deterministic function ${\gamma }_0\left(t\right)$ such that ${\gamma }_0\left(t\right)+{\gamma }^{\top }X\left(t\right)=0$ with probability one, then ${\gamma }_0\left(t\right)=0$ and $\gamma =0$ for any $t\in \left[0,\tau \right]$.

Condition 4. The transformation function $G$ is thrice continuously differentiable on $\left[0,\infty \right)$ with $G\left(0\right)=0$, $G^{\prime }\left(x\right)>0$ and $G\left(\infty \right)=\infty$.

Condition 5. Let ${\dot{\text{Ψ}}}_{{\theta }_0}$ be the Fréchet derivative of $\text{Ψ}\left(\theta \right)$ with respect to $\theta$ at $\theta ={\theta }_0$. See Web Appendix C for detailed expressions of ${\dot{\text{Ψ}}}_{{\theta }_0}$. We assume that ${\dot{\text{Ψ}}}_{{\theta }_0}$ is an invertible map.

Remark 4: Conditions 1 and 2 state the boundedness of the covariates and the compactness of the Euclidean parameter space, which are conventional conditions used in most regression analyses. Condition 3 ensures the existence and uniqueness of the jump sizes in (14). Condition 4 ensures that the transformation function $G$ is strictly increasing on $\left[0,\infty \right)$. Condition 5 is a classical condition for Z-estimators.

Theorem 1: Under Conditions 1 – 5, the proposed ES estimator ($\widehat{\beta }$, $\widehat{A}$) is strongly consistent to (${\beta }_0$, $A_0$).

Theorem 2: Under Conditions 1 – 5, $\sqrt{n}\left(\widehat{\beta }-{\beta }_0,\widehat{A}-A_0\right)$ converges weakly to a zero-mean Gaussian process in the metric space ${\mathcal{R}}^d\times {\overline{lin}}^q\left(B{V}_1\left[0,\tau \right]\right)$.

Here, we let $\overline{\text{lin}}\left(B{V}_1\left[0,\tau \right]\right)$ be the closed linear span for linear functionals of $B{V}_1\left[0,\tau \right]$. For each $j\left(j=1,\dots ,q\right)$, $A_j$ is contained in the Banach space $\overline{\text{lin}}\left(B{V}_1\left[0,\tau \right]\right)$, where $A_j\left[h\right]=\int h\left(t\right)d{A}_j\left(t\right)$ for $h\in BV\left[0,\tau \right]$. Thus, $A={\left(A_1,\dots ,A_q\right)}^{\top }$ is contained in the Banach space ${\overline{\text{lin}}}^q\left(B{V}_1\left[0,\tau \right]\right)$. Here, ${\overline{\text{lin}}}^q\left(B{V}_1\left[0,\tau \right]\right)$ stands for the product space $\overline{\text{lin}}\left(B{V}_1\left[0,\tau \right]\right)\times \cdots \times \overline{\text{lin}}\left(B{V}_1\left[0,\tau \right]\right)$. Detailed proofs of the above theorems are presented in Web Appendix C.

4. Simulation Studies

We carried out extensive simulation studies to evaluate the finite-sample performance of the proposed estimation and inference procedures. Suppose that the failure time $T$ follows the Cox-Aalen transformation model with the cumulative hazard function

$$\text{Λ}\left(t\left|X\left(\cdot \right),Z\left(\cdot \right)\right.\right)=G\left[{{\displaystyle \int }}_0^t\exp \left\{{\beta }_1{Z}_1\left(s\right)+{\beta }_2{Z}_2\right\}d{\text{Λ}}_X\left(s\right)\right].$$

Here, $Z_1\left(t\right)=B_{1}I\left(t⩽V\right)+B_{2}I\left(t>V\right)$ is a time-dependent covariate where $B_1$ and $B_2$ are independent $\text{Ber}\left(0.5\right)$, $V\sim \text{Unif}\left(0,3\right)$, and $Z_2\sim \text{Unif}\left(0,1\right)$ is a time-independent covariate. We set ${\beta }_1=0.5$, ${\beta }_2=-0.5$, and consider four different configurations for ${\text{Λ}}_X\left(s\right)={\int }_0^s{X}^{\top }\left(v\right)dA\left(v\right)$, $A\left(t\right)={\left(A_1\left(t\right),\dots ,A_q\left(t\right)\right)}^{\top }$:

Scenario 1. $X={\left(1,X_2\right)}^{\top }$ with $X_2\sim \text{Ber}\left(0.4\right)$, $A_1\left(t\right)=\log \left(1+t/4\right)$ and $A_2\left(t\right)=0.1t$.

Scenario 2. $X={\left(1,X_2\right)}^{\top }$ with $X_2\sim \text{Unif}\left(0,1\right)$, $A_1\left(t\right)=\log \left(1+t/4\right)$ and $A_2\left(t\right)=0.1t$.

Scenario 3. $X\left(t\right)={\left(1,X_2\left(t\right)\right)}^{\top }$ with $X_2\left(t\right)=B_3+B_{4}t$, where $B_3\sim \text{Unif}\left(1,2\right)$ and $B_4\sim \text{Unif}\left(0.1,0.5\right)$, $A_1\left(t\right)=\log \left(1+t/4\right)$ and $A_2\left(t\right)=0.1t$.

Scenario 4. Let $D$ be a categorical variable that takes values in $\left\{1,2,3\right\}$ with equal probability. $X={\left(1,X_2,X_3\right)}^{\top }$, where $X_2=I\left(D=2\right)$, $X_3=I\left(D=3\right)$, $A_1\left(t\right)=\log \left(1+t/4\right)$, $A_2\left(t\right)=0.1t$ and $A_3\left(t\right)=0.05t$.

For the transformation functions, we consider the class of logarithmic transformations $G\left(x\right)=r^{-1}\log \left(1+rx\right)$ with $r=0,0.5$ and 1, where $r=0$ specifies the Cox-Aalen model. For all setups, we let $\tau =1$ be the duration of the study. For each study participant, we generate one censoring time $C\sim \text{Exponential}\left(0.5\right)$. We set $\text{Δ}=1$ if $T⩽\min \left(C,\tau \right)$, and 0 otherwise. This process yields about 75 – 85% right-censored observations for $r=0,0.5$ and 1. For each dataset, we applied the proposed ES algorithm by setting the initial value of $\beta$ to 0 and the initial value of $a_k$ to be $\left(1/m,0,\dots ,0\right)$ for each $k=1,\dots ,m$. We also tried other initial values, yielding almost identical results. We set $n=200$, 500 or 800, and all simulation results are based on 1000 replicates.

Table 1 summarizes the results for estimation of ${\beta }_1$ and ${\beta }_2$ for all scenarios. Despite the high censoring percentage, from Table 1, one can see that the proposed procedures perform well in several ways: (i) the estimators are virtually unbiased; (ii) the estimated standard error is fairly close to the empirical standard error; (iii) the empirical coverage probability of 95% confidence intervals are all close to the nominal 95% level; (iv) when the sample size increases, the bias, and the variability of the parameter estimator, decreases. Thus, our proposed estimation procedures are reliable for various Cox-Aalen transformation models.

Table 1.

Simulation results for estimation of the regression parameters under Scenarios 1 to 4

		${\beta }_1=0.5$				${\beta }_2=-0.5$
$r$	$n$	Bias	SE	SEE	CP	Bias	SE	SEE	CP
	Scenario 1
0	200	0.003	0.350	0.340	0.950	−0.014	0.587	0.574	0.947
	500	0.007	0.212	0.212	0.952	−0.005	0.354	0.359	0.956
	800	−0.003	0.172	0.167	0.948	−0.001	0.279	0.285	0.951
0.5	200	−0.001	0.380	0.369	0.949	−0.014	0.639	0.630	0.950
	500	0.007	0.227	0.230	0.961	−0.002	0.388	0.395	0.957
	800	−0.004	0.185	0.181	0.951	−0.001	0.302	0.313	0.951
1	200	−0.002	0.402	0.402	0.956	−0.020	0.690	0.699	0.957
	500	0.008	0.246	0.252	0.957	0.002	0.415	0.437	0.968
	800	−0.005	0.198	0.198	0.946	−0.003	0.323	0.347	0.957
	Scenario 2
0	200	0.004	0.337	0.334	0.954	−0.002	0.574	0.563	0.942
	500	0.006	0.208	0.209	0.962	−0.004	0.348	0.353	0.960
	800	−0.002	0.169	0.164	0.945	−0.006	0.275	0.280	0.949
0.5	200	−0.002	0.363	0.362	0.951	−0.014	0.624	0.620	0.948
	500	0.008	0.223	0.227	0.954	−0.000	0.384	0.389	0.963
	800	−0.003	0.184	0.179	0.946	−0.003	0.300	0.308	0.948
1	200	−0.005	0.389	0.396	0.957	−0.019	0.672	0.690	0.958
	500	0.007	0.240	0.248	0.957	0.002	0.412	0.432	0.965
	800	−0.004	0.197	0.195	0.944	−0.005	0.325	0.342	0.961
	Scenario 3
0	200	0.005	0.288	0.287	0.958	−0.009	0.494	0.486	0.947
	500	0.002	0.180	0.180	0.949	−0.004	0.305	0.305	0.953
	800	−0.001	0.146	0.141	0.949	−0.009	0.245	0.241	0.950
0.5	200	0.001	0.319	0.321	0.954	−0.009	0.552	0.555	0.953
	500	0.001	0.198	0.202	0.956	−0.004	0.348	0.348	0.953
	800	−0.001	0.160	0.159	0.947	−0.009	0.276	0.276	0.942
1	200	0.010	0.343	0.365	0.964	−0.002	0.624	0.647	0.962
	500	−0.002	0.216	0.229	0.959	−0.002	0.380	0.403	0.963
	800	−0.006	0.175	0.180	0.963	−0.003	0.305	0.318	0.960
	Scenario 4
0	200	0.010	0.339	0.334	0.951	−0.011	0.572	0.562	0.938
	500	0.005	0.211	0.209	0.948	−0.003	0.348	0.353	0.958
	800	−0.000	0.169	0.164	0.948	−0.000	0.280	0.279	0.948
0.5	200	0.007	0.366	0.362	0.946	−0.014	0.615	0.619	0.947
	500	0.003	0.228	0.227	0.950	−0.005	0.378	0.389	0.968
	800	0.001	0.183	0.179	0.950	−0.001	0.308	0.307	0.949
1	200	0.002	0.389	0.396	0.951	−0.008	0.657	0.690	0.960
	500	0.002	0.244	0.248	0.957	0.002	0.412	0.433	0.967
	800	0.001	0.195	0.196	0.956	0.000	0.330	0.341	0.954

Note: Bias, bias of the parameter estimator; SE, empirical standard error of the parameter estimator; SEE, mean of the standard error estimator; CP, empirical coverage percentage of the 95% confidence interval.

Figure 1 shows the estimation results for the cumulative regression functions $A\left(\cdot \right)$ in Scenario 1. The proposed estimators are again virtually unbiased and the estimated curves are able to capture the shapes of the true cumulative regression functions very well; the estimated standard errors are close to the empirical standard errors; and the confidence intervals have reasonably accurate coverage probabilities. To save space, estimation results for $\alpha \left(\cdot \right)$ via the kernel smoothing approach with bandwidth $h=0.1$ are provided in Web Appendix D for Scenario 1. In addition, estimation results for $A\left(\cdot \right)$ and $\alpha \left(\cdot \right)$ under Scenarios 2 and 4 are also presented in Web Appendix D. These results further confirm the satisfactory performance of our proposed method in various numerical settings. We also conducted simulation studies to investigate the robustness of the proposed estimator under the misspecification of the $G$ function. The setups were the same as Scenario 3, and simulation results are displayed in Web Appendix D. The results suggested that the misspecification of the transformation function led to biased estimates and lower coverage probabilities than the nominal levels.

Figure 1.

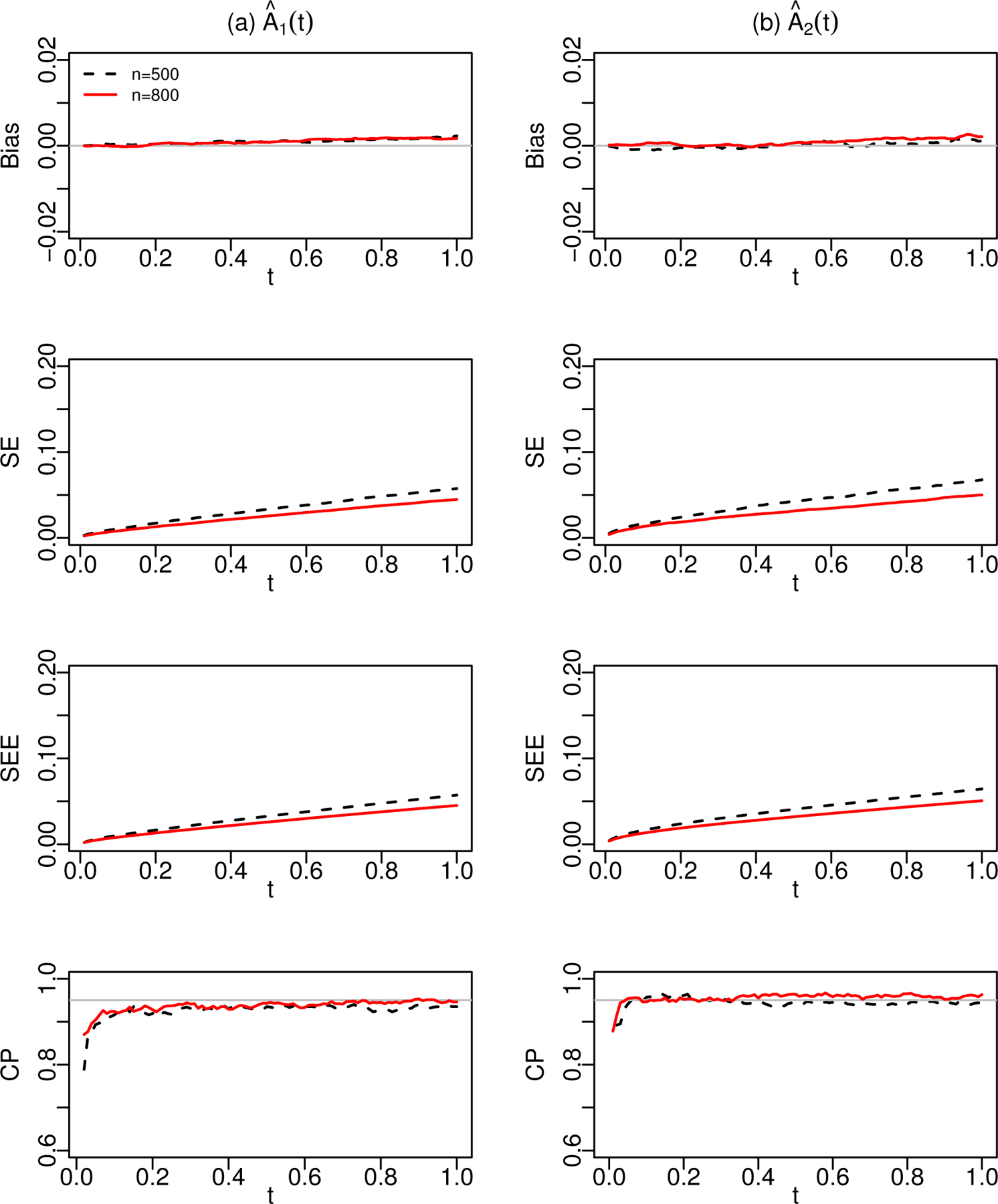
Estimation results for (a) $A_1\left(t\right)=\log \left(1+t/4\right)$ and (b) $A_2\left(t\right)=0.1t$ in Scenario 1, under the logarithmic transformation $G\left(x\right)=r^{-1}\log \left(1+rx\right)$ with $r=0$. The dashed and solid lines are for data sets with $n=500$ and $n=800$, respectively. Bias, SE, SEE, and CP stand, respectively, for the bias, empirical standard error, mean of the standard error estimator, and empirical coverage probability of the 95% confidence interval.

Moreover, we demonstrate the superiority of our proposed model over Zeng and Lin’s model in one simulation example. Specifically, we generated the data from our proposed Cox-Aalen transformation model where one covariate has a multiplicative effect, and the other has an additive effect. If we falsely assume that both covariates have multiplicative effects and fit Zeng and Lin’s model, we will obtain biased estimates of the survival function and cumulative hazard. Thus, our proposed model can better capture complex hazard functions. See Web Appendix D for details.

5. An HIV Prevention Study Example

In this section, we apply the proposed model and methods to two harmonized randomized trials, HIV Vaccine Trials Network (HVTN) 704/HIV Prevention Trials Network (HPTN) 085 and HVTN 703/HPTN 081 (Corey et al., 2021), designed to determine whether a broadly neutralizing monoclonal antibody (bnAb) can prevent the acquisition of human immunodeficiency virus type 1 (HIV). The HVTN 704/HPTN 085 trial enrolled 2687 men who have sex with men and transgender persons in the Americas and Europe, and HVTN 703/HPTN 081 enrolled 1924 females in sub-Saharan Africa. For each trial, HIV uninfected participants were randomly assigned in 1:1:1 ratio to receive infusions of a bnAb (VRC01) at a dose of 10 mg per kilogram of body weight (low-dose group), VRC01 at 30 mg per kilogram (high-dose group) or saline placebo, administered at 8-week intervals for 10 total infusions. The primary efficacy endpoint was diagnosis of HIV infection by the week 80 trial visit, and HIV testing was conducted at each 4-week trial visit starting at week 0. For participants acquiring HIV infection, the diagnosis date was determined by the adjudicated diagnosis date based on validated assays (Corey et al., 2021). Participant follow-up is right-censored by the minimum of their last negative HIV sample collection date and $\tau =85.9$ weeks (Corey et al., 2021). Therefore, the observed data consist of exact and right-censored observations.

Among the 4559 HIV negative participants from both trials, 1401 are in the U.S. and Switzerland, 1249 in Brazil and Peru, 1009 in South Africa, and 900 in other sub-Saharan African countries (Switzerland was pooled with the U.S. given few participants in Switzerland). We analyze the two trials pooled together, which is valid given the harmonized protocols such that essentially the study is one trial in two distinct study populations. There were a total of 174 HIV infection diagnosis endpoints in the two trials pooled, including 60 out of 1520 participants in the low-dose group, 47 out of 1520 in the high-dose group, and 67 out of 1519 in the placebo group. The numbers of HIV infection diagnosis endpoints by region are reported in Web Appendix E. Participants were categorized by age (in years old) into four groups, [17, 20], [21, 30], [31, 40] and [41, 52], with 540, 2651, 1102 and 266 participants, respectively.

Figure 2 reveals that the risk of HIV infection diagnosis in different regions crosses over. Therefore, without imposing proportional hazards for different regions, we consider the following Cox-Aalen transformation model to assess the association between treatment assignment, age, and region with the time since the first infusion to HIV infection diagnosis:

$$\text{Λ}\left(t\left|X,Z\right.\right)=G\left\{{{\displaystyle \int }}_0^t\exp \left({\beta }^{\top }Z\right)d{\text{Λ}}_X\left(s\right)\right\},$$

Figure 2.

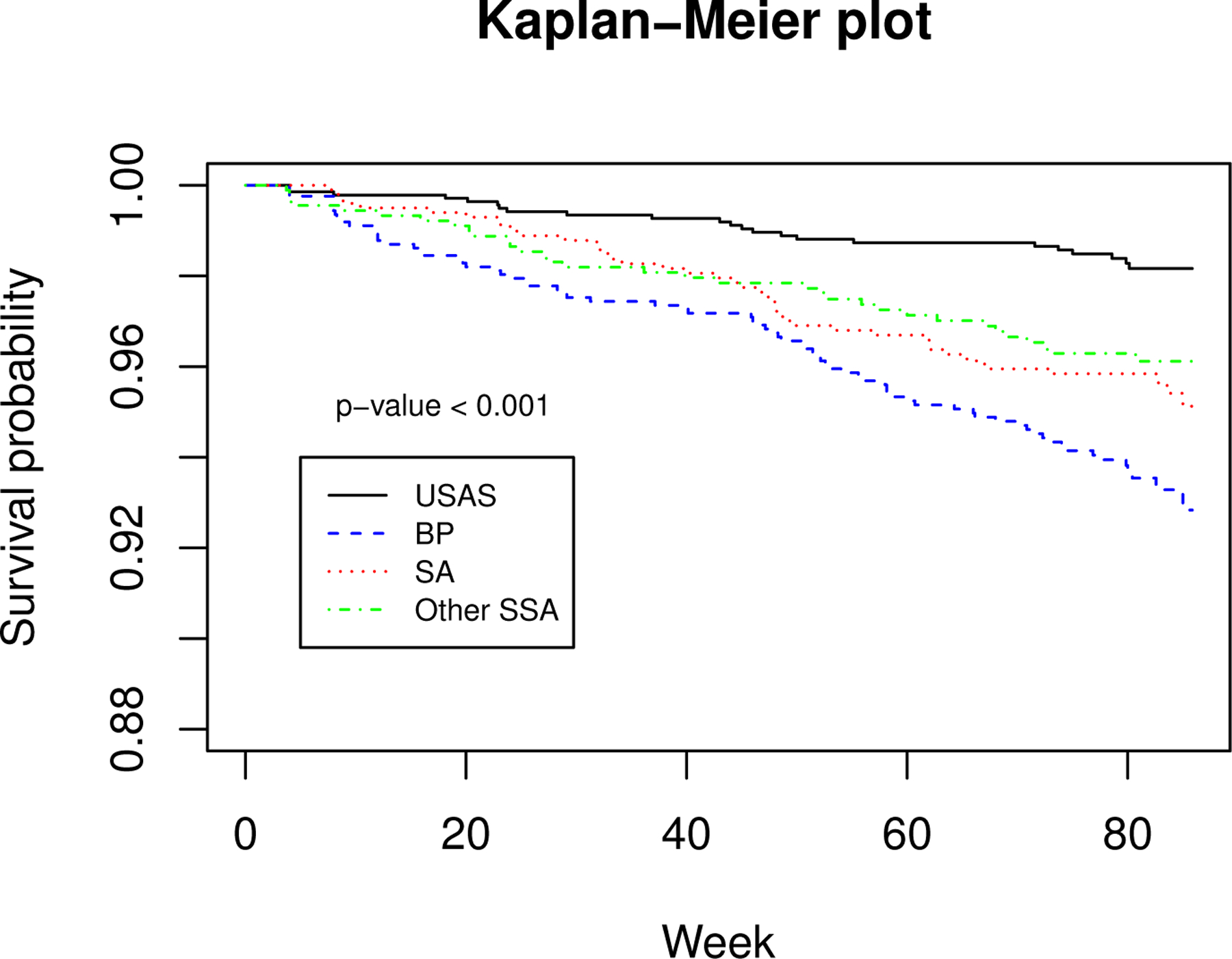
Kaplan-Meier plot for four regions in the full cohort. Here, “USAS”, “BP”, “SA” and “Other SSA” represent USA and Switzerland, Brazil and Peru, South Africa and other sub-Saharan African countries, respectively.

where $\beta$ is the unknown regression coefficients and ${\text{Λ}}_X\left(s\right)={\int }_0^s\left\{X^{\top }\alpha \left(v\right)\right\}dv=X^{\top }A\left(s\right)$ with $A\left(s\right)={\left(A_1\left(s\right),\dots ,A_4\left(s\right)\right)}^{\top }$. Here, $Z={\left(Z_1,Z_2,Z_3,Z_4,Z_5\right)}^{\top }$, where $Z_1$ and $Z_2$ are indicators of being assigned to the low-dose and high-dose group, respectively, with the placebo group as the reference group; $Z_3$, $Z_4$, $Z_5$ are indicators of the age groups [21, 30], [31, 40] and [41, 52], respectively, with [17, 20] as the reference age group. In addition, let $X={\left(1,X_2,X_3,X_4\right)}^{\top }$, where $X_2$, $X_3$, $X_4$ are indicators of participants from Brazil and Peru, South Africa, and other sub-Saharan African countries, respectively. The participants from USA and Switzerland are considered as the reference group.

We conducted the analysis using the class of logarithmic transformations $G\left(x\right)=r^{-1}\log \left(1+rx\right)$, with $r$ values ranging from 0 to 3 with an increment of 0.1. The $r$ value that maximizes the log-likelihood function evaluated at the final parameter estimates was selected. The log-likelihood is maximized at $r=0$, though the values do not change greatly for different values of $r$ due to a high censoring rate (about 96.2%); this phenomenon is verified in our simulation studies (see Web Appendix E for details).

The lower panel of Table 2 shows the regression parameter estimates for the selected transformation function ($r=0$). High-dose VRC01 significantly lowers the risk of HIV infection diagnosis, while low-dose VRC01 does not. The model fit also shows a significant association between older age and a lower risk of HIV infection diagnosis. Figure 3 displays the estimated baseline cumulative hazard function $\widehat{\text{Λ}}\left(t\left|X,Z=0\right.\right)$ for the four different regions. The risk of HIV infection diagnosis is the highest in Brazil and Peru and lowest in the U.S. and Switzerland. The estimates for South Africa and other sub-Saharan African countries cross; in particular, South Africa has a lower risk at early times after the first infusion but a higher risk at later times. In addition, Figure 3 shows that the HIV infection diagnosis hazards are not proportional across geographic regions. Figure 4 plots the estimates of conditional survival functions at sixteen different combinations of covariates: four age groups crossed with four regions. This figure further confirms our findings above. In Web Appendix E, we also report the analysis results under other values of r and observe the same patterns.

Table 2.

Regression analysis results for the HIV trials from Zeng and Lin’s model fit to each of the four geographic regions separately and the proposed Cox-Aalen transformation model based on the full cohort data with the logarithmic transformation $G\left(x\right)=r^{-1}\log \left(1+rx\right)$ with $r=0$

	USA/Switzerland			Brazil/Peru
Covariates	Est	SE	p-value	Est	SE	p-value
Low-dose	−0.107	0.484	0.825	−0.167	0.276	0.545
High-dose	−0.437	0.524	0.404	−0.279	0.283	0.325
21 − 30	−0.454	0.630	0.472	−0.525	0.262	0.045
31 − 40	−2.709	1.141	0.018	−1.283	0.396	0.001
41 − 52	−1.152	0.903	0.202	−16.859	1.668	< 0.001
	South Africa			Other SSA
Covariates	Est	SE	p-value	Est	SE	p-value
Low-dose	−0.025	0.354	0.943	−0.080	0.400	0.842
High-dose	−0.392	0.392	0.317	−0.509	0.449	0.258
21 – 30	−0.187	0.380	0.623	−0.480	0.498	0.335
31 – 40	−0.954	0.601	0.112	−0.719	0.586	0.220
41 – 52	−13.867	2.366	< 0.001	−13.871	2.626	< 0.001
	The Proposed Model
Covariates	Est	SE	p-value
Low-dose	−0.108	0.178	0.542
High-dose	−0.363	0.190	0.056
21 – 30	−0.429	0.187	0.022
31 – 40	−1.219	0.274	< 0.001
41 – 52	−1.989	0.721	0.006

Note: Est and SE stand for the estimates of the regression parameters and the estimated standard errors, respectively. “Other SSA” is for other sub-Saharan African countries. “USA/Switzerland”, “Brazil/Peru”, “South Africa”, and “Other SSA” correspond to the estimation results by fitting Zeng and Lin’s model to each geographic region. “The Proposed Model” corresponds to the estimation results when fitting the proposed Cox-Aalen transformation models to the full cohort data.

Figure 3.

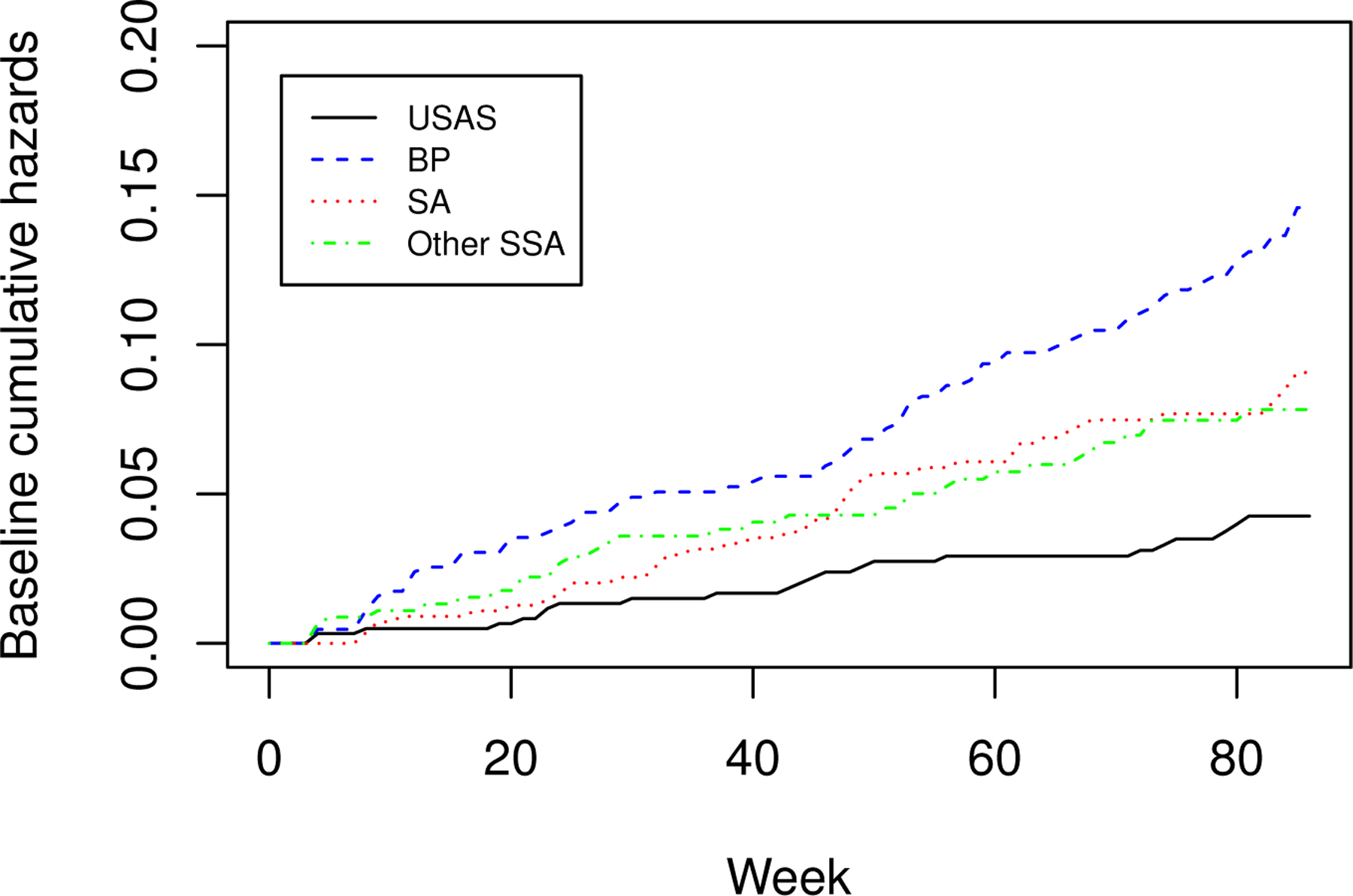
Estimated baseline cumulative hazard function for four regions under the logarithmic transformation $G\left(x\right)=r^{-1}\log \left(1+rx\right)$ with $r=0$. Here, “USAS”, “BP”, “SA” and “Other SSA” represent USA and Switzerland, Brazil and Peru, South Africa and other sub-Saharan African countries, respectively.

Figure 4.

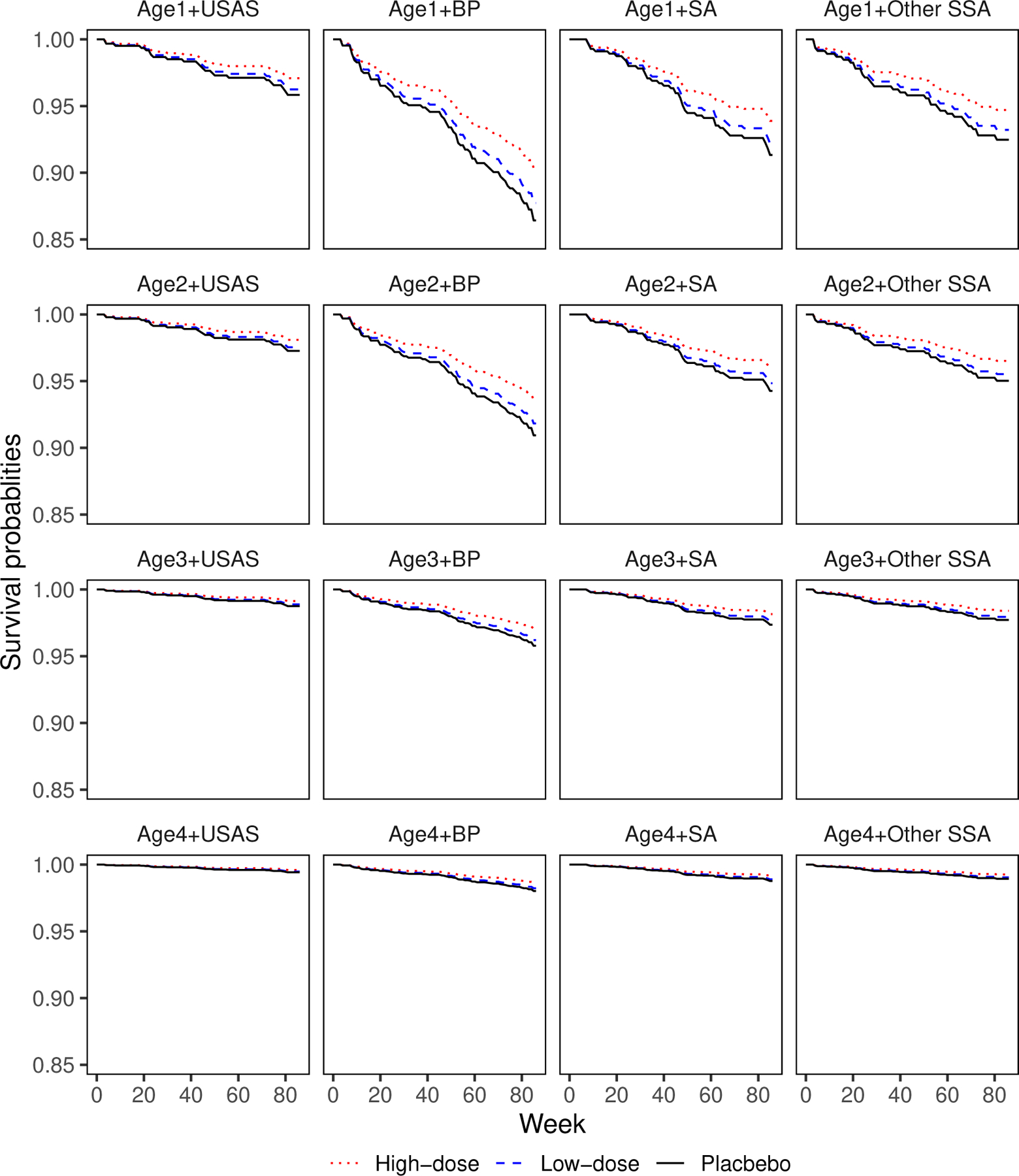
Estimated survival functions by considering different combinations of covariates under the proposed model with the transformation $G\left(x\right)=r^{-1}\log \left(1+rx\right)$ with $r=0$. Here, “Age1”, “Age2”, “Age3” and “Age4” stand for the age goups, [17, 20], [21, 30], [31, 40] and [41, 52], respectively. “USAS”, “BP”, “SA” and “Other SSA” represent USA and Switzerland, Brazil and Peru, South Africa and other sub-Saharan African countries, respectively.

The four other panels of Table 2 (upper panels) show results from Zeng and Lin’s model fit to each of the four geographic regions separately; this method was not applied to the full cohort (pooled) data because it cannot flexibly model the differences in baseline cumulative hazards and the diagnostics support lack of fit. In these results, the p-values for the effect of high-dose VRC01 markedly increase, and the coefficient estimates for the age group [41, 52] are unstable because there are very few HIV infection diagnosis endpoints in this age group in the three regions Brazil and Peru, South Africa, and other sub-Saharan African countries. Therefore, the results from the Cox-Aalen transformation modeling –which could be based on the full cohort data through flexible specifications of the baseline cumulative hazard functions – provide new insights with improved precision and power beyond insights achieved from the application of Zeng and Lin’s model.

6. Discussion

In this article, we proposed a class of semiparametric Cox-Aalen transformation models that includes Zeng and Lin’s model (Zeng and Lin, 2006; Zeng et al., 2016) and the Cox-Aalen model (Scheike and Zhang, 2002) as special cases. By considering the class of frailty-induced transformations, we successfully developed a fast and stable ES algorithm to estimate the parametric and nonparametric components of the proposed model along with easy-to-compute variance estimators. In addition, the asymptotic properties of our proposed estimators are rigorously studied. Elashoff and Ryan (2004) pointed out that an ES algorithm can be regarded as a block Newton-Gauss-Seidel algorithm (see Ortega 1972, p.146). Following Ortega (1972, p.147), an ES algorithm converges locally to the solution, $\widehat{\theta }$, of $U\left(\theta \right)=0$ if the Jacobian matrix $D=\partial U/\partial \theta$ is nonsingular at $\theta =\widehat{\theta }$ and the largest eigenvalue of $D^{-1}\left(\widehat{\theta }\right)$ is less than 1. For general estimating equations, the two conditions above are difficult to verify in advance, especially for the second condition. Nevertheless, the matrix $D$ is needed to calculate the variance of $\widehat{\theta }$ in (16), and hence one can check the required conditions numerically.

In real data applications, we ascertain whether a covariate has a multiplicative or additive effect based on the following criteria. First, we may employ the underlying biological, physical meaning, or other domain knowledge for decision-making. Second, initial data exploration can be performed for each covariate, such as drawing the Kaplan-Meier (KM) plot. If the KM curves cross, this covariate should be modeled additively. Third, similar to Qu and Sun (2019), Yu et al. (2019), we may employ some AIC or BIC-based procedures. In particular, all possible combinations of covariate effects will be examined. However, it is easy to see that this is inefficient when there are many covariates. In addition, Scheike and Zhang (2003) proposed supremum tests to determine the multiplicative and additive parts of the Cox-Aalen model. It is worthwhile to investigate if similar testing procedures can be constructed for our proposed model. More theoretical and numerical studies are needed, which we leave for future work.

Indeed, the outlined procedures for determining the covariates for the multiplicative or additive components are valid for a given class of the Cox-Aalen transformation model. In practice, when the KM curves corresponding to different values or groups of values of a certain covariate, say $X$, cross, the effects of this covariate are not necessarily additive. In addition to the possibility that the effect of $X$ is additive, there are a number of ways that the proportionality can fail, e.g., $X$ not as a part of $Z$ under the Cox-Aalen transformation model. For example, the effect of $X$ could be time-varying as in the Cox model with time-varying regression coefficients studied by Cai and Sun (2003). In another scenario, the contributions from the additive components and the multiplicative components of the model may not be in the multiplicative form. In addition to choosing the right covariates for the multiplicative and additive components of the model, mis-specifying the transformation function can result in erroneous inferences.

Assessing the adequacy of the proposed model is crucial because model misspecification affects the validity of inference and prediction accuracy. For Zeng and Lin’s model, Chen et al. (2012) considered appropriate time-dependent residuals and constructed various graphical and numerical procedures for model assessment. In our analysis of the HIV prevention trial data, we use the log-likelihood to select the transformation function, even though the log-likelihood surface is relatively flat. Similar to Chen et al. (2012), we suggest constructing the cumulative sums of residuals over the argument of the transformation function, i.e., $W\left(x,t\right)=n^{-1/2}{\sum }_{i=1}^n{\int }_0^{t}I\left({\int }_0^u{Y}_i\left(s\right)e^{\widehat{\beta }\top Z_i\left(s\right)}{X}_i^{\top }\left(s\right)d\widehat{A}\left(s\right)⩽x\right)d{M}_i\left(u;\widehat{\beta },\widehat{A}\right)$ to check the transformation form, where $M_i\left(t;\beta ,A\right)=N_i\left(t\right)-G\left\{{\int }_0^t{Y}_i\left(s\right)e^{\beta \top Z_i\left(s\right)}{X}_i^{\top }\left(s\right)dA\left(s\right)\right\}$. A thorough theoretical and numerical investigation of model misspecification is still needed for the proposed model. We are currently pursuing this direction.

Data Availability Statement

The data that support the findings of this paper are available in the Supporting Information of this article.