u-track3D: Measuring, navigating, and validating dense particle trajectories in three dimensions

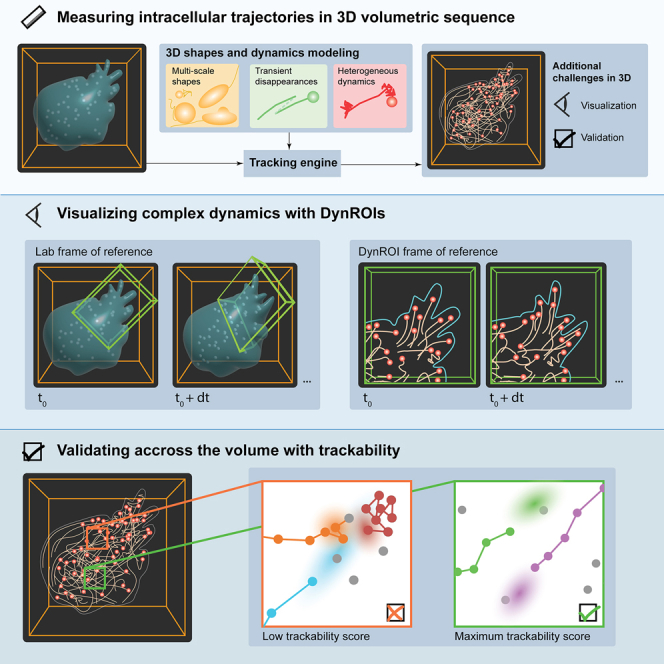
Summary

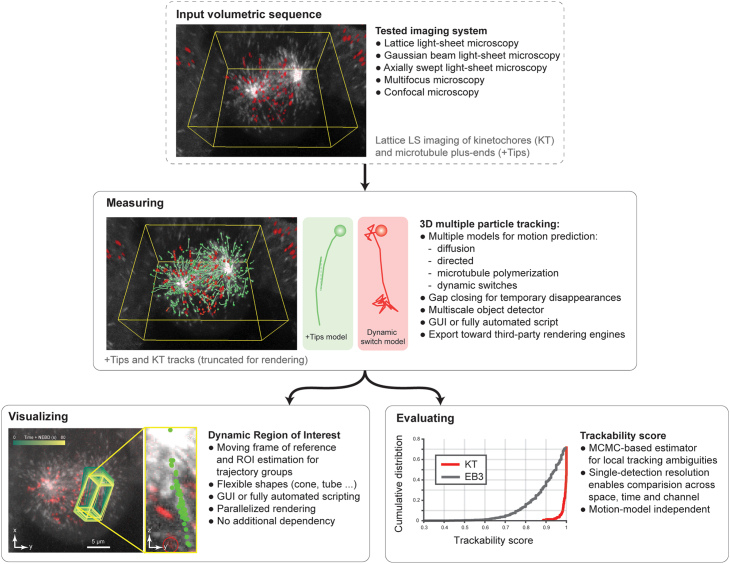
We describe u-track3D, a software package that extends the versatile u-track framework established in 2D to address the specific challenges of 3D particle tracking. First, we present the performance of the new package in quantifying a variety of intracellular dynamics imaged by multiple 3D microcopy platforms and on the standard 3D test dataset of the particle tracking challenge. These analyses indicate that u-track3D presents a tracking solution that is competitive to both conventional and deep-learning-based approaches. We then present the concept of dynamic region of interest (dynROI), which allows an experimenter to interact with dynamic 3D processes in 2D views amenable to visual inspection. Third, we present an estimator of trackability that automatically defines a score for every trajectory, thereby overcoming the challenges of trajectory validation by visual inspection. With these combined strategies, u-track3D provides a complete framework for unbiased studies of molecular processes in complex volumetric sequences.

Graphical abstract

Highlights

• •u-track3D provides an improved algorithm and workflow for particle tracking
• •The algorithm quantifies molecular trafficking, polymerization, and transcription
• •Dynamic regions of interest reveal collective events nested in the cellular volume
• •Trackability score enables the automatic localization of tracking errors

Motivation

Particle tracking is a ubiquitous task in the study of dynamic molecular and cellular processes through microscopy. Light-sheet microscopy has opened a path to acquiring complete cell volumes for investigation in three dimensions. However, hypothesis formulation and quantitative analysis have remained difficult due to fundamental challenges in the visualization and the verification of large and dense sets of three-dimensional (3D) particle trajectories. New software tools are required that allow microscopists to automatically track diverse particle movements in 3D, inspect the resulting trajectories in an informative manner, and receive unbiased assessments of the quality of trajectories.

3D microscopy of entire cells presents an image complexity that challenges the computation and observation of measurements such as particle trajectories. Roudot et al. introduce u-track3D, a package that combines robust particle tracking with image navigation and track validation algorithms for the discovery and unbiased analysis of dynamic processes.

Introduction

Light-sheet fluorescence microscopy (LSFM) achieves three-dimensional (3D) imaging with minimal phototoxicity, fast sampling, and near-isotropic resolution,^1,2 allowing the study of dynamic intracellular processes in the entire cellular volume.^1,2,3,4 While computer vision techniques are well established for interrogating cell biological processes in 2D,⁵ these tools do not translate to both the visualization of measurement results and their validation in 3D. A key challenge for image analysis in 3D is the user interaction with the data. The manipulation of time-lapse 3D image volumes is often cumbersome, and any of the projection mechanisms necessary to map the 3D volume into a 2D representation on a screen is prone to artifacts that may cause erroneous conclusions.⁶ Thus, computational tools for 3D image analysis must be able to reveal the complexity of 3D cellular and sub-cellular processes while being as automated as possible to avoid selection and perception biases.

The most elementary way to measure the behavior of intracellular processes is particle tracking. Particles can comprise sub-diffraction-sized objects that appear in the image volume as bona fide spots, objects of an extended size that appear as a rigid structure, and larger deformable objects. The more complex the object’s shape is, the more sophisticated the methods needed for particle detection. The problem of particle tracking is then defined as the reconstruction of plausible trajectories from the coordinates [x(t), y(t), z(t)] of the identified particles. Because the number of hypothetical trajectories grows super-exponentially over time, many approaches have been proposed to approximate the best solution.^7,8,9 They typically combine a modeling of intracellular dynamics and transient disappearances (or mis-detection), statistical approaches,^{10,11,12,13,14,15,16} or recursive neural networks^17,18,19 to estimate the likelihood of trajectory-to-measurement associations and discrete optimization^10,20,21,22 to select the best set of associations at each time point. Only a few of these methods have been implemented in 3D^7,11,23,24 and even fewer tackle the visualization and validation challenges in dense sets of trajectories.

Several open-source^{25,26,27,28,29} and commercial^30,31,32 software packages have been released to make volumetric rendering technology amenable to time-resolved 3D bioimaging data. Together they have proposed advances in accelerating sequence rendering,^26,28 modularity and extensibility,^25,27 annotation tools,^33,34 or scalable raytracing for high-quality rendering.^29,35 Those approaches provide an outside view of the 3D data and a range of tools to investigate the volume manually (e.g., in focused regions of interest [ROIs] or slices). They also reveal many challenges associated with visual occlusions, 3D perception on a flat screen, interactions, and time-consuming volume exploration. BigDataViewer³⁶ has tackled the occlusion and perception challenges indirectly by focusing on the caching and rendering of 2D slices at arbitrary orientations. The primary effect is to accelerate rendering at the expense of 3D context, but it also avoids distortion of pixel-level information. As such, the Mamut software has demonstrated that combining BigDataViewer and 3D rendering of vectorial information enables annotation in large and complex 3D trajectories.³⁷ The immersive quality of virtual reality (VR) headsets has also been exploited to better perceive and interact with complex 3D datasets.^{38,39,40,41,42} Finally, a complementary approach to full volume visualization is the presentation of software-defined ROIs. The embryoMiner package⁴³ implements this idea by building static ROIs from groups of trajectories that are then used to systematically visualize the data in a series of 3D tiles. The approaches implemented in u-track3D also belong to this category; however, the ROIs adapt over time to the changing geometry of collective processes. Hence, u-track3D allows the inspection of specific particle dynamics in a crowded and dynamic surrounding.

Considerably fewer works have been dedicated to trajectory validation. Previous work can be categorized into ground-truth-based approaches and error-inference-based approaches. Within the former category, a time-consuming but widely accessible approach consists in using manual annotations to build a ground truth to be compared to the measured dataset.^24,44,45 Already in 2D, these techniques are subject to selection bias, as it is easier to annotate bright and well-separated objects. In 3D, these challenges are compounded by the complexity of visualization and selection of particles. Another ground-truth-based approach relies on the simulation of image sequences that mimic the acquisition.^7,46,47,48 In contrast to the annotation-based approach, simulation can automate the prediction of tracking performance for simplified scenarios in which image formation and particle dynamics are known perfectly a priori. The second category of methods attempts to infer the likelihood of tracking errors directly on the data. Early efforts proposed heuristics that combine motions and density measurements to identify error-prone areas.^2,49 Arguably, a more elegant approach would be a direct analysis of the optimality of the reconstructed trajectories. This idea has been proposed by Cardinale and colleagues⁵⁰ and applied to estimating the scale, intensity, position, and associated confidence intervals of the spindle pole body. While this confidence interval reflects the uncertainty about positions and velocities, the correctness of trajectory-to-measurement matches is not evaluated. Our goal was to design an algorithm for tracking error inference that does not require annotation or specific simulations, does not rely on heuristics other than those considered by the tracking algorithm, can handle heterogeneous scenarios, scales with the computational complexity of the tracker itself, and provides an interpretable output for mis-matched, spurious, and missing trajectories comparable to conventional benchmarks.⁷

Building upon our previous particle tracking work,^2,10,13 we thus designed the software package u-track3D to enable the measurement, observation, and validation of dynamic processes in 3D (Figure 1). u-track3D can detect and track morphologically and dynamically diverse cellular structures, including single molecules, adhesion complexes, and larger macromolecular structures such as growing microtubules. The software design is open, allowing users to import the coordinate files from other detection routines and then apply the u-track3D framework only for trajectory reconstruction. We introduce a library for visualization and mapping of dynamic ROIs (dynROIs) that move with the biological structure under evaluation and enable an intuitive visualization of particle behaviors. Finally, we present a scalable approach for automatic assessment of trackability of each particle throughout the image volume by evaluating the stability of trajectory-to-assignment associations.

Figure 1.

u-track3D is a complete pipeline for the measurement, visualization, and evaluation of large sets of 3D trajectories

The pipeline is here illustrated on lattice light-sheet imaging of HeLa cells undergoing mitosis labeled with eGFP-labeled EB3 (marking microtubule plus-ends, rendered in gray) and mCherry-labeled centromere protein A (marking kinetochores, rendered in red).

Results

Measuring, visualizing, and validating 3D trajectories with the u-track3D pipeline

Multiple particle tracking

To generate a 3D particle tracking package, we adopted and modified features that were critical for accurate particle tracking in 2D.¹⁰ This includes the breakdown of trajectory reconstruction into a frame-by-frame association of corresponding particles followed by an association of the resulting track segments into full-length trajectories. Both steps rely on the same solution for optimal one-to-one assignments of particle detections and track segments in a bipartite graph.^10,51 The two-step approach permits the closing of temporal gaps in the detection of a particle as well as the handling of particle merging and splitting events. U-track3D incorporates a Kalman filtering approach to model on the fly the characteristics of a particle’s Brownian, directed, and heterogeneous motion, which supports both the procedure for frame-by-frame particle association and the one of track segment association. To support the concurrent tracking of objects of variable sizes, we implemented a multiscale particle detector equipped with a generalized adaptive thresholding approach (see section “Multiscale particle detector” in STAR Methods).

DynROIs

Moving from 2D to 3D images complicates the interaction of a human observer with both raw and derived data. Widely used global image projections, including maximum intensity projection (MIP), and other volume rendering techniques are limited by the overlap of many dynamic structures along the viewing axis.⁶ However, detailed visualization of 3D images and trajectories in their local context is essential for a user to adjust software control parameters and to interpret the underlying biology. Projection approaches have to be tailored to emphasize a subset of selected voxel or aspects of highest interest. Such projections should not only bring the particle or group of particles of interest into focus but also continuously adapt as the particles move. To meet this requirement, u-track3D incorporates a framework for rendering particle-centric dynROIs, thereby allowing the user to follow the particle behavior throughout its lifetime in a visually comprehensible format. DynROIs are implemented in a hierarchical object structure across molecular, macromolecular, and cellular scales (see section “dynamic region of interest estimation” in STAR Methods). First, u-track3D provides a variety of shapes (rectangle cuboids, spheres, cones, tubes, and rounded tubes) to define an ROI encompassing one, two, or three trajectories. Second, to manage larger sets of tracks, dynROIs are built by estimating an affine transform between the associated point cloud in consecutive time points. Finally, the top-level dynROI is defined for the cell. For example, cells embedded in a 3D environment are often randomly oriented, and their orientation changes over time. While image-based registration can be used to correct changes in cell orientation, it is computationally expensive, especially as the size of the volume and length of the sequence grow. To reduce the computational burden, we segment and transform the cell mask into a randomly downsampled point cloud, which is then used to estimate an affine transform.

Trackability score

Validation of tracking results is crucial for proper parameter adjustment during image acquisition and analysis as well as the biological interpretation of integrated measurements. However, it remains an extremely challenging task in 3D datasets, particularly when the particle density is high. Contrary to a scenario in 2D where a single field of view presents a wide range of trajectories for visual inspection, dynROIs in 3D tend to capture only a few trajectories and cannot represent the heterogeneity of local image quality, particle density, and dynamic properties, which all affect the tracking accuracy. To solve this problem, we complemented u-track3D with an option to compute a local trackability score. We use Monte Carlo simulation to determine for every trajectory and every time point the confidence by which the algorithm was able to assign the chosen particle to the trajectory (see section “stochastic programming for the evaluation of trackability” in STAR Methods). Specifically, we exploit the particle history, the detection accuracy, and the associated motion model(s) to derive a trackability metric that represents the likelihood of each of the chosen associations vis-à-vis the set of alternative associations with neighboring particles. We demonstrate the performance of the resulting score and how it can be used to compare trackability across space, time, and the molecules under study.

Measurement of the kinetics of endocytosis in 3D

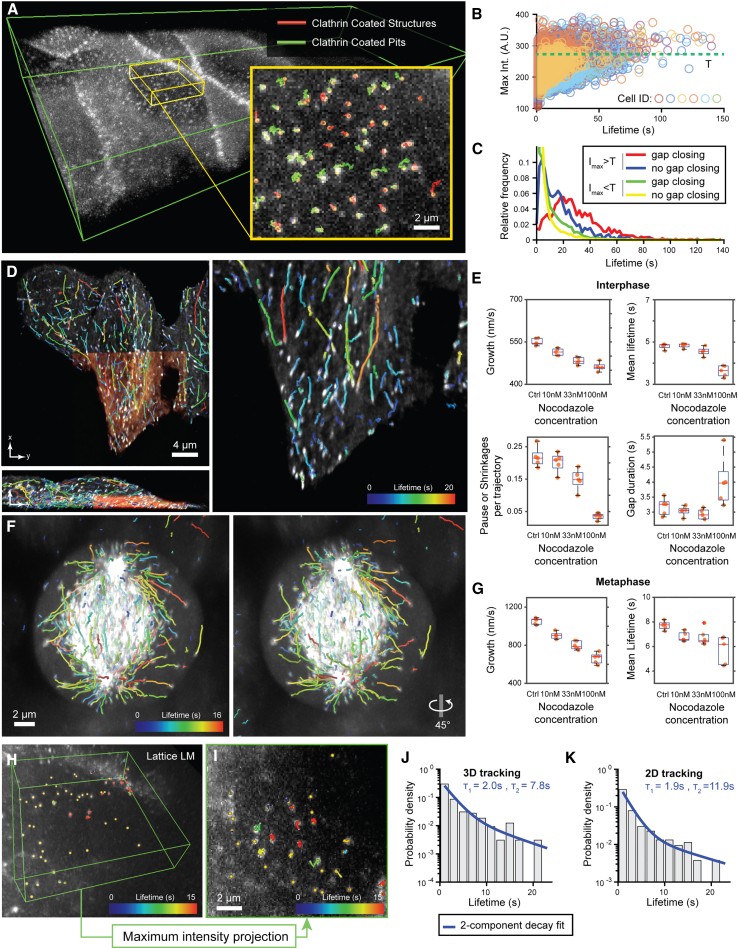
To assess the performance of u-track3D, we investigated the dynamics of various cellular structures imaged by light-sheet microscopy (Figure 2). As reported with u-track,¹⁰ gap closing is a crucial step in 2D particle tracking because of frequent, transient disappearances: particles might not be detected, particles move in and out of the microscope’s in-focus volume, or particles can temporarily overlap in space. While the latter two sources of disappearance are largely eliminated by proper 3D imaging, the challenges of false or missing detections remain. To test the performance of u-track3D in closing gaps, we examined the lifetimes of clathrin-coated structures forming at the cell plasma membrane (Figures 2A–2C). These structures represent mostly sub-diffraction objects; i.e., they appear in an imaging volume as 3D point-spread functions. We used high-resolution diagonally swept light-sheet microscopy² to sample every second a full volume of puncta generated by the GFP-labeled AP2 subunit of the endocytic coat. U-track3D recovered the canonical lifetime distributions of abortive and maturing clathrin-coated pits,^52,53 that is, an exponential decay for abortive pits and Rayleigh-like distribution with maximal probability around 20 s for maturing pits (Figure 2C; Data S1; see section “clathrin-mediated endocytosis study on a glass coverslip” in STAR Methods). While in 2D the identification of those two populations relied on extensive trajectory analysis to discount incomplete trajectories,⁵³ our u-track3D software achieves accurate trajectory classification directly by thresholding the maximum intensity of trajectories in 3D (Figures 2B and 2C). Importantly, the distinction of two lifetime distributions can only be obtained with the support of gap closing (Figure 2C), suggesting that gaps remain a hurdle for accurate tracking in 3D.

Figure 2.

u-track3D supports a variety of imaging and biological scenarios

(A) Maximum intensity projections (MIPs) of a rat kidney cell layer imaged with diagonally scanned light-sheet microscopy (diaSLM). Cells are expressing eGFP-labeled alpha subunit of the AP-2 complex. Green box is 160 × 40 × 12 μm. Inset shows trajectories of clathrin aggregates classified as clathrin-coated structures or maturing pits.

(B) Normalized maximum intensity of each trajectory as a function of lifetime plotted for six cellular layers composed of multiple cells each. The green line denotes the median of the cumulated distribution (value T).

(C) Probability density of lifetime for the set of trajectories above and below the threshold value T, with and without gap closing (n = 6 cellular layers, pooled trajectories lifetimes).

(D) MIP of HeLa cells in interphase imaged with lattice light-sheet microscopy (LLSM) expressing eGFP-labeled EB1 (orange area is 30 × 32 × 7 μm). Overlay highlights EB1 trajectories.

(E) Average microtubule lifetimes, microtubule growth rate, as well as average number and duration of pause and shrinkage events per trajectory for increasing concentrations of nocodazole (n = 5 per conditions; center line, median; box limits, 25 and 75 percentiles; whiskers, extremum).

(F) MIP of HeLa cells in metaphase imaged with LLSM along with 45°rotation around the vertical axis. Overlay highlights EB1 trajectories.

(G) Same as (E) measured for cells in metaphase (n = 5 per conditions).

(H) MIP of mouse embryonic stem (ES) cell nucleus imaged with LLSM expressing GFP-labeled TFs. Green box is 13 × 13 × 3 μm. Overlay highlights SOX2 trajectories. (I) MIP of ES cell nucleus imaged with LLSM expressing GFP-labeled TFs. Overlay highlights SOX2 trajectories tracked after MIP transformation.

(J) Probability density of SOX2 binding time measured in LLSM overlaid with a two-component decay fit (n = 1 cell).

(K) Probability density of SOX2 binding time measured in projected LLSM data overlaid with a two-component decay fit (n = 1 cell).

Measurement of instability in microtubule dynamics across dense 3D mitotic spindles

With limited sampling frequency in volumetric imaging, particle tracking can be improved by dynamic motion models through Kalman filtering. To assess the performance of a 3D implementation of previously published motion models for 2D tracking of microtubule polymerization dynamics,^54,55 we imaged and tracked microtubule dynamics in HeLa cells by following GFP fusions of the microtubule plus-end tracking protein EB1 sampled at 1 Hz by lattice light-sheet imaging.¹ We quantified metrics such as growth rate, growth lifetime, and pause frequency (see section “microtubule instability measurement” in STAR Methods). The latter is a measure for the probability that a stalled or shrinking microtubule, which is accompanied by disappearance of the EB1 particle in the video, is rescued to renewed growth (see Figure S1 and Data S1). Consistent with our previous observations in 2D,⁵⁴ u-track3D faithfully detected a dose-dependent decrease in all three metrics upon treatment of cells with the microtubule-destabilizing drug nocodazole (Figures 2D–2E). We also investigated the destabilizing effect of nocodazole on the number and duration of pauses or shrinkages (Figure 2E). We then extended our analyses to mitotic cells, where the density of EB1 particles is much higher in central regions of the mitotic spindle (see Data S1). Both scenarios show a strong response in nocodazole concentration, indicating that u-track3D properly captures the drug-induced variation of growth rate and lifetime (Figures 2F and 2G), despite strong variations in particle density.

Measurement of interaction between transcription factors and chromatin

We then sought to investigate the impact of the depth information on the measurement of biological quantities when compared to 2D particle tracking. We employed a lattice light-sheet microscope to image the interactions between transcription factors (TFs) and chromatin in embryonic stem cells. In a study using the same biological system but performed with 2D imaging, Chen et al.⁵⁶ had shown that TFs alternate between short-lived binding events at non-specific chromatin sites (residence time ∼0.75 s), 3D diffusion (average duration ∼3 s), and longer lived transcription events where the TF is bound at specific chromatin sites (residence time ∼12 s). We performed the same analysis, now applying 3D tracking, and contrasted the results to the tracking of 2D projections of the same 3D volumes (Figures 2H–2K and section “single molecule dynamics study with lattice light-sheet microscopy” in STAR Methods). An analysis on 2D projections reproduced the results of the original study. However, with 3D analysis, the residence time of specific binding events was reduced by one-third (∼7.8 s in 3D vs. 11.9 s in 2D). Interestingly, the shorter binding time extracted from 3D trajectories is consistent with measurements performed in nuclear receptors studies.^57,58 Together, these data suggest that the overlap caused by axial projections for 2D tracking may bias kinetic measurements.

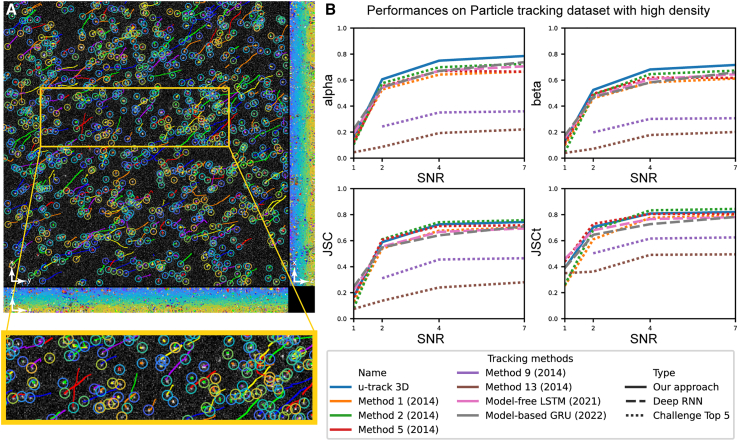
U-track3D leads the field of algorithms evaluated in the particle tracking challenge

We evaluated u-track3D’s competitiveness using the standard 3D test dataset of the particle tracking challenge.⁷ We compared u-track3D against the top five approaches competing in the original benchmark as well as two tracking approaches that make use of recent advances in recursive neural networks (RNNs)^17,18 (see Figures 3 and S2). The dataset is designed to mimic viral dynamics alternating between confined and directed displacements that are large enough to create significant ambiguities in the densest scenarios (Figure 3A). The dataset includes 12 sequences representing four signal-to-noise ratios and three density levels (see Figure S2). The challenge prescribes four metrics to compare the precision and accuracy of each approach. The first precision metric, alpha, relates to the Euclidean distance between the real trajectories and measured trajectories, while beta weighs this by the rate of spurious tracks. The accuracy metrics ignore distance and instead count the points within 5 pixels of a real detection. The Jaccard similarity coefficient (JSC) or Jaccard index (JI) is computed as (TP/N + FP) where N is the number of real particles, TP is the number of true-positive matches, and FP is the number of false-positive matches. The JSCt describes the same metric using the count of trajectories that match at least 50% of the segments; the rest is considered FP.

Figure 3.

u-track3D performance in comparison to existing methods evaluated on a standard 3D test dataset with high particle density

(A) MIP of the simulated virus dynamics overlayed with trajectories reconstructed by u-track3D. Trajectories are colored following a random colormap.

(B) Performance metrics for precision (alpha and beta) and accuracy (JSC and JSCt) to compare different tracking pipelines.

Our results can be summarized as follows: first, u-track3D ranks first on all metrics and densities for signal-to-noise ratio (SNR) 4 and SNR 7 except for one data point where it ranks second (Figures 3B and S2). Also, u-track3D ranks first or among the top three approaches for lower SNR data. Strikingly, deep-learning approaches are outperformed by conventional methods, except at the level SNR = 1. Of note, this scenario represents a breakpoint dataset that is not representative of the typical image quality targeted for a meaningful analysis of trajectory counts and lifetimes. At this low SNR, RNN-based approaches provide the best performance; however, they are nonetheless insufficiently robust to generate accurate trajectory estimates.

While a precise ablation study is out of the scope of this paper, an analysis of the design of competing approaches can help in discussing these performances. First, the most competitive approaches in the original challenge^20,23,59 present differences in their design but they all rely on similar strategies: object detection is based on some type of adaptive thresholding, they use motion modeling for displacement prediction, they use a discrete optimization approach to assign predictions to measurements, and they employ various techniques to detect and correct for transient object disappearances. The u-track framework pursues the same strategies but incorporates piecewise-stationary motion modeling and gap closing to enhance tracking robustness during transitions between dynamic regimes. The competing approaches assume stationarity in motion type (mostly Brownian²⁰) or smooth transitions.^23,59 Second, the main difference between u-track3D and RNN-based tracking lies in the method that evaluates the cost of each trajectory-to-measurement association and the detection of transient disappearances. Both approaches employ a conventional detector and temporally greedy assignments. The techniques based on RNNs also use a locally adaptive detector and a discrete combinatorial optimization approach to assign prediction to measurement.⁵¹ As such, the difference in performances must lie in the method for motion and gap prediction. In a nutshell, the first RNN technique uses a long/short-term memory (thus, in Figure 3 it is referred to as model-free LSTM) network to filter and predict particle position. The second, more recent, RNN technique by the same authors uses gated recurrent units (referred to as model-based GRU) and reduces the parameter space needed for prediction by learning the moment and the covariance of a normal distribution associated with the state of each trajectory. Both approaches are trained on a simulated dataset presenting a mixture of Brownian, directed, and heterogeneous motions. In the original paper,¹⁸ the model-based approach performs better than both the conventional and the model-free RNN on the “vesicle scenario,” which simulates free diffusion. However, the difference is not as clear in the “virus scenario,” where the model-free approach often outperforms the latter. This suggests that the performance of RNNs can improve upon the state of the art when taking a priori knowledge into account to constrain the parameter space. However, as demonstrated in our previous work,¹³ the sudden transition between confined and directed displacement are poorly approximated by a normal distribution and better modeled by a piecewise-stationary constraint. This qualitative analysis does not imply that deep-learning approaches cannot be competitive but that further improvement requires the consideration of a priori knowledge on molecular dynamics in the design of the network architecture. Our performance analysis shows that, with the motion models implemented in the package, u-track3D remains a state-of-the-art tracker, despite the advances deep learning and other pipelines deploy.

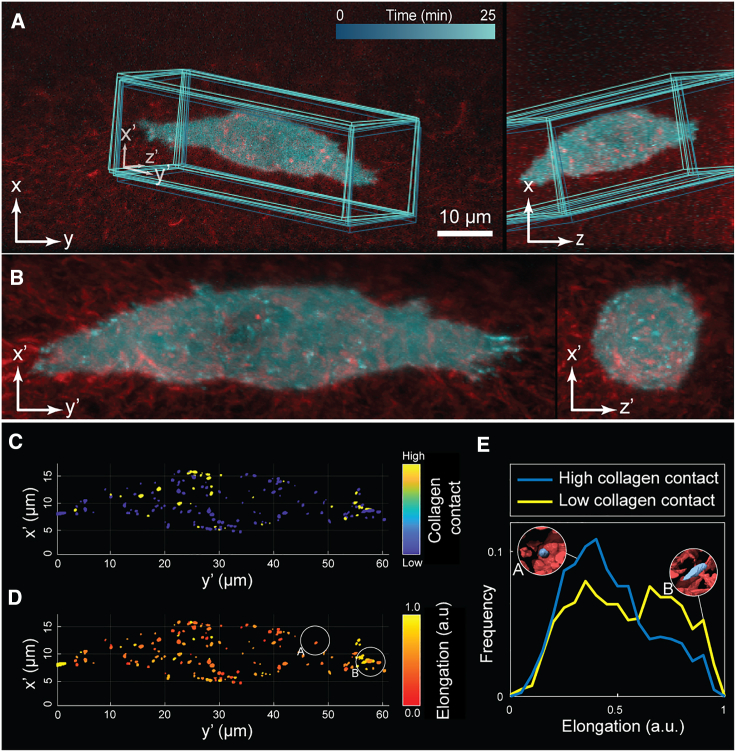
Visualization of adhesion formation in 3D

We illustrate the application of a whole-cell dynROI with the study of spatial interactions between cell-matrix adhesions and fluorescently labeled 3D collagen fibers in osteosarcoma cells imaged by axially swept light-sheet microscopy³ (Figure 4A; Data S2). The dynROI allowed us to visualize the relationship between adhesion shapes and its proximity to collagen fibrils, showing two populations of globular and elongated adhesions (Figures 4B–4D). The most elongated adhesions are located predominantly at the tip of pseudopodial extensions and align with the protrusive direction, while globular adhesions concentrate in the quiescent part of the membrane. Our measurements show that this elongation distribution can be decomposed further (Figure 4E). We found a unimodal distribution of mostly globular adhesions in close contact with collagen fibers (see section “adhesions and collagen interaction imaging and analysis” in STAR Methods). In contrast, adhesions with a lesser degree of collagen contact display a bimodal distribution of globular and elongated adhesions. These data suggest—quite unexpectedly from what is known in 2D—that the most mechanically engaged adhesions may be the least elongated.⁶⁰ We conjecture that adhesion elongation in 3D may be less driven by a zippering of an integrin-mediated plaque along a collagen fiber but rather dictated by the organization of cell-cortical actin fibers or the local collagen architecture. Indeed, this behavior becomes apparent by replay of time-lapse sequences of the proximity and elongation parameters in the spatially stabilized dynROI (Data S2). DynROIs are thus a powerful way to assess the spatial distribution and heterogeneity of molecular interactions in highly dynamic cells.

Figure 4.

DynROIs reveal the behavior of molecular adhesions in 3D environments

(A) Dual-colored orthogonal MIP of osteocarcinoma cells expressing eGFP-labeled paxillin and embedded in collagen labeled with Alexa Fluor 568. Overlay highlights dynROI.

(B) View of the dynROI.

(C and D) Detection of adhesions colored as a function of the degree of collagen contact and elongation.

(E) Probability density of elongation for adhesions with high and low degree of contact with collagen fibers (n = 1 cell).

DynROI applied to mitotic spindle dynamics

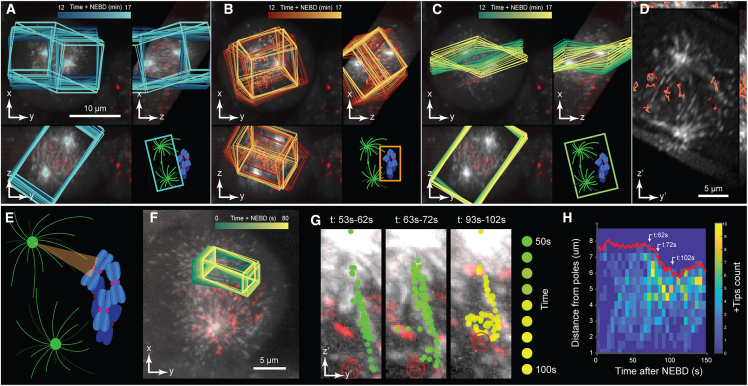
Many cellular processes involve a large-scale reorganization of macromolecular structures, which challenges 3D analysis. A good example is the vertebrate mitotic spindle.⁶¹ Thousands of microtubules form a dense bipolar array while the two spindle poles move apart and rotate back and forth. Concurrently, spindle microtubules establish contacts with chromosomes at kinetochores and subsequently move chromosomes toward poles or the spindle center. This process is virtually impossible to understand by mere visual inspection of volume renderings. We therefore assessed how u-track3D and dynROIs may facilitate the analysis. The image dataset comprises dual-channel time-lapse sequences of GFP-labeled microtubule plus ends and mCherry-labeled centromeres protein A marking kinetochores in mitotic HeLa cells acquired at 0.1 Hz by lattice light-sheet microscopy⁶² from prometaphase to metaphase. Microtubule plus ends, kinetochores, and spindle poles were localized by multiscale particle detection. Pole trajectories can then be used to define a dynROI that follows the spindle motion (Figure 5A and section “dynamic region of interest estimation” in STAR Methods). An embedded second dynROI follows the point cloud formed by the kinetochore trajectories (Figure 5B and section “dynamic region of interest estimation” in STAR Methods). Based on the pair of dynROIs, we further construct a planar dynROI with an orientation that is defined by the interpolar axis and a vector following the kinetochore-associated dynROI motion (Figures 5C and 5D; Data S3; section “dynamic region of interest estimation” in STAR Methods). Our framework for dynROI estimation thus enables the visualization of mesoscale structures composed of different molecular assemblies.

Figure 5.

DynROIs drive the visualization of chromosome capture by microtubules and reveal possible interactions between neighboring kinetochore fibers

(A–D) Dual-colored orthogonal MIP of HeLa cells undergoing mitosis labeled with eGFP-labeled EB3 (marking microtubule plus-ends rendered in gray) and mCherry-labeled centromere protein A (marking kinetochores rendered in red). Overlays highlight (A) a dynROI built around centrosome trajectories, (B) a dynROI built around kinetochores trajectories, and (C) a plane built to visualize the dynamics of chromosomes relative to the spindle location. (D) View of the dynROI following description in (H).

(E) Definition of a conical dynROI between a centrosome and a kinetochore.

(F) Dual-colored orthogonal MIP of HeLa cells during prometaphase. Overlay highlights the motion of the dynROI.

(G) Cumulative overlays of the detected microtubule plus-end position for three periods of 10 s between 53 and 102 s post nucleus envelope breakage.

(H) Plus-ends count function of time and distance from the pole (n = 1 dynROI).

In previous work,⁶² using volume acquired at 1 Hz, we showed with spindle-wide statistics and indirect modeling that kinetochore fiber formation is accelerated by an augmin-dependent nucleation and directional growth along the fiber toward kinetochores. We now use dynROIs to directly visualize the dynamic space between spindle poles and kinetochores (Figures 5E–5G; Video S1). We define a kinetochore fiber assembly dynROI by a cone whose medial axis connects spindle pole and target kinetochore (see section “dynamic region of interest estimation” in STAR Methods). Using such dynROIs, we noted a directional bias in microtubule polymerization toward kinetochores, consistent with previous observations.⁶² However, we also observed microtubule polymerization branching off a kinetochore fiber and polymerizing toward another kinetochore (circled in red in Figure 5G, time 53–72 s). The branching was followed by rapid poleward movement of the targeted kinetochore and an increase of plus-end count in the dynROI (Figure 5G and 5H, time 93–102 s) suggesting that the target kinetochore was captured, generating a new avenue for microtubule amplification. The example underscores how the dynROI library implemented in u-track3D enables the visual discovery of dynamic processes that are obscured in 3D image volumes.

Video S1. DynROIs drive the visualization of chromosome capture by microtubules and reveal possible interactions between neighboring kinetochore fibers, related to Figure 5

Left: dual-colored orthogonal MIP of HeLa cells during prometaphase acquired with a volumetric frequency of 1 Hz. Overlay highlights the motion of the dynROI. Right: rendering of the volume described by the dynROI in its associated frame of reference. Green dots highlight plus ends inside the mapping cone and red circle describes the motion of the target kinetochore.

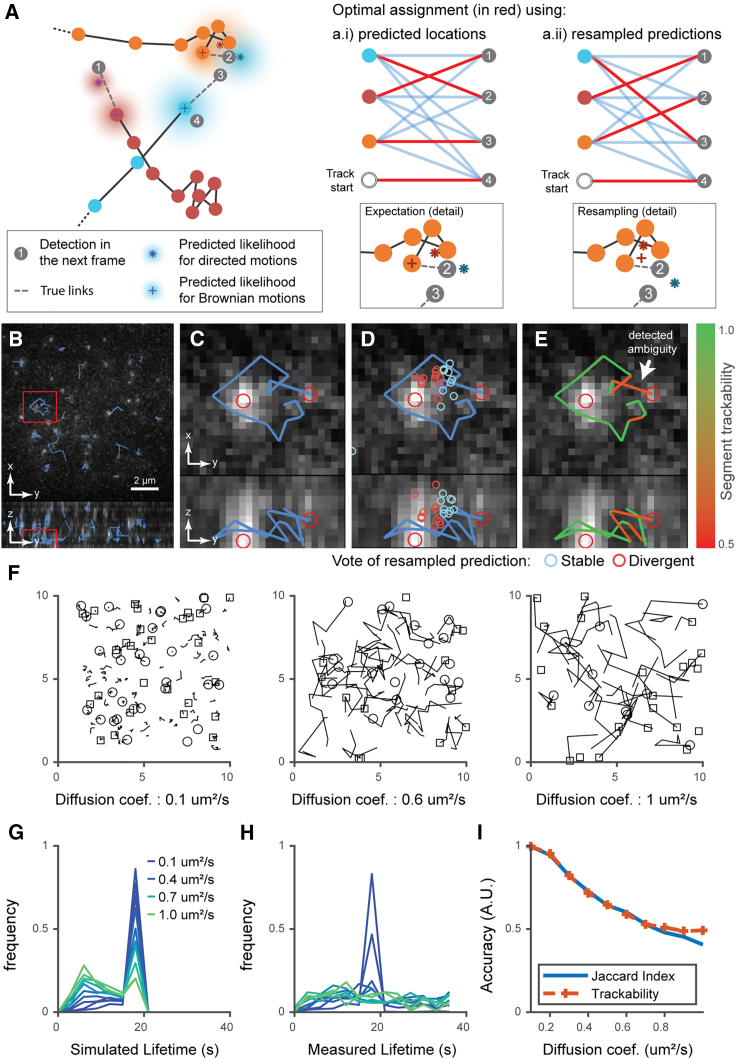
Trackability score to detect tracking ambiguities

We developed a pipeline to assign a trackability score to every trajectory, based on the ambiguity of trajectory-to-measurement associations (Figure 6 and section “stochastic programming for the evaluation of trackability” in STAR Methods). Figure 6A shows an ambiguous association between time $t-1$ and $t$ where two hypotheses for the assignment of new detections to track heads have a similar association cost. The bipartite graph matching identifies a single optimal solution (see Figure 6A.i). To determine the level of ambiguity in the solution, we resample all track head predictions $N$ times and test the stability of the original assignment (one resampling example is shown in Figure 6A.ii). The approach is illustrated in Figures 6B–6D based on the tracking of a TF in previously published multifocus microscopy data.⁶³ Each dot indicates a resampled prediction of the particle location at $t$, and blue versus red defines whether the newly computed local assignment matches or differs from the original solution. The trackability score is defined as the fraction of matching samples. Hence, the score accounts for the local competition among detections for track head associations and the uncertainty of motion prediction for each track head.

Figure 6.

The trackability score relies on the stochastic footprint of each trajectory to infer tracking accuracy

(A) Example of a tracking ambiguity due to three trajectories in close proximity (orange, blue, and red). Dashed lines represent the true motion between track heads at time $t-1$ and detections at time $t$, represented by gray dots. Colored gradients represent the likelihood of each expected particle location at time $t$, estimated using the history of positions up to time $t-1$ and considering multiple motion model hypotheses. The optimal assignment between the expected and detected particle positions at time $t$ in this case yields an erroneous assignment from the orange track head to detection 2 and from the blue track head to detection 3 (graph A.i). Resampling of the expected locations results in a new assignment (graph A.ii), this time without error.

(B) Orthogonal MIP of ES cells expressing eGFP- labeled Sox2 molecules imaged by multifocus microscopy. Overlaid boxes highlight the ROI enlarged in (C)–(E).

(C) Orthogonal MIP of ROI. Overlay shows a trajectory where two close detections create assignment ambiguity.

(D) Overlay illustrates the stochastic resampling of the predicted particle positions at this time point; blue circles, assignments in agreement with the original solution; red circles, assignments that differ from the original solution.

(E) Overlay shows trajectory segments colored according to estimated trackability scores.

(G) Examples of simulated trajectories with diffusion coefficients ranging from 0.1 to 1 μm²/s with a fixed particle density of 0.1 μm⁻³. Visualization is limited to five consecutive frames to reduce clutter.

(F) Lifetime of simulated trajectories (the change in distribution is due to trajectories leaving the field of view as the diffusion coefficient increases).

(H) Lifetime distribution measured through tracking shows a loss of the original distributions when the diffusion coefficient exceeds 0.2 μm²/s.

(I) Accuracy measured through the Jaccard index (JI, blue); the trackability score (orange, dashed), which is derived without external ground truth, closely follows the JI up to a diffusion coefficient 0.6 μm²/s beyond which tracking is random.

We evaluated the capacity of our score to predict tracking quality in several scenarios. We simulated trajectory sets of increasing stochasticity along with a noisy detector and applied u-track3D to trace the particle movements (parameters are described in Tables S1 and S2). Using the ground truth, we then classified each link of the extracted traces as a TP or FP. This classification allows us to compute for each simulated set the true JI $JI=\frac{TP}{TP+FP+FN}=\frac{TP}{FP+L}$, with L denoting the number of simulated links. Figure 6F presents simulated trajectories with increasing diffusion coefficients; the display is truncated to five consecutive time points to improve visibility. With a detection density fixed to 0.1 μm⁻³ and increasing speed of diffusion, the tracking performance rapidly deteriorates to completely inaccurate links and trajectory lifetime distributions (see Figures 6G and 6H). The trackability score follows the decrease in the JI until it plateaus at 0.5 for very challenging conditions (Figure 6I). The initially close match between trackability score and JI is expected as larger diffusion speeds increase ambiguities in parallel to FPs and false negatives. However, beyond a diffusion of 0.6 μm²/s, the prediction of the particle location in the next frame is less likely centered on the correct detection. As such, during the resampling of the expected particle location, the rate of samples in agreement versus disagreement with the original link is defined by chance; hence, the score plateaus at 0.5. We also simulated a scenario in which the particle density increases at a diffusion fixed to 0.3 μm²/s. Analogous to the increase in diffusion, the trackability score follows the JI up to a density of 0.25 μm⁻³ where the two performance measurements start to diverge (see Figure S3). In the case of directed displacements and a given density of 0.1 μm⁻³, our trackability score also follows the true JI up to a critical velocity of 1.8 μm/s, which is more than twice the average distance between a particle and its closest neighbor (see Figure S4). Finally, we sought to test our approach in a scenario in which trajectories undergo sudden transitions between diffusive and directed motion (see Figure S5). Of note, the densities, diffusion coefficients, and velocities are fixed in this scenario and the only parameter that varies is the transition rate, ranging from 0 (no transition) to 0.5 (on average one transition every two frames). Our results show that the trackability score correctly predicts the reduction in tracking accuracy as increasing transition rates render tracking more ambiguous. A quasi-plateau is reached due to the high frequency of dynamic transitions. In conclusion, the proposed trackability score is able to detect changes in tracking quality in a variety of scenarios.

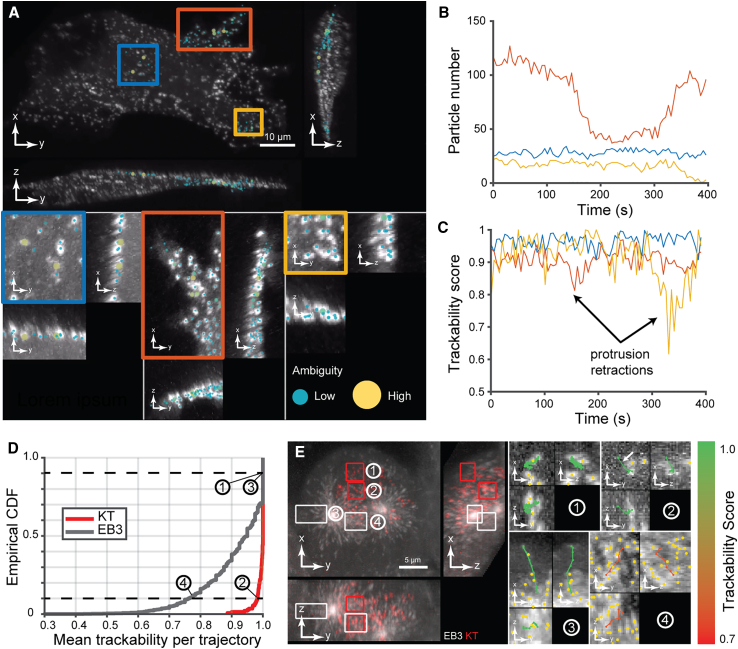
Trackability score to compare tracking quality across time, space, and fluorescent channels

To test the trackability score in real-world tracking, we first analyzed the spatiotemporal variation in the tracking quality of endocytic pits (see section “endosome trackability on cell cultured on top of collagen” in STAR Methods) associated with quiescent and protrusive parts of a cell membrane (Figure 7A). We manually selected dynROIs to capture a quiescent area, a slow fluctuating protrusion-retraction cycle, and an abrupt and rapid protrusion. These dynROIs were selected within a larger dynROI compensating whole-cell movement (see Video S2). Trackability scores were consistently high in the quiescent dynROI, cyclically decreased in the fluctuating protrusion, and showed a sharp decrease where and when the fastest protrusion was located (Figures 7B and 7C). The score thus accurately reflects variations in particle trackability across space and time and detects time points of high ambiguity due to rapid movement.

Figure 7.

Demonstration of trackability score on experimental data

(A) Orthogonal MIP of breast cancer cells imaged with diaSLM expressing eGFP-labeled alpha subunit of the AP-2 complex. Boxes show ROIs with quiescent (blue ROI) and slow/fast protrusion-retraction activity (orange and yellow ROIs). Dot overlays show local level of ambiguity.

(B) Number of track segments over time for the three ROIs (n = 1 cell).

(C) Trackability score over time for the three ROIs (n = 1 cell).

(D) Cumulative distribution of the average trackability score of trajectories for both EB3 and kinetochore channels sampling the dynamics of the mitotic spindle shown in Figure 5.

(E) Four ROIs (two for each channel) showing trajectories colored according to their mean trackability score. Trajectories were selected near the 10th and 90th percentiles of the cumulative distribution. Yellow dots show surrounding detections.

Video S2. The trackability score reflects local tracking ambiguities to compare trajectory quality across cellular locations, related to Figure 7

Top: orthogonal MIP of breast cancer cells imaged with diaSLM expressing eGFP-labeled alpha subunit of the AP-2 complex acquired with a volumetric frequency of 1 Hz. Rectangular overlays show dynROIs with different types of dynamic of activity. Dot overlays show local level of ambiguity. Bottom: rendering of the volume described by the dynROI in the associated frames of reference.

In a second experiment, we analyzed the spindle assembly dataset shown in Figures 5F–5H. The cumulative distributions of trajectory-averaged trackability scores showed that kinetochore trajectories overall are more reliably reconstructed compared to microtubule plus-end trajectories (Figure 7D). The score also enables trackability analysis on a per-trajectory basis. Trajectories with a score near the 90th percentile of the cumulative distribution appear to be error free for both plus end and kinetochore channels (Figure 7E). In contrast, a plus-end trajectory with a score near the 10^th percentile shows a likely erroneous path in an area of dense, crisscrossing microtubules. Because of the overall much higher trackability of the kinetochore channel, a trajectory near the 10^th percentile shows only one likely wrong link caused by FP particle detection (see arrow in Figure 7E detail of ROI 2). Hence, the trackability score is a faithful reporter of the overall accuracy of tracking results, and it assists the selection of correctly tracked objects in dense trajectory populations.

Discussion

We describe a new version of the popular tracking framework u-track, which now enables the study of particle dynamics in 3D live microscopy and tackles key challenges in the exploration and analysis of those complex datasets.

The u-track3D software is implemented in MATLAB and distributed with a user-friendly graphical user interface (GUI) and tutorial scripts. The GUI is designed for testing the software and for the interactive visualization of the particle detections, trajectories, and dynROI locations overlaid onto the raw data. In particular, both raw voxels and measurements can be observed using either slice-by-slice visualization or MIPs in the frame of reference of the laboratory or in a frame of reference of a dynROI. The scripts are primarily used for batch processing and analysis at scale, and they enable the systematic visualization of tracking results across a full dataset. Our rendering engine is designed for automated and parallelized visualization of raw data and overlaid measurements, taking advantage of the asynchronous nature of processing jobs. Montages of raw and overlaid images can be easily specified and saved in a variety of formats (png, avi, and gifs). The script interface also provides a finer control of the shape of dynROIs than the GUI (cone, tube, rounded tubes, etc.). Finally, both detection and tracking can be limited to a dynROI, enabling the rapid adjustment of algorithm parameters before processing a full dataset. Two datasets are provided to test the software, one extracted from the endocytosis imaging introduced in Figure 7A and the other extracted from the mitosis imaging experiment introduced in Figure 5. Computation time and memory usage for the complete pipeline, including detection, tracking with trackability inference, and dynROI definition, has been benchmarked using the endocytosis dataset on a standard computing workstation and office laptop (see “Benchmarking computational time and memory usage” in STAR Methods).

Limitations of the study

While the robustness and applicability of the software have been tested in several studies,^62,64 challenges remain toward a generic approach for automated exploration of 3D sequences. A chief bottleneck comes with the multiple sources of motions occurring across scales. While a given frame rate may be sufficient to sample and track the motion of particles on a static substrate, the object may not be trackable when the particle-embedding volume moves rapidly. u-track3D addresses this problem with the estimation of dynROIs, which allow the pre-alignment of particle groups associated with an entire cell or sub-cellular structure. However, the automated estimation of the scale, type, clusters, and magnitude of those displacements remains an open problem for heterogeneous groups of objects. New developments in stochastic filtering approaches for multiscale displacements are thus necessary.

Another key challenge in the analysis of dynamic 3D data is the quantification of the motion of diffuse signaling molecules or macromolecular structures that do not present a well-defined particle in the imaged volume. These motions can be estimated coarsely using 3D optic flow approaches, for which a few promising methods tailored to fluorescence imaging have been proposed.^65,66,67

Finally, the visualization and interaction with large multidimensional data remain difficult. While we believe the proposed dynROIs add a powerful tool for exploration of 3D sequences, the underlying rendering engine is limited to MIPs or slide-by-slide visualization. Community efforts are currently underway to provide a generic and versatile graphic library along with GUI interface such as Napari²⁸ and Sciview.²⁷ They could complete the capabilities of our renderer with more advanced volumetric rendering (alpha, ray casting) as well as surface rendering.

We thus introduce u-track3D as feature-complete software for the quantification and analysis of particle-like trajectories in 3Ds but also as a stepping-stone toward automated and unbiased exploration of any type of dynamic datasets. As we deliver the software to the community, we are continuously improving the software by fixing bugs and evaluating suggestions for improvements made by the community.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Chemicals, peptides, and recombinant proteins
DMEM	Thermo Fisher Scientific	12491015
DMEM without phenol red	Invitrogen	N/A
Antibiotic/antimycotic for IMCD cells	Thermo Fisher Scientific	15240062
DMEM HeLa Cells	Institute of Molecular Biotechnology of the Austrian Academy of Sciences	N/A
penicillin–streptomycin	Sigma-Aldrich	P0781
GlutaMAX	Thermo Fisher Scientific	35050061
rat tail-derived Collagen Type I	Corning	354236
truncated CMV promoter	Addgene	110718
mNeonGreen-Paxillin	Allele Biotechnology	N/A
Alexa Fluor 568	Thermo Fisher Scientific	A20003
Deposited data
Raw test dataset	This paper	https://zenodo.org/record/6881276
Experimental models: Cell lines
Inner medulla collecting duct (IMCD) mouse epithelial cells	ATCC	ATCC: CRL-2123, RRID: CVCL_0429
U2OS female cells	ATCC	ATCC: HTB-96 RRID:CVCL_0042
Sum159O breast cancer cells	Whitehurst68,69	N/A
HeLa Kyoto line	S. Narumiya	RRID:CVCL_1922
Stable Embryonic Stem Cells	Liu56	N/A
Software and algorithms
u-track3D	This paper	https://doi.org/10.5281/zenodo.10055024
MATLAB 2015a-2023a	Mathworks	RRID:SCR_001622
Gmic	D. Tschumperlé/GREYC/CNRS	https://gmic.eu/
AMIRA v6	Thermo Fisher Scientific	RRID:SCR_007353
LabView	Emerson	RRID:SCR_014325
Other
FCS	Thermo Fisher Scientific	A5256701
FBS U2OS	Sigma	F0926-500ML
5 mm diameter coverslips	Thomas Scientific	64–0700
NA 0.71 water dipping illumination objective	Special Optics	54-10-7
25X/NA 1.1 water dipping detection objective	Nikon Instruments	CFI75 Apo LWD 25XY
Camera ORCA-Flash 4.0	Hamamatsu Photonics	C11440-22C
Bidirectional scan unit	Cambridge Technology	6215
Remote focusing system	Nikon Instruments	CFI S Plan Fluor ELWD
Achromatic doublet	Edmund Optics	49–396
Filters	Chroma Technology Corporation	ZET405/488/561/640, ZT568rdc, ET525/50m, ET600/50m
Piezzo Actuator	Physik Instrumente	P-603.1S2
Piezzo controller	Physik Instrumente	E−709.SRG

Resource availability

Lead contact

Further information and requests for resources should be directed to and will be fulfilled by the lead contact, Philippe Roudot (philippe.roudot@univ-amu.fr).

Materials availability

This study did not generate new unique reagents.

Data and code availability

• •Raw TIFF light-sheet imaging data used in Figures 5 and 7 have been deposited in https://zenodo.org/record/6881276 and are publicly available as of the date of publication. DOIs are listed in the key resources table. They are automatically downloaded by the tutorial scripts. The full imaging datasets used in this paper represent tens of Terabyte of data and are too large to be made available on a server maintained for public access. However, this data can be made available through other means (such as mail, or large file transfer sev) upon request to the lead contact author.
• •All original code has been deposited at https://zenodo.org/records/10055024 and is publicly available as of the date of publication. DOIs are listed in the key resources table. A user’s guide for both GUI and scripts and test datasets are available within the same repository. The repository used for update and bugfixes is at https://github.com/DanuserLab/u-track3D.
• •Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.

Experimental model and study participant details

Clathrin-mediated endocytosis in an epithelial cell layer

Inner medulla collecting duct (IMCD) mouse epithelial cells stably expressing alpha-adaptin GFP⁵³ were cultured in in Dulbecco’s modified Eagle’s medium (DMEM) supplemented with 10% fetal calf serum (FCS) and 1% antibiotic/antimycotic at 37°C.

Mitosis in HeLa cells

HeLa cell lines stably expressing fluorescent reporter proteins were derived from a HeLa Kyoto line obtained from S. Narumiya (Kyoto University, Kyoto, Japan) and cultured in DMEM (produced in-house at Institute of Molecular Biotechnology of the Austrian Academy of Sciences) supplemented with 10% FCS (Thermo Fisher Scientific), 1% (v/v) penicillin–streptomycin (Sigma-Aldrich), and GlutaMAX (Thermo Fisher Scientific) at 37°C with 5% CO2 in a humidified incubator.

Transcription factors activity in embryonic stem cells

Stable Embryonic Stem (ES) cell lines were generated and cultured as described in.⁵⁶ Briefly, ES cell-imaging experiments were performed in Dulbecco’s modified Eagle’s medium (DMEM) without phenol red (Invitrogen), 15% FBS, 1 mM GlutaMAX at 37°C.

Adhesions in collagen-embedded osteosarcoma cells

Mycoplasma-free U2OS female cells were cultured in DMEM with 10% FBS (Sigma; F0926-500ML) at 5% CO2 and 37°C.

Trackability of endocytic pits in collagen-embedded breast cancer cells

Sum159O breast cancer cells stably expressing alpha-adaptin GFP are a derivative of Sum159 cells obtained from Angelique Whitehurst and prepared as in.^68,69 Cells were plated on a ∼2 mm thick bed of rat tail-derived Collagen Type I (354236, Corning) at 37°C.

Method details

Multiscale particle detector

Three-dimensional microscopy imposes specific constraints on the design of a particle detector. First, the diversity of shapes and sizes of intracellular structures may not be visible to the naked eye in a volumetric rendering, we must thus design a detector that is responsive to those variations. Second, light scattering and variation in signal intensity create large changes in signal-to-noise ratio (SNR) across space that are also difficult to assess visually. Our detector must then be adapted to those changes from low to high SNR. Finally, the large dimension of 3D data sets requires the design of computationally efficient approaches. Following, we describe a multiscale detector equipped with an adaptive thresholding approach that tests multiple possible scales at each location through the implementation of multiple iterations of filtering. This tool is similar in spirit to other multiscale detectors that combine the localization task with the scale selection task using either Gaussian kernels⁷⁰ or the wavelet transforms.⁷¹ The main difference is the combination of multiple thresholding masks obtained through the evaluation of a statistical test for each voxel and for each of the evaluated scales.

We first developed a multiscale adaptive thresholding approach inspired by our previous work focused on the sensitive detection limited to the case of diffraction-limited fluorescent structures.⁵³ Let us consider the following image model:

$$M\left(\mathit{x},A,\sigma ,\mu ,C\right)=A{\left(\mathit{x}\right)G}_{\sigma ,\mu }\left(\mathit{x}\right)+C\left(\mathit{x}\right)+ϵ\left(\mathit{x}\right)$$

where $A$ denotes the spot amplitude, $\mathit{x}$ the 3D position, $G_{\sigma ,\mu }\left(\mathit{x}\right)$ is a Gaussian function with standard deviation $\sigma$ and mean $\mu$, $C$ is the background signal and $ϵ\left(\mathit{x}\right)$ is the additive noise following a Poisson-Gaussian stochastic footprint. The least-square formulation of our optimization problem as

$$\underset{A\left(\mathit{x}\right),C\left(\mathit{x}\right)}{\mathrm{argmin}}\sum _{x\in W}{\left(A\left(\mathit{x}\right)G_{\sigma ,\mu }\left(\mathit{x}\right)+C\left(\mathit{x}\right)-I\left(\mathit{x}\right)\right)}^{\mathbf{2}}\text{,}$$

where $I(.)$ denotes the image volume and $W$ is a 3D box of size $8\sigma$, can be simplified to the resolution of a linear system that can be decomposed in multiple filtering passes:

$$A\left({\mathit{x}}_{\mathbf{0}}\right)=\frac{\left(I\ast G_{\sigma ,0}\right)\left({\mathit{x}}_{\mathbf{0}}\right)-\left(\overline{G_{\sigma ,0}}\ast {\mathbf{1}}_w\right)\left({\mathit{x}}_0\right)}{n\overline{{G_{\sigma ,0}}^{\mathbf{2}}}+n{\overline{G_{\sigma ,0}}}^{\mathbf{2}}}$$

and,

$$C\left({\mathit{x}}_{\mathbf{0}}\right)=\frac{\left(I\ast {\mathbf{1}}_w\right)\left({\mathit{x}}_{\mathbf{0}}\right)-n\overline{G_{\sigma ,0}}A\left({\mathit{x}}_{\mathbf{0}}\right)}{n}$$

where ${\mathit{x}}_0$ is the fixed voxel position ${\mathbf{1}}_w$ is a unitary convolution kernel along $W$, n is the number of voxels encompassed in $W$. The statistical analysis of the local residuals resulting from the fit

$$r\left(\mathit{x}\right)=\left(A\left({\mathit{x}}_{\mathbf{0}}\right)G_{\sigma ,\mu }\left(\mathit{x}\right)+C\left({\mathit{x}}_{\mathbf{0}}\right)-I\left(\mathit{x}\right)\right)\text{,}$$

with $\mathit{x}\in W$, provides a p-value-based threshold for testing for the hypothesis that $A\left({\mathit{x}}_{\mathbf{0}}\right)\gg C\left({\mathit{x}}_{\mathbf{0}}\right)$ as described in.⁵³ This approach yields a sensitive binary map $H_{0,\sigma }(.)$ for the detection of the voxel describing a fluorescence object at scale $\sigma$. This approach avoids the fitting of an object template in order to reduce computation time.

Next, we carry out this adaptive thresholding step at multiple scale to obtain a vote map.

$$V\left(\mathit{x}\right)=\sum _{\sigma \in \mathrm{\Omega }}{H}_{0,\sigma }\left(\mathit{x}\right)$$

where $\mathrm{\Omega }$ is the scale range, typically ranging between 0.120 and 1 μm. The resulting object mask $V(.)$ thus summarizes the presence of particles at any scale at a given voxel (see Figure S6) using only filtering operations that can process each voxel in a parallelized fashion. In order to refine the localization of objects present in contiguous object masks, we implemented a multiscale Laplacian of a Gaussian filtering framework⁷² to estimate a map of scale response $S(.)$ for each voxel defined as:

$$S\left(\mathit{x}\right)=\underset{\sigma \in \mathrm{\Omega }}{\mathrm{argmax}}{\sigma }^2{\nabla }^2\left(I\left(\mathit{x}\right)\ast G_{\sigma ,0}\left(\mathit{x}\right)\right)$$

where ${\nabla }^2(.)$ denotes the Laplacian operator. The watershed algorithm is then applied to further segment this scale response map to detect touching objects. The center of object is determined through the weighted centroid of the voxels belonging to a same object mask.

Dynamic region of interest estimation

In order to visualize and map the molecular processes nested in volumetric time lapse sequences, we propose a framework for the definition of dynamic regions of interest (dynROI) from point cloud sequences. Those dynROIs are described by dynamic bounding boxes (or rectangular cuboids) that are sized to fit the data optimally and oriented according to a moving frame of reference. In this note, we describe the general principles underpinning the estimation of those dynROIs from dynamic point clouds and their implementation across scales: from cellular down to molecular dynROIs.

Generic point cloud tracking principle

We first define an optimal frame of reference in the first time point of the sequence with an origin $O_0$ described by the average point cloud position and with unit vectors $\left(u_0,v_0,w_0\right)$ described by the eigenvectors of the covariance matrix of the point positions (a.k.a. principal component analysis). The orientation of the dynROI box in the first frame is described by this frame of reference and its size is defined by the boundaries of the point cloud augmented by a tunable margin (default is set to 5 voxel).

The frame of reference at time t is then estimated through a rigid transform as:

$$\widehat{\left(O_t,R_t\right)}=\underset{O_t,R_t}{\mathrm{argmin}}\sum _{\begin{array}{c}{\mathit{x}}_t\in {\mathrm{\Omega }}_{\mathrm{t}}\\ x_0\in {\mathrm{\Omega }}_0\end{array}}\Vert {\mathit{x}}_t-\left(R_t{\mathit{x}}_0+O_t\right)\Vert$$

using the Iterative closest point algorithm,⁷³ where ${\mathrm{\Omega }}_t$ denotes the set of points coordinate at time $t$. The unit vector $\left(u_t,v_t,w_t\right)$ are then estimated by applying the rigid transform to $\left(u_0,v_0,w_0\right)$. At each time point the size of the box is adjusted to fit the extension of the current point cloud in the current orientation with the additional margin. Multiple dynROI shapes have then been implemented to adjust to the local process (box, sphere, tube, rounded tube, plane and cone).

Dynamic region of interest estimation for the cell

The cell is first segmented using the Otsu algorithm and the point cloud representing the cell mask is downsampled randomly to reduce its density by 90% and speed up computations. The generic point cloud tracking principle described above is applied to the downsampled sequence with a margin set to 30 voxels and a box-shaped dynROI (see Figure S7).

Dynamic region of interest for the spindle

Spindle poles were detected using the multiscale detector with the default p value (set to 0.005) and scales ranging from 0.4 to 0.8 ums. The motion of poles was modeled with a piecewise stationary Brownian and Directed motion model with a maximum instantaneous displacement set to 3 times the process noise estimated from a Kalman filtering of the trajectory, a lower bound set at 0.5 μm and upper bound set at 0.8 μm. Failure to detect the very dynamic aggregate on nucleating microtubules is handled with gap closing, the maximum gap is set to 2 s (or 2 frames) with a minimum length of 2 s for the track segment. The resulting dynROI was built has a rounded tube center with a fringe of 9 microns around the segment formed by the two brightest objects present during the complete sequence.

Dynamic region of interest for the chromosomes

The kinetochores marking the center of chromosomes were detected using the multiscale detector with the default p value (set to 0.005) and scales ranging from 0.15 to 0.25 voxels. Motion was modeled with a Brownian motion model with a maximum instantaneous displacement set to 5 times the process noise estimated by Kalman filtering of the trajectory, a lower bound set at 0.4 μm and upper bound set at 0.6 μm. Variation in SNR were managed with a maximum gap set to 4 s (or frames) with a minimum length of 2 s for the track segment. The dynROI was estimated using the generic point cloud tracking principles described above using all the trajectories detected inside the spindle dynROI with a box-shaped dynROI and a margin of 0.1 μm.

Dynamic region of interest estimation for the interpolar region

Let $\left(O_t^s,u_t^s,v_t^s,w_t^s\right)$ and $\left(O_t^k,u_t^k,v_t^k,w_t^k\right)$ denote the frames of reference estimated for the spindle and the chromosome respectively. We want to build a frame of reference $\left(O_t^i,u_t^i,v_t^i,w_t^i\right)$ that follows an interpolar plane showing how microtubule nucleation events inside the spindle are orchestrated to capture chromosomes efficiently. We first set the origin to $O_t^i=O_t^s$ and $w_t^i=w_t^s$ so that one axis is following the spindle at all time. For the plane to describe the motion of the chromosome population, the second unit vector follows a slice of the kinetochore-associated dynROI ${v_t^k}^{\prime }=\cos \left(\theta \right)u_t^k+\sin \left(\theta \right)w_t^k$ projected to ensure orthogonality as $v_t^i={v_t^k}^{\prime }.\left(1-{w_t^i}^{\mathrm{T}}{w}_t^i\right)$. Finally the last unit vector is set as $u_t^i=v_t^i\times w_t^i$. The dynROI type is a plane with a lateral fringe of 50 voxels, a height of 4 voxels and an angle $\theta$ set to $\frac{\pi }{2}$.

Dynamic region of interest estimation for the kinetochore fibers

Assuming K-fibers to span the region between poles and kinetochores as a straight polymer, its associated microtubule dynamics was observed using a conical dynROIs with an angle of $\frac{\pi }{12}$.

Stochastic programming for the evaluation of trackability

The association of particle detections with trajectory heads is performed in a temporally greedy fashion, i.e., particles detected at time $t$ are linked to the heads of track segments defined up to time $t-1$ without consideration of the track segments beyond $t$ and only indirect consideration of track segment before t-1. Therefore, our definition of trackability relates to the level of ambiguity in assigning particles detected in time point t to track segment heads in t – 1. The optimal association is obtained by linear assignment of heads to particles in a bipartite graph:

$$\underset{{\{a}_{ij}\}}{\mathrm{argmin}}\sum _{i\in \mathrm{\Omega },j\in {\mathrm{D}}_{\mathrm{t}}}{c}_{ij}{a}_{ij}\mathrm{s}.\mathrm{t}.\sum _{i\in \mathrm{\Omega }}{a}_{ij}=1\mathrm{and}\sum _{j\in {\mathrm{D}}_{\mathrm{t}}}{a}_{ij}=1\text{,}$$

where $\mathrm{\Omega }$ is the set of track segment heads, $D_t$ is the set of detections measured at time $t$, $a_{ij}\in \left\{\mathrm{0,1}\right\}$ denotes the assignement of the ith track segment to the jth particle and $c_{ij}\mathbb{\in }\mathbb{R}$ is the cost associated to making that association. The association cost $c_{ij}$ typically reflects the distance between the predicted location of the $i$ th track segment at $t$ and the $j$ th detection at this same time point. This assignment problem is convex, hence with a guaranteed unique solution, and can be solved using a variety of linear programming algorithms.^51,74,75 However, a key challenge in our framework is the deterministic aspect of this solution. There is no measure of uncertainty attributed to the final graph of associations (see Figure 5A). While several algorithms have been proposed to estimate the uncertainty related to the total optimal cost of a linear programming problem, a.k.a. stochastic programming,⁷⁶ they do not focus on the detection of local changes in association made in the bipartite graph. In this Section, we will first detail how we consider the randomness present in the history of each track to estimate the probability distribution associated to all assignment costs $c_{ij}$. We will then describe how these uncertainties can then be exploited to detect local ambiguities in the assignment problem, which subsequently define a score of trackability.

Stochastic filtering approaches are routinely used to estimate the parameter describing the dynamic properties of tracked particles from their position history. They enable the prediction of particle location from one frame to the next to refine the cost used for linear assignment. Those temporally recursive algorithms also provide inferences of track segment prediction uncertainty from t-1 to t. Briefly, let ${\mathit{x}}_t$ be a variable describing the state of the track segment. For a particle moving in a directed fashion, it is defined as:

$${\mathit{x}}_t=\left(x,y,z,dx,dy,dz\right)\text{.}$$

The associated probability $p\left({\mathit{x}}_t|{\mathit{z}}_{1:t}\right)$ can be estimated recursively thanks to the Bayes rule:

$$p\left({\mathit{x}}_t|{\mathit{z}}_{1:t}\right)\propto p\left({\mathit{z}}_t|{\mathit{x}}_t\right)\int p\left({\mathit{x}}_t|{\mathit{x}}_{t-1}\right)p\left({\mathit{x}}_{t-1}|{\mathit{z}}_{1:t-1}\right)d{\mathit{x}}_{t-1}\text{,}$$

where ${\mathit{z}}_{\mathbf{1}:\mathit{t}}$ represents the past measured positions assigned to a particular track. Kalman filtering is a scalable and flexible way to model the motions of thousands of particles in parallel, and as such is used in the majority of tracking approaches,⁷ including u-track. In this framework, the relationships between random variables are assumed to be linear and described as follows:

$${\mathit{x}}_t=\mathit{F}{\mathit{x}}_{t-1}+{\mathit{w}}_t$$

$${\mathit{z}}_t=\mathit{H}{\mathit{x}}_t+{\mathit{v}}_t$$

where $\mathit{F}$ is the state transition matrix between consecutive time points, $\mathit{H}$ is the observation matrix, and ${\mathit{w}}_t$ and ${\mathit{v}}_t$ are the model and measurement noise respectively, both assumed to be Gaussian with covariance matrices ${\mathit{Q}}_t$ and ${\mathit{R}}_t$. The Gaussian and linear assumption provides an analytical solution with a computationally efficient implementation to estimate $p\left({\mathit{x}}_t|{\mathit{z}}_{1:t}\right)\sim N\left({\hat{\mathit{x}}}_t,{\hat{\mathit{P}}}_t\right)$ (see our previous work¹³ for a detailed review). Before optimal assignment between a track segment at $t-1$ and the object detected on frame $t$, the probability distribution of the predicted particle positon at time $t$ is then described by $p\left({\mathit{x}}_t|{\mathit{z}}_{1:t-1}\right)\sim N\left({\mathit{F}\hat{\mathit{x}}}_{t-1},{\mathit{F}\hat{\mathit{P}}}_{t-1}{\mathit{F}}^T+{\mathit{Q}}_t\right)$. As such the variation of the cost to associate the ith track segment to the $j$ th measurement can be expressed, without loss of generality as:

$$c_{ij}\sim \Vert \mathit{H}\mathit{x}-{\mathit{z}}_t^j\Vert \mathrm{s}.\mathrm{t}.\mathit{x}\sim \mathit{p}\left({\mathit{x}}_t^i|{\mathit{z}}_{1:t-1}^{\mathit{i}}\right)\text{.}$$

This expression provides us with a direct way to explore the space of possible combination of cost values through Monte Carlo simulations. u-track 3D implements several types of stochastic filtering approaches such as unimodal and multimodal Kalman filtering as well as piecewise stationary motion filtering or smoothing approaches, where the same principles can be straightforwardly applied.

The principle underlying the use of our predicted probability distribution to evaluate assignment stability is described graphically in Figure 6. Our local trackability score is defined as:

$$T_t^i=\frac{1}{N}\sum _{n=1}^N\left[a_{i{j}^{\ast }}=a_{i{j}^n}\right]$$

where $a_{i{j}^{\ast }}$ is the initial assignment found for the $i$ th trajectory, $a_{i{j}^n}$ is a newly computed assignment resulting from the $n$ th out of a total of N simultaneous resampling rounds of all costs $c_{ij}$ and [.] denotes the Iverson bracket. Each new assignment result, or vote, is considered different if the track segment is assigned to another detection, or determined to be a track termination. As such, a lower score $T_t^i$ reflect a larger instability in the optimal assignment, hence a higher ambiguity and lower trackability. In our experiments, the number of resampling rounds is set to N = 20.

Clathrin-mediated endocytosis study on a glass coverslip

Cell preparation and imaging

Inner medulla collecting duct (IMCD) mouse epithelial cells were plated on 5 mm diameter coverslips (64–0700, Thomas Scientific) and mounted to a custom machined holder for imaging with a high-NA version of diagonally scanned light-sheet microscopy.² This microscope is equipped with an NA 0.71 water dipping illumination objective (54-10-7, Special Optics), and a 25X/NA 1.1 water dipping detection objective (CFI75 Apo LWD 25XY, Nikon Instruments), and a Hamamatsu Flash 4.0 sCMOS camera. Briefly, 500 time points were acquired with 30 μW of 488 nm illumination (measured at the back pupil of the illumination objective) and a 15 ms camera exposure. Each image stack was 106.5 × 39.9 × 23.1 μm, with a lateral and axial voxel size of 104 and 350 nm, respectively, resulting in a 1.008 Hz volumetric image acquisition rate.

Clathrin structure trajectory estimation and post-processing

Clathrin structure aggregates, labelled by alpha-adaptin GFP were detected using a multiscale particle detector with a p value set to 0.05 and scales ranging from 0.15 to 0.5 μm. For tracking, the motion of particles was modeled with a Brownian motion model with a maximum instantaneous displacement set as three times the process noise estimated by Kalman filtering of the trajectory, a lower bound set at 0.1 μm and upper bound set at 0.3 μm. When detection gaps are enabled, the maximum gap length is set to 3 s (or frames) with a minimum length of 3 s for any track segment allowable to be connected by the gap closing algorithm.¹⁰

The median of the maximum intensity reached per track was then used to discriminate between abortive and maturing CCPs. To account for the variation of fluorescence signal across acquisitions, the maximum intensities were scaled such that the empirical cumulative distribution function (cdf) of maximum intensities computed for each acquisition matched the median cdf of all acquisitions, as previously described in ref. 53.

Microtubule instability measurement

Cell preparation and imaging

HeLa cells stably expressing EB3-EGFP alone or along with mCherry-CENPA were plated on coverslips mounted on the microscope in CO2-independent L15 medium containing 10% FBS, without phenol red, and maintained at 37°C for the duration of the experiment. All images were recorded with an Orca Flash 4.0 v2 sCMOS camera (C11440-22C; Hamamatsu). Images were acquired in sample-scan imaging mode with a lateral translation of 0.4 μm and subsequently deskewed in postprocessing. Final voxel dimensions for all lattice light-sheet image datasets were 104 nm × 104 nm × 210–217 nm. The microscope was controlled by custom-made software. Acquisition frequency was adapted for each experiment and is specified in the main text.

Plus-ends trajectory estimation

Plus-ends, labelled through GFP tagging of EB1, were detected using a multiscale detector with the default p value (set to 0.005) and scales ranging from 0.15 μm to 0.25 μm. The polymerization of microtubule was modeled with a directed displacement estimated through a Kalman filtering of the trajectory, similar to,⁵⁵ but now in 3D. The random component of this displacement was estimated as 3 times the process noise of the Kalman filter with a lower bound of 0.3 μm and an upper bound of 0.6 μm.

The shrinkages and pauses detection framework proposed in⁵⁵ has also been translated to 3D plus-ends trajectories. The detection of both shrinkages and pauses is carried out by closing gaps between track segments, which implicitly delineate phases of microtubule growth. In our experiment, the minimum growth duration to consider gap closing was set to 4 s (or frames) and the maximum gap duration was set to 8 s. In order to detect pauses, the maximum angle between a speed vector estimated immediately prior and posterior to the pause event was set to 30°, the maximum positional fluctuation in the plus-ends location during a pause is set to 0.5 μm. To detect a shrinkage event between two segments, we first measure the distance D between the termination point of the earlier segment (which is equivalent to the potential locus of a catastrophe event) and the initiation point of the later segment (which is equivalent to the potential locus of a rescue point) along the path of the earlier segment. The two segments are connected by the gap closer if the distance between the initiation point to the closest point along the trajectory of the first segment does not exceeds $Dsin\left(\theta \right)$ with $\theta$ set to 20° in our experiment.

Single molecule dynamics study with lattice light-sheet microscopy

Cell preparation and imaging

Fluorescently labelled Sox2 transcription factors were imaged over 100 time points with Lattice light-sheet microscopy imaging. Nine planes spaced 500nm apart were acquired at 50 ms of camera exposure, resulting in a 2 Hz volumetric image acquisition rate. Each image stack was 50 × 50 × 5 μm, then cropped around the nucleus, with a lateral and axial voxel size of 100 and 500 nm, respectively.

Estimation of transcription factor binding times

Transcription factor single molecules were detected using a multiscale detector using a p value of 0.01 and a scale ranging from 0.15 to 0.3 μm. Transcription factor motion was modeled using a Brownian motion model with a maximum instantaneous displacement estimated as 6 times the process noise estimated by Kalman filtering of trajectory to account for speed variations during long periods of confined diffusion, a lower bound set at 0.3 μm and upper bound set at 0.5 μm. The maximum gap is set to 4 s (or frames) with a minimum length of 2 s for any track segment allowable to be connected by the gap closing algorithm. We assume that if the single molecule is detectable it immobilized at the DNA. Accordingly, characteristic binding times $\tau$ are estimated by a double exponential fit to the lifetime distribution.

Adhesions and collagen interaction imaging and analysis

Cell preparation and imaging

U2OS Cells were lentivirally transduced with a truncated CMV promoter (Addgene #110718) driving the expression of mNeonGreen-Paxillin (Allele Biotechnology). Cells were seeded into a pH-neutralized collagen solution (∼2 mg/mL) that, when polymerized, fully embedded cells in a three-dimensional extracellular matrix environment. For visualization of the extracellular matrix, a small concentration of the collagen was fluorescently conjugated with Alexa Fluor 568 NHS Ester (A20003, ThermoFisher). Samples were imaged with a high-NA variant of Axially Swept Light-Sheet Microscopy using 488 nm and 561 nm lasers for illumination (OBIS LX, Coherent, Inc.). The details of this microscope will be published elsewhere. Briefly, lasers are combined, spatially filtered, expanded, and shaped into a light-sheet with a cylindrical lens. This light-sheet was relayed to a bidirectional scan unit (6215, Cambridge Technology), a remote focusing system (CFI S Plan Fluor ELWD, Nikon Instruments), and eventually to the illumination objective (54-10-7, Special Optics). Fluorescence was detected in a widefield format with a water-dipping objective (CFI75 Apo LWD 25SW, Nikon Instruments) and imaged onto two sCMOS cameras (ORCA-Flash4.0, Hamamatsu Photonics) with a 500 mm achromatic doublet (49–396, Edmund Optics), laser line filter, a dichroic, and bandpass filters (ZET405/488/561/640, ZT568rdc, ET525/50m, and ET600/50m, Chroma Technology Corporation). The laser laterally dithered for shadow reduction and scanned synchronously with the detection objective (P-603.1S2 and E−709.SRG, Physik Instrumente) to acquire a three-dimensional stack of images. All equipment was controlled with custom LabVIEW software, which is available from UTSW upon completion of a material transfer agreement.

Adhesion detection and elongation analysis

Paxillin aggregates as a surrogate for adhesions were detected using the multiscale detector described in Section “Multiscale particle detector” based on a p value of 0.001 and a scale ranging from 0.3 to 0.5 μm. The elongation of each detected adhesion is computed through a tubularity metric evaluated for each voxel and averaged across all the voxels associated to a single adhesion. Similar to the classic vesselness estimator by Frangi and colleagues,⁷⁷ our tubularity metric is based on the eigen values of the Hessian matrix to describe local curvature,. Let $\left({\lambda }_1<{\lambda }_2<{\lambda }_3\right)$ be the three eigenvalues of the Hessian matrix computed at each voxel, the tubularity metric $T=1-|{\lambda }_1/{\lambda }_2|$ yields a value between 0 and 1 increasing with the elongation of the adhesions. As such, a noteworthy difference between the classic score described in Frangi’s approach is the use of the two lowest eigen-values (associated with the two axis of lowest curvature direction) to discriminate between flat and elongated adhesions.

Collagen detection and distance analysis

Collagen was detected using the 3D implementation of steerable filtering as described in.⁷⁸ An adhesion was considered in close contact with collagen if the center of at least one voxel belonging to its mask was less than 100 nm away from any voxels of the collagen mask.

Endosome trackability on cell cultured on top of collagen

Cell preparation and imaging

Sum159O breast cancer cells⁶⁹ stably expressing alpha-adaptin GFP were imaged similarly to the one platted on glass coverslip, with the exception that they were plated on a ∼2 mm thick bed of rat tail-derived Collagen Type I (354236, Corning).

Clathrin structure trajectory estimation

Clathrin structure aggregates, labelled by alpha-adaptin GFP were detected using a multiscale particle detector with a p value set to 0.01 and scales ranging from 0.125 to 0.5 μm. For tracking, the motion of particles was modeled with a Brownian motion model. In order to follow the erratic displacements caused by large protrusive motions, the maximum instantaneous displacement was set to 5 times the process noise estimated by Kalman filtering of the trajectory, a lower bound set at 0.3 μm and upper bound set at 0.6 μm. The maximum gap length is set to 3 s (or frames) with a minimum length of 3 s for any track segment allowable to be connected by the gap closing algorithm.¹⁰

Benchmarking computational time and memory usage

Computational time and memory consumption have been tested on a computing workstation and office laptop (see specification below). The test includes detection, tracking with trackability and dynROI definition on the endocytosis test dataset (400 Mb) provided along with this manuscript. Runtime takes an average of 17.3 s (s.d. 0.2 s) seconds on the workstation and 2 min 29 s (s.d. 6 s) on the laptop. The maximum memory used by the pipeline was 12Gb on the workstation and 0.5 Gb on the office laptop.

Office laptop.

• •Model: X1 Carbon 6^th gen
• •Year: 2018
• •CPU: Intel i7-8550U @ 1.80GHz, 4 Cores
• •RAM: 16 Gb
• •GPU: integrated
• •Disk: 1 Tb
• •OS: Windows 11
• •MATLAB version: 2023a

Computing Workstation.

• •Model: Colfax SX6300
• •Year: 2020
• •CPU: Intel Xeon 6242R @ 3.10GHz, 80 cores
• •GPU: Nvidia A6000
• •Disk: 16 Tb
• •OS: Ubuntu 20.04.3 LTS
• •MATLAB version: 2021a

Quantification and statistical analysis

Statistical analysis was performed by considering either intracellular processes or cells as independent observations as specified in the manuscript. Each statistic considering intracellular processes (either experimental or simulated data) includes more than a thousand events. Statistical details of all experiments at the cellular level can be found in the figure legends including exact value of n, clear descriptions of what n represents and box-plot representations.

Published: December 1, 2023

Supplemental information

Data S1. Videos illustrating the recovery of transient disappearance to capture endocytic events and microtubule instability, related to Figure 2

Individual files: Video-1-v1.mp4: detail of a rat kidney cells layer expressing GFP-AP2 subunit imaged with diagonally scanned light-sheet microscopy (diaSLM) acquired with a volumetric frequency of 1 Hz and rendered with MIP. Overlay highlights trajectories colored according to maturing events (green), aborting events (orange), and tracks discarded because their lifetimes are cut by the acquisition beginning and end (blue). The red spheres highlight gap location. Video-2-v1.mp4: details of HeLa cell in interphase expressing GFP-EB1 imaged with lattice light-sheet microscopy, rendered with MIP, and acquired with a volumetric frequency of 1 Hz under control condition (left) and after treatment with 33 nM nocodazole (right). Overlay highlights trajectories, colored uniquely, and yellow circles highlight location of pauses and rescues. Video-3.mp4: HeLa cell in metaphase expressing GFP-EB1 imaged with lattice light-sheet microscopy, rendered with MIP, and acquired with a volumetric frequency of 1 Hz. Overlay highlights trajectories. Rendering using the Amira rendering software.

Data S2. Videos illustrating the visualization and quantification of adhesions in 3D, related to Figure 4

Individual files: Video-4-v3.mp4: dual-colored orthogonal MIP of osteocarcinoma cells expressing eGFP-labeled paxillin and embedded in collagen labeled with Alexa Fluor 568 acquired with a volumetric frequency of 0.07 Hz. Overlay highlights dynROI. Video-5-v5.mp4: mask of detected adhesions colored according to their proximity to the closest collagen fiber. Video-6-v2.mp4: mask of detected adhesions colored according to their elongations. Video-7-v1.mp4: slice of the mask of detected adhesions and collagen fibers taken at the center of cell dynROI described in Figure 2A and Video 3.

Data S3. Videos illustrating the estimation of a dynROI for the visualization of the mitotic spindle from prometaphase to metaphase, related to Figure 5

Individual files: Video-8.mp4: dual-colored orthogonal MIP of HeLa cells undergoing mitosis labeled with eGFP-labeled EB3 and mCherry-labeled Centrome Protein A acquired with a volumetric frequency of 0.1 Hz. From left to right, overlays highlight a dynROI built around centrosome trajectories, a dynROI built around centromere trajectories, and a plane built to visualize the dynamics of chromosomes relative to the spindle location. Video-9-v2.mp4: dual-colored orthogonal MIP of HeLa cells undergoing mitosis labeled with eGFP-labeled EB3 and mCherry-labeled Centrome Protein A acquired with a volumetric frequency of 0.1 Hz. The red overlay highlights the dynROI tracking a plane built to visualize the dynamics of chromosomes relative to the spindle location.