Effect of constitutive law on the erythrocyte membrane response to large strains

Abstract

Three constitutive laws, that is the Skalak, neo-Hookean and Yeoh laws, commonly employed for describing the erythrocyte membrane mechanics are theoretically analyzed and numerically investigated to assess their accuracy for capturing erythrocyte deformation characteristics and morphology. Particular emphasis is given to the nonlinear deformation regime, where it is known that the discrepancies between constitutive laws are most prominent. Hence, the experiments of optical tweezers and micropipette aspiration are considered here, for which relationships between the individual shear elastic moduli of the constitutive laws can also be established through analysis of the tension-deformation relationship. All constitutive laws were found to adequately predict the axial and transverse deformations of a red blood cell subjected to stretching with optical tweezers for a constant shear elastic modulus value. As opposed to Skalak law, the neo-Hookean and Yeoh laws replicated the erythrocyte membrane folding, that has been experimentally observed, with the trade-off of sustaining significant area variations. For the micropipette aspiration, the suction pressure-aspiration length relationship could be excellently predicted for a fixed shear elastic modulus value only when Yeoh law was considered. Importantly, the neo-Hookean and Yeoh laws reproduced the membrane wrinkling at suction pressures close to those experimentally measured. None of the constitutive laws suffered from membrane area compressibility in the micropipette aspiration case.

1. Introduction

The dynamics of single red blood cells (RBCs) – commonly modelled as capsules of biconcave resting shape, composed of an infinitely thin membrane accounting for the mechanical properties of the lipid bilayer and elastic cytoskeleton, and an internal fluid, the cytoplasm – have been extensively studied for over half a century. Yet, theoretical, computational, and experimental works are further shedding light on how various physical and mechanical properties of the capsule, such as the shape [1, 2, 3, 4, 5, 6, 7, 8, 9], the membrane constitutive law [8, 9, 10, 11], the rheology of the internal and suspending mediums [4, 12, 13, 14, 15, 16, 17], and the membrane viscosity [18, 19, 20, 21, 22, 23, 24], affect the deformation and motion of single erythrocytes. Among these properties, the study of the effects of the constitutive law, governing the mechanical response of the erythrocyte membrane to the external applied stresses, has received less attention despite its paramount importance on the accurate modelling of red blood cells. Not only does the choice of the constitutive law affect the capsule behaviour, but it also influences the evaluation of the membrane mechanical properties, for example the shear elastic modulus, from experimental measurements [11, 25].

Even though few studies have dealt with the effect of constitutive law on the response of the almost area-incompressible red blood cells to the surrounding flow, a multitude of works have explored the impact of constitutive laws on the dynamics of area-compressible, spherical and ellipsoidal capsules in various flow conditions. Theoretically, different constitutive laws have been compared for capsules undergoing uniaxial extension and isotropic dilatation [25]. The influence of constitutive laws on the capsule behaviour has been computationally examined in diverse flow situations, for instance in shear flow [25, 26, 27, 28], planar hyperbolic flow [27, 29], axisymmetric elongational flow [27], capillary flow [30], and radially oscillatory flow [31]. Theoretical predictions have been compared with experimental data to identify plausible constitutive laws for the membrane material of bioartificial capsules [32]. The previous work has been extended to compare numerical results of several constitutive laws with experiments [33, 34]. Simulations have also been employed in conjunction with experiments to determine the membrane mechanical properties of capsules circulating in a square-section microfluidic channel [35], capsules in elongation flow [36], and cells undergoing compression [37]. For comprehensive reviews regarding the effect of constitutive laws on the dynamics of area-compressible, spherical and ellipsoidal capsules, the reader is referred to the works of Pozrikidis [38] and Barthès-Biesel [39]. This plethora of literature articulates the importance of understanding the impact that the choice of constitutive law has on the capsule response and the determination of its mechanical properties. The aforementioned studies have, however, focused on area-compressible capsules of initially spherical or ellipsoidal shape, and their findings cannot thus be straightforwardly extended to the case of red blood cells, whose response to the surrounding flow will be further affected by their membrane surface incompressibility and complex shape.

With respect to red blood cells, Mills et al. [10] have performed optical tweezers experiments, and compared the experimental results for the axial and transverse diameters of the stretched erythrocytes with computational ones considering the neo-Hookean and Yeoh laws. Dimitrakopoulos [11] has reviewed numerous studies in the literature so as to analyze the variation in the evaluation of the shear elastic modulus of the erythrocyte membrane obtained from fitting different constitutive laws to measurements of various experiments, namely experiments of optical tweezers, micropipette aspiration, low-viscosity ektacytometry, electrically-induced deformation, and capillary flow. To validate their numerical framework, Sinha & Graham [8] have performed simulations of the optical tweezers experiment for three different constitutive laws, that is the Skalak, neo-Hookean and Yeoh laws. Finally, Siguënza et al. [9] have compared in detail computational results for the axial and transverse diameters, in-plane and folding lengths, area variation, and resulting shape of RBCs subjected to optical tweezers stretching, when either Skalak or Yeoh law is employed for the modelling of the erythrocyte membrane.

However, a careful comparison between the values of shear elastic modulus selected for the different constitutive laws has in general been omitted in the aforementioned studies. The purpose of the present work is to meticulously compare constitutive laws, whose chosen elastic parameters follow theoretical relations, by means of simulations in scenarios for which experimental data exist. Further, we are interested in cases where the erythrocyte undergoes moderate and large deformations, as it has been shown that all constitutive laws produce identical behaviour for the same value of shear elastic modulus in the small deformation regime, corresponding to extensions of less than 15% [11, 25]. The focus on this deformation regime is also physiologically relevant. RBCs are subjected to large deformations when flowing within capillaries [38] or passing through slits of the venous sinuses, such as in the spleen [40].

Here, we have chosen to computationally realize the optical tweezers [4, 10, 41, 42] and micropipette aspiration [43, 44, 45, 46, 47] experiments, which have been widely used to measure the mechanical properties of the erythrocyte membrane. In both experiments, the red blood cell sustains moderate and large deformations, specifically up to 100% extension in the axial and lateral directions for the optical tweezers and micropipette aspiration experiments, respectively. Moreover, correlations between the shear elastic moduli of different constitutive laws can be deduced through theoretical analysis in both cases. The following constitutive laws have been considered in the present work: Skalak, neo-Hookean, and Yeoh laws. The strain-hardening Skalak law is typically employed for modelling cellular-scale blood flow [48]. The strain-softening neo-Hookean model has also been considered in earlier studies due to its simplicity [49, 50, 51, 52]. Through the optical tweezers studies of Mills et al. [10] and Sigüenza et al. [9], Yeoh law, whose nature varies with the deformation, has emerged as an alternative owing to its capability of capturing the RBC’s deformation characteristics and morphology. Balogh & Bagchi [53] have also reported that Yeoh law predicts the experimental results of micropipette aspiration better than Skalak law, without, however, exploring the effect of different constitutive laws as it was not within the scope of their work. It is worth mentioning that the erythrocyte membrane nature coincides with that of Skalak and Yeoh laws at large strains, namely being strain-hardening [11]. Despite the difference in nature, the neo-Hookean model is considered here also for comparison purposes with Yeoh law, which constitutes an extension of it.

To facilitate our study on the effect of constitutive laws, certain assumptions have been made allowing us to restrict the parameter space. Although the erythrocyte properties, such as the shape, dimensions, and cytoplasmic viscosity, may vary considerably with cell age [46, 54], temperature [55], and disease [56], their variation poses an additional modelling challenge as it consequently alters the RBC’s mechanical properties. For this reason, only healthy human RBCs have been considered here, with the aforementioned properties being kept invariant. The effect of the erythrocyte membrane viscosity has been omitted in the current study, as it has been shown that the membrane viscosity does not influence significantly the steady-state deformation of a RBC subjected to optical tweezers stretching [4, 20]. Lastly, the bending elastic modulus of the erythrocyte membrane has been kept constant throughout our simulations, since it has been demonstrated that, for the optical tweezers experiment, its variation has a negligible effect on the RBC deformation [8].

The article is organized as follows. In Section 2, the in-house massively parallel computational fluid dynamics solver, HARVEY [57], used to perform simulations is presented. HARVEY is based on the lattice Boltzmann method (LBM), described in Section 2.1, to solve the fluid flow governing equations on a uniform, Cartesian grid. Details of the erythrocyte model considered here are given in Section 2.2. The finite element method (FEM), employed for evolving the RBC’s membrane equations of motion in a Lagrangian description, is discussed in Section 2.3. Lastly, the immersed boundary method (IBM), coupling the fluid and structure solvers, is presented in Section 2.4. (For the readers interested in HARVEY’s computational performance, we refer them to the works of Randles et al. [57, 58, 59] for bulk blood flow simulations, and the works of Roychowdhury et al. [60] and Ames et al. [61] for blood flow simulations at the cellular level.) In Section 3, theoretical relations between the shear elastic moduli of the constitutive laws examined here are derived. In particular, the case of uniaxial extension, the theoretical equivalent of the optical tweezers experiment, is treated in Section 3.1, and the micropipette aspiration case is analyzed in Section 3.2. The computational results of the optical tweezers and micropipette aspiration are, respectively, presented in Sections 4.1 and 4.2. Finally, the key contributions of the present work are summarized in Section 5.

2. Computational framework: HARVEY

2.1. Lattice Boltzmann method

To resolve the flow field in the cytoplasm within the erythrocyte membrane and its surrounding fluid, which are both assumed to be incompressible and Newtonian, we employ the lattice Boltzmann method. In the LBM framework, distribution functions $f_i(\mathit{x},t)$ representing the density of particles at position $\mathit{x}$ and time $t$ with velocity ${\mathit{c}}_i$ along the $i^{th}$ lattice direction are tracked. The evolution of the distribution functions is governed by the lattice Boltzmann equation, where the Bhatnagar-Gross-Krook collision operator [62] and the forcing scheme of Guo et al. [63] are used

$$f_i\left(\mathit{x}+{\mathit{c}}_i\text{Δ}t,t+\text{Δ}t\right)=f_i(\mathit{x},t)-\frac{\text{Δ}t}{\tau }\left[f_i(\mathit{x},t)-f_i^{\text{eq}}(\rho ,\mathit{u})\right]+\text{Δ}t{F}_i.$$ (1)

The relaxation time $\tau$ is related to the kinematic viscosity $\nu$ by

$$\nu =c_s^2\left(\tau -\frac{\text{Δ}t}{2}\right),$$ (2)

where $c_s=\text{Δ}x/(\sqrt{3}\text{Δ}t)$ is the speed of sound, and $\text{Δ}x$, $\text{Δ}t$ are the lattice spacing and time step, respectively. To allow for the ambient fluid and cytoplasm to have different viscosities, we follow the approach of Zhang et al. [64]. For the fluid component at position $\mathit{x}$, its kinematic viscosity is given by

$$\nu (\mathit{x})={\nu }_{\text{amb}}+\left({\nu }_{\text{cyto}}-{\nu }_{\text{amb}}\right)\text{H}(d(\mathit{x},\mathit{X})),$$ (3)

where ${\nu }_{\text{amb}}$ and ${\nu }_{\text{cyto}}$ denote respectively the ambient and cytoplasmic viscosities. The Heaviside function H is defined as

$$\text{H}(d)=\{\begin{array}{ll}0,& d<-2\text{Δ}x\\ \frac{1}{2}\left[1+\frac{d}{2\text{Δ}x}+\frac{1}{\pi }\sin \left(\frac{\pi d}{2\text{Δ}x}\right)\right],& -2\text{Δ}x\le d\le 2\text{Δ}x\\ 1,& d>2\text{Δ}x.\end{array}$$ (4)

The variable $d(\mathit{x},\mathit{X})$ denotes the shortest distance from the fluid component at position $\mathit{x}$ to the erythrocyte membrane located at $\mathit{X}$. This distance is assigned to be positive for the cytoplasm, and negative for the ambient fluid.

The equilibrium distribution function $f_i^{\text{eq}}$ is expressed as

$$f_i^{\text{eq}}(\rho ,\mathit{u})=w_i\rho \left[1+\frac{{\mathit{c}}_i\cdot \mathit{u}}{c_s^2}+\frac{(\mathit{u}\otimes \mathit{u}):\left({\mathit{c}}_i\otimes {\mathit{c}}_i-c_s^2\mathbf{I}\right)}{2c_s^4}\right],$$ (5)

where $w_i$ are weight coefficients depending on the chosen lattice arrangement for the velocity discretization, and $\mathbf{I}$ is the identity tensor. Guo’s forcing $F_i$ takes the form

$$F_i=\left(1-\frac{1}{2\tau }\right)w_i\left[\frac{{\mathit{c}}_i-\mathit{u}}{c_s^2}+\frac{\left({\mathit{c}}_i\cdot \mathit{u}\right){\mathit{c}}_i}{c_s^4}\right]\cdot \mathit{f}.$$ (6)

The force term $\mathit{f}$ is the sum of two contributions: ${\mathit{f}}_{\text{ext}}$ accounting for external forces, and ${\mathit{f}}_{\text{IB}}$ taking into account the interaction between the erythrocyte membrane and its ambient and enclosed uid components

$$\mathit{f}={\mathit{f}}_{\text{ext}}+{\mathit{f}}_{\text{IB}}.$$ (7)

The form of the force ${\mathit{f}}_{\text{IB}}$ is discussed in § 2.4.

The fuid density $\rho$ and velocity $\mathit{u}$ are defined as the 0^th and 1^st moments of the distribution function

$$\rho (\mathit{x},t)=\sum _i{f}_i(\mathit{x},t),$$ (8a)

$$\mathit{u}(\mathit{x},t)=\left[\sum _i{\mathit{c}}_i{f}_i(\mathit{x},t)+\frac{\text{Δ}t}{2}\mathit{f}(\mathit{x},t)\right]/\rho (\mathit{x},t).$$ (8b)

For simplicity, the lattice spacing is set here equal to the time step as $\text{Δ}x=\text{Δ}t=1$ in lattice units, resulting in $c_s=1/\sqrt{3}$. We employ the D3Q19 lattice arrangement, for which the lattice velocities (in columns) are defined as

$${\mathit{c}}_i=\left[\begin{array}{ccccccccccccccccccc}0& 1& -1& 0& 0& 0& 0& 1& -1& 1& -1& 0& 0& 1& -1& 1& -1& 0& 0\\ 0& 0& 0& 1& -1& 0& 0& 1& -1& 0& 0& 1& -1& -1& 1& 0& 0& 1& -1\\ 0& 0& 0& 0& 0& 1& -1& 0& 0& 1& -1& 1& -1& 0& 0& -1& 1& -1& 1\end{array}\right],$$

and the weight coeffcients are given by

$$w_0=1/3,w_{1-6}=1/18,w_{7-18}=1/36.$$

2.2. Erythrocyte model

The red blood cell is modelled as a capsule of biconcave shape containing the cytoplasm enclosed by the cell’s infinitely thin membrane. Its stress-free biconcave shape is described by the following parametric equation, similarly to the one in the work of Pivkin & Karniadakis [65]

$$z=R\sqrt{1-\frac{x^2+y^2}{R^2}}\left[C_0+C_1\frac{x^2+y^2}{R^2}+C_2\frac{{\left(x^2+y^2\right)}^2}{R^4}\right],$$ (9)

where $\left(R,C_0,C_1,C_2\right)=(3.90\text{μm},0.1035805,1.001279,-0.561381)$. This results in a cell of diameter $D_0=7.80\text{μm}$ and maximum thickness $W_0=2.56\text{μm}$ with surface area and volume of $A_0=133{\text{μm}}^2$ and $V_0=93{\text{μm}}^3$, respectively. These measurements fall well within the range of those reported for healthy human RBCs [66]. As mentioned earlier, the cytoplasm is considered to be an incompressible and Newtonian fluid with kinematic viscosity about five times that of the blood plasma [48], that is ${\nu }_{\text{cyto}}=6.0\times {10}^{-6}{\text{m}}^2/\text{s}$.

The erythrocyte membrane is composed of an isotropic and elastic material. As discussed in §1, several constitutive laws have been proposed throughout the years to model the response of such membranes. Here, we focus the discussion on the Skalak, neo-Hookean and Yeoh laws.

In Skalak (SK) law [67], the strain energy function $W_{\text{s}}$ is given by

$$W_{\text{s}}^{\text{SK}}=\frac{G_{\text{s}}^{\text{SK}}}{4}\left(I_1^2+2I_1-2I_2+C^{\text{SK}}{I}_2^2\right),$$ (10)

where $G_{\text{s}}^{\text{SK}}$ denotes the surface shear elastic modulus associated with this law, and $C^{\text{SK}}$ is a dimensionless parameter representing area incompressibility. Large values of $C^{\text{SK}}$ ensure that the erythrocyte membrane is almost area-incompressible. $I_1$ and $I_2$ are the strain invariants of the Green-Lagrange strain tensor, and further details are provided in the Appendix.

For the neo-Hookean (NH) law, the strain energy function takes the form [27]

$$W_{\text{s}}^{\text{NH}}=\frac{G_{\text{s}}^{\text{NH}}}{2}\left(I_1-1+\frac{1}{I_2+1}\right).$$ (11)

This law does not restrict the area dilatation.

Yeoh (YE) law [68] is a cubic extension of the neo-Hookean model, for which the strain energy function is expressed as

$$W_{\text{s}}^{\text{YE}}=\frac{G_{\text{s}}^{\text{YE}}}{2}\left(I_1-1+\frac{1}{I_2+1}\right)+C^{\text{YE}}{\left(I_1-1+\frac{1}{I_2+1}\right)}^3,$$ (12)

where $C^{\text{YE}}$ is a parameter taken equal to $G_{\text{s}}^{\text{YE}}/30$. This value of $C^{\text{YE}}$ corresponds to the one found by Mills et al. [10] that best matches force-extension data from the optical tweezers experiment. Likewise to the neo-Hookean model, the area dilatation is unrestricted in Yeoh law.

The bending resistance of the erythrocyte membrane is described by the Helfrich bending energy [69] as follows

$${ℰ}_{\text{b}}=\frac{k_{\text{b}}}{2}\underset{S}{\int }{\left(2\kappa -c_0\right)}^2\text{d}S,$$ (13)

where $k_{\text{b}}$ denotes the bending elastic modulus, and $\kappa$, $c_0$ are the mean and spontaneous curvatures, respectively. The bending modulus takes the value $k_{\text{b}}=1.8\times {10}^{-19}\text{N}\cdot \text{m}$, as measured by Evans [70] via micropipette aspiration experiments. Here, the spontaneous curvature is set equal to 0. It is worth noting that the bending energy proposed by Helfrich [69] includes also a Gaussian curvature term, which can however be omitted here as its integral over a closed surface is a topological invariant according to the Gauss-Bonnet theorem.

Finally, in order to conserve the RBC volume, we consider the following volume conservation energy [71]

$${ℰ}_{\text{v}}=\frac{k_{\text{v}}}{2}\frac{{\left(V-V_0\right)}^2}{V_0},$$ (14)

where $k_{\text{v}}$ is a volume penalty coefficient, $V_0$ and $V$ represent respectively the RBC volume at time $t=0$ and subsequent times $t$. The volume penalty coefficient is set here equal to $k_{\text{v}}=0.1$, resulting in volume variations of less than 1%.

2.3. Finite element method

The erythrocyte membrane surface is discretized using Loop subdivision elements [72, 73], composed of linear triangles refined by a subdivision process. Here, we consider successive refinements of an icosahedron, known as the control mesh or level 0 of the subdivision, and project them onto the initial RBC biconcave shape, resulting in a triangular mesh of high homogeneity and isotropy [74]. After $N_{\text{ref}}$ refinements, the mesh is composed of $N_{\text{elem}}=20\times 4^{N_{\text{ref}}}$ triangular elements, and $N_{\text{ver}}=N_{\text{elem}}/2+2$ nodes, also known as vertices. The Loop subdivision surfaces offer improved numerical stability and accuracy due to their higher regularity compared to the standard linear or quadratic Lagrange $C^0$ elements. In the limit of infinite subdivisions, the triangular mesh, referred to as the limit surface, is $C^2$ continuous everywhere except at the so-called irregular vertices, namely the vertices that are not linked to exactly 6 elements, where it is only $C^1$. In the case of an icosahedron as the control mesh, there are 12 irregular vertices that are linked to only 5 elements. Any vertex introduced during the Loop subdivision process is by default regular. The surface force density ${\mathit{F}}_m^l$ exerted by the $l^{\text{th}}$ vertex located at ${\mathit{X}}_l$ onto the surrounding fluids can be computed as discussed in the Appendix.

2.4. Immersed boundary method

To reproduce the effect of ${\mathit{F}}_m^l$ on the fluid flow, denoted here by ${\mathit{f}}_{\text{IB}}$, the following spreading operation is used

$${\mathit{f}}_{\text{IB}}(\mathit{x},t)=𝓢\left[{\mathit{F}}_m^l\right](\mathit{x})=\sum _{l=1}^{N_{\text{ver}}}{\mathit{F}}_m^l{\delta }_h\left(\mathit{x}-{\mathit{X}}_l\right)\text{Δ}s,$$ (15)

where ${\delta }_h$ denotes the discretized Dirac delta function, and $\text{Δ}s$ represents the initial distance between two neighboring vertices. For the discretized Dirac delta function, the following formulation is considered here [75]

$${\delta }_h(r)=\{\begin{array}{ll}\frac{1}{4}\left[1+\cos \left(\frac{\pi r}{2}\right)\right],\hfill & \left|r\right|\le 2,\hfill \\ 0,\hfill & \left|r\right|>2.\hfill \end{array}$$ (16)

In the case of $r$ being a vector, $\mathit{r}=\left(r_x,r_y,r_z\right)$, the multidimensional ${\delta }_h$ is then given by ${\delta }_h(\mathit{r})={\delta }_h\left(r_x/\text{Δ}x\right){\delta }_h\left(r_y/\text{Δ}x\right){\delta }_h\left(r_z/\text{Δ}x\right)/\text{Δ}{x}^3$. Once the force ${\mathit{f}}_{\text{IB}}(\mathit{x},t)$ is known, the flow field, Eq. (8), can be obtained at the next time step $t+\text{Δ}t$ by solving the lattice Boltzmann equation, Eq. (1). The known velocity field $\mathit{u}(\mathit{x},t+\text{Δ}t)$ is then interpolated at the vertices as

$$\mathit{U}\left({\mathit{X}}_l,t+\text{Δ}t\right)=ℐ[\mathit{u}]\left({\mathit{X}}_l\right)=\sum _{\mathit{x}}\mathit{u}{\delta }_h\left(\mathit{x}-{\mathit{X}}_l\right){(\text{Δ}x)}^d,$$ (17)

with $d$ being the domain dimensionality, here $d=3$. The updated vertices position can be subsequently found by Euler’s rule

$${\mathit{X}}_l(t+\text{Δ}t)={\mathit{X}}_l(t)+\mathit{U}\left({\mathit{X}}_l,t+\text{Δ}t\right)\text{Δ}t.$$ (18)

This concludes one simulation time step.

3. Comparison of constitutive laws

3.1. Uniaxial extension

We consider here the case of an erythrocyte membrane subjected to uniaxial extension, where the principal tensions satisfy the conditions: ${\text{T}}_1\ne 0$ and ${\text{T}}_2=0$. As mentioned earlier, the uniaxial extension can be considered as the theoretical equivalent of the optical tweezers experiment. The following analysis provides relationships between the shear elastic moduli of the constitutive laws considered here, which will be employed in Section 4.1 to determine the appropriate values of $G_{\text{s}}^{\text{SK}}$, $G_{\text{s}}^{\text{NH}}$, and $G_{\text{s}}^{\text{YE}}$, allowing for a direct comparison between them.

It can readily be shown that the principal tension ${\text{T}}_1$ takes, respectively, the following form when the Skalak, neo-Hookean or Yeoh law is considered [11, 34]

$${\text{T}}_1^{\text{SK}}=\frac{G_{\text{s}}^{\text{SK}}}{{\lambda }_1{\lambda }_2}\left\{{\lambda }_1^2\left({\lambda }_1^2-1\right)+C^{\text{SK}}{\left({\lambda }_1{\lambda }_2\right)}^2\left[{\left({\lambda }_1{\lambda }_2\right)}^2-1\right]\right\},$$ (19a)

$${\text{T}}_1^{\text{NH}}=\frac{G_{\text{s}}^{\text{NH}}}{{\lambda }_1{\lambda }_2}\left[{\lambda }_1^2-\frac{1}{{\left({\lambda }_1{\lambda }_2\right)}^2}\right],$$ (19b)

$${\text{T}}_1^{\text{YE}}=\frac{G_{\text{s}}^{\text{YE}}}{{\lambda }_1{\lambda }_2}\left[{\lambda }_1^2-\frac{1}{{\left({\lambda }_1{\lambda }_2\right)}^2}\right]\times \left\{1+3C^{\text{YE}}{\left[{\lambda }_1^2+{\lambda }_2^2+\frac{1}{{\left({\lambda }_1{\lambda }_2\right)}^2}-3\right]}^2\right\}.$$ (19c)

Since the erythrocyte membrane is commonly modelled as an area-incompressible elastic material, the below area-incompressibility constraint should be considered: ${\lambda }_1{\lambda }_2=1$ [76]. Taking this constraint into account, Eqs. (19) can be simplified as

$${\text{T}}_1^{\text{SK}}=G_{\text{s}}^{\text{SK}}{\lambda }_1^2\left({\lambda }_1^2-1\right),$$ (20a)

$${\text{T}}_1^{\text{NH}}=G_{\text{s}}^{\text{NH}}\left({\lambda }_1^2-1\right),$$ (20b)

$${\text{T}}_1^{\text{YE}}=G_{\text{s}}^{\text{YE}}\left({\lambda }_1^2-1\right)\left[1+3C^{\text{YE}}{\left({\lambda }_1^2+\frac{1}{{\lambda }_1^2}-2\right)}^2\right].$$ (20c)

It should be mentioned that, under uniaxial extension, the Skalak law is strain-hardening, that is its tension grows superlinearly with the strain, whereas the neo-Hookean law is strain-softening, i.e. its tension increases sublinearly with the strain [25]. The Yeoh law exhibits a more complicated behaviour. At small deformations, it performs similarly to the neo-Hookean law. However, at moderate and large deformations, its nature, i.e. strain-softening or strain-hardening, varies due to the cubic term in Eq. (12) [68].

To correlate the shear elastic moduli of the neo-Hookean and Yeoh laws with respect to $G_{\text{s}}^{\text{SK}}$, the principal tensions ${\text{T}}_1^{\text{NH}}$ and ${\text{T}}_1^{\text{YE}}$, Eqs. (20b) and (20c), can be equated to ${\text{T}}_1^{\text{SK}}$, Eq. (20a). This equating results in the following relations

$$G_{\text{s}}^{\text{NH}}={\lambda }_1^2{G}_{\text{s}}^{\text{SK}},\text{and}$$ (21a)

$$G_{\text{s}}^{\text{YE}}=\frac{{\lambda }_1^2{G}_{\text{s}}^{\text{SK}}}{1+3C^{\text{YE}}{\left({\lambda }_1^2+{\lambda }_1^{-2}-2\right)}^2}.$$ (21b)

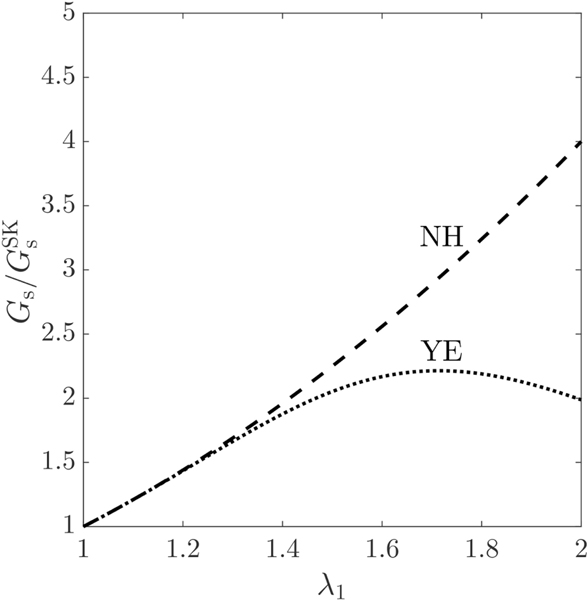
The dependence of the shear elastic modulus ratios $G_{\text{s}}^{\text{NH}}/G_{\text{s}}^{\text{SK}}$ and $G_{\text{s}}^{\text{YE}}/G_{\text{s}}^{\text{SK}}$ in Eqs. (21) on the principal extension ratio ${\lambda }_1$ is depicted in Fig. 1. As seen, the shear elastic modulus ratio for the neo-Hookean law increases monotonically with regard to ${\lambda }_1$. The ratio $G_{\text{s}}^{\text{YE}}/G_{\text{s}}^{\text{SK}}$ performs similarly to $G_{\text{s}}^{\text{NH}}/G_{\text{s}}^{\text{SK}}$ up to ${\lambda }_1\approx 1.3$, with differences being notable for ${\lambda }_1\ge 1.4$. It subsequently displays an increase up to ${\lambda }_1\approx 1.7$, with its degree of strain-softening, however, being less than that of the neo-Hookean law. After this point, a decrease in the dependence of $G_{\text{s}}^{\text{YE}}/G_{\text{s}}^{\text{SK}}$ on ${\lambda }_1$ can be observed. This trend variation physically represents the change in the nature of Yeoh law, from strain-softening to strain-hardening material. It should be noted that the threshold value of ${\lambda }_1$ for the change in Yeoh law’s nature to occur depends on the particular choice of the dimensionless parameter $C^{\text{YE}}$ in Eq. (12). As we are interested in the regime of moderate and large deformations, that is ${\lambda }_1\ge 1.4$, the following relations can be deduced from Fig. 1

$$G_{\text{s}}^{\text{NH}}\approx 2G_{\text{s}}^{\text{SK}},G_{\text{s}}^{\text{YE}}\approx 1.90G_{\text{s}}^{\text{SK}}\text{for}{\lambda }_1\approx 1.4,$$ (22a)

$$G_{\text{s}}^{\text{NH}}\approx 4G_{\text{s}}^{\text{SK}},G_{\text{s}}^{\text{YE}}\approx 1.99G_{\text{s}}^{\text{SK}}\text{for}{\lambda }_1=2.$$ (22b)

Figure 1:

Variation of the shear elastic modulus $G_{\text{s}}$ of the neo-Hookean (NH) and Yeoh (YE) laws, normalized with the shear elastic modulus of Skalak law $\left(G_{\text{s}}^{\text{SK}}\right)$, with respect to the principal extension ratio ${\lambda }_1$, so that all constitutive laws produce the same principal tension ${\text{T}}_1$.

3.2. Micropipette aspiration analysis

Through the following micropipette aspiration analysis, relationships between the shear elastic moduli of the constitutive laws are established, which will later be used in Section 4.2 to choose the $G_{\text{s}}^{\text{SK}}$, $G_{\text{s}}^{\text{NH}}$ and $G_{\text{s}}^{\text{YE}}$ values. It is worth noting that micropipette aspiration allows us to additionally compare the effect of constitutive law on the erythrocyte membrane response to deformations in the lateral plane, as opposed to the optical tweezers experiment where RBCs are subjected to axial and transverse deformations.

Evans [76, 77] proposed the following homonymous constitutive law, which has been extensively employed for fitting data in micropipette aspiration experiments

$$W_{\text{s}}^{\text{EV}}=\frac{G_{\text{s}}^{\text{EV}}}{2}\left[\frac{I_1+2}{\sqrt{I_2-1}}-1+C^{\text{EV}}{\left(\sqrt{I_2-1}-1\right)}^2\right].$$ (23)

$G_{\text{s}}^{\text{EV}}$ is the shear elastic modulus associated with this law, and the dimensionless parameter $C^{\text{EV}}$ represents the area dilatation modulus. The principal tension can be found as [11, 34]

$${\text{T}}_1^{\text{EV}}=G_{\text{s}}^{\text{EV}}\left[\frac{{\lambda }_1^2-{\lambda }_2^2}{2{\left({\lambda }_1{\lambda }_2\right)}^2}+C^{\text{EV}}\left({\lambda }_1{\lambda }_2-1\right)\right],$$ (24)

which, under the constraint of area-incompressibility [76], reduces to

$${\text{T}}_1^{\text{EV}}=G_{\text{s}}^{\text{EV}}\frac{{\lambda }_1^2+1}{2{\lambda }_1^2}\left({\lambda }_1^2-1\right).$$ (25)

It has been shown that, under uniaxial tension, the Evans law is strain-softening [34].

Following the analysis of Waugh & Evans [45], the principal extension ratio ${\lambda }_1$ at a point on the erythrocyte membrane outside the micropipette entrance is given by

$${\lambda }_1^2=1+{\left(\frac{R_{\text{pip}}}{r}\right)}^2\left(\frac{2L_{\text{asp}}}{R_{\text{pip}}}-1\right)\text{for}{L}_{\text{asp}}\ge R_{\text{pip}},$$ (26)

with $R_{\text{pip}}$ being the inner radius of the micropipette, and $L_{\text{asp}}$ the length of the RBC’s aspirated part. For the desired resultant ${\lambda }_1$, the micropipette suction pressure $\text{Δ}P$ can be found by integrating in the plane of the membrane from the micropipette tip outward as

$$\text{Δ}P=\frac{4}{R_{\text{pip}}}{\int }_{R_{\text{pip}}}^{\infty }\frac{{\text{T}}_s}{r}\text{d}r.$$ (27)

The maximum membrane shear resultant ${\text{T}}_s$ is given by the deviator of the principal tensions, namely ${\text{T}}_s=\left({\text{T}}_1-{\text{T}}_2\right)/2$. The principal tension ${\text{T}}_2$ for each law can be readily determined by substituting ${\lambda }_2=1/{\lambda }_1$, owing to the area-incompressibility constraint, into the corresponding formulation of ${\text{T}}_1$. Therefore, as shown in the work of Waugh & Evans [45], the maximum membrane shear resultant for Evans law can be expressed as

$${\text{T}}_s^{\text{EV}}=\frac{G_{\text{s}}^{\text{EV}}}{2}\left({\lambda }_1^2-{\lambda }_1^{-2}\right),$$ (28)

with the resulting suction pressure taking the form

$$\text{Δ}P=\frac{G_{\text{s}}^{\text{EV}}}{R_{\text{pip}}}\left[\frac{2L_{\text{asp}}}{R_{\text{pip}}}-1+\ln \left(\frac{2L_{\text{asp}}}{R_{\text{pip}}}\right)\right].$$ (29)

To establish the relations of the shear elastic moduli of the Skalak, neo-Hookean and Yeoh laws with respect to $G_{\text{s}}^{\text{EV}}$, we follow the same procedure as above. The maximum membrane shear resultants for the Skalak, neo-Hookean and Yeoh laws are found, respectively, to be

$${\text{T}}_s^{\text{SK}}=\frac{G_{\text{s}}^{\text{SK}}}{2}\left({\lambda }_1^2-{\lambda }_1^{-2}\right)\left({\lambda }_1^2+{\lambda }_1^{-2}-1\right),$$ (30a)

$${\text{T}}_s^{\text{NH}}=\frac{G_{\text{s}}^{\text{NH}}}{2}\left({\lambda }_1^2-{\lambda }_1^{-2}\right),$$ (30b)

$${\text{T}}_s^{\text{YE}}=\frac{G_{\text{s}}^{\text{YE}}}{2}\left({\lambda }_1^2-{\lambda }_1^{-2}\right)\left[1+3C^{\text{YE}}{\left({\lambda }_1^2+{\lambda }_1^{-2}-2\right)}^2\right],$$ (30c)

with the corresponding suction pressure being formulated as

$$\text{Δ}P=\frac{G_{\text{s}}^{\text{SK}}}{R_{\text{pip}}}\left(\frac{2L_{\text{asp}}}{R_{\text{pip}}}-1\right)\left(\frac{L_{\text{asp}}}{R_{\text{pip}}}+\frac{R_{\text{pip}}}{2L_{\text{asp}}}+\frac{1}{2}\right),$$ (31a)

$$\text{Δ}P=\frac{G_{\text{s}}^{\text{NH}}}{R_{\text{pip}}}\left[\frac{2L_{\text{asp}}}{R_{\text{pip}}}-1+\ln \left(\frac{2L_{\text{asp}}}{R_{\text{pip}}}\right)\right],$$ (31b)

$$\begin{gathered} \text{Δ}P=\frac{G_{\text{s}}^{\text{YE}}}{R_{\text{pip}}}\{\frac{2L_{\text{asp}}}{R_{\text{pip}}}-1+\ln 2+C^{\text{YE}}[8{\left(\frac{L_{\text{asp}}}{R_{\text{pip}}}\right)}^3-18{\left(\frac{L_{\text{asp}}}{R_{\text{pip}}}\right)}^2+12\frac{L_{\text{asp}}}{R_{\text{pip}}}+\frac{9}{2}\frac{R_{\text{pip}}}{L_{\text{asp}}}-\frac{3}{8}{\left(\frac{R_{\text{pip}}}{L_{\text{asp}}}\right)}^2 \\ -10+\ln 64]+\left(1+6C^{\text{YE}}\right)\ln \left(\frac{L_{\text{asp}}}{R_{\text{pip}}}\right)\}. \end{gathered}$$ (31c)

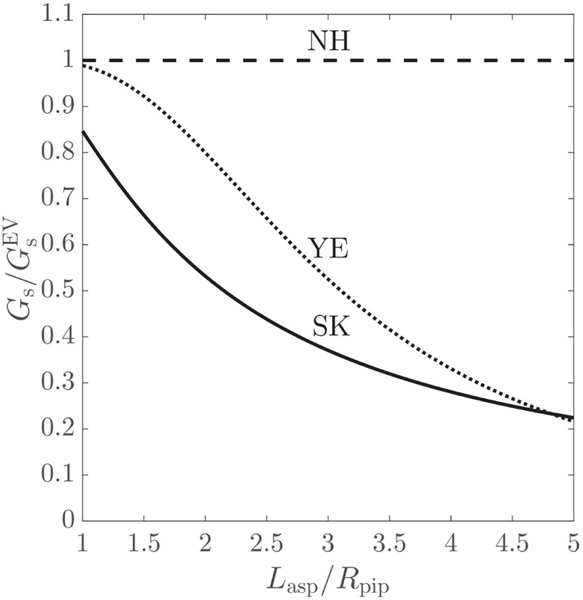
By combining Eqs. (31) with Eq. (29), the ratios $G_{\text{s}}^{\text{SK}}/G_{\text{s}}^{\text{EV}}$, $G_{\text{s}}^{\text{NH}}/G_{\text{s}}^{\text{EV}}$ and $G_{\text{s}}^{\text{YE}}/G_{\text{s}}^{\text{EV}}$ can be deduced, which, for simplicity, are illustrated in Fig. 2. For Skalak law, its shear elastic modulus, $G_{\text{s}}^{\text{SK}}$, drops for increasing dimensionless aspiration length. For neo-Hookean law, its shear elastic modulus does not change with varying $L_{\text{asp}}/R_{\text{pip}}$, remaining constant to $G_{\text{s}}^{\text{EV}}$. Yeoh law performs similarly to the neo-Hookean law for $L_{\text{asp}}/R_{\text{pip}}\le 1.5$, when the differences between the estimated $G_{\text{s}}^{\text{NH}}$ and $G_{\text{s}}^{\text{YE}}$ are less than 10%. At $L_{\text{asp}}/R_{\text{pip}}\approx 2.25$, a change in the curvature of the ratio $G_{\text{s}}^{\text{YE}}/G_{\text{s}}^{\text{EV}}$ line can be noted, from concave to convex, coinciding with the shift in Yeoh law’s nature, from strain-softening to strain-hardening. Yeoh law becomes more and more strain-hardening as the aspiration length increases, and, for $L_{\text{asp}}/R_{\text{pip}}\ge 4.85$, it has a higher degree of strain-hardening than Skalak law.

Figure 2:

Variation of the shear elastic modulus $G_{\text{s}}$ of the Skalak (SK), neo-Hookean (NH) and Yeoh (YE) laws, scaled with the shear elastic modulus of Evans law $\left(G_{\text{s}}^{\text{EV}}\right)$, with regard to the dimensionless aspiration length $L_{\text{asp}}/R_{\text{pip}}$, so that all constitutive laws result the same micropipette suction pressure $\text{Δ}P$.

4. Results

4.1. Optical tweezers

4.1.1. Computational setup

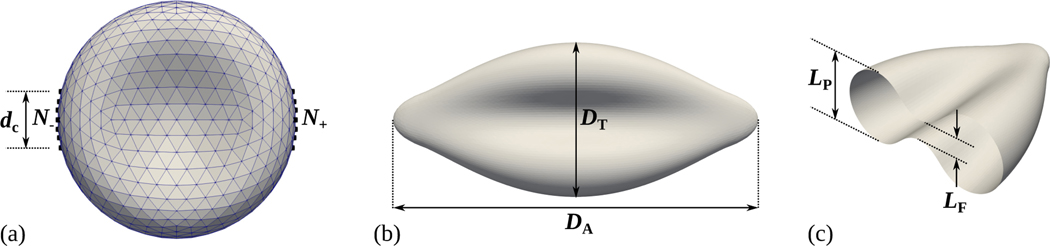
In the optical tweezers experiment of Mills et al. [10], two silica microbeads of diameter 4.12 μm are attached to diametrically opposite ends of a RBC. One microbead is optically trapped by a laser beam, thus remaining stationary, while the other one is binded to the surface of a glass slide allowing for motion and consequently stretching of the RBC. To computationally reproduce the physics of this experimental setup, a force ${\mathit{F}}_{\text{OT}}$ is applied to $N_{+}=\epsilon N_{\text{ver}}$ vertices, denoted by black square symbols in Fig. 3(a), of the erythrocyte membrane with the largest x-coordinates in the positive x-direction, and a force $-{\mathit{F}}_{\text{OT}}$ is correspondingly acting on $N_{-}=N_{+}$ vertices with the smallest x-coordinates in the negative x-direction. Hence, the force ${\mathit{F}}_{\text{OT}}^l=\pm {\mathit{F}}_{\text{OT}}/\left(\epsilon N_{\text{ver}}\right)$ is exerted on each vertex $l$ in ${\mathbb{N}}_{+}$ or ${\mathbb{N}}_{-}$, with ${\mathbb{N}}_{+}$ and ${\mathbb{N}}_{-}$ denoting the sets of the $N_{+}$ and $N_{-}$ vertices with the largest and smallest x-coordinates respectively, and it is simply added to Eq. (40) when the vertex $l\in {\mathbb{N}}_{+}\cup {\mathbb{N}}_{-}$. The vertex fraction $\epsilon$ is related to the diameter $d_c$ of the contact area between the microbeads and the RBC. When the RBC reaches mechanical equilibrium with the ambient fluid, its deformed shape can be characterized by an axial $D_{\text{A}}$ and transverse $D_{\text{T}}$ diameter, as shown in Fig. 3(b). The axial diameter is computed as $D_{\text{A}}=\left|x_{\max }-x_{\min }\right|$, where $x_{\max }$ and $x_{\min }$ are the maximum and minimum x-coordinates among the $N_{+}$ and $N_{-}$ vertices, respectively. The transverse diameter is calculated as $D_{\text{T}}=2\times {\max }_{l=1,\dots ,N_{\text{ver}}}\sqrt{{\left(y_l-c_y\right)}^2+{\left(z_l-c_z\right)}^2}$, with $c_y$ and $c_z$ being the $y$- and $z$-coordinates of the RBC’s center of mass. Following Sigüenza et al. [9], the in-plane $L_{\text{P}}$ and folding $L_{\text{F}}$ lengths, as defined in Fig. 3(c), are also measured at the deformed state.

Figure 3:

(a) Illustration of the computational setup used to simulate the optical tweezers experiment [10]. A stretching force is applied to $N_{+}$ and $N_{-}$ vertices, depicted by black square markers, representing physically the contact area of diameter $d_c$ between the silica microbeads and the RBC. (b, c) The axial $D_{\text{A}}$ and transverse $D_{\text{T}}$ diameters along with the in-plane $L_P$ and folding $L_{\text{F}}$ lengths characterize the deformation of the RBC, once the latter reaches mechanical equilibrium.

In our simulations, a RBC of diameter $D_0$ is immersed at the center of a rectangular domain of size $\left[-2D_0,2D_0\right]\times \left[-D_0,D_0\right]\times \left[-D_0/2,D_0/2\right]$, as in the work of Sigüenza et al. [9]. A domain resolution of $D_0/39$ is found to result in grid-independent solutions. In the experiment of Mills et al. [10], the ambient fluid is a phosphate-buffered saline (PBS) solution with bovine serum albumin (BSA) addition. Although the fluid dynamic viscosity is measured to be 1.3 × 10⁻³ Pa · s, no value is reported for the fluid density, which varies depending on the room temperature and the BSA percentage in the PBS solution between 1000 to 1100 kg/m³ [78]. Due to this uncertainty, the ambient fluid is considered to be blood plasma in our simulations, whose density and kinematic viscosity values are close to those of the fluid used in experiments. It should be noted that, although the choice of the fluid properties may have an effect on the transient phase, it does not affect the deformation of the RBC when the latter reaches mechanical equilibrium with the ambient fluid [8, 9]. A relaxation time of 1 is chosen for the ambient fluid, resulting in a value of 3 in the cytoplasmic region following the approach of Zhang et al. [64]. To accurately capture the deformation of the RBC, 5 successive refinements of an icosahedron are considered in the discretization process of the erythrocyte membrane. The ensuing mesh resolution of the RBC, $\text{Δ}s\approx 0.12\text{μm}$, is comparable to that employed by Mills et al. [10] in their simulations performed with the commercial software ABAQUS and finer than the one used in the work of Sigüenza et al. [9]. The resulting mesh resolution ratio, $\text{Δ}s/\text{Δ}{x}^{\prime }=0.6$, lies within the suggested IBM range, that is $0.5\le \text{Δ}s/\text{Δ}{x}^{\prime }\le 1.5$ [74]. Finally, the vertex fraction is taken equal to 0.02, corresponding to a contact area diameter of $2.0\text{μm}$ [79].

4.1.2. Choice of the shear elastic modulus value

Hénon et al. [41] measured the shear elastic modulus to be $G_{\text{s}}=2.5\pm 0.4\text{μN}/\text{m}$. However, this value was obtained by performing optical tweezers experiments in the linear, small strain regime $\left(\left|{\mathit{F}}_{\text{OT}}\right|\le 15\text{pN}\right)$. Yoon et al. [42] found experimentally the shear modulus to be $G_{\text{s}}=3-6\text{μN}/\text{m}$ in the moderate deformation regime $\left(\left|{\mathit{F}}_{\text{OT}}\right|<50\text{pN}\right)$. Mills et al. [10] predicted a value of $G_{\text{s}}=5.5\text{μN}/\text{m}$ by fitting the experimental mean values for the axial and transverse diameters considering $\left|{\mathit{F}}_{\text{OT}}\right|\le 88\text{pN}$ to the strain-softening Evans law [76] under a constant area constraint. Here, $G_{\text{s}}^{\text{SK}}=\{4.0,5.0\}\text{μN}/\text{m}$ is chosen to perform simulations with Skalak law, and these values lie well within the aforementioned experimental ranges. The parameter $C^{\text{SK}}$ in Eq. (10) is set equal to 100, which has been shown to ensure area incompressibility [9, 25]. Taking into account Eqs. (22a) and (22b), the shear elastic moduli for the neo-Hookean and Yeoh laws should be in the range of [8.0, 20.0] and $\left[7.6,10.0\right]\text{μN}/\text{m}$, respectively. The shear elastic moduli considered here for the neo-Hookean and Yeoh laws take respectively the values: $G_{\text{s}}^{\text{NH}}=\{10.0,12.0\}\text{μN}/\text{m}$ and $G_{\text{s}}^{\text{YE}}=10.0\text{μN}/\text{m}$. These values are within the expected theoretical range and the numerical limits found by Dao et al. [4] and Mills et al. [10] - $G_{\text{s}}^{\text{NH}}\in [11.1,17.7]\text{μN}/\text{m}$ and $G_{\text{s}}^{\text{NH}/\text{YE}}\in [5.3,11.3]\text{μN}/\text{m}$ in the corresponding works. The simulation parameters are finally summarized in Table 1.

Table 1:

Summary of the parameters for the optical tweezers simulation.

Parameter	Value
Computational domain size, $L\times H\times W$	$\left[-2D_0,2D_0\right]\times \left[-D_0,D_0\right]\times \left[-D_0/2,D_0/2\right]$
Domain resolution, $\text{Δ}{x}^{\prime }$	$D_0/39$
Fluid density, $\rho ={\rho }_{\text{plasma}}$	1025 kg/m3
Plasma kinematic viscosity, ${\nu }_{\text{amb}}={\nu }_{\text{plasma}}$	1.2 × 10−6 m2/s
Cytoplasm kinematic viscosity, ${\nu }_{\text{cyto}}$	6.0 × 10−6 m2/s
Kinematic viscosity ratio, $\lambda ={\nu }_{\text{cyto}}/{\nu }_{\text{amb}}$	5.0
Relaxation time, $\tau$	1 for the plasma and 3 for the cytoplasm
RBC’s center of mass, $\left(c_x,c_y,c_z\right)$	(0,0,0)
RBC discretization, $\left(N_{\text{ref}},N_{\text{elem}},N_{\text{ver}}\right)$	(5,20480,10242)
Shear elastic modulus, $G_{\text{s}}$	$G_{\text{s}}^{\text{SK}}=\{4.0,5.0\}\text{μN}/\text{m}\left(C^{\text{SK}}=100\right)$ $G_{\text{s}}^{\text{NH}}=\{10.0,12.0\}\text{μN}/\text{m}$ $G_{\text{s}}^{\text{YE}}=10.0\text{μN}/\text{m}$
Bending elastic modulus, $k_{\text{b}}$	$1.8\times {10}^{-19}\text{N}\cdot \text{m}$
Volume penalty coefficient, $k_{\text{v}}$	0.1
Vertex fraction, $\epsilon$	0.02
Contact area diameter, $d_{\text{c}}$	$2.0\text{μm}$

4.1.3. Effect on the axial and transverse diameters

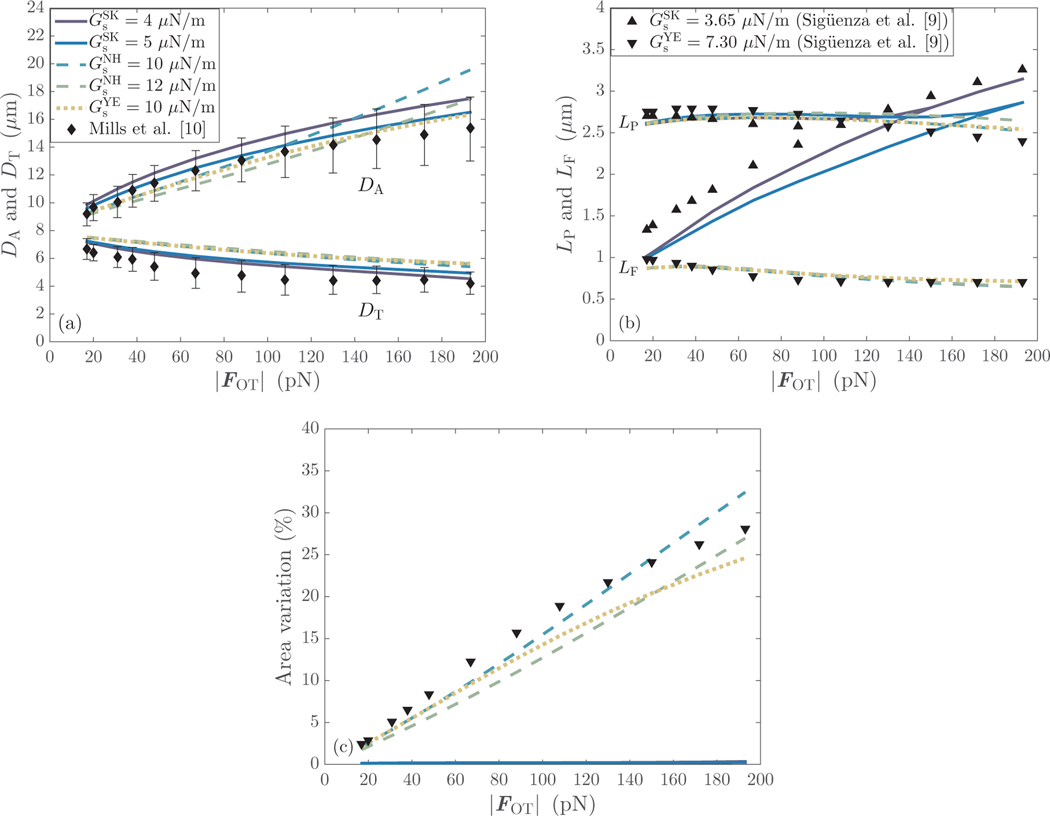
Figure 4(a) shows the results for the axial and and transverse diameters as obtained by the different constitutive laws. For Skalak law with $G_{\text{s}}^{\text{SK}}=4\text{μN}/\text{m}$, the results for both $D_{\text{A}}$ and $D_{\text{T}}$ fall within the experimental limits of Mills et al. [10]. When $G_{\text{s}}^{\text{SK}}=5\text{μN}/\text{m}$, the axial diameter is captured perfectly, while small discrepancies from the upper limit of the experimental range can be observed for the transverse diameter at $\left|{\mathit{F}}_{\text{OT}}\right|\le 108\text{pN}$. These discrepancies are, however, less than 1.5%. This data indicates that the range of [4.0,5.0] $\text{μN}/\text{m}$ is the recommended one for Skalak law. It is clear from Fig. 4(a) that lower values of $G_{\text{s}}^{\text{SK}}$ may result in an overprediction of $D_{\text{A}}$, while higher values may cause an overprediction of $D_{\text{T}}$. For the neo-Hookean model with $G_{\text{s}}^{\text{NH}}=10\text{μN}/\text{m}$, deviations from the experimental results occur for the axial diameter at $\left|{\mathit{F}}_{\text{OT}}\right|>150\text{pN}$, while the transverse diameter is consistently overpredicted with an average relative error of ∼ 8%. A similar trend can be noted for $D_{\text{T}}$ in the simulations performed with the neo-Hookean and Yeoh laws by Mills et al. [10]. It is noteworthy that the axial diameter of a RBC undergoing large deformations can be adequately captured at a higher value of $G_{\text{s}}^{\text{NH}}$, without the latter having a significant effect, however, on the transverse diameter. For Yeoh law, the axial diameter is resolved well, while the transverse one is overestimated, as expected. It is worth mentioning that the neo-Hookean with $G_{\text{s}}^{\text{NH}}=10\text{μN}/\text{m}$ and Yeoh laws produce identical results for both $D_{\text{A}}$ and $D_{\text{T}}$ at $\left|{\mathit{F}}_{\text{OT}}\right|\le 48\text{pN}$ when the RBC stretches up to ∼ 40% of its original size. Notable differences in $D_{\text{A}}$ between the two models occur at $\left|{\mathit{F}}_{\text{OT}}\right|>88\text{pN}$ when the RBC deforms up to ∼ 65% of its initial size. The variations in $D_{\text{T}}$ are visible only after $\left|{\mathit{F}}_{\text{OT}}\right|>130\text{pN}$. Finally, the results for $D_{\text{A}}$ of Yeoh law can be seen to tend to those of Skalak law with $G_{\text{s}}^{\text{SK}}=5\text{μN}/\text{m}$ for high values of the stretching force.

Figure 4:

(a) Comparison of the axial ($D_{\text{A}}$) and transverse ($D_{\text{T}}$) diameters obtained for the different constitutive laws with the experimental results of Mills et al. [10]. (b) Evolution of the in-plane ($L_P$) and folding ($L_{\text{F}}$) lengths with the stretching force magnitude, and comparison with the numerical results of Sigüenza et al. [9]. (c) Variation of the erythrocyte membrane area with $\left|{\mathit{F}}_{\text{OT}}\right|$.

4.1.4. Effect on the in-plane and folding lengths

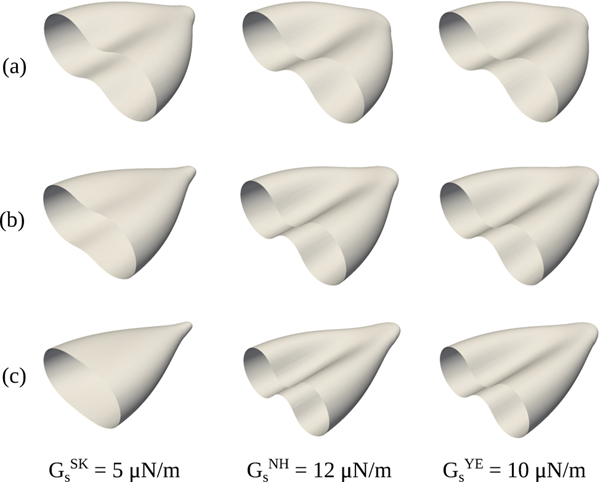
The results for the in-plane and folding lengths are presented in Fig. 4(b) and compared qualitatively with those of Sigüenza et al. [9] due to the differences in $G_{\text{s}}$. For Skalak law, the in-plane length does not experience initially significant changes, while the folding length increases considerably with $\left|{\mathit{F}}_{\text{OT}}\right|$. At a certain stretching force magnitude, depending on the stiffness of the erythrocyte membrane, the in-plane and folding lengths become identical, indicating that the RBC transitions from a biconcave to a rounded shape. This is clearly demonstrated in Fig. 5. After this transition point, a further increase in $\left|{\mathit{F}}_{\text{OT}}\right|$ results in a more circular RBC shape. It is worth noting that this transition occurs at $\left|{\mathit{F}}_{\text{OT}}\right|=\{150,172\}\text{pN}$ when $G_{\text{s}}^{\text{SK}}=\{4.0,5.0\}\text{μN}/\text{m}$, respectively. For the neo-Hookean and Yeoh laws, the in-plane and folding lengths evolve in parallel, suggesting that the RBC retains its biconcave shape, as illustrated in Fig. 5. The in-plane length varies slightly with $\left|{\mathit{F}}_{\text{OT}}\right|$. The following mean and deviation values for $L_{\text{P}}$ are reported: $\overline{L_{\text{P}}}\pm L_{\text{P}}^{\prime }=\{2.60\pm 0.08,2.67\pm 0.06,2.61\pm 0.07\}\text{μm}$ for the neo-Hookean with $G_{\text{s}}^{\text{NH}}=\{10.0,12.0\}\text{μN}/\text{m}$ and Yeoh laws, respectively. The folding length initially experiences a modest increase, with a relative difference of less than 3.5% in all cases, and then gradually decreases to ∼ 18 − 26% of its initial folding length. It is worth noting that the neo-Hookean and Yeoh laws predict almost identical values of $L_{\text{P}}$, with the mean relative discrepancy being 0.1%, for the same shear elastic modulus $G_{\text{s}}=10.0\text{μN}/\text{m}$. For the increased $G_{\text{s}}^{\text{NH}}=12.0\text{μN}/\text{m}$, the results of the in-plane length deviate from those of $G_{\text{s}}^{\text{NH}}=10.0\text{μN}/\text{m}$ at $\left|{\mathit{F}}_{\text{OT}}\right|\ge 48\text{pN}$. The above observations indicate that differences in the predicted in-plane length occur due to a variation in $G_{\text{s}}$ rather the cubic extension term in Yeoh law. Interestingly, Skalak law with $G_{\text{s}}^{\text{SK}}=4.0$ and $5.0\text{μN}/\text{m}$ predicts similar values of $L_{\text{P}}$ to those corresponding to $G_{\text{s}}^{\text{NH}/\text{YE}}=10.0\text{μN}/\text{m}$ and $G_{\text{s}}^{\text{NH}}=12.0\text{μN}/\text{m}$ at $\left|{\mathit{F}}_{\text{OT}}\right|\le 108$ and 150 pN, respectively. Regarding the folding length, the results for the neo-Hookean model overlap, while those of Yeoh increasingly deviate when $\left|{\mathit{F}}_{\text{OT}}\right|>108\text{pN}$. Finally, the results of both $L_{\text{P}}$ and $L_{\text{F}}$ considering Yeoh law are close to the reference ones of Sigüenza et al. [9] despite the difference in $G_{\text{s}}^{\text{YE}}$.

Figure 5:

Visualization of the deformed red blood cell shape at: (a) $\left|{\mathit{F}}_{\text{OT}}\right|=67\text{pN}$, (b) $\left|{\mathit{F}}_{\text{OT}}\right|=130\text{pN}$, and (c) $\left|{\mathit{F}}_{\text{OT}}\right|=193\text{pN}$. Due to symmetry, only half of the erythrocyte membrane is presented.

4.1.5. Effect on the erythrocyte membrane area

The area variation, defined as: $\left|A-A_0\right|/A_0\times 100(\text{\%})$, with $\left|{\mathit{F}}_{\text{OT}}\right|$ is shown in Fig. 4(c). It is obvious that Skalak law causes negligible variations in the erythrocyte membrane area when $C=100$. The results at $G_{\text{s}}^{\text{SK}}=4.0$ and $5.0\text{μN}/\text{m}$ are superimposed, and a maximum area variation of 0.35% and 0.25% is respectively found for each case. This agrees well with the value of 0.30% reported by Sigüenza et al. [9] where $G_{\text{s}}^{\text{SK}}=3.65\text{μN}/\text{m}$ and $C=100$ are considered. For the neo-Hookean model, the area dilatation increases linearly with the stretching force magnitude, and reaches a maximum value of 32.5% and 27.0% at $G_{\text{s}}^{\text{NH}}=10.0$ and $12.0\text{μN}/\text{m}$, correspondingly. Similarly to the observations made for $D_{\text{A}}$, Yeoh law results in the same area dilatation as in the case of $G_{\text{s}}^{\text{NH}}=10.0\text{μN}/\text{m}$ at $\left|{\mathit{F}}_{\text{OT}}\right|\le 67\text{pN}$. It is worth noting that the results curve follows a similar trend to that of Sigüenza et al. [9]. The maximum area dilatation is, however, lower than the reference one, 25.0% as opposed to 28.0%, due to the stiffer erythrocyte membrane considered in the current work.

4.1.6. Effect on the erythrocyte morphology

Finally, the red blood cell shapes are depicted for different magnitudes of the stretching force and constitutive laws in Fig. 5. The most important feature to note here is the transition of the erythrocyte membrane from a biconcave to a rounded shape in the case of Skalak law, and the conservation of the RBC’s biconcave shape when the neo-Hookean or Yeoh model is considered, as mentioned earlier. Sigüenza et al. [9] reported that the same shape transition as for Skalak law could be observed when simulations were performed with Yeoh law while imposing an area conservation constraint at the same time. This implies that the shape transition occurs due to the area incompressibility, rather than Skalak law itself. Although the erythrocyte membrane is known to be area incompressible, with an area increase of 3 to 4% resulting in cell lysis [80], the current constitutive laws are unable to capture accurately the shape of a red blood cell undergoing moderate/large deformations under the physically correct area incompressibility constraint. The rounded shape found numerically does not correspond to reality, as Mills et al. [10] reported that a similar folding to the one occuring for the neo-Hookean or Yeoh law, when the area dilatation is not restrained, in Fig. 5 could be experimentally observed. Lastly, it would be worth exploring in future studies whether a non-zero spontaneous curvature affects the erythrocyte morphology. Sinha & Graham [8] studied the effect of spatially-varying spontaneous curvature, that is biconcave discoid, oblate spheroid, and sphere spontaneous shapes, on the axial and transverse diameters of a red blood cell subjected to optical tweezers stretching, when the Skalak law is considered, and they found that its effect is negligible. However, it is not mentioned whether the different spontaneous curvatures influenced the morphology of the deformed red blood cell.

4.2. Micropipette aspiration

4.2.1. Computational setup

In the experiment of Waugh & Evans [45], flaccid red blood cells are aspirated into a pipette by a suction pressure $\text{Δ}P$. This pressure difference is computationally realized by implementing the Zou-He boundary scheme adapted to the D3Q19 lattice arrangement [81] at the faces perpendicular to the pipette axis. Once the RBC is in mechanical equilibrium with the surrounding fluid for a given $\text{Δ}P$, the length $L_{\text{asp}}$ of its aspirated part, shown in Fig. 6(a), is computed as the distance from the tip of the pipette to the vertex of the erythrocyte membrane located along the pipette axis with the largest x-coordinate [3].

Figure 6:

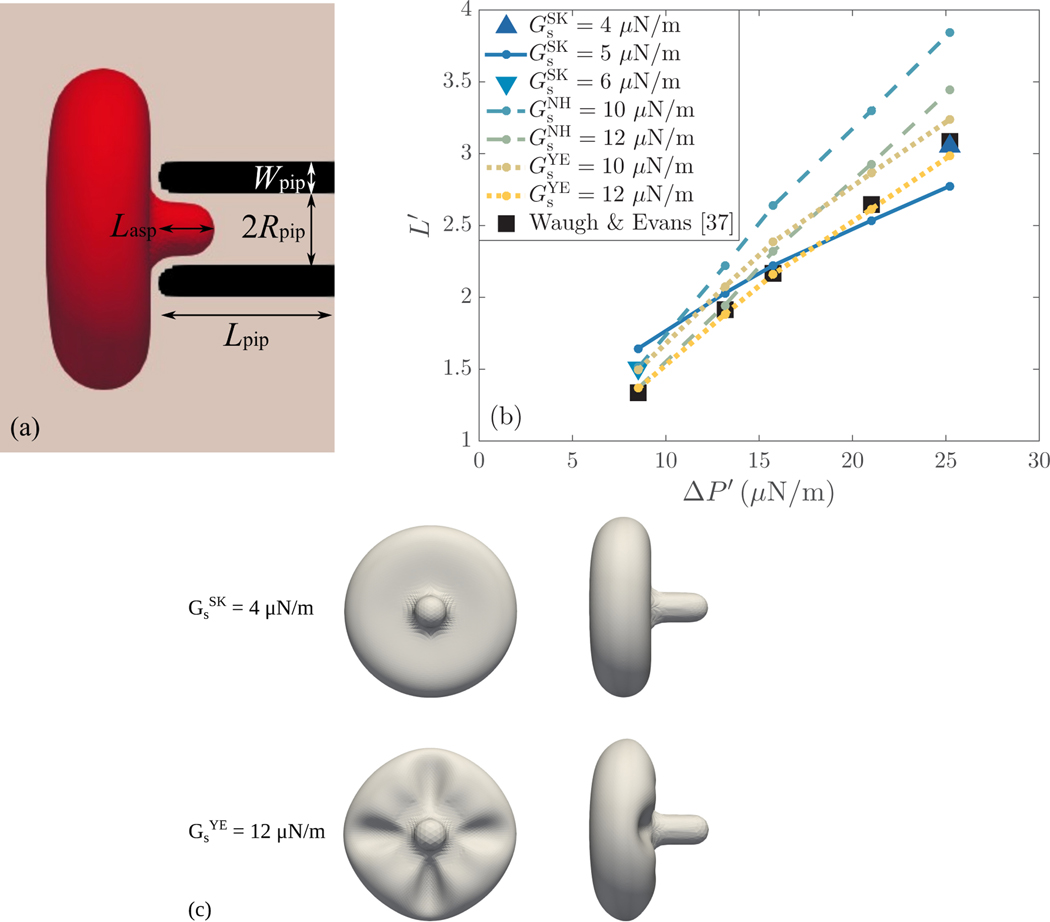
(a) Schematic diagram of the computational setup employed in the micropipette aspiration simulations. A red blood cell is aspirated into a pipette of length $L_{\text{pip}}$, inner radius $R_{\text{pip}}$ and thickness $W_{\text{pip}}$. When the RBC reaches mechanical equilibrium, its deformation is characterized by the aspiration length $L_{\text{asp}}$. (b) Comparison of the dimensionless aspiration lengths $L^{\prime }=L_{\text{asp}}/R_{\text{pip}}$ found by the different constitutive laws at various (normalized) pressure differences $\text{Δ}{P}^{\prime }=\text{Δ}P\cdot R_{\text{pip}}/2$ with the experimental results of Waugh & Evans [45]. (c) Visualization of the aspirated RBC shape for $G_{\text{s}}^{\text{SK}}=4.0\text{μN}/\text{m}$ and $G_{\text{s}}^{\text{YE}}=12.0\text{μN}/\text{m}$ at $\text{Δ}{P}^{\prime }=25.2\text{μN}/\text{m}$.

In the simulations, the RBC and micropipette are immersed inside a rectangular domain of dimensions $L\times H\times W=8.6\text{μm}\times 11.5\text{μm}\times 11.5\text{μm}$, similarly to the work of Balogh & Bagchi [53]. The pipette is modelled as a rigid, solid cylinder with rounded inlet end and thickness $W_{\text{pip}}=0.8\text{μm}$. Its inner radius $R_{\text{pip}}$ and length $L_{\text{pip}}$ are 0.9 and $4.3\text{μm}$, respectively. The pipette dimensions considered here are the same as those in Balogh & Bagchi [53]. The no-slip condition is enforced at the pipette walls by the half-way bounce-back boundary scheme [82]. The RBC’s center of mass is initially placed at a horizontal distance of $1.6\text{μm}$ from the tip of the pipette. Both the RBC and micropipette are surrounded by a fluid with density and viscosity similar to water. Finally, a resolution of $0.088\text{μm}$ and 5 successive refinements are employed respectively in the discretization of the computational domain and erythrocyte membrane, resulting in $\text{Δ}s/\text{Δ}{x}^{\prime }\approx 1.4$. These resolutions are on a par with those in Balogh & Bagchi [53].

4.2.2. Choice of the shear elastic modulus value

Using micropipettes of inner radius $<0.5\text{μm}$, Evans & La Celle [43] estimated the shear elastic modulus to be $G_{\text{s}}=7.0\text{μN}/\text{m}$ by fitting the experimental data for the aspiration length to Evans law. Considering the spherical cap model, Chien et al. [44] found a good agreement with experimental results for $G_{\text{s}}=4.2\text{μN}/\text{m}$. Waugh & Evans [45] studied the effect of temperature variations on the shear elastic modulus. At 35.3 ^°C, they obtained a value of $6.07\pm 1.08\text{μN}/\text{m}$ for $G_{\text{s}}$ and its standard deviation. Similarly, Linderkamp & Meiselman [46] measured $G_s=6.0\pm 1.1\text{μN}/\text{m}$. In a later study, Evans et al. [47] re-evaluated based on Evans law the shear elastic modulus to be $G_{\text{s}}=9.0\pm 1.7\text{μN}/\text{m}$ by accurately measuring the inner diameter of the micropipettes. As pointed out by Hochmuth & Waugh [83], greater weight should be given to this value, as a 20% error in the measurement of $R_{\text{pip}}$ results in a 40% error in the $G_{\text{s}}$ estimation. Assuming thus that $G_{\text{s}}^{\text{EV}}=9.0\pm 1.7\text{μN}/\text{m}$ and taking into account the micropipette aspiration analysis in §3.2, the corresponding values of the shear elastic modulus can be obtained for the Skalak, neo-Hookean and Yeoh laws. For the range of pressure differences and, therefore, aspiration lengths considered here, it is found that $G_{\text{s}}^{\text{SK}}\in [2.6,7.7]\text{μN}/\text{m}$, $G_{\text{s}}^{\text{NH}}\in [7.3,10.7]\text{μN}/\text{m}$ and $G_{\text{s}}^{\text{YE}}\in [3.7,10.2]\text{μN}/\text{m}$. As mentioned by Dimitrakopoulos [11], the values range of $G_{\text{s}}$ for the neo-Hookean and Yeoh laws should be scaled up by a factor of $1.\overline{3}$, resulting in $G_{\text{s}}^{\text{NH}}\in [9.7,14.3]\text{μN}/\text{m}$ and $G_{\text{s}}^{\text{YE}}\in [4.9,13.6]\text{μN}/\text{m}$, to implicitly account for the area incompressibility constraint, which is satisfied in the cases of Evans and Skalak laws by explicitly assigning a large value to the area dilatation modulus. Here, we have chosen: $G_{\text{s}}^{\text{SK}}=\{4.0,5.0,6.0\}\text{μN}/\text{m}$ and $G_{\text{s}}^{\text{NH}/\text{YE}}=\{10.0,12.0\}\text{μN}/\text{m}$, which are within the theoretically predicted ranges. Although the values of $G_{\text{s}}^{\text{YE}}$ lie towards the upper theoretical limit, they were chosen such that a one-to-one comparison is allowed between the results of the neo-Hookean and Yeoh laws. The summary of the simulation parameters is finally shown in Table 2.

Table 2:

Summary of the parameters for the micropipette aspiration simulation.

Parameter	Value
Computational domain size, $L\times H\times W$	$8.6\text{μm}\times 11.5\text{μm}\times 11.5\text{μm}$
Pipette’s length, radius, thickness, $\left(L_{\text{pip}},R_{\text{pip}},W_{\text{pip}}\right)$	(4.3, 0.9, 0.8) μm
Domain resolution, $\text{Δ}{x}^{\prime }$	0.088 μm
Fluid density, $\rho ={\rho }_{\text{water}}$	1000 kg/m3
Water kinematic viscosity, ${\nu }_{\text{amb}}={\nu }_{\text{water}}$	1.0 × 10−6 m2/s
Cytoplasm kinematic viscosity, ${\nu }_{\text{cyto}}$	6.0 × 10−6 m2/s
Kinematic viscosity ratio, $\lambda ={\nu }_{\text{cyto}}/{\nu }_{\text{amb}}$	6.0
Relaxation time, $\tau$	1 for the water and 3.5 for the cytoplasm
RBC’s center of mass, $\left(c_x,c_y,c_z\right)$	(−1.6,0,0) μm
RBC discretization, $\left(N_{\text{ref}},N_{\text{elem}},N_{\text{ver}}\right)$	(5,20480, 10242)
Shear elastic modulus, $G_{\text{s}}$	$G_{\text{s}}^{\text{SK}}=\{4.0,5.0,6.0\}\text{μN}/\text{m}\left(C^{\text{SK}}=100\right)$
	$G_{\text{s}}^{\text{NH}}=\{10.0,12.0\}\text{μN}/\text{m}$
	$G_{\text{s}}^{\text{YE}}=\{10.0,12.0\}\text{μN}/\text{m}$
Bending elastic modulus, $k_{\text{b}}$	1.8 × 10−19 N · m
Volume penalty coefficient, $k_{\text{v}}$	0.1

4.2.3. Effect on the aspiration length and the erythrocyte membrane area

Figure 6(b) presents the results of the dimensionless aspiration length $L^{\prime }=L_{\text{asp}}/R_{\text{pip}}$ as a function of the normalized pressure difference $\text{Δ}{P}^{\prime }=\text{Δ}P\cdot R_{\text{pip}}/2$. The results for the different constitutive laws are compared with the experimental ones of Waugh & Evans [45]. Considering Skalak law with $G_{\text{s}}^{\text{SK}}=5.0\text{μN}/\text{m}$, a good agreement with the experimental results can be reached only for the intermediate pressure differences, with the relative error in $L^{\prime }$ being less than 6.1%. At $\text{Δ}{P}^{\prime }=8.5$ and $25.2\text{μN}/\text{m}$, the discrepancy in the prediction of $L^{\prime }$ is higher than 20 and 10%, respectively. By increasing the erythrocyte membrane stiffness to $G_{\text{s}}^{\text{SK}}=6.0\text{μN}/\text{m}$, a better agreement with the experimental estimation of $L^{\prime }$ can be obtained at $\text{Δ}{P}^{\prime }=8.5\text{μN}/\text{m}$, with the relative error reduced to 12.8%. A further increase in $G_{\text{s}}^{\text{SK}}$, such as $7.0\text{μN}/\text{m}$, would improve the agreement with the reference result of Waugh & Evans [45] for the lowest $\text{Δ}{P}^{\prime }$. Similarly, the computationally predicted $L^{\prime }$ at $\text{Δ}{P}^{\prime }=25.2\text{μN}/\text{m}$ agrees excellently with the corresponding experimentally determined value when reducing the RBC stiffness to $G_{\text{s}}^{\text{SK}}=4.0\text{μN}/\text{m}$. The relative error is less than 1.1%. It is noteworthy that both $G_{\text{s}}^{\text{SK}}=7.0$ and $4.0\text{μN}/\text{m}$ for which an excellent agreement with the reference results at the lowest and highest $\text{Δ}{P}^{\prime }$ can be respectively expected or observed correspond to values of $G_{\text{s}}^{\text{EV}}$ close its upper limit, that is $G_{\text{s}}^{\text{EV}}=10.7\text{μN}/\text{m}$. For the neo-Hookean law with $G_{\text{s}}^{\text{NH}}=10.0\text{μN}/\text{m}$, corresponding to $G_{\text{s}}^{\text{EV}}=7.5\text{μN}/\text{m}$, the aspiration length is significantly overestimated in all cases, with the relative error being 13 − 25%. Increasing $G_{\text{s}}^{\text{NH}}$ to $12.0\text{μN}/\text{m}$, corresponding to $G_{\text{s}}^{\text{EV}}=9.0\text{μN}/\text{m}$, results in a good agreement with the experimental data at $\text{Δ}{P}^{\prime }<20.0\text{μN}/\text{m}$. The relative differences in $L^{\prime }$ are less than 2.5% at $\text{Δ}{P}^{\prime }=8.5$ and $13.2\text{μN}/\text{m}$ and 7.0% at $\text{Δ}{P}^{\prime }=15.8\text{μN}/\text{m}$. The deviation observed for the higher pressure differences could be reduced if a higher value of $G_{\text{s}}^{\text{NH}}$ was considered, for example $14.0\text{μN}/\text{m}$. This value corresponds to $G_{\text{s}}^{\text{EV}}=10.5\text{μN}/\text{m}$. The Yeoh law with $G_{\text{s}}^{\text{YE}}=10.0\text{μN}/\text{m}$ performs adequately with the discrepancies in the estimated aspiration length ranging from 5% to 12%. An excellent agreement can be achieved by increasing $G_{\text{s}}^{\text{YE}}$ to $12.0\text{μN}/\text{m}$, with the relative error in $L^{\prime }$ being less than 3.5% in all cases. It is worth mentioning that, as expected by the micropipette aspiration analysis in §3.2, the neo-Hookean and Yeoh laws predict similar aspiration lengths for the same value of shear elastic modulus at $\text{Δ}{P}^{\prime }<10.0\text{μN}/\text{m}$, for which $L^{\prime }\le 1.5$. It is clear that only Yeoh law is capable of accurately estimating the aspiration length at the whole range of pressure differences for a single value of shear elastic modulus. Finally, it should be noted that, despite the large deformations the aspirated RBC undergoes, the variations in the erythrocyte membrane area are negligible for all constitutive laws. For Skalak law, the area dilatation is restricted to 0.15%. For neo-Hookean and Yeoh laws, the maximum area dilatation is respectively found to be 0.8% and 0.3%.

4.2.4. Effect on the erythrocyte morphology

Although both the neo-Hookean and Yeoh laws satisfy implicitly the area-incompressibility constraint in the micropipette aspiration simulations performed here, differences in the aspirated RBC shape found by the aforementioned and Skalak laws were observed. Figure 6(c) illustrates the erythrocyte membrane shapes as obtained by Skalak and Yeoh laws at the highest pressure difference, $\text{Δ}{P}^{\prime }=25.2\text{μN}/\text{m}(\text{Δ}P=56\text{Pa})$. Results are presented for $G_{\text{s}}^{\text{SK}}=4.0\text{μN}/\text{m}$ and $G_{\text{s}}^{\text{YE}}=12.0\text{μN}/\text{m}$ since an excellent agreement with the experimentally estimated aspiration length could be achieved for these values of shear elastic modulus in both cases. The shapes resulting by the use of the neo-Hookean law are omitted as they are identical to those found by employing Yeoh law. As can be seen, the erythrocyte membrane exhibits wrinkling at the part of its exterior surface being close to the pipette tip when Yeoh law is considered. At $\text{Δ}{P}^{\prime }<15.0\text{μN}/\text{m}$, all constitutive laws produce the same RBC shape. The wrinkling appears slightly in the neo-Hookean and Yeoh law cases at $\text{Δ}{P}^{\prime }=15.8\text{μN}/\text{m}(\text{Δ}P=35\text{Pa})$, and it becomes more apparent at the higher pressure differences $(\text{Δ}P\ge 45\text{Pa})$. Folding/buckling of the erythrocyte membrane has been reported to occur during micropipette aspiration experiments [44, 46]. Evans et al. [47] observed such wrinkling when performing aspiration experiments with normal and sickle erythrocytes in micropipettes with inner diameter of 1.5 μm at a suction pressure of 45 Pa. It is expected that wrinkling will appear at lower suction pressures for micropipettes of higher inner diameter, which facilitate the aspiration of erythrocytes. Here, the threshold suction pressure for wrinkling to occur is evaluated at 35 Pa for micropipettes with inner diameter of $1.8\mathrm{\mu m}$, while it can be easily observed at $\text{Δ}P\ge 45\text{Pa}$. These experimental observations suggest that the RBC shape found by the neo-Hookean and Yeoh laws may correspond to reality; however, more evidence should be provided in future micropipette aspiration experiments to verify the exact wrinkling morphology.

5. Conclusions

Given the molecular structure complexity of red blood cells, it should not be expected that any of the constitutive laws, currently available in the literature, may accurately predict all potential erythrocyte behaviours [48]. Yet, it is essential to elucidate their capability of accurately capturing the erythrocyte behaviour in terms of different levels of deformation. The present work provides insight into the range of applicability of the most commonly used constitutive laws in the modelling of the erythrocyte membrane response, that is the Skalak, neo-Hookean, and Yeoh laws. We have focused on the moderate and large deformation regime, which is commonly encountered also in physiological settings. Two configurations, namely optical tweezers and micropipette aspiration, have been examined here by means of computational modelling. These configurations allow us to rigorously compare constitutive laws for two reasons. First, experimental measurements are available in the literature, and, second, relationships between the shear elastic modulus values of the different constitutive laws can be theoretically derived. Finally, these configurations allow us to cover deformations across all planes, with the erythrocyte being subjected to deformations in the axial and transverse planes in the optical tweezers experiment, and in the lateral plane during micropipette aspiration.

For the optical tweezers experiment, it has been found that all constitutive laws considered here are able to adequately predict the force-extension experimental data, i.e. the axial and transverse diameters, over the full deformation range for a constant value of their shear elastic modulus. For Skalak law, the optimal value of $G_{\text{s}}$ lies between 4.0 and $5.0\text{μN}/\text{m}$, while this value raises up to 12.0 and $10.0\text{μN}/\text{m}$ when considering, respectively, the neo-Hookean and Yeoh laws. Although these values of $G_{\text{s}}^{\text{NH}}$ and $G_{\text{s}}^{\text{YE}}$ result in a good agreement with experimental data for the axial diameter of the stretched erythrocyte, a slight overprediction of ∼ 8% appeared to occur for the transverse diameter. It is worth mentioning that, as predicted by the theoretical analysis of uniaxial extension, the neo-Hookean and Yeoh laws produce identical deformation in the axial direction at $\left|{\mathit{F}}_{\text{OT}}\right|\le 48\text{pN}$, corresponding to a maximum extension of ∼ 40%, for the same value of $G_{\text{s}}$. The differences in $D_{\text{A}}$ between these two laws become apparent at $\left|{\mathit{F}}_{\text{OT}}\right|>88\text{pN}$, when the RBC has stretched at least ∼ 65% of its initial size, and can be attributed to the change in Yeoh law’s nature (from strain-softening to strain-hardening) which occurs at a RBC extension of ∼ 70%. It should also be noted that the results for $D_{\text{A}}$ of Yeoh law match those of Skalak law at $\left|{\mathit{F}}_{\text{OT}}\right|>170\text{pN}$, corresponding to extensions of ∼ 100%, when $G_{\text{s}}^{\text{YE}}=2G_{\text{s}}^{\text{SK}}$, as anticipated by theory. With respect to the transverse diameter, the following trends have been revealed: 1. varying the shear elastic modulus value does not influence significantly the estimation of $D_{\text{T}}$ for any constitutive law, and 2. the neo-Hookean and Yeoh laws predict similar results, demonstrating that the cubic extension term in Yeoh law has a negligible effect on the RBC deformation in the transverse direction. Regarding the morphology, a folding on the erythrocyte membrane, similar to that observed in experiments, can be seen when considering the neo-Hookean and Yeoh laws, indicating that these laws maintain the RBC’s biconcave shape. On the contrary, the erythrocyte shape gradually transitions from biconcave to rounded with increasing $\left|{\mathit{F}}_{\text{OT}}\right|$ for Skalak law. This transition is delayed with increasing value of the shear elastic modulus. Lastly, the erythrocyte membrane area does not sustain significant variations in the case of Skalak law, when sufficiently high values of its dilatational modulus are considered, as opposed to the neo-Hookean and Yeoh laws. A short summary of the findings for the optical tweezers experiment can be found in Table 3.

Table 3:

Summary of the optical tweezers findings.

	Skalak	neo-Hookean	Yeoh
Shear elastic modulus, $G_{\text{s}}$	[4.0, 5.0] μN=m	12.0 μN/m	10.0 μN/m
Axial diameter, $D_A$	✔	✔	✔
Transverse diameter, $D_{\text{T}}$	✔	slightly overpredicted	slightly overpredicted
Erythrocyte folding	✘	✔	✔
Area-incompressibility	✔	✘	✘

For the micropipette aspiration experiment, it has been demonstrated that only Yeoh law is able to precisely predict the aspiration length across the entire range of suction pressures considered here for a fixed shear elastic modulus value, found to be $G_{\text{s}}^{\text{YE}}=12.0\text{μN}/\text{m}$. For the Skalak and neo-Hookean laws, the shear elastic modulus value, for which a good agreement can be obtained with the experimental results, is dependent on the applied suction pressure, and, thus, the resultant deformation. It has been shown that the $G_{\text{s}}$ value should vary between 4.0 to $7.0\text{μN}/\text{m}$ for Skalak law, and 12.0 to $14.0\text{μN}/\text{m}$ for the neo-Hookean model. In accordance with the theoretical analysis, similar aspiration lengths are predicted by the neo-Hookean and Yeoh laws for the same value of shear elastic modulus when $L^{\prime }\le 1.5$. Importantly, it has been revealed that wrinkling occurs on the erythrocyte membrane for suction pressures $\text{Δ}P\ge 35\text{Pa}$ when considering the neo-Hookean and Yeoh laws, but not the Skalak law. It is noteworthy that the threshold suction pressure for wrinkling to appear in our simulations, i.e. $\text{Δ}P=35\text{Pa}$, is close to that experimentally observed, that is 45 Pa [47]. The discrepancy between the two may be attributed to the difference in the inner diameter of the pipette considered here ($1.8\text{μm}$) and used in the experiments ($1.5\text{μm}$). Finally, negligible variations in the erythrocyte membrane area have been reported for all constitutive laws. The computational findings for the micropipette aspiration experiment are summarized in Table 4.

Table 4:

Summary of the micropipette aspiration findings.

	Skalak	neo-Hookean	Yeoh
Shear elastic modulus, $G_{\text{s}}$	[4.0, 7.0] μN/m	[12.0, 14.0] μN/m	12.0 μN/m
Aspiration length, $L^{\prime }$	$G_{\text{s}}$-dependent	$G_{\text{s}}$-dependent	$G_{\text{s}}$-independent
Erythrocyte wrinkling	✘	✔	✔
Area-incompressibility	✔	✔	✔

The current study paves the way for further investigations on the effect of constitutive law on the erythrocyte behaviour. More physiologically relevant configurations, such as the flow of red blood cells through narrow slits similar to those encountered in the spleen, are worth exploring in the future. Varying the erythrocyte properties also merits further study, as any variation will reflect on the shear elastic modulus value predicted by each constitutive law.

Appendix: Stresses and forces computation

Stresses computation

Following Green & Adkins [84], we express the erythrocyte membrane mechanics problem in the curvilinear coordinate system defined by ${\xi }_1$ and ${\xi }_2$. Let ${\mathit{X}}^0\left({\xi }_1,{\xi }_2\right)$ and $\mathit{X}\left({\xi }_1,{\xi }_2,t\right)$ be the position of a given membrane material point in the reference and deformed states, respectively. To describe elastic deformations of a curved surface, it is convenient to use the local covariant $\left({\mathit{A}}_1,{\mathit{A}}_2,\mathit{n}\right)$ and contravariant $\left({\mathit{A}}^1,{\mathit{A}}^2,\mathit{n}\right)$ bases in the deformed state, composed of the tangent vectors

$${\mathit{A}}_{\alpha }={\mathit{X}}_{,\alpha }=\frac{\partial \mathit{X}}{\partial {\xi }_{\alpha }},\alpha =1,2,$$ (32)

and the outward unit normal vector $\mathit{n}$. The covariant metric and curvature tensors are defined in the deformed state as

$${\text{A}}_{\alpha \beta }={\mathit{A}}_{\alpha }\cdot {\mathit{A}}_{\beta },$$ (33a)

$${\text{B}}_{\alpha \beta }={\mathit{A}}_{\alpha ,\beta }\cdot \mathit{n}=\frac{\partial {\mathit{A}}_{\alpha }}{\partial {\xi }_{\beta }}\cdot \mathit{n},$$ (33b)

where $\alpha ,\beta =1,2$. The contravariant representations ${\text{A}}^{\alpha \beta }$ and ${\text{B}}^{\alpha \beta }$ of the metric and curvature tensors are defined similarly to Eq. (33), and satisfy the following conditions: ${\text{A}}^{\alpha \gamma }{\text{A}}_{\gamma \beta }={\delta }_{\beta }^{\alpha }$ and ${\text{B}}^{\alpha \gamma }{\text{B}}_{\gamma \beta }={\delta }_{\beta }^{\alpha }$, where ${\delta }_{\beta }^{\alpha }$ is the Kronecker delta. The same quantities can be defined in the reference state, i.e. ${\mathit{A}}_{\alpha }^0$, ${\text{A}}_{\alpha \beta }^0$, ${\text{B}}_{\alpha \beta }^0$, etc.

The surface deformation gradient tensor $\mathbf{F}={\mathit{A}}_{\alpha }\otimes {\mathit{A}}^{0^{\alpha }}$ is such that $\text{d}\mathit{X}=\mathbf{F}\cdot \text{d}{\mathit{X}}^0$. The Green-Lagrange strain tensor $\mathbf{E}$ is defined as $\mathbf{E}=\frac{1}{2}(\mathbf{C}-\mathbf{I})$, where $\mathbf{C}={\mathbf{F}}^T\cdot \mathbf{F}$ is the right Cauchy-Green tensor, and its strain invariants are given by

$$I_1=2\text{tr}(\mathbf{E})=\text{tr}(\mathbf{C})-2={\lambda }_1^2+{\lambda }_2^2-2,$$ (34a)

$$I_2=2\det (\mathbf{E})=\det (\mathbf{C})-1={\lambda }_1^2{\lambda }_2^2-1,$$ (34b)

with ${\lambda }_1$ and ${\lambda }_2$ being the principal extension ratios. The Cauchy tension tensor $\mathbf{T}$, which depends on the strain energy function of the chosen constitutive law, is expressed as

$$\mathbf{T}=\frac{1}{J_s}\mathbf{F}\cdot \frac{\partial W_{\text{s}}}{\partial \mathbf{E}}\cdot {\mathbf{F}}^T,$$ (35)

where the Jacobian $J_s={\lambda }_1{\lambda }_2$ represents physically the ratio between the deformed and reference local surface areas. The contravariant representation of $\mathbf{T}$ takes thus the form [27, 85]

$${\text{T}}^{\alpha \beta }=\frac{2}{J_s}\frac{\partial W_{\text{s}}}{\partial I_1}{\text{A}}^{0^{\alpha \beta }}+2J_s\frac{\partial W_{\text{s}}}{\partial I_2}{\text{A}}^{\alpha \beta }.$$ (36)

Finally, the membrane and bending stresses due to the Helfrich bending energy, Eq. (13), can be found as [86]

$${\sigma }^{\alpha \beta }=\frac{2}{\sqrt{A}}\frac{\partial \left(\sqrt{A}{ℰ}_{\text{b}}\right)}{\partial {\text{A}}_{\alpha \beta }}=\frac{k_{\text{b}}}{2}\left(4{\kappa }^2{\text{A}}^{\alpha \beta }-8\kappa {\text{B}}^{\alpha \beta }\right),$$ (37a)

$${\text{μ}}^{\alpha \beta }=\frac{\partial {ℰ}_{\text{b}}}{\partial {\text{B}}_{\alpha \beta }}=\frac{k_{\text{b}}}{2}\left(4\kappa {\text{A}}^{\alpha \beta }\right),$$ (37b)

with $A$ being the determinant of the local metric.

Forces computation

The characteristic feature of the Loop subdivision surfaces is that the displacement field within an element does not depend on the displacements of only the vertices composing the element, but also of its 1-ring neighboring vertices, that is the vertices sharing 1 edge with it. For a given element $e$, the limit position ${\mathit{X}}_e$ can be computed as [87]

$${\mathit{X}}_e\left({\xi }_1,{\xi }_2\right)=\sum _{n\in E_n}{N}_n^e\left({\xi }_1,{\xi }_2\right){\mathit{X}}_n,$$ (38)

where the node $n$ belongs to the 1-ring $E_n$ about the element $e$, $N_n^e$ are the shape functions, and ${\mathit{X}}_n$ denotes the nodal coordinates. In the current work, we employ the box-spline shape functions as presented in the work of Cirak et al. [73].

To calculate the surface force density ${\mathit{F}}_m$ exerted by the membrane onto the surrounding fluids, the weak form of the equation describing the quasistatic mechanical equilibrium of the erythrocyte membrane

$${\nabla }_s\cdot \left({\text{T}}^{\alpha \beta }+{\text{σ}}^{\alpha \beta }+{\text{μ}}^{\alpha \beta }\right)+{\mathit{F}}_{\text{v}}-{\mathit{F}}_m=\mathbf{0}$$ (39)

needs to be solved, where ${\nabla }_s$ denotes the surface gradient and ${\mathit{F}}_{\text{v}}$ is the volume penalty force density corresponding to Eq. (14). The detailed solution process can be found in [86]. The surface force density of the l^th vertex located at ${\mathit{X}}_l$ can then be computed as [88]

$${\mathit{F}}_m^l=\frac{{\mathit{F}}_m}{{\int }_S{N}_l^e\text{d}S}.$$ (40)