Latent Class Proportional Hazards Regression with Heterogeneous Survival Data

Abstract

Heterogeneous survival data are commonly present in chronic disease studies. Delineating meaningful disease subtypes directly linked to a survival outcome can generate useful scientific implications. In this work, we develop a latent class proportional hazards (PH) regression framework to address such an interest. We propose mixture proportional hazards modeling, which flexibly accommodates class-specific covariate effects while allowing for the baseline hazard function to vary across latent classes. Adapting the strategy of nonparametric maximum likelihood estimation, we derive an Expectation-Maximization (E-M) algorithm to estimate the proposed model. We establish the theoretical properties of the resulting estimators. Extensive simulation studies are conducted, demonstrating satisfactory finite-sample performance of the proposed method as well as the predictive benefit from accounting for the heterogeneity across latent classes. We further illustrate the practical utility of the proposed method through an application to a mild cognitive impairment (MCI) cohort in the Uniform Data Set.

1. INTRODUCTION

The problem of exploring heterogeneous survival data often arises in studies of neurodegenerative diseases such as mild cognitive impairment (MCI). For example, amnestic MCI and non-amnestic MCI represent different etiologies that manifest different risk of progression to dementia [22]. Accurately classifying MCI into meaningful subtypes has played an important role in disease prognosis. Traditionally based on the number and the type of affected cognitive domains [28], classification of MCI subtypes has evolved toward data-driven approaches that permit flexible utilization of various phenotype measurements collected from MCI patients, such as cognitive tests in different domains [11] and neuroimaging biomarkers [9]. However, little investigation has been made to delineate the subtypes of MCI and the associated heterogeneity directly with respect to the timing of landmark disease events (e.g., diagnosis of dementia), which may provide useful insight to help develop early and precise intervention.

To fill in such a gap, a natural venue is to consider latent class analysis (LCA) of the time-to-event outcome of interest, which takes the perspective that the observed survival data (e.g., time to dementia) are manifestations from distinct latent classes or subgroups. In literature, the LCA of a survival outcome has often been investigated in conjunction with latent class modeling of other types of outcomes, such as longitudinal outcomes [15, 23, 24, 29, among others] and questionnaire responses [14]. These methods generally require imposing assumptions regarding the relationship between the survival outcome and the other outcomes, such as the conditional independence given the latent class membership, which are difficulty to verify with the observed data. More importantly, the interpretation of the latent classes under such joint LCA models can be largely attributed to the variations in the non-survival outcomes, and thus may considerably deviate from the survival heterogeneity of interest.

LCA methods tailored to probe the heterogeneity solely pertaining to a survival outcome, however, are sparse. Relevant existing work includes the mixture Weibull models [4, 16, for example] and mixture exponential models [13, for example], which were proposed to investigate heterogeneous event time distributions for two or more underlying classes. However, these methods assumed parametric distributions, and thus may be in jeopardy of generating biased inference when these parametric assumptions are not adequate for the real data. Rosen and Tanner [26] developed an estimation procedure for a mixture of Cox’s proportional hazards (PH) models [5] under the concept of “mixture-of-experts”. However, their model assumed a common baseline hazard function for all component Cox models within the mixture. Note that even when considering the Cox PH modeling under the joint LCA modeling of survival and longitudinal data, additional model restrictions were often imposed, such as a spline formulation of the baseline hazard function [23] or a common covariate effect across different latent classes [15, 14]. More recently, a deep neural network approach [21] was proposed to tackle a mixture of Cox models; however such an approach lacks a clear statistical framework for studying asymptotic behaviors of the resulting estimates.

Motivated by the limitations of the existing methods, we propose a semi-parametric approach to conducting latent class proportional hazards (PH) regression analysis of survival data to help reveal the heterogeneity of disease population and its implications on disease progression. In this work, we adopt flexible latent class PH modeling which permits the nonparametric baseline hazard function to vary across different latent classes, and also allows for class-specific covariate effects. To estimate the proposed model which involves an infinite-dimensional parameter (i.e. the unspecified baseline cumulative hazard function), we employ the technique of non-parametric maximum likelihood [32, NPMLE] and properly adapt it to deal with the extra challenges associated with the unobservable latent class label or membership. Following the lines of [17], we rigorously establish the asymptotic properties of the proposed estimators through employing empirical process arguments [27] and semi-parametric efficiency results [2]. We also investigate different inference strategies, including utilizing the information matrix or employing the profile likelihood [19]. Finally, we derive a stable expectation-maximization (E-M) algorithm to implement the proposed estimation and inference. Our algorithm can be easily carried out with existing software or algorithms. According to our numerical experience, the proposed EM algorithm is robust to initialization and performs well with non-informative initial values.

2. DATA AND MODELS

2.1. Data and notations

Let $T$ denote time to the event of interest and let $C$ denote time to independent censoring of $T$. Let $\mathit{x}$ denote a $p\times 1$ vector of baseline covariates. Define $\tilde{T}=T\wedge C$ and $\mathrm{\Delta }=I(T\le C)$, where $\wedge$ is the minimum operator. The observed data consist of $n$ independent and identically distributed replicates of $\mathit{O}=(\tilde{T},\mathrm{\Delta },\mathit{x})$, denoted by $\left\{{\mathit{O}}_i=\left({\tilde{T}}_i,{\mathrm{\Delta }}_i,{\mathit{x}}_i\right),i=1,\dots ,n\right\}$. The latent class membership is indicated by $\mathit{\xi }=\left({\xi }_1,\dots ,{\xi }_L\right)$, where $L$ denotes the number of latent classes, and ${\xi }_l=1$ if the underlying latent class is the $l$-th class and 0 otherwise.

2.2. The assumed models

We assume that the whole population consists of $L$ latent classes, within each of which, $T$ follows a class-specific semiparametric proportional hazards model. We further assume that the class-specific baseline hazard functions are proportional to each other. To formulate class-specific baseline hazard functions under this proportionality assumption, we first choose a reference class and then define the baseline hazard functions for the other classes as some constants multiplying the baseline hazard function for the reference class. Specifically, without loss of generality, we let class 1 (i.e. ${\xi }_1=1$) be the reference class, where $T$ has the hazard function $\lambda (t\mid {\xi }_1=1,\overline{\mathit{x}})={\lambda }_0(t)\mathrm{e}\mathrm{x}\mathrm{p}({\overline{x}}^T{\mathit{\zeta }}_1)$. Here ${\lambda }_0(t)$ is the unspecified baseline hazard function for the reference class, $\overline{\mathit{x}}$ is a $q\times 1$ subvector of $\mathit{x}$ with $q\le p$, and ${\mathit{\zeta }}_1$ is a $q\times 1$ vector representing unknown covariate effects in the reference class. For the other classes, we assume ${\lambda (t\mid {\xi }_l=1,\overline{\mathit{x}})=\lambda }_0(t)\mathrm{e}\mathrm{x}\mathrm{p}\{a_l+{\overline{\mathit{x}}}^T({\mathit{\zeta }}_1+{\mathit{\zeta }}_l)\},l=2,\dots ,L$, where $a_l$ is an unknown parameter with $\mathrm{e}\mathrm{x}\mathrm{p}(a_l)$ representing the constant hazard ratio between class $l$ and class 1, and ${\mathit{\zeta }}_l$ is a $q\times 1$ vector of unknown coefficients representing the differences in covariate effects between class $l$ and class 1. Define ${{\mathit{z}}_l=({\overline{\mathit{x}}}^T,{\mathbf{0}}_{(q+1)\times (L-1)}^T)}^T\cdot I(l=1)+{({\overline{\mathit{x}}}^T,{({\mathit{e}}_{l-1}\otimes \check{\mathit{x}})}^T)}^T\cdot I(l>1)$ and $\mathit{\gamma }={({\mathit{\zeta }}_1^T,a_2,{\mathit{\zeta }}_2^T,a_3,{\mathit{\zeta }}_3^T,\dots ,a_L,{\mathit{\zeta }}_L^T)}^T$, where ${\mathbf{0}}_d$ represents a $d$-vector of zeros, $e_{l-1}$ represents a vector of length $(L-1)$, where the $(l-1)$ th element is 1 and the other elements are equal to zero, $\breve{\mathit{x}}={(1,{\overline{\mathit{x}}}^T)}^T$, and $\otimes$ denotes Kronecker product operator. With these notations, it is easy to see that a unified expression for the class-specific hazard functions is given by

$$\lambda \left(t\mid {\xi }_l=1\right)={\lambda }_0\left(t\right)\mathrm{e}\mathrm{x}\mathrm{p}\left({\mathit{z}}_l^T\mathit{\gamma }\right),l=1,\dots ,L$$ (1)

By the definition, $\gamma$ is the vector of unknown parameters with length $q\times L+(L-1)$.

We also adopt a standard latent polytomous logistic regression model [1] to model the latent class probabilities. That is, we assume

$$\mathrm{P}\mathrm{r}\left({\xi }_l=1\mid \mathit{x}\right)=p_l(\mathit{x};\mathit{\alpha })=\frac{\mathrm{e}\mathrm{x}\mathrm{p}\left({\tilde{\mathit{x}}}^T{\mathit{\alpha }}_l\right)}{\sum _{d=1}^L\mathrm{e}\mathrm{x}\mathrm{p}\left({\tilde{\mathit{x}}}^T{\mathit{\alpha }}_d\right)},l=1,\dots ,L,$$ (2)

where $\tilde{\mathit{x}}={\left(1,{\mathit{x}}^T\right)}^T,{\mathit{\alpha }}_1=\mathbf{0}$ for the identifiability consideration, and $\mathit{\alpha }={\left({\mathit{\alpha }}_2,\dots ,{\mathit{\alpha }}_L\right)}^T$ is a vector of unknown parameters with length $(p+1)\times (L-1)$.

Define ${\mathrm{\Lambda }}_0(t)={\int }_0^t{\lambda }_0(s)ds$ and let $\mathit{\theta }={\{{\mathit{\gamma }}^T,{\mathrm{\Lambda }}_0(\cdot )\}}^T$. Under models (1) and (2), the conditional density of $(\tilde{T},\mathrm{\Delta })$ given $\mathit{x}$ can be written as

$$f(\tilde{T},\mathrm{\Delta }\mid \mathit{x};\mathit{\alpha },\mathit{\theta })=\sum _{l=1}^L{p}_l(\mathit{x},\mathit{\alpha })f_l(\tilde{T},\mathrm{\Delta }\mid \mathit{x};\mathit{\theta }),$$ (3)

where $f_l(\tilde{T},\mathrm{\Delta }\mid \mathit{x};\mathit{\theta })={\{{\lambda }_0(\tilde{T})e^{{\mathit{z}}_l^T\mathit{\gamma }}\}}^{\mathrm{\Delta }}\mathrm{e}\mathrm{x}\mathrm{p}\{-{\mathrm{\Lambda }}_0(\tilde{T})e^{{\mathit{z}}_l^T\mathit{\gamma }}\}$, standing for the class-$l$ l density of $(\tilde{T},\mathrm{\Delta })$ implied by model (1).

In the sequel, we shall use ${\mathit{\alpha }}_0,{\gamma }_0$, and ${\mathrm{\Lambda }}_0$ to denote the true parameters in model (1) and model (2), and use $\mathit{\alpha },\mathit{\gamma }$, and $\mathrm{\Lambda }$ to denote elements in the parameter spaces for ${\mathit{\alpha }}_0,{\gamma }_0$, and ${\mathrm{\Lambda }}_0$ respectively.

3. ESTIMATION AND INFERENCE

In this section, we derive the estimation procedure for ${\mathit{\alpha }}_0,{\mathit{\theta }}_0$, and ${\mathrm{\Lambda }}_0(\cdot )$. We also study the theory and inference associated with the proposed estimators.

3.1. The observed data likelihood

Under models (1) and (2), the observed data likelihood can be written as

$$\begin{gathered} L(\mathit{\alpha },\mathit{\gamma },\mathrm{\Lambda };\mathit{O})=\prod _{i=1}^n\{\sum _{l=1}^L{p}_l\left({\mathit{x}}_i;\mathit{\alpha }\right){\left\{\lambda \left({\tilde{T}}_i\right)\exp \left({\mathit{z}}_{il}^T\mathit{\gamma }\right)\right\}}^{{\mathrm{\Delta }}_i} \\ \exp \left\{-\mathrm{\Lambda }\left({\tilde{T}}_i\right)\exp \left({\mathit{z}}_{il}^T\gamma \right)\right\}\}{f}_{\mathit{X}}\left({\mathit{x}}_i\right), \end{gathered}$$ (4)

where $f_{\mathit{X}}(\cdot )$ is the density function of $\mathit{x}$. Note that $f_{\mathit{X}}\left({\mathit{x}}_i\right)$ does not involve the unknown parameters, $\mathit{\alpha },\mathit{\gamma }$, and $\mathrm{\Lambda }$, and thus is omitted in further derivations.

It is challenging to directly maximize the observed data likelihood $L(\mathit{\alpha },\gamma ,\mathrm{\Lambda };\mathit{O})$ due to the structure of mixture distributions and the involvement of the nonparametric parameter $\mathrm{\Lambda }(\cdot )$. To conquer these difficulties, we derive an Expectation-Maximization (EM) algorithm which naturally accommodates the unobservable latent class membership and incorporates the strategy of NPMLE for the estimation of ${\mathrm{\Lambda }}_0(\cdot )$.

3.2. The proposed EM algorithm

Suppose $\mathit{\xi }$ is observed. The likelihood corresponding to the complete data $(\mathit{\xi },\mathit{O})$ takes the form,

$$\begin{gathered} L_c(\mathit{\alpha },\mathit{\gamma },\mathrm{\Lambda };\mathit{\xi },\mathit{O})=\prod _{i=1}^n\prod _{l=1}^L\{p_l\left({\mathit{x}}_i;\mathit{\alpha }\right){\left\{\lambda \left({\tilde{T}}_i\right)\exp \left({\mathit{z}}_{il}^T\mathit{\gamma }\right)\right\}}^{{\mathrm{\Delta }}_i} \\ {\exp \left\{-\mathrm{\Lambda }\left({\tilde{T}}_i\right)\exp \left({\mathit{z}}_{il}^T\mathit{\gamma }\right)\right\}\}}^{I\left({\xi }_{il}=1\right)}. \end{gathered}$$

Following the NPMLE strategy, we further treat $\mathrm{\Lambda }(\cdot )$ as piecewise constant between the observed event times. That is, we let $\mathrm{\Lambda }(t)={\sum }_{j:t_j\le t}\mathrm{\Lambda }\left\{t_j\right\}$ with $\mathrm{\Lambda }\left\{t_j\right\}=d_j$, where $t_1<t_2<\dots <t_m$ are distinct uncensored event times. Denote the cumulative hazard function $\mathrm{\Lambda }\left(t_j\right)$ at $t_j$ by ${\mathrm{\Lambda }}_j(j=1,\dots ,m)$. Then the corresponding log complete data likelihood can be expressed as

$$\begin{gathered} {\ell }_c(\mathit{\alpha },\mathit{\gamma },\mathrm{\Lambda };\mathit{\xi },\mathit{O})= \\ \sum _{j=1}^m\sum _{l=1}^L{\xi }_{(j)l}\left\{\log \mathrm{\Lambda }\left\{t_j\right\}+{\mathit{z}}_{(j)l}^T\mathit{\gamma }-e^{{\mathit{z}}_{(j)l}^T\mathit{\gamma }}{\mathrm{\Lambda }}_j\right\} \\ -\sum _{j=1}^m\sum _{k:t_j\le {\tilde{T}}_k<t_{j+1}}I\left({\mathrm{\Delta }}_k=0\right)\sum _{l=1}^L{\xi }_{kl}{e}^{{\mathit{z}}_{kl}^T\mathit{\gamma }}{\mathrm{\Lambda }}_j \\ +\sum _{i=1}^n\sum _{l=1}^L{\xi }_{il}\log p_l\left({\mathit{x}}_i;\mathit{\alpha }\right), \end{gathered}$$ (5)

where ${\xi }_{\left(j\right)l}$ and ${\mathit{z}}_{\left(j\right)l}$ respectively represent the membership indicator ${\xi }_l$ and covariate vector ${\mathit{z}}_l$ for the observation with uncensored failure time $t_j(j=1,\dots ,m)$.

In the E-step, we calculate the expectation of the log complete data likelihood conditioned on the observed data $\mathit{O}$ and the current estimates of unknown parameters ${\mathit{\alpha }}^{\left(j\right)},{\mathit{\gamma }}^{\left(j\right)}$, and ${\mathrm{\Lambda }}^{\left(j\right)}$ at the $j$ th iteration, namely, $E\{{\ell }_c(\mathit{\alpha },\mathit{\gamma },\mathrm{\Lambda };\mathit{\xi },\mathit{O})\mid \mathit{O},{\mathit{\alpha }}^{\left(j\right)},{\mathit{\gamma }}^{\left(j\right)},{\mathrm{\Lambda }}^{\left(j\right)}\}$. Given the linearity with respect to $\mathit{\xi }$ in (5), it is straightforward to see

$$\begin{gathered} E\{{\ell }_c(\mathit{\alpha },\mathit{\gamma },\mathrm{\Lambda };\mathit{\xi },\mathit{O})\mid \mathit{O},{\mathit{\alpha }}^{(j)},{\mathit{\gamma }}^{(j)},{\mathrm{\Lambda }}^{(j)}\}= \\ {\ell }_c\{\mathit{\alpha },\mathit{\gamma },\mathrm{\Lambda };\widehat{E}(\mathit{\xi }),\mathit{O}\}, \end{gathered}$$

where $\hat{E}(\mathit{\xi })=\{\hat{E}\left({\xi }_{il}\right):i=1,\dots ,n;l=1,\dots ,L\}$ with $\hat{E}\left({\xi }_{il}\right)=E({\xi }_{il}\mid {\mathit{O}}_i;{\mathit{\alpha }}^{(j)},{\mathit{\gamma }}^{(j)},{\mathrm{\Lambda }}^{\left(j\right)})$. Note that $E\left({\xi }_{il}\mid {\mathit{O}}_i;\mathit{\alpha },\mathit{\gamma },\mathrm{\Lambda }\right)=\mathrm{P}\mathrm{r}\left({\xi }_{il}=1\mid {\mathit{O}}_i;\mathit{\alpha },\mathit{\gamma },\mathrm{\Lambda }\right)$. By applying the Bayes’ Rule, we get

$$\begin{gathered} \widehat{E}({\xi }_{il})=\mathrm{Pr}({\xi }_{il}=1\mid {\mathit{O}}_i;{\mathit{\alpha }}^{(h)},{\mathit{\gamma }}^{(h)},{\mathrm{\Lambda }}^{(h)}) \\ =\frac{p_l({\mathit{x}}_i;{\mathit{\alpha }}^{(h)})f_l({\tilde{T}}_i,{\mathrm{\Delta }}_i\mid {\mathit{x}}_i;{\mathit{\gamma }}^{(h)},{\mathrm{\Lambda }}^{(h)})}{{\sum }_{d=1}^L{p}_d({\mathit{x}}_i;{\mathit{\alpha }}^{(h)})f_d({\tilde{T}}_i,{\mathrm{\Delta }}_i\mid {\mathit{x}}_i;{\mathit{\gamma }}^{(h)},{\mathrm{\Lambda }}^{(h)})}. \end{gathered}$$ (6)

Denote the resulting conditional expectation ${\ell }_c\{\mathit{\alpha },\mathit{\gamma },\mathrm{\Lambda };\hat{E}(\mathit{\xi }),\mathit{O}\}$ by $Q(\mathit{\alpha },\mathit{\gamma },\mathrm{\Lambda })$. In the subsequent M-step, $Q(\mathit{\alpha },\mathit{\gamma },\mathrm{\Lambda })$ serves as the target function to maximize.

In the M-step, we adopt a profile likelihood strategy to maximize $Q(\mathit{\alpha },\mathit{\gamma },\mathrm{\Lambda })$ that profiles out $\mathrm{\Lambda }$, where $\mathrm{\Lambda }$ is treated as an $m$-dimensional unknown parameter $\left\{d_k:k=\right.1,\dots ,m\}$ with $d_k=\mathrm{\Lambda }\left\{t_k\right\}$. First, with fixed $\mathit{\alpha }$ and $\mathit{\gamma }$, we obtain $\stackrel{\mathrm{ˆ}}{\mathrm{\Lambda }}(t;\mathit{\alpha },\mathit{\gamma })=\mathrm{a}\mathrm{r}\mathrm{g}{\mathrm{m}\mathrm{a}\mathrm{x}}_{\mathrm{\Lambda }}Q(\mathit{\alpha },\mathit{\gamma },\mathrm{\Lambda })$ by solving

$$\begin{gathered} \frac{\partial }{\partial d_k}Q(\mathit{\alpha },\mathit{\gamma },\mathrm{\Lambda }) \\ =\frac{1}{d_k}-\sum _{i:{\tilde{T}}_i\ge t_k}\sum _{l=1}^L\hat{E}\left({\xi }_{il}\right)e^{{\mathit{z}}_{il}^T\mathit{\gamma }}=0,k=1,\dots ,m. \end{gathered}$$

This gives ${\widehat{d}}_k(\mathit{\gamma })={\{{\sum }_{i:{\tilde{T}}_i\ge t_k}\sum _{l=1}^L\widehat{E}\left({\xi }_{il}\right)e^{{\mathit{z}}_{il}^T\mathit{\gamma }}\}}^{-1}$, $k=1,\dots m,$ and

$$\widehat{\mathrm{\Lambda }}(t;\mathit{\alpha },\mathit{\gamma })=\sum _{k:t_k\le t}{\widehat{d}}_k(\mathit{\gamma })={\int }_0^t\frac{{\sum }_{i=1}^{n}d{N}_i(s)}{{\sum }_{i=1}^n{\sum }_{l=1}^L\widehat{E}\left({\xi }_{il}\right)Y_i(s)e^{{\mathit{z}}_{il}^T\mathit{\gamma }}},$$ (7)

where $N_i\left(t\right)=I\left({\tilde{T}}_i\le t,\mathrm{\Delta }=1\right)$ and $Y_i\left(t\right)=I\left({\tilde{T}}_i\ge t\right)$. Then by plugging in $\stackrel{\mathrm{ˆ}}{\mathrm{\Lambda }}(t;\mathit{\alpha },\mathit{\gamma })$ into $Q(\mathit{\alpha },\mathit{\gamma },\mathrm{\Lambda })$, we obtain the profile complete data $\log$ likelihood $Q_p(\mathit{\alpha },\mathit{\gamma })\equiv Q\{\mathit{\alpha },\mathit{\gamma },\stackrel{\mathrm{ˆ}}{\mathrm{\Lambda }}(t;\mathit{\alpha },\mathit{\gamma })\}$:

$$\begin{gathered} Q_p(\mathit{\alpha },\mathit{\gamma })=\sum _{i=1}^n\sum _{l=1}^L\widehat{E}\left({\xi }_{il}\right)\left[\log p_l\left({\mathit{x}}_i;\mathit{\alpha }\right)+ \\ {\int }_0^{t^{*}}\{\log \frac{1}{{\sum }_{i=1}^n{\sum }_{l=1}^L\widehat{E}\left({\xi }_{il}\right)Y_i(s)e^{{\mathit{z}}_{il}^T\mathit{\gamma }}}+{\mathit{z}}_{il}^T\mathit{\gamma }\}d{N}_i(s)\right], \end{gathered}$$ (8)

where $t^{\mathrm{*}}$ is a finite constant satisfying $t^{\mathrm{*}}>t_m$. Then we can find $\stackrel{\mathit{ˆ}}{\mathit{\alpha }}=\mathrm{a}\mathrm{r}\mathrm{g}{\mathrm{m}\mathrm{a}\mathrm{x}}_{\mathit{\alpha }}{Q}_p(\mathit{\alpha },\mathit{\gamma })$ and $\stackrel{\mathit{ˆ}}{\mathit{\gamma }}=\mathrm{a}\mathrm{r}\mathrm{g}{\mathrm{m}\mathrm{a}\mathrm{x}}_{\mathit{\gamma }}{Q}_p(\mathit{\alpha },\mathit{\gamma })$ by solving

$$\frac{\partial }{\partial \mathit{\alpha }}{Q}_p(\mathit{\alpha },\mathit{\gamma })=\sum _{i=1}^n\sum _{l=1}^L\hat{E}\left({\xi }_{il}\right)\frac{\partial }{\partial \mathit{\alpha }}\mathrm{l}\mathrm{o}\mathrm{g}{p}_l\left({\mathit{x}}_i;\mathit{\alpha }\right)=\mathbf{0}$$

and

$$\begin{gathered} \frac{\partial }{\partial \gamma }{Q}_p(\mathit{\alpha },\gamma )=\sum _{i=1}^n\sum _{l=1}^L{\int }_0^{t^{\mathrm{*}}}\hat{E}\left({\xi }_{il}\right)\left({\mathit{z}}_{il} \\ -\frac{\sum _{j=1}^n\sum _{k=1}^L\hat{E}\left({\xi }_{jk}\right)Y_j(u){\mathit{z}}_{jk}\mathrm{e}\mathrm{x}\mathrm{p}\left({\mathit{z}}_{jk}^T\mathit{\gamma }\right)}{\sum _{j=1}^n\sum _{k=1}^L\hat{E}\left({\xi }_{jk}\right)Y_j(u)\mathrm{e}\mathrm{x}\mathrm{p}\left({\mathit{z}}_{jk}^T\mathit{\gamma }\right)}\right)d{N}_i(u)=\mathbf{0}. \end{gathered}$$

The resulting estimator of ${\mathrm{\Lambda }}_0\left(t\right)$ is given by $\widehat{\mathrm{\Lambda }}(t)=\widehat{\mathrm{\Lambda }}(t;\widehat{\mathit{\alpha }},\widehat{\gamma })$.

Remark:

It is easy to see that solving $\frac{\partial }{\partial \alpha }{Q}_p(\mathit{\alpha },\mathit{\gamma })=0$ is equivalent to fitting a weighted multinomial logistic regression with weights $\widehat{E}(\mathit{\xi })$, which can be easily implemented by $\mathrm{R}$ package VGAM [30]. In addition, equation $\frac{\partial }{\partial \gamma }{Q}_p(\mathit{\alpha },\mathit{\gamma })=0$ can be viewed as the score equation corresponding to the partial likelihood of the proportional hazards regression with data $\left\{\left({\tilde{T}}_{il},{\mathrm{\Delta }}_{il},z_{il}\right):i=1,\dots ,n;l=1,\dots ,L\right\}$ with ${\tilde{T}}_{il}={\tilde{T}}_i,{\mathrm{\Delta }}_{il}={\mathrm{\Delta }}_i$, and weights $\hat{E}\left({\xi }_{il}\right)$. Nevertheless, we choose not to solve $\frac{\partial }{\partial \gamma }{Q}_p(\mathit{\alpha },\mathit{\gamma })=0$ by fitting a weighted Cox regression. This is because an existing computational routine for the weighted Cox regression would exercise a special tie treatment for the pseudo ties caused by repeatedly counting each observed event time for multiple latent classes (i.e. ${\left\{{\tilde{T}}_{il}\right\}}_{l=1}^L$), making the resulting estimates not accurately correspond to a solution to $\frac{\partial }{\partial \gamma }{Q}_p(\mathit{\alpha },\gamma )=0$. Instead, we implement an efficient Newton-Raphson algorithm under Rcpp environment [6] to directly solve the equation $\frac{\partial }{\partial \gamma }{Q}_p(\mathit{\alpha },\mathit{\gamma })=0$

To implement the proposed EM algorithm, we begin with an initial guess of $\hat{E}(\mathit{\xi })$, which can be a random guess or obtained in an informative way such as K-means clustering of $\tilde{T}$. Then we repeat the M-step and E-step until a stopping criterion is satisfied. We propose to use an Aitken acceleration-based stopping criterion as described in [18, page 52]. Denote $l^{(k)}$ as the logarithm of the observed-data likelihood (4) evaluated with the parameter estimates at the $k$th iteration. Define $a^{(k)}=(l^{(k+1)}-l^{(k)})/(l^{(k)}-l^{(k-1)})$ and $l_A^{(k+1)}=l^{(k)}+(l^{(k+1)}-l^{(k)})/(1-a^{(k)})$. The algorithm is stopped when $\left|l_A^{(k+1)}-l_A^{(k)}\right|<tol$, where $tol$ is a pre-specified tolerance parameter. In our numerical studies, we set $tol={10}^{-7}$ to ensure convergence to a local optimum.

3.3. Asymptotic properties and inference procedures

We establish desirable asymptotic properties of the estimators obtained from the proposed estimation procedure by using the NPMLE arguments similar to those used in [31] and [17].

We assume the following regularity conditions:

(C1) There exists $t^{\mathrm{*}}>0$ such that $\mathrm{P}\mathrm{r}\left(C=t^{\mathrm{*}}\right)>0$ and $\mathrm{P}\mathrm{r}\left(C>t^{\mathrm{*}}\right)=0$;

(C2) For $l=1,\dots ,L,\mathrm{P}\mathrm{r}\left({\xi }_l=1\mid \mathit{x};\mathit{\alpha }\right)\in (\mathrm{0,1})$.

(C3) $∥{\mathit{\alpha }}_0∥<\mathrm{\infty };∥{\gamma }_0∥<\mathrm{\infty };∥{\mathit{z}}_l∥<\mathrm{\infty }$ for $l=1,\dots ,L;{\mathrm{\Lambda }}_0(\cdot )$ is continuously differentiable with ${\mathrm{\Lambda }}_0^{\prime }(t)>0$ on $\left[0,t^{\mathrm{*}}\right]$, where $\parallel \cdot \parallel$ denotes the Euclidean norm.

Conditions (C1)-(C3) are reasonable in practical applications. Condition (C1) is often satisfied in the presence of administrative censoring. This condition helps prove the uniform consistency of $\stackrel{\mathrm{ˆ}}{\mathrm{\Lambda }}(\cdot )$ on $\left[0,t^{\mathrm{*}}\right]$. Condition (C2) ensures that the latent class membership probabilities $p_l(\mathit{x};\mathit{\alpha })$ is greater than zero, which further guarantees that $\mathrm{l}\mathrm{o}\mathrm{g}{p}_l(\mathit{x};\mathit{\alpha })$ has a finite lower bound. Condition (C3) assumes the smoothness of $\mathrm{\Lambda }(\cdot )$ and the boundedness of ${\mathit{\alpha }}_0,{\gamma }_0$ and baseline covariates $\mathit{x}$.

We establish the asymptotic properties of the proposed estimators in the following two theorems with proofs provided in Web Appendix A.

Theorem 3.1.

Under regularity conditions (C1)-(C3), $\stackrel{\mathit{ˆ}}{\mathit{\alpha }},\stackrel{\mathit{ˆ}}{\mathit{\gamma }}$, and $\stackrel{\mathrm{ˆ}}{\mathrm{\Lambda }}(\cdot )$ are strongly consistent. That is, $∥\stackrel{\mathit{ˆ}}{\mathit{\alpha }}-{\mathit{\alpha }}_0∥+∥\hat{\gamma }-{\gamma }_0∥+{\mathrm{s}\mathrm{u}\mathrm{p}}_{t\in \left[0,t^{\mathrm{*}}\right]}\left|\stackrel{\mathrm{ˆ}}{\mathrm{\Lambda }}(t)-{\mathrm{\Lambda }}_0(t)\right|\to 0$ almost surely.

Theorem 3.2.

Under regularity conditions (C1)-(C3), $\sqrt{n}\left(\stackrel{\mathit{ˆ}}{\mathit{\alpha }}-{\mathit{\alpha }}_0\right)$ and $\sqrt{n}\left(\stackrel{\mathit{ˆ}}{\mathit{\gamma }}-{\mathit{\gamma }}_0\right)$ converges to multivariate mean zero Gaussian distributions; $\sqrt{n}\{\hat{\mathrm{\Lambda }}(t)-{\mathrm{\Lambda }}_0(t)\}$ converges weakly to a univariate mean zero Gaussian process on $t\in \left[0,t^{\mathrm{*}}\right]$. In addition, $\stackrel{\mathit{ˆ}}{\mathit{\alpha }}$ and $\stackrel{\mathit{ˆ}}{\mathit{\gamma }}$ are semiparametric efficient as defined in [2].

Based on the developed theory, we propose to conduct variance estimation based on the information matrix of the observed-data profile log-likelihood [19], defined as $\mathrm{p}\mathrm{l}(\mathit{\alpha },\mathit{\gamma })\equiv \ell \{\mathit{\alpha },\mathit{\gamma },\stackrel{\mathrm{ˆ}}{\mathrm{\Lambda }}(\mathit{\alpha },\mathit{\gamma });\mathit{O}\}$. Define $\widehat{pl}(\stackrel{\mathit{ˆ}}{\mathit{\alpha }},\stackrel{\mathit{ˆ}}{\mathit{\gamma }})=\ell \{\stackrel{\mathit{ˆ}}{\mathit{\alpha }},\stackrel{\mathit{ˆ}}{\mathit{\gamma }},\stackrel{\mathrm{ˆ}}{\mathrm{\Lambda }}(\stackrel{\mathit{ˆ}}{\mathit{\alpha }},\stackrel{\mathit{ˆ}}{\mathit{\gamma }});\mathit{O}\}$, and let ${\stackrel{\mathrm{ˆ}}{\mathrm{p}\mathrm{l}}}_j(\stackrel{\mathit{ˆ}}{\mathit{\alpha }},\stackrel{\mathit{ˆ}}{\mathit{\gamma }})$ be the subject $j$’s contribution to $\stackrel{\mathrm{ˆ}}{\mathrm{p}\mathrm{l}}(\stackrel{\mathit{ˆ}}{\mathit{\alpha }},\stackrel{\mathit{ˆ}}{\mathit{\gamma }})$. The covariance matrix of ${\stackrel{\mathit{ˆ}}{\mathit{\theta }}\equiv ({\stackrel{\mathit{ˆ}}{\mathit{\alpha }}}^T,{\stackrel{\mathit{ˆ}}{\mathit{\gamma }}}^T)}^T\in {\mathbb{R}}^r$ can be estimated by the inverse of

$$\sum _{j=1}^n{\left(\begin{array}{c}\frac{{\widehat{pl}}_j\left(\stackrel{\mathit{ˆ}}{\mathit{\theta }}+h_n{\mathit{ϵ}}_1\right)-{\stackrel{\mathrm{ˆ}}{\mathrm{p}\mathrm{l}}}_j\left(\stackrel{\mathit{ˆ}}{\mathit{\theta }}-h_n{\mathit{ϵ}}_1\right)}{2h_n}\\ ⋮\\ \frac{{\stackrel{\mathrm{ˆ}}{\mathrm{p}\mathrm{l}}}_j\left(\stackrel{\mathit{ˆ}}{\mathit{\theta }}+h_n{\mathit{ϵ}}_r\right)-{\stackrel{\mathrm{ˆ}}{\mathrm{p}}}_j\left(\stackrel{\mathit{ˆ}}{\mathit{\theta }}-h_n{\mathit{ϵ}}_r\right)}{2h_n}\end{array}\right)}^{\otimes 2},$$

where $r=(p+1)\times (L-1)+q\times L+L-1,{\mathit{ϵ}}_k$ is the $k$th canonical vector in ${\mathbb{R}}^r,{\mathit{d}}^{\otimes 2}=\mathit{d}{\mathit{d}}^T$, and $h_n$ is a constant of order $n^{-1/2}$. In our numerical studies, we choose $h_n=5n^{-1/2}$ by following [8]. Instead of using the numerical approximation of Hessian matrix as in [19], we utilize the outer product of the first order numerical differences, which is more computationally affordable and guarantees that the resulting covariance matrix estimator is positive definite.

Alternatively, an analytical consistent variance estimator based on observed-data log-likelihood can be constructed by adapting the arguments of [31], which enable inference for $\stackrel{\mathrm{ˆ}}{\mathrm{\Lambda }}(t)$ in addition to $\stackrel{\mathit{ˆ}}{\mathit{\alpha }}$ and $\hat{\gamma }$. Details about the analytical variance estimator are provided in Web Appendix A. The analytical variance estimator typically requires inverse matrix computation for a large covariance matrix due to the inclusion of the cumulative hazard function, which may cause numerical instability. In practice, we recommend using the profile likelihood approach to obtain variance estimates for $\stackrel{\mathit{ˆ}}{\mathit{\alpha }}$ and $\hat{\gamma }$, and making inference on ${\mathrm{\Lambda }}_0(t)$ based on the analytical approach.

3.4. Selection of the number of latent classes

In practice, the number of latent classes, $L$, can be selected by using domain knowledge or some data-driven criteria. The commonly used data-driven criteria include standard model selection criteria, for example, the Akaike information criterion (AIC) defined as $-2\mathrm{l}\mathrm{o}\mathrm{g}L(\mathit{\alpha },\mathit{\gamma },\mathrm{\Lambda };\mathit{O})+2r$, where $r=(p+1)\times (L-1)+q\times L+L-1$, and the Bayesian information criterion (BIC) defined as $-2\mathrm{l}\mathrm{o}\mathrm{g}L(\mathit{\alpha },\mathit{\gamma },\mathrm{\Lambda };\mathit{O})+r\mathrm{l}\mathrm{o}\mathrm{g}n$, and entropy-based criteria, such as the standardized entropy index $1-{\sum }_{i=1}^n{\sum }_{l=1}^L\hat{E}\left({\xi }_{il}\right)\{-\mathrm{l}\mathrm{o}\mathrm{g}\hat{E}\left({\xi }_{il}\right)\}/n\mathrm{l}\mathrm{o}\mathrm{g}L$ [20], and integrated complete-data likelihood (ICL-BIC) [3, 12], which is defined as $-2\mathrm{l}\mathrm{o}\mathrm{g}L(\mathit{\alpha },\mathit{\gamma },\mathrm{\Lambda };\mathit{O})+r\mathrm{l}\mathrm{o}\mathrm{g}(n)-2{\sum }_{i=1}^n{\sum }_{l=1}^L\hat{E}\left({\xi }_{il}\right)\mathrm{l}\mathrm{o}\mathrm{g}\hat{E}\left({\xi }_{il}\right)$. We investigate the performance of using different criteria for determining the number of latent classes through the simulation studies reported in Section 4.2.

3.5. Survival prediction

Precise survival prediction is of great practical interest. Based on the models (1) and (2), we propose to predict the survival function for a subject with covariates $\mathit{x}$ by

$$\widehat{S}(t\mid \mathit{x})=\sum _{l=1}^L{p}_l(\mathit{x};\widehat{\mathit{\alpha }})\exp \{-\widehat{\mathrm{\Lambda }}(t)\exp ({\mathit{z}}_l^T\widehat{\mathit{\gamma }})\}.$$ (9)

As shown by our numerical studies, the survival prediction by $\hat{S}(t\mid \mathit{x})$ properly accounts for the heterogeneity across latent classes and can be more precise than the predictions that ignore the existence of latent classes.

To evaluate the performance of survival prediction, we propose to utilize the Brier Score, defined as $E[\{I(T\ge t)-\hat{S}(t\mid \mathit{x}){\}}^2]$. In practice, we observe $Y(t)=I(\tilde{T}\ge t)$ instead of $I(T\ge t)$. To accommodate censoring to $T$, we consider the following two estimators of the Brier Score which are adapted from the estimators presented in [25]: (a) databased Brier score,

$$\begin{gathered} {\stackrel{\mathrm{ˆ}}{\mathrm{B}\mathrm{S}}}_1(t)=\frac{1}{n}\sum _{i=1}^n\left\{\frac{I\left({\tilde{T}}_i>t\right)}{\hat{G}(t)}{\{1-\hat{S}\left(t\mid {\mathit{x}}_i\right)\}}^2 \\ +\frac{{\mathrm{\Delta }}_{i}I\left({\tilde{T}}_i\le t\right)}{\hat{G}\left({\tilde{T}}_i\right)}{\{0-\hat{S}\left(t\mid {\mathit{x}}_i\right)\}}^2\right\}; \end{gathered}$$

(b) model-based Brier score,

$$\begin{gathered} {\stackrel{\mathrm{ˆ}}{\mathrm{B}\mathrm{S}}}_2(t)=\frac{1}{n}\sum _{i=1}^n\left[I\left({\tilde{T}}_i>t\right){\left\{1-\hat{S}\left(t\mid {\mathit{x}}_i\right)\right\}}^2+\right. \\ {\mathrm{\Delta }}_{i}I\left({\tilde{T}}_i\le t\right){\left\{0-\hat{S}\left(t\mid {\mathit{x}}_i\right)\right\}}^2 \\ +\left(1-{\mathrm{\Delta }}_i\right)I\left({\tilde{T}}_i\le t\right)\left\{{\left\{1-\hat{S}\left(t\mid {\mathit{x}}_i\right)\right\}}^2\frac{\hat{S}\left(t\mid {\mathit{x}}_i\right)}{\hat{S}\left({\tilde{T}}_i\mid {\mathit{x}}_i\right)}+\right. \\ \left.\left.{\left\{0-\hat{S}\left(t\mid {\mathit{x}}_i\right)\right\}}^2\left(1-\frac{\hat{S}\left(t\mid {\mathit{x}}_i\right)}{\hat{S}\left({\tilde{T}}_i\mid {\mathit{x}}_i\right)}\right)\right\}\right]. \end{gathered}$$

Here $\hat{G}(\cdot )$ is the Kaplan-Meier estimator of $G(u)\equiv \mathrm{P}\mathrm{r}(C\ge u$) under the assumption that $C$ is independent of $\mathit{x}$. We may replace $\hat{G}(\cdot )$ by an estimate for $\mathrm{P}\mathrm{r}(C\ge u\mid \mathit{x})$ obtained through regressing $C$ over $\mathit{x}$ to allow for covariate-dependent censoring.

4. SIMULATION STUDY

We conducted simulation studies to evaluate the finite-sample performance of the proposed method. We considered data scenarios with $L=2$ or 3. We generated a two-dimensional baseline covariate vector $\mathit{x}=\left(x_1,x_2\right)$, where $x_1$ is a binary Bernoulli (0.5) random variable and $x_2$ is a continuous Uniform (0, 1) random variable. Then the latent class label vector $\mathit{\xi }$ was generated from a Multinomial $(1,{\left\{p_1(\mathit{x};\mathit{\alpha }),\dots ,p_L(\mathit{x};\mathit{\alpha })\right\}}^T)$ distribution following model (2). Given $\mathit{\xi }$, the time-to-event $T$ was generated from the class-specific distribution function $F_T\left(t\mid {\xi }_l=\right.1)=1-\mathrm{e}\mathrm{x}\mathrm{p}\left\{0.1\left(1-e^t\right)\mathrm{e}\mathrm{x}\mathrm{p}\left({\mathit{z}}_l^T\mathit{\gamma }\right)\right\}(l=1,\dots ,L)$ which satisfied model (1) with ${\mathrm{\Lambda }}_0(t)=0.1\left(e^t-1\right)$. Then we generated independent censoring time $C$ as the minimum of an $Exponential(r)$ variable and a Uniform(5, 6) variable.

Supplementary Table S.1 summarizes the choice of $r,\mathit{\alpha }$ and $\mathit{\gamma }$ in five simulation scenarios. Among scenarios with $L=2$ (i.e., (I), (II), (III), and (IV)), scenario (I) served as a benchmark with relatively light censoring rate and less overlapped survival distributions among the two classes. In contrast, scenario (II) involved more overlapped survival distributions while heavy censoring is present in scenario (III). Scenario (IV) considered a special situation where covariate $x_1$ had a large effect size on class probability $p_l(\mathit{x};\mathit{\alpha })$ but zero covariate effect on survival, while $x_2$ had zero covariate effect on latent class probability but a large effect size on survival. Compared to scenario (I), scenario (IV) had slightly heavier censoring but with similar level of overlapping of the survival distributions among the two classes. Scenario (V) concerned three latent classes and was comparable to scenario (I) in terms of censoring and the overlapping among class-specific survival distributions. Empirical metrics of censoring and overlapping among classes for the five scenarios can be found in Supplementary Table S.2.

4.1. Parameter estimation

To evaluate parameter estimation, we conducted 10,000 simulations with sample size $n=1000$ under scenarios (I)-(IV) and sample sizes n = 1000, 2000 and 3000 under scenario (V). To initialize the algorithm, we used a perturbed $\hat{E}(\mathit{\xi })$ from the true latent class labels $\mathit{\xi }$. In addition, the variance estimation for ${\{{\stackrel{\mathit{ˆ}}{\mathit{\alpha }}}^T,{\stackrel{\mathit{ˆ}}{\mathit{\gamma }}}^T\}}^T$ was conducted using both the profile likelihood and the analytical approaches, while the variance estimation for $\stackrel{\mathrm{ˆ}}{\mathrm{\Lambda }}(\cdot )$ was conducted using the analytical approach. We considered an outlying estimate as non-convergent if its $L_2$ norm (i.e., $\sqrt{{∥\stackrel{\mathit{ˆ}}{\mathit{\alpha }}-{\mathit{\alpha }}_0∥}^2+{∥\stackrel{\mathit{ˆ}}{\mathit{\gamma }}-{\mathit{\gamma }}_0∥}^2})$ was greater than the median $L_2$ norm (out of 10,000 simulation runs) plus 5 times median absolute deviation (MAD). Supplementary Table S.2 displays the estimation convergence rate along with median standardized entropy index and median censoring rate under different simulation scenarios. Supplementary Table S.2 indicates that the convergence rates are generally acceptable in all settings.

The simulation results on the estimates for the four representative parameters, ${\alpha }_{\mathrm{2,2}},$ ${\zeta }_{\mathrm{1,1}},a_2$, and $\mathrm{\Lambda }(3)$, are shown in Table 1. Full estimation results for all unknown parameters are available in supplementary Tables S.3 and S.4, which also compares the two variance estimation approaches for $\stackrel{\mathit{ˆ}}{\mathit{\alpha }}$ and $\hat{\gamma }$. We observe that under scenarios (I) and (IV), the proposed estimator achieved very small median biases and accurately estimated standard errors. The coverage probabilities of the 95% confidence intervals are close to 0.95 for both regression coefficients ${\mathit{\alpha }}_0$ and ${\gamma }_0$ and the infinitedimensional baseline cumulative hazard ${\mathrm{\Lambda }}_0(t)$. We also note that, compared to scenarios (I) and (IV), a fuzzier mixture pattern of distributions in scenario (II) and heavier censoring in scenario (III) may result in larger median biases for most parameters. In addition, slight underestimation of the standard errors is observed for scenario (II) and scenario (III). That is, the empirical coverage probabilities are slightly lower than 0.95, in particular for $a_2$. For scenario (V) with three latent classes, unstable estimation may occur with the smaller sample size 1000, as reflected by the higher estimation biases for parameters $a_2$ and $a_3$ and regression parameters ${\zeta }_{21}$ and ${\zeta }_{22}$ as compared to those given the larger sample sizes 2000 or 3000. This observation suggests that recovering the information on a larger number of latent classes may warrant a larger sample size. In scenarios (I)-(IV), the two variance estimators behave similarly, both achieving satisfactory standard error estimation and coverage probabilities for all unknown parameters. In scenario (V) with sample size 1000, both approaches yield empirical coverage probabilities considerably lower than the nominal value for some parameters, such as $a_2$ and $a_3$. However, the under-coverage issue is resolved with increased sample sizes very quickly by the profile likelihood approach but rather slowly by the analytical approach. This may suggest better finite-sample performance of the profile likelihood based variance estimation as compared to the analytic variance estimation.

Table 1.

Median bias (M.Bias), standard deviation (SE), median standard error estimate (SEE), and coverage probability (CP) of parameters ${\hat{\alpha }}_{\mathrm{2,2}}$, ${\hat{\zeta }}_{\mathrm{1,1}}$, ${\hat{a}}_2$ and $\stackrel{\mathrm{ˆ}}{\mathrm{\Lambda }}(3)$ out of 10000 simulations. Profile likelihood variance estimation approach was used for ${\hat{\alpha }}_{\mathrm{2,2}}$, ${\hat{\zeta }}_{\mathrm{1,1}}$, and ${\hat{a}}_2$. Analytical approach based on observed-data log-likelihood was used for $\stackrel{\mathrm{ˆ}}{\mathrm{\Lambda }}(3)$.

n	Scenarios	${\hat{\alpha }}_{\mathrm{2,2}}$				${\hat{\zeta }}_{\mathrm{1,1}}$
		M.Bias	SE	SEE	CP	M.Bias	SE	SEE	CP
1000	(I)	−0.020	0.302	0.296	0.949	−0.024	0.199	0.201	0.956
1000	(II)	−0.007	0.522	0.500	0.945	−0.045	0.318	0.314	0.958
1000	(III)	−0.037	0.410	0.380	0.936	−0.063	0.427	0.403	0.963
1000	(IV)	0.010	0.665	0.696	0.968	−0.011	0.205	0.207	0.952
1000	(V)	0.039	0.581	0.515	0.908	−0.042	0.236	0.216	0.938
2000	(V)	0.034	0.389	0.371	0.929	−0.022	0.151	0.146	0.946
3000	(V)	0.036	0.311	0.305	0.940	−0.014	0.121	0.118	0.946
		${\hat{a}}_2$				$\hat{\mathrm{\Lambda }}(3)$
		M.Bias	SE	SEE	CP	M.Bias	SE	SEE	CP
1000	(I)	0.011	0.449	0.412	0.940	−0.010	0.351	0.344	0.951
1000	(II)	0.032	0.451	0.406	0.926	0.003	0.545	0.504	0.949
1000	(III)	0.016	0.733	0.616	0.914	−0.018	0.759	0.661	0.942
1000	(IV)	0.002	0.310	0.309	0.954	0.016	0.481	0.449	0.945
1000	(V)	−0.256	1.160	0.787	0.791	0.117	0.585	0.520	0.910
2000	(V)	−0.122	0.828	0.628	0.872	0.062	0.390	0.367	0.925
3000	(V)	−0.074	0.631	0.534	0.932	0.038	0.315	0.298	0.927

We repeated the above simulations with non-informative initial values, $\hat{E}\left({\xi }_{il}\right)=1/L(i=1,\dots ,n,l=1,\dots ,L)$. The results are presented in Supplementary Tables S.5–S.7, indicating similar performances to that shown in Table 1. This demonstrates the robustness of the proposed E-M algorithm to different initial values.

4.2. Selecting the number of latent classes

We further conducted 1000 simulations for each of the five simulation scenarios with sample size $n=1000$. Given each simulated dataset, we fitted the assumed latent class PH model with the proposed E-M algorithm initiated by K-means clustering, and then applied the four data-driven criteria, AIC, BIC, the standard entropy index, and the integrated complete-data likelihood BIC (ICL-BIC), to select $L$ among the candidate values, {2, 3, 4, 5}. Figure 1 shows the empirical percentages of selecting each candidate value of $L$ by the different selection criteria.

Figure 1.

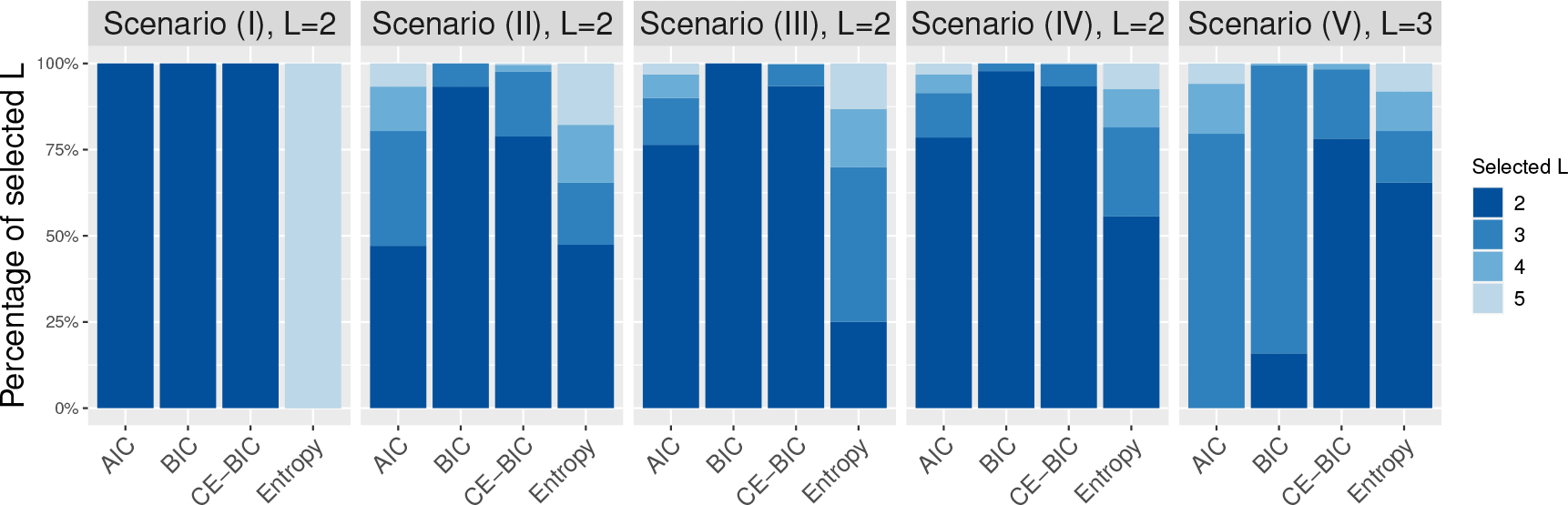
Percentage of latent classes selected by different model selection criteria out of 1000 simulations under simulation scenarios (I)-(V).

As shown in Figure 1, BIC correctly selected $L$ in all 1000 simulations when the two latent classes are well separated (see scenario (I)), even with heavily censoring (see scenario (III)). BIC also performed well under heavy distribution overlapping (see scenario (II)), with separated covariate effects on survival and marginal latent class probability (see scenario (IV)), and with three latent classes (see scenario (V)). Compared to BIC, AIC tended to select a larger number of latent classes, particularly for the heavy distribution overlapping scenario (see scenario (II)). In terms of entropy-based criteria, we find that the standardized entropy index tended to select incorrect $L$, and accordingly ICL-BIC performed worse than the stand-alone BIC. Similar results were also observed when there were three latent classes in scenario (V). The superiority of BIC over entropy-based criteria may relate to the fact that the proposed method is a likelihood-based method. Based on our simulation results, we recommend using BIC to select $L$ when applying the proposed method.

4.3. Assessing prediction performance

For each of the five simulation scenarios, we further simulated 1000 datasets with sample size 1000. For each simulated dataset, we conducted five-fold cross-validation to assess the survival prediction performance of the proposed latent class PH regression and the standard PH regression. Specifically, we fit models on the training dataset, and estimate the Brier Score ${\stackrel{\mathrm{ˆ}}{\mathrm{B}\mathrm{S}}}_j^{(f)}(t)(j=\mathrm{1,2})$ based on the testing set, where $f$ indicates one of the five random folds $(f=1,\dots ,5)$. Then we compute the average Brier score ${\overline{\widehat{BS}}}_j^{(f)}(t)=\frac{1}{5}{\sum }_{f=1}^5{\widehat{\text{BS}}}_j^{(f)}(t)$ for a range of $t$’s within the timeinterval $\left[0,t^{\mathrm{*}}\right]$. We set the upper bound of time interval $t^{\mathrm{*}}=5$ for scenarios (I) - (IV) and $t^{\mathrm{*}}=5.75$ for scenarios (V) to cover the support of the generated event times.

Supplementary Figures S.1–S.5 plot the estimated Brier Scores over time under scenarios (I)-(V), respectively. In all simulation scenarios, the proposed latent class PH regression analysis consistently achieved lower median average Brier Score estimates as compared to the standard PH regression which ignores the existence of latent classes. While the improvement in survival prediction is rather minor under scenarios (I), (II), (III) and (V), we observe quite major improvement under scenario (IV), particularly for the survival prediction at early time points. Note that under scenario (IV), covariates have different effects on the latent class probability and class-specific survival. The large difference in prediction error in this setting suggests that the standard PH regression analysis may have inadequate capacity to capture such complex data heterogeneity.

5. REAL DATA EXAMPLE

We applied our method to a subset of the Uniform Data Set, which included 5348 patients who were followed-up between September 2005 and June 2015 by the National Alzheimer’s Coordinating Center. The goal of our analyses is to understand potential subtypes of MCI directly linked to the heterogeneity in the time to the onset of dementia. In this dataset, 1501 patients developed dementia during the follow-up, resulting in a censoring rate of 72%. The censoring occurred mostly due to reasons such as moving out of area, and hence we deem the random censoring assumption as reasonable for this dataset. We fit the model given by (1) and (2) with covariates that measure various baseline cognitive characteristics, including overall cognition (Mini-mental state examination, MMSE), executive functions (Trail making test B, TB, and Digit symbol, DS), memory (logical memory delayed, LMD, and category fluency, CF), language (Boston naming, BN), and attention (Trail making test A, TA, and digit span forward, DSF). All the cognitive scores were normed based on age, race, and educational attainment. In addition, baseline number of impaired instrumental activities of daily living (IADLs), number of neuropsychiatric symptoms (NPI-Q), binary measure of depression (GDS), indicator of cerebrovascular disease (EH), and baseline age centered at 75 years (AGE) were also included as covariates in our models. A more detailed descriptions of this dataset can be found in [10].

We first determined the number of latent classes $L$ for our latent class PH analysis. As suggested by the simulation studies, we employed BIC as the data-driven criterion to select $L$. The 2-class model yielded the smallest BIC, 24481, as compared to the 3-class model which yielded BIC= 24625 and the 4-class model which yields BIC = 24797. By these results, we selected $L=2$.

In Table 2, we present the parameter estimates along with the corresponding 95% confidence intervals which were obtained from fitting the model given by (1) and (2) with $L=2$ or fitting the standard PH regression model. Based on the results from the standard PH regression (see $\hat{\zeta }$ in Table 2), we see that patients with worse baseline conditions in different cognitive domains (executive function, memory, language and attention), functional abilities, behavioral features and aging tended to have increased risk, or earlier onset, of dementia. However, these results do not directly reveal a finite number of potential MCI subtypes pertaining to the progression to dementia.

Table 2.

Point estimates and 95% confidence intervals for the covariate effects obtained by Cox model and the latent class model with two classes for the MCI data application.

		Cox model (1 class)		Latent class model (2 classes)
				Class probability		Class-specific survival submodel
Domains	Covariates	$\hat{\mathit{\zeta }}$	95% CI	$\hat{\mathit{\alpha }}$	95% CI	${\hat{\mathit{\zeta }}}_1$	95% CI	${\hat{\mathit{\zeta }}}_1+{\hat{\mathit{\zeta }}}_2$	95% CI
	Intercept	NA	NA	−2.94*	(−5.00,−0.88)	NA	NA	2.03*	(1.26,2.80)
Overall cognition	MMSE	−0.12*	(−0.15,−0.10)	−0.17	(−0.40, 0.07)	−0.14*	(−0.21,−0.07)	−0.09*	(−0.16,−0.03)
Executive function	TB	0.08*	(0.05,0.12)	0.20*	(0.00, 0.40)	−0.01	(−0.14, 0.11)	0.12*	(0.04,0.19)
	DS	−0.11*	(−0.17,−0.05)	−0.77*	(−1.28,−0.26)	0.03	(−0.20, 0.26)	−0.17*	(−0.30,−0.03)
Memory	LMD	−0.41*	(−0.46,−0.35)	0.23	(−0.40, 0.86)	−0.63*	(−0.80,−0.46)	−0.27*	(−0.39,−0.15)
	CF	−0.21*	(−0.27,−0.14)	−0.74	(−1.73, 0.26)	−0.17	(−0.36, 0.02)	−0.13	(−0.29,0.03)
Language	BN	−0.03*	(−0.06,0.00)	0.35*	( 0.15, 0.55)	−0.17*	(−0.26,−0.07)	0.04	(−0.07,0.15)
Attention	TA	−0.04*	(−0.08,0.00)	−0.15	(−0.49, 0.19)	−0.10	(−0.21, 0.01)	0.01	(−0.07,0.10)
	DSF	0.05	(−0.00,0.10)	0.06	(−0.32, 0.44)	0.01	(−0.11, 0.13)	0.07	(−0.10,0.25)
Cerebrovascular	EH	−0.02	(−0.23,0.18)	−1.10	(−2.53, 0.34)	0.39	(−0.16, 0.93)	−0.11	(−0.55,0.33)
Functional abilities	IADLs	0.12*	(0.10,0.14)	0.40*	( 0.03, 0.76)	0.21*	( 0.14, 0.28)	0.03	(−0.05,0.10)
Behavioral assessment	NPI-Q	0.06*	(0.04,0.09)	0.19	(−0.17, 0.55)	0.11*	( 0.03, 0.19)	0.00	(−0.08,0.08)
	GDS	0.07	(−0.07,0.21)	−0.70	(−2.03, 0.62)	0.09	(−0.33, 0.50)	0.12	(−0.30,0.55)
Aging	AGE	0.27*	(0.20,0.33)	0.90*	( 0.39, 1.42)	0.38*	( 0.20, 0.56)	0.01	(−0.20,0.22)

^*Statistically signficant covariate effect based on 95% confidence interval.

Higher scores on TB and TA indicated worse conditions.

The proposed latent class PH regression analyses can help fill in this gap. Specifically, the parameter estimates for model (2) (see $\stackrel{\mathit{ˆ}}{\mathit{\alpha }}$ in Table 2) suggest that younger MCI patients with more severe problems in language domain (BN) were more likely to belong to the latent class 1, while older MCI patients with worse executive functions (TB and DS) and impaired functional abilities (IADLs) were more likely to be belong to class 2. The parameter estimates for the class-specific survival model (1) help delineate the heterogeneity in covariate effects on time-to-dementia between the two latent classes (see ${\hat{\zeta }}_1$ and ${\hat{\zeta }}_1+{\hat{\zeta }}_2$ in Table 2). We first note that for both classes, worse baseline overall cognition (MMSE) is statistically significantly associated with higher risk of developing dementia. In addition, memory loss (LMD) has a significant effect within both classes but its effect sizes are fairly different. In addition, the effects of worse executive functions (TB and DS) are statistically significant only for class 2, while problems in language domain (BN), functional abilities (IADLs), behaviors (NPI-Q) and age (AGE) have significant effects on time-to-dementia only for class 1. Combing these results, we are able to correspond the two data-driven classes to meaningful clinical MCI subgroups. Patients in class 1 tended to be younger with milder baseline impairment and are prone to a wider range of baseline risk factors including memory, language, functional abilities, and behavioral assessment domains. This suggests a more diverse manifestation of disease progression for the MCI patients in class 1. In contrast, class 2 were comparably older patients who exhibited amnestic impairment at baseline, with executive function and memory domains as the only risk factors, which may correspond to the typical phenotypes of Alzheimer’s Disease.

Based on the estimation results, we assigned each patient to one of the two latent classes according to the modal rule. That is, we assigned patient i to the class associated with the highest posterior membership probability $\widehat{E}({\xi }_{il})$. This led to 69% of the patients assigned to class 1 and 31% of the patients assigned to class 2. Table 3 summarizes patient characteristics by the latent class assignment. Comparing the two classes, patients in class 1 have higher MMSE compared to those in class 2, showing better overall cognitive status. Moreover, class 1 is generally better than class 2 in most of the domain-specific scores, except for the Boston Naming test attached to the language domain. In addition, patients in class 2 are older than those in class 1. In terms of time-to-dementia, patients in class 1 generally show slower progression to dementia than patients in class 2. This is consistent with the observation that only 18% of patients in class 1 developed dementia in contrast to half of patients in class 2.

Table 3.

Summary statistics of the survival outcome and baseline covariates for the two MCI latent classes, based on modal assignment of class identity.

	Class 1, N=37141	Class 2, N=16341
$\tilde{T}$	1.8 (0.0, 3.4)	1.1 (0.0, 2.1)
Δ2	683 (18%)	818 (50%)
MMSE	−0.99 (−2.2, 0.0)	−2.1 (−3.8, −0.9)
TB4	0.4 (−0.2, 1.4)	1.7 (0.5, 4.0)
DS	−0.5 (−1.2, 0.1)	−1.4 (−2.0, −0.8)
LMD	−1.2 (−2.1, −0.4)	−1.5 (−2.3, −0.7)
CF	−0.8 (−1.4, −0.1)	−1.3 (−1.9, −0.7)
BN	−0.6 (−1.9, 0.2)	−0.5 (−1.6, 0.3)
TA3	0.1 (−0.4, 0.9)	0.7 (−0.1, 1.7)
DSF	−0.3 (−0.9, 0.5)	−0.4 (−1.0, 0.4)
EH	224 (6.0%)	104 (6.4%)
IADLs	1 (0, 2)	4 (2, 6)
NPI-Q	1 (0, 2)	2 (1, 4)
GDS	694 (19%)	279 (17%)
AGE	−0.2 (−0.8, 0.4)	0.2 (−0.4, 0.8)

¹Median (IQR); n (%)

²Number of patients diagnosed with dementia

³Larger TB and TA scores indicate worse conditions.

We also assessed the goodness-of-fit of our latent class PH models by comparing the empirical Kaplan-Meier curve of time-to-dementia versus the estimated overall survival function based on models (1) and (2), which was calculated as $n^{-1}{\sum }_{i=1}^n\hat{S}\left(t\mid {\mathit{x}}_i\right)$. As shown in Figure 2, the empirical Kaplan-Meier curve (referred to as “K-M”) is very close to the estimated survival curve based on the proposed models (referred to as “Overall”), indicating reasonable goodnessof-fit of the two-class PH regression model to the MCI dataset. In Figure 2, we also plot the estimated class-specific survival functions, ${\sum }_{i=1}^{n}I\left(i\in C_l\right)\hat{S}\left(t\mid {\mathit{x}}_i\right)/{\sum }_{i=1}^{n}I\left(i\in C_l\right)$, where $C_l$ denotes the set of patients assigned to class $l(l=\mathrm{1,2})$. We see that the estimated survival curve for class 1 is higher than the curve for class 2, indicating that patients in class 1 had slower progression towards dementia. This result is consistent with the observation from Table 3.

Figure 2.

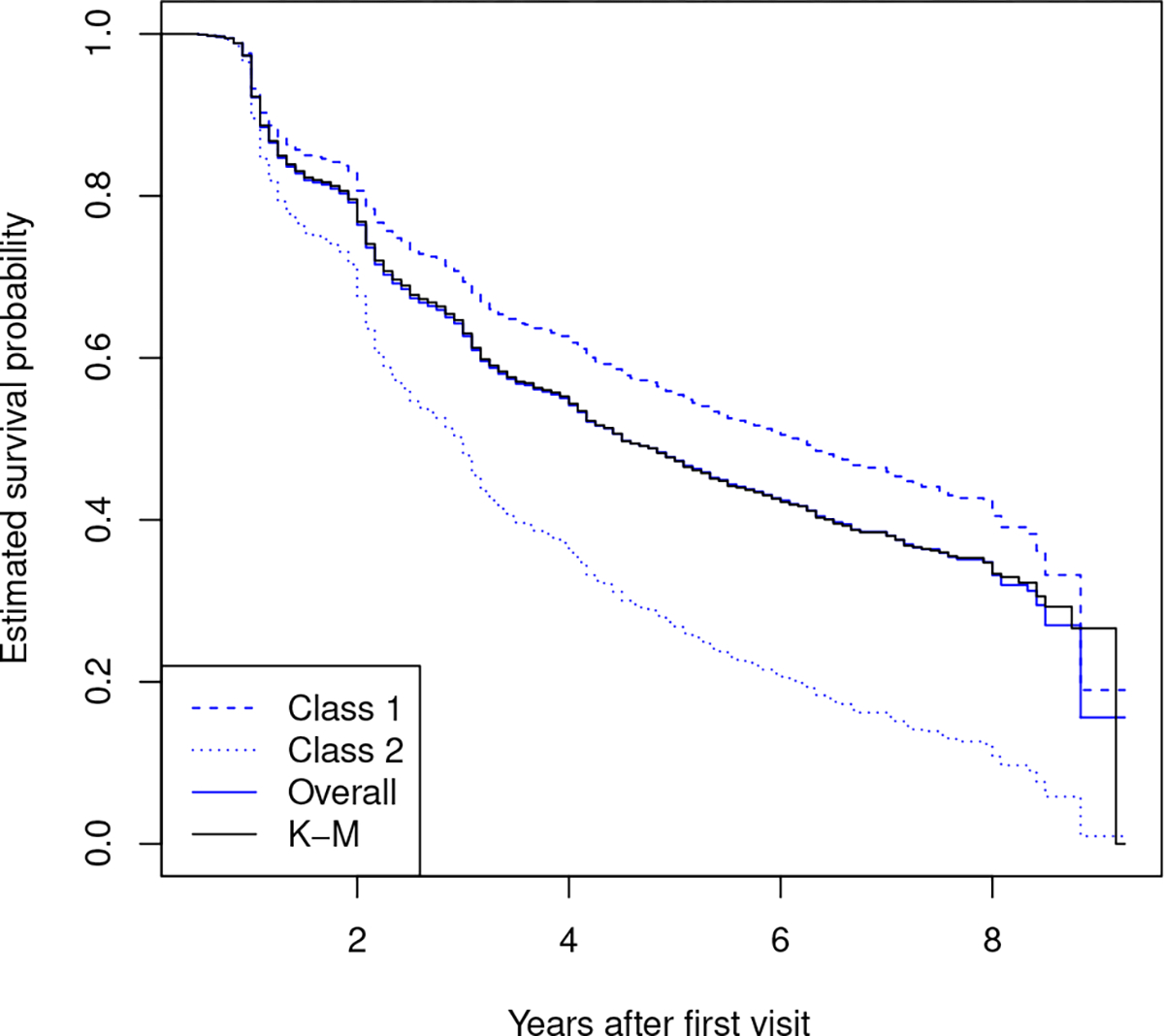
Blue dashed and dotted lines (Class 1 and Class 2): Estimated class-specific survival probabilities by the latent class model. Blue solid line (Overall): Estimated overall survival probability by the latent class model. K-M: Estimated Kaplan-Meier curve for overall survival probability.

We compared the predictive performance of the proposed latent class PH regression versus the standard PH regression using the estimated Brier Scores ${\overline{\widehat{\text{BS}}}}_1(t)$ and ${\overline{\widehat{\text{BS}}}}_2(t)$ for $t\in (\mathrm{0,8}]$ computed via 5-fold cross-validation. Figure 3 shows that the proposed latent class PH regression achieved lower Brier Scores than the standard PH regression. This evidences a gain in survival prediction accuracy from properly accounting for the heterogeneity across latent classes.

Figure 3.

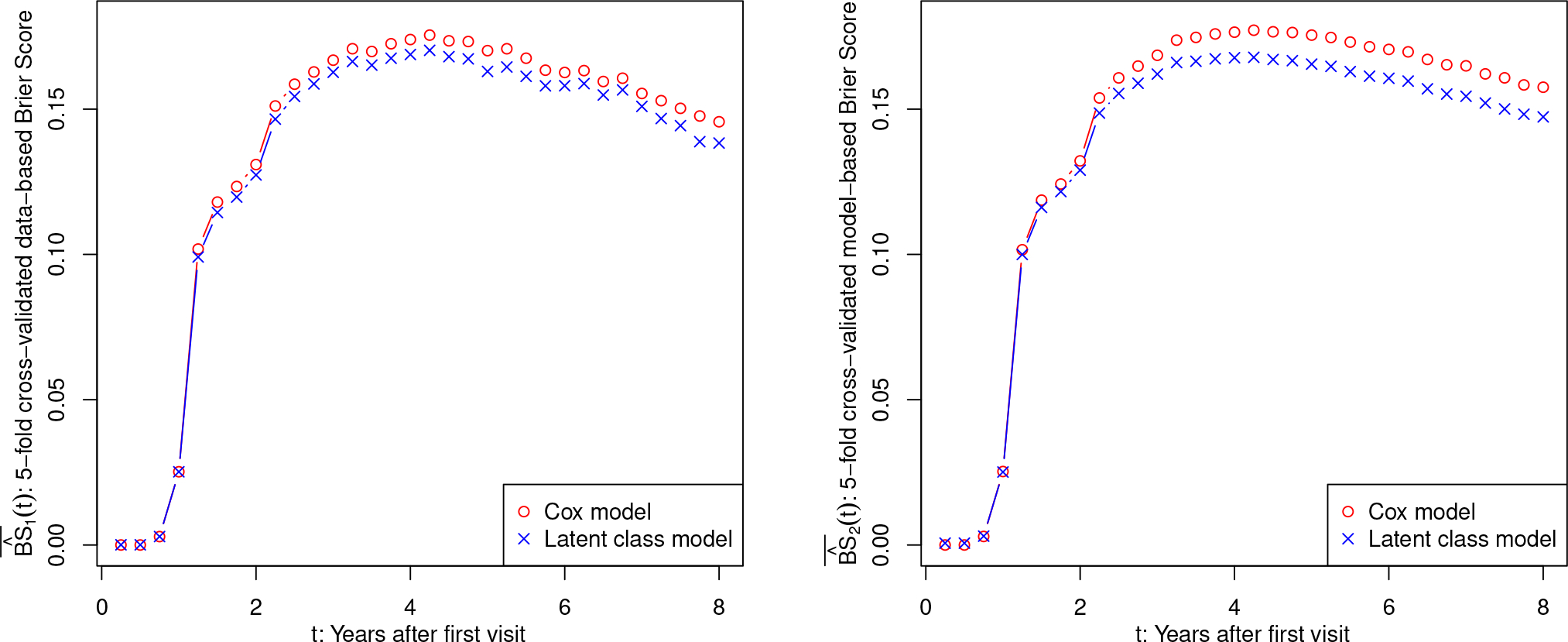
Average of 5-fold cross-validated Brier Scores, ${\overline{\widehat{BS}}}_j(t),j=\mathrm{1,2}$, obtained by the Cox model and the proposed latent class model with $L=2$, for the MCl data application.

6. DISCUSSION

In this work, we propose a semi-parametric approach to conducting latent class PH regression, which can lead to improved understanding of heterogeneous survival data and generate useful scientific implications. Our numerical studies consistently suggest empirical gains in survival prediction benefited from properly accounting for survival heterogeneity across latent classes. This justifies a recommendation of considering latent class PH regression as a useful complementary analysis of survival data in practice. We develop an efficient and stable E-M algorithm which has a solid theoretical underpinning from the general NPMLE framework. The algorithm is efficiently implemented in Rcpp [7] format and is publicly available as an R package.

In our work, the class-specific baseline hazard functions are assumed to be proportional to each other. To assess the method’s robustness when the proportionality assumption is violated, we conducted an additional simulation study as described in Appendix B, and the results are shown in supplementary Table S.8 and Figure S.6. As observed, when the proportionality assumption is violated, the proposed method can still reasonably delineate survival heterogeneity across latent classes and achieve better predictive performance compared to the standard Cox regression.

It is worth mentioning that the proposed latent class PH regression framework can be extended to handle time-dependent covariates with delicate modifications to the complete data likelihood and the corresponding algorithm. When competing risks are present in addition to random censoring to the event time outcome, the proposed method is still applicable as long as regression coefficients are properly interpreted as covariate effects on cause-specific hazard. The proposed work is confined to handle a finite number of covariates. Extensions for handling survival data with a large number of covariate merit future research.