A SIMPLE, CONSISTENT ESTIMATOR OF SNP HERITABILITY FROM GENOME-WIDE ASSOCIATION STUDIES

Abstract

Analysis of genome-wide association studies (GWAS) is characterized by a large number of univariate regressions where a quantitative trait is regressed on hundreds of thousands to millions of single-nucleotide polymorphism (SNP) allele counts, one at a time. This article proposes an estimator of the SNP heritability of the trait, defined here as the fraction of the variance of the trait explained by the SNPs in the study. The proposed GWAS heritability (GWASH) estimator is easy to compute, highly interpretable, and is consistent as the number of SNPs and the sample size increase. More importantly, it can be computed from summary statistics typically reported in GWAS, not requiring access to the original data. The estimator takes full account of the linkage disequilibrium (LD) or correlation between the SNPs in the study through moments of the LD matrix, estimable from auxiliary datasets. Unlike other proposed estimators in the literature, we establish the theoretical properties of the GWASH estimator and obtain analytical estimates of the precision, allowing for power and sample size calculations for SNP heritability estimates, and forming a firm foundation for future methodological development.

1. Introduction.

Genome-wide association studies (GWAS) attempt to describe an observed trait or phenotype, typically assuming a polygenic additive linear model, in terms of a large number of single-nucleotide polymorphisms (SNPs), each captured by the number of copies of a reference allele (0, 1 or 2). The sample size in typical GWAS may be in the order of tens to hundreds of thousands, while the number of SNPs may be ten to one hundred times as large, in the order of millions. Since the number of SNP predictors is larger than the sample size, the linear model is under-determined and it is impossible to estimate the coefficients simultaneously without additional assumptions. Low-dimensional summaries, however, are estimable. In particular, in this paper we focus on the SNP heritability (Yang et al., 2010), defined as the proportion of variance of the outcome explained by the measured SNPs.

While heritability has traditionally been assessed via familial studies, the concept and estimation of SNP heritability have recently become of great interest in the field (for example, Yang et al. (2010) has been cited more than 2800 times to date). This is because GWAS for most human traits have not yet discovered loci accounting for a majority of heritability estimated via familial studies. The invention of the SNP-heritability concept was critical for explaining why this might be because for many traits, most of the variance is distributed across very many loci with small effects that GWAS have not yet been powered to fully discover. With this insight there has been a rejuvenated interest in pursuing larger GWAS and also in the possibility of effective genome-wide predictions. SNP heritability is thus an extremely important parameter that quantifies the proportion of the observed outcome that can be predicted from common SNPs and so defines the amount of information available in the GWAS. It has been a critical parameter in motivating the continued application of GWAS and the utility of GWAS data for predictions (Visscher et al., 2017).

In addition to estimating the heritability of phenotypes based on additive effects of assayed SNPs, the prototypical GWAS analysis also aims to identify individually important genetic loci. This is typically done by regressing the outcome variable on each SNP, one at a time, selecting only the most stringently significant SNPs $\left(p<5\times {10}^{-8}\right)$ as discoveries. Thousands of studies have been performed and tens of thousands of candidate causal variants have been cataloged for all variety of trait and disease (MacArthur et al. (2017), www.ebi.ac.uk/gwas/). In part due to funding institution data sharing mandates, to increase transparency, and to fuel post-hoc and secondary analysis of GWAS results (Pasaniuc and Price, 2017), per-SNP univariate regression statistics (beta coefficients, $t$-statistics, $p$-values, standard errors, etc.) are now regularly published along with GWAS articles. While privacy concerns often prevent the sharing of subject level genotypes and phenotypes, these summary statistics are readily available for hundreds of individual GWAS studies (e.g., www.ebi.ac.uk/gwas/downloads/summary-statistics).

It is of practical interest, therefore, to develop an estimator of SNP heritability that can provide accurate estimates using only summary statistics from GWAS. Computational efficiency is another desired property given the large size of the data. And, as with any estimation procedure, interpretability is also desired in order to gain further insights into the data. For example, we wish to understand how SNP heritability estimates are affected by the correlation between the predictor genomic markers, called linkage disequilibrium (LD) in the context of GWAS. Finally, it is crucial that the theoretical properties of a SNP heritability estimator from GWAS summary statistics are well understood to understand the conditions under which the performance of the estimator is likely to be adequate and to facilitate development of extensions to SNP heritability estimates.

In this paper, we propose an estimator called GWAS heritability (GWASH) estimator. The estimator is based on the variance-fraction estimator in Dicker (2014) and is astonishingly simple. For a GWAS with $m$ predictors and $n$ independent subjects, the estimator is

$${\hat{h}}_{\text{GWASH}}^2=\frac{m}{n{\hat{\mu }}_2}\left(s^2-1\right),$$

where $s^2$ is the empirical variance of the GWAS t-statistics (up to a small transformation) and ${\hat{\mu }}_2$ is an estimate of the second spectral moment of the LD matrix, capturing the effect of LD in a single number.

The GWASH estimator is not only easy to remember and compute as a simple formula. It also has an interpretation as being proportional to the excess empirical variance of the univariate t-statistics with respect to the complete null hypothesis of independence between the outcome and the predictors, in which case the the empirical variance is about 1. The empirical variance $s^2$ is in itself an intuitive quantity that summarizes the strength of the relationship between the predictors and the outcome, and has been used as a simple measure of enrichment in GWAS contexts (Schork et al., 2013). Thus, the proposed estimator has the nice property that it increases linearly with enrichment, where the proportionality constant depends on LD.

Moreover, the formula dictates that LD affects the estimation of SNP heritability as a scaling factor, yielding a definition of the effective number of SNPs involved. Computing the factor ${\hat{\mu }}_2$ to find the effective number of predictors is the only relatively difficult part of the estimation. The factor ${\hat{\mu }}_2$ estimates ${\mu }_2=\text{tr}\left({\tilde{\mathbf{\Sigma }}}^2\right)/m$, where $\tilde{\mathbf{\Sigma }}$ is the correlation matrix of the predictors, the LD matrix. As a first approximation, the patterns of correlations among SNPs can be taken as a feature of a given population and estimated from publicly-available data resources such as the 1000 genomes project (1KGP) (Genomes Project et al. (2015), http://www.internationalgenome.org/.). This approach has been reasonable when the reference sample plausibly represents the same population as the GWAS sample in contexts including imputation (Li et al., 2009), heritability estimation (e.g., Bulik-Sullivan et al. (2015)), functional fine-mapping (e.g., Spain and Barrett (2015)) and various post-hoc burden tests (e.g., de Leeuw et al. (2015)). One of the key contributions of this work is that we propose an efficient way of calculating the factor ${\hat{\mu }}_2$ so that the entire LD matrix need not be computed.

As an alternative method, Linkage Disequilibrium Score (LDSC) regression (Bulik-Sullivan et al., 2015) has become the most popular approach for estimating SNP heritability from summary statistics. LDSC estimates SNP heritability by regressing squared per-SNP univariate regression scores $(t$ or Wald statistics) on corresponding “LD Scores,” defined as estimates of the sum of squared correlations for a given SNP and all others. While an effective and computationally efficient approach, LDSC was not motivated by a well-specified generative model and relies on a number of heuristics, including binning LD scores, censoring outlying values, and empirical approximations to standard errors. These features are difficult to consider analytically and limit assessment of theoretical properties, opportunities for further methodological development, and use in power analyses.

As a real data example, Table 1 shows the estimated SNP heritability using GWASH and LDSC regression from publicly available GWAS summary statistics for three phenotypes. This analysis used a subset of SNPs of size $m=\mathrm{872,188}$ that was available in all four GWAS, in LDSC regression, and in the 1KGP data to calculate ${\hat{\mu }}_2$ and other auxiliary quantities. Owing to a model where samples are taken from a single population, LDSC regression was applied here with a fixed intercept equal to 1. As Table 1 shows, GWASH yields very similar estimates to LDSC regression, confirming its validity in real data, but also produces smaller standard errors. More details about this table are given in Section 7.

Table 1.

Heritability estimates for three complex traits: IQ (Sniekers et al., 2017), years of education (Okbay, 2016) and body mass index (BMI) (Locke, 2015). Estimated SEs are given in parentheses. The last column is the heritability attributed to SNPs found significant in those studies.

Trait	n	m (total)	m (used)	GWASH	LDSC (int=1)	Attr.
IQ	75,270	12,104,295	872,188	0.21 (0.006)	0.20 (0.008)	0.048
EduYears	328,917	9,444,231	872,188	0.10 (0.002)	0.10 (0.003)	0.01
BMI	233,018	2,554,638	872,188	0.05 (0.002)	0.05 (0.006)	0.027

In addition to its simplicity and interpretability, the main strength of the GWASH estimator is its solid theoretical foundation. Following Dicker (2014), we show that the GWASH estimator is consistent as $m$ and $n$ increase to a limiting fixed ratio, which could be greater than 1. We also provide a formula for estimating the asymptotic standard error (SE). For ease of comparison both analytically and in small scale simulations, we consider a stylized version of LDSC regression (intercept = 1) without binning, bootstrap and other elements. We find that both estimators are, in fact, asymptotically equivalent, suggesting avenues to further improve the theoretical foundation for both methods.

We wish to emphasize that accurately computing SNP heritability is of very substantial interest within the field of genetics, as evidenced by the large numbers of publications that use current approaches. To date, this literature has focused on a simple random effects model where a Gaussian distribution was proposed for genetic effects. Closer scrutiny as to the scale at which the single Gaussian was specified (with respect to standardized genotypes in Yang et al. (2010)) revealed implicit assumptions surrounding dependencies between allele frequency and effect sizes. This has resulted in a hotly-contested debate about which set of assumptions provides in the most robust estimates of SNP heritability (see, for example, Speed et al. (2017)). Emerging from this has been a series of post hoc methods which split genetic markers into different bins, estimating heritability per bin and summing, each attempting to counter challenges about specific alternate models (see, as examples, Gazal et al. (2017); Yang et al. (2015)). Part of the problem with development of novel approaches is the lack of a well-grounded theoretical framework, wherein assumptions and limitations are rigorously specified.

The current paper thus has a critically-important aim with regards to the state of the field in SNP-heritability estimation: introducing a principled theoretical framework with well-specified assumptions and consistency properties. This should have the beneficial impact of clarifying the debate and spurring development of models with desirable theoretical properties.

In the rest of the paper we derive the GWASH estimator, show its asymptotic properties, evaluate its performance in non-asymptotic settings via simulations comparing with LDSC regression, and provide further details on the data analysis. We conclude with a discussion of how the GWASH asymptotic SE formula may be used to perform power analysis in prospective GWAS.

2. GWAS.

2.1. The classic polygenic linear model.

Suppose that a continuous outcome variable or phenotype is measured together with a panel of genotype markers at $m$ loci for each of $n$ independent subjects. Let $y_i$ and ${\overrightarrow{\mathit{x}}}_i=\left(x_{i1},\dots ,x_{im}\right)$ denote the outcome and genomic panel for subject $i=1,\dots ,n$. According to the classic polygenic model (Fisher, 1918; Lynch and Walsh, 1998), the outcome is generated according to the linear model

$$y_i={\overrightarrow{x}}_i\beta +{\epsilon }_i,i=1,\dots ,n,$$ (1)

where the error terms ${\epsilon }_i$ are independent with mean 0 and variance ${\sigma }^2$. This model may also be written in matrix form as

$$y=X\beta +\epsilon ,$$ (2)

where $\mathit{y}={\left(y_1,\dots ,y_n\right)}^{\mathrm{T}},\mathit{\beta }={\left({\beta }_1,\dots ,{\beta }_m\right)}^{\mathrm{T}},\mathit{\epsilon }={\left({\epsilon }_1,\dots ,{\epsilon }_n\right)}^{\mathrm{T}}$ and $\mathit{X}$ is the regression matrix with rows ${\overrightarrow{\mathit{x}}}_i,i=1,\dots ,n$. It is also useful to write the regression matrix in terms of its columns as $\mathit{X}=\left({\mathit{x}}_1,\dots ,{\mathit{x}}_m\right)$.

True to the sampling scheme, we shall consider the genomic panels ${\overrightarrow{\mathit{x}}}_i$ to be randomly drawn from the population together with the associated phenotypes. Let $\mathbf{\Sigma }=\text{Cov}\left({\overrightarrow{\mathit{x}}}_i\right)$ denote the $m\times m$ covariance matrix between genomic markers in the underlying population. The corresponding correlation matrix, which we shall denote $\tilde{\mathbf{\Sigma }}=\text{Cor}\left({\overrightarrow{\mathit{x}}}_i\right)$, is the so-called LD matrix and contains the marginal correlations between SNP counts. The entries of this matrix tend to decay away from the diagonal, and we shall exploit this structure in our calculations below.

For simplicity, our model does not explicitly include other fixed covariates (e.g. age, gender, ethnicity factors, etc.) but rather we shall assume that a regression model has adjusted for these other covariates. The interpretation of the coefficients and the SNP heritability shall be conditional on having accounted for those other covariates and is the same as if those covariates had been included in the full model.

Similarly, rather than including an intercept term, we may equivalently assume that the vector $\mathit{y}$ and the columns ${\mathit{x}}_1,\dots ,{\mathit{x}}_m$ of $\mathit{X}$ have been centered by subtracting the vector average, so that $1^{\mathrm{T}}\mathit{y}=0$ and $1^{\mathrm{T}}{\mathit{x}}_j=0$ for $j=1,\dots ,m$. A nice consequence of centering is that, for the centered data, $\mathrm{E}\left(\mathit{y}\right)=0$ and $\mathrm{E}\left(\mathit{X}\right)=0$, where the expectation is taken with respect to the population distribution. Hence, the model (1) or (2) have no intercept term.

2.2. SNP heritability.

The SNP heritability $h^2$ is defined as the variance explained by the predictors in model (2). Specifically, model (1) has the variance decomposition

$$\text{Var}\left(y_i\mid \beta \right)=\text{E}\left({\beta }^{\text{T}}{\overrightarrow{x}}_i^{\text{T}}{\overrightarrow{x}}_i\beta \mid \beta \right)+\text{E}\left({\epsilon }_i^2\right)={\beta }^{\text{T}}\Sigma \beta +{\sigma }^2.$$ (3)

since $\mathrm{E}\left({\overrightarrow{\mathit{x}}}_i\right)=0$. Let ${\tau }^2={\mathit{\beta }}^{\mathrm{T}}\mathbf{\Sigma }\mathit{\beta }$. The SNP heritability is the quantity (Falconer and Mackay, 1996; Lynch and Walsh, 1998)

$$h^2=\frac{{\tau }^2}{{\tau }^2+{\sigma }^2}.$$ (4)

Note that in this model the vector $\mathit{\beta }$ is fixed and arbitrary, with no prespecified distribution. The model places no restrictions on the distribution of model coefficients as long as they yield the proper SNP heritability. Thus, as opposed to other methods such as Yang et al. (2010); Bulik-Sullivan et al. (2015); Zhou, Carbonetto and Stephens (2013), no distributional assumptions are required on $\mathit{\beta }$ in order to estimate SNP heritability, an important point given recent debate in the literature (Speed et al., 2017).

2.3. GWAS univariate regressions.

In GWAS, the vector of SNP effects $\mathit{\beta }$ is estimated by univariate regression coefficients. Since $\mathit{y}$ and the columns ${\mathit{x}}_j$ are assumed centered, there is no need to fit an intercept term and the slope parameters ${\beta }_j$ for each SNP $j=1,\dots ,m$ are estimated via

$${\hat{\beta }}_j={\left(x_j^{\text{T}}{x}_j\right)}^{-1}{x}_j^{\text{T}}y={\Vert x_j\Vert }^{-2}{x}_j^{\text{T}}y.$$ (5)

The univariate regression estimates are typically converted into t-scores by dividing by an estimate of SE at each SNP. For each $j=1,\dots ,m$, the residual variance is

$${\hat{\sigma }}_j^2=\frac{1}{n-2}{\Vert y-x_j{\hat{\beta }}_j\Vert }^2.$$ (6)

yielding the t-score

$$t_j=\frac{{\hat{\beta }}_j}{\sqrt{{\hat{\sigma }}_j^2{\left(x_j^{\text{T}}{x}_j\right)}^{-1}}}=\frac{\Vert x_j\Vert {\hat{\beta }}_j}{{\hat{\sigma }}_j}.$$ (7)

The goal is to produce an estimator of SNP heritability that relies on the above so-called summary statistics ${\hat{\beta }}_j,{\hat{\sigma }}_j^2$ and $t_j,j=1,\dots ,m$. We describe the SNP heritability estimator in general in Section 3 and return to the summary statistics in Section 5.1.

3. The Dicker estimator.

To better describe the derivation of the GWASH estimator, we first discuss the estimator proposed by Dicker (2014). Addressing the high-dimensional case where $m$ is greater than $n$, and separately from the GWASSH problem, Dicker (2014) proposes an estimator of the fraction of variance explained by $\mathit{X}$ in model (2) when the vector of coefficients $\mathit{\beta }$ is fixed. While not called heritability there, this fraction is the same as the SNP heritability defined in (4). Since ordinary least squares methods fail when $m>n$, Dicker’s estimator is based instead on a clever use of the method of moments. Dicker proposes two forms of the estimator depending on whether the covariance matrix $\mathbf{\Sigma }$, typically unknown, is estimable or not.

3.1. The Dicker estimator for estimable covariance.

An estimable covariance matrix $\mathbf{\Sigma }$ presumes the existence of a norm-consistent positive definite estimator $\stackrel{\mathit{ˆ}}{\mathbf{\Sigma }}$, despite the dimension $m$ being larger than the sample size $n$. Examples of estimable covariance matrices are a diagonal $\mathbf{\Sigma }$, so that the columns of $\mathit{X}$ are uncorrelated but have different variances, or matrices where the correlation structure is captured by a fixed number of parameters, such as autoregressive (AR) and exchangeable correlation models.

Written in our notation, the Dicker estimator of $h^2$ for estimable covariance (Dicker, 2014, Sec. 4.1) can be simplified to

$${\hat{h}}_I^2=\frac{m}{n}\left(\frac{{\Vert {\hat{\Sigma }}^{-1/2}{X}^{\text{T}}y\Vert }^2}{m\parallel y{\parallel }^2}-1\right)$$ (8)

(see Supplementary Material), where $n$ is replaced by $n-1$, owing to the centering of $\mathit{y}$ and the columns of $\mathit{X}$ (Dicker, 2014, Sec. 1). This estimator requires a consistent estimator $\stackrel{\mathit{ˆ}}{\mathbf{\Sigma }}$ of the covariance matrix $\mathbf{\Sigma }$, which is not available without further assumptions. The sample covariance matrix

$$S=\frac{1}{n-1}{X}^{\text{T}}X,$$ (9)

whose entries are the sample covariances of the columns of $\mathit{X}$, is an unbiased estimator of $\mathbf{\Sigma }$, satisfying $\mathrm{E}\left(\mathit{S}\right)=\mathbf{\Sigma }$. It is, however, not norm-consistent in general if the dimension $m$ is larger than the sample size $n$.

Assuming that the true correlation is nonzero only close to the diagonal, as is the case with human population genetics, consistent estimators may be obtained, for example, by banding the sample covariance matrix (Bickel and Levina, 2008; Cai, Zhang and Zhou, 2010). Even so, the estimator (8) requires computation of the inverse square root ${\stackrel{\mathit{ˆ}}{\mathbf{\Sigma }}}^{-1/2}$. This is computationally taxing for the typical large matrix size $m$ in GWAS in the order of magnitude of a million. Dicker’s estimator for unestimable covariance avoids this problem.

3.2. The Dicker estimator for unestimable covariance.

When a model for $\mathbf{\Sigma }$ is not sufficiently specified to be estimable, Dicker (2014) offers another form of the estimator that replaces estimation of $\mathbf{\Sigma }$ by estimation of its first few moments. Written in our notation, the Dicker estimator of $h^2$ for unestimable covariance (Dicker, 2014, Sec. 4.2) can be simplified to

$${\hat{h}}_{II}^2=\frac{m{\hat{m}}_1^2}{n{\hat{m}}_2}\left(\frac{{\Vert X^{\text{T}}y\Vert }^2}{m{\hat{m}}_1\parallel y{\parallel }^2}-1\right)$$ (10)

(see Supplementary Material), where

$${\hat{m}}_1=\frac{1}{m}\text{tr}\left(S\right),{\hat{m}}_2=\frac{1}{m}\text{tr}\left(S^2\right)-\frac{m}{n-1}{\hat{m}}_1^2,$$ (11)

and $\mathit{S}$ is the sample covariance matrix (9).

Proposition 2 of Dicker (2014) states that if the entries of $\mathit{X}$ and $\mathit{\epsilon }$ are Gaussian and $\mathbf{\Sigma }$ is not too far from the identity matrix (technical details omitted here), then ${\hat{h}}_{II}^2$ satisfies a CLT and is approximately Gaussian with mean $h^2$ and variance

$$\frac{{\psi }_{II}^2}{n}=\frac{2}{n}\left(\frac{m{m}_1^2}{n{m}_2}+2\frac{m_1{m}_3}{m_2^2}{h}^2-h^4\right),$$ (12)

for large $m$ and $n$ such that $m/n$ is bounded, where

$$m_1=\frac{1}{m}\text{tr}\left(\Sigma \right),m_2=\frac{1}{m}\text{tr}\left({\Sigma }^2\right),m_3=\frac{1}{m}\text{tr}\left({\Sigma }^3\right).$$ (13)

By the commutative property of the trace, it can be shown that the quantities in (13) correspond to the first, second and third moments of the eigenvalues of $\mathbf{\Sigma }$. In that sense they can be called spectral moments.

An estimate of SE for ${\hat{h}}_{II}^2$ can be obtained as the square root of (12) by plugging in the estimate of $h^2$ and those of $m_1$ and $m_2$ given by (11). As an estimate of $m_3$, Dicker (Dicker, 2014, Remark 12) suggests

$${\hat{m}}_3=\frac{1}{m}\text{tr}\left(S^3\right)-\frac{3m}{n-1}{\hat{m}}_1{\hat{m}}_2-\frac{m^2}{{(n-1)}^2}{\hat{m}}_1^3\text{.}$$ (14)

4. The GWASH estimator.

In GWAS, it is feasible to implement Dicker’s estimator (10) if the entire dataset composed of $\mathit{X}$ and $\mathit{y}$ is available. However, often only GWAS summary statistics are avaiable. The GWASH estimator is essentially a modification of the Dicker estimator where the columns of $\mathit{X}$ are standardized. This standardization allows writing the estimator in terms of the correlation scores defined next, which easily translate into summary statistics.

4.1. Correlation scores.

Let $\tilde{\mathit{y}}=\sqrt{n-1}\mathit{y}/\parallel \mathit{y}\parallel$ be the standardized vector $\mathit{y}$ so that $\parallel \tilde{\mathit{y}}{\parallel }^2/(n-1)=1$. Similarly, let $\tilde{\mathit{X}}=\left({\tilde{\mathit{x}}}_1,\dots ,{\tilde{\mathit{x}}}_m\right)$ be the result of standardizing the matrix $\mathit{X}$ by columns, so that the standardized columns ${\tilde{\mathit{x}}}_j=\sqrt{n-1}{\mathit{x}}_j/∥{\mathit{x}}_j∥$ satisfy ${∥{\tilde{\mathit{x}}}_j∥}^2/(n-1)=1$, for $j=1,\dots ,m$. Because of the original centering, $1^{\mathrm{T}}\tilde{\mathit{y}}=0$ and $1^{\mathrm{T}}{\tilde{\mathit{x}}}_j=0$.

The main idea of the GWASH estimator is to replace $\mathit{X}$ and $\mathit{y}$ in (10) by their standardized versions $\tilde{\mathit{X}}$ and $\tilde{\mathit{y}}$. Because (10) depends on the summary statistic ${∥{\mathit{X}}^{\mathrm{T}}\mathit{y}∥}^2$, to become ${∥{\tilde{\mathit{X}}}^{\mathrm{T}}\tilde{\mathit{y}}∥}^2$, it is convenient here to define what we call the correlation scores

$$u_j=\frac{1}{\sqrt{n-1}}{\tilde{x}}_j^{\text{T}}\tilde{y}=\sqrt{n-1}\frac{x_j^{\text{T}}y}{\Vert x_j\Vert \parallel y\parallel },j=1,\dots ,m,$$ (15)

or in vector form, $\mathit{u}={\tilde{\mathit{X}}}^{\mathrm{T}}\tilde{\mathit{y}}/\sqrt{n-1}$.

The score $u_j$ is equal to $\sqrt{n-1}$ times the sample correlation between ${\mathit{x}}_j$ and $\mathit{y}$. Under the null hypothesis of no heritability $\left(h^2=0\right)$, so that ${\mathit{x}}_j$ and $\mathit{y}$ are independent, the score (15) is asymptotically normal with mean zero and variance one. In this sense it plays the role of a z-score.

4.2. The LD matrix.

By standardization, we may define the sample covariance matrix of the columns of $\tilde{\mathit{X}}$,

$$\tilde{S}=\frac{1}{n-1}{\tilde{X}}^{\text{T}}\tilde{X}.$$ (16)

By definition, this is the sample correlation matrix with ones on the diagonal and can be referred to as the sample LD matrix.

Let $\tilde{\mathbf{\Sigma }}=\text{Cor}\left({\overrightarrow{\mathit{x}}}_i\right)$ be the population correlation matrix corresponding to the covariance matrix $\mathbf{\Sigma }$. Analogous to (13), we can define the first three spectral moments of $\tilde{\mathbf{\Sigma }}$ by

$${\mu }_1=\frac{1}{m}\text{tr}\left(\tilde{\Sigma }\right)=1,{\mu }_2=\frac{1}{m}\text{tr}\left({\tilde{\Sigma }}^2\right),{\mu }_3=\frac{1}{m}\text{tr}\left({\tilde{\Sigma }}^3\right).$$ (17)

These quantities capture the total effect of LD between the genomic markers. If the genomic markers are independent with $\tilde{\mathbf{\Sigma }}=\mathit{I}$, then ${\mu }_2={\mu }_3=1$; otherwise both moments are greater than 1.

4.3. The GWASH estimator from subject-level data.

The GWASH estimator is defined as a modification of the Dicker estimator where: 1) $\mathit{X}$ and $\mathit{y}$ in (10) are replaced by their standardized versions $\tilde{\mathit{X}}$ and $\tilde{\mathit{y}}$; 2) the moment estimators ${\hat{m}}_1,{\hat{m}}_2$ and ${\hat{m}}_3$ in (10), (11) and (14) are replaced by moment estimators ${\hat{\mu }}_1=1,{\hat{\mu }}_2$ and ${\hat{\mu }}_3$ based on the correlation matrix (16) instead (details on these are given in sections 4.4 and 5.3 below).

Performing the replacements outlined above yields the expression

$${\hat{h}}_{\text{GWASH}}^2=\frac{m}{n{\hat{\mu }}_2}\left(\frac{{\Vert {\tilde{X}}^{\text{T}}\tilde{y}\Vert }^2}{m\left(n-1\right)}-1\right).$$ (18)

However, this expression can be written succinctly in terms of the correlation scores. We may now define our estimator.

Definition 1. The GWAS heritability (GWASH) estimator is given by

$${\hat{h}}_{\text{GWASH}}^2=\frac{m}{n{\hat{\mu }}_2}\left(s^2-1\right),$$ (19)

where $s^2$ is the empirical second moment of the correlation scores:

$$s^2=\frac{1}{m}{\Vert u\Vert }^2=\frac{1}{m}\sum _{j=1}^m{u}_j^2,$$ (20)

and ${\hat{\mu }}_2$ is an estimator of ${\mu }_2$ in (17).

The GWASH estimator depends on the data only through two summary statistics, $s^2$ and ${\hat{\mu }}_2$. Under the null hypothesis of no heritability $\left(h^2=0\right),s^2\to 1$ for large $m$ by the law of large numbers. Thus, (19) expresses the estimate of SNP heritability as proportional to the excess variance of the scores with respect to the null variance 1.

The quantity ${\hat{\mu }}_2$ contains all the necessary information about the correlation between the predictors. From (17), if the predictors are independent, ${\mu }_2=1$. Otherwise, ${\mu }_2>1$. This implies that ignoring LD causes overestimation of the SNP heritability. Taking account of LD is equivalent to using a smaller number of predictors. In this sense, we may define ${\hat{m}}_{\text{eff}}=m/{\hat{\mu }}_2$ as the estimated effective number of markers: the higher the LD, i.e. the higher the correlation between the predictors, the lower their effective number.

4.4. Estimation of the LD second spectral moment ${\mu }_2$.

From (11), an appropriate estimate of ${\mu }_2$ is

$${\hat{\mu }}_2=\frac{1}{m}\text{tr}\left({\tilde{S}}^2\right)-\frac{m-1}{n-1}=1+\frac{1}{m}\sum _{i\ne j}\left({\tilde{S}}_{ij}^2-\frac{1}{n-1}\right).$$ (21)

The expression on the left, in comparison to (11), uses $\tilde{\mathit{S}}$ instead of $\mathit{S}$ and uses ${\hat{\mu }}_1=1$ instead of ${\hat{m}}_1$. The replacement of $m-1$ instead of $m$ is more clearly understood in the expression on the right, obtained by replacing $\text{tr}\left({\tilde{\mathit{S}}}^2\right)=m+{\sum }_{i\ne j} {\tilde{S}}_{ij}^2$. Here we can see that ${\hat{\mu }}_2$ is equal to 1 (the value of ${\mu }_2$ under no correlation) plus $1/m$ times the total squared correlation observed in the sample LD matrix $\tilde{\mathit{S}}$, after subtracting from each term a bias correction of $1/(n-1)$. The extra term $1/(n-1)$ is the approximate second moment, for large $n$, of the empirical correlation ${\tilde{S}}_{ij}$ when the true underlying correlation ${\tilde{\Sigma }}_{ij}$ is zero. It is pervasive in the LD matrix and we may refer to it as a “correlation floor”.

The following lemma, whose proof is in Section S2 in the Supplementary Material, states that ${\hat{\mu }}_2$ is a consistent estimator of ${\mu }_2$.

Lemma 1. Assume the spectral moments $m_k=tr\left({\mathbf{\Sigma }}^k\right)/m,k=1,\dots ,4$, are bounded as $m$ gets large. Then, as $m$ and $n$ get large such that $m/n$ converges to a constant (which may be zero),

$${\hat{\mu }}_2={\mu }_2+O_P\left(\frac{1}{n}\right).$$ (22)

4.5. Asymptotic properties of the GWASH estimator.

By construction, the GWASH estimator has similar asymptotic properties to the Dicker estimator (10), namely consistency and asymptotic normality. Theorem 1 below shows this formally and gives the theoretical justification for using the GWASH estimator in GWAS.

Assumption 1. Suppose that the assumptions of Proposition 2 of Dicker (2014) hold, namely:

• The variance components ${\sigma }^2$ and ${\tau }^2$, as well as the spectral moments $m_k=\text{tr}\left({\mathbf{\Sigma }}^k\right)/m,k=1,\dots ,4$, are bounded.

• Let ${\tau }_k^2={\mathit{\beta }}^{\mathrm{T}}{\mathbf{\Sigma }}^k\mathit{\beta },{\Delta }_k={\sum }_{\ell =1}^k \left|{\tau }_{\ell }^2-{\tau }_0^2{m}_{\ell }\right|$, and suppose ${\Delta }_3=o(1/\sqrt{n})$.

Theorem 1. Under Assumption 1, as $m$ and $n$ get large such that $m/n$ converges to a constant (which may be zero), the GWASH estimator (19) satisfies the $CLT\sqrt{n}\left({\hat{h}}_{\text{GWASH}}^2-h^2\right)/\psi \to N\left(\mathrm{0,1}\right)$, where

$$\frac{{\psi }^2}{n}=\frac{2}{n}\left(\frac{m}{n{\mu }_2}+2\frac{{\mu }_3}{{\mu }_2^2}{h}^2-h^4\right).$$ (23)

Theorem 1 implies consistency of the estimator for large $m$ and $n$. The proof is given in Section S3 in the Supplementary Material. Moreover, notice that the theorem allows for $m>n$ as well as $m<n$. In particular, the GWASH estimator may be used to estimate the heritability of a fixed set of $m$ SNPs for increasing $n$, as long as model (1) holds.

For large $m$ and $n$, the GWASH estimator is approximately Gaussian with mean $h^2$ and variance (23). In this scenario, an estimate of SE for ${\hat{h}}^2$ can be obtained as the plug-in estimate $\hat{\psi }/\sqrt{n}=\sqrt{{\hat{\psi }}^2/n}$, where

$$\frac{{\hat{\psi }}^2}{n}=\frac{2}{n}\left(\frac{m}{n{\hat{\mu }}_2}+2\frac{{\hat{\mu }}_3}{{\hat{\mu }}_2^2}{\hat{h}}^2-{\hat{h}}^4\right)$$ (24)

and ${\hat{\mu }}_3$ is an estimator of ${\mu }_3$ (see Section 5.3). The asymptotic normality of ${\hat{h}}^2$ allows constructing an approximate two-sided 95% confidence interval for $h^2$ of the form ${\hat{h}}^2\pm 1.96\hat{\psi }/\sqrt{n}$. In addition, the null hypothesis $H_0:h^2=0$ may be tested against the alternative $H_A:h^2>0$ using the Wald statistic $\sqrt{n}{\hat{h}}^2/\hat{\psi }$ and declaring it significant at the $\alpha$ level if it exceeds the normal quantile $z_{1-\alpha }$.

4.6. Aggregation and partition of SNP heritability.

The GWASH estimator (19) can be applied to any set of SNPs, large or small. Here we show how the heritability of several sets of SNPs can be aggregated to estimate the total SNP heritability, or conversely, how the total SNP heritability can be partitioned into SNP subsets. Suppose we have $K$ subsets of SNPs defined by the index sets ${𝒥}_1,\dots ,{𝒥}_K$. The sets may be partially overlapping. Let $m_k$ be the number of SNPs in the index set ${𝒥}_k,k=1,\dots ,K$. Applying (19), the SNP heritability estimate of the set ${𝒥}_k$ is

$${\hat{h}}_{\text{GWASH},k}^2=\frac{m_k}{n{\hat{\mu }}_{2,k}}\left(s_k^2-1\right),s_k^2=\frac{1}{m_k}\sum _{j\in {𝒥}_k}{u}_j^2,$$ (25)

where $s_k^2$ is the empirical second moment of the correlation scores within the set $J_k$. Similar to (21),

$${\hat{\mu }}_{2,k}=\frac{1}{m_k}\text{tr}{\left({\tilde{S}}^{\left(k\right)}\right)}^2-\frac{m_k-1}{n-1}=1+\frac{1}{m_k}\sum _{i\ne j\in {𝒥}_k}\left[{\left({\tilde{S}}_{ij}^{\left(k\right)}\right)}^2-\frac{1}{n-1}\right]$$ (26)

applies to the submatrix ${\tilde{\mathit{S}}}^{\left(k\right)}$ including only the indices in ${𝒥}_k$. From (25), using (19) and (20), we obtain the following result.

Proposition 1. The total SNP heritability estimate ${\hat{h}}_{\text{GWASH}}^2$ of the set $𝒥={𝒥}_1\cup \dots \cup {𝒥}_K$ can be computed as

$${\hat{h}}_{\text{GWASH}}^2=\sum _{k=1}^K\frac{{\hat{\mu }}_{2,k}}{{\hat{\mu }}_2}{\hat{h}}_{\text{GWASH},k}^2.$$ (27)

Moreover, if the K sets of SNPs are independent,

$${\hat{\mu }}_2=\sum _{k=1}^K\frac{m_k}{m}{\hat{\mu }}_{2,k}+o\left(\frac{1}{n}\right).$$ (28)

Proposition 1 indicates that the total SNP heritability is a weighted sum of the contributions of the various subsets, where the weights depend on the amount of LD in each subset relative to the total. Note that this is not a weighted average, as the weights ${\hat{\mu }}_{2,k}/{\hat{\mu }}_2$ may be smaller or larger than 1. For example, if the sets are dependent, the total ${\hat{\mu }}_2$ may be larger than the individual values ${\hat{\mu }}_{2,k}$ in each set. On the other hand, if the amount of LD within each set is larger than between sets, the total ${\hat{\mu }}_2$, which is an average over a larger number of SNPs, may be smaller than the individual values ${\hat{\mu }}_{2,k}$ in each set.

Another way to interpret Proposition 1 is as follows. Recall that ${\hat{\mu }}_{2,k}$ is the ratio between the number of SNPs $m_k$ and the corresponding effective number of SNPs, measuring SNP redundancy. The weight of each set is the ratio between the redundancy in the set and the redundancy of all sets put together.

5. Practical aspects in the context of GWAS.

5.1. The GWASH estimator from summary statistics.

In publicly available GWAS results, the original data $\mathit{y}$ and $\mathit{X}$ required to compute the correlation scores (15) are typically not available. Instead, it is possible to access the t-statistics (7) from the univariate regressions. The next result shows that the original data is not necessary, but it is possible to convert the squared t-statistics to squared correlation scores by a simple formula.

Proposition 2. The square of the correlation scores (15) can be obtained from the squared $t$-statistics (7) via

$$u_j^2=\left(\frac{n-1}{n-2}\right)\frac{t_j^2}{1+t_j^2/\left(n-2\right)}.$$ (29)

The squared correlation scores and the squared t-statistics are very close for large $n$, but not exactly. The transformation is needed because the residual variance (6) typically used in GWAS is a biased estimator of the true noise variance. The effect of the transformation is to “undo” the division by (6) and turn the t-statistic into a more appropriate score.

To compute the GWASH estimator (19), $s^2$ can be computed directly from the u-scores (29). The LD second spectral moment ${\hat{\mu }}_2$ cannot be computed from summary statistics. However, ${\hat{\mu }}_2$ is a property of the population from which the GWAS data was sampled. Following others, we make the assumption that the sampled population has similar properties to those in public datasets such as the 1000 genomes project (1KGP) (Genomes Project et al., 2015). Under this assumption, ${\hat{\mu }}_2$ can be estimated from any random sample assayed on the same set of predictors, even if the representative sample is of a different size. For example, if a representative auxiliary dataset of size $\tilde{n}$ is available on the same set of SNPs, then ${\hat{\mu }}_2$ can be estimated using the methods of Section 4.4 with $\tilde{n}$ instead of $n$. The same holds for ${\hat{\mu }}_3$ (see Section 5.3).

5.2. Efficient computation of the LD second moment estimator ${\hat{\mu }}_2$.

From a computational point of view, we may take advantage of the fact that, in a randomly mating population, SNPs appreciably far away within the same chromosome, or on different chromosomes, should be segregating independently. For independent markers $i,j$, their squared correlation ${\tilde{S}}_{ij}^2$ has mean of about $1/(n-1)$ (see Eq. (S1)), and so the terms ${\tilde{S}}_{ij}^2-1/(n-1)$ in (21) far from the diagonal are small and can be excluded from the calculation.

In general, suppose that only a set ${ℐ}_2$ of index pairs $(i,j),i\ne j$, are included in the calculation of ${\hat{\mu }}_2$. This results in the modified estimator

$${\hat{\mu }}_{2,{ℐ}_2}=1+\frac{1}{m}\sum _{\left(i,j\right)\in {ℐ}_2}\left({\tilde{S}}_{ij}^2-\frac{1}{n-1}\right)=1+\frac{1}{m}\left[\sum _{\left(i,j\right)\in {ℐ}_2}{\tilde{S}}_{ij}^2-\frac{\left|{ℐ}_2\right|}{n-1}\right],$$ (30)

where $\left|{ℐ}_2\right|$ is the number of elements in the set ${ℐ}_2$. Note that the bias correction of $1/(n-1)$ is applied to only the terms included in the sum.

Specifically, for a single chromosome with $m_k$ markers, $k=1,\dots ,K$, excluding all pairs more than $q>0$ indices away is equivalent to applying formula (21) to the restricted matrix ${\tilde{\mathit{S}}}_q^{\left(k\right)}$ with entries

$${\left({\tilde{S}}_q^{\left(k\right)}\right)}_{ij}=\{\begin{array}{ll}1\hfill & i=j\hfill \\ {\tilde{S}}_{ij}\hfill & i\ne j,\left(i,j\right)\in {ℐ}_2^{\left(k\right)}\hfill \\ 0\hfill & i\ne j,\left(i,j\right)\notin {ℐ}_2^{\left(k\right)}\hfill \end{array},$$ (31)

where ${ℐ}_2^{\left(k\right)}=\left\{\right(i,j):1<|i-j|\le q\}$ with indices $i,j$ within chromosome $k$. It can be shown that $\left|I_q^{\left(k\right)}\right|=q\left(2m_k-q-1\right)$, yielding the formula

$${\hat{\mu }}_{2,q}^{\left(k\right)}=\frac{1}{m_k}\left[\text{tr }{\left({\tilde{S}}_q^{\left(k\right)}\right)}^2-\frac{q\left(2m_k-q-1\right)}{n-1}\right].$$ (32)

In practice, the restricted matrix (31) can be stored as a sparse matrix and the trace above computed using the property that for any squared matrix $\mathit{A},\text{tr}\left({\mathit{A}}^2\right)={\sum }_{i,j} A_{ij}^2$.

For a set of $K$ chromosomes with $m_1+\cdots +m_K=m$, the overall estimate ${\hat{\mu }}_{2,q}$ is calculated, using (28), as the weighted average of the per-chromosome estimates (32), weighted by the number of markers $m_k$ in each chromosome. In what follows, we refer to the distance $q$ as correlation bandwidth.

5.3. Estimation of the LD third spectral moment ${\mu }_3$.

To compute the variance (24), we need an estimator of ${\mu }_3$. From (14), an appropriate estimate of ${\mu }_3$ is

$$\begin{gathered} {\hat{\mu }}_3=\frac{1}{m}\text{tr}\left({\tilde{S}}^3\right)-3\frac{m-1}{n-1}{\hat{\mu }}_2-\frac{\left(m-1\right)\left(m-2\right)}{{(n-1)}^2} \\ =\frac{1}{m}\left[\text{tr}\left({\tilde{S}}^3\right)-3\frac{m\left(m-1\right)}{n-1}{\hat{\mu }}_2-\frac{m\left(m-1\right)\left(m-2\right)}{{(n-1)}^2}\right]. \end{gathered}$$ (33)

To understand this estimator, we realize that

$$\begin{gathered} \text{tr}\left({\tilde{S}}^3\right)=\text{tr}\left(\tilde{S}{\tilde{S}}^2\right)=\sum _{i,j=1}^m{\tilde{S}}_{ij}{\left({\tilde{S}}^2\right)}_{ij}=\sum _{i,j,k=1}^m{\tilde{S}}_{ij}{\tilde{S}}_{jk}{\tilde{S}}_{ik} \\ =m+\sum _{i\ne j}{\tilde{S}}_{ij}^2+\sum _{i\ne k}{\tilde{S}}_{ik}^2+\sum _{j\ne k}{\tilde{S}}_{jk}^2+\sum _{i\ne j\ne k}{\tilde{S}}_{ij}{\tilde{S}}_{jk}{\tilde{S}}_{ik}, \end{gathered}$$ (34)

where we have replaced ${\tilde{S}}_{ii}=1,i=1,\dots ,m$. Thus, the first subtracted term in (33) makes a bias correction of ${\hat{\mu }}_2/(n-1)$ for each of the $3m(m-1)$ second order terms in the sum above, while the second subtracted term makes a bias correction of $1/(n-1{)}^2$ for each of the $m(m-1)(m-2)$ third order terms. A computationally efficient approximation for ${\hat{\mu }}_3$ is given in Section S4 in the Supplementary Material.

5.4. Relationship to LDSC regression.

The LDSC regression method (Bulik-Sullivan et al. (2015)) is derived under different modeling assumptions to ours, the most important being the assumption that the $\mathit{\beta }$ coefficients are random. In addition, the corresponding software is written for large GWAS applications and is not amenable to smaller scale simulations as we do here. To allow direct comparison both analytically and in simulations, here we consider a stylized version of LDSC regression that closely matches the GWASH estimator.

Assuming independent subjects from a single population, the LDSC method is essentially based on the approximation

$$\text{E}\left[u_j^2\mid {\hat{\ell }}_j\right]\approx h^2\left(\frac{n}{m}{\hat{\ell }}_j-1\right)+1,j=1,\dots ,m,$$ (35)

written in our notation (see Section S5 in the Supplementary Material), where ${\hat{\ell }}_j={\sum }_{k=1}^m {\tilde{r}}_{jk}^2$ are the so-called LD-scores and ${\tilde{r}}_{jk}$ are the entries of $\tilde{\mathit{S}}={\tilde{\mathit{X}}}^{\mathrm{T}}\tilde{\mathit{X}}/(n-1)$. The LDSC method estimates $h^2$ by fitting a linear model based on (35) plus observation noise. Defining ${\mathit{u}}^2={\left(u_1^2,\dots ,u_m^2\right)}^{\mathrm{T}}$ and $\mathcal{l}={\left((n/m){\hat{\ell }}_1-1,\dots ,(n/m){\hat{\ell }}_m-1\right)}^{\mathrm{T}}$, the model (35) reads $\mathrm{E}\left({\mathit{u}}^2\right)=h^2\mathcal{l}+1$, leading to the least squares estimator

$${\hat{h}}_{\text{LD}}^2=|\mathit{\ell }{|}^{-2}{\mathit{\ell }}^{\text{T}}\left(u^2-1\right),$$ (36)

fitted with a fixed intercept equal to 1.

The GWASH estimator is related to the LDSC regression estimator above in the following way. In linear regression, the fitted line always goes through the average of the point cloud. Therefore, the average $\left(\bar{\ell },\stackrel{-}{u^2}\right)=\left(1^{\mathrm{T}}\mathcal{l}/m,1^{\mathrm{T}}{\mathit{u}}^2/m\right)$ must satisfy the equation

$$\overline{u^2}={\hat{h}}_{\text{LD}}^2\overline{\ell }+1.$$ (37)

We show in Section S5 in the Supplementary Material that this implies

$${\hat{h}}_{\text{LD}}^2=\frac{\overline{u^2}-1}{\overline{\ell }}={\hat{h}}_{\text{GWASH}}^2+O\left(\frac{1}{n}\right).$$ (38)

In other words, if we consider a scatterplot of $u_j^2$ as a function of the LD scores ${\hat{\ell }}_j$, LDSC fits the least-squares straight line through the distribution, while GWASH targets the mean of the distribution directly, and the two are asymptotically equivalent. We will see in the simulations and data analysis that both give similar estimates but have different SEs.

6. Finite sample performance.

The following simulations evaluate the performance of the GWASH estimator under various finite sample scenarios. To push the limits of the estimator, we consider an autoregressive (AR) covariance structure for the predictor matrix $\mathit{X}$ where the AR parameter $\rho$ ranges from 0 to 0.8 and where the variances of the columns of $\mathit{X}$ have a wide spread from 1 to $m$. We consider two different distributions for the entries of $\mathit{X}$:

• The rows of $\mathit{X}$ are i.i.d. multivariate normal with mean 0 and covariance matrix $\mathbf{\Sigma }=[\text{Diag}(\mathbf{\Sigma }\left){]}^{1/2}\tilde{\mathbf{\Sigma }}\right(\rho \left)\right[\text{Diag}\left(\mathbf{\Sigma }\right){]}^{1/2}$, where $\text{Diag}\left(\mathbf{\Sigma }\right)=$ $\text{Diag}(\mathrm{1,2},\dots ,m)$ and $\tilde{\mathbf{\Sigma }}\left(\rho \right)$ is the $m\times m$ AR correlation matrix with entries ${\tilde{\Sigma }}_{ij}={\rho }^{|i-j|}$.

• The rows of $\mathit{X}$ are i.i.d. multivariate binomial, generated using a Gaussian multivariate copula (Hofert et al., 2014; Kojadinovic and et al., 2010). According to this method, a multivariate normal vector is generated with the same covariance matrix $\mathbf{\Sigma }$ as above and AR parameter ${\rho }^{*}$. The multivariate normal vector is then transformed to binomial by a quantile transformation with the corresponding variance. Because of the copula, the correlation between the binomial variables is not exactly AR and we use the notation ${\rho }^{*}$ as a reminder of this.

For the vector of coefficients $\mathit{\beta }$, we consider two different structures:

• $\mathit{\beta }$ is a single realization of $m$ i.i.d. $N\left(\mathrm{0,1}\right)$ variables.

• $\mathit{\beta }$ is a mixture, containing 90% of 0 ‘s and 10% i.i.d. $N$(0,1) variables.

Note that $\mathit{\beta }$ is generated once in each case and then fixed for all simulations. In all cases, the outcome $\mathit{y}$ is generated according to model (2) with i.i.d. Gaussian errors. Given $\mathit{\beta }$ and $\mathbf{\Sigma }$, for any desired SNP heritability $h^2>0$, the error variance is set to ${\sigma }^2={\tau }^2\left(1-h^2\right)/h^2$ so that (4) gives SNP heritability $h^2$. For $h^2=0$, we set $\mathit{\beta }=0$.

6.1. Estimation of SNP heritability.

Figure 1 shows the estimates of $h^2$ under the aforementioned combinations. The estimation methods shown are:

• The GWASH estimator (19) using the full sample correlation matrix $(q=m-1)$ to estimate ${\mu }_2$, as in (21).

• The GWASH estimator (19) using only $q$ off-diagonals of the sample correlation matrix to estimate ${\mu }_2$, as in (32) (only when $\rho >0$).

• The Dicker estimator for unestimable covariance (10).

• The simple LD regression estimator (36).

All $h^2$ estimates are hardly distinguishable and close to the true values (grey diagonal line) within simulation error. This is precisely the desired behavior, as it shows that the GWASH estimator can estimate SNP heritability just as well as the Dicker and LDSC estimators using only summary statistics. Note too that the correlation bandwidth $q$ has little influence on the results.

FIG 1.

Average estimates of $h^2(m=2000,n=\mathrm{1000,\; 100}$ repetitions) and empirical standard deviations (bars) for: $\mathit{\beta } normal and \mathit{X} normal \left(left column\right); \mathit{\beta }\mathrm{ }\mathrm{m}\mathrm{i}\mathrm{x}\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{e}\mathrm{ }\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{ }\mathit{X}\mathrm{ }\mathrm{n}\mathrm{o}\mathrm{r}\mathrm{m}\mathrm{a}\mathrm{l}\mathrm{ }\left(\mathrm{c}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{ }\mathrm{c}\mathrm{o}\mathrm{l}\mathrm{u}\mathrm{m}\mathrm{n}\right);\mathrm{ }\mathit{\beta }\mathrm{ }\mathrm{m}\mathrm{i}\mathrm{x}\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{e}\mathrm{ }\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{ }\mathit{X}$ binomial (right column).

6.2. Estimation of spectral moments and SE.

To understand the effect of LD on the spectral moment estimators, estimates of ${\mu }_2$ and ${\mu }_3$ are shown in Table 2 under the different $\mathit{X}$ structures considered above. Both ${\hat{\mu }}_2$ and ${\hat{\mu }}_3$ match their true values whether the full or partial sample correlation matrix is used in their estimation. Note that the empirical SE when using the partial $\tilde{\mathit{S}}$ is slightly smaller than that when using the full $\tilde{\mathit{S}}$.

Table 2.

Estimates of ${\mu }_2$ and ${\mu }_3(m=1000)$: values presented are the mean and empirical standard deviation over 100 repetitions. The symbol ${\rho }^{*}$ represents the AR parameter of the Gaussian copula.

X	AR	μ2 true	${\widehat{\mu }}_2$ Full $\tilde{S}$	${\widehat{\mu }}_{2,q}$ Partial $\tilde{S}$	μ3 true	${\widehat{\mu }}_3$ Full $\tilde{S}$	${\widehat{\mu }}_{3,q}$ Partial $\tilde{S}$
normal	ρ = 0.8	4.55	4.53 (0.03)	4.50 (0.02)q=11	30.49	30.2 (0.48)	29.1 (0.32)q=11
	ρ = 0.4	1.38	1.38 (0.006)	1.38 (0.003)q=5	2.36	2.35 (0.04)	2.35 (0.01)q=5
	ρ = 0.2	1.08	1.08 (0.004)	1.08 (0.001)q=3	1.26	1.26 (0.02)	1.26 (0.004)q=3
	ρ = 0	1	1.00 (0.004)		1	1.00 (0.01)
binomial	ρ* = 0.8	2.54	2.55 (0.02)	2.55 (0.02)q=11	10.42	10.48 (0.24)	10.28 (0.18)q=11
	ρ* = 0.4	1.13	1.13 (0.005)	1.13 (0.003)q=5	1.44	1.44 (0.02)	1.44 (0.009)q=5
	ρ* = 0.2	1.03	1.03 (0.004)	1.03 (0.001)q=3	1.08	1.08 (0.01)	1.08 (0.003)q=3
	ρ* = 0	1	1.00 (0.004)		1	1.00 (0.01)

Finally, Figure 2 compares estimates of SE according to the following methods:

FIG 2.

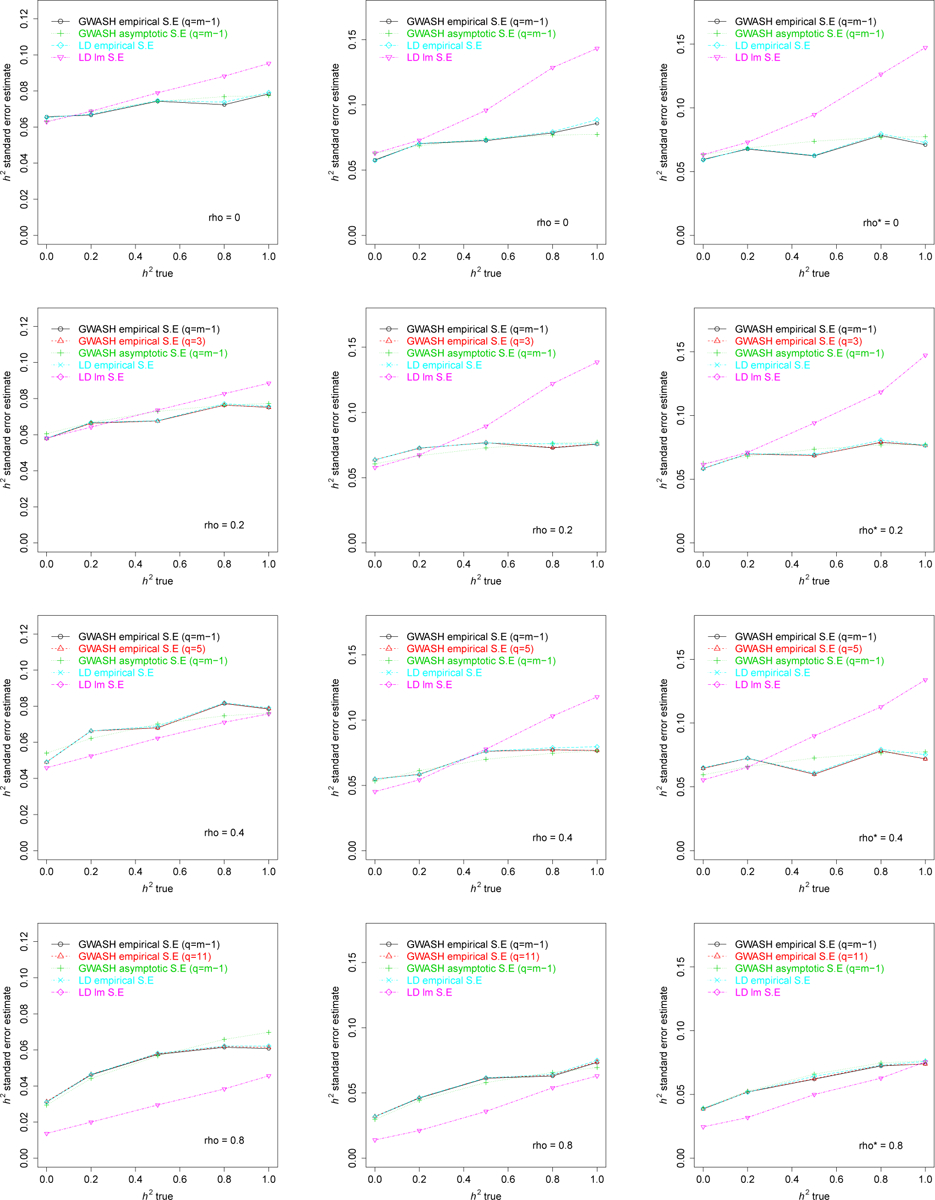
SEs of $h^2$ estimates $(m=2000,n=\mathrm{1000,\; 100}$ repetitions) for: $\mathit{\beta } normal and \mathit{X}\mathrm{ }\mathrm{n}\mathrm{o}\mathrm{r}\mathrm{m}\mathrm{a}\mathrm{l}\mathrm{ }\left(\mathrm{l}\mathrm{e}\mathrm{f}\mathrm{t}\mathrm{ }\mathrm{c}\mathrm{o}\mathrm{l}\mathrm{u}\mathrm{m}\mathrm{n}\right);\mathrm{ }\mathit{\beta }\mathrm{ }\mathrm{m}\mathrm{i}\mathrm{x}\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{e}\mathrm{ }\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{ }\mathit{X}\mathrm{ }\mathrm{n}\mathrm{o}\mathrm{r}\mathrm{m}\mathrm{a}\mathrm{l}\mathrm{ }\left(\mathrm{c}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{ }\mathrm{c}\mathrm{o}\mathrm{l}\mathrm{u}\mathrm{m}\mathrm{n}\right);\mathrm{ }\mathit{\beta }\mathrm{ }\mathrm{m}\mathrm{i}\mathrm{x}\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{e}\mathrm{ }\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{ }\mathit{X}$ binomial (right column).

• Empirical SE of the GWASH estimator (19) using the full sample correlation matrix $(q=m-1)$ to estimate ${\mu }_2$.

• Empirical SE of the GWASH estimator (19) using only $q$ off-diagonals of the sample correlation matrix to estimate ${\mu }_2$ (only when >0).

• Theoretical asymptotic SE of the GWASH estimator (square root of (24)), using the full sample correlation matrix $(q=m-1)$ to estimate ${\mu }_2$ and ${\mu }_3$.

• Theoretical asymptotic SE of the GWASH estimator (square root of (24)), using only $q$ off-diagonals of the sample correlation matrix to estimate ${\mu }_2$ and ${\mu }_3$.

• Empirical SE of the LDSC regression estimator (36).

• Theoretical SE of the LDSC regression estimator (36) obtained from the linear model fit.

In all plots, the asymptotic SE formula for the GWASH estimator approximates the empirical SE closely. LDSC regression, however, overestimates or underestimates the corresponding empirical SE, explaining why the estimation of SE in Bulik-Sullivan et al. (2015) requires computational methods such as jackknife and bootstrapping to estimate the SE more accurately.

7. Application to GWAS data.

GWASH and LDSC regression (intercept = 1) estimates were obtained for three complex traits (Table 1). To enable comparison between the two approaches, we used a subset of SNPs that was present in each of the four GWAS, had an LD score that had been precomputed by the LDSC authors, and had genotype data available in the 1KGP data. We also excluded SNPs with a minor allele frequency less than 0.1% in any of the five 1KGP European subpopulations as these may be less reliably genotyped or vary more in frequency among populations, limiting their representativeness. After these exclusions, $m=\mathrm{872,188}$ SNPs remained for analysis for each GWAS. The SNP heritability was estimated using (27), aggregating by chromosomes. (A more extensive study using all available SNPs is shown in Section 8.3 below.)

For our estimator, calculation of ${\hat{\mu }}_2$ and ${\hat{\mu }}_3$ requires LD information not provided with summary statistics. To compute representative values, we used a sample of the same 1KGP data with a correlation bandwidth of $q=1000$, yielding the values ${\hat{\mu }}_2=16.93$ and ${\hat{\mu }}_3=617.35$. Further details on data pre-processing, application of LDSC regression and calculation of ${\hat{\mu }}_2$ and ${\hat{\mu }}_3$ are given in Section A in the Supplementary Material.

7.1. Results and interpretation.

The estimated values by GWASH and LDSC regression in Table 1 are very similar. Considering LDSC as the current leading standard, these results validate the GWASH estimator. However, the SEs for the GWASH estimator are smaller, owing to its simplicity.

All SNP heritability estimates are highly significantly greater than zero and significantly different from each other. Based on the common set of SNPs analyzed, we may infer that height has a stronger correlation with these SNPs at the population level than IQ, and more so than BMI and Educ. Attain., suggesting that the latter traits may be more influenced by other genetic factors or the environment. For all traits, the SNP heritability explained by the specific SNPs that were found as statistically significant in those studies is much lower (Table 1, last column). The difference suggests that there are many SNP effects on these traits that remain undiscovered.

7.2. Choice of correlation bandwidth.

To evaluate the choice of correlation bandwidth $q$, the GWASH estimate was recomputed for a range of values of $q$ up to 5000 used in the calculation of ${\hat{\mu }}_2$. Figure 3 (left panel) shows that the GWASH estimate is fairly insensitive to the correlation bandwidth $q$, the chosen value $q=1000$ being a reasonable compromise between accuracy and computation. At this value of $q$ and larger, the GWASH and LDSC estimates are statistically the same.

FIG 3.

Left: Sensitivity of GWASH estimates to the correlation bandwidth $q$ in the calculation of ${\hat{\mu }}_2$. The LDSC (int=1) estimator is added in gray for reference. Standard errors are indicated as vertical lines for GWASH and as dashed horizontal lines for LDSC. Right: Computation time of GWASH for the largest chromosome as a function of the correlation bandwidth $q$.

7.3. Computation time.

Figure 3 (right panel) shows the computation time for the chromosome with the largest number of SNPs as a function of the correlation bandwidth $q$, broken down by the various computation components. Most of the computation time is spent pre-computing ${\hat{\mu }}_2$ and ${\hat{\mu }}_3$. As indicated by Eqs. (32) and (S10), the computation time for ${\hat{\mu }}_2$ grows linearly with $q$ while the computation time for ${\hat{\mu }}_3$ grows quadratically.

Once ${\hat{\mu }}_2$ and ${\hat{\mu }}_3$ are computed, estimating the SNP heritability is fast. For example, for $q=1000$ used in the data analysis above, calculation of ${\hat{\mu }}_2$ and ${\hat{\mu }}_3$ took 3.4 min. and 14.5 min., respectively, with the remaining calculation of ${\hat{h}}^2$ taking only 0.07 min. In contrast, calculation of the LDSC estimate took 0.5 min. using their already pre-computed parameters and not assessing its uncertainty. Note that LDSC requires a list of LD scores that is as long as the number of SNPs, while GWASH requires only a single number ${\hat{\mu }}_2$. The third moment ${\hat{\mu }}_3$ is needed only to estimate the standard error of GWASH using formula (24); the accuracy of LDSC is estimated using a computationally intensive jackknife procedure.

8. Discussion.

The key advantages of the GWASH estimator are its simplicity and grounding in statistical theory, both of which can be leveraged to better understand the empirical properties of SNP heritability estimates, as well as serving as a basis for future methods development. We now discuss several practical implications of the GWASH estimator for GWAS analysis and understanding of genetic inheritance.

8.1. Estimation of SE.

A nice property of the GWASH estimator, inherited from the Dicker estimator and not available with other currently used estimators, is that the precision (23) of the estimator is known theoretically based on the number of SNPs $m$, the sample size $n$, the second and third spectral moments ${\mu }_2$ and ${\mu }_3$ of the LD matrix, and the true SNP heritability $h^2$. The first two quantities are known from the study, while the second two can be estimated from a public resource (e.g. 1KGP). The true SNP heritability is unknown. In this paper we have substituted for $h^2$ an estimate from the study itself.

To assess the sensitivity of the $\text{SE}$ to the value of $h^2$, Figure 4 shows the SE (square root of (24)) as a function of the sample size $n$ and the true SNP heritability $h^2$ using the values $m=\mathrm{872,\; 188},{\mu }_2=16.93$ and ${\mu }_3=617.35$ from the data analysis. The plot shows that the SE is almost insensitive to the value of $h^2$, increasing only slightly as $h^2$ increases for any fixed $n$. As a consequence, a slightly conservative but more stable estimate of the SE can be obtained by simply using the worst-case value $h^2=1$ instead of the estimated value ${\hat{h}}^2$.

Fig 4.

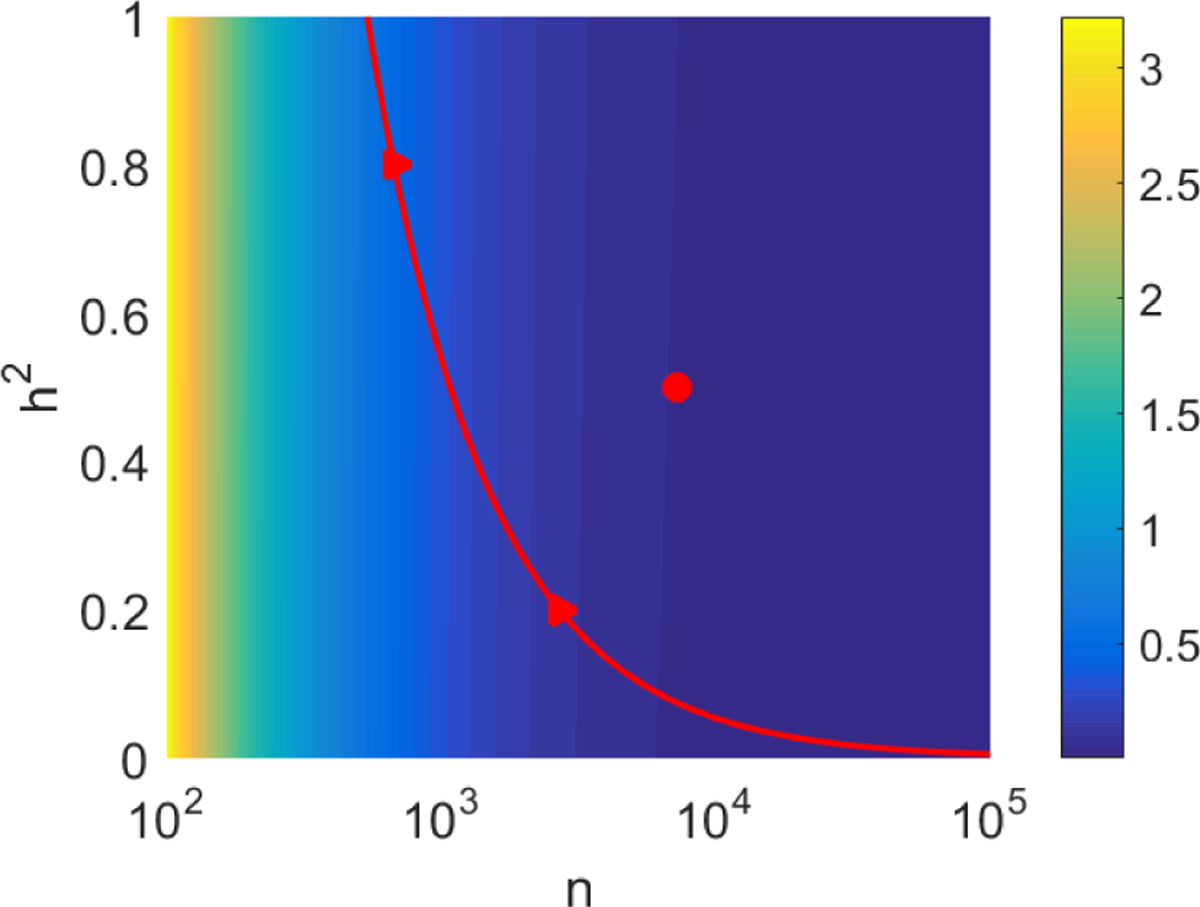
The SE of the GWASH estimator as a function of $n$ and $h^2$, for $m=\mathrm{872,188},{\mu }_2=16.93$ and ${\mu }_3=617.35$. The red curve indicates the pairs $\left(n,h^2\right)$ for which $h^2=1.645\text{ SE}$; values of $n$ to the right of the curve allow detection of a non-zero SNP heritability at the $5\%$ level.

8.2. Sample size and power calculations for prospective GWAS.

Relation (23) can be used in a prospective study to determine the number of subjects required to estimate SNP heritability according to a desired accuracy. Given any fixed set of $m$ SNPs, the values of ${\mu }_2$ and ${\mu }_3$ may be estimated from a public resource (e.g. 1KGP) and then the SE can be designed as a function of $n$ and the targeted $h^2$. For the values of $m,{\mu }_2$ and ${\mu }_3$ in the data analysis, Figure 4 shows that the SE can be quite large for small $n$, but it drops as $n$ increases.

From a design point of view, the sample size $n$ can be chosen to achieve a desired SE. For example, for a SNP heritability of $h^2=0.5$, an SE of 0.05 is achieved with $n=7234$ (red circle in Figure 4). The SE can also help design studies with the goal of detecting a SNP heritability that is significantly greater than zero. As mentioned at the end of Section 4.5, a one-sided Wald test will be significant at the 5% level if the estimate of $h^2$ is greater than 1.645 SEs. In Figure 4, this corresponds to choosing $n$ to the right of the red curve. For example, to detect a SNP heritability of $h^2=0.8$, the minimal sample size is $n=673$; to detect a SNP heritability of $h^2=0.2$, the minimal sample size is $n=2699$ (red triangles).

8.3. How many SNPs are needed to estimate SNP heritability?

In the data analysis above, we chose to use the same SNP set for all datasets to have the same basis of comparison with LDSC in terms of the LD content, captured by ${\mu }_2$ and ${\mu }_3$. Different SNPs sets may represent different portions of the total genetic variance and give discrepant results. To demonstrate that GWASH behaves as expected, we estimated the SNP heritability from different random subsets of the total SNP set available for each GWAS. Figure 5 shows that the estimates of $h^2$ rise sharply until around 1,000,000 SNPs and then begin to asymptote. In the most extreme example, increasing the SNP size more than seven times for EduYears from 1,000,000 to 7,500,000 results in a negligible increase in SNP heritability. Interestingly, these results suggest that little information is gained by increasing the number of SNPs beyond about 2,000,000.

FIG 5.

Dependence of GWASH estimates on the number of SNPs included in the estimation, for three traits: IQ (top line), EduYears (middle line) and BMI (bottom line).

We note here that producing Figure 5 required changing the correlation bandwidth from the previous analysis. The $q=1000$ SNP correlation bandwidth was tuned to the original SNP set of 872,188 SNPs. In this analysis, a new value of $q$ would have to be tuned for every new SNP set. To facilitate the multiple computations in Figure 5, we instead used genetic distance to band the LD matrix, estimating all correlations within 1 centimorgan. The value of ${\hat{\mu }}_2$ was then calculated using (30), the value of ${ℐ}_2$ obtained by explicitly counting the number of estimated paired correlations. The required computations for calculating ${\hat{\mu }}_3$ were prohibitive for the large SNP sets, so we omit standard errors in Figure 5.

8.4. Precomputation of ${\hat{\mu }}_2$.

The value of ${\mu }_2$ depends on the specific collection of SNPs used in a GWAS. However, it seems to be highly predictable once certain features of the SNP set are fixed. Figure 6 shows the estimate ${\hat{\mu }}_2$ of random subsets of SNPs for various imputation panels (HM2, hapmap2; HM3, hapmap3; HRC, haplotype reference consortium; KGP, thousand genomes project), genetic ancestry populations (AFR, African; EAS, East Asian; EUR, European) and minor allele frequency (MAF) thresholds, as a function of the size $m$ of post-MAF thresholded subset of the imputation panel SNPs. Details are given in Section A.

FIG 6.

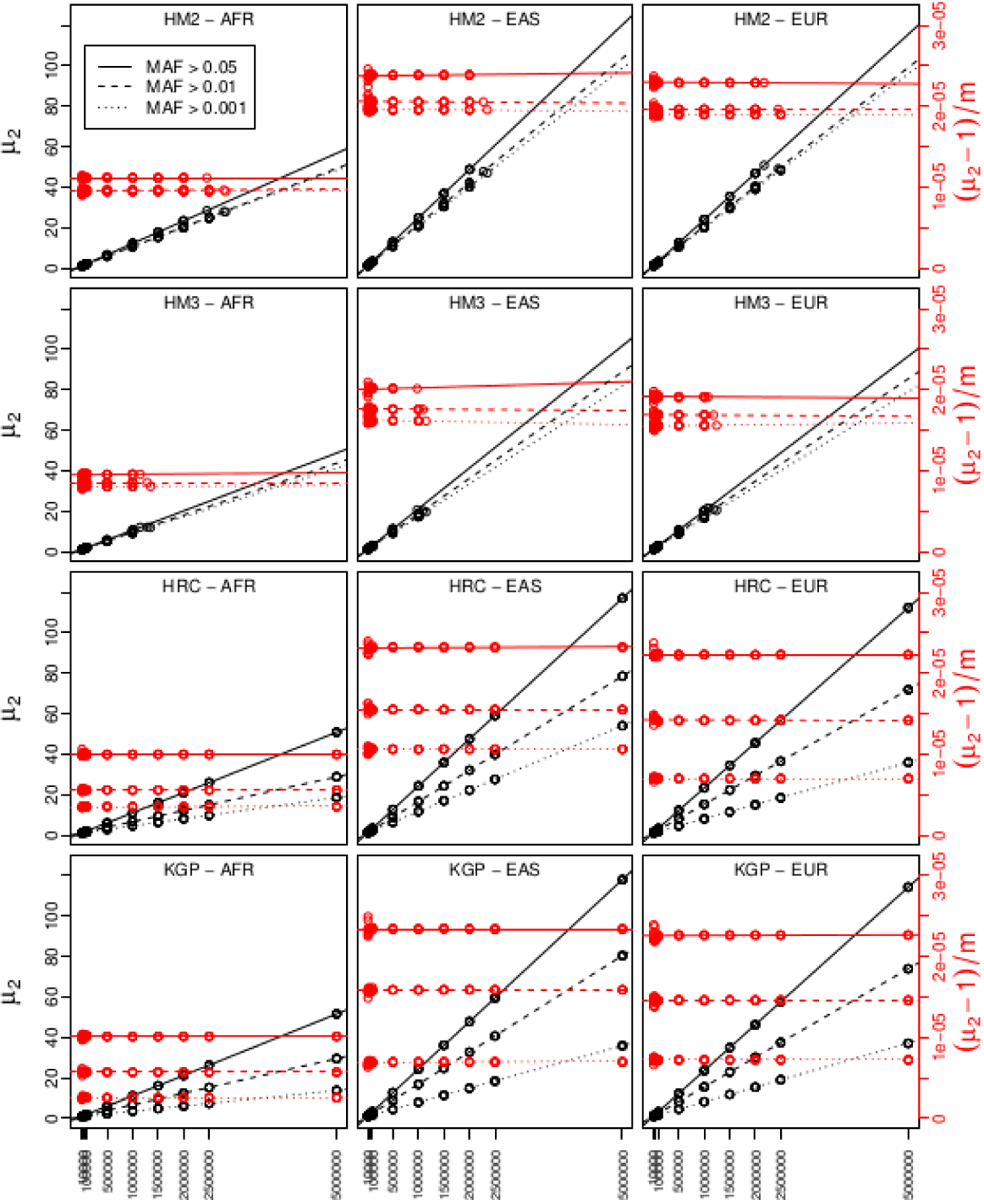
Values of ${\hat{\mu }}_2$ (increasing lines, left scale) and $\left({\hat{\mu }}_2-1\right)/m$ (nearly constant lines, right scale) for random SNP subsets of size $m$ for various imputation panels, genetic ancestry populations and MAF thresholds.

Interestingly, random sub-selections of different sized SNP sets from a given super-collection results a linear increase in ${\hat{\mu }}_2$ such that $\left({\hat{\mu }}_2-1\right)/m$ converges to a constant. From (21), this constant is the limit

$$r^2=\underset{m\to \infty }{\text{lim}}\frac{{\hat{\mu }}_2-1}{m}=\underset{m\to \infty }{\text{lim}}\frac{1}{m^2}\sum _{i\ne j}\left({\tilde{S}}_{ij}^2-\frac{1}{n-1}\right),$$

which is the average squared correlation above the correlation floor per SNP pair. This relationship allows one to calculate an approximate ${\hat{\mu }}_2$ as

$${\hat{\mu }}_2\approx 1+m{r}^2$$

for any GWAS that can be considered as studying a random collection of SNPs from a reference set as described above. Values of $r^2$ for each of the 36 super-collections described above is given in Table 3.

Table 3.

Values of the constant $r^2\left(\times {10}^{-6}\right)$ for each of the 36 super-collections in Figure 6.

	African			East Asian			European
MAF >	0.05	0.01	0.001	0.05	0.01	0.001	0.05	0.01	0.001
HM2	11.2	9.64	9.46	23.7	20.6	19.6	23.0	19.6	19.0
HM3	9.50	8.53	8.02	20.1	17.6	16.2	19.1	16.9	15.5
HRC	9.97	5.53	3.48	23.1	15.5	10.5	22.3	14.2	6.99
KGP	10.1	5.73	2.56	23.4	15.8	6.92	22.6	14.6	7.24

8.5. Fixed effects vs. random effects.

In this paper, the vector of coefficients $\mathit{\beta }$ was treated as fixed and arbitrary, allowing for the greatest flexibility in the model. LDSC regression assumes instead the SNP effects to be random. If the entries of $\mathit{\beta }$ are drawn independently from a distribution with mean 0 and variance ${\varsigma }^2$ then, from (3),

$$\begin{gathered} \text{Var}\left(y_i\right)=\text{E}\left[\text{Var}\left(y_i\mid \beta \right)\right]+\text{Var}\left[\text{E}\left(y_i\mid \beta \right)\right]=\text{E}\left[{\beta }^{\text{T}}\Sigma \beta +{\sigma }^2\right]+\text{Var}\left[\text{E}\left({\overrightarrow{x}}_i\right)\beta \right] \\ =\text{tr}\left[\Sigma \text{E}\left(\beta {\beta }^{\text{T}}\right)\right]+{\sigma }^2={\varsigma }^2\text{tr}\left(\Sigma \right)+{\sigma }^2. \end{gathered}$$

Thus, as opposed to (4), the SNP heritability estimated by LDSC regession is the quantity $h^2={\varsigma }^2\text{tr}\left(\mathbf{\Sigma }\right)/\left[{\varsigma }^2\text{tr}\left(\mathbf{\Sigma }\right)+{\sigma }^2\right]$. In Bulik-Sullivan et al. (2015), it is assumed that the phenotype and genomic markers have variance 1 so that $\text{Var}\left(y_i\right)=1$ and $\mathbf{\Sigma }$ has ones on the diagonal. Thus $\text{tr}\left(\mathbf{\Sigma }\right)=m$ and a desired SNP heritability of $h^2$ is achieved by setting ${\varsigma }^2=h^2/m$ and ${\sigma }^2=1-h^2$.

The two models have different interpretations. The fixed-effects model assumes that the effect of each SNP is consistent across samples within a population, while in the random-effects model, the SNP effects may change across samples. The fixed-effects model is more consistent with the original formulations of heritability (Falconer and Mackay, 1996; Lynch and Walsh, 1998). It is interesting that both LDSC and GWASH reach the same estimates, even though they have been derived from different data models.

8.6. Epistasis.

Epistasis refers to the contribution of interaction between SNPs in model (1) (Hill, Goddard and Visscher, 2008). In principle, epistasis can be incorporated simply by adding columns to the $\mathit{X}$ matrix that contain all the desired interaction terms between SNPs and then proceeding as prescribed by the estimator. This can be done for a limited number of interaction terms, but considering all $m(m-1)/2$ interactions in addition to the $m$ main effects is computationally intractable, as this would lead to an LD matrix of size $m(m+1)/2\times m(m+1)/2$ (e.g. take $\left.m~{10}^6\right)$.

There is also some debate in the genetics literature surrounding the practical evidence for a large epistatic component. To date, only a small amount of variance was explained by these higher order effects (Hill, Goddard and Visscher, 2008; Hemani et al., 2014a) and this was challenged as potentially erroneous (Hemani et al., 2014b; Wood et al., 2014). There are in fact theoretical grounds as to why interactions may not explain a large portion of variance in most complex traits (Hill, Goddard and Visscher, 2008). Nonetheless, it remains an interesting topic and one which could be pursued in future studies.

8.7. Connections to enrichment.

Schork et al. (2013) used the quantity $s^2-1$ as a measure of enrichment to compare different functional classes of SNPs. Being proportional to this quantity, the GWASH estimator can be viewed as a correction that accounts for the LD between SNPs through the factor ${\mu }_2$. Hence, the GWASH estimator may be used in a similar way to partition SNP heritability among different functional classes of SNPs and help narrow down the most important SNPs involved in genetic inheritance of complex traits. This extension of GWASH is left for future work.

APPENDIX A: DATA PROCESSING

Pre-processing of GWAS summary statistics.

Summary statistics from the three GWAS studies listed in Table 4 were downloaded from the authors’ cited public repositories. For each study we kept the SNP name, effect allele (A1), non-effect allele (A2), per SNP sample size $\left(n\right)$, association p-value $\left(p\right)$ and corresponding test statistic $\left(t\right)$. Where per SNP sample sizes were not available (Edu. Attain.), we used the sample size reported in the paper for each SNP. Where test statistics were not reported (BMI, Edu. Attain), we converted two-tailed p-values to z-scores via the inverse of the normal CDF, maintaining the sign from the regression coefficients.

Table 4.

Reference information on the three GWAS studies used in this paper

Trait	Ref.	Data source (website)
IQ	Sniekers et al. (2017)	https://ctg.cncr.nl/documents/p1651/sumstats.txt.gz
EduYears	Okbay (2016)	http://ssgac.org/documents/SSGAC_Rietveld2013.zip
BMI	Locke (2015)	http://portals.broadinstitute.org/collaboration/giant/images/1/15/SNP_gwas_mc_merge_nogc.tbl.uniq.gz

Application of LDSC regression.

To perform LDSC regression for each of the four GWAS studies, we downloaded all necessary software and reference data from the authors repository (https://github.com/bulik/ldsc). Both GWASH and LDSC require information about the LD among SNPs that is not typically made available alongside summary statistics. The LDSC authors address this by providing pre-computed LD scores estimated from a subset of representative individuals’ genotypes, available as part of the 1KGP data. We used these pre-computed values and their recommended protocols as faithfully as possible, following their provided tutorial.

Estimation of ${\mathit{\mu }}_2$ and ${\mathit{\mu }}_3$ from the 1KGP data.

A sample of 503 individuals of European ancestry were used to compute representative values of ${\hat{\mu }}_2$ and ${\hat{\mu }}_3$. Genome-wide genotypes are available for these individuals through the 1KGP data, phase 36 (http://www.internationalgenome.org/).

To compute the LD matrix, we used the statistical genetic software package plink2 (Chang et al., 2015), which provides fast routines for manipulating large genotype data sets. Restriction to the correlation bandwidth $q=1000$ was achieved using the plink2 commands --r and --ld-window 1000, which returns correlations up to only 1000 rows off the diagonal, for each chromosome in parallel. Similar commands were used for other values of $q$. To compute pairwise LD within 1 centimorgan for Figure 5, we used the plink2 commands --r and --ld-window-cm 1. Matrix calculations for ${\hat{\mu }}_2$ and ${\hat{\mu }}_3$, as described in Sections 4.4 and S4 in the Supplementary Material, were performed in an R routine using sparse matrix operations in the package matrix.

Precomputation of ${\stackrel{\mathit{ˆ}}{\mathit{\mu }}}_2$ in Figure 6.

To study the predictability of ${\hat{\mu }}_2$ shown in Figure 6, we estimated LD among different collections of SNPs, in different collections of individuals, using individual genotype data released as part of the 1KG project. First, we collected lists of SNPs available in four of the most common imputation reference panels: HapMap2 (version 22; HM2; YRI 2,852,185 SNPs; JPT+CHB 2,416,664 SNPs; CEU 2,543,888 SNPs), HapMap3 (release 2; HM3; 1,387,467 SNPs), the Haplotype Reference Consortium (version 1.1; HRC; 40,405,530 SNPs) and the 1000 Genome Project (version 5a; KGP; 81,271,745 SNPs). For HapMap studies, SNP lists were obtained from pre-processed data made available for imputations on the IMPUTE website (http://mathgen.stats.ox.ac.uk/impute/impute_v1.haplotypes.html), where for HRC and KGP, SNP lists were taken from original data sources.

Next, for each of the four imputation panels, we extracted the genotypes of subjects in three different ancestry groups (AFR, African, $n=661$; EAS, East Asian, $n=504$; EUR, European, $n=503$) at the overlapping SNPs. From each of the twelve resulting ancestry-specific imputation panel genotype sets, we created three subsets including only genotypes above selected minor allele frequencies (MAF > 0.05, > 0.01, > 0.001). This resulted in 36 collections of genotypes meant to represent the potentially unique patterns of LD that could arise when choosing SNP subsets based on an imputation panel or minor allele frequency threshold for GWAS in samples from different genetic ancestries. For each of the 36 KGP data subsets, we calculated ${\hat{\mu }}_2$ for differently sized random subsets of SNPs $(m=$10,000, 25,000, 50,000, 100,000, 500,000, 1,000,000, 1,500,000, 2,000,000, 2,500,000, 5,000,000 and the complete set, if it was less than 5,000,000), repeating each sampling five times.