Analyzing Clustered Continuous Response Variables with Ordinal Regression Models

SUMMARY:

Continuous response data are regularly transformed to meet regression modeling assumptions. However, approaches taken to identify the appropriate transformation can be ad hoc and can increase model uncertainty. Further, the resulting transformations often vary across studies leading to difficulties with synthesizing and interpreting results. When a continuous response variable is measured repeatedly within individuals or when continuous responses arise from clusters, analyses have the additional challenge caused by within-individual or within-cluster correlations. We extend a widely used ordinal regression model, the cumulative probability model (CPM), to fit clustered, continuous response data using generalized estimating equations (GEE) for ordinal responses. With the proposed approach, estimates of marginal model parameters, cumulative distribution functions (CDFs), expectations, and quantiles conditional on covariates can be obtained without pre-transformation of the response data. While computational challenges arise with large numbers of distinct values of the continuous response variable, we propose feasible and computationally efficient approaches to fit CPMs under commonly used working correlation structures. We study finite sample operating characteristics of the estimators via simulation, and illustrate their implementation with two data examples. One studies predictors of CD4:CD8 ratios in a cohort living with HIV, and the other investigates the association of a single nucleotide polymorphism and lung function decline in a cohort with early chronic obstructive pulmonary disease.

1. Introduction

Analyses of quantitative response variables are often challenged by distributions that do not follow standard parametric assumptions. While it is common in such settings to transform the response variables to satisfy model assumptions, such transformations are often ad hoc and model parameters can be difficult to interpret on their natural, untransformed scale. For example, researchers are interested in studying factors associated with longitudinal measures of CD4:CD8 ratio among people with HIV on antiretroviral therapy (ART). CD4:CD8 ratio is the ratio of CD4 lymphocyte count (cells/mm³) to CD8 lymphocyte count (cells/mm³), and a low CD4:CD8 ratio has been associated with immune senescence, inflammation, and comorbidities for people with HIV (Castilho et al., 2016). CD4:CD8 ratio tends to be right-skewed (Web Appendix A), so it is often transformed prior to analysis; however, there is no standard accepted transformation and results may be sensitive to the choice of transformation. Researchers have analyzed CD4:CD8 ratio with no transformation (Castilho et al., 2016), log-transformation (Sauter et al., 2016), square-root transformation (da Silva et al., 2018), fifth-root transformation (Gras et al., 2019), and various categorizations (Petoumenos et al., 2017).

As a second example, the Lung Health Study was a randomized clinical trial of smokers with early chronic obstructive pulmonary disease (COPD) to examine whether a smoking cessation intervention and inhaled bronchodilator use could slow lung function decline (Anthonisen et al., 1994). Lung function was measured with forced expiratory volume in the first second of exhalation (FEV1), and thresholds defined by FEV1 are commonly used to define the severity of chronic obstructive pulmonary disease (Global Initiative for Chronic Obstructive Lung Disease, 2021). An analysis that fits a binary regression model to a dichotomized lung function measure loses a substantial amount of information compared to an analysis that treats lung function (e.g., FEV1) on its natural, continuous scale. However, with standard regression analyses of continuous scales, parametric assumptions on the distribution are required to capture important quantities, such as exceedance probabilities.

A compelling approach to tackle the challenges associated with non-standard response distribution modeling is to treat continuous response variables as if they were ordinal using cumulative probability models (CPMs), also known as cumulative link models (Liu et al., 2017; Agresti, 2010). The CPM is a semi-parametric linear transformation model (Zeng and Lin, 2006) that assumes a linear model following an unspecified response transformation. Rather than making an assumption about the appropriate transformation to apply, CPM fitting uses the data to estimate the transformation nonparametrically with a step function. The CPM is invariant to any monotonic transformation of the response variable because only order information is used for regression parameter estimation. Therefore, no pre-transformation of the response variable is needed. A nice feature of CPMs is that regression parameters from CPMs are interpretable (based on the chosen link function), and because the cumulative distribution function (CDF) is modeled, conditional (on covariates) means, quantiles, and exceedance probabilities can be extracted from the CPM fit. The use of CPMs for cross-sectional continuous response variables, even with thousands of unique outcomes, is computationally feasible with applications of sparse matrix calculations, and it has been implemented in the orm() function in the rms R package (Harrell, 2020).

Although CPMs have been shown to be an excellent tool for the analysis of cross-sectional continuous response data, they are not directly applicable to the CD4:CD8 study or the Lung Health Study because these studies include repeated measures on individuals. Clustered continuous data are common in practice and important for studying exposure-response associations. Generalized estimating equations (GEE; Liang and Zeger (1986); Zeger and Liang (1986)) extends quasi-likelihood estimation (Wedderburn, 1974) for generalized linear models (GLMs) (McCullagh and Nelder, 1983), from independent to correlated data settings. However, even though valid inferences are possible with GEE when second and higher order moments are misspecified, GEE for correlated data is challenged by non-standard distributions in the same way linear regression is for cross-sectional response data.

Extending Liu et al. (2017) that discussed CPMs for scalar response data, we present CPMs for cluster-correlated continuous response variables. Specifically, we demonstrate that 1) CPMs can be fit to quantitative correlated data using GEE methods for ordinal data, and 2) GEE for ordinal data can be applied to non-standard, quantitative response distributions. Our proposed approach estimates time- and covariate-dependent CDFs, from which estimates of the mean, quantiles, and exceedance probabilities can be derived. In addition, we present software and strategies for implementing GEE methods for ordinal data to settings with large numbers (i.e., hundreds or thousands) of distinct levels.

2. Review of Existing Methods

The CPM is a class of models for scalar ordinal response data (Liu et al., 2017). Let $Y$ be a continuous response variable, and $Y^{\ast }=h(Y)$ be a transformation of $Y$ with $h(\cdot )$ an unspecified non-decreasing function. Let $\mathit{X}$ be a vector of covariates with $\mathit{X}=0$ as a reference value. Let $ϵ$ be an error term. We assume the relationship between the transformed variable and covariates is linear, $Y^{\ast }={\beta }^T\mathit{X}+ϵ$, where $ϵ$ follows a known distribution $F_{ϵ}$ and $\beta$ is a vector of regression parameters. It follows that

$$Y=h^{-1}(Y^{\ast })=h^{-1}({\beta }^T\mathit{X}+ϵ).$$ (1)

Letting $G=F_{ϵ}^{-1}$ be a link function, (1) can be expressed as a CPM with $F(y\mid \mathit{X})=P(Y\le y\mid \mathit{X})=P(ϵ\le h(y)-{\beta }^T\mathit{X}\mid \mathit{X})=F_{ϵ}(h(y)-{\beta }^T\mathit{X})$, which implies $G\{F(y\mid \mathit{X})\}=h(y)-{\beta }^T\mathit{X}$. The intercept $h(y)=G\{F(y\mid \mathit{X}=0)\}$ represents the link-transformed CDF for $\mathit{X}=0$ (i.e. the reference CDF), and ${\beta }^T\mathit{X}$ represents shifts in this CDF that depend on the values of $\mathit{X}$. The interpretation of $\beta$ depends on the choice of the link function. For example, $\beta$ is interpreted as a log odds ratio with the logit link (i.e., $F_{ϵ}$ logistic distribution) and a log hazard ratio with the complementary log-log link (i.e., $F_{ϵ}$ extreme value distribution).

Assume there are $N$ subjects and denote $y_{(j)}$ to be the jth smallest observed response value ($j=1,\dots ,J$). Rather than specifying a functional form for $h(\cdot )$, we can estimate it using a step function with ${\gamma }_j=h(y_{(j)})$. Since $h(\cdot )$ is estimated nonparametrically, CPMs belong to the class of semi-parametric linear transformation models (Zeng and Lin, 2006). For $(y_i,{\mathit{X}}_i)$, $i\in 1,\dots ,N$ with $y_i$ equal to the jth ordered value, $y_{(j)}$, the CPM is given by

$$G\{F(y_i\mid {\mathit{X}}_i)\}=G\{F(y_{(j)}\mid {\mathit{X}}_i)\}={\gamma }_j-{\beta }^T{\mathit{X}}_i.$$ (2)

Letting $\theta ={(\gamma }^T,{{\beta }^T)}^T$ and $\gamma ={({\gamma }_1,\dots ,{\gamma }_{J-1})}^T$, the likelihood for $\theta$ is

$$L(\theta )=\prod _{j=1}^J\prod _{i:y_i=y_{(j)}}\{F(y_i\mid {\mathit{X}}_i)-F(y_i^{-}\mid {\mathit{X}}_i)\},$$ (3)

where $F(y_i^{-}\mid {\mathit{X}}_i)={\text{lim}}_{t\uparrow y_i}F(t\mid {\mathit{X}}_i)$. A nonparametric likelihood can be obtained by substituting $F(y_{(j-1)}\mid {\mathit{X}}_i)$ for $F(y_{(j)}^{-}\mid {\mathit{X}}_i)$ as follows

$$L(\theta )=\prod _{j=1}^J\prod _{i:y_i=y_{(j)}}\{G^{-1}({\gamma }_j-{\beta }^T{\mathit{X}}_i)-G^{-1}({\gamma }_{j-1}-{\beta }^T{\mathit{X}}_i)\},$$ (4)

where $-\infty \equiv {\gamma }_0<{\gamma }_1<\cdots <{\gamma }_{J-1}<{\gamma }_J\equiv \infty$. From this likelihood, nonparametric maximum likelihood estimates (NPMLEs) of $\theta$ can be obtained.

The CPM in (2) is identical to the cumulative link model used for ordinal data. For example, CPMs with the logit link are referred to as proportional odds models. The likelihood in (4) is identical to the multinomial likelihood used to estimate parameters of cumulative link models for ordinal data (McCullagh, 1980). It follows that a semi-parametric linear transformation model can be fitted with an ordinal CPM where each distinct value of the continuous $Y$ is treated as its own ordinal category. There will be $N$ categories for truly continuous $Y$. CPMs model the continuous response variable CDF as a linear function of covariates after an unspecified, monotonic transformation has been applied. The transformation is estimated nonparametrically from the observed data with a step function.

CPMs have several attractive properties for fitting continuous response data (Liu et al., 2017; Tian et al., 2020). Since only ordinal information is used for estimating $\beta$, CPMs are invariant to any monotonic transformation of the response, which means no transformation is needed. They have been shown to work well with continuous response variables subject to detection limits (Tian et al., 2022), and under some mild conditions, CPMs yield estimates that are consistent and asymptotically normal (Li et al., 2022) with variances that can be estimated with the inverse of the observed information matrix. Other quantities, such as quantiles, exceedance probabilities, and expectations conditional on covariates can be derived from the CPM model fit. For example, the expectation can be estimated with $\widehat{E}(Y\mid \mathit{X})={\sum }_{j=1}^J{\sum }_{i:y_i=y_{(j)}}{y}_{(j)}\left\{\widehat{F}(y_{(j)}\mid \mathit{X})-\widehat{F}(y_{(j-1)}\mid \mathit{X})\right\}$. Standard errors for CDFs and expectations can be calculated using the delta method, and quantiles can be estimated with linear interpolations of the inverse of the CDFs (Liu et al., 2017; Tian et al., 2022).

Until recently, use of CPMs for continuous responses was rare due, in part, to computational costs. The orm() function in the rms package in R is a computationally efficient implementation of CPMs that can be fit with tens of thousands of distinct responses. It takes advantage of the sparse structure of the Hessian matrix which permits efficient inversion by Cholesky decomposition in a Newton-Raphson algorithm (Harrell, 2020; Liu et al., 2017).

3. Methods

3.1. CPMs for Clustered Continuous Response Variables

We extend CPMs to the cluster correlated response setting for the same reason they were developed in the cross-sectional response setting; namely, we would like to avoid parametric and often ad hoc transformations of the response to satisfy modeling assumptions. Although our notation throughout suggests we are in a setting with longitudinal data, our methodology applies to more general clustered data.

Let $N$ be the number of subjects in a sample with $i\in \{1,\dots ,N\}$ indexing subjects (clusters), and $M_i$ being the number of observations for subject $i$. Denote the response for subject $i$ at time $t$ with $Y_{it}$, and ${\mathit{Y}}_i={(y_{i1,\dots ,Y_{i{M}_i}})}^T$. Across all subjects, $\mathit{Y}={({\mathit{Y}}_1,\dots ,{\mathit{Y}}_N)}^T$ has a total of $J$ distinct values; with truly continuous $\mathit{Y}$, $J={\sum }_{i=1}^N{M}_i$. Let $Z_{it,j}=I(Y_{it}\le y_{(j)})$ and ${\mu }_{it,j}=E(Z_{it,j}\mid {\mathit{X}}_{it})=P(Y_{it}\le y_{(j)}\mid {\mathit{X}}_{it})=F(y_{(j)}\mid {\mathit{X}}_{it})$, where $y_{(j)}$ corresponds to the jth smallest value among the $J$ levels of the response variable, and ${\mathit{X}}_{it}$ is the design vector (without an intercept) for subject $i$ at time $t$. Let the vector of binary indicator variables for subject $i$ at time $t$ be ${\mathit{Z}}_{it}=(Z_{it,1},{\dots ,Z_{it,J-1})}^T$, and ${\mu }_{it}=({\mu }_{it,1},{\dots ,{\mu }_{it,J-1})}^T$. Finally, for subject $i$, let ${\mathit{Z}}_i=({\mathit{Z}}_{i1}^T,{\dots ,{\mathit{Z}}_{i{M}_i}^T)}^T$ and ${\mu }_i=({\mu }_{i1}^T,{\dots ,{\mu }_{i{M}_i}^T)}^T$.

Suppose $Y_{it}$ has a linear relationship with the covariates ${\mathit{X}}_{it}$ after an unspecified monotonic transformation $h(\cdot )$ has been applied. This leads to a linear transformation model

$$Y_{it}=h^{-1}(Y_{it}^{\ast })=h^{-1}({\beta }^T{\mathit{X}}_{it}+{ϵ}_{it}),$$ (5)

where ${ϵ}_{it}$ follows a specified distribution and ${ϵ}_{it}$ is independent of ${ϵ}_{i^{\prime }{t}^{\prime }}$ for $i\ne i^{\prime }$, but not if $i=i^{\prime }$. By linear transformation models, we have ${\mu }_{it,j}=P(Y_{it}\le y_{(j)}\mid {\mathit{X}}_{it})=P({ϵ}_{it}\le h(y{(}_{(j)})-{\beta }^T{\mathit{X}}_{it}\mid {\mathit{X}}_{it})=F_{ϵ}(h(y_{(j)})-{\beta }^T{\mathit{X}}_{it})$, which implies $F_{ϵ}^{-1}({\mu }_{it,j})=h(y_{(j)})-{\beta }^T{\mathit{X}}_{it}$. Then the CPM for a clustered continuous response variable is

$$G({\mu }_{it,j})={\gamma }_j-{\beta }^T{\mathit{X}}_{it},$$ (6)

where $G=F_{ϵ}^{-1}$ is the specified link function, ${\gamma }_j=h(y_{(j)})$, and $\theta ={({\gamma }^T,{\beta }^T)}^T$. The interpretation of $\beta$ depends on the link function. For example, if $G(\cdot )$ is the log odds link, $\beta$ is a log odds ratio; if $G(\cdot )$ is the log-log link, $\beta$ is a log hazard ratio. The intercepts $\gamma$ are the link function transformed CDFs when all covariates set equal to 0. This also represents the transformation needed for the response variable to be modeled by a linear model.

With clustered data, we cannot directly fit NPMLEs for CPMs because observations are not independent. However, since the CPM is parameterized as an expectation ${\mu }_{it,j}=E(Z_{it,j}\mid {\mathit{X}}_{it})$, we can rely on GEE techniques to estimate parameters in (6). For valid inference, GEE requires correct specification of the marginal model for the response mean. GEE also permits specification of within cluster response dependence with a working correlation structure. The working correlation structure does not have to represent the true structure; however, to the extent that it differs from the true structure, efficiency losses incur (Liang and Zeger, 1986; Zeger and Liang, 1986). GEE methods for clustered ordinal responses have been developed (Heagerty and Zeger, 1996; Lipsitz et al., 1994; Huang et al., 2002; Parsons et al., 2006; Touloumis et al., 2013).

We estimate $\theta$ in (6) using ordinal GEE methods by solving the equation

$$A_{\theta }(\theta ;\alpha )=\sum _{i=1}^N{\mathit{D}}_i^T{\mathit{W}}_i^{-1}({\mathit{Z}}_i-{\mu }_i)=0,$$ (7)

where ${\mathit{D}}_i=\frac{\partial {\mu }_i}{\partial \theta }$, ${\mathit{W}}_i={\mathit{S}}_i^{\frac{1}{2}}{\mathit{R}}_i(\alpha ){\mathit{S}}_i^{\frac{1}{2}}$, and $\alpha$ is a vector of association parameters. ${\mathit{R}}_i(\alpha )$ is a working correlation matrix for ${\mathit{Z}}_i$ and ${\mathit{S}}_i$ is a $M_i(J-1)\times M_i(J-1)$ block matrix with elements based on the variance of $Z_{it,j}$, $\{{\mu }_{it,j}(1-{\mu }_{it,j})\}$. ${\mathit{W}}_i^{-1}$ can be considered as a weight matrix for subject $i$. Efficiency is improved to the extent that the working correlation matrix ${\mathit{R}}_i(\alpha )$ is a better approximation to the true correlation structure of ${\mathit{Z}}_i$. The structure of ${\mathit{R}}_i(\alpha )$ is assumed by the analyst and $\alpha$ can then be estimated with a second estimating function that will be described in more detail in Section 3.3. The covariance of $\widehat{\theta }$ is given by

$$V_{\theta }(\alpha )={\left(\sum _{i=1}^N{\mathit{D}}_i^T{\mathit{W}}_i^{-1}{\mathit{D}}_i\right)}^{-1}\left(\sum _{i=1}^N{\mathit{D}}_i^T{\mathit{W}}_i^{-1}\text{Cov}({\mathit{Z}}_i){\mathit{W}}_i^{-1}{\mathit{D}}_i\right){\left(\sum _{i=1}^N{\mathit{D}}_i^T{\mathit{W}}_i^{-1}{\mathit{D}}_i\right)}^{-1},$$ (8)

which can estimated by replacing $\theta$ with $\widehat{\theta }$ and $\text{Cov}({\mathit{Z}}_i)$ with $({\mathit{Z}}_i-{\mu }_i){({\mathit{Z}}_i-{\mu }_i)}^T$.

Since ${\mu }_{it,j}=F(y_{(j)}\mid {\mathit{x}}_{it})$ is a CDF, other quantities can be readily obtained from a fitted CPM. The CDF can be calculated with $\widehat{F}(y\mid \mathit{X})=G^{-1}({\widehat{\gamma }}_j-{\widehat{\beta }}^T\mathit{X})$, where $j$ is the index such that $y_{(j)}=\max \{j^{\prime }\in \{1,\dots ,J\}:y_{(j^{\prime })}\le y\}$. We can derive its standard error with the delta method. Similar to the scalar response setting, cross-sectional summaries (e.g., quantiles and expectations) and confidence intervals can be calculated from $\widehat{\theta }$ and ${\widehat{V}}_{\theta }(\alpha )$.

Fitting ordinal GEE methods to clustered continuous response data is computationally challenging. Specifically, for each observation $Y_{it}$, we need $J-1$ indicators $Z_{it,j}=I(Y_{it}\le y_{(j)})$, and $J$ is usually a large number for continuous data, which implies that ${\mathit{W}}_i$ and ${\mathit{D}}_i$ in (7) and (8) can be high-dimensional. In the following subsections, we introduce two computationally efficient implementations, first with independent working correlation structures and second with more complex working correlation structures commonly used for GEE-based estimation.

3.2. CPMs with Independent Working Correlation

It is well known that working covariance weighting can be more efficient than working independent weighting, particularly for parameters corresponding to time-varying covariates. However, the independent working correlation structure is simpler and therefore easier to implement than other structures because it does not require estimating $\alpha$, and the computational burden of matrix inversion is reduced with a diagonal structure. In addition, there are settings where using an independent working correlation structure is recommended for statistical reasons, the most common of which occurs when interest is in the cross-sectional $E(Y_{it}\mid {\mathit{X}}_{it})$ but where $E(Y_{it}\mid {\mathit{X}}_{it})\ne E(Y_{it}\mid {\mathit{X}}_{i1},\dots ,{\mathit{X}}_{i{M}_i})$. In such settings, one must use an independent working correlation to ensure consistent estimates of time-varying covariate parameters (Pepe and Anderson, 1994; Schildcrout and Heagerty, 2005; Diggle et al., 2002).

CPMs for scalar response data can be fitted when there are thousands of distinct values. With an independent working correlation structure, solving (7) for $\theta$ and plugging $\widehat{\theta }$ into (8) to estimate the variance is equivalent to treating the response data as unclustered, computing the NPMLEs of CPMs as described in Section 2, and then correcting estimates of uncertainty by using a sandwich-variance estimate (see Web Appendix B). Specifically, we fit CPMs to clustered continuous response variables by maximizing the marginal likelihood

$$\begin{gathered} L(\theta )=\prod _{j=1}^J\prod _{i,t:y_{it}=y_{(j)}}(G^{-1}({\gamma }_j-{\beta }^T{\mathit{X}}_{it})-G^{-1}({\gamma }_{j-1}-{\beta }^T{\mathit{X}}_{it})) \\ =\prod _{j=1}^J\prod _{i,t:y_{it}=y_{(j)}}({\mu }_{it,j}-{\mu }_{it,j-1}). \end{gathered}$$ (9)

To correct for correlated responses within each cluster, we use the Huber-White sandwich estimator for covariance (Freedman, 2006). Since the clusters are independent but observations within clusters are dependent, we group within-cluster observations. Let

$$l(\theta )=\log (L(\theta ))=\sum _{j=1}^J\sum _{i,t:y_{it}=y_{(j)}}\log (f_{it,j})$$

be the log-likelihood of (9) under the assumption of independent observations, where $f_{it,j}={\mu }_{it,j}-{\mu }_{it,j-1}$. The first and second order partial derivatives of $l(\theta )$ with respect to $\theta$ are

$$\begin{gathered} l^{\prime }(\theta )=\frac{\partial l(\theta )}{\partial \theta }=\sum _{j=1}^J\sum _{i,t:y_{it}=y_{(j)}}\frac{\partial \log (f_{it,j})}{\partial \theta }=\sum _{j=1}^J\sum _{i,t:y_{it}=y_{(j)}}{g}_{it,j}, \\ {l}^{″}(\theta )=\frac{{\partial }^{2}l(\theta )}{\partial {\theta }^2}=\sum _{j=1}^J\sum _{i,t:y_{it}=y_{(j)}}\frac{{\partial }^2\log (f_{it,j})}{\partial {\theta }^2}, \end{gathered}$$

and the Huber-White sandwich estimator for $\text{Cov}(\widehat{\theta })$ is given by

$${\left(l^{″}(\widehat{\theta }\right)}^{-1}\left(\sum _{i=1}^N\left(\sum _{t=1}^{M_i}{\widehat{g}}_{it,j}\right){\left(\sum _{t=1}^{M_i}{\widehat{g}}_{it,j}\right)}^T\right){\left(l^{″}(\widehat{\theta })\right)}^{-1},$$ (10)

where ${\sum }_{t=1}^{M_i}{\widehat{g}}_{it,j}$ is the sum of the plug-in estimators for the first partial derivative elements within a cluster. Consistency and asymptotic normality of estimates and the validity of the sandwich estimators are shown under the conditions provided in Web Appendix C (Li et al., 2022). Point estimates and robust covariances for CPMs can be obtained with the orm() and robcov() functions in the rms package in R (Harrell, 2020).

3.3. CPMs with Exchangeable/AR1 Working Correlation

Though computationally efficient, CPMs with an independent working correlation structure can be statistically inefficient if the within cluster correlation is high and/or clusters are large. GEE methods for ordinal response variables allow for more complicated working correlation structures to improve efficiency, and approaches have been proposed. For example, Lipsitz et al. (1994) estimated association parameters with Pearson residuals; Heagerty and Zeger (1996) extended alternating logistic regression for binary longitudinal outcomes to ordinal longitudinal outcomes with pairwise log-odds ratio parameters as the association parameters (Lipsitz et al., 1991; Carey et al., 1993); and Touloumis et al. (2013) captured response association with local odds ratios based on Goodman’s row and column effects models.

To improve efficiency over the independent working correlation approach described above, we appeal to the framework proposed by Parsons et al. (2006, 2009) that specifies the association parameter $\alpha$ as a correlation and that estimates the parameter iteratively by minimizing the determinant of $V_{\theta }(\alpha )$. This method, which Parsons et al. (2009) called “repolr” (repeated measures proportional odds logistic regression), estimates $\alpha$ based on the covariance matrix, whose dimension is relatively manageable. In contrast, other ordinal GEE methods require enumerating all pairs of observations within each cluster to estimate $\alpha$, which is computationally intensive for continuous response data.

In repolr, ${\mathit{R}}_i(\alpha )$ is constructed as ${\mathit{R}}_i(\alpha )={\mathit{K}}_i(\alpha )\otimes \mathit{C}$, where ${\mathit{K}}_i(\alpha )$ is a $M_i\times M_i$ within-cluster working correlation matrix and $\mathit{C}$ is a $(J-1)\times (J-1)$ matrix of correlations among elements in ${\mathit{Z}}_{it}$. $\mathit{C}$ is set to be common for every pair of binary, ordinal-level indicators for each subject at each time point, so that

$$\mathit{C}=\left[\begin{array}{ccc}\hfill {\rho }_{11}\hfill & \hfill \cdots \hfill & \hfill {\rho }_{1(J-1)}\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill {\rho }_{(J-1)1}\hfill & \hfill \cdots \hfill & \hfill {\rho }_{(J-1)(J-1)}\hfill \end{array}\right],$$

where ${\rho }_{pq}$ is expected correlation between $Z_{itp}$ and $Z_{itq}$ for $i=1,\dots ,N$. With the logit link, ${\rho }_{pq}={\rho }_{qp}=\{\text{exp}{({\gamma }_p-{\gamma }_q)\}}^{\frac{1}{2}}$ where $p<q$ (Kenward et al., 1994). Two common structures for $\mathit{K}(\alpha )$ are exchangeable (also called uniform or compound symmetric) and first-order autoregressive (AR1) structures (Diggle et al., 2002). For the exchangeable structure, ${\mathit{K}}_{(p,q)}(\alpha )=1$ if $p=q$ and ${\mathit{K}}_{(p,q)}(\alpha )=\alpha$ otherwise; for the AR1 structure, ${\mathit{K}}_{(p,q)}(\alpha )=1$ for $p=q$ and ${\mathit{K}}_{(p,q)}(\alpha )={\alpha }^{\mid t_p-t_q\mid }$ otherwise. Note that the working correlation structure is specified for $\mathit{Y}$, not $\mathit{Z}$; this is illustrated in Web Appendix D with a simple example. The additional estimating equation for the association parameter $\alpha$ in repolr is

$$\frac{\partial \log \mid V_{\theta }(\alpha )\mid }{\partial \alpha }=0,$$ (11)

which is equivalent to estimating $\alpha$ by minimizing $\log \mid V_{\theta }(\alpha )\mid$. The equation solves for $\alpha$ that minimizes the confidence region size of the $\theta$. The algorithm iterates between solving (7) for $\widehat{\theta }$ and solving (11) for $\widehat{\alpha }$ until convergence. This approach can be applied with the repolr() function in the repolr package in R (Parsons, 2017) for complete data and for the logit link.

With continuous response variables, it may still be expensive to run a fully-iterated repolr model; hence, we propose a one-step GEE estimator for repolr (Lipsitz et al., 2017). In our setting, instead of iterating between the two estimating equations (7) and (11) until convergence, we start with an estimate of $\theta$ under an independent working correlation structure, ${\widehat{\theta }}_I$, which can be efficiently estimated with CPMs. We then obtain the association parameter $\widehat{\alpha }$ by solving (11) with $V_{{\widehat{\theta }}_I}(\alpha )$. Finally, we solve (7) using $\widehat{\alpha }$ to get $\widehat{\theta }$, which is asymptotically equivalent to the fully-iterated GEE estimator (Lipsitz et al., 2017).

We built an R package, cpmgee (Tian, 2022), that applies this one-step estimation procedure for exchangeable and AR1 working correlation structures. This package also fits CPMs with independent working correlation.

Although the one-step GEE estimator for repolr can substantially reduce the computational burden, computation with exchangeable and AR1 working correlation structures may still be intensive if the number of distinct values of a continuous response variable is large. One may seek to reduce the number of distinct values in the response by binning. Specifically, the $N^{\prime }={\sum }_{i=1}^N{M}_i$ observations can be divided into ${ℳ}_b$ bins, where the value assigned to each observation in the bin is the median value for observations in that bin. The median is a natural choice to capture the center of the bin, although it should be noted that $\beta$ coefficients are not impacted by the chosen value as long as the order of the bins is preserved. Approximately equal-quantile binning can be achieved by expressing $N^{\prime }$ as

$$N^{\prime }={ℳ}_{b}q+r=({ℳ}_b-r)q+r(q+1),$$

where $q$ is the integer quotient of $N^{\prime }∕{ℳ}_b$ and $r$ is the remainder. Thus, ${ℳ}_b-r$ bins have $q$ observations, and $r$ bins have $q+1$ observations. Rounding to a decimal place is yet another way to reduce the number of distinct values. Strategies for binning and rounding cross-sectional CPMs with very large sample sizes are provided elsewhere (Li et al., 2022).

4. Simulations

We studied the performance of our estimators applying CPMs with independent, exchangeable, and AR1 working correlation to continuous clustered data under various simulation settings. Responses were generated in the following manner for subject $i$ at time $t$:

$$Y_{it}=\text{Inv-}{\chi }^2(\Phi (Y_{it}^{\ast })∕2,\text{df}=5),\text{and}{Y}_{it}^{\ast }=X_i{\beta }_X+T_{it}{\beta }_X+T_{it}{\beta }_T+{ϵ}_{it},$$

where $\text{Inv-}{\chi }^2(\cdot ,\text{df}=5)$ is the inverse of the CDF for a chi-square distribution with 5 degrees of freedom and $\Phi (\cdot )$ is the probability density function of the standard normal distribution. The transformation has been used in earlier work (Tian et al., 2020) and was chosen because it does not correspond to a commonly-used closed-form transformation.

In the primary study setting, we set the sample size $N=1000$, $X_i$ was a time-invariant covariate with standard normal distribution, and $T_{it}$ represented time, a time-varying covariate, with values {0, 0.2, 0.4, 0.6, 0.8, 1}. We imposed dropout completely at random uniformly across $t\in \{3,4,5,6\}$, such that the number of observations per subject varied from 2 to 6. A logistic residual distribution was used and the correlation structure was exchangeable with $\alpha =0.7$. We set ${\beta }_X=1$ and ${\beta }_T=1$. For CPMs with exchangeable and AR1 working correlation structures, we fit models using equal-quantile binning with ${ℳ}_b=300$.

We also explored scenarios with a smaller $\alpha$, different values of ${ℳ}_b$ for binning, and rounding with different decimal places. Additional simulation settings including the identity transformation; complete data; differing sample sizes, cluster sizes, time effects, and correlation structures; and link function misspecification are shown in Web Appendix E.

We replicated each scenario 1000 times and evaluated for percent bias, root mean squared error (RMSE), empirical standard error, average estimated standard error, and coverage of 95% confidence intervals. We compared our methods with a gold standard for estimating $\beta$, in which GEE with an identity link and the correct working correlation structure was fit to the correctly transformed continuous response variable. We also investigated the performance of estimates of the conditional expectation, median, and CDF – specifically, $E(Y\mid X=1,T=0.2))$, $Q(0.5\mid X=1,T=0.2)$, and $F(5\mid X=1,T=0.2)$, respectively – that were estimated from the fitted CPMs. We do not show the average estimated standard error of $Q(0.5\mid X=1$, $T=0.2$) because its confidence interval was obtained from linear interpolation of the inverse of the confidence interval for the conditional CDF (Liu et al., 2017).

Computation times for our CPM methods are shown in Web Appendix F. CPM fits with independent working correlation structure are computationally efficient and can handle thousands of distinct values in the response variable. CPM fits with exchangeable working correlation are much slower, although they can be sped up by binning the outcome.

4.1. The Primary Setting

Simulation results under the primary study setting with $N=1000$ and $\alpha =0.7$ as well as a secondary setting with $\alpha =0.3$ are shown in Table 1. For the primary setting ($\alpha =0.7$), CPMs performed quite well with low bias and generally good coverage for ${\beta }_X$, ${\beta }_T$, $E(Y\mid X=1,T=0.2)$, $Q(0.5\mid X=1,T=0.2)$, and $F(5\mid X=1,T=0.2)$. CPMs with an independent working correlation structure had minimal bias and coverage near 0.95. Estimates of ${\beta }_T$ from CPMs with a properly-specified, exchangeable working correlation structure exhibited modest bias (~3%) that resulted in somewhat lower coverage (0.91). As expected, the exchangeable working correlation structure was much more efficient than the independent structure (e.g., empirical SE equal to 0.069 versus 0.091).

Table 1.

Simulation results for CPMs for the primary setting and its modifications with lower within cluster correlation ($\alpha =0.3$). For comparison, gold standard models were fit using GEE with the identity link and the correct exchangeable working correlation structure after correctly transforming the response variable.

$\alpha$	Method	Metric	${\beta }_X$	${\beta }_T$	$E(Y\mid X=1,T=0.2)$	$Q(0.5\mid X=1,T=0.2)$	$F(5\mid X=1,T=0.2)$
0.7	Gold Standard	Bias(%)	−0.010	0.087	-	-	-
		RMSE	0.050	0.060	-	-	-
		Empirical SE	0.050	0.060	-	-	-
		Average SE	0.051	-	-	-	-
		Coverage	0.953	0.944	-	-	-
		RE	reference	reference	-	-	-
	CPM (ind)	Bias(%)	0.129	0.270	−0.009	−0.074	−0.169
		RMSE	0.054	0.091	1.232	1.199	0.171
		Empirical SE	0.054	0.091	0.139	0.132	0.016
		Average SE	0.055	0.088	0.142	-	0.016
		Coverage	0.957	0.942	0.956	0.958	0.956
		RE	1.129	2.279	-	-	-
	CPM (ex)	Bias(%)	0.234	2.983	−0.181	−0.270	−0.077
		RMSE	0.052	0.075	1.224	1.191	0.170
		Empirical SE	0.052	0.069	0.135	0.130	0.015
		Average SE	0.053	0.067	0.137	-	0.016
		Coverage	0.957	0.910	0.948	0.956	0.958
		RE	1.047	1.310	-	-	-
0.3	Gold Standard	Bias(%)	−0.061	0.127	-	-	-
		RMSE	0.040	0.089	-	-	-
		Empirical SE	0.040	0.089	-	-	-
		Average SE	0.040	0.087	-	-	-
		Coverage	0.955	0.943	-	-	-
		RE	reference	reference	-	-	-
	CPM (ind)	Bias(%)	0.063	0.254	−0.015	−0.054	−0.069
		RMSE	0.041	0.092	1.236	1.204	0.171
		Empirical SE	0.041	0.092	0.107	0.105	0.013
		Average SE	0.042	0.091	0.105	-	0.013
		Coverage	0.959	0.946	0.957	0.952	0.959
		RE	1.063	1.073	-	-	-
	CPM (ex)	Bias(%)	0.160	2.929	−0.196	−0.249	0.023
		RMSE	0.041	0.091	1.227	1.195	0.170
		Empirical SE	0.041	0.086	0.105	0.105	0.013
		Average SE	0.041	0.085	0.109	-	0.013
		Coverage	0.961	0.936	0.953	0.943	0.959
		RE	1.041	0.943	-	-	-

The average computation time for the gold standard, CPM(ind) and CPM(ex) estimators under the primary setting ($\alpha =0.7$) was 0.13s, 42s, and 2937s. The time was based on 100 simulation replications performed on a 64 bit Linux server equipped with 24 Intel Xeon E5-2620 processors running at 2.40GHz.

We observed efficiency losses when fitting CPMs with an exchangeable working correlation (empirical SE equal to 0.069) compared to the gold standard GEE estimator that applies the appropriate transformation and then uses an identity link with an exchangeable working correlation structure (empirical SE equal to 0.060). However, it is important to note that in practice, the appropriate transformation is not known to the analyst. Further, estimates of the conditional expectation cannot be extracted from the gold standard GEE estimator because $h\{E(Y^{\ast }\mid X=1,T=0.2)\}\ne E\{h(Y^{\ast })\mid X=1,T=0.2\}=E(Y\mid X=1,T=0.2)$, nor can estimates of the conditional quantiles and exceedence probabilities without making additional distributional assumptions. Working exchangeable and independent structures yielded approximately equal precision when estimating the conditional mean, median, and CDF. This is not surprising because the conditional quantities are estimated using linear combinations of the estimated $\gamma$, ${\beta }_X$, and ${\beta }_T$ values, and substantive efficiency gains associated with the exchangeable structure are only observed for ${\beta }_T$ estimates.

In the secondary setting, when the within cluster correlation was relatively low ($\alpha =0.3$), CPMs were approximately valid and all relative efficiencies compared to the gold standard GEE analysis were much closer to 1. We note that for the CPM with an exchangeable working correlation structure, the bias in the parameter estimate was similar to the primary data setting (~ 3%). However, because there was more uncertainty (empirical SE equal to 0.086 versus 0.069) the impact of the biased parameter estimate had less impact on coverage.

4.2. Equal-quantile Binning and Rounding

In the primary simulation setting, when applying CPMs with exchangeable working correlation, we used equal-quantile binning with ${ℳ}_b=300$. We observed substantial efficiency gains for estimating ${\beta }_T$ compared CPMs with independent working correlation that used no binning, but we also observed a small bias in the parameter estimate. To investigate the sensitivity of the procedure to binning choice, we repeated simulations while imposing different binning/rounding strategies. Table 2 shows results.

Table 2.

Simulation results for fitting CPMs with exchangeable working correlation with equal-quantile binned and rounded response data based on the primary setting. For equal-quantile binning, we show results of ${ℳ}_b=25,50,100$ and 200. Results of rounding to 0 and 1 decimal place are also shown.

Scenario	Metric	${\beta }_X$	${\beta }_T$	$E(Y\mid X=1,T=0.2)$	$Q(0.5\mid X=1,T=0.2)$	$F(5\mid X=1,T=0.2)$
Binning ${ℳ}_b=25$	Bias(%)	0.171	0.548	−1.064	−2.258	0.142
	RMSE	0.052	0.068	1.205	1.107	0.170
	Empirical SE	0.052	0.067	0.134	0.132	0.018
	Average SE	0.053	0.067	0.129	-	0.016
	Coverage	0.956	0.945	0.889	0.881	0.901
Binning ${ℳ}_b=50$	Bias(%)	0.174	0.757	−0.039	−0.053	−0.233
	RMSE	0.052	0.068	1.205	1.166	0.171
	Empirical SE	0.052	0.068	0.135	0.131	0.016
	Average SE	0.053	0.067	0.133	-	0.016
	Coverage	0.958	0.942	0.929	0.923	0.935
Binning ${ℳ}_b=100$	Bias(%)	0.187	1.193	−0.316	−0.493	−0.174
	RMSE	0.052	0.069	1.217	1.181	0.171
	Empirical SE	0.052	0.068	0.135	0.130	0.016
	Average SE	0.053	0.067	0.135	-	0.016
	Coverage	0.957	0.936	0.945	0.948	0.953
Binning ${ℳ}_b=200$	Bias(%)	0.208	2.069	−0.197	−0.311	−0.112
	RMSE	0.052	0.071	1.223	1.189	0.170
	Empirical SE	0.052	0.068	0.135	0.131	0.015
	Average SE	0.053	0.067	0.136	-	0.016
	Coverage	0.957	0.924	0.946	0.952	0.958
Rounding 0 decimal place	Bias(%)	0.196	0.799	−0.015	−7.316	−20.965
	RMSE	0.052	0.070	1.231	0.940	0.222
	Empirical SE	0.054	0.069	0.136	0.155	0.014
	Average SE	0.053	0.068	0.139	-	0.014
	Coverage	0.959	0.937	0.952	0.244	0.004
Rounding 1 decimal place	Bias(%)	0.210	3.180	−0.123	−0.693	−2.147
	RMSE	0.052	0.076	1.229	1.175	0.176
	Empirical SE	0.052	0.070	0.136	0.130	0.015
	Average SE	0.053	0.067	0.138	-	0.016
	Coverage	0.957	0.907	0.953	0.942	0.943

As we decreased ${ℳ}_b$ from 200 to 25, we observed that the bias in the ${\beta }_T$ estimate effectively vanished, and the coverage improved. Importantly, there was no noticeable change in estimation precision from coarsening the data. With that said, we observed slightly worse performance in estimates of the conditional quantities with fewer bins, particularly when ${ℳ}_b$ was quite low (25 or 50). In contrast, rounding to 0 decimal places resulted in 169 categories in the response variable on average, resulting in poor performance for estimating $Q(0.5\mid X=1,T=0.2)$ and $F(5\mid X=1,T=0.2)$. Rounding is a sub-optimal choice for such right-skewed responses because many distinct values at the lower end of the distribution are rounded to a single value. There were 498 ordinal levels on average if the response variable was rounded to 1 decimal place; consistent with binning results for ${ℳ}_b=300$, coverage for ${\beta }_T$ was 0.91, but the performance of the conditional estimators was quite good.

To summarize, as expected, working correlation structures can improve efficiency compared to working independent structures, particularly for estimating coefficients for time-varying covariates when correlation within clusters is high. This is the primary motivation for their use. However, CPMs with non-independent working correlation may require binning fully quantitative response data. A large number of bins can lead to slightly biased estimates of coefficients for time-varying covariates. In contrast, a small number of bins can lead to slightly biased estimates of conditional quantities due to over-coarsening.

4.3. Other Simulation Results

Results for other simulation settings are in Web Appendix E. With complete data and the same time-varying covariate pattern across all subjects, CPMs with independent working correlation were as efficient as those with exchangeable working correlation structure (Table S1 in Web Appendix). This is consistent with other studies of the performance of GEE with exchangeable versus independent structures with balanced and complete data (Mancl and Leroux, 1996). With $N=100$, CPMs with independent working correlation showed good performance while CPMs with exchangeable correlation had substantial bias; this bias decreased as sample size increased. With $N=500$, the relationship between the number of bins and bias for ${\beta }_T$ with exchangeable working correlation was similar to that seen with $N=1000$, and was seemingly dependent on $N∕{ℳ}_b$ (Table S4 in Web Appendix). With data generated with AR1 correlation, CPMs with AR1 working correlation performed well and were almost as efficient as the gold standard GEE with the identity link under the correct transformation with AR1 working correlation structure (Table S7 in Web Appendix). CPMs had reasonable performance with moderate link function misspecification, i.e., when data were generated with normal residuals but fit using the logit link function (Table S8 in Web Appendix).

5. Applications

To illustrate the use of the proposed CPM methods, we applied them on the CD4:CD8 ratio and Lung Health Study datasets presented in the Introduction.

5.1. CD4:CD8 Ratio

Longitudinal measures of CD4:CD8 ratio were collected on 1763 adults with HIV on stable ART (one year on ART with undetectable viral load) at the Vanderbilt Comprehensive Care Clinic. We are interested in modeling CD4:CD8 ratio during the second year on ART. A mean of 2.9 CD4:CD8 measurements per subject were available (median = 3; range = 1-7) with 3862 distinct outcome values. Time-invariant covariates considered were calendar year at baseline (one year after ART initiation), race, baseline age, sex, probable route of infection, hepatitis C virus (HCV) infection status, and hepatitis B virus (HBV) infection status. Time (in years) after baseline was the only time-varying covariate.

CPMs with independent working correlation is able to handle 3862 ordinal levels efficiently, while CPMs with exchangeable/AR1 working correlation require binning or rounding due to computational complexities. Thus, we divided the outcome into 1000 bins and rounded to 2 decimal places. Equal-quantile binning resulted in 979 ordinal levels due to ties. The 2 decimal place rounding led to 234 levels. The logit link was used in all models.

Odds ratio estimates and 95% confidence intervals from the fitted CPMs are shown in Table 3. The results suggest that time, race, baseline age, and sex are associated with CD4:CD8 ratio. For example, fixing other variables, a 10-year increase in baseline age is associated with 33% decrease in the odds of having higher CD4:CD8 ratio based on the CPM with an independent working correlation. Results are fairly similar across all three fitted CPMs.

Table 3.

Odds ratio estimates of higher CD4:CD8 ratios with pointwise 95% confidence intervals from CPMs with independent working correlation and CPMs with exchangeable working correlation with binning (1000 equal-quantile bins) and rounding (2 decimal places) are shown. Variance ratios (VRs) are calculated by the variances of the log-odds ratios from CPMs with exchangeable working correlation divided by the variances of the log-odds ratios from CPMs with independent working correlation. Notably, VRs are the same up to two decimals for binning and rounding.

Predictor	Independent	Exchangeable (Binning)	Exchangeable (Rounding)	VR
Time (years)	1.22 (1.08, 1.37)	1.23 (1.14, 1.33)	1.23 (1.13, 1.32)	0.43
Enrollment Year	1.01 (0.98, 1.04)	1.01 (0.99, 1.04)	1.014 (0.99, 1.04)	0.81
Race
African American	(Reference)
Caucasian	1.01 (0.83, 1.24)	1.07 (0.89, 1.29)	1.06 (0.88, 1.28)	0.88
Hispanic	0.68 (0.46, 0.99)	0.73 (0.50, 1.06)	0.72 (0.50, 1.05)	0.98
Other	0.72 (0.47, 1.12)	0.74 (0.49, 1.12)	0.73 (0.48, 1.11)	0.89
Baseline Age (10 years)	0.67 (0.61, 0.74)	0.68 (0.62, 0.74)	0.68 (0.62, 0.74)	0.88
Sex
Male	(Reference)
Female	1.72 (1.32, 2.25)	1.80 (1.40, 2.32)	1.80 (1.40, 2.32)	0.90
Route
Heterosexual	(Reference)
Injection Drug Use	0.99 (0.68, 1.46)	0.93 (0.64, 1.35)	0.93 (0.64, 1.35)	0.93
MSM	0.90 (0.70, 1.17)	0.90 (0.71, 1.15)	0.90 (0.71, 1.14)	0.89
Other/Unknown	0.79 (0.47, 1.35)	0.86 (0.54, 1.38)	0.85 (0.53, 1.37)	0.79
HCV	0.82 (0.60, 1.14)	0.81 (0.60, 1.09)	0.81 (0.60, 1.09)	0.85
HBV	0.99 (0.66, 1.49)	0.92 (0.64, 1.31)	0.92 (0.64, 1.32)	0.77

There were some differences in efficiency of estimates across different CPM estimating procedures. The variance ratios in Table 3 correspond to the variances of the log-odds ratios from CPMs with exchangeable working correlation divided by the variances of the log-odds ratios from CPMs with independent working correlation. The variances for the estimated log-odds ratio for the time-varying covariate, time, for the two exchangeable working correlation models was 0.43 times that for the independent working correlation model. We saw variance ratios ranging from 0.77 to 0.98 for time-invariant covariate parameter estimates.

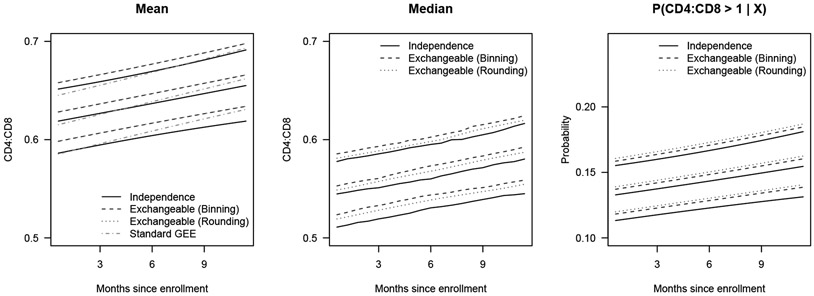
In additional to odds ratios, other quantities can be estimated from the fitted CPMs. Conditional means, medians, and probabilities of CD4:CD8 being greater than 1 are shown as a function of time in Figure 1 with other covariates fixed at their median (for continuous covariates) or mode (for categorical covariates) levels. CD4:CD8 ratio above 1 is considered normal for people without HIV (Petoumenos et al., 2017). Results from the three models were generally very close. We also included the conditional mean obtained by a standard GEE model with an identity link and independent working correlation without transforming the response data for purpose of comparison; results from this analysis are also fairly similar.

Figure 1.

The estimated conditional mean CD4:CD8 ratio, median CD4:CD8 ratio, and the conditional probability that CD4:CD8 ratio is greater than 1 as functions of months since enrollment while fixing other covariates at their medians (for continuous covariates) or modes (for categorical covariates). Pointwise 95% confidence intervals are also shown. The estimated conditional means from the two models with exchangeable working correlation structure (binning and rounding) were almost identical.

5.2. Lung Function Health Study

The purpose of the Lung Health Study was to determine whether a smoking intervention program and the use of an inhaled bronchodilator could slow the rate of decline in lung function in participants with early COPD (Anthonisen et al., 1994). Our interest was in the association of a single nucleotide polymorphism (SNP), rs12194741, with lung function decline over 5 years as measured with FEV1 (Hansel et al., 2013). rs12194741 was represented with a binary indicator for the presence of at least 1 copy of the T allele. We evaluate the genetic contribution to lung function decline by the interaction of rs12194741 and visit with data collected from participants’ annual visits. We included participants who were continuous smokers (dropping observations after smoking stopped) with at least 2 observations. 2562 subjects were included and 1694 (66%) completed 5 visits. Baseline adjustment covariates included age, study site, body mass index (BMI, weight(kg)/height(m²)), lifetime smoking status (in pack years), and average number of cigarettes smoked per day over the year prior to enrollment. BMI change from baseline and study visit were included as time-varying covariates. The distribution of the responses, FEV1, was fairly symmetric (Web Appendix G).

We applied CPMs with independent and AR1 working correlation structures and used the logit link function. Neither binning nor rounding were applied prior to fitting the models as we felt data from 2562 participants was more than sufficient to support the 361 distinct values of the outcome. Table 4 shows odds ratio estimates of higher FEV1 and 95% confidence intervals obtained from the two methods. The odds ratios from the two models were very close. The variance ratios shown in the last column indicate that, as expected, the log-odds ratio estimates obtained by CPMs with the AR1 working correlation structure were more precise than those from CPMs with the independent structure, particularly for time-varying covariates (visit and BMI change). The confidence interval for the interaction term did not cover 1, consistent with rs12194741 being associated with more rapid lung function decline.

Table 4.

Odds ratios estimates for higher FEV1 with 95% confidence intervals from CPMs with independent and AR1 working correlation. The last column shows the variance ratios (VRs) calculated by the variances of the log-odds ratios from CPMs with AR1 working correlation divided by the variances the log-odds ratios from CPMs with independent working correlation. Nine site indicators (LHS was a 10-site study) were also included in the regression analyses but are not shown.

Predictor	Independent	AR1	VR
Visit	0.86 (0.84, 0.88)	0.86 (0.85, 0.87)	0.64
rs12194741	1.12 (0.97, 1.29)	1.12 (0.97, 1.29)	0.97
Visit × rs12194741 interaction	0.97 (0.94, 0.99)	0.97 (0.95, 0.99)	0.61
BMI Change (per 5 kg/m2)	0.65 (0.53, 0.80)	0.66 (0.56, 0.76)	0.56
Baseline Age (per 10–year)	0.34 (0.30, 0.39)	0.34 (0.30, 0.39)	0.90
Baseline BMI (per 5 kg/m2)	1.48 (1.34, 1.63)	1.48 (1.35, 1.62)	0.88
Cigarettes/day (per 10 cigs/day)	0.98 (0.92, 1.03)	0.98 (0.92, 1.03)	0.96
Pack Years (per 20 pack year)	1.19 (1.09, 1.30)	1.19 (1.09, 1.30)	0.98

Conditional quantities including means, medians, and $P(\text{FEV}1\le 2\mid \mathit{X})$ as a function of study visit and genotype were derived from the models and are in Web Appendix G.

6. Discussion

We extended CPMs, a class of ordinal regression models for cross-sectional responses, to analyze clustered continuous response data. In scalar-response settings, CPMs have been used to fit different types of continuous response variables (Liu et al., 2017). Only rank information is used in CPMs when estimating $\beta$, and thus fitting such ordinal regression models can avoid transformations of response variables. To account for correlation between observations within each cluster, we estimated parameters in CPMs using GEE techniques. We proposed feasible and computationally efficient approaches for fitting CPMs with independent, exchangeable, and AR1 working correlation structures. With the estimated parameters, we can obtain CDFs, expectations and quantiles conditional on covariates to help interpret regression results. Our approaches work well under a variety of simulation settings studied for this paper. We built an R package, cpmgee, for CPMs with independent, exchangeable and AR1 working correlation.

Fitting CPMs with an exchangeable/AR1 working correlation structure is more computationally burdensome than using an independent working correlation structure and often requires binning/rounding. In addition, exchangeable/AR1 working correlation structures can be problematic when the full covariate conditional model is not equal to the fitted cross-sectional model ((Pepe and Anderson, 1994); see Section 5.7 in Web Appendix E for brief simulation and discussion). However, the goal of using a working covariance weighting over independent weighting is statistical efficiency. With time-varying covariates, unequal cluster sizes, and high within cluster correlation, our simulations are consistent with prior studies in that substantial efficiency gains can be realized by appropriately employing exchangeable/AR1 working correlation structures. This holds even after binning. Considerations for the extent of binning should depend on analytical goals. A smaller number of bins is more computationally efficient and provides highly efficient and approximately valid inferences for both time-invariant and time-varying covariate coefficients. In contrast, if one is focused on estimating conditional expectations, medians, or exceedance probabilities, we recommend using a larger number of bins or using an independent working correlation structure.

There are several avenues of interest that were not addressed fully in this paper and warrant further study. These include: 1) The semi-parametric method proposed herein requires specifying a link function. Characterizing the extent to which the inference is impacted under misspecified link functions would be useful, though some small-scale simulations are presented in Table S7 of the Web Appendix. 2) A deeper study that provides additional guidance on binning strategies is warranted. 3) In simulation studies that are not shown, we noticed circumstances where the one-step repolr estimator appeared more efficient than a fully-iterated repolr estimator. This observation was surprising to us and warrants further investigation. 4) In future research, we plan to extend CPMs to include sampling weights, which we believe will allow us to fit fully continuous clustered data with more complex working correlation structures. Implemention of weights would also allow us to extend these methods to address challenges associated with missing data and/or confounding.

Data Availability Statement

The data for CD4:CD8 ratio in this paper will not be made publicly available for ethical, and privacy reasons. The dataset contains sensitive information. Furthermore, we do not own the data, and we made an agreement with those who collected the data that we will not share it. We are happy to provide others with the relevant information for how they might be able to obtain the data under reasonable requests (please contact Bryan Shepherd at bryan.shepherd@vumc.org). Data from the Lung Health Study are available from the National Institutes of Health’s database of Genotypes and Phenotypes (dbGaP, https://www.ncbi.nlm.nih.gov/gap/), and one may request access to these data by using the Study Accession number: phs000335.v3.p2.