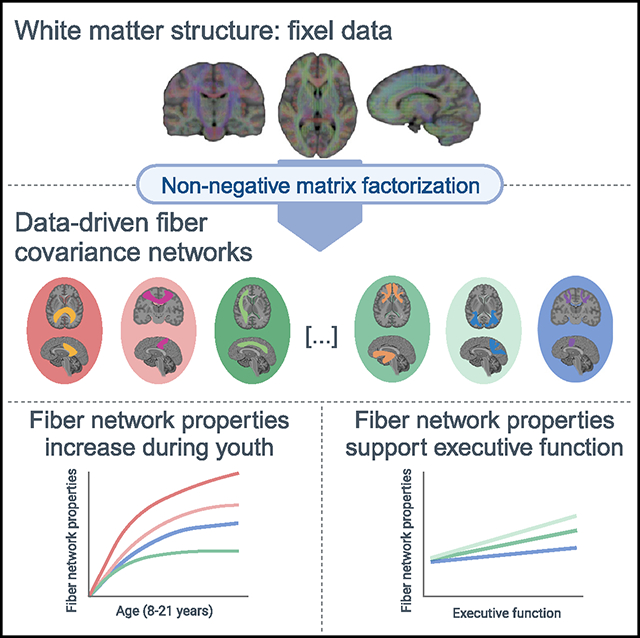
SUMMARY
During adolescence, the brain undergoes extensive changes in white matter structure that support cognition. Data-driven approaches applied to cortical surface properties have led the field to understand brain development as a spatially and temporally coordinated mechanism that follows hierarchically organized gradients of change. Although white matter development also appears asynchronous, previous studies have relied largely on anatomical tract-based atlases, precluding a direct assessment of how white matter structure is spatially and temporally coordinated. Harnessing advances in diffusion modeling and machine learning, we identified 14 data-driven patterns of covarying white matter structure in a large sample of youth. Fiber covariance networks aligned with known major tracts, while also capturing distinct patterns of spatial covariance across distributed white matter locations. Most networks showed age-related increases in fiber network properties, which were also related to developmental changes in executive function. This study delineates data-driven patterns of white matter development that support cognition.
In brief
Bagautdinova et al. use machine learning to reveal fiber covariance networks in white matter in a large sample of youth. Most fiber covariance networks show age-related increases in fiber network properties, which are also related to developmental changes in executive function.
Graphical Abstract
INTRODUCTION
Throughout childhood and adolescence, cerebral white matter expands dramatically and is extensively remodeled.1,2 In tandem with this macrostructural expansion, microstructural properties of white matter also undergo substantial change, including increases in myelination, axonal density, and axonal caliber.3,4 Cognition also develops rapidly during this period, with executive function undergoing a particularly protracted improvement throughout adolescence and young adulthood.5–7 The maturation of white matter architecture is thought to facilitate the efficient and coordinated relay of information between brain regions and to support the development of executive function.8 Quantifying how development of white matter structure supports executive function is a critical prerequisite for normative accounts of brain development as well as for studies of youth-onset psychiatric disorders that are characterized by both deficits in executive functions9,10 and differences within white matter.11
Increasingly, we understand brain development as a spatially and temporally coordinated mechanism that progresses along major axes of brain organization.12–14 For example, cortical development has been shown to follow a continuous sensorimotor-to-association (S-A) gradient during childhood and adolescence, whereby lower-order sensory areas mature earliest and transmodal association areas show more prolonged age-related changes.12 These synchronized maturational processes across hierarchically similar cortical regions are thought to contribute to the appearance of large-scale spatial covariance of brain structure in adulthood,15,16 whereby regions that grow simultaneously will have similar cortical properties, likely due to shared underlying biological mechanisms. Evidence for these hierarchical and heterochronous developmental gradients has now been observed using various cortical measures derived from neuroimaging, including cortical thickness, functional connectivity, intracortical myelination, and intrinsic activity amplitude.12,17,18 More important, the existence of fundamental gradients of cortical organization has been discovered by shifting toward data-driven approaches, as opposed to conventional region of interest analyses investigating predetermined sets of anatomically defined brain regions.
In contrast to research on cortical surface properties, work on white matter development has relied largely on anatomical atlases to characterize white matter tracts. Interestingly, findings suggest that, similar to cortical surface organization, white matter tracts exhibit asynchronous maturational timing, with projection and commissural tracts maturing earlier than association tracts.19 Although inconsistencies exist, the available data suggest simultaneous inferior-to-superior and posterior-to-anterior patterns of white matter maturation.20 Notably, white matter maturation along these two anatomical axes could mirror the maturation of gray matter along the S-A axis.12 Findings thus point to a hierarchically organized developmental program, possibly driven by common underlying biological mechanisms that orchestrate the rate of maturation in distant white matter regions. Analogous to cortical properties, such synchronized maturational processes should ultimately also contribute to generating spatial covariance in white matter structure. However, tract-of-interest–based approaches do not directly capture the spatial covariance that may exist across distributed white matter locations.
Understanding the ways in which white matter connections spatially covary is particularly important, given that covariance in brain structure is thought to result from coordinated maturational processes.15,16 Characterizing the spatial and developmental covariance of white matter structure would provide a new perspective on white matter structure that may capture biologically meaningful organizational principles of white matter and overcome purely anatomically defined structures. Given that white matter tracts connect widespread and spatially distant brain areas, it is likely that certain white matter areas display similar microstructural profiles, even though they belong to anatomically distinct tracts. Conversely, microstructural properties of subregions within the same anatomically defined white matter tract may vary significantly. Given that spatial organization is likely driven by synchronized maturational processes, it is likely that structurally similar white matter regions follow the same developmental trajectories. Data-driven machine learning approaches are well suited to detect the intrinsic spatial organization of the brain, because they can accurately capture the covariance that exists across large-scale networks of structurally covarying areas. One recently developed approach for identifying covariance networks within high-dimensional neuroimaging data is non-negative matrix factorization (NMF), an unsupervised machine learning approach.21–23 NMF has been used to define data-driven covariance networks across the cortex using gray matter features such as cortical thickness and volume.24–26 NMF has also been used to identify partitions of single anatomical regions.27–29 However, applications to white matter specifically remain quite rare.30
Here, we leveraged NMF to uncover how structurally covarying areas of white matter cooperatively develop to support executive function in a large sample of youth from the Philadelphia Neurodevelopmental Cohort.31 Specifically, we delineated white matter fiber covariance networks based on both macrostructural and microstructural fiber properties. We identified 14 fiber covariance networks that mapped well onto the known architecture of white matter while additionally capturing distinct spatial and temporal patterns of coordinated maturation in structurally similar brain regions. Most fiber covariance networks showed age-related increases in fiber micro- and macrostructure, which were further related to normative developmental improvements in executive function. Together, our findings provide insight into how development unfolds across the brain’s white matter and contributes to the maturation of cognition in youth.
RESULTS
We identified fiber covariance networks to study how structural properties of the white matter of the brain are related across spatially distributed areas and are refined in an age-dependent manner. To delineate these covariance networks, we applied the fixel-based analysis (FBA) pipeline4 with single-shell three-tissue constrained spherical deconvolution32 to diffusion-weighted magnetic resonance imaging (DWI) data from 939 youth aged 8–22 years (see Figure S1 for sample selection). This approach minimizes extra-axonal signal contributions from gray matter and cerebrospinal fluid, resulting in more accurate estimations of white matter structure for single-shelled data. Moreover, unlike voxel-based diffusion modeling approaches, FBA gives a more accurate description of the underlying white matter geometry because it can identify multiple fiber populations within a voxel. These individual fiber populations in each voxel are referred to as fixels.4,33 For each fixel, a fiber density and cross-section (FDC) measure was calculated that quantifies both microscopic (intraaxonal volume) and macroscopic (morphology differences in fiber bundle size) properties of white matter.4 We then applied orthonormal projective NMF (opNMF),23 a data-driven unsupervised machine learning method, to fixel-wise FDC data to identify spatial networks in which FDC covaries consistently across participants. The combination of a fixel-based approach with machine learning enabled us to both account for multiple crossing fibers within a single voxel and allow different fiber populations at a single voxel to be assigned to distinct covariance networks, resulting in an accurate representation of white matter maturation. opNMF produces a network matrix, containing the networks and their respective loadings on each fixel, and a participant-specific matrix, reflecting the average FDC value of each participant in a given covariance network (Figure 1). These participant-specific average FDC values for each network were then used as the dependent variable in subsequent group-level analyses.
Figure 1. Identifying fiber covariance networks using NMF.
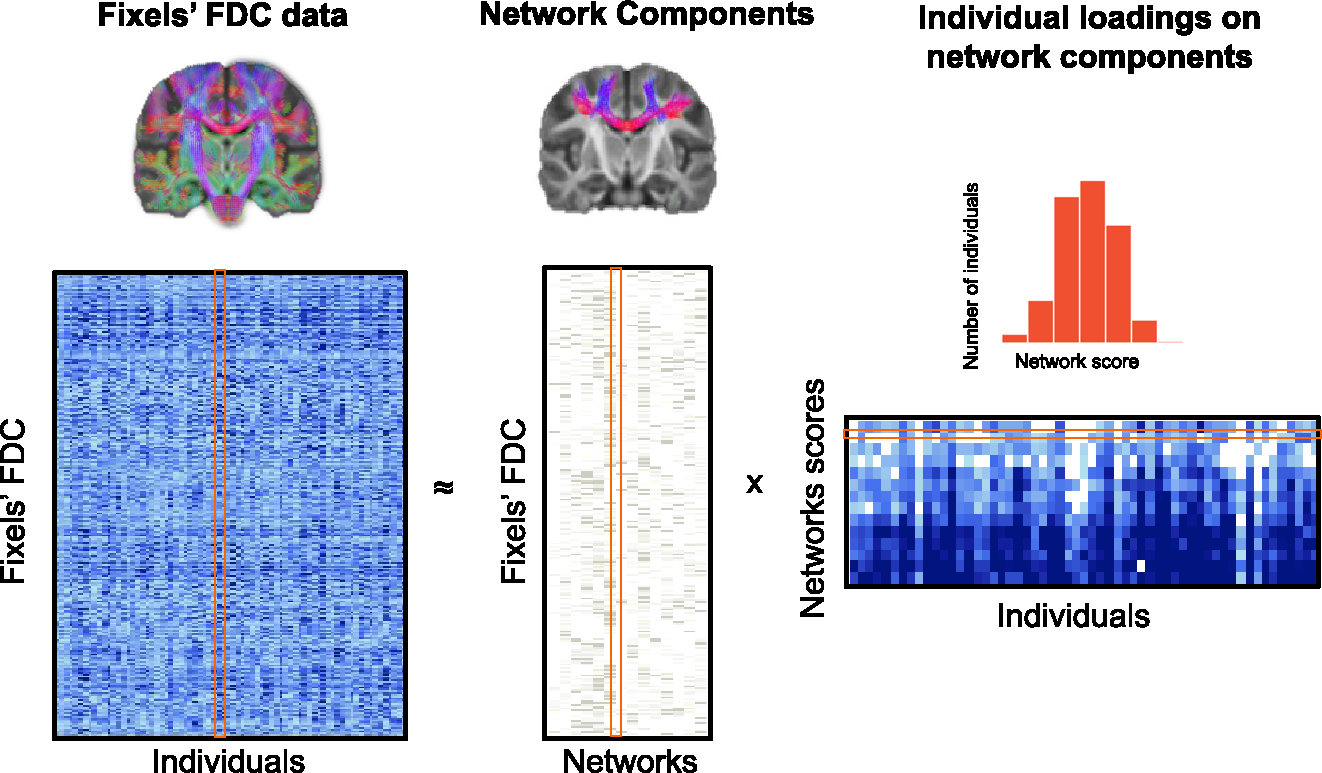
In this schematic, the original whole-brain FDC data for each fixel (rows) and for all individuals (columns) are fed into opNMF, which then decomposes the data into a matrix of network components and a matrix of individual loadings in each network. The network components matrix contains the loadings of each fixel in each of the 14 networks. Above the network components matrix is one example of fixel loadings onto an opNMF network. The individual loadings matrix contains the participant-specific scores for each network. The histogram above shows a sample row of the matrix with scores for all of the participants in one network. More important, both output matrices are ≥0 (e.g., elements of the factorization are nonnegative). The individual network loadings were used as the dependent variable in group-level analyses.
opNMF identifies anatomically meaningful fiber covariance networks
We applied opNMF to segment whole-brain white matter into a low-dimensional number of networks, each comprising white matter areas wherein FDC covaries in an organized fashion across individuals. Segmenting the white matter of the brain into 14 covariance networks parsimoniously captured FDC variability in a reproducible manner with low reconstruction error (see Figure S2A for reconstruction errors of all network solutions). As in prior work using NMF on gray matter,21,24 the 14 networks were sparse and highly symmetric bilaterally (Figure 2). Moreover, the networks were stable in a split-half reliability analysis (based on cosine similarity; Figures S2B and S2C), and each network explained similar levels of variance in the data (Figure S2D), confirming the generalizability and broad utility of data-driven opNMF solutions to unseen data. Furthermore, they corresponded to known fiber bundles, including commissural fibers (networks 1, 6, and 7), association fibers (5, 9, 10, and 14), projection fibers (3, 4, and 8), and cerebellar white matter (11, 12, and 13); one network included a mix of association and projection fibers (network 2). These covariance networks, however, also differed from known white matter bundle atlases in certain aspects. For example, different fiber bundles were in some cases aggregated into one network, such as the superior longitudinal and arcuate fasciculi that form one covariance network (network 5). Moreover, in some components, the data-driven covariance networks also split different portions of a canonical fiber bundle into different networks, such as the inferior and superior/anterior corticospinal tract (CST; networks 3 and 8). Thus, while covariance networks efficiently mapped major white matter bundles, they simultaneously revealed distinct patterns of shared structural properties. To facilitate their identification in subsequent sections, we labeled the 14 networks based on the tracts that are most strongly represented in them (Figure 2).
Figure 2. Delineating fiber covariance networks with orthogonal projective NMF.
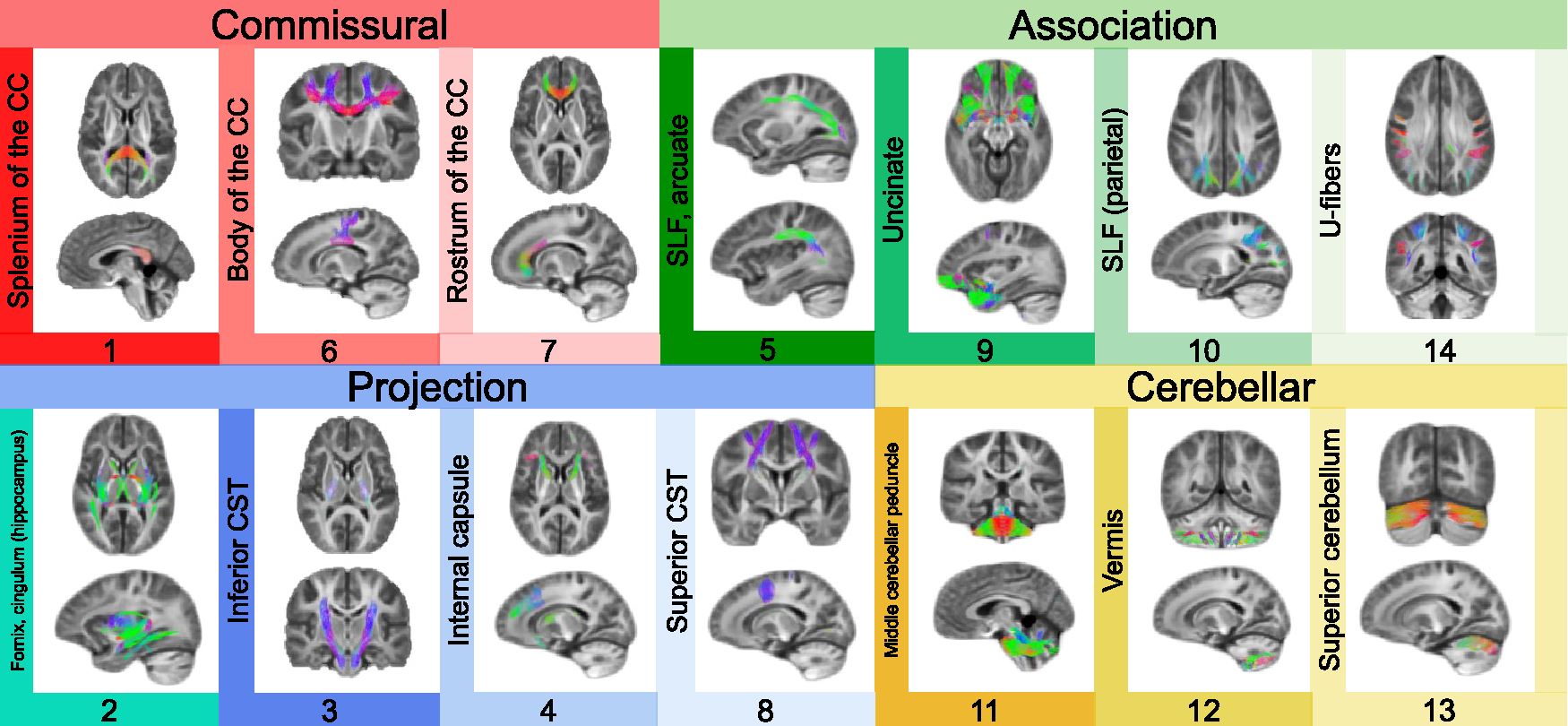
opNMF yields a probabilistic parcellation such that each fixel receives a loading score onto each of the 14 networks quantifying the extent to which the fixel belongs to each network. Here, the probabilistic parcellation was converted into discrete covariance network definitions for display by labeling each fixel according to its highest loading. The coloring of fixels is based on the red-green-blue (RGB) convention, which encodes the left-right, anterior-posterior, and inferior-superior directions, respectively. The networks identified include commissural bundles (1, 6, and 7), cerebellar white matter (11, 12, and 13), association bundles (5, 9, 10, 14, and 2), and projection bundles (2, 3, 4, and 8). Network 2 is included both in the association and projection networks because it encompasses the fornix and the cingulum (hippocampus). Network 10 refers to the parietal portion of the superior longitudinal fasciculus (SLF). CC, corpus callosum; CST, corticospinal tract.
Fiber covariance networks show widespread development
A primary goal of this study was to characterize how macro- and microstructural properties cooperatively develop across different white matter areas. Therefore, we investigated whether the identified fiber covariance networks displayed any developmental changes throughout childhood and adolescence. Because brain maturation is a nonlinear process, we modeled age associations using generalized additive models (GAMs) with penalized splines, which rigorously capture nonlinear effects while avoiding overfitting. All of the models included sex and in-scanner head motion as covariates. Our developmental models revealed that 12 of the 14 fiber covariance networks exhibited significant age-related changes in FDC (Figures 3A and 3B), indicative of widespread white matter development. To determine the magnitude of the age effect in each covariance network, we computed effect sizes as the partial R2, the proportion of variance explained by age. The largest effect sizes (partial R2 > 0.10) were found in networks encompassing the body of the corpus callosum (CC), the superior longitudinal fasciculus and arcuate fasciculus (SLF), the splenium of the CC, and the inferior CST. These results indicate that most fiber covariance networks undergo maturational changes throughout adolescence, with the strongest age-related changes generally observed in networks connecting unimodal sensorimotor regions (with the exception of the network containing the superior longitudinal and arcuate fasciculi, which connects frontoparietal regions).
Figure 3. Developmental refinement of fiber covariance networks.
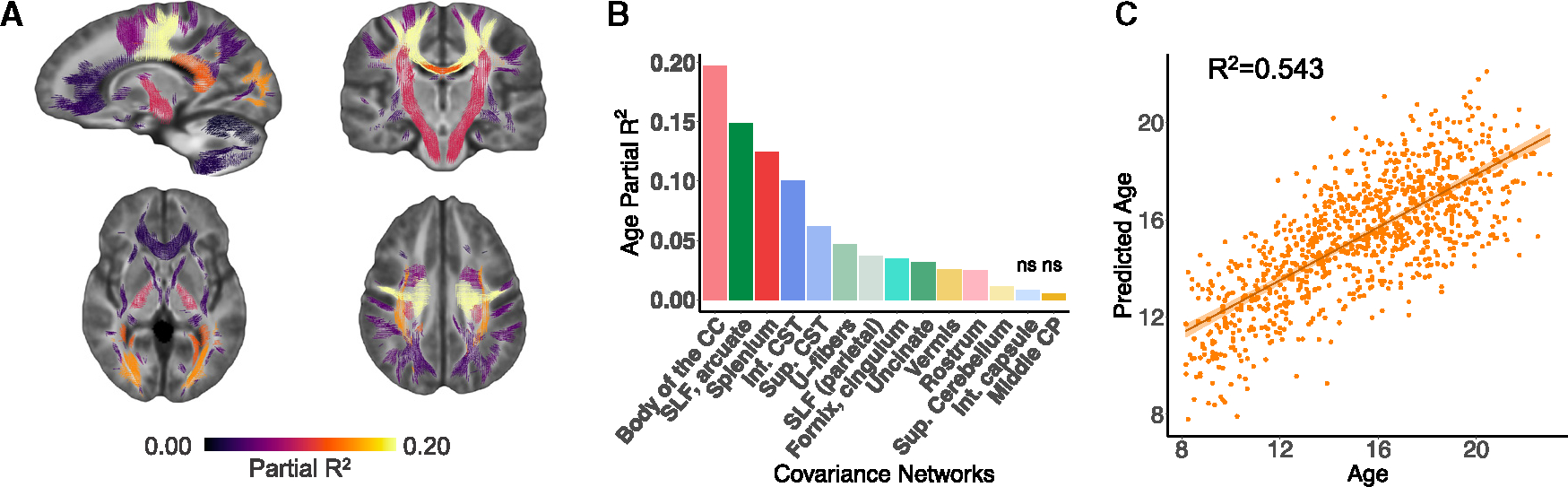
(A) Mass-univariate analyses using GAMs revealed that age was associated with significant changes in FDC in 12 of 14 networks. The coloring of the fixels of the covariance networks is based on the variance explained (partial R2). Multiple comparisons were accounted for using the FDR (q < 0.05).
(B) Bar graph depicting the effect size (partial R2) of the developmental effect for each network. The greatest effect sizes were seen in networks such as the body of the corpus callosum (CC), the superior longitudinal (SLF) and arcuate fasciculi, and the splenium of the CC (networks 6 and 5 and 1). Nonsignificant associations are marked by “ns.”
(C) We tested whether the multivariate signature of fiber covariance networks could predict age above and beyond sex and data quality by comparing a full model to a null model excluding the 14 covariance networks. We found a significant difference between a reduced covariate-only model (i.e., sex, motion, and image quality) and a full model that included both the fiber covariance networks and covariates (F = 76.3, df = 14, p < 0.001). The proportion of variance in age explained by the 14 covariance networks was R2 = 0.543, resulting in a good correspondence between age and predicted age. CST, corticospinal tract; CP, cerebellar peduncle; Int, internal; Sup, superior.
The above quantified the magnitude of the relationship with age of each individual fiber covariance network. As a next step, we sought to determine the degree to which the multivariate signature of fiber covariance networks encoded development. We used a linear model to test whether participants’ covariance network scores, representing participants’ network-specific FDC, could predict age above and beyond demographic and diffusion data quality measures. We found a significant difference between a reduced covariate-only model (i.e., sex, motion, and image quality) and a full model that included both the fiber covariance networks and covariates (F = 76.3, df = 14, p < 0.001). The proportion of variance in age explained by the 14 covariance networks was R2 = 0.543 (Figure 3C). These results demonstrate that fiber covariance networks effectively predicted the age of a participant, and indicate that childhood and adolescence are a time frame of robust refinement of fiber covariance network properties.
Having established that age effects were robust, we sought to obtain a more fine-grained representation of the maturational profile of each covariance network. We thus plotted network-specific developmental trajectories and quantified the direction and magnitude of maturational changes in FDC (Figure 4). The age-related changes were characterized by increasing FDC in most of the networks, with the exception of the fornix/cingulum (hippocampus), vermis, and superior cerebellum, where FDC decreased with age. To identify the developmental windows of significant white matter maturation, we quantified the first derivative of the age smooth term, which represents the change in FDC at a given age. Age fit derivatives revealed distinct timings of developmental changes in different covariance networks. Specifically, the uncinate fasciculus, the parietal portion of the SLF, the splenium of the CC, the inferior CST, and superficial U-fibers showed increased FDC most significantly during childhood and the beginning of adolescence (i.e., from age 8 to before age 16). Other networks, including the body of the CC, the SLF/arcuate fasciculus, the superior CST, and the rostrum of the CC, displayed protracted increases in FDC throughout childhood and adolescence (i.e., until age 18). The FDC of the fornix/cingulum (hippocampus) network continued declining from age 8 through early adulthood (i.e., age 22). Conversely, the vermis and the superior cerebellum showed only brief windows of declining FDC. Thus, covariance networks captured temporally distinct patterns of coordinated white matter changes across different brain areas.
Figure 4. Development is associated with increased FDC in most fiber covariance networks.
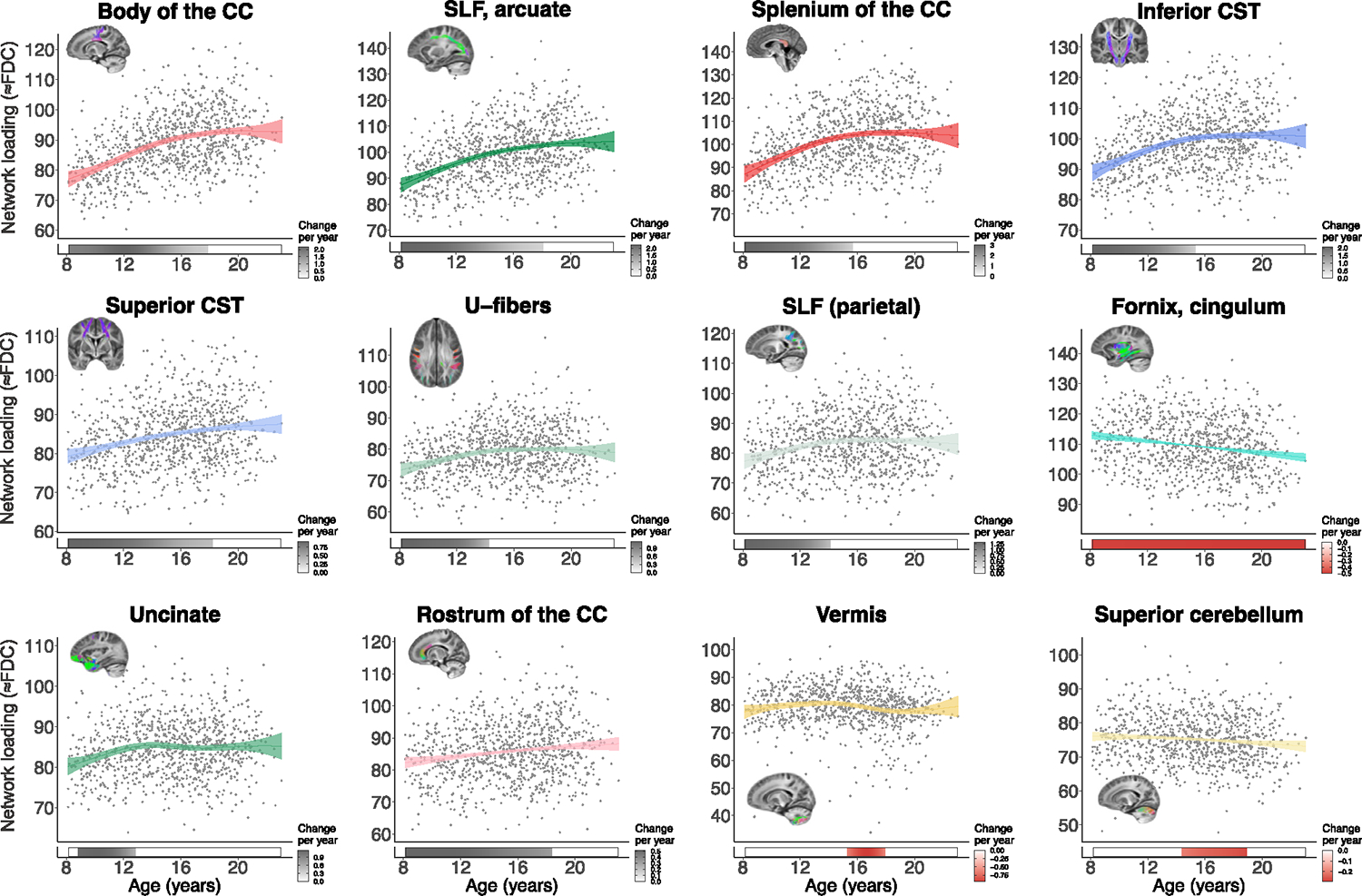
Plots display relationships quantified by GAMs between FDC and age for each covariance network. Significant age-related changes were characterized by increasing FDC in most networks, with the exception of the fornix/cingulum (network 2), vermis (network 12), and superior cerebellum (network 13). Bars below the x axis depict the derivative of the fitted GAM smooth function and correspond to developmental windows of significant white matter maturation. The filled portion of the bar indicates periods in which the magnitude of the derivative is significant. A gray bar color indicates significant FDC increases (i.e., a positive derivative), and a red bar color indicates significant FDC decreases (negative derivative). CC, corpus callosum; CST, corticospinal tract; SLF, superior longitudinal fasciculus.
Executive function is associated with variation in fiber covariance networks linking limbic and association cortex
Executive function is known to undergo considerable improvements during adolescence and young adulthood,5–7 and evidence from diffusion tensor imaging studies suggests that these improvements are linked to white matter microstructural development.8 Based on these findings, we next examined whether variation in fiber covariance networks was related to differences in executive function. We found that better executive function was associated with higher FDC in 13 of 14 covariance networks while controlling for age, sex, motion, and image quality (Figures 5A and 5B). Although significant, these univariate relationships showed modest effect sizes (partial R2 < 0.06). The three covariance networks with the greatest effect sizes include bundles such as the fornix/cingulum (hippocampus), the parietal section of the SLF, and the combined SLF and arcuate fasciculus network (Figure 5D). Thus, differences in executive function appear to be most strongly linked to limbic and association networks.
Figure 5. Fiber covariance network features are associated with executive function in youth.
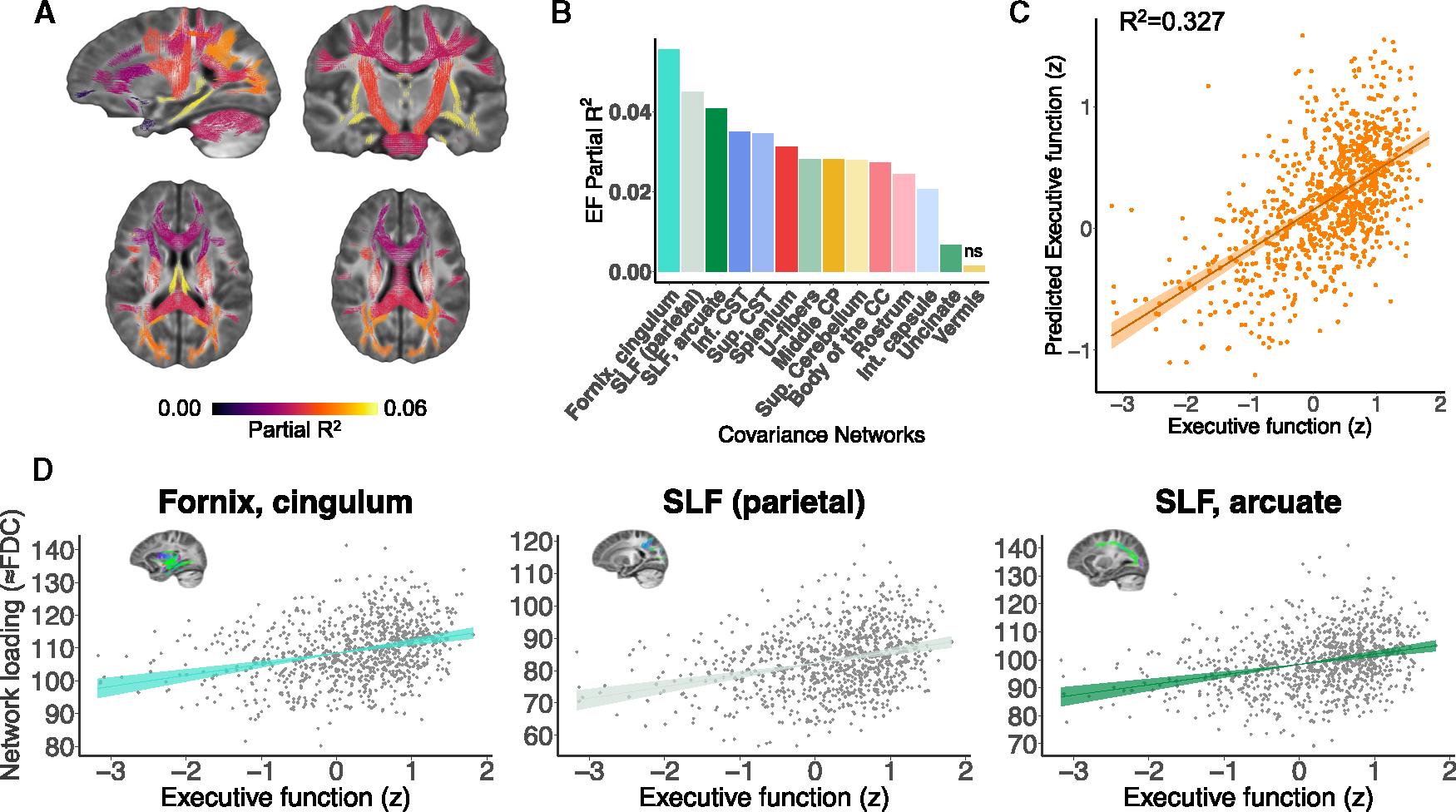
(A) Univariate analyses using GAMs that controlled for sex, motion, and image quality revealed that executive function was associated with higher FDC in 13 of 14 networks. The coloring of the fixels of the covariance networks is based on the partial R2 scores of executive function. Multiple comparisons were accounted for using the FDR (q < 0.05).
(B) Bar graph depicting the effect size of executive function for each network (partial R2). These partial R2 magnitudes were highest in association networks such as the fornix/cingulum (hippocampus), the parietal part of the superior longitudinal fasciculus (SLF), and the superior longitudinal and arcuate fasciculi (networks 2, 5, and 10).
(C) We tested whether the multivariate signature of the fiber covariance networks could predict executive function above and beyond sex and data quality by comparing a full model to a null model excluding the 14 covariance networks. We found a significant difference between a reduced covariate-only model (i.e., sex, motion, and image quality) and a full model that included both the fiber covariance networks and covariates (F = 6.56, df = 14, p < 0.001). The proportion of variance in executive function explained by the 14 covariance networks was R2 = 0.327, resulting in a good correspondence executive function and predicted executive function.
(D) The association between executive function and FDC is shown for the covariance networks with the highest partial R2 scores. EF, executive function; CC, corpus callosum; CST, corticospinal tract; CP, cerebellar peduncle; Int, internal; Sup, superior.
Having examined associations between executive function and each individual fiber covariance network, we next evaluated whether the multivariate pattern of covariance network FDC could jointly predict executive function performance over and above age, sex, and data quality. Of note, due to regression to the mean, predicted executive function scores are expected to be closer to the mean compared to the original variance of the data. Nevertheless, we found that fiber covariance networks could explain over 30% of the variance in executive function beyond demographics and image quality (R2 = 0.327; F = 6.56, df = 14, p < 0.001; see Figure 5C). Together, these findings suggest that fiber covariance networks may support executive function.
Sensitivity analyses provide convergent results
As a final step, we conducted sensitivity analyses to evaluate potentially confounding variables. All of the associations between FDC and age remained significant following false discovery rate correction after controlling for either total brain volume (TBV), maternal education, or overall psychopathology (Figure S3). Similarly, the majority of the associations between FDC and executive function remained significant when TBV, maternal education, or overall psychopathology were added as covariates (Figure S4). Exceptions included the rostrum of the CC, the internal capsule, the uncinate fasciculus, and the U-fibers. To further examine the ability of fiber covariance networks to predict age above and beyond TBV, we compared a full model that included all 14 fiber covariance networks and covariates (including TBV) to a reduced model that included only TBV and covariates. We found a significant difference between the reduced and the full model (F = 77.5, df = 14, p < 0.001), and the 14 covariance networks jointly explained over half of all of the variance in age above and beyond covariates such as sex, mean FD, and TBV (R2 = 0.54). Finally, we addressed the potential impact of outliers by excluding individuals with executive function Z scores below −2. Fiber covariance networks remained a highly significant predictor of executive function above and beyond covariates (F = 6.54, df = 14, p < 0.001) and the proportion of explained variance (R2 = 0.307) remained similar, indicating that the outliers did not exert undue leverage on the model fit (Figure S5).”
DISCUSSION
We uncovered how structurally covarying areas of white matter cooperatively develop during childhood and adolescence to support executive function. Specifically, we identified white matter structural networks based on covarying micro- and macrostructural properties and delineated their age-dependent changes. The majority of these structural covariance networks showed age-related increases in FDC, which were further related to normative developmental improvements in youth executive function. Notably, the most pronounced developmental changes were found in more superior and anterior fiber covariance networks. Furthermore, limbic and association networks were most strongly associated with executive function. As described below, these findings suggest that white matter development follows inferior-to-superior and posterior-to-anterior axes that could influence the hierarchical maturation of the cortex.
Networks derived from opNMF complement anatomically defined white matter bundles
We derived data-driven fiber covariance networks using an advanced machine learning technique, opNMF.23 In comparison to the sparse, positively signed networks produced by opNMF, principal-component analysis and other techniques produce widely dispersed networks with a mix of positive and negative weights, which often limit interpretability. Using a completely data-driven approach that did not incorporate explicit spatial constraints, opNMF revealed networks exhibiting both spatial contiguity within hemispheres and high bilateral symmetry. The identified 14 networks were stable, indicating that data-driven white matter covariance networks generalize well to unseen data. Our covariance networks aligned well with existing definitions of major white matter pathways, while also differing in certain aspects. First, because individual fiber populations were modeled within each voxel using FBA, multiple fiber populations present within a given voxel could be assigned to distinct networks. This contrasts with most currently available white matter tract atlases, wherein each voxel is assigned to a single white matter bundle or network. Second, our hypothesis-free, data-driven approach was able to capture distinct patterns of spatially covarying white matter structure that have not been described previously. For example, distinct white matter tracts were in some cases aggregated into one network. This was observed in network 5, which encompassed both the superior longitudinal and arcuate fasciculi. Interestingly, this indicates that although the superior longitudinal and arcuate fasciculi are analyzed independently in atlas-based analyses, these tracts in fact display similar white matter architecture and organizational features, suggesting that they may be governed by common underlying biological mechanisms. Conversely, other anatomical tracts were split across different networks. For example, the CST was divided into an inferior and superior/anterior portion, and the SLF was divided into frontal and parietal connections, each with unique developmental trajectories. This suggests that although these tracts are conventionally studied as a whole, certain subregions are in fact characterized by distinct patterns of spatial and temporal organization that can be disambiguated. Fiber covariance networks thus offer complementary information to standard anatomically defined atlases.
Together, these findings suggest that relative to conventional anatomical atlases, data-driven atlases derived from covariance networks provide an efficient way to describe white matter structure that aligns with organizational properties of the brain, which may be shaped through shared developmental processes.15 Data-driven maps may be particularly useful to study brain organization from multimodal neuroimaging-derived microstructural properties34 and from comparison across different species.35 Future research could leverage our white matter network data-driven atlas to better understand how brain structural development underlies the development of functional brain networks.
Covariance networks capture temporally distinct patterns of coordinated white matter maturation
We found that fiber covariance networks underwent different developmental patterns, with variations in both the magnitude and the timing of maturation. In general, findings aligned with recent white matter development studies using advanced diffusion modeling strategies, which reported similar developmental time frames.36,37
The greatest magnitudes of structural age-related change detected in the present study were found in networks primarily comprising the body and splenium of the CC, as well as the superior longitudinal and arcuate fasciculi. Interestingly, it appears that these networks are located at intermediate stages along known inferior-to-superior and posterior-to-anterior axes of cortical organization. This is to be expected, given that the present study encompasses late childhood, adolescence, and early adulthood, as opposed to early childhood (most inferior/posterior changes) and mid-adulthood (most superior/anterior changes). These major axes of brain organization have been highlighted from a lifespan developmental perspective of both gray and white matter1,38–40 and from specific developmental periods such as infancy41 and youth.42,43
The timing of maturation varied considerably across fiber covariance networks, with some networks maturing in early childhood, some plateauing in adolescence, and some plateauing only by the end of adolescence. More specifically, fiber networks encompassing the cerebellum, fornix, and parahippocampal cingulum showed either no change or decreasing FDC during adolescence. Early maturation of the cerebellum and fornix aligns with prior lifespan studies44–48 and suggests that these regions mature early. Interestingly, the cingulum is most commonly studied as a whole (including both cingulate gyrus and parahippocampal sections) and has typically been related to prolonged maturation. However, in line with our results, recent fixel-based findings indicate that only the cingulate portion of the cingulum shows age-related increases.36 This suggests that the more inferior, parahippocampal regions of the cingulum may mature earlier. In contrast to these early maturing networks, the uncinate fasciculus, the parietal portion of the SLF, the splenium of the CC, the inferior CST, and superficial U-fibers matured until mid-adolescence (i.e., from age 8 to before age 16). Finally, some of the most prolonged age-related changes were observed in more superior and anterior fiber covariance networks, including the rostrum of the CC, the superior longitudinal and arcuate fasciculi, the body of the CC, and the superior CST, all of which continued maturing throughout adolescence (i.e., until age 18). Interestingly, the identified patterns of maturation across different covariance networks are again suggestive of a hierarchical patterning of development, whereby inferior and posterior white matter regions tend to mature earlier than superior and anterior areas. Of note, the S-A axis has been proposed as a more parsimonious way to capture the combination of inferior-to-superior and posterior-to-anterior developmental patterns.12 Although further studies are needed to directly assess this, the data-driven networks identified in this study suggest that a hierarchical pattern may also orchestrate the timing of age-related changes in white matter structure. Of note, it is likely that white matter connections linking to the most anterior areas connecting to regions subserving higher-order functions would show another wave of maturational changes going into the third decade of life.44 Further data-driven approaches using data that encompass a larger age range would be better suited to capture this. Overall, these findings indicate that white matter structure is spatially and temporally coordinated in a manner that aligns with major inferior-to-superior and posterior-to-anterior axes of cortical organization.
Association covariance networks are linked to executive function
Having characterized the development of fiber covariance networks during adolescence, we lastly evaluated the cognitive impact of these developmental effects. While controlling for age, we found that an increase in FDC was associated with higher executive performance in all but one covariance network. The associations between FDC and executive function were most robust in frontoparietal and temporal association networks, namely the parahippocampal cingulum as well as the SLF and arcuate fasciculus. Higher FDC values may reflect increases in axonal packing and count and/or increases in the number of voxels that a bundle occupies.4 Of note, childhood developmental studies that have separately investigated FD, fiber cross-section (FC), and their combination FDC, show more widespread and pronounced increases in cross-sectional fiber bundle size relative to increases in FD.49,50 Applying this observation to the present results suggests that the changes in FDC may be mostly driven by changes in FC. Both microstructural (FD) and morphological changes (FC) may allow for more efficient signaling between distributed frontoparietal and temporal regions that are critical for executive function. This result adds to prior work reporting associations between executive function and localized increases in white matter integrity in relatively small samples.8 Furthermore, it directly coheres with observations that greater cortical representation of association networks is linked to better general cognition in youth51,52 and suggests that the expansion of white matter underlying limbic and association cortices may contribute to these findings. Of note, although the fornix/cingulum was positively associated with executive function, FDC values of this network decreased with age. Importantly, the positive association between FDC and executive function in this network was found while controlling for age effects. Such potentially counterintuitive associations with development and cognition have been reported for structural brain features such as cortical thickness; the cortex tends to thin with development, but in general, children who perform better on cognitive tasks tend to have thicker cortex.53,54
Limitations of the study
Despite the strengths of this study, several limitations should be noted. We used a cross-sectional design, which precludes inference regarding within-individual developmental effects. However, it is worth mentioning that the present developmental effects of FDC agree with results from smaller-scale longitudinal studies.36,49 Larger-scale longitudinal studies such as the IMAGEN study55 and the Adolescent Brain Cognitive Development Study56 could eventually provide estimates of within-person change in fiber covariance networks at the population level. Second, the b-value of the diffusion imaging protocol is somewhat low (b = 1,000 s/mm2), which may result in less accurate FDC measures due to contamination from extra-axonal signal.36 In the present study, we addressed this caveat by using a single-shell multi-tissue modeling approach, which minimizes extra-axonal signal contributions. In addition, we chose to quantify white matter development using a combined measure of FD and FC, which limited the biological specificity from the FD metric. Of note, prior work using FBA has shown that the development of white matter is driven mostly by morphological changes from FC.36,49,50
Conclusions
We introduced a data-driven approach for defining fiber covariance networks that are distinct from typical tract-based anatomical atlases and have unique associations with age in youth. Our findings suggest that developmental patterns of white matter follow large-scale anatomical gradients, in a way that may support heterochronous patterns of cortical maturation. Notably, specific limbic and association networks were associated with individual differences in executive function. Taken together, these results provide a data-driven framework to understand adolescent white matter organization and maturation using high-order diffusion modeling and multivariate analysis techniques.
STAR★METHODS
RESOURCE AVAILABILITY
Lead contact
Further information and requests for resources should be directed to and will be fulfilled by the lead contact, Dr. Theodore Satterthwaite (sattertt@pennmedicine.upenn.edu).
Materials availability
This study did not generate new unique reagents.
Data and code availability
This paper analyzes existing, publicly available data from the Philadelphia Neurodevelopmental Cohort.31 Data is available at the database of Genotypes and Phenotypes (dbGaP): https://www.ncbi.nlm.nih.gov/projects/gap/cgi-bin/study.cgi?study_id=phs000607.v3.p2. To request access, an authorization request can be completed via https://dbgap.ncbi.nlm.nih.gov/aa/wga.cgi?%20page=login&page=login.
All original code for image preprocessing, evaluating opNMF solutions, and all statistical analyses has been deposited at https://github.com/PennLINC/Fixel_NMF_development and on Zenodo at https://zenodo.org/records/10064924, https://doi.org/10.5281/zenodo.10064924. All code is publicly available as of the date of publication. DOIs are listed in the key resources table.
Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.
KEY RESOURCES TABLE.
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
|
| ||
| Deposited data | ||
| Raw and preprocessed structural T1-weighted images, diffusion images, clinical and cognitive data | Philadelphia Neurodevelopmental Cohort | https://www.ncbi.nlm.nih.gov/projects/gap/cgi-bin/study.cgi?study_id=phs000607.v3.p2 |
|
| ||
| Software and algorithms | ||
|
| ||
| R 4.1.2 | R Foundation | https://cran.r-project.org/bin/macosx/ |
| MATLAB R2018a | MathWorks | https://www.mathworks.com/ |
| Nipype | NiPy | https://pypi.org/project/nipype/ |
| QSIprep | PennLINC | https://github.com/PennBBL/qsiprep |
| FSL 6.0.3 | FSL | https://fsl.fmrib.ox.ac.uk/fsl/fslwiki/ |
| MRtrix3 v3.0RC3 | MRtrix | http://www.mrtrix.org/ |
| Confixel | PennLINC | https://github.com/PennLINC/ConFixel |
| BrainParts (non-negative matrix factorization) | BrainParts | https://github.com/asotiras/brainparts |
| Statistical analyses of fiber covariance networks | This paper | https://doi.org/10.5281/zenodo.10064923 |
EXPERIMENTAL MODEL AND STUDY PARTICIPANT DETAILS
Participants
Participants were drawn from the Philadelphia Neurodevelopmental Cohort (PNC).31 Among the original 1,601 individuals who participated in the PNC, 340 were excluded due to clinical factors, including medical disorders that could affect brain function, current use of psychoactive medications, prior inpatient psychiatric hospitalizations, or an incidentally encountered structural brain abnormality. Among the 1,261 participants eligible for inclusion in this study, 174 participants were excluded for missing either a B0 field map or diffusion weighted MRI data. Data from the remaining 1,087 participants underwent both manual and automated quality assurance protocol for DWI57,58 and T1w datasets, which excluded 146 participants for poor quality data (see below for details and Figure S1). This set of exclusion criteria resulted in a final sample of 941 participants, with mean age 15.3 years, standard deviation (SD) = 3.4 years (n = 522 females). All participants or their parent/guardian provided informed consent, and minors provided assent. All study procedures were approved by the Institutional Review Boards of both the University of Pennsylvania and the Children’s Hospital of Philadelphia.
METHOD DETAILS
Cognitive assessment
The Penn computerized neurocognitive battery (CNB) was administered to all participants. The CNB consists of 14 tests adapted from tasks applied in functional neuroimaging to evaluate a broad range of cognitive domains.5,59 These domains include executive control (abstraction and flexibility, attention, working memory), episodic memory (verbal, facial, spatial), complex cognition (verbal reasoning, nonverbal reasoning, spatial, processing), social cognition (emotion identification, emotion intensity differentiation, age differentiation), motor and sensorimotor speed. As in prior work,58,60 the z-transformed accuracy and speed of each test were averaged to yield an integrated measure of cognitive efficiency (excluding motor and sensorimotor speed because they do not produce accuracy measures) that reflects accurate and rapid responding. These efficiency scores were then summarized by an exploratory factor analysis, which delineated four correlated factors (complex cognition, executive function, social cognition, and memory).60 Two participants from the full n = 941 sample had incomplete cognitive datasets, thus group-level statistical analyses examining associations between fiber covariance networks and executive function focused on the remaining 939 participants.
Image acquisition
All MRI scans were acquired on the same 3T Siemens Tim Trio scanner and 32-channel head coil at the Hospital of the University of Pennsylvania.31
T1 weighted MRI
T1-weighted structural images were acquired prior to DWI acquisition with a 5-min magnetization-prepared, rapid acquisition gradient-echo T1-weighted (MPRAGE) image with the following parameters: repetition time = 1810 ms, echo time = 3.51 ms, inversion time = 1100 ms, flip angle = 9°, field of view = 180 × 240 mm, matrix = 192 × 256, slice number = 160, voxel resolution = 0.94 × 0.94 × 1 mm).
Diffusion MRI
Diffusion scans were acquired using a twice-refocused spin-echo (TRSE) single-shot echo-planar imaging (EPI) sequence (TR = 8100 ms, TE = 82 ms, FOV = 240 × 240 mm, matrix = 128 × 128, slices = 70, slice thickness/gap = 2/0 mm, flip angle = 90/180/180, voxel resolution = 1.875 × 1.875 × 2 mm, volumes = 71). A 64-direction set was divided into two independent 32-directions imaging runs - for a total scanning time of ~11 min. Each 32-direction sub-set was chosen to be maximally independent such that they separately sampled the surface of a sphere. The complete sequence consisted of 64 directions with b = 1000 s/mm2 and 7 interspersed scans with b = 0 s/mm2.
Field map
In addition, a map of the main magnetic field (i.e., B0) using phase-difference images was derived from a double-echo, gradient-re-called echo (GRE) sequence, allowing us to estimate field distortions in each dataset (TR = 1000 ms; TE1 = 2.69 ms; TE2 = 5.27 ms; 44 slices; slice thickness/gap = 4/0 mm; FOV = 240 mm; effective voxel resolution = 3.8 × 3.8 × 4 mm).
Image quality assurance
All T1-weighted anatomical images were independently rated by three highly trained image analysts (see61 for a detailed description); participants with low quality structural images were excluded. Similarly, all dMRI images were subject to a rigorous manual quality assessment procedure involving visual inspection of all 71 gradient volumes.57 Each volume was evaluated for the presence of artifact, with the total number of volumes impacted summed over the series. Data was considered “Poor” if more than 14 (20%) volumes contained artifact, “Good” if it contained 1–14 volumes with artifact, and “Excellent” if no visible artifacts were detected in any volumes. All 941 participants included in the present study had diffusion datasets identified as “Good” or “Excellent” and also had less than 2 mm mean relative displacement between interspersed b = 0 volumes. Finally, to further mitigate potential effects of image quality on our DWI findings, measures of quality were included as covariates in all group-level analyses.
Image processing
All images were processed with QSIprep, version 0.8.0RC3 (https://github.com/PennBBL/qsiprep),62 which is based on Nipype 1.1.9.63 A total of 2 DWI series in the j-distortion group were concatenated, with preprocessing operations performed on individual DWI series before concatenation. Any image with a b-value less than 100 s/mm2 was treated as a b = 0 image. MP-PCA denoising as implemented in MRtrix3’s dwidenoise64 was applied with a 5-voxel window. After MP-PCA, Gibbs unringing was performed using Mrtrix3’s mrdegibbs.65 Following unringing, B1 field inhomogeneity was corrected using dwibiascorrect from Mrtrix3 with the N4 algorithm.66 After B1 bias correction, the mean intensity of the DWI series was adjusted so all the mean intensity of the b = 0 images matched across each separate DWI scanning sequence.
Prelude from FSL (https://fsl.fmrib.ox.ac.uk/fsl/fslwiki/, version 6.0.3) was used to estimate the susceptibility distortion correction. FSL’s eddy was used for head motion and Eddy current correction.67 Eddy was configured with a q-space smoothing factor of 10, a total of 5 iterations, and 1000 voxels used to estimate hyperparameters. A linear first level model and a linear second level model were used to characterize Eddy current-related spatial distortion. Q-space coordinates were forcefully assigned to the shell. Field offset was attempted to be separated from participant movement. Shells were aligned post-eddy. Eddy’s outlier replacement was run.67 Data were grouped by slice, only including values from slices determined to contain at least 250 intracerebral voxels. Groups deviating by more than 4 standard deviations (SD) from the prediction had their data replaced with imputed values. Final interpolation was performed using the jac method.
The DWI time-series were resampled to the anterior-to-posterior commissure (ACPC) generating a preprocessed DWI run in AC-PC space with 1.25mm isotropic voxels. Several confounding time-series were calculated: framewise displacement (FD) based on the preprocessed DWI using the implementation in Nipype (following the definitions by68) and the number of bad slices in raw images. These two metrics - mean framewise displacement and number of bad slices - were included in all group-level statistical analyses.
Fixel-based analysis
We pursued a modeling technique that models information from multiple distinct fiber populations within a given voxel: the fixel-based analysis (FBA) pipeline.4 In this pipeline, an individual fiber population within a voxel (fixel) is derived from fiber orientation distributions (FODs) estimated by a CSD technique.32 This approach minimizes extra-axonal signal contributions from gray matter and cerebrospinal fluid, resulting in more accurate estimations of white matter structure for single shelled data. Moreover, unlike voxel-based diffusion modeling approaches, FBA gives a more accurate description of the underlying white matter geometry as it can identify multiple fiber populations within a voxel.
Diffusion images were further processed using MRtrix3 (v3.0RC3, http://www.mrtrix.org/)69 according to the FBA pipeline,4 which involves the following steps. First, we calculated study-specific response functions for white matter, gray matter, and cerebrospinal fluid70 using data from 30 representative study participants (1 female and 1 male from each of fifteen age bins: 8–9 years old, 9–10 years old, up to 22–23 years old). Study-specific average response functions were then used to estimate FODs for all individuals with single-shell three tissue CSD.32 Following group-wise intensity normalization of the FOD images, we generated a study-specific FOD template (with the same 30 participants) and each individual’s FOD image was registered to the study template. The resulting participants’ transformed FOD images in template space were segmented along their main directions to delineate individual fiber bundle elements in each voxel, referred to as “fixels” (main manuscript Figure 1).4,33 Apparent fiber density (FD) was calculated for each fixel as the integral of the FOD lobe. Fiber cross-section (FC) was computed using the spatial warps generated during registration of each participant’s FOD image toward the common FOD template.4 Finally, a combined fiber density and cross-section (FDC) measure was calculated that quantifies both microscopic (intra-axonal volume) and macroscopic (morphology differences in fiber bundles) properties of white matter. FDC has previously been found to be more sensitive to detect change in white matter properties relative to FD and fiber cross-section alone.4 After calculating FDC for each fixel, the FDC values were smoothed to increase the signal-to-noise ratio. However, it is important to smooth fixel-specific metrics only with other fixels that share common streamlines, and not with all adjacent fixels.33 Therefore, to appropriately smooth fixels’ FDC values, we first generated a whole-brain probabilistic tractogram from the FOD template – in this case, a 20-million streamlines tractogram. The tractogram was reduced to a 2-million streamlines tractogram using the Spherical-deconvolution Informed Filtering of Tractograms algorithm (SIFT)71 for which streamlines density is proportional to FD as estimated with CSD. Lastly, we computed a fixel-fixel connectivity matrix based on the reduced tractogram to inform smoothing of the fixel data at 10mm Full-Width at Half Maximum. Smoothed FDC metric for 602,229 fixels was used as input to the unsupervised machine learning approach using opNMF.
Non-negative matrix factorization
We employed orthonormal projective NMF23 to identify networks where fibers’ FDC covaried consistently across participants. opNMF produces sparse, positively-signed components that form a purely additive and non-overlapping parts-based representation.23 opNMF decomposes the input matrix X containing fixel-wise FDC estimates ⎯ of dimensions F × N (F = 602,229 fixels, N = 941 participants) -into a network matrix W (of dimension F × K; K = user-specified number of networks) and a weight matrix H (of dimension K × N; main manuscript Figure 1). The network and weight matrices are estimated such that their multiplication reconstructs the input matrix as best as possible by minimizing the reconstruction error between the original and the reconstructed input – the Frobenius norm. The network matrix W contains the estimated non-negative networks and their respective loadings on each of the fixels. This probabilistic (soft) definition of networks can be converted into discrete (hard) network definitions for visualization by labeling each fixel according to its highest network loading. The weight matrix H contains participant-specific scores for each network. These participant-specific scores are equivalent to an average of FDC values for each covariance network. Consequently, the higher the participant score on a network, the higher that participant’s FDC value within that network. The participants’ scores from matrix H for each network were then used as the dependent variable in the subsequent group-level univariate analyses.
We used ConFixel72 (https://github.com/PennLINC/ConFixel) to convert participants’ FDC data at every fixel into a readable Hierarchical Data Format 5 (HDF5) file format for opNMF. Then, we used Brainparts (https://github.com/asotiras/brainparts) and MATLAB R2018a to run the opNMF decomposition. Consistent with prior studies using this technique,21,73 we evaluated multiple opNMF solutions from 2 to 30 networks (in steps of two) to obtain a range of possible solutions. We selected the optimal network solution using the reconstruction error criterion. This involves a visualization of the residual error after estimating different numbers of components (Figure S2A) (see21 for a detailed description). The inflection point of the reconstruction error slope indicates the optimal number of components, given that adding more components than the intrinsic data dimension only results in minor decreases in reconstruction error. The stability of the identified 14 fiber covariance networks was evaluated in a split-half reliability analysis by computing the cosine similarity between matched components of data splits 1 and 2 (Figure S2B). Cosine similarity range from 0 to 1, with higher values indicating greater stability of a given component across different data splits. To further contextualize the obtained stability values, we generated a null distribution of cosine similarity values by permuting fixel loadings on the 14 networks in each data split, reflecting random fixel loadings onto the 14 networks. Null cosine similarity values were then recomputed between matched pairs of permuted components. This procedure was repeated 10,000 times (Figure S2C). Cosine similarity values were expected to be higher for observed networks compared to permuted networks. The explained variance was computed for each of the 14 networks by calculating the reconstruction error between the original input X matrix and the reconstructed matrix for a given opNMF network (Figure S2D). The amount of variance explained by each opNMF network is expected to be distributed across all 14 networks.
QUANTIFICATION AND STATISTICAL ANALYSIS
After delineating fiber covariance networks, we evaluated associations between network FDC and both age and executive function. As brain maturation is a nonlinear process, we modeled age associations using generalized additive models (GAMs) with penalized splines in the R package “mgcv”.74 GAMs assess a penalty with increasing nonlinearity to avoid overfitting the data. Due to this penalty, GAMs designate nonlinearities only when they explain additional variance in the data above and beyond linear effects. All models used up to four basis functions, which were selected using the restricted maximum likelihood framework (REML) to produce estimates of variance parameters. For each white matter covariance network, we examined associations between age and FDC while controlling for sex, mean framewise displacement during the diffusion scan, and the number of slices with signal dropout (“bad slices”) observed in diffusion volumes, using the following formula:
To identify developmental windows of significant white matter maturation, we quantified the first derivative of the smooth age term, which represents the slope of the spline fit, at every age. Using the gratia package in R, we operationalized the window of significant age-related change as the period at which the 95% point-wise confidence interval of the spline’s estimated slope did not include 0.
To investigate whether executive function performance was associated with each network’s FDC above and beyond the effect of age, we included the executive efficiency factor score as a linear variable in the model above. In each set of analyses, multiple comparisons were controlled for using the False Discovery Rate (q < 0.05) and effect sizes were quantified as the partial R2. The partial R2 is the proportion of variance explained by a full model that is not explained by a reduced model. For example, when investigating the relationship between age and FDC, the full GAM model includes age and the aforementioned covariates while the reduced model includes only covariates.
Following the investigation of the developmental and executive function effects of each covariance network separately, we next explored how well FDC of all these covariance networks jointly encode age and individual differences in executive function. Using a linear model, we tested whether the 14 covariance networks’ FDC jointly predicted age above and beyond sex, in-scanner motion, and quality of diffusion data. We used an F-test to compare the full linear model predicting age to a reduced model that excluded the 14 covariance networks. Similarly, we explored whether a network’s FDC predicted executive function above and beyond covariates and compared this full model to a reduced model excluding the 14 covariance networks. Finally, we calculated the proportion of variance explained (partial R2 coefficient) by the 14 covariance networks in predicting age and executive functioning.
Sensitivity analyses
We conducted sensitivity analyses to ensure our results were not influenced by confounding variables. First, we repeated all group-level statistical analyses while including maternal education level as an additional covariate. Second, we included total brain volume in all group-level analyses to evaluate whether our results were driven by gross differences in brain volume. Third, we evaluated the ability of fiber covariance networks to predict age above and beyond TBV, by comparing a full model that included TBV, all 14 fiber covariance networks and covariates to a reduced model that included only TBV and covariates. Fourth, we addressed the potential impact of outliers by excluding individuals with executive function z-scores below −2 and regenerating executive function predictions using fiber covariance networks. Finally, we included a summary measure of overall lifetime psychopathology from a bifactor model, a dimensional approach to psychopathology that has been widely used in past work in this sample.73,75–79
Supplementary Material
Highlights.
We define spatially covarying fiber covariance networks using machine learning
Networks align with major tracts, while also capturing distinct spatial patterns
Most networks show age-related increases in fiber network properties
Fiber covariance networks are linked to developmental changes in executive function
ACKNOWLEDGMENTS
This study was supported by grants from the National Institutes of Health: R01MH112847 (to T.D.S. and R.T.S.); R01MH120482, R37MH125829, R01MH113550, and RF1MH116920 (to T.D.S.); R01MH133843 (to A.F.A.-B.); R01MH119219 (to R.C.G.); K99MH127293 and R00MH127293 (to B.L.); R01MH119185 and R01MH120174 (to D.D.R.); R01MH123550 (to R.T.S.); R01AG067103 (to A.S.); and R01EB022573 (to C.D.). Additional support was provided by the AE Foundation, the Penn Center for Biomedical Image Computing and Analytics, and the Penn/CHOP Lifespan Brain Institute. J.B. was supported by Canadian Institutes of Health Research Postdoctoral Fellowship CIHR-396349. V.J.S. was supported by National Science Foundation Graduate Research Fellowship DGE-1845298.
Footnotes
DECLARATION OF INTERESTS
The authors declare no competing interests.
SUPPLEMENTAL INFORMATION
Supplemental information can be found online at https://doi.org/10.1016/j.celrep.2023.113487.
REFERENCES
- 1.Lebel C, and Beaulieu C (2011). Longitudinal development of human brain wiring continues from childhood into adulthood. J. Neurosci. 31, 10937–10947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Westlye LT, Walhovd KB, Dale AM, Bjørnerud A, Due-Tønnessen P, Engvig A, Grydeland H, Tamnes CK, Østby Y, and Fjell AM (2010). Life-span changes of the human brain white matter: Diffusion tensor imaging (DTI) and volumetry. Cereb. Cortex 20, 2055–2068. [DOI] [PubMed] [Google Scholar]
- 3.Paus T (2010). Growth of white matter in the adolescent brain: Myelin or axon? Brain Cogn. 72, 26–35. [DOI] [PubMed] [Google Scholar]
- 4.Raffelt DA, Tournier JD, Smith RE, Vaughan DN, Jackson G, Ridgway GR, and Connelly A (2017). Investigating white matter fibre density and morphology using fixel-based analysis. Neuroimage 144, 58–73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Gur RC, Richard J, Calkins ME, Chiavacci R, Hansen JA, Bilker WB, Loughead J, Connolly JJ, Qiu H, Mentch FD, et al. (2012). Age group and sex differences in performance on a computerized neuro-cognitive battery in children age 8–21. Neuropsychology 26, 251–265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Ferguson HJ, Brunsdon VEA, and Bradford EEF (2021). The developmental trajectories of executive function from adolescence to old age. Sci. Rep. 11, 1382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Tervo-Clemmens B, Calabro FJ, Parr AC, Fedor J, Foran W, and Luna B (2022). A Canonical Trajectory of Executive Function Maturation During the Transition from Adolescence to Adulthood. Preprint at PsyArXiv. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Goddings AL, Roalf D, Lebel C, and Tamnes CK (2021). Development of white matter microstructure and executive functions during childhood and adolescence: a review of diffusion MRI studies. Dev. Cogn. Neurosci. 51, 101008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Paus T, Keshavan M, and Giedd JN (2008). Why do many psychiatric disorders emerge during adolescence? Nat. Rev. Neurosci. 9, 947–957. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Johnson MH (2012). Executive function and developmental disorders: The flip side of the coin. Trends Cognit. Sci. 16, 454–457. [DOI] [PubMed] [Google Scholar]
- 11.Koshiyama D, Fukunaga M, Okada N, Morita K, Nemoto K, Usui K, Yamamori H, Yasuda Y, Fujimoto M, Kudo N, et al. (2020). White matter microstructural alterations across four major psychiatric disorders: mega-analysis study in 2937 individuals. Mol. Psychiatr. 25, 883–895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Sydnor VJ, Larsen B, Bassett DS, Alexander-Bloch A, Fair DA, Liston C, Mackey AP, Milham MP, Pines A, Roalf DR, et al. (2021). Neurodevelopment of the association cortices: Patterns, mechanisms, and implications for psychopathology. Neuron 109, 2820–2846. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Goulas A, Margulies DS, Bezgin G, and Hilgetag CC (2019). The architecture of mammalian cortical connectomes in light of the theory of the dual origin of the cerebral cortex. Cortex 118, 244–261. [DOI] [PubMed] [Google Scholar]
- 14.Cahalane DJ, Charvet CJ, and Finlay BL (2012). Systematic, balancing gradients in neuron density and number across the primate isocortex. Front. Neuroanat. 6, 28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Alexander-Bloch A, Giedd JN, and Bullmore E (2013). Imaging structural co-variance between human brain regions. Nat. Rev. Neurosci. 14, 322–336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Alexander-Bloch A, Raznahan A, Bullmore E, and Giedd J (2013). The convergence of maturational change and structural covariance in human cortical networks. J. Neurosci. 33, 2889–2899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Baum GL, Flournoy JC, Glasser MF, Harms MP, Mair P, Sanders AFP, Barch DM, Buckner RL, Bookheimer S, Dapretto M, et al. (2022). Graded Variation in T1w/T2w Ratio during Adolescence: Measurement, Caveats, and Implications for Development of Cortical Myelin. J. Neurosci. 42, 5681–5694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Pines AR, Larsen B, Cui Z, Sydnor VJ, Bertolero MA, Adebimpe A, Alexander-Bloch AF, Davatzikos C, Fair DA, Gur RC, et al. (2022). Dissociable multi-scale patterns of development in personalized brain networks. Nat. Commun. 13, 2647. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Lebel C, and Beaulieu C (2011). Longitudinal Development of Human Brain Wiring Continues from Childhood into Adulthood. J. Neurosci. 31, 10937–10947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Lebel C, Treit S, and Beaulieu C (2019). A review of diffusion MRI of typical white matter development from early childhood to young adulthood. NMR Biomed. 32, e3778. [DOI] [PubMed] [Google Scholar]
- 21.Sotiras A, Toledo JB, Gur RE, Gur RC, Satterthwaite TD, and Davatzikos C (2017). Patterns of coordinated cortical remodeling during adolescence and their associations with functional specialization and evolutionary expansion. Proc. Natl. Acad. Sci. USA 114, 3527–3532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Yang Z, and Oja E (2010). Linear and nonlinear projective nonnegative matrix factorization. IEEE Trans. Neural Network. 21, 734–749. [DOI] [PubMed] [Google Scholar]
- 23.Sotiras A, Resnick SM, and Davatzikos C (2015). Finding imaging patterns of structural covariance via Non-Negative Matrix Factorization. Neuroimage 108, 1–16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Kaczkurkin AN, Park SS, Sotiras A, Moore TM, Calkins ME, Cieslak M, Rosen AFG, Ciric R, Xia CH, Cui Z, et al. (2019). Evidence for dissociable linkage of dimensions of psychopathology to brain structure in youths. Am. J. Psychiatr. 176, 1000–1009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Nassar R, Kaczkurkin AN, Xia CH, Sotiras A, Pehlivanova M, Moore TM, Garcia De La Garza A, Roalf DR, Rosen AFG, Lorch SA, et al. (2019). Gestational age is dimensionally associated with structural brain network abnormalities across development. Cereb. Cortex 29, 2102–2114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Sun D, Adduru VR, Phillips RD, Bouchard HC, Sotiras A, Michael AM, Baker FC, Tapert SF, Brown SA, Clark DB, et al. (2021). Alcohol Use Disrupts Age-Appropriate Cortical Thinning in Adolescence: A Data Driven Approach. Preprint at bioRxiv. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Robert C, Patel R, Blostein N, Steele CJ, and Chakravarty MM (2022). Analyses of microstructural variation in the human striatum using non-negative matrix factorization. Neuroimage 246, 118744. [DOI] [PubMed] [Google Scholar]
- 28.Patel R, Steele CJ, Chen AGX, Patel S, Devenyi GA, Germann J, Tardif CL, and Chakravarty MM (2020). Investigating microstructural variation in the human hippocampus using non-negative matrix factorization. Neuroimage 207, 116348. [DOI] [PubMed] [Google Scholar]
- 29.Ochi R, Plitman E, Patel R, Tarumi R, Iwata Y, Tsugawa S, Kim J, Honda S, Noda Y, Uchida H, et al. (2022). Investigating structural subdivisions of the anterior cingulate cortex in schizophrenia, with implications for treatment resistance and glutamatergic levels. J. Psychiatry Neurosci. 47, E1–E10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Nazeri A, Krsnik Ž, Kostović I, Ha SM, Kopić J, Alexopoulos D, Kaplan S, Meyer D, Luby JL, Warner BB, et al. (2022). Neurodevelopmental patterns of early postnatal white matter maturation represent distinct underlying microstructure and histology. Neuron 110, 4015–4030.e4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Satterthwaite TD, Elliott MA, Ruparel K, Loughead J, Prabhakaran K, Calkins ME, Hopson R, Jackson C, Keefe J, Riley M, et al. (2014). Neuroimaging of the Philadelphia Neurodevelopmental Cohort. Neuroimage 86, 544–553. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Tournier JD, Calamante F, and Connelly A (2007). Robust determination of the fibre orientation distribution in diffusion MRI: Non-negativity constrained super-resolved spherical deconvolution. Neuroimage 35, 1459–1472. [DOI] [PubMed] [Google Scholar]
- 33.Raffelt DA, Smith RE, Ridgway GR, Tournier J-D, Vaughan DN, Rose S, Henderson R, and Connelly A (2015). Connectivity-based fixel enhancement: Whole-brain statistical analysis of diffusion MRI measures in the presence of crossing fibres. Neuroimage 117, 40–55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Huntenburg JM, Bazin PL, and Margulies DS (2018). Large-Scale Gradients in Human Cortical Organization. Trends Cognit. Sci. 22, 21–31. [DOI] [PubMed] [Google Scholar]
- 35.Xu T, Nenning KH, Schwartz E, Hong SJ, Vogelstein JT, Goulas A, Fair DA, Schroeder CE, Margulies DS, Smallwood J, et al. (2020). Cross-species functional alignment reveals evolutionary hierarchy within the connectome. Neuroimage 223, 117346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Genc S, Malpas CB, Gulenc A, Sciberras E, Efron D, Silk TJ, and Seal ML (2020). Longitudinal patterns of white matter fibre density and morphology in children are associated with age and pubertal stage. Dev. Cogn. Neurosci. 45, 100853. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Pines AR, Cieslak M, Larsen B, Baum GL, Cook PA, Adebimpe A, Dá vila DG, Elliott MA, Jirsaraie R, Murtha K, et al. (2020). Leveraging multi-shell diffusion for studies of brain development in youth and young adulthood. Dev. Cogn. Neurosci. 43, 100788. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Bethlehem R.a.I., Seidlitz J, White SR, Vogel JW, Anderson KM, Adamson C, Adler S, Alexopoulos GS, Anagnostou E, Areces-Gonzalez A, et al. (2022). Brain charts for the human lifespan. Nature 604, 525–533. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Slater DA, Melie-Garcia L, Preisig M, Kherif F, Lutti A, and Draganski B (2019). Evolution of white matter tract microstructure across the life span. Hum. Brain Mapp. 40, 2252–2268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Chen Z, Zhang H, Yushkevich PA, Liu M, and Beaulieu C (2016). Maturation along white matter tracts in human brain using a diffusion tensor surface model tract-specific analysis. Front. Neuroanat. 10, 9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Grotheer M, Rosenke M, Wu H, Kular H, Querdasi FR, Natu VS, Yeatman JD, and Grill-Spector K (2022). White matter myelination during early infancy is linked to spatial gradients and myelin content at birth. Nat. Commun. 13, 997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Krogsrud SK, Fjell AM, Tamnes CK, Grydeland H, Mork L, Due-Tønnessen P, Bjørnerud A, Sampaio-Baptista C, Andersson J, Johansen-Berg H, and Walhovd KB (2016). Changes in white matter microstructure in the developing brain—A longitudinal diffusion tensor imaging study of children from 4 to 11 years of age. Neuroimage 124, 473–486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Colby JB, Van Horn JD, and Sowell ER (2011). Quantitative in vivo evidence for broad regional gradients in the timing of white matter maturation during adolescence. Neuroimage 54, 25–31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Lebel C, Gee M, Camicioli R, Wieler M, Martin W, and Beaulieu C (2012). Diffusion tensor imaging of white matter tract evolution over the lifespan. Neuroimage 60, 340–352. [DOI] [PubMed] [Google Scholar]
- 45.Yap QJ, Teh I, Fusar-Poli P, Sum MY, Kuswanto C, and Sim K (2013). Tracking cerebral white matter changes across the lifespan: Insights from diffusion tensor imaging studies. J. Neural. Transm. 120, 1369–1395. [DOI] [PubMed] [Google Scholar]
- 46.Dubois J, Dehaene-Lambertz G, Perrin M, Mangin JF, Cointepas Y, Duchesnay E, Le Bihan D, and Hertz-Pannier L (2008). Asynchrony of the early maturation of white matter bundles in healthy infants: Quantitative landmarks revealed noninvasively by diffusion tensor imaging. Hum. Brain Mapp. 29, 14–27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Hermoye L, Saint-Martin C, Cosnard G, Lee SK, Kim J, Nassogne MC, Menten R, Clapuyt P, Donohue PK, Hua K, et al. (2006). Pediatric diffusion tensor imaging: Normal database and observation of the white matter maturation in early childhood. Neuroimage 29, 493–504. [DOI] [PubMed] [Google Scholar]
- 48.Leitner Y, Travis KE, Ben-Shachar M, Yeom KW, and Feldman HM (2015). Tract Profiles of the Cerebellar White Matter Pathways in Children and Adolescents. Cerebellum 14, 613–623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Genc S, Smith RE, Malpas CB, Anderson V, Nicholson JM, Efron D, Sciberras E, Seal ML, and Silk TJ (2018). Development of white matter fibre density and morphology over childhood: A longitudinal fixel-based analysis. Neuroimage 183, 666–676. [DOI] [PubMed] [Google Scholar]
- 50.Dimond D, Rohr CS, Smith RE, Dhollander T, Cho I, Lebel C, Dewey D, Connelly A, and Bray S (2020). Early childhood development of white matter fiber density and morphology. Neuroimage 210, 116552. [DOI] [PubMed] [Google Scholar]
- 51.Cui Z, Li H, Xia CH, Larsen B, Adebimpe A, Baum GL, Cieslak M, Gur RE, Gur RC, Moore TM, et al. (2020). Individual Variation in Functional Topography of Association Networks in Youth. Neuron 106, 340–353.e8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Keller AS, Pines AR, Sydnor VJ, Cui Z, Bertolero MA, Barzilay R, Alexander-Bloch AF, Byington N, Chen A, Conan GM, et al. (2022). Personalized Functional Brain Network Topography Predicts Individual Differences in Youth Cognition. Preprint at bioRxiv. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Burgaleta M, Johnson W, Waber DP, Colom R, and Karama S (2014). Cognitive ability changes and dynamics of cortical thickness development in healthy children and adolescents. Neuroimage 84, 810–819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Karama S, Colom R, Johnson W, Deary IJ, Haier R, Waber DP, Lepage C, Ganjavi H, Jung R, and Evans AC; Brain Development Cooperative Group (2011). Cortical thickness correlates of specific cognitive performance accounted for by the general factor of intelligence in healthy children aged 6 to 18. Neuroimage 55, 1443–1453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Schumann G, Loth E, Banaschewski T, Barbot A, Barker G, Büchel C, Conrod PJ, Dalley JW, Flor H, Gallinat J, et al. (2010). The IMAGEN study: Reinforcement-related behaviour in normal brain function and psychopathology. Mol. Psychiatr. 15, 1128–1139. [DOI] [PubMed] [Google Scholar]
- 56.Casey BJ, Cannonier T, Conley MI, Cohen AO, Barch DM, Heitzeg MM, Soules ME, Teslovich T, Dellarco DV, Garavan H, et al. (2018). The Adolescent Brain Cognitive Development (ABCD) study: Imaging acquisition across 21 sites. Dev. Cogn. Neurosci. 32, 43–54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Roalf DR, Quarmley M, Elliott MA, Satterthwaite TD, Vandekar SN, Ruparel K, Gennatas ED, Calkins ME, Moore TM, Hopson R, et al. (2016). The impact of quality assurance assessment on diffusion tensor imaging outcomes in a large-scale population-based cohort. Neuroimage 125, 903–919. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Baum GL, Ciric R, Roalf DR, Betzel RF, Moore TM, Shinohara RT, Kahn AE, Vandekar SN, Rupert PE, Quarmley M, et al. (2017). Modular Segregation of Structural Brain Networks Supports the Development of Executive Function in Youth. Curr. Biol. 27, 1561–1572.e8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Gur RC, Richard J, Hughett P, Calkins ME, Macy L, Bilker WB, Brensinger C, and Gur RE (2010). A cognitive neuroscience-based computerized battery for efficient measurement of individual differences: Standardization and initial construct validation. J. Neurosci. Methods 187, 254–262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Moore TM, Reise SP, Gur RE, Hakonarson H, and Gur RC (2015). Psychometric properties of the penn computerized neurocognitive battery. Neuropsychology 29, 235–246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Rosen AFG, Roalf DR, Ruparel K, Blake J, Seelaus K, Villa LP, Ciric R, Cook PA, Davatzikos C, Elliott MA, et al. (2018). Quantitative assessment of structural image quality. Neuroimage 169, 407–418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Cieslak M, Cook PA, He X, Yeh F-C, Dhollander T, Adebimpe A, Aguirre GK, Bassett DS, Betzel RF, Bourque J, et al. (2021). QSI-Prep: an integrative platform for preprocessing and reconstructing diffusion MRI data. Nat. Methods 18, 775–778. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Gorgolewski K, Burns CD, Madison C, Clark D, Halchenko YO, Waskom ML, and Ghosh SS (2011). Nipype: A flexible, lightweight and extensible neuroimaging data processing framework in Python. Front. Neuroinf. 5, 13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Veraart J, Fieremans E, and Novikov DS (2016). Diffusion MRI noise mapping using random matrix theory. Magn. Reson. Med. 76, 1582–1593. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Kellner E, Dhital B, Kiselev VG, and Reisert M (2016). Gibbs-ringing artifact removal based on local subvoxel-shifts. Magn. Reson. Med. 76, 1574–1581. [DOI] [PubMed] [Google Scholar]
- 66.Tustison NJ, Avants BB, Cook PA, Zheng Y, Egan A, Yushkevich PA, and Gee JC (2010). N4ITK: Improved N3 bias correction. IEEE Trans. Med. Imag. 29, 1310–1320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Andersson JLR, and Sotiropoulos SN (2016). An integrated approach to correction for off-resonance effects and subject movement in diffusion MR imaging. Neuroimage 125, 1063–1078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Power JD, Mitra A, Laumann TO, Snyder AZ, Schlaggar BL, and Petersen SE (2014). Methods to detect, characterize, and remove motion artifact in resting state fMRI. Neuroimage 84, 320–341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Tournier JD, Smith R, Raffelt D, Tabbara R, Dhollander T, Pietsch M, Christiaens D, Jeurissen B, Yeh CH, and Connelly A (2019). MRtrix3: A fast, flexible and open software framework for medical image processing and visualisation. Neuroimage 202. [DOI] [PubMed] [Google Scholar]
- 70.Dhollander T, and Connelly A (2016). A novel iterative approach to reap the benefits of multi-tissue CSD from just single-shell (+b=0) diffusion MRI data. In 24th International Society of Magnetic Resonance in Medicine, p. 3010. [Google Scholar]
- 71.Smith RE, Tournier J-D, Calamante F, and Connelly A (2013). SIFT: Spherical-deconvolution informed filtering of tractograms. Neuroimage 67, 298–312. [DOI] [PubMed] [Google Scholar]
- 72.Zhao C, Tapera TM, Bagautdinova J, Bourque J, Covitz S, Gur RE, Gur RC, Larsen B, Mehta K, Meisler SL, et al. (2023). ModelArray: An R package for statistical analysis of fixel-wise data. Neuroimage 271, 120037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Kaczkurkin AN, Park SS, Sotiras A, Moore TM, Calkins ME, Cieslak M, Rosen AFG, Ciric R, Xia CH, Cui Z, et al. (2019). Evidence for Dissociable Linkage of Dimensions of Psychopathology to Brain Structure in Youths. Aust. J. Pharm. 176, 1000–1009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Wood SN (2004). Stable and efficient multiple smoothing parameter estimation for generalized additive models. J. Am. Stat. Assoc. 99, 673–686. [Google Scholar]
- 75.Shanmugan S, Wolf DH, Calkins ME, Moore TM, Ruparel K, Hopson RD, Vandekar SN, Roalf DR, Elliott MA, Jackson C, et al. (2016). Common and Dissociable Mechanisms of Executive System Dysfunction Across Psychiatric Disorders in Youth. Aust. J. Pharm. 173, 517–526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Kaczkurkin AN, Moore TM, Calkins ME, Ciric R, Detre JA, Elliott MA, Foa EB, Garcia de la Garza A, Roalf DR, Rosen A, et al. (2018). Common and dissociable regional cerebral blood flow differences associate with dimensions of psychopathology across categorical diagnoses. Mol. Psychiatr. 23, 1981–1989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Cui Z, Pines AR, Larsen B, Sydnor VJ, Li H, Adebimpe A, Alexander-Bloch AF, Bassett DS, Bertolero M, Calkins ME, et al. (2022). Linking Individual Differences in Personalized Functional Network Topography to Psychopathology in Youth. Biol. Psychiatr. 92, 973–983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Moore TM, Calkins ME, Satterthwaite TD, Roalf DR, Rosen AFG, Gur RC, and Gur RE (2019). Development of a computerized adaptive screening tool for overall psychopathology (“p”). J. Psychiatr. Res. 116, 26–33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Parkes L, Moore TM, Calkins ME, Cook PA, Cieslak M, Roalf DR, Wolf DH, Gur RC, Gur RE, Satterthwaite TD, and Bassett DS (2021). Transdiagnostic dimensions of psychopathology explain individuals’ unique deviations from normative neurodevelopment in brain structure. Transl. Psychiatry 11, 232. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
This paper analyzes existing, publicly available data from the Philadelphia Neurodevelopmental Cohort.31 Data is available at the database of Genotypes and Phenotypes (dbGaP): https://www.ncbi.nlm.nih.gov/projects/gap/cgi-bin/study.cgi?study_id=phs000607.v3.p2. To request access, an authorization request can be completed via https://dbgap.ncbi.nlm.nih.gov/aa/wga.cgi?%20page=login&page=login.
All original code for image preprocessing, evaluating opNMF solutions, and all statistical analyses has been deposited at https://github.com/PennLINC/Fixel_NMF_development and on Zenodo at https://zenodo.org/records/10064924, https://doi.org/10.5281/zenodo.10064924. All code is publicly available as of the date of publication. DOIs are listed in the key resources table.
Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.
KEY RESOURCES TABLE.
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
|
| ||
| Deposited data | ||
| Raw and preprocessed structural T1-weighted images, diffusion images, clinical and cognitive data | Philadelphia Neurodevelopmental Cohort | https://www.ncbi.nlm.nih.gov/projects/gap/cgi-bin/study.cgi?study_id=phs000607.v3.p2 |
|
| ||
| Software and algorithms | ||
|
| ||
| R 4.1.2 | R Foundation | https://cran.r-project.org/bin/macosx/ |
| MATLAB R2018a | MathWorks | https://www.mathworks.com/ |
| Nipype | NiPy | https://pypi.org/project/nipype/ |
| QSIprep | PennLINC | https://github.com/PennBBL/qsiprep |
| FSL 6.0.3 | FSL | https://fsl.fmrib.ox.ac.uk/fsl/fslwiki/ |
| MRtrix3 v3.0RC3 | MRtrix | http://www.mrtrix.org/ |
| Confixel | PennLINC | https://github.com/PennLINC/ConFixel |
| BrainParts (non-negative matrix factorization) | BrainParts | https://github.com/asotiras/brainparts |
| Statistical analyses of fiber covariance networks | This paper | https://doi.org/10.5281/zenodo.10064923 |


