On the surprising effectiveness of a simple matrix exponential derivative approximation, with application to global SARS-CoV-2

Significance

Recent work uses a simplistic approximation to the matrix exponential derivative to apply gold-standard models from evolutionary biology to a collection of challenging data analyses. Whereas one may expect the naive approach to break down with increasing model dimensionality, empirical results show no such failure. Here, we 1) develop rigorous error bounds that improve—in a certain sense—as model dimension grows and 2) demonstrate the scalability of the naive approach to a higher-dimensional analysis of the global spread of the virus responsible for the COVID-19 pandemic.

Abstract

The continuous-time Markov chain (CTMC) is the mathematical workhorse of evolutionary biology. Learning CTMC model parameters using modern, gradient-based methods requires the derivative of the matrix exponential evaluated at the CTMC’s infinitesimal generator (rate) matrix. Motivated by the derivative’s extreme computational complexity as a function of state space cardinality, recent work demonstrates the surprising effectiveness of a naive, first-order approximation for a host of problems in computational biology. In response to this empirical success, we obtain rigorous deterministic and probabilistic bounds for the error accrued by the naive approximation and establish a “blessing of dimensionality” result that is universal for a large class of rate matrices with random entries. Finally, we apply the first-order approximation within surrogate-trajectory Hamiltonian Monte Carlo for the analysis of the early spread of Severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) across 44 geographic regions that comprise a state space of unprecedented dimensionality for unstructured (flexible) CTMC models within evolutionary biology.

Phylogeographic methods (1–4) model large-scale viral transmission between human populations as a function of the shared evolutionary history of the viral population of interest. Data take the form of dates, locations, and genome sequences associated with individual viral samples. Spatiotemporal structure interfaces with network structure given by the phylogeny, or family tree, describing the viruses’ collective history beginning with the most recent common ancestor. While one cannot directly observe this history, one may statistically reconstruct the phylogenetic tree by positing that changes in the viral genome happen randomly at regular intervals, thereby capturing the intuition that viral samples with more differences between their (aligned) sequences should find themselves further apart on the family tree.

The continuous-time Markov chain (CTMC) (5) represents the gold-standard mathematical model for such evolution of characters (e.g., nucleotides) within a fixed span of evolutionary time. A CTMC defined over a discrete, $d$-element state space consists of a row vector ${\mathbf{\pi }}_0$ whose individual components describe the probability of inhabiting each of the possible states at time $t=0$ as well as a $d\times d$ infinitesimal generator (or rate) matrix $\mathbf{Q}$ with nonnegative off-diagonal elements $q_{\mathit{ij}}$, $i\ne j$, and nonpositive diagonal elements $q_{\mathit{ii}}=-\sum _j{q}_{\mathit{ij}}$. For any lag $t\ge 0$, the matrix exponential (6, 7) provides the Markov chain’s transition probability matrix

$$\begin{array}{c}\hfill {\mathbf{P}}_t:=e^{t\mathbf{Q}}:={\displaystyle \sum _{n=0}^{\infty }}\frac{t^n{\mathbf{Q}}^n}{n!},\end{array}$$ [1]

which has elements ${[{\mathbf{P}}_t]}_{\mathit{ij}}$ that dictate the probability of the process jumping from state $i$ to state $j$ after time $t$. It is straightforward to verify that ${\mathbf{P}}_t$ is a valid transition matrix, having probability vectors for rows: If $\mathbf{1}$ and $\mathbf{0}$ are the column vectors of ones and zeros, respectively, then $\mathbf{Q}\mathbf{1}=\mathbf{0}$ and, therefore, ${\mathbf{P}}_t\mathbf{1}=\mathbf{1}$. The law of total probability then provides the marginal probability of the process at any time $t\ge 0$ as ${\mathbf{\pi }}_t={\mathbf{\pi }}_0{e}^{t\mathbf{Q}}$.

Whether frequentist (8) or Bayesian (9–12) likelihood-based approaches to phylogenetic reconstruction allow phylogenetic tree branch lengths to parameterize time lags within the CTMC framework. We present the exact statement of the phylogenetic CTMC paradigm below (Section 3). Here, we note that the historical importance of tree-reconstruction from aligned sequences leads to an early emphasis on the sparse specification of $\mathbf{Q}$ based on biologically motivated assumptions (13–15). Classical Markov chain Monte Carlo (MCMC) procedures (16, 17) work well for such low-dimensional models. But the phylogenetic CTMC framework has applications beyond simple nucleotide substitution models. Within, e.g., Bayesian phylogeography, the work in ref. 1 provides a phylogenetic CTMC model for the spread of avian influenza across $d=20$ global geographic locations but, for computational reasons, favors a low-dimensional $\mathcal{O}\left(d\right)$ parameterization of $\mathbf{Q}$. Similarly, Lemey et al. (2) model the spread of influenza A H1N1 and H3N2 between as many as $d=26$ geographic regions but—again for computational reasons—fit the model with approximation techniques that provide no inferential guarantees.

Recently, Magee et al. (18) demonstrate the feasibility of approximate gradient-based methods for both maximum a posteriori and full Bayesian inference of flexible and fully-parameterized rate models and apply these methods to a gold-standard $\mathcal{O}\left(d^2\right)$ mixed-effect CTMC model for the spread of A H3N2 influenza between $d=14$ geographic locations. The usual CTMC log-likelihood gradient calculations feature the matrix exponential derivative (Eqs. 13 and 15)

$${\nabla }_{{\displaystyle J}}{e}^{tQ}:=\underset{ϵ\to 0}{\text{lim}}\frac{e^{t(Q+ϵJ)}-e^{tQ}}{ϵ}$$ [2]

$$\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=e^{tQ}{\displaystyle \sum _{n=0}^{\infty }}\frac{t^{n+1}}{(n+1)!}\left({\displaystyle \sum _{\mathcal{l}=0}^n}{(-1)}^{\mathcal{l}}\left(\begin{array}{c}n\\ \mathcal{l}\end{array}\right)Q^{\mathcal{l}}J{Q}^{n-\mathcal{l}}\right)$$ [3]

computed in the direction $\mathbf{J}$ of each of the $d^2$ natural basis elements ${\mathbf{J}}_{\mathit{ij}}$ spanning the space of real-valued, $d\times d$ matrices $\mathcal{M}(d)=\mathcal{M}(d,\mathbb{R})$, thereby requiring at least $\mathcal{O}\left(d^5\right)$ floating point operations (19).

Within the phylogenetic CTMC models of Section 3, log-likelihood derivative computations that require ${\mathrm{\nabla }}_{\mathbf{J}}{e}^{t\mathbf{Q}}$ balloon to $\mathcal{O}\left(KN{d}^5\right)$, for $N$ the number of biological specimens observed and $K$ the number of parameters parameterizing $\mathbf{Q}$. To address this overwhelming computational cost, Magee et al. (18) leverage the simplistic approximation obtained by setting $n=0$ within Eq. 3:

$$\begin{array}{c}\hfill {\tilde{\mathrm{\nabla }}}_{\mathbf{J}}{e}^{t\mathbf{Q}}:=t{e}^{t\mathbf{Q}}\mathbf{J}.\end{array}$$ [4]

Ref. 18 show that this approximation helps reduce total cost to $\mathcal{O}\left(K{d}^2+N{d}^3\right)$ and use this speedup within surrogate-trajectory Hamiltonian Monte Carlo (HMC) (SI Appendix) to obtain a 34-fold improvement in effective sample size per second (ESS/s) over random-walk MCMC within their 14-region phylogeographic example. When trying to explain the remarkable empirical performance of the naive approximation, the authors derive an error upper bound (for an arbitrary matrix norm)

$$\begin{array}{c}\hfill ||{\tilde{\mathrm{\nabla }}}_{\mathbf{J}}{e}^{t\mathbf{Q}}-{\mathrm{\nabla }}_{\mathbf{J}}{e}^{t\mathbf{Q}}||\le \frac{\Vert \mathbf{J}\Vert ||\mathbf{Q}||}{2}(e^{2t}-2t-1)\end{array}$$ [5]

that fails to leverage the specific forms of $\mathbf{Q}$ and $\mathbf{J}$. Notably, this bound explodes as either $t$ or $||\mathbf{Q}||$ diverges to $\infty$. Of course, the latter quantity would be expected to grow large with dimension $d$ without more careful structural assumptions, e.g., that $\mathbf{Q}$ is a rate matrix belonging to the class

$$\begin{array}{c}\hfill \mathcal{R}(d):=\{\mathbf{Q}\in \mathcal{M}(d)|{\mathbf{Q}}_{\mathit{ij}}\ge 0\text{for} j\ne i,{\displaystyle \sum _{j=1}^d}{\mathbf{Q}}_{\mathit{ij}}=0\}.\end{array}$$ [6]

In the following, we use the finer structural properties of $\mathbf{Q}$ to obtain more precise bounds on

$$\begin{array}{c}\hfill \mathbf{E}(t):={\mathrm{\nabla }}_{\mathbf{J}}{e}^{t\mathbf{Q}}-t{e}^{t\mathbf{Q}}\mathbf{J}.\end{array}$$ [7]

In Theorem 1, we provide an affine (in $t$) correction to the approximation Eq. 4 that yields an exponentially tight $t\to \infty$ asymptotic for the error Eq. 7. Then, in Theorem 3, we establish precise probabilistic bounds in the high-dimensional $d\to \infty$ limit for a large class of randomly drawn rate matrices $\mathbf{Q}\in \mathcal{R}$. Here, we show, for any $\mathbf{Q}\in \mathcal{R}$ whose off-diagonal elements are determined by independently and identically distributed (iid) draws from a positive, sub-exponential distribution $F$, that all of the nonzero singular values grow as ${\sigma }_j(\mathbf{Q})\sim d$ along with asymptotically valid almost sure bounds for these rates as $d\to \infty$.

In regards to this second result, Theorem 3, note that random rate (or “Laplacian”) matrices have attracted a great deal of attention from the probability research community, especially in regard to their high-dimensional properties; see e.g., refs. 20, 21, 22, 23, 24, 25. In particular, seminal papers such as refs. 26, 27, 28 establish broad characterizations of bulk behavior for the Laplacian eigenspectrum. One contribution of this paper, of independent interest, is a short and self-contained construction of useful bounds for the singular values of $\mathbf{Q}\in \mathcal{R}$.

In Theorem 2 and Corollary 1, we show how Theorems 1 and 3 combine to provide a more refined analysis of $\mathbf{E}$ for suitable randomly generated $\mathbf{Q}\in \mathcal{R}(d)$. In Theorem 2, we establish that particular terms appearing in the bound Eq. 24 in Theorem 1 decay with a rate on the order of $1/d$ in the operator norm topology for large $d$ for certain classes of symmetric generators $\mathbf{Q}$. This class includes the random elements considered in Theorem 3. Here, although Corollary 1 applies only for symmetric matrices composed of sub-exponential draws, we provide strong supplemental numerical evidence that our bounds remain valid well beyond this special symmetric, sub-exponential special case (Remark 5 and Fig. 1).

Fig. 1.

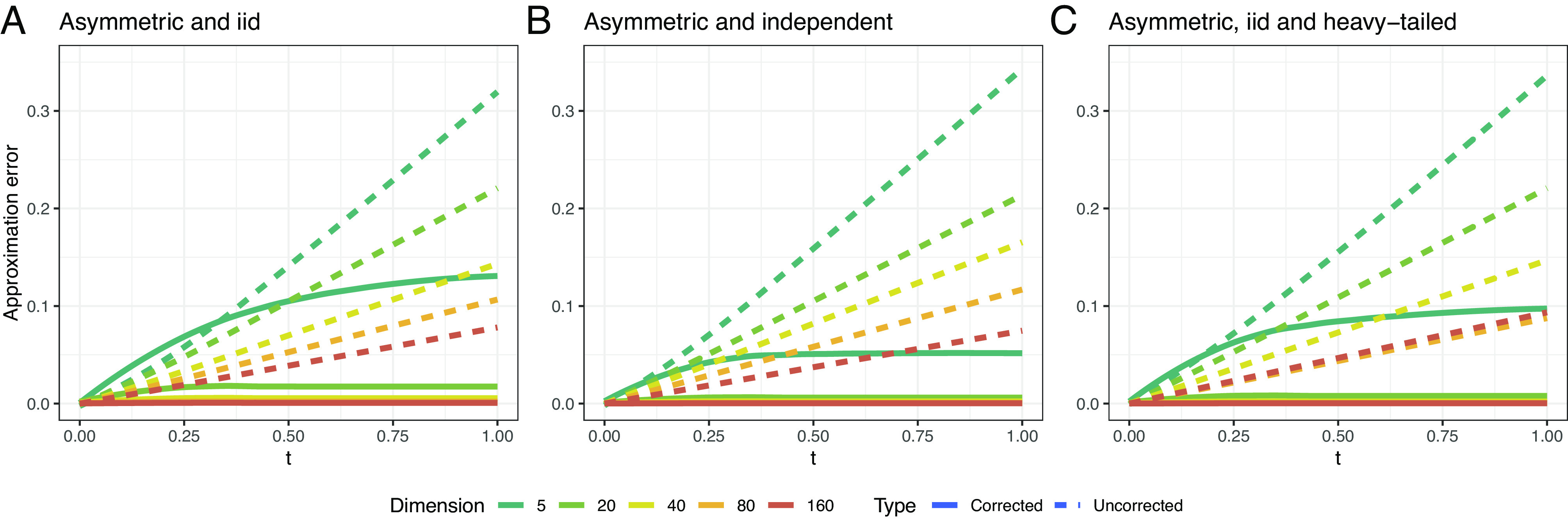
Frobenius norm errors obtained by first-order approximation $t{e}^{t\mathbf{Q}}\mathbf{J}$ and by affine-corrected first-order approximation $t{e}^{t\mathbf{Q}}\mathbf{J}-t(\mathbf{I}-{\mathbf{Q}}^{+}\mathbf{Q})\mathbf{J}\mathbf{Q}{\mathbf{Q}}^{+}$ (Theorem 2) under increasingly relaxed assumptions. Within each assumption set, we average over 20 independent Monte Carlo simulations of random generator matrices for each dimension. Plot A corresponds to asymmetric generators with off-diagonal elements having independent and iid standard exponential random variables that correspond to the sub-exponential distribution hypothesis. Plot B drops the identical distribution assumption by allowing each row and column of the generator matrix to additively contribute its own mean—itself given by a standard exponential—to its corresponding exponentially distributed entries. Plot C features rate matrices with iid Cauchy entries truncated to be positive. Empirically, the results of Corollary 1 extend beyond the symmetric, iid, and sub-exponential hypotheses, suggesting scope of future work.

One notable practical implication of Theorem 2, Corollary 1 and Remark 5 is the identification of a further correction to Eq. 4. Crucially, this correction has the same $\mathcal{O}\left(d^3\right)$ computational cost as Eq. 4 while leading to an asymptotically temporally uniformly accurate approximation of ${\mathrm{\nabla }}_{\mathbf{J}}{e}^{t\mathbf{Q}}$ (Remark 5 and Eq. 46).

Section 2 contains simulation studies comparing accuracy of matrix exponential derivative approximations for different distributional assumptions on the generator matrix; the posterior distributions obtained using surrogate-trajectory HMC and traditional HMC; and parameter identification under different priors on generator matrix elements.

In Section 3, we follow these theoretical and empirical investigations with an application of the naive, first-order gradient approximation Eq. 4 to a challenge in phylogeography requiring Bayesian inference of a rate-matrix of unprecedented dimensionality. Namely, we apply the approximation to a gold-standard mixed-effects, phylogenetic CTMC model that uses 1,897 parameters to describe the spread of SARS-CoV-2 across a $d=44$ dimensional state space consisting of different global geographic locations. Such an application complements the empirical studies of ref. 18 in a manner that emphasizes the naive approximation’s potential for impact.

1. Rigorous Results

This section lays out our rigorous results Theorems 1–3 and Corollary 1, the proofs of which appear in SI Appendix.

In what follows, we adopt the following notational conventions. For any $\mathbf{A}\in \mathcal{M}(d)$, we list the associated (not necessarily distinct) eigenvalues of $\mathbf{A}$ in ascending order according to their real part, namely,

$$\begin{array}{c}\hfill \mathfrak{R}{\lambda }_1(\mathbf{A})\le \cdots \le \mathfrak{R}{\lambda }_d(\mathbf{A}).\end{array}$$ [8]

Similarly, the singular values of $\mathbf{A}$ are written in ascending order

$$\begin{array}{c}\hfill {\sigma }_1(\mathbf{A})\le \cdots \le {\sigma }_d(\mathbf{A}).\end{array}$$ [9]

We let $\mathcal{S}(d)=\mathcal{S}(d,\mathbb{R})$ and $\mathcal{S}(d,\mathbb{C})$ represent the spaces of $d\times d$ symmetric and Hermitian matrices, respectively.

We make use of multiple matrix norms leading to materially different bounds as $d\to \infty$ (29). Take

$$\begin{array}{c}\hfill {\Vert \mathbf{A}\Vert }_F:=\sqrt{{\displaystyle \sum _{i,j=1}^d}{\mathbf{A}}_{\mathit{ij}}^2}=\sqrt{{\displaystyle \sum _{j=1}^d}{\sigma }_j{(\mathbf{A})}^2}\end{array}$$ [10]

for the Frobenius norm and

$$\begin{array}{c}\hfill {\Vert \mathbf{A}\Vert }_{\mathit{op}}:=\sqrt{{\lambda }_d({\mathbf{A}}^{\ast }\mathbf{A})}=\sqrt{{\lambda }_d(\mathbf{A}{\mathbf{A}}^{\ast })}={\sigma }_d(\mathbf{A})\end{array}$$ [11]

for the operator norm of $\mathbf{A}$. Finally, note that when we simply write $\Vert ·\Vert$; the statement then holds for any valid matrix norm as in our formulation of Theorem 1.

1.1. Deterministic Bounds on Approximation Error in Time.

We begin by deriving a dynamical equation for the error $\mathbf{E}(t)$, defined in Eq. 7. Recall that $\mathbf{X}(t):=e^{t\mathbf{Q}}$ for any $\mathbf{Q}\in \mathcal{M}(d)$ obeys the (matrix-valued) ordinary differential equation

$$\begin{array}{c}\hfill \frac{d\mathbf{X}}{\mathit{dt}}=\mathbf{Q}\mathbf{X},\mathbf{X}(0)=\mathbf{I}.\end{array}$$ [12]

Setting ${\mathbf{Y}}^{ϵ}={ϵ}^{-1}(e^{t(\mathbf{Q}+ϵ\mathbf{J})}-e^{t\mathbf{Q}})$ and taking a limit as $ϵ\to 0$, we find that $\mathbf{Y}={\mathrm{\nabla }}_{\mathbf{J}}{e}^{t\mathbf{Q}}$ obeys

$$\begin{array}{c}\hfill \frac{d\mathbf{Y}}{\mathit{dt}}=\mathbf{Q}\mathbf{Y}+\mathbf{J}\mathbf{X}=\mathbf{Q}\mathbf{Y}+\mathbf{J}{e}^{t\mathbf{Q}},\mathbf{Y}(0)=\mathbf{0}.\end{array}$$ [13]

Thus, variation of constants yields that, for any $t\ge 0$,

$${\nabla }_J{e}^{tQ}=e^{tQ}{{\displaystyle \int }}_0^t{e}^{-sQ}J{e}^{sQ}ds$$ [14]

$$\begin{array}{l}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=e^{tQ}{\displaystyle \sum _{k,m=0}^{\infty }}{\int }_0^t\frac{{(-s)}^k{Q}^{k}J{s}^m{Q}^m}{k!m!}ds\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=e^{tQ}{\displaystyle \sum _{n=0}^{\infty }}\frac{t^{n+1}}{(n+1)!}\left({\displaystyle \sum _{\mathcal{l}=0}^n}{(-1)}^{\mathcal{l}}\left(\begin{array}{c}n\\ \mathcal{l}\end{array}\right)Q^{\mathcal{l}}J{Q}^{n-\mathcal{l}}\right).\hfill \end{array}$$ [15]

Taking the first-order ($n=0$) approximation in Eq. 15 produces Eq. 4. Note that, from Eq. 14, this approximation $\tilde{\mathrm{\nabla }}{e}^{t\mathbf{Q}}\mathbf{J}$ is evidently exact in the special case when $\mathbf{J}$ and $\mathbf{Q}$ commute.

Next notice that, if we differentiate $\tilde{\mathbf{Y}}:=t{e}^{t\mathbf{Q}}\mathbf{J}$ in $t$, we find that $\tilde{\mathbf{Y}}$ obeys

$$\begin{array}{c}\hfill \frac{d\tilde{\mathbf{Y}}}{\mathit{dt}}=\mathbf{Q}\tilde{\mathbf{Y}}+e^{t\mathbf{Q}}\mathbf{J},\tilde{\mathbf{Y}}(0)=\mathbf{0}.\end{array}$$ [16]

Thus, taking the error $\mathbf{E}(t)$ as in Eq. 7 and combining Eq. 13 with Eq. 16 yields

$$\begin{array}{c}\hfill \frac{d\mathbf{E}}{\mathit{dt}}=\mathbf{Q}\mathbf{E}+\mathbf{J}{e}^{t\mathbf{Q}}-e^{t\mathbf{Q}}\mathbf{J},\mathbf{E}(0)=\mathbf{0}.\end{array}$$ [17]

Hence, again integrating this expression, we find

$$E(t)=e^{tQ}{{\displaystyle \int }}_0^t(e^{-sQ}J{e}^{sQ}-J)ds$$ [18]

$$\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=e^{tQ}{\displaystyle \sum _{n=1}^{\infty }}\frac{t^{n+1}}{(n+1)!}\left({\displaystyle \sum _{\mathcal{l}=0}^n}{(-1)}^{\mathcal{l}}\left(\begin{array}{c}n\\ \mathcal{l}\end{array}\right)Q^{\mathcal{l}}J{Q}^{n-\mathcal{l}}\right)$$ [19]

as could also be directly deduced from Eqs. 14 to 15.

Given a rate matrix $\mathbf{Q}$ in $\mathcal{R}(d)$, recall that $\mathfrak{R}{\lambda }_{d-1}(\mathbf{Q})\le {\lambda }_d(\mathbf{Q})=0$ by the Gershgorin circle theorem (30, Theorem 6.1.1). Imposing a further non-degeneracy assumption (e.g., that $\mathfrak{R}{\lambda }_{d-1}(\mathbf{Q})<0$) we therefore have an exponential decay in $\mathbf{Q}{e}^{t\mathbf{Q}}$. This starting point suggests that, under fairly general conditions, we may decompose Eq. 18 into a component where $\mathbf{Q}{e}^{t\mathbf{Q}}$ induces an exponential decay in time and a complementary component taking the form of a time-affine correction term.

These observations lead to the following theorem, the proof of which appears in SI Appendix.

Theorem 1.

Suppose that $\mathbf{Q},\mathbf{J}\in \mathcal{M}(d)$ for some $d\ge 1$. We assume that we can find an element ${\mathbf{Q}}^{+}\in \mathcal{M}(d)$ such that $\mathbf{Q}$ is a generalized inverse of ${\mathbf{Q}}^{+}$, namely,

$$\begin{array}{c}\hfill {\mathbf{Q}}^{+}\mathbf{Q}{\mathbf{Q}}^{+}={\mathbf{Q}}^{+}\end{array}$$ [20]

and such that

$$\begin{array}{c}\hfill e^{\tau \mathbf{Q}}(\mathbf{I}-{\mathbf{Q}}^{+}\mathbf{Q})=\mathbf{I}-{\mathbf{Q}}^{+}\mathbf{Q},(\mathbf{I}-\mathbf{Q}{\mathbf{Q}}^{+})e^{\tau \mathbf{Q}}=\mathbf{I}-\mathbf{Q}{\mathbf{Q}}^{+},\end{array}$$ [21]

for any $\tau \in \mathbb{R}$. Furthermore, we suppose that ${\mathbf{Q}}^{+}$ and $\mathbf{Q}$ commute

$$\begin{array}{c}\hfill \mathbf{Q}{\mathbf{Q}}^{+}={\mathbf{Q}}^{+}\mathbf{Q}.\end{array}$$ [22]

Finally, taking $\Vert ·\Vert$ be any matrix norm, we assume that

$$\begin{array}{c}\hfill \Vert \mathbf{Q}{e}^{\tau \mathbf{Q}}\Vert \le C_0{e}^{-\kappa \tau },\mathit{for\; all} \tau \ge 0,\end{array}$$ [23]

where the constants $C_0>0,\kappa >0$ are independent of $\tau$. Then, under these circumstances,

$$\begin{array}{cc}\hfill \Vert {\mathbf{Q}}^{+}\mathbf{J}(\mathbf{I}-\mathbf{Q}{\mathbf{Q}}^{+})& -(\mathbf{I}-{\mathbf{Q}}^{+}\mathbf{Q})\mathbf{J}{\mathbf{Q}}^{+}+t(\mathbf{I}-{\mathbf{Q}}^{+}\mathbf{Q})\mathbf{J}\mathbf{Q}{\mathbf{Q}}^{+}\hfill \\ \hfill & +{\mathrm{\nabla }}_{\mathbf{J}}{e}^{t\mathbf{Q}}-t{e}^{t\mathbf{Q}}\mathbf{J}\Vert \le C(1+t)e^{-\kappa t}\hfill \\ \hfill \end{array}$$ [24]

for any $t\ge 0$. Here, $C>0$ is a $t$-independent constant which is given explicitly as

$$\begin{array}{cc}\hfill C_0(\Vert (\mathbf{I}-{\mathbf{Q}}^{+}\mathbf{Q})\mathbf{J}{({\mathbf{Q}}^{+})}^2\Vert & +\Vert {({\mathbf{Q}}^{+})}^2\mathbf{J}(\mathbf{I}-\mathbf{Q}{\mathbf{Q}}^{+})\Vert +\Vert {\mathbf{Q}}^{+}\mathbf{J}\Vert )\hfill \\ \hfill & +C_0^2\Vert {\mathbf{Q}}^{+}\mathbf{J}{\mathbf{Q}}^{+}\Vert .\hfill \end{array}$$ [25]

Remark 1:

To illuminate the scope of Theorem 1, we have the following three classes of matrices maintaining the conditions Eqs. 20–23 as follows.

• (i)
  Suppose that $\mathbf{Q}\in \mathcal{M}(d)$ is such that

  $$\begin{array}{c}\hfill \mathfrak{R}{\lambda }_{d-1}(\mathbf{Q})<\mathfrak{R}{\lambda }_d(\mathbf{Q})\le 0,{\lambda }_d(\mathbf{Q})\text{is simple}\end{array}$$ [26]

  and such that, if ${\lambda }_d(\mathbf{Q})$ has an imaginary component, then its real part is strictly negative. Under these circumstances, writing $\mathbf{Q}$ in its Jordan canonical form yields, for some $m\ge 1$,

  $$\begin{array}{c}\hfill \mathbf{Q}=\mathbf{M}\text{diag}(J_1,\cdots ,J_{m-1},{\lambda }_d(\mathbf{Q})){\mathbf{M}}^{-1}.\end{array}$$ [27]

  Here, under Eq. 26 each of these blocks $J_j$ must be invertible and so we may take

  $$\begin{array}{c}\hfill {\mathbf{Q}}^{+}:=\mathbf{M}\text{diag}(J_1^{-1},\cdots ,J_{m-1}^{-1},{\lambda }_d{(\mathbf{Q})}^{+}){\mathbf{M}}^{-1},\end{array}$$ [28]

  where

  $$\begin{array}{c}\hfill {\lambda }_d{(\mathbf{Q})}^{+}=\left\{\begin{array}{cc}0\hfill & \text{if} {\lambda }_d(\mathbf{Q})=0,\hfill \\ {\lambda }_d{(\mathbf{Q})}^{-1}\hfill & \text{otherwise.}\hfill \end{array}\right.\end{array}$$ [29]
• (ii)
  We next consider the case where $\mathbf{Q}\in \mathcal{M}(d)$ is diagonalizable and its spectrum lies strictly on the left half plane or at the origin. This time, we can write

  $$\begin{array}{c}\hfill \mathbf{Q}=\mathbf{M}\mathbf{\Lambda }{\mathbf{M}}^{-1}\text{where} \mathbf{\Lambda }=\text{diag}({\lambda }_1(\mathbf{Q}),\dots ,{\lambda }_d(\mathbf{Q}))\end{array}$$ [30]

  and we set

  $$\begin{array}{c}\hfill {\mathbf{Q}}^{+}=\mathbf{M}{\mathbf{\Lambda }}^{+}{\mathbf{M}}^{-1}\text{with} {\mathbf{\Lambda }}^{+}=\text{diag}({\lambda }_1{(\mathbf{Q})}^{+},\dots ,{\lambda }_d{(\mathbf{Q})}^{+}).\end{array}$$ [31]

  The complex numbers ${\lambda }_j{(\mathbf{Q})}^{+}$, $j=1,\dots ,d$ are defined as in Eq. 29.
• (iii)
  Finally, we specialize to the case where $\mathbf{Q}\in \mathcal{S}(d)$ is symmetric. In this case, $\mathbf{Q}=\mathbf{U}\mathbf{\Lambda }{\mathbf{U}}^{\ast }$, where $\mathbf{U}$ is a unitary matrix and $\mathbf{\Lambda }=diag({\lambda }_1(\mathbf{Q}),\dots ,{\lambda }_d(\mathbf{Q}))$, ${\lambda }_j(\mathbf{Q})$ are its (real) eigenvalues. We suppose that these eigenvalues are all nonpositive,

  $$\begin{array}{c}\hfill {\lambda }_d(\mathbf{Q})\le 0.\end{array}$$ [32]

  Here, we take ${\mathbf{Q}}^{+}$ as the Moore-Penrose inverse, namely,

  $$\begin{array}{c}\hfill {\mathbf{Q}}^{+}=\mathbf{U}{\mathbf{\Lambda }}^{+}{\mathbf{U}}^{\ast },\end{array}$$ [33]

  where ${\mathbf{\Lambda }}^{+}$ is as in Eq. 31.

In anticipation of Theorem 3 and our desired application in Section 3, we are preoccupied with the dimensional dependence of the constants in Eqs. 23, 24, 25 in our formulation of Theorem 1. We next provide some such desirable bounds in case (iii) of Remark 1. Note that analogous results for generators $\mathbf{Q}$ in the classes (i) or (ii) would seemingly require a delicate analysis of the associated eigenspaces, i.e., of the structure of $\mathbf{M}$ in Eq. 27 or Eq. 30 respectively. However, Remark 4 and Fig. 1 provide numerical evidence of a broader scope for dimensionally improving approximations beyond the symmetric case, at least for certain classes of randomly drawn matrices.

Theorem 2.

Let symmetric $\mathbf{Q}\in \mathcal{S}(d)$ be nonpositive, i.e., suppose that Eq. 32 holds. Take ${\mathbf{Q}}^{+}$ as in Eq. 33 and define

$$\begin{array}{c}\hfill d_{-}= max\{1\le j\le d|\mathfrak{R}{\lambda }_j(\mathbf{Q})<0\}.\end{array}$$ [34]

Then, for any $\mathbf{J}\in \mathcal{M}(d)$,

$$\begin{array}{cc}\hfill \Vert t(\mathbf{I}& -{\mathbf{Q}}^{+}\mathbf{Q}{)\mathbf{J}\mathbf{Q}{\mathbf{Q}}^{+}+{\mathrm{\nabla }}_{\mathbf{J}}{e}^{t\mathbf{Q}}-t{e}^{t\mathbf{Q}}\mathbf{J}\Vert }_F\hfill \\ \hfill \le & (\sqrt{d_{-}}|{\lambda }_1(\mathbf{Q})|·[2\sqrt{d-d_{-}}\Vert {\mathbf{Q}}^{+}{\Vert }_F^2+{\Vert {\mathbf{Q}}^{+}\Vert }_F\hfill \\ \hfill & +\sqrt{d_{-}}|{\lambda }_1(\mathbf{Q})|\Vert {\mathbf{Q}}^{+}{\Vert }_F^2](1+t)e^{-t|{\lambda }_{d-}(\mathbf{Q})|}\hfill \\ \hfill & +2\sqrt{d-d_{-}}\Vert {\mathbf{Q}}^{+}{\Vert }_F){\Vert \mathbf{J}\Vert }_F\hfill \end{array}$$ [35]

with $\Vert {\mathbf{Q}}^{+}{\Vert }_F^2:=\sum _{k=1}^{d_{-}}\frac{1}{{\lambda }_k^2(\mathbf{Q})}$, whereas

$$\begin{array}{cc}\hfill \Vert t(& \mathbf{I}-{\mathbf{Q}}^{+}\mathbf{Q}{)\mathbf{J}\mathbf{Q}{\mathbf{Q}}^{+}+{\mathrm{\nabla }}_{\mathbf{J}}{e}^{t\mathbf{Q}}-t{e}^{t\mathbf{Q}}\mathbf{J}\Vert }_{\mathit{op}}\hfill \\ \hfill \le & (\frac{|{\lambda }_1(\mathbf{Q})|(2+|{\lambda }_{d_{-}}(\mathbf{Q})|+|{\lambda }_1(\mathbf{Q})|)}{{\lambda }_{d-}^2(\mathbf{Q})}(1+t)e^{-t|{\lambda }_{d_{-}}(\mathbf{Q})|}\hfill \\ \hfill & +\frac{2}{|{\lambda }_{d_{-}}(\mathbf{Q})|}){\Vert \mathbf{J}\Vert }_{\mathit{op}}.\hfill \end{array}$$ [36]

Under the further assumption that ${\lambda }_d(\mathbf{Q})=0$ and

$$\begin{array}{c}\hfill {\mu }_{1}d\le |{\lambda }_{d-1}(\mathbf{Q})|\le |{\lambda }_1(\mathbf{Q})|\le {\mu }_{2}d\end{array}$$ [37]

for some $0<{\mu }_1\le {\mu }_2$, we have

$$\begin{array}{cc}\hfill \Vert t(& \mathbf{I}-{\mathbf{Q}}^{+}\mathbf{Q}{)\mathbf{J}\mathbf{Q}{\mathbf{Q}}^{+}+{\mathrm{\nabla }}_{\mathbf{J}}{e}^{t\mathbf{Q}}-t{e}^{t\mathbf{Q}}\mathbf{J}\Vert }_F\hfill \\ \hfill \le & (\frac{{\mu }_2}{{\mu }_1^2}·[2\sqrt{d}+{\mu }_{1}d+{\mu }_2{d}^2]{(1+t)}^{-t{\mu }_{1}d}+\frac{2}{{\mu }_1\sqrt{d}}){\Vert \mathbf{J}\Vert }_F\hfill \end{array}$$ [38]

and that

$$\begin{array}{cc}\hfill \Vert t(\mathbf{I}& -{\mathbf{Q}}^{+}\mathbf{Q}{)\mathbf{J}\mathbf{Q}{\mathbf{Q}}^{+}+{\mathrm{\nabla }}_{\mathbf{J}}{e}^{t\mathbf{Q}}-t{e}^{t\mathbf{Q}}\mathbf{J}\Vert }_{\mathit{op}}\hfill \\ \hfill \le & (\frac{{\mu }_2}{{\mu }_1^2}·[\frac{2}{d}+{\mu }_1+{\mu }_2](1+t)e^{-t{\mu }_{1}d}+\frac{2}{{\mu }_{1}d}){\Vert \mathbf{J}\Vert }_{\mathit{op}}.\hfill \end{array}$$ [39]

1.2. High-Dimensional Asymptotics via Random Matrix Theory.

We turn to our probabilistic bounds on the singular values of randomly generated rate matrices, Theorem 3. Although interesting in its own right, this result leads to consequences for the bounds in Eqs. 23 and 24 when applied in Theorem 2. Before proceeding, we briefly introduce further mathematical preliminaries associated with the so-called sub-exponential random variables. To avoid confusion, note that the following definition uses the term in the same way as, e.g., ref. 31, but that other definitions that mean quite the opposite (i.e., heavier than exponential tails) appear in the literature (32).

Definition 1:

A random variable $X$ is called sub-exponential if there exists some constant $K>0$ for which its tails satisfy

$$\begin{array}{c}\hfill \mathbb{P}(|X|\ge t)\le 2e^{-t/K},\forall t\ge 0.\end{array}$$ [40]

In this case, the sub-exponential norm of $X$ is defined by

$$\begin{array}{c}\hfill {\Vert X\Vert }_{{\psi }_1}= inf\{s>0:\mathbb{E}{e}^{|X|/s}\le 2\}.\end{array}$$ [41]

The class of sub-exponential distributions is denoted by

$$\begin{array}{c}\hfill L_{{\psi }_1}=\{F_X(dx):{\Vert X\Vert }_{{\psi }_1}<\infty \}.\end{array}$$

Remark 2:

In fact, by Vershynin (31, Proposition 2.7.1, p. 33), condition Eq. 40 is equivalent to the existence of some $s_0>0$ such that $\mathbb{E}{e}^{|X|/s_0}\le 2$, namely, ${\Vert X\Vert }_{{\psi }_1}<\infty$ in Eq. 41. As a notable example, if $X\sim exp(\lambda )$, $\lambda >0$, then it is easy to see that $X\in L_{{\psi }_1}$, indeed.

We formulate our second major result as follows.

Theorem 3.

Let $F_X\in L_{{\psi }_1}$ be a distribution such that $X\ge 0$ a.s., $\mathbb{E}X=\mu >0$ and $VarX={\sigma }^2>0$. We consider a sequence of random matrices $\mathbf{Q}\equiv \mathbf{Q}(d)={\{q_{\mathit{ij}}\}}_{i,j=1,\cdots ,d}\in \mathcal{R}(d)$, $d\in \mathbb{N}$, where either

$$\begin{array}{c}\hfill \begin{array}{cc}& {\{q_{\mathit{ij}}\}}_{i,j=1,\cdots ,d,i\ne j}\stackrel{\mathit{iid}}{\sim }{F}_X\text{and}\hfill \\ \hfill & -q_{\mathit{ii}}={\displaystyle \sum _{j\in \{1,\cdots ,d\}\backslash \{i\}}}{q}_{\mathit{ij}},i=1,\cdots ,d\hfill \end{array}\end{array}$$ [42]

or we impose that $\mathbf{Q}\in \mathcal{R}(d)\cap \mathcal{S}(d)$ as

$$\begin{array}{c}\hfill \begin{array}{cc}& {\{q_{\mathit{ij}}\}}_{i,j=1,\cdots ,d, i>j}\stackrel{\mathit{iid}}{\sim }{F}_X,q_{\mathit{ij}}:=q_{\mathit{ji}}\text{for} i<j\text{and}\hfill \\ \hfill & -q_{\mathit{ii}}={\displaystyle \sum _{j\in \{1,\cdots ,d\}\backslash \{i\}}}{q}_{\mathit{ij}},i=1,\cdots ,d.\hfill \end{array}\end{array}$$ [43]

Then, in either of these cases, for any $d\in \mathbb{N}\backslash \{1\}$, we have

$$\begin{array}{cc}\hfill \mu +O_{a.s.}(\sqrt{\frac{logd}{d}})\le & \frac{{\sigma }_2(\mathbf{Q})}{d}\hfill \\ \hfill \le & \frac{{\sigma }_d(\mathbf{Q})}{d}\le \mu +O_{a.s.}(\sqrt{\frac{logd}{d}})\hfill \end{array}$$ [44]

almost surely.

Remark 3:

The bounds constructed in Theorem 3 are strongly reminiscent of the bounds for eigenvalues provided in Theorem 1.5 of the seminal paper (28) (see also, for instance, Corollary 1.6 in ref. 26 and Corollary 1.1 in ref. 27).

Finally, let us observe that Theorems 2 and 3 as well as the fact that

$$\begin{array}{c}\hfill {\sigma }_j(\mathbf{Q})=|{\lambda }_{d-j+1}(\mathbf{Q})|,\text{for e.g., any} \mathbf{Q}\in \mathcal{S}(d)\cap \mathcal{R}(d)\end{array}$$ [45]

combine to produce the following immediate corollary.

Corollary 1.

Consider any sequence of random matrices $\mathbf{Q}\equiv \mathbf{Q}(d)={\{q_{\mathit{ij}}\}}_{i,j=1,\cdots ,d}\in \mathcal{R}(d)$, $d\in \mathbb{N}$, as in Theorem 3 under the second (symmetric) case Eq. 43. Then, taking ${\mu }_1={\mu }_1(d)$ and ${\mu }_2={\mu }_2(d)$ as the resulting lower and upper bounds defined by Eq. 44, we have that $\mathbf{Q}$ satisfies both Eqs. 38 and 39, cf. Eq. 45 relative to this sequence of ${\mu }_1,{\mu }_2$ for any $\mathbf{J}\in \mathcal{M}(d)$.

Remark 4:

Our rigorous formulation of Corollary 1 is limited to symmetric random rate matrices whose above diagonal elements are independent and iid draws from a sub-exponential distribution. However, strong numerical evidence suggests that the scope of the approximations Eqs. 38 and 39 reach far beyond the limitations of Corollary 1 in several different ways. Fig. 1 explores the consequences of relaxing various assumptions of Corollary 1. The third plot involves folded Cauchy random variables, the heavy tails of which violate the sub-exponential assumption (Definition 1). There appears to be no significant departure from the idea that the form $t(\mathbf{I}-{\mathbf{Q}}^{+}\mathbf{Q})\mathbf{J}\mathbf{Q}{\mathbf{Q}}^{+}$ corresponds increasingly well to the true approximation error [Eq. 7] as the dimension increases.

Remark 5:

Calculation of ${\tilde{\mathrm{\nabla }}}_{\mathbf{J}}{e}^{t\mathbf{Q}}:=t{e}^{t\mathbf{Q}}\mathbf{J}$ requires $\mathcal{O}\left(d^3\right)$ operations by, e.g., computing the spectral decomposition $\mathbf{Q}$ as in Eq. 30. One may then recycle this decomposition to determine the additional term $t(\mathbf{I}-{\mathbf{Q}}^{+}\mathbf{Q})\mathbf{J}\mathbf{Q}{\mathbf{Q}}^{+}$ for little extra cost. In view of Corollary 1 and Fig. 1,

$$\begin{array}{c}\hfill {\widehat{\mathrm{\nabla }}}_{\mathbf{J}}{e}^{t\mathbf{Q}}:=t{e}^{t\mathbf{Q}}\mathbf{J}-t(\mathbf{I}-{\mathbf{Q}}^{+}\mathbf{Q})\mathbf{J}\mathbf{Q}{\mathbf{Q}}^{+}\end{array}$$ [46]

provides an accurate approximation of ${\mathrm{\nabla }}_{\mathbf{J}}{e}^{t\mathbf{Q}}$ for asymptotically for large $d$. Thus, we anticipate further computational improvements when fitting large, gold-standard models using this refined approximation. That said, we leave the efficient and scalable application of ${\widehat{\mathrm{\nabla }}}_{\mathbf{J}}{e}^{t\mathbf{Q}}$ to future work.

2. Empirical Studies

Before applying the naive matrix exponential derivative approximation to the phylogeographic analysis of SARS-CoV-2, we carry out a few targeted studies that illustrate the empirical performance of the approximate derivative and its affine correction Eq. 46 (Fig. 1); agreement between CTMC generator matrix empirical posterior distributions generated by surrogate-trajectory HMC algorithms using approximate derivatives and the truth (Fig. 2); and point estimation of generator matrix element values under different sparsity regimes and different CTMC state space dimensionalities $d$ (Fig. 3).

Fig. 2.

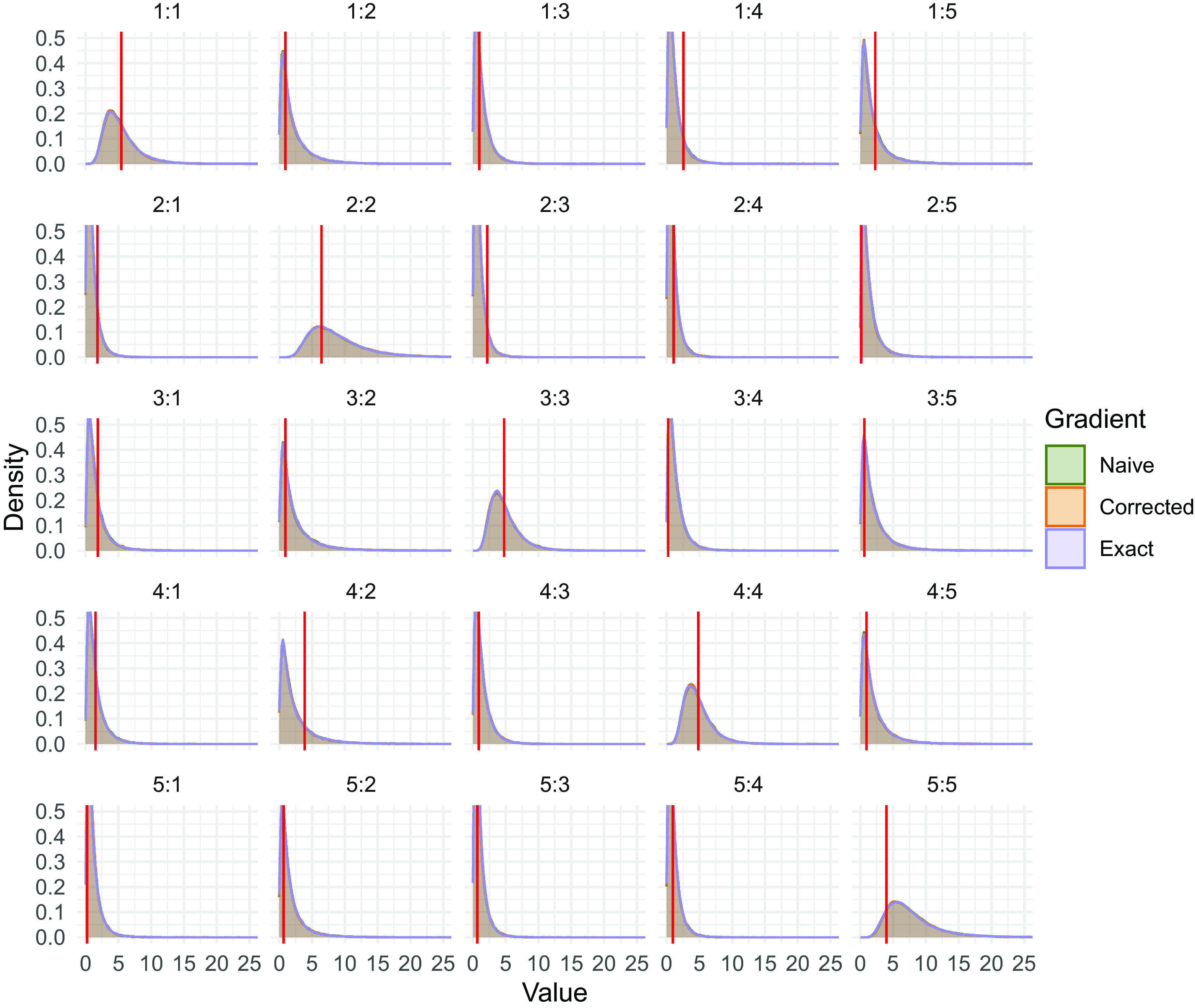
Posterior density plots for surrogate-trajectory HMC using the naive approximate derivative, the corrected approximation Eq. 46 and the exact matrix exponential derivative for elements of a $5\times 5$ generator matrix. The near-perfect overlap reflects the fact that each algorithm’s transition kernel leaves the posterior distribution invariant (33). To generate data, we randomly draw standard normal generator entries once and simulate 20 independent initial/final position pairs from a CTMC with time interval $t=1$. We show the true value in red and negate diagonal elements to simplify presentation.

Fig. 3.

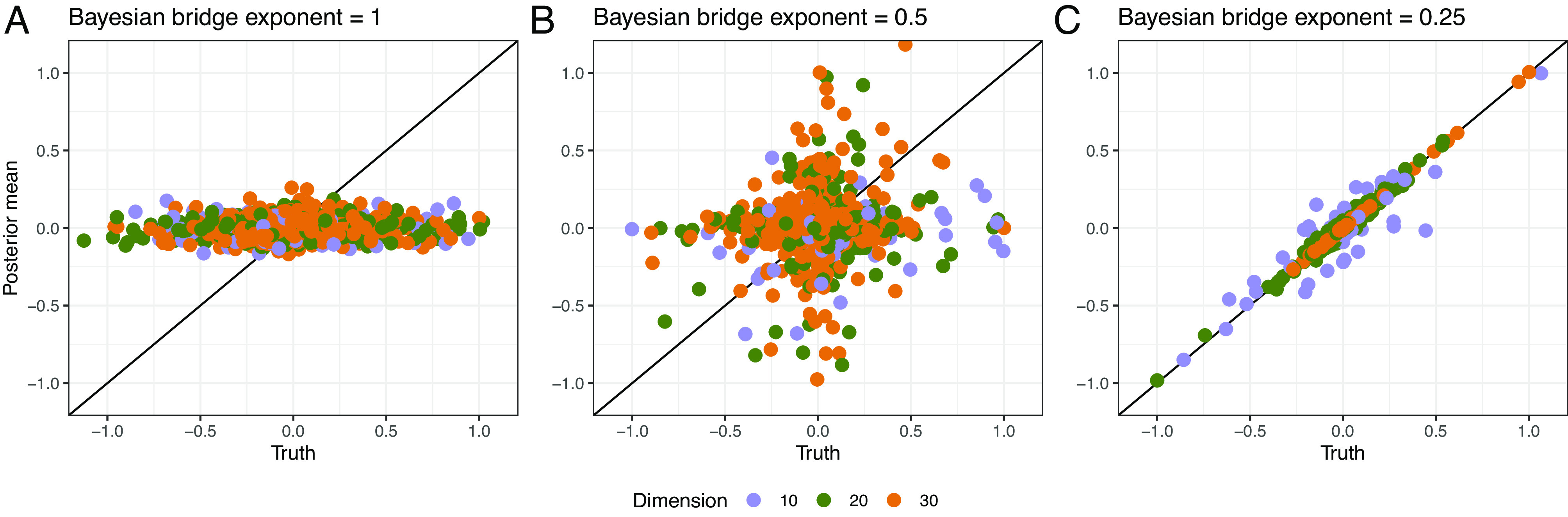
Posterior means versus truth for CTMC generator matrix elements within differing sparsity regimes and with different dimensionalities $d$, holding observation count fixed at 300. We generate posteriors using surrogate-trajectory HMC with the naive matrix exponential derivative. To affect sparsity levels, we generate generator matrix entries according to the Bayesian bridge distribution (34) with different exponents ($\alpha \in \{1,1/2,1/4\}$ for plots A, B and C, respectively), normalizing by the largest absolute values to ease comparison. Smaller $\alpha$ values encode more peaked distributions with heavier tails and thus enforce greater sparsity. Plot C reflects the fact that the Bayesian bridge prior with exponent $\alpha =1/4$ helps identify non-null parameters in small sample contexts (18). With this intuition in mind, we specify such a prior on generator random effects in Section 3.

Here, we fill in remaining simulation details not included in figure captions. In the simulations contributing to Fig. 1, we randomly generate new, independent direction matrices $\mathbf{J}$ at each time step within each of the 20 independent runs. The results are not sensitive to $\mathbf{J}$ in general. We also note that under Definition 1 the Cauchy distribution is not sub-exponential and therefore represents a deviation from core assumptions of Section 1. Using varying distributions on the elements of generator matrices $\mathbf{Q}$, the simulations contributing to Figs. 2 and 3 both randomly generate $N$ independent initial states ${\mathbf{y}}_1^0,\cdots ,{\mathbf{y}}_N^0$ according to uniform distributions over their respective CTMC state spaces. For each of these initial states ${\mathbf{y}}_0$, we then simulate from the CTMC for time interval $t=1$ to obtain samples ${\mathbf{y}}_1^1,\cdots ,{\mathbf{y}}_N^1$. The likelihood then takes the form $\prod _n{({\mathbf{y}}_n^0)}^T{e}^{\mathbf{Q}}{\mathbf{y}}_n^1$. For the simulation contributing to Fig. 2, we specify standard normal priors and sample from the posterior by generating 100,000 iterations from each algorithm. For the simulation contributing to Fig. 3, we generate 500,000 MCMC samples using surrogate-trajectory HMC with the naive matrix exponential derivative and calculate the posterior mean of each generator matrix element using the final 100,000 samples.

3. Application: Global Spread of SARS-CoV-2

Ref. 18 consider phylogenetic models that involve CTMC priors and show that the first-order approximation Eq. 4 of the matrix exponential derivative Eq. 2 performs remarkably well within surrogate HMC (SI Appendix), achieving an over 30-fold efficiency gain compared to random-walk Metropolis for a 14-state model with over 180 model parameters. Here, we demonstrate similar strong performance of the first-order approximation within surrogate HMC for a 44-state model with almost 1,900 model parameters.

3.1. Phylogenetic CTMC.

Start with a (possibly unknown) rooted and bifurcating phylogenetic tree $\mathcal{T}$ consisting of $N$ leaf nodes that correspond to observed biological specimens and $N-1$ internal nodes that correspond to unobserved ancestors. The tree also contains $2N-2$ branches of length $t_v$ connecting each child node $v$ to its parent $u$.

Given $\mathcal{T}$, we model the evolution of $d$ characters along each branch of the tree according to a CTMC model with $d\times d$ generator matrix $\mathbf{Q}$ and stationary distribution $\mathbf{\pi }=({\pi }_1,\cdots ,{\pi }_d)=\underset{t\to \infty }{lim}\tilde{\mathbf{\pi }}{e}^{t\mathbf{Q}}$, for $\tilde{\mathbf{\pi }}$ any arbitrary probability vector. Examples of characters are the $d=4$ nucleotides within a set of aligned genome sequences (13) and the set of $d=15$ geographic regions visited by an influenza subtype (2). We may scale $t_v$ to be raw time (e.g., years) or the expected number of substitutions with respect to $\mathbf{\pi }$ depending on the given problem. In the former case, one may augment the model with a rate scalar $\gamma$ that modulates the expected number of substitutions across all branches, and the finite-time transition probability matrix along branch $v$ becomes ${\mathbf{P}}_v:=e^{\gamma t_v\mathbf{Q}}$. In the following, we further posit $\mathbf{Q}=\mathbf{Q}(\mathit{\theta })$ for $\mathit{\theta }$ a vector of parameters.

Let data $\mathbf{Y}$ be the $d\times N$ matrix with columns ${\mathbf{y}}_n$, $n\in \{1,\cdots ,N\}$, each having a single nonzero entry (set to 1) corresponding to the observed state of the biological specimen. One may use any node $v$ to express the likelihood

$$\begin{array}{c}\hfill p(\mathbf{Y}|\mathit{\theta })={\mathbf{p}}_v^T{\mathbf{q}}_v,\end{array}$$ [47]

where ${\mathbf{p}}_v$ and ${\mathbf{q}}_v$ are the post-order and pre-order partial likelihood vectors, respectively (35). The former describes the probability of the observed states for all observed specimens (i.e., leaf nodes) that descend from node $v$, conditioned on the state at node $v$. The latter describes analogous probabilities for all observed specimens not descending from node $v$. For leaf nodes, ${\mathbf{p}}_n:={\mathbf{y}}_n$, $n\in \{1,\cdots ,N\}$, and one may specify the root node’s pre-order partial likelihood to be any arbitrary probability vector a priori. Let “ᴏ” denote the Hadamard or elementwise product between matrices or vectors of equal dimensions. If we suppose that node $u$ gives rise to two child nodes, $v$ and $w$, then

$$\begin{array}{c}\hfill {\mathbf{p}}_u={\mathbf{P}}_v{\mathbf{p}}_v ᴏ {\mathbf{P}}_w{\mathbf{p}}_w,{\mathbf{q}}_v={\mathbf{P}}_v^T\left({\mathbf{q}}_uᴏ{\mathbf{P}}_w{\mathbf{p}}_w\right).\end{array}$$ [48]

Using the chain rule and the fact that ${\mathbf{p}}_v$ does not depend on ${\mathbf{P}}_v$, one may write the likelihood’s derivative with respect to a single parameter ${\theta }_k$ thus:

$$\begin{array}{cc}\hfill \frac{\partial }{\partial {\theta }_k}p(\mathbf{Y}|\mathit{\theta })& \propto {\displaystyle \sum _{v=1}^{2N-2}}\text{tr}\left(\frac{\partial ({\mathbf{p}}_v^T{\mathbf{q}}_v)}{\partial {\mathbf{P}}_v}\frac{\partial {\mathbf{P}}_v^T}{\partial {\theta }_k}\right)\hfill \\ \hfill & ={\displaystyle \sum _{v=1}^{2N-2}}\text{tr}\left(({\mathbf{q}}_u°{\mathbf{P}}_w{\mathbf{p}}_w){\mathbf{p}}_v^T(\frac{\partial e^{\gamma t_v\mathbf{Q}}}{\partial {\theta }_k}{)}^T\right)\hfill \\ \hfill & ={\displaystyle \sum _{v=1}^{2N-2}}{\mathbf{p}}_v^T({\displaystyle \sum _{i,j=1}^d}\frac{\partial e^{\gamma t_v\mathbf{Q}}}{\partial q_{\mathit{ij}}}\frac{\partial q_{\mathit{ij}}}{\partial {\theta }_k}{)}^T({\mathbf{q}}_u°{\mathbf{P}}_w{\mathbf{p}}_w),\hfill \end{array}$$ [49]

where we suppress the dependence of $u$ and $w$ on $v$.

Whereas the recursions of Eq. 48 facilitate fast likelihood computation, inferring $\mathit{\theta }$ using gradient-based approaches such as HMC requires a large number of repeated evaluations of the matrix exponential derivative. These computations become particularly onerous when one opts for a gold-standard mixed-effects model (18) and specifies

$$\begin{array}{c}\hfill log{q}_{\mathit{ij}}=b_{\mathit{ij}}+{ϵ}_{\mathit{ij}},i\ne j.\end{array}$$ [50]

Here, the fixed effects $b_{\mathit{ij}}$ are elements of some non-random matrix $\mathbf{B}$, and the random effects ${ϵ}_{\mathit{ij}}$ are mutually independent a priori and inferred as model parameters. The dimension $K$ of $\mathit{\theta }$ in this model is $\mathcal{O}(d^2)$, so the $\mathcal{O}(KN{d}^5)$ cost of the log-likelihood derivative Eq. 49 becomes a massive $\mathcal{O}(N{d}^7)$. In this context, Magee et al. (18) shows that an approximate log-likelihood derivative based on the first-order approximation to the matrix exponential helps achieve a considerable speedup over the exact derivative, requiring only $\mathcal{O}(d^4+N{d}^3)$ floating-point operations yet facilitating high-quality proposals in the context of surrogate HMC.

In the following section, we use this method to analyze the global spread of SARS-CoV-2 and show that the first-order approximation maintains its performance for an even higher-dimensional problem than previously considered.

3.2. Bayesian Analysis of SARS-CoV-2 Contagion.

We use the phylogenetic CTMC framework to model the early spread of SARS-CoV-2—the virus responsible for the ongoing COVID-19 pandemic—based on $N=285$ observed viral samples collected from $31$ regions worldwide between 24 December 2019 and 19 March 2020. These regions comprise 13 provinces within China and 18 countries without. Understanding the manner in which viruses travel between human populations is an object of ongoing study, and phylogeographic analyses point to the central role of travel networks including those measured by airline passenger counts (3) or Google mobility data (36). Here, we include three such predictors of travel in our CTMC model by expanding the fixed effects in regression model Eq. 50 to take the form

$$\begin{array}{c}\hfill \mathbf{B}={\theta }_1{\mathbf{X}}_1+{\theta }_2{\mathbf{X}}_2+{\theta }_3{\mathbf{X}}_3\end{array}$$ [51]

for ${\mathbf{X}}_1$, ${\mathbf{X}}_2$, and ${\mathbf{X}}_3$ fixed 44 $\times$ 44 matrix predictors and ${\theta }_1$, ${\theta }_2$, and ${\theta }_3$ real-valued regression coefficients. Note we have expanded the number of regions between which viruses may travel to $d=44$ by including two additional Chinese provinces and 11 additional countries. Fig. 4 presents the three predictors of interest: ${\mathbf{X}}_1$ contains air travel proximities between locations as measured by annualized air passenger counts between airports contained within a region (3); ${\mathbf{X}}_2$ contains intracontinental proximities arising from physical distances when two regions inhabit the same continent and fixed at the minimum otherwise; finally, ${\mathbf{X}}_3$ describes the Hubei asymmetry, i.e., the nonexistence of human travel out of the Hubei province in early 2020.

Fig. 4.

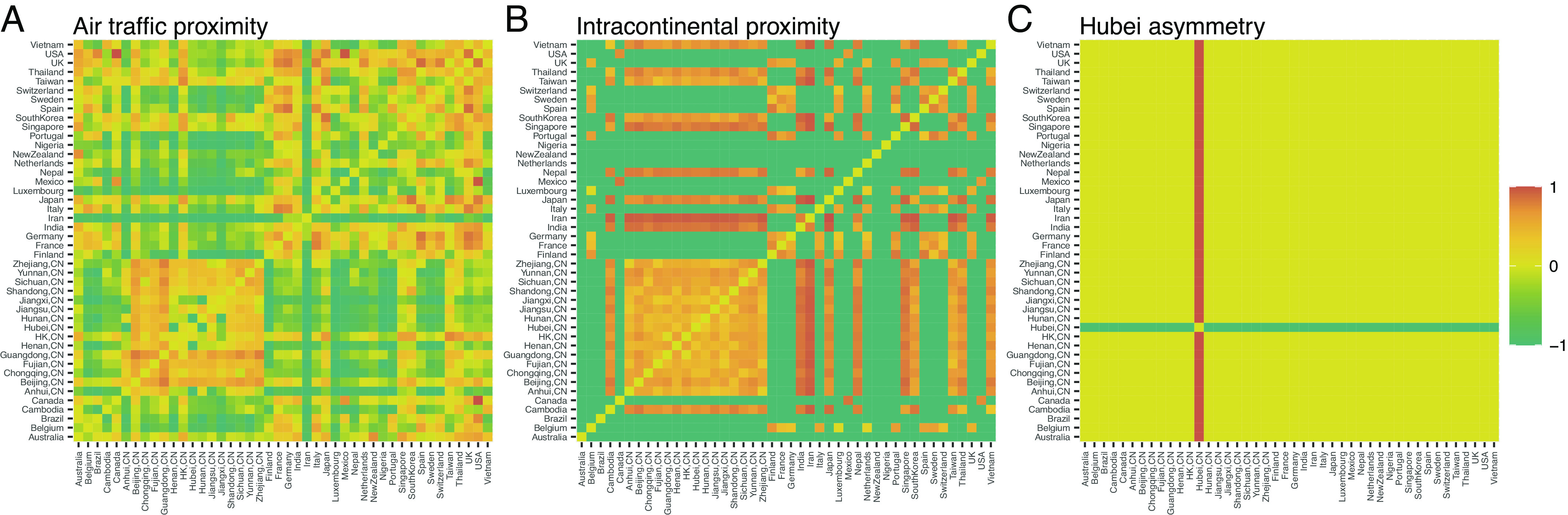
Matrix predictors described in Eq. 51 combine in a linear manner to form the fixed-effect matrix $\mathbf{B}$ featured within the mixed-effects regression model Eq. 50. Air traffic proximities (A) are proportional to the number of air passengers exchanged between airports within respective regions (3). Intracontinental proximities (B) take values between $-$1 for regions on different continents to 1 for adjacent regions. The Hubei asymmetry (C) roughly characterizes the Hubei quarantine of early 2020.

In the context of a Bayesian analysis, we specify independent normal priors on ${\theta }_1$, ${\theta }_2$, and ${\theta }_3$ with means of 0 and variances of 2. We also assume that the 1,892 random effects ${ϵ}_{\mathit{ij}}$ follow sparsity-inducing Bayesian bridge priors with global scale parameter $\tau$ and exponent $\alpha =0.25$. Here, we follow ref. 37 and specify a Gamma prior on ${\tau }^{-\alpha }$ with a shape parameter of 1 and a rate parameter of 2. Finally, we place a flat prior on the rate scalar $\gamma$. Inferring the posterior distribution of all 1,897 model parameters requires an advanced MCMC strategy. Namely, we adopt an HMC-within-Gibbs approach, updating the scalars $\gamma$ and $\tau$ independently but updating all 1,895 regression parameters (both fixed and random effects) using surrogate HMC accomplished with the first-order approximation

$$\begin{array}{c}\hfill \gamma t_v{e}^{\gamma t_v\mathbf{Q}}{\mathbf{J}}_{\mathit{ij}}\approx \frac{\partial e^{\gamma t_v\mathbf{Q}}}{\partial q_{\mathit{ij}}}\end{array}$$

within Eq. 49.

We generate 8 million MCMC samples in this manner, saving 1 in 10,000 Markov chain states, in order to guarantee a minimum ESS greater than 100. By far, the worst-mixing parameter is the global scale $\tau$, which obtains an ESS of 185. The three fixed-effects regression coefficients ${\theta }_1$, ${\theta }_2$, and ${\theta }_3$ obtain ESS’s of 721, 721, and 644, respectively. The median and minimum ESS for the 1,892 random effects ${ϵ}_{s{s}^{\prime }}$ are 721 and 190, respectively. We note that, after thinning and removing burn-in, the sample only consists of 721 states, so ESS of 721 implies negligible autocorrelation between samples.

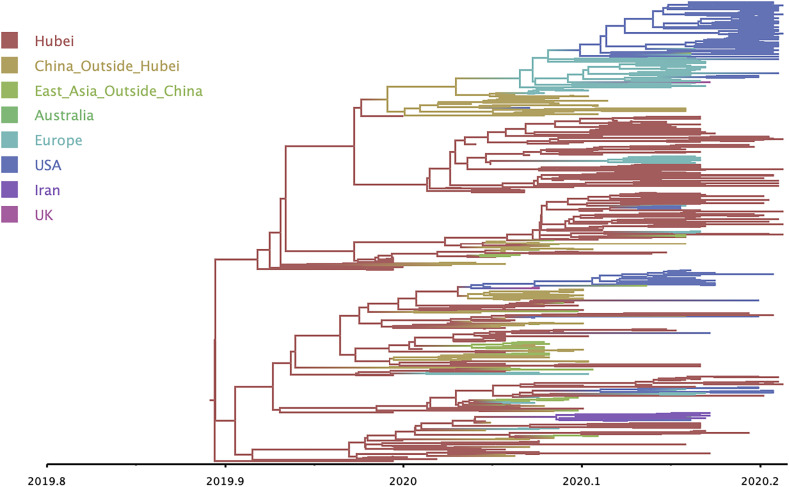
The Left plot of Fig. 5 presents posterior densities for the fixed-effect coefficients from regression Eq. 50. The air traffic proximity, intracontinental proximity and Hubei asymmetry coefficients have posterior means and 95% credible intervals of 0.76 (0.50, 1.03), 0.04 ($-$0.04, 0.12), and 0.27 ($-$0.39, 0.78), respectively. While these results suggest a positive association between each predictor matrix and the infinitesimal generator matrix $\mathbf{Q}$, the only predictor with a statistically significant association is air traffic proximity. This result agrees with a previous phylogeographic analysis of the global spread of influenza (3). The Right plot of Fig. 5 presents the posterior mean for generator $\mathbf{Q}$. As one may expect, the matrix looks similar to that of the air traffic predictor matrix in Fig. 4, but one may also see the influence of the Hubei asymmetry in, e.g., the squares corresponding to travel between Guangdong and Hubei provinces. Finally, we randomly generate regions of unobserved ancestors from their posterior predictive distributions every 100-thousandth MCMC iteration. After collapsing regions into 8 major blocks, Fig. 6 projects the empirical posterior predictive mode of these blocks onto the phylogenetic tree $\mathcal{T}$. The general pattern looks similar to that of figure 1 from ref. 38, although the geographic blocking scheme differs slightly.

Fig. 5.

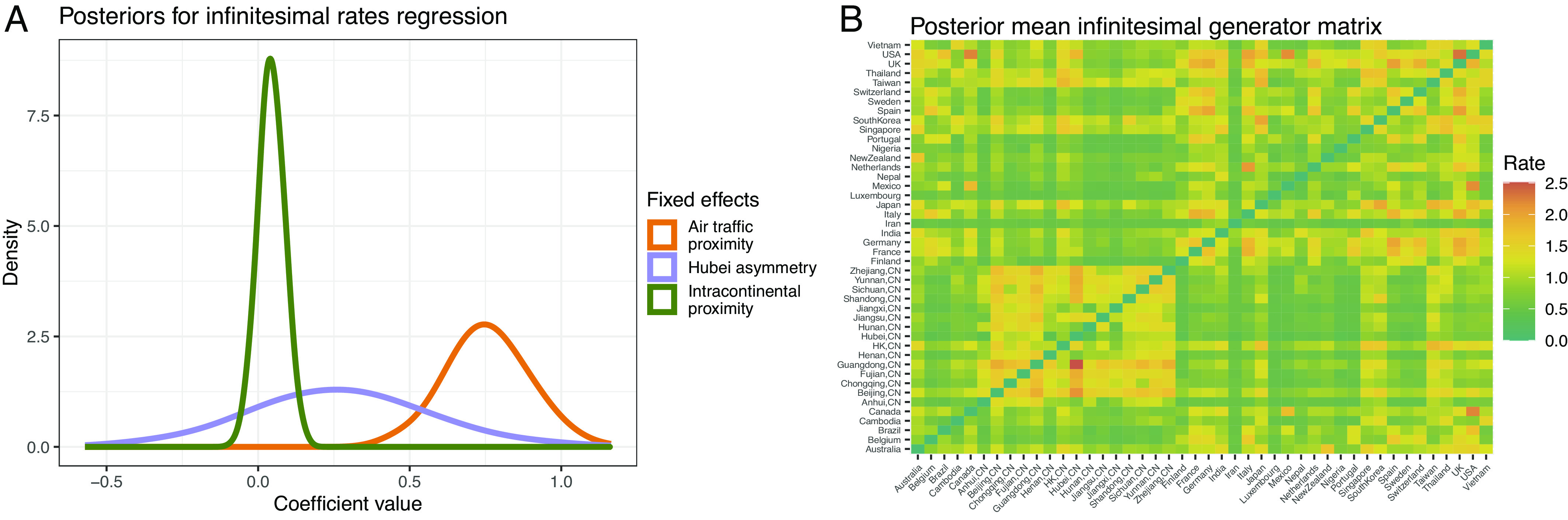
Posterior inference. Posterior densities (A) for the three fixed-effect regression coefficients corresponding to the predictor matrices of Fig. 4 reflect largely positive associations between predictors and infinitesimal rate matrix, although air traffic proximity has the only statistically significant coefficient with posterior mean of 0.76 and 95% credible interval of (0.50, 1.03). The posterior mean (B) infinitesimal rate matrix closely resembles the air traffic predictor, while reflecting the Hubei asymmetry to a lesser extent.

Fig. 6.

Posterior predictive modes for (unobserved) ancestral locations color a phylogenetic tree that describes the shared evolutionary history of 285 SARS-CoV-2 samples.

In addition to these scientific questions of interest, we are interested in the performance of the first-order approximation as a surrogate gradient for HMC in such a high-dimensional setting. Whereas we know that the surrogate-trajectory HMC transition kernel leaves its target distribution invariant regardless of the approximation quality (33), transitions that rely on poor gradient approximations result in small acceptance rates, more random walk behavior and high autocorrelation between samples. Since ESS is inversely proportional to a Markov chain’s asymptotic autocorrelation, larger ESS suggests a useful gradient approximation. To isolate the approximation’s performance, we fix the Bayesian bridge global-scale $\tau$ at 2.5$\times {10}^{-5}$. We generate a Markov chain with 80,000 states, saving every tenth state and removing the first 1,000 states as burn-in. Despite the relatively small number of iterations, we observe large ESS that suggest satisfactory accuracy of the first-order approximation within the context of high-dimensional surrogate HMC. The ESS for the three fixed-effect regression coefficients ${\theta }_1$, ${\theta }_2$, and ${\theta }_3$ are 1,053, 1,343, and 498, respectively. The median and minimum ESS for the 1,892 random effects ${ϵ}_{\mathit{ij}}$ are 1,514 and 1,161, respectively.

4. Discussion

We develop tight probabilistic bounds on the error associated with a simplistic approximation to the matrix exponential derivative for a large class of CTMC infinitesimal generator matrices with random entries. Our “blessing of dimensionality” result shows that this error improves for higher-dimensional matrices. We apply the numerically naive approach to the analysis of the global spread of SARS-CoV-2 using a mixed-effects model of unprecedented dimensions. The results obtained herein suggest the further study of CTMCs through the lens of random matrix theory. Furthermore, this analysis suggests a refinement of the first-order approximation to the matrix exponential derivative that may be particularly useful within modern, high-dimensional settings.

Supplementary Material

Appendix 01 (PDF)

Data, Materials, and Software Availability

Public data have been deposited in Github (39).