Much more to explore with an oxidation state of nearly four: Pr valence instability in intermetallic m-Pr₂Co₃Ge₅

Abstract

For some intermetallic compounds containing lanthanides, structural transitions can result in intermediate electronic states between trivalency and tetravalency; however, this is rarely observed for praseodymium compounds. The dominant trivalency of praseodymium limits potential discoveries of emergent quantum states in itinerant 4f¹ systems accessible using Pr⁴⁺-based compounds. Here, we use in situ powder x-ray diffraction and in situ electron energy-loss spectroscopy (EELS) to identify an intermetallic example of a dominantly Pr⁴⁺ state in the polymorphic system Pr₂Co₃Ge₅. The structure-valence transition from a nearly full Pr⁴⁺ electronic state to a typical Pr³⁺ state shows the potential of Pr-based intermetallic compounds to host valence-unstable states and provides an opportunity to discover previously unknown quantum phenomena. In addition, this work emphasizes the need for complementary techniques like EELS when evaluating the magnetic and electronic properties of Pr intermetallic systems to reveal details easily overlooked when relying on bulk magnetic measurements alone.

An example of a dominantly Pr⁴⁺ intermetallic compound is reported using complementary in situ techniques.

INTRODUCTION

Crystalline structure plays a key role in controlling thermal decomposition in batteries, improving catalyst efficiency, and the development of quantum materials due to its explicit relationship with electronic structure and chemical behavior. In the latter group, electron-electron interactions result in the formation of strongly correlated electronic states that can be linked to emergent quantum phenomena depending on the presence of specific structural elements (1). For example, in combination with strong electron interactions, nonsymmorphic symmetry elements give rise to topological electronic states (2, 3) and geometrically frustrated lattices to magnetic spin-liquid behavior (4–6), both of which find applications in spintronic and quantum computing (7).

Often, materials obtain their strongly correlated nature from the presence of lanthanide elements with 4f electrons at the limit between local moment and itinerant behavior (8–12). Valence instabilities in lanthanide compounds can have substantial impacts on crystal structure and physical properties (13–16). Targeting systems with structural phase transformations can provide an exciting path forward for strongly correlated materials, specifically in identifying valence-unstable states in dominantly trivalent lanthanides like Pr with the opportunity to access technologically relevant quantum states (17–20). Still, Pr compounds are typically trivalent, with only a small number of dominantly tetravalent Pr-containing oxides and fluorides reported (21). Critically, there are no examples of dominantly tetravalent intermetallic compounds leaving much more to explore regarding the impact of Pr⁴⁺ ions on their magnetic properties. Given the link between structural and valence transitions, one avenue for identifying an intermetallic system capable of hosting tetravalent Pr is to target structure types where instabilities in electronic structure and valence are already present.

A particularly deep reservoir for studies of interesting electronic states are compounds with the formula A₂M₃X₅ (A = lanthanide, actinide, Y, Sc; M = transition metal; X = main group metal) where various examples exhibit quantum critical points, unstable valence states, superconductivity, topological semimetallic states, charge density waves, and other phenomena (22). These compounds crystallize in eight known structure types and can be considered polyanionic three-dimensional frameworks of transition and main group metals that are most commonly filled with lanthanide or actinide cations (23). Polymorphism and structural phase transformations between the U₂Co₃Si₅ (Ibam) (24), Lu₂Co₃Si₅ (C2/c or the nonstandard equivalent I2/c) (25), and Sc₂Fe₃Si₅ (P4/mnc) (26) structure types have opened avenues of investigation as the formation of metastable structures often leads to emergent physical properties (27–30).

Intrigued by the unstable electronic states and polymorphism in the group 9 germanides (31–35), we recently showed that large single crystals of both m-Pr₂Co₃Ge₅ (Lu₂Co₃Si₅ type, I2/c) (36) and o-Pr₂Co₃Ge₅ (U₂Co₃Si₅ type, Ibam) (37) can be stabilized at room temperature. In this work, we reveal a second-order structural phase transition between two polymorphs of Pr₂Co₃Ge₅ through complementary in situ powder x-ray diffraction (PXRD) and in situ electron energy-loss spectroscopy (EELS). We demonstrate a relationship between the structural phase transformation and a change in Pr valence from Pr^3.80(5)+ to Pr^3.00(5)+, the first of its kind for an intermetallic compound. We discuss the hallmarks of valence changes and delocalization evident in the Pr and Co electron energy-loss spectra and show how the anisotropic magnetic properties are affected with this change in structure and valence. This work demonstrates how minor changes in crystal structure can be indicative of substantial reconfigurations in electronic and magnetic interactions leading to unexplored and exciting avenues for quantum materials investigations.

RESULTS

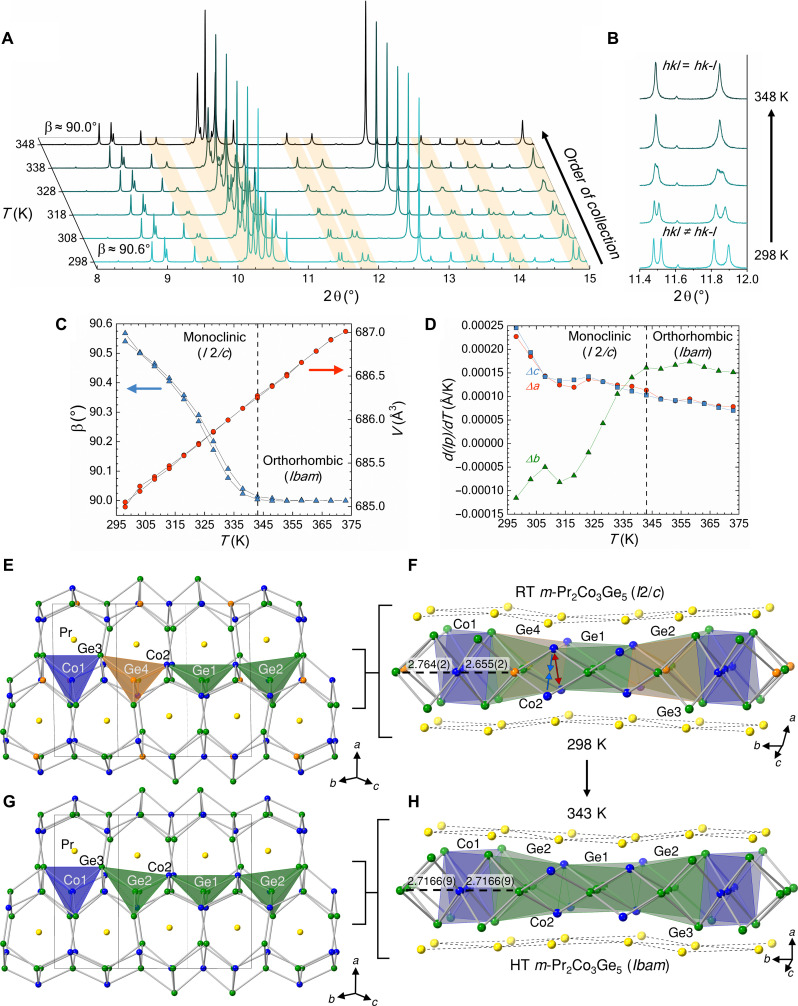
Figure 1A shows the temperature-dependent PXRD patterns from 298 to 348 K taken for m-Pr₂Co₃Ge₅. The convergence of the hkl and hk-l reflections (Fig. 1B) demonstrates that the structure of m-Pr₂Co₃Ge₅ undergoes a second-order structural phase transformation from the space group I2/c (Lu₂Co₃Si₅ structure type) to Ibam (U₂Co₃Si₅ structure type). The β angle, the angle between the a and c lattice directions, of m-Pr₂Co₃Ge₅ begins converging homogeneously toward 90° immediately upon heating from room temperature indicating the beginning of the structural phase transformation and concludes at approximately 343 K. The high-temperature diffraction pattern of m-Pr₂Co₃Ge₅ matches exceedingly well with the room-temperature powder diffraction pattern of o-Pr₂Co₃Ge₅. For comparison, Rietveld refinements of synchrotron PXRD for room-temperature m-Pr₂Co₃Ge₅ and o-Pr₂Co₃Ge₅ are shown in fig. S1, and atomic position and bond distance tables for all structures are provided in tables S1 and S2. Figure 1C shows that while the β angle converges to 90° upon heating, the volume increases linearly with temperature giving no clear indication of a valence change. The first derivative of the change in lattice parameters of m-Pr₂Co₃Ge₅ (Fig. 1D) shows nonlinear change in the b lattice direction in contrast to the a and c directions corresponding with a transformation to the orthorhombic structure type. The length of the b axis is directly related to the β angle of m-Pr₂Co₃Ge₅. As the β angle approaches 90° across the phase transition, the b axis must elongate to compensate for the change since the volume of the Pr₂Co₃Ge₅ unit cell of changes minimally as a function of temperature.

Fig. 1. In situ x-ray diffraction and crystal structure of m-Pr₂Co₃Ge₅ and o-Pr₂Co₃Ge₅.

(A and B) Temperature-dependent x-ray diffraction of m-Pr₂Co₃Ge₅ (λ = 0.458977 Å) highlighting the structural phase transformation from I2/c to Ibam. The change in angle β as related to the change in volume and the change in lattice parameters (lp) are given in (C) and (D), respectively. Dashed lines indicate the conclusion of the second-order structural phase transformation. Crystal structure of room-temperature (E and F) and 343-K (G and H) m-Pr₂Co₃Ge₅ obtained from synchrotron PXRD where Pr, Co, and Ge are represented with yellow, blue, and green/orange spheres, respectively. Select Co-Ge distances (Å) are shown to illustrate the distortion of the basal atoms of the tetrahedral slab along the crystallographic b direction. Red and blue arrows indicate the separation and contraction of the Co2 dimerization, respectively.

The structural differences of room-temperature and high-temperature m-Pr₂Co₃Ge are shown in Fig. 1 (E to H). Notably, the five coordinate Co2 atoms that were dimerized along the c direction at room temperature undergo the largest change in bond distance within the framework, expanding from d_Co2-Co2 = 3.464(2) Å to d_Co2-Co2 = 3.5838(7) Å at 343 K. The distortion of the [Co₃Ge₅] framework across the phase transition leads to an increase in Pr local environment symmetry from C₁ to C_s as the Pr-Ge2/4 and Pr-Co2 distances undergo contractions ranging from Δ_Pr-Ge4 = −0.029(1) Å to Δ_Pr-Ge2 = −0.019(1) Å and elongations ranging from Δ_Pr-Ge2 = 0.010(1) Å to Δ_Pr-Ge4 = 0.028(1) Å. With the existence of a structural phase transformation confirmed in m-Pr₂Co₃Ge₅, temperature-dependent EEL spectra were obtained to determine the structure-valence relationship of the two polymorphs.

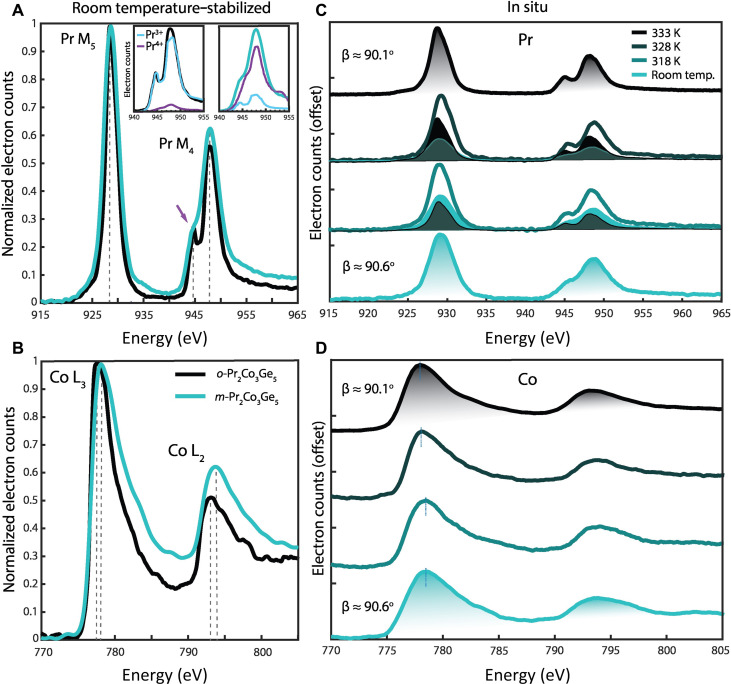
In situ EELS collects quantitative information regarding the 4f electronic states of the lanthanide without the influence of sample contributions like thickness and compositional inhomogeneities. Monochromated EELS data were acquired during in situ heating of m-Pr₂Co₃Ge₅ within the TEAM I S/TEM from room temperature to 333 K with an energy resolution of 0.25 eV. The final state of the Pr and Co edges after heating (shown in black in Fig. 2, C and D, respectively) were compared to a sample produced in the room-temperature orthorhombic phase (shown in black in Fig. 2, A and B, respectively) to confirm that the sample had been fully transformed in situ under vacuum. A description of the room-temperature EELS for each polymorph can be found in the Supplementary Materials. During the heating process, the Pr M_4,5 and Co L_2,3 edges representing the excitation of core electrons to the partially filled higher energy 4f and 3d orbitals, respectively, were recorded at two intermediate temperature steps.

Fig. 2. Room-temperature and in situ EEL spectra of m-Pr₂Co₃Ge₅ and o-Pr₂Co₃Ge₅.

Core-loss EELS of the Pr M_4,5 (A) and Co L_2,3 edges (B) for room-temperature m-Pr₂Co₃Ge₅ (blue) and o-Pr₂Co₃Ge₅ (black). Dashed lines indicate the peak maxima, highlighting differences in the distribution of density of states between the two structures. Pr valency was determined by fitting reference M_4,5 spectra for Pr³⁺ and Pr⁴⁺ (see Methods) to the acquired data, as shown in the inset of (A). The M₄ edge feature at 945 eV (marked with an arrow) is a signature of Pr³⁺. This feature increases in prominence when the sample undergoes transformation. Temperature-dependent EEL spectra across the structural phase transformation are shown in (C and D). The Pr M_4,5 edges correspond to 4f orbital occupancy and the Co L_2,3 edges to 3d occupancy. The shading in (C) shows the linear fit contributions of the initial and final structures’ M_4,5 edges to the spectra of the intermediate structures, indicating a gradual transition in Pr valency with structural transformation. The total integrated area of the spectra taken at room temperature and 333 K are shaded beneath their respective curves. Data were normalized on the basis of the M₅ or L₃ edge maxima.

Upon heating, several changes are observed in the Pr EEL spectra. A lower-energy satellite edge emerged on the Pr M₄ edge of m-Pr₂Co₃Ge₅ (see arrow in Fig. 2A), indicating a change in Pr valence from a dominantly Pr⁴⁺ state to a dominantly Pr³⁺ state most likely due to an increase in electron filling of the 4f orbitals and reconfiguration of the Pr 4f electronic states. In addition, the edge onset, defined as 10% the peak maxima, increases from 925.02 to 925.65 eV, indicating that the ionization energy required for an electron to transition from the core level to the 4f valence band is greater at 333 K. We also observe an increase in both the M₅:M₄ edge height ratio and a decrease in total integrated area (see Supplementary Materials) upon heating. The reduction in unoccupied 4f states indicated by the decrease in integrated area implies a greater filling of the 4f orbitals in the high-temperature state of m-Pr₂Co₃Ge₅. Multiple linear least squares (MLLS) fits (see Methods) of room-temperature m-Pr₂Co₃Ge₅ reveals a valence state of Pr^3.80(5)+ compared to Pr^3.00(5)+ in room-temperature o-Pr₂Co₃Ge₅. At 333 K, the MLLS fits of m-Pr₂Co₃Ge₅ yield a valence of Pr^3.16(5)+, in good agreement with the in situ PXRD, which indicate a β angle slightly greater than 90°. It is important to note that the MLLS method relies on the precision of the reference spectra and does not account for differences in coordination environment or data collection methods. While the exact values of the Pr oxidation state may differ from the determined values, the change from tetravalent to trivalent with heating is clear.

The maxima of the Co L_2,3 edges in m-Pr₂Co₃Ge₅, shown with dotted lines in Fig. 2D, shift to lower energy upon heating while the edge onsets remain relatively constant or shift slightly higher in energy. The L₃:L₂ edge height ratio remains constant across the phase transition. Given the alteration to the Co interatomic distances during the phase transition, it is not unexpected that we observe corresponding energy shifts in the Co L_2,3 edge maxima and smaller peaks in the edge tails. Specifically, we observe a broader energy-loss range for electron transitions in the room-temperature m-Pr₂Co₃Ge₅ Co spectra compared to those measured at 333 K, indicating an increased diversity in energy transition pathways and, consequently, a greater variety of potentially unoccupied final 3d states.

EEL spectra of Pr valence transitions in cobalt containing oxides indicate nearly identical modifications of Pr M_4,5 edges as reported here; however, large changes in the Co L_2,3 edges were not observed despite O K edge modifications indicating alterations to the Co oxidation state (38). Ultimately, in situ EELS conclusively demonstrates that the observed variations in the electronic states of Co and Pr are inherent to the structural differences of the Pr₂Co₃Ge₅ polymorphs.

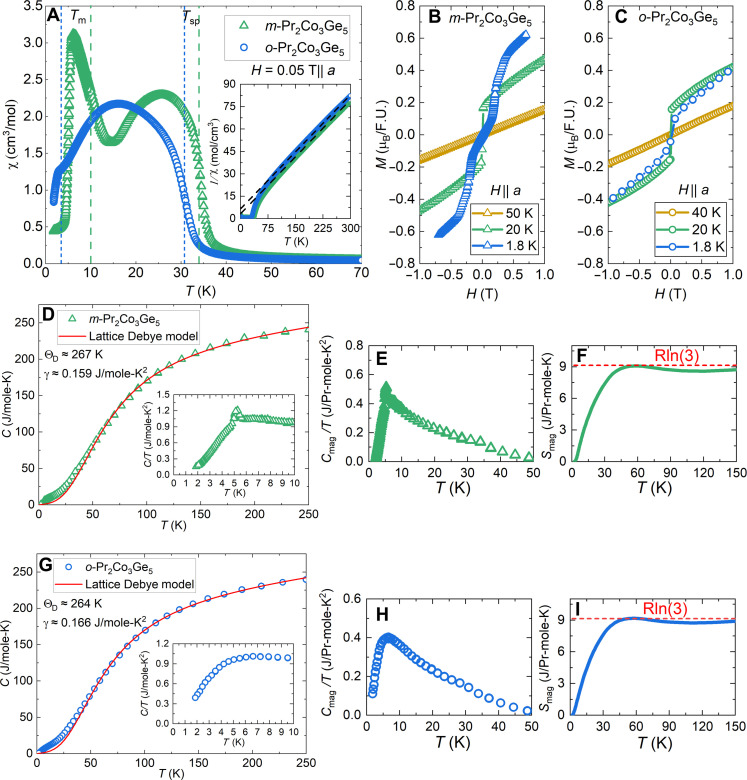
While we would expect a reduction in effective magnetic moment, magnetic saturation moment, and magnetic entropy associated with the nearly tetravalent Pr state of m-Pr₂Co₃Ge₅ when compared to the room-temperature stabilized o-Pr₂Co₃Ge₅, magnetic and transport measurements of both polymorphs indicate that this is not the case. The temperature-dependent magnetic susceptibility is shown in Fig. 3 and fig. S5 and are summarized in table S3. The differences in the magnetic ordering of the two polymorphs is most visible with applied fields of H = 0.05 T parallel to the a crystallographic direction, where two ordering events, T_sp = 30.8 K and T_M = 3.4 K, are visible for o-Pr₂Co₃Ge₅ that shift to higher temperatures, T_sp = 35.3 K and T_M = 10 K, for m-Pr₂Co₃Ge₅ (Fig. 3A).

Fig. 3. Magnetic and transport properties of m-Pr₂Co₃Ge₅ and o-Pr₂Co₃Ge₅.

(A) Zoomed temperature-dependent magnetic susceptibility of m-Pr₂Co₃Ge₅ and o-Pr₂Co₃Ge₅ at H = 0.05 T||a. The inset shows the inverse magnetic susceptibility and Curie-Weiss fit for the entire temperature range. (B and C) Zoomed field-dependent magnetization with H||a per formula unit of m-Pr₂Co₃Ge₅ (triangles) and o-Pr₂Co₃Ge₅ (circles) at T = 1.8, 20, and 40, or 50 K (blue, green, and yellow, respectively). Magnetic data for o-Pr₂Co₃Ge₅ were obtained from prior work (37). (D and G) Temperature-dependent heat capacity with a Lattice Debye fit for m-Pr₂Co₃Ge₅ and o-Pr₂Co₃Ge₅, respectively. The insets feature the low-temperature behavior of the heat capacity. (E and H) Magnetic contribution to the heat capacity. (F and I) Temperature-dependent magnetic entropy.

The inverse susceptibility data indicates a linear Curie-Weiss dependence. Both polymorphs have an effective magnetic moment μ_eff ~ 4.0 μ_B/Pr, elevated from the calculated value of a Pr³⁺ ion, μ_calc = 3.58μ_B/Pr³⁺, implying a Co contribution to the magnetic moment. Weiss constants for o-Pr₂Co₃Ge₅ and m-Pr₂Co₃Ge₅, summarized in table S3, are consistent from H = 0.05 to 0.5 T and indicate dominant antiferromagnetic interactions along the a direction and dominant ferromagnetic interactions along the c direction. The potential for Co magnetic contribution prevents an unambiguous quantification of Pr moment between the two polymorphs through bulk magnetic measurement and will require magnetic structure determination (e.g., using neutron scattering). However, the magnetic contribution of Co can be estimated using the oxidation states determined from EELS (see Methods), resulting in μ_calc = 2.32 μ_B/Co for Pr^3.80(5)+ in m-Pr₂Co₃Ge₅ and μ_calc = 1.35 μ_B/Co for Pr^3.00(5)+ in o-Pr₂Co₃Ge₅. On the basis of these calculations, the Co contribution to the magnetic moment is decreased in o-Pr₂Co₃Ge₅, countering the increased Pr magnetic contribution from the trivalent oxidation state.

From field-dependent magnetization applied along the a direction at 20 K (Fig. 3, B and C, and figs. S6 and S7), o-Pr₂Co₃Ge₅ attains a saturation moment of μ_sat = 1.36 μ_B/F.U. and m-Pr₂Co₃Ge₅ a value of μ_sat = 1.66 μ_B/F.U., far below the expected saturation moment for Pr³⁺ (μ_sat = 6.40μ_B/F.U.) or Pr⁴⁺ (μ_sat = 4.28 μ_B/F.U.) assuming no Co contribution. When measured along the c direction at 1.8 K (figs. S6 and S7), the magnetic saturation is higher, μ_sat = 3.66 and 2.60 μ_B/F.U. for o-Pr₂Co₃Ge₅ and m-Pr₂Co₃Ge₅, respectively, but this is still less than half the expected value based on the oxidation states determined from EELS. In both cases, it is likely that the reduced magnetic saturation value can be attributed to crystal electric field splitting of the full J multiplets; however, additional measurements such as inelastic neutron scattering are needed to understand the crystal electric field splitting. The monoclinic polymorph exhibits multiple metamagnetic transitions at fields less than 0.7 T applied along the a direction while the orthorhombic polymorph does not. In addition, m-Pr₂Co₃Ge₅ saturates more rapidly up to 0.7 T than o-Pr₂Co₃Ge₅, attaining magnetizations of 0.60 and 0.30 T, respectively. Similar behavior is observed with magnetic field applied along the c-direction, where the monoclinic polymorph is more responsive to weak magnetic fields.

The heat capacity data of the two polymorphs is shown in Fig. 3, D and G. Above 50 K, the two polymorphs are indistinguishable, which is expected given that the similarities between the lattices are likely to produce similar phonon behaviors. The broad magnetic contributions below 50 K in both polymorphs are expected from the ferromagnetic ordering observed in susceptibility measurements and show that the initial ordering for both polymorphs is not abrupt, possibly because of magnetic frustration. The distinct lambda feature at 5 K in m-Pr₂Co₃Ge₅ (Fig. 3D, inset, and E) is absent in o-Pr₂Co₃Ge₅ (Fig. 3, G, inset, and H) and corresponds to the prominent spin reorientation observed at 10 K in temperature-dependent magnetic susceptibility measurements. To obtain the magnetic contribution to the specific heat and the magnetic entropy of m-Pr₂Co₃Ge₅ and o-Pr₂Co₃Ge₅, we fit the heat capacity to a lattice-Debye model (Methods) and subtracted it from the measured heat capacities of each polymorph (Fig. 3, F and I, respectively). For both polymorphs, the experimental magnetic entropy is reduced from a theoretical value of either Rln(9) for Pr³⁺ or Rln(6) for Pr⁴⁺ each attaining a value of Rln(3) at 50 K. This is consistent with the effects of crystal field splitting but may be difficult to interpret because of the presence of Co magnetism. The Sommerfeld coefficients are approximately γ = 0.159 J/mol-K² for m-Pr₂Co₃Ge₅ and γ = 0.166 J/mol-K² for o-Pr₂Co₃Ge₅ indicating a moderately correlated system that, when considered with the broad curvature in electrical resistivity measurements observed in prior work (36, 37), could suggest Kondo lattice behavior.

DISCUSSION

The large change in Pr valence is notable given the unit cell volume of room-temperature m-Pr₂Co₃Ge₅ sees a contraction of only ΔV = −0.52(1) ų when compared to the high-temperature transformed m-Pr₂Co₃Ge₅. In addition, neither the Pr-Ge, nor the Pr-Co interatomic distances undergo substantial contraction to accommodate the smaller atomic radii of the Pr⁴⁺ dominant state in room-temperature m-Pr₂Co₃Ge₅ relative to the Pr³⁺ state at 343 K. However, lattice volume contraction does not always directly correlate with the degree of valence transition (39). Upon heating, Pr transforms from an 8-coordinate system in m-Pr₂Co₃Ge₅ to a 12-coordinate system in o-Pr₂Co₃Ge₅, which could motivate a change in interaction of the Pr 4f and conduction electrons. The effects of local point group symmetry on the valence behavior of Pr are well known, where loss of cubic symmetry typically generates a singlet ground state and lack of strong Kondo interactions unless a low-lying singlet state can form (40–43). The increase in point symmetry from m-Pr₂Co₃Ge₅ to o-Pr₂Co₃Ge₅ could tune the crystal electric field of Pr from a quasi-doublet state to a singlet state that, given strong enough hybridization with neighboring p and d electrons, could motivate a transition from an intermediate valent state like what has been described for Pr-based skutterudites (44) to a fully trivalent sate. The largely reduced saturation magnetic moments and experimental magnetic entropies for both polymorphs suggest strong crystal electric field splitting of the Pr J multiplets. However, in this case, larger differences between the two polymorphs’ experimental magnetic entropies and Sommerfeld coefficients would be expected, as these metrics are strongly tied to the crystal field splitting schemes. It is possible that the Co contribution to the magnetic moment is adding additional complexity to the interpretation of ΔS_mag and γ.

The loss of Co dimerization across the structural phase transformation of m-Pr₂Co₃Ge₅ suggests that the structural dimorphism could be motivated by an electronic instability due to an unfilled transition metal valence shell, as previously shown for many binary intermetallic compounds (45). To account for this lack of electrons, transition metal–transition metal (M─M) bonding occurs, effectively reducing the required electron count from 18 e⁻/M to some 18-n e⁻/M, where n is the number of electron pairs formed via M─M bonding. While more complex bonding analysis is required to fully grasp the influence of Co─Co bonding on the oxidation state of Pr in Pr₂Co₃Ge₅, it would not be an isolated case. On the basis of spectral and structural evidence, however, the behavior of m-Pr₂Co₃Ge₅ is distinct from these previous observations in that both the lanthanide and transition metal become more oxidized without marked changes in bond lengths or unit cell size. The lack of electron transfer between the lanthanide and transition metals, as observed in other systems like CeRhGe (46), suggests that the Ge atoms are withdrawing electrons. The determination of electron transfer and bonding in lanthanide–transition metal–germanides is a complex issue that is still under investigation due to the similar electronegativities of group 8 to 10 transition metals and Ge (47). Still, Ge has been determined to participate in strong polar-covalent interactions with alkali metals and La (48). It is possible that the strong lanthanide–transition metal interactions exhibited in the 4d transition metal lanthanide germanide systems (49, 50) departs from what is observed for Pr₂Co₃Ge₅ because of the lower electronegativities of the 3d transition metals. While the role of the transition metal and tetrel elements in the formation of tetravalent Pr are not presently clear, we can broadly state that further investigations should be focused toward 3d transition metal germanides that likely have electronic instabilities, i.e., structural phase transformations. Naturally, this demonstrates the importance of future temperature-dependent spectroscopic and structural investigations in the A₂M₃X₅ family of compounds, but other tetragonal to monoclinic deformations have been found in systems of the ThCr₂Si₂ (51), BaNiSn₃ (52), and CaBe₂Ge₂ structure types (53) which may also host Pr intermediate valence behavior.

While a combination of computational and inelastic scattering experiments would be required to fully elucidate the mechanism responsible for the nearly Pr⁴⁺ valence state in m-Pr₂Co₃Ge₅, it is most likely that a combination of changing symmetry and 4f hybridization across the structural phase transformation are responsible. Tangentially, lattice vibrations could also be playing a role in the structural phase transformation of m-Pr₂Co₃Ge₅. The configuration of bonds within the constraints of the 18-n rule can undergo rearrangement due to electron-phonon interactions as illustrated by the temperature-dependent phase transformation of IrIn₃ (54). The presence of charge density waves in compounds isostructural to Pr₂Co₃Ge₅ seems to suggest a complicated interplay between valence, vibrational, and electronic states.

We have shown a marked hidden valence change in a Pr-based intermetallic compound linked to a monoclinic to orthorhombic second-order phase transformation in Pr₂Co₃Ge₅. The nature of the Pr valence state in m-Pr₂Co₃Ge₅ and o-Pr₂Co₃Ge₅ was confirmed through in situ PXRD and in situ EELS across the structural phase transformation of m-Pr₂Co₃Ge₅. While the origin of the Pr valence transition is not clear on the basis of bulk heat capacity and magnetic measurements, its implications for understanding the duality between local/itinerant 4f states and the moderately correlated nature of Pr₂Co₃Ge₅ make it a promising platform for future investigations of Pr-based mixed valent intermetallic compounds. Given the ubiquity of the U₂Co₃Si₅ structure type, many more examples of structural phase transformations might be found in the A₂M₃X₅ system. Developing our understanding of the relationship between valence and structure in Pr-based intermetallic compounds enables design of strongly correlated materials capable of accessing presently unfound quantum states based on magnetic lanthanides and actinides with unstable valences.

METHODS

Synthesis

o-Pr₂Co₃Ge₅ and m-Pr₂Co₃Ge₅ were synthesized using the flux growth method, where Sn was the low–melting metal flux and elements were weighed out in the stoichiometric ratio of 3 Pr:2 Co:7 Ge:50 Sn. The reactants were transferred into an alumina Canfield crucible set (55) and sealed in a fused silica tube with ~1/3-atm argon gas. For o-Pr₂Co₃Ge₅, the ampoule was placed in a furnace set to 300°C, raised to 1175°C at a rate of 150°C/hour, and dwelled for 6 hours, whereas for m-Pr₂Co₃Ge₅, the ampoule was raised to 1175°C at a slower rate of 100°C/hour and dwelled for longer (24 hours). In both cases, the samples were cooled to 815°C at a rate of 3°C/hour before being removed, inverted, and centrifuged at 815°C to separate excess Sn from the large (1 to 5 mm in length) polyhedral crystals. The remaining Sn flux was etched using 1:1 HCl:H₂O, with a yield of approximately 80%. Almost all reactions produced members of the Pr_n+1Co_nGe_3n+1 homologous series (56) as a side product, but this phase was easily removed because of its plate like morphology and size (~2 mm by ~2 mm). In addition, trace amounts of PrCoGe₃ are evident in high-resolution PXRD.

While the synthetic conditions presented above are different for each polymorph, the formation of o-Pr₂Co₃Ge₅ is challenging. We initially attempted to reproduce o-Pr₂Co₃Ge₅ by varying the duration of the high-temperature dwell step ranging from 4 to 48 hours but obtained only the monoclinic polymorph. From here, we investigated the possibility that o-Pr₂Co₃Ge₅ was a metastable high-temperature polymorph. Reheating and annealing of m-Pr₂Co₃Ge₅ sealed in an evacuated quartz ampoule followed by quenching in either ice water, icy brine, or liquid nitrogen were also unsuccessful in stabilizing o-Pr₂Co₃Ge₅, but this could be due to the reduced rate of heat transfer caused by the quartz ampoule. We then moved to altering the postsynthetic conditions directly from the final dwell temperature of 815°C including varying the centrifugation speed, precooling the centrifuge with dry ice, and inverting the reaction ampoule directly into liquid nitrogen but were unsuccessful in obtaining the orthorhombic polymorph. While some reactions have been successful in synthesizing o-Pr₂Co₃Ge₅, m-Pr₂Co₃Ge₅ is the more common product.

Powder x-ray diffraction

High-resolution in situ PXRD data (λ = 0.458977 Å) were collected in the 2θ range from 0.5° to 28° on a ground single crystal of m-Pr₂Co₃Ge₅ at the 11-BM beamline at the Advanced Photon Source of Argonne National Laboratory. TOPAS was used to perform a sequential Rietveld refinement, identifying m-Pr₂Co₃Ge₅ as the dominant phase with PrCoGe₃ (less than 1 wt %) and Sn (less than 4 wt %) as impurity phases. The PrCoGe₃ and residual Sn from flux growth most likely originate from excess flux that remained on the surface of the crystal after acid etching. For in situ experiments, samples were placed in Kapton capillaries and heated using a hot gas blower in 5-K increments from 298 to 373 K and back. For each measurement, the sample was held for 30 min at temperature before diffraction data were collected to ensure the sample was at equilibrium.

Anisotropic susceptibility and transport measurements

Magnetic properties measurements were performed on oriented single crystals of m-Pr₂Co₃Ge₅ and o-Pr₂Co₃Ge₅ using a Quantum Design VSM magnetic property measurement system. For m-Pr₂Co₃Ge₅, all anisotropic measurements were performed with crystal oriented relative to the I-centered monoclinic unit cell to allow direct comparison between the two polymorphs. The magnetization measurements were performed at constant temperatures of T = 1.8, 10, 20, 30, 40, and 50 K for o-Pr₂Co₃Ge₅ and T = 1.8 K under applied magnetic fields (H) from −7 to 7 T. For the zero field–cooled and field-cooled magnetic susceptibility measurements, the sample was cooled down to 1.8 K with no applied field before heating to 300 K and cooling back down to 1.8 K with an applied field of H = 0.2 T. In both cases, single crystals were mounted such that the magnetic fields were parallel to a, b, and c axes. Heat capacity (C) was measured from 1.8 to 250 K using a Quantum Design physical property measurement system.

The magnetic contribution of Co can be estimated using Eq. 1

$${{\mathrm{\mu }}_{\text{eff}}}^2=n_{\text{Pr}}{({\mathrm{\mu }}_{\text{calc}})}^2+n_{\text{Co}}{({\mathrm{\mu }}_{\text{calc}})}^2$$ (1)

where μ_eff is the effective magnetic moment per formula unit determined from Curie-Weiss fit of the inverse magnetic susceptibility (Fig. 3A, inset), μ_calc is the calculated Pr or Co contribution based on valences determined from EELS, n_Pr is the number of moles of Pr per formula unit, and n_Co is the number of moles of Co per formula unit. For m-Pr₂Co₃Ge₅ with μ_eff = 5.58 μ_B/F.U. (H = 0.05 T||a) and μ_calc = 2.74 μ_B/Pr for a valence of Pr^3.80(5)+, then the expected Co contribution to the effective magnetic moment is μ_calc = 2.32 μ_B/Co. Following the same procedure for Pr³⁺ in o-Pr₂Co₃Ge₅, we obtain a Co contribution of μ_calc = 1.35 μ_B/Co.

The heat capacity was fit to a lattice-Debye model shown in Eq. 2

$$C=\mathrm{\gamma }T+C_{\mathrm{D}}{\left(\frac{T}{{\mathrm{\theta }}_{\mathrm{D}}}\right)}^3{\int }_0^{{\mathrm{\theta }}_{\mathrm{D}}/T}\frac{x^4{e}^x}{{(e^x-1)}^2}\mathit{dx}$$ (2)

where x = hω/κ_BT, ω is the Debye frequency, θ_D is the Debye temperature, and C_D is a constant containing numbers of oscillators and degrees of freedom. To obtain the magnetic contribution to the specific heat and the magnetic entropy, these fits were subtracted from the measured heat capacities of each polymorph.

Energy-dispersive x-ray spectroscopy

Elemental maps were collected in a FEI ThemIS operated at 300 kV with a Super-X energy-dispersive x-ray spectroscopy (EDS) detector. The energy resolution of the system is 140 eV. The composition of m-Pr₂Co₃Ge₅ was measured as 17.9–atomic % (at %) Pr, 35.2–at % Co, and 46.9–at % Ge (Pr₂Co_3.9Ge_5.2). The composition of o-Pr₂Co₃Ge₅ was measured as 17.8–at % Pr, 31.5–at % Co, and 50.7–at % Ge (Pr₂Co_3.5Ge_5.7). EDS maps were acquired over 5 min from bulk regions of the sample with drift correction enabled. No other elements, including Sn, which is used during flux synthesis, were detected in quantities above their fit errors.

Electron energy-loss spectroscopy

The TEAM I, an aberration-corrected transmission electron microscope, was used to collect dual EELS spectral images in probe-corrected scanning transmission electron microscopy mode that include the zero-loss peak and either the L_2,3 edges (2p → 3d) of Co or the M_4,5 edges (3d → 4f) of Pr. The following acquisition parameters were used: a 17-mrad convergence angle, 400-mm camera length, 90-meV dispersion, and 2.5-mm energy filtering slit. Core-loss EELS was collected from a 40-nm-thick region of an electron-transparent lamella of m-Pr₂Co₃Ge₅. The lamella was tilted off zone axis to avoid orientation-specific channeling effects.

The room-temperature orthorhombic and monoclinic Pr M_4,5 edges were fit using MLLS to determine the Pr oxidation state. MLLS fits were performed using spectra obtained from Pr₂O₃ and BaPrO₃ as references for Pr³⁺ and Pr⁴⁺, respectively (57, 58). Fitting the edges indicates that the orthorhombic sample is 90 to 100% Pr³⁺ and 0 to 10% Pr⁴⁺ (95% +/− 5% Pr³⁺). As for the monoclinic sample, the valence states are 75 to 85% Pr⁴⁺ and 15 to 25% Pr³⁺ (20% +/− 5% Pr³⁺). The MLLS fits require a trade-off between fitting the fine features and fitting the general edge shapes. The fine features were weighted more heavily, particularly those visible in the M₄ edge, in determination of oxidation state because of the broadening issues that would influence peak shapes and the dependency of location on the energy axis on crystal structure.

Using a Gatan model 652 double-tilt heating holder, the temperature of the lamella was raised from room temperature (approximately 297 K) until changes in the Pr were first observed. This occurred around 318 K. The temperature was held for 2 min, and then EELS images from both the Co L_2,3 and Pr M_4,5 energy regimes were collected. The temperature was then raised to 328 K, and spectral images were collected again following the same procedure. Last, the holder temperature was raised to 333 K, held at that temperature for 2 min, and then allowed to cool back to room temperature before EELS was performed. There is an estimated 5-K systematic error in the temperature control of the heating holder within this temperature range.

Supplementary Materials

This PDF file includes:

Supplementary Text

Figs. S1 to S7

Tables S1 to S3

References