Abstract
The current study is carried out to find out the stable wheat genotype in ambient and high temperature planting conditions. The objective was to estimate the genotype x environment interactions through various univariates and multivariate techniques. Twenty wheat genotypes were evaluated at Jabalpur, Narmadapuram, and Sagar districts of Madhya Pradesh, India, across cropping years 2019–20 and 2021–21, considering both timely and late planting conditions. The univariate and multivariate stability analysis were performed based on per-plant grain yield and grain filling rate. Our result revealed that environment, genotype, and GEI effects were significant (P < 0.001) across all the environments. The wheat genotypes JW3288, L8, and L13 have been discerned as top performers, exhibiting remarkable stability in grain yield per plant. Similarly, for grain filling rate, genotypes L11 and L13 have emerged as superior and consistently stable performers. Notably, the AMMI and GGE models demonstrated superior effectiveness and accuracy compared to the linear regression model. In conclusion, based on thorough univariate and multivariate stability analyses, L13 emerges as the most stable genotype across all environments under both planting conditions. Consequently, L13 holds promise for inclusion in future breeding programs. It's noteworthy that Jabalpur stands out as the most discriminating and representative environment among all the conditions assessed.
Subject terms: Plant sciences, Plant breeding
Wheat (triticum aestivum L.) is a most widely consumed cereal crop in the world1. It undergoes widespread cultivation on a global scale, with India assuming a pivotal role as a primary region where it serves as an indispensable staple food. In the prevailing circumstances, high temperatures have been identified as a foremost determinant in the reduction of wheat yield2–7. Predictable wheat yield nearly suffers from 6 to 10 percent per one ◦C increase in temperature at the grain-filling stage8–10. Rao et al.11 described 0.28 ◦C and 0.32 ◦C per decade increase in the least and extreme temperatures, respectively over wheat-growing parts of India. The central zone of India is determined as the most heat-prone area12. Nearly ~ 42%, wheat cultivating area has suffered by heat stress in the central zone of India13.
In earlier studies, researchers predominantly identified wheat genotypes demonstrating stable yield in the North Plain Zone of India14–16. Nevertheless, the exigency for a stable, heat-tolerant wheat variety is notably urgent in Central India16. While specific research has historically focused on the stability of wheat grain yield, recent studies have appropriately shifted their focus towards elucidating the genotype-environment interaction (GEI) for grain yield17,18. The meticulous control of grain yield involves a substantial number of genes with a heritability ranging from low to moderate19. The analysis of multi-environmental data under both heat stress and non-stress conditions, researchers sought to unravel the intricate interactions between genotype and environment for heat stress and non-stress conditions14,20–22.
The elucidation of genotype by environment interaction (GEI) patterns is facilitated through the application of two principal methodological approaches: regression-based models, as showcased by the frameworks established by Eberhart and Russell; and advanced multivariate stability prediction methods, exemplified by additive main effects and multiplicative interaction (AMMI), as well as genotypic main effects plus genotype by environment interaction (GGE) biplot analysis20,23,24. A biplot is like a special chart that helps show information from a table in two directions. It lets us see how things in rows are related and how things in columns are related at the same time. This helps us understand the connections between both rows and columns in a simple picture25,26. The first-time people used biplots to study farm data and pick the best model, when they looked at information from a multilocation trials of cotton27. After that, biplots were used to study tables that show how different types of plants interact with different environments28. Many plant breeders and agricultural researchers using the biplot tool because it's helpful in evaluating crop plants in different environments. Its popularity grew after it was successfully used for these purposes29,30. The additive main effects and multiplicative interaction (AMMI) model, characterized by its multiplicative nature, effectively gauges genotype by environment interaction (GEI) components through sophisticated multidimensional methodologies, demonstrating high discriminatory power in the estimation of such components31,32. Concurrently, the genotypic main effects plus genotype by environment interaction (GGE) biplot analysis serves as a valuable tool for delineating mega-environments, establishing stable genotype rankings, and pinpointing ideal varieties with consistent performance over the heat stress and non-stress conditions16,33. The GGE biplot was evaluated by Gauch et al.34 for decomposing G + G x E, while they still appealed that GGE biplots interpret G + G x E more exactly than AMMI stability35–37. The GGE biplot studies have been extensively used to describe macro environments, aspect genotype ranks, and correspondingly to find environments that are representative and discriminative7. By incorporating both main effects and interaction effects, AMMI and GGE biplots provide a comprehensive understanding of how wheat varieties respond in different climatic regimes of Central India. However, the primary objective of current study was to organize different places where plants experience stress into specific large categories called mega-environments. This helps us decide which locations affect plants in similar ways, and we can then exclude certain places from future testing. Additionally, we aim to find the best places for future tests and figure out which plant types are stable and superior in heat stress and non-stress environment. These high-quality plant types can be used as different varieties or sources for a particular mega-environment or even for adapting to a wide range of environments with heat stress tolerance.
Materials and methods
Experimental material
A set of 240 recombinant inbred lines was meticulously bred at the Indian Institute of Wheat and Barley Research in Karnal. This was accomplished through a meticulous crossing of the heat-susceptible parent (MACS2496) and the heat-tolerant parent (WH730), a contrast pairing that has been confirmed and validated by many researchers5,38–41. Among the 240 recombinant inbred lines fifteen-heat tolerant recombinant inbred lines were recognised by Department of Plant Breeding and Genetics JNKVV Jabalpur based on their performance and heat susceptibility index. Hence the identified stable recombinant inbred lines were still not registered anywhere. To further identification of stable performing recombinant inbred lines for ambient and high-temperature planting conditions. The analysis of genotype-environment interaction was meticulously conducted. To performing the analysis the selected heat tolerant recombinant inbred lines along with two parents (WH730 and MACS2496) and three commercial checks (GW322, JW3382, and JW3288), were planted at three locations (Jabalpur, Narmadapuram and Sagar), two cropping years (2019–20 and 2020–21) and two planting conditions (timely and late) of Madhya Pradesh (Table 1 and Supplemental Table s1 and s2).
Table 1.
Pedigree and heat susceptibility indices of studied wheat genotypes.
| Genotypes | Y(hsi) | Pedigree | Origin |
|---|---|---|---|
| Heat tolerant recombinant inbred lines | |||
| L1 | 0.03 | MACS2496/WH730 | IIWBR, Karnal |
| L2 | 0.12 | MACS2496/WH730 | IIWBR, Karnal |
| L3 | 0.21 | MACS2496/WH730 | IIWBR, Karnal |
| L4 | 0.23 | MACS2496/WH730 | IIWBR, Karnal |
| L5 | 0.25 | MACS2496/WH730 | IIWBR, Karnal |
| L6 | 0.28 | MACS2496/WH730 | IIWBR, Karnal |
| L7 | 0.28 | MACS2496/WH730 | IIWBR, Karnal |
| L8 | 0.37 | MACS2496/WH730 | IIWBR, Karnal |
| L9 | 0.38 | MACS2496/WH730 | IIWBR, Karnal |
| L10 | 0.38 | MACS2496/WH730 | IIWBR, Karnal |
| L11 | 0.41 | MACS2496/WH730 | IIWBR, Karnal |
| L12 | 0.42 | MACS2496/WH730 | IIWBR, Karnal |
| L13 | 0.43 | MACS2496/WH730 | IIWBR, Karnal |
| L14 | 0.44 | MACS2496/WH730 | IIWBR, Karnal |
| L15 | 0.44 | MACS2496/WH730 | IIWBR, Karnal |
| Parents | |||
| WH730 | 0.45 | CPAN2092/Improved Lok 1 | HAU, Hisar |
| MACS2496 | 1.7 | SERI "S" | ARI, Pune |
| Commercial checks | |||
| GW322 | 1.69 | GW173/GW196 | SDAU, VIJAPUR |
| JW3382 | 0.66 | CHOIX/STAR/3/HE1/3*CNO79//2*SERI/4/GW273 | JNKVV, Jabalpur |
| JW3288 | 1.24 | DOVE/BUC/DL 788–2 | JNKVV, Jabalpur |
Y(hsi) = heat susceptibility index based on grain yield.
Testing environment
Selected heat-tolerant recombinant inbred lines, their parents and commercial checks were tested into timely sown and late sown planting conditions. Timely sown environments designated as NSE (normal sown environment) and late sown environment designated as HSE (heat stressed environment). Under NSE the experimental material was screened in two cropping years (2019–20 and 2020–21) at three locations (Jabalpur, Sagar and Narmadapuram) on the other hand under HSE the experimental material was screened in two cropping years (2019–20 and 2020–21) at two locations (Jabalpur and Narmadapuram). The maximum and minimum day—night temperatures during two cropping years (2019–20 and 2020–21), under NSE, 36.8/16.7–21.4/4.8 °C, 39.1/22.8–23.1/02.1 °C and 39.1/22.8–23.1/02.1 °C, were recorded at Jabalpur, Sagar and Narmadapuram, respectively while under HSE, 39.3/23.2–22/4.8 °C and 41.5/12.2–20.5/2.9 °C, were recorded at Jabalpur and Narmadapuram, respectively (Supplemental Table s5, s6 and s7). Geographically the experimental field of Jabalpur, Sagar and Narmadapuram were located at 23.21, 23.83, and 21.50, latitudes (N) 79.95, 78.71, and 76.43, longitudes (E) and heights from mean sea level were recorded 392, 433, and 229 m, respectively. Geographically, JNKVV's College of Agriculture Jabalpur, Regional Agriculture Research Centre Sagar, and College of Agriculture Narmadapuram were located at latitudes (N) of 23.21, 23.83, and 21.50, longitudes (E) of 79.95, 78.71, and 76.43, and heights(m) from mean sea level of 392, 433, and 229, respectively (Table 2). For the experimental fields in Jabalpur, Sagar, and Narmadapuram, the soil pH values were 7.61, 6.96, and 8.10, respectively (Table 2). Throughout the cropping period, adherence to recommended packages and practices, coupled with the implementation of an optimal number of irrigations, was rigorously maintained.
Table 2.
Experimental details.
| General detail of experimental locations | |||||
|---|---|---|---|---|---|
| Environment | Locations | Planting year | Planting Date | Day night temperature range (°C) | |
| NSE1 | Jabalpur | 2019–20 | 2nd Dec | 36.8/20.4—21.0/6.3 | |
| NSE2 | Sagar | 2019–20 | 2nd Dec | 39.1/22.8—19.5/5.8 | |
| NSE3 | Narmadapuram | 2019–20 | 2nd Dec | 37.6/14.6—17.1/3.1 | |
| NSE4 | Jabalpur | 2020–21 | 2nd Dec | 36.3/16.7—21.4/4.8 | |
| NSE5 | Sagar | 2020–21 | 2nd Dec | 38.1/23.5—23.1/2.1 | |
| NSE6 | Narmadapuram | 2020–21 | 2nd Dec | 36.1/22.5—12.5/4.2 | |
| HSE1 | Jabalpur | 2019–20 | 4th Jan | 39.3/24.0—22.0/7.5 | |
| HSE2 | Narmadapuram | 2019–20 | 4th Jan | 41.5/12.2—20.2/2.9 | |
| HSE3 | Jabalpur | 2020–21 | 4th Jan | 38.8/23.2—21.4/4.8 | |
| HSE4 | Narmadapuram | 2020–21 | 4th Jan | 40.3/24.5—20.5/4.2 | |
| Geographical detail of experimental locations | |||||
|---|---|---|---|---|---|
| Latitude (N) | Longitude (E) | Altitude (a.m.s.l.) | Soil Colour | Soil pH | Locations |
| 23.21 | 79.95 | 392 | Dark grey | 7.61 | Jabalpur |
| 23.83 | 78.71 | 433 | Black soils | 6.96 | Sagar |
| 21.5 | 76.43 | 229 | Deep black soil | 8.1 | Narmadapuram |
N = North, E = East, a.m.s.l. = Above mean sea level, NSE = normal sown environment, HSE = Heat stress environment, Dec = December, Jan = January.
Design of experiment and data collections
Each experimental trial was conducted in randomised block design with three replications. Numerous component traits were observed manually, including days to heading, days to maturity, thousand kernel weight, grain filling duration, grain filling rate and grain yield per plant. Grain filling rate and grain yield per plant were subjected to the current study. As per Dias and Lidon's42 methodology, the comprehensive span from anthesis to maturity was considered as the grain filling duration. This duration was subsequently utilized to calculate the grain filling rate in grams per day using the formula (total grain yield per plant/grain filling duration).
Statistical analysis
Analysis of variance and association study
Fischer and Maurer's43 method, 1-(ys/yp)/1-(xs/xp), was used to estimate the heat susceptibility index (HSI). Ys stands for yield under stress, Yp for yield without stress, and Xs and Xp stand for mean yields across all cultivars under stress and non-stress circumstances, respectively. "Stress intensity" is the definition of the expression (1- Xs/Xp). To ascertain the variance among grain yield per plant and grain filling rate, a combined ANOVA was performed through various packages of R software version 4.2. Whereas genotypes were measured as fixed factors, environments were measured as random variables. The "corroplot" package of R software was used to perform the pearson association between studied traits and heat susceptibility index, and the resulting model is given as: rG = cov (A, B)/var(A), var(B), where cov (A, B) designates the covariance present among traits, and var (A), and similarly, var (B), displays the genetic alteration of trait44.
Regression based stability analysis
Initially genotype x environment interactions were estimated through regression-based stability models. Eberhart and Russell's model45, the regression coefficient (bi), and the deviation from regression (S2di) are all stability indicators based on regression. These parameters collectively govern the performance of a genotype across a variety of contexts46. The Eberhart and Russell’s stability model45 is given as: Yij = μi + βiIj + δij, where the Yij designates the assessment of ith (i = 1, 2, 3, . . .. . ., x) genotype across the jth (1, 2, 3, . . .. . ., n) environment, μi is the genotype mean, βi designates the regression coefficient, δij demonstrations the deviation from the regression coefficient, and Ij is the environmental index acknowledged by deducting the total mean from each environmental mean47.
AMMI and GGE biplot analysis
Additionally, the multivariate method for stability analysis were directed rendering to AMMI and GGE biplot by means of different statistical packages obtainable in R studio. The “metan” package of R studio was practical for AMMI analysis, while the GGE Biplot GUI package was working for GGE biplot based analysis. In the AMMI model, the ANOVA and PCA are compound collected into an individual statistical package. Therefore, GEI exposed to PCA investigation only when key authentication has already been accomplished by means of ANOVA48. The equation for AMMI model is specified as below: Yge = μ + αg + βe + Σnλnγgnδen + ρge, where in circumstance of the additive factors, Yge is display the grain yield and grain filling rate for a specific (g) genotype in an (e) environment, where μ stand for grand mean, αg designates deviation of genotype from the mean, βe is deviation of environment from the mean, λn stands for singular value of n component, γgn designates the value of eigenvector for genotype (g) and δen is the value of eigenvector for e and ρge; which is known as residual49. The AMMI stability values (ASV) were estimated as per Rad et al.49, ASV = √[(SSIPCA1/SSIPCA2) (IPCA1)2] + (IPCA2)2, Where, SSIPCA1 and SSIPCA2 are sum of squares of IPCA1 and IPCA2, respectively and IPCA1 and IPCA2 are the genotypic scores in the AMMI model. Moreover, the equation for GGE biplot model is characterized as: Pij = (yij—μ—δj)/λj = (βi + ϵij)/λj, where Pij is the matrix for genotype i and environment j, μ denotes the grand mean, δj is the column (environment) main effect, λj is an evaluating factor, βi is the row (genotype) main effect, and ϵij characterizes genotype x environment interaction, and yij is genotype and environment, two-way table50. The GGE biplot also includes a group of biplot-based platforms for interpreting interactions between the environment and the genotype. In a general context, for addressing inquiries related to Genotype by Environment (G x E), both GGE biplot and AMMI utilize graphical representations51. In total, the results of both biplot analyses are further interpreted based on the standards established by Khan et al15.The Genomic Selection Index (GSI) was computed following Farshadfar's methodology43, where GSI is defined as the sum of the rank of ASV (RASV) and the mean grain yield rank of the genotype (Rgm).
Bioethical statement
The seed material remains unregistered and has not been submitted to any publicly accessible herbarium. It was acquired from IIWBR, Karnal, through a legally binding agreement, without any associated costs. We emphasize our unwavering commitment to strict adherence to all local, national, and international guidelines and legislation governing the use of plants in this study, as delineated in the editorial policies for research involving plants (https://www.nature.com/srep/journal-policies/editorialpolicies#research-involving-plants).
Results
Combined analysis of variance
The pooled analysis of variance (ANOVA) was used to identify interactions between and within the sources of variation that were examined in this investigation. Table 3 contains the results of the combined ANOVA for grain yield and grain filling rate. Under normal and heat stress environment, omitting the year for grain filling rate under heat stress, replication for grain yield under normal and heat stress environment, the variation owing to genotype (G), location (L), year (Y), G x Y, G x L, and G x Y x L interactions for all two characters was significant, either at 0.001% or 0.05% level of significance. For grain yield and grain filling rate, wheat genotypes shown a considerable degree of heterogeneity.
Table 3.
Combined analysis of variances for wheat genotypes under normal and heat stress environment.
| Sources | Normal sown environment (NSE) | Heat stress environment (HSE) | ||||
|---|---|---|---|---|---|---|
| DF | YLD | GFR | DF | YLD | GFR | |
| Genotype (G) | 19 | 57.81*** | 0.078*** | 19 | 42.97*** | 0.014*** |
| Replication (R) | 2 | 0.82 ns | 0.001* | 2 | 0.0001 ns | 0.006* |
| Location (L) | 2 | 23.78*** | 0.281*** | 1 | 34.77*** | 0.059*** |
| Year (Y) | 1 | 55.36*** | 0.005* | 1 | 13.45*** | 0.001 ns |
| G x L | 38 | 16.81*** | 0.579*** | 19 | 15.89*** | 0.014*** |
| G x Y | 19 | 15.55*** | 0.013*** | 19 | 26.57*** | 0.007*** |
| L x Y | 2 | 14.78*** | 0.043*** | 1 | 33.89*** | 0.041*** |
| G x L x Y | 38 | 15.44*** | 0.012*** | 19 | 22.84*** | 0.008*** |
| Residual | 120 | 0.851 | 0.111 | 80 | 0.317 | 0.001 |
DF = degree of freedom, YLD = grain yield, GFR = grain filling rate, G x L = Genotype x Location, G x Y = Genotype x Year, L x Y = Location x Year, G x L x Y = Genotype x Location x Year, *P < 0.05, ***P < 0.001, ns = non-significant.
Association study
Supplemental Figure s1 illustrates a highly significant correlation (P = 0.001%) between grain filling rate and heat susceptibility index with grain yield. The strong positive and negative correlation originated among grain yield in normal sown environment (r = 0.80) and heat stress environment (r = − 0.82) with heat susceptibility index, respectively. The grain filling rate (r = 0.79) was found significance (P = 0.001%)) strong and positive correlation with grain yield.
Regression based stability analysis
The slope of linear regression (bi) and deviation from regression (S2di) displayed a vast range, for heat tolerant wheat genotypes (Tables 4 and 5). Across normal sown environments, bi for grain yield ranged from 0.22 (L2) to 1.76 (L5), and absolute values of S2di ranged from 0.35 (L12) to 11.20 (WH730) while for grain filling rate bi range from 0.05 (L9) to 2.65 (WH730), and absolute value of s2di ranged from zero (L11) to 0.027 (WH730) (Table 4). On the other hand, across heat stress environments for grain yield, bi ranged from − 1.91 (L10) to 3.13 (MACS2496), with the absolute values of S2diranging from − 0.05 (L15) to 12.4 (L5) (Table 5). Among the wheat genotypes for grain yield, L12 (S2di = 0.35) and L13 (S2di = 0.84) under normal sown environment, L15 (S2di = − 0.05) and L9 (S2di = 0.25) under heat stress environment showed lower S2divalue (Tables 4 and 5). Similarly, for grain filling rate, L11 (S2di = 0.0) under normal sown environment while under heat stress environment WH730, MACS2496 and GW322 (0.0) showed lower S2di value (Tables 4 and 5). Under normal sown environments (NSE) L12 (bi = 1.44, S2di = 0.35) for grain yield and L11 (bi = 1.14, S2di = 0.0) for grain filling rate were identified as most stable genotypes (Table 4). For grain yield L3 (bi = 0.79, S2di = 0.18) and for grain filling rate L6 (bi = 0.85, S2di = 0.007) were identified as most stable wheat genotype under heat stress environments (HSE) (Table 5). Across all the environments, good levels of stability for grain yield were exhibited by WH730 (bi = 0.78, S2di = 0.05), while for grain filling rate L6 (bi = 0.97, S2di = 0.0) followed by JW3382 (bi = 0.93, S2di = 0.0) were found most stable genotype (Supplemental Table s3).
Table 4.
Stability parameters for grain yield and grain filling rate under normal sown environment.
| Genotype | Grain yield | Grain filling rate | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Gm | Rgm | bi | S2di | ASV | RASV | GSI | Gm | Rgm | bi | S2di | ASV | RASV | GSI | |
| Heat tolerant recombinant inbred lines | ||||||||||||||
| L1 | 11.38 | 16 | 0.64 | 2.95 | 1.31 | 7 | 23 | 0.30 | 16 | 0.18 | 0.001 | 0.05 | 1 | 17 |
| L2 | 10.75 | 19 | 0.22 | 4.88 | 2.32 | 11 | 30 | 0.29 | 17 | 0.33 | 0.006 | 0.47 | 13 | 30 |
| L3 | 10.65 | 20 | 0.29 | 8.71 | 1.87 | 9 | 29 | 0.31 | 14 | 0.88 | 0.012 | 0.62 | 17 | 31 |
| L4 | 12.37 | 12 | 0.63 | 0.89 | 0.46 | 2 | 14 | 0.28 | 19 | 0.87 | 0.002 | 0.27 | 9 | 28 |
| L5 | 12.98 | 7 | 1.76 | 9.42 | 3.90 | 17 | 24 | 0.41 | 4 | 1.98 | 0.006 | 0.79 | 18 | 22 |
| L6 | 12.13 | 13 | 0.98 | 4.11 | 1.70 | 8 | 21 | 0.29 | 18 | 0.69 | 0.004 | 0.20 | 6 | 24 |
| L7 | 11.18 | 17 | 1.57 | 5.16 | 2.53 | 12 | 29 | 0.31 | 13 | 1.49 | 0.004 | 0.25 | 8 | 21 |
| L8 | 12.63 | 9 | 0.30 | 7.34 | 3.52 | 16 | 25 | 0.31 | 12 | 0.20 | 0.003 | 0.55 | 14 | 26 |
| L9 | 10.91 | 18 | 0.45 | 10.3 | 4.21 | 19 | 37 | 0.30 | 15 | 0.05 | 0.009 | 0.83 | 19 | 34 |
| L10 | 11.93 | 15 | 0.85 | 5.17 | 2.65 | 13 | 28 | 0.32 | 11 | 0.83 | 0.004 | 0.43 | 12 | 23 |
| L11 | 13.74 | 6 | 1.42 | 2.96 | 1.18 | 5 | 11 | 0.39 | 6 | 1.14 | 0.000 | 0.07 | 2 | 8 |
| L12 | 12.57 | 10 | 1.44 | 0.35 | 0.41 | 1 | 11 | 0.33 | 10 | 1.47 | 0.001 | 0.21 | 7 | 17 |
| L13 | 12.92 | 8 | 1.48 | 0.84 | 0.74 | 3 | 11 | 0.39 | 7 | 1.55 | 0.005 | 0.28 | 10 | 17 |
| L14 | 12.38 | 11 | 0.91 | 6.35 | 2.68 | 15 | 26 | 0.36 | 9 | 0.73 | 0.007 | 0.58 | 16 | 25 |
| L15 | 11.96 | 14 | 0.75 | 6.11 | 2.68 | 14 | 28 | 0.27 | 20 | 0.84 | 0.001 | 0.20 | 5 | 25 |
| Parents | ||||||||||||||
| WH730 | 19.10 | 1 | 1.74 | 11.20 | 5.95 | 20 | 21 | 0.62 | 1 | 2.65 | 0.027 | 1.55 | 20 | 21 |
| MACS2496 | 15.67 | 2 | 1.65 | 10.60 | 3.98 | 18 | 20 | 0.44 | 2 | 1.62 | 0.006 | 0.31 | 11 | 13 |
| Commercial checks | ||||||||||||||
| GW322 | 14.47 | 5 | 1.33 | 3.73 | 1.26 | 6 | 11 | 0.40 | 5 | 1.47 | 0.001 | 0.18 | 4 | 9 |
| JW3382 | 14.83 | 3 | 1.07 | 8.67 | 1.96 | 10 | 13 | 0.38 | 8 | 0.97 | 0.005 | 0.11 | 3 | 11 |
| JW3288 | 14.59 | 4 | 0.51 | 3.58 | 1.10 | 4 | 8 | 0.43 | 3 | 0.06 | 0.009 | 0.56 | 15 | 18 |
Gm = Grand mean, Rgm = Rank of genotypes based grand mean, bi = Regression coefficient of Eberhart and Russell model, S2di = Deviation form regression of Eberhart and Russel model, ASV = AMMI stability value, RASV = Stability rank based on AMMI stability value, GSI = Genomic selection index.
Table 5.
Stability parameters for grain yield and grain filling rate under heat stress environment.
| Genotypes | Grain yield | Grain filling rate | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Gm | Rgm | bi | S2di | ASV | RASV | GSI | Gm | Rgm | bi | S2di | ASV | RASV | GSI | |
| Heat tolerant recombinant inbred lines | ||||||||||||||
| L1 | 11.29 | 10 | 2.44 | 0.97 | 0.498 | 4 | 14 | 0.366 | 17 | 0.61 | 0.002 | 0.2 | 7 | 24 |
| L2 | 10.45 | 17 | − 0.7 | 1.34 | 0.911 | 12 | 29 | 0.352 | 18 | − 1.58 | 0.001 | 0.5 | 17 | 35 |
| L3 | 9.76 | 18 | 0.79 | 0.18 | 0.323 | 2 | 20 | 0.423 | 9 | 2.76 | 0.003 | 0.42 | 15 | 24 |
| L4 | 11.66 | 5 | 1.8 | 6.4 | 1.458 | 17 | 22 | 0.424 | 8 | 2.04 | 0.001 | 0.16 | 5 | 13 |
| L5 | 11.88 | 3 | 0.52 | 12.4 | 2.214 | 20 | 23 | 0.469 | 2 | 0.64 | 0.006 | 0.24 | 9 | 11 |
| L6 | 11.01 | 14 | 0.61 | 3.51 | 1.017 | 13 | 27 | 0.382 | 16 | 0.85 | 0.007 | 0.06 | 1 | 17 |
| L7 | 10.48 | 16 | 1.83 | 1.03 | 0.778 | 11 | 27 | 0.456 | 5 | 1.95 | 0.001 | 0.27 | 11 | 16 |
| L8 | 11.99 | 2 | 0.72 | 1.29 | 0.66 | 7 | 9 | 0.347 | 20 | 0.61 | 0.001 | 0.06 | 2 | 22 |
| L9 | 9.7 | 20 | 1.75 | 0.25 | 0.499 | 5 | 25 | 0.351 | 19 | 1.9 | 0.001 | 0.21 | 8 | 27 |
| L10 | 11.19 | 13 | − 1.91 | 3.14 | 0.726 | 9 | 22 | 0.476 | 1 | 1.29 | 0.02 | 0.51 | 18 | 19 |
| L11 | 12.29 | 1 | − 0.41 | 6.47 | 1.47 | 18 | 19 | 0.429 | 7 | − 0.82 | 0.004 | 0.34 | 12 | 19 |
| L12 | 11.5 | 7 | − 0.31 | 6.18 | 1.61 | 19 | 26 | 0.461 | 4 | − 1.54 | 0.003 | 0.54 | 20 | 24 |
| L13 | 11.54 | 6 | 1.48 | 1.49 | 0.693 | 8 | 14 | 0.454 | 6 | 0.51 | 0.003 | 0.11 | 3 | 9 |
| L14 | 11.2 | 12 | 2.27 | 0.92 | 0.607 | 6 | 18 | 0.467 | 3 | 2.66 | 0.004 | 0.25 | 10 | 13 |
| L15 | 11.4 | 9 | 0.04 | − 0.05 | 0.115 | 1 | 10 | 0.385 | 14 | − 1.29 | 0.001 | 0.44 | 16 | 30 |
| Parents | ||||||||||||||
| WH730 | 11.84 | 4 | 2.59 | 3.35 | 1.31 | 16 | 20 | 0.414 | 11 | 3.33 | 0 | 0.4 | 14 | 25 |
| MACS2496 | 9.71 | 19 | 3.13 | 1.81 | 1.056 | 14 | 33 | 0.39 | 13 | 3.97 | 0 | 0.52 | 19 | 32 |
| Commercial checks | ||||||||||||||
| GW322 | 11.23 | 11 | − 0.87 | 0.89 | 0.426 | 3 | 14 | 0.414 | 12 | − 1.46 | 0 | 0.39 | 13 | 25 |
| JW3382 | 11.44 | 8 | 1.36 | 1.33 | 0.75 | 10 | 18 | 0.416 | 10 | 1.46 | 0.002 | 0.15 | 4 | 14 |
| JW3288 | 10.53 | 15 | 2.85 | 3.63 | 1.291 | 15 | 30 | 0.385 | 15 | 2.09 | 0.004 | 0.2 | 6 | 21 |
Gm = Grand mean, Rgm = Rank of genotypes based grand mean, bi = Regression coefficient of Eberhart and Russell model, S2di = Deviation form regression of Eberhart and Russel model, ASV = AMMI stability value, RASV = Stability rank based on AMMI stability value, GSI = Genomic selection index.
Additive main effect and multiplicative interactions (AMMI) analysis
AMMI based ANOVA
The AMMI-based analysis of variance (ANOVA) results for the current study's evaluations of grain yield and grain filling rate are shown in Table 6 and supplemental table s4. The results showed that G, E, and GEI significantly influenced by grain yield and grain filling rate. The first two interaction principal component analysis (IPCA) axes explained about 68.9, 78.2 and 68.9% of the GEI across normal sown, heat stressed and across all the environments for grain yield, respectively while 68.9, 78.2 and 59.5% of GEI were explained by first two IPCA for grain filling rate in normal sown, heat stress and across all the environments, respectively (Table 6 and supplemental table s4). Across all the environments proportion of total variation contributed by G, E, and GEI were executed for grain yield was 12.8, 12.3, and 35.8, percentage, respectively while for grain filling rate 15.4, 14.5 and 33.7 percentage, respectively (Supplemental table s4).
Table 6.
AMMI-based ANOVA for grain yield and grain filling rate.
| Source | DF | Grain yield | Grain filling rate | ||||
|---|---|---|---|---|---|---|---|
| MSS | Percent explained | p value | MSS | Percent explained | p value | ||
| Under normal sown environment | |||||||
| Environment | 5 | 132.08 | 15.4 | < 0.001 | 0.131 | 13.54 | < 0.001 |
| Block | 6 | 1.14 | 0.2 | 0.234 | 0 | 0.03 | 0.941 |
| Genotype | 19 | 49.17 | 21.8 | < 0.001 | 0.079 | 30.97 | < 0.001 |
| G x E | 95 | 13.61 | 30.2 | < 0.001 | 0.014 | 26.58 | < 0.001 |
| PC1 | 23 | 32.3 | 57.4 | < 0.001 | 0.029 | 52.2 | < 0.001 |
| PC2 | 21 | 13.37 | 21.7 | < 0.001 | 0.01 | 16.7 | < 0.001 |
| PC3 | 19 | 10.07 | 14.8 | < 0.001 | 0.01 | 14.2 | < 0.001 |
| PC4 | 17 | 4.62 | 6.1 | < 0.001 | 0.008 | 10.2 | < 0.001 |
| PC5 | 15 | 0 | 0 | < 0.001 | 0.006 | 6.7 | < 0.001 |
| Residuals | 114 | 0.84 | - | - | 0.001 | - | - |
| Total | 334 | 12.82 | - | - | 0.014 | - | - |
| Under heat stress environment | |||||||
| Environment | 3 | 12.219 | 9.74 | < 0.001 | 0.033 | 6.5 | 0.02 |
| Block | 4 | 0.806 | 0.42 | 0.082 | 0.003 | 0.77 | 0.009 |
| Genotype | 19 | 4.677 | 19.5 | < 0.001 | 0.014 | 17.35 | < 0.001 |
| G x E | 57 | 5.401 | 39.83 | < 0.001 | 0.01 | 35.69 | < 0.001 |
| PC1 | 21 | 6.722 | 45.9 | < 0.001 | 0.014 | 54.3 | < 0.001 |
| PC2 | 19 | 5.635 | 34.8 | < 0.001 | 0.007 | 23.9 | < 0.001 |
| PC3 | 17 | 3.508 | 19.4 | < 0.001 | 0.007 | 21.8 | < 0.001 |
| Residuals | 76 | 0.374 | - | - | 0.001 | - | - |
| Total | 216 | 3.578 | - | - | 0.007 | - | - |
DF = Degree of freedom, MSS = Means of sum squire, G x E = Genotype x Environment and PC = Principal component.
Stable genotypes identified based on AMMI-ASV and GSI value
The AMMI, additive main effects and multiplicative interaction stability value (ASV) is presented for grain yield and grain filling rate under normal sown, heat stress and across all the environments in the Tables 4, 5 and supplemental table s3. The range of ASV value from 0.41 (L12) to 5.95 (WH730) and 0.05 (L1) to 1.55 (WH730) were observed for grain yield and grain filling rate respectively, in normal sown environments (Table 4). Similarly, the range of ASV value from 0.115 (L15) to 2.21 (L5) and 0.06 (L6) to 0.54 (L12) were observed for grain yield and grain filling rate respectively, in heat stress environments (Table 5). For grain yield L12 (ASV = 0.41) in normal sown, L15 (ASV = 0.41) in heat stress and WH730 (ASV = 0.20) across all the environments while for grain filling rate L1 (ASV = 0.05) in normal sown, L6 (ASV = 0.06) in heat stress and L1 (ASV = 0.02) across all the environments were observed as most stable genotypes (Tables 4, 5 and supplemental table s3). The genomic selection index was estimated and presented for grain yield and grain filling rate in Table 4, 5 and supplemental table s3. Genotype with the lowest stability parameter was deemed stable, and that with a lower GSI value had higher mean yield and higher stability. For grain yield the JW3288 (GSI rank = 8) in normal sown, L8 (GSI rank = 9) in heat stress and L13 (GSI rank = 9) in all the environments while for grain filling rate L11 (GSI rank = 8) in normal sown, L13 (GSI rank = 9) in heat stress and GSI rank = 9 was achieved by L11 and L13 in all the environments, suggested that high stable and well performed genotypes (Table 4, 5 and supplemental table s3).
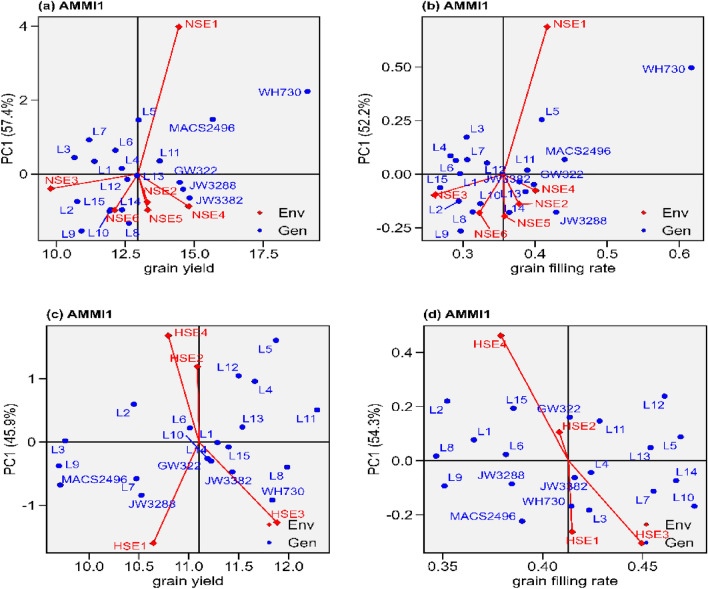
AMMI 1
The AMMI biplots of 20 (Supplemental table s1 and s2) heat stress tolerance wheat genotypes across normal sown, heat stress sown and across both the environmental conditions are presented in Figs. 1, 2, supplemental fig. s2 and s3. In the current study, IPCA1 for grain yield explained 57.4, 45.9, and 46.2% while for grain filling rate 52.2, 54.3 and 39.6% of the variation attributed to GEI in normal sown, heat stress and across both the environmental conditions, respectively (Fig. 1. and supplemental fig. s2). Based on AAMI1, for grain yield NSE4 and HSE3 (Fig. 1a and c) while for grain filling rate NSE1 and HSE3 (Fig. 1b and d) are high-potential environments under normal sown and heat stress environments, respectively. Similarly for grain yield NSE3 and HSE1 (Fig. 1a and b) while for grain filling rate NSE3 and HSE4 (Fig. 1c and d) are low-potential environments under normal sown and heat stress environments, respectively. Similarly, for grain yield and grain filling rate, WH730 are specifically adapted to high-potential environments in normal sown environments while respectively, for grain yield and grain filling rate L11 and L10 are specifically adapted to high-potential environments in heat stress environments, (Fig. 1.). With an almost zero IPCA1 score, the cultivar is said to have a poor interaction with its environment it means the cultivar have high stability. For grain yield and grain filling rate NSE3 (Fig. 1a and b) across normal sown environments while HSE2 (Fig. 1b and d) across heat stress environments had a PCA1 score or vector nearer to zero compared to other environments, specifies lower interaction effect which nearly ensures the better performance of all genotypes in that environment. Hence, for grain yield L1, L13 and GW322 (Fig. 1a) while for grain filling rate L6, L12, L11 and GW322 (Fig. 1b) might be the utmost stable genotypes among the normal sown environments based on IPCA1. Similarly, for grain yield L3, L1 and L15 (Fig. 1c) while for grain filling rate L8, L6, L4 and L13 (Fig. 1d) identified as most stable genotype among heat stress environment. Across all the environments for grain yield and grain filling rate, NSE3 and NSE6 identified as most stable environment respectively, on the other hand, for grain yield L13, L1, L12, L13 and GW322 while for grain filling rate L1, L6, JW3382 and GW322 identified as most stable genotype across all the environments (Supplemental fig. s1).
Figure 1.
The “AMMI1” graphs displays the main effect and IPC1 effect values describing relationship among examined wheat genotypes and environments. (a) grain yield under normal sown environment, (b) grain filling rate under normal sown environment, (c) grain yield under heat stress environment (d) grain filling rate under heat stress environment.
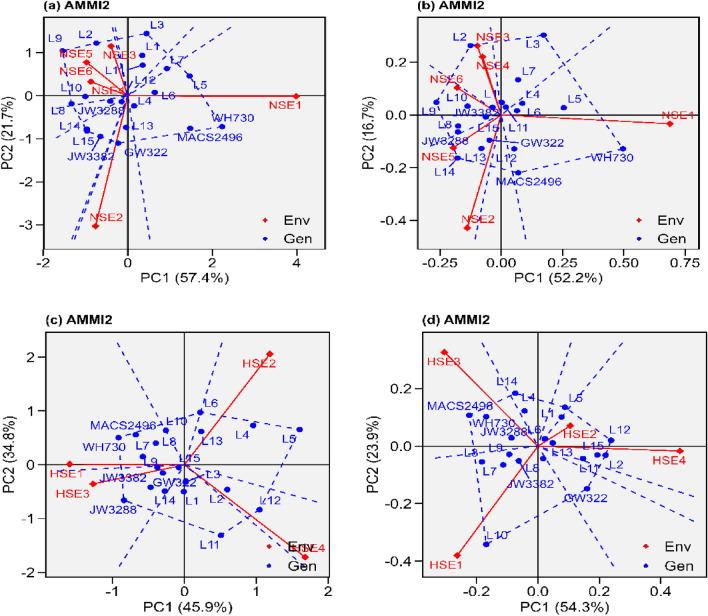
Figure 2.
“AMMI2” graphs displays both the axes of interaction (IPCA1 and IPCA2) values for genotype effect and genotype by environment interaction effect. (a) grain yield under normal sown environment, (b) grain filling rate under normal sown environment, (c) grain yield under heat stress environment (d) grain filling rate under heat stress environment.
AMMI 2
The AMMI2 expose and inferring the difficult GEI that comprises significant multi-environments and finding of genotypes with also broad or narrow spectrum adaptability. For grain yield and grain filling rate under normal sown environments, NSE1 (Fig. 2a and b) while under heat stressed environments, HSE4 for grain yield and HSE1 for grain filing rate was farthest from the origin, suggesting that the best discriminatory ability but was not stable. In contrast, for grain yield NSE4 (Fig. 2a) and for grain filling rate NSE6 (Fig. 2b), across normal sown environments while for grain yield HSE3 (Fig. 2c) and for grain filling rate HSE2 (Fig. 2d) was nearest to the origin, suggesting that was the most stable environment across heat stressed environments. Across all the tested environments NSE3 and NSE4 were very closer to the origin suggested as most stable environments for grain yield and grain filling rate, respectively (Supplemental fig. s2). In contrast to genotypes that are placed apart from one another, genotypes that assemble together on the biplot origin suggested that genotypes have identical response to all tested environment. Also, compared to genotypes that are near positioned to the biplot origin, those that are located away are more vulnerable to environmental interactions.
GGE Biplot analysis
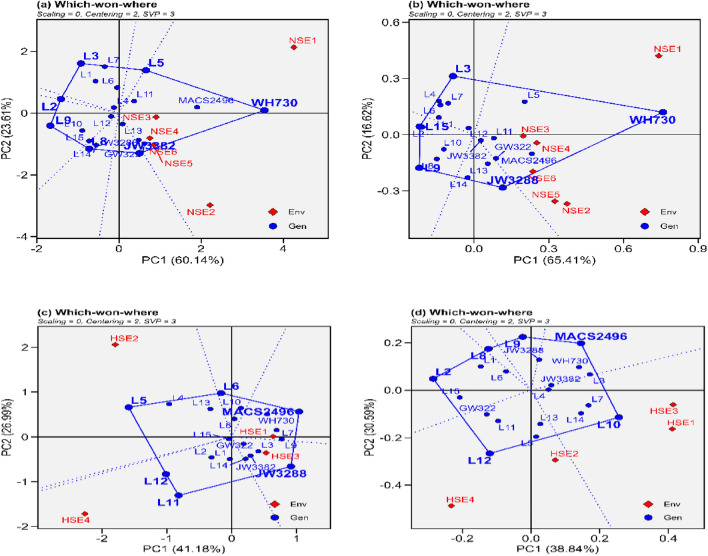
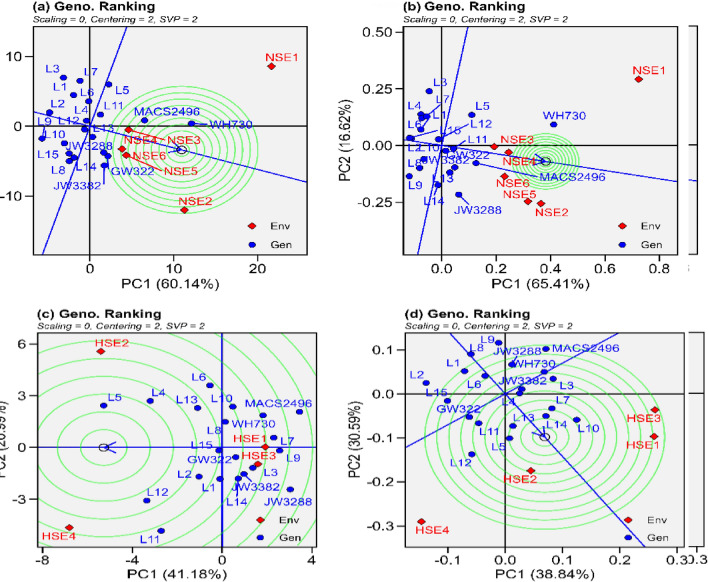
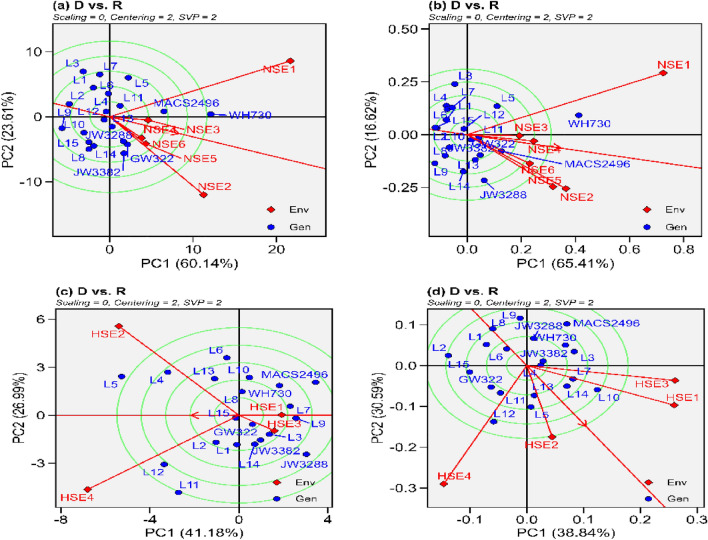
The GGE biplots for grain yield and grain filling rate of 20 selected heat tolerant wheat genotypes are shown in Figs. 3, 4, 5, and 6. As the x axis and y axis, the first and second principal component scores, respectively.
Figure 3.
The polygon view of “Which-won-where” model of GGE biplot representing the performance of wheat genotypes and their interactions with environment. (a) grain yield under normal sown environment, (b) grain filling rate under normal sown environment, (c) grain yield under heat stress environment (d) grain filling rate under heat stress environment.
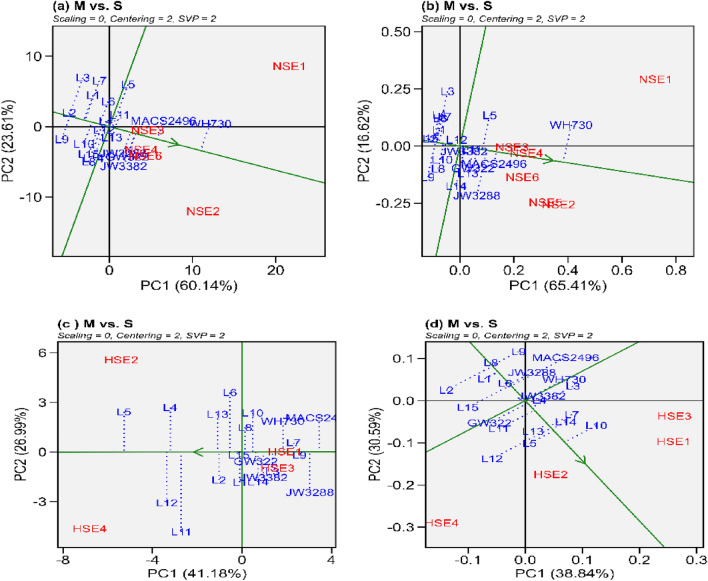
Figure 4.
The “mean versus stability” model describe the interaction effect of wheat genotypes. (a) grain yield under normal sown environment, (b) grain filling rate under normal sown environment, (c) grain yield under heat stress environment (d) grain filling rate under heat stress environment.
Figure 5.
“Ranking of genotypes” model of biplot assess other wheat genotypes against the ideal genotype conferring genotype interaction and genotype x environment interactions. (a) grain yield under normal sown environment, (b) grain filling rate under normal sown environment, (c) grain yield under heat stress environment (d) grain filling rate under heat stress environment.
Figure 6.
The “Discrimitiveness vs. Representativeness” model of biplot evaluate the wheat genotypes against the ideal genotypes, conferring genotype interaction and genotype x environment interactions. (a) grain yield under normal sown environment, (b) grain filling rate under normal sown environment, (c) grain yield under heat stress environment (d) grain filling rate under heat stress environment.
“Which-Won-Where” approaches
A "which-won-where" polygon view of the biplot showing which wheat genotype did best in which environment is shown in Fig. 3a to d and supplemental fig. s4. For grain yield and grain filling rate, respectively the biplots accounted variation approximately 83.75% and 82.03% (Fig. 3a and b) across normal sown environments, 68.17% and 69.43% (Fig. 3c and d) across heat stressed environments, 73.42% and 66.19% (Supplemental fig. s4) across all the environments from total variation related to genotype and GEI. The vertex wheat genotypes in each sector of the biplots represented the top-performing wheat genotypes in the environments that fell within that sector. Wheat genotypes that were positioned nearer the biplot's origin were more stable than vertex genotypes. The genotypes that formed the corners of the polygon for grain yield in the normal sown (L3, L5, WH730, GW322, L14, L9 and L2) (Fig. 3a) and in heat-stressed environments (L5, L6, MACS2496, JW3288, L11 and L12) (Fig. 3c) were utmost responsive genotypes to environments in their corresponding directions compared with the other genotypes. Similarly, for grain filling rate in normal sown environment (L3, WH730, JW3288, L9 and L15) (Fig. 3b) and in heat stressed environment (L2, L8, L9, MACS2496, L10 and L12) (Fig. 3d) genotypes were outmost responsive genotypes compared with other genotypes. The biplot was divided into several sectors by a line drawn perpendicular to the sides of the polygon and extending from the biplot's origin. For grain yield under normal sown environments, WH730 was the highest performing genotype at NSE1; JW3382 was the best genotype at NSE2, NSE3, NSE4, NSE5 and NSE6 (Fig. 3a), similarly for grain filling rate WH730 was the highest performing genotype at NSE1, NSE3 and NSE4; JW3288 was best at NSE2, NSE5 and NSE6 (Fig. 3b). Under heat stressed environments for grain yield, L5 at HSE2, L11 at HSE4, W3288 at HSE3 and MACS2496 at HSE1 were the winner genotypes (Fig. 3c) while for grain filling rate L10 was at HSE1, HSE2 and HSE3; L12 was at HSE4 identified as best performing genotypes, nevertheless L2, L8, L9 and MACS2496 did not win in any of the environments (Fig. 3d). Across all the environments for grain yield L5 was at HSE2; WH730 was at NSE1and NSE3; L2 was at HSE4; JW3382 was at NSE4, HSE3, HSE1, NSE6, NSE2 and NSE5 while for grain filling rate L3 was at HSE2; WH730 was at NSE5, NSE2, NSE6 and NSE3; L15 was at HSE4; L5 was at HSE3 and NSE1 identified as best performing genotypes (Supplemental fig. s4).
Mean vs. stability and ranking of genotypes
If single value portioning or SVP = 1, the biplot's origin is intersected by the average environment coordinate (AEC) line (single value portioning). The "Mean vs. stability" view often referred to as AEC and SVP, helps to simplify genotype assessment by focusing on mean performance and stability over different environmental conditions (Fig. 4). The biplot graph is made up of two straight lines: I the AEC ordinate (horizontal) and (ii) the AEC abscissa (vertical). The arrow on line one of Fig. 4 indicated in the direction of higher mean performance for the characteristic under this study. It can be seen that for grain yield and grain filling rate in normal sown environments WH730 (Fig. 4a and b) had the highest performing ability while L3 (Fig. 4a and b) had the lowest performing ability. Moreover, MACS2496 (Fig. 4a and b) had the highest performing stability, while L3 (Fig. 4a and b) had the lowest performing stability, and other cultivars had general stability in normal sown environments. In heat stressed environments for grain yield L5 (Fig. 4c) had the highest performing ability while MACS2496 (Fig. 4c) had the lowest performing ability. Whereas, for grain yield L2 (Fig. 4c) had the highest performing stability, while JW3288 (Fig. 4c) had the lowest performing stability in heat stress environments. Similarly, for grain filling rate L10 (Fig. 4d) had the highest performing ability while L2 (Fig. 4d) had the lowest performing ability in heat stress environments. Additionally, L4 (Fig. 4d) had the highest performing stability, while L2 (Fig. 4d) had the lowest performing stability. Across all the environments MACS2496 and L13 (Supplemental fig. s5) had the highest performing stability, while L3 and L9 (Supplemental fig. s5) had the lowest performing stability for grain yield and grain filling rate, respectively. The most stable genotypes for grain yield and grain filling rate were identified as JW3288 and L11 (Fig. 5a and b) in environments where seeds were sown timely, L15 and L13 (Fig. 5c and d) in heat-stressed environments, and L13 and L11 (Supplemental fig. s6) in both of these environmental conditions, respectively. These genotypes had above-average yields and were located on the AEC abscissa with zero (very low) projection onto the AEC ordinate. In contrast, L5 and L10 under heat stressed environment for grain yield and grain filling rate respectively (Fig. 5c and d), while for grain yield and grain filling rate WH730 under normal sown and across all the environmental conditions was identified as highest performing but less stable (Fig. 5a, b and supplemental fig. s6), as evident from greater projection onto the AEC ordinate.
Relationships, discrimination and representativeness of the test environments
Figure 6a to d and Supplemental fig. s7 present a vector view of the GGE biplot, elucidating the relationships between environmental interactions and the biplot origin through depicted vectors. All of the normal sown environments showed positive correlation (< 90°) for grain yield and grain filling rate (Fig. 6a and b). On the other hand, under heat stressed environments HSE1 and HSE3; HSE2 and HSE4 were positively correlated (Fig. 6c) for grain yield while for grain filling rate excluding HSE4 all the tested environments associated positively (Fig. 6d). Across all the environments for grain yield excluding HSE1 and HSE4 all the environments associated positively (Fig. S6) while for grain filling rate excluding HSE2 and HSE4 all the environments associated positively (Supplemental fig. s7). The "ideal environment" in Fig. 6 is represented by the circle at the centre of the concentric circle; it is a virtual environment with the longest vector (most discriminating) of all environments and is fully representative (i.e., it has no significant contribution to GEI and thus is positioned on the AEC abscissa). Similarly, for grain yield and grain filling rate, a cultivar closer to the centre has more stability, as shown in Fig. 6a to d, for grain yield L4 and L12, for grain filling rate L10 and L11 under normal sown environments while for grain yield L15 and GW322, for grain filling rate L4 and JW3382 in heat stressed environments had relatively high performing ability with good stability. Similarly, L12 for grain yield and grain filling rate has high performing ability and stability across all the environments (Supplement fig. s7).
Discussion
In central India, a region heavily reliant on wheat for daily dietary needs, the identification of heat-tolerant, high-performing wheat varieties surpassing commercial checks is crucial for advancing nutritional security. Numerous studies have previously shown the potential for concurrent enhancement of wheat grain yield and grain filling rate under both heat stress and nonstress conditions7,16,52. The observed variations in grain yield and grain filling rate among the experimental genotypes, under both heat-stressed and non-stressed conditions, imply the possibility of identifying preferred genotypes that exhibit favourable traits across both environments. Prior investigations have documented significant variances among tested wheat genotypes concerning the examined traits in both heat-stressed and non-stress environments40,53,54. The discernible interactions observed between wheat genotype and environment, coupled with stability estimates derived from the univariate and multivariate stability analysis, imply the existence of a GEI interaction55. This suggests a dynamic alteration in the response patterns and ranking of wheat genotypes in response to diverse environmental conditions. Consistent findings were observed in prior research concerning wheat genotypes, encompassing both heat-stressed and non-stressed environments40,56,57. As indicated by the outcomes of preceding research, the environmental influences were notably significant across diverse environmental conditions7,16,52,58. As anticipated, environments subjected to heat stress demonstrated a diminished mean grain yield compared to non-stressed environments2,4,41.Previous reports in India have documented the grain yield superiority of newly developed recombinant lines over commercial checks16,40,59. This suggested that the newly created recombinant lines outperformed over the commercial checks under heat stress situations.
Elevated bi values observed in the majority of high-yielding and fast grain-filling wheat genotypes in this study suggest their heightened adaptability to high-yield environments45. As per Betrán et al.60, a positive correlation was observed between high mean performance and regression coefficient across diverse environmental conditions. According to univariate stability analysis, L12 and L11 exhibited the highest stability (low S2divalues) for grain yield and grain filling rate, respectively, under normal sown conditions. For both traits under heat stress, L3 and L6 displayed superior stability, while WH730 and L6 were identified as the most stable across all environments.
The predominance of genotype-environment interaction (GEI) over genotype suggests that the AMMI biplot is effective for visualizing genotype evaluation. Similar investigations were conducted in other crops to explore genotype-environment interaction (GEI) through the AMMI model61–63. Efficient selection of genotypes excelling in both stability and performance can be achieved through the Genomic Selection Index (GSI), calculated from AMMI stability values. Hence, JW3288, L8, and L13 emerged as superior genotypes for grain yield under normal sowing conditions, heat stress, and across all environments, respectively. This approach has been efficiently employed in other crops64,65. While AMMI can aid in selecting stable cultivars achieving both high and low yields, it often overlooks numerous high-yielding cultivars with poor stability34,66.
By segmenting the biplot, the GGE biplot provides a polygonal perspective, facilitating a clearer examination of 'which-won-where' patterns. "When diverse test environments cluster into distinct segments, it signifies the presence of diverse high-performing genotypes for those segments, indicating the existence of genotype-environment interaction (GEI)66. The polygonal view divided the biplot into two sectors: one represented by NSE1 and the other by all remaining environments, consistently observed across normal sown conditions for both grain yield and grain filling rate. In grain yield under heat stress, four sectors were identified across different environments, and for grain filling rate, two sectors represented by HSE3 and HSE4. Across all environments, both grain yield and grain filling rate exhibited two sectors represented by NSE1 and HSE. This data is essential for categorizing environments into distinct mega-environments and recommending specific wheat genotypes for each environment21,67,68. An optimal genotype, defined by Yan and Kang69 as one that excels in performance while maintaining stability. The most desired genotypes in this study were those that were closest to the ideal genotype in each environment. Across all of the test environments genotype L12 as the best genotype, telling this genotype's inherent capacity for superior performance and added adaptability. Yan70,71, declares that the association among the vectors of binary test environments is resolute via the cosine of the angle among them. Angles > 90° advised a negative association of genotype presentation among these environments, whereas lesser angles (< 90°) designated resemblance in genotype presentation among these environments. Right angles (90°) designated orthogonality and absence of association. It was obvious after the GGE biplot's vector interpretation that convinced environments had positive relationships while others showed negative relationships. While negative or low associations indicate considerable dissimilarity among environments resultant strongly influenced by Genotype-Environment Interaction (GEI) however, positive relationships suggest similarity in genotype performance across various environments72,73. When assessing crops, environments with long vectors and modest angles with the AEC abscissa are beneficial66,74.
Conclusion
The present study identified the most promising stable heat tolerant wheat genotypes for the central India. Under various heat stress regimes L8, L15 and L1 were identified as most stable recombinant lines for grain yield while for grain filling rate L13, L5 and L4identified as most stable lines based on univariate stability analysis. Whereas, across heat stress and non-stressed environments GW322, L11, L12, and L13were identified as most stable lines for both the traits. When choosing outstanding wheat genotypes in terms of stability, the multivariate stability analysis performed better than the univariate stability model. The NSE3 and HSE2 identified as most stable environments. In heat stress regimes, L8 was identified as the most stable recombinant inbred line, determined through comprehensive analyses encompassing both univariate and multivariate stability assessments. The recombinant inbred line, L8, could be further tested and utilized in future breeding programs.
Supplementary Information
Acknowledgements
I am very thankful to Indian Council of Agricultural Research, New Delhi, for awarding the Junior/Senior Research Fellowship during my Ph.D. degree. I would like to thanks to Department of Plant Breeding and Genetics, Jawaharlal Nehru Krishi Vishwavidyalaya, Jabalpur, Madhya Pradesh for facilitate and funding the all experimentation. I am also thankful to Indian Institute of Wheat and Barley Research, Karnal for sharing the experimental material.
Author contributions
Conceptualization, R.S.S. and V.K.; Experimental material developed, C.S.: methodology, V.K. and S.P.; investigation, S.K.S.; writing — original draft, V.K.; writing — review and editing, R.S.S.; funding acquisition, R.S.S. and S.P.
Data availability
The datasets of the current study can be requested from corresponding author with strong reason.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
The online version contains supplementary material available at 10.1038/s41598-024-53052-w.
References
- 1.Pal, N., Saini, D.K. & Kumar, S. Breaking yield ceiling in wheat: Progress and future prospects. In Wheat (Intech.Open 2022).
- 2.Gourdji SM, Sibley AM, Lobell DB. Global crop exposure to critical high temperatures in the reproductive period: historical trends and future predictions. Environ. Res. Lett. 2013;8:1–10. doi: 10.1088/1748-9326/8/2/024041. [DOI] [Google Scholar]
- 3.Joshi AK, Mishra B, Chatrath R, Ortiz Ferrara G, Singh RP. Wheat improvement in India: present status, emerging challenges and future prospects. Euphytica. 2007;157:431–446. doi: 10.1007/s10681-007-9385-7. [DOI] [Google Scholar]
- 4.Lobell DB, Sibley A, Ortiz-Monasterio JI. Extreme heat effects on wheat senescence in India. Nat. Clim. Change. 2012;2:86–189. doi: 10.1038/nclimate1356. [DOI] [Google Scholar]
- 5.Pask A, et al. A wheat phenotyping network to incorporate physiological traits for climate change in South Asia. Field Crops Res. 2014;168:156–167. doi: 10.1016/j.fcr.2014.07.004. [DOI] [Google Scholar]
- 6.Sharma RC, et al. Wheat grain yield and stability assessed through regional trials in the Eastern Gangetic Plains of South Asia. Euphytica. 2007;157:457–464. doi: 10.1007/s10681-007-9470-y. [DOI] [Google Scholar]
- 7.Verma A, Chatrath R, Sharma I. AMMI and GGE biplots for G×E analysis of wheat genotypes under rain fed conditions in central zone of India. J. Appl. Nat. Sci. 2015;7(2):656–661. doi: 10.31018/jans.v7i2.662. [DOI] [Google Scholar]
- 8.Asseng S, et al. Rising temperatures reduce global wheat production. Nat. Clim. Chang. 2015;5(2):143–147. doi: 10.1038/nclimate2470. [DOI] [Google Scholar]
- 9.Lobell DB, et al. Prioritizing climate change adaptation needs for food security in 2030. Science. 2008;319:607–610. doi: 10.1126/science.1152339. [DOI] [PubMed] [Google Scholar]
- 10.Mondal S, et al. Earliness in wheat: A key to adaptation under terminal and continual high temperature stress in South Asia. Field Crops Res. 2013;151:19–26. doi: 10.1016/j.fcr.2013.06.015. [DOI] [Google Scholar]
- 11.Rao BB, Chowdary PS, Sandeep VM, Pramod VP, Rao VUM. Spatial analysis of the sensitivity of wheat yields to temperature in India. Agric. For. Meterol. 2014;200:192–202. doi: 10.1016/j.agrformet.2014.09.023. [DOI] [Google Scholar]
- 12.Sonkar G, et al. Vulnerability of Indian wheat against rising temperature and aerosols. Environ. Pollut. 2019;254:1129–1146. doi: 10.1016/j.envpol.2019.07.114. [DOI] [PubMed] [Google Scholar]
- 13.Kumar SN, et al. Vulnerability of wheat production to climate change in India. Clim. Res. 2014;59(3):173–187. doi: 10.3354/cr01212. [DOI] [Google Scholar]
- 14.Hilmarsson HS, Rio S, Sanchez JIY. Genotype by environment interaction analysis of agronomic spring barley traits in Iceland using AMMI, factorial regression model and linear mixed model. Agronomy. 2021;11(3):1–15. doi: 10.3390/agronomy11030499. [DOI] [Google Scholar]
- 15.Khan MMH, Rafii MY, Ramlee SI, Jusoh M, Al-Mamun M. AMMI and GGE biplot analysis for yield performance and stability assessment of selected Bambara groundnut (Vigna subterranea L Verdc) genotypes under the multi-environmental trials (METs) Sci. Rep. 2021;11(1):1–17. doi: 10.1038/s41598-021-01411-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Singh C, et al. Genotype x environment interaction analysis of multi-environment wheat trials in India using AMMI and GGE biplot models. Crop Breed. Appl. Technol. 2019;19(3):309–318. doi: 10.1590/1984-70332019v19n3a43. [DOI] [Google Scholar]
- 17.Khazratkulova S, et al. Genotype environment interaction and stability of grain yield and selected quality traits in winter wheat in Central Asia. Turk. J. Agric. For. 2015;39:920–929. doi: 10.3906/tar-1501-24. [DOI] [Google Scholar]
- 18.Tremmel-Bede K, et al. Stability analysis of wheat lines with increased level of arabinoxylan. PLoS ONE. 2020;15:1–15. doi: 10.1371/journal.pone.0232892. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Khazratkulova S, et al. Genotype × environment interaction and stability of grain yield and selected quality traits in winter wheat in Central Asia. Turk. J. Agric. For. 2015;39:920–929. doi: 10.3906/tar-1501-24. [DOI] [Google Scholar]
- 20.Gauch HG. A simple protocol for AMMI analysis of yield trials. Crop Sci. 2013;53:1860–1869. doi: 10.2135/cropsci2013.04.0241. [DOI] [Google Scholar]
- 21.Gauch HG, Zobel RW. Identifying mega-environments and targeting genotypes. Crop Sci. 1997;37:311–326. doi: 10.2135/cropsci1997.0011183X003700020002x. [DOI] [Google Scholar]
- 22.Modeling genotype-by-environment interaction and its genetic basis Malosetti, M., Ribaut, J.M. & VAN-Eeuwijk, F.A. The statistical analysis of multi-environment data. Front. Physiol. 2013;4:44–17. doi: 10.3389/fphys.2013.00044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Myint KA, et al. Genetic diversity and selection criteria of MPOB Senegal oil palm (Elaeisguineensis Jacq.) germplasm by quantitative traits. Ind. Crops Prod. 2019;139:1–11. doi: 10.1016/j.indcrop.2019.111558. [DOI] [Google Scholar]
- 24.Gupta V, et al. AMMI and GGE biplot analysis of yield under terminal heat tolerance in wheat. Mol. Biol. Rep. 2023;50(4):3459–3467. doi: 10.1007/s11033-023-08298-4. [DOI] [PubMed] [Google Scholar]
- 25.Shahriari Z, Heidari B, Dadkhodaie A. Dissection of genotype × environment interactions for mucilage and seed yield in Plantago species: Application of AMMI and GGE biplot analyses. PloS One. 2018;13(5):e0196095–e196133. doi: 10.1371/journal.pone.0196095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Elias AA, Robbins KR, Doerge RW, Tuinstra MR. Half a century of studying genotype × environment interactions in plant breeding experiments. Crop Sci. 2016;56:2090–2105. doi: 10.2135/cropsci2015.01.0061. [DOI] [Google Scholar]
- 27.Bocianowski J, Tratwal A, Nowosad K. Genotype by environment interaction for main winter triticale varieties characteristics at two levels of technology using additive main effects and multiplicative interaction model. Euphytica. 2021;217:1–30. doi: 10.1007/s10681-020-02756-x. [DOI] [Google Scholar]
- 28.Bocianowski J, Warzecha T, Nowosad K, Bathelt R. Genotype by environment interaction using AMMI model and estimation of additive and epistasis gene effects for 1000-kernel weight in spring barley (Hordeum vulgare L.) J. Appl. Genet. 2019 doi: 10.1007/s13353-019-00490-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Yan W. Singular-value partitioning in biplot analysis of multi environment trial data. Agron. J. 2002;94:990–996. [Google Scholar]
- 30.Yan W, Kang MS, Ma B, Woods S, Cornelius PL. GGE biplot vs AMMI analysis of genotype-by-environment data. Crop Sci. 2007;47:643–655. doi: 10.2135/cropsci2006.06.0374. [DOI] [Google Scholar]
- 31.Sabaghnia N, Sabaghpour SH, Dehghani H. The use of an AMMI model and its parameters to analyse yield stability in multi-environment trials. J. Agric. Sci. 2008;146(5):571–581. doi: 10.1017/S0021859608007831. [DOI] [Google Scholar]
- 32.Sharifi P, Aminpanah H, Erfani R, Mohaddesi A, Abbasian A. Evaluation of genotype × environment interaction in rice based on AMMI model in Iran. Rice Sci. 2017;24(3):173–180. doi: 10.1016/j.rsci.2017.02.001. [DOI] [Google Scholar]
- 33.Shrestha J, Subedi S, Acharya R, Sharma S, Subedi M. Grain yield stability of maize (Zea mays L) hybrids using ammi model and GGE biplot analysis. SAARC J. Agric. 2021;19(2):107–121. doi: 10.3329/sja.v19i2.57675. [DOI] [Google Scholar]
- 34.Gauch HG, Piepho HP, Annicchiarico P. Statistical analysis of yield trials by AMMI and GGE: Further considerations. Crop Sci. 2008;48:866–889. doi: 10.2135/cropsci2007.09.0513. [DOI] [Google Scholar]
- 35.Bishnoi OP. GGE biplot based stability analysis of durum wheat genotypes using statistical package GGE Biplot GUI. Int. J. Agric. Environ. Biotechnol. 2020;13(2):149–153. doi: 10.30954/0974-1712.02.2020.5. [DOI] [Google Scholar]
- 36.Mostafavi K, Imeni SH, Zare M. Stability analysis of rice genotypes based GGE biplot Method in North of Iran. J. Appl. Sci. Res. 2011;7(11):1690–1694. [Google Scholar]
- 37.Ruswandi D, et al. GGE biplot analysis for stability and adaptability of maize hybrids in western region of Indonesia. Int. J. Agron. 2021;2021:1–9. doi: 10.1155/2021/2166022. [DOI] [Google Scholar]
- 38.Garg D, Sareen S, Dalal S, Tiwari R, Singh R. Heat shock protein-based SNP marker for terminal heat stress in wheat ('triticumaestivum'L) Austral. J. Crop Sci. 2012;6(11):1516–1521. [Google Scholar]
- 39.Kumar A, Kumar P, Singh G. Assessment and role of genetic diversity of component traits for improving grain yield and heat tolerance in bread wheat (Triticum aestivum) Indian J. Agric. Sci. 2019;89(7):103–115. [Google Scholar]
- 40.Sareen S, Tyagi BS, Sarial AK, Tiwari V, Sharma I. Trait analysis, diversity, and genotype x environment interaction in some wheat landraces evaluated under drought and heat stress conditions. Chilean J. Agric. Res. 2014;74(2):135–42. doi: 10.4067/S0718-58392014000200002. [DOI] [Google Scholar]
- 41.Sharma D, Mamrutha HM, Gupta VK, Tiwari R, Singh R. Association of SSCP variants of HSP genes with physiological and yield traits under heat stress in wheat. Res. Crops. 2015;16(1):139–146. doi: 10.5958/2348-7542.2015.00020.0. [DOI] [Google Scholar]
- 42.Dias AS, Lidon FC. Evaluation of grain filling rate and duration in bread and durum wheat, under heat stress after anthesis. J. Agronomy Crop Sci. 2009;195(2):137–147. doi: 10.1111/j.1439-037X.2008.00347.x. [DOI] [Google Scholar]
- 43.Farshadfar E. Incorporation of AMMI stability value and grain yield in a single non-parametric index (GSI) in bread wheat. Pak. J. Biol. Sci. 2008;11:1791–1796. doi: 10.3923/pjbs.2008.1791.1796. [DOI] [PubMed] [Google Scholar]
- 44.Sandhu KS, Mihalyov PD, Lewien MJ, Pumphrey MO, Carter AH. Combining genomic and phenomic information for predicting grain protein content and grain yield in spring wheat. Front. Plant Sci. 2021;12:1–14. doi: 10.3389/fpls.2021.613300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Eberhart SA, Russell WA. Stability parameters for comparing varieties 1. Crop Sci. 1966;6:36–40. doi: 10.2135/cropsci1966.0011183X000600010011x. [DOI] [Google Scholar]
- 46.Changizi M, Choukan R, Heravan EM, Bihamta MR, Darvish F. Evaluation of genotype × environment interaction and stability of corn hybrids and relationship among univariate parametric methods. Can. J. Plant Sci. 2014;94(7):1255–1267. doi: 10.4141/cjps2013-386. [DOI] [Google Scholar]
- 47.Fischer RA, Maurer R. Drought resistance in spring wheat cultivars I. Grain yield responses. Austral. J. Agric. Res. 1978;9(5):897–912. doi: 10.1071/AR9780897. [DOI] [Google Scholar]
- 48.Neisse AC, Kirch JL, Hongyu K. AMMI and GGE biplot for genotype environment interaction: A medoid–based hierarchical cluster analysis approach for high–dimensional data. Biom. Lett. 2018;55(2):97–121. doi: 10.2478/bile2018-0008. [DOI] [Google Scholar]
- 49.Rad MN, et al. Genotype environment interaction by AMMI and GGE biplot analysis in three consecutive generations of wheat (Triticum aestivum) under normal and drought stress conditions. Aust. J. Crop Sci. 2013;7(7):956–961. [Google Scholar]
- 50.Yan W, Tinker NA. Biplot analysis of multi-environment trial data: Principles and applications. Can. J. Plant Sci. 2006;86(3):623–645. doi: 10.4141/P05-169. [DOI] [Google Scholar]
- 51.Pour-Aboughadareh A, Khalili M, Poczai P, Olivoto T. Stability indices to deciphering the genotype-by-environment interaction (GEI) effect: An applicable review for use in plant breeding programs. Plants. 2022;11(3):414–424. doi: 10.3390/plants11030414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Amare K, Zeleke H, Bultosa G. Variability for yield, yield related traits and association among traits of sorghum (Sorghum Bicolor (L) Moench) varieties in Wollo, Ethiopia. J. Plant Breed. Crop Sci. 2015;7:125–133. doi: 10.5897/JPBCS2014.0469. [DOI] [Google Scholar]
- 53.Qaseem MF, Qureshi R, Shaheen H. Effects of pre-anthesis drought, heat and their combination on the growth, yield and physiology of diverse wheat (Triticum aestivum L.) genotypes varying in sensitivity to heat and drought stress. Sci. Rep. 2019;9:1–12. doi: 10.1038/s41598-019-43477-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Rattey A, Shorter R, Chapman S, Dreccer F, Herwaarden AV. Variation for and relationships among biomass and grain yield component traits conferring improved yield and grain weight in an elite wheat population grown in variable yield environments. Crop & Pasture Sci. 2009;60:717–729. doi: 10.1071/CP08460. [DOI] [Google Scholar]
- 55.Khan I, et al. Stability analysis of wheat through genotype by environment interaction in three regions of Khyber Pakhtunkhwa Pakistan. SABRAO J. Breed. Genet. 2023;55(1):50–60. doi: 10.54910/sabrao2023.55.1.5. [DOI] [Google Scholar]
- 56.Elbasyoni IS. Performance and stability of commercial wheat cultivars under terminal heat stress. Agronomy. 2018;8(4):37. doi: 10.3390/agronomy8040037. [DOI] [Google Scholar]
- 57.Kamara MM, et al. Combining ability and gene action controlling grain yield and its related traits in bread wheat under heat stress and normal conditions. Agronomy. 2021;1(8):1450. doi: 10.3390/agronomy11081450. [DOI] [Google Scholar]
- 58.Tembo B. Genotype by environment interaction analysis of wheat (Triticum aestivum L.) grain yield under rainfed conditions in Zambia. SABRAO J. Breed Genet. 2021;53(4):609–619. doi: 10.54910/sabrao2021.53.4.5. [DOI] [Google Scholar]
- 59.Tanin MJ, et al. Ascertaining yield and grain protein content stability in wheat genotypes having the Gpc-B1 gene using univariate, multivariate, and correlation analysis. Front Genet. 2022;13:1001904. doi: 10.3389/fgene.2022.1001904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Betrán FJ, Ribaut JM, Beck DL, Gonzalez-de LD. Genetic analysis of inbred and hybrid grain yield under stress and non-stress environments. Crop Sci. 2003;43:807–817. doi: 10.2135/cropsci2003.8070. [DOI] [Google Scholar]
- 61.Bashir EM, Ali AM, Ismail MI, Parzies HK, Haussmann BI. Patterns of pearl millet genotype-by-environment interaction for yield performance and grain iron (Fe) and zinc (Zn) concentrations in Sudan. Field Crop Res. 2014;166:82–91. doi: 10.1016/j.fcr.2014.06.007. [DOI] [Google Scholar]
- 62.Nzuve F, Githiri S, Mukunya DM, Gethi J. Analysis of genotype × environment interaction for grain yield in Maize hybrids. J. Agric. Sci. 2013;5(11):75–85. [Google Scholar]
- 63.Vaezi B, et al. GGE biplot and AMMI analysis of barley yield performance in Iran. Cereal. Res. Commun. 2017;45:500–511. doi: 10.1556/0806.45.2017.019. [DOI] [Google Scholar]
- 64.Donkor EF, Nyadanu D, Akromah R, Osei K. Genotype-by environment interaction and stability of taro [Colocasia esculenta (l) Schott] genotypes for yield and yield components. Ecol Genet Genom. 2020;17:100070. doi: 10.1016/j.egg.2020.100070. [DOI] [Google Scholar]
- 65.Nduwumuremyi A, Melis R, Shanahan P, Theodore A. Interaction of genotype and environment effects on important traits of cassava (Manihot esculenta Crantz) Crop J. 2017;5(5):373–386. doi: 10.1016/j.cj.2017.02.004. [DOI] [Google Scholar]
- 66.Yan W, Kang MS, Ma S, Woods B, Cornelius PL. GGE biplot vs AMMI analysis of genotype-by-environment data. Crop Sci. 2007;47:643–655. doi: 10.2135/cropsci2006.06.0374. [DOI] [Google Scholar]
- 67.Abakemal D, Shimelis H, John D. Genotype-by environment interaction and yield stability of quality protein maize hybrids developed from tropical-highland an inbred line. Euphytica. 2016;209:757–769. doi: 10.1007/s10681-016-1673-7. [DOI] [Google Scholar]
- 68.Badu-Apraku B, et al. Yield gains in extra-early maize cultivars of three breeding eras under multiple environments. Agron. J. 2017;109:418–431. doi: 10.2134/agronj2016.10.0566. [DOI] [Google Scholar]
- 69.Yan W, Kang MS. GGE biplot analysis a graphical tool for breeders, geneticists, and agronomists (CRC Press. FL): Boca Raton; 2002. pp. 126–138. [Google Scholar]
- 70.Gasura E, Setimela P, Souta C. Evaluation of the performance of sorghum genotypes using GGE biplot. Can. J. Plant Sci. 2015;95:1205–1214. doi: 10.4141/cjps-2015-119. [DOI] [Google Scholar]
- 71.Yan W. Singular-value partitioning in biplot analysis of multi-environment trial data. Agron. J. 2002;94:990–996. [Google Scholar]
- 72.Makumbi D, Diallo A, Kanampiu F, Mugo S, Karaya H. Agronomic performance and genotype x environment interaction of herbicide-resistant maize varieties in eastern Africa. Crop Sci. 2015;55:540–555. doi: 10.2135/cropsci2014.08.0593. [DOI] [Google Scholar]
- 73.Sserumaga JP, et al. Genotype by environment interactions and agronomic performance of doubled haploids testcross maize (Zea mays L) hybrids. Euphytica. 2016;207:353–365. doi: 10.1007/s10681-015-1549-2. [DOI] [Google Scholar]
- 74.Tukamuhabwa P, Assiimwe M, Nabasirye M, Kabayi P, Maphosa M. Genotype by environment interaction of advanced generation soybean lines for grain yield in Uganda. Afr. Crop Sci. J. 2012;20:107–115. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The datasets of the current study can be requested from corresponding author with strong reason.