Computational discovery of microstructured composites with optimal stiffness-toughness trade-offs

Abstract

The conflict between stiffness and toughness is a fundamental problem in engineering materials design. However, the systematic discovery of microstructured composites with optimal stiffness-toughness trade-offs has never been demonstrated, hindered by the discrepancies between simulation and reality and the lack of data-efficient exploration of the entire Pareto front. We introduce a generalizable pipeline that integrates physical experiments, numerical simulations, and artificial neural networks to address both challenges. Without any prescribed expert knowledge of material design, our approach implements a nested-loop proposal-validation workflow to bridge the simulation-to-reality gap and find microstructured composites that are stiff and tough with high sample efficiency. Further analysis of Pareto-optimal designs allows us to automatically identify existing toughness enhancement mechanisms, which were previously found through trial and error or biomimicry. On a broader scale, our method provides a blueprint for computational design in various research areas beyond solid mechanics, such as polymer chemistry, fluid dynamics, meteorology, and robotics.

Experiments informed computational discovery of microstructured composites with optimal stiffness-toughness trade-offs.

INTRODUCTION

Stiffness—the ability to resist deformation in response to an applied force—and toughness—the ability to resist cracks—are two quintessential properties in most engineering materials because these materials must resist nonrecoverable deformation and prevent catastrophic failure under external loading in structural applications. Unfortunately, stiffness and toughness are often mutually exclusive because, to be tough, a material must be ductile enough to tolerate long cracks and absorb more energy before fracturing (1). Although a few exceptions have been found among microstructured composites through trial-and-error approaches or biomimicry (2–7), there is no systematic way to design and fabricate these materials. Recent development in additive manufacturing allows materials to be arranged combinatorially in space, enabling designs that were impossible to physically realize before, including high-performance structural materials (8–10) and functional objects (7, 11). Furthermore, computational methods (e.g., structural optimization) allow for efficient exploration of optimal designs inside a parameterized design space with the help of numerical simulation (12–17). However, all reliable computational explorations require simulation models to accurately match the corresponding experimental measurements over the entire design space. This is still very difficult for toughness prediction as current simulations—despite harnessing advanced fracture theories—are unable to fully model the fracture of structured materials (18–20). Moreover, the computational process for finding microstructured composites that are both stiff and tough is also challenging because their conflicting nature dictates that there is not a single best solution but a set of Pareto-optimal solutions. To obtain the entire Pareto front where one can make simple trade-off decisions among optimal designs, existing structural optimization algorithms typically execute many single-objective optimization routines or rely on evolutionary strategies (21). Both of these strategies incur a large number of simulations. Therefore, finding Pareto-optimal designs using these approaches imposes contradictory demands on the simulator: The simulator not only should model all physical details to be accurate, but it must also run extremely fast to reduce computational cost. These simulators have to undergo careful design by field experts, which is normally unrealistic, especially for microstructured composites with complicated geometries and abundant material interfaces.

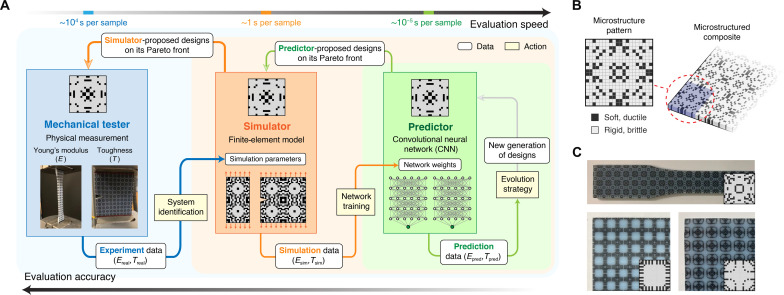
Here, we present an efficient and expert-knowledge–free approach for the automatic discovery of microstructured composite designs with optimal stiffness-toughness trade-offs (where stiffness is measured using Young’s modulus), tackling all of the aforementioned challenges simultaneously. Our approach uses three evaluators (Fig. 1A): (i) a mechanical tester that conducts physical measurements, (ii) a finite-element method (FEM)–based simulator that performs virtual mechanical testing in moderate complexity, and (iii) a convolutional neural network (CNN)–based predictor that executes machine learning inference. All evaluators take an arbitrary microstructure design as input and then measure or predict its Young’s modulus and toughness as output, with varying evaluation speed and accuracy. The mechanical tester runs very slowly due to labor-intensive specimen fabrication and testing (~10⁴ s per sample), but this provides ground truth performance values for a microstructure design. At the opposite end of the spectrum, we have the predictor, which runs extremely fast (~10⁻⁵ s per sample) but yields relatively inaccurate results. In between, we have the simulator, which runs reasonably fast (~1 s per sample) given its moderate complexity and delivers intermediate accuracy. The full pipeline executes in a nested-loop fashion. Faster evaluators, acting as surrogate models, conduct multi-objective structural optimization and propose microstructure designs on the Pareto front to slower evaluators (from right to left, top, Fig. 1A). Slower evaluators, being more accurate, validate the performance of these designs and use them as additional training data to improve the accuracy of the faster evaluators (from left to right, bottom, Fig. 1A). As faster evaluators become increasingly accurate throughout the process, they are able to propose higher-quality designs to the slower evaluators. Overall, our nested-loop pipeline effectively improves sample efficiency in finding microstructure designs with optimal stiffness-toughness trade-offs. The inner loop between the simulator and the predictor reduces the number of numerical simulations for finding the simulator’s Pareto front by an order of magnitude compared with other state-of-the-art structural optimization algorithms. The outer loop between the mechanical tester and the simulator simultaneously closes the sim-to-real gap and finds experimentally verified Pareto-optimal microstructure designs based on only a few dozen physical measurements. This is accomplished with a physics-based simulator that does not incorporate sophisticated or advanced modeling of material inelasticity or fracture. Despite the limited modeling capability, the simulator autonomously learns to match the behavior of Pareto-optimal microstructures with physical experiments.

Fig. 1. Schematic of our approach.

(A) Workflow of the proposed nested-loop pipeline. Our system integrates three distinctive evaluators: a mechanical tester, an FEM-based simulator, and a CNN-based predictor, which vary in evaluation speed and accuracy. Data flow directions are indicated by colored arrows. Arrows from slower, more accurate evaluators to faster, less accurate evaluators illustrate the propagation of microstructure performance data for improving the latter’s accuracy. Arrows pointing in the opposite direction represent proposed Pareto-optimal designs from faster evaluators to slower ones for validation. The self-loop at the predictor depicts an evolutionary strategy for finding its Pareto front. (B) Illustration of a microstructure and the corresponding microstructured composites. The microstructure is defined by a two-dimensional pattern that demonstrates the spatial arrangement of two base materials with contrasting properties. (C) Sample photographs of manufactured microstructured composites, annotated by the source microstructure patterns.

RESULTS

The microstructured composites in this study consist of two acrylic-based photopolymers, one rigid and one soft, which contrast in stiffness and ductility (table S2). The unit cell of a microstructure, which we call a microstructure pattern (Fig. 1B and fig. S1), is constructed by digitally arranging the base materials in a 20 × 20 regular grid through three-dimensional (3D) printing (Fig. 1C). The Young’s modulus and toughness of a microstructure are measured on fabricated specimens via tensile mechanical testing. To obtain reliable physical measurements that are comparable in horizontal and vertical directions, we limit the volume fraction of the rigid material in a microstructure pattern between 50 and 85% and further enforce symmetry along axes and diagonals (see note S1). Even under these constraints, the design space of microstructures is sufficiently large to render exhaustive search methods infeasible.

At the foundation of our approach, the FEM-based simulator is constructed with simplified specimen geometry and material modeling. The FEM grid comprises three types of elements: soft, rigid, and interface elements (see left-hand side of Fig. 2A). To simulate mechanical testing of a microstructured composite, each element type is characterized by three essential material parameters: Young’s modulus, Poisson’s ratio, and maximal strain energy density (the energy density beyond which an element fails and becomes void). Above them, a global damping coefficient is added to capture energy dissipation and suppress numerical oscillations, resulting in a total of 10 exposed parameters. The exposed parameters are initially optimized to match experimental measurements of base materials, namely, homogeneous composites fabricated with soft, rigid, and interface materials, respectively (22). To minimize the expert knowledge required, advanced material parameters that control the fracture behavior, such as strength surface and critical energy release rate (23–25), are omitted from the simulator. This precludes tedious implementation and allows for substantial evaluation throughput. With a customized high-performance explicit solver for dynamic finite-element analysis (see note S3), it takes around 0.015 s for every Young’s modulus evaluation and 0.2 s for toughness at maximum throughput (fig. S6).

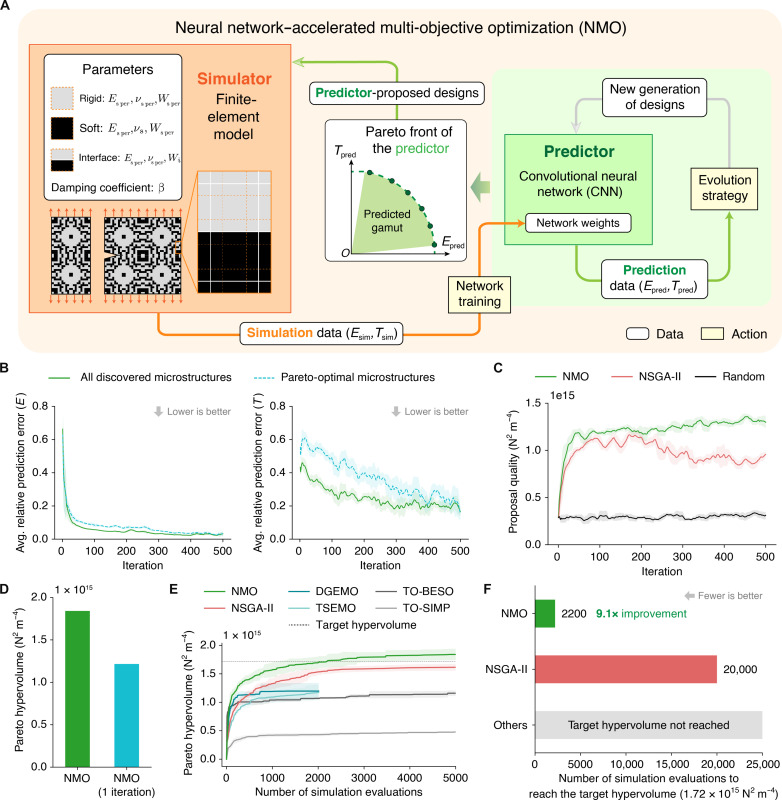
Fig. 2. The inner loop of the proposed workflow with neural network-accelerated multi-objective optimization (NMO).

(A) Workflow of NMO, illustrated by a zoomed-in snapshot of Fig. 1A. The simulator has 10 exposed parameters, including material model parameters of rigid, soft, and interface base materials plus a global damping coefficient. (B) Average prediction errors of Young’s modulus and toughness in NMO over 500 iterations, calculated for all discovered microstructures and specifically those on the simulation Pareto front. Shaded regions indicate SDs estimated from adjacent data points. (C) Evolution of design proposal quality, as characterized by the Pareto hypervolume of 10 proposed designs in each iteration, over 500 iterations. NMO is compared with NSGA-II and a random sampling strategy. (D) Comparison of the final Pareto hypervolumes from NMO and its simplified alternative (NMO one iteration) that only trains the predictor with 5000 random designs and proposes designs back to the simulator once. (E) Comparison between NMO and other multi-objective optimization algorithms in Pareto hypervolume growth within a budget of 5000 simulation evaluations. The baselines comprise our modified NSGA-II algorithm, topology optimization (TO) [e.g., BESO (27, 57) and SIMP (58)], and multi-objective Bayesian optimization (MOBO) [e.g., diversity-guided efficient multiobjective optimization (DGEMO) (29) and Thompson sampling efficient multiobjective optimization (TSEMO) (30)]. MOBO algorithms are stopped at 2000 simulations due to exceeding a time limit of 24 hours. Each solid curve is an average of repeats using five random seeds, and the colored region around each curve indicates SD. (F) Number of evaluations required for NMO and other baseline algorithms to reach a target hypervolume, marked by the dashed black line in (E).

The inner loop of our nested-loop pipeline explores the maximal simulated performance range of microstructured composites (i.e., the simulated performance gamut) and finds designs on the simulation Pareto front. Because the complex, discontinuous nature of fracture makes it almost impossible to reach theoretically Pareto-optimal microstructures without exhaustive search, the goal of the inner loop is to find the largest Pareto front possible using a limited number of simulations. Unlike traditional methods that conduct structural optimization using the simulator exclusively, the inner loop of our approach uses the CNN-based predictor as a surrogate model to guide the optimization process (see note S3 for details), hence named neural network–accelerated multi-objective optimization (NMO) (Fig. 2A). Starting from a dataset of 10 random microstructures (fig. S15), NMO repeats the following steps for 500 iterations in total (Fig. 2A). First, the two neural networks of the predictor, one for Young’s modulus and one for toughness, are trained using simulated properties of all microstructures in the current dataset. Then, the Pareto front of the trained predictor is computed using an evolutionary multi-objective optimization algorithm (right part of Fig. 2A; in our case, we use a modified non-dominated sorting genetic algorithm II (NSGA-II) (26); see Materials and Methods). Each of these Pareto front computations incurs a negligible time cost because the predictor runs orders of magnitude faster than the simulator. Last, the predictor proposes 10 Pareto-optimal designs to the simulator for validation. The validated designs are used to augment the microstructure dataset to serve as additional training data in the next iteration.

In early iterations, the predictor is very inaccurate due to limited training data. Predictions for Pareto-optimal designs are particularly inaccurate because they are far away from the microstructures in the initial dataset. Nonetheless, as the algorithm proceeds, the predictor becomes more accurate by virtue of accumulating training data from the simulator. This is evidenced by the decreasing prediction errors in both Young’s modulus and toughness over iterations (Fig. 2B). The prediction errors of Pareto-optimal microstructures decline even faster (the blue lines in Fig. 2B), indicating that the predictor improves its inference near the simulation Pareto front considerably after retraining.

Meanwhile, the self-learning predictor is able to propose increasingly better microstructure designs to the simulator, which we quantify using the Pareto hypervolume (namely, the area enclosed by the Pareto front) of 10 validated designs in each NMO iteration (Fig. 2C). Compared with a direct application of NSGA-II and random sampling, our approach shows consistently higher design proposal quality over the entire algorithm. Eventually, the repetitive proposal-validation workflow allows NMO to reach a Pareto hypervolume of 1.84 × 10¹⁵ N² m⁻⁴ after 500 iterations (5000 simulation evaluations excluding random initial designs). This is notably better than simply training the predictor via 5000 random samples and validating Pareto optimal designs once (NMO one iteration in Fig. 2D), which only achieves 66.1% of our achieved hypervolume.

NMO outperforms state-of-the-art optimization algorithms in terms of exploration efficiency within the design space, including NSGA-II (26), topology optimization (TO) (27, 28), and other surrogate model–based algorithms such as multi-objective Bayesian optimization (MOBO) (29, 30). As shown in Fig. 2E, NMO covers the largest Pareto hypervolume within a budget of 5000 simulations, surpassing TO and MOBO algorithms by a notable margin. This demonstrates promising opportunities for NMO to tackle structural design problems involving complex, nonlinear mechanical properties, where TO exhibits severe limitations. To further distinguish NMO in sample efficiency, we run both NMO and NSGA-II until reaching a target hypervolume of 1.72 × 10¹⁵ N² m⁻⁴ and then observe the number of simulations required (Fig. 2F). Here, NMO takes an order of magnitude fewer simulation evaluations to achieve the target hypervolume, demonstrating evidently superior sample efficiency. Aside from the modified NSGA-II in this study, NMO is also compatible with other optimization algorithms for finding the predictor’s Pareto front. In practice, it is recommended to choose appropriate algorithms based on problem characteristics to maximize the advantage of the predictor.

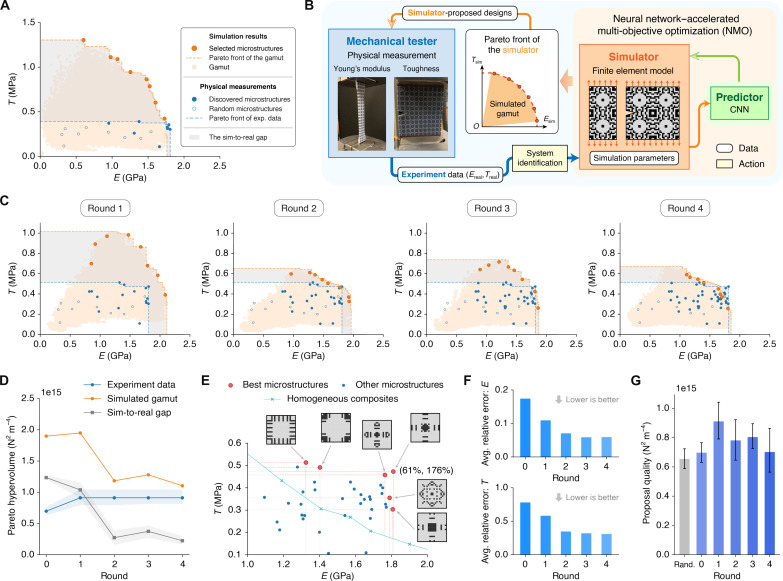
Following the inner loop, we select eight Pareto-optimal microstructure designs from the simulation Pareto front, fabricate specimens, and mechanically test their actual performance, which concludes round 0 of the outer loop. However, because our simulator does not incorporate sophisticated constitutive models or advanced fracture mechanics, the simulated properties of these microstructure designs deviate notably from their physical measurements. Unpredictable manufacturing flaws introduced by the 3D printer and measurement errors due to, e.g., boundary effects, further contribute to the sim-to-real gap. At this stage, the less accurate simulator normally tends to overestimate the performance of microstructures on its Pareto front because the optimization algorithm tries to exploit the discrepancies between simulation and reality. Thus, the experimental Pareto front of the selected microstructure designs is much smaller than the simulation Pareto front (Fig. 3A).

Fig. 3. The outer loop of the proposed workflow.

(A) Experiment data of discovered microstructures and the simulation gamut at the end of round 0. The sim-to-real gap is defined as the symmetric difference between the Pareto hypervolumes of the experimental Pareto front and the simulation Pareto front. (B) Workflow illustration of the outer loop as simplified from Fig. 1A. (C) Evolution of experiment data and the simulation gamut within four rounds of the outer loop, where the sim-to-real gap shrinks substantially. (D) Pareto hypervolume of experiment data and the simulation gamut, and the area of the sim-to-real gap over four rounds of the outer loop. (E) Representative microstructures found by the pipeline with optimal trade-offs. Numbers in parentheses indicate the improvement of a design in Young’s modulus and toughness compared to homogeneous composites with various volume fractions of the rigid material. (F) Average relative simulation error on Young’s modulus and toughness in each round of the outer loop. The error is calculated for all 50 discovered microstructures to showcase the improvement in simulation accuracy. (G) Quality of microstructure designs proposed by the simulator over the entire outer loop. Proposal quality is evaluated by the experimental Pareto hypervolume of eight proposed designs in each round. The quality of the 10 randomly chosen microstructures before round 1 (Rand.) is used as a reference.

To close the sim-to-real gap, the outer loop of our pipeline improves the accuracy of the simulator through system identification (Fig. 3B), where the exposed parameters of the simulator are optimized to match simulation outputs with physical measurements for all discovered microstructure designs (fig. S7). Rather than setting simulation parameters using physical measurements of base materials directly, our approach computes parameters that holistically match the properties of a diverse set of microstructures. The sim-to-real gap is effectively treated as a black box, and system identification automatically absorbs all sources of errors into the exposed parameters of the simulator, including modeling, fabrication, and measurement errors. This effectively compensates for the omission of advanced material models and fracture mechanisms. We choose Bayesian optimization (BO) as the solver for system identification, an algorithm frequently used to optimize complex, nonconvex functions with many local optima. The BO solver is instantiated from multiple random seeds for better robustness. Moreover, by assigning different weights to the source microstructures, we are able to prioritize matches for near–Pareto-optimal designs, so that the simulator generalizes better to other designs with desirable performance (see note S3). This allows the simulator to propose designs that more likely expand the experimental Pareto front instead of spending its modeling capacity on designs far from optimal.

The outer loop uses the same proposal-validation workflow as the inner loop. Here, the simulator serves as a surrogate model for the mechanical tester to search for experimental Pareto-optimal microstructure designs with high sample efficiency. After round 0, we assemble a dataset of 18 discovered microstructures, including 8 proposed Pareto-optimal designs from round 0 and 10 additional random designs for regularization in system identification (hollow blue markers in Fig. 3A). In each subsequent round, our pipeline updates the simulator via system identification, searches for the simulation Pareto front through the inner loop (NMO), proposes eight Pareto-optimal microstructure designs to the mechanical tester (Fig. 3B), validates their performance by physical measurements, and lastly adds them to the dataset of discovered microstructures. We run the outer loop for four rounds and visualize the evolution of experiment data and simulated gamut in Fig. 3C. For a quantitative comparison, the advancement of their Pareto hypervolumes is illustrated in Fig. 3D. As the pipeline proceeds, the Pareto front of experiment data gradually converges to the simulation Pareto front and the sim-to-real gap ultimately decreases by an order of magnitude. Among 50 microstructures found by the pipeline in total, we select 6 designs on or near the experimental Pareto front as the best examples and present their patterns in Fig. 3E. Compared with homogeneous composites fabricated by mixing base materials at various ratios during 3D printing, they achieve up to 175.6% higher toughness under the same Young’s modulus or 61.0% higher Young’s modulus at the same toughness, demonstrating much better trade-offs between stiffness and toughness.

Intuitively, the outer loop parallels the inner loop as an automated self-learning process for the simulator (31–33). Because the microstructure dataset is augmented by eight new microstructures per round, the simulator becomes more accurate over time as depicted by its decreasing error from ground truth physical measurements (Fig. 3F). With higher accuracy, the simulator is able to propose increasingly better microstructure designs in each round, as characterized by the improving Pareto hypervolume of their physically validated properties (Fig. 3G). Therefore, even with our relatively simple simulator—which omits complex, advanced modeling techniques—our pipeline simultaneously bridges the sim-to-real gap and finds microstructures with experimentally verified Pareto-optimal performance.

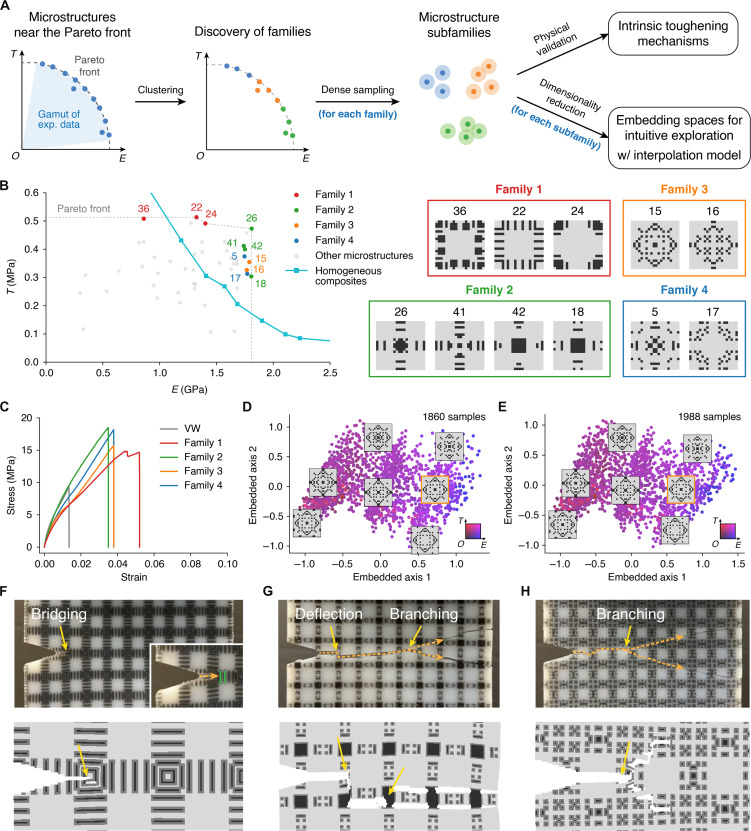
From a methodology perspective, our data-driven computational approach inverts the standard design process: Instead of implementing handcrafted or bioinspired toughening mechanisms to fabricate synthetic composites (4, 6, 34), we can interpret these mechanisms from automatically discovered Pareto-optimal designs even without any prior knowledge (Fig. 4A). To that end, we first notice that microstructures near the experimental Pareto front can be clustered into four major families, where designs in the same family are structurally similar (Fig. 4B) (13). The representative stress-strain curve from each family exemplifies how these designs improve fracture resistance considerably over the rigid base material while maintaining comparable Young’s moduli, resulting in optimal stiffness-toughness trade-offs (Fig. 4C). Therefore, the microstructure families allow for extracting and interpreting toughening mechanisms by groups rather than individual designs. To verify the discovered families, we treat the physically measured microstructures as seeds and generate a local performance gamut for each family through dense sampling, from which three validation samples near the Pareto front of each family are selected and validated by the mechanical tester (fig. S16 and table S13). Moreover, to intuitively explore microstructures with similar appearance and performance, we take advantage of our well-trained simulator to generate a local gamut for each seed design near the experimental Pareto front and compute a low-dimensional embedding space using Isomap (Fig. 4D) (35). We additionally build an interpolation model for neighboring patterns in the embedding space (see note S4 and fig. S16) to generate patterns that are potentially missed in dense sampling, which eventually refines the embedding space (Fig. 4E).

Fig. 4. Analysis of families and intrinsic toughening mechanisms using discovered Pareto-optimal microstructures.

(A) Schematic of the analysis workflow. Microstructures near the Pareto front are grouped into families and further split into subfamilies (see note S4 and fig. S17). The mechanical performance of each family is verified, while the pattern variation in each subfamily is studied in a low-dimensional embedding space. (B) Seed microstructures of four families and their mechanical performance compared with homogeneous composites. (C) Representative stress-strain curves of microstructures in each family collected from mechanical testing. (D and E) Isomap embedding space of an example subfamily before (D) and after (E) interpolation. Some representative patterns are illustrated. Microstructure properties are encoded in colors (Young’s modulus: the blue channel; toughness: the red channel). Seed patterns are highlighted in orange boxes. (F to H) Toughening mechanisms observed in experiment and simulation: bridging, deflection, and branching. Snapshots are taken from validation microstructures in family 1 (F), family 2 (G), and family 3 (H).

By analyzing tested specimens and simulation videos, the discovered microstructure families allow us to successfully identify some well-known mechanisms of toughness enhancement, such as bridging, deflection, and branching (18, 36–39) (Fig. 4, F to H). These mechanisms resist crack growth and prevent the formation of clean cleavage as observed in homogeneous composites (fig. S33). Their prominence varies depending on the distribution of soft material. Bridging is mostly observed in family 1, where parallel bars of soft material absorb more energy through elastic deformation and introduce additional stress resistance by crack blunting to slow down crack propagation (Fig. 4F and fig. S22). Deflection is witnessed in both family 1 and family 2, as characterized by chunks of soft material that withstand a large strain and disturb the cracks (Fig. 4G and figs. S22 and S3). Conversely, branching effects are predominant in family 3 and family 4, which feature scattered elements of soft material. In this case, the propagation energy of the cracks dissipates in the form of branched cracks due to the trapping effect from soft material (Fig. 4H and figs. S24 and S25) (40). In addition, we also observed other toughing mechanisms that do not obviously fall into the three prevailing categories. For example, some isolated soft material elements are assigned to the edge of a microstructure pattern (fig. S24), either near the notch tip or on the path of crack propagation. Despite not being organized into shapes such as bars or circles, these elements still effectively dissipate energy and delay crack propagation (1). Overall, it is common among discovered families that soft material elements enhance toughness through crack blunting, while stiff material elements are integrally connected to maintain Young’s modulus (see note S4). Our pipeline automatically finds the critical soft and stiff elements that contribute to balanced Young’s modulus and toughness without prescribed knowledge of existing toughening mechanisms. These structural features are generated using a fully computational method instead of biomimics or experimental trial and error. Therefore, they may pave the way for novel physical insights, provided that further characterization and analysis are conducted by experts in fracture mechanics.

In addition, our computational pipeline has adequate scalability to solve Pareto-optimal microstructure discovery problems in higher-design resolutions. For example, we applied our pipeline to find the Pareto front between stiffness and porosity in isotropic porous materials (see note S5 for details about fabrication, experiment, and simulation). The microstructure patterns in this case study are represented by 182 × 104 grids, constituting a considerably larger design space. Nonetheless, our pipeline still maintains excellent sample efficiency in Pareto front discovery (fig. S29). Moreover, our approach manages to identify designs with theoretically optimal performance as prescribed by the Hashin-Shtrikman upper bound (41, 42) (fig. S28).

DISCUSSION

In conclusion, we have presented a generalizable, scalable, and efficient computational approach that does not require expert knowledge to automatically find microstructured composites with optimal trade-offs between stiffness and toughness. We integrate three distinct evaluation methods—experimental measurement, numerical simulation, and machine learning inference—in a data-driven proposal-validation framework. The essence of our approach is a nested-loop workflow that improves the sample efficiency of slow, accurate evaluators by harnessing fast, approximate evaluators as surrogate models and progressively improving their accuracy. Our pipeline achieves superior sample efficiency when discovering the simulation Pareto front, running an order of magnitude fewer simulations than other state-of-the-art structural optimization algorithms. With a data-driven self-learning simulator, we find the experimental Pareto front of Young’s modulus and toughness using only a few dozen physical measurements. Furthermore, our automated strategy is able to identify prevailing toughening mechanisms that were initially found by field experts based on intuition or biomimicry and through experimental trial and error. This is an inversion of traditional composite design approaches since toughening mechanisms stem from Pareto-optimal designs. Our pipeline circumvents the time-consuming, labor-intensive development of advanced simulation models and eliminates the need for any prerequisite knowledge of toughness enhancement. Therefore, our pipeline is readily applicable to various trade-off problems well beyond the field of solid mechanics, especially where simulation struggles to match reality, such as polymer chemistry (43), computational biology (44, 45), fluid dynamics (46, 47), meteorology (48, 49), and robotics (50).

MATERIALS AND METHODS

Specimen manufacturing

All homogeneous and microstructured composites were manufactured on a Stratasys Object 260 Connex multimaterial 3D printer with a nominal resolution of 300, 600, and 800 dpi in x, y, and z directions, respectively. VeroWhitePlus (VW+) and TangoBlackPlus (TB+), two acrylic-based photopolymers, were used as base materials. The model orientation is visualized by the coordinate axes in fig. S2. Specifically, microstructure patterns are located on the x-y plane and sweep along the z direction, where the longest dimension of the model aligns with the y direction. Regarding the scale of printed specimens, each pixel in a microstructure pattern is calculated to be a 260 μm², a reasonable approximation to the least common multiple of the droplet dimensions in x and y directions.

To enable droplet-level control, we used a voxel printing approach supported by the printer. In the voxel printing mode, droplet configurations were precomputed locally and sent to the printer in real-time. This allows for printing homogeneous composites mixed with base materials at a given ratio. For any volume fraction of the rigid base material, denoted by ϕ a printing model was created by probabilistically assigning base materials to droplets, where each droplet was assigned with the rigid material at a probability of ϕ. Because the base materials are miscible, homogeneous composites were printed by mixing the droplets on the fly. Homogeneous composite materials with ϕ = 0.5, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, and 0.9 were printed as benchmarks.

Physical measurement

For Young’s modulus measurements, all testing specimens were printed following the dimensions recommended in ASTM D638. For toughness measurements, as there is no standard reference for heterogeneous composites, we devised our specimens shown in fig. S2. The dimensions of a toughness specimen are 104 mm by 52 by 3.2 mm. A notch with a length of 10.4 mm was printed, equivalent to 20% of the specimen’s width. After that, a triangle cut was added using a milling machine at a depth of 7.8 mm, which is 15% of the specimen’s width. The length of the gripper area on either side is 25 mm, leaving a 54-mm gauge area in the middle.

After printing, all specimens were carefully cleaned to remove support material and dried at room temperature. An ultraviolet (UV) light post-curing process was conducted on both the top and bottom sides of the sample to get more uniform curing. This step was performed in a Fusion UV system with a constant belt speed of around 2 cm/s. In addition, the printed notch of each toughness specimen was cleaned by a new razor blade to avoid the influence of residual support material at the tip.

All specimens were tested on an Instron 5984 universal testing machine with a maximum load of 150 kN. Tensile tests for Young’s modulus measurements were conducted according to ASTM D638. Four specimens were tested for each composite, and the results were averaged. On the toughness side, there is no existing standard targeting heterogeneous composites. Thus, we used the following tensile test method. The specimen was pulled at a rate of 2 mm/min. Data acquisition stopped once the crack propagated entirely through the specimen. Because crack propagation in microstructured composites is nonlinear, the toughness is defined as the energy absorbed and dissipated per unit volume, namely, the area under the stress-strain curve (2). At least four specimens were tested for each composite, where at least three specimens that manifested the most common and consistent fracture behaviors were considered valid. These valid toughness measurements were averaged, from which a representative stress-strain curve was selected. The same procedure was followed when testing homogeneous composites for consistency. Measured stress-strain curves from the toughness test of several representative microstructures are provided in fig. S8. For each microstructure design, four specimens were fabricated and measured (distinguished by color). The stress-strain curves of the same microstructure pattern are generally consistent, with SDs consistently less than 5% of the mean for Young’s modulus and less than 20% for toughness.

Interface engineering

Interfaces between the rigid and soft base materials are engineered by applying crafted droplet patterns in interface areas, i.e., half-pixel wide areas around shared edges and vertices of adjacent pixels (fig. S3). The droplet patterns approximate a 50/50 mixture of the base materials and vary depending on the orientation of shared edges. On the basis of the coordinates defined in fig. S3, droplets are arranged in alternate columns for edges along the x direction (vertices included) and alternate rows for edges along the y direction (vertices excluded; see note S1). The droplet patterns remain consistent in the z direction during 3D printing. Figure S4 compares the performance of five random microstructures manufactured with engineered interfaces, nonengineered interfaces, and default interfaces to the printer. The results demonstrate that our interface engineering method yields the best trade-off between Young’s modulus and toughness in printed specimens. In addition, the engineered interfaces are modeled using an interface material in simulation and count as the third base material.

Simulation

The simulator comprises a pair of FEM-based virtual testers, which predict Young’s modulus, toughness, and nonlinear stress-strain response given a microstructure pattern. The Neo-Hookean material model is used for all three base materials (VW+, TB+, and interface material) in a 2D setting (see the Supplementary Materials for details). The FEM grids represent simplified geometries of manufactured specimens. To model the interfaces between the rigid and soft materials, microstructure units in the FEM grids are upsampled by two times, and elements located at interfaces are assigned with the interface material (fig. S5). Dirichlet boundary conditions are enforced on displacements in the pulling direction. An explicit solver is used for time integration as it is usually preferred for dynamic simulations, and it is simple to implement. Material viscosity is modeled using numerical damping and controlled by a global damping coefficient. For toughness, crack initiation and propagation are modeled by thresholding the strain energy density of each element as derived from the Neo-Hookean model, where the element is removed upon exceeding a material-specific strain energy density threshold. The simulation stops when the gauge stress drops below 20% of the ultimate strength, and toughness is calculated using the area beneath the stress-strain curve. For Young’s modulus, a small constant strain is applied, and the grid is allowed to converge to an equilibrium within a fixed number of timesteps. Young’s modulus is then obtained from the measured gauge stress. Algorithmic details and parameter values of the virtual testers can be found in the Supplementary Materials.

Our simulator was implemented using the high-performance Taichi programming language (51) to harness the tremendous acceleration power of graphics processing units (GPUs). To further increase the throughput, multiple microstructures were batched and simulated simultaneously to enable maximum GPU utilization (fig. S6).

System identification

The simulated behaviors of a microstructure are contingent on several tunable parameters in the simulator, including Young’s moduli, Poisson’s ratios, and strain energy density thresholds of the base materials plus a global damping coefficient. These parameters are optimized in system identification for a close match between the simulation output and the physical measurements. Here, the objective function accounts for multiple sources of errors, including modeling (the Neo-Hookean constitutive model and a simplified fracture mechanism), fabrication (from 3D printing and specimen preparation), and measurement (inaccuracies of the equipment and other random influences from the environment). For Young’s modulus, the mean relative prediction error is minimized over a collection of composites, referred to as the system identification dataset. For toughness, the minimization objective is a combination of mean relative prediction errors on both the toughness value and the stress-strain curve, where the relative error of the curve is defined as the area between simulated and experimental stress-strain curves divided by experimental toughness. To fully use the modeling capabilities of the virtual testers, we keep parameter values separated between Young’s modulus and toughness simulation. Furthermore, microstructures in the dataset are weighted to reflect priority in system identification (fig. S9). First, microstructures closer to the experimental Pareto front have larger weights since we mainly focus on near–Pareto-optimal designs. Second, to alleviate possible bias from an uneven performance distribution in the dataset, weight penalties are inflicted upon clusters of microstructures whose physical measurements are too close to one another. A more detailed mathematical formulation of system identification is provided in the Supplementary Materials. We used batch BO to solve the minimization problem due to its excellent data efficiency and compatibility with our batch simulation mechanism. The BO algorithm was repeated for five times using different random seeds, after which the best solution was selected (see note S3 for implementation details).

Neural network–accelerated multi-objective optimization

We developed the NMO algorithm to explore the design space of microstructures and discover Pareto-optimal samples in high sample efficiency. The exploration started from randomly generated microstructures as the first generation. Unlike NSGA-II algorithms that compute offsprings from mutation and crossover operations, NMO uses the predictor, which contains a pair of residual CNNs (52), as a surrogate model to guide the proposal of the next generation (see the Supplementary Materials for details). Both networks are instantiated from the same architecture template, but the network for toughness is much larger (fig. S10). This allows for greater learning capacity to capture the complex mapping from microstructure patterns to toughness. In each iteration, the networks were trained on the simulation results of all discovered microstructures. On the basis of their predictions, a modified NSGA-II algorithm was run to propose Pareto-optimal samples that likely expand the hypervolume of the current gamut. The proposed samples became the next generation of microstructures once their performance was validated by the simulator.

The modified NSGA-II algorithm within NMO has a custom mutation operator and an additional hash-table-based deduplication mechanism. The custom mutation operator substitutes the original mutation and crossover operators in offspring generation. It changes a microstructure pattern at varied scales probabilistically, including flipping a single pixel, drawing a rasterized line, or overwriting a rectangular area of pixels. Symmetry and structure constraints are subsequently enforced on the mutated pattern. The hash table–based deduplication mechanism prevents microstructures from being added to the next generation if they have already been found and is a faster alternative to exhaustive match in existing patterns. The NMO algorithm stores found microstructures in a global hash table, while each individual run of the modified NSGA-II algorithm uses a separate hash table. More implementation details are provided in the Supplementary Materials.

We note that the validation of the inner loop and the outer loop were conducted separately. While NMO was evaluated for the inner loop in Fig. 2, we directly used the modified NSGA-II to verify the outer loop and generate the results in Fig. 3. Despite being evaluated independently, NMO is readily applicable to the computational discovery pipeline because our modularized implementation switches between optimization algorithms very easily.

Sample selection for physical validation

In each round of the outer loop, several microstructures near the simulation Pareto front were selected for physical validation (fig. S14). The selection algorithm has two stages. First, to identify microstructures that are sufficiently close to the Pareto front, we associated each microstructure with a rank induced by Pareto dominance. By our definition, the first rank comprises microstructures on the Pareto front of the whole gamut, and the i-th rank contains microstructures on the Pareto front of a partial gamut where those in higher ranks are excluded. Then, a microstructure qualified as a selection candidate if the following three criteria were satisfied: (i) it is in the third rank or higher; (ii) its simulated performance trade-off is better than the actual performance trade-off of homogeneous composites; and (iii) its toughness is higher than the microstructure with the largest Young’s modulus in the gamut. Second, we chose eight microstructures from the candidates to cover a wide range of mechanical performance and improve the diversity among discovered microstructures. To that end, the candidate microstructures were divided into eight radial bins according to their normalized mechanical performance. Then, we solved a combinatorial optimization problem, where one microstructure was chosen in each bin such that the selected microstructures were maximally distinguished from the discovered ones and from each other. The optimization problem was tackled using a beam search algorithm that finds an approximated best solution in a few seconds. In the Supplementary Materials, we provide a more detailed description of the selection algorithm, including a mathematical formulation of the combinatorial optimization problem.

Analysis of microstructure families and toughening mechanisms

After the nested-loop pipeline terminated, 11 microstructures with near-optimal trade-offs between experimental Young’s modulus and toughness were categorized into four families (Fig. 4B). We refer to these microstructures as seed microstructures. They were used to generate more pattern variations in each family and verify that the similarity in mechanical performance is preserved. This procedure breaks down into the following steps. To start, a family-specific simulator was obtained in each family from system identification on all near–Pareto-optimal microstructures. In this case, the seed microstructures were assigned with large identical weights, while others outside the family were assigned with small identical weights for regularization purposes. These family-specific simulators have much lower prediction errors on the seed microstructures in the family compared to the global simulator in round 4 (table S7). Then, on the basis of simulation results from the family-specific simulators, we ran a dense evolutionary sampling algorithm around seed microstructures to generate a local gamut for each family. The sampling algorithm is akin to the modified NSGA-II algorithm but limits the mutated patterns within a maximum of 16-pixel difference from seed microstructures. There is neither tournament selection of parents nor competition among the population; hence, the target is simply to generate a gamut as dense as possible. Last, three near–Pareto-optimal microstructures were chosen from the resulting local gamut for physical validation (fig. S16), whose physical measurements were demonstrated to be comparable to seed microstructures (table S13). Therefore, we confirmed that the discovered families contain microstructures with similar patterns and mechanical performance.

To visualize the pattern variation in each microstructure family, we divided each family into subfamilies by extracting microstructures within a 16-pixel radius from each seed microstructure, allowing any microstructure to occur in multiple subfamilies. For every subfamily, a 2D embedding space was computed for all microstructure patterns using Isomap (35). The first Wasserstein distance (53), i.e., the earth mover’s distance (EMD), was used as the distance metric between microstructure patterns instead of the Euclidean distance (fig. S18) because EMD takes into account pixel distributions in microstructure patterns and better reflects differences in geometric shapes. Figures S17 and S30 illustrate the visualized embedding spaces of 11 subfamilies across four families. Furthermore, we built an interpolation model for neighboring microstructures in the Isomap embedding space to generate more microstructures that might be missing in our dense sampling (fig. S17). Our interpolation method is based on Wasserstein barycenters from optimal transport theory (54, 55), which has been successfully demonstrated as a robust, intuitive interpolation scheme among voxelized shapes (56). In this way, we generated around 5% more microstructure patterns in each subfamily, on average, and used them to refine the Isomap embedding spaces. A comparison between the embedding spaces before and after interpolation is illustrated in figs. S21, S31, and S32. A mathematical formulation of EMD and our interpolation scheme can be found in note S4.

The identification of microstructure families simplifies the analysis of intrinsic toughening mechanisms leading to near-optimal trade-offs between Young’s modulus and toughness. As microstructures have similar patterns and performance in each family, they typically share common structural features that enhance fracture resistance. Thus, we used video recordings of seed microstructures and validation microstructures in each family to observe and interpret several predominant toughening mechanisms. For each microstructure, the simulation video produced by family-specific simulators was validated against actual footage from mechanical testing to verify that the mechanisms were properly captured by the simulator. The representative mechanisms of each microstructure family are thoroughly discussed in the Supplementary Materials.

Supplementary Materials

This PDF file includes:

Notes S1 to S5

Figs. S1 to S33

Tables S1 to S15

References