Revealing emergent magnetic charge in an antiferromagnet with diamond quantum magnetometry

Abstract

Whirling topological textures play a key role in exotic phases of magnetic materials and are promising for logic and memory applications. In antiferromagnets, these textures exhibit enhanced stability and faster dynamics with respect to their ferromagnetic counterparts, but they are also difficult to study due to their vanishing net magnetic moment. One technique that meets the demand of highly sensitive vectorial magnetic field sensing with negligible backaction is diamond quantum magnetometry. Here we show that an archetypal antiferromagnet—haematite—hosts a rich tapestry of monopolar, dipolar and quadrupolar emergent magnetic charge distributions. The direct read-out of the previously inaccessible vorticity of an antiferromagnetic spin texture provides the crucial connection to its magnetic charge through a duality relation. Our work defines a paradigmatic class of magnetic systems to explore two-dimensional monopolar physics, and highlights the transformative role that diamond quantum magnetometry could play in exploring emergent phenomena in quantum materials.

Diamond quantum magnetometry is utilized to directly read the vorticity of antiferromagnetic spin textures through coupled multi-polar emergent magnetic charge distributions.

Main

Topologically protected states in magnetic materials are promising candidates for next-generation spintronics architectures^1,2. In particular, topological textures in antiferromagnets (AFMs) could provide additional advantages over their ferromagnetic counterparts including enhanced stability as well as faster and richer dynamics^3–17. However, the vanishing net moment renders the detection of AFM textures difficult. Synchrotron-based dichroic X-ray techniques are at the imaging forefront and have—for the first time—revealed the existence of two-dimensional (2D) topological AFM spin textures in haematite, namely, α-Fe₂O₃ (refs. ^18,19). Although sensitive to staggered magnetization, this technique is insensitive to its sign and thus the associated vorticity, that is, the whirling of the spin textures is not observed.

When viewed through the lens of canted magnetization, instead of the Néel vector, we uncover weak magnetic fields emanating from the divergence of the canted moments. Such fields can be equivalently described by the magnetic analogue of Gauss’s law²⁰, thereby pointing to the existence of emergent magnetic charges in a topologically rich AFM landscape. Diamond quantum magnetometry (DQM), employing a single nitrogen-vacancy (NV) colour centre as a point field sensor, enables weak field sensing^21–25, thereby putting it in a unique position to study the above proposed concept of emergent magnetic charges in a new class of magnetic materials—canted AFMs.

In this Article, we demonstrate the DQM imaging of topological textures in the AFM α-Fe₂O₃ and show that these textures host a rich tapestry of magnetic charge distribution. In particular, the duality relation between staggered vorticity and magnetic charge allows us to associate the AFM Bloch meron with a spatially extended emergent magnetic monopole. Distinct from emergent magnetic monopoles in other realizations, such as spin ice²⁶, we observe that the positively and negatively charged monopolar textures are topologically equivalent, whereas the topological antiparticle (AFM antimeron) has a quadrupolar character. Our results demonstrate the potential of DQM to discover and investigate emergent magnetic phenomena.

Properties of α-Fe₂O₃ and DQM

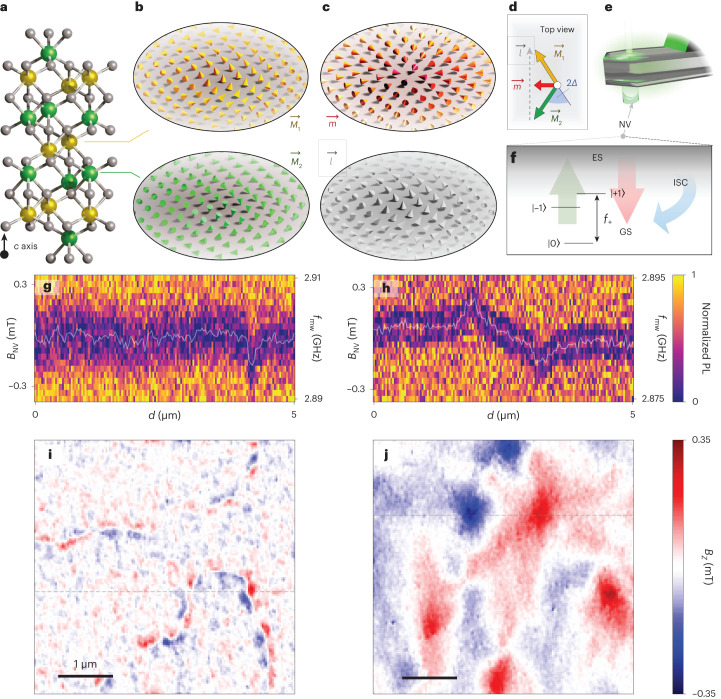
Haematite α-Fe₂O₃ is an AFM oxide insulator, which hosts a variety of topological spin textures^18,27,28. Figure 1a illustrates the atomic structure of α-Fe₂O₃. It comprises a stack of anti-parallel ferromagnetic sublattices along the c axis, with magnetization textures $\overrightarrow{M_1}$ and $\overrightarrow{M_2}$ (Fig. 1b). Spin re-orientation occurs at the Morin transition temperature, T_M ≈ 200 K (ref. ¹⁸) (Supplementary Section 1); below and above T_M, the ferromagnetic sublattices lie predominantly out of plane and in plane, respectively. The Néel vector $\overrightarrow{l}=\overrightarrow{M_1}-\overrightarrow{M_2}$ characterizes the AFM order, whereas $\overrightarrow{m}=\overrightarrow{M_1}+\overrightarrow{M_2}$ is the net magnetization (Fig. 1c,d). Above T_M, $\overrightarrow{m}$ has a predominantly in-plane orientation with an average magnitude m_Δ ≈ 2 × 10³ A m^–1. This weak magnetization is due to the slight in-plane canting of Δ ≈ 1.1 mrad (Supplementary Section 1) between $\overrightarrow{M_1}$ and $\overrightarrow{M_2}$, as a consequence of the bulk Dzyalonshinskii–Moriya interaction (DMI) vector along the c axis²⁹ (Supplementary Section 5). Consequently, $\overrightarrow{m}$ lies in plane and satisfies $\overrightarrow{m}\cdot \overrightarrow{l}=0$. Since m_Δ is much weaker than $\mid \overrightarrow{l}\mid$, this weak magnetization has no discernible effect on the AFM character of α-Fe₂O₃. Finally, $\overrightarrow{m}$ vanishes where $\overrightarrow{l}$ turns out of plane below T_M or due to the formation of AFM spin textures.

Fig. 1. Signatures of emergent magnetic fields in α-Fe₂O₃.

a, Atomic structure of α-Fe₂O₃ (Fe and O atoms in the yellow/green and grey spheres, respectively). b, Discrete representation of the alternating ferromagnetic sublattice magnetization $\overrightarrow{M_1}$ (yellow cones) and $\overrightarrow{M_2}$ (green cones) with AFM coupling along the c axis shown in a. c, Illustration of the whirling staggered magnetization $\overrightarrow{l}$ (grey cones), forming an anti-clockwise a-Bloch meron, and the resultant canted magnetic moment $\overrightarrow{m}$ (red cones). d, Illustration showing the relationship between $\overrightarrow{l}$, $\overrightarrow{m}$, $\overrightarrow{M_1}$ and $\overrightarrow{M_2}$ and the canting angle Δ. e, A scanning diamond sensor with a single NV centre maps out the magnetic ($\overrightarrow{B}$) field generated near the sample surface. f, Energy diagram of the NV ground states (GS) of |±1〉 and |0〉 sublevels. A microwave field drives the GS spin transition, whereas a 532 nm laser excites the NV to the excited state (ES) (green arrow). The NV then undergoes a radiative decay to GS (red arrow) or a non-radiative and spin-selective path via the intersystem crossing (ISC) (blue arrow), enabling ODMR acquisition. g,h, ODMR (mapped as the normalized photoluminescence (PL)) along the fast-scan direction, measured on the α-Fe₂O₃ thin film at T = 4 K (g) and across T_M at 300 K (h). The fitted f₊(B_NV) is plotted as a white line in each panel. i,j, B_z images retrieved from fitted B_NV maps reveal distinct field signatures across T_M. The dashed lines in i and j correspond to fitted B_NV traces in g and h, respectively. Scale bars, 1 μm.

We quantify the magnetic field distribution from these spin textures via DQM (Supplementary Section 2). Figure 1e illustrates our diamond probe hosting a single NV centre, which is scanned at a constant height above the sample. The NV centre is a spin defect with a paramagnetic ground-state manifold and state-selective optical transitions. This allows the Zeeman splitting between the ground states |±1〉 and |0〉 to be probed with a microwave frequency f_mw sweep and optical excitation via optically detected magnetic resonance (ODMR). In the weak-field approximation³⁰ with negligible strain, we infer the magnetic field projected onto the NV axis (B_NV) from the energy difference between |0〉 and |+1〉 given by $\Delta E_{+}=h\left(\mid f_{+}-D\mid -\tilde{\gamma }{B}_{\mathrm{bias}}\right)=h\tilde{\gamma }{B}_{\mathrm{NV}}$, where h is Planck’s constant, f₊ is the resonant frequency corresponding to the transition, D ≈ 2.87 GHz and $\tilde{\gamma }$ = 28 MHz mT^–1. A bias field B_bias ≈ 0.5 mT is applied along the NV axis to enable the extraction of field orientation. Figure 1g,h illustrates the variation in ODMR frequency across a linescan over the α-Fe₂O₃ surface at T = 4 and 300 K, respectively. The colour plot displays the signal amplitude, whereas the white curves demarcate f₊ used to extract B_NV. An ODMR raster scan across the sample surface provides a B_NV image. We transform this to the laboratory coordinates (B_x,y,z) via the Fourier reconstruction technique³¹, where z coincides with the c axis of the crystal. Figure 1i,j presents images of B_z collected at 4 and 300 K, respectively. The observed qualitative differences reveal distinct magnetic phases for temperatures below and above T_M (ref. ¹⁸). The image below T_M comprises narrow features in an almost-zero field background, consistent with the absence of net magnetization. By contrast, the image above T_M displays larger features within a non-zero field background, expected from a non-zero net magnetization.

Emergent properties in α-Fe₂O₃

To gain a physical interpretation of magnetization distribution from the measured B_z images, we begin from a thin-film approximation (Supplementary Section 4.1):

$$B_z={\alpha }_{xy}\left(t,d\right)*\overrightarrow{\nabla }\cdot {\overrightarrow{m}}_{xy}+{\alpha }_z\left(t,d\right)*{\nabla }^2{m}_z,$$ 1

where * indicates convolution; α_i (i = xy, z) are the effective point spread functions³²; t is the film thickness; d is the height above the film surface; and ${\overrightarrow{m}}_{xy}$ and m_z are the in-plane and out-of-plane components of $\overrightarrow{m}$, respectively. ${\overrightarrow{m}}_{xy}$ and m_z contribute to B_z through the divergence and Laplacian, respectively. The α_i functions account for the magnetic field decay above the surface, acting as blurring kernels with size of ~d. Hence, the spatial resolution of DQM is set by the NV-sample distance d_NV (Supplementary Section 3). Due to DMI symmetry in α-Fe₂O₃ (Supplementary Section 5), m_z = 0 and ${\overrightarrow{m}}_{xy}\ne 0$, rendering the second term in equation (1) zero. Therefore, B_z images are the divergence of the canted magnetization $\overrightarrow{\nabla }\cdot {\overrightarrow{m}}_{xy}$, convolved with α_xy. Moreover, for a $\widehat{z}$-oriented DMI, the net magnetization is given by $\overrightarrow{m}=\mathrm{\Delta }\left(\widehat{z}\times \overrightarrow{l}\right)$, where Δ is the DMI-set canting angle. This yields the expression $\overrightarrow{\nabla }\cdot {\overrightarrow{m}}_{xy}=\mathrm{\Delta }\left[\widehat{z}\cdot \left(\overrightarrow{\nabla }\times \overrightarrow{l}\right)\right]$ (Supplementary Section 5). The striking consequence is that the B_z images also offer a projected measure of staggered vorticity, that is, the curl of the Néel vector $\overrightarrow{\mathcal{V}}=\overrightarrow{\nabla }\times \overrightarrow{l}$.

Characteristic field signatures and vorticity read-out

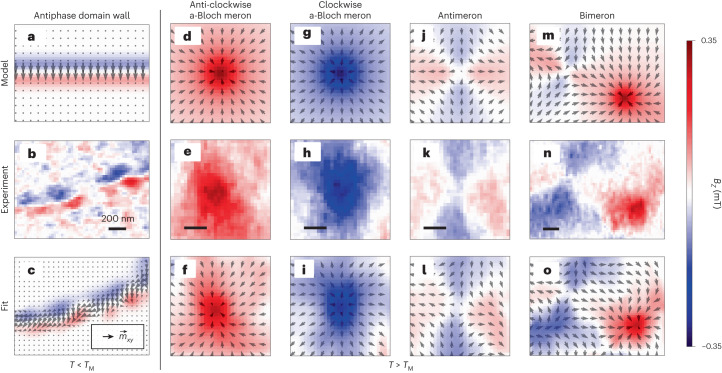
After establishing the relationship between B_z and ${\overrightarrow{m}}_{xy}$, next we show that the images obtained in Fig. 1 are produced by AFM antiphase domain walls (ADWs), merons, antimerons and bimerons—consistent with recent observations in α-Fe₂O₃ (ref. ¹⁸). Below T_M, we model the B_z images with a linear AFM domain wall¹⁸, characterized by width w and phase ξ_a (Supplementary Section 5.1). The phase ξ_a controls the spatial variation of $\overrightarrow{l}$, resulting in an AFM Néel (a-Néel) or an AFM Bloch (a-Bloch) ADW profile for (ξ_a = 0, π) and (${\xi }_{\mathrm{a}}=\frac{\mathrm{\pi }}{2}$, $\frac{3\pi }{2}$), respectively. For a linear ADW profile centred at x = 0 along the x axis, $\overrightarrow{\nabla }\cdot {\overrightarrow{m}}_{xy}=$ $m_{\mathrm{\Delta }}\left(\frac{\mathrm{\pi }}{w}\right)\sin \left(\frac{\mathrm{\pi }x}{w}\right)\sin \left({\xi }_{\mathrm{a}}\right)$ for $\mid x\mid \le \frac{w}{2}$, and zero elsewhere¹⁸ (Supplementary Section 5.1). Hence, we expect ADWs to display a sinusoidal profile in $\overrightarrow{\nabla }\cdot {\overrightarrow{m}}_{xy}$ and in B_z, with zero crossing at the centre, and amplitude and sign modulated by sin(ξ_a). In particular, an a-Néel ADW will not yield a B_z signal as $\overrightarrow{\nabla }\cdot {\overrightarrow{m}}_{xy}=0$, whereas an a-Bloch counterpart will show the maximal signal. Based on equation (1), these characteristics are reflected in the calculated B_z image of an ADW model in Fig. 2a (Supplementary Section 5.4), assuming a phase of ξ_a = π. The measured B_z image (Fig. 1i) and a close-up image (Fig. 2b) capture the signature zero crossing of an ADW. DQM also reveals variations in B_z along the wall boundary, capturing the spatially varying phase ξ_a in α-Fe₂O₃ (ref. ¹⁸). This phase dependence of B_z allows the unambiguous identification of the zero-signal sections along the wall with varying ξ_a as a-Néel ADWs. Figure 2c presents a reconstruction of the ${\overrightarrow{m}}_{xy}$ distribution of the multi-chiral ADW (illustrated by arrows), obtained by fitting B_z to the data in Fig. 2b through systematic regularization (Supplementary Section 7).

Fig. 2. Classification of topological AFM textures via DQM.

a–c, Topological AFM textures observed below T_M. A distinct B_z signature of an ADW calculated (a) and measured (b) above the sample surface. The reconstructed ${\overrightarrow{m}}_{xy}$ (black arrows) from b and its B_z distribution (c). d–o, Topological AFM textures observed above T_M. Calculated (d) and measured (e) B_z-field signatures of an anti-clockwise a-Bloch meron and the reconstructed ${\overrightarrow{m}}_{xy}$ (black arrows) of e and its associated B_z (f). Similarly, the calculated and measured B_z signatures and the ${\overrightarrow{m}}_{xy}$ reconstruction of a clockwise a-Bloch meron, an antimeron and a bimeron are given in g–i, j–l and m–o, respectively. Supplementary Section 7 provides the details and limitations of ${\overrightarrow{m}}_{xy}$ reconstruction. Scale bars, 200 nm.

In contrast, DQM at 300 K captures larger spatial features of a strong B_z signal (Fig. 1j). In the above-T_M regime, we anticipate finite net magnetization forming whirling topological structures, such as multi-chiral merons and antimerons¹⁸, as well as topologically trivial in-plane domain walls. Topological textures can be characterized by the topological charge $\mathcal{Q}$ and topological winding $\mathcal{N}$. Each AFM texture produces a distinctive B_z signal, allowing us to develop a systematic procedure to differentiate them (Supplementary Section 5). Here we focus on 2D topological textures and model isolated (anti)merons based on a linear ansatz^18,33, described by phase ξ_a and winding number $\mathcal{N}$ (Supplementary Section 5.3). The corresponding divergence in polar coordinates (r, ϕ) is $\overrightarrow{\nabla }\cdot {\overrightarrow{m}}_{xy}=m_{\mathrm{\Delta }}\sin \left(\varphi \left(1-\mathcal{N}\right)-{\xi }_a\right)f\left(r\right)$, where f(r) is a radial function dependent on the (anti)meron phase (Supplementary Section 5.3). A meron ($\mathcal{N}=+1$) produces a radially symmetric B_z distribution about its core with magnitude and polarity controlled by sin(ξ_a). Analogous to ADWs, a-Néel merons (ξ_a = 0, π) are divergence-free and exhibit B_z = 0, whereas a-Bloch counterparts $\left(\right){\xi }_{\mathrm{a}}=\frac{\mathrm{\pi }}{2}$, $\frac{3\mathrm{\pi }}{2}\left)\right)$ show the maximal B_z amplitude. In contrast, for an antimeron ($\mathcal{N}=-1$), the B_z distribution is two-fold symmetric and ξ_a controls an azimuthal offset. The calculated B_z images in Fig. 2d,g,j of the a-Bloch meron model of both polarities and the antimeron model reinforce these observations (Supplementary Section 5.4). Thus, DQM unambiguously reveals the topological winding number $\mathcal{N}$ and staggered vorticity $\overrightarrow{\mathcal{V}}$ for each spin texture. DQM cannot distinguish the sign of the topological charge of the spin texture due to the vanishing canted moment at its core. Figure 2e,h,k presents the measured B_z images of an anti-clockwise a-Bloch meron ($\mathcal{N}=+1,{\xi }_{\mathrm{a}}=\mathrm{\pi }/2$), a clockwise a-Bloch meron ($\mathcal{N}=+1,{\xi }_{\mathrm{a}}=3\mathrm{\pi }/2$) and an antimeron ($\mathcal{N}=-1$), respectively, in good agreement with their modelled counterparts. Further, in Fig. 2f,i,l, we reconstruct the ${\overrightarrow{m}}_{xy}$ distributions and use them to calculate the measured B_z image for each texture discussed above (Supplementary Section 7). Given the density of spin textures evident in Fig. 1j, the reconstructed ${\overrightarrow{m}}_{xy}$ approach better captures the finer details of the measured B_z images in the absence of true isolation. We note that although several simplifying steps are considered in our magnetization reconstruction (Supplementary Section 7), the insights presented in the main text, including those on staggered vorticity, remain valid. We further note that the density of (anti)merons can be reduced via meron–antimeron annihilation mediated by an external in-plane magnetic field¹⁸ (Supplementary Section 8). Finally, a meron and an antimeron in close proximity can form a stable bimeron. Figure 2m displays the corresponding calculated B_z image of an isolated bimeron model, whereas Fig. 2n shows the measured B_z image of one such occurrence. Similarly, Fig. 2o displays the calculated B_z image from its reconstructed ${\overrightarrow{m}}_{xy}$. Although (anti)merons are always topologically protected, this is not necessarily true for meron–antimeron pairs. Labelling a meron–antimeron pair as topologically protected would require the knowledge of the topological charge sign of its constituents^29,34.

Emergent magnetic charge

The fact that DQM provides a direct measure of $\overrightarrow{\nabla }\cdot {\overrightarrow{m}}_{xy}$ creates a unique opportunity to consider a magnetic analogue of the electric Gauss’s law. Namely, the non-zero divergence of magnetization manifests the existence of an areal magnetic charge density via ${\sigma }_{\mathrm{m}}=-t\left(\overrightarrow{\nabla }\cdot {\overrightarrow{m}}_{xy}\right)$. Here ${\overrightarrow{m}}_{xy}$ is independent of t—valid in the thin-film limit¹⁸. Therefore, AFM textures in α-Fe₂O₃ have associated emergent magnetic charge distributions, which locally act as sources or sinks of the magnetic field. We can define a formal duality relation that connects the magnetic charge density σ_m to the staggered vorticity $\overrightarrow{\mathcal{V}}$ via

$${\sigma }_m/t=-\overrightarrow{\nabla }\cdot {\overrightarrow{m}}_{xy}=\mathrm{\Delta }\left(\widehat{z}\cdot \overrightarrow{\mathcal{V}}\right),$$ 2

which scales with sin(ξ_a), highlighting the influence of the texture phase. Crucially, retrieving the emergent charge density σ_m only requires the Fourier deconvolution of the measured B_z images from the transfer function α_xy (Supplementary Section 4.2). We can also perform a downward (upward) continuation³⁵ (Supplementary Section 4.2) of the planar $\overrightarrow{B}$ distribution captured in Fig. 2b,e,h,k,n, down to (away from) the sample surface. This allows a three-dimensional visualization of $\overrightarrow{B}$ ($=\overrightarrow{H}$ in a vacuum) in the volume above the magnetic charge distribution. Note that this charge and field retrieval process is independent of the ${\overrightarrow{m}}_{xy}$ reconstruction and the linear meron model assumption.

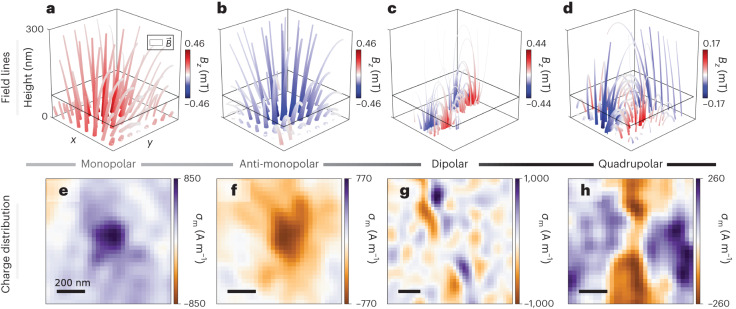
Figure 3a–d illustrates the field lines of $\overrightarrow{B}$ above the (anti-)clockwise a-Bloch meron, ADW and antimeron. For the two Bloch merons, $\overrightarrow{B}$ is consistent with the profile expected for spatially extended sources and sinks of the magnetic field emanating from a monopolar distribution, which we retrieved via equation (2) in Fig. 3e,f. This implies that a-Bloch merons host a class of emergent monopoles piggybacking on the topologically protected AFM textures. Interestingly, such monopolar magnetic distributions are not observed in ferromagnetic materials, as the presence of long-range demagnetizing fields favours divergence-free Bloch textures. In our case, we are freed from this constraint due the presence of a weak demagnetizing contribution relative to the stronger AFM exchange in α-Fe₂O₃. In contrast to merons, the ADW in Fig. 3c and the antimeron in Fig. 3d are associated with σ_m distributions that exhibit dipolar and quadrupolar characters, respectively (Fig. 3g,h). Finally, we emphasize that the observation of emergent monopoles is fully consistent with the modelling of AFM topological textures in Fig. 2 and does not violate Maxwell’s equation as they are, in fact, sinks and sources of the $\overrightarrow{H}$ field. Although $\overrightarrow{\nabla }\cdot \overrightarrow{H}\ne 0$ in the material, the condition of $\overrightarrow{\nabla }\cdot \overrightarrow{B}=0$ is still conserved since $\overrightarrow{B}={\mu }_0\left(\overrightarrow{H}+\overrightarrow{m}\right)$ and in the absence of any free electric current, $\nabla \cdot \overrightarrow{H}=-\nabla \cdot \overrightarrow{m}$. Therefore, when probing the fields outside the material, where ${\mu }_0\overrightarrow{H}=\overrightarrow{B}$, one sees a field $\overrightarrow{B}$ that appears as if it is emerging from sources and sinks given by $\overrightarrow{\nabla }\cdot \overrightarrow{m}$ (refs. ^26,36,37).

Fig. 3. Emergent magnetic charge distributions.

a–d, Three-dimensional visualization of $\overrightarrow{B}$ in the volume above an assortment of topological AFM textures. The streamtubes illustrate the magnetic field lines of $\overrightarrow{B}$ above an anti-clockwise a-Bloch meron (a), a clockwise a-Bloch meron (b), an ADW (c) and an antimeron (d). The girth and colour of each streamtube vary with the magnetic field norm $\mid \overrightarrow{B}\mid$ and the z component of field (B_z), respectively. e–h, Magnetic charge density (σ_m) distributions retrieved from the downward continuation of a–d reveal a magnetic monopolar (e), anti-monopolar (f), dipolar (g) and quadrupolar (h) charge character associated to an anti-clockwise a-Bloch meron, clockwise a-Bloch meron, ADW and antimeron, respectively. Scale bars, 200 nm.

Based on the above analysis, it is tempting to attribute a non-zero net monopolar charge to isolated a-Bloch merons, quantified by Q_m ≡ ∫_Sσ_mdS within area S. We pick a circular integration area S of radius r centred on a given spin texture. Figure 4a,b illustrates an example in the case of antimerons. The (1/r) dependence of $\overrightarrow{\nabla }\cdot {\overrightarrow{m}}_{xy}$ for 2D magnetic charges hosted by spin textures then yields (Supplementary Section 5.9)

$$Q_{\mathrm{m}}\left(r\right)=\left\{\begin{array}{cc}2\mathrm{\pi }{m}_{\mathrm{\Delta }}\sin \left({\xi }_{\mathrm{a}}\right)\sin \left(\frac{\mathrm{\pi }r}{2R_{\mathrm{M}}}\right)rt\hfill & ,\mathcal{N}=+1,r\le R_{\mathrm{M}}\hfill \\ 2\mathrm{\pi }{m}_{\mathrm{\Delta }}\sin \left({\xi }_{\mathrm{a}}\right)rt\hfill & ,\mathcal{N}=+1,r>R_{\mathrm{M}}.\hfill \\ 0\hfill & ,\mathcal{N}=-1\hfill \end{array}\right)$$ 3

Figure 4c presents the radial dependence of Q_m for four measured merons (light-blue dashed curves) and antimerons (light-red dashed curves), whereas the dark-blue (red) dashed curve is the average Q_m radial dependence for merons (antimerons). For an isolated linear meron model, Q_m scales linearly with r, and the measured Q_m radial dependence is in agreement with this. Q_m itself is not a topological invariant, as a smooth transformation of an a-Bloch meron to an a-Néel meron would tune Q_m from non-zero to zero. For an isolated antimeron, the two-fold rotational symmetry ensures Q_m = 0 for all r values (Supplementary Section 5.9) and at short distances, the experimental Q_m value of an antimeron agrees well with this prediction. Beyond measurement-induced variations, deviation from the strict Q_m = 0 condition arises when an antimeron is influenced by neighbouring spin textures. This reduces the two-fold symmetry and reveals a finite Q_m. Figure 4a,b captures this reduced symmetry as well as the consequential bias towards negative and positive Q_m, respectively. Finally, as r goes to infinity, the integration area would overlap with the surrounding spin textures, leading to a further deviation from the Q_m = 0 condition.

Fig. 4. Scaling of 2D integrated magnetic charges.

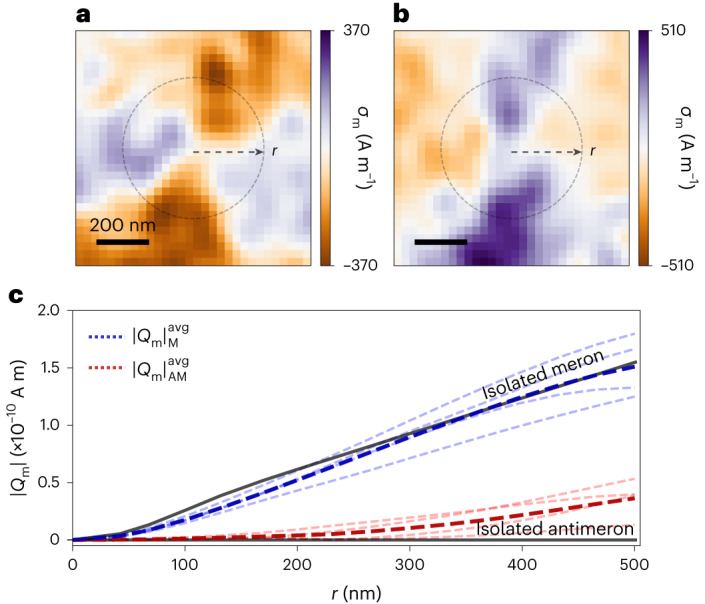
a,b, Reconstructed magnetic charge distribution (σ_m) of two experimentally observed antimerons (AM 1 and AM 2) with slightly distorted quadrupolar characters. AM 1 and AM 2 display a bias towards positive and negative charges, respectively. The dashed circle in a and b illustrates the circular integration area S of radius r, centred at the core of the antimeron, to obtain |Q_m|. Scale bars, 200 nm. c, Experimentally retrieved magnitude of the total integrated magnetic charge of multiple merons (|Q_m|_M, light-blue dashed curves) and antimerons (|Q_m|_AM, light-red dashed curves) plotted as a function of integration radius r. Their average experimental |Q_m| profiles, namely, $\mid Q_{\mathrm{m}}{\mid }_{\mathrm{M}}^{\mathrm{avg}}$ and $\mid Q_{\mathrm{m}}{\mid }_{\mathrm{AM}}^{\mathrm{avg}}$, are represented by dark-blue and dark-red curves, respectively. The solid black curves plot the theoretically predicted Q_m radial dependence based on equation (3) for isolated merons and antimerons.

The assumption that we have a collection of isolated spin textures oversimplifies the reality. Although the AFM topological textures are mesoscopically discernible and thus appear localized, they are, in fact, the constituents of the complex multi-textural ensemble that interacts via a 2D magnetic charge canvas. The magnetic charge per constituent is not just dictated by their nature as merons and antimerons, but modified through their interaction with other constituents. For example, an isolated meron and antimeron pair forming an AFM bimeron (Fig. 2n) would have a non-zero Q_m, whose sign is predominantly determined by its meron (Supplementary Section 5.9). However, this clearly cannot be the case for a bimeron embedded in a uniform magnetization field in the far field (Supplementary Section 5.10), since the divergence theorem ensures that Q_m = 0. This indicates that the interaction among AFM textures produces additional magnetic charge density away from the cores and highlights the interactive nature of this multi-textural ensemble.

Discussion and outlook

Our ability to identify the duality between topological AFM textures and magnetic charges is due to the direct read-out of staggered vorticity enabled by DQM. Specifically, the NV centre senses the amplitude of the magnetic field projected onto the NV axis, allowing us to deduce the three field components via their linear dependence. This enables us to independently reconstruct the magnetic charge and local magnetization. As such, we go beyond detecting antimerons and merons, to further distinguish between clockwise and anti-clockwise a-Bloch components, which otherwise appear indistinguishable in X-ray dichroic images. Our imaging approach can be extended to a wider family of topological textures, including skyrmions, a-Néel merons and bimerons, as well as distorted AFM textures that are otherwise divergence-free (Supplementary Section 5.6–5.8), relevant for topological AFM circuitry^7,27,38.

Although haematite provides favourable conditions for DQM imaging due to spin canting, it is, by no means, unique among AFMs in possessing a weak net magnetization or quasi-isotropic spins in two dimensions. It may be possible to observe topological phenomenology in similar canted AFMs, including orthoferrites, orthochromites and iron borate^39–42. In compensated AFMs without bulk DMI, staggered spin textures can also generate a local net magnetization, either statically or dynamically^8,43,44. Moreover, DQM can be useful in detecting preferential vorticity in ultrathin films induced by interfacial interactions—a key requirement for applications in topological spintronics^27,28.

The reported duality between magnetic charges and topological AFM textures sheds light on a new class of materials hosting 2D monopolar physics in contrast with other systems that harbour emergent magnetic monopoles, such as the pyrochlore spin ice²⁶. Although intriguing, monopoles in spin ice are intrinsically distinct, as they have an underlying gauge charge, which is topological and quantized. Conversely, the emergent magnetic charges in haematite are 2D, not quantized and are topological in the sense that they dress topological AFM textures underpinning them. We have demonstrated that haematite supports a rich tapestry of interacting magnetic charge distributions that could open up new and complementary ways to detect, manipulate and functionalize—via their magnetic charge—AFM topological textures. Our capability to classify different AFM spin textures could be combined with conventional spin manipulation techniques such as spin torques, allowing for read-out and write-in schemes. Realizing this in a complex manifold of states endowed with highly nonlinear interactions could be attractive for unconventional computing^1,2. Finally, the intriguing physical insights revealed in α-Fe₂O₃ are a testament to the relevance and potential of DQM as a versatile table-top platform to explore emergent phenomena in AFMs and other quantum materials.

Online content

Any methods, additional references, Nature Portfolio reporting summaries, source data, extended data, supplementary information, acknowledgements, peer review information; details of author contributions and competing interests; and statements of data and code availability are available at 10.1038/s41563-023-01737-4.

Author contributions

A.K.C.T., M.H., H.J., P.G.R. and M.A. conceived the experiments. A.K.C.T. and M.H. performed the DQM measurements with assistance from L.S., D.B., A.G., A.M. and M.S.G.F. H.J. fabricated and characterized the samples. A.K.C.T., H.J., M.H., D.B. and A.G. performed the data analysis with inputs from L.S., C.C., P.G.R. and M.A. All authors contributed to the discussion of the results. All authors contributed to the preparation of the manuscript.

Peer review

Peer review information

Nature Materials thanks Ulrich Nowak, Uri Vool and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Data availability

All data needed to evaluate the conclusions in the paper are available in this Article or its Supplementary Information. The data that support the findings of this study are available from the corresponding authors upon reasonable request.

Competing interests

The authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s41563-023-01737-4.