Examining the Influence of Imbalanced Social Contact Matrices in Epidemic Models

Mackenzie A Hamilton; Jesse Knight; Sharmistha Mishra

doi:10.1093/aje/kwad185

. 2023 Sep 15;193(2):339–347. doi: 10.1093/aje/kwad185

Examining the Influence of Imbalanced Social Contact Matrices in Epidemic Models

Mackenzie A Hamilton, Jesse Knight, Sharmistha Mishra ^✉

PMCID: PMC10840077 PMID: 37715459

Abstract

Transmissible infections such as those caused by severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) spread according to who contacts whom. Therefore, many epidemic models incorporate contact patterns through contact matrices. Contact matrices can be generated from social contact survey data. However, the resulting matrices are often imbalanced, such that the total number of contacts reported by group A with group B do not match those reported by group B with group A. We examined the theoretical influence of imbalanced contact matrices on the estimated basic reproduction number (R₀). We then explored how imbalanced matrices may bias model-based epidemic projections using an illustrative simulation model of SARS-CoV-2 with 2 age groups (<15 and ≥15 years). Models with imbalanced matrices underestimated the initial spread of SARS-CoV-2, had later time to peak incidence, and had smaller peak incidence. Imbalanced matrices also influenced cumulative infections observed per age group, as well as the estimated impact of an age-specific vaccination strategy. Stratified transmission models that do not consider contact balancing may generate biased projections of epidemic trajectory and the impact of targeted public health interventions. Therefore, modeling studies should implement and report methods used to balance contact matrices for stratified transmission models.

Keywords: contact balance, contact mixing, contact reciprocity, infectious disease modeling, SARS-CoV-2, vaccine policy

Abbreviations

SARS-CoV-2: severe acute respiratory syndrome coronavirus 2
SEIR: susceptible-exposed-infectious-recovered

Contact patterns (i.e., who contacts whom) are a fundamental component of infectious disease transmission dynamics. Such patterns, and the role of highly connected subgroups, can determine the size of epidemics, the incidence of infection among subgroups of a population, and whether epidemics emerge and persist (1). Mathematical models are widely used to study transmission dynamics and evaluate public health interventions; therefore, such models are often structured to consider population and contact heterogeneity (2–6).

Models with population and contact heterogeneity require estimates of contact within and between subgroups, represented through a contact matrix. Data to generate contact matrices are often obtained from contact diaries and surveys, with the POLYMOD social contact study (7) among the most commonly used data sources for models of respiratory pathogens (2–5). POLYMOD collected data on daily age-stratified social contacts of almost 8,000 individuals across 8 European countries. To enable broader application of POLYMOD data, several techniques were then developed to project contact matrices to other countries (8–10). For example, Prem et al. (8, 9) used a Bayesian hierarchical model with country-specific data on population demographic structure, school enrollment, workforce participation, and household makeup to project POLYMOD contact matrices to 177 different countries around the world.

When using empirical contact data to structure the underlying contact patterns in a population, analysts must consider the balanced (i.e., reciprocal) nature of measured contacts (11, 12). In reality, the total number of contacts that individuals in subgroup i form with individuals in subgroup j must be equal to the total number of contacts that individuals in subgroup j form with individuals in subgroup i, such that:

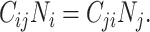(1)

where 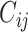Inline graphic is the number of contacts an individual in subgroup 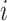forms with individuals in subgroup 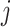per day; 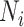is the size of subgroup 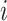; and likewise for 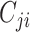and 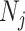. Here “measured contacts,” which may not always lead to transmission, are distinguished from “effective contacts,” which do lead to transmission (by definition). The measured contact matrix (“who contacts whom”) must be balanced, but the transmission matrix (“who infects whom”) is often asymmetrical (13). This is because effective contacts that lead to transmission are a function of measured contacts and biological probabilities of transmission per contact (i.e., infectiousness and susceptibility, e.g., modified by vaccination). However, perfect reciprocity is rarely observed in measured contacts from survey data. Imbalances in empirical contact data often arise due to measurement error in survey responses (e.g., recall bias or social desirability bias). However, even when measurement error is absent, imbalances can arise due to selection bias (e.g., differential sampling of subgroups across the network). That is, contact surveys rarely sample from closed, perfectly defined networks, and sampling frames are seldom designed to reflect network structures (11, 12).

Numerous mathematical transmission models have used contact data from POLYMOD and Prem et al., but many lack description of methods applied to handle the imbalanced (i.e., nonreciprocal) nature of these matrices (6, 14–16). For example, in some early models examining age-based prioritization of severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) vaccination, there was either no mention of whether or not measured contacts were balanced or how they were balanced (6, 14–16). As such, it is not always clear if and when age-structured transmission models used balanced or imbalanced contact patterns. Moreover, how imbalanced contact matrices affect modeling projections has yet to be quantified.

We sought to examine how imbalances in measured contact matrices influence infection transmission dynamics. First, we examined the theoretical influence of imbalanced contact matrices on the estimated basic reproduction number (R₀). We then conducted an illustrative simulation study, using a SARS-CoV-2 age-stratified compartmental model as an example, to explore the influence of imbalanced contact matrices on the temporal epidemic dynamics, cumulative infections among age groups, and potential impact of age-specific vaccination strategies.

METHODS

Study design

We conducted an analytical and simulation (mathematical modeling) study to examine 3 key characteristics of a model’s underlying transmission dynamics that can be modified by a network structure: the basic reproduction number, the temporal pattern of an epidemic, and the epidemic size. First, we compared the basic reproduction number R₀ of an epidemic in a population stratified into 2 age groups (<15 and ≥15 years) when parameterized with imbalanced versus balanced contact matrices across all 177 demographic settings studied by Prem et al. (8). We used contact matrices from Prem et al. to inform parametrization because of their use in most SARS-CoV-2 transmission models to date.

Next, we conducted a theoretical SARS-CoV-2 simulation study using an SEIR (susceptible-exposed-infectious-recovered) mathematical model in 3 demographic settings where imbalanced contacts reported by persons aged ≥15 with those aged <15 were 1) larger than (Singapore), 2) equal to (Luxembourg), and 3) less than (Gambia) balanced contacts between those aged ≥15 and those aged <15. We compared the timing and magnitude of peak infection incidence, cumulative infections after 1 year of seeding, and cumulative infections averted in the context of age-specific vaccination strategies after 1 year of seeding, when models were parameterized with imbalanced versus balanced matrices.

Age-stratified social contact data

We obtained age-stratified social contact matrices and population data from Prem et al. (8). Raw matrices were imbalanced and stratified into 16 age groups, with each matrix element, C_ij, representing the mean number of contacts that a person in age group i reported with a person in age group j per day. To simplify our analysis, we transformed the age structure of the matrices into 2 age groups: individuals less than 15 years of age, and those aged 15 or older. Imbalanced contact matrices for these age groups were derived by calculating the population-weighted average contacts per person per day of contributing age groups (e.g., ages 0–4, 5–9, and 10–14 years for the new age group of <15 years) from the raw, imbalanced, contact matrices from Prem et al.

Derivation of balanced social contact matrices

As has been done previously (10, 17, 18), we estimated the balanced contacts between individuals in age groups 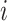Inline graphic and 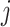(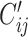) per day by averaging reported contacts from Prem as follows:

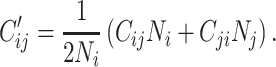(2)

Derivation of R₀

We used methodology from Diekmann et al. (19) to calculate R₀. In brief, R₀ is the dominant eigenvalue of the next generation matrix (i.e., the number of secondary infectious persons that result in each age group). In a population divided into 2 age groups, the dominant eigenvalue is the maximum solution of:

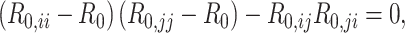(3)

where 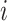Inline graphic and 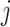denote the 2 age groups (i.e., <15 and ≥15 years of age), and 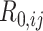is the number of secondary infectious individuals in age group 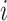that result from contact with an infectious person in age group 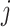in a completely susceptible population, calculated as:

(4)

where 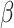Inline graphic is the probability of transmission of an infectious disease upon contact, and 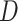is the duration of infectiousness. We calculated R₀ with imbalanced and balanced matrices from 177 demographic settings studied in Prem et al. (8). We then calculated a relative 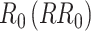under imbalanced versus balanced conditions where:

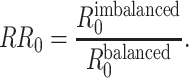(5)

We assumed the probability of transmission and the duration of infectiousness was constant across age groups (and therefore had no impact on the relative reproduction number); thus, our estimate of the influence of imbalanced matrices is independent of a specific infectious disease.

SEIR transmission model

For our simulations, we used a deterministic, compartmental transmission model of SARS-CoV-2 using a simplified SEIR system. Susceptible (S) individuals transitioned to an exposed health state (E) via a force of infection, defined by a probability of contact and probability of transmission per contact with a person in the infectious (I) health state. Individuals in the exposed health state became infectious after a latent period. After an average period of infectiousness, individuals in the infectious health state moved to the recovered health state (R), where they could not be reinfected. Model equations and details are outlined in Web Appendix 1 (supplementary equations; available at https://doi.org/10.1093/aje/kwad185). Table 1 summarizes model parameter values.

Table 1.

SEIR Transmission Model Parameters

Parameter	Symbol	Value	Source: First Author, Year (Reference No.)
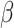
Probability of transmission per contact		0.015	Davies, 2020 (26)
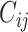
Contact rate per day		Supplementary data^a	Prem, 2021 (8)
Duration of pre-infectious (latent) period	1/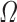	5.5 days	Xin, 2022 (27), Cheng, 2021 (28)
Duration of infectious period	1/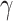	10 days	Walsh, 2020 (29)
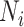
Population size		Supplementary data^a	Prem, 2021 (8)

Open in a new tab

Abbreviation: SEIR, susceptible-exposed-infectious-recovered.

^a Parameter varies by age group.

We made 3 key assumptions to simplify our model and focus the analysis on the influence of imbalanced matrices. First, we assumed the population size was fixed (i.e., the model simulates a closed system with no births or deaths) to avoid changes in the probability of contact over time. Second, we assumed that there were no interventions to mitigate the spread of SARS-CoV-2 (e.g., isolation of infected individuals, reduction in contacts in response to increases in infection rates) as we were interested in isolating the effect of imbalanced matrices rather than infection prevention and control strategies. Finally, we assumed the probability of transmission of, and duration of infectiousness with, SARS-CoV-2 was fixed across age groups to estimate the impact of imbalanced matrices independent of infection properties by age.

Simulation of SARS-CoV-2 transmission

We simulated SARS-CoV-2 transmission in 3 demographic settings from Prem et al. (8), where imbalanced contacts of ages ≥15 years reported with those of <15 years were: larger than (Singapore), equal to (Luxembourg), and less than (Gambia) balanced contacts between those aged ≥15 and those aged <15 (Web Figure 1). Models were seeded with 1 individual in the infectious state per age group for all simulations. We then compared the magnitude and time to peak incidence, and the percent difference in cumulative infections 1 year after seeding, when models were parameterized with imbalanced versus balanced matrices.

Transmission impact of a targeted public health intervention

To explore the influence of imbalanced matrices on the impact of prioritized public health interventions, we simulated 2 age-specific SARS-CoV-2 vaccination scenarios in all models: one in which vaccines were administered to individuals of <15 years, and another where vaccines were administered to individuals ≥15. We assumed that 50% of the vaccinated age group were immune prior to seeding, and these individuals could not be infected (i.e., were permanently immune). We compared cumulative infections overall and per age group in the presence and absence of vaccination over 1 year, to calculate cumulative infections averted from vaccination. Then, we calculated the percent difference in cumulative infections averted between models parameterized with imbalanced versus balanced matrices.

Validation analyses

To validate robustness of findings, we conducted 2 additional analyses. First, we assessed how imbalanced matrices affected R₀ in a population stratified into different age groups: individuals younger than 40 years of age, and 40 or older. Next, we assessed how imbalanced matrices affected R₀ when biases in raw contact matrices were opposite to original observations from Prem et al. (8). For example, if reported contacts between those aged <15 and ≥15 were larger than balanced contacts between those aged <15 and ≥15 (e.g., Gambia), we forced those aged <15 to underestimate contacts with those aged ≥15. We conducted this analysis to assess how systematic bias in contact patterns from Prem may have influenced our results.

RESULTS

Imbalance in contact matrices by demographic setting

In comparison with balanced matrices, imbalanced matrices from countries with older populations overestimated total contacts reported by those ≥15 years of age with those <15, and underestimated total contacts reported by those who were <15 with those who were ≥15 (Web Figure 1). The opposite pattern was observed in countries with younger populations, where contacts reported by those aged <15 with those age ≥15 were overestimated and contacts reported by those aged ≥15 with those aged <15 were underestimated (Web Figure 1). For example, in Singapore (median age, 42.2 years) the number of imbalanced contacts reported by those aged ≥15 with those aged <15 were 1.5 times the balanced contacts between those aged ≥15 and those aged <15, whereas in Gambia (median age, 17.8 years), imbalanced contacts reported by those aged ≥15 with those aged <15 were 0.45 times the balanced contacts between those aged ≥15 and those aged <15.

Influence of imbalanced contact matrix on R₀ and epidemic trajectory

In comparison with models with balanced matrices, models with imbalanced matrices consistently underestimated R₀ (Figure 1, Web Figure 2, Web Figure 3). For example, R₀ was 5.7% and 3.1% smaller in Gambia and Singapore, respectively, when matrices were imbalanced versus balanced. Models with imbalanced matrices also underestimated the magnitude of, and had delayed time to, peak incidence of SARS-CoV-2 (Web Figure 4). Peak incidence was most dampened and delayed among the age group that underestimated their contacts (i.e., ages ≥15 in Gambia and <15 in Singapore).

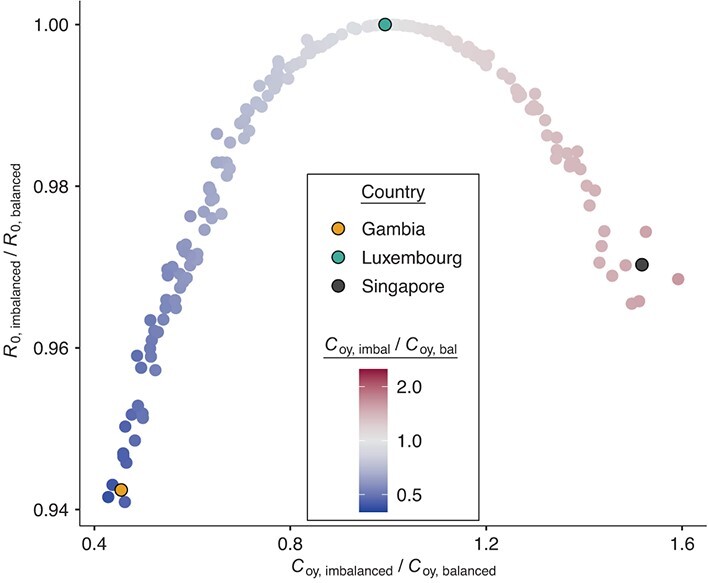
Models with imbalanced (imbal) contact matrices underestimate R₀. Underestimation of R₀ in models with imbalanced contact matrices using data from Prem et al. (8, 9). bal, balanced; C, population contact rate; o, “old” (≥15 years); R₀, basic reproduction number; y, “young” (<15 years).

When imbalanced and balanced contacts between those aged ≥15 and those aged <15 were similar, there was minimal influence on R₀ and on the epidemic trajectory of SARS-CoV-2. For example, in Luxembourg imbalanced contacts reported by those aged ≥15 with those aged <15 were 0.99 times the balanced contacts; therefore, R₀ was nearly the same under imbalanced and balanced conditions (difference in R₀ = 0.0003%).

Influence of imbalanced contact matrix on cumulative infections after 1 year of transmission

Models with imbalanced contacts consistently overestimated cumulative infections in the age group that overestimated their contacts, and underestimated cumulative infections in the age group that underestimated their contacts (Figure 2). For example, cumulative infections were 3.2% larger among those aged <15 years and 6.7% smaller among those aged ≥15 in imbalanced versus balanced models in Gambia, whereas cumulative infections were 1.6% larger among those aged ≥15 and 10.2% smaller among those who were <15 in imbalanced versus balanced models in Singapore.

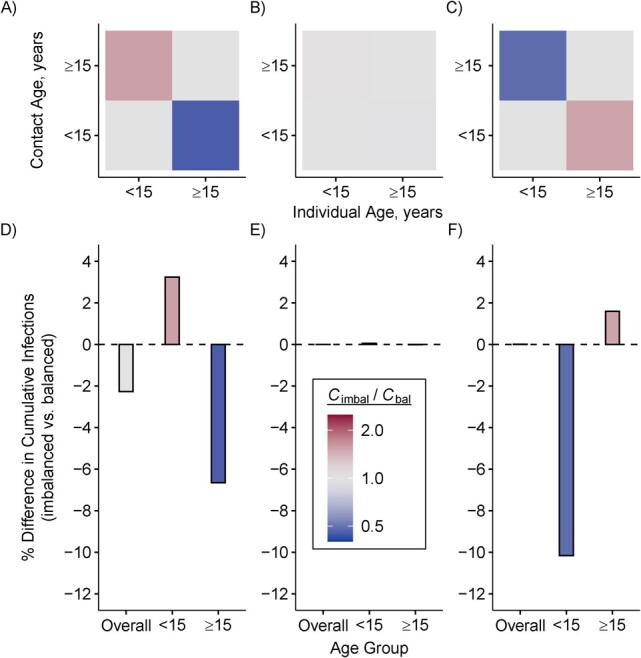
Imbalanced (imbal) contact matrices bias estimates of cumulative severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) infections overall and among subgroups. Direction and magnitude of imbalance in synthetic contact matrices from Gambia (A), Luxembourg (B), and Singapore (C). Percent difference in cumulative infections overall and per age group from models parameterized with imbalanced versus balanced (bal) contact matrices in Gambia (D), Luxembourg (E), and Singapore (F). One infected individual was seeded per age group per model. Cumulative infections were compared 1 year after seeding in a completely susceptible and closed population in the absence of public health interventions. Contact matrices from Prem et al. (8, 9).

Influence of imbalanced contact matrix on age-specific vaccination strategies

Imbalanced matrices also directly and indirectly biased projected infections averted from age-specific SARS-CoV-2 vaccination strategies (Figure 3). For example, when vaccines were prioritized for individuals younger than 15, imbalanced models underestimated infections averted among those aged ≥15 in Gambia (percent difference = −24.4) and overestimated infections averted among those aged ≥15 in Singapore (percent difference = 38.8). When vaccines were prioritized to individuals 15 or older, imbalanced models overestimated infections averted among those aged <15 in Gambia (percent difference = 20.2) and Singapore (percent difference = 25.5).

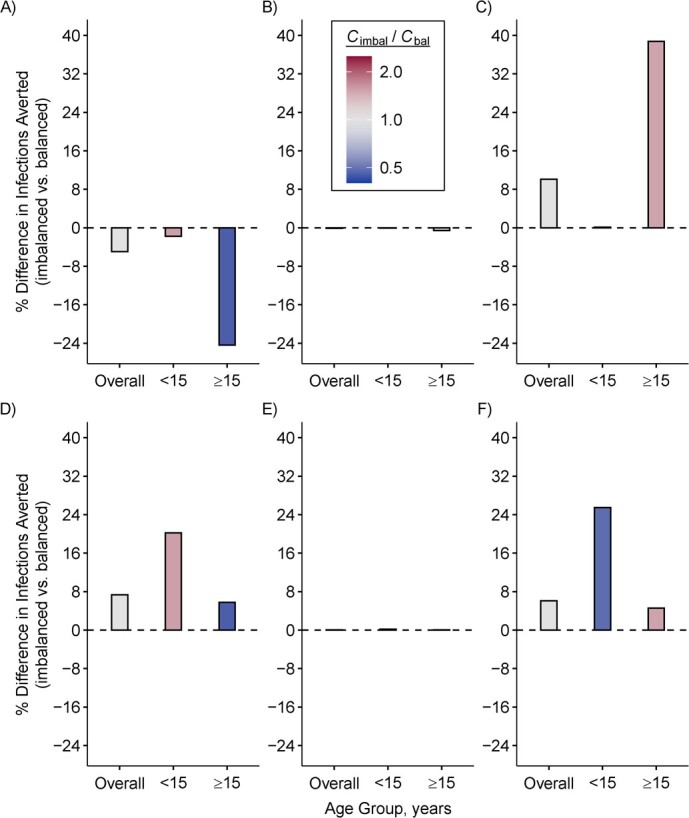
Imbalanced (imbal) contact matrices bias the impact of age-specific severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) vaccination strategies. Percent difference in cumulative infections averted in models parameterized with imbalanced versus balanced (bal) contact matrices when 50% of the population aged <15 years was vaccinated, using examples of different age-demographic settings: Gambia (A), Luxembourg (B), and Singapore (C). Percent difference in cumulative infections averted in models parameterized with imbalanced versus balanced contact matrices when 50% of the population ≥15 was vaccinated, using examples of different age-demographic settings: Gambia (D), Luxembourg (E), and Singapore (F). One infected individual was seeded per age group, per model. Cumulative infections averted were compared 1 year after seeding in a completely susceptible and closed population, in the absence of additional public health interventions other than vaccination. Contact matrices from Prem et al. (8, 9).

Validation analyses

Our results were robust to changes in stratification of age groups (Web Figure 5A). For example, imbalanced contacts reported by persons aged ≥40 years with those aged <40 were 1.4 and 0.38 times the balanced contacts reported by persons aged ≥40 years with those aged <40 in Singapore and Gambia, respectively. In these 2 settings, models with imbalanced matrices underestimated R₀ by 2.5% and 5.4% respectively.

Results were also robust to assumptions regarding which age group over- or underestimated their contacts (Web Figure 5B). For example, when we forced imbalanced contacts reported by those 15 years or older with those aged <15 to be 0.48 and 1.6 times the balanced contacts between those aged ≥15 and aged <15 in Singapore and Gambia, respectively (i.e., opposite the original imbalance direction observed in Prem et al.), models with imbalanced matrices still underestimated R₀ by 3.0% and 5.8%, respectively.

DISCUSSION

Using a combination of analytical and simulation methods, we found that the use of imbalanced contact matrices reshaped the underlying transmission dynamics of SARS-CoV-2. Models with imbalanced matrices consistently underestimated R₀, leading to: 1) biased time to, and magnitude of, peak infection incidence, 2) biased estimates of subgroup-specific cumulative infections, and 3) biased impact of age-specific SARS-CoV-2 vaccination strategies. Biases resulting from imbalanced matrices persisted as we varied age group definitions, and as we transformed assumptions regarding which age group over- or underestimated their contacts per demographic setting.

The finding that R₀ is always smaller when models are parameterized with imbalanced versus balanced matrices can be explained mathematically. In simplifying equation3, we see that R₀ is monotonically related to the product of R_0,ij and R_0,ji (proof provided in Web Appendix 1; supplementary equations S5 to S8). We can also see that R_0,ij and R_0,ji are proportionate to 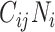Inline graphic and 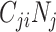, respectively (i.e., equation4). Following the isoperimetric theorem for rectangles, given a fixed sum of population contacts between age groups 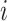and 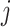(i.e., 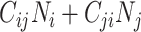), the product of 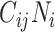and 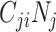will be maximized when 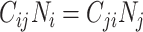(i.e., equation1; conditions for balanced mixing). Since we assumed all other parameters in equation4 were fixed across age groups, and the sum of population contacts was constant between imbalanced and balanced matrices (i.e., equation2), the product of R_0,ij and R_0,ji will maximize when 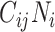Inline graphic and 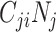are equal. Therefore, under our model and assumptions, R₀ will always be largest under balanced conditions.

It may also be intuitive that biases in cumulative infections per age group are related to biases in contact patterns from imbalanced matrices. The number of infections among subgroup 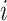Inline graphic is dependent on the “force of infection” ():

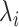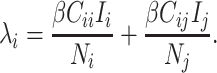(6)

As 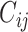Inline graphic increases or decreases, the force of infection among subgroup 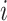will also increase or decrease, as will the number of infections observed within the subgroup.

Given that infection transmission dynamics were biased by imbalanced contact patterns, it was expected that they would also bias impact of subgroup-specific public health interventions. This is because biases in contact patterns influence both risk of infection acquisition and transmission potential once infected. That is, if a model underestimates contacts that subgroup 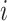Inline graphic makes with subgroup 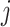, the model also underestimates the transmission potential of subgroup 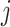to subgroup 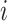. This was most notable when vaccine was administered to 50% of the population aged <15 years, where models that underestimated transmission potential of those aged <15 underestimated infections averted among those aged ≥15 (i.e., Gambia), and models that overestimated transmission potential of those aged <15 overestimated infections averted among those aged ≥15 (i.e., Singapore). Counterintuitively, when vaccine was administered to 50% of the population aged ≥15, imbalanced models overestimated infections averted among those aged <15 in both Gambia and Singapore (i.e., regardless of direction of bias in transmission potential of those aged ≥15). We hypothesize that imbalanced models from Singapore overestimated infections averted among those aged <15 (despite underestimating transmission potential of those aged ≥15) because of indirect bias in infection transmission dynamics. In addition to underestimating transmission potential of those aged ≥15, imbalanced models from Singapore overestimated transmission potential of those aged <15. Therefore, in the absence of vaccination, there were more infections observed among persons who were ≥15 years of age in imbalanced models from Singapore. This provided more opportunity for vaccination to stop transmission of infection from those aged ≥15 to those aged <15.

To our knowledge, this is the first study to quantitatively assess bias associated with imbalanced contact matrices on compartmental models of infectious diseases. Our work builds on a previous study by Arregui et al. (10) that demonstrated that the way in which contact matrices are balanced and projected to new demographic settings can influence the epidemic trajectory observed. The issue of nonreciprocity has been well-recognized in survey data on sexual partnerships, where various methods have been developed to balance sexual partnerships, and balancing is an established component of the modeling of sexually transmitted infections (11, 20, 21). However, the importance of balanced contacts has been less discussed, and not yet established, as part of standard practice and reporting of transmission modeling studies with non–sexually transmitted infections (22). Given that imbalanced matrices can create error in model projections, and models with population heterogeneity are increasingly used to inform public health decisions (23–25), modelers should ensure and report on balancing of their contact matrices.

Limitations

The simplicity of our analytical study and simulation model allowed us to quantitatively assess and interpret the influence of imbalanced versus balanced matrices irrespective of other infection transmission parameters. As such, important sources of variability in transmission risk that lead to asymmetry in effective contact matrices could potentially amplify or dampen the influence of imbalanced measured contact matrices, and would benefit from further examination. Our results may also vary when studied in open populations (with births, deaths, and/or movement of individuals) or when considering infection prevention and control measures such as school closures or isolation procedures. Bias may also vary when considering heterogeneity in biological characteristics, such as immunity to infection, duration of infectiousness, and probability of transmission once infected. For example, we assumed that the probability of transmission and duration of infectiousness was constant across age groups. If older individuals were more likely to transmit SARS-CoV-2 than those in younger age groups, and had a longer duration of infectiousness, they would have greater transmission potential and we might see even greater bias in models that overestimate the contacts that those aged <15 made with those aged ≥15. Our examination was restricted to direct transmission of respiratory pathogens in the context of close contacts and, thus, via droplet or close-range aerosolized transmission. Other modes of transmission, such as transmission via fomites, blood products, or in the context of waterborne (e.g., fecal-oral) pathogens require different types of contacts in their force of infection. The survey data used to generate symmetrical measured contact matrices also do not capture the potential for point-source transmission events, including those that may occur via long-range aerosolized pathogens.

There are different ways to balance a measured contact matrix. Thus, differences in epidemic dynamics between models with imbalanced versus balanced matrices could differ based on the balancing method used. We used a population-weighted average of reported contacts given that the matrices were synthetic (8). However, when using survey data (e.g., POLYMOD (7)), it is more common to calculate respondent weighted averages of population contacts (10), or use statistical techniques to infer patterns across the population according to participant demographic information (12). Therefore, the balancing method used may change the extent to which raw contacts are considered imbalanced, and thus the magnitude and direction of potential bias. Finally, our balancing approach (as with many others) assumes that self-reported numbers from each group are equally subject to measurement error. That is, no age group’s answers are more or less reliable than any other.

Conclusions

We showed that compartmental models of infectious diseases parameterized with imbalanced contact matrices may produce biased estimates of initial epidemic characteristics (e.g., R₀), epidemic trajectory (e.g., timing and magnitude of peak infection incidence), cumulative impact on populations (e.g., cumulative infections per age group), and impact of prioritized public health interventions. To avoid biases in projections, stemming from how the model is parameterized, modelers should account for and report reciprocity of contact matrices in their stratified transmission models.

Supplementary Material

Web_Material_kwad185

Click here for additional data file.^{(383.3KB, pdf)}

ACKNOWLEDGMENTS

Author affiliations: MAP Centre for Urban Health Solutions, Li Ka Shing Knowledge Institute, St. Michael’s Hospital, Unity Health Toronto, Toronto, Ontario, Canada (Mackenzie A. Hamilton, Jesse Knight, Sharmistha Mishra); Institute of Medical Science, University of Toronto, Toronto, Ontario, Canada (Jesse Knight, Sharmistha Mishra); Institute of Health Policy, Management and Evaluation, University of Toronto, Toronto, Ontario, Canada (Sharmistha Mishra); Department of Medicine, St. Michael’s Hospital, Unity Health Toronto, Toronto, Ontario, Canada (Sharmistha Mishra); and Institute for Clinical Evaluative Sciences (ICES), Toronto, Ontario, Canada (Sharmistha Mishra).

This work was supported by the Canadian Institutes of Health Research (grant number VR5-172683) and unrestricted research operating funds from the St. Michael’s Hospital Foundation.

Age-stratified contact matrices analyzed in this study were obtained from Prem et al. (8) Their contact matrices are available for download at https://github.com/kieshaprem/synthetic-contact-matrices. The codes to transform and balance source contact matrices, and generate results for this analysis are available on GitHub at https://github.com/mishra-lab/imbalanced-contact-matrices.

J.K. was supported by a doctoral award from the National Sciences and Engineering Research Council of Canada (NSERC CGS-D). S.M. is supported by a Tier 2 Canada Research Chair in Mathematical Modeling and Program Science (CRC grant number 950-232643). We thank Dr. Korryn Bodner, Linwei Wang, and Ekta Mishra for helpful discussions. We thank Siyi Wang for the technical revisions and Kristy Yiu and Samantha Lo for coordination support.

This work was presented at the Society for Medical Decision Making 44th Annual North American Meeting, October 23–26, 2023, Seattle, Washington (poster PP-248).

A preprint of this article has been published online. Hamilton MA, Knight J, Mishra S. Failure to balance social contact matrices can bias models of infectious disease transmission. medRxiv. 2020. (https://doi.org/10.1101/2022.07.28.22278155).

The views expressed in this article are those of the authors and do not reflect those of University of Toronto or Unity Health Toronto. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Conflict of interest: none declared.

REFERENCES

1. Wallinga J, Boven M, Lipsitch M. Optimizing infectious disease interventions during an emerging epidemic. Proc Natl Acad Sci U S A. 2010;107(2):923–928. [DOI] [PMC free article] [PubMed] [Google Scholar]
2. Tuite A, Fisman DN, Kwong JC, et al. Optimal pandemic influenza vaccine allocation strategies for the Canadian population. PLoS Curr. 2010;2:RRN1144. [DOI] [PMC free article] [PubMed] [Google Scholar]
3. Yamin D, Jones FK, DeVincenzo JP, et al. Vaccination strategies against respiratory syncytial virus. Proc Natl Acad Sci U S A. 2016;113(46):13239–13244. [DOI] [PMC free article] [PubMed] [Google Scholar]
4. Medlock J, Galvani AP. Optimizing influenza vaccine distribution. Science. 2009;325(5948):1705–1708. [DOI] [PubMed] [Google Scholar]
5. Mulberry N, Tupper P, Kirwin E, et al. Vaccine rollout strategies: the case for vaccinating essential workers early. PLOS Glob Public Health. 2021;1(10):e0000020. [DOI] [PMC free article] [PubMed] [Google Scholar]
6. Bubar KM, Reinholt K, Kissler SM, et al. Model-informed COVID-19 vaccine prioritization strategies by age and serostatus. Science. 2021;371(6532):916–921. [DOI] [PMC free article] [PubMed] [Google Scholar]
7. Mossong J, Hens N, Jit M, et al. Social contacts and mixing patterns relevant to the spread of infectious diseases. PLoS Med. 2008;5(3):e74. [DOI] [PMC free article] [PubMed] [Google Scholar]
8. Prem K, Zandvoort KV, Klepac P, et al. Projecting contact matrices in 177 geographical regions: an update and comparison with empirical data for the COVID-19 era. PLoS Comput Biol. 2021;17(7):e1009098. [DOI] [PMC free article] [PubMed] [Google Scholar]
9. Prem K, Cook AR, Jit M. Projecting social contact matrices in 152 countries using contact surveys and demographic data. PLoS Comput Biol. 2017;13(9):e1005697. [DOI] [PMC free article] [PubMed] [Google Scholar]
10. Arregui S, Aleta A, Sanz J, et al. Projecting social contact matrices to different demographic structures. PLoS Comput Biol. 2018;14(12):e1006638. [DOI] [PMC free article] [PubMed] [Google Scholar]
11. Morris M. A log-linear modeling framework for selective mixing. Math Biosci. 1991;107(2):349–377. [DOI] [PubMed] [Google Scholar]
12. Wallinga J, Teunis P, Kretzschmar M. Using data on social contacts to estimate age-specific transmission parameters for respiratory-spread infectious agents. Am J Epidemiol. 2006;164(10):936–944. [DOI] [PubMed] [Google Scholar]
13. Vynnycky E, White R. An Introduction to Infectious Disease Modelling. Oxford, UK: Oxford University Press; 2010. [Google Scholar]
14. Hogan AB, Winskill P, Watson OJ, et al. Within-country age-based prioritisation, global allocation, and public health impact of a vaccine against SARS-CoV-2: a mathematical modelling analysis. Vaccine. 2021;39(22):2995–3006. [DOI] [PMC free article] [PubMed] [Google Scholar]
15. Jentsch PC, Anand M, Bauch CT. Prioritising COVID-19 vaccination in changing social and epidemiological landscapes: a mathematical modelling study. Lancet Infect Dis. 2021;21(8):1097–1106. [DOI] [PMC free article] [PubMed] [Google Scholar]
16. Foy BH, Wahl B, Mehta K, et al. Comparing COVID-19 vaccine allocation strategies in India: a mathematical modelling study. Int J Infect Dis. 2021;103:431–438. [DOI] [PMC free article] [PubMed] [Google Scholar]
17. Willem L, Van Hoang T, Funk S, et al. SOCRATES: an online tool leveraging a social contact data sharing initiative to assess mitigation strategies for COVID-19. BMC Res Notes. 2020;13(1):293. [DOI] [PMC free article] [PubMed] [Google Scholar]
18. Buckner JH, Chowell G, Springborn MR. Dynamic prioritization of COVID-19 vaccines when social distancing is limited for essential workers. Proc Natl Acad Sci U S A. 2021;118(16):e2025786118. [DOI] [PMC free article] [PubMed] [Google Scholar]
19. Diekmann O, Heesterbeek JA, Metz JA. On the definition and the computation of the basic reproduction ratio 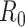in models for infectious diseases in heterogeneous populations. J Math Biol. 1990;28(4):365–382. [DOI] [PubMed] [Google Scholar]
20. Garnett GP, Hughes JP, Anderson RM, et al. Sexual mixing patterns of patients attending sexually transmitted diseases clinics. Sex Transm Dis. 1996;23(3):248–257. [DOI] [PubMed] [Google Scholar]
21. Côté AM, Sobela F, Dzokoto A, et al. Transactional sex is the driving force in the dynamics of HIV in Accra, Ghana. AIDS. 2004;18(6):917–925. [DOI] [PubMed] [Google Scholar]
22. Pitman R, Fisman D, Zaric GS, et al. Dynamic transmission modeling: a report of the ISPOR-SMDM Modeling Good Research Practices Task Force Working Group-5. Med Decis Making. 2012;32(5):712–721. [DOI] [PubMed] [Google Scholar]
23. Buchwald AG, Bayham J, Adams J, et al. Estimating the impact of statewide policies to reduce spread of severe acute respiratory syndrome coronavirus 2 in real time, Colorado, USA. Emerg Infect Dis. 2021;27(9):2312–2322. [DOI] [PMC free article] [PubMed] [Google Scholar]
24. James LP, Salomon JA, Buckee CO, et al. The use and misuse of mathematical modeling for infectious disease policymaking: lessons for the COVID-19 pandemic. Med Decis Making. 2021;41(4):379–385. [DOI] [PMC free article] [PubMed] [Google Scholar]
25. Biggerstaff M, Slayton RB, Johansson MA, et al. Improving pandemic response: employing mathematical modeling to confront coronavirus disease 2019. Clin Infect Dis. 2022;74(5):913–917. [DOI] [PMC free article] [PubMed] [Google Scholar]
26. Davies NG, Klepac P, Liu Y, et al. Age-dependent effects in the transmission and control of COVID-19 epidemics. Nat Med. 2020;26(8):1205–1211. [DOI] [PubMed] [Google Scholar]
27. Xin H, Li Y, Wu P, et al. Estimating the latent period of coronavirus disease 2019 (COVID-19). Clin Infect Dis. 2022;74(9):1678–1681. [DOI] [PubMed] [Google Scholar]
28. Cheng C, Zhang D, Dang D, et al. The incubation period of COVID-19: a global meta-analysis of 53 studies and a Chinese observation study of 11 545 patients. Infect Dis Poverty. 2021;10(1):119. [DOI] [PMC free article] [PubMed] [Google Scholar]
29. Walsh KA, Spillane S, Comber L, et al. The duration of infectiousness of individuals infected with SARS-CoV-2. J Infect. 2020;81(6):847–856. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Web_Material_kwad185

Click here for additional data file.^{(383.3KB, pdf)}

[ref1] 1. Wallinga J, Boven M, Lipsitch M. Optimizing infectious disease interventions during an emerging epidemic. Proc Natl Acad Sci U S A. 2010;107(2):923–928. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref2] 2. Tuite A, Fisman DN, Kwong JC, et al. Optimal pandemic influenza vaccine allocation strategies for the Canadian population. PLoS Curr. 2010;2:RRN1144. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref3] 3. Yamin D, Jones FK, DeVincenzo JP, et al. Vaccination strategies against respiratory syncytial virus. Proc Natl Acad Sci U S A. 2016;113(46):13239–13244. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref4] 4. Medlock J, Galvani AP. Optimizing influenza vaccine distribution. Science. 2009;325(5948):1705–1708. [DOI] [PubMed] [Google Scholar]

[ref5] 5. Mulberry N, Tupper P, Kirwin E, et al. Vaccine rollout strategies: the case for vaccinating essential workers early. PLOS Glob Public Health. 2021;1(10):e0000020. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref6] 6. Bubar KM, Reinholt K, Kissler SM, et al. Model-informed COVID-19 vaccine prioritization strategies by age and serostatus. Science. 2021;371(6532):916–921. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref7] 7. Mossong J, Hens N, Jit M, et al. Social contacts and mixing patterns relevant to the spread of infectious diseases. PLoS Med. 2008;5(3):e74. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref8] 8. Prem K, Zandvoort KV, Klepac P, et al. Projecting contact matrices in 177 geographical regions: an update and comparison with empirical data for the COVID-19 era. PLoS Comput Biol. 2021;17(7):e1009098. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref9] 9. Prem K, Cook AR, Jit M. Projecting social contact matrices in 152 countries using contact surveys and demographic data. PLoS Comput Biol. 2017;13(9):e1005697. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref10] 10. Arregui S, Aleta A, Sanz J, et al. Projecting social contact matrices to different demographic structures. PLoS Comput Biol. 2018;14(12):e1006638. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref11] 11. Morris M. A log-linear modeling framework for selective mixing. Math Biosci. 1991;107(2):349–377. [DOI] [PubMed] [Google Scholar]

[ref12] 12. Wallinga J, Teunis P, Kretzschmar M. Using data on social contacts to estimate age-specific transmission parameters for respiratory-spread infectious agents. Am J Epidemiol. 2006;164(10):936–944. [DOI] [PubMed] [Google Scholar]

[ref13] 13. Vynnycky E, White R. An Introduction to Infectious Disease Modelling. Oxford, UK: Oxford University Press; 2010. [Google Scholar]

[ref14] 14. Hogan AB, Winskill P, Watson OJ, et al. Within-country age-based prioritisation, global allocation, and public health impact of a vaccine against SARS-CoV-2: a mathematical modelling analysis. Vaccine. 2021;39(22):2995–3006. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref15] 15. Jentsch PC, Anand M, Bauch CT. Prioritising COVID-19 vaccination in changing social and epidemiological landscapes: a mathematical modelling study. Lancet Infect Dis. 2021;21(8):1097–1106. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref16] 16. Foy BH, Wahl B, Mehta K, et al. Comparing COVID-19 vaccine allocation strategies in India: a mathematical modelling study. Int J Infect Dis. 2021;103:431–438. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref17] 17. Willem L, Van Hoang T, Funk S, et al. SOCRATES: an online tool leveraging a social contact data sharing initiative to assess mitigation strategies for COVID-19. BMC Res Notes. 2020;13(1):293. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref18] 18. Buckner JH, Chowell G, Springborn MR. Dynamic prioritization of COVID-19 vaccines when social distancing is limited for essential workers. Proc Natl Acad Sci U S A. 2021;118(16):e2025786118. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref19] 19. Diekmann O, Heesterbeek JA, Metz JA. On the definition and the computation of the basic reproduction ratio in models for infectious diseases in heterogeneous populations. J Math Biol. 1990;28(4):365–382. [DOI] [PubMed] [Google Scholar]

[ref20] 20. Garnett GP, Hughes JP, Anderson RM, et al. Sexual mixing patterns of patients attending sexually transmitted diseases clinics. Sex Transm Dis. 1996;23(3):248–257. [DOI] [PubMed] [Google Scholar]

[ref21] 21. Côté AM, Sobela F, Dzokoto A, et al. Transactional sex is the driving force in the dynamics of HIV in Accra, Ghana. AIDS. 2004;18(6):917–925. [DOI] [PubMed] [Google Scholar]

[ref22] 22. Pitman R, Fisman D, Zaric GS, et al. Dynamic transmission modeling: a report of the ISPOR-SMDM Modeling Good Research Practices Task Force Working Group-5. Med Decis Making. 2012;32(5):712–721. [DOI] [PubMed] [Google Scholar]

[ref23] 23. Buchwald AG, Bayham J, Adams J, et al. Estimating the impact of statewide policies to reduce spread of severe acute respiratory syndrome coronavirus 2 in real time, Colorado, USA. Emerg Infect Dis. 2021;27(9):2312–2322. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref24] 24. James LP, Salomon JA, Buckee CO, et al. The use and misuse of mathematical modeling for infectious disease policymaking: lessons for the COVID-19 pandemic. Med Decis Making. 2021;41(4):379–385. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref25] 25. Biggerstaff M, Slayton RB, Johansson MA, et al. Improving pandemic response: employing mathematical modeling to confront coronavirus disease 2019. Clin Infect Dis. 2022;74(5):913–917. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref26] 26. Davies NG, Klepac P, Liu Y, et al. Age-dependent effects in the transmission and control of COVID-19 epidemics. Nat Med. 2020;26(8):1205–1211. [DOI] [PubMed] [Google Scholar]

[ref27] 27. Xin H, Li Y, Wu P, et al. Estimating the latent period of coronavirus disease 2019 (COVID-19). Clin Infect Dis. 2022;74(9):1678–1681. [DOI] [PubMed] [Google Scholar]

[ref28] 28. Cheng C, Zhang D, Dang D, et al. The incubation period of COVID-19: a global meta-analysis of 53 studies and a Chinese observation study of 11 545 patients. Infect Dis Poverty. 2021;10(1):119. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref29] 29. Walsh KA, Spillane S, Comber L, et al. The duration of infectiousness of individuals infected with SARS-CoV-2. J Infect. 2020;81(6):847–856. [DOI] [PMC free article] [PubMed] [Google Scholar]

PERMALINK

Examining the Influence of Imbalanced Social Contact Matrices in Epidemic Models

Mackenzie A Hamilton

Jesse Knight

Sharmistha Mishra

Abstract

Abbreviations