First-order ultrasensitivity in phosphorylation cycles

Abstract

Cellular signal transduction takes place through a network of phosphorylation cycles. These pathways take the form of a multi-layered cascade of cycles. This work focuses on the sensitivity of single, double and n length cycles. Cycles that operate in the zero-order regime can become sensitive to changes in signal, resulting in zero-order ultrasensitivity (ZOU). Using frequency analysis, we confirm previous efforts that cascades can act as noise filters by computing the bandwidth. We show that n length cycles display what we term first-order ultrasensitivity which occurs even when the cycles are not operating in the zero-order regime. The magnitude of the sensitivity, however, has an upper bound equal to the number of cycles. It is known that ZOU can be significantly reduced in the presence of retroactivity. We show that the first-order ultrasensitivity is immune to retroactivity and that the ZOU and first-order ultrasensitivity can be blended to create systems with constant sensitivity over a wider range of signal. We show that the ZOU in a double cycle is only modestly higher compared with a single cycle. We therefore speculate that the double cycle has evolved to enable amplification even in the face of retroactivity.

1. Introduction

Protein signalling pathways communicate information from external signals to processes in both the nucleus and cytoplasm to modulate cell responses. These pathways engage in various types of signal processing, such as integrating signals over time [1], converting signal strength to signal duration [2] and converting graded signals to switch-like behaviours [3]. In eukaryotes especially, these pathways tend to be highly interconnected, encompassing cross-talk and signal processing between multiple pathways. For example, a large number of signalling pathways exist that include the RTK/RAS/MAP-kinase pathway such as PI3K/Akt signalling, WNT signalling, as well as many others [4].

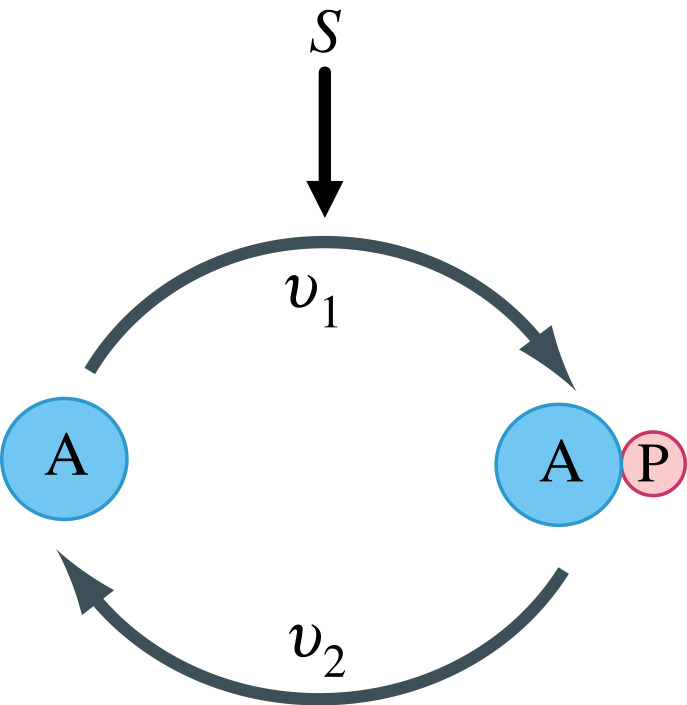
A common motif found in signalling pathways is the phosphorylation cycle. In these cycles, a protein is phosphorylated in response to a signal and dephosphorylated to return the protein to its original state. Often, such cycles form layers or cascades, where one cycle activates the next. Given the ubiquity of phosphorylation cycles, one might be inclined to consider such cycles as fundamental processing units in biochemical cascades [5]. Many signalling proteins are also phosphorylated at more than one site. For example, the proteins MEK and ERK can be doubly phosphorylated. In this case, phosphorylation is processive, meaning that phosphorylation occurs in a strict order, resulting in a two-cycle motif structure (figure 8). We call these a double cycle and the case with a single phosphorylation, a single cycle (figure 1). Some signalling proteins are phosphorylated on many sites.

Figure 8.

Double cycle model where signal S activate both forward arms, v₁ and v₃.

Figure 1.

Single phosphorylation cycle with protein A and phosphorylated protein AP. v₁ and v₂ are the reaction rates for the phosphorylation and dephosphorylation reactions, respectively, with signal S activating the forward arm, v₁.

There are many functions that can be performed by multi-site phosphorylation. Makevich et al. [6] showed it was possible for a multi-site phosphorylation cycle to exhibit bistability, and Chickarmane et al. [7] showed how oscillations could be obtained from competitive inhibition and multi-site phosphorylation. Finally, Thomson et al. [8] made the intriguing observation that multi-site systems could display many stable and unstable steady-states. Multi-site systems are therefore known to generate a wide variety of dynamic behaviours [9].

The essential steady-state properties of phosphorylation cycles, particularly the single cycle, have been well documented by many authors dating from the late 1970s [10] to the present day [11,12]. As detailed above, there has also been some interesting work done on multi-site systems.

This work focuses on the sensitivity analysis of single, double and n length phosphorylation cycles. Note that when we refer to sensitivity, or ultrasensitivity we will always be referring to a logarithmic gain. This concept will be described more fully in the following section. We will first outline the results of the paper:

• 1. The frequency response for a single cycle shows that the cycle behaves as a low-pass filter. The bandwidth of the system (that is, its ability to response to changing signals) is at a minimum at the steepest point on the steady-state sigmoid response curve. That is, where the steady-state is most responsive, the system has the least ability to respond to varying signals. This confirms work done previously by others [11,13]. The Jacobian is also at a minimum at the most sensitive point on the steady-state response curve.
• 2. A double phosphorylation cycle displays a modest amount of ultrasensitivity even when the kinases and phosphatases that phosphorylate and dephosphorylate the cycle proteins are operating below their Michaelis constant (km). We refer to this property as the first-order ultrasensitivity. In addition, the sensitivity of the first-order ultrasensitivity response has an upper bound equal to the number of cycles. For example, a double cycle will display a maximum sensitivity of two at low signal levels which then declines slowly to zero as the level of signal increases. This is in contrast to the zero-order ultrasensitivity which starts at one, rises to a peak, then falls back to zero.
• 3. The first-order and zero-order ultrasensitivity can be blended so that the ultrasensitivity starts higher and remains at the higher value over a wider range of signal.
• 4. We extend the first-order ultrasensitivity analysis to n cycles and show that n cycles can yield a maximum first-order ultrasensitivity sensitivity of n.
• 5. We conduct an empirical study of how much more sensitivity a double cycle can achieve compared to a single cycle. We find that a double cycle can have approximately 1.6 times more sensitivity.
• 6. Finally, we investigate briefly the effect of retroactivity on the first-order ultrasensitivity and find that first-order ultrasensitivity is immune to retroactivity. This is in contrast to zero-order ultrasensitivity where retroactivity can greatly diminish the ultrasensitivity [14].

1.1. Biological perspective

The potential for high sensitivity in protein cascades is thought to offer important benefits to an organism. In particular, protein cascades give an organism the ability to amplify small signals that it receives from the environment and thereby influence its phenotype. The ability to amplify signals in these systems has been attributed to the zero-order ultrasensitivity that phosphorylation cycles can generate. Amplification also brings other benefits including the ability to generate bistable [15] as well as oscillatory behaviour [16]. The literature has reported many such examples.

One of the main conclusions of the current work is that while a single cycle only shows one kind of ultrasensitivity, that is the zero-order ultrasensitivity [17], the double cycle (and n cycles in general) shows an additional form of ultrasensitivity which we call the first-order ultrasensitivity. The first-order ultrasensitivity has unique properties: (i) the magnitude of the sensitivity has an upper bound n where n is the number of cycles; and (ii) the amplification potential of a double cycle appears to be immune to the effects of retroactivity. Given that retroactivity can diminish the amplification potential of protein cascades [15], we can speculate that some of the loss could be made up through the presence of the first-order ultrasensitivity.

A further consideration is frequency response, that cycles operate as low-pass filters. A low-pass filter provides noise rejection, an important feature for biological systems which operate in noisy environments.

In the following, §2 will consider the properties of a single phosphorylation cycle, its frequency response and sensitivity properties. In §3, we will consider the double phosphorylation cycle, its sensitivity, a comparison with the single cycle and the effect of retroactivity. Finally, in §4 we will consider the properties of n cycles.

1.2. Terminology

Some of the terminology we use in this paper may be unfamiliar to readers, we have therefore added a glossary at the end which defines some of the most common terms we use.

In the following text, upper-case letters will be used to denote the name of the species, for example, A or AP. We will use lower-case lettering to indicate a concentration, for example, a or ap. This is to avoid unnecessary clutter when using the more traditional square brackets for concentration. Symbols such as AP, BP, APP, BPP refer to the A or B protein having been phosphorylated once, AP, or twice APP.

1.3. Logarithmic gains

When we indicate the magnitude of a sensitivity or ultrasensitivity, we will always be referring to a logarithmic gain [18]. This is a standard, unit-less measure in metabolic control analysis [19]. A logarithmic gain is described by the expression:

$$\text{L}og\hspace{0.17em}gain=\frac{\mathrm{\partial }\ln Y}{\mathrm{\partial }\ln X},$$

where Y and X are the dependent and independent variables, respectively. The gain indicates how a variable Y responds to changes in X. The derivative of a logarithmic function, d lnf(x)/dx = 1/f(x)df(x)/dx, allows us to write the above expression in a more intuitive way:

$$\text{L}og\hspace{0.17em}gain=\frac{\mathrm{\partial }Y}{\mathrm{\partial }X}\frac{X}{Y}\approx \frac{Y\mathrm{\%}}{X\mathrm{\%}},$$

which is a ratio of relative changes. The logarithmic gains can therefore be interpreted approximately as a ratio of percentage changes. This makes the logarithmic gain much easier to measure experimentally since the experimenter need only consider ratios of fold changes without any concern for the units of the actual measurement.

Whenever we refer to a sensitivity we will use the symbol $C_X^Y$. The superscript represents the dependent variable and the subscript the independent variable. In metabolic control analysis, the sensitivities are called control coefficients [20].

2. Single phosphorylation cycle

The single phosphorylation cycle is shown in figure 1. It involves two proteins, unphosphorylated protein A, and phosphorylated protein AP. Phosphorylation is catalysed by a kinase, and dephosphorylation by a phosphatase. We assume that the kinase is represented by the signal, S. We examine the properties of the cycle as a function of the signal. This system can be modelled using the following set of differential equations:

$$\frac{\mathrm{d}\text{a}}{\mathrm{d}t}=v_2-v_1$$

and

$$\frac{\mathrm{d}\text{a}p}{\mathrm{d}t}=v_1-v_2.$$

Throughout, we use upper-case letters to indicate chemical species and the corresponding lower-case letter to indicate the concentration of the chemical species. Note that these equations are linearly dependent since either one can be obtained from the other by multiplying by minus one. This is due to mass conservation between A and AP. The moiety, A, is conserved during its transformation to AP and in its conversion from AP to A [21,22]. Therefore, the total mass of moiety A in the system is fixed and does not change as the system evolves in time. In other words, a + ap = T where T is the fixed total mass of moiety. This makes the assumption that the synthesis and degradation of protein A and degradation of protein AP is negligible compared to the cycling rate.

Mathematically, the presence of the conservation law means that there is only one independent variable. If we designate the independent variable to be AP, then the dependent variable becomes A and can be computed using a trivial rearrangement of the conservation law: a = T − ap where T is the total mass in the cycle.

If we initially assume linear irreversible mass-action kinetics on the forward and reverse limbs, we can write:

$$\frac{\mathrm{d}\text{a}}{\mathrm{d}t}=k_2\text{a}p-k_{1}s.\text{a}\mathrm{and}\frac{\mathrm{d}\text{a}p}{\mathrm{d}t}=k_{1}s.\text{a}-k_2\text{a}p.$$

Note that a period separating two variables indicates multiplication of concentrations. We have assumed, without loss of generality, that the stimulus, S, is a simple linear multiplier into the rate law, v₁. We can readily solve for the steady-state levels of A and AP by setting the independent differential equation to zero, from which we obtain the well-known result:

$$\text{a}p=\frac{\text{T}.s\hspace{0.17em}{k}_1}{s\hspace{0.17em}{k}_1+k_2}\mathrm{and}\text{a}=\frac{\text{T}{k}_2}{s\hspace{0.17em}{k}_1+k_2}$$ 2.1

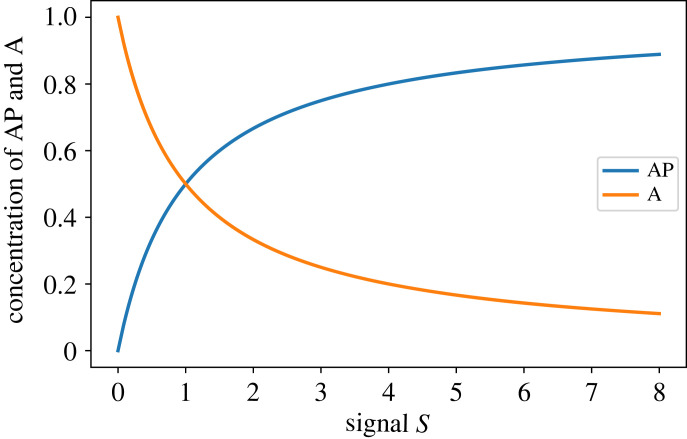
Note that the steady-state level of A is determined from the relation a = T − ap. The input to the cycle can be modelled by changes to S. We can, therefore, plot the steady-state concentration of AP as a function of the input signal S. This is shown in figure 2 and illustrates a well-known result.

Figure 2.

Steady-state plot of AP and A versus signal S for a system with mass-action kinetics. The plot shows the expected and well-known hyperbolic response. The sensitivity, $C_S^{\mathrm{AP}}$, is always less than or equal to one in this system.

The response is a rectangular hyperbola (cf. Michaelis–Menten equation). As the stimulus increases, AP increases with a corresponding drop in A due to mass conservation.

2.1. Sensitivity analysis

Of particular interest in this article is to consider the sensitivity of AP to changes in signal S. This can be computed by taking the derivative of the solution (2.1) and scaling by signal, S, and AP. This is in accordance with the previous definition of a logarithmic gain and yields:

$$\begin{array}{cc}& C_S^{\text{A}P}=\frac{k_2}{s\hspace{0.17em}{k}_1+k_2}\\ \mathrm{and}& C_S^{\text{A}P}=\frac{\mathrm{d}\text{a}p}{\mathrm{d}s}\frac{s}{\text{a}p}\end{array}\}$$ 2.2

This is a well-known result showing that the sensitivity is always less than or equal to one; that is, a 1% change in S always generates less than a 1% change in AP. Interestingly, the sensitivity of the system is independent of the total mass in the system.

In order to examine the sensitivity of systems that use nonlinear rate laws, we need to introduce a frequently used concept from metabolic control analysis (MCA) [19], the elasticity or local response.

2.2. Sensitivity in terms of local responses

A key advantage to using the MCA formalism is that it is it possible to relate the system responses (2.2) to the local responses or elasticities. This makes it possible to understand how a given system response is generated from the local behaviour of the system components.

In MCA, local responses are described using elasticity coefficients [19,20]. These coefficients measure how the reaction rate of a given system component is responsive to changes to one of its modulators. For example, an enzyme that converts a single substrate to a single product, the reaction rate is influenced by changes in the substrate, product and the enzyme itself. As a result, the enzyme can be described by three elasticities. More formally, we defined the elasticity as the scaled partial derivative:

$${\epsilon }_{s_i}^v={\left(\frac{\mathrm{\partial }v}{\mathrm{\partial }{s}_i}\frac{s_i}{v}\right)}_{s_j,s_k,\dots }.$$ 2.3

A unimolecular reaction catalysed by an enzyme, E, with substrate S and product P can be characterized by the elasticities:

$${\epsilon }_s^v,\hspace{0.17em}{\epsilon }_p^v\text{a}nd{\epsilon }_e^v.$$

Since the reaction rate laws, v, are often nonlinear, the elasticities are a function of the reactant concentrations. Hence it is common to consider elasticities at a specific operating point of the system, which is often the steady state.

Elasticities are also known as kinetic orders in chemical network theory [23] and biochemical systems theory [24].

We can illustrate what the elasticities look like for a simple mass-action reaction and the irreversible Michaelis–Menten model as follows. For a mass-action rate law such as:

$$v=ks.$$

The elasticity is

$${\epsilon }_s^v=\frac{\mathrm{\partial }(k\hspace{0.17em}s)}{\mathrm{\partial }s}\frac{s}{k\hspace{0.17em}s}=1.$$

The elasticity is a constant with a value of one and indicates that the reaction is the first-order in s. For the irreversible Michaelis–Menten model:

$$v=\frac{V_{m}s}{K_m+s},$$

we can do the same derivation to yield:

$${\epsilon }_s^v=\frac{\mathrm{\partial }(V_{m}s/(K_m+s))}{\mathrm{\partial }s}\frac{s}{(V_{m}s/(K_m+s))}=-\frac{V_{m}s}{{(K_m+s)}^2}\frac{s}{(V_{m}s/(K_m+s))}=\frac{K_m}{K_m+s}.$$

In this case, the elasticity is not a constant but is a function of the substrate concentration, S. At low substrate, the elasticity is close to one, indicating the reaction has the first-order properties but as the substrate concentration increases the elasticity tends to zero (as the enzyme saturates) showing that the reaction shows the zero-order properties.

2.3. Response of a nonlinear system

Much more interesting behaviour, but also well known, is observed if the kinase and phosphatase activity is no longer modelled using simple mass-action kinetics but is modelled using saturable nonlinear Michaelis–Menten rate laws [25]. In this case, the steady-state behaviour shows a marked sigmoid response (figure 3), often termed zero-order ultrasensitivity [3,17,26] because the behaviour appears when the kinase and/or phosphatase start to operate near the zero-order region of the Michaelis–Menten rate law. The degree of sigmoidicity is determined by the degree of saturation of the kinase and phosphatase. This is a well-known result that was shown by Goldbeter & Koshland using a detailed mechanistic model [17] of enzyme binding and catalysis. Later, Small & Fell [27] showed that zero-order ultrasensitivity could also be demonstrated more generally using MCA without having to consider a detailed mechanistic model. This analysis also highlighted the essential properties of a network that were responsible for the zero-order ultrasensitivity. Figure 3 shows the sigmoid response and the scaled and unscaled sensitivities as a function of signal. Of interest is that the peak of the unscaled derivative appears to match the inflection point while the scaled derivative peak is shifted to the left. The proof in appendix A.1 provides conditions under which this may occur.

Figure 3.

Steady-state plot of AP, the unscaled control coefficient dap/ds, and the scaled control coefficient (dap/ds)(s/ap) over a range of signal, S, values. The kinetics are given by saturable Michaelis–Menten rate laws. Note the sigmoid response in AP and the spike in sensitivity due to the zero-order ultrasensitivity. See Model 5.1 in appendix A.

2.4. Frequency response of a single cycle

The frequency response describes the steady-state response of a system to sinusoidal inputs at varying frequencies. In general, the sinusoidal inputs are small in amplitude so that even if the system is nonlinear, analytical solutions can be obtained through linearization. Linear systems exhibit three important characteristics in terms of their response to sinusoidal inputs. First, the output signal has the same frequency as the input signal. Second, the amplitude of the signal can be amplified or attenuated. Third, due to inherent delays in the system (for example, the time it takes molecular pools to fill or empty), sinusoidal signals tend to get delayed, resulting in phase shifts. Interestingly, the frequency component of a signal is unaltered when assuming linearity [28]. By examining how a system alters the amplitude and phase of a sinusoidal input, information on the system’s characteristics can be determined. Moreover, a range of sinusoidal frequencies is tested since changes in amplitude and phase are often a function of the input frequency. The result is a particular form of graphical rendering called a Bode plot [29]. These plots invariably come in pairs, one indicating the effect on the amplitude and a second on the phase.

We use the extension of metabolic control analysis to the frequency domain as developed by Ingalls [29] to compute the frequency response. A similar extension was developed by Rao et al. [30], which emphasized the application of signal-flow graphs within the context of a frequency response.

The following study includes both analytical analysis and numeric simulations. For the simulations, we assume the model in appendix A.5.1 written using the Antimony format [31], which can be readily translated to SBML via the online tool makeSBML (https://sys-bio.github.io/makesbml/). We begin by looking at the Jacobian matrix. The transitional approach to deriving the Jacobian is to differentiate the differential equations with respect to the state variables. However, in this case we need the Jacobian expressed in terms of the elasticities. Owing to the conservation law, there is also only one independent variable and hence the full Jacobian will be singular. We can avoid both issues by using a result from metabolic control analysis [32] where the Jacobian is expressed in terms of a reduced stoichiometry matrix, N_r, the unscaled elasticity matrix, $\mathcal{E}$, and the link matrix, L. Further details of the link matrix as well as a derivation of the following Jacobian equation [33] can be found in appendix A.2.

$$\text{J}acobian={\mathbf{N}}_{\mathbf{r}}\times \mathcal{E}\times \mathbf{L},$$ 2.4

where N_r is the reduced stoichiometry matrix, $\mathcal{E}$ the matrix of unscaled elasticities and L the link matrix [32]. The multiplication symbols indicate matrix products. The unscaled elasticity matrix is a two by two matrix:

$$\mathcal{E}=\left[\begin{array}{cc}{\mathcal{E}}_{\text{A}P}^{v_2}& 0\\ 0& {\mathcal{E}}_{\text{A}}^{v_1}\end{array}\right].$$ 2.5

The unscaled elasticity is simply the partial derivative of the reaction rate with respect to a given concentration, hence:

$${\mathcal{E}}_{\text{A}P}^{v_2}=\frac{\mathrm{\partial }{v}_2}{\mathrm{\partial }\text{a}p}\mathrm{and}{\mathcal{E}}_{\text{A}}^{v_1}=\frac{\mathrm{\partial }{v}_1}{\mathrm{\partial }\text{a}}.$$

The Link matrix relates the reduced stoichiometry matrix to the full stoichiometry matrix via:

$$\mathbf{N}=\mathbf{L}\times {\mathbf{N}}_{\mathbf{r}}.$$

It is relatively easy to manually compute L for a single cascade by inspection but there are number of software packages [34–37] that can compute these matrices automatically. The reduced stoichiometry and Link matrix are shown in equations (2.6):

$${\mathbf{N}}_{\mathbf{r}}=\left[\begin{array}{cc}1& -1\end{array}\right]\mathrm{and}L=\left[\begin{array}{c}1\\ -1\end{array}\right].$$ 2.6

With this information, the Jacobian can be shown to be:

$$\text{J}acobian=\frac{\mathrm{d}}{\mathrm{d}\text{a}p}\left(\frac{\mathrm{d}\text{a}p}{\mathrm{d}t}\right)=-({\mathcal{E}}_{\text{A}P}^{v_2}+{\mathcal{E}}_{\text{A}}^{v_1}).$$ 2.7

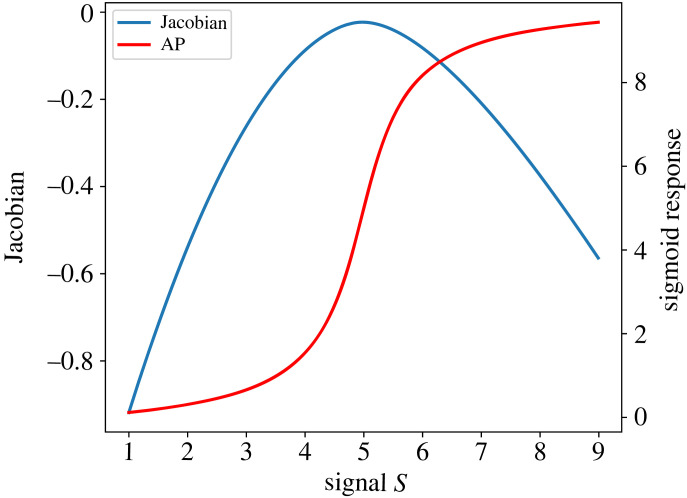
Since the two unscaled elasticities are positive, the Jacobian is negative. Moreover, since the Jacobian is the sum of the two unscaled elasticities, near the steepest portion of the sigmoid curve, these unscaled elasticities are at their minimum. This is what elicits the steep rise in AP but it also means that the Jacobian is at a minimum. This is more easily illustrated in a simulation shown in figure 4. This result may appear to be counterintuitive since one might expect the sharpest transition in the zero-order ultrasensitive response to be the most responsive and, thereby have the largest value for the Jacobian.

Figure 4.

Value of the Jacobian as a function of the input signal. The absolute value of the Jacobian reaches a minimum near or at the steepest point on the sigmoid curve for AP.

The frequency response can be derived analytically using the frequency domain extension by Ingalls [29], Since the system is nonlinear this approach necessitates the linearization of the system. The details of the derivation are given in appendix A.2. The result is the following transfer function where s is a complex variable:

$$H_s(j\omega )=\frac{\mathrm{\partial }{v}_1/\mathrm{\partial }\text{s}}{j\omega +\mathrm{\partial }{v}_1/\mathrm{\partial }\text{a}+\mathrm{\partial }{v}_2/\mathrm{\partial }\text{a}p}.$$ 2.8

This is a classic first-order system. Its pole is −(∂v₁/∂a + ∂v₂/∂ap). Note that the pole is always negative, and so the system is stable. Further, the speed of response is faster as (∂v₁/∂a) + (∂v₂/∂ap) increases. Equation (2.8) can be written in standard form [28]:

$$H_x(j\omega )=\frac{K}{\tau j\omega +1},$$

where K is given by K = (∂v₁/∂s)/((∂v₁/∂a) + (∂v₂/∂ap)) and τ, the time constant by:

$$\tau =\frac{1}{(\mathrm{\partial }{v}_1/\mathrm{\partial }\text{a})+(\mathrm{\partial }{v}_2/\mathrm{\partial }\text{a}p)}.$$

The time constant indicates the responsiveness of the system. The smaller τ is, the more responsive the system will be, and τ is smaller if the pole has a larger magnitude.

Put differently, the smaller the unscaled elasticities (and hence more zero-order ultrasensitivity), the slower the system is to respond.

The bandwidth (the frequency where the amplitude ratio drops by a factor of 0.707) of a first-order system is 1/τ [28]. Hence, when the system moves through the steepest portion of the sigmoid curve, its bandwidth is at a minimum. This is also shown in figure 5, which plots the bandwidth as a function of the signal. This also matches the earlier observation that at the steepest point in the sigmoid curve, the system is least responsive in time. Hence when the system is most responsive to steady-state changes, it is least responsive in time.

Figure 5.

Bandwidth as a function of the input signal for a single cycle. The bandwidth reaches a minimum near or at the steepest point of the sigmoid curve for AP.

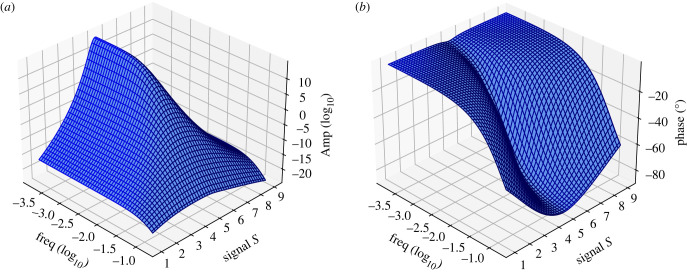
The frequency response can be obtained by plotting the Bode plots for the amplitude and phase. These plots are shown in figure 6 and were computed using the Python Tellurium [37] utility, ‘frequencyResponse’ found at https://github.com/sys-bio/frequencyResponse. This shows a typical response for a low-pass filter. Of more interest is plotting the Bode plots as a function of signal. This results in two three-dimensional (3D) plots for amplitude and phase, figure 7. The amplitude plot clearly shows the reduction in the bandwidth as the signal passes the point of steepest response in the sigmoid curve (at around S = 5). At low and high signal levels the bandwidth increases. The work by Gomez-Uribe et al. [11] came to a similar conclusion but by doing simulations on a specific mechanism, and some limited analytical work. Moreover, Thattai & Oudenaarden [13] investigated the effect of zero-order ultrasensitivity on how noise is transmitted and showed attenuation in noise which is consistent with this result.

Figure 6.

Bode plot for the single cycle system showing the response of AP as a function of signal frequency. The plots show the typical behaviour of a low-pass filter with the phase shift reaching a maximum shift of 90°. Both curves were computed when the signal, S, equalled 5.

Figure 7.

3D Bode plots for amplitude (a) and phase (b) as functions of frequency and signal S for a single cycle system with output AP.

3. Double phosphorylation cycle

It is very common to find double phosphorylation cycles in protein signalling networks (figure 8 and appendix A.5.3 for the Antimony model). For example, the MAPK cascade contains two such double cycles. Previous work [5,38,39] has reported on some of the zero-order ultrasensitivity properties of such systems. A key feature of double cycles is that they can elicit moderate ultrasensitivity even when the reaction kinetics are governed by simple first-order mass-action kinetics. However, as we will see, the nature of the ultrasensitivity is different from zero-order ultrasensitivity.

We first consider the case when each reaction is governed by simple linear mass-action kinetics. If we assume a stimulus, S, activates v₁ and v₃ we can write the differential equations for this system as:

$$\begin{array}{rl}\frac{\mathrm{d}\text{a}}{\mathrm{d}t}& =k_2\hspace{0.17em}\text{a}p-k_1\hspace{0.17em}\text{a}.s,\\ \frac{\mathrm{d}\text{a}p}{\mathrm{d}t}& =k_1\hspace{0.17em}\text{a}.s-k_2\hspace{0.17em}\text{a}p+k_4\hspace{0.17em}\text{a}pp-k_3\hspace{0.17em}\text{a}p.s,\\ \frac{\mathrm{d}\text{a}pp}{\mathrm{d}t}& =k_3\hspace{0.17em}\text{a}p.s-k_4\hspace{0.17em}\text{a}pp.\end{array}$$

Noting that the total mass of the system is a + ap + app = T, we can solve for the steady-state to yield:

$$\begin{array}{rl}\text{a}& =\frac{k_2{k}_4\text{T}}{k_1{k}_3\hspace{0.17em}{s}^2+k_1{k}_4\hspace{0.17em}s+k_2{k}_4},\\ \text{a}p& =\frac{k_1{k}_4\hspace{0.17em}s.\text{T}}{k_1{k}_3{s}^2+k_1{k}_4\hspace{0.17em}s+k_2{k}_4},\hspace{0.17em}\\ \text{a}pp& =\frac{k_1{k}_3\hspace{0.17em}{s}^2.\text{T}}{k_1{k}_3\hspace{0.17em}{s}^2+k_1{k}_4\hspace{0.17em}s+k_2{k}_4}.\end{array}$$

The response of APP to changes in signal can be evaluated by differentiating with respect to signal S:

$$C_S^{\text{A}PP}=\frac{k_4(k_1\hspace{0.17em}s+2k_2)}{k_{1}s(k_3\hspace{0.17em}s+k_4)+k_2{k}_4}.$$ 3.1

We note that $C_S^{\mathrm{APP}}\le 2$ for all positive values of signal strength and parameters k₁ to k₄ (see appendix A.6 for a proof). A useful analysis can be obtained by applying metabolic control analysis and expressing the sensitivity in terms of the component elasticities. The proof is given in appendix A.4, but the response of APP to changes in the stimulus is given by:

$$C_S^{\text{A}PP}=\frac{\text{a}({\epsilon }_2^3+{\epsilon }_2^2)+\text{a}p\hspace{0.17em}{\epsilon }_1^1}{\text{a}\hspace{0.17em}{\epsilon }_2^2{\epsilon }_3^4+\text{a}p\hspace{0.17em}{\epsilon }_1^1{\epsilon }_3^4+\text{a}pp\hspace{0.17em}{\epsilon }_1^1{\epsilon }_2^3},$$ 3.2

where the ${\epsilon }_j^i$ are the elasticity coefficients. Equation (3.2) looks a little complicated but can be simplified by assuming all reactions are first-order. Under these conditions, all the elasticities equal one (because its first-order) so that the equation reduces to something much more manageable:

$$C_S^{\text{A}PP}=\frac{2\text{a}+\text{a}p}{\text{a}+\text{a}p+\text{a}pp}.$$ 3.3

This indicates that given the right ratios for A, AP, and APP, it is possible for $C_S^{\mathrm{APP}}>1$. The maximum value the equation can reach is when AP and APP are zero, where at this point $C_S^{\mathrm{APP}}=2$. Thus, the maximum is 2, this matches the result in equation (3.1).

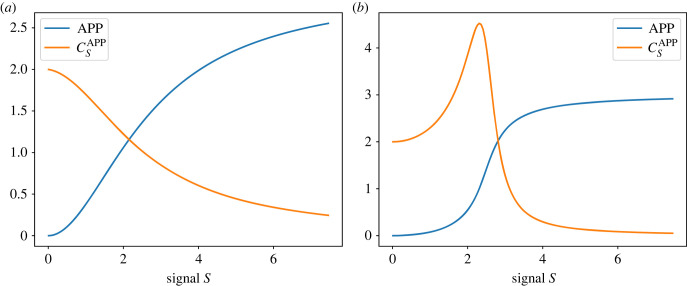
An important observation is that the character of the response given in equation (3.2) is very different from the more well-known zero-order ultrasensitivity. We can see the difference by looking at the sensitivities shown in figure 9. Figure 9a, we see the response when the rate laws are linear mass-action kinetic laws. This results in what we call first-order ultrasensitivity. It is characterized by the response starting at the maximum value at zero signal and then decreasing to zero at high signal levels.

Figure 9.

Response of a double cycle, figure 8, to an input signal S. (a) Linear mass-action kinetics illustrating first-order ultrasensitivity where $C_S^{APP}$ starts at a value of two then declines to zero at high signal levels. (b) Model based on saturable Michaelis–Menten kinetics showing, in this case, a blend of first- and zero-order ultrasensitivity. Note how the sensitivity, $C_S^{\mathrm{APP}}$, starts at two, not one, as it would in a purely zero-order response which is shown in figure 3.

By contrast, on the right panel, we see the effect of using saturable Michaelis–Menten kinetics. However, this is not a purely zero-order ultrasensitivity response. A purely zero-order sensitive response starts at one, spikes close to the inflection point, then rapidly decreases (figure 3). For a double cycle, we get a blend of first- and zero-order ultrasensitivity. We can see this more clearly in figure 10 where we have plotted the response at different Michaelis constant (Km) values. At a moderate level of zero-order ultrasensitivity (Km < 6), we achieve a relatively constant sensitivity from the system up to the inflection point. Km values below this (e.g. Km = 0.5) result in the appearance of the characteristic spike. This is an interesting behaviour that may permit evolution to develop amplifiers with a relatively constant sensitivity without the need for negative feedback [5,40].

Figure 10.

The result of blending first and zero-order responses in a double cycle. High Kms (Michaelis constant) result in pure first-order ultrasensitivity. As the Kms are reduced, more zero-order sensitivity is blended into the first-order ultrasensitive response. Zero-order ultrasensitivity gives a spike at higher saturation. The blending of the two effects allows a wider range of signal over which we can achieve higher sensitivity.

We see a similar response when comparing the response of a Hill equation to the more complex Monod–Wyman–Changeux model in enzyme kinetics [25,41]. The sensitivity of a Hill equation to ligand is to first start at the maximum sensitivity and then decrease. This is similar to the first-order ultrasensitivity response. By contrast, the response to a ligand for a Monod–Wyman–Changeux model is for the sensitivity to start at 1.0, then peak to a maximum, and decrease after. This is very similar to the zero-order response.

To summarize, a double cycle can show two kinds of ultrasensitivity, the classical zero-order ultrasensitivity and what we term first-order ultrasensitivity.

3.1. Comparisons of single and double cycles

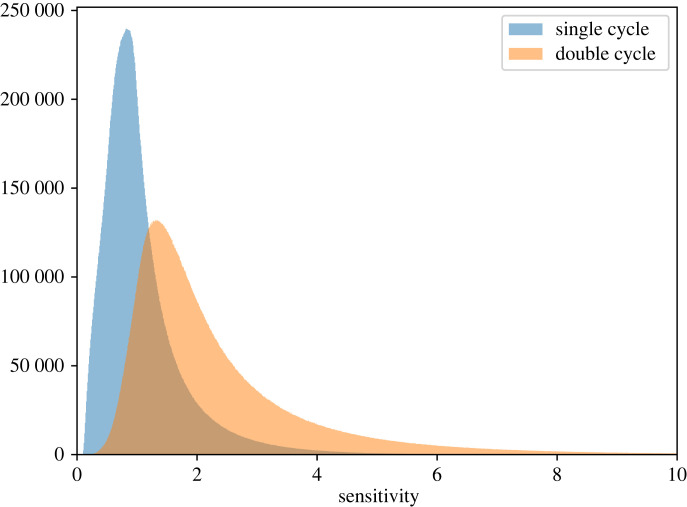
Sauro & Kholodenko [5] noted that a double cycle will show more zero-order ultrasensitivity compared to a single cycle. This can be understood from equation (3.2) where the denominator contains products of the elasticities. When operating in the zero-order regime the elasticities are small (because the enzymes are near saturation) and the product of small elasticities is an even smaller number. As the elasticities become smaller, the denominator decreases faster than the numerator, hence the sensitivity will be higher compared to a single cycle. To investigate this further we conducted an empirical study using equation (3.2) for the sensitivity of a double cycle system and the equivalent equation for a single cycle system $C_S^{\mathrm{AP}}=\mathrm{ap}/(\mathrm{a}\hspace{0.17em}{\epsilon }_2^1+\mathrm{ap}\hspace{0.17em}{\epsilon }_1^2)$. To do this, we sampled 25 000 000 networks with randomly assigned elasticities (between 0.1 and 1.0) and the mass of the systems by sampling the molar fractions (also between 0.1 and 1.0) with a total mass of 1. Note that this is a global survey of possible mass and elasticity distributions and does not account for a number of factors (steady-state condition, enzyme concentration, rate parameters, etc.) that may determine which states of the system are accessible. The results of this study are shown in figure 11 and show how the sensitivities are distributed. The modes of plots for the single and double cycle sensitivities were 0.81 and 1.33, respectively. This suggests a somewhat modest improvement that a double-cycle has over a single cycle of about 1.64-fold.

Figure 11.

The x-axis represents the value of the sensitivity $C_S^{\mathrm{AP}}$ for a single cycle or for the double cycle $C_S^{\mathrm{APP}}$. The histograms were generated by sampling 25 000 000 networks and thus represents the distribution of sensitivities. The modes are 0.81 for a single cycle and 1.33 for a double cycle. These numbers vary slightly between runs so that these are not exact but it allows us to state that a double cycle shows approximately 1.64 times more sensitivity compared with an equivalent single cycle.

In summary, we conclude that a double cycle only adds modestly to the sensitivity of a system compared to a single cycle.

3.2. Effect of retroactivity

Retroactivity [42] is an effect where a downstream system causes upstream systems to change their behaviour. This is a common effect in electronics where a downstream circuit may draw too much current from an upstream circuit causing voltage drops at the point where they contact. A common remedy to this problem is to introduce a negative feedback loop. This is especially common in devices such as op amps.

The same phenomena can occur in biochemical pathways [42]. For example, assume we have two double phosphorylation/dephosphorylation cycles forming a cascade (figure 12) where the first cycle generates active kinase, APP, to phosphorylate the forward arms, v₅ and v₇, of the second cycle that in turn creates active BPP. At the molecular level, active kinase APP must physically bind to inactive B and BP in order to phosphorylate B and BP to generate active BPP. This results in sequestration of mass from the first layer and changing the total mass of the cycle will thereby alter its behaviour.

Figure 12.

A system of two double cycles forming a cascade.

Previous studies [14] have shown that the zero-order ultrasensitivity appears to be sensitive to this sequestration, even to the extent of eliminating it completely. However, experimental studies such as the work by Ferrell [43] has observed ultrasensitivity in oocytes, and Wiley [16] has observed sustained oscillations in active ERK protein which is the final protein in the MAPK cascade and attributed to the negative feedback and the ultrasensitivity of the MAPK stack. It would seem there is sufficient ultrasensitivity in the pathway to generate these behaviours. One possibility is that the first-order ultrasensitivity is contributing to it, but this depends on whether it is sensitive to sequestration effects. To investigate this we can mimic sequestration by looking at how sensitive a double cycle is to changes in the total mass by looking at any variation in $C_S^{\mathrm{APP}}$.

To do this, we computed the sensitivity over a range of total mass in the cycle. The results in table 1 show that the sensitivity is independent of total mass. The reason for this is that changes to the total mass simply scales everything so that the ratio of the different species in the double cycle remains the same. This in turn results in an unchanged sensitivity.

Table 1.

Effect of removing mass, to mimic retroactivity, from a double cycle on the sensitivity of APP with respect to signal S. The model uses linear mass-action kinetics so that the observed ultrasensitivity is due entirely to the first-order effects. Note the first-order ultrasensitivity remains unchanged although the gain, as defined by d APP/dS, decreases because the total mass of the system decreases.

total mass in cycle	concentration of APP	sensitivity of APP to signal: $C_S^{\mathrm{APP}}$	gain (dAPP/dS)
5.0	0.6397	1.6820	1.076
1.0	0.1279	1.6820	0.215
0.9	0.1151	1.6820	0.194
0.4	0.0511	1.6820	0.086

In summary, we conclude that the first-order ultrasensitivity is immune to retroactivity. This is unlike zero-order ultrasensitivity which can be markedly affected by retroactivity.

4. Single layer with many cycles

This section provides results for single-layer cascades with an arbitrary number of cycles. A cascade has N species (or states, such as phosphorylation levels), and so there are N − 1 cycles. In this model, we use S_i to indicate the ith species in the system, species ordered left to right. Mass is conserved, and so $\sum _n{S}_n=T$.

Our focus is on control coefficients. There are two ways to derive the control coefficient relationships. The first approach is we can assume linear mass-action kinetics for all steps and solve for the steady-state concentrations as we did in the last section. We can then derive the scaled derivatives from the analytical solutions. The second approach is to assume nonlinear kinetics and linearize the system and express the response in terms of the system elasticities. We describe both approaches.

4.1. Responses based on mass-action kinetics

Here, we assume mass-action kinetics. That is, for the reaction A → B, the reaction rate is kA, where k is the kinetic constant for the reaction.

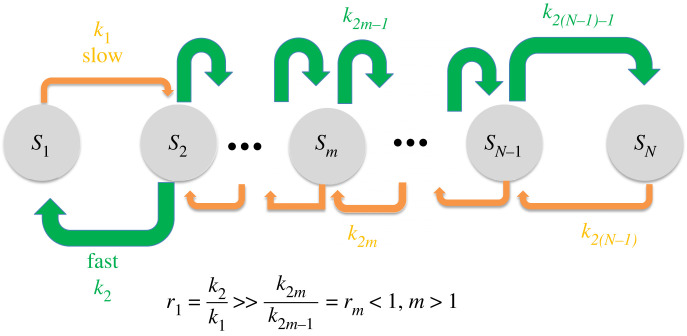
The leftmost species is S₁. S₂ is to the right of S₁, and so on, with the rightmost species being S_N. Species S₁ and S_N have one outgoing reaction and one incoming reaction. All other species have two incoming and two outgoing reactions. Odd-numbered kinetic constants refer to reactions that produce a species with a larger subscript. So, S_m → S_m+1 proceeds at the rate k_2m−1 S_m, and S_m+1 → S_m proceeds at the rate k_2m S_m+1.

Appendices A.7 and A.8 derive control coefficients for the last stage in the cascade, S_N. The derivation is done in terms of P(l) = S_l/S_N; that is, P(l) is the mass of S_l relative to S_N. The result is

$$C_{r_m}^{S_N}=\frac{\sum _{l=1}^{m}P(l)}{1+\sum _{l=1}^{N-1}P(l)},$$ 4.1

where r_m = k_2m/k_2m−1.

Equation (4.1) provides an interesting insight. Control of S_N by S_m is possible only if we can transfer mass between S_N and S_m. In general, we want S_N to be small so that little mass needs to be transferred to achieve greater control. So for S_m to control S_N, either S_m must be large or S_m must mediate mass transfers from S_n, n < m. That is, the control coefficient $C_{r_m}^{S_N}$ is large if the sum of the mass of S_n, n ≤ m is large.

We can use equation (4.1) to design a cascade to control species S_N. By design, we mean specifying values of the r_m (i.e. relative values of kinetic constants). The primary objective of the design is to provide effective control by making the control coefficients $C_{k_{2m-1}}^{S_N}$ as large as possible. A secondary consideration in the design is determining the fraction of mass for each species since there may be constraints related to species concentrations. Note that r_m can be increased by increasing k_2m or decreasing k_2m−1.

Our first observation from equation (4.1) is that $C_{r_m}^{S_N}$ has a maximum value of 1. This is apparent since the summation in the numerator is part of the summation in the denominator. We maximize $C_{r_m}^{S_N}$ by making the numerator of the summation very large. Note that P(l) > 0 and there are more terms in the numerator summation for larger m. So, control coefficients are monotonically increasing in m. That is, $C_{r_{m+1}}^{S_N}>C_{r_m}^{S_N}$.

From the foregoing, we can make $C_{r_m}^{S_N}\to 1$ by having $\sum _{l=1}^{l=m}P(l)\approx \sum _{l=1}^{l=N-1}P(l)$. We can make all of these control coefficients large if $P(1)\approx \sum _{l=1}^{l=N-1}P(l)$. P(1) is large if k₁ is small and/or k₂ is large. However, smaller kinetic constants also result in longer settling times. Intuitively, this is clear because reaction rates are slower. The formal reason for this is that the resulting transfer function has poles close to 0.

Figure 13 displays the design of a cascade in which P(1) ≫ P(l) for l > 1. Note that by simultaneously controlling all cycles in the cascade, we achieve a control of $\sum _{m=1}^{N-1}{C}_{k_{2m-1}}^{S_N}\approx N-1$. It is interesting to note that the behaviour the system exhibits when activating one cycle is very similar to how a linear metabolic pathway responds. While a metabolic pathway relies on product inhibition to transmit changes [44], a series of protein cycles uses movement in a fixed amount of mass to elicit transmission changes. One major difference is that the sum of control coefficients in a metabolic pathway is one, while in the sequence of cycles, the maximum value is equal to the number of cycles. Here we show that simultaneously manipulating the reaction rates for the N − 1 cycles results in a control coefficient of N − 1. Since $P(1)\gg P(l)\hspace{0.17em}\mathrm{for}\hspace{0.17em}l>1$, we know that most of the mass in the cascade is S₁.

Figure 13.

Designing a controllable cascade for changing S_N. The cascade has large values of control coefficients for each S_n, $C_{k_{2n-1}}^{S_N}$, n < N. The key to the design is that S₁ has most of the mass so that k_2n−1 mediates the transfer of mass between S₁ and S_N.

Figure 14 displays control coefficients obtained from Tellurium simulations of a four cycle (five species) cascade (see appendix A.5.4). The plot in the upper left displays the control coefficients as we vary the value of r₁ for which the control coefficients are calculated. A small value of r₁ results in a small $C_{k_1}^{S_N}$. The mass is equally distributed among the other species, and so species closer to S_N mediate the transfer of more mass and hence have larger control coefficients. A large value of r₁ results in most of the mass being S₁, a situation that provides more control when adjusting the kinetic constants. Indeed, a very large r₁ results in the control coefficients converging to 1.

Figure 14.

Control coefficients for S₅ in a five species cascade. Better control is achieved by having r₁ large (e.g. by making k₁ small). A large r₁ means that most mass is S₁ and so that S₁–S₄ mediate the transfer of mass between S₁ and S₅.

The other plots explore the effect of varying r_m, m ∈ {2, 3, 4}. Large values of r₂ result in S₂ having most of the mass. Since S₁ lies to the left of S₂, adjusting k₁ transfers little mass to S_N. As a result, $C_{k_1}^{S_N}$ is much smaller in the upper right plot than in the upper left plot. Similar effects can be seen in the bottom row of plots.

4.2. Responses in terms of control coefficients

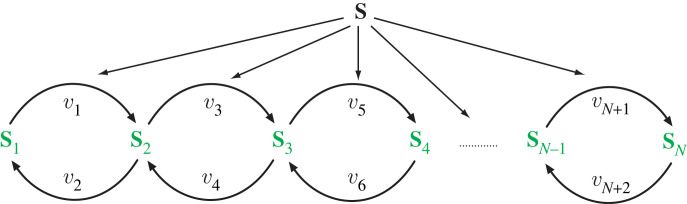
In this section, we derive the control coefficients in terms of elasticities for the model shown in figure 15.

Figure 15.

Multiple cycles with S as the stimulus signal.

The proof can be found in appendix A.4, which illustrates the case for a two-cycle system but the proof can easily be generalized to multiple cycles. For a three-cycle system, where APPP is the output, the response when the signal S activates each forward arm is given by:

$$C_S^{\text{A}PPP}=\frac{3M_1+2M_2+M_3}{M_1+M_2+M_3+M_4}.$$ 4.2

The maximum value that $C_S^{\mathrm{APPP}}$ can reach in this case is three. This can be generalized to a system with N − 1 cycles (or N proteins) where it can be shown that the maximum response is N − 1. The response of a system with N cycles is given by:

$$C_S^{S_N}=\frac{\sum _{i=1}^{N-1}(N-i)M_i}{\sum _{i=1}^N{M}_i}.$$ 4.3

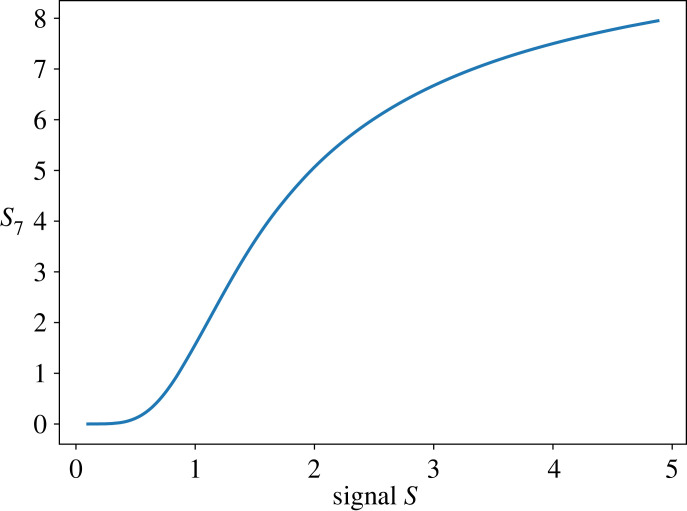
For example, a system that has six cycles displays a maximum response of six.

Figure 16 shows a plot of the response of a six-cycle system that uses first-order mass-action kinetics for each step.

Figure 16.

Multiple cycles with S as the stimulus signal.

5. Conclusion

In this paper, we examine some of the frequency response and sensitivity characteristics of single-, double- and multiple-cycle systems. We use a combination of metabolic control analysis and related control engineering techniques to analyse the systems. There are other more recent sensitivity analysis formalisms, such as those found in chemical network theory (CNT) [45,46]. However, these are generally much more complex to use and less developed. However, CNT has traditionally been more geared towards stability analysis, especially through the pioneering works of Clarke [23] and Feinberg [47]. The systems we consider in this article are stable and only have a single steady-state and therefore do not require the use of stability analysis. This is not to say that such systems cannot exhibit more interesting behaviours, and we have published other work where stability was a consideration [7].

A summary of the most notable results are as follows.

• 1. The frequency response for a single cycle shows that the cycle behaves as a low-pass filter. The bandwidth of the system (its ability to respond to changing signals) is at a minimum at the steepest point on the steady-state sigmoid response curve. This is equivalent to the Jacobian being at a minimum at this point. Although not discussed in the main text, the frequency response of two layers of single cycles reveals similar behaviour. The only difference is that the system is now a second-order system that shows damped behaviour as indicted by the damping ratio ζ. These results are shown in appendix A.3 for reference.
• 2. A double cycle phosphorylation cycle displays ultrasensitivity even when the kinases and phosphatases that phosphorylate and dephosphorylate the cycle proteins are operating below their Michaelis constants. We refer to this as first-order ultrasensitivity in contrast to the more well-known zero-order ultrasensitivity. However, the magnitude of first-order ultrasensitivity is more modest and has an upper bound equal to the number of cycles. The first-order logarithmic gain starts at two at low signal levels then declines as the signal increases. This is in contrast to the zero-order ultrasensitivity which starts at one at low signal levels, rises to a peak, then declines to zero as the signal increases.
• 3. First-order and zero-order ultrasensitivity can be blended so that the ultrasensitivity starts higher and remains at the higher value over a wider range of signal.
• 4. We extend the first-order ultrasensitivity analysis to n cycles and show that n cycles can yield a maximum first-order ultrasensitivity of n.
• 5. We conduct an empirical study of how much more ultrasensitivity a double cycle can achieve compared to a single cycle. We find that a double cycle can have approximate 1.6 times more logarithmic gain. This seems to be only a modest improvement.
• 6. We investigate the effect of retroactivity on first-order ultrasensitivity and find that first-order ultrasensitivity is immune to retroactivity. This is in contrast to zero-order ultrasensitivity where retroactivity can greatly diminish the ultrasensitivity.

We therefore speculate that the double phosphorylation cycles found, for example, in the MAPK cascade have evolved to enable reasonable levels of amplification even in the face of retroactivity.

A single cycle behaves as a classic low-pass filter and when operating under zero-order conditions, the bandwidth of the system is a minimum at the most sensitive steady-state point on the sigmoid ultrasensitivity curve. This indicates that the system acts as a noise filter in this region of the response. When cascading two single cycles, the system acts as a second-order system and we show that the damping ratio for such a system cannot go below one. This means that all transient dynamics as a result of perturbations to the input signal are always monotonic. We did not discover any other special features based on the frequency response for a double cycle. This may be due to the linearization procedure we use and that more pronounced effects happen in the nonlinear region. This would require an empirical study where we physically inject sinusoidal signals of varying amplitude and frequency and observe the effect on the outputs of the pathway. This could be used to investigate in more detail the frequency response.

We also examined double cycle sensitivities. Double cycles can show a degree of ultrasensitivity even when the kinases and phosphatases are operating below their Michaelis constants, that is, outside the zero-order regime. We show that a double cycle under these conditions can have a maximum response sensitivity of 2. We call this effect first-order ultrasensitivity to contrast it with the more well-known zero-order sensitivity. We show that first-order ultrasensitivity has unique response properties compared with zero-order ultrasensitivity. The first-order ultrasensitivity has a maximum at zero signal, then decreases to zero at high signal levels. There is also an accompanying characteristic plateau near the start before the response starts to decline. If the Michaelis constants are reduced so that the kinase and phosphatases tend to become more saturated, zero-order ultrasensitivity emerges but is blended in with the first-order ultrasensitivity. This allows a unique behaviour not found in single cycles. Whereas in a single cycle, zero-order ultrasensitivity peaks near the steepest portion, then declines rapidly, a blended response allows the sensitivity to remain relatively constant over a wider range of signal. This may have evolutionary significance as it allows the system to maintain a constant sensitivity over a wider range of signal.

On theoretical grounds it is known that zero-order ultrasensitivity can be significantly reduced in the presence of retroactivity [14] which is where a downstream system can adversely affect up stream system behaviour due to loading effects. We show that the first-order ultrasensitivity is immune to retroactivity. This may allow a cascade of phosphorylation cycles to maintain its ability to amplify even in the presence of retroactivity.

Finally, we look at the sensitivity of multiple cycles in a single layer and note that under the first-order ultrasensitivity conditions, the maximum sensitivity is equal to the number of cycles. We also note that the response to changes at individual cycle points can be explained in a similar manner to how control coefficients are distributed in a linear metabolic pathway.

There are some areas we have not considered in this paper and some unanswered questions. The first is how the frequency response of a single cycle and double cycle compare. Some initial investigations suggest that very little difference exists and a double cycle behaves as a simple over-damped system. This may be due to the linearization procedure we use and that more pronounced effects happen in the nonlinear region. Of more interest is that the in vivo concentrations of the kinases and phosphatases are comparable to the levels of the cycle substrates. In the current study, we used simple Michaelis–Menten kinetics to model behaviour and it is possible that under in vivo conditions the use of Michaelis–Menten kinetics might not be valid. This has been highlighted by a number of published works [48,49] where better approximations have been proposed. Further studies are need to investigate how ultrasensitivity and retroactivity are influenced by the choice of kinetic model.

Appendix A

A.1. Proposition 1

Let U = dap/ds be the unscaled steady-state sensitivity of the variable AP with respect to the signal S and let C = (dap/ds)(s/ap) = U.R be the corresponding scaled steady-state sensitivity where R = s/ap is the scaling term. Suppose (d/ds)C(σ) = 0 for some value of signal σ > 0, AP(σ) > 0, and U(σ) > 0. Then (d/ds)U(σ) = 0, if and only if (d/ds)R(σ) = 0.

Proof. —

Setting the derivative of the scaled sensitivity to 0 yields, by the product rule:

$$\frac{\mathrm{d}}{\mathrm{d}s}C=\frac{\mathrm{d}}{\mathrm{d}s}\left(\frac{\mathrm{d}\mathrm{ap}}{\mathrm{d}s}\frac{s}{\mathrm{ap}}\right)$$ A 1

$$=R\frac{{\mathrm{d}}^2\mathrm{ap}}{\mathrm{d}{s}^2}+\frac{\mathrm{d}\mathrm{ap}}{\mathrm{d}s}\frac{\mathrm{d}}{\mathrm{d}s}(R)$$ A 2

$$=R\frac{\mathrm{d}}{\mathrm{d}s}U+U\frac{\mathrm{d}}{\mathrm{d}s}(R)$$ A 3

$$=0$$ A 4

Rearranging we have

$$\frac{\mathrm{d}}{\mathrm{d}s}C=0\hspace{0.17em}⟹\hspace{0.17em}\frac{\mathrm{d}}{\mathrm{d}s}U=-\frac{U}{R}\frac{\mathrm{d}}{\mathrm{d}s}R.$$ A 5

Thus, d/dsU = 0 if and only if d/dsR = 0. □

A.2. Derivation of the frequency response for a single cycle (equation (2.8))

The basis for the derivation is [29]:

$${\mathbf{H}}_x(i\omega )={(\hspace{0.17em}j\omega \mathbf{I}-{\mathbf{N}}_{\mathbf{r}}\frac{\mathrm{\partial }\mathbf{v}}{\mathrm{\partial }\mathbf{x}}\mathbf{L})}^{-1}{\mathbf{N}}_{\mathbf{r}}\frac{\mathrm{\partial }\mathbf{v}}{\mathrm{\partial }\mathbf{p}},$$

where N_r is the reduced stoichiometry matrix, L the link matrix, ∂v/∂x the unscaled species elasticity matrix and ∂v/∂p the parameter elasticity matrix.

Using Tellurium, the following was obtained:

$${\mathbf{N}}_{\mathbf{r}}=\left[\begin{array}{cc}1& -1\end{array}\right]\mathbf{L}=\left[\begin{array}{c}1\\ -1\end{array}\right].$$

The independent species is AP; hence, the single row in the stoichiometry matrix corresponds to AP. The two columns correspond to v₁ and v₂. The unscaled elasticity matrix is a two by two matrix given by:

$$\left[\begin{array}{cc}0& {\mathcal{E}}_{\text{A}}^1\\ {\mathcal{E}}_{\text{A}P}^2& 0\end{array}\right]=\left[\begin{array}{cc}0& \frac{\mathrm{\partial }{v}_1}{\mathrm{\partial }\text{A}}\\ \frac{\mathrm{\partial }{v}_2}{\mathrm{\partial }\text{A}P}& 0\end{array}\right].$$

Two entries are zero because we assume no product inhibition on the kinase (v₁) phosphatase (v₂) by AP and A, respectively. The parameter unscaled elasticity matrix is given by:

$$\frac{\mathrm{\partial }\mathbf{v}}{\mathrm{\partial }\mathbf{p}}=\left[\begin{array}{c}{\mathcal{E}}_s^1\\ 0\end{array}\right].$$

The parameter elasticity matrix only has a single non-zero term because we assume that the only interaction is by signal, S, on v₁. Insertion of these terms into the frequency response expression leads to:

$$H_x(j\omega )=\frac{\mathrm{\partial }{v}_1/\mathrm{\partial }x}{j\omega +\mathrm{\partial }{v}_1/\mathrm{\partial }\text{a}+\mathrm{\partial }{v}_2/\mathrm{\partial }\text{a}p}.$$ A 6

The fact that the system is first-order makes this a simple derivation.

A.3. Derivation of the frequency response for two-layers of single cycles

Tellurium was used to derive the reduced stoichiometry (N_r) and link matrix (L):

$${\mathbf{N}}_{\mathbf{r}}=\left[\begin{array}{cccc}1& -1& 0& 0\\ 0& 0& 1& -1\end{array}\right]\mathbf{L}=\left[\begin{array}{cc}1& 0\\ 0& 1\\ 0& -1\\ -1& 0\end{array}\right].$$

The order of the species in the model was set to ensure that the top two rows of the stoichiometry matrix were AP and BP, respectively. This resulted in the two independent species being AP and BP. As a result, the unscaled elasticity matrix was:

$$\frac{\mathrm{\partial }\mathbf{v}}{\mathrm{\partial }\mathbf{x}}=\left[\begin{array}{cccc}0& 0& 0& {\mathcal{E}}_{\text{A}}^1\\ {\mathcal{E}}_{\text{A}P}^2& 0& 0& 0\\ {\mathcal{E}}_{\text{A}P}^3& 0& {\mathcal{E}}_{\text{B}}^3& 0\\ 0& {\mathcal{E}}_{\text{B}P}^4& 0& 0\end{array}\right]=\left[\begin{array}{cccc}0& 0& 0& \frac{\mathrm{\partial }{v}_1}{\mathrm{\partial }\text{A}}\\ \frac{\mathrm{\partial }{v}_2}{\mathrm{\partial }\text{A}P}& 0& 0& 0\\ \frac{\mathrm{\partial }{v}_3}{\mathrm{\partial }\text{A}P}& 0& \frac{\mathrm{\partial }{v}_3}{\mathrm{\partial }\text{B}}& 0\\ 0& \frac{\mathrm{\partial }{v}_4}{\mathrm{\partial }\text{B}P}& 0& 0\end{array}\right]$$

The parameter elasticity is the same as for the single layer except the number of rows is extended to four:

$$\frac{\mathrm{\partial }\mathbf{v}}{\mathrm{\partial }\mathbf{p}}=\left[\begin{array}{c}{\mathcal{E}}_s^1\\ 0\\ 0\\ 0\end{array}\right]$$

The entry ${\mathcal{E}}_{\mathrm{AP}}^3$ represents the elasticity that connects the two layers together. As before, the frequency response can be derived by inserting these terms into the equation:

$${\mathbf{H}}_x(i\omega )={(\hspace{0.17em}j\omega \mathbf{I}-{\mathbf{N}}_{\mathbf{r}}\frac{\mathrm{\partial }\mathbf{v}}{\mathrm{\partial }\mathbf{x}}\mathbf{L})}^{-1}{\mathbf{N}}_{\mathbf{r}}\frac{\mathrm{\partial }\mathbf{v}}{\mathrm{\partial }\mathbf{p}}.$$

This leads to a second-order system:

$$H_{\text{B}P}(s)=\frac{{\mathcal{E}}_{\text{A}P}^3\hspace{0.17em}{\mathcal{E}}_{\text{S}}^1}{({\mathcal{E}}_{\text{A}}^1+{\mathcal{E}}_{\text{A}P}^2+s)({\mathcal{E}}_{\text{B}}^3+{\mathcal{E}}_{\text{B}P}^4+s)}.$$ A 7

When the denominator is expanded this gives:

$$H_{\text{B}P}(s)=\frac{{\mathcal{E}}_{\text{A}P}^3\hspace{0.17em}{\mathcal{E}}_{\text{S}}^1}{s^2+(({\mathcal{E}}_{\text{A}}^1+{\mathcal{E}}_{\text{A}P}^2)+({\mathcal{E}}_{\text{B}}^3+{\mathcal{E}}_{\text{B}P}^4))s+({\mathcal{E}}_{\text{A}}^1+{\mathcal{E}}_{\text{A}P}^2)({\mathcal{E}}_{\text{B}}^3+{\mathcal{E}}_{\text{B}P}^4)}.$$ A 8

This can be converted into the standard form for a second-order system by dividing top and bottom by $({\mathcal{E}}_{\mathrm{A}}^1+{\mathcal{E}}_{\mathrm{AP}}^2)({\mathcal{E}}_{\mathrm{B}}^3+{\mathcal{E}}_{\mathrm{BP}}^4)$, and setting $1/(({\mathcal{E}}_{\mathrm{A}}^1+{\mathcal{E}}_{\mathrm{AP}}^2)({\mathcal{E}}_{\mathrm{B}}^3+{\mathcal{E}}_{\mathrm{BP}}^4))$ to $1/{\omega }_n^2$, such that ${\omega }_n=\sqrt{({\mathcal{E}}_{\mathrm{A}}^1+{\mathcal{E}}_{\mathrm{AP}}^2)({\mathcal{E}}_{\mathrm{B}}^3+{\mathcal{E}}_{\mathrm{BP}}^4)}$. This allows us to rewrite the transfer function as:

$$H_{\text{B}P}(s)=\frac{K}{(s^2/{\omega }_n^2)+(1/{\omega }_n^2)(({\mathcal{E}}_{\text{A}}^1+{\mathcal{E}}_{\text{A}P}^2)+({\mathcal{E}}_{\text{B}}^3+{\mathcal{E}}_{\text{B}P}^4))s+1},$$ A 9

where K is called the gain in classical control theory. Finally, we define:

$$2\zeta {\omega }_n=({\mathcal{E}}_{\text{A}}^1+{\mathcal{E}}_{\text{A}P}^2)+({\mathcal{E}}_{\text{B}}^3+{\mathcal{E}}_{\text{B}P}^4),$$ A 10

and multiplying top and bottom by ${\omega }_n^2$, results in:

$$H_{\text{B}P}(s)=K\frac{{\omega }_n^2}{s^2+2\zeta {\omega }_{n}s+{\omega }_n^2}.$$

The transfer function is now in the standard form where ζ is the damping ratio. Equation (A 10) can be rearranged to give:

$$\zeta =\frac{1}{2}\frac{({\mathcal{E}}_{\text{A}}^1+{\mathcal{E}}_{\text{A}P}^2)+({\mathcal{E}}_{\text{B}}^3+{\mathcal{E}}_{\text{B}P}^4)}{\sqrt{({\mathcal{E}}_{\text{A}}^1+{\mathcal{E}}_{\text{A}P}^2)({\mathcal{E}}_{\text{B}}^3+{\mathcal{E}}_{\text{B}P}^4)}}.$$

This equation is of the form:

$$\frac{1}{2}\frac{x+y}{\sqrt{xy}},$$

which can be shown to have a value greater than one as follows.

$$\begin{array}{rl}& {(\sqrt{x}+\sqrt{y})}^2\ge 0\\ & x+y-2\sqrt{xy}\ge 0\\ & x+y\ge 2\sqrt{xy}\end{array}$$

Hence:

$$\frac{1}{2}\frac{x+y}{\sqrt{xy}}\ge 1.$$

This means that the damping ratio, ζ is greater than one. Second-order systems with a damping ratio greater than one cannot admit any damped periodic behaviour. This means all dynamic behaviour of the two-cycle system must be monotonic.

A.4. Proof for equation (3.2)

Consider the double cycle model shown in figure 17.

Figure 17.

Double cycle model with signal S activating both v₁ and v₂.

To keep things simple, we assume no product inhibition or reversibility in the cycle reactions. Although we are doing a manual derivation for the expression, it is possible to use PyscesToolbox [51], which is an extremely effective tool for deriving control coefficient expressions symbolically and we highly recommend using it in such cases. However, the manual derivation illustrates the deductive approach that can be used to derive sensitivities within the framework of metabolic control analysis.

Our objective is to derive the equation for $C_S^{\mathrm{APP}}$. To do this we first note that the response $C_S^{\mathrm{APP}}$ is given by the sum (based on a theorem described in [32,52]):

$$C_s^{APP}=C_{e_1}^{\text{A}PP}{\epsilon }_S^{v_1}+C_{e_3}^{\text{A}PP}{\epsilon }_S^{v_3}.$$

We can make the derivation simpler by noting that the elasticity of S to v₁ and v₃ is one. This is a reasonable assumption since S is usually a kinase, and catalysis is normally first-order. This means we only have to find the expressions for $C_{e_1}^{\mathrm{APP}}$ and $C_{e_3}^{\mathrm{APP}}$. We will show the derivation for $C_{e_1}^{\mathrm{APP}}$. The derivation for $C_{e_3}^{\mathrm{APP}}$ can be done in a similar manner.

In the model in figure 17, S is the signal, v₁ is catalysed by enzyme e₁, v₂ by e₂, etc. where e_i is concentration of enzyme i. To derive $C_{e_1}^{\mathrm{APP}}$, we perturb v₁ by changing e₁ by an amount δe₁. This changes the steady state from which the following local equations can be obtained. For an understanding of what a local equation is see appendix A and especially B, in the paper by Kacser & Burns [19]. Briefly, a local equation is the sum total of local changes that gives rise to the net change in a given reaction rate. For example, given a reaction S → P, the net change in the reaction rate of this reaction is the sum of the changes of contributions from S and P. In this case, S will contribute positively while P, due to product inhibition, will contribute negatively to the forward reaction rate.

Note that subscripts on the following elasticities, 1 = a, 2 = ap and 3 = app. This is to reduce clutter. For example, ${\epsilon }_2^3$ represents the elasticity of rate v₃ with respect to species AP.

$$\frac{\delta v_1}{v_1}={\epsilon }_1^1\frac{\delta \text{a}}{\text{a}}+\frac{\delta e_1}{e_1},\frac{\delta v_2}{v_2}={\epsilon }_2^2\frac{\delta \text{a}p}{\text{a}p}$$

and

$$\frac{\delta v_3}{v_3}={\epsilon }_2^3\frac{\delta \text{a}p}{\text{a}p},\frac{\delta v_4}{v_4}={\epsilon }_3^4\frac{\delta \text{a}pp}{s_3}.$$

At steady state it must be true that v₁ = v₂ and v₃ = v₄, though it is not necessarily the case that v₁ = v₃. This means that when the steady state changes and thereby the rates change, it must be the case that δv₁ = δv₂ and δv₃ = δv₄. In relative terms, we can also assert that: δv₁/v₁ = δv₂/v₂ and δv₃/v₃ = δv₄/v₄. By equating the local equations δv₁/v₁ and δv₂/v₂, we obtain:

$${\epsilon }_2^1\frac{\delta \text{a}}{\text{a}}+\frac{\delta e_1}{e_1}={\epsilon }_2^2\frac{\delta \text{a}p}{\text{a}p}.$$

Both sides of the equation can be divided by δe₁/e₁ to give:

$${\epsilon }_2^1\left(\frac{\delta \text{a}}{\text{a}}\right)/\left(\frac{\delta e_1}{e_1}\right)+1={\epsilon }_2^2\frac{\delta \text{a}p}{\text{a}p}/\left(\frac{\delta e_1}{e_1}\right).$$

In the limit as the delta changes tend to zero, we obtain:

$${\epsilon }_2^1{C}_{e_1}^{\text{A}}+1={\epsilon }_2^2{C}_{e_1}^{\text{A}P}.$$ A 11

A similar equation can be derived for $C_{e_1}^{\mathrm{AP}}$ and $C_{e_1}^{\mathrm{A}}$ using the v₃, v₄ pair of local equations. In this case, the result is simpler:

$$C_{e_1}^{\text{A}P}=C_{e_1}^{\text{A}PP}.$$ A 12

As a result we have two equations and three unknowns $C_{e_1}^{\mathrm{A}},C_{e_1}^{\mathrm{AP}}$ and $C_{e_1}^{\mathrm{APP}}$. To solve for the three unknowns, a third equation is necessary. The double cycle has a single conservation equation, a + ap + app = T. Perturbing e₁ by δe₁ does not disturb the total T but changes the distribution of species such that the change in species must be constrained by δa + δap + δapp = 0. We next adjust each term in this expression as follows:

$$\text{a}\frac{\delta \text{a}}{\text{a}}+\text{a}p\frac{\delta \text{a}p}{\text{a}p}+\text{a}pp\frac{\delta \text{a}pp}{\text{a}pp}=0,$$

and dividing throughout by δe₁/e₁ and taking the delta limit to zero, yields:

$$\text{a}\hspace{0.17em}{C}_{e_1}^{\text{A}}+\text{a}p\hspace{0.17em}{C}_{e_1}^{\text{A}P}+\text{a}pp\hspace{0.17em}{C}_{e_1}^{\text{A}PP}=0.$$ A 13

We now have three equations (A 11), (A 12) and (A 13) in three unknowns, which can be solved. For example, solving for $C_{e_1}^{\mathrm{APP}}$ gives:

$$C_{e_1}^{\text{A}PP}=\frac{\text{a}pp\hspace{0.17em}{\epsilon }_2^3}{\text{a}\hspace{0.17em}{\epsilon }_2^2{\epsilon }_3^4+\text{a}p\hspace{0.17em}{\epsilon }_1^1{\epsilon }_3^4+\text{a}pp\hspace{0.17em}{\epsilon }_1^1{\epsilon }_2^3}.$$

Using the same technique, a solution to $C_{e_3}^{\mathrm{APP}}$ can also be found as follows:

$$C_{e_3}^{\text{A}PP}=\frac{\text{a}\hspace{0.17em}{\epsilon }_2^2+\text{a}pp\hspace{0.17em}{\epsilon }_1^1}{\text{a}\hspace{0.17em}{\epsilon }_2^2{\epsilon }_3^4+\text{a}p\hspace{0.17em}{\epsilon }_1^1{\epsilon }_3^4+\text{a}pp\hspace{0.17em}{\epsilon }_1^1{\epsilon }_2^3}.$$

The influence of an external signal, S, is the sum of its interactions therefore $C_S^{\mathrm{APP}}=C_{e_1}^{\mathrm{APP}}+C_{e_3}^{\mathrm{APP}}$ where we assume that the elasticity of the signal on v₁ and v₃ is one. This gives us the total response of s₃ due to changes in the signal S. The sum is given by equation (A 14):

$$C_S^{\text{A}PP}=\frac{\text{a}({\epsilon }_2^3+{\epsilon }_2^2)+\text{a}p\hspace{0.17em}{\epsilon }_1^1}{\text{a}\hspace{0.17em}{\epsilon }_2^2{\epsilon }_3^4+\text{a}p\hspace{0.17em}{\epsilon }_1^1{\epsilon }_3^4+\text{a}pp\hspace{0.17em}{\epsilon }_1^1{\epsilon }_2^3}.$$ A 14

This is equation (3.2) in the main text.

A.5. Antimony models

A.5.1. Single cycle

  # Declaring AP first ensures that the first row

# of the stoichiometry matrix will be AP

# This forces the independent variable to be AP

species AP, P

A -> AP; k1*S*A/($Km$ + A)

AP -> A; k2*AP/($Km$ + AP)

k1 = 0.14; k2 = 0.7

A = 10; S = 1; $Km$ = 0.5

A.5.2. Single cycle two layers

species AP, BP, A, B

v1: A -> AP; k1*S*A/($Km$ + A)

v2: AP -> A; k2*AP/($Km$ + AP)

v3: B -> BP; k3*AP*B/($Km$ + B)

v4: BP -> B; k3*BP/($Km$ + BP)

k1 = 0.4 # 0.5

k2 = 0.7; k3 = 0.7

k4 = 0.7 # 3.5

$Km$ = 0.5

A = 10; B = 10; S = 1

A.5.3. Double cycle

species APP, AP, A

J1: A -> AP; k1*S*A/($Km$ + A)

J2: AP -> A; k2*AP/($Km$ + AP)

J3: AP -> APP; k3*S*AP/($Km$ + AP)

J4: APP -> AP; k4*APP/($Km$ + APP)

k1 = 0.14; k2 = 0.7

k3 = 0.7; k4 = 0.7; $Km$ = 0.5

A = 10; S = 1

A.5.4. N cycle model

  J1f: S1 -> S2; S1*k1;

J1b: S2 -> S1; S2*k2;

J2f: S2 -> S3; S2*k3;

J2b: S3 -> S2; S3*k4;

J3f: S3 -> S4; S3*k5;

J3b: S4 -> S3; S4*k6;

J4f: S4 -> S5; S4*k7;

J4b: S5 -> S4; S5*k8;

k1 = 1; k2 = 1.0;

k3 = 1; k4 = 1.0;

k5 = 1; k6 = 1.0;

k7 = 1; k8 = 1.0;

S1 = 100; S2 = 0;

S3 = 0; S4 = 0;

S5 = 0;

A.6. Proposition 2

Suppose that

$$C_S^{\text{A}PP}=\frac{k_4(k_1\hspace{0.17em}s+2k_2)}{k_{1}s(k_3\hspace{0.17em}s+k_4)+k_2{k}_4},$$ A 15

where $C_S^{\mathrm{APP}}$ is the response of APP with respect to the non-negative signal S, and non-negative parameters k_i : i ∈ {1, 2, 3, 4}. Then $C_S^{\mathrm{APP}}\le 2$ $\mathrm{\forall }$ values of S and parameters k_i.

Proof. —

Suppose $\mathrm{\exists }$ a non-negative signal strength S and/or non-negative parameters k₁ − k₄ such that

$$C_S^{\text{A}PP}>2.$$

Then

$$\begin{array}{rl}{C}_S^{\text{A}PP}& =\frac{k_4(k_{1}s+2k_2)}{k_{1}s(k_{3}s+k_4)+k_2{k}_4}>2\\ & \hspace{0.17em}⟹\hspace{0.17em}{k}_4(k_{1}s+2k_2)>2(k_{1}s(k_{3}s+k_4)+k_2{k}_4)\\ & \hspace{0.17em}⟹\hspace{0.17em}{k}_1{k}_{4}s+2k_2{k}_4>2k_1{k}_3{s}^2+2k_1{k}_{4}s+2k_2{k}_4\\ & \hspace{0.17em}⟹\hspace{0.17em}0>2k_1{k}_3{s}^2+k_1{k}_{4}s.\end{array}$$

This violates our non-negative S and k_i conditions as at least one value must be negative. Thus $C_S^{\mathrm{APP}}\le 2$ must hold. □

A.7. Proof for steady state, multiple cycles

We begin by considering the steady-state mass or concentration (we use the two interchangeably) of S_n for a cascade with mass-action kinetics. At steady state, the rate at which mass leaves S_n to the right has to be the same as the rate at which mass enters S_n from the right. Or, v_2n−1 = v_2n, and hence k_2n−1 S_n = k_2n S_n+1, where k_i > 0. From this, we infer

$$S_n=S_N\prod _{l=n}^{N-1}{r}_l,$$

where r_n = k_2n/k_2n−1. The product of the ratio of the kinetic constants occurs frequently in our analysis, and so we define

$$P(n)=\prod _{l=n}^{N-1}{r}_l.$$ A 16

P(n) is the relative mass of species S_n; that is relative to the concentration of S_N. Using the constraint that mass is constant,

$$\begin{array}{rl}T& =\sum _{n=1}^N{S}_n\\ & =S_N+S_N\sum _{n=1}^{N-1}P(n).\end{array}$$

From this, we obtain the steady-state solutions.

$$S_N=\frac{T}{1+\sum _{\hspace{0.17em}j=1}^{N-1}P(j)}$$ A 17

and

$$S_n=\frac{TP(n)}{1+\sum _{\hspace{0.17em}j=1}^{N-1}P(j)},\hspace{0.17em}n<N$$ A 18

The denominator in these equations is the total relative mass. The numerator is the relative mass for a particular species multiplied by the total mass.

A.8. Control coefficients with mass-action kinetics

Control coefficients are calculated relative to the ratios r_m; that is, we have a signal that only affects the ratio r_m associated with S_m. From this, we calculate $C_{k_{2n-1}}^{S_N}$ and $C_{k_{2n}}^{S_N}$.

Consider $C_{r_m}^{S_N}=(\mathrm{\partial }{S}_N/\mathrm{\partial }{r}_m)(r_m/S_N)$. Note that

$$\begin{array}{rl}\frac{\mathrm{\partial }P(n)}{\mathrm{\partial }{r}_m}& =\frac{P(n)}{r_m}\text{i}f\hspace{0.17em}n\le m\\ & =0\hspace{0.17em}\text{o}therwise\end{array}$$

and so

$$\frac{\mathrm{\partial }{S}_N}{\mathrm{\partial }{r}_m}=-\frac{T\sum _{l=1}^{m}P(l)}{r_m(1+\sum _{l=1}^{N-1}P{(l))}^2}.$$

We now calculate the control coefficients as

$$\begin{array}{rl}{C}_{r_m}^{S_N}& =-\frac{\sum _{l=1}^{m}P(l)}{1+\sum _{l=1}^{N-1}P(l)}\\ C_{k_{2m}}^{S_N}& =C_{r_m}^{S_N}\\ C_{k_{2m-1}}^{S_N}& =-C_{r_m}^{S_N}\end{array}$$ A 19

$$=\frac{\sum _{l=1}^{m}P(l)}{1+\sum _{l=1}^{N-1}P(l)}$$ A 20

A.9. Link matrix

We define the stoichiometry matrix N as an m by n matrix where m is the number of species and n the number of reactions. Each entry in the matrix represents the stoichiometric coefficient for a given reaction with respect to a given species.

A pathway may include one or more conservation laws where the sum of amounts of a set of species is constant regardless of the kinetic properties of the pathway. For example, the simple pathway S₁ → S₂ and S₂ → S₁ has a single conservation law where the sum, s₁ + s₂, is constant. Such conservation laws are manifest in the stoichiometry matrix as dependent rows which splits the matrix into a set of dependent and independent species. For convenience, the rows of the stoichiometry matrix can be reordered so that the independent rows are the top most rows. We can extract the top independent rows into a new matrix with the symbol N_r, meaning the reduced stoichiometry matrix.

The number of rows in N_r is the rank of the stoichiometry matrix which we denote by m_o. The dependent rows, of which there are m − m_o, can be derived from N_r by application of a set of elementary operations which we denote by the matrix L_o.

The link matrix is now defined as an identity matrix of size m_o combined with the L_o matrix:

$$\mathbf{L}=\left[\begin{array}{c}{\mathbf{I}}_{m_o}\\ {\mathbf{L}}_{\mathbf{o}}\end{array}\right].$$

The full stoichiometry matrix can now be defined in terms of the product of the link matrix and the reduced stoichiometry matrix:

$$\mathbf{N}=L\times N_r.$$ A 21

In practice, the factorization of the stoichiometric matrix is accomplished using either LU or QR factorization [53,54]. Most mainstream modelling packages [34–37,55,56] carry out this reduction in order to ensure numerical stability.

Given this background, we can now derive the following Jacobian expression used in the main text:

$$\text{J}acobian={\mathbf{N}}_{\mathbf{r}}\times \mathcal{E}\times \mathbf{L}.$$

The proof is given by Hofmeyr in [33] but is buried among other material and so we repeat it here for convenience to the reader.

The system of differential equations describing the time course behaviour of the pathway can be written in terms of the stoichiometry matrix and the rate vector as:

$$\frac{\mathrm{d}s}{\mathrm{d}t}=Nv.$$

Let us designate the vector of independent species using s_i and the vector of dependent species s_d. This allows us to write the system of differential equations as:

$$\left[\begin{array}{c}\frac{\mathbf{d}{\mathbf{s}}_{\mathbf{i}}}{\mathrm{d}\mathbf{t}}\\ \frac{\mathbf{d}{\mathbf{s}}_{\mathbf{d}}}{\mathrm{d}\mathbf{t}}\end{array}\right]=\left[\begin{array}{c}{\mathbf{I}}_{m_o}\\ {\mathbf{L}}_{\mathbf{o}}\end{array}\right]{\mathbf{N}}_{\mathbf{r}}\mathbf{v}.$$

Inspection of this equation reveals that:

$${\mathbf{L}}_{\mathbf{o}}\frac{\mathrm{d}{\mathbf{s}}_{\mathbf{i}}}{\mathrm{d}\mathbf{t}}=\frac{\mathrm{d}{\mathbf{s}}_{\mathbf{d}}}{\mathrm{d}\mathbf{t}}.$$

Integration of this yields:

$${\mathbf{s}}_{\mathbf{d}}\mathbf{(}\mathbf{t}\mathbf{)}\mathbf{-}{\mathbf{s}}_{\mathbf{d}}\mathbf{(}\mathbf{0}\mathbf{)}\mathbf{=}{\mathbf{L}}_{\mathbf{o}}\mathbf{(}{\mathbf{s}}_{\mathbf{i}}\mathbf{(}\mathbf{t}\mathbf{)}\mathbf{-}{\mathbf{s}}_{\mathbf{i}}\mathbf{(}\mathbf{0}\mathbf{)}\mathbf{)}\mathbf{,}$$

where s_i(0) and s_d(0) are the quantities of species at time zero. Introducing the constant vector T = s_d (0) − L_o s_i (0) we can write the relationship as:

$${\mathbf{s}}_{\mathbf{d}}\mathbf{(}\mathbf{t}\mathbf{)}\mathbf{=}\mathbf{T}\mathbf{+}{\mathbf{L}}_{\mathbf{o}}{\mathbf{s}}_{\mathbf{i}}\mathbf{(}\mathbf{t}\mathbf{)}\mathbf{.}$$ A 22

This gives the explicit relationship between the dependent and independent species. We will first be more explicit about the rate vector in the system of differential equations by writing it as follows:

$$\frac{\mathrm{d}\mathbf{s}}{\mathrm{d}\mathbf{t}}=\mathbf{N}\mathbf{v}\mathbf{(}\mathbf{s}\mathbf{(}\mathbf{p}\mathbf{)}\mathbf{,}\mathbf{p}\mathbf{)},$$

where we have included the vector of species concentrations s (of size m), v is the vector of rate laws of size n, and p is a vector of model parameters (its size is unimportant for our purpose). We can focus on the rate of change of independent species and split the s vector into the dependent and independent species to give equation (A 21) as:

$$\frac{\mathrm{d}{\mathbf{s}}_{\mathbf{i}}}{\mathrm{d}\mathbf{t}}={\mathbf{N}}_{\mathbf{r}}\mathbf{v}\mathbf{(}{\mathbf{s}}_{\mathbf{i}}\mathbf{(}\mathbf{p}\mathbf{)}\mathbf{,}{\mathbf{s}}_{\mathbf{d}}\mathbf{(}{\mathbf{s}}_{\mathbf{i}}\mathbf{(}\mathbf{p}\mathbf{)}\mathbf{)}\mathbf{,}\mathbf{p}\mathbf{)}.$$

At steady-state the left-hand side is zero:

$${\mathbf{N}}_{\mathbf{r}}\mathbf{v}\mathbf{(}{\mathbf{s}}_{\mathbf{i}}\mathbf{(}\mathbf{p}\mathbf{)}\mathbf{,}{\mathbf{s}}_{\mathbf{d}}\mathbf{(}{\mathbf{s}}_{\mathbf{i}}\mathbf{(}\mathbf{p}\mathbf{)}\mathbf{)}\mathbf{,}\mathbf{p}\mathbf{)}=0.$$

Differentiating this with respect to p gives:

$${\mathbf{N}}_{\mathbf{r}}\frac{\mathrm{\partial }\mathbf{v}}{\mathrm{\partial }{\mathbf{s}}_{\mathbf{i}}}\frac{\mathrm{d}{\mathbf{s}}_{\mathbf{i}}}{\mathrm{d}\mathbf{p}}+{\mathbf{N}}_{\mathbf{r}}\frac{\mathrm{\partial }\mathbf{v}}{\mathrm{\partial }{\mathbf{s}}_{\mathbf{d}}}\frac{\mathrm{\partial }{\mathbf{s}}_{\mathbf{d}}}{\mathrm{\partial }{\mathbf{s}}_{\mathbf{i}}}\frac{\mathrm{\partial }{\mathbf{s}}_{\mathbf{i}}}{\mathrm{\partial }\mathbf{p}}+N_r\frac{\mathrm{\partial }\mathbf{v}}{\mathrm{\partial }\mathbf{p}}=0.$$

Note that the dependent species is a function of the independent species by way of equation (A22) so that:

$$\frac{\mathrm{\partial }{\mathbf{s}}_{\mathbf{d}}}{\mathrm{\partial }{\mathbf{s}}_{\mathbf{i}}}={\mathbf{L}}_{\mathbf{o}}$$

and

$${\mathbf{N}}_{\mathbf{r}}\frac{\mathrm{\partial }\mathbf{v}}{\mathrm{\partial }{\mathbf{s}}_{\mathbf{i}}}\frac{\mathrm{d}{\mathbf{s}}_{\mathbf{i}}}{\mathrm{d}\mathbf{p}}+{\mathbf{N}}_{\mathbf{r}}\frac{\mathrm{\partial }\mathbf{v}}{\mathrm{\partial }{\mathbf{s}}_{\mathbf{d}}}{\mathbf{L}}_{\mathbf{o}}\frac{\mathrm{\partial }{\mathbf{s}}_{\mathbf{i}}}{\mathrm{\partial }\mathbf{p}}+{\mathbf{N}}_{\mathbf{r}}\frac{\mathrm{\partial }\mathbf{v}}{\mathrm{\partial }\mathbf{p}}=0.$$

Rearranging this equation gives:

$${\mathbf{N}}_{\mathbf{r}}\left[\frac{\mathrm{\partial }\mathbf{v}}{\mathrm{\partial }{\mathbf{s}}_{\mathbf{i}}}\frac{\mathrm{\partial }\mathbf{v}}{\mathrm{\partial }{\mathbf{s}}_{\mathbf{d}}}\right]\left[\begin{array}{c}\mathbf{I}\\ {\mathbf{L}}_{\mathbf{o}}\end{array}\right]\frac{\mathrm{d}{\mathbf{s}}_{\mathbf{i}}}{\mathrm{d}\mathbf{p}}+{\mathbf{N}}_{\mathbf{r}}\frac{\mathrm{\partial }\mathbf{v}}{\mathrm{\partial }\mathbf{p}}=0.$$

Replacing terms gives:

$${\mathbf{N}}_{\mathbf{r}}\hspace{0.17em}\mathcal{E}\hspace{0.17em}\mathbf{L}\hspace{0.17em}\frac{\mathrm{d}{\mathbf{s}}_{\mathbf{i}}}{\mathrm{d}\mathbf{p}}+{\mathbf{N}}_{\mathbf{r}}\frac{\mathrm{\partial }\mathbf{v}}{\mathrm{\partial }\mathbf{p}}=0$$

In appendix A, Hofmeyr [33] shows that the expression:

$${\mathbf{N}}_{\mathbf{r}}\hspace{0.17em}\times \mathcal{E}\hspace{0.17em}\times \mathbf{L},$$

is the Jacobian matrix. We do not repeat the proof here which is given in appendix A of [33] but involves expanding the system of differential equations in a Taylor series and truncating high terms and then equating the formal definition of the Jacobian matrix that appears in the Taylor series with the above expression.

Ethics

This work did not require ethical approval from a human subject or animal welfare committee.

Data accessibility

All Python scripts used to generate the figures and simulations can be found at: https://github.com/sys-bio/frequency_response_paper.

Declaration of AI use

We have not used AI-assisted technologies in creating this article.

Authors' contributions

M.A.K.: formal analysis, writing—original draft, writing—review and editing; J.L.H.: conceptualization, writing—original draft, writing—review and editing; H.M.S.: conceptualization, formal analysis, writing—original draft, writing—review and editing. All authors gave final approval for publication and agreed to be held accountable for the work performed therein.

Conflict of interest declaration

We declare we have no competing interests.

Funding

The research reported in this article was supported by the National Institute of Cancer of the National Institutes of Health under award no. U01CA227544. This work was supported in part by the Washington Research Foundation and by a Data Science Environments project award from the Gordon and Betty Moore Foundation (Award no. 2013-10-29) and the Alfred P. Sloan Foundation (Award no. 3835) to the University of Washington eScience Institute.

Glossary

Some of the terminology we use may be unfamiliar to readers, such terminology is defined here:

First-order kinetics: first-order kinetics [50] refers to the property where increasing the concentration of a reactant in a chemical reaction leads to a proportional increase in the reaction rate. That is, the reaction rate is proportional to reactant concentration.

Zero-order kinetics: zero-order kinetics [50] refers to the property where increasing the concentration of a reactant in a chemical reaction results in no change to the rate of reaction. That is, the reaction rate is independent of the reactant concentration.

Saturable kinetics: saturable kinetics relates to reactions catalysed by enzymes where the enzyme can become saturated by substrate [25] leading to zero-order kinetics at high reactant concentrations.

Km (Michaelis constant): the Km is a fundamental parameter often used in describing enzyme kinetics [25]. It is numerically equal to the concentration of substrate that results in half the maximal enzymatic rate. Thus, an enzyme where the substrate is above the Km is more saturated with substrate than an enzyme where the substrate is below the Km.

Zero-order ultrasensitivity: zero-order ultrasensitivity is when the cycle kinase and phosphatase of a phosphorylation cycle are operating above their Km values. This leads to the kinase and phosphatase operating closer to the saturating region of the reaction profile and gives rise to high sensitivity in the cycles response to changes in an input signal.

Signal elasticity: the elasticity is defined in the main text but in brief it is the logarithmic gain of a reaction rate with respect to a specified modulator. When referring to the ‘signal elasticity' the modulator is in this case a signal or modulator of some kind. Hence the signal elasticity is the elasticity of the signal. Throughout this article, the signal is always the effector that activates the phosphorylation cycle. Details can be found in the original publication from 1973 [19]. There is a specific Wikipedia page on the topic of elasticities (https://en.wikipedia.org/wiki/Elasticity_coefficient) which might be easier to access.