Quantitative Prediction of Right Ventricular Size and Function From the ECG

Abstract

Background

Right ventricular ejection fraction (RVEF) and end‐diastolic volume (RVEDV) are not readily assessed through traditional modalities. Deep learning–enabled ECG analysis for estimation of right ventricular (RV) size or function is unexplored.

Methods and Results

We trained a deep learning–ECG model to predict RV dilation (RVEDV >120 mL/m²), RV dysfunction (RVEF ≤40%), and numerical RVEDV and RVEF from a 12‐lead ECG paired with reference‐standard cardiac magnetic resonance imaging volumetric measurements in UK Biobank (UKBB; n=42 938). We fine‐tuned in a multicenter health system (MSH_original [Mount Sinai Hospital]; n=3019) with prospective validation over 4 months (MSH_validation; n=115). We evaluated performance with area under the receiver operating characteristic curve for categorical and mean absolute error for continuous measures overall and in key subgroups. We assessed the association of RVEF prediction with transplant‐free survival with Cox proportional hazards models. The prevalence of RV dysfunction for UKBB/MSH_original/MSH_validation cohorts was 1.0%/18.0%/15.7%, respectively. RV dysfunction model area under the receiver operating characteristic curve for UKBB/MSH_original/MSH_validation cohorts was 0.86/0.81/0.77, respectively. The prevalence of RV dilation for UKBB/MSH_original/MSH_validation cohorts was 1.6%/10.6%/4.3%. RV dilation model area under the receiver operating characteristic curve for UKBB/MSH_original/MSH_validation cohorts was 0.91/0.81/0.92, respectively. MSH_original mean absolute error was RVEF=7.8% and RVEDV=17.6 mL/m². The performance of the RVEF model was similar in key subgroups including with and without left ventricular dysfunction. Over a median follow‐up of 2.3 years, predicted RVEF was associated with adjusted transplant‐free survival (hazard ratio, 1.40 for each 10% decrease; P=0.031).

Conclusions

Deep learning–ECG analysis can identify significant cardiac magnetic resonance imaging RV dysfunction and dilation with good performance. Predicted RVEF is associated with clinical outcome.

Nonstandard Abbreviations and Acronyms

AUPRC

area under the precision‐recall curve

CNN

convolutional neural network

DL

deep learning

MSH

Mount Sinai Hospital

RVEDV

right ventricular end‐diastolic volume

UKBB

UK Biobank

Research Perspective.

What Is New?

• We developed and fine‐tuned a deep learning algorithm on ECGs that estimates right ventricular volume and ejection fraction; the ECG‐predicted right ventricular ejection fraction was significantly associated with composite cardiac outcome.

What Questions Should Be Addressed Next?

• How does this deep learning model perform across a wider range of pathological conditions?

• How does the model perform in external validation across multiple centers?

Right ventricular (RV) size and functional metrics have important prognostic implications for many diseases, including cardiomyopathy, pulmonary hypertension, and structural heart disease. ¹ Volumetric measurements such as RV ejection fraction (RVEF) and end‐diastolic volume (RVEDV) are correlated with major adverse outcomes ² and have particular importance in patients with congenital heart disease ³ and pulmonary hypertension. ⁴

However, current tools for accurate quantification of RVEF and RVEDV are limited. Estimation of volumes by traditional 2‐dimensional echocardiographic RV measurements are not recommended in adults or children ⁵ , ⁶ due to poor reproducibility, especially in the setting of significant pathology. ⁷ Three‐dimensional echocardiography is a promising novel technology but has significant technical and processing limitations and is not broadly available. ⁸ , ⁹ Cardiac magnetic resonance imaging (cMRI) is the clinical reference standard for volumetric quantification, but cMRI is not globally accessible, is time and resource intensive, and cannot be performed in some patients, such as those with implanted devices and those who will not tolerate the examination.

There is an urgent clinical need for novel methods to assess RV size and function that are validated against gold‐standard metrics, widely available, and simple to perform. We sought to develop such a method through application of modern machine learning techniques to a ubiquitous clinical tool: the ECG.

Recent developments in deep learning (DL) technology have produced models to interpret ECG for accurate diagnosis of structural heart disease and prognosis, ¹⁰ but the use of DL on ECG to quantify RVEDV and RVEF has not been explored. We hypothesized that we could develop a DL algorithm to accurately quantify RVEDV and RVEF from a pathological clinical cohort and a large healthy registry of paired ECG and cMRI and that ECG assessment of RV function was associated with clinical outcome.

Methods

This project was approved by the institutional review board of the Icahn School of Medicine at Mount Sinai School of Medicine and waiver of informed consent was obtained. The code pipeline is available at https://github.com/akhilvaid/RVSizeFunction. The code provided in the repository contains all functions required to load and analyze data using a choice of models. The ECG data and some specialized code for preprocessing these data cannot be released due to concerns of patient privacy and institutional intellectual property, respectively.

Overview

Broadly, we trained a convolutional neural network (CNN) on a larger data set of paired ECG and cMRI data from the UK Biobank (UKBB) and then fine‐tuned the model on a smaller, retrospectively collected cohort of clinically indicated cMRI–ECG pairs from a single urban referral center. We then performed a prospective validation on the subsequent 4 months following the model training/testing set.

UKBB Data Set

We accessed paired ECG and cMRI data from the UKBB. Participant enrollment and cMRI acquisition parameters have been described previously. ¹¹ We used a previously validated automated segmentation method to obtain RVEDV and RVEF ¹² from the balanced steady‐state free precession cine short‐axis stack. This method contours the right ventricle to include the papillary muscles within the RV volume. A cMRI‐trained cardiologist (S.D.) performed manual segmentation of 10 randomly selected studies for comparison with the automated method, with Bland–Altman analysis results shown in Figure S1. RVEF mean difference was 3.7 (95% upper limit of agreement, 12.8%; lower limit of agreement, −5.4%), and RVEDV indexed to body surface area mean difference was −2.9 mL/m² (95% upper limit of agreement, 17.7; lower limit of agreement, −23.5%). We excluded entries with RVEF values <10% or >80%. Per the UKBB study protocol, a standard 12‐lead ECG was obtained at the same visit as cMRI. ECG acquisition parameters have been previously published ¹³ and were accessed in Extensible Markup Language format with preprocessing per below.

Clinical Data Set

As the UKBB did not contain a high prevalence of dilated or dysfunctional RV measurements, we fine‐tuned the model on a clinical cohort of diverse patients in a large urban health system with 5 hospitals (MSH_original [Mount Sinai Hospital, New York, NY]). We queried our cMRI reporting software (Precession, Intelerad, Montreal, Canada) for studies performed from April 4, 2012, to November 22, 2022, in patients aged ≥18 years and collected clinically indicated cMRI reports paired with ECGs within 2 weeks before or 2 weeks after cMRI examination. The MUSE Cardiology Information System (GE, Boston, MA) ECG database was queried for relevant patient medical record numbers, filtered by date of acquisition, and exported as Extensible Markup Language files. We excluded patients with congenital heart disease as an indication for MRI, or without a recorded ECG within the inclusion time frame. Like the UKBB data set, we excluded entries with RVEF values <10% or >80%. We extracted clinically measured RVEDV and RVEF from reports. MRI is typically performed on a 1.5T scanner using balanced steady‐state free precession sequences with manual contouring of the cine short‐axis stack to include RV papillary muscles within the blood pool for the RV, though all reports were included. Left ventricular volume (contoured to exclude the papillary muscles from the blood pool) and ejection fraction were also collected. Patient age at cMRI, sex, indication for cMRI, cardiac rhythm at cMRI, weight, and height were also collected from the report.

ECG Preprocessing

ECG waveforms represented as a time series of voltage sampled at 500 Hz in each lead were extracted as Extensible Markup Language files from both the UKBB and MSH data sets. We included 8 channels from the 12‐lead ECG: leads I, II, and V1 to V6 as the other leads are linear transformations without additional information. Our ECG preprocessing pipeline was described in detail previously. ¹⁴ Briefly, we corrected for baseline wander through the application of a median filter applied over a 2‐second window and a subsequent Butterworth bandpass filter applied to a 0.5‐ to 40‐Hz range. We excluded low‐quality ECG recordings/ECGs with missing lead information by discarding ECGs with variations in QRS amplitude or frequency greater than +/−3 SD of the population mean for that lead. A total of 633 (3.4%) ECGs in the MSH data set and 549 (1.3%) ECGs in the UKBB data set were removed (see Figure 1). ECGs were then restricted to the first 5 seconds to ensure all patients had equivalent data and plotted to images with standardization of lead amplitude to the minimum and maximum voltages within each preprocessed lead.

Figure 1. Study Inclusion flow diagram.

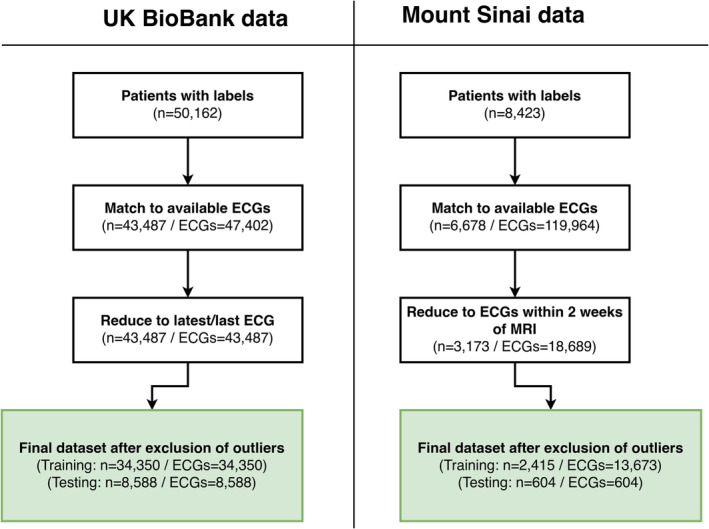
Cardiac MRI and ECG inclusion diagram chart for UK Biobank (left) and Mount Sinai Hospital data sets (right). MRI indicates magnetic resonance imaging.

Model Construction and Training

The model input was the preprocessed cMRI‐paired ECG. The model outputs of interest were numerical RVEF (%) and RVEDV/body surface area (mL/m²) (ie, supervised learning for regression tasks) as well as these values dichotomized into pathological thresholds of RVEF<40% and RVEDV ≥120 mL/m² (ie, supervised learning for classification tasks). Thus, for each data set, 4 separate models were trained: (1) RVEF regression, (2) RVEF classification, (3) RVEDV regression, and (4) RVEF classification. In the UKBB study protocol, only 1 ECG was obtained per subject and cMRI, which was randomly split into 80% training and 20% testing subsets. For the MSH_original data set, as multiple ECGs per cMRI could occur within the inclusion time frame, patients were group shuffle split into 80% train and 20% test groups. This method ensured that no patient was represented both in the test and training set but allowed multiple ECGs obtained in the inclusion period for a patient to be considered in the training set. For the MSH_original test set, only 1 subject with 1 paired ECG closest to the time of cMRI was included.

We selected a DenseNet‐201 2‐dimensional CNN architecture that had been previously trained on >700 000 ECGs ¹⁴ as initialization parameters. Neural network architectures are uniquely able to extract information‐rich features from complex waveform data and form the basis of several published DL‐ECG models. ¹⁴ , ¹⁵ , ¹⁶ , ¹⁷ , ¹⁸ We trained the network using the Adam optimizer with cross‐entropy as the loss function for classification and mean absolute error for regression tasks, respectively. To minimize overfitting, we monitored train‐test loss over training epochs against an internal validation set of 5% of ECGs within the training cohort. Training was stopped at the epoch that performed best with respect to this internal validation set, despite continuing training with an adaptive learning rate for several more epochs. This method is functionally equivalent to early stopping as a form of regularization.

We first trained on the UKBB data set as a way of training features specific to the right ventricle, but the data set has a low prevalence of RV pathology. We then fine‐tuned the model to predict outcomes in the MSH cohort, which had a higher outcome prevalence to learn features specific to RV pathology. Fine‐tuning a neural network refers to the process of using pretrained parameters (as opposed to random parameters) from a related task as a starting point for training on a new task or data set. This may potentially improve model performance on smaller data sets because the network may have already learned the basic features needed for the new task. We also tested whether using a pretrained model resulted in better performance compared with random initialization of parameters and found that use of the pretrained model increased model performance in the MSH_original (Tables S1 and S2) and UKBB test sets.

Model Evaluation

We evaluated model performance with area under the receiver operating characteristic curve (AUROC) and area under the precision‐recall curve (AUPRC) for classification tasks. Precision‐recall curves are generated by plotting the precision (ie, the positive predictive value) against the recall (ie, the sensitivity) over the range of predictions generated. AUPRC, by emphasizing the ability of the classifier to predict outcomes, is useful to evaluate the performance of a classifier in the setting of class imbalance where outcomes are more important to detect than nonoutcomes. ¹⁹ Unlike AUROC, AUPRC depends on the baseline prevalence of disease and therefore can be interpreted as the ability of the classifier to identify a group “enriched” for disease over the baseline. We reported sensitivity, specificity, positive predictive value, negative predictive value, positive likelihood ratio (LR), and negative LR with bootstrapped 95% CIs at the probability threshold defined by the maximum sum of sensitivity and specificity (Youden's J). We also evaluated classification model performance in key subgroups, including sex, left ventricular (LV) dysfunction (defined as left ventricular ejection fraction [LVEF] <50%), arrhythmia, obesity (body mass index ≥30), and age ≥60 years. We performed AUROC comparisons and tested for effect modification between subgroups using the method of DeLong. ²⁰ Patients with missing subgroup data (see Table 1) were excluded from subgroup analysis. For regression tasks, we visualized predicted versus expected scatterplots and described the relationship using nonparametric Passing–Bablok regression analysis, which is commonly used to compare 2 measurement methods. ²¹ The relationship between the predicted (ECG) and expected (cMRI) RV metric was also evaluated with linear R ² calculation and Lin's concordance correlation coefficient. Difference plots in which the difference between ECG‐predicted and cMRI RV metric were plotted against the cMRI reference standard, and a linear slope with prediction CIs based on 1.96*SD of the residuals were reported as recommended by Bland and Altman. ²² Mean absolute error of the models with 95% CI was calculated through 500 bootstrap iterations. We also performed saliency mapping using the GradCAM library to highlight the regions of a given ECG input image that were most associated with a prediction.

Table 1.

Demographic and Clinical Characteristics in Mount Sinai Data Set

	MSHoriginal training set (n=2415)	MSHoriginal test set (n=604)	MSHvalidation temporal validation (n=115)
Age, y, mean (SD)	56.0 (16.4)	55.9 (17.0)	56.3 (16.1)
Sex, female, n (%)	865 (37.5)*	209 (36.3)†	45 (39.8)‡
Sex, male, n (%)	1550 (62.5)	395 (63.7)	70 (60.2)
Race or ethnicity, n (%) White	995 (41.2)	258 (42.7)	41 (35.7)
Black	476 (19.7)	101 (16.7)	28 (24.4)
Other/Unknown	944 (39.1)	245 (40.6)	46 (40)
BSA, m2, mean (SD)	1.95 (0.29)	1.96 (0.27)	1.95 (0.29)
BMI	27.7 (6.4)*	27.6 (5.8)†	27.6 (6.2)
BMI ≥30 kg/ht2, n (%)	663 (28.5)*	152 (26)†	36 (31.3)
Indication for cMRI, n (%) Cardiomyopathy	1959 (81.1)	485 (80.3)	86 (74.8)
Abnormal ECG	183 (7.6)	56 (9.3)	1 (0.9)
Tumor	107 (4.4)	22 (3.6)	8 (7.0)
Valvular function	20 (0.8)	5 (0.8)	0 (0)
Other/unknown	146 (6.0)	36 (6.0)	20 (17.4)
Rhythm at cMRI, n (%) Normal sinus	1957 (91.1)*	476 (90.5) †	106 (95.5) ‡
Sinus with ectopic beats	97 (4.5)	25 (4.8)	2 (1.8)
Atrial fibrillation/flutter	78 (3.6)	21 (4.0)	1 (0.9)
Other	15 (0.7)	4 (0.7)	2 (1.8)
Admitted as inpatient at time of MRI	863 (35.7)	217 (35.9)	45 (39.1)
LVEF, median (IQR)	53 (36–61)*	53 (36–62)	52 (34–63)
LVEF <50%, n (%)	1016 (42)*	261 (43.4)	44 (38.3)
RVEF, median (IQR)	54 (46–61)	53 (46–60)	54 (47–59)
RVEF ≤40%, n (%)	411 (17.0)	109 (18.0)	18 (15.7)
LVEDVi, median (IQR)	84 (69–110)*	84 (70–108)†	85 (65–107)
RVEDVi, median (IQR)	78 (63–95)*	80 (64–99)†	70 (58–81)
RVEDVi ≥120, n (%)	202 (8.7)	62 (10.6)	5 (4.3)

BMI indicates body mass index; BSA, body surface area; cMRI, cardiac magnetic resonance imaging; IQR, interquartile range; LVEF, left ventricular ejection fraction; LVEDVi, left ventricular end‐diastolic volume indexed to body surface area; MRI, magnetic resonance imaging; MSH, Mount Sinai Hospital; RVEDVi, right ventricular end‐diastolic volume indexed to body surface area; and RVEF, right ventricular ejection fraction.

^*Training set missing data: rhythm at cMRI, n=268; patient sex, n=108; LVEDVi, n=91; BSA; BMI; RVEDVi, n=87; LVEF, n=4.

^† Test set missing data: rhythm at cMRI, n=78; BSA; BMI; LVEDVI; RVEDVI, n=20 missing; LVEF, n=3 missing; patient sex, n=28 missing.

^‡ Temporal validation set missing data: patient rhythm, n=4; patient sex, n=2.

Temporal Validation

We performed temporal validation (MSH_validation) of the final classification models in the period of November 23, 2022 to March 21, 2023, from a cohort of patients with clinically indicated cMRI and paired ECG within +/−14 days of cMRI like the MSH_original data set. Patients with prior ECG or cMRI included in the MSH_original data set were excluded. AUROC and AUPRC metrics were reported as above.

Survival Analysis for Composite Outcome

We reviewed the medical records of patients included within the MSH_original test set to ascertain date of last known follow‐up, death, and date of heart transplant if performed. We performed survival analysis to evaluate the association between predicted numerical RVEF and the combined outcome of death or heart transplantation. This composite outcome is commonly used to represent end‐stage heart failure in heart failure prediction models. ²³ Kaplan–Meier survival plots stratified by MRI‐LVEF and ECG‐predicted RVEF were generated. Using Cox proportional hazards for multivariable modeling, we tested several variables associated with heart failure outcome including MRI–quantified LVEF, age, sex, obesity (body mass index >30), hospitalization at time of MRI (as a proxy for severe heart failure), ²³ and self‐reported race or ethnicity. ²⁴ Variable selection was determined using the Akaike information criterion for the model excluding RVEF, and then the additive value of ECG‐predicted RVEF versus MRI‐quantified RVEF was evaluated using Akaike information criterion and Harrell's C‐statistic. The linear risk assumption for continuous variables was assessed visually through martingale residual plots with a running mean smoother line plotted to identify nonlinearity. A nonlinear inflection point in risk related to age at around 60 years old was identified, and therefore age was dichotomized at ≥60 years old. We tested proportional hazards assumptions in the final model by evaluating the relationship between scaled Schoenfeld residuals and time. A P value <0.05 was considered statistically significant.

Software

Model training was performed in Python (version 3.8; Python Software Foundation, Beaverton, OR) with pandas, numpy, scipy, scikit‐learn, PyTorch, torchvision, PIL, matplotlib, seaborn, and GradCAM packages. Data visualization and descriptive statistics were performed in R (R Foundation for Statistical Computing, Vienna, Austria) and Stata13 (StataCorp, College Station, TX). Continuous metrics are reported as mean (SD).

Results

Demographic and Clinical Information

We included 42 938 patient MRI‐ECG pairs from UKBB after quality control. Mean age was 64.7 years, 48% were men, 96.5% were White individuals, and the most common comorbidities were hypertension (22.5%) and hyperlipidemia (17.3%). Heart surgery and history of myocardial infarction were reported in 1.8% and 1.4%, respectively. The mean RVEF was 57% (SD, 6.3), with RV dysfunction (RVEF ≤40%) present in 425 (1.0%). Mean RVEDV was 82 (15.6) mL/m², with RV dilation (RVEDV ≥120 mL/m²) in 680 (1.6%).

The MSH_original data set consisted of 3019 patients that were split 80% to 20% into training and test cohorts. The training set consisted of 2415 patients and 13 673 ECG recordings meeting the inclusion criteria. The test set contained 604 patients, each with 1 paired cMRI and ECG. Test set mean age was 56 (17) years, and cardiomyopathy was the predominant indication for cMRI (80%). Prevalence of RV dysfunction was 18%, and prevalence of RV dilation was 11%. Demographic, clinical, and MRI characteristics of the MSH_original cohorts split by test and training groups are listed in Table 1. A comparison between the available overlapping variables of the MSH and UKBB data sets are shown in Table S3. A graphical overview of patient and ECG inclusion is shown in Figure 1.

The MSH_validation group consisted of 115 patients, each with 1 paired ECG and cMRI. Demographic and clinical characteristics were concordant with the MSH_original group, except for smaller RVEDV measurements and a lower prevalence of RV dilation (n=5; 4.3%). However, presence of RV systolic dysfunction was similar (n=18; 15.7%). Clinical and demographic information of the MSH training, test, and temporal validation cohorts is shown in Table 1.

RVEF Classification Models

Model performance characteristics to classify RV systolic dysfunction (defined as RVEF ≤40%) in UKBB and MSH data sets are shown in Figure 2. In UKBB (baseline prevalence 1.0%), AUROC was 0.86 (0.80–0.90), and AUPRC was 0.17 (0.11–0.26). In the MSH_original data set (baseline prevalence, 18.0%), AUROC was 0.81 (0.77–0.86), and AUPRC was 0.59 (0.49–0.69). At Youden's J threshold, there was a sensitivity of 65% (95% CI, 57–75), specificity of 86% (83–89), positive predictive value of 51% (43–59), negative predictive value of 92% (89–94), positive LR of 4.7 (3.7–6.2), and negative LR of 0.40 (0.29–0.50) in the MSH_original test data set. Performance between clinically relevant subgroups in the MSH_original test data set is shown in Table 2. RVEF model AUROC did not differ between any tested subgroup, including those with and without LV dysfunction.

Figure 2. Classification of abnormal right ventricular ejection fraction and end‐diastolic volume.

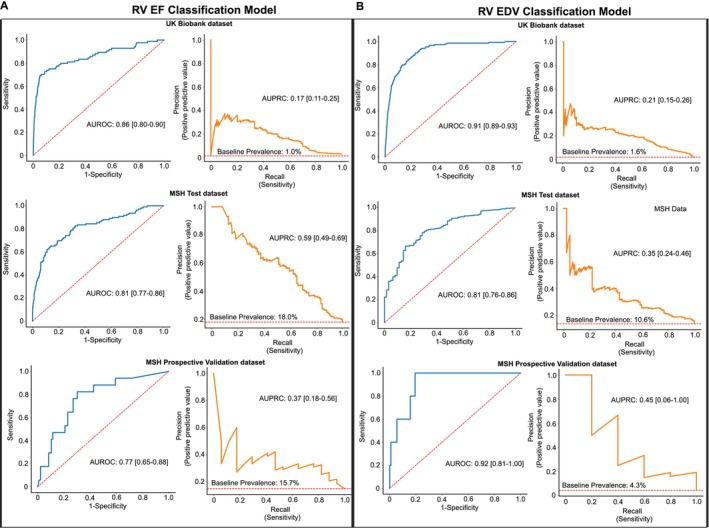
Receiver operating characteristic curves (blue) and precision recall curves (orange) to classify RV systolic dysfunction (A, left) and RV dilation (B, right) in UK Biobank data set (top), MSH data set (middle), and MSH prospective validation data set (bottom). Red dashed lines on receiver operating characteristic curves represent no model skill, and on precision recall curves represent baseline incidence of disease. AUROC indicates area under the receiver operating characteristic curve; AUPRC, area under the precision‐recall curve; MSH, Mount Sinai Hospital; and RV, right ventricular.

Table 2.

Classification Model Performance, MSH Subgroup Analysis

		Model AUROC (95% CI)		Model AUROC (95% CI)
	n	MSH RVEDV classification	P value*	MSH RVEF classification	P value*
Overall	604	0.81 (0.76–0.86)		0.81 (0.77–0.86)
Subgroup
Female	209	0.72 (0.62–0.81)	0.40	0.79 (0.69–0.90)	0.46
Male	395	0.77 (0.70–0.83)		0.84 (0.79–0.89)
Age ≥60 y	272	0.67 (0.57–0.76)	0.015	0.80 (0.72–0.87)	0.58
Age <60 y	332	0.81 (0.74–0.87)		0.82 (0.76–0.89)
Arrhythmia†	50	0.74 (0.53–0.94)	0.56	0.81 (0.67–0.94)	0.69
Nonarrhythmia	476	0.80 (0.74–0.86)		0.84 (0.79–0.89)
LVEF <50%	261	0.87 (0.81–0.94)	0.024	0.74 (0.68–0.81)	0.93
LVEF ≥50%	340	0.75 (0.67–0.83)		0.75 (0.53–0.98)
BMI ≥30 kg/ht2	152	0.80 (0.75–0.88)	0.79	0.88 (0.73–0.86)	0.053
BMI <30 kg/ht2	432	0.80 (0.68–0.91)		0.79 (0.73–0.86)
Race
White	258	0.83 (0.74–0.92)	0.83	0.82 (0.74–0.91)	0.90
Black	101	0.78 (0.64–0.92)		0.82 (0.74–0.91)
Other/Unknown	245	0.82 (0.75–0.89)		0.79 (0.72–0.88)

BMI indicates body mass index; and LVEF, left ventricular ejection fraction; RVEDV, right ventricular end‐diastolic volume; and RVEF, right ventricular ejection fraction.

^* P value for comparison of area under the receiver operating characteristic curves between subgroups.

^† Defined as normal sinus rhythm vs sinus with atrial/ventricular ectopy, atrial fibrillation/flutter, or other.

RVEDV Classification Models

Model performance to classify RV dilation (defined as RVEDV ≥120 mL/m²) is shown in Figure 2B. In UKBB (baseline prevalence, 1.6%), AUROC was 0.91 (0.89–0.93), and AUPRC was 0.21 (0.15–0.26). In the MSH_original data set (baseline prevalence, 10.6%), AUROC was 0.81 (0.76–0.86), and AUPRC was 0.35 (0.24–0.46). At Youden's J threshold, there was a sensitivity of 84% (95% CI, 75–93), specificity of 66% (63–71), positive predictive value of 23% (18–29), negative predictive value of 97% (95–99), positive LR of 2.5 (2.1–3.0), and negative LR of 0.24 (0.10–0.38) in the MSH_original test data set. Classification performance between clinically relevant subgroups in the MSH data set is shown in Table 2. RVEDV model performance differed in patients aged ≥60 versus <60 years (AUROC, 0.67 versus 0.81; P=0.015) and those with LV systolic dysfunction versus normal LV function (AUROC, 0.87 versus 0.75; P=0.024).

Prospective Validation

The RVEDV and RVEF classification models were further tested in a temporal validation data set consisting of ≈4 months of data collected after development of the final models, the MSH_validation group. For RV systolic dysfunction classification, model AUROC was 0.77 (0.65–0‐88), and AUPRC was 0.37 (0.18–0.56). For RV dilation classification, model AUROC was 0.92 (0.81–1.00), and AUPRC was 0.45 (0.06–1.00).

RVEDV and RVEF Regression Models

We developed models to predict the numerical value of RVEDV and RVEF. They were subsequently fine‐tuned in the MSH data set, with test set regression results shown in Figure 3. For RVEF prediction, the mean absolute error between predicted and expected RVEF was clinically reasonably low at 7.8%, the R ²=0.360 for the linear fit between the 2 measures, and there was moderate agreement (concordance correlation coefficient, 0.57). Passing–Bablok regression analysis demonstrated systematic differences between the ECG‐predicted and cMRI RVEF evidenced by significant differences in the regression intercept and slope from 0 and 1, respectively (see Figure 3A). Difference plots for RVEF are shown in Figure 3B. The errors are nonnormally distributed, with ECG overestimating cMRI RVEF at low (pathological) values and ECG underestimating cMRI RVEF at higher values, and 95% prediction CI of +/− 14.0%. In the RVEDV model, the mean absolute error was 17.6 mL/m², R ²=0.250, and the concordance correlation coefficient was 0.43. Like the RVEF models, Passing–Bablok regression demonstrated systematic differences between methods (Figure 3C), and difference plots exhibited nonnormally distributed error with a 95% prediction CI of +/− 27.5 mL/m². ECG overestimated cMRI RVEDV at low values, and ECG underestimated cMRI RVEDV at higher (pathological) values (Figure 3D).

Figure 3. RVEF and RVEDV regression models, MSH data set.

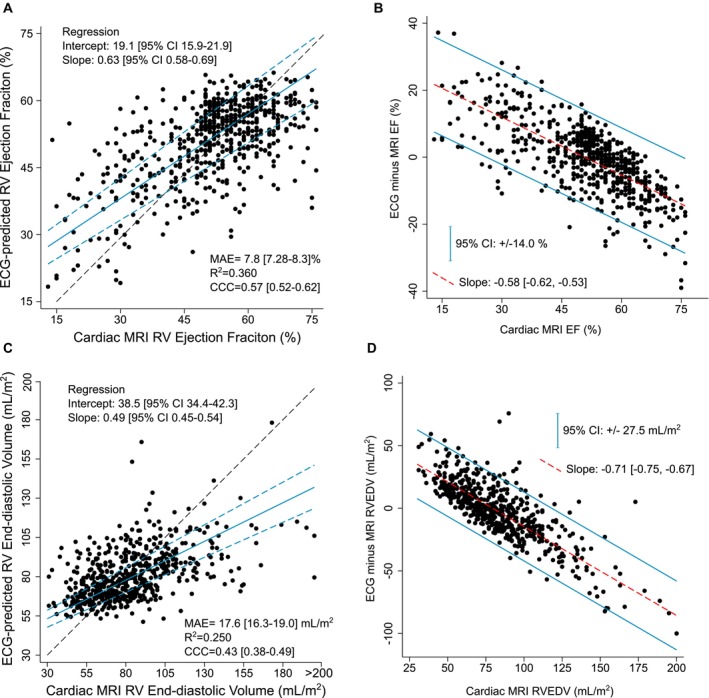
MSH_original regression model with ECG‐predicted vs cMRI‐expected scatter plots to predict numerical RVEF (A) and numerical RVEDV (C). Scatter plots plotted with line of perfect concordance (dashed black line) and Passing–Bablok regression best‐fit line (solid blue) with 95% CIs (dashed blue line). Difference plots analysis of RVEF (B) and RVEDV (D) with regression slope (red line) and 95% CIs of the errors (blue line) displayed. CCC indicates concordance correlation coefficient; EF ejection fraction; MAE, mean absolute error; MRI, magnetic resonance imaging; MSH, Mount Sinai Hospital; RV, right ventricle; and RVEDV, right ventricular end‐diastolic volume.

Saliency Mapping

RV dilation and RV dysfunction classification model saliency mapping examples from the MSH_original test set are shown in Figure 4. Qualitative review of several saliency mapping examples suggested that P waves and QRS complexes in leads II, V1, and V5/6 are particularly influential.

Figure 4. Saliency mapping.

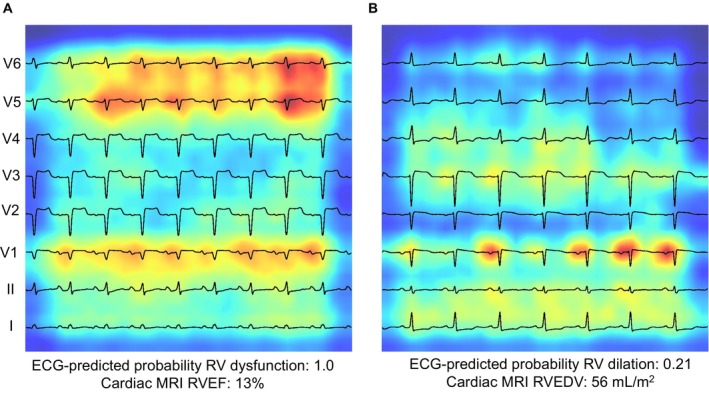
Saliency mapping ECG examples from the MSH_original test set. Leads are arranged from bottom to top: lead I, II, V1‐V6. Increasing shades of red indicate increasingly influential pixels in the model. A shows a true‐positive example of RV dysfunction. The P and QRS portions of V1, V5, and V6 are particularly influential. B shows a true‐negative example of RV dilation. QRS complex of lead I and P‐wave in V1 is particularly influential. MRI indicates magnetic resonance imaging; RVEF, right ventricular ejection fraction; and RVEDV, right ventricular end‐diastolic volume.

Survival Analysis

Follow‐up information was available for 575 of 604 (95%) patients in the MSH_original test cohort, with a median follow‐up time of 2.27 (interquartile range, 0.67–5.03) years. The combined outcome of death or heart transplantation occurred in 65 of 604 (10.8%; n=59 deaths and n=6 heart transplants) patients. Kaplan–Meier survival curves are illustrated in Figure 5. Multivariable modeling excluding RVEF as a predictor identified the optimal baseline model including LVEF, age (dichotomized at ≥60 years), and hospitalized status to be by Akaike information criterion (Table S4). Addition of either ECG‐predicted or MRI‐quantified RVEF to the baseline model modestly improved Akaike information criterion and C‐statistic, though MRI‐quantified RVEF resulted in greater improvement of the baseline model compared with ECG‐predicted RVEF (Table S5). The final multivariable survival model including ECG‐predicted RVEF is shown in Table 3. In a model including MRI‐quantified LVEF and age and hospitalized status, ECG‐predicted RVEF was significantly associated with increased risk of death/transplant (hazard ratio, 1.40 for each 10% decrease in RVEF; P=0.031). No significant interaction was identified between LVEF and RVEF. The proportional hazards assumption and linearity assumptions for the remaining continuous variables (LVEF and RVEF) were satisfied (Figure S2). We repeated the analysis using MRI‐quantified RVEF and found similar results (Table S6).

Figure 5. Unadjusted survival curves.

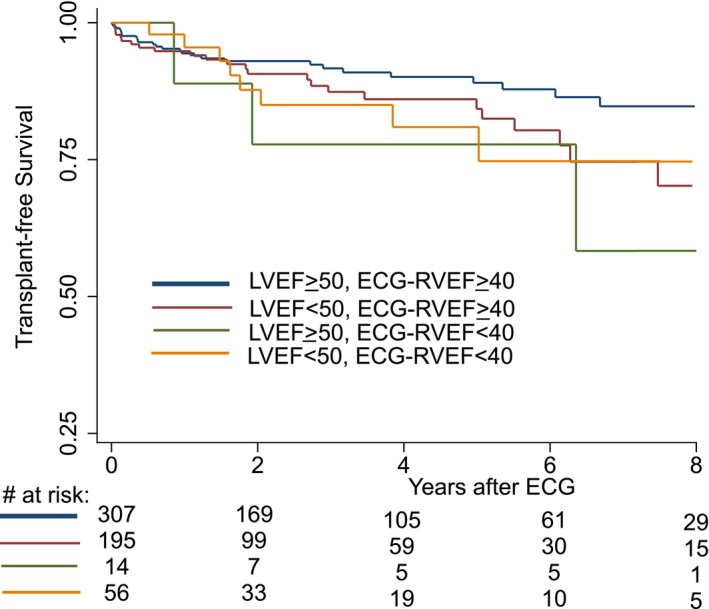
Kaplan–Meier survival curves by presence of LVEF and RVEF dysfunction. Note that curves are truncated at 8 years due to low sample size after this time point. Risk table is displayed at bottom of figure. LVEF indicates left ventricular ejection fraction; and ECG‐RVEF, electrocardiogram‐predicted right ventricular ejection fraction.

Table 3.

Survival Analysis for Freedom From Death/Heart Transplant, Bivariable and Multivariable Analyses

Model variable	HR (95% CI)	P value
ECG‐predicted RVEF (every 10% decrease)	1.40 (1.03–1.91)	0.031
cMRI LVEF (every 10% decrease)	0.98 (0.83–1.17)	0.86
Age ≥60 y	2.81 (1.65–4.79)	<0.001
Hospitalized at cMRI	1.86 (1.10–3.15)	0.022

cMRI indicates cardiac magnetic resonance imaging; HR, hazard ratio; LVEF, left ventricular ejection fraction; and RVEF, right ventricular ejection fraction.

Discussion

In summary, we used DL on ECGs to quantify RVEDV and RVEF on the basis of paired cMRI as reference standard. We first developed this model in a large cohort of mostly healthy participants in the UKBB registry, then further fine‐tuned the model in a smaller cohort of clinically indicated paired ECG and cMRI samples from MSH. Finally, we prospectively validated the model in the subsequent ≈4 months after model development. The classification models to detect RV dilation (RVEDV ≥120 mL/m²) and RV dysfunction (RVEF ≤40%) have good performance in a clinical cohort. Regression models demonstrated moderate predictive ability of ECG for numerical estimation of cMRI‐measured RVEDV and RVEF, and ECG‐predicted RVEF was associated with worse short‐term freedom from death/heart transplantation. Saliency mapping suggested P‐wave and QRS complexes of leads II, V1, and V5/V6 as particularly important. This represents a significant advancement in prediction of RV enlargement by 12‐lead ECG, which is known to be insensitive by traditional methods (eg, voltage criteria), ²⁵ and this work is the first to show that RV volumetric markers of dilation and dysfunction can be predicted from ECG.

We find the classification models to be more clinically applicable, as they provide good test performance characteristics at clinically important RVEF and RVEDV values on the basis of AUROC and AUPRC metrics. We provided test statistics at probability thresholds on the basis of statistical criteria (Youden's J) for the MSH RVEDV and RVEF classification models, but it is important to note that selection of an appropriate threshold is a clinical decision based on the use‐case of the model. It is also worth noting that AUROC may be deceivingly inflated in the setting of class imbalance, as is the case in the UKBB data set, and therefore AUPRC is an important metric to consider in this case. However, AUPRC should be interpreted in relation to the baseline prevalence of disease, which explains why AUPRC is lower in the UKBB cohort compared with the MSH cohort. As an example of this, at a baseline prevalence of RV dysfunction of ≈18% in the MSH data set, examination of the AUPRC reveals that at a prediction threshold recall (sensitivity) of ≈50%, the precision (positive predictive value) is ≈60%. In other words, an ECG in this population could alert the practitioner to half of all cases of RV dysfunction in the population, and of cases identified, over half would have true RV dysfunction. Contrast this with the performance of the UKBB model, with only a 1% baseline prevalence of RV dysfunction. At a similar recall (sensitivity) of 50%, the precision (positive predictive value) is ≈20%, demonstrating a higher false‐positive rate despite a higher AUROC value, but still a large enrichment in positive cases over random selection from the baseline population. Future clinical implementation should take into consideration the population distribution of disease when determining the clinical utility of this algorithm and in development of appropriate probability thresholds for model prediction.

In contrast to the classification model performance, our regression model performance is less clinically applicable at this time, as difference plot analysis suggested there is high bias at the extremes of measurement (which are the pathological cases) and wide limits of agreement between ECG and MRI. Passing–Bablok regression confirms that the 2 measurement methods are not equivalent. However, the fact that a correlation is detected at all is itself a novel breakthrough in DL‐ECG analysis. Additionally, ECG‐predicted RVEF added predictive performance to a multivariable survival model and was associated with combined outcome of death/heart transplant in short‐term follow‐up. This demonstrates the potential clinical utility of this algorithm for prediction of patient outcome. It is interesting that both ECG‐predicted RVEF and MRI‐quantified RVEF were associated with poorer short‐term survival, whereas LVEF was not in our multivariable model. Low RVEF is a strong risk factor for poor outcome in several conditions, including myocarditis and ischemic cardiomyopathy. We suspect that LVEF was not a significant predictor of outcome for reasons related to cohort and follow‐up time. As the most common cause of RV dysfunction is pulmonary hypertension due to left heart dysfunction, RV dysfunction is observed to be a “common final pathway” in heart failure. ¹ Thus, it is possible that RVEF may be a more sensitive marker for short‐term outcomes than LVEF, and the statistical observation of LVEF nonsignificance, therefore, might be explained as a statistical adjustment for a mediator (ie, RVEF) in the causal pathway of poor short‐term outcome. It is possible that in a larger sample size or longer follow‐up time LVEF would become a significant predictor, as is well described in established risk prediction models. ²³ Further exploration of this is beyond the scope of this report, as our intention was to demonstrate clinical utility of ECG‐predicted RV.

DL‐ECG models have been shown to predict LV systolic dysfunction, elevated LV mass, and primarily left‐sided structural heart disease. ¹⁴ , ¹⁶ , ²⁶ , ²⁷ ECG detection of LVEF has been incorporated into clinical workflow to increase detection of asymptomatic low LVEF in the primary care setting. ²⁸ The right heart is largely uninvestigated in this field. We have previously shown that DL‐ECG analysis can detect the qualitative presence of RV systolic dysfunction or RV dilation by 2‐dimensional echocardiography. ¹⁴ However, the limitations of 2‐dimensional echocardiography in quantitative assessment of the right ventricle are well described, and our model represents an advancement over this prior work through training on a diverse group of data sets with paired reference standard cMRI RV measurements, thus allowing us to quantify RV size and systolic function by an important clinical metric. Although further work is needed, this algorithm might eventually be incorporated into on‐cart analysis to provide a useful screening tool for RV health that is validated against reference standard metrics. This may allow for better assessments of the RV with a simple test to further inform the need for further diagnostics or therapies. Additional possible benefits of developing non–cMRI‐based automated methods for RV quantification include a possible reduction in variability of measurement, as manually contoured RV volumes from cardiac MRI have increased variability compared with the left ventricle with coefficients of variation in the 6% to 9% range for RVEDV, and 8% to 12% for RVEF. ²⁹ , ³⁰ , ³¹

In the MSH cohort, LV and RV dysfunction were often found together, but our model performed well in the subgroups with and without concomitant LV dysfunction. This suggests that our model can distinguish RV systolic dysfunction separately from LV dysfunction. Similarly, equivalent performance in those with and without arrhythmia suggests that the model recognizes RV systolic dysfunction independently of cardiomyopathy associated with abnormal rhythm. Our subgroup analysis suggests the classification models have robust performance across subgroups with described differences in ECG morphology including body mass index, sex, and race, which suggests demographic parity in potentially vulnerable groups that may be affected by model unfairness. A more detailed examination of model fairness is an important future step in model deployment. ³² Finally, we did identify differences in the RVEDV (but not RVEF model) in performance across age and LVEF subgroups. This should be addressed in future work through expansion of the training set to include additional patients from these subgroups in a multicenter fashion.

Although the depolarization and repolarization patterns on the 12‐lead ECG are dominated by the higher myocardial mass of the left ventricle, prior work has described crude correlations between ECG pattern and RV systolic function, ³³ , ³⁴ , ³⁵ which provide a potential scientific rationale for our findings. In our study, saliency mapping demonstrated the importance of lead V1 in evaluating the right ventricle, which may be physiologically explained by its proximity to the right atrium and right ventricle. Further study to differentiate how and why these models can evaluate RV dysfunction independently from LV dysfunction are needed to enhance the explainability of DL‐ECG RV models.

We chose a 2‐dimensional CNN architecture for deep learning because this theoretically allows us to input images of ECGs (eg, .pdf files, pictures). Not all centers may store ECG data as 1‐dimensional vectors, which makes an image‐based approach more universally acceptable. Additionally, a 2‐dimensional approach allows us to take advantage of availability of 2D CNN models pretrained on millions of images which may enhance performance. The use of 2‐dimensional image–based input for DL‐ECG analysis may have superior performance compared with 1‐dimensional signal‐based ECG input methods, ³⁶ though several groups also report excellent results using a non–image‐based approach. ¹⁵ , ¹⁶ , ¹⁷ Further research to determine the generalizability of our models using different sources of ECG images is required.

This work should be viewed in the light of some limitations. First, model training and fine‐tuning was performed in only 2 data sets in 2 settings, which may limit the generalizability of these models to other relevant cardiac conditions. The overwhelming majority of patients in the MSH cohort had indication of cardiomyopathy for cMRI, and a higher‐than‐expected number of patients were admitted to the hospital at the time of MRI. This was likely in part due to the tight inclusion period imposed on paired MRI‐ECG samples to ensure that ECGs were valid representations of RV health. However, as MRI is more commonly a scheduled outpatient procedure, it is possible that other important patient subgroups are underrepresented. Additionally, we did not subtype the cardiomyopathy due to limitations in the reporting fields in which the indication for MRI was extracted. Therefore, external validation in other populations where ECG patterns are likely to differ, for instance, in pulmonary hypertension, congenital heart disease, and across different forms of cardiomyopathy, will ensure the generalizability and clinical applicability of these models. The LVEF ECG model used for pretraining was trained on a similar cohort of patients from similar institutions. In experiments performed after our initial model trainings, we identified that ≈30% of cases were present in both the original LVEF model and the MSH RVEF and EDV models (in the MSH_original test set, 183/604 patients overlapped with the original LVEF pretrained model). We examined the model performance between groups with overlap and without and found no difference in model performance (AUROC for overlapping data was 0.82 [95% CI, 0.72–0.89], AUROC for nonoverlapping samples was 0.81 [95% CI, 0.75–0.87]; data not shown above). We therefore believe the effect of this possible “data leakage” (in which the model makes predictions for data on which it has already been trained) is minimal. Furthermore, the MSH_validation set, due to temporal inclusion criteria, does not contain patients included in the original LVEF model and exhibited generally stable performance characteristics. The theoretical effect of data leakage is to inflate the performance of the model in the validation set through overfitting to nongeneralizable aspects of the overlapping data. We believe we did not observe this because the labels between the current and pretrained models, RVEF and RVEDV versus LVEF, are biologically different enough phenomena that this overlap does not make a difference. Still, this concern, in addition to other concerns raised about the need to ensure generalizability across health care systems and patient groups, emphasizes the need for external validation of this model.

Second, we did not compare performance across different CNN architectures because the chosen Densenet‐201 architecture had been pretrained to detect LVEF from prior works, ¹⁴ which we demonstrated had superior accuracy compared with a nonpretrained model (Table S1). To judge whether alternate architectures are superior, we would need to retrain several model architectures across a large corpus of ECGs for LVEF prediction and subsequently use this model as pretraining for the current task. These experiments are important from a data science perspective, but beyond the scope of the current project goals to demonstrate the feasibility of DL‐ECG analysis to quantify metrics of RV size and systolic function. Similarly, our decision to include 8 of 12 available leads in the model was based on a priori knowledge that the augmented leads aVF, aVL, and aVR, and lead III are linear transformations of the other leads and should theoretically not provide additional information to the model. As these models have been built on prior works, we are unable to test model performance across different lead configurations without significant model retraining. Further work to describe the optimal lead configuration for DL‐ECG models should be an area of further research.

Third, we trained models on the large UKBB data set, in which RV volumes were automatically contoured through a cMRI segmentation algorithm. This method may be more prone to error and systematically biased compared with clinician labeling, and this method differed from the MSH cohort in which we derived RV measurements from clinician‐verified cMRI reports. We performed a comparison between manual and automated contouring methods and found minimal mean differences between methods, though some variability was observed (Figure S1). We fine‐tuned the model on MSH data to account for the differences in distribution between data sets, but it is possible that we might have obtained better performance if the UKBB data set were contoured by clinicians. However, this is infeasible due to the large number of studies (> 40 000) in UKBB. It is also important to note that we did not conduct experiments to demonstrate the added value of using the large amounts of UKBB data that went into model training (total n>42 000 ECGs with paired cMRI). Our group has demonstrated that CNN architectures continue to increase performance with increasing amounts of ECG data even above 500 000 training examples. ¹⁸ Given these prior works, we did not seek to demonstrate the additive value of UKBB data, which would require multiple model retrainings at different training sample sizes. This is an interesting direction of research in the data science realm and would be useful to establish minimum sample size estimates for neural network training in the ECG analysis.

Finally, our regression models demonstrate the potential of DL analysis to derive unseen functional data from the ECG; however, currently they exhibit clinically unacceptable limits of agreement with cMRI. The regression models demonstrate the tendency for the networks to predict closer to the population mean. The model architecture we selected is complex enough to fit the training data; however, high variance still exists. Further steps to improve prediction may require experimentation with different model architectures and training on additional pathological cases (increasing sample size), but it may also be that the ECG is too limited to allow for accurate numerical prediction, in which case the classification models may still be useful to rule in or rule out cases. Performance appeared stable in prospective validation, but due to small sample size of the validation group and a shift in baseline prevalence, we may miss subtle differences in performance. As these models improve, research into the usefulness of serial DL‐ECG analysis to trend RV size or function should be explored, as trending of RV metrics over time is an important clinical application of this technology that may reduce the need for serial cMRI.

In summary, we developed and validated a DL algorithm to predict RV dilation or systolic dysfunction as defined by reference standard cMRI metrics. This method can provide novel RV quantification from a simple and globally available tool. These prediction tools may be useful in decreasing the need for costly cMRI, with implications for disease screening, risk stratification, and progression of disease. Future work to improve accuracy of prediction to validate findings in heterogeneous clinical populations, and clinical trials to show improved workflow and outcomes are required.

Sources of Funding

This study was supported by the National Heart, Lung, and Blood Institute, National Institutes of Health (R01HL155915), and National Center for Advancing Translational Sciences, National Institutes of Health (CTSA grant UL1TR004419).

Disclosures

Dr Nadkarni reports consultancy agreements with AstraZeneca, BioVie, GLG Consulting, Pensieve Health, Reata, Renalytix, Siemens Healthineers, and Variant Bio; reports research funding from Goldfinch Bio and Renalytix; honoraria from AstraZeneca, BioVie, Lexicon, Daiichi Sankyo, Menarini Health, and Reata; reports patents or royalties with Renalytix; owns equity and stock options in Pensieve Health and Renalytix as a scientific cofounder; owns equity in Verici Dx; has received financial compensation as a scientific board member and advisor to Renalytix; serves on the advisory board of Neurona Health; and serves in an advisory or leadership role for Pensieve Health and Renalytix. R. Do reports receiving grants from AstraZeneca; receiving grants and nonfinancial support from Goldfinch Bio; being a scientific cofounder, consultant, and equity holder for Pensieve Health (pending); and being a consultant for Variant Bio, all not related to this work. The remaining authors have no disclosures to report.

Supporting information

Tables S1–S6

Figures S1–S2