Adaptation of a mutual exclusivity framework to identify driver mutations within oncogenic pathways

Summary

Distinguishing genomic alterations in cancer-associated genes that have functional impact on tumor growth and disease progression from the ones that are passengers and confer no fitness advantage have important clinical implications. Evidence-based methods for nominating drivers are limited by existing knowledge on the oncogenic effects and therapeutic benefits of specific variants from clinical trials or experimental settings. As clinical sequencing becomes a mainstay of patient care, applying computational methods to mine the rapidly growing clinical genomic data holds promise in uncovering functional candidates beyond the existing knowledge base and expanding the patient population that could potentially benefit from genetically targeted therapies. We propose a statistical and computational method (MAGPIE) that builds on a likelihood approach leveraging the mutual exclusivity pattern within an oncogenic pathway for identifying probabilistically both the specific genes within a pathway and the individual mutations within such genes that are truly the drivers. Alterations in a cancer-associated gene are assumed to be a mixture of driver and passenger mutations with the passenger rates modeled in relationship to tumor mutational burden. We use simulations to study the operating characteristics of the method and assess false-positive and false-negative rates in driver nomination. When applied to a large study of primary melanomas, the method accurately identifies the known driver genes within the RTK-RAS pathway and nominates several rare variants as prime candidates for functional validation. A comprehensive evaluation of MAGPIE against existing tools has also been conducted leveraging the Cancer Genome Atlas data.

Cancer is known to arise after a cell experiences multiple driver mutations that allow it to grow uncontrollably and ultimately metastasize to distant anatomic sites. In this paper, we introduce a computational approach for identifying driver mutations by leveraging the mutual exclusivity of genes and variants within oncogenic pathways.

Introduction

It is now well known that cancer is a genetic disease that develops through the accumulation of somatic mutations. When individual tumors are subjected to mutation analysis, countless mutations are identified. A major challenge is to identify genes that carry driver mutations, the ones that are pivotal in producing uncontrolled tumor growth. Such genes are known as driver genes. A number of computational methods and tools have been developed, falling within several overarching categories. MutSigCV,¹ DriverML,² ActiveDriver,³ and OncodriveFML⁴ are frequency-based approaches that target genes exhibiting mutation rates surpassing anticipated levels; OncoDriverCLUST⁵ and MSEA⁶ operate as hotspot-based methods, excelling in the detection of gain-of-function mutations within specific protein domains; DawnRank⁷ and DriverNet⁸ are network-based methods aiming to uncover clusters of driver genes through leveraging prior knowledge of pathways, proteins, or genetic interactions.

Another major technical concept that has influenced research in this field is mutual exclusivity. If somatic mutations in two (or more) genes tend not to occur together in the same tumor, then this is evidence that the disruption of the genes involved are leading to similar effects. Presence of such mutual exclusivity is strong evidence that the genes are cancer-associated genes.⁹ Important findings on mutual exclusivity through existing large-scale sequencing studies include EGFR and KRAS in lung adenocarcinoma (LUAD)^10,11,12 and the RTK-RAS pathway primarily involving BRAF, NRAS, and NF1 in melanoma.^13,14 Studies of this phenomenon usually involve searching for evidence of mutual exclusivity of genes in a “pathway” of genes that are believed to possess related effects. A number of authors have studied this problem from a statistical perspective, developing several techniques. The methods called Dendrix¹⁵ and Mutex¹⁶ define criteria or score metrics based on searching for the mutually exclusive gene sets using a greedy approach. MEMo⁹ and gcMECM¹⁷ are based on a search for mutually exclusive genes using graph or network-based approaches. WeSME¹⁸ and FaME¹⁹ employ computational-oriented methods that can scale up to genome-wide analysis. CoMEt²⁰ and WExT²¹ employ a permutation-based test for mutual exclusivity. A method by Szczurek et al.,²² MEGSA,²³ DISCOVER,²⁴ TiMEx,²⁵ and MEScan²⁶ utilize probabilistic model-based tests to assess the significance of mutual exclusivity in a given gene set.

Most of these methods focus on de novo search of gene sets (from the around 22,000 genes in the human genome) that display mutual exclusivity. In this article, we turn our attention to leveraging the mathematical property of mutual exclusivity for identifying probabilistically both the specific genes within a pathway and the individual mutations within such genes that are truly the drivers. The evaluation of mutual exclusivity occurs within pre-defined pathways of genes, i.e., collections of genes that have been shown in previous research to share biological functions.²⁷ A major assumption is that, within any given pathway, only one of the mutations observed can be the “driver” for that tumor, though there could be additional drivers in other pathways.

We build our method around the likelihood function developed by Hua et al.²³ In their model, a mutation in a given gene can represent either a driver or a passenger mutation. Passenger mutations in this context represent random, non-consequential background somatic mutations that are a result of the genetic instability commonplace in tumor cells. We limit attention to non-synonymous mutations, except for the calculation of tumor mutational burden (TMB), a confounding factor. The global patterns of mutual exclusivity in the data allow the model to identify the proportion of tumors that possess a driver in the pathway based on the assumption that the driver mutations are completely mutually exclusive, i.e., a tumor can contain at most 1 driver in the pathway under investigation. A test of the hypothesis that this proportion is zero thus represents a test of mutual exclusivity of the set of genes under consideration. By applying this repeatedly to different subsets of genes in the pathway, one can find the most significant subset, and thus conclude that this subset of genes consists of the drivers. Hua et al. made the assumption that the relative proportions of drivers versus passengers in each gene have a common proportionality.²³ In our approach, we relax this assumption, allowing us to estimate the proportions of driver mutations for each gene and then, through Bayes’ rule, to determine probabilistically which mutations in each tumor are drivers and which ones are passengers. By mapping all of these probabilities, we can determine for which genes drivers predominate. Also, these individual probabilities allow us to shed light on which types of mutation within any given gene show up as drivers frequently. These results are driven fundamentally by the global empirical patterns of mutual exclusivity in the dataset.

In summary we show that our method goes beyond using statistical tests for mutual exclusivity to create a framework for inferring probabilistically which genes have the strongest evidence as drivers and which mutations within these genes are specifically identified as drivers. We show through detailed analysis of the RTK-RAS pathway in a large sample of melanomas how the method confirms the prominence of a small number of recurring mutations in well-known genes in this pathway and identifies some rare individual mutations that appear to be important. We benchmark our method against seven existing tools for driver-gene nomination, leveraging the Cancer Genome Atlas (TCGA) data from 11 cancer sites for a comprehensive evaluation under real-world scenarios. The method has been implemented in a Python package named MAGPIE (mutual exclusivity analysis of cancer-associated genes and variants and their probability of being driver) and is available on GitHub at https://github.com/tarot0410/MAGPIE.

Material and methods

Our data framework involves a set of $N$ tumors, and the analysis is restricted to a set of $M$ genes in the pathway under consideration. That is, the analytic framework is pathway specific. The data could include sequencing of genes in other pathways, but analyses of these other pathways would be conducted independently. That is, any given tumor may have multiple driver genes, but a key assumption is that there can only be one driver mutation in the pathway under consideration.

MEGSA framework

We initially construct our strategy on the MEGSA (mutually exclusive gene set analysis) likelihood-based analysis introduced by Hua et al.²³ Let ${\mathit{x}}_{\mathit{i}}=\left(x_{i1},\dots ,x_{iM}\right)$ denote the observed binary mutation status of tumor $i$ ($i=1,\dots ,N$), where $x_{ij}=1$ if a non-synonymous alteration is observed in the $j^{th}$ gene ($j=1,\dots ,M$) and 0 otherwise. Any observed mutation must be either a driver mutation or a passenger mutation. Only one driver mutation from the pathway is possible in a given tumor. As a result, all driver mutations observed must be mutually exclusive, i.e., no two drivers can occur in a given tumor. We define $\gamma$ ($0\le \gamma \le 1)$ as the proportion of tumors in the study cohort that have a driver mutation in the pathway under investigation. Let $p_j$ denote the relative frequency of such tumors that possess a driver mutation in the $j^{th}$ gene in the pathway with ${\sum }_{j=1}^M{p}_j=1$ and $0\le p_j\le 1$. Independent of driver mutations, each gene has a constant passenger mutation rate, denoted by ${\pi }_j$ for the $j^{th}$ gene. The log likelihood of the observed data is

$$logL\left(\gamma ,\pi ;X\right)=\sum _{i=1}^N\log \left\{\left(1-\gamma \right)\prod _{j=1}^M{\pi }_j^{x_{ij}}{\left(1-{\pi }_j\right)}^{1-x_{ij}}+\gamma \sum _{j=1}^M{p}_j{I}_{\left\{x_{ij}=1\right\}}\prod _{k\ne j}{\pi }_k^{x_{ik}}{\left(1-{\pi }_k\right)}^{1-x_{ik}}\right\}\text{.}$$ (Equation 1)

For the purpose of developing a statistical test of mutual exclusivity, Hua et al. made the assumption that the relative frequencies of driver mutations in each gene are proportional to the passenger mutation rates, i.e., $p_j\propto {\pi }_j$. Thus, the log likelihood is reduced to

$$logL\left(\gamma ,\mathit{\pi };X\right)=\sum _{i=1}^N\log \left\{\left(1-\gamma \right)\prod _{j=1}^M{\pi }_j^{x_{ij}}{\left(1-{\pi }_j\right)}^{1-x_{ij}}+\gamma \frac{1}{\sum _{k=1}^M{\pi }_k}\sum _{j=1}^M{\pi }_j{I}_{\left\{x_{ij}=1\right\}}\prod _{k\ne j}{{\pi }_k^{x_{ik}}\left(1-{\pi }_k\right)}^{1-x_{ik}}\right\}\text{.}$$ (Equation 2)

To test the fundamental null hypothesis that there is no mutual exclusivity in the pathway, a likelihood ratio test can be employed. This is, in effect, a test of the hypothesis $H_0:\gamma =0$ versus the alternative $\left(H_1\right)$ that $\gamma >0$, where the test statistic has a null distribution of ${0.5\chi }_0^2+{0.5\chi }_1^2\text{.}$²³

Proposed approach

MEGSA is a powerful tool to quantify the overall mutual exclusivity in the pathway or to select a subset of genes that reflect mutual exclusivity most strongly. Although the method we propose in this article is adapted from the MEGSA framework, the problem it solves is fundamentally different. Our method is designed to identify specifically which tumors possess a driver mutation and to identify the driver if more than one mutation in the pathway is present. It is further able to identify which variants within a given gene have the capacity to be driver variants.

We follow the model proposed in Equation 1. However, unlike Hua et al. we do not assume $p_j\propto {\pi }_j$, a critical assumption in the MEGSA approach. We further reformulate the likelihood into a mixture model framework. Assume that the gene membership of the driver mutation for tumor $i$ in the study cohort is denoted by ${\mathit{z}}_{\mathit{i}}=(z_{i0},z_{i1},\dots ,z_{iM}$). Tumors with $z_{ik}=1,k>0$ have driver mutations in the $k^{th}$ gene. Tumors with $z_{i0}=1$ do not possess a driver mutation. We emphasize that ${\mathit{z}}_{\mathit{i}}$ is unobserved and must be inferred. Let $\mathit{\tau }=\left({\tau }_0,{\tau }_1,\dots ,{\tau }_M\right)$ denote the vector of proportions of tumors having each gene-specific driver mutation, i.e., ${\tau }_k=p(z_{ik}=1$). Note that in this new notation ${\tau }_k$ represents the absolute relative frequency of tumors with drivers in the $k^{th}$ gene (or no driver in the case of $k=0$), while in the earlier notation $p_j$ represents the corresponding relative frequency of the presence of a driver in the $j^{th}$ gene among tumors that have drivers in the pathway. Following a standard mixture model framework, the log likelihood of the observed data is

$$logL\left(\mathit{\tau },\mathit{\pi };X\right)=\sum _{i=1}^N\log \left\{\sum _{k=0}^M{\tau }_k{f}_k\left({\mathit{x}}_{\mathit{i}}|\mathit{\pi }\right)\right\}$$ (Equation 3)

where $f_k\left({\mathit{x}}_{\mathit{i}}|\mathit{\pi }\right)=\{\begin{array}{cc}\prod _{j=1}^M{{\pi }_j}^{x_{ij}}{\left(1-{\pi }_j\right)}^{1-x_{ij}},& k=0\\ \frac{x_{ik}}{{{\pi }_k}^{x_{ik}}{\left(1-{\pi }_k\right)}^{1-x_{ik}}}\prod _{j=1}^M{{\pi }_j}^{x_{ij}}{\left(1-{\pi }_j\right)}^{1-x_{ij}},& k>0\end{array}$is the cluster-specific probability density function of ${\mathit{x}}_{\mathit{i}}$.

Equations 3 and 1 are in fact equivalent. To be specific, ${\tau }_0=1-\gamma$ and ${\tau }_k=\gamma p_k$ for $k>0$. As before, $\gamma =1-{\tau }_0$ quantifies the overall influence of a pathway, i.e., the proportion of tumors with a driver mutation in the pathway, while ${\tau }_k,k>0$, quantifies the relative frequency for which gene $k$ is the driver. One of the advantages of using a mixture model framework is that ${{\tau }_k}^{\prime }s$ are defined both under the null hypothesis of no driver mutations in the cohort (i.e., ${\tau }_0=1$ or $\gamma$ = 0) and under the alternative (i.e., ${\tau }_0<1$ or $\gamma >0$: there exists evidence of a mutually exclusive pattern), while for the MEGSA model the ${p_j}^{\prime }s$ are undefined under the null hypothesis.

Parameters ${\{\tau }_k\}$ and $\left\{{\pi }_j\right\}$ can be estimated using the expectation-maximization (EM) algorithm.²⁸ The complete data log likelihood is

$$logL\left(\mathit{\tau },\mathit{\pi },\mathit{z}|X\right)=\sum _{i=1}^N\sum _{k=0}^M{z}_{ik}\log \left\{{\tau }_k{f}_k\left({\mathit{x}}_{\mathit{i}}|\mathit{\pi }\right)\right\}\text{.}$$ (Equation 4)

In the E step, we compute the posterior probability $w_{ik}=p\left(z_{ik}=1|{\mathit{x}}_{\mathit{i}}\right)$ at the $t^{th}$ iteration:

$$w_{ik}^{\left(t\right)}=\frac{{\hat{\tau }}_k^{\left(t\right)}{f}_k\left({\mathit{x}}_{\mathit{i}}|{\hat{\mathit{\pi }}}^{\left(t\right)}\right)}{\sum _{s=0}^M{{\hat{\tau }}_s^{\left(t\right)}f}_s\left({\mathit{x}}_{\mathit{i}}|{\hat{\mathit{\pi }}}^{\left(t\right)}\right)}\text{.}$$

In the M step, Equation 4 is maximized in terms of ${\{\tau }_k\}$ and ${\{\pi }_j\}$ with $w_{ik}$ fixed at $w_{ik}^{\left(t\right)}$:

$${\hat{\tau }}_k^{\left(t+1\right)}=\frac{W_k^{\left(t\right)}}{N}and{\hat{\pi }}_j^{\left(t+1\right)}=\frac{\sum _{i=1}^N{x}_{ij}\left(1-w_{ij}^{\left(t\right)}\right)}{N-W_j^{\left(t\right)}}$$

where $W_k^{\left(t\right)}=\sum _{i=1}^N{w}_{ik}^{\left(t\right)}$.

In general, given initial estimates ${\{\hat{\tau }}_k^{\left(0\right)}\}$ and ${\{\hat{\pi }}_j^{\left(0\right)}\}$, the EM algorithm then iterates between E step and M step until the estimates converge.

Adjustment for tumor mutational burden

Up to now, the model has been based on the assumption that the passenger mutation rates ${\{\pi }_j\}$ are considered constant across the set of tumors. In fact, this assumption is quite unrealistic since the overall TMB is known to vary widely across tumors and is, in many oncologic settings, an influential prognostic factor.²⁹ To address this important potential confounder, we extend the method to allow adjustment for the effect of mutational burden in the model. Let $y_i$ denote the TMB score for tumor $i$. We have elected to compute the raw TMB score for each tumor by counting the total number of observed mutations (including both synonymous and non-synonymous mutations) among all sequenced genes and use a centered log-scaled score as the input to the model. This represents the overall propensity for mutations to occur in a specific tumor. Due to this dependency, we now identify the passenger mutation rates using $\left\{{\pi }_{ij}\right\}$ rather than $\left\{{\pi }_j\right\}$. In our later example mutational burden is represented by the total number of mutations observed across all genes that are genotyped, not just those in the pathway under investigation. Since ${\pi }_{ij}$ is bounded by 0 and 1, a natural approach to adjust for mutational burden is to use

$$logit\left({\pi }_{ij}\right)={\beta }_{0j}+{\beta }_1{y}_i\text{,}$$ (Equation 5)

where ${\beta }_{0j}$ represents the baseline log odds of the passenger mutation rate for the $j^{th}$ gene, and ${\beta }_1$ measures the common influence of mutational burden on the passenger mutation rate for all genes in the pathway. Since we are primarily interested in estimating the probabilities ${\{\tau }_k\}$, which represent the relative frequencies for which each gene is the driver, $\left\{{\beta }_{0j}\right\}$ and ${\beta }_1$ are effectively nuisance parameters in the model. The conditional data density for ${\mathit{x}}_{\mathit{i}}$ |$y_i$ is

$$p\left({\mathit{x}}_{\mathit{i}}|y_i\right)=\sum _{k=0}^{M}p\left({\mathit{x}}_{\mathit{i}},z_{ik}=1|y_i\right)=\sum _{k=0}^{M}p\left({\mathit{x}}_{\mathit{i}}|y_i,z_{ik}=1\right)p\left(z_{ik}=1|y_i\right)\text{.}$$ (Equation 6)

We assume ${\mathit{z}}_{\mathit{i}}\perp y_i$ s.t. $p\left(z_{ik}=1|y_i\right)=p\left(z_{ik}=1\right)={\tau }_k$, and as a result Equation 6 is reduced to

$$p\left({\mathit{x}}_{\mathit{i}}|y_i\right)=\sum _{k=0}^M{\tau }_{k}p\left({\mathit{x}}_{\mathit{i}}|y_i,z_{ik}=1\right)\text{.}$$ (Equation 7)

The log likelihood of the observed data adjusting for mutational burden is

$$logL\left(\mathit{\tau },{\mathit{\beta }}_{\mathbf{0}},{\beta }_1;X,Y\right)=\sum _{i=1}^N\log \left\{\sum _{k=0}^M{\tau }_k{g}_k\left({\mathit{x}}_{\mathit{i}}|y_i,z_{ik}=1\right)\right\}$$ (Equation 8)

where

$$g_k\left({\mathit{x}}_{\mathit{i}}|y_i,z_{ik}=1,{\mathit{\beta }}_{\mathbf{0}},{\beta }_1\right)=\{\begin{array}{cc}\prod _{j=1}^M{{\pi }_{ij}}^{x_{ij}}{\left(1-{\pi }_{ij}\right)}^{1-x_{ij}},& k=0\\ \frac{x_{ik}}{{{\pi }_{ik}}^{x_{ik}}{\left(1-{\pi }_{ik}\right)}^{1-x_{ik}}}\prod _{j=1}^M{{\pi }_{ij}}^{x_{ij}}{\left(1-{\pi }_{ij}\right)}^{1-x_{ij}},& k>0\end{array}$$

is the cluster-specific probability density function of ${\mathit{x}}_{\mathit{i}}$ conditional on $y_i$ and ${\pi }_{ij}=\frac{1}{1+e^{-\left({\beta }_{0j}+{\beta }_1{y}_i\right)}}$. There are no analytical solutions for ${\hat{\beta }}_{0j}^{\left(t+1\right)}$ and ${\hat{\beta }}_1^{\left(t+1\right)}$ in the M step if using the EM algorithm. Thus, we use limited-memory BFGS (L-BFGS)³⁰ implemented in PyTorch to minimize the negative log likelihood function and estimate $\left\{{\tau }_k\right\}$, $\left\{{\beta }_{0j}\right\}$, and ${\beta }_1$.

A statistical test to establish mutual exclusivity

Our proposed methodology seeks to identify drivers from a framework of observed mutual exclusivity. However, before performing such an analysis on a chosen pathway we propose first conducting a statistical test of the null hypothesis of no mutual exclusivity, i.e., a test of the hypothesis that $\gamma =0$, or equivalently, $\mathit{\tau }=\left({\tau }_0,{\tau }_1,\dots ,{\tau }_M\right)=\left(\mathrm{1,0},\dots ,0\right)$. In their original development of the MEGSA model, Hua et al. derived an asymptotic likelihood ratio test. Their limiting distribution depends crucially on the assumption that the relative frequencies of driver mutations in each gene are proportional to the passenger mutation rates, an assumption we dropped as indicated earlier. Consequently, we propose to compute the empirical p value by using a parametric bootstrap approach.

Let $\theta =\left(\mathit{\tau },{\mathit{\beta }}_{\mathbf{0}},{\beta }_1\right)$ denote the parameters in our model. We introduce the following bootstrap estimator for the restricted (under null) and unrestricted settings, respectively.

$$\tilde{\theta }=\underset{\theta \in {\Theta }_{H_0}}{\arg \mathit{max}}logL\left(\theta \right),and\hat{\theta }=\underset{\theta \in \Theta }{\arg \mathit{max}}logL\left(\theta \right)$$ (Equation 9)

where $\Theta ={\Theta }_{\mathit{\tau }}\times {\Theta }_{{\mathit{\beta }}_{\mathbf{0}}}\times {\Theta }_{{\beta }_1}$ is the full parameter space and ${\Theta }_{H_0}=\{\theta \in \Theta :\mathit{\tau }=\left(\mathrm{1,0},\dots ,0\right)\}$.

We propose the bootstrap likelihood ratio statistic

$$LR=-2\left(logL\left(\tilde{\theta }\right)-logL\left(\hat{\theta }\right)\right)$$ (Equation 10)

as the test statistic for the null hypothesis.

To construct the test, we generate $B$ bootstrap samples (algorithm will be introduced later) denoted by $X^{\left(b\right)},b=\mathrm{1,2},\dots ,B$. Denoting by ${LR}^{\ast }$ the test statistic from the observed dataset and ${LR}^{\left(b\right)}$ its value from the $b^{th}$ bootstrap dataset, the empirical p value is

$$p=\frac{1+{\sum }_{b=1}^B{I}_{\left\{{LR}^{\left(b\right)}\ge {LR}^{\ast }\right\}}}{1+B}\text{.}$$ (Equation 11)

The following data generation algorithm is employed both to create the null distribution (when $\gamma =0)$ and to generate datasets under positive levels of mutual exclusivity for our later simulations of model properties. (1) Generate the latent gene membership ${\mathit{z}}_{\mathit{i}}=(z_{i0},z_{i1},\dots ,z_{iM}$) of the driver mutation in each tumor $i$ (note that $z_{i0}=1,\forall i$ when we are generating a reference distribution under the null hypothesis). Specifically, $z_{ij}\stackrel{i.i.d.}{\sim }Multinomial\left(1,\mathit{\tau }\right)$ where $\mathit{\tau }=\left({\tau }_0,{\tau }_1,\dots ,{\tau }_M\right)$. Tumor $i$ has a driver mutation in the $k^{th}$ gene ($k=1,\dots ,M$) if $z_{ik}=1$. Otherwise, it does not possess a driver mutation and $z_{i0}=1$. (2) Generate the centered log-scale mutational burden ($y_i$) for each tumor $i$: $y_i\stackrel{i.i.d.}{\sim }N\left(0,\sigma \right)$. (3) Generate the individual mutations as $x_{ij}=1$ if $z_{ij}=1$ and $x_{ij}\sim Binomial\left(1,{\pi }_{ij}\right)$ otherwise, where ${\pi }_{ij}$ is computed using Equation 5 with given $\left\{{\beta }_{0j}\right\},{\beta }_1$ and $y_i$. For simulating data replicates, $\sigma ,\left\{{\beta }_{0j}\right\}$ and ${\beta }_1$ are pre-specified. For generating bootstrap data samples, we set ${\beta }_1$ = ${\hat{\beta }}_1$, the estimated ${\beta }_1$ by fitting our model to the observed data, and then solved for ${\beta }_{0j}$ using the following equation

$$q_j=\frac{1}{N}\sum _{i=1}^N{\pi }_{ij}=\frac{1}{N}\sum _{i=1}^N\frac{1}{1+e^{-\left({\beta }_{0j}+{\beta }_1{y}_i\right)}}$$ (Equation 12)

where $q_j$ denotes the overall mutation rate for $j^{th}$ gene in the observed data. Equation 12 allows for the bootstrap samples to maintain the association between ${\pi }_{ij}$ and $y_i$ while controlling the similar overall mutation rate for each gene. There is no closed-form solution for ${\beta }_{0j}$ in Equation 12, so we solved for ${\beta }_{0j}$ numerically using Newton’s method.

Identifying driver mutation for each tumor and specific variants within a gene

For every tumor we seek to identify the driver mutation or to determine that there is no driver mutation in the pathway. This can be inferred probabilistically from the posterior probabilities computed through Bayes’ rule. In the absence of adjustment for mutational burden the posterior probability that the mutation in the $k^{th}$ gene ($k>0$) in the pathway is the driver is

$$w_{ik}=p\left(z_{ik}=1|{\mathit{x}}_{\mathit{i}}\right)=\frac{{\hat{\tau }}_k{f}_k\left({\mathit{x}}_{\mathit{i}}|\hat{\mathit{\pi }}\right)}{\sum _{s=0}^M{\hat{\tau }}_s{f}_s\left({\mathit{x}}_{\mathit{i}}|\hat{\mathit{\pi }}\right)}\text{.}$$ (Equation 13)

When $k=0$, Equation 13 provides the probability that tumor $i$ does not have any driver mutation in the pathway. If a tumor is observed to have mutations in multiple genes, the most-likely driver mutation can be determined using

$$z_i^{\ast }={\arg \max }_k{w}_{ik}\text{.}$$ (Equation 14)

Similarly, the posterior probability under the scenario of adjusting for mutational burden is

$$w_{ik}=p\left(z_{ik}=1|{\mathit{x}}_{\mathit{i}},y_i\right)=\frac{{\hat{\tau }}_k{g}_k\left({\mathit{x}}_{\mathit{i}}|y_i,{\stackrel{\mathbf{ˆ}}{\mathit{\beta }}}_{\mathbf{0}},{\hat{\beta }}_1\right)}{\sum _{s=0}^M{\hat{\tau }}_s{g}_s\left({\mathit{x}}_{\mathit{i}}|y_i,{\stackrel{\mathbf{ˆ}}{\mathit{\beta }}}_{\mathbf{0}},{\hat{\beta }}_1\right)}\text{.}$$ (Equation 15)

Further, we can gauge the relative influence of individual variants within genes as drivers by averaging these posterior probabilities across the tumors in which the specific variant was observed. Let $x_{ij\left(l\right)}$ denote the mutation status (1 = yes; 0 = no) of variant $l$ from gene $j$ in tumor $i$, where variant $l$ is nested within gene $j$. The observed mutation frequency for variant $l$ (in gene $j$) is

$$N_{j\left(l\right)}=\sum _{i=1}^N{x}_{ij\left(l\right)}\text{,}$$ (Equation 16)

and the average posterior probability that variant $l$ is a driver is

$$P_{j\left(l\right)}=\frac{1}{N_{j\left(l\right)}}\sum _{i=1}^N{x}_{ij\left(l\right)}{w}_{ij,}$$ (Equation 17)

a term we refer to as the “driver frequency.”

Application of MAGPIE: The InterMEL study

The InterMEL study involves genomic sequencing of primary tumors from individuals with stage IIA–IIIB melanomas. Data from the InterMEL study serve as an illustrative example for demonstrating the application of MAGPIE. The InterMEL study protocol was approved by the institutional review boards (ethics committees) at each participating institution, material and data user agreements are in place, and research has been conducted according to the principles expressed in the Declaration of Helsinki. The need for informed consent was waived by the ethics committees due to the retrospective nature of the study.

Results

We apply the method to the InterMEL consortium dataset of early-stage melanoma tumors^31,32 (Database of Genotypes and Phenotypes [dbGaP] study accession: phs003099.v1.p1) and conduct an analysis on the RTK-RAS pathway for an illustration of how MAGPIE works and what it delivers. We then apply the method to three different pathways within 11 different cancer sites from TCGA data and benchmark its performance with several other existing methods. Lastly, we explore, via simulations, the properties of the method.

Illustration of MAGPIE: Data from the InterMEL study

Our analysis is based on 495 tumor samples genotyped to date through the InterMEL study. DNA samples were sequenced at Memorial Sloan Kettering Cancer Center using the Integrated Mutation Profiling of Actionable Cancer Targets, or MSK-IMPACT, a clinically validated and US Food and Drug Administration (FDA)-approved hybridization capture-based, next-generation sequencing assay developed to guide cancer treatment.^33,34 This involved sequencing of 468 cancer-associated genes.

For our illustration of the method, we focus solely on mutations in the RTK-RAS pathway, the major known pathway that influences the development of melanomas.^14,35 The MSK-IMPACT panel includes 38 genes from the RTK-RAS pathway where the list of pathway genes are as defined by Sanchez-Vega et al.²⁷ It is well known that mutations occur in melanomas frequently in several genes in this pathway, most prominently the genes BRAF and NRAS. Mutations in these two genes are almost always mutually exclusive. However, mutual exclusivity has not been studied systematically for other genes in this pathway. Also, hotspot mutations occur very frequently at the 600^th residue in BRAF (hereafter referred to as BRAF Val600 variant) and the 61^st residue in NRAS (hereafter referred to as NRAS Gln61 variant), but the importance of mutations altering other residues is less clear.

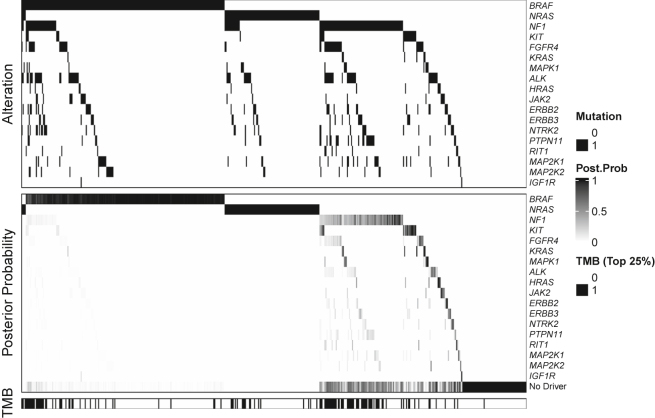
The data reveal that 91% of the 495 tumors had a mutation in the RTK-RAS pathway. However, our estimate of $\hat{\gamma }$ = 0.76 (p value = 0.001) indicates that in only 76% of the tumors is one of the mutations considered to be the driver. TMB varies widely with a standard deviation of 1.1 for the log tumor burden and an estimated effect of ${\beta }_1$ = 1.21. Figure 1 displays data (top) and model estimates (bottom) for the 18 genes with the highest estimated values of ${\tau }_j$ (proportion of tumors carrying a driver mutation in gene j). Figure S1 displays the results for all 38 genes. The top panel displays a structured waterfall plot of the observed mutations. The two most frequently occurring genes at the top of the figure, BRAF and NRAS, are almost always mutually exclusive, the exceptions being the 4 cases at the extreme left of the figure. It is further noticeable that mutations in these genes frequently occur in the absence of mutations in any of the other genes in the pathway (see the right-most columns in the BRAF and NRAS rows). This high degree of general mutual exclusivity is the key pattern in the data that influences our analysis, confirming a high probability of a driver for mutations observed in these two genes. This is reflected in the bottom panel of Figure 1 where the depth of the shade indicates the strength of evidence that the mutation in question is the driver. Quantitative details are provided in Table 1, which displays the relative frequencies for which mutations in the genes occur alongside the portion of these occurrences that are flagged as drivers by our method. This gene-specific driver frequency is the estimated ${\tau }_j$. Interestingly, the method suggests that NRAS is the driver in all tumors involving NRAS mutations, notably the 4 tumors in which BRAF and NRAS mutations occurred simultaneously. Moving down the gene list, the analysis suggests that KIT mutations, which occur in about 5% of tumors, is the driver about half of the time, NF1 mutations are drivers in about ¼ of the 26% of tumors that harbor NF1 mutations, and that there is limited evidence of driver status for the low-frequency genes. Although NF1 has a relatively high mutation rate, our method downgrades its importance as a driver gene because of its strong association with high TMB, which is displayed in the bottom panel of Figure 1 where a dark line indicates that the mutational burden for that tumor is in the top 25^th percentile. In general, tumors with high mutational burden are less likely to have a driver mutation identified after model adjustment, but the final posterior probability vector for each tumor computed with the estimated parameter values also depends on other factors (e.g., the proportion of tumors with mutation in a given gene that are singletons). Table S1 summarizes the results for all 38 genes.

Figure 1.

Illustration of the observed binary mutation status, estimated posterior probability of driver mutation, and the distribution of binary tumor mutational burden for the 18 genes with the highest estimated driver frequency in the RTK-RAS pathway

Table 1.

Summary of the observed mutation frequency and the estimated driver frequency for each gene among the top genes ranked by the estimated driver frequency in the RTK-RAS pathway from the InterMEL study

Gene	Mutation frequency	Driver frequency
BRAF	0.402	0.382
NRAS	0.196	0.196
NF1	0.261	0.069
KIT	0.051	0.026
FGFR4	0.091	0.010
KRAS	0.014	0.010
MAPK1	0.032	0.009
ALK	0.131	0.009
HRAS	0.026	0.008
JAK2	0.040	0.007
ERBB2	0.065	0.006
ERBB3	0.057	0.006
NTRK2	0.065	0.005
PTPN11	0.065	0.004
RIT1	0.024	0.004
MAP2K1	0.071	0.004
MAP2K2	0.046	0.003
IGF1R	0.004	0.002

Finally, we illustrate results for individual variants within driver genes. In Table 2, we provide the frequencies and average posterior probabilities for each of the 48 distinct variants observed in BRAF. High probabilities are generally assigned when the variant occurs as a singleton, and lower probabilities are assigned when other variants in the pathway occur. Very low probabilities occur when a driver variant in a different gene is observed. Thus, the 4 variants at the bottom of this table are the variants (on the extreme left in Figure 1) that occurred alongside an NRAS mutation.

Table 2.

Variant analysis

BRAF Mutationa	Type	Prob.	Freq.	OncoKB	Classification	Co-occurring mutations
c.1406G>C (p.Gly469Ala)	missense	>0.99	1	oncogenic	class 2	–
c.2209G>A (p.Gly737Ser)	missense	>0.99	1	–	–	BRAF c.1799T>A (p.Val600Glu)a
c.1799T>G (p.Val600Gly)	missense	>0.99	2	likely oncogenic	class 1	–
c.2191C>T (p.Pro731Ser)	missense	>0.99	2	–	–	BRAF c.1798G>A (p.Val600Met)a; BRAF c.1799T>G (p.Val600Gly)a
c.1457_1471delATGTGAC AGCACCTA (p.Asn486_Pro490del)	in frame	>0.99	1	likely oncogenic	class 2	–
c.1843G>A (p.Gly615Arg)	missense	>0.99	1	–	–	–
c.1756G>A (p.Glu586Lys)	missense	>0.99	2	likely oncogenic	–	BRAF c.1799T>A (p.Val600Glu)a
c.1404_1406delTGGinsAAA (p.Phe468_Gly469delinsLeuLys)	missense	0.99	1	–	–	–
c.1997T>A (p.Ile666Asn)	missense	0.99	1	–	–	BRAF c.1799T>A (p.Val600Glu)a
c.1798G>A (p.Val600Met)	missense	0.99	3	inconclusive	class 1	–
c.1799T>A (p.Val600Glu)	missense	0.99	116	oncogenic	class 1	–
c.1801A>G (p.Lys601Glu)	missense	0.98	4	likely oncogenic	class 2	–
c.1798_1799delGTinsAG (p.Val600Arg)	missense	0.98	8	oncogenic	class 1	–
c.1798_1799delGTinsAA (p.Val600Lys)	missense	0.98	31	oncogenic	class 1	–
c.1808G>A (p.Arg603Gln)	missense	0.97	1	–	–	–
c.1790T>G (p.Leu597Arg)	missense	0.97	1	likely oncogenic	class 2	–
c.95_100delGCGCCG (p.Gly32_Ala33del)	in frame	0.97	1	–	–	–
c.1405G>A (p.Gly469Arg)	missense	0.96	3	oncogenic	class 2	–
c.1789_1790delCTinsTC (p.Leu597Ser)	missense	0.96	2	likely oncogenic	class 2	–
c.983C>T (p.Pro328Leu)	missense	0.95	1	–	–	–
c.2212T>C (p.Phe738Leu)	missense	0.94	1	–	–	–
c.950C>T (p.Ser317Phe)	missense	0.94	1	–	–	–
c.1750C>T (p.Leu584Phe)	missense	0.93	1	inconclusive	–	–
c.1397G>A (p.Gly466Glu)	missense	0.93	1	oncogenic	class 3	–
c.952C>T (p.Pro318Ser)	missense	0.92	2	–	–	BRAF c.1798_1799delGTinsAA (p.Val600Lys)a
c.1781A>C (p.Asp594Ala)	missense	0.92	1	oncogenic	–	–
c.990T>G (p.Ile330Met)	missense	0.92	1	–	–	–
c.1780G>A (p.Asp594Asn)	missense	0.91	2	oncogenic	class 3	–
c.421C>T (p.Pro141Ser)	missense	0.91	1	–	–	–
c.1454T>G (p.Leu485Trp)	missense	0.90	1	likely oncogenic	class 2	–
c.1781A>G (p.Asp594Gly)	missense	0.90	2	oncogenic	class 3	–
c.1796C>T (p.Thr599Ile)	missense	0.85	1	likely oncogenic	class 2	–
c.1495A>G (p.Lys499Glu)	missense	0.85	1	likely oncogenic	–	–
c.1244C>T (p.Ala415Val)	missense	0.85	1	–	–	–
c.1033C>T (p.Pro345Ser)	missense	0.85	1	–	–	–
c.1397G>C (p.Gly466Ala)	missense	0.85	1	oncogenic	class 3	–
c.1391G>A (p.Gly464Glu)	missense	0.80	1	oncogenic	class 2	–
c.2203C>T (p.Arg735Trp)	missense	0.75	1	–	–	–
c.1165C>T (p.Arg389Cys)	missense	0.74	1	–	–	–
c.755G>A (p.Arg252Gln)	missense	0.74	1	–	–	–
c.1753C>T (p.His585Tyr)	missense	0.68	1	–	–	–
c.2195C>T (p.Ser732Phe)	missense	0.66	1	–	–	–
c.980G>A (p.Gly327Glu)	missense	0.66	1	–	–	–
c.1400C>T (p.Ser467Leu)	missense	0.59	3	oncogenic	class 3	NRAS c.181C>A (p.Gln61Lys)b
c.31G>A (p.Gly11Ser)	missense	<0.01	1	–	–	NRAS c.37G>T (p.Gly13Cys)b
c.1352A>T (p.Glu451Val)	missense	<0.01	1	–	–	NRAS c.37G>T (p.Gly13Cys)b
c.1501G>A (p.Glu501Lys)	missense	<0.01	1	inconclusive	–	NRAS c.35_36delGTinsAG (p.Gly12Glu)b
c.1733A>T (p.Lys578Met)	missense	<0.01	1	–	–	NRAS c.181C>A (p.Gln61Lys)b

^aGenBank: NM_004333.4 (BRAF).

^bGenBank: NM_002524.4 (NRAS).

BRAF variants have been studied extensively and classified into a few major classes with varying potency in oncogenicity based on differences in dimerization requirement and RAS dependency (class 1 mutations are Val600 mutations that activate the pathway downstream as monomers; class 2 comprises RAS-independent dimers that activate kinase activity; class 3 variants show diminished kinase activity but signal as RAS-dependent dimers).^36,37,38,39 Table 2 shows that the BRAF variants with high estimated probability of being a driver (>90%) include most of the functionally potent class 1 and class 2 variants. OncoKB is a widely popular evidence-based variant annotation tool that integrates such known biologic and oncogenic effects,⁴⁰ which can provide orthogonal evidence about the classifications. Notably, the probabilities are generally higher for variants classified as oncogenic by OncoKB. Furthermore, we observed that c.1781A>C (GenBank: NM_004333.4) (p.Asp594Ala) variant, despite not being classified as a BRAF class 1–3 mutation, exhibits a high estimated driver probability of 0.92 and is categorized as oncogenic by OncoKB. Other rare BRAF variants identified with high estimated probabilities, such as c.1843G>A (p.Gly615Arg), c.1404_1406delTGGinsAAA (p.Phe468_Gly469delinsLeuLys), c.1808G>A (p.Arg603Gln), c.95_100delGCGCCG (p.Gly32_Ala33del), and c.983C>T (p.Pro328Leu), currently lack established biological and clinical evidence. These variants merit investigation for functional validation. Individual variant analyses of four additional genes are provided in Table S2. For KIT, KRAS, and STK11, there is clearly a strong correlation between the MAGPIE classification and the OncoKB reference, with truncation mutations having notably higher probabilities in the case of the tumor suppressor STK11. For NRAS, almost all of the observed variants both have a high assigned probability and are classified as either oncogenic or likely oncogenic by OncoKB.

Benchmarking MAGPIE against existing tools using TCGA data

To further assess MAGPIE’s performance in real-world scenarios, we applied it to a comprehensive set of independent analyses involving three distinct pathways (RTK-RAS, PI3K, and Wnt) across 11 cancer sites, utilizing TCGA data. Pathway genes are defined based on the framework established by Sanchez-Vega et al.²⁷ Table 3 summarizes the following descriptive statistics and estimates for individual tumor sites and/or pathways: the number of tumors from each tumor site (# of tumors); relative frequency of observed mutations (mut freq); estimated proportion of tumors possessing a driver mutation (driver freq); p value of the corresponding significance test for mutual exclusivity (p val). The results reveal that the RTK-RAS pathway exhibits significant mutual exclusivity (p value < 0.05) in eight distinct cancer sites, encompassing breast cancer (BRCA), lower-grade glioma (LGG), uterine corpus endometrial carcinoma (UCEC), LUAD, head and neck squamous cell carcinoma (HNSC), papillary thyroid carcinoma (THCA), urothelial bladder cancer (BLCA), and cutaneous melanoma (SKCM). The PI3K pathway is deemed significant in five cancer sites—BRCA, LGG, UCEC, LUAD, and SKCM—and nearly reaches the threshold for significance in HNSC (p value = 0.051). The Wnt pathway shows a significant mutually exclusive pattern in seven cancer sites, namely LGG, UCEC, LUAD, HNSC, prostate adenocarcinoma (PRAD), BLCA, and SKCM.

Table 3.

Results of independent MAGPIE analyses on individual pathways in each tumor site

Sitea	# of tumors	RTK-RAS			PI3K			Wnt
		Mut freq	Driver freq	p val	Mut freq	Driver freq	p val	Mut freq	Driver freq	p val
BRCA	987	0.217	0.090	0.017	0.475	0.400	<0.001	0.098	0.039	0.266
LGG	520	0.221	0.115	0.033	0.187	0.095	0.032	0.056	0.034	0.029
UCEC	508	0.614	0.385	<0.001	0.904	0.719	<0.001	0.575	0.309	<0.001
LUAD	503	0.809	0.632	<0.001	0.400	0.205	0.002	0.314	0.140	0.002
HNSC	489	0.409	0.177	0.024	0.317	0.246	0.051	0.225	0.093	0.011
THCA	486	0.728	0.723	<0.001	0.047	0.008	0.599	0.037	0.010	0.249
PRAD	477	0.117	0.069	0.370	0.094	0.044	0.313	0.094	0.062	0.004
LUSC	464	0.597	0.213	0.356	0.407	0.221	0.186	0.349	0.157	0.288
BLCA	399	0.684	0.398	<0.001	0.451	0.194	0.435	0.291	0.145	0.049
SKCM	365	0.942	0.895	<0.001	0.504	0.228	0.005	0.553	0.188	0.014
KIRC	353	0.235	0.080	0.317	0.195	0.054	0.909	0.079	0.049	0.129

^aTCGA disease codes and abbreviations: BRCA, breast cancer; LGG, lower grade glioma; UCEC, uterine corpus endometrial carcinoma; LUAD, lung adenocarcinoma; HNSC, head and neck squamous cell carcinoma; THCA, papillary thyroid carcinoma; PRAD: Prostate adenocarcinoma; LUSC, lung squamous cell carcinoma; BLCA, urothelial bladder cancer; SKCM, cutaneous melanoma; KIRC: clear cell kidney carcinoma.

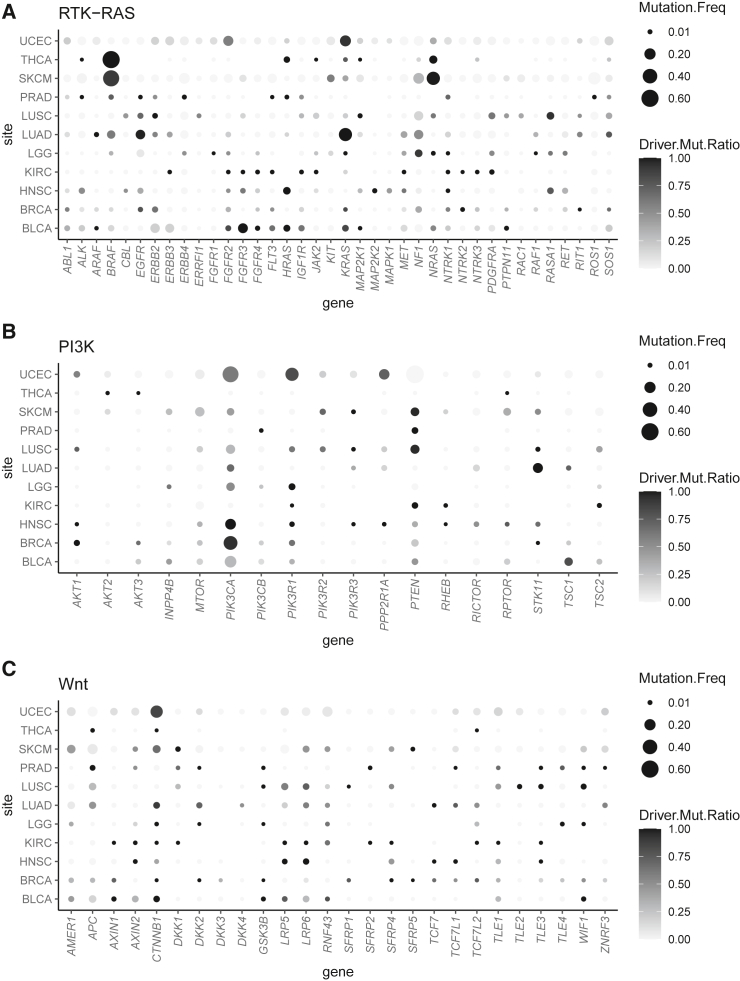
Figure 2 provides a comprehensive overview of the driver genes identified. The size of the bubbles in the graph corresponds to the relative frequency of mutations associated with a specific gene (x axis) within the corresponding cancer site (y axis). The depth of shade of these bubbles indicates the ratio of the estimated driver mutation rate to the observed mutation rate for a given gene. This ratio effectively represents the conditional probability that an observed mutation is considered a driver alteration. Strong driver genes are expected to exhibit a substantial bubble size and a dark tone, ensuring easy visual discernment.

Figure 2.

Bubble plots showing the likelihood of individual genes within a pathway as driver across different tumor sites

(A) RTK-RAS pathway.

(B) PI3K pathway.

(C) Wnt pathway. TCGA disease codes and abbreviations: BRCA, breast cancer; LGG, lower-grade glioma; UCEC, uterine corpus endometrial carcinoma; LUAD, lung adenocarcinoma; HNSC, head and neck squamous cell carcinoma; THCA, papillary thyroid carcinoma; PRAD, prostate adenocarcinoma; LUSC, lung squamous cell carcinoma; BLCA, urothelial bladder cancer; SKCM, cutaneous melanoma; KIRC, clear cell kidney carcinoma.

Within the RTK-RAS pathway, several potent driver genes emerge across diverse cancer sites. Specifically, BRAF is identified as a strong driver gene in THCA and SKCM, as is EGFR in LUAD. The roster of strong drivers includes FGFR2 in UCEC, FGFR3 in BLCA, KRAS in UCEC and LUAD, and NRAS in SKCM. In the context of the PI3K pathway, strong driver genes are as follows: PIK3CA in UCEC, HNSC, BRCA, and BLCA; PIK3R1 in UCEC; PPP2R1A in UCEC; and STK11 in LUAD. In the Wnt pathway, the strong drivers encompass AMER1 in SKCM and CTNNB1 in UCEC and SKCM. A number of driver genes displaying moderate or weaker significance are also identified. These genes, though challenging to discern from bubble charts, can be identified from their estimated driver frequencies in Tables S3–S5.

Next, we benchmark the performance of MAGPIE against existing methods for driver gene identification. Although MAGPIE is designed to identify driver genes and individual variants at any frequency, in fact the identification of rare drivers is a unique strength. For the purpose of comparing it with existing frequency-based methods, we have restricted attention to genes that have both been identified as statistically significant for mutual exclusivity and have an estimated driver frequency of at least 1%. We compare MAGPIE with published results from seven existing methods: MutSigCV,¹ DriverML,² ActiveDriver,³ and OncodriveFML⁴—each a frequency-based approach targeting genes exhibiting mutation rates surpassing anticipated levels. OncoDriverCLUST⁵ focuses on hotspot detection and identifying genes displaying a marked bias toward mutations clustering within regions encoding specific protein domains; DawnRank⁷ employs a sub-network framework to rank genes based on their downstream impact within interaction networks; and Dendrix¹⁵ is devoted to identifying mutually exclusive gene sets through a measure quantifying the intricate balance between coverage and exclusivity. The driver genes, identified through these competing methods applied to TCGA data, are comprehensively documented in Han et al.²

In Figure 3, we present a concise summary of the results from four cancer sites (SKCM, LUAD, UCEC, and BLCA) that compares the driver genes identified by the different methods, facilitating a comprehensive comparative analysis. The complete results for all 11 cancer sites are summarized in Figure S3. Given that there is limited ground truth to judge if a gene is indeed a driver, we focus on the extent of agreement between MAGPIE’s selections and those of other methodologies.

Figure 3.

Driver gene nomination by different methods (selected cancer sites)

(A) RTK-RAS pathway.

(B) PI3K pathway.

(C) Wnt pathway. TCGA disease codes and abbreviations: SKCM, cutaneous melanoma; LUAD, lung adenocarcinoma; UCEC, uterine corpus endometrial carcinoma; BLCA, urothelial bladder cancer.

The overall impression from these results is that the methods broadly target the same genes but there are wide discrepancies in the results. The major, known driver genes, such as BRAF, NRAS, EGFR, KRAS, and NF1 in the RTK-RAS pathway; PIK3CA, PTEN, and PIK3R1 in the PIKS pathway; and APC and CTNNB1 for Wnt, are all identified for their key cancer sites by multiple methods. Of note, MAGPIE is generally consistent in identifying these key genes, unlike some of the competitors. Some particular observations include the following. In RTK-RAS, MAGPIE uniquely identifies KRAS in SKCM and RIT1 in LUAD, and the results supported are by previous research.^41,42 Conversely, for PI3K, MAGPIE fails to identify PTEN as a driver for UCEC. However, in this site PTEN’s omission as a driver stems from the fact that a substantial majority of PTEN mutations co-occur with mutations in PIK3CA and PIK3R1. Furthermore, mutations in PIK3CA and PIK3R1 exhibit a notable level of mutual exclusivity (Figure S2). Consequently, the algorithm’s preference leans toward selecting PIK3CA and PIK3R1 as driver genes while excluding PTEN. Finally, MAGPIE nominates CTNNB1 and APC as drivers in SKCM, LUAD, and BLCA. This aligns with findings by Karachaliou et al., who observed a mutually exclusive mutation pattern of APC and CTNNB1 in TCGA-SKCM data, and further established an association between APC/CTNNB1 mutations and adverse outcomes in stage IV melanoma.⁴³ The implications of APC/CTNNB1 in LUAD and BLCA, however, warrant further comprehensive examination.

We further evaluated the performance of each method with quantitative metrics by using the driver genes curated in the Catalogue of Somatic Mutations in Cancer (COSMIC) Cancer Gene Census (CGC) as the benchmark. The current release of the CGC includes over 700 evidence-based, manually curated cancer-driver genes (release v98, May 23, 2023).⁴⁴ We consider all genes in the three pathways as the gene pool, among which the true positive genes are those collected in the CGC. Sensitivity and specificity are summarized for each method within individual tumor types along with the average Youden’s index across all tumor types (Table S6). Here, we excluded KIRC from the analysis because there is no associated driver gene found in the CGC, and we further combined LUAD and LUSC into one category named “LUNG” following the CGC’s coding convention. Overall, MAGPIE is ranked 3^rd among all eight methods according to the average Youden’s index. Finally, we want to clarify that this quantitative evaluation could be biased because the CGC classifies driver genes using a conservative approach, and thus the reference driver gene list used in the analysis is unlikely to be a complete set.

Operating characteristics of the method

We have conducted simulations to examine the properties of the method. There are many different features of a pathway that could potentially affect these properties. We have elected to generate data by using selected features of the RTK-RAS pathway that were estimated from the InterMEL data and then to vary some key aspects of these results to explore the influence of selected features. Specifically, we focus on a pathway with three types of genes: (1) strong driver genes that function as drivers most of the time (like BRAF and NRAS), (2) moderate driver genes that sometimes function as drivers and sometimes do not (like NF1), and (3) genes that are presumed to never be drivers. Details of their overall and driver frequencies are provided in Table 4. We consider two general configurations, denoted by $A$ and $B$. Configuration $A$ refers to the low-noise setting in which two genes are generated from each type. Configuration $B$ refers to the high-noise setting in which the number of non-driver genes is increased to 10. The probabilities in Table 4 correspond to pathways where mutual exclusivity is present. When we evaluate the test size under the null hypothesis of no exclusivity (Table S7), we use configuration $A$ under the assumption that all genes in the configuration have driver rates of 0%. As previously described in the data generation algorithm, the centered log-scale mutational burden was generated from a normal distribution with standard deviation $\sigma =1$. ${\beta }_{0j}$ was set to maintain the designed overall and driver mutation frequency under each setting as summarized in Table 4. For all settings, we simulated 1,000 data replicates under our model structure, and for each test, we generated 1,000 bootstrap samples.

Table 4.

Characteristics of simulated genes

Gene type	Mutation frequencies		Configuration (# genes)
	Overall	Driver	A low noise	B high noise
Strong sriver	20%	20%	2	2
Moderate driver	20%	10%	2	2
Non-driver	20%	0%	2	10

We first examined the properties of the initial significance test to determine the evidence that mutual exclusivity exists in the pathway, using Equation 11. We calculated the size of the test for sample sizes ranging from 500 to 5,000 under a model in which there was no effect of TMB (${\beta }_1=0$) and under a model in which the effect of TMB was in the range of that observed in the real dataset (${\beta }_1=1$). The results are summarized in Table S7, where the test size is computed as the average proportion of null hypothesis rejections among the 1,000 simulated data replicates. We observe that the test size of our proposed bootstrap-based test is, in general, close to the nominal level of 5% across different settings.

Next, we explored the ability of the model to identify drivers in individual tumors. We used two distinct statistics for this purpose. First, we evaluated overall measures that characterize the true-positive rates (TPRs) and false-positive rates (FPRs) for identifying whether or not a tumor has a driver in the pathway. For this calculation, the overall FPR is given by

$$OverallFPR=\frac{1}{\sum _{i=1}^N{I}_{z_{i0}=1}}\sum _{i=1}^N{I}_{z_{i0}=1}{I}_{{\mathit{argmax}}_k{w}_{ik}>0}\text{.}$$ (Equation 18)

The corresponding TPR is given by

$$CrudeoverallTPR=\frac{1}{\sum _{i=1}^N{I}_{z_{i0}\ne 1}}{\sum }_{i=1}^N{I}_{z_{i0}\ne 1}{I}_{{\mathit{argmax}}_k{w}_{ik}>0}\text{.}$$ (Equation 19)

Table 5 summarizes the results of overall accuracy, where FPR and TPR in the table are calculated as the average among the 1,000 simulated data replicates. We observe that, in general, FPR decreases and TPR increases with larger sample size. When there exists an association between passenger mutation rate and TMB (i.e., ${\beta }_1=1$), our method tends to classify fewer mutations as drivers, reducing both FPR and TPR. Conversely, elevation in pathway noise tends to make our method nominate more driver mutations, increasing both FPR and TPR. However, the effect of such noise diminishes with a larger sample size.

Table 5.

Overall accuracy

Configuration	Sample size	Mutational burden	Accuracy
			FPR	TPR
A Low noise	500	${\beta }_1=0$	0.210	0.994
		${\beta }_1=1$	0.156	0.968
	1,000	${\beta }_1=0$	0.211	0.999
		${\beta }_1=1$	0.154	0.969
	5,000	${\beta }_1=0$	0.212	1.000
		${\beta }_1=1$	0.153	0.971
B High noise	500	${\beta }_1=0$	0.247	0.997
		${\beta }_1=1$	0.187	0.973
	1,000	${\beta }_1=0$	0.213	0.999
		${\beta }_1=1$	0.166	0.973
	5,000	${\beta }_1=0$	0.212	1.000
		${\beta }_1=1$	0.155	0.972

Finally, we explored diagnostic accuracy at a more granular level, seeking to determine the accuracy of driver identification for the different individual gene configurations. For this purpose, we define the gene-specific false-positive and true-positive rates (gFPR and gTPR). That is, our FPR in this context measures, among tumors with a mutation in gene $j$ that is not a driver, what proportion are incorrectly flagged as a driver:

$$gFP{R}_j=\frac{1}{\sum _{i=1}^N{I}_{x_{ij}=1}{I}_{z_{ij}=0}}\sum _{i=1}^N{I}_{x_{ij}=1}{I}_{z_{ij}=0}{I}_{{\mathit{argmax}}_k{w}_{ik}=j}\text{.}$$ (Equation 20)

The corresponding true gene-specific positive rate measures, among tumors with a mutation in gene $j$ that is a driver, what proportion are correctly flagged as a driver:

$$gTP{R}_j=\frac{1}{\sum _{i=1}^N{I}_{x_{ij}=1}{I}_{z_{ij}=1}}\sum _{i=1}^N{I}_{x_{ij}=1}{I}_{z_{ij}=1}{I}_{{\mathit{argmax}}_k{w}_{ik}=j}\text{.}$$ (Equation 21)

Results are provided in Table S8, where, as before, the gFPR and gTPR values are averages across all simulated datasets. It is worth noting that the previously defined overall FPR and crude overall TPR are not simple weighted averages of gFPR or gTPR across genes, as the denominators in those formulas are not the same. We do not compute gFPR for strong driver genes because in our simplified construct there are no tumors that have non-driver mutations in these genes (i.e., no passenger mutations identified). Similarly, we do not compute gTPR for non-driver genes. For strong driver genes, we observe that the average gTPR is close to 1 in almost all scenarios (e.g., small sample size or high noise). Similarly, the method also performs well in screening out non-driver genes, evidenced by the extremely small gFPR across different scenarios. For moderate driver genes, those that can often be either a driver or a passenger, it is clearly more challenging for the method to identify drivers accurately, with gFPRs ranging from 0.340 to 0.477 across our various configurations, while the gTPRs range from 0.851 to 0.942. As was shown previously in Table 5, with greater association between passenger mutation rate and TMB, our method tends to classify fewer mutations as drivers, reducing both FPR and TPR. Conversely, the presence of increasing noise has minimal impact at an individual gene level.

Discussion

Our goals in developing this methodology were to find a strategy for identifying potential driver mutations in a tumor and assigning probabilities to the potential candidates. We built our strategy on a model that frames the selection on the presence of mutual exclusivity patterns in the data. Among the many groups that have studied mutual exclusivity in this context, we elected to build on the ideas of Hua et al.²³ since their model was firmly based on well-established statistical principles. The underlying model is structured around the assumption that there can be at most 1 driver in the pathway in any individual tumor, and this is in itself an assumption that may not be correct. However, this assumption does provide a solid framework in which to examine mutual exclusivity. We observe in our detailed analysis of data from the InterMEL study that the method produces results that appear to be highly plausible in that they align with known evidence about the RTK-RAS pathway. However, the RTK-RAS example represents a pathway for which the mutual exclusivity between BRAF and NRAS is especially profound, and thus may present an easier task than for pathways without highly prevalent variants that are very strongly mutually exclusive. However, our more comprehensive analysis of multiple pathways and cancer sites using TCGA data also demonstrates that MAGPIE generally identifies the known cancer-associated genes in addition to identifying other genes worthy of further investigation. The comparative analyses using multiple methods demonstrate wide variation in the results, demonstrating only modest levels of agreement among the methods. However, without a gold standard reference it is difficult to distinguish the methods on the basis of accuracy in identifying driver genes.

We believe that our method has strong potential for shedding light on which mutations are potentially pathogenic in a specific gene. In the melanoma BRAF example we presented, the Val600 variants identified as pathogenic are well characterized and are targets for FDA-approved therapies. However, approximately 35% of all BRAF mutations occur outside the Val600 codon.³⁸ The functional impact and therapeutic potential of non-Val600 BRAF mutations is an active research topic, yet existing knowledge in this area is limited. Our analysis of BRAF identified variants other than the common Val600 variants that may be potentially pathogenic. These represent the kinds of variants that could be prime candidates for experimental validation using modern in vitro and in vivo strategies.⁴⁵

We emphasize that our strategy is focused on a single pathway and is based on the pivotal assumption that there can be only one driver in the pathway in any given tumor. However, in any given tumor there are very likely multiple drivers, each occurring in distinct pathways. While one could perform our analysis independently for distinct pathways in order to identify a more complete set of drivers, a future research task is to expand our approach to permit a simultaneous analysis of multiple pathways.

Web resources

• Mutation Data from the InterMEL study, https://www.ncbi.nlm.nih.gov/projects/gap/cgi-bin/study.cgi?study_id=phs003099.v1.p1

• GitHub, MAGPIE, https://github.com/tarot0410/MAGPIE

• NIH National Cancer Institute, Genomic Data Commons, https://gdc.cancer.gov/about-data/publications/mc3-2017

• Sanger Institute, COSMIC, https://cancer.sanger.ac.uk/cosmic/download

Published: January 16, 2024