Joint Structural Break Detection and Parameter Estimation in High-Dimensional Non-Stationary VAR Models

Abstract

Assuming stationarity is unrealistic in many time series applications. A more realistic alternative is to assume piecewise stationarity, where the model can change at potentially many change points. We propose a three-stage procedure for simultaneous estimation of change points and parameters of high-dimensional piecewise vector autoregressive (VAR) models. In the first step, we reformulate the change point detection problem as a high-dimensional variable selection one, and solve it using a penalized least square estimator with a total variation penalty. We show that the penalized estimation method over-estimates the number of change points, and propose a selection criterion to identify the change points. In the last step of our procedure, we estimate the VAR parameters in each of the segments. We prove that the proposed procedure consistently detects the number and location of change points, and provides consistent estimates of VAR parameters. The performance of the method is illustrated through several simulated and real data examples.

1. Introduction

Emerging applications in biology (Smith 2012; Fujita et al. 2007) and finance (De Mol et al. 2008; Fan et al. 2011) have sparked an interest in methods for analyzing high-dimensional time series. Recent work includes new regularized estimation procedures for vector autoregressive (VAR) models (Basu and Michailidis 2015; Nicholson et al. 2017), high-dimensional generalized linear models (Hall et al. 2016) and high-dimensional point processes (Hansen et al. 2015; Chen et al. 2017). Related methods have also focused on joint estimation of multiple time series (Qiu et al. 2016), estimation of (inverse) covariance matrices (Xiao and Wu 2012; Chen et al. 2013; Tank et al. 2015), and estimation of high-dimensional systems of differential equations (Lu et al. 2011; Chen et al. 2016).

Despite considerable progress on both computational and theoretical fronts, the vast majority of existing work on high-dimensional time series assumes that the underlying process is stationary. However, multivariate time series observed in many modern applications are non-stationary. For instance, Clarida et al. (2000) show that the effect of inflation on interest rates varies across Federal Reserve regimes. Similarly, as pointed out by Ombao et al. (2005), electroencephalograms (EEGs) recorded during an epileptic seizure display amplitudes and spectral distribution that vary over time. This nonstationarity in EEG signals is illustrated in Figure 1, which shows the signals recorded at 18 EEG channels during an epileptic seizure from a patient diagnosed with left temporal lobe epilepsy (Ombao et al. 2005). The sampling rate in this data is 100 Hz and the total number of time points per EEG is $T=\mathrm{22,768}$ over ~228 seconds. Based on the neurologist’s estimate, the seizure took place at $t=~85s$. Figure 1 also suggests that the magnitude and the variability of EEG signals change around that time.

Figure 1:

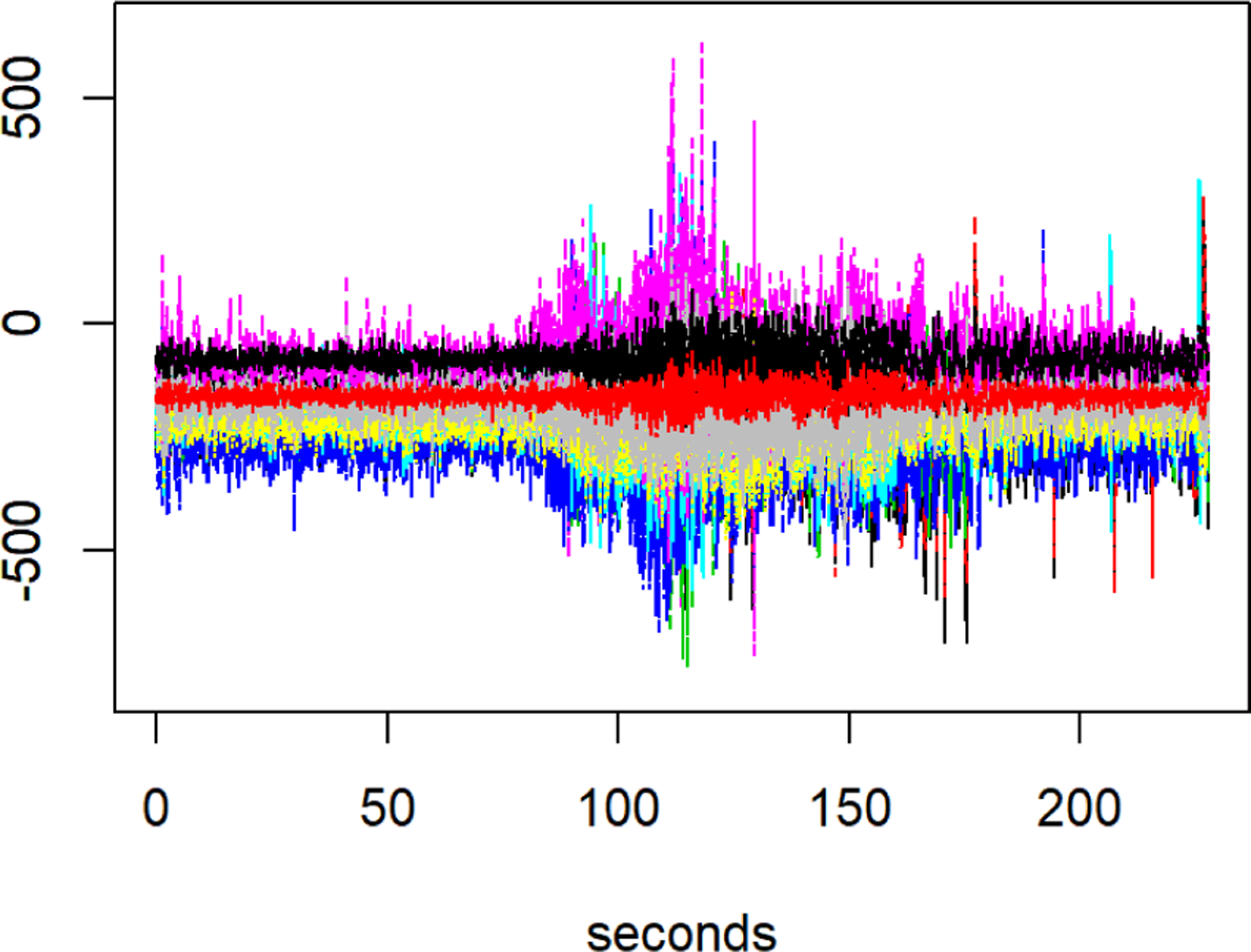
EEG signals from a patient diagnosed with left temporal lobe epilepsy. The data was recorded at 18 locations on the scalp during an epileptic seizure over 22,768 time points.

Detecting structural break points in high-dimensional time series and obtaining reliable estimates of model parameters are important from multiple perspectives. First, structural breaks often reveal important changes in the underlying system and are scientifically important. In our EEG example, automatic detection of structural breaks can assist clinicians in identifying seizures. Second, changes in model parameters before and after break points often provide important scientific insight. For instance, the occurrence of epileptic seizure is expected to change the mechanism of interactions among brain regions. Such changes can be seen in Figure 2. The figure shows networks of interactions among EEG channels before and after seizure. These networks are obtained from estimates using our proposed method, as described in Section 8. Briefly, edges in the first two networks correspond to Granger causal relations (Granger 1969) among EEG channels before and after the period of seizure; the occurrence of seizure is also automatically detected using our proposed method. It can be seen that while the two networks share many edges, they also exhibit important differences. Perhaps most notable are changes in connectivity patterns of channels T5, P3 and Pz, which measure brain activity in the left temporal lobe, the cite of epilepsy in the patient. Without reliable estimates of model parameters, gaining such scientific insight may not be feasible. Third, identifying structural breaks in time series is crucial for proper data analysis. The last plot in Figure 2 shows the network of interactions obtained from the full EEG data, ignoring the structural break due to seizure. This network is much more dense than the other two, and is almost fully connected, which is rather unexpected (Achard et al. 2006). This example underscores that ignoring the break points and assuming stationarity when analyzing times series can result in severe estimation bias.

Figure 2:

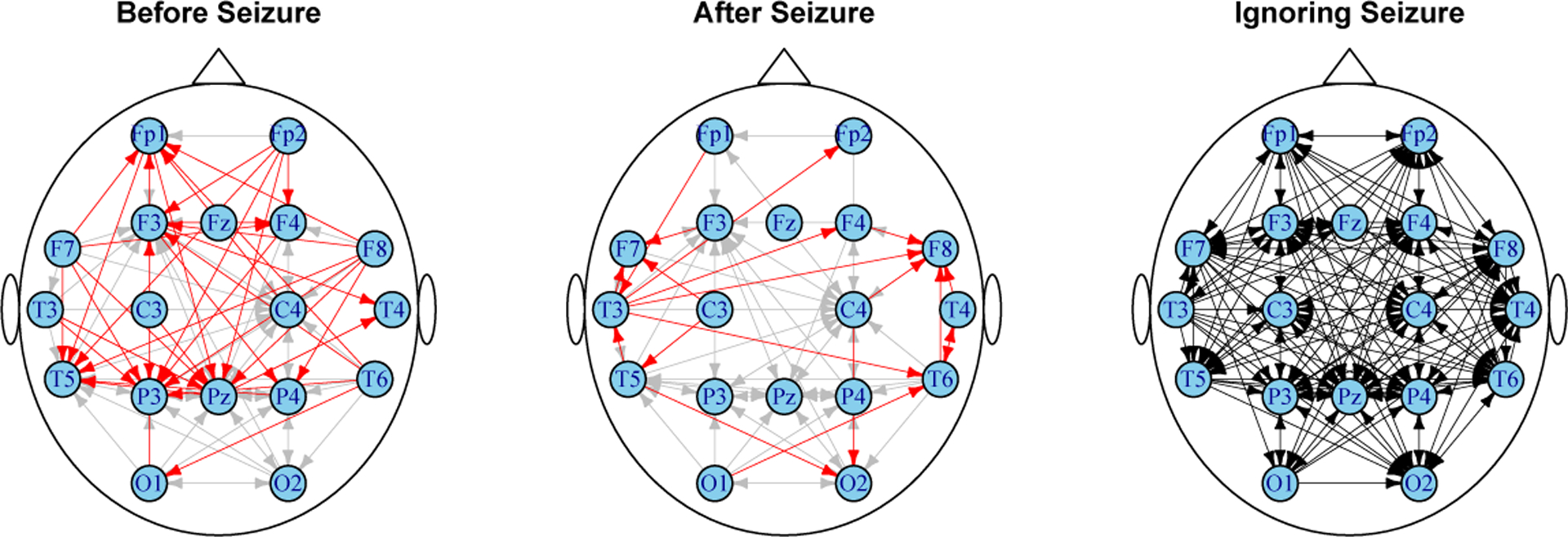
Network of Granger causal interactions among EEG channels based on data from Figure 1. The plots show the schematic locations of the EEG channels. The first two figures show interactions among EEG channels before and after the period of seizure. Gray edges in these two networks show common edges, while red edges show interactions identified either before or after seizure. The rightmost network shows interactions from an estimate obtained by ignoring the structural break in the time series.

In this paper, we develop a regularized estimation procedure to simultaneously detect the structural break points, and estimate the model parameters in high-dimensional piecewise stationary VARs with possibly many break points. We show that our proposed three-stage procedure is consistent for identifying the number and location of structural breaks in the covariance structure of multivariate time series, and for estimating the model parameters. To the best of our knowledge, ours is the first method that can simultaneously identify the change points and estimate the model parameters in high-dimensional non-stationary time series with growing number of break points. In fact, while change point detection in multivariate time series has been an active area of recent research (see the review in Section 1.1), existing procedures do not provide consistent estimates of model parameters. This is in part due to the difficulty of change point detection, especially in high dimensions. More specifically, high-dimensional change point detection methods, including ours, only provide consistent estimates of the relative location of change points. As a result, a naïve approach based on using the estimated change points to break the time series into ‘stationary’ pieces, and then using high-dimensional parameter estimation procedures, may lead to inferior, or even inconsistent, estimates of model parameters. This point is formalized at the end of Section 5 (Remark 6) and is illustrated in our simulation studies, where it can be seen that combining the state-of-the-art change point detection procedure with regularized parameter estimation methods results in inferior estimates of model parameters. The third step of our procedure circumvent this difficulty by utilizing our improved rates of consistency of change point detection to remove a small number of observations around the estimated change points in order to obtain stationary segments at which we could perform usual high-dimensional parameter estimation.

Another advantage of our method is that it can handle high-dimensional VAR models with diverging number of structural breaks, where the number of time series components can grow exponentially fast with respect to the number of time points. This is in contrast to most existing methods for change point detection, which can only handle univariate or multivariate processes where the number of time series components grows at most polynomially with the number of time points (see, e.g., Chan et al. 2014; Cho and Fryzlewicz 2015). The high-dimensionality of time series brings new challenges in deriving asymptotic results, compared to univariate or finite-dimensional cases. We derive rates of consistency that are better than the previously established rates, and require less stringent assumptions in some cases; see Section 4.1 for detailed comparison of our method with existing procedures.

The rest of this paper is organized as follows. Before describing the piecewise stationary model in Section 2, we review related procedures for non-stationary time series in Section 1.1. An initial estimation procedure and its asymptotic properties are discussed in Section 3. In Section 4, we show that under reasonable assumptions, structural breaks in high-dimensional VAR models can be consistently estimated. Our procedure for consistent parameter estimation is presented in Section 5 and finite sample tuning parameters selection for the procedure are discussed in Section 6. Results of simulation experiments are presented in Section 7. In Section 8, we illustrate the utility of the proposed method by applying it to identify structural break points in two multivariate time series. We conclude the paper with a discussion in Section 9. Technical lemmas, proofs, algorithmic details and additional simulation results are gathered in the Appendix.

1.1. Related Methods for Non-Stationary Time Series

Non-stationary VAR models have been primarily studied in univariate or low-dimensional settings. Existing approaches include models that fully parameterize the evolution of the transition matrices of time-varying VARs, or enforce a Bayesian prior on the structure of the time dependence (Primiceri 2005).

A popular approach for analyzing non-stationary time series is assuming local stationarity, which means that in each small time interval, the process is well-approximated by a stationary one. This notion has been studied in low dimensions by, e.g., Dahlhaus (2012); Sato et al. (2007) proposed a wavelet-based method for estimating time-varying VAR coefficients. Recently, Ding et al. (2016) considered estimation of high-dimensional time-varying VARs by solving time-varying Yule-Walker equations based on kernelized estimates of auto-covariance matrices.

Methods based on local stationarity are theoretically appealing and suitable in certain applications. However, local stationarity may not hold in many applications. For instance, in the above EEG example, assuming that the process can be locally approximated by a stationary one at the time of seizure may be unrealistic. A more natural assumption in such settings is that the process is piecewise stationary — i.e., it is stationary in each of (potentially many) regions, e.g., before and after seizure.

A number of methods have been proposed for analyzing univariate piecewise stationary time series. For instance, Davis et al. (2006), Chan et al. (2014) and Bai (1997) propose different methods for identifying structural break points in univariate time series. Various methods have also been proposed for detecting changes in multivariate time series. One of the early contributions to this literature was the SLEX method of Ombao et al. (2005), which uses time-varying wavelets to detect changes in the covariance structure of multivariate time series. The test procedure of Aue et al. (2009) addresses a similar problem in possibly nonlinear time series, whereas Aue et al. (2017) takes a functional data perspective in order to identify changes in the mean structure of multivariate time series. More recent approaches by Cho and Fryzlewicz (2015) and Cho (2016) use variants of CUSUM statistic in order to detect structural break points in high-dimensional time series.

Despite significant progress, existing multivariate approaches do not provide estimates of model parameters. For instance, to deal with the large number of time series, Ombao et al. (2005) apply a dimension reduction step, whereas Aue et al. (2009), Cho and Fryzlewicz (2015) and Cho (2016) use some variation of CUSUM statistic. Consequently, these methods only estimate the structural break points. In the EEG example, these methods can identify the structural breaks, but do not reveal mechanisms of interactions among brain regions, which is of key interest for understanding changes in brain function before and after seizure. As discussed in Section 5, consistent estimation of model parameters in high-dimensional piecewise stationary VAR models introduces new challenges. Addressing these challenges and providing interpretable estimates of parameters in high-dimensional piecewise stationary VAR models are two key contributions of the current paper.

2. Piecewise Stationary VAR Models

A piecewise stationary VAR model can be viewed as a collection of separate VAR models concatenated at multiple break points over the observed time period. More specifically, suppose there exist $m_0$ break points $0=t_0<t_1<\cdots <t_{m_0}<t_{m_0+1}=T+1$ such that for $t_{j-1}\le t<t_j,j=1,\dots ,m_0+1$,

$$y_t={\mathrm{\Phi }}^{(1,j)}{y}_{t-1}+\cdots +{\mathrm{\Phi }}^{(q,j)}{y}_{t-q}+{\mathrm{\Sigma }}_j^{1/2}{\epsilon }_t.$$ (1)

Here, $y_t$ is the $p$-vector of observed time series at time $t;{\mathrm{\Phi }}^{(l,j)}\in {\mathbb{R}}^{p\times p}$ is the (sparse) coefficient matrix corresponding to the $l$th lag of a VAR process of order $q$ during for the $j$th segment, where $j=1,\cdots ,m_0+1;{\epsilon }_t$ is a multivariate Gaussian white noise with independent components, and ${\mathrm{\Sigma }}_j$ is the covariance matrix of the noise for the $j$th segment. To simplify the notations, we sometime denote the noise as ${\epsilon }_t$ without specifying the covariance ${\mathrm{\Sigma }}_j$; however, throughout the paper, we allow for different covariance matrices in each segment. Note that the first few observations in each segment are, in fact, affected by the last few observations from the previous segment. Thus, the break points do not really divide the time series into stationary segments; hence, strictly speaking, model (1) is not piecewise stationary. This feature can, in general, lead to additional challenges when estimating the parameters, but is circumvented by the third step of our procedure discussed in Section 5.

Our goal is to detect the break points, $t_j$, together with estimates of the coefficient parameters ${\mathrm{\Phi }}^{(l,j)}$ in the high-dimensional case, where $p>T$. To this end, we generalize the change-point detection ideas of Harchaoui and Lévy-Leduc (2010) and Chan et al. (2014) to the multivariate, high-dimensional setting, and extend them to obtain consistent estimates of model parameters. More specifically, our estimation procedure utilizes the following linear regression representation of the VAR process

$$\left(\begin{array}{c}{y}_q^{\prime }\\ y_{q+1}^{\prime }\\ ⋮\\ y_T^{\prime }\end{array}\right)=\left(\begin{array}{llllllllll}{y}_{q-1}^{\prime }\hfill & \dots \hfill & y_0^{\prime }\hfill & & 0\hfill & & \dots \hfill & & 0\hfill & \\ y_q^{\prime }\hfill & \dots \hfill & y_1^{\prime }\hfill & y_q^{\prime }\hfill & \dots \hfill & y_1^{\prime }\hfill & & & 0\hfill & \\ & ⋮\hfill & & & & & \ddots \hfill & & & \\ y_{T-1}^{\prime }\hfill & \dots \hfill & y_{T-q}^{\prime }\hfill & y_{T-1}^{\prime }\hfill & \dots \hfill & y_{T-q}^{\prime }\hfill & \dots \hfill & y_{T-1}^{\prime }\hfill & \dots \hfill & y_{T-q}^{\prime }\hfill \end{array}\right)\left(\begin{array}{c}{\theta }_1^{\prime }\\ {\theta }_2^{\prime }\\ ⋮\\ {\theta }_n^{\prime }\end{array}\right)+\left(\begin{array}{c}{\epsilon }_q^{\prime }\\ {\epsilon }_{q+1}^{\prime }\\ ⋮\\ {\epsilon }_T^{\prime }\end{array}\right),$$ (2)

where $n=T-q+1$. Throughout the paper, the transpose of a matrix $A$ is denoted by $A^{\prime }$. Denoting ${\mathrm{\Phi }}^{(.,j)}=\left({\mathrm{\Phi }}^{(1,j)}\dots {\mathrm{\Phi }}^{(q,j)}\right)\in {\mathbb{R}}^{p\times pq}$, we set ${\theta }_1={\mathrm{\Phi }}^{(.,1)}$; for $i=\mathrm{2,3},\dots ,n$, we let

$${\theta }_i=\left\{\begin{array}{ll}{\mathrm{\Phi }}^{(.,j+1)}-{\mathrm{\Phi }}^{(.,j)},& \text{when }i=t_j\text{ for some }j\\ 0,& \text{otherwise.}\end{array}\right.$$ (3)

Note that in this parameterization, ${\theta }_i\ne 0$ for $i\ge 2$ implies a change in the VAR coefficients. Therefore, for $j=1,\dots ,m_0$, the structural break points $t_j$ can be estimated as time points $i\ge 2$, where ${\theta }_i\ne 0$.

Noting that (2) is a linear regression of the form $𝒴=𝒳\mathrm{\Theta }+E$, and letting $\mathbf{Y}=\mathrm{v}\mathrm{e}\mathrm{c}\left(𝒴\right)$, $\mathbf{Z}=I_p\otimes 𝒳$, and $\mathbf{E}=\mathrm{v}\mathrm{e}\mathrm{c}\left(E\right)$, we rewrite it in vector form as

$$\mathbf{Y}=\mathbf{Z}\mathrm{\Theta }+\mathbf{E},$$ (4)

where $\otimes$ denotes the tensor product of two matrices. Denoting $\pi =n{p}^{2}q,\mathbf{Y}\in {\mathbb{R}}^{np\times 1},\mathbf{Z}\in {\mathbb{R}}^{np\times \pi },\mathrm{ }\mathrm{\Theta }\in {\mathbb{R}}^{\pi \times 1}$, and $\mathbf{E}\in {\mathbb{R}}^{np\times 1}$.

3. An Initial Estimator

The linear regression representation in (4) suggests that the model parameters $\mathbf{\Theta }$ can be estimated via regularized least squares. The regularization is necessary to both handle the growing number of parameters corresponding to potential change points, as well as the number of time series $p$. A simple initial estimate of parameters $\mathbf{\Theta }$ can thus be obtained by using an ${\ell }_1$-penalized least squares regression of the form

$$\widehat{\Theta }={\text{argmin}}_{\Theta }\frac{1}{n}\parallel Y-Z\Theta {\parallel }_2^2+{\lambda }_{1,n}\parallel \Theta {\parallel }_1+{\lambda }_{2,n}\sum _{k=1}^n\underset{j=1}{\overset{k}{\Vert \sum }}{\theta }_j{\Vert }_1.$$ (5)

Problem (5) uses a fused lasso penalty (Tibshirani et al. 2005), with two ${\ell }_1$ penalties controlling the number of break points and the sparsity of the VAR model. The problem is convex and can be solved efficiently. In fact, by Proposition 1 of Friedman et al. (2007), it can be solved by first finding a solution, ${\tilde{\mathrm{\Theta }}}^{\left(0\right)}$, for ${\lambda }_{2,n}=0$ and then applying element-wise soft-thresholding to the partial sums of ${\tilde{\mathrm{\Theta }}}^{\left(0\right)}$ in order to obtain the final estimate for ${\lambda }_{2,n}\ne 0$. Details of this algorithm are described in Appendix C.

Despite its convenience and computational efficiency, estimates from (5) do not correctly identify the structural break points in the piecewise VAR process. In fact, our theoretical analysis in the next section shows that the number of estimated break points from (5), i.e., the number of nonzero ${\widehat{\theta }}_i\ne 0,i\ge 2$, over-estimates the true number of break points. This is because the design matrix $\mathbf{Z}$ may not satisfy the restricted eigenvalue condition (Bickel et al. 2009) needed for consistent estimation of parameters. However, as we show in Section 3.1, the model from (5) does achieve prediction consistency. In Section 4 we show that this initial estimator can be refined in order to obtain consistent estimates of structural break points.

3.1. Asymptotic Properties

Let ${\widehat{𝒜}}_n=\left\{i\ge 2:{\widehat{\theta }}_i\ne 0\right\}$ be the set of estimated change points from (5). The total number of estimated change points is then the cardinality of the set ${\widehat{𝒜}}_n$; denote $\widehat{m}=\left|{\widehat{𝒜}}_n\right|$. Let ${\widehat{t}}_j$ be the estimated break points for $j=1,\dots ,\widehat{m}$. Then, the relationship between ${\widehat{\theta }}_j$ and ${\widehat{\mathrm{\Phi }}}^{(.,j)}$ in each of the estimated segments can be seen as:

$${\widehat{\Phi }}^{\left(.,1\right)}={\widehat{\theta }}_1,\hspace{1em}{\text{and}\hspace{1em}\widehat{\Phi }}^{\left(.,j\right)}=\sum _{i=1}^{{\widehat{t}}_j}{\widehat{\theta }}_i,\hspace{1em}j=1,2,\dots ,\widehat{m}.$$ (6)

In this section, we show that with high probability $\widehat{m}\ge m_0$, and that there exist $m_0$ points within ${\widehat{𝒜}}_n$ that are ‘close’ to the true break points. To this end, we first establish the prediction consistency of the estimator (5). Using a more careful analysis, we then show that the penalized least squares in (5) identifies a larger set of candidate break points. These result justify the second step of our estimation procedure described in the Section 4, which searches over the break points in ${\widehat{𝒜}}_n$ to find an optimal set of break points.

Before stating our assumptions, we define a few notations. Denote the number of nonzero elements in the $k$-th row of ${\mathrm{\Phi }}^{(.,j)}$ by $d_{kj},k=\mathrm{1,2},\dots ,p$ and $j=\mathrm{1,2},\dots ,m_0$. Further, for each $j=\mathrm{1,2},\dots ,m_0+1$ and $k=1,\dots ,p$, let ${ℐ}_{kj}$ be the set of all column indexes of ${\mathrm{\Phi }}_k^{(.,j)}$ at which there is a nonzero term, where ${\mathrm{\Phi }}_k^{(.,j)}$ denotes the $k$-th row of ${\mathrm{\Phi }}^{(.,j)}$. Let $ℐ={\cup }_{k,j}{ℐ}_{kj}$, and define $d_n={\mathrm{m}\mathrm{a}\mathrm{x}}_{1\le k\le p,1\le j\le m_0+1}\left|{ℐ}_{kj}\right|$. Further, let $d_n^{\star }={\sum }_{j=1}^{m_0+1}{\sum }_{k=1}^p{d}_{kj}$ be the total sparsity of the model. Note that our theoretical analysis concerns the high-dimensional case with many break points, where $p,m_0$ and the network sparsity increase with the number of time points, $T$. More specifically, $p\equiv p\left(n\right)$ and $m_0\equiv m_0\left(n\right)$ and $d_{kj}\equiv d_{kj}\left(n\right)$, where $n=T-q+1$. To simplify the notation, we suppress the $n$-index.

A1 For each $j=\mathrm{1,2},\dots ,m_0+1$, the process $y_t^{\left(j\right)}={\mathrm{\Phi }}^{(1,j)}{y}_{t-1}^{\left(j\right)}+\cdots +{\mathrm{\Phi }}^{(q,j)}{y}_{t-q}^{\left(j\right)}+{\mathrm{\Sigma }}_j{ }^{1/2}{\epsilon }_t$ is a stationary Gaussian time series. Denote the covariance matrices ${\mathrm{\Gamma }}_j\left(h\right)=\mathrm{c}\mathrm{o}\mathrm{v}\left(y_t^{\left(j\right)},y_{t+h}^{\left(j\right)}\right)$ for $t,h\in \mathbb{Z}$. Also, assume that for $\kappa \in [-\pi ,\pi ]$, the spectral density matrices $f_j\left(\kappa \right)=\left(2\pi {)}^{-1}{\sum }_{l\in \mathbb{Z}}{\mathrm{\Gamma }}_j\right(l)e^{-\sqrt{-1}\kappa l}$ exist; moreover,

$$\underset{1\le j\le m_0+1}{\mathrm{m}\mathrm{a}\mathrm{x}}ℳ\left(f_j\right)=\underset{1\le j\le m_0+1}{\mathrm{m}\mathrm{a}\mathrm{x}}\left(\underset{\kappa \in [-\pi ,\pi ]}{\mathrm{s}\mathrm{u}\mathrm{p}}{\mathrm{\Lambda }}_{\mathrm{m}\mathrm{a}\mathrm{x}}\left(f_j\left(\kappa \right)\right)\right)<+\mathrm{\infty },$$

$$\underset{1\le j\le m_0+1}{\mathrm{m}\mathrm{i}\mathrm{n}}\mathbf{m}\left(f_j\right)=\underset{1\le j\le m_0+1}{\mathrm{m}\mathrm{i}\mathrm{n}}\left(\underset{\kappa \in [-\pi ,\pi ]}{\mathrm{s}\mathrm{u}\mathrm{p}}{\mathrm{\Lambda }}_{\mathrm{m}\mathrm{i}\mathrm{n}}\left(f_j\left(\kappa \right)\right)\right)>0,$$

where ${\mathrm{\Lambda }}_{\mathrm{m}\mathrm{a}\mathrm{x}}\left(A\right)$ and ${\mathrm{\Lambda }}_{\mathrm{m}\mathrm{i}\mathrm{n}}\left(A\right)$ are the largest and smallest eigenvalues of the symmetric or Hermitian matrix $A$, respectively.

A2 The matrices ${\mathrm{\Phi }}^{(.,j)}$ are sparse. More specifically, for all $k=\mathrm{1,2},\dots ,p$ and $j=\mathrm{1,2},\dots ,m_0,\mathrm{ }{d}_{kj}\ll p$, i.e., $d_{kj}/p=o\left(1\right)$. Moreover, there exists a positive constant $M_{\mathrm{\Phi }}>0$ such that

$$\underset{1\le j\le m_0+1}{\mathrm{m}\mathrm{a}\mathrm{x}}{∥{\mathrm{\Phi }}^{(.,j)}∥}_{\mathrm{\infty }}\le M_{\mathrm{\Phi }}.$$

A3 There exists a positive constant $v$ such that

$$\underset{1\le j\le m_0}{\mathrm{m}\mathrm{i}\mathrm{n}}{∥{\mathrm{\Phi }}^{(.,j+1)}-{\mathrm{\Phi }}^{(.,j)}∥}_2\ge v>0.$$

Moreover, there exists a vanishing positive sequence ${\gamma }_n$ such that, as $n\to \mathrm{\infty }$,

$$\underset{1\le j\le m_0+1}{\mathrm{m}\mathrm{i}\mathrm{n}}\left|t_j-t_{j-1}\right|/\left(n{\gamma }_n\right)\to +\mathrm{\infty },,\hspace{1em}\text{and}\hspace{1em}{d}_n^{\star }\sqrt{\frac{\text{log}p}{n{\gamma }_n}}\to 0.$$

Assumption A1 allows us to obtain appropriate probability bounds in high dimensions. This assumption does not restrict the applicability of the method since it is valid for large families of VAR models (Basu and Michailidis 2015). The second part of A1 will also be needed in the proof of consistency of VAR parameters once the break points are detected. The first part of Assumption A2 characterizes the sparsity of the model, and is common in the high-dimensional linear regression literature. The second part bounds the ${\ell }_{\mathrm{\infty }}$-norm of transition matrices, and is needed to quantify the effect of misspecification in the model, which arises because we are not able to exactly locate the break points. Since this effect needs to be accounted for in the sum of squared errors, the magnitude of elements in the true transition matrices becomes important. See Remark 3 for further discussions on the necessity of this assumption and potential relaxations. The sequence ${\gamma }_n$ is directly related to the detection rate of the break points $t_j;j=1,\dots ,m_0$. Assumption A3 connects this detection rate to the tuning parameter chosen in the estimation procedure. Also, this assumption puts a minimum distance-type requirement on the coefficients in different segments. This can be regarded as the extension of Assumption H2 in Chan et al. (2014) for univariate time series to the high-dimensional case. Finally, the last part of this assumption restricts the total sparsity of the model, in order to accommodate the high-dimensional regime $p>T$. While somewhat common in the high-dimensional time series literature (see, e.g., Basu and Michailidis 2015), this assumption may be restrictive in some applications, if the network corresponding to the transition matrices is dense. As discussed in Appendix E, this assumption can be relaxed using a secondary analysis.

As pointed out earlier, and discussed in Chan et al. (2014) and Harchaoui and Lévy-Leduc (2010), the design matrix $\mathbf{Z}$ in (5) may not satisfy the restricted eigenvalue condition needed for parameter estimation consistency (Bickel et al. 2009). Thus, as a first step towards establishing the consistency of the proposed procedure, we next establish the prediction consistency of the estimator from (5).

Theorem 1. Suppose $A1$ and $A2$ hold. Choose ${\lambda }_{1,n}=2C\sqrt{\frac{\mathrm{l}\mathrm{o}\mathrm{g}\left(n\right)+2\mathrm{l}\mathrm{o}\mathrm{g}\left(p\right)+\mathrm{l}\mathrm{o}\mathrm{g}\left(q\right)}{n}}$ for some $C>0$ and ${\lambda }_{2,n}=o\left({\left(n{d}_n^{\star }\right)}^{-1}\right)$, and assume $m_0\le m_n$ with $m_n=o\left({\lambda }_{1,n}^{-1}\right)$. Then, with high probability approaching 1 as $n\to +\mathrm{\infty }$,

$$\frac{1}{n}\parallel \mathit{Z}\left(\widehat{\Theta }-\Theta \right){\parallel }_2^2\le 2M_{\Phi }{\lambda }_{1,n}{m}_n\underset{1\le j\le m_0+1}{\text{max}}\left\{\sum _{k=1}^p\left(d_{kj}+d_{k\left(j-1\right)}\right)\right\}+{\lambda }_{2,n}n{d}_n^{\star }.$$ (7)

Theorem 1 is proved in Appendix B. Note that this theorem imposes an upper bound on the model sparsity, as the right hand side of (7) must go to zero as $n\to \mathrm{\infty }$. In Section 4, we specify the limit on the sparsity needed for consistent identification of structural break points.

We now turn to the original problem of estimating the number of break points and locating them. The next result shows that the number of selected change points, $\widehat{m}$, based on (5) will be at least as large as the true number, $m_0$. Moreover, there exists at least one estimated change point in $n{\gamma }_n$-radius neighborhood of each each true change point. Before stating the theorem, we need some additional notation. Let ${𝒜}_n=\left\{t_1,t_2,\dots ,t_{m_0}\right\}$ be the set of true change points. Following Boysen et al. (2009) and Chan et al. (2014), define the Hausdorff distance between two countable sets in real line as

$$d_H(A,B)=\underset{b\in B}{\mathrm{m}\mathrm{a}\mathrm{x}}\underset{a\in A}{\mathrm{m}\mathrm{i}\mathrm{n}}|b-a|.$$

Note that the above definition is not symmetric and therefore not a real distance. However, this is the version of function $d_H(A,B)$ used in our next theorem.

Theorem 2. Suppose A1–A3 hold. Choose ${\lambda }_{1,n}=2C_1\sqrt{\frac{\mathrm{l}\mathrm{o}\mathrm{g}\left(n\right)+2\mathrm{l}\mathrm{o}\mathrm{g}\left(p\right)+\mathrm{l}\mathrm{o}\mathrm{g}\left(q\right)}{n}}$, and ${\lambda }_{2,n}=\frac{C_2}{n}\sqrt{\frac{\mathrm{l}\mathrm{o}\mathrm{g}p}{n{\gamma }_n}}$ for some large constants $C_1,C_2>0$. Then, as $n\to +\mathrm{\infty }$,

$$\mathbb{P}\left(\left|{\widehat{𝒜}}_n\right|\ge m_0\right)\to 1,\hspace{1em}\mathit{\text{and}}\hspace{1em}\mathbb{P}\left(d_H\left({\widehat{𝒜}}_n,{𝒜}_n\right)\le n{\gamma }_n\right)\to 1.$$

For this theorem, ${\lambda }_{1,n}$ could be as large as ${\lambda }_{1,n}=O\left(\sqrt{\frac{{\gamma }_n\mathrm{l}\mathrm{o}\mathrm{g}p}{n}}\right)$. However, for compatibility, we use the same rate as in Theorem 1. The rate of consistency for break point detection in Theorem 2 is $n{\gamma }_n$, which can be chosen as small as possible assuming that Assumptions A2 and A3 hold. ${\gamma }_n$ also depends on the minimum distance between consecutive true break points, as well as the number of time series, $p$. When $m_0$ is finite, one can choose ${\gamma }_n=\left(\mathrm{l}\mathrm{o}\mathrm{g}n\mathrm{l}\mathrm{o}\mathrm{g}p\right)/n$ or ${\gamma }_n=\left(\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{l}\mathrm{o}\mathrm{g}n\mathrm{l}\mathrm{o}\mathrm{g}p\right)/n$. This means that the convergence rate for estimating the relative locations of the break points, i.e., $t_j/T$ using ${\widehat{t}}_j/T$, could be as low as $(\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{ }\mathrm{l}\mathrm{o}\mathrm{g}n\mathrm{l}\mathrm{o}\mathrm{g}p)/n$. In Section 4.1, we compare these rates with those obtained in related procedures.

Remark 1. When $m_0$ is known, arguments similar to the proof of Theorem 2 lead to the same consistency rate, i.e., $n{\gamma }_n$, for locating the break points. In Theorem 3, we consider the case of unknown $m_0$ and show that the consistency rate for this general case is of order $O\left(m_{0}n{\gamma }_n{d}_n^{\star 2}\right)$. Compared to the known $m_0$ case, the additional term $m_0{d}_n^{\star 2}$ quantifies the additional complexity of estimating the number of break points.

The second part of Theorem 2 shows that even though we select more points than needed, there exists a subset of the estimated points, with cardinality $m_0$ that and estimates the true break points at the same rate as if $m_0$ was known. This result motivates the second stage of our estimation procedure, discussed in the next section, which removes the redundant break points.

4. Consistent Estimation of Structural Breaks

Theorem 2 shows that the penalized estimation procedure (5) over-estimates the number of break points. A second stage screening is thus needed to remove the redundant estimated change points and consistently estimate the true change points. To this end, we propose a screening procedure, based on a modification of the procedure in Chan et al. (2014). The main idea is to develop an information criterion based on a new penalized least squares estimation procedure, in order to screen the candidate break points found in the first estimation stage. Formally, for a fixed $m$ and estimated change points $s_1,\dots ,s_m$, let ${\mathbf{X}}_{\left({\ell }_{\mathrm{m}\mathrm{i}\mathrm{n}},{\ell }_{\mathrm{m}\mathrm{a}\mathrm{x}}\right)}={\left(Y_{{\ell }_{\mathrm{m}\mathrm{i}\mathrm{n}}}^{\prime },\dots ,Y_{{\ell }_{\mathrm{m}\mathrm{a}\mathrm{x}}}^{\prime }\right)}^{\prime }$, and consider the linear regression

$$\left(\begin{array}{c}{y}_q^{\prime }\\ y_{q+1}^{\prime }\\ ⋮\\ y_T^{\prime }\end{array}\right)=\left(\begin{array}{cccc}{\mathbf{X}}_{\left(q-1,s_1-1\right)}& 0& \dots & 0\\ 0& {\mathbf{X}}_{\left(s_1,s_2-1\right)}& \dots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \dots & {\mathbf{X}}_{\left(s_m,T-1\right)}\end{array}\right)\left(\begin{array}{c}{\theta }_{\left(q,s_1\right)}^{\prime }\\ {\theta }_{\left(s_1,s_2\right)}^{\prime }\\ ⋮\\ {\theta }_{\left(s_m,T\right)}^{\prime }\end{array}\right)+\left(\begin{array}{c}{\xi }_q^{\prime }\\ {\xi }_{q+1}^{\prime }\\ ⋮\\ {\xi }_T^{\prime }\end{array}\right),$$ (8)

or, more compactly,

$$𝒴={𝒳}_{s_1,\dots ,s_m}{\theta }_{s_1,\dots ,s_m}+\mathrm{\Xi },$$

where ${𝒳}_{s_1,\dots ,s_m}\in {\mathbb{R}}^{n\times {\pi }_m},{\theta }_{s_1,\dots ,s_m}={\left({\theta }_{\left(q,s_1\right)}^{\prime },{\theta }_{\left(s_1,s_2\right)}^{\prime },\dots ,{\theta }_{\left(s_m,T\right)}^{\prime }\right)}^{\prime }\in {\mathbb{R}}^{{\pi }_m\times p}$, with ${\pi }_m=(m+1)pq$. We estimate ${\theta }_{s_1,\dots ,s_m}$ as the solution of a penalized regression,

$${\widehat{\theta }}_{s_1,\dots ,s_m}={\text{argmin}}_{{\theta }_{s_1,\dots ,s_m}}\sum _{i=1}^{m+1}\left(\frac{1}{s_i-s_{i-1}}\sum _{t=s_{i-1}}^{s_i-1}\Vert y_t-{\theta }_{\left(s_{i-1},s_i\right)}{Y}_{t-1}{\Vert }_2^2+{\eta }_{\left(s_{i-1},s_i\right)}\Vert {\theta }_{\left(s_{i-1},s_i\right)}{\Vert }_1\right),$$ (9)

with tuning parameters ${\eta }_n=\left({\eta }_{\left(s_0,s_1\right)},\dots ,{\eta }_{\left(s_m,s_{m+1}\right)}\right)$, where $s_0=q$ and $s_{m+1}=T$.

Now, let

$$L_n\left(s_1,s_2,\dots ,s_m;{\eta }_n\right)={\Vert 𝒴-{𝒳}_{s_1,\dots ,s_m}{\widehat{\theta }}_{s_1,\dots ,s_m}\Vert }_F^2+\sum _{i=1}^{m+1}{\eta }_{\left(s_{i-1},s_i\right)}{\Vert {\widehat{\theta }}_{\left(s_{i-1},s_i\right)}\Vert }_1,$$ (10)

where $\parallel .{\parallel }_F$ is the Frobenius norm of the matrix. Then, for a suitably chosen sequence ${\omega }_n$, specified in Assumption A4 below, consider the following information criterion:

$$\text{IC}\left(s_1,\dots ,s_m;{\eta }_n\right)=L_n\left(s_1,s_2,\dots ,s_m;{\eta }_n\right)+m{\omega }_n.$$ (11)

The second stage of our procedure selects a subset of initial $\widehat{m}$ break points from (5) by solving

$$\left(\tilde{m},{\tilde{t}}_j;j=1,\dots ,\tilde{m}\right)={\text{argmin}}_{0\le m\le \widehat{m},\mathbf{s}=\left(s_1,\dots ,s_m\right)\in {\widehat{𝒜}}_n}\mathrm{I}\mathrm{C}\left(\mathbf{s};{\eta }_n\right).$$ (12)

To establish the consistency of the screening procedure (12), we need two additional assumptions, involving the total sparsity of the model, $d_n^{\star }={\sum }_{j=1}^{m_0+1}{\sum }_{k=1}^p{d}_{kj}$.

A4 Let ${\mathrm{\Delta }}_n={\mathrm{m}\mathrm{i}\mathrm{n}}_{1\le j\le m_0}\left|t_{j+1}-t_j\right|$. Then, $m_{0}n{\gamma }_n{d}_n^{\star 2}/{\omega }_n\to 0$, and ${\mathrm{\Delta }}_n/\left(m_0{\omega }_n\right)\to +\mathrm{\infty }$.

A5 There exist a large positive constant $c>0$ such that (a) if $\left|s_i-s_{i-1}\right|\le n{\gamma }_n$, then ${\eta }_{\left(s_{i-1},s_i\right)}=c\sqrt{n{\gamma }_n\mathrm{l}\mathrm{o}\mathrm{g}p}$; (b) if there exist $t_j$ and $t_{j+1}$ such that $\left|s_{i-1}-t_j\right|\le n{\gamma }_n$ and $\left|s_i-t_{j+1}\right|\le n{\gamma }_n$, then, ${\eta }_{\left(s_{i-1},s_i\right)}=2\left(c\sqrt{\frac{\mathrm{l}\mathrm{o}\mathrm{g}p}{s_i-s_{i-1}}}+M_{\mathrm{\Phi }}{d}_n^{\star }\frac{n{\gamma }_n}{s_i-s_{i-1}}\right)$; (c) otherwise, ${\eta }_{\left(s_{i-1},s_i\right)}=2\left(c\sqrt{\frac{\mathrm{l}\mathrm{o}\mathrm{g}p}{s_i-s_{i-1}}}+M_{\mathrm{\Phi }}{d}_n^{\star }\right)$.

Assumption A4 plays an important role in characterizing the rate of consistency of locating the break points by connecting the rate of the minimum spacing between consecutive break points, ${\mathrm{\Delta }}_n$, the detection rate quantity, ${\gamma }_n$, and the penalty term needed in the screening step, ${\omega }_n$. Since ${\mathrm{\Delta }}_n\le n/m_0$, this assumption implicitly restricts the total number of change points. More specifically, the assumption translates to $n{\left(m_0^2{\omega }_n\right)}^{-1}\to +\mathrm{\infty }$, as $n\to +\mathrm{\infty }$, which requires $m_0=o\left(\sqrt{n/{\omega }_n}\right)$; this restricts the rate of $m_0$, but still allows $m_0$ to diverge with $n$.

Assumption A5 specifies the rates of tuning parameters in the second step of our procedure. While somewhat involved, the segment-specific tuning parameters specified in this assumption help achieve sharp rates of consistency. A more comprehensive discussion on this assumption is provided in Remark 5.

We can now state our main result on consistency of change point detection.

Theorem 3. Suppose $A1-A5$ hold. Then, as $n\to +\mathrm{\infty }$, the minimizer $\left(\tilde{m},{\tilde{t}}_j,j=1,\dots ,\tilde{m}\right)$ of (12) satisfies

$$\mathbb{P}\left(\tilde{m}=m_0\right)\to 1.$$

Moreover, there exists a positive constant $B>0$ such that

$$\mathbb{P}\left(\underset{1\le j\le m_0}{\mathrm{m}\mathrm{a}\mathrm{x}}\left|{\tilde{t}}_j-t_j\right|\le B{m}_{0}n{\gamma }_n{d}_n^{\star 2}\right)\to 1.$$

The proof of Theorem 3, given in Appendix B, relies heavily on the result presented in Lemma 4, which is stated and derived in Appendix A. While the statement of Lemma 4 is similar to Lemma 6.4 in Chan et al. (2014), its proof has important differences to address the additional challenges that arise in our setting. The first difference is due to our definition of information criterion (IC). The IC in (11) includes three parts: the sum of squared errors, the $L_1$ norm of the estimated VAR parameters in (9), and the penalty on the number of break points, ${\omega }_n$. In contrast, the IC in Equation 2.9 of Chan et al. (2014) does not include an $L_1$ penalty. The reason for including this additional penalty is the high-dimensional nature of our problem. Specifically, when the distance between two consecutive estimated break points in the first step is less than $n{\gamma }_n$, the restricted eigenvalue condition cannot be verified for the segment defined by these two break points. Therefore, the behavior of the estimated VAR parameters within this segment cannot be controlled. This makes the evaluation of the effect of wrong estimation in the sum of squared term more difficult. The addition of the $L_1$ penalty circumvents this problem. The second key difference is that the proof of Lemma 6.4 in Chan et al. (2014) relies on the fact that for each candidate segment, the least squared estimator of the AR parameter has a closed-form representation, which can be utilized to quantify the effect of missing a true break point on the sum of squared error. In contrast, in our high-dimensional setting, there is no closed form solution for (9). Thus, in proof of Lemma 4, each candidate segment in the first step may need a different treatment; also, for some segments, specific restricted eigenvalue and deviation bounds need to be verified in order to characterize the asymptotic behavior of VAR parameters.

Remark 2. For the case when $m_0$ is finite, we can set ${\gamma }_n=(\mathrm{l}\mathrm{o}\mathrm{g}n\mathrm{l}\mathrm{o}\mathrm{g}p)/n,{\lambda }_n=o\left(\right(\mathrm{l}\mathrm{o}\mathrm{g}n\mathrm{l}\mathrm{o}\mathrm{g}p)/np)$, and ${\omega }_n=(\mathrm{l}\mathrm{o}\mathrm{g}n\mathrm{l}\mathrm{o}\mathrm{g}p{)}^{1+\nu }$ for some positive $\nu >0$. For these rates, the model can have total sparsity $d_n^{\star }=o\left((\mathrm{l}\mathrm{o}\mathrm{g}n\mathrm{l}\mathrm{o}\mathrm{g}p{)}^{\nu /2}\right)$.

Remark 3. The second part of Assumption A2 puts an upper bound on the ${\ell }_{\mathrm{\infty }}$-norm of transition matrices. This assumption is needed in Theorems 1 and 3 in order to quantify the effect of misspecification in our model—due to the inaccuracy in locating the break points. The magnitude of elements in the true transition matrices becomes important when accounting for this effect in the sum of squared errors. Nonetheless, it is possible to relax this assumption and allow the ${\ell }_{\mathrm{\infty }}$-norm of transition matrices to diverge at a certain rate at the price of worsening the rate of consistency of break points detection by the same magnitude. For example, when $m_0$ is finite, we can assume ${\mathrm{m}\mathrm{a}\mathrm{x}}_{1\le j\le m_0+1}{∥{\mathrm{\Phi }}^{(.,j)}∥}_{\mathrm{\infty }}=O(\mathrm{l}\mathrm{o}\mathrm{g}n\mathrm{l}\mathrm{o}\mathrm{g}p{)}^r$, set ${\gamma }_n=(\mathrm{l}\mathrm{o}\mathrm{g}n\mathrm{l}\mathrm{o}\mathrm{g}p)/n$ and total sparsity $d_n^{\star }=o\left((\mathrm{l}\mathrm{o}\mathrm{g}n\mathrm{l}\mathrm{o}\mathrm{g}p{)}^{\nu /2}\right)$, and achieve the consistency rate of order $O\left((\mathrm{l}\mathrm{o}\mathrm{g}n\mathrm{l}\mathrm{o}\mathrm{g}p{)}^{1+r+\nu }\right)$. Here, the consistency rate is not affected severely, but the ${\ell }_{\mathrm{\infty }}$-norm of transition matrices can diverge with the sample size.

Remark 4. The proposed procedure can be also applied to low-dimensional time series. For example, with $p=c{n}^a$ for positive constants $c$ and a, the probability bounds derived in Lemma 3 would be sharp enough to achieve the desired consistency results similar to those for the high-dimensional case in Theorem 3.

Remark 5. Selecting the tuning parameter $\eta$ in Assumption A5 is challenging in practice, since the distance between candidate break points from the initial estimation to the true break points is unknown. Thus, while the specified tuning parameters achieve optimal consistency rates for locating the break points, they are not practical in finite sample settings and applications. To overcome this challenge, we can instead consider a fixed tuning parameter $\eta$ in all the candidate segments as $\eta =C{m}_0\sqrt{{\mathrm{\Delta }}_n^{\star }\mathrm{l}\mathrm{o}\mathrm{g}p}/n$ for some large enough positive constant $C>0$, where ${\mathrm{\Delta }}_n^{\star }={\mathrm{m}\mathrm{a}\mathrm{x}}_{1\le j\le m_0}\left|t_{j+1}-t_j\right|$. We can still show the consistency of the proposed procedure in (12) with this fixed $\eta$. However, the consistency rate for locating the break points using this fixed rate would be different from that achieved in Theorem 3. For finite $m_0$, the rate would be of order $(n\mathrm{l}\mathrm{o}\mathrm{g}p{)}^{1/2+\nu }$ for some positive $\nu >0$ as compared to the rate $(\mathrm{l}\mathrm{o}\mathrm{g}n\mathrm{l}\mathrm{o}\mathrm{g}p{)}^{1+\nu }$ when the tuning parameters are selected as in Assumption A5. In all simulation studies and real data applications, $\eta$ was selected according to the fixed rate mentioned in this remark.

When the number of change points at the first stage $\widehat{m}=\left|{\widehat{𝒜}}_n\right|$ is large, the second screening step for finding the minimizer of the information criterion IC could be computationally demanding. In order to reduce the computational cost, we can use a backward elimination algorithm (BEA), similar to Chan et al. (2014), to approximate the optimal point at a lower computational cost. The idea of this algorithm is to start with the full set of selected points, ${\widehat{𝒜}}_n$, and remove an unnecessary point in each step, until no further reduction is possible. See Appendix C for details.

While the proposed BEA algorithm is not guaranteed to achieve the minimizer of (12), it only requires to search ${\widehat{m}}^2$ sets in order to find the break points. The algorithm thus results in a significant reduction in the computational time when $\widehat{m}$ is large. The proposed BEA algorithm was used in simulation studies of Section 7 and real data examples of Section 8, and seems to perform very well in all cases.

4.1. Comparison with Other Methods

Before discussing the parameter estimation consistency in Section 5, in this section, we compare our rates of consistency for break point estimation with related methods. That is because existing approaches do not provide consistent parameter estimation. By Theorem 3, our rate is of order $m_{0}n{\gamma }_n{d}_n^{\star 2}$. Thus, the exact rate depends on values of $m_0,{\gamma }_n$, and $d_n^{\star }$, which are governed by Assumptions A1–A5.

Chan et al. (2014) consider structural break detection in univariate AR processes. When $m_0$ is finite, their rate of consistency for estimating the location of break points is of order $\mathrm{l}\mathrm{o}\mathrm{g}n$ under the assumption that the distance between two consecutive break points is at least $(\mathrm{l}\mathrm{o}\mathrm{g}n{)}^{1+\nu }$ for some positive $\nu >0$. Our method can be seen as an extension of this work to high dimensions: choosing ${\gamma }_n=\mathrm{l}\mathrm{o}\mathrm{g}n\mathrm{l}\mathrm{o}\mathrm{g}p/n$, our rate of consistency is of order $\mathrm{l}\mathrm{o}\mathrm{g}n\mathrm{l}\mathrm{o}\mathrm{g}p{d}_n^{\star 2}$ assuming that consecutive break point distances are at least of the same order. The additional factor $\mathrm{l}\mathrm{o}\mathrm{g}p{d}_n^{\star 2}$ quantifies the complexity of the problem in the high-dimensional setting. In the univariate case, or even in multivariate case with fixed dimension $p$, our method achieves the same rates of consistency as Chan et al., i.e., $\mathrm{l}\mathrm{o}\mathrm{g}n$.

The test procedure of Aue et al. (2009) can locate break points in the covariance structure of multivariate time series, and achieve a rate of consistency of order $\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{l}\mathrm{o}\mathrm{g}n$. Interestingly, we can also set ${\gamma }_n=\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{l}\mathrm{o}\mathrm{g}n\mathrm{l}\mathrm{o}\mathrm{g}p/n$. In this case, for finite number of break points, our rates for consistently locating the break points can be $\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{l}\mathrm{o}\mathrm{g}n\mathrm{l}\mathrm{o}\mathrm{g}p{d}_n^{\star 2}$, which differs with the rate derived in Aue et al. (2009) by a factor of order $\mathrm{l}\mathrm{o}\mathrm{g}p{d}_n^{\star 2}$. This factor is, again, due to the fact in our analysis the number of time series, $p$, is allowed to grow exponentially with $n$. In contrast, the analysis in Aue et al. (2009) does not directly take the rate of increase in $p$ into account. For fixed $p$, both methods give similar rates for locating the break points, i.e., $\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{l}\mathrm{o}\mathrm{g}n$.

The recent proposal of Cho and Fryzlewicz (2015) uses a CUSUM statistic to identify the number of break points together with their locations. The proposal of Cho and Fryzlewicz (2015) is the closest in spirit to our approach as it also identifies structural breaks in high-dimensional time series. However, aside from consistent estimation of model parameters discussed in the Introduction, the two methods have a number of differences. First, in Cho and Fryzlewicz (2015), the number of time series $p$ is allowed to grow polynomially with the number of time points $T$. In contrast, we allow $p$ to grow exponentially with $T$. Second, the minimum distance between two consecutive break points allowed in Cho and Fryzlewicz (2015) is of order ${\mathrm{\Delta }}_n=T^{\psi }$ for some $\psi \in (6/\mathrm{7,1})$. In our setting, depending on the sparsity of the model, this rate could be as low as ${\mathrm{\Delta }}_n=(\mathrm{l}\mathrm{o}\mathrm{g}n\mathrm{l}\mathrm{o}\mathrm{g}p{)}^{1+\nu }{d}_n^{\star 2}$ for some positive $\nu >0$. Therefore, for sparse enough VARs, our method can detect considerably closer break points. Finally, our rate of consistency for estimating the break point locations is of order $m_{0}n{\gamma }_n{d}_n^{\star 2}$, which could be as $\mathrm{l}\mathrm{o}\mathrm{w}$ as $(\mathrm{l}\mathrm{o}\mathrm{g}n\mathrm{l}\mathrm{o}\mathrm{g}p{)}^{1+\nu }$ if we set ${\gamma }_n=\mathrm{l}\mathrm{o}\mathrm{g}n\mathrm{l}\mathrm{o}\mathrm{g}p/n$ and $d_n^{\star }=O\left((\mathrm{l}\mathrm{o}\mathrm{g}n\mathrm{l}\mathrm{o}\mathrm{g}p{)}^{\nu /2}\right)$. Cho and Fryzlewicz (2015) can achieve a similar rate when ${\mathrm{\Delta }}_n$ is of order $T$. However, when ${\mathrm{\Delta }}_n$ is smaller and is of order $T^{\psi }$ for some $\psi \in (6/\mathrm{7,1})$, Cho and Fryzlewicz’s rate of consistency will be of order $T^{2-2\psi }$, which is larger than our logarithmic rate. More generally, comparing our rate of consistency with the rate in Cho and Fryzlewicz (2015) is difficult, since our rate explicitly depends on the sparsity of the model while this sparsity level does not appear in their analysis.

5. Consistent Parameter Estimation

Theorems 2 and 3 suggest that we can consistently estimate the location (and number) of change points in high-dimensional time series. However, even with such estimates, consistent estimation of ${\mathrm{\Phi }}^{(.,j)}$ parameters in non-stationary high-dimensional VAR models remains challenging. This challenge primarily stems from the inexact nature of structural break estimation. More specifically, while we know that the estimated break points are in some neighborhood of the true break points, they are not guaranteed to segment the time series into stationary components. A more careful analysis is thus needed to ensure the consistency of VAR parameters.

The key to our approach for consistent parameter estimation is that Theorems 2 and 3 imply that removing the selected break points together with large enough $R_n$-radius neighborhoods will also remove the true break points. We can thus obtain stationary segments at the cost of discarding some portions of the observed time series. Theorem 2 suggests that the radius $R_n$ can be as small as $n{\gamma }_n$. However, based on Theorem 3, in order not to keep any redundant break points, $R_n$ needs to be at least $B{m}_{0}n{\gamma }_n{d}_n^{\star 2}$ for a large value $B>0$.

Given the results in Theorems 3, suppose, without loss of generality, that we have selected $m_0$ break points using the procedure developed in Section 4. Denote these estimated break points by ${\tilde{t}}_1,\dots ,{\tilde{t}}_{m_0}$. Then, by Theorem 3,

$$\mathbb{P}\left(\underset{1\le j\le m_0}{\mathrm{m}\mathrm{a}\mathrm{x}}\left|{\tilde{t}}_j-t_j\right|\le R_n\right)\to 1$$

as $n\to \mathrm{\infty }$. Denote $r_{j1}={\tilde{t}}_j-R_n-1,r_{j2}={\tilde{t}}_j+R_n+1$ for $j=1,\dots ,m_0$, and set $r_{02}=q$ and $r_{\left(m_0+1\right)1}=T$. Further, define the intervals $I_{j+1}=\left[r_{j2},r_{(j+1)1}\right]$ for $j=0,\dots ,m_0$. The idea is to form a linear regression on ${\cup }_{j=0}^{m_0}{I}_{j+1}$ and estimate the auto-regressive parameters by minimizing an ${\ell }_1$-regularized least squares criterion. More specifically, denoting ${\mathbf{y}}_{\left({\ell }_{\mathrm{m}\mathrm{i}\mathrm{n}},{\ell }_{\mathrm{m}\mathrm{a}\mathrm{x}}\right)}={\left(y_{{\ell }_{\mathrm{m}\mathrm{i}\mathrm{n}}}^{\prime },\dots ,y_{{\ell }_{\mathrm{m}\mathrm{a}\mathrm{x}}}^{\prime }\right)}^{\prime },\mathrm{ }{\mathbf{X}}_{\left({\ell }_{\mathrm{m}\mathrm{i}\mathrm{n}},{\ell }_{\mathrm{m}\mathrm{a}\mathrm{x}}\right)}={\left(Y_{{\ell }_{\mathrm{m}\mathrm{i}\mathrm{n}}}^{\prime },\dots ,Y_{{\ell }_{\mathrm{m}\mathrm{a}\mathrm{x}}}^{\prime }\right)}^{\prime }$, and ${\mathbf{e}}_{\left({\ell }_{\mathrm{m}\mathrm{i}\mathrm{n}},{\ell }_{\mathrm{m}\mathrm{a}\mathrm{x}}\right)}={\left({\zeta }_{{\ell }_{\mathrm{m}\mathrm{i}\mathrm{n}}}^{\prime },\dots ,{\zeta }_{{\ell }_{\mathrm{m}\mathrm{a}\mathrm{x}}}^{\prime }\right)}^{\prime }$, we form the following linear regression:

$$\left(\begin{array}{c}{\mathbf{y}}_{\left(q,r_{11}\right)}\\ {\mathbf{y}}_{\left(r_{12},r_{21}\right)}\\ ⋮\\ {\mathbf{y}}_{\left(r_{m_{0}1},T\right)}\end{array}\right)=\left(\begin{array}{cccc}{\mathbf{X}}_{\left(q-1,r_{11}-1\right)}& 0& \dots & 0\\ 0& {\mathbf{X}}_{\left(r_{12}-1,r_{21}-1\right)}& \dots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \dots & {\mathbf{X}}_{\left(r_{m_{0}2}-1,T-1\right)}\end{array}\right)\left(\begin{array}{c}{\beta }_1^{\prime }\\ {\beta }_2^{\prime }\\ ⋮\\ {\beta }_{m_0+1}^{\prime }\end{array}\right)+\left(\begin{array}{c}{\mathbf{e}}_{\left(q,r_{11}\right)}\\ {\mathbf{e}}_{\left(r_{12},r_{21}\right)}\\ ⋮\\ {\mathbf{e}}_{\left(r_{m_{0}1},T\right)}\end{array}\right)$$ (13)

This regression can be written in compact form as ${𝒴}_{\mathbf{r}}={𝒳}_{\mathbf{r}}B+E_{\mathbf{r}}$, or, in a vector form, as

$${\mathbf{Y}}_{\mathrm{r}}={\mathbf{Z}}_{\mathbf{r}}\mathbf{B}+{\mathbf{E}}_{\mathbf{r}}$$ (14)

where ${\mathbf{Y}}_{\mathbf{r}}=\mathrm{v}\mathrm{e}\mathrm{c}\left({𝒴}_{\mathbf{r}}\right),{\mathbf{Z}}_{\mathbf{r}}=I_p\otimes {𝒳}_{\mathbf{r}},\mathbf{B}=\mathrm{v}\mathrm{e}\mathrm{c}\left(B\right),{\mathbf{E}}_{\mathbf{r}}=\mathrm{v}\mathrm{e}\mathrm{c}\left(E_{\mathbf{r}}\right)$, and $\mathbf{r}$ is the collection of all $r_{j1}$ and $r_{j2}$ for $j=0,\dots ,m_0+1$. Let $\tilde{\pi }=\left(m_0+1\right)p^{2}q,N_j=\mathrm{l}\mathrm{e}\mathrm{n}\mathrm{g}\mathrm{t}\mathrm{h}\left(I_{j+1}\right)=r_{(j+1)1}-r_{j2}$ for $j=0,\dots ,m_0$ and $N={\sum }_{j=1}^{m_0}{N}_j$. Then, ${\mathbf{Y}}_{\mathbf{r}}\in {\mathbb{R}}^{Np\times 1},{\mathbf{Z}}_{\mathbf{r}}\in {\mathbb{R}}^{Np\times \tilde{\pi }},\mathbf{B}\in {\mathbb{R}}^{\tilde{\pi }\times 1}$, and ${\mathbf{E}}_{\mathbf{r}}\in {\mathbb{R}}^{Np\times 1}$. We estimate the VAR parameters by solving

$$\widehat{\mathbf{B}}={\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}\mathrm{n}}_{\mathbf{B}}{N}^{-1}{∥{\mathbf{Y}}_{\mathbf{r}}-{\mathbf{Z}}_{\mathbf{r}}\mathbf{B}∥}_2^2+{\rho }_n\parallel \mathbf{B}{\parallel }_1.$$ (15)

We obtain the following consistency result.

Theorem 4. Suppose $A1-A5$ hold and $m_0$ is unknown and $R_n=B{m}_{0}n{\gamma }_n{d}_n^{\star 2}$. Assume also that ${\Delta }_n>\epsilon n$ for some large positive $\epsilon >0$ and ${\rho }_n=C\sqrt{\frac{\mathrm{l}\mathrm{o}\mathrm{g}\tilde{\pi }}{N}}$ for large enough $C>0$. (Note that $N/n=O\left(1\right)$.) Then, as $n\to +\mathrm{\infty }$, the minimizer $\widehat{\mathit{B}}$ of (15) satisfies

$$\parallel \widehat{\mathbf{B}}-\mathrm{\Phi }{\parallel }_{\ell }=O_p\left({\left(d_n^{\star }\right)}^{1/\ell }{\rho }_n\right)\hspace{1em}\mathit{\text{for}}\hspace{1em}\ell =\mathrm{1,2}\text{. }$$

Theorem 4 is proved in Appendix B, where it is also shown that, if $m_0$ is known, then it is enough to set $R_n=n{\gamma }_n$. The next remark emphasizes that removing the $R_n$-radius of estimated break points and fast rates of convergence play a crucial role in consistent parameter estimation.

Remark 6. Existing approaches for change point detection in multivariate and high-dimensional settings, including ours and the proposal of Cho and Fryzlewicz (2015), are only able to consistently estimate the relative location of change points, $t_j/T$. As a result, using the estimated change points to partition the time series into ‘stationary’ segments, and then estimating the VAR parameters of each segment using a regularized estimation procedure may lead to inferior, or even inconsistent, estimates of VAR parameters. On the one hand, using our sharper rates of consistency for change point detection, it is indeed possible to verify parameter estimation consistency without removing any portion of the data. However, the consistency rate will be different (worse in some settings) due to having misspecified models in the intervals of type $\left[{\tilde{t}}_j,t_j\right]$ or $\left[t_j,{\tilde{t}}_j\right],j=\mathrm{1,2},\dots ,m_0$. Rates for such a procedure are provided in Appendix F. On the other hand, the slower rates of consistency in Cho and Fryzlewicz (2015) may result in inconsistent estimates of VAR parameters. This is because if the distance between the break point $t_j$ and its estimation ${\tilde{t}}_j$ is large relative to the minimum distance between two consecutive break points, then the restricted eigenvalue (RE) condition may not hold for that segment. As discussed in Bickel et al. (2009), the RE condition is critical for establishing the consistency of parameter estimation in high-dimensional settings. To see this, note that the consistency rate for locating break points using the method of Cho and Fryzlewicz (2015) is of order $T^{2-2\psi }$ with $\psi \in (6/\mathrm{7,1})$. Now, if, similar to our setting, the minimum distance between two consecutive break points is of order $(\mathrm{l}\mathrm{o}\mathrm{g}T\mathrm{l}\mathrm{o}\mathrm{g}p{)}^{1+\nu }$ for some $\nu >0$, then the estimated break points might be far from the true break points since $T^{2-2\psi }/(\mathrm{l}\mathrm{o}\mathrm{g}T\mathrm{l}\mathrm{o}\mathrm{g}p{)}^{1+\nu }$ may diverge. This violates the RE condition and may result in inconsistent parameter estimation using $L_1$-regularization.

6. Tuning Parameter Selection

Our proposed three-stage procedure relies on multiple tuning parameters, ${\lambda }_{1,n},{\lambda }_{2,n},{\eta }_n,{\omega }_n,{\rho }_n$ and $R_n$. Although the theoretical rates for these parameters are derived in previous sections, their selection in finite sample applications needs further discussion. In this section, we provide guidance on selecting these tuning parameters.

• ${\lambda }_{1,n}$: We select ${\lambda }_{1,n}$ by cross-validation. Let $𝒯$ be a set of equally spaced time points, starting from a randomly selected initial time point. The data without observations in $𝒯$ can be used in the first step of our procedure to estimate $\mathrm{\Theta }$ for a range of values for ${\lambda }_{1,n}$. The estimated $\mathrm{\Theta }$ are then used to predict the series at time points in $𝒯$. The value of ${\lambda }_{1,n}$ which minimizes the mean squared prediction error over $𝒯$ is the cross-validated choice of ${\lambda }_{1,n}$.

• ${\lambda }_{2,n}$: As described previously, the rate for ${\lambda }_{2,n}$ vanishes fast as $T$ increases. Thus for simplicity, we suggest setting ${\lambda }_{2,n}$ to zero. This choice was used in all of the numerical analyses in the paper—both simulations studies and real data applications—and seems to give satisfactory results.

• ${\eta }_n$: Following Remark 5, we suggest a fixed rate for this parameter, and, based on the theoretical rate in Remark 5, set ${\eta }_n=(\mathrm{l}\mathrm{o}\mathrm{g}n\mathrm{l}\mathrm{o}\mathrm{g}p)/n$. This choice was used in all of the numerical analyses in the paper and provides very good results.

• ${\omega }_n$: Selecting ${\omega }_n$ is difficult, since it depends on how large changes in the VAR parameters must be in order to consider them as break points in finite sample applications. A similar tuning parameter appears in other work on the topic, including Cho and Fryzlewicz (2015) and Chan et al. (2014). Following Assumption A4, in our analysis we set ${\omega }_n=C(\mathrm{l}\mathrm{o}\mathrm{g}n\mathrm{l}\mathrm{o}\mathrm{g}p{)}^{3/2}$ for some $C>0$. The range for the constant $C$ used in our analysis is within the interval [0, 1].

• ${\rho }_n$: Finally, we select the tuning parameter ${\rho }_n$ for parameter estimation as the minimizer of the combined Bayesian Information Criterion (BIC) for all the segments. Following Lütkepohl (2005) and Zou et al. (2007), for $j=0,\dots ,\tilde{m}$ we define the BIC on the interval $I_{j+1}=$ $\left[r_{j2},r_{(j+1)1}\right]$ as

  $$\mathrm{B}\mathrm{I}\mathrm{C}\left(j,{\rho }_n\right)=\mathrm{l}\mathrm{o}\mathrm{g}\left(\mathrm{d}\mathrm{e}\mathrm{t}{\widehat{\mathrm{\Sigma }}}_{\epsilon ,j}\right)+\frac{\mathrm{l}\mathrm{o}\mathrm{g}\left(r_{(j+1)1}-r_{j2}\right)}{\left(r_{(j+1)1}-r_{j2}\right)}{∥{\widehat{\beta }}_{j+1}∥}_0,$$

  where ${\widehat{\mathrm{\Sigma }}}_{\epsilon ,j}$ is the residual sample covariance matrix with $\widehat{\mathbf{B}}$ estimated in (15), and ${∥{\widehat{\beta }}_{j+1}∥}_0$ is the number of nonzero elements in ${\widehat{\beta }}_{j+1}$; then ${\rho }_n$ is selected as

  $${\widehat{\rho }}_n={\text{argmin}}_{{\rho }_n}\sum _{j=0}^{\tilde{m}}\text{BIC}\left(j,{\rho }_n\right).$$ (16)
• $R_n$: Recall from Section 5 that we need to remove the selected break points together with their $R_n$-radius neighborhood before estimating the parameters using (15). In practice, the radius $R_n$ needs to be estimated. However, a closer look at the proof of Theorem 3 together with Assumption A4 suggest that ${\omega }_n$ can be chosen as an upper bound for the selection radius $R_n$. In other words, in the statement of Theorem 3, the radius $B{m}_{0}n{\gamma }_n{d}_n^{\star 2}$ can be replaced by ${\omega }_n$ and the result would still hold. Formally, as $n\to \mathrm{\infty }$,

  $$\mathbb{P}\left(\underset{1\le j\le m_0}{\mathrm{m}\mathrm{a}\mathrm{x}}\left|{\tilde{t}}_j-t_j\right|\le {\omega }_n\right)\to 1.$$

  Therefore, in all simulation scenarios and data applications, we set $R_n={\omega }_n$.

Additional discussions on tuning parameters are given in Section 7.4, where we investigate the robustness of our procedure to the recommended tuning parameters.

7. Simulation Studies

7.1. Preliminaries

We evaluate the performance of the proposed three-stage estimator with respect to both structural break detection and parameter estimation. In this section, we consider three simulations scenarios. The first two scenarios examine low-dimensional settings, with $T=300,p=20,q=1$ and $m_0=2$; the third scenario examines a high-dimensional setting with $T=80,p=100,q=1$ and $m_0=1$. Detail of simulation settings in each scenario are explained in Section 7.2 and Appendix D, where results from two additional simulation settings are also presented¹. In all, except Scenario 5 in Appendix D, results are averaged over 100 randomly generated data sets with mean zero and ${\mathrm{\Sigma }}_{\epsilon }=0.01I_T;$ a non-diagonal ${\mathrm{\Sigma }}_{\epsilon }$ is considered in Scenario 5.

For structural break detection, we compare our method with the sparsified binary segmentation-multivariate time series (SBS-MVTS) approach of Cho and Fryzlewicz (2015). For both methods, we report the locations of the estimated break points and the percentage of simulations where each break point is correctly identified. This percentage is calculated as the proportion of simulations, where selected break points are close to each of the true break points. More specifically, a selected break point is counted as a ‘success’ for the first true break point, $t_1$, if it is in the interval $\left[0,t_1+0.5\left(t_2-t_1\right)\right)$; similarly, a selected break point is counted as a ‘success’ for the second true break point, $t_2$, if it falls in the interval $\left[t_1+0.5\left(t_2-t_1\right),T\right]$. For our method, we also report the percentage of cases where the break point is correctly estimated in the $R_n$-radius of truth. The results are reported in Table 1.

Table 1:

Mean and standard deviation of estimated break point locations, the percentage of simulation runs where break points are correctly detected (selection rate)

	method	break point	truth	mean	std	selection rate
Scenario 1
	SBS-MVTS	1	0.3333	0.3513	0.039	0.85
		2	0.6667	0.6425	0.0558	0.87
	Our method	1	0.3333	0.3318	0.0104	1
Scenario 2		2	0.6667	0.6584	0.0153	1
	SBS-MVTS	1	0.1667	0.31	0.0802	0.94
		2	0.8333	0.6414	0.102	0.68
	Our method	1	0.1667	0.1763	0.022	1
Scenario 3		2	0.8333	0.7971	0.023	1
	SBS-MVTS	1	0.5	0.4688	0.1504	0.64
	Our method	1	0.5	0.4975	0.0223	1

For parameter estimation, we evaluate the performance of our procedure by reporting the (relative) estimation error, as well as true and false positive rates, calculated by comparing the nonzero patterns of true and estimated coefficient matrices. Since existing procedures do not provide consistent estimates of piecewise stationary VAR parameters, we compare our procedure to a procedure based on the state-of-the-art methods in high-dimensional change point detection and VAR estimation. More specifically, we use the estimated change points from SBS-MVTS to partition the time series into ‘stationary’ segments, without removing the $R_n$-radius of selected break points. We then use our ${\ell }_1$-penalized procedure (15) to estimate the VAR parameters in each segment. The results in Table 2 clearly show the advantages of our procedure and highlight the importance of removing the $R_n$-radius of selected break points in the third step of our procedure; see Section 7.2 for details.

Table 2:

Results of parameter estimation for all three simulation scenarios. The table shows mean and standard deviation of relative estimation error (REE), true positive rate (TPR), and false positive rate (FPR) for estimated coefficients.

	Method	REE	SD(REE)	TPR	FPR
Simulation 1	Our Method	0.3385	0.0282	1.00	0.036
	SBS-MVTS	0.4113	0.2678	1.00	0.039
Simulation 2	Our Method	0.654	0.052	0.72	0.03
	SBS-MVTS	0.901	0.154	0.63	0.03
Simulation 3	Our Method	0.6422	0.0234	0.91	0.003
	SBS-MVTS	0.8023	0.089	0.67	0.003

7.2. Simulation Scenarios

Simulation Scenario 1 (Simple $\mathbf{\Phi }$ and break points close to the center).

In the first scenario, the autoregressive coefficients have the same structure but different values; see Appendix D for details. In this scenario, $t_1=100$ and $t_2=200$, which means that break points are not close to the boundaries.

Before comparing our procedure with the SBS-MVTS method of Cho and Fryzlewicz (2015), we take a closer look at the first two steps of our procedure in this simulation setting. To this end, we plot the break points in one simulated data sets in the left panel of Figure 3. As expected from Theorem 2, more than 2 break points are detected using the first stage estimator. However, some break points are indeed in a small neighborhood of true change points. Our second-stage screening procedure eliminates the extra candidate points, leaving only the two closest points to the true change points. The final selected points in all 100 simulation runs are shown in the right panel of Figure 3, and confirm the consistency of the proposed method in selecting the break points.

Figure 3:

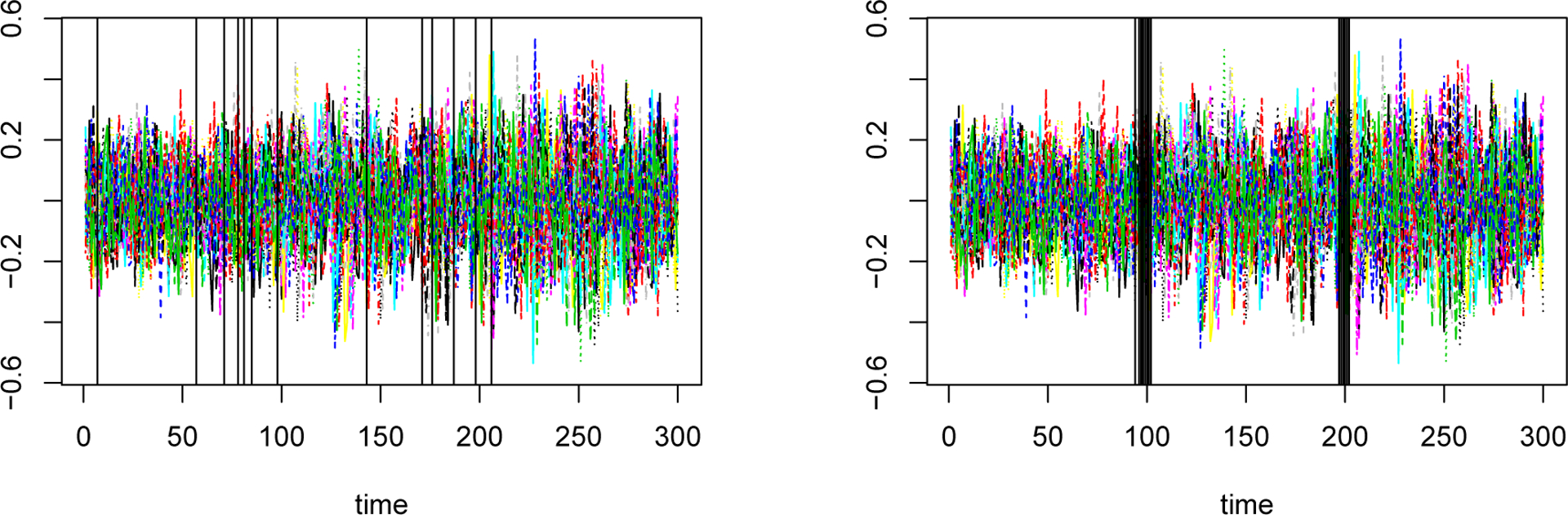
Left: Estimated break points from the first stage of our proposed procedure (Equation 5) for a single runs in Simulation Scenario 1; on average ~13 points are selected in the first stage. Right: Final selected break points for all 100 simulation runs in Simulation Scenario 1.

Simulation Scenario 2 (Simple $\mathbf{\Phi }$ and break points close to the boundaries).

The coefficient matrices in this scenario are similar to those in Scenario 1. However, the break points are closer to the boundaries. Specifically, $t_1=50$ and $t_2=250$.

Simulation Scenario 3 (High-dimensional setting with simple $\mathbf{\Phi }$).

In this scenario, $T=80,\mathrm{ }p=100$ and there is a single break point at $t=40$. The autoregressive coefficients have the same structure as the first two VAR matrices in Scenario 1.

7.3. Simulation Results

Mean and standard deviations of locations of selected break points, relative to the sample size $T$ — i.e., ${\tilde{t}}_1/T$ and ${\tilde{t}}_2/T$ — for all simulation scenarios are summarized in Table 1. The results clearly indicate that, in all settings, our procedure accurately detects the number of break points and their locations. They also suggest that our procedure produces more accurate estimates of break points than the SBS-MVTS method. The advantage of our method is more pronounced when comparing the percentage of times where the break points are correctly detected using each method.

In addition to overall improvement in detecting break points, the simulation results also indicate that our procedure offers significant advantages over SBS-MVTS in in Simulation Scenarios 2 and 3. In Scenario 2, where the break points are closer to the boundaries, the detection performance of our procedure does not deviate much from Scenario 1, but the performance on locating the break points seems to be slightly worse. This is in stark contrast to SBS-MVTS, which gives worse estimates of break points in this simulation setting. Similarly, our procedure continues to perform well in the high-dimensional setting of Scenario 3, whereas SBS-MVTS performs considerably worse than Scenario 1.

Table 2 summarizes the results for autoregressive parameter estimation in all three simulation scenarios. The table shows mean and standard deviation of relative estimation error (REE), as well as true positive (TPR) and false positive rates (FPR) of the estimates. The results suggest that our method also performs well in terms of parameter estimation. However, true positive rates are low in Scenario 2. One potential explanation for the reduced TPR in this scenario is that the first and third segments used for estimation in this scenario contain less than 40 time points, compared to 90 time points in Scenario 1. This shorter length makes it harder to estimate the parameters and correctly select zero and nonzero coefficients. Comparing our procedure and the naïve procedure based on SBS-MVTS, introduced in Section 7.1, indicates that our procedure is superior in all simulation scenarios, both in terms of estimation error and variable selection. Since the two methods use the same estimation procedure, this advantage can be attributed to our proposal, and, in particular, to removing the $R_n$-neighborhood of the estimator break points. These findings affirm our theoretical results.

7.4. Robustness of Tuning Parameter Selection

To address the challenges of selecting 6 tuning parameters for our method, in Section 6 we proposed data-driven procedures for selecting ${\lambda }_{1,n}$ (cross-validation), ${\rho }_n$ (minimizing BIC), and $R_n$. We also made recommendations on how to select the other three tuning parameters. To assess the robustness of our method to these recommendations, in this section, we conduct two simulation studies to investigate how the method performs with other choices of ${\lambda }_{2,n}$ and ${\eta }_n$. We also propose a data-driven procedure for choosing ${\omega }_n$ and conduct a third simulation to check its performance. All three additional simulation cases are repeated 100 times and the results are averaged over these iterations.

The simulation settings for checking the robustness with respect to ${\lambda }_{2,n}$ and ${\eta }_n$ are the same as Simulation 1. In each iteration of the first simulation (Case 1), we choose ${\lambda }_{2,n}$ uniformly randomly from the interval $\left(0,n^{-3/2}\sqrt{\mathrm{l}\mathrm{o}\mathrm{g}p/{\gamma }_n}\right)$, instead of simply setting it to zero as recommended in Section 6. (This interval corresponds to the rate assumed in Theorem 2, with constants 0 and 1.) Similarly, in the second simulation (Case 2), we choose ${\eta }_n$ as ${\eta }_n=c(\mathrm{l}\mathrm{o}\mathrm{g}n\mathrm{l}\mathrm{o}\mathrm{g}p)/n$ with the constant $c$ chosen uniformly randomly from the interval (0.5, 1.5) instead of setting it to $c=1$ as recommended in Section 6. The results for break point detection are presented in Table 3. Comparing these with our previous results on Simulation 1 reported in Table 1, we see no significant changes which confirm the robustness of our method with respect to selecting these two tuning parameters.

Table 3:

Sensitivity analysis for tuning parameters. The table shows mean and standard deviation of estimated break point locations, as well as the percentage of simulation runs where break points are correctly detected (selection rate) for the three simulations in Section 7.4.

	break point	truth	mean	std	selection rate
Case 1	1	0.3333	0.3302	0.0108	1
	2	0.6667	0.6715	0.0088	1
Case 2	1	0.3333	0.3313	0.0098	1
	2	0.6667	0.6704	0.0082	1
Case 3	1	0.3333	0.3313	0.0098	1
	2	0.6667	0.6702	0.0086	1

For the last tuning parameter ${\omega }_n$, the recommendation in Section 6 was to set ${\omega }_n=C(\mathrm{l}\mathrm{o}\mathrm{g}n\mathrm{l}\mathrm{o}\mathrm{g}p{)}^{3/2}$ for some $C>0$. The range for the constant $C$ used in our analysis is within the interval [0, 1]. Here, we propose a data-driven method to select ${\omega }_n$. The idea is to first finish the backward elimination algorithm (BEA) until no break points are left. Then, we cluster the jumps in the objective function $L_n$ in Equation (10) into two subgroups, small and large. We then use the minimum value in the large subgroup as the optimal value for ${\omega }_n$. Details of this approach are presented in Appendix G. Intuitively, if removing a break point leads to a small jump in $L_n$, then the break point is likely redundant. In contrast, larger jumps correspond to true break points. The smallest jump in the second group is thus a reasonable candidate for ${\omega }_n$. The detailed algorithm in Appendix G also includes a provision for cases with no break points.

To assess the performance of the above data-driven procedure, in our third simulation in this section (Case 3), we repeat Simulation 1 but use the above procedure to choose ${\omega }_n$. The results in Table 3 show that this approach performs satisfactorily.

8. Applications

8.1. EEG Data

In this section, we revisit the EEG data discussed in Section 1. Recall that the data consists of electroencephalogram (EEG) signals recorded at 18 locations on the scalp of a patient diagnosed with left temporal lobe epilepsy during an epileptic seizure. The sampling rate is 100 Hz and the total number of time points per EEG is $T=\mathrm{22,768}$ over 228 seconds. The time series for all 18 EEG channels are shown in Figure 1. The seizure was estimated to take place at $t=85s$. Examining the EEG plots, it can be seen that the magnitude and the volatility of signals change simultaneously around that time. To speed up the computations, we select ten observation per second and reduce the total time points to $T=2276$.

Data from one of the EEG channels (P3) was previously used by Davis et al. (2006) and Chan et al. (2014) for detecting structural breaks in the time series. As a comparison, we apply the SBS-MVTS method of Cho and Fryzlewicz (2015) as well as our procedure to detect the break points based on changes in all 18 time series. Table 4 shows the location of the selected break points using the Auto-PARM method of Davis et al. (2006) and the two-stage procedure of Chan et al. (2014), based on data from channel P3, as well as those estimated using our method and SBS-MVTS based on all 18 channels. The selected break points by our method are also shown in Figure 4.

Table 4:

Location of break points detected in the EEG data using four estimation methods. The locations are rounded to the closest integer.

Methods	1	2	3	4	5	6	7	8	9	10	11
Auto–PARM	86	90	106	121	133	149	162	175	206	208	326
Chan et al. (2014)	84	106	120	134	155	177	206	225	–	–	–
SBS–MVTS	84	107	114	126	133	143	157	176	–	–	–
Our method	83	111	114	121	130	138	144	162	–	–	–

Figure 4:

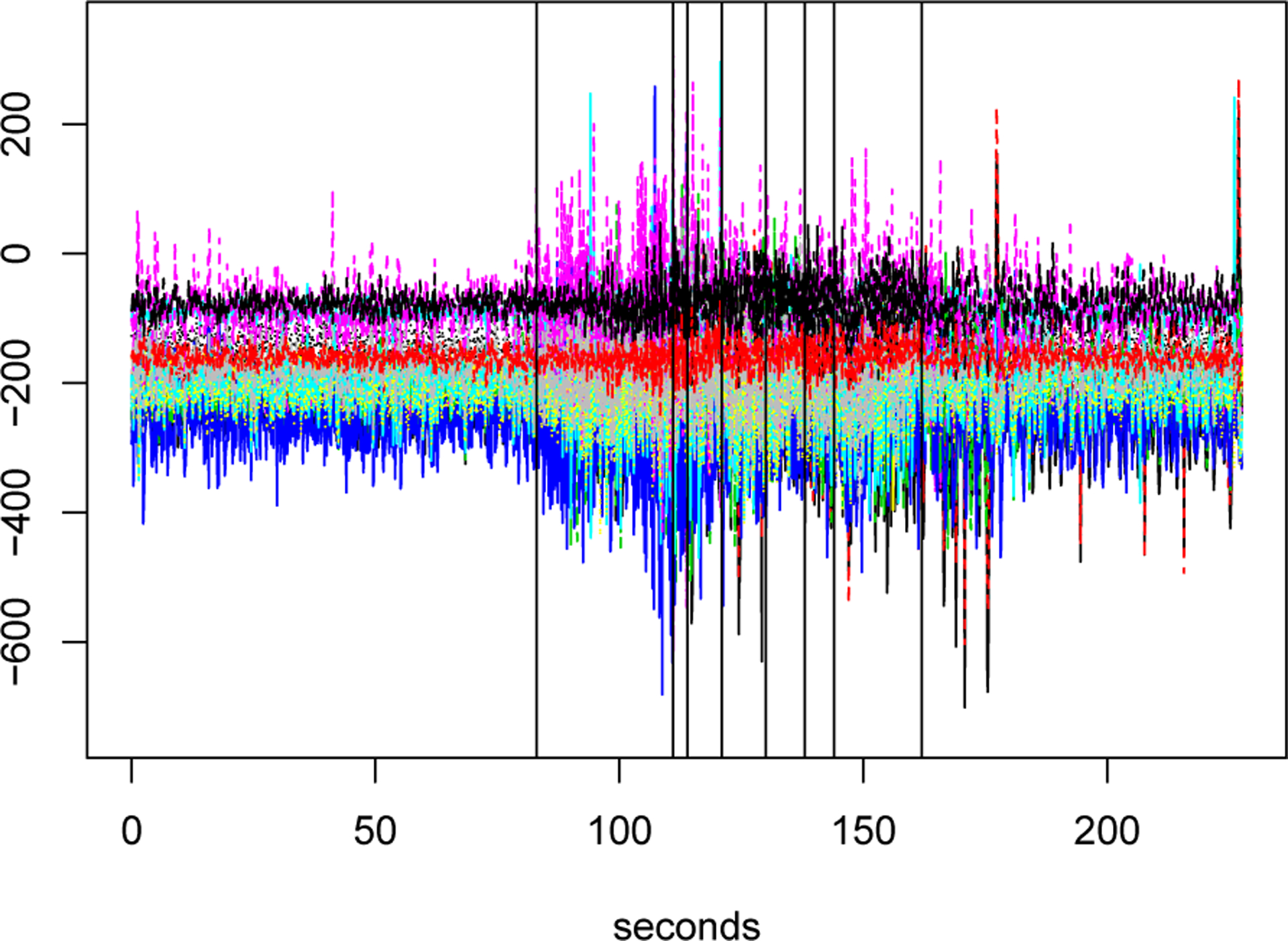
EEG data over 228 seconds with the 8 selected break points using our method

Our method detects a break point at $t=83$, which is close to the seizure time identified by neurologists. Most other break points selected by our method are also close to those detected by the two univariate approaches and SBS-MVTS. However, the main advantage of our method is that it also provides consistent estimates of VAR parameters. As shown in Figure 2, these estimates can be used to gain novel insight into changes in mechanisms of neuronal interactions before and after seizure.

Given the proximity of selected break points between $t=83$ and $t=162$, in order to obtain the networks in Figure 2, we consider the time segments before and after these two time points. More specifically, using the procedure of Section 5, we discard observations in the $R_n$ radius before $t=83$ and after $t=162$ in order to ensure the stationarity of remaining observations. We then use the ${\ell }_1$-penalized least square estimator of (15), with tuning parameter selected by BIC (16), to obtain estimates of VAR parameters before and after seizure. Network edges in Figure 2 correspond to nonzero estimated coefficients larger than 0.05 in magnitude. This thresholding is motivated by the known over-selection property of lasso (Shojaie et al. 2012) and is used to improve the interpretability of estimated networks.

8.2. Yellow Cab Demand in NYC

As a second example, we apply our method and SBS-MVTS to the yellow cab demand data in New York City (NYC), obtained from the NYC Taxi & Limousine Commission’s website². Here, the number of yellow cab pickups are aggregated spatially over the zipcodes and temporally over 15 minute intervals during April 16th, 2014. We only consider the zipcodes with more than 50 cab calls to obtain a better approximation using linear VAR models. This results in time series for 39 zipcodes observed over 96 time points. To identify structural break points, we consider a differenced version of the data in order to remove first order non-stationarities.

Table 5 shows the 5 break points detected by our method, along with two break points identified by SBS-MVTS; the differenced time series and detected break points by our method are also shown in Figure 5. Based on data from NYC Metro (MTA), morning rush hour traffic in the city occurs between 6:30AM and 9:30AM, whereas the afternoon rush hour starts from 3:30PM and continues until 06:00PM. Interestingly, the selected break points by our method are very close to the rush hour start/end times during a typical day. Specifically, the selected break points at 7AM, 10AM, and 6PM are close to rush hour periods in NYC. These results suggest that the covariance structure of cab demands between the zipcodes in NYC may significantly change before and after the rush hour periods. Even with the least conservative tuning parameters, SBS-MVTS only selects two break points in this example, and does not identify any break points in the afternoon rush hour period.

Table 5:

The location of break points for the NYC Yellow Cab Demand data.

	1	2	3	4	5
SBS–MVTS	6am	11:30am	–	–	–
Our method	7am	8:15am	10am	6pm	7pm

Figure 5:

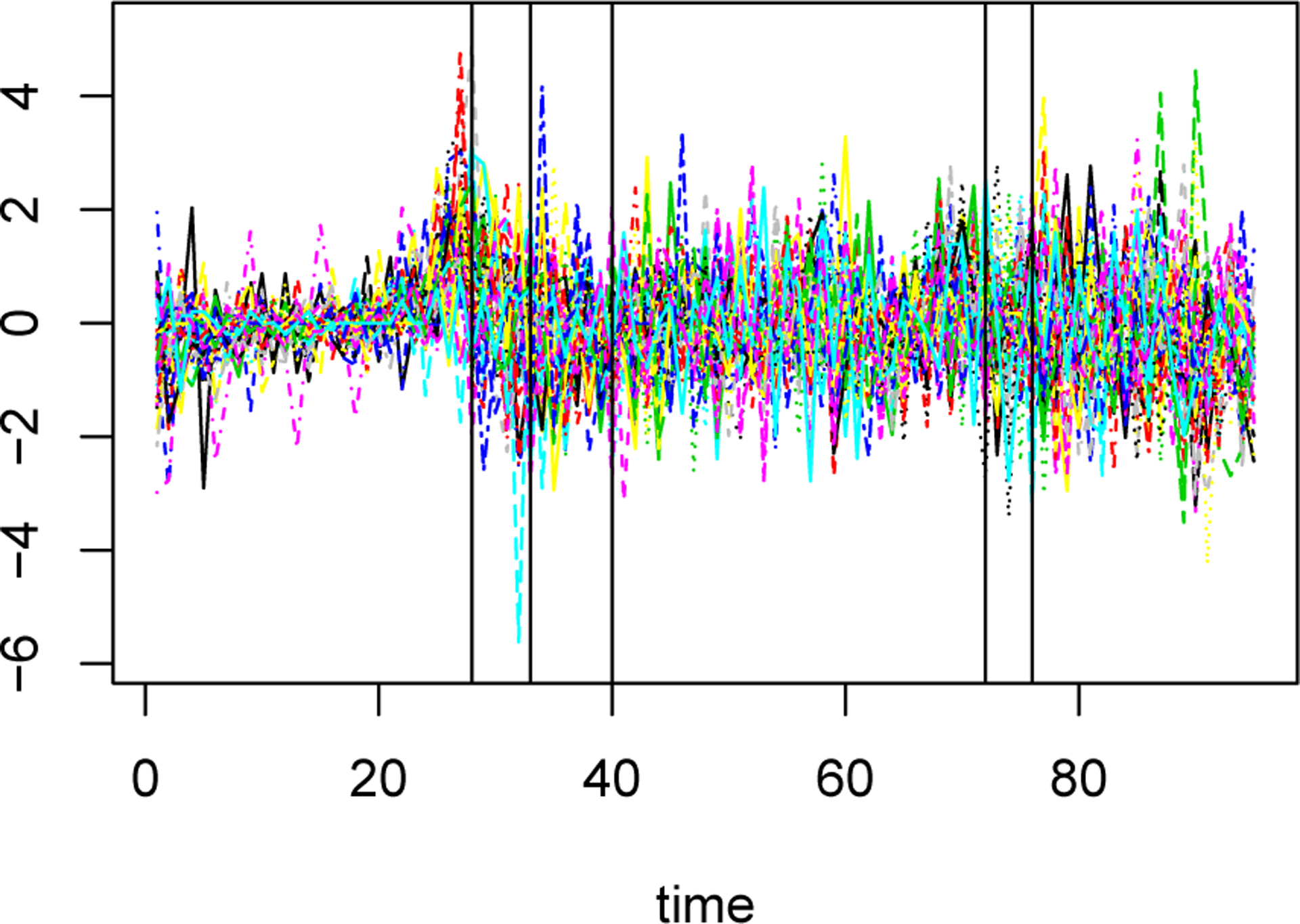
The NYC Yellow Cab Demand differenced time series from 39 different zipcodes over a single day with 96 time points. The 5 selected break points by the proposed method are shown as vertical lines.

9. Discussion

We proposed a three-stage method for simultaneous change point detection and parameter estimation in high-dimensional piecewise stationary VAR models.

We showed that the proposed method consistently estimates the total number and location of break points, and also the parameters of the underlying high-dimensional sparse piecewise stationary VAR model. Numerical experiments in three simulation settings and two real data applications corroborate these theoretical findings. In particular, in both real data examples considered, the break points detected using the proposed method are in agreement with the nature of the data sets.

When the total number of break points, $m_0$, is finite, the rate of consistency for detecting break point locations relative to the sample size $T$ depends on three factors: (1) the number of time points, $T,$ (2) the number of time series, $p$, and (3) the total sparsity of the model, $d_n^{\star }$. In the univariate case, Chan et al. (2014) obtained a consistency rate of order $(\mathrm{l}\mathrm{o}\mathrm{g}n)/n$. In the high-dimensional case, the rate shown here is of order $\left(d_n^{\star 2}\mathrm{l}\mathrm{o}\mathrm{g}n\mathrm{l}\mathrm{o}\mathrm{g}p\right)/n$. The $\mathrm{l}\mathrm{o}\mathrm{g}p$ and $d_n^{\star }$ factors in this rate highlight the challenges of change point detection in high dimensions. The proposed procedure also allows the number of break points to increase with the sample size, as long as the minimum distance between consecutive break points is large enough, as characterized by Assumptions A3 and A4.

A limitation of the proposed procedure is the need to select multiple tuning parameters. In Section 6, we proposed data-driven strategies or made specific recommendations for choosing the tuning parameters. While it is possible to devise cross-validation type procedures for selecting all tuning parameters, this would increase computational burden of our method. However, the sensitivity analyses in Section 7.4 indicate that deviations from the recommendations of Section 6 do not impact the performance of our method. Therefore, we leave further investigations of data-driven choices of tuning parameters to future research. We note, however, that selecting the penalty parameter for the second stage estimator (9) can be challenging in practice. In our numerical studies, a simplified version of this tuning parameter was used. This simplified version does not guarantee optimal rates of consistency for break point estimation. Investigating optimal tuning parameters for this step, using e.g. the procedure of Feng and Simon (2018), and analyzing their theoretical properties can be fruitful areas of future research.

We end this discussion by noting that our method can be applied to cases where the jumps occur only in the means across different segments with fixed transition matrices. In this case, all design matrices will be deterministic. Therefore, technical proofs, including verifying the restricted eigenvalue condition and deviation bound will be simpler. Another possibility is to allow both mean vectors and transition matrices to change at certain locations. This makes our design matrices deterministic in some parts and random in others. Finding sufficient conditions on the jumps sizes in both mean vectors and transition matrices in order to consistently locate their changes over time could be an interesting problem.