A Bayesian Approach to Sequential Analysis in Post-licensure Vaccine Safety Surveillance

Abstract

With rapid development of computing technology, Bayesian statistics have increasingly gained more attention in various areas of public health. However, the full potential of Bayesian sequential methods applied to vaccine safety surveillance has not yet been realized, despite acknowledged practical benefits and philosophical advantages of Bayesian statistics. In this paper, we describe how sequential analysis can be performed in a Bayesian paradigm in the field of vaccine safety. We compared the performance of the frequentist sequential method, specifically, Maximized Sequential Probability Ratio Test (MaxSPRT), and a Bayesian sequential method using simulations and a real world vaccine safety example. The performance is evaluated using three measurements: false positive rate, false negative rate, and average earliest time to signal. Depending on the background rate of adverse events, the Bayesian sequential method could significantly improve the false negative rate and decrease the earliest time to signal. We consider the proposed Bayesian sequential approach to be a promising alternative for vaccine safety surveillance.

1. Introduction

Because vaccine adverse events (AE), especially rare AE, may not be detected during pre-licensure clinical trials due to limited sample size, it is crucial to continually monitor the safety of vaccines in the larger population after they are approved for use. To ensure that any unexpected elevated risks of AE are detected at the earliest possible time, sequential analyses are performed as data accumulate. For example, the Centers for Disease Control and Prevention (CDC) has routinely performed rapid-cycle sequential analyses to monitor the safety of newly approved vaccines, including seasonal influenza vaccines [1,2,3], rotavirus vaccines [4], Tdap vaccines [5], and human papillomavirus vaccines [6].

In a frequentist paradigm, when data are accumulated and analyzed sequentially, the issue of multiple testing is raised, and therefore efforts are made to find appropriate stopping boundaries to control the overall type I error rate below a pre-specified significance level, such as 0.05. Various stopping boundaries have been proposed in a group sequential setting, such as the constant Pocock [7] boundary, the conservative O’Brien and Flemming [8] boundary, and boundaries that utilize alpha spending functions [9,10]. Those boundaries are most suitable for clinical trial studies, wherein there are a small number of discrete analysis time points. In post-licensure vaccine safety monitoring, the most commonly used statistical method for sequential analysis is Maximized Sequential Probability Ratio Test (MaxSPRT) [11], which is similar to group sequential methods, but can continuously analyze data without the interim sample size constraint. The stopping boundaries in MaxSPRT are determined in advance through exact calculations based on an estimated total length of surveillance and a predefined significance level. The limitations of the above frequentist sequential analysis (group and continuous) have been discussed in much literature [12–14]. Most notably, frequentist inference, especially some group sequential inference, on the parameter of interest is indirectly estimated by calculating Prob(Data|parameter), and the p-value based on this indirect calculation is often misinterpreted. For example, it is often wrongly believed that p-value represents probability that the null hypothesis is true. Frequentist sequential methods also suffer from the dilemma whether the analysis should continue once the stopping boundary is exceeded. According to the statistical inference theory, the surveillance should stop as soon as we detect a signal since further analyses or statistical tests are not valid due to the fact that no more type I error is to be spent. However, in reality in many situations it is desirable to continue the surveillance regardless of a signal being detected or not because of minimal effort in accruing data. In addition to the above frequentist philosophical limitations, the MaxSPRT method in specific has some drawbacks. First, in the design stage, the upper limit of the surveillance length needs to be pre-specified, but it is difficult to precisely determine this value due to effects of this value on overall Type I error rate, overall power, the minimization of expected time to signal and the realistic consideration of surveillance ending time. In most situations, the value of the upper limit is selected with some component of arbitrariness, e.g. it was set as 20% more than the maximum observed number of AEs in previous years in one of influenza vaccine sequential surveillance studies. A wrong choice of upper limit would affect critical value (threshold) and thus significantly decrease or increase the designed type I error rate and statistical power. Second, although point estimates of the relative risk are usually reported using the MaxSPRT method, confidence intervals are difficult to derive and generally not reported. Third, if the true relative risk is low and the upper limit is also low, which is the case for most rare AEs, the type II error using the MaxSPRT method is considerably high, e.g. with a true relative risk of 1.2 and a upper limit of 40, the type II error can be as high as 80% [11].

The nature of sequential analysis, i.e. continuously updating analyses as data accumulate, is more in line with the Bayesian paradigm than with the frequentist approach because results from previous interim analyses can be used to form a new prior for the current and future analyses. With a Bayesian approach, we directly measure the probability of the parameter of interest greater or lesser than certain values or any other characteristics of the parameter (such as CI) from posterior distributions. Bayesian sequential methods have been recently adopted for monitoring clinical trials [13,15], and meta-analysis [16], however, the full potential of Bayesian sequential methods applied to post-licensure vaccine or drug surveillance has not yet been realized.

Our paper is organized as follows. In Section 2, we review the concept, assumptions and the basic statistical design and model form used in the frequentist MaxSPRT method for monitoring elevated safety risks of AEs following vaccination. In Section 3 we present the general Bayesian paradigm and how a sequential Bayesian approach is applied to vaccine safety surveillance. In Section 4 we evaluate the performance of the frequentist method MaxSPRT and the Bayesian approach through simulations. In Section 5 we provide an example of using a sequential Bayesian method to estimate the relative risk of febrile seizure following influenza vaccines during 2010–2011 influenza season, and then compare Bayesian sequential results with MaxSPRT results. We then conclude in Section 6 and discuss pros and cons of using a Bayesian approach in a post-licensure vaccine surveillance setting.

2. Frequentist sequential methods in post-licensure safety surveillance

For frequentist sequential methods, both group and continuous sequential methods have been proposed to monitor post-licensure vaccine safety, although disagreement exists in which method performs best [16,17]. We provide a brief overview of the two methods below in the context of vaccine safety surveillance. In both methods the null hypothesis is formulized as

$$H_0:\theta ={\theta }_0$$

The composite alternative hypothesis is formulized as

$$H_1:\theta >{\theta }_0,$$

where $\theta$ represents the relative risk of an $\mathrm{A}\mathrm{E}$ following vaccination, and in most cases ${\theta }_0$ is set as one. Let $Y_t$ be a random variable representing the number of patients who have the $\mathrm{A}\mathrm{E}$ after vaccination up to time $t$. For most rare $\mathrm{A}\mathrm{E}\mathrm{s}$, it is reasonable to assume that $Y_t$ follows a Poisson distribution with a mean of $\theta {\mu }_t$, where ${\mu }_t$ represents the estimated number of patients who have the $\mathrm{A}\mathrm{E}$ during the time interval $[0,t]$ if they had not received vaccination, which reflects a known background rate of the $\mathrm{A}\mathrm{E}.{\mu }_t$ can be derived from the historical data or previous literature. Thus we have that

$$Y_t\sim \mathit{Poisson}\left(\theta {\mu }_t\right),$$

with $\theta =1$ under the null hypothesis, and $\theta >1$ under the alternative.

For both group and continuous sequential methods, we can use the likelihood ratio as the test statistic.

$$\mathrm{\Lambda }=\frac{sup\left\{L\left(\theta \mid Y_t:\theta \in \mathrm{\Theta }\right)\right\}}{L\left(\theta \mid Y_t:\theta =1\right)},$$

where $\mathrm{\Theta }$ is the parameter space under the alternative hypothesis $H_1.L\left(\theta \mid Y_t\right)$ is the likelihood function. After substituting the likelihood function with the Poisson density function and replacing the sup function with the maximum likelihood estimator $\hat{\theta }=\frac{y_t}{{\mu }_t}$, the $\mathrm{l}\mathrm{o}\mathrm{g}$ likelihood ratio test statistic is

$$ln\left(\mathrm{\Lambda }\right)=\left({\mu }_t-y_t\right)+y_{t}ln\left(y_t/{\mu }_t\right),$$

where $y_t$ is the observed number of patients who experienced the AE. For continuous sequential methods, $t$ represents the time when every new case is collected, while for group sequential methods, $t$ represents the interim time when analysis is performed. Assuming $N$ is the maximum surveillance length in terms of expected number of cases, the stopping boundary for the continuous MaxSPRT is

$$T=min(\hat{T},N)$$

where

$$\hat{T}=inf\left\{t>0:\mathit{ln}\left(\mathrm{\Lambda }\right)>=B\left(t\right)\right\},$$

which is the time we reject $H_0.B\left(t\right)$ is a function of time $t$, which can be a time-invariant flat constant proposed in the original MaxSPRT paper [11] or a time-varying boundary which changes over time [18, 19]. For group sequential method, the stopping boundary can be defined as $B(t)=a{\left(N/Y_t\right)}^{1-2\delta }$ [20]. When $\delta =0$, it gives the O’Brien-Fleming boundary, and when $\delta =1$, it gives a Pocock boundary. Other boundary functions can be defined in a similar fashion. Although $B\left(t\right)$ can be defined differently in continuous and group sequential methods, the key difference between the two methods lies in how to define $t$. For the group sequential method, $t=1,\dots ,G$, where the sample size at each time point $n_1,n_2-n_1,n_3-n_2,\dots ,n_G-n_{G-1}>>1$. When $n_G-n_{G-1}=\dots =n_3-n_2=n_2-n_1=1$, it becomes the continuous sequential method. In reality, due to various reasons, we may not perform analysis each time the sample size increases, and may instead analyze data based on calendar time, such as weekly.

3. Bayesian sequential approach

Bayesian statistical inference is built upon Bayes’ rule, which can be expressed as

$$p(\theta \mid y)=\frac{p\left(\theta \right)p(y\mid \theta )}{p\left(y\right)}.$$

That is, the posterior distribution of the parameter $\theta$ given the observed data $y$ can be obtained if we know the prior probability of $\theta$ and the conditional probability $p(y\mid \theta )$. In vaccine safety surveillance, most often the parameter of interest $\theta$ represents relative risk or risk difference between the exposed group and the control group.

If $\theta$ represents relative risk, we propose to use a Gamma distribution as one of the priors, because 1) the relative risk is always greater than or equal to zero, and the Gamma distribution models a random variable that is restricted to nonnegative values; and 2) Gamma and Poisson are conjugate, therefore we can obtain the posterior as a Gamma distribution analytically. Assuming the number of AEs $Y_t$ during the time interval $[0,t]$ follows the Poisson distribution with a mean of $\theta {\mu }_t$,

$$Y_t\sim \mathit{Poisson}\left(\theta {\mu }_t\right).$$

If the prior is the Gamma distribution

$$\theta \sim \mathit{Gamma}\left(\alpha ,\beta \right),$$

then the resulting posterior distribution is

$$\theta \mid Y_t\sim \mathit{Gamma}\left(\alpha +y_t,\beta +{\mu }_t\right).$$

We can also use other non-negative priors, such as lognormal, chi-squared, or uniform with a non-negative range. For those priors, a Markov Chain Monte Carlo (MCMC) algorithm is used to obtain the posterior distribution. Note, we can add any covariate or confounders in the model, for example, we can define

$${\mu }_t=b_1{x}_{1_t}+b_2{x}_{2_t}+\dots b_3{x}_{n_t},$$

where $x_{1_t},x_{2_t}$ represent any confounder, such as age, site, and season.

If the risk difference is the parameter of interest, we can use a Beta-Binomial model described in Tang et al. [21]. Specifically, the risk difference can be modeled using the following Bayesian approach. We assume the number of patients who experienced an AE $Y_{ijt}$ follows a Binomial distribution, i.e.

$$Y_{ijt}\sim Binomial\left(n_{ijt},p_{ijt}\right),$$

where $j=0,1$ indicating the control group and the exposed group respectively, $i=1\dots k$ representing $k$ strata, such as age, sex, site, etc, and $t=1\dots ,T$ represents each analysis time point. We set the prior as

$$p_{ijt}\sim Beta\left({\alpha }_{ijt},{\beta }_{ijt}\right).$$

$\alpha$ and $\beta$ can follow any hyper prior distribution, such as Gamma distribution. The risk difference $\delta$ is calculated as

$${\delta }_t=E\left(p_{i1t}\right)-E\left(p_{i0t}\right).$$

Whether the parameter of interest is relative risk or risk difference, at each interim analysis the posterior distribution of $\theta$ or $\delta$ fully summarizes all current information about this parameter, including a measure of central tendency and uncertainties. It is common to use the highest density interval (HDI) to form stopping boundaries and decide when to report a signal and possibly stop the surveillance [16]. For example, if the relative risk is the parameter of interest, we recommend reporting a signal if a highest density interval excludes one (Figure 1). That is, we conclude there is an elevated risk of $\mathrm{A}\mathrm{E}$ at time $T$, where

$$T=inf\left\{t>0:P\left(\theta >={\zeta }_1\text{and}\theta <={\zeta }_2,1<{\zeta }_1<{\zeta }_2\mid Y_t\right)>=1-ϵ\right\}\text{,}$$ (1)

$ϵ$ is analogous to type I error rate in the frequentist approach, which can be set as 0.05 or 0.025. In some studies, especially clinical trial studies, a stopping boundary is also defined when

$$P\left(\theta <={\zeta }_1\text{or}\theta >={\zeta }_2,{\zeta }_1<1<{\zeta }_2\mid Y_t\right)<=ϵ,$$ (2)

indicating that a large area under the posterior density curve includes one (Figure 2). However, in vaccine safety surveillance, because of minimal effort in accruing data, we do not stop the surveillance if there’s not enough evidence to show an elevated risk. That is, if the above stopping boundary (eq. 1) is not reached at the current analysis time point, the surveillance continues to the next analysis. In some situations, we continue the surveillance even if the stopping boundary (eq. 1) is exceeded. In reality, eq. 1 serves more as a signal detection rule rather than a stopping rule. In a Bayesian sequential paradigm, we do not distinguish between continuous and group sequential analyses. The next analysis can occur at any time point with just one additional sample or with thousands more new cases. Unlike frequentist sequential methods wherein the stopping rule is designed to maintain the overall type I error rate at a pre-specified level, with Bayesian methods the decision of stopping is completely based on the current posterior distribution of the parameter and is not impacted by future unhappened decisions. Therefore, adjusting the overall type I error is never a goal of any Bayesian sequential study, not to mention the type I error is a concept only in the frequentist method. However, we do want to evaluate and minimize the false positive rate regardless of the method we used, which we describe in the following section.

Figure 1:

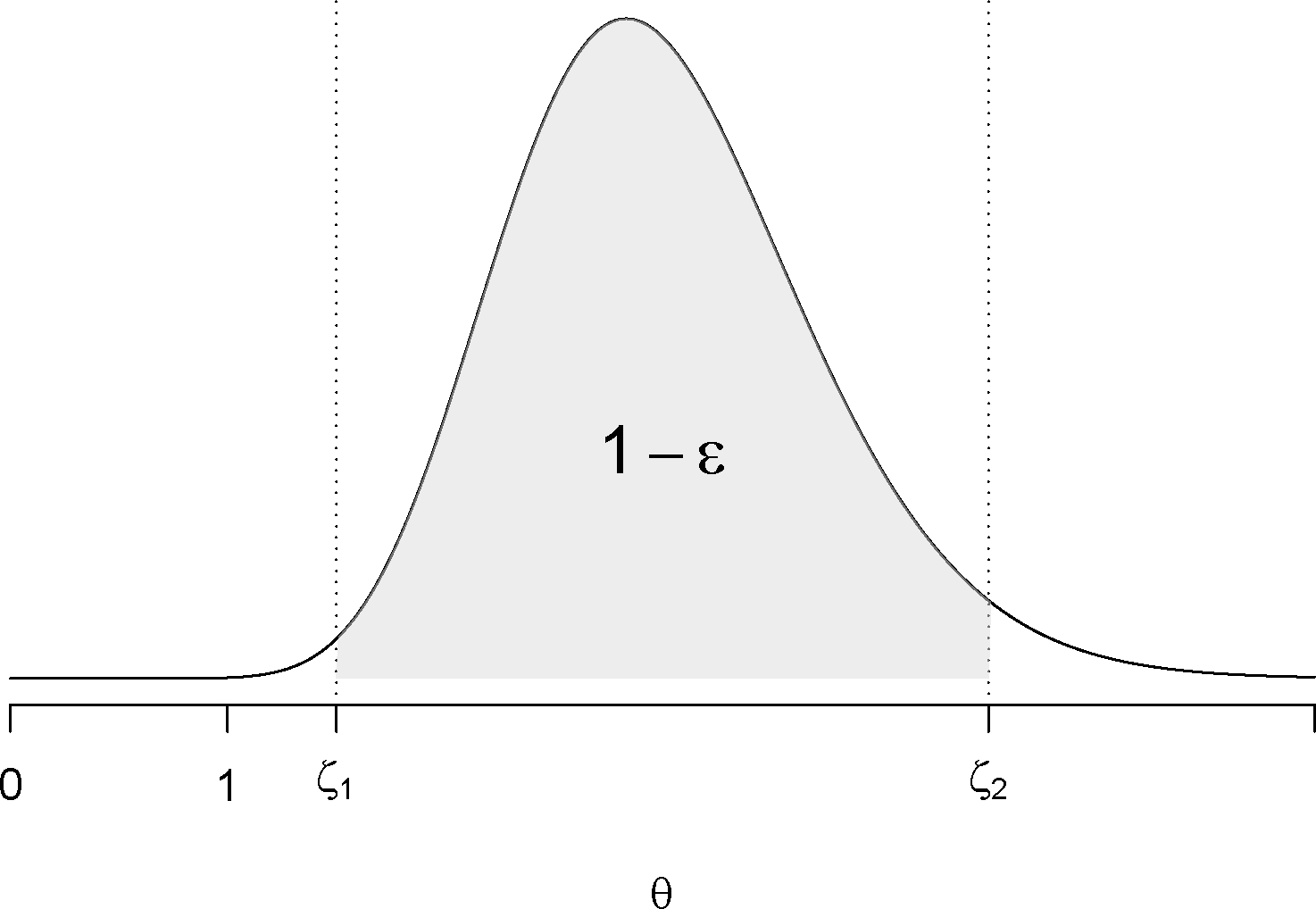
A stopping rule using highest density interval (HDI). The gray area shows the probability of the parameter value in the interval of $\left({\zeta }_1,{\zeta }_2\right)$ (interval excludes 1 ) is $1-ϵ$.

Figure 2:

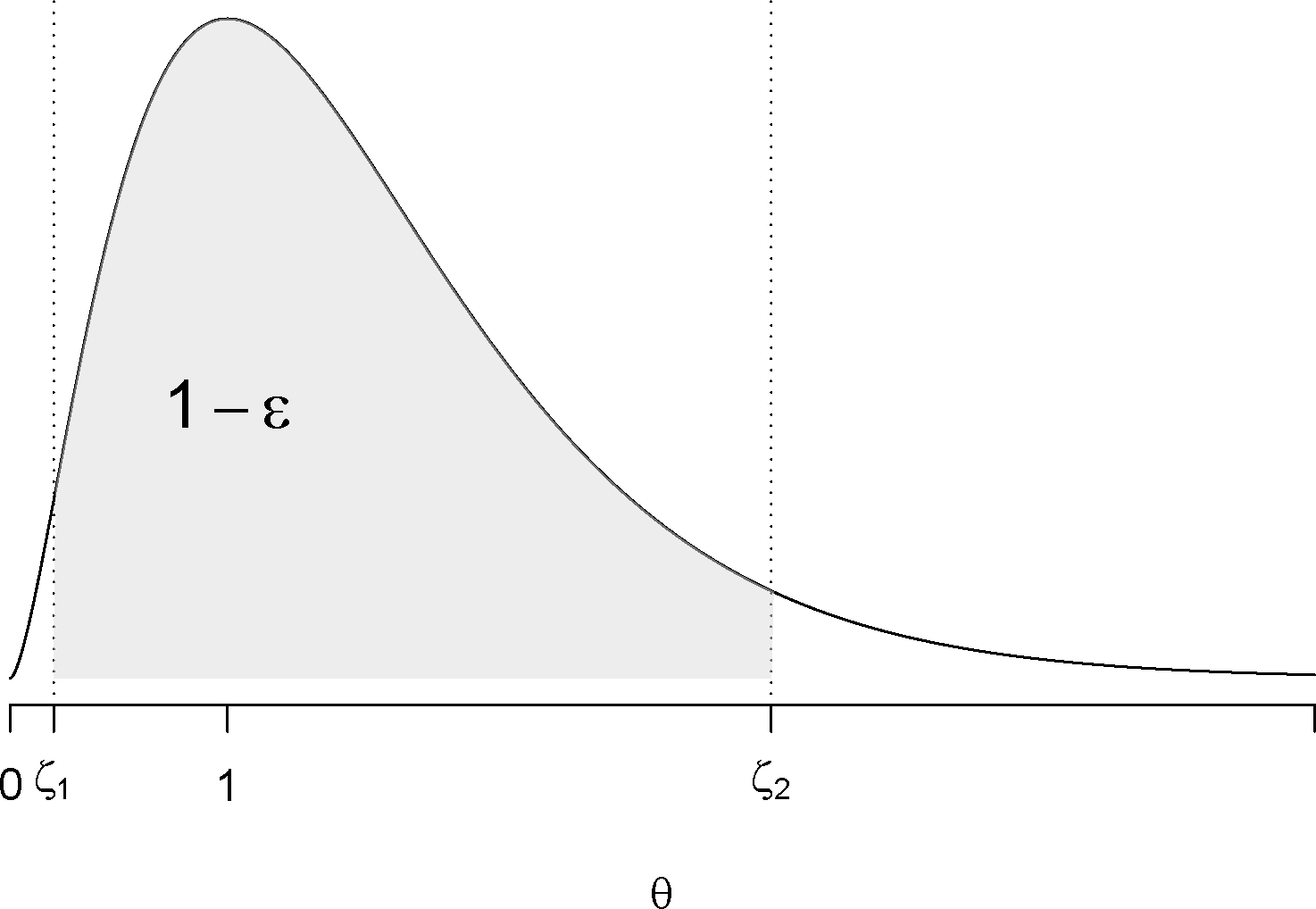
A stopping rule using highest density interval (HDI). The gray area shows the probability of the parameter value in the interval of $\left({\zeta }_1,{\zeta }_2\right)$ (interval includes 1) is $1-ϵ$.

4. Simulations

We simulated data under different scenarios with three background rates to evaluate the performance using both the frequentist (MaxSPRT) approach and the Bayesian sequential approach described above. Suppose there are three AEs following vaccination under surveillance with three different background rates. We set the background rate of the first event as 12.7 per 1000 person-years, which converts to 2.8e-4 in an 8-day risk window. We obtained this number based on the rate of febrile seizures following varicella vaccine [22]. We set the background rate of the second event as 25.4 per 1000 person-years, which is twice as high as the background rate of the first event. We then set the background rate of the third event as 6.35 per 1000 person-years, which is half of the background rate of the first event. We assumed the number of the events occurring follow three separate Poisson processes with different means. We also assumed vaccine doses were evenly distributed across 10 time points with 50,000 doses accumulated at each time point. The true relative risks were set as 1.2, 1.5, and 2, respectively. 1000 replicates were generated for each scenario with a different background rate and a different relative risk. We then applied both the MaxSPRT method and the Bayesian sequential method to each set of simulated data. For the MaxSPRT method, Type I error rate was pre-specified as 0.05. Critical values used to reject the null hypothesis and declare a signal were obtained based on maximum surveillance lengths expressed as expected number of events. For the Bayesian method, we reported a signal if a 95% highest density interval excluded one. That is, $ϵ=0.05$ in eq (1). If we failed to report a signal by the end of the analysis, we concluded the risk of event following vaccination is not elevated. In each analysis we reported and examined the estimated false positive rate (FPR) and false negative rate (FNR). We also compared the average earliest time to signal using both methods. For the Bayesian approach, we also evaluated the sensitivity of priors with different parameters. We chose a Gamma distribution as the prior for evaluation with mode=1 and variance as 0.1, 0.5, 1, 2, and 5 respectively. The mode was set as one because we believe there was no elevated risk before we analyzed the data.

The simulation results based on 3 different background rates are shown in Tables 1–3, respectively. When the background rate is 12.7 per 1000 person-years, the FPR using a Bayesian method ranges between 6–10% for priors with different variances, while the FPR using the MaxSPRT method is around 0.8%. However, FNRs using a Bayesian method are much lower than ones with the MaxSPRT (26–30% vs. 62%) when the relative risk is 1.2. When the relative risk is 1.5, the difference in the FNR using the two methods is minimal, with the Bayesian approach slightly lower(0.1% vs. 0.3%). When the relative risk is further increased to 2, there’s no difference in the estimated FNR between the two methods (0%). When the background rate is doubled to 25.4 per 1000 person-years (Table 2), the FPR using a Bayesian method ranges from 9% to 11%, while FPR using the MaxSPRT method is 0.6%. However, the FNR using a Bayesian approach is lower than using the MaxSPRT method (6% vs. 29%) when the relative risk is 1.2. No difference was found when relative risk is 1.5 or 2. When the background rate is decreased to 6.35 per 1000 person-years, we found similar results. FPRs are higher (6–10%) for the Bayesian method than for the MaxSPRT method (2%), while FNRs are lower for the Bayesian method (48%−56%) than for the MaxSPRT method (79%) with a relative risk of 1.2. When the relative risk is set as 1.5, the FNR using a Bayesian method ranges from 2–3% while the FNR for the MaxSPRT approach is more than 13%. No difference in the FNR exists when the relative risk is increased to 2.

Table 1.

Comparing false positive rates (FPR), false negative rates (FNR) and earliest time to signal using the Bayesian sequential method with a 95% credible interval as the signal criterion and the frequentist MaxSPRT method when the background rate is 12.7 per 1000 person-years.

		FPR	FNR			Earliest time to signal
Methods	Variance	RR=1	RR=1.2	RR=1.5	RR=2	RR=1.2	RR=1.5	RR=2
Bayesian	0.1	0.055	0.294	0.001	0	5.082	2.525	1.280
	0.5	0.077	0.262	0.001	0	4.614	2.233	1.177
	1.0	0.091	0.259	0.001	0	4.556	2.193	1.163
	2.0	0.093	0.257	0.001	0	4.490	2.165	1.158
	5.0	0.096	0.258	0.003	0	4.443	2.148	1.157
MaxSPRT		0.008	0.616	0.003	0	6.156	3.395	1.385

## Warning: package ‘xtable’ was built under R version 3.5.3

The unit for time is the number of analysis time points.

Table 3.

Comparing false positive rates (FPR), false negative rates (FNR) and earliest time to signal using the Bayesian sequential method with a 95% credible interval as the signal criterion and the frequentist MaxSPRT method when the background rate is 6.35 per 1000 person-years.

		FPR	FNR			Earliest time to signal
Methods	Variance	RR=1	RR=1.2	RR=1.5	RR=2	RR=1.2	RR=1.5	RR=2
Bayesian	0.1	0.061	0.564	0.029	0	5.688	4.111	2.038
	0.5	0.088	0.493	0.024	0	4.943	3.450	1.675
	1.0	0.093	0.483	0.021	0	4.799	3.392	1.622
	2.0	0.101	0.479	0.020	0	4.747	3.339	1.595
	5.0	0.104	0.476	0.019	0	4.687	3.308	1.568
MaxSPRT		0.016	0.789	0.134	0	6.095	4.857	2.206

The unit for time is the number of analysis time points.

Table 2.

Comparing false positive rates (FPR), false negative rates (FNR) and earliest time to signal using the Bayesian sequential method with a 95% credible interval as the signal criterion and the frequentist MaxSPRT method when the background rate is 25.4 per 1000 person-years.

		FPR	FNR			Earliest time to signal
Methods	Variance	RR=1	RR=1.2	RR=1.5	RR=2	RR=1.2	RR=1.5	RR=2
Bayesian	0.1	0.087	0.060	0	0	4.122	1.557	1.010
	0.5	0.095	0.056	0	0	3.847	1.437	1.007
	1.0	0.103	0.056	0	0	3.847	1.437	1.007
	2.0	0.105	0.056	0	0	3.825	1.427	1.007
	5.0	0.107	0.055	0	0	3.821	1.423	1.007
MaxSPRT		0.006	0.286	0	0	5.647	2.041	1.061

The unit for time is the number of analysis time points.

With regards to the average earliest time to signal, the Bayesian method performed better regardless of the relative risk and the background rate. The difference is most prominent (32% earlier for the Bayesian method) when the background rate is higher (25.4 per 1000 person-years) and the RR is lower (1.2), which means on average 70,400 doses and 47 cases might be avoided if we use the Bayesian approach in this scenario. For the Bayesian method with a Gamma prior, with the increase of the variance of the prior, the FPR increases while the FNR and earliest time to signal decrease (Figure 3), but not by a substantial amount, especially for the FNR. For example, when the background rate is 12.7 per 1000 person-years, the FPR is 5.5% with a variance of 0.1 in a gamma prior; the FPR increases to 9.6% with a variance of 5. The FNR is 2.9% with a variance of 0.1 and decreases to 2.6% with a variance of 5 when RR is 1.2. In addition, when the variance is greater than 1, the variance has very minimal impact on FPR, FNR, or earliest time to signal.

Figure 3:

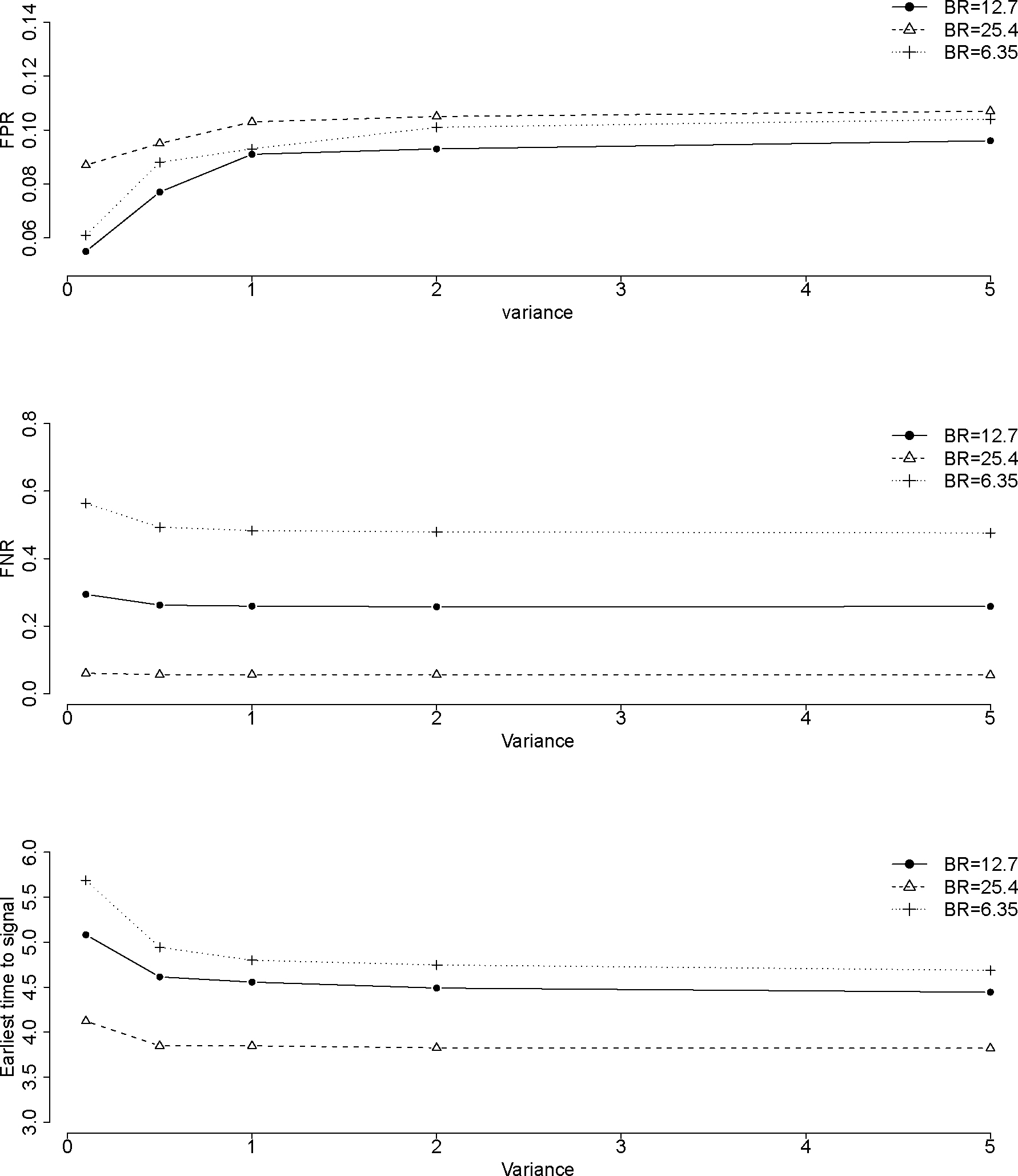
Impact of FPR, FNR and average earliest time to signal by variances in a Gamma prior for different scenarios with RR=1.2 and background rate (BR)=12.7, 25.4, and 6.35 per 1000 person-years. The unit for time is the number of analysis time points.

5. An example

We illustrate here the Bayesian sequential analysis method applied to the real-world vaccine safety data. We also present and compare results with those from the frequentist MaxSPRT method. The increased risk of febrile seizure following the administration of influenza vaccines is of concern for children younger than 5 years old. The CDC-sponsored Vaccine Safety Datalink established surveillance activity to monitor whether influenza vaccines are positively associated with an elevated risk of febrile seizure in young children. The sequential monitoring was conducted during the 2010–2011 influenza season for children aged 6 – 59 months who received their first dose of the trivalent inactivated influenza vaccine. A statistical signal of febrile seizure was found using a frequentist approach [23]. We re-analyzed the data using both MaxSPRT and Bayesian methods. For the Bayesian method, we chose to use a Gamma prior for the same reasons we described above:

$$Y_p\sim Gamma(\alpha ,\beta ),$$

and we set $\alpha$ as 2.618 and $\beta$ as 1.618 to ensure both the mode and the variance to be 1. Similarly as the above, the resulting posterior distribution is

$$\theta \mid Y_t\sim \mathit{Gamma}\left(\alpha +y_t,\beta +{\mu }_t\right),$$

where $y_t$ and ${\mu }_t$ are the observed number of cases and the expected number of cases at week $\mathrm{t}$, respectively. Table 4 shows signals generated using both the MaxSPRT method and the Bayesian method. The first signal generated by the Bayesian approach occurred during the week of October 10, 2010 (week 11) after 54,904 doses of influenza vaccines were administered, while the MaxSPRT produced a signal during the week of October 24, 2010 after 88,592 doses of influenza vaccines were administered, which was two weeks later and 33k more doses. Figure 4 shows the posterior curves for the parameter of relative risk during week 7, 10, 13, 16, and 20. It shows strong evidence that the parameter of relative risk moved to higher values as the time passed. The estimated relative risk stabilized around 2.98.

Table 4.

Signals generated by MaxSPRT and Bayesian methods using VSD influenza vaccine safety data during 2010–2011 influenza season.

Week	Observed	Expected	Cumulative doses	LLR	Critical value	Bayes lower CI	Bayes upper CI	Signal (MaxSPRT)	Signal (Bayesian)
week 1	0	0.0000635	2	0.000	3.468	0.141	3.660	No	No
week 2	0	0.0004074	10	0.000	3.468	0.141	3.659	No	No
week 3	0	0.0006361	16	0.000	3.468	0.141	3.659	No	No
week 4	0	0.0015739	48	0.000	3.468	0.141	3.657	No	No
week 5	0	0.0149011	299	0.000	3.468	0.139	3.627	No	No
week 6	0	0.0530657	955	0.000	3.468	0.136	3.544	No	No
week 7	0	0.1538906	2808	0.000	3.468	0.129	3.342	No	No
week 8	1	0.3755498	7729	0.355	3.468	0.345	3.888	No	No
week 9	2	0.8393673	17822	0.576	3.468	0.308	3.492	No	No
week 10	3	1.6540956	35663	0.440	3.468	0.455	3.103	No	No
week 11	7	2.5440721	54904	2.629	3.468	1.042	3.834	No	Yes
week 12	9	3.3651772	72542	3.219	3.468	1.153	3.727	No	Yes
week 13	15	4.1043193	88592	8.544	3.468	1.791	4.577	Yes	Yes
week 14	17	4.7263061	101862	9.487	3.468	1.860	4.513	Yes	Yes
week 15	18	5.4139540	116501	9.039	3.468	1.790	4.245	Yes	Yes
week 16	21	5.9908531	128847	11.331	3.468	1.969	4.400	Yes	Yes
week 17	23	6.3116437	135672	13.053	3.468	2.094	4.525	Yes	Yes
week 18	24	6.7721527	145642	13.138	3.468	2.076	4.419	Yes	Yes
week 19	25	7.1411842	153628	13.466	3.468	2.082	4.368	Yes	Yes
week 20	25	7.4691285	160766	12.672	3.468	2.007	4.211	Yes	Yes
week 21	26	7.6449998	164584	13.470	3.468	2.057	4.255	Yes	Yes
week 22	26	7.8169554	168370	13.064	3.468	2.020	4.177	Yes	Yes
week 23	26	8.0741988	173899	12.479	3.468	1.966	4.066	Yes	Yes
week 24	26	8.3038506	178849	11.980	3.468	1.921	3.972	Yes	Yes
week 25	26	8.4930151	182989	11.583	3.468	1.885	3.898	Yes	Yes
week 26	26	8.6873295	187172	11.189	3.468	1.849	3.824	Yes	Yes
week 27	26	8.8479430	190705	10.874	3.468	1.821	3.766	Yes	Yes

Figure 4.

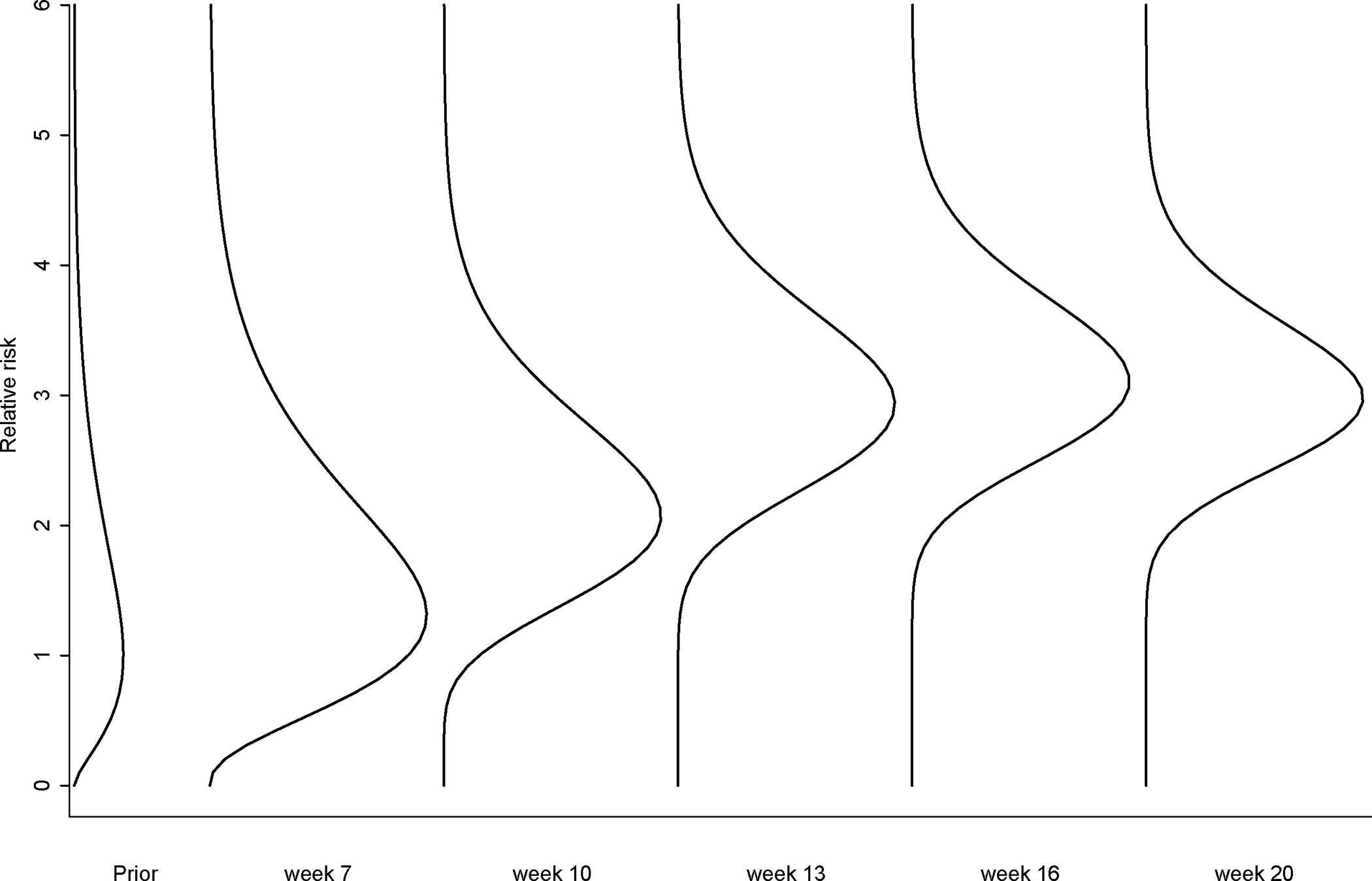
Posterior distribution curves of relative risks of febrile seizure following influenza vaccines during 2010–2011 season (the analysis signaled in week 11).

6. Conclusions and discussion

In this study, we presented a Bayesian sequential approach used for continuously monitoring vaccine safety. We demonstrated how the Bayesian approach can be applied to vaccine safety surveillance in a sequential setting through both simulations and a real-world data example. We compared Bayesian and frequentist MaxSPRT results using both simulations and an example. We found the Bayesian approach can provide better performance in terms of the FNR and average earliest time to signal. On the other hand, the FPR using the Bayesian approach was slightly higher than using the MaxSPRT approach, especially when the background rate is low. Note that there is a tradeoff between the FPR and the FNR and earliest time to signal. Any single measurement does not fully assess the performance. We also need to notice that the Bayesian method has the flexibility to balance the FNR and the FPR to achieve desirable results. For example, in the above simulations, if we choose 97.5% instead of 95% credible interval as a signal reporting criterion, with a background rate of 12.7 per 1000 person-years, the FPR would be reduced to 3%, and the FNR is still much lower than its frequentist counterpart (39% vs. 62%, Table 5). When we use the frequentist approach for sequential monitoring, the FPR (type I error) is usually pre-set at below 0.05. This is based on the implicit default assumption that false positive results are far more costly than false negative ones [24]. Much attention and efforts are often directed towards minimizing the FPR with little attention on the fact that the FNR may be dramatically increased. In vaccine safety, we believe the FNR is as important as the FPR, especially for rare and serious outcomes, such as Guillain-barré syndrome (GBS) and death. A large FNR indicates that we are not able to capture most real AE signals. Fortunately, for the MaxSPRT method this only occurs when the relative risk is below 1.5. When the relative risk is large enough, such as 2, both methods can well capture true signals. It is worth noting that the MaxSPRT method is designed on the assumption of continuous testing, which means a statistical test needs to be performed whenever a new case is observed. However, in reality it is not feasible nor desirable to have very frequent analyses. Therefore, in our simulations we simulated data and performed analyses in a way that is more likely to represent real world vaccine safety surveillance. This also explains why the FPR in the MaxSPRT method is much lower than the pre-defined Type I error rate (0.05).

Table 5.

Comparing false positive rates (FPR), false negative rates (FNR) and earliest time to signal using the Bayesian sequential method with a 97.5% credible interval as the signal criterion and the frequentist MaxSPRT method when the background rate is 12.7 per 1000 person-years.

		FPR	FNR			Earliest time to signal
Methods	Variance	RR=1	RR=1.2	RR=1.5	RR=2	RR=1.2	RR=1.5	RR=2
Bayesian	0.1	0.030	0.393	0.001	0.000	5.662	2.904	1.396
	0.5	0.040	0.362	0.001	0.000	5.141	2.556	1.249
	1.0	0.041	0.360	0.001	0.000	5.023	2.503	1.228
	2.0	0.044	0.360	0.001	0.000	4.967	2.466	1.216
	5.0	0.045	0.359	0.001	0.000	4.941	2.440	1.208
MaxSPRT		0.008	0.616	0.003	0.000	6.156	3.395	1.385

The unit for time is the number of analysis time points.

In the past, one obstacle to adopting Bayesian sequential methods in vaccine safety is that extensive computer resources are required during Bayesian MCMC optimization routines [25]. However, with recent computing technology improvement and Bayesian software development, implementation of Bayesian sequential methods are neither difficult nor time-prohibitive.

One of the criticism in using a Bayesian approach is that subjective information is incorporated through priors and different priors may lead to different conclusions. There is much debate in the literature on whether the Bayesian method should be subjective or more objective [26,27]. Since posterior distributions are actually weighted results between the prior and the likelihood, we can assess sensitivity of results to different priors. Emerson et al. [28] recommended that sensitivity analyses be performed and a contour plot be presented under varying prior parameters and important measures. Because the purpose of this paper is mainly for demonstration and comparison between Bayesian and frequentist sequential methods for hypothesis testing, for the purposes of brevity and to be consistent with frequentist null hypothesis we chose priors with a mode=1, that means we assume the relative risk is most likely to be one. Under such a prior that favors no elevated risk, if we are still able to find strong evidence of an increased risk, then other priors that less favor no elevated risk would not change the direction of the results. This provides further support and credibility to positive signal reports. We did examine how the variance parameter of the prior affected the results, and we found larger variance would increase the FPR and decrease the FNR, because as the variance increases more weight is given to the parameter with values larger than one instead of closely centering around one.

Our study had several limitations. The first was that the simulation was based on only three background rates (6.35, 12.7, and 25.4 per 1000 person-years). We used 12.7 per 1000 person-years to represent febrile seizure background rate, and we then doubled it to 25.4 and also decreased by half to 6.35. Although febrile seizure is a relatively uncommon medical outcome, there are other very rare outcomes such as GBS which might be less than 1 per 100,000 person-years. Future simulation work might be needed for rare outcomes with very low background rates. Another potential limitation was that we compared the Bayesian approach with the original flat boundary MaxSPRT method. A variant MaxSPRT with a time-varying boundary was recently introduced [29] and claims to reduce the time to signal. However, because most if not all vaccine safety sequential studies used the flat boundary MaxSPRT, we believe it is more meaningful to use the original MaxSPRT as a benchmark. In addition, we believe even if the Bayesian approach is not the best performed method, it has advantages, such as continuous surveillance, that other frequentiest methods can not provide.

The Bayesian sequential approach is an attractive alternative to the frequentist MaxSPRT method in vaccine safety surveillance. Although the FPR using the Bayesian method may be slightly higher than 0.05 with a 95% credible interval criterion depending on the background rate, the FNR is significantly decreased (e.g. from 80% to 50% or from 60% to 30%) for low relative risks, such as 1.2. In vaccine safety, we understand that high false positives can lead to additional work in terms of checking data quality and medical chart reviews, but with rare outcomes and often low relative risks, it is also important to lower the FNR so that we are able to capture most true AE signals in our routine surveillance. We favor using Bayesian sequential methods in vaccine safety surveillance because of following three main benefits: 1) the Bayesian approach provides full posterior distribution(s) of the parameter(s) of interest instead of only point estimates and test statistics, which means more information can be obtained from the posterior distribution, including interval estimates; 2) the philosophical awkwardness or the dilemma of whether the surveillance should continue once the stopping boundary is exceeded can be avoided in a Bayesian paradigm. In our perspective, it is extremely important to continue the surveillance as long as new data continue to be accrued; 3) the Bayesian method can model any parameter (such as risk difference) or any algebraic formulation of parameters, not restricted to only relative risk. In addition, it can directly incorporate confounders in the model, while in the frequentist MaxSPRT method, confounding variables can only be stratified and included through baseline value estimation. However, since the Bayesian sequential approach does not specify a Type I error rate, it may not be suitable for clinical trial analysis wherein a strict false positive rate is required.