Using independent open-to-closed transitions to simplify aggregated Markov models of ion channel gating kinetics

Abstract

Deducing plausible reaction schemes from single-channel current traces is time-consuming and difficult. The goal is to find the simplest scheme that fits the data, but there are many ways to connect even a small number of states (>2 million schemes with four open and four closed states). Many schemes make identical predictions. An exhaustive search over model space does not address the many equivalent schemes that will result. We have found a canonical form that can express all reaction schemes for binary channels. This form has the minimal number of rate constants for any rank (number of independent open-closed transitions), unlike other canonical forms such as the well established “uncoupled” scheme. Because all of the interconductance transitions in the new form are independent, we refer to it as the manifest interconductance rank (MIR) form. In the case of four open and four closed states, there are four MIR form schemes, corresponding to ranks 1-4. For many models proposed in the literature for specific ion channels, the equivalent MIR form has dramatically fewer links than the uncoupled form. By using the MIR form we prove that all rank 1 topologies with a given number of open and closed states make identical predictions in steady state, thus narrowing the search space for simple models. Moreover, we prove that fitting to canonical form preserves detailed balance. We also propose an efficient hierarchical algorithm for searching for the simplest possible model consistent with a given data set.

Ion channels participate in many cell signaling pathways. They allow spatial and temporal control of calcium ions that regulate processes as diverse as fertilization, memory, muscle contraction (1), and immune response (2, 3). Abnormal channel function is implicated in pathologies such as cystic fibrosis (4), ataxia (5), and overresponse to anesthesia (6).

Patch-clamp recordings (7) reveal that ion channels open and close spontaneously and that the kinetics can be complex. This complexity can be ascribed to multiple open and closed states, corresponding to different channel conformations. Changes in conformation may occur because of the intrinsic dynamics of the protein or in response to external events such as ligand binding. The pathways and transition rates between the various conformation states constitute an intrinsic component of the cell's signal-processing apparatus. Therefore, the study of gating kinetics can shed light on both normal and abnormal cell signaling.

To analyze a given channel, discrete Markov models (8-16) are fit to patch-clamp recordings of its current. However, it is known that different models can make identical predictions of steady-state gating statistics (17, 18), so that attempts to find the best-fitting model can uncover many models that all fit equally well. We introduce a class of models that avoids this problem; when restricting to these models, the mapping between model parameters and gating statistics is one-to-one. These models allow for a physical interpretation of the interconductance “rank,” a quantity that can be extracted directly from the data, and that corresponds to the number of independent routes between open and closed states. Furthermore, these models allow optimal fitting of data with a minimum number of parameters.

A Markov model for the dynamics of a channel consists of a reaction scheme or topology of allowed transitions between states, together with rate constants for these transitions. For the typical case of binary channels studied here, all open states have the same current, so the states can each be labeled by “O” for open or “C” for closed. The indistinguishability of the closed (or open) states from one another causes ambiguity in fitting models to data. Kienker (17) showed that the two topologies C-C-O and C-O-C are “equivalent”: for every set of rates for one there is a set of rates for the other such that both have identical steady-state behavior.

The space of topologies grows rapidly with the number of states. Our goal is to provide tools and strategies for navigating this space, allowing researchers to focus on a small, tractable set. The fitting of rate constants then can be carried out with existing ion channel analysis software, such as qub (19), that is capable of handling any desired topology.

Methods

Here, we discuss the established concepts used in this work. Beyond these concepts, we allude to the mathematical techniques used after each result. Detailed proofs are contained in the supporting information, which is published on the PNAS web site. These proofs mainly depend on linear algebra, especially Kienker transformations (17), which are briefly reviewed there as well.

Most of the results presented here have exceptions which are, literally, infinitely uncommon. These exceptions happen when certain relationships among the rate constants cause degeneracies, such as two exactly identical decay rates in the open-time distribution. In the statements of the theorems below, those exceptions are indicated by the mathematical terms “almost all” or “almost every,” meaning “with infinitely rare exceptions.” Throughout, the term “topology” means the reaction scheme, usually displayed in a state transition diagram, without regard to reaction rates. “Model” means a Markov model with a particular topology and a particular set of reaction rates.

Equivalence and Canonical Forms. There are two related notions of equivalence: equivalent models and equivalent topologies. “Equivalent models” have identical steady-state dwell-time distributions. “Equivalent topologies” are capable of modeling the same range of steady-state behaviors, and therefore almost every model with one topology is equivalent to some model with the other (as in Definition 1 in the supporting information). Equivalent topologies will have the same number N_o of open states and the same number N_c of closed states, and in fact they must have the same number of “independent” O-C links (defined below). Beyond these constraints, it has so far been nontrivial to say whether two topologies are equivalent. Steady-state experiments can never distinguish among equivalent topologies.

Any collection of equivalent models may be viewed as ways in which different dynamics can generate the same steady-state statistics. Any prescription for expressing any set of equivalent entities in a unique way is called a “canonical form.” Representing a model in canonical form means finding an equivalent model with canonical topology, which should always be feasible for a good canonical form. The choice of canonical forms has previously been limited to just two, as discussed below, for which it was known how to find canonical models equivalent to almost any model.

Equivalent models are equivalent to a single model in canonical form, and this fact can be used to test whether two models are equivalent. Equivalent models will fit data equally well, regardless of the fitting technique (e.g., maximum likelihood or least squares). To obtain the best possible fit to steady-state data, it suffices to fit the data to models in canonical topologies, because models in other topologies are always equivalent to canonical models.

Known Canonical Forms. We will compare the canonical form introduced below to the canonical form described by Bauer et al. (12) and Kienker (17), which we refer to as Bauer-Kienker uncoupled (BKU) form. In BKU form, every open state is connected to every closed state and vice versa, but there are no open-to-open or closed-to-closed connections. This form has 2N_oN_c rate constants.

Physical models must have positive reaction rates. Negative reaction rates can lead to negative probabilities for individual states and consequently are difficult to interpret. Kienker noted (17) that models equivalent to a physical model can have negative rates. For example, it can be shown that any four-state model in BKU form must have negative rates to be equivalent to any physical model with topology C-O-O-C (see C-O-O-C Has Negative Rates in BKU Form in the supporting information). This result implies that negative rates should be allowed when fitting data to a canonical form. If the resulting canonical model is nonphysical, it can still be viewed as a parsimonious representation of the data using a generalized Markov process (20). Below, we show that negative rates can sometimes be avoided.

If the principle of detailed balance (DB) is not obeyed, BKU form models may require rates that are complex numbers to achieve the best fit. A generally applicable canonical form given by Larget (18) is similar to BKU form. Both have the same number of parameters, and both minimize the number of intraconductance reactions. In Larget's form, complex numbers are never required, unlike in BKU form. Larget's form always has negative rates, whereas the complex rates in BKU form can be removed by a slight change in the form that adds no more parameters (see Real and Complex Rates in the supporting information).

Dwell-Time Distributions. The dwell-time distribution f_o(t_o) is the probability density that the time interval for which the channel is open has duration t_o. Likewise, f_oc(t_o, t_c) is the probability density consecutive open and closed intervals have durations t_o and t_c. Colquhoun et al. (8, 9) derived expressions for these distributions in terms of the “generator matrix,” Q_ij, which is the matrix of transition rates between the various states. Fredkin et al. (10, 11) showed that f_oc and f_co are sufficient to fully characterize the steady-state data, under certain technical conditions that are almost always satisfied. All of the dwell-time distributions are sums of decaying exponentials. For example,

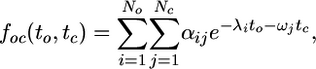[1]

where λ_i and ω_j are the open and closed decay constants, respectively, and α_ij is a matrix of amplitudes.

Identifiability. If different models make identical predictions about a particular class of experiments, the models are not “identifiable” with respect to those experiments. A topology is identifiable provided any changes to its rate constants result in changes to the steady-state dwell-time distributions. Conversely, topologies that have more parameters than there are degrees of freedom in the data are not identifiable. In this case, there is a continuum of rate constants for the topology that all yield identical statistics, and thus values for these rates cannot be uniquely determined from steady-state data, regardless of the quantity or quality of data. A trivial example of a nonidentifiable topology is one with two closed states and no open states. Obviously, patch-clamp current traces could not be used to infer the transition rates between the two states.

It has long been known (10) that there are at most 2N_oN_c degrees of freedom in steady-state data. Therefore, topologies with more than N_oN_c links are not identifiable. The bound on the number of degrees of freedom can be improved (11) to 2R(N_o + N_c - R), where R is the interconductance rank defined below. Topologies with more than this many rates are not identifiable; topologies with fewer rates may or may not be identifiable. The problem of determining which topologies are identifiable remains unsolved (10).

Interconductance Rank. The canonical form that we introduce in this work makes explicit use of R, the interconductance rank. Before giving the physical interpretation of rank, we review the mathematical definition. The rank of a model is defined as the matrix rank (number of independent rows or columns) of the matrix Q_oc, which is the block of Q_ij

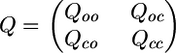[2]

representing open to closed transitions. We assume the ranks of Q_oc and Q_co are equal, which is generally true for reversible reactions. These ranks also equal the matrix rank of α_ij, which can be estimated directly from the data without reference to a model (11). Therefore, equivalent models must have the same interconductance rank. The rank of a topology is defined as the maximal rank of any model with that topology, and this rank equals the number of “independent” O-C links, where different independent links do not link to the same state; this equality is proved in Rank and Independent Reactions in the supporting information.

If a model is fit to data, the rank of the resulting model will equal either the rank of the data (α_ij) or the rank of the topology of the model, whichever is smaller. For a model to have plausibly generated the data, the two ranks should be equal. If the topology used for the fitted model has a larger rank, then there will be linear dependencies among the rates that cannot be justified biochemically, unless there is a symmetry that can explain them.

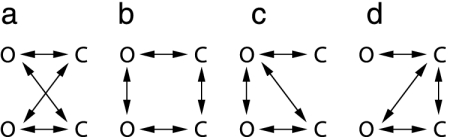
The ranks of a few illustrative topologies are shown in Fig. 1. The rank of the topology in Fig. 1a is 1. The topologies shown in Fig. 1 b-d all have rank 2. Note that in Fig. 1d there are three Os connected to Cs and three Cs connected to Os, but the rank of the topology is only 2. Fredkin and Rice (11) noted that the lesser of the number of Os connected to Cs and the number of Cs connected to Os is an upper bound on a topology's rank. Fig. 1d shows that this bound is not tight; note that no three of the O-C links are independent. Incidentally, this example is a subtopology (or special case) of BKU form, because it has no O-O or C-C links.

Fig. 1.

Examples of simple rank 1 and rank 2 topologies. (a) A rank 1 topology with one O-C link. (b) A rank 2 topology with two O-C links. (c) A rank 2 topology with four O-C links. (d) A rank 2 topology with five O-C links. Both c and d can accommodate only two independent O-C links.

It can be shown (Theorem 8 in the supporting information) that when rank 1 data are fit to BKU form, the resulting number of nonzero rate parameters is 2 N_oN_c, far more than the 2(N_o + N_c - 1) necessary when R = 1. In this case the rank of the topology is the lesser of N_o and N_c, whereas the rank of the model is 1. If N_o and N_c are both >1, then it is generally not plausible that rank 1 data were generated by a BKU form model; the model may fit the data, but there is no explanation for the linear dependencies of the rates. Thus, BKU form often obscures the rank, uses more links than necessary, and usually does not lead to plausible models.

Results

Manifest Interconductance Rank (MIR) Form. MIR form is defined by the following requirements: (i) all interconductance links are independent, and (ii) all intraconductance links involve at least one state with an interconductance link. The MIR form is illustrated in Figs. 2b and 3b. Fig. 2b shows how states can be arranged into four columns. The two central columns contain the same number of states, with Cs in one and Os in the other. These states are linked in horizontal pairs to form the R interconductance O-C links. The remaining Cs and Os are in the first and last columns, respectively. Every C in the second column is connected to every other C, and Cs in the first column are not connected to each other. Connections for the Os follows the same pattern. The total number of reactions in MIR form is R(N_o + N_c - R), which gives the Fredkin bound of 2R(N_o +N_c - R) independent rate constants that can be recovered from steady-state data. The MIR form can be constructed for any rank up to the maximum possible rank (the lesser of N_o and N_c). Because all interconductance links are independent, the rank of the topology equals the number of O-C links. The maximum-rank MIR form has all lower rank MIR forms as subtopologies, making the full-rank MIR form as powerful as BKU form. A comparison of the two forms expressed as matrices of rate parameters is shown schematically in Fig. 3, in a case where the rank is not full.

Fig. 2.

Examples of reaction diagrams for canonical forms. (a) BKU canonical form for N_c = 6 and N_o = 5. The number of reversible reactions is N_oNc = 30. (b) MIR canonical form for N_c = 6, N_o = 5, and R = 3. The number of reversible reactions is R(N_o + N_c - R) = 24.

Fig. 3.

Comparison of transition matrices for canonical forms. (a) BKU “uncoupled” form. (b) MIR form. White space denotes regions of the matrix filled with zeros. Shaded regions have nonzero values. Diagonal lines indicate a single diagonal strip of nonzero values. In b, the width of the gray regions is equal to the rank R. When R takes its maximum value, the number of nonzero values is the same in the two forms.

There are two steps required to show that MIR form is canonical. The first step is to show that for almost any model, there is an equivalent model in canonical form and to give a prescription for how to find that model.

Theorem. Almost every model can be expressed in MIR form.

Mathematically, the MIR form corresponds to “diagonalizing” the interconductance transition matrices Q_oc and Q_co. This transformation is almost always possible. The nondegeneracy conditions that comprise the exceptions are comparable to ones required for BKU form (see Manifest Interconductance Rank Form in the supporting information). The required diagonalization is performed by first diagonalizing the products Q_coQ_oc and Q_ocQ_co. The mathematics of this procedure have been exploited previously in other fields such as canonical correlation analysis (21) and partial least-squares (22).

The topologies in Fig. 2 both have N_o = 5, N_c = 6. The rank of the MIR form topology in Fig. 2b is given by R = 3. The rank of the BKU form topology is fixed by R = min(N_o, N_c), which is 5 in this case. In BKU form (Fig. 2a), there are 30 reversible transitions, whereas in MIR form (Fig. 2b), there are only 24. If one were to fit data generated by a rank-3 topology to BKU form, one could recover as many as 60 reaction rates (30 reactions), but these parameters would not all be independent. If one were to fit the same data to MIR form, one would recover at most 48 parameters (24 reactions), and these parameters would almost always be independent.

The second part of showing that MIR form is canonical is proving that its topology is identifiable. If this condition were not true, then expression of a model in MIR form would not be unique. We state our result as follows.

Theorem. MIR and BKU forms are identifiable for almost all parameters.

Proofs for the two forms are presented as Theorems 1 and 2 in the supporting information. Both are related to the fact that there is only one normalized similarity transformation, neglecting permutations, that can diagonalize a nondegenerate matrix.

Although generically MIR form has fewer links than BKU form, there are special topologies that have fewer links when expressed in BKU form. One example is the topology in Fig. 1d. This topology can be constructed by removing four links from the general BKU form, leaving the five links shown. Equivalent models in MIR form have eight links. Conversely, starting from MIR form and removing links results in topologies requiring more links when expressed in BKU form, regardless of rank. Thus, if models in nature tend to resemble simplified special cases of one form or the other, fitting to that form may result in simpler models, as the following examples will show.

Many channel models in the literature conform or nearly conform to MIR form. In Table 1, we count the number of MIR- and BKU-compatible reactions in four publications by different authors. Compatible reactions are those that are in the equivalent model in canonical form. A topology with all reactions compatible is already in the given canonical form. We shall see that when only a few reactions are not compatible, the canonical version of the model may have only a few more links than the original model.

Table 1. Resemblance of models proposed by different authors to BKU and MIR canonical forms.

Ref.	No. of models	Links	BKU links, %	MIR links, %
29	11	131	31	76
10	6	25	36	80
30	2	15	47	93
31	1	14	29	93
Total	20	185	33	79

Of the 20 models discussed in these articles, 7 are in MIR form, and none are in BKU form. Also, models in the literature tend to have substantially more MIR-compatible than BKU-compatible links. Fig. 4 illustrates two of the cases where only one link was not compatible with MIR form.

Fig. 4.

Two topologies proposed in the literature and the topologies of the equivalent models in BKU and MIR forms. (a) A full rank model of the nicotinic acetylcholine receptor described in ref. 30. Of its eight links, seven are MIR-form compatible, whereas four are BKU-form compatible. Equivalent BKU form models have 13 links, compared with 10 links for MIR form. (b) A rank 4 model of the inositol trisphosphate receptor described in ref. 31. There are 14 links, 13 of which are compatible with MIR form, whereas only 4 are compatible with BKU form. As shown, equivalent MIR form models have 15 links, whereas equivalent BKU form models have 36 links.

Fig. 4 shows both proposed topologies, together with the MIR and BKU form topologies that can model the same data. These topologies are found by the transformation techniques described in Manifest Interconductance Rank Form and Kienker Transformations in the supporting information, and they will give the same results for almost any rate constants. In Fig. 4a, the resulting MIR form requires only two more links than the original topology to fit the same data. BKU form requires an additional five links as shown. Similarly, Fig. 4b shows a proposed topology with 14 links, only 1 of which is not MIR-form compatible. The MIR form topology has 15 links. The BKU form topology has 36 links.

In both examples in Fig. 4, when either canonical form is used, the number of links will be less than the R(N_o + N_c - R) bound, because both topologies are sparsely linked to begin with. However, using MIR form results in significantly fewer links because these models are topologically close to being simplified special cases of MIR form.

The tendency for models in the literature to resemble MIR form more than BKU form may indicate a tacit belief among researchers that nonindependent O-C links are rare. This belief implies that usually, when the channel opens from a particular closed state, it arrives in a particular open state.

Canonical Forms and Detailed Balance. At thermodynamic equilibrium, chemical reaction kinetics are governed by the principle of microscopic reversibility, or DB. DB implies no net circulation around reaction cycles at steady state. One proposed mechanism for voltage-gated ion channels explicitly violates DB and consumes free energy (23); note that at thermodynamic equilibrium, the membrane potential would be zero. Several authors have discussed tests for DB violations in ion channel data (24-27). We have proven (see Theorem 5 in the supporting information) the following.

Theorem. If a model satisfies DB, then the equivalent models in both BKU and MIR form satisfy DB.

However, note that for any model satisfying DB, there are many models equivalent to it that violate DB. Our result implies that if violations of DB are required to fit data using canonical form, then there is no model obeying DB that can fit the data as well.

Rank 1 Topologies. Topologies with only one independent interconductance transition, implying a “gateway” state between open and closed states, are rank 1 topologies. As stated previously, negative rate constants may be required to find a canonical form model that is equivalent to some physical models. Rank 1 topologies do not suffer from this complication.

Theorem. Nonnegativity of rates is preserved when a rank 1 model satisfying DB is expressed in either MIR or BKU forms.

The proof (see Theorem 7 in the supporting information) relies on the special structure of these canonical forms in the rank 1 case. The proof is easy compared with the related result (28) that amplitudes α_ij in the dwell-time distribution f_oc (see Eq. 1) are positive if the open and closed dwell times are uncorrelated and DB is satisfied. Uncorrelated open and closed dwell times imply that f_oc(t_o, t_c) = f_o(t_o) f_c(t_c), which is true for all rank 1 models (10). This fact is intuitive; if there is only a single gateway state linking the Os and Cs in a Markov model, there is no way to generate correlated open and closed times, because an individual Markov state has no memory. Note that the theorem does not apply to rank 2 topologies, such as the C-O-O-C example described earlier that does have negative rates in BKU form (but is already in MIR form).

The above result is not the only simplification that applies in the rank 1 case. We have proven for fixed N_o and N_c the following.

Theorem. All rank 1 topologies are equivalent.

This result is somewhat surprising. It does not hold for rank 2 (see None of C-O-O-C, O-C-C-O, and C-O-C-O are equivalent to each other in the supporting information). The rank 1 equivalence proof uses induction on the number of open and closed states (see Theorem 6 in the supporting information). The proof also can be adapted to show that given a rank 1 model with nonnegative rates obeying DB, every rank 1 topology has an equivalent model with nonnegative rates. This means that the “all rank 1 topologies are equivalent” result holds when restricting to physical models if DB is satisfied. It also implies that the presence of a negative rate in a rank 1 model indicates DB violation in any equivalent physical model. This is another result that does not hold for rank 2.

The MIR rank 1 form has only N_o + N_c - 1 bidirectional reactions as shown in Fig. 5. The BKU rank 1 form has N_oN_c bidirectional reactions, none of which can have a zero rate (see Theorem 8 in the supporting information). Thus, BKU form maximally obscures the rank; a rank 1 model will have a topology with the largest possible rank for given N_o and N_c.

Fig. 5.

Rank 1 MIR form with N_o = 3 and N_c = 4. With fewer links, the topology would not be connected.

Discussion

The four main results presented here reduce the amount of work needed to find simple models that can account for steady-state channel data. Fitting to MIR canonical form produces simpler models than in BKU form. If a fit to canonical form violates DB, then there is no equivalent model in which DB is satisfied. All rank 1 topologies are equivalent, so they all will fit steady-state data equally well. For rank 1, if DB is satisfied, fits to canonical form can be restricted to positive rates. Thus, in the rank 1 case, the statistical test of whether DB is violated is reduced to testing whether any rates are significantly negative. The rank 1 equivalence and positivity results explain reports in the literature that best fits of data to various rank 1 topologies all yield the same likelihood (16).

Canonical form reaction rates that yield the best fit to the data can be complex numbers if DB is violated. To ensure that the best fit has been obtained, either Larget's canonical form should be fit (real rates suffice) or MIR or BKU form can be fit with complex eigenvalues (see Real and Complex Rates in the supporting information). In any event, negative reaction rates are necessary to ensure the best fit, except in the rank 1 DB case.

Fredkin et al. (10) suggested a procedure for estimating rank from covariance functions of the data. MIR form allows rank to be estimated by using the statistical framework of nested models. Here, nested means that every MIR topology contains the lower-rank MIR topologies as special cases. For example, the rank 3 MIR topology in Fig. 2b can be converted to rank 2 by setting the rates for six bidirectional reactions to zero: the links connecting the bottommost C and O states to different columns.

MIR form has the fewest reactions that a canonical form can have. A form with fewer would have less parameters than Fredkin and Rice's calculation of the generic number of parameters in the data (11). In contrast, the well known BKU “uncoupled” form has the most reactions a canonical form can have. A form with more rates would not be identifiable (10).

We have seen that models in the literature are closer to MIR than to BKU form. If data are generated by a process with fewer than R(N_o + N_c - R) reactions, then fitting to a topology similar to the true topology can yield a model that also has fewer reactions. For example, the topology in Fig. 4b can be fit by using 15 reactions in MIR form but would require 36 reactions in BKU form.

The reason that MIR-like models are so much more prevalent in the literature than BKU-like models may be because different O and C states often represent different states of ligand binding that persist when the protein opens or closes. Such an O state is expected to link to only one C state and vice versa. In contrast, many O states will be linked to each other (as will C states), but there are no such links in BKU form.

Recent determination of atomic resolution structures of some ion channels have made possible molecular dynamics simulations of the opening or closing of these channels. These simulations are far too short (tens of nanoseconds) to compare with current traces, which describe events on the millisecond scale and longer. However, it could be possible to use numerical techniques to identify quasi-stable conformations of an ion channel that are candidates for the multiple open and closed states evidenced by patch-clamp experiments. To the extent that some of the relevant coordinates are preserved when the channel opens and closes, MIR form should allow simplification of the model, beyond any guaranteed simplification owing to the rank, as was seen in Table 1 and Fig. 4. If a ligand can be bound with the channel open or closed, then the ligand-binding coordinate would constitute an example of such preservation.

Atomic structures also can inform the choice of N_o and N_c, based on the number of predicted ligand-binding sites, for example. Symmetries observed in the structure should also be reflected in the model, although the implications for the canonical forms are not clear. Molecular dynamics simulations also might shed light on the number of independent pathways between open and closed states, which should then be reflected in the rank R of the model.

Exhaustive Search

The brute force approach to exhaustive search is to search over all topologies. The optimization criterion should take into account the quality of the fit and the simplicity of the model; an established one that has been applied in this setting is the Bayesian Information Criterion (BIC) (15). The brute force approach has the advantage that only positive rates are needed to find the greatest likelihood. It has the disadvantage that there are >10 trillion topologies for the case of 6 open and 6 closed states.

A more sophisticated exhaustive strategy would be to search over only one model in every class of equivalent models. This strategy avoids the problem of sorting through many models with exactly equal likelihoods. This approach still leaves a very large search space and is currently infeasible because it requires enumeration of the equivalence classes, which is unsolved. Because this approach relies on equivalence, negative rates must be allowed to guarantee that the highest likelihood is found. Nonequilibrium dynamical experiments might in principle be used to help choose among multiple models in the best-fitting equivalence class.

This strategy is very effective for rank 1 topologies because there is only one equivalence class for fixed N_o and N_c. The identifiable rank 1 topologies all have the same number of links, N_o + N_c - 1, and thus the same BIC score. Moreover, they all have positive rates if DB is satisfied. Thus, there is no point in fitting to more than one rank 1 topology.

Whatever the search strategy, there is no point in searching nonidentifiable topologies, because they will always fit the data equally well in a continuum of ways and no better than the special case topologies that are identifiable. In general, it is not known which are the identifiable topologies, but we do know they can have no more than R(N_o + N_c - R) reactions, where R is the rank of the topology. Some of these topologies can be shown, using methods to be discussed elsewhere, to be nonidentifiable and may be omitted. Beyond rank 1, the space of such topologies is still exponentially large and contains many equivalences.

Hierarchical Search

We propose an alternative strategy. When fitting to a topology that contains the best topology as a subtopology, this fact should be indicated by very small rate constants for the links that should be removed. This observation suggests the following hierarchical search method:

1. Ascertain the rank, R, by successive fits to MIR form for the various ranks. (N_o and N_c are assumed known from the dwell-time distributions.)

2. Fit to all topologies with R(N_o + N_c - R) links.

3. For fits that yield links with small rates, remove all combinations of those links and reevaluate the simplicity criterion (such as BIC) for the resulting topologies.

Again, for the sake of efficiency, one can omit remaining nonidentifiable topologies, to the extent they are known. We emphasize that the hierarchical search only helps to find simpler models; the fit will not improve beyond the MIR fits in step 1. In fact, we believe that the quality of all fits in step two will be identical, according to the following proposition.

Conjecture. All identifiable rank R topologies with R(N_o + N_c - R) links are equivalent.

The number of equations to be solved to put a canonical form model into such a topology equals the number of unknowns. Thus, the conjecture is true if these equations are all mutually consistent. Although the conjecture does not address which topologies are identifiable, the nonidentifiable topologies will have a lower, or at best equal, likelihood score because some of their parameters have no effect on the fit.

Example. C-O-O-C.

Here, we discuss the hierarchical search strategy and the conjecture for the case N_o = N_c = 2. There are four rank 2 topologies with four links, as shown in Fig. 6. These four topologies are identifiable, and each is equivalent to the others (see Identifiability and Equivalence of all 4-link Topologies with N_o = N_c = R = 2 in the supporting information). Moreover, they contain (as subtopologies) all identifiable topologies of all ranks (R = 1 and R = 2) with N_o = N_c = 2. All topologies with more links, or with four links but lower rank, are not identifiable. Consider the hypothetical search in which the true topology is C-O-O-C. From the one-dimensional dwell-time distributions, we ascertain that N_o = N_c = 2. We fit the MIR form rank 2 topology (Fig. 6b) and the MIR form rank 1 topology, C-C-O-O, and find that the quality of fit is significantly better for the R = 2 MIR form. By using a fitting algorithm that allows negative rates, we fit the remaining topologies in Fig. 6, obtaining the same likelihood for all. The topologies shown in Fig. 6 a and d yield unphysical models with negative rates (see C-O-O-C Has Negative Rates in BKU Form in the supporting information). (If we had used fitting algorithm with positivity constraints, the two topologies a and d would have significantly lower likelihood than the other four-link topologies.) The MIR form topology (Fig. 6b) has a near zero rate for the C-C reaction. The topology shown in Fig. 6c has a near zero rate for the diagonal C-O link. Thus, fits to both topologies Fig. 6 b and c indicate C-O-O-C as a candidate topology. We now fit to C-O-O-C to find that C-O-O-C has the best BIC score, because it has six reaction rates compared with eight.

Fig. 6.

An exhaustive list of four-link rank 2 topologies for N_o = N_c = 2. All these topologies are identifiable, and together they contain all three-link topologies including both ranks 1 and 2.

All of the four-link topologies have identical BIC scores because they are all equivalent. As we fit longer records, two things happen: the BIC score for the C-O-O-C reaction improves relative to the 4-link candidates, and simultaneously the two physical candidates both become closer to C-O-O-C. Thus, we recover C-O-O-C.

The benefits of this approach increase as the number of states increases, although it too becomes impractical fairly quickly. For N_o = 2 and N_c = 3, there are 22 rank 2 topologies with six links, at least two of which are not identifiable. For N_o = N_c = 3, there are 116 rank 3 topologies with 9 links, and for N_o = N_c = 4 there are 47,677 rank 4 topologies with 16 links. In the latter case, there are >2.5 million connected topologies, so restricting to the 16-link topologies reduces the computational burden by a factor of >50. Unfortunately, we estimate that the search space for the hierarchical strategy contains 200 million topologies for N_o = N_c = 5 and 10 trillion for N_o = N_c = 6. The hierarchical strategy makes it practical to search up to N_o = N_c = 4.

The first step is always to estimate N_o and N_c. We have shown that the rank R is also of fundamental importance. All three quantities can in principle be extracted from current traces without reference to any specific topology. Other biochemical data also might help to constrain these values. MIR form allows one to make use of the rank and is closer than BKU form to most proposed topologies in the literature we examined. The number of topologies very close to MIR form, which will have few or no nonindependent O-C links, is manageable. An effective strategy thus might be to start with MIR form and greedily move one link at a time, keeping the rank fixed.

The results presented here can be extended. In their current form they provide a number of useful tools for the identification of binary channel gating kinetics.

Note Added in Proof. It has come to our attention that Flomenbom et al. (32) give additional arguments and discussion relevant to the rank 1 equivalence theorem presented here.