Bootstrap-adjusted quasi-likelihood information criteria for mixed model selection

Abstract

We propose two model selection criteria relying on the bootstrap approach, denoted by QAICb1 and QAICb2, in the framework of linear mixed models. Similar to the justification of Akaike Information Criterion (AIC), the proposed QAICb1 and QAICb2 are proved as asymptotically unbiased estimators of the Kullback–Leibler discrepancy between a candidate model and the true model. However, they are defined on the quasi-likelihood function instead of the likelihood and are proven to be asymptotically equivalent. The proposed selection criteria are constructed by the quasi-likelihood of a candidate model and a bias estimation term in which the bootstrap method is adopted to improve the estimation for the bias caused by using the candidate model to estimate the true model. The simulations across a variety of mixed model settings are conducted to demonstrate that the proposed selection criteria outperform some other existing model selection criteria in selecting the true model. Generalized estimating equations (GEE) are utilized to calculate QAICb1 and QAICb2 in the simulations. The effectiveness of the proposed selection criteria is also demonstrated in an application of Parkinson's Progression Markers Initiative (PPMI) data.

1. Introduction

During the process of model selection, model selection criteria play a vital role to choose the most appropriate model. A well-known model selection criterion is AIC [1], which assesses a model through two aspects, the goodness of fit and simplicity. Originated from the information theory, AIC utilizes the likelihood function of a candidate model to evaluate how well the model fits the data set and a bias correction to measure the complexity of a model. Due to its simple form of the bias correction term, AIC tends to choose more complex or overfitted models rather than simpler ones, especially in the small sample scenario [9,19]. More importantly, the distribution assumption of the data is not always satisfied and the computation cost of likelihood functions significantly increases when it comes to the mixed model for highly correlated data.

The quasi-likelihood function [20] shares similar properties of the traditional likelihood function but can be well-defined as long as the mean and variance of the distribution for the data set are specified. The lack of distribution assumptions makes the quasi-likelihood more applicable to various models, including linear and generalized linear mixed models. Furthermore, with the introduction of an over-dispersion parameter, the quasi-likelihood function is capable of reducing the influence brought by overdispersion. When the quasi-likelihood function is applied to correlated data, the method of GEE [13] is commonly used to estimate model parameters.

To improve the quality of model selection, resampling approaches can be incorporated, of which the most influential technique is the bootstrap [5–7] method. A typical bootstrap approach takes three forms: parametric, semiparametric and nonparametric bootstrap. The nonparametric bootstrap is the most widely used because it is free from the parametric distribution of the data by using the bootstrap distribution [7]. AIC could be improved by absorbing the bootstrap approach, as shown in Cavanaugh and Shumway [4]. Ishiguro and Morita [10] proposed WIC through bootstrap followed by a successful application to a practical problem. Ishiguro et al. [11] proposed the extended information criterion (EIC) to extend the usage of AIC by estimating the bias correction term based on the bootstrap resample. When it comes to the mixed model with dependent data, Shang and Cavanaugh [19] brought out two bootstrap-based selection criteria, AICb1 and AICb2, which are efficient especially in small sample scenarios. Unfortunately, these bootstrap utilizations rely on the likelihood function of a data set which furthermore depends on the distribution assumption.

To extend the justification of AIC, QIC(R) [16] was proposed as a model selection criterion by mimicking the construction of AIC and modifying the Kullback–Leibler (K-L) discrepancy [12] using the quasi-likelihood function and estimators from GEE. However, the performance of QIC(R) is not consistent. In the context of linear mixed models, when the correlation within groups becomes large, QIC(R) is less likely to select the most appropriate model.

Motivated to overcome the above disadvantages in selecting overfitted models, in distribution assumptions, and in consistency of selection criteria for mixed model selection, we propose two model selection criteria, denoted by QAICb1 and QAICb2, based on the quasi-likelihood function and bootstrap method for correlated data in linear mixed models, as an extension and modification of QIC(R) in Pan [16] and of AICb1 and AICb2 in Shang and Cavanaugh [19]. We apply the GEE estimator along with the bootstrap approach to compute the quasi-likelihood of the data and to estimate the bias term.

In Section 2, we present the linear mixed models and the quasi-likelihood function. In Section 3, we propose the bootstrap-adjusted quasi-likelihood-based model selection criteria, denoted by QAICb1 and QAICb2. They are proved to be asymptotically unbiased estimators of the K-L discrepancy between a candidate and the true model in the Supplemental Appendix. In Section 4, the simulations in various settings are conducted to illustrate the selection performance of QAICb1 and QAICb2 for linear mixed models using both nonparametric and semi-parametric bootstrap methods, along with the comparison with other two existing criteria. An application of the proposed selection criteria in the PPMI data is presented in Section 5. Section 6 concludes and discusses.

2. Linear mixed models and quasi-likelihood

Let N be the number of total observations with $N=\sum _{i=1}^n{n}_i$, the linear mixed model for n clusters takes the form of

$$y_i=X_i\beta +Z_i{b}_i+{ϵ}_i,i=1,\dots ,n,$$ (1)

where $y_i$ is the response vector, $X_i$ and $Z_i$ are the design matrices for the fixed and random effects, respectively, with i as the index for the clusters, β is a $(p+1)\times 1$ vector of fixed coefficients, $b_i$ is a $q\times 1$ vector of random effects with $E(b_i)=0$ and $\mathrm{Var}(b_i)=\mathrm{\Delta }$, ${ϵ}_i$ is an $n_i\times 1$ vector of error terms with $E({ϵ}_i)=0$ and $\mathrm{Var}({ϵ}_i)={\sigma }^2{I}_{n_i}$. The matrix Δ is positive definite, and $I_{n_i}$ is an $n_i\times n_i$ identity matrix. Combining all the responses in one vector, Equation (1) can be expressed as

$$Y=\mathrm{X\beta }+\mathrm{Zb}+ϵ.$$ (2)

In model (2), $Y=(y_1^{\mathrm{\prime }},\dots ,y_n^{\mathrm{\prime }}{)}^{\mathrm{\prime }}$ is an $N\times 1$ vector of all the responses, $b=(b_1^{\mathrm{\prime }},\dots ,b_n^{\mathrm{\prime }}{)}^{\mathrm{\prime }}$ is an $\mathrm{nq}\times 1$ vector for random effects, $ϵ=({ϵ}_1^{\mathrm{\prime }},\dots ,{ϵ}_n^{\mathrm{\prime }}{)}^{\mathrm{\prime }}$ is an $N\times 1$ error vector, $X=(X_1^{\mathrm{\prime }},\dots ,X_n^{\mathrm{\prime }}{)}^{\mathrm{\prime }}$ is an $N\times (p+1)$ matrix and assumed to be full rank, and Z is an $N\times \mathrm{nq}$ block diagonal matrix with diagonal elements $Z_1,\dots ,Z_n$.

We note that even though a typical linear mixed model requires random effects to follow a multivariate normal distribution with mean $00$ and covariance matrix Δ, the distribution of random effects in model (1) is not specified or unknown in many situations, and it is the same for the distribution of error terms ${ϵ}_i$. As quasi-likelihood functions only require the first two moments of the distribution, more flexibility exists when it comes to the distribution of random effects. In other words, the quasi-score equation could be constructed when the mean and variance of Y are specified.

To further simplify the notation, it is assumed that $n_i=m$ for all $i=1,\dots ,n$ and $\mathrm{Var}({ϵ}_i)={\sigma }^{2}I$, where I is an $m\times m$ identity matrix. In a linear mixed model, let ${\mu }_i=E(y_i)=X_i\beta$ and $V_i=\mathrm{Var}(y_i)=Z_i\mathrm{\Delta }{Z}_i^{\mathrm{\prime }}+\mathrm{Var}({ϵ}_i)=Z_i\mathrm{\Delta }{Z}_i^{\mathrm{\prime }}+{\sigma }^{2}I$, then the response vector $y_i$ has mean ${\mu }_i$ and variance covariance matrix $V_i$. Thus, the log quasi-likelihood $Q({\mu }_i;y_i)$ is defined through the following differential equation:

$$\frac{\mathrm{\partial }Q({\mu }_i;y_i)}{\mathrm{\partial }{\mu }_i}=V_i^{-1}(y_i-{\mu }_i).$$ (3)

Note that $\mathrm{\partial }{\mu }_i/\mathrm{\partial }{\beta }_i=X_i$, and Equation (3) could be written in terms of β by:

$$\frac{\mathrm{\partial }Q({\mu }_i;y_i)}{\mathrm{\partial }\beta }=X_i^{\prime }{V}_i^{-1}(y_i-X_i\beta ).$$ (4)

Moreover, using Equation (4), the estimated $\hat{\beta }$ can be achieved by solving the following quasi-score equation

$$U(\beta )=\sum _{i=1}^n{X}_i^{\prime }{V}_i^{-1}(y_i-X_i\beta )=0.$$ (5)

Note that we have

$$E(U(\beta ))=\sum _{i=1}^n{X}_i^{\prime }{V}_i^{-1}(E(y_i)-X_i\beta )=0,$$

which means when the first moment of the distribution is correctly specified, the root of Equation (5), $\hat{\beta }$, is consistent. Moreover, the robust variance estimate of $\hat{\beta }$ given by White [21],

$$V_{\hat{\beta }}={\left(\sum _{i=1}^n{X}_i^{\prime }{V}_i^{-1}{X}_i\right)}^{-1}\{\sum _{i=1}^n{X}_i^{\prime }{V}_i^{-1}(y_i-X_i\hat{\beta })(y_i-X_i\hat{\beta }{)}^{\prime }{V}_i^{-1}{X}_i\}{\left(\sum _{i=1}^n{X}_i^{\prime }{V}_i^{-1}{X}_i\right)}^{-1},$$

which is consistent as well provided that $E(y_i)=X_i\beta$ [22]. Note that we do not include the overdispersion parameter when constructing the quasi-likelihood function here. As the mean and variance of Y are independently distributed, the parameter estimation of the linear mixed model will not encounter overdispersion.

3. Bootstrap-adjusted quasi-likelihood information criteria: QAICb1 and QAICb2

In this section, we propose two model selection criteria, denoted by QAICb1 and QAICb2, based on the quasi-likelihood function and bootstrap approach and start by extending the likelihood-based K-L discrepancy [12] to the quasi-likelihood-based function. Bootstrapping is applied to establish these two selection criteria, named QAICb1 and QAICb2. We prove that QAICb1 and QAICb2 are asymptotically equivalent and asymptotically unbiased estimators of the quasi-likelihood-based K-L discrepancy between the true model and a candidate model in the Supplemental Appendix. Therefore, QAICb1 and QAICb2 are proposed to serve as two criteria for mixed model selection. In fact, these two criteria can also be extended to generalized linear models with random effects in future analysis.

3.1. K-L discrepancy based on quasi-likelihood

Similar to the K-L discrepancy in Shang and Cavanaugh [19] and Cavanaugh and Shumway [4] using the likelihood function, we will define the K-L discrepancy using the quasi-likelihood function. Let ${\beta }_0$ and β denote the parameters for the true model and a candidate model, respectively. The quasi-likelihood function corresponding to the parameters β for a candidate model is denoted by $Q(\beta ,\varphi ;Y)$, where ϕ denotes the nuisance parameters containing all covariance parameters. Following Pan [17] and the definition of K-L discrepancy, the K-L discrepancy based on the quasi-likelihood function between the true model and a candidate model is defined as

$$d(\beta ,{\beta }_0,\varphi ;Y)=E_0[-2Q(\beta ,\varphi ;Y)],$$

where the expectation $E_0$ is taken under the true model. Since the quasi-likelihood owns the same properties as the likelihood function, this discrepancy can reflect the distance between a fitted model and the true model, indicating the goal of this discrepancy is similar to that defined based on the likelihood function. As discussed in the Supplemental Appendix, the discrepancy $d(\beta ,{\beta }_0,\varphi ;Y)$ is valid for β for each of all candidate models in the neighborhood of ${\beta }_0$ with ${\beta }_0$ being the local minimizer of $d(\beta ,{\beta }_0,\varphi ;Y)$. More importantly, the unbiased estimator or asymptotically unbiased estimator of this discrepancy can serve as a model selection criterion, and the minimized criterion value shows the fitted model is the most appropriate one because it has closest distance with the true model.

Let $\hat{\beta }$ be the estimator of β from a candidate model. Here, $\hat{\beta }$ is the estimator derived by solving the corresponding quasi-score Equation (5). Then, the corresponding discrepancy can be written as

$$d(\hat{\beta },{\beta }_0,\varphi ;Y)=E_0[-2Q(\beta ,\varphi ;Y)]{|}_{\beta =\hat{\beta }}.$$ (6)

It is not possible to evaluate the quantity in Equation (6) because the parameters corresponding to ${\beta }_0$ is usually unknown. Let $d({\beta }_0,\varphi ,k)$ be the expectation of the discrepancy in Equation (6) under the true model, and k is the number of estimated parameter for the candidate model, we now have

$$\begin{array}{rl}d({\beta }_0,\varphi ,k)& =E_0[d(\hat{\beta },{\beta }_0,\varphi ;Y)]\\ & =E_0[E_0\{-2Q(\beta ,\varphi ;Y)\}{|}_{\beta =\hat{\beta }}]\\ & =E_0[-2Q(\hat{\beta },\varphi ;Y)]\\ & +E_0[E_0\{-2Q(\beta ,\varphi ;Y)\}{|}_{\beta =\hat{\beta }}]-E_0[-2Q(\hat{\beta },\varphi ;Y)].\end{array}$$ (7)

According to construction of AIC in Akaike [1], as shown in Equation (7), the quantity $-2Q(\hat{\beta },\varphi ;Y)$ is a biased estimator of $d({\beta }_0,\varphi ,k)$ and the bias term is

$$E_0[E_0\{-2Q(\beta ,\varphi ;Y)\}{|}_{\beta =\hat{\beta }}]-E_0[-2Q(\hat{\beta },\varphi ;Y)].$$ (8)

The selection criteria based on the discrepancy in Equation (7) should serve as the unbiased estimators or asymptotically unbiased estimators and then can measure the distance between the true model and a candidate model. Next, we will propose two selection criteria named QAICb1 and QAICb2, which own such properties, as proved in the Supplemental Appendix.

3.2. Selection criteria: QAICb1 and QAICb2

Let $\{Y^{\ast }(i),i=1,\dots ,B\}$ be the B bootstrap samples obtained through Y by resampling on the individual level and $\{{\hat{\beta }}^{\ast }(i),i=1,\dots ,B\}$ be the corresponding estimators from the bootstrap samples. As discussed in the Supplemental Appendix, we can replace the terms of the original sample by the related ones from the bootstrap samples. For the brevity of notation, we remove the ϕ from the notation of a quasi-likelihood because in a set of candidate models, we let the covariance structure be fixed and only make a selection from the fixed effects.

Thus, the quantity in expression (8) of the bias correction term could be expressed as

$$E_{\ast }[E_{\ast }\{-2Q(\beta ;Y^{\ast })\}{|}_{\beta ={\hat{\beta }}^{\ast }}]-E_{\ast }[-2Q({\hat{\beta }}^{\ast };Y^{\ast })],$$ (9)

where the expectation $E_{\ast }$ is taken with respect to the empirical distribution of the bootstrap sample $Y^{\ast }$, and fortunately, the expectation of expression (9) can be estimated numerically through estimators obtained using the bootstrap samples.

Motivated by the construction of EIC in Ishiguro et al. [11] and AICb1 and AICb2 in Shang and Cavanaugh [19], the bootstrap estimation of the expectation in expression (9) relies on a crucial assumption, which is expressed as

$$E_{\ast }\{-2Q(\beta ;Y^{\ast })\}=-2Q(\beta ;Y),$$ (10)

under the parametric, semiparametric or nonparametric bootstrap approaches. The detailed proof of the assumption in Equation (10) is provided in the Supplemental Appendix. Taking advantage of assumption (10), the expectation in Equation (9) can be expressed as

$$\begin{array}{rl}{E}_{\ast }[E_{\ast }\{-2Q(\beta ;Y^{\ast })\}{|}_{\beta ={\hat{\beta }}^{\ast }}]& =E_{\ast }[-2Q(\beta ;Y){|}_{\beta ={\hat{\beta }}^{\ast }}]\\ & =E_{\ast }[-2Q({\hat{\beta }}^{\ast };Y)].\end{array}$$ (11)

The bootstrap expectation in Equation (11) can be estimated by

$$\frac{1}{B}\sum _{i=1}^B-2Q({\hat{\beta }}^{\ast }(i);Y).$$ (12)

As $B\to \mathrm{\infty }$, we have

$$\frac{1}{B}\sum _{i=1}^B-2Q({\hat{\beta }}^{\ast }(i);Y)⟶E_{\ast }\{-2Q({\hat{\beta }}^{\ast };Y)\}\mathrm{a}.\mathrm{s}.,$$

according to the law of large numbers (LLN).

Similarly, we can employ the bootstrap approach to directly estimate the quantity in expression (9) by

$$\frac{1}{B}\sum _{i=1}^B-2Q(\hat{\beta }(i{)}^{\ast };Y(i{)}^{\ast }).$$ (13)

As $B\to \mathrm{\infty }$, we have

$$\frac{1}{B}\sum _{i=1}^B-2Q({\hat{\beta }}^{\ast }(i);Y^{\ast }(i))⟶E_{\ast }\{-2Q({\hat{\beta }}^{\ast };Y^{\ast })\}\mathrm{a}.\mathrm{s}.$$

By utilizing the two bootstrap estimates in expressions (12) and (13), the following expression, denoted by $\mathrm{b}1$, is to estimate the bias term in expression (9):

$$\begin{array}{rl}\mathrm{b}1& =\frac{1}{B}\sum _{i=1}^B-2Q({\hat{\beta }}^{\ast }(i);Y)-\frac{1}{B}\sum _{i=1}^B-2Q({\hat{\beta }}^{\ast }(i);Y^{\ast }(i))\\ & =\frac{1}{B}\sum _{i=1}^B-2\frac{Q({\hat{\beta }}^{\ast }(i);Y)}{Q({\hat{\beta }}^{\ast }(i);Y^{\ast }(i))}.\end{array}$$ (14)

In fact, the expression of b1 in Equation (14) is asymptotically unbiased estimator of the bias term in expression (8). We, therefore, propose the first bootstrap-adjusted quasi-likelihood information criteria QAICb1 for the linear mixed model as

$$\mathrm{QAICb}1=-2Q(\hat{\beta };Y)+\frac{1}{B}\sum _{i=1}^B-2\frac{Q({\hat{\beta }}^{\ast }(i);Y)}{Q({\hat{\beta }}^{\ast }(i);Y^{\ast }(i))}.$$ (15)

Equation (15) is an asymptotically unbiased estimator of the discrepancy between a candidate model and the true model in Equation (7) as proved in the Supplemental Appendix.

The second bootstrap-adjusted variant is similarly constructed following the development of the AICb in Cavanaugh and Shumway [4] and AICb2 in Shang and Cavanaugh [19]. The bias term in expression (8) can be written as

$$\begin{array}{rl}& E_0[E_0\{-2Q(\beta ;Y)\}{|}_{\beta =\hat{\beta }}]-E_0\{-2Q({\beta }_0;Y)\}\end{array}$$ (16)

$$\begin{array}{rl}& +E_0\{-2Q({\beta }_0;Y)\}-E_0[-2Q(\hat{\beta };Y)].\end{array}$$ (17)

By replacing the expectations in expressions (16) and (17) and using the bootstrap expectation and applying the crucial assumption in Equation (10), we have

$$\begin{array}{rl}& E_{\ast }[E_{\ast }\{-2Q(\beta ;Y^{\ast })\}{|}_{\beta ={\hat{\beta }}^{\ast }}]-E_{\ast }\{-2Q({\beta }_0;Y^{\ast })\}\\ & =E_{\ast }\{-2Q({\hat{\beta }}^{\ast };Y^{\ast })\}-\{-2Q({\beta }_0;Y)\}\end{array}$$ (18)

and

$$\begin{array}{rl}& E_{\ast }\{-2Q({\beta }_0;Y^{\ast })\}-E_{\ast }[-2Q(\hat{\beta };Y^{\ast })]\\ & =-2Q({\beta }_0;Y)-2Q(\hat{\beta };Y).\end{array}$$ (19)

Under certain conditions, we can show that both quantities in Equations (18) and (19) will converge as follows when $n\to \mathrm{\infty }$:

$$\begin{array}{rl}& E_{\ast }[-2Q({\hat{\beta }}^{\ast };Y)-\{-2Q(\hat{\beta };Y)\}]\\ & ⟶E_{\ast }\{-2Q({\hat{\beta }}^{\ast };Y^{\ast })\}-\{-2Q({\beta }_0;Y)\}\mathrm{a}.\mathrm{s}.\end{array}$$ (20)

and

$$\begin{array}{rl}& E_{\ast }[-2Q({\hat{\beta }}^{\ast };Y)-\{-2Q(\hat{\beta };Y)\}]\\ & ⟶-2Q({\beta }_0;Y)-2Q(\hat{\beta };Y)\mathrm{a}.\mathrm{s}.\end{array}$$ (21)

We now define b2 as a mean over the bootstrap samples and sum up the left-hand side of expressions (20) and (21), then we have

$$\begin{array}{rl}\mathrm{b}2& =2\{\frac{1}{B}\sum _{i=1}^B-2Q({\hat{\beta }}^{\ast }(i);Y)-\frac{1}{B}\sum _{i=1}^B-2Q(\hat{\beta };Y)\}\\ & =2\{\frac{1}{B}\sum _{i=1}^B-2\frac{Q({\hat{\beta }}^{\ast }(i);Y)}{Q(\hat{\beta };Y)}\}.\end{array}$$ (22)

Because of convergences in expressions (20), (21) combining with Equation (22), the quantity of b2 in Equation (22) will be used to estimate the sum of the converged parts in Equations (18) and (19), and this sum is equal to the bias term of the discrepancy in expression (9). We therefore propose the second bootstrap-adjusted quasi-likelihood information criterion QAICb2 for the linear mixed model as

$$\mathrm{QAICb}2=-2Q(\hat{\beta };Y)+2\{\frac{1}{B}\sum _{i=1}^B-2\frac{Q({\hat{\beta }}^{\ast }(i);Y)}{Q(\hat{\beta };Y)}\}.$$ (23)

Therefore, two model selection criteria in Equations (15) and (23) are proposed.

4. Simulations in linear mixed models

In this section, the performance of selection criteria QIC(R) in Equation (24), ${\mathrm{QAIC}}_u(R)$ in Equation (25), QAICb1 in Equation (15), and QAICb2 in Equation (23) is compared in the simulated correlated data from model (1). When the nested models are utilized in the simulations, there are total 10 subsequently nested candidate models with the largest model containing all the 10 covariates. Let ${\beta }_0=(2,2,1,1,0.5,0,0,0,0,0,0{)}^{\mathrm{\prime }}$ be true parameters for the fixed effects. The covariates $X_1,\dots ,X_{10}$ are independently generated from the standard normal distribution. The error term is generated from a normal distribution with mean 0 and standard deviations $\sigma =1$, 1.3, and 1.5, respectively. Let the sample size be n = 25, n = 50, n = 100, and $n=200,$ respectively. With each sample size, let m = 3 be the number of repeated measurements. The number of bootstrap samples B is set to be 250, which is the minimum value of B in which the simulation results can be well obtained. The true correlation matrix is chosen as EX(ρ) or AR(ρ) or a mixture of different correlation matrices with $\rho =0.2$, 0.4, 0.6, 0.8, and the fitting correlation matrix is exchangeable or autoregressive.

There are three covariance matrices used in generating the data: exchangeable, first-order autoregressive, and unstructured. Under these three covariance structures, the variance for the random effects is determined by specifying the correlations, and the random effects are generated from a normal distributions. For example, when $\rho =0.2$ and ${\sigma }^2=1$ and an exchangeable covariance structure is utilized, we can obtain that $\mathrm{Var}(b_i)=\mathrm{\Delta }=0.25$ in model (1) because $\rho =\mathrm{\Delta }/(\mathrm{\Delta }+{\sigma }^2)$ and $b_i$ are generated from normal distribution with mean zero and variance 0.25. We note that an exchangeable covariance structure is also called a compound symmetric structure or a random intercept model. When a first-order autoregressive model is utilized, the covariance structure is presented as

$$\frac{{\sigma }^2}{1-{\rho }^2}\left[\begin{array}{ccc}1& \rho & {\rho }^2\\ \rho & 1& \rho \\ {\rho }^2& \rho & 1\end{array}\right].$$

If ρ and ${\sigma }^2$ are given, the covariance structure is determined. Such a first-order autoregressive model serves as linear mixed model and the random effects and error terms are generated from a normal distribution with mean zero and this covariance structure. We note that autoregressive linear mixed effects models in which the current response is regressed on the previous response, fixed effects, and random effects [8]. When an unstructured covariance is utilized, the data are constructed from a combination of data generated with exchangeable, autoregressive, and self-defined covariances which will be described in related simulation parts.

This section is divided into two subsections. The simulations in the first subsection are via nonparametric bootstrap, and those in the second part are via semi-parametric bootstrap. We investigate the model selection performance of QAICb1 and QAICb2 using a set of nested candidate models pairing with different true correlations. When bootstrap is utilized, the performance of QAICb1 and QAICb2 is also examined using candidate models constructed by different combinations of predictor variables.

We will incorporate GEE in the calculation of the proposed selection criteria, QAICb1 and QAICb2 in Equations (15) and (23). Two different covariance structures are adopted: exchangeable and first-order autoregressive. They are easy to be computed when GEE is utilized to estimate the model parameters under the quasi-likelihood setting. However, when the number of observations within the same individual is large, it is very challenging to estimate the parameters because of high-dimensional parameters under which McCullagh and Nelder [15] pointed out that the quasi-likelihood function may not exist until certain requirements are met. In the process of selecting the most appropriate model in a candidate pool, the model with the smallest value of QAICb1 or QAICb2 is considered to be the best model. We present a selection criterion now for comparison in the simulations. Pan [16] proposed an information criterion-based on the quasi-likelihood function for correlation R, QIC(R), as

$$\mathrm{QIC}(R)=-2Q(\hat{\beta }(R),\hat{\varphi };Y)+2\mathrm{trace}(\hat{\mathrm{\Sigma }}\hat{J}),$$ (24)

where $\hat{\varphi }$ is estimated ϕ based on the largest candidate model. In addition, J is the covariance of $\hat{\beta }$ and can be estimated by the robust or sandwich covariance estimator. Additionally, $\hat{\mathrm{\Sigma }}$ is the estimated of Σ, and to estimate $Q(\beta ,\varphi ;Y)$ and Σ, we have the following properties:

$$\begin{array}{rl}& E_0\{-{\frac{\mathrm{\partial }Q(\beta ,\varphi ;Y)}{\mathrm{\partial }\beta }|}_{\beta ={\beta }_0}\}=0\mathrm{and}\\ & \mathrm{\Sigma }=E_0\{-{\frac{{\mathrm{\partial }}^{2}Q(\beta ,\varphi ;Y)}{\mathrm{\partial }\beta \mathrm{\partial }{\beta }^{\mathrm{\prime }}}|}_{\beta ={\beta }_0}\}=\sum _{i=1}^n{X}_i^{\mathrm{\prime }}{V}_i{X}_i.\end{array}$$

We note that $\hat{\mathrm{\Sigma }}$ can be consistently estimated by its empirical estimator $-{\mathrm{\partial }}^{2}Q(\beta ,\varphi ;Y)/\mathrm{\partial \beta }\mathrm{\partial }{\beta }^{\mathrm{\prime }}{|}_{\beta =\hat{\beta }}$. QIC(R) in Equation (24) is used to select the most appropriate mixed model by fitting models and selecting the one with the smallest QIC(R). QIC(R) partially under the independence assumption. QIC(R) treats all the within-individual observations to be mutually independent. The parameters estimated in QIC(R) are based on the GEE approach such that QIC(R) is distribution free compared to other AIC-type selection criteria.

Before going deep into the performance of the proposed criteria QAICb1 and QAICb2, we now introduce another criterion ${\mathrm{QAIC}}_u$ defined in Pan [16]. Given a GEE estimator $\hat{\beta }(R)$ of β, ${\mathrm{QAIC}}_u(R)$ is expressed as

$${\mathrm{QAIC}}_u(R)=-2Q(\hat{\beta }(R),\hat{\varphi };Y)+2k.$$ (25)

Note that k is the number of parameters to be estimated. It has been found in the simulations that ${\mathrm{QAIC}}_u(R)$ is more efficient when the correlation of the data is relatively large, compared to the $\mathrm{QIC}(R)$. A possible reason would be the use of the bias correction term $2k$ for ${\mathrm{QAIC}}_u(R)$. Notice that the term $2k$ is only associated with the dimension of the candidate models and independent of the correlation structure. As there exist similarities between the log-likelihood and log quasi-likelihood functions, especially when the normal models are used, ${\mathrm{QAIC}}_u(R)$ shares similar properties of AIC, and it is also the asymptotic result of the QIC(R). Unlike $\mathrm{QIC}(R)$, which tends to underestimate the corresponding discrepancy when the correlation is large, the bootstrap-adjusted criteria QAICb1 and QAICb2 perform better in model selection across different correlation structures.

4.1. Simulations via nonparametric bootstrap approach

We will conduct simulations using a nonparametric approach. In real data sets, it is usually unknown that the correlation matrix is correctly specified or not. Therefore, the simulations are conducted in the settings where the true correlation matrix is not correctly specified to investigate the performance of QAICb1 and QAICb2 in model selection, which means the true correlation and the fitting correlation matrices are distinct. In the first setting, EX(ρ) is the true correlation and autoregressive (AR(ρ)) is the fitting correlation. The second setting is the opposite, with AR(ρ) being the true correlation and exchangeable (EX(ρ)) being the fitting correlation.

4.1.1. True correlation is not correctly specified

Tables 1– 3 feature the simulation results corresponding to three different true variances. A clear trend observed is that regardless of the correlation coefficient ρ and the standard deviation σ (or variance ${\sigma }^2$), as the sample size n increases, the rate of selecting the true model turns larger, i.e. the performance of model selection becomes better, indicating the consistency of the proposed selection criteria QAICb1 and QAICb2. The criterion $\mathrm{QIC}(\mathrm{R})$ performs poorly in selecting the correct model, and it is less effective than the others. As the correlation ρ increases, its selection performance turns worse.

Table 1.

True model selection rates under $\sigma =1$ (nonparametric).

True correlation		EX(ρ)				AR(ρ)
Fitting correlation		Autoregressive				Exchangeable
n	ρ	0.2	0.4	0.6	0.8	0.2	0.4	0.6	0.8
25	QIC(R)	50.4	50.1	49.7	44.1	54.0	48.8	47.1	43.3
	${\mathrm{QAIC}}_u(R)$	74.0	76.8	82.7	90.5	76.7	74.5	80.8	86.6
	QAICb1	61.9	66.1	72.0	80.3	65.0	63.7	70.4	76.2
	QAICb2	67.4	71.2	75.5	83.1	70.0	68.9	74.9	79.3
50	QIC(R)	60.3	60.0	56.3	49.8	63.4	62.1	57.4	49.8
	${\mathrm{QAIC}}_u(R)$	71.9	78.5	81.8	91.5	74.4	77.4	81.6	88.9
	QAICb1	66.0	72.5	74.4	86.5	69.6	72.0	76.0	83.3
	QAICb2	68.1	74.9	76.8	88.1	72.0	73.9	77.4	84.7
100	QIC(R)	66.1	63.5	60.8	55.3	66.1	64.8	56.9	49.9
	${\mathrm{QAIC}}_u(R)$	75.0	77.4	84.3	91.6	73.9	76.7	80.9	90.8
	QAICb1	70.6	72.4	80.5	88.9	69.1	73.8	77.2	88.7
	QAICb2	71.4	74.7	81.9	89.3	70.2	74.8	78.3	88.8
200	QIC(R)	70.2	66.6	67.8	58.0	70.3	65.6	62.7	55.0
	${\mathrm{QAIC}}_u(R)$	75.6	77.1	85.7	92.1	74.9	77.0	84.0	91.0
	QAICb1	72.8	75.1	83.6	90.4	72.8	74.8	82.1	88.7
	QAICb2	73.5	75.9	84.7	90.7	73.2	75.6	82.1	89.5

Table 3.

True model selection rates under $\sigma =1.5$ (nonparametric).

True correlation		EX(ρ)				AR(ρ)
Fitting correlation		Autoregressive				Exchangeable
n	ρ	0.2	0.4	0.6	0.8	0.2	0.4	0.6	0.8
25	QIC(R)	48.4	47.0	48.5	41.2	48.8	48.7	44.9	40.8
	${\mathrm{QAIC}}_u(R)$	34.7	38.9	51.3	61.5	32.8	37.7	45.5	59.7
	QAICb1	59.5	60.6	64.5	69.7	59.2	60.4	61.5	70.6
	QAICb2	63.1	63.8	67.8	71.5	62.4	64.5	65.8	73.8
50	QIC(R)	59.0	61.8	57.0	51.5	60.6	59.3	55.2	46.4
	${\mathrm{QAIC}}_u(R)$	33.0	41.8	52.6	68.4	31.7	36.8	46.7	62.2
	QAICb1	64.8	71.3	75.8	83.4	66.9	69.6	74.2	81.4
	QAICb2	67.3	73.8	77.0	85.9	69.7	72.1	76.3	82.7
100	QIC(R)	66.0	64.3	63.3	54.7	67.0	63.6	60.4	53.3
	${\mathrm{QAIC}}_u(R)$	30.9	40.2	54.0	68.6	31.9	38.1	48.1	63.1
	QAICb1	70.0	75.7	80.5	86.7	69.2	71.5	79.9	86.4
	QAICb2	70.3	76.8	81.8	87.2	70.9	73.9	79.9	87.3
200	QIC(R)	67.4	66.8	65.7	55.4	68.9	64.1	65.1	52.0
	${\mathrm{QAIC}}_u(R)$	31.7	38.2	53.4	70.1	30.8	34.7	48.5	62.9
	QAICb1	70.2	76.9	83.2	91.4	71.5	71.1	82.1	87.7
	QAICb2	71.2	76.8	84.3	91.2	72.5	71.1	82.3	88.2

Selection criterion ${\mathrm{QAIC}}_u(R)$ is not consistent for different values of ρ, although it performs better as ρ becomes large. Using $2k$ to estimate the bias correction term, the ρ values will only affect the quasi-likelihood estimation because $2k$ is not associated with the correlation structure but with the dimension of the candidate models. Under the circumstances that ρ is small and σ is large, $2k$ is not able to penalize the quasi-likelihood enough to satisfy the selection evaluation. The size of variances heavily affects the effectiveness of ${\mathrm{QAIC}}_u(R)$. As the sample size n escalates, the correctly selected rates tend to increase as the correlation size going up. So, ${\mathrm{QAIC}}_u(R)$ performs better than $\mathrm{QIC}(\mathrm{R})$ when ρ is large and σ is small.

We observe that the selection criteria QAICb1 and QAICb2 outperform ${\mathrm{QAIC}}_u(R)$ and QIC(R), and the QAICb2 behaves better than the other criteria in the tables. With the escalation of ρ, the behavior of QAICb1 and QAICb2 becomes significantly remarkable in model selection. The performance of QAICb2 is preferred compared with that of QAICb1.

The proposed selection criteria QAICb1 and QAICb2 are much more effective than the other two in different sample sizes. For example, in Table 2 with an exchangeable fitting correlation, $\rho =0.6$ and n = 100, both the QIC(R) and ${\mathrm{QAIC}}_u(R)$ have a selection rate of around $60\mathrm{\%}$ while QAICb1 and QAICb2 have a selection rate close to $80\mathrm{\%}$. Even though with a small sample size n = 25, their selection rates of around $63\mathrm{\%}$ and $67\mathrm{\%}$ are better than the other two criteria.

Table 2.

True model selection rates under $\sigma =1.3$ (nonparametric).

True correlation		EX(ρ)				AR(ρ)
Fitting correlation		Autoregressive				Exchangeable
n	ρ	0.2	0.4	0.6	0.8	0.2	0.4	0.6	0.8
25	QIC(R)	50.4	49.3	46.1	43.3	50.0	47.5	44.6	39.2
	${\mathrm{QAIC}}_u(R)$	46.7	52.5	59.3	75.5	45.9	48.6	55.8	69.5
	QAICb1	59.0	62.0	66.2	77.0	62.2	63.4	63.0	72.9
	QAICb2	64.6	62.7	70.0	79.3	66.8	67.8	67.3	75.8
	Run-time	8.76 seconds				9.74 seconds
50	QIC(R)	59.3	59.3	53.0	49.2	62.5	60.8	56.9	48.0
	${\mathrm{QAIC}}_u(R)$	42.5	53.7	59.0	77.9	48.3	54.3	60.2	72.9
	QAICb1	64.9	70.8	75.0	85.3	68.1	70.6	75.9	82.9
	QAICb2	67.4	73.1	78.5	85.8	70.8	72.8	78.0	83.7
	Run-time	10.98 seconds				12.44 seconds
100	QIC(R)	70.1	64.0	62.0	54.8	67.3	64.9	58.2	54.5
	${\mathrm{QAIC}}_u(R)$	47.9	51.5	65.0	78.4	46.0	51.9	58.9	76.6
	QAICb1	72.5	72.8	82.0	89.4	69.5	72.5	76.7	88.3
	QAICb2	73.6	74.5	83.5	90.0	71.5	73.1	78.7	88.9
	Run-time	17.82 seconds				16.47 seconds
200	QIC(R)	70.1	65.3	67.7	57.7	70.4	68.0	62.1	54.6
	${\mathrm{QAIC}}_u(R)$	46.5	51.5	67.4	80.0	45.5	52.7	60.8	76.1
	QAICb1	72.9	74.1	83.2	91.5	72.4	76.2	78.5	89.0
	QAICb2	73.9	74.3	83.7	91.6	72.5	76.7	79.2	89.5
	Run-Time	25.12 seconds				29.74 seconds

The selection criteria QAICb1 and QAICb2 not only own the property of ${\mathrm{QAIC}}_u(R)$ that being relatively consistent throughout different correlation coefficients, but also remain effective with respect to various sample sizes with noise σ. Tables 1 – 3 show that when the sample size is large, QAICb1 and QAICb2 are much more effective than ${\mathrm{QAIC}}_u(R)$ especially for larger variances.

The overall performance of QAICb1 and QAICb2 significantly outperforms the other two criteria, and generally QAICb2 outperforms QAICb1, which means the two proposed criteria are appropriate for mixed model selection.

We select the setting under $\sigma =1.3$ in Table 2 to record the running times for programming in computing the simulation results. We can see the running speed is generally fairly fast for the simulations via nonparametric bootstrap when the true correlation is not correctly specified.

4.1.2. Discussion on selecting overfitted candidate models

This section conducts the simulations for selecting nested models and with the true covariance as a mixture of several covariance matrices to show that QAICb1 and QAICb2 are less likely to select overfitted candidate models. The data are generated using a mixture of true covariance structures with $30\mathrm{\%}$ of the observations from EX(0.5), $30\mathrm{\%}$ from AR(0.5), and the rest $40\mathrm{\%}$ from a self-defined matrix as the following:

$${\sigma }^2\left[\begin{array}{ccc}1& 0.9& 0.4\\ 0.9& 1& 0.8\\ 0.4& 0.8& 1\end{array}\right].$$

Tables 4 – 6 feature the results of selecting the nested models with the largest 10 predictors, and the 10 candidate models are denoted by M1, M2,…, M10. M4 is the true model. M5 to M10 are the overfitted models, and M1 to M4 are the underfitted models. The selection rates are recorded in 1000 repetitions.

Table 4.

Selection results under n = 100 and $\sigma =1.3$ (nonparametric).

True correlation: EX(0.6)				Fitting correlation: exchangeable
Criteria	M1	M2	M3	TRUE	M5	M6	M7	M8	M9	M10
QIC(R)	0	0	0	587	119	77	69	43	53	52
${\mathrm{QAIC}}_u(R)$	0	0	0	656	114	75	51	37	43	24
QAICb1	0	0	0	818	74	48	27	9	17	7
QAICb2	0	0	0	828	70	52	22	7	15	6
Run-time	15.99 seconds

Table 6.

Selection results under n = 100 and $\sigma =1.5$ (nonparametric).

True correlation: mixture				Fitting correlation: autoregressive
Criteria	M1	M2	M3	TRUE	M5	M6	M7	M8	M9	M10
QIC(R)	0	0	0	581	133	81	46	55	46	58
${\mathrm{QAIC}}_u(R)$	0	0	0	640	130	78	39	38	35	40
QAICb1	0	0	0	806	116	42	12	8	6	10
QAICb2	0	0	0	816	114	38	10	7	7	8
Run-time	13.37 seconds

The results in Tables 4 – 6 show that all of the four criteria have similar selection patterns that they are more likely to choose overfitted candidate models than underfitted candidate models. However, QAICb1 and QAICb2 significantly reduce the chance in selecting overfitted candidate models. In other words, the true model selection rates of QAICb1 and QAICb2 are much higher than those of QIC(R) and ${\mathrm{QAIC}}_u(R)$ by not selecting overfitted models. Focusing on Table 5, the percentages of choosing M5 as the final model for QIC(R) and ${\mathrm{QAIC}}_u(R)$ are $13.0\mathrm{\%}$ and $13.3\mathrm{\%},$ respectively, while the percentages for QAICb1 and QAICb2 are $10.6\mathrm{\%}$ and $10.0\mathrm{\%}$, which is a noticeable decrease by around $3\mathrm{\%}$ on only one overfitted model.

Table 5.

Selection results under n = 100 and $\sigma =1.3$ (nonparametric).

True correlation: AR(0.6)				Fitting correlation: exchangeable
Criteria	M1	M2	M3	TRUE	M5	M6	M7	M8	M9	M10
QIC(R)	0	0	0	582	130	83	65	55	48	37
${\mathrm{QAIC}}_u(R)$	0	0	0	589	133	86	64	49	43	36
QAICb1	0	0	0	767	106	54	30	16	19	8
QAICb2	0	0	0	787	100	45	31	15	17	5
Run-time	16.03 seconds

The simulation results in Table 6 demonstrate that when the true covariance is a mixture of different covariance matrices, QAICb1 and QAICb2 are less likely to select highly overfitted candidate models compared to the results in the previous two tables. The selection rates for candidate models M8 to M10 are all less than $1\mathrm{\%}$ which are lower than the corresponding rates in the previous two tables.

The simulation results demonstrate that QAICb1 and QAICb2 are more likely to avoid overfitted candidate models than QIC(R) and ${\mathrm{QAIC}}_u(R)$ along with the result of more consistent performance. As a result, the highly overfitted candidate models will be rarely chosen as the final model via QAICb1 and QAICb2.

We record the running times in Tables 4 – 6, and the results can be obtained within several seconds.

4.1.3. Simulations for candidate models with combinations of predictors

In this section, we will use models in different combinations of predictor variables to select the most appropriate model. We have 5 different covariates $X_1$ to $X_5$ independently generated from the standard normal distribution and set the true model parameter to be ${\beta }_0=(1,-1,0.5,0,-0.5{)}^{\prime }$. Always keeping the intercept, the different combinations of models are summarized in Table 7.

Table 7.

Description of candidate models.

Model	Covariates	Model	Covariates
M1	$X_1$, $X_2$	M5	$X_1$, $X_2$, $X_3$, $X_4$
M2	$X_1$, $X_2$, $X_3$	M6	$X_1$, $X_2$, $X_3$, $X_5$
M3	$X_1$, $X_2$, $X_4$	M7	$X_1$, $X_2$, $X_4$, $X_5$
M4 (True)	$X_1$, $X_2$, $X_5$	M8	$X_1$, $X_2$, $X_3$, $X_4$, $X_5$

We evaluate the performance of the selection criteria with different sample sizes n = 25, n = 50, n = 100, and n = 200 and a fixed standard deviation of $\sigma =1.3$. The true correlation matrix is set as EX(ρ) or AR(ρ) with $\rho =0.2$, 0.4, 0.6, 0.8. Again, the number of bootstrap samples B is chosen to be 250 in all settings. For the mixed true covariance structure, $30\mathrm{\%}$ of the observations are from EX(0.5), another $30\mathrm{\%}$ come from AR(0.5), and the rest $40\mathrm{\%}$ from a self-defined matrix as the following:

$${\sigma }^2\left[\begin{array}{ccc}1& 0.8& 0.3\\ 0.8& 1& 0.6\\ 0.3& 0.6& 1\end{array}\right].$$

Tables 8– 10 feature the selection rates for the proposed criteria and the other two criteria used for comparison. We observe that the selection rates of QIC(R) decrease with the increase of the correlation coefficient ρ while ${\mathrm{QAIC}}_u(R)$, QAICb1, and QAICb2 have higher selection rates with relatively larger ρ. Of all the simulation settings, the performance of QAICb1 and QAICb2 is almost the same and is generally much more significant than ${\mathrm{QAIC}}_u(R)$. The selection rates of ${\mathrm{QAIC}}_u(R)$ are about $5\mathrm{\%}$ to $18\mathrm{\%}$ less than those from QAICb1 and QAICb2.

Table 8.

True model selection rates via variable combinations (nonparametric).

True correlation		EX(ρ)				AR(ρ)
Fitting correlation		Exchangeable				Autoregressive
n	ρ	0.2	0.4	0.6	0.8	0.2	0.4	0.6	0.8
25	QIC(R)	57.3	52.4	53.6	48.6	56.6	55.9	52.2	44.0
	${\mathrm{QAIC}}_u(R)$	53.8	53.2	64.4	72.5	53.3	56.5	61.3	70.1
	QAICb1	63.4	60.6	68.2	72.6	62.1	64.5	66.3	71.1
	QAICb2	66.3	62.8	69.9	74.0	64.4	67.6	68.7	72.4
50	QIC(R)	66.1	60.3	59.8	53.4	64.3	61.2	60.1	51.9
	${\mathrm{QAIC}}_u(R)$	54.5	56.9	65.7	78.3	52.3	55.0	61.6	74.0
	QAICb1	68.7	70.0	75.0	84.6	67.1	66.8	74.2	81.5
	QAICb2	71.0	70.6	75.5	85.6	68.2	67.7	75.8	82.2
100	QIC(R)	68.5	64.3	60.7	53.6	67.8	67.2	59.5	56.8
	${\mathrm{QAIC}}_u(R)$	56.5	58.5	65.7	77.2	54.6	59.8	62.8	77.3
	QAICb1	70.4	72.3	77.0	86.2	69.9	73.5	75.2	85.0
	QAICb2	71.0	71.9	77.7	87.3	71.1	74.5	75.9	85.5
200	QIC(R)	66.5	62.9	59.9	55.4	69.5	68.2	63.4	56.1
	${\mathrm{QAIC}}_u(R)$	51.9	56.4	63.8	76.2	54.5	58.3	62.4	70.8
	QAICb1	70.5	71.1	77.6	87.2	70.3	73.4	76.0	83.8
	QAICb2	70.0	71.3	78.2	87.5	71.6	73.2	75.9	83.7

Table 10.

True model selection rates via variable combinations (nonparametric).

True correlation	Mixture			Mixture
Fitting correlation	Exchangeable			Autoregressive
n	50	100	200	50	100	200
QIC(R)	63.1	63.6	64.5	61.1	61.5	62.2
${\mathrm{QAIC}}_u(R)$	62.7	62.6	62.2	64.6	63.6	62.7
QAICb1	74.7	74.7	75.9	73.5	78.8	79.0
QAICb2	75.5	77.4	76.6	74.5	78.8	79.2
Run-time (s)	7.98	10.73	16.29	6.81	9.49	14.97

The simulation results show that the selection effectiveness of QAICb1 and QAICb2 improves as the sample size increases, especially in the setting where the true covariance is a mixture. Furthermore, starting from n = 50, when the sample size is large enough, the selection rates in selecting the true model are hardly impacted by the sample size. As a result, QAICb1 and QAICb2 perform consistently with smaller n and therefore will be more capable than QIC(R) and ${\mathrm{QAIC}}_u(R)$ in small-sample model selection.

In addition to the consistency of QAICb1 and QAICb2 over different sample sizes, the impact from the true correlation coefficient ρ is not as large as expected. In Table 9, when $n=100$ and the fitting correlation is autoregressive, the selection rates of ${\mathrm{QAIC}}_u(R)$ under $\rho =0.2$ and $\rho =0.8$ are $50.8\mathrm{\%}$ and $76.5\mathrm{\%},$ respectively, with a difference $25.7\mathrm{\%}$ while the rate differences in QAICb1 and QAICb2 are all around $16\mathrm{\%}$.

Table 9.

True model selection rates via variable combinations (nonparametric).

True correlation		EX(ρ)				AR(ρ)
Fitting correlation		Autoregressive				Exchangeable
n	ρ	0.2	0.4	0.6	0.8	0.2	0.4	0.6	0.8
25	QIC(R)	57.8	55.8	55.8	48.0	58.0	56.0	50.9	50.5
	${\mathrm{QAIC}}_u(R)$	54.0	56.7	56.7	69.4	51.6	55.8	55.1	68.4
	QAICb1	63.0	64.8	64.8	70.4	63.3	63.4	61.2	70.8
	QAICb2	65.3	67.3	67.3	72.8	65.7	65.5	63.5	72.9
50	QIC(R)	64.7	63.4	59.3	53.2	65.1	63.6	61.2	55.8
	${\mathrm{QAIC}}_u(R)$	54.9	60.1	66.2	76.6	53.5	56.6	63.6	71.8
	QAICb1	68.2	71.2	74.1	83.2	66.9	69.3	73.0	78.4
	QAICb2	68.8	71.8	75.6	84.3	68.5	71.1	74.4	80.0
100	QIC(R)	66.7	68.2	61.6	57.7	67.0	64.8	62.3	57.1
	${\mathrm{QAIC}}_u(R)$	50.8	60.2	63.3	76.5	54.3	56.4	62.1	73.6
	QAICb1	68.0	74.3	75.9	84.5	68.2	70.7	75.4	83.0
	QAICb2	69.2	74.9	76.3	85.0	69.2	71.9	76.1	83.7
200	QIC(R)	67.4	66.4	63.3	60.5	69.3	65.5	66.5	56.4
	${\mathrm{QAIC}}_u(R)$	51.5	58.1	63.9	74.2	52.5	55.0	65.0	74.2
	QAICb1	68.6	71.5	76.8	85.6	71.8	71.2	78.5	86.2
	QAICb2	69.1	71.7	77.2	86.4	71.8	71.5	78.2	86.6

Therefore, the simulation results demonstrate that QAICb1 and QAICb2 have more outstanding selection performance with respect to both the sample size and correlation coefficient. More importantly, the proposed selection criteria behaves effectively in a small sample setting.

We select the settings via variable combinations in Table 10 to record the running times. We can see the running speed is fairly fast, which indicates that the proposed selection criteria are applicable and feasible with respect to the computational time.

4.2. Simulations via semiparametric bootstrap approach

The semiparametric bootstrap is utilized to construct the bootstrapping samples. The semiparametric bootstrap involves sampling with replacement over the residuals after deducting the mean estimated by a parametric method from the responses under each of the candidate models. In what follows, the simulation results are presented and discussed in similar settings as those for the nonparametric method. The sample size n is chosen to be 15, 25, 35 and 50.

4.2.1. Linear mixed models involving different correlation structures

This section will present simulation results when the sample is constructed by observations from a mixture of three different covariance structures. That is, $40\mathrm{\%}$ of the observations are from EX(0.5), $40\mathrm{\%}$ come from AR(0.5), and the rest $20\mathrm{\%}$ from a self-defined matrix as following:

$${\sigma }^2\left[\begin{array}{ccc}1& 0.4& 0.6\\ 0.4& 1& 0.3\\ 0.6& 0.3& 1\end{array}\right].$$

Both the exchangeable and autoregressive fitting correlations are used to fit candidate models and three values of σ are considered.

The simulation results are summarized in Tables 11 – 13. Firstly, as the sample size n increases, the selection rates for all four selection criteria go up. When both n and σ are small, ${\mathrm{QAIC}}_u(R)$ performs better than the other three selection criteria in selecting the correct model. In Table 11 when $\sigma =1$, n = 25 and the fitting correlation is exchangeable, the true model selection rate of ${\mathrm{QAIC}}_u(R)$ is $77.2\mathrm{\%}$ higher than $62.3\mathrm{\%}$ of QAICb2. When n is 50, the selection rate of QAICb2 is $74.8\mathrm{\%}$ lower than $79.0\mathrm{\%}$ of ${\mathrm{QAIC}}_u(R)$. In addition, when $\sigma =1.5$ and n = 50 with the exchangeable fitting correlation, Table 13 shows that ${\mathrm{QAIC}}_u(R)$ has $43.8\mathrm{\%}$ of the true model selection rate while QAICb2 achieves a much higher rate of $75.2\mathrm{\%}$. With the increase of n, QAICb2 becomes more and more effective in selecting the best model, especially in the cases where σ is relatively large ( $\sigma =1.3$ or 1.5), QAICb2 has noticeably higher true model selection rates than $\mathrm{QIC}(R)$ and ${\mathrm{QAIC}}_u(R)$.

Table 11.

True model selection rates under $\sigma =1$ (semiparametric).

True correlation	Mixture				Mixture
Fitting correlation	Exchangeable				Autoregressive
n	15	25	35	50	15	25	35	50
QIC(R)	37.5	49.4	54.3	58.0	42.4	50.6	54.3	59.8
${\mathrm{QAIC}}_u(R)$	73.8	77.2	80.8	79.0	75.2	76.7	77.7	78.8
QAICb1	43.8	53.6	57.5	58.8	47.2	53.0	55.5	55.9
QAICb2	49.4	62.3	72.6	74.8	52.5	61.1	70.3	76.2
Run-time (s)	18.10	20.21	25.08	29.34	17.29	19.84	24.29	28.14

Table 13.

True model selection rates under $\sigma =1.5$ (semiparametric).

True correlation	Mixture				Mixture
Fitting correlation	Exchangeable				Autoregressive
n	15	25	35	50	15	25	35	50
QIC(R)	31.9	45.4	53.6	58.5	35.6	44.8	56.0	59.1
${\mathrm{QAIC}}_u(R)$	37.4	40.6	42.4	43.8	39.5	40.9	43.6	44.1
QAICb1	37.5	46.8	54.3	57.2	40.7	49.4	54.5	54.7
QAICb2	40.6	56.2	66.8	75.2	42.9	58.0	66.8	72.3

Table 12.

True model selection rates under $\sigma =1.3$ (semiparametric).

True correlation	Mixture				Mixture
Fitting correlation	Exchangeable				Autoregressive
n	15	25	35	50	15	25	35	50
QIC(R)	35.6	48.3	55.2	58.0	35.5	47.4	57.3	56.9
${\mathrm{QAIC}}_u(R)$	49.8	56.7	59.8	55.3	49.0	54.9	56.9	55.3
QAICb1	39.9	52.0	56.5	57.8	39.4	50.0	56.0	58.1
QAICb2	45.1	59.1	69.7	74.2	44.0	60.6	69.6	72.7

Secondly, in general, QAICb2 has the best overall selection performance while QAICb1 is not as effective as QAICb2 across all model settings. When the true correlation is a mixture of several correlation structures and the semiparametric bootstrap is utilized, QAICb2 has the most consistent and effective overall selection performance than the others. Possibly affected by the bias introduced from overfitted candidate models, the performance of QAICb1 is not optimal when compared to the results from the nonparametric bootstrap.

We want to remark that the program running times under semiparametric bootstrap are slightly longer than those for nonparametric bootstrap with computation in selected simulation settings, as shown in Table 11, but sufficiently short.

4.2.2. Discussion on selecting overfitted candidate models

In this section, we intend to show that QAICb2 is less likely to select overfitted candidate models while QAICb1 is more likely to do so, which results in the nonoptimal performance of QAICb1. The simulation results are presented in Tables 14 – 16.

Table 14.

Selection results under n = 100 and $\sigma =1.3$ (semiparametric).

True correlation: EX(0.6)				Fitting correlation: exchangeable
Criteria	M1	M2	M3	TRUE	M5	M6	M7	M8	M9	M10
QIC(R)	0	0	0	576	132	81	70	42	56	43
${\mathrm{QAIC}}_u(R)$	0	0	0	648	129	68	58	33	39	25
QAICb1	0	0	0	535	247	111	52	27	14	14
QAICb2	0	0	0	849	103	19	17	4	6	2

Table 16.

Selection results under n = 100 and $\sigma =1.3$ (semiparametric).

True correlation: mixture				Fitting correlation: exchangeable
Criteria	M1	M2	M3	TRUE	M5	M6	M7	M8	M9	M10
QIC(R)	0	0	0	627	110	66	53	57	48	39
${\mathrm{QAIC}}_u(R)$	0	0	0	584	118	75	56	66	50	51
QAICb1	0	0	0	529	236	94	56	43	23	19
QAICb2	0	0	0	811	97	40	20	19	8	5

From the three tables, we can see that all of the four selection criteria do not select candidate models smaller than the true model, and QAICb2 owns the highest true model selection rates by not selecting relatively large candidate models. In Table 14, the selection rates of M6 for QIC(R) and ${\mathrm{QAIC}}_u(R)$ are $8.1\mathrm{\%}$ and $6.8\mathrm{\%},$ respectively, while the corresponding rate for QAICb2 is $1.9\mathrm{\%}$; QAICb2 rarely chooses highly overfitted candidate models M8 to M10. Similar pattern can be found in Tables 15 and 16, where the selection of candidate model M5 is avoided by QAICb2. Tables 14 – 16 also demonstrate that QAICb1 is not as effective as QAICb2 because QAICb1 tends to choose more relatively larger models than QAICb2.

Table 15.

Selection results under n = 100 and $\sigma =1.3$ (semiparametric).

True correlation: AR(0.6)				Fitting correlation: autoregressive
Criteria	M1	M2	M3	TRUE	M5	M6	M7	M8	M9	M10
QIC(R)	0	0	0	599	113	91	68	51	40	38
${\mathrm{QAIC}}_u(R)$	0	0	0	654	112	82	57	42	30	23
QAICb1	0	0	0	550	237	104	60	25	13	11
QAICb2	0	0	0	875	68	30	20	5	2	0

In the semiparametric bootstrap process, the resampling accommodates the residuals obtained from the candidate models. The bootstrap estimation in Equation (14) relies on the candidate model, and both the numerator and denominator are calculated using GEE estimators from the bootstrap samples, and also the denominator in the fraction of Equation (14) utilizes the $Y^{\ast }(i)$ from the bootstrap samples. Because the value of QAICb1 heavily depends on the semiparametric bootstrap samples, if a candidate model is biased, the estimation in Equation (14) tends to be biased.

5. Application

To further investigate the performance of the proposed two criteria in mixed model selection, an application in Parkinson's Progression Markers Initiative (PPMI) data is conducted in this section. Within the application, we construct the candidate models first and then apply QAICb1 and QAICb2 to obtain the most appropriate model.

5.1. Data description

The PPMI [14] is a longitudinal clinical study trying to identify the significant factors contributing to the progression of Parkinson's disease. Taking place at various sites from four different countries, the PPMI comprehensively evaluated the characteristics of participated subjects based on different perspectives, including brain imaging, genetics, behavioral assessments. The data of the PPMI study was provided by The Michael J. Fox Foundation for Parkinson's Research.

There are 441 subjects participated in this clinical study with each measured by the baseline and 3 follow-ups, so there are total 1764 data points with 4 repeated measurements for each individual. For simplification, we choose 12 predictor variables featuring genetics and individual assessments out of the original variables. A detailed description of all the variables is displayed in Table 17. It is worth noting that the rating scale is one of the fundamental tools used to evaluate the stage of Parkinson's disease in patients. The usual rating scales consist of 5 different segments covering different movement hindrances of Parkinson's disease while in our data only 3 segments are available with Mentation, Behavior, and Mood in Part I (RS1), Activities of Daily Living in Part II (RS2), and Motor Examination in Part III (RS3). The variables GP1-GP6 measure different gene pieces for possibly controlling the motion of an individual.

Table 17.

A description of predictor variables.

Name	Description
PD	Status of Parkinson's disease, ‘yes’ = 1, ‘no’ = 0
GP1	Genetic piece: chr12 rs34637584 GT
GP2	Genetic piece: chr17 rs11868035 GT
GP3	Genetic piece: chr17 rs11012 GT
GP4	Genetic piece: chr17 rs393152 GT
GP5	Genetic piece: chr17 rs12185268 GT
GP6	Genetic piece: chr17 rs199533 GT
RS1	Part I of the unified Parkinson's disease rating scale
RS2	Part II of the unified Parkinson's disease rating scale
RS3	Part III of the unified Parkinson's disease rating scale
Sex	Index of an individual's sex, ‘female’ = 0, ‘male’ = 1
Weight	Numerical value of an individual's age
Age	Numerical value of an individual's age
ID	Index of an individual

5.2. Data processing and candidate models

The PPMI data encounters missing values. One way to deal with this issue is to remove the data points with missing inputs if the percentage of missing points is low and missing data are at random. However, the missing rate is high for this data set, we consider using multiple imputation and obtain the complete data by the weighted predictive mean matching imputation approach and all of our model selection analysis is based on the imputed data set.

There are total of 12 predictor variables except the response variable ‘PD’ and the indexing variable ‘ID’. As described in Table 17, ‘PD’ is an indicator of Parkinson's disease status, and the response variable is the logit of probability of having the Parkinson's disease. The model is to predict this probability using the most appropriate fixed effects and random effects. ‘ID’ denotes the index of patients. With each index of ‘ID’, the measures are repeated 4 times for each individual. So, the ‘ID’ variable has random effects in the model and the covariance structure is exchangeable.

If we consider all the possible candidate models, there are $2^{12}$ possibilities, which is not realistic. So, we first go through a pre-screening procedure in which we select the predictor variables by applying the step-wise model selection approaches. In this pre-screening procedure, we use ${\mathrm{QAIC}}_u(R)$, and no bootstrapping is needed for it, the forward and backward step-wise approaches give us different fixed effects but both with ‘ID’ as the random effects in the models: both the forward and backward step-wise approaches select ‘Sex’, ‘RS1’, ‘RS2’, and ‘RS3’, but the forward approach also selects ‘GP1’; the backward approach also selects ‘Weight’ and ‘Age’. Therefore, after this pre-screening procedure, we will keep ‘Sex’, ‘RS1’, ‘RS2’, and ‘RS3’ as the fixed effects and will select the predictor variables among ‘GP1’, ‘Age’, and ‘Weight’ because the two step-wise approaches have distinct selections among these 3 predictor variables. We, therefore, have 8 candidate models in the candidate pool, which are presented in Table 18. From the table, we can see that in the pre-screening, the forward step-wise method chooses the model ‘M2’; the backward step-wise chooses the model ‘M7’.

Table 18.

Candidate models for PPMI data analysis.

Name	GP1	Age	Weight	Sex	RS1	RS2	RS3
M1				$\times \times$	$\times \times$	$\times \times$	$\times \times$
M2	$\times \times$			$\times \times$	$\times \times$	$\times \times$	$\times \times$
M3		$\times \times$		$\times \times$	$\times \times$	$\times \times$	$\times \times$
M4	$\times \times$	$\times \times$		$\times \times$	$\times \times$	$\times \times$	$\times \times$
M5			$\times \times$	$\times \times$	$\times \times$	$\times \times$	$\times \times$
M6	$\times \times$		$\times \times$	$\times \times$	$\times \times$	$\times \times$	$\times \times$
M7		$\times \times$	$\times \times$	$\times \times$	$\times \times$	$\times \times$	$\times \times$
M8	$\times \times$	$\times \times$	$\times \times$	$\times \times$	$\times \times$	$\times \times$	$\times \times$

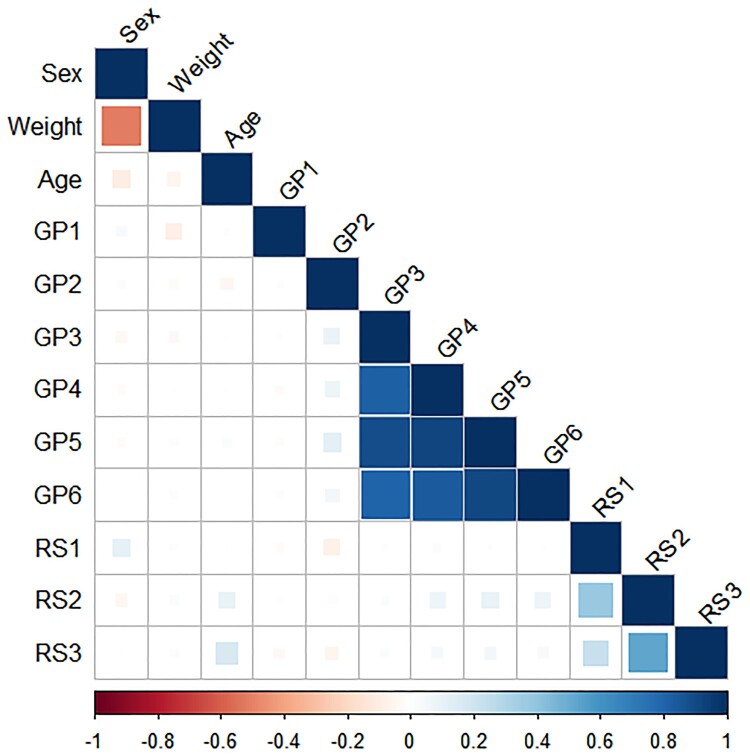
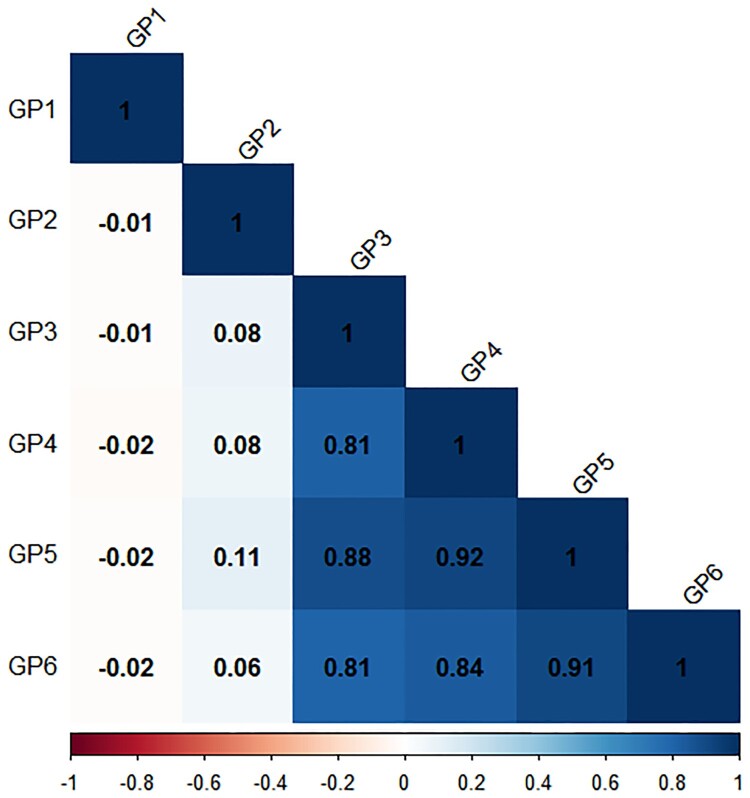
We can further remark on why we have these candidate models. Based on the correlations in Figure 1, we notice that there are two sets of variables that are highly correlated with each other, and the correlations for each of the two sets are shown in Figures 2 and 3 respectively. Based on the correlations in Figure 2, the first set contains six variables from ‘GP1’ to ‘GP6’, and these are measures of genetic pieces. Five of these variables from ‘GP2’ to ‘GP6’ are not considered because ${\mathrm{QAIC}}_u(R)$ does not select them in the pre-screening. So, only ‘GP1’ is selected in the model from the first correlated set by the forward step-wise approach, indicating that only ‘GP1’ is a potential gene that may relate to Parkinson's disease.

Figure 1.

Visualization of PPMI correlation matrix.

Figure 2.

Correlation of gene expression.

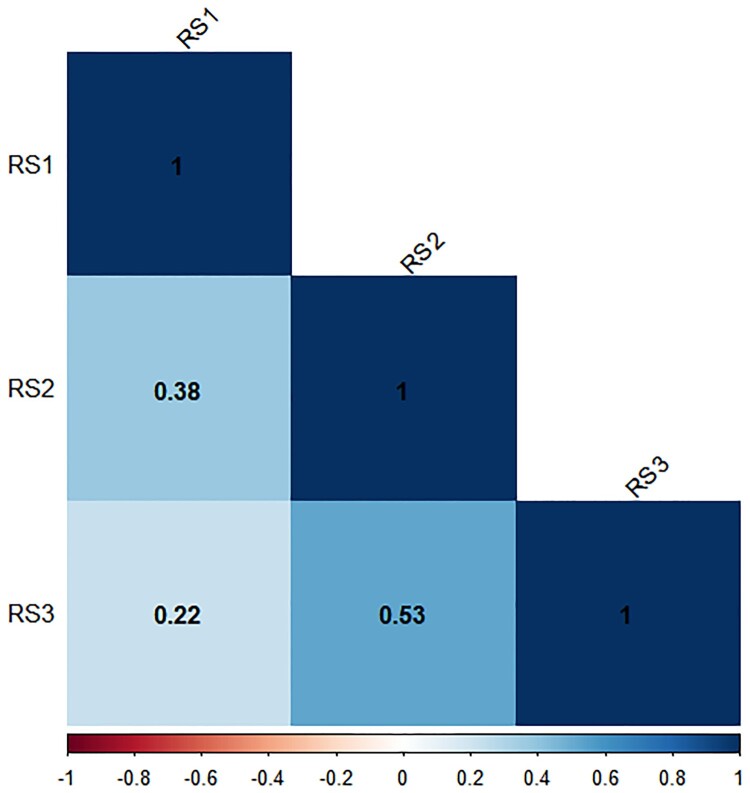
Figure 3.

Correlation of RS.

The second set consists of 3 variables: ‘RS1’, ‘RS2’, and ‘RS3’, as shown in Figure 3, which are the measures of a person's stage of Parkinson's disease. As the two pre-screening approaches select ‘RS1’, ‘RS2’, and ‘RS3’, and the correlation between them are not very high, we keep them in our candidate models.

We will also include the predictor variables ‘Weight’ and ‘Age’ into the candidate models to better characterize a subject. Considering these 2 variables and ‘GP1’ will greatly simplify the process of model selection, we test all the variable combinations of the 3 predictor variables ‘GP1’, ‘Weight’, and ‘Age’, which results in the selection of 8 possible candidate models. The summary of all the candidate models is in Table 18.

5.3. Presentation of selection results

After the four different model selection criteria are applied to select the candidate models, the selection results are presented in Table 19. The number of bootstrap samples is set to be 250. This number is the minimum value which can achieve efficient and effective results for the bootstrap method, and a larger number of the sample size can be used but does not improve the results much.

Table 19.

Selection results using different selection criteria.

Criterion	Final model	Criterion	Final model
QIC(R)	M2	QAICb1	M4
${\mathrm{QAIC}}_u(R)$	M4	QAICb2	M4

From the table, we can see QIC(R) selects the model ‘M2’ and QAICb1, QAICb2, and ${\mathrm{QAIC}}_u(R)$ all select the model ‘M4’ as the most appropriate model, which adds ‘Age’ to the model ‘M2’.

The selection results show that model ‘M4’ is more likely to be the most appropriate model. This model ‘M4’ shows that the status of Parkinson's disease can be effectively predicted by ‘Age’, ‘Sex’, rating scales for movement hindrances ‘RS1’, ‘RS2’, ‘RS3’, and a gene-piece measure ‘GP1’, which complies with a common understanding about Parkinson's disease. In this particular data set, although QAICb1, QAICb2, and ${\mathrm{QAIC}}_u(R)$ all select the same model, the previous simulation results show that QAICb2 outperforms the other compared criteria in selecting a correct model.

6. Concluding remarks and discussion

We propose two criteria QAICb1 in Equation (15) and QAICb2 in Equation (23) for mixed model selection by adopting the quasi-likelihood function and bootstrap approaches.

Fully specifying the distribution of the data may not be realistic when it comes to some practical problems. To overcome the limitations of the traditional model selection criteria on distributions, we propose the selection criteria depending less on the parametric distribution and is easy to fulfill. We replace the log-likelihood function in the K-L discrepancy by the log quasi-likelihood, in which the approach depends less on the parametric distribution and much easier to calculate with the existence of correlation in the data. QAICb1 and QAICb2 are developed to serve as asymptotically unbiased estimators of the quasi-likelihood based on K-L discrepancy between a candidate model and the true model. We can therefore utilize them as model selection criteria to select the most appropriate model among a candidate pool in mixed models.

The proposed selection criteria QAICb1 and QAICb2 consist of two components: the log quasi-likelihood and an estimation of the bias correction term. To compute the log quasi-likelihood function, we utilize GEE to obtain the model parameters from the original data with a prespecified fitting correlation matrix. The estimation of the bias correlation term is based on the bootstrap approach, which provides us with more significant selection performance of QAICb1 and QAICb2 for mixed models.

Both QAICb1 and QAICb2 are based on the quasi-likelihood functions without assumptions of distributions, so these two model selection criteria are general methods when the distribution is not specified or unknown in linear mixed models. When the distribution is specified, not only nonparametric bootstrap but also parametric bootstrap can be utilized for calculating QAICb1 and QAICb2. In the parametric bootstrap, the distribution information can be well employed.

To extensively study the model selection performance of QAICb1 and QAICb2, the simulations with different model settings are conducted. The simulation results demonstrate that the proposed criteria generally outperform some other selection criteria such as $\mathrm{QIC}(\mathrm{R})$ and ${\mathrm{QAIC}}_u(R)$ in selecting the best model. With the escalation of the correlation ρ, the behavior of QAICb1 and QAICb2 becomes significantly remarkable in model selection. The results also show that the performance of QAICb1 and QAICb2 is almost the same in large samples except for the situation where the semiparametric bootstrap approach is used to generate bootstrap samples. The selection performance of QAICb1 is not as optimal as that of QAICb2 for the semiparametric bootstrap. Based on the simulation results, QAICb2 is preferred when the semiparametric bootstrap is utilized.

We note that there exist many model selection criteria, and it is common sense that no unique selection criterion can take all advantages for model selection. Although the recent trend towards variable selection in linear mixed models adopts many penalized methods for high-dimensional situations, for small to medium size of predictors involved in the model selection, the proposed QAICb1 and QAICb2 perform effectively and focus on the performance improvement in model selection over $\mathrm{QIC}(\mathrm{R})$ and ${\mathrm{QAIC}}_u(R)$ using the quasi-likelihood functions and bootstrap methods. For high-dimensional cases where the number of predictors is very large, the proposed selection criteria QAICb1 and QIACb2 do not perform as well as in small to medium-dimensional settings. Therefore, we prefer to adopt QAICb1 and QAICb2 for small or medium-dimension model selection.

A suitable number of bootstrap samples B should be considered to achieve the best selection performance of QAICb1 and QAICb2 in bootstrapping. In the simulations, B is chosen to be 250, which serves as the minimal number of bootstrap samples needed to effectively estimate the bias term in QAICb1 and QAICb2, respectively. Increasing B from 250 does not significantly increase the performance of the proposed selection criteria.

To compare other selection criteria with the proposed QAICb1 and QAICb2, we can remark on the Information Complexity Criteria (ICOMP) [2,3] performance in the settings where we conduct the simulations. We compute some ICOMP values in the simulation settings, but not presented here. When the distribution is normal, the ICOMP significantly outperforms the proposed selection criteria QAICb1 and QAICb2, and the ICOMP computation relies on the distribution in a mixed model. Based on the ICOMP, Shang [18] developed a diagnostic of influential cases in generalized linear mixed models. However, for the unknown distributions in mixed models and other distributions (e.g. logistic regression), the proposed selection criteria outperform the ICOMP in selecting the true model. We address that the proposed QAICb1 and QAICb2 focus on the performance improvement in model selection over $\mathrm{QIC}(\mathrm{R})$ and ${\mathrm{QAIC}}_u(R)$ using the quasi-likelihood functions and bootstrap methods.

When establishing theoretical properties and conducting simulations, we initially propose QAICb1 and QAICb2 for linear mixed models. The utilization of the quasi-likelihood and GEE could also be extended to typical generalized linear mixed effects models with both fixed and random effects included in Zeger et al. [22]. We will extend QAICb1 and QAICb2 to generalized linear models with random effects by including the estimation of overdispersion parameter in future research. Also, we plan to develop the proposed selection criteria into an R function accessible to general users.

Disclosure statement

No potential conflict of interest was reported by the author(s).