Modeling tissue co-regulation estimates tissue-specific contributions to disease

Abstract

Integrative analyses of genome-wide association studies and gene expression data have implicated many disease-critical tissues. However, co-regulation of genetic effects on gene expression across tissues impedes distinguishing biologically causal tissues from tagging tissues. Here, we introduce tissue co-regulation score regression (TCSC), which disentangles causal tissues from tagging tissues by regressing gene-disease association statistics (from transcriptome-wide association studies) on tissue co-regulation scores reflecting correlations of predicted gene expression across genes and tissues. We applied TCSC to 78 diseases/traits (average N = 302K) and gene expression prediction models for 48 GTEx tissues. TCSC identified 21 causal tissue-trait pairs at 5% FDR, including well-established findings, biologically plausible novel findings (e.g. aorta artery and glaucoma), and increased specificity of known tissue-trait associations (e.g. subcutaneous adipose, but not visceral adipose, and HDL). TCSC also identified 17 causal tissue-trait covariance pairs at 5% FDR. In conclusion, TCSC is a precise method for distinguishing causal tissues from tagging tissues.

Introduction

Most diseases are driven by tissue-specific or cell-type-specific mechanisms, thus the inference of causal disease tissues is an important goal¹. For many polygenic diseases and complex traits, disease-associated tissues have previously been identified via the integration of genome-wide association studies (GWAS) with tissue-level functional data characterizing expression quantitative trait loci (eQTLs)^2–5, gene expression^6–9, or epigenetic features^10–17. However, it is likely that most disease-associated tissues are not actually causal, due to the high correlation of eQTL effects (resp. gene expression or epigenetic features) across tissues; the correlation of eQTL effects across tissues, i.e. tissue co-regulation, can arise due to shared eQTLs or distinct eQTLs in linkage disequilibrium (LD)^2,18,19,5. One approach to address this involves comparing eQTL-disease colocalizations across different tissues² while another approach leverages multi-trait fine-mapping to simultaneously evaluate all tissues for disease colocalization⁵; both methods risk implicating co-regulated tagging tissues that colocalize with disease. To our knowledge, no previous study has formally modeled genetic co-regulation across tissues to statistically disentangle causal from tagging tissues.

Here, we introduce a new method, tissue co-regulation score regression (TCSC), that disentangles causal tissues from tagging tissues and partitions disease heritability (or genetic covariance of two diseases/traits) into tissue-specific components. TCSC leverages gene-disease association statistics across tissues from transcriptome-wide association studies (TWAS)^20,21,18. A challenge is that TWAS association statistics include the effects of both co-regulated tissues (see above) and co-regulated genes^18,22. To address this, TCSC regresses TWAS chi-square statistics (or products of z-scores for two diseases/traits) on tissue co-regulation scores reflecting correlations of predicted gene expression across genes and tissues. Distinct from previous methods that analyze each tissue marginally, TCSC jointly models contributions from each tissue to identify causal tissues (analogous to the distinction in GWAS between marginal association and fine-mapping²³). We validate TCSC using extensive simulations using real genotypes with LD, including comparisons to RTC Coloc², RolyPoly⁶, LDSC-SEG⁷, and CoCoNet⁹ (reviewed in ^1,24). We apply TCSC to 78 diseases and complex traits (average N = 302K) and 48 GTEx tissues¹⁹, showing that TCSC recapitulates known biology and identifies biologically plausible novel tissue-trait pairs (or tissue-trait covariance pairs) while attaining increased specificity relative to previous methods.

Results

Overview of TCSC regression

TCSC estimates the disease heritability explained by cis-genetic components of gene expression in each tissue when jointly modeling contributions from each tissue. We refer to tissues with nonzero contributions as “causal” tissues (with the caveat that joint-fit effects of gene expression on disease may not reflect biological causality; see Discussion). TCSC assumes that gene expression-disease effect sizes are independent and identically distributed (i.i.d.) across genes and tissues (while accounting for the fact that cis-genetic components of gene expression are correlated across genes and tissues); violations of this model assumption are explored via simulations below. TCSC leverages the fact that TWAS ${\chi }^2$ statistics for each gene and tissue include both causal effects of that gene and tissue on disease and tagging effects of co-regulated genes and tissues. We define co-regulation based on squared correlations in cis-genetic expression, which can arise due to shared causal eQTLs and/or LD between causal eQTLs¹⁸. TCSC determines that a tissue is causal for disease if genes and tissues with high co-regulation to that tissue have higher TWAS ${\chi }^2$ statistics than genes and tissues with low co-regulation to that tissue.

In detail, let $h_{ge\left(t^{\prime }\right)}^2$ denote the disease heritability explained by the cis-genetic component of gene expression in tissue $t^{\prime }$. The expected TWAS ${\chi }^2$ statistic for gene $g$ and tagging tissue $t$ is

$$E\left[{\chi }_{g,t}^2\right]=N{\sum }_{t\prime }{l\left(g,t;t^{\prime }\right)h}_{ge\left(t^{\prime }\right)}^2/G_{t\prime }+1,$$ (1)

where $N$ is GWAS sample size, $t^{\prime }$ indexes causal tissues, $l\left(g,t;t^{\prime }\right)$ are tissue co-regulation scores (defined as $l\left(g,t;t^{\prime }\right)={\sum }_{g\prime }{r}^2\left({\widehat{W}}_{g,t},W_{g^{\prime },t^{\prime }}\right)$, where $W$ denotes the cis-genetic component of gene expression for a gene-tissue pair across individuals, $\widehat{W}$ denotes the cis-predicted expression for a gene-tissue pair, the sum is over genes $g^{\prime }$ within +/− 1 Mb to gene $g$), and $G_{t\prime }$ is the number of significantly cis-heritable genes in tissue $t^{\prime }$. A derivation of Equation (1) is provided in the Methods section. Equation (1) allows us to estimate $h_{ge\left(t^{\prime }\right)}^2$ via a multiple linear regression of TWAS ${\chi }^2$ statistics (for each gene and tagging tissue) on tissue co-regulation scores (Fig. 1).

Figure 1. Overview of TCSC regression.

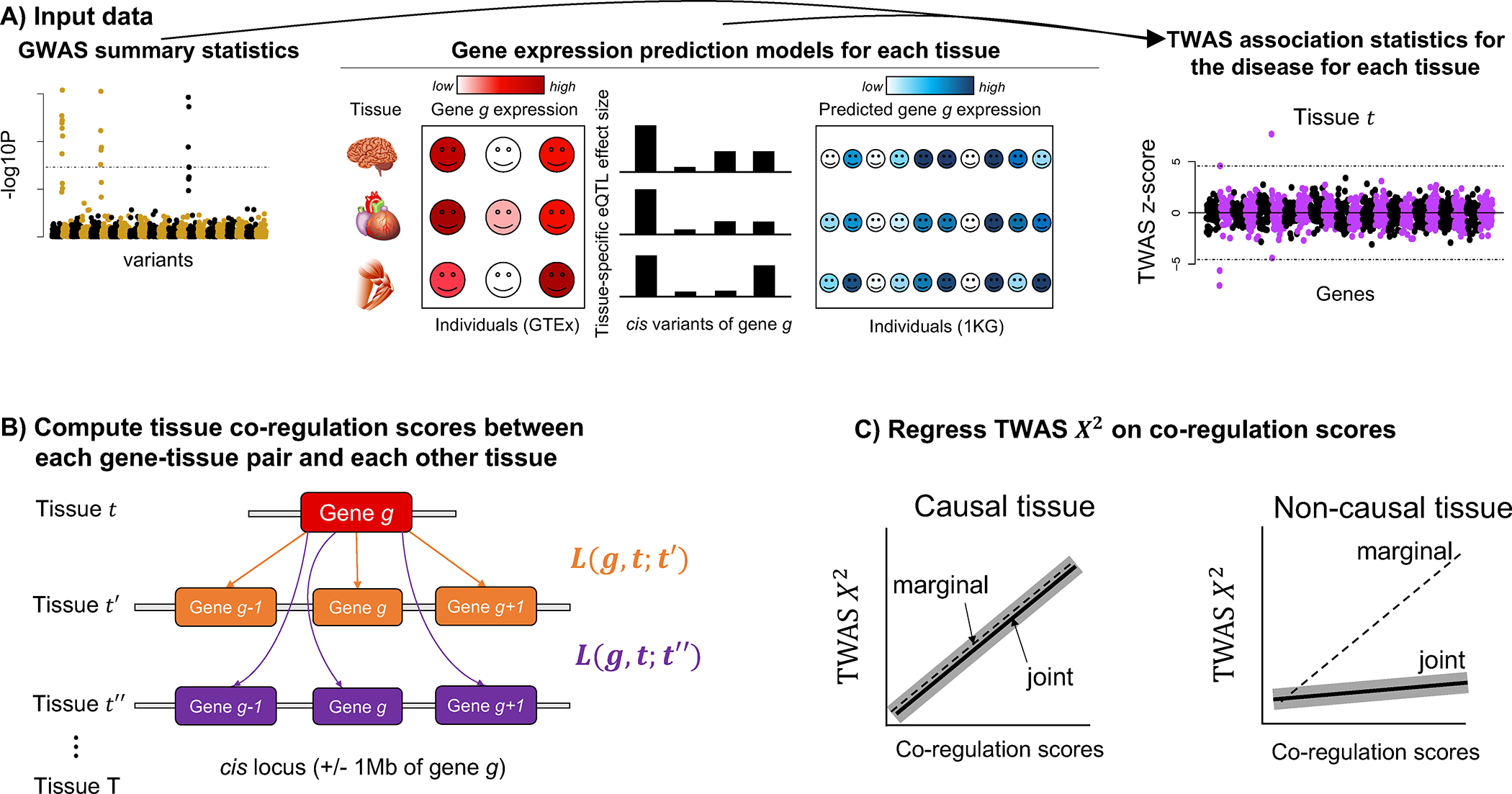
(A) Input data to TCSC includes (1) GWAS summary statistics for a disease and (2) gene expression prediction models for each tissue, which are used to produce (3) TWAS summary statistics for the disease for each tissue. (B) TCSC computes tissue co-regulation scores $L(g,t;t^{\prime })$ for each gene-tissue pair $(g,t)$ with potentially causal tissues $t^{\prime }$. (C) TCSC regresses TWAS chi-squares on tissue co-regulation scores to estimate tissue-specific contributions to disease. Solid lines represent hypothetical TCSC estimates; dashed lines represent hypothetical TWAS associations; shadows represent hypothetical TCSC estimates +/− jackknife standard errors (joint models only).

TCSC can also estimate the genetic covariance between two diseases explained by cis-genetic components of gene expression in each tissue, using products of TWAS z-scores. In detail, let ${\omega }_{ge\left(t^{\prime }\right)}$ denote the genetic covariance explained by the cis-genetic component of gene expression in tissue $t^{\prime }$(Methods). The expected product of TWAS z-scores in disease 1 and disease 2 for gene $g$ and tagging tissue $t$ is

$$E\left[z_{gt}^1\times z_{gt}^2\right]=\sqrt{N_1{N}_2}{\sum }_{t^{\prime }}l\left(g,t;t^{\prime }\right){\omega }_{ge\left(t^{\prime }\right)}/G_{t^{\prime }}+\rho N_s/\sqrt{N_1{N}_2}$$ (2)

where $N_1$ is GWAS sample size for disease 1, $N_2$ is GWAS sample size for disease 2, $t^{\prime }$ indexes causal tissues, $l\left(g,t;t^{\prime }\right)$ are tissue co-regulation scores, $G_{t\prime }$ is the number of significantly cis-heritable genes in tissue $t^{\prime }$ (Methods), $\rho$ is the phenotypic correlation between disease 1 and disease 2, and $N_s$ is the number of overlapping GWAS samples between disease 1 and disease 2. Equation (2) allows us to estimate ${\omega }_{ge\left(t^{\prime }\right)}$ via a multiple linear regression of products of TWAS z-scores in disease 1 and disease 2 (for each gene and tagging tissue) on tissue co-regulation scores. We note that the last term in Equation (2) is not known a priori but is accounted for via the regression intercept, analogous to previous work²⁵.

Further details, including a formal definition of $h_{ge\left(t^{\prime }\right)}^2$ in terms of SNP-level effects, quality control of gene expression models and TWAS statistics, estimation of standard errors, correcting for bias in tissue co-regulation scores (analogous to GCSC²²), are provided in the Methods section. We have publicly released open-source software implementing TCSC regression (see Code Availability), as well as all GWAS summary statistics, TWAS association statistics, tissue co-regulation scores, and TCSC output from this study (see Data Availability).

Simulations

We performed extensive simulations to evaluate the robustness and power of TCSC, using the TWAS simulator of Mancuso et al.²⁶ (see Code Availability). We used real genotypes from the 1000 Genomes Project²⁷ to simulate gene expression values (for each gene and tissue) and complex trait phenotypes, and then computed TWAS association statistics for each gene and tissue and estimated co-regulation scores. Primary simulations partitioned trait heritability across 10 highly correlated tissues (one of which contained causal gene-trait effects explaining 100% of trait heritability). We evaluated TCSC while varying many parameters including trait heritability explained by the causal tissue, trait heritability not explained by gene expression, and the number of causal tissues and the number of tagging tissues; more details are provided in the Supplementary Note: Simulation Framework. We also compared the type I error and power of TCSC to four previously published methods: RTC Coloc², RolyPoly⁶, LDSC-SEG⁷, and CoCoNet⁹.

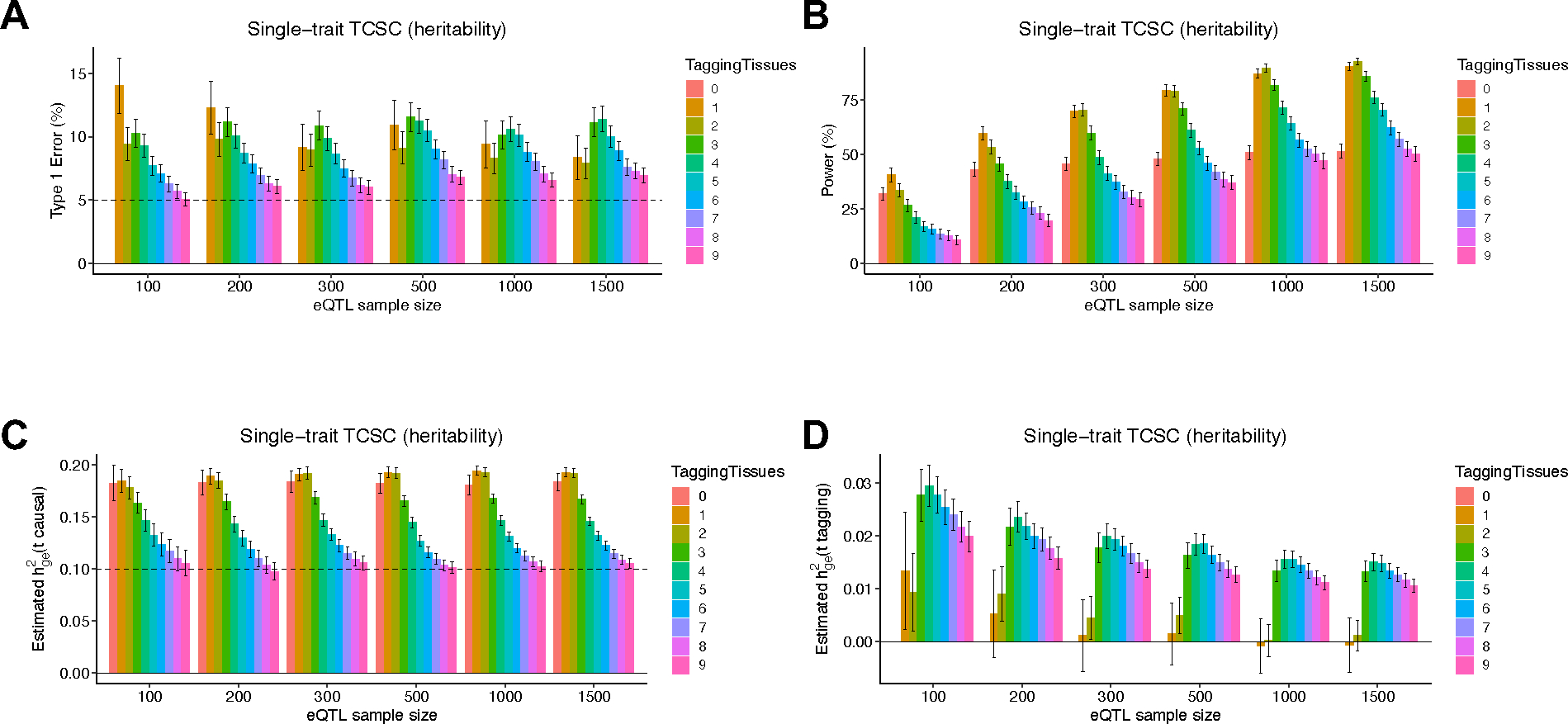
We first evaluated the bias in TCSC estimates of the disease heritability explained by the cis-genetic component of gene expression in tissue $t^{\prime }(h_{ge\left(t\prime \right)}^2)$, for both causal and non-causal tissues. For causal tissues, TCSC produced unbiased estimates of $h_{ge\left(t\prime \right)}^2$ (Fig. 2A, Supplementary Table 1); this implies that error in eQTL effect size estimates, which impacts TWAS statistics and co-regulation scores, does not bias TCSC estimates for causal tissues. A subtlety is that, as noted above, estimates of $h_{ge\left(t\prime \right)}^2$ are impacted by the number of significantly cis-heritable genes in tissue $t^{\prime }(G_{t^{\prime }}$), which may be sensitive to eQTL sample size. For non-causal tissues, TCSC produced estimates of $h_{ge\left(t\prime \right)}^2$, that were significantly positive when averaged across all simulations, but not large enough to substantially impact type I error (see below).

Figure 2. Robustness and power of TCSC regression in simulations.

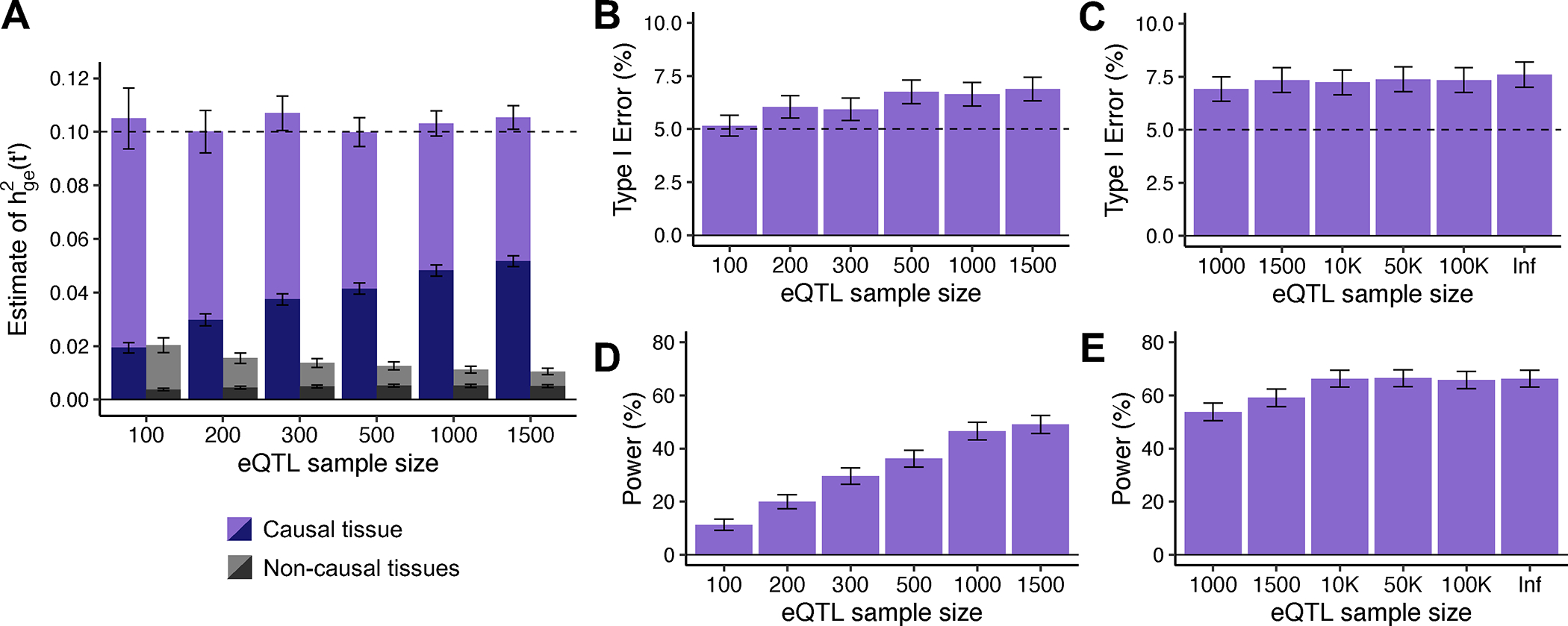
(A) Bias in estimates of disease heritability explained by the cis-genetic component of gene expression in tissue $t^{\prime }(h_{ge\left(t\prime \right)}^2)$ for causal (purples) and non-causal (grays) tissues. $G_{t\prime }$ was set to the total number of true cis-heritable genes across tissues for light purple (resp. gray) or to the number of significantly cis-heritable genes in each tissue for dark purple (resp. gray). The dashed line indicates the true value of $h_{ge\left(t\prime \right)}^2$ for causal tissues. (B) Percentage of estimates of $h_{ge\left(t\prime \right)}^2$ for non-causal tissues that were significantly positive at p < 0.05 per eQTL sample size (n = 100, 200, 300, 500, 1000, 1500). (C) Percentage of estimates of $h_{ge\left(t\prime \right)}^2$ for non-causal tissues that were significantly positive at p < 0.05 per larger eQTL sample size (n = 1000, 1500, 10K, 50K, 100K, Infinite). (D) Percentage of estimates of $h_{ge\left(t\prime \right)}^2$ for causal tissues that were significantly positive at p < 0.05 per eQTL sample size (n = 100, 200, 300, 500, 1000, 1500). (E) Percentage of estimates of $h_{ge\left(t\prime \right)}^2$ for causal tissues that were significantly positive at p < 0.05 per larger eQTL sample size (n = 1000, 1500, 10K, 50K, 100K, Infinite). For panels B-E, we used a one-sided z-test to obtain p-values. For panels A, B and D, we performed n = 1,000 independent simulations per eQTL sample size. For panels C and E, we performed n = 2,000 independent simulations per eQTL sample size and used cross-validation adjusted-R² > 0 instead of GCTA to define significantly cis-heritable genes in these analyses. In all panels, data are presented as mean values +/− 1.96 × SEM. Numerical results are reported in Supplementary Table 1.

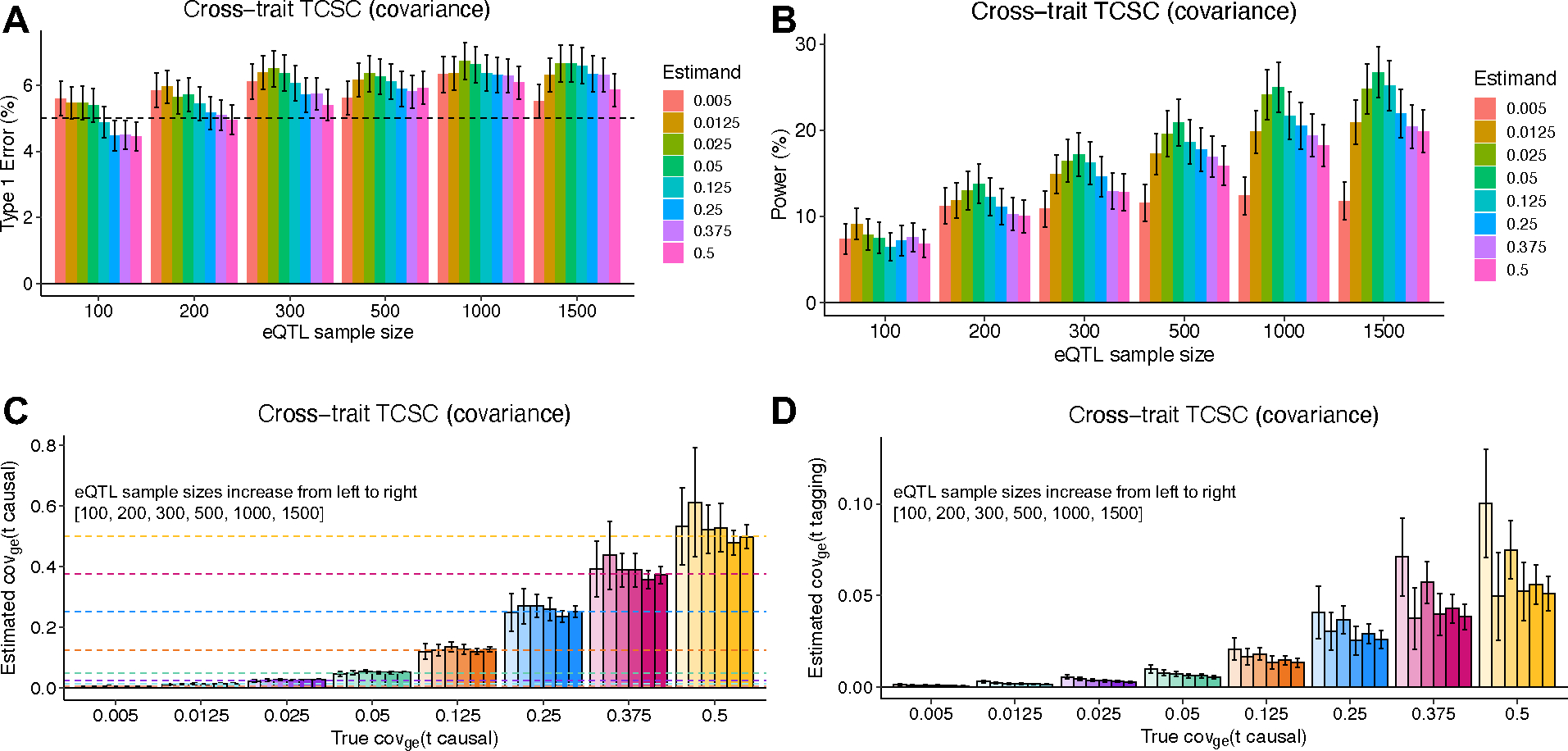
We next evaluated the type I error of TCSC for non-causal tissues. The type I error of TCSC was approximately well-calibrated, ranging from 5.2% to 6.9% across eQTL sample sizes of 100–1,500 at a significance threshold of p = 0.05 (Fig. 2B, Supplementary Table 1). In comparison, we observed type I errors from 53%–86% for RTC Coloc, 32%–33% for LDSC-SEG, 11%–12% for RolyPoly, and 32%–38% for CoCoNet, substantially greater than the type I error of TCSC (Extended Data Fig. 1, Supplementary Table 2). We confirmed that the type I error of TCSC does not increase further at larger gene expression sample sizes (Fig. 2C, Supplementary Note: Single-trait simulation analysis at large sample size).

We next evaluated the power of TCSC for causal tissues. We determined that TCSC was moderately well-powered to detect causal tissues, with power ranging from 11%–49% across eQTL sample sizes at a nominal significance threshold of p < 0.05 (Fig. 2D, Supplementary Table 1). As noted above, the power of TCSC varies greatly with the choice of parameter settings (see below), thus the power of TCSC in real-world settings is best evaluated using real trait analysis. As expected, power increased at larger eQTL sample sizes, due to lower standard errors on point estimates of $h_{ge\left(t\prime \right)}^2$ (Fig. 2A). We also evaluated the power of RTC Coloc, RolyPoly, LDSC-SEG, and CoCoNet. For the only other method with type I error less than 15% (RolyPoly), power ranged from 14%–17% across eQTL sample sizes, substantially lower than TCSC (Extended Data Fig. 1, Supplementary Table 2). We also used ROC curves to assess the relationship between the sensitivity (power) and specificity (one minus the false positive rate) of all 5 methods across 1,000 uniformly spaced p-value thresholds. TCSC attained the largest AUC (0.78, vs. 0.54–0.59 for other methods) (Extended Data Fig. 1). We also evaluated the power of TCSC at four larger gene expression sample sizes (see above) and determined that power plateaus at 10,000 individuals (Fig. 2E).

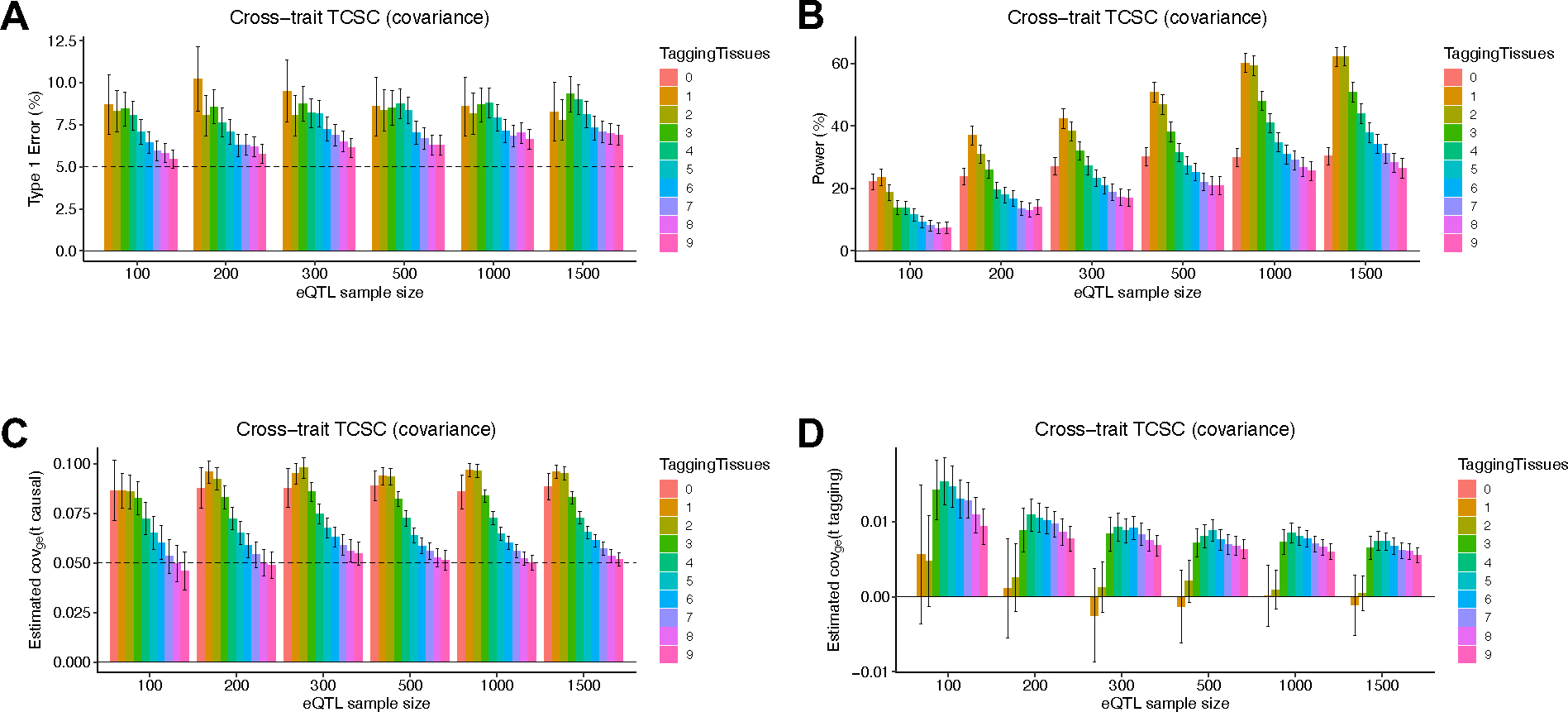
We similarly evaluated cross-trait TCSC for simulated traits with a genetic correlation of 0.5. Cross-trait simulations produced similar conclusions to the single trait analysis above (Extended Data Figs. 1–2, Supplementary Table 3, Supplementary Note). We also performed 12 secondary simulation analyses showing the performance of TCSC across a diverse parameter space (Extended Data Figs. 3–6, Supplementary Figs. 2–21, Supplementary Note).

Tissue-specific contributions to 78 diseases/traits

We applied TCSC to publicly available GWAS summary statistics for 78 diseases and complex traits (average N = 302K; Methods, Supplementary Table 4) and gene expression data for 48 GTEx tissues¹⁹ (Table 1). The 48 GTEx tissues were aggregated into 39 meta-tissues (average N = 266, range: N = 101–320 individuals, 23 meta-tissues with N = 320) in order to reduce variation in eQTL sample size across tissues (Table 1 and Supplementary Note: Analyzing GTEx tissues) and referred to as “tissues” below. We constructed gene expression prediction models for an average of 3,993 significantly cis-heritable protein-coding genes (as defined above) in each tissue. We primarily report the proportion of disease heritability explained by the cis-genetic component of gene expression in tissue $t^{\prime }({{\pi }_{t^{\prime }}=h}_{ge\left(t\prime \right)}^2/h_g^2)$, where $h_g^2$ is the common variant SNP-heritability estimated by S-LDSC^13,28,29.

Table 1. GTEx meta-tissues and constituent tissues analyzed.

For each meta-tissue we list the constituent tissue(s) and total sample size. Daggers denote meta-tissues with more than one constituent tissue; for these meta-tissues, each constituent tissue has equal sample size up to rounding error (an exception is the transverse intestine meta-tissue, which includes 176 transverse colon samples and all 144 small intestine samples).

Meta-tissue	Constituent Tissue(s)	Sample Size
Adipose Subcutaneous	Adipose Subcutaneous	320
Adipose Visceral Omentum	Adipose Visceral Omentum	320
Adrenal Gland	Adrenal Gland	200
Aorta Artery	Aorta Artery	320
† Brain Basal Ganglia	Putamen, Caudate, Nucleus Accumbens	320
† Brain Cereb.	Cerebellum, Cerebellar Hemisphere	320
† Brain Cortex	Frontal, Anterior, Cingulate	320
† Brain Limbic	Amygdala, Hippocampus, Hypothalamus	320
Brain Spinal Cord	Brain Spinal Cord	115
Brain Substantia Nigra	Brain Substantia Nigra	101
Breast Mammary Gland	Breast Mammary Gland	320
Coronary Artery	Coronary Artery	180
Cultured Fibroblasts	Cultured Fibroblasts	320
Esophagus Mucosa	Esophagus Mucosa	320
Esophagus Muscularis	Esophagus Muscularis	320
Heart Atrial Appendage	Heart Atrial Appendage	320
Heart Left Ventricle	Heart Left Ventricle	320
LCLs	LCLs	116
Liver	Liver	183
Lung	Lung	320
Minor Salivary Gland	Minor Salivary Gland	118
Muscle Skeletal	Muscle Skeletal	320
Ovary	Ovary	140
Pancreas	Pancreas	252
Pituitary	Pituitary	220
Prostate	Prostate	186
Skin (sun exposed)	Skin (sun exposed)	320
Skin (sun unexposed)	Skin (sun unexposed)	320
† Sigmoid Intestine	Sigmoid Colon, Gastroesophageal Junction	320
Spleen	Spleen	185
Stomach	Stomach	269
Tibial Artery	Tibial Artery	320
Tibial Nerve	Tibial Nerve	320
Testis	Testis	277
Thyroid	Thyroid	320
† Transverse Intestine	Transverse Colon, Small Intestine	320
Uterus	Uterus	108
Vagina	Vagina	122
Whole Blood	Whole Blood	320

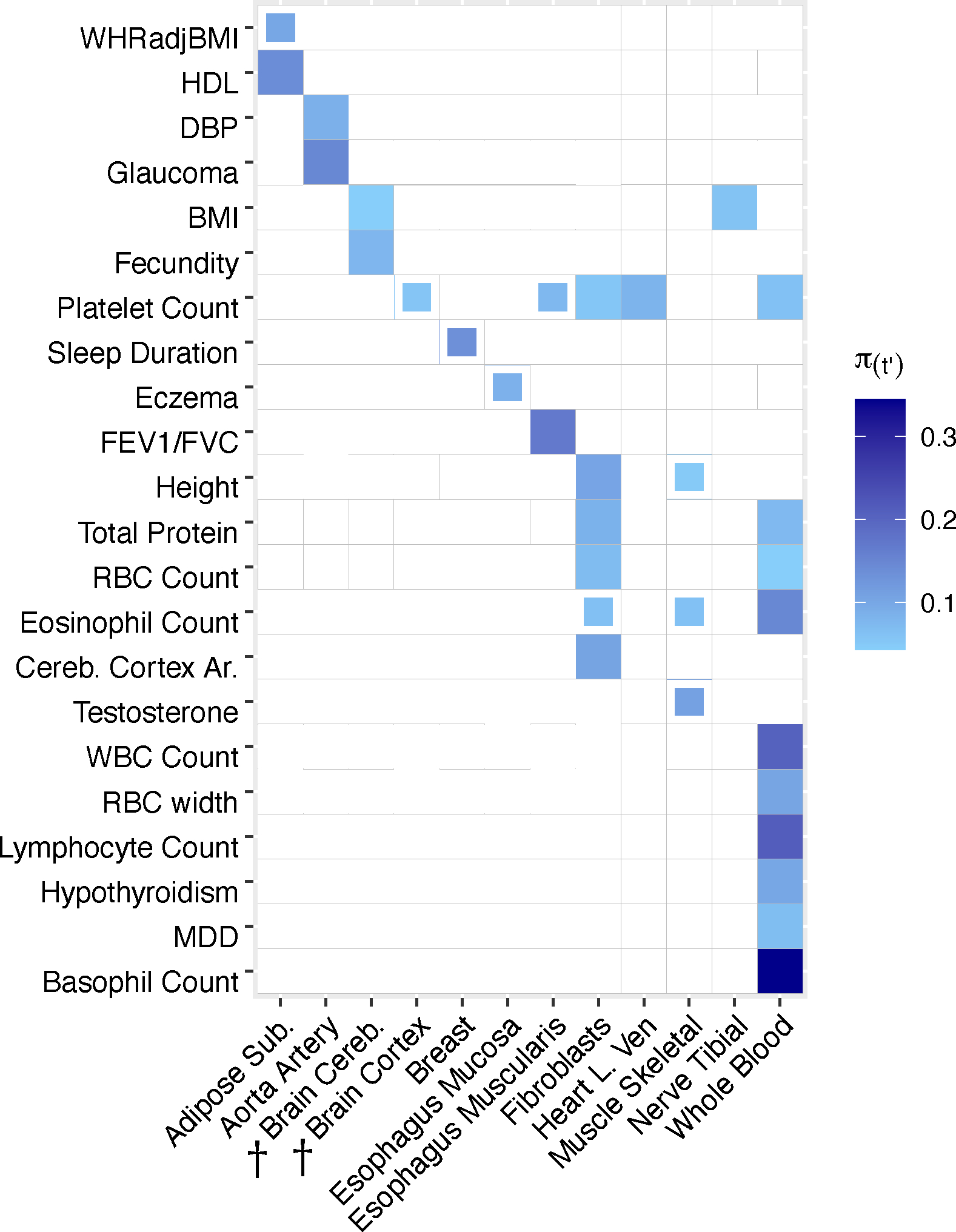
TCSC identified 21 causal tissue-trait pairs with significantly positive contributions to disease/trait heritability at 5% per-trait FDR, spanning 7 distinct tissues and 17 distinct diseases/traits (Fig. 3, Methods, Supplementary Table 5, Supplementary Fig. 22). Many of the significant findings recapitulated known biology, including associations of whole blood with blood cell traits such as white blood cell count (${\pi }_{t^{\prime }}=0.21$, s.e. = 0.064, $P=5.7\times {10}^{-4}$) and liver with lipid traits such as LDL (${\pi }_{t^{\prime }}=0.20$, s.e. = 0.050, $P=2.9\times {10}^{-5}$). TCSC also identified several biologically plausible findings not previously reported in the genetics literature. First, aorta artery was associated with glaucoma (${\pi }_{t^{\prime }}=0.15$, s.e. = 0.051, $P=1.3\times {10}^{-3}$) and also with diastolic blood pressure (DBP) (${\pi }_{t^{\prime }}=0.078$, s.e. = 0.024, $P=5.1\times {10}^{-4}$), which is consistent with DBP measuring the pressure exerted on the aorta³⁰ and high blood pressure being a known risk factor for glaucoma^31–35. Second, TCSC identified heart left ventricle as a causal tissue for platelet count (${\pi }_{t^{\prime }}=0.091$, s.e. = 0.031, $P=1.7\times {10}^{-3}$), consistent with the role of platelets in the formation of blood clots in cardiovascular disease^36–39; in fact, antiplatelet drugs have been successful at reducing adverse cardiovascular outcomes⁴⁰. Moreover, the left ventricle serves as a muscle to pump blood throughout the body⁴¹, likely modulating platelet and other blood cell counts. Other significant findings are reported in Supplementary Table 6 and the Supplementary Note.

Figure 3. TCSC estimates tissue-specific contributions to disease and complex trait heritability.

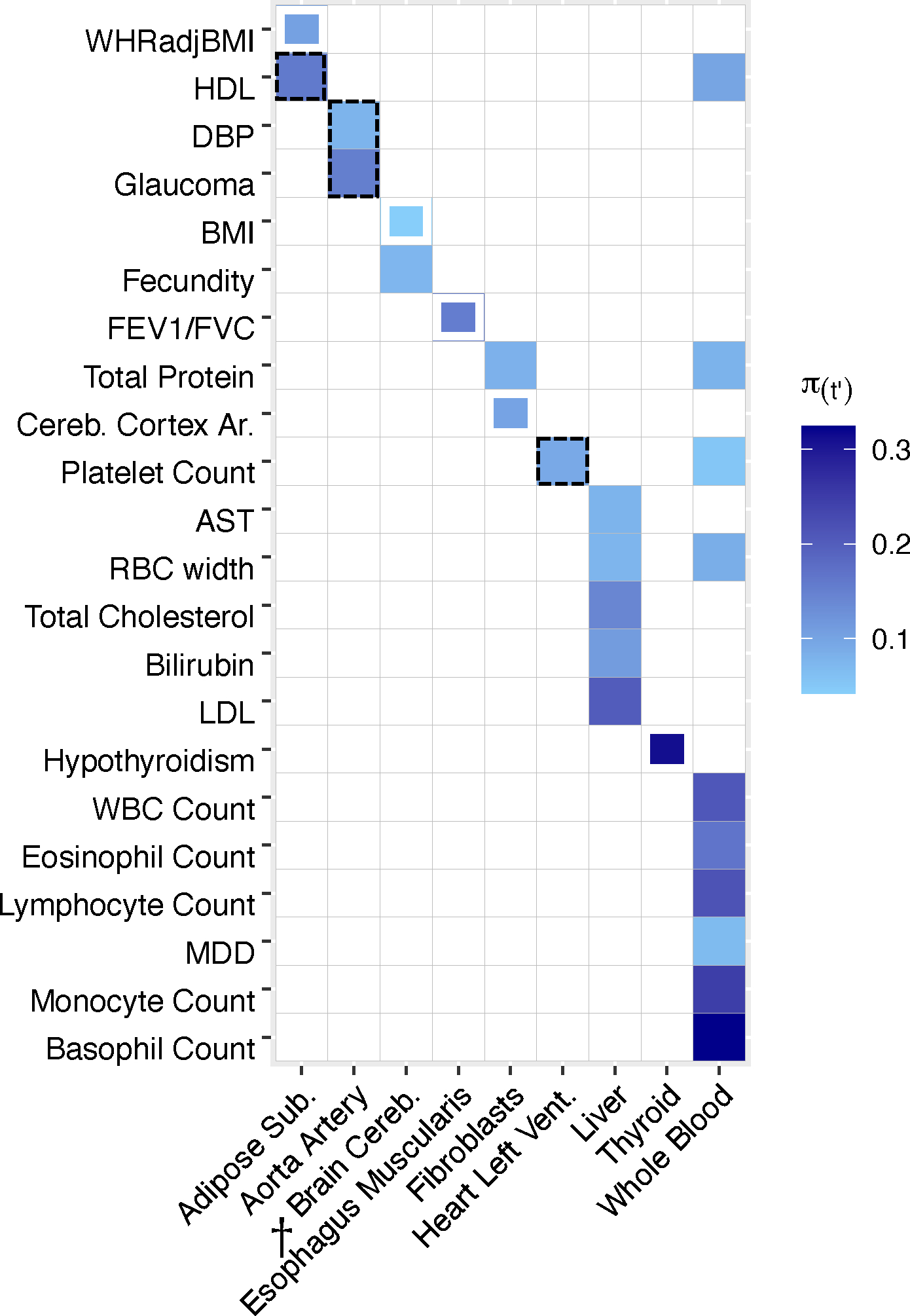
We report estimates of the proportion of disease heritability explained by the cis-genetic component of gene expression in tissue $t^{\prime }({\pi }_{t^{\prime }}$). We report tissue-trait pairs with FDR of 10% or lower, where full boxes denote FDR of 5% or lower and partial boxes denote FDR between 5% and 10%. Dashed boxes denote results that are highlighted in the main text. Tissues are ordered alphabetically. Daggers denote meta-tissues with more than one constituent tissue. Diseases/traits are ordered with respect to causal tissues. Numerical results are reported in Supplementary Tables 5–6. WHRadjBMI: waist-hip-ratio adjusted for body mass index. HDL: high-density lipoprotein. DBP: diastolic blood pressure. BMI: body mass index. FEV1/FVC: forced expiratory volume in one second divided by forced vital capacity. Cereb. Cortex Ar.: cerebral cortex surface area. AST: aspartate aminotransferase. LDL: low-density lipoprotein. WBC Count: white blood cell count. MDD: major depressive disorder.

TCSC also increased the specificity of known tissue-trait associations. For high density lipoprotein (HDL), previous studies reported that deletion of a cholesterol transporter gene in adipose tissue reduces HDL levels^42,43. TCSC specifically identified subcutaneous adipose (${\pi }_{t^{\prime }}=0.16$, s.e. = 0.054, $P=1.5\times {10}^{-3}$; Fig. 3), but not visceral adipose or breast adipose tissue (P > 0.05; Supplementary Table 6), as a causal tissue for HDL. Previous studies have established that levels of adiponectin, a hormone released by adipose tissue to regulate insulin, are positively correlated with HDL^44–46 and more recently, a study has reported that adiponectin levels are associated specifically with subcutaneous adipose tissue and not visceral adipose tissue⁴⁷. We note that TCSC did not identify liver as a causal tissue for HDL (FDR > 5%), which may be due to limited power in liver due to smaller eQTL sample size. For waist-hip ratio adjusted for BMI (WHRadjBMI), previous studies reported colocalization of WHRadjBMI GWAS variants with cis-eQTLs in subcutaneous adipose, visceral adipose, liver, and whole blood⁴⁸, consistent with WHRadjBMI measuring adiposity in the intraabdominal space, which is likely regulated by metabolically active tissues⁴⁹. TCSC specifically identified subcutaneous adipose as a suggestive finding (${\pi }_{t^{\prime }}=0.10$, s.e. = 0.037, $P=2.4\times {10}^{-3}$, 5% < FDR < 10%; Fig. 3), but not visceral adipose, breast, liver, or whole blood (P > 0.05; Supplementary Table 6). The causal mechanism may again involve adiponectin, which is negatively correlated with WHRadjBMI⁵⁰. We note that the P value distributions across traits are similar for adipose tissues (Supplementary Table 7). For BMI, previous studies have broadly implicated the central nervous system, but did not reveal more precise contributions^{51,13,52,53,7,54}. TCSC specifically identified brain cereb. as a suggestive finding (${\pi }_{t^{\prime }}=0.042$, s.e. = 0.015, $P=2.6\times {10}^{-3}$, 5% < FDR < 10%), but not brain cortex or brain limbic (P > 0.05; Supplementary Table 6), as a causal tissue for BMI. This finding is consistent with a known role for brain cerebellum in biological processes related to obesity including endocrine homeostasis⁵⁵ and feeding control⁵⁶; recently, a multi-omics approach has revealed cerebellar activation in mice upon feeding⁵⁷.

We performed several secondary analyses. First, we removed tissues with eQTL sample size less than 320 individuals, as these tissues may often be underpowered (Fig. 2C). We identified 23 significant tissue-trait pairs, reflecting a gain of 8 newly significant tissue-trait pairs (Extended Data Fig. 7, Supplementary Table 8, Supplementary Note). We also performed a brain-specific analysis in which we applied TCSC to 41 brain traits (average N = 226K) while restricting to 13 individual GTEx brain tissues (Supplementary Tables 10–11, Supplementary Note). TCSC identified 8 brain tissue-brain trait pairs at 5% FDR, including the brain hippocampus as a causal tissue for ADHD consistent with dopamine regulation^58–60 (Extended Data Fig. 8, Supplementary Table 12).

Comparisons of TCSC to other methods

We compared TCSC to two methods, RTC Coloc² and LDSC-SEG⁷, that use gene expression data to identify disease-critical tissues based on tissue specificity of eQTL-GWAS colocalizations or heritability enrichment of specifically expressed genes, respectively. Both methods analyze each tissue marginally; thus, RTC Coloc and LDSC-SEG may output more significantly associated tissues per trait than TCSC (analogous to the distinction in GWAS between marginal association and fine-mapping²³). To assess whether TCSC attains higher specificity, we applied each method to 7 traits with at least one tissue-trait association for each of the three methods (Methods) and compared results across causal tissues identified by TCSC and across the most strongly co-regulated tagging tissue (based on Spearman $\rho$ for estimated eQTL effect sizes, averaged across genes, from ref.¹⁹).

Results for the 7 traits are reported in Fig. 4 and Supplementary Table 13; results for all 17 diseases/traits with causal tissue-trait associations identified by TCSC are reported in Extended Data Fig. 9 and Supplementary Table 14, and results for all diseases/traits and tissues are in Supplementary Table 15. We reached three main conclusions. First, RTC Coloc implicates a broad set of tissues (not just strongly co-regulated tissues) for each trait (Fig. 4A); for example, for WBC count, RTC Coloc implicated 8 of 10 tissues. This is consistent with our simulations, in which RTC Coloc suffered a high type I error rate and had a substantially lower AUC than TCSC (Extended Data Fig. 1). Second, LDSC-SEG implicates a small set of strongly co-regulated tissues for each trait (Fig. 4B); for WBC count, LDSC-SEG typically implicated 3 of 10 tissues, consisting of whole blood, spleen, and breast tissue. This is consistent with our simulations, in which LDSC-SEG suffered a substantial type I error rate and had a substantially lower AUC than TCSC (Extended Data Fig. 1). Third, TCSC typically implicates one causal tissue per trait (Fig. 4C); for WBC count, TCSC implicated only whole blood as a causal tissue. This is consistent with our simulations, in which TCSC attained moderate power to identify causal tissues with approximately well-calibrated type I error. However, the higher specificity of TCSC may be accompanied by incomplete power to identify secondary causal tissues; we observed less significant (lower −log₁₀P-value and lower −log₁₀FDR) results for causal tissues from TCSC than by RTC Coloc or LDSC-SEG (Supplementary Table 14). We also observed similar patterns when comparing TCSC to RTC Coloc and LDSC-SEG in the brain-specific analysis (Extended Data Fig. 10, Supplementary Table 16, Supplementary Note).

Figure 4. Comparison of disease-critical tissues identified by RTC Coloc, LDSC-SEG and TCSC.

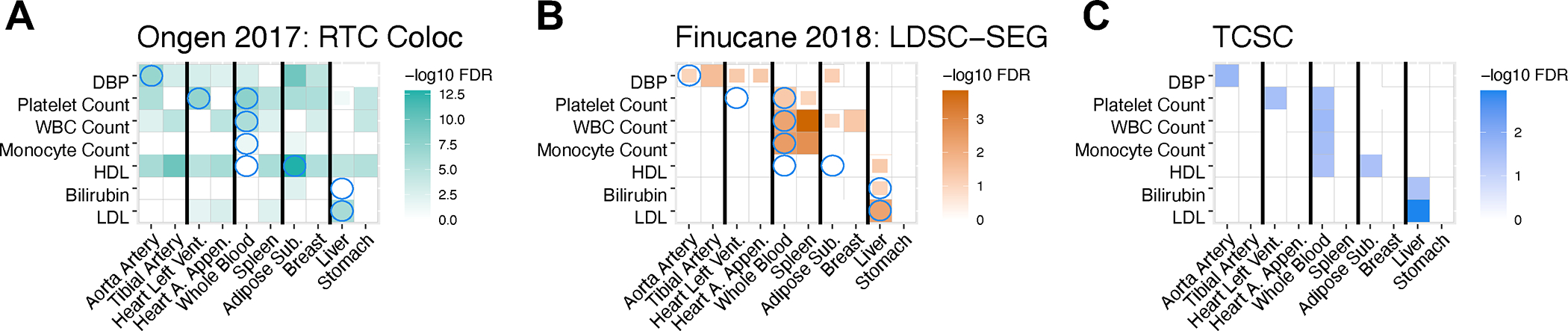
We report -log₁₀FDR values for (A) RTC Coloc, (B) LDSC-SEG, (C) TCSC, across 7 traits with at least one significantly associated tissues (at FDR 5%) for each of the three methods and 10 tissues consisting of the causal tissues identified by TCSC and the most strongly co-regulated tagging tissues, ordered consecutively. We report tissue-trait pairs with FDR of 10% or lower, where full boxes denote FDR of 5% or lower and partial boxes denote FDR between 5% and 10%. Blue circles in panels (A) and (B) denote the causal tissue-trait pairs identified by TCSC. Numerical results are reported in Supplementary Table 13.

Tissue-specific contributions to cross-trait covariance

We applied cross-trait TCSC to 262 pairs of disease/traits (e.g. pairs with significantly nonzero genetic correlation, Methods, Supplementary Table 17) and gene expression data for 39 meta-tissues (Table 1). We primarily report the signed proportion of genetic covariance explained by the cis-genetic component of gene expression in tissue $t^{\prime }({{\zeta }_{t^{\prime }}=\omega }_{ge\left(t\prime \right)}/{\omega }_g)$, where ${\omega }_g$ is the common variant genetic covariance estimated by cross-trait LDSC⁶¹. TCSC identified 17 causal tissue-trait covariance pairs with significant contributions to trait covariance at 5% per-trait FDR, spanning 12 distinct tissues and 13 distinct trait pairs (Fig. 5A, Supplementary Table 18).

Figure 5. Cross-trait TCSC estimates tissue-specific contributions to the genetic covariance of two diseases/traits.

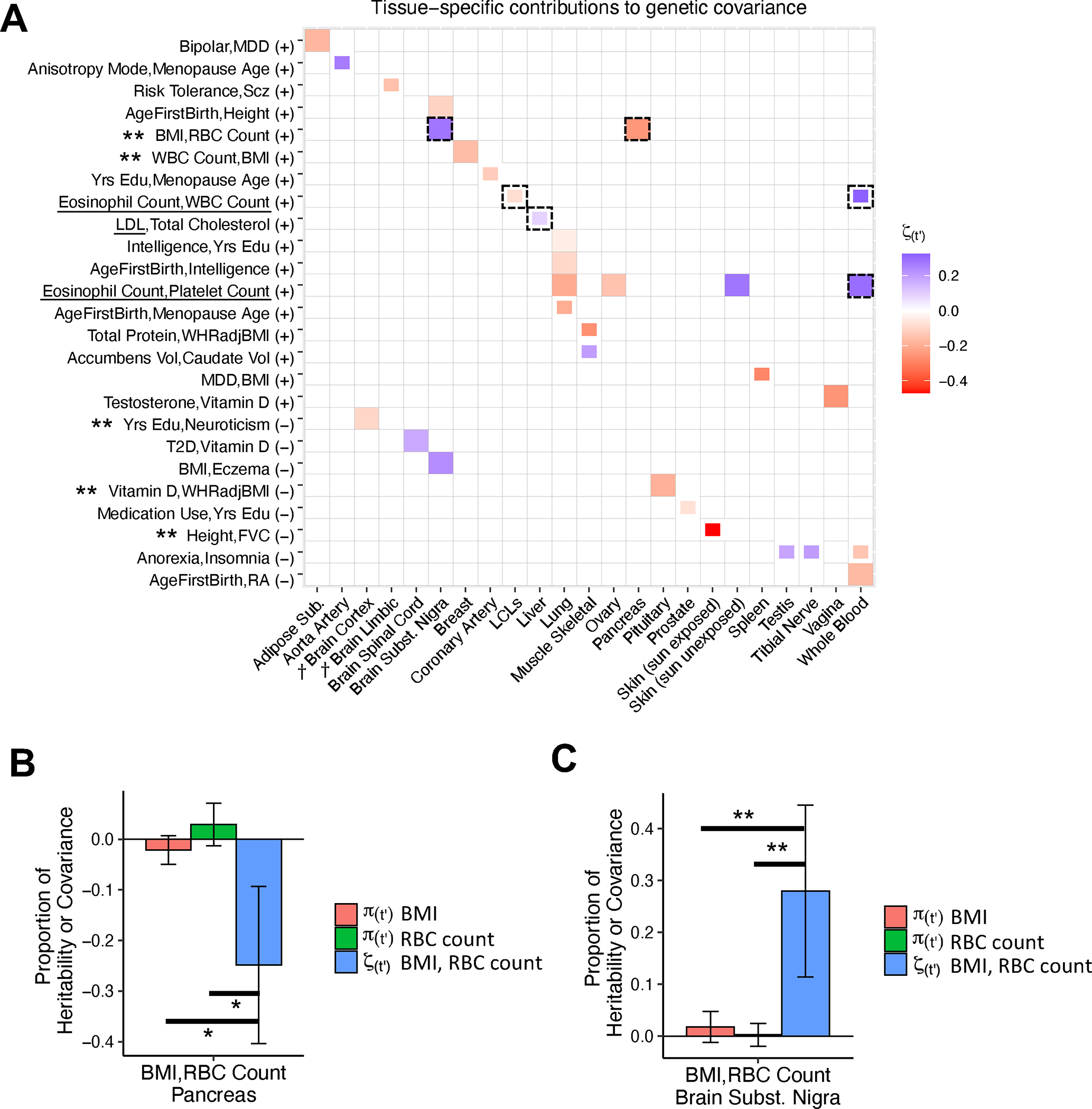
(A) Estimates of the signed proportion of genetic covariance explained by the cis-genetic component of gene expression in tissue $t^{\prime }({\zeta }_{t^{\prime }}$). Full boxes denote FDR < 5% and partial boxes denote 5% < FDR < 10%. Dashed boxes are highlighted in the main text. Tissues are ordered alphabetically. Daggers denote meta-tissues with >1 constituent tissue. Trait pairs are ordered by positive (+) or negative (−) genetic covariance, and then with respect to causal tissues. Underlined traits were shown in Fig. 3. Double asterisks denote trait pairs with significant differences between tissue-specific contributions to covariance and heritability, the latter of which was non-significant for both traits. Numerical results are reported in Supplementary Tables 18–19. BMI: body mass index. RBC Count: red blood cell count. WBC Count: white blood cell count. LDL: low-density lipoprotein. Yrs Edu: years of education. WHRadjBMI: waist-hip-ratio adjusted for body mass index. Accumbens Vol: brain accumbens volume. Caudate Vol: brain caudate volume. MDD: major depressive disorder. Scz: Schizophrenia. T2D: type 2 diabetes. FVC: forced vital capacity. RA: rheumatoid arthritis. (B) For BMI and RBC Count, estimates of the proportion of trait heritability and covariance explained by the cis-genetic component of gene expression in pancreas. Asterisks denote the difference between the covariance and heritability estimates was significantly < 0 at 10% FDR using a genomic block jackknife to estimate the standard error. (C) Same as (B), but for the brain substantia nigra. Double asterisks denote the difference between the covariance and heritability estimates was significantly > 0 at 5% FDR using a genomic block jackknife to estimate the standard error. Data in (B) and (C) are presented as TCSC estimates +/− 1.96 × the jackknife standard error. Numerical results are reported in Supplementary Table 21.

Several results recapitulated known biology. Consistent with the significant contribution of liver to LDL heritability in Fig. 3, TCSC identified a suggestive positive contribution of liver to the covariance of LDL and total cholesterol (${\zeta }_{t^{\prime }}=0.090$, s.e. = 0.029, $P=1.0\times {10}^{-3}$, 5% < FDR < 10%), and consistent with the positive contributions of whole blood to blood cell count heritabilities in Fig. 3, TCSC identified a significant positive contribution of whole blood to the covariance of eosinophil and platelet counts (${\zeta }_{t^{\prime }}=0.30$, s.e. = 0.10, $P=2.3\times {10}^{-3}$).

TCSC identified several biologically plausible findings not previously reported in the genetics literature. First, brain substantia nigra had a significantly positive contribution to the genetic covariance of BMI and red blood cell count (RBC count) (${\zeta }_{t^{\prime }}=0.28$, s.e. = 0.084, $P=4.6\times {10}^{-4}$), while pancreas had a significantly negative contribution (${\zeta }_{t^{\prime }}=-0.25$, s.e. = 0.079, $P=8.7\times {10}^{-4}$). In the brain, energy metabolism is regulated by oxidation and previous work has shown that red blood cells play a large role in these metabolic processes as oxygen sensors⁶²; in addition, previous studies have reported differences in the level of oxidative enzymes in red blood cells between individuals with high BMI and low BMI^63,64, suggesting that genes regulating oxidative processes might have pleiotropic effects on RBC count and BMI. In the pancreas, pancreatic inflammation (specifically acute pancreatitis) is associated with reduced levels of red blood cells, or anemia⁶⁵, while pancreatic fat is associated with metabolic disease and increased BMI⁶⁶. Second, LCLs had a suggestive negative contribution to the genetic covariance of eosinophil count and white blood cell count (${\zeta }_{t^{\prime }}=-0.081$, s.e. = 0.028, $P=1.8\times {10}^{-3},$ 5% < FDR < 10%, in contrast to the suggestive positive contribution of whole blood: ${\zeta }_{t^{\prime }}=0.32$, s.e. = 0.12, $P=2.4\times {10}^{-3}$, 5% < FDR < 10%). This is plausible as previous studies have reported the suppression of proliferation of lymphocytes (the white blood cell hematopoietic lineage from which LCLs are derived) by molecules secreted from eosinophils^67–69. Other significant findings are reported in Supplementary Table 19 and the Supplementary Note.

For 16 of the 17 causal tissue-trait covariance pairs, the causal tissue was non-significant for both constituent traits. We sought to formally assess whether tissue-specific contributions to covariance could exceed contributions to heritability. Specifically, for each causal tissue-trait covariance pair, we estimated the differences between the tissue-specific contribution to covariance (${\zeta }_{t^{\prime }}$) and the tissue-specific contributions to heritability for each constituent trait (${\pi }_{t^{\prime }}$) (and estimated standard errors by jackknifing differences across the genome). We identified five tissue-trait covariance pairs for which these differences were statistically significant at 5% FDR for both traits and ${\pi }_{t^{\prime }}$ was non-significant for both traits (marked by double asterisks in Fig. 5A, results reported in Supplementary Table 20 and the Supplementary Note). The negative contribution of pancreas (Fig. 5B) and the positive contribution of brain substantia nigra (Fig. 5C) to the covariance of BMI and RBC count were larger than tissue-specific contributions to heritability, which were each non-significant. Even in simulations, TCSC often detected tissue-specific contributions to covariance without detecting tissue-specific contributions to heritability for both traits, especially when contributions to heritability substantially differed (Supplementary Table 21).

Discussion

We developed a new method, tissue co-regulation score regression (TCSC), that disentangles causal tissues from tagging tissues and partitions disease heritability (or cross-trait covariance) into tissue-specific components. We applied TCSC to 78 diseases and complex traits and 48 GTEx tissues, identifying 21 tissue-trait pairs (and 17 tissue-trait covariance pairs) with significant tissue-specific contributions. TCSC identified biologically plausible novel tissue-trait pairs, including associations of aorta artery with glaucoma, heart left ventricle with platelet count, and brain hippocampus with ADHD. TCSC also identified biologically plausible novel tissue-trait covariance pairs, including a positive contribution of brain substantia nigra and a negative contribution of pancreas to the covariance of BMI and red blood cell count; in particular, our findings suggest that genetic covariance may reflect distinct tissue-specific contributions.

TCSC differs from previous methods in jointly modeling contributions from each tissue to disentangle causal tissues from tagging tissues (analogous to the distinction in GWAS between marginal association and fine-mapping²³). We briefly discuss several other methods that use eQTL or gene expression data to identify disease-associated tissues. RTC Coloc identifies disease-associated tissues based on tissue specificity of eQTL-GWAS colocalizations²; this study made a valuable contribution in emphasizing the importance of tissue co-regulation, but did not model tissue-specific effects, such that RTC Coloc may implicate many tissues (Fig. 4A). LDSC-SEG identifies disease-critical tissues based on heritability enrichment of specifically expressed genes⁷; this distinguishes a focal tissue from the set of all tissues analyzed but does not distinguish closely co-regulated tissues (Fig. 4B). We discuss four other methods in the Supplementary Note: Other tissue-trait association methods.

We note several limitations of our work. First, TCSC requires tissue-specific eQTL data (thus requiring genotype/gene expression data in substantial sample size), whereas some methods (LDSC-SEG⁷, RolyPoly⁶, and CoCoNet⁹) only require gene expression data in limited sample size. Second, joint-fit effects of gene expression on disease may not reflect biological causality; if a causal tissue or cell type is not assayed, TCSC may identify a co-regulated tissue (e.g. a tissue whose cell type composition favors a causal cell type) as causal. We anticipate that this limitation will become less severe as potentially causal tissues, cell types and contexts are more comprehensively assayed. Third, TCSC does not achieve a strict definition or estimation of mediated effects; this is conceptually appealing and can, in principle, be achieved by modeling non-mediated effects, but may result in limited power to distinguish disease-critical tissues⁷⁰. Fourth, TCSC performs less well in the presence of disease heritability that is not mediated through gene expression (Supplementary Figs. 16–19). We discuss other limitations in the Supplementary Note: Other limitations. Despite these limitations, TCSC is a powerful and generalizable approach for modeling tissue co-regulation to estimate tissue-specific contributions to disease.

Methods

Our research complies with all relevant ethnical regulations; no specific approval was needed.

TCSC regression

TCSC leverages the fact that the TWAS ${\chi }^2$ statistic for a gene-tissue pair includes the direct effects of the gene on the disease as well as the tagging effects of co-regulated tissues and genes with shared eQTLs or eQTLs in LD. Thus, genes that are co-regulated across many tissues will tend to have higher ${\chi }^2$ statistics than genes regulated in a single tissue. TCSC determines that a tissue causally contributes to disease if genes with high co-regulation to the tissue have higher TWAS ${\chi }^2$ statistics than genes with low co-regulation to the tissue.

We model the genetic component of gene expression as a linear combination of SNP-level effects:

$$W_{jgt\prime }=\sum _m{X}_{jm}{\beta }_{gt\prime m},$$ (3)

where $W_{jgt}$ is the cis-genetic component of gene expression in individual $j$ for gene $g$ and tissue $t^{\prime },X_{jm}$ is the standardized genotype of individual $j$ for SNP $m$, and ${\beta }_{gtm}$ is the standardized effect of the m^th SNP on the cis-genetic component of gene expression of gene $g$ in tissue $t^{\prime }$. We define the cis-genetic component of gene expression $W_{jgt}$ to have mean 0 and variance 1 and ${\beta }_{gt\prime m}$ to have mean 0 and variance $\frac{1}{M_g}$, where $M_g$ is the number of cis variants for gene g.

TCSC assumes that true gene-disease effects are identically distributed (i.i.d.) across genes and tissues while accounting for the fact that cis-genetic components of gene expression (and cis-genetic predictions of gene expression) are correlated¹ (see Supplementary Figs. 12–15 for simulations where gene expression-trait effect sizes are not i.i.d. across genes and tissues; TCSC performs well despite violations of model assumptions). The high correlation of cis-eQTLs across tissues leads to tagging from co-regulated tissues². We model phenotype as a linear combination of genetic components of gene expression across genes in different tissues:

$$Y_j=\sum _{t\prime }\sum _g{W}_{jgt}{\alpha }_{gt\prime }+{ϵ}_j,$$ (4)

where $Y_j$ is the (binary or continuous-valued) phenotype of individual $j,{\alpha }_{gt}$ is the standardized effect size of the cis-genetic component of gene expression on disease and ${ϵ}_j$ is the component of phenotype not explained by cis-genetic components of gene expression. We emphasize that we model disease as a function of the unobserved true cis-genetic component of gene expression $W_{jgt\prime }$, not the genetically predicted value ${\widehat{W}}_{jgt\prime }$ obtained from gene expression prediction models. Equation (4) can be rewritten in terms of SNP-level effects:

$$Y_j=\sum _i{X}_{ji}{{\beta }^{\prime }}_i+\sum _{t\prime }\sum _g\sum _m{X}_{jm}{\beta }_{gt\prime m}{\alpha }_{gt}+{ϵ}_j,$$ (5)

where ${{\beta }^{\prime }}_i$ are direct SNP-disease effects not mediated through gene expression.

We define the disease heritability explained by cis-genetic expression across all tissues as follows:

$$h_{ge}^2=var(\sum _{t\prime }\sum _g\sum _m{X}_{jm}{\beta }_{gt\prime m}{\alpha }_{gt})$$ (6)

Because $W_{jgt}$ has mean 0 and variance 1 and ${\alpha }_{gt}$ are assumed to be i.i.d. across genes and tissues (see above), Equation (5) implies that:

$$h_{ge}^2=\sum _{t\prime }\sum _g{\alpha }_{gt\prime }^2,$$ (7)

analogous to the relationship between SNP effect sizes and SNP-heritability²⁵: $h_g^2=var\left(\sum _i{X}_j{\beta }_i\right)$. We emphasize that the respective terms in Equation (5) for each tissue t’ are independent as ${\alpha }_{gt\prime }$ are assumed to be i.i.d. across genes and tissues. It follows that the disease heritability explained by a particular tissue $t^{\prime }$ is

$$h_{ge\left(t^{\prime }\right)}^2=var\left(\sum _g\sum _m{X}_{jm}{\beta }_{gt\prime m}{\alpha }_{gt\prime }\right),$$ (8)

which given that $W_{jgt\prime }$ has mean 0 and variance 1 and ${\alpha }_{gt\prime }$ is i.i.d. across genes, reduces to:

$$h_{ge\left(t^{\prime }\right)}^2=\sum _g{\alpha }_{gt\prime }^2.$$ (9)

Equation (7) and Equation (9) imply that $h_{ge}^2=\sum _{t\prime }{h}_{ge\left(t\prime \right)}^2.$ Now, let ${\alpha }_{gt\prime }$ be a random variable drawn from a normal distribution with mean zero and tissue-specific variance $var\left({\alpha }_{g{t}^{\prime }}\right)={\tau }_{t\prime }.$ Then

$$h_{ge\left(t^{\prime }\right)}^2=\sum _{g}var\left({\alpha }_{g{t}^{\prime }}\right)={\tau }_{t\prime }{G}_{t\prime },$$ (10)

where $G_{t\prime }$ is the number of significantly cis-heritable genes in the model. In simulations, we demonstrate that when there are similar numbers of cis-heritable genes across tissues, setting $G_{t\prime }$ to the total number of unique cis-heritable genes produces unbiased estimates in TCSC for the causal tissue; however, when there are varying numbers of cis-heritable genes across tissues (fewer in the causal tissue), this produces upward biased estimates (Supplementary Fig. 3–4) and thus setting $G_{t\prime }$ to the number of significantly cis-heritable genes in tissue t’ is recommended. With this variance term, we can define a polygenic model that relates TWAS ${\chi }^2$ statistics to co-regulation scores, which explicitly model the covariance structure of the ${\chi }^2$ statistics. This strategy is analogous to modeling the dependence of GWAS ${\chi }^2$ statistics on LD scores²⁵.

In a TWAS, the estimated value of the gene-disease effect size ${\alpha }_{g{t}^{\prime }}$ is proportional to the correlation of the cis-genetic components of gene expression and their true gene-disease effect sizes for nearby genes across tissues, analogous to GCSC²²:

$$E\left[{\widehat{\alpha }}_{gt}\right]=\sum _{t^{\prime }}\sum _{g^{\prime }}{r({\widehat{W}}_{gt},W_{g\prime t\prime })\alpha }_{g^{\prime }{t}^{\prime }}+{ϵ}_g,$$ (11)

where $r({\widehat{W}}_{gt},W_{g\prime t\prime })$ is the estimated correlation in cis-genetic predicted expression between gene $g$ in tissue $t$ and genes $g^{\prime }$ in tissue $t^{\prime }.{ϵ}_g$ is the component of phenotype not explained by cis-genetic components of gene expression, with mean 0 and variance ${\sigma }_e^2/N$.

The value of the TWAS ${\chi }^2$ is proportional to the squared estimated disease-gene effect size and the GWAS sample size N as follows:

$${\chi }_{gt}^2=N{\widehat{\alpha }}_{gt}^2$$ (12)

Using the equations (9) and (10), we can write the expectation of TWAS ${\chi }^2$ as follows:

$$\mathrm{E}\left[{\chi }_{gt}^2\right]=\mathrm{E}\left[{N\widehat{\alpha }}_{gt}^2\right]$$ (13)

$$=N\mathrm{E}\left[{\left(\sum _{t^{\prime }}\sum _{g^{\prime }}{{\widehat{r}}_{gg\prime t\prime }\alpha }_{g\prime t\prime }+{ϵ}_g\right)}^2\right]$$ (14)

$$=N\sum _{t^{\prime }}\sum _{g^{\prime }}\mathrm{E}\left[{\widehat{r}}_{gg\prime t\prime }^2\right]\mathrm{E}\left[{\alpha }_{g\prime t\prime }^2\right]+N\mathrm{E}\left[{ϵ}_g^2\right]$$ (15)

$$\approx N\sum _{t^{\prime }}\sum _{g^{\prime }}{(r}_{gg\prime t\prime }^2{+\frac{1}{N})h_{ge(t\prime )}^2/G}_{t\prime }+N{\sigma }_e^2/N$$ (16)

$$=N\sum _{t^{\prime }}\sum _{g^{\prime }}{(r}_{gg\prime t\prime }^2+\frac{1}{N}){\tau }_{t\prime }+{\sigma }_e^2$$ (17)

$$=N\sum _{t^{\prime }}\sum _{g^{\prime }}{r}_{gg\prime t\prime }^2{\tau }_{t\prime }+\sum _{t^{\prime }}\sum _{g^{\prime }}{\tau }_{t\prime }+{\sigma }_e^2$$ (18)

$$=N\sum _{t^{\prime }}\sum _{g^{\prime }}{r}_{gg\prime t\prime }^2{\tau }_{t\prime }+\sum _{t\prime }var({\alpha }_{g\prime t\prime })+{\sigma }_e^2$$ (19)

$$=N\sum _{t^{\prime }}l\left(g,t;t^{\prime }\right){\tau }_{t\prime }+1$$ (20)

$$=N\sum _{t^{\prime }}l\left(g,t;t^{\prime }\right)h_{ge\left(t^{\prime }\right)}^2/G_{t\prime }+1$$ (1)

To go from Equation (15) to Equation (16) we use the following relationship from the derivation of LDSC¹³:

$$\mathrm{E}\left[{\widehat{r}}_{gg\prime t\prime }^2\right]\approx r_{gg\prime t\prime }^2+\frac{1}{N}$$ (21)

We go from Equation (19) to Equation (20) because the variance of the phenotype $Y_j$ is $\sum _{t^{\prime }}var\left({\alpha }_{g\prime t\prime }\right)+{\sigma }_e^2$ and is equal to one. We also introduce the notation that $\sum _{g^{\prime }}{r}_{gg\prime t\prime }^2$ are the tissue and gene co-regulation scores $l\left(g,t;{\mathrm{t}}^{\prime }\right),$ see below. We are interested in estimating ${\tau }_{t\prime }$, the per-gene disease heritability explained by the cis-genetic component of gene expression in tissue $t^{\prime }$. From the derivation, the genome-wide tissue-specific contribution to disease heritability is estimated as

$$h_{ge\left(t^{\prime }\right)}^2=G_{t\prime }{\tau }_{t\prime }.$$ (22)

For the analysis of tissue-specific contributions to the covariance between two diseases, we can extend TCSC by using products of TWAS z-scores. Following the polygenic model described above, the expected product of TWAS z-scores in disease 1 and disease 2 for gene $g$ and tagging tissue $t$ is

$$E\left[z_{gt}^1\times z_{gt}^2\right]=\sqrt{N_1{N}_2}{\sum }_{t^{\prime }}l\left(g,t;t^{\prime }\right){\omega }_{ge\left(t^{\prime }\right)}/G_{t^{\prime }}+\rho N_s/\sqrt{N_1{N}_2}$$ (23)

where $N_1$ is GWAS sample size for disease 1, $N_2$ is GWAS sample size for disease 2, $t^{\prime }$ indexes causal tissues, $l\left(g,t;t^{\prime }\right)$ are tissue co-regulation scores (see below), ${\omega }_{ge\left(t^{\prime }\right)}$ is the genetic covariance explained by the cis-genetic component of gene expression in tissue $t^{\prime },G_{t^{\prime }}$ is the number of significantly cis-heritable genes in tissue $t^{\prime }$ (see below), $\rho$ is the phenotypic correlation between disease 1 and disease 2, and $N_s$ is the number of overlapping GWAS samples between disease 1 and disease 2. The last term represents the intercept⁶¹, and while we use a free intercept in the multivariate regression on co-regulation scores, the estimation of this term only plays a role in the estimation of regression weights (see below).

For estimates of $h_{ge\left(t\prime \right)}^2$ and ${\omega }_{ge\left(t^{\prime }\right)},$ we use a free intercept; the estimation of $\rho N_s\sqrt{N_1{N}_2}$ serves only to inform the heteroscedasticity weights (see below) and is not used in the multivariate TCSC regression to estimate ${\omega }_{ge\left(t^{\prime }\right)}.$ To estimate standard errors, we use a genomic block jackknife over 200 genomic blocks with an equal number of genes in each. The standard deviation is computed as the square root of the weighted variance across the jackknife estimates (where the weight of each block is equal to the sum of the regression weights for the genes in that block) multiplied by 200 blocks. We expect that the jackknife standard error will be conservative relative to the empirical standard error across estimates due to variation in causal signal across loci⁷¹.

Estimating tissue co-regulation scores and correcting for bias

We define the co-regulation score of gene $g$ with tissues $t$ and $t^{\prime }$ as

$$l\left(g,t;t^{\prime }\right)={\sum }_{g^{\prime }}{r}^2\left({\widehat{W}}_{g,t},W_{g^{\prime },t^{\prime }}\right),$$ (24)

where $W$ denotes the cis-genetic component of gene expression for a gene-tissue pair across individuals, $\widehat{W}$ denotes the cis-predicted expression for a gene-tissue pair, and genes $g^{\prime }$ are within +/− 1 Mb of the focal gene $g$. TCSC corrects for bias in tissue co-regulation scores arising from differences between cis-genetic vs. cis-predicted expression (analogous to GCSC²²). We apply bias correction to co-regulation scores in the special case when $g=g^{\prime }$ and $t=t^{\prime }$. While co-regulation scores aim to estimate $r^2\left({\widehat{W}}_{g,t},W_{g^{\prime },t^{\prime }}\right)$, the squared correlation of the predicted cis-genetic component of expression of gene $g$ and tissue $t$ (corresponding to the TWAS ${\chi }_{g,t}^2$ statistic) with the actual cis-genetic component of gene expression of gene $g^{\prime }$ in tissue $t^{\prime }$, when $g=g^{\prime }$ and $t=t^{\prime }$, the estimated value of $r^2\left({\widehat{W}}_{g,t},W_{g^{\prime },t^{\prime }}\right)$ will always equals one because the estimate is based on $r^2\left({\widehat{W}}_{g,t},{\widehat{W}}_{g^{\prime },t^{\prime }}\right)$. However, this implies that predictions of the cis-genetic component of expression are perfectly accurate, which is unlikely to be the case. Therefore, the estimated value of $r^2\left({\widehat{W}}_{g,t},W_{g^{\prime },t^{\prime }}\right)$ if left to equal one will cause co-regulation scores to be systematically inflated.

Therefore, when $g=g^{\prime }$ and $t=t^{\prime }$, we set

$$r^2\left({\widehat{W}}_{g,t},W_{g^{\prime },t^{\prime }}\right)=R^2/h_{GCTA}^2,$$ (25)

where $R^2$ is the cross-validation prediction statistic of the gene expression model for gene $g$ in tissue $t$ and $h_{GCTA}^2$ is the GCTA-estimated cis-heritability of gene expression for gene $g$ in tissue $t$. The quotient $R^2/h_{GCTA}^2$ is the accuracy of the gene expression prediction model, which reflects the upper bound on how much the cis-predicted expression can be correlated with the true cis-genetic component of gene expression. While we only consider genes with $h_{GCTA}^2$ p < 0.01, the uncertainty in $h_{GCTA}^2$ estimates should be modest and therefore not greatly impact our bias correction. We note that TWAS tests the null hypothesis that a specific weighted linear combination of SNPs is not associated with disease (and does not test the null hypothesis that the cis-genetic component of gene expression is not associated with disease).

TCSC regression weights

TCSC uses three sets of regression weights to increase power (analogous to GCSC²²). The first regression weight is inversely proportional to $L\left(g,t\right),$ the total co-regulation score of each gene-tissue pair summed across tissues $t^{\prime }$:

$$L\left(g,t\right)=\sum _{t^{\prime }}{\sum }_{g^{\prime }}{r}^2\left({\widehat{W}}_{g,t},W_{g^{\prime },t^{\prime }}\right)$$ (26)

(without applying bias correction; see above), which allows TCSC to properly account for redundant contributions of co-regulated genes to TWAS ${\chi }^2$ statistics.

The second regression weight is inversely proportional to $T\left(g,t\right),$ the number of tissues in which a gene is significantly cis-heritable:

$$T\left(g,t\right)=\sum _{t^{\prime }\in g,t^{\prime }significantlycis-heritable}1,$$ (27)

thereby up-weighting signal from genes that are regulated in a limited number of tissues and preventing TCSC from attributing more weight to genes that are co-regulated across many tissues.

The third regression weight is inversely proportional to $H_{h^2}\left(g,t\right)$, the heteroscedasticity of ${\chi }^2$ statistics, and is computed differently for estimates of $h_{ge\left(t^{\prime }\right)}^2$ than for estimates of ${\omega }_{ge\left(t^{\prime }\right)}$ (analogous to GCSC²² and cross-trait LDSC⁶¹, respectively).

For estimates of $h_{ge\left(t\prime \right)}^2,$ we estimate $H_{h^2}\left(g,t\right)$ in two steps. First, we make a crude estimate of heritability explained by predicted expression ($h_{ge}^2$) as follows:

$${\mu }_{\chi }=N{\mu }_L{h}_{ge}^2+1,$$ (28)

where ${\mu }_{\chi }$ is the mean ${\chi }^2$ statistic:

$${\mu }_{\chi }=\frac{\sum _{t\prime }{\sum }_{g\prime }{\chi }_{g\prime ,t\prime }^2}{{\sum }_{t^{\prime }}{G}_{t\prime }},$$ (29)

where $N$ is the GWAS sample size, $g^{\prime }$ iterates over significantly cis-heritable genes and $t^{\prime }$ iterates over tissues, and ${\mu }_L$ is the mean value of total co-regulation across tissues $t^{\prime }$,

$${\mu }_L=\frac{\sum _{t\prime }{\sum }_{g\prime }L\left(g\prime ,t\prime \right)}{{\sum }_{t^{\prime }}{G}_{t\prime }}.$$ (30)

Then, we compute the heteroscedasticity for each significantly cis-heritable gene-tissue pair as

$${H_{h^2}\left(g,t\right)=\left(NL\left(g,t\right)h_{ge}^2+1\right)}^2.$$ (31)

Finally, we combine the three regression weights as follows:

$${Weight}_{h^2}\left(g,t\right)=\frac{1}{L\left(g,t\right)T\left(g,t\right)H_{h^2}(g,t)}.$$ (32)

For estimates of ${\omega }_{ge\left(t^{\prime }\right)},$ we estimate $H_{\omega }(g,t)$ in two steps. First, we regress the products of TWAS z-scores on total tissue co-regulation scores, $L\left(g,t\right)$, using regression weights, ${Weight}_{\omega }\left(g,t\right),$ computed as follows:

$${Weight}_{\omega }\left(g,t\right)=\frac{1}{L\left(g,t\right)T\left(g,t\right)H_{\omega }(g,t)}$$ (33)

where $H_{\omega }(g,t)$ is first estimated as follows:

$$H_{\omega }\left(g,t\right)=\left(N_{1}L\left(g,t\right)h_{ge}^2\left(trait1\right)+1\right)\left(N_{2}L\left(g,t\right)h_{ge}^2\left(trait2\right)+1\right)+{\left(\frac{\sqrt{N_1{N}_2}{\omega }_{ge}L\left(g,t\right)}{\sum _{t^{\prime }}\frac{G_{t^{\prime }}}{T^{\prime }}}\right)}^2,$$ (34)

where $h_{ge}^2\left(trait1\right)$ is the crude heritability estimate for trait 1 and $h_{ge}^2\left(trait2\right)$ is the crude heritability estimate for trait 2, ${\omega }_{ge}$ is estimated as $\frac{\sum _{t^{\prime }}{\sum }_{g^{\prime }}{z}_{{\mathrm{g}}^{\prime }{\mathrm{t}}^{\prime }}^{\left(1\right)}{z}_{{\mathrm{g}}^{\prime }{\mathrm{t}}^{\prime }}^{\left(2\right)}}{\sqrt{N_1{N}_2}},N_1$ is the sample size of the first GWAS, $N_2$ is the sample size of the second GWAS, and $T^{\prime }$ is the total number of tissues in the regression.

Second, we use the regression intercept to estimate the product $\rho N_s:$

$$\rho N_s=intercept\mathrm{*}\sqrt{N_1{N}_2},$$ (35)

where $\rho$ represents the phenotypic correlation between trait 1 and 2 and $N_s$ represents the number of shared samples between GWAS 1 and 2. We also use the coefficient of the regression to update our estimate of ${\omega }_{ge}$, such that we may update the heteroscedasticity weight as follows:

$$H_{\omega }\left(g,t\right)=\left(N_{1}L\left(g,t\right)h_{ge}^2\left(trait1\right)+1\right)\left(N_{2}L\left(g,t\right)h_{ge}^2\left(trait2\right)+1\right)+{\left(\frac{\sqrt{N_1{N}_2}{\omega }_{ge}L\left(g,t\right)}{\sum _{t^{\prime }}\frac{G_{t^{\prime }}}{T^{\prime }}}+\rho N_s\sqrt{N_1{N}_2}\right)}^2.$$ (36)

Finally, we combine the three regression weights as follows:

$${Weight}_{\omega }\left(g,t\right)=\frac{1}{L\left(g,t\right)T\left(g,t\right)H_{\omega }(g,t)}.$$ (37)

Gene expression prediction models and tissue co-regulation scores in GTEx data

To construct gene expression prediction models, we applied FUSION²¹ (Code Availability) to individual-level GTEx data by regressing measured gene expression on genotypes of common variants (MAF > 0.05) and covariates provided by GTEx¹⁹. FUSION uses several different regression models: single eQTL, elastic net, lasso, and BLUP and the following covariates: sex, 5 genotyping principal components, PEER factors⁷², and assay type. We defined significantly cis-heritable genes as protein-coding genes with GCTA heritability p < 0.01²¹, heritability estimate > 0, and adjusted-R² > 0 in cross-validation prediction.

We used gene expression prediction models of significantly cis-heritable genes to predict expression into 489 European individuals from 1000 Genomes²⁷. We then estimated tissue co-regulation scores using Equation (24) and Equation (25)⁷³, where cis-predicted gene expression is used to estimate the cis-genetic component of gene expression.

GWAS summary statistics and TWAS association statistics

We collected GWAS summary statistics from 78 relatively independent heritable complex diseases and traits (average N = 302K) with heritability z-score > 6, including 33 diseases/traits from UK Biobank⁷⁴. We estimated the heritability of all summary statistics and genetic correlation of all pairs of summary statistics. We excluded traits with heritability z-score < 6, using S-LDSC with the baseline-LD v2.2 model^13,28,29 and as done previously²⁸. We excluded one of each pair of traits that are both genetically correlated and have significantly overlapping samples. Specifically, for any pair of non-UK Biobank traits with an estimated sample overlap greater than the following threshold -- squared cross-trait LDSC intercept / (trait 1 S-LDSC intercept * trait 2 S-LDSC intercept) > 0.1⁶¹ -- the trait with the larger SNP heritability z-score was retained. For any pair of UK Biobank traits with a squared genetic correlation > 0.1, the trait with the larger SNP heritability z-score was retained⁷⁵. In total, this procedure resulted in 78 sets of relatively independent GWAS summary statistics. We limited all analyses (including cross-trait analyses) to the 78 relatively independent traits in order to avoid redundant findings across single-trait (and cross-trait) analyses. For the brain-specific analysis, we first selected brain-related diseases and complex traits, e.g. psychiatric disorders and behavioral phenotypes, excluding multi case-control studies and case vs case studies. Then, we applied our standard filters as described above, but relaxing the threshold of squared genetic correlation to 0.25.

We used FUSION²¹ (Code Availability) to compute TWAS association statistics for each pair of signed GWAS summary statistics and each significantly cis-heritable gene-tissue pair, across the two scenarios described above. We restrict gene expression prediction models and TWAS association statistics for each tissue to significantly cis-heritable genes in that tissue, defined as genes with significantly positive cis-heritability (2-sided p < 0.01; estimated using GCTA⁷⁶) and positive adjusted-$R^2$ in cross-validation prediction. We further removed genes within the MHC (chromosome 6, 29 Mb - 33 Mb) and TWAS ${\chi }^2>80$ or ${\chi }^2>0.001N$, where $N$ is the GWAS sample size, as previously used for quality control in the heritability analysis of GWAS summary statistics¹³. TCSC scales linearly with the number of genes and quadratically with the number of tissues. After all input datasets are created and processed, running TCSC on a single real GWAS trait with 39 tissues takes about two minutes⁷³. We employ a per-trait FDR (as in ref.^77,78) rather than a global FDR (as in ref.⁷), because power is likely to vary across traits and there are a sufficiently large number of independent quantities estimated per trait (${\pi }_{t^{\prime }}$ jointly estimated across 39 tissues); a global FDR is more appropriate when there are far fewer independent quantities estimated per trait, e.g. due to non-independent, marginal tissue associations in ref.⁷ For cross-trait analysis, we estimated the genetic correlation of each of 3,003 pairs of the 78 disease/traits analyzed in this study; the 262 pairs analyzed by cross-trait analysis had significantly nonzero genetic correlation (p < 0.05 / 3,003).

RTC Coloc and LDSC-SEG analysis of GWAS summary statistics and GTEx tissues

We downloaded supplementary tables for the RTC coloc method² and for LDSC-SEG⁷. For traits in our set of 78 GWAS summary statistics that were not analyzed by the LDSC-SEG study and for traits that are inherently brain-related (as these traits require a different procedure for generating tissue-specific gene sets), we ran LDSC-SEG ourselves. To this end, we downloaded LD scores for GTEx tissues and specifically expressed gene set SNP-level annotations (https://alkesgroup.broadinstitute.org/LDSCORE/LDSC_SEG_ldscores/) and ran LDSC-SEG⁷ using S-LDSC v1.0.0. For brain-related traits, we additionally ran a brain-specific analysis using LDSC-SEG⁷. Briefly, specifically expressed genes were determined via a t-test of the sentinel brain tissue against all other brain tissues, rather than against all other non-brain GTEx tissues, as done in the primary analysis of the LDSC-SEG study. For traits in our set that were not analyzed by the RTC Coloc study, of which there were few, we did not apply their method, as it was too computationally intensive to apply to real trait data.

Statistics and Reproducibility

First, as described above, we downsampled or meta-analyzed GTEx tissues to reduce the potential for type I error in our analysis; downsampling was performed randomly. Second, as described above, GWAS summary statistics with a SNP heritability z-score < 6 were excluded, due to the potential to have low power. Third, in analyses of real diseases/traits, we verified that we obtained consistent results when analyzing different GWAS cohorts. We obtained independent GWAS summary statistics for 10 traits implicated in 13 significant tissue-trait pairs (Supplementary Table 4) and confirmed the same direction of effect for 13 of 13 tissue-trait pairs (including FDR < 5% for 7 of 13 tissue-trait pairs, FDR < 10% for 9 of 13 tissue-trait pairs) (Supplementary Table 5). Fourth, 1,000 independent genetic architectures were simulated to robustly evaluate TCSC performance. Randomization and blinding were not pertinent to our study.

Extended Data

Extended Data Figure 1. Comparison of tissue-trait association methods with TCSC in simulations.

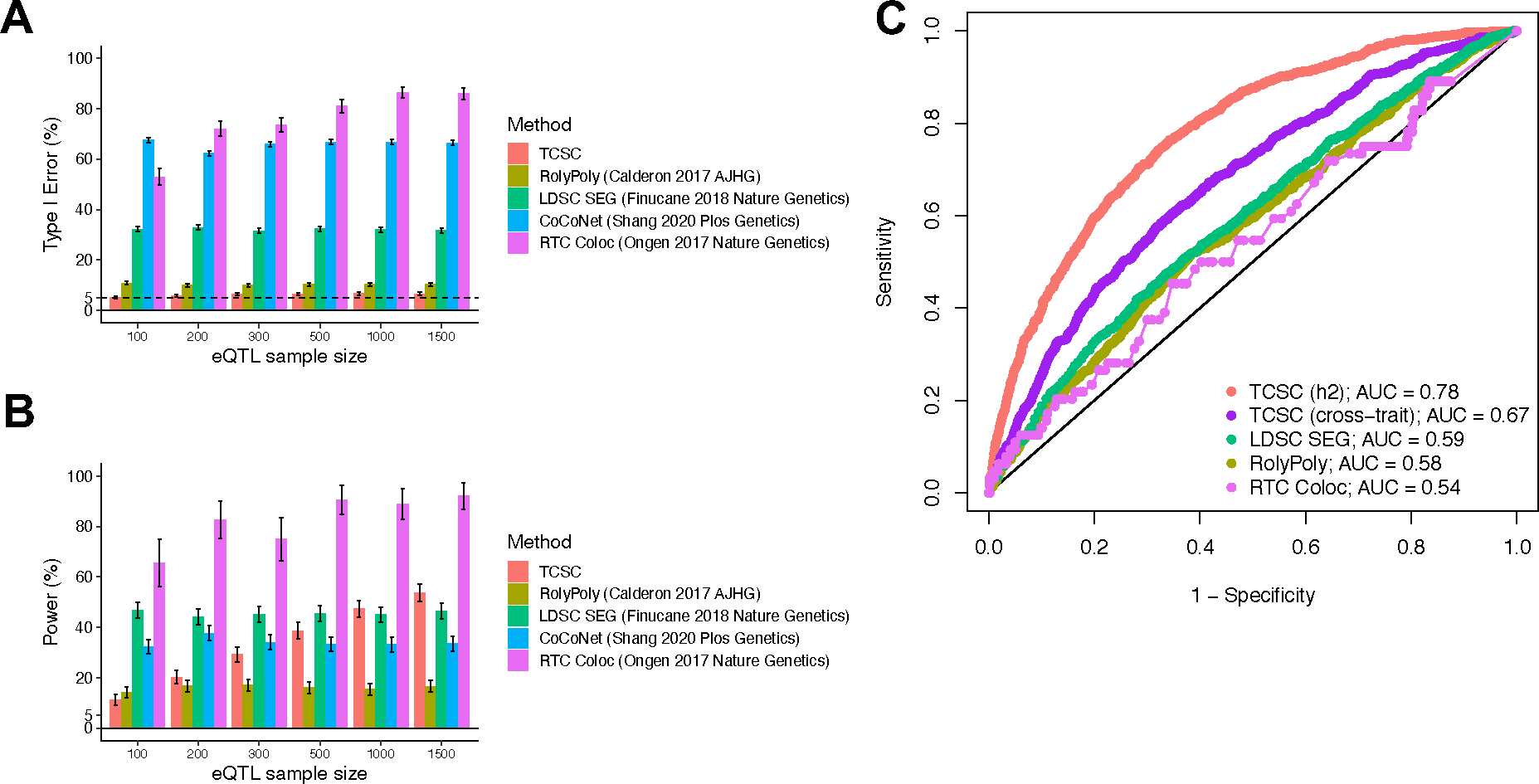
(A) Percentage of estimates of $h_{ge\left(t\prime \right)}^2$ for non-causal tissues that were significantly positive at p < 0.05. $h_{ge\left(tcausal\right)}^2$ is set to 10% and GWAS sample size is set to 10,000. (B) Percentage of estimates of $h_{ge\left(t\prime \right)}^2$ for causal tissues that were significantly positive at p < 0.05. In panels A and B, we performed n = 1,000 independent simulated genetic architectures for TCSC, LDSC-SEG, CoCoNet, and RolyPoly and n = 100 independent simulated genetic architectures for RTC Coloc due to the computationally intensive nature of the method across each eQTL sample size (n = 100, 200, 300, 500, 1000, 1500); we used a one-sided z-test and the genomic block jackknife standard error to obtain p-values and data are presented as mean values +/− 1.96 × SEM. (C) Receiver operating characteristic (ROC) curves for each method, including cross-trait TCSC, across 1,000 uniformly spaced p-values between 0 and 1 used as the threshold to identify a causal tissue at a simulation eQTL sample size of 300, most closely matching real data analysis. We note that CoCoNet cannot be compared here because the method identifies the single most likely causal tissue using maximum likelihood estimation rather than via p-value. Numerical results are provided in Supplementary Tables 1 and 2.

Extended Data Figure 2. Robustness and power of cross-trait TCSC in simulations.

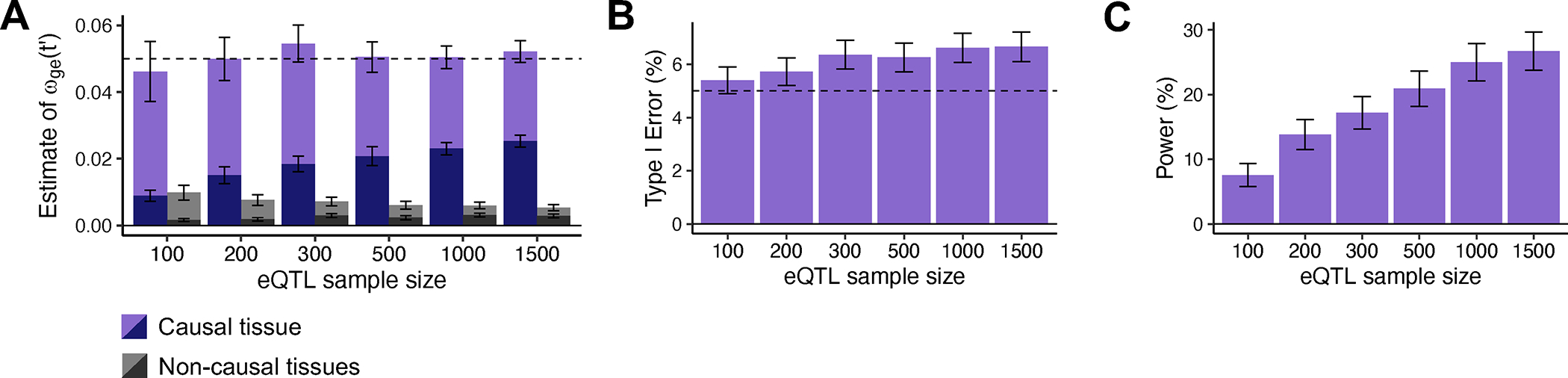
(A) Bias in estimates of genetic covariance explained by the cis-genetic component of gene expression in tissue $t^{\prime }({\omega }_{ge\left(t\prime \right)}$) for causal (purples) and non-causal (grays) tissues, across n = 1,000 independent simulations per eQTL sample size (n = 100, 200, 300, 500, 1000, 1500). Light purple (resp. gray) indicates that $G_{t\prime }$ was set to the total number of true cis-heritable genes across tissues, dark purple (resp. gray) indicates that $G_{t\prime }$ was set to the number of significantly cis-heritable genes detected in each tissue. The dashed line indicates the true value of ${\omega }_{ge\left(t\prime \right)}$ for causal tissues. (B) Percentage of estimates of ${\omega }_{ge\left(t\prime \right)}$ for non-causal tissues that were significantly positive at p < 0.05. (C) Percentage of estimates of ${\omega }_{ge\left(t\prime \right)}$ for causal tissues that were significantly positive at p < 0.05. For panels B and C, we performed n = 1,000 independent simulations per eQTL sample size (n = 100, 200, 300, 500, 1000, 1500) and used a one-sided z-test to obtain p-values. In all panels, data are presented as mean values +/− 1.96 × SEM. Numerical results are reported in Supplementary Table 3.

Extended Data Figure 3. Robustness and power of TCSC regression in simulations with different values of ${\mathit{h}}_{\mathit{g}\mathit{e}\left(\mathit{t}\prime \right)}^2.$

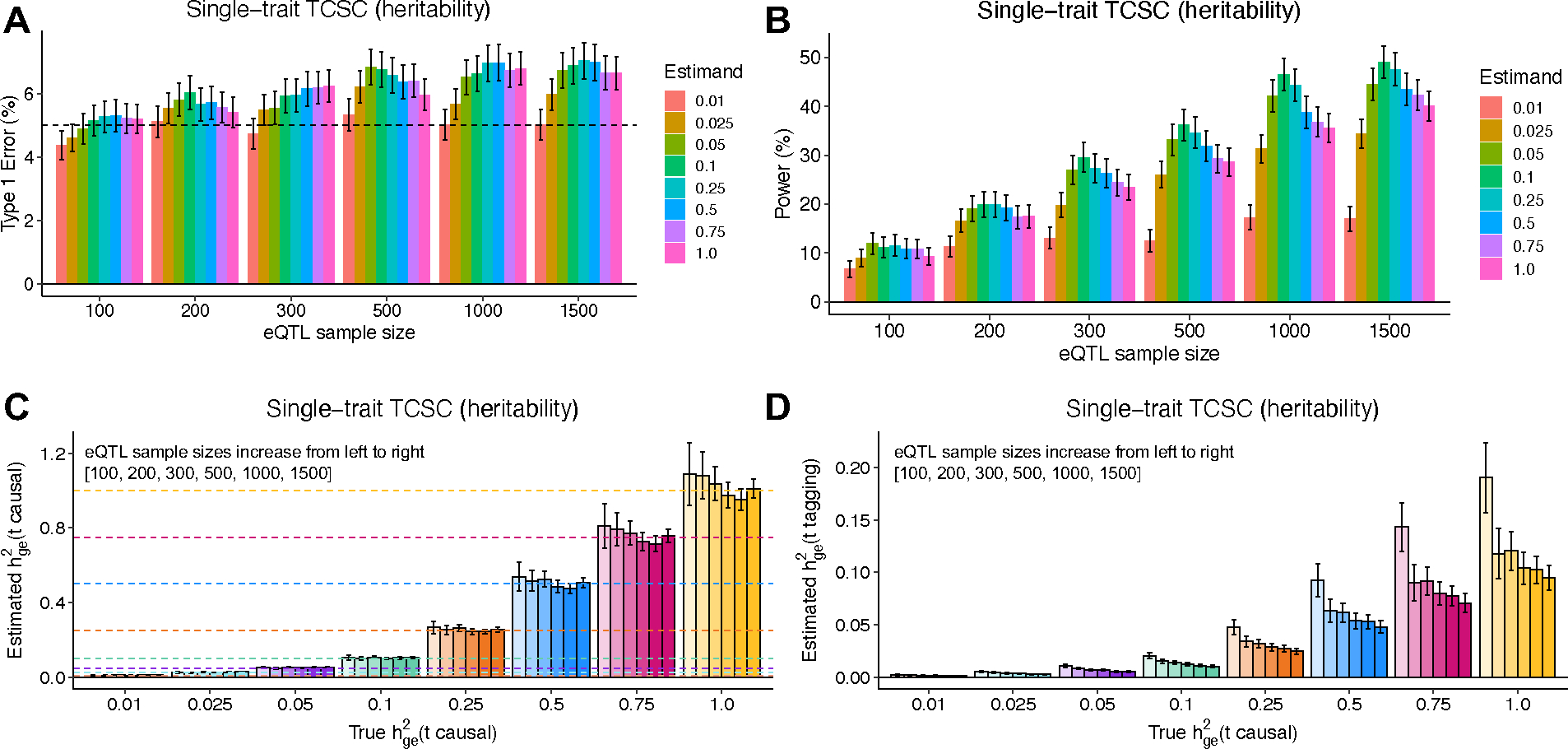
(A) Type I error per true value of $h_{ge\left(t\prime \right)}^2$ in the causal tissue. False positive event is defined as $h_{ge\left(t\prime \right)}^2>0$ for non-causal tissues at p < 0.05. (B) Power to detect the causal tissue per true value of $h_{ge\left(t\prime \right)}^2$ in the causal tissue. A true positive event is defined as $h_{ge\left(t\prime \right)}^2$ > 0 for causal tissues at p < 0.05. (C) Bias on causal estimates of $h_{ge\left(t\prime \right)}^2$ for different true values of the causal tissue $h_{ge\left(t\prime \right)}^2$. Dashed lines indicate true values of $h_{ge\left(t\prime \right)}^2$. (D) Bias on non-causal estimates of $h_{ge\left(t\prime \right)}^2$ for different true values of the causal tissue $h_{ge\left(t\prime \right)}^2$. In all panels, we performed n = 1,000 independent simulated genetic architectures across different eQTL sample sizes (n = 100, 200, 300, 500, 1000, 1500); we used a one-sided z-test and the genomic block jackknife standard error to obtain p-values and data are presented as mean values +/− 1.96 × SEM. The value of $G_{t\prime }$ is set to the total number of unique cis-heritable genes across all tissues.

Extended Data Figure 4. Robustness and power of cross-trait TCSC regression in simulations with different values of ${\mathit{\omega }}_{\mathit{g}\mathit{e}\left(\mathit{t}\prime \right)}$.

(A) Type I error per true value of ${\omega }_{ge\left(t\prime \right)}$ in the causal tissue. False positive event is defined as ${\omega }_{ge\left(t\prime \right)}>0$ for non-causal tissues at p < 0.05. (B) Power to detect the causal tissue per true value of ${\omega }_{ge\left(t\prime \right)}$ in the causal tissue. A true positive event is defined as ${\omega }_{ge\left(t\prime \right)}>0$ for causal tissues at p < 0.05. (C) Bias on causal estimates of ${\omega }_{ge\left(t\prime \right)}$ for different true values of the causal tissue ${\omega }_{ge\left(t\prime \right)}$. Dashed lines indicate true values of ${\omega }_{ge\left(t\prime \right)}$. (D) Bias on non-causal estimates of ${\omega }_{ge\left(t\prime \right)}$ for different true values of the causal tissue ${\omega }_{ge\left(t\prime \right)}$. In all panels, we performed n = 1,000 independent simulated genetic architectures across different eQTL sample sizes (n = 100, 200, 300, 500, 1000, 1500); we used a one-sided z-test and the genomic block jackknife standard error to obtain p-values and data are presented as mean values +/− 1.96 × SEM. The value of $G_{t\prime }$ is set to the total number of unique cis-heritable genes across all tissues.

Extended Data Figure 5. Robustness and power of TCSC regression in simulations with different numbers of non-causal tissues.

(A) Type I error involving a variable number of non-causal tissues in the presence of a single causal tissue. False positive event defined as $h_{ge\left(t\prime \right)}^2$ > 0 for non-causal tissues at p < 0.05. Note, when there are 0 tagging tissues, there is no measurement of type I error. (B) Power to detect the causal tissue in which $h_{ge\left(t\prime \right)}^2>0$ for causal tissues at p < 0.05. (C) Bias on estimates of $h_{ge\left(t\prime \right)}^2$ for the causal tissue, while changing the number of non-causal tissues in the model. The dashed line indicates that the true value of $h_{ge\left(t\prime \right)}^2$. (D) Bias on estimates of $h_{ge\left(t\prime \right)}^2$ for non-causal tissues, while changing the number of non-causal tissues in the model. In all panels, we performed n = 1,000 independent simulated genetic architectures across different eQTL sample sizes (n = 100, 200, 300, 500, 1000, 1500); we used a one-sided z-test and the genomic block jackknife standard error to obtain p-values and data are presented as mean values +/− 1.96 × SEM. The value of $G_{t\prime }$ is set to the total number of unique cis-heritable genes across all tissues.

Extended Data Figure 6. Robustness and power of cross-trait TCSC regression in simulations with different numbers of non-causal tissues.

(A) Type I error involving a variable number of non-causal tissues in the presence of a single causal tissue. False positive event defined as ${\omega }_{ge\left(t\prime \right)}$ > 0 for non-causal tissues at p < 0.05. Note, when there are 0 tagging tissues, there is no measurement of type I error. (B) Power to detect the causal tissue in which ${\omega }_{ge\left(t\prime \right)}>0$ for causal tissues at p < 0.05. (C) Bias on estimates of ${\omega }_{ge\left(t\prime \right)}$ for the causal tissue, while changing the number of non-causal tissues in the model. The dashed line indicates that the true value of ${\omega }_{ge\left(t\prime \right)}$. (D) Bias on estimates of ${\omega }_{ge\left(t\prime \right)}$ for non-causal tissues, while changing the number of non-causal tissues in the model. In all panels, we performed n = 1,000 independent simulated genetic architectures across different eQTL sample sizes (n = 100, 200, 300, 500, 1000, 1500); we used a one-sided z-test and the genomic block jackknife standard error to obtain p-values and data are presented as mean values +/− 1.96 × SEM. The value of $G_{t\prime }$ is set to the total number of unique cis-heritable genes across all tissues.

Extended Data Figure 7. Tissue-specific contributions to disease and complex trait heritability in secondary analysis of 23 tissues, removing tissues with small eQTL sample size.

We report estimates of the proportion of disease heritability explained by the cis-genetic component of gene expression in tissue $t^{\prime }({\pi }_{t^{\prime }}$). Results are shown for tissue-trait pairs with FDR <= 10%; full boxes denote FDR of 5% or lower and partial boxes denote FDR between 5% and 10%. Tissues are ordered alphabetically. Color corresponds to ${\pi }_{t^{\prime }}$, the proportion of common variant heritability causally explained by predicted gene expression in tissue $t^{\prime }$. These results are largely consistent with the analysis of 39 GTEx tissues (Figure 4). WHRadjBMI: waist-hip-ratio adjusted for body mass index. HDL: high-density lipoprotein. DBP: diastolic blood pressure. BMI: body mass index. FEV1/FVC: forced expiratory volume in one second divided by forced vital capacity. Cereb. Cortex Ar.: cerebral cortex surface area. WBC Count: white blood cell count. RBC Count: red blood cell count. MDD: major depressive disorder. Daggers next to a tissue indicate a meta-tissue.

Extended Data Figure 8. Tissue-specific contributions to disease and complex trait heritability in brain-specific analysis.

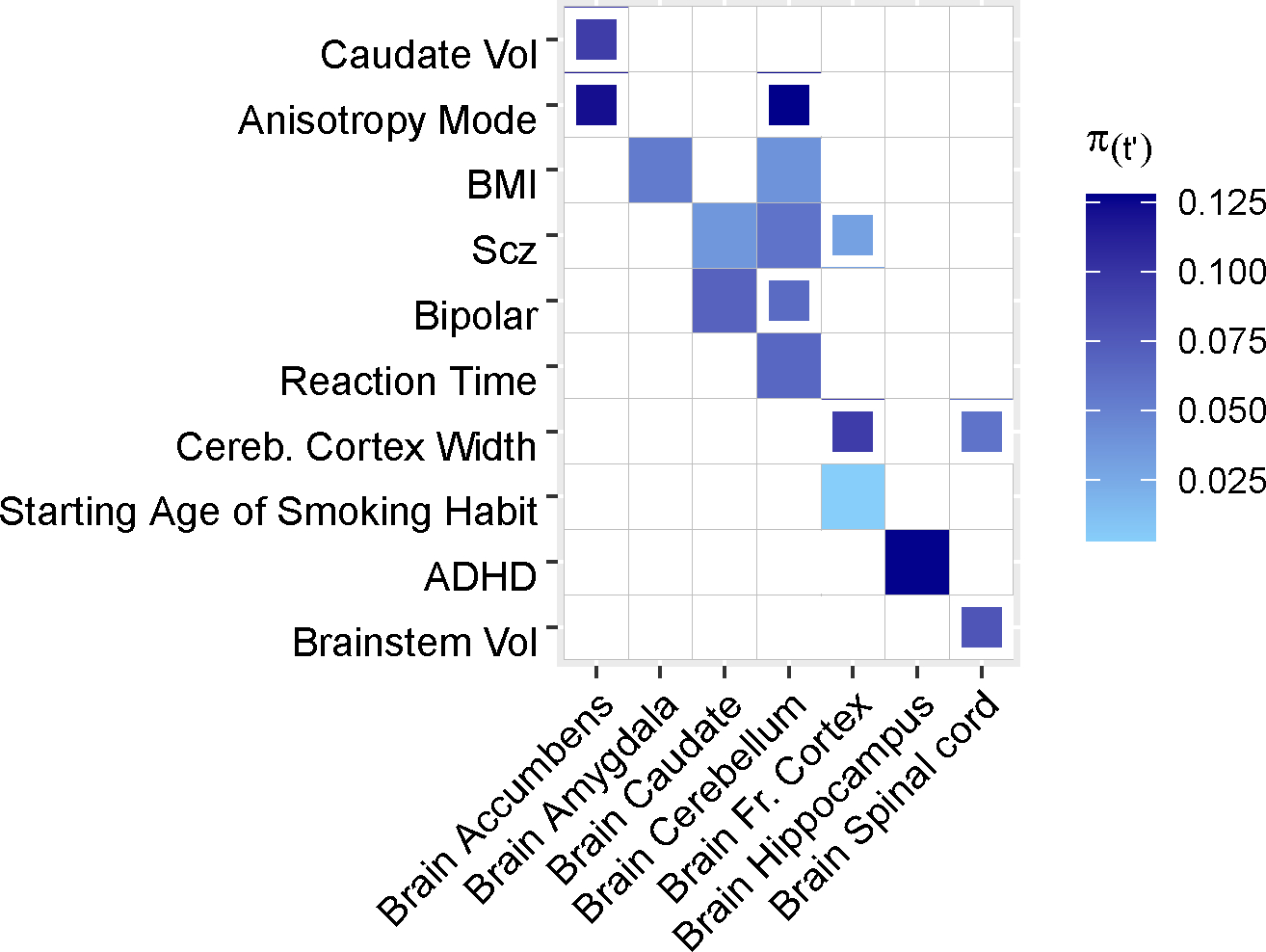
We separately analyzed results for 41 brain-related diseases and complex traits and 13 brain tissues. Results are shown for tissue-trait pairs with FDR <= 10%; full boxes denote FDR of 5% or lower and partial boxes denote FDR between 5% and 10%. Tissues are ordered alphabetically. Each tissue has an eQTL sample size ranging from 101 to 189 individuals. Color corresponds to ${\pi }_{t^{\prime }}$, the proportion of common variant heritability causally explained by predicted gene expression in tissue $t^{\prime }$. Caudate Vol: caudate volume. BMI: body mass index. Scz: schizophrenia. Bipolar: bipolar disorder. Brainstem Vol: brainstem volume. Cereb. Cortex Width: cerebral cortex width. ADHD: attention-deficit/hyperactivity disorder. Brainstem Vol: brainstem volume.

Extended Data Figure 9. Comparison of disease-critical tissues identified by RTC Coloc, LDSC-SEG and TCSC for all 17 disease/traits with causal tissue-trait associations identified by TCSC.

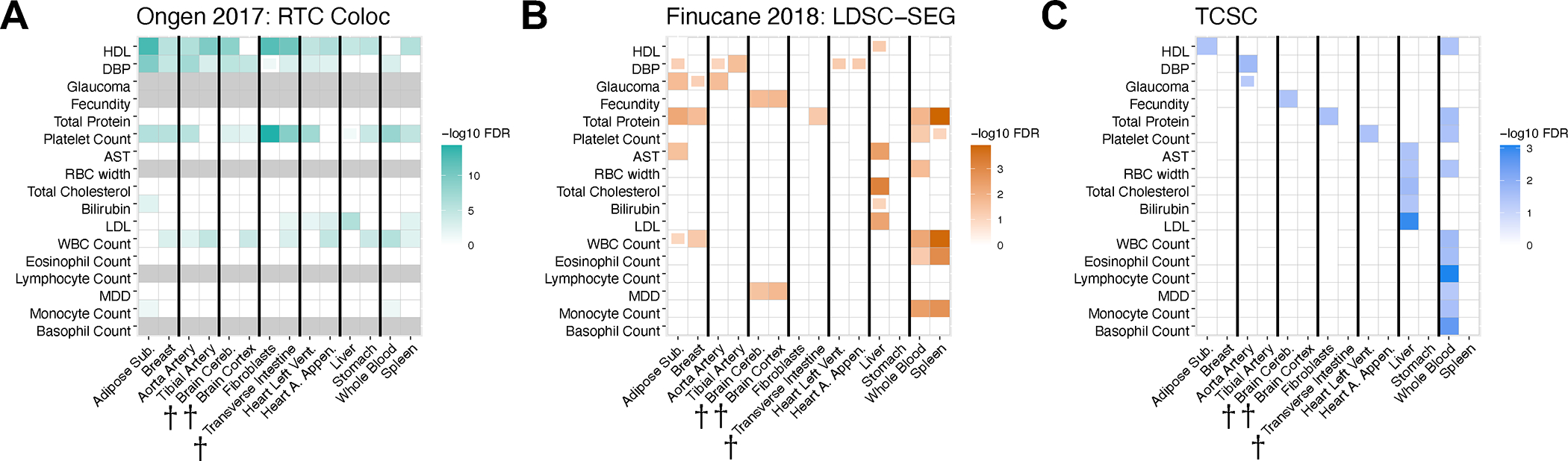
FDR significance of trait-tissue associations across three different methods for each of 17 traits with a significant tissue found by TCSC from Fig. 3 and 7 causal tissues, plus each tissue’s most highly genetically correlated GTEx tissue. Full boxes denote FDR of 5% or lower and partial boxes denote FDR between 5% and 10%. Thicker black lines separate the causal tissue found in the primary TCSC analysis (left) from its most highly genetically correlated GTEx tissue (right), with two exceptions. First, breast tissue was the most highly genetically correlated tissue for two causal tissues, adipose subcutaneous and thyroid; therefore, these three tissues appear as a trio. Second, the aorta artery and tibial artery are each other’s most highly genetically correlated tissue and both are a causal tissue different traits by TCSC. (A) RTC Coloc (Ongen 2017 Nat Genet), (B) LDSC-SEG (Finucane 2018 Nat Genet), (C) TCSC. Per-trait FDR in panels A and C, FDR across traits and tissues in panel B. WHRadjBMI: waist-hip-ratio conditional on body mass index. HDL: high-density lipoprotein. DBP: diastolic blood pressure. BMI: body mass index. FEV1/FVC: forced expiratory volume in one second divided by forced vital capacity. Cereb. Cortex Ar.: cerebral cortex surface area. AST: aspartate aminotransferase. LDL: low-density lipoprotein. WBC: white blood cell count. MDD: major depressive disorder. Daggers next to a tissue indicate a meta-tissue. For BMI, fecundity, and cereb. cortex ar., LDSC-SEG brain-specific analysis results are used.

Extended Data Figure 10. Comparison of disease-critical tissues identified by RTC Coloc, LDSC-SEG and TCSC for brain-specific analysis.

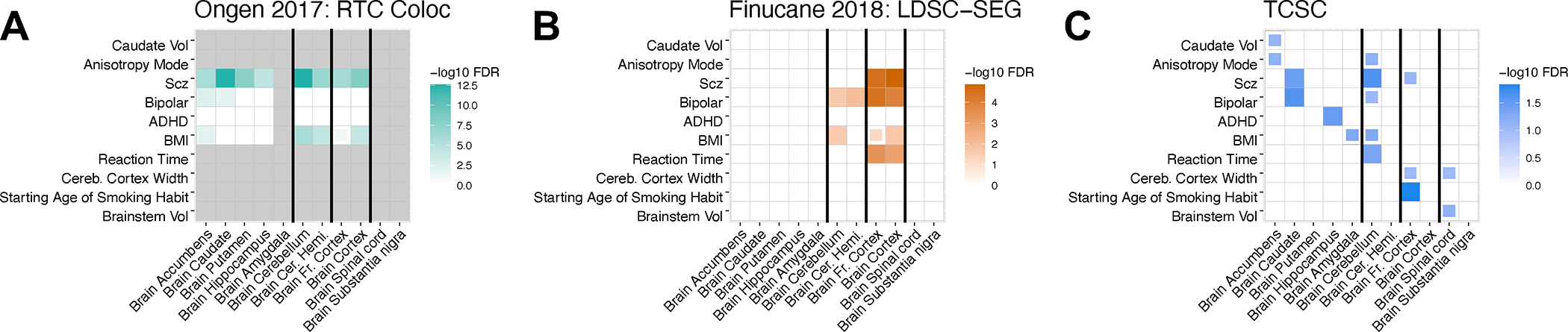
Brain-specific tissue-trait pairs identified by three methods: RTC Coloc, LDSC-SEG, and TCSC. Full boxes denote FDR of 5% or lower and partial boxes denote FDR between 5% and 10%. Each tissue has an eQTL sample size ranging from 100 to 189 individuals. Additionally, we include each tissue’s most highly genetically correlated GTEx tissue. Thicker black lines separate the causal tissue found in the primary TCSC analysis (left) from its most highly genetically correlated GTEx tissue (right), with one exception: brain accumbens, caudate, putamen, hippocampus, and amygdala are all highly genetically correlated, with no pairs of exclusively high genetic correlation. Caudate Vol: caudate volume. BMI: body mass index. Scz: schizophrenia. Bipolar: bipolar disorder. Brainstem Vol: brainstem volume. Cereb. Cortex Width: cerebral cortex width. ADHD: attention-deficit/hyperactivity disorder. Brainstem Vol: brainstem volume.

Data Availability

We have made 78 GWAS summary statistics and 41 brain-specific summary statistics publicly available at https://github.com/TiffanyAmariuta/TCSC/tree/main/sumstats (DOI: 10.5281/zenodo.8030594)⁷³, gene expression prediction models publicly available at https://alkesgroup.broadinstitute.org/TCSC/GeneExpressionModels/, TWAS association statistics publicly available at https://alkesgroup.broadinstitute.org/TCSC/TWAS_sumstats/, tissue co-regulation scores publicly available at https://github.com/TiffanyAmariuta/TCSC/tree/main/coregulation_scores, and TCSC output publicly available at https://github.com/TiffanyAmariuta/TCSC/tree/main/results. Gene expression and genotype data were acquired from the GTEx v8 eQTL dataset (dbGaP Accession phs000424.v8.p2) and 1000 Genomes phase 3 data were downloaded from https://data.broadinstitute.org/alkesgroup/FUSION/LDREF.tar.bz2.