Abstract
The biomechanical and biochemical processes in the biological systems of living organisms are extremely complex. Advances in understanding these processes are mainly achieved by laboratory and clinical investigations, but in recent decades they are supported by computational modeling. Besides enormous efforts and achievements in this modeling, there still is a need for new methods that can be used in everyday research and medical practice. In this report, we give a view of the generality of the finite element methodology introduced by the first author and supported by his collaborators. It is based on the multiscale smeared physical fields, termed as Kojic Transport Model (KTM), published in several journal papers and summarized in a recent book (Kojic et al., 2022) [1]. We review relevant literature to demonstrate the distinctions and advantages of our methodology and indicate possible further applications. We refer to our published results by a selection of a few examples which include modeling of partitioning, blood flow, molecular transport within the pancreas, multiscale-multiphysics model of coupling electrical field and ion concentration, and a model of convective-diffusive transport within the lung parenchyma. Two new examples include a model of convective-diffusive transport within a growing tumor, and drug release from nanofibers with fiber degradation.
Keywords: Convective-diffusive transport, Kojic transport model, Multiscale-multiphysics models, Composite smeared finite element, Lung parenchyma
1. Introduction
Biological systems in living organisms are generally more complex when compared to others in nature. Physico-chemical laws are equally applicable to mechanical systems within the living as in the general environment. But, there are specific processes in the living systems, such as, for example, a transformation of the biochemical into mechanical energy with temporarily succeeding events occurring in orders of magnitude different time and length scales. Or, the heart represents an electro-mechanical system that involves the generation of electrical impulses with strictly determined waves, transferred through a neural fiber network to reach muscle cell membranes, and causing a change of the membrane potential; further, change of calcium concentration within cells ultimately produces conformational changes of molecules of the sarcomere to produce mechanical force. The internal mechanical force represents the heart muscle's action to pump the blood from the heart to the arterial network.
There is a huge number of scientific papers, books, and reports on computational methods applied to model mechanics and physical fields in biomedical engineering. Before the computer era, starting in the nineteen-fifties, the methods were based, as in other fields of science and engineering, on analytically derived expressions with various functional forms such as special functions, integral transforms, finite and infinite series, etc. The development of computational methods, with the use of computers and specific software, revolutionalized mathematical modeling in science and applied fields, and even in medicine. The most generally used is the Finite Element Method (FEM) which also is the basic methodology of this report.
This paper aims to emphasize the generality of the Kojic Transport Model (KTM) which is based on the concept of smeared physical fields in biomedical engineering. The KTM has a strong distinction from other approaches and we first refer to a few references which illustrate this distinction. This way we also provide an insight into the advantages and generality of our methodology.
In [2] it is introduced an n-compartment mammillary distributed-parameter model for the estimation of physiological parameters in tumors, such as perfusion, mean transit time, fractional volumes, and transfer and rate constants. The idea consists of the division of the tumor's space into the capillary compartment to which other compartments, called the peripheral interstitial compartments, are connected. The diffusion of the tracer is governed by the convective-diffusive mass balance equations within the capillary, while diffusion only is taken within the compartments. Mass transport within the capillary of a length L is given by the following convective-diffusion equation
| (1) |
while diffusion within compartments is governed by equations
| (2) |
where c1 and ci are concentrations; rV1 and rVi are volumetric fractions within capillary and compartments, respectively; Q is volumetric flux per unit mass of tissue within the capillary, ρ is transported mass density; Ki1 and K1i are transport coefficients from capillary to the compartment and vice-versa; and qV is a volumetric term associated with capillary. Equations (1), (2) are solved in analytical form by the integral Laplace transformation and results are fitted to the experimental data to obtain material coefficients.
Another example that is related to the KTM is the determination of perfusion within an arterial blood vessel of the heart [3,4]. These authors introduced compartments for arterial blood vessels according to the lengths and diameters of capillaries within reference volumes around selected points within the heart tissue wall. The governing equations for blood flow within a compartment i have a usual form based on the Darcy law,
| (3) |
and the mass balance equation is
| (4) |
where are Darcy velocities, is Darcy permeability tensor, p is pressure, , is a source term, and are inter-compartment coupling (transport) coefficients. The capillary flow is represented in a continuum form by a permeability tensor evaluated within a reference volume. This tensor is analogous to our transport tensor given in the next section. Volumetric participations within compartments are taken into account by specifying a continuum porosity. The same approach to modeling perfusion is applied in Ref. [5].
Finally, we in this section refer to the modeling of electrical signal propagation in heart electrophysiology. The so-called phenomenological models are continuum models which can be compared with our KTM methodology. There are two types of these – initial monodomain followed by bidomain model. In the case of the monodomain model, the membrane potential (difference between cell internal and external electrical potentials) field is determined taking into account ionic fluxes through membranes and the volumetric fraction of the cells. We here give the fundamental balance equations for current density in the case of a bidomain model, called the extended bidomain model, according to Ref. [6]. The model includes two cell groups, group 1 and group 2, with their conduction characteristics, and the equations are, according to the notation used in our KTM representation,
| (5) |
where the upper indices 1 and 2 correspond to the first and second group of cells, while ‘ext’ stands for the extracellular space; rAV is the area-to-volume ratio for cells; Cm is membrane electrical capacitance; G is electrical conductivity for cells and extracellular space, respectively; Iion is ionic membrane flux, and Ve is electrical potential within cells and extracellular space.
2. Methodology
2.1. Gradient-driven physical fields and Kojic transport model (KTM)
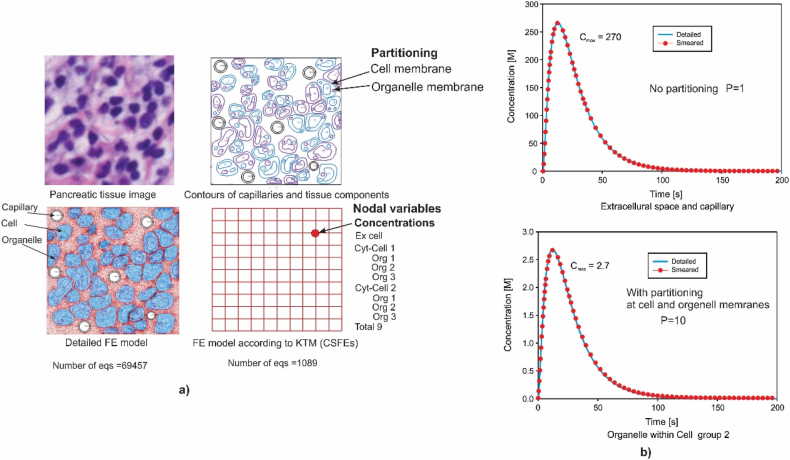
Here we summarize the FE formulation according to Ref. [7]. Application of this methodology is given in a number of our references [[8], [9], [10], [11], [12], [13], [14], [15], [16], [17]], and is described and summarized in Ref. [1]. This methodology is built into our FE software package PAK-BIO [18]. The background of the smeared concept and the KTM formulation of the composite smeared finite element (CSFE) are shown in Fig. 1. We further summarize the formulation of this element.
Fig. 1.
Composite smeared finite element (CSFE) with coupled physical fields within volumetric domains occupying the element space. According to Ref. [7].
First, we note that gradient-driven physical fields of interest in biomedical engineering considered here, are governed by a gradient law
| (6) |
where is the physical field depending on spatial coordinates xi and time t, Ji is the flux of (per unit surface and unit time), and Dij is the constitutive transport tensor. The fundamental balance equation, which has to be satisfied at any spatial point and any time for the field, can be written in the following form,
| (7) |
where c is the rate coefficient, and qV is the source term representing the rate of per unit volume. For diffusion, the rate coefficient is c = 1 and is concentration; c = ρcT for heat transfer, where ρ is density, cT is specific heat and is temperature; c = 0 for flow through porous media and is pressure. Transport tensor is the diffusion tensor, heat conduction tensor, and Darcy's tensor - for diffusion, heat transfer, and flow through porous media, respectively. In the case of electrical conduction, equation (6) is applicable, where Ji is current density, Dij is a diagonal conductivity tensor and is electrical potential. The above equations correspond to a general 3D or 2D continuum space, but they can be reduced to the 1D conditions which are present in biological systems as flow or mass or transport within small vessels, or electrical signal propagation by nerve network.
The important step in the formulation of the CSFE is a transformation of the 1D transport equations to a continuum form to treat the 1D transport as in other continuum domains within the CSFE. This is achieved by a consistent derivation of the expression for the transport tensor [1], which can be written as
| (8) |
where DK is the transport coefficient of a K-th 1D structural element in the vicinity of a considered spatial point of the physical field; AK are cross-sectional areas of the elements, is the sum of all AK, and are directional cosines of the 1D elements. This detail in the KTM contributes not only to the generality but also to simplicity in applications. An analogous expression to our expression in equation (8) is used in Refs. [3,4], equation (3).
The continuum balance equation (7) are further transformed into the FE format for each domain by a standard Galerkin method [1]. These balance equations for each domain K, a time step of size , and equilibrium iteration i can be written as,
| (9) |
where element matrices M and K take into account transitional and transport characteristics, while and are external (to the element) and volumetric fluxes; and , and are nodal vectors, nodal increments, and vectors at the start of a time step, respectively. The specificity of the matrices and nodal vectors is that they include the volumetric fractions of the domains. For example, the transport matrix K for a domain K is
| (10) |
where is the volumetric fraction, and NI, NJ are the FE interpolation functions.
A very important step in the formulation of the CSFE is how to couple mutually dependent physical fields within the continuum domains. This is achieved by introducing connectivity elements at each FE node. There are as many of these elements at a node as there are the coupling of the fields. Moreover, these practically fictitious elements represent biological barriers as capillary walls or cell membranes. The balance equation for a connectivity element at node J between domains m and n is (dropping out the rate terms)
| (11) |
where the connectivity matrix is
| (12) |
In the above equations (11), (12), and are the nodal values of the volumetric fraction, area-to-volume coefficient, wall transport coefficient, and volume (of the FE assembly) belonging to the node, respectively. The area coefficient is for capillaries with dcap being the capillary diameter, while for spherical cells with diameter dcell, it is .
To illustrate the KTM generality, here is given application to modeling mass release from a nanofiber network to the surrounding. This process is particularly suitable for medical implants where the drug release to tissue can be adjusted. Using electrospinning, it is possible to generate a nanofiber network containing a certain concentration of drug which is released by diffusion to the surroundings. An image of these nanofibers is shown in Fig. 2.
Fig. 2.
Image of nanofiber network with axial diffusion with fibers and radial diffusion to the surrounding. Lab of the Faculty of Technology and Metallurgy, University of Belgrade, Serbia [15,16].
The axial diffusion along the fibers is transformed to the continuum format as for the other 1D structures, with the evaluation of the diffusion tensor according to equation (8), while the governing balance equation has the form (9). The drug release from the fibers is achieved by connectivity elements (displaced in Fig. 2) according to the FE balance equation (9), with the matrices (for a node J)
| (13) |
In this equation (13) RJ is the fiber radius; and DfibJ are partitioning and diffusion coefficient, respectively; and , where is the area-to-volume ratio and VJ is the volume of the continuum belonging to node J.
The accuracy of this model is assessed by comparing the KTM solution with that obtained using the model with specific composite finite elements for fibers [11].
2.2. The generality of the KTM and comparison with other methods
In this section, we summarize the generality of the KTM and then give some evidence of the advantages of our computational models compared to other methodologies for the gradient-driven physical fields within biological systems.
In the previous section, we presented the fundamental assumptions in the formulation of the CSFE. Following that, we can emphasize several key facts which illustrate the generality of the KTM.
-
1)
The KTM, based on the multiscale composite finite element (CSFE) with smeared fields, can be considered a new avenue that offers a simple straightforward consistent formulation for modeling gradient-driven physical fields in biological systems.
-
2)
The CSFE is a continuum multiscale finite element composed of different physical fields (domains) which are mutually dependent. These domains have different spatial scales from macro to nanoscale. For example, the physical fields are related to the mass transport from capillaries through capillary walls, to extracellular space, further through cell membranes to cell interior cytosol, and through organelle membranes to the organelle interior. In applications, we have used the same time steps within the models, but a subdivision of the time step for lower scales can simply be employed.
-
3)
The 1D detailed models, with the use of 1D finite elements to follow the networks within which the process (transport) occurs, as in capillaries, neural networks, or nanofibers, are applicable to small spatial domains due to the complexity of geometry and the requirement of huge effort for model generation. On the other hand, our equivalent 3D continuum models are simple for space discretization and need appropriate transport tensor evaluation according to (8). This tensor can be associated with FE nodes to take the heterogeneity of parameters within the space.
-
4)
The accuracy of the KTM model has been assessed in a number of our publications, summarized in Ref. [1]. The original formulation was improved by correction functions introduced in Refs. [15,16], here illustrated in solutions in Fig. 3. Generally, the smeared physical fields can be considered as the mean value solutions in a vicinity of a considered spatial point.
-
5)
The KTM generality is particularly notable in modeling the biological barriers between the continuum domains. We illustrate the effects of partitioning at the biological barrier interfaces in an example following solutions in Ref. [12]. Fig. 3a shows detailed and the KTM FE models where we can see that the detailed model, with the use of standard 2D FEs, leads to 69,457 equations to be solved, while the KTM model, with the use of only 100 CSFEs, has 1089 equations. The reduction in the number of equations is around 70 times, hence the efficiency is increased by approximately the same number. It is assumed a bolus-type prescribed concentration within capillaries and concentration fields are calculated within two types of cells and organelles. Fig. 3b shows solutions for the mean concentrations in the
Fig. 3.
a) Image of a 50x50 μm tissue domain of pancreatic cancer, contours of two groups of cells with two organelles (upper panel); detailed 2D FE model of tissue with 6 capillaries normal to the image plane, and simple model with CSFE (lower panel). b) Mean concentration evolution within capillaries (prescribed) and in extracellular space (upper panel), and organelles of Cell group 2 – with partitioning (lower panel). According to Ref. [12] with small modifications.
extracellular space (upper panel) and organelles (lower panel). It can be seen a 100 times reduction of concentration within organelles due to partitioning (partitioning coefficient at the cell and organelle equal to 10). This effect of partitioning is a measure of hydrophobicity important in drug delivery. Other solutions are given in Ref. [1].
This example illustrates the generality of the KTM by including the hydrophobicity of molecules at the biological barriers, as well as the accuracy of the KTM since practically there is no difference between the two solutions in Fig. 3b.
By comparing our concept of connectivity elements with, for example, the approach given in Ref. [2], it can be seen that in equation (2) there is no explicit measure of the surface at a FE node through which the transfer from capillary occurs - as we have in expressions (13). The same conclusion can be drawn when comparing our connectivity elements with expressions (4) of reference [3,4]. Other specific molecular processes occurring at the cell membranes and within cells, which are fundamental for drug delivery, can be incorporated straightforwardly into our connectivity elements and continuum subdomains. For example, specific properties of the functionalization of nanoparticle surfaces [19], can be included. Or, the kinetics of the ligand-receptor binding can be incorporated. This kinetics, according to Ref. [20], is described by equation (14) of molecular interactions,
| (14) |
where Cbs, Cb, Ci, and C are concentrations of unbound binding sites, bound vesicles, internalized vesicles, and free vesicles per tumor volume, respectively; ka, kd, and kint are the association, dissociation, and internalization rate constants, respectively; and Rs is synthesis rate of new binding sites.
-
6)
Further, we refer to models applied in electrophysiology. A detailed comparison of the traditional bidomain models, as the one described by equation (5), and the KTM, is given in Refs. [1,14]. We here notify few of the differences between our and traditional models. Unlike the previous models which consider the entire continuum without compartments with their own volumes, in the KTM we treat each compartment separately with their specific transport properties. The physical fields are computed within the compartments, organized in a natural way and hierarchically according to the transport process; the fields are connected by the appropriate connectivity elements. As stated earlier, the connectivity elements represent biological barriers, and in the case of electrophysiology they specify the conductances from the neural fibers to the surrounding, and through cell membranes. According to the KTM, the governing balance equations refer to each tissue domain separately, with the volumetric fractions (K is compartment number), while in the previous models they correspond to the entire continuum, e.g. equation (5). The KTM hierarchy and multiscale character can be seen from the expression for the volume of a cell subdomain (here given by equation (15)):
| (15) |
where is the relative volume ratio of the subdomain with respect to the cell volume, whose ratio is related to the finite element volume V. Accuracy of the KTM is demonstrated and assessed by comparison with respect to the detailed FE models of a composite tissue [1,[8], [9], [10], [11], [12], [13]].
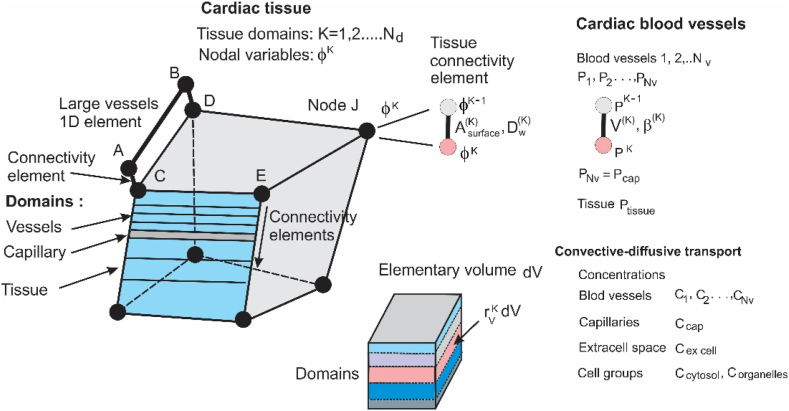
Finally, we indicate applications of the KTM which are not considered in our publications. The first example is related to an extension of our models to heart perfusion where blood vessels larger than capillaries are classified according to their diameters. The corresponding CSFE is shown in Fig. 4. Besides perfusion, the model may also include mass transport by diffusion and.
Fig. 4.
Composite smeared finite element (CSFE) with subdomains for cardiac blood vessels classified according to vessel diameters. The first equivalent continuum vessel domain is connected to 1D large vessel network, while the last is connected to the capillary continuum domain. Tissue nodal variables may include pressure, concentration, and electrical potential.
electrical field. Our model has advantages with respect to the multi-compartment Darcy perfusion models of [[3], [4], [5]], as already discussed, but also it is more general.
The second example of further application of the KTM is related to mass transport within the lungs. The concept of this model is shown in Fig. 5. The model assumes coupled mechanics and mass transport (airflow and diffusion). The lung function involves a large change of the lung geometry, therefore the airways within parenchyma are subjected to significant cyclic changes in size over breathing cycles. For mechanics, 1D finite elements can be used for large airways, while for parenchyma 3D FEs with internal microstructure [21] may be implemented. Regarding mass transport – airflow and particulate transport by diffusion, 1D or 3D FEs can be employed for large airways. The parenchyma consists of small airways classified as airway generations and KTM applies, with equivalent 3D domains for each generation or a group of generations. A transport matrix KJk,k+1 at node J between two domains, k and k+1, can be expressed in a form given in Fig. 5, where DJk+1 and VJk+1 are transport coefficient and continuum volume of the domain k+1 belonging to the node, respectively. We give the first results of this model in the next section.
Fig. 5.
A FE model for lung mechanics, airflow, and diffusion. Mechanics: 1D, and a multiscale 3D continuum FEs with internal microstructure [21]. Mass transport: 1D and KTM for large airways and parenchyma.
2.3. A few selected examples for demonstrating the generality of the KTM
In this section, we have selected a few examples from our earlier publications to illustrate the statements on the generality of the KTM.
Fig. 6a and b show the modeling of mass release from a nanoparticle according to Ref. [22]. The goal was to find the effective partitioning coefficient for the release of molecule Rhodamine B from a.
Fig. 6.
Determination of the effective partitioning coefficient for the release of Rhodamine B from a nanoparticle to the surrounding (According to Ref. [22]).
nanoparticle to its surroundings. The partitioning coefficient as a measure of hydrophobicity is further built in our KTM models. As stated in Section 2.1, it is an important feature for the KTM that partitioning is included in the connectivity elements for any boundary between the domains (e.g. vessel walls or membranes). The 2x2 connectivity matrix is modified to include partitioning according to (13).
Another example demonstrates the application of the KTM to large-scale models. In Ref. [13]) it was considered mass transport in the pancreas when a bolus-type entering of mass occurs in the pancreas main artery. A constant pressure is assumed at the entrance. The model is generated from imaging data obtained at a lab in MD Anderson Cancer Center in Houston. The model includes large blood vessels, capillary system, lymphatic system, extracellular space, and two types of cells with their organelles. There are 7 continuum subdomains with their volumetric fractions, diffusion characteristics, and partitioning at cell and organelle membranes. Each node has 10 variables – 3 pressures and 7 concentrations. The number of equations to be solved is 1,025,502. Other details are given in reference [13]. In Fig. 7 are shown.
Fig. 7.
Concentration fields within the pancreas at time t = 20s. Concentration for the Cell 2 group (portioning P = 10 at cell membrane) is significantly smaller than for Cell 1 (P = 5) due to partitioning. (According to Ref. [13]).
concentration fields in different domains, where differences can be noticed due to partitioning effects. Fig. 8 shows the evolution of the mean concentration in different domains which also demonstrates the effects of the diffusion and partitioning characteristics.
Fig. 8.
Evolution of concentration in different domains of the pancreas (According to Ref. [13]).
We further give an example that shows an application of the KTM to the diffusion of ions (charged molecules), where we have a coupling of electrical and concentration fields [14]. The mass balance equation here includes concentration and electrical potential,
| (16) |
where cm is the concentration of ion m, Ve is the electrical potential, D is the diffusion coefficient, zm is molecule valence, F is the Faraday constant, T is the absolute temperature, and R is the universal gas constant. To illustrate the generality of the KTM we show schematics of connectivity elements in case of electrical conduction through nerves and cell membranes (Fig. 9a and b)
Fig. 9.
Schematic of nerve fibers and cells. a) Dendritic tree and 1D finite elements along the nerve fibers with connectivity elements 1,2; b) Cell with current IV through membrane due to potential difference membrane, and ionic current Iion due to molecule flow modeled by connectivity elements 1,2. (According to Ref. [14]).
We modeled a tissue sample of the shape as in Fig. 3, isolated and with 6 neural fibers normal to the plane using a detailed 2D model and the KTM model. It was assumed that there are two groups of cells, that electrical potential in fibers is constant, and that there are ionic currents of potassium and sodium through cell membranes (details are given in Ref. [14]). The evolution of electrical potential within extracellular space and cells is shown in Fig. 10.
Fig. 10.
Evolution of the mean potential in extracellular space and cells, detailed
and smeared solutions; with ionic currents of potassium and sodium included. (According to Ref. [14]).
Finally, we show in this section one of the results recently obtained to be used for lung modeling according to Fig. 5. Fig. 11 shows a model of airflow that includes a 3D/2D axisymmetric domain connected to 1D pipe elements immersed within a 3D domain of lung parenchyma. The first FE domain is based on the Navier-Stokes equations, while the second domain is modeled by 1D pipe elements connected to our general lung multiscale-multiphysics FEs (GLFEs). It is taken that air velocities and concentrations are given on the left side of the fluid domain, while zero pressure and zero concentrations are specified for 1D pipe elements on the right boundary. We here give (Fig. 12a and b) a change with time of concentration within pipe elements and at a point within the parenchyma. Details of the model and other solutions are given in the cited reference.
Fig. 11.
Two models coupled - 3D or axisymmetric fluid domain (left) coupled to 1D (pipe) model within a 3D parenchyma model (3D GLFE elements). Boundary fluid elements 5–8 are connected to boundary pipe nodes 3,4,19,22. (According to Ref. [23]).
Fig. 12.
a) Concentration at the connection of pipes with fluid over time; b) Concentration over time at a point close to pipe connection with fluid, for the small airway domains. (According to Ref. [23]).
3. Results – additional examples
Application of the KTM has been demonstrated in a number of our publications, with a few examples in Section 2.3, while a summary is provided in the book [1]. Here, we present solutions for two new examples – one related to molecular convective-diffusive transport within a tumor, and another shows computation of drug delivery from nanofibers.
3.1. Convective-diffusive transport within a tumor
Data for this model comes from a laboratory from the Department of Nanomedicine at Houston Methodist Institute. A tumor growth within a mouse is recorded and we consider a middle cross-section for which data for the geometry, capillary distribution and diameters, and volumetric fraction of cells are provided during the tumor evolution. The data are assigned to a 10x10 regular mesh from which are calculated values for the finite element mesh. Using these data a study of perfusion is considered in Ref. [24]. Here, we extend that analysis to include diffusion. The data used in this example are:
Volumetric fractions of capillaries and cells – nodal variable dependent on deformation, input from imaging data;
Darcy tensor (diagonal): kDii = 1e−2 [mm2/(Pa s)];
The hydraulic coefficient for the capillary wall: h = 12.5 [ml/min/mmHg];
Diffusion tensor for extracellular space and cells (diagonal): Dii = 1 [mm2/s];
Diffusion transport coefficient for capillary wall and cell membrane: Dw = 1 [mm/s].
It is taken that the pressure in capillaries is uniform and constant, equal to 10 mmHg, while the concentration of transported drug molecules has a bolus shape as shown in Fig. 14. It is adopted that both pressure and concentration in the extracellular space at the tumor boundary are equal to zero. On the other hand, it is taken that there is no diffusion at the boundary between cells within the tumor and surrounding tissue.
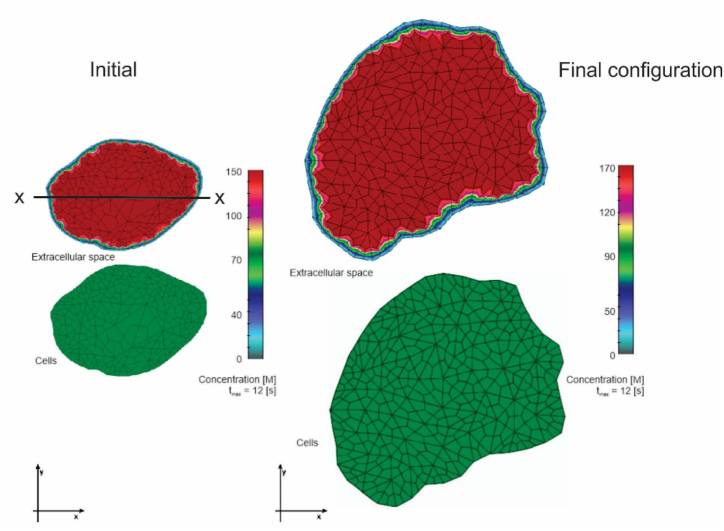
Fig. 14.
a) Mean concentration over time for capillaries, extracellular space, and cells; b), c) Distribution of concentration along the x-x line (Fig. 13) for extracellular space and cells at three times. No partitioning.
Fig. 13 shows concentration fields at the initial position, and final configuration, at the time tmax = 12s, when the concentration within capillaries reaches a maximum (at each configuration). It can be seen that concentrations are quite uniform within both extracellular and cell domains, with significantly smaller values within cells. This difference comes from diffusion as a time-dependent process.
Fig. 13.
Concentration fields at initial and final configurations, time is tmax = 12s when the bolus of capillary concentration reaches the maximum (shown in Fig. 14).
Fig. 14a displays the mean concentration over time for the extracellular space and cells, while Fig. 14b and c shows concentration distibutions along the x-x line in Fig. 13. It can be seen that concentration within the extracellular space is smaller than in the capillaries and further decreases in the cells. Also, a hindrance of the concentration maximum can be noticed between these curves. These effects result from the presence of capillary walls and cell membranes as biological barriers. Fig. 15(a–c) show the results as in Fig. 14, but assuming that there is a partitioning (effect of hydrophobicity) at the interface between the capillary wall and extracellular space. It is taken that the partitioning coefficient is P = 10. Now, concentrations within extracellular space and cells are reduced due to partitioning.
Fig. 15.
Initial configuration. a) Mean concentration over time for extracellular space and cells; b), c) Distribution of concentration along the x-x line (Fig. 13) for extracellular space and cells at three times. Partitioning between capillary walls and extracellular space, P = 10.
Finally, in Fig. 16a-c we show the results as in Fig. 15, but for the final configuration. It can be seen that the solutions at these two figures have the same character, hence the change of geometrical data and other model parameters affect mainly the values of concentration. The same findings apply to the case with partitioning P = 10 (results not shown).
Fig. 16.
Final configuration. a) Mean concentration over time for extracellular space and cells; b), c) Distribution of concentration along the x-x line (Fig. 13) for extracellular space and cells at three times. Partitioning between capillary walls and extracellular space, P = 10.
3.2. Drug delivery from nanofibers
We modeled drug delivery from nanofibers in our previous publications ([1,[15], [16], [17]]). Here we extend these models to the investigations of the effects of degradation and hydrophobicity on drug release.
The drug release from nanofibers has been thoroughly studied experimentally, and here are cited some of these studies. Poly (D, L-lactic-co-glycolic acid) - (PLGA) is the most commonly used polymer to create 3D scaffolds in tissue engineering [25,26]. PLGA can be prepared in several forms according to the different ratios of its constituents, lactic (LA) and glycolic acid (GA). It has been shown that the rate of degradation (i.e. the weight loss of polymer) is affected by the percentage of glycolic acid (GA) in PLGA [27,28], where the fastest degradation occurs for PLGA 50:50 (LA/GA) and the slowest for PLGA 85:15 (LA/GA). We here consider a model for a three-layer PCL/PLGA/PCL implant shown in Fig. 17a, as in Ref. [17], with the corresponding equations for mass transport and degradation, and the LA/GA ratio of 50:50, 65:35, 75:25, and 85:15. According to the measurements [17] we used the volume fraction (rV) of nanofibers of 78% for PLGA 50:50 and 59% for PLGA 65:35, while for PLGA 75:25 and PLGA 85:15, the porosities were 50% and 43%, respectively. Based on the data from Ref. [28], we use the following parameters for hydrophobicity (higher partitioning coefficient means lower hydrophobicity) in the numerical simulation: P = 1 × 10−5 (50:50), 1 × 10−6 (65:35), 5 × 10−7 (75:25), and 1 × 10−7 (85:15). These data are in accordance with the findings in Ref. [29] that larger presence of GA in PLGA reduces the degradability of the polymer and increases hydrophobicity. The following values were used for coefficients of degradation: = 2.5 × 10−7 (50:50), 2.0 × 10−7 (65:35), 1.5 × 10−7 (75:25), and 1 × 10−7 (85:15) s−1.
Fig. 17.
Three-layered PCL/PLGA/PCL scaffold. a) Geometry of the model, b) Concentration field within the fibers (fiber domain of the KTM) at t = 50 days; c) Cumulative drug release (in percent) vs. time for the RhB impregnated into standard PLGA complexes with the LA/GA ratio: 50:50, 65:35, 75:25, and 85:15; d) Drug release vs. time for RhB complex impregnated into 24 wt% 65:35 PLGA, for several volume fractions of fibers within the PCL layer.
Concentration fields within the fibers of the PCL/PLGA/PCL scaffold at time t = 50 days are shown in Fig. 17b. Mass release curves in the case of the RhB complex impregnated into standard PLGA complexes: 50:50, 65:35, 75:25, are shown in Fig. 17c. It can be noticed that drug release increases with a decrease of the PLGA ratio, which can be attributed to an increased mass loss due to degradation and decreased hydrophobicity. Dependence of the mass release on the fiber density within the math, expressed by the volumetric fraction rV of the fibers, is shown in Fig. 17d, for several values of the rV: 0.2, 0.3, 0.423, 0.5, and 0.6. The results show that the mass release is faster when the fiber density is smaller. This occurs because the effective diffusion coefficient increases with a decrease of the fiber density. Namely, during diffusion within a porous medium, there exists the interaction between the solid phase (here fibers) and transported molecules width reduced diffusivity. This phenomenon was analyzed and quantified in Ref. [1] (Chapter 5), and [30]. The effective diffusion coefficients for the PCL layer were found to be: Dequiv = 0.008, 0.0071, 0.006, 0.0053, and 0.0044 μm2/s, for the volumetric fractions of rV = 0.2, 0.3, 0.423, 0.5, and 0.6, respectively. It was assumed that the diameter of the fibers in the PCL layer is the same for all three cases and equals D = 2.5 μm. For the PLGA layer, the values for rV and Dequiv were as in Ref. [17]. The drug release curves show a delay of the drug passage through the math, which is a desirable effect in the implant design.
4. A summary and concluding remarks
We have briefly summarized the main characteristics of the KTM model. The generality and robustness of this methodology are illustrated by comparison with other typical approaches available in the literature. The goal of this short study was to emphasize that this quite straightforward method also provides a basis for further additions of specificities in medicine, biology, and science to model various complex multiscale and multiphysics problems. For example, it is suggested to include in the KTM the kinetics of the ligand-receptor binding as a straightforward generalization. We have illustrated the KTM generality by a selection of a few characteristic examples from our earlier publications. The first example demonstrates the determination of the effective partitioning coefficients in drug release from nanoparticles. These coefficients are further implemented in our connectivity elements within the KTM as a unique feature in modeling biological barriers. The next example serves to show the applicability of the KTM to large-scale models, with a multiscale description. The FE model of the entire pancreas is generated from images and it includes large vessels, extracellular space, capillary and lymphatic systems; and two groups of cells with their organelles and hydrophobic properties of transported molecules. Further, the multiphysics character of the KTM is shown in an example where the electrical field and diffusive transport of ions are coupled. Furthermore, this example demonstrates how general and complex phenomena in transport through biological barriers (here coupled cell membrane electrical potential and diffusion) can be included in the KTM. Finally, a simple example from our recent study of lung modeling is presented where the mechanics of lung deformation (with its microstructural deformation) is coupled to multiscale particulate transport within the lung airway generations. Additional two examples are given in support of the KTM generality – drug transport through a growing tumor (the KTM model generated from images), and a drug release from nanofibers with fiber degradation.
From the presented short analysis and illustrative examples that outline the concept and uniqueness of the KTM, it can be concluded that the KTM, due to its generality, ease and straightforward application, and efficiency, can serve as a tool in the development of today's important expert systems for everyday medical practice.
5. Data availability statement
The data that has been used is confidential.
Funding statement
This research was funded by the National Institute of Health (grant U01CA244107), as well as the Ministry of Education, Science and Technological Development of the Republic of Serbia, contract numbers 451-03-68/2023-14/200107 (Faculty of Engineering, University of Kragujevac), 451-03-66/2024-03/200378 (Institute for Information Technologies Kragujevac, University of Kragujevac); grant number F-134 (Serbian Academy of Sciences and Arts). The research was partially funded by the Golfers Against Cancer (C.S.F.) and funds from Houston Methodist Research Institute (C.S.F.). The authors are thankful to the City of Kragujevac, Serbia.
CRediT authorship contribution statement
Milos Kojic: Writing – original draft, Methodology, Conceptualization. Miljan Milosevic: Writing – review & editing, Software, Methodology. Vladimir Simic: Writing – review & editing, Visualization, Validation, Software. Bogdan Milicevic: Writing – review & editing, Visualization, Validation, Software. Rossana Terracciano: Writing – review & editing, Validation, Investigation, Data curation. Carly S. Filgueira: Writing – review & editing, Validation, Investigation, Data curation.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- 1.Kojic Milos, Milosevic Miljan, Ziemys Arturas. Elsevier; 2022. Computational Models in Biomedical Engineering - Finite Element Models Based on Smeared Physical Fields: Theory, Solutions, and Software. [Google Scholar]
- 2.Koh T.S., Cheong L.H., Hou Z., Soh Y.C. A physiologic model of capillary–tissue exchange for dynamic contrast-enhanced imaging of tumor microcirculation. IEEE Trans. Biomed. Engrg. 2003;50(2):159–167. doi: 10.1109/TBME.2002.807657. [DOI] [PubMed] [Google Scholar]
- 3.Hyde Eoin R., Cookson Andrew N., Lee Jack, Michler Christian, Goyal Ayush, Taha Sochi, Chabiniok Radomir, Sinclair Matthew, Nordsletten David A., Spaan Jos, Jeroen P., van den Wijngaard H.M., Siebes Maria, Smith Nicolas P. Multi-scale Parameterisation of a Myocardial perfusion model using Whole-Organ arterial networks. Ann. Biomed. Eng. 2013 doi: 10.1007/s10439-013-0951-y. [DOI] [PubMed] [Google Scholar]
- 4.Hyde Eoin R., Michler Christian, Lee Jack, Cookson Andrew N., Chabiniok Radek, Nordsletten David A., Smith Nicolas P. Parameterisation of multi-scale continuum perfusion models from discrete vascular netwok. Med. Biol. Eng. Comput. 2013;51:557–570. doi: 10.1007/s11517-012-1025-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Di Gregorio S., Fedele M., Pontone G., Corno A.F., Zunino P., Vergara C., Quarteroni A. MOX, Dipartimento di Matematica Politecnico di Milano; 2019. A Multiscale Computational Model of Myocardial Perfusion in the Human Heart. [Google Scholar]
- 6.Corrias A., Pathmanathan P., Gavaghan D.J., Buista M.L. Modelling tissue electrophysiology with multiple cell types: applications of the extended bidomain framework. Integr. Biol. 2012;4:192–201. doi: 10.1039/c2ib00100d. [DOI] [PubMed] [Google Scholar]
- 7.Kojic Milos. Smeared concept as a general methodology in finite element modeling of physical fields and mechanical problems in composite media. J. Serb. Soc. Comp. Mech. 2018;12(No.2):1–16. [Google Scholar]
- 8.Kojic M., Milosevic M., Simic V., Koay E.J., Fleming J.B., Nizzero S., Kojic N., Ziemys A., Ferrari M. A composite smeared finite element for mass transport in capillary systems and biological tissue. Comp. Meth. Appl. Mech. Engrg. 2017;324:413–437. doi: 10.1016/j.cma.2017.06.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Kojic M., Milosevic M., Simic V., Koay E.J., Kojic N., Ziemys A., Ferrari M. Extension of the composite smeared finite element (CSFE) to include lymphatic system in modeling mass transport in capillary systems and biological tissue. J. Serb. Soc. Comp. Mech. 2017;11(No.2):108–120. doi: 10.24874/jsscm.2017.11.02.09. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Kojic Milos, Simic Vladimir, Milosevic Miljan. Composite smeared finite element – some aspects of the formulation and accuracy. IPSI Transactions on Advanced Research. 2017;13(2) | ISSN 1820 – 4511. July2017. [Google Scholar]
- 11.Kojic M., Milosevic M., Simic V., Stojanovic D., Uskokovic P. A radial 1D finite element for drug release from drug Loaded nanofibers. J. Serb. Soc. Comp. Mech. 2017;11(1):82–93. [Google Scholar]
- 12.Kojic M., Milosevic M., Kojic N., Koay E.J., Fleming J.B., Ferrari [ M., Ziemys A. Mass release curves as the constitutive curves for modeling diffusive transport within biological tissue. Comput. Biol. Med. 2018;92:156–167. doi: 10.1016/j.compbiomed.2016.06.026. 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Kojic M., Milosevic M., Simic V., Koay E.J., Kojic N., Ziemys A., Ferrari M. Multiscale smeared finite element model for mass transport in biological tissue: from blood vessels to cells and cellular organelles. Comput. Biol. Med. 2018;99:7–23. doi: 10.1016/j.compbiomed.2018.05.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kojic M., Milosevic M., Simic V., Ziemys A., Filipovic N., Ferrari M. Smeared multiscale finite element model for electrophysiology and ionic transport in biological tissue. Comput. Biol. Med. 2019;108:288–304. doi: 10.1016/j.compbiomed.2019.03.023. [DOI] [PubMed] [Google Scholar]
- 15.Milosevic M., Simic V., Milicevic B., Koay E.J., Ferrari M., Ziemys A., Kojic M. Correction function for accuracy improvement of the Composite Smeared Finite Element for diffusive transport in biological tissue systems. Comp. Meth. Appl. Mech. Engrg. 2018 doi: 10.1016/j.cma.2018.04.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Milosevic Miljan, Dusica Stojanovic, Simic Vladimir, Milicevic Bogdan, Radisavljevic Andjela, Uskokovic Petar, Kojic Milos. A computational model for drug release from PLGA implant. Materials. 2018;11(12):2416. doi: 10.3390/ma11122416. 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Milosevic M., Stojanovic D.B., Simic V., Grkovic M., Bjelovic M., Uskokovic P.S., Kojic M. Preparation and modeling of three-layered PCL/PLGA/PCL fibrous scaffolds for prolonged drug release. Sci. Rep. 2020 Jul 7;10(1) doi: 10.1038/s41598-020-68117-9. Erratum in: Sci Rep. 2021 Aug2;11(1):16028, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Kojic M., Filipovic N., Milosevic M., Pak-Bio . Bioengineering R&D Center, and University of Kragujevac; Serbia: 2020. Finite Element Program for Bioengineering Problems. [Google Scholar]
- 19.Ozcelikkale Altug, Moon Hye-ran. Michael Linnes and Bumsoo Han, In vitro microfluidic models of tumor microenvironment to screen transport of drugs and nanoparticles. WIREs Nanomed Nanobiotechnol. 2017 doi: 10.1002/wnan.1460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ying Chong T., Wang Juntian, Lamm Robert J., Kamei Daniel T. Mathematical modeling of vesicle drug delivery systems 2: Targeted vesicle interactions with cells, tumors, and the Body. J. Lab. Autom. 2013;18(1):46–62. doi: 10.1177/2211068212458265. [DOI] [PubMed] [Google Scholar]
- 21.Kojic M. Multiscale composite 3d finite element for lung mechanics. J. Serbian Soc. Comp. Mech. 2020;14(1):1–11. [Google Scholar]
- 22.Kojic M., Milosevic M., Wu Blanco E., Ferrari M., Ziemys A. Mass partitioning effects in diffusion transport. Phys. Chem. Chem. Phys. 2015;17:20630–20635. doi: 10.1039/c5cp02720a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Kojic M. A multiscale multiphysics finite element for lung. J. Serbian Soc. Comp. Mech. 2023 submitted for publication. [Google Scholar]
- 24.Terracciano R., Milićević B., Milošević M., Simić V., Carcamo-Bahena Y., Royal A.L.R., Carcamo-Bahena A.A., Butler E.B., Grattoni A., Kojić M., Filgueira C.S. 2023. An Insight into Perfusion Anisotropy within Solid Murine Lung Cancer Tumors. in preparation. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Mano J.F., Sousa R.A., Boesel L.F., Neves N.M., Reis R.L. Bloinert, biodegradable and injectable polymeric matrix composites for hard tissue replacement: State of the art and recent developments. Compos. Sci. Technol. 2004;64:789–817. [Google Scholar]
- 26.Lin H.R., Kuo C.J., Yang C.Y., Shaw S.Y., Wu Y.J. Preparation of macroporous biodegradable PLGA scaffolds for cell attachment with the use of mixed salts as porogen additives. J. Biomed. Mater. Res. 2002;63:271–279. doi: 10.1002/jbm.10183. [DOI] [PubMed] [Google Scholar]
- 27.Lu L., Peter S.J., Lyman M.D., Lai H., Leite S.M., Tamada J.A., Uyama S., Vacanti J.P., Langer R., Mikos A.G. In vitro and in vivo degradation of porous poly(-lactic-co-glycolic acid) foams. Biomaterials. 2000;21:1837–1845. doi: 10.1016/s0142-9612(00)00047-8. [DOI] [PubMed] [Google Scholar]
- 28.Park T.G. Degradation of poly (lactic- co-glycolic acid) microspheres: effect of copolymer composition. Biomaterials. 1995;16:1123–1130. doi: 10.1016/0142-9612(95)93575-x. [DOI] [PubMed] [Google Scholar]
- 29.Makadia H.K., Siegel S.J. Poly lactic-co-glycolic acid (PLGA) as biodegradable Controlled drug delivery Carrier. Polymers. 2011;3(3):1377–1397. doi: 10.3390/polym3031377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Ziemys A., Kojic M., Milosevic M., Kojic N., Hussain F., Ferrari M., Grattoni A. Hierarchical modeling of diffusive transport through nanochannels by coupling molecular dynamics with finite element method. J. Comput. Phys. 2011;230:5722–5731. doi: 10.1016/j.jcp.2011.03.054. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data that has been used is confidential.