ProtWave-VAE: Integrating Autoregressive Sampling with Latent-Based Inference for Data-Driven Protein Design

Abstract

Deep generative models (DGMs) have shown great success in the understanding and data-driven design of proteins. Variational autoencoders (VAEs) are a popular DGM approach that can learn the correlated patterns of amino acid mutations within a multiple sequence alignment (MSA) of protein sequences and distill this information into a low-dimensional latent space to expose phylogenetic and functional relationships and guide generative protein design. Autoregressive (AR) models are another popular DGM approach that typically lacks a low-dimensional latent embedding but does not require training sequences to be aligned into an MSA and enable the design of variable length proteins. In this work, we propose ProtWave-VAE as a novel and lightweight DGM, employing an information maximizing VAE with a dilated convolution encoder and an autoregressive WaveNet decoder. This architecture blends the strengths of the VAE and AR paradigms in enabling training over unaligned sequence data and the conditional generative design of variable length sequences from an interpretable, low-dimensional learned latent space. We evaluated the model’s ability to infer patterns and design rules within alignment-free homologous protein family sequences and to design novel synthetic proteins in four diverse protein families. We show that our model can infer meaningful functional and phylogenetic embeddings within latent spaces and make highly accurate predictions within semisupervised downstream fitness prediction tasks. In an application to the C-terminal SH3 domain in the Sho1 transmembrane osmosensing receptor in baker’s yeast, we subject ProtWave-VAE-designed sequences to experimental gene synthesis and select-seq assays for the osmosensing function to show that the model enables synthetic protein design, conditional C-terminus diversification, and engineering of the osmosensing function into SH3 paralogues.

Graphical Abstract

INTRODUCTION

A long-standing goal in protein engineering and chemistry has been the design of novel synthetic proteins with engineered functions and properties. Natural proteins have evolved under genetic drift and natural selection to robustly perform complex functions such as ligand binding, molecular recognition, and substrate-specific catalysis. With the exponential growth of sequenced protein data sets and the advent of mature deep learning models, modern machine learning tools have become ubiquitous in the engineering of novel proteins with desired functions.¹ In particular, deep generative models (DGMs) offer a powerful modeling paradigm to learn sequence-to-function mappings and employ these relations for synthetic protein design.^2–5 Two primary DGM paradigms have demonstrated substantial success in protein engineering: autoregressive (AR) language models^6–11 and variational autoencoders (VAEs).^{12–15,15–20} AR models can operate on variable length sequences, meaning that they do not require the construction of multiple sequence alignments and can be used to learn and generate novel sequences with high variability and diverse lengths.^7,8 Since protein sequences from nonhomologous families or within homologous families with high variability present challenges in constructing alignments,⁷ AR generative models are well suited for alignment-free training, prediction, and design. AR models have been shown to successfully engineer novel nanobodies by designing the complementarity-determining region (CDR) 3,⁷ demonstrate competitive performance in mutation and contact prediction,²¹ and have been used to design functional synthetic proteins across diverse protein families.⁸ A limitation of autoregressive models is their typical lack of a low-dimensional learned latent space that exposes interpretable phylogenetic and functional relationships and can be used to guide the conditional generation of synthetic sequences.

In contrast, VAEs naturally infer a latent space that is subsequently used for the conditional generation of novel sequences. VAE models have been shown to accurately predict single mutant effects,¹³ infer a homologous family’s phylogeny and fitness within the latent space,¹² design in vivo signaling of orthologue proteins,¹⁴ and diversify synthetic AAV capsids.²² While these models are often capable of identifying biological patterns in the data corresponding to ancestral history or evolved function, there is a challenge known as “posterior collapse”²³ wherein the model might not use these patterns effectively, thereby hampering its ability to design sequences. This means that when using certain techniques like autoregressive decoders, these models can face challenges in producing diverse, variable-length synthetic sequences or learning from protein data sets that do not rely on sequence alignments.

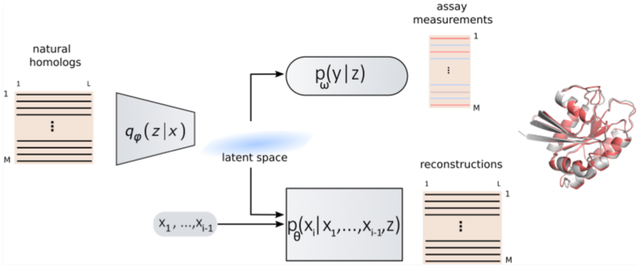
In this work, we propose ProtWave-VAE as a new DGM architecture integrating the desirable features of the AR and VAE paradigms (Figure 1). In summary, this model uses a neural network architecture capable of operating on variable-length protein sequences and discovering a low-dimensional projection of these sequences. These two features enable us to train the model over nonhomologous, unaligned sequence data, to identify clusters, gradients, and patterns in the sequence data within the low-dimensional space that can be useful in designing novel protein sequences with desirable properties, and to generate variable-length synthetic sequences. Full details of the approach are presented in Materials and Methods, but for the reader interested in the technical details of the architecture, some of the key architectural design choices of our approach are as follows. To address the challenges associated with learning VAEs with autoregressive decoders and to enhance our models’ design capabilities, we adopted an Information Maximizing (InfoMax) approach.²⁴ This differs from traditional methods by adjusting weights and introducing mutual information regularization terms, ultimately aiming to improve the relationship between input data and the patterns that the model identifies. We used a WaveNet decoder²⁵ that is designed to handle data more efficiently and avoids common optimization issues by using special techniques like dilated causal convolutions. Previously, models have been developed that combine VAEs with dilated causal convolutions as the decoder for text generation,²⁶ but this approach has yet to be explored for protein design and fitness prediction. These convolutions are much faster than recurrent networks during training time, offer superior inference of long-range correlations, and are computationally less expensive than large-scale language models. We note that the AR-VAE model can be modularly extended to use other powerful and expressive decoders, such as autoregressive transformer-based decoders.²⁷

Figure 1.

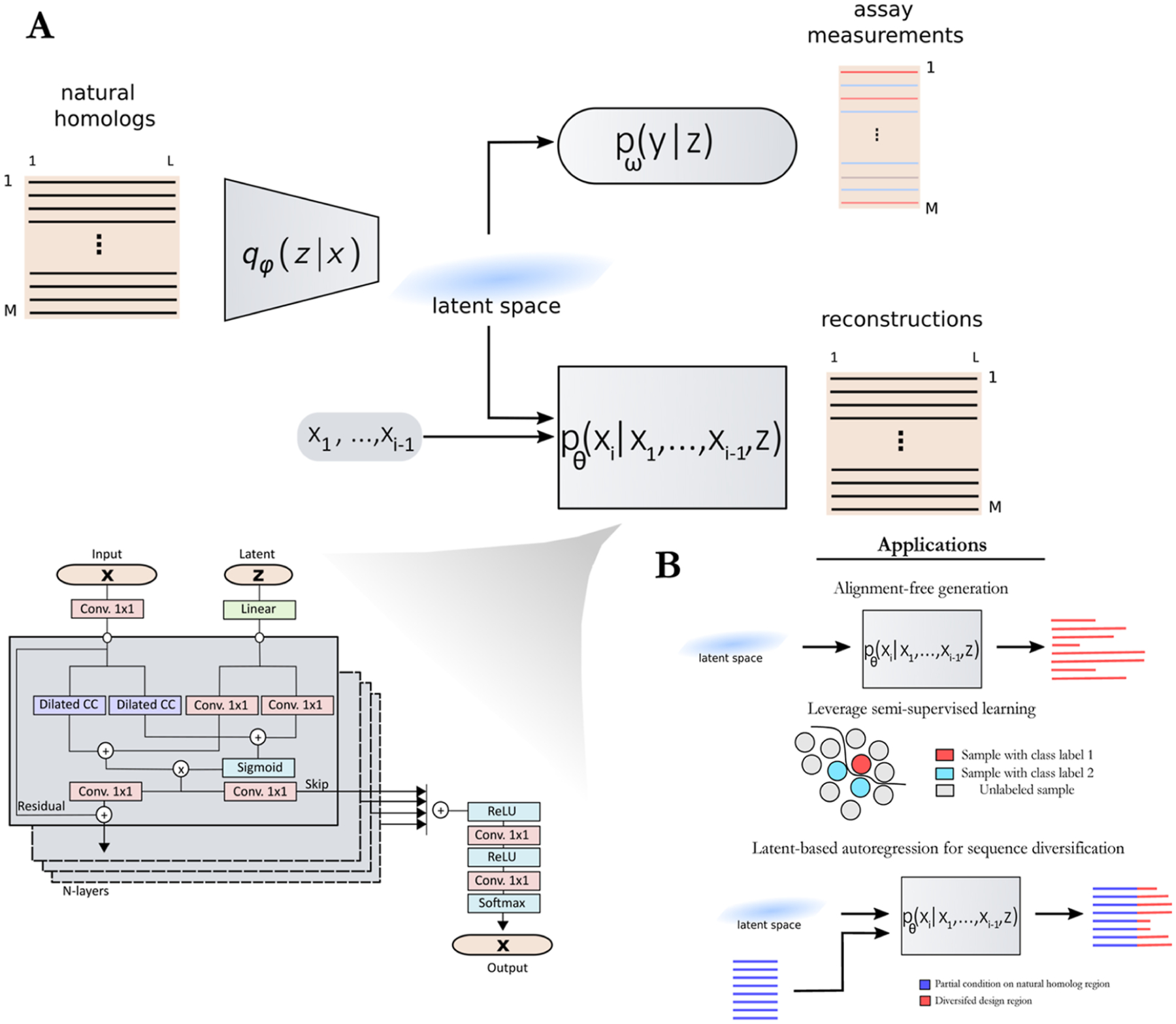
(A) Schematic illustration of the ProtWave-VAE model integrating an InfoMax VAE with a convolutional encoder and WaveNet autoregressive decoder. This unsupervised learning model may be made semisupervised by incorporating an optional top model comprising a discriminative multilayer perception to regress the function on the protein location within the latent space embedding. The model architecture employs a gated dilated convolutional encoder q_φ(z|x), a WaveNet (i.e., gated dilated causal convolution) autoregressive decoder p_θ(x_i|x₁, …, x_i−1, z), and a supervised neural regression model p_ω(y|z) to predict the functional assay measurements when available. The variable x corresponds to the amino acid sequence of the entire protein, z corresponds to the latent space coordinates associated with the protein sequence x, and y corresponds to the functional assay associated with protein x. The variable x_i corresponds to the amino acid identity in position i of the protein sequence. (B) By combining latent inference and autoregressive generation, our model enables (i) alignment-free inference and variable-length generation, (ii) semisupervised learning, and (iii) conditional generation based on N-terminal residues and latent space conditioning vectors. The first application allows for training models on protein families that require no multiple sequence alignments (MSAs). The second application provides and leverages assay measurements during the generative learning process and reshapes the latent space for better control of the functional design of proteins. The third application permits sequence diversification by conditioning on an N-terminus sequence motif of a natural homologue and conditioning on latent embeddings to generate and inpaint the C-terminus region. This final application is not restricted to the C-terminus diversification of natural homologues; rather, it can also be utilized by conditioning protein tags (such as expression tags or affinity tags) and filling in missing protein sequences through inpainting.

ProtWave-VAE shares similarities with, but is differentiated from, a number of related approaches in the literature. The ProT-VAE model of Sevgen et al.¹⁹ uses a VAE architecture employing a large-scale pretrained ProtT5 encoder and decoder and has shown substantial promise for alignment-free protein design. ProtWave-VAE is distinguished by its incorporation of latent conditioning and autoregressive sampling along the decoder path and its lightweight architecture comprising ~10⁶–10⁷ trainable parameters relative to ~10⁹ for ProT-VAE. Prior work using WaveNet autoregressive models demonstrated competitive prediction of mutant effects and the design of novel nanobodies,⁷ but the absence of a latent space precluded these approaches from leveraging latent conditioning for controlled protein generation by selectively sampling regions within a latent space associated with specific protein properties. By virtue of the variational inference of meaningful biological latent codes, latent conditioning is available to ProtWave-VAE. Similar to other autoregressive models for protein design which leverage a large transformer (e.g., ProGen1⁸) and LSTM architecture (e.g., UniRep⁶), our approach infers a regularized latent space for meaningful conditional information for the autoregressive decoder. Hawkins et al.¹⁸ have previously demonstrated the use of an AR-VAE model for protein design, but our model employs a powerful WaveNet decoder instead of a GRU decoder, which was enabled by our use of an Information Maximizing VAE loss to prevent posterior collapse.²⁴

We demonstrate and test ProtWave-VAE in applications to both retrospective protein function prediction tasks and synthetic protein design, wherein the sequences designed by the model are experimentally synthesized and tested. First, we show that our approach can infer biologically meaningful latent spaces while incorporating an expressive autoregressive generator and learning on alignment-free sequences for four selected protein families.²⁸ To assess the generative capacity of our model to synthesize well-folded tertiary structures, we sampled novel sequences and predicted their tertiary structures using AlphaFold2.^29,30 Despite not being exposed to any structural information during training, we find that the predicted structures of the synthetic sequences recapitulate the native folds corresponding to the protein family. Second, we extend the training objective to a semisupervised learning paradigm³¹ for fitness landscape prediction and benchmark our semisupervised model variant on four fitness landscape predictions within TAPE and FLIP protein function prediction tasks.^32,33 Our model predictions are competitive or superior to the current state-of-the-art approaches employing models typically using approximately an order of magnitude more trainable parameters. Third, using the AroQ chorismate mutase family with fitness assay measurements³⁴ as a training set, we demonstrate that our model can reshape the latent space to induce functional gradients valuable for the conditional generation of novel synthetic proteins with elevated functionality without losing generative capabilities. Fourth, we introduce a method to perform C-terminal diversification of natural protein sequences by conditioning on a user-specified number of N-terminal residues and latent space-conditioning vectors. This enables us to introduce sequence diversity into the C-terminal region of the sequence while also engineering the desired phylogeny and/or function through latent space conditioning. We demonstrate this approach in applications to homologues of the CM protein. Fifth, to experimentally verify our model’s generative capacity, we used a high-throughput in vivo select-seq to measure the binding of the Src homology 3 (SH3) domain in Saccharomyces cerevisiae (i.e., baker’s yeast) to its cognate pbs2 ligand within an osmosensing pathway that protects the cell from high salt conditions by activating a homeostatic response.^14,35 Using this assay, we generated novel sequences that rescue the osmosensing function and partially diversified natural SH3 homologues that maintain or elevate the functionality. In summary, the ProtWave-VAE model presents a novel AR-VAE DGM to learn informative and meaningful low-dimensional latent space embeddings from unaligned training sequences and permit the conditional autoregressive generation of variable-length synthetic sequence with engineered N-terminal residues and/or latent vectors informing desired phylogeny and/or function.

RESULTS AND DISCUSSION

Alignment-Free Learning of Latent Space Embeddings.

Our first test of the model was to assess the degree to which the latent space can expose biologically meaningful representations of phylogenetic and functional patterns in unaligned homologous protein data sets. Identifying these “design rules” (i.e., correlated patterns of amino acid mutations underpinning phylogeny and function) is a prerequisite to the tailored design of synthetic functional proteins.¹⁵ To do so, we trained independent ProtWave-VAE models over four protein families:²⁸ G-protein (GTPase, Ras-like; PFAM PF00071), dihydrofolate reductase (DHFR; PFAM PF00186), beta-lactamase (PFAM PF13354), and S1A serine protease.³⁶ Full details of the model training and hyperparameter optimization, including latent space dimensionality, are provided in Materials and Methods. For visual clarity and consistency, irrespective of the latent space dimensionality, we present 2D latent space projections into the top two principal components identified by principal component analysis (PCA). By annotating the PCA projections of the latent embeddings with the known phylogenetic and functional information for the natural homologues, we find that in all four cases ProtWave-VAE learns to disentangle the training sequences into their phylogenetic groups and functional subclasses (Figures 2A and S2A). For G-protein, the model inferred disentangled representations in terms of functional subclasses (Ras, Rab, Rac, and Rho) and phylogeny (Metazoa, Amoebozoa, Viridiplantae, Fungi, and Alveolata (Figure 2A–i)). For DHFR, the latent embeddings show well-defined clusters annotated by phylogenic groups: eukaryota, firmicutes, and actinobacteria (Figure 2A-ii). Similarly, for the lactamase family, the PCA projections of the latent space show disentangled phylogenic groups (Figure S2A-ii). Interestingly, for the S1A family, the model can infer meaningful representations in terms of functional specificity, trypsin versus chymotrypsin, and homologues by their corresponding species information, vertebrate or invertebrate species and warm or cold environment species (Figure S2A-i).

Figure 2.

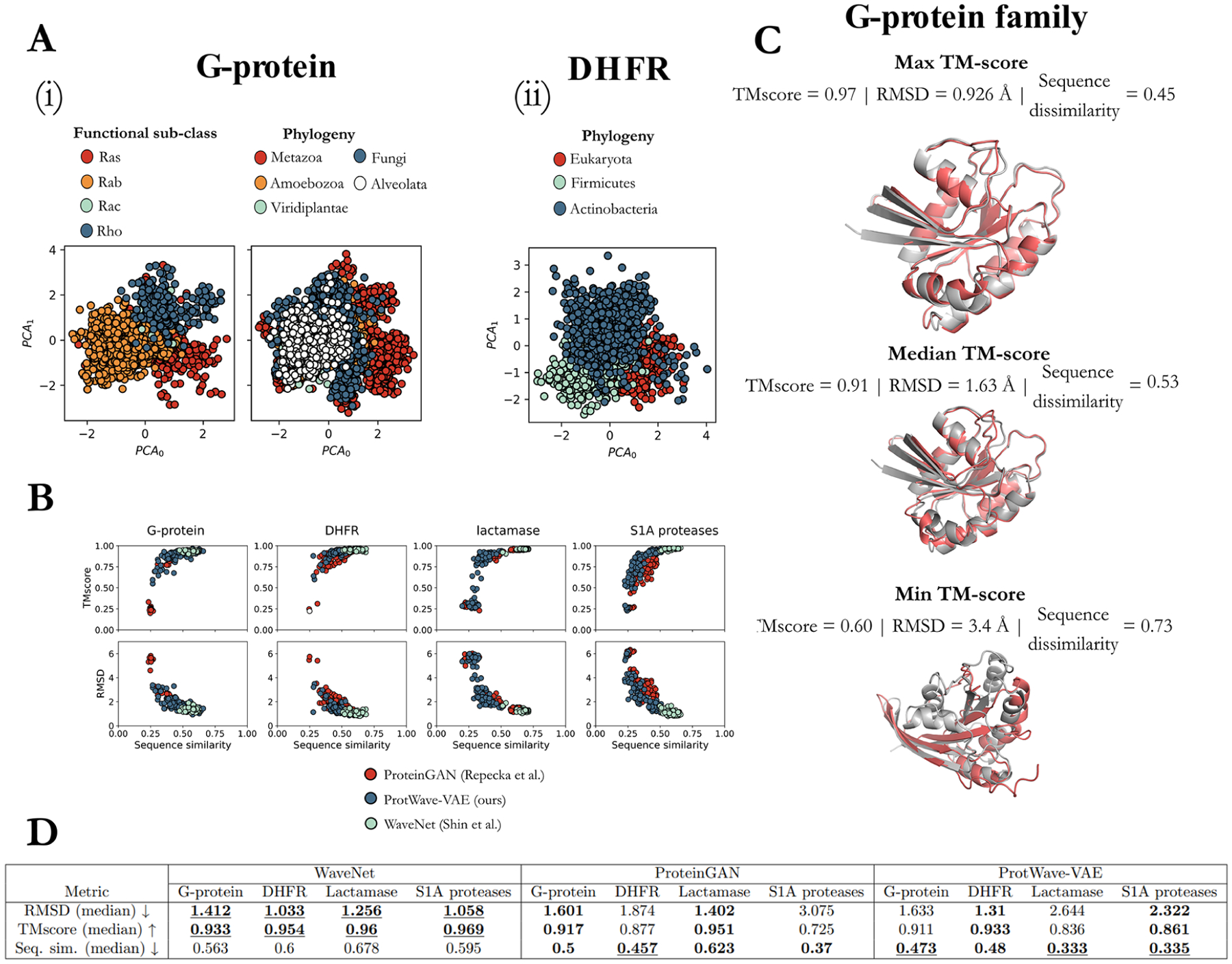
ProtWave-VAE can infer meaningful biological representations of alignment-free protein families. (A) Here, we present the principal component analysis (PCA) projections of the inferred latent spaces for the (i) G-protein and (ii) DHFR families. For the G-protein family, we find that the unsupervised model disentangles homologues within the inferred latent space based on functional subclasses and phylogeny. Similarly, with the DHFR family, the model learns to disentangle homologues in the inferred space in terms of the phylogeny. (B) To test the ProtWave-VAE generative capacity, we randomly sampled 100 latent vectors z for each protein family from a normal distribution 𝒩 (0,I), corresponding to the latent prior. Then, using a computational structure prediction workflow (ColabFold + TMalign), we predicted each structure of the sample sequences and compared the predicted structure against a natural homologue that defines the corresponding protein family, retrieving TMscores and root-mean-square distance (RMSD) scores. We computed the minimum Levenshtein distance between the sampled novel sequence and training sequences normalized by the length of the longer sequence in the pair. We also benchmarked ProtWave-VAE’s generative performance against sequences derived from an unconditionally sampled WaveNet decoder⁷ and 100 sequences randomly sampled from the ProteinGAN³⁷ latent space. (C) Using the G-protein structure predictions of ProtWave-VAE novel design sequences (red), we visualize the alignment of maximum, median, and minimum TMscore synthetic sequences (gray). Figure S2 illustrates the latent spaces, structure predictions, and TMscores of the remaining protein families. (D) Median scores of the four protein families, as generated by the three distinct models in terms of RMSD, TMscore, and sequence similarity (seq sim.). In the table, values that are both bold and underlined indicate the best scores, while values in bold only signify the second best.

Our computational results suggest that combining an autoregressive decoder with a latent-based inference model exposes meaningful biological representations within a learned low-dimensional latent space. While ProtWave-VAE is not the only method capable of inferring meaningful protein representations in low-dimensional latent spaces—the elegant work of Ding, Zou, and Brooks¹² demonstrates that simple VAE models are capable of learning latent spaces exposing functional and phylogenetic clusters and relationships—our model achieves this while being trained on unaligned sequences and employing autoregressive sampling for decoding. This method of inferring representations from unaligned sequences sets our model apart from position weight matrices (PWMs), which typically require aligned sequences. This distinction underscores the unique approach of our inference in comparison to those of these techniques. However, can our approach still generate novel samples indistinguishable from the training data distribution? To test the generated alignment-free sequences, we used AlphaFold2 with MMSeqs2 (i.e., ColabFold^29,30) to predict the tertiary structure of the generated sequences and determine whether the predictions recapitulate the tertiary structure of the natural homologues. To showcase our model’s ability to infer meaningful representations from protein families, we randomly sampled 100 latent vectors from an isotropic Gaussian distribution and used the trained ProtWave-VAE WaveNet-based autoregressive decoder to generate novel sequences for each protein family. To measure the novelty of the generated sequences, we computed the minimum Levenshtein distance from any homologue in the training data set normalized by the length of the longer sequence within the pair. Additionally, we sought to assess whether the generated sequences were predicted to adopt a tertiary fold consistent with the homologous family. We compared the predicted tertiary structure of each ProtWave-VAE-designed sequence to a prototypical member of the homologous family with a known crystal structure available within the Protein Data Bank:³⁸ 5P21 for G-protein, 1XR2 for DHFR, 3TGI for S1A serine protease, and 1FQG for beta-lactamase. To quantify the similarity of the folds, we computed the TMscores and heavy-atom root-mean-squared distances (RMSDs) using the TMalign algorithm.³⁹ We present scatterplots of TMscore against sequence novelty and RMSD against sequence novelty for the 100 designed proteins in Figure 2B. Our results show that the artificial proteins possess TMscores in the range 0.2–1.0⁴⁰ and RMSDs in the range 0–6 Å, with TMscores having a strong positive correlation with sequence similarity and RMSDs having a strong negative correlation with sequence similarity.

Furthermore, we demonstrate the model’s ability to generate sequences with tertiary structures similar to the native fold without being exposed to any structural information during training. In Figures 2C and S2B, we show the AlphaFold-predicted tertiary structures of three representative synthetic sequences with maximum, median, and minimum TMscores. The similarity of the synthetic sequence tertiary structures to the native folds, as quantified by high TMscores and low RMSDs for all four protein families, supports that the correlated patterns of amino acid mutations learned by the model within the unaligned sequence data are sufficient to generate tertiary structures representative of the homologous family’s native fold.

In addition to analyzing the generative performance of ProtWave-VAE, we also compared the generative performance against the WaveNet decoder by Shin et al.,⁷ which is an autoregressive generative model, and the ProteinGAN by Repecka et al.,³⁷ which is a latent-only Generative Adversarial Network that was experimentally shown to be able to design novel functional sequences (Figure 2B). In terms of the comparison between the three generative models, the WaveNet decoder performs better than both the ProteinGAN and ProtWave-VAE models in terms of TMscores and RMSD values; however, ProteinGAN and ProtWave-VAE perform better in terms of sampling novel sequences defined by sequence similarity (Figure 2D and Table S1). ProtWave-VAE outperforms ProteinGAN on sequence similarity (median) for G-protein, lactamase, and S1A protease family while maintaining good TMscore values. ProtWave-VAE achieves 0.91, 0.93, 0.84, and 0.86 median TMscore values for G-protein, DHFR, lactamase, and S1 protease protein family design, which are significantly greater than a TMscore of 0.5, which is regarded as a threshold to classify a protein pair as belonging to the same fold.⁴⁰ In addition, the metric of sequence novelty for protein design plays the role of a proxy for the model’s ability to sample further out in an unexplored sequence space and has direct real-world value in applications where sequence diversity is a priority such as the diversification of viral capsid designs,²² diversification of complementarity-determining regions in nanobodies or antibodies,⁷ and in generating sequence-divergent libraries of catalytic enzymes.¹⁴

In summary, the ProtWave-VAE model demonstrates the capability to infer meaningful biological representations and generate novel sequences possessing tertiary structures with native-like folds on par with the performance of leading generative protein models.

Fitness Landscape Benchmarking Using Semisupervised Learning.

We subsequently evaluated the capabilities of the ProtWave-VAE model in semisupervised downstream fitness prediction tasks and compared its performance against a number of leading methodologies. The primary rationale behind semisupervised learning approaches is that latent representations z become more informative for predicting downstream functional properties y when they are also employed for reconstructing sequences x.^31,41 In a similar vein, it is plausible to suggest that unlabeled protein sequences contain considerable information about their structure and function.^42,43 In addition, semisupervised learning is beneficial when labels are scarce, and unlabeled data are abundant, which is generally the case for protein design applications where only a small fraction of entries within large sequence databases is annotated with functional assays. One advantage of the AR-VAE architecture of ProtWave-VAE is that it can employ semisupervised learning via its learned latent space in a straightforward manner that can be more difficult to achieve for standalone AR approaches. We benchmark our model on four popular semisupervised downstream function and fitness prediction tasks from two popular community benchmarks: Task Assessing Protein Embeddings (TAPE)³³ and Fitness Landscape Inference for Protein (FLIP)³² baselines. The four semisupervised prediction tasks are (1) the highly epistatic mutational landscape of GB1 (FLIP),⁴⁴ (2) mutational screening of the fitness landscape of VP-1 AAV (FLIP),^45,46 (3) stability landscape prediction (TAPE),⁴⁷ and (4) epistatic green fluorescent protein (GFP) landscape prediction (TAPE).⁴⁸

Our benchmark evaluations show that ProtWave-VAE either rivals or surpasses a number of state-of-the-art (SOTA) models, including large language models (ESM-1b and ESM-1v),^49,50 transformer-based models (TAPE Transformer),^33,51 and masked dilated convolution-based architectures (CARP-640 M)⁵² (Table 1). In the GB1 task, ProtWave-VAE exceeds SOTA models in random split and 3-vs-rest split, while remaining competitive in the 1-vs-rest and 2-vs-rest splits based on the Spearman ρ rank correlation. These findings imply strong extrapolation capabilities in the genotype space for the model. Nonetheless, it underperforms on the low-versus-high split in the GB1 data set, suggesting effective learning from the low-fitness mode (training samples) but more limited accuracy in extrapolating and capturing the high-fitness mode (test samples). In the AAV task, where the model aims to predict the fitness measurements of AAV capsid mutants, ProtWave-VAE surpasses SOTA models in random splits, design mutant split, and 1-vs-rest, while competing effectively on mutant-design split and 2-vs-rest against large language models using either transformer or dilated convolution architectures. Only in the stability task does our model underperform in stability regression predictions based on the Spearman ρ correlation and again remains on par with SOTA models when it comes to fluorescence regression prediction in the GFP task.

Table 1.

Protein Property Prediction Results on FLIP and TAPE Benchmarks^a

architecture	GB1 (FLIP) benchmarks
	random split (sampled)	low-vs-high	1-vs-rest	2-vs-rest	3-vs-rest
	ρ	ρ	ρ	ρ	ρ
ESM-1b (per AA)32		0.59	0.28	0.55	0.79
ESM-1b (mean)32	0.92	0.13	0.32	0.36	0.54
ESM-1v (per AA)32	0.92	0.51	0.28	0.28	0.82
Ridge32	0.82	0.34	0.28	0.59	0.76
CNN32	0.91	0.51	0.17	0.32	0.83
CARP-640 M (pt-ft)52		0.43	0.19	0.73	0.87
ProtWave-VAE (our model)	0.94	0.14	0.29	0.70	0.87
ProtWave-VAE (ΔInfoMax)	0.93	0.02	0.29	0.56	0.85
ProtWave-VAE (Δdilations)	0.91	0.23	0.28	0.55	0.85
ProtWave-VAE (Δgates)	0.88	0.11	0.26	0.62	0.82

architecture	AAV (FLIP) benchmarks
	random split (sampled)	Mut-Des	Des-Mut	1-vs-rest	2-vs-rest	7-vs-rest	low-vs-high
	ρ	ρ	ρ	ρ	ρ	ρ	ρ
ESM-1b (per AA)32	0.90	0.76		0.03	0.65	0.65	0.39
ESM-1v (per AA)32	0.92	0.79		0.10	0.70	0.70	0.34
Ridge32	0.83	0.64	0.53	0.22	0.03	0.65	0.12
CNN32	0.92	0.71	0.75	0.48	0.74	0.74	0.34
CARP-640 M (pt-ft)52		0.85		0.73	0.81	0.77	0.19
ProtWave-VAE (our model)	0.93	0.82	0.83	0.73	0.77	0.72	0.23
ProtWave-VAE (ΔInfoMax)				0.70	0.74	0.73	0.19
ProtWave-VAE (Δdilations)				0.53	0.76	0.71	0.31
ProtWave-VAE (Δgates)				0.57	0.48	0.65	0.18

Stability (TAPE) Benchmarks
architecture	TAPE split
	ρ
ESM32	0.71
TAPE transformer32	0.73
UniRep6,32	0.73
linear regression32	0.48
CNN Dallago32	0.51
CARP-640 M52	0.72
ProtWave-VAE (our model)	0.51
ProtWave-VAE (ΔInfoMax)	0.46
ProtWave-VAE (Δdilations)	0.55
ProtWave-VAE (Δgates)	0.61
GFP (TAPE) Benchmarks
architecture	TAPE split
	ρ
ESM32	0.68
TAPE transformer32	0.68
UniRep6,32	0.67
linear regression32	0.68
CNN32	0.50
CARP-640 M52	0.68
ProtWave-VAE (our model)	0.67
ProtWave-VAE (ΔInfoMax)	0.62
ProtWave-VAE (Δdilations)	0.66
ProtWave-VAE (Δgates)	0.66

^aThe best results and second-best results are marked. The ablated models are listed below the primary ProtWave-VAE model architecture for comparison, where the symbol Δ denotes an ablation: ProtWave-VAE (ΔInfoMax) refers to the replacement of the InfoMax loss with a standard ELBO objective, ProtWave-VAE (Δdilations) refers to the ProtWave-VAE model with the dilated convolution removed and replaced with simple convolutions, and ProtWave-VAE (Δgates) refers to the omission of the gated convolutions. Blank entries in the table correspond to property prediction calculations that were not conducted, typically due to the high computational expense involved.

We also performed an ablation analysis of our ProtWave-VAE model by selectively removing or replacing certain model components and subsequently benchmarking on the FLIP and TAPE tasks. Maintaining the same hyperparameters and model architecture, we (i) replaced the InfoMax loss with the standard ELBO objective, (ii) substituted the dilated convolutions in the encoder and generator decoder with simpler convolutions, and (iii) omitted the gated convolutions, a component that has proven to be highly effective in generative Gated PixelCNNs and WaveNets.^25,53,54 These ablations were designed to expose the role of these three model components on the overall performance. A key observation from this analysis is the consistent underperformance of the model when the InfoMax loss was replaced with the standard ELBO objective [ProtWave-VAE (ΔInfoMax)]. For instance, in the GB1 task, the 2-vs-rest score dropped from 0.70 to 0.56, and similar trends were observed across other tasks. In the AAV task, the ProtWave-VAE (ΔInfoMax) model achieved a 1-vs-rest score of 0.70 compared to the score of 0.73 achieved by our original model. Similarly, in the GFP and stability tasks, the performance of the ProtWave-VAE (ΔInfoMax) model was consistently lower than that of the original ProtWave-VAE model. These findings underscore the importance of the InfoMax loss in our model’s performance and highlight its importance over the standard ELBO objective in the context of our model architecture. In the architecture modification study, where we replaced dilated convolutions with simple convolutions [ProtWave-VAE (Δdilations)] or eliminated gated signals [ProtWave-VAE (Δgates)], we observed a notable decrease in performance on GB1 2-vs-rest and AAV 1-vs-rest tasks. On the other hand, for tasks such as GB1 1-vs-rest and GFP, the performance metrics remained more or less stable. Even though there was a minor boost in the model performance on the stability task, it still lagged considerably behind the state-of-the-art benchmarks. In summary, features such as dilated convolutions and gated architecture contribute positively to leading-edge performance on certain tasks but are not consistently as important as using InfoMax loss over the ELBO objective.

Overall, these results demonstrate that the ProtWave-VAE model performs well on semisupervised downstream functional and fitness prediction at a level competitive with the state-of-the-art models such as ESM and CARP-640M. This demonstrates that ProtWave-VAE is learning internal latent space representations that expose the ancestral and functional relationships necessary to both generatively design novel synthetic sequences and accurately predict their functional properties. Furthermore, we observe that the ProtWave-VAE model is much more lightweight than typical SOTA models, containing 100-fold fewer trainable parameters than the most lightweight transformer model (ESM^49,50) considered in the benchmark suite, conveying advantages and savings in terms of cost and time for model training and deployment.

Generative Modeling with Semisupervised Learning for the Chorismate Mutase Family.

We next sought to explore the potential impact of incorporating experimental knowledge into generative learning tasks by employing semisupervised learning to reshape the latent space based on functional measurements.⁵⁵ The goal of many protein engineering campaigns is to design proteins with elevated functions along one or more dimensions. We hypothesized that the incorporation of functional measurements into the training of the ProtWave-VAE model within a semisupervised paradigm could induce functional gradients within the learned latent space and partially disentangle the latent representation to foreground the functional property of interest. We further hypothesized that this reshaped latent space would support the superior conditioning and generative decoding of synthetic mutants with elevated function.

To test these hypotheses, we compared unsupervised and semisupervised learning for the chorismate mutase (CM) protein family.³⁴ We found that semisupervised learning infers a gradient in fitness, whereas unsupervised learning does not (Figure 3A), indicating that information from experimental assays can be leveraged to sculpt the latent space to induce gradients in the properties of interest. To test whether the introduction of the second decoder for the semisupervised regression task harms the model’s generative capacity, we generatively designed 100 sequences for both unsupervised and semisupervised trained models by randomly sampling 100 latent vectors z for each protein family from a normal distribution N(0,I) corresponding to the latent prior and computing the TMscore and RMSD scores between predicted structures and natural Escherichia coli crystal structures (PDB: 1ECM) using ColabFold (Figure 3B,C). Our results demonstrate no performance degradation in terms of TMscore or RMSD values between unsupervised and semisupervised models and show that the predicted structures of the designed sequences accurately recapitulate the native fold. This result demonstrates that semisupervised learning can reshape the latent space to induce a gradient in the property of interest while maintaining the generative capabilities of the ProtWave-VAE model. Determining whether the designed synthetic CM sequences do indeed possess elevated functions as one advances up and extrapolates beyond the induced functional gradient can, of course, only be ascertained by experimental gene synthesis and functional assays.

Figure 3.

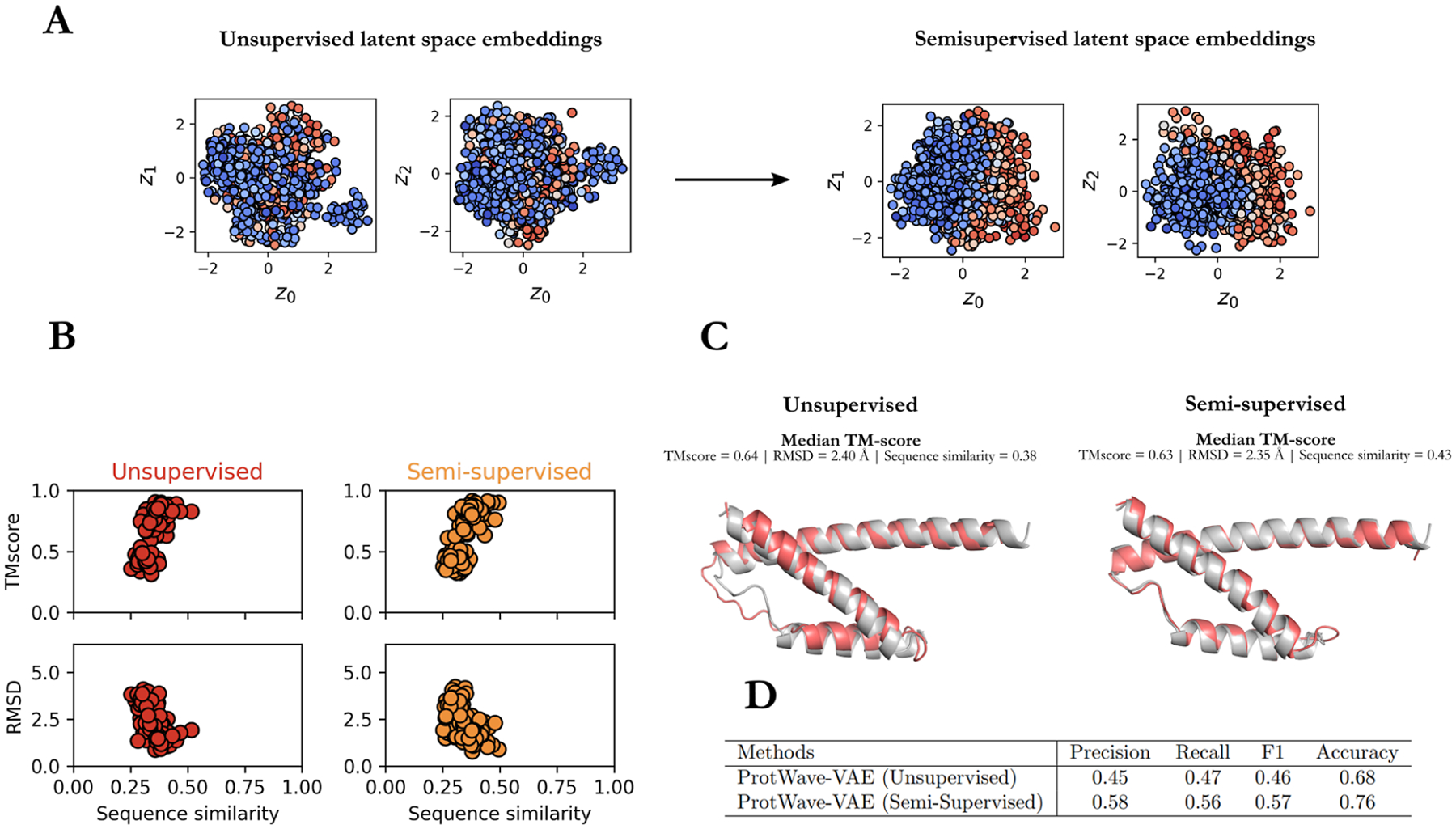
Comparison of unsupervised and semisupervised learning for generative design of the chorismate mutase (CM) proteins. (A) Semisupervised learning allows us to infer and reshape the latent space, so that latent coordinates correlate more strongly with CM fitness, as measured by the relative enrichment select-seq assay scores. (B) To verify that reshaping the latent space does not lead to a loss of generative capabilities for the model, we used the ColabFold plus TMalign algorithm to demonstrate no significant loss of generative performance in the RMSD and TMscores of the predicted tertiary structures generated by unsupervised and semisupervised ProtWave-VAE models. (C) Superposition of the wild-type E. coli crystal structure (PDB: 1ECM) (gray) and the ColabFold predicted structure of the ProtWave-VAE design sequence possessing the median TMscore (red), showing excellent agreement for both the unsupervised and semisupervised models. (D) Classification metric results show that KNN classification improves in predicting functional CM sequences when using semisupervised latent representations over unsupervised representations.

To discern the comparative benefits of semisupervised learning over unsupervised learning in predicting protein function, we utilized a k-nearest neighbor (KNN) classifier employing k = 5 neighbors. The model was trained on training latent embeddings of 1130 natural CM homologues, and the relative enrichment (r.e.) scores determined experimentally by Russ et al. as a measure of biological function³⁴ were reconfigured into classification labels defining active r.e. (≥ 0.5) and inactive r.e. (< 0.5). The hold-out set incorporated the 1618 CM sequences originally devised by Russ et al.³⁴ Following the evaluation of our classification results, recall, precision, F1 score, and accuracy, it was observed that semisupervised learning produced a marked enhancement in predictive capacity compared to unsupervised learning (Figure 3D).

Introducing Novel Latent-Based Autoregression for Sequence Diversification.

The integrated AR-VAE architecture of the ProtWave-VAE model enables a potentially useful form of synthetic protein generative design that we refer to as C-terminal diversification with latent conditioning. By combining latent inference, conditioning, and autoregressive amino acid generation, our model allows us to condition on both the latent vector within the VAE latent space and an arbitrary number of N-terminal residues in the generated protein to diversify the C-terminal region. Simple latent-based generative models such as standard VAEs allow for generating a whole sequence by conditioning on latent embeddings but typically cannot also condition on amino acids from a known natural protein of interest and then diversify (i.e., “inpaint”) the missing region of interest. In contrast, AR generative models generate sequences by predicting subsequent amino acids while conditioning on previously predicted amino acids but cannot conduct latent inference and use those latent embeddings to control the design of synthetic sequences. Autoregressive generation in this manner has proven to be a successful strategy and valuable tool in, for example, nanobody design, by diversifying the complementarity-determining region CDR3 while conditioning on CDR1 and CDR2.⁷ However, the absence of a biologically meaningful latent space to condition latent codes to inpaint missing regions means that the generation process cannot be readily guided to introduce particular ancestral or functional characteristics. We propose that the capability of the ProtWave-VAE model to perform simultaneous N-terminal and latent conditioning may prove valuable in applications to nanobodies, antibodies, enzymes, signaling domains, linkers, and multimeric proteins, where it is desirable to maintain some structural and/or functional properties of the N-terminal region and introduce new capabilities by the redesign of the C-terminus. We demonstrate this novel generative approach in an application to C-terminal diversification of the E. coli CM homologue (PDB: 1ECM).

We sampled 100 latent embeddings from a normal distribution 𝒩 (0,I) over each latent space of the unsupervised and semisupervised ProtWave-VAE models (Figure 3). These latent codes were then used to perform latent-only conditional synthetic generation of novel CM sequences (Algorithm 1), where L represents the maximum sequence length that can be generated by the model and x_<i corresponds to the sequence of amino acids between the N-terminus and positions (i − 1) that have previously been generated by the model. We then performed N-terminus plus latent conditional generation of CM sequences using the same latent codes, but also fixed the identity of the N-terminal residues 1–40 and inpainted the remaining C-terminal residues 41–96 using autoregressive sampling (Algorithm 2) (Figure 4A). We hypothesized that the sequences generated by the two approaches should possess ColabFold-predicted tertiary structures in equally good agreement to the wild-type E. coli crystal structure but that the C-terminal region (residues 41–96) should follow a different distribution in the two ensembles reflecting the impact of N-terminal conditioning on the autoregressive generation process. Specifically, the sequences generated by latent-only conditioning should access a more diverse sequence space compared to those additionally constrained by N-terminal conditioning on the wild-type sequence.

Figure 4.

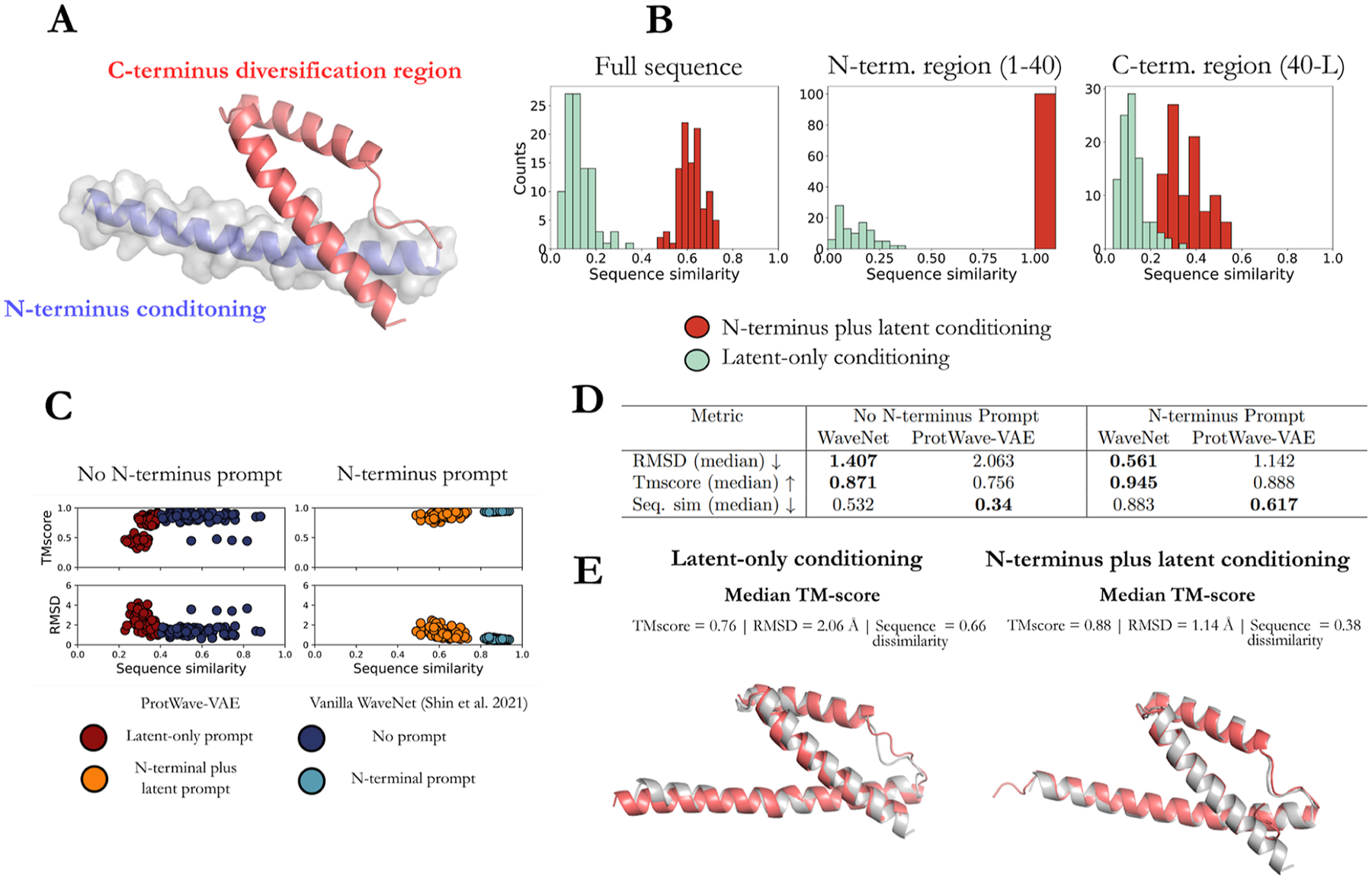
Introduction of C-terminus diversification with N-terminus and latent conditioning. (A) Tertiary structure of the E. coli CM wild-type protein (PDB: 1ECM) illustrating the N-terminal region (residues 1–40) used for N-terminal conditioning (blue) and the remaining C-terminal region (residues 41–96) subject to generative diversification (red). (B) We generated 100 novel latent conditioning vectors by sampling from a 𝒩 (0,I) prior over each of the supervised and semisupervised latent spaces and used each latent vector to generate a novel synthetic protein with and without N-terminal conditioning. We compare the sequence similarity of the full sequence, N-terminal conditioning, and C-terminal diversification regions between the latent-only (green) and N-terminal plus latent (red) conditioned generated sequence ensembles. (C) Vanilla WaveNet performs better than ProtWave-VAE in terms of TMscore and RMSD values for both no N-terminus and N-terminus prompting; however, during N-terminus prompting, ProtWave-VAE generated more diverse and novel sequences indicated by the lower sequence similarities while maintaining good TMscores and RMSD values. (D) Median statistic computed over the performance metrics (RMSD, TMscore, and sequence similarity) to compare the generative ability between the vanilla WaveNet model vs ProtWave-VAE model. Bold text indicates best values between the WaveNet decoder and ProtWave-VAE model. (E) Structure prediction (red) of the median TMscore sequence for ProtWave-VAE latent-only and N-terminal plus latent conditioned designs against the E. coli wild-type crystal structure; PDB: 1ECM (gray).

As anticipated, the sequences designed by latent-only conditioning were more dissimilar to the E. coli wild-type than those produced by N-terminal and latent conditioning (Figure 4B). Of course, this follows because the N-terminal region comprising residues 1–40 is identical to the wild-type for all sequences generated by the N-terminal conditioned approach, resulting in 100% sequence similarity within the N-terminal region for these sequences, whereas the latent-only sequences possess sequence similarities in the range of 0–50%. Further, the sequence similarity of the C-terminal region comprising residues 41–96 is higher for the N-terminal and latent conditioned sequences than the latent-only sequences. This is a direct result of the autoregressive nature of the model, wherein the fixed N-terminal region conditions the generation of the C-terminal region to remain closer to the wild-type for the same latent vector. ColabFold structure predictions and RMSD and TMscore evaluation of the generated protein sequences demonstrate the anticipated positive correlation between sequence similarity and TMscore and negative correlation between sequence similarity and RMSD (Figure 4C). The smaller diversity of the N-terminal and latent conditioned sequences means that they exhibit a tighter distribution than those produced by latent-only conditioning. Comparison of the ColabFold structure predictions for the synthetic sequences with the median TMscore shows that they possess tertiary structures visually indistinguishable from the E. coli wild-type crystal structure for both the N-terminal and latent conditioning and latent-only conditioning generation processes (Figure 4E).

We also utilized a WaveNet decoder model⁷ to train and generate 100 sequences for both scenarios—with and without an N-terminus prompt. The WaveNet model outperforms ProtWave-VAE in terms of TMscore and RMSD metrics, but ProtWave-VAE excels in generating sequences that exhibit greater diversity and novelty (cf. Figure 4D and Table S2). This enhanced capacity for novel sequence generation, especially when the sequence is conditioned on a wild-type N-terminus prompt, could be attributed to the use of latent space conditioning, which may facilitate the exploration of diverse design patterns. WaveNet, being an unsupervised autoregressive generative model, provides functionality for N-terminal prompting but does not possess the capacity to condition latent space vectors associated with different protein properties. By permitting both forms of conditioning, ProtWave-VAE can use latent conditioning to introduce superior diversity into the sequences resulting from a single N-terminal prompt.

Taken together, these results demonstrate that N-terminal conditioning can be used to effectively constrain the degree of C-terminal diversification by providing additional conditioning of the autoregressive sequence generation process. The structural similarity of the synthetic sequences to the native fold of the protein family, at least for this application, is insensitive to whether or not N-terminal conditioning is used in the generation procedure.

Experimental Validation of Latent-Based Autoregression for Synthetic Protein Design and Natural Sequence Diversification.

So far, we have demonstrated the ability of the ProtWave-VAE model to infer biologically meaningful latent space embeddings, perform downstream functional prediction tasks competitive with the state-of-the-art approaches, operate in a semisupervised fashion without compromising generative capacity, and perform N-terminal conditioned sequence generation. All of these demonstrations have been performed by the retrospective analysis of existing data sets and comparison of tertiary structures generated by ColabFold. To rigorously validate our ProtWave-VAE capabilities in the functional protein design, it is necessary to experimentally synthesize and assay the sequences generatively designed by the model. To do so, we trained a ProtWave-VAE model to design synthetic Src homology 3 (SH3) sequences capable of functioning like natural SH3^Sho1 domains by binding its cognate pbs2 ligand and effecting the osmosensing mechanism in S. cerevisiae, as assessed by a a select-seq assay^14,35 (Figure 5A). This assay couples a high-osmolarity challenge with next-generation sequencing to measure the relative enrichment (r.e.) of the postselection population in a particular mutant relative to a null gene and wild-typeS. cerevisiae.¹⁴ The r.e. score provides a quantitative measurement of the degree to which our designed SH3 domains are functional in vivo and capable of activating a homeostatic osmoprotective response. The assay shows good reproducibility in independent trials (R² = 0.94; Figure S3). We trained a semisupervised ProtWave-VAE model on an SH3 data set consisting of natural SH3 proteins, mostly from the fungal kingdom and synthetic proteins designed using our previous generation unsupervised learning VAE models for which we possess functional assay measurements.¹⁴ The semisupervised nature of the model is observed to induce a strong r.e. gradient in the latent space (Figure 5B), allowing us to condition the generative sequence design by drawing latent vectors in the functional region of the latent space using our latent-only (Algorithm 1) and N-terminal and latent conditioned (Algorithm 2) strategies (Figure 5C).

Figure 5.

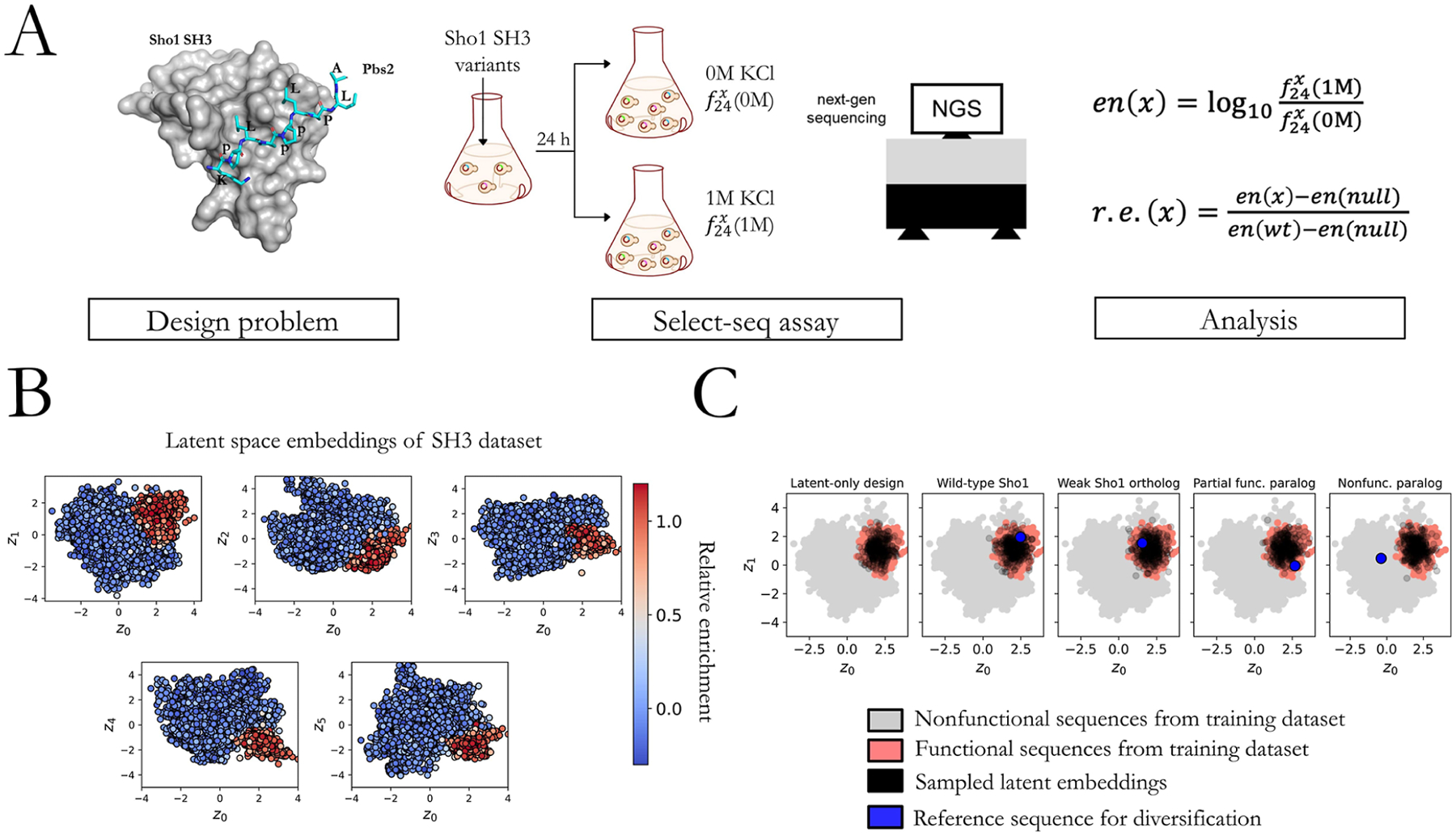
Experimental assessment of ProtWave-VAE generatively designed synthetic Sho1^SH3 domains. (A) Crystal structure (PDB: 2VKN) of the S. cerevisiae wild-type (wt) Sho1^SH3 binding to the pbs2 ligand (blue sticks) is shown along with an illustrative cartoon of the select-seq assay and next-gen sequencing platform for measuring relative enrichment (r.e.) scores as a measure of fitness. The enrichment en(x) of mutant protein x is the logarithm of the ratio $f_{24}^x(1M)/f_{24}^x(0M)$, where $f_{24}^x(kM)$ is the frequency of mutant x in the population after being subjected to 24 h of kM KCl solution. The relative enrichment r.e.(x) of mutant x is a normalized enrichment score relative to the wild-type protein and a null protein such that r.e.(x) = 1 indicates the same functional performance as the wild-type protein, and r.e.(x) = 0 indicates the same functional performance as the null gene. (B) Six-dimensional latent space spanned by latent vectors z = {z₀, z₁, z₂, z₃, z₄, z₅} of a trained semisupervised ProtWave-VAE model exposes clear gradients in the r.e. scores in all 2D projections of this space. The high-fitness training sequences (red) are clustered and segregated from the low-fitness training sequences (blue). (C) We generated synthetic ProtWave-VAE sequences for experimental testing by five separate protocols: (I) latent-only conditioning, (II) N-terminal and latent conditioning of wild-type Sho1^SH3, (III) N-terminal and latent conditioning of a weak binding Sho1 orthologue, (IV) N-terminal and latent conditioning of a partial rescuing SH3 paralogue, and (V) N-terminal and latent conditioning of a SH3 paralogue that does not rescue Sho1 functionality. We illustrate the nonfunctional (gray, r.e. < 0.5) and functional (red, r.e.≥ 0.5) sequences within the z₀ – z₁ projection of the latent space together with the sampled latent space embeddings (black) and, if appropriate, the reference sequence used for N-terminal conditioning (blue). In all cases, latent vectors were drawn from the region of the latent space containing the functional training sequences to guide the generation of functional synthetic Sho1^SH3 orthologues. We did so by fitting an anisotropic Gaussian to the r.e.≥ 0.5 (red) training points and randomly sampling from this distribution to generate the latent conditioning vectors (black).

We employed the trained ProtWave-VAE model to devise sequences using five distinct protocols, resulting in five subgroups of designed sequences (I–V). Subgroup (I) utilized latent vectors for conditioning the generative design of synthetic sequences. Latent vectors were extracted from the ProtWave-VAE latent space by fitting a 6D anisotropic Gaussian to the embedding of training sequences with select-seq measurements of r.e. ≥ 0.5 and randomly sampling from this distribution (Figure 5C, black points). This ensured that the latent vectors originated from a region of latent space containing functional training sequences, which in turn conditioned the generation of functional sequences. The other four subgroups were designed by using the N-terminal and latent conditioning approach. To assess our model’s capability in producing functional designs, we chose four reference proteins for N-terminus conditioning, defining subgroups (II) wild-type S. cerevisiae Sho1^SH3, (III) a weak binding Sho1 orthologue, (IV) a partial rescuing SH3 paralogue drawn from the Hof1 paralogue group, and (V) a nonfunctional S. cerevisiae paralogue drawn from the actin-binding protein (ABP1) paralogue group. The latent embeddings for these conditioning sequences are denoted by blue points in Figure 5C. We observed that the nonfunctional SH3 paralogue was situated outside the functional niche, as it could not rescue Sho1 functionality. In the latent-only design subgroup (I), we generated 150 sequences. In each of the four N-terminal and latent conditioned subgroups (II–V), we produced 150 (II–IV) and 99 (V) designs subdivided into three equal-sized subcategories differentiated by the fraction of the sequence used for N-terminal conditioning: 25%, 50%, and 75%. Subgroups (II–V) were intended to assess various protein design goals, including: (II) preserving function, (III–IV) enhancing existing function, and (V) gain of function. Finally, we included two control subgroups (VI) and (VII), each comprising 150 sequences, for the N-terminal and latent conditioning subgroups (III) (N-terminal conditioning on a weak binding Sho1 orthologue) and (IV) (N-terminal conditioning on a partial rescuing SH3 paralogue), to verify that our model’s capacity to improve the function was not simply due to chance. Within these control subgroups, we introduced random mutations in the designable C-terminal region until the distribution of the 50 sequences within each subgroup subcategory matched the Levenshtein distances to the wild-type S. cerevisiae of the 50 sequences designed by the ProtWave-VAE (Figure S1).

Figure 6A displays the experimental measurements for sequences belonging to the latent-only conditioning subgroup (I). Out of the 150 gene designs, 148 were successfully assembled and tested experimentally. The first two plots are scatterplots, where each point represents a designed sequence, the y-axis denotes the relative enrichment score, and the x-axis indicates the sequence similarity relative to the most similar sequence in the training data set and to the wild-type SH3^Sho1 S. cerevisiae. For the latent-only conditioning subgroup (I), the designed sequences exhibit the ability to rescue functionality (i.e., r.e. ≥ 0.5) while covering a broad spectrum of normalized Levenshtein distances, ranging from the sequence similarities of 75–100% and 45–70% relative to the training data set and wild-type SH3^Sho1. This suggests that the ProtWave-VAE model can produce highly diverse sequences that significantly deviate from the wild type yet retain the correlated amino acid residue patterns necessary for maintaining the osmosensing function. The final bar graph highlights the superior performance of ProtWave-VAE compared to our previously reported InfoVAE and VanillaVAE models when designing sequences using local sampling.¹⁴ The ProtWave-VAE model outperforms the two VAE models, rescuing functionality at a level of 51% (76 out of 148) versus 48% and 21%, respectively. In addition to its high performance in designing synthetic functional sequences with latent-only conditioning, ProtWave-VAE, unlike our previous two VAE approaches, does not require training over a multiple-sequence alignment and can readily generate variable-length sequences.

Figure 6.

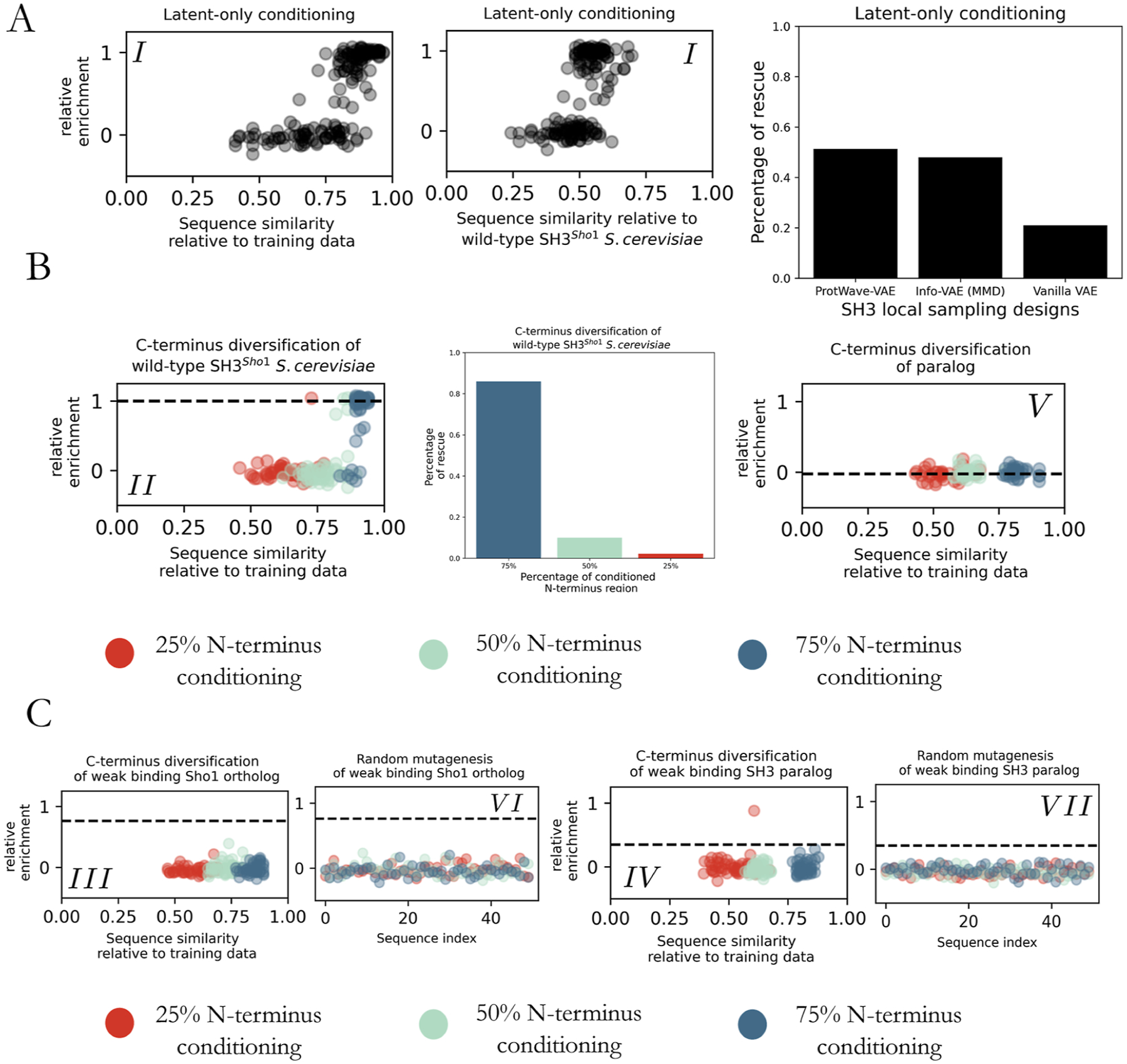
Experimental outcomes of ProtWave-VAE generated sequences. (A) Subgroup (I)—latent-only synthetic design. Scatterplots illustrate the sequence similarity measured by normalized Levenshtein distance and relative enrichment (r.e.) scores for the synthetic designs. The bar graph demonstrates the ProtWave-VAE performance through local sampling compared to the synthetic generative designs previously reported for our VAE-based DGM using an Info-VAE employing a max-mean discrepancy (MMD) loss and a Vanilla VAE employing the standard ELBO loss.¹⁴ The ProtWave-VAE generates diverse sequences with a high probability of functional rescue. (B) Subgroups (II)—maintaining function with C-terminus diversification for SH3 wild-type—and (V)—elevating function of a nonfunctional paralogue using C-terminus diversification. Experimental measurements for design groups employed 25% (red), 50% (green), and 75% (blue) of the sequence length for N-terminal conditioning. The scatterplot on the left displays the r.e. scores for subgroup (II) versus sequence similarity to the training data set. The bar graph reveals the rescue percentage within the design pool for subgroup (II) at varying N-terminus conditioned percentages. The scatterplot on the right presents r.e. vs sequence similarity to the training data set for subgroup (V). None of these sequences rescued the osmosensing function. The horizontal dotted line for both scatterplots corresponds to the relative enrichment score of the homologue used for N-terminus conditioning. (C) Subgroups (III) and (VI)—elevating function of a weak binding Sho1 orthologue using C-terminus diversification and its random mutagenized control—and (IV) and (VII)—elevating function of a partial rescuing SH3 paralogue using C-terminus diversification and its random mutagenized control. The two left scatterplots pertaining to subgroups (III) and (VI) failed to show any rescue at any level of N-terminal conditioning. The two right scatterplots pertaining to subgroups (IV) and (VII) show that one of the generatively designed sequences with 25% N-terminal conditioning did rescue function.

Figure 6B showcases the experimental outcomes for sequences belonging to the N-terminus plus latent conditioning for C-terminus diversification of the wild-type SH3^Sho1 (subgroup (II)) and paralogue SH3 that fails to rescue function (subgroup (V)). Considering first the left scatterplot displaying the r.e. measurements and sequence similarities for the generatively designed sequences in subgroup (II) that were successfully assembled and tested, we find the number of functional sequences for each N-terminus percentage prompt to be 1 out of 46 for 25% N-terminal conditioning (red), 5 out of 50 for 50% (green), and 43 out of 50 for 75% (blue). The bar graph presents the percentage of rescue, which amounts to 86%, 10%, and 2.2% for 75%, 50%, and 25% N-terminal conditioning, respectively. These results suggest that conditioning on both the N-terminus and the latent vectors to inpaint the remaining C-terminus can lead to functional synthetic sequences, but the success rates decrease with the increasing degree of C-terminus inpainting and number of amino acid positions to diversify. We propose that this decaying success rate may result from an incompatibility of the two conditioning goals such that the latent vector seeks to generate a C-terminal sequence incompatible with the predefined N-terminal sequence. Turning to the right scatterplot presenting the data for the C-terminus diversified paralogue designs in subgroup (V), we find that none of the generatively designed sequences that were successfully assembled and subjected to experimental testing were capable of rescuing function: 0 out of 32 for 25% N-terminal conditioning (red), 0 out of 33 for 50% (green), and 0 out of 33 for 75% (blue). Together with the potential incompatibility of the two conditioning goals, it is also possible that if any N-terminal residues are indispensable to protein function–either directly through binding to the target ligand or indirectly via their participation in critical multibody interaction networks with other amino acids–and these are conditioned to contain mutant residues via the N-terminal conditioning, then no C-terminal inpainting can lead to functional rescue.

Figure 6C displays the experimental outcomes for sequences belonging to the N-terminus plus latent conditioning for C-terminal diversification of the weak orthologue SH3^Sho1 (subgroup (III)) and partial paralogue SH3 (subgroup (IV)). The design goal for these two subgroups was to enhance functionality by inpainting the C-terminus. As a control to demonstrate that the generative model performs better than random mutagenesis, we experimentally tested mutants in subgroups (VI) and (VII). The first scatterplot corresponds to subgroup (III). Similar to our results for the SH3 paralogue (subgroup (V)), we find that none of the designed sequences were able to rescue function: 0 out of 50 for 25% N-terminal conditioning (red), 0 out of 50 for 50% (green), and 0 out of 50 for 75% (blue). The second scatterplot contains data for the subgroup (VI) control, in which we randomly mutated the C-terminal region of the weak orthologue to produce the same distribution of Levenshtein distances to the S. cerevisiae wild-type, as generated in the subgroup (III) treatment group. Again, we observe no sequences capable of functional rescue: 0 out of 50 for 25% N-terminal conditioning (red), 0 out of 50 for 50% (green), and 0 out of 50 for 75% (blue). These results indicate that ProtWave-VAE was unable to improve the functionality of the weak orthologue using N-terminus and latent conditioning.

The third scatterplot in Figure 6C corresponds to subgroup (IV), in which we considered C-terminal diversification of a partial rescuing SH3 paralogue. In this case, we observe one success out of the 48 designed sequences with 25% N-terminal conditioning (red) that resulted in a boost of the r.e. score from an initial value of 0.35 for the partially rescuing paralogue to a value of 0.88, corresponding to a 2.5× enhancement in functionality by inpainting the missing C-terminus region. Interestingly, with a sequence similarity of just 61% to any training sequence, this C-terminus-diversified design is the most novel functional artificial sequence, even when compared to any of the synthetic designs with latent-only conditioning in subgroup (I). None of the other generated sequences, 0 out of 50 for 50% (green), and 0 out of 50 for 75% (blue), were capable of rescue. The control subgroup (VII) is presented in the fourth scatterplot, within which no sequences exhibited functionality. This result implies that N-terminus plus latent-only conditioning can serve as an approach for designing novel sequences by conditioning on distant paralogues and inpainting the C-terminus to elevate function, although the overall hit rate of functional sequences is relatively low. Again, we conjecture that this may result from an inherent incompatibility of the latent vector and N-terminal conditions and that the successful rescue resulted from a generative design in which these conditions were mutually compatible.

The experimental results reveal that our proposed model can effectively design synthetic proteins with functional properties on par with those of their natural counterparts. Additionally, the model is capable of venturing into unexplored regions of sequence space that have not been traversed by natural evolution. Our study also presents a novel protein engineering technique for diversifying the C-terminus of proteins, contributing to the preservation and enhancement of their functionality. Among the findings, the most noteworthy is the ability of the ProtWave-VAE model to imbue a weak binding SH3 paralogue from the Hof1 paralogue group with osmosensing function, resulting in a 2.5× increase in relative enrichment and generating the most novel sequence among all synthetic designs, sharing only 61% sequence similarity to any training sequence.

CONCLUSIONS

In this work, we introduce ProtWave-VAE as a DGM for data-driven protein design blending desirable aspects of VAE and autoregressive (AR) sequence generation. The ProtWave-VAE model combines an InfoMax VAE with a dilated convolutional encoder and WaveNet autoregressive decoder and optional semisupervised regression decoder. This permits model training over unaligned and potentially nonhomologous protein families, learning of a meaningful low-dimensional latent space exposing phylogeny and function, reshaping of the latent space and induction of gradient values by semisupervised training, and autoregressive generation of variable length sequences conditioned on latent vectors and, optionally, N-terminal residues.

We demonstrate and test the predictive and generative capabilities of the ProtWave-VAE model in five applications: (i) learning of biologically meaningful latent space embeddings of four protein families and generative design of novel protein sequences with tertiary structures in close agreement with the natural native folds, (ii) accurate prediction of protein fitness and function in community TAPE and FLIP benchmarks with competitive or superior performance to state-of-the-art architectures, (iii) semisupervised training over annotated chorismate mutase training data to disentangle functional gradients within the latent space and enable generative design of novel sequences conditioned on high functionality, (iv) C-terminal diversification of synthetic chorismate mutase proteins using N-terminus and latent conditioning, and (v) design and experimental testing of novel SH3 proteins to demonstrate the maintenance and elevation of function.

These studies demonstrate the capabilities of the ProtWave-VAE model in data-driven generative protein design. Its capacity to learn over unaligned sequence data means that it eschews the need for multiple sequence alignments that can introduce bias into the training data and typically restricts training to homologous protein families. Its capacity for N-terminal conditioning enables directed diversification of the C-terminal region of proteins guided by latent conditioning to introduce or elevate function. Its capacity for semisupervised retraining makes it well suited for multiround protein engineering campaigns within virtuous cycles of model training and synthetic sequence design and testing.^55,56 In future work, rather than limiting ourselves to interpolative sampling from a Gaussian distribution that defines the functional cluster, we plan to investigate the potential extrapolative sampling by performing gradient ascent up the functional gradients exposed by the semisupervised latent space embeddings.^55,57,58 Specifically, we intend to explore the use of Bayesian optimization or continuous optimization strategies that can inform iterative rounds of machine learning-guided directed evolution (MLDE) campaigns.⁵⁹

ProtWave-VAE exhibits competitive performance in downstream functional prediction relative to state-of-the-art networks based on large language models but is much smaller in size, possessing approximately 100-fold fewer trainable parameters. This makes ProtWave-VAE attractive in reducing the cost of training and deployment and accelerating innovation via rapid ablation studies, hyperparameter optimization, and development and testing cycles. The N-terminal conditioning is anticipated to be valuable in protein engineering applications, where it is desired to keep part of the protein sequence fixed (e.g., the framework region within an antibody) and generatively design the remainder (e.g., the hypervariable region). Another application is to condition on protein tags (e.g., His-tags or expression-tags) and leverage iterative exploration in the latent space to improve protein expression, stability, or other properties.⁸ The capacity of ProtWave-VAE to generate highly diverse and novel sequences with native-like folds, both with and without N-terminal conditioning, makes it particularly well suited to design applications where sequence diversification is a priority, including diversifying complementarity-determining regions in antibodies or producing sequence-diverse libraries of catalytic enzymes. A deficiency of the autoregressive nature of ProtWave-VAE is that the conditioning can only be applied unidirectionally, here from the N-terminus to C-terminus. This means it is currently not possible to condition on amino acid residues in arbitrary and noncontiguous regions of the sequence and allow the model to generatively inpaint the remaining residues. A second deficiency is the potential incompatibility of the latent vector and N-terminal conditions in guiding sequence generation. This sets the stage for further innovation to combine latent inference and order-agnostic autoregressive generation for novel protein engineering and techniques for harmonizing multiple conditioning goals. We would also like to apply ProtWave-VAE to the design of larger and more biologically and biomedically relevant proteins, including multichain protein complexes with quaternary structure, and also to fields beyond protein engineering that may also benefit from alignment-free, latent-conditioned generative design, including the design of small molecules, nucleic acids, prose, and music.

MATERIALS AND METHODS

Data Collection and Preparation.

Each protein sequence employed in the protein family task, fitness benchmark task, chorismate mutase unsupervised versus semisupervised task, and SH3 design task was transformed into one-hot encoded tensors with a length of 21, which includes the 20 amino acid labels and padded tokens. Additional information regarding data set collection, preprocessing, training protocols, and hyperparameter optimization can be found in the Supporting Information

Integrating Latent-Based Inference with an Autoregressive Decoder.

To overcome posterior collapse issues and improve variational inference when integrating latent-based inference with autoregressive decoding, we implemented an Information Maximizing VAE model.²⁴ Our unsupervised loss function for the ProtWave-VAE model is

$$\begin{gathered} {ℒ}_{US}=\xi {\mathbb{E}}_{z~q_{\varphi }(z\mid x)}\left[\text{log}{p}_{\theta }(x\mid z)\right]-(1-\alpha ) \\ {𝒟}_{\text{KL}}\left(q_{\theta }(z\mid x)\Vert p(z)\right)-(\alpha +\lambda -1) \\ {𝒟}_{\text{MMD}}\left(q_{\varphi (z)}\Vert p(z)\right) \end{gathered}$$ (1)

where p_θ(x|z) is the decoder model, 𝔇_KL is the Kullback–Leibler divergence between the variational posterior approximation q_ϕ(z|x) and normal prior distribution p(z). The third term 𝔇_MMD is the max-mean discrepancy (MMD) that helps penalize the aggregated posterior distribution and improves amortized inference. We introduce an autoregressive decoder employing a WaveNet-based architecture, where p_θ(x|z) = p_θ(x₀|z)∏_i=1p_θ(x_i|x_<i, z). The MMD divergence term becomes

$${𝒟}_{\text{MMD}}={\mathbb{E}}_{z,z\prime ~p(z),p(z\prime )}\left[k\left(z,z^{\prime }\right)\right]-2{\mathbb{E}}_{z,z\prime ~q(z),p(z\prime )}\left[k\left(z,z^{\prime }\right)\right]+{\mathbb{E}}_{z,z\prime ~q(z),q(z\prime )}\left[k\left(z,z^{\prime }\right)\right]$$

where k(·, ·) is a positive definite kernel and 𝒟_MMD=0 if and only if p(z) = q(z). We choose the Gaussian kernel $k\left(z,z^{\prime }\right)={\text{e}}^{{\left(z-z\prime \right)}^2/{\sigma }^2}$ as our characteristic kernel k(·, ·), and σ is a hyperparameter defining the bandwidth of our Gaussian kernel. The prefactor loss weights ξ, α, and λ scale the contribution of the reconstruction loss, weights the mutual information between x and z, and scales the penalization of MMD divergence. The prefactor loss weight hyperparameters were optimized using grid search for each protein family task. Full details of the hyperparameter optimization procedure are provided in the Supporting Information. To overcome posterior collapse²³ and enable the use of expressive AR VAE decoders, we incorporated an Information Maximizing (InfoMax) loss objective instead of the common ELBO training objective.²⁴ The InfoMax loss is similar to ELBO, but prefactor weights and additional max-mean discrepancy regularization terms are introduced to motivate better inference and regularization. A mutual information maximization term is introduced to encourage high mutual information between the input vectors and latent space embeddings.

In Figure 1, the overall architecture of our model is shown, along with three main applications of our approach in protein engineering: alignment-free generation, semisupervised learning, and C-terminus diversification. The protein sequences, which need not be aligned during either training or deployment, are embedded in a lower-dimensional latent space using a gated dilated convolution neural network encoder q_ϕ(z|x). The decoder (i.e., generator) p_θ(x|z) is a WaveNet-based architecture (i.e., gated dilated causal convolution), which samples from the latent space and predicts amino acid residues while conditioning on previous amino acids p_θ(x|z) = p(x₀|z)∏_i=1p(x_i|x_<i, z). Generally, when using a dilated causal convolution, we use teacher forcing, which leverages true previous labeled amino acids as the previous conditional information for predicting the following amino acid label. In contrast to recurrent neural networks or causal masked transformers as the autoregressive decoders, the causal convolutional architectures with teacher forcing allows for fast training with time complexity for the forward pass 𝒪 (1) instead of 𝒪(L), where L is the length of the sequence. Recurrent architectures can be prone to vanishing or exploding gradients, whereas this is a deficiency from which convolutional architectures typically do not suffer.

Extending ProtWave-VAE to a Semisupervised Learning Paradigm.

The semisupervised training objective is the following

$${ℒ}_{SS}={ℒ}_{US}+\gamma {\mathbb{E}}_{(x,y)\in {𝒟}_{\text{L}}}\left[\text{log}{p}_{\omega }(y\mid z)\right]$$ (2)

where p_ω(y|z) is a regression decoder comprising a simple fully connected neural network parametrized with training parameters ω. In practice, we minimize the mean-squared error objective $\frac{1}{2}|y-\tilde{y}{|}^2$, where y and $\tilde{y}$ are the ground truth and predicted regression value. (x, y) ∈ 𝒟_L denotes that the samples which are fed through the supervised branch are only sequences x with assay measurements y. In the semisupervised paradigm, the discriminative and generative losses are learned together. In essence, during fitness prediction benchmarking on TAPE and FLIP, or generative evaluation with chorismate mutase enzymes, the encoder model infers latent space embeddings of the sequences, while the generative decoder and regression head reconstruct sequences and predict fitness. Hyperparameters were tailored for each task, with full details in the Supporting Information. Compared to unsupervised learning, semisupervision provides the model with functional information on a subset of the sequences and helps to shape the latent space to better expose functional localization and gradients, thereby enhancing control over the design of function-specific synthetic sequences.

Model Architecture, Hyperparameter Optimization, and Training.

The encoder architecture included gated nonlinear activation with dilated convolutions and multilayer perceptrons (MLP) to map the encoder logits to latent vectors. The decoder utilized an autoregressive WaveNet-based architecture with gated activation and dilated causal convolutions. When generating sequences, we first transform the model’s logits into probabilities for each amino acid location and then select an amino acid label by sampling from the predicted categorical distribution. For certain tasks, such as chorismate mutase semisupervised learning and SH3 design, a predictive top model was implemented. This model samples the latent vectors and maps them to protein property predictions by using a simple MLP architecture. Hyperparameters were optimized using grid search, and training was conducted using the stochastic gradient descent optimizer Adam.⁶⁰ Full details regarding the architectures, training, and hyperparameter optimization are provided in the Supporting Information, and the source code can be found at: https://github.com/PraljakReps/ProtWaveVAE.

ColabFold Structure Prediction.

To predict protein structures for each sequence in the ProtWave-VAE data set, we employed AlphaFold ColabFold Batch v1.2^29,30 for AlphaFold2 structure prediction. We generated three structures for each sequence in each task, which has been a standard method testing protein sequence-based generative model performance.¹⁰ We note, however, that relying solely on AlphaFold2 for synthetic protein design can be misleading due to certain known failure modes. For example, AlphaFold2’s confidence scores often poorly correlate with point mutation stability.^61,62 As such, it is often also desirable, where possible, to perform experimental analysis of the structure or function of the generative protein designs.

TMalign Prediction.

We utilized the TMalign algorithm³⁹ to calculate the TMscore and heavy-atom root-mean-squared distance (RMSD) between the predictions of natural homologue and design structures. The presented TMscore and RMSD values are the mean values of the three-ensemble AlphaFold2 ColabFold predictions. The designed sequences with structures that aligned most closely with the natural homologues were considered the best structural matches based on TMscore. These TMscores have been shown to be a good metric for predicting the accuracy of agreement between the experimentally solved structures versus AlphaFold2 predictions.²⁹

Sequence Novelty.

The method for calculating the sequence novelty of the designed samples differs depending on whether the designed sequences are produced by latent-only conditioning or N-terminal and latent conditioning. In the former case, we compute the novelty measurement by determining the minimum Levenshtein distance between the design sample and any natural training sample and then dividing it by the length of the longer sequence in the pair. In the latter case, since we are diversifying a single natural homologue, we calculate the Hamming distance instead of the Levenshtein distance and normalize the Hamming distance by the sequence length of the natural homologue to obtain the sequence dissimilarity. The sequence similarity is commensurately defined as (1 – sequence dissimilarity).

Gene Construction.

Experimental protocols follow our previous work.¹⁴ S. cerevisiae codon-optimized genes coding for all synthetic SH3 proteins were amplified from a mixed pool of oligonucleotide fragments synthesized on microarray chips (Twist). The oligonucleotides corresponding to each gene were designed with primer annealing sites and a padding sequence to make them uniform 250 mer. PCR was performed using KAPA-Hifi polymerase with 1X KAPA HiFi Buffer (Roche), 0.2 mM dNTPs, and 1.0 μm of each forward (5′-CCGGTTGTACC-TATCGAGTG-3′) and reverse primers (5′-GACCATGCAAG-GAGAGGTAC-3′) in 25 μL total volume, with an initial activation (95 °C, 2 min), followed by 14 cycles of denaturation (95 °C, 20 s), annealing (65 °C, 10 s), and primer extension (70 °C, 10 s). A final extension step (70 °C, 2 min) was subsequently performed. Amplified products were column-purified (Zymo Research), digested with EcoR1 and BamH1, ligated into the digested PRS316 plasmid with the N-terminal membrane domain of Sho1,³⁵ and transformed into Agilent Electro-competent XL1-Blues to yield >250× transformants per gene. The entire transformation was cultured in 50 mL of LB media containing 100 μg/mL sodium ampicillin (Amp) at 37 °C overnight, after which plasmids were purified and pooled.

Sho1 Osmosensing High-Throughput Select-Seq Assay.

Experimental protocols follow our previous work.¹⁴ The haploid S. cerevisiae strain SS101 was constructed on the W303 background gifted by Wendell Lim (UCSF).³⁵ Genetic knockouts of Ssk2 and Ssk22 were created to remove the Sho1-independent branch of the osmoresponse pathway.⁶³ The pooled pRS316 plasmids with the SH3 gene library were transformed into SS101 cells using the LiAc-PEG high-efficiency transformation protocol.⁶⁴ Plate checks were performed to confirm that at least 50 copies of each gene were successfully transformed. Transformed SS101 cells were grown in liquid Sc-Ura media for 24 h (20 mL Sc-Ura media for each 10⁸ total transformed cells) at 30 °C and then passaged to 250 mL of fresh liquid Sc-Ura media to make OD = 0.05. After another 24 h of growth at 30 °C, the Sc-Ura culture can be kept at 4 °C for up to 2 weeks.

All growth was at 30 °C on a shaker. The stock Sc-Ura culture was transferred to YPD media for 24 h growth to get the t₀ sample. The culture was diluted every 8 h to keep the cell density below 0.2 OD₆₀₀. A small volume of the t₀ sample was transferred to YPD media supplemented with either (1) no KCl (nonselective) or (2) 1 M KCl (selective), and the rest was spun down and mini-prepped to extract plasmids from yeast. Both nonselective and selective cultures were grown for 24 h, with OD₆₀₀ maintained under 0.2 to obtain the t₂₄ samples. The two t₂₄ samples were span down and minipreped using the same protocol as the t₀ sample.

Plasmids purified from both t₀ and t₂₄ samples were amplified using two rounds of PCR with Q5 polymerase (New England Biolabs) to add adapters and indices for Illumina sequencing. In the first round, the DNA was amplified using primers that add from six to nine random bases (Ns) for initial focusing, as well as part of the i5 or i7 Illumina adapters. Six cycles were used to minimize the amplification-induced bias, followed by AMPure purification before the second round of PCR. In the second round of PCR, the remaining adapter sequence and TruSeq indices were added, and 20 cycles were used. The final products were gel-purified (Zymo Research), quantified using Qubit (ThermoFisher), and sequenced in an Illumina MiSeq system with a paired-end 300 cycle kit. Allele counts were obtained by using standard procedures. Paired-end reads were joined using FLASH, trimmed to the EcoR1 and BamH1 cloning sites, and translated. Only exact matches to the designed genes were counted. Enrichment (en) and relative enrichment (r.e.) values for each gene x of the three growth conditions were defined as

$$\text{en}(x)={\text{log}}_{10}\left(\frac{f_{24}^x(1\text{M})}{f_{24}^x(0\text{M})}\right)$$ (3)

and

$$\text{r. e.}(x)=\frac{\text{en}(x)-\text{en}(\text{null})}{\text{en}(\text{wt})-\text{en}(\text{null})}$$ (4)

where ${f_{24}}^x(1\text{M})$ and $f_{24}^x(0\text{M})$ represent the frequency of observing gene x after being subjected to a 24 h exposure to 1 and 0 M, respectively, KCl solution. The wild-type (wt) sequence is the Sho1 gene of S. cerevisiae, and the null gene is TAGNTAATTTCGGCGTGGGTATGG-TGGCAGGCCCCGTGGCCGGGACTGTTGGGCGCCATCTCCTTGCATGCAC-CATTCCTTGCGGCGGCGGTGCTCAACGGCCT-CAACCTACTACTGGGCTGC TTCCTAATGCAG-GAGTCGCATAAGGGAGAGCGTCGAGAT, where the stop codon TAG produces Sho1 without the C-terminal SH3 domain. A second independent selection assay was performed to ensure reproducibility (Figures 5A and S3). The average en of the two trials was used to calculate r.e., and the r.e. values of SH3 variants with at least five counts in the 0 M at 24 h population in both trials were used for analysis.

ABBREVIATIONS

AR

autoregressive

CDR

complementarity-determining region

CM

chorismate mutase

DGM

deep generative model

DHFR

dihydrofolate reductase

ELBO

evidence lower bound

FLIP

Fitness Landscape Inference for Proteins

MSA

multiple sequence alignment

PCA

principal component analysis

RMSD

root-mean-squared distance

SH3

Src homologue 3

TAPE

Task Assessing Protein Embeddings

VAE

variational autoencoder

wt

wild-type