A new method for multiancestry polygenic prediction improves performance across diverse populations

Abstract

Polygenic risk scores (PRSs) increasingly predict complex traits; however, suboptimal performance in non-European populations raise concerns about clinical applications and health inequities. We developed CT-SLEB, a powerful and scalable method to calculate PRSs, using ancestry-specific genome-wide association study summary statistics from multiancestry training samples, integrating clumping and thresholding, empirical Bayes and superlearning. We evaluated CT-SLEB and nine alternative methods with large-scale simulated genome-wide association studies (~19 million common variants) and datasets from 23andMe, Inc., the Global Lipids Genetics Consortium, All of Us and UK Biobank, involving 5.1 million individuals of diverse ancestry, with 1.18 million individuals from four non-European populations across 13 complex traits. Results demonstrated that CT-SLEB significantly improves PRS performance in non-European populations compared with simple alternatives, with comparable or superior performance to a recent, computationally intensive method. Moreover, our simulation studies offered insights into sample size requirements and SNP density effects on multiancestry risk prediction.

Genome-wide association studies (GWASs) have identified tens of thousands of single nucleotide polymorphisms (SNPs) associated with complex traits and diseases¹. PRSs summarize the combined effect of individual SNPs, offering the potential to improve risk stratification for various diseases and conditions^2–7. However, to date, GWASs have primarily focused on populations predominately comprising European (EUR)-origin individuals⁸. Consequently, the PRSs generated from these studies tend to underperform in non-EUR populations, particularly in African (AFR)-ancestry populations^9–12. The limited representation of non-EUR populations in PRS research raises concerns that using current PRSs for clinical applications may exacerbate health inequities^13–16.

In addition to the critical importance of addressing inequalities in the representation of a non-EUR population in genetic research, there is also an important need to develop statistical methods that leverage genetic data across populations to develop better-performing PRSs. Most existing PRS methods have been developed to analyze data from a single-ancestry group^17–26 and, subsequently, their performance was primarily evaluated in EUR populations^3–6. Although the same methods can also be used to build PRSs in non-EUR populations, the resulting PRSs tend to have limited performance due to smaller training data sample sizes compared with EUR populations^9,14. Some studies have conducted meta-analyses of GWASs across diverse populations to develop a multiancestry PRS^27–29. Although this approach may lead to a single PRS that performs more ‘equally’ across diverse groups, it does not account for heterogeneity in linkage disequilibrium (LD) and effect sizes across populations, and is not designed to derive the best PRS possible for each population^30,31.

Recent methods aim to develop more optimal PRSs in non-EUR populations by combining available GWASs from the target population with ‘borrowed’ information from larger GWASs in the EUR populations. One such study developed PRSs in separate populations and then combined them by optimal weighting to maximize target-population performance³². Other studies proposed Bayesian methods using multivariate priors for effect-size distribution to borrow information across populations^30,33,34. Despite these developments, methods leveraging multiancestry datasets for PRSs remain limited. Both theoretical and empirical studies have indicated that the optimal PRS building depends on multiple factors^17,35,36, including sample size, heritability, effect-size distribution, and LD, and thus exploration of alternative methods with complementary advantages is needed to build optimal PRSs in any given setting. Moreover, and perhaps more importantly, evaluation of multiancestry methods for building improved PRSs remains quite limited to date owing to the lack of large GWASs for various non-EUR populations, especially of AFR origin, where risk prediction remains the most challenging.

In the present Technical Report, we propose CT-SLEB, a computationally simple and powerful method for generating PRSs using GWASs across diverse ancestry populations. CT-SLEB is a model-free approach that combines multiple techniques, including a two-dimensional (2D) extension of the popular clumping and thresholding (CT) method^17,18, a superlearning (SL) model for combining multiple PRSs and an empirical Bayes (EB) approach for effect-size estimation. We compared CT-SLEB’s performance with nine alternative methods using large-scale simulated GWASs across five ancestry groups. In addition, we developed and validated population-specific PRSs for 13 complex traits using GWAS data from 23andMe, Inc., the Global Lipids Genetics Consortium (GLGC)³⁷, All of Us (AoU) and UK Biobank (UKBB) across EUR (n ≈ 3.91 million), AFR (primarily African American (AA), n ≈ 265,000), Latino (n ≈ 574,000), East Asian (EAS, n ≈ 270,000) and South Asian (SAS, n ≈ 77,000) populations. Both simulation studies and empirical data analyses indicated CT-SLEB as a scalable and powerful method for generating PRSs for non-EUR populations. Furthermore, our simulation studies and evaluation of various methods in large datasets provided insights into the future yield of multiancestry PRSs because GWASs in diverse populations continue to grow.

Results

Method overview

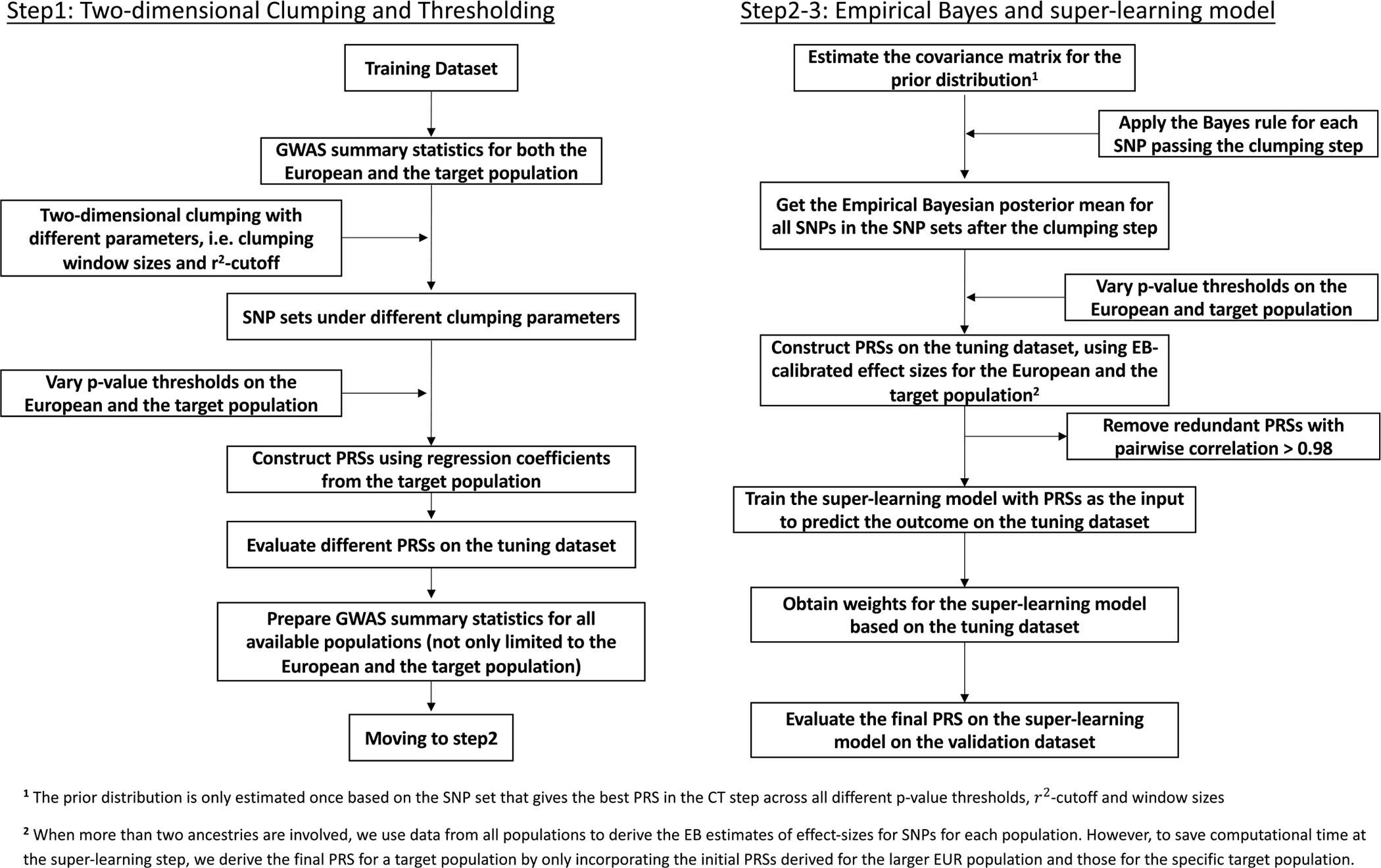
CT-SLEB is designed to generate multiancestry PRSs, incorporating large GWASs from the EUR population and smaller GWASs from non-EUR populations. The method has three key steps (Fig. 1 and Extended Data Fig. 1): (1) CT method for selecting SNPs to be included in a PRS for the target population; (2) EB method for SNP coefficient estimation; and (3) SL model to combine a series of PRSs generated under different SNP selection thresholds. CT-SLEB requires three independent datasets: (1) GWAS summary statistics from training datasets across EUR and non-EUR populations; (2) a tuning dataset for the target population to determine optimal model parameters; and (3) a validation dataset for the target population to report the final prediction performance.

Fig. 1 |. CT-SLEB workflow.

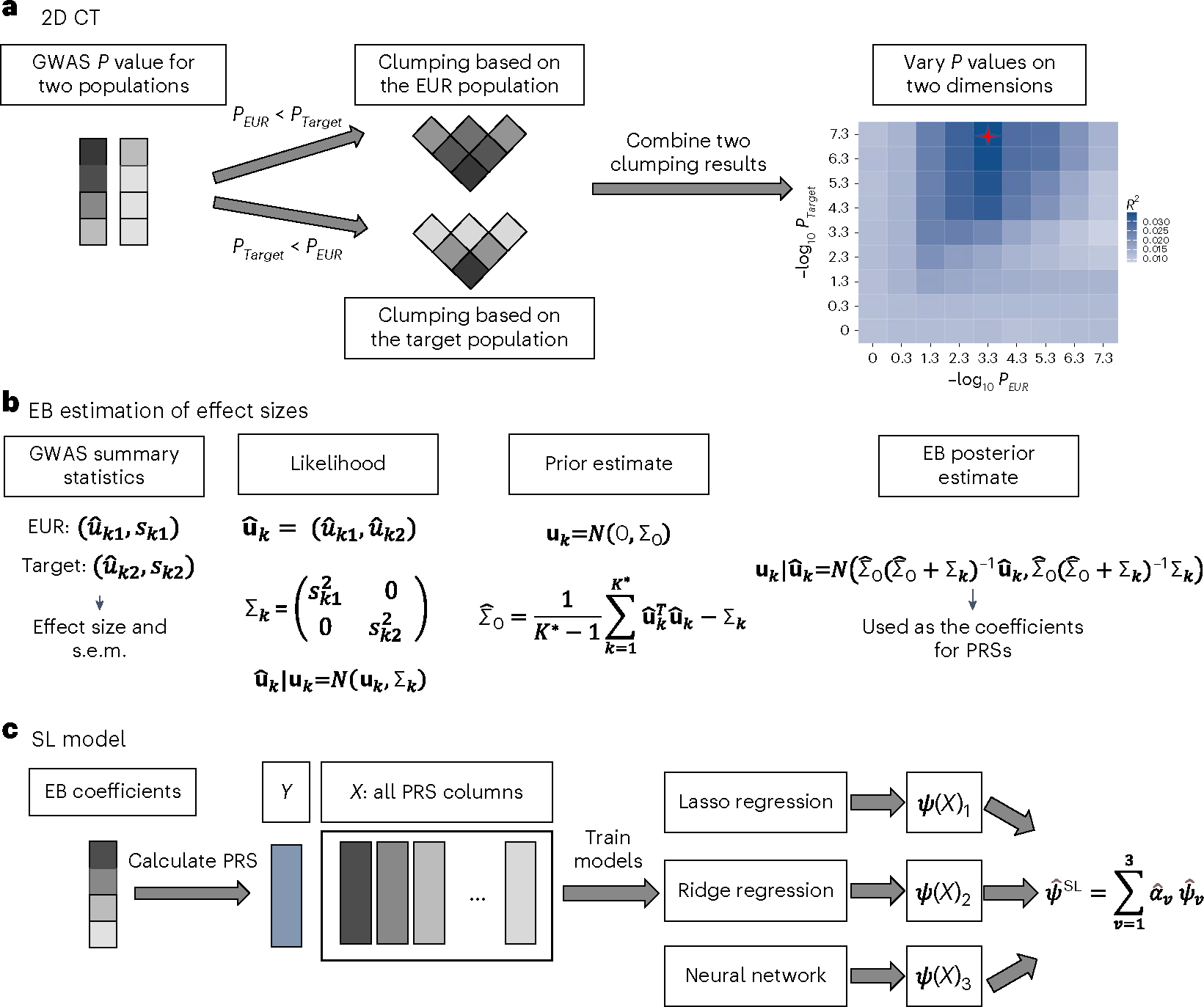
a–c, The method has three key steps: CT method for selecting SNPs (a); EB procedure for incorporating correlation in effect sizes of genetic variants across populations (b); and SL model for combining the PRSs derived from the first two steps under different tuning parameters (c). GWAS summary statistics data were obtained from the training data. The tuning dataset was used to train the SL model. The final prediction performance was evaluated using an independent validation dataset. s.e.m., standard error of the mean.

Two-dimensional CT.

In step 1, CT-SLEB uses 2D CT on GWAS summary statistics data to incorporate SNPs with either shared effects across the EUR and the target populations or population-specific effects in the target population (Fig. 1a). Each SNP is assigned to one of two groups based on the P value from the EUR and target populations: (1) SNPs with a P value smaller in the EUR population; or (2) SNPs with a P value smaller in the target population or those that exist only in the target population. SNPs in the first group are ranked by the EUR P value (from smallest to largest) and then clumped using LD estimates from the EUR reference sample. SNPs in the second group are ranked by the target-population P value and clumped using LD estimates from the target-population reference sample. Clumped SNPs from both groups form a candidate set for the next step. In the thresholding step, P-value thresholds vary over a 2D grid. Each dimension corresponds to the threshold for the P value from one population. At any threshold combination, a SNP may be included in the target-population PRSs if its P value from either the EUR or the target population achieves the corresponding threshold.

EB estimation of effect sizes.

As SNP effect sizes are expected to be correlated across populations^38,39, we proposed an EB method to efficiently estimate effect sizes for SNPs to be included in the PRSs (Fig. 1b). Based on the selected SNP set from the CT step, we first estimated a ‘prior’ covariance matrix of effect sizes between the EUR and the target population. Then, we estimated each SNP’s effect size in the target population using the corresponding posterior mean, which weights the effect-size estimate from each population based on the bias-variance trade-off (Methods).

Superlearning.

Previous research has shown that combining PRSs under different P-value thresholds can effectively increase prediction performance²⁰. Therefore, we proposed an SL model to predict the outcome using PRSs generated under different tuning parameters as training variables (Fig. 1c). The SL model is a linear combination of predictors based on multiple supervised learning algorithms^40–42. The set of prediction algorithms can be self-designed or chosen from classical prediction algorithms. We used the R package SuperLearner v.2.0–26 (ref. 43) and chose Lasso⁴⁴, ridge regression⁴⁵ and neural networks⁴⁶ as three different candidate models in the implementation. We trained the SL model on the tuning dataset and evaluated the final PRS performance using the independent validation dataset.

Design of simulation studies.

We conducted simulation studies comparing ten methods across five broad categories: (1) single-ancestry methods using only target-population data; (2) EUR PRSs, generated using single-ancestry methods on EUR-only GWAS data; (3) weighted PRSs, applying single-ancestry PRSs separately to the EUR and target populations, and deriving an optimal linear combination of the two; (4) Bayesian methods, assuming a multivariate Bayesian framework for PRS construction; and (5) our proposed approach, CT-SLEB. The single-ancestry methods include CT^17,18 and LDpred2 (refs. 19,26). EUR PRSs are generated using CT and LDpred2. Weighted PRS approaches include: CT based, LDpred2 based and PolyPred-S+ (ref. 47). The last method linearly combines PRSs using EUR and target-population PRSs from SBayesR²¹ and EUR PRS from PolyFun-pred⁴⁸, which integrates functional annotation information to identify causal variants across the genome and thus uses additional information that is not incorporated into the other methods compared. Bayesian methods include the following: (1) XPASS method³⁴, assuming a multivariate normal distribution for effect size and using the posterior mean of the target population to construct PRS; and (2) PRS-CSx³⁰, using a continuous shrinkage Bayesian framework to calculate the posterior mean of effect sizes for EUR and non-EUR populations, and subsequently deriving an optimal linear combination of all populations using a tuning dataset.

All methods used the target and EUR population training data to construct PRSs for the target population. In addition, CT-SLEB and PRS-CSx were evaluated using data from all five ancestries. For computational efficiency, most analyses were restricted to ~2.0 million SNPs included in Hapmap3 (HM3) (ref. 49) or the Multi-Ethnic Genotyping Arrays (MEGA)⁵⁰ chip array, or both. However, the PolyPred-S+ and PRS-CSx methods were currently limited to ~1.3 million HM3 SNPs in the provided software.

Simulation study results

Results from simulation studies (Fig. 2 and Supplementary Figs. 1–5) show that multiancestry methods generally lead to the most accurate PRSs in different settings. When the training data sample size for the target population is small (Fig. 2a and Supplementary Figs. 1a and 2–5a), PRSs from single-ancestry methods perform poorly compared with EUR-based PRSs. Conversely, when the target-population training sample size is large (Fig. 2b and Supplementary Figs. 1b and 2–5b–d), PRSs from single-ancestry methods can outperform EUR PRSs. PRSs generated from multiancestry methods can achieve substantial improvement in either setting.

Fig. 2 |. Simulation results of various PRS methods in multiancestry settings.

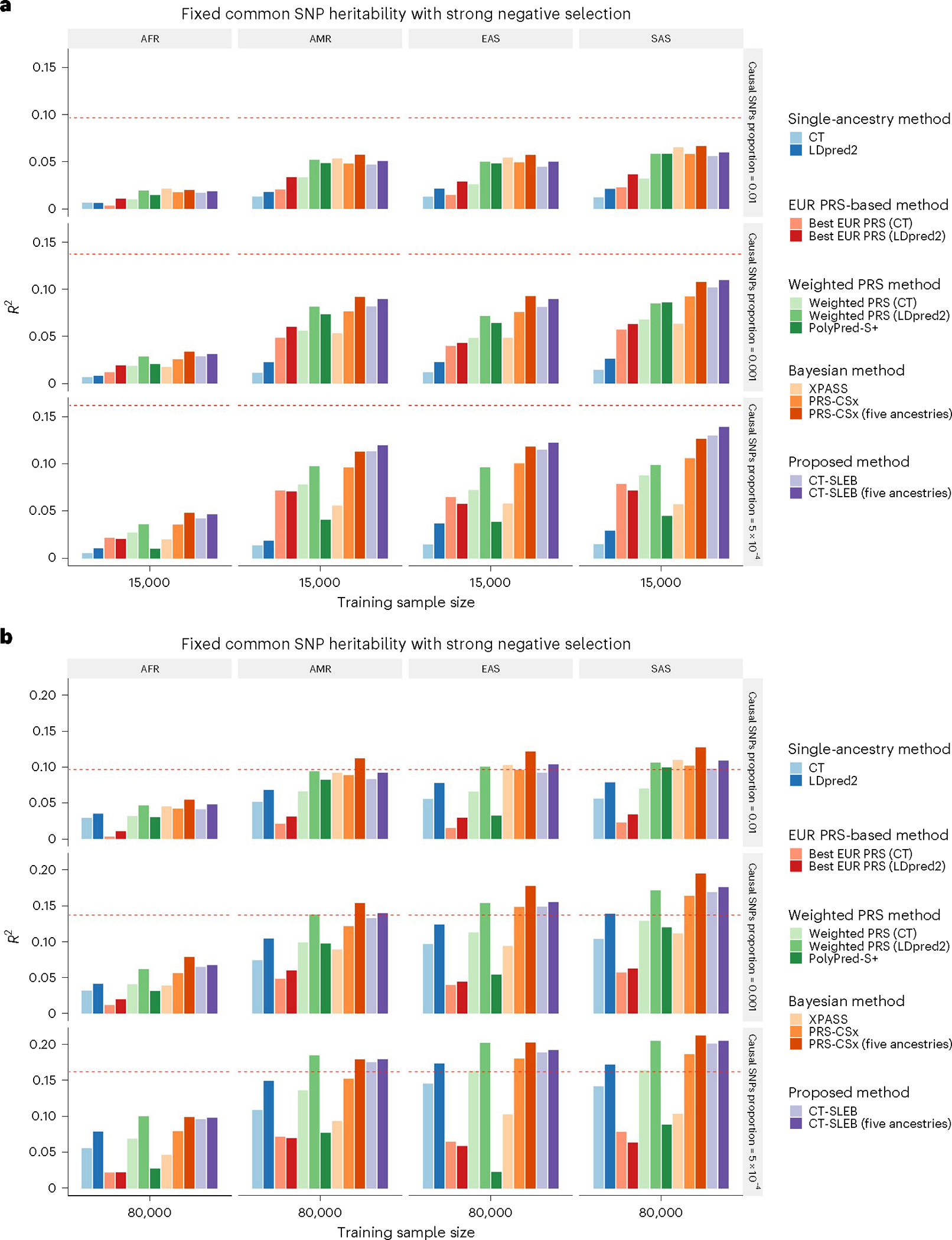
a,b, Each of the four non-EUR populations with a training sample size of 15,000 (a) or 80,000 (b). For the EUR population, the size of the training sample was set at 100,000. The tuning dataset included 10,000 samples per population. Prediction R² values were reported based on an independent validation dataset with 10,000 subjects per population. Common SNP heritability was assumed to be 0.4 across all populations, and effect-size correlation was assumed to be 0.8 across all pairs of populations. The proportion of causal SNPs varies across 0.01 (top), 0.001 (middle), 5 × 10⁻⁴ (bottom), and effect sizes for causal variants are assumed to be related to allele frequency, under a strong negative selection model. Data were generated based on ~19 million common SNPs across the 5 populations, but analyses were restricted to ~2.0 million SNPs that were used on Hapmap3 + MEGA chip array. PolyPred-S+ and PRS-CSx analyses were further restricted to ~1.3 million HM3 SNPs. All approaches were trained using data from the EUR and target populations. CT-SLEB and PRS-CSx were also evaluated using data from all five ancestries as training data. The red dashed line shows the prediction performance of EUR PRSs generated using the single-ancestry method (best of CT or LDpred2) in the EUR population.

When using only EUR and target-population data, both CT-SLEB and PRS-CSx can lead to improvements over other candidate methods in most settings. When the target-population sample size is large, weighted LDpred2 performs comparably to CT-SLEB and PRS-CSx. Between CT-SLEB and PRS-CSx, neither method is uniformly superior across all scenarios. With a smaller target-population sample size $(n=\mathrm{15,000})$, PRS-CSx often outperforms CT-SLEB at the highest degree of polygenicity ($P_{\text{causal}}=0.01$), whereas CT-SLEB excels at the lowest polygenicity $\left(P_{\text{causal}}=5\times {10}^{-4}\right)$. The difference between the two methods narrows with larger sample sizes $(n=\mathrm{45,000}-\mathrm{100,000})$. When using data from all five ancestries simultaneously, CT-SLEB and PRS-CSx improve by 6.8% and 23.7% on average, respectively, compared with only using EUR and target-population data. PRS-CSx outperforms CT-SLEB in many settings (Fig. 1b and Supplementary Figs. 1a,b and 2–5b–d). Under different simulation settings, the number of SNPs used by CT-SLEB ranged from 549,000 to 933,000, while PRS-CSx retained all HM3 SNPs (Supplementary Table 1).

Comparing the runtime for constructing AFR PRSs on chromosome 22 data (Methods and Supplementary Table 2), CT-SLEB is, on average, almost 25× faster than PRS-CSx (4.35 versus 109.11 min) in two ancestries analyses and 91× faster than that of PRS-CSx in five ancestries setting (4.62 minutes versus 420.96 minutes) using a single core with Intel E5–26840v4 central processing unit (CPU). Sensitivity analyses assessing the required tuning and validation sample size for CT-SLEB (Extended Data Fig. 2) demonstrated that prediction performance improves with larger sizes. Meanwhile, CT-SLEB’s performance remained robust when the tuning and validation sample sizes were around 2,000. Additional sensitivity analyses compared CT-SLEB and PRS-CSx performance when both methods used HM3 SNPs. CT-SLEB held an advantage in low polygenicity setting with a training sample size of 15,000 or 45,000 (Supplementary Fig. 6a,b). However, with a training sample size >80,000, both methods showed similar performance in a low polygenicity setting (Supplementary Fig. 6c,d).

Unequal predictive performance of PRSs across populations presented an ethnic barrier for implementing this technology in healthcare. We examined the required training GWAS sample size for minority populations to bridge the performance gap compared with the EUR population. Results indicated that, when effect sizes for shared causal SNPs are similar across populations (genetic correlation = 0.8), the gap is mostly eliminated for all populations except AFR when the sample size reaches between 45% and 80% of the EUR population (Fig. 3 and Supplementary Fig. 7). However, for the AFR population, sample size requirements can vary dramatically depending on the genetic architecture of traits. When we assumed equal common SNP heritability for AFR and other populations, the AFR sample size requirement appeared dauntingly large due to smaller per-SNP heritability (Fig. 3a,b and Supplementary Fig. 7a,b). If per-SNP heritability remained the same across populations, but heritability varied proportionately to the number of common variants, the AFR sample size requirement aligned with those of other minority populations (Fig. 3c,d and Supplementary Fig. 7c).

Fig. 3 |. Comparison of CT-SLEB PRSs across different ancestries with single-ancestry EUR PRSs in the EUR population.

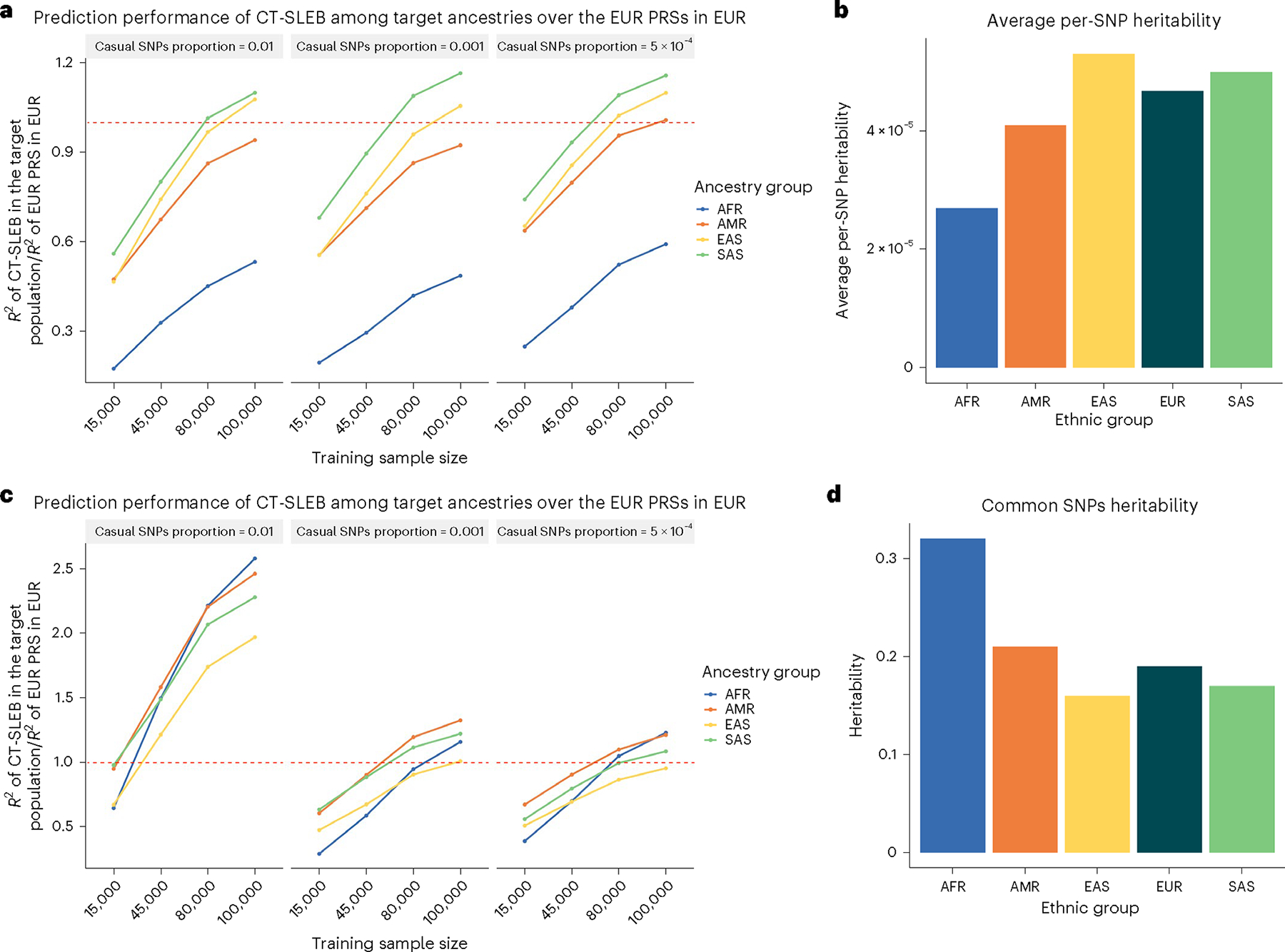
a–d, The training sample size for each of the four non-EUR populations is 15,000, 45,000, 80,000 or 100,000. The training sample size for the EUR population is fixed at 100,000 and PRS performance is evaluated using single-ancestry CT or LDpred2, depending on whichever performs the best in each setting. a,b, Under the genetic architecture where common SNP heritability is fixed at 0.4, (a) depicts the relative performance of CT-SLEB in non-European populations compared to EUR PRSs, while (b) shows the averaged per-SNP heritability across different ancestries. Then under the genetic architecture where per-SNP heritability is fixed. c,d, (c) demonstrates the relative performance of CT-SLEB in non-European populations relative to EUR PRSs.) The effect-size correlation was assumed to be 0.8 across all pairs of populations. The effect sizes for causal variants were assumed to be related to allele frequency under a strong negative selection model. CT-SLEB uses the summary statistics from all five ancestries.

CT-SLEB has a major advantage over PRS-CSx in computational scalability, allowing it to handle a much larger number of SNPs. We used CT-SLEB to study the effect of SNP density on PRS performance by considering three SNP sets for PRS building: (1) ~1.3 million SNPs in HM3 (ref. 49); (2) ~2.0 million SNPs, which included all HM3 SNPs and additional SNPs in the MEGA chips array; and (3) all ~19 million common SNPs included in the 1000 Genomes Project (phase 3) (ref. 51), which were used to generate the traits in our simulation studies. We observed that PRS performance in various US minority populations could be substantially enhanced by including SNPs in denser panels. This benefit, resulting from denser panels, was more enhanced when the target-population sample size was larger and in settings with fewer causal SNPs (Fig. 4 and Supplementary Fig. 8).

Fig. 4 |. Prediction performance of CT-SLEB PRS under varying SNP densities.

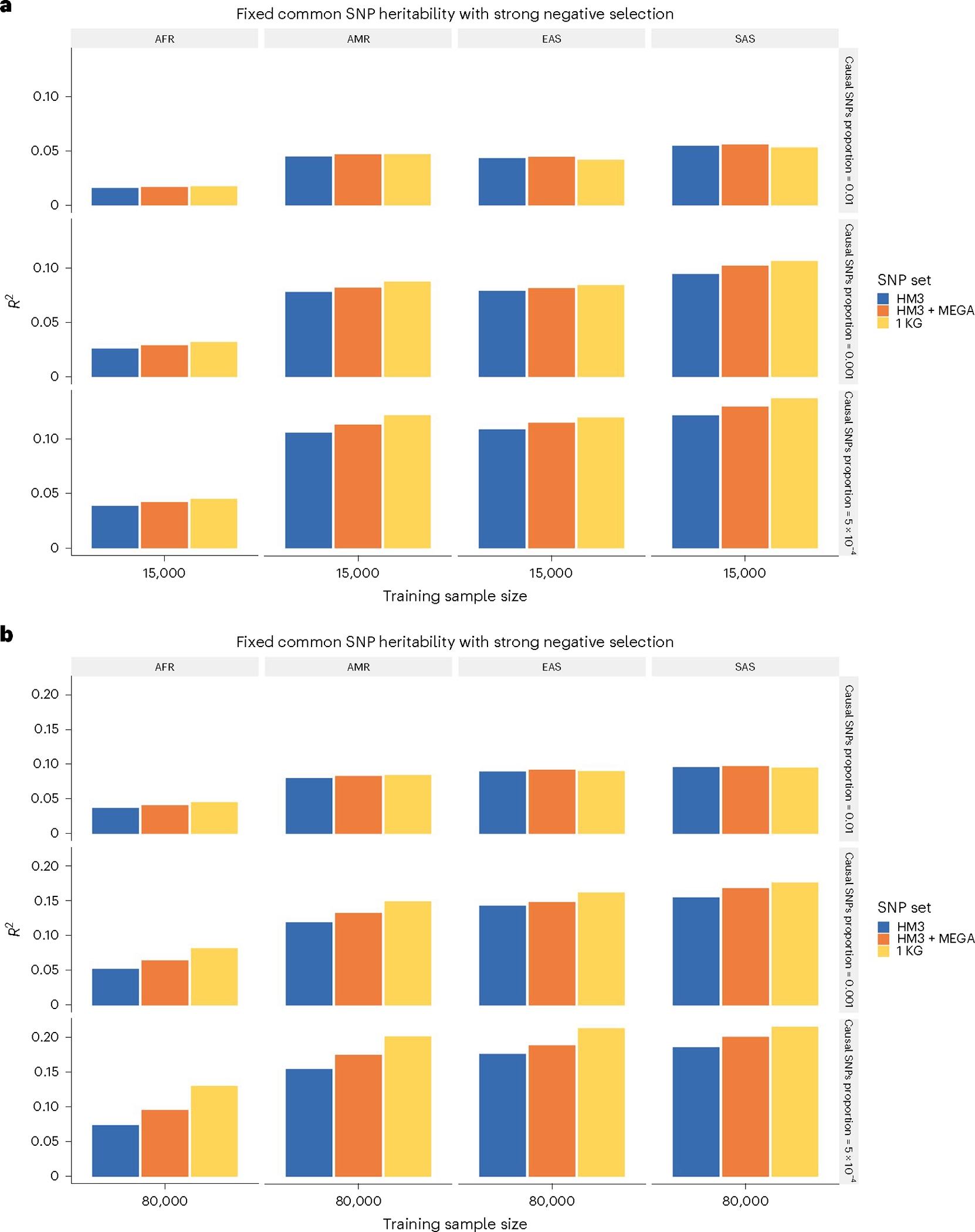
a,b, The analysis of simulated data based on ~19 million SNPs was limited to 3 different SNP sets: Hapmap3 (~1.3 million SNPs), Hapmap3 + MEGA chips array (~2.0 million SNPs) and 1000 Genomes Project (1KG; ~19 million SNPs). a,b, The training sample size for each of the four non-EUR populations was 15,000 (a) or 80,000 (b). The training sample size for the EUR population was fixed at 100,000. Prediction R² values are reported based on an independent validation dataset with 10,000 subjects per population. Common SNP heritability was assumed to be 0.4 across all populations and effect-size correlation was assumed to be 0.8 across all pairs of populations. The proportion of causal SNPs varied across 0.01 (top), 0.001 (middle) and 5 × 10⁻⁴ (bottom). Lastly, effect sizes for causal variants were assumed to be related to allele frequency under a strong negative selection model.

23andMe data analysis results

We developed and validated population-specific PRSs for seven complex traits using GWAS data from 23andMe, Inc. (Methods, Supplementary Tables 3 and 4 and Supplementary Data). We conducted GWASs using a training dataset for each population adjusting for principal components (PCs) 1–5, sex and age (Methods). The Manhattan plots and Q–Q (quantile–quantile) plots for GWASs are shown in Supplementary Figs. 9–15 and no inflation was observed (Supplementary Table 5). We estimated heritability for the seven traits in the EUR population using LD-score regression⁵² (Supplementary Table 6 and Methods).

The results for heart metabolic disease burden and height (Fig. 5 and Supplementary Table 7) followed a similar pattern to our simulation studies. The PRS-CSx using five ancestries generally yielded to the best performing PRSs across different populations. With only EUR and target-population data, both CT-SLEB and PRS-CSx performed well across different populations. The relative gain was often large, especially for the AA population, compared with the best performing EUR or single-ancestry PRS. Weighted methods did not excel with the AA population, but showed substantial improvement compared with each component PRS (EUR and single ancestry) for other populations. PolyPred-S+ had comparable performance to PRS-CSx and CT-SLEB on EAS and SAS populations, but was notably worse on the AA population. We also observed that, even with the best performing method and large sample, a substianial gap remained for PRS performance in non-EUR populations compared with the EUR population (Fig. 5).

Fig. 5 |. Prediction accuracy of PRSs for heart metabolic disease burden and height in 23andMe, Inc. datasets.

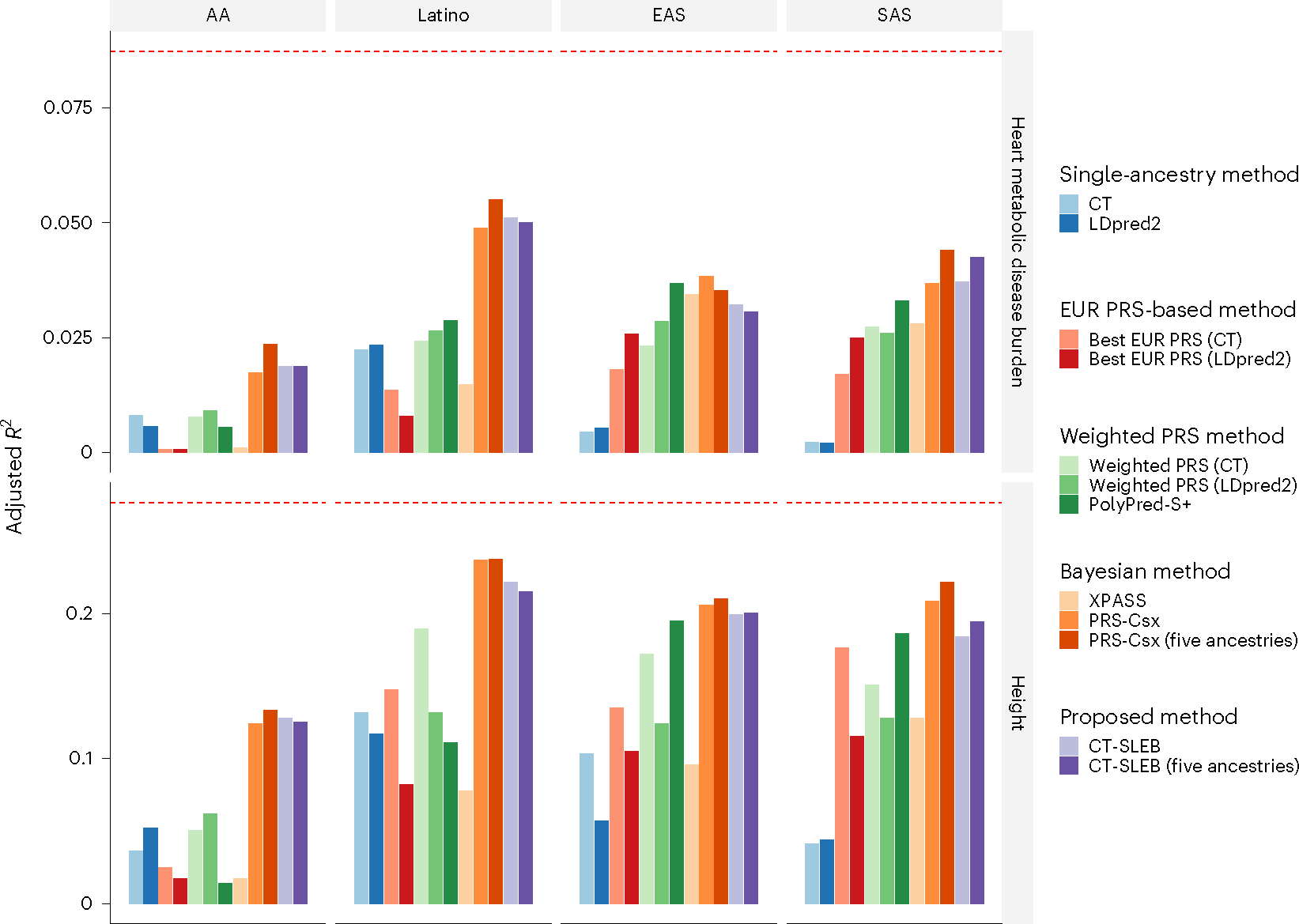
The total sample size for heart metabolic disease burden and height was, respectively, 2.46 million and 2.93 million for EUR, 131,000 and 141,000 for AFR, 375,000 and 509,000 for Latino, 110,000 and 121,000 for EAS and 29,000 and 32,000 for SAS, respectively. The dataset was randomly split into 70%, 20%, and 10% for training, tuning, and validation datasets, respectively. The adjusted R² values were reported based on the PRS performance in the validation dataset, accounting for PCs 1–5, sex, and age. The red dashed line represents the prediction performance of EUR PRS generated using a single-ancestry method (best of CT or LDpred2) in the EUR population. Analyses were restricted to ~2.0 million SNPs that are included in Hapmap3, or the MEGA chips array or both. PolyPred-S+ and PRS-CSx analyses were further restricted to ~1.3 million HM3 SNPs. All approaches were trained using data from the EUR and the target population. CT-SLEB and PRS-CSx were also evaluated using training data from all five ancestries. From top to bottom, two continuous traits are displayed in the following order: (1) heart metabolic disease burden and (2) height.

We observed similar trends in the 23andMe data analysis for five binary traits: any cardiovascular disease (CVD), depression, migraine diagnosis, morning person and sing back musical note (SBMN) (Fig. 6 and Supplementary Table 7). In most settings, CT-SLEB, PRS-CSx and PolyPred-S+ often produced superior PRSs, improving on the best EUR or single-ancestry PRSs. For CVD, which is the clinically most relevant trait for risk prediction and preventive intervention, CT-SLEB outperformed PRS-CSx and PolyPred-S+ by a notable margin except for the EAS population. For the AFR population, particularly underrepresented in genetic research, CT-SLEB outperformed PRS-CSx and PolyPred-S+ by a notable margin for several traits (for example, CVD and morning person). Conversely, PRS-CSx and PolyPred-S+ significantly outperformed CT-SLEB for predicting migraine diagnosis and SBMN in the SAS population. Despite the best performing methods and large GWASs in non-EUR populations, a major gap remains for PRS performance compared with the EUR population.

Fig. 6 |. Prediction accuracy of five binary traits in 23andMe, Inc. datasets.

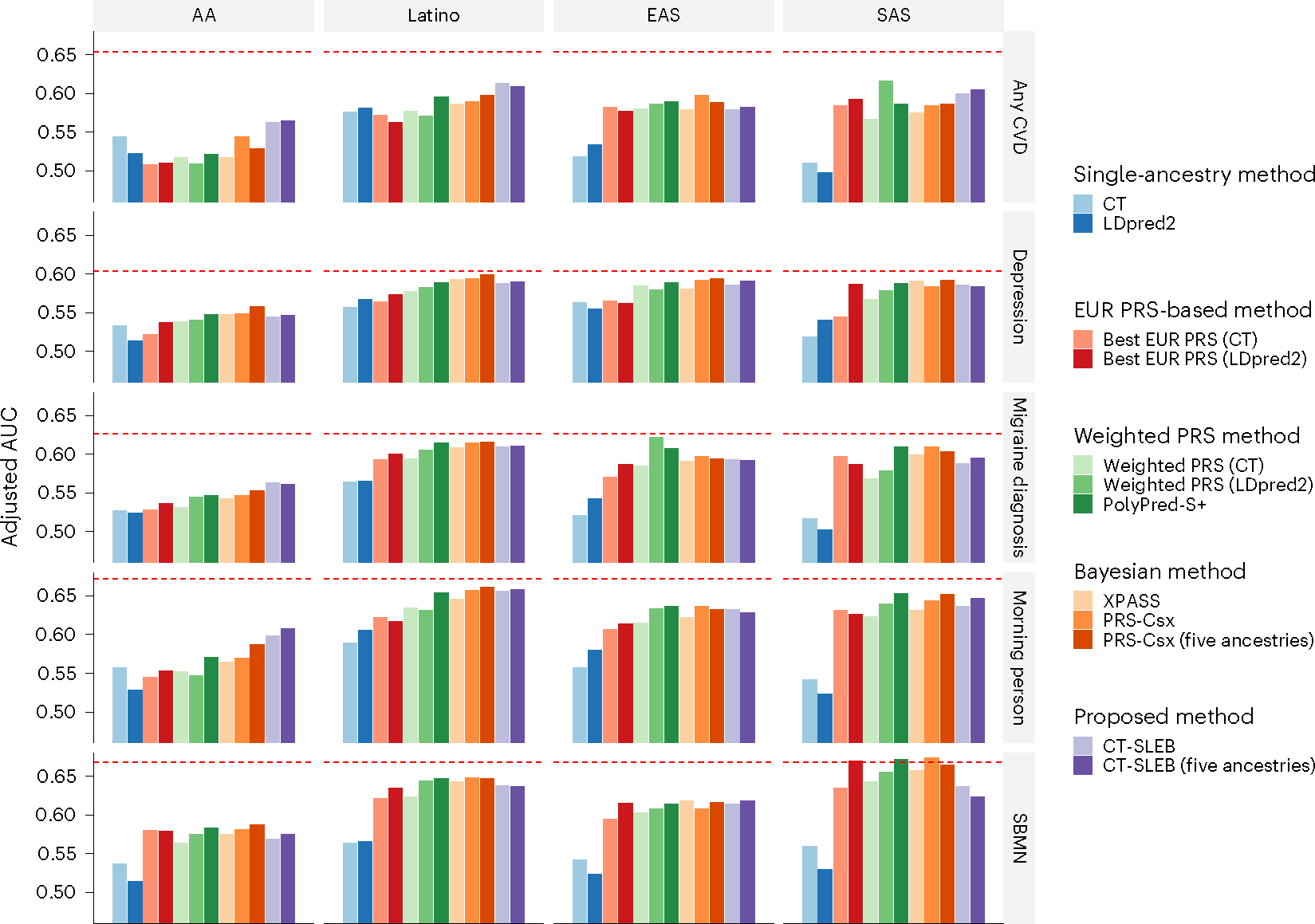
The data are from five populations: EUR (averaged n ≈ 2.37 million), AFR (averaged n ≈ 109,000), Latino (averaged n ≈ 401,000), EAS (averaged n ≈ 86,000) and SAS (averaged n ≈ 24,000). The datasets are randomly split into 70%, 20% and 10% for training, tuning and validation datasets, respectively. The adjusted AUC values were reported based on the validation dataset accounting for PCs 1–5, sex and age. The red dashed line represents the prediction performance of EUR PRS generated using a single-ancestry method (best of CT or LDpred2) in the EUR population. Analyses were restricted to the ~2.0 million SNPs that are included in Hapmap3, the MEGA chips array or both. PolyPred-S+ and PRS-CSx analyses were further restricted to ~1.3 million HM3 SNPs as implemented in the provided software. All approaches were trained using data from the EUR and the target populations. CT-SLEB and PRS-CSx were also evaluated using training data from five ancestries. From top to bottom, five binary traits are displayed in the following order: (1) any CVD; (2) depression; (3) migraine diagnosis; (4) SBMN; and (5) morning person.

GLGC and AoU analysis results with UKBB as validation dataset

We developed and validated population-specific PRSs using GWAS summary data for four traits from GLGC—high-density lipoprotein (HDL)-cholesterol, low-density lipoprotein (LDL)-cholesterol, log(triglycerides) (log(TGs)) and total cholesterol (TC)—and two traits from AoU—height and body mass index (BMI) (Methods and Supplementary Tables 4 and 8). We evaluated the methods using individual-level data from UKBB (Supplementary Table 9). The Manhattan plots and Q–Q plots for GWASs are shown in Supplementary Figs. 16–21, with no inflation observed given the genomic inflation factor for most ancestries, except height for the Latino population in AoU (${\lambda }_{\mathrm{1,000}}=1.0$; Supplementary Table 5). We estimated heritability for the four traits in the EUR population using LD-score regression⁵² (Supplementary Table 6 and Methods).

In GLGC data analyses, CT-SLEB, PRS-CSx and PolyPred-S+ outperformed the other approaches (Fig. 7). CT-SLEB demonstrated superior performance in the AFR population, improving adjusted R² for log(TGs) and LDL-cholesterol by 140% and 66.4%, respectively, compared with PRS-CSx. This highlighted the advantage of the model-free approach CT-SLEB in handling biomarker traits, with some SNPs having unusually large effects. Conversely, PRS-CSx outperformed CT-SLEB in the EAS population. For log(TGs) and LDL-cholesterol, the adjusted R² ratio between CT-SLEB and PRS-CSx was only 89.8% and 52.9%, respectively. It is interesting that, for LDL-cholesterol and TC, PRSs generated by CT-SLEB and five ancestries PRS-CSx demonstrated superior performance in the AFR population compared with EUR PRSs in the EUR population (Fig. 7). Finally, in AoU data analyses, CT-SLEB performed better in predicting BMI, whereas PRS-CSx predicted height more accurately (Fig. 8). These results highlight the importance of generating PRSs using multiple alternative methods in multiancestry settings.

Fig. 7 |. Prediction accuracy of four blood lipid traits from the GLGC.

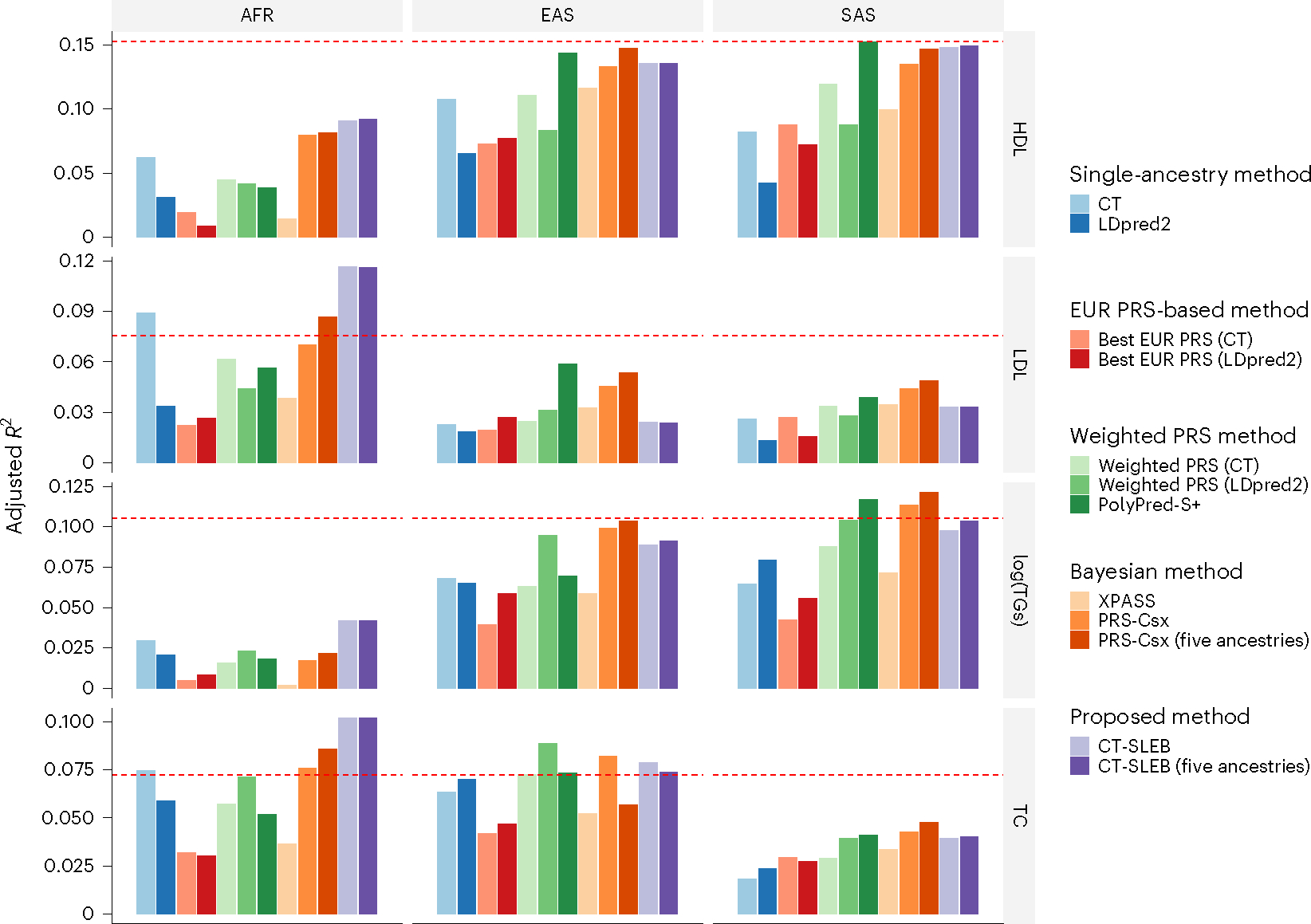
We used the GWAS summary statistics from five populations as the training data: EUR (n ≈ 931,000), AFR (primarily AA, n ≈ 93,000), Latino (n ≈ 50,000), EAS (n ≈ 146,000) and SAS (n ≈ 34,000). The tuning and validation datasets are from UKBB data with three different ancestries: AFR (n = 9,042), EAS (n = 2,009) and SAS (n = 10,615). The tuning and validation were split half and half. The adjusted R² values were reported based on the performance of the PRS in the validation dataset, while accounting for PCs 1–10, sex and age. The red dashed line represents the prediction performance of EUR PRSs generated using a single-ancestry method (best of CT or LDpred2) in the EUR population. Analyses were restricted to ~2.0 million SNPs that are included in Hapmap3, the MEGA chips array or both. PolyPred-S+ and PRS-CSx analyses were further restricted to ~1.3 million HM3 SNPs as implemented in the provided software. All approaches were trained using data from the EUR and the target populations. CT-SLEB and PRS-CSx were also evaluated using training data from five ancestries. From top to bottom, four traits are displayed in the following order: (1) HDL-cholesterol, (2) LDL-cholesterol, (3) log(TGs) and (4) TC.

Fig. 8 |. Prediction accuracy of two traits from the AoU dataset.

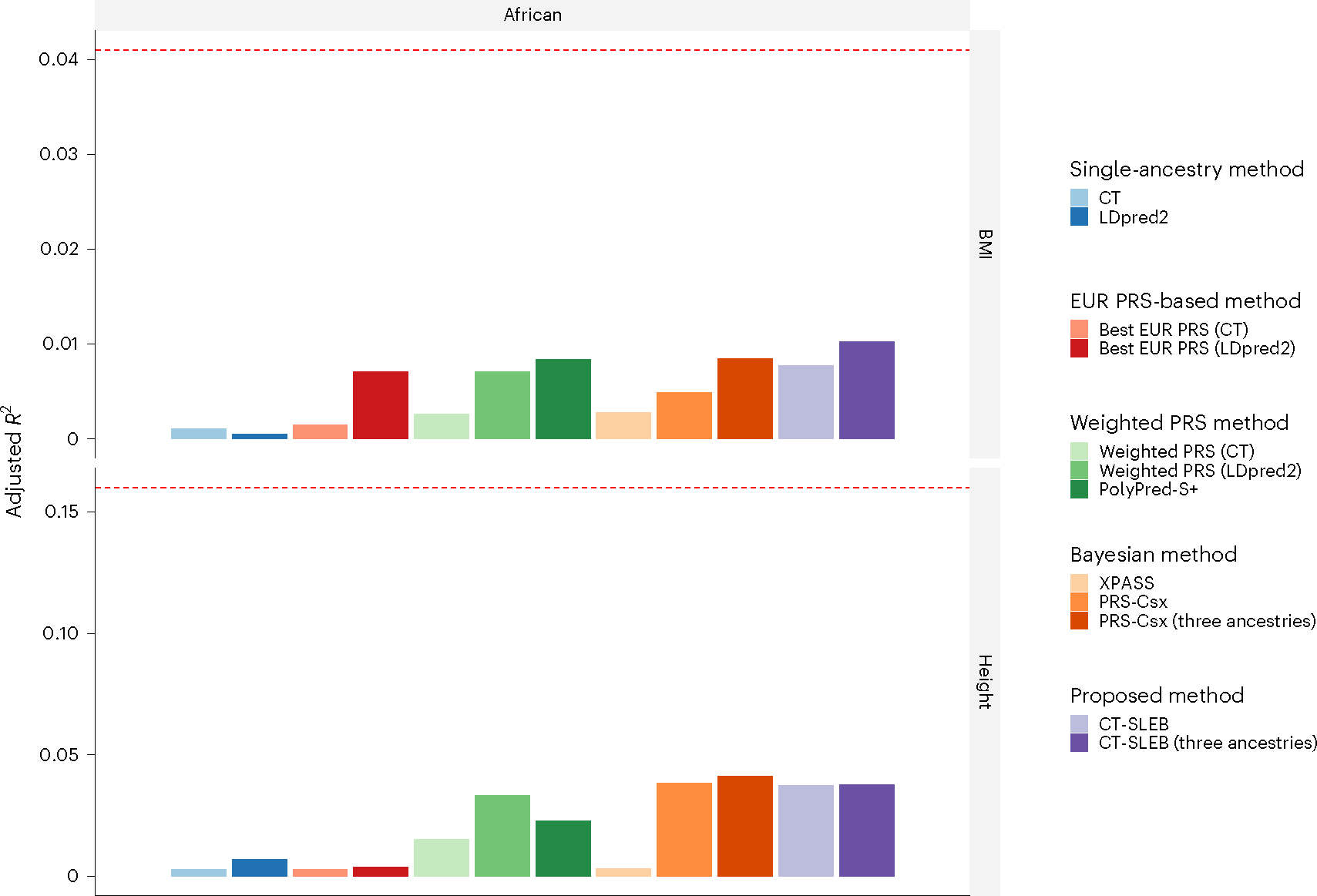
We used the GWAS summary statistics from three populations as the training data: EUR (n ≈ 48,000), AFR (n ≈ 22,000) and Latino (averaged n ≈ 15,000). The tuning and validation datasets are from UKBB data with AFR (n = 9,042). The tuning and validation were split half and half. The adjusted R² values were reported based on the performance of the PRSs in the validation dataset, while accounting for PCs 1–10, sex and age. The red dashed line represents the prediction performance of EUR PRSs generated using a single-ancestry method (best of CT or LDpred2) in the EUR population. Analyses were restricted to around 800,000 SNPs that were genotyped in the AoU dataset for different ancestries. All approaches were trained using data from the EUR and AFR populations. CT-SLEB and PRS-CSx were further evaluated using training data from three ancestries: AFR, EUR and Latino. From top to bottom, two traits are displayed in the following order: (1) BMI and (2) height.

To directly compare CT-SLEB and PRS-CSx, we reported the prediction performance R² (for continuous traits) or logit-scale variance (converted from the area under the receiver operating characteristic curve (AUC) for binary traits; Supplementary Note) between CT-SLEB and PRS-CSx, averaging over the 13 traits within each ancestry in 23andMe, GLGC and AoU data analyses (Supplementary Table 10). When only EUR and the target-population data were used for PRS construction, the averaged performance ratio between CT-SLEB and PRS-CSx was 144%, 88.5%, 103%, and 92.1% for AFR (primarily AA), EAS, Latino and SAS, respectively. When data from five ancestries or three ancestries (AoU) were used for PRS construction, the averaged performance ratio was 143%, 91.7%, 94.5%, and 89.6% for AFR (primarily AA), EAS, Latino and SAS, respectively.

Discussion

In summary, we proposed CT-SLEB as a powerful and computationally scalable method to generate optimal PRSs across ancestrally distinct groups using GWASs across diverse populations. We compared CT-SLEB’s performance with various simple and complex methods, in large-scale simulation studies and datasets. Results showed that no single method was uniformly the best across all scenarios, and it was important to generate PRSs using alternative methods across multiple ancestries. Encouragingly, CT-SLEB led to marked improvement in PRS performance compared with alternatives for AFR origin populations, where polygenic prediction has been most challenging. Computationally, CT-SLEB is an order of magnitude faster than a recently proposed Bayesian method, PRS-CSx³⁰, and can more easily handle much larger SNP contents and additional populations.

A unique contribution of our study is the evaluation of a variety of PRS methodologies in the unprecedentedly large and diverse datasets from the 23andMe, GLGC, AoU and UKBB GWASs. Our findings offer crucial insights into the future yield of emerging large multiancestry GWASs. Adult height is often used as a model trait to explore the genetic architecture of complex traits, and the potential for polygenic prediction. The standard CT method, when trained in ~2 million EUR individuals from 23andMe data, leads to a PRS with a prediction R² of approximately 0.276. Using LD-score regression, we estimated GWAS heritability of height using the 23andMe data to be 0.395, indicating that the PRS had achieved about 69.8% (0.276 of 0.395) of its maximum potential in the 23andMe EUR population. However, even with the best method and large 23andMe GWAS sample ($n_{\text{Latino}}\approx \mathrm{350,000}$ and $n_{\text{AFR}}\approx \mathrm{100,000}$), the highest prediction accuracy of height PRS for non-EUR populations was substantially lower compared with that of the EUR population (relative R² of ~0.48 (0.133 of 0.276) for AFR, 0.76 (0.210 of 0.276) for EAS, ~0.86 (0.237 of 0.276) for Latino, and ~0.80 (0.222 of 0.276) for SAS compared with that for EUR). The average relative R² (continuous traits) or logit-scale variance (binary traits) for AFR, EAS, Latino and SAS across the 13 evaluated traits was 0.50, 0.76, 0.77 and 0.79, respectively (Supplementary Table 11).

We observed similar patterns for other traits, including disease outcomes for which risk prediction is of the most interest. For CVD, for example, the CT method, trained in a sample of ~700,000 cases and ~1.3 million controls from the EUR population, produced a PRS with a prediction accuracy of an AUC of 0.65. For other populations with considerable but smaller sample sizes than the EUR population ($n_{\text{case}}/n_{\text{control}}=\mathrm{32,000}/66,$ for AA and $n_{\text{case}}/n_{\text{control}}=\mathrm{84,000}/\mathrm{270,000}$ for Latino populations), the AUCs for the best performing PRSs are close to 60% or lower. Furthermore, sample size is not the only factor for differential PRS performances across populations. For example, the performance of the best CVD PRS for Latino and SAS populations are similar, despite a much smaller sample size for the latter population. Collectively, these findings and additional simulation study results indicated that bridging the PRS performance gap across populations required greater parity in GWAS sample sizes.

Our simulation studies and data analyses showed that no single PRS method is uniformly most powerful in all settings. In the analysis of GLGC data, for example, CT-SLEB greatly improved PRS performance compared with PRS-CSx for the AFR population, but the opposite was true for the EAS population. The optimal method for generating PRSs depended on the underlying multivariate effect-size distribution of the traits across different populations. Although Bayesian methods, in principle, could generate optimal PRS under correct specification of underlying effect-size distribution^19,26,30,34, modeling this distribution in multiancestry settings could be challenging. In the analysis of lipid traits in GLGC, for example, we found that the Bayesian methods could not account well for the existence of large-effect SNPs in the AFR population owing to the inadequacy of the underlying model for the effect-size distribution. Conversely, the CT method and their extensions, although they do not require strong modeling assumptions about effect-size distribution, cannot optimally incorporate LD among SNPs. Our analysis revealed the advantages of alternative methods in different settings by comparing results across various complex traits with distinct architecture in terms of heritability, polygenicity, and number of clusters of distinct effect sizes^53,54. We thus advocate that, in future applications, researchers consider generating and evaluating a variety of PRSs obtained from complementary methods. As different PRSs may contain some orthogonal information, the best strategy could be to combine them using a final SL step, rather than choosing one best PRS.

Our study has several limitations. Although 23andMe datasets have extremely large sample sizes, the power of genetic risk prediction is likely to be blunted in this population, compared with other settings, owing to higher environmental heterogeneity. For example, a recent study⁵⁵ reported achieving prediction R² for height of ~41% for the EUR individuals within UKBB using a PRS developed with ~1.1 million individuals from UKBB (n = 400,000) and 23andMe (n = 700,000). In comparison, the PRS prediction R² for height that we achieved within the 23andMe EUR population was only ~30% despite doubling the sample size of the training dataset. However, we also noted that the heritability estimate in 23andMe $\left(h_{\mathrm{S}\mathrm{N}\mathrm{P}}^2=0.395\right)$) is substantially smaller than those previously reported^56,57 based on UKBB ($h_{\mathrm{S}\mathrm{N}\mathrm{P}}^2\approx 0.5-0.7$). When comparing the results across the two studies using prediction R² relative to the underlying heritability of the respective populations, we observed a significant gain in performance due to the increased sample size of the present study. Thus, although caution is needed to extrapolate the 23andMe study results to other populations, the relative performance of PRSs across different methods and different ancestry groups within this population is probably generalizable to other settings.

Although we conducted large-scale simulation across various scenarios, the simulated genotype data from HapGen2 may not fully reflect the levels of differentiation within and across ancestries due to limited haplotype data within the 1000 Genomes Project. Furthermore, our proposed method, as well as many existing methods, primarily focused on generating PRSs across ancestrally distinct populations. However, highly admixed populations such as the AFR and Latino origin in the USA could benefit from methods that explicitly account for individual-level estimates of admixture proportions⁵⁸. In addition, our method assumes that individual-level data are available for model tuning and validation, but this is not a fundamental limitation because summary statistics-based methods^59,60 could also be used in these steps. Moreover, although we observed a consistent increase of five ancestries CT-SLEB over two ancestries CT-SLEB in simulations, real data analyses did not show the same consistent pattern (Figs. 5–7), potentially owing to the complexity of underlying effect sizes across different ancestries compared with simulations.

In conclusion, we have proposed a new and computationally scalable method for generating powerful PRSs using data from GWASs in diverse populations. Furthermore, our simulation studies and data analysis across multiple traits involving large 23andMe Inc., GLGC, AoU and UKBB studies will provide unique insight into the potential outcomes of future GWASs in diverse populations for years to come.

Online content

Any methods, additional references, Nature Portfolio reporting summaries, source data, extended data, supplementary information, acknowledgements, peer review information; details of author contributions and competing interests; and statements of data and code availability are available at https://doi.org/10.1038/s41588-023-01501-z.

Methods

We assumed that there were $l=1,\dots L$ populations, with $l=1$ indexing the EUR population. We assumed that, for each population, summary statistics data from underlying GWASs were available in the form of $({\hat{\beta }}_{kl},{\hat{\sigma }}_{kl},P_{kl})$ for $k=1,2,\dots ,K_L$ SNPs, where $\hat{\beta },\hat{\sigma }$ and $P$ denote effect-size estimates, standard error of the mean (s.e.m.) values and $P$ values for individual SNPs, respectively. We also assumed that additional datasets were available for each target population, which can be split into tuning and validation sets. Our proposed CT-SLEB method contained three steps: (1) 2DCT; (2) EB procedure; and (3) SL algorithm, detailed in the following subsections.

CT

In this step, we extended the traditional CT to a 2D setting so that PRSs for a target population could be built using approximately independent SNPs that showed significant associations in at least one of the two populations (majority population and target population). The CT method has two components: clumping and thresholding. In the 2D setting where the lead SNPs might be informed by GWASs of either the EUR or the target population, it is unclear which reference sample is the most suited for LD clumping. After initial exploration of alternative approaches through simulation studies, we found that the most informative approach was to split the SNPs into two sets depending on which population they showed stronger signals and then to perform LD clumping for each set separately, based on the reference sample from respective populations. For the thresholding step, we selected SNPs based on two distinct thresholds for their respective P values in the two populations. As the optimal threshold for P-value selection depends on sample size^18,35,36, and sample sizes for GWASs across EUR and minority populations are highly differential, we anticipated (and confirmed through simulation studies) that a 2D approach for threshold selection was more optimal than using a single P-value threshold across both populations. The CT step details are as follows:

1. The clumping $r^2$-cutoff and base size of the clumping window size $w_{\mathrm{b}}$ vary across 0.01, 0.05, 0.1, 0.2, 0.5 and 0.8, and 50 kb and 100 kb, respectively. The clumping window size $w_{\mathrm{s}}$ is defined as $w_{\mathrm{b}}/r^2$ because LD is inversely proportional to the genetic distance between variants^20,61.

2. Select all variants with smaller $P$ values in EUR $\left(P_{k1}<P_{k2}\right)$ and clump based on $P_{k1}$ using LD estimates from EUR reference samples with selected $r^2$ and $w_{\mathrm{s}}$.

3. Select all variants with smaller P values in the target population $\left(P_{k2}<P_{k1}\right)$ and the population-specific SNPs and, then, clump based on $P_{k2}$ using LD estimates from the target-population’s reference samples with the same $r^2$ cutoff and $w_{\mathrm{b}}$.

4. Combine the postclumping variants from steps 2 and 3 as the candidate variant set.

5. Define two different P-value cutoffs $\left(P_{t1},P_{t2}\right)$ for the EUR and target populations. A variant was selected if $P_{k1}<P_{t1}$ or $P_{k2}<P_{t2}$. We allowed $P_{t1}$ and $P_{t2}$ to vary in the set: 5 × 10⁻⁸, 5 × 10⁻⁷, 5 × 10⁻⁶, …, 5 × 10⁻¹, 1.0. With the cross-combination of $P_{t1}$ and $P_{t2}$, a total of 81 different P-value cutoffs were applied.

6. With the cross-combination of $P_{t1},P_{t2},r^2$ and $w_{\mathrm{b}}$, a total of 972 PRSs $(6r^2\mathrm{t}\mathrm{h}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{h}\mathrm{o}\mathrm{l}\mathrm{d}\mathrm{s}\times 2w_{\mathrm{b}}\mathrm{w}\mathrm{i}\mathrm{n}\mathrm{d}\mathrm{o}\mathrm{w}\mathrm{s}\times 81\mathrm{v}\mathrm{a}\mathrm{l}\mathrm{u}\mathrm{e}\mathrm{t}\mathrm{h}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{h}\mathrm{o}\mathrm{l}\mathrm{d}\mathrm{s})$ were evaluated on the tuning dataset using estimated regression coefficients (${\hat{\beta }}_{k2}$ from the target-population’s GWAS.

EB to calibrate regression coefficients

In the CT step, we used ${\hat{\beta }}_{k2}$ from the target population to calculate PRS. However, ${\hat{\beta }}_{k2}$ can be noisy with small target-population GWAS sample sizes. Meanwhile, given the high genetic correlations across ancestries^38,39, effect sizes from other populations can calibrate regression coefficients for PRSs. Although we only used P values from GWASs for the EUR and the target populations for selecting SNPs in the CT step, the EB step leveraged GWASs from multiple populations. Suppose ${\stackrel{\mathbf{ˆ}}{\mathbf{u}}}_k=\left({\hat{u}}_{k1},\dots ,{\hat{u}}_{kL}\right)=({\hat{\beta }}_{k1}\sqrt{2f_{k1}\left(1-f_{k1}\right)},\dots ,{\hat{\beta }}_{kL}\sqrt{2f_{kl}\left(1-f_{kL}\right)})$ is the vector of the standardized effect size for the kth SNP in L different populations, with ${\stackrel{\mathbf{ˆ}}{\mathbf{s}}}_k^{\mathrm{*}}=\left(s_{k1},\dots ,s_{kL}\right)=\left({\hat{\sigma }}_{k1}\sqrt{2f_{k1}\left(1-f_{k1}\right)},\dots ,{\hat{\sigma }}_{kL}\sqrt{2f_{kL}\left(1-f_{kL}\right)}\right)$ being the vector of the corresponding s.e.m. values of ${\stackrel{\mathbf{ˆ}}{\mathbf{u}}}_k$. We assumed that ${\widehat{\mathbf{u}}}_k\mid u_k\approx N\left({\mathbf{u}}_k,{\mathrm{\Sigma }}_k\right)$, where ${\mathrm{\Sigma }}_k=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left\{s_k^2\right\}$ and given that the GWASs for different populations were independent. In addition, we assumed that the prior distribution of the mean of ${\widehat{\mathbf{u}}}_k$ is ${\mathbf{u}}_k\approx N\left(0,{\Sigma }_{\mathbf{0}}\right)$, which assumed that the effect size followed the strong negative selection model. By integrating the conditional and prior distribution, we obtained the marginal distribution of ${\widehat{\mathbf{u}}}_k$ as $N\left(0,{\Sigma }_0+{\mathrm{\Sigma }}_k\right)$. Supposing that the SNP set selected from the CT step had $K^{\mathrm{*}}$ variants overlapped across all the populations, we estimated the prior covariance matrix ${\Sigma }_0$ using the $K^{\mathrm{*}}$-overlapped variants shared across all populations as:

$${\stackrel{\mathrm{ˆ}}{\mathrm{\Sigma }}}_0=\frac{1}{K^{\mathrm{*}}-1}\sum _{k=1}^{K^{\mathrm{*}}} {\stackrel{\mathbf{ˆ}}{\mathbf{u}}}_k^T{\stackrel{\mathbf{ˆ}}{\mathbf{u}}}_k-{\mathrm{\Sigma }}_k.$$

We note that we ignored potential correlation across selected SNPs in this step, but the estimate was still expected to be consistent for ${\Sigma }_0$ which represents marginal variance–covariance matrices for effect sizes associated with an individual SNP across populations. Applying the Bayes formula, the posterior distribution of ${\mathbf{u}}_k$ became:

$${\mathit{u}}_k\mid {\stackrel{\mathit{ˆ}}{\mathit{u}}}_k\approx N\left({\stackrel{\mathrm{ˆ}}{\mathrm{\Sigma }}}_0{({\stackrel{\mathrm{ˆ}}{\mathrm{\Sigma }}}_0+{\mathrm{\Sigma }}_k)}^{-\mathbf{1}}{\stackrel{\mathit{ˆ}}{\mathit{u}}}_k,{\stackrel{\mathrm{ˆ}}{\mathrm{\Sigma }}}_0{({\stackrel{\mathrm{ˆ}}{\mathrm{\Sigma }}}_0+{\mathrm{\Sigma }}_k)}^{-1}{\mathrm{\Sigma }}_k\right).$$

The EB coefficients for the $k$th SNP were defined as:

$${\widehat{\mathit{\beta }}}_k^{\mathrm{E}\mathrm{B}}=F_k{\stackrel{\mathrm{ˆ}}{\mathrm{\Sigma }}}_0{({\stackrel{\mathrm{ˆ}}{\mathrm{\Sigma }}}_0+{\mathrm{\Sigma }}_k)}^{-1}{\stackrel{\mathbf{ˆ}}{\mathbf{u}}}_k,$$

where ${\widehat{\mathit{\beta }}}_k^{\mathrm{E}\mathrm{B}}$ is an $L\times 1$ vector for the posterior effect size of the $k$th SNP for each of the $L$ populations and $F_k=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}{\left\{\frac{1}{\sqrt{2f_{kl}\left(1-f_{kl}\right)}}\right\}}_{L\times L}$ is the scaling matrix to scale effect sizes from the standardized scale back to the original scale. Preliminary simulation studies indicated that the EB step of effect-size calibration led to distinct improvement in PRS performance (compared with using effect-size estimates from the target population) irrespective of all other steps.

To save computational time, we estimated ${\stackrel{\mathrm{ˆ}}{\mathrm{\Sigma }}}_0$, based on the SNP set that gives the best PRS in the CT step and applied the same ${\stackrel{\mathrm{ˆ}}{\mathrm{\Sigma }}}_0$ to derive the EB-calibrated effect sizes for all PRSs corresponding to a cross-combination of $P_{t1},P_{t2},r^2$ cutoff and $w_{\mathrm{b}}$. Using EB-calibrated effect sizes, we computed 972 PRSs for each population $(6r^2\mathrm{t}\mathrm{h}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{h}\mathrm{o}\mathrm{l}\mathrm{d}\mathrm{s}\times 2w_{\mathrm{b}}\mathrm{w}\mathrm{i}\mathrm{n}\mathrm{d}\mathrm{o}\mathrm{w}\mathrm{s}\times 81\mathrm{v}\mathrm{a}\mathrm{l}\mathrm{u}\mathrm{e}\mathrm{t}\mathrm{h}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{h}\mathrm{o}\mathrm{l}\mathrm{d}\mathrm{s})$. In all analyses, we computed the 1,944 PRSs using EB-calibrated effect sizes of the target population and EUR. When more than two ancestries were involved, we used data from all populations to derive EB estimates (Supplementary Note). However, to save computational time at the SL step, we derived the final PRS for the target population by only incorporating the 1,944 PRSs derived for the larger EUR population and the target population. All 1,944 PRSs were used as input for the SL step to predict the outcome for the target population. As many PRSs are highly correlated, we filtered out redundant ones with pairwise correlations >0.98. In the simulations, 369 of the 1,944 PRSs were kept on average after the filtering.

Superlearning

We combined all PRSs generated from the previous steps into an input dataset and trained them on the tuning dataset to predict the outcome Y. The SL algorithm generated an optimally weighted combination from a set of distinct prediction algorithms^40–42,62 (Supplementary Note). The set of prediction algorithms could be self-designed or chosen from classical prediction algorithms, for example, Lasso⁴⁴, ridge regression⁴⁵ and neural networks⁴⁶. We used three different prediction algorithms implemented in the SuperLearner package⁴³ to generate the SL estimate: Lasso⁴⁴, ridge regression⁴⁵ and neural networks⁴⁶. For binary traits, as ridge regression was currently not supported by the SuperLearner package, we used Lasso and neural network in data analysis. To use AUC as the objective function, we used the flag ‘method = method.AUC’ in the SuperLearner package.

Simulation

Large-scale, multiancestry genotype data were generated using HAPGEN2 (v.2.1.2) (ref. 63) mimicking the LD of EUR, AFR, Americas (AMR), EAS and SAS. The 1000 Genomes Project (phase 3) (ref. 51) served as the reference panel, including 503 EUR, 661 AFR, 347 AMR, 504 EAS and 489 SAS subjects. Biallelic SNPs with mean allele frequency (MAF) > 0.01 in any of the populations were kept, resulting in ~8.6 million SNPs for EUR, ~14.8 million SNPs for AFR, ~9.8 million SNPs for AMR, ~7.6 million SNPs for EAS and ~9.0 million SNPs for SAS. The genotype data were generated with a total of ~19.2 million SNPs. The set of simulated variants for all five ancestries was the same. Population-specific SNP proportions ranged from 2.92% for AMR to 43.84% for AFR, respectively (Supplementary Fig. 22). SNPs with MAF < 0.01 in a population were excluded from PRS calculation owing to unstable LD estimation. A total of 120,000 independent subjects were simulated for each of the populations.

Trait values were generated by selecting causal SNPs randomly across the genome, with the causal SNP proportion set to 0.01, 0.001 or 5 × 10⁻⁴. We considered two models for heritability distribution: (1) constant common SNP heritability; and (2) constant per-SNP heritability which implied that the total heritability was proportional to the number of common SNPs. We also considered three negative selection patterns: strong, mild and no negative selection.

We denoted $u_{kl}$ as the standardized effect size for the $k$th causal SNP of the $l$th population. Under strong negative selection and constant heritability model, standardized effect sizes were drawn from a multivariate normal distribution of the form:

$$u_{kl}\approx N\left(0,\frac{h^2}{C_l}\right),\mathrm{c}\mathrm{o}\mathrm{v}\left(u_{k{l}_1},u_{k{l}_2}\right)=\frac{\rho h^2}{\sqrt{C_{l_1}{C}_{l_2}}},$$

where $C_l$ is the number of causal SNPs with $\mathrm{M}\mathrm{A}\mathrm{F}>0.01$ in the $l\text{th}$ population, the heritability $h^2$ associated with common SNPs for each population is set to 0.4, and the genetic correlation $\rho$ is set to 0.8. We then generated the phenotype using linear model of the form $Y_{il}={\sum }_{k=1}^{C_l} \frac{G_{ikl}}{\sqrt{2f_{kl}\left(1-f_{kl}\right)}}{u}_{kl}+{ϵ}_{il}$ for the $i$th subject in the $l$th population, where $f_{kl}$ is the effect allele frequency for the $k$th causal SNP in the $l$th population. The error terms were generated as ${ϵ}_{il}\approx N\left(0,1-h^2\right)$. We also considered mild negative selection $(u_{kl}^2\propto {\left[f_{kl}\left(1-f_{kl}\right)\right]}^{0.75})$ and no negative selection $\left(u_{kl}^2\propto \left[f_{kl}\left(1-f_{kl}\right)\right]\right.$) scenarios (Supplementary Note). Finally, we assumed total heritability of all ~19 million SNPs to be 0.4 across all populations, but with common SNP heritability varying proportionally to their number within each population. The model assumed equal per-SNP heritability across populations, leading to the common SNP heritability values of 0.32, 0.21, 0.16, 0.19 and 0.17 for AFR, AMR, EAS, EUR and SAS, respectively. Genetic correlation was set to 0.8 or 0.6.

We set the training sample sizes for each target population to 15,000, 45,000, 80,000 or 100,000. GWAS summary statistics for each population were generated based on the training samples using PLINK v.1.90 with the command ‘--linear’. We fixed the EUR sample size at 100,000 and simulated the tuning and validation dataset of 10,000 for each target population. The final prediction R² is the average of ten independent simulation replicates. For CT-SLEB and PRS-CSx, incorporating data across all five ancestries, we assumed non-EUR training sample sizes to be equal to the target population’s.

Existing PRS methods

The CT method selects clumped SNPs with varying P-value thresholds and chooses an optimal PRS based on its performance on the tuning dataset. We implemented CT using PLINK v.1.90 (ref. 64) with the clumping step command ‘--clump --clump-r2 0.1 --clump-kb 500’. We estimated LD based on 3,000 randomly selected unrelated subjects from the training dataset for each population. We set candidate P-value thresholds as 5 × 10⁻⁸, 1 × 10⁻⁷, 5 × 10⁻⁷, 1 × 10⁻⁶, …, 5 × 10⁻¹ and 1.0 and we used the PLINK command ‘--score no-sum no-mean-imputation’ for computing PRS. The optimal P-value threshold is determined based on prediction R² on the tuning dataset.

The LDpred2 method infers SNP effect sizes by a shrinkage estimator, combining GWAS summary statistics with a prior on effect sizes while leveraging LD information from an external reference panel. LDpred2 is implemented using the R package ‘bigsnpr’²⁶. The tuning parameters were: (1) the proportion of causal SNPs, with candidate values set to sequences of length 17 that are evenly spaced on a logarithmic scale from 10⁻⁴ to 1; (2) per-SNP heritability, with candidate values set to 0.7, 1 or 1.4× the total heritability estimated by LD-score regression divided by the number of causal SNPs; and (3) the ‘sparse’ option, which was set to ‘yes’ or ‘no’ (the ‘sparse’ option sets some weak effects to zero). The method selected tuning parameters based on the performance on the tuning dataset.

The EUR PRS based on CT or LDpred2 was built using a EUR training dataset from the EUR population and estimated tuning parameters based on the EUR tuning sample. When evaluating the EUR PRSs in the target population, we excluded the SNPs that do not exist in the target population.

Weighted PRS linearly combined the CT or LDpred2 PRSs generated from the EUR and target populations. The weights for EUR PRSs and for target-population PRSs are estimated using the target-population’s tuning dataset through a linear regression. We implemented weighted PRSs using R v.4.0.0.

PolyPred-S+ consists of a PolyFun-pred predictor trained on the EUR population and two SBayesR predictors using training data from the EUR and target populations, respectively. On a target-population tuning dataset, PolyPred-S+ performed non-negative least squares regression to compute the mixture weights and linearly combined the predictors. PolyFun-pred leveraged genome-wise functional annotations for prior causal probabilities, fed into the SuSiE fine-mapping method for the posterior causal effect estimation. SBayesR estimated posterior tagging effects with a finite normal mixture prior on effect sizes. For PolyFun-pred, we used precomputed prior causal probabilities provided by the authors, extracted LD information using the EUR population in the 1000 Genomes Project (phase 3) and assumed 10 causal SNPs per locus. Using GCTB (2.03 beta version), we trained SBayesR with the sparse shrunk LD matrix for HapMap3 variants published by the SBayesR authors. Currently, the shrunk LD matrix is available only for EUR populations. Therefore, both SBayesR predictors for EUR and target populations used the shrunk LD matrix for EUR. Model parameters and MCMC (Markov Chain Monte Carlo) settings followed the same way as the PolyPred-S+ authors’ UKBB simulations.

XPASS leverages the genetic correlation between the target and EUR populations, assuming a bivariate normal distribution with nonzero covariance for effect-size pairs corresponding to the same SNP in both populations. It can incorporate population-specific covariates as fixed effects to improve weight estimation accuracy. We extracted the top 20 PCs from the reference genome for each population as the covariates. When estimating LD matrices, ancestry-specific reference data were inputted. LD matrices were estimated based on EUR LD blocks for all datasets, because the XPASS package offered only EUR and EAS options.

PRS-CSx estimated population-specific SNP effect sizes using a Bayesian framework with continuous shrinkage priors to jointly model GWAS summary statistics from multiple populations. In addition, PRS-CSx conducted a step similar to weighted PRSs, linearly combining PRSs based on the posterior effect sizes from EUR and target populations, with weights estimated based on the target-population’s tuning dataset. We implemented PRS-CSx following https://github.com/getian107/PRScsx. We set the gamma-gamma prior hyperparameters a and b to default values of 1 and 0.5, respectively. Furthermore, the parameter $\varphi$ varied over the default set of values 10⁻⁶, 10⁻⁴, 10⁻² and 1, with optimal $\varphi$ being determined based on tuning dataset performances.

Runtimes and memory usage comparison

We compared the computation time and memory usage of CT-SLEB (two ancestries and five ancestries) and PRS-CSx (two ancestries and five ancestries) based on their performance on chromosome 22, assuming AFR as the target population. All analyses used a single core with an Intel E5–26840v4 CPU. Performance was averaged over 100 replicates. The training dataset consisted of GWAS summary statistics for AFR (n_GWAS = 15,000) and EUR (n_GWAS = 100,000) populations. Tuning and validation datasets each contained 10,000 subjects. For the five ancestries analyses, training GWAS sample sizes for AMR, EAS and SAS were set to 15,000 each.

23andMe data analysis

The individuals in our analyses are part of the 23andMe participant cohort. All participants provided informed consent and answered surveys online according to our human subject protocol, reviewed and approved by Ethical and Independent Review Services, a private institutional review board (http://www.eandireview.com). Detailed information about genotyping, quality control, imputation, removing related individuals and ancestry determination has been provided in Supplementary Note. Participants were included in the analysis based on consent status as checked when data analyses were initiated.

Our analysis involved five ancestries (AA, EAS, EUR, Latino and SAS), and included two continuous and five binary traits: (1) heart metabolic disease burden; (2) height; (3) any CVD; (4) depression; (5) migraine diagnosis; (6) morning person; and (7) SBMN. Data for each population were randomly split into training, tuning and validation datasets (70%, 20% and 10%, respectively), with detailed sample size in Supplementary Table 3. We performed GWASs for the seven traits using each population’s training dataset, adjusting for PCs 1–5, sex and age with standard quality control procedures (Supplementary Note). SNPs with MAF > 0.01 in at least one population were kept in the analyses. We further restricted analyses to SNPs that were on HM3 + MEGA chips array with ~2.0 million SNPs. LDSC v.1.01 (ref. 52) was used to estimate the heritability with the EUR population GWAS summary statistics for the seven traits. LD scores were estimated using the 503 unrelated EUR samples from the 1000 Genomes Project. Heritability analyses were limited to EUR populations due to insufficient sample size in non-EUR populations for stable LD-score regression estimates.

We compared PRS prediction performance for ten methods: CT, LDPred2, best EUR PRS based on CT and LDpred2, weighted PRS based on CT and LDpred2, PolyPred-S+, XPASS, PRS-CSx (using EUR and target-population data or all five populations) and CT-SLEB (using EUR and target-population data or all five populations). As individual-level data were unavailable in the training step, we used the 1000 Genomes Project (phase 3) reference data to estimate LD for each population. Specifically, AFR and AMR from the 1000 Genomes Project served as references for the AA and Latino populations in 23andMe, respectively. PRS prediction performance was reported based on the independent validation dataset, separate from training and tuning datasets. To calculate the adjusted R² for continuous traits, we first regressed the traits on covariates and then evaluated PRS performance by predicting residualized trait values. The adjusted AUC for binary traits was calculated using roc.binary function in the R package RISCA v.1.01 (ref. 65).

GLGC data analysis

We obtained GWAS summary statistics of four blood lipid traits from publicly available GLGC databases (http://csg.sph.umich.edu/willer/public/glgc-lipids2021/results/ancestry_specific). UKBB data were removed from the GWAS summary statistics. The details of study design, genotyping, quality control and GWASs have been described elsewhere³⁷. Training data were available for the four blood lipid traits, LDL-cholesterol, HDL-cholesterol, log(TGs) and TC, from five different ancestries: EUR, AFR (primarily AA), Latino, EAS and SAS (Supplementary Table 8). Tuning + validation data from UKBB dataset were from EUR, AFR, EAS and SAS ancestries (Supplementary Table 9). Details of ancestry prediction for UKBB have been described in Supplementary Note. As a result of poor ancestry classification and low sample size, the Latino population was not evaluated using UKBB data. The implementation of the ten different PRS approaches followed the same steps as in the 23andMe data analyses. We used the 1000 Genomes Project (phase 3) reference data to estimate the LD for each population. The adjusted R² values were adjusted by sex, age and genetic PCs 1–10.

AoU data analysis

The individuals included in our analyses were part of the AoU participant cohort. All these individuals’ information has been collected according to the AoU Research Program Operational Protocol (https://allofus.nih.gov/sites/default/files/aou_operational_protocol_v1.7_mar_2018.pdf).

Detailed information about genotyping, ancestry determination, quality control and removing related individuals can be found in the AoU Research Program Genomic Research Data Quality Report (https://www.researchallofus.org/wp-content/themes/research-hub-wordpress-theme/media/2022/06/All%20Of%20Us%20Q2%202022%20Release%20Genomic%20Quality%20Report.pdf).

We analyzed three ancestries (EUR, AFR and Latino/AA) and two continuous traits (height and BMI). GWASs for these traits were performed using unrelated samples for each population, adjusting for PCs 1–16, sex and age, with quality control steps provided by the AoU platform.

The AoU platform provided whole-genome sequencing (WGS) data and array data. Although the WGS data have fewer samples than array data (98,590 WGS and 165,127 array samples, 22 June 2022 version), quality control information and relatedness of samples were provided only within the WGS data. For GWASs with respect to each population, we performed sample-level quality control within the WGS data. Due to computation burden, analyses were conducted using array SNPs with subjects passing the WGS data quality control. SNPs with MAF > 0.01 in at least one of the three populations were kept, whereas analyses were restricted to SNPs available on HM3 + MEGA chips array. As the analyses were constrained to array data, all analyses involved up to 800,000 SNPs (Supplementary Table 4). We used the reference data from the 1000 Genomes Project (phase 3) to estimate the LD for each population.

Tuning + validation data from UKBB dataset were from EUR and AFR ancestries. The Latino population was not evaluated on UKBB for the same reason as in GLGC analyses. The implementation of the ten different PRS approaches followed the same steps as the 23andMe data analyses. The adjusted R² was adjusted by sex, age and PCs 1–10.

Extended Data

Extended Data Fig. 1 |. CT-SLEB detailed flowchart.

The method contains three major steps: 1. Two-dimensional clumping and thresholding; 2. Empirical-Bayes procedure for utilizing genetic correlations of effect sizes across populations; 3. Super-learning model for combining PRSs under different tuning parameters. The tuning dataset is used to train the super learning model. The final prediction performance is evaluated based on an independent validation dataset. For continuous traits, the prediction is evaluated using R² obtained from the linear regression between outcome and PRS after adjusting for covariates (Methods). For binary traits, the prediction is evaluated using the area under the ROC curve (AUC).

Extended Data Fig. 2 |. Performance of CT-SLEB with different tuning and validation sample sizes.

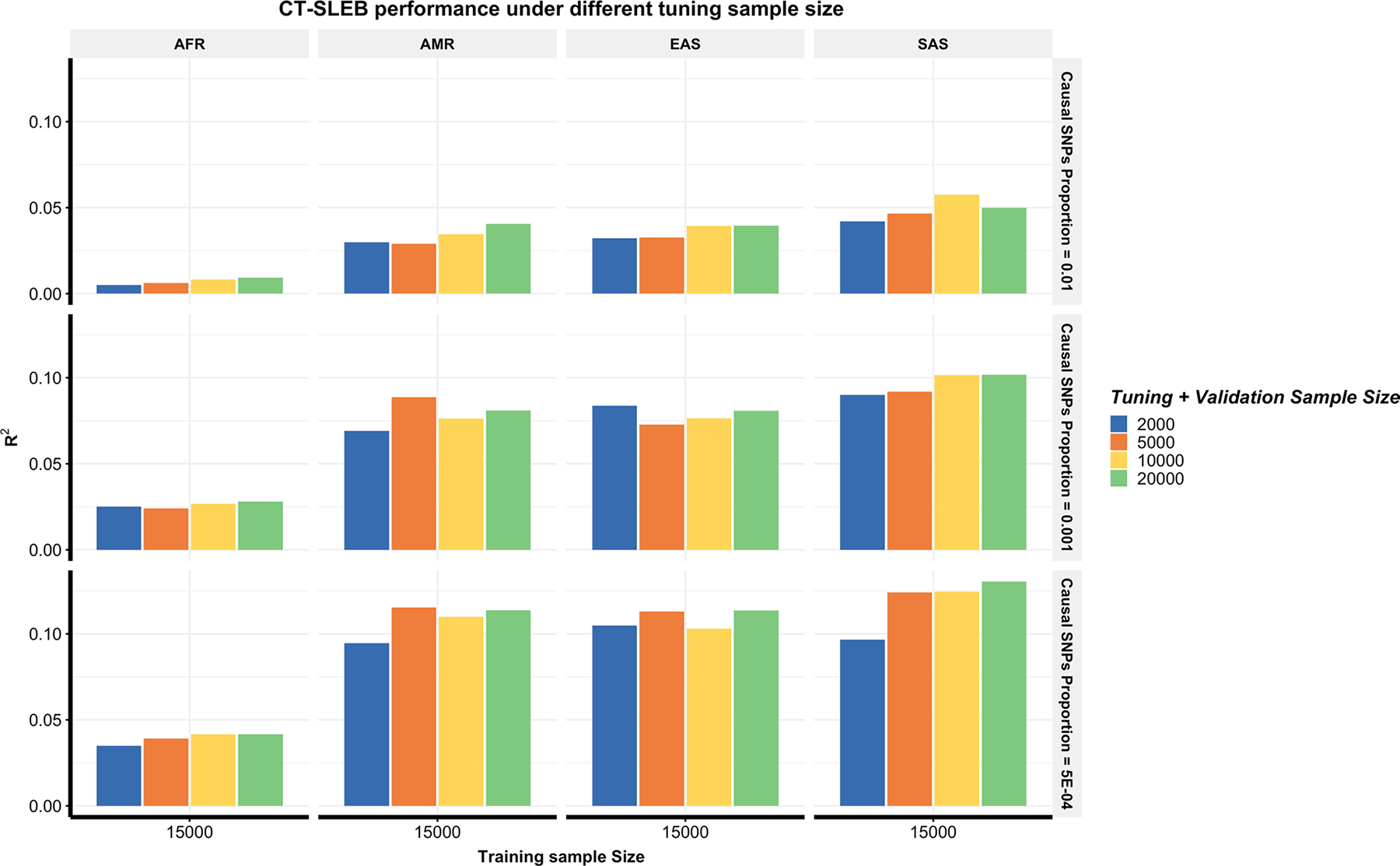
The total tuning and validation sample size is set as 2000, 5000, 100,000 and 200,000 with half for tuning and half for validation. Analyses are conducted in the multiancestry setting under a strong negative selection model. The training sample size for the AFR population is 15,000. The training sample size for EUR is 100,000. The sample size for the tuning dataset and validation for each population is fixed at 10,000, respectively. Common SNP heritability is assumed to be 0.4 across all populations and effect-size correlation is assumed to be 0.8 across populations. The causal SNPs proportion is varied across 0.01 (top panel), 0.001 (medium panel), or 5 × 10⁻⁴ (bottom panel). The final prediction R² is reported as the average of ten independent simulation replicates.

Data availability

Simulated genotype data for 600,000 subjects from 5 ancestries are at: https://dataverse.harvard.edu/dataset.xhtml?persistentId=doi:10.7910/DVN/COXHAP. GWAS summary level statistics for five ancestries from GLGC are at: http://csg.sph.umich.edu/willer/public/glgc-lipids2021/results/ancestry_specific. GWAS summary statistics for three ancestries are from AoU at: https://dataverse.harvard.edu/dataset.xhtml?persistentId=doi:10.7910/DVN/FAWEQK. The PRSs developed for six traits for GLGC and AoU have been released through the PGS Catalog (https://www.pgscatalog.org) with publication ID PGP000489 and score IDs PGS003767–PGS003848. The 23andMe GWAS summary statistics for the top 10,000 genetic markers associated with 3 traits (height, morning person and SBMN) across 5 diverse ancestries have been made available as Supplementary Data and are also available at: https://dataverse.harvard.edu/dataset.xhtml?persistentId=doi:10.7910/DVN/3NBNCV. The full GWAS summary statistics and the final PRSs for these three traits (height, morning person and SBMN) are available through 23andMe, Inc. to qualified researchers under an agreement with 23andMe, Inc. that protects the privacy of the 23andMe participants. Please visit research.23andme. com/dataset-access for more information and to apply for access to the data. The summary statistics for the four other traits used in the paper (any CVD, heart metabolic disease burden, depression and migraine) will not be made available because of 23andMe’s business requirements. Participants provided informed consent and participated in the research online, under a protocol approved by the external AAHRPP-accredited institutional review board, Ethical & Independent Review Services.