Skip to main content
PMC home page
IEEE Open Journal of Engineering in Medicine and Biology logoLink to IEEE Open Journal of Engineering in Medicine and Biology
. 2024 Jan 26;5:157–162. doi: 10.1109/OJEMB.2024.3358989

The Contribution of Secondary Particles Following Carbon Ion Radiotherapy to Soft Errors in CIEDs

Yudai Kawakami 1, Makoto Sakai 2,✉, Hiroaki Masuda 3, Masami Miyajima 3, Takao Kanzaki 3, Kazutoshi Kobayashi 4, Tatsuya Ohno 2, Hiroshi Sakurai 1
PMCID: PMC10939317  PMID: 38487101

Abstract

Introduction: While carbon ion radiotherapy is highly effective in cancer treatment, it has a high risk of causing soft error, which leads to malfunctions in cardiac implantable electrical devices (CIEDs). To predict the risk of malfunction prior to treatment, it is necessary to measure the reaction cross-sections and contributions to the soft error of secondary particles generated during treatments. Methods: A field-programmable gate array was used instead of CIEDs to measure soft errors by varying the energy spectrum of secondary particles. Results and discussion: The reaction cross-sections measured for each secondary particle were 3.0 × 10−9, 2.0 × 10−9, 1.3 × 10−8, and 1.5 × 10−8 [cm2/Mb] for thermal neutrons, intermediate-energy neutrons, high-energy neutrons above 10 MeV, and protons, respectively. The contribution of high-energy neutrons was the largest among them. Our study indicates that to reduce the risk of soft errors, secure distance and appropriate irradiation directions are necessary.

Keywords: Carbon ion radiotherapy, cardiac implantable electrical device (CIED), cross-section, neutron, soft error

I. Introduction

The number of radiotherapy treatments for patients with cardiac implantable electronic devices (CIEDs), such as pacemakers and defibrillators, is continuously increasing annually [1]. Notably, there is a risk of CIED malfunction caused by radiotherapy [2], [3], [4], [5], [6], [7]. For example, there have been reports of malfunctioning Implantable cardioverter-defibrillators causing ventricular tachycardia, necessitating cardiopulmonary resuscitation [8]. In other cases, the malfunctioning of pacemakers resulted in premature atrial pacing, causing symptoms, such as chest agony, shortness of breath, and hypotension, which required intensive care [9]. CIED malfunctions are believed to be caused by soft errors in their random-access memory [10]. In 1998, the American Association of Physicists in Medicine considered the risk of soft errors in relation to the cumulative dose to CIEDs and set a threshold of 2 Gy [11]. However, the American Society for Radiation Oncology guidelines for radiotherapy in patients with CIEDs suggest that there might be no association between CIED malfunction and cumulative dose [12]. Daniel et al. confirmed no correlation between soft errors and cumulative dose, suggesting an association with neutrons [13]. With the development of space exploration and automated driving, studies on soft errors have increased. Iwashita et al. measured the cross-section of soft errors for 10–800 MeV neutrons using field-programmable gate arrays (FPGAs) [15], [18]. Currently, neutrons originating from cosmic rays are considered a source of naturally occurring soft errors. Therefore, it is highly likely that neutrons also cause soft errors in CIEDs during radiation therapy.

The possibility of device malfunction due to computed tomography is not clinically significant [14]. Regarding radiation therapy, guidelines state that the risk of soft errors is high for high-energy X-ray therapy, particle therapy, and boron neutron capture therapy because of the large number of generated neutrons. Despite this, the quantitative risk of soft errors caused by radiotherapy has not been sufficiently described, and no relationship with neutron energy or quantity has been established. In particular, carbon-ion radiotherapy (CIRT) produces large quantities of high-energy neutrons as secondary radiation through a nuclear reactions of a primary carbon beam; thus, risks must be assessed to ensure safe treatment.

In this study, we measured the soft errors in CIRT using an FPGA and evaluated the cross-section and the contribution of secondary particles. By evaluating the contribution of each secondary particle, it should be possible to assess the risk of soft errors occurring during treatment and devise strategies for efficiently shielding against secondary particles.

II. Materials and Methods

A. FPGAs

FPGAs are integrated circuits that can be configured by the purchaser or designer [15]. They are widely used in electronic devices, including CIEDs, and contain numerous radiation-sensitive memory units. FPGAs have also been used to measure soft errors caused by cosmic rays in electronic devices [15], [17]. Thus, we used an FPGA as an alternative to CIEDs to measure the number of soft errors generated.

B. The Soft Error Principle

The process of soft error generation differs for high- (above 10 MeV) and low-energy neutrons (thermal neutron). High-energy neutrons cause spallation reactions with the Si atoms in the device, resulting in charge generation. The accumulation of charges can invert memory and lead to soft errors [15], [16]. For low-energy neutrons, the boron neutron capture reaction (10B(n, α)7Li) generates charged particles. High-energy ion particles also generate high-density ionization, directly or indirectly.

If a memory that is directly related to the operation of CIEDs is inverted, device behavior may become unpredictable, such as temporary errors in pacing or resetting to backup settings [16].

C. Soft Error Measurement

Soft errors generated via carbon-beam irradiation were measured using an FPGA (Cmod s7, Digilent). First, 9.93 Mb of data were written onto the FPGA using Vivado 2019.2 (Xilinx). The FPGA was then placed in a phantom and irradiated with a carbon beam for 10 min. The number of soft errors or memory inversions was determined by comparing the post-irradiation memory data with written data.

D. Classification of Secondary Particles

Neutrons are considered the primary source of soft errors, especially at energies above 10 MeV [15], [17], [18]. However, previous studies have reported non-negligible contributions from thermal neutrons [1], [17], [19]. Protons have also been found to cause soft errors [13], [20]. Therefore, we evaluated four secondary particles as contributors to the soft errors, including thermal neutrons (1–0.5 eV), intermediate-energy neutrons (0.5 eV–10 MeV), high-energy neutrons (10 MeV), and protons.

E. Experimental Setup

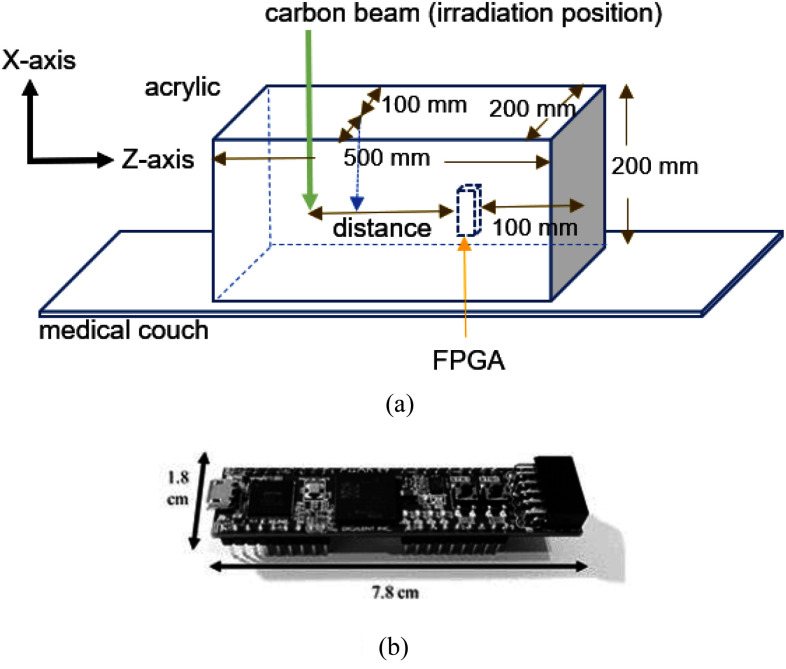
The experiments were performed at the Gunma University Heavy Ion Medical Center, Japan. We used a pencil beam with a Gaussian distribution of σ = 11 mm, energy of 290 MeV/u, and beam intensity of 1.0 × 109 particles/s (same as the clinical intensity). The phantom used in the experiment was a 200 mm × 200 × 500 mm3 PMMA block (Fig. 1). The phantom density is homogeneous, and the density is 1.18 g/cm3. A cavity sufficiently large to fit the FPGA board was positioned 100 mm from the edge of the phantom. The FPGA was placed at the center and connected to a personal computer located outside the irradiation room.

Fig. 1.

Fig. 1.

Open in a new tab

Experimental setup (a) and FPGA board used (b).

F. Experiment With Distance Variation

The irradiation position and distance from the FPGA were varied from 50 mm to 200 mm at 10 mm intervals. The number of memory inversions was measured for each condition after irradiation for 10 min; approximately 10 measurements were performed for each condition.

G. Radiation Quality Variation

The quality of the secondary particles irradiated toward the FPGA was altered using different materials on the front and back. Polyethylene containing 10% 10B2O3 (P.E. with 10B), Fe, Ni, Pb, and graphite plates were used to change the radiation quality. Soft-error measurements were performed under nine different conditions (Table I). Approximately 7–10 repeated measurements were performed for each condition with 10 min of irradiation. The distance between the irradiation position and the FPGA was fixed at 80 mm.

TABLE I. Experimental Conditions.

Condition number Front of FPGA Back of FPGA
0 PMMA 80 mm PMMA 100 mm
1 PMMA 40 mm, Al 30 mm, and PMMA 10 mm Fe 10 mm
2 PMMA 50 mm, Fe 20 mm, and PMMA 10 mm Fe 20 mm
3 PMMA 50 mm and Pb 30 mm PMMA 50 mm
4 PMMA 50 mm, Fe 20 mm, and Ni 10 mm Ni 10 mm and Fe 20 mm
5 PMMA 40 mm, Graphite 20 mm and PE with 10B 20 mm Ni 20 mm and Fe 40 mm
6 PMMA 25 mm, Al 5 mm, and PE with 10B 50 mm PMMA 50 mm
7 PMMA 30 mm, Ni 20 mm, and PE with 10B 30 mm PMMA 50 mm
8 PMMA 30 mm and Fe 50 mm Fe 40 mm
Open in a new tab

“Front” and “Back” indicate that the material is placed between the irradiation position and the FPGA or the opposite side of the irradiation position. They are described in the order of irradiation position.

H. Monte Carlo Simulation

A Monte Carlo simulation was performed to calculate the distribution of secondary particles using PHITS [21]. The experimental setup was reproduced to calculate the neutron and proton fluxes at the FPGA location. The energy was set to 290 MeV/u, the source nuclide was 12C, the beam shape was a Gaussian distribution with σ = 11 mm, and the number of particles generated was set to 1 × 107. The library of cross- sections was JENDL-4.0 [22]. The number of histories was set so that the calculation error was less than 5%.

I. Multivariate Analysis

A multivariate analysis was performed to evaluate the contribution of each secondary particle to soft error generation. The soft error number is expressed by (1). The data in Figs. 3, 4, and 5 were used in the analysis.

I.

where, y indicate the expected number of soft errors. β1, β2, β3, and β4 represent the cross-sections of thermal neutrons, intermediate-energy neutrons, high-energy neutrons, and protons, respectively. Meanwhile, x1, x2, x3, and x4 indicate the number of thermal neutrons, intermediate-energy neutrons, high-energy neutrons, and protons, respectively.

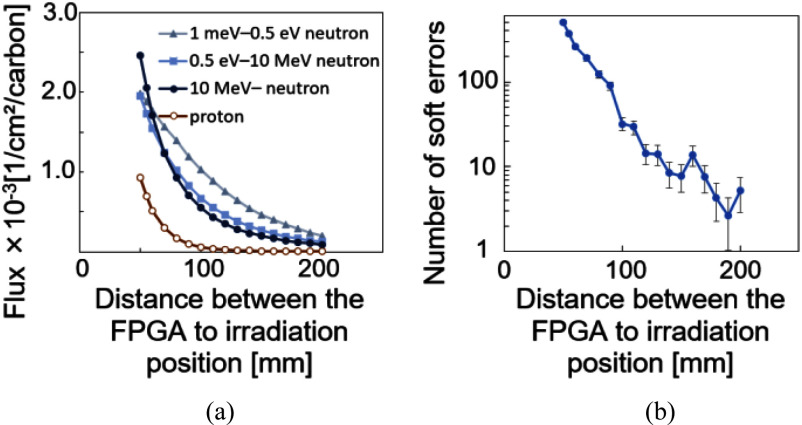
Fig. 3.

Fig. 3.

Open in a new tab

Secondary particle distribution calculated via PHITS simulation (a), and the number of soft errors generated with varying distances from the irradiation position (b). Error bars indicate standard deviation.

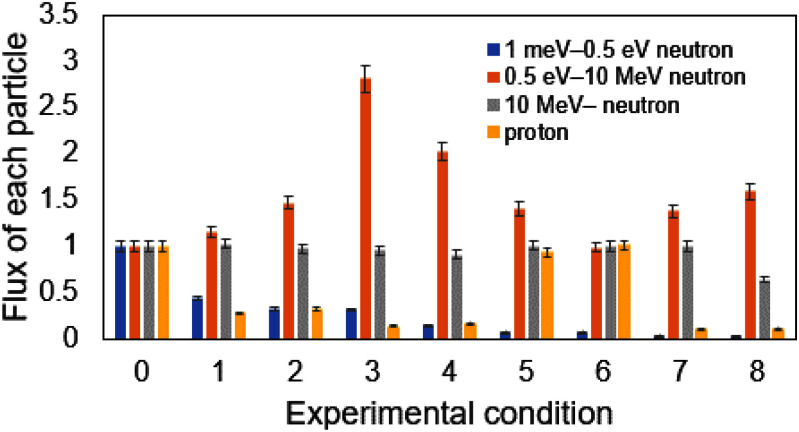
Fig. 4.

Fig. 4.

Open in a new tab

Radiation quality with each condition normalized with condition 0, in which only acrylic was used. Blue: thermal neutrons (1 meV–0.5 eV), Orange: intermediate-energy neutrons (0.5 eV–10 MeV), Gray: high-energy neutrons (>10 MeV), and Yellow: protons. The error bars indicate the error considering error propagation as a ratio to condition 0.

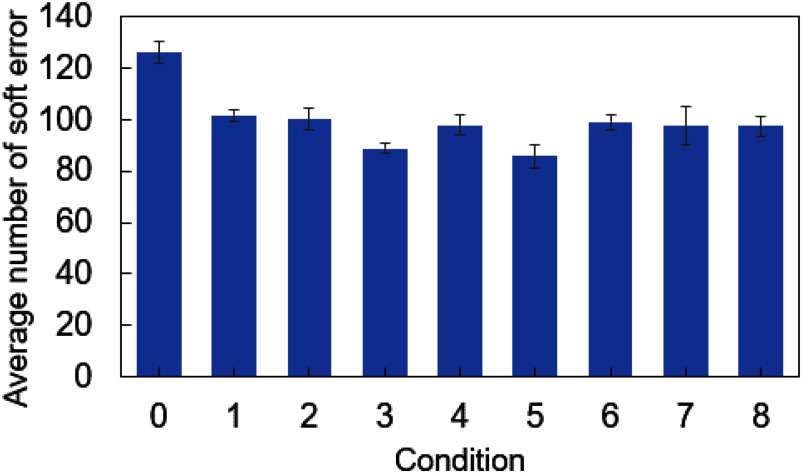
Fig. 5.

Fig. 5.

Open in a new tab

Variation in the average number of soft errors for each experimental condition. Error bars indicate standard deviation.

The cross section (regression coefficient) was calculated to minimize (2).

I.

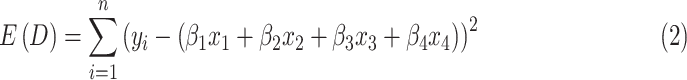where, E(D) is the error function, n is the number of data, and yi is the number of soft errors measured.

The Dannett test was used to assess the contribution of high-energy neutrons compared to that of other particles. The significance level was set at p < 0.05.

III. Results

A. Neutron Distribution

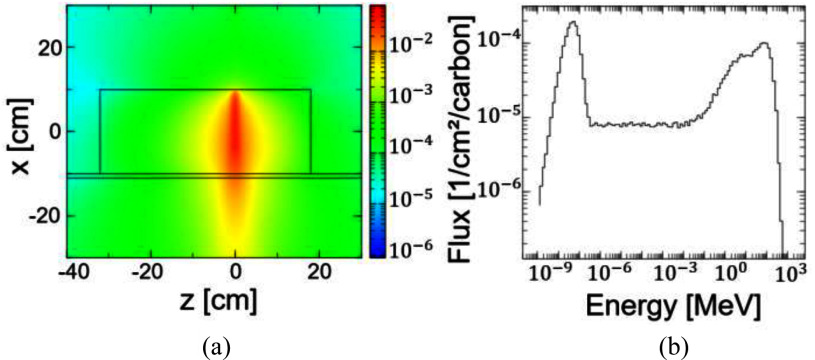
Fig. 2 shows the flux distribution of high-energy (>10 MeV) neutrons and the neutron spectrum at z = 8 cm. The carbon beam is irradiated from the upper side of the figure. A large number of neutrons were produced in the axial direction of the beam and fewer in the lateral direction. Many high-energy neutrons were generated along the beam axis. The peak was generated on the high energy side due to the high energy of the carbon beam. The high-energy neutrons collided with the nucleus, lost energy, and reached equilibrium with the thermal motion of the molecule, thus producing a peak on the low energy side as well.

Fig. 2.

Fig. 2.

Open in a new tab

Monte Carlo simulation results. Carbon ions (290 MeV/u) were irradiated from the upper side of (a) to a PMMA phantom on a couch made of carbon fiber reinforced plastic. A: (a) shows the flux distribution of high-energy neutrons >10 MeV assuming FPGA at z = 8 cm. B: Neutron spectrum at the FPGA position (x = 0 and z = 8 cm).

B. Distance Dependence

Fig. 3 shows the change in the secondary-particle fluxes calculated by PHITS and the number of soft errors as a function of distance from the irradiation position. We confirmed that the flux of secondary particles decreased rapidly as the distance between the irradiation position and the FPGA increased. Consequently, the number of soft errors decreased rapidly with distance.

C. Radiation Quality Variation

Fig. 4 shows the changes in the fluxes of thermal, intermediate-energy, and high-energy neutrons, as well as protons, under different conditions calculated by PHITS. We observed clear variations in radiation quality.

Fig. 5 shows the number of soft errors generated under different conditions. The number of soft errors generated varied depending on radiation quality.

D. Multiple Regression Analysis

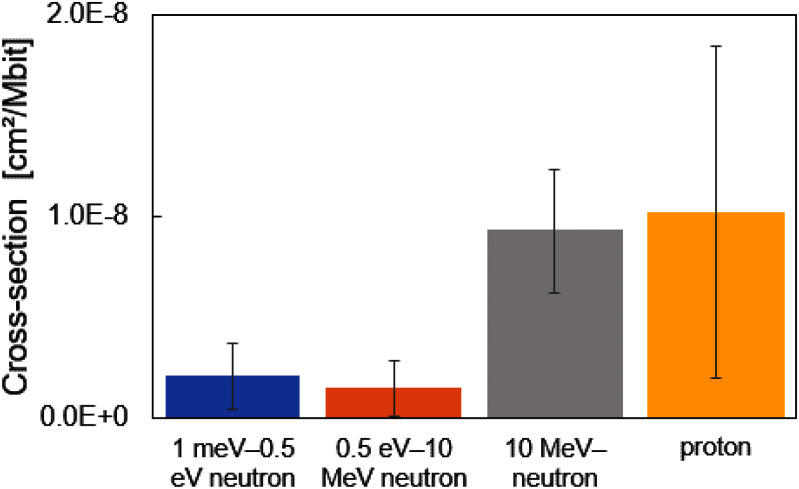
A multiple regression analysis was conducted using the results shown in Figs. 3, 4, and 5 (Fig. 6). The data on the number of soft errors and the number of secondary particles for each condition at a distance of 80 mm were analyzed to obtain cross-sections. The contribution of each secondary particle, calculated from the results obtained in Fig. 6, as well as the contributions of each radiation source to condition 0 are shown in Table II, considering neutron and proton fluences (to obtain the contribution, the product of the cross section and fluence was divided by the number of errors).

Fig. 6.

Fig. 6.

Open in a new tab

Results of multiple regression analysis. Cross-sections are shown for each particle type. Error bars indicate standard deviation. In this study, cross- section is defined as the probability of soft errors per megabit (Mbit).

TABLE II. Percentage of Errors Caused by Each Particle Out of 116 Errors in Condition 0.

Particle Energy Contribution [%] Error range [%]
Neutron 1 meV–0.5 eV 16.6 ±6.9
Neutron 0.5 eV–10 MeV 9.1 ±8.7
Neutron 10 MeV - 58.5 ±16.2
Proton all 15.8 ±5.0
Open in a new tab

The contribution of high-energy neutrons (>10 MeV) was significantly higher than that of other particles (p < 0.05, Table II). Although other particles are also considered to contribute to soft errors, the magnitude of their contribution was smaller than that of the high-energy neutrons.

IV. Discussion

In this study, we measured soft errors generated from CIRT and evaluated the contribution of secondary particles.

The fraction of high-energy neutrons decreased as the distance increased because the energy of high-energy neutron is reduced by collisions with nuclei, resulting in an increase in the fraction of thermal neutrons (Fig. 3(a)). The risk of soft errors decreased rapidly as the distance between the irradiation position and FPGA increased (Fig. 3(b)). The highest probability of soft errors was observed for high-energy neutrons.

Scattering by many nuclei is important for neutron shielding. However, high-density materials do not necessarily reduce soft errors efficiently, because the scattering cross-section is not proportional to the atomic number, hydrogen efficiently removes neutron energy, and the absorption cross-section of thermal neutrons varies greatly from nuclide to nuclide (Supplemental Fig. 2).

Neutrons lose their energy through elastic scattering and become thermal neutrons. As hydrogen efficiently takes energy from neutrons, the use of acrylic or polyethylene with high hydrogen content decreases the number of high-energy neutrons and increases the number of thermal neutrons. In contrast, boron has a large absorption cross section for thermal neutrons; therefore, polyethylene with boron can thermalize and absorb neutrons. Graphite, aluminum, iron, nickel, and lead are materials with different densities and atomic numbers and have different scattering cross sections and thermalization rates for high-energy neutrons. Lead has the highest density but also the highest atomic number; hence, the neutron energy is hardly reduced. Iron and nickel have nearly the same atomic number and are close in density. However, they have different cross sections for generating protons, and the number of protons increases with nickel compared to that in iron.

Of the nine conditions shown in Figs. 4 and 5, the number of soft errors decreases under conditions where low-energy neutrons, high-energy neutrons, and protons can be shielded. Although there are some conditions in which the number of soft errors decreases even without a substantial decrease in the number of high-energy neutrons, it can be inferred that many low-energy neutrons and protons are shielded in these conditions, indicating that the contribution of low-energy neutrons and protons cannot be negligible. In contrast, even if intermediate-energy neutrons increase, soft errors do not increase, which may indicate that the contribution of intermediate-energy neutrons is minor.

The cross-sections for soft errors with thermal, intermediate-energy, and high-energy neutrons, as well as protons, were 2.08 × 10−9 [cm2/Mb], 1.43 × 10−9 [cm2/Mb], 9.29 × 10−9 [cm2/Mb], and 1.02 × 10−8 [cm2/Mb], respectively. The contribution of high-energy neutrons was the highest, accounting for approximately 58.5% of the secondary particles (Table II).

Our results are comparable with those of previous studies. The cross-sections estimated by Iwashita et al. were 8–10 × 10−10 [cm2/Mb] for thermal neutrons and 2–3 × 10−9 [cm2/Mb] for high-energy neutrons [17]. Xilinx's Device Reliability Report showed that the cross-section for neutrons at the Los Alamos Neutron Science Center was 6.99 × 10−9 [cm2/Mb] [23]. Although the obtained cross-sections for the intermediate-energy neutrons were large, this may be due to a measurement error, as indicated by the large error bars. Nevertheless, the contribution of secondary particles to soft error was considered reasonable based on past results.

Andrea et al. demonstrated that the cross-section of a single-event upset for protons was slightly larger than that for neutrons [24]. The same trend is observed in Fig. 6, which is considered a reasonable result. This contribution was small because of the small number of protons used in this study. However, because the cross-sections were comparable to those of high-energy neutrons, the risk was considered higher if a treatment generated more protons.

Soft errors can also be generated by ions other than neutrons and protons (e.g., deuterons, tritons, and alpha-rays); however, the amount produced by these ions was much lower than that produced by protons. Alpha particles and deuterons generate approximately 1/10 the number of protons. Their contribution to soft errors was considered to be small and was not considered in this study.

CIRT produces many high-energy (>10 MeV) neutrons. The contribution of high-energy neutrons decreased as the distance increased, resulting in a rapid decrease in the number of soft errors. The differential cross-section (angular distribution) of high-energy neutron generation is also important when considering its effect on CIEDs. A large number of high-energy neutrons were produced in the axial direction of the beam, whereas the number produced in the transverse and upstream directions was small (Supplemental Figs. 1, 5) [25]. CIEDs, such as pacemakers, are typically placed around the left clavicle. For example, when a patient is in the supine position and irradiated from above, relatively few high-energy neutrons reach the frontal body surface. Therefore, if CIEDs are placed on the upstream side of the beam or at a sufficient distance in the lateral direction, the risk of soft errors is reduced. However, if the CIEDs are located downstream of the beam axis (i.e., irradiated from the back or right side of the patient), the number of high-energy neutrons increases along with the risk of soft errors. Under clinical conditions, the risk would be higher than that in this study owing to neutron generation from dose monitors, range shifters, and collimators, which are installed upstream of the patient. The MLC, range shifter, and spreader Bragg peaks also produce neutrons and protons, which complicate the evaluation. They were, therefore, not considered in this study.

Scanning irradiation is a potential method for reducing the contribution of neutrons because it decreases the neutron dose compared with passive irradiation [26]. Henrik et al. demonstrated that the risk of a CIED malfunction during scanning proton irradiation was sufficiently low [27]. We also consider it noteworthy to compare our findings with proton therapy but quantitative comparisons between carbon beam therapy and proton beam therapy are difficult. However, the risk of proton therapy may be greater because previous studies have shown that proton therapy produces more secondary neutrons even when the dose in [Gy (RBE)] is the same.

Shielding of neutrons can also reduce this risk, as shown by Kakino et al. [18]. However, this study focused on X-ray therapy (photoneutrons), in which the energy of the generated neutrons was much lower (up to ∼1 MeV) than that in CIRT (up to ∼100 MeV). Neutrons with energies of ∼100 MeV have a small reaction cross-section, making effective shielding challenging. Therefore, more effective methods for shielding high-energy neutrons must be developed.

In this study, bit flips are counted as soft errors. One soft error does not necessarily mean one malfunction; a soft error can probabilistically cause a malfunction if it occurs in an important memory directly related to the operation of the CIEDs.

This study had several limitations. The results were obtained from only one type of FPGA, and we did not evaluate the soft-error probability with a clinical device. The risk of soft errors varies with the process size and circuit design [29]. The risk during clinical exposure may also vary depending on the process size of the CIEDs. The process size of CIEDs varies from product to product, with semiconductors of various process sizes used in a single product. FPGA manufacturers have published failure in time numbers [23]. By evaluating similar risk coefficients for CIEDs, the risk of soft errors can be assessed using simulations or simple measurements.

The risk during clinical exposure may be several times higher than that in this study, considering the irradiation time. The treatment involves 12–16 fractions of 1–2 min of irradiation with a dose of 50–70 Gy, depending on the tumor-type and tumor site. However, it is difficult to accurately assess the risk in treatment irradiation by solely relying on the results in this study. As the purpose of this study was to determine the contribution of secondary particles to soft errors, a simple geometry was created. The effects of MLCs, range shifters, and spread-out Bragg-peaks must be considered in treatment irradiation because they also produce neutrons and protons. Further experiments under clinical conditions are required.

Therefore, the accuracy of this study was insufficient for clinical application. Devices that can measure soft errors are required to improve simulation accuracy. Irradiating only protons or neutrons with specific energies would provide a more accurate confirmation of the contribution of each secondary particle. Despite needing improvements in measurement accuracy, our study provides a quantitative framework for evaluating and comparing the risk of soft error occurrence and a useful basis for future risk assessments.

V. Conclusion

We successfully measured soft errors exerted by CIRT and evaluated the contribution of secondary particles. High-energy neutrons (>10 MeV) were the main contributors among the secondary particles. To reduce the risk of soft errors, it is necessary to maintain a sufficient transverse distance and avoid placing the CIEDs downstream of the beam. These findings provide valuable insights for future risk assessments in the field of radiotherapy.

Supplementary Materials

Supplementary materials
supp1-3358989.pdf (152.2KB, pdf)

Acknowledgment

This work was conducted as part of the Research Project with Heavy Ions at the GHMC.

Statement of Contribution: The authors confirm their contribution to the paper as follows: Y. Kawakami and M. Sakai contributed to the conception and design of the study, code writing, interpretation of results and the manuscript writing. H. Masuda, M. Miyajima and T. Kanzaki contributed to the performance of the experiments and the review and editing. K. Kobayashi contributed to the design of the study, interpretation of results and the review and editing. T. Ohno and H. Sakurai contributed to the interpretation of results and review and editing. All authors contributed to the article edition and approved the submitted version.

Conflicts of Interest: All authors declare no conflicts of interest.

Funding Statement

This work was supported in part by JSPS KAKENHI under Grant JP21H02864 and in part by Takahashi Industrial and Economic Research Foundation.

Contributor Information

Yudai Kawakami, Email: t221d026@gunma-u.ac.jp.

Makoto Sakai, Email: sakai-m@gunma-u.ac.jp.

Hiroaki Masuda, Email: ma.hiro@gunma-u.ac.jp.

Masami Miyajima, Email: m-miyajima@gunma-u.ac.jp.

Takao Kanzaki, Email: tkanzaki@gunma-u.ac.jp.

Kazutoshi Kobayashi, Email: kazutoshi.kobayashi@kit.ac.jp.

Tatsuya Ohno, Email: tohno@gunma-u.ac.jp.

Hiroshi Sakurai, Email: sakuraih@gunma-u.ac.jp.

References

  • [1].Matsubara H. et al. , “Prediction of radiation-induced malfunction for cardiac implantable electronic devices (CIEDs),” Med. Phys., vol. 47, no. 4, pp. 1489–1498, Apr. 2020, doi: 10.1002/mp.14057. [DOI] [PubMed] [Google Scholar]
  • [2].Okano N. et al. , “Safety verification of carbon-ion radiotherapy for patients with cardiac implantable electronic devices (CIEDs),” J. Radiat. Res., vol. 63, no. 1, pp. 122–127, 2022, doi: 10.1093/jrr/rrab105. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [3].Solan A. et al. , “Treatment of patients with cardiac pacemakers and implantable cardioverter-defibrillators during radiotherapy,” Int. J. Radiat. Oncol., Biol., Phys., vol. 59, no. 3, pp. 897–904, Jul. 2004, doi: 10.1016/j.ijrobp.2004.02.038. [DOI] [PubMed] [Google Scholar]
  • [4].Zaremba T. et al. , “The effect of radiotherapy beam energy on modern cardiac devices: An in vitro study,” EP Europace, vol. 16, pp. 612–616, Apr. 2014. [DOI] [PubMed] [Google Scholar]
  • [5].Elders J. et al. , “High incidence of implantable cardioverter defibrillator malfunctions during radiation therapy: Neutrons as a probable cause of soft errors,” Europace, vol. 15, no. 1, pp. 60–65, Jan. 2013, doi: 10.1093/europace/eus197. [DOI] [PubMed] [Google Scholar]
  • [6].Hashimoto T. et al. , “Particle therapy using protons or carbon ions for cancer patients with cardiac implantable electronic devices (CIED): A retrospective multi-institutional study,” Jpn. J. Radiol., vol. 40, no. 5, pp. 525–533, 2022, doi: 10.1007/s11604-021-01218-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [7].Gumuser E. et al. , “Effect of proton radiation therapy on cardiovascular implantable electronic devices [CIED],” Eur. Heart J., vol. 43, no. suppl. 2, Oct. 2022, Art. no. 747, doi: 10.1093/eurheartj/ehac544.747. [DOI] [Google Scholar]
  • [8].Nemec J., “Runaway implantable defibrillator–A rare complication of radiation therapy,” Pacing Clin. Electrophysiol., vol. 30, no. 5, pp. 716–718, 2007, doi: 10.1111/j.1540-8159.2007.00735.x. [DOI] [PubMed] [Google Scholar]
  • [9].Zweng A. et al. , “Life-threatening pacemaker dys therapeutic radiation: A case report,” Angiology, vol. 60, no. 4, pp. 509–512, 2009, doi: 10.1177/0003319708315305. [DOI] [PubMed] [Google Scholar]
  • [10].Azraai M. et al. , “Current clinical practice in patients with cardiac implantable electronic devices (CIED) undergoing radiotherapy (RT),” Heart, Lung Circulation, vol. 31, no. 3, pp. 327–340, 2022, doi: 10.1016/j.hlc.2021.10.020. [DOI] [PubMed] [Google Scholar]
  • [11].Marbach J. et al. , “Management of radiation oncology patients with implanted cardiac pacemakers: Report of AAPM task group, american association of physicists in medicine,” Med. Phys., vol. 21, no. 1, pp. 85–90, 1994, doi: 10.1118/1.597259. [DOI] [PubMed] [Google Scholar]
  • [12].Indik J. et al. , “2017 HRS expert consensus statement on magnetic resonance imaging and radiation exposure in patients with cardiovascular implantable electronic devices,” Heart Rhythm, vol. 14, no. 7, pp. e97–e153, Jul. 2017, doi: 10.1016/j.hrthm.2017.04.025. [DOI] [PubMed] [Google Scholar]
  • [13].Daniel G. et al. , “Malfunction of implantable cardiac devices in patients receiving proton beam therapy: Incidence and predictors,” Int. J. Radiat. Oncol., Biol., Phys., vol. 87, no. 3, pp. 570–575, 2013, doi: 10.1016/j.ijrobp.2013.07.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [14].Krames E. S., “Possible malfunction of electronic medical devices caused by computed tomography scanning,” Neuromodulation, vol. 12, pp. 5–7, Jan. 2009. [DOI] [PubMed] [Google Scholar]
  • [15].Iwashita H. et al. , “Energy-resolve soft-error rate measurements for 1-800 MeV neutrons by the time-of-flight technique at LANSCE,” IEEE Trans. Nucl. Sci., vol. 67, no. 11, pp. 2363–2369, Nov. 2020. [Google Scholar]
  • [16].Kobayashi K., “Endurance measurement of semiconductor chips–Beam test by particle accelerator for single event effects,” Kasokuki, vol. 13, no. 4, pp. 245–252, 2016. [Google Scholar]
  • [17].Iwashita H. et al. , “Energy-resolved SEU cross section from 10-meV to 800-MeV neutrons by time-of-flight measurement,” IEEE Trans. Nucl. Sci., vol. 70, no. 3, pp. 216–221, Mar. 2023, doi: 10.1109/TNS.2023.3245142. [DOI] [Google Scholar]
  • [18].Kakino R. et al. , “Photoneutron-induced damage reduction for cardiac implantable electronic devices using neutron-shielding sheets in high-energy X-ray radiotherapy: A phantom study,” Phys. Med., vol. 89, pp. 151–159, 2021, doi: 10.1016/j.ejmp.2021.07.036. [DOI] [PubMed] [Google Scholar]
  • [19].Daniel O. et al. , “High-energy versus thermal neutron contribution to processor and memory error rates,” IEEE Trans. Nucl. Sci., vol. 67, no. 6, pp. 1161–1168, Jun. 2020. [Google Scholar]
  • [20].Weulersse C. et al. , “Prediction of proton sections for SEU in SRAMs and SDRAMs using the METIS engineer tool,” Microelectronics Rel., vol. 55, no. 9-10, pp. 1491–1495, 2015, doi: 10.1016/j.microrel.2015.06.117. [DOI] [Google Scholar]
  • [21].Sato T. et al. , “Features of particle and heavy ion transport code system (PHITS), version 3.02,” J. Nucl. Sci. Technol., vol. 55, pp. 684–690, 2018. [Google Scholar]
  • [22].Shibata K. et al. , “JENDL-4.0: A new library for nuclear science and engineering,” J. Nucl. Sci. Technol., vol. 48, no. 1, pp. 1–30, 2011, doi: 10.1080/18811248.2011.9711675. [DOI] [Google Scholar]
  • [23].Xilinx, “Device reliability report first half 2021,” virsion 10.15, 2021. [Online]. Available: https://docs.xilinx.com/r/en-US/ug116/The-Reliability-Program
  • [24].Coronetti A. et al. , “Proton direct ionization upsets at tens of MeV,” IEEE Trans. Nucl. Sci., vol. 70, no. 4, pp. 314–321, Apr. 2023, doi: 10.1109/TNS.2022.3207877. [DOI] [Google Scholar]
  • [25].Satoh D. et al. , “Distributions of neutron yields and doses around a water phantom bombarded with 290-MeV/nucleon and 430-MeV/nucleon carbon ions,” Nucl. Instrum. Methods Phys. Res. B, vol. 387, pp. 10–19, 2016, doi: 10.1016/j.nimb.2016.09.011. [DOI] [Google Scholar]
  • [26].Brenner D. and Hall E., “Secondary neutrons in clinical proton radiotherapy: A charged issue,” Radiotherapy Oncol., vol. 86, no. 2, pp. 165–170, 2008, doi: 10.1016/j.radonc.2007.12.003. [DOI] [PubMed] [Google Scholar]
  • [27].Henrik B. et al. , “Risk of cardiac implantable electronic device malfunctioning during pencil beam proton scanning in an in vitro setting,” Int. J. Radiat. Oncol., Biol., Phys., vol. 111, no. 1, pp. 186–195, Sep. 2021, doi: 10.1016/j.ijrobp.2021.03.053. [DOI] [PubMed] [Google Scholar]
  • [28].Yonai S. et al. , “Measurement of neutron ambient dose equivalent in passive carbon-ion and proton radiotherapies,” Med. Phys., vol. 35, no. 11, pp. 4782–4792, 2008, doi: 10.1118/1.2989019. [DOI] [PubMed] [Google Scholar]
  • [29].Bernardi P., Reorda M. S., Sterpone L., and Violante M., “On the evaluation of SEU sensitiveness in SRAM-based FPGAs,” in Proc. IEEE 10th Int. -Line Testing Symp., 2004, pp. 115–120, doi: 10.1109/OLT.2004.1319668. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary materials
supp1-3358989.pdf (152.2KB, pdf)

Articles from IEEE Open Journal of Engineering in Medicine and Biology are provided here courtesy of Institute of Electrical and Electronics Engineers

RESOURCES