gPKPDviz: A flexible R shiny tool for pharmacokinetic/pharmacodynamic simulations using mrgsolve

Abstract

GPKPDviz is a Shiny application (app) dedicated to real‐time simulation, visualization, and assessment of the pharmacokinetic/pharmacodynamic (PK/PD) models. Within the app, gPKPDviz is capable of generating virtual populations and complex dosing and sampling scenarios, which, together with the streamlined workflow, is designed to efficiently assess the impact of covariates and dosing regimens on PK/PD end points. The actual population data from clinical trials can be loaded into the app for simulation if desired. The app‐generated dosing regimens include single or multiple dosing, and more complex regimens, such as loading doses or intermittent dosing. When necessary, the dosing regimens can be defined externally and loaded to the app for simulation. Using mrgsolve as the simulation engine, gPKPDviz is typically used for population simulation, however, with a slight modification of the mrgsolve model, gPKPDviz is capable of performing individual simulations with individual post hoc parameters, individual dosing logs, and individual sampling timepoints through an external dataset. A built‐in text editor has a debugging feature for the mrgsolve model, providing the same error messages as model compilation in R. GPKPDviz has had stringent validation by comparing simulation results between the app and using mrgsolve in R. GPKPDviz is a member of the suite of Modeling and Simulation Shiny apps developed at Genentech to facilitate the typical modeling work in Clinical Pharmacology. For broader access to the Pharmacometric community, gPKPDviz has been published as an open‐source application in GitHub under the terms of GNU General Public License.

INTRODUCTION

Simulations based on available pharmacokinetic/pharmacodynamic (PK/PD) models are critical to explore PK/PD relationships, support clinical trial designs, and facilitate dose and regimen selections. Graphical user interfaces (GUIs) that facilitate these simulations can greatly enhance the communication and influence of modeling and simulation (M&S) in multi‐functional team settings. Such GUIs also allow M&S tools to be made accessible to a wider audience with limited programming skills.

There are few MATLAB‐based open‐source GUIs that are capable of PK/PD simulations, including gPKPDsim ¹ (for any model implemented in SimBiology), A4S ² (for the predefined model library), MatVPC ³ (for any model implemented in MATLAB; focus on visual predictive checks), and ATLAS mPBPK ⁴ (for minimal physiologically‐based PD model). GPKPDsim and ATLAS mPBPK also have data fitting capabilities. Simulx‐GUI ⁵ was recently released for the advanced clinical trial simulations as part of the Monolix Suite. Berkeley Madonna ⁶ , ⁷ software is capable of real‐time simulation and visualization of PK/PD models, however, the implementation of interindividual variability and complex dosing scenarios are not straightforward. In addition, both tools require a commercial license.

Shiny is an open‐source R package that builds interactive user interfaces straight from R. ⁸ Shiny applications (will be referred to as “Shiny apps” hereinafter) can be deployed over the web for local hosting or a hosting service with broader access. Shiny apps are being increasingly used by pharmacometricians and clinical pharmacologists ⁹ , ¹⁰ , ¹¹ due to their flexible interfaces and the rich ecosystem of R packages. A suite of M&S Shiny apps, called R‐Shiny Exploratory Analysis Platform in Clinical Pharmacology ¹² has been developed by Genentech for internal use to facilitate the typical modeling work performed in clinical pharmacology, including the PK/PD simulation application in this manuscript.

To perform simulations in R for the ordinary differential equation (ODE)‐based PK/PD models, the open‐source R package with an ODE solver must be used. Packages developed in the PK/PD field include mrgsolve, ¹³ , ¹⁴ PKPDsim, ¹⁵ , ¹⁶ and RxODE/rxode2. ¹⁷ , ¹⁸ , ¹⁹ The deSolve ²⁰ and diffeqr ²¹ packages have more broader applications, covering ODE, partial differential equation, and delayed differential equation, etc. In this regard, mrgsolve was intentionally designed to be similar to NONMEM syntax, in addition, it has an efficient simulation engine and is easy to integrate with Shiny.

Combining Shiny and mrgsolve, we developed gPKPDviz (Genentech PK/PD visualizer), which allows real‐time simulation and visualization of PK/PD models. It comes packaged with a library of mrgsolve models for the Roche/Genentech molecules on the internal server, and some template models and the public available models in the open‐source version (currently limited, but to be expanded). GPKPDviz has gone through stringent validation by comparing outputs from the app to simulation results performed in R (Supplementary Rmd S1). For broader access to the pharmacometrics community, gPKPDviz was published as an open‐source application in GitHub under the terms of GNU General Public License version 3. ²²

ModVizPop ⁹ is another open‐source Shiny app for PK/PD simulations using mrgsolve as the simulation engine. Different from some model‐specific Shiny apps, ²³ , ²⁴ , ²⁵ ModVizPop and gPKPDviz are both considered as the Shiny “Platform,” in the way they were created to work with any ODE‐based models in mrgsolve format. ModVizPop is unable to simulate virtual populations within the app, and it relies on the external dataset to read in covariate information. ModVizPop also needs to load external dataset for complex dosing and sampling schedules, as the in‐app simulation capability is limited. In comparison, gPKPDviz is capable of simulating virtual populations and complex dosing and sampling schedules within the app, and, when needed, it can also load external datasets to take on whatever complexities for covariate, dosing, and sampling schedules. Given the flexible settings and the streamlined workflow, gPKPDviz was designed to effectively evaluate the impact of covariates and dosing regimens on PK (exposure) or PD (response) end points. GPKPDviz can efficiently address clinical pharmacology questions such as, “what is the impact of a dose delay or alternative dosing regimen, knowing the target PK threshold?” or “from the PK point of view, is there a benefit of fixed dosing over body size‐based dosing for heavier patients?”

Recently, e‐Campsis ²⁶ , ²⁷ was released by calvagone as a Shiny “Platform” for population PK/PD simulations using R packages campsis ²⁸ and campsismod, ²⁹ which provides a powerful front end to run simulations with mrgsolve or RxODE/rxode2. It comes with the free or pro version, and both required the comprehension of campsis model syntax. The free version has limited functionality. The covariate distribution can be flexible, as long as it is defined in R in the covariate field. E‐Campsis does not allow loading external datasets for simulation, thus it has limited flexibility to handle complex dosing scenarios or individual simulations. Once the simulation is fully configured, e‐Campsis generates the complete R code for the users to reproduce or refine the simulation offline; such functionality is not available for gPKPDviz or ModVizPop.

This tutorial for gPKPDviz starts with the description the app workflow and the key features of each tab, followed by two comprehensive clinical applications, including dose delay or alternative dosing regimen assessment for pertuzumab, and body size‐based dosing regimen assessment for polatuzumab vedotin. The animated demonstrations are provided in the GitHub repository using pertuzumab simulations as examples. ²²

APP DESCRIPTION

App workflow

GPKPDviz is comprised of five tabs: (1) Model, (2) Population, (3) Dosing, (4) Simulate, and (5) Results. A typical workflow of use of the app is shown in Figure 1. However, users can repeatedly update certain tabs to simulate multiple scenarios for comparison purposes, such as updating the Dosing and Simulate tabs for simulation of different dosing regimens or updating the Model and Simulate tabs for simulation of different parameter values. It is also feasible to run the Population and Simulate tabs iteratively to assess the impact of population distribution on simulations.

FIGURE 1.

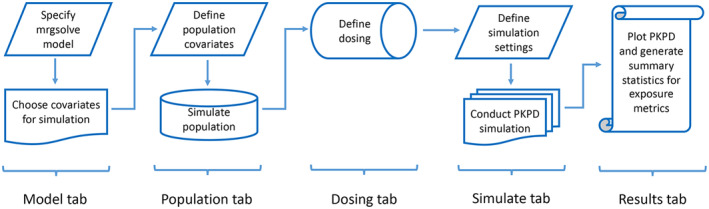
Typical workflow of gPKPDviz. PK/PD, pharmacokinetic/pharmacodynamic.

Mrgsolve model

Mrgsolve is an R package actively maintained by Metrum Research Group. ¹³ , ¹⁴ The mrgsolve model is the backbone for all the simulations in gPKPDviz. It has similar annotations and code blocks as NONMEM, but is more flexible and efficient for simulation. The model specification file consists of R and C++ code that is parsed, compiled, and dynamically loaded into the R session. The commonly used code blocks for mrgsolve include $PROB (notes about the model), $PREAMBLE (initialize the C++ variables), $CMT (declare model compartments), $PARAM (declare model parameters), $OMEGA, $SIGMA, $MAIN (alias $PK), $ODE (alias $DES), $TABLE (alias $ERROR), and $CAPTURE (declare output variables).

For details about the mrgsolve package, readers can refer to the mrgsolve user guide. ¹³ It is worth emphasizing here that any variable defined in the $PARAM block can only be updated by the individual values outside of the model, but not re‐defined within the model by other blocks. Similar to NONMEM, mrgsolve has the $PRED block and $PKMODEL block (equivalent to ADVAN 1~4 in NONMEM). Any mrgsolve models that translated from NONMEM code should be validated against NONMEM simulations, for both typical and individual predictions. ³⁰ , ³¹

Model tab

The first step in the app workflow is to specify an mrgsolve model in the “Model” tab, either by loading an external model or choosing one from the built‐in library. Once the model is loaded, users are required to select the variables from the drop‐down menu to generate the population data (see the “Population” tab). To make certain variables available in the drop‐down menu, they need to be first defined in the $PARAM block of the model. For each selected variable, the user can specify the data type as either continuous (default) or categorical. Such information is required in the “Population” tab for virtual simulation, and the “Result” tab for stratifications. The user also needs to specify the time unit from the drop‐down list, as either day or hour, according to the time unit of the model. It is critical to specify the appropriate model time unit, which otherwise will lead to wrong simulation outcomes. The loaded model code can be manually edited without affecting the source code. This is particularly useful to allow quick exploration of different parameter values. The model will be compiled after the initial loading and re‐compiled whenever changes are made. The built‐in text editor has a debugging feature that provides the same error message as the mrgsolve code compilation in R, facilitating efficient model development.

Users have the option to define a seed in the Model tab to make the simulations reproducible. Once defined, the same seed will be used across the app to control all the randomization processes, including the virtual population simulation and sampling with replacement (see the “Population tab” section), and the simulations (see the “Simulate tab” section).

Population tab

The population data are defined based on the variables selected in the Model tab. The user can either simulate the virtual population within the app (i.e., covariates simulated as per certain distribution or proportion), or load the actual covariate data from an external dataset (in .csv format). The population data is automatically summarized in tables and histogram plots for verifications and visualization purposes.

The selected variables in the Model tab typically represent the model covariates for the virtual population generation. Continuous covariates are simulated based on a truncated multivariate normal distribution with user‐specified parameters (mean, standard deviation, bounds, and correlations). Categorical covariates are simulated based on binomial distributions with user‐defined proportions. The correlation between continuous and categorical variables is achieved by allowing different distributions for each category. The continuous covariates can be further categorized into bins for stratification of simulated output. Of note, only the categorical variables and categorized continuous variables are used for stratifications.

The selected variables can also include any variables that serve as the data input for simulation, (such as the post hoc parameters for individual simulation) as long as they are defined in $PARAM block of the model.

Compared to the app‐generated virtual population, the user‐loaded actual population data have certain advantages. First, it naturally reflects the actual covariate correlations and covariate distributions in the clinical data. Second, it can handle time‐varying covariates and inter‐occasion variability. Finally, it could incorporate the post hoc parameters for individual simulations. The user‐loaded population data could be further enlarged by sampling with replacement.

Dosing tab

Dosing regimens for the virtual populations are defined in the “Dosing” tab. Users have the option to generate the dosing regimen within the app or load the dosing data through an external dataset. The app can generate up to three unique dosing interventions. Each intervention is configured individually by the dose amount, number of doses, dosing interval, dosing compartment, and route of administration, which can all be combined in a sequential or simultaneous manner when needed. The app provides two options of defining doses: flat dosing and covariate‐based dosing (e.g., body weight‐based dosing).

Within the app, it is straightforward to define the regular dosing regimens using only one dosing intervention (e.g., single dose, or repeated dose with equal interval). The irregular dosing regimens, such as loading dose, step‐up dosing, and intermittent dosing, can be defined by combining several interventions in a sequential manner. A “Dosing Sequence Table” would be automatically created to reflect the dosing regimens.

Although less frequently used, when combining interventions in a simultaneous manner, it can handle models with more than one dosing compartment, with each compartment defined by a unique intervention. The models that fall into this category include, for example, a PK/PD model for combination therapy where the PD is driven by the PK from each treatment, or a PK model with concurrent absorption process (or different absorption sites) where the PK is driven by each absorption process (or site). Combining interventions in a simultaneous manner also allows the users to explore concurrent intravenous and subcutaneous dosing scenarios for compounds that are eligible for both dosing routes.

Despite its convenience, the app‐generated dosing regimen has several limitations. First, it can only handle up to three unique interventions (although in most cases it is enough). Second, it does not allow individualized dosing regimens (i.e., the app‐generated regimen is always applied to the entire population). The user‐uploaded dosing dataset, on the other hand, can take on whatever complexity is required. The individual dosing regimen, coupling with the post hoc parameters and individual sampling time, can be used for the simulation of individual profiles.

Simulate tab

The next step is to conduct simulations in the “Simulate” tab, using the loaded mrgsolve model, the previously defined population data, the dosing information, and the sampling times. Depending on the loaded mrgsolve model, either population simulation (random sampling from OMEGA and SIGMA metrics) or individual simulation (reading from individual post hoc parameters) would be performed.

The simulation can be conducted according to the app‐generated time grid with equal interval (i.e., the fine time grid), user‐defined timepoints with irregular interval, or a combination of both. When the app finds records with actual sampling times (evid = 0) in the dosing dataset loaded in the dosing tab, the simulations can follow the actual sampling times, alone or augmented with the fine time grid. If necessary, the typical profile could be simulated, using the “zero_re” function on the back‐end. ¹³

Mrgsolve uses the C++ translation of DLSODA solver from ODEPACK. ³² The ‘simulate’ tab allows for the adjustment of key solver settings, ¹³ including hmax (maximum step size), maxsteps (maximum steps between adjacent simulation time points), atol (absolute tolerance), and rtol (relative tolerance). Whereas the default values are sufficient for most cases, any modifications should be based on a deep understanding of the system dynamics.

As described in the app workflow, the user can conduct batches of simulations that differ only in dosing regimen, which can be done iteratively between “Dosing” and “Simulate” tabs. It is also possible to conduct and compare simulations with different populations or even different model parameters.

Results tab

The simulated data is composed of the generic variables (i.e., model unspecific) and the model‐specific variables. The generic variables include dosing and sampling information (SIM_TYPE, REC_TYPE), subject identifier (USUBJID, ID), simulation identifier (SIM_ID), time, event identification (EVID), dosing amount (AMT), and cumulative dose count. The model‐specific variables include state variables (defined in $CMT or $PKMODEL), output variables (defined in $CAPTURE), and model covariates (including binned covariate derivatives). The state variables and output variables are populated automatically from the loaded mrgsolve model. To include a covariate in the simulated data, it must be defined in $PARAM and selected in the drop‐down menu. A snapshot of the simulated data is shown in Figure S1.

SIM_TYPE defines the data source, including “Simulation,” “User Specified,” and “User Overlay.” “Simulation” data source corresponds to the three record types in REC_TYPE, including the “Population” type for covariate data (at time 0 for baseline covariates and non‐zero times for time‐varying covariates), the “Dose” type for dosing records (at the dosing times), and the “Observation” type for sampling records (at the sampling times). EVID of 2, 1, and 0 are assigned to the “Population,” “Dose,” and “Observation” types, respectively. The definition of evid in the app is the same as NONMEM. To ensure the proper order of the simulated data from different record types, the tiny time shifts are automatically added to the “Dose” (1E‐10) and “Observation” (1E‐11) types.

Of note, only the simulated fine time grid with equal interval belongs to the “Observation” type of “Simulation” data source; the user‐defined sampling times with irregular interval or the actual sampling time loaded from external data belongs to the “Observation” type of “User Specified” data source. The overlaid observed data, if any, belong to the “Observation” type of “User Overlay” data source.

Filtering of the simulated data can be applied prior to plotting or the calculation of summary stats. Typically, users would filter “Observation” type in REC_TYPE, because only the simulations at the sampling times are of interest for plotting or summary stats. The output variables declared in $CAPTURE and the state variables defined in $CMT or $PKMODEL will be automatically available for plotting or summary stats. The plots can be shown side‐by‐side when there are two or more variables selected for the same SIM_ID (e.g., PK and PD outputs), or different SIM_IDs for the same variable (e.g., PK output across regimens). The users also have the option to overlay the outputs from different SIM_IDs in the same plot with different colors. Further stratifications can be made by categorical covariates or categorized continuous covariates, or by subject ID to the extreme. Users have the option to further customize the plot, such as median with 90% interval in log scale. To enhance efficiency in updating the plots, it is preferred to make several changes before hitting the “Update Results” button, so that all the changes can be rendered at once.

One important goal of the simulation is to compare the exposure metrics across dosing regimens or covariate categories. The exposure metrics provided by the app include area under the curve (AUC), concentration at the last time point (LAST, or C _trough), maximum concentration (MAX), and minimum concentration (MIN). AUC is calculated by PK/PDmisc using the trapezoidal method. ³³ MAX, MIN, and LAST are captured directly from the simulation output. Of note, the “LAST” and “MIN” can be different in the case of oral or subcutaneous dosing. The summary statistics and box plots are generated to enable comparisons across scenarios. The options for summary statistics include mean, median, geometric mean, standard deviation, 90% confidence interval (CI), coefficient of variation (CV%), and geometric coefficient of variation (geoCV%). A reference line (e.g., IC₉₀ from preclinical studies) can be applied to the exposure metric (e.g., C _trough), thus the percentage above the reference level can be derived and included to the summary stats table. Another feature of the app is to check for agreement between simulation and observations, by allowing the user to upload observed data (e.g., from on‐going studies).

Finally, users can export the entire simulation as a zip file, including the model code, seed number (if defined), population data with the associated user‐specified parameters (if simulated within the app), dosing table, simulated data, plots, and summary stats. The zip file contains all the information needed for reproducing the simulations. The downloaded data can be further analyzed by other programs, if desired.

CASE EXAMPLES

Case 1: Impact of dose delays and alternative dosing regimens on pertuzumab PK following intravenous infusion

Background

The first case demonstrated how to use the app to conduct simulations of various dosing regimens using pertuzumab as an example. The impact of dose delays and alternative dosing regimens on pertuzumab PK was previously published by Liu et al. ³⁴

Perjeta (generic name pertuzumab) as an intravenous (i.v.) infusion was initially approved in 2012 ³⁵ in combination with trastuzumab, to treat patients with HER2‐positive breast cancer across the neoadjuvant, adjuvant, and metastatic treatment settings. The approved dose is 420 mg every 3‐week cycle following an initial loading dose of 840 mg (i.e., 840 mg/420 mg every 3 weeks). A reloading dose of 840 mg is required if the dose interval is 6 weeks or longer. This approved regimen will be hereafter referred to as the base case. The dose‐delay simulations have the same regimen as the base case, except that the dosing interval between the third and fourth doses is extended to 4, 6, or 9 weeks (i.e., DL4W, DL6W, and DL9W). Two alternative‐dosing regimens were tested, that is, 840 mg/420 mg every 4 weeks and 840 mg every 6 weeks (i.e., ALTQ4W and ALTQ6W).

Pertuzumab PK following i.v. infusion was best described by a two‐compartment model with linear elimination. Baseline serum albumin (ALBU) and lean body weight (LBW) were identified as covariates on clearance (CL), while LBW as covariates on central (V ₁) and peripheral volume of distribution (V ₂). ³⁶ The mrgsolve model of pertuzumab PK was implemented (Perjeta_valid.cpp; Supplementary Model S1) and validated against the NONMEM simulations (shown in HTML S1 from R Markdown).

Preclinical xenograft efficacy models indicated that the target steady‐state C _trough for pertuzumab is 20 μg/mL for maximum tumor growth suppression. ³⁷ The approved regimen for HER2‐positive breast cancer (i.e., the base case) demonstrated favorable efficacy when C _troughgreater than 20 μg/mL was achieved in 90% of patients. ³⁸ Thus, the percentage of the simulated patients with C _trough above 20 μg/mL was used as the criteria for the assessment of various regimens.

Model tab

After loading the model (Perjeta_valid.cpp), a pop‐up window appeared to define the “Model Covariates” (select “ALBU” and “LBW”), “Covariate Types” (select “Continuous”), and the “Model Time Unit” (select “day”). A randomization seed was provided to ensure reproducibility. A “Model Summary” was automatically created for verification, and the complete mrgsolve code was also displayed (Figure 2).

FIGURE 2.

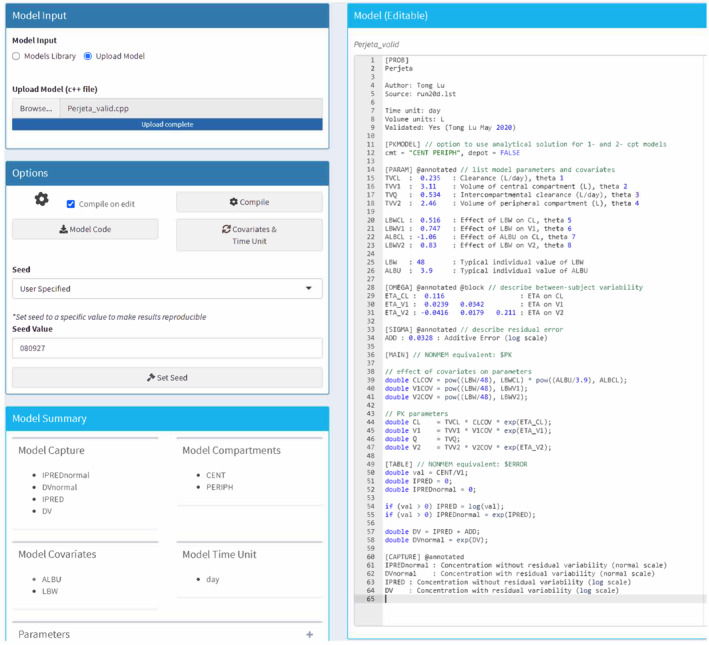
Model tab for pertuzumab population simulation in gPKPDviz. Select model covariates (albumin [ALBU] and lean body weight [LBW]); set model time unit (day); set random seed (080927) for replicable simulation.

Population tab

In the paper by Liu et al., ³⁴ LBW and ALBU were simulated by gPKPDviz assuming a truncated normal distribution. In this analysis, the dataset containing actual values of LBW and ALBU (population.data.csv; n = 477) were loaded for simulation (Figure S2). Data from representative individuals were included in the supplementary file as Data S1. The requirements for the format of external data sets are shown under “Data Upload Criteria” after clicking “Upload Dataset.” One thousand virtual patients were further generated by sampling with replacement (Figure 3), which was summarized with a table and histogram plot. By default, the population data for the first 10 individuals is shown under the “Data” sub‐tab. The data distribution as histogram plots can be revealed under the “Baseline Values” sub‐tab. The histogram plots for the 477 and the 1000 patients confirmed the data similarity (data not shown). LBW and ALBU were categorized into four bins for plotting and summarization purposes, and were appended to the original data (Figure 3).

FIGURE 3.

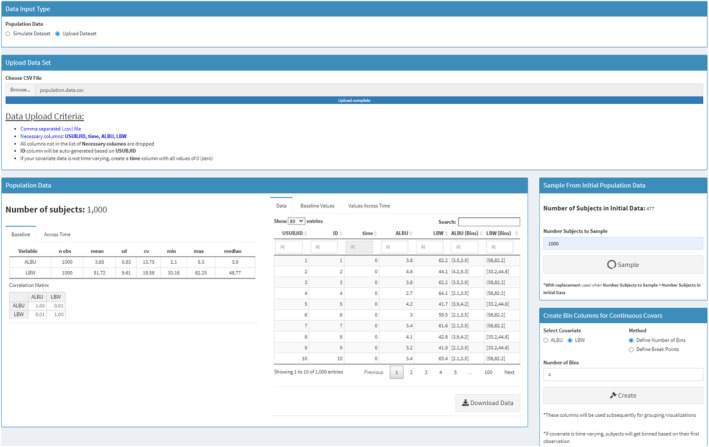
Population tab for pertuzumab population simulation in gPKPDviz: sampling with replacement. First, upload covariate values from the external dataset (population.data.csv; n = 477); second, sample with replacement to generate 1000 virtual patients from the 477 actual patients; third, generate binned covariates for albumin (ALBU) and lean body weight (LBW).

Dosing tab

The dosing regimen for all the cases (i.e., base case [BASE], delay‐4‐week [DL4W], delay‐6‐week [DL6W], delay‐9‐week [DL9W], alternative‐q4‐week [ALTQ4W], and alternative‐q6‐week [ALTQ6W]) were defined as external datasets for loading (Data S1). The doses were given as i.v. infusions over 1‐h for 840 mg or 30‐min for 420 mg, for a total of eight cycles.

It is also feasible to define the base case and alternative regimens within the app. Shown in Figure S3 is an example of defining the base case, where two dose interventions describing loading and maintenance phases separately were combined sequentially. However, the app could not generate the delayed regimens, given that more than three interventions would be needed.

Simulate tab

For the base case, the user‐specified sampling times relative to the most recent dose were defined in “Additional (Optional) inputs,” according to the Garg analysis, ³⁶ as day 0, 0.021 (30‐min), 0.0625 (90‐min), and each day from day 1 to day 21. For the delayed regimens or alternative regimens, one sample right before the next dose was added automatically to the user‐specified sampling times, which captured the C _trough for every regimen without needing to manually revise the sampling times. To simulate only by user‐specified sampling times, the “Sampling Interval” and “Sampling Duration” were set to zero. The snapshot for defining sampling times for the base case is shown in Figure S4. As explained in the App overflow section, the simulated data at the user‐specified sampling times will correspond to the “Observation” type with “User Specified” data source.

The process of defining the Dosing tab and Simulation tab can be repeated for all cases, with corresponding SIM_IDs (BASE, DL4W, DL6W, DL9W, ALTQ4W, and ALTQ6W).

Result tab

The structure of the simulated data is shown in Figure S1 for the BASE case. The variables that are unique to the pertuzumab case are ALBU, LBW (model covariates), CENT, PERIPH (state variables), IPRED_normal, DV_normal, IPRED, DV (output variables), and ALBU_bin and LBW_bin (binned derivatives for covariates).

The simulation exercises shown below were to reproduce the key results from Liu et al. ³⁴

1. Pertuzumab base case PK

First, filter BASE under “SIM_ID” variable to extract the base case simulations. By clicking “Update Results,” the plots under default settings were created, which was the pooled individual PK predictions over time (i.e., IPRED_normal), colored by SIM_TYPE (Figure S5). It was generated by default due to the fact that IPRED_normal was the first output variable listed in $CAPTURE.

Several steps were taken to customize the plot (Figure S6A). First, for data source, filter “User Specified” under SIM_TYPE (or filter “Observation” under REC_TYPE); second, for plot display, select “Percentiles” for “User Specified” data; third, for reference line, enter 20 as reference value; fourth, for time scale, adjust “Time Unit” to Week; fifth, for color, set “Color by” to “None” (i.e., gray color); and sixth, for Y‐Axis, set “Y‐Axis Max” to 400. After clicking “Update Results”, the updated plot was shown as median and 90% interval in the time scale of week (Figure 4a; refer to figure 1 from Liu et al. ³⁴ ).

FIGURE 4.

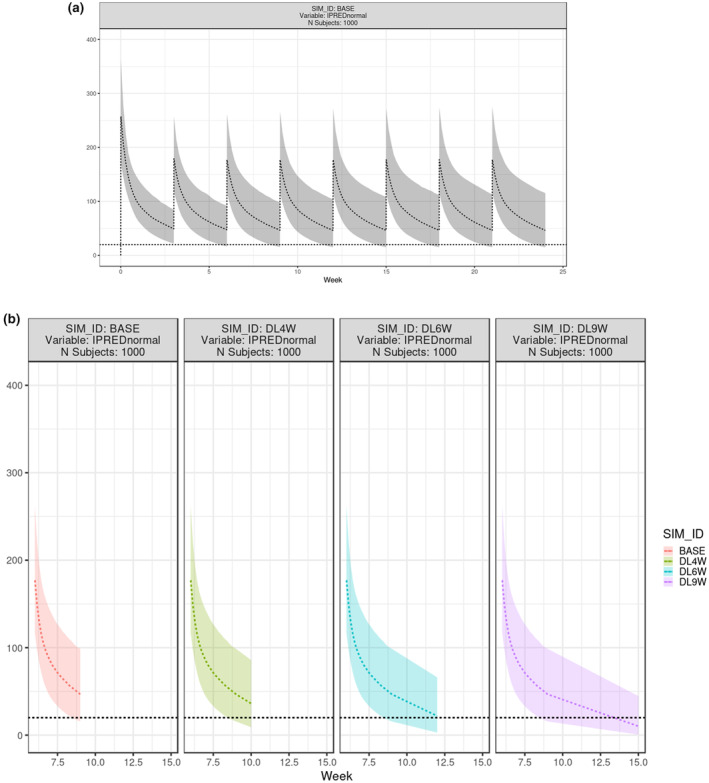
Result tab for pertuzumab population simulation in gPKPDviz: PK profiles. (a) Simulation of individual prediction (IPRED) for pertuzumab base case, shown as median and 90% interval from 1000 virtual patients for 8 cycles; X axis is in week, and Y axis is in μg/mL; (b) Effect of dose delay on pertuzumab PK at cycle 3, shown as median and 90% interval of IPRED from 1000 virtual patients. X axis is in week, and Y axis is in μg/mL; Plots were laid out side‐by‐side for base case (BASE) and the dose delay cases (DL4W, DL6W, and DL9W). PK, pharmacokinetic; SIM, simulated.

To derive the summary stats for AUC, C _max, and C _trough in the first four cycles (Table 1; refer to table 1 from Liu et al. ³⁴ ), first extract the cycle one to four data (filters 1, 2, 3, and 4 under “Cumulative Dose Count” variable), choose the exposure metrics (tick AUC, LAST, MAX in “Stats Display”), choose the summary stats of interests (tick median/5th percentile/95th percentile in “Stats Type”), and then summarize by “Cumulative Dose Count” (Figure S6B). The 20 μg/mL threshold was defined under the “Summary Stats” sub‐tab for C _trough (“LAST” Threshold), in order to derive the percentage above threshold for the simulated C _trough values in the summary stats table.

TABLE 1.

Result tab of gPKPDviz for pertuzumab population simulation: summary statistics.

Summarized by	% Above LAST Threshold (20)	AUC stats	LAST stats	MAX stats
Summary Stats Table (for base case in the first four cycles)
SIM_ID BASE Cumulative dose count 1 Variable: IPREDnormal N subjects: 1000	96.9	Median: 1990 5th Percentile: 1350 95th Percentile: 2830	Median: 49.3 5th Percentile: 23.3 95th Percentile: 83.4	Median: 254 5th Percentile: 176 95th Percentile: 366
SIM_ID BASE cumulative dose count 2 Variable: IPREDnormal N subjects: 1000	93.7	Median: 1700 5th Percentile: 982 95th Percentile: 2710	Median: 47.6 5th Percentile: 17.8 95th Percentile: 90.4	Median: 178 5th Percentile: 122 95th Percentile: 259
SIM_ID BASE cumulative dose count 3 Variable: IPREDnormal N subjects: 1000	92.5	Median: 1680 5th Percentile: 949 95th Percentile: 2860	Median: 47.1 5th Percentile: 16.2 95th Percentile: 97.7	Median: 177 5th Percentile: 120 95th Percentile:261
SIM_ID BASE cumulative dose count 4 Variable: IPREDnormal N subjects: 1000	92.2	Median: 1680 5th Percentile: 931 95th Percentile: 2940	Median: 46.7 5th Percentile: 15.9 95th Percentile: 101	Median: 177 5th Percentile: 119 95th Percentile: 264
Summary Stats Table (for base case and dose delay cases at cycle 3)
SIM_ID BASE Variable: IPREDnormal N subjects: 1000	92.5	Median: 1680 5th Percentile: 949 95th Percentile: 2860	Median: 47.1 5th Percentile: 16.2 95th Percentile: 97.7	Median: 177 5th Percentile:120 95th Percentile: 261
SIM_ID DL4W Variable: IPREDnormal N subjects: 1000	80.7	Median: 1980 5th Percentile: 1040 95th Percentile: 3480	Median: 36 5th Percentile: 9.89 95th Percentile: 83.2	Median: 177 5th Percentile:120 95th Percentile: 261
SIM_ID DL6W Variable: IPREDnormal N subjects: 1000	52.8	Median: 2410 5th Percentile: 1170 95th Percentile: 4480	Median: 21.3 5th Percentile: 3.46 95th Percentile: 62	Median: 177 5th Percentile:120 95th Percentile: 261
SIM_ID DL9W Variable: IPREDnormal N subjects: 1000	24.5	Median: 2890 5th Percentile: 1320 95th Percentile: 5700	Median: 9.78 5th Percentile: 0.655 95th Percentile: 42.2	Median: 177 5th Percentile:120 95th Percentile: 261

Note: Summary statistics include the median, 5th and 95th percentile for AUC, C _max (MAX), and C _trough (LAST) from the 1000 virtual patients, and the percent of patients with C _trough above 20 μg/mL threshold; The dose delay cases have the same regimen as the base case, except that the dosing interval between the 3rd and 4th dose is extended to 4‐, 6‐, or 9‐weeks (i.e., DL4W, DL6W, and DL9W).

Abbreviations: AUC, area under the curve; C _max, maximum plasma concentration; C _trough, trough plasma concentration; LAST, concentration at the last time point; MAX, maximum concentration.

Using the BASE case simulation, the impact of ALBU on the steady‐state PK at cycle four can be easily explored by the stratified covariate ALBU_bin (i.e., summarized by ALBU_bin). By providing 20 μg/mL as threshold for C _trough, the percentage above threshold for each category was also included in the summary stats table (Figure S7, Table S1). The animated demonstrations for the BASE case simulation stratified by ALBU_bin were provided on GitHub. ²²

• 2Effect of dose delay on pertuzumab PK

To assess the impact of the extended dose interval (i.e., dose delay) on the C _trough at cycle 3, BASE, DL4W, DL6W, DL9W were filtered under “SIM_ID,” and “3” was filtered under “Cumulative Dose Count.” Once summarized by SIM_ID, the PK profiles at cycle three were plotted across regimens (Figure 4b). Similarly, the summary stats table was generated to compare across regimens (Table 1, refer to table 3 from Liu et al. ³⁴ ). The animated demonstration for comparing BASE and DL6W was provided on GitHub. ²²

• 3Effect of alternative dosing on pertuzumab PK

To assess the impact of the alternative dosing regimen (ALT4W and ALT6W), the PK profiles following eight cycles of dosing were compared to the BASE case in Figure S8 (refer to figure 3 in Liu et al. ³⁴ ). The summary stats for cycle one or four were derived and compared across regimens in Table S2 (i.e., summarized by both SIM_ID and cumulative dose count) (refer to table 4 in Liu et al. ³⁴ ).

Individual simulation and sensitivity analysis

The simulation exercises shown below were to illustrate additional features of the app, including individual simulation and sensitivity analysis:

1. Individual simulation

To illustrate the features of individual simulation, the dataset containing post hoc estimates was compiled for the population tab (population.data.indpara.csv; representative individuals in Data S1), and the dataset containing individual dosing and sampling records was compiled for the dosing tab (SamplingDosing.ind.csv; representative individuals in Data S1). The mrgsolve code for population simulation was modified for individual simulations (Perjeta.ind.cpp; Model S1), including (1) replace $PARAM block with a list of post hoc parameters (use the population estimates as placeholder); (2) remove $OMEGA block, and (3) redefine the PK parameter in $MAIN block with the post hoc parameters. During the simulation process, the post‐hoc parameters in the $PARAM block were updated seamlessly with the individual estimates from the population data (population.data.indpara.csv), for the variables with common names (i.e., CL_ind, V _1ind, Q _ind, and V _2ind).

After loading SamplingDosing.ind.csv in the dosing tab, the following message popped up: “Non‐dosing rows found in dosing data set. These records will be used as additional observation time points in the simulated data.” In addition, the fine time grid was also simulated at every half hour for 120 days, overlaying the simulations at the actual observation time points (colored by SIM_TYPE). Of note, the simulations from fine time grid and actual sampling times have SIM_TYPE as “Simulation” and “User Specific,” respectively. The individual simulations were displayed when further stratifying the plots by subject ID (i.e., summarized by USUBJID), shown in Figure 5 for the representative subjects. To label the dose time and amount on the individual plots, the box for “Show dose events” was ticked. The animated demonstration for individual simulation was provided on GitHub. ²²

• 2Sensitivity analysis

FIGURE 5.

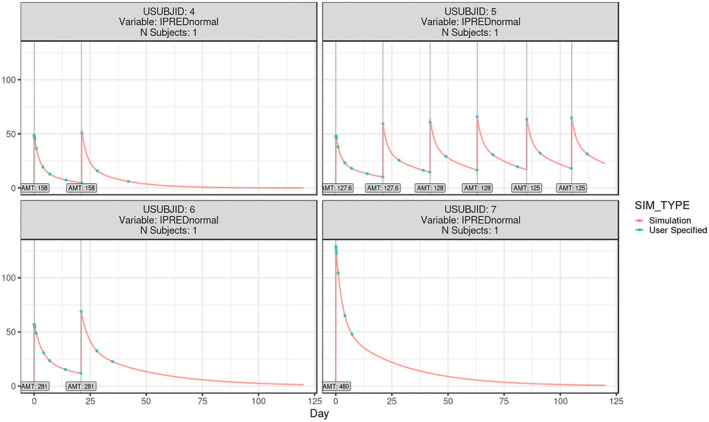
Individual simulation of pertuzumab PK in gPKPDviz for the representative individuals. The individual simulations were based on the individual dosing history, post hoc PK parameters, and the actual sampling time (green dots) augmented with the fine time grid (red curve); the vertical lines represented the dose time and amount; X axis is in day, and Y axis is in μg/mL. IPRED, individual prediction; PK, pharmacokinetic.

Sensitivity analysis here refers to how sensitive the model prediction is to the change of a structural parameter, whereas all the other parameters are fixed. It is meant to evaluate the contribution/importance of a structural parameter to the model overall, through graphical visualization. ⁶ , ³⁹ The population prediction is usually used for this purpose, without accounting for the interindividual variability. The following steps are needed to perform the sensitivity analysis in the app for all the parameters at once. The structural parameters being tested included CL, V ₁, inter‐compartmental clearance, and V ₂.

1. Dataset: create a dataset containing a list of individuals with varying parameter values, sorted by PARA (set to 1 when CL varies and 2 when V ₁ varies, etc.) and RANK (set to 1 for the lowest value tested and 5 as the highest, etc., increased gradually by a 2‐fold magnitude; population.data.sensitivity.allpara.csv; Data S1).

2. Model file: modify Perjeta_valid.cpp by adding PARA and RANK to $PARAM block (Perjeta.sensitivity.cpp; Model S1).

3. Model tab: select PARA, RANK, and all the structural parameters from the drop‐down list; set “Model Time Unit” to day; set PARA and RANK as categorical covariate.

4. Population tab: load the dataset created in step a.

5. Dosing tab: load the dosing regimen from the external dataset (e.g., Base.csv).

6. Simulate tab: simulate the population prediction by ticking the box for “PRED Simulation”, using the user‐specified sampling time defined in “Simulate tab” of Case 1.

7. Results tab: summarize the plots by PARA, and color by RANK; untick “Share Y‐Axis” under “Axis”.

The resulting sensitivity plots were shown in Figure 6 for the base case. The users can conduct the sensitivity analysis more efficiently in R using the mrgsim.sa package, which is showcased in the mrgsolve gallery. ⁴⁰

Case 2

Body weight‐based dosing versus fixed dosing of polatuzumab vedotin for heavier patients

FIGURE 6.

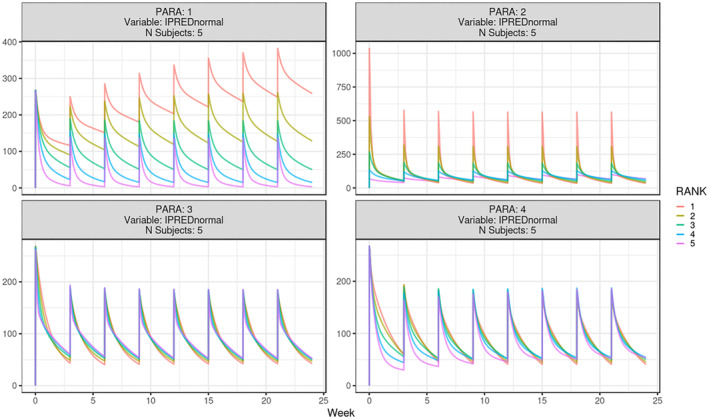
Sensitivity analysis of pertuzumab PK in gPKPDviz. Sensitivity simulation of individual prediction (IPRED) for pertuzumab base case; PARA 1, 2, 3, 4 represent CL, V ₁, Q, and V ₂, respectively; for each parameter, set RANK to 1, 2, 3, 4, 5, with 1 as the lowest value tested and 5 as the highest value (increase gradually by a two‐fold magnitude); X axis is in week, and Y axis is in μg/mL. CL, clearance; Q, inter‐compartmental clearance; V ₁, central volume of distribution; V ₂, peripheral volume of distribution.

The second case was to demonstrate how to use gPKPDviz to efficiently assess body weight‐based dosing versus flat dosing for a heavier patient population, using polatuzumab vedotin as an example.

Polivy (generic name polatuzumab vedotin; pola) is a CD79b‐directed antibody‐drug conjugate with activity against dividing B cells. The small molecule, Monomethyl auristatin E (MMAE), is an anti‐mitotic agent covalently attached to the antibody via a cleavable linker. Pola was approved as the combination therapies to treat adult patients with previously untreated or treated diffuse large B‐cell lymphoma. ⁴¹ , ⁴² The recommended dosing regimen is 1.8 mg/kg (i.v. infusion over 90 min) every 3 weeks for six cycles. A two‐analyte integrated population PK (PopPK) model ⁴³ for pola (antibody‐conjugated MMAE [acMMAE] and unconjugated MMAE) has been developed based on data from 460 patients in four clinical studies. The mrgsolve code for pola PopPK model was developed and validated against the NONMEM output (Pkcase_Polatuzumab.valid.cpp; included in the published model library). It was modified for the individual simulation purpose (Pola.ind.cpp; Model S1).

Given that pola dosing is based on body weight, there is a risk of overdosing for patients with heavier body weights (≥100 kg) considering that acMMAE clearance increases less than proportionally to body weight ⁴³ ; a flat dose of 180 mg could be a better regimen for this subpopulation. To compare PK between the two regimens, the 460 patients were stratified into two subgroups, that is, 100~146 kg versus 38~100 kg within the app, and their cycle six exposures were simulated following either six cycles of bodyweight‐based dosing at 1.8 mg/kg or flat dosing at 180 mg. The simulations were conducted based on the user‐loaded post hoc estimates, app‐generated dosing regimens, and the fine time grid for simulation (every 2 h sample for 18 weeks). Figure 7 illustrates the implementation of covariate‐based dosing in gPKPDviz. Comparisons were made between the two regimens for the heavier bodyweight subgroup, and also between the two subgroups following the bodyweight‐based dosing (published previously ⁴⁴ ).

FIGURE 7.

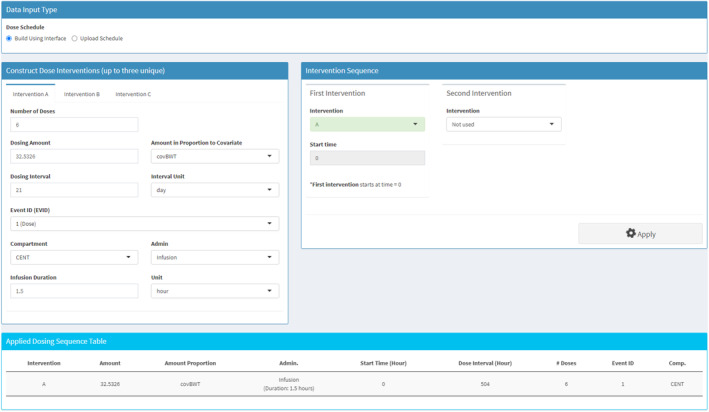
Implementation of body weight‐based dosing in gPKPDviz for polatuzumab. The polatuzumab was dosed at 1.8 mg/kg (corresponding to 32.5326 μg/kg acMMAE), by intravenous.v. infusion of 1.5 h every 3 weeks for six cycles. acMMAE, antibody‐conjugated monomethyl auristatin E.

For the heavier bodyweight subgroup, the cycle six PK profiles for acMMAE and MMAE were shown in Figure S9 following bodyweight‐based or flat dosing; the geometric mean ratio of cycle six AUC for bodyweight‐based versus flat dosing were 1.13 and 1.17, respectively, for acMMAE and MMAE (derived from Table S3). The magnitude of increase (<=17%) for bodyweight‐based dosing was considered not of clinical relevance. Similarly, following bodyweight‐based dosing, the geometric mean ratio for higher versus lower bodyweight subgroups were 1.08 and 1.27, respectively, for acMMAE and MMAE (Figure S10, Table S4). The magnitude of increase for heavier subgroup was relatively higher for MMAE (27%) but was still small compared with the interindividual variability as indicated by coefficient of variation of the geometric mean (geoCV%: 40.5~53%; Table S4). The comparison outcomes for C _max were very similar to those for AUC (results not shown). Overall, dose capping of 180 mg for patients with bodyweight greater than or equal to 100 kg is not warranted based on the available data, supporting bodyweight‐based dosing for pola. ⁴⁴

Model validation

To validate the mrgsolve models used in the app, we compared the simulations from the mrgsolve model to the corresponding NONMEM model. The original NONMEM dataset was fed into both models to check the discrepancies for population prediction (PRED), individual prediction (IPRED), and individual prediction with residual error (DV).

Any noticeable discrepancies at the PRED level would be indicative of misspecification in the structural component of the mrgsolve model. To assess the discrepancies at the IPRED and DV levels, population simulation with 1000 replicates was conducted. For each individual, the median, 5th, and 95th of the 1000 simulated profiles were plotted and compared between the two models. The 5th and 95th percentiles from mrgsolve might deviate slightly from NONMEM purely due to the randomness, even for a correctly implemented mrgsolve model. To reduce the impact from randomness, the VPC–like plots (with CIs around the prediction intervals ⁴⁵ ) were generated for IPRED and DV using the nominal time. To complete this, first extract a subset of the dataset; ideally, it would be a group of patients (n > 50) taking the same dose level with similar sampling and dosing schedules. Second, for each replicate, derive the median, 5th, and 95th percentiles (i.e., prediction intervals) for the patient subset at each nominal timepoint. Third, calculate the median, 5th, and 95th percentiles (i.e., CIs) around each prediction interval.

The mrgsolve code for pertuzumab population PK model (Perjeta_valid.cpp) is validated. See the html output (Supplementary Rmd S2) generated from R markdown.

App validation

The gPKPDviz app itself was also validated by confirming that the key results from mrgsolve simulations outside of the app by R matched the output from the app, when applying the identical seed. The simulation of pertuzumab base case was used for the validation. Specifically, it is 420 mg every 3‐week cycle following an initial loading dose of 840 mg, for a total of eight cycles. The user‐defined sampling times relative to the most recent dose were defined according to the Garg analysis ³⁶ as day 0, 0.021 (30‐min), 0.0625 (90‐min), and each day from day 1 to day 21.

The key simulations performed for validation purpose include the following:

• Case 1: population simulation based on the simulated covariates (1000 virtual individuals), the simulated dosing regimen and the user‐defined sampling times; set seed to for randomization control;

• Case 2: population simulation based on the actual covariates (sampling with replacement from the 477 individuals to generate 1000 individuals), the simulated dosing regimen and the user‐defined sampling time; set seed to for randomization control;

• Case 3: case 2 with simulation of typical profile (PRED);

• Case 4: case 2 filtered by cycle eight and stratified by ALBU_bin;

• Case 5: individual simulation of the actual patients (n = 477) based on the post hoc parameters, the individual dosing history, and the individual sampling time augmented with the fine time grid.

The key app features being validated directly or indirectly include the following:

1. Population tab: truncated multi‐normal distribution, sampling‐with‐replacement, binning of continuous covariates, randomization control.

2. Dosing tab: regimen simulation with two interventions (840 mg loading dose and 420 mg maintenance dose), individual dosing history filtering for individual simulation.

3. Simulate tab: population simulation, typical profile simulation, fine time grid simulation, simulation as per individual sampling time with or without the fine time grid, randomization control.

4. Result tab: data assembly and filtering, median time‐profile with 90% CI, stratifications, exposure metrics derivation, percent above threshold derivation, and summary statistics.

The detailed validation process is included in the Supplementary Rmd S1 file generated from R markdown. The testing of time‐varying covariates and correlation between continuous variables are not covered here because they did not apply to the pertuzumab case; those features were validated in‐house by other case examples (results not shown).

DISCUSSION

We have developed and showcased a powerful and flexible PK/PD model simulator (gPKPDviz), with an intuitive interface to cover most needs for the scenario simulations in clinical pharmacology. Although all the simulations done in this app could be achieved in R using mrgsolve package, gPKPDviz is an attractive tool for the real‐time simulations in a project team setting, with fast turnaround time. Developing mrgsolve models is the prerequisite for using the app. Once the mrgsolve models are developed by the PK/PD scientists, it can be loaded onto the app for applications by team members who know PKs but have limited programming skills. This app can also serve as an exploratory tool to unveil the impact of various components of the model on the outcomes. Furthermore, it offers an interactive, open‐source platform for teaching mrgsolve or pharmacometrics in general in an academic context.

We internally use gPKPDviz as a platform to host models for the selected Roche/Genentech molecules. As an open‐source platform, ²² we offer a selection of basic model templates in the library including one, two, three compartment PopPK models and indirect response model, and some publicly available models including PopPK models (pertuzumab and polatuzumab) and PK/PD model (Neutropenia model for Paclitaxel ⁴⁶ ). More model codes will be added into the library.

In this manuscript, we selected two PopPK cases to demonstrate the actual clinical applications of the app. Although adding a PK/PD case would be beneficial, we chose to provide such model in the model library (i.e., neutropenia PK/PD model for paclitaxel), without further expanding the manuscript. The app is capable of describing paclitaxel PK and neutrophil count profile side‐by‐side for various dosing regimens. Users can use the app to derive the nadir of neutrophil count profile and compare across regimens.

In gPKPDviz, the derivation of AUC (trapezoidal method) or MAX and MIN (capture from simulation output) are sensitive to the sampling time. One can use this feature to evaluate how different sampling intervals might impact the assessment of these parameters. Whereas increasing sampling intensity can improve accuracy, it will prolong run time and increase the chance of the termination due to memory limit. Alternatively, MAX or MIN can be estimated within the ODE system. However, such estimates could be affected by overshooting which is inherent to the ODE solver. In mrgsolve, the impact of overshoot can be properly managed by reducing the hmax, ⁴⁷ which is the trade‐off of estimation accuracy and simulation time. Mrgsolve code is provided in the model library to showcase the ODE‐based derivation of AUC, MAX (and T _max), MIN (and T _min) after each dose, using pertuzumab PopPK model as the template.

Currently, there are no tools available yet to fully automate the model translation process from NONMEM (or other model estimation software) to mrgsolve syntax, although in most cases the translations are straightforward. The $NMXML and $NMEXT blocks in mrgsolve allow to import the estimates of $THETA, $OMEGA, and $SIGMA from the NONMEM run files (.xml file and .ext file) into the mrgsolve model, ¹⁴ which helps to simplify the translation process and reduce the translation error considerably. Among the code blocks, there are four C++ functions that mrgsolve manages: PREAMBLE, MAIN, ODE, and TABLE. There is a specific calling order for those functions, although they can be specified in any order in the model. Understanding the calling order and calling nature of the C++ functions is the key for proper model translation/development. ¹³ For instance, PREAMBLE is called only once at the first record of the data set, whereas $MAIN is called repeatedly as per the data record. For the variables that need to be re‐defined within the model, they can be declared either in the $MAIN block (e.g., time after dose TAD ⁴⁸ ), or the $PREAMBLE block (e.g., the variables for adaptive simulation ⁴⁹ ), depending on the nature of the variable.

Formal validation of the mrgsolve model is highly recommended before applying it for the decision making. The validation of the mrgsolve model is essential at the PRED level, considering most errors in translation are related to the structure model and the covariate model. The validation at IPRED and DV level is also preferred to verify the random effect model, especially for models with atypical random effects, such as Box‐Cox transformation. The topic regarding mrgsolve model validation was discussed in the mrgsolve blog by the package developer. ³⁰ , ³¹ The gPKPDviz app itself was also extensively validated against the mrgsolve simulations outside of the app by R, which, together with the validated mrgsovle model, would ensure the accuracy of the app‐generated outputs when being operated properly by the users. We opted for manual validation of the app, utilizing pre‐defined case examples to assess its key functionalities. In contrast to automated testing methods, such as shinytest ⁵⁰ (tests user interface) and testthat ⁵¹ (assesses R functionality), manual testing leverages the tester's contextual understanding and domain knowledge. Although manual testing requires less initial setup, it can be more time‐consuming, especially for repetitive tasks, and does not offer the consistent reproducibility inherent in automated tests. Given the scope of enhancements to gPKPDviz is expected to be modest, we are inclined to continue with manual validation for the newly incorporated features. Ideally, utilizing a combination of manual and automated testing would ensure the most thorough validation of an app.

GPKPDviz is under continuous development in collaboration with Metrum Research Group. Although gPKPDviz was originally developed for simulating continuous endpoints, it can handle categorical end points well, except that, in the current version, the postprocessing is designed exclusively for continuous endpoints (i.e., exposure metrics derivation and summary statistics).

Additional features under consideration include simulating truncated log‐normal distribution with correlation for continuous covariates, providing a last observation carried forward (locf) option for the simulation of time‐varying covariates, ¹³ adding T _max to the summary table, handling longitudinal categorical endpoints in the graphical visualization, and report generation of key results in a certain format. ¹⁰ Some exposure metrics that are unique to the infection diseases, including time above minimum inhibitory concentration (MIC), C _max/MIC ratio, and AUC/MIC ratio, ⁵² , ⁵³ are also under consideration for future implementation. The population simulation feature involving repeated simulation with randomly sampled parameter sets ⁵⁴ is not available in gPKPDviz. Considering the aim of replicated stimulation is mainly for VPCs, we plan to develop a stand‐alone Shiny app for VPCs, by leveraging mrgsolve and the VPC packages, and dedicate the use of gPKPDviz for the scenario simulations.

Simulations in mrgsolve outpace NONMEM and native R significantly, particularly for ODE‐based models, in part due to its seamless integration with C++. The simulation process in gPKPDviz is nearly as efficient as running mrgsove in R, yet the most time and memory consuming step it to load the simulated data. For instance, on our Shiny server, it took 15 s to simulate the pertuzumab PopPK model for 500 subjects with hourly sample for 27 weeks, but it costs around 2 min to load the simulated data with 2 million entries. The suggestion is to choose the sampling interval wisely to reduce the size of simulated data and thus the loading time. Given the overhead from Shiny's web framework and added data loading/processing needs, running mrgsolve within a Shiny app might demand more memory in general than run it directly in R. We recommend deploying gPKPDviz on a robust server to allocate ample session memory, particularly when simulating complex ODE‐based model with intensive sampling, like every hour, spanning prolonged durations such as daily dose over a year.

Despite being powered by mrgsolve, there are certain limitations for gPKPDviz that are inherent to the app‐based simulations. Besides the previously mentioned high memory demand and limited session memory allocation, there are other limitations. These includes limited flexibility (compared with mrgsolve in R), reliance on the web server, and, most importantly, the difficulty to be QCed because most Shiny apps, including gPKPDviz, lack the ability to output reproducible R code after running the simulations. Shinymeta package provides functionality to capture and export the underlying code of a Shiny app, ⁵⁵ allowing users to reproduce the Shiny outcomes outside of the app. However, it would be less efficient to implement it at the late stage of the app development. Thus, the current gPKPDviz app is primarily intended for exploratory analyses and internal decision making, and may not be suitable when source code is required, for example, in regulatory submissions. It is at the user's discretion to determine the most appropriate situations for the application.

ACCESSING THE APPLICATION

GPKPDviz can be accessed as an open‐source application on GitHub. ²² To create a stable and reproducible environment, the application is distributed as a docker image that can be loaded in the host computer either through docker desktop or through docker commands in the terminal. Once the docker image is loaded into the host computer, the user can access the application using a local port (by default, it is programmed to be http://localhost:3838/).

FUNDING INFORMATION

The analysis was sponsored by Genentech, Inc., a member of the Roche group.

CONFLICT OF INTEREST STATEMENT

T.L., V.P., L.B., J.Y.J., and M.K. are full‐time employees of Genentech, Inc., and own Roche stock. E.V. is the Drug Development Training Program (DDTP) fellow in Department of Clinical Pharmacology, Genentech, Inc. E.A. and K.B. are employees of Metrum Research Group.

Supporting information

Figures S1–S10.

Tables S1–S4.

Data S1.

Data S2.

Data S3.

Data S4.

Lu T, Poon V, Brooks L, et al. gPKPDviz: A flexible R shiny tool for pharmacokinetic/pharmacodynamic simulations using mrgsolve. CPT Pharmacometrics Syst Pharmacol. 2024;13:341‐358. doi: 10.1002/psp4.13096