Abstract
Exogenous high-voltage pulses increase cell membrane permeability through a phenomenon known as electroporation. This process may also disrupt the cell cytoskeleton causing changes in cell contractility; however, the contractile signature of cell force after electroporation remains unknown. Here, single-cell forces post-electroporation are measured using suspended extracellular matrix-mimicking nanofibers that act as force sensors. Ten, 100 μs pulses are delivered at three voltage magnitudes (500, 1000, and 1500 V) and two directions (parallel and perpendicular to cell orientation), exposing glioblastoma cells to electric fields between 441 V cm−1 and 1366 V cm−1. Cytoskeletal-driven force loss and recovery post-electroporation involves three distinct stages. Low electric field magnitudes do not cause disruption, but higher fields nearly eliminate contractility 2–10 min post-electroporation as cells round following calcium-mediated retraction (stage 1). Following rounding, a majority of analyzed cells enter an unusual and unexpected biphasic stage (stage 2) characterized by increased contractility tens of minutes post-electroporation, followed by force relaxation. The biphasic stage is concurrent with actin disruption-driven blebbing. Finally, cells elongate and regain their pre-electroporation morphology and contractility in 1–3 h (stage 3). With increasing voltages applied perpendicular to cell orientation, we observe a significant drop in cell viability. Experiments with multiple healthy and cancerous cell lines demonstrate that contractile force is a more dynamic and sensitive metric than cell shape to electroporation. A mechanobiological understanding of cell contractility post-electroporation will deepen our understanding of the mechanisms that drive recovery and may have implications for molecular medicine, genetic engineering, and cellular biophysics.
Keywords: electroporation, nanofibers, cytoskeleton, forces, mechanobiology, pulsed electric fields, actin
Graphical Abstract

Exogenous electric fields, applied as short, high-voltage pulses can disrupt the cell through a process known as electroporation. Electroporation increases membrane permeability, enabling molecular and ionic diffusion across the cell membrane.1,2 Electroporation techniques such as gene transfection,3 electrofusion,4 and electrochemotherapy5 exploit a transient increase in membrane permeability, while irreversible electroporation induces cell death through a loss of homeostasis for nonthermal tumor ablation.6–8
Developed over five decades, the classical theory on electroporation focuses on the mechanisms and time scales of membrane disruption.1,9–11 While it is now widely accepted that hydrophilic pores, electrically altered lipids, and modulated voltage-gated ion channels increase membrane permeability within microseconds of intense electric field application, the mechanisms and time scale (minutes to hours) of membrane resealing remain only partially understood.2,12–14 Recently, there is a growing appreciation that pulsed electric fields cause disruption to the cell cytoskeleton.15–34 The cytoskeleton generates contractile forces that maintain tensional homeostasis required for survival while also dynamically connecting to the cell membrane. Studies show that chemically or physically disrupting the cytoskeleton alters membrane permeability after electroporation27,35,36 and affects cell viability.19,20,22,28 Electric fields may also decrease the elastic modulus of cells.18,29,37 However, the dynamic changes in cell contractility and tensional homeostasis after electroporation have not been quantified yet.
Here, we use a custom-built microfluidic device to enclose suspended extracellular matrix-mimicking fibers that act as force sensors (nanonet force microscopy, NFM),38–40 enabling us to causally link cell contractility, shape, and viability of single cells undergoing electroporation. We describe a biphasic mechanical response and remodeling of the cytoskeleton post-electroporation. Our analysis of multiple cell types reveals three distinct stages during the recovery process: an initial loss in contractility immediately post-electroporation (stage 1), a biphasic force response (stage 2), and a final force recovery stage to pre-electroporation contractility (stage 3). Cytoskeletal staining reveals that the biphasic response is concurrent with actin-mediated bleb retraction and is most pronounced when the electric field direction is parallel to the axis of cell elongation, which interestingly also results in higher cell viability. Altogether, our data suggest targeted opportunities to optimize electroporation for genetic engineering, gene therapy, and molecular medicine.
RESULTS AND DISCUSSION
Microfluidic Chip Integrates Force-Sensing Nanofibers.
We fabricated a custom microfluidic device that integrates the nanofiber scaffold between two needle electrodes spaced 1 cm apart (Figure 1a). Using the previously reported non-electrospinning STEP technique,41,42 we generated suspended polystyrene nanofiber networks: 250 nm-diameter nanofibers spaced 15 μm apart were fused to larger, 2 μm-diameter orthogonal fibers spaced 275 μm apart. Rotation of the nanofiber scaffold 90° reoriented the electric field from a “parallel” configuration that aligned the electric field direction from being parallel to the nanofibers to a “perpendicular” orientation that placed the nanofibers perpendicular to the field (Figure 1b). We refer to these orientations simply as the parallel (∥) and perpendicular (⊥) orientations. Cells elongate between adjacent nanofibers and deflect them according to the cell’s inherent contractility (Figure 1c). In this study, we subjected human glioblastoma cells (U251, Sigma-Aldrich) to 10, 100 μs square-wave pulses at 1 Hz delivered at 500, 1000, or 1500 V, generating approximately uniform electric fields across the scaffold region (Figure 1d, Figure S1c–f). At applied voltages of 500, 1000, and 1500 V, our models indicated that the scaffold region-of-interest (cut-out region of scaffold, see Figure 1d) experienced electric field magnitudes of 441 ± 12 V cm−1, 882 ± 23 V cm−1, and 1323 ± 35 V cm−1, respectively, for the parallel orientation and 455 ± 12 V cm−1, 911 ± 24 V cm−1, and 1366 ± 36 V cm−1, respectively, for the perpendicular orientation. The contractile force of a cell was calculated by the deflection of the flexible nanofibers.38,43 To calculate the contractile force from fiber deflection, we model a deflecting nanofiber as a fixed–fixed beam with two point-source loads, , acting at the two primary adhesion sites, one at either end of the cell.38,44–46 The direction of the force application, , was determined from the orientation of the actin stress fibers, actin-rich retraction fibers, or as specified in the Methods (Figure 1e). In general, is approximately linearly dependent on the cell length for , but constant (~12.4°) for (Figure 1f).
Figure 1.

Nanofiber force sensing. (a) A microfluidic PDMS device encloses a nanofiber network spun on a hollow substrate. The cells are electroporated via a high-voltage pulse generator connected to two needle electrodes. Precisely controlled nanofiber networks are fabricated using the non-electrospinning STEP technique: ø250 nm fibers (15 μm spacing) are deposited orthogonal to ø2 μm fibers (275 μm spacing) and fused at their intersections. Scale bar 20 μm (lower), and 1 μm (upper). b) Parallel orientation, cell long-axis aligned with the electric field; perpendicular orientation, cell long-axis perpendicular to the electric field. (c) Single cells attach to parallel nanofibers, causing visible fiber deflection. Scale bar 25 μm. The deflecting fiber is modeled as a fixed–fixed beam with two point-loads, F, located at the attachment points of the cells and at an angle . (d) A finite element model indicates that the electric field is approximately uniform within the region of interest at the center of the scaffold. (e) An elongated cell shows f-actin stress fibers (red) and focal adhesions (green) along the fibers. Contractile force is applied along the f-actin stress fibers (e, bottom left), retraction fibers (e, bottom center), or at the bisection of the membrane angle (e, bottom right). The dashed lines indicate fiber location. Scale bars 10 μm (top) and 5 μm (bottom). (f) The angle is well approximated by a two-segment line when plotted against cell length. For cells longer than 63.4 μm, is constant at 12.4°. For cells shorter than 63.4 μm, is approximated as a linear function of cell length. Inset images show a round and elongated cell with corresponding data points. Scale bars 5 μm. EP, electroporation.
Contractility as a Biophysical Metric of Electroporation.
Almost immediately after electroporation, cell elongation decreased and membrane blebs formed. In the parallel orientation, cell rounding became appreciable with increasing field strengths (Figure 2a). Interestingly, in the perpendicular orientation, cells largely retained their elongated morphology (Figure 2b) unless the field strength was high (1500 V), which resulted in high levels of blebbing and cell rounding. Membrane blebbing decreased over a span of several minutes, after which the cells respread along the fibers. We quantified the temporal dynamics of the cell length, average fiber deflection (measured at cell attachment points), and contractile force response for different field strengths both in the parallel (Figure 2c) and perpendicular orientations (Figure 2d).
Figure 2.

Cell shape and contractile force response to electroporation. (a, b) Cell responses to electroporation at 500 V, 1000 V, and 1500 V in the (a) parallel orientation (441 V cm−1, 882 V cm−1, and 1323 V cm−1 respectively) and (b) perpendicular orientation (455 V cm−1, 911 V cm−1, and 1366 V cm−1 respectively). The onset of membrane disruption by electroporation is visualized for 1000 V∥ by the inclusion of YO-PRO-1 (green, background subtraction and thresholding used to remove background signal, see the Methods). Cells show rounding, membrane blebbing, and an eventual return to a characteristic elongated state in a voltage- and orientation-dependent manner. Scale bars are 25 μm. (c, d) Average fiber deflection, cell length, and contractile force post-EP for cells in the parallel (c) and perpendicular orientation (d). Cells in the parallel orientation show rapidly decreased length and contractility and recovery within 1–2 h. For the perpendicular orientation, no response occurs at 500 V, a moderate response occurs at 1000 V, and an extreme response is seen at 1500 V. Unexpectedly, fiber deflection and force plots show a transitory increase shortly after electroporation (see arrows on plots), indicating multiple stages in the recovery process. Error bands show standard error. (e, f) Maximum percent decrease in force and cell length is greatest at high voltages. (g) Electroporation at high electric fields causes significant cell death, particularly in the perpendicular orientation.
In the parallel orientation, all applied voltages immediately reduced the average contractile force and showed complete recovery within 1–2 h (Figure 2c). Increasing the applied voltage caused a larger decrease in the cell force (Figure 2e) and length (Figure 2f). Unexpectedly, we discovered a transitory biphasic rebound in the cell contractile force immediately after the initial decrease in force post-electroporation, as indicated by the black arrows in Figure 2c. Analysis of individual force responses in the parallel orientation reveals that a majority of the cells (50 of 75 of sampled cells, 67%) underwent a multistage force response, discussed in detail later in this paper.
In the perpendicular orientation, higher electric fields caused a greater decrease in force (Figure 2e) and length (Figure 2f) after electroporation; however, cell response was quite different from the parallel orientation. Contractile force and cell length did not change after electroporation of 500 V, similar to steady-state cell behavior observed in control (sham) experiments (Figure S2f). Application of 1000 V⊥ decreased contractile force and elongation, but this decrease was smaller (Figure 2e, Figure S2a,b), more gradual, and recovery occurred sooner than 1000 V∥. Few cells survived 1500 V⊥, but surviving cells showed higher-than-average prepulse contractility (Figure S3a), had dramatically reduced force and lengths after treatment, and had a long recovery to near pre-electroporation conditions. Interestingly, cell death (Figure S3b) was higher for cells treated in the perpendicular orientation than in the parallel orientation (Figure 2g, Table S2). At 1500 V, the percent cell death increased dramatically from 46 ± 10% (∥ orientation) to 98 ± 1% (⊥ orientation). At the end of data collection post-electroporation (3–4 h), we did not find any significant differences in cell length or contractile force compared to pre-electroporation values for either cell orientation (Figure S2c,d).
Contractility Reveals a Multistage Cell Recovery Post-Electroporation.
The recovery process can be divided into the following stages (Figure 3a,b, Movie S1): a cell-rounding stage (stage 1) of decreasing force and cell rounding, a biphasic stage (stage 2) characterized by a transient rebound of force and subsequent relaxation, and a cell-spreading stage (stage 3) during which the cell recovers its pre-electroporation force and length. In Figure 3c, we show the multistage dynamics of contractile force and fiber deflection for a single cell in each treatment condition. We found that this response occurs more frequently in the parallel orientation (for example, 20 of 26 cells for 1000 V∥ (77%) versus 8 of 22 cells for 1000 V⊥ (36%)). See Table S1 for all percentages.
Figure 3.

Electroporated cells show a biphasic force recovery. (a) A sample contractile force profile for a cell treated at 500 V∥. The cell-rounding stage (stage 1) begins after electroporation and ends at the first force minimum. Contractile forces increase during phase I of the biphasic stage (stage 2) before decreasing again in phase II. The cell-spreading stage (stage 3) begins after the second force minimum during which the cell recovers its pre-electroporation contractility. (b) Images of a cell showing a multistage response (1000 V∥). Corresponding force values are presented for each image, and the stages of recovery are schematically represented above. Scale bar 25 μm. (c) Contractile force and deflection for a representative cell from each treatment demonstrating a multistage response. Note a minimal response for 500 V⊥. (d) Cells in the perpendicular orientation have significantly less change in force and length in the first 2 min after electroporation, except at very high voltages (1500 V). (e) The biphasic stage lasts 20–30 min (longer for 1500 V⊥) with higher voltages causing slightly longer durations. The duration of phase I is nearly equivalent to phase II. (f) Force significantly increases during the biphasic response. The first and second minimum values are not significantly different. During the biphasic stage, cell length does not change significantly. (g) Image sequence of a representative cell electroporated (1000 V∥) in calcium-free media. Scale bar 25 μm. Cell force and length remain unaffected in calcium-free DMEM during the first 2 min after electroporation (1000 V∥).
Stage 1:
Recovery begins with a cell-rounding stage that typically occurs within the first 5 min (longer for 1500 V⊥) after pulsing and is characterized by a rapid reduction of force. Cell extremities retract along the fibers (via actin retraction fibers (Figure 1e)) causing rounding and membrane blebbing (Figure 3b, t = 0–2 min). At 500 and 1000 V, cell length decreases significantly more in the parallel orientation than the perpendicular orientation during the first 2 min post-electroporation (Figure 3d). Since calcium is known to breakdown cell focal adhesions47 and is also an important ion regulating cell response to electroporation,48 we repeated experiments in calcium-free DMEM (see Methods). For electroporation of 1000 V∥ in serum-free media with no extracellular calcium, cells universally remained elongated on the fibers shortly after electroporation (Figure 3g), in stark contrast to the ubiquitous rounding that occurred after the same electroporation conditions in standard cell culture media.
Stage 2:
The biphasic stage begins at a force minimum following the cell rounding stage, in a state of high membrane blebbing. A significant increase of contractile force (Figure 3f) occurs during the first half of this stage (phase I), averaging 11 ± 1 nN or 14% of the average pre-electroporation value. Some cells show force increases up to 40 nN or 48% of the average pre-electroporation force value. The maximum force during this stage is reached when nearly all membrane blebs have disappeared (Figure 3b, t = 16–24 min). Following the local force maximum, contractility decreases (Figure 3b, t = 16–32 min) to a local minimum value that is not statistically different from first minimum (phase II) (Figure 3f). The duration of phase I and phase II is nearly equal (Figure 3e). During the entire biphasic stage, cell length remained almost unchanged (Figure 3f). The total duration of the biphasic stage increased with increasing field strength (Figure 3e) in both the parallel orientation (500 V: 21 ± 1 min; 1000 V: 25 ± 3 min; 1500 V: 32 ± 4 min) and in the perpendicular orientation (500 V: no response; 1000 V: 22 ± 1 min; 1500 V: 47 ± 19 min).
Stage 3:
The cell spreading phase is characterized by a gradual recovery of contractility as the cell respreads along the fibers (Figure 3b, t = 32–192 min). Cells eventually recover their pre-electroporation elongation as well as their pre-electroporation contractile force.
Cytoskeletal Reorganization Drives Cell Contractile Response Post-Electroporation.
The cytoskeleton plays a major role in regulating the contractile response of cells. We performed immunofluorescent staining for the major cytoskeletal components, actin (Figure 4) and microtubules (Figure S4), on fixed cells at various time points post-electroporation (1000 V∥; 0.5, 2, 8, 16, 32, 128 min and 24 h) and compared cytoskeletal structure with non-electroporated cells. Non-electroporated cells show well-developed actin stress fibers and continuous microtubules aligned with cell elongation (Figure 4a,b, Figure S4). During the cell-rounding stage (Figure 3b, Figure 4a,b, 0.5 and 2 min time points) as cells begin to detach from the fibers and decrease in length, the aligned actin fibers and microtubules get disrupted and blebs form on the cell membrane. By 8 min, the f-actin stress fibers are nearly nonexistent, and cells take on a rounded shape with the actin primarily localized at the cortex or on actin-rich retraction fibers originating from prior adhesion sites along the nanofibers. Throughout the cell-rounding stage and at the early phases of the biphasic force response stage (2, 8 min post-electroporation), we observed high levels of membrane blebbing (Figure 3b) with very large individual blebs (up to 20–30 μm 2 projected area). Using two metrics for blebbing, bleb size49 and membrane “roughness” (see Methods for details), we found blebbing to be maximal at 2 min post-electroporation, with significant decreases by 16 min, and baseline values by 32 min (Figure 4c–f). Also, at 32 min, we observed the formation of actin stress fibers, indicating the start of stage 3 (cell-spreading stage) of force recovery. At 128 min, electroporated cells show a fully recovered cytoskeletal structure with well-defined actin stress fibers and aligned, continuous microtubules. Blebbing dynamics in calcium-free media followed similar trends, but the bleb recovery was faster (Figure S5a,b).
Figure 4.

Electroporation disrupts the cytoskeleton. (a) Maximum intensity projections of cells stained for actin before electroporation and during various stages of recovery post-electroporation (1000 V∥). (b) A single confocal z-slice taken in the nanofiber plane. Pre-EP, actin cytoskeleton consists primarily of well-defined stress fibers (yellow markers). During the cell-rounding stage (2, 8 min), both stress fibers and blebs (blue markers) are present. During the biphasic stage (8, 16 min), cells are rounded with cortical actin and no stress fibers. Eventually, stress fibers begin to reform (32 min), and blebbing is reduced as the cell enters the cell-spreading stage and regains its characteristic cytoskeletal structure. (c, d) Bleb size analysis. Large blebs form immediately after electroporation (maximum at 2 min), but are reduced to baseline values within 32 min. (e, f) Membrane roughness is quantified by the ratio of the contour length of the membrane along the nanofiber by the cell length end-to-end distance. Membrane roughness is at its maximum at 2 min after electroporation and returns to pre-EP values after 32 min. All scale bars 10 μm. EP, electroporation.
Cell Membrane Permeability Aligns with Electric Field Orientation.
Given our observations that the electric field orientation with respect to cell shape altered cell responses in contractile force and cell length, we wanted to determine how orientation affected membrane permeability. Using propidium iodide (PI) as a marker of membrane permeability, we visualized the temporal dynamics of PI uptake during and after the application of 10, 1000 V pulses delivered at 1 Hz. We found that PI entered cells at both the anodic (hyperpolarized) and cathodic (depolarized) sides of the cells (with respect to electric field): near the cell’s end points (protrusions) in the parallel orientation and along the cell’s width in the perpendicular orientation (Figure 5, Movie S2). Incidentally, we observed that PI uptake was biased toward the cathodic side of the cell (Figure 5c) with the initial rate of fluorescence intensity change (au/s) nearly two times greater compared to the anodic side in the parallel orientation (22.9 ± 3.7 vs 10.7 ± 1.1 au/s), while the perpendicular orientation showed a smaller but still significant difference between the cathodic and anodic side (26.1 ± 5.7 vs 18.5 ± 3.7 au/s). To investigate if PI uptake was dependent upon calcium in the buffer, we repeated experiments in calcium-free media at 1000 V. We found that the temporal uptake of PI in calcium-free media at 1000 V followed similar trends as in regular media at 1000 V (Figure S5c,d) with no significant difference in PI uptake 60 s after electroporation (Figure S5e).
Figure 5.
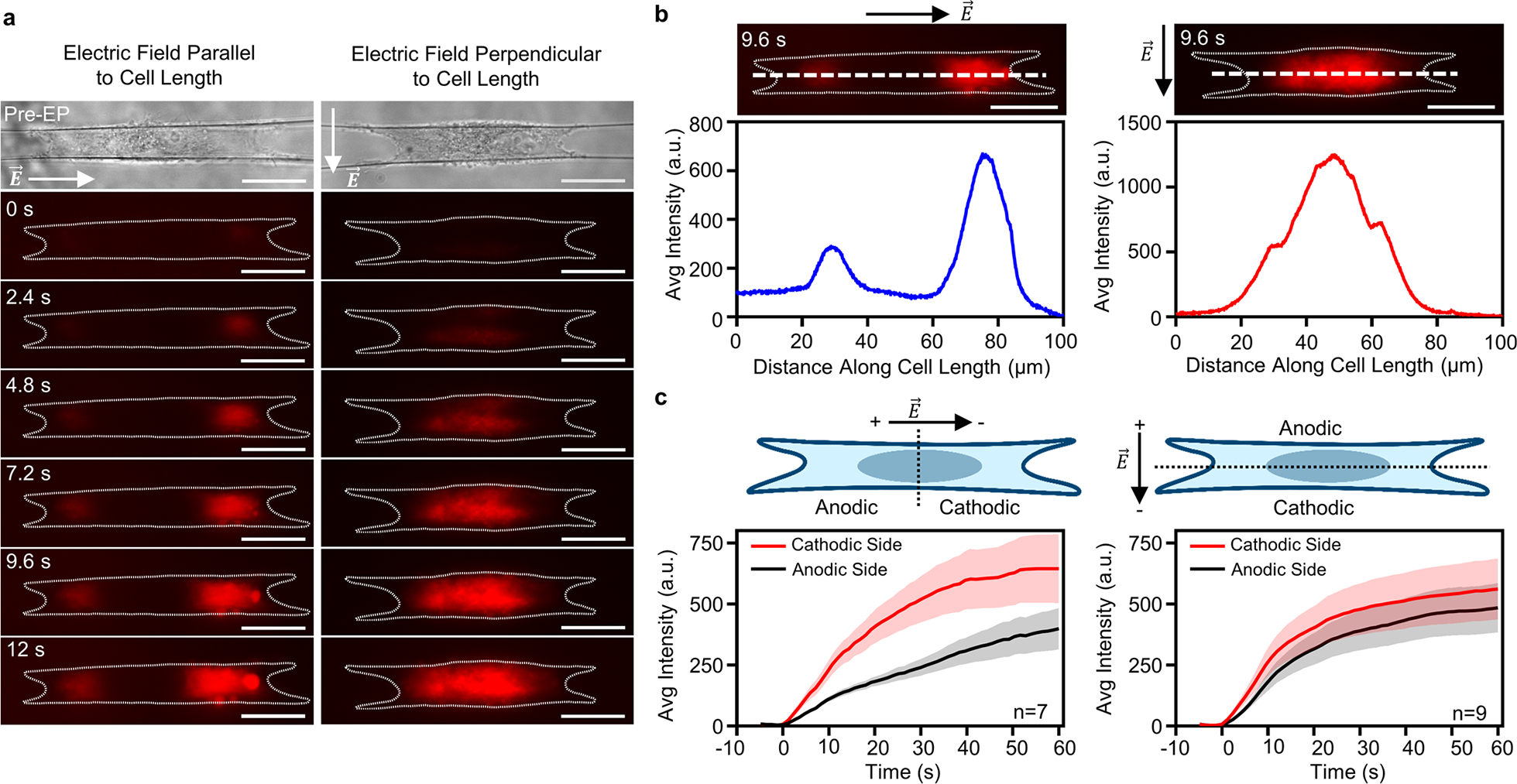
Cell orientation affects membrane permeability after electroporation. (a) Cells show uptake of PI during and after the application of 10, 1000 V pulses (∥: 882 V cm−1; ⊥: 911 V cm−1) delivered at 1 Hz. Time t = 0 indicates the end of the first pulse. PI uptake reveals distinct spatial distributions of membrane permeability for the parallel and perpendicular orientations. In the parallel orientation (a, left column), PI uptake is located near the cell attachment points. However, in the perpendicular orientation (a, right column), uptake is near the central sidewalls. White dashed lines show cell boundary pre-electroporation. The time series indicates that membrane permeability and the influx of PI precedes cell rounding. See Movie S2. Scale bars 20 μm. (b) Representative intensity plots taken along the cell length (large white dashed lines) demonstrate the distinct spatial distributions of membrane permeability in the parallel and perpendicular orientations. (c) PI uptake is biased toward the cathodic (depolarized) side of the cell. Error bands show standard error.
Cell Contractility and Not Necessarily Cell Shape Is Sensitive to Pulsed Electric Fields.
We wanted to inquire if our findings of cell shape and force recovery were generalizable to other cell types, so we investigated electroporation effects to five other cell lines: VAMT cells (human mesothelioma), human thyroid cancer cells, CHO-K1 cells (Chinese hamster ovary), C2C12 cells (mouse myoblasts), and HeLa cells (human cervical cancer). We performed electroporation experiments with cells in the parallel orientation (Figure 6a,b). Although the magnitude of contractile force pre-electroporation varied between cell lines, all cells lines demonstrated a rapid and significant loss in force after electroporation, followed by an eventual recovery of force in 1–2 h. Importantly, experiments with all cell types showed instances of cells undergoing biphasic force responses (stage 2) during recovery (Figure 6c). Furthermore, we found that contractile force is a much more sensitive indicator of cell recovery compared to cell shape (length) alone, as HeLa and CHO cells showed minimal rounding, but a significant loss of contractile force after electroporation. Overall, our experiments with additional cell types, healthy and cancerous, demonstrate that the loss of contractile force after electroporation was cell line independent, while a severe loss of cell shape was cell line dependent.
Figure 6.

Electroporation experiments on five additional cells lines conducted at 1500 or 2000 V in the parallel orientation. (a) Brightfield images of cell responses to electroporation. Scale bar is 25 μm. (b) Cell length and contractile force responses for five cell types after electroporation. Note that the cell contractile force is more dynamic than the cell shape. All cell types demonstrate a robust loss and recovery of forces post-electroporation, but do not necessarily show any significant changes in the cell shape. (c) An example of a multistage response for each additional cell type.
Despite the extensive development and use of electroporation technologies in various biological applications, the dynamics of mechanical recovery to tensional homeostasis in cells post-electroporation remain poorly understood. Complementary to membrane-centric approaches to electroporation reported in literature, here we provide a mechanobiological investigation of electroporated cells by measuring the contractile forces of single cells adherent to extracellular matrix-mimicking suspended fibers. Our network of suspended nanofibers constrains cells to be elongated, in high-aspect ratio shapes with inherent mechanical, biological, and spatial anisotropy, properties that we investigate with two electric field directions (Figure 1). We demonstrate that both electric field magnitude and direction significantly impact the contractile response of cells, which exhibits three distinct stages (Figure 2): an initial loss in contractility immediately post-electroporation (stage 1), a biphasic force response (stage 2), and force recovery to prepulse contractility (stage 3).
Cells attached to our parallel network of fibers form clusters of focal adhesions at their extremities, and upon electroporation, the adhesions are broken, leading to cell rounding (stage 1). Our observations of minimal cell rounding in the absence of extracellular calcium (Figure 3g) implicate extracellular Ca2+-induced focal adhesion disassembly as a possible contributing factor to the cell-rounding stage. It is well established that electroporation disrupts the transmembrane Ca2+ gradient48,50 and causes an influx of extracellular calcium inside the cell, and that locally elevated intracellular calcium levels can lead to disassembly of focal adhesions within minutes.47,51–53 This conclusion is reinforced by our observation that significant PI uptake occurs prior to cell rounding (Figure 5 and Movie S2). To disambiguate the role of serum and calcium in cell rounding, we performed experiments in both serum-free and calcium-free media. Our findings that cell rounding was observed after electroporation in calcium-containing DMEM (1.8 mM calcium, no serum) and minimal rounding in calcium-free media further confirm the role of calcium in cell rounding (Figure S5f). Cell rounding after electroporation has been previously attributed to colloid-osmotic swelling,17,37,54,55 and our results suggest that extracellular calcium is an additional factor driving the loss of cell adhesion. Incidentally, we found some evidence that cells with higher levels of prepulse contractility undergo a faster cell-rounding stage, suggesting a “slingshot effect” caused by the contractile actin stress fibers that accelerate the rounding process (Figure S2e). Independent of the magnitude of prepulse contractility, we observe a rapid loss of actin stress fibers and microtubule structure following the electric field treatment, as prior studies have also noted.15,25,37,56 Cytoskeletal disruption was concomitant with the formation of blebs, with a peak bleb size observed at 2 min post-electroporation (1000 V∥) corresponding closely with the maximal loss of cell contractility. Bleb elimination by 32 min (1000 V∥) post-electroporation is in reasonable agreement with the time scales of membrane resealing previously reported.11,13,27,57,58
Membrane disruption during electroporation is driven by an induced transmembrane potential (ITP), causing pore formation if ITP values exceed a “critical” threshold (~0.2–1 V).2,9,59–63 Our simple ITP models (Figure S6, steady-state, constant membrane conductivity) predict pore formation (ITP ≥ 1.0 V) for all conditions except 500 V perpendicular, in good agreement with our experimental results demonstrating the loss of contractility and cell length for these conditions. However, a maximal ITP value of 0.5 V for cells treated at 500 V in the perpendicular orientation indicates minimal (or no) electroporation, a result consistent with minimal changes to contractile force or length and no YO-PRO-1 uptake observed (data not shown). Incidentally, our experiments showed that PI uptake was asymmetric with a bias toward the cathodic (depolarized) side of the cell, a finding consistent with previous studies but not explained by our ITP models or electroporation theory.64,65 Our models indicate that cells in the parallel orientation should have greater overall disruption compared to the perpendicular orientation due to higher ITP values. However, our experiments revealed a higher cell viability for cells electroporated in the parallel orientation. Modifying our model to include dynamic membrane conductivity,66,67,68 electric field disruption near the nanofibers, pore characteristics (number and radii),68 and/or total mass transport across the membrane69,70 might reconcile the differences between experimental viability results and model predictions. Cell shape-change after pulsing, which is more rapid and prominent after electroporation in the parallel orientation, may also contribute to increased viability in this orientation, as rounding may promote cell recovery by reducing membrane tension or by reducing the cell’s surface area, thereby reducing transport across the disrupted membrane.
As cells become rounded at the end of the cell-rounding stage (stage 1), the contractility measurements demonstrate a biphasic response with a significant rise in forces but with a minimal change in cell length during the first half of this stage (stage 2). Although the exact mechanisms responsible for the biphasic force response remain unknown, we suggest three likely contributing factors. First, during the initial phase of force recovery, contractility increases as blebbing decreases. Bleb reduction by contraction of cortical actin likely contributes to the increased contractility we observe.71,72 Second, cell volume may decrease slightly after electroporation (Figure S3c,d), likely due to cytoskeleton tension-mediated water efflux,73,74 thus leading to an increase in force. Third, increased levels of intracellular Ca2+ have been shown to cause an aggregation of endoplasmic reticulum Ca2+ sensor STIM1, which then leads to the recruitment of the force-bearing focal adhesion protein, talin, and could thereby account for the increased cell contractility in the first phase of this biphasic stage.75 The reduced contractility seen in phase II is most likely indicative of a reorganization of actin, possibly from a bleb-reduction configuration to a spreading configuration, yet the specific mechanisms are unknown.
Irrespective of the electric field strength and orientation, cells that were viable post-electroporation (see Methods for viability criteria) had fully restored contractility typically within the first 1–3 h post-electroporation (stage 3). Such time scales for cell contractile recovery fall within the reported range of cytoskeletal recovery times (minutes to hours).23,25,26,32,37,76 Cell force recovery has been previously investigated in the context of rapid mechanical stretching events,77–82 and not for electroporation, which we show here. While mechanical stretching and electric field treatment are fundamentally different cues, the cellular contractility response to perturbation bears similarities. Studies show that rapid mechanical stretching disrupts tensional homeostasis, leading to rapid disruption of the actin cytoskeleton, followed by recovery of cell contractility either in single or multistages. For example, Nekouzadeh et al. demonstrated that rapid stretching induced a multistage recovery process: a stage of rapid force increase and relaxation (>1 min), a force plateau stage, and finally a gradual active force recovery stage that lasted around 20 min.82 Loss and recovery of cell force were attributed to cytoskeletal fluidization (depolymerization of the actin cytoskeleton) and cytoskeletal resolidification (actin stress fiber recovery), respectively. While these force response patterns resemble the multistage force dynamics reported by us, we note the importance of membrane disruption linked with integrity of cytoskeletal networks in electroporation. The large-scale bleb formation and recession observed in our studies post-electroporation are synchronized with disruption and formation of actin fibers (Figure 4), which might explain why the time scales of electroporation-mediated biphasic force recovery (few minutes) differ from the stretch-mediated shedding of forces occurring typically within a few seconds. Additionally, while mechanical stretching induces a loss in contractility without affecting the overall cell shape, electroporation-mediated disruption can have a loss of cell shape (rounding) followed by recovery (spreading). Such substantial cell shape recoveries may further explain the longer time scales of force recovery (2–3 h) compared with mechanical stretching (~30 min).79,82
CONCLUSION
In conclusion, the prevailing paradigm in electroporation emphasizes membrane disruption and resealing as the key metrics in cell recovery, yet from our study across multiple cell types, it is increasingly clear that cytoskeletal dynamics play a significant role in cell shape and force recovery. Our ECM-mimicking nanofiber-based platform demonstrates that mechanical force recovery is a robust metric to evaluate cell recovery after electroporation. We anticipate our mechanobiological approach to cell recovery will yield insights clarifying the relationship between membrane dynamics (permeability, tension, composition) and cytoskeletal dynamics (structure, contractility) and show how these properties impact cell survival. Fundamental knowledge on the relationship between cell mechanics and membrane permeability may link membrane resealing times with the force response, knowledge that may reveal the mechanisms of pore resealing and enable optimizations for electroporation technologies such as gene transfection. We expect that a better understanding of the mechanical response to electroporation will present target opportunities in reversible electroporation applications such as genetic engineering, gene therapy, and molecular medicine.
METHODS
Device Fabrication and Fiber Deposition.
Scaffold bases consisting of a hollow square region (see Figure 1; outer scaffold dimensions: 8 × 8 mm; inner region: 3 × 3 mm) were laser cut from ~250 μm-thick polystyrene coverslips (Fisher Scientific). Using our previously reported non-electrospinning spinneret-based tunable engineered parameters (STEP) technique, we fabricated force-sensing nanofiber networks consisting of a horizontal array of densely spaced (interfiber spacing: 14.5 ± 0.7 μm) small diameter (~250 nm, 233 ± 4 nm) nanofibers deposited on a vertical array of widely spaced (interfiber spacing: 279 ± 9 μm) large diameter (diameter ~2 μm, 1.92 ± 0.11 μm) support fibers. Fiber networks were fused at their junctions using a custom fusing chamber. The 250 nm-diameter fibers were prepared using a 7 wt % solution of polystyrene (MW: 2000 000 g/mol; category no. 829; Scientific Polymer Products, Ontario, NY, USA) in p-xylene (X5–500; Thermo Fisher Scientific, Waltham, MA, USA), while a 2 wt % solution (polystyrene MW: 15,000 000 g/mol; category no. PL2014–9001, Agilent Technologies, Santa Clara, CA, USA) was used for the large, 2 μm support fibers. Individual fiber diameter and interfiber spacing were confirmed via scanning electron microscopy (SEM) images. Mechanical properties of the fibers are listed in Table S3.
A single channel in polydimethylsiloxane (PDMS) was bonded to a glass coverslip to contain a plastic scaffold placed between two electrodes spaced 1 cm apart. A master mold for the PDMS channel was fabricated on a glass slide using acrylic. A 1/16 in. acrylic sheet was laser-cut to form the channel region (30 × 10 × 1.6 mm) and epoxied onto the glass slide. Acrylic walls surrounding the channel region were laser cut from 3/16 in. acrylic and epoxied in place. PDMS was mixed in 10:1 (w/w) base to cross-linker, degassed, and cast-molded using the master mold. After curing at 80 °C for 2–3 h, the PDMS was removed from the mold, and inlet and outlet holes were punched with a 0.75 mm biopsy punch. Before bonding to a glass coverslip, high-vacuum grease (Dow Corning, Midland, MI) was used to tack the scaffold in place on the glass slide. Bonding of the PDMS to the coverslip was achieved using a plasma cleaner (Harrick Plasma). To complete the device assembly, stainless steel acupuncture needles (diameter 0.18 mm) were carefully inserted through the device at a spacing of 1 cm and epoxied in place. The assembled device was placed under vacuum until use.
Cell Culture and Experimental Procedure.
The glioblastoma cell line U251 (Sigma-Aldrich) was cultured according to standard practices in growth media consisting of Dulbecco’s modified Eagle media (DMEM) with l-glutamine, 4.5 g/L glucose, and sodium pyruvate (Corning) supplemented with 10% fetal bovine serum (FBS, R&D Systems) and 1% penicillin streptomycin (Gibco). The growth media had a conductivity of 12.8 mS/cm and an osmolarity of 355 mOsm and contained 1.95 mM calcium. U251 cells tested negative for mycoplasma. Cells were passaged at 70–90% confluency. Both C2C12 mouse myoblasts (ATCC) and HeLa cells83 were cultured in growth media consisting of DMEM with l-glutamine, 4.5 g/L glucose, and sodium pyruvate (Corning) supplemented with 10% FBS (R&D Systems). VAMT cells were cultured in RPMI 1640 medium supplemented with 10% FBS (R&D Systems). Chinese hamster ovary (CHO-K1, ATCC) cells were cultured in growth media consisting of DMEM/F12 (DMEM:nutrient mixture F-12, Thermo Fischer Scientific) supplemented with 10% FBS (R&D Systems). Thyroid cancer cells84 (isolated from young mouse tumors) were cultured in F12 medium (Ham’s F-12 nutrient mixture, Thermo Fischer Scientific) supplemented with 10% FBS (R&D Systems).
To prepare a device, the device was sterilized with ethanol, washed with PBS, and incubated for 45 min with 4 μg/mL Fibronectin in PBS. Cells were trypsinized, centrifuged at 150 × g for 5 min, and resuspended in media at 0.1 × 106 cells/mL. Cells in suspension were added to the device and incubated at 37 °C and 5% CO2 for 20–40 min. The device was then transferred to the microscope and incubated for 2 h at 30 °C and 5% CO2 before data collection. Contractile force experiments were performed on a Zeiss microscope (Zeiss AxioObserver Z1) with an incubation chamber maintaining a 30 °C and 5% CO2 environment throughout the entirety of the experiments. The incubation temperature was decreased from standard 37 °C incubation to 30 °C to remove the potential of thermal damage caused by Joule heating during pulsing (Figure S3e,f; see Mitigation of Thermal Effects subsection). Bright-field data were captured at 20× (phase objective, 0.8 NA) at intervals of 2 min. For each experiment, approximately 25–50 locations on the fiber network were imaged every 2 min. Imaging locations frequently contained more than one cell. For U251 experiments, 20 min of baseline data were collected before electroporation and cells were maintained in growth media for the duration of the experiment. For consistency with U251 experiments, experiments with other cell types were all performed in DMEM growth media (devices flushed ~20 min pre-experiment for cells not cultured in DMEM growth media). Ten min of baseline data were collected before pulsing.
To prepare cells for treatment in calcium-free DMEM, cells were seeded in complete growth media and allowed to adhere and spread on the fibers for at least 2 h under incubation at 37 °C and 5% CO2. After incubation, devices were removed from the incubator and flushed thoroughly (2×, each flush with 2× device volume) with calcium-free DMEM (DMEM with 4.5 g/L glucose and without l-glutamine, sodium pyruvate, and calcium chloride; Gibco, 21068–028). The free calcium concentration was measured to be approximately 50 μM (Cell Biolabs Inc., MET-5121), and free calcium was not chelated to prevent alterations in cell morphology.85,86 The device was then immediately placed on the microscope, incubated at 30 °C and 5% CO2 as in the other experiments. A brief acclimation period of approximately 20 min was given prior to data collection. Baseline (pre-electroporation) images were acquired for 10 min before applying the electroporation pulses. Cells were maintained in calcium-free DMEM for the duration of the experiment.
Sample Size and Inclusion Criteria.
We analyzed U251 cells from three independent experiments for each voltage (500 V, 1000 V, 1500 V) and orientation (∥, ⊥) condition. Table 1 presents the number of cells analyzed for the force analysis from each independent experiment. For each voltage and orientation tested, three independent experiments were conducted, with 20 or more total cells analyzed where possible. Ultralow viability for the 1500 V⊥ condition limited the sample number. Cells selected for analysis were well-centered on the fibers (for the duration of the experiment), had no interference from other cells, were adhered to nanofibers with fixed end points (orthogonal fibers well-fused), and showed an elongated and contractile phenotype. We performed three independent experiments of the 1000 V∥ condition in calcium-free DMEM and analyzed the response of 24 cells. Additionally, we performed two control (“sham”) experiments (Figure S2f). For our force analysis on additional cell types presented in Figure 6, we analyzed ≥8 cells from a single experiment for each cell type. C2C12 cells were electroporated at 2000 V due to their greater resistance to electroporation effects.
Table 1.
Sample size for Force Analysis of U251 Cells
| number of cells analyzed per independent experiment |
||||
|---|---|---|---|---|
| condition | Exp1 | Exp2 | Exp3 | total cells analyzed |
|
| ||||
| 500 V‖ | 6 | 6 | 9 | 21 |
| 1000 V‖ | 9 | 6 | 11 | 26 |
| 1500 V‖ | 9 | 11 | 8 | 28 |
| 500 V⊥ | 7 | 7 | 9 | 23 |
| 1000 V⊥ | 8 | 6 | 8 | 22 |
| 1500 V⊥ | 0a | 0a | 4 | 4 |
| 1000 V‖ Ca2+-free | 13 | 7 | 4 | 24 |
| control (sham) | 8 | 5 | – | 13 |
No cells viable for analysis.
Viability of U251 cells post-electroporation was analyzed from at least three independent experiments for each voltage (500 V, 1000 V, 1500 V) and orientation (∥, ⊥, 2D flat). Table 2 presents the number for cells analyzed for each independent experiment. Viability was assessed 180 min post-electroporation for 500 V experiments and 240 min post-electroporation for 1000 and 1500 V experiments. (Note: 2D flat data were collected from experiments investigating the ⊥ or ∥ orientations.)
Table 2.
Sample Size for Viability Analysis
| number of cells analyzed per independent experiment |
||||||||
|---|---|---|---|---|---|---|---|---|
| condition | Exp1 | Exp2 | Exp3 | Exp4 | Exp5 | Exp6 | Exp 7 | total cells analyzed |
|
| ||||||||
| 500 V‖ | 66 | 55 | 112 | – | – | – | – | 233 |
| 500 V⊥ | 68 | 25 | 37 | 26 | 25 | – | – | 181 |
| 500 V 2D flat | 34 | 26 | 32 | 103 | – | – | – | 195 |
| 1000 V‖ | 60 | 62 | 60 | 33 | 27 | 48 | 126 | 416 |
| 1000 V⊥ | 39 | 45 | 93 | 21 | – | – | – | 198 |
| 1000 V 2D flat | 37 | 23 | 42 | – | – | – | – | 102 |
| 1500 V‖ | 101 | 65 | 71 | – | – | – | – | 237 |
| 1500 V⊥ | 33 | 74 | 201 | – | – | – | – | 308 |
| 1500 V 2D flat | 15 | 24 | 20 | 93 | 48 | 126 | – | 326 |
High-resolution bright-field data of individual cells enabled us to assess viability without the need for conventional live/dead staining. Viability was assessed at the single-cell level from bright-field data based on several criteria. Cells considered viable had (visually) intact membranes, had respread on the fibers, and were able to apply contractile forces to the fibers (i.e., deflected parallel nanofibers). Cells considered “dead” did not have (visually) intact membranes (cell lysis), did not respread on the fibers, and did not apply contractile forces (i.e., no fiber deflections). Using these criteria, cells considered “viable” were very distinct from cells considered “dead.” Figure S3b shows several examples of “viable” vs “dead” cells. As shown in this figure, cell death generally occurred immediately following electroporation, suggesting necrosis (accidental cell death). For all experiments, all cells elongated between two parallel fibers with the characteristic elongated shape shown in Figure 1c were included in the viability analysis.
Electroporation Parameters.
Cells were electroporated with a high-voltage pulse generator (BTX ECM 830, Harvard Apparatus). Ten, 100 μs square-wave pulses were delivered at 500, 1000, or 1500 V to the device electrodes. Pulses were delivered at a frequency of 1 Hz. Measured current and voltage waveforms approximated ideal square waves (Figure S1a,b). Voltage waveforms were not affected by pulse number. Electrical current increased slightly with pulse number due to Joule heating. Finite element modeling of the electric field within the device indicated that at applied voltages of 500, 1000, and 1500 V, the cells within the scaffold region-of-interest (cut-out region of scaffold, 250 μm from edges) experienced electric field magnitudes of 441 ± 12 V cm−1, 882 ± 23 V cm−1, and 1323 ± 35 V cm−1, respectively, for the parallel orientation and 455 ± 12 V cm−1, 911 ± 24 V cm−1, and 1366 ± 36 V cm−1, respectively, for the perpendicular orientation. See the Finite Element Modeling subsection for more details.
Pulse application resulted in micron-diameter bubble formation on both electrodes, but did not result in electrical arcing. Undesired electrochemical effects were minimized by incorporating a large volume of fluid outside the electrode region (~2.5 times the volume of fluid between the electrodes) and locating the fiber network region several millimeters away from both electrodes. Media pH was minimally affected by electroporation (no electroporation (sham): 7.11 ± 0.06; 1500 V: 7.16 ± 0.06; pH measured 3 h after electroporation).
Immunostaining and Confocal Microscopy.
Cells were fixed and stained for actin, paxillin, and microtubules according to standard practices. Cells were fixed with 10% formalin for 10 min, permeabilized with 0.1% Triton-X 100 in PBS for 15 min, and blocked with 5% goat serum in PBS for 30 min. Focal adhesion antibody (Paxillin, TYR31) (5 μg/mL) and microtubule antibody (β-tubulin) (1 μg/mL) were prepared in an antibody dilution buffer (PBS with 10 mg/mL BSA and 1 μL/mL Triton X-100) and were added to the cells and incubated at room temperature for 3 h. The device was washed with PBS and antibody dilution buffer supplemented with actin stain (rhodamine phalloidin, sc-301530; Santa Cruz Biotechnology, Dallas, TX, USA) diluted in a 1:80 ratio, and secondary antibodies (Alexa Fluor 488 Goat Antibody (green), Alexa Fluor 647 Goat Antibody (cyan) both diluted in a 1:400 ratio) were added for 45 min at room temperature while protected from light. The device was then washed with PBS, and 300 nM DAPI diluted in PBS was added to the device for 5 min in the dark. The device was then washed with PBS and imaged using a 63× (1.15 NA) water-immersion objective on a confocal microscope (Zeiss LSM 880). The z-slice thickness was kept at either 0.36 or 0.5 μm.
Cell volume calculations were performed in MATLAB from z-stacks of fluorescent images (stained for actin, microtubules, and the nucleus) of fixed cells at various time points (prepulse, 0.5, 2, 8, 16, 32, and 128 min) after electroporation (n = 6, 10, 8, 13, 7, 9, and 5 cells corresponding to prepulse, 0.5, 2, 8, 16, 32, and 128 min time points, respectively). In MATLAB, images were converted into grayscale and subsequently binarized using a custom MATLAB routine to calculate the projected cell area as shown in Figure S3c. Cell volume was calculated as thickness.
Bleb analysis was performed in ImageJ. Bleb area was measured on the z-slice corresponding to the bleb’s greatest diameter (n = 82, 126, 214, 131, and 23 blebs from 12, 12, 13, 11, and 4 cells for 0.5, 2, 8, 16 and 32 min time points, respectively). A membrane roughness ratio (Figure 4e) was used to quantify the increased length of the cell contour along the nanofiber due to the presence of blebs and was measured as the ratio of the contour length to the cell end-to-end length (n = 6, 14, 16, 9, 10, and 6 for −2 (prepulse), 0.5, 2, 8, 16, and 32 min time points, respectively). Non-electroporated cells demonstrated negligible blebbing and thus had a roughness ratio very close to 1. Bleb analysis for calcium-free experiments (Figure S5a,b) followed the same procedure, however bright-field images were used to calculate the roughness ratio.
Membrane Permeability Imaging.
To experimentally confirm membrane disruption by electroporation, we used YO-PRO-1 and propidium iodide (PI), both membrane-impermeant dyes. Membrane disruption by electroporation was visually demonstrated by the fluorescence of the membrane-impermeant dye YO-PRO-1 (1000 V∥ condition shown in Figure 2a). For clarity in Figure 2a, we used a background subtraction technique (via a Gaussian-blur) and a lower intensity threshold to remove background YO-PRO-1 signal, and thus these images are for illustration purposes only. Experiments were performed with 1 μL/mL (1 μM) YO-PRO-1 (Thermo Fisher Scientific) in media.
We visualized the spatial distribution of PI uptake during the first 60 s after electroporation at 1000 V (∥: 882 V/cm; ⊥: 911 V/cm). A high concentration of PI (0.17 mg/mL) (Fisher Scientific) was used as in similar studies87 to enable high frame-rate data collection (short exposure times) while maintaining a strong fluorescence signal. We added media containing PI immediately prior to imaging and electroporating the cells. Ten, 1000 V pulses were delivered at 1 Hz. Images were captured at 1.2 s intervals at 63× magnification.
Force Calculation.
Contractile force was calculated in MATLAB by comparing the deflection profile of the fiber with the best fit profile of a loaded fixed–fixed beam subjected to the cell forces at an angle, , measured as the angle between the resultant force vector and the undeflected nanofiber direction. Details on force analysis formulation and numerical scheme have been published previously.39 The cell’s applied load to the fiber is assumed to be at each end point of the cell’s protrusions where the f-actin stress fibers are anchored to the nanofibers via focal adhesions (Figure 1e).
The direction of the resultant force, , is estimated based on physiological structures from fixed cells. Elongated cells (cells before electroporation or long after electroporation) have well-defined stress fibers which are ~12.4° from the horizontal (Figure 1e, bottom left). In instances where stress fibers were not present in recovering cells, we deferred to the angle of the dominant retraction fibers, (Figure 1e bottom center) known for their force bearing capabilities.88,89 In cases where neither stress fibers were visible and the cell was highly rounded, we took the resultant angle to be the bisection of the angle created by the membrane at the point of attachment to the fiber (Figure 1e, bottom right). For these situations, mechanical forces must be applied in-line with the membrane; thus, the resultant force would be the sum of the vectors radiating outward along the membrane, resulting in half the angle formed by the membrane. For a completely spherical cell, the half angle created by the membrane would point the force vector directly to the cell centroid. We fixed cells and imaged their cytoskeleton under no-electroporation conditions and 0.5, 2, 8, 16, 32, 128 min after electroporation at 1000 V∥. When was averaged for each cell, we arrived at the plot in Figure 1f (n = 119). When cell length is <63.4 μm in length, the angle of force application increases and can be approximated as linear. Minimizing error for the data results in the following best fit:
| (1) |
where is in degrees and is in μm. At each time point during cell recovery, the cell length was computed and the corresponding force angle was an input to the finite element model.
The deflection profiles were measured by marking the fiber end points and eight points along the fiber length including the two end points of the cell. Fiber properties used in the computation of contractile force can be found in Table S3. Cell elongation was defined to be the length between a cell’s end points on a fiber.
Finite Element Modeling.
COMSOL 5.4 was used to model the electric field distribution in the device. We used the AC/DC module to perform a steady-state simulation. Computational models of the electric field within the device are shown in Figure 1d and Figure S1. Our models indicated that the scaffold region-of-interest (cut-out region of scaffold, 250 μm from edges) experienced electric field magnitudes of 0.88 V cm−1 for every 1 V delivered when the scaffold was in the parallel orientation and 0.91 V cm−1 for every 1 V delivered when the scaffold was in the perpendicular orientation. Cells adherent to the glass slide (2D flat) experienced electric field magnitudes of 0.93 V cm−1 and 0.90 V cm−1 for every 1 V delivered when the scaffold was in the parallel orientation and perpendicular orientation, respectively. Scaffold rotation is the cause of the slight increase in the electric field in the perpendicular orientation.
COMSOL was used to model the induced transmembrane potential (ITP) on cells. An accurate cell volume was reconstructed using 3D Slicer from a z-stack of images of a fixed, actin-stained cell. Cell volume was meshed using 3-Matic. We performed a steady-state model and neglected the effect of electroporation-induced conductivity changes to the cell membrane.90 Over the volume, the Laplace (eq 2) was solved:
| (2) |
where is voltage. A contact impedance boundary condition was used to model the boundary condition across the cell membrane:
| (3) |
where and are the conductivity and thickness of the cell membrane, respectively, and and are the voltages on either side of the cell membrane. Model parameters are presented in Table S4.
Mitigation of Thermal Effects.
We performed experiments at 30 °C to mitigate thermal effects due to Joule heating. We analytically and experimentally determined Joule heating to be no greater than 8 °C (Figure S3). We calculated the worst-case scenario for Joule heating by assuming that all electrical energy was immediately converted to thermal energy to cause an instantaneous temperature rise.87 Worst-case Joule heating was calculated for the delivery of 10 pulses at 1500 V using the equation:
| (4) |
where is the change in temperature within the device, is the voltage applied (measured), is the current through the device (measured), is the specific heat capacity of the media (approximated as water: 4.184 kJ/(kg·K)), and is the mass of the media being heated. Mass is calculated as , where is the density (approximated as water: 1 kg/m3), is distance between electrodes (1 cm), is width of the channel (1 cm), and is height of the channel (1.6 mm). We calculated that the worst-case scenario Joule heating would cause a temperature rise of <8 °C.
Fiber optic temperature probe measurements within the device demonstrated that at the maximum electroporation condition of 10 pulses at 1500 V cm−1, the temperature rise was under 7 °C (Figure S3e–f). Our analytical temperature rise calculation is thus in good agreement with experiments. The rapid temperature rise was quickly dissipated by the surrounding fluid in the channel, and the temperature returned to within 2 °C of the pretreatment temperature within a few minutes.
Statistical Analysis.
All data is presented as mean ± SEM. Statistical analysis was performed in JMP and Graphpad Prism. Student t tests were performed to determine significance between data sets. The significance level for Student t tests was .
Supplementary Material
ACKNOWLEDGMENTS
We would like to thank I. Varella and S. Overton for their support on this project. The authors would like to thank A. Vadlamani, N. Alinezhadbalalami, K. Aycock, and A. Mukherjee for reviewing the manuscript and A. Padhi for his help with experiments. HeLa cells were kindly provided by Dr. Jennifer DeLuca, Colorado State University. The mesothelioma (VAMT) cell line was kindly provided by Dr. Emil Lou, University of Minnesota Twin Cities. Thyroid cancer cells were kindly provided by Dr. Aime Franco, Children’s Hospital of Philadelphia. P.M.G. and R.V.D. acknowledge support from the NIH (P01CA207206). A.J. and A.S.N. acknowledge support from the NSF (no. 1762634). The authors acknowledge support from the ICTAS Center for Engineered Health and thank Macromolecules Innovation Institute at Virginia Tech. P.M.G. is a trainee in the BIOTRANS IGEP program at Virginia Tech.
Footnotes
The authors declare no competing financial interest.
ASSOCIATED CONTENT
Supporting Information
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsnano.0c07020.
Sample size of cells analyzed for force response and percent of cells showing a biphasic stage of their response (T1); sample size of cells analyzed for viability response and percent cell death for each experiment (T2); mechanical properties of the nanofibers used for force calculations (T3); parameters for ITP models (T4); electroporation waveforms and the electric field within the device (S1); supplemental analysis of force and length changes after electroporation (S2); additional analysis of cell death, cell volume, and Joule heating (S3); microtubule dynamics after electroporation (S4); analysis of blebbing, dye uptake, and cell rounding in calcium-free DMEM (S5); ITP model of a 3D cell in two orientations (S6) (PDF)
Movie S1: Multistage force response after electroporation (MP4)
Movie S2: Propidium iodide uptake in the parallel and perpendicular orientations (MP4)
Contributor Information
Philip M. Graybill, Department of Mechanical Engineering, Virginia Tech, Blacksburg, Virginia 24061, United States.
Aniket Jana, Department of Mechanical Engineering, Virginia Tech, Blacksburg, Virginia 24061, United States.
Rakesh K. Kapania, Department of Aerospace and Ocean Engineering, Virginia Tech, Blacksburg, Virginia 24061, United States
Amrinder S. Nain, Department of Mechanical Engineering, Virginia Tech, Blacksburg, Virginia 24061, United States; School of Biomedical Engineering and Sciences, Virginia Tech-Wake Forest University, Blacksburg, Virginia 24061, United States
Rafael V. Davalos, Department of Mechanical Engineering, Virginia Tech, Blacksburg, Virginia 24061, United States; School of Biomedical Engineering and Sciences, Virginia Tech-Wake Forest University, Blacksburg, Virginia 24061, United States
REFERENCES
- (1).Weaver JC; Chizmadzhev YA Theory of Electroporation: A Review. Bioelectrochem. Bioenerg. 1996, 41, 135–160. [Google Scholar]
- (2).Kotnik T; Rems L; Tarek M; Miklavcic D Membrane Electroporation and Electropermeabilization: Mechanisms and Models. Annu. Rev. Biophys. 2019, 48, 63–91. [DOI] [PubMed] [Google Scholar]
- (3).Potter H; Heller R Transfection by Electroporation. Curr. Protoc Mol. Biol. 2018, 121, 9.3.1–9.3.13. [DOI] [PubMed] [Google Scholar]
- (4).Hu N; Yang J; Joo SW; Banerjee AN; Qian S Cell Electrofusion in Microfluidic Devices: A Review. Sens. Actuators, B 2013, 178, 63–85. [Google Scholar]
- (5).Mali B; Jarm T; Snoj M; Sersa G; Miklavcic D Antitumor Effectiveness of Electrochemotherapy: A Systematic Review and Meta-Analysis. Eur. J. Surg Oncol 2013, 39, 4–16. [DOI] [PubMed] [Google Scholar]
- (6).Davalos RV; Mir IL; Rubinsky B Tissue Ablation with Irreversible Electroporation. Ann. Biomed. Eng. 2005, 33, 223–231. [DOI] [PubMed] [Google Scholar]
- (7).Scheffer HJ; Nielsen K; de Jong MC; van Tilborg AA; Vieveen JM; Bouwman AR; Meijer S; van Kuijk C; van den Tol PM; Meijerink MR Irreversible Electroporation for Nonthermal Tumor Ablation in the Clinical Setting: A Systematic Review of Safety and Efficacy. J. Vasc Interv Radiol 2014, 25, 997–1011. [DOI] [PubMed] [Google Scholar]
- (8).Geboers B; Scheffer HJ; Graybill PM; Ruarus AH; Nieuwenhuizen S; Puijk RS; van den Tol PM; Davalos RV; Rubinsky B; de Gruijl TD; Miklavcic D; Meijerink MR High-Voltage Electrical Pulses in Oncology: Irreversible Electroporation, Electrochemotherapy, Gene Electrotransfer, Electrofusion, and Electroimmunotherapy. Radiology 2020, 295, 254–272. [DOI] [PubMed] [Google Scholar]
- (9).Tsong TY Electroporation of Cell Membranes. In Electroporation and Electrofusion in Cell Biology; Jordan CA.; Neumann E.; Sowers AE., Eds.; Springer: Boston, MA, 1989; pp 149–163. [Google Scholar]
- (10).Rols MP; Teissie J Electropermeabilization of Mammalian Cells. Quantitative Analysis of the Phenomenon. Biophys. J. 1990, 58, 1089–1098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (11).Saulis G; Venslauskas MS; Naktinis J Kinetics of Pore Resealing in Cell Membranes after Electroporation. J. Electroanal. Chem. Interfacial Electrochem. 1991, 321, 1–13. [Google Scholar]
- (12).Pavlin M; Miklavcic D Theoretical and Experimental Analysis of Conductivity, Ion Diffusion and Molecular Transport during Cell Electroporation–Relation between Short-Lived and Long-Lived Pores. Bioelectrochemistry 2008, 74, 38–46. [DOI] [PubMed] [Google Scholar]
- (13).Teissie J Membrane Permeabilization Lifetime in Experiments. In Handbook of Electroporation; Miklavčič D., Ed.; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2017; pp 61–75. [Google Scholar]
- (14).Weaver JC; Vernier PT Pore Lifetimes in Cell Electroporation: Complex Dark Pores? arXiv (Biological Physics), August 24, 2107, 1708.07478, ver. 1. https://arxiv.org/abs/1708.07478 (accessed 2019-09-26). [Google Scholar]
- (15).Berghofer T; Eing C; Flickinger B; Hohenberger P; Wegner LH; Frey W; Nick P Nanosecond Electric Pulses Trigger Actin Responses in Plant Cells. Biochem. Biophys. Res. Commun. 2009, 387, 590–595. [DOI] [PubMed] [Google Scholar]
- (16).Hohenberger P; Eing C; Straessner R; Durst S; Frey W; Nick P Plant Actin Controls Membrane Permeability. Biochim. Biophys. Acta, Biomembr. 2011, 1808, 2304–2312. [DOI] [PubMed] [Google Scholar]
- (17).Pakhomov AG; Xiao S; Pakhomova ON; Semenov I; Kuipers MA; Ibey BL Disassembly of Actin Structures by Nanosecond Pulsed Electric Field Is a Downstream Effect of Cell Swelling. Bioelectrochemistry 2014, 100, 88–95. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (18).Thompson GL; Roth C; Tolstykh G; Kuipers M; Ibey BL Disruption of the Actin Cortex Contributes to Susceptibility of Mammalian Cells to Nanosecond Pulsed Electric Fields. Bioelectromagnetics 2014, 35, 262–272. [DOI] [PubMed] [Google Scholar]
- (19).Stacey M; Fox P; Buescher S; Kolb J Nanosecond Pulsed Electric Field Induced Cytoskeleton, Nuclear Membrane and Telomere Damage Adversely Impact Cell Survival. Bioelectrochemistry 2011, 82, 131–134. [DOI] [PubMed] [Google Scholar]
- (20).Rols MP; Teissie J Experimental Evidence for the Involvement of the Cytoskeleton in Mammalian Cell Electropermeabilization. Biochim. Biophys. Acta, Biomembr. 1992, 1111, 45–50. [DOI] [PubMed] [Google Scholar]
- (21).Goswami I; Perry JB; Allen ME; Brown DA; von Spakovsky MR; Verbridge SS Influence of Pulsed Electric Fields and Mitochondria-Cytoskeleton Interactions on Cell Respiration. Biophys. J. 2018, 114, 2951–2964. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (22).Xiao D; Tang L; Zeng C; Wang J; Luo X; Yao C; Sun C Effect of Actin Cytoskeleton Disruption on Electric Pulse-Induced Apoptosis and Electroporation in Tumour Cells. Cell Biol. Int. 2011, 35, 99–104. [DOI] [PubMed] [Google Scholar]
- (23).Steuer A; Wende K; Babica P; Kolb JF Elasticity and Tumorigenic Characteristics of Cells in a Monolayer after Nanosecond Pulsed Electric Field Exposure. Eur. Biophys. J. 2017, 46, 567–580. [DOI] [PubMed] [Google Scholar]
- (24).Carr L; Bardet SM; Burke RC; Arnaud-Cormos D; Leveque P; O’Connor RP Calcium-Independent Disruption of Microtubule Dynamics by Nanosecond Pulsed Electric Fields in U87 Human Glioblastoma Cells. Sci. Rep. 2017, 7, 41267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (25).Harkin DG; Hay ED Effects of Electroporation on the Tubulin Cytoskeleton and Directed Migration of Corneal Fibroblasts Cultured within Collagen Matrices. Cell Motil. Cytoskeleton 1996, 35, 345–357. [DOI] [PubMed] [Google Scholar]
- (26).Kanthou C; Kranjc S; Sersa G; Tozer G; Zupanic A; Cemazar M The Endothelial Cytoskeleton as a Target of Electroporation-Based Therapies. Mol. Cancer Ther. 2006, 5, 3145–3152. [DOI] [PubMed] [Google Scholar]
- (27).Teissie J; Rols MP Manipulation of Cell Cytoskeleton Affects the Lifetime of Cell Membrane Electropermeabilization. Ann. N. Y. Acad. Sci. 1994, 720, 98–110. [DOI] [PubMed] [Google Scholar]
- (28).Thompson GL; Roth C; Tolstykh G; Kuipers M; Ibey BL, Role of Cytoskeleton and Elastic Moduli in Cellular Response to Nanosecond Pulsed Electric Fields. In Terahertz and Ultrashort Electromagnetic Pulses for Biomedical Applications; Wilmink GJ., Ibey BL., Eds.; SPIE Press: Bellingham, WA, 2013; Vol. 8585, p 85850T. [Google Scholar]
- (29).Louise C; Etienne D; Marie-Pierre R AFM Sensing Cortical Actin Cytoskeleton Destabilization During Plasma Membrane Electropermeabilization. Cytoskeleton 2014, 71, 587–594. [DOI] [PubMed] [Google Scholar]
- (30).Pehlivanova VN; Tsoneva IH; Tzoneva RD Multiple Effects of Electroporation on the Adhesive Behaviour of Breast Cancer Cells and Fibroblasts. Cancer Cell Int. 2012, 12, 9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (31).Perrier DL; Vahid A; Kathavi V; Stam L; Rems L; Mulla Y; Muralidharan A; Koenderink GH; Kreutzer MT; Boukany PE Response of an Actin Network in Vesicles under Electric Pulses. Sci. Rep. 2019, 9, 8151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (32).Meulenberg CJ; Todorovic V; Cemazar M Differential Cellular Effects of Electroporation and Electrochemotherapy in Monolayers of Human Microvascular Endothelial Cells. PLoS One 2012, 7, e52713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (33).Čemažar M, Effects of Electroporation of Mammalian Cells on Cytoskeleton and Intercellular Connections. In Handbook of Electroporation; Miklavčič D., Ed.; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2017; pp 307–321. [Google Scholar]
- (34).Graybill PM; Davalos RV Cytoskeletal Disruption after Electroporation and Its Significance to Pulsed Electric Field Therapies. Cancers 2020, 12, 1132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (35).Mussauer H; Sukhorukov VL; Haase A; Zimmermann U Resistivity of Red Blood Cells against High-Intensity, Short-Duration Electric Field Pulses Induced by Chelating Agents. J. Membr. Biol. 1999, 170, 121–133. [DOI] [PubMed] [Google Scholar]
- (36).Neamtu S; Morariu VV; Turcu I; Popescu AH; Copaescu LI Pore Resealing Inactivation in Electroporated Erythrocyte Membrane Irradiated with Electrons. Bioelectrochem. Bioenerg. 1999, 48, 441–445. [DOI] [PubMed] [Google Scholar]
- (37).Chopinet L; Roduit C; Rols MP; Dague E Destabilization Induced by Electropermeabilization Analyzed by Atomic Force Microscopy. Biochim. Biophys. Acta, Biomembr. 2013, 1828, 2223–2229. [DOI] [PubMed] [Google Scholar]
- (38).Sheets K; Wang J; Zhao W; Kapania R; Nain AS Nanonet Force Microscopy for Measuring Cell Forces. Biophys. J. 2016, 111, 197–207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (39).Tu-Sekine B; Padhi A; Jin S; Kalyan S; Singh K; Apperson M; Kapania R; Hur SC; Nain A; Kim SF Inositol Polyphosphate Multikinase Is a Metformin Target That Regulates Cell Migration. FASEB J. 2019, 33, 14137–14146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (40).Padhi A; Thomson AH; Perry JB; Davis GN; McMillan RP; Loesgen S; Kaweesa EN; Kapania R; Nain AS; Brown DA Bioenergetics Underlying Single-Cell Migration on Aligned Nanofiber Scaffolds. Am. J. Physiol Cell Physiol 2020, 318, C476–C485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (41).Wang J; Nain AS Suspended Micro/Nanofiber Hierarchical Biological Scaffolds Fabricated Using Non-Electrospinning Step Technique. Langmuir 2014, 30, 13641–13649. [DOI] [PubMed] [Google Scholar]
- (42).Nain AS; Wang J Polymeric Nanofibers: Isodiametric Design Space and Methodology for Depositing Aligned Nanofiber Arrays in Single and Multiple Layers. Polym. J. 2013, 45, 695–700. [Google Scholar]
- (43).Padhi A; Singh K; Franco-Barraza J; Marston DJ; Cukierman E; Hahn KM; Kapania RK; Nain AS Force-Exerting Perpendicular Lateral Protrusions in Fibroblastic Cell Contraction. Communications biology 2020, 3, 390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (44).Jana A; Nookaew I; Singh J; Behkam B; Franco AT; Nain AS Crosshatch Nanofiber Networks of Tunable Interfiber Spacing Induce Plasticity in Cell Migration and Cytoskeletal Response. FASEB J. 2019, 33, 10618–10632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (45).Sheets K; Wunsch S; Ng C; Nain AS Shape-Dependent Cell Migration and Focal Adhesion Organization on Suspended and Aligned Nanofiber Scaffolds. Acta Biomater. 2013, 9, 7169–7177. [DOI] [PubMed] [Google Scholar]
- (46).Meehan S; Nain AS Role of Suspended Fiber Structural Stiffness and Curvature on Single-Cell Migration, Nucleus Shape, and Focal-Adhesion-Cluster Length. Biophys. J. 2014, 107, 2604–2611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (47).Giannone G; Rondé P; Gaire M; Beaudouin J; Haiech J; Ellenberg J; Takeda K Calcium Rises Locally Trigger Focal Adhesion Disassembly and Enhance Residency of Focal Adhesion Kinase at Focal Adhesions. J. Biol. Chem. 2004, 279, 28715–28723. [DOI] [PubMed] [Google Scholar]
- (48).Gissel H; Lee RC; Gehl J Electroporation and Cellular Physiology. In Clinical Aspects of Electroporation; Kee ST, Gehl J, Lee EW, Eds.; Springer New York: New York, NY, 2011; pp 9–17. [Google Scholar]
- (49).Sharma P; Sheets K; Elankumaran S; Nain AS The Mechanistic Influence of Aligned Nanofibers on Cell Shape, Migration and Blebbing Dynamics of Glioma Cells. Integr Biol. (Camb) 2013, 5, 1036–1044. [DOI] [PubMed] [Google Scholar]
- (50).Frandsen SK; Gissel H; Hojman P; Tramm T; Eriksen J; Gehl J Direct Therapeutic Applications of Calcium Electroporation to Effectively Induce Tumor Necrosis. Cancer Res. 2012, 72, 1336–1341. [DOI] [PubMed] [Google Scholar]
- (51).Conklin MW; Lin MS; Spitzer NC Local Calcium Transients Contribute to Disappearance of Pfak, Focal Complex Removal and Deadhesion of Neuronal Growth Cones and Fibroblasts. Dev. Biol. 2005, 287, 201–212. [DOI] [PubMed] [Google Scholar]
- (52).D’Souza RS; Lim JY; Turgut A; Servage K; Zhang J; Orth K; Sosale NG; Lazzara MJ; Allegood J; Casanova JE CalciumStimulated Disassembly of Focal Adhesions Mediated by an ORP3/IQSec1 Complex. eLife 2020, 9, e54113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (53).Giannone G; Ronde P; Gaire M; Haiech J; Takeda K Calcium Oscillations Trigger Focal Adhesion Disassembly in Human U87 Astrocytoma Cells. J. Biol. Chem. 2002, 277, 26364–26371. [DOI] [PubMed] [Google Scholar]
- (54).Nesin OM; Pakhomova ON; Xiao S; Pakhomov AG Manipulation of Cell Volume and Membrane Pore Comparison following Single Cell Permeabilization with 60- and 600-ns Electric Pulses. Biochim. Biophys. Acta, Biomembr. 2011, 1808, 792–801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (55).Ušsaj M; Trontelj K; Hudej R; Kandušer M; Miklavčič Dˇ Cell Size Dynamics and Viability of Cells Exposed to Hypotonic Treatment and Electroporation for Electrofusion Optimization. Radiol. Oncol. 2009, 43, 108–119. [Google Scholar]
- (56).Steuer A; Schmidt A; Laboha P; Babica P; Kolb JF Transient Suppression of Gap Junctional Intercellular Communication after Exposure to 100-ns Pulsed Electric Fields. Bioelectrochemistry 2016, 112, 33–46. [DOI] [PubMed] [Google Scholar]
- (57).Kanduser M; Sentjurc M; Miklavcic D Cell Membrane Fluidity Related to Electroporation and Resealing. Eur. Biophys. J. 2006, 35, 196–204. [DOI] [PubMed] [Google Scholar]
- (58).Saulis G Pore Disappearance in a Cell after Electroporation: Theoretical Simulation and Comparison with Experiments. Biophys. J. 1997, 73, 1299–1309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (59).Kotnik T; Pucihar G; Miklavcic D Induced Transmembrane Voltage and Its Correlation with Electroporation-Mediated Molecular Transport. J. Membr. Biol. 2010, 236, 3–13. [DOI] [PubMed] [Google Scholar]
- (60).Hibino M; Itoh H; Kinosita K Jr Time Courses of Cell Electroporation as Revealed by Submicrosecond Imaging of Transmembrane Potential. Biophys. J. 1993, 64, 1789–1800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (61).Maswiwat K; Wachner D; Gimsa J Effects of Cell Orientation and Electric Field Frequency on the Transmembrane Potential Induced in Ellipsoidal Cells. Bioelectrochemistry 2008, 74, 130–141. [DOI] [PubMed] [Google Scholar]
- (62).Teissie J; Rols MP An Experimental Evaluation of the Critical Potential Difference Inducing Cell Membrane Electropermeabilization. Biophys. J. 1993, 65, 409–413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (63).Towhidi L; Kotnik T; Pucihar G; Firoozabadi SM; Mozdarani H; Miklavcic D Variability of the Minimal Transmembrane Voltage Resulting in Detectable Membrane Electroporation. Electromagn. Biol. Med. 2008, 27, 372–385. [DOI] [PubMed] [Google Scholar]
- (64).Sozer EB; Pocetti CF; Vernier PT Asymmetric Patterns of Small Molecule Transport after Nanosecond and Microsecond Electropermeabilization. J. Membr. Biol. 2018, 251, 197–210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (65).Tekle E; Astumian RD; Chock PB Selective and Asymmetric Molecular Transport across Electroporated Cell Membranes. Proc. Natl. Acad. Sci. U. S. A. 1994, 91, 11512–11516. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (66).Pucihar G; Miklavcic D; Kotnik T A Time-Dependent Numerical Model of Transmembrane Voltage Inducement and Electroporation of Irregularly Shaped Cells. IEEE Trans. Biomed. Eng. 2009, 56, 1491–501. [DOI] [PubMed] [Google Scholar]
- (67).Rems L; Ušaj M; Kandušer M; Reberšek M; Miklavčič D; Pucihar G Cell Electrofusion Using Nanosecond Electric Pulses. Sci. Rep. 2013, 3, 3382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (68).Krassowska W; Filev PD Modeling Electroporation in a Single Cell. Biophys. J. 2007, 92, 404–417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (69).Sweeney DC; Douglas TA; Davalos RV Characterization of Cell Membrane Permeability in Vitro Part II: Computational Model of Electroporation-Mediated Membrane Transport. Technol. Cancer Res. Treat. 2018, 17, 1533033818792490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (70).Yu M; Lin H Modeling Transport across the Electroporated Membrane. In Handbook of Electroporation; Miklavčič D., Ed.; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2017; pp 1089–1110. [Google Scholar]
- (71).Charras GT; Hu CK; Coughlin M; Mitchison TJ Reassembly of Contractile Actin Cortex in Cell Blebs. J. Cell Biol. 2006, 175, 477–90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (72).Chikina AS; Svitkina TM; Alexandrova AY Time-Resolved Ultrastructure of the Cortical Actin Cytoskeleton in Dynamic Membrane Blebs. J. Cell Biol. 2019, 218, 445–454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (73).Guo M; Pegoraro AF; Mao A; Zhou EH; Arany PR; Han Y; Burnette DT; Jensen MH; Kasza KE; Moore JR; et al. Cell Volume Change through Water Efflux Impacts Cell Stiffness and Stem Cell Fate. Proc. Natl. Acad. Sci. U. S. A. 2017, 114, E8618–E8627. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (74).Platonova A; Ponomarchuk O; Boudreault F; Kapilevich LV; Maksimov GV; Grygorczyk R; Orlov SN Role of Cytoskeleton Network in Anisosmotic Volume Changes of Intact and Permeabilized A549 Cells. Biochim. Biophys. Acta, Biomembr. 2015, 1848, 2337–2343. [DOI] [PubMed] [Google Scholar]
- (75).Chen Y-T; Chen Y-F; Chiu W-T; Wang Y-K; Chang H-C; Shen M-R The Er Ca2+ Sensor Stim1 Regulates Actomyosin Contractility of Migratory Cells. J. Cell Sci. 2013, 126, 1260–1267. [DOI] [PubMed] [Google Scholar]
- (76).Jarm T; Cemazar M; Miklavcic D; Sersa G Antivascular Effects of Electrochemotherapy: Implications in Treatment of Bleeding Metastases. Expert Rev. Anticancer Ther. 2010, 10, 729–746. [DOI] [PubMed] [Google Scholar]
- (77).Chen C; Krishnan R; Zhou E; Ramachandran A; Tambe D; Rajendran K; Adam RM; Deng L; Fredberg JJ Fluidization and Resolidification of the Human Bladder Smooth Muscle Cell in Response to Transient Stretch. PLoS One 2010, 5, e12035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (78).Krishnan R; Canovic EP; Iordan AL; Rajendran K; Manomohan G; Pirentis AP; Smith ML; Butler JP; Fredberg JJ; Stamenovic D Fluidization, Resolidification, and Reorientation of the Endothelial Cell in Response to Slow Tidal Stretches. Am. J. Physiol Cell Physiol 2012, 303, C368–375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (79).Krishnan R; Park CY; Lin YC; Mead J; Jaspers RT; Trepat X; Lenormand G; Tambe D; Smolensky AV; Knoll AH; Butler JP; Fredberg JJ Reinforcement versus Fluidization in Cytoskeletal Mechanoresponsiveness. PLoS One 2009, 4, e5486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (80).Lan B; Krishnan R; Park CY; Watanabe RA; Panganiban R; Butler JP; Lu Q; Cole WC; Fredberg JJ Transient Stretch Induces Cytoskeletal Fluidization through the Severing Action of Cofilin. Am. J. Physiol Lung Cell Mol. Physiol 2018, 314, L799–L807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (81).Lee SL; Nekouzadeh A; Butler B; Pryse KM; McConnaughey WB; Nathan AC; Legant WR; Schaefer PM; Pless RB; Elson EL; Genin GM Physically-Induced Cytoskeleton Remodeling of Cells in Three-Dimensional Culture. PLoS One 2012, 7, e45512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (82).Nekouzadeh A; Pryse KM; Elson EL; Genin GM Stretch-Activated Force Shedding, Force Recovery, and Cytoskeletal Remodeling in Contractile Fibroblasts. J. Biomech 2008, 41, 2964–2971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (83).Sundin LJ; Guimaraes GJ; DeLuca JG The NDC80 Complex Proteins Nuf2 and Hec1Make Distinct Contributions to Kinetochore–Microtubule Attachment in Mitosis. Mol. Biol. Cell 2011, 22, 759–768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (84).Jolly LA; Novitskiy S; Owens P; Massoll N; Cheng N; Fang W; Moses HL; Franco AT Fibroblast-Mediated Collagen Remodeling within the Tumor Microenvironment Facilitates Progression of Thyroid Cancers Driven by BrafV600E and Pten Loss. Cancer Res. 2016, 76, 1804–1813. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (85).Bird SD Calcium Mediates Cell Shape Change in Human Peritoneal Mesothelial Cells. Cell Calcium 2018, 72, 116–126. [DOI] [PubMed] [Google Scholar]
- (86).Mermelstein CS; Rebello MI; Amaral LM; Costa ML Changes in Cell Shape, Cytoskeletal Proteins and Adhesion Sites of Cultured Cells after Extracellular Ca2+ Chelation. Braz. J. Med. Biol. Res. 2003, 36, 1111–1116. [DOI] [PubMed] [Google Scholar]
- (87).Sweeney DC; Rebersek M; Dermol J; Rems L; Miklavcic D; Davalos RV Quantification of Cell Membrane Permeability Induced by Monopolar and High-Frequency Bipolar Bursts of Electrical Pulses. Biochim. Biophys. Acta, Biomembr. 2016, 1858, 2689–2698. [DOI] [PubMed] [Google Scholar]
- (88).Thery M; Jimenez-Dalmaroni A; Racine V; Bornens M; Julicher F Experimental and Theoretical Study of Mitotic Spindle Orientation. Nature 2007, 447, 493–496. [DOI] [PubMed] [Google Scholar]
- (89).Schaub S; Bohnet S; Laurent VM; Meister JJ; Verkhovsky AB Comparative Maps of Motion and Assembly of Filamentous Actin and Myosin II in Migrating Cells. Mol. Biol. Cell 2007, 18, 3723–3732. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (90).Pucihar G; Kotnik T; Valic B; Miklavcic D Numerical Determination of Transmembrane Voltage Induced on Irregularly Shaped Cells. Ann. Biomed. Eng. 2006, 34, 642–652. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


