Abstract
Quantitative measurements produced by tandem mass spectrometry proteomics experiments typically contain a large proportion of missing values. Missing values hinder reproducibility, reduce statistical power, and make it difficult to compare across samples or experiments. Although many methods exist for imputing missing values, in practice, the most commonly used methods are among the worst performing. Furthermore, previous benchmarking studies have focused on relatively simple measurements of error such as the mean-squared error between imputed and held-out values. Here we evaluate the performance of commonly used imputation methods using three practical, “downstream-centric” criteria. These criteria measure the ability to identify differentially expressed peptides, generate new quantitative peptides, and improve the peptide lower limit of quantification. Our evaluation comprises several experiment types and acquisition strategies, including data-dependent and data-independent acquisition. We find that imputation does not necessarily improve the ability to identify differentially expressed peptides but that it can identify new quantitative peptides and improve the peptide lower limit of quantification. We find that MissForest is generally the best performing method per our downstream-centric criteria. We also argue that existing imputation methods do not properly account for the variance of peptide quantifications and highlight the need for methods that do.
Keywords: quantitative mass spectrometry, proteomics, imputation, machine learning, statistics, differential expression, lower limit of quantification
Graphical Abstract
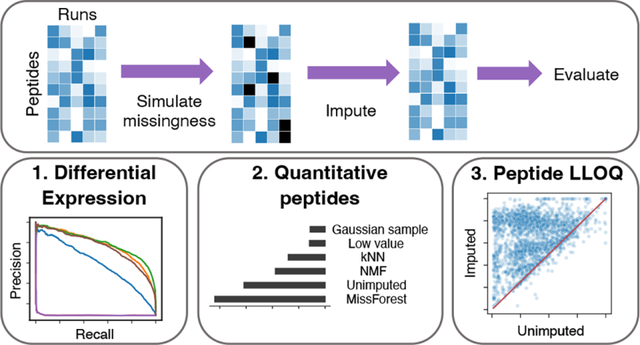
1. INTRODUCTION
The quantitative accuracy and sensitivity of tandem mass spectrometry proteomics have increased dramatically in the past decade. In spite of this trend, proteomics experiments are still limited by excessive “missingness,” which refers to peptides that are present in the sample matrix but are not assigned an abundance value. Missingness can be attributed to a variety of technical factors including ion suppression, coeluting peptides, the lower limit of quantification of the instrument, and the failure to confidently assign peptides to all observed spectra.1,2 Although low abundance peptides are generally more likely to be missing, peptides may be missing across the entire range of intensities. Missingness decreases the statistical power of proteomics experiments, hinders reproducibility, and makes it difficult to compare across batches or experiments.1,2
Imputation is a bioinformatic solution to the missingness problem. Imputation refers to the use of statistical or machine learning procedures to estimate missing values in a data set. While still relatively new within the proteomics community, imputation has long been standard practice for analysis of gene expression,3 clinical and epidemiological data,4 and more recently astronomy5,6 and single-cell transcriptomic data.7,8 Imputation methods for proteomics data (Table 1) fall into three broad categories: “single-value replacement” methods, in which all missing values are filled in with a single replacement value; “local similarity” methods, which use statistical models to learn patterns of local similarity in the data, for example, between subsets of similar peptides or runs; and “global similarity” methods, which learn broad patterns of similarity across all peptides and runs.
Table 1.
Existing Proteomics Imputation Methodsa
| Method | Type | Description | Examples |
|---|---|---|---|
| Zero replacement | S | Replace missing values with zeros | |
| Mean replacement | S | Replace missing values with the mean peptide intensity for a peptide or sample | |
| Low value replacement | S | Replace missing values with the lowest observed intensity in any sample (sample minimum) or peptide (peptide minimum) | |
| Gaussian random sample | S | Randomly sample from a Gaussian distribution centered around the lowest observed intensity | Perseus9 |
| Regression | L | Linear regression is used to estimate missing values | lm, glm |
| kNN | L | Weighted average intensity of k most similar peptides | impute.knn,3 VIM10 |
| MissForest | G | Nonparametric method to impute missing values using a random forest classifier trained on the observed parts of the data set, repeated until convergence | MissForest11 |
| PCA | G | Run principal component analysis, impute missing values with the regularized reconstruction formulas and repeat until convergence | pcaMethods,12 missMDA13 |
Descriptions of generalized imputation strategies and examples of specific tools that implement each strategy. The “Type” column indicates whether the method uses single-value replacement (S), local similarity (L), or global similarity (G).
It is not always clear what imputation method is best for a given proteomics data set. A number of studies benchmark imputation methods and offer guidelines for selecting an appropriate method.1,2,14–17 A general recommendation is that single-value replacement strategies rarely work well. Another is that the optimal imputation method depends on the structure of the missingness in the data. Mass spectrometry-based proteomics experiments exhibit two major forms of missingness: missing completely at random (MCAR) and missing not at random (MNAR). MCAR describes missingness that does not depend on any observed variable; that is, missingness occurs independent of peptide intensity or relationships between samples. For MNAR, missingness is dependent on some observed variable. For example, in mass spectrometry-based proteomics, missingness is often a function of peptide intensity, with more missingness occurring in peptides closer to the instrument’s lower limit of quantification (LLOQ).
When comparing the performance of imputation methods, it is commonplace to use relatively simple criteria that are easy to compute but not necessarily relevant to most proteomics researchers. One example is calculating the mean squared error (MSE) between imputed and ground truth peptide quantifications for a withheld set of matrix entries. As an alternative, we introduce “downstream-centric,” criteria focused on differential expression, peptide LLOQ, and the total number of quantitative peptides in an experiment. We argue that these downstream-centric criteria are more relevant to the questions that proteomics researchers typically seek to answer. Furthermore, we observe that the best-performing imputation methods per traditional criteria often differ from the best performing methods per our downstream-centric criteria.
To decide which imputation methods to include in our study, we carried out a systematic literature review. All Journal of Proteome Research articles published between January 1, 2019 and January 31, 2023 were searched for the following terms: “impute,” “imputed,” “imputation.” For this survey, we excluded methodological and benchmarking studies. On the basis of the resulting citation counts (Figure 1), we selected four of the most popular imputation methods: k-nearest neighbor (kNN),3 MissForest,11 Gaussian sampling,9 and low value replacement. We also include a non-negative matrix factorization (NMF) imputation method, which has recently been proposed for proteomics.18–20 By focusing on only the most commonly used imputation methods, our aim is to provide a practical comparison that will be beneficial to experimental proteomicists. For this reason, seldom used R packages (e.g., imp4p, impSeqRob, and QRLIC) have been omitted from our analysis. We also omit PCA-based methods, as they did not come up in our literature review.
Figure 1.
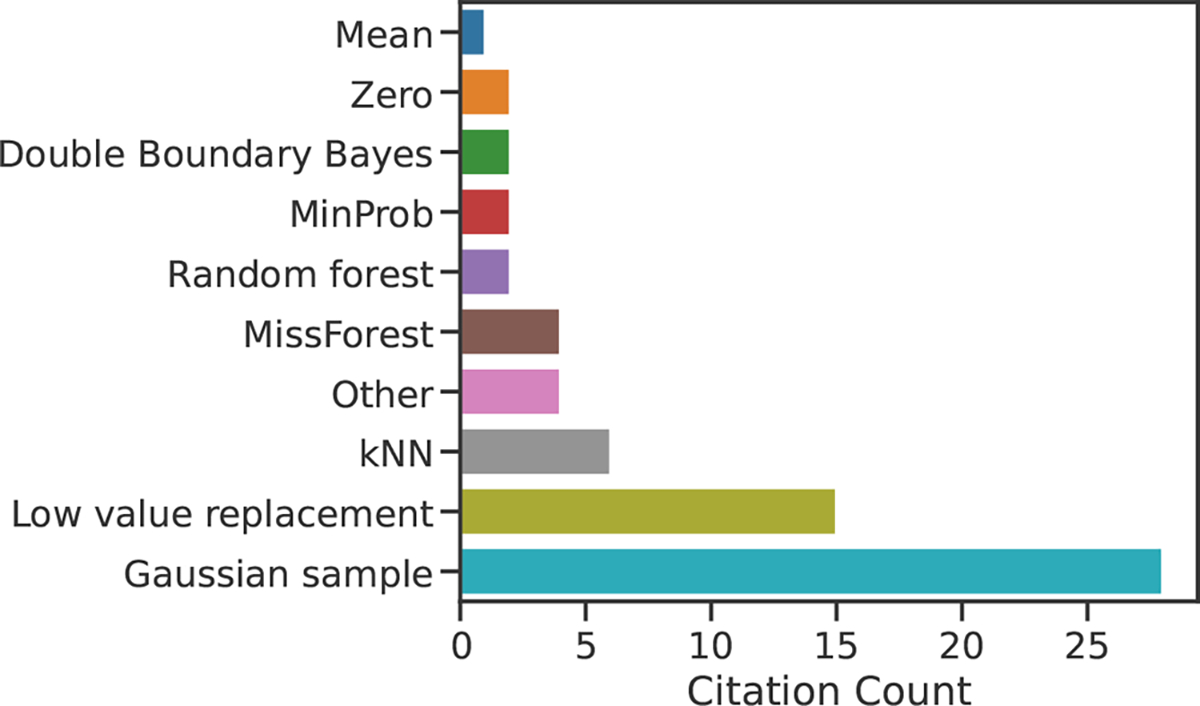
Identifying the most commonly used proteomics imputation methods. Results of a literature survey of Journal of Proteome Research articles from January 2019 to January 20, 2023 are shown. Methods labeled “Other” appear in just a single publication, and refer to the imp4p and QRLIC R packages, as well as methods based on Euclidean distances and randomly drawing from the entire peptide intensity range. The full results of this literature search, including the names and DOIs of the identified studies, are included as Data 1.
Additionally, we choose to conduct our analysis primarily on peptide-level quantifications. Our reason for this is severalfold: (i) summarizing peptide quantifications at the protein level reduces often-critical data heterogeneity,21 (ii) protein roll-up can introduce statistical bias,22 and (iii) imputation may perform better at the peptide level.15
We evaluate the performance of the five imputation methods with both traditional and downstream-centric criteria. The latter include the ability to (i) identify differentially expressed peptides, (ii) generate new quantitative peptides, and (iii) improve peptide LLOQ. Our benchmarking study comprises a variety of experiment types including serial dilution series, data-dependent acquisition (DDA), data-independent acquisition (DIA), label-free, and isobaric labeled experiments. Critically, we include an unimputed condition in all three downstream-centric evaluation experiments for evaluating whether imputation should be performed at all. Our findings suggest that imputation may not improve detection of differentially expressed peptides but that it can identify new quantitative peptides and improve peptide LLOQ.
We also demonstrate that the variance among the measured peptide intensities is greater than expected. Peptide quantifications from ion-counting mass spectrometers are often assumed to be well approximated by Poisson statistics.23–25 We demonstrate that peptide quantifications are overdispersed relative to a Poisson model for multiple mass spectrometry acquisition strategies. Furthermore, we demonstrate that the commonly used logarithmic transformation does not result in a uniform variance of peptide quantifications. These findings suggest that the statistical assumptions made by several prominent imputation methods are not met in the proteomics data. They also suggest the need for methods that employ variance stabilization prior to imputation, similar to strategies taken in genomics.26–28
2. METHODS
2.1. Data Sets
For this study, we used 12 public quantitative proteomics data sets (Table 2). Eight of the 12 data sets were accessed via the Proteomics Identification Database (PRIDE, https://www.ebi.ac.uk/pride/),29 and are indicated with their ProteomeXchange (PXD) labels.30 Two data sets were obtained from the National Cancer Institute’s Clinical Proteomic Tumor Analysis Consortium (CPTAC) data portal (https://proteomic.datacommons.cancer.gov/pdc/).31 The remaining two data sets, PXD034525 and PXD014815, were obtained from Panorama (https://panoramaweb.org/home/project-begin.view). Additional details on data set acquisition are provided in Data 2.
Table 2.
Data Set Characteristicsa
| Identifier | Peptides | Runs | % Missing | Quantification Software | Experiment Type | Citation |
|---|---|---|---|---|---|---|
| PXD016079 | 32999 | 31 | 45 | MaxQuant, MBR | DDA, LFQ | 32 |
| PXD006109 | 38124 | 20 | 17 | MaxQuant, MBR | DDA (BoxCar) | 33 |
| PXD014525 | 17208 | 36 | 92 | MaxQuant | DDA, LFQ | 34 |
| PXD034525 | 40346 | 10 | 13 | EncyclopeDIA, Skyline | DIA | 35 |
| PXD014815 | 24204 | 42 | 29 | EncyclopeDIA, Skyline | DIA | 36 |
| PXD013792 | 2224 | 12 | 72 | MaxQuant | DDA, LFQ | 37 |
| PXD014156 | 697 | 20 | 55 | MaxQuant | DDA, LFQ | 38 |
| PXD006348 | 10362 | 24 | 72 | MaxQuant | DDA, LFQ | 39 |
| PXD011961 | 23415 | 23 | 46 | MaxQuant, MBR | DDA, LFQ | 40 |
| CPTAC-S047 | 40000 | 30 | 54 | Philosopher | DDA, TMT | 41 |
| CPTAC-S051 | 40000 | 30 | 41 | Spectrum Mill | DDA, TMT | 42 |
| PXD007683 | 38921 | 11 | 0 | Custom pipeline | DDA, TMT | 43 |
Description of the proteomics data sets used in this study. The two CPTAC data sets were downsampled by randomly selecting 40,000 peptides and 30 runs each. “MBR” stands for “match between runs,” “LFQ” for “label-free quantification,”, and “TMT” for “tandem mass tag.” References for quantification software: MaxQuant,44 EncyclopeDIA,45 Skyline,46 Philosopher.47.
For experiments processed with MaxQuant, we used the.txt output files to generate peptide-by-run intensity matrices by selecting only the “Sequence” and “Intensity” columns. For the CPTAC experiments, we obtained peptide-spectral match files (.psm) from the CPTAC data portal and converted them to matrix format with custom scripts (available at https://github.com/Noble-Lab/2023-prot-impute-benchmark). The peptide-by-run matrices from these CPTAC studies were large (S047: 110,000 peptides × 226 samples; S051: 291,000 peptides × 35 samples). For efficiency, we downsampled these matrices by randomly selecting 40,000 peptides and 30 runs from each.
For the two DIA data sets, peptide quantification matrices were obtained directly from Panorama.
2.2. Traditional Evaluation Measures
We first used a traditional machine learning-style train-test setup to evaluate the performance of imputation methods. With this approach, the values in the peptide-by-run matrix were randomly partitioned into two groups: a training set and a test set. The imputation method was trained on the training set values, and we measured how well the method imputed the values in the test set. For each data set, peptides with fewer than four present values in the training set were removed prior to imputation.
The training/test partitioning was performed with two different procedures: MCAR and MNAR. For MCAR, 25% of the present (i.e., nonmissing) matrix entries were randomly selected for the test set. The remaining matrix entries were used as the training set. For MNAR, we took a similar approach to the one described by Lazar et al.15 For a given peptide-by-run matrix, we constructed an equally sized threshold matrix filled with values sampled from a Gaussian distribution centered about the 30th percentile of the distribution of quantifications, with a standard deviation 0.6. For each element Xij in the peptide-by-run matrix, if the corresponding thresholds matrix element Tij < Xij, then Xij was assigned to the training set. Otherwise, a single Bernoulli trial with a probability of success of 0.75 was conducted. If the Bernoulli trial was successful, then Xij was assigned to the test set. Otherwise Xij was assigned to the training set. The Bernoulli success probability and the Gaussian distribution mean and standard deviation were selected in such a way that 25% of the present matrix entries were ultimately assigned to the test set. The remaining 75% were assigned to the training set. The distributions of the training and test set values following the MCAR and MNAR partitions are shown in Supplementary Figure 1, for experiment PXD034525.
Once the peptide-by-run matrices were partitioned into train/test, imputation was performed with five procedures: NMF, kNN, MissForest, low value replacement (run minimum), and Gaussian sample impute. A custom PyTorch model was used for NMF imputation. This model used an MSE loss function and stochastic gradient descent to converge on an ideal matrix factorization. This model is available at https://github.com/Noble-Lab/MSFactor. For kNN, we used the KNNImputer implementation from scikit-learn. MissForest version 1.5 was used (https://CRAN.R-project.org/package=missForest).11 Custom code was used for the low value replacement and Gaussian sample impute procedures. For Gaussian sample impute we replicated the procedure taken by Perseus.9 For low value replacement, we filled in missing values with the lowest measured peptide intensity for each run. NMF and kNN analyses were performed with four latent factors and neighbors, respectively. MissForest was performed with 100 trees, the default setting.
Following imputation, we computed the MSE between the observed and imputed values for each test set (Figure 2).
Figure 2.
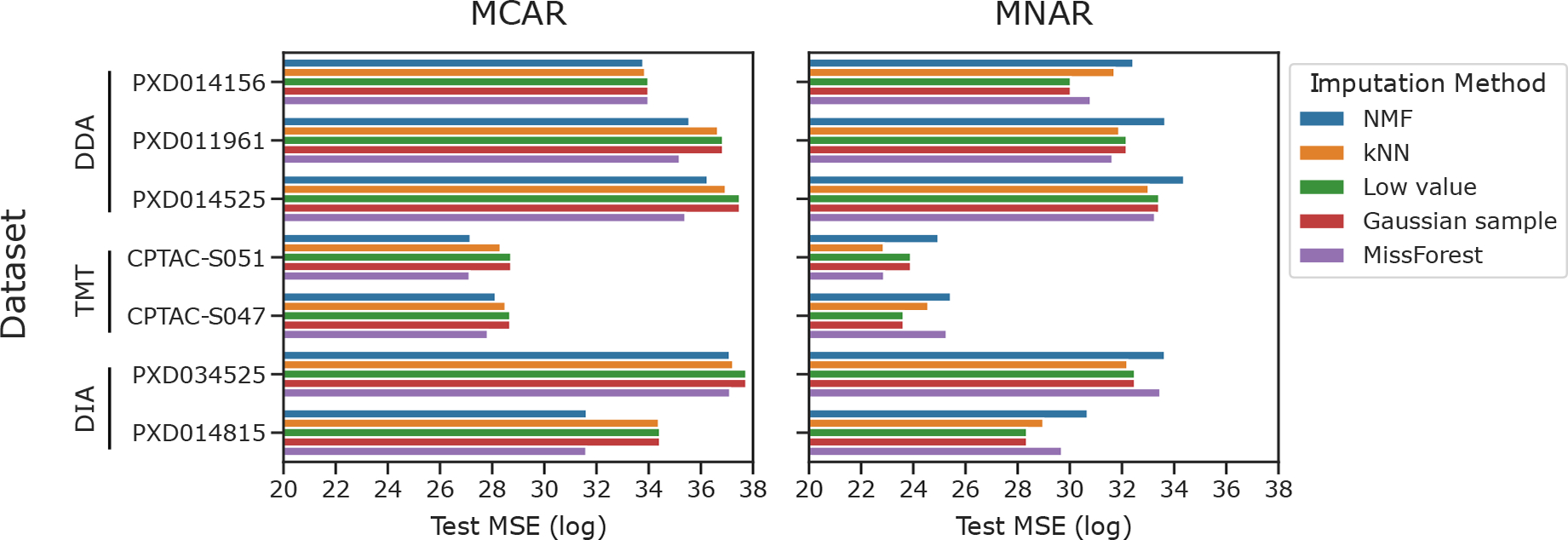
Evaluating imputation methods with traditional criteria. Test set reconstruction error (MSE) for imputation with five methods is shown for seven proteomics data sets. MCAR and MNAR procedures were used to simulate the missing values
2.3. Downstream-Centric Evaluation Measures
2.3.1. Differential Expression.
For differential expression analysis we obtained data from PXD034525, a DIA study of Alzheimer’s disease.35 Clinical samples had previously been assigned to experimental groups based on several genetic, histopathological, and cognitive criteria. We compared differentially expressed peptides between (i) autosomal dominant Alzheimer’s disease dementia and (ii) high cognitive function and low Alzheimer’s disease neuropathologic change. Both experimental groups were composed of nine patient samples and 32,614 detected peptides.
Ground truth differentially expressed peptides were determined by performing two-sample t tests between experimental groups for each detected peptide. P-values were corrected for multiple hypothesis testing using the Benjamini-Hochberg procedure.48 Peptides with corrected p-values <0.01 were considered ground truth differentially expressed.
MCAR and MNAR partitioning was performed similar to above, but this time we created three disjoint sets: training, validation, and test. For the MCAR partition, 15% of matrix entries were randomly selected without replacement for the validation set, and a separate 15% was selected for the test set. For the MNAR partition, matrix entries corresponding to successful Bernoulli trials were assigned in an alternating fashion to either the validation or the test set. The Bernoulli success probability and Gaussian distribution mean and standard deviation were tuned so as to generate a 70%/15%/15% train/validation/test split.
The validation sets were used to select the optimal hyperparameters for NMF and kNN. For MissForest a full hyperparameter search proved computationally unfeasible, so we again selected the default value of 100 for the n trees parameter. None of the other methods had tunable hyperparameters. The following values were included in our hyperparameter searches for n latent factors and k neighbors: [1,2,4,8,16,32].
Following hyperparameter selection, imputation was performed with each method. Differentially expressed peptides were determined for the imputed matrices, as previously described. Precision-recall curves comparing ground truth to imputed differentially expressed peptides were generated with scikit-learn (Figure 3). For the unimputed condition, the differential expression calculation was performed as previous while simply ignoring the missing matrix entries. That is, the differential expression test was performed on training set values only.
Figure 3.
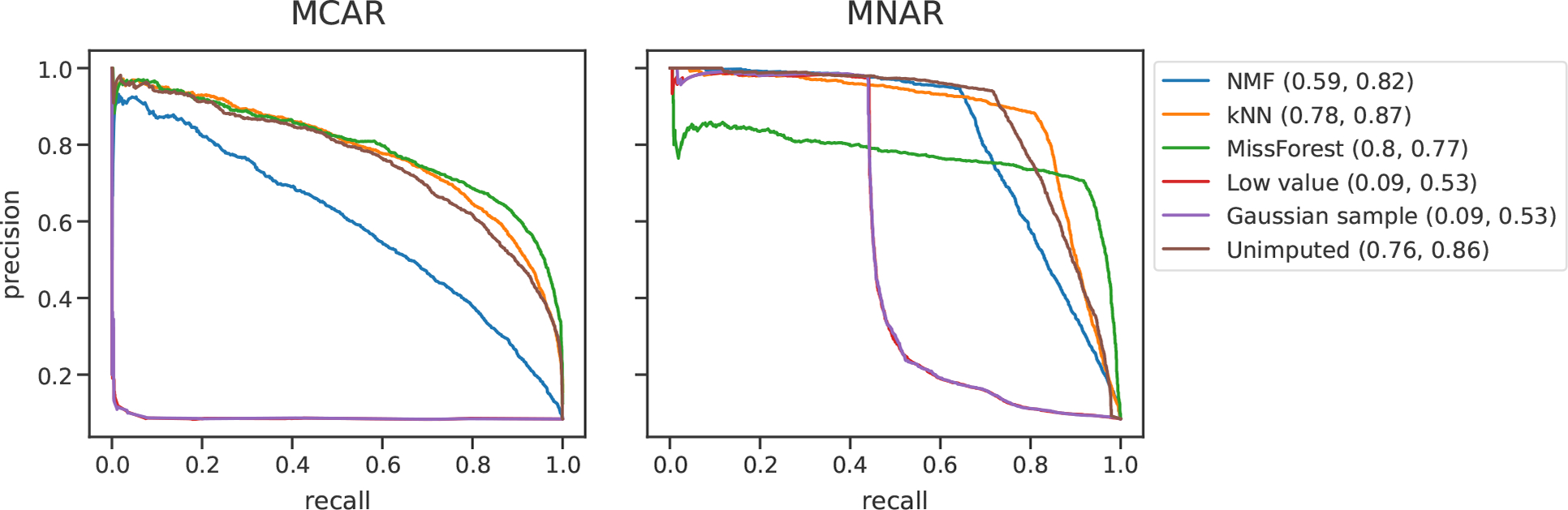
Comparing the abilities of imputation methods to identify differentially expressed peptides. Precision-recall curves are shown for MCAR and MNAR simulated missingness. Data were obtained from PXD034525, a DIA study of Alzheimer’s disease. Differentially expressed peptides were identified between two clinically annotated Alzheimer’s disease groups.35 The areas under the precision-recall curves (AUCs) for the MCAR and MNAR are indicated.
We performed an additional differential expression experiment for PXD034525 in which we varied the missingness fraction from 25% to 30% to 50% (Supplementary Figure 2). For MNAR, this was accomplished through tuning the Bernoulli success probability and Gaussian distribution mean and standard deviation parameters in order to achieve the desired missingness fraction.
The differential expression procedure was repeated for a TMT data set, CPTAC-S04741 (Supplementary Figure 3). This was a study of pediatric brain cancer. We compared clinical samples annotated as “Low-grade glioma/astrocytoma” to “Ependymoma”. Twenty-three patient samples were used for each condition, and 26,923 detected peptides. We performed a 70%/15%/15% train/validation/test split.
The differential expression test was repeated for protein-level quantifications of PXD034525 (Figure 4). Once again, we performed a 70%/15%/15% train/validation/test split. 4,999 proteins were included in this analysis.
Figure 4.
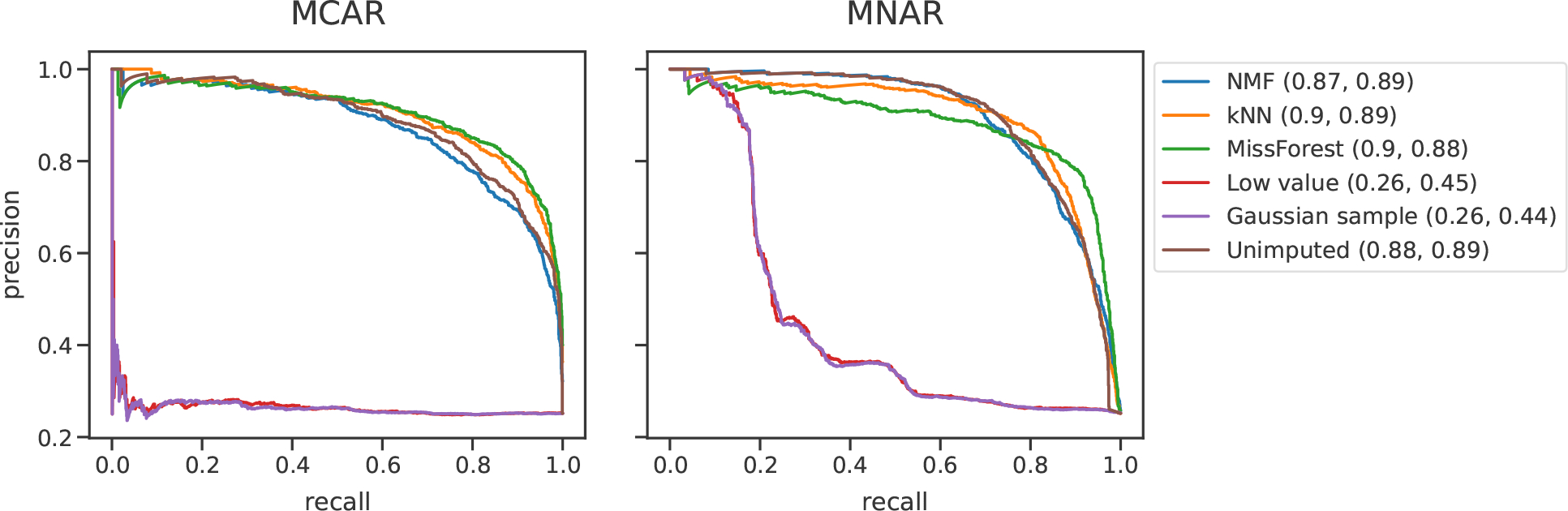
Comparing the abilities of imputation methods to identify differentially expressed proteins. DIA data were obtained from PXD034525. Differentially expressed proteins were identified between two clinically annotated Alzheimer’s disease groups. Missingness was simulated by MCAR and MNAR. AUC values are given in parentheses.
2.3.2. Quantitative Peptides.
To examine the effects of imputation on the number of quantitative peptides in a proteomics experiment, we obtained data from PXD014815.36 This was a serial dilution experiment in which peptides were successively diluted by increasing the concentration of a matched background matrix. As a result, the total protein concentration in each sample was known. The authors then used a custom statistical model to fit the relationship between observed and expected signal and to determine whether increases in signal corresponded to proportional increases in peptide abundance. Peptides in which the increase in signal did indeed correspond to increases in quantity across a linear range were considered quantitative.
We used this statistical model to assess the number of quantitative peptides before and after imputation of the serial dilution series data set (Figure 5). MCAR partitioning was performed as described above. Hyperparameter tuning for kNN and NMF was performed as described above. The peptide-by-run matrix was imputed with each method, and quantitative peptides were identified in the imputed matrices. The UpsetR package was used to generate Figure 5.49
Figure 5.
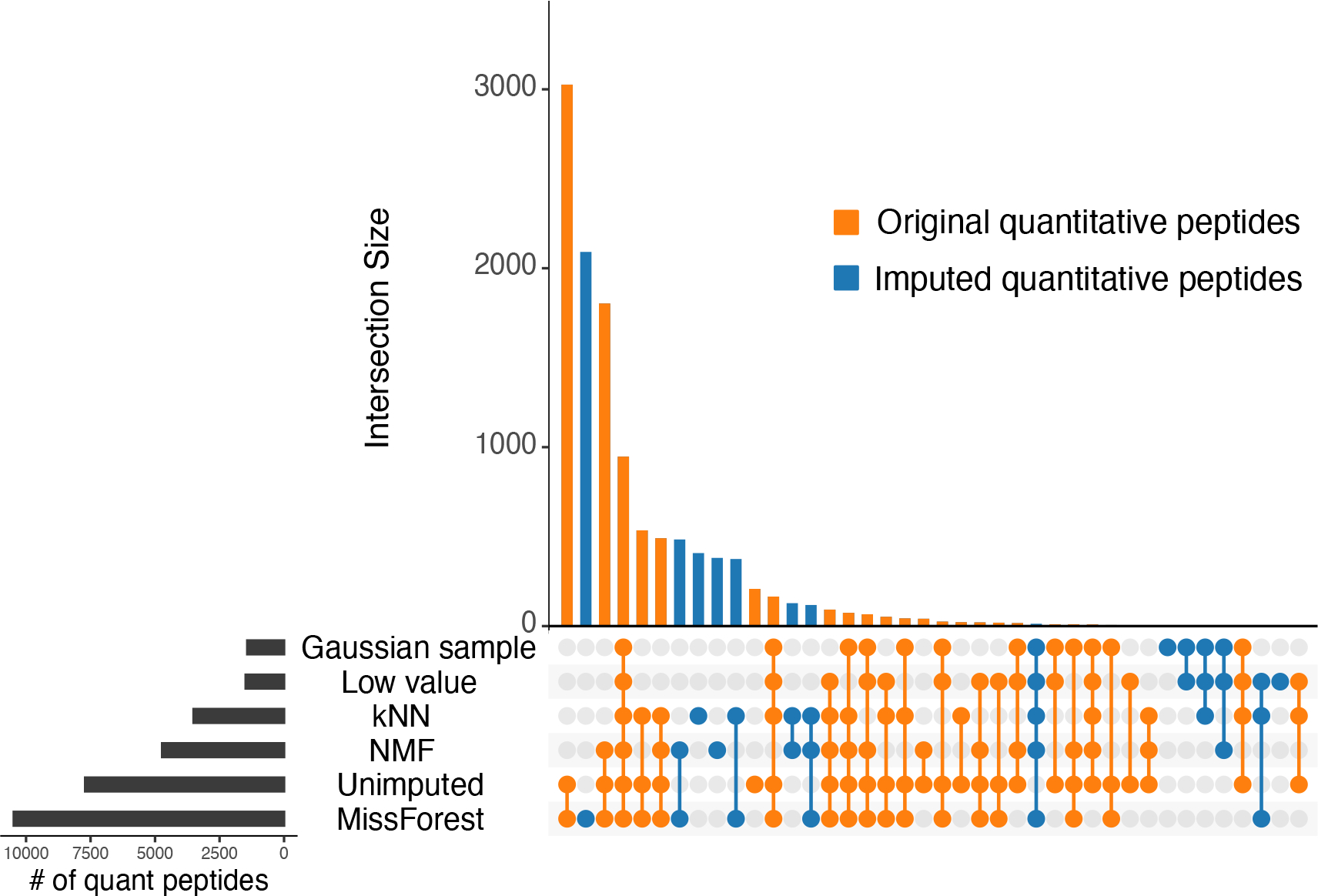
Comparing the abilities of imputation methods to generate additional quantitative peptides. Orange indicates peptides that were quantitative in both the imputed and the unimputed data sets. Blue indicates peptides that were only quantitative after imputation. Data were obtained from PXD014815.36
2.3.3. Lower Limit of Quantification.
We used the serial dilution experiment from PXD014815 to examine the effects of imputation on the peptide LLOQ (Figure 6). We again used the statistical model from Pino et al.36 to determine the LLOQ of each detected peptide before and after imputation. One-sided binomial tests were performed to determine whether each imputation method decreases the LLOQ for significantly more peptides than it increases. Binomial p-values were corrected with the Benjamini–Hochberg procedure.
Figure 6.
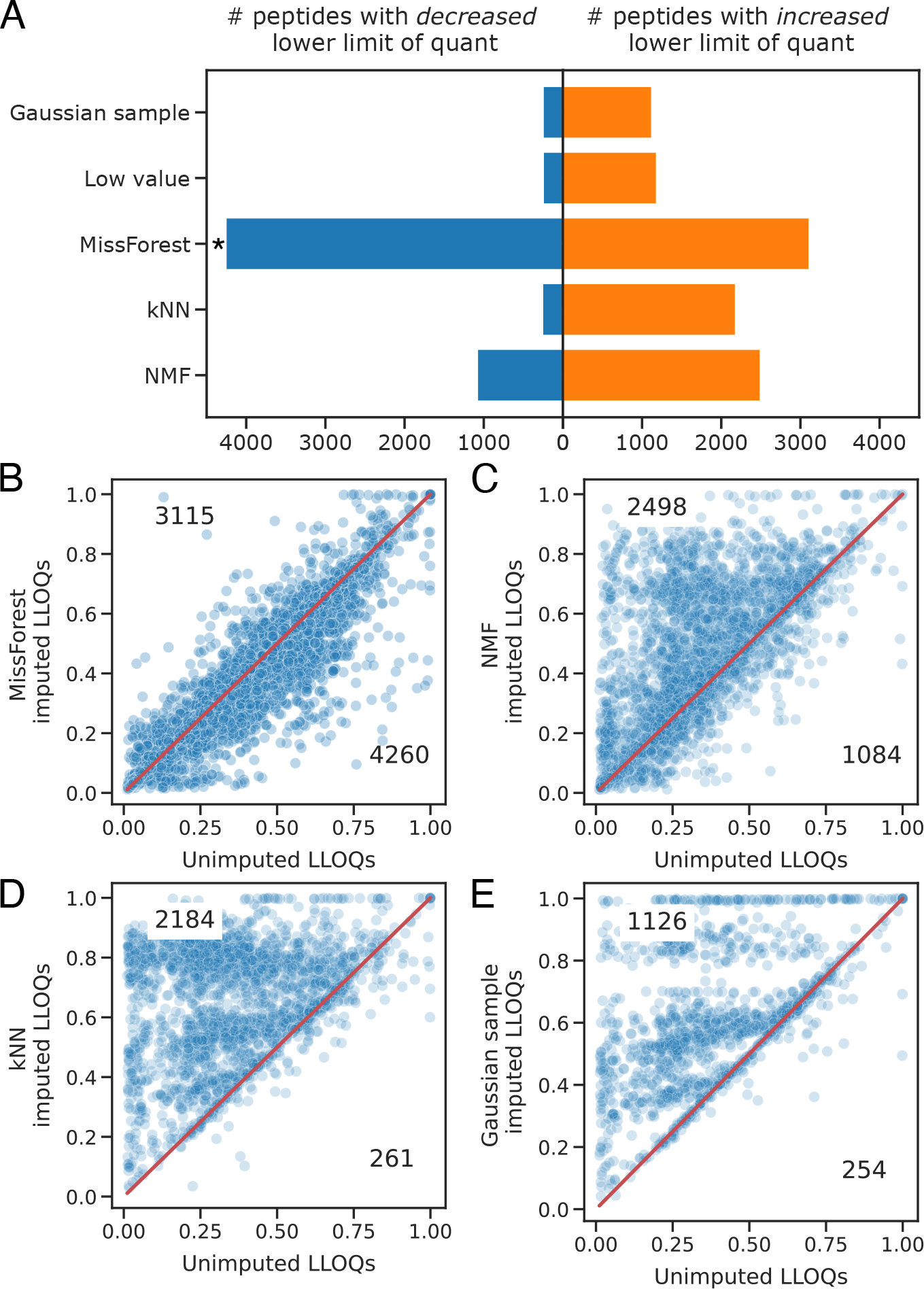
Comparing the abilities of imputation methods to decrease peptide LLOQ. In (A) the asterisk indicates a one-sided binomial Benjamini-Hochberg corrected p-value <0.01. In panels B–E the LLOQs of unimputed peptides are plotted against the LLOQs of the same imputed peptides. Only peptides with changes in LLOQ following imputation are plotted. Data were obtained from PXD014815.36
2.4. Runtime Evaluation
We used Python’s time module to compare the runtimes of the various imputation methods (Figure 7). NMF, kNN, low value replacement, Gaussian sample, and MissForest were run on 14 public proteomics data sets accessed from PRIDE. This experiment was performed on a dual CPU Intel Xeon E5–2620 machine with 32 GB RAM, running CentrOS 7.6. NMF was specified to run on a maximum of 10 cores, and the remaining methods were run on a single core. This was because the kNN implementation we used, scikit-learn’s KNNImputer, does not support multiprocessing, nor do our custom implementations of low value replacement and Gaussian sample impute. MissForest does support multiprocessing, though in our experience, the parallelized version of MissForest proved nearly impossible to run to completion. Thus, we choose to limit MissForest to a single core.
Figure 7.
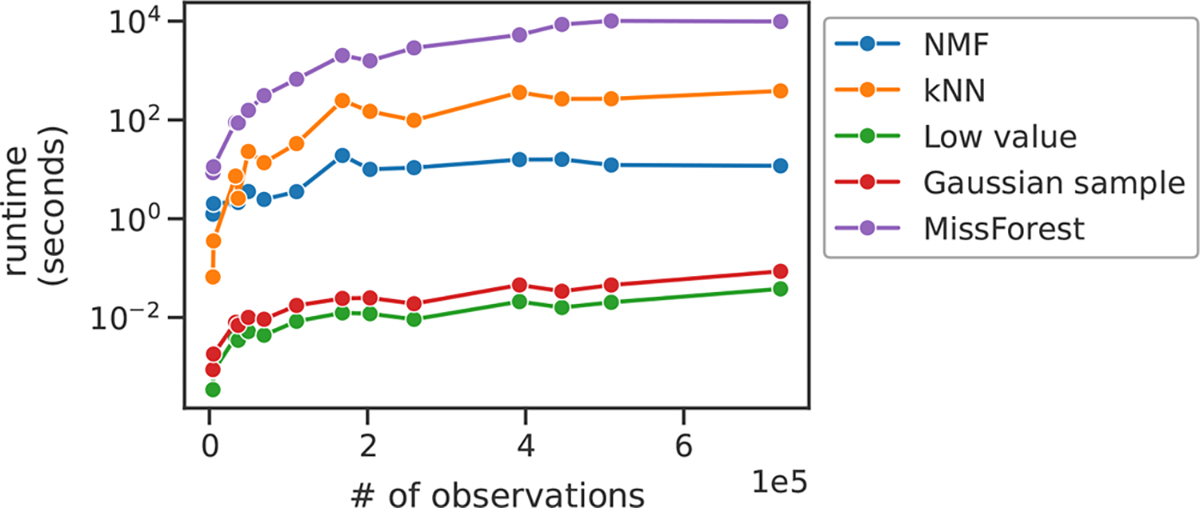
Runtime comparison for the imputation methods. Each point represents a data set. Data sets are ordered by the number of nonmissing observations in their training sets after an 80%/20% MCAR train/test partition.
3. RESULTS
3.1. Evaluating with Traditional Criteria
We began by assessing the performance of popular imputation methods with a traditional machine learning criterion: prediction error on a withheld test set. Accordingly, we obtained peptide-level quantifications for seven of the experiments shown in Table 2. These included DIA, DDA and TMT experiments, with a missingness range of 0 to 92%. We assessed the ability of the imputation methods to reconstruct missing values after MCAR and MNAR procedures were used to simulate an additional 25% missing in each data set.
Our results (Figure 2) demonstrate that the relative performance of imputation methods depends on the type of missingness. MissForest and NMF perform the best for all seven data sets under the MCAR condition. In the MNAR condition, the two single-value imputation methods—Gaussian sample and low value replacement—appear to work the best, though MissForest also performs well for some data sets. In both conditions, the two TMT data sets—CPTAC-S047 and CPTAC-S051—yield lower reconstruction errors across all imputation methods when compared to the DDA and DIA data sets.
3.2. Evaluating with Downstream-Centric Criteria
Although traditional machine learning-style evaluations such as shown in Figure 2 are informative, we argue that prediction error on a held-out set is neither the most convincing nor the most relevant metric for most proteomics researchers. Additionally, good performance per traditional evaluation criteria may not translate to good performance on downstream analysis tasks. Furthermore, recent benchmarking studies have made the assumption that imputation will improve performance on downstream analysis tasks relative to no imputation. This assumption is generally unfounded, as imputation can introduce bias even when used appropriately.50,51 With these considerations in mind, we compared the performance of five commonly used imputation methods on three downstream analysis tasks that we argue are more congruent with the questions proteomicists typically seek to answer.
3.2.1. Differential Expression.
We began with a differential expression analysis. We obtained peptide-level quantifications from a DIA-based clinical study of Alzheimer’s disease.35 Patient-derived brain samples had been assigned to experimental groups based on several genetic, histopathological, and cognitive criteria. We compared samples belonging to two experimental groups: (i) autosomal dominant dementia and (ii) high cognitive function and low Alzheimer’s disease neuropathologic change. These experimental groups represent opposite ends of the spectrum of Alzheimer’s disease severity and Merrihew et al. found significant biological heterogeneity between them.
We compared the abilities of imputation methods to identify differentially expressed peptides after simulating missingness with either MCAR or MNAR (Figure 3). To perform this experiment, we identified ground truth differentially expressed peptides in the low-missingness Alzheimer’s disease DIA data set, simulated 30% missingness, then imputed with various methods, and identified differentially expressed peptides in the imputed matrices. We also included an unimputed condition in which differentially expressed peptides were identified directly from the unimputed training set. The sharp elbows in the MNAR precision-recall curves are due to the fact that an alpha value of 0.01 was used for determining significantly differential peptides for both ground truth and imputed matrices. It is likely that many peptides had p-values very close to the 0.01 threshold but were not considered differentially expressed, resulting in sharp decreases in precision as soon as this threshold was crossed.
In the MCAR condition, MissForest, kNN and no imputation all performed well, with areas under the curve (AUCs) of 0.80, 0.78, and 0.76, respectively. In the MNAR condition, kNN, no imputation, and NMF performed the best, with respective AUCs of 0.87, 0.86, and 0.82. While the two single-value imputation methods performed well in the MNAR condition of the traditional evaluation experiment (Figure 2), they performed poorly on the differential expression test, with the lowest AUCs for both MCAR and MNAR. In both conditions, no imputation performed nearly the same or better than the five imputation methods.
We also performed differential expression experiments for a TMT (Figure 3) and a label-free DDA (Figure 4) data set. For the TMT data set, no imputation performed the best for MCAR, and was slightly outperformed by kNN for MNAR. For the label-free DDA data set, no imputation performed the best for both MCAR and MNAR. For the label-free DDA data set the single-value impute methods were the worst performing for both MCAR and MNAR.
We revisited the Alzheimer’s disease DIA data set to perform a final differential expression experiment for protein-level quantifications (Figure 4). In both MCAR and MNAR conditions, the single-value imputation strategies performed the worst. Interestingly, the AUCs of the nonsingle value imputation strategies were all in the range of 0.87–0.9. This indicates that for this particular DIA data set differential expression analysis was more accurate at the protein level. We again observed that no imputation performs remarkably well relative to commonly used imputation methods with AUCs of 0.88 and 0.89 for MCAR and MNAR, respectively.
3.2.2. Quantitative Peptides.
Next, we assessed whether imputation can generate quantitative peptides. While peptide detection rates have increased significantly over the past decade, not every detected peptide is necessarily quantitative. For a peptide to be considered quantitative, increases in measured signal must correspond to increases in peptide abundance, across a linear range.36 We obtained data from a serial dilution series experiment (PXD014815) in which the protein concentration was known for each sample. We used a statistical model developed by Pino et al. to determine whether each detected peptide was quantitative before and after imputation.36
The results of this experiment (Figure 5) show that several imputation methods produce new quantitative peptides. MissForest, kNN and NMF each generated large sets of peptides that were quantitative only after imputation (2,768 for MissForest; 1,050 for kNN; 1,128 for NMF). However, MissForest was the only method that increased the total number of quantitative peptides relative to no imputation, producing 10,475 quantitative peptides relative to the 7,707 obtained with no imputation.
3.2.3. Lower Limit of Quantification.
We also assessed whether imputation can improve the peptide LLOQ, which refers to the minimum abundance at which a peptide can be considered quantitative. For this analysis, we again used the serial dilution data set from Pino et al. We found that while imputation did indeed decrease the LLOQ for many peptides, it also increased the LLOQ for some peptides, which was the opposite of the intended effect. Strikingly, MissForest was the only method that decreased the LLOQ of significantly more peptides than it increased (Figure 6, one-sided binomial p-value corrected with Benjamini–Hochberg < 0.01).
3.3. Runtime
For imputation methods to be incorporated into existing proteomics data processing workflows, they must be runnable in a reasonable time frame. With this in mind, we compared the runtimes of our five imputation methods (Figure 7). The two simplest methods, Gaussian sample and low value replacement, ran in a matter of seconds; NMF and kNN ran in a matter of minutes; and MissForest took several hours to complete. Thus, with the possible exception of MissForest, runtime should not present a barrier for incorporation into data processing workflows.
3.4. Variance in Quantitative Proteomics Data
We investigated the statistical assumptions underlying several imputation approaches. Peptide quantifications are often modeled with Poisson statistics.23–25 One feature of a Poisson distribution is that the variance is equivalent to the mean. Additionally, it is commonplace to logarithmically transform quantifications prior to analysis. One assumption with a logarithmic transformation is that the variance of the transformed quantifications will be uniform. Parametric imputation methods with a Gaussian prior include least-squares regression, the Gaussian sample impute method, and standard NMF.
To empirically investigate the variance of peptide quantifications, we obtained data from four experiments, each of which contained technical replicates (Table 2). We used three DDA experiments and one DIA. We calculated the means and variances of peptide quantifications across technical replicates for each detected peptide for each experiment. We found that peptide quantifications are overdispersed relative to the Poisson distribution (Figure 8, left); that is, for nearly every peptide, the variance across replicates was greater than the mean intensity across replicates. Log transformation resulted in more uniform variance across intensities, but many peptides still displayed extraordinarily high variances (Figure 8, right).
Figure 8.
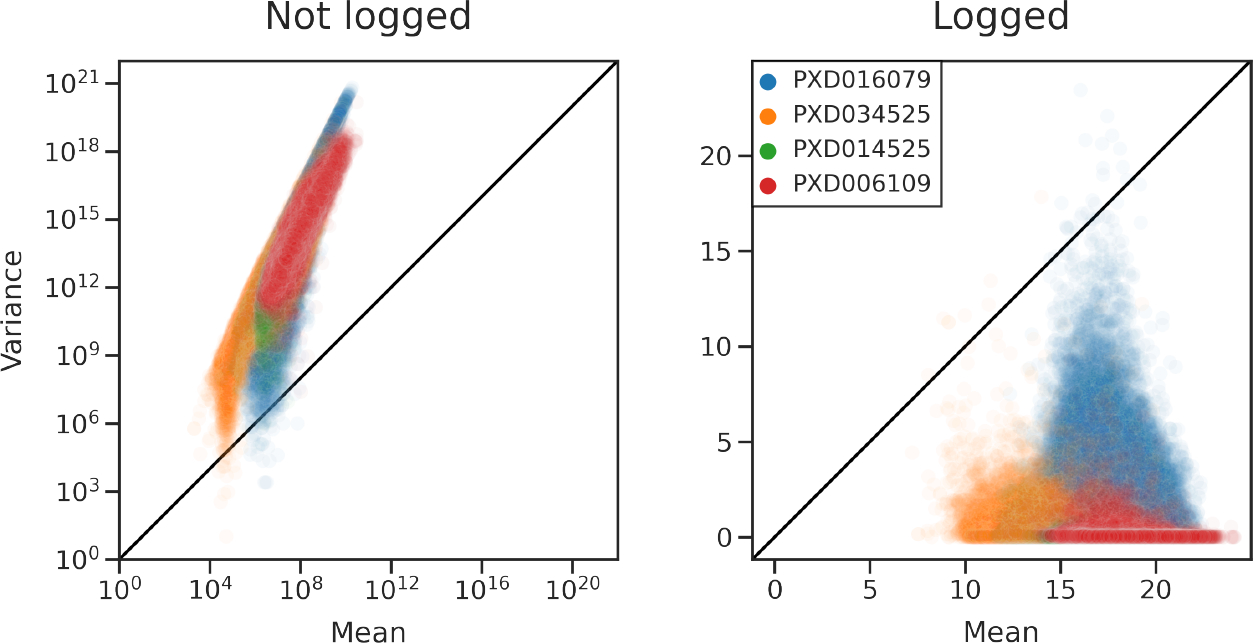
Variance of peptide quantifications is greater than expected. Means and variances were calculated across technical replicates for every detected peptide. Each dot corresponds to a peptide. Data from DIA (PXD034525) and DDA (PXD016079, PXD014525, PXD006109) experiments are plotted.
We found that for multiple data sets obtained with both DDA and DIA acquisition strategies neither Poisson nor Gaussian assumptions hold. This suggests that parametric imputation methods with implicit Gaussian assumptions may be ill-suited for these data.
We also observed that imputation with NMF and MissForest had little effect on the variance of peptide quantifications (Figure 5). The Gaussian sample method, however, introduced additional variance. This finding suggests that while NMF and MissForest imputation do not profoundly affect the underlying distribution of peptide quantifications, single-value impute strategies may do so. In this way, single-value impute strategies may introduce artifacts into proteomics data when their underlying assumptions are not met.
4. DISCUSSION
The two most popular imputation methods—Gaussian sampling and low value replacement—performed poorly in our downstream-centric experiments. These single-value imputation strategies were the worst perfoming for peptide-level differential expression detection in DIA data (Figure 3), protein-level differential expression in DIA data (Figure 4), and peptide-level differential expression in label-free DDA data (Supplementary Figure 4), generating quantitative peptides (Figure 5) and decreasing peptide LLOQ (Figure 6).
However, the results of the downstream-centric experiments did not always agree with those of the traditional evaluation experiment. In particular, the single-value imputation strategies often outperformed the local and global similarity strategies for the traditional benchmarking experiment shown in Figure 2, especially for MNAR. This was likely because the single-value imputation strategies assume that missing values are drawn from the low end of the distribution of peptide quantifications, and this assumption was met in the MNAR condition of the traditional evaluation experiment. We argue that traditional evaluation experiments such as Figure 2 are misleading because they inflate the performance of single-value impute strategies. Performance on our downstream-centric criteria is more relevant than the test set MSE, because the downstream criteria are more congruent with questions proteomics researchers typically seek to answer. Thus, we urge the community to move away from traditional performance evaluations in favor of the downstream-centric criteria presented here.
Our results suggest that imputation may not be necessary for the differential expression analysis. For a DIA experiment with MCAR and MNAR simulated missingness, no imputation worked roughly as well as the best imputation methods (Figure 3). In the MCAR condition, the largest AUC value belonged to MissForest at 0.8, only slightly higher than that of unimputed at 0.76. In the MNAR condition, kNN had the highest AUC at 0.87, and unimputed was close behind, with 0.86. This result generalized to a label-free DDA data set (Supplementary Figure 4), in which no imputation outperformed all imputation methods for MCAR and MNAR. For a TMT data set, no imputation had the highest AUC for MCAR and was tied for the second highest for MNAR (Supplementary Figure 3).
We found that as the missingness fraction increased, unimputed performed better and better relative to the five imputation methods (Supplementary Figure 2). For example, in the case of MNAR with a 50% missingness fraction, unimputed had an AUC of 0.65, whereas the best imputation method was MissForest with an AUC of 0.55.
We also found that for a DIA experiment differential expression analysis was more accurate when performed at the protein level (Figure 4). This makes sense because protein roll-up reduces missingness and hides variability between peptides of the same protein, therefore making the differential expression identification task easier.21 Researchers should approach protein-level analysis with caution, however, because protein roll-up may introduce statistical bias and reduce data heterogeneity.21,22 It should be noted that once again, the unimputed condition had one of the highest AUC values for both MCAR and MNAR.
Taken together, our differential expression results cast doubt on the practice of imputing missing values prior to differential expression analysis. We have shown that at the peptide and protein level, for DIA, label-free DDA and TMT experiments, no imputation generally works, as well as the most commonly used imputation methods. Our results are in line with Wolski et al., who suggest that statistical models of differential expression that do not impute, but rather explicitly model missingness, tend to outperform traditional models.52
As we performed differential expression analysis on only three data sets, we do not claim our results will generalize to all proteomics data. Instead, our results suggest that researchers should empirically evaluate whether imputation improves accuracy of their differential expression analysis on a case-by-case basis, using procedures similar to the one we introduce here.
Bai et al. have shown that the choices in normalization procedure and statistical analysis method can affect differential expression results.53 The normalization procedures used by the data sets we analyzed are provided as Supplementary Table 1. We acknowledge that differences in normalization may have introduced variation that cannot be explained by imputation methods alone. It is also possible that the spectral processing tools themselves—for example, MaxQuant versus Skyline—may have contributed additional variation. Future work will aim to repeat our benchmark analysis with standardized spectral processing and normalization procedures.
We choose a two-sample sample t test for differential expression analysis because it represents a simple, transparent and commonly used procedure.54,43,39,32 Furthermore, the three data sets that we analyzed all had relatively simple experimental designs. For the DIA35 and TMT41 data sets, each analyzed sample came from a different individual, and serial biopsies and time series data were excluded from our analysis. For the label-free DDA data set,39 biological replicates from two Brucella species were compared. For simple experimental designs such as these, differential expression analysis does not require complicated statistical procedures. For more complex designs we recommend MSstats, which can model a variety of experimental designs in a statistically rigorous manner.55
We found that imputation can identify new quantitative peptides (Figure 5). As modern proteomics techniques increase the number of identifications, it is important to remember that not all of the detected peptides are quantitative. Here we show that MissForest can be used as a postprocessing tool to generate additional quantitative peptides in a proteomics experiment (Figure 5). Additionally, NMF and kNN can produce new subsets of quantitative peptides even though they may still decrease the total number of quantitative peptides. Increasing the number of quantitative peptides will increase the statistical power of any downstream prediction or inference task that relies on peptide abundances. Such tasks include identifying differentially expressed peptides, clustering samples or peptides, dimensionality reduction, and identifying coexpression modules and protein–protein interaction networks.
Imputation with MissForest can also improve the peptide LLOQ (Figure 6). It is worth acknowledging that while MissForest decreased the LLOQ of significantly more peptides than it increased, it did still increase the LLOQ for a large number of peptides (3,115/24,204 detected peptides). That said, any proteomics study that examines biologically important low-abundance peptides may still benefit from MissForest imputation. As the scale and sensitivity of proteomics experiments increase, MissForest—and future imputation methods—may help researchers study key peptides derived from ever-smaller sample volumes.
Finally, we provide empirical evidence that peptide quantifications exhibit more variance than can be explained under Poisson or Gaussian modeling assumptions (Figure 8). While ion counting may be a Poisson process,23–25 it is clear that the resulting quantifications are not Poisson distributed. One property of a Poisson distribution is that the mean and variance are equal. We found that this property was violated by several proteomics data sets: the variance among peptide quantifications across technical replicates was greater than the corresponding means (Figure 8). This result held true for both DDA and DIA experiments and for protein-level quantifications (Figure 6). We speculate that this additional variance may be due to an unaccounted-for noise source such as electrospray ionization. Another assumption is that log-transformed intensities are roughly Gaussian. Under this model, variance would be uniform across mean intensities. We show this assumption is also violated in DIA and DDA data: we observed nonuniform variance after log transformation (Figure 8, right). It is worth noting that Poisson is a discrete probability distribution, whereas Gaussian is continuous. From a statistical standpoint, it should not be assumed that a logarithmic transformation can convert a discrete probability distribution into a continuous one.
Future imputation methods should explicitly model the variance present in the proteomics data. One obvious choice of generating distribution is the negative binomial distribution, which has an additional parameter that can account for variance independent of the mean. This strategy has been employed previously to model counts from single-cell RNA sequencing experiments.27,28 Another option would be to perform variance stabilization prior to imputation. This is the goal with the log transformation; however, as we have shown, logging does not successfully stabilize variance. VSN, a custom variance stabilizing transformation originally developed for microarrays, has been shown to stabilize the variance of protein quantifications,16,56 as has the generalized log transformation.57 However, the proteomics community has yet to broadly adopt these methods. Proteomics may also benefit from the variance stabilization technique developed by Bayat et al., in which a variance stabilizing function is empirically learned from the data.26 Successful modeling and variance stabilization approaches could benefit not just imputation but also data analysis for proteomics more broadly.
We speculate that the unusual dimensionality of peptide-by-run matrices, generally thousands of peptides by fewer than 100 runs, may cause problems for existing imputation methods. Many proteomics imputation methods were originally developed for microarrays and relatively square matrices. Future imputation methods may benefit from explicitly accounting for the dimensionality of peptide-by-run matrices.
The proteomics community would benefit from easy-to-use and broadly applicable imputation methods. As previously reported,1,2,14,15 we found that the best choice in imputation method depends on the analysis task and the details of the experiment. This suggests the need for new imputation methods that are generalizable enough to accurately handle data from any acquisition strategy and type of missingness. Deep neural networks have proven to be highly generalizable in other contexts. Recent “deep” impute methods may be a step in the right direction,20 though much work remains to be done. In the future, data-driven imputation methods may be broadly adopted as part of general signal processing workflows for proteomics.
Supplementary Material
Supplementary Table 1. Normalization methods applied to the data sets included in this study; Supplementary Figure 1. Distributions of train and test sets following MCAR and MNAR partitioning procedures; Supplementary Figure 2. Comparing the abilities of imputation methods to identify differentially expressed peptides, as a function of missingness fraction; Supplementary Figure 3. Comparing the abilities of imputation methods to identify differentially expressed peptides for a TMT data set; Supplementary Figure 4. Comparing the abilities of imputation methods to identify differentially expressed peptides for a label-free DDA data set; Supplementary Figure 5. Variance of peptide quantifications is greater than expected following imputation; Supplementary Figure 6. Variance of protein quantifications is greater than expected (PDF)
ACKNOWLEDGMENTS
The authors thank Michael J. MacCoss of the University of Washington’s Department of Genome Sciences for helpful discussions. This work was supported by National Institute on Aging grant number 1F31AG082395–01.
Footnotes
The authors declare no competing financial interest.
Complete contact information is available at: https://pubs.acs.org/10.1021/acs.jproteome.3c00205
ASSOCIATED CONTENT
Supporting Information
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jproteome.3c00205.
Contributor Information
Lincoln Harris, Department of Genome Sciences, University of Washington, Seattle, Washington 98195, United States.
William E. Fondrie, Talus Biosciences, Seattle, Washington 98112, United States
Sewoong Oh, Paul G. Allen School of Computer Science and Engineering, University of Washington, Seattle, Washington 98195, United States.
William S. Noble, Department of Genome Sciences and Paul G. Allen School of Computer Science and Engineering, University of Washington, Seattle, Washington 98195, United States
Data Availability Statement
The code used to generate all the figures in this paper can be found at: https://github.com/Noble-Lab/2023-prot-impute-benchmark. The custom NMF imputation model can be found at https://github.com/Noble-Lab/MSFactor. All data sets used in this study are publicly available and can be found on PRIDE, CPTAC or Panorama.29,31,58 In addition, Data 1 provides the full results of our literatures search, including names and DOIs of the identified studies, and Data 2 provides a complete list of file names obtained for each PRIDE, CPTAC and Panorama experiment. Data 1 and 2 can be found at: https://github.com/Noble-Lab/2023-prot-impute-benchmark/tree/main/supplemental.
REFERENCES
- (1).Bramer L; Irvahn J; Piehowski P; Rodland K; Webb-Robertson BJ A review of imputation strategies for isobaric labeling-based shotgun proteomics. J. Proteome Res. 2021, 20 (1), 1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (2).Webb-Robertson BJ; Wiberg H; Matzke M; Brown J; Wang J; McDermott J; Smith R; Rodland K; Metz T; Pounds J; Waters K Review, evaluation and discussion of challenges of missing value imputation for mass spectrometry-based label-free global proteomics. J. Proteome Res. 2015, 14, 1993–2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (3).Troyanskaya O; Cantor M; Sherlock G; Brown P; Hastie T; Tibshirani R; Botstein D; Altman R Missing value estimation method for DNA microarrays. Bioinformatics 2001, 17, 520–525. [DOI] [PubMed] [Google Scholar]
- (4).Sterne J; White I; Carlin J; Spratt M; Royston P; Kenward M; Wood A; Carpenter J Multiple imputation for missing data in epidemiological and clinical research: potential and pitfalls. BMJ. 2009, 338, b2393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (5).Keerin P; Boongoen T Estimation of missing values in astronomical survey data: An improved local approach using cluster directed neighbor selection. Information Processing and Management 2022, 59, 102881. [Google Scholar]
- (6).Luken K; Padhy R; Wang XR Missing data imputation for galaxy redshift estimation. In NeurIPS; Fourth Workshop on Machine Learning and the Physical Sciences, Virtual, December 13, 2021; 2021. [Google Scholar]
- (7).Linderman G; Zhao J; Roulis M; Bielecki P; Flavell R; Nadler B; Kluger Y Zero-preserving imputation of single-cell RNA-seq data. Nat. Commun. 2022, 13 (192), DOI: 10.1038/s41467-021-27729-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (8).van Dijk D; Sharma R; Nainys J; Yim K; Kathail P; Carr A; Burdziak C; Moon K; Chaffer C; Pattabiraman D; Bierie B; Mazutis L; Wolf G; Krishnaswamy S; Pe’er D Recovering gene interactions from single-cell data using data diffusion. Cell 2018, 174, 716–729. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (9).Tyanova S; Temu T; Sinitcyn P; Carlson A; Hein M; Geiger T; Mann M; Cox J The Perseus computational platform for comprehensive analysis of (prote)omics data. Nat. Methods 2016, 13, 731–740. [DOI] [PubMed] [Google Scholar]
- (10).Kowarik A; Templ M Imputation with the R package VIM. Journal of Statistical Software 2016, 74 (7), DOI: 10.18637/jss.v074.i07. [DOI] [Google Scholar]
- (11).Stekhoven D; Buhlmann P MissForest – non-parametric missing value imputation for mixed-type data. Bioinformatics 2012, 28, 112–118. [DOI] [PubMed] [Google Scholar]
- (12).Stacklies W; Redestig H; Scholz M; Walther D; Selbig J pcaMethodsa bioconductor package providing PCA methods for incomplete data. Bioinformatics 2007, 23, 1164–1167. [DOI] [PubMed] [Google Scholar]
- (13).Josse J; Husson F missMDA: a package for handling missing values in multivariate data analysis. Journal of Statistical Software 2016, 70 (1), DOI: 10.18637/jss.v070.i01. [DOI] [Google Scholar]
- (14).Egert J; Brombacher E; Warscheid B; Kreutz C DIMA: Data-driven selection of an imputation algorithm. J. Proteome Res. 2021, 20, 3489–3496. [DOI] [PubMed] [Google Scholar]
- (15).Lazar C; Gatto L; Ferro M; Bruley C; Burger T Accounting for the Multiple Natures of Missing Values in Label-Free Quantitative Proteomics Data Sets to Compare Imputation Strategies. J. Proteome Res. 2016, 15, 1116–1125. [DOI] [PubMed] [Google Scholar]
- (16).Välikangas T; Suomi T; Elo L A comprehensive evaluation of popular proteomics software workflows for label-free proteome quantification and imputation. Briefings in Bioinformatics 2017, 19, 1344–1355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (17).Dabke K; Kreimer S; Jones M; Parker S A simple optimization workflow to enable precise and accurate imputation of missing values in proteomic data sets. J. Proteome Res. 2021, 20, 3214–3229. [DOI] [PubMed] [Google Scholar]
- (18).Xu J; Wang Y; Xu X; Cheng KK; Raftery D; Dong J NMF-Based Approach for Missing Values Imputation of Mass Spectrometry Metabolomics Data. Molecules 2021, 26, 5787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (19).Hediyeh-Zadeh S; Webb A; Davis M MsImpute: Estimation of missing peptide intensity data in label-free quantitative mass spectrometry. Mol. Cell. Proteomics 2023, 22, 100558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (20).Webel H; Niu L; Nielsen AB; Locard-Paulet M; Mann M; Jensen LJ; Rasmussen S Mass spectrometry-based proteomics imputation using self supervised deep learning. bioRxiv, 2023, DOI: 10.1101/2023.01.12.523792. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (21).Plubell D; Kall L; Webb-Robertson BJ; Bramer L; Ives A; Kelleher N; Smith L; Montine T; Wu C; MacCoss M Putting Humpty Dumpty Back Together Again: What Does Protein Quantification Mean in Bottom-Up Proteomics? J. Proteome Res. 2022, 21, 891–898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (22).Boekweg H; Payne S Challenges and opportunities for single-cell computational proteomics. Mol. Cell. Proteomics 2023, 22 (4), 100518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (23).Ipsen A Derivation from first principles of the statistical distribution of the mass peak intensities of MS data. Anal. Chem. 2015, 87, 1726–1734. [DOI] [PubMed] [Google Scholar]
- (24).Ipsen A; Ebbels T Prospects for a statistical theory of LC/TOFMS data. Journal of the American Society of Mass Spectrometry 2012, 23, 779–791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (25).Kimmel J; Kyu Yoon O; Zuleta I; Trapp O; Zare R Peak height precision in Hadamard transform time-of-flight mass spectra. American Society of Mass Spectrometry 2005, 16, 1117–1130. [DOI] [PubMed] [Google Scholar]
- (26).Bayat F; Libbrecht M VSS: variance-stabilized signals for sequencing-based genomic signals. Bioinformatics 2021, 37, 4383–4391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (27).Risso D; Perraudeau F; Gribkova S; Dudoit S; Vert JP A general and flexible method for signal extraction from single-cell RNA-seq data. Nat. Commun. 2018, 9 (284), DOI: 10.1038/s41467-017-02554-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (28).Hafemeister C; Satija R Normalization and variance stabilization of single-cell RNA-seq data using regularized negative binomial regression. Genome Biology 2019, 20 (1), 296. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (29).Perez-Riverol Y; Csordas A; Bai J; Bernal-Llinares M; Hewapathirana S; Kundu D; Inuganti A; Griss J; Mayer G; Eisenacher M; Perez E; Uszkoreit J; Pfeuffer J; Sachsenberg T; Yilmaz S; Tiwary S; Cox J; Audain E; Walzer M; Jarnuczak A; Ternent T; Brazma A; Vizcaino JA The PRIDE database and related tools and resources in 2019: improving support for quantification data. Nucleic Acids Res. 2019, 47 (D1), D442–D450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (30).Vizcaíno J; Deutsch E; Wang R; Csordas A; Reisinger F; Ríos D; Dianes J; Sun Z; Farrah T; Bandeira N; Binz PA; Xenarios I; Eisenacher M; Mayer G; Gatto L; Campos A; Chalkley R; Kraus HJ; Albar JP; Martinez-Bartolomé S; Apweiler R; Omenn G; Martens L; Jones A; Hermjakob H ProteomeXchange provides globally coordinated proteomics data submission and dissemination. Nat. Biotechnol. 2014, 32, 223–226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (31).Edwards N; Oberti M; Thangudu R; Cai S; McGarvey P; Jacob S; Madhavan S; Ketchum K The CPTAC Data Portal: A Resource for Cancer Proteomics Research. J. Proteome Res. 2015, 14, 2707–2713. [DOI] [PubMed] [Google Scholar]
- (32).Selamoglu N; Onder O; Ozturk Y; Khalfaoui-Hassani B; Blaby-Haas CE; Garcia BA; Koch H-G; Daldal F Comparative differential cuproproteomes of Rhodobacter capsulatus reveal novel copper homeostasis related proteins. Metallomics 2020, 12, 572–591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (33).Meier F; Geyer P; Virreira Winter S; Cox J; Mann M BoxCar acquisition method enables single-shot proteomics at a depth of 10,000 proteins in 100 minutes. Nat. Methods 2018, 15, 440–448. [DOI] [PubMed] [Google Scholar]
- (34).Bekker-Jensen D; Bernhardt O; Hogrebe A; Martinez-Val A; Verbeke L; Gandhi T; Kelstrup C; Reiter L; Olsen J Rapid and site-specific deep phosphoproteome profiling by data-independent acquisition without the need for spectral libraries. Nat. Commun. 2020, 11 (787) DOI: 10.1038/s41467-020-14609-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (35).Merrihew G; Park J; Plubell D; Searle B; Keene D; Larson E; Bateman R; Perrin R; Chhatwal J; Farlow M; McLean C; Ghetti B; Newell K; Frosch M; Montine T; MacCoss M A peptide-centric quantitative proteomics dataset for the phenotypic assessment of Alzheimer’s disease. Scientific Data 2023, 10 (206) DOI: 10.1038/s41597-023-02057-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (36).Pino L; Searle B; Yang HY; Hoofnagle A; Noble W; MacCoss M Matrix-matched calibration curves for assessing analytical figures of merit in quantitative proteomics. J. Proteome Res. 2020, 19, 1147–1153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (37).Nitschko V; Kunzelmann S; Frohlich T; Arnold G; Forstemann K Trafficking of siRNA precursors by the dsRBD protein blanks in Drosophila. Nucleic Acids Res. 2020, 48, 3906–3921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (38).Azizan A; Kaschani F; Barinas H; Blaskowski S; Kaiser M; Denecke M Using proteomics for an insight into the performance of activated sludge in a lab-scale WWTP. International Biodeterioration and Biodegradation 2020, 149, 104934. [Google Scholar]
- (39).Murugaiyan J; Eravci M; Weise C; Roesler U; Sprague L; Neubauer H; Wareth G Pan-proteomic analysis and elucidation of protein abundance among the closely related Brucella species, Brucella abortus and Brucella melitensis. Biomolecules 2020, 10 (6), 836. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (40).Rodrigues D; Mufteev M; Weatheritt R; Djuric U; Ha K; Ross PJ; Wei W; Piekna A; Sartori M; Byres L; Mok R; Zaslavsky K; Pasceri P; Diamandis P; Morris Q; Blencowe B; Ellis J Shifts in ribosomal engagement impact key gene sets in neurodevelopment and ubiquitination in Rett syndrome. Cell Reports 2020, 30, 4179–4196. [DOI] [PubMed] [Google Scholar]
- (41).Petralia F; Tignor N; Reva B; Koptyra M; Chowdhury S; Rykunov D; Krek A; Ma W; Zhu Y; Ji J; Calinawan A; Whiteaker J; Colaprico A; Stathias V; Omelchenko T; Song X; Raman P; Guo Y; Brown M; Ivey R; Szpyt J; Thakurta SG; Gritsenko M; Weitz K; Lopez G; Kalayci S; Gumus Z; Yoo S; da Veiga Leprevost F; Chang HY; Krug K; Katsnelson L; Wang Y; Kennedy J; Voytovich U; Zhao L; Gaonkar K; Ennis B; Zhang B; Baubet V; Tauhid L; Lilly J; Mason J; Farrow B; Young N; Leary S; Moon J; Petyuk V; Nazarian J; Adappa N; Palmer J; Lober R; Rivero-Hinojosa S; Wang LB; Wang J; Broberg M; Chu R; Moore R; Monroe M; Zhao R; Smith R; Zhu J; Robles A; Mesri M; Boja E; Hiltke T; Rodriguez H; Zhang B; Schadt E; Mani DR; Ding L; Iavarone A; Wiznerowicz M; Schurer S; Chen XS; Heath A; Rokita JL; Nesvizhskii A; Fenyo D; Rodland K; Liu T; Gygi S; Paulovich A; Resnick A; Storm P; Roo B; Wang P Children’s Brain Tumor Network, and Clinical Proteomic Tumor Analysis Consortium. Integrated proteogenomic characterization across major histological types of pediatric brain cancer. Cell 2020, 183, 1962–1985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (42).Satpathy S; Jaehnig E; Krug K; Kim BJ; Saltzman A; Chan D; Holloway K; Anurag M; Huang C; Singh P; Gao A; Namai N; Dou Y; Wen B; Vasaikar S; Mutch D; Watson M; Ma C; Ademuyiwa F; Rimawi M; Schiff R; Hoog J; Jacobs S; Malovannaya A; Hyslop T; Clauser K; Mani D; Perou C; Miles G; Zhang B; Gillette M; Carr S; Ellis M Microscaled proteogenomic methods for precision oncology. Nat. Commun. 2020, 11, 532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (43).O’Connell J; Paulo J; O’Brien J; Gygi S Proteome-wide evaluation of two common protein quantification methods. J. Proteome Res. 2018, 17, 1934–1942. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (44).Cox J; Mann M MaxQuant enables high peptide identification rates, individualized p.p.b.-range mass accuracies and proteome-wide protein quantification. Nat. Biotechnol. 2008, 26, 1367–1372. [DOI] [PubMed] [Google Scholar]
- (45).Searle B; Pino L; Egertson J; Ting Y; Lawrence R; MacLean B; Villen J; MacCoss M Chromatogram libraries improve peptide detection and quantification by data independent acquisition mass spectrometry. Nat. Commun. 2018, 9 (5128), DOI: 10.1038/s41467-018-07454-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (46).MacLean B; Tomazela D; Shulman N; Chambers M; Finney G; Frewen B; Kern R; Tabb D; Liebler D; MacCoss M Skyline: an open source document editor for creating and analyzing targeted proteomics experiments. Bioinformatics 2010, 26, 966–968. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (47).da Veiga Leprevost F; Haynes S; Avtonomov D; Chang HY; Shanmugam A; Mellacheruvu D; Kong A; Nesvizhskii A Philosopher: a versatile toolkit for shotgun proteomics data analysis. Nat. Methods 2020, 17, 869–870. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (48).Benjamini Y; Hochberg Y Controlling the false discovery rate: a practical and powerful approach to multiple testing. Journal of the Royal Statistical Society 1995, 57, 289–300. [Google Scholar]
- (49).Conway J; Lex A; Gehlenborg N UpSetR: an R package for the visualization of intersecting sets and their properties. Bioinformatics 2017, 33, 2938–2940. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (50).Andrews T; Hemberg M False signals induced by single-cell imputation. F1000 Research 2018, 7, 1740. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (51).Ly LH; Vingron M Effect of imputation on gene network reconstruction from single-cell RNA-seq data. Patterns 2022, 3, 100414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (52).Wolski W; Nanni P; Grossmann J; d’Errico M; Schlapbach R; Panse C prolfqua: A comprehensive R-package for proteomics differential expression analysis. J. Proteome Res. 2023, 22, 1092–1104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (53).Bai M; Deng J; Dai C; Pfeuffer J; Sachsenberg T; Perez-Riverol Y LFQ-based peptide and protein intensity differential expression analysis. J. Proteome Res. 2023, 22, 2114–2123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (54).Brunner AD; Thielert M; Vasilopoulou C; Ammar C; Coscia F; Mund A; Hoerning O; Bache N; Apalategui A; Lubeck M; Richter S; Fischer D; Raether O; Park M; Meier F; Theis F; Mann M Ultra-high sensitivity mass spectrometry quantifies single-cell proteome changes upon perturbation. Molecular Systems Biology 2022, 18, No. e10798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (55).Kohler D; Staniak M; Tsai T-H; Huang T; Shulman N; Bernhardt OM; MacLean BX; Nesvizhskii AI; Reiter L; Sabido E; Choi M; Vitek O MSstats Version 4.0: Statistical Analyses of Quantitative Mass Spectrometry-Based Proteomic Experiments with Chromatography-Based Quantification at Scale. J. Proteome Res. 2023, 22, 1466–1482. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (56).Huber W; von Heydebreck A; Sultmann H; Poustka A; Vingron M Variance stabilization applied to microarray data calibration and to the quantification of differential expression. Bioinformatics 2002, 18, S96–104. [DOI] [PubMed] [Google Scholar]
- (57).Anderle M; Roy S; Lin H; Becker C; Joho K Quantifying reproducibility for differential proteomics: noise analysis for protein liquid chromatography-mass spectrometry of human serum. Bioinformatics 2004, 20, 3575–3582. [DOI] [PubMed] [Google Scholar]
- (58).Sharma V; Eckels J; Schilling B; Ludwig C; Jaffe J; MacCoss M; MacLean B Panorama Public: A Public Repository for Quantitative Data Sets Processed in Skyline. Mol. Cell. Proteomics 2018, 17, 1239–1244. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Table 1. Normalization methods applied to the data sets included in this study; Supplementary Figure 1. Distributions of train and test sets following MCAR and MNAR partitioning procedures; Supplementary Figure 2. Comparing the abilities of imputation methods to identify differentially expressed peptides, as a function of missingness fraction; Supplementary Figure 3. Comparing the abilities of imputation methods to identify differentially expressed peptides for a TMT data set; Supplementary Figure 4. Comparing the abilities of imputation methods to identify differentially expressed peptides for a label-free DDA data set; Supplementary Figure 5. Variance of peptide quantifications is greater than expected following imputation; Supplementary Figure 6. Variance of protein quantifications is greater than expected (PDF)
Data Availability Statement
The code used to generate all the figures in this paper can be found at: https://github.com/Noble-Lab/2023-prot-impute-benchmark. The custom NMF imputation model can be found at https://github.com/Noble-Lab/MSFactor. All data sets used in this study are publicly available and can be found on PRIDE, CPTAC or Panorama.29,31,58 In addition, Data 1 provides the full results of our literatures search, including names and DOIs of the identified studies, and Data 2 provides a complete list of file names obtained for each PRIDE, CPTAC and Panorama experiment. Data 1 and 2 can be found at: https://github.com/Noble-Lab/2023-prot-impute-benchmark/tree/main/supplemental.


