Comparative analysis of models in predicting the effects of SNPs on TF-DNA binding using large-scale in vitro and in vivo data

Abstract

Non-coding variants associated with complex traits can alter the motifs of transcription factor (TF)–deoxyribonucleic acid binding. Although many computational models have been developed to predict the effects of non-coding variants on TF binding, their predictive power lacks systematic evaluation. Here we have evaluated 14 different models built on position weight matrices (PWMs), support vector machines, ordinary least squares and deep neural networks (DNNs), using large-scale in vitro (i.e. SNP-SELEX) and in vivo (i.e. allele-specific binding, ASB) TF binding data. Our results show that the accuracy of each model in predicting SNP effects in vitro significantly exceeds that achieved in vivo. For in vitro variant impact prediction, kmer/gkm-based machine learning methods (deltaSVM_HT-SELEX, QBiC-Pred) trained on in vitro datasets exhibit the best performance. For in vivo ASB variant prediction, DNN-based multitask models (DeepSEA, Sei, Enformer) trained on the ChIP-seq dataset exhibit relatively superior performance. Among the PWM-based methods, tRap demonstrates better performance in both in vitro and in vivo evaluations. In addition, we find that TF classes such as basic leucine zipper factors could be predicted more accurately, whereas those such as C2H2 zinc finger factors are predicted less accurately, aligning with the evolutionary conservation of these TF classes. We also underscore the significance of non-sequence factors such as cis-regulatory element type, TF expression, interactions and post-translational modifications in influencing the in vivo predictive performance of TFs. Our research provides valuable insights into selecting prioritization methods for non-coding variants and further optimizing such models.

INTRODUCTION

Up to date, genome-wide association studies (GWASs) have identified about 400 000 single-nucleotide polymorphism (SNP)–trait associations [1]. However, most variants are located in non-coding deoxyribonucleic acid (DNA) [2], leading to a major challenge in deciphering their biological functions. A possible mechanism for functional non-coding variants involves the disruption of canonical transcription factor binding sites (TFBSs), impacting the in vivo binding of transcription factors (TFs) to cis-regulatory elements (CREs) such as promoters and enhancers [3]. Some SNPs associated with complex diseases identified by GWASs have been proven to alter the expression of target genes by influencing the binding of TFs. For example, the major allele of the genetic variant rs12740374, located in the 3′ untranslated region of the CELSR2 gene, disrupts the binding of the TF C/EBP, leading to the downregulation of SORT1 gene expression in mice liver cells, ultimately contributing to elevated LDL-C levels [4]. Similarly, the BMI-raising allele of variant rs1421085 within the first intron of FTO disrupts a conserved motif of the ARID5B repressor, resulting in overexpression of IRX3 and IRX5. This leads to the differentiation of mesenchymal adipocyte precursor shifting from energy-dissipating beige adipocytes to energy-storing white adipocytes [5]. Although TFBS polymorphisms account for only 8% of genome polymorphisms, they represent 31% of the trait-associated polymorphisms identified by GWASs [6]. Furthermore, variants leading to differential TF binding are highly enriched in the set of causal variants reported for traits across several independent studies [7]. These findings suggest that TFBS variants play an important role in downstream gene expression and phenotypic variation.

TFs bind to DNA in a sequence-specific manner, and their motifs are typically 6–20 bp long [8, 9]. The specificity of TF-DNA binding can be examined using advanced high-throughput sequencing technologies. The in vitro methods mainly include protein binding microarrays (PBMs), systematic evolution of ligands by exponential enrichment (SELEX) and selective microfluidics-based ligands enrichment (SMiLE), and the in vivo methods include chromatin immunoprecipitation–based sequencings such as ChIP-seq, ChIP-exo and ChIP-nexus [9]. PBM experiments construct oligonucleotide sequence microarrays covering all k-mers to measure the binding specificity of specific proteins to oligonucleotide sequences [10]. In each high-throughput SELEX (HT-SELEX) experiment, random 40 bp DNA sequences are incubated with a recombinant TF protein in vitro to quantitatively assess the binding strength through multiple rounds of elution, PCR-amplification and sequencing [11]. Whereas HT-SELEX uses randomized DNA sequences as input, SNP-SELEX uses a library of 40 bp DNA matching the reference human genomic sequence [7]. The center position of each sequence corresponds to tested SNPs permutated to all four bases, enabling the estimation of binding differences between allelic sequences. ChIP-seq provides a deep read coverage of TF binding regions, facilitating the exploration of specific TF binding sequences. Furthermore, the statistical biases between the number of mapped reads containing reference or alternate allele reveal so-called allele-specific binding (ASB) events, indicating the preferential binding of a TF to one of the two alleles at the heterozygous sites [12]. These technologies have made a success and generated huge amounts of TF binding data. However, given the high experiment cost [9], exploring the effects of non-coding variants on TF binding remains a challenging aspect in elucidating their roles in phenotypic and pathogenetic mechanisms.

Position weight matrices (PWMs) and machine learning methods have been widely used to predict TFBS and extended to predict the effects of SNPs on TF-DNA binding. A classical PWM contains weights for each base at each position of a TF binding motif [13]. The weights are summed to compute the binding affinity of a candidate DNA sequence to a TF, enabling the prediction of regulatory SNPs using tools such as atSNP [14], motifbreakR [15] and tRap [16]. Machine learning, particularly deep learning methods, can mitigate the occurrence of false positives by capturing the intricate complexity of TF-DNA binding [17]. Kmer-support vector machine (SVM) or gkm-SVM classifier generates a weighted vocabulary of all possible k-mers based on training data of putative regulatory sequences, which quantify their contribution to the prediction of regulatory functions. The binding change of variants in TFBS is computed by comparing the sum of weights between all k-mers overlapping the reference and alternative allele [18, 19]. In recent years, deep neural networks (DNNs) have made great progress in characterizing the regulatory potential of non-coding variants. Convolutional neural networks (CNNs) have been successfully applied to analyze in vivo TF-DNA interactions [20]. A lot of CNN-based models have been also designed for variant impact prediction, such as DeepBind [21], DeepSEA [22], Basset [23], DeFine [24] and DeepFun [25]. CNN-based models predict possible regulatory effects of variants based on disruption or creation of TF motifs discovered by convolutional filters [25]. These models can dissect causal variants in a tissue- or cell-type-specific manner and exhibit great advantages when dealing with larger datasets. Models recently introduced, such as BPNet [26], Leopard [27], FCNA [28], FCNsignal [29] and FCNGRU [30], have demonstrated the capability to achieve base-resolution predictions, which have great potential to assess and interpret variant effects on epigenomic profiles [31]. As far as we know, these models use different training data in addition to different algorithms during the training process. Positive training sets are mostly sequences binding with TFs, and negative sets are randomly shuffled sequences or randomly selected sequences from the genome with similar features as the positive sets, such as length and GC content. Importantly, the aforementioned training data are not directly employed to discern the effects of SNPs on TF binding, and no SNP information is incorporated or provided in the entire training process.

Several benchmark studies have evaluated the prediction performance of models for the regulatory effects of SNPs on TF binding. Wagih et al. collected and curated 132 373 potential ASB variants of 101 TFs, comparing the performance of five models based on PWMs, deep learning and kmer-based machine learning [17]. They found that deep learning and kmer-based machine learning methods were more accurate than PWMs. However, due to variations in the TFs predicted by these models, only 11 common TFs were used for comparison. They also investigated the performance of individual TFs, identifying those with accurately predictable variant effects and those that were not. Furthermore, they explored mechanisms that might explain undesirable performance in variant impact prediction [17]. Yan et al. used preferential binding scores (PBSs) of 270 TFs to 95 886 non-coding SNPs detected by SNP-SELEX to demonstrate that deltaSVM models outperformed ΔPWM in predicting differential TF binding to non-coding variants [7]. This finding was also validated using their independent data. However, these studies incorporated a limited number of TFs or models, highlighting the need for a comprehensive large-scale comparative analysis.

In this study, we aimed to conduct a systematic and unbiased analysis of model performance in predicting the effects of variants on TF binding. We gathered and curated in vitro binding affinity data for 407 TFs and ~15 000 SNPs identified through SNP-SELEX, alongside in vivo ASB data for 380 TFs and over 3 million SNPs identified by ChIP-seq, to serve as benchmarks. We compared the performance of 14 models in predicting SNP impacts, including PWMs, kmer/gkm-based machine learning and DNN methods trained on different in vitro and/or in vivo data. Our study revealed significant differences in the accuracy of predictive models for SNP effects on TF binding between in vitro and in vivo. Specifically, deltaSVM_HT-SELEX and QBiC-Pred, trained on in vitro datasets, demonstrated superior performance for in vitro variant impact prediction. In contrast, DNN-based multitask models like DeepSEA, Sei and Enformer, trained on ChIP-seq datasets, exhibit the most favorable predictive capabilities in vivo. We also investigated the effects of training data, model architecture and PWM databases on predictive accuracy. Finally, we explored the relationship between prediction performance and properties of TFs, such as DNA binding domains (DBDs), evolutionary conservation, binding motifs, gene expression, protein interactions and post-translational modifications (PTMs). Our study serves as a valuable reference for the selection of suitable models to predict the effects of variants on TF binding, both in vitro and in vivo. In addition, it contributes to an enhanced understanding of how specific features impact TF and model prediction performance.

MATERIAL AND METHODS

Overview of state-of-the-art models

We conducted a comprehensive survey of all models used to predict the impact of SNPs on TF-DNA binding (Supplementary Table S1). Subsequently, we selected 14 models based on PWM, SVM, ordinary least squares (OLS) and DNN (Table 1). These models were trained using in vitro or in vivo experimental data, either cell-type-specific or non-specific. The models included four PWM-based methods (atSNP [14], motifbreakR [15], tRap [16] and FABIAN-variant [32]), three kmer/gkm-based machine learning methods (deltaSVM_HT-SELEX [7], deltaSVM_ChIP-seq [18, 19] and QBiC-Pred [33]) and seven DNN-based methods (DeepBind_HT-SELEX [21], DeepBind_ChIP-seq [21], DeepSEA [22], Beluga [34], DeepFun [25], Sei [35] and Enformer [36]). We did not choose base-resolution DNN models, as the number of TFs that could be predicted by these models were limited. More detailed description of models and prediction of SNP impact on TF-DNA binding is available in Supplementary Methods.

Table 1.

Basic information of 14 models for variant impact prediction

Model	Model type	Training data/database	Data type/PWM	Platform	Publication year	TF number	TFs evaluated in SNP-SELEX First Batch	TFs evaluated in SNP-SELEX Novel Batch	TFs evaluated in ASB
atSNP	PWM	HOCOMOCO V11; JASPAR 2022	PWM	R	2015	700	146	311	210
motifbreakR	PWM	HOCOMOCO V11; JASPAR 2022	PWM	R	2015	700	146	311	210
tRap	PWM	HOCOMOCO V11; JASPAR 2022	PWM	R	2011	700	146	310	210
FABIAN-variant	PWM	HOCOMOCO V11; JASPAR 2022	PWM	Web	2022	700	145	310	206
deltaSVM_HT-SELEX	gkm-SVM	HT-SELEX [63]	In vitro	C++; Perl; Python	2021	533	162	340	126
deltaSVM_ChIP-seq	gkm-SVM	ENCODE v3 ChIP-seq	In vivo	Python	2019	465	43	90	247
QBiC-Pred	kmer-OLS	PBM dataset [33, 40, 64]	In vitro	Web	2019	582	129	280	138
DeepBind_HT-SELEX	DNN-single-task	HT-SELEX [11]	In vitro	Python(kipoi)	2015	375	115	222	94
DeepBind_ChIP-seq	DNN-single-task	ENCODE v2 ChIP-seq	In vivo	Python(kipoi)	2015	134	23	40	77
DeepSEA	DNN-multitask	ENCODE v2 ChIP-seq	In vivo	Python(kipoi)	2015	153	25	44	86
Beluga	DNN-multitask	ENCODE v2 ChIP-seq	In vivo	Python(kipoi)	2018	154	25	45	86
DeepFun	DNN-multitask	ENCODE v2, v3 ChIP-seq	In vivo	Web	2021	291	31	63	159
Sei	DNN-multitask	Cistrome; ENCODE v2 ChIP-seq	In vivo	Python	2022	1006	79	165	302
Enformer	DNN-multitask	ENCODE v2, v3 ChIP-seq; GEO	In vivo	Python	2021	678	53	113	284

Note: The ‘TF number’ column represents the number of TFs with standard HGNC symbol.

Evaluation datasets preprocessing

SNP-SELEX data collection

Two batches of the SNP-SELEX data were downloaded from GVAT [7] (Table 2). The First Batch subset characterized the in vitro allelic binding of 95 886 common human SNPs (MAF > 1% in European and Asian populations) to 270 distinct TFs. SNPs were selected from neighboring regions (≤500 kb) of 83 type-2 diabetes (T2D) risk loci identified in several GWASs. The Novel Batch subset included SNPs from islet enhancer regions or randomly chosen from the human genome. In addition, four cycles of SELEX experiments were conducted for the Novel Batch subset, while the First Batch subset underwent six cycles. The database provides information on TF name, position of oligo sequence (hg19), the reference and alternative alleles of the SNP, oligo binding score (OBS, defined by area under the curve (AUC) of oligo enrichment per TF, a score to assess TF binding to the 40 bp sequence), PBS (defined by AUC of differential allelic enrichment per TF) and P-value of PBS for each SNP-TF pair.

Table 2.

Basic information of evaluation datasets

Data set	Subset	SNP	TF	SNP-TF pair	TFs for evaluation	Website
SNP-SELEX	First Batch	90 035	270	1 612 172	167	http://renlab.sdsc.edu/GVATdb/search.html
SNP-SELEX	Novel Batch	66 329	487	1 048 486	374	http://renlab.sdsc.edu/GVATdb/search.html
ASB	–	3 684 496	1140	14 575 885	380	https://adastra.autosome.org/bill-cipher/downloads

Definition of positive and negative samples in SNP-SELEX

To evaluate the model’s performance using the SNP-SELEX data, we used pbSNPs with PBS P-value <0.01 as the criteria. Positive samples comprised pbSNPs, while negative samples included SNPs with PBS P-value >0.5. We removed SNPs in the Novel Batch subset that were duplicates from the First Batch subset.

ASB data collection

In vivo ASB data were downloaded from ADASTRA v5.1.2 [12] (Table 2). It resulted from a meta-analysis of more than 7000 ChIP-Seq data, considering the possible false positives from aneuploidy and local copy number variation [12]. It encompassed comprehensive information on ASBs across 1140 TFs, including position of SNPs, alleles, reference SNP IDs (rsIDs), count of ChIP-seq peak calls overlapping the allele, mean background allelic dosage of the genomic segment encompassing the variant, allele-wise effect size (ES) for quantifying ASB allelic imbalance (calculated by weighted-average of log-ratios of observed and expected allelic read counts), allele-wise logit-aggregated and FDR-corrected P-values (SNPs with a P-value of reference or alternative allele less than 0.05 were considered ASBs) and P-value for the best motif occurrence of the PWM (HOCOMOCO v11) for reference or alternative allele. The ASB data coordinates were based on hg38 genome assembly, and we utilized LiftOver [37] to perform conversion of genomic coordinates when necessary.

Definition of positive and negative samples in ASB

For the ASB data, Abramov et al. [12] computed the P-values for the best motif occurrence of the PWM in the HOCOMOCO v11 core collection for reference or alternative allele using SPRY-SARUS. We initially divided the dataset into two subsets based on the sequence motifs of TFs in HOCOMOCO v11: Motif_Available (TFs with a sequence motif) and Motif_None (TFs without a sequence motif). We then applied simple filtering to two subsets, including (1) removing pairs with a null effect size for any alleles, (2) removing pairs with max (fdrp_bh_Ref, fdrp_bh_Alt) < 0.05 and (3) retaining pairs with min (motif_p_Ref, motif_p_Alt) < 0.05 for the Motif_Available subset. To more effectively distinguish positive samples from negative samples, we used the allelic effect size difference (ΔES = es_mean_ref-es_mean_alt) as a measure of the differential TF binding ability between the two alleles [12]. Positive samples were defined as SNPs with min(fdrp_bh_Ref, fdrp_bh_Alt) < 0.05 & |ΔES| > = 2, while negative samples consisted of SNPs with min(fdrp_bh_Ref, fdrp_bh_Alt) > 0.5 & |ΔES| < = 1.

All TF names were checked and adjusted to the standard HGNC symbol. TFs that couldn’t be converted were retained with their original names.

Evaluation metrics

We primarily used the AUROC as a metric for evaluating the models, complemented by AUPRC and Spearman rank correlation coefficients. The AUROC and AUPRC for each TF was computed using R package PPROC [38]. We retained TFs with at least 20 positive samples and an equal number of negative samples for sufficient statistical power in subsequent evaluation analysis.

If there were multiple models of a TF trained on data of different cell types or batches, we selected the model with the highest AUROC value.

Annotations of TFs and TF property analysis

To study the relationship between TFs and their properties, we selected the maximum AUROC value across all models as a measure of performance for each TF within each evaluation dataset subset.

TF DBD information

DBD information of TFs was obtained from TFClass [39], which classified human TFs across four hierarchical levels: superclass, class, family and subfamily. To identify TF classes with better or worse prediction performance than the average, we implemented a linear model: AUROC ~ class + batch and set the sum contrast. For each TF, ΔAUROC represents the difference between its AUROC and the mean of means across all classes. We then calculated the mean of ΔAUROCs for shared TFs in the two batches of the SNP-SELEX data.

Conservation levels of TFs

We acquired TF conservation data from Lambert et al. [8], categorizing 1639 human TFs into seven conservation levels representing approximate gene age, determined by the presence or absence of their orthologs across 32 eukaryotic genomes. These levels included opisthokont, bilateria, vertebrata, tetrapoda, mammalia, boreoeutherian and primates and were ascribed to two major stages: whole genome duplication (WGD) and Krüppel-associated box (KRAB) expansion, based on the divergence time between human TF-TF paralogs. ΔAUROCs were calculated using the same strategy as in the ‘TF DBD information’. The comparison between two stages was performed using two-sided Wilcoxon test.

Sequence motifs of TFs

We searched sequence motifs of TFs using established PWM databases such as CISBP [40], HOCOMOCO [41] and JASPAR [42]. TFs were divided into two groups, one with known sequence motifs and the other without, and we compared them using a two-sided Wilcoxon test.

SNPs in promoter/enhancer regions

SNPs were allocated to candidate promoter and enhancer regions (hg38) obtained from SCREEN [43]. We selected TFs with equal numbers of positive and negative samples (≥20) from promoters, enhancers and other genomic regions and computed individual TF AUROCs within each region. The SNP coordinates in the SNP-SELEX data were converted from hg19 to hg38 using LiftOver [37]. Possible prediction difference between different regions was conducted by an ANOVA analysis: AUROC~TF + Model + Type, ‘Model’ and ‘Type’ represented different models and genomic regions, respectively. Multiple comparisons were performed by two-sided Tukey’s test.

SNPs in CpG islands or non-CpG islands

We downloaded the regions of CpG islands from UCSC genome browser [37] and subsequently annotated the SNPs within the ASB dataset. Comparisons between these two regions, CpG islands or non-CpG islands, among multiple models were performed by an ANOVA analysis: AUROC~TF + Model + Type and two-sided Tukey’s test.

Expression quantitative trait loci (eQTL) annotation of SNPs

We downloaded fine-mapping cis-eQTL data from GTEx v8 [44, 45] and subsequently annotated the SNPs within the ASB dataset. Comparisons between eQTL and non-eQTL groups among multiple models were performed by an ANOVA analysis: AUROC~TF + Model + Type and two-sided Tukey’s test.

Expression, TF-TF/transcription co-factors interactions and PTMs of TFs

RNA-seq data of 1554 human TFs detected in 37 adult tissues were obtained from the study of Lambert et al. [8, 46]. For each TF, we calculated the maximum expression value across all tissues as the cross-tissue expression level. The specificity of a TF was calculated using the function ‘entropySpecificity’ of R package BioQC v1.22.0 [47]. A value of zero would be given if the gene was transcribed at the same frequency in all tissues and a maximum value of 1 if the gene was expressed in a single tissue. We collected known TF-TF/transcription co-factors (TcoF) interactions from TcoF-DBv2 [48], and information on seven types of PTMs of TF proteins was obtained from PhosphoSitePlus v6.7.0.1 [49]. TFs were equally divided into three groups based on their various properties, and multiple comparisons were performed using a two-sided Dunn’s test.

RESULTS

Overview of two evaluation datasets

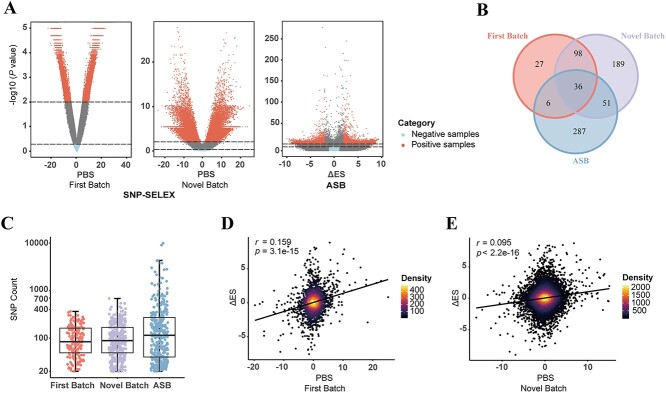
To assess the performance of 14 models in predicting the effects of non-coding variants on TF-DNA binding (Table 1), we collected large-scale experimental data that measured the differential TF binding between the reference and alternative allele of each SNP (Table 2). We obtained two batches of SNP-SELEX data, the First Batch subset and the Novel Batch subset, from the GVAT database [7]. The First Batch subset contained 90 035 SNPs and 270 TFs, resulting in 1 612 172 SNP-TF pairs with binding affinity differences. The Novel Batch subset contained 66 329 SNPs and 487 TFs, resulting in 1 048 486 SNP-TF pairs. In addition, we downloaded ASB data from the ADASTRA database [12], which included binding strengths of 14 575 885 SNP-TF pairs across 1140 TFs based on a meta-analysis of over 7000 ChIP-seq datasets. The ASB data also incorporated P-values for the best motif occurrence of the PWM for reference or alternative alleles, according to the availability of annotated motifs of TFs in the HOCOMOCO v11 database [41]. We utilized these datasets to benchmark the predictive power of the 14 models. The allocation of positive and negative samples (SNP-TF pairs) in each subset was based on the differential TF binding scores and P-values, where the differential TF binding scores were measured using the PBSs in the SNP-SELEX data and ΔES in the ASB data. To ensure adequate statistical power, we only included TFs with at least 20 positive samples for all subsets, each with an equal number of positive and negative samples.

The distribution of positive and negative samples in each subset is shown in Figure 1A, illustrating that they can be well distinguished based on the defined criteria (Supplementary Figure S1). The SNP-SELEX data exhibited high Spearman rank correlation coefficients between differential binding scores and P-values for SNP-TF pairs, particularly the First Batch subset (r = −0.939, 95% confidence interval [CI]: −0.941 to -0.933, P-value <2.2e-16, Novel Batch: r = −0.888, 95% CI: −0.893 to −0.882, P-value <2.2e-16, two-sided t-test) (Supplementary Table S2), which benefited from purer experimental conditions of in vitro binding and more stringent settings. The lower Spearman rank correlation coefficient observed in the ASB data (r = −0.572, 95% CI: −0.586 to −0.555, P-value <2.2e-16, two-sided t-test) might be attributed to the influence of various technical and biological factors on in vivo binding. After filtering TFs with at least 20 positive samples, 167 (First Batch), 374 (Novel Batch), 380 (ASB) TFs were preserved in each subset (Figure 1B, Table 2). Detailed TFs incorporated in each model are available in Supplementary Data 1. The number of positive samples for each TF in the SNP-SELEX data ranged from approximately 20 to 700, with a median value of around 88 (Figure 1C). In the ASB data, the number of positive samples ranged from approximately 20 to 10 000, and the median value for the data was 115 (Figure 1C). All the assessed TFs accounted for 40.14% (582/1450) of the human TFs collected in the TFClass database [39], covering 82.05% of TF DBD classes (32/39) (Supplementary Figure S2A and B). By computing the Spearman rank correlation coefficients between the PBS values in the SNP-SELEX dataset and the ΔES values in the ASB dataset for common SNP-TF pairs, we found significant positive correlations between the two datasets. Specifically, the First Batch subset and the Novel Batch subset showed significant positive correlation coefficients of 0.159 (95% CI: 0.119–0.199, P-value = 3.1e-15, two-sided t-test) and 0.095 (95% CI: 0.075–0.115, P-value <2.2e-16, two-sided t-test) with the ASB dataset, respectively (Figure 1D and E). Although the correlations were not strong, the two datasets would complement each other due to their ability to capture different aspects of TF-DNA binding between in vitro and in vivo experiments.

Figure 1.

Overview of in vitro and in vivo evaluation datasets. (A) Distribution of positive and negative samples in the SNP-SELEX and ASB data. 1/4 ASB data with random selection are shown. PBS: preferential binding score, the differential binding ability of two alleles to a TF. ΔES: the difference between reference and alternative allele effect size. The horizontal dashed line in the SNP-SELEX data denotes the PBS P-value threshold for selecting positive and negative samples (positive samples: P-value <0.01, negative samples: P-value >0.5). The horizontal dashed line in the ASB data denotes the threshold of ES P-values selected for positive and negative samples (positive samples: min (fdrp_bh_Ref, fdrp_bh_Alt) < 0.05 & |ΔES| ≥ 2, negative samples: min (fdrp_bh_Ref, fdrp_bh_Alt) > 0.5 & |ΔES| < = 1). Each dot represents one SNP-TF pair. (B) The number of TFs to be evaluated in each subset of evaluation datasets and their intersection. (C) The number of positive samples per TF in each subset of evaluation datasets. (D, E) Correlation between the PBS values of the SNP-SELEX data and ΔES values of the ASB data. Spearman rank correlation coefficients and P-values are calculated by the R function cor.test.

Evaluation of the models using the SNP-SELEX data

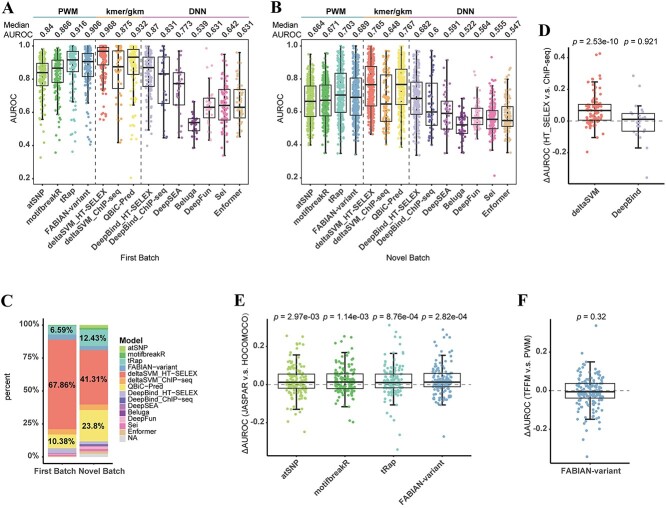
We first systematically compared the performance of the 14 models using the in vitro SNP-SELEX data. In the First Batch subset, most models achieved satisfactory performance with median AUROCs ≥ 0.8 (Figure 2A). However, in the Novel Batch subset, we observed a decrease in performance, with only half of the models having median AUROCs ≥ 0.65 (Figure 2B). This trend was similarly reflected in AUPRCs (Supplementary Figure S3A and B). Detailed results of AUROCs and AUPRCs for each TF are available in Supplementary Data 2, and summary statistics of AUROCs and AUPRCs for each model are available in Supplementary Tables S3 and S4. Among the models, two kmer/gkm-based machine learning methods, namely, deltaSVM_HT-SELEX and QBiC-Pred, exhibited optimal performance in the two subsets (First Batch: median AUROC = 0.968 and 0.932, Novel Batch: median AUROC = 0.765 and 0.767) (Figure 2A and B). The P-values and 95% CIs obtained from pairwise paired Wilcoxon tests between all models are listed in Supplementary Data 3. Among all TFs’ optimal variant impact predictors, 67.86% (First Batch) and 41.31% (Novel Batch) of them in the two subsets were deltaSVM_HT-SELEX, while 10.38% (First Batch) and 23.8% (Novel Batch) were QBiC-Pred (Figure 2C). Similar results were obtained through a comparative analysis using the Spearman rank correlation coefficients for all SNP-TF pairs, not just the positive and negative ones (Supplementary Figure S3C and D, Supplementary Data 4). The finding that kmer/gkm-based machine learning methods outperformed PWMs was consistent with previous reports [7]. It was proposed that the PWMs ignored dependencies between binding sites in TF-DNA interactions and the influence of flanking DNA sequences [7, 50]. In addition, kmer/gkm-based models could overcome the limitation of low-affinity TFBS [7]. The third highest-ranking method was the PWM-based tRap, with median AUROCs of 0.916 (First Batch) and 0.703 (Novel Batch) (Figure 2A and B). Despite using the same PWMs from the JASPAR 2022 and HOCOMOCO v11 databases as atSNP, motifbreakR and FABIAN-variant, tRap employed different algorithm to measure variant impact scores. Furthermore, we did not observe a significant advantage of DNN-based methods in predicting the effects of SNPs on in vitro TF-DNA binding, even for DeepBind_HT-SELEX, which was trained on in vitro data.

Figure 2.

Evaluation of the models using the SNP-SELEX data. (A, B) Comparison of performance of 14 models evaluated respectively by (A) First Batch subset and (B) Novel Batch subset of the SNP-SELEX data. It shows that kmer/gkm-based machine learning methods (deltaSVM_HT-SELEX, QBiC-Pred) outperform PWMs and DNN-based methods in predicting in vitro SNPs’ effect on TF-DNA binding. Each dot represents one TF. (C) The proportion of the optimal prediction model for all TFs based on the First Batch subset and the Novel Batch subset. (D) Comparison of individual TF’s performance of deltaSVM and DeepBind models using in vitro or in vivo training data. P-value calculated by two-sided paired Wilcoxon test is shown. (E) Comparison of individual TF’s performance using four models with PWMs from JASPAR 2022 or HOCOMOCO v11 databases. P-value calculated by two-sided paired Wilcoxon test is shown. (F) Comparison of individual TF’s performance using FABIAN-variant with TFFMs or PWMs from JASPAR 2022 databases. P-value calculated by two-sided paired Wilcoxon test is shown.

To explore whether training data affected predictive power, we compared the AUROCs between models of the same method trained on different in vitro or in vivo data. As expected, given the in vitro evaluation dataset, deltaSVM_HT-SELEX exhibited significantly higher AUROCs compared to deltaSVM_ChIP-seq (91 common TFs, pseudo-median = 0.064, 95% CI: 0.048–0.086, P-value = 2.53e-10, two-sided paired Wilcoxon test) (Figure 2D). However, there was no significant difference in the AUROCs of TFs predicted by DeepBind_HT-SELEX and DeepBind_ChIP-seq (26 common TFs, pseudo-median = −0.004, 95% CI: −0.036 to 0.034, P-value = 0.921, two-sided paired Wilcoxon test) (Figure 2D).

JASPAR [42] and HOCOMOCO [41] are commonly used open-access databases containing TF binding motifs. JASPAR comprises manually curated and non-redundant PWMs across eukaryotes determined by multiple high-throughput in vitro and in vivo methods. HOCOMOCO provides PWMs for 680 human and 453 mouse TFs only by large-scale ChIP-seq analysis. We compared the AUROCs between the two motif databases by using the four PWM-based models and found a slight advantage with the JASPAR database (Figure 2E, Supplementary Table S5). Transcription factor flexible models (TFFMs), which leverage hidden Markov models to account for complex positional dependencies, have been introduced and shown to be more accurate than PWMs [32]. FABIAN-variant offers 1224 TFFMs from the JASPAR database and is the first web application that can analyze variant effects with TFFMs. Given that, we explored the possible difference in predictive performance between PWMs or TFFMs. However, our analysis failed to reveal any substantial differences between the two (165 common TFs, pseudo-median = −0.005, 95% CI: −0.015 to 0.005, P-value = 0.32, two-sided paired Wilcoxon test), highlighting the robustness of both approaches in SNP impact prediction (Figure 2F).

Evaluation of the models using the ASB data

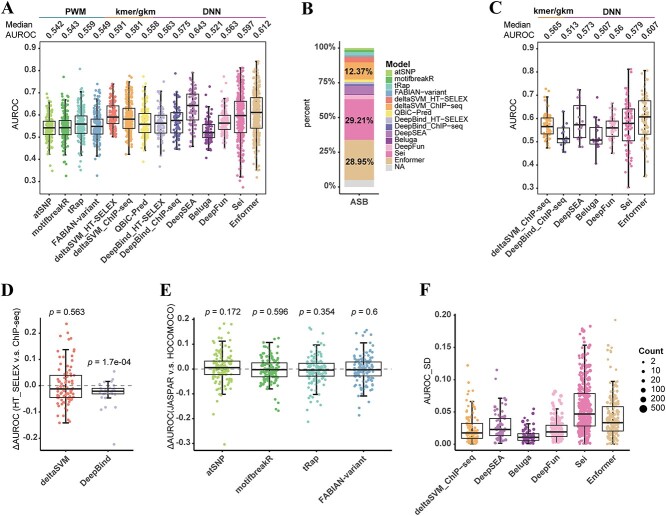
We then conducted a comprehensive comparative analysis of the 14 models using the in vivo ASB data as a benchmark. Upon comparing the AUROCs of the 14 models, we observed that only two DNN-based models, DeepSEA and Enformer, attained a median AUROC exceeding 0.6 (Figure 3A). The third highest-ranking method was the DNN-based Sei, with a median AUROC of 0.597 (Figure 3A). The AUPRCs also supported the relatively high-ranking predictive performance of these three models (Supplementary Figure S4A). In comparison to SNP-SELEX data, the generally and significantly lower AUROC values of these models on the ASB data (Supplementary Tables S6 and S7) could be ascribed to the more complex TF-DNA binding context in vivo. Among the evaluated TFs, DeepSEA, Sei and Enformer were the best models for 6.05%, 29.21% and 28.95% of the TFs, respectively (Figure 3B). The Spearman rank correlation coefficients for all SNP-TF pairs also showed that Sei, DeepSEA and Enformer were among the top models, along with DeepFun (Supplementary Figure S4B, Supplementary Data 5). These deep learning methods outperformed PWM-based models in predicting the impact of SNPs on TF binding in vivo, which agreed with the findings of Wagih et al. [17]. DeltaSVM_ChIP-seq, trained on the ENCODE v3 data, was also capable of predicting a large proportion of TFs, accounting for 12.37% of the optimal predictors (Figure 3B). Among the four PWM-based methods, tRap had the highest predictive accuracy (median AUROC = 0.559) as evaluation on the SNP-SELEX data (Figure 3A). Detailed results of AUROCs and AUPRCs for each TF are available in Supplementary Data 6, and summary statistics of AUROCs and AUPRCs for each model are available in Supplementary Table S8. The P-values and 95% CIs for the pairwise paired Wilcoxon test between all models are listed in Supplementary Data 7. For the same model, we calculated the Pearson correlation coefficients between the AUROCs evaluated using the SNP-SELEX data and ASB data. There was a positive correlation between the two benchmark results for each model (Supplementary Figure S4C, Supplementary Table S9). In addition, we searched binding motifs of TFs in several commonly used motif databases and observed that 34.47% (131/380) of TFs in the ASB data lacked known binding motifs (Supplementary Figure S4D). For these TFs, we predicted SNP effects on TF binding exclusively using machine learning and deep learning models. Notably, Enformer (median AUROC = 0.607) exhibited the best performance for those TFs without known motifs (Figure 3C, Supplementary Figure S4E, Supplementary Table S10).

Figure 3.

Evaluation of the models using the ASB data. (A) Comparison of performance of 14 models evaluated by the ASB data. It shows that DNN-based methods (DeepSEA, Sei, Enformer) perform best in predicting in vivo SNPs’ effect on TF-DNA binding. Each dot represents one TF. (B) The proportion of the optimal prediction model for all TFs. (C) Enformer performs best indicated by AUROCs of TFs without known sequence motifs among several machine learning models. (D) Comparison of individual TF’s performance of deltaSVM and DeepBind models using in vitro or in vivo training data. P-value calculated by two-sided paired Wilcoxon test is shown. (E) Comparison of individual TF’s performance using four models with PWMs from JASPAR 2022 or HOCOMOCO v11 databases. P-value calculated by two-sided paired Wilcoxon test is shown. (F) Standard deviation (SD) of AUROCs with cell-type-specific models. Each dot represents a TF, and the size of the dots represents the number of cell-type-specific predictors for the TF.

Using the ASB data as the evaluation dataset, we also investigated the effects of in vitro and in vivo training data, model architectures, PWM databases and cell-type-specific training data on model prediction performance. The deltaSVM_HT-SELEX and deltaSVM_ChIP-seq models did not show significant differences in distinguishing ASB variants from non-ASB variants in vivo (85 common TFs, pseudo-median = −0.005, 95% CI: −0.019 to 0.013, P-value = 0.563, two-sided paired Wilcoxon test), whereas DeepBind_ChIP-seq outperformed DeepBind_HT-SELEX (30 common TFs, pseudo-median = −0.022, 95% CI: −0.032 to −0.013, P-value = 1.7e-04, two-sided paired Wilcoxon test) (Figure 3D). These results suggested that, at least for common TFs, the performance of models trained on in vitro and in vivo data partly depended on the evaluation dataset. Both DeepBind and DeepSEA models used ChIP-seq data from ENCODE v2 for training, but they adopted single-task and multitask architectures, respectively. We observed that DeepSEA had better performance than DeepBind_ChIP-seq (76 common TFs, pseudo-median = −0.072, 95% CI: −0.088 to −0.056, P-value = 3.53e-09, two-sided paired Wilcoxon test) (Supplementary Figure S4F). This suggested that the DNN-based multitask model was superior to the single-task model for in vivo prediction task. The comparison between the two PWM databases, JASPAR and HOCOMOCO, showed no significant difference for all four PWM models (Figure 3E, Supplementary Table S11). Some TFs in deltaSVM_ChIP-seq and most of DNN-based models had multiple predictors trained on ChIP-seq data from different cell types. To assess the consistency of these predictions, we calculated the SD of AUROCs for all predictors of the same TF. For six models with cell-type-specific predictions, Sei and Enformer had relatively higher SD of AUROCs across cell types (Figure 3F). This indicated that these two models might capture more cell-type-specific effects. Specifically, we could see that CTCF (Supplementary Figure S5) had low SD because of its general role and CTCF binding sites were relatively invariant across diverse cell types [51]. Several TFs (SOX2, ATF2, FOSL1, JUND) with high SD might be attributed to the formation of heteromeric complexes that enables these TFs to bind longer motifs with specificities [50, 52, 53] (Supplementary Figure S5).

Relationship between prediction performance of TFs and their DBDs

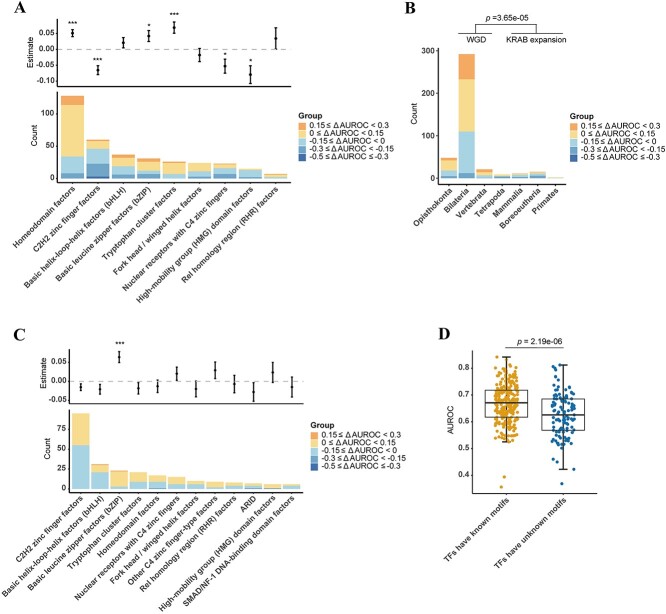
TFs interact with target sequences through DBDs, and the way they bind is highly dependent on the domain’s specific structural features. To explore the predictive performance of TFs with different DBDs, we conducted TF annotation using the DBD information from the TFClass database [39]. This enabled us to categorize the 407 TFs, evaluated in two batches of the SNP-SELEX data, into 23 distinct characterized classes (Supplementary Figure S2A). The ‘Homeodomain factors’ class and the ‘C2H2 zinc finger factors’ class were the most abundant (Figure 4A). To facilitate meaningful analysis, we conducted additional filtering on the classes, retaining those that encompassed a minimum of 10 TFs across the two batches of SNP-SELEX data. This refined filtering yielded a subset of nine classes for subsequent analysis. For each TF within these classes, we calculated the maximum AUROC across all models. Subsequently, we compared the relative AUROC change observed in each class to the mean AUROC across all classes. This comparative analysis was accomplished through the implementation of a linear regression model, with the batch effect of SNP-SELEX data corrected (adjusted 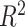= 0.362, F-statistic = 30.217, P-value <2.2e-16). Classes with better performance included ‘Basic leucine zipper factors’ (ΔAUROC = 0.042, 95% CI: 0.008–0.075, P-value = 0.026, two-sided t-test), ‘Homeodomain factors’ (ΔAUROC = 0.051, 95% CI: 0.029–0.072, P-value = 1.90e-05, two-sided t-test) and ‘Tryptophan cluster factors’ (ΔAUROC = 0.068, 95% CI: 0.034–0.103, P-value = 3.76e-04, two-sided t-test), while classes with lower AUROCs were ‘C2H2 zinc finger factors’ (ΔAUROC = −0.065, 95% CI: −0.093 to −0.038, P-value = 1.90e-05, two-sided t-test), ‘High-mobility group domain factors’ (ΔAUROC = −0.079, 95% CI: −0.134 to −0.025, P-value = 0.01, two-sided t-test) and ‘Nuclear receptors with C4 zinc fingers’ (ΔAUROC = −0.053, 95% CI: −0.096 to −0.009, P-value = 0.026, two-sided t-test) (Figure 4A, Supplementary Table S12). Interestingly, we found that the performance of these TF classes showed an association with the similarity of TF-DNA binding motifs. Specifically, for many TFs belonging to the ‘Basic leucine zipper factors’ or ‘Homeodomain factors’ classes, which recognized similar motifs [8], their predictive performance was consistently high. In contrast, C2H2 zinc finger proteins contributed most of the diversity to the motif collection that involved changes in DNA-sequence preference [8].

Figure 4.

Relationship between prediction performance of TFs and their DBDs. (A, C) Relative prediction performance of TFs with different DBD classes in the (A) SNP-SELEX data or (C) ASB data. Several classes show higher or lower AUROCs than the average. Bar plots showing the number of TFs with different ΔAUROC values in each class, and scatter plots showing the average AUROCs of TFs in each class. The horizontal dashed line denotes no change from AUROCs of all TFs which belong to known DBD classes, ^*P < 0.05, ^**P < 0.01, ^***P < 0.001. The DBD class information comes from the TFClass database. (B) Performances of TFs benchmarked on the SNP-SELEX data in the WGD stage are significantly higher than that of TFs in the KRAB expansion stage. Bar plots showing the number of TFs with different ΔAUROC values in each gene age. P-values calculated by two-sided Wilcoxon test are indicated: ^***P < 0.001. WGD: whole genome duplication. (D) Performance of TFs with known sequence motifs is significantly better than TFs without known motifs. P-value calculated by two-sided Wilcoxon test is shown.

Furthermore, we investigated whether the performance of TFs correlated with their evolutionary conservation levels. Lambert et al. [8] classified 1639 human TFs into seven conservation levels (approximated gene age) based on their distribution across 32 eukaryotic genomes. These gene ages can be roughly divided into two stages: WGD and KRAB expansion (Figure 4B). The WGD stage involved duplications across diverse TF families, while the KRAB expansion stage was dominated by duplications of KRAB C2H2 zinc fingers [8]. The ΔAUROCs of TFs in the WGD stage was significantly higher than that of TFs in the KRAB expansion stage (difference = 0.114, 95% CI: 0.062–0.166, P-value = 3.65e-05, two-sided Wilcoxon test) (Figure 4B). As most Homeodomain TFs with better predictive performance were generated during or before WGD, and lots of C2H2 zinc finger TFs with poorer performance were generated during KRAB expansion, the findings regarding DBD classes and the evolutionary conservation of TFs remained consistent.

We then classified 380 TFs that can be evaluated in the ASB data into 28 known DBD classes. It is worth noting that 105 TFs fell into the unknown class (Supplementary Figure S2B). Twelve classes with not less than five TFs were remained and subjected to multiple linear regression (adjusted 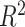= 0.086, F-statistic = 3.12, P-value = 6.01e-04). we found that the ‘Basic leucine zipper factors’ class could be better predicted in both in vitro and in vivo evaluation data (Figure 4C, Supplementary Table S13).

Based on the availability of motif information, TFs of the in vivo ASB data fell into two groups. Expectedly, for TFs that have a known motif, they could be predicted more accurately than those without known motifs (difference = 0.043, 95% CI: 0.026–0.062, P-value = 2.19e-06, two-sided Wilcoxon test) (Figure 4D). Especially, 13.54% (13/96) TFs of ‘C2H2 zinc finger factors’, which showed overall poor performance, did not have known motifs.

Performance of TFs is influenced by in vivo properties of DNA and TFs

In addition to specific sequence motifs, the binding of TFs to genomic regions in vivo depends on various properties of both DNA and TFs [9]. The complexity of the TF-DNA binding in vivo has led to poor performance of some TF models that rely solely on sequence information [17]. As TFs are often found in CREs, this led us to question whether the predictive accuracy of our models differs when assessing differential TF binding to SNPs within different CRE types, including enhancer, promoter or other genomic regions. The CRE annotations were obtained from the SCREEN website [43]. Specifically, we focused on three models, DeepSEA, Sei and Enformer, known for their superior in vivo performance. Using common TFs with at least 20 positive SNPs, we observed different prediction performance among these CRE types (Supplementary Table S14). Specifically, SNPs in promoters had lower AUROCs compared to those in enhancers (difference = −0.023, 95% CI: −0.037 to −0.009, P-value = 3.92e-04, two-sided Tukey’s test) and other genomic regions (difference = −0.015, 95% CI: −0.029 to −0.001, P-value = 0.015, two-sided Tukey’s test) (Figure 5A, Supplementary Table S15) after accounting for the variation of TFs and models. Since CpG islands often overlap with promoter regions [54], we performed the comparative analysis between SNPs in CpG islands and non-CpG islands. As expected, SNPs in CpG islands showed poorer performance than those in non-CpG islands (difference = −0.024, 95% CI: −0.035 to −0.013, P-value = 3.98e-05, two-sided Tukey’s test) (Figure 5B, Supplementary Table S16). Interestingly, the difference in allelic TF binding among the CRE types was evident only in the ASB data, but not in the SNP-SELEX data as predicted by the best in vitro model deltaSVM_HT-SELEX (Supplementary Figure S6A), highlighting the important role of CRE types in vivo. In addition, we conducted a comparison of the predictive performance of TFs with SNPs categorized by whether they are eQTLs or not. However, we found no significant difference between these two groups (difference = −0.007, 95% CI: −0.015 to −0.0009, P-value = 0.081, two-sided Tukey’s test) (Supplementary Figure S7, Supplementary Table S17).

Figure 5.

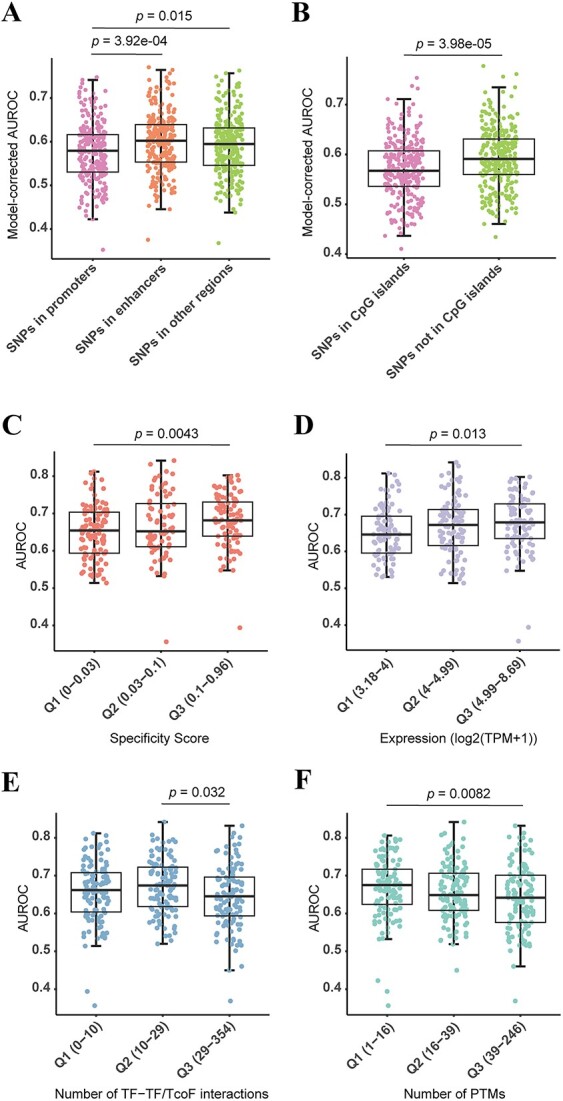
Performance of TFs is influenced by in vivo properties of DNA and TFs. (A, B) Box plot showing the model-corrected AUROCs of TFs with SNPs, where (A) the SNPs are located in enhancers, promoters and other genomic regions, and (B) the SNPs are located in CpG islands and non-CpG islands. AUROCs are predicted by the ASB data. Each dot represents one TF. P-values calculated by two-sided Tukey’s test and corrected by Benjamini–Hochberg (BH) method are shown. (C–F) Performances of TFs have some associations with their properties based on in vivo ASB data. Performances of TFs in different groups of expression specificity (0, if a gene was transcribed at the same frequency in all tissues; 1, if a gene was expressed in only one tissue) (C), expression levels (D), TF-TF/TcoF interactions (E) and PTMs (F). Each dot represents one TF. The groups are divided according to the tertiles (Q1–Q3). P-values calculated by two-sided Dunn’s test and corrected by BH method are shown.

We next explored the relationship between the prediction performance and various in vivo properties of TFs, including TFs’ expression, TF-TF/TcoF interactions and PTMs by using the maximum AUROC value across the 14 models for each TF. We first downloaded RNA-seq profiles of 1554 human TFs from Lambert et al. [8] to study the influence of TF expression specificity and expression level. Using BioQC [47], entropy-based gene expression-specific scores were calculated. We categorized TFs into three groups based on the tertiles of the specificity scores (Q1–Q3, the tertiles were used for all subsequent analyses). Our results revealed significant variation in TF performance among these groups (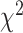 = 10.162, P-value = 6.21e-03, Kruskal–Wallis rank sum test). The Q3 group, characterized by higher expression specificity scores, exhibited higher median AUROCs compared to the Q1 group (Z-statistic = −3.187, P-value = 4.31e-03, two-sided Dunn’s test) (Figure 5C, Supplementary Table S18). In addition, we calculated the maximum expression value across all tissues for each TF as a measurement of cross-tissue expression level. The TF performance also varied significantly across groups with different expression levels ( 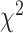= 8.307, P-value = 0.016, Kruskal–Wallis rank sum test). Subsequent pairwise comparisons indicated that TFs in the Q3 group outperformed those in the Q1 group (Z-statistic = −2.847, P-value = 0.013, two-sided Dunn’s test) (Figure 5D, Supplementary Table S19).

TFs interact with various proteins during transcriptional regulation, forming complexes crucial for DNA accessibility and gene transcription [55]. To investigate whether the degree of interactions influenced TF prediction performance, we obtained TF-TF/TcoF interaction data for 339 TFs from TcoF-DB [48]. We observed significant differences between groups with varying numbers of TF-TF/TcoF interactions (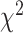 = 6.515, P-value = 0.038, Kruskal–Wallis rank sum test). TFs with the most TF-TF/TcoF interactions (Q3) performed more poorly than the Q2 group (Z-statistic = 2.552, P-value = 0.032, two-sided Dunn’s test) (Figure 5E, Supplementary Table S20), although TFs in the Q1 group did not show the best performance. We finally explored the effects of PTMs on the prediction of allelic TF binding, as they could impact TF localization, stability, activity and interactions with other proteins [56]. We collected information of seven PTM types for 358 TFs from PhosphoSitePlus [49]. The performance of TFs significantly differed among the three groups with different numbers of PTMs ( 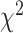= 8.984, P-value = 0.011, Kruskal–Wallis rank sum test). TFs in the Q3 group had lower AUROCs than TFs in the Q1 Group (Z-statistic = 2.996, P-value = 0.0082, two-sided Dunn’s test) (Figure 5F, Supplementary Table S21). This result revealed that TFs with extensive modifications performed worse compared to those with fewer modifications, which was consistent with the observations of Wagih et al. [17].

DISCUSSION

Interpreting the impact of non-coding variants on transcriptional regulation remains an important challenge. In recent years, numerous computational tools and methods have been developed to predict the effects of SNPs on TF-DNA binding. However, the accuracy of these models, which are primarily based on sequence context, has not been thoroughly assessed. In our study, we evaluated 14 models (Table 1) that could predict the impact of SNPs on TFBS by using large-scale in vitro and in vivo TF binding data (Table 2). The in vitro analysis incorporated a substantial cohort of 407 TFs with a minimum of 20 positive samples and encompassed approximately 32 000 pbSNPs. In parallel, our investigation of in vivo ASB data included 380 TFs and about 100 000 potential ASBs. Notably, our evaluation datasets reached an unprecedented scale in terms of the number of SNPs and TFs, providing a robust foundation for model evaluation and analysis. Furthermore, more models were evaluated in this study than previous studies. For example, Martin et al. employed PBM data of 6 TFs and ASB data of 14 TFs, respectively, to verify that the OLS model could accurately predict the impact of variants on TF binding in vitro and in vivo and was better than the widely used PWM models and the deep learning model DeepBind [33]. Beer found that gkm-SVM could identify a validated prostate cancer–associated SNP rs339331, whereas DeepSEA could not [57]. Wagih et al. evaluated the performance of five models using potential ASB variants of 101 TFs [17]. Yan et al. used SNP-SELEX data to demonstrate that deltaSVM models outperformed ΔPWM when predicting allelic TF binding [7].

We observed that most models were significantly more accurate in predicting the effects of SNPs in vitro compared to in vivo (Supplementary Tables S6 and S7). Specifically, most models achieved median AUROC values greater than 0.8 when evaluated using the First Batch subset of the SNP-SELEX data (Figure 2A). In contrast, for the evaluation using the ASB data, only DeepSEA and Enformer attained median AUROCs above 0.6 (Figure 3A). Regarding the prediction of SNPs’ impact on in vitro TF-DNA binding, kmer/gkm-based machine learning methods (deltaSVM_HT-SELEX, QBiC-Pred) trained on in vitro data performed the best. On the other hand, DNN-based multitask models (DeepSEA, Sei, Enformer) had better performance in vivo than other models, followed by two SVM-based models (deltaSVM_HT-SELEX, deltaSVM_ChIP-seq). In addition, we observed that TFs in the ‘Basic leucine zipper factor’ class were better predicted both in vitro and in vivo, whereas TFs belonging to the ‘C2H2 zinc finger factors’ class performed worse (Figure 4A and C). This result was consistent with the evolutionary ages of these TF classes (Figure 4B). We also found that it was more difficult to predict allelic binding for TFs without known motifs (Figure 4D). ASBs located in promoters or CpG islands were also more difficult to predict than those in other genomic regions in vivo (Figure 5A and B). Finally, the analysis between the prediction performance of TFs and some of their in vivo properties showed that TFs with higher expression specificity or cross-tissue expression levels were more likely to be predicted better, whereas TFs with more TF-TF/TcoF interactions or more extensive PTMs had poorer predictive performance (Figure 5C–F).

There is an obvious discrepancy between the results of in vitro and in vivo prediction, which is probably ascribed to the varying complexity between the two types of experimental conditions. SNP-SELEX synthesizes TF proteins in vitro and constructs a library of 40 bp DNA centered on the location of SNPs to evaluate the binding ability of sequence to TF through co-incubation, elution, amplification and sequencing [7]. This technique enables direct quantification of SNPs’ effects on TF binding. In contrast to the SNP-SELEX data, the ASB data are generated through ChIP-seq, which can detect indirect binding and is susceptible to false positives and false negatives due to external factors such as cross-linkers and antibodies [8, 20]. In addition, accurately measuring imbalances between reference and alternative allele reads remains a challenge. The criteria of ASB variants also significantly influences the model performance, with smaller P-value thresholds leading to higher AUROCs [17]. Moreover, to increase the statistical power for ASB identification, current large-scale ASB data are compiled through a meta-analysis of many heterogeneous ChIP-seq datasets, which further adds to their complexity. Biologically, TF-DNA binding in vivo is influenced by many factors, such as chromosome structure, nucleosome location and cofactors [58]. Our analysis also found that the in vivo properties of both DNA and TFs were related to the models’ predictive power. These factors were not incorporated into models trained primarily on sequence information.

Machine learning approaches, as opposed to PWMs, can capture more sequence determinants of structural properties of TF-DNA interactions, such as the impact of flanking sequences on the enhancer–promoter regulatory complex’s activity or stability and dinucleotide interdependency in some TF dimers [7, 18]. For the SNP-SELEX data, kmer/gkm-based machine learning models (deltaSVM, QBiC-Pred) had the highest accuracy (Figure 2A and B), indicating that these traditional machine learning methods were sufficient to capture sequence features that affect TF binding. For the ASB data, DNN-based models, particularly the CNN-based multitask model, showed larger median AUROCs (Figure 3A), indicating that deep learning methods could capture more complex features of TF-DNA binding in vivo.

Although the binding motifs of individual TFs do not typically vary depending on cell type or conditions, there are some cases where differential TF binding has been characterized [50]. Cell-type-specific TF binding locations and patterns have been observed in many studies [53]. Such cell-type-specific binding is determined by the TF’s intrinsic sequence preferences, cooperative interactions with co-factors, cell-type-specific chromatin landscapes and three-dimensional chromatin interactions [50, 53, 59]. Although our ASB data were compiled across diverse cell types, the Sei and Enformer model trained on different cell types exhibited higher variance in prediction (Figure 3F), implying they might capture more cell-type-specific allelic TF binding because of a wider variety of TFs and cell types used for training. Recently, a dataset of tissue-specific allele effects on TF binding has emerged [60], offering potential benefits for tissue-specific model training and evaluation if expanded further.

Despite PWMs not showing optimal predictive performance and assuming independent nucleotide binding energies [61], they remain popular due to their simplicity and interpretability, as evidenced by their use in many analytical platforms [13]. Among the four PWM-based models (tRap, atSNP, motifbreakR and FABIAN-variant), tRap outperformed the others in both in vitro (Figure 2A and B) and in vivo predictions (Figure 3A). Notably, the algorithms used by these models to calculate binding scores differed. atSNP reported the maximum affinity value of any subsequence with a reference or alternate allele as the sequence’s affinity score to the TF, allowing for inconsistent positions between subsequences [14]. motifbreakR represented differential binding by comparing the binding specificities of two subsequences at the same position and strand [15]. FABIAN-variant used same strategy as atSNP but calculated a joint score between −1 and 1 to represent TFBS loss or gain [32]. Conversely, tRap summed the binding scores of all subsequences to obtain the sequence’s total affinity [16]. Regarding the PWM databases, PWMs from the JASPAR database showed only slightly higher predictive performance than those from the HOCOMOCO database in vitro (Figure 2E) but no significant difference in vivo (Figure 3E). This suggested that the PWM-based methods were relatively insensitive to the source of training data, at least for in vivo prediction.

In our study, we assessed a total of 14 models that could predict SNPs’ effects on 1546 TFs. This comprehensive coverage accounted for nearly all of the 1639 known human TFs documented in the work by Lambert et al [8]. However, it is worth noting that despite the substantial expansion of our benchmark datasets, they encompassed only 694 TFs, revealing a notable discrepancy. Furthermore, the pressing need for evaluation datasets of higher quality remains evident. As for benchmarking against in vivo data, the use of the latest CUT&Tag technology [62] as an alternative to ChIP-seq can help reduce experimental noise. In addition, incorporating more in vivo features into models, such as epigenetic modifications, TF expressions, interactions and PTMs, may improve the prediction of ASB variants beyond sequence context.

Key Points

• The performance of 14 computational models that can predict the effects of non-coding variants on TF binding was assessed using in vitro and in vivo benchmarks.

• For in vitro variant impact prediction, kmer/gkm-based machine learning methods (deltaSVM, QBiC-Pred) trained on in vitro datasets performed the best.

• For in vivo variant impact prediction, DNN-based multitask models (DeepSEA, Sei, Enformer) trained on the ChIP-seq datasets exhibited the best performance.

• The prediction performance of TFs is associated with their DNA binding domains (DBDs) and in vivo properties.

Author Biographies

Dongmei Han is a PhD student at the Shanghai Institute of Nutrition and Health, University of Chinese Academy of Sciences, China.

Yurun Li is a PhD student at the Shanghai Institute of Nutrition and Health, University of Chinese Academy of Sciences, China.

Linxiao Wang is a PhD student at the Shanghai Institute of Nutrition and Health, University of Chinese Academy of Sciences, China.

Xuan Liang is a PhD student at the Shanghai Institute of Nutrition and Health, University of Chinese Academy of Sciences, China.

Yuanyuan Miao is a PhD student at the Shanghai Institute of Nutrition and Health, University of Chinese Academy of Sciences, China.

Wenran Li is a postdoctoral fellow at the Shanghai Institute of Nutrition and Health, University of Chinese Academy of Sciences, China.

Sijia Wang is a full professor at the Shanghai Institute of Nutrition and Health, University of Chinese Academy of Sciences, China.

Zhen Wang is an associate professor at the Shanghai Institute of Nutrition and Health, University of Chinese Academy of Sciences, China.

FUNDING

This work was supported by the National Key R&D Program of China (2021YFA1100501) and National Natural Science Foundation of China (32370690).

AUTHOR CONTRIBUTIONS

D.H. and Z.W. conceived the study. D.H. collected data. D.H., L.W. and Z.W. constructed methodology. D.H., Y.L., L.W. and Y.M. implemented computer codes. D.H. and Z.W. performed the formal analysis. Y.L. and Y.M. performed validation. D.H. and Z.W. wrote the manuscript. X.L. and W.L. revised the manuscript. S.W. and Z.W. supervised the study. The authors read and approved the final manuscript.

CODE AVAILABILITY

The codes used to process and generate the results of this study are available at GitHub (https://github.com/hdm2020/benchmark).

DATA AVAILABILITY

The benchmark datasets generated in this study and the prediction performance of the 14 models for each TF are available at Figshare (https://doi.org/10.6084/m9.figshare.24961908). SNP-SELEX data used in this study are available in the GVAT database (http://renlab.sdsc.edu/GVATdb/), and ASB data are available in the ADASTRA database (https://adastra.autosome.org/bill-cipher/downloads). Other data sets we used include: PWM data and sequence motifs of TFs from the JASPAR 2022 database (https://jaspar.genereg.net/) and HOCOMOCO v11 database (https://hocomoco11.autosome.org/), sequence motif information also from CISBP (http://cisbp.ccbr.utoronto.ca/), TF DBD information from the TFClass database (http://tfclass.bioinf.med.uni-goettingen.de/), candidate enhancers or promoters from the SCREEN website (https://screen.encodeproject.org/), eQTL annotation from GTEx v8 (https://www.gtexportal.org/), conservation levels and expression of TFs (http://humantfs.ccbr.utoronto.ca/download.php), TF-TF/TcoF interactions from the TcoF-DB v2 database (https://tools.sschmeier.com/tcof/home/), PTMs of TFs from the PhosphoSitePlus v6.7.0.1 database (https://www.phosphosite.org/).