I’m not sure that curve means what you think it means: Toward a [more] realistic understanding of the role of eye-movement generation in the Visual World Paradigm

Abstract

The Visual World Paradigm (VWP) is a powerful experimental paradigm for language research. Listeners respond to speech in a “visual world” containing potential referents of the speech. Fixations to these referents provides insight into the preliminary states of language processing as decisions unfold. The VWP has become the dominant paradigm in psycholinguistics and extended to every level of language, development, and disorders. Part of its impact is the impressive data visualizations which reveal the millisecond-by-millisecond time course of processing, and advances have been made in developing new analyses that precisely characterize this time course. All theoretical and statistical approaches make the tacit assumption that the time course of fixations is closely related to the underlying activation in the system. However, given the serial nature of fixations and their long refractory period, it is unclear how closely the observed dynamics of the fixation curves are actually coupled to the underlying dynamics of activation. I investigated this assumption with a series of simulations. Each simulation starts with a set of true underlying activation functions and generates simulated fixations using a simple stochastic sampling procedure that respects the sequential nature of fixations. I then analyzed the results to determine the conditions under which the observed fixations curves match the underlying functions, the reliability of the observed data, and the implications for Type I error and power. These simulations demonstrate that even under the simplest fixation-based models, observed fixation curves are systematically biased relative to the underlying activation functions, and they are substantially noisier, with important implications for reliability and power. I then present a potential generative model that may ultimately overcome many of these issues.

Introduction

In the past 25 years, few empirical methods in cognitive science have had the wide-ranging impact of the Visual World Paradigm (VWP; Tanenhaus et al., 1995) on language research (Magnuson, 2019; Salverda et al., 2011, for reviews). The VWP starts from a simple premise. Subjects are situated in a visual world. This could be as simple as four pictures on a computer screen or as complex as a real-world conversation over real objects. They then hear spoken language referring to those objects. Objects represent possible interpretations of the speech. While they perform this task (or just scan the scene), eye movements are monitored. Since eye movements unfold continuously as the subjects interpret the speech, they thus provide insight into the degree to which listeners consider various interpretations over time.

This was initially applied to sentence processing (Eberhard et al., 1995) and word recognition (Allopenna et al., 1998). However, the ultimate impact of the VWP was inconceivable in 1995. It rapidly spread down the language chain to speech perception (McMurray et al., 2002), and up to pragmatics (Hanna & Tanenhaus, 2004; Keysar et al., 2000). It has become important in understanding development (Fernald et al., 1998; Rigler et al., 2015; Snedeker & Trueswell, 2004), and bilingualism (Spivey & Marian, 1999), and for characterizing language comprehension in clinical populations including people who have dyslexia (Desroches et al., 2006), autism (Brock et al., 2008), schizophrenia (Rabagliati et al., 2019), developmental language disorder (McMurray et al., 2010), and brain damage (Mack et al., 2013; Mirman et al., 2011). It has even been applied outside of spoken language, to reading (Hendrickson et al., 2021) and speech production (Griffin, 2001).

The VWP is not a panacea. There are limits on the types of words or objects that can be studied (picturable nouns), and it can be difficult to map complex sentences onto a visual scene while preserving some kind of task for the subject. There are ongoing concerns about whether the visual scene constrains linguistic processing (Magnuson, 2019). Such constraints could be theoretically important as a marker of the embodiment and interactivity of language and vision (Spivey, 2007). They could also be a confound, as in arguments that fixations in the VWP only reflects objects that have been “prenamed” in working memory (see Huettig et al., 2011, for a discussion), though concern has been ruled out empirically at least for word recognition (Apfelbaum et al., in press). Despite these ongoing concerns, the VWP has remained highly influential for three reasons.

First, unlike techniques such as priming, the task of the VWP is natural: understanding language. Thus, it is more ecological and more suitable for populations who may lack the meta-linguistic awareness needed for tasks like lexical decision. Second, most alternatives—including reaction times, but also neuroimaging approaches like MRI and ERPs—make only indirect inferences about language processing by identifying conditions in which processing is difficult. In contrast, the VWP offers more direct access to what interpretations are considered during processing: If a subject is fixating a referent (more than unrelated object), they are considering it.

Perhaps the most important reason for the VWP’s impact is time. The VWP has long been touted as a “real-time” measure, estimating the state of the system while processing unfolds. It is not the first real-time method, but it is richer than many. In prior approaches like cross-modal priming or response deadlines, the researcher defines a small number of time points of interest, and these are probed on distinct trials. For example, if one wanted to use priming to assess processing at 200 and 500 ms after word onset, one would present the orthographic target 200 ms after the word on half the trials, and 500 ms on the other half. Each trial assesses one time point, and the number of total time points that can be measured is limited. In contrast, VWP has been claimed to assess processing nearly continuously in time on all trials. This is an inconceivably large advance in the richness of the data.

Part of this claim rests on the temporally rich visualizations of the data. From the beginning, researchers adopted visualizations like Fig. 1 (Allopenna et al., 1998) to depict the time course of fixations (termed “fixation curves” here). Multiple studies have illustrated a close correspondence between these kinds of visualizations and continuous output from models such as TRACE (McClelland & Elman, 1986) and TISK (Allopenna et al., 1998; Dahan et al., 2001; Hannagan et al., 2013; McMurray et al., 2009). And this is not mere observation—one can manipulate parameters of the model and show systematic distortions that mimic differences among people with language disorders or brain damage (Dahan et al., 2001; McMurray et al., 2010; Mirman et al., 2011). This has yielded a collective sense that these curves fairly precisely characterize the time course of processing.

Fig. 1.

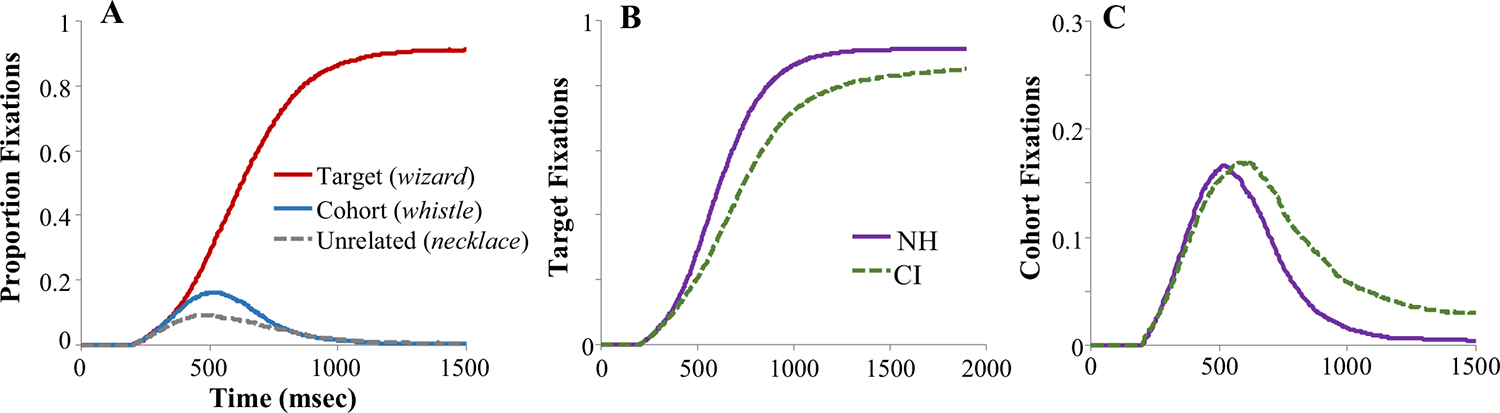
Typical Visual World Paradigm (VWP) visualizations (adapted from Farris-Trimble et al., 2014, Exp. 1). In this experiment, participants (normal hearing or cochlear implant [CI] users) heard an isolated word (e.g., wizard) and selected the referent from a screen containing pictures of the target (wizard), a cohort competitor (whistle), a rhyme (lizard, not shown), and an unrelated (necklace). a Proportion fixations to the target, cohort, and unrelated in the normal hearing listeners show a precise time-locking to the unfolding ambiguity in the signal: Early on, listeners fixate the target and cohort as the input they have heard thus far (wi-) is consistent with both. Later, they suppress the competitor to hone in on the target. b–c Fixations to the target (b) or cohort (c) as a function of listener group (NH: normal hearing; CI: cochlear implant users) can reveal precise quantitative differences in the time course of processing. (Color figure online)

The power of these visualizations has led to an explosion of techniques for making precise statistical estimates about the dynamics of the fixation curve (Cho et al., 2018; McMurray et al., 2010; Porretta et al., 2018; Seedorff et al., 2018). These approaches offer evermore mathematically and statistically precise ways to characterize these nonlinear functions, and the factors that affect them. All of these approaches—including ones I helped develop—assume the face validity of the fixation curve. This validity has not been questioned.

This manuscript starts from the premise that all of these approaches fail to take seriously the nature of the fixation record as a stochastic series of discrete and fairly long-lasting physiologically constrained events. A model of this process is implemented to determine whether the form of this stochastic process alters the observed fixation curves that one should expect from a given underlying function. The short answer to this question is that the regularities of this stochastic process have both systematic and unpredictable effects on the observed fixation curves; they add not only noise but also bias. As a result, the fixation curves do not always resemble the underlying dynamics of the system, and this may necessitate alternative statistical models and caution in interpreting existing models. Critically, as the field moves to issues of power, reliability, and replicability, understanding the contributions of this stochastic component to the data is critical for designing experiments, identifying indices of psychological constructs in the fixation record, and evaluating the rigor of VWP studies more broadly.

This manuscript starts with a brief review of current analytic approaches. It then turns to a detailed discussion of how fixation curves are derived and the linking hypotheses that conceptualize the relationship between the underlying activation in the system and observed fixations before presenting the simulations.

Analytic approaches to the VWP

This project’s goal is not to evaluate analytic approaches, but its questions are motivated by current analysis methods. Three broad classes of analytic approaches have been used.

Fixation-driven approaches

The earliest studies used fixation-driven approaches, which emphasize specific properties of the fixation record: the number of fixations to an object, the duration, the likelihood of transition from one object to another, and so forth (e.g., see McMurray et al., 2008a, 2009; Spivey & Marian, 1999; Tanenhaus et al., 1995). Such approaches are historically related to work done on eye-movement control in reading, which has led to fixation-driven measures tied to theoretical constructs (e.g., first fixation duration, regressions; cf. Rayner et al., 1998). These measures are highly physiologically grounded and straightforward to estimate. However, there are several limits.

First, there are many such measures in principle. In reading, measures like first fixation time or the likelihood of refixation are linked to theoretical concepts about reading, lexical access, and sentence processing, permitting a hypothesis-driven approach. However, eye-movement control in reading may be somewhat simpler than in the VWP. In reading, eye-movement control is routinized (overpracticed) and largely directed by the problem of extracting information. However, in the VWP, eye movements simultaneously reflect visual information uptake, language processing (matching lexical activation to the scene), and response planning (and this may differ as the task/decision unfolds; Magnuson, 2019). With no clear theory to guide variable selection, this can lead to too many researcher degrees of freedom.

Second, this problem is exacerbated by the fact that an effect on the underlying decision function may be spread across multiple fixation variables. For example, increased competitor activation could increase the probability of fixating an object, extend the fixation’s duration, or increase the likelihood of returning to it. Any single measure may lack power to detect effects.

Finally, fixation-driven measures are not always temporally precise, and there are fundamental limitations on this. Consider a simple measure like the likelihood of fixating the competitor. One might like to estimate this at multiple times (e.g., between 100 and 200 ms, 200 and 300). However, given the low likelihood of fixating the competitor overall, there may be very few trials to contribute to any individual bin for a given subject.¹

Fixation curves: Indices

Using the fixation curves (Fig. 1) as the basis of analysis overcomes some of these limits. When the VWP was developed, we lacked statistical tools to fully characterize these functions in time. Consequently, many studies started from these curves as a visualization tool but derived individual indices to assess aspects of them. An example is area under the curve (AUC), in which one simply averages over the time span of interest and uses that as a measure of how much the subject is fixating a given object.

Index approaches offer some advantages over fixation-based ones. First, the fixation curve is simultaneously affected by many properties of the fixation record (likelihood of fixating, transitions, duration, and so forth). These would all be independent Dependent Variables (DVs) in a fixation-based analyses (with lower power). In contrast, the fixation curves functionally collapse across these properties to a single DV. A subject could have a higher AUC because fixations were longer, they were more likely to look at the competitor, or they fixated it twice. Thus, indices may overcome some of the degrees of freedom associated with fixation-based approaches. Of course, they add their own degrees of freedom. AUC, for example, requires the researcher to specify a time window. However, recent approaches like permutation-based clustering (Maris & Oostenveld, 2007) and BDOTS (Oleson et al., 2017) can detect that there is a difference and also the time window over which it occurs.

Second, these measures can be much more temporally specific than fixation-based measures. They do not rely on having some quantity of fixation that precisely starts or stops at certain times, and the temporal precision is limited only by the sampling period.

Third, index approaches are not limited to the overall degree of looking. This can lead to measures that are highly theoretically informed, provided we accept the validity of the fixation curves. For example, indices have been identified to determine when the fixation curve crosses a threshold (Ben-David et al., 2011), to estimate the peak looking to a competitor, or the duration over which competitor fixations were above threshold (Rigler et al., 2015). Perhaps the most sophisticated approach is an onset detection technique developed by me and my colleagues (Galle et al., 2019; McMurray et al., 2008b; and see Reinisch & Sjerps, 2013). These combine both target and competitor fixations to estimate when the fixations record is biased by different factors in the input.

In the best versions, indices are hypothesis driven; some (like onset detection) have been in use sufficiently across papers that they are fairly standard (minimizing researcher degrees of freedom [d.f.]). Such indices can serve as a confirmatory hypothesis test in which the researcher proposes a measure—in advance—and tests only that DV. However, at worst, they can also be unconstrained.

These approaches have fallen out of favor, but not for the reasons you think. In their heyday, questionable research practices were not the concern that they are now. Instead, researchers saw a different glaring weakness: While they start from the fixation curves, index approaches do not model the full time course. To many (including me), this felt like a missed opportunity.

Time course analyses

In the past decade, new approaches have been developed to more precisely model the fixation curve. The first used polynomial growth curves in a mixed model (Mirman et al., 2008). Shortly later, my lab introduced nonlinear curvefitting (Farris-Trimble & McMurray, 2013; McMurray et al., 2010) to more intuitively capture the shape of the fixation curve, though only when it fit a predefined form. Newer approaches offer more flexibility and precision. generalized additive mixed models (GAMMS; Porretta et al., 2018) use “smoothing” functions to capture virtually any nonlinear effect of time. Cho et al. (2018) propose a more radical auto-regressive framework in which time is not an explicit factor. Rather, the proportion of fixations at each time is modeled as a function of the proportion at the previous time. These approaches offer even more flexibility and can accommodate curves of virtually any shape, and in a mixed-model framework that can handle cross-random effects.

The current zeitgeist—as seen in the evolution of these statistical approaches—is to model the precise time course of fixations with evermore precision and rigor. These precise specifications are then interpreted as reflecting precise read outs of cognitive states. However, this rests on the assumption of a direct linking function between underlying decision dynamics and measurable fixation curves. This linking function has not been explicitly investigated.

What are fixation curves, and where do they come from?

Typical fixation curves appear to be continuous and smooth, but they are actually built from discontinuous and “chunky” data. Saccades are relatively ballistic, and fixations are discrete. Listeners can only fixate one thing at a time, and once they get there, there is a roughly 200-ms refractory period until they can move. Figure 2 shows a schematic of how these smooth curves are built from this data. In this example, the visual display (Fig. 2a) might contain a target object (sandal, in purple), a cohort (sandwich, in blue), a rhyme (candle, in red), and an unrelated object (necklace, in gray). On each trial, subjects make a series of discrete fixations to these objects (Fig. 2b). On Trial 1, for example, they may look at the correct object and stay there, while on Trial 3, they may briefly fixate the cohort before moving to the target.

Fig. 2.

Schematic illustrating the source of the fixation curves (courtesy Richard Aslin). a A typical screen in the Visual World Paradigm (VWP) used to study word recognition may contain four objects: a target (corresponding to the auditory stimulus, sandal, in green), a cohort or onset competitor (sandwich, in blue), a rhyme (candle, in red), and an unrelated object. b On each trial, listeners launch a discrete series of fixations. On some trials, they may look at the target and stay; on others, they may look briefly at a competitor before the target. c To obtain the time course of fixations, one computes the proportion of trials in which the participant is fixating each object at each time slice. (Color figure online)

To construct the fixation curves, the researcher averages across trials, within times, to compute the proportion of trials on which subjects were fixating a class of referents (Fig. 2c).² Two-hundred ms is marked here as a rough estimate of the time it takes to plan and launch an eye movement (Viviani, 1990)—fixations initiated before then are not thought to be driven by the auditory input, and a saccade launched at 600 ms (for example) was likely planned at 400 ms. It also thus represents the refractory period before the subject can make another fixation.

These curves are used to make inferences about activation that is presumed to be continuous over time. The typical (unspoken) assumption in analyzing these data can be termed the high-frequency sampling (HFS) assumption. Under this assumption, the underlying activation of a word or interpretation determines the probability of fixating the corresponding object. If the researcher is sampling at 4 ms intervals, the fixation curve thus derives from a probabilistic sample every 4 ms. To account for the oculomotor delay, the likelihood of fixating an object at a given time is a function of the underlying probability 200 ms prior.

The HFS sampling assumption is most clear in studies using the Luce Choice rule to generate VWP predictions from continuous activation models (Allopenna et al., 1998; Dahan et al., 2001; Hannagan et al., 2013; McMurray et al., 2010; Mirman et al., 2011). Here, the underlying activation is given by a model (TRACE or TISK), and this activation is transformed into a likelihood of fixating each object at each timestep. This is done with no attempt to model the intervening fixations (though see Chapter 7 in Spivey, 2007). To be fair, this works well; these studies show a very high concordance between model predictions and fixation curves.

The labs that have used HFS in this explicit way typically treat HFS as a simplifying assumption that enables one to make theoretical claims about underlying decision dynamics from the data. It has never been treated as a strong theoretical claim about how fixations are linked to underlying activation. In fact, the HFS assumption is patently untrue. Subjects cannot move their eyes every 4 ms. Once a subjects’ gaze lands on something, they must stay there for about 200 ms; and saccades (which typically last 30–50 ms) can only be altered in flight in rare circumstances. Moreover, the duration of fixations to competitors can be related to experimental conditions (such as the degree of phonemic ambiguity: McMurray et al., 2008a), and people are more likely to look at some screen locations (e.g., top left > top right > bottom left; Salverda et al., 2011), or are more likely to make transitions between nearby objects but not more distal (e.g., diagonal). The common defense is that when sampling across a reasonably large number of trials, the precise timing and duration of eye movements is fairly random. Consequently, it is reasonable to treat each time slice as an independent sample from the underlying activation function 200 ms prior. But is it safe to assume that noise across trials uniformly smears over the discrete nature of fixations?

Current statistical approaches attack this issue around the edges. For example, one of the consequences of the fact that fixations unfold as a series of discrete events is that the fixation curve at each step is related to prior steps, since adjacent samples are likely to be influenced by the same fixation. Models then may be improved by assuming autocorrelated errors (Oleson et al., 2017), or by modeling the mean in terms of this autocorrelation (Cho et al., 2018). However, this still assumes each time point is an independent draw from the underlying probability function (even though the mean or variance of that distribution might be related to prior times).

The open question addressed here is whether these systematic effects on fixations can be treated as noise or if they bias the fixation curves away from the underlying decision curves that generated them. If HFS does not hold, this may not be a major problem for index approaches as these do not attempt to precisely capture the entire time course. However, the goal of all existing time-course-based approaches is to extract precise estimates of when the fixation curves affected by experimental conditions. If the HFS does not hold, this raises a conundrum. These approaches may be more accurate at modeling the data, but the fine-grained dynamics they purport to capture may not accurately reflect the underlying dynamics we wish to assess.

Goals of the present study

As psychology and cognitive science have begun to pay more attention to methodological rigor, it has become clear that in addition to issues of statistical impropriety and researcher degrees of freedom (Bakker et al., 2012; Open Science Collaboration, 2015; Stroebe et al., 2012), one contributor to the replication crisis is poor theoretical specificity (Oberauer & Lewandowsky, 2019). There is a chain of assumptions that allow researchers to derive predictions of behavioral data from a theory that is rarely couched in behavioral terms (Meehl, 1990; Scheel et al., 2021). Fleshing out this derivation chain and validating its components are essential for generating accurate empirical predictions from theory. Without confidence in what a theory predicts, a theory could be true, but this cannot be detected by available empirical evidence. Or conversely, it may be falsely assumed to be true on the basis of invalid predictions. In this context, understanding how the sequential and chunky nature of the fixation system contributes to the smooth fixation curves is an essential component of the derivation chain for the VWP.

To accomplish this, a series of Monte Carlo simulations were run, in which an underlying activation function for a given “subject” was known, and a series of fixations were generated using both the HFS model as well as more sophisticated models that capture the chunkiness of the fixation system. The observed fixation curves were then related to the underlying activation to characterize the role of the fixation-generating system in shaping this common visualization.

This study addressed six key questions. However, it is important to note the context. Many VWP experiments ask essentially either/or questions. For example, they might ask whether listeners fixate a competitor more or less in some or are faster to converge on the target in conditions than others. These are referred to as ordinal questions. For these coarser questions, perhaps the HFS assumption is close enough. But even in this case, there are three questions that remain relevant to ordinal designs.

First, do the assumptions about the underlying generating function lead to differences in the statistical properties of the fixation curves? Does the stochasticity lead to reduced power or create the possibility of a Type I error?

Second, and relatedly, as the VWP is increasingly applied to individual differences or correlational designs, its reliability is of concern (though this is also relevant for experimental work: Hedge et al., 2018; Schmidt, 2010). Reliability is clearly a function of the task itself, but in any system in which results are sampled stochastically, some portion derives from the laws of probabilistic sampling. This is particularly unpredictable in a complex system such as the saccade system. Thus, we ask if some portion of the reliability of the VWP derives from the fixation system? This is essential for knowing the upper limit of efforts to improve reliability by improving items, task properties, and so on.

Third, since the data are probabilistic, power, Type I error, and reliability are all likely shaped by the number of samples (trials).

Understanding these factors are important for designing more rigorous experiments, planning power, identifying the cause of null effects, and avoiding spurious significant effects. Moreover, fixation-generating function clearly accounts for some proportion of the variance. To the extent that this can be understood or even modeled, we can attain a more complete characterization of the data (and this may help reveal small effects).

There is also increasing interest in going beyond simple differences, to use the fixation curves to make fine-grained claims about the time course of processing using what I term termed continuous-in-time experiments. This is seen in evermore sophisticated statistical approaches (Cho et al., 2018; Mirman et al., 2008; Porretta et al., 2018). Such designs raise new questions.

Fourth, we ask whether it is necessary to model the time course with such accuracy, or conversely, if failing to do so leads to Type I error or loss of power.

Fifth, theoretical accounts have argued that different aspects of the fixation curves mean different things. For example, we have proposed that typical development is reflected in differences in the slope of the target function (reflecting increasing rate of spreading activation) while language disorders are reflected in the asymptote (reflecting failure to resolve competition; McMurray et al., 2022a). Thus, it is important to understand the degree to which specific assertions such as these can be tested: Can a difference in the underlying slope appear as a difference in the asymptote because of the fixation-generating system? Are some aspects of the curves more corrupted by the fixation-generating functions than others?

Sixth, studies are increasingly time locking analysis of the fixation curves (and theoretical claims) to the time of linguistic events in the real world. For example, they may analyze fixations prior to a particular event to document anticipation (Altmann & Kamide, 1999; Salverda et al., 2014), or they may examine only fixations after a particular event to ask if information or decision processes persist (Dahan & Gaskell, 2007; McMurray et al., 2009). However, it is possible that the inherent dynamics of the fixation system could systematically bias the ability to map the time of change in the fixation curve to real time. Thus, it is important to know the circumstances under which such inferences can be made.

More broadly, the VWP is often used to make claims like an effect occurs as soon as incoming speech hits the language system, or that competitor activation persists surprisingly long. This is supported by modeling work showing a close time-locking of VWP results to computational models (Allopenna et al., 1998; Hannagan et al., 2013; McMurray et al., 2010; Mirman et al., 2011). This modeling work—and these colloquial assumptions—assume a linear mapping from time in the world to the timing of the fixation curves. But this assumption may not be guaranteed given the nature of the fixation system. A broader investigation could either support this conceptualization or raise the need for more cautious interpretations of VWP data.

Simulation 0: Stochastic sampling

Before discussing simulations of actual fixation curves, it is helpful to consider the simple math of random sampling. If one flips a coin four times, the most likely value is to get two heads and two tails. But that is only likely to occur on 37.5% of the “runs.” That is, less than half the time, the outcome of this experiment does not reflect the true underlying probability (it has low validity). If one were to perform this twice (test–retest reliability), reliability would be poor: On many tests, you might get three heads on one run but two on another. In fact, the chances of observing two heads on two consecutive runs is only 14%! However, in a run of 100 flips, things might look quite different—one is much more likely to get an observed value close to 50%, and to be to obtain something close to that twice in a row. These properties are also a consequence of the probability. What if the coin were loaded such that likelihood of a head is only 0.25? Here, if the coin is flipped four times, the most likely outcome is one head and three tails. That will occur slightly more often than the mostly likely outcome for a fair coin (42.2%) and the chances of getting it twice in a row is higher (17%). Thus, validity and reliability are lawful consequences of the number of coin-flips or draws and the probability.

The stochastic generation of eye movements must obey these simple principles. For example, the underlying probability of a cohort fixation may be quite low, whereas the target could be closer to 50%. This will clearly influence the reliability and power of an experiment that relies on the target or the competitor; and such considerations should be taken into account when choosing the number of trials. Thus, it was important to visualize the consequences of these simple principles of stochastic sampling before considering the more complex consequences of an eye-movement generating function.

Virtually all tests based on accuracy fall prey to this issue. However, I have found no published descriptions of the relationship between number of samples, the baseline probability, and the validity/reliability of a measure. Thus, a simple simulation (see Supplement S1 for methods) was conducted in which an underlying probability was chosen, some number of draws were performed, and the mean was saved. This was done twice, and the whole process repeated for 50 subjects. The correlation (across subjects) between the mean and the original probability, and between the means from the two runs was then computed. This was done for a range of underlying probabilities, from low values like.15 (typical of cohort fixations) to higher values like.8 (typical of target fixations). This was done with a range of draws (from 5 to 300), even though typical VWP experiments might only include 15–30 trials (repetitions) per condition.

Figure 3 shows the results. At low numbers of repetitions (5–10 trials), validity is poor and only greater than 0.6 when the underlying probability was near the middle of the range. Reliability was extremely poor and did not crest 0.5 in even the best of circumstances. In fact, at low or high underlying probabilities, reliability didn’t cross 0.2! At a more reasonable 50 trials, when the underlying probability was 0.5, validity (r >.9) and reliability (r ~.8) were strong. But, at more extreme values typical of the VWP, both fell precipitously. And only with more than 150 repetitions were validity and reliability reasonable at all underlying probabilities.

Fig. 3.

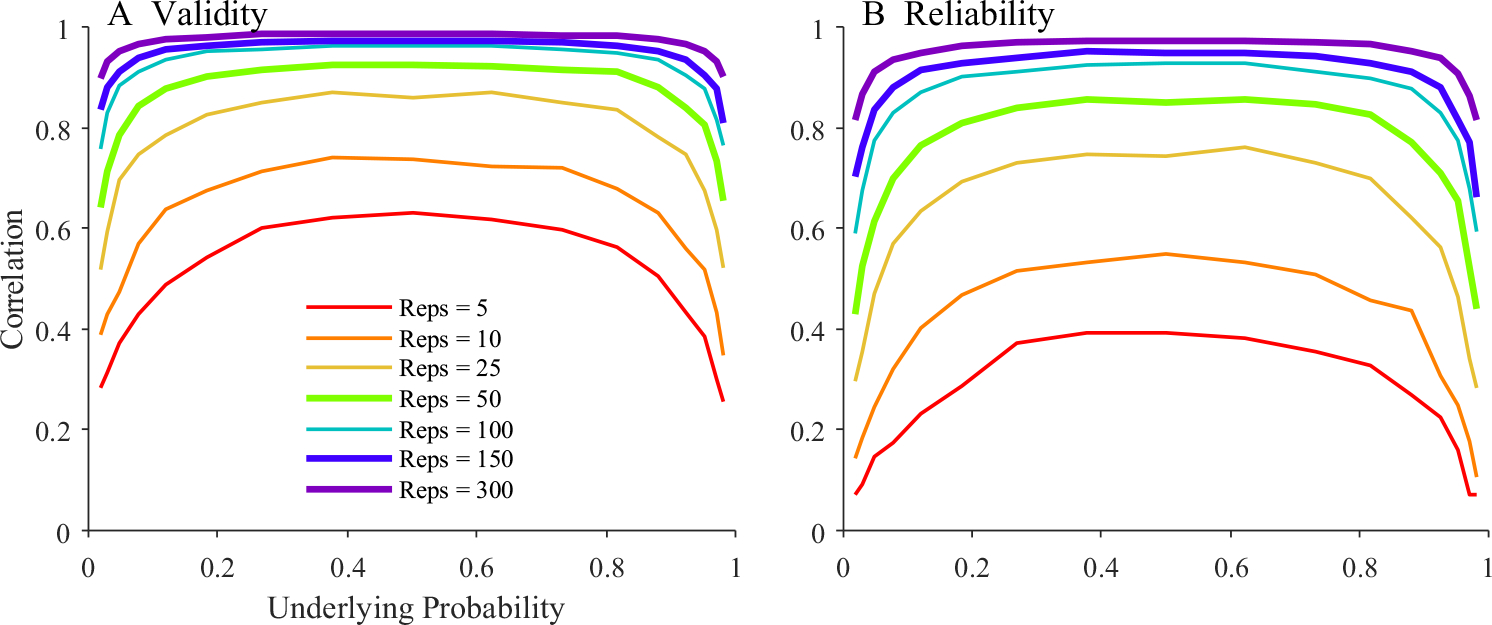
Results of a simple probability sampling procedure as a function of the underlying probability and the number of trials sampled. a Validity—the correlation between underlying and observed probability. b Test–retest reliability (correlation between two runs). Thicker lines represent the numbers of repetitions used in the simulations of fixation curves below

Of course, a fixation analysis is more complex than this simple simulation—typical measures for the VWP pool across multiple samples and extract complex values (e.g., the slope). This could enhance reliability and validity (since each trial effectively contributes multiple draws) or threaten it (from compounding noise). Thus, this simulation offers only a baseline for validity and reliability; it is unclear to what extent the fixation model may impact these psychometric properties.

Overview and methods of simulations

To investigate the role of the fixation-generating model, a series of simple simulations were developed.³ These simulations started by first selecting a function that describes the probability of fixating the target (or a competitor) over time. Parameters of this function are then randomly selected to simulate a single subject. This is termed the underlying or generating function. I next randomly generated a series of fixations from this underlying function using various assumptions about how eye movements are generated. This was then done for 300 trials, and the data were averaged to produce a fixation curve for that subject. Next, new parameters of the underlying function were selected for 1,000 subjects, and the process was repeated. Finally, results were analyzed, using a curvefitting technique, and the estimated fixation curves were compared with the underlying functions.

For both the generating (underlying) function and the analysis of the derived data, a nonlinear curvefitting approach (McMurray, 2017; McMurray et al., 2010) was used for several reasons. First, it was easy to randomly select the parameters to describe a single subject (e.g., the slope and asymptotes) and still get reasonable curves (e.g., between 0 and 1). This would have been harder with polynomial growth curves (for example), where the parameters do not map clearly onto the shape of the resulting function, nor is the function limited to be between 0 and 1.

Second, this approach can precisely characterize the data in a way that is independent of the full data set. In contrast, mixed-model approaches like growth curves or GAMMs cannot analyze subjects individually. When a subject-specific parameter (e.g., a subject’s slope) is estimated, values are not based only on that subject’s data and are biased toward the mean (shrinkage). While this is a strength for analysis, it makes the interpretation of results less clear here, where the goal is to ask if a subject’s observed data matches their underlying function.

Finally, the parameters of the nonlinear function are meaningful descriptors of the fixation curves. Parameters like slope and asymptote are meaningful descriptors—even if researchers use a different approach for statistical modeling—because they describe readily observable aspects of the functions. This allows clear questions such as whether a particular fixation model makes the slope of the target function shallower than the underlying function.

Methods

Source code for all of the simulations presented here is available online (https://osf.io/wbgc7/). Curvefitting was performed using functions in McMurray (2017, Version 24), available as a standalone package at (https://osf.io/4atgv/).

Target and competitor fixations were modeled with separate functions. Each describes the (binomial) probability that the subject fixated the target (or competitor) at that time or not. This is an oversimplification: In a real experiment, probabilities would be related in a multinomial distribution (e.g., if the subject fixates the target, he or she cannot be fixating the competitor). However, the binomial case is a reasonable starting place as most studies analyze fixations to each object separately. Supplement S3 presents a multinomial model showing similar results.

Target fixations

Target fixations were modeled with a four-parameter logistic (Equation 1, Fig. 4a), as in McMurray et al. (2010):

$$p(\mathit{target})=\frac{max-b}{1+\mathrm{e}\mathrm{x}\mathrm{p}\left(4\cdot \frac{s}{max-b}(xo-t)\right)}+b.$$ (1)

Fig. 4.

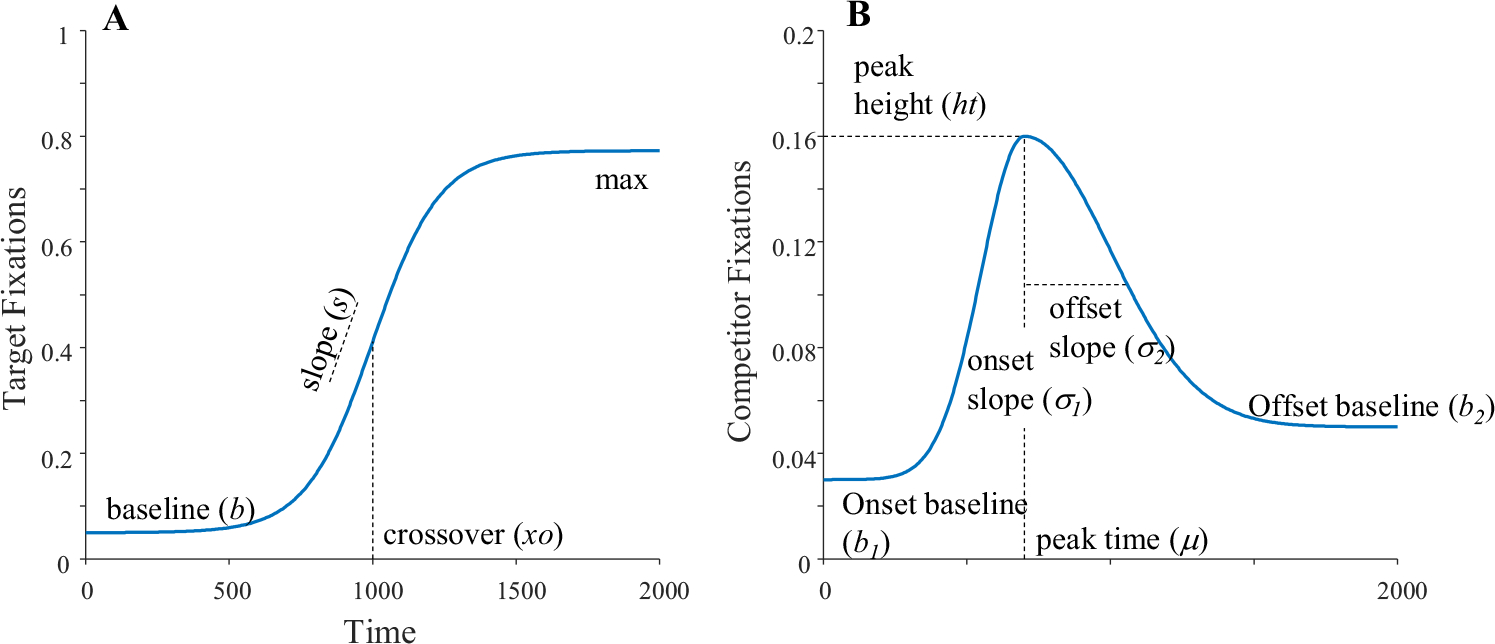
Functions used to generate and fit the fixation functions, annotated with the free parameters. a A four-parameter logistic function. b An asymmetric Gaussian

This function starts from a lower asymptote or baseline ($b$), and transitions to an upper asymptote ($max$). The transition is at $xo$ (crossover), and the slope ($s$) is the derivative at the crossover.

Parameters for the underlying function were selected randomly for each run of the model. Each parameter was selected from a random normal distribution whose means and standard deviations were based on the normal hearing participants in (Farris-Trimble et al., 2014). Some constraints were put on these functions to ensure the resulting fixation function took a reasonable form (e.g., the crossover was between 0 and 2,000). See Supplement S2.

Competitors

Competitors were modeled with the asymmetric Gaussian (Equation 2, Fig. 4b):

$$p(\mathit{competitor})=\left\{\begin{array}{l}\mathrm{e}\mathrm{x}\mathrm{p}\left(\frac{(\mu -t{)}^2}{-2{\sigma }_1^2}\right)\left(ht-b_1\right)\text{if}t<\mu \\ \mathrm{e}\mathrm{x}\mathrm{p}\left(\frac{(\mu -t{)}^2}{-2{\sigma }_2^2}\right)\left(ht-b_2\right)\text{if}t\ge \mu \end{array}\right.\text{.}$$ (2)

This function consists of two Gaussians, each with their own asymptotes ($b_1$ and $b_2$) and their own slopes (onset slope $\left[{\sigma }_1\right]$ and offset slope $\left[{\sigma }_1\right]$). They share a common peak height ($ht$) and a common time at which peak is reached (peak time, $\mu$).

As before, parameters for the underlying functions were drawn from constrained normal distributions whose means and variances were taken from prior work (Farris-Trimble et al., 2014). Constraints were designed to keep the values in a reasonable range (e.g., competitors should peak below 0.4, and above the baselines).

Fixation generation

After selecting the parameters of the underlying function, a series of fixations were generated for a set number of trials to simulate an experiment. These models started from the underlying function as the probability of fixating the object, and models made progressively more sophisticated assumptions about the fixation-generating system. Data were then averaged to compute a fixation curve for that subject.

Analysis

Fixation curves were fit using a constrained gradient descent procedure used in prior studies (Farris-Trimble & McMurray, 2013; Farris-Trimble et al., 2014; McMurray et al., 2010). This uses a constrained gradient descent technique to find the parameters that minimize the least squared error between the observed fixation curve and the predicted function. There is no analytic solution to this problem, so suboptimal fits (local minima) can occur. Typically, one should visually inspect fits, and poor fits can often be corrected with hand-selected starting parameters. However, with the large number of fits here, this was impossible. Thus, three steps were taken. First, starting parameter estimates were improved with new techniques. Second, around 100 fits for each simulation were manually inspected to ensure fits were good. Finally, any fit whose correlation to the observed data was below 0.8 (across all runs) was dropped.

After obtaining fits, the parameters of the function (e.g., the slope, crossover, peak height) were the unit of analysis. Since these parameters were of the same form as the generating function, this permitted simple analyses asking whether the observed and underlying parameters were correlated, if there was bias, and so forth.

Overview of simulations

Our first simulation examined the high-frequency sampling (HFS) assumption. While this assumption is unrealistic (and one might say, inconceivable), these simulations document what the results of this Monte Carlo procedure look like under ideal circumstances. Simulation 2 turns to a simple fixation-based sampling (FBS) model in which fixations are a series of discrete units. Simulation 3 follows that up with a slightly more complex sampling scheme that acknowledges that eye movements may persist longer than average on activated objects (fixation-based sampling with enhanced target duration [FBS+T]), and Simulation 4 (Supplement S3) generalizes these to a multinomial model. The next simulations investigate the consequences of these models for measurement: Simulation 5 investigates test–retest reliability, and Simulation 6 investigates power and Type I error. Finally, Simulation 7 presents an exploratory new analysis that builds a fixation-generating model into the analysis.

Simulation 1: Stochastic high-frequency sampling

Approach

Figure 5 shows an overview of the approach. First, the parameters of a subjects’ underlying function were randomly generated. Next, 300 trials were generated. At each 4-ms time slice, the probability of fixating the target or competitor was computed from the subject’s underlying function (Eqs. 1 or 2, respectively). This probability was used to determine whether the subject was looking at the object or not at that time at each 4-ms time slice. To simulate the assumed 200-ms oculomotor delay, when computing the likelihood of fixating, the time was shifted by 200 ms. Thus, the likelihood of fixating the target at 600 ms was based on the logistic function at 400 ms. The series of fixations was then averaged across trials to generate the observed fixation curve. This was curvefit and compared with the underlying parameters.

Fig. 5.

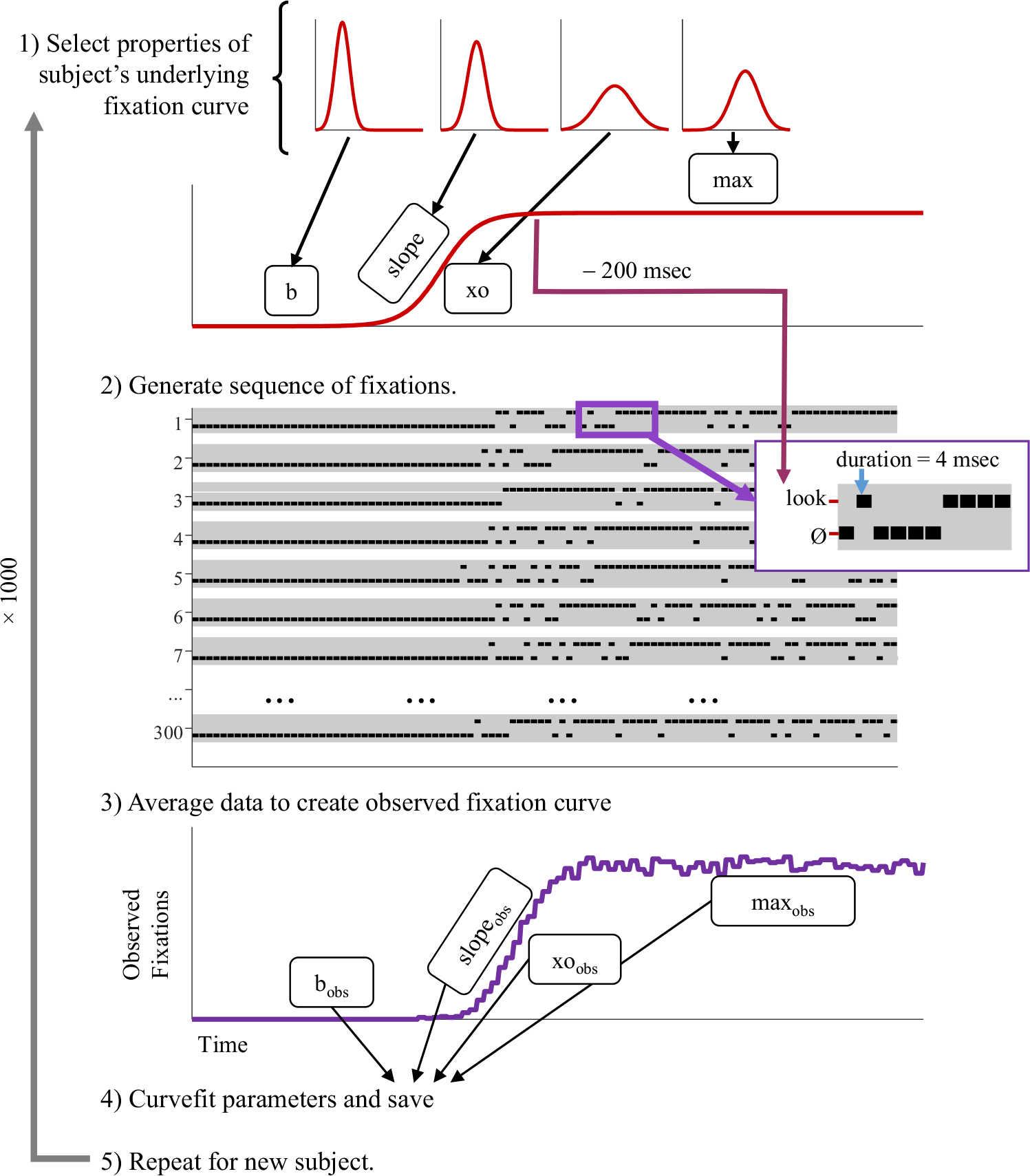
Overview of Simulation 1. (1) Parameters of the underlying function are selected from Gaussian distributions derived from empirical data (b [baseline], xo [crossover], slope, and max). These are used to define the underlying function specifying the likelihood of looking at each time. (2) Next, a series of fixations is generated. These are sampled every 4 ms. The likelihood of fixating comes from the underlying function at 200 ms before the current fixation. (3) Next, the data are averaged to compute the observed fixations. (4) Observed functions are fitted to extract observed parameters. (5) This is repeated for 1,000 subjects and the estimated and observed parameters are compared

Results and discussion

Target

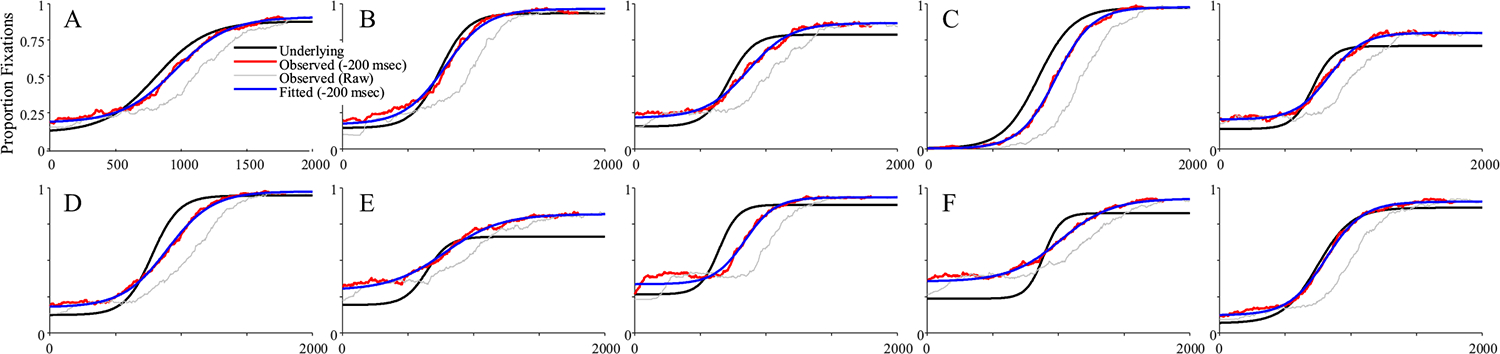
Figure 6 shows 10 representative subjects.⁴ Shown in black is the underlying function for that subject, and in gray is the observed data. To facilitate comparison to the underlying curves, red curves show the observed data after accounting for the oculomotor delay (200 ms). Fitted functions are shown in blue, also shifted for the oculomotor delay. Fits were good with an average correlation of 0.997 between the fits and the data, and no fits were dropped for poor correlations to the observed data.

Fig. 6.

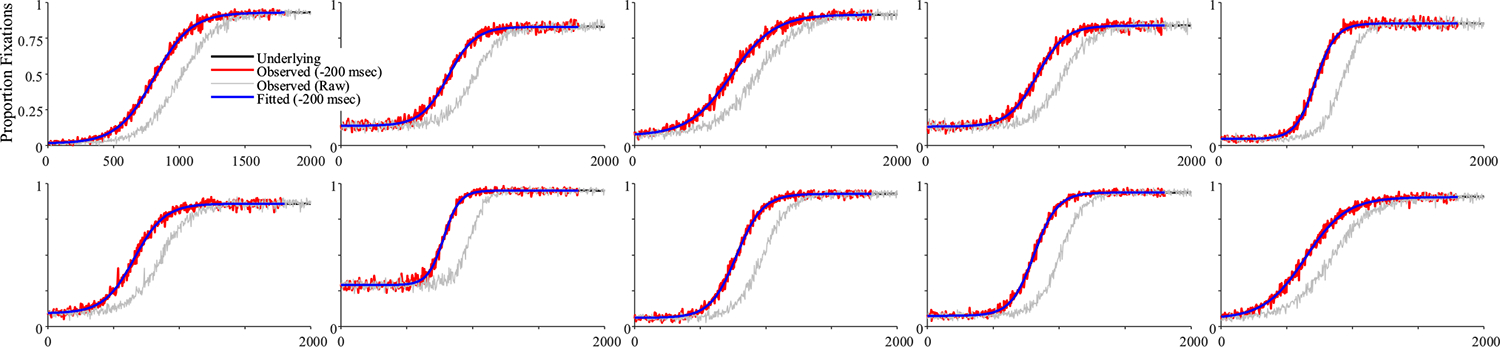
Representative subjects from the high-frequency stochastic sampling (HFS) simulations of target fixations. Shown is the underlying and observed likelihood of fixating the target over time for a single subject (in each panel). In black is the underlying function. In gray is the observed (generated data). Red shows the same data but shifted by 200 ms to account for the oculomotor delay. Blue is the logistic curve fit to the observed data (also shifted by 200 ms). Note that in all cases shown here, the fitted curve is directly over the underlying. Under HFS assumptions, once the oculomotor delay is accounted for, the observed data are a close match to the underlying function. (Color figure online)

The fitted curves were almost uniformly on top of the underlying curves (the reason you cannot see the black curves in Fig. 6). This is supported by the high correlations between the underlying parameter values and the fitted values (Table 1, Column 1): the baseline, peak, and crossover were all at 1.0 and slope was at 0.998. A high correlation could still be observed even if the data were systematically biased (e.g., if fitted crossovers were consistently later than the true crossovers). Thus, for each run, a difference score was computed (underlying − observed). Table 1 shows the average bias. As Fig. 7 shows, these were near zero for all parameters except crossover, which had a bias of −200 ms (the oculomotor delay), and standard deviations were very small. Finally, the correlation among observed parameters (Table 1) was computed to determine whether anything about our sampling procedure was imposing structure on the data that was not there in underlying latent functions (the underlying parameters were uncorrelated). Cross-correlations among the observed parameters were very low and always less than.05.

Table 1.

Summary statistics for the target simulations assuming a high-frequency sampling (HFS) eye-movement model

Parameter	Correl with underlying	Mean	Bias			Cross correlations among observed parameters
			M	SD	D	b	max	xo	s
Baseline (b)	1.0	.135	<.001	0.002	−.025		−.016	.005	.008
Max	1.0	.852	≥.001	0.0018	−.062	−.016		−.007	.036
Crossover (xo)	1.0	969.3	−200.0	2.26	−88.68	.0005	−.007		.007
Slope (s)	.998	.0019	<.0001	<0.0001	.0019	.008	.036	.008

The first column shows the correlation between the observed fits and the underlying function. Mean bias refers to the average difference between observed and underlying value for that parameter (note the −200-ms bias for crossover matches the oculomotor delay). SD refers to the standard deviation (across subjects) for bias. b: initial asymptote; max: upper asymptote, xo: crossover, s: slope

Fig. 7.

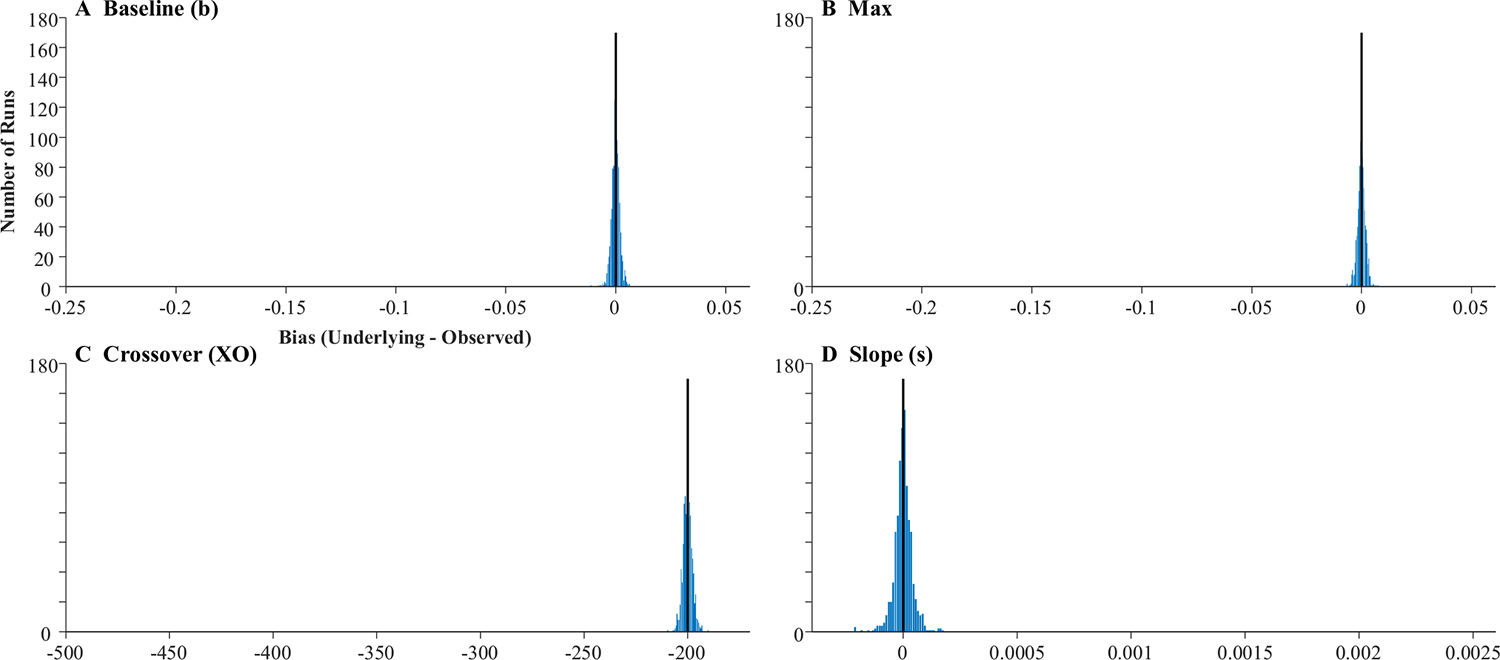
Histograms showing distribution of bias across subjects in the four parameters of the target model assuming high-frequency stochastic sampling (HFS). Histograms include 40 evenly sized bins, optimally spaced to reflect the distribution of the data. Axes are expanded to match the other histograms in this manuscript. The black line indicates what would be expected for an unbiased measure

Competitor fixations

A similar pattern was observed for competitor fixations. Figure 8 shows representative subjects. Fits were good with an average correlation of.919 (68/1,000 fits were dropped⁵). Again, observed fixations curves showed a very close match to the underlying curves, with the blue curves masking the black in virtually all conditions, and very high correlations between the observed and underlying parameters (Table 2; all rs >.94, and 5 were >.98). Examination of the difference scores (underlying − observed) showed little bias. The mean bias was very low, except for peak time, which was biased at −200 ms (again, the oculomotor delay). Histograms (Fig. 9) were centered where expected. Standard deviations of the bias were very low—μ, for example, scaled in ms, and had a standard deviation of only 11.7 ms.

Fig. 8.

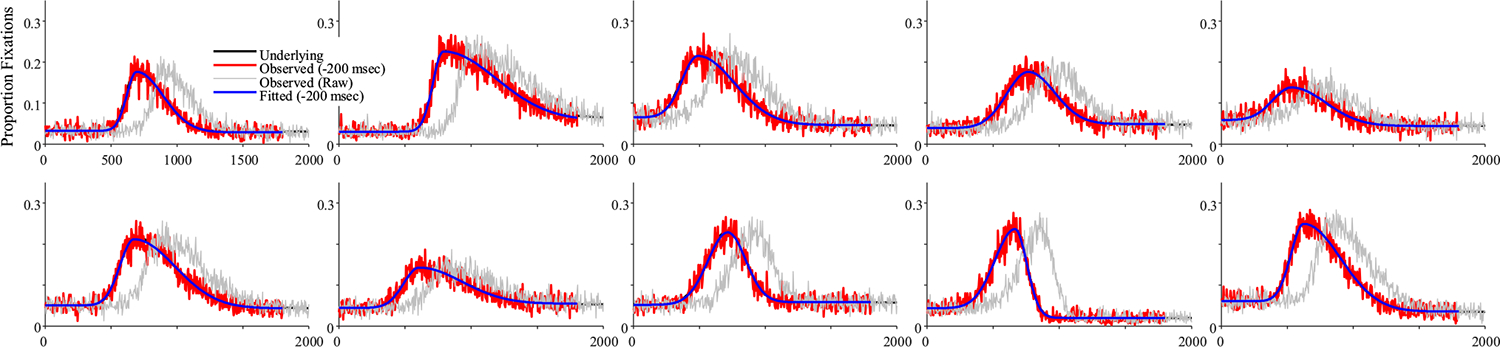
Representative subjects from the high-frequency stochastic sampling (HFS) simulations of competitor fixations. Shown is the underlying and observed likelihood of fixating the competitor over time for a single subject (in each panel). Note that in all cases shown here, the fitted curve is directly over the underlying. Under HFS assumptions, once the oculomotor delay is accounted for, the observed data are a close match to the underlying probability function. (Color figure online)

Table 2.

Summary statistics for the competitor simulations assuming a high-frequency sampling (HFS) eye-movement model

Parameter	Correl with underlying	Mean	Bias			Cross correlations among observed parameters
			M	SD	D	μ	ht	σ1	σ1	b1	b2
Peak time (μ)	.988	828.2	−200.0	11.8	−16.80		.001	.069	−.002	.008	−.004
Peak height (ht)	.997	.187	≥.0002	0.003	−.056	.001		.059	−.025	.054	.050
Onset slope (σ1)	.946	130.7	−.06	10.2	−.033	.069	.059		.008	.009	.009
Offset slope (σ2)	.990	240.0	.13	12.9	.014	−.002	−.025	.008		.024	−.043
Onset asymp (b1)	.996	.049	<.0001	.0012	−.002	.008	.054	.009	.024		−.021
Offset asymp (b2)	.996	.049	<.0001	.0013	.003	−.004	.050	.009	−.043	−.021

μ: Time of peak; ht: peak height; σ₁: onset slope; σ₂: offset slope_; b₁: onset asymptote; b₂: offset asymptote

Fig. 9.

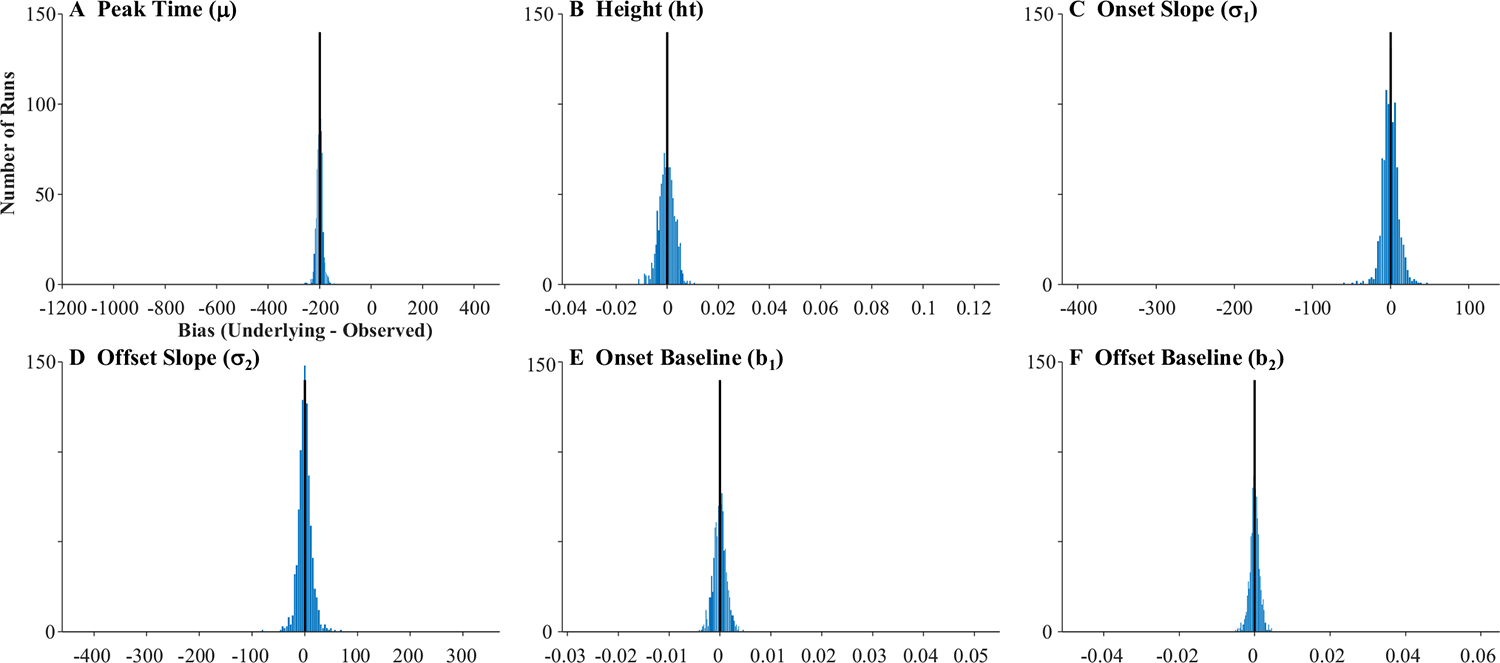
Histograms showing distribution of bias across subjects in the six parameters of the competitor model assuming high-frequency stochastic sampling (HFS). Histograms include 40 evenly sized bins, optimally spaced to reflect the distribution of the data. Axes are expanded to match the other histograms in this manuscript. The black line indicates what would be expected for an unbiased measure

Discussion

These simulations largely validate the modeling approach. When data were explicitly generated using an HFS model, underlying parameters of both targets and competitors could be reliably estimated. Estimates had low variance, were unbiased, and the curvefitting approach does not impose correlations on the estimated parameters. Moreover, validity was stronger than what would be expected based on the number of trials alone—even cohort asymptotes, with a mean of.05 showed correlations of greater than 0.996 (by comparison, Fig. 2 suggests these should be at.95). This is likely because these curvefit parameters are implicitly pooling across many draws (successive samples). HFS is, of course, implausible. However, this offers a picture of what results should look like when the assumptions of the analysis hold.

Simulation 2: Fixation-based sampling

Approach

Simulation 2 developed a rudimentary fixating generating model. The fixation-based sampling (FBS) model derives fixation curves from a series of discrete fixations with a reasonable refractory period. This model treats the fixations as primarily a read out of the unfolding decision. While this ignores the role of the fixation as an information gathering behavior, this is consistent with some views of the VWP that treat the fixation as primarily reflecting motor preparation (which is based on the unfolding decision), the parallel contingent independence assumption of Magnuson (2019). This is not intended as a complete model of fixations in the VWP. Rather, this model asks if the ballistic and chunky nature of the saccade/fixation system alone is sufficient to create noise and/or bias in the observed fixation curves. If even this minimal model shows enhanced noise and bias in the observed data, any more complex model is likely to as well.

In the FBS model (Fig. 10), the underlying curves for each subject were randomly generated in the same way as Simulation 1. Unlike that model, data on each trial is generated as a series of fixations whose duration were randomly determined from fixation to fixation. Once a fixation was “drawn,” the subject was presumed to be fixating on a single object throughout this time. The likelihood of fixating the target (or competitor) or not over this fixation was again determined by the underlying time-course function (either the logistic or asymmetric Gaussian), using the onset of the previous fixation as the time parameter. This assumes that at fixation onset, the subject immediately plans whether or not to look at the next object, but then wait through the fixation (the refractory period) before fixating it.

Fig. 10.

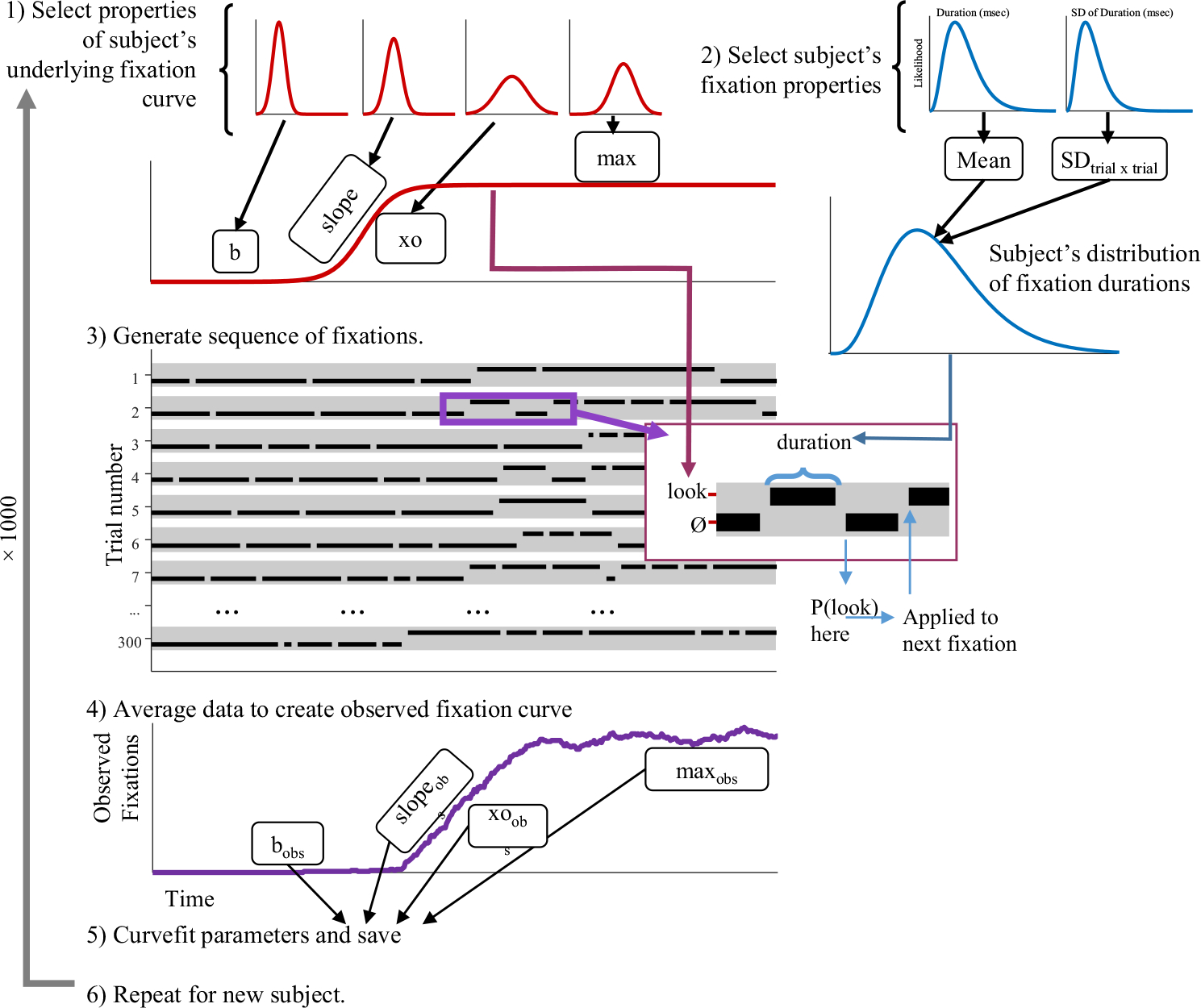
Overview of Simulation 2 (fixation-based sampling [FBS]). (1) Parameters of the underlying function (b [baseline], xo [crossover], slope, and max) are selected from Gaussian distributions derived from empirical data, as in Simulation 1. (2) A mean fixation duration, and a trial × trial SD of fixation duration are randomly selected from Gamma distributions derive from empirical data. (3) A series of fixations is then randomly generated. For each fixation (inset) the duration is randomly chosen from that subject’s distribution of fixation durations. The likelihood of fixating the object comes from the underlying function sampled from the onset of the previous fixation. (4) Next the data are averaged to compute the observed fixations. (5) Observed functions are fitted to extract observed parameters. (6) This is repeated for 1,000 subjects, and the estimated and observed parameters are compared

In addition to each subject’s own parameters for the underlying curves, each subject had their own unique distribution of fixation durations (the mean and SD), randomly chosen for that subject. These distributions (Table 3) were based on an analysis of the normal hearing participants (N = 37 subjects, 290 trials each) of Farris-Trimble et al. (2014). Across subjects, the mean fixation duration (to nontarget objects) was about 200 ms for nontarget objects, and subjects did not vary substantially (SD ~ 30 ms). Fixations were longer to the target than to other objects (or to nothing). Simulation 2 ignored this to create a minimal contrast with the HFS model (but Simulation 3 tests this). The mean duration was thus set to the average of the three nontarget objects (the last row). This was 204 ms, a close analogue to conventional estimates of the oculomotor planning time. Each subject also had their own trial-to-trial variability. These were estimated from the within-subject standard deviation in duration (Table 3, the within-subject-columns). These standard deviations were high, with individual fixations varying by 90–100 ms (the mean of SD column). Both the mean and within-trial standard deviation were chosen randomly and fixed for that subject.

Table 3.

Properties of fixation durations

Object	b/w Subject Mean Duration		w/in Subject (Trial × Trial) SD
	M	SD	Mean of SD	SD of SD
Target	360.3	65.8	195.1	39.04
Cohort	211.3	31.1	91.0	14.7
Unrelated	202.8	32.9	80.1	17.1
None	200.1	33.9	118.6	41.9
All nontarget	204.7	32.6	96.6	24.6

The random duration of a specific fixation, and the general properties of a subject (e.g., their mean distribution), were generated from a gamma distribution. This distribution (unlike a Gaussian ) is zero bounded with a long tail, so it matches the distribution of real fixations well. It has two free parameters—shape and scale. To convert means and standard deviations of the empirical data to shape and scale, shape was set to M²/SD² and scale to SD²/M.

Once a subject’s underlying distribution of fixations was selected, a series of trials was simulated. On these trials, fixations were simulated sequentially, so the second fixation was not randomly selected until after the first. For each fixation, the duration was selected randomly from a gamma distribution with the subject’s shape and scale. Whether or not a fixation was directed to the object (e.g., to the target or not) was based on the time of the onset of the prior fixation.

After generating a series of trials, data were averaged and analyzed as in Simulation 1. For display, when adjusting for the oculomotor delay, time was shifted by the mean fixation duration for that subject (which on average was about 200 ms).

Results and discussion

Target

Figure 11 shows representative subjects for the target simulation. Fits were good, with an average correlation of.998 and no excluded fits. Asymptotes generally lined up fairly well between the observed and underlying function. However, FBS created a much larger delay between the raw data (in gray) and the underlying function (in black) than the HFS model: Even after adjusting for that subject’s mean fixation duration (red for data, blue for fits), the observed curves were still delayed relative to the underlying curves. Slopes and crossovers were not only delayed but also less consistent. For example, in Fig. 11a, the delay was carried by a difference in crossover (slope was the same between observed and underlying), while in Fig. 11b, slope was shallower in the observed data. These observations are mimicked in the validity estimates (Table 4). While correlations between the observed and underlying values were above 0.98 for the asymptotes, they were lower (but still high) for crossover (r = .855) and slope (r = .751).

Fig. 11.

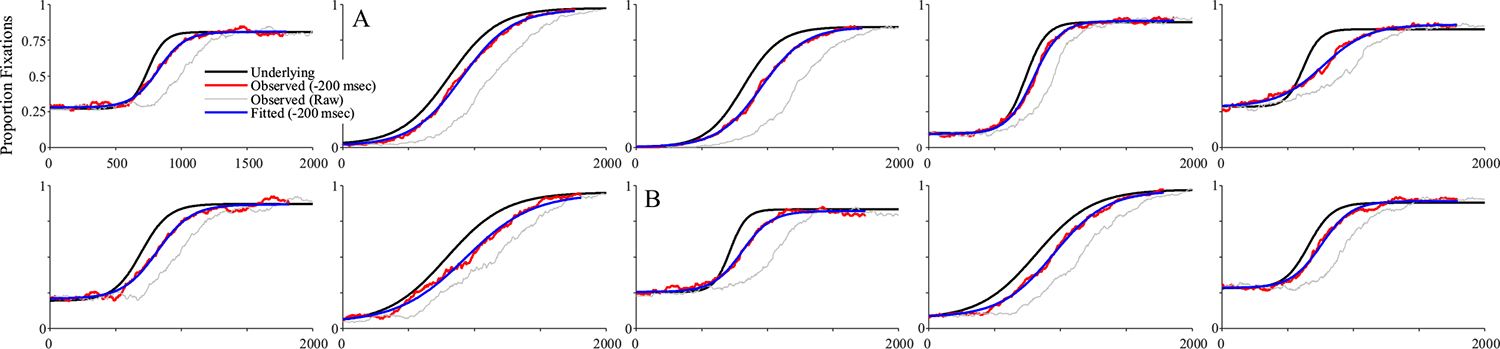
Representative subjects for target fixations assuming fixation-based sampling (FBS). Two patterns are highlighted: a The slope of the underlying function is preserved, but the crossover is delayed (even beyond the oculomotor delay). b The slope of the observed data is shallower than that of the observed data. (Color figure online)

Table 4.

Summary statistics for the target simulations assuming the fixation-based sampling eye-movement model

Parameter	Correl with underlying	Mean	Bias			Cross correlations among observed parameters
			M	SD	D	b	max	xo	s
Lower asymp (b)	.987	.132	.003	.012	.24		.008	.059	−.155
max	.986	.848	.0014	.016	.09	.008		.006	.237
crossover (xo)	.855	1094.0	−327.5	50.8	−6.44	.059	.006		−.071
slope (s)	.751	.0014	.0005	.0004	1.22	−.155	.237	−.071

b: initial asymptote; max: upper asymptote, xo: crossover, s: slope

Bias (Fig. 12) showed a similar pattern. The asymptotes were unbiased, with means near zero and fairly low variance. In contrast, the crossover was significantly biased; on average, the underlying crossover was 327.5 ms earlier than the observed. This was substantially more than one would have expected given the mean fixation duration of 203.7. Slope was also biased downward, as observed data showed generally shallower slopes than the underlying.

Fig. 12.

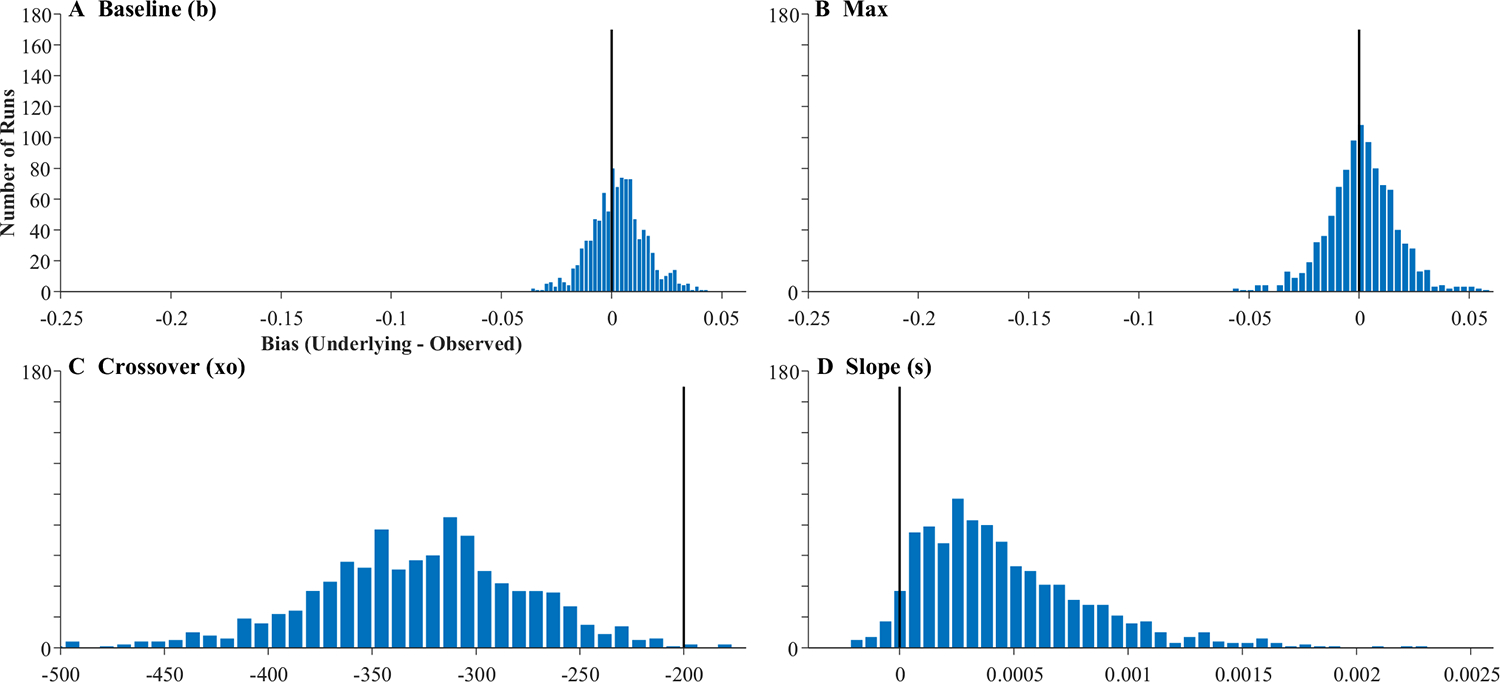
Histograms showing distribution of bias across subjects in the four parameters of the target model assuming fixation-based sampling (FBS). Histograms include 40 evenly sized bins, optimally spaced to reflect the distribution of the data. Axes are expanded to match the other histograms in this manuscript. The black line indicates what would be expected for an unbiased measure

Bias was highly related to the mean and standard deviation of the subject’s fixation durations. The bias in the crossover was correlated at r = −.897 with the mean duration: Subjects with longer fixations tended to have crossovers that were even later than the underlying crossover. To understand this, consider a fixation that was initiated at 500 ms—a time when the underlying probability function is just starting to rise. Whether or not it was directed to the target, however, is not dictated by the probability function at 500 ms, but by the function at 300 ms (when it was planned). However, for a participant with even longer fixation durations, it would have been planned even earlier (when the function was even lower). This would then slow the ultimate rise of the fixation curve. Moreover, once the subject decides to look (or not) that outcome is locked for the duration of the fixation, even if the underlying curve rises during that time. Thus, a long mean fixation duration acts as a drag, delaying the growth of the observed fixation curve. In contrast, the bias in slope was not highly related to the mean duration (r = .045) but was moderately related to the standard deviation (r = .269): Greater variability in the durations tended to smooth out the functions, resulting in slopes that were shallower than expected.

Finally, unlike the HFS model, the fixation-generating model appeared to impose correlations on the parameter estimates. There were moderate correlations between slope and the asymptotes (onset: r = −.155, offset: r = .237; Table 4 for complete matrix). Subjects with more extreme asymptotes tended to have larger slopes. Neither of these correlations were present in the underlying values (onset: r = .032; offset: r = .021). Thus, the fixation-generating model may make it difficult to achieve an unbiased estimate of a subject’s underlying fixation curve.

Competitor

Fits were good with an average correlation of 0.958, and 23 dropped runs. Figure 13 shows results. Competitors were much less consistent than targets. In some cases, the observed and underlying data matched (Fig. 13a); in others, there was a delayed onset, but otherwise similar functions (Fig. 13c), and in others the function was stretched (Fig. 13b). Some runs showed higher peaks (Fig. 13d), but others, lower (Fig. 13e). Thus, even with a large number of trials (300), most FBS runs were unlikely to approximate the underlying function.

Fig. 13.

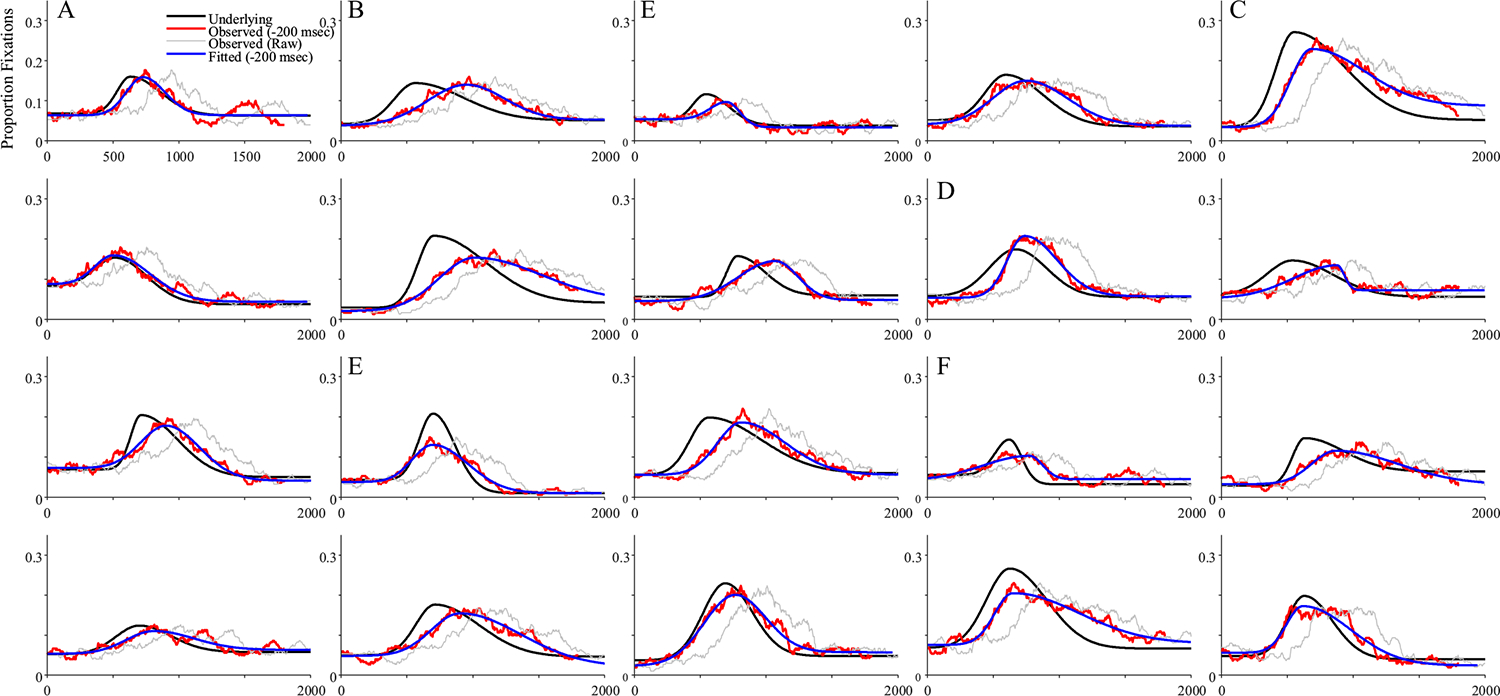
Representative subjects from the fixation-based sampling (FBS) simulations of competitor fixations. Shown is the underlying and observed likelihood of fixating the competitor over time for a single subject (in each panel). Several patterns emerged: a The observed data matched the underlying (after accounting for the oculomotor delay). b The observed function is delayed and slower to build and fall. c The observed function is delayed but otherwise similar. d The observed function has a higher peak than the underlying. e The observed data have a lower peak. (Color figure online)

This was reflected in the correlations between underlying and observed parameters (Table 5). Here, only parameters directly related to the overall amount of looking (peak height and asymptotes) were reasonably correlated with their underlying values (r ~.7). Peak timing (μ) was correlated but lower (r = .50), and the slope parameters had only small correlations. This lack of validity was not directly related to any of the eye movement parameters. Only peak timing was correlated with the mean fixation duration (r = .357; other parameters |r| < .1).

Table 5.

Summary statistics for the competitor simulations assuming a fixation-based sampling (FBS) eye-movement model

Parameter	Correl with underlying	Mean	Bias			Cross Correlations among Observed parameters
			M	SD	D	μ	ht	σ1	σ1	b1	b2
peak time (μ)	.502	976.2	−351.3	126.4	−2.13		−.030	.493	−.233	−.104	.038
peak height (ht)	.845	.158	.0245	.025	.85	−.030		−.169	−.082	.178	.188
onset slope (σ1)	.112	202.4	−72.0	121.2	−.55	.493	−.169		−.145	−.319	−.015
offset slope (σ2)	.327	271.4	−37.3	140.8	−.27	−.233	−.082	−.145		−.019	−.453
onset asymp (b1)	.799	.048	.0019	.011	.20	−.104	.178	−.319	−.019		.053
offset asymp (b2)	.681	.048	.0019	.015	.14	.038	.188	−.015	−.453	.053

μ: Time of peak; ht: peak height; σ₁: onset slope; σ₂: offset slope; b₁: onset asymptote; b₂: offset asymptote

This lack of systematicity was also seen in bias (Fig. 14). While b₁ and b₂ were unbiased, peak timing (μ) was biased well beyond the 200-ms oculomotor delay. Height was biased downward, with lower values than the underlying. However, in quite a few runs (139/1,000), the observed ht was higher than the underlying value. Onset and offset slopes were generally lower (steeper) than the underlying values. Bias was related to the properties of the subject’s fixations. Predictably, the bias in peak timing (μ) was negatively related to the mean fixation duration (r = −.383): subjects with longer fixation durations showed more delayed peak timing values relative to their underlying values. Bias in peak height (ht) was correlated with the variability in a subject’s fixations (r = .248): subjects with more variable fixations tended to have lower heights relative to the underlying. Importantly, all parameter estimates showed substantially more variance than the HFS model (Fig. 8). Thus, with a more realistic fixation model, the observed data are biased in some parameters and there is dramatically more noise.

Fig. 14.

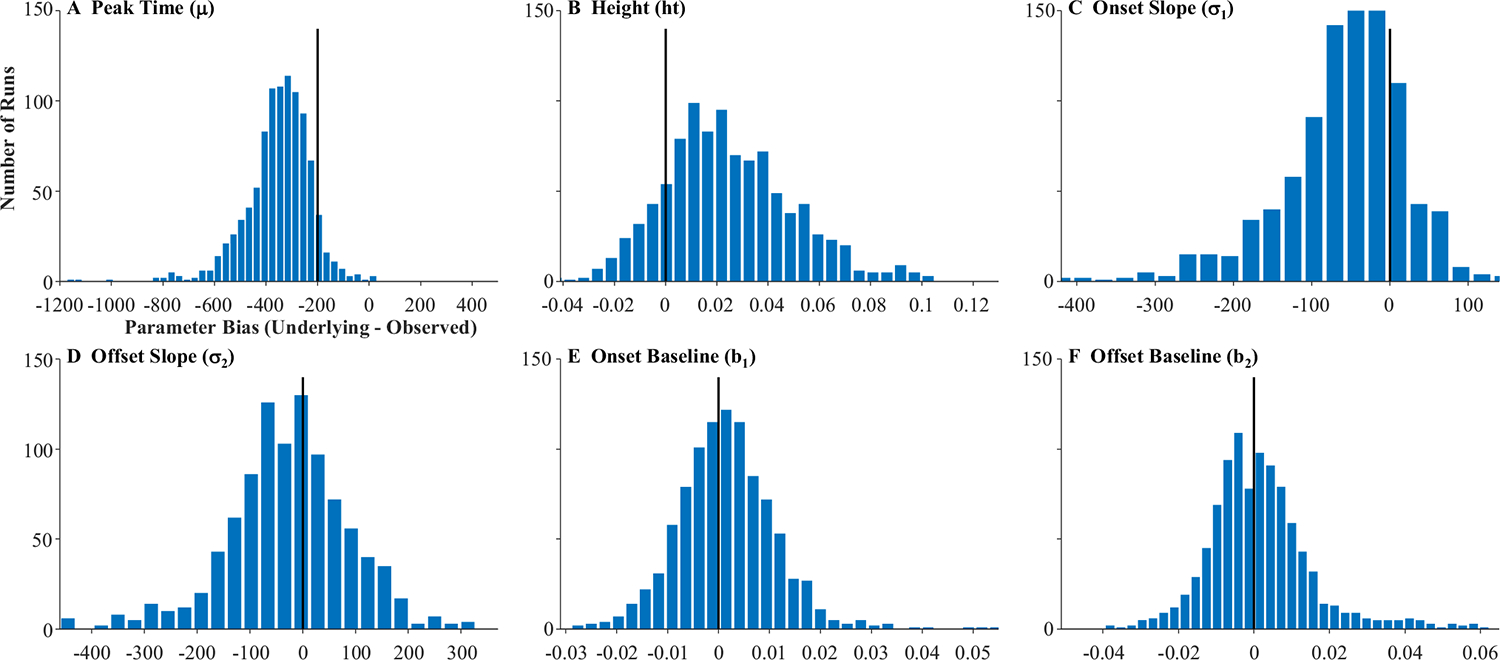
Histograms showing distribution of bias across subjects in the six parameters of the competitor model assuming fixation-based sampling. Histograms include 40 evenly sized bins, optimally spaced to reflect the distribution of the data. Axes are expanded to match the other histograms in this manuscript. The black line indicates what would be expected for an unbiased measure

Finally, even as the underlying parameters were uncorrelated, the FBS generating model imposed moderate correlations among several observed parameters (Table 5). Onset slope (σ₁) was strongly correlated with peak timing (μ) and had a small correlation with b₁. Offset slope (σ₂) was also correlated with b₂. All of the parameters had small but non negligible correlations above 0.1. Thus, the fixation-generating model created spurious correlations among estimates.

Discussion

These simulations suggest that assuming even a simple serial fixation model has substantial effects on the observed data. Observed target fixations rose more slowly and were delayed far beyond the expected 200 ms oculomotor delay. Competitor fixations were also delayed. Moreover, there was large variance across subjects, and in many individual runs, the competitor fixations did not provide a close fit to the underlying data. One bright spot was the asymptotes which tended to be unbiased for both types of fixations (even as the variance was higher), which seemed to be reliable even when the FBS model was assumed.

Competitor estimates were noticeably poorer—particularly for parameters related to timing (slopes and peak time). To some extent this drop in validity is to be expected. These parameters are working from a portion of the underlying curve that is low (e.g., Fig. 3a); but these estimates are far lower than would be expected by stochastic sampling alone (with 300 trials, the lowest correlation in Simulation 0 was still greater than.9). Thus, this suggests that the FBS system is creating additional (and complex) noise in the system.

Notably, when the underlying function showed only a small peak (e.g., Fig. 13e–f) the fixation curve tended to show an even smaller peak. This is because if the heightened underlying activation was short lived, it was less likely that there would be a fixation launched in that window (to reflect that). This may explain why Simmons and Magnuson (2018) did not find evidence for rhyme activation in one-syllable words and Teruya and Kapatsinski (2019) did not observe it for one-phoneme overlap cohorts. It is not that these competitors were inactive; rather, the stochastic process of generating fixations made it difficult to see it.

Simulation 3: Fixation-based sampling with enhanced target duration

Approach

In the empirical record (Table 3; Farris-Trimble et al., 2014), target fixations were about 160-ms longer than fixations to other objects: Once the subject fixated something reasonably active, they were more likely to stay. This was not accounted for by the FBS model, and it was unclear how this would change the results. It could further delay target fixations. However, it also could enhance overall target looking, speeding the function.

This simulation thus implemented a simple modification to the FBS model. Fixations were randomly selected as before. However, if a given fixation was to be to the target, its duration was drawn from a distribution with longer mean and standard deviation (Table 3). If the fixation was to be away from the target, it was drawn from the same distribution as before (shorter durations). Since this effect was not observed in competitor fixations, Simulation 3 only considered targets.

Results

Fits were good averaging r = .998, and no subjects were dropped. Figure 15 shows representative results. It is noteworthy that many of these functions are no longer symmetrical and could have shallower slopes at early times and steeper slopes at later ones (Fig. 15b), or the converse (Fig. 15e). This is commonly observed in real data (and a limit of using the four-parameter logistic). This finding suggests this asymmetry may come in part from fixation sampling issues. The degree of match between underlying and observed fixation curves was much more variable. In Fig. 15a, for example, the observed data matched the underlying data fairly closely, and do not even show the heightened delay seen of the FBS models (see Fig. 11). However, this was not consistent across runs (cf. Fig. 15c). For the first time, there was also a significant failure of the observed data to preserve the asymptotes. In Fig. 15d, for example the observed lower asymptote is above the underlying, while in Fig. 15f, both asymptotes are off. As a result, estimated parameters are less correlated with their true values than in Simulation 2 (Table 6). The asymptotes are off ceiling (though still high), and crossover (r = .792) and slope (r = .616) are quite a bit lower.

Fig. 15.

Representative subjects for target fixations assuming fixation-based sampling with enhanced target duration (FBS+T). Two patterns are highlighted: a The underlying and observed data are a fairly close match. b There is an additional delay but otherwise a close match in slope. c The slope is shallower. d Asymptotes of the observed data exceed the underlying. (Color figure online)

Table 6.

Summary statistics for the target simulations assuming a fixation-based sampling with enhanced target duration (FBS+T) eye-movement model

Parameter	Correl with under	Mean	Bias			Cross correlations among observed parameters
			M	SD	D	b	max	xo	s
Lower asymp (b)	.935	.187	−.051	.047	−1.08		.147	.002	−.528
max	.892	.895	−.050	.044	−1.12	.147		−.209	−.049
crossover (xo)	.792	1,087.9	−322.6	66.2	−4.88	.002	−.209		0.114
slope (s)	.616	.0012	.0007	.0005	1.41	−.528	−.049	.114

b: initial asymptote; max: upper asymptote, xo: crossover, s: slope

There was bias in all four parameters (Fig. 16). Both asymptotes were systematically shifted to be greater than observed values. The crossover was later, and slope was systematically higher. We also saw increased variance—particularly in the asymptotes—over Simulation 2. However, correlations between the estimated parameters were only a little worse than in Simulation 2 (Table 6). Slope was highly correlated with the lower asymptotes (but not the upper), and crossover and the upper asymptote had a small correlation.

Fig. 16.

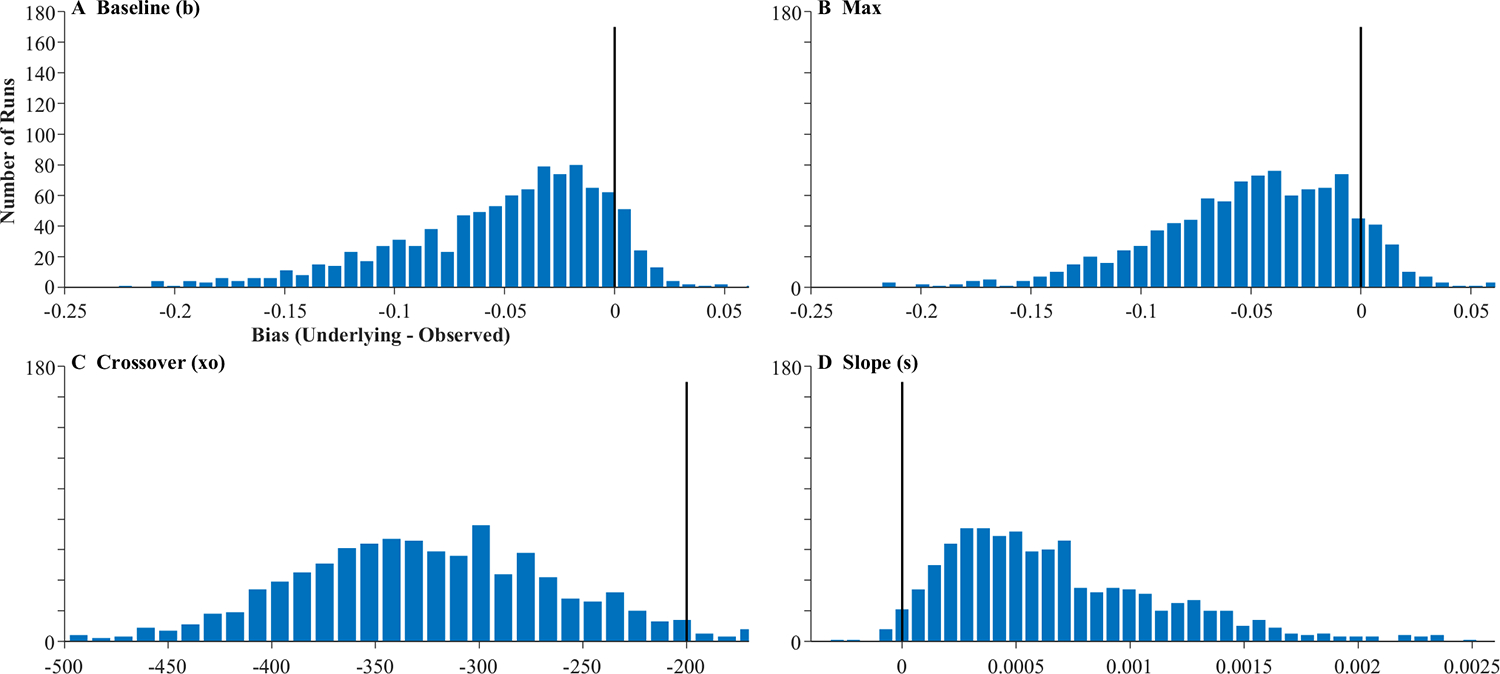
Histograms showing distribution of bias across subjects in the four parameters of the target model assuming fixation-based sampling with enhanced target duration (FBS+T). Histograms include 40 evenly sized bins, optimally spaced to reflect the distribution of the data. Axes are expanded to match the other histograms in this manuscript. The black line indicates what would be expected for an unbiased measure

Discussion

This simulation added realism to the FBS model in one small step: If the subject fixated the target at a given moment, that fixation was lengthened by about 160 ms. Doing so added even more variability—even to the asymptotes—and bias to all parameters.

Simulation 4 (supplement)

The forgoing simulations treated fixations to each object (target or competitor) as deriving from a binomial distribution (is the participant fixating the target/competitor or not). This is an oversimplification of the true, multinomial process, in which the participant must choose which object (of the four) to fixate. Supplement S3 thus constructed a multinomial version of Simulations 1–3. Findings were similar with a fairly close alignment between the underlying and observed fixation curves under the HFS fixation model and increasing variability and bias under more realistic FBS and FBS+T models.

Simulation 5: Reliability

Approach

Simulations 1–4 suggest that more realistic fixation-generating models lead to systematic and unsystematic differences between the observed data and the underlying function. While the systematic differences (bias) pose a problem for interpretating the data, unsystematic differences (noise) may impact the psychometric properties of the VWP: reliability, power, and Type I error (TIE). For example, in competitor models, the observed peak was sometimes higher than underlying and sometimes lower (Fig. 12d–e). This raises the question of whether the observed data are reliable. That is, if one generated a series of fixations from the same underlying function twice, would the fixation curves from each run match? It is possible that even with a reasonable number of trials, there would not be sufficient samples to converge on the “true” observed data (e.g., Fig. 3b). In contrast, the observed data could be reliable from run to run, and the unpredictability across different runs in the prior simulations is stable. This would imply that the mapping between underlying and observed functions is lawful, but highly complex.

This is a question of reliability. This issue is being confronted throughout our field as experimental measures are adapted to individual difference metrics (Enkavi et al., 2019; Hedge et al., 2018). As the replication crisis in experimental psychology has unfolded (Open Science Collaboration, 2015), there has been significant attention paid to poor scientific (Bakker et al., 2012) and statistical (J. P. Simmons et al., 2011) practices and to small effect sizes. However, equally important is reliability: A true effect may fail because the empirical measure is not reliable (Schmidt, 2010). This is particularly a problem for measures adapted from experimental psychology, which are often optimized to minimize within-subject variability (Hedge et al., 2018). In that way a failure to understand (and report) the reliability of the VWP is an example of a questionable measurement practice (Flake & Fried, 2020).

This is increasingly important for the VWP. As the VWP is applied to clinical populations, individual differences and development (Desroches et al., 2006; McMurray et al., 2019b; Mirman et al., 2008; Rigler et al., 2015; Yee et al., 2008), its reliability is the upper limit of what effect sizes can be detected. If a measure is only correlated with itself at r = .6 (test–retest reliability), it cannot have a higher correlation than.6 with any other factor. There is only one published study of the test–retest reliability of the VWP (though one hopes for more; Farris-Trimble & McMurray, 2013). It showed good to moderate (r = .5–.75) reliability depending on which aspects of the fixation curves were examined.

Test–retest reliability in the real world is a product of two things. The first is how stable the latent trait is. In the framework developed here, this corresponds to the underlying curve. Second, reliability is a product of how consistently the test assesses those latent values. Usually, we think of measurement accuracy as a function of properties of the test: The items, the timing of the stimuli, fatigue, and so on. However, the previous simulations suggest that in the VWP substantial noise may derive from the stochastic fixation-generating function. If the stochasticity of the eye-movement system also contributes to lack of reliability, there may be an upper limit to what can be achieved by optimizing the VWP along traditional dimensions (items, trial design, etc.).

Simulation 5 thus ask how much the fixation-generating process contributes to a lack of reliability by locking the underlying latent curve and examining reliability solely as a function of the stochasticity of the generating process. On each “trial” a subject’s underlying fixation curve was randomly selected. Next, fixations were generated for a fixed number of trials and fit as before. After that, a new set of trials was generated from the same underlying function. This was done for 1,000 subjects, and the estimated parameters of the fixation curve were correlated across test and retest. This was done for all three eye-movement-generating models (HFS, FBS, and FBS+T), and for three different sizes of experiments (50, 150, and 300 trials).

Note that these estimates will be higher than empirically estimated reliability, as they only reflect a single source of lack of noise (the stochasticity of the eye movements) and assume perfect stability of the latent trait. Moreover, these simulations used the Pearson correlation to estimate reliability; better estimates would be obtained with the concordance or interclass correlations (Bartko, 1966; Lin, 1989), both of which test for a one-to-one relationship (rather than mere predictability). The simpler Pearson coefficient was used for comparability to the only published work on the reliability of the VWP (Farris-Trimble & McMurray, 2013). Estimates with the concordance or interclass correlation are likely to be smaller.

Results

Figure 17 shows reliability of each parameter as a function of the number of trials, and the fixation-generating function (Table 7 for numerical results). Under the HFS assumption (blue lines), reliability was strong for almost all parameters, even with only 50 trials (r >.89, for all but σ₁). Moreover, for targets, the fixation-based generation was not a huge factor, as long as there were sufficient trials. At 300 trials, all four parameters could be estimated at r >.82, even assuming FBS or FBS+T generating models (though that this would be expected from randomness alone: Fig. 3b). With fewer trials, reliability was generally preserved at r >.7 levels for baseline, max, and crossover, but not slope. Moreover, the difference between the generating models was minimal. Thus, even though Simulations 1–3 suggest that FBS and FBS+T models bias the observed data relative to the underlying function, this bias is consistent, and properties of the observed data can be estimated reliably.

Fig. 17.

Test–retest reliability for parameter estimates as a function of number of trials (x-axis) and generating model (curves). a Target parameters: baseline (b), max, crossover (xo), and slope (s). b Competitor/asymmetric Gaussian parameters: peak time (μ), peak height (ht), onset slope (σ₁), offset slope (σ₂), initial asymptote (b₁) and final asymptote (b₂). HFS: high-frequency stochastic sampling; FBS: fixation-based sampling; FBS+T: fixation-based sampling with enhanced target duration. (Color figure online)

Table 7.

Test–retest reliability (Pearson correlation) for parameter estimates as a function of fixation model and number of trials

Parameter			HFS			FBS			FBS+T
			300	150	50	300	150	50	300	150	50	# trials
Target	Reliab	b	.999	.999	.997	.976	.954	.867	.971	.943	.831
		max	1.000	.999	.998	.974	.950	.852	.954	.905	.779
		xo	.999	.998	.995	.954	.914	.770	.943	.885	.680
		s	.996	.991	.976	.820	.683	.359	.852	.703	.457
	Validity	b	1.000	.999	.998	.988	.977	.932	.943	.928	.873
		max	1.000	1.000	.999	.986	.974	.925	.907	.893	.807
		xo	1.000	.999	.998	.840	.828	.769	.806	.774	.668
		s	.998	.996	.988	.739	.683	.510	.611	.564	.484
Competitor	Reliab	μ	.979	.965	.896	.585	.452	.184
		ht	.994	.987	.968	.775	.651	.332
		σ1	.933	.880	.613	.189	.001	−.041
		σ2	.985	.968	.914	.233	.115	.005
		b1	.988	.985	.959	.675	.491	.194
		b2	.992	.983	.944	.452	.263	.175
	Validity	μ	.986	.976	.950	.584	.510	.375
		ht	.997	.994	.983	.787	.687	.465
		σ1	.782	.764	.795	.177	.153	.070
		σ2	.992	.981	.957	.440	.289	.189
		b1	.486	.487	.471	.401	.336	.213
		b2	.996	.992	.974	.641	.535	.401

Validity rows show average of the correlation of the derived estimates and the underlying parameters (averaged across the two runs). Note that the fixation-based sampling with enhanced target (FBS+T) simulations were not run for the competitors as this model is not different from the fixation-based sampling (FBS) model for competitors. Target parameters: baseline (b), max, crossover (xo), and slope (s). Competitor/asymmetric Gaussian parameters: peak time (μ), peak height (ht), onset slope (σ₁), offset slope (σ₂), initial asymptote (b₁), and final asymptote (b₂)

This pattern was not observed for competitors. With the FBS generating model, reliability dropped from >0.95 in most cases to.7 or below at 300 trials. They fell off precipitously with fewer trials. These estimates (even at 300 trials) are below what one would have expected from mere random sampling alone (Fig. 3b). This suggests the fixation-generating function added additional noise. The lack of reliability suggests the diverse of patterns of observed data in Fig. 13 are not systematic: Sometimes the same underlying function can produce a delayed and shallow function, and sometimes a higher peak. This is particularly true with few trials.

Discussion

For target fixations the more realistic fixation models reduce reliability but only somewhat. The exception was slope at low numbers of trials where reliability was not acceptable. Thus, while the observed data may be systematically biased (delayed) by the fixation-generating function, the pattern of data is at least reliable. This can also be seen in the raw fixation curves data (Supplement S4, Fig. S4.1,2). In the real world, factors like the number of trials, the set of items, or the testing conditions may be more important drivers of reliability (or lack thereof) than the stochasticity of the oculomotor system.

In contrast, for competitors, more plausible generating models reduced reliability to well below acceptable ranges. This was particularly true when small numbers of trials were tested. This was not due to poorly shaped data or to bad fits—I excluded all of the bad fits before computing reliability. Rather the same underlying function can give rise to differently shaped data. This is also not a function of the statistical analysis—the same lack of reliability can be observed in the observed fixation curves, prior to analysis with the curvefitter (Supplement Fig. S4.3). This suggests that the stochasticity of the eye movements is likely a reason why Farris-Trimble and McMurray (2013) found generally lower reliability estimates for most parameters describing cohort and rhyme fixations than for those describing target fixations.

These results stand in contrast with the fact that reliability in the HFS model was relatively high across all parameters for both targets and cohorts. This is important as it suggests that it is not just the random sampling (e.g., the number of trials), driving lower reliability but the nature of the fixation-generating scheme.

One caveat is that these reliability estimates are for single indices of the curves (e.g., the slope of the target in one condition). This is appropriate for individual difference designs (e.g., McMurray et al., 2010); however, in experimental conditions it may be that the difference of these estimates (e.g., between conditions) is of greater importance. Reliability of differences is likely to be lower as the variance in each condition compounds.

Simulation 6: Power and Type I error

Approach

The prior simulations suggest that the stochasticity of the fixation-generating function reduces reliability in some indices—even when the underlying function did not change from test to retest. This raises the question of whether power (the likelihood of detecting a true effect) or Type I error (TIE, the likelihood of detecting an effect that is not there) is affected by the fixation-generating functions. These were investigated in a series of simulated experiments.

In experiments assessing power, subjects were tested twice with some difference in the underlying parameters to simulate an experimental condition. The size of this difference varied randomly across subjects (e.g., as a random slope) to achieve a predefined power. Next, data were generated for each condition for each subject and the time course functions were fit. The resulting parameters was then analyzed to determine if condition was significant. One thousand experiments were run to compute the overall likelihood of detecting an effect in some underlying parameter. Separate simulations were run shifting each underlying parameter (e.g., a difference in slope, peak etc.), and for each of the three fixation-generating models (for target: HFS, FBS and FBS+T; for competitors, HFS and FBS). Two experiments were also conducted in which two parameters were shifted together: slope and crossover for target, and height and offset baseline for competitors (these are commonly correlated in real data).

A second set of experiments assessed Type I error. These used the same procedure as those assessing power, with two exceptions. First, the randomly selected experimental difference had a mean of zero, but the variance was the same as in the power analyses. Second, a random difference for all parameters was tested in the same experiment.

In addition to using the parameters as DVs, a variety of commonly used single indices like AUC, or the peak of the fixation curves were computed (Table 8). The rationale for this was that these common indices—though they less precisely characterize the curves—may capture more global changes as well as or better than more precise measures. Finally, as our prior simulations suggested that some parameters were affected by the mean and variance of the fixation durations, for each DV, statistical tests were conducted both with a traditional t test and with an analysis of covariance (ANCOVA), which controlled for the mean and standard deviation of fixation duration.

Table 8.

Individual indices of the fixation curves

Used for	Estimate	Analog	Description
Target+Competitor	AUCearly	max, ht, b2	Average fixations (area under curve) from 200 to 1,200 ms
	AUClate	max, b2	Area under curve from 1,000 to 2,000
Competitor	AUCfull	ht, b2	Area under curve from 200 to 2,000
Target	maxDeriv	slope	Maximum derivative. Data smoothed with a 96-ms triangular window. Derivative computed as regression slope in a 7-frame window. Maximum slope across the time course.
	maxDerivtime	xo	The time of the maximum derivative.
	Threshold75	xo	The time at which fixations crossed 75% of that subjects maximum fixations (Ben-David et al., 2011). Data were first smoothed with a 48-ms window.
	Time25/75	slope	Time between the point at which fixations first cross 25% of that subject’s maximum, and when they cross 75%.
	Timing	slope + xo	Composite of slope and crossover (McMurray et al., 2019a). slope and xo are estimated from curvefitter. Next is log scaled and multiple by -1. Finally, both estimates are converted to z-scores and averaged.
Competitor	Peaklooks	ht	Maximum over the full time course. Data were first smoothed with a 48-ms window.
	Peaktime	μ	Time at which Peaklooks is observed
	Extent	σ1+σ2	The duration over which fixations were greater than .05. Data were smoothed with a 48-ms window.

Analogs refer to which parameters of the logistic or asymmetric Gaussian functions are likely reflected by a given index. max: upper asymptote of logistic; ht: Peak of asymmetric Gaussian; b₂: final asymptote of asymmetric Gaussian; slope: slope of logistic; xo: crossover point of logistic; μ: Time of peak in asymmetric Gaussian; σ₁, σ₂: Initial/final slope of asymmetric Gaussian

All experiments used 300 trials per condition to eliminate the number of trials as a factor driving any differences in power. The sample size was 50 subjects. This was chosen as a reasonable sample size that could accommodate two covariates. I computed the minimum detectable effect (using traditional power analyses) to determine what effect size could be detected for a given power. I assumed a power of 0.7—deliberately less than the standard 0.8—to avoid potential ceiling effects. This suggested an effect size of d = .358, which is not an effect of unusual size for the VWP. For simulations manipulating two parameters this was divided by the square root of two, leading to a difference of.253 on each individual parameter, but a difference of.358 along the diagonal (i.e., in both dimensions together).

To simulate an experimental condition, subjects’ baseline parameters for their logistic or asymmetric Gaussian were first selected along with a mean difference for that subject on the parameter of interest. This difference came from a normal distribution with a fixed mean (specified in advance), and whose standard deviation was the mean difference divided by the targeted effect size. As a result, most subjects would have the expected difference, but some could have a larger difference and others might have no difference. Random generation of the differences was constrained such that parameters could not be outside of the ranges in Supplement S2 (e.g., crossover must be between 300 and 1,100). It was also constrained in other ways—for example, the height of the competitor fixations could not be lower than the baselines. If the randomly selected difference led to an invalid value, it was reselected. This tended to alter the variance in unexpected ways, often leading observed power (in the underlying parameters) that was lower than the targeted 0.7. To accommodate this, the same parameters of the underlying functions were analyzed to capture the true power absent the fixation-generating functions.

Results

Power

In none of the analyses was power markedly changed by the inclusion of the mean and standard deviation of the fixation durations as a covariate: No individual analysis showed more than a.01 increase in power in the ANCOVA over the standard t test, and many showed a small decrease. Thus, the ANCOVAs were not considered further.

Figure 18 shows selected results for power simulations using T tests. Each grouping shows the results of one type of experiment manipulating a single parameter of the underlying function. Black lines show the likelihood of a significant effect on the underlying parameters, absent the noise imposed by the fixation-generating function (α = .05 is also marked). Colored lines show the likelihood of detecting an effect in each parameter or index.

Fig. 18.

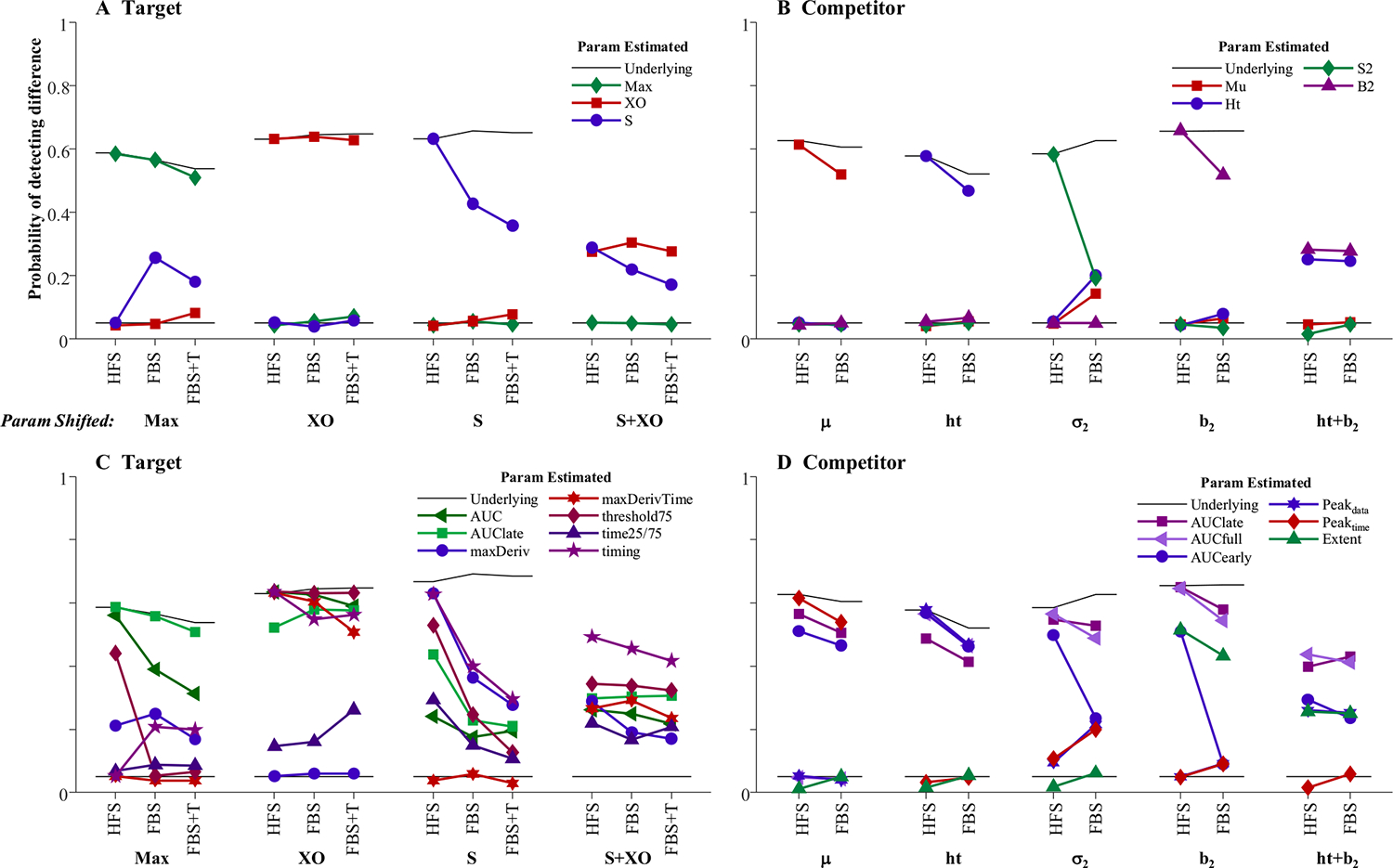
Power to detect a significant effect as a function of the parameter that differed in the underlying curves, and the fixation-generating function. On each experiment, a single parameter of the underlying function was “shifted” by (on average) 0.35 SD (for a power of.6). The parameter that was shifted is indicated below each grouping of curves. The observed power in the underlying parameters is indicated by the black curve. Different estimates are indicated by different colored curves within each group. a Parametric analysis of target fixations. Parameters include baseline (b), max, crossover (xo), and slope (s). b Parametric analysis of competitors. Parameters include peak time (μ), peak height (ht), onset slope (σ₁), offset slope (σ₂), initial asymptote (b₁) and final asymptote (b₂). c Results of nonparametric, single estimate measures on the same data as a (see Table 8 for description of the estimates). d Results of single estimate measures on the same data as d. HFS: high-frequency stochastic sampling; FBS: fixation-based sampling; FBS+T: fixation-based sampling with enhanced target duration. (Color figure online)

Figure 18a–b shows the result for the curvefit parameters (numerical results are too big to print, but available as an excel pivot table at https://osf.io/wbgc7/). In the first grouping of Fig. 18a, the underlying max was shifted by.358 standard deviations. The green curve there shows that a curvefitting approach could reliably detect this shift in the maximum at a power of about 0.6 (the same power observed for the underlying maximum assuming no fixation-generating model); in contrast, when max was shifted, the crossover (in red) was only significant on 0.05 of experiments for all generating functions. This suggests a high degree of specificity.

Looking across analyses, when the (unrealistic) HFS eye-movement-generating function was assumed (the first point in each grouping), the likelihood of detecting an effect in the observed estimates matched the likelihood of the underlying estimates. That is, when crossover (for example) was manipulated, and a statistical test was conducted on that parameter, the first point in each grouping showed strong power, and the same power if as the underlying functions were analyzed. Moreover, the likelihood of detecting a spurious effect (e.g., an effect on crossover when peak was shifted) was near.05. This suggests that under the HFS model, the analytic approach behaves as expected, with good power and specificity.

With more realistic generating functions (the second and third points), a different pattern emerged. When peak and crossover of the target were manipulated, this generally showed good power and specificity. Differences in peak or crossover were detected at the same rate as present in the underlying functions (black lines). Moreover, there were few spurious effects (e.g., an effect on max when the underlying difference was in crossover) except slope, which responded to changes in underlying peak at greater than.05 (Fig. 18a, first grouping, blue line).

In contrast, when the underlying change was in slope, results were markedly different: Power dropped off substantially for both the FBS and FBS+T models.

A similar story was observed for the competitors. For peak time, height, and baseline, power showed only a small reduction (of about 0.1) with the FBS generating model. However, for the slope parameter (σ₂), it showed a dramatic reduction.

In both simulations that manipulated multiple underlying parameters (Fig. 18a–b, last groupings), power was reduced. This makes sense as the t test only considered an individual parameter and the effect size was spread among two. This suggests reduced power when of overrelying on single estimates of the curves (particularly when the true effect spans multiple parameters). This conclusion was largely unaffected by the nature of the generating function.

Next, the nonparametric indices were examined (Fig. 18c–d). This addressed two questions. First, do any of these indices offer similar power to parametric approaches? Second, are any more robust to the fixation-generating function than the parametric estimates?

Results were mixed. For targets, maxDeriv (red lines) was only sensitive to changes in slope: it showed excellent power when the underlying slope was shifted, and near.05 when it was not. That may be a reasonable way to detect changes in target slope when a parametric approach is not advised. Surprisingly, AUC performed well in different situations: AUC_early was sensitive to changes in peak, but also changes in crossover; AUC_late detected underlying changes in all of the parameters. These may be useful when there are no prior hypotheses, as they can detect a variety of more precise changes in the time course. The slope+xo composite, timing, was the best option when both slope and crossover changed (outperforming all other measures). Surprisingly, it did not suffer when only of those two measures changed. Thus, when it is unclear whether effects will appear in slope or crossover, this could be useful. Finally, while some of these indices performed well, all showed a similar power reduction between HFS and FBS models as the parametric estimates. The competitor (Fig. 18d) showed a similar story. Max_time was highly sensitive to peak location and nothing else. All three AUC measures were broadly useful, particularly when both height and offset baseline were manipulated. And none of these factors countered the loss of power seen in the FBS (though they were not worse).

TIE

Results of the TIE analysis suggest very little effect on Type I error (Table 9, with violations of α < .05 shaded in gray). In all cases, TIE was low, under.07 and close to the desired alpha of.05. In many cases where TIE was greater than.05, this was often due to sampling error. For example, with the FBS generating function, there were 19 cases where either the t test, ANCOVA or both yielded TIE >.05 (all less than.06). However, in five of those cases that was also true for analysis of the underlying parameters, and in two cases, the underlying function violated α < .05, and the observed data did not. Crucially, there was little difference between results for the HFS models or the other two generating models. Equally importantly, while the power analysis suggested that many single estimate measures (e.g., AUC) were sensitive to multiple changes in the underlying function, this was not spurious—when there were no true changes, they did not show enhanced TIE.

Table 9.

Results of the Type I error (TIE) analysis

	Parameter/Measure	HFS		FBS			FBS+T
		T test (Und)	T Test	T test (Und)	T test	ANCOVA	T test (Und)	T test	ANCOVA
Target	max	.064	.065	.045	.043	.042	.051	.049	.047
	xo	.060	.059	.051	.053	.052	.047	.050	.050
	s	.048	.046	.046	.058	.060	.044	.043	.039
	AUCearly	.050	.045	.052	.062	.061	.048	.049	.053
	AUClate	.064	.062	.051	.041	.040	.048	.048	.049
	maxDeriv	.048	.048	.046	.061	.061	.043	.049	.048
	maxDerivtime	.060	.048	.050	.057	.057	.048	.042	.043
	threshold75	.058	.057	.051	.043	.046	.049	.060	.055
	time25/75	.033	.030	.025	.045	.047	.031	.049	.052
	timing	.057	.059	.052	.059	.059	.036	.065	.062
Competitor	μ	.062	.061	.041	.048	.047
	ht	.055	.054	.059	.059	.056
	σ2	.042	.044	.033	.050	.049
	b2	.058	.060	.046	.056	.057
	AUCfull	.052	.054	.053	.057	.055
	AUCearly	.057	.056	.055	.046	.043
	AUClate	.058	.056	.045	.038	.041
	Peakdata	.056	.054	.059	.057	.058
	Peaktime	.062	.057	.042	.045	.049
	Extent	.047	.048	.039	.038	.042

In each experiment, all parameters of the underlying function were “shifted” (similar to the power analysis), though with a mean difference of 0. Shown is the likelihood of detecting a significant effect for curvefitting parameters and single-estimate measures via a paired t test on (a) that property of the underlying curves, (b) the estimate performed on the generated data, and (c) an ANCOVA on those estimates accounting for the mean and SD of each subjects fixation durations. Shaded cells indicate cells where p > .05. Target parameters include max, xo (crossover), and s (slope) from curvefits, along with derived measures described in Table 8. Competitor estimates include peak time (μ), peak height (ht), offset slope (σ₂), and final asymptote (b₂) along with derived measures described in Table 8. HFS: high-frequency sampling; FBS: fixation-based sampling; FBS+T: fixation-based sampling with enhanced target duration

Discussion

These simulations showed effects of the eye-movement generating function on power. Particularly for aspects of the fixation curves involving rate of change, the more realistic generating functions yielded far lower than expected power. In contrast, more stable aspects such as the time of the crossover or peak competitor, the peak of the competitor, and the asymptote of the targets showed no decrement in power with better fixation-generating functions. This suggests a need for experimenters to consider which aspect of the fixation function they are interested in when planning power for a given study. In contrast, TIE was held stable at.05 across all of the generating functions and measures, suggesting the primary concern is obtaining sufficient power to detect true effects, not avoiding spurious ones.

Many of the single indices performed well. Some like timing were uniquely suitable when the effect spanned several underlying parameters; others like the AUCs could be sensitive to multiple changes; and others like the maxDeriv were highly specific. All held TIE at.05. This again speaks to the need for thinking about the specific components of the fixation function that may be affected by an experimental manipulation when planning a study. These less parametric measures may be useful for confirmatory hypothesis testing when the function does not fit a standard form, and there is no evidence that these are any less powerful or more TIE prone than parametric measures that intricately capture the time course of processing.

Critically, while power was reduced in many cases by fixation-generating function, TIE was mostly held constant near α = .05. This is very important as it suggests that we do not need worry that a failure to account for the fixation-generating function, or the use of an inappropriate analysis (e.g., the nonparametric indices) will lead to false discovery; rather, our concern as experiments should be about whether an underpowered design may miss effect true effects.

Simulation 7: An (exploratory) generative approach to analysis

The foregoing simulations show that with a more realistic fixation-generating model, the observed data do not always closely match the underlying probability function which generated them. Some estimated parameters were biased relative to the underlying parameters (e.g., target crossover, and cohort peak height, and even target maximum with the FBS+T model). These biases may make it difficult to characterize (in absolute terms) the unfolding decision. For example, it might not be straightforward to ask if the cohort hit peak before or after the uniqueness point of the stimulus, as the bias in μ makes it difficult to align fixation time and real time. Even worse, there was increased variance in all parameters. The result of this was lower test–retest reliability and a loss of power.

These results cannot solely be attributed to the nonlinear curvefitting approach used to characterize these data. The same analysis scheme under HFS assumptions showed strong correlations between underlying and observed parameters and strong power and reliability. Moreover, this lack of validity and reliability is plainly visible in the generated fixation functions even before curvefitting (e.g., Figs. 11, 13, 15), and the reduced power appears in many nonparametric indices. Thus, these concerns are likely to apply to all analytic approaches. This calls for an analytic approach that does not accurately describe just the observed data (as existing approaches do) but also the processes that generated it: a generative model.

Generative models work backwards from traditional statistical approaches. Rather than attempting to describe the data as observed (using the richest description possible), a generative model starts from assumptions about how the observed data were generated. It then finds the generating model that was most likely to have created the observed data. Consider the contrast with a traditional model of fixation curves. The standard approach assumes that the data came from a logistic (or a growth curve, or a series of smooths) with some noise. That is, the logistic (or other function) is assumed to describe the central tendency of the data. It then optimizes the free parameters of this function to find the most likely outcome. In contrast, the generative model assumes the data came from a logistic with a stochastic eye-movement model layered on top. In this case, the logistic does not describe the data, it describes the underlying activation function that would have generated the data (with the assumption of a fixation system).

Generative models are often used in quantitative psychology, for example, in the long-running debate between exemplar and prototype theories of categorization (cf. Smith, 2014), or in drift-diffusion approaches to reaction time (Ratcliff & Rouder, 1998). However, their application to complex behaviors is not widely advanced (though see Haines et al., 2022, for an excellent discussion and examples).

A generative model starts by assuming some underlying description of the participant. For a drift-diffusion model, for example, this might be a participant’s drift rate and decision threshold. In this case, we assume that the underlying description of a subject is their own internal likelihood of considering the target or the competitor. These are simplified as the logistic and asymmetric Gaussian functions used here. Note that many (but not all) generative models assume this description derives from a process model (Ratcliff & Rouder, 1998), though others may assume only a latent trait (Haines et al., 2022). The corresponding process model for this approach might be something like TRACE (McClelland & Elman, 1986). In that sense, our curves are not process models, but a reasonable parametric description of that process—target curves from interactive activation models are almost always logistic in some form, and competitors can usually be described with an asymmetric Gaussian. Thus, these are reasonable ways to describe the latent likelihood of considering the target or competitor.

Note that unlike the traditional approach, these curves do not describe the probability of fixating that object. Rather these, curves describe the probability of considering it (e.g., lexical activation). The probability of fixating the object is then generated by a process model—in this case, the FBS or FBS+T models. This model is presumed to generate the distribution of fixations, and consequently the fixation curve most likely to have been derived from the underlying activation curve. The generative model thus works by optimizing the parameters of the underlying activation curve that yield the generated data most similar to the observed data.

Any generative model must make simplifying assumptions. Typical generative models would evaluate the likelihood of observing a specific sequence of fixations (and their durations) given the underlying parameters and the generative model. However, this means optimizing the model on the raw (fixation-by-fixation) data, not the averaged fixation curves. That is the model should not only predict the correct average curves but also the distribution of possibilities across trials. This would entail huge data sets. But it may also require much more detailed knowledge about the factors that drive individual fixations (visual salience or meaning, transitions between objects). Moreover, such a model would need to start from an underlying function that yields a multinomial distribution (the likelihood at looking at each object, not the likelihood of looking at one object or not at that object). Such a function has not currently been proposed.

The model proposed here makes a number of simplifications as a first step. The generative side starts from an underlying binomial function (e.g., the logistic function for target looking), generates a series of fixations, and averages the data to create a predicted fixation curve. Then, parameters of the underlying function are optimized such that the averaged predicted fixation function matches the observed data. Rather than optimizing the model to the likelihood of a given sequence, it is optimized to generate the averaged fixation curve. Critically, the generative function that creates the data is given the mean and standard deviation of the subject’s fixations so that it can generate distribution of fixations that match a subject’s own. These are not free parameters. Thus, generative model is optimized only to mean performance (not the distribution) and treat the data as binomial. However, it is also computationally tractable and eliminates many unknowns.

The final simulations implement this simplified generative approach. The goal of a generative model is to not just fit the data but to approximate the true latent (but unobservable) curve. This makes it difficult to validate as we have no secondary measures of the latent function, and the fixation models are admitted simplifications. In this context, while this investigation demonstrates the feasibility of this approach, it should not be seen as validating the method for statistical use. However, while our simulations can only demonstrate feasibility, this is important for two reasons. First, there were large technical hurdles to overcome in implementing and optimizing such a model. These are described below and in Supplement S5; code is available to aid in further development. Second, given the prior simulations, it was possible that the fixation-generating system could introduce so much randomness that underlying functions could not be reliably estimated. That is, there may be cases where the same observed fixation curve could have derived from multiple underlying curves. Thus, test–retest reliability as a key metric of success: Can this approach obtain the same estimates twice in a row (given the noise in both the fixation data [across test and retest], and the noise inherent in the model). If the model fails on this metric, it may not be worth further development as fixation is just too underspecified to properly identify the underlying curve.

Approach

The generative model was implemented in two parts. First, a function was developed that takes the parameters of the latent function (e.g., slope and crossover [etc.] for the logistic; μ, and ht [etc.], for the asymmetric Gaussian) as well as the mean and standard deviation of the subject’s fixations. It then generates the average of 10,000 trials worth of fixations as the predicted data. Finally, this function computes the least squared error between the predicted and observed data.

In the second part, a search process was implemented which estimates starting underlying parameters and adjusts them iteratively to minimize the least squared error. This was implemented using a patternsearch algorithm, which minimizes the error between the function and the data but does not make strong assumptions about the smoothness of the error function.

Note that while the mean and standard deviation of the subject’s fixation data are parameters, they are not free parameters and so are not optimized by the fitter. They are estimated directly from the participants data, and then used to generate the predicted pattern of fixations. A complete instantiation of this is available for the logistic and asymmetric Gaussians functions, under both FBS and FBS+T assumptions. This can be found as part of the code shared for this paper and is also embedded in the freely available curvefitter for use with live data⁶ (McMurray, 2017). Several tricky issues arose in implementing the model, including how to implement a gradient descent search of the parameter space when the function generates noisy data, and how to estimate starting parameters for a latent function that by definition does not match the observed data. Solutions to these are described in Supplement S5. Even so, this was computationally intensive. A single fit for the generative logistic function required about 4.36 seconds assuming FBS and 5.18 for FBS+T [using 20 cores]. In contrast the traditional logistic only required 0.13 seconds. While this is certainly reasonable for analysis of regular data sets, it was not possible to run thousands of simulations. Thus, smaller scale simulations were run to assess validity and bias (N = 500) and reliability (N = 250). Power and Type I error—which require running hundreds of experiments each consisting of 50 or so subjects—were infeasible. Reliability was the most important metric as it addresses the question of whether the stochastic fixation-generating process leads to an essentially insolvable problem.

One concern is that this approach assumes a fixation-generating model that we already know is oversimplified (though more plausible than the HFS model assumed by other approaches). Thus, robustness was evaluated by examining mis-specified models (e.g., when the data were generated under FBS+T, but the model assumed FBS). This was only done for the logistic function where two models were available. This yielded four simulations: (1) an FBS–match model, in which the data came from an FBS model and the fitted model assumed it; (2) an FBS+T–matched model, in which the data and fitting functions both assumed FBS+T; (3) an FBS–underspecified model, in which the data came from FBS+T, but the fitting model assumed only FBS (it was underspecified relative to the data); and (4) an FBS–overspecified model, in which the data came from FBS, but the fitting model assumed FBS+T.

Results

Target

Fits were very good. The average correlation between the observed data and the fixation curves predicted by the generating model was greater than.996 in each of the four simulations, and no run was dropped. This was far superior to the traditional approach applied to FBS and FBS+T generated data. The fact that fits were good even in the misspecified models is an important caution—a model that does not capture the generating function of the data may nonetheless yield a close match (even as the estimated parameters may be wrong).

Figure 19 shows representative results from each of the four simulations. Analysis began with the two simulations in which the fixation-generating function matched the function used to fit the data (Fig. 19a–b). These functions showed a very strong match between the underlying and observed results in two ways. First, with the simpler, FBS-generating model, the predicted (blue) and observed (red) fixation curves were on top of each other in every run. Second and more impressively, the estimated latent functions (green) completely overlapped the true underlying function (black), despite the fact that the fitting procedure had no access to this latent function (e.g., it was only optimized to match the observed data). The FBS+T–match simulations (Fig. 19b) showed similarly impressive fits. For all of them the observed and predicted data were quite close. The latent and underlying functions also matched closely though there were several whose slope (cf. subpanel a) or asymptotes (b) were off.

Fig. 19.

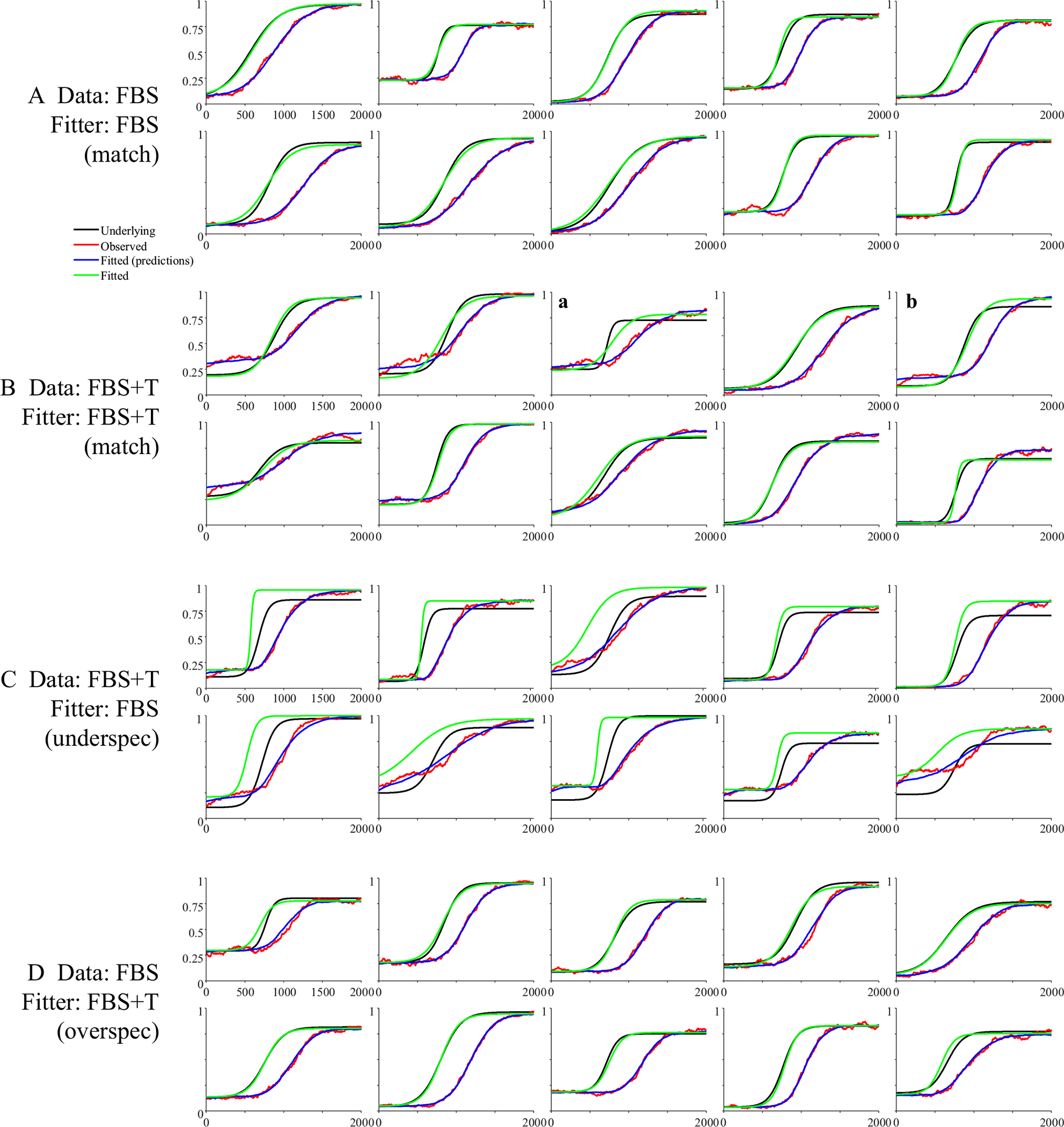
Representative runs of the generative target model. Red lines show observed competitor looks as a function of time. Black lines are the underlying fixation function. Green lines show the latent fixation function that is estimated from the data (and should match the black). Blue lines (fitted predicted) are the predicted fixations from that function. The function is optimized to minimize the least squared error between the blue and red curves. Panels marked by lowercase letters are described in the text. a Data are generated by the fixation-based sampling (FBS) model, and the fitted model assumes FBS. b Data are generated by the more complex fixation-based sampling with enhanced target duration (FBS+T) model, which is also assumed by the fitting model. c Data are generated by the FBS+T model, but the generative model only assumes the simpler FBS model (it is underspecified). d Data are generated by the simpler FBS model, but the generative model assumes FBS+T (overspecified). (Color figure online)

Figure 19c suggests the importance of properly specifying the model. When the data came from an FBS+T model, but the fitting model was underspecified (FBS), we saw poorer performance. While the predicted data completely matched the observed data in all displayed runs, the underlying and latent functions rarely matched (green vs. black lines). In contrast, Fig. 19d shows an overspecified model in which the model expected FBS+T situation but got FBS data. This showed similarly good fits as the two match models. This is not surprising—the model took as input the separate mean and standard deviation of the fixation durations for both fixations toward the target and fixations elsewhere. Since the data came from FBS (not FBS+T) these were very similar, and the fitted model functionally behaved like FBS. It may be of value then to over-parameterize generative models with respect to the properties of the fixations (e.g., assume separate fixation durations for all four objects). These are estimated directly from the data (they are not fit), so do not cost degrees of freedom, and could help ensure an adequate model.

Figure 20a–d shows the correlation between the parameters of the estimated underlying generating function and those of the true generating function; Fig. 20e–h shows test–retest reliability, and Fig. 21 shows mean bias. For comparison, both figures report (in blue) the corresponding values from earlier simulations using traditional approaches. Recall that for the baseline and max parameters (logistic), the traditional curvefitter (blue bars) did a good job of extracting those parameters with an FBS generating model, with high validity and reliability, and bias near zero. Not surprisingly, all four generative simulations showed similarly good performance. However, with FBS+T data (right groupings in each panel), the traditional approaches broke down with lower validity and reliability and more bias. In contrast, the generative model that was expecting FBS+T data coped with this much better. Its validity estimates were much higher than either the traditional or the mismatched generative model, and its bias was restored to near zero.

Fig. 20.

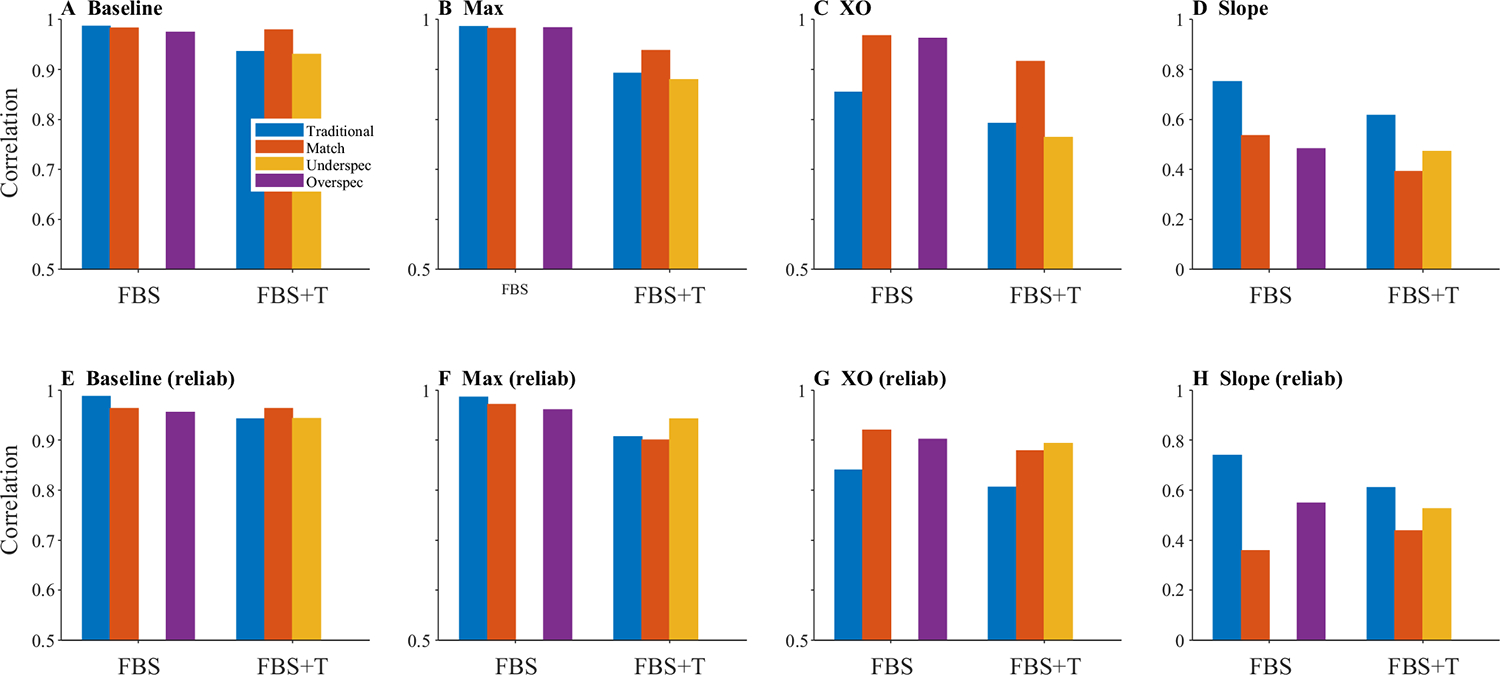
Validity (top row) and reliability (bottom row) estimates for each estimated parameters of the generative model. Validity correlations represent the correlation between the estimated parameters of the underlying function and their true values. Reliability estimates are test–retest reliability when the function was held constant, and two batches of data (300 trials) were generated and analyzed. Estimates labeled traditional are the corresponding numbers for the regular logistic curvefitting analyses in Simulations 2 and 3. Match models are models in which the eye-movement generating function that created the data was the same as in the fitter. underspecified models are models in which the generating function assumed by the analysis (fixation-based sampling [FBS]) was less complex than what generated the data (fixation-based sampling with enhanced target [FBS+T]). These were not possible for FBS data. In overspecified models, the generating function assumed by the analysis (FBS+T) was more complex than what generated the data (FBS). These were not possible for FBS+T data. Target estimates include baseline (b), max, crossover (xo), and slope (s). (Color figure online)

Fig. 21.

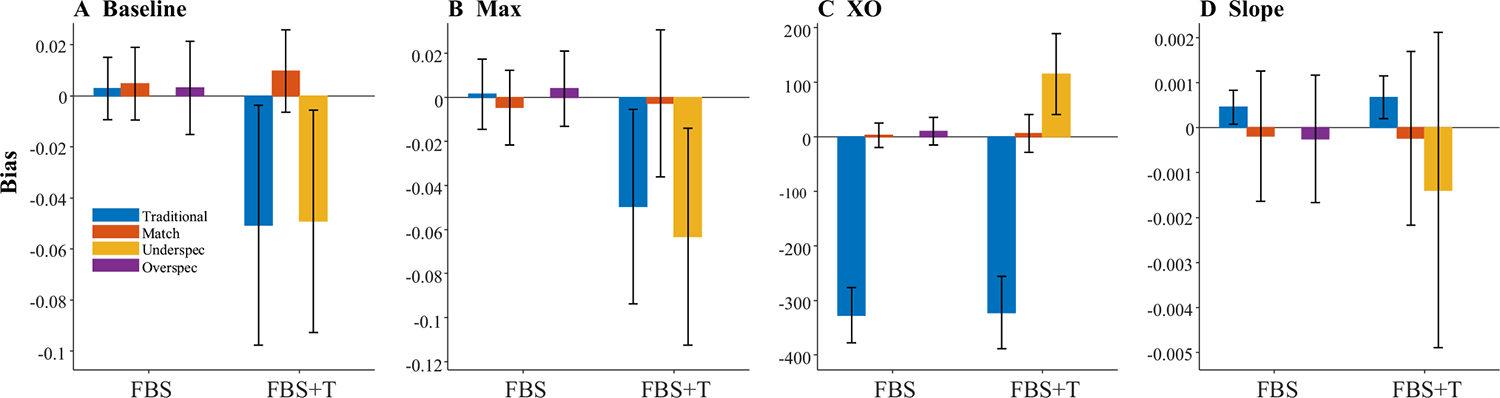
Mean bias (underlying parameter estimate minus observed) for each parameter of the logistic as a function of the generating model of the data (x-axis), and the model used for analysis. Target indices include (a) baseline (b), (b) max, (c) crossover (xo), and (d) slope (s). (Color figure online)

Our prior simulations also suggested that crossover (Fig. 20c, g; Fig. 21) showed some of the most deleterious effects of more realistic generating models. With traditional analysis techniques (blue bars) and both FBS and FBS+T-generated data, there was substantial bias and lower validity (FBS: r = .85; FBS+T: r = .79) and reliability (FBS: r = .84; FBS+T: r = .81) than with HFS-generated data (r >.999 for both). In contrast, when the data were fit with a generative model that matched the data, there were sharp improvements in validity and reliability: In the FBS condition validity leaped to 0.967 (reliability: r = .920), and in the FBS+T condition it rose to.915 (reliability: r = .879). Most importantly, when the generating function was not underspecified (it matched the data or was over-specified), bias was eliminated (Fig. 20c)—the generative model can yield a true estimate of the crossover (though underspecified models introduced some bias). Slope was more challenging: generative models were not as accurate at detecting the true slope as more traditional approaches, in either simulation. While they did reduce bias to near zero (Fig. 21d), they did so at the cost of increased variability.

Competitors

Results for the competitor models were somewhat more straightforward as there was only one generating model (which always matched the data). As with traditional approaches, fitting competitor fixations proved more challenging. Thus, fits between the predicted and observed data were poorer than for the target (though on par with traditional competitor analyses). Fits averaged r = .930, and 31 of 500 models were dropped.

Figure 22 shows representative results. As in target models, the predicted (blue) and observed (red) data were close matches. While the underlying function (black) and the estimated latent function (green) were fairly close, there were also cases where they diverged. However, this divergence appeared to be more noise than bias. For example, in Fig. 22b, height was underestimated, whereas in Fig. 22c, it was overestimated. Others showed extremely steep onset or offset slopes (Fig. 22d–e), although there were also examples of under estimated slopes (Fig. 22a). Generally speaking, there was good concordance between the estimated latent and the underlying functions. This was strikingly unlike what was observed with traditional fitting approaches which did not approximate the underlying function well (e.g., Fig. 12).

Fig. 22.

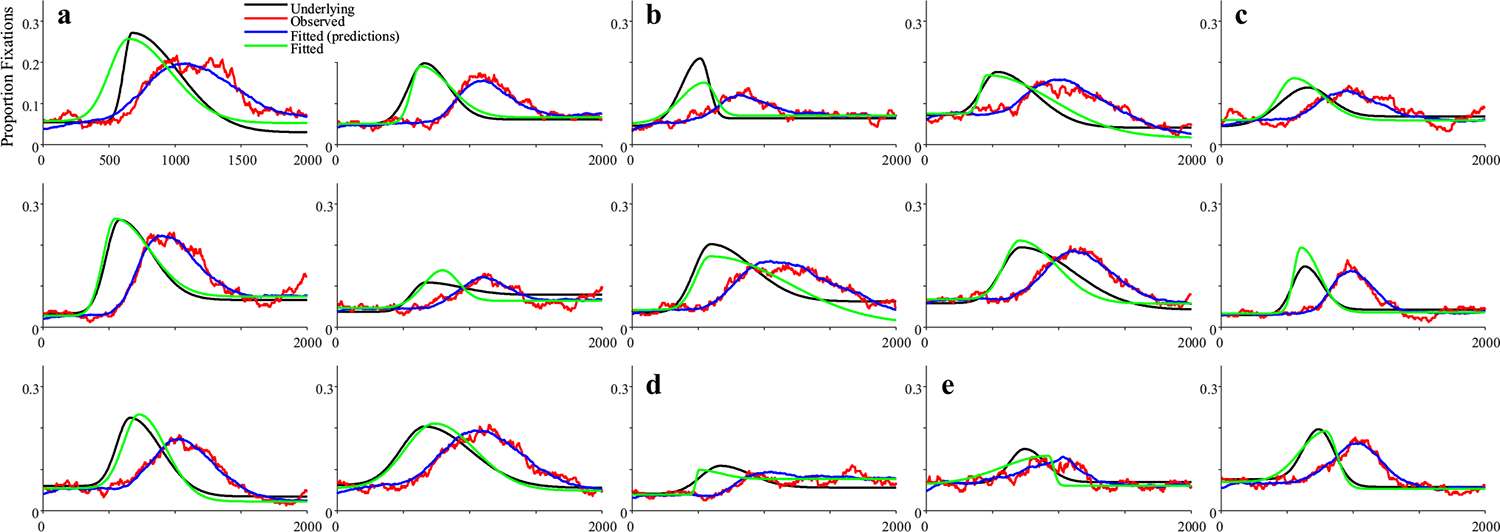
Representative runs of the generative competitor model. Red lines refer to the observed competitor looks as a function of time. Black lines are the underlying fixation function. Green lines refer to the estimated latent curve (and should match the black). Blue lines (fitted predicted) are the predicted fixation curves from that latent curve. FBS: fixation-based sampling; FBS+T: fixation-based sampling with enhanced target duration

Analysis of validity reliability, and bias (Fig. 23) suggested a modest improvement over the traditional approach. Peak time (μ) and offset slope (σ₂) showed validity gains of about 0.2. As both parameters showed relatively low validity to begin with (r < .4) this was meaningful. Other parameters had similar validity as standard approaches. For reliability, most parameters were similar across the two approaches except peak time (μ) and onset slope (σ₁), which were lower. As with the target, bias was reduced. Peak time (μ) and height both showed large bias with traditional approaches, but this was eliminated in the generative model.

Fig. 23.

Results of validity and reliability analyses for competitors assuming an fixation-based sampling (FBS) generating and analysis model. Competitor indices include peak time (μ), peak height (ht), onset slope (σ₁), offset slope (σ₂), initial asymptote (b₁) and final asymptote (b₂). a Validity: Correlation between observed and underlying parameters for each parameter in the traditional (blue) and generating (red) model. b Test–retest reliability for each parameter. c Bias for each parameter. (Color figure online)

Discussion

These foregoing simulations offer several conclusions and avenues for future research. First, when the assumed generating function matched the underlying data, performance was very good. This was particularly true of the logistic models, where validity, reliability and bias were improved for the baseline, max, and crossover (but not slope). However, even in competitor models, most parameters showed improved validity, and reliability and less bias. The success of these models is clear in Figs. 19 and 22, where the model could recover the true unobserved curve (in black) despite only having access to the observed fixations (red).

Second, getting the right fixation model matters, to a point. If the model is too simple (Fig. 19c), the observed and predicted data can be a close match (blue vs. red), but the underlying curves will not be accurate. This appears to come mostly at a cost to validity and reliability; bias was acceptable. Even then, validity and reliability were no worse than traditional models (Fig. 20, compare yellow bars to blue), so perhaps this is acceptable. However, the real risk is that the experimenter rarely has access to the true underlying function, so it is difficult to evaluate the accuracy of the estimated latent functions if the predicted data are a close match. Instead, researchers must rely on things like outliers to determine whether a spurious fit was obtained.

Third, there was little cost of overspecifying the model. This makes sense as the additional parameters (the mean and standard deviation of the target fixation durations) are not free parameters (in the sense that the fitter must estimate them)—they are measured directly from the data. If no systematic variance is captured by them, they will have little effect (or cost). This suggests a path forward: researchers should create and test probabilistic models of the generating function itself, particularly for aspects that can be implemented without free parameters.

Finally, and most importantly, the high reliability of most parameters estimated by the generative model suggests that at a fundamental level, this probabilistic system is not underspecified. That is, even though there were cases where distinct underlying functions could give rise to the same data (e.g., Fig. 22a–b), these were relatively rare, and the procedure generally obtained similar estimates for two runs of the data. This is notable despite two sources of noise: the variability in the fixations that generated the data (on test and retest) and the variability of the fixations in the generative model. This meets the bar to warrant further development.

It is premature to recommend utilizing this generative approach as an analysis tool yet (at least by itself). There are too many unknowns about the fixation-generating function, and there is no clear way to evaluate the estimated underlying functions. However, even as more sophisticated generating models may be out of reach for the reasons described earlier, this approximation is highly feasible and may serve as a path for future work.

General discussion

These simulations attempted a serious look at the nature of the processes that lie between the underlying unfolding decision and observed fixation curves in the VWP. The goal was to computationally flesh out the derivation chain (Meehl, 1990; Scheel et al., 2021) by which inferences about the underlying activation curve can lead to predictions about fixations. This was done with a model in which the true underlying function was known allowing us to observe the consequences of various fixation-generating models for the observed fixation curves.

The simulations started by considering the high-frequency sampling (HFS) assumption. This generating model assumes independent sampling at the sample rate of the eye tracker, with some fixed oculomotor delay. No serious person would claim it is true. Yet it is often justified as reasonable by reference to the general noise across fixations and trials, and it is quite clearly assumed by modeling approaches for linking computational models to fixation data via the Luce choice decision rule (Allopenna et al., 1998; McMurray et al., 2010; Mirman et al., 2008).

The simulations of HFS showed that if this were the true generating function, then all is well. The observed data were a close match to the underlying function, and the parameters of the underlying function can be estimated reliably, with low bias, and few spurious correlations among estimated parameters. Power was not affected by the stochasticity of the fixation system, and TIE is at.05. This validates the curvefitting approach for analysis of the later simulations: When the assumptions of such models are met, the paradigm performs wells.

However, things broke down with more sophisticated fixation-generating models. In the FBS model, results were problematic but straightforward. Target looking was biased (delayed) by well more than the standardly assumed 200 ms; the function was shallower, and every parameter showed increased variability. The situation was worse for competitors, and for targets in the FBS+T model (in which fixation duration was affected by what the subject was fixating). Fixation curves were noisier for all parameters, and often did not resemble the underlying functions. In addition, for targets, asymptotes now showed bias and spurious correlations.

Critically, correlations between the underlying and observed parameters were reduced under FBS and FBS+T models (validity; Table 10). Under the HFS assumption correlations were above.99 for the targets, and.94 for competitors, with the FBS model, validity for the target crossover and slope, and for all competitor parameters dropped below.9, and some competitor parameters were below.4. Moving to the more realistic FBS+T model, the slope went as low as.616. This is not a function of our estimating/fitting procedure. As Figs. 11, 13, and 15 show, the observed data just does not match the underlying function regardless of the analytic model.

Table 10.

Validity (correlation between underlying and observed parameters) for each simulation. HFS: high-frequency sampling; FBS: fixation-based sampling; FBS+T: fixation-based sampling with enhanced target duration

	Parameter	HFS	FBS	FBS+T
Target	Baseline (b)	1.0	.987	.935
	Max	1.0	.986	.892
	Crossover (xo)	1.0	.855	.792
	Slope (s)	.998	.751	.616
Competitor	Peak time (μ)	.988	.502	N/A
	Peak height (ht)	.997	.845
	Onset slope (σ1)	.946	.112
	Offset slope (σ2)	.990	.327
	Onset asymp (b1)	.996	.799
	Offset asymp (b2)	.996	.681

More realistic fixation-generating functions also created systematic biases in some parameters. For targets, slopes were shallower and crossovers later than their true values; for competitors, peak times were later, and peaks were lower. There were also spurious correlations among the observed parameters, correlations that were not present in the underlying parameters. That is, these correlations do not reflect correlations among latent traits (e.g., the slope and maximum are not really correlated), but rather appear to be imposed by the generating function.

Both the FBS and FBS+T models also reduced test–retest reliability (Fig. 17, Table 7), and for some parameters to correlations below 0.4 (target slope, and virtually all competitor parameters except height). This is a serious concern for using these aspects of the curves to make inferences. This is likely because even with over 50 trials, when there are only 3–4 fixations per trial, there are just not enough fixations to smooth out the noise and generate a reliable fixation curve. Some part of this is sampling error. Figure 3 shows that even in a simple coin-flipping experiment, when there are a small number of trials there is a dramatically reduced likelihood of both estimating a mean probability and of observing the same probability in two runs. This is particularly problematic when the underlying probability is below 0.2 (typical values for competitors in the VWP) or above 0.8 (typical target asymptotes in the VWP). However, the FBS and FBS+T models clearly add additional noise beyond sampling error: In some cases, reliability and validity were lower than what would be predicted from sampling alone.

Finally, simulations examined the consequences of the fixation-generating model for power and Type I error. Fortunately, TIE was held at.05 even under the FBS+T model for both curvefitting analyses and nonparametric indices. This suggests fixation-generating function is not likely a driver of TIE in prior studies. In contrast, the story with power was more complex (Fig. 18). For some properties of the curves (target max and crossover), power was preserved and similar across the HFS and FBS or FBS+T models. However, for target slope and parameters describing the competitor, power was dramatically reduced with more complex generating models. This suggests two important points. First, when null effects are observed in these measures empirically, these needed to be treated with particular care, as the underlying power may be much less than expected by the number of subjects. Second, when effects are detected on these properties of the curve, the underlying difference may be bigger than what is observed. It is not clear if these issues can be worked into Bayesian analyses that are used to evaluate the strength of evidence for null effects; this may be a useful avenue of future work.

There’s a shortage of perfect data visualizations in the world—it would be a pity to spoil yours

Simple fixation-generating models yielded (1) larger variances in estimates, with meaningful effects on reliability for some aspects of the curve; (2) systematic bias in some places; (3) a nonlinear mapping between underlying and observed functions; (4) systematic correlations among observed parameters that were not present in the underlying data; and (5) reduced power in some circumstances. Yet, despite these issues, the bulk of the early VWP work has largely asked simple questions answered with ordinal experiments: Under which condition is a competitor more or less active or is a target activated faster or slower? These simulations suggest that such inferences may be fine: There were no situations where the FBS appeared to reverse the direction of such effects, and α was preserved at 0.05. Yet, even for this purpose, the issues of reduced reliability and power are concerning. Moreover, the fixation curves may be problematic for more specific purposes such as identifying properties of the curves that differ or time locking the fixation curves to real events.

The question is where to go from here. In the long run, a generative analytic approach may overcome many of these issues. However, the preliminary version presented here comes with significant concerns that are not yet resolved. While a comprehensive and perfect analytic technique may be currently beyond reach, there are lessons to be learned about experimental design and planning, visualizing and interpreting of results, and broader issues on replicability and rigorous science. Before discussing lessons, I briefly address limitations of this work.

Limitations

The analytic approach

Analysis of these simulations used nonlinear curvefitting (Farris-Trimble & McMurray, 2013; McMurray et al., 2010). This was adopted because unlike growth curve analysis and to some extent GAMMs, the parameters offer meaningful descriptions of the curves. More importantly, each subject’s data are fit independently of other subjects, unlike mixed models in which all subjects’ data are fit simultaneously and show shrinkage toward the group trends. Here, this enabled a cleaner estimate of validity and reliability. However, these models have been rightly criticized for their inability to handle crossed random effects, and for their requirement that the data “obey” the expected form of the function.

Would the results be any different if this study had used a different approach? This is unlikely. Most of the findings are visible directly in the observed data: under FBS assumptions, observed target curves are shallower than expected, competitor curves are more variable, and so forth. Thus, one should interpret these results not in terms of the specific analytic approach, but in terms of general properties of the fixation curves that are susceptible to noise or bias under realistic generating functions. Even if you use a polynomial growth curve and do not intend to estimate the target slope, a fixation-generating function will still lead to a shallower linear trend or quadratic effect than is present in the underlying activation curve. Future work should simulate a realistic generating function (FBS or FBS+T) in these other frameworks.

What to look at…

These simulations largely used a binomial model, capturing fixations to one object at a time. However, the true function should be multinomial—the system is not deciding to look at the target or not; rather, it is deciding whether to look at the target, the cohort, the unrelated or nothing at all. Supplement S2 presents a simplified multinomial model that illustrates many of the same trends as the binomial model. However, the lack of multinomial models is an omnipresent issue—all available analysis techniques typically examine looks to each object separately. The development of a true multinomial model could be crucial for better analysis and for better generative models.

… And when to look at it

Both the FBS and FBS+T models assumed people make the decision to look at the next object at the moment that their eyes land on the current object. That assumes that fixations are solely a stochastic readout of the underlying decision state. That cannot be true—fixations also serve to obtain (visual) information that may alter the underlying decision state (see Magnuson, 2019, for an excellent discussion of various mechanisms). Most likely, people take a brief period to take in the visual information from the current fixation before deciding where to move next. It is not clear how long it would take an observer to estimate the properties of the kind of simple clip art images used in the VWP (particularly if they are repeated). However, ERP and eye-movement studies suggest people can read a word in about 50–60 ms (Sereno & Rayner, 2003), and extract key information from a visual scene in even less time (Bacon-Macé et al., 2005). Given that simulated saccades were on the order of 200 ms, it was unlikely that implementing this delay would have made a large difference, and it may have even introduced noise. However, answering the question of when the decision to move is made is crucial for building better fixation (and generative) models.

… And how long do you look there?

The FBS model assumes fixation duration is entirely random over time. The FBS+T model was slightly more realistic in this regard, but even it assumed that the “boost” to duration for target looks is uniform across time. Most likely the duration of target fixations is even longer at later times and may be non-existent at early times (since the target is not known). Similarly, the analysis of earlier empirical data showed no difference between the durations of fixations to competitors and other objects; however, there could be a short-lived difference during the brief period when the competitor is more active (see McMurray et al., 2008a, for an example). A more comprehensive understanding of duration could also improve these models like (cf. Walshe & Nuthmann, 2021).

It is also helpful to consider more global effects on the sequence of fixations. Perhaps there are contingent effects: Are people quicker to leave a less active item to move to a more active item than the converse? Moreover, these models assume the overall rate of fixations is fairly constant: The time of each fixation is based on the duration of the previous (and that is constant across the trial). However, studies suggest that the overall rate of saccade generation is modulated by listeners expectations, even in purely auditory tasks (Abeles et al., 2020). A better model of these things could be crucial for building a better generative model, and a variant of the FBS+T model would be the place to start.

Summary

The above factors are unlikely to dramatically change the conclusions here. Recall, a primary findings was that parameters related to the slope and timing of the fixation curves were most affected by the generating model. Thus, seems unlikely that moving to a more complex generating model—with more sources of noise—would mitigate these effects. Even with these simplifications, these simulations suggest that fixation curve is profoundly shaped by the basic properties of fixations as a chunky series events with a roughly 200-ms refractory period.

This is not to dismiss these issues. Resolving these questions could refine or understanding of the fixation curves and lead more accurate generative models which—unlike the one presented here—have enough independent empirical support for actual use. Across the large number of labs using the VWP, there are likely to be reams of data on the precise duration and sequence of fixations—this could be potentially mined to develop such a model, and the OSF website for this project may be a useful repository.

Why does this matter?

The point of this exercise was not simply to tear down the existing paradigm—indeed, I have been a beneficiary of it. We should not stop analyzing data in the usual ways, and my own lab is continuing to submit papers and grants with traditional models. However, after working with these simulations now for several years, it is clear that the field needs to understand the role of the fixation-generating function in creating the visualizations and measures we rely on. Though this study only offers the beginning of a solution, there are a number of important takeaways—even if we want to continue with business as usual. That is, now that we know the dangers of the fixation curve swamp, what are we to do? In discussing these issues, we simultaneously focus on implications for ordinal designs and for continuous-in-time designs.

How does time in the fixation curve relate to real time?

Standard practice since Allopenna et al. (1998) is to assume a 200-ms oculomotor delay. At the level of a single saccade, this is certainly correct—it was based on strong psychophysical work on single fixations (Viviani, 1990), and is supported by empirical data presented here on saccade latency (Table 3). However, the way this 200-ms estimate is used may be wrong.

The typical approach is to simply shift the x-axis of the fixation curve by 200 ms and call it a day. These simulations suggest minimally a longer delay is necessary: Even as fixation durations were assumed to average about 200 ms here, the crossover of the target and peak time of the competitor were delayed by much more than that in the FBS and FBS+T models. However, time is not simply delayed by a fixed amount—target curves are not just shifted, their slopes are shallower, and for competitors, things can go in any number of ways. The mapping of time between observed and underlying functions is not linear. This is clearly seen in Fig. 24, which captures the time lag at which the underlying activation is maximally related to the observed fixations (see Supplement 6). While the HFS model generally maintains this around 200 ms throughout most of the trial, the FBS and FBS+T models show increasing lag over the course of the trial.

Fig. 24.

Relationship between real time and observed time in the fixation curve for (a) targets and (b) competitors. At each time slice (x-axis), the lag at which the maximum correlation between the underlying activation and the observed fixations is shown. The black line represents the 200-ms oculomotor delay (see Supplement 6 for methods). (Color figure online)

This has implications for both ordinal and continuous-in-time studies. For ordinal studies, AUCs are often identified on the basis of events in the stimulus (e.g., the average length of the word); this challenges these inferences. Moreover, ordinal studies examining at timing (e.g., a delayed cohort peaks, target slope) may be more problematic. While the rank order of a timing parameter is likely preserved (e.g., a condition leads to earlier fixations will still be earlier under reasonable fixation-generating assumptions), indices of timing are less reliable than of overall looking (Fig. 17). They may require more power (subjects and trials). Continuous-in-time studies could suffer more. Certainly, this finding makes it more difficult to be confident to precisely time lock the fixation curve to real world events. The disruption of later times also has clear effects on the shape of the competitor curves, potentially making it more problematic to draw direct inferences about the shape. At this point there are not yet clear solutions (outside of potentially a generative model), but these findings should serve as warning to interpret temporal aspects of the fixation curves cautiously.

Power and reliability

There were strong effects of the fixation-generating model on power and reliability. Several potential sources can be ruled out. First, this was not due to the analysis technique—the same technique applied to HFS data showed good reliability and power, and nonparametric index approaches applied to FBS data showed lower power. Importantly, unlike a real test–retest study, this could not have been due to bad items or procedures and underlying function did not vary from test to retest. Here, the only reason power and reliability could be lower was the fixation-generating model.

This issue is relevant to both ordinal and continuous-in-time studies. How should we approach it? First, we need to consider overpowering VWP studies. This requires more than just more subjects. As show by Simulation 0 (Fig. 3) and later reliability simulations (Fig. 17), this has to be also considered in terms of the number of trials. In these simulations, 150 trials (which many would consider to be an overpowered experiment!) was not enough to yield good reliability for some aspects of the curves. A traditional power analysis that assumes a power of.7 on the basis of number of subjects alone will have a true power that is much lower when we consider the role of the fixation-generating function. Importantly for continuous-in-time studies, the effects of this may vary across different indices, and the data presented here (Fig. 18) offer a rough guide as to which indices may need even more power.

Second, we may want to restrict hypotheses to indices that can be estimated reliably (e.g., competitor height, target asymptote) and accept the fact that there may be some hypotheses that cannot be tested with current methods (Meehl, 1990). It may help to conduct simulations applying these simulations to real or hypothesized studies as a tool for identifying which indices would be reliable in a given study (code is available at: https://osf.io/wbgc7/).

Third, and relatedly, in ordinal experiments, null effects are to be predicted in certain aspects of the function. For example, effects on portions of the curve that are low or high probability may be difficult to detect (Fig. 3), and slope-based effects are hard to detect (Fig. 18a, s grouping; Fig. 18b, σ₂ grouping). But there are also more complex patterns. For example, when the underlying competitor function has a short-duration peak (Fig. 12e–f), there may be few visible fixations (which may explain the inability of Teruya & Kapatsinski, 2019, to find cohort effects for short overlap cohorts). This needs to be taken into account when interpreting small effects and null results. It may be more helpful to talk about more general patterns of fixations than diving into more specific aspects of the curves.

Spurious correlations

The VWP is increasingly used to document individual differences and development (e.g., Law et al., 2017; McMurray et al., 2010; Rigler et al., 2015; Sekerina & Brooks, 2007). In doing this, a desirable direction is to identify certain properties of real-time processing that may be useful descriptors of latent traits. For example, my laboratory is testing the hypothesis that development of spoken word recognition is characterized by changes in activation rate (timing based parameters like slope and crossover; McMurray et al., 2018), while differences due to language disorders are more reflective of the asymptotes (McMurray et al., 2019b, 2010; e.g., differences in the speed of activation vs. the degree of resolution).

These simulations suggest caution in interpreting single parameters—there may be no effect on target slope, but one is observed anyways due to a real effect on the initial asymptote (Table 6), or there may be no difference in competitor onset slope (σ₁), but there appears to be due to a difference in peak time (μ) (Table 5). These correlations may be imposed by the fixation-generating function—not systematicities across subjects in word recognition. These simulations suggest the need to understand these things so as to not interpret them as meaningful. This is not to argue that we should not be making these inferences; but rather we need to be cautious about their potential causes, and the correlations presented here in Tables 4, 5 and 6 suggest particular places of caution. When working in these domains, researchers should consider basing simulation studies (like these) based on the observed properties of their own data to figure out how much correlation should be expected by chance in a given data set.

Theory building

Finally, these findings are important for theory building. The common HFS assumption assumes that observed fixation curves are fairly close read-outs of the underlying activation function (accounting for the oculomotor delay). However, taking this assumption too seriously risks building a theory of language processing which is biased with respect to time. Models of word recognition (McClelland & Elman, 1986; Norris & McQueen, 2008) are typically exquisitely timed to real events in the world—the unfolding stimulus or the uniqueness point of the words. If the time axis of our measure is not linearly related to the model, that is a problem—models might assume aspects of word recognition happen earlier or later than they really do. This is not likely a problem for the macro structure of the model—indeed, TRACE was well validated long before we had the VWP to help characterize the precise shapes of the model. But the field should be cautious about overinterpreting the shape of these functions.

The bottom line

Unfortunately, there are not yet perfect solutions to these problems. Though ultimately a generative model may help, the most important contribution of this work at a purely empirical level is to raises these issues and encourage researchers to caution—both in study design and in interpretation—when working with specific indices of the fixation curve.

Toward a generative model

A well supported generative model could in principle solve many of these issues (see Haines et al., 2022, for an analogy). This is likely out of reach at the moment. At a purely technical level, it was not possible to implement a state-of-the-art model (e.g., a multinomial model of the underlying activation, which predicts individual trials, and computes the likelihood of specific patterns of fixations). However, the workaround introduced here was reasonable. It simplified the problem by (1) assuming a binomial function for the underlying curves; (2) basing the fixation model on observed properties of each subjects’ fixations (rather than fitting it); and (3) optimizing the fit to the expected mean fixation curve (not the distribution of fixations). This approach was feasible. It runs in a reasonable time. Importantly, when the assumed fixation model matches the true one, the generative model accurately recovers the underlying function, and for the most part shows better validity and reliability than approaches based on the observed data alone. This was not guaranteed: given the indeterminacy of the fixation-generating function (and the fact that this stochasticity appears twice in the generative model) it was possible that multiple underlying curves would be consistent with the observed data, and the model would not reliably extract the correct latent curve. However, the strong reliability suggests this is not the case (with sufficient trials).

However, there are technical limitations. This generative model is sensitive to initial parameter estimates of the underlying function. Right now, initial estimates are based solely on the simulations—there is no way to know if they are correct for real data. They also require many trials. As the reliability simulations show (Supplement S4), with only a small number of trials the same underlying function can generate a variety of observed functions. As there is no independent way to characterize the true underlying function, these issues are real concerns for real data. In these simulations, the underlying function was known, and it was clear if the estimated latent function matched it. However, in a real experiment these will be unknown, and as Fig. 19c shows occasionally two distinct underlying functions (the black and green) can generate two similar observed functions (the red and blue) but still show a near perfect fit to the data. We need to develop better ways to evaluate model fit such as looking for outliers (many invalid fits also had overly steep slopes) or patterns of covariance. Or we may need better ways to fit the model such as better starting parameters, or priors or constraints on the parameters.

But the real limits are not technical limits of implementation. Rather, we need to get the model of fixations right. This need was raised by simulations when the wrong fixation-generating approach was underspecified relative to the data: this model (which assumed FBS for fixation curves generated by FBS+T) generally did not get the true underlying function (Fig. 19c) and showed lower reliability and validity than the true model. However, this was not without hope. While validity (Fig. 20a) and bias (Fig. 21) of baseline, max, and crossover were lower for the underspecified generative model than the correct one, they were on par with the traditional analyses and max and crossover actually showed better reliability for the underspecified generative models than for traditional analyses (Fig. 20b)! Further, an overspecified model was not problematic. Thus, the right approach may be to develop more complex generative models than needed (if they do not add free parameters).

What is truly needed however, is a better understanding of how eye movements are planned. Within the VWP there are many relevant factors that were not captured here. Our models, for example, just predict the likelihood of fixating the target and treat the duration of the fixation as random variation. However, informal analyses of VWP data suggest, the likelihood of transitioning between competitors may be more relevant. For example, subjects may be more likely to move their eyes from a less active interpretation (e.g., the competitor late in the trial) to a more active one (e.g., the target late in a trial) than to do so in the other direction (over and above the base probabilities). Subjects may also fixate longer on more active objects than others. And the act of fixating an object may build activation for its word (Chen & Mirman, 2012, 2015). Thus, the fixation-generating function may be more intricately linked to the activation function than is simulated here.

But even beyond the VWP, developing an accurate fixation model should be based on empirical work on eye-movement control and object recognition that is independent of work on language processing. Work on scene semantics (Henderson et al., 2019) may offer ways to integrate low-level visual salience with the meaning of objects; work on visual search and models like Walshe and Nuthmann (2021) can describe accurately describe the durations of saccades as they relate to visual information in the scene. But ultimately, these models should also be informed by the role of fixations not just in picking up visual information, but in guiding motor behavior—as in the VWP. A fixation-generating model built on these sources of information could provide independent support for this sort of analysis. To the extent that these can be implemented in simple schemes such as this one (and preferably with few free parameters), such insight could be incorporated into future generative models.

Source code is available for the generative approaches to support this development. This is integrated into a user-friendly curvefitting package (McMurray, 2017), which can handle both generative and traditional models used here (along with other functions such as the rotated logistic and ex-Gaussian functions). The generative model is not yet appropriate as an analysis tool, but by providing the code, it may serve as a framework for further thinking and development. Long term, whether the field adopts a generative approach must depend on the degree to which we can support the specific assumptions built into the generative model. At this point, the true fixation-generating system is severely under modeled here. However, at the same time, all of the existing models largely assume HFS. The present study suggests that HFS is clearly the wrong assumption, and perhaps more wrong than the oversimplified FBS model assumed here. There is a need to do better.

HFS, you seemed like a decent linking function. I hate to kill you

At the broadest level, these simulations suggest the need to reconsider the linking function that binds together an underlying theory and the observed data. This is a critical part of the derivation chain, and even a “mostly good” linking function needs to be better understood in order to make precise predictions from theory (Meehl, 1967; Scheel et al., 2021). HFS has gotten us a long way, but these simulations make it clear that any reasonable assumption about fixations does not lead to data that accurately reflect the underlying activation curve. A major portion of the variance is the systematic (and nonsystematic) noise induced by the fixation-generating system. These simulations, however, suggest that it is possible to create a new linking function. Stochastic models of the fixation generation process are straightforward to implement and can be integrated in both simulations and potentially into analytic tools. We just need to know more about how and when fixations are planned in these tasks.

But this is only a small piece of the linking function. These simulations start from the likelihood of fixating something or not. However, computational models and theories do not work at that level—they may predict the activation of hundreds of words or interpretations, which then need to be mapped to the available items on the screen, and then need be mapped to a probability. Thus, we need to consider the mapping between underlying activation states and the likelihood of fixating at all. Teruya and Kapatsinski (2019), for example, argue that this may be nonlinear (activation may need to reach a threshold before an eye movement is launched). Other studies, focus on the role of the preview period (Apfelbaum et al., in press; Huettig & Altmann, 2011; Huettig & McQueen, 2007) in potentially priming semantic features or names in advance of the speech. Magnuson (2019) offers the most systematic review to date of the variety of cognitive processes that may take place to link speech to the world.

All of this must be considered. However, before we do, the basic properties of the fixation system—which can be measured and simulated—must be accounted for first. For example, Teruya and Kapatsinski (2019) find that cohorts which overlap with the target by one (and perhaps two) phonemes (e.g., cat and cove) do not lead to measurable fixations. They argue that since all models of word recognition predict some activation, this must mean that a low level of activation has not crossed the threshold; they put this failure on a mechanism that links the decision to fixate with the visual objects. In contrast our simulations suggest that if the activation is short lived, the dynamics of fixating may cause it to be missed (Fig. 13d, f)—even if the underlying probability curve has a peak. The fixation system is the aspect of the linking function closest to the data. While the other aspects must be fleshed out as well, understanding the actual behavior we are studying—fixations—is a crucial first step.

Where do we go from here?

Without a true generative model, how can we keep doing what we are doing? We have been in the fixation curve business for so long, now that it’s over, what do we do with the rest of our data? One thing that needs to be strongly considered is greater use of converging methodologies. Mouse tracking (Spivey et al., 2005) and other continuous motor-based task (grip force, reach tracking) offer an analogous approach but built on a motor behaviors that are fundamentally continuous. However, it is not clear that the entire issue with eye movements is their serial nature; rather, there is a broader need to understand how the inherent dynamics of a given response system (oculomotor, reaching, etc.) may alter the mapping between underlying and observed data. Thus, without a more comprehensive model of the motor system in question (the derivation chain), it may not be safe to assume that some other continuous motor behavior will solve the problem. Hence, these techniques may be most helpful as converging evidence.

EEG and MEG approaches may also be of use. Of course, there are deep questions about what it means when scalp voltage or magnetic potentials are elevated or lower—the linking hypothesis or derivation chain, again. However, recent studies have attempted to by-pass some of these concerns raised by traditional ERP approaches by using regression and mixed models to predict neural activity at each time slice from a range of interesting psycholinguistic factors (Brodbeck et al., 2018; Kocagoncu et al., 2017; Sarrett et al., 2020); here, the analysis is not tied to specific components; rather, the question is when some factor (e.g., the number of competitors) affects distribution of activity. Work in my own lab has coupled EEG with temporally sensitive machine learning (McMurray et al., 2022b) to construct something analogous to fixation curves. Such techniques may also offer useful points of convergence.

But for the psycholinguist who has already invested substantial funds, training, infrastructure, and intellectual effort in eye-tracking, what is to be done? It seems to me that fixation curves are only mostly dead. These simulations suggest that we should not take the precise time course (as depicted in the fixation curves) too seriously. But we should not ignore it. In almost all of the simulations, the observed fixation curves were systematically related to the underlying curve. Moreover, such curves may be a crucial bridge to generative models. We just cannot treat them as a read-out anymore.

For simpler ordinal predictions, this may be sufficient. The zeitgeist now is to develop ever more precise tools for characterizing the fixation curves. I have developed some of them myself. However, the fact that now out-of-favor indices like AUC show as good reliability, power and TIE as more precise parametric approaches suggest that the situation may be acceptable for ordinal experiments (as long as we heed warnings about power, reliability, and null effects). These indices can be used to conduct targeted hypothesis tests. Indeed, simulation 6 suggests that even indices of the overall amount of looking seem to be fairly unbiased, as powerful as anything more sophisticated, and do not show increased TIE. Was area under the curve okay all along?

If we go down this route, the field needs to converge on standard measures to minimize researcher degrees of freedom. A good example of a subfield which has done this is reading research, where measures like first fixation time and regressions are now standard (Rayner et al., 1998), and even implemented by commercial eye-tracking manufacturers. But similar standardization is also seen in mouse tracking (Freeman & Ambady, 2010) and pupillometry/listening effort (Winn et al., 2018). We need something similar for the VWP. The onset detection techniques (McMurray et al., 2008b) already offers some standardization across studies. But there should be a standard approach to identifying time windows for area under the curve, or for estimating when two curves separate. And newer approaches like the bootstrapped difference of time series (Seedorff et al., 2018) or permutation-based clustering (Darvas et al., 2004) can offer ways to do AUC with fewer researcher degrees of freedom as they automatically estimate both the difference between the curves, and the time window over which they are significant (though perhaps don’t take the time estimates too seriously!). A corollary to all of this is that in our zest for ever greater statistical precision, we may want to stop encouraging authors to adopt the latest, greatest time-course approach (listen up, Reviewer 2)—a well-justified index may be more appropriate, just as powerful, and unlikely to lead to Type I errors.

However, researchers should also consider a more serious exploration of the sequence of fixations (rather than fixation curves). In addition to their use as dependent variables, such measures could serve as independent variables or covariates in an analysis of fixation curves (Apfelbaum et al., 2022). Does the latency or duration of looking (at the subject level) predict anything about their fixation curves? Or does the likelihood of fixating one thing alter fixations downstream? Again, this needs to be standardized. But we must also consider the sequence of fixations in a task like this as an interesting behavior in its own right, divorced from any psycholinguistic hypotheses we may want to test. Or we may wish to estimate the time course of fixations using nonlinguistic analogue tasks (Farris-Trimble & McMurray, 2013) as a covariate to remove variance from the fixation system.

Rigor and reproducibility

Perhaps no other issue has animated the behavioral sciences quite like the so-called replication crisis (Bakker et al., 2012; Open Science Collaboration, 2015; Schmidt, 2010). There are many factors that contribute. Outright dishonesty and sloppiness, or the abuse of researcher degrees of freedom are problems, and inexcusable ones. However, lack of replicability may also derive from chasing weak effects with low-powered studies, or unreliable methods. These simulations speak to issues of power and reliability. They suggest that attaining methodological rigor in the VWP requires deeper thinking about power and reliability that is more intricately tied to the contribution of the chunky stochastic nature of the fixation-generating system.

Oberauer and Lewandowsky (2019) offer a compelling theoretical addition to this list, and one that may be most important issue. They argue that a major contributor is that most theories are under-constrained in their ability to make clear predictions about the data. This harkens back to earlier work by (Meehl, 1990; and see Scheel et al., 2021, for a more recent synthesis) calling for the need to understand the entire derivation chain—from latent theoretical construct to observable behavior. Oberauer and Lewandowsky (2019) build on this with a Bayesian analysis that models the likelihood of a prediction given the theory, the likelihood of the data given the prediction, and so forth. They show that if the likelihood of a prediction given a theory has any uncertainty in it, a failure to replicate is depressingly likely, as the uncertainty at this lowest level of the chain cascades through the system.

How does this apply here? Theories of language processing are usually described as theories of activation or consideration, not fixations. That is, a theory predicts that a given word (or interpretation) is more active under one condition than another. The problem is that researchers often assume a direct relationship between heightened or delayed activation and increased or later fixations. Our simulations suggest concrete cases where this assumption is not warranted, where activation or the timing of activation does not predict increased activation: Even if the theory predicts heightened activation or a difference in the timing, this may not consistently appear as corresponding differences in the fixation curve.

First, whenever the competitor is predicted to be only briefly active (a few hundred ms), it may not be fixated very much—even if it is highly active (e.g., Fig. 13e). This may underly the failure to observe predicted effects of short competitors (Teruya & Kapatsinski, 2019). Second, effects on the timing of the function seem to cascade over time in the trial to where the timing of the underlying activation is less reliably reflected in the fixation curves at later points in the trials. Thus, theories that predict differences later in the trial may be less testable than those that predict early effects.

Third, theories are moving beyond simple ordinal claims to more precise claims about quantitative indices such as the slopes or asymptotes (e.g., McMurray et al., 2022a). A realistic fixation model makes such predictions more challenging. A theory may predict an effect on the final asymptote of the cohort competitor (e.g., McMurray et al., 2022a), but our simulations suggest the asymptote is strongly collinear with the offset slope (r=−.453, Table 5) even in the absence of such a correlation in the underlying data. This may make it challenging to test theories that make more precise claims about the time course of processing.

Finally, more broadly, reliability and validity were lower across all parameters due to the fixation-generating function. This is true for all indices when there are few trials, and some even when there were a lot of trials (e.g., slopes of the competitor fixations). In many cases reliability and power are poor enough that one should not predict differences in the fixations even if underlying activation is changing in the correct direction. This has to be considered as a source variance in mapping the theory to the predictions—the source of noise highlighted by the Oberauer and Lewandowsky (2019) analysis. This needs to be considered in any analysis of replicability or reliability of the VWP.

Thus, at multiple levels, the ability to make precise predictions from a theory of activation to the observed fixation data results is compromised when we consider more complex generating functions. That is, even when we know the underlying function, the observed fixation curves are not always predictable. And just as described by Oberauer and Lewandowsky (2019), this cascades through the inferential chain to impact reliability and power. Oberauer and Lewandowsky’s approach applied here suggests that even the simplest change in this linking assumption creates large uncertainty in the predicted fixation data. That is, without really knowing the fixation-generating function is, it may not be possible for a theory to make accurate predictions about the data in all cases.

A second key issue in rigor is the distinction between confirmatory and nonconfirmatory (or exploratory) research. The mounting drive toward preregistration is a consequence of this. Is psycholinguistics ready for this? Are we truly doing confirmatory research? Our field is young, and particularly as the VWP is applied to special populations and development, theories do not make predictions that are sufficiently quantitatively precise for confirmatory work. These simulations, which severely oversimplify the fixation system, suggest we do not fully understand the link between underlying activation and observed data.

Particularly given the uncertainty in the linking function, the goal of precisely modeling the time course of fixations with ever more precision (and without strong theories to guide it) risks a nonconfirmatory approach. While it is certainly possible to make precise predictions with such models, most of the time predictions are ordinal—the competitor should receive “more” fixations—even if this difference cannot be pinpointed to an interaction of condition with the quadratic or cubic terms of a growth curve model. However, by testing every aspect of the time course and when the precise interactions cannot be specified, these ordinal predictions give the veneer of confirmatory research to a fundamentally nonconfirmatory analysis. In principle, this may be appropriate: Perhaps psycholinguistic theory and our understanding of the VWP does not yet have the quantitative precision to be truly confirmatory. It is not unreasonable to separate registration of qualitative hypotheses from registration of statistical models and predictions (Petersen et al., in press). But, if so, we should acknowledge it, embrace it, and frame the work appropriately.

Alternatively, if predictions are ordinal, perhaps a simpler index approach would be superior—one could propose an index and test just that. This has the possibility of being truly confirmatory, but we are not there yet. Common indices like AUC are underconstrained; Everyone likes to invent them; and they are ripe for p-hacking. However, the simulations here show that when used appropriately they do have similar power and TIE to full time course approaches. With appropriate standardization (much as in the reading literature), researcher degrees of freedom could be minimized. Ideally, the specifics of such measures are developed independently of the study at hand⁷ based on theory or from meta-analytic work across multiple studies. And then these measures should undergo empirical evaluation: using Monte Carlos to ensure they avoid TIE; and empirical work to establish reliability and discriminant validity from other measures. The final stage of course is external validity. This is not news to anyone with introductory training in psychometrics. But it is worth considering in psycholinguistics.

In 25 years, VWP analyses have advanced from the extremely simple to the extremely complex. We can now characterize the observed fixation curve extremely precisely using several techniques. But should we? As these simulations show, our understanding of how underlying activation in the system maps to the observed fixation curves is not where it should be, and we do not understand the complete derivational chain from theory to behavior. We may have been led astray by the quest to characterize the curves better and ignored the basic fixation behavior which is the basis of our technique. Perhaps we need to focus less on what the right statistical approach is for capturing the fixation curves, and instead focus more what are the questions we attempt to ask, and the fundamentals of the behavior that link these questions to data.