Benchmarking digital PCR partition classification methods with empirical and simulated duplex data

Abstract

Digital PCR (dPCR) is a highly accurate technique for the quantification of target nucleic acid(s). It has shown great potential in clinical applications, like tumor liquid biopsy and validation of biomarkers. Accurate classification of partitions based on end-point fluorescence intensities is crucial to avoid biased estimators of the concentration of the target molecules. We have evaluated many clustering methods, from general-purpose methods to specific methods for dPCR and flowcytometry, on both simulated and real-life data. Clustering method performance was evaluated by simulating various scenarios. Based on our extensive comparison of clustering methods, we describe the limits of these methods, and formulate guidelines for choosing an appropriate method. In addition, we have developed a novel method for simulating realistic dPCR data. The method is based on a mixture distribution of a Poisson point process and a skew-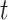 distribution, which enables the generation of irregularities of cluster shapes and randomness of partitions between clusters (‘rain’) as commonly observed in dPCR data. Users can fine-tune the model parameters and generate labeled datasets, using their own data as a template. Besides, the database of experimental dPCR data augmented with the labeled simulated data can serve as training and testing data for new clustering methods. The simulation method is available as an R Shiny app.

INTRODUCTION

In recent years, there has been a growing interest in digital PCR (dPCR) for nucleic acid sequence quantification, as the technology offers numerous appealing features such as high accuracy, repeatability and calibration-free absolute quantification [1]. It also demonstrates high resistance to a sub-optimal amplification efficiency, often caused by PCR inhibitors. Consequently, dPCR is increasingly applied in a wide array of domains. These include the detection of genetically modified organisms, molecular pathology, liquid biopsy analyses in oncology [2, 3], as well as clinical and environmental microbiology, including viral load monitoring [4, 5]. The recent technological improvements in dPCR allow for the use of up to six different fluorescent colors, enabling the simultaneous analysis of multiple target nucleic acids. To make dPCR terminology easier to grasp, we have added a glossary (see Table S1 in the Supplementary).

dPCR has a straightforward reaction readout. In contrast to qPCR, which requires real-time monitoring for quantification, dPCR primarily relies on end-point fluorescence detection. First, a sample is partitioned into numerous individual PCR reactions each resulting in its own end-point fluorescence intensity. Quantification relies on Poisson statistics and the fraction of positive partitions [5]. The analysis revolves around the binary outcome of each partition, namely positive or negative. For a singleplex experiment where only one target is quantified, the classification into positive and negative partitions is based on a threshold [6].

For multiplex experiments where multiple targets are quantified in the same reaction, classification of multi-dimensional dPCR partition data can be challenging. One can either do the classification dimension-by-dimension by setting thresholds, or one can consider all channels simultaneously. In the latter case, particularly for duplex experiments, manual clustering is often applied, based on a visual inspection of the two-dimensional scatter plot of the fluorescence intensities. However, this manual procedure may introduce bias and lower precision [7]. As misclassification can significantly impact the accuracy of estimates [8], and with higher-throughput instruments being introduced, there is a growing need for automated partition classification methods.

However, designing a robust classification method is not straightforward [6]. Many methods are unsupervised because the true positive/negative partition labels are typically unknown. Although some methods make use of negative and positive controls, there are often deviations between the controls and actual samples due to variability in fluorescence readout or due to sample matrix effects.

This paper evaluates the performance of clustering methods for the classification of partitions in duplex experiments, using both simulated and empirical data. We consider three types of clustering methods: methods specifically developed for dPCR partition classification, general clustering algorithms and clustering methods designed for flow cytometry data. We assess the applicability and performance of 11 different methods, discuss when and why specific methods fail, and finally provide guidelines for method selection in a variety of biologically relevant scenarios. Further, a novel simulation method is developed to guide users in the selection of the most suitable method tailored to their specific data.

MATERIALS AND METHODS

Methodology overview

The adequacy of a clustering method hinges on the accurate classification of partitions, but the partition labels are often unavailable in dPCR data. Furthermore, the performance of a clustering method can vary significantly across different datasets due to biological and technical variability. Factors such as cluster size and proximity play pivotal roles in influencing the clustering outcome. As such, the effectiveness of clustering is related to these dataset-specific characteristics.

To overcome these problems, we will use two different simulation methodologies. The first starts from an empirical dataset for which the classification has been done by three experts (manually defined clusters). In the event of a dispute, the decision aligned with the majority viewpoint. This is subsequently considered as the ground truth. From this dataset, partitions are randomly sampled to form a new dataset to which the clustering methods are applied. This process is repeated many times, and the average performance of the clustering methods is reported. We have used this approach starting from three different datasets (see Section 3.3). The advantage of this approach is that the (resampled) data are very realistic, but a shortcoming is that the data characteristics (e.g. resolution of clusters, rain, target concentration, …) cannot be varied, and hence the conclusions from this study are limited to situations similar to the original empirical datasets.

The second simulation method starts from a probabilistic model from which endpoint intensities can be sampled. The model generates realistic data, with parameters to tune cluster resolution, rain, target concentration, among others. Since the parameters are under our control, the clustering methods can be evaluated for a large set of scenarios (see Section 3.4.).

Clustering methods

Clustering methods can be broadly categorized into partitioning, hierarchical, density-based, model-based, and graph-based approaches [9]. Based on this categorization and the availability of R packages or code, we selected kmeans and cmeans (partitioning-based), DBSCAN (density-based), flowclust and flowmerge (model-based), flowSOM (hierarchical clustering), samSPECTRAL (graph-based), dpcp, calico (partitioning-based and density-based), flowpeaks (density-based and model-based) and ddPCRclust (concensus clustering based on flowdensity, flowpeaks and samSPECTRAL). This gives 11 clustering algorithms in total that have been utilized for flow cytometry, and dPCR, as well as all-purpose clustering methods (Table 1).

Table 1.

Overview of the clustering evaluated in this study

Method	Environment and availability	Short description	reference
kmeans	R package (stats)	Iterative partitioning algorithm; used with or without good initial values (centroids).	[10]
cmeans	R package (e1071)	Iterative soft partitioning algorithm; with or without good initial values.	[11]
DBSCAN	R package (dbscan)	Density-based clustering algorithm; the number of sufficient neighbours and radius has to be pre-specified.	[12]
dpcp	R code from GitHub; R shiny app	Two-step approach; DBSCAN is utilized to identify the locations of first-order clusters, then cmeans is applied.	[13]
flowSOM	R package from Bioconductor	Self-organizing map to find winning nodes, followed by hierarchical clustering on those representatives.	[14]
flowPeaks	R package from Bioconductor	Based on finite Gaussian mixture models; start with kmeans to compute smooth density function empirically, then merging is performed; no need to specify the number of clusters.	[15]
flowClust	R package from Bioconductor	Based on t mixture models with Box-Cox transformation; model parameters are inferred using an Expectation-Maximization algorithm; the number of clusters can be pre-specified or automatically chosen by the Bayesian information criterion (BIC).	[16]
flowMerge	R package from Bioconductor	Extension of flowClust and is intended to solve the issue of flowClust producing too many clusters in the automatic mode; the best model is selected by the change point in entropy.	[17]
SamSPECTRAL	R package from Bioconductor	Graph-based method; starts with data reduction due to the computational cost, then computes the similarity matrix, followed by spectral clustering, then kmeans; the number of clusters can be pre-specified or automatically determined by the knee point of the eigenvalue plot.	[18]
calico	R code from GitHub; R shiny app	Based on gridding and kmeans; starts with sample space gridding to reduce the differences in density, then the first round of kmeans is implemented on the gridded data to obtain centroid for the second round of kmeans.	[19]
ddPCRclust	R package from Bioconductor	Ensemble-based approach that combines the outcomes of flowDensity, SamSPECTRAL and flowPeaks.	[20]

Additional details including software package versions used for each clustering method are included in Appendix Table S2.

We compared all these algorithms using their default parameter settings in the R packages, except for dpcp. The use of the latter with its default values does not work for the standardized data (see Section 3.3). The dpcp method utilizes DBSCAN as the first step for the identification of cluster centers. The default value for ‘neighborhood distance’ in this step ranges from 100 to 150, which leads to one single cluster when applied to the standardized data. Thus, we had to change this distance parameter to 0.15 (the same as used for the standalone DBSCAN algorithm). This method also requires clean references (with few rain and single-target clusters identified), but since we do not have references in the simulations, we performed the two-step approach on the same data twice. This is allowed when the sample itself is clean and all lower-order clusters are present [13]. With respect to the initial values for kmeans and cmeans, we simply estimated the mean of cluster centers after manual clustering. For the empirical datasets, these will be accurate centroids, but for the simulated data, there may be small deviations. ddPCRclust fails to perform effectively on standardized data, consistently producing only one cluster. As a workaround, we conducted this method on the original, unstandardized data.

Empirical datasets

For the evaluation of the clustering methods, we selected three empirical datasets (Figure 1).

Figure 1.

(A) HR (high-resolution) dataset, (B) MM (multi-mode) dataset (C), LR (low-resolution) dataset.

The selected datasets encompass clusters of varying sizes, as can be seen from the Poisson parameter estimates in Table 2. The table also describes the amount of rain in the data, and the resolution of the clusters. The latter is quantified as follows. First, for each cluster , the scaled distances to neighbouring clusters 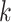are calculated:

Table 2.

Summary of the empirical datasets and their characteristics

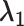
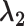
D ataset	Number of partitions			rain	resolution	short description
HR	18 233	0.036	0.036	Not many, but some outliers	sep=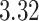 (good)	good separation but some crosstalk; RPP30 genomic DNA assay, refer to [21]
MM	14 277	0.28	0.28	Continuous rain	sep=3.30 (medium)	Obvious multimodality; HIV gblock sequences, refer to [22]
LR	22 723	0.69	0.19	Rain mainly along the x-axis	sep=2.34 (poor)	Barely separable on x-axis; The development of assays for the genotyping plants various primers/probes and conditions for each target are evaluated.

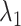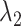and are the average number of target molecules per partition (for target 1 and target 2), see Figure 1 for more details.

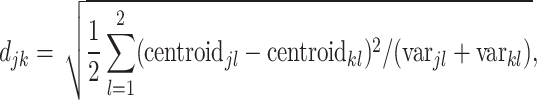(1)

where 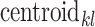is the fluorescence intensity values in channel 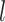of the centroid of cluster 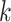, and 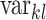is the variance of the intensities in channel 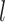of cluster 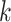. For a given cluster 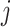, the smallest of these distances between cluster centers is a measure of the resolution of cluster 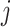from its neighbouring clusters. Let 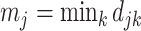denote this minimum distance for cluster 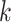. As an overall measure for resolution, for the complete dataset, we calculated the smallest of the 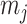, i.e. 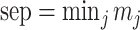. Thus, a small value for sep means that there are at least two clusters that are close to one another, and a large value for sep means that all clusters are well separated.

To make sure that different methods are compared fairly and to avoid any biases caused by differences in intensity scales between channels, we perform channel-by-channel standardization. The standardized data will have mean of 0 and standard deviation of 1. This way, we prevent methods, such as kmeans, from favoring channels with larger scales and ensure unbiased comparisons.

For the evaluation of the clustering methods, 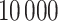bootstrap samples were generated from each of the three datasets, and all 11 clustering methods were applied to each bootstrap sample. Details on how the performance of the clustering methods were quantified will be given in Section 3.7.

Probabilistic model

The model, which will be used for the simulation of synthetic data, is based on a non-homogeneous Poisson point process, which is a stochastic point process where the intensity of point occurrences varies across the spatial domain [23–25]. In a two-dimensional space, let 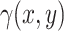be the intensity function, where (x,y) represents the coordinates in the spatial domain. In our context, 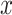and 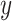refer to the intensities in the two channels. The intensity function specifies the expected number of points per unit area at a given location. Assume that the number of partitions in a small area near point (x,y), denoted as 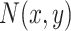, can be described by a Poisson distribution with mean 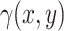. This mean parameter 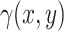is subsequently modelled as in a log-linear model. Here we suggest

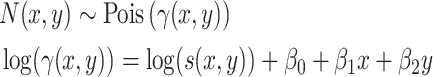(2)

where 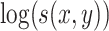is an offset that in itself comes from a working probabilistic model. If 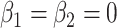, the Poisson point process would be only an approximation of that working model, but the term 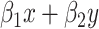allows the model to smoothly deviate from the working model. As a working model, we consider the multivariate skew- 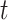distribution [26]. With 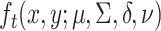the density function of this distribution, where 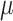is the location parameter, 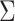is the covariance matrix, 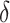regulates the slant of the density, and 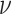is the degrees of freedom, we have 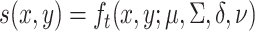[27]. The parameters are estimated from fitting individual clusters of the empirical datasets. After obtaining the parameters of the skewed-t distribution, the log densities of the data points are computed, which serve as the offset in the non-homogeneous Poisson process.

Because rain is typically present along the directions connecting any two clusters, a constraint on the density is imposed as a further refinement of the model. The model for cluster 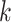is then given by

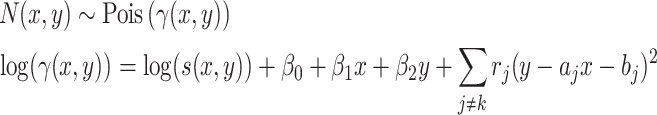(3)

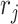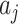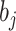where the summation is over all other clusters, is a penalty parameter, and and are the slope and intercept of the line connecting the centers of clusters 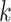and 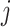. Again, the parameters will be estimated from empirical data, and, when simulating new data from this model, the structure of the rain can be altered by changing the values of 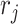. In particular, a large value of 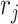forces the rain to be concentrated near the line connecting the centers of clusters 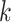and 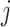(see Figure 2). Figure S1 in the Supplementary is an example with small values of .

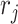Figure 2.

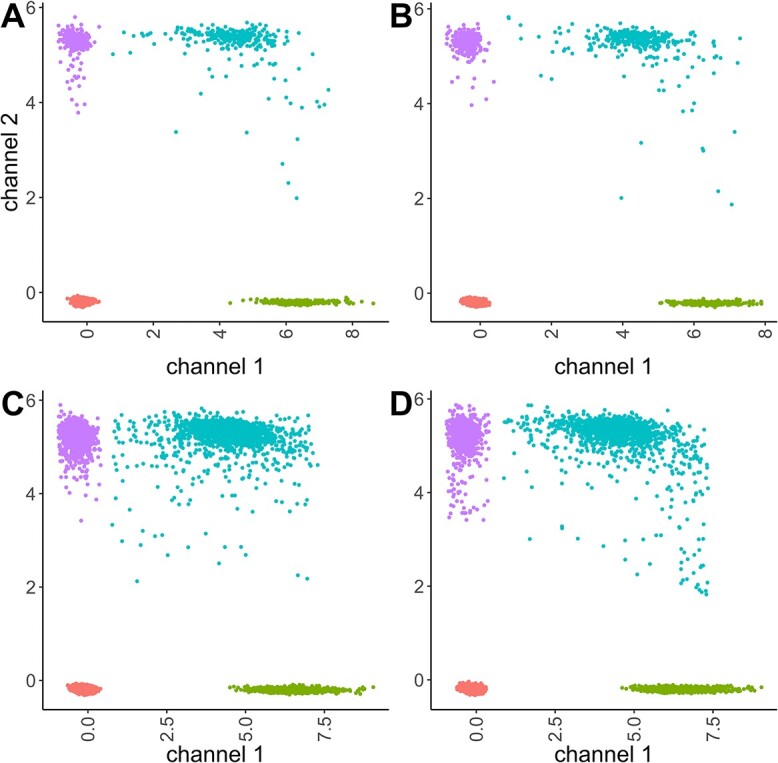
(A) HR dataset with the removal of data points that deviate substantially from the lines constructed by the centers of double positive and negative clusters. (B) Simulated data using the method described in Section 3.4. (C) Simulated data with no constraints imposed. (D) Simulated data with constraints imposed. Note: to emphasize the effect, we increased the concentration of the original dataset by a factor of 6.

A visual examination of the two-dimensional scatter and density plots, and projection depth plots [28] is employed to assess the goodness-of-fit of the probabilistic model.

Simulation set-up

We consider a two-color system and two assays in our simulation study. In most of the scenarios, we will have four clusters: one negative population, two single positive populations and one double positive population. The double positive group may disappear in the case of very low target concentrations.

We aim to investigate the impact of several factors on the clustering performance, including the following:

• Cluster resolution: good, medium, and poor.

• Concentration: expressed as the partition occupancy, which is the percentage of positive partitions. This number directly relates to the average number of molecules per partition (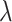). We considered four levels: high (80% partition occupancy for each target), low (10%), very low (2%) and rare ( 0.1%). From the partition occupancies of the targets, we deduced the expected cluster sizes for single positive, double positive, and negative instances. These actual cluster sizes were then simulated from a multinomial distribution.

• Rain percentage: from 0 to 10% of the cluster size, in steps of 2%. The control of rain percentage is achieved by manipulating the parameter 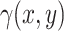in Equation 3. To generate the desired amount of rain in the dataset, we adjust the rain intensity by multiplying 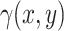with a scalar. However, it is important to note that this adjustment also affects the intensity of non-rain points. To maintain the desired ratio of rain to non-rain, a two-step process is implemented. Firstly, we generate the data with the required amount of rain by scaling 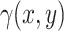. For instance, if we aim to increase the rain percentage from the initial 10–20%, we multiply 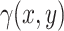by a factor of 2.25. We then proceed to remove non-rain points based on their silhouette coefficients’ rankings. By retaining only the lowest 10% of silhouette coefficients, we preserve the required number of rain points in the dataset. Subsequently, the original non-rain points are reintroduced to complete the dataset.

• Orthogonality: yes or no. Orthogonality means that the cluster centers are positioned in a squared pattern. We have generated non-orthogonal clusters by applying a rotation matrix 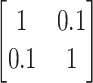to the orthogonal data.

• Modality: uni- or bimodal. A mode refers to a local density peak within a cluster. If there are multiple modes, we also consider the distance between those modes. To create a bimodal cluster, we simulate two clusters. The covariance matrix 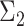(of the second population) differs slightly from 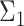(of the first population). We manipulate this deviation by sampling the values of 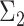from a normal distribution with 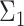as mean and 10% of this mean as standard deviation (coefficient of variation). The final bimodal cluster is then constructed by sampling 80% of partitions from the first simulated cluster, and 20% from the second. The partitions from the second cluster are translated along the vertical direction with a Mahalanobis distance [29] of 3, 7 or 10 from the first cluster center. In this way the overlap between the two populations is varied from large to small.

• Equal concentration: yes or no. If ‘no’, the concentration of target 2 will be set at half the concentration of target 1.

Each combination of these factors makes up a simulation scenario. However, the total number of combinations of all these factors is large, and performing 1152 simulations for each factor combination would take too much computation time. We have therefore selected 150 factor combinations (i.e. 150 scenarios) by constructing a factorial empirical design with the JMP software (version 16). The design was constructed such that it allows us to estimate all main effects and all two-way interactions in a linear model.

To assess the impact of variables on the model’s goodness-of-fit, we conducted step-by-step variable elimination. Starting with the full model, we removed one variable at a time and observed the change in mean squared error (MSE). A significant drop suggested the variable’s importance, while minimal change indicated modest influence.

In each simulation, we start with sampling the total number of partitions from a normal distribution with a mean of 20 000 and a standard deviation of 1000; this number is rounded to an integer. Next, based on the concentration levels, we sample the cluster sizes from a multinomial distribution. Subsequently, for each cluster the endpoint intensities are sampled from the Poisson process (Equation 3) according to the simulation scenario as specified by one of the 150 factor combinations.

Parameter optimization

We optimized the tuning parameter values of the clustering algorithms whenever possible. Two distinct methods were employed to search for the optimal tuning parameter values.

The first method is manual or instructed search. Flowclust, SamSPECTRAL, ddPCRclust and dpcp provide specific instructions on how to select tuning parameter values or to make use of the prior knowledge, and we adhered to these guidelines. For methods without predefined optimization procedures, we employed a manual search. We initially identified key tuning parameters, assigning each a range of values spanning different magnitudes. Subsequently, the algorithms were tested with all combinations of these parameters, and the resulting clustering outcomes were visually inspected.

The second method is an automatic search that aims to optimise the adjusted Rand index (ARI) or silhouette coefficient. In particular, ranges of possible values were assigned to the key tuning parameters. Then the optimization algorithm automatically searched for tuning parameter values that can achieve the highest ARI or silhouette coefficient. The automatic search was implemented using Bayesian optimization with the ‘mlrMBO’ R package (version 1.1.5.1, [30]). It is a more exhaustive algorithm than then manual approach.

We then manually compared the best clustering results given by manual/instructed search and automatic search. We did this for all three empirical datasets. For more details, please see Parameter optimization in the Supplementary.

For the simulated data, a comprehensive manual search for tuning parameters was deemed impractical as there are 150 scenarios, but an automatic search may be possible. To explore this possibility, we implemented the automatic search based on the silhouette coefficient on the empirical datasets (no prior knowledge about grouping is required). However, we have observed that the automatic search procedure can yield quite wrong results (Figures S6G, S13G and S15G). This could be attributed to the optimization algorithm getting stuck in local minima, and the silhouette coefficient may not always be a reliable indicator. After all, the silhouette coefficient does not make use of the manual grouping information. We thus decided not to adjust the tuning parameters for each simulation scenario. Instead, as the simulation models were based on empirical data, we clustered the simulated data with the tuning parameters that were optimised for the empirical data. Notably, the three empirical datasets align with three different levels of resolution (see Table 2). Consequently, we applied the corresponding tuning parameter values to simulated datasets sharing the same level of resolution.

Performance evaluation

The clustering performance is assessed using ARI [31] and the relative bias of the 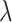estimates.

The ARI measures the similarity or agreement between two different clusterings of the same dataset. Here we compare the results of one of the 11 clustering methods with the ground truth. The ARI ranges from -1 to 1, where 1 indicates a perfect match between the two clusterings, 0 indicates random agreement, and -1 indicates complete disagreement.

We examined the ARI not only for the entire dataset but also for data points located on the periphery of clusters, as our interest also lies in rain classification. The edge data points are identified based on the ranking of silhouette coefficients within each cluster. We consider the percent of data points (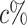) with the lowest silhouette coefficients as rain. To determine this, we need some prior knowledge about the rain percentage .

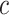The relative bias of 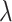refers to the deviation between an estimated value and the true value relative to the actual value itself, which is 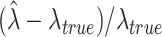. The average of this quantity over the 100 simulations, gives the relative bias of the estimator.

To match the clusters to the reference populations, we use the Hungarian assignment algorithm [32], which solves the linear assignment problem by finding a one-to-one mapping that minimizes the sum of distance between the cluster centers given by those methods and those of the references (the known true cluster centers).

We also recorded the runtime for the empirical data analysis. To investigate the stability of the clustering results, we ran the methods with different random starts on 100 bootstrap samples of size 10 000 from the original datasets.

We evaluated the overall performance as well as individual failure cases. We chose methods that demonstrated promising overall performance in both simulation and on the empirical data to perform further investigation.

Implementation, data and code availability

All the analyses were conducted using R (version 4.2.2) [33]. In addition, we have developed a Shiny app that enables end-users to interactively explore different parameters and simulate their own data for algorithm testing (see https://dpcr-ugent.shinyapps.io/DigitalPCRDataSimulator/). R code is available on GitHub (see https://github.com/digpcr/comparative_study_clustering/tree/main).

RESULTS

Empirical data

When comparing the different methods on empirical datasets, we observed that flowmerge, dpcp, kmeans_initials and cmeans_initials (with good initials provided), calico and flowpeaks work consistently well across datasets, both with default parameters and optimised tuning parameter values (refer to Table 3, S4 and S5). In contrast, cmeans without initials performed comparatively poor for all datasets. The performance of flowclust (manual or automatic) and SamSPECTRAL (manual) varied between datasets.

Table 3.

Performance metrics from the resampling study of the HR dataset

Method	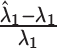(%)	(%)	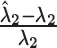ARI	ARI non-central	Number of clusters
ddPCRclust	0.40∥1.11	−0.55∥−0.32	0.999∥0.999	0.987∥0.986	/
flowmerge	−0.84	−0.55	0.999	0.987	4
dpcp	−2.09∥−1.94	−0.97∥−0.77	0.998∥0.998	0.985∥0.984	/
flowSOM	−1.66∥−3.13	−1.44∥−1.54	0.998∥0.997	0.979∥0.973	/
flowpeaks	−2.15∥−4.27	−0.96∥−4.01	0.998∥0.999	0.980∥0.991	4∥8.61
kmeans with initials	−2.29	−1.09	0.998	0.979	/
cmeans with initials	−2.29	−1.14	0.998	0.979	/
calico	−3.12∥−2.82	−2.06∥−1.90	0.996∥0.996	0.975∥0.962	/
DBSCAN	−3.35∥-49.70	−2.83∥-46.85	0.999∥0.998	0.993∥0.996	5∥8.26
SamSPECTRAL	−14.18	−1.17	0.998	0.986	/
SamSPECTRAL auto	−30.57	−25.71	0.998	0.985	8.31
flowclust	18.02	707.55	0.649	0.636	/
flowclust auto	28.25	422.53	0.783	0.768	4
kmeans	15.16	578.35	0.730	0.717	/
cmeans	172.37	1045.16	0.414	0.399	/

Average relative bias of 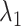and 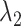, the ARI calculated for all resampled 10 000 data points and for the data points on the edge only, and the average number of clusters identified. When two values are separated with ‘∥’, the result with the optimal tuning parameter value is shown before the ∥, and the result with the default parameter value is shown behind ∥. For those methods that have only value, either no optimal tuning parameter values are available or the optimal ones coincide with the default ones. The methods are ranked from low to high relative bias (sum of the absolute relative biases 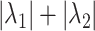) based on the results with optimal tuning parameter values. ‘/’: the number of clusters is pre-defined.

With the optimal tuning parameter values, the overall performance of the clustering methods has improved, especially for DBSCAN and SamSPECTRAL_auto. DBSCAN and SamSPECTRAL, which appeared as overall successful methods in our simulation study (see further), faced challenges for the HR dataset. DBSCAN overestimated the number of clusters, hampering the subsequent automatic labeling process (Figure S43A in the Supplementary). This overestimation may stem from rain scattering over many locations. Yet, post-clustering manual merging can yield accurate estimates, a finding supported by the disconnection between the observed ARI (high) and the relative bias (high). This problem was solved by using the optimal tuning parameter values. The relative bias of 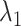and 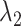dropped from 49.7% and 46.85% to 3.35% and 2.83%, respectively, and the estimated cluster number was reduced from 8.26 to 5. SamSPECTRAL proved sensitive to outliers and misidentified a minor cluster comprising two data points (Figure S43B in Supplementary). The alterations in parameters exhibit a minimal impact on the performance of SamSPECTRAL, as evidenced by only small changes in both the relative bias and ARI. Nonetheless, big improvements were observed in SamSpectral_auto when optimal tuning parameter values were applied to the MM dataset (refer to Table S4). The relative bias showed a significant improvement, decreasing from approximately 30% to 2%.

Flowclust (model-based) and kmeans and cmeans without initials (partitioning-based) suffered stability issues: in some cases, these methods split the negative cluster, resulting in high relative bias and low ARI (Figure S43 in the Supplementary).

Per sample run-times range from 6 ms (kmeans with initials) to 14 s (SamSPECTRAL in automatic mode; Table S6), demonstrating feasible execution time overall.

We also applied the clustering results to the duplex RPP30 host genomic DNA assay [21] for the absolute quantification of target DNA. The RPP30 assay can be used to correct for DNA shearing during the technical procedures [22, 34].

In terms of the confidence intervals (CIs) for the HR dataset, most of CIs covered the true values except for samspectral_auto where 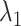and 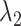are always underestimated (e.g. for 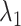, 59.90% bias, 95% CI [14.54–38.30 ], see Figure 3). ddPCRclust (4.63% bias, 95% CI [36.52–42.09]), flowmerge (7.03% bias, 95% CI [35.79–41.67]), flowSOM (7.48% bias, 95% CI [35.62–41.00]), flowPeaks (8.43% bias, 95% CI [35.41–41.28]), kmeans_initials (8.70% bias, 95% CI [35.41–41.21]), cmeans_initials (8.71% bias, 95% CI [35.41–41.21]), dpcp (9.36% bias, 95% CI [33.73–41.30]) and calico (9.62% bias, 95% CI [35.12–41.05]) gave accurate and narrow CIs. kmeans (8.53% bias, 95% CI [35.58–59.14]), SamSPECTRAL (13.09% bias, 95% CI [16.32–41.56]), DBSCAN (15.68% bias, 95% CI [16.57–40.90]), flowclust_auto (59.79% bias, 95% CI [35.58–60.07]) and SamSPECTRAL_auto (59.90% bias, 95% CI [14.54–38.30]) gave quite wide CIs, which indicates that the clustering results produced by those methods are inconsistent.

Figure 3.

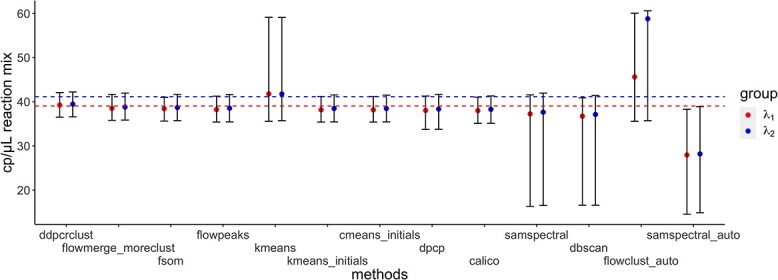
CI of 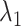and 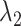for HR dataset. The confidence interval is calculated based on the resampled 10, 000 data points with the optimal tuning parameter values. The 95% confidence interval spans from the 2.5th to the 97.5th percentile of all estimates. The red dashed line in the plot represents the true value for 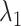, while the blue line represents the true value of 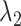. The methods are ordered by the relative bias of the mean concentration to the true value.

Data generation model: goodness-of-fit

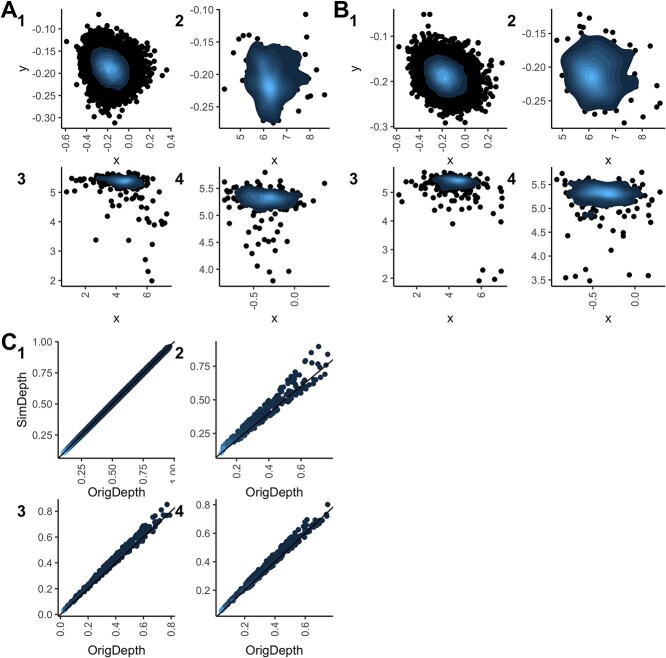
The density plots and depth-depth plots (Figures 4 and S2, S3 in the Supplementary) suggest that simulated aligns closely with the empirical data. While overall agreement looks good, deviations become noticeable as observations approach the center.

Figure 4.

Goodness-of-fit for the HR dataset. (A)–(B) Density plots of the original and simulated data, respectively, and (C) depth-depth plots. 1, 2, 3 and 4 represent the negative population, single positive 1, double positive and single positive 2, respectively. The further the data points from the cluster center, the darker those data points are. Depth values indicate how deep a data point is within the data distribution, with more central or typical points having higher depths and outliers having lower depths [35].

Global method performance on simulated data

We conducted a comparison of clustering results obtained through different methods using default parameter values and optimal tuning parameter values (Figure 5 vs. Figure S17). Notably, the application of optimal tuning parameter values derived from the empirical data did not enhance the overall performance in terms of average ARI and relative bias. In fact, it led to more extreme cases, particularly evident for flowpeaks and flowSOM. Consequently, we will only discuss here the simulation results obtained with default parameter values.

Figure 5.

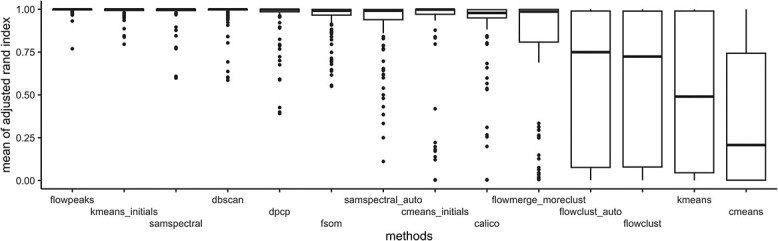
Averaged ARI across the 150 factor combinations.

Across the simulation scenarios, we observed large performance disparities among the methods (mean ARI range [0.2, 0.99]; Figure 5). Overall, flowpeaks, kmeans_initials, SamSPECTRAL and DBSCAN showed the best performance with mean ARIs of 0.99, 0.99, 0.98 and 0.97 respectively). In contrast, simple partitioning methods like cmeans and kmeans often yielded low ARI values (mean ARI of 0.2 and 0.5, respectively). Still, when provided with appropriate initial centroid values (cmeans_initials and kmeans_initials), better results were obtained (mean ARI of 0.87 and 0.99, respectively). Model-based algorithms like flowclust (in manual and automatic mode) and flowmerge generally exhibited subpar performance (mean ARI of 0.54, 0.54 and 0.79, respectively).

Of note, larger variation is observed when considering edge data points only (Figure S21 in Supplementary). flowpeaks and SamSPECTRAL demonstrated superior performance (mean ARI of 0.97 and 0.96, respectively). Regarding the relative bias of 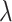estimates, most methods perform well (mean relative bias lower than 5%; Figures 6 and S22 in the Supplementary). However, some outliers indicate that these methods can sometimes suffer from large relative biases (over 50%).

Figure 6.

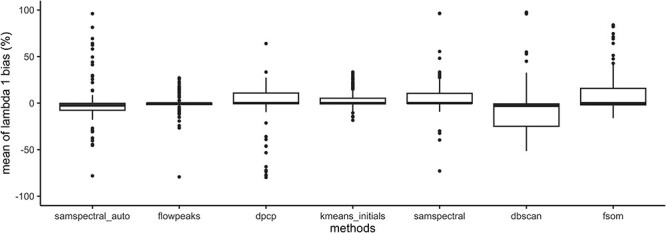
Relative bias of 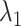across the 150 factor combinations. Note: cmeans, kmeans, flowclust, flowclust in automatic mode, flowmerge and calico were omitted from the bias analysis since their overall performance is poor.

The linear model results indicate that target concentration and resolution greatly impact the clustering performance across all methods (Figures S23–S38, Appendix 2 for the linear model fit results). Likewise, changes in MSE identified ‘concentration’ and ‘resolution’ as the most influential variables for the model’s performance (Figure 7). Equal concentration, cluster orthogonality and multi-modality had minimal impact on most methods’ clustering performance. One exception is the model-based method flowmerge that is sensitive to multiple modes.

Figure 7.

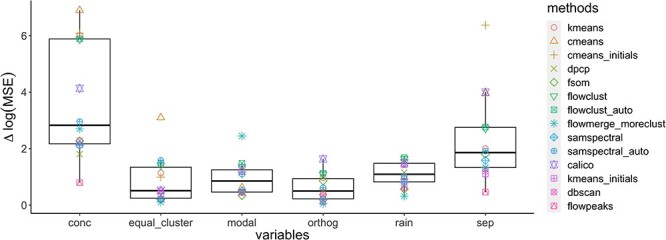
Changes in log(MSE) with variable elimination. The x-axis represents the variable removed at each step, while the y-axis shows the change in log(MSE). This change was calculated by subtracting the log(MSE) of the full model from that of the model with the variable removed. A high 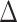log(MSE) indicates a big drop if this variable is removed, signifying its substantial contribution to the response variable.

calico, cmeans, cmeans_initials, kmeans, flowclust, flowclust_auto, flowSOM and samspectral_auto struggle to accurately classify data points at low concentration levels (0.1–2% partition occupancy, Figure S39). Interestingly, we observed a positive impact on ARI due to the interaction between low concentration levels and rain percentage. This suggests that at extremely low concentrations, the presence of rain may increase the effective concentration and assist algorithms in identifying the correct clusters.

Failure cases on simulated data

In terms of failure scenarios (ARI < 0.9), there are 20% of cases for calico, 9% for DBSCAN, 12% for dpcp, 29% for flowmerge, 0.66% for flowpeaks, 14% for flowSOM, 3.3% for kmeans_initials, 6.6% for SamSPECTRAL and 23% for SamSPECTRAL_auto.

An examination of the failure cases allowed the identification of scenarios for which some methods struggled to accurately identify the clusters. For instance, calico showed poor performance at very low concentrations and could also make mistakes at high concentrations if the grid number was misspecified (Figures 8A and S40 in Supplementary). DBSCAN failed primarily when confronted with high concentrations alongside medium or poor resolution, characterized by continuous rain between clusters (Figure 8B). dpcp failed in similar situations (Figure 8C). Flowpeaks struggled with high concentrations and double modalities where the sub-cluster centroids were clearly apart (Figure 8E). flowSOM encountered difficulties when the resolution was poor at high concentrations. Additionally, flowSOM sometimes failed to identify small clusters and incorrectly split the negative cluster (Figure 8F). kmeans_initials only failed when the resolution was poor at high concentrations (Figure 8G). SamSPECTRAL also struggled at high concentrations and in cases of poor resolution, but instead of splitting the negative population, it identified some rain as a distinct cluster (Figure 8H). Furthermore, in automatic mode without pre-specified cluster numbers, SamSPECTRAL occasionally produced only one or two clusters when the clusters were too small to be identified (Figure 8I). Flowmerge struggled to find the small clusters (Figure 8D) but also defined sub-clusters when the two clusters were clearly separated.

Figure 8.

Scenarios where methods fail: calico (A), DBSCAN (B), dpcp (C), flowmerge (D), flowpeaks (E), flowSOM (F), kmeans with initials (G), samspectral (H), sampectral in automatic mode (I).

We reapplied the clustering methods to the failure cases presented in Figure 8, this time utilizing optimal tuning parameter values. Notably, adjusting the tuning parameters resulted in an improved performance of DBSCAN, dPCP and flowSOM (see Figure S41), with which fewer data points were misclassified. However, for flowPeaks and SamSPECTRAL, parameter adjustment did not yield improvements.

DISCUSSION

Method strengths and limitations

We conducted a comprehensive comparison of various clustering algorithms, including those specifically designed for dPCR and for flow cytometry. Each method has strengths and limitations. While simpler, general methods or dPCR approaches may outperform more intricate flow cytometry methods in certain scenarios, the latter can excel when dealing with more complex datasets such as when the separation is poor.

The flow cytometry methods can be directly applied to (higher-order) multiplexing dPCR data. Many flow cytometry clustering algorithms start with a larger number of clusters and merge them based on criteria like distance and density, these merging criteria often rely on experience rather than being data-driven. Besides, in flow cytometry, cluster centers and sizes are unpredictable. Conversely, in dPCR data, we can have prior knowledge about cluster positions and sizes. For instance, the positions of higher-order clusters can be approximated as the vector sum of primary clusters [36]. However, such information is not incorporated into flow cytometry methods.

Existing dPCR clustering methods are typically limited to two-dimensional data, but some one-dimensional methods have the potential to be extended to multiple dimensions [6]. Prior knowledge on the cluster centroids can help with clustering, as shown in our study. dpcp depends on the presence of a well-separated reference sample for the initial identification of primary clusters, whereas ddPCRclust relies on accurately identifying the primary clusters within the samples. Obtaining good centroids is realistic as we can have control samples that closely resemble the target sample. On the other hand, if the controls significantly deviate from the target samples, then the resulting centroids may be misleading for the algorithms.

Insights from the simulation study

We developed a simulation method which is capable of generating data that closely resemble empirical dPCR data. Empirical data can often be complex and challenging to handle due to factors such as heavy noise, irregular shapes and overlapping clusters. In contrast, simulation studies provide more controllable conditions where the classification is known in advance, enabling easier and more accurate comparisons. With the simulation model, we do not make assumptions of the fluorescence intensities, which is often not normally distributed and may be long-tailed due to the presence of rain. In this way, we avoided the bias introduced by making a normal distributional assumption. Our model used skew- distribution as an offset, which takes into account the wide spread of the data and the irregular shape of the clusters. The Poisson point process also captures the rain well. Simulated data allow us to explore the underlying theories, application conditions, and limitations of various clustering methods.

Among the evaluated methods, kmeans_initials, DBSCAN and flowpeaks consistently exhibited strong performance across most simulation setups. Simple kmeans can be highly effective when provided with good centroids. While DBSCAN and flowpeaks occasionally produced a higher number of clusters than expected, they demonstrated low relative bias in 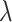estimates.

Conversely, model-based methods like flowclust and flowmerge faced challenges in many cases, potentially due to their reliance on likelihood estimation. These likelihood-based methods tend to perform well when the concentration is high. However, they may disregard small clusters as the sparse data points contribute little to the likelihood.

The dPCR methods dpcp, calico and ddPCRclust also failed on many occasions. The performance of dpcp, which utilizes DBSCAN as the initial step for identifying centroids, is not on par with DBSCAN as stand-alone. In many instances where DBSCAN fails to produce reasonable centroids, such as in cases of very low concentration or poor resolution, dpcp fails to function. In the study by [13], a reference sample with distinct resolution, minimal rain and identifiable first-order clusters was employed. This discrepancy in performance could be attributed to the fact that the two-step dpcp method may not be as effective as DBSCAN alone, when applied to noisy data. Calico, on the other hand, faces challenges when classifying data points with clear resolution at high concentration levels. This difficulty may stem from the dependence of this method on grid size. When too many grid cells are employed, the size discrepancies become magnified. ddPCRclust is an ensemble-based approach. However, when confronted with challenging dPCR data, individual models within the ensemble may exhibit subpar performance, leading to unsatisfactory results or even worse results compared to using them individually. Apart from that, ddPCRclust cannot work on the standardized data.

We identified resolution and concentration level as the most influential factors impacting clustering performance. Many methods encountered difficulties when dealing with extremely low concentrations, a problematic observation as this is one of the major application area of dPCR [37]. On the other hand, orthogonality and modality had negligible effects on clustering performance. Notably, when the concentration level was low, equal concentration and rain proved beneficial in aiding algorithms to accurately identify clusters.

Recommendation for clustering methods

The simulation study shows that at high to medium concentration levels with good resolution (from cluster sizes of hundreds of partitions to thousands), almost all methods work quite well. However, at very low concentration, many methods will struggle. In real-life, users generally have some prior knowledge about the target concentration. For example, dPCR has been applied for the detection of somatic mutations, both for absolute allele quantification and for rare mutation detection [3].

When selecting clustering methods, we recommend considering both the concentration and resolution levels. Among the tested methods, DBSCAN, kmeans_initials and flowpeaks are good generic choices. For the remaining methods, we provide specific recommendations in terms of concentration and resolution, as outlined in Table 4.

Table 4.

Recommendations for clustering methods

Concentration levels	Resolution	Recommended methods
High	Good	cmeans with initials, dpcp, flowmerge, flowSOM, kmeans, SamSPECTRAL
	Medium	cmeans with initials, dpcp, flowmerge, flowSOM, SamSPECTRAL
	Poor	flowmerge, flowSOM, SamSPECTRAL
Low	Good	calico, cmeans with initials, dpcp, flowmerge, flowSOM, SamSPECTRAL
	Medium	calico, cmeans with initials, dpcp, flowmerge, flowSOM, SamSPECTRAL
	Poor	flowmerge, flowSOM, SamSPECTRAL
Very low	Good	dpcp, SamSPECTRAL
	Medium	dpcp, SamSPECTRAL
	Poor	/
Rare	Good	SamSPECTRAL
	Medium	SamSPECTRAL
	Poor	/

‘/’ means the methods other than DBSCAN, kmeans_initials and flowpeaks do not work well under those circumstances. Note: by the simulation results, a high to low concentration level means cluster sizes of thousands to hundreds of positive partitions.

Here we offer a general recommendation. However, for selecting the most suitable clustering method tailored to a specific assay, we recommend utilizing our interactive Shiny application. With this tool, the user can construct a model based on their own data, generate synthetic data and assess the performance of various methods across different simulation scenarios. Access to the evaluation code, including ARI and relative bias calculations, is available from GitHub.

Guidance and future perspectives in dPCR clustering

Our findings provide valuable guidance for selecting appropriate clustering methods for dPCR data analysis. We only explored absolute quantification, but it would also be interesting to study other applications, e.g. CNV. However, we believe that the conclusions from our examples translate to other applications, such as CNV. The reason is that all types of applications rely on the clustering of the partitions. If a clustering method does not work well for absolute quantification, then it will also not work well for CNV. Additionally, the database of empirical dPCR data augmented with the labeled simulated data can serve as training and testing data for other clustering methods.

Optimizing tuning parameter values resulted in improved clustering on the three empirical datasets. Similarly, some failure cases in the simulation study were rectified through parameter adjustments. However, using the optimized tuning parameter values did not lead to an improvement in the overall performance on the simulated data. This could be attributed to the fact that parameters derived from the empirical data may not be universally optimal for all simulated data, given the diverse simulation scenarios that were considered. This indicates that parameter optimization can be helpful when analyzing specific datasets, but one should be cautious when using parameter values optimised for a single dataset to cluster many datasets when a case-by-case parameter optimization is not feasible. Therefore, for future dPCR clustering endeavors, we recommend the establishment of guidelines for selecting optimal tuning parameter values tailored to the specific characteristics of the dPCR data. Additionally, the development of an effective automated aberrant classification flagging system would be a welcome addition to warn users of potential poor classifications.

Furthermore, the latest generation of dPCR instruments now enable analysis of up to six colors [4]. Our study focused on two-color settings for which it is possible to do an extensive and thorough benchmarking of clustering methods. Today, applications with two colors are still much more common than with six or seven colors, and hence we consider our study as very relevant. The generalisation of our findings to more challenging scenarios with higher-order multiplexing, requires further investigation. Although the clustering methods for general purposes or flow cytometry can be directly applied to multiplex dPCR data, they may not perform so well. Therefore, the development of better methods and methods that can cope with more than two colors will be needed.

Key Points

• We evaluated the performance of clustering methods for the classification of partitions in duplex experiments, using both simulated and empirical data. Three types of methods are considered: methods specifically developed for dPCR, also general clustering algorithms, and clustering methods designed for flow cytometry data.

• We developed a novel simulation method to generate realistic dPCR data, which enables an extensive evaluation of clustering methods. The simulation method incorporates many biologically relevant characteristics, such as concentration and resolution. The method is available as a R Shiny app.

• We discuss when and why specific methods fail, and finally provide guidelines for method selection in a variety of biologically relevant scenarios.

COMPETING INTERESTS

JV is co-founder of Pxlence.

FUNDING

Y.C. and D.G. are funded by Ghent University’s Special Research Fund (BOF, grant 01IO0420 awarded to O.T. and W.D.S.). M.V. is funded by Stilla Technologies (grant awarded to O.T. and W.D.S.).

AUTHOR CONTRIBUTIONS

Conceptualization: Y.C., O.T., M.V.; implementation: Y.C.; supervision: O.T., M.V.; original draft: Y.C.; review and editing: Y.C., W.D.S., W.T., D.G., J.V., A.L., M.V., O.T.

Author Biographies

Yao Chen is a third-year PhD candidate at the Department of Applied Mathematics, Computer Science and Statistics at Ghent University, working on an interdisciplinary project of statistical analysis of digital PCR data.

Ward De Spiegelaere is an associate professor at Ghent University, where he heads the dPCR facility at the Faculty of Veterinary Medicine. He works on higher order multiplexing and partition clustering for various dPCR applications, including pathogen detection, mutation analysis and quality control of RNA and DNA by dPCR.

Wim Trypsteen is a postdoctoral research. His research interests lie in threshold setting, applications of dPCR in absolute HIV DNA and RNA quantification and analysis of HIV intactness.

David Gleerup is a third-year PhD candidate. His work focuses on designing and validating new higher order multiplex assays for digital PCR within the fields of both veterinary and human medicine.

Jo Vandesompele is a professor at Ghent University and group leader at the Cancer Research Institute in Ghent where he co-supervises the OncoRNALab. Jo has a long-standing track record in method development for PCR based quantification of nucleic acids. The lab focuses on PCR primer design, the study of pre-analytical variables, and data-analysis. Applications are being developed in the context of oncology and liquid biopsies.

Antoon Lievens is molecular biologist and statistician with a career in method qPCR and dPCR development in the fields of GMO, Food Fraud, and plant breeding. He focuses on research and development of (d)dPCR analysis tools.

Matthijs Vynck a postdoctoral researcher with molecular biology background focussing on clustering analysis of dPCR data and statistical data analysis of dPCR experiments.

Olivier Thas is a Professor of Biostatistics at Hasselt University, Guest Professor at the Faculty of Sciences at Ghent University and Honorary Professor at the University of Wollongong. His research focusses on the development and application of flexible statistical methods for the analysis of biomolecular quantitation experiments.