Transfer Learning under High-dimensional Generalized Linear Models

Abstract

In this work, we study the transfer learning problem under highdimensional generalized linear models (GLMs), which aim to improve the fit on target data by borrowing information from useful source data. Given which sources to transfer, we propose a transfer learning algorithm on GLM, and derive its ℓ₁ / ℓ₂-estimation error bounds as well as a bound for a prediction error measure. The theoretical analysis shows that when the target and source are sufficiently close to each other, these bounds could be improved over those of the classical penalized estimator using only target data under mild conditions. When we don’t know which sources to transfer, an algorithm-free transferable source detection approach is introduced to detect informative sources. The detection consistency is proved under the high-dimensional GLM transfer learning setting. We also propose an algorithm to construct confidence intervals of each coefficient component, and the corresponding theories are provided. Extensive simulations and a real-data experiment verify the effectiveness of our algorithms. We implement the proposed GLM transfer learning algorithms in a new R package glmtrans, which is available on CRAN.

1. Introduction

Nowadays, a great deal of machine learning algorithms has been successfully applied in our daily life. Many of these algorithms require sufficient training data to perform well, which sometimes can be limited. For example, from an online merchant ‘s view, it could be difficult to collect enough personal purchase data for predicting the customers’ purchase behavior and recommending corresponding items. However, in many cases, some related datasets may be available in addition to the limited data for the original task. In the merchant-customer example, we may also have the customers’ clicking data in hand, which is not exactly the same as but shares similarities with the purchase data. How to use these additional data to help with the original target task motivates a well-known concept in computer science: transfer learning (Torrey and Shavlik, 2010; Weiss et al., 2016). As its name indicates, in a transfer learning problem, we aim to transfer some useful information from similar tasks (sources) to the original task (target), in order to boost the performance on the target. To date, transfer learning has been widely applied in a number of machine learning applications, including the customer review classification (Pan and Yang, 2009), medical diagnosis (Hajiramezanali and Zamani, 2018), and ride dispatching in ride-sharing platforms (Wang et al., 2018), etc. Compared with the rapidly growing applications, there has been little discussion about the theoretical guarantee of transfer learning. Besides, although transfer learning has been prevailing in computer science community for decades, far less attention has been paid to it among statisticians. More specifically, transfer learning can be promising in the high-dimensional data analysis, where the sample size is much less than the dimension with some sparsity structure in the data (Tibshirani, 1996). The impact of transfer learning in high-dimensional generalized linear models (GLMs) with sparsity structure is not quite clear up to now. In this paper, we are trying to fill the gap by developing transfer learning tools in high-dimensional GLM inference problem, and providing corresponding theoretical guarantees.

Prior to our paper, there are a few pioneering works exploring transfer learning under the high-dimensional setting. Bastani (2021) studied the single-source case when the target data comes from a high-dimensional GLM with limited sample size while the source data size is sufficiently large than the dimension. A two-step transfer learning algorithm was developed, and the estimation error bound was derived when the contrast between target and source coefficients is ℓ₀-sparse. Li et al. (2021) further explored the multi-source high-dimensional linear regression problem where both target and source samples are high-dimensional. The ℓ₂-estimation error bound under ℓ_q-regularization (q ∈ [0, 1]) was derived and proved to be minimax optimal under some conditions. In Li et al. (2020), the analysis was extended to the Gaussian graphical models with false discovery rate control. Other related research on transfer learning with theoretical guarantee includes the non-parametric classification model (Cai and Wei, 2021; Reeve et al., 2021) and the analysis under general functional classes via transfer exponents (Hanneke and Kpotufe, 2020a,b), etc. In addition, during the past few years, there have been some related works studying parameter sharing under the regression setting. For instance, Chen et al. (2015) and Zheng et al. (2019) developed the so-called “data enriched model” for linear and logistic regression under a single-source setting, where the properties of the oracle tuned estimator with a quadratic penalty were studied. Gross and Tibshirani (2016) and Ollier and Viallon (2017) explored the so-called “data shared Lasso” under the multi-task learning setting, where ℓ₁ penalties of all contrasts are considered.

In this work, we contribute to transfer learning under a high-dimensional context from three perspectives. First, we extend the results of Bastani (2021) and Li et al. (2021), by proposing multi-source transfer learning algorithms on generalized linear models (GLMs) and we assume both target and source data to be high-dimensional. We assume the contrast between target and source coefficients to be ℓ₁-sparse, which differs from the ℓ₀-sparsity considered in Bastani (2021). The theoretical analysis shows that when the target and source are sufficiently close to each other, the estimation error bound of target coefficients could be improved over that of the classical penalized estimator using only target data under mild conditions. Moreover, the error rate is shown to be minimax optimal under certain conditions. To the best of our knowledge, this is the first study of the multi-source transfer learning framework under the high-dimensional GLM setting. Second, as we mentioned, transferring sources that are close to the target can bring benefits. However, some sources might be far away from the target, and transferring them can be harmful. This phenomenon is often called negative transfer in literature (Torrey and Shavlik, 2010). We will show the impact of negative transfer in simulation studies in Section 4.1. To avoid this issue, we develop an algorithm-free transferable source detection algorithm, which can help identify informative sources. And with certain conditions satisfied, the algorithm is shown to be able to distinguish useful sources from useless ones. Third, all aforementioned works of transfer learning on high-dimensional regression only focus on the point estimate of the coefficient, which is not sufficient for statistical inference. How transfer learning can benefit the confidence interval construction remains unclear. We propose an algorithm on the basis of our two-step transfer learning procedure and nodewise regression (Van de Geer et al., 2014), to construct the confidence interval for each coefficient component. The corresponding asymptotic theories are established.

The rest of this paper is organized as follows. Section 2 first introduces GLM basics and transfer learning settings under high-dimensional GLM, then presents a general algorithm (where we know which sources are useful) and the transferable source detection algorithm (where useful sources are automatically detected). At the end of Section 2, we develop an algorithm to construct confidence intervals. Section 3 provides the theoretical analysis on the algorithms, including ℓ₁ and ℓ₂-estimation error bounds of the general algorithm, detection consistency property of the transferable source detection algorithm, and asymptotic theories for the confidence interval construction. We conduct extensive simulations and a real-data study in Section 4, and the results demonstrate the effectiveness of our GLM transfer learning algorithms. In Section 5, we review our contributions and shed light on some interesting future research directions. Additional simulation results and theoretical analysis, as well as all the proofs, are relegated to supplementary materials.

2. Methodology

We first introduce some notations to be used throughout the paper. We use bold capitalized letters (e.g. X, A) to denote matrices, and use bold little letters (e.g. x, y) to denote vectors. For a p-dimensional vector x = (x₁, …, x_p)^T we denote its ℓ_q-norm as $\Vert \mathit{x}\Vert =(\sum _{i=1}^p\mid x_i{\mid }^q{)}^{1∕q}(q\in (0,2])$, and ℓ₀-“norm” ∥ x ∥₀ = #{j : x_j ≠ 0}. For a matrix A_{p × q} = [a_ij]_{p × q}, its 1-norm, 2-norm, ∞-norm and max-norm are defined as $\Vert \mathit{A}{\Vert }_1=\underset{j}{\text{sup}}\sum _{i=1}^p\mid a_{ij}\mid ,\Vert \mathit{A}{\Vert }_2={\max }_{\mathit{x}:\Vert \mathit{x}{\Vert }_2=1}\Vert \mathit{A}\mathit{x}{\Vert }_2,\Vert \mathit{A}{\Vert }_{\infty }=\underset{i}{\text{sup}}\sum _{j=1}^q\mid a_{ij}\mid$ and $\Vert \mathit{A}{\Vert }_{\max }=\underset{i,j}{\text{sup}}\mid a_{ij}\mid$, respectively. For two non-zero real sequences ${\{a_n\}}_{n=1}^{\infty }$ and ${\{b_n\}}_{n=1}^{\infty }$, we use a_n ≪ b_n, b_n ≫ a_n or a_n = ^𝒪 (b_n) to represent ∣ a_n / b_n ∣→ 0 as n → ∞. And a_n ≲ b_n or a_n = ^𝒪 (b_n) means $\underset{n}{\text{sup}}\mid a_n∕b_n\mid <\infty$. Expression a_n ≍ b_n means that a_n / b_n converges to some positive constant. For two random variable sequences ${\{x_n\}}_{n=1}^{\infty }$ and ${\{y_n\}}_{n=1}^{\infty }$, notation x_n ≲ _py_n or x_n = ^𝒪 _p(y_n) means that for any ϵ > 0, there exists a positive constant M such that $\underset{n}{\text{sup}}\mathbb{P}(\mid x_n∕y_n\mid >M)\le ∊$. And for two real numbers a and b, we use a ∨ b and a ∧ b to represent max(a, b) and min(a, b), respectively. Without specific notes, the expectation $\mathbb{E}$, variance Var, and covariance Cov are calculated based on all randomness.

2.1. Generalized linear models (GLMs)

Given the predictors $\mathit{x}\in {\mathbb{R}}^p$, if the response yfollows the generalized linear models (GLMs), then its conditional distribution takes the form

$$y\mid \mathit{x}\sim \mathbb{P}(y\mid \mathit{x})=\rho (y)\text{exp}\{y{\mathit{x}}^T\mathit{w}-\psi ({\mathit{x}}^T\mathit{w})\},$$

where $\mathit{w}\in {\mathbb{R}}^p$ is the coefficient, ρ and ψ are some known univariate functions. $\psi \prime ({\mathit{x}}^T\mathit{w})=\mathbb{E}(y\mid \mathit{x})$ is called the inverse link function (McCullagh and Nelder, 1989). Another important property is that Var(y ∣ x) = ψ″(x^T w), which follows from the fact that the distribution belongs to the exponential family. It is ψ that characterizes different GLMs. For example, in linear model with Gaussian noise, we have a continuous response y and $\psi (u)=\frac{1}{2}{u}^2$; in the logistic regression model, y is binary and ψ(u) = log(1 + e^u); and in Poisson regression model, y is a nonnegative integer and ψ(u) = e^u. For most GLMs, ψ is strictly convex and infinitely differentiable.

2.2. Target data, source data, and transferring level

In this paper, we consider the following multi-source transfer learning problem. Suppose we have the target data set (X⁽⁰⁾, y⁽⁰⁾) and K source data sets with the k-th source denoted as (X^(k), y^(k)), where ${\mathit{X}}^{(k)}\in {\mathbb{R}}^{n_k\times p},{\mathit{y}}^{(k)}\in {\mathbb{R}}^{n_k}$ for k = 0, …, K. The i-th row of X^(k) and the i-th element of y^(k) are denoted as ${\mathit{x}}_i^{(k)}$ and $y_i^{(k)}$, respectively. The goal is to transfer useful information from source data to obtain a better model for the target data. We assume the responses in the target and source data all follow the generalized linear model:

$$y^{(k)}\mid \mathit{x}\sim \mathbb{P}(y\mid \mathit{x})=\rho (y)\text{exp}\{y{\mathit{x}}^T{\mathit{w}}^{(k)}-\psi ({\mathit{x}}^T{\mathit{w}}^{(k)})\},$$ (1)

for k = 0, …, K, with possibly different coefficient ${\mathit{w}}^{(k)}\in {\mathbb{R}}^p$, the predictor $\mathit{x}\in {\mathbb{R}}^p$, and some known univariate functions ρ and ψ. Denote the target parameter as β = w⁽⁰⁾. Suppose the target model is ℓ₀-sparse, which satisfies ∥ β ∥₀ = s ≪ p. This means that only s of the p variables contribute to the target response. Intuitively, if w^(k) is close to β, the k-th source could be useful for transfer learning.

Define the k-th contrast δ^(k) = β − w^(k) and we say ∥ δ^(k) ∥₁ is the transferring level of source k. And we define the level-h transferring set 𝒜_h = {k :∥ δ^(k) ∥₁ ≤ h} as the set of sources which has transferring level lower than h. Note that in general, h can be any positive values and different h values define different 𝒜_h set. However, in our regime of interest, h shall be reasonably small to guarantee that transferring sources in 𝒜_h beneficial. Denote $n_{{𝒜}_h}=\sum _{k{\in }^{{𝒜}_h}}{n}_k,{\alpha }_k=\frac{n_k}{n_{{𝒜}_h}+n_0}$ for k ∈ {0} ∪ 𝒜_h and K_𝒜h = ∣ 𝒜_h ∣.

Note that in (1), we assume GLMs of the target and all sources share the same inverse link function ψ. After a careful examination of our proofs for theoretical properties in Section 3, we find that these theoretical results still hold even when the target and each source have their own function ψ, as long as these GLMs satisfy Assumptions 1 and 3 (to be presented in Section 3.1). It means that transferring information across different GLM families is possible. For simplicity, in the following discussion, we assume all these GLMs belong to the same family and hence have the same function ψ

2.3. Two-step GLM transfer learning

We first introduce a general transfer learning algorithm on GLMs, which can be applied to transfer all sources in a given index set 𝒜. The algorithm is motivated by the ideas in Bastani (2021) and Li et al. (2021), which we call a two-step transfer learning algorithm. The main strategy is to first transfer the information from those sources by pooling all the data to obtain a rough estimator, then correct the bias in the second step using the target data. More specifically, we fit a GLM with ℓ₁-penalty by pooled samples first, then fit the contrast in the second step using only the target by another ℓ₁-regularization. The detailed algorithm (𝒜-Trans-GLM) is presented in Algorithm 1. The transferring step could be understood as to solve the following equation w.r.t. $\mathit{w}\in {\mathbb{R}}^p$:

$$\sum _{k\in \{0\}\cup 𝒜}\left[({\mathit{X}}^{(k)}{)}^T{\mathit{y}}^{(k)}-\sum _{i=1}^{n_k}{\psi }^{\prime }((\mathit{w}{)}^T{\mathit{x}}_i^{(k)}){\mathit{x}}_i^{(k)}\right]=0_p,$$

which converges to the solution of its population version under certain conditions

$$\sum _{k\in \{0\}\cup 𝒜}{\alpha }_k\mathbb{E}\left\{[{\psi }^{\prime }(({\mathit{w}}^{𝒜}{)}^T{\mathit{x}}^{(k)})-{\psi }^{\prime }(({\mathit{w}}^{(k)}{)}^T{\mathit{x}}^{(k)})]{\mathit{x}}^{(k)}\right\}=0_p,$$ (2)

where ${\alpha }_k=\frac{n_k}{n_{𝒜}+n_0}$. Notice that in the linear case, w^𝒜 can be explicitly expressed as a linear transformation of the true parameter w^(k), i.e. ${\mathit{w}}^{𝒜}={\mathbf{\Sigma }}^{-1}\sum _{k\in \{0\}{\cup }^{𝒜}}{\alpha }_k{\mathbf{\Sigma }}^{(k)}{\mathit{w}}^{(k)}$, where ${\mathbf{\Sigma }}^{(k)}=\mathbb{E}[{\mathit{x}}^{(k)}({\mathit{x}}^{(k)}{)}^T]$ and $\mathbf{\Sigma }=\sum _{k\in \{0\}{\cup }^{𝒜}}{\alpha }_k\mathbb{E}[{\mathit{x}}^{(k)}({\mathit{x}}^{(k)}{)}^T]$ (Li et al., 2021).

To help readers better understand the algorithm, we draw a schematic in Section S.1.1 of supplements. We refer interested readers who want to get more intuitions to that.

Algorithm 1: 𝒜 -Trans-GLM

$$\begin{array}{cc}\hfill & \mathrm{Input}:\text{target data}({\mathit{X}}^{(0)},{\mathit{y}}^{(0)}),\text{source data}\{({\mathit{X}}^{(k)},{\mathit{y}}^{(k)})\}k=1K,\text{penalty parameters}{\lambda }_w\text{and}\hfill \\ \hfill & {\lambda }_{\delta },\text{transferring set}𝒜\hfill \\ \hfill & \mathrm{Output}:\text{the estimated coefficient vector}\mathit{\beta }\hfill \\ \hfill & 1\mathbf{Transferring}\mathrm{step}:\text{Compute}\hfill \\ \hfill & {\mathit{w}}^{𝒜}\leftarrow \text{arg}{\text{min}}_{\mathit{w}}\left\{\frac{1}{n_{𝒜}+n_0}\sum _{k\in \{0\}{\cup }^{𝒜}}\left[-{({\mathit{y}}^{(k)})}^T{\mathit{X}}^{(k)}\mathit{w}+\sum _{i=1}^{n_k}\psi ({\mathit{w}}^T{\mathit{x}}_i^{(k)})\right]+{\lambda }_{\mathit{w}}\Vert \mathit{w}{\Vert }_1\right\}\hfill \\ \hfill & 2\mathbf{Debiasing}\mathrm{step}:\text{Compute}\hfill \\ \hfill & {\mathit{\delta }}^{𝒜}\leftarrow \text{arg}{\text{min}}_{\mathit{\delta }}\left\{-\frac{1}{n_0}({\mathit{y}}^{(0)}{)}^T{\mathit{X}}^{(0)}({\mathit{w}}^{𝒜}+\mathit{\delta })+\frac{1}{n_0}\sum _{i=1}^{n_0}\psi (({\mathit{w}}^{𝒜}+\mathit{\delta }{)}^T{\mathit{x}}_i^{(0)})+{\lambda }_{\mathit{\delta }}\Vert \mathit{\delta }{\Vert }_1\right\}\hfill \\ \hfill & 3\mathbf{Let}\mathit{\beta }\leftarrow {\mathit{w}}^{𝒜}+{\mathit{\delta }}^{𝒜}\hfill \\ \hfill & 4\mathbf{Output}\mathit{\beta }\hfill \end{array}$$

2.4. Transferable source detection

As we described, Algorithm 1 can be applied only if we are certain about which sources to transfer, which in practice may not be known as a priori. Transferring certain sources may not improve the performance of the fitted model based on only target, and can even lead to worse performance. In transfer learning, we say negative transfer happens when the source data leads to an inferior performance on the target task (Pan and Yang, 2009; Torrey and Shavlik, 2010; Weiss et al., 2016). How to avoid negative transfer has become an increasingly popular research topic.

Here we propose a simple, algorithm-free, and data-driven method to determine an informative transferring set 𝒜. We call this approach a transferable source detection algorithm and refer to it as Trans-GLM.

We sketch this detection algorithm as follows. First, divide the target data into three folds, that is, ${\{({\mathit{X}}^{(0)[r]},{\mathit{y}}^{(0)[r]})\}}_{r=1}^3$. Note that we choose three folds only for convenience. We also explored other fold number choices in the simulation. See Section S.1.3.3 in the supplementary materials. Second, run the transferring step on each source data and every two folds of target data. Then, for a given loss function, we calculate its value on the left-out fold of target data and compute the average cross-validation loss ${\widehat{L}}_0^{(k)}$ for each source. As a benchmark, we also fit Lasso on every choice of two folds of target data and calculate the loss on the remaining fold. The average cross-validation loss ${\widehat{L}}_0^{(0)}$ is viewed as the loss of target. Finally, the difference between ${\widehat{L}}_0^{(k)}$ and ${\widehat{L}}_0^{(0)}$ is calculated and compared with some threshold, and sources with a difference less than the threshold will be recruited into 𝒜. Under the GLM setting, a natural loss function is the negative log-likelihood. For convenience, suppose n₀ is divisible by 3. According to (1), for any coefficient estimate w. the average of negative log-likelihood on the r-th fold of target data (X^(0)[r], y^(0)[r]) is

$${\widehat{L}}_0^{[r]}(\mathit{w})=-\frac{1}{n_0∕3}\sum _{i=1}^{n_0∕3}\log \rho (y_i^{(0)[r]})-\frac{1}{n_0∕3}({\mathit{y}}^{(0)[r]}{)}^T{\mathit{X}}^{(0)}\mathit{w}+\frac{1}{n_0∕3}\sum _{i=1}^{n_0∕3}\psi ({\mathit{w}}^T{\mathit{x}}_i^{(0)[r]}).$$ (3)

The detailed algorithm is presented as Algorithm 2.

Algorithm 2: Trans-GLM

$$\begin{array}{cc}\hfill & \mathrm{Input}:\text{target data}({\mathit{X}}^{(0)},{\mathit{y}}^{(0)}),\text{all source data}\{({\mathit{X}}^{(k)},{\mathit{y}}^{(k)}){\}}_{k=1}^K,\text{a constant}{C}_0>0,\hfill \\ \hfill & \text{penalty parameters}\{\{{\lambda }^{(k)[r]}{\}}_{k=0}^K{\}}_{r=1}^3\hfill \\ \hfill & \mathrm{Output}:\text{the estimated coefficient vector}\mathit{\beta },\text{and the determind transferring set}𝒜\hfill \\ \hfill & 1\mathbf{Transferable}\mathbf{source}\mathrm{detection}:\text{Randomly divide}({\mathit{X}}^{(0)},{\mathit{y}}^{(0)})\text{into three sets of equal}\hfill \\ \hfill & \text{size as}\{({\mathit{X}}^{(0)[i]},{\mathit{y}}^{(0)[i]}){\}}_{i=1}^3\hfill \\ \hfill & 2\mathbf{for}r=1\mathbf{to}3\mathbf{do}\hfill \\ \hfill & 3{\mathit{\beta }}^{(0)[r]}\leftarrow \text{fit the Lasso on}\{({\mathit{X}}^{(0)[i]},{\mathit{y}}^{(0)[i]}){\}}_{i=1}^3\setminus ({\mathit{X}}^{(0)[r]},{\mathit{y}}^{(0)[r]})\text{with penalty parameter}\hfill \\ \hfill & {\lambda }^{(0)[r]}\hfill \\ \hfill & 4{\mathit{\beta }}^{(k)[r]}\leftarrow \text{run step}1\text{in Algorithm}1\text{with}\hfill \\ \hfill & (\{({\mathit{X}}^{(0)[i]},{\mathit{y}}^{(0)[i]}){\}}_{i=1}^3\setminus ({\mathit{X}}^{(0)[r]},{\mathit{y}}^{(0)[r]}))\cup ({\mathit{X}}^{(k)},{\mathit{y}}^{(k)})\text{and penalty parameter}{\lambda }^{(k)[r]}\text{for all}\hfill \\ \hfill & k\ne 0\hfill \\ \hfill & 5\text{Calculate the loss function}{\widehat{L}}_0^{[r]}({\mathit{\beta }}^{(k)[r]})\text{on}({\mathit{X}}^{(0)[r]},{\mathit{y}}^{(0)[r]})\text{for}k=1,\dots ,K\hfill \\ \hfill & 6\mathbf{end}\hfill \\ \hfill & 7{\widehat{L}}_0^{(k)}\leftarrow \sum _{r=1}^3{\widehat{L}}_0^{[r]}({\mathit{\beta }}^{(k)[r]})∕3,{\widehat{L}}_0^{(0)}\leftarrow \sum _{r=1}^3{\widehat{L}}_0^{[r]}({\mathit{\beta }}^{(0)[r]})∕3,\widehat{\sigma }=\sqrt{\sum _{r=1}^3({\widehat{L}}_0^{[r]}({\mathit{\beta }}^{(0)[r]})-{\widehat{L}}_0^{(0)}{)}^2∕2}\hfill \\ \hfill & 8𝒜\leftarrow \{k\ne 0:{\widehat{L}}_0^{(k)}-{\widehat{L}}_0^{(0)}\le C_0(\widehat{\sigma }\vee 0.01)\}\hfill \\ \hfill & 9𝒜-\mathbf{Trans}-\mathrm{GLM}:\mathit{\beta }\leftarrow \text{run Algorithm}1\text{using}\{({\mathit{X}}^{(k)},{\mathit{y}}^{(k)})\}k\in \{0\}{\cup }^{𝒜}\hfill \\ \hfill & 10\text{Output}\mathit{\beta }\text{and}𝒜\hfill \end{array}$$

It’s important to point out that Algorithm 2 does not require the input of h. We will show that 𝒜 = 𝒜_h for some specific h if certain conditions hold, in Section 3.2. Furthermore, under these conditions, transferring with 𝒜 will lead to a faster convergence rate compared to Lasso fitted on only the target data, when target sample size n₀ falls into some regime. This is the reason that this algorithm is called the transferable source detection algorithm.

2.5. Confidence intervals

In previous sections, we’ve discussed how to obtain a point estimator of the target coefficient vector β from the two-step transfer learning approach. In this section, we would like to construct the asymptotic confidence interval (CI) for each component of β based on that point estimate.

As described in the introduction, there have been quite a few works on high-dimensional GLM inference in the literature. In the following, we will propose a transfer learning procedure to construct CI based on the desparsified Lasso (Van de Geer et al., 2014). Recall that desparsified Lasso contains two main steps. The first step is to learn the inverse Fisher information matrix of GLM by nodewise regression (Meinshausen and Bühlmann, 2006). The second step is to “debias” the initial point estimator and then construct the asymptotic CI. Here, the estimator β from Algorithm 1 can be used as an initial point estimator. Intuitively, if the predictors from target and source data are similar and satisfy some sparsity conditions, it might be possible to use Algorithm 1 for learning the inverse Fisher information matrix of target data, which effectively combines the information from target and source data.

Before formalizing the procedure to construct the CI, let’s first define several additional notations. For any $\mathit{w}\in {\mathbb{R}}^n$, denote ${\mathit{W}}_{\mathit{w}}^{(k)}=\text{diag}\left(\sqrt{{\psi }^{″}(({\mathit{x}}_1^{(k)}{)}^T\mathit{w})},\dots ,\sqrt{{\psi }^{″}(({\mathit{x}}_{n_k}^{(k)}{)}^T\mathit{w})}\right)$, ${\mathit{X}}_{\mathit{w}}^{(k)}={\mathit{W}}_{\mathit{w}}^{(k)}{\mathit{X}}^{(k)},{\mathbf{\Sigma }}_{\mathit{w}}^{(k)}=\mathbb{E}[{\mathit{x}}^{(k)}({\mathit{x}}^{(k)}{)}^T{\psi }^{″}(({\mathit{x}}^{(k)}{)}^T\mathit{w})]$ and ${\mathbf{\Sigma }}_{\mathit{w}}^{(k)}=n_k^{-1}({\mathit{X}}_{\mathit{w}}^{(k)}{)}^T{\mathit{X}}_{\mathit{w}}^{(k)}$. ${\mathit{X}}_{\mathit{w},j}^{(k)}$ represents the j-th column of ${\mathit{X}}_{\mathit{w}}^{(k)}$ and ${\mathit{X}}_{\mathit{w},-j}^{(k)}$ represents the matrix ${\mathit{X}}_{\mathit{w}}^{(k)}$ without the j-th column. ${\mathbf{\Sigma }}_{\mathit{w},j,-j}^{(k)}$ represents the j-th row of ${\mathbf{\Sigma }}_{\mathit{w}}^{(k)}$ without the diagonal (j, j) element, and ${\mathbf{\Sigma }}_{\mathit{w},j,j}^{(k)}$ is the diagonal (j, j) element of ${\mathbf{\Sigma }}_{\mathit{w}}^{(k)}$.

Next, we explain the details of the CI construction procedure in Algorithm 3. In step 1, we obtain a point estimator β from 𝒜 -Trans-GLM (Algorithm 1), given a specific transferring set 𝒜. Then in steps 2-4, we estimate the target inverse Fisher information matrix $({\mathbf{\Sigma }}_{\mathit{\beta }}^{(0)}{)}^{-1}$ as

$$\mathbf{\Theta }=\text{diag}({\widehat{\tau }}_1^{-2},\dots ,{\widehat{\tau }}_p^{-2})\left(\begin{array}{cccc}\hfill 1\hfill & \hfill -{\widehat{\gamma }}_{1,2}^{(0)}\hfill & \hfill \cdots \hfill & \hfill -{\widehat{\gamma }}_{1,p}^{(0)}\hfill \\ \hfill -{\widehat{\gamma }}_{2,1}^{(0)}\hfill & \hfill 1\hfill & \hfill \cdots \hfill & \hfill -{\widehat{\gamma }}_{2,p}^{(0)}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill -{\widehat{\gamma }}_{p,1}^{(0)}\hfill & \hfill -{\widehat{\gamma }}_{p,2}^{(0)}\hfill & \hfill \cdots \hfill & \hfill 1\hfill \end{array}\right)$$ (4)

.

Finally in step 5, we “debias” β using the target data to get a new point estimator b which is asymptotically unbiased as

$$\mathit{b}+\mathit{\beta }+\frac{1}{n_0}\mathbf{\Theta }({\mathit{X}}^{(0)}{)}^T[{\mathit{Y}}^{(0)}-{\mathit{\psi }}^{\prime }({\mathit{X}}^{(0)}\mathit{\beta })],$$ (5)

where ${\mathit{\psi }}^{\prime }({\mathit{X}}^{(0)}\mathit{\beta })≔({\psi }^{\prime }(({\mathit{x}}_1^{(0)}{)}^T\mathit{\beta }),\dots ,{\psi }^{\prime }(({\mathit{x}}_{n_0}^{(0)}{)}^T\mathit{\beta }){)}^T\in {\mathbb{R}}^{n_0}$.

It’s necessary to emphasize that the confidence level (1 − α) is for every single CI rather than for all p CIs simultaneously. As discussed in Sections 2.2 and 2.3 of Van de Geer et al. (2014), it is possible to get simultaneous CIs for different coefficient components and do multiple hypothesis tests when the design is fixed. In other cases, e.g., random design in different replications (which we focus on in this paper), multiple hypothesis testing might be more challenging.

Algorithm 3: Confidence interval construction via nodewise regression

$$\begin{array}{cc}\hfill & \mathrm{Input}:\text{target data}({\mathit{X}}^{(0)},{\mathit{y}}^{(0)}),\text{source data}\{({\mathit{X}}^{(k)},{\mathit{y}}^{(k)}){\}}_{k=1}^K,\text{penalty parameters}\{{\lambda }_j{\}}_{j=1}^p\hfill \\ \hfill & \text{and}\{{\tilde{\lambda }}_j{\}}_{j=1}^p,\text{transferring set}𝒜,\text{confidence level}(1-\alpha )\hfill \\ \hfill & \mathrm{Output}:\text{Level-}(1-\alpha )\text{confidence interval}{I}_j\text{for}{\beta }_j\text{with}j=1,\dots ,p\hfill \\ \hfill & 1\text{Compute}\mathit{\beta }\text{via Algorithm 1}\hfill \\ \hfill & 2{\text{Compute}}^{{\widehat{\mathit{\gamma }}}_j^{𝒜}\leftarrow {\text{arg min}}_{\mathit{\gamma }}\left\{-\frac{1}{2(n_{𝒜}+n_0)}\sum _{k\in \{0\}{\cup }^{𝒜}}\Vert {\mathit{X}}_{\mathit{\beta },j}^{(k)}-{\mathit{X}}_{\mathit{\beta },-j}^{(k)}\mathit{\gamma }{\Vert }_2^2+{\lambda }_j\Vert \mathit{\gamma }{\Vert }_1\right\}}\text{for}j=1,\dots ,p\hfill \\ \hfill & 3\text{Compute}{\mathit{\varrho }}_j\leftarrow {\text{arg min}}_{\mathit{\varrho }}\left\{-\frac{1}{2n_0}{\Vert {\mathit{X}}_{\mathit{\beta },j}^{(0)}-{\mathit{X}}_{\mathit{\beta },-j}^{(0)}({\widehat{\mathit{\gamma }}}_j^{𝒜}+\mathit{\varrho })\Vert }_2+{\tilde{\lambda }}_j{\Vert \mathit{\varrho }\Vert }_1\right\}\hfill \\ \hfill & 4\text{Compute}{\widehat{\mathit{\gamma }}}_j^{(0)}\leftarrow {\widehat{\mathit{\gamma }}}_j^{𝒜}+{\mathit{\varrho }}_j,{\mathbf{\Sigma }}_{\mathit{\beta }}\leftarrow \sum _{k\in \{0\}{\cup }^{𝒜}}\frac{n_k}{n_{𝒜}+n_0}{\mathbf{\Sigma }}_{\mathit{\beta }}^{(k)},{\widehat{\tau }}_j^2={\mathbf{\Sigma }}_{\mathit{\beta },j,j}-{\mathbf{\Sigma }}_{\mathit{\beta },j,-j}{\widehat{\mathit{\gamma }}}_j\text{and calculate}\hfill \\ \hfill & \mathbf{\Theta }\text{via}(6),\text{where}{\widehat{\mathit{\gamma }}}_j^{(0)}=({\widehat{\gamma }}_{j,1}^{(0)},\dots ,{\widehat{\gamma }}_{j,j-1}^{(0)},{\widehat{\gamma }}_{j,j+1}^{(0)},\dots ,{\widehat{\gamma }}_{j,p}^{(0)}{)}^T.\hfill \\ \hfill & 5\text{Compute}{I}_j\leftarrow [{\widehat{b}}_j-{\mathbf{\Theta }}_j^T{\mathbf{\Sigma }}_{\mathit{\beta }}{\mathbf{\Theta }}_j{q}_{\alpha ∕2}∕\sqrt{n_0},{\widehat{b}}_j+{\mathbf{\Theta }}_j^T{\mathbf{\Sigma }}_{\mathit{\beta }}{\mathbf{\Theta }}_j{q}_{\alpha ∕2}∕\sqrt{n_0}]\text{for}j=1,\dots ,p,\text{where}\hfill \\ \hfill & {\widehat{b}}_j\text{is the}j-\text{th component of}\mathit{b}\text{in}(7),\text{and}{q}_{\alpha ∕2}{\text{is the}}^{\alpha ∕2}-{\text{left tail quantile of}}^{N(0,1)}\hfill \\ \hfill & 6\text{Output}{\{I_j\}}_{j=1}^p\hfill \end{array}$$

3. Theory

In this section, we will establish theoretical guarantees on the three proposed algorithms. Section 3.1 provides a detailed analysis of Algorithm 1 with transferring set 𝒜_h, which we denote as 𝒜_h-Trans-GLM. Section 3.2 introduces certain conditions, under which we show that the transferring set 𝒜 detected by Algorithm 2 (Trans-GLM) is equal to 𝒜_h for some h with high probability. Section 3.3 presents the analysis of Algorithm 3 with transferring set 𝒜_h, where we prove a central limit theorem. For the proofs and some additional theoretical results, refer to supplementary materials.

3.1. Theory on 𝒜_h-Trans-GLM

We first impose some common assumptions about GLM.

Assumption 1. ψ is infinitely differentiable and strictly convex. We call a second-order differentiable function ψ strictly convex ifψ′′ (x) > 0.

Assumption 2. For any $\mathit{a}\in {\mathbb{R}}^p$, ${\mathit{a}}^T{\mathit{x}}_i^{(k)}$, s are i.i.d. ${\kappa }_u\Vert \mathit{a}{\Vert }_2^2$-subGaussian variables with zero mean for all k = 0, … , K, where k_u is a positive constant. Denote the covariance matrix of x^(k) as Σ^(k), with $\underset{k}{\text{inf}}{\lambda }_{\text{min}}({\mathbf{\Sigma }}^{(k)})\ge {\kappa }_l>0$, where κ_l is a positive constant.

Assumption 3. At least one of the following assumptions hold: (M _ψ, U and$\overline{U}$ are some positive constants)

1. ∥ψ′′∥_∞ ≤ M_ψ < ∞ a.s.;

2. $\underset{k}{\text{sup}}\Vert {\mathit{x}}^{(k)}{\Vert }_{\infty }\le U<\infty$ a.s., $\underset{k}{\text{sup}}\underset{\mid z\mid \le \overline{U}}{\text{sup}}{\psi }^{″}(({\mathit{x}}^{(k)}{)}^T{\mathit{w}}^{(k)}+z)\le M_{\psi }<\infty$ a.s.

Assumption 1 imposes the strict convexity and differentiability of ψ, which is satisfied by many popular distribution families, such as Gaussian, binomial, and Poisson distributions. Note that we do not require ψ to be strongly convex (that is, ∃C > 0, such that ψ′′(x) > C), which relaxes Assumption 4 in Bastani (2021). It is easy to verify that ψ in logistic regression is in general not strongly convex with unbounded predictors. Assumption 2 requires the predictors in each source to be subGaussian with a well-behaved correlation structure. Assumption 3 is motivated by Assumption (GLM 2) in the full-length version of Negahban et al. (2009), which is imposed to restrict ψ′′ in a bounded region in some sense. Note that linear regression and logistic regression satisfy condition (i), while Poisson regression with coordinate-wise bounded predictors and ℓ₁-bounded coefficients satisfies condition (ii).

Besides these common conditions on GLM, as discussed in Section 2.3, to guarantee the success of 𝒜_h-Trans-GLM, we have to make sure that the estimator from the transferring step is close enough to β. Therefore we introduce the following assumption, which guarantees w ^𝒜_h defined in (2) with 𝒜 = 𝒜_h is close to β.

Assumption 4. Denote ${\mathbf{\Sigma }}_h=\sum _{k\in \{0\}{\cup }^{{𝒜}_h}}{\alpha }_k\mathbb{E}\left[{\int }_0^1{\psi }^{″}(({\mathit{x}}^{(k)}{)}^T\mathit{\beta }+t({\mathit{x}}^{(k)}{)}^T({\mathit{w}}^{{𝒜}_h}-\mathit{\beta }))dt\cdot {\mathit{x}}^{(k)}({\mathit{x}}^{(k)}{)}^T\right]$ and ${\mathbf{\Sigma }}_h^{(k)}=\mathbb{E}\left[{\int }_0^1{\psi }^{″}(({\mathit{x}}^{(k)}{)}^T\mathit{\beta }+t({\mathit{x}}^{(k)}{)}^T({\mathit{w}}^{(k)}-\mathit{\beta }))dt\cdot {\mathit{x}}^{(k)}({\mathit{x}}^{(k)}{)}^T\right]$. It holds that $\underset{k\in \{0\}{\cup }^{{𝒜}_h}}{\text{sup}}\Vert {\mathbf{\Sigma }}_h^{-1}{\mathbf{\Sigma }}_h^{(k)}{\Vert }_1<\infty$.

Remark 1. A sufficient condition for Assumption 4 to hold is ${({\mathbf{\Sigma }}_{{\mathit{w}}^{{𝒜}_h},\mathit{\beta }}^{(k)})}^{-1}{\mathbf{\Sigma }}_{{\mathit{w}}^{(k^{\prime })},\mathit{\beta }}^{(k^{\prime })}$ has positive diagonal elements and is diagonally dominant, for any k ≠ k′ in 𝒜_h, where ${\mathbf{\Sigma }}_{\mathit{w},\mathit{\beta }}^{(k)}≔\mathbb{E}\left[{\int }_0^1{\psi }^{″}(({\mathit{x}}^{(k)}{)}^T\mathit{\beta }+t({\mathit{x}}^{(k)}{)}^T(\mathit{w}-\mathit{\beta }))dt\cdot {\mathit{x}}^{(k)}({\mathit{x}}^{(k)}{)}^T\right]$ for any $\mathit{w}\in {\mathbb{R}}^p$.

In the linear case, this assumption can be further simplified as a restriction on heterogeneity between target predictors and source predictors. More discussions can be found in Condition 4 of Li et al. (2021). Now, we are ready to present the following main result for the 𝒜_h-Trans-GLM algorithm. Define the parameter space as

$$\Xi (s,h)=\left\{\mathit{\beta },\{{\mathit{w}}^{(k)}{\}}_{k\in {𝒜}_h}:\Vert \mathit{\beta }{\Vert }_0\le s,\underset{k\in {𝒜}_h}{\text{sup}}\Vert {\mathit{w}}^{(k)}-\beta {\Vert }_1\le h\right\}.$$

Given s and h, we compress parameters β, {w ^(k)}_k∈𝒜h into a parameter set ξ for simplicity.

Theorem 1 (ℓ₁/ℓ₂-estimation error bound of 𝒜_h-Trans-GLM with Assumption 4).

Assume Assumptions 1, 2 and 4 hold. Suppose $h\ll \sqrt{\frac{n_0}{\log p}},h\le C\sqrt{s}$, n₀ ≥ C log p and n_Ah ≥ Cs log p, where C > 0 is a constant. Also assume Assumption 3.(i) holds or Assumption 3.(ii) with $h\le C\prime U^{-1}\overline{U}$ for some C′ > 0 holds. We take ${\lambda }_{\mathit{w}}=C_{\mathit{w}}\sqrt{\frac{\log p}{n_{{𝒜}_h}+n_0}}$ and ${\lambda }_{\mathit{\delta }}=C_{\mathit{\delta }}\sqrt{\frac{\log p}{n_0}}$, where C_w and C_δ are sufficiently large positive constants. Then

$$\underset{\xi \in \Xi (s,h)}{\text{sup}}\mathbb{P}\left(\Vert \mathit{\beta }-\mathit{\beta }{\Vert }_2\lesssim {\left(\frac{s\log p}{n_{{𝒜}_h}+n_0}\right)}^{1∕2}+\left[{\left(\frac{\log p}{n_0}\right)}^{1∕4}{h}^{1∕2}\right]\wedge h\right)\ge 1-n_0^{-1},$$ (6)

$$\underset{\xi \in \Xi (s,h)}{\text{sup}}\mathbb{P}\left(\Vert \mathit{\beta }-\mathit{\beta }{\Vert }_1\lesssim s{\left(\frac{\log p}{n_{{𝒜}_h}+n_0}\right)}^{1∕2}+h\right)\ge 1-n_0^{-1}.$$ (7)

Remark 2. When $h\ll s\sqrt{\frac{\log p}{n_0}},n_{{𝒜}_h}\gg n_0$, the upper bounds in (6) and (7) are better than the classical Lasso ℓ₂-bound $O_p\left(\sqrt{\frac{s\log p}{n_0}}\right)$ and ℓ₁-bound $O_p\left(s\sqrt{\frac{\log p}{n_0}}\right)$ using only target data.

Similar to Theorem 2 in Li et al. (2021), we can show the following lower bound of ℓ₁/ℓ₂-estimation error in regime Ξ(s, h) in the minimax sense.

Theorem 2 (ℓ₁/ℓ₂-minimax estimation error bound). Assume Assumptions 1, 2 and 4 hold. Also assume Assumption 3.(i) holds or Assumption 3.(ii) with n₀ ≳ s² log p. Then

$$\begin{gathered} \underset{\mathit{\beta }}{\text{inf}}\underset{\xi \in \Xi (s,h)}{\text{sup}}\mathbb{P}\left(\Vert \mathit{\beta }-\mathit{\beta }{\Vert }_2\gtrsim {\left(\frac{s\log p}{n_{{𝒜}_h}+n_0}\right)}^{1∕2}+{\left(\frac{s\log p}{n_0}\right)}^{1∕2}\wedge \left[{\left(\frac{\log p}{n_0}\right)}^{1∕4}{h}^{1∕2}\right]\wedge h\right)\ge \frac{1}{2}, \\ \underset{\mathit{\beta }}{\text{inf}}\underset{\xi \in \Xi (s,h)}{\text{sup}}\mathbb{P}\left(\Vert \mathit{\beta }-\mathit{\beta }{\Vert }_1\gtrsim s{\left(\frac{\log p}{n_{{𝒜}_h}+n_0}\right)}^{1∕2}+\left[s{\left(\frac{\log p}{n_0}\right)}^{1∕2}\right]\wedge h\right)\ge \frac{1}{2}. \end{gathered}$$

Remark 3. Theorem 2 indicates that under conditions on h required by Theorem 1 ( $h\lesssim s\sqrt{\log p∕n_0}$), 𝒜_h-Trans-GLM achieves the minimax optimal rate of ℓ₁/ℓ₂-estimation error bound.

Next, we present a similar upper bound, which is weaker than the bound above but holds without requiring Assumption 4.

Theorem 3 (ℓ₁/ℓ₂-estimation error bound of 𝒜_h-Trans-GLM without Assumption 4). Assume Assumptions 1 and 2 hold. Suppose $h\ll \sqrt{\frac{n_0}{\log p}},h\le C{s}^{-1∕2},n_0\ge C\log p$ and n_Ah ≥ Cs log p, where C > 0 is a constant. Also assume Assumption 3.(i) holds or Assumption 3.(ii) with $h\le C\prime U^{-1}\overline{U}$ for some C′ > 0 holds. We take ${\lambda }_{\mathit{w}}=C_{\mathit{w}}\left(\sqrt{\frac{\log p}{n_{{𝒜}_h}+n_0}}+h\right)$ and ${\lambda }_{\mathit{\delta }}=C_{\mathit{\delta }}\sqrt{\frac{\log p}{n_0}}$, where C_w and C_δ are sufficiently large positive constants. Then

$$\begin{gathered} \underset{\mathit{\xi }\in \Xi (s,h)}{\text{sup}}\mathbb{P}\left(\Vert \mathit{\beta }-\mathit{\beta }{\Vert }_2\lesssim {\left(\frac{s\log p}{n_{{𝒜}_h}+n_0}\right)}^{1∕2}+\sqrt{s}h+\left[{\left(\frac{\log p}{n_0}\right)}^{1∕4}{h}^{1∕2}\right]\wedge h\right)\ge 1-n_0^{-1}, \\ \underset{\mathit{\xi }\in \Xi (s,h)}{\text{sup}}\mathbb{P}\left(\Vert \mathit{\beta }-\mathit{\beta }{\Vert }_1\lesssim s\sqrt{\frac{\log p}{n_{{𝒜}_h}+n_0}}+sh\right)\ge 1-n_0^{-1}. \end{gathered}$$

Remark 4. When $h\ll \sqrt{\frac{\log p}{n_0}}$ and n_Ah ≫ n₀, the upper bounds in (i) and (ii) are better than the classical Lasso bound $O_p\left(\sqrt{\frac{\log p}{n_0}}\right)$ with target data.

Comparing the results in Theorems 1 and 3, we know that with Assumption 4, we could get sharper ℓ₁/ℓ₂-estimation error bounds.

3.2. Theory on the transferable source detection algorithm

In this section, we will show that under certain conditions, our transferable set detection algorithm (Trans-GLM) can recover the level-h transferring set 𝒜_h for some specific h, that is, 𝒜 = 𝒜_h with high probability. Under these conditions, transferring with 𝒜 will lead to a faster convergence rate compared to Lasso fitted on the target data, when the target sample size n₀ falls into certain regime. But as we described in Section 2.4, Algorithm 2 does not require any explicit input of h.

The corresponding population version of ${\widehat{L}}_0^{[r]}(\mathit{w})$ defined in (3) is

$$\begin{gathered} L_0(\mathit{w})=-\mathbb{E}[\log \rho (y^{(0)})]-\mathbb{E}[y^{(0)}{\mathit{w}}^T{\mathit{x}}^{(0)}]+\mathbb{E}[\psi ({\mathit{w}}^T{\mathit{x}}^{(0)})] \\ =-\mathbb{E}[\log \rho (y^{(0)})]-\mathbb{E}[{\psi }^{\prime }({\mathit{w}}^T{\mathit{x}}^{(0)}){\mathit{w}}^T{\mathit{x}}^{(0)}]+\mathbb{E}[\psi ({\mathit{w}}^T{\mathit{x}}^{(0)})]. \end{gathered}$$

Based on Assumption 6, similar to (2), for {k}-Trans-GLM (Algorithm 1 with 𝒜 = {k}) used in Algorithm 2, consider the following population version of estimators from the transferring step with respect to target data and the k-th source data, which is the solution β^(k) of equation $\sum _{j\in \{0,k\}}{\alpha }_j^{(k)}\mathbb{E}\left\{[{\psi }^{\prime }(({\mathit{\beta }}^{(k)}{)}^T{\mathit{x}}^{(k)})-{\psi }^{\prime }(({\mathit{w}}^{(k)}{)}^T{\mathit{x}}^{(k)})]{\mathit{x}}^{(k)}\right\}=0$, where ${\alpha }_0^{(k)}=\frac{2n_0∕3}{2n_0∕3+n_k}$ and ${\alpha }_k^{(k)}=\frac{n_k}{2n_0∕3+n_k}$. Define β⁽⁰⁾ = β. Next, let’s impose a general assumption to ensure the identifiability of some 𝒜_h by Trans-GLM.

Assumption 5 (Identifiability of 𝒜_h). Denote ${𝒜}_h^c=\{1,\dots ,K\}\setminus {𝒜}_h$. Suppose for some h, we have

$$\begin{gathered} \mathbb{P}\left(\underset{r}{\text{sup}}\mid {\widehat{L}}_0^{[r]}({\mathit{\beta }}^{(k)[r]})-{\widehat{L}}_0^{[r]}({\mathit{\beta }}^{(k)})\mid >{\mathrm{Y}}_1^{(k)}+\zeta {\Gamma }_1^{(k)}\right)\lesssim g_1^{(k)}(\zeta ), \\ \mathbb{P}\left(\underset{r}{\text{sup}}\mid {\widehat{L}}_0^{[r]}({\mathit{\beta }}^{(k)})-L_0({\mathit{\beta }}^{(k)})\mid >\zeta {\Gamma }_2^{(k)}\right)\lesssim g_2^{(k)}(\zeta ), \end{gathered}$$

where $g_1^{(k)}(\zeta )$, $g_2^{(k)}(\zeta )\to 0$ as ζ → ∞. Assume $\underset{k{\in }^{{𝒜}_h^c}}{\text{inf}}{\lambda }_{\text{min}}(\mathbb{E}[{\int }_0^1{\psi }^{″}((1-t)({\mathit{x}}^{(0)}{)}^T\mathit{\beta }+t({\mathit{x}}^{(0)}{)}^T{\mathit{\beta }}^{(k)})dt\cdot {\mathit{x}}^{(0)}({\mathit{x}}^{(0)}{)}^T])≔\underset{¯}{\lambda }>0$, and

$$\Vert {\mathit{\beta }}^{(k)}-\mathit{\beta }{\Vert }_2\ge {\underset{¯}{\lambda }}^{-1∕2}\left[C_1\left(\sqrt{{\Gamma }_1^{(0)}}\vee \sqrt{{\Gamma }_2^{(0)}}\vee 1\right)+\sqrt{2{\mathrm{Y}}_1^{(k)}}\right],\forall k\in {𝒜}_h^c$$ (8)

$${\mathrm{Y}}_1^{(k)}+{\Gamma }_1^{(k)}+{\Gamma }_2^{(k)}+h^2=O(1),\forall k\in {𝒜}_h;{\Gamma }_1^{(k)}=O(1),{\Gamma }_2^{(k)}=O(1),\forall k\in {𝒜}_h^c,$$ (9)

where C₁ > 0 is sufficiently large.

Remark 5. Here we use generic notations ${\mathrm{Y}}_1^{(k)}$, ${\Gamma }_1^{(k)}$, ${\Gamma }_2^{(k)}$, $g_1^{(k)}(\zeta )$ and $g_2^{(k)}(\zeta )$. We show their explicit forms under linear, logistic, and Poisson regression models in Proposition 1 in Section S. 1.2.1 of supplements.

Remark 6. Condition (8) guarantees that for the sources not in 𝒜_h, there is a sufficiently large gap between the population-level coefficient from the transferring step and the true coefficient of target data. Condition (9) guarantees the variations of $\underset{r}{\text{sup}}\mid {\widehat{L}}_0^{[r]}({\mathit{\beta }}^{(k)[r]})-{\widehat{L}}_0^{[r]}({\mathit{\beta }}^{(k)})\mid$ and $\underset{r}{\text{sup}}\mid {\widehat{L}}_0^{[r]}({\mathit{\beta }}^{(k)})-L_0({\mathit{\beta }}^{(k)})\mid$ are shrinking as the sample sizes go to infinity.

Based on Assumption 5, we have the following detection consistency property.

Theorem 4 (Detection consistency of 𝒜_h). For Algorithm 2 (Trans-GLM), with Assumption 5 satisfied for some h, for any δ > 0 there exist constants C′(δ) and N = N (δ) > 0 such that when C₀ = C′(δ) and m in _{k∈{0}∪𝒜h} n_k > N (δ), $\mathbb{P}{(}^{𝒜}={𝒜}_h)\ge 1-\delta$.

Then Algorithm 2 has the same high-probability upper bounds of ℓ₁/ℓ₂-estimation error as those in Theorems 1 and 3 under the same conditions, respectively.

Remark 7. We would like to emphasize again that Algorithm 2 does not require the explicit input of h. Theorem 4 tells us that the transferring set𝒜 suggested by Trans-GLM will be 𝒜_h for some h, under certain conditions.

Next, we attempt to provide a sufficient and more explicit condition (Corollary 1) to ensure that Assumption 5 hold. Recalling the procedure of Algorithm 2, we note that it relies on using the negative log-likelihood as the similarity metric between target and source data, where the accurate estimation of coefficients or log-likelihood for GLM under the high-dimensional setting depends on the sparse structure. Therefore, in order to provide an explicit and sufficient condition for Assumption 6 to hold, we now impose a “weak” sparsity assumption on both w ^(k) and β^(k) with $k\in {𝒜}_h^c$ for some h. Note that the source data in 𝒜_h automatically satisfy the sparsity condition due to the definition of 𝒜_h.

Assumption 6. For some h and any $k\in {𝒜}_h^c$, we assume w ^(k) and β^(k) can be decomposed as follows with some s′ and h′ > 0 :

1. w(k) = ς(k) + ϑ(k), where ∥ς(k)∥₀≤ s′ and ∥ϑ(k)∥₁≤ h′ ;

2. β(k) = l(k) + ϖ(k), where ∥l(k)∥₀≤ s′ and ∥ϖ(k)∥₁≤ h′.

Corollary 1. Assume Assumptions 1, 2, 6 and $\underset{k{\in }^{{𝒜}_h^c}}{\text{inf}}{\lambda }_{\text{min}}\left(\mathbb{E}[{\int }_0^1{\psi }^{″}((1-t)({\mathit{x}}^{(0)}{)}^T\mathit{\beta }+t({\mathit{x}}^{(0)}{)}^T{\mathit{\beta }}^{(k)})dt\cdot {\mathit{x}}^{(0)}({\mathit{x}}^{(0)}{)}^T]\right)≔\underset{¯}{\lambda }>0$ hold. Also assume $\underset{k{\in }^{{𝒜}_h^c}}{\text{sup}}\Vert {\mathit{\beta }}^{(k)}{\Vert }_{\infty }<\infty ,\underset{k}{\text{sup}}\Vert {\mathit{w}}^{(k)}{\Vert }_{\infty }<\infty$. Let ${\lambda }^{(k)[r]}=C\left(\sqrt{\frac{\log p}{n_k+n_0}}+h\right)$ when $k\in {𝒜}_h,{\lambda }^{(k)[r]}=C\sqrt{\frac{\log p}{n_k+n_0}}\cdot (1\vee \Vert {\mathit{\beta }}^{(k)}-\mathit{\beta }{\Vert }_2\vee \Vert {\mathit{w}}^{(k)}-\mathit{\beta }{\Vert }_2)$ when $k\in {𝒜}_h^c$ and ${\lambda }^{(0)}=C\sqrt{\frac{\log p}{n_0}}$ for some sufficiently large constant C > 0. Then we have the following sufficient conditions to make Assumption 5 hold for logistic, linear and Poisson regression models. Denote

$$\Omega =\sqrt{h^{\prime }}{\left(\frac{\log p}{{\text{min}}_{k{\in }^{{𝒜}_h}}{n}_k+n_0}\right)}^{1∕4}+{\left(\frac{s^{\prime }\log p}{{\text{min}}_{k{\in }^{{𝒜}_h}}{n}_k+n_0}\right)}^{1∕4}[(s\vee s^{\prime }{)}^{1∕4}+\sqrt{h^{\prime }}]+{\left(\frac{\log p}{{\text{min}}_{k{\in }^{{𝒜}_h}}{n}_k+n_0}\right)}^{1∕8}(h^{\prime }{)}^{1∕4}[(s\vee s^{\prime }{)}^{1∕8}+(h^{\prime }{)}^{1∕4}]$$

1. For logistic regression models, we require

   $$\begin{gathered} \underset{k{\in }^{{𝒜}_h}}{\text{inf}}{n}_k\gg s\log p,n_0\gg \left\{[s\vee s^{\prime }+(h^{\prime }{)}^2]\vee {\Omega }^2\right\}\cdot \log K, \\ \underset{k{\in }^{{𝒜}_h^c}}{\text{inf}}\Vert {\mathit{\beta }}^{(k)}-\mathit{\beta }{\Vert }_2\gtrsim {\left(\frac{s\log p}{n_0}\right)}^{1∕4}\vee 1+\Omega ,h\ll s^{-1∕2}. \end{gathered}$$
2. For linear models, we require

   $$\begin{gathered} \underset{k{\in }^{{𝒜}_h}}{\text{inf}}{n}_k\gg s^2\log p,n_0\gg \left\{[(s\vee s^{\prime }{)}^2+(h^{\prime }{)}^4]\vee [(s\vee s^{\prime }+(h^{\prime }{)}^2){\Omega }^2]\right\}\cdot \log K, \\ \underset{k{\in }^{{𝒜}_h^c}}{\text{inf}}\Vert {\mathit{\beta }}^{(k)}-\mathit{\beta }{\Vert }_2\gtrsim {\left(\frac{s^2\log p}{n_0}\right)}^{1∕4}\vee 1+\left[(s^{\prime }{)}^{1∕4}+\sqrt{h^{\prime }}\right]\Omega ,h\ll s^{-1}. \end{gathered}$$
3. For Poisson regression models, we require

   $$\begin{gathered} \underset{k{\in }^{{𝒜}_h}}{\text{inf}}{n}_k\gg s^2\log p,n_0\gg \left[(s\vee s^{\prime }+h^{\prime })\vee {\Omega }^2\right]\cdot \log K,U(s\vee s^{\prime }+h\vee h^{\prime })\lesssim 1, \\ \underset{k{\in }^{{𝒜}_h^c}}{\text{inf}}\Vert {\mathit{\beta }}^{(k)}-\mathit{\beta }{\Vert }_2\gtrsim {\left(\frac{s\log p}{n_0}\right)}^{1∕4}\vee 1+\left[(s^{\prime }{)}^{1∕4}+\sqrt{h^{\prime }}\right]\Omega ,h\ll s^{-1}. \end{gathered}$$

Under Assumptions 1, 2, and the sufficient conditions derived in Corollary 1, by Theorem 4, we can conclude that 𝒜 = 𝒜_h for some h. Note that we don’t impose Assumption 4 here. Remark 4 indicates that, for 𝒜_h-Trans-GLM to have a faster convergence rate than Lasso on target data, we need $h\ll \sqrt{\frac{\log p}{n_0}}$ and n_Ah ≫ n₀. Suppose s′≍s, h′ ≲ s^1/2. Then for logistic regression models, when s log K ≪ n₀ ≪ s log p, the sufficient condition implie $h\ll s^{-1∕2}\ll \sqrt{\frac{\log p}{n_0}}$. For linear models, when $s^2\log K\ll n_0\ll s^2\log p,h\ll s^{-1}\ll \sqrt{\frac{\log p}{n_0}}$. And for Poisson models, when $s\log K\ll n_0\ll s^2\log p,h\ll s^{-1}\ll \sqrt{\frac{\log p}{n_0}}$. This implies that when target sample size n₀ is within certain regimes and there are many more source data points than target data points, Trans-GLM can lead to a better ℓ₂-estimation error bound than the classical Lasso on target data.

3.3. Theory on confidence interval construction

In this section, we will establish the theory for our confidence interval construction procedure described in Algorithm 3. First, we would like to review and introduce some notations. In Section 2.5, we defined ${\mathbf{\Sigma }}_{\mathit{\beta }}^{(k)}=\mathbb{E}[{\mathit{x}}^{(k)}({\mathit{x}}^{(k)}{)}^T{\psi }^{″}(({\mathit{x}}^{(k)}{)}^T\mathit{\beta })]$. Let $\mathbf{\Theta }=({\mathbf{\Sigma }}_{\mathit{\beta }}^{(0)}{)}^{-1}$ and K_Ah = ∣𝒜_h∣. Define

$${\mathit{\gamma }}_j^{(k)}={\underset{{\mathit{\gamma }}^{{\in }^{\mathbb{R}p-1}}}{\text{arg}\text{min}}}^{\mathbb{E}}\left\{{\psi }^{″}({\mathit{\beta }}^T{\mathit{x}}^{(k)})\cdot [{\mathit{x}}_j^{(k)}-({\mathit{x}}_{-j}^{(k)}{)}^T\mathit{\gamma }{]}^2\right\}=({\mathbf{\Sigma }}_{\mathit{\beta },-j,-j}^{(k)}{)}^{-1}{\mathbf{\Sigma }}_{\mathit{\beta },-j,-j}^{(k)},$$

which is closely related to $({\mathbf{\Sigma }}_{\mathit{\beta }}^{(k)}{)}^{-1}$ and ${\mathit{\gamma }}_j^{(0)}$ can be viewed as the population version of ${\widehat{\mathit{\gamma }}}_j^{(0)}$. And ${\mathbf{\Sigma }}_{\mathit{\beta },j,-j}^{(k)}$ represents the j-th row without the (j, j) diagonal element of ${\mathbf{\Sigma }}_{\mathit{\beta }}^{(k)}$. ${\mathbf{\Sigma }}_{\mathit{\beta },-j,-j}^{(k)}$ denotes the submatrix of ${\mathbf{\Sigma }}_{\mathit{\beta }}^{(k)}$ without the j-th row and j-th column. Suppose

$$\begin{gathered} \underset{k{{\in }^{𝒜}}_h,j=1:p}{\text{sup}}\Vert ({\mathbf{\Sigma }}_{\mathit{\beta },-j,-j}^{(0)}{)}^{-1}{\mathbf{\Sigma }}_{\mathit{\beta },-j,j}^{(0)}-({\mathbf{\Sigma }}_{\mathit{\beta },-j,-j}^{(k)}{)}^{-1}{\mathbf{\Sigma }}_{\mathit{\beta },-j,-j}^{(k)}{\Vert }_1\le h_1, \\ \underset{k{{\in }^{𝒜}}_h,j=1:p}{\text{sup}}\left[\mid {\mathbf{\Sigma }}_{\mathit{\beta },j,j}^{(k)}-{\mathbf{\Sigma }}_{\mathit{\beta },j,j}^{(0)}\mid \vee \mid ({\mathbf{\Sigma }}_{\mathit{\beta },j,-j}^{(k)}-{\mathbf{\Sigma }}_{\mathit{\beta },j,-j}^{(0)}){\mathit{\gamma }}_j^{(0)}\mid \right]\le h_{\max }. \end{gathered}$$

Then by the definition of ${\mathit{\gamma }}_j^{(k)}$,

$$\underset{k{{\in }^{𝒜}}_h,j=1:p}{\text{sup}}\Vert {\mathit{\gamma }}_j^{(k)}-{\mathit{\gamma }}_j^{(0)}{\Vert }_1\lesssim h_1,$$

which is similar to our previous setting $\underset{k{\in }^{𝒜h}}{\text{sup}}\Vert {\mathit{w}}^{(k)}-\mathit{\beta }{\Vert }_1\le h$. This motivates us to apply a similar two-step transfer learning procedure (steps 2-4 in Algorithm 3) to learn ${\mathit{\gamma }}_j^{(0)}$ for j = 1,… , p. We impose the following set of conditions.

Assumption 7. Suppose the following conditions hold:

1. $\underset{k\in \{0\}{\cup }^{{𝒜}_h}}{\text{sup}}\Vert {\mathit{x}}^{(k)}{\Vert }_{\infty }\le U<\infty$, $\underset{k\in \{0\}{\cup }^{{𝒜}_h}}{\text{sup}}\mid ({\mathit{x}}^{(k)}{)}^T{\mathit{w}}^{(k)}\mid \le U\prime <\infty$ a.s.;

2. $\underset{j}{\text{sup}}\Vert {\mathit{\gamma }}_j^{(0)}{\Vert }_0∕s<\infty$, $\underset{j\in 1:p,k\in \{0\}{\cup }^{{𝒜}_h}}{\text{sup}}\mid ({\mathit{x}}^{(k)}{)}^T{\mathit{\gamma }}_j^{(0)}\mid \le U″<\infty$ a.s.;

3. $\underset{k\in \{0\}{\cup }^{{𝒜}_h}}{\text{inf}}{\lambda }_{\text{min}}({\mathbf{\Sigma }}_{{\mathit{w}}^{(k)}}^{(k)})\ge \underset{¯}{U}>0$;

4. $\underset{k\in \{0\}{\cup }^{{𝒜}_h}}{\text{sup}}\underset{\mid z\mid \le \overline{U}}{\text{sup}}{\psi }^{″\prime }(({\mathit{x}}^{(k)}{)}^T{\mathit{w}}^{(k)}+z)\le M_{\psi }<\infty$ a.s.

5. $\underset{k\in \{0\}{\cup }^{{𝒜}_h}}{\text{sup}}\Vert ({\mathbf{\Sigma }}_{\mathit{\beta },-j,-j}^{{𝒜}_h}{)}^{-1}{\mathbf{\Sigma }}_{\mathit{\beta },-j,-j}^{(k)}{\Vert }_1<\infty$, where ${\mathbf{\Sigma }}_{\mathit{\beta }}^{{𝒜}_h}=\sum _{k\in \{0\}{\cup }^{{𝒜}_h}}{\alpha }_k{\mathbf{\Sigma }}_{\mathit{\beta }}^{(k)}$;

6. ${\text{min}}_{k{\in }^{{𝒜}_h}}{n}_k\gtrsim n_0,n_0\gg \frac{s^3(\log p{)}^2}{K_{{𝒜}_h}^2}\vee K_{{𝒜}_h},n_{{𝒜}_h}+n_0\gg s^2\log p$;

7. $$\begin{gathered} h_1\lesssim s^{-1∕2}\wedge \left[\sqrt{\frac{n_0}{\log p}}\left(\frac{\sqrt{K_{{𝒜}_h}}}{s}\wedge 1\right)\right],h_1\vee h\ll \frac{K_{{𝒜}_h}{n}_0^{1∕2}}{s^2{(\log p)}^{3∕2}}\wedge \frac{n_0^{1∕4}}{s^{1∕2}{(\log p)}^{1∕4}},h{h}_1^{1∕2}\ll \\ {n}_0^{-1∕4}{(\log p)}^{-1∕4}\left(\frac{K_{{𝒜}_h}}{s}\wedge 1\right),h^{5∕2}{h}_1\ll n_0^{-3∕4}{(s\log p)}^{-1∕4},h_1\ll \frac{K_{{𝒜}_h}^{1∕2}{n}_0^{1∕2}}{s^{3∕2}{(\log p)}^{1∕2}}\wedge \frac{K_{{𝒜}_h}^{3∕2}{n}_0^{1∕2}}{s^{5∕2}{(\log p)}^{3∕2}}, \\ {h}_1{h}^{1∕2}\ll \frac{n_0^{1∕4}}{s{(\log p)}^{1∕4}}\wedge \frac{K_{{𝒜}_h}{n}_0^{1∕4}}{s^2{(\log p)}^{5∕4}},h\ll \frac{K_{{𝒜}_h}^{1∕2}}{{(s\log p)}^{1∕2}}\wedge \frac{1}{n_0^{1∕4}{(\log p)}^{1∕2}},h_{\max }\ll s^{-1∕2}\wedge \left(\frac{1}{s}\sqrt{\frac{K_{{𝒜}_h}}{\log p}}\right), \\ h{h}_{\max }\ll n_0^{-1∕2} \end{gathered}$$.

Remark 8. Conditions (i)-(iii) are motivated from conditions of Theorem 3.3 in Van de Geer et al. (2014). Note that in Van de Geer et al. (2014), they define $s_j={\Vert {\mathit{\gamma }}_j^{(0)}\Vert }_0$ and treat s_j and s as two different parameters. Here we require $\underset{j}{\text{sup}}{s}_j\lesssim s$ just for simplicity (otherwise condition (vii) would be more complicated). Condition (iv) requires the inverse link function to behave well, which is similar to Assumption 3. Condition (v) is similar to Assumption 4 to guarantee the success of the two-step transfer learning procedure to learn γ⁽⁰⁾ in Algorithm 3 with a fast rate. Without condition (v), the conclusions in the following Theorem 5 may still hold but under a stronger condition on h, h₁ and h_max, and the rate (34) may be worse. We do not explore the details in this paper and leave them to interested readers. Conditions (vi) and (vii) require that the sample size is sufficiently large and the distance between target and source is not too large. In condition (vi), min _k∈𝒜h n_k ≳ n₀ is not necessary and the only reason we add it here is to simplify condition (vii).

Remark 9. When x^(k)’s are from the same distribution, h₁ = h_max = 0. In this case, we can drop the debiasing step to estimate ${\widehat{\mathit{\gamma }}}_j^{(0)}$ in Algorithm 3 as well as condition (v). Furthermore, condition (vii) can be significantly simplified and only $h\ll \frac{K_{{𝒜}_h}{n}_0^{1∕2}}{s^2{(\log p)}^{3∕2}}\wedge \frac{n_0^{1∕4}}{s^{1∕2}{(\log p)}^{1∕4}}\wedge \frac{K_{{𝒜}_h}^{1∕2}}{{(s\log p)}^{1∕2}}\wedge \frac{1}{n_0^{1∕4}{(\log p)}^{1∕2}}$ is needed.

Remark 10. From conditions (vi) and (vii), we can see that as long as K_Ah ≲ s(log p)^2/3, the conditions become milder as K_Ah increases.

Now, we are ready to present our main result for Algorithm 3.

Theorem 5. Under Assumptions 1-4 and Assumption 7,

$$\frac{\sqrt{n_0}({\widehat{b}}_j-{\beta }_j)}{\sqrt{{\mathbf{\Theta }}_j^T{\mathbf{\Sigma }}_{\mathit{\beta }}{\mathbf{\Theta }}_j}}-\stackrel{d}{\to }N(0,1),$$ (10)

and

$$\begin{gathered} \mid {\mathbf{\Theta }}_j^T{\mathbf{\Sigma }}_{\mathit{\beta }}{\mathbf{\Theta }}_j-{\mathbf{\Theta }}_{jj}\mid \lesssim s\sqrt{\frac{\log p}{n_{{𝒜}_h}+n_0}}+\sqrt{s}\left[h^{1∕2}{\left(\frac{\log p}{n_0}\right)}^{1∕4}\wedge h\right]+{(s{h}_1)}^{1∕2}{\left(\frac{\log p}{n_0}\right)}^{1∕4} \\ +{(s{h}_1)}^{1∕2}\left[{\left(\frac{s\log p}{n_{{𝒜}_h}+n_0}\right)}^{1∕4}+\left(h^{1∕4}{\left(\frac{\log p}{n_0}\right)}^{1∕8}\right)\wedge h^{1∕2}\right]+\sqrt{s}{h}_{max}, \end{gathered}$$ (11)

for j = 1,… , p , with probability at least $1-K_{{𝒜}_h}{n}_0^{-1}$.

Theorem 5 guarantees that under certain conditions, the (1 − α)-confidence interval for each coefficient component obtained in Algorithm 3 has approximately level (1 − α) when the sample size is large. Also, if we compare the rate of (34) with the rate $O_p(s\sqrt{\log p∕n_0})$ in Van de Geer et al. (2014) (see the proof of Theorem 3.1), we can see that when $h\ll s\sqrt{\frac{\log p}{n_0}}$, $h_1\ll \sqrt{\frac{s\log p}{n_0}}\cdot \left[s^{1∕2}\wedge {\left(\frac{n_{{𝒜}_h}+n_0}{n_0}\right)}^{1∕4}\right]$, $h_1^{1∕2}{h}^{1∕4}\ll s^{1∕2}{\left(\frac{\log p}{n_0}\right)}^{3∕8}$ and $h_{\max }\ll \sqrt{\frac{s\log p}{n_0}}$, the rate is better than that of desparsified Lasso using only target data.

4. Numerical Experiments

In this section, we demonstrate the power of our GLM transfer learning algorithms via extensive simulation studies and a real-data application. In the simulation part, we study the performance of different methods under various settings of h. The methods include Trans-GLM (Algorithm 2), naïve-Lasso (Lasso on target data), 𝒜_h-Trans-GLM (Algorithm 1 with 𝒜 = 𝒜_h) and Pooled-Trans-GLM (Algorithm 1 with all sources). In the real-data study, besides naïve-Lasso, Pooled-Trans-GLM, and Trans-GLM, additional methods are explored for comparison, including support vector machines (SVM), decision trees (Tree), random forests (RF) and Adaboost algorithm with trees (Boosting). We run these benchmark methods twice. First, we fit the models on only the target data, then at the second time, we fit them a combined data of target and all sources, which is called a pooled version. We use the original method name to denote the corresponding method implemented on target data, and add a prefix “Pooled” to denote the corresponding method implemented on target and all source data. For example, Pooled-SVM represents SVM fitted on all data from target and sources.

All experiments are conducted in R. We implement our GLM transfer learning algorithms in a new R package glmtrans, which is available on CRAN. More implementation details can be found in Section S. 1.3.1 in the supplements.

4.1. Simulations

4.1.1. Transfer learning on 𝒜_h

In this section, we study the performance of 𝒜_h-Trans-GLM and compare it with that of naïve-Lasso. The purpose of the simulation is to verify that 𝒜_h-Trans-GLM can outperform naïve-Lasso in terms of the target coefficient estimation error, when h is not too large.

Consider the simulation setting as follows. We set the target sample size n₀ = 200 and source sample sample size n_k = 100 for each k ≠ 0. The dimension p = 500 for both target and source data. For the target, the coefficient is set to be β = (0.5·1_s, 0_p−s)^T, where 1_s has all s elements 1 and 0_p−s has all (p − s) elements 0, where s is set to be 5. Denote $R{p}^{(k)}$ as p independent Rademacher variables (being −1 or 1 with equal probability) for any k. $R{p}^{(k)}$ is independent with $R{p}^{(k\prime )}$ for any k ≠ k2. For any source data k in 𝒜_h, we set ${\mathit{w}}^{(k)}=\mathit{\beta }+{(h∕p)}^{R_p^{(k)}}$. For linear and logistic regression models, predictors from target ${\mathit{x}}_i^{(0)}\stackrel{i.i.d.}{\sim }N(0_p,\mathbf{\Sigma })$ with Σ = [Σ _jj2]_p×p where Σ _jj2 = 0.5^{∣j−j′∣}, for all i = 1, … , n. And for $k\in {𝒜}_h$, we generate p-dimensional predictors from $N(0_p,\mathbf{\Sigma }+\mathit{∊}{\mathit{∊}}^T)$, where $\mathit{∊}\sim N(0_p,{0.3}^2{\mathit{I}}_p)$ and is independently generated. For Poisson regression model, predictors are from the same Gaussian distributions as those in linear and binomial cases with coordinate-wise truncation at ±0.5.

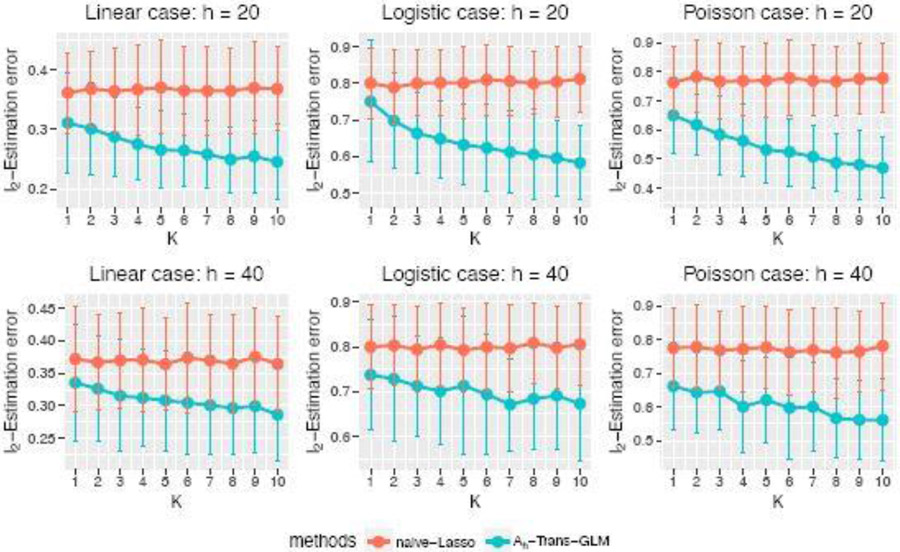
Note that naïve-Lasso is fitted on only target data, and 𝒜_h-Trans-GLM denotes Algorithm 1 on source data in 𝒜_h as well as target data. We train naïve-Lasso and 𝒜_h-Trans-GLM models under different settings of h and K_𝒜h, then calculate the ℓ₂-estimation error of β. All the experiments are replicated 200 times and the average ℓ₂-estimation errors of 𝒜_h-Trans-GLM and naïve-Lasso under linear, logistic, and Poisson regression models are shown in Figure 1.

Fig. 1.

The average ℓ₂-estimation error of 𝒜_h-Trans-GLM and naïve-Lasso under linear, logistic and Poisson regression models with different settings of h and K. n₀ = 200 and n_k = 100 for all k = 1, … , p, p = 500, s = 5. Error bars denote the standard deviations.

From Figure 1, it can be seen that 𝒜_h-Trans-GLM outperforms naïve-Lasso for most combinations of h and K. As more and more source data become available, the performance of 𝒜_h-Trans-GLM improves significantly. This matches our theoretical analysis because the ℓ₂-estimation error bounds in Theorems 1 and 3 become sharper as n_𝒜h grows. When h increases, the performance of 𝒜_h-Trans-GLM becomes worse.

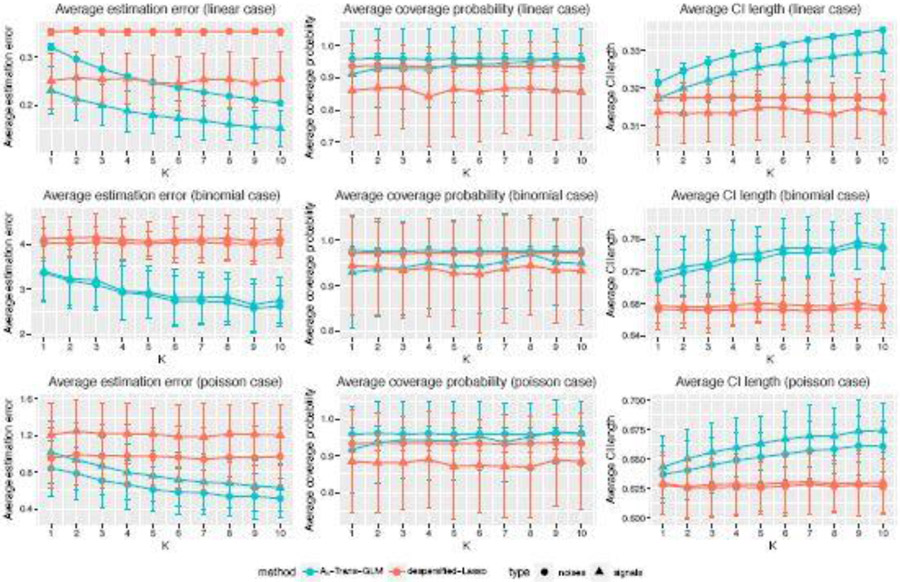
We also apply the inference algorithm 3 with 𝒜_h and compare it with desparsified Lasso (Van de Geer et al., 2014) on only target data. Recall the notations we used in Section 3.3. Here we consider 95% confidence intervals (CIs) for each component of coefficient β, and report three evaluation metrics in Figure 2 when h = 20 under different K_𝒜h : (i) the average of estimation error of Θ _jj over variables in the signal set S and noise set S^c (including the intercept), respectively (which we call “average estimation error”); (ii) the average CI coverage probability over variables in the signal set S and noise set S^c; (iii) the average CI length over j ∈ signal set S and noise set S^c. Note that there is no explicit formula of Θ for logistic and Poisson regression models. Here we approximated it through 5 × 10⁶ Monte-Carlo simulations. Notice that the average estimation error of 𝒜_h-Trans-GLM declines as K increases, which agrees with our theoretical analysis in Section 3.3. As for the coverage probability, although CIs obtained by desparsified Lasso can achieve 95% coverage probability on S^c in linear and binomial cases, it fails to meet the 95% requirement of coverage probability on S in all three cases. In contrast, CIs provided by 𝒜_h-Trans-GLM can achieve approximately 95% level when K is large on both S and S^c. Finally, the results of average CI length reveal that the CIs obtained by 𝒜_h-Trans-GLM tend to be wider as K increases. Considering this together with the average estimation error and coverage probability, a possible explanation could be that desparsified Lasso might down-estimate Θ _jj which leads to too narrow CIs to cover the true coefficients. And 𝒜_h-Trans-GLM offers a more accurate estimate of Θ _jj which results in wider CIs.

Fig. 2.

Three evaluation metrics of Algorithm 3 with 𝒜_h (we denote it as 𝒜_h-Trans-GLM) and desparsified Lasso on target data, under linear, logistic and Poisson regression models, with different settings of K. h = 20. n₀ = 200 and n_k = 100 for all k = 1, … , p, p = 500, s = 5. Error bars denote the standard deviations.

We also consider different $(\{n_k{\}}_{k=0}^K,p,s)$ settings with the results in the supplements.

4.1.2. Transfer learning when 𝒜_h is unknown

Different from the previous subsection, now we fix the total number of sources as K = 10. There are two types of sources, which belong to either 𝒜_h or ${𝒜}_h^c$. Sources from 𝒜_h have similar coefficients to the target one, while the coefficients of sources from 𝒜_h can be quite different. Intuitively, using more sources from 𝒜_h benefits the estimation of the target coefficient. But in practice, 𝒜_h may not be known as a priori. As we argued before, Trans-GLM can detect useful sources automatically, therefore it is expected to be helpful in such a scenario. Simulations in this section aim to justify the effectiveness of Trans-GLM.

Here is the detailed setting. We set the target sample size n₀ = 200 and source sample sample size n_k = 200 for all k ≠ 0. The dimension p = 2000. Target coefficient is the same as the one used in Section 4.1.1 and we fix the signal number s = 20. Recall $R_p^{(k)}$ denotes p independent Rademacher variables and $R_p^{(k^{\prime })}$ are independent for any k ≠ k2. Consider h = 20 and 40. For any source data k in 𝒜_h, we set ${\mathit{w}}^{(k)}=\mathit{\beta }+(h∕p)R_p^{(k)}$. For linear and logistic regression models, predictors from target ${\mathit{x}}_i^{(0)}\stackrel{i.i.d.}{\sim }N(0,\mathbf{\Sigma })$ with Σ = [Σ _jj2]_p×p where Σ _jj2 = 0.9^∣j−j2∣, for all i = 1, …, n₀. For the source, we generate p-dimensional predictors from independent t-distribution with degrees of freedom 4. For the target and sources of Poisson regression model, we generate predictors from the same Gaussian distribution and t-distribution respectively, and truncate each predictor at ±0.5.

To generate the coefficient w^(k) for $k\notin {𝒜}_h$, we randomly generate S^(k) of size s from {2s + 1, … , p}. Then, the j-th component of coefficient w^(k) is set to be

$$w_j^{(k)}=\{\begin{array}{cc}0.5+2h{r}_j^{(k)}∕p,\hfill & j\in \{s+1,\dots ,2s\}\cup S^{(k)},\hfill \\ 2h{r}_j^{(k)}∕p,\hfill & \text{otherwise},\hfill \end{array}\phantom{\}}$$

where $r_j^{(k)}$ is a Rademacher variable. We also add an intercept 0.5. The generating process of each source data is independent. Compared to the setting in Section 4.1.1, the current setting is more challenging because source predictors come from t-distribution with heavier tails than sub-Gaussian tails. However, although Assumption 2 is violated, in the following analysis, we will see that Trans-GLM can still succeed in detecting informative sources.

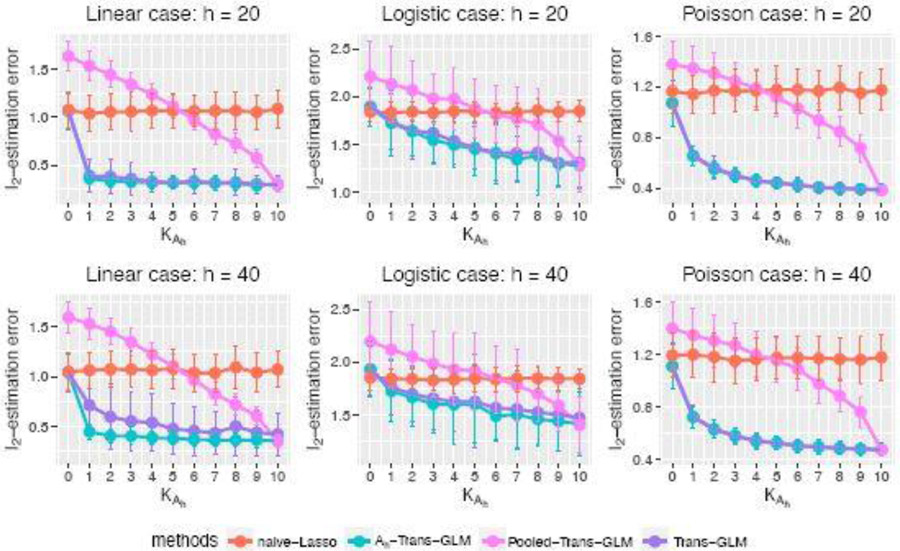
As before, we fit naïve-Lasso on only target data. 𝒜_h-Trans-GLM and Pooled-Trans-GLM represent Algorithm 1 on source data in 𝒜_h and target data or all sources and target data, respectively. Trans-GLM runs Algorithm 2 by first identifying the informative source set 𝒜, then applying Algorithm 1 to fit the model on sources in 𝒜. We vary the values of K_𝒜h and h, and repeat simulations in each setting 200 times. The average ℓ₂-estimation errors are summarized in Figure 3.

Fig. 3.

The average ℓ₂-estimation error of various models with different settings of h and K_𝒜h when K = 10. n_k = 200 for all k = 0, … , K, p = 2000, s = 20. Error bars denote the standard deviations.

From Figure 3, it can be observed that in all three models, 𝒜_h-Trans-GLM always achieves the best performance as expected since it transfers information from sources in 𝒜_h. Trans-GLM mimics the behavior of 𝒜_h-Trans-GLM very well, implying that the transferable source detection algorithm can successfully recover 𝒜_h. When K_𝒜h is small, Pooled-Trans-GLM performs worse than naïve-Lasso because of the negative transfer. As K_𝒜h increases, the performance of Pooled-Trans-GLM improves and finally matches those of 𝒜_h-Trans-GLM and Trans-GLM when K_𝒜h = K = 10.

4.2. A real-data study

In this section, we study the 2020 US presidential election results of each county. We only consider win or lose between two main parties, Democrats and Republicans, in each county. The 2020 county-level election result is available at https://github.com/tonmcg/US_County_Level_Election_Results_08-20. The response is the election result of each county. If Democrats win, we denote this county as class 1, otherwise, we denote it as class 0. And we also collect the county-level information as the predictors, including the population and race proportions, from https://www.kaggle.com/benhamner/2016-us-election.

The goal is to explore the relationship between states in the election using transfer learning. We are interested in swing states with a large number of counties. Among 49 states (Alaska and Washington, D.C. excluded), we select the states where the proportion of counties voting Democrats falls in [10%,90]%, and have at least 75 counties as target states. They include Arkansas (AR), Georgia (GA), Illinois (IL), Michigan (MI), Minnesota (MN), Mississippi (MS), North Carolina (NC), and Virginia (VA).

The original data includes 3111 counties and 52 county-level predictors. We also consider the pairwise interaction terms between predictors. After pre-processing, there are 3111 counties and 1081 predictors in the final data, belonging to 49 US states.

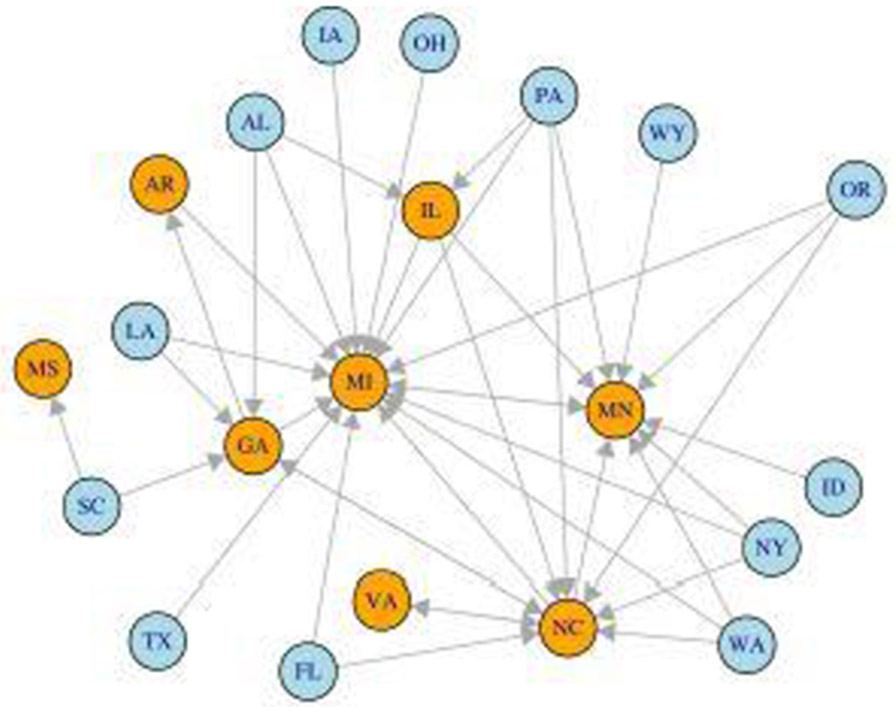
We would like to investigate which states have a closer relationship with these target states by our transferable source detection algorithm. For each target state, we use it as the target data and the remaining 48 states as source datasets. Each time we randomly sample 80% of target data as training data and the remaining 20% is used for testing. Then we run Trans-GLM (Algorithm 2) and see which states are in the estimated transferring set 𝒜. We repeat the simulation 500 times and count the transferring frequency between every state pair. The 25 (directed) state pairs with the highest transferring frequencies are visualized in Figure 4. Each orange node represents a target state we mentioned above and blue nodes are source states. States with the top 25 transferring frequencies are connected with a directed edge.

Fig. 4.

The transferability between different states for Trans-GLM.

From Figure 4, we observe that Michigan has a strong relationship with other states, since there is a lot of information transferable when predicting the county-level results in Michigan, Minnesota, and North Carolina. Another interesting finding is that states which are geographically close to each other may share more similarities. For instance, see the connection between Indiana and Michigan, Ohio and Michigan, North Carolina and Virginia, South Carolina and Georgia, Alabama and Georgia, etc.

In addition, one can observe that states in the Rust Belt also share more similarities. As examples, see the edges among Pennsylvania, Minnesota, Illinois, Michigan, New York, and Ohio, etc.

To further verify the effectiveness of our GLM transfer learning framework on this dataset and make our findings more convincing, we calculate the average test misclassification error rates for each of the eight target states. For comparison, we compare the performances of Trans-GLM and Pooled-Trans-GLM with naïve-Lasso, SVM, trees, random forests (RF), boosting trees (Boosting) as well as their pooled version. Average test errors and the standard deviations of various methods are summarized in Table 1. The best method and other top three methods for each target are highlighted in bold and italics, respectively.

Table 1.

The average test error rate (in percentage) of various methods with different targets among 500 replications. The cutoff for all binary classification methods is set to be 1/2. Numbers in the subscript indicate the standard deviations.

Methods	Target states
	AR	GA	IL	MI	MN	MS	NC	VA
naïve-Lasso	4.793.36	6.983.90	5.734.14	11.492.44	12.462.70	7.536.57	15.606.73	9.484.88
Pooled-Lasso	3.594.71	9.984.22	7.895.56	7.045.80	10.38 5.18	22.017.18	12.735.35	21.445.46
Pooled-Trans-GLM	1.83 3.12	4.86 3.60	2.52 3.55	5.62 4.54	10.755.60	7.23 6.65	9.71 5.75	7.15 4.23
Trans-GLM	1.54 2.94	4.74 3.54	2.51 3.45	5.53 4.73	10.34 5.73	7.246.81	9.34 5.57	7.18 4.67
SVM	6.711.70	17.093.89	7.005.40	12.591.87	13.292.29	23.928.90	12.666.86	10.785.29
Pooled-SVM	7.846.32	13.474.73	7.755.24	7.586.40	13.015.69	27.328.72	12.305.75	17.315.46
Tree	2.23 3.58	8.374.40	4.625.27	10.055.53	10.978.42	5.97 5.26	18.298.01	14.466.88
Pooled-Tree	7.816.89	7.684.59	4.634.26	7.426.18	10.535.91	16.737.30	14.767.26	17.435.85
RF	3.603.57	6.043.59	4.083.98	6.424.79	10.51 5.10	7.275.72	11.296.29	7.734.77
Pooled-RF	3.734.82	7.493.90	4.353.63	5.34 4.99	10.864.96	12.566.88	11.046.03	10.405.18
Boosting	2.233.58	4.65 3.77	2.55 3.82	7.795.52	10.646.51	5.28 5.16	10.886.47	7.53 5.10
Pooled-Boosting	3.104.84	5.713.53	3.823.85	5.815.27	11.215.13	14.317.42	10.82 5.99	11.955.25

Table 1 shows that in four out of eight scenarios, Trans-GLM performs the best among all approaches. Moreover, Trans-GLM is always ranked in the top three except in the case of target state MS. This verifies the effectiveness of our GLM transfer learning algorithm. Besides, Pooled-Trans-GLM can always improve the performance of naïve-Lasso, while for other methods, pooling the data can sometimes lead to worse performance than that of the model fitted on only the target data. This marks the success of our two-step transfer learning framework and the importance of the debiasing step. Combining the results with Figure 4, it can be seen that the performance improvement of Trans-GLM (compared to naïve-Lasso) for the target states with more connections (share more similarities with other states) are larger. For example, Trans-GLM outperforms naïve-Lasso a lot on Michigan, Minnesota and North Carolina, while it performs similarly to naïve-Lasso on Mississippi.

We also try to identify significant variables by Algorithm 3. Due to the space limit, we put the results and analysis in Section S.1.3.4 of supplements. Interested readers can find the details there. Furthermore, since we have considered all main effects and their interactions, one reviewer pointed out that besides the classical Lasso penalty, there are other variants like group Lasso (Yuan and Lin, 2006) or Lasso with hierarchy restriction (Bien et al., 2013), which may bring better practical performance and model interpretation. To be consistent with our theories, we only consider the Lasso penalty here and leave other options for future study.

5. Discussions

In this work, we study the GLM transfer learning problem. To the best of our knowledge, this is the first paper to study high-dimensional GLM under a transfer learning framework, which can be seen as an extension to Bastani (2021) and Li et al. (2021). We propose GLM transfer learning algorithms, and derive bounds for ℓ₁/ℓ₂-estimation error and a prediction error measure with fast and slow rates under different conditions. In addition, to avoid the negative transfer, an algorithm-free transferable source detection algorithm is developed and its theoretical properties are presented in detail. Moreover, we accommodate the two-step transfer learning method to construct confidence intervals of each coefficient component with theoretical guarantees. Finally, we demonstrate the effectiveness of our algorithms via simulations and a real-data study.

There are several promising future avenues that are worth further research. The first interesting problem is how to extend the current framework and theoretical analysis to other models, such as multinomial regression and the Cox model. Second, Algorithm 1 is shown to achieve the minimax ℓ₁/ℓ₂ estimation error rate when the homogeneity assumption (Assumption 4) holds. Without homogeneity of predictors between target and source, only sub-optimal rates are obtained. This problem exists in the line of most existing high-dimensional transfer learning research (Bastani, 2021; Li et al., 2021, 2020). It remains unclear how to achieve the minimax rate when source predictors’ distribution deviates a lot from the target one. Another promising direction is to explore similar frameworks for other machine learning models, including support vector machines, decision trees, and random forests.