Estimating geographic variation of infection fatality ratios during epidemics

Abstract

Objectives

We aim to estimate geographic variability in total numbers of infections and infection fatality ratios (IFR; the number of deaths caused by an infection per 1,000 infected people) when the availability and quality of data on disease burden are limited during an epidemic.

Methods

We develop a noncentral hypergeometric framework that accounts for differential probabilities of positive tests and reflects the fact that symptomatic people are more likely to seek testing. We demonstrate the robustness, accuracy, and precision of this framework, and apply it to the United States (U.S.) COVID-19 pandemic to estimate county-level SARS-CoV-2 IFRs.

Results

The estimators for the numbers of infections and IFRs showed high accuracy and precision; for instance, when applied to simulated validation data sets, across counties, Pearson correlation coefficients between estimator means and true values were 0.996 and 0.928, respectively, and they showed strong robustness to model misspecification. Applying the county-level estimators to the real, unsimulated COVID-19 data spanning April 1, 2020 to September 30, 2020 from across the U.S., we found that IFRs varied from 0 to 44.69, with a standard deviation of 3.55 and a median of 2.14.

Conclusions

The proposed estimation framework can be used to identify geographic variation in IFRs across settings.

1. Introduction

During the course of an epidemic, accurate estimation of the infection fatality ratio (“IFR”) – the number of deaths caused by an infection per 1,000 infected people – is crucial for planning and developing risk mitigation strategies. IFRs may vary by age distribution of the population, distribution of infection across demographic groups, prevalence of underlying health conditions, access to healthcare resources, and other factors (Shen et al., 2021; Wood et al., 2021). Therefore, a flexible framework for estimating IFRs among different populations that vary across geographic regions is essential.

Accurately ascertaining both components of the IFR, the number of deaths and the number of infections, can be challenging (Dana Flanders & Kleinbaum, 1995). While the number of deaths may be under- or over-reported in some settings (Aron et al., 2020), even more problematic are potential inaccuracies in ascertaining the number of infections. While case mortality data may provide an upper bound for the IFR, the total number of infections is likely to be dramatically underestimated because infected people may not be tested or report illness. This issue was well-documented during the COVID-19 pandemic (Campbell et al., 2020; Orin & Topol, 2020; Rubin, 2020). In addition, the availability and uptake of testing, as well as the reliability of testing data, may also vary over time and geography. For example, during the COVID-19 pandemic, the number of SARS-CoV-2 nucleic acid amplification tests (NAATs) administered was not consistently recorded for all counties (The Atlantic, 2021).

Here we develop an inferential framework for estimating area-level variation in IFRs and the total numbers of infections to address common data limitations. We utilize a non-central hypergoemetric model to derive estimators, and validate these estimators with simulations. To demonstrate their application, we use the estimators to assess geographic patterns in the number of SARS-CoV-2 infections and IFRs across the U.S. during the COVID-19 pandemic, finding novel patterns.

2. Methods

2.1. Overview of estimators

2.1.1. Definitions

Our goal is to estimate, over a specified period of time, the total numbers of infections and IFRs for a pathogen within discrete geographic subregions contained within a larger region. For example, the period of time may be a month or year; the subregions may be states or provinces; and the larger region may be the country or continent containing the subregions.

We suppose that infections with the pathogen can be detected reliably with testing, but that there is a bias toward testing infected individuals. Over the period of time, across geographic subregion j, let T_j denote the number of tests for the pathogen that are administered, D_j denote the number of deaths caused by the pathogen, and C_j denote the number of observed disease cases (i.e., positive tests). Let P_j be the population size of the subregion, assumed effectively constant. Let the number of infections (both observed and unobserved) be denoted ι_j. Define ω_j as the odds ratio of testing an infected vs. an uninfected individual. Let φ_j be the IFR in subregion j. Across the entire region, as opposed to the subregions, we will denote the total numbers of tests, deaths, and observed cases, and the overall population, number of infections, odds ratio, and IFR without subscripts (i.e., T, D, C, P, ι, ω, and φ, respectively). We denote estimators for parameters with “hat” notation; e.g., an estimator for ω will be denoted by $\widehat{\omega }$.

2.1.2. General Assumptions

To derive an estimator for the number of infections and IFR in each subregion j, we make three assumptions:

• 1.Odds ratios (ω and ω_j): Although it is not necessary to assume actual values of ω and ω_j, it is necessary to assume that the odds ratio of testing an infected vs. an uninfected person is constant across geographic subregions, so that for all subregions i and j, ω = ω_i = ω_j.
• 2.Global IFR (φ): To estimate geographic variation in IFR, in our framework it is necessary to assume that the baseline IFR (φ) for the entire region under consideration is known.
• 3.Observed quantities: we assume that the population (P_j) and numbers of deaths (D_j), observed cases (C_j), and tests (T_j) in each subregion are known, as well as P, D, C, and T for the entire region.

We conceptualize the process by which people are tested with a noncentral hypergeometric model, wherein each test is administered to either a sick or healthy person with some bias toward administering tests to symptomatic people (e.g., because sick people are more likely to seek testing (Campbell et al., 2020); quantified by ω). For estimation, we utilize an approximation for the mean of the Wallenius’ noncentral hypergeometric distribution (Equation 16 in reference Fog, 2008):

$$\frac{C}{\iota }+{\left(1-\frac{T-C}{P-\iota }\right)}^{\omega }\approx 1$$ (1)

and

$$\frac{C_j}{{\iota }_j}+{\left(1-\frac{T_j-C_j}{P_j-{\iota }_j}\right)}^{{\omega }_j}\approx 1.$$ (2)

The noncentral hypergeometric process is appropriate because it results from randomly picking balls without replacement from an urn, where there are two types of balls (in this case sick and healthy people from a finite population) and there is a bias toward picking one type of ball (sick people). Although Expressions (1) and (2) are close approximations, for clarity, in the following we will refer to them as equalities.

2.1.3. Estimators

We develop a moments estimator ${\widehat{\iota }}_j$ for ι_j based on Expressions (1) and (2). Because by Assumptions 2 and 3 the region-wide IFR (φ) and the total number of deaths (D) are known, a moments estimator $\widehat{\iota }$ for ι is given by

$$\widehat{\iota }\equiv 1000\cdot D/\phi$$ (3)

(By definition, φ ≡ 1000 ⋅ D/ι.) A moments estimator $\widehat{\omega }$ for the odds ratio (ω) then follows by plugging C, $\widehat{\iota }$, T, and P into Expression (1) and solving for ω; that is,

$$\widehat{\omega }=\left(\left(1-\frac{C}{\widehat{\iota }}\right)\right./\log \left(1-\frac{T-C}{P-\widehat{\iota }}\right)$$ (4)

It follows from Assumption 1 that a moments estimator ${\widehat{\iota }}_j$ for ι_j can be found by substituting $\widehat{\omega }$ for ω_j in Expression (2) and solving for ι_j; that is, solving the following equation for ${\widehat{\iota }}_j$:

$$\frac{C_j}{{\widehat{\iota }}_j}+{\left(1-\frac{T_j-C_j}{P_j-{\widehat{\iota }}_j}\right)}^{\hat{\omega }}=1$$ (5)

Although there is no general closed form solution for ${\widehat{\iota }}_j$, the appropriate root can easily be found numerically with the constraint that ${\widehat{\iota }}_j\ge 0$. A moments estimator ${\widehat{\phi }}_j$ for the IFR in subregion j is then given by

$${\widehat{\phi }}_j=1000\cdot D_j/{\widehat{\iota }}_j.$$ (6)

To estimate the variance of these estimators, a parametric bootstrap can be utilized: that is, parametric bootstrap resamples using the Wallenius’ noncentral hypergeometric model can be generated using the parameter estimates, and estimates of variance and confidence intervals calculated via usual bootstrap methods.

2.2. Validation and application to COVID-19

We now use data from the COVID-19 pandemic to validate and apply these estimators. We utilize the observed numbers of COVID-19 cases and deaths, and the numbers of SARS-CoV-2 NAAT tests from the U.S. between April 1, 2020 and September 30, 2020 as the basis for an extensive numerical analysis assessing the robustness, accuracy, and precision of the estimators. We then estimate the numbers of SARS-CoV-2 infections and IFRs across counties and states in the U.S. during this same period.

2.2.1. Data

For validation and application analyses, we utilize publicly-available case and mortality data from the COVID-19 Data Repository by the Center for Systems Science and Engineering (CSSE) at Johns Hopkins University (Dong et al., 2020). These case and mortality data, which are at a daily temporal resolution, are shifted by 14 days to account for the fact that COVID-19 deaths result from SARS-CoV-2 infections acquired approximately two weeks prior to death rather than at the time of death. We utilize NAAT testing data from The U.S. Covid Atlas (Kolak et al., 2021).

2.2.2. Definitions

For estimation purposes, we divide the period between April 1, 2020 and September 30, 2020 into seven-day intervals, hereafter referred to as “weeks.” Following the terminology developed above, we treat the entire U.S. as the “region,” and counties and states as “subregions” where the number of infections and IFRs are to be estimated. In the U.S., each state contains multiple counties, so we make two sets of estimates, one for each state and one for each county.

County- and state-level variables are denoted with the subscripts c and s respectively (following the notation developed above, country-wide variables lack a subscript). For instance the number of observed cases in state j will be denoted C_sj and the number of cases across the entire U.S. will be denoted C. Where distinguishing between individual counties and states is unnecessary, we omit the j subscript for clarity; for instance denoting C_sj by C_s.

2.2.3. COVID Case Study Assumptions

To apply the estimators to the COVID-19 pandemic, we further specify the above assumptions.

• 1.1Odds ratios (ω, ω_c, ω_s): Following Assumption 1 (above) here we assume that for a given week in the pandemic, the odds ratio of testing an individual infected vs. uninfected with SARS-CoV-2 is the same for all counties, states, and the entire U.S; that is, for any county i and state j, ω = ω_ci = ω_sj. However, the odds ratios may change across weeks.
• 2.1Regional-wide IFR (φ): Following Assumption 2 (above), we assume that the SARS-CoV-2 IFR across the entire U.S. was five deaths per 1,000 infections from April 1, 2020 to September 30, 2020, a widely agreed upon value (O’Driscoll et al., 2021).
• 3.1Observed quantities: Following Assumption 3 (above), we assume that the population (P_c, P_s, P), and the numbers of COVID-19 deaths (D_c, D_s, D) and cases (C_c, C_s, C) in each county, state, and across the entire U.S. are known. Likewise, we assume that the number of SARS-CoV-2 NAAT tests in each state (T_s) and consequently across the entire U.S. (T) is known. However, we assume that the number of tests in some counties (T_c) for some weeks is unknown. The latter assumption reflects the actual situation where, in the U.S., the number of SARS-CoV-2 NAATs in some counties was not consistently recorded during 2020, despite the fact that it was recorded in other counties and in aggregate for each state. For instance, reliable testing data are unavailable for all counties in the state of Washington, but they are available for all counties in neighboring states (Holmgren et al., 2020; The Atlantic, 2021)
• 3.2
  Number of tests in each county (T_c): Heuristically, having data on testing is needed, because otherwise it is impossible to know whether observing few cases in a county is indicative of low infection rates or just a limited testing effort, and vice versa for high rates. Because the number of SARS-CoV-2 NAATs in some counties in some weeks is unknown, it is necessary to estimate it. To do so, we assume that the number of tests administered T_cj in county j can be predicted by some subset of the population size P_cj, number of observed cases C_cj, and number of COVID-19 deaths D_cj. Specifically, we start with the following full model:

  $$\log (T_{cj})={\beta }_0+{\beta }_1\log (P_{cj})+{\beta }_2\log (C_{cj})+{\beta }_3\log (D_{cj})+{ϵ}_j$$ (7)

• where ϵ_j is a normal random variable with mean 0 (log transformations were implemented to improve the linearity of empirical relationships). This linear model was strongly-supported by regression diagnostics. For each week, we fit this model using the counties where NAAT testing data are available, and all-subsets model selection with 51-fold cross validation, omitting the counties for each state and the District of Columbia separately in each fold (Fig. S1A). The selected models consistently had cross-validation coefficients of determination in the range 0.8–0.95, giving us high confidence in their predictive power (Fig. S1B). For each time point, we then use the fitted model to interpolate the number of NAATs in the counties where testing data were unavailable.

2.2.4. Estimates

Following the sequence in which the estimators in Section 2.1.3 are developed, we first estimate ι and ω at the country level, and then ι_c, ι_s, φ_c, and φ_s at the county and state levels (Table 1; Supplementary Information, Section 1.1). As an added step specific to COVID-19, we initially estimate T_c in counties where testing data is unavailable. To calculate the uncertainty of these point estimates, we use a parametric bootstrap. Specifically, using the point estimates for the odds ratio and the number of infections, for each time point and region, we generate 100 parametric bootstrap resamples using the Wallenius’ noncentral hypergeometric model in Expressions (1) and (2). Dividing the observed mortality by the resulting bootstrap estimates of the number of infections yields an estimate of the sampling distribution of the estimator for the IFR $({\widehat{\phi }}_j)$.

Table 1.

Estimators used for finding unobserved quantities (see Table S1). Bold numbers indicate the order of calculation. The estimators for the total number of infections at the state and county levels [(7) and (10); ${\hat{\iota }}_s$ and ${\hat{\iota }}_c$] are defined implicitly and are found by solving the given equations numerically. These estimators and $\hat{\omega }$ are based on the approximation for the mean of the Wallenius’ noncentral hypergeometric distribution given in Expression (1). Time (t), state (j), and county (i) subscripts are omitted for readability, but all estimators are time-, state-, and county-specific.

Region	Infection fatality ratio	Infections	Tests	Odds ratio
Country	φ = 5 (observed)	(4)$\hat{\iota }=\frac{1000D}{\varphi }$	(3)$\hat{T}=\sum {\hat{T}}_s$	(5)$\hat{\omega }=\frac{\log \left(1-\frac{C}{\hat{\iota }}\right)}{\log \left(1-\frac{\hat{T}-C}{P-\hat{\iota }}\right)}$
State	(8)${\hat{\phi }}_s=\frac{1000D_s}{{\hat{\iota }}_s}$	(7)$\frac{C_S}{{\widehat{\iota }}_S}+{\left(1-\frac{{\widehat{T}}_S-C_S}{P_S-{\widehat{\iota }}_S}\right)}^{{\hat{\omega }}_S}=1$	(2)${\hat{T}}_s=\sum {\hat{T}}_c$	(6)${\hat{\omega }}_s=\hat{\omega }$
County	(11)${\hat{\phi }}_c=\frac{1000D_c}{{\hat{\iota }}_c}$	(10)$\frac{C_c}{{\hat{\iota }}_c}+{\left(1-\frac{{\hat{T}}_c-C_c}{P_c-{\hat{\iota }}_c}\right)}^{{\hat{\omega }}_c}=1$	(1)${\hat{T}}_c$ (linear model)	(9)${\hat{\omega }}_c=\hat{\omega }$

2.2.5. Validation: performance when assumptions are met

Under scenarios with set numbers of infections, we generated simulated COVID-19 case data from April 1, 2020 to September 30, 2020 (Supplementary Information, Section 1.2). Using the simulated values of the known quantities in the original data set (black quantities in Table S1) and the estimation procedure described above, we found estimates of all of the unknown quantities (red quantities in Table S1), and also the country-wide IFR, φ. Comparing estimates from 100 iterations of the sampling process to the known values yielded measures of the performance of the estimators.

2.2.6. Validation: performance when assumptions are violated

We performed simulations to assess the performance of the estimators when (a) odds ratios varied spatially in addition to temporally, a violation of Assumption 1.1, and (b) the region-wide IFR differed from five deaths per 1,000 infections, a violation of Assumption 2.1. Specifically, to simulate data from a model where Assumption 1.1 was violated, we multiplied the odds ratio for each state by a factor of (a) 0.9 to 1.1, which equaled 0.896 + 0.004 ⋅ S and (b) 0.5 to 1.5, which equaled 0.482 + 0.018 ⋅ S, where S is the numeric FIPS code of the state (a pseudo-random factor). To simulate data from a model where Assumption 2.1 was violated, we substituted a value of 0.005 and 0.5 for 0.0196 in Step 3, above, giving an overall infection fatality ratio of approximately 0.21 and 18 deaths per 1,000 infections rather than 5, respectively. In addition, for the real (unsimulated) case data, we compared the summed county-level infection estimates within each state to the state-level infection estimates to check for consistency.

2.2.7. Validation: comparison to published seroprevalence IFR estimates

We compared the IFR estimates from the hypergeometric estimators $({\widehat{\phi }}_j)$ to those from seroprevalence studies summarized in reference (Ioannidis, 2021). We matched the geographic regions (e.g., counties containing cities where seroprevalence estimates are available) and time periods as closely as possible, calculating estimates based on the number of infections and deaths integrated over three months before the date of the seroprevalence estimate. All seroprevalence IFR estimates considered were from between April and August 2020.

3. Results

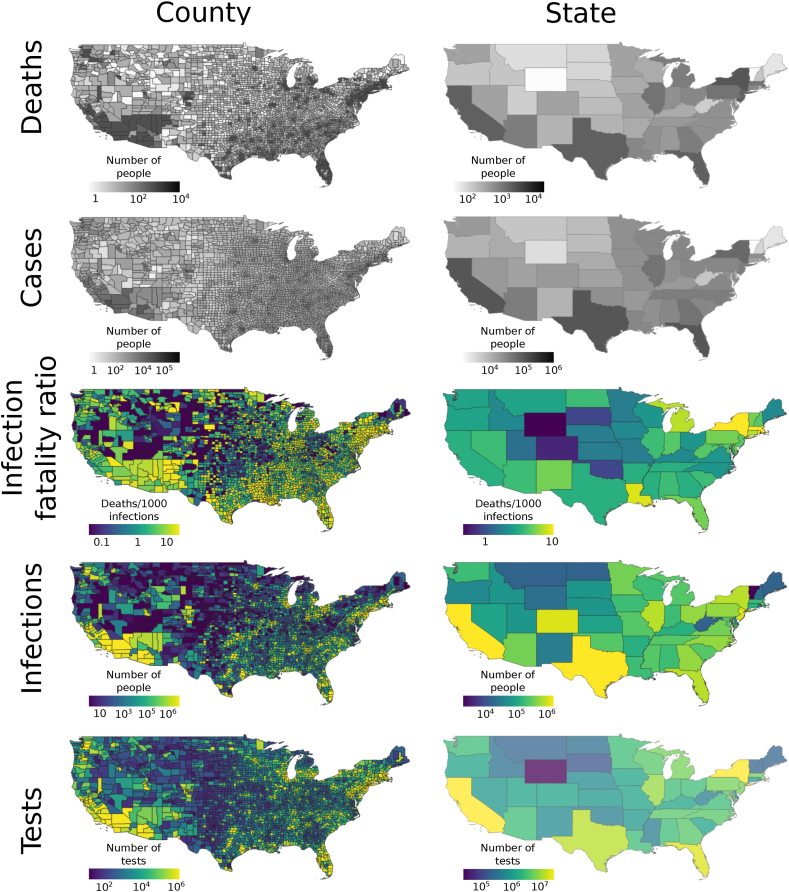
Applying the county-level estimators to the real, unsimulated, COVID-19 data spanning April 1, 2020 to September 30, 2020 from across the U.S., we found that IFRs varied across counties from 0 to 44.69, with a mean of 3.15 and a median of 2.14 (standard deviation 3.55). IFRs were the lowest in the Intermountain West, High Plains, and New England, and the highest in Arizona, Western New Mexico, and scattered other regions of the U.S. The number of SARS-CoV-2 infections (not corrected for population) was highest in the Southwest and scattered other parts of the U.S. County-level IFRs showed a relatively low degree of spatial autocorrelation. Similar trends were evident at the state level, with lower spatial grain (Fig. 1). All of the estimators had low variance (Fig. S2).

Fig. 1.

Maps showing estimated and observed values of the number of COVID-19 deaths and cases, and SARS-CoV-2 IFRs, number of infections, and number of NAATs in the U.S. over the period spanning March 1, 2020 to October 31, 2020. Estimated quantities are shown in color, while observed quantities are shown in gray. The number of SARS-CoV-2 NAATs was estimated in some counties, while observed in others.

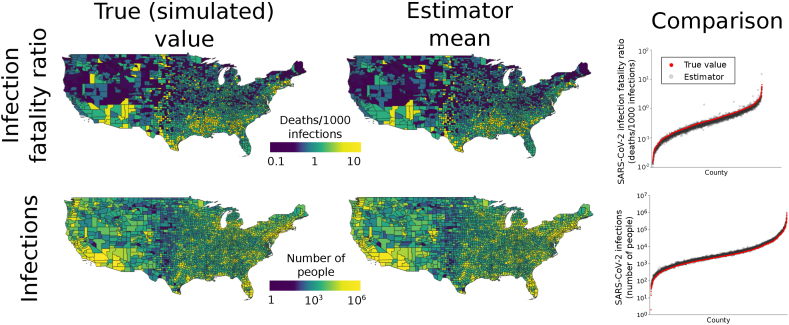
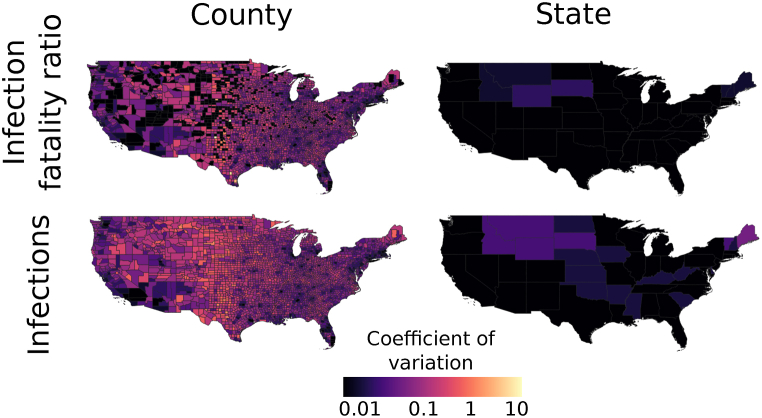
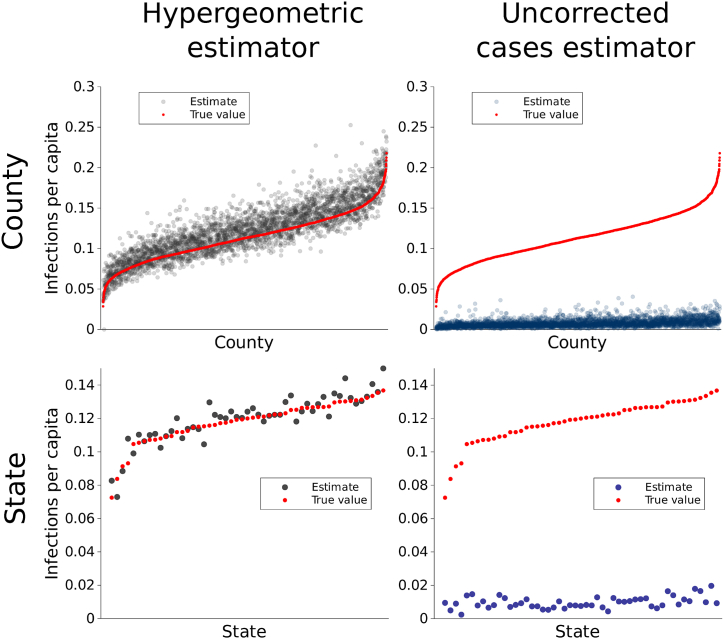
In our validation, we found that the mean of the county-level estimates of IFRs and number of SARS-CoV-2 infections had high accuracy (Fig. 2; Pearson correlation coefficients for estimator means and true values 0.927 and 0.996 respectively). Likewise, at the state level, the mean of the estimates for IFRs and number of infections had high accuracy and precision (Fig. S3; Pearson correlation coefficients for estimator means and true values 0.991 and 0.996, respectively). Moreover, the estimators had coefficients of variation below 1 for almost all counties and states (Fig. 3; for example, for IFR, 99.7%, 96.7%, and 40.1% of counties had coefficients of variation below 1, 0.5, and 0.1, respectively). In contrast, estimates of the number of infections and IFR obtained simply by using the raw numbers of cases and case fatality ratios, respectively, were biased by up to several orders of magnitude and had low precision (Fig. S4). These results also held for per capita infection estimates (Fig. 4), indicating that the performance was not driven by varying populations across counties and states. The estimator was robust against deviations from Assumption 1: when odds ratios varied spatially, performance remained good (Figs. S5A–B, S6A-B). When the global IFR differed from five deaths per 1,000 infections, the estimator became biased, as would be expected. However, it continued to correctly estimate the relative values of the county-level IFRs; that is, to indicate area-level variation in IFRs (Figs. S5C–D, S6C-D). Using the observed (non-simulated) numbers of cases, the summed county level estimates of the number of infections within each state matched the number of infections directly estimated for those states (Fig. S7). At both the state level and county level, seroprevalence IFR estimates matched the IFR estimates from the hypergeometric estimator (Fig. S8), further indicating its validity.

Fig. 2.

Performance of county-level estimators. Maps in the first column show true (simulated) SARS-CoV-2 IFRs and numbers of infections. All values were conditioned on observed numbers of COVID-19 deaths. Counties with zero COVID-19 deaths are omitted from the SARS-CoV-2 IFR estimation results because they have ratios of zero. The second column gives the means of the estimates over 100 simulated data sets for each county. The close match between true values and estimates indicates that the estimators have high accuracy. The accuracy is further illustrated by the graphs in the third column, which plot the true values in each county compared to the mean of the estimator. In each plot, counties (x-axis) are ordered by increasing value.

Fig. 3.

The estimators for IFRs and the number of infections have high precision. At both the county and state levels, the estimators have low coefficients of variation, generally below 0.1 and often below 0.01.

Fig. 4.

Performance of county-level estimators for SARS-CoV-2 infections with population taken into account. The hypergeometric infections estimator per capita had low bias and high precision (column 1), displaying superior performance to a naive estimator that used the uncorrected number of COVID-19 cases (column 2). On the x-axis, counties and states are ordered by increasing number of SARS-CoV-2 infections, shown in red.

4. Discussion

We present an inferential framework for estimating the geographic variation in the total number of infections of a pathogen and its IFR. We apply this framework to SARS-CoV-2 and the COVID-19 pandemic, finding that it is robust and performs accurately and precisely. The approach relies on a noncentral hypergeometric model that accounts for differential probabilities of positive tests (i.e. because sick individuals are more likely to seek testing than healthy individuals (Campbell et al., 2020)), which we show is well-suited for estimating IFRs.

Most studies utilize an averaged IFR, despite known geographic and temporal variation in this parameter. The problematic nature of variation in IFR estimates is well-documented in the literature; for example, multiple systematic reviews have highlighted differences in SARS-CoV-2 IFRs across time and geographic settings (Ioannidis, 2021; O'Driscoll et al., 2021; Verity et al., 2020). Although in limited settings, comprehensive case reporting and tracking enable more accurate estimation of the IFR, most estimates are based on a snapshot of seroprevalence data, which may not be representative of the population of interest and is subject to information delays and issues around accuracy of testing. (Levin et al., 2020; Takahashi et al., 2020).

Our framework helps to address the challenges of IFR estimation posed by incompletely observed data. There are sparse examples of other approaches to address this issue: for example, Reich et al. (Reich et al., 2012) propose using a log-linear model to estimate the relative case fatality ratio, and this approach has been applied to the SARS-CoV-2 epidemic to develop a corrected estimator of case fatality rate that accounts for time lag and imperfect reporting of deaths and recoveries (Angelopoulos et al., 2020). Similarly, Brazeau et al. (Brazeau et al., 2022) used serologic test sensitivity and specificity alongside a Bayesian framework to account for uncertainties in the parameters for determining IFR, including consideration of delay-distributions from time from infection to seroconversion, time to death, and time to seroreversion (i.e., antibody waning), and showed improvements in state-level estimates of SARS-CoV-2 infections in the U.S.

Our approach differs in that we use data on testing effort, where reliably reported, to address incompletely observed seroprevalence data, which are widely used to estimate IFR. Most seroprevalence data are limited geographically, may have non-representative samples, or fail to account for potential delays from onset to seroconversion. Therefore, our framework can be seen as complementary to the methods described above.

The number of excess deaths is another frequently used metric of the burden of mortality, particularly with regard to the COVID-19 pandemic. Typically defined as the difference between the observed number of deaths and the expected number of deaths across a given time period (Centers for Disease Control and Prevention, 2021), it includes changes in mortality that may directly or indirectly be attributable to COVID-19 (such as from delayed care or behavioral health crises). While useful in some settings, excess death estimates are highly sensitive to the reference time period used and negative estimates often occur in younger age strata (Woolf et al., 2021; Excess Deaths Associated with COVID). Our proposed method allows for more detailed area-level estimates of mortality directly attributable to an infection.

As with all statistical tools, the accuracy and precision of our method are limited by the quality of the data that are available. An advantage of our approach is that it allows investigators to rely on the best available data and estimate quantities where data may be lacking. In the application to COVID-19, our estimates use data on NAAT (also known as molecular or PCR tests) and do not include data from antigen tests including home tests, which did not receive FDA approval until late 2020. The NAAT are the most reliable for detecting infections and were the most widely used during the study period.

Our approach is also limited by a number of assumptions, though our numerical analyses show that the performance of the approach is robust to many violations of these assumptions. However, as with any inferential approach, sufficiently extreme violations of assumptions will reduce the performance of the method, and in these situations, it may be necessary to modify the method. Specifically, Assumption 1 – that the odds testing an infected vs. an uninfected individual is the same across geographic regions – can be relaxed in numerous ways. While some geographic or temporal structure must be assumed to estimate the odds ratios, which are latent variables, this structure does not need to be geographically homogeneous. With additional covariates (e.g., data on demographics, health care access), it may also be possible to further infer specific aspects of the odds ratios. Second, regarding Assumption 2, while an overall IFR must be assumed, this value can in principle be any number between 0 and 1 dependent on the disease, time, location, and other factors. Moreover, when the aim is to rank IFRs in subregions relative to each other instead of estimate their precise values, the assumed overall IFR may not matter. And third, an added degree of complexity specific to COVID-19 in the U.S. is imparted here because the number of NAATs in each state, but not every county, are known. In a more typical scenario, when testing effort is recorded for each subregion, one could directly make estimates for a single class of subregions (e.g., counties) from a superregion (e.g., country). This would omit the need for our Assumption 3.2. It should be possible to adapt our approach for application at different geographic and temporal scales, and it may be particularly useful in settings in which resources to carry out large, representative seroprevalence studies are unavailable.

Local estimates are likely to be more accurate and useful for policy planning purposes than generalized or country-level estimates. The importance of flexible estimates is highlighted by the work of Solis et al. (Solís et al., 2021), who examined how COVID-related models performed differently in different states and the impact on morbidity with respect to state-level policy decisions driven by a lack of fit. Our approach can serve as an extension to other methods for estimation of epidemic burden to allow for greater precision around geographic and temporal population subgroups.

In summary, we propose versatile inference methods that leverage the best available data to yield comprehensive estimates that allow for variance in IFRs across geographic regions or time intervals. We show in validation models that our method can be used to accurately and precisely estimate SARS-CoV-2 IFR at the county level in the U.S.

CRediT authorship contribution statement

Joshua Ladau: Writing – review & editing, Writing – original draft, Visualization, Validation, Software, Project administration, Methodology, Investigation, Formal analysis, Data curation, Conceptualization. Eoin L. Brodie: Writing – review & editing, Writing – original draft, Project administration, Funding acquisition, Conceptualization. Nicola Falco: Writing – review & editing, Writing – original draft, Conceptualization. Ishan Bansal: Writing – review & editing, Writing – original draft, Investigation, Conceptualization. Elijah B. Hoffman: Writing – review & editing, Writing – original draft, Investigation, Conceptualization. Marcin P. Joachimiak: Writing – review & editing, Writing – original draft, Investigation, Conceptualization. Ana M. Mora: Writing – review & editing, Writing – original draft, Methodology. Angelica M. Walker: Writing – review & editing, Writing – original draft, Investigation, Conceptualization. Haruko M. Wainwright: Writing – review & editing, Writing – original draft, Conceptualization. Yulun Wu: Writing – review & editing, Writing – original draft, Validation, Methodology, Investigation, Formal analysis. Mirko Pavicic: Writing – review & editing, Writing – original draft, Investigation. Daniel Jacobson: Writing – review & editing, Writing – original draft, Validation, Supervision, Project administration, Methodology, Investigation, Funding acquisition, Data curation, Conceptualization. Matthias Hess: Writing – review & editing, Writing – original draft, Supervision, Project administration, Investigation, Conceptualization. James B. Brown: Writing – review & editing, Writing – original draft, Visualization, Validation, Supervision, Project administration, Methodology, Investigation, Funding acquisition, Formal analysis, Data curation, Conceptualization. Katrina Abuabara: Writing – review & editing, Writing – original draft, Visualization, Supervision, Project administration, Methodology, Investigation, Funding acquisition, Data curation, Conceptualization.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Handling Editor: Dr Daihai He

Appendix A. Supplementary data

The following is the Supplementary data to this article: