Abstract
Interfaces between molecular organic architectures and oxidic substrates are a central feature of biosensors and applications of biomimetics in science and technology. For phospholipid bilayers, the large range of pH- and ionic strength-dependent surface charge densities adopted by titanium dioxide and other oxidic surfaces leads to a rich landscape of phenomena that provides exquisite control of membrane interactions with such substrates. Using neutron reflectometry measurements, we report sharp, reversible transitions that occur between closely surface-associated and weakly coupled states. We show that these states arise from a complex interplay of the tunable length scale of electrostatic interactions with the length scale arising from other forces that are independent of solution conditions. A generalized free energy potential, with its inputs only derived from established measurements of surface and bilayer properties, quantitatively describes these and previously reported observations concerning the unbinding of bilayers from supporting substrates.
Graphical abstract

INTRODUCTION
Oxidic surfaces are widely employed as substrates for a broad range of applications relevant for catalysis,1 biosensing,2 chromatography, and separation technology,3,4 as well as in fundamental studies of biomembrane properties and structures, 5−8 inert coatings, and intermolecular forces.9 Lipid bilayers on such substrates are frequently used to investigate the interaction of proteins and peptides with membranes or to prepare biosensors, i.e., interfacial devices that rely on biorelevant interactions in their sensing schemes.10 Looking ahead to an anticipated marriage of synthetic biology and semiconductor technology,11,12 fully controllable membrane-like surface architectures will be a crucial ingredient of cell/semiconductor interfaces that enable the transfer of stimuli from and to CMOS ICs.13,14 Similarly, the current disruptive transition from in vitro to in vivo medical diagnostics15,16 depends on engineering proximity contacts between biological interfaces and sensor devices. By its very conception, such engineered cell−semiconductor interfaces require nanoscale control of the underlying interfacial architectures and their responses to a variable environment.
Exploitation of the appealing features of the solid-state/soft material interfaces and their broad application potential is confounded by several factors. The complex chemistry of silica surfaces17 results in complex interactions with their environment, especially aqueous electrolytes. Lipid membranes and detergent aggregates on such surfaces add an idiosyncratic set of interaction mechanisms, such as repulsion due to thermally excited undulations18−20 and their surface hydration dynamics 21 which have led to the prediction that membranes stacked in multilayers will unbind from each other under suitable conditions.22 Finally, conventional preparation schemes employing bilayer deposition or self-organization rarely lead to the conceived idealized structures. For example, wetting instabilities can lead to locally pinned bilayer areas and disrupt the continuity of transferred bilayer membranes,23,24 while the rearrangement of bilayer structures upon vesicle fusion to planar substrates can lead to local inhomogeneities.25 These issues limit our quantitative understanding of the interfacial forces that act in such nanoscale systems. Whereas the components of interfacial forces and their potentials, as well as interrelations among them, have been extensively studied, 26,27 a generalized quantitative picture has not yet emerged. In part, this is due to the lack of a sufficiently simple experimental system whose key interaction parameters are well known and continuously variable under experimental control.
In this study, we demonstrate such a system, achieving the predictive control of unpinned, large-scale homogeneous zwitterionic phospholipid bilayers (1,2-dioleoyl-sn-3-glycerophosphatidylcholine, DOPC) that explore the complex interaction potential above planar, atomically flat silica (SiO2) and titania (TiO2) surfaces. Our measurements leverage recent developments on the preparation of unpinned, defect-free bilayers on substrates that were previously found difficult to coat by using more established techniques28,29 and shed light on the mechanism of bilayer formation. State-of-the-art NR measurements yield ångström-level precision in structural characterization. We control the bilayer position above the oxidic surfaces by adjusting the pH (between 4 and 11) and ionic strength ([NaCl] = 10−1000 mM; M = mol/L). We show that the bilayers can be reversibly driven from close contact with their supporting substrates to ~4 nm distance, where they fluctuate freely. The results are analyzed as a superposition of the van der Waals (vdW) interactions in this asymmetric system with Poisson−Boltzmann electrostatics, bilayer-inherent fluctuation repulsion, and short-range repulsion due to hydration forces.30,31 Applying only well-established values of the model parameters in these four components, the resulting free energy, , describes the distance dependence of the bilayers quantitatively. is thus a generalized potential, which, as we demonstrate, is also adequate to quantify the behavior of similar systems that have been previously reported in the literature. The complexity of this generalized potential gives rise to a dependence of the bilayer distance from a TiO2 surface that is reminiscent of a phase transition, with possible applications to the sensitive detection of changes in surface potential. The findings reported here have implications for the development of capacitive coupling techniques of single cells to electronic readouts for establishing long-term cell viability on semiconductor substrates and for the facile preparation of biomedical devices in personalized medicine and theranostics. They further address the technological need to design and construct artificial sensor structures with incorporated membrane proteins for which the lack of space between the membrane and substrate is a fundamental limitation.
EXPERIMENTAL SECTION
Experimental Design.
This study was designed to determine the bilayer membrane morphology on oxidic surfaces and its response to environmental changes with ångström resolution using neutron reflectometry. Measurement protocols that afford such precision,32 data modeling, and evaluation33 as well as the information content of such measurements and its optimization in experimentation34 have been established in a previous work. In particular, it has been shown that isotopic variation of the neutron scattering contrast, which can be isomorphically achieved on a sample by the exchange of the aqueous solvent, in combination with composition-space refinement35 of the underlying structure using chemical and volumetric constraints, is a facile method to achieve a high resolution (ref 32 and works cited within). To ensure consistency across structural determinations at different pH and/or ionic strengths, the same oxidic substrates were used for measurement at each condition. A pseudo-random scheme was used to probe different conditions to ensure that significant changes in the sample did not occur over the course of these measurements.
Sample Preparation.
Industry-quality silicon wafers (1,0,0; surface roughness: <5 Å) of 5 mm thickness and 3 in. (76.2 mm) diameter n-doped to a conductivity between 1 and 100 Ωcm were coated with 100−200 Å nominal thickness amorphous SiO2 by dry thermal oxidation or with 140 Å nominal thickness TiO2 by magnetron sputtering (300 W, 11 sccm Ar flow rate, chamber pressure: <1 mTorr) on a Denton Vacuum Discovery 550 sputtering system at the NIST Center for Nanoscale Science and Technology cleanroom. Samples were vacuum sealed until further use. The sample wafer was mounted with its coated surface facing a 100 μm fluid-filled reservoir defined by a 65 mm inner diameter cylindrical Viton gasket separating it from a roughened backing wafer, thus assembling a fluid cell for NR measurements. The backing wafer was perforated by a single inlet and outlet, which were coupled by flat-bottomed fittings (IDEX Health and Science, Oak Harbor, WA) to external tubing for solution exchanges.
Solvent-Assisted Lipid Bilayer (SLB) Formation.
DOPC (Avanti Polar Lipids, Alabaster, AL) was dissolved in 2-propanol, typically at a concentration of 3 mg/mL, and injected into the fluid cell. An aqueous solution (Millipore) of the desired NaCl concentration, buffered at pH 7.4 by 10 mM tris(hydroxymethyl)-aminomethane (“Tris”) or 5 mM 4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid (“HEPES”), was then injected via a syringe pump at a rate of 0.057 mL/min. At this flow rate, the average fluid velocity through the flow cell was ~2 × 10−4 m/s, comparable to a previous work by Tabaei et al.,36 for a total of 5.13 mL (about 12 cell volumes).
Buffer Exchanges.
Subsequent buffer exchanges were performed using the same slow exchange rate (0.057 mL/min) and volume (5.13 mL) as for SLB formation. For measurements at different ionic strengths, the NaCl concentration was varied in the order [NaCl] = 150 mM, 1 M, 10 mM. At each NaCl concentration, the pH was varied in a pseudo-random fashion to minimize systematic errors potentially arising from changing the pH in a single direction. For 150 mM and 1 M NaCl, two measurements at pH 5 were performed, each separated by measurement of at least eight other buffer conditions, to demonstrate reproducibility and accurate error estimation.
Neutron Reflectometry.
Specular NR experiments were carried out on the MAGIK reflectometer37 at the National Institute for Standards and Technology (NIST) Center for Neutron Research (NCNR) with a setup and sample environment as described38 in which a monochromatic beam (wavelength, = 5.000 Å) impinged on the interface between the coated surface and the liquid reservoir at an angle of (Figure 1A). The pre-sample collimating slits were chosen to maintain a constant illuminated footprint area for each measurement at a scattering angle of 2. The post-sample collimation was chosen to allow the entire reflected beam to impinge on the detector to measure specular reflection. Reflectivity curves covered a range in the scattering vector from 0.008 to 0.20 or 0.25 Å−1. The reflectivity was calculated as
| (7) |
Here, is the measured count rate normalized to a much larger monitor count rate to correct for fluctuations in beam intensity. is the background intensity, primarily from incoherent scattering from the liquid reservoir, which is calculated by linear interpolation of the scattering intensity measured with the detector positioned at 1.5 and 2.5. , the incident beam intensity, is directly measured through the silicon substrate at with the detector positioned in line with the incident beam.
Figure 1.
Measurement of DOPC bilayer formation on oxidic surface films. (A) Principle of bilayer formation monitored by specular reflection of a neutron beam at grazing incidence. Phospholipid dissolved in 2-propanol is allowed to incubate oxidic surface films (TiO2 or SiO2) supported by Si wafers, leading to the formation of incomplete lipid monolayers (characterized in panels (B) and (C)). Subsequent gradated buffer exchange with an aqueous solution transforms the lipidic surface structure into continuous, complete phospholipid bilayers (characterized in panels (D−F)). (B, C) Resolved structures of the surface-adsorbed, incomplete DOPC monolayers under 2-propanol show that aliphatic lipid chains are primarily in contact with the moderately hydrophilic solvent. (D, E) After buffer exchange, NR shows the formation of essentially defect-free lipid bilayers on both oxidic surfaces. However, while the membrane is tightly adsorbed to SiO2 (D), it is separated from the TiO2 surface by an aqueous cushion (E), the extent of which can be manipulated by changes of the pH and/or ionic strength of the buffer as shown for pH 11 in panel (F). Confidence intervals on are reported at the 68% level and are calculated as described in the Experimental Section.
Statistical Analysis.
NR data were modeled using the composition space modeling procedures described previously for supported lipid bilayers.33 Optimizations were performed on the Bridges high-performance computing system39 using the DREAM Markov chain Monte Carlo (MCMC) algorithm40 implemented in the software package Refl1D.41 Confidence intervals on parameters and model predictions were calculated from parameter distributions derived from at least 3.2 million DREAM samples after the optimizer had reached a steady state.
RESULTS AND DISCUSSION
Experimental Results.
Solvent-assisted lipid bilayer (SLB) formation is a facile method for the one-step preparation of substrate-supported membranes through the gradual exchange of an alcoholic solution of phospholipids, which bathes a solid substrate, with aqueous buffer.28,29 However, there is limited information about the SLB formation mechanism and structural details of the resulting membranes,28 particularly in comparison with more established membrane preparation methods.2,7,42,43 To characterize the mechanism of membrane formation, we used neutron reflection (NR), a technique that probes structures on a planar interface with ångström-level precision in the out-of-plane direction, (Figure 1A). Taking advantage of the neutron scattering length (nSLD) contrast variation capability of NR, in the form of isomorphic in situ solvent exchange to replace hydrogen-based solvents or buffers with their deuterated counterparts, the structure of interest is characterized in local environments of low and high nSLD.32,34 These related measurements are evaluated in a composition-space model35 that is parametrized by molecular component distributions (component−volume occupancies, CVOs32) along that are, in their sum, space filling.33
We first characterized the bare surfaces of the amorphous, thermally oxidized SiO2 and the sputtered TiO2 films with NR under fully protiated and fully deuterated 2-propanol, then we measured samples again upon exposure to DOPC solutions in 2-propanol (Figure S1). Joint optimization of the composition-space model of a monolayer lipid film resolved the headgroup and lipid chain distributions shown in Figure 1B,C. Dashed lines indicate the total volume occupancy of the lipid; the space above is occupied by solvent. Lipid headgroups were proximal to the oxidic surface in both cases. The interfacial lipid density, expressed as the fractional density of a fully hydrated DOPC bilayer leaflet, A = (72.4 ± 0.5) Å2 per lipid,44 was (38.6 ± 0.8) % and (58.5 ± 0.8) % on SiO2 for 0.3 mg/mL and 3.0 mg/mL DOPC in 2-propanol, respectively; on TiO2, it was (47.8 ± 2.5) % for 3.0 mg/mL DOPC (68% confidence intervals). We conclude that DOPC forms a hydrophobically terminated monolayer on these oxidic surfaces under 2-propanol whose completeness depends on the lipid concentration in the solution. It is then comprehensible that such a monolayer provides a template for bilayer completion when the adjacent bulk solvent phase becomes continuously more aqueous in the course of replacement with the gradated solvent mixture.
Following the gradual exchange of 2-propanol by aqueous buffer in the procedure that leads to SLB formation (see Experimental Section), the interfacial structures on SiO2 and TiO2 were further characterized with NR in fully hydrogenated (H2O) and deuterated (D2O) buffers (150 mM NaCl, 10 mM Tris, pH 7). The resulting CVO profiles are shown in Figure 1D,E and the NR data in Figure S2. The bilayers were more than 95% complete on both substrates. On TiO2, a contiguous water cushion with a thickness separated the membrane from the substrate (Figure 1E). On SiO2, the major difference was the lack of such a water cushion (Figure 1D). The root-mean-square surface corrugations of the bilayers, defined as the quadratic sum of bilayer fluctuations and substrate roughness , , were similar to those of the bare substrates ( ≈ 4 Å for TiO2 in Figure 1E), which implies that the bilayers were essentially conformal with the surfaces. At least for the bilayer prepared on TiO2, this further implies that the membrane was not locally pinned to the substrate surface. Because all subsequent measurements at different ionic strengths and pH values (see below) were performed on the same bilayers after the appropriate solvent exchanges, this further demonstrates that the observed membrane structures under these varied conditions were those of freely fluctuating bilayers. Representative for our data analysis, Table S1 provides a detailed set of model fit parameters for DOPC on TiO2 at pH 7 (structure shown in Figure 1E).
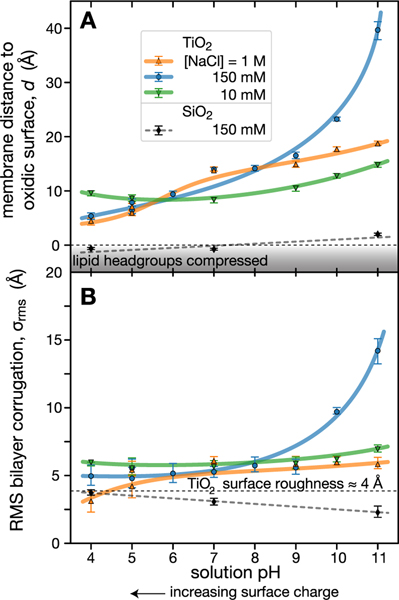
When we changed the pH of the aqueous buffer from 7 to 4 or 11, the structural responses of the membranes differed widely between the SiO2- and TiO2-terminated substrates. On silica, the DOPC bilayer structures were essentially insensitive to variations within the entire pH range, while they varied significantly on titania, both in terms of the substrate distance and apparent surface roughness. At high pH on TiO2, the membrane was found to be displaced by several nanometers away from the substrate, to , and showed large undulations as deduced from the high surface roughness, (Figure 1F). To obtain a more comprehensive picture of membrane interactions with titania, we systematically varied the pH from 4 to 11 at [NaCl] = 10 mM, 150 mM, and 1 M. NR data are shown in Figure S3. A compilation of results is shown in Figure 2 in terms of the membrane−substrate distance (panel (A)) and apparent surface roughness (panel (B)). We observed that bilayers stay in close contact with the SiO2 surface at all pH values; at pH 7 and below, the membrane-substrate distance is formally negative, suggesting headgroup deformation due to its strong adsorption to the substrate (Figure 1D). By comparison, bilayers are located further away but still in close contact with the TiO2 surface, except at 150 mM NaCl and high pH. In this regime, bilayers are no longer tightly associated with the interface but are suspended between 20 and 40 Å away at pH 10 and 11, respectively, with a commensurate increase in their fluctuation amplitudes. The observed structural changes upon variation of pH and ionic strength were reproducible in independent sample preparations, independent of sample history, and fully reversible upon changes in opposite directions. In other words, the structural characteristics we observe bear the signatures of equilibrium properties.
Figure 2.
Dependence of DOPC membrane disposition near oxidic surfaces on pH and ionic strength. (A) Bilayer distances from the oxidic surface. (B) Bilayer undulation amplitudes. Bilayers prepared on SiO2 are strongly coupled to the solid surface. By contrast, bilayers prepared on TiO2 reside on an aqueous cushion under otherwise identical conditions ([NaCl] = 150 mM, pH 7, 10 mM Tris), showing only slight variations in their substrate distances and fluctuation amplitudes at pH 4 and pH 7 for all ionic strengths but large variations at intermediate ionic strengths and high pH. Lines overlaid on data are guides for the eye. Error bars are 68% confidence intervals and are calculated as described in the Experimental Section.
Analysis.
We generalized an analysis by Israelachvili and co-workers for bilayers on glass9 to the oxidic surfaces studied here, composing a free energy function, , that contains four contributions: van der Waals interactions, electrostatic interactions, confinement entropy, and hydration forces. It will be shown from the analysis of our experimental data that this mean-field approach is fully appropriate at distances beyond , even in the linear approximation to Poisson−Boltzmann electrostatics, which we compare with the fully non-linear treatment in the Supporting Information. is not expected to be valid at the atomistic level, and significant corrections may be required for .
First, the vdW interaction for a slab in proximity to an infinite half-space is27
| (1) |
Here, the slab represents a bilayer with its acyl chain and headgroup layer thicknesses and , respectively, where the value for is from NR measurements presented in Figure 1 and that for emerges from the parameterization of the bilayer.33 The inner surface of the bilayer slab is located at a distance from the substrate. The Hamaker parameters A132, for TiO2 and SiO2 (1) interacting with hydrocarbons (3) across water (2), were computed using the summation method45 with the dielectric dispersion of the bilayer represented using a four-damped-oscillator model with values for tetradecane and water from tabulated data.27 A two-damped-oscillator model was used to describe the infrared and ultraviolet dielectric dispersion of TiO2 and SiO2. Importantly, screening of the vdW term by electrolytes, which affects frequencies of 109 Hz or less, can reduce the attraction by up to 50% between two bilayers or a bilayer and a SiO2 substrate.46,47 For TiO2, with very different low-frequency dielectric properties from SiO2, estimation using the dielectric dispersions shows that the screening effect is negligible.
Second, electrostatic interactions were modeled as
| (2) |
using the Hogg−Healy−Fuerstenau (HHF) approach,48 where and are the surface potentials of the substrate and bilayer, respectively, and is the Debye screening length. This approximation assumes small values of the potentials but was reported to be valid for higher potentials as well.9 A comparison between results calculated from eq 2 and a numerical solution of the nonlinear Poisson−Boltzmann equation can be found in Figure S4 and demonstrates close correspondence in the regions of experimental interest. For surfaces with charges of the same sign, the HHF equation (eq 2) predicts attraction at small separations and repulsion at intermediate length scales that vanishes at a large . While DOPC bilayers are formally zwitterionic, electrophoretic liposome measurements established that their effective surface potential is slightly negative,49−51 which is likely due to water ordering at the headgroups.52 For DOPC liposomes in NaCl at pH 7.4, the surface potential is negative, with a magnitude of 6 mV or smaller at electrolyte concentrations from 10 to 90 mM.53 At a lower ionic strength, other studies report higher magnitudes and show modest changes of the DOPC surface potential with pH.52 For simplicity, we adopted a constant value, = −5 mV. This value is of the opposite sign and larger in magnitude than that expected from protonation of the PC phosphate (pKa ≈ 1; ref 54) at pH 4.
Third, the free energy of the bilayer confinement near a surface is of the form18
| (3) |
where is the bending modulus of the membrane and is an empirically determined force constant. Experiment and simulation have converged to a value of = 0.111 (refs 55 and 56); was determined from the interpolation of reported values57 to T = 22 °C.
Fourth and finally, mean-field approximations of the short-range repulsive hydration force58
| (4) |
typically put its decay length in the range of 1 Å to 2 Å. Experimental data are consistent with = 0.02 J/m2 and = 1.88 Å.21 Note that despite its short range makes a significant contribution to the overall potential at as shown in Figure 4A (see below). For separations , hydration forces have been shown to be strongly oscillatory,59 while has a weak dependence on surface charge.60 Hydration effects can also be responsible for exclusion of ions from between bilayer stacks.61 Because these effects are significant only at bilayer−substrate separations , they are not included in our calculations.
Figure 4.
Sections at constant surface potentials through the free energy landscape of a DOPC membrane on a TiO2 surface. (A) Decomposition of the overall free energy into its components as defined in eq 5. Only the electrostatic contribution depends on the ionic strength and surface charge so that the remaining terms are referred to as “invariant”; their sum has an intrinsic free energy minimum at ≈ 18 Å. Panels (B−D) show sections at = −30 mV, 0 mV, and +30 mV for increasing [NaCl]. Arrows indicate the positions of the local minima of . Insets in panels (B) and (C) show magnified views of the potentials within the boxed areas.
Summing over these contributions, we obtain the total free energy of a bilayer near its oxidic substrate:
| (5) |
Each component in eq 5 has been more rigorously explored in the literature21,31,57,62,63 than we treat them here, but such sophistication is not required for the quantitative interpretation of the experimental results we discuss below, particularly for . Visualizing its dependence on the substrate surface potential and distance from the bilayer, Figure 3 shows the generalized potential that acts on a prototypical bilayer membrane (DOPC) for three ionic strengths of the adjacent solution, with [NaCl] as indicated and, to match the experiments reported above, 10 mM Tris as the pH buffer. The Hamaker parameter chosen in the calculations for Figure 3 was that for TiO2 as the substrate, but because |A132| for SiO2 is only about 30% smaller than that for TiO2, the results are qualitatively also valid for silica-terminated substrates (Figure S5). Blue and red shadings indicate regions of negative and positive free energy, respectively, and black and white dashed lines, respectively, indicate the locations where has local minima and maxima. Thus, for a given surface potential , the bilayer is predicted to be observed at a corresponding local minimum.
Figure 3.
Interaction free energy landscapes for a DOPC membrane on TiO2 at different ionic strengths of the intervening buffer. Debye constants, , are for values of that include 10 mM Tris buffer. The color scale is linear for and logarithmic beyond; blue and red areas represent regions of negative and positive free energies, respectively. Lines of zero potential are shown in black. Black (white) dashed lines indicate trajectories of the local potential minima (maxima) as changes. Because the dependences of on pH and are vastly different for TiO2 and SiO2, the interaction energy of membranes with these substrates is located in different regions of the free energy landscape as indicated in (B). While changes in pH at constant drive of TiO2 from moderately positive at pH 4 to moderately negative at pH 11,66 remains strongly negative with little variation for SiO2.52
Figure 3 demonstrates how strongly the free energy landscape and the predicted trajectories of the local minima depend on the electrostatic parameters and (i.e., on ionic strength, I). is symmetric in at close distances to the substrate and strongly asymmetric beyond. This asymmetry at high distances is introduced by the product term in eq 2, , which is attractive for (because is negative in this calculation) and repulsive for . As expected, surface potentials stabilize the bilayer at very short distance from the substrate surface for all ionic strengths, and a strong attraction is also predicted for a membrane brought into close contact with the substrate at a large negative due to the term proportional to in eq 2. Between these extremes, membrane association with the substrate varies strongly with changes of the buffer conditions. While local potential minima are located at at all for [NaCl] = 10 mM and [NaCl] = 1 M, the contours that separate regions of attraction and repulsion, as well as the trajectories of local minima, are highly complex at physiological ionic strength ([NaCl] = 150 mM). This indicates that such intermediate ionic strengths offer the opportunity to manipulate bilayers near the oxidic interface.
Figure 4A disentangles the HHF potential from the other contributions to , which are invariant to the electrostatic parameters. The aggregate contributions of these invariant terms are represented as a solid gray line. Movie S1 shows the interplay of these terms continuously as a function of ionic strength at = −20 mV, demonstrating how the properties of the HHF potential can be exploited for experimental control of the bilayer interaction with the substrate. The invariant terms create a potential minimum at at a shallow depth of about −10 μJ/m2 or −2 × 10−3 kBT/lipid at a lipid area of 72 Å2. Figure 4B−D provide isopotential () sections through that show how the progression of minima positions upon going from positive (= 30 mV) to negative (= −30 mV) potentials is straightforward at low ([NaCl] = 10 mM) and high ([NaCl] = 1 M) ionic strengths, where the range of is mismatched with . However, at intermediate and negative , the range and magnitude of compensate the invariant terms; the isopotential sections become contorted, and the distance of the local minimum of is much larger and its depth (−1 μJ/m2 or −2 × 10−4 kBT/lipid) much shallower than those of the invariant profile.
Generalization.
The energetics of bilayer membranes adsorbed to oxidic surfaces and of bilayers assembled in multilayer stacks have been a rich field of study for decades. In particular, a recent work by Daillant and co-workers went a long way toward a quantitative characterization of the free energy of “floating bilayers” near solid surfaces.64 The results presented here take this further in two important ways. First, by performing these studies in a simple, rigorously quantifiable experimental setting, manipulation of the substrate surface charge enables control of the electrostatic free energy term in both its range and magnitude. This enables us to explore the formidable complexity of the overall free energy landscape shown in Figure 3. Second, the composite free energy function expressed in eq 5 describes this simple system in full quantitative detail without any free parameters because all characteristic constants that collectively determine are independently established from general principles or experimentally determined. We thus propose that this description of the energetics provides a generalized interaction potential for zwitterionic membranes in the vicinity of solid-state surfaces. If true, then this generality should allow us to reinterpret a bounty of experimental data on similar systems in the literature in fully quantitative terms. We show below that this is indeed the case by mapping reported experimental conditions in two prominent examples onto the substrate and bilayer surface potentials. The generality of this treatment also implies that our experimental results provide a critical test of the underlying theoretical concepts at the ångström length scale.
Central to the interpretation of our NR results for DOPC bilayers on TiO2 and SiO2 are the localizations of these systems within the free energy landscape as a function of pH and ionic strength. For [NaCl] = 150 mM, these are shown in Figure 3B. The surface potential of SiO2 is strongly negative, −50 mV > > −100 mV, over the entire pH range,52 and the bilayer is both predicted (Figure S5) and observed (Figures 1D and 2A) to be strongly ( per lipid) and tightly associated with the surface. This rationalizes why glass surfaces have been the substrates of choice for the formation of solid-supported bilayers by vesicle fusion.65 The mapping of this bilayer−substrate system to the minima in the free energy landscape clearly indicates that zwitterionic bilayers on SiO2-terminated substrates are locked in close proximity to the substrate surface at all pH and ionic strength values.
Entirely different is the situation for bilayers on TiO2. Figure 3B also shows the mapping of this system onto the predicted free energy minima at various pH values. A rough correlation between pH and substrate surface potential was obtained from experimental data on free TiO2 (anatase) particle surfaces.66 (We expect the values to be shifted to marginally more negative potential because the slightly anionic bilayer surface decreases the interfacial pH values from their nominal bulk values indicated in the plot; the surface chemistry of the amorphous sputtered film may also differ somewhat from that of crystalline anatase nanoparticles.) Because the TiO2 surface potential is near zero at pH 7, bilayers are formed under conditions represented by the right-hand region of the free energy landscape and are thus locked on the right branch of the free energy minima. For the low and high ionic strength, the free energy landscape (Figure 3A,C, respectively) limits variations of the equilibrium bilayer distance from the TiO2 substrate to values below 20 Å with modest changes expected over the entire pH range. At intermediate , however, the equilibrium distances vary widely, owing to a fine balance between the invariant components and the electrostatic attraction that depends sensitively on the ionic environment (see Figure 4A and Movie S1). This sensitivity to is maximal near −20 mV in the pH range between 8 and 10, where increases steeply upon reduction of by just a few mV (Figure 3B).
Because the uncertainty in the projection of pH values onto interferes with direct verification, we investigated the correlation between bilayer fluctuation amplitudes and the bilayer−substrate separation to establish a quantitative agreement between predictions from eq 5 and our experimental data. As shown in Figure 2B, NR is sensitive to the root-mean-square (rms) amplitudes, , of the overall corrugation of a bilayer. This corrugation has two components: the substrate surface roughness and the intrinsic membrane fluctuations . Membrane fluctuation amplitudes can be predicted from as67
| (6) |
where . For the bilayer in 150 mM NaCl, the predicted overall bilayer roughness (solid line) is overlaid on the experimental data in Figure 5. As with the data presented in Figure 3, no adjustable parameter was required to obtain quantitative agreement between prediction and observation. At small bilayer−substrate separations, the membrane is conformal to the substrate. As the bilayer drifts away from the surface when bathed in buffers of increasing pH, the fluctuation amplitudes increase rapidly; above 25 Å, approaches the Helfrich level for free bilayer undulations, and fluctuation amplitudes increase more slowly with further bilayer−substrate separation.
Figure 5.
RMS corrugation amplitudes vs distance from the substrate of a DOPC membrane on a TiO2 surface in buffers of different ionic strengths. Corrugation is defined as the apparent roughness of the fluctuating bilayer near a substrate given the substrate roughness: .Following ref 67, bilayer fluctuation amplitudes were predicted using eq 6. values were determined by NR in the measurements of the bare substrates under 2-propanol, for example, . The measurements on each substrate were performed on one sample with multiple exchanges of the buffer. Error bars and the uncertainty of denote 68% confidence intervals determined by a Markov chain Monte Carlo (MCMC) fitting algorithm41 applied to the substrate/bilayer model.33
Previous reports in the literature are consistent, and can be quantitatively interpreted, with our hypothesis that eq 5 provides a generalized free energy interaction potential for bilayers with supporting substrates. A series of publications described adsorbed DSPC (1,2-distearoyl-sn-3-glycero-PC) bilayers deposited on substrate-grafted DSPC, referred to as “floating” bilayers, and reported temperature-driven transitions between states of distinct substrate separations. Upon heating the system across the main bilayer phase transition , substrate separation of the free DSPC membrane increased vastly, from tightly bound to a few nanometers,68−70 before the bilayer unbound at still higher temperature. Variations of such experiments with DMPC (1,2-dimyristoyl-sn-3-glycero-PC) have also been described by Hughes and co-workers,71 and later work of Fragneto and co-workers showed directly that bilayer separation is controlled by the surface potential of the substrate.72 Related observations were more recently reported with zwitterionic POPC (1-palmitoyl-2-oleoyl-sn-3-glyceroPC) bilayers on carboxyl-terminated surfaces as a function of ionic strength.47 When the ionic strength of the medium was adjusted to intermediate values (200 mM), the bilayer “floated” above the carboxylated surface and the separation increased when the ionic strength was decreased.
The observations reported in both lines of work are readily accounted for by the theoretical framework developed here. A carboxylated surface carries a modestly negative surface charge,47 similar to that of titania at high pH. Figure 6 shows the application of eq 5 to this situation, adopting all parameters from Figure 3 except the Debye length, which was calculated for [NaCl] buffered with 20 mM HEPES. At the estimated = −20 mV, the potential minimum drifts away from the surface as the ionic strength is increased then approaches the surface again with further increases in I. Movie S2 shows this dynamically. The observed sequence of bilayer separations from the surface following changes in salt concentrations reported in Figure 5 of ref 47 is quantitatively described, within a few ångströms, by the generalized potential, eq 5.
Figure 6.
Interaction free energy landscapes for a POPC membrane on a carboxyl-terminated substrate. Free energies were computed from eq 5 with parameters intended to reproduce experimental data reported in Figure 5 of ref 47. Lines of zero potential are shown in black. Black (white) dashed lines represent trajectories of the local free energy minima (maxima). The substrate’s surface potential was estimated to be −20 mV (vertical dotted line). Yellow points represent the positions of the lowest free energy. (A) At low , the bilayer is predicted to be stably bound to the substrate at a distance of . (B) As [NaCl] is increased to 100 mM, the bilayer is pushed out to . (C) Further increase in [NaCl] to 200 mM moves the bilayer to . See also a related animation in Movie S2.
Similarly, a fully quantitative description of the behavior of a DSPC bilayer on substrate-grafted DSPC68,69 is accounted for by invoking electrostatic effects. A decrease in the bending modulus by about an order of magnitude across the phase transition69 is largely responsible for destabilizing the bilayer on the substrate, as observed in Figure S6A where we determined the interaction free energy by neglecting electrostatic interactions (, no salt). Under these conditions, eq 5 predicts that the bilayer will be stably associated with the substrate at high values of and steeply gain distance from the substrate when falls below 10−19 J upon chain melting. However, it should remain loosely associated with the substrate at least up to distances around = 60 Å. A better description of the experimental outcome is obtained by accounting for the fact that the bilayer surfaces are indeed slightly anionic (Figure S6B). While the general behavior is qualitatively similar as in panel (A), the bilayer is now predicted to unbind at a significantly lower distance, , as experimentally observed.67 To account for the ion-free medium, the nonlinear Poisson−Boltzmann equation was used in the absence of anions for these calculations.68,70,73 Chain melting in the “floating” bilayer is also associated with an increase in the anionic charge density of the bilayer surface,50 which further promotes the detachment.
The underlying mechanism in all three cases discussed here is the same: when the range and magnitude of the electrostatic interaction disrupt the delicate balance with the other contributions to the adsorption free energy (≈ 2 × 10−4 kBT/lipid), large effects on the position of the potential minimum and the observed interfacial structure are observed. As a result, the range of conditions that control the bilayer separation from its substrate is rather narrow, and exerting control over the interfacial structure in applications thus requires each component of the system to be carefully controlled. The substrate surface charge is the most critical element. As demonstrated for silica and titania, their distinct surface chemistries presented to the aqueous medium can be exploited to control bilayer association. Strong adhesion, as observed on silica, is advantageous for spontaneous vesicle fusion74 but cannot be sufficiently weakened to support bilayers in a disjoined configuration. Conversely, bilayers that interact weakly with surfaces such as titania do not spontaneously form by vesicle fusion36,75 but can be formed using the solvent exchange techniques adopted here.
Figure 3B shows the coexistence of multiple free energy minima at different bilayer−substrate separations for certain substrate and bilayer potentials. As a result, the observed membrane−substrate separation may depend not only on the buffer conditions but also on the method of bilayer preparation and sample history. Movie S3 shows that multiple free energy minima can also be quite close in spacing and total free energy , particularly at small , suggesting the possibility that the coexistence of phases with distinct membrane−membrane or membrane−substrate distances could be experimentally realized. In multilamellar systems, a similar behavior has been induced by association of various ion and buffer species with bilayer surfaces.76−78 Such states of phase coexistence are often observed in multi-component bilayer systems and have also been induced by pH and ionic strength tuning in POPC bilayer stacks in contact with simple buffers.79
The results and analyses presented here establish that even a minimal set of bilayer/substrate interactions can be responsible for complex behaviors. Conversely, this minimal set provides the backdrop for exquisitely sensitive surface property measurement. For example, the extremely shallow free energy minima that we showed to be experimentally accessible on TiO2 surfaces allow exploration of small alterations to surface properties based on solution chemistry. This is shown in Figure S7, in which we used 5 mM HEPES as a buffer instead of 10 mM Tris for a complementary set of measurements to those presented in Figure 2. This supplemental experiment shows the same progression of with pH for the two buffer conditions. With HEPES buffer, the pH response is offset by approximately 2 units; this is naturally attributed to a shift in surface potential of a few mV due to differences in buffer adsorption. These observations also highlight an important limitation of the techniques developed here: changes in bilayer stiffness and surface charge, e.g., from adsorption of ions or macromolecules, not only will both affect the measured bilayer−substrate distance but will also be strongly coupled. Further study by complementary experimental and computational techniques will be essential to disentangling these effects.
CONCLUSIONS
We presented a practical and theoretical framework for tuning experimental parameters of the substrate, lipid bilayer composition, and aqueous medium to control the morphology of the supported bilayer systems. We showed that the SLB solvent exchange method is suitable to form bilayers on weakly interacting substrates when the preparation conditions provide sufficient association of lipid headgroups with the substrate in a hydrophobic solvent to form a monolayer template for bilayer formation. Once formed, bilayers can be driven away from the substrate surface and their separation tuned with ångström precision. For large separations from the substrate surface, the tuning of the bilayer−substrate distance can be quantitatively accounted for entirely by the electrostatic component of the overall free energy. The complexity of the electrostatic free energy profile gives rise to a rich landscape of predicted phenomena, including multiple free energy minima for identical substrate and bilayer potentials. We expect that exploration of this complex phase behavior will yield important insights into the role of the basic forces governing membrane−substrate interactions and may lead to the discovery of new effects and possibilities in the coupling of biological systems to semiconductor devices.
Supplementary Material
ACKNOWLEDGMENTS
Helpful discussions with Drs. Elizabeth Kelley, Markus Deserno, and John F. Nagle; technical advice by Dr. Nam-Joon Cho; as well as technical assistance by Drs. Eric Rus, Joseph Dura, Katie Weigandt, and Steven Hudson are gratefully acknowledged. We thank Matthew Robinson and Peter Litwinowicz at the NIST Center for Nanoscale Science and Technology for the substrate preparation and the NIST Center for Neutron Research for the beam time. This project was funded in part by the U.S. Department of Commerce (MSE award no. 70NANB17H299 to M.L.) and used the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation grant number ACI-1548562. Access to the XSEDE Bridges system at the Pittsburgh Supercomputing Center was provided through allocations TG-MCB160127 to D.P.H. and TGMCB190007 to M.L. Certain commercial materials, equipment, and instruments are identified in this work to describe the experimental procedure as completely as possible. In no case does such an identification imply a recommendation or endorsement by NIST nor does it imply that the materials, equipment, or instrument identified are necessarily the best available for the purpose.
Footnotes
ASSOCIATED CONTENT
Supporting Information
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.langmuir.1c00214.
Raw data and derived neutron scattering length density profiles that resulted in the data shown in Figures 1 and 2, an evaluation of the differences in free energy based on linearized and non-linear solutions of the Poisson−Boltzmann equation, a rigorous calculation of the free energy landscape of a DOPC membrane on a SiO2-terminated substrate, a semi-quantitative account of the behavior of a DSPC membrane on a surface-grafted PC bilayer in water to account for experimental results published in references 66 and 67, an estimate of the differences in the behavior of a DOPC membrane on TiO2 in Tris and HEPES buffer, and a table of model fit parameters exemplary for a DOPC bilayer on TiO2 at pH 7 and [NaCl] = 150 mM (PDF)
Changes of membrane free energy on TiO2 as a function of ionic strength (MP4)
POPC bilayer on a carboxylated substrate as a function of ion concentration in the buffer in reference to ref 47 (MP4)
Membrane on TiO2 as a function of bilayer surface potential, (MP4)
Complete contact information is available at: https://pubs.acs.org/10.1021/acs.langmuir.1c00214
The authors declare no competing financial interest.
Contributor Information
Dennis J. Michalak, Department of Physics, Carnegie Mellon University, Pittsburgh, Pennsylvania 15213, United States
Mathias Lösche, Department of Physics and Department of Biomedical Engineering, Carnegie Mellon University, Pittsburgh, Pennsylvania 15213, United States; Center for Neutron Research, National Institute of Standards and Technology, Gaithersburg, Maryland 20899, United States.
David P. Hoogerheide, Center for Neutron Research, National Institute of Standards and Technology, Gaithersburg, Maryland 20899, United States
REFERENCES
- (1).Youngblood WJ; Lee S-HA; Maeda K; Mallouk TE. Visible light water splitting using dye-sensitized oxide semiconductors. Acc. Chem. Res. 2009, 42, 1966–1973. [DOI] [PubMed] [Google Scholar]
- (2).Cornell BA; Braach-Maksvytis VLB; King LB; Osman PDJ; Raguse B; Wieczorek L; Pace RJ. A biosensor that uses ion-channel switches. Nature 1997, 387, 580–583. [DOI] [PubMed] [Google Scholar]
- (3).Loidl-Stahlhofen A; Kaufmann S; Braunschweig T; Bayerl TM. The thermodynamic control of protein binding to lipid bilayers for protein chromatography. Nat. Biotechnol. 1996, 14, 999–1002. [DOI] [PubMed] [Google Scholar]
- (4).Loidl-Stahlhofen A; Schmitt J; Nöller J; Hartmann T; Brodowsky H; Schmitt W; Keldenich J. Solid-supported biomolecules on modified silica surfaces − A tool for fast physicochemical characterization and high-throughput screening. Adv. Mater. 2001, 13, 1829–1834. [Google Scholar]
- (5).Groves JT; Boxer SG; McConnell HM. Electric field-induced reorganization of two-component supported bilayer membranes. Proc. Natl. Acad. Sci. 1997, 94, 13390–13395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (6).Nagle JF; Tristram-Nagle S. Structure of lipid bilayers. Biochim. Biophys. Acta 2000, 1469, 159–195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (7).Tanaka M; Sackmann E. Polymer-supported membranes as models of the cell surface. Nature 2005, 437, 656–663. [DOI] [PubMed] [Google Scholar]
- (8).Clifton LA; Holt SA; Hughes AV; Daulton EL; Arunmanee W; Heinrich F; Khalid S; Jefferies D; Charlton TR; Webster JRP; Kinane CJ; Lakey JH. An accurate in vitro model of the E. coli envelope. Angew. Chem., Int. Ed. 2015, 54, 11952–11955. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (9).Anderson TH; Min Y; Weirich KL; Zeng H; Fygenson D; Israelachvili JN. Formation of supported bilayers on silica substrates. Langmuir 2009, 25, 6997–7005. [DOI] [PubMed] [Google Scholar]
- (10).Atanasov V; Knorr N; Duran RS; Ingebrandt S; Offenhäusser A; Knoll W; Köper I. Membrane on a chip: A functional tethered lipid bilayer membrane on silicon oxide surfaces. Biophys. J. 2005, 89, 1780–1788. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (11).Müller J; Ballini M; Livi P; Chen Y; Radivojevic M; Shadmani A; Viswam V; Jones IL; Fiscella M; Diggelmann R; Stettler A; Frey U; Bakkum DJ; Hierlemann A. High-resolution CMOS MEA platform to study neurons at subcellular, cellular, and network levels. Lab Chip 2015, 15, 2767–2780. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (12).Park JS; Grijalva SI; Aziz MK; Chi T; Li S; Sayegh MN; Wang A; Cho HC; Wang H. Multi-parametric cell profiling with a CMOS quad-modality cellular interfacing array for label-free fully automated drug screening. Lab Chip 2018, 18, 3037–3050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (13).Fromherz P. Electrical interfacing of nerve cells and semiconductor chips. ChemPhysChem 2002, 3, 276–284. [DOI] [PubMed] [Google Scholar]
- (14).Eickenscheidt M; Jenkner M; Thewes R; Fromherz P; Zeck G. Electrical stimulation of retinal neurons in epiretinal and subretinal configuration using a multicapacitor array. J. Neurophysiol. 2012, 107, 2742–2755. [DOI] [PubMed] [Google Scholar]
- (15).Xie J; Lee S; Chen X. Nanoparticle-based theranostic agents. Adv. Drug Delivery Rev. 2010, 62, 1064–1079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (16).Choi S; Lee H; Ghaffari R; Hyeon T; Kim D-H. Recent advances in flexible and stretchable bio-electronic devices integrated with nanomaterials. Adv. Mater. 2016, 28, 4203–4218. [DOI] [PubMed] [Google Scholar]
- (17).Schrader AM; Monroe JI; Sheil R; Dobbs HA; Keller TJ; Li Y; Jain S; Shell MS; Israelachvili JN; Han S. Surface chemical heterogeneity modulates silica surface hydration. Proc. Natl. Acad. Sci. 2018, 115, 2890–2895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (18).Helfrich W. Steric interaction of fluid membranes in multilayer systems. Z. Naturforsch. 1978, 33, 305–315. [Google Scholar]
- (19).Evans EA; Parsegian VA. Thermal-mechanical fluctuations enhance repulsion between bimolecular layers. Proc. Natl. Acad. Sci. 1986, 83, 7132–7136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (20).Wennerström H; Olsson U. The undulation force; theoretical results versus experimental demonstrations. Adv. Colloid Interface Sci. 2014, 208, 10–13. [DOI] [PubMed] [Google Scholar]
- (21).Mennicke U; Constantin D; Salditt T. Structure and interaction potentials in solid-supported lipid membranes studied by X-ray reflectivity at varied osmotic pressure. Eur. Phys. J. E 2006, 20, 221–230. [DOI] [PubMed] [Google Scholar]
- (22).Lipowsky R; Leibler S. Unbinding transitions of interacting membranes. Phys. Rev. Lett. 1986, 56, 2541–2544. [DOI] [PubMed] [Google Scholar]
- (23).Spratte K; Chi LF; Riegler H. Physisorption instabilities during dynamic Langmuir wetting. Europhys. Lett. 1994, 25, 211–217. [Google Scholar]
- (24).Li L; Köpf MH; Gurevich SV; Friedrich R; Chi L. Structure formation by dynamic self-assembly. Small 2012, 8, 488–503. [DOI] [PubMed] [Google Scholar]
- (25).Goksu EI; Vanegas JM; Blanchette CD; Lin W-C; Longo ML. AFM for structure and dynamics of biomembranes. Biochim. Biophys. Acta 2009, 1788, 254–266. [DOI] [PubMed] [Google Scholar]
- (26).Israelachvili JN. Intermolecular and Surface Forces; 2nd Ed.; Academic Press: San Diego, 1992. [Google Scholar]
- (27).Parsegian VA. Van der Waals Forces − A Handbook for Biologists, Chemists, Engineers, and Physicists; Cambridge University Press: Cambridge (U.K.), 2006. [Google Scholar]
- (28).Hohner AO; David MPC; Rädler JO. Controlled solvent-exchange deposition of phospholipid membranes onto solid surfaces. Biointerphases 2010, 5, 1–8. [DOI] [PubMed] [Google Scholar]
- (29).Ferhan AR; Yoon BK; Park S; Sut TN; Chin H; Park JH; Jackman JA; Cho N-J. Solvent-assisted preparation of supported lipid bilayers. Nat. Protoc. 2019, 14, 2091–2118. [DOI] [PubMed] [Google Scholar]
- (30).Rand RP; Parsegian VA. Hydration forces between phospholipid bilayers. Biochim. Biophys. Acta 1989, 988, 351–376. [Google Scholar]
- (31).Israelachvili JN; Wennerstroem H. Entropic forces between amphiphilic surfaces in liquids. J. Phys. Chem. 1992, 96, 520–531. [Google Scholar]
- (32).Heinrich F; Lösche M. Zooming in on disordered systems: Neutron reflection studies of proteins associated with fluid membranes. Biochim. Biophys. Acta 2014, 1838, 2341–2349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (33).Shekhar P; Nanda H; Lösche M; Heinrich F. Continuous distribution model for the investigation of complex molecular architectures near interfaces with scattering techniques. J. Appl. Phys. 2011, 110, 102216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (34).Treece BW; Kienzle PA; Hoogerheide DP; Majkrzak CF; Lösche M; Heinrich F. Optimization of reflectometry experiments using information theory. J. Appl. Crystallogr. 2019, 52, 47–59. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (35).Wiener MC; White SH. Fluid bilayer structure determination by the combined use of x-ray and neutron diffraction. II. ″Composition-space″ refinement method. Biophys. J. 1991, 59, 174–185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (36).Tabaei SR; Choi J-H; Haw Zan G; Zhdanov VP; Cho N-J. Solvent-assisted lipid bilayer formation on silicon dioxide and gold. Langmuir 2014, 30, 10363–10373. [DOI] [PubMed] [Google Scholar]
- (37).Dura JA; Pierce DJ; Majkrzak CF; Maliszewskyj N; McGillivray DJ; Lösche M; O’Donovan KV; Mihailescu M; Perez-Salas U; Worcester DL; White SH. AND/R: Advanced neutron diffractometer/reflectometer for investigation of thin films and multilayers for the life sciences. Rev. Sci. Instrum. 2006, 77, No. 074301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (38).Eells R; Hoogerheide DP; Kienzle PA; Lösche M; Majkrzak CF; Heinrich F. Structural investigations of membrane-associated proteins by neutron reflectometry. In Characterization of Biological Membranes: Structure and Dynamics; Nieh M-P; Heberle FA; Katsaras J, Eds.; De Gruyter: Berlin, 2019; pp. 87–130. [Google Scholar]
- (39).Towns J; Cockerill T; Dahan M; Foster I; Gaither K; Grimshaw A; Hazlewood V; Lathrop S; Lifka D; Peterson GD; Roskies R; Scott JR; Wilkins-Diehr N. XSEDE: Accelerating Scientific Discovery. Comput. Sci. Eng. 2014, 16, 62–74. [Google Scholar]
- (40).Vrugt JA; ter Braak CJF; Diks CGH; Robinson BA; Hyman JM; Higdon D. Accelerating Markov Chain Monte Carlo Simulation by Differential Evolution with Self-Adaptive Randomized Subspace Sampling. Int. J. Nonlinear Sci. Numer. Simul. 2009, 10, 273–290. [Google Scholar]
- (41).Kirby BJ; Kienzle PA; Maranville BB; Berk NF; Krycka J; Heinrich F; Majkrzak CF. Phase-sensitive specular neutron reflectometry for imaging the nanometer scale composition depth profile of thin-film materials. Curr. Opin. Colloid Interface Sci. 2012, 17, 44–53. [Google Scholar]
- (42).McGillivray DJ; Valincius G; Vanderah DJ; Febo-Ayala W; Woodward JT; Heinrich F; Kasianowicz JJ; Lösche M. Molecular-scale structural and functional characterization of sparsely tethered bilayer lipid membranes. Biointerphases 2007, 2, 21–33. [DOI] [PubMed] [Google Scholar]
- (43).Wacklin HP. Neutron reflection from supported lipid membranes. Curr. Opin. Colloid Interface Sci. 2010, 15, 445–454. [Google Scholar]
- (44).Kučerka N; Tristram-Nagle S; Nagle JF. Structure of fully hydrated fluid phase lipid bilayers with monounsaturated chains. J. Membr. Biol. 2005, 208, 193–202. [DOI] [PubMed] [Google Scholar]
- (45).Bergström L. Hamaker constants of inorganic materials. Adv. Colloid Interface Sci. 1997, 70, 125–169. [Google Scholar]
- (46).Petrache HI; Tristram-Nagle S; Harries D; Kučerka N; Nagle JF; Parsegian VA. Swelling of phospholipids by monovalent salt. J. Lipid Res. 2006, 47, 302–309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (47).Clifton LA; Paracini N; Hughes AV; Lakey JH; Steinke N-J; Cooper JFK; Gavutis M; Skoda MWA. Self-assembled fluid phase floating membranes with tunable water interlayers. Langmuir 2019, 35, 13735–13744. [DOI] [PubMed] [Google Scholar]
- (48).Hogg R; Healy TW; Fuerstenau DW. Mutual coagulation of colloidal dispersions. Trans. Faraday Soc. 1966, 62, 1638–1651. [Google Scholar]
- (49).Chibowski E; Szcześ A. Zeta potential and surface charge of DPPC and DOPC liposomes in the presence of PLC enzyme. Adsorption 2016, 22, 755–765. [Google Scholar]
- (50).Morini MA; Sierra MB; Pedroni VI; Alarcon LM; Appignanesi GA; Disalvo EA. Influence of temperature, anions and size distribution on the zeta potential of DMPC, DPPC and DMPE lipid vesicles. Colloids Surf., B 2015, 131, 54–58. [DOI] [PubMed] [Google Scholar]
- (51).Smith MC; Crist RM; Clogston JD; McNeil SE. Zeta potential: a case study of cationic, anionic, and neutral liposomes. Anal. Bioanal. Chem. 2017, 409, 5779–5787. [DOI] [PubMed] [Google Scholar]
- (52).Zimmermann R; Küttner D; Renner L; Kaufmann M; Zitzmann J; Müller M; Werner C. Charging and structure of zwitterionic supported bilayer lipid membranes studied by streaming current measurements, fluorescence microscopy, and attenuated total reflection Fourier transform infrared spectroscopy. Biointerphases 2009, 4, 1–6. [DOI] [PubMed] [Google Scholar]
- (53).Maity P; Saha B; Kumar GS; Karmakar S. Binding of monovalent alkali metal ions with negatively charged phospholipid membranes. Biochim. Biophys. Acta 2016, 1858, 706–714. [DOI] [PubMed] [Google Scholar]
- (54).Marsh D. CRC Handbook of Lipid Bilayers; CRC Press: Boca Raton, LA, 1990. [Google Scholar]
- (55).Gouliaev N; Nagle JF. Simulations of interacting membranes in the soft confinement regime. Phys. Rev. Lett. 1998, 81, 2610–2613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (56).Gordeliy VI; Cherezov V; Teixeira J. Strength of thermal undulations of phospholipid membranes. Phys. Rev. E 2005, 72, No. 061913. [DOI] [PubMed] [Google Scholar]
- (57).Pan J; Tristram-Nagle S; Kučerka, N.; Nagle, J. F. Temperature dependence of structure, bending rigidity, and bilayer interactions of dioleoylphosphatidylcholine bilayers. Biophys. J. 2008, 94, 117–124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (58).Parsegian VA; Fuller N; Rand RP. Measured work of deformation and repulsion of lecithin bilayers. Proc. Natl. Acad. Sci. 1979, 76, 2750–2754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (59).Israelachvili JN; Pashley RM. Molecular layering of water at surfaces and origin of repulsive hydration forces. Nature 1983, 306, 249–250. [Google Scholar]
- (60).Sasaki S; Maeda H. Electrostatic effect on the hydration layer of colloidal silica particles. J. Colloid Interface Sci. 1994, 167, 146–149. [Google Scholar]
- (61).Petrache HI; Kimchi I; Harries D; Parsegian VA. Measured depletion of ions at the biomembrane interface. J. Am. Chem. Soc. 2005, 127, 11546–11547. [DOI] [PubMed] [Google Scholar]
- (62).Petrache HI; Zemb T; Belloni L; Parsegian VA. Salt screening and specific ion adsorption determine neutral-lipid membrane interactions. Proc. Natl. Acad. Sci. 2006, 103, 7982–7987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (63).Tristram-Nagle S; Nagle JF. Lipid bilayers: thermodynamics, structure, fluctuations, and interactions. Chem. Phys. Lipids 2004, 127, 3–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (64).Hemmerle A; Malaquin L; Charitat T; Lecuyer S; Fragneto G; Daillant J. Controlling interactions in supported bilayers from weak electrostatic repulsion to high osmotic pressure. Proc. Natl. Acad. Sci. 2012, 109, 19938–19942. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (65).Castellana ET; Cremer PS. Solid supported lipid bilayers: From biophysical studies to sensor design. Surf. Sci. Rep. 2006, 61, 429–444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (66).Gustafsson J; Mikkola P; Jokinen M; Rosenholm JB. The influence of pH and NaCl on the zeta potential and rheology of anatase dispersions. Colloids Surf., A 2000, 175, 349–359. [Google Scholar]
- (67).Mecke KR; Charitat T; Graner F. Fluctuating lipid bilayer in an arbitrary potential: Theory and experimental determination of bending rigidity. Langmuir 2003, 19, 2080–2087. [Google Scholar]
- (68).Fragneto G; Charitat T; Graner F; Mecke K; Perino-Gallice L; Bellet-Amalric E. A fluid floating bilayer. Europhys. Lett. 2001, 53, 100–106. [Google Scholar]
- (69).Daillant J; Bellet-Amalric E; Braslau A; Charitat T; Fragneto G; Graner F; Mora S; Rieutord F; Stidder B. Structure and fluctuations of a single floating lipid bilayer. Proc. Natl. Acad. Sci. 2005, 102, 11639–11644. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (70).Charitat T; Lecuyer S; Fragneto G. Fluctuations and destabilization of single phospholipid bilayers. Biointerphases 2008, 3, FB3–FB15. [DOI] [PubMed] [Google Scholar]
- (71).Hughes AV; Roser SJ; Gerstenberg M; Goldar A; Stidder B; Feidenhans’l R; Bradshaw J. Phase behavior of DMPC free supported bilayers studied by neutron reflectivity. Langmuir 2002, 18, 8161–8171. [Google Scholar]
- (72).Lecuyer S; Fragneto G; Charitat T. Effect of an electric field on a floating lipid bilayer: A neutron reflectivity study. Eur. Phys. J. E 2006, 21, 153–159. [DOI] [PubMed] [Google Scholar]
- (73).Charitat T; Bellet-Amalric E; Fragneto G; Graner F. Adsorbed and free lipid bilayers at the solid-liquid interface. Eur. Phys. J. B 1999, 8, 583–593. [Google Scholar]
- (74).Reimhult E; Zäch M; Höök F; Kasemo B. A multitechnique study of liposome adsorption on Au and lipid bilayer formation on SiO2. Langmuir 2006, 22, 3313–3319. [DOI] [PubMed] [Google Scholar]
- (75).Reviakine I; Rossetti FF; Morozov AN; Textor M. Investigating the properties of supported vesicular layers on titanium dioxide by quartz crystal microbalance with dissipation measurements. J. Chem. Phys. 2005, 122, 204711. [DOI] [PubMed] [Google Scholar]
- (76).Rappolt M; Pabst G; Amenitsch H; Laggner P. Salt-induced phase separation in the liquid crystalline phase of phosphatidylcholines. Colloids Surf., A 2001, 183–185, 171−181. [Google Scholar]
- (77).Pabst G; Hodzic A; Štrancar J; Danner S; Rappolt M; Laggner P. Rigidification of neutral lipid bilayers in the presence of salts. Biophys. J. 2007, 93, 2688–2696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (78).Yamada NL; Hishida M; Seto H; Tsumoto K; Yoshimura T. Unbinding of lipid bilayers induced by osmotic pressure in relation to unilamellar vesicle formation. Eur. Phys. Lett. 2007, 80, 48002. [Google Scholar]
- (79).Johnson MA; Seifert S; Petrache HI; Kimble-Hill AC. Phase Coexistence in Single-Lipid Membranes Induced by Buffering Agents. Langmuir 2014, 30, 9880–9885. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.