Significance
Contingency tables are pervasive across quantitative research and data-science applications. Existing statistical tests fall short, however; none provide robust, computationally efficient inference and control type I error. In this work, motivated by a recent advance in reference-free genomic inference, we propose a family of tests on contingency tables called Optimized Adaptive Statistic for Inferring Structure (OASIS). OASIS utilizes a linear test-statistic, enabling the computation of closed form P-value bounds, exact asymptotic ones, and interpretable rejection of the null. In genomic applications, OASIS performs reference-free and metadata-free variant detection in SARS-CoV-2 and Mycobacterium tuberculosis and is robust to noise in single-cell RNA sequencing, all tasks without existing solutions.
Keywords: computational genomics, reference genome free inference, contingency table, finite-sample P-value
Abstract
Contingency tables, data represented as counts matrices, are ubiquitous across quantitative research and data-science applications. Existing statistical tests are insufficient however, as none are simultaneously computationally efficient and statistically valid for a finite number of observations. In this work, motivated by a recent application in reference-free genomic inference [K. Chaung et al., Cell 186, 5440–5456 (2023)], we develop Optimized Adaptive Statistic for Inferring Structure (OASIS), a family of statistical tests for contingency tables. OASIS constructs a test statistic which is linear in the normalized data matrix, providing closed-form P-value bounds through classical concentration inequalities. In the process, OASIS provides a decomposition of the table, lending interpretability to its rejection of the null. We derive the asymptotic distribution of the OASIS test statistic, showing that these finite-sample bounds correctly characterize the test statistic’s P-value up to a variance term. Experiments on genomic sequencing data highlight the power and interpretability of OASIS. Using OASIS, we develop a method that can detect SARS-CoV-2 and Mycobacterium tuberculosis strains de novo, which existing approaches cannot achieve. We demonstrate in simulations that OASIS is robust to overdispersion, a common feature in genomic data like single-cell RNA sequencing, where under accepted noise models OASIS provides good control of the false discovery rate, while Pearson’s consistently rejects the null. Additionally, we show in simulations that OASIS is more powerful than Pearson’s in certain regimes, including for some important two group alternatives, which we corroborate with approximate power calculations.
Discrete data on contingency tables are ubiquitous in data science and are central in the social sciences and quantitative research disciplines, including biology. In modern applications, these tables are frequently large and sparse, leading to a continued interest in new statistical tests for contingency tables (1). One recent motivating application is SPLASH (2), a method for genomic inference which maps myriad problems in genomic sequence analysis to the study of contingency tables. These disparate applications include detecting phylogenetically distinct strains or alternative splicing in single-cell RNA sequencing, among others.
There is a rich literature that addresses testing for row and column independence in contingency tables beginning with the work of Pearson, who designed the widely used test in the early 1900s (3, 4). Other approaches include the likelihood ratio test, permutation, or Markov chain Monte Carlo (MCMC) methods (5), limited-information methods (6), and modeling parametric deviations from the null with log–linear models (4).
Despite the prominence of Pearson’s test, it suffers from multiple statistical drawbacks which limit its utility for scientific inference. First, the test lacks robustness: it has high power against many scientifically uninteresting alternatives, for example against models where technical or biological noise causes a table to formally deviate from the specified null. We expand on this point in Section 6.1 and provide simulation evidence for noise stemming from biological overdispersion and contamination.
Second, the test does not provide statistically valid P-values for any finite number of observations. There is substantial work on estimating significance thresholds, primarily centered on an asymptotic theory that assumes a fixed table size with the number of observations tending to infinity. For example, common guidelines (4) indicate that the distribution is a bad approximation when more than 20% of the entries take a value less than 5. However, in modern tables of interest, this is often the case; the biological tables which motivated this test’s design have many rows (tens or hundreds) relative to the total number of observations per column (similarly in the tens or hundreds), violating use guidelines (2).
Other methods such as log–linear models suffer from similar limitations: namely, lack of robustness and of calibration for finite observations (4). Limited-information tests (6), developed for multidimensional contingency tables modeling user responses to questions each with options (i.e., possible rows), consider quadratic forms of univariate or bivariate residuals. Specializing to , a standard contingency table, this method can be seen as working to denoise by ignoring higher-order dependencies. While this method has good empirical performance in sparse multidimensional settings, it is conceptually and statistically distinct from OASIS and is critically only able to provide asymptotic P-values, relying on the same distributional assumptions as . MCMC-based methods have also been developed, which provide statistically valid P-values, but despite significant recent works, the sampling required renders them too computationally intensive for large tables in practice (1, 5). Additionally, for resampling-based tests, samples from the null can at best yield a P-value of 1/(B + 1). Thus, many samples are required to obtain sufficiently small P-values to reject the null, especially under the burden of multiple hypothesis correction. Finally, MCMC-based methods suffer from the same robustness issues as . To our knowledge, no nontrivial P-values exist for contingency tables that are computable in closed form and are valid for a finite number of observations.
In this work, we introduce OASIS, a powerful and general family of interpretable tests, motivated by and building on earlier work in genomic inference (2). OASIS provides P-value bounds that 1) are valid for a finite number of observations, 2) have a closed-form expression, 3) are empirically robust to small deviations from the null, and 4) in practice enable scientific inference that cannot be achieved with .
To build intuition for a task we seek OASIS to perform, consider the following setting generated by SPLASH (2) (discussed further in Section 6). A total of 103 patients are infected with potentially different variants of SARS-CoV-2 (7). For each, a black box produces counts of the nucleotide composition of a segment of the SARS-CoV-2 variant’s genome, which can be considered a categorical variable. Under the null hypothesis, each patient is infected with the same variant of the virus, and so all columns in the table will be drawn from the same distribution over rows. If a new strain has infected a group of patients, then the row distribution for these patients will be different. The desired test should detect this deviation and provide post-inferential guidance on why the table was rejected, ideally discriminating populations of patients on the basis of which strains infected them.
To understand why an alternative test is needed, we consider Pearson’s in more detail. The test statistic sums squared residuals after normalization (Fig. 1B and Eq. 3). The resulting sum is asymptotically distributed under the null, but can significantly deviate from this for a finite number of observations. When it rejects the null, Pearson’s test provides no framework for interpreting why, leading practitioners to develop and use exploratory data-analysis tools such as correspondence analysis (8–11).
Fig. 1.
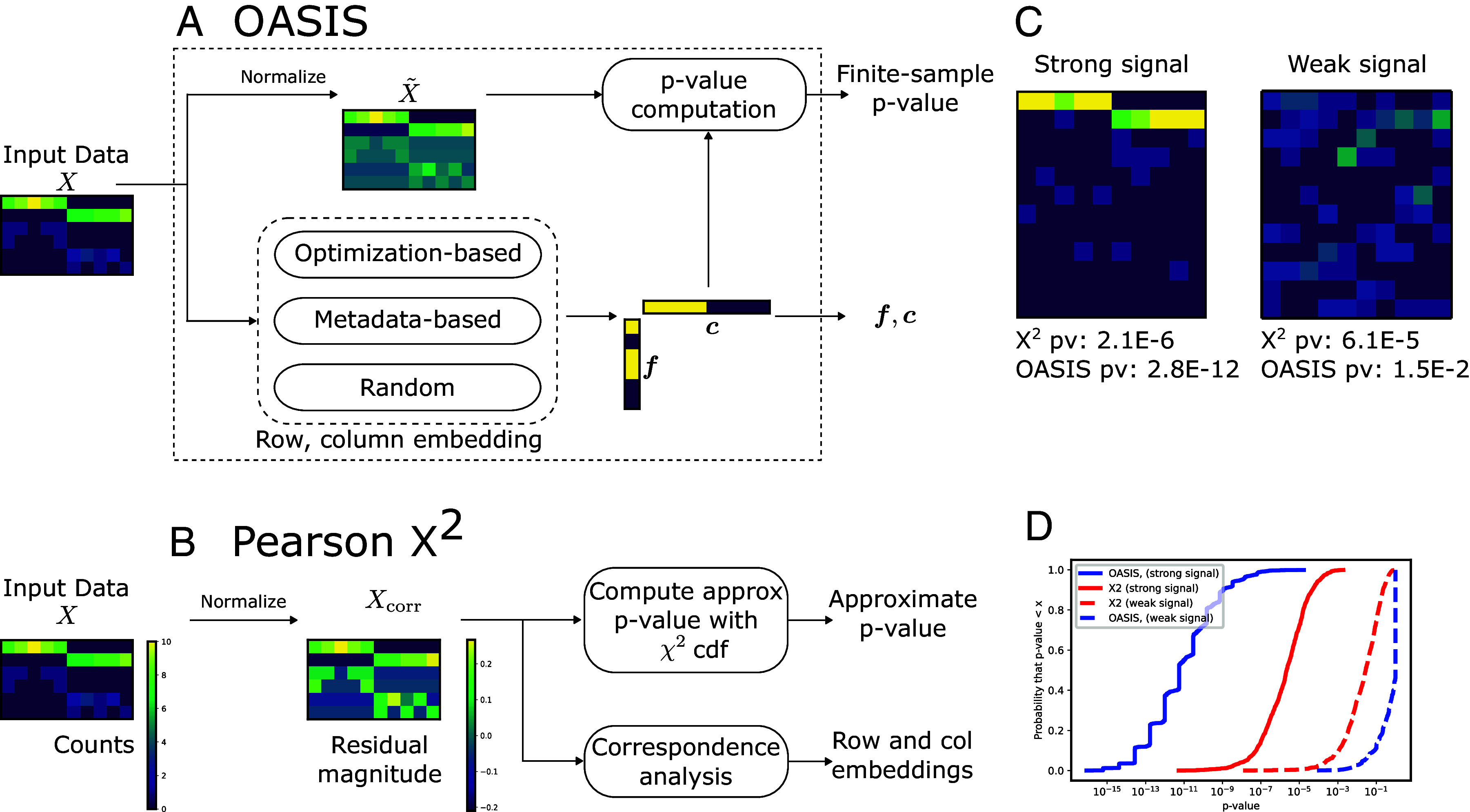
Comparison of OASIS and Pearson’s test for input matrix . (A) OASIS computes a matrix of residuals as in Eq. 2. Row (column) embeddings () are generated by one of several options. These vectors are used to compute the OASIS test statistic in Eq. 1, which admits a finite-sample P-value bound using classical concentration inequalities. (B) computes a matrix of residuals as in Eq. 4, which is sensitive to deviations in low count rows, as seen in the Bottom four rows in the example matrix and . The test then provides an asymptotically valid P-value via a distributional approximation. For interpretability, practitioners often use correspondence analysis (4) to interpret rejection of the null, a procedure with no statistical guarantees, which can fail to detect the desired structure. (C) depicts two example counts tables. The one on the left corresponds to concentrated (strong) signal, while the one on the right corresponds to diffuse (weak) signal. Both tables have 100 counts distributed evenly over 10 columns, with 12 rows. assigns both of them similar significance, but OASIS assigns a much smaller P-value to the Left table than the Right, agreeing with our intuition. (D) plots the empirical CDF of the P-values of OASIS and Pearson’s . This is shown for the two classes of tables; ones with a strong concentrated two-group signal, and ones with a diffuse signal. OASIS yields significantly improved P-values for the case with strong signal, and substantially worse power than in the weak signal case, which visually looks like noise. on the other hand yields much more similar performance in the two settings. Here, OASIS-opt is shown, which is run over five independent splits of the dataset. The generative model for these tables is detailed in SI Appendix, section S.6.A, with additional plots showing e.g., the spectra of the centered and normalized contingency tables in (C), illustrating that OASIS prioritizes the first table with a more concentrated spectrum.
OASIS seeks to improve these shortcomings by building in interpretability and analytic tractability in its construction of a linear test statistic (Fig. 1A and Eq. 2). This construction enables the use of classical concentration inequalities to yield P-value bounds that are valid for finite numbers of observations. As opposed to which sums squared residuals, OASIS computes a bilinear form of residuals, similar in spirit but methodologically distinct from a Lancaster decomposition of (12) and related polynomial decomposition methods (13). Residuals lacking structure are thus averaged out and are unlikely to generate a large test statistic. We make this observation precise via linear algebraic characterizations of these approaches. The most similar method to OASIS regarding interpretable decompositions of contingency tables is correspondence analysis, (8–11), an exploratory method for post facto interpretation with no statistical guarantees.
One recent work which shares some similarities with ours provides a method for estimating graph dimension with cross-validated eigenvalues (14). Their method, like ours, is based on splitting the data into two portions, generating embeddings on one part, and testing the signal strength on the held-out portion. While general, this method requires additional assumptions on the embeddings used for inference and critically is only able to provide asymptotically valid P-values. In this work, with our more analytically tractable test statistic, we construct a closed-form P-value bound which is valid for any number of observations.
In the rest of this paper, we formalize OASIS, state several of its theoretical properties, contrast it with , and present several variants and extensions of the OASIS test. We do not seek to expound on the full theoretical generality of OASIS, but instead provide an applied exposition and disciplined framework for computing some optimization-based instantiations of the statistic, illustrating the performance of OASIS in simulations and in real biological data. Simulations show that OASIS is a robust test with low statistical power against a variety of alternatives where the null is formally violated, but without a biological or scientific meaning. Simulated alternatives show that OASIS has power in many settings of interest, and in fact has more power than in a variety of settings including for some important two group alternatives. Biological examples show that, with no parameter tuning, OASIS enables scientific inference currently impossible with Pearson’s test; for example, OASIS has 100% accuracy in distinguishing patient populations infected with Omicron-BA.1 and BA.2 from those infected with the Delta variant without knowledge of a reference genome or any sample metadata (7). In a different biological domain, analyzing M. tuberculosis sequencing data, OASIS precisely partitions samples from two sub-sub-lineages, again with no metadata or reference genome (15). Finally, the OASIS framework enables more general tests and analyses which we discuss in the conclusion, including a disciplined alternative statistical framework for matrix decomposition beyond the singular value decomposition (SVD), and inference on multiple tables defined on the same set of columns.
1. Problem Formulation
As is standard in contingency table analysis, the observed matrix of counts is taken as . Defining , a contingency table is then defined by pairs of observations of a row (-valued) categorical random variable, and a column (-valued) categorical random variable. In this work, we focus on the case where the columns correspond to biological samples (explanatory random variable) and the rows correspond to the response variable (4). Thus, we are interested in whether the conditional row distribution is the same for each column. Define as the -th column of , and as the total number of counts in column . Without loss of generality, we assume that , as otherwise this column can be omitted. Let be the total number of counts in the table, equivalently obtainable by summing row or column sums. The null model studied is:
Definition 1 (Null Model).
Conditional on the column totals , each column of the contingency table is , drawn independently for all , for some common vector of (unknown) row probabilities .
Contingency tables are well studied, and we refer the reader to ref. 4 for further background. A classical example studies the relationship between aspirin use and heart attacks, where the columns correspond to aspirin or placebo use, and the rows correspond to Fatal Attack, Nonfatal Attack, or No Attack. It is found that conditioning on whether the subject takes aspirin or not yields a statistically significant difference in outcome.
Notationally, denotes the vector norm or spectral norm for matrices, unless otherwise specified. denotes the Frobenius norm of a matrix . denotes a principal eigenvector of a symmetric matrix (any unit eigenvector with maximal eigenvalue). The operation maps a length vector to an matrix , where all off diagonal entries of are 0 and for . denotes the - th column of a matrix. When applied to a vector, scalar operators (such as or ) are applied entrywise. () is the all ones (zeros) vector of appropriate dimension. denotes the CDF of a standard Gaussian random variable, and we use to denote convergence in distribution. For two probability distributions over , is the total variation distance between the two, and is the symmetric chi-squared distance. sign is 1 if , 0 if , and if .
2. OASIS Test Statistic
The OASIS test statistic has a natural linear algebraic formulation Eq. 1. This statistic is computed using two input vectors and , where a significant P-value will be obtained if the contingency table can be well partitioned according to and . These vectors should be thought of as row and column embeddings respectively and can be generated with the assistance of metadata (if available), by random selection, or through an optimization framework we develop in Section 4. To compute the OASIS test statistic , we first define the expected matrix and the centered and normalized table :
| [1] |
| [2] |
is normalized so that under the null, the variance of is constant across all up to the dependence between and . This linearity enables the construction of a finite-sample valid P-value bound for any fixed and . In preliminary work, these vectors were chosen randomly (2), leading to a specific case of the OASIS test we call OASIS-rand, albeit with a looser analysis and worse P-value bound. In this work, we construct and by directly optimizing the P-value bound. Other approaches based on experimental design or interpretability criterion are also possible.
2.1. Comparison with Pearson’s .
The linear algebraic formulation of Pearson’s statistic reveals its fundamental differences from OASIS. is computed as:
| [3] |
| [4] |
In contrast, OASIS’s P-value depends on in Eq. 2, highlighting two main differences between and OASIS. First, left normalizes using empirical row frequencies, which from a technical perspective makes finite-sample analysis of the test statistic difficult, and from a practical perspective upweights minor deviations in low count rows. OASIS treats rows and columns asymmetrically and only normalizes by column frequencies, which are given by the model. Second, squares each residual, and then sums these quantities. OASIS computes a bilinear form of the residual matrix with and and squares the resulting sum. This allows residuals resulting from unstructured deviations to average out, focusing the power of the test on structured deviations from the null. We make this intuition precise in Section 4.1.
Since Pearson’s test does not provide guidance for the reason the null is rejected, practitioners commonly employ correspondence analysis for this task (9). Correspondence analysis studies the matrix of standardized residuals defined in Eq. 4. This method computes the SVD of , and projects rows and columns along the first few principal vectors to obtain low dimensional embeddings for both the rows and the columns. As we show, OASIS provides a statistically grounded alternative to this approach by analyzing , which in our experiments better identifies latent structure.
In addition, the power of Pearson’s test decays as the table size increases, as is approximated as being -distributed with degrees of freedom under the null for an table. This yields several important classes of alternative hypotheses where OASIS is predicted (and empirically shown) to have higher power than , such as time series or 2-group alternatives when the total number of counts is small relative to (details in Section 6.2).
3. Analysis of OASIS
The bilinear form of OASIS’s test statistic admits both an exact asymptotic P-value, and a finite-sample P-value bound. We additionally construct an effect size measure which quantifies the magnitude of deviation from the null, deconfounding the total number of observations .
3.1. P-Value Bound.
A preliminary version of OASIS was designed so that P-value bounds could easily be obtained via classical concentration inequalities (2); here, we improve these bounds, derive the asymptotic distribution of the test statistic, and show the finite-sample bounds that we derive have a matching form with the asymptotic P-value. For notational convenience, we define the quantity which measures the similarity between the column embedding vector and the vector of column counts as
| [5] |
where we drop the dependence on and when clear from context. Observe that by Cauchy–Schwarz. While the P-value bound can be computed for any , we provide a constrained variant below for simplicity.
Proposition 1.
Under the null hypothesis, for any fixed and with , if , the OASIS test statistic satisfies
We prove this proposition by rewriting as a weighted sum of the observations, which are independent and identically distributed under the null, enabling the use of Hoeffding’s inequality to bound the probability that is large. We provide an unconstrained version of this bound along with the proof details in SI Appendix, section S.2.B.
3.2. Asymptotic Normality.
As intuition predicts, since the OASIS test statistic is a sum of independent increments, it converges in distribution to a Gaussian as the number of observations goes to infinity, as long as . For any fixed , define the row variance , where is the common row distribution under the null. Then, we can state the following asymptotic normality result.
Proposition 2.
Consider any fixed probability distribution with , and any sequence of column counts where each , with and for all . Then, the random sequence of OASIS test statistics , where and independently across and , satisfies
The intuition for this result is that each entry of is asymptotically distributed as , up to the negative correlation stemming from the unknown . Then, is a linear combination of with weights , and so has variance up to the factor. We prove this proposition using a Lyapunov central limit theorem in SI Appendix, section S.2.C.
As a direct corollary, by Slutsky’s theorem an asymptotically valid P-value can be constructed using the sample variance , based on the empirical row distribution .
Corollary 1.
Under the conditions of Proposition 2,
is an asymptotically valid P-value.
Using a standard Gaussian tail bound this asymptotic P-value can be upper bounded as
| [6] |
for . This exactly matches the upper bound derived in Proposition 1 up to , which essentially upper bounds the variance of , a -valued random variable, as .
3.3. Effect Size.
Through and , OASIS assigns scalar values to each row and column. The preliminary version of OASIS (2) assigned each sample to one of two groups by utilizing . Building on this, we formalize an effect size measure for OASIS, which is computed as the difference in mean as measured by between the two sample groups induced by the sign of . Defining and , the effect size is computed as
| [7] |
where . Defining as the empirical row distribution over samples in (similarly for ), the effect size measure in Eq. 7 satisfies for all that
The proof of the relationship between effect size and total variation distance and the motivation for this effect size measure stem from a simple two group alternative (SI Appendix, section S.2.D). Empirically, this effect size measure allows OASIS to prioritize scientifically interesting tables.
4. Optimization-Based Approach to Constructing f, c
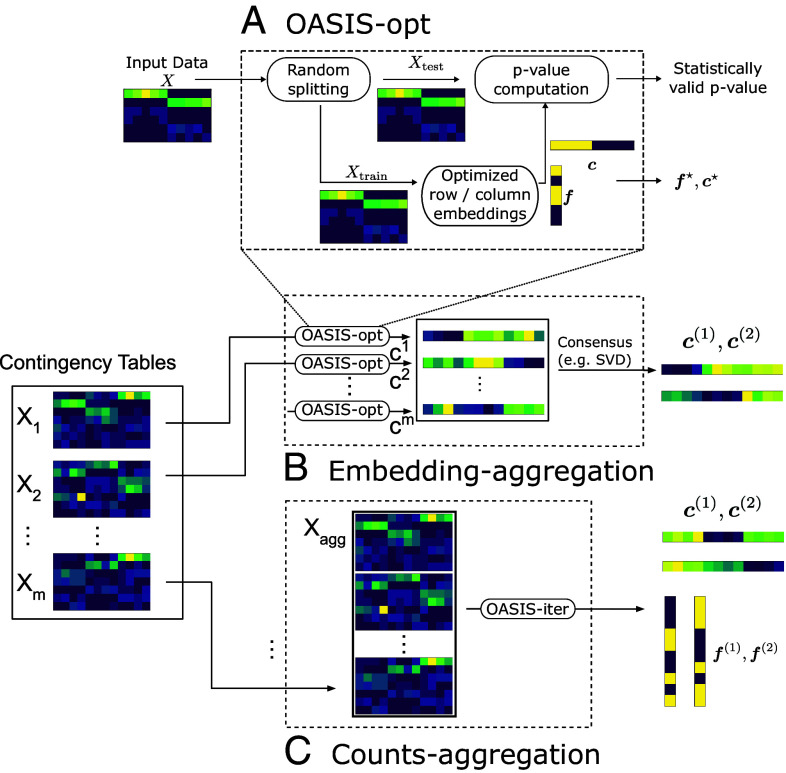
Discussion heretofore has focused on studying OASIS’s test statistic for a fixed and . The natural question is then, how to choose and ? Here, we focus on an intuitive method, OASIS-opt, that partitions the observed counts into independent “train” and “test” datasets, constructs and that optimize the P-value (bound) on the training data, and computes a statistically valid P-value (bound) on the held-out test data (Fig. 2A and SI Appendix, section S.2.E).
Fig. 2.
Figure showing the algorithms we build using OASIS. (A) OASIS-opt employs data-splitting to generate optimized, data-dependent and , before generating a statistically valid P-value bound using the held-out test data. (B and C) depict two algorithms we propose for inferring latent structure from a collection of tables defined on the same set of columns. As building blocks, we use OASIS-opt for embedding-aggregation, and OASIS-iter (Section 5.1) for counts-aggregation. (B) Embedding-aggregation (Algorithm 2) performs inference on each table marginally using OASIS-opt and aggregates the resulting sample embeddings. (C) Counts-aggregation (Algorithm 1) stacks the contingency tables into one large matrix , and performs iterative analysis on this aggregated table using OASIS-iter.
4.1. Minimizing the P-value bound.
Examining Proposition 1, our goal is to identify that minimize this P-value bound. We begin by simplifying the optimization objective, observing that the P-value bound is minimized by maximizing the test statistic. Defining the two optimization problems:
| [8] |
| [9] |
we prove the following lemma (details in SI Appendix, section S.3.A).
Lemma 1.
The set of optimal solutions to Eq. 9 is contained within the set of optimal solutions to Eq. 8.
Thus, to identify an optimal solution to Eq. 8, it suffices to optimize Eq. 9. Since the objective is bilinear the maximum value must be attained at a corner point. Further, since is self-dual, an optimal in Eq. 9 can be identified as
| [10] |
In graph contexts, a similar combinatorial optimization problem arises in the determination of the max-cut, which is known to be NP-complete. In particular, Eq. 10 is in general APX-hard, meaning that no polynomial-time approximation scheme exists for arbitrarily good approximations (16). For small , the problem can be solved exactly by enumerating all possible . For large more sophisticated algorithms can be used, such as SDP relaxations (discussed in SI Appendix, section S.3.D). However, due to the structure of and the biconvex nature of Eq. 9, alternating maximization is computationally efficient and yields empirically good performance.
Alternating maximization converges to a local maximum, computing iterates as , implicitly computing . Due to the nonconvexity of the overall objective, several random initializations are used in practice, which we encapsulate in an algorithm called OASIS-opt (details in SI Appendix, section S.3). Note that there are two sources of randomness in OASIS-opt; statistical randomness in data-splitting, and the random initializations for approximately solving the inner maximization problem. These are distinct, with the former being necessary and the latter being a computational tool to improve alternating maximization. Additional random train/test splits can be utilized with Bonferroni correction to improve empirical performance, ensuring rejection of highly significant tables at the expense of a higher burden of multiple hypothesis correction (discussed in SI Appendix, section S.6.A).
4.2. Relation to the Singular Value Decomposition.
Examining the optimization problem in Eq. 9, observe that if were constrained then the optimal solution would take (resp. ) as the principal left (resp. right) singular vector of , where the optimal value would be the maximum singular value by the variational characterization of the SVD. OASIS-opt provides an alternative decomposition of a contingency table to the ubiquitous SVD, within a disciplined statistical framework. While the SVD has a statistical interpretation in some settings (e.g., under additive white Gaussian noise), OASIS-opt’s alternative decomposition is tailored for multinomial data, a better fit for the application at hand (17).
As in Eq. 3, the test statistic can be expressed as , where . Comparatively, the OASIS test statistic attains a maximum value (up to the as opposed to constraint on ) of . Note that the ball is contained within the ball, so the optimal value of the OASIS test statistic is in fact lower bounded by . The Frobenius norm is the sum of squared singular values, and so is summing over all possible directions of deviation. This makes it powerful, but overpowered against uninteresting alternatives such as those with a flat spectrum. OASIS on the other hand computes significance by projecting deviations from the expectation in a single direction. Intuitively, this denoises all the lower signal components, and ensures that OASIS remains robust to biological noise and yields interpretable results. This is exactly why fails to distinguish between the two tables in Fig. 1C (spectra plotted in SI Appendix, Fig. S1).
An SVD of or offers one approach to generating for inference with OASIS. However, this choice gives worse P-value bounds (as the SVD is optimizing a fundamentally different objective), with empirically less meaningful and than OASIS-opt, as shown for SARS-CoV-2 data in Section 6.3, and a toy example in SI Appendix, Fig. S8. From a statistical perspective, directly optimizing OASIS’s -constrained P-value bound naturally yields improved P-value bounds to optimizing the SVD’s -constrained objective. OASIS-opt provides a promising alternative to correspondence analysis, but further experiments and analysis are required to validate the quality of these embeddings in more general settings.
4.3. Minimizing the Asymptotic P-Value.
While optimizing the finite-sample P-value bound yields a combinatorially hard optimization problem, the asymptotic P-value can be optimized efficiently. As we detail in SI Appendix, section S.3.C, an optimal which minimizes the asymptotic P-value objective given in Corollary 1 can be efficiently computed as
| [11] |
where and is a principal eigenvector of . A corresponding is then computed as . This provides an interesting contrast with the classical SVD, where correspondence analysis would take as the row embeddings a principal eigenvector of the matrix . While correspondence analysis primarily places weight on high count rows, OASIS upweights low count rows, prioritizing those that have meaningful between-class differences. Note that the optimal is continuous-valued in this setting; the binary nature of in the finite-sample case is due to the use of Hoeffding’s inequality in the construction of the P-value bound. Alternative finite-sample bounds based on Bernstein’s inequality, for example, would also yield continuous-valued optimal .
5. A Statistical Framework for Subgroup Classification with OASIS-opt
OASIS at its core is a statistical test for contingency tables. However, after the null has been rejected, many follow-up questions often remain. One natural question, after the samples have been found to violate the null when combined using , is whether there exist different ways of grouping samples to still yield statistically significant deviations. A more general question is whether, studying many tables defined on the same sets of columns, there is some global inference that can be drawn regarding the underlying clustering of the samples. Some related data fusion methods have been proposed, and we refer the reader to ref. 18 for a more complete survey.
5.1. Iterative Analysis of Contingency Tables with OASIS-iter.
Addressing the first question of iterative testing of a single contingency table, we first define a method OASIS-perp, which takes in a table and a set of vectors , and optimizes the following objective:
| [12] |
This objective is identical to that of OASIS-opt, with the added constraint that is orthogonal to all vectors in . This retains the biconvexity of the original problem, enabling the use of alternating maximization.
To iteratively analyze a table, we propose a simple wrapper on top of OASIS-perp called OASIS-iter. OASIS-iter decomposes a contingency table by first identifying from OASIS-opt, then iteratively identifying optimizing Eq. 12 subject to the identified being orthogonal to . This provides a statistical stopping criterion for cluster identification; for each pair we compute OASIS’s P-value bound, and once the obtained exceeds the desired significance level (e.g., ), the number of clusters can be estimated as . Each outputted by this procedure represents an orthogonal direction along which this table can be partitioned so as to yield a significant partitioning. The algorithm is made explicit in SI Appendix, section S.3.B.
5.2. Counts-Aggregation.
With this primitive of iterative analysis of a single table, one candidate approach to identifying clusters across multiple tables is by aggregating counts across many tables, and running OASIS-iter to iteratively identify underlying clusters. We design a method for this task called counts-aggregation (Algorithm 1), shown graphically in Fig. 2B. Counts-aggregation takes as input a set of tables, which are defined on the same set of columns and should have shared latent structure. In our setting, these tables are generated by SPLASH, where we filter OASIS-opt’s calls for tables with a large effect size, many observations, and a significant P-value bound after performing Benjamini–Yekutieli (BY) correction (19) across a much larger list of tables outputted from SPLASH (2). These tables are then vertically concatenated into one larger table, , upon which OASIS-iter is run. For ease of visualization, we only utilize the first two outputted and as the 2D sample embeddings.
Note that this aggregated table need not satisfy the contingency table null, due to the correlation in entries from different subtables. Algorithmically, we discard rows in this table with fewer than 10 observations to minimize the computational burden. Additionally, to avoid having a single high-count subtable dominate all the others in this computation, we normalize the counts in each subtable by , the total number of counts in that subtable.
5.3. Embedding-Aggregation.
Due to the statistical dependencies and practical issues with normalizing and aggregating tables before performing statistical testing, we additionally propose a second clustering approach which independently identifies 1D embeddings for each table and then aggregates these results. Embedding-aggregation (Algorithm 2), utilizes OASIS-opt to generate a vector for each table, collects these vectors into a matrix , and then computes a low dimensional embedding for the samples with an SVD (Fig. 2C). As before, the tables used as input could be SPLASH outputs filtered for those with a large effect size, many observations, and a significant postcorrection P-value bound. Entries may be missing from due to samples not appearing in all tables: We impute these with a value of 0 for simplicity, but more sophisticated approaches are possible.
6. Numerical Results
Many problems in modern data science, including in genomics, map to contingency tables. We show that OASIS is robust to some important classes of noise models, and that OASIS has substantial power against several classes of alternative hypotheses of interest. Analyzing raw sequencing data, OASIS can perform classification tasks not possible with Pearson’s , enabling reference-free strain classification in SARS-CoV-2 and M. tuberculosis.
6.1. Robustness against Uninteresting Alternatives.
Next-generation sequencing data are commonly treated as matrices of discrete counts, for example, with single-cell RNA sequencing data often represented as a cell-by-gene counts matrix. While the statistical null posits that observations in each sample are identically distributed, biochemical noise introduced during sampling generates overdispersed counts, violating this null. The field has converged on modeling such data with negative binomial distributions (20, 21). Probabilistically, a negative binomial random variable is equivalent to a Poisson random variable with a random, gamma-distributed, mean. This yields an alternative probabilistic model where , , is the expected number of observations, and under the true null counts would be observed (). This does not satisfy the contingency table null for , but also does not represent biologically meaningful deviation.
To test the robustness of OASIS and , we simulate this uninteresting alternative in Table 1, showing the fraction of rejected tables (for ) at the level of negative binomial overdispersion predicted by the sampling depth (20). As expected, Pearson’s rejects nearly all tables generated under this negative binomial sampling model, while OASIS retains robustness across a wide range of parameters, due to the unstructured deviations. For all tests, the rejection fraction is monotonic in the number of rows and columns. Taking a table with a mean of observations per sample with a uniform row distribution, for 20 rows and 10 columns OASIS-opt rejects 7.5% of tables, while Pearson’s test rejects 95.7% of tables. Additional experiments and simulation details in SI Appendix, section S.6.B.1.
Table 1.
Power against negative binomial overdispersion
| num rows | num cols | OASIS-rand | OASIS-opt | |
|---|---|---|---|---|
| 5 | 10 | 0.143 | 0.003 | 0.010 |
| 50 | 0.318 | 0.006 | 0.019 | |
| 400 | 0.318 | 0.006 | 0.019 | |
| 20 | 10 | 0.957 | 0.054 | 0.075 |
| 50 | 1.000 | 0.065 | 0.193 | |
| 400 | 1.000 | 0.078 | 0.874 | |
| 100 | 10 | 1.000 | 0.947 | 0.996 |
| 50 | 1.000 | 0.996 | 1.000 | |
| 400 | 1.000 | 0.998 | 1.000 |
Uniform target distribution, expected number of counts per column , full plots and details in SI Appendix, section S.6.B.1.
Power against null generated by negative binomial sampling as modeled for single-cell sequencing data (20).
More generally, an applied task in genomics and other applications is to reject the null only when it is “interesting.” Below, we refer to an alternative as uninteresting if it can be explained by a small number of outlying matrix counts, or from sampling from a set of distributions where is the row distribution of the -th column, and for all . Such distributions, while statistically deviant from the null, represent small effects that may be due to contamination or equipment error, and are not a priority to detect. OASIS provides robustness against these sources of unstructured noise that represent biologically uninteresting alternatives, as we show with simulations against corruption of each individual column’s probability distribution (SI Appendix, Fig. S5).
6.2. Power against Simulated Alternatives.
OASIS has substantial power (in some regimes more than ) against large, structured deviations from independence, such as when the samples can be partitioned into two groups with nearly disjoint supports. These examples arise in important applications, such as detecting viral mutations, recombination in B cells that generate antibodies—V(D)J recombination—and differentially regulated alternative splicing, among others.
We show this empirically in SI Appendix, section S.6.C, and provide approximate power calculations in SI Appendix, section S.7 that corroborate these numerical results. Approximate power calculations are derived, for a given alternative, by considering the toy setting where we observe the expected underlying alternative matrix. Concretely, for sample with row probabilities , we assume that we observe instead of the random draw . In this deterministic setting, OASIS’s P-value bound is comparable to and in some regimes better than , in particular when the number of rows is large, as shown in Table 2. We conjecture that while OASIS may not exhibit the optimal asymptotic rate against certain classes of alternatives (as shown by the unique per-sample expression setting), it does have power going to 1 as the number of observations goes to infinity across a broad class of alternatives.
Table 2.
Summary of approximate power calculations
| Alternative | OASIS P-value bound | Pearson’s asymptotic P-value | Notes |
|---|---|---|---|
| Two-group | OASIS is more powerful when is small | ||
| Time series | Same behavior as two group setting | ||
| Unique per-sample expression | more powerful, but OASIS has power going to 1 | ||
| One deviant sample | has too much power |
are distributions, indicating the target distributions of the two groups in the first setting, and the extremal distributions in the time series setting. Constants omitted for clarity. Details in SI Appendix, section S.7.
6.3. SARS-CoV-2 Variant Detection.
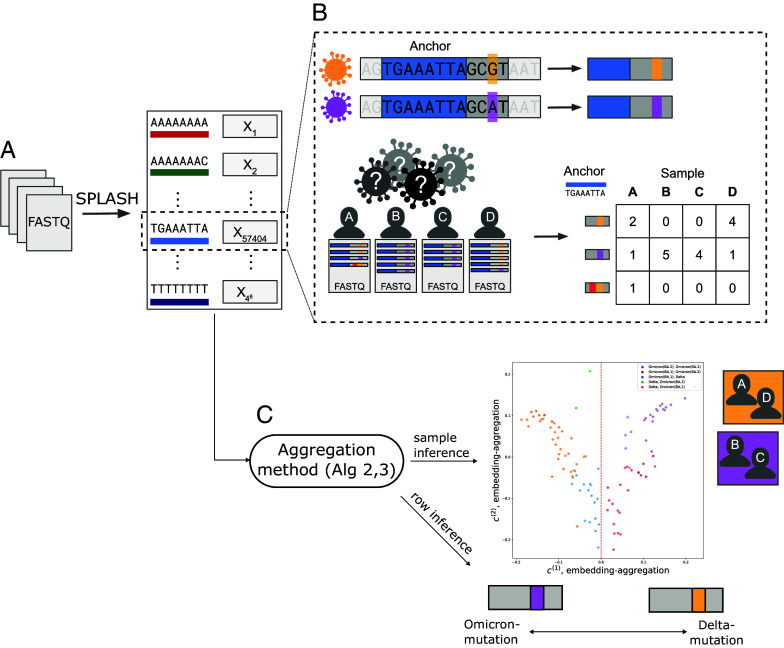
To illustrate OASIS’s performance, we study a public dataset of SARS-CoV-2 coinfections generated in France, which sequences patients during a period of Omicron and Delta cocirculation (7). We show that OASIS detects variants in SARS-CoV-2 by analyzing sequencing data from 103 patients’ nasal swabs as contingency tables via SPLASH, as described in ref. 2. SPLASH generates a contingency table for each length -subsequence present (called an anchor -mer) from genomic sequencing (Fig. 3). A statistical test with good scientific performance will identify anchors near known mutations in the SARS-CoV-2 genome that distinguish Omicron and Delta. Data processing details are deferred to SI Appendix, section S.4.
Fig. 3.
(A) SPLASH (2) generates contingency tables from genomic sequencing data, here FASTQ files, for all possible anchor k-mers (length genomic sequences). (B) Shown in greater detail is the process for one specific anchor, TGAAATTA. This anchor highlights a mutation between two strains of SARS-CoV-2, Omicron (purple) and Delta (orange). Below, viral sequencing data from four individuals (samples) infected with SARS-CoV-2 is shown. However, it is a priori unknown which strain each individual was infected with, and no reference genome is available. For the fixed anchor sequence (shown in blue), SPLASH counts for each sample the frequency of sequences that occur immediately after (target sequence), and generates a contingency table, where the columns are indexed by the samples and the rows are indexed by the sequences. Shown in (B) is one read in sample A which underwent sequencing error, highlighted in red, and thus yielded an additional discrete observation—a sequence—resulting in an extra row. Sequencing error leads to tables with many rows with low counts. Note that we cannot know a priori which rows of this table are due to sequencing error, as we simply observe raw sequencing data. (C) The contingency tables generated by SPLASH are defined over the same set of samples (patients), so we can use these tables to jointly infer sample origin. The plot shown depicts the results of embedding-aggregation (Algorithm 2) on SARS-CoV-2 data (7), perfectly predicting whether a patient has Delta or not, and yielding high predictive accuracy () for subvariant classification (Omicron BA.1 versus BA.2). Counts-aggregation (Algorithm 1) can also be used to predict the strain of mutated targets, with 93% classification accuracy of whether a target was Delta or not. In the depicted toy example, this would correspond to grouping targets and individuals by strain as shown.
OASIS and yield substantially different results on the 100,914 tables generated by SPLASH. We demonstrate the improvement in biological inference enabled by OASIS, utilizing as a measure of biological relevance for each method’s called tables how well these calls can predict sample metadata. For each sample, we have associated metadata indicating the clinical ground truth of whether the patient (sample) was infected with Delta. For each table called by OASIS-opt, we use as its 1D sample embedding the vector , taking the sign of each entry to generate a two-group partitioning. The measure of biological relevance used is then computed as the absolute cosine similarity, , between the sample metadata and the sign of . This corresponds to the fraction of agreed-upon coordinates in (up to a global sign flip). For this process is mirrored, where instead of , the principal right singular vector for correspondence analysis is used.
Out of the 100,914 tables, OASIS rejects 28,430, and Pearson’s test rejects 71,543 tables. However, when the tables that rejects are decomposed, they do not yield signal that correlates well with the ground truth (Table 3). Examining quantiles of the two empirical distributions of absolute cosine similarities, the 0.5 and 0.9 quantiles of these distributions are 0.22 and 0.66 for OASIS, as opposed to 0.10, 0.52 for . For these significant tables correspondence analysis yields similarly high correlation, indicating that in this setting it is primarily the focused rejection of OASIS that is yielding the larger similarities (SI Appendix, Fig. S9). In addition, of the 389 anchors that OASIS calls that does not, the 0.5 and 0.9 quantiles of the absolute cosine similarities are 0.15 and 0.76, showing that many biologically relevant tables were missed by .
Table 3.
Concordance between sample metadata and identified embeddings
| OASIS | OASIS called, did not | pv 0 | OASIS pv 0 | OASIS filtered | ||
|---|---|---|---|---|---|---|
| Number of anchors | 71,543 | 28,430 | 389 | 16,611 | 2,114 | 2,495 |
| 0.5 quantile cosine similarity | 0.10 | 0.22 | 0.15 | 0.09 | 0.69 | 0.72 |
| 0.9 quantile cosine similarity | 0.52 | 0.66 | 0.76 | 0.40 | 0.79 | 0.82 |
For each set of calls, we display the number of anchors called, the median cosine similarity, and the 90-th quantile of cosine similarity.
Absolute cosine similarities between ground truth clinical metadata (whether a sample is infected with Delta or not) and the binarized sample embeddings identified by (correspondence analysis) and OASIS-opt ( vector).
Analyzing all 16,611 tables rejected by with a P-value of 0 (up to numerical precision), the 1D embeddings obtained from correspondence analysis had low absolute cosine similarity with the biological ground truth, with 0.5 and 0.9 quantiles of 0.087 and 0.40. In SI Appendix, Fig. S11 we zoom in on two of the most significant tables rejected by but not by OASIS-opt. Correspondence analysis yields embeddings with minimal correlation with the ground truth, 0.15 and 0.02 for the two tables selected, one of which visually appears to have just detected one deviating sample.
In contrast, OASIS-opt yields significantly more biologically relevant calls. For the 2,114 tables that OASIS-opt assigns a P-value bound of 0, the absolute cosine similarities with ground truth have 0.5 and 0.9 quantiles of 0.69 and 0.79. We similarly see that OASIS-opt’s filtered significance calls have extremely high concordance with clinical metadata. We filter for significant tables with effect size in the top 10% and total counts as these are predicted to delineate strains, yielding 2,495 tables. Of these, the absolute cosine similarity has 0.5 and 0.9 quantiles of 0.72 and 0.82. The ECDF of the absolute cosine similarities of all of OASIS-opt’s and ’s calls are shown in SI Appendix, Fig. S9, highlighting an order of magnitude difference in the fraction of identified tables with, e.g., 0.6 absolute cosine similarity.
Comparing with the original statistic used in SPLASH (2), OASIS-rand identifies 5,932 significant tables. All except 48 of these are identified by OASIS-opt. The two most significant tables that are called by OASIS-opt (with an effect size in the top 10% and counts greater than 1,000) and not by OASIS-rand are shown in SI Appendix, Fig. S10, both having high absolute cosine similarity with sample metadata, 0.76, showing that the additional calls OASIS-opt provides are biologically relevant. We further show that OASIS provides calls beyond those possible with , showing in SI Appendix, Fig. S12 the five tables in the reduced anchor list above (effect size and counts filtered), which all have large cosine similarities with the ground truth metadata.
6.3.1. Counts-aggregation.
Running counts-aggregation (Algorithm 1) on the SARS-CoV-2 dataset yields valuable inference on both targets and samples. We select the first two components for simplicity of visualization, as the first component contains 57% of the total power as measured by , and with the second contains 76% of the cumulative power (full spectrum shown in SI Appendix, Fig. S9). Focusing first on samples, the first two identified by counts-aggregation have high predictive power over strain information. A simple threshold on yields perfect prediction of whether a patient has Delta or not. The second vector, , enables classification of Omicron subvariants. A linear predictor on and yields 94/103 (91%) accuracy in predicting whether the primary strain is Omicron BA.1, shown in Fig. 4B.
Fig. 4.
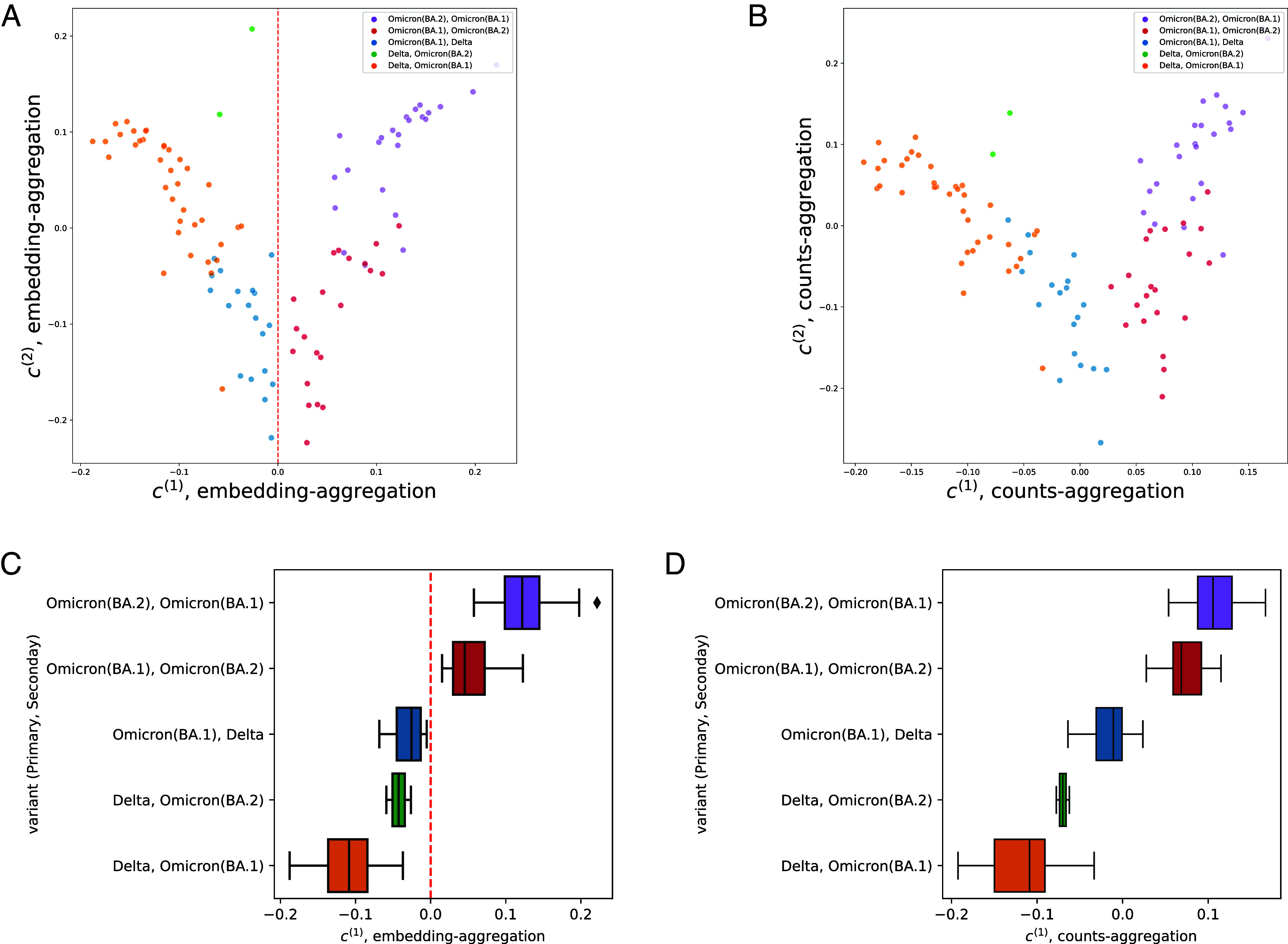
Analysis of SARS-CoV-2 coinfection data (7). Tables were generated by SPLASH (2) and tested with OASIS-opt. (A and B) depict the two dimensional embeddings generated by embedding-aggregation and counts-aggregation respectively, and (C and D) show only the one dimensional embedding. (A and C) depict the results of embedding-aggregation (Algorithm 2). (A) shows the generated 2D embeddings, which perfectly classify whether a patient has Delta or not at , highlighted in (C). (B and D) depict the results of counts-aggregation (Algorithm 1). Perfect separation of Delta versus non-Delta samples, no longer at . Analysis details in SI Appendix, section S.4.
Running counts-aggregation on these matrices also enables joint inference on targets from different tables. The outputted of this procedure has significant predictive power over whether a target corresponds to an Omicron mutation or not. We validate this by using Bowtie (22) to check whether a target perfectly aligns to the Wuhan reference, a Delta assembly, an Omicron BA.1 assembly, or an Omicron BA.2 assembly (details in SI Appendix, section S.4). Comparing with this ground truth vector of whether a target was classified as Delta or not, correctly classified 4,496/4,836 (93%) targets (up to a global flip). This is with no parameter tuning. The targets that are incorrectly classified have the potential to uncover novel biology, which is beyond the scope of this paper. Analyzing the first two anchors with targets that are considered misclassified, the first corresponds to a known Omicron deletion not present in the used reference genome, while the second perfectly identifies and predicts an annotated Omicron deletion; however, due to parameter choices (SPLASH’s “lookahead distance” (2)), both targets perfectly map to the Wuhan reference. We provide alignments for these results in SI Appendix, Fig. S13.
6.3.2. Embedding-aggregation.
We additionally run embedding-aggregation (Algorithm 2) on this SARS-CoV-2 dataset, restricting our attention to the first two right singular vectors of . The first singular vector of the matrix perfectly partitions individuals infected with the Delta strain from those that were not (at the threshold ). The second singular vector differentiates between the Omicron BA.1 and BA.2 subvariants as shown in Fig. 4A where the x-axis is the principal right singular vector and the y-axis is the second right singular vector. When tasked with predicting whether a sample has BA.1 as its primary variant, a simple linear classifier in this two dimensional space is able to correctly classify 95/103 (92%) of the samples (details in SI Appendix, section S.4.A).
Since embedding-aggregation provides inference on the samples, it can be used to indirectly provide inference on the targets. We show this by utilizing as a predictor of whether a patient is infected with Delta or not, which yields correct predictions on 4,357/4,836 targets (90%), up to a global flip. This highlights the power of counts-aggregation in performing joint inference directly on the rows.
Together, these analyses suggest that OASIS finds tables representing important biological differences and generates scientifically valuable low-dimensional embeddings through a disciplined statistical framework, features absent from .
6.4. M. tuberculosis Lineage Identification.
We tested the generality of OASIS-opt’s inferential power to classify microbial variants in a different microorganism, the bacterium M. tuberculosis. We processed data from 25 isolates from two sub-sub-lineages known to derive from sublineage 3.1: 3.1.1 and 3.1.2 (15). Currently, bacterial typing is based on manual curation and SNPs, is highly manually intensive, and requires mapping to a reference genome.
As with SARS-CoV-2, we utilized SPLASH to generate tables which we tested with OASIS-opt. 80,519 tables were called by OASIS-opt (BY corrected P-value bound ), 258 with effect size in the 90-th quantile and total count 1,000. To avoid biological noise, we preemptively filtered out tables with targets with repetitive sequences (10 repeated basepairs). OASIS-opt was run blind to sample metadata and the M. tuberculosis reference genome.
6.4.1. Counts-aggregation.
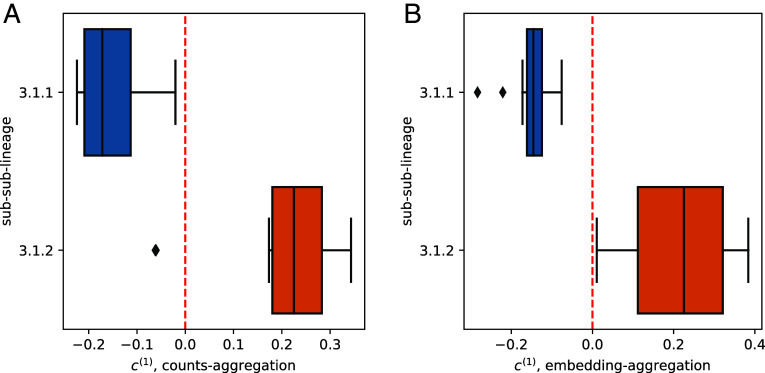
We run counts-aggregation on the filtered M. tuberculosis tables described above. The first identified vector yields a well-separated partitioning in terms of sub-sub-lineage as shown in Fig. 5A. Two samples are misclassified, with the rest being perfectly predicted by , yielding an accuracy of 23/25 (92%).
Fig. 5.
Interpretation of OASIS-rejected null from M. tuberculosis data (7). Tables were generated by SPLASH (2) and tested with OASIS. (A) shows the generated 1D embeddings from embedding-aggregation (Algorithm 2), which perfectly classifies patients based on sub-sub-lineage at . (B) depicts the results of counts-aggregation (Algorithm 1). Two samples are misclassified (visually, one on top of the other), but with a much larger margin for the rest. 2D plots with shown in SI Appendix, Fig. S14.
6.4.2. Embedding-aggregation.
We run embedding-aggregation on the same set of filtered tables. The first singular value constitutes 50% of the power in the matrix, and the top two singular values comprise 72% of the spectrum’s power. A 1D embedding from the first singular vector leads to a perfectly separation of sub-sub-lineages, classifying at the threshold , as shown in Fig. 5B.
7. Discussion
In this paper, we proposed a framework for interpretable and finite-sample valid inference for contingency tables, describing several applications and extensions of OASIS. There are many exciting directions of ongoing and future work, some of which we discuss below (details in SI Appendix, section S.5). A known failing of is its inability to utilize available metadata regarding the rows and columns of the matrix (e.g., ordinal structure). OASIS however can incorporate this knowledge in its construction of and . Additionally, with its natural effect size measure, OASIS can be used as a coefficient of correlation between two random variables, even continuous valued ones. While Hoeffding’s inequality for sums of bounded random variables provides one candidate P-value bound, alternatives can be constructed using different methods, such as empirical variants of Bernstein’s inequality (23) or ones based on Stein’s method (24), leading to alternative optimization objectives for . OASIS’s statistic can also be extended to different nulls, e.g., volume-based (25), by using alternative concentration inequalities (26). While OASIS currently analyzes two-dimensional tables, its simple and theoretically tractable approach of centering, normalizing, and projecting naturally extends to tensors. As we have shown, OASIS empirically has power against a wide variety of alternatives, outperforming Pearson’s test in some regimes (SI Appendix, section S.7); a more precise power analysis would help practitioners know when to best use OASIS. Finally, as currently presented, in a setting with large numbers of tables generated in a single experiment over the same set of samples, OASIS performs testing on each table independently. We have introduced two approaches for jointly analyzing tables, counts-aggregation, and embedding-aggregation, to identify latent relationships between samples. Ongoing and future work investigates other approaches, including adaptive ones, to perform this statistical inference and testing on tensors. While we would not be surprised if such tests have been previously introduced, we have not been able to locate them in the literature.
8. Conclusion
This paper provides a theoretical framework for and an applied extension of OASIS, a test that maps statistical problems involving discrete data to a statistic that admits a closed-form finite-sample P-value bound. Here, we focused on practical scientific problems, applying OASIS to data in contingency tables. We develop OASIS with an emphasis toward genomics applications, a rapidly expanding field with diverse scientific applications from single-cell genomic inference to viral and microbial strain detection. The field still relies heavily on classical statistical tests and parametric models. OASIS provides an alternative to these approaches that is both empirically robust and scientifically powerful. On real and simulated data, OASIS-opt prioritizes biologically significant signals: Without a reference genome, any metadata, or specialization to the application at hand, it can classify viral variants including Omicron subvariants and Delta in SARS-CoV-2 as well as sub-sub-lineages of M. tuberculosis. Moreover, it is robust to noise introduced during sequencing, the genomic data generation process, including in single-cell genomics (27). OASIS provides a tool toward answering questions in mechanistic biology that are manual labor intensive (7) or impossible to address with current statistical approaches. In addition to its statistically calibrated output, OASIS’s lineage assignment is performed in a rigorous statistical framework that promises further theoretical extensions in clustering.
In summary, OASIS is a finite-sample valid test that has many important statistical properties not enjoyed by which will enable its use across many disciplines in modern data science. It is computationally simple, robust against deviations from the null in scientifically uninteresting directions, and provides a statistical method for the analyst to interpret rejections of the null hypothesis. In addition to a finite-sample P-value bound, we characterize the asymptotic distribution of OASIS’s test statistic under the null. We construct an optimization framework for generating row and column embeddings that optimize the P-value bound or the asymptotic P-value. Simulations corroborate the theoretical guarantees provided for OASIS, with experiments on genomic data showing a glimpse of the discovery power enabled by OASIS.
Supplementary Material
Appendix 01 (PDF)
Acknowledgments
Author contributions
T.Z.B., D.T., and J.S. designed research; T.Z.B., D.T., and J.S. performed research; T.Z.B. and J.S. analyzed data; and T.Z.B., D.T., and J.S. wrote the paper.
Competing interests
T.Z.B. and J.S. have submitted a provisional patent no. 63/366,444 relating to this work.
Footnotes
This article is a PNAS Direct Submission.
Data, Materials, and Software Availability
Previously published data were used for this work (7, 15). M. tuberculosis data is publicly available under Accession ID PRJEB41116 (28). SARS-CoV-2 data is publicly available under Accession ID PRJNA817806 (29). Software available at: https://github.com/refresh-bio/SPLASH (30).
Supporting Information
References
- 1.Chen Y., Diaconis P., Holmes S. P., Liu J. S., Sequential Monte Carlo methods for statistical analysis of tables. J. Am. Stat. Assoc. 100, 109–120 (2005). [Google Scholar]
- 2.Chaung K., et al. , Splash: A statistical, reference-free genomic algorithm unifies biological discovery. Cell 186, 5440–5456 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Pearson K., On the criterion that a given system of deviations from the probable in the case of a correlated system of variables is such that it can be reasonably supposed to have arisen from random sampling. London, Edinb. Dublin Philosoph. Magaz. J. Sci. 50, 157–175 (1900). [Google Scholar]
- 4.Agresti A., Categorical Data Analysis (John Wiley& Sons, 2012), vol. 792. [Google Scholar]
- 5.Diaconis P., Sturmfels B., Algebraic algorithms for sampling from conditional distributions. Ann. Stat. 26, 363–397 (1998). [Google Scholar]
- 6.Maydeu-Olivares A., Joe H., Limited information goodness-of-fit testing in multidimensional contingency tables. Psychometrika 71, 713–732 (2006). [Google Scholar]
- 7.Bal A., et al. , Detection and prevalence of SARS-CoV-2 co-infections during the omicron variant circulation in France. Nat. Commun. 13, 1–9 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Iversen G. R., Decomposing chi-square: A forgotten technique. Sociol. Methods Res. 8, 143–157 (1979). [Google Scholar]
- 9.Greenacre M. J., Correspondence analysis. Wiley Interdisc. Rev. Comput. Stat. 2, 613–619 (2010). [Google Scholar]
- 10.Hsu L. L., Culhane A. C., Correspondence analysis for dimension reduction, batch integration, and visualization of single-cell RNA-seq data. Sci. Rep. 13, 1–17 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Salzman J., Spectral Analysis with Markov Chains (Citeseer, 2007), vol. 68. [Google Scholar]
- 12.Lancaster H., The derivation and partition of χ2 in certain discrete distributions. Biometrika 36, 117–129 (1949). [PubMed] [Google Scholar]
- 13.Diaconis P., Griffiths R. C., Reproducing kernel orthogonal polynomials on the multinomial distribution. J. Approx. Theory 242, 1–30 (2019). [Google Scholar]
- 14.Chen F., Roch S., Rohe K., Yu S., Estimating graph dimension with cross-validated eigenvalues. arXiv [Preprint] (2021). http://arxiv.org/abs/2108.03336 (Accessed 10 June 2023).
- 15.Dreyer V., et al. , High fluoroquinolone resistance proportions among multidrug-resistant tuberculosis driven by dominant l2 mycobacterium tuberculosis clones in the Mumbai metropolitan region. Genome Med. 14, 95 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Papadimitriou C., Yannakakis M., “Optimization, approximation, and complexity classes” in Proceedings of the Twentieth Annual ACM Symposium on Theory of Computing (1988), pp. 229–234. [Google Scholar]
- 17.Townes F. W., Hicks S. C., Aryee M. J., Irizarry R. A., Feature selection and dimension reduction for single-cell RNA-seq based on a multinomial model. Genome Biol. 20, 1–16 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Feng Q., Jiang M., Hannig J., Marron J., Angle-based joint and individual variation explained. J. Multivar. Anal. 166, 241–265 (2018). [Google Scholar]
- 19.Benjamini Y., Yekutieli D., The control of the false discovery rate in multiple testing under dependency. Ann. Stat., 1165–1188 (2001). [Google Scholar]
- 20.Love M. I., Huber W., Anders S., Moderated estimation of fold change and dispersion for RNA-seq data with DESeq2. Genome Biol. 15, 1–21 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Jiang R., Sun T., Song D., Li J. J., Statistics or biology: The zero-inflation controversy about scRNA-seq data. Genome Biol. 23, 1–24 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Langmead B., Trapnell C., Pop M., Salzberg S. L., Ultrafast and memory-efficient alignment of short DNA sequences to the human genome. Genome Biol. 10, 1–10 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Maurer A., Pontil M., “Empirical Bernstein bounds and sample variance penalization” in The 22nd Conference on Learning Theory, Montreal, Quebec, Canada, June 18–21, 2009 (COLT, 2009). [Google Scholar]
- 24.Chatterjee S., Stein’s method for concentration inequalities. Probab. Theory Relat. Fields 138, 305–321 (2007). [Google Scholar]
- 25.Diaconis P., Efron B., Testing for independence in a two-way table: New interpretations of the chi-square statistic. Ann. Stat. 13, 845–874 (1985). [Google Scholar]
- 26.Hoeffding W., The large-sample power of tests based on permutations of observations. Ann. Math. Stat. 169–192 (1952).
- 27.Dehghannasiri R., et al. , Unsupervised reference-free inference reveals unrecognized regulated transcriptomic complexity in human single cells. bioRxiv [Preprint] (2022). https://www.biorxiv.org/content/10.1101/2022.12.06.519414v1 (Accessed 12 December 2022).
- 28.CRyPTIC Consortium, CRyPTIC. Foundation for Medical Research India. Mumbai. NIH short read archive. https://www.ncbi.nlm.nih.gov/bioproject/PRJEB41116. Accessed 5 March 2022.
- 29.Bal A., et al. , Detection and prevalence of SARS-CoV-2 co-infections during the omicron variant circulation in France. NIH short read archive. https://www.ncbi.nlm.nih.gov/bioproject/?term=PRJNA817806. Accessed 5 March 2022. [DOI] [PMC free article] [PubMed]
- 30.Kokot M., Dehghannasiri R., Baharav T. Z., Salzman J., Deorowicz S., Splash2 provides ultra-efficient, scalable, and unsupervised discovery on raw sequencing reads. Github. https://github.com/refresh-bio/SPLASH. Accessed 20 November 2022.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Appendix 01 (PDF)
Data Availability Statement
Previously published data were used for this work (7, 15). M. tuberculosis data is publicly available under Accession ID PRJEB41116 (28). SARS-CoV-2 data is publicly available under Accession ID PRJNA817806 (29). Software available at: https://github.com/refresh-bio/SPLASH (30).