3D Printable Modular Soft Elastomers from Physically Cross-linked Homogeneous Associative Polymers

Abstract

Three-dimensional (3D) printing of elastomers enables the fabrication of many technologically important structures and devices. However, there remains a critical need for the development of reprocessable, solvent-free, soft elastomers that can be printed without the need for post-treatment. Herein, we report modular soft elastomers suitable for direct ink writing (DIW) printing by physically cross-linking associative polymers with a high fraction of reversible bonds. We designed and synthesized linear-associative-linear (LAL) triblock copolymers; the middle block is an associative polymer carrying amide groups that form double hydrogen bonding, and the end blocks aggregate to hard glassy domains that effectively act as physical cross-links. The amide groups do not aggregate to nanoscale clusters and only slow down polymer dynamics without changing the shape of the linear viscoelastic spectra; this enables molecular control over energy dissipation by varying the fraction of the associative groups. Increasing the volume fraction of the end linear blocks increases the network stiffness by more than 100 times without significantly compromising the extensibility. We created elastomers with Young’s moduli ranging from 8 kPa to 8 MPa while maintaining the tensile breaking strain around 150%. Using a high-temperature DIW printing platform, we transformed our elastomers to complex, highly deformable 3D structures without involving any solvent or post-print processing. Our elastomers represent the softest melt reprocessable materials for DIW printing. The developed LAL polymers synergize emerging homogeneous associative polymers with a high fraction of reversible bonds and classical block copolymer self-assembly to form a dual-cross-linked network, providing a versatile platform for the modular design and development of soft melt reprocessable elastomeric materials for practical applications.

1. Introduction

Three-dimensional (3D) printing of elastomers enables the fabrication of various technologically important structures and devices, such as soft robots,^1,2 stretchable electronics,³ sensors,^4,5 actuators,^6,7 and dissipative structures.^8,9 Among various kinds of 3D printing methods, direct ink writing (DIW) printing elastomers,^10,11 a process based on materials extrusion, offers great versatility in material selection as long as the materials exhibit rheological properties for extrusion and deposition.¹² For successful DIW, materials should be liquid-like during extrusion to readily flow through the nozzle and then transition to solid-like after exiting the nozzle to retain their as-deposited shape. Thermoplastics, a kind of polymer that undergoes reversible solid-to-liquid-like transitions triggered by solvents and/or heat, are a commonly utilized feedstock for DIW.^13,14 However, most thermoplastics are inherently stiff with Young’s modulus greater than 10⁶ Pa.¹⁵ Lowering the stiffness of elastomers could significantly expand their applications where materials are required to comply with the shape of the object they are in contact with; a prominent example is soft hydrogels.¹⁶⁻¹⁸ However, hydrogels contain a significant amount of water that can evaporate or leach out, thereby compromising the materials properties. As a result, it is of great technological importance to develop 3D printable, soft, yet solvent-free elastomers.

Leveraging the self-assembly of responsive bottlebrush-based triblock copolymers, we previously developed a class of soft elastomers suitable for DIW printing.¹⁹ However, making these elastomers suitable for DIW requires dissolving the polymers in a solvent. After deposition, the solvent evaporates, leading to volumetric shrinkage and warping in the printed structures, ultimately reducing print fidelity. The need for solvents can be circumvented using photocurable bottlebrush polymer melts as inks, which can be solidified by UV light after deposition.²⁰ However, this material design requires sophisticated chemistry, and the printed parts are cross-linked by permanent covalent bonds and are not reprocessable. Additionally, the photo-cross-linking process is sensitive to the intensity of light, which inevitably diminishes as the size of printed objects increases. This may result in uncontrollable cross-linking and mechanical properties. Moreover, in a bottlebrush polymer, the highly overlapping side chains undergo steric repulsion, generating tension that prestrains the bottlebrush backbone.²¹⁻²³ Consequently, bottlebrush elastomers are often brittle.²⁴ It is highly desirable to develop DIW printable elastomers that provide modular control over stiffness and toughness and can be printed without the need for solvents or post-print treatment.

Recently, we developed a new class of associative polymers that carry an unprecedentedly high fraction of stickers that is no less than 0.8 sticker per Kuhn segment.²⁵ The stickers are amide groups that can form pairwise double hydrogen bonds without microphase separation. This starkly contrasts with the behavior observed in most existing associative polymers, where sticker interactions often result in nanoscale aggregations or even microphase separation.^26,27 In our homogeneous associative polymers, the reversible bonds significantly slow down the polymer dynamics without creating a rubbery network. This finding highlights the potential of using associative polymers with high fractions of stickers to control energy dissipation, an important mechanism for toughening elastomers.²⁵

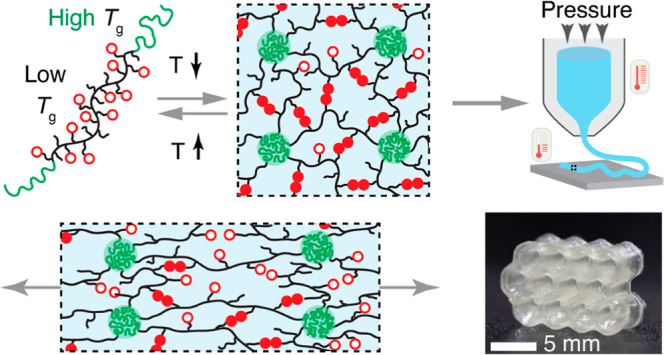
Herein, we developed a new class of DIW printable and reprocessable elastomers with modular controllable stiffness and toughness by physically cross-linking associative polymers with high fractions of stickers. This was achieved by designing a linear-associative-linear (LAL) triblock copolymer consisting of linear polymer end blocks with a glass-transition temperature T_g above room temperature and an associative polymer middle block with a T_g below room temperature (Figure 1a). At room temperature, the distinct blocks microphase separate into a network with the associative polymer being cross-linked by hard glassy nodules (Figure 1b). At relatively low temperatures, the glassy nodules effectively act as strong cross-links to maintain the material’s integrity during deformation, while the associative bonds break and reform to dissipate energy and increase material toughness (Figure 1c). The stiffness of the network is enhanced by increasing the volume fraction of the glassy nodules. At elevated temperatures, the glassy nodules dissociate, allowing the polymers to be suitable for DIW printing (Figure 1d,e). The LAL polymers represent a modular elastomeric ink for DIW printing: the fraction of stickers controls the network toughness, and the volume fraction of the glassy domains determines the network stiffness.

Figure 1.

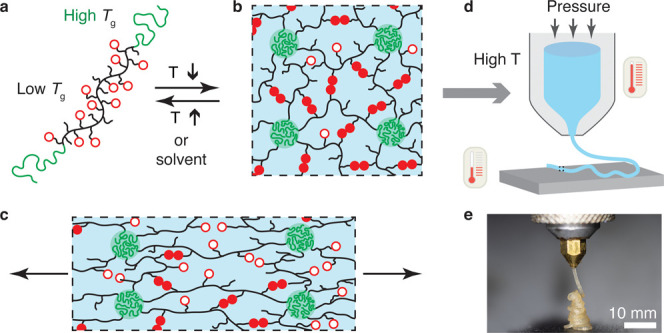
Design concept of DIW printable modular soft elastomers. (a) Illustration of a linear-associative-linear (LAL) triblock copolymer, in which the end blocks are a linear polymer with a relatively high T_g and the middle block is a low T_g polymer carrying many stickers that can form pairwise reversible bonds without aggregating to nanoscale clusters. (b) At relatively low temperatures, the LAL triblock copolymer self-assembles into a microstructure in which the middle block forms an associative polymer network and the end blocks form hard glassy domains. Open circles: open stickers; filled circles: bonded stickers. (c) In the network, the glassy domains effectively act as strong cross-links and maintain the material integrity upon deformation, whereas the reversible bonds break and reform to dissipate energy and enable high toughness. The volume fraction f of glassy domains is adjusted to tune the network stiffness. Thus, the self-assembled network represents a modular elastomeric ink for DIW printing: (1) the fraction of stickers determines the efficiency of energy dissipation or network toughness; (2) the volume fraction of glassy domains determines network stiffness. (d) The glassy domains and reversible bonds dissociate at high temperatures, resulting in a yield-stress fluid suitable for DIW printing. (e) An optical image of extruding the LAL elastomer at 170 °C.

2. Results and Discussion

We denote the LAL triblock copolymer as A_y(B_1−λC_λ)_xA_y, in which y is the number of chemical monomers A per end block, x is the degree of polymerization per middle block, which is a random copolymer consisting of monomers B and C, and λ is the fraction of monomer C in the middle block. In our polymer design, the end A blocks were poly(benzyl methacrylate) (PBnMA), which has a T_g,PBnMA at 54 °C and a melting point, T_m,PBnMA, near 200 °C (Figure S6). For the middle block (B_1−λC_λ)_x, we used hexyl acrylate (HA) as a spacer monomer B and 5-acetamido-1-pentyl acrylate (AAPA) as a sticky monomer C, which was separately synthesized by following previous methods^28,29 (step 1 in Scheme 1 and Polymer synthesis and characterization in Supporting Information Materials and Methods). B and C are essentially the same except that C carries an amide group. Thus, the size of a Kuhn monomer of the middle block nearly does not change with the fraction λ of reversible groups.²⁵ Moreover, an amide–amide hydrogen bond has a strength of ϵ_b ≈ 20k_BT,³⁰ which is weak enough to dissociate at laboratory time scales at room temperature yet strong enough for efficient energy dissipation. Such a balance between dissociation and association is critical to achieving a combination of high toughness and rapid self-healing, as both theoretically³¹ predicted and experimentally³² demonstrated in previous studies. Increasing the fraction of reversible bonds from λ = 0 to λ = 1 results in the increase of T_g from −64.5 to −16.5 °C.²⁵ All the reversible blocks explored in this study have T_g below −40 °C²⁵ and remain elastomeric at room temperature.

Scheme 1. Synthesis of LAL triblock copolymers.

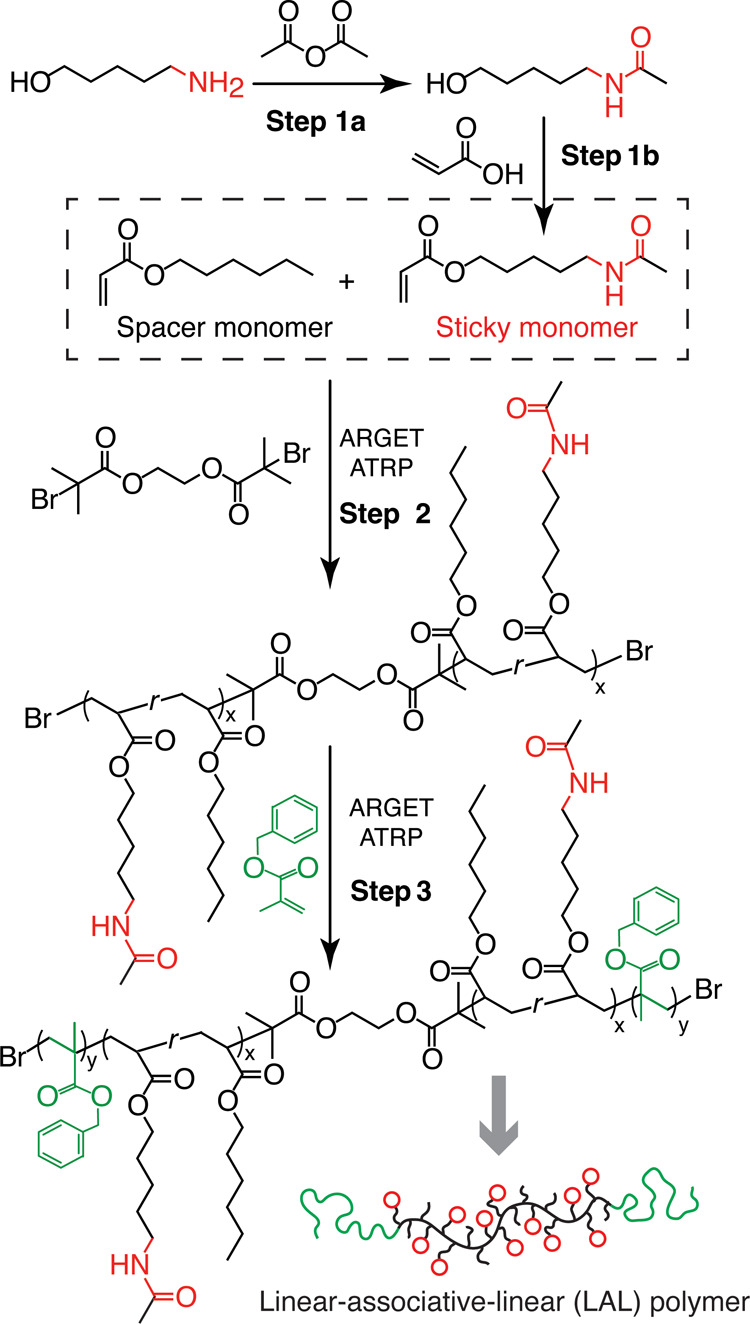
Step 1: synthesis of the sticky monomer that carries an amide group. Step 2: activators-regenerated-by-electron-transfer (ARGET) atom-transfer radical polymerization (ATRP)³³ of the sticky and non-sticky spacer monomers to form a middle block carrying amide groups. Step 3: ARGET-ATRP polymerization of linear PBnMA blocks.

We developed a procedure for synthesizing LAL triblock copolymers with precisely controlled molecular architecture (steps 2 and 3 in Scheme 1 and Polymer synthesis and characterization in Supporting Information Materials and Methods) By adjusting the molar ratio between the sticky monomer AAPA and the spacer monomer HA, we can control the fraction of reversible groups λ (Step 2). By adjusting the molar ratio of the initiator to the spacer and sticky monomers, we can control the absolute molecular weight (MW) of the reversible middle block, M_R. Furthermore, tuning the amount of feed BnMA monomers controls the MW or the volume fraction f of the end PBnMA blocks (step 3). The synthesis method therefore allows precise control over f, λ, and M_R, three of the most important molecular parameters of LAL triblock copolymers.

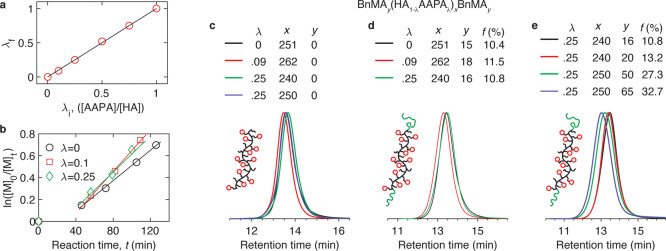
We start with quantifying the reaction kinetics of the spacer and sticky monomers using proton nuclear magnetic resonance spectroscopy (¹H NMR characterization in Supporting Information Materials and Methods). Because both monomers have the same acrylate functional group and a similar molecular structure, they exhibit the same reaction rate, as shown by the same fraction of sticky monomers before and after polymerization (Figure 2a). The conversion rate increases linearly with the reaction time regardless of the fraction of reversible groups explored in this study (Figure 2b). This informs the successful synthesis of a set of LAL triblock polymers with fixed f ≈ 10% but various λ = 0, 0.09, and 0.25 (Figure 2c,d, and synthesis conditions in Table S1), which, respectively, corresponds to an average of 0, 0.8, and 2.2 amide groups per Kuhn segment,²⁵ as well as fixed λ = 0.25 but various f ≈ 10, 13, 27, and 32% (Figure 2e). Importantly, the MW of all polymers is fixed near 40 kg/mol, which is below the critical MW of poly(hexyl acrylate) (PHA), 46 kg/mol, above which the effects of entanglements become noticeable. This set of triblock polymers allows exploration of the effects of reversible bonds on the properties of unentangled polymer networks.

Figure 2.

Characterization of LAL polymers. (a) Dependence of the fraction of reversible groups λ_f in a polymer on the initial feed ratio λ_i between AAPA sticky monomers and HA spacer monomers. (b) Dependence of conversion on the reaction time for different fractions of sticky AAPA monomers. (c) Gel permeation chromatography (GPC) of the reversible middle blocks. (d,e) GPC traces of triblock copolymers: (d) fixed end block volume fraction (f ≈ 10%) but various fractions of reversible bonds (λ = 0, 0.09, and 0.25); (e) fixed λ = 0.25 but increasing f from 10 to 33%.

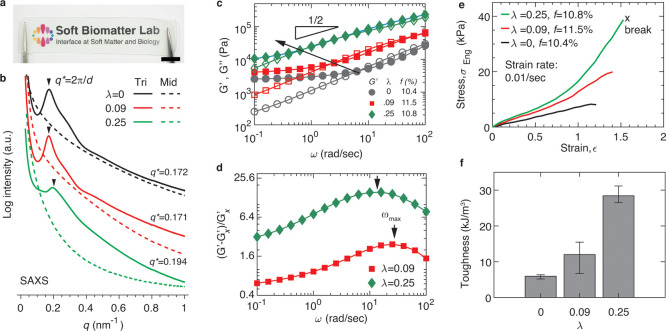
At room temperature, the LAL polymers form a colorless and optically transparent solid, as shown by a representative photograph in Figure 3a. Yet, small-angle X-ray scattering (SAXS) reveals a pronounced primary scattering peak, as shown by the radially integrated 1D intensity profiles in Figure 3b. This peak, denoted as q*, corresponds to the average center-to-center distance between neighboring glassy domains, d = 2π/q*, where the peak location is determined by a previous method.³⁴ Interestingly, as λ increases, the position of q* moves toward higher wavevector numbers. This indicates that the distance between two neighboring spherical domains decreases at higher concentrations of reversible bonds (see Table 1 and SAXS measurements in Supporting Information Materials and Methods). By contrast, in a spherical microstructure self-assembled by conventional triblock copolymers without reversible bonds, to balance the interfacial repulsion between incompatible blocks, the middle block is stretched to a size R that is determined by its MW M_R and the end block volume fraction f: R ∼ f^2/9M^2/3_R.³⁵ Such a difference is likely attributed to the inter- and intramolecular interactions of stickers on the middle block, which help balance the interfacial repulsion between the incompatible end blocks and the middle block to result in less stretched network strands. Further understanding of the effects of reversible bonds on block copolymer self-assembly is beyond the scope of this paper and will be subjected to future explorations. Nevertheless, the LAL polymers self-assemble into an elastomer consisting of a strong network cross-linked by glassy nodules and an associative polymer network cross-linked by hydrogen bonds.

Figure 3.

Introduction of reversible bonds enhances the stiffness and extensibility of polymer networks. (a) Representative optical image of an LAL polymer (sample TV 1, Table 1). Scale bar: 10 mm. (b) Radially averaged 1D SAXS intensity I as a function of the magnitude of wavevector q. The triblock polymers have nearly the same end block volume fraction, f ≈ 10%, but various fractions of amide groups, λ = 0, 0.09, and 0.25. Dashed lines: melts of middle block polymer; solid lines: polymer networks self-assembled by triblock copolymers. The primary scattering peak, q*, is associated with the average center-to-center distance between two neighboring glassy domains (green spheres in Figure 1): d = 2π/q*. (c) Frequency dependence of storage (solid symbols, G′) and loss (empty symbols, G″) moduli of the self-assembled polymer networks measured at 20 °C at a fixed strain of 0.5%. The slope 1/2 corresponds to the Rouse dynamics of the network strands. The arrow represents the trend of the crossover frequency ω_c below which G′ becomes greater than G″. (d) Contribution to shear storage modulus from reversible bonds, (G′ – G^′_x)/G^′_x, in which G^′_x is the shear storage modulus of the polymer without reversible bonds. (e) Dependence of engineering stress, σ_eng, on strain, ϵ, at a fixed strain rate of 0.01/s. (f) Dependence of the tensile toughness on the fraction of amide bonds. Error bar: standard deviation from measurements for the same sample reprocessed using solvents (n = 3).

Table 1. Molecular Parameters of LAL Triblock Copolymers^a.

sample	middle block					triblock			G (kPa)	tensile fracture strain	SAXS
	nHA	nAAPA	ntot	λ	D̵	nBnMA	fBnMA (%)	D̵			q* (nm–1)	d (nm)
TR1	251	0	251	0	1.26	30	10.4	1.28	2.52	1.22 ± 0.02	0.172	36.5
TR2	239	23	262	0.09	1.19	36	11.5	1.23	4.07	1.39 ± 0.05	0.171	36.7
TR3	180	60	240	0.25	1.22	32	10.8	1.26	10.55	1.57 ± 0.05	0.194	32.4
TV1	180	60	240	0.25	1.22	40	13.2	1.28	12.14	1.60 ± 0.17	0.218	28.8
TV2	188	62	250	0.25	1.22	102	27.3	1.35	67.25	0.95 ± 0.15	0.160	39.2
TV3	188	62	250	0.25	1.22	132	32.7	1.33	2730.00	0.82 ± 0.06	0.168	37.4

^an_HA, number of HA repeating units per middle block; n_AAPA, number of AAPA repeating units per middle block; n_tot, total number of repeating units per middle block; n_BnMA, number of BnMA repeating units for each end linear PBnMA blocks; λ, fraction of AAPA repeating units per middle block; f_BnMA, volume fraction of PBnMA end blocks; D̵, polydispersity index (PDI); G, shear storage modulus G′ at 0.1 rad/s; q*, wavenumber of the primary scattering peak; d = 2π/q*, average center-to-center distance between two neighboring glassy domains; TR: triblock copolymers with different fractions of reversible bonds; TV: triblock copolymers with various volume fractions of end blocks. Error: standard deviation for n ≥ 3.

We used a stress-controlled rheometer to quantify the dynamic mechanical properties of the polymer networks. At room temperature, the shear storage modulus G′ of polymer networks is nearly constant at low frequencies, as shown by solid symbols in Figure 3c. We take the value of G′ at the lowest oscillatory shear frequency, 0.1 rad/s, as the network shear modulus G. As λ increases from 0 to 0.25, corresponding to an average of 2.2 amide groups per Kuhn segment,¹⁹G increases by nearly 4 times from 2.52 to 10.55 kPa. This increase suggests that at a relatively high fraction of associative groups the contribution to the network stiffness from reversible bonds dominates the contribution from glassy nodules.

Unlike typical glassy nodules that are permanent at room temperature, the reversible hydrogen bonds can break and reform, slowing down the dynamics of polymer networks. As the fraction of associative groups increases, the relaxation time of the network strand increases. This effect is evident in the reduction of the crossover frequency ω_c, below which G′ becomes higher than G″, as denoted by the arrow in Figure 3c and shown in Figure S7. To quantify the contribution of reversible bonds to the network stiffness, we introduce a parameter (G′ – G^′_x)/G^′_x, in which G^′_x is the shear storage modulus for the network without reversible bonds. As expected, (G′ – G^′_x)/G^′_x becomes higher as λ increases from 0.09 to 0.25 because of the contribution from reversible bonds. Interestingly, the value of (G′ – G^′_x)/G^′_x exhibits a nonmonotonic dependence on the probing frequency (Figure 3d). This behavior is characteristic of reversible polymer networks, in which the fraction of unrelaxed reversible bonds increases at higher frequencies or shorter probing time scales. This trend ends at time scales shorter than the lifetime of a reversible association, as the contribution from reversible bonds to the network modulus is exhausted.³¹

Surprisingly, when λ increases from 0.09 to 0.25, the extent of the increase for (G′ – G^′_x)/G^′_x with frequency remains the same up to ω_max, at which point (G′ – G^′_x)/G^′_x is maximized, as shown by the two nearly parallel curves in Figure 3d. This behavior is attributed to the similar relaxation dynamics of the associative polymers despite different fractions of reversible groups. Because the two polymers carry high fractions of associative groups that are no less than 0.8 sticker per Kuhn monomer, they can be considered as a homopolymer consisting of renormalized Kuhn monomers.²⁵ Thus, all polymers follow the same Rouse dynamics, and the only difference is that the basic time scale—the relaxation time of a renormalized Kuhn monomer τ_s—increases with λ. Recently, we experimentally showed that at room temperature τ_s increases exponentially with the fraction of associative groups: τ_s = τ₀ exp(αλ), in which τ₀ is the monomer relaxation time without associative groups and α is a constant equal to 8.6 ± 1.2.²⁵ It is expected that the Rouse dynamics of a polymer with λ reversible groups slow by a factor of exp(αλ). Consistent with this understanding, the crossover frequency ω_c inversely scales with the monomer relaxation time: ω_c(λ) = ω_c(0)exp(−9λ), as shown by the solid line in Figure S7. Together, our results demonstrate that the addition of reversible bonds slows polymer dynamics and makes the polymer networks more dissipative.

The enhanced energy dissipation was further confirmed by uniaxial tensile tests. Introducing associative groups increases the network breaking strain from 1.22 ± 0.02 to 1.57 ± 0.05 (Figure 3e) and the network tensile toughness by nearly 5 times from 5.90 ± 0.66 to 28 ± 2.42 kJ/m³ (Figure 3f). However, the absolute values of stiffness and toughness are relatively low compared to the existing double-network³² or interpenetrating-network elastomers,³⁶ which approximately have a stiffness of 10⁶ Pa and a tensile toughness of 10⁶ J/m³.

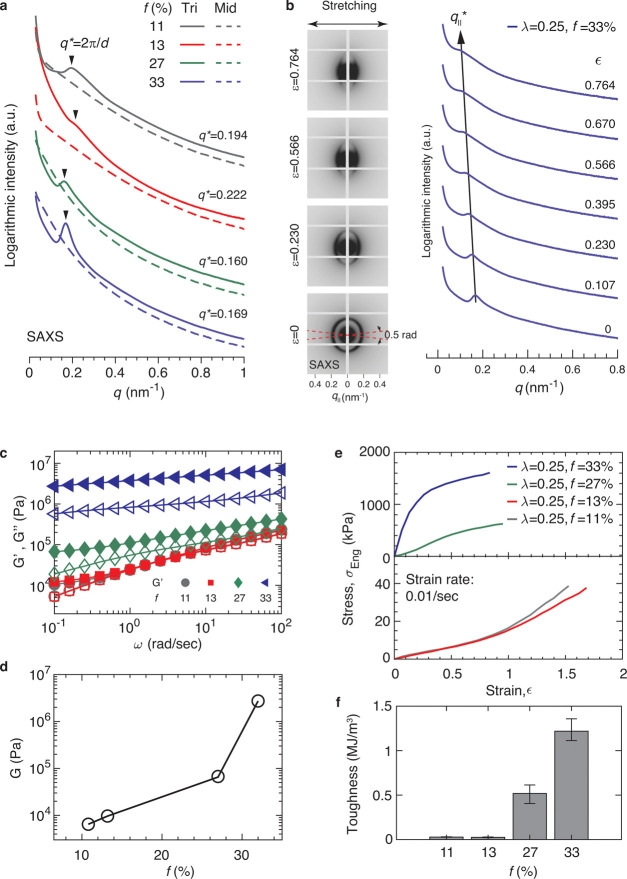
To further improve the network mechanical properties, we increased the volume fraction of the glassy domains. In block copolymer self-assembly, at high volume fractions, the glassy domains may percolate throughout the whole microstructure to result in a high stiffness.^37,38 To this end, we used the middle block with the highest fraction of reversible bonds (λ = 0.25) and increased f from 11 to 33%. As f increases, the primary SAXS scattering peak becomes more pronounced (Figure 4a). For the sample with f = 33%, in situ SAXS/tensile measurements reveal the increase of the distance between two neighboring glassy domains along the direction of stretching, as shown by the shift of the q* toward lower wavenumbers in Figure 4b. Moreover, the primary scattering peaks become more broad and less pronounced, suggesting less ordered glassy domains along the direction of stretching. Yet, the polymer remains transparent because the average center-to-center distance between two glassy domains, ∼37 nm, is much smaller than the wavelength of visible light (Table 1). Macroscopically, as f increases, G′ becomes much larger than G″ over a wide range of shear frequency (Figure 4c) and the loss factor becomes smaller (Figure S8), suggesting that the network becomes less dissipative. However, the network stiffness increases by more than 2 orders of magnitude from ∼10 kPa to ∼3 MPa (Figure 4d). As a result, although the network becomes less stretchable (Figure 4e), the tensile toughness increases by nearly 40 times from 28 ± 2.42 kJ/m³ to 1.2 ± 0.12 MJ/m³ (Figure 4f).

Figure 4.

Increasing the volume fraction of glassy domains dramatically enhances polymer stiffness and toughness. (a) SAXS patterns for the triblock polymers with the same MW of the middle block and fraction of amide groups (λ = 0.25) but various end block volume fractions, f ≈ 11, 13, 27, and 33%. (b) In situ tensile/SAXS test of the sample with f = 33% and λ = 0.25. ϵ is the tensile strain. (c) Frequency dependence of storage (solid symbols, G′) and loss (empty symbols, G″) moduli of the self-assembled polymer networks measured at 20 °C at a fixed strain of 0.5%. (d) Dependence of the equilibrium shear modulus G on f. (e) Stress–strain curves for polymer networks at room temperature. (f) Tensile toughness of polymer networks with different fractions of amide groups. Error bar: standard deviation from measurements for the same sample reprocessed using solvents (n = 3).

Unlike conventional elastomers that are cross-linked by permanent covalent bonds, LAL polymers are a kind of thermoplastic-like elastomers physically cross-linked by nodules of glassy polymers. Similar to the melting of traditional thermoplastics, these nodules are expected to dissociate at high temperatures. We explore the effects of temperature for two polymers with nearly the same end block volume fraction of f ≈ 31% but with different fractions of associative groups of λ = 0 and λ = 0.25. The end block volume fraction of 31% is close to the highest value explored in this study (Table 1); this corresponds to the LAL polymer possessing the strongest glassy domains. At room temperature, these two polymers exhibit shear moduli of 48 and 375 kPa, respectively (Figure S9). At a relatively high temperature of 170 °C, which is much higher than the glass transition temperature T_g ≈ 54 °C but lower than the melting point T_m ≈ 200 °C of end PBnMA blocks, the polymers remain a solid with G′ of ∼2 kPa (λ = 0.25) and 700 Pa (λ = 0), much larger than G″ of ∼500 Pa (λ = 0.25) and 250 Pa (λ = 0) (Figure S10). However, both polymers become a yield-stress fluid, so that they transition from solid to liquid above a critical stress (Figure S10). These behaviors are consistent with the creep/recovery measurements, which show that the LAL polymer is an elastic solid at 20 °C but can flow like a liquid under a shear stress of 200 Pa at 200 °C (Figure S11). Importantly, at 170 °C, the yield stresses, 829 Pa (λ = 0.25) and 459 Pa (λ = 0), are low enough that the polymers can be readily extruded but high enough to maintain their as-deposited shape (Figure 1e).

To enable DIW printing of the LAL polymer at elevated temperatures, we integrated a heated extruder into a customized linear driving stage. The heated extruder consists of a metal syringe surrounded by a heating jacket and a stepper motor that mechanically drives the syringe plunger to control the rate of extrusion. We directly loaded chunks of the solid LAL polymer into the syringe barrel, heated the syringe to 170 °C, and extruded the polymer onto the build plate that was maintained at 80 °C. The temperature of the build plate was higher than the T_g = 54 °C of the PBnMA blocks, so that the extruded filaments can establish relatively strong adhesion among their neighbors. Importantly, we kept the extrusion speed relatively low at 0.3 mm³/s to avoid die swelling; this often occurs at high extrusion speeds and results in extrudate with diameter much larger than the nozzle diameter to impair printing fidelity.^39,40 The combination of precise control over the extrusion speed and temperature produces smooth and continuous extrusion of LAL filaments, as shown by a representative image in Figure 1e.

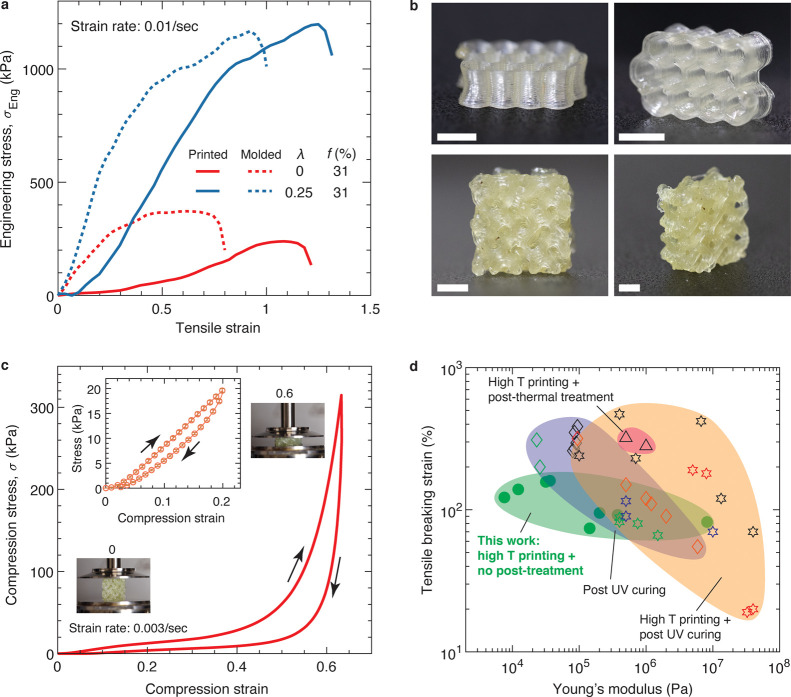
To evaluate the quality of DIW printing, we compared the mechanical properties of the printed tensile bars to those of their molded counterparts. The printed specimens exhibit tensile moduli of 652.5 and 89.7 kPa for λ = 0.25 and λ = 0, respectively (Figure 5a, Table S3). The tensile moduli are lower than the cast specimens, likely attributed to the imperfect welding between neighboring filaments, a caveat common to filament-based DIW printing.⁴¹ As expected, introducing associative groups significantly enhanced the mechanical properties of printed tensile bars, increasing the tensile breaking strain from 1.15 to 1.25 and the tensile strength from 239 to 1190 kPa with the corresponding tensile toughness increasing from 132 to 939 kJ/m³.

Figure 5.

DIW printing of LAL polymers to produce highly deformable 3D structures. (a) Stress–strain behavior of 3D printed and molded tensile bars of LAL polymers tested at room temperature and 0.01/s strain rate. (b) Photos of honeycomb (upper) and gyroid (lower) structures printed using an LAL polymer (f = 31%, λ = 0.25%). The light yellowish color is attributed to reprocessing of the polymers at high temperatures and contamination by the extruder. Scale bars: 5 mm. (c) Compression stress–strain behavior of the 3D printed gyroid in (b). The compression strain rate is 0.003/s. Inset: cyclic compression–release profile exhibits a hysteresis for the deformation of 20%. Error bar: standard deviation for n = 4. (d) Ashby-type plot comparing elastomers for solvent-free DIW printing based on tensile breaking strain and Young’s modulus. Filled green circles: our modular soft elastomers; other symbols: literature data (Table S2).

Using the same printing parameters, we successfully transformed the LAL polymer (f ≈ 31%, λ = 0.25) into more complex 3D structures. Specifically, we printed a 3D honeycomb structure with a layer thickness of 300 μm (Figure 5b, upper panel; Movie S1). Due to the melt-based processing approach, there is no observable volumetric shrinkage in the printed structure, in contrast to the significant shrinkage of ∼50% in prior solvent-assisted DIW printing of elastomers.¹⁹ Leveraging the inherent reprocessability of the LAL polymers, we recycled the printed honeycomb structure and used it as the feedstock for printing a gyroid, a type of 3D structure with a complex internal feature that is typically not possible to create by conventional molding. Because the printing process is solvent-free and the deposited material does not shrink or warp significantly, we can create a gyroid with good fidelity, as shown in the bottom panel of Figure 5b and Movie S2.

To explore the mechanical properties of the printed gyroid, we performed a uniaxial compression test at a fixed strain rate of 0.003/s. Interestingly, the stress–compression profile reveals two distinct regimes. At compressive strains below ∼30%, the compressive stress increases nearly linearly with strain and corresponds to an apparent elastic modulus of 18 kPa. When comparing the loading and unloading cycles, the printed gyroid exhibits a hysteresis associated with 25% energy dissipation (inset, Figure 5c). This energy dissipation is primarily attributed to the breakage and reformation of the reversible hydrogen bonds. Above 30% strain, the stress begins to increase more rapidly with a maximum stress of 325 kPa reached at 60% strain, the highest value due to the instrumentation limit in measuring stress. The corresponding energy dissipation efficiency is remarkably high of 62%. Importantly, the printed gyroid can be repeatedly compressed up to 60% compression strain without noticeable damage or plastic deformation, as shown by the cyclic compression test in Figure 5c and Movie S3. Taken together, our results demonstrate that the LAL elastomers are amenable to the solvent-free DIW printing of complex, reprocessable, deformable, and dissipative 3D structures without the need for a sacrificial supporting matrix or post-curing.

3. Conclusions

We developed melt reprocessable and DIW printable modular soft elastomers based on physically cross-linked associative polymers with high fractions of reverisble bonds. The developed linear-associative-linear polymer synergizes the emerging homogeneous associative polymers and the existing success of block copolymer self-assembly (ref (42) and references therein) to produce elastomers that span 3 orders of magnitude in Young’s modulus from ∼8 kPa to ∼8 MPa while maintaining the tensile breaking strain around 150% (Figure 5d). At elevated temperatures, the self-assembled glassy nodules and reversible bonds dissociate, leading to a reversible solid-like to liquid-like transition under shear stress. This property makes the self-assembled polymer networks suitable for DIW without the need for any additional solvents. The lower limit of stiffness for our elastomers is more than three times lower than the softest solvent-free DIW elastomers in literature (Figure 5d),²⁰ about 20 times softer than the solvent-free DIW printable polymer composites (Figure S12),³ and more than 6 times softer than the currently available thermoplastic polymers printed using other additive manufacturing techniques (Figure S13).⁴³ Moreover, because the networks are physically cross-linked by glassy nodules, they are intrinsically reprocessable with heating or using solvents such as dichloromethane, as visualized by the optical images in Figure S14a. Compared to the original polymer, the reprocessed polymer exhibits nearly the same mechanical properties (Figure S14b). Despite their inherent melt reprocessability, these polymers are mechanically stable up to a relatively high temperature of 150 °C (Figure S15). The exceptional combination of a wide range of accessible mechanical properties, reprocessability, and thermostability highlights the potential of linear-associative-linear polymers as a new class of soft DIW printable elastomers.

We note a few open questions that should be addressed in future explorations. Our polymers explored here are limited in stretchability up to 150%. This is likely attributed to the relatively low MW of the associative polymers, which are chosen to ensure that the middle blocks remain unentangled. Using longer associative polymers would enhance the stretchability of the elastomers.⁴⁴ In the context of polymer science, the influence of the reversible associations on block copolymer self-assembly has yet to be understood. Despite these unanswered questions, the introduced LAL polymers provide a promising platform for the modular design and development of reprocessable polymeric elastomers for practical applications.

4. Experimental Section

4.1. Materials

HA (98%), acetic anhydride (≥98%), 5-amino-1-pentanol (≥92%), acrylic acid (99%), K₂CO₃ (≥99%), N-(3-(dimethylamino)propyl)-N′-ethylcarbodiimide hydrochloride (98%), N,N-diisopropylethylamine (>99%), benzyl methacrylate (96%), copper(II) chloride (99.999%), tris[2-(dimethylamino)ethyl]amine, ethylene bis(2-bromoisobutyrate) (97%), tin(II) 2-ethylhexanoate (92.5–100%), and anisole (≥99.7%) were purchased from Sigma-Aldrich and used as received. Methanol (Certified ACS), ethyl acetate (Certified ACS), hexanes (Certified ACS), dichloromethane (Certified ACS), diethyl ether (Certified ACS), dimethylformamide (Certified ACS), tetrahydrofuran (THF, Certified ACS), and THF (HPLC) were purchased from Fisher and used as received.

4.2. Polymer Synthesis and Characterization

The synthesis of a LAL triblock copolymer consists of two steps: (1) synthesis of the reversible middle block and (2) using the middle block as a macroinitiator to grow the two end linear blocks. We synthesized the reversible block by copolymerizing HA with AAPA which carries an amide group at one of its two ends and serves as the sticky monomer. Detailed synthesis procedures are presented in the Supporting Information, and the reaction conditions for the synthesis are summarized in Table S1.

4.3. ¹H NMR Characterization

We used 600 MHz ¹H NMR (Varian, INOVA) to determine the conversion of HA and AAPA and the volume fraction of PBnMA. Chemical shifts for ¹H NMR spectra are reported in parts per million (ppm) compared to a singlet at 7.26 ppm in CDCl₃. Details are presented in the Supporting Information.

4.4. Gel Permeation Chromatography

We used gel permeation chromotography (GPC) to determine the polydispersity index (PDI) of polymers. GPC measurements were performed using a TOSOH EcoSEC HLC-8320GPC system with two TOSOH Bioscience TSKgel GMH_HR-M 5 μm columns in series and a refractive index detector at 40 °C. HPLC grade THF was used as the eluent with a flow rate of 1 mL/min. The samples were dissolved in THF with a concentration around 5 mg/mL.

4.5. Rheology

Rheological measurements were performed using a stress-controlled rheometer (Anton Paar MCR 302) equipped with a plate–plate geometry of diameter 8 mm. We exploited the solvent reprocessability of the LAL polymer to prepare samples in situ. Specifically, we dissolved LAL polymers in dichloromethane to make a homogeneous mixture with a concentration of 300 mg/mL. We pipetted about 1 mL of solution onto the bottom plate, allowed the solution to dry in air at room temperature, and then heated the bottom plate to 40 °C for an additional 20 min. This allowed us to prepare a relatively thick film of ∼0.3 mm without the formation of cavities due to the evaporation of solvent. Then, we lowered the upper plate and trimmed the excess sample at the edge of the geometry.

For frequency sweep at various temperatures, we fixed the oscillatory shear strain at 0.5% while varying the shear frequency from 0.1 to 100 rad/s. When changing the temperature, we used a slow temperature ramping rate of 1 °C/min and waited for 2 min at each temperature point before collecting data; this ensured that the self-assembled microstructure is in equilibrium at each temperature point.

4.6. Tensile Test

To prepare a sample for the tensile test, we dissolved a triblock copolymer in dichloromethane at a concentration of 300 mg/mL in a glass vial. Then, we transferred the solution to a Teflon mold and allowed the solvent to slowly evaporate for 24 h to avoid the formation of bubbles in the sample. The polymer film with a thickness of 0.5 mm was formed and peeled off from the Teflon mold. The film was cut into three identical rectangular pieces with a length of 1.5 cm and a width of 2.5 mm. The two ends of the film were glued to two pieces of hard paper using epoxy with a gap of 5 mm; this was done to avoid possible damage to the sample from grips during the tensile test.

We performed tensile tests using a Mark-10 ESM303 Motorized Test Stand equipped with a 2.5 N load cell. The two hard papers were fixed to the load cell and moving stage, respectively. Uniaxial tensile measurements were conducted at room temperature in air under a strain rate of 0.01 s^–1. The strain was measured by monitoring the change of the tensile stress using MESUR Mark-10 software. Each measurement was repeated at least three times.

To demonstrate the reprocessability of the self-assembled elastomers, we cut the elastomer into small pieces, dissolved them in dichloromethane, and redried the solution to obtain an elastomer (Figure S9a). From the tensile test, the solvent-reprocessed elastomer exhibits negligible changes in stress–strain curves, as shown by Figure S9b.

4.7. SAXS Measurements

To prepare a sample for SAXS measurement, we dissolved a triblock copolymer in dichloromethane at a concentration of 300 mg/mL in a glass vial. Then, we added 150 μL of solution on a 1.2 × 1.2 cm glass substrate and allowed the solvent to slowly evaporate for 24 h. For each sample, the smallest dimension after solvent evaporation is larger than 0.5 mm, more than 10⁴ times the size of a triblock copolymer; this prevents the substrate or boundary effects on self-assembly.

We used the Soft Matter Interfaces (12-ID) beamline⁴⁵ at the Brookhaven National Laboratory to perform SAXS measurements on annealed bulk polymers. The sample-to-detector distance was 8.3 m, and the radiation wavelength was λ = 0.77 Å. The scattered X-rays were recorded using an in-vacuum Pilatus 1 M detector, consisting of 0.172 mm square pixels in a 941 × 1043 array. The raw SAXS images were converted into q-space, visualized in Xi-CAM software⁴⁶ and radially integrated using a custom Python code. The 1D intensity profile, I(q), was plotted as a function of the scattering wave vector, |q⃗| = q = 4πλ^–1 sin(θ/2), where θ is the scattering angle.

The LAL and control triblock copolymers with a volume fraction f of PBnMA around 0.11 were self-assembled into a spherical structure, as indicated by the characteristic peaks in Figure 3b. The domain distance calculated from SAXS measurements almost did not change when λ was increased to 0.09, but it abruptly decreased from 36.5 to 32.4 nm when λ was increased to 0.25 (Table 1). This contrasts with the behavior of conventional triblock copolymers without reversible bonds, in which the domain distance is constant at a fixed molecular weight and weight fraction of end blocks. Such a difference is likely attributed to the intramolecular interactions of stickers on the middle block, which help balance the interfacial repulsion between the incompatible end and middle blocks to result in less stretched network strands.

4.8. DIW Printing

Unlike classical stiff plastics for filament-based 3D printers, our polymers are soft and can be easily deformed. To this end, inspired by previously reported method for printing liquid crystal elastomers,⁴⁷ we developed a high-temperature DIW printing platform by integrating a heated printhead (modified from Hyrel TAM-15) into a 3-axis Aerotech gantry (AGS1500). Within the heating jacket of the extruder, we loaded a metal syringe with a plunger actuated by a stepper motor (Aerotech SM35). Importantly, the step motor for extrusion is independent of yet integrated into the controlling software for the gantry. This feature allows for precise control over the extrusion speed in relation to the moving speed of the printhead to enable smooth, consistent deposition of the LAL polymer filaments as the printhead accelerates and decelerates.

In a typical printing experiment, we cut the LAL polymer sample (λ = 0.25; f = 0.31) into small pieces and then loaded them into the syringe barrel equipped with a nozzle diameter of 500 μm. We heated the extruder to 170 °C, slightly lower than the melting point, T_m ≈ 200 °C, but much higher than the glass-transition temperature, T_g ≈ 54 °C, of the glassy nodules in the dual-cross-linked network. To avoid typical die swell in polymer extrusion, in which the extrudate diameter is usually greater than the channel size,³⁹ we used a relatively low extrusion rate of 0.3 mm³/s to ensure that the extruded filament has a diameter comparable to the nozzle diameter. Synchronizing with the extrusion rate, we used a translation speed of the printhead at 100 mm/min. Moreover, we set the spacing between extruded beads at 400 μm, slightly smaller than the diameter of the extruded filament. Additionally, we used a heated build plate and maintained its temperature at 80 °C, slightly higher than T_g ≈ 54 °C but significantly lower than T_m ≈ 200 °C of the glassy nodules in the dual-cross-linked network. These printing parameters allow a deposited filament to immediately solidify while facilitating welding between neighboring filaments, improving the strength of the interface between layers in a printed object. Using the same set of printing parameters, we successfully created tensile bars, honeycombs, and gyroid structures with good fidelity.

4.9. Compression Tests

Because our elastomers are soft, the force required to deform the material is very small. To this end, we used a rheometer (Anton Paar MCR 302) with a normal force resolution of 0.5 mN to perform the compression tests. The sample, in the form of a printed cubic gyroid, was fixed onto the bottom geometry. We lowered the upper geometry to contact the sample, at which the normal force is slightly above 0. During the compression measurements, the moving profile of the upper plate was preset to exert cyclic and subsequent large compression at a fixed strain rate of 0.003/s. We recorded the normal force, gap size, and time and calculated the stress and strain based on the premeasured dimensions of the samples. The measurement was conducted with the compression strain up to 60%, which is the highest value afforded by our instrument due to its limitation in measuring stress.

4.10. Yield-Stress Behavior Measurement

To evaluate the yield-stress behavior of LAL polymers at high temperatures, we used a rheometer (Anton Paar MCR 302) equipped with a plate–plate geometry of 8 mm diameter. For sample preparation, we dissolved LAL polymers in dichloromethane, creating a homogeneous mixture with a concentration of 300 mg/mL. Subsequently, we pipetted 1 mL of the solution onto the bottom plate, covering it to create a closed environment, allowing the solution to dry slowly at room temperature. During the measurement, we maintained a constant temperature of 170 °C and an oscillatory frequency of 1 rad/s while varying the shear rate from 0.01 to 10⁴%. To ensure the equilibrium of the self-assembled microstructure at the desired temperature, we used a slow temperature ramping rate of 1 °C/min and allowed 2 min of waiting period at 170 °C before data collection. This ensured the self-assembly of the end-blocks at elevated temperatures.

4.11. Differential Scanning Calorimetry

We determined the glass-transition temperature T_g,PBnMA and the melting temperature T_m,PBnMA of the LAL polymer (f = 31%; λ = 0.25) using a differential scanning calorimeter (DSC Q20, TA Instruments). Before characterization, the sample was dried at room temperature (∼293 K) under vacuum (30 mbar) for at least 24 h. A standard aluminum DSC pan was used for the measurements with approximately 10 mg of sample loaded. The sample was first heated from 20 to 250 °C at 10 °C/min, followed by cooling at 5 °C/min to 20 °C with the temperature modulation of 1.2 K every 60 s and then heating at 5 °C/min to 250 °C. Our results show a well-defined T_m at 202 °C (Figure S6a). Moreover, the LAL polymer exhibits a T_g at 54 °C (Figure S6b).

Note that when determining the T_g, we followed the conventional way by using the second heating curve DSC from measurements, as it often requires a heating/cooling cycle to erase the thermal history of polymers. By contrast, when determining the T_m, we used the first heating curve from DSC measurements. This is because, for triblock copolymers with high end block volume fractions, such as our system, the ability for the end blocks to crystallize depends on appropriate annealing. In our measurements, we used a combination of solvent and temperature annealing to equilibrate the sample, as detailed in our previous publications.³⁴ However, the heating–cooling process involved in the DSC measurements is insufficient to equilibrate the polymer. Indeed, the melting peak disappears after the first heating (Figure S6b).

4.12. Creep/Recovery Measurement

To perform the creep/recovery measurement, we used a rheometer (Anton Paar MCR 302) equipped with a plate–plate geometry with a diameter of 8 mm. For sample preparation, we dissolved an LAL polymer (f = 31%, λ = 0.25) in dichloromethane at a concentration of 300 mg/mL in a glass vial. We then pipetted 1 mL of solution onto the bottom plate, covering it to create a closed environment to dry it slowly at room temperature. We applied the stress for 300 s, released the load, and continued to monitor the deformation of the polymer for 600 s.

In the first set of measurements, we fixed the shear stress at 200 Pa but increased the temperature from 20 to 200 °C. At 50 °C, slightly below the T_g,PBnMA = 54 °C, the residual strain remains small at 1.5% (thick red line, Figure S11a). By contrast, at 200 °C, close to the T_m,PBnMA, the polymer exhibits a significant residual strain of 60%. Interestingly, under a constant shear stress of 200 Pa, the polymer flows at a strain rate of 1.45 × 10^–3/s (Figure S11b). This finding is consistent with our discovery that the polymer is a yield-stress fluid at high temperatures (Figure S10).

In the second set of measurements, we fixed the temperature at 20 °C but increased the shear stress from 100 to 200 Pa. At 100 Pa, the polymer exhibits elastic deformation, and the deformation is fully recovered once the stress is unloaded, as shown by the thick blue line in Figure S11c. When being applied to a relatively high stress of 200 Pa, the polymer does not recover to its initial state and exhibits plastic deformation. Yet, the extent of plastic deformation is very small of 1% (think black line, Figure S11c). These results show that the polymer can nearly recover to its original shape at room temperature.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acspolymersau.3c00021.

• Procedures for the synthesis of middle block and triblock polymers; methods of using ¹H NMR to determine the degree of polymerization of middle block and triblock polymers; supporting data for GPC, rheological measurement, creep-recovery measurement, tensile test, reprocessability test, and SAXS measurements; ¹H NMR spectra of all middle block and triblock polymers; and list and references of existing solvent-free polymers for DIW printing (PDF)

• 3D DIW printing of a honeycomb structure (MP4)

• 3D DIW printing of a cubic gyroid structure (MP4)

• Cyclic compression test of a printed gyroid (MP4)

Author Contributions

M.K., S.N., and D.A.R. contributed equally. L.H.C., S.N., M.K., and D.R. designed the research. S.N., M.K, D.R., and L.H.C. performed the research. S.N., L.H.C., M.K., and D.R. analyzed the data. B.H., J.Z., G.F., and M.Z. helped with SAXS/WAXS measurements and data analysis. L.H.C. and M.K. wrote the paper. All authors reviewed and commented on the paper. L.H.C. conceived and supervised the study. CRediT: Myoeum Kim data curation, investigation, methodology, visualization, writing-review & editing; Shifeng Nian data curation, formal analysis, investigation, methodology, visualization, writing-review & editing; Daniel A. Rau data curation, investigation, methodology, writing-review & editing; Baiqiang Huang investigation, methodology; Jinchang Zhu investigation, methodology; Guillaume Freychet investigation, methodology; Mikhail Zhernenkov investigation, methodology; Li-Heng Cai conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, project administration, supervision, visualization, writing-original draft, writing-review & editing.

The authors declare the following competing financial interest(s): L.H.C. and S.N. have filed a patent application (U.S. Provisional Patent Application Serial No. 63/345,749) based on linear-associative-linear polymers.

Special Issue

Published as part of ACS Polymers Auvirtual special issue “2023 Rising Stars”.