Geometric framework for statistical analysis of eye tracking heat maps, with application to a tobacco waterpipe study

Abstract

Health warning labels have been found to increase awareness of the harmful effects of tobacco products. An eye tracking study was conducted to determine the optimal placement and type of a health warning label on tobacco waterpipes. Participants viewed images that contained one of (1) four waterpipes, (2) three different types of warning labels, (3) placed in three locations. Typically, statistical analysis of eye tracking data is conducted based on summary statistics such as total dwell time, duration score, and number of visits to an area of interest. However, these summary statistics fail to capture the complete variability in a participant's eye movement. Instead, we propose to estimate heat maps defined on the entire image domain using the raw two-dimensional coordinates of eye movement via kernel density estimation. For statistical analysis of heat maps, we adopt the Fisher–Rao Riemannian geometric framework, which enables computationally efficient comparisons of heat maps, statistical summarization and exploration of variability in a sample of heat maps, and metric-based hierarchical clustering. We apply this framework to eye tracking data from the tobacco waterpipe study and comment on the results in the context of the optimal placement and type of health warning labels on tobacco waterpipes.

1. Introduction

Exposure to misleading tobacco packaging and pro-tobacco advertising can lead to misinformation and misperception about potential health risks associated with the use of tobacco products [3,11,29,31]. Health warning labels on packaging and in advertisements can help increase awareness of the harmful effects of these products [13,14]. However, the particular placement and type of warning label can generate vastly different responses from a tobacco user. Eye tracking studies, wherein a participant is presented with an image (or video) and measurements of their eye movements are recorded, have become an effective tool in assessing the variability associated with people's attentiveness to different placements and types of warning labels on tobacco products shown in the image. In particular, eye tracking studies have been used to avoid the issue of recall error, e.g. of survey-based studies, since they record direct measures of attention [19,48]. In the context of tobacco regulation, current statistical approaches for assessing attention in eye tracking studies have primarily focused on crude summaries generated from the eye tracker such as the number of saccades (rapid movement between fixation points), total fixation times, and total number of fixations in an area of interest (AOI) in an image [5,21,25–27,33,45,47]. Fixation points are calculated using eye movement event-detection algorithms from raw x and y eye coordinates; see [2] for an evaluation and discussion of various eye movement event-detection algorithms. Henceforth, we refer to raw x and y eye coordinates, i.e. the raw eye tracking data without saccades, simply as raw eye coordinates.

A qualitative way to analyze attention is by using a heat map, which is a richer representation of eye tracking data and is used to represent the full behavior of a person's eye movement across an image domain [42]. A common way of producing a heat map is from a fixation map, which is an ordered set of fixation points, sized according to the viewing duration, that are connected by lines that represent saccades. In other words, a fixation map represents the full ordered trajectory of a person's eye movement, while its corresponding heat map generally ignores the ordering of fixation points. Thus a heat map can be viewed as a summary of a fixation map. A major benefit of the heat map representation, compared to a fixation map, is its ability to better separate different levels of observation intensity, by using color mappings or varying transparency levels. Due to proprietary restrictions, specifications for the eye movement event-detection algorithms are not always provided, making results difficult to reproduce [30]. Beyond eye tracking, heat maps have been used in various imaging applications including robot navigation [34], transport geography [49], group activity recognition [23], predictions of thermal comfort [10], biopsy [12], and fire risk analysis [24]. However, each application utilizes its own definition of a heat map. As mentioned earlier, heat maps are most commonly used for qualitative assessment of the data with a primary role in data visualization.

In this work, we seek a definition of a heat map that can be estimated from raw eye coordinates and that is amenable to quantitative statistical analysis. We derive heat maps via kernel density estimation (KDE) applied to raw eye coordinates. The proposed heat map representation eliminates the need to calculate fixations and consequently avoids the use of eye movement event-detection algorithms. In our implementation of KDE, we use a product of two support constrained Gaussian kernels as the smoothing function, and Silverman's rule with a robust estimate for the standard deviation to select the optimal value of the bandwidth parameter [20,39,41]. Various methods have been proposed to determine the optimal bandwidth size, with plug-in selectors, cross-validation selectors, and normal optimal smoothers proving very useful for a wide range of data sets [6,7,15,35,40,41]. Our choice of Silverman's rule for the smoothing bandwidth parameter was determined based on the sparsity of the data and primary interest in smooth estimated heat maps to represent a qualitative measure of participants' overall attention patterns. Thus our definition of a heat map is a nonparametric, bivariate probability density function (pdf) over the image domain. For statistical analysis of heat maps, we use a Riemannian geometric framework based on the nonparametric Fisher–Rao metric, which has shown promise in multiple application domains [22,28,32,36,37,44]. As seen later, this framework allows us to (1) compare heat maps via a formal geodesic distance on the space of pdfs, (2) summarize a sample of heat maps using their mean and principal component analysis-based directions of variability, and (3) cluster heat maps according to their similarity. For each of the tasks, we additionally provide effective visualizations of the generated quantitative results. The proposed framework is applied to eye tracking data from a study that considered an optimal placement of health warning labels on various types of waterpipes (also commonly referred to as hookah pipes) [21].

The rest of this paper is organized as follows. Section 2 describes the Fisher–Rao Riemannian-geometric framework for statistical analysis of heat maps. Section 3 describes the waterpipe eye tracking study and associated data that motivates our analysis. Section 4 applies the presented methodology to analyze the effectiveness of different placements and types of health warning labels for four waterpipes. Section 5 contains a brief discussion and directions for future work.

2. Statistical analysis framework for heat maps

Our representation of a heat map as a nonparametric, bivariate pdf allows us to exploit an existing metric-based statistical framework for analyzing pdfs. In particular, we use the Riemannian-geometric approach based on the Fisher–Rao metric. Details of this framework for univariate pdfs are provided in [43,44]. Here, our focus lies in specifying this framework for bivariate pdfs.

Each heat map is a pdf with domain corresponding to the image domain. Without loss of generality, we rescale the domain of each image to $[0,1{]}^2$, resulting in a representation space of heat maps given by $\mathcal{F}=\{f:[0,1{]}^2\to {\mathbb{R}}_{>0}\mid {\int }_0^1{\int }_0^{1}f(x,y)\mathrm{d}x\mathrm{d}y=1\}$. A natural metric structure on $\mathcal{F}$ is given by the Fisher–Rao (FR) Riemannian metric. Loosely speaking, a Riemannian metric on $\mathcal{F}$ is a family of smoothly varying inner products on tangent spaces of $\mathcal{F}$. Thus, to define the FR metric, we first define the tangent space to $\mathcal{F}$ at a heat map $f\in \mathcal{F}$ as $T_f\left(\mathcal{F}\right)=\{\mathrm{\delta f}:[0,1{]}^2\to \mathbb{R}\mid {\int }_0^1{\int }_0^1\mathrm{\delta f}(x,y)\mathrm{d}x\mathrm{d}y=0\}$; intuitively, the tangent space contains all possible perturbations of the heat map f. Then, for two tangent vectors $\delta f_1,\delta f_2\in T_f\left(\mathcal{F}\right)$, the FR Riemannian metric is defined as

$$\langle \langle \delta f_1,\delta f_2\rangle {\rangle }_f={\int }_0^1{\int }_0^1\delta f_1(x,y)\delta f_2(x,y)\frac{1}{f(x,y)}\mathrm{d}x\mathrm{d}y.$$ (1)

Importantly, the FR Riemannian metric (and associated geodesic distance) is invariant to smooth, one-to-one transformations of pdfs [8]. But, as clearly seen in Equation (1), the metric changes for every point $f\in \mathcal{F}$, making computation of geodesic paths and distances under this metric a difficult task; one has to resort to numerical algorithms, which tend to be computationally inefficient in practice.

However, as shown by Bhattacharya [4], a simple square-root transformation simplifies the complicated FR Riemannian metric to the standard ${\mathbb{L}}^2$ metric, and maps the space of heat maps $\mathcal{F}$ to the positive orthant of the Hilbert sphere. Define the mapping $\varphi :\mathcal{F}\to \mathrm{\Psi }$ as $\varphi \left(f\right)=+\sqrt{f}:=\psi$. Henceforth, we refer to ψ as the square-root density (SRD) of the heat map f. The inverse mapping ${\varphi }^{-1}:\mathrm{\Psi }\to \mathcal{F}$ is simply given by ${\varphi }^{-1}\left(\psi \right)={\psi }^2=f$. The representation space of SRDs is $\mathrm{\Psi }=\{\psi :[0,1{]}^2\to {\mathbb{R}}_{>0}\mid {\int }_0^1{\int }_0^1{\psi }^2(x,y)\mathrm{d}x\mathrm{d}y=1\}$. The tangent space to Ψ at a point $\psi \in \mathrm{\Psi }$ is given by $T_{\psi }\left(\mathrm{\Psi }\right)=\{\mathrm{\delta \psi }:[0,1{]}^2\to \mathbb{R}|{\int }_0^1{\int }_0^1\mathrm{\delta \psi }(x,y)\psi (x,y)\mathrm{d}x\mathrm{d}y=0\}$. One can show that, under the SRD representation, the FR Riemannian metric on $\mathcal{F}$, given in Equation (1), simplifies to the standard ${\mathbb{L}}^2$ Riemannian metric on Ψ, i.e. for two tangent vectors $\delta {\psi }_1,\delta {\psi }_2\in T_{\psi }\left(\mathrm{\Psi }\right)$, $\langle \delta {\psi }_1,\delta {\psi }_2\rangle ={\int }_0^1{\int }_0^1\delta {\psi }_1(x,y)\delta {\psi }_2(x,y)\mathrm{d}x\mathrm{d}y$. Note that this metric remains unchanged as one traverses tangent spaces defined at different $\psi \in \mathrm{\Psi }$. Further, since ${\int }_0^1{\int }_0^{1}f(x,y)\mathrm{d}x\mathrm{d}y={\int }_0^1{\int }_0^1{\psi }^2(x,y)\mathrm{d}x\mathrm{d}y=\Vert \psi {\Vert }^2=1$ ( $\Vert \cdot \Vert$ denotes the ${\mathbb{L}}^2$ norm) and $\psi (x,y)>0\mathrm{\forall }(x,y)\in [0,1{]}^2$, Ψ is the positive orthant of the unit sphere in ${\mathbb{L}}^2$. The geometry of the sphere under the ${\mathbb{L}}^2$ metric is well known, resulting in analytical expressions for the geodesic path and distance. This, in turn, results in efficient computation on Ψ, and coupled with the inverse mapping ${\varphi }^{-1}$, can be exploited to define various statistical analysis tasks for heat maps computed from raw eye coordinates. Further, geodesic paths can be used for effective visualization of heat map deformations.

The FR distance between two heat maps, $f_1,f_2\in \mathcal{F}$, is defined using their corresponding SRDs, $\varphi \left(f_1\right)={\psi }_1,\varphi \left(f_2\right)={\psi }_2\in \mathrm{\Psi }$, as the length of the great circle path connecting them on Ψ:

$$d_{\mathrm{FR}}(f_1,f_2)=d_{{\mathbb{L}}^2}({\psi }_1,{\psi }_2)={\cos }^{-1}(\langle {\psi }_1,{\psi }_2\rangle )=\theta ,$$ (2)

where $\langle {\psi }_1,{\psi }_2\rangle ={\int }_0^1{\int }_0^1{\psi }_1(x,y){\psi }_2(x,y)\mathrm{dxdy}$. The corresponding geodesic path is given by

$$\alpha \left(t\right)=\frac{1}{\sin \left(\theta \right)}(\sin (\theta (1-t)){\psi }_1+\sin (\mathrm{\theta t}\left){\psi }_2\right).$$ (3)

Based on this framework, the geodesic distance provides a quantitative measure of differences between heat maps, while the geodesic path provides a qualitative visual assessment of the corresponding deformation. Importantly, both are easy to compute.

Using the distance in Equation (2), we define a sample mean on Ψ. Let $f_1,\dots ,f_n\in \mathcal{F}$ denote a sample of heat maps and ${\psi }_1,\dots ,{\psi }_n\in \mathrm{\Psi }$ their SRDs. The sample Karcher mean of ${\psi }_1,\dots ,{\psi }_n$ is given by

$$\overline{\psi }=\arg \underset{\psi \in \mathrm{\Psi }}{min}\sum _{i=1}^n{d}_{{\mathbb{L}}^2}(\psi ,{\psi }_i{)}^2,$$ (4)

i.e. $\overline{\psi }\in \mathrm{\Psi }$ minimizes the sum of squared pairwise distances from each datum in the sample. Further, the Karcher variance of ${\psi }_1,\dots ,{\psi }_n$ is given by

$$\rho \left(\overline{\psi }\right)=\frac{1}{n}\sum _{i=1}^n{d}_{{\mathbb{L}}^2}(\overline{\psi },{\psi }_i{)}^2.$$ (5)

To compute the solution to the optimization problem in Equation (4) via a gradient descent algorithm, we require two additional tools from differential geometry: the exponential and inverse-exponential maps. The exponential map, $\exp :T_{\psi }\left(\mathrm{\Psi }\right)\to \mathrm{\Psi }$, maps points from the tangent space at a point ψ to the representation space Ψ, and is defined as (for $\psi \in \mathrm{\Psi },\mathrm{\delta \psi }\in T_{\psi }\left(\mathrm{\Psi }\right)$)

$${\exp }_{\psi }\left(\mathrm{\delta \psi }\right)=\cos (\Vert \mathrm{\delta \psi }\Vert )\psi +\sin (\Vert \mathrm{\delta \psi }\Vert )\frac{\mathrm{\delta \psi }}{\Vert \mathrm{\delta \psi }\Vert }.$$ (6)

Conversely, the inverse-exponential map (also commonly referred to as the log map), ${\exp }_{{\psi }_1}^{-1}:\mathrm{\Psi }\to T_{{\psi }_1}\left(\mathrm{\Psi }\right)$, maps points from Ψ to the tangent space at a point ${\psi }_1$, and is defined as (for ${\psi }_1,{\psi }_2\in \mathrm{\Psi }$)

$${\exp }_{{\psi }_1}^{-1}\left({\psi }_2\right)=\frac{\theta }{\sin \left(\theta \right)}({\psi }_2-\cos (\theta \left){\psi }_1\right),\theta =d_{{\mathbb{L}}^2}({\psi }_1,{\psi }_2)={\cos }^{-1}(\langle {\psi }_1,{\psi }_2\rangle ).$$ (7)

Briefly, the gradient descent algorithm to compute the Karcher mean proceeds as follows.

1. Initialize with a point ${\overline{\psi }}^0\in \mathrm{\Psi }$ and set iteration counter k = 0.

2. Project ${\psi }_1,\dots ,{\psi }_n$ to $T_{{\overline{\psi }}^k}\left(\mathrm{\Psi }\right)$ using the inverse-exponential map (Equation 7), resulting in tangent vectors ${\exp }_{{\overline{\psi }}^k}^{-1}\left({\psi }_1\right)=\delta {\psi }_1,\dots ,{\exp }_{{\overline{\psi }}^k}^{-1}\left({\psi }_n\right)=\delta {\psi }_n$.

3. Compute the sample average of $\delta {\psi }_1,\dots ,\delta {\psi }_n$, $\overline{\mathrm{\delta \psi }}=\frac{1}{n}\sum _{i=1}^n\delta {\psi }_i$.

4. Update the current sample mean using the exponential map (Equation 6), resulting in ${\overline{\psi }}^{k+1}={\exp }_{{\overline{\psi }}^k}\left(ϵ\overline{\mathrm{\delta \psi }}\right)$, where $ϵ>0$ is a small step size.

5. Check for convergence, and if not converged, return to step (ii) and set k = k + 1.

Variability among a sample of SRDs ${\psi }_1,\dots ,{\psi }_n$, representing heat maps $f_1,\dots ,f_n$, can be studied via principal component analysis (PCA) in the tangent space at the estimated Karcher mean. In particular, it involves the following steps.

1. Compute $\overline{\psi }$, the Karcher mean of ${\psi }_1,\dots ,{\psi }_n$ (solve optimization problem in Equation 4).

2. For $i=1,\dots ,n$, compute $\delta {\psi }_i={\exp }_{\overline{\psi }}^{-1}\left({\psi }_i\right)$ using the inverse-exponential map (Equation 7). In practice, each ${\psi }_i$ and the corresponding $\delta {\psi }_i$ are sampled using a grid of $N\times N$ points on $[0,1{]}^2$.

3. For $i=1,\dots ,n$, vectorize $\delta {\psi }_i\in {\mathbb{R}}^{N\times N}$ resulting in ${\widetilde{\mathrm{\delta \psi }}}_i\in {\mathbb{R}}^{N^2}$.

4. Compute the $N^2\times N^2$ sample covariance matrix given by $K=\frac{1}{n-1}\sum _{i=1}^n{\widetilde{\mathrm{\delta \psi }}}_i{\widetilde{\mathrm{\delta \psi }}}_i^{\mathrm{\top }}$.

5. Perform singular value decomposition (SVD): $K=U\mathrm{\Sigma }{U}^{\mathrm{\top }}$. The resulting diagonal matrix Σ contains the ordered principal component variances, while columns of the orthogonal matrix U are the principal modes of variation in the data.

To visualize a particular mode of variation, we first reshape the corresponding column of U (of size $N^2\times 1$) into an $N\times N$ matrix, denoted by $\tilde{u}$, approximating the corresponding functional object in the tangent space $T_{\overline{\psi }}\left(\mathrm{\Psi }\right)$. We then apply the exponential map and the inverse mapping ${\varphi }^{-1}$. For example, to visualize the first principal mode of variation, we compute and display the path

$$f_t={\varphi }^{-1}({\exp }_{\overline{\psi }}(t\sqrt{{\mathrm{\Sigma }}_{11}}{\tilde{u}}_1\left)\right),t=-0.1,-0.05,0,0.05,0.1,$$ (8)

where ${\mathrm{\Sigma }}_{11}$ denotes the first diagonal entry of Σ and ${\tilde{u}}_1$ is the first mode of variation; the path then captures heat maps that are $-0.1,-0.05,0,0.05,0.1$ standard deviations from the mean in the direction specified by ${\tilde{u}}_1$. We only visualize these paths locally since the representation space of SRDs of heat maps, Ψ, is constrained and the dimensionality of $\tilde{u}$ is very large, e.g. $N^2=10,000$ if we sample the domain $[0,1{]}^2$ using a $100\times 100$ grid.

To summarize, the Riemannian-geometric framework based on the FR metric provides tools for (1) comparison of heat maps via the geodesic distance, (2) summarization of a sample of heat maps via the Karcher mean, and (3) assessment of variability in a sample of heat maps via principal component analysis in the tangent space at the Karcher mean. The geodesic distance can also be used for other statistical tasks such as hierarchical clustering of heat maps.

3. Description of the waterpipe eye tracking study and associated data

Waterpipe tobacco smoking has become more socially acceptable among young adults in the USA, and over 40% of adults ages 18–24 years have tried waterpipe smoking [9,18,38,46]. Young adults primarily smoke in a social setting such as hookah cafes and rarely see the health warning label that comes with the tobacco pack [1,18]. Klein et al. performed an eye tracking study to find the optimal placement of a graphic warning label for hookah pipes by applying standard total fixation time comparisons [21]. The study assessed three warning labels: a lung image with a text warning (lung+text), a mouth image with a text warning (mouth+text), and a text warning only (text). The warning read, ‘WARNING: Hookah smoke contains poisons that can cause mouth and lung cancer.’ The top panel in Figure 1 displays the three types of warning labels. This warning message was different than the text-only FDA-approved message (‘Warning: This product contains nicotine. Nicotine is an addictive chemical.’), because the FDA-approved message was not perceived to be effective among a convenience sample of young adults [21].

Figure 1.

Top: Three types of warning labels used in the waterpipe eye tracking study (lung+text, mouth+text, text-only). Middle: Cropped images of waterpipes 1-4 (left to right). Bottom: Three locations of the warning label shown on pipe 1 (stem, hose, and water bowl).

The following waterpipe eye tracking study recruitment information is given in [21] with further details. The majority of study participants were recruited from The Ohio State University and surrounding areas through social media advertisements, flyers, and word-of-mouth. Only young adults between the ages of 18 and 29 who had previously smoked a waterpipe and did not have any eye conditions that could hinder the recording of eye tracking data, e.g. glaucoma, macular degeneration, cataracts, eye implants, permanently dilated pupils, inability to see out of both eyes, were eligible to participate in the single session in-person eye tracking study. Table 1 provides a summary of demographics for the participants in the study. The participants consisted of roughly the same proportion of males ( $48.7\mathrm{\%}$) and females ( $51.3\mathrm{\%}$), and were primarily White Americans with lower-middle class and middle class socioeconomic status.

Images presented to the study participants consisted of high-quality photos of four waterpipes with the health warning labels placed in three different, standardized locations: water bowl, stem and hose. The images of the four waterpipes and the three warning label placements are shown in the middle and bottom panels of Figure 1, respectively. Study participants were seated between 24 and 32 inches from a monitor equipped with an infrared camera of the eye tracking system. Experiment Suite software (SensoMotoric Instruments, 120 Hz REDm System) was used to display the images and capture the eye movement data. Each participant viewed 72 waterpipe images: three warning labels (text+lung, text+mouth and text) × four waterpipes × three placements of the warning label × two image types (full and cropped image). Each waterpipe image was viewed for five seconds to standardize total viewing time, and the order of the images was randomized.

Previous studies have shown that overall awareness of warning labels increases with the size of the label and presence of graphics [16,17]. Readability is also improved as the size of the warning label increases. Thus, our analysis focuses on eye tracking data corresponding to the cropped images, since the warning labels appear larger in these images.

Table 1.

Summary of demographics for study participants (n = 74).

	n	$\mathrm{\%}$
Gender
Female	36	48.7
Male	38	51.3
Race
White	42	56.8
African American	18	24.3
Other	14	18.9
Country of Birth
US	65	87.8
Non-US	9	12.2
Socioeconomic Status
Working/Lower-Middle Class	17	23.0
Middle Class	44	59.5
Upper Class	9	12.1
Don't Know/Other	4	5.4
Age
18-20	20	27.0
21-23	42	56.8
24-29	12	16.2

3.1. Kernel density estimation of heat maps

To estimate smooth heat maps based on the raw eye coordinates, we use a standard product Gaussian kernel density estimator of the form ${\hat{f}}_{(h_1,h_2)}(x_1,x_2)=\frac{1}{n{h}_1{h}_2}\sum _{i=1}^{n}K\left(\frac{x_1-x_{i1}}{h_1}\right)K\left(\frac{x_2-x_{i2}}{h_2}\right)$, where $x_1$ and $x_2$ denote the image coordinates, n is the total number of raw eye coordinate points, K is a standard normal kernel, and $h_1$ and $h_2$ are the bandwidths for the $x_1$ and $x_2$ coordinates, respectively. Since eye coordinates were recorded on a restricted (image) domain, we modify this estimator by using the reflection boundary correction method to obtain a proper density with bounded support on the image domain via

$${\hat{f}}_{(h_1,h_2)}(x_1,x_2)=\sum _{i=1}^n\prod _{j=1}^2[K\left(\frac{x_j-x_{\mathrm{ij}}^{-}}{h_j}\right)+K\left(\frac{x_j-x_{\mathrm{ij}}}{h_j}\right)+K\left(\frac{x_i-x_{\mathrm{ij}}^{+}}{h_j}\right)],$$ (9)

where $L_j\le x_j\le U_j$, $x_{\mathrm{ij}}^{-}=2L_j-x_{\mathrm{ij}}$, $x_{\mathrm{ij}}^{+}=2U_j-x_{\mathrm{ij}}$ and $L_j,U_j,j=1,2$ represent the lower and upper bounds of the image domain for each dimension, respectively [39]. The vast majority of participants' data did not lie too close to the boundaries of the image support, and we found that the reflection method used for boundary correction had little to no impact on the heat map estimates.

To select the bandwidths $(h_1,h_2)$, we use Silverman's rule with a robust estimate of the standard deviation [20,41]. Silverman's rule is given by $h_j={\sigma }_j(\frac{1}{n}{)}^{1/6},j=1,2$, and minimizes the mean integrated squared error $\mathrm{MISE}\left(\right(h_1,h_2\left)\right)=E[\int \int ({\hat{f}}_{h_1,h_2}(x_1,x_2)-f(x_1,x_2){)}^2\mathrm{d}{x}_1\mathrm{d}{x}_2]$ when the underlying density being estimated, f, is Gaussian. Furthermore, to accommodate for long tailed distributions and possible outliers, we use the median absolute deviation estimator for ${\sigma }_j,j=1,2$ given by ${\tilde{\sigma }}_j=\mathrm{median}(|x_{\mathrm{ij}}-{\tilde{\mu }}_j|)/0.6745,j=1,2$, where ${\tilde{\mu }}_j,j=1,2$ is the median of the sample of raw eye coordinates [20].

Furthermore, we compared Silverman's rule with the robust standard deviation estimate for bandwidth selection to the Improved Sheather–Jones method, which has the following desirable features: (i) it optimizes the mean integrated squared error without using a normal reference rule, (ii) it fixes boundary problems, using a method similar to the reflection method, to accurately estimate a density on a bounded support, and (iii) it has been shown to perform better for multimodal data [6]. However, as seen in Figure 2, we found that due to the sparsity of the data in our study, the Improved Sheather–Jones method selected very small bandwidths and resulted in overfitting; this drawback was previously pointed out in [6].

Figure 2.

Each row compares the kernel density estimate for a different participant. Column 1: Pipe 1 image with lung+text label on water bowl. Column 2: Raw eye coordinates overlaid on the pipe image. Column 3: Kernel density estimate of heat map using Silverman's rule with robust standard deviation estimate for bandwidth selection. The bandwidth values from top to bottom are $\left\{\right(0.0114,0.0340),(0.0126,0.0092),(0.0146,0.0144\left)\right\}$. Column 4: Kernel density estimate using the Improved Sheather-Jones method for bandwidth selection. The bandwidth values from top to bottom are $\left\{\right(0.0039,0.0045),(0.0026,0.0031),(0.0048,0.0048\left)\right\}$.

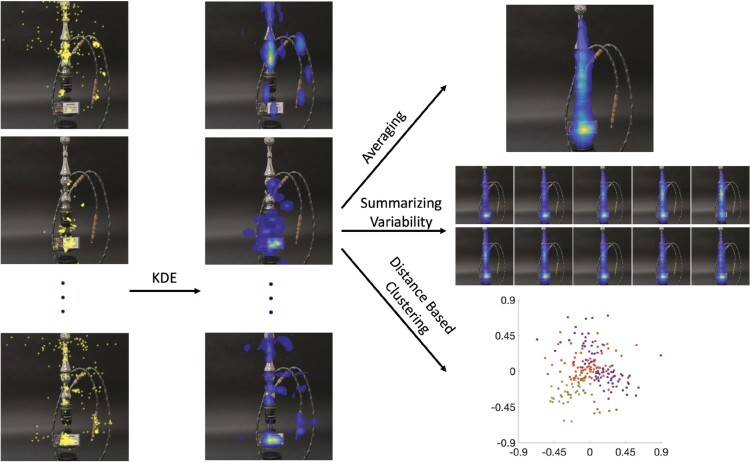
To summarize, Figure 3 presents the full analysis pipeline of the proposed approach. We begin with images of raw eye coordinates (yellow points in left column) for each participant, and apply KDE as described in this section to generate a pdf-based heat map for each image (middle column). The heat maps are then used for statistical summarization and distance-based clustering (right column).

Figure 3.

We start with images of the raw eye coordinates (yellow points in the left column) for each participant and apply kernel density estimation to generate a pdf-based heat map representation of the data (middle column). The heat maps are then used for statistical summarization and analysis (right column): (1) sample averaging (top), (2) summarization of variability through principal component analysis (middle), and (3) distance-based hierarchical clustering (bottom).

4. Statistical analysis of heat maps from waterpipe study

We apply the methodology described in Section 2 to investigate the effects of placement and type of health warning label on waterpipes, based on heat maps estimated from raw eye coordinates. As mentioned before, we consider eye tracking data corresponding to cropped images of four different waterpipes (middle row in Figure 1). For each waterpipe, there are three different placements of the label, water bowl, hose and stem, and three different types of warning label, lung+text, mouth+text and text, for a total of 36 waterpipe images for each participant. For each waterpipe image viewed by the participants, the eye tracker recorded the $x_1$ and $x_2$ coordinates of their eye movement during viewing time on a $[0,1280]\times [0,1024]$ image domain. Due to issues with the eye tracking device, we deleted outlier coordinates for some of the images prior to estimation of the heat maps; outliers were defined as any points that fell outside of the image domain or that had missing $x_1$ or $x_2$ coordinates. Out of the 74 participants enrolled in the study, 66 had reliable eye tracking data for each image after removal of outliers. All eye coordinates were mapped to the domain $[0,1{]}^2$, and we applied KDE, as described in Section 3.1, on a $100\times 100$ grid to obtain heat maps for each participant and waterpipe image. The middle panel in Figure 4 displays the raw eye coordinates recorded for one participant when viewing waterpipe 1 with a lung+text label placed on the water bowl; the right panel displays the corresponding heat map. For improved visualization, when displaying a heat map on top of the corresponding waterpipe image, we do not show values that are close to 0.

Figure 4.

Left: Pipe 1 image with lung+text label on the water bowl. Middle: Eye coordinates recorded for a participant viewing the image of waterpipe 1 with the lung+text label placed on the water bowl. Right: Corresponding heat map overlaid on top of the waterpipe image.

4.1. Quantitative/qualitative comparison of heat maps via geodesic distance/ path

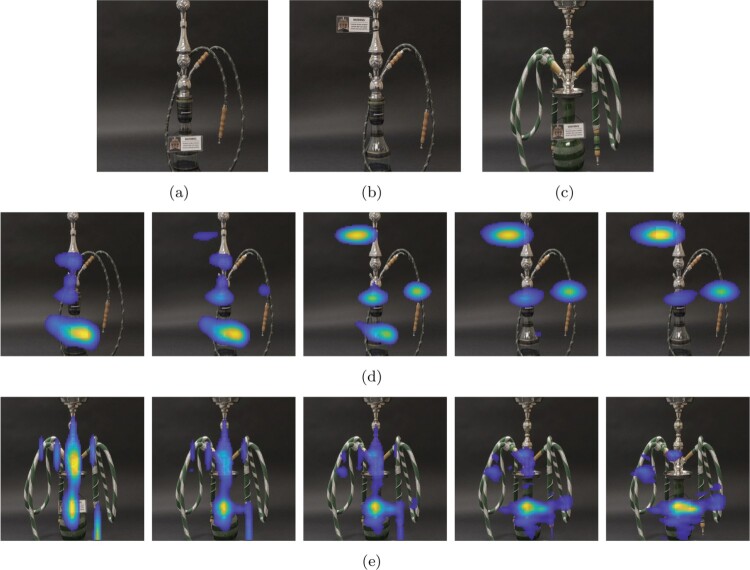
We first present two examples of comparisons of heat maps via the FR geodesic distance and path. Since the geodesic distance is the length of the geodesic path, these results enable us to assess the types of deformations between heat maps that are captured by the distance. The second and third rows in Figure 5 display two geodesic paths between heat maps. In the second row, we compare heat maps for two different participants viewing waterpipe 1 with the lung+text label; the label was placed on the water bowl in the leftmost image and on the stem in the rightmost image. In the third row, we compare heat maps for two different participants viewing waterpipe 2 with the lung+text label placed on the water bowl. The two geodesic paths represent natural deformations between heat maps and allow us to visually interpret the associated geodesic distances, which are 1.28 and 1.05 for the second and third rows, respectively. Further, we discover something interesting in the geodesic presented in the third row. Although the two participants are viewing the same exact image, they tend to focus on different features of the waterpipe. The second participant (rightmost heat map in the geodesic path) directs most of their attention to the warning label located on the water bowl. On the other hand, the first participant directs some of their attention to the warning label, but also fixates on the shiny stem, which is a prominent feature of this waterpipe. This represents natural variability in eye tracking data, where different features of the image, e.g. warning label, shiny stem, elaborate hose, etc., may capture some or the majority of a participant's attention during viewing time. This also highlights the challenges associated with determining the optimal placement and type of warning label on waterpipes.

Figure 5.

(a) Waterpipe 1 with lung+text label on water bowl. (b) Waterpipe 1 with lung+text label on stem. (c) Waterpipe 2 with lung+text label on waterbowl. (d) Geodesic path between heat maps for a participant viewing image in (a) (start of path) and image in (b) (end of path). (e) Geodesic path between heat maps for two participants viewing image in (c) (same for start and end of path). The associated FR geodesic distances are 1.28 for (d) and 1.05 for (e).

4.2. Hierarchical clustering of heat maps

To assess the effectiveness of the FR distance in capturing variability and discriminating across different placements of the warning labels on the four waterpipes, we implement and assess results of hierarchical clustering. For each waterpipe and type of label, we compute the $198\times 198$ pairwise distance matrix (66 participants ×3 different label placements). Using each distance matrix, we perform hierarchical clustering with complete linkage; we set the desired number of clusters to 3. In Table 2, we report the resulting rand indices for each waterpipe and type of label, with the three label placements serving as a ground truth partition of the heat maps; best performance is italicized for each waterpipe. The rand index takes values between 0 and 1 (with 1 indicating perfect agreement) and is used to assess clustering performance. The proposed FR distance is effective in discriminating across heat maps based on different label placements. In particular, the warning labels with lung/mouth images produce the best clustering results, indicating that they are more effective at capturing the participants' attention than the text label.

Table 2.

Rand indices to assess heat map hierarchical clustering performance based on the FR distance.

Waterpipe	Lung+Text	Mouth+Text	Text
1	0.639	0.505	0.512
2	0.666	0.567	0.613
3	0.586	0.663	0.494
4	0.641	0.658	0.627

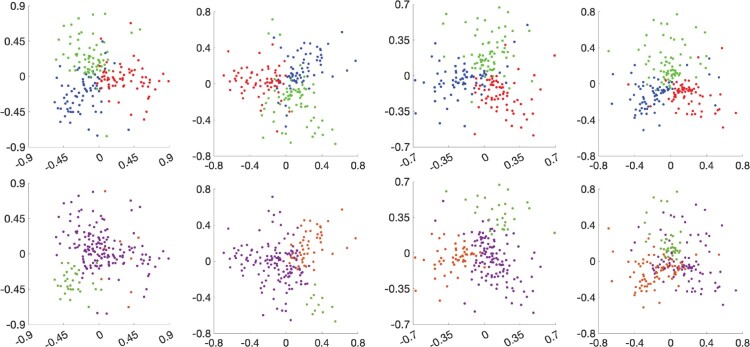
To visualize the ground truth partitions and the hierarchical clustering results, we apply multidimensional scaling (MDS) to the distance matrices, focusing on the mouth+text label. Briefly, MDS allows us to visualize the similarity across heat maps, as well as their cluster-based grouping, in a low dimensional Euclidean space. The top row of Figure 6 displays the heat map data of the participants after MDS, for waterpipes 1–4 (left to right), with colors indicating the placement of the warning label (water bowl=blue, hose=green and stem=red). The points are well-separated based on the three placements. In the bottom row of Figure 6, we display the same sets of points, but color them according to the partitions produced via hierarchical clustering. The three estimated clusters are more distinguishable for waterpipes 2–4. Similar patterns can be observed in the MDS plots for the lung+text and text labels, which are presented in Section 1 of the Supplementary Materials.

Figure 6.

Heat map data after MDS, for waterpipes 1–4 (left to right), colored according to the placement (water bowl=blue, hose=green, stem=red) of the mouth+text label (top row), and the partitions estimated via hierarchical clustering (bottom row).

4.3. Sample averaging of heat maps

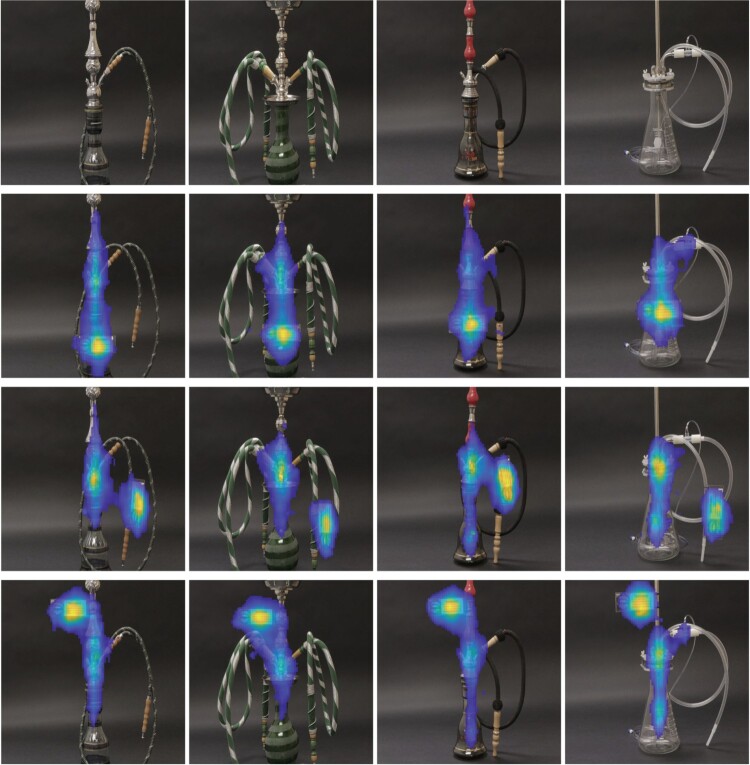
Next, we summarize the overall attention of the participants as they viewed images of each of the four waterpipes by computing the sample Karcher mean, given in Equation (4), of the corresponding heat maps. Figure 7 displays 12 Karcher means with different waterpipe images along the bottom three rows (pipes 1–4 from left to right) and different warning label placements along the columns (water bowl, hose and stem from top to bottom). We only focus on the mouth+text warning label here and note that the results are similar for the lung+text and text labels (see Section 2 of the Supplementary Materials). The sample size for each Karcher mean computation is n = 66 corresponding to the 66 participants. Although there is considerable variation in the heat maps across participants, the estimated sample means tend to show a high level of consistency across the waterpipes and label placement. In particular, on average, attention is heavily focused on the warning label. However, participants also direct significant attention to prominent features of the waterpipes, especially if the warning label is placed near these features. For example, waterpipe 4 appears the most unique, and attention is drawn toward the center of the waterpipe where the hose connects to the stem, irrespective of where the label is placed. For waterpipes 1–3, participants tend to focus on the shiny stems in addition to the label.

Figure 7.

Karcher means of participants' heat maps for pipe images with mouth+text label. Waterpipes 1–4 are shown along the rows from left to right, respectively. Starting from the second row, the label placements are shown along the columns with the water bowl, hose and stem from top to bottom, respectively.

4.4. Assessment of variability among heat maps

In the previous section, we used the Karcher mean to visualize and assess overall attention while study participants viewed different waterpipe images. The Karcher mean is defined as the minimizer of the Karcher variance. Thus, in Table 3, we report the Karcher variances of the heat map samples, computed using Equation (5), for each label placement and type for the four different waterpipes. For each combination of label type and waterpipe, we italicized the placement of the label that results in the lowest variance. Interestingly, for waterpipe 4, the stem placement of the label always results in the lowest variance, irrespective of the type of label, indicating that this may be the most effective location for a warning label on this waterpipe to capture the participants' attention. For waterpipe 1, the stem also appears to be the most effective label location. This is intuitive since the stem is a prominent feature of this waterpipe. For waterpipe 2, with the lung+text and text labels, it appears that the hose placement is most effective. Again, the hose appears to be the most interesting part of this waterpipe. For waterpipe 3, with the mouth+text and text labels, it appears that the stem placement is most effective. Overall, effectiveness of warning label placement heavily depends on the type of waterpipe under consideration.

Table 3.

Karcher variances of heat maps for waterpipes 1–4, with different warning label placements and types.

	Lung+Text			Mouth+Text			Text
Waterpipe	Base	Hose	Stem	Base	Hose	Stem	Base	Hose	Stem
1	0.793	0.925	0.731	0.822	0.769	0.771	0.730	0.831	0.658
2	0.868	0.700	0.711	0.773	0.820	0.711	0.833	0.707	0.733
3	0.839	0.659	0.725	0.846	0.811	0.737	0.771	0.743	0.606
4	0.789	0.672	0.662	0.797	0.831	0.674	0.774	0.734	0.647

Finally, Figure 8 provides a visual assessment of the first principal mode of variability in the heat map data for three different cases: (i) waterpipe 2, text label, water bowl placement (top row), (ii) waterpipe 3, text label, stem placement (middle row), and (iii) waterpipe 4, mouth+text label, stem placement (bottom row). The displayed paths were generated using Equation (8). In case (i), we see a deviation of attention from the label on the water bowl to the intricate stem of the waterpipe, i.e. the mode captures vertical eye movement. In case (ii), there is deviation of attention from the warning label (placed at the stem) to the rest of the stem and part of the water bowl; this mode also reflects variation in how attention is directed at the label as evidenced by the changing shape of the yellow region. Finally, in case (iii), there is a shift in attention from the stem and water bowl to the label (placed at the stem). Overall, these modes of variation represent natural variability in the heat map data. The second modes of variability for the same three cases are presented in Section 3 of the Supplementary Materials, and tend to capture residual variability that directs attention to the stem of the different waterpipes.

Figure 8.

First principal mode of variation for three cases: (i) waterpipe 2, text, water bowl (top), (ii) waterpipe 3, text, stem (middle), and (iii) waterpipe 4, mouth+text, stem (bottom).

5. Discussion and future work

We use a Riemannian-geometric framework based on the Fisher–Rao metric for statistical analysis of heat maps, which until recently have been primarily used as a qualitative measure. We apply this method to eye tracking data obtained from a waterpipe tobacco study that endeavored to find the optimal placement of health warning labels on hookah pipes. We computed averages of heat maps, studied variability via principal component analysis, and used the FR distance for hierarchical clustering to quantify the attention of study participants to different features of the waterpipe images.

In general, determining the optimal placement and type of warning label on tobacco waterpipes, based on eye tracking data, is a very difficult problem. Heat maps estimated from eye tracking data usually exhibit large amounts of complex variability that depends on the prominent features of the pipe under consideration. However, our analysis reveals some consistent, intuitive patterns across the four waterpipes. First, the hierarchical clustering results show better separation, as determined by higher rand indices, between partitions corresponding to different label placements, when the warning label includes a graphic, i.e. lung+text or mouth+text. This may indicate that the warning labels which include a graphic in addition to text are better at capturing and holding participants' attention than the text only label. This finding complements results seen in previous studies, where awareness to warning labels increased in the presence of a graphic. Additionally, it highlights the capability of the FR metric to capture meaningful differences between heat maps. Second, our analysis reveals that the majority of participants' attention is devoted to prominent features of the waterpipes, i.e. the stem and hose. Across all four waterpipes and three types of label, we find that these two placements result in lowest overall variability among the heat maps. This suggests that these two locations may be more effective as warning label placements than the water bowl. We note that these findings are based on fixed waterpipe images and further studies are needed to corroborate these results when the waterpipes appear in videos.

Two natural extensions of the proposed framework are to consider (1) hypothesis testing and (2) regression models with heat maps serving as predictors and/or responses; these developments are complicated by the nonlinear representation space of heat maps. While our analysis considered fixed images of waterpipes, there is great interest in eye tracking data collected during viewing of videos. In this case, one must develop a time-varying heat map representation. The FR metric-based framework can still be applied in this setting, but the underlying data objects are more complex since they represent a trajectory of heat maps indexed by video frames.

Human subjects approval statement

The Ohio State University Institutional board reviewed this study protocol.

Funding Statement

Research reported in this publication was supported by the National Cancer Institute of the National Institutes of Health under Award Number R01 CA229306. The research was also supported, in part, by NSF CCF 1740761, NSF CCF 1839252, NSF DMS 2015226 and NIH R37 CA214955 (to SK), and The Ohio State University Comprehensive Cancer Center and the National Institutes of Health under grant number P30 CA016058. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health or the Food and Drug Administration.

Disclosure statement

No potential conflict of interest was reported by the author(s).