Distribution-free Phase II triple EWMA control chart for joint monitoring the process location and scale parameters

ABSTRACT

Distribution-free or nonparametric control charts are used for monitoring the process parameters when there is a lack of knowledge about the underlying distribution. In this paper, we investigate a single distribution-free triple exponentially weighted moving average control chart based on the Lepage statistic (referred as TL chart) for simultaneously monitoring shifts in the unknown location and scale parameters of a univariate continuous distribution. The design and implementation of the proposed chart are discussed using time-varying and steady-state control limits for the zero-state case. The run-length distribution of the TL chart is evaluated by performing Monte Carlo simulations. The performance of the proposed chart is compared to those of the existing EWMA-Lepage (EL) and DEWMA-Lepage (DL) charts. It is observed that the TL chart with a time-varying control limit is superior to its competitors, especially for small to moderate shifts in the process parameters. We also provide a real example from a manufacturing process to illustrate the application of the proposed chart.

1. Introduction

Statistical Process Control (SPC) is one of the widely used techniques for keeping the quality characteristics of a process in an acceptable and stable level. Control charts are the most important tool of SPC and are used for monitoring shifts in the location and/or scale parameter(s) of the underlying process distribution. Shewhart [56] first introduced a memory-less control chart where the charting statistic is based on the current observation. Shewhart's control charts are easy to use and effective in detecting large shifts in the process parameters; however, they do not have good detection ability for small and moderate shifts. For this reason, Page [50] and Roberts [53] proposed the cumulative sum (CUSUM) and exponentially weighted moving average (EWMA) charts respectively, which are memory-type as their charting statistics are based on both the past and current observations. Many other memory-type control charts have been proposed to improve the performance of the CUSUM and EWMA charts, especially for small shifts. Shamma and Shamma [55] proposed the double EWMA (DEWMA) chart with steady-state control limits by combining two EWMA charts and they showed that it is superior to the Shewhart chart for small and moderate shifts, while it has similar detection ability with the EWMA chart. Zhang and Chen [65] studied the DEWMA chart using the time-varying control limits and they found it more effective than the EWMA chart for small shifts. Sheu and Lin [56] presented the generally weighted moving average (GWMA) chart which is an extension of the EWMA chart with an additional adjustment parameter. Abbas et al. [2] developed the mixed EWMA-CUSUM (MEC) chart, while Abbas [1] introduced the homogeneously weighted moving average (HWMA) chart. Recently, Alevizakos et al. [5] developed the triple EWMA (TEWMA) chart by combining three EWMA charts. Alevizakos et al. [5] found that the TEWMA chart with time-varying control limits is more effective than the EWMA, DEWMA, and GWMA charts for small shifts, while it is comparable with them for moderate and large shifts. On the other hand, using steady-state control limits, it is shown that the EWMA and GWMA charts have a slightly better detection ability than the DEWMA and TEWMA charts, especially for small and moderate shifts.

In many real-life applications where a shift in both location and scale parameters exists, practitioners use two independent control charts; one for detecting shifts in the location parameter and one for the scale parameter. However, using two separate charts may result in invalid conclusion about the state of the process because a simultaneously shift in the location and scale parameters is a bi-aspect phenomenon. Thus, single charts for joint monitoring of location and scale parameters have been introduced. Gan [25] developed an EWMA chart for joint monitoring of the process mean and variance of normally distributed data while Chen and Cheng [15] proposed the max-chart by combining the Shewhart $\overline{X}$ and S charts. An overview of the single charts for joint monitoring of the mean and variance is presented by Cheng and Thaga [16] and McCracken and Chakraborti [41]. Recent papers about this topic are those of Mukherjee et al. [18], Zafar et al. [63], Chong et al. [19] and Chatterjee et al. [14].

All the above-mentioned control charts assume that the underlying process distribution (the normal one in the most cases) is known. However, this assumption is often violated. In recent years, researchers have introduced distribution-free (or nonparametric) control charts. We recommend Amin and Searcy [7], Li et al. [36], Graham et al. [27], Chakraborty et al. [12], Li et al. [34,35] Alevizakos et al. [3,4] and Perdikis et al. [51] for distribution-free Phase I charts for monitoring the location parameter and Das [22], Das and Bhattacharga [23], Yang and Arnold [62] and Haq [29] for monitoring the scale parameter. On the other hand, distribution-free Phase II charts for monitoring shifts in the location parameter can be found in the works of Chakraborti and Van de Wiel [11], Graham et al. [28], Malela-Majika and Rapoo [40], Mukherjee et al. [45], Mabube et al. [37,38], Malela-Majika [39] and Letshedi et al. [33].

In the last decades, distribution-free Phase II control charts have been introduced for joint monitoring the location and scale parameters using a reference sample from Phase I. There are several types of statistics for these charts, such as the Cucconi, Lepage, Cramér–von Mises (CvM), and Kolmogorov-Smirnov (KS). Ross and Adams [54] developed two distribution-free charts based on the CvM and KS statistics to detect a general shift on the process distribution. Mukherjee and Chakraborti [44] presented the Shewhart-Lepage (SL) chart for joint monitoring of the location and scale parameters while Chowdhury et al. [20] presented the Shewhart-Cucconi (SC) chart and they found that it performs better or similar to the SL chart. Chowdhury et al. [21] introduced the CUSUM-Lepage (CL) chart and they showed that it is more effective than other distribution-free CUSUM schemes and the SL chart. Zhang et al. [64] presented the EWMA chart based on the CvM statistic (ECvM) which is robust to non-normality data and more sensitive than the SL and SC charts. Mukherjee and Marozzi [44] introduced the CUSUM-Cucconi (CC) chart where it outperforms the SL, SC, and CL charts for various shifts in location and/or scale parameters. Mukherjee and Marozzi [47] presented a modified SL chart and they introduced a new type of charts; the circular-grid charts. Mukherjee [43] presented the EWMA-Lepage (EL) chart using a structure of charting statistic for reducing the inertia problem and comparing to the SL and CL charts, it was found more effective for several ranges of shifts. Mukherjee and Sen [49] investigated the optimal design of SL type schemes while Chong et al. [17] presented four SL type schemes for monitoring one-sided shifts in the location and scale parameters. Song et al. [59] presented several EWMA schemes based on the Lepage and Cucconi statistics. Chong et al. [18] presented distribution-free Shewhart-type charts based on the combination of p-values for simultaneously monitoring of shifts in location and scale parameters. Song et al. [60] studied the EL and EWMA-Cucconi (EC) charts with dynamic fast initial response (FIR). Song et al. [58] proposed several distribution-free circular-grid charts based on the Cucconi and percentile modified Lepage (PML) statistics. Chan et al. [13] investigated the DEWMA-Lepage (DL) and HWMA-Lepage (HL) charts with time-varying and steady-state control limits and they showed that both of them are more effective than the EL chart when time-varying control limits are used. For more discussion on distribution-free control charts, the reader are referred to Gibbons and Chakraborti [26], Qiu [52] and Chakraborti and Graham [9,10].

In the SPC literature, the development and study of distribution-free charting schemes is very popular in the recent years. To the best of our knowledge, a TEWMA chart for joint monitoring of location and scale parameters has not been introduced. In this article, motivated by the works of Alevizakos et al. [5], Mukherjee [43], and Chan et al. [13], we present a distribution-free TEWMA chart based on the Lepage statistic (denoted as TL chart) for joint monitoring of shifts in the location and scale parameters. We study its performance in terms of the run-length characteristics using time-varying and steady-state control limits for the zero-state case and we also compare it with the EL and DL charts. Although, many distribution-free control charts based on Lepage statistic have been developed, we decided to compare the proposed TL chart with the DL and EL charts because (i) the TEWMA scheme is an extension of the EWMA scheme and (ii) the EL and DL charts are more effective than the Shewhart and CUSUM schemes in a wide range of shifts, as shown in Mukherjee [43] and Chan et al. [13]

The rest of this article is organized as follows: In Section 2, we provide the statistical background of the Lepage statistic as well as the structure of the EL and DL charts. In Section 3, we present the proposed TL chart and a step-by-step procedure for it. The in-control (IC) and out-of-control (OOC) performances of the TL chart as well as a comparison study with EL and DL charts are given in Section 4. An illustrative example is provided in Section 5 to demonstrate the application of the proposed chart. Finally, conclusions and recommendations are given in Section 6.

2. Distribution-free Phase II control charts based on the Lepage statistic

2.1. Lepage statistic for two-sample test

Assume that ${\mathbf{X}}_{\mathbf{m}}=(X_1,X_2,\dots ,X_m)$ is a reference (or Phase I) sample of size m with unknown continuous cumulative distribution function (cdf) F(x). Moreover, let ${\mathbf{Y}}_{\mathbf{tj}}=(Y_{1j},Y_{2j},\dots ,Y_{\mathrm{nj}})$, with $t=1,2,\dots ,n$ and j = 1, 2, …, denoted as Y, be the jth Phase II (test) sample of size n with cdf G(y). Note that the Phase II samples are assumed to be independent and identically distributed (iid) and mutually independent from the Phase I sample. The cdf F and G satisfy the relation $G(x)=F(\frac{x-\theta }{\delta })$, where $\theta \in \mathbb{R}$ and δ > 0 represent the shifts in the location and scale parameters, respectively. The process is considered to be IC if θ = 0 and δ = 1. When θ ≠ 0 and δ = 1, we have a pure location shift, while θ = 0 and δ ≠ 1 indicates a pure scale shift. Finally, if θ ≠ 0 and δ ≠ 1, then we have a shift in both location and scale parameters. In the above three cases, the process is declared as OOC.

Wilcoxon [61] proposed a statistic, named as Wilcoxon rank sum (WRS) statistic, to test the equality of the two location parameters by merging the m observations of the Phase I and the n observations of the jth test sample. Define an indicator variable I_k = 0 or 1 if the kth order statistic of the combined sample N = m + n is a X or Y observation, respectively. The WRS statistic, say T₁, is defined as

$$\begin{array}{r}{T}_1=\sum _{k=1}^{N}k{I}_k.\end{array}$$ (1)

The IC expected value and variance of the T₁ statistic are given by

$$\begin{array}{r}E\left(T_1|\mathrm{IC}\right)={\mu }_{T_1}=\frac{n(N+1)}{2}\end{array}$$ (2)

and

$$\begin{array}{r}\mathrm{Var}\left(T_1|\mathrm{IC}\right)={\sigma }_{T_1}^2=\frac{\mathrm{mn}(N+1)}{12}.\end{array}$$ (3)

Ansari and Bradley [8] proposed a statistic, named as AB statistic, to test the equality of the two scale parameters. The AB statistic, say T₂, is defined as

$$\begin{array}{r}{T}_2=\sum _{k=1}^N|k-\frac{1}{2}(N+1)|I_k.\end{array}$$ (4)

The IC expected value and variance of the AB statistic are given by

$$\begin{array}{r}E(T_2|\mathrm{IC})={\mu }_{T_2}=\{\begin{array}{ll}{\displaystyle \frac{\mathrm{nN}}{4}},& \text{if}N\text{is even},\\ {\displaystyle \frac{n(N^2-1)}{4N}},& \text{if}N\text{is odd}\end{array}\end{array}$$ (5)

and

$$\begin{array}{r}\mathrm{Var}(T_2|\mathrm{IC})={\sigma }_{T_2}^2=\{\begin{array}{ll}{\displaystyle \frac{\mathrm{mn}(N^2-4)}{48(N-1)}},& \text{if}N\text{is even},\\ {\displaystyle \frac{\mathrm{mn}(N+1)(N^2+3)}{48N^2}},& \text{if}N\text{is odd}.\end{array}\end{array}$$ (6)

For more information about the T₁ and T₂ statistics, the reader is referred to Gibbons and Chakraborti [26]. Note that for the jth test sample, the WRS and AB statistics are denoted as T_1j and T_2j, respectively, while the corresponding standardized statistics are denoted as

$$S_{1j}=\frac{T_{1j}-{\mu }_{T_1}}{{\sigma }_{T_1}}\text{and}{S}_{2j}=\frac{T_{2j}-{\mu }_{T_2}}{{\sigma }_{T_2}}.$$

Lepage [32] introduced a statistic to test the equality of both the location and scale parameters of the two samples, given by

$$\begin{array}{r}{L}_j=S_{1j}^2+S_{2j}^2.\end{array}$$ (7)

It should be pointed out that E(S_1j|IC) = E(S_2j|IC) = 0 and $E(S_{1j}^2|\mathrm{IC})=E(S_{2j}^2|\mathrm{IC})=1$. Thus, E(L_j|IC) = 2. The L_j statistic is non-negative by definition and a large value of L_j means that a shift in the process location and/or scale parameter(s) exists. As a result, the distribution-free Phase II control charts based on the Lepage statistic have been designed with an upper control limit (UCL). Furthermore, there is no explicit form of the conditional variance of the Lepage statistic and it depends on the values of m and n.

2.2. The EL control chart

The charting statistic of the EL scheme, as proposed by Mukherjee [43], is given by

$$\begin{array}{r}E{L}_j=max\{2,\lambda L_j+(1-\lambda )E{L}_{j-1}\},\end{array}$$ (8)

where 0 < λ ≤ 1 is the smoothing parameter and EL₀ = 2. According to Song et al. [59], this type of scheme helps in reducting the inertia problem of the EWMA chart. The charting statistic of the traditional EL chart, as discussed by Chakraborti and Graham [9] and studied by Song et al. [59] and Chan et al. [13], is defined as

$$\begin{array}{r}E{L}_j=\lambda L_j+(1-\lambda )E{L}_{j-1},\end{array}$$ (9)

where EL₀ = E(L_j|IC) = 2. The time-varying UCL is given by

$$\begin{array}{r}\mathrm{UC}{L}_j=2+L\sqrt{\frac{\lambda }{2-\lambda }[1-(1-\lambda {)}^{2j}]{\xi }_1+{[1-(1-\lambda {)}^j]}^2{\xi }_2},\end{array}$$ (10)

where L>0 is the width of control limits, ξ₁ = E[Var(L_j|X_m, IC)] and ξ₂ = Var[E(L_j|X_m, IC)]. Chan et al. [13] computed the values of ξ₁ and ξ₂ for m = 100, 300 and n = 5, 10, 15 by performing Monte Carlo simulations. Table 1 reproduces the values of ξ₁ and ξ₂ from Table 1 of Chan et al. [13]. For large values of j, the steady-state UCL becomes

$$\begin{array}{r}\mathrm{UC}{L}_j=2+L\sqrt{\frac{\lambda }{2-\lambda }{\xi }_1+{\xi }_2}.\end{array}$$ (11)

A process is considered to be OOC if a charting statistic exceeds the UCL; otherwise, the process is said to be IC. Note that the EL chart reduces to the SL chart [44] for λ = 1.

Table 1.

Values of ξ₁ and ξ₂ connected to the Lepage statistic.

m	n	ξ1	ξ2
100	5	3.5257	0.02665
100	10	3.6909	0.04684
100	15	3.7288	0.07875
300	5	3.5758	0.00755
300	10	3.7673	0.01052
300	15	3.8306	0.01474

2.3. The DL control chart

The DEWMA scheme is a combination of two EWMA schemes. The charting statistic of the DL chart is given via the system of equations

$$\begin{array}{r}\{\begin{array}{l}E{L}_j=\lambda L_j+(1-\lambda )E{L}_{j-1},\\ D{L}_j=\mathrm{\lambda E}{L}_j+(1-\lambda )D{L}_{j-1},\end{array}\end{array}$$ (12)

where EL₀ = DL₀ = 2. The time-varying UCL is given by

$$\begin{array}{r}\mathrm{UC}{L}_j=2+L\sqrt{K_{D_j}{\xi }_1+{[1-(1+\mathrm{\lambda j})(1-\lambda {)}^j]}^2{\xi }_2},\end{array}$$ (13)

where

$$K_{D_j}=\frac{\begin{array}{c}{\lambda }^4[1+(1-\lambda {)}^2-(j+1{)}^2(1-\lambda {)}^{2j}\\ +(2j^2+2j-1)(1-\lambda {)}^{2j+2}-j^2(1-\lambda {)}^{2j+4}]\end{array}}{[1-(1-\lambda {)}^2{]}^3}.$$

For large values of j, the steady-state UCL becomes

$$\begin{array}{r}\mathrm{UCL}=2+L\sqrt{\frac{\lambda (2-2\lambda +{\lambda }^2)}{(2-\lambda {)}^3}{\xi }_1+{\xi }_2}.\end{array}$$ (14)

A process is considered to be OOC if a charting statistic DL_j exceeds the UCL; otherwise, the process is declared as IC.

As we mentioned earlier, the DL control chart was studied by Chan et al. [13] using time-varying and steady-state control limits. They showed that the DL chart is superior to the EL chart in detecting small and moderate pure or mixed shifts.

3. The proposed TL control chart

3.1. Structure of the TL chart

The charting statistic of the TL control chart is defined via the system of equations

$$\begin{array}{r}\{\begin{array}{l}E{L}_j=\lambda L_j+(1-\lambda )E{L}_{j-1},\\ D{L}_j=\mathrm{\lambda E}{L}_j+(1-\lambda )D{L}_{j-1},\\ T{L}_j=\mathrm{\lambda D}{L}_j+(1-\lambda )T{L}_{j-1},\end{array}\end{array}$$ (15)

where EL₀ = DL₀ = TL₀ = 2. The charting statistic TL_j can also be written as

$$\begin{array}{r}T{L}_j=\frac{{\lambda }^3}{2}\sum _{i=1}^j(1-\lambda {)}^{j-i}(j-i+1)(j-i+2)L_j+(1-\lambda {)}^j[\mathrm{\lambda j}(\mathrm{\lambda j}+\lambda +2)+2].\end{array}$$ (16)

Using Equation (16), it is easy to prove that E(TL_j|IC) = 2, while following the approach of Mukherjee [43] and Chan et al. [13], where Var(TL_j|IC) = E[Var(TL_j|X_m, IC)] + Var[E(TL_j|X_m, IC)], the IC variance of the statistic TL_j is given by

$$\begin{array}{r}\mathrm{Var}(T{L}_j|\mathrm{IC})=K_{T_j}{\xi }_1+{[1-\frac{(1-\lambda {)}^j}{2}[\mathrm{\lambda j}(\mathrm{\lambda j}+\lambda +2)+2]]}^2{\xi }_2,\end{array}$$ (17)

where

$$\begin{array}{rl}{K}_{T_j}& =[\frac{d^3{\lambda }^6}{4}[-\frac{j(j^2-1)(j-2)d^{j-3}}{1-d}-\frac{4j(j^2-1)d^{j-2}}{(1-d{)}^2}-\frac{12j(j+1)d^{j-1}}{(1-d{)}^3}\\ -\frac{24(j+1)d^j}{(1-d{)}^4}+\frac{24(1-d^{j+1})}{(1-d{)}^5}]+2d^2{\lambda }^6[-\frac{j(j^2-1)d^{j-2}}{1-d}\\ -\frac{3j(j+1)d^{j-1}}{(1-d{)}^2}-\frac{6(j+1)d^j}{(1-d{)}^3}+\frac{6(1-d^{j+1})}{(1-d{)}^4}]\\ +\frac{7d{\lambda }^6}{2}[-\frac{j(j+1)d^{j-1}}{1-d}-\frac{2(j+1)d^j}{(1-d{)}^2}+\frac{2(1-d^{j+1})}{(1-d{)}^3}]\\ +{\lambda }^6[\frac{1-d^{j+1}}{(1-d{)}^2}-\frac{(j+1)d^j}{1-d}]],\end{array}$$

with d = (1 − λ)². The proof is derived in the Supplementary Material. More information about the mean and variance of the TEWMA statistic can be found in Alevizakos et al. [5]. The time-varying UCL of the TL chart is given by

$$\begin{array}{r}\mathrm{UC}{L}_j=2+L\sqrt{\mathrm{Var}(T{L}_j|\mathrm{IC})},\end{array}$$ (18)

where Var(TL_j|IC) is given by Equation (17). For large values of j, the steady-state UCL becomes

$$\begin{array}{r}\mathrm{UCL}=2+L\sqrt{[\frac{6(1-\lambda {)}^6\lambda }{(2-\lambda {)}^5}+\frac{12(1-\lambda {)}^4{\lambda }^2}{(2-\lambda {)}^4}+\frac{7(1-\lambda {)}^2{\lambda }^3}{(2-\lambda {)}^3}+\frac{{\lambda }^4}{(2-\lambda {)}^2}]{\xi }_1+{\xi }_2}.\end{array}$$ (19)

The TL chart gives an OOC signal at the jth test sample if the charting statistic TL_j plots on or over the UCL.

3.2. Implementation of the TL chart

The proposed TL chart can be implemented using the following steps:

• Step 1:

  Select a Phase I sample ${\mathbf{X}}_{\mathbf{m}}=(X_1,X_2,\dots ,X_m)$ from an IC process.

• Step 2:

  Select a Phase II (or test) sample ${\mathbf{Y}}_{\mathbf{tj}}=(Y_{1j},Y_{2j},\dots ,Y_{\mathrm{nj}})$, where $j=1,2,\dots$ Note that the test samples are themselves independent and also independent from the Phase I sample. When the process is IC, the distributions of the two samples are the same (i.e. θ = 0 and δ = 1). On the other hand, when the process is OOC, the distribution of the test sample is taken to be of the same form as that of the Phase I sample, but with a shift in the location and/or scale parameters(s).

• Step 3:

  Calculate the WRS (T_1j) and AB (T_2j) statistics using Equations (1) and (4) respectively, the standardized S_1j and S_2j statistics and the Lepage L_j statistics using Equation (7). After that, compute the TL_j statistic using Equation (16).

• Step 4:

  Compute the time-varying or steady-state UCL using Equation (18) or (19) respectively, and compare each charting statistic with them.

• Step 5:

  If TL_j ≥ UCL_j (or UCL), then the process is considered to be OOC at the jth test sample. Otherwise, the process is considered to be IC and we proceed to the next test sample.

• Step 6:
  Follow-up procedure: When the process is OOC, compute the p-values for the WRS test for location parameters (denoted as p₁) and the AB test for scale parameters (denoted as p₂) on the basis of the Phase I sample with m observations and the jth test sample with n observations. The following four states are considered:

  • If p₁ is significant (or low) but not p₂, then only a shift in the location parameter has been occurred.
  • If p₂ is significant but not p₁, then only a shift in the scale parameter has been occurred.
  • If both p₁ − and p₂ −values are significant, then a shift in both the location and scale parameters is indicated.
  • If both p₁ − and p₂ −values are insignificant, then either there is an interaction between location and scale shifts or because of a false alarm.

The above follow-up procedure has also been used by Chowdhury et al. [20,21], Mukherjee [43] and Chan et al. [13]. Note that the EL and DL charts can also be implemented in a similar way.

4. Performance analysis and comparison

The performance of a control chart is usually measured in terms of the run-length distribution and its associated characteristics. The average run-length (ARL) is the most popular performance measure of a control chart and is defined as the expected number of charting statistics that must be plotted before the chart gives an OOC signal [42]. When the process is IC, the ARL is denoted as ARL₀ and should be large to avoid false alarms. On the other hand, when the process is OOC, the ARL is denoted as ARL₁ and should be small to detect the shift quickly. Except for the ARL, the standard deviation of the run-length (SDRL) and several percentile points are also evaluated to obtain more information about the run-length distribution.

In this Section, there are many tables which present the IC and OOC performance of the TL, DL and EL control charts for several continuous distributions. In order to be more easier for the reader to focus on the conclusions of this study, we have put tables into an ”Online Supplement”.

4.1. Monte Carlo simulation approach

The ARL₀ is a function of the design parameters of a control chart and can be computed using Markov chain approach, integral equations and Monte Carlo simulations. In this study, we perform the latter method because the charting statistic and the time-varying UCL are too complex. Thus, numerical computations in R software are used to determine the value of L on the basis of 25,000 replications. As the proposed chart is distribution-free, we generate m observations (Phase I) from a standard normal distribution and 15,000 Phase II samples, each of size n, from the same distribution; however any continuous probability distribution can be considered. Following the steps described in subsection 3.2 and changing only the value of L, we determine the appropriate one, so that the ARL₀ be approximately equal to a desired value. We consider m = 100 and 300 for the Phase I sample, n = 5, 10 and 15 for the Phase II sample and λ = 0.05, 0.10, 0.25 and 0.50 for the smoothing parameter. Table 2 presents the L values for several combinations of (m, n, λ) for the TL chart, so that the ARL₀ be approximately equal to 500. From this table, we observe that for a fixed value of m (n), the L value decreases (increases) as the value of n (m) increases in order to achieve the desired ARL₀ value. The same applies when the sample sizes m and n are fixed and the λ value increases. In order to compute the run-length characteristics of the TL chart under the OOC condition, we consider that a shift in the location and/or scale parameter(s) occurs at the start, ie, from the first Phase II sample. In addition, we follow the same steps as earlier to evaluate the zero-state run-length characteristics. The steady-state run-length characteristics are computed in a similar way, but the shift in the process parameter(s) occurs not from the first Phase II sample, but later. Steps 1 to 5 are repeated 25,000 times and the run-length characteristics are evaluated using the 25,000 values of the run-length. In this study, like the majority of the cited papers on joint monitoring the unknown values of location and scale parameters, we investigate the zero-state run-length characteristics.

Table 2.

Values of L for different combinations of (m, n, λ) for the TL control chart in order to achieve an ARL₀ ≈ 500.

		Time-varying UCL				Steady-state UCL
m	n	λ = 0.05	0.10	0.25	0.50	0.05	0.10	0.25	0.50
100	5	0.648	1.236	2.140	3.020	0.500	1.161	2.114	3.011
100	10	0.462	1.045	1.971	2.892	0.325	0.966	1.945	2.883
100	15	0.261	0.804	1.753	2.716	0.137	0.721	1.722	2.707
300	5	1.127	1.670	2.461	3.306	0.999	1.607	2.433	3.297
300	10	1.101	1.628	2.424	3.256	0.953	1.560	2.399	3.247
300	15	1.007	1.562	2.375	3.213	0.871	1.493	2.347	3.202

4.2. The IC run-length distribution

The TL chart is distribution-free, so the IC run-length characteristics remain the same for all continuous distributions. To investigate the IC and OOC performance of the proposed TL chart, we consider two symmetric and two asymmetric distributions. Those are: (i) the normal distribution with location parameter θ and scale parameter δ, denoted by N(θ, δ), (ii) the Laplace or double exponential distribution with location parameter θ and scale parameter $\delta /\sqrt{2}$, denoted by $L(\theta ,\delta /\sqrt{2})$, (iii) the shifted exponential distribution with shift parameter θ and scale parameter δ, denoted by SE(θ, δ) and the Gumbel distribution with location parameter θ and scale parameter δ, denoted by Gumbel(θ, δ). We remind that the IC values of location and scale parameters are θ = 0 and δ = 1, respectively. Table 3 presents the probability density functions (pdf) as well as the mean and the variance of the above distributions. Note that γ in the mean value of Gumbel distribution represents the Euler-Mascheroni constant. Based on the L values of Table 2, we evaluated the IC run-length characteristics of the TL chart under the N(0, 1) distribution. These values are approximately the same for any continuous distribution because the proposed chart is distribution-free. This can be concluded from Tables S2-S9, where ARL₀ and IC SDRL (SDRL₀) are approximately the same for all considered distributions. The results are presented in Table S1. More specifically, the first row of each cell in Table S1 presents the ARL₀ and the SDRL₀ while the second row presents the 5th, 25th, 50th, 75th and 95th percentile points of the IC run-length distribution. From Table S1, we observe the following:

1. The IC run-length distribution is highly positively skewed as the ARL₀ is larger than the 50th percentile point (MRL₀). The difference between the ARL₀ and the MRL₀ is large when the TL chart is designed with a time-varying UCL and a small value of λ (0.05 or 0.10) and a practitioner uses a small value of m and a large value of n. For example, when a time-varying UCL is used, the MRL₀ of a TL chart with (m = 100, n = 15, λ = 0.05, L = 0.261) is 15 while the corresponding value of the TL chart with (m = 300, n = 5, λ = 0.25, L = 2.461) is 284.

2. Generally, for fixed values of m and λ, the SDRL₀ and the 95th percentile point increase as the value of n increases while the 5th, 25th and 50th percentile points decrease. As regard as the 75th percentile point, we observe that it decreases, especially for small values of λ. For instance, when a steady-state UCL is used, the SDRL₀ and the percentile points of the TL chart with (m = 100, n = 5, λ = 0.10, L = 1.161) are 1133.47, 22, 70, 184, 472 and 1872 while the corresponding values of the TL charts with (m = 100, n = 10, λ = 0.10, L = 0.966) and (m = 100, n = 15, λ = 0.10, L = 0.721) are 1202.85, 19, 58, 165, 451, 1923 and 1242.44, 16, 44, 138, 427, 2054, respectively.

3. For fixed values of n and λ, the SDRL₀ and the 95th percentile point decrease as the value of m increases while the other percentile points increase. For example, when a time-varying UCL is used, the SDRL₀ and the percentile points of the TL chart with (m = 100, n = 5, λ = 0.25, L = 2.140) are 953.59, 3, 68, 210, 547, 1882 while the corresponding values of the TL chart with (m = 300, n = 5, λ = 0.25, L = 2.461) are 673.52, 8, 101, 284, 640, 1697.

4. For fixed values of m and n, the SDRL₀ and the 95th percentile point decrease as the λ value increases and vice versa for the other percentile points. For example, when a time-varying UCL is used, the SDRL₀ and the percentile points of the TL chart with (m = 300, n = 10, λ = 0.05, L = 1.101) are 998.59, 1, 20, 175, 559, 2015 while the corresponding values of the TL chart with (m = 300, n = 10, λ = 0.25, L = 2.424) are 661.54, 6, 97, 277, 643, 1720.

5. For fixed values of (m, n, λ), most of the percentile points, except for the 95th, are larger when one uses a steady-state UCL instead of a time-varying UCL. Moreover, the SDRL₀ value is smaller. For example, when (m = 100, n = 5, λ = 0.05), the SDRL₀ and the percentile points of a TL chart with a time-varying UCL and L = 0.648 are 1560.69, 1, 3, 65, 329, 2185 while the corresponding values of a TL chart a steady-state UCL and L = 0.500 are 1340.46, 25, 56, 150, 404, 1873.

To sum up, a small value of m and a large value of n in combination with a small value of λ may result in a large number of false alarms as the SDRL₀ value is very high. For this reason, we recommend practitioners to use a large value of m (say, m = 300) and a medium value of λ to avoid many OOC signals.

Table 3.

Distributions used in the OOC performance study.

Distribution	pdf	Mean	Variance
Normal	$f(x)={\displaystyle \frac{1}{\delta \sqrt{2\pi }}}{\text{e}}^{-{\displaystyle \frac{1}{2}}({\displaystyle \frac{x-\theta }{\delta }}{)}^2},x\in \mathrm{\Re }$	θ	δ2
Laplace	$f(x)={\displaystyle \frac{1}{\delta \sqrt{2}}}{\text{e}}^{-{\displaystyle \frac{|x-\theta |\sqrt{2}}{\delta }}},x\in \mathrm{\Re }$	θ	δ2
Shifted exponential	$f(x)={\displaystyle \frac{1}{\delta }}{\text{e}}^{{\displaystyle \frac{x-\theta }{\delta }}},x\ge \theta$	θ + δ	δ2
Gumbel	$f(x)={\displaystyle \frac{1}{\delta }}{\text{e}}^{-({\displaystyle \frac{x-\theta }{\delta }}+\text{e}-{\displaystyle \frac{x-\theta }{\delta }})},x\in \mathrm{\Re }$	θ + δγ	${\displaystyle \frac{{\pi }^2{\delta }^2}{6}}$

4.3. The OOC performance

To study the effect of shift(s) in the location and/or scale parameter(s), we consider 35 combinations of (θ, δ) where θ ∈ {0, 0.1, 0.25, 0.5, 1, 1.5, 2} and δ ∈ {1, 1.1, 1.25, 1.5, 2}. Tables S2-S9 present the ARL and SDRL (given in the parenthesis) values of the TL, DL and EL charts when m = 100, n = 5 and ARL₀ ≈ 500 for both time-varying and steady-state UCL. Moreover, the performance of the TL chart is evaluated for λ ∈ {0.05, 0.10, 0.25, 0.50} while the performance of the DL and EL charts for λ ∈ {0.05, 0.25}.

4.3.1. OOC performance under a normal distribution

Tables S2 and S3 show the OOC performance of the TL, DL and EL charts with a time-varying and a steady-state UCL respectively, under a N(θ, δ) distribution. Bold fonts in Table S2 indicate the smallest ARL₁ values for each shift.

From Table S2, we observe that the TL chart with λ = 0.05 is the most effective control chart at almost all levels of shifts, except for (θ, δ) = (0.1, 1) and (0.5, 1.5) where the DL chart with λ = 0.05 has the best detection ability. The OOC performance of all charts deteriorates as the value of λ increases. However, a larger value of λ results in a smaller SDRL₀, ie, in a smaller probability of false OOC signal. We notice that when λ = 0.25, the TL chart is superior to the DL chart, especially for a pure scale shift (θ = 0, δ ≠ 1) and small shifts in both parameters (0.1 ≤ θ ≤ 0.5, 1.1 ≤ δ ≤ 1.25). For the rest range of shifts, the TL chart performs a slightly better or similarly to the DL chart. Both of the TL and DL charts outperform the EL chart over the entire ranges of shifts.

From Table S3, where the charts are designed with a steady-state UCL, the results are different from those observed in Table S2. It is seen that a small value of λ is preferred to detect a pure small shift in one of two parameters or a small shift in both parameters simultaneously while a larger value of λ is more effective for moderate to large shifts. For example, a TL chart with λ = 0.50 outperforms the other TL charts with smaller values of λ for a pure and moderate to large location shift (1 ≤ θ ≤ 2, δ = 1), for moderate to large location shifts and small scale shifts (1 ≤ θ ≤ 2, 1.1 ≤ δ ≤ 1,.25), for moderate to large location shifts and a moderate scale shift (0.5 ≤ θ ≤ 2, δ = 1.5) and for a pure and large scale shift (δ = 2). Comparing with the DL and EL charts, the DL chart with λ = 0.05 is the best-performing scheme for a pure and small location shift (0.1 ≤ θ ≤ 0.5, δ = 1), for small shifts in both parameters (0.1 ≤ θ ≤ 0.25, δ = 1.1) and for (θ, δ) = (0, 1.25), (0.1, 1.25). On the other hand, the TL chart is the most effective chart for a pure and very small shift in scale parameter, ie, (θ = 0, δ = 1.1). Finally, the EL charts are superior to its competitors for the rest ranges of shifts, especially for mixed shifts with a moderate to large scale shift (δ ≥ 1.5).

Finally, comparing each scheme with a time-varying UCL with its corresponding with a steady-state UCL for the same value of λ, we observe that the differences between the ARL₁ values are large when λ = 0.05. These differences decrease as the value of λ increases. However, a TL chart with λ = 0.25 and a time-varying UCL provides a good detection ability for a large range of shifts comparing to DL and EL charts while it also has an acceptable SDRL₀ value.

4.3.2. OOC performance under a Laplace distribution

The OOC performance of the TL, DL and EL charts with a time-varying and a steady-state UCL under a $L(\theta ,\delta /\sqrt{2})$ distribution is presented in Tables S4 and S5, respectively. Note that using θ and $\delta /\sqrt{2}$ as location and scale parameters for the Laplace distribution, the mean/median and variance are equal to the corresponding values under a N(θ, δ) distribution, ie, θ and δ², respectively. Bold fonts in Table S4 indicate the smallest ARL₁ values for each shift. Generally, the results are similar to the results observed under the N(θ, δ) distribution, but with some minor differences.

From Table S4, it is seen that the TL chart with λ = 0.05 outperforms the other charts over the entire ranges of shifts, except for a pure and large location shift (θ = 0, δ = 2) and mixed small to moderate location and large scale shifts (0.1 ≤ θ ≤ 0.5, δ = 2) where the DL chart with λ = 0.05 performs a slightly better. Like to the N(θ, δ) distribution, the detection ability of all charts deteriorates as the value of λ increases. Furthermore, the TL chart with λ = 0.25 is more effective than the DL chart with λ = 0.25 for the same ranges of shifts with those under the normal distribution, ie, (θ = 0, δ ≠ 1) and (0.1 ≤ θ ≤ 0.5, 1.1 ≤ δ ≤ 1.25).

The results about the OOC performance of control charts with a steady-state UCL are very close to those under the N(θ, δ) distribution. A minor difference is that the TL chart with λ = 0.05 is the most effective chart for pure and small location shifts (0.1 ≤ θ ≤ 0.25, δ = 1) and for very small shifts in both parameters (θ = 0.1, δ = 1.1) while the DL chart with λ = 0.05 is the most sensitive for a pure and small scale shift (θ = 0, 1.1 ≤ δ ≤ 1.25) and for small shifts in both parameters, ie, (θ = 0.25, δ = 1.1) and (0.1 ≤ θ ≤ 0.25, δ ≤ 1.25). The EL chart is superior to its competitors for the rest ranges of shifts.

Finally, we observe that the ARL₁ values under the Laplace distribution are smaller than those under the normal distribution for a pure location shift and for mixed shifts with θ ≥ 0.5 and vice versa for the rest ranges of shifts.

4.3.3. OOC performance under a shifted exponential distribution

The results about the OOC performance of the TL, DL and EL charts with a time-varying and a steady-state UCL under a SE(θ, δ) distribution are shown in Tables S6 and S7, respectively where bold fonts in Table S6 indicate the smallest ARL₁ values for each shift. The results are quite similar to those of the symmetric distributions; however, there are some differences.

From Table S6, we observe that the TL chart with λ = 0.05 is the best-performing chart, especially for pure and small to moderate location shifts (θ ≤ 1, δ = 1) and for mixed shifts with a small to moderate location shift, except for the cases of (θ, δ) = (0.1, 1) and (0.1, 1.1) where the TL chart with λ = 0.5 and the EL chart with λ = 0.25 are the most sensitive, respectively. Moreover, the control charts are ARL-biased for a pure and small shift in the location parameter (θ = 0.1, δ = 1) and in some cases for mixed small shifts in both parameters (θ = 0.1, δ = 1.1). It is to be noted that the ARL₁ values for (θ, δ) = (0.1, 1), (0.1, 1.1) and (0.1, 1.25) are larger than the corresponding values of (θ, δ) = (0, 1), (0, 1.1) and (0, 1.25), respectively. The performances of control charts deteriorate as the value of λ increases, except for shifts of (θ = 0.1, δ ≤ 0.1) where charts with large values of λ perform better. Finally, the TL chart with λ = 0.25 is more effective than the DL and EL charts with λ = 0.25 for pure and small to moderate location shifts (0.1 ≤ θ ≤ 0.5, δ = 1) or mixed shifts with a small to moderate location shift (0.1 ≤ θ ≤ 0.5, δ ≠ 1), except for shifts of (θ = 0.1, δ ≤ 1.1) where the EL chart is more effective.

Among the charts with a steady-state UCL, it is seen that a small value of λ is preferred to detect small shifts in parameters and medium to large values of λ are more effective for detecting moderate to large shifts. The TL chart with λ = 0.50 has the smallest ARL₁ value for (θ = 0.1, δ = 1) while the TL chart with λ = 0.05 is the most effective for (θ = 0, δ = 1.25). On the other hand, the DL chart with λ = 0.05 is very sensitive for a pure and small to moderate scale shift [(θ = 0, δ = 1.1) and (θ = 0, δ = 1.5)] as well as for mixed small shifts in both parameters; those are (θ, δ) = (0.25, 1), (0.25, 1.1), (0.1, 1.25), (0.25, 1.25). The EL chart outperforms the other charts for the rest ranges of shifts, ie, for mixed moderate to large shifts in both parameters.

4.3.4. OOC performance under a Gumbel distribution

The OOC performance of the competing charts with a time-varying and a steady-state UCL under a Gumbel(θ, δ) distribution is provided in Tables S8 and S9, respectively. Bold fonts indicate the smallest ARL₁ values for each shift. The results are similar to those under the SE(θ, δ) distribution.

From Table S8, we observe that the TL chart with λ = 0.05 outperforms the DL and EL charts over the entire ranges of shifts, except for (θ = 0.1, δ = 1) and (θ ≤ 0.1, δ = 2) where the EL chart with λ = 0.25 and DL chart with λ = 0.05 respectively, are the most effective. The charts are ARL-biased only for (θ = 0.1, δ = 1) while the ARL₁ values of shifts with θ = 0.1 are always larger than those with θ = 0 for the same amount of scale shift. Comparing the charts with λ = 0.25, the proposed TL chart is more effective than the DL chart, especially for pure and small to moderate location shifts (0.1 ≤ θ ≤ 1, δ = 1) and for mixed small shifts in both parameters (0.1 ≤ θ ≤ 1, 1.1 ≤ δ ≤ 1.25). The two charts perform similarly for pure and large location shifts (θ ≥ 1.5, δ = 1) and mixed large shifts in both parameters (θ ≥ 1.5, δ ≥ 1.5). We note that both of TL and DL charts are more effective than the EL chart at the whole of shifts.

From Table S9, we observe that the TL chart with λ = 0.05 is the most effective chart for the cases of (θ, δ) = (0.25, 1), (0.1, 1.1) and (0.25, 1.1) while the DL chart with λ = 0.05 has the best detection ability against the other charts for (θ, δ) = (0.5, 1), (0, 1.1), (0.5, 1.1) and (θ ≤ 0.25, δ = 1.25). The EL chart outperforms its competitors for the rest ranges of shifts.

5. Illustrative example

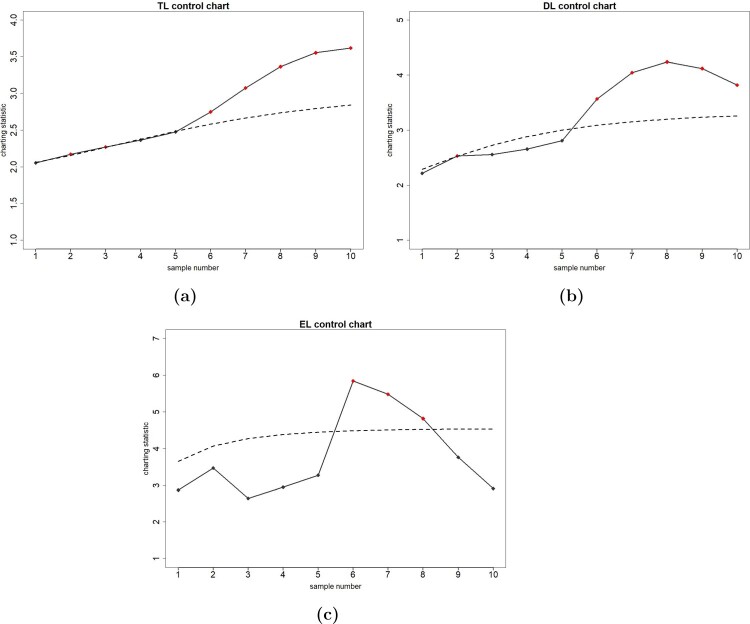
In order to demonstrate the application of the proposed TL chart, we use a dataset, given by Figueiro and Gomes [24], about the lengths (in mm) of cork stoppers. The dataset is presented in Table 4. The first 100 observations represent the Phase I sample and therefore, m = 100. The Phase II dataset consists of 10 samples, each of size n = 5. It should be noted that according to Figueiro and Gomes [24] and Song et al. [60] who also studied this dataset, the lengths of cork stoppers can be considered to be right-skewed. It is not necessary to estimate the unknown values of process parameters from the Phase I dataset because the proposed chart does not require the knowledge of them. The Lepage statistic uses the Phase I and each of Phase II samples to test the equality of both the location and scale parameters. Setting an ARL₀=500 and using (m, n, λ) = (100, 5, 0.25), we construct the TL, DL and EL charts with a time-varying UCL. Table 5 shows the charting statistics of the control charts with the corresponding UCL_j values while Figure 3 displays the control charts. Bold fonts in Table 5 and red dots in Figure 1 indicate the charting statistics that lie over the corresponding UCL_j values. From Figure 1, we observe that the TL chart gives OOC signals at test samples 2, 3 and from 6 until 10, while the DL chart produces OOC signals at test samples 2 and from 6 until 10. Finally, the EL chart offers OOC signals at test samples 6, 7 and 8.

Table 4.

Lengths (in mm) of cork stoppers.

Sample number	Phase I					Sample number	Phase II
1	44.55	44.78	44.88	44.78	44.73	1	45.25	45.12	44.65	45.02	45.08
2	44.68	44.96	45.20	44.72	45.21	2	44.80	44.86	45.03	44.86	44.84
3	44.82	44.88	45.65	44.48	44.76	3	44.68	45.10	45.02	44.79	44.79
4	45.15	44.79	45.11	44.51	44.92	4	45.00	45.00	44.95	45.01	45.12
5	44.73	44.69	44.93	44.98	45.47	5	44.77	45.06	45.27	45.23	44.94
6	44.78	44.48	44.89	44.77	45.03	6	45.21	45.16	45.07	45.21	45.17
7	44.78	44.96	44.77	45.19	45.12	7	45.18	45.14	45.01	44.96	44.93
8	45.09	44.83	44.98	45.05	44.75	8	45.00	44.93	45.06	45.06	44.86
9	44.91	44.76	44.83	44.77	45.08	9	44.86	44.70	45.21	44.59	44.96
10	44.90	45.34	44.84	44.94	44.90	10	44.82	44.95	44.79	45.05	44.76
11	44.86	44.79	45.07	44.90	44.99
12	44.98	44.61	44.75	44.82	44.86
13	45.18	44.64	45.10	45.02	44.87
14	45.02	44.84	44.93	44.66	44.78
15	44.75	44.83	44.89	44.72	44.82
16	44.85	44.73	44.73	44.80	44.90
17	44.78	44.82	44.99	45.15	45.32
18	44.68	45.07	44.79	44.86	45.04
19	44.52	45.02	44.85	44.79	45.19
20	44.90	44.89	44.91	45.24	44.86

Table 5.

Charting statistics and UCL_j values of control charts and follow-up procedure.

		EL chart		DL chart		TL chart		p1-value		p2-value
j	Lj	ELj	UCLj	DLj	UCLj	TLj	UCLj	$p_1^{-}$	$p_1^{+}$	$p_2^{-}$	$p_2^{+}$
1	5.4666	2.8667	3.6478	2.2167	2.2912	2.0542	2.0630	0.9358	0.0661	0.9629	0.0371
2	5.2706	3.4677	4.0671	2.5294	2.5268	2.1730	2.1556	0.5390	0.4670	0.0183	0.9817
3	0.1635	2.6416	4.2742	2.5575	2.7241	2.2691	2.2648	0.4254	0.5805	0.6602	0.3398
4	3.8564	2.9453	4.3864	2.6544	2.8802	2.3654	2.3774	0.9757	0.0252	0.4911	0.5089
5	4.2515	3.2719	4.4499	2.8088	2.9994	2.4763	2.4848	0.9562	0.0452	0.8786	0.1214
6	13.5538	5.8423	4.4869	3.5672	3.0882	2.7490	2.5816	0.9988	0.0013	0.9822	0.1780
7	4.3909	5.4795	4.5089	4.0452	3.1532	3.0731	2.6656	0.9818	0.0189	0.5866	0.4134
8	2.8446	4.8207	4.5222	4.2391	3.2002	3.3646	2.7362	0.9386	0.0633	0.2419	0.7581
9	0.5946	3.7642	4.5305	4.1204	3.2337	3.5535	2.7942	0.3760	0.6297	0.7758	0.2242
10	0.3383	2.9077	4.5358	3.8172	3.2576	3.6195	2.8409	0.4461	0.5598	0.3077	0.6923

Figure 1.

Distribution-free Phase II control charts for the lengths of cork stoppers data (a) the TL chart, (b) the DL chart, and (c) the EL chart).

Next, we apply a follow-up procedure by computing the p₁ and p₂ values for the WRS and AB tests, respectively. In order to specify the direction of shift (upward or downward), we compute the $p_k^{+}$ and $p_k^{-}$, k = 1, 2, values. The test sample 2 shows an OOC behavior for the TL and DL charts. As $p_2^{-}$-value is significantly lower than 5% ( $p_2^{-}=0.0183$) and $p_1^{+}$, $p_1^{-}$ and $p_2^{+}$-values are significantly higher than 5%, we conclude that there is an evidence of a downward shift in the scale parameter and no evidence in the location parameter. Similarly, for the test samples 6 and 7, $p_1^{+}$-values are significantly lower than 5%, while $p_1^{-}$, $p_2^{+}$ and $p_2^{-}$-values are significantly higher than 5%. Thus, there is an evidence of an upward shift in the location parameter. For the test sample 8, the $p_1^{+}$-value is marginally higher than 5% ( $p_1^{+}=0.0633$) and $p_1^{-}$, $p_2^{+}$ and $p_2^{-}$-values are significantly higher than 5%; thus, one may conclude that there is an evidence of an upward shift in the location parameter. Finally, for the test samples 3, 9 and 10, the p-values are not significant and either there is an interaction between location and scale shifts or there is a false alarm.

To sum up, TL and DL charts are more effective than the EL chart as they detect an OOC earlier than the EL chart. Moreover, the TL chart gives more OOC signals than the DL chart.

6. Conclusions and recommendations

In this article, we propose a distribution-free Phase II TEWMA control chart based on the Lepage statistic for joint monitoring the location and scale parameters of an unknown and continuous distribution. The proposed chart is referred as TL chart. Performing Monte Carlo simulations, we evaluated its IC and OOC performances with time-varying and steady-state UCL in terms of the run-length characteristics. We also compared its performance with other distribution-free Phase II charts based on the Lepage statistic, such as the EL and the DL charts. Using a time-varying UCL, we observe that the TL chart outperforms its competitors, especially for small to moderate shifts in one of two parameters or in both parameters simultaneously. Due to a large value of SDRL₀ for small values of smoothing parameter λ, we recommend practitioners to implement the TL chart with medium values of λ, such as λ = 0.25. On the other hand, using a steady-state UCL, the DL and TL charts are more effective than the EL chart for a pure and small shift in one of parameters or in small shifts in both of parameters while the EL chart is the best-performing for moderate to large shifts.

Knoth et al. [30,31] advised practitioners against the use of the TEWMA scheme, as well as many other memory-type control charts, such as DEWMA, GWMA, HWMA and MEC charts, when the process parameters are assumed to be known. They put emphasis on the weights of data and they compared different control charts with design parameters which have been arisen from the equality of the asymptotic variances of the different charting statistics. They considered only the ARL value and not other run-length characteristics. This criterion should be considered as arbitrary. In our opinion, a holistic approach should take into consideration not only the ARL, but also other characteristics of the run-length distribution, as well as the properties of control charts in robustness and inertia problem, where the DEWMA and TEWMA schemes have better properties rather than the EWMA scheme [5]. This topic has been studied by Alevizakos et al. [6] who concluded that some of the extensions and modifications of the EWMA chart are more effective than the traditional EWMA chart, especially for small and moderate shifts for both the zero-state and steady-state cases.

For future research, it would be of interest to study distribution-free Phase II TEWMA charts for joint monitoring the process parameters based on the Cucconi or Cramér–von Mises statistics.

Disclosure statement

No potential conflict of interest was reported by the author(s).