Foveal blur-boosted segmentation of nuclei in histopathology images with shape prior knowledge and probability map constraints

Abstract

Motivation

In most tissue-based biomedical research, the lack of sufficient pathology training images with well-annotated ground truth inevitably limits the performance of deep learning systems. In this study, we propose a convolutional neural network with foveal blur enriching datasets with multiple local nuclei regions of interest derived from original pathology images. We further propose a human-knowledge boosted deep learning system by inclusion to the convolutional neural network new loss function terms capturing shape prior knowledge and imposing smoothness constraints on the predicted probability maps.

Results

Our proposed system outperforms all state-of-the-art deep learning and non-deep learning methods by Jaccard coefficient, Dice coefficient, Accuracy and Panoptic Quality in three independent datasets. The high segmentation accuracy and execution speed suggest its promising potential for automating histopathology nuclei segmentation in biomedical research and clinical settings.

Availability and implementation

The codes, the documentation and example data are available on an open source at: https://github.com/HongyiDuanmu26/FovealBoosted.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Pathology image analysis is a crucial step to support accurate cancer mechanism research, disease grading, diagnosis and treatment planning (Elmore et al., 2015). Although there is a high demand for precise nuclei morphology analyses, nuclei segmentation, the prerequisite step, very often is completed manually by pathologists in practice. In spite of a large number of studies on this topic (Hayakawa et al., 2021), there is still a lack of robust, accurate and efficient methods that can be widely deployed. Thus, it remains high demands and priority to develop effective and precise nuclei segmentation methods.

By far, numerous studies have been initiated for robust nuclei segmentation (Hayakawa et al., 2021). Thresholding is an easy and straightforward method for segmentation (Kumar et al., 2017). However, neither simple Otsu thresholding nor advanced methods such as adaptive thresholding can accommodate crowded nuclei that challenge these methods on touching nuclei division (Kumar et al., 2017). With the usage of efficient radial line scanning, system mRLS (multiscale Radial Line Scanning) improves segmentation performance but cannot meet the accuracy requirement for clinical use (Xu et al., 2017). The use of such watershed-based algorithms as MOW (Jung and Kim, 2010) and IVW (Xu et al., 2014) was reported to segment nuclei with promising results (Veta et al., 2013). Representing the input image as a topographic surface, watershed methods simulate the flooding process from all markers defined either by manual annotations or other automated algorithms. Thus, their performances highly depend on the marker initialization and can be significantly deteriorated by over-segmentation (Kumar et al., 2017). Active contour model (ACM)-based algorithms are also widely used for pathology nuclei segmentation (Zhang et al., 2019). Although promising segmentation performance can be achieved, it is time-consuming for such algorithms as RACM (Xing et al., 2014) to complete segmentation.

Recently, deep learning methods have drawn dramatic attention in numerous fields and achieved great progress in a large variety of analysis tasks including medical image analysis (Kumar et al., 2017; Naylor et al., 2017). Thanks to its outstanding ability to automatically capture image patterns, Convolutional Neural Network (CNN) has been reported effective for image related analysis tasks (LeCun et al., 1998). For example, U-Net, one classic segmentation system has demonstrated inspiring performance in numerous segmentation tasks and evolved to multiple variations (Ronneberger et al., 2015). In addition, DeepLab and its variants enabled by numerous advanced techniques such as Atrous Convolution, Atrous Spatial Pyramid Pooling and fully connected Conditional Random Field (CRF) module, have achieved great success in multiple semantic segmentation tasks (Chen et al., 2018). Generative adversarial network (GAN) is another successful type of CNN design for segmentation systems. Its advanced variant, conditional GAN (cGAN), has shown great potential for medical image analysis (Shin et al., 2018). Mask R-CNN and YOLACT++ are two representative segmentation models derived from two- and one-stage detector, respectively. They have been successfully used in numerous challenges with promising segmentation precision and effectiveness (Bolya et al., 2019a,b; He et al., 2017). Based on these general CNN architectures, numerous deep learning systems are specifically designed to tackle the challenge in nuclei segmentation. For example, a famous nuclei segmentation system CIA-Net uses a newly designed information aggregation module and the bootstrapped loss, achieving first place in MICCAI’18 MoNuSeg challenge (Zhou et al., 2019). In addition, HoVer-Net achieves inspiring performance in segregating overlapping nuclei instances by predicting both horizontal and vertical distances of nuclear pixels to nuclei centers (Graham et al., 2019). Another such representative state-of-the-art method is Bi-directional O-shaped CNN (BiO-Net) (Xiang et al., 2020). Thanks to its recurrent usage of convolutional blocks, it produces promising segmentation results.

Although multiple studies report inspiring segmentation performance, deep learning systems generally have two main drawbacks. First, performances of deep learning segmentation systems highly depend on the scale of the dataset and the quality of the ground truth for training (Naylor et al., 2017). As it is difficult to collect sufficient high-quality image data and precise ground truth from experts in most cases, the development of effective solutions that can assure and boost the training success with limited annotated data becomes an important but challenging research subject. Second, it is noted that most conventional energy-based methods, such as watershed and ACM algorithms, can explicitly use such morphology information as shape prior for enhanced nuclei contour identification (Zhang et al., 2019). By contrast, CNN models cannot explicitly leverage the prior knowledge on nuclei shapes. It remains an unsolved and challenging problem to explicitly integrate nuclei morphological knowledge into CNN models.

To address these two problems critical to CNN performance and usability, we have developed two methods for better nuclei segmentation performance. (i) We propose to enrich the limited datasets and boost the CNN training process by foveal blur, a blurring method emulating human vision behaviors. To our best knowledge, this is the first time that foveal blur is introduced for nuclei segmentation with a clear algorithm description. With foveal blurring for each nucleus in a histopathology image, it can efficiently scale up the training dataset by producing a large number of foveal-blurred nuclei-level image instances. Thus, our foveal blur-based solution ensures effective deep learning training when the training image set is limited. (ii) To explicitly inform the CNN model of nuclei morphological knowledge, we design two new loss function terms on shape prior and smoothness constraints. Specifically, we create a nuclei shape prior dictionary that penalizes prediction results aberrant from nuclei shape priors. In this way, it encourages the CNN system to predict nuclei contours compatible with representative nuclei shapes. The second new term evaluates the smoothness of the predicted probability map by the first- and second-order gradient. By explicitly teaching deep learning system nuclei segmentation principles, we propose our human-knowledge boosted deep learning system for enhanced model learning. Our method is tested with three independent datasets. Results from all three datasets show that our method outperforms other state-of-the-art non-deep learning and deep learning systems for comparison by both segmentation accuracy and speed. With the promising segmentation accuracy and computational efficiency, our proposed human-knowledge boosted deep learning system presents its promising potential for accurate and efficient nuclei segmentation for biomedical research and clinical practice.

2 Materials and methods

2.1 Foveal blurred image generation

Enlightened by research findings in neuropsychology and psychophysics, foveal blur was originally proposed to simulate human visual attention in digital image processing research (Perry and Geisler, 2002). The relative spatial frequency map representing human vision acuity over the gaze direction has been modeled and idealized in image processing tasks in 2002 (Perry and Geisler, 2002). It is noticed that the resolution close to the gaze point is high and regions divergent from the gaze point are gradually blurred due to the decrease in the vision acuity. We illustrate in Figure 1, a typical relative spatial frequency map and multiple sample foveal blurred pathology image patches focusing on different nuclei.

Fig. 1.

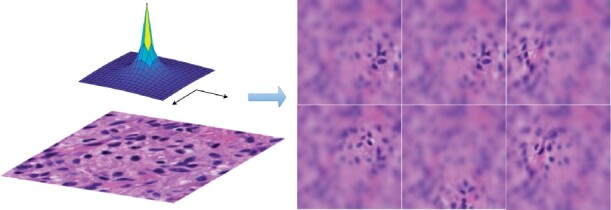
We present an idealized spatial frequency map (top left), a raw histopathology image patch (bottom left) and multiple foveal blurred sample images (right) derived from the raw histopathology image patch

No study has provided an accurate and clear algorithmic description of foveal blur image generation to our best knowledge. Therefore, we provide the detailed procedure of our complete foveal blurring process below. For different levels of blurring effect on each pixel, the original image is first convoluted with one Gaussian kernel with a standard deviation of 0.248 (Jiang et al., 2015). Blurred images at six different levels are generated recursively and used to form the multi-resolution pyramid. The distance between the fixation (x_c, y_c) and blur pixel (x, y) is measured by the angle between two sight trajectories to these two points from one person in distance p: $\theta =\mathit{atan}(\sqrt{{(x-x_c)}^2+{(y-y_c)}^2}/p)$. We set p = 7.5 to lead to a comfortable and natural experience (Jiang et al., 2015). Using such computed angles, we produce the spatial frequency based on the relative spatial frequency map. The idealized function is $F=\frac{\alpha }{\alpha +\theta }$, where α is set 2.5 for compliance with the actual acuity of the human retina (Pointer and Hess, 1989). Next, we calculate blending coefficients for the linear combination of the blurred images in the multi-resolution pyramid. As we have six images in the multi-resolution pyramid, we partition the spatial frequency range into five intervals by six cutoff values: 0, $\frac{1}{5},\hspace{0.17em}\frac{2}{5},\hspace{0.17em}\frac{3}{5},\hspace{0.17em}\frac{4}{5},\hspace{0.17em}\frac{5}{5}$. The spatial frequency F determines the image level in the multi-resolution pyramid. If the pixel has a spatial frequency F in $(\frac{2}{5},\frac{3}{5})$ level, for example, the blurred representation of this pixel is a linear combination of the third and the fourth image in the multi-resolution pyramid with weight $|F-\frac{2}{5}|$, and $|F-\frac{3}{5}|$, respectively. The detailed algorithmic descriptions are given in Algorithm 1.

Processed by the proposed foveal blur method with a focus on nuclei centroids, numerous images focusing on individual nuclei can be derived from each pathology image. On average, there are more than 100 nuclei in each histopathology image patch from all our three testing datasets. Therefore, this process can readily scale up each dataset by more than 100 times. In addition to the proposed foveal blurred image generation for the system input module, we have also proposed methods for better learning nuclei contour ground truth explicitly on the system output side. As the foveal blurred histopathology images are images focusing on individual nuclei, we ‘down-sample’ the ground truth annotations to the nuclei level and only retain the corresponding nucleus mask to train the CNN segmentation system. The proposed methods for both system input and output modules are designed to make the system learn nuclei information on a one-by-one case rather than as a whole, enabling a boosted learning from a given small-scaled dataset.

Algorithm 1: Algorithm for foveal blurred image generation.

Data: Raw image I(x, y), and fixation (x_c, y_c).

Result: Foveal blurred image $\tilde{I}(x,y)$.

Initial: # of images in multi-resolution pyramid: k, retina configuration: α, p, and Gaussian kernel: G.

/* multi-resolution pyramid images */

$$P_i\leftarrow \{\begin{array}{cc}I\hfill & \text{if}\hspace{0.17em}i=k\hfill \\ P_{i+1} \mathrm{\otimes G}\hfill & \text{if}\hspace{0.17em}i=1,\dots ,k-1\hfill \end{array}$$

/* relative spacial frequency map */

$$\theta (x,y)\leftarrow \mathit{atan}(\sqrt{{(x-x_c)}^2+{(y-y_c)}^2}/p)$$

$$F(x,y)\leftarrow \frac{\alpha }{\alpha +\theta }$$

/* blending coefficients */

$$B_i\leftarrow \{\begin{array}{cc}|F-\frac{i-1}{k-1}|\hfill & \text{if}\hspace{0.17em}\frac{i-2}{k-1}<F<\frac{i}{k-1}\hfill \\ 0\hfill & \text{else};\hfill \end{array}$$

/* linear combination of pyramid images with blending coefficients */

$$\tilde{I}(x,y)\leftarrow \sum _{i=1}^k{B}_i{P}_i$$

2.2 Shape prior generation

We have created a shape reference library to explicitly teach the CNN model the prior knowledge on nuclei shapes. Although it is easy to acquire numerous nuclei samples, it is not straightforward to identify representative shapes to be included in the shape library. Taking the computational efficiency into account, we cluster N nuclei samples from a large number of histology images into K groups where $K\ll N$. Following the method in prior research work, K is set to 100 in this work, and it can be changed depending on the specific task and dataset (Zhang et al., 2019). All training nuclei samples are aligned by the generalized Procrustes analysis (Goodall, 1991). In this way, we exclude rotation effect from the shape learning process. We identify representative nuclei instances capturing as much group representative morphology information as possible by solving the following optimization problem.

$$\widehat{d}=\arg \underset{d}{\min }{\Vert {\psi }_i-B{d}_i\Vert }_2^2+\lambda {\Vert d_i\Vert }_{1}s.t.d_{ii}=0$$ (1)

where d_i denotes the linear combination coefficients to the ith nucleus sample; ψ denotes the distance map of the centered nucleus binary mask that presents the distance from each pixel to the nearest edge pixel of a nucleus sample; $B=\left\{{\psi }_1,{\psi }_2,{\psi }_3\dots {\psi }_N\right\}$ denotes the library consisting of the N nuclei samples distance maps with size 32 × 32 in pixels. By minimizing the difference between the nucleus sample and the optimal linear combination of all other nuclei samples in the shape library, we obtain distance coefficients between all sample pairs. Given $\widehat{d_i}$ is the best linear combination coefficient vector for shape reconstruction of nucleus sample i, we denote $\widehat{d_{ij}}$ as the jth entry of $\widehat{d_i}$. Each element D_ij of the symmetric distance matrix D representing the distance between ith and jth nucleus sample is computed as the average of the distance coefficients:

$$D_{ij}=({\widehat{d}}_{ij}+{\widehat{d}}_{ji})/2$$ (2)

After the distance similarity matrix D is formulated, the un-normalized spectral clustering method is used to partition the shape priors into K clusters (Mohar, 1997). Then, The cluster representative nucleus is calculated by pixel-wise average in each cluster. The resulting K nuclei $\Psi ={\Psi }_1,{\Psi }_2,{\Psi }_3,\dots ,{\Psi }_K$ encoded by the distance map are the most cluster representative nuclei samples for the shape library. Finally, we transfer these distance map representations to binary nuclei masks. We demonstrate a panel of representative nuclei and the resulting nuclei shape library in Figure 2.

Fig. 2.

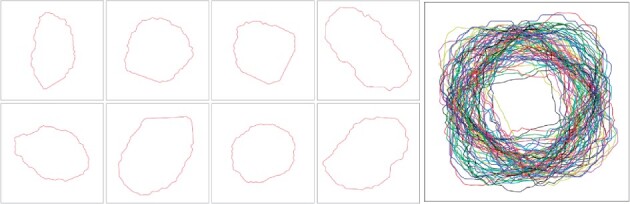
Representative nuclei and the resulting nuclei shape prior library

2.3 Loss function

A deep learning segmentation system $f(·)$ having a large set of hyperparameters θ maps a given image x to its segmentation prediction $f(x|\theta )$. Its loss function $\mathcal{L}$ measures the performance of the segmentation by the difference between the system predictions $f(x|\theta )$ and golden standard y provided. The segmentation system updates its trainable parameters to minimize such loss function over the training set by computing the gradient of the loss function with respect to each parameter in the deep learning system with back-propagation.

$$\widehat{\theta }=\arg \underset{\theta }{\min }\sum _{i=1}^N\mathcal{L}(f(x_i|\theta ),y_i)$$ (3)

To make our system explicitly learn nuclei shape prior knowledge and follow shape constraints, we have designed two new terms in the loss function in addition to the cross entropy loss.

2.3.1 Term of cross entropy

Cross entropy is widely used in the loss function for segmentation tasks, measuring the difference between two probability distributions:

$${\mathcal{L}}_{CE}=-\sum _{i=1}^N{\int }_{z\in \Omega }{y}_i\hspace{0.17em}\text{log}(f(x_i(z)|\theta ))dz$$ (4)

where Ω denotes the image domain and N is the total number of image patches in the training batch. In addition to cross entropy, this component of loss can be replaced with some other loss function such as Dice loss, one common loss function option in segmentation tasks (Zhou et al., 2019). This term serves as a fundamental component in our loss function measuring the difference between ground truth and system prediction.

However, both cross entropy and Dice loss treat all pixels equally and individually. It can explicitly capture neither human prior knowledge of the nuclei morphology nor local information on relationships across neighboring pixels. To address these problems, we next propose two additional terms in the loss function.

2.3.2 Term of shape prior

As we intend to make our system prediction results similar to representative nuclei $\Psi$ in the shape prior library by shape, we have developed a new loss function term on shape compatibility assessed by the convolution operation. By traversing all samples in the shape prior library, we find the nucleus presenting the maximum autocorrelation with the prediction nucleus, and take it as the shape prior representation of the prediction. The closer the prediction is to the shape priors in the library, the less the loss term is. Therefore, this shape prior term penalizes the system when predictions are divergent from nuclei samples in the shape library.

$${\mathcal{L}}_{SP}=-\sum _{i=1}^N\underset{k}{\max }{\int }_{z\in \Omega }{\Psi }_k\otimes f(x_i(z)|\theta )dz$$ (5)

where the operator ⊗ represents the convolution operation.

2.3.3 Term of smoothness in the prediction map

To further constrain the morphological smoothness of the resulting prediction map, we have designed a new loss function term to restrain the system from producing sharp or irregular prediction probability maps. This smoothness term is enlightened by the fact that similar inputs for a robust system lead to similar outputs. Notably, the prediction result for each image pixel by CNN systems is primarily determined by the corresponding local receptive image field, while predictions for neighboring pixels are determined by local overlapped receptive image fields. Thus, similar input local receptive image fields would lead to similar prediction results for neighboring pixels in a robust CNN system. However, local drastic changes in the prediction result can deteriorate CNN system robustness. Therefore, our smoothness term is designed to strengthen the system robustness by means of penalizing such local drastic changes in the prediction results. Specifically, we constrain magnitudes of the first and second-order gradient of the predicted probability maps for guided nuclei segmentation. Any dramatic change in the prediction map over the nuclei regions is penalized by this term, encouraging the CNN system to pay attention to the local information of pixels in close proximity. The hyperparameter α is introduced to balance the first and second-order components in the prediction smoothness term:

$${\mathcal{L}}_{SM}=\sum _{i=1}^N{\int }_{z\in \Omega }({\Vert \nabla f(x_i(z)|\theta )\Vert }_1+\alpha {\Vert {\nabla }^{2}f(x_i(z)|\theta )\Vert }_1)dz$$ (6)

Combining all these components, the overall loss function in our proposed human-knowledge boosted deep learning system has three individual terms. We have a basic cross entropy term measuring the pixel-wise difference between the prediction and the ground truth. In addition, two human-knowledge-based terms are designed, one on nuclei shape prior learning and another on smoothness regulation penalizing morphological irrationality in the predicted probability map. Making balance over the different restrictions on the system, the overall loss function is a linear combination of these three loss terms:

$$\mathcal{L}(x|\theta ,y)={\mathcal{L}}_{CE}+{\lambda }_{SP}{\mathcal{L}}_{SP}+{\lambda }_{SM}{\mathcal{L}}_{SM}$$ (7)

where λ_SP and λ_SM are two weights to balance the loss function terms, making three different terms approximately on the same scale by numerical values. In our experimental configuration, weights are set as $\alpha =0.1,\hspace{0.17em}{\lambda }_{SP}=0.5$ and ${\lambda }_{SM}=0.5$, respectively.

2.4 The deep learning model architecture

We illustrate the schema of the proposed deep learning-based segmentation system in Figure 3. Before the deep learning system training, the shape prior library is built to capture representative nuclei. Next, training image pairs, i.e. one foveal blurred image and the corresponding fixation nucleus mask, are provided to the CNN backbone. Finally, three loss terms are computed. By backpropagation, weights of the CNN backbone are updated until the system converges to the best performance. Note that testing images in our experiments are not processed with foveal blur. In the testing phase, the inputs to our proposed system are raw histopathology images that are neither pre-processed nor manually labeled.

Fig. 3.

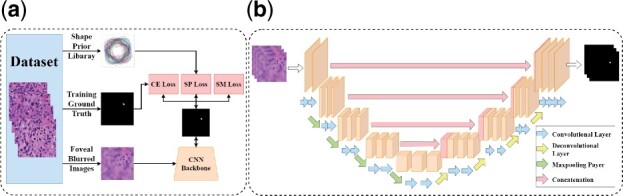
We present the system schema with details of (a) the proposed system, and (b) CNN backbone architecture

A large pool of deep learning models is open to serve as the CNN backbone based on our approach design. In our experiments, we use one classical version of U-Net (Ronneberger et al., 2015) to demonstrate the effectiveness of our proposed method for enhanced model training. However, the U-Net model can be replaced with other deep learning architectures. The paired symmetric down-sampling and up-sampling procedure is the signature characteristic of the U-Net model. In the down-sampling component, there are four convolutional blocks, each consisting of two convolutional layers and one maxpooling layer. Likewise, the deconvolutional block consisting of two convolutional layers and one deconvolutional layer is repeated four times in the up-sampling part, making the system output of the same size as that of the input. Four intermediate connections between the down-sampling and the up-sampling module are deployed to avoid critical information loss due to sampling. In addition, we keep the number of channels the same as that of the original U-Net architecture (Ronneberger et al., 2015).

Because the proposed deep learning system is a segmentation system rather than an instance segmentation system, post-processing is needed to segregate all contoured nuclei. After our deep learning system produces the binary nuclei segmentation masks, distance transform, h-minima transform and watershed are used to generate final instance-level nuclei segmentation results (Malpica et al., 1998).

3 Results and discussion

3.1 Data description

In this study, we comprehensively test our proposed systems with three independent datasets, namely GBM (local images and local annotations), TCGA (public images and local annotations) and MoNuSeg dataset (public images and public annotations), respectively. Three independent datasets include in total 41 960 nuclei boundary annotations from 119 histopathology images.

GBM dataset This dataset includes 40 H&E histopathology image regions of interest of glioblastoma tissues produced at Emory University Hospital at 40× magnification. Each pathology image region has a size of 512 × 512 in pixels and contains on average 150 nuclei with their contours delineated by our domain experts. We randomly split the dataset into seven images for training and the remaining for testing. To demonstrate the merit of our system that can be trained with a very limited number of images, we intentionally choose a small portion of the dataset as the training set.

TCGA dataset This is a publicly available dataset that includes 36 pathology image patches from nine brain tumor patients at 40× magnification from TCGA public archive (TCGA, 2020). Each patch is in 512 × 512 pixels and contains on average 122 nuclei that are well annotated by our domain experts. This dataset is randomly divided into nine and 27 images for training and testing, respectively.

MoNuSeg dataset The third dataset comes from the MICCAI’2018 Multi-organ Nuclei Segmentation Challenge (MoNuSeg) (MoNuSeg Challenge, 2018). This public dataset provides H&E stained tissue images captured at 40× magnification from the TCGA archive. All nuclei boundary annotations are provided by the Challenge hosts. In total, 44 images are produced with seven distinct organs (i.e. Breast, Kidney, Liver, Prostate, Bladder, Colon and Stomach) from 44 patients. Training and testing sets are split by the Challenge hosts. Specifically, the training dataset contains 30 images of size 1000 × 1000 in pixels and around 22 000 nuclear boundary annotations, while the testing set has 14 pathology images of size 1000 × 1000 in pixels with additional 7000 nuclear boundary annotations.

3.2 Progressive performance improvement from backbone

For model training, stochastic gradient descent (SGD) is used as the learning strategy. Nesterov momentum is used and set with 0.9. The learning rate is initiated with 0.001 and gradually decayed by one-tenth every 1000 epochs. The loss function of the system converges after 3000 epochs. The training and testing are completed on a computer cluster with NVIDIA Tesla V100 GPU and 88 Intel Xeon CPUs. Three models are fully trained to the best performance, including (i) only foveal blur component (named as FB-Net), (ii) the combination of foveal blur in training image patches with shape prior learning in the loss function (FB+SP) and (iii) foveal blur, shape prior term and morphology smoothness term in the loss function (FB+SP+SM).

We compare performances of our proposed three systems with the three independent datasets, and present qualitative and quantitative results in Figure 4 and Table 1, respectively. Multiple evaluation metrics are used for performance assessment, including Jaccard Coefficient (J), Precision (P), Recall (R), Dice Coefficient (DC), Accuracy (Acc), Panoptic Quality (PQ) and Hausdorff distance (HD) (Bertels et al., 2019; Graham et al., 2019; Kirillov et al., 2019; Rockafellar and Wets, 2009). The first five metrics are pixel-level segmentation metrics. By contrast, Hausdorff distance evaluates the system performance at the instance-level. Notably, Panoptic Quality is a metric assessing method performance at both the pixel and instance-level. The averages by these metrics are computed with all three testing datasets. We notice that performances from the U-Net systems trained with cross entropy and Dice loss are approximately the same. Thus, while the cross entropy term in our proposed systems can be replaced with Dice loss, the resulting system performances remain similar. As U-Net is the backbone of our proposed systems, our proposed systems, consistent with our anticipations, are better than U-Net trained with either cross entropy loss or Dice loss. Overall, we notice a strong trend of progressive improvements by all performance metrics in all three datasets as we gradually add FB, SP and SM components into our system. This manifests that all our three major contributions to the human-knowledge boosted deep learning model play an important role in system performance enhancement. Specifically, our FB+SP+SM system achieves the best segmentation results both by visual inspections and quantitative metrics, with nearly 5% improvement from FB-Net system by Jaccard coefficient for the GBM and TCGA dataset, and 3% improvement for the MoNuSeg dataset. Because of the large image size and high cellular density in the MoNuSeg dataset, the performance of systems for the MoNuSeg dataset is worse than that for the other two datasets. As the MoNuSeg dataset contains pathology images of seven different organs, such diversity makes it more difficult for segmentation. However, with the MoNuSeg dataset, our best system (i.e. FB+SP+SM) demonstrates a 7%, 4% and 10% improvement from the baseline U-Net model by Jaccard coefficient, Dice coefficient and Panoptic Quality.

Fig. 4.

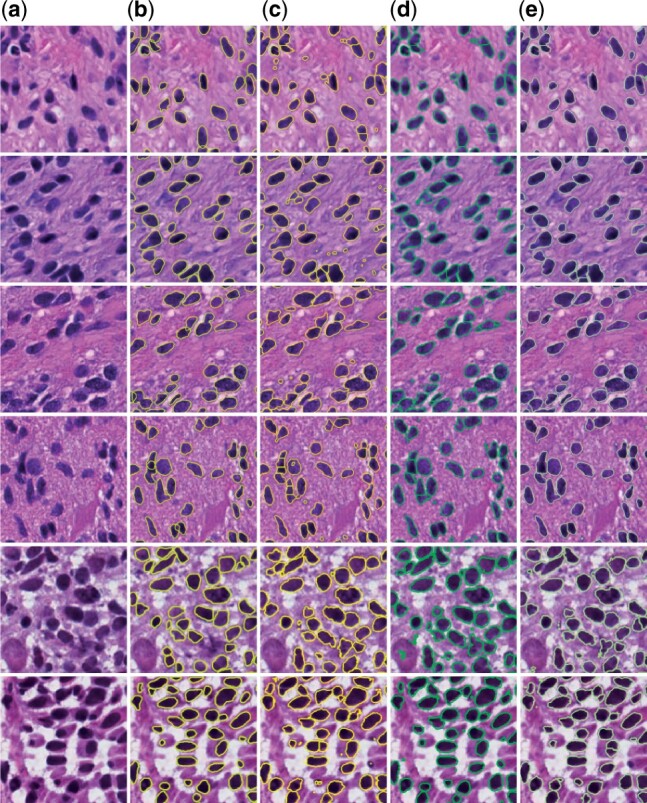
Typical segmentation results of our proposed systems. (a) original pathology images, (b) ground truth and results from (c) FB-Net, (d) FB+SP and (e) FB+SP+SM; The first, the second and the last two rows present images from GBM, TCGA and MoNuSeg datasets, respectively

Table 1.

Progressively improved results from our proposed systems are compared with the backbone U-Net model

Metrics		U-Net+DC	U-Net+CE	FB-Net	FB+SP	FB+SP+SM
GBM	J (%)	68.70	70.96	75.36	77.92	80.02
	P (%)	83.76	82.90	87.04	90.32	91.75
	R (%)	83.48	83.16	84.91	85.11	86.27
	DC (%)	83.57	83.01	85.94	87.59	88.90
	Acc (%)	90.83	92.14	93.58	94.43	95.03
	PQ (%)	56.72	58.91	61.76	68.25	69.13
	HD (pixels)	41.07	41.12	39.47	39.02	37.21
TCGA	J (%)	72.60	72.26	76.78	78.28	81.80
	P (%)	86.81	83.23	86.50	87.13	91.32
	R (%)	85.07	84.30	87.10	88.52	88.90
	DC (%)	85.93	83.73	87.09	87.81	89.95
	Acc (%)	92.75	93.10	93.86	94.96	95.74
	PQ (%)	58.38	57.96	61.86	65.73	68.57
	HD (pixels)	49.56	49.02	48.37	46.72	44.98
MoNuSeg	J (%)	65.02	65.64	69.81	70.11	72.59
	P (%)	85.29	70.06	76.87	77.13	79.86
	R (%)	73.64	91.40	88.57	88.72	88.85
	DC (%)	78.71	79.21	82.17	82.38	84.03
	Acc (%)	90.34	89.63	91.66	91.77	92.66
	PQ (%)	47.35	50.43	55.48	54.01	60.84
	HD (pixels)	56.77	57.37	55.93	56.72	55.17

Note: The average Jaccard coefficient (J), Precision (P), Recall (R), Dice coefficient (DC), Accuracy (Acc), Panoptic Quality (PQ) and Hausdorff distance (HD) for three independent datasets are presented, respectively. The best performance by each metric and dataset is bolded.

As a biology terminology, the foveation and foveal blur were first introduced into the image processing field in 2002 (Perry and Geisler, 2002). Multiple studies have reported the foveal blur is beneficial to numerous tasks, such as image coding (Wang et al., 2001), video detection (Boccignone et al., 2005) and visual search (Zelinsky et al., 2019). In the medical image analysis field, only one study was inspired by foveal blur to our best knowledge (Ciresan et al., 2012). This study reports that neuronal membrane segmentation in electron microscopy images can achieve better performance by foveal blur (Ciresan et al., 2012). This study uses foveal blur only at the center of each input image, while we utilize foveal blur to generate individual images focusing on each nucleus for dataset enrichment and boosted training. It is well known that the dataset scale is a decisive factor in the final system performance in the deep learning field. In addition to the perspective of biomimetics on simulating human vision acuity (Perry and Geisler, 2002), another more straight-forward explanation on the resulting superior performance of our systems is that foveal blurring can produce multiple images of different attention modes from the original image. Note that foveal blur is only utilized for enhanced model training in the training phase by dataset augmentation. With such a mechanism, our method provides an effective vehicle to fully extract information from each nucleus and enables deep learning models to effectively learn information critical for nuclei segmentation even with a very small scaled image dataset. Thanks to the minor modification to the architecture and no additional computing burden in the testing phase, the foveal blur strategy is demonstrated to be more effective and efficient. More experiments and quantitative analysis are illustrated in Supplementary Section S1 of Supplementary Materials.

The merits of our proposed two loss function terms unfold in mainly two aspects. (i) Although CNN is specially designed to capture the local image information on the relationships among neighboring pixels, its commonly used loss function treats all pixels equally and individually, such as cross entropy, Dice loss or mean square error loss. Thus, we have proposed a new loss function to enhance the inter-pixel relationship characterizations by new terms on shape priors and smoothness constraints. (ii) When pathologists manually delineate nuclei, they avoid candidates that are not eligible by size or shape, fully leveraging the prior knowledge they gain in their medical training. By contrast, CNN cannot explicitly learn these important characteristics or prior knowledge. To address this problem, we explicitly make CNN models learn representative nuclei by the new loss function terms on shape priors and smoothness constraint on the predicted probability map. In addition, it is noticed that most deep learning systems tend to produce a large number of small false positive segmentation results. By the inclusion of the new loss function terms on shape priors and smoothness penalizing small false positive contours, the proposed human-knowledge boosted deep learning system can have substantially enhanced performance. More experiments and quantitative analysis are illustrated in Supplementary Section S2 of Supplementary Materials.

3.3 Comparison with state-of-the-art systems

We include numerous state-of-the-art nuclei segmentation systems for performance comparison. Both conventional and deep learning methods are selected for fair and comprehensive comparisons, including mRLS (Xu et al., 2017), MOW (Jung and Kim, 2010), IVW (Xu et al., 2014), RACM (Xing et al., 2014), U-Net (Ronneberger et al., 2015), DeepLabV3+ (Chen et al., 2018), conditional GAN (cGAN) (Mirza and Osindero, 2014), Mask R-CNN (He et al., 2017) and YOLACT++ (Bolya et al., 2019a,b). Specifically, the first four systems are non-deep learning methods using watershed, ACM and RLS-based algorithms. The last five systems are state-of-the-art deep learning-based models that have been proved outstanding for nuclei segmentation. In Table 2, we compare the results of four non-deep learning and five deep learning methods with those from our best proposed method (i.e. FB+SP+SM) on three independent datasets. For a fair comparison, the same data augmentation (i.e. normalization, random shift, flip and rotation) are deployed to all deep learning systems. All systems are fully trained to their own best performances according to the hyperparameter configuration and loss function from the original literature. Deep learning methods are trained and tested with the same data partitioning configurations, while non-deep learning methods, having no training process, are applied to the same test set.

Table 2.

Performance comparison between state-of-the-art methods (both non-deep learning and deep learning models) and our proposed system (mean, std). The best performance by each metric and dataset is bolded.

Metrics		mRLS	MOW	IVW	RACM	U-Net + CE	DLV3+	cGAN	Mask R-CNN	YOLCAT++	FB + SP + SM
GBM	J (%)	61.88 (4.88)	68.00 (2.27)	69.17 (1.79)	53.17 (3.05)	70.96 (1.88)	75.29 (1.93)	72.45 (1.35)	72.89 (1.91)	67.16 (5.54)	80.02 (0.97)
	P (%)	78.35 (2.00)	73.77 (1.88)	76.38 (2.03)	62.15 (2.11)	82.90 (2.17)	86.61 (1.70)	84.24 (1.37)	86.53 (0.69)	90.66 (1.10)	91.75 (2.17)
	R (%)	74.97 (7.89)	89.72 (3.28)	88.12 (3.65)	78.85 (6.35)	83.16 (1.91)	85.27 (3.36)	83.83 (1.65)	82.24 (2.32)	72.14 (6.06)	86.27 (1.88)
	DC (%)	76.35 (3.75)	80.93 (1.62)	81.76 (1.25)	69.38 (2.63)	83.01 (1.29)	85.89 (1.26)	84.02 (0.91)	84.31 (1.28)	80.22 (3.92)	88.90 (0.60)
	Acc (%)	86.47 (1.37)	90.15 (1.62)	90.32 (1.64)	84.47 (2.46)	92.14 (1.15)	93.53 (1.04)	92.63 (1.13)	92.65 (1.33)	91.62(2.35)	95.03 (0.70)
	PQ (%)	55.63 (1.86)	53.76 (2.34)	59.64 (2.66)	37.36 (4.24)	58.91 (2.53)	64.66 (1.89)	60.57 (2.07)	66.10 (1.79)	58.11 (7.33)	68.09 (1.57)
	HD (pixels)	47.58 (6.16)	40.48 (7.20)	39.05 (9.48)	42.69 (5.31)	41.12 (7.59)	39.39 (8.53)	40.91 (7.26)	39.53 (15.01)	37.45 (6.77)	37.21 (5.96)
TCGA	J (%)	56.08 (5.99)	74.31 (4.63)	72.86 (4.54)	57.44 (3.69)	72.26 (6.56)	76.68 (1.41)	74.65 (2.21)	81.84 (3.15)	61.44 (10.87)	81.80 (3.62)
	P (%)	86.15 (2.16)	87.66 (2.68)	89.00 (1.97)	73.92 (1.53)	83.23 (5.52)	87.33 (2.00)	92.92 (0.97)	91.50 (1.54)	97.37 (1.52)	91.32 (3.73)
	R (%)	61.67 (6.88)	83.08 (5.52)	80.07 (4.94)	72.22 (6.11)	84.30 (3.91)	86.31 (1.62)	81.42 (2.45)	88.58 (3.32)	62.22 (11.27)	88.90 (4.75)
	DC (%)	71.68 (5.00)	85.18 (3.11)	84.22 (3.09)	72.90 (3.01)	83.73 (4.53)	85.86 (2.35)	86.77 (1.41)	89.98 (1.93)	77.24 (9.69)	89.95 (2.21)
	Acc (%)	85.99 (1.96)	93.56 (2.02)	92.94 (2.18)	88.12 (2.16)	93.10 (2.17)	94.35 (0.83)	95.03 (0.58)	95.81 (1.10)	80.31 (6.73)	95.74 (1.13)
	PQ (%)	53.11 (6.07)	56.37 (1.35)	60.05 (2.92)	45.18 (0.94)	57.96 (2.10)	64.60 (1.93)	63.60 (2.01)	68.09 (2.80)	56.06 (8.51)	69.91 (2.16)
	HD (pixels)	54.66 (16.72)	48.54 (4.12)	46.11 (8.38)	45.08 (8.26)	49.02 (9.10)	47.88 (8.69)	48.72 (10.17)	47.48 (20.14)	65.87 (21.77)	44.98 (10.44)
MoNuSeg	J (%)	53.40 (4.37)	55.57 (13.41)	67.77 (5.60)	44.27 (8.68)	65.64 (3.44)	69.38 (3.81)	67.99 (3.32)	66.24 (6.32)	51.24 (4.97)	72.59 (5.14)
	P (%)	87.61 (4.43)	92.39 (4.81)	90.80 (3.24)	75.09 (3.92)	70.06 (3.95)	76.08 (4.43)	73.96 (3.69)	78.25 (9.29)	68.92 (6.97)	79.86 (5.05)
	R (%)	57.83 (5.09)	58.95 (16.17)	72.70 (5.15)	52.35 (12.81)	91.40 (3.86)	88.94 (4.38)	89.57 (4.28)	81.99 (5.64)	67.05 (6.46)	88.85 (3.62)
	DC (%)	69.55 (3.70)	70.80 (11.14)	80.70 (4.06)	61.04 (8.21)	79.21 (2.54)	81.86 (2.63)	80.91 (2.39)	79.51 (4.72)	67.62 (4.44)	84.03 (3.39)
	Acc (%)	83.32 (1.53)	82.50 (9.44)	90.55 (1.86)	78.81 (5.58)	89.63 (1.05)	91.46 (1.34)	90.86 (1.01)	91.56 (2.70)	85.28 (0.83)	92.66 (1.65)
	PQ (%)	49.55 (1.54)	34.68 (13.82)	51.00 (8.89)	30.78 (4.42)	50.43 (2.60)	57.30 (2.35)	53.58 (2.63)	60.33 (6.98)	54.17 (8.40)	60.84 (3.47)
	HD (pixels)	68.86 (11.96)	57.47 (7.39)	56.54 (6.61)	56.31 (8.47)	57.37 (6.63)	55.86 (7.52)	56.38 (7.15)	55.76 (15.22)	66.99 (9.92)	55.17 (7.07)

Within the non-deep learning method group, the multi-resolution method derived from the radial line scanning model (i.e. mRLS) and a variant of the active contour map algorithm (i.e. RACM) tend to generate a large number of false positive predictions that deteriorate method performance. By contrast, the watershed-based methods, i.e. MOW and IVW, achieve better performances than mRLS and RACM. Of deep learning methods for comparison in this study, experimental results suggest that U-Net segmentation is less competitive than DeepLabV3+ or conditional GAN by performance due to its relatively simple architecture. Furthermore, YOLACT++, a one-stage detector-based segmentation system derived from YOLO, is not good at recognizing small or overlapped objects. Due to this weakness shared by methods in the YOLO system family, YOLACT++ does not work as well with the MoNuSeg dataset as the other two datasets because the MoNuSeg dataset includes a large number of small nuclei in a high cellular density. In the GBM and MoNuSeg dataset, our proposed system (FB+SP+SM) outperforms other methods by most metrics. For the TCGA dataset, our method and Mask R-CNN are the best by three metrics each. Note the performance difference between our method and Mask R-CNN is negligible when Mask R-CNN is the best for the TCGA dataset. Our system outperforms all other methods by most metrics for the GBM and MoNuSeg dataset. Although in the TCGA dataset Mask R-CNN performs the best by Jaccard coeffient, Dice coefficient and Accuracy, it is highly comparable to our method by these metrics, but at a much higher computational cost than ours. More segmentation results are demonstrated in Supplementary Figures S4 and S5 in Supplementary Materials.

By evaluation results, conventional methods using watershed and ACM techniques are not as competitive as deep learning methods in general. As the MoNuSeg dataset includes larger pathology images of higher nuclei density, conventional methods have better Precision but worse Recall compared to deep learning methods. This suggests conventional methods tend to produce fewer false positive nuclei than such generative models as deep learning methods. The development of our new loss function terms on nuclei shape prior knowledge and smoothness constraints, however, can help reduce such false positive errors from deep learning methods. As each histology slide has about 5 mm in thickness and represents a two-dimensional projection of tissues in a three-dimensional space, some vague nuclei are inevitably found in the resulting scanned pathology images. In practice, pathologists use personal and time-variant criteria to decide if such nuclei belong to a tissue slide and are properly focused by a digital scanner case by case. By contrast, our systems tend to delineate these vague nuclei and result in more false positive nuclei than human annotations, thus lowering the performance by Recall. Note that such a property of our methods can be a valuable merit for studies where all nuclei, including those out of focus, are preferred for analysis.

3.4 Comparison with state-of-the-art nuclei segmentation systems on MoNuSeg challenge

For more in-depth performance comparisons, six other state-of-the-art deep learning systems specifically designed for nuclei segmentation are compared with our system (FB+SP+SM) by the dataset from the Multi-Organ Nuclei Segmentation Challenge (MoNuSeg). MoNuSeg is a popular challenge that provides a large dataset of pathology images and nuclei annotations (MoNuSeg Challenge, 2018). Numerous deep learning models specifically designed for nuclei segmentation have been evaluated by this gold standard dataset. The comparison results in the metric of the Jaccard coefficient are presented in Figure 5. Same data augmentation is deployed to all deep learning systems. All systems are fully trained to their own best performances according to the hyperparameter configuration and loss function from the original literature.

Fig. 5.

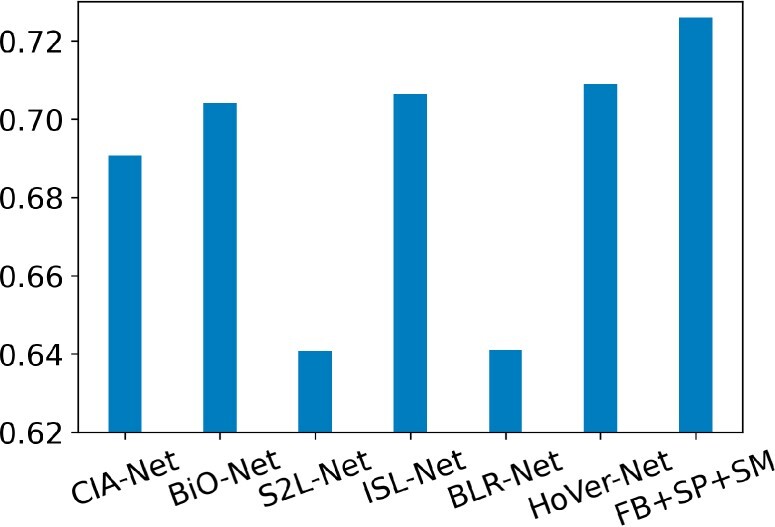
Jaccard coefficient comparison of our proposed method with the state-of-the-art deep learning models specifically designed for nuclei segmentation evaluated by the MoNuSeg dataset

CIA-Net is the winning model of MoNuSeg Challenge with 0.6907 by Jaccard coefficient (Zhou et al., 2019). It has two decoder modules for nuclei and contour recognition separately. The resulting two modules are further integrated with a Contour-aware Information Aggregation module. By contrast, our system explicitly incorporates information of nuclei shape priors from a well-defined nuclei shape library. Although CIA-Net uses one smooth loss function (i.e. bootstrapped loss) to address noisy and incomplete labeling issues, it is fundamentally different from our proposed smoothness (SM) term that is designed to smooth the prediction probability map. Bi-directional O-shaped CNN (BiO-Net) is another successful deep learning nuclei segmentation system for our comparison study. It yields 0.704 by Jaccard coefficient for the MoNuSeg Challenge dataset (Xiang et al., 2020). With skip connections, BiO-Net is an encoder-decoder system that fully recurrently utilizes building blocks with a minor extra burden to the computation. For performance comparison, another nuclei segmentation focused deep learning model S2L-Net is included. It is trained by manual- and pseudo-annotations along with a specially designed loss function. The trained system produces pseudo-annotation and achieves 0.6408 by Jaccard coefficient for the MoNuSeg challenge dataset (Lee and Jeong, 2020). The loss function of this network is specifically tailored to combine manual- and pseudo-annotations. By contrast, our novel contribution to the loss function in the proposed system is to enable deep learning models to explicitly learn human-knowledge boosted nuclei morphology information in a direct way.

We also include ISL-Net, a popular nuclei segmentation deep learning method for comparison. In a self-supervised manner, ISL-Net attempts to leverage the nuclei size and quantity information with triplet learning and the count ranking loss, achieving 0.7063 by Jaccard coefficient with the MoNuSeg challenge dataset (Xie et al., 2020). Although ISL-Net and our proposed models both aim to utilize nuclei morphology information, our strategy is to explicitly teach deep learning models with human prior knowledge of nuclei shape and global morphology smoothness constraints on the resulting prediction maps. By contrast, such information as nuclei size and count is implicitly represented by the ISL-net model, which is not beneficial to the system’s robustness and generalizability. BLR-Net is another nuclei segmentation model we compare with. By adding one loss term on the prediction blending energy, it yields 0.641 by Jaccard coefficient with the same MoNuSeg challenge dataset (Wang et al., 2020). Such a deep learning model attempts to utilize nuclei morphology information by punishing the bad boundary predictions. By comparison, our model focuses on achieving the global smoothness of the prediction map and explicitly learning human-knowledge derived shape prior information. Finally, we also compare our model with HoVer-Net, a popular nuclei segmentation system based on deep learning architecture (Graham et al., 2019). Tested in the MoNuSeg dataset, it achieves a Jaccard coefficient of 0.7089. By contrast, our best model (FB+SP+SM) achieves a Jaccard coefficient of 0.7259. Compared with all these state-of-the-art deep learning methods specifically tailored to nuclei segmentation, our developed model has demonstrated superior performance with substantial result improvement.

3.5 Effectiveness and efficiency

In the testing phase, the inputs to our proposed system are raw histopathology images that are neither foveal blurred nor manually labeled. This good merit enables our proposed system to be promising for effectively and widely deployed to a large set of research studies and clinical sites. We run all analyses on a cluster with one NVIDIA GTX V100 GPU. Figure 6 presents the segmentation performance in Jaccard coefficient and testing speed for image patches of two sizes, i.e. 512 × 512 (GBM) and 1000 × 1000 (MoNuSeg). Regardless of the image size, our proposed systems present the best effectiveness and efficiency balance. It takes 0.05 s for our system FB+SP+SM to process one 512 × 512 pathology image patch. By contrast, the fastest system U-Net is nearly 10% worse than our most advanced system FB+SP+SM by Jaccard coefficient. The most competitive method DeepLabV3+ is two times slower and 5% worse than our FB+SP+SM model by Jaccard coefficient. For image patches of 1000 × 1000 pixels, similar result patterns are presented for the effectiveness and efficiency investigations. In conclusion, our proposed systems present a high potential for high-throughput nuclei segmentation in an accurate and efficient manner.

Fig. 6.

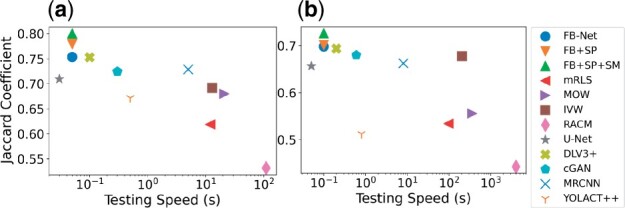
Scatter plots of the average Jaccard coefficient and testing speed for the (a) GBM and (b) MoNuSeg dataset

Funding

This research was supported by the National Institute of Health [U01CA242936, R01EY028450, R01CA214928], National Science Foundation [ACI 1443054, IIS 1350885] and CNPq.

Conflict of Interest: none declared.